Optimization of the generalized covariance estimator in noncausal processes

Abstract

This paper investigates the performance of routinely used optimization algorithms in application to the Generalized Covariance estimator (GCov) for univariate and multivariate mixed causal and noncausal models. The GCov is a semi-parametric estimator with an objective function based on nonlinear autocovariances to identify causal and noncausal orders. When the number and type of nonlinear autocovariances included in the objective function are insufficient/inadequate, or the error density is too close to the Gaussian, identification issues can arise. These issues result in local minima in the objective function, which correspond to parameter values associated with incorrect causal and noncausal orders. Then, depending on the starting point and the optimization algorithm employed, the algorithm can converge to a local minimum. The paper proposes the Simulated Annealing (SA) optimization algorithm as an alternative to conventional numerical optimization methods. The results demonstrate that SA performs well in its application to mixed causal and noncausal models, successfully eliminating the effects of local minima. The proposed approach is illustrated by an empirical study of a bivariate series of commodity prices.

1 Introduction

In recent years, there has been a growing interest in employing mixed causal-noncausal processes for the analysis of economic and financial time series (Lanne and Saikkonen 2013; Hecq et al. 2016; Gourieroux and Jasiak 2022, 2023; Swensen 2022, and Cavaliere et al. 2020). These models have gained popularity due to their ability to incorporate both causal and noncausal components to accurately capture the intricate nonlinear dynamics feature of economic and financial processes. In economics, the integration of both causal and noncausal components is particularly valuable when it comes to modeling rational expectations. Unlike traditional autoregressive models, mixed models offer insight into how economic variables are influenced by their expectations and the mechanisms underlying the formation of these expectations (see Lanne and Saikkonen 2011, 2013). In the financial domain, these models capture nonlinear dynamics, including local trends, commonly referred to as speculative bubbles. Speculative bubbles are explosive financial patterns that frequently emerge in highly volatile markets, such as the cryptocurrency and commodity markets. These bubbles represent periods of excessive prices (rates), driven more by market psychology and speculation than by the underlying fundamentals. During such episodes, asset prices rise to unsustainable levels, often followed by a sudden and sharp decline, leading to adverse economic outcomes. Therefore, the identification and analysis of speculative bubbles are of crucial importance to avoid possible disruptions of economic stability and resource allocation (see Gourieroux and Jasiak 2017; Fries and Zakoian 2019, and Hecq and Voisin 2021).

The estimation techniques available for mixed causal-noncausal processes fall into two main categories: parametric and semi-parametric estimators. The parametric (approximate) maximum likelihood method yields efficient estimates only when the error distribution is specified correctly. In contrast, semi-parametric methods offer the advantage of robustness to specification errors and do not require a distributional assumption on the errors of the model (Gourieroux and Jasiak 2017, 2023, and Hecq and Velasquez-Gaviria 2022). As a consequence, the benefit of employing a semi-parametric estimator is evident. Currently, GCov is the only semi-parametric estimator in the time domain available for the estimation of mixed causal-noncausal models. It was introduced by Gourieroux and Jasiak (2017) and subsequently extended to a semi-parametrically efficient estimator in Gourieroux and Jasiak (2023). The GCov is characterized by an objective function based on the autocovariances of linear and nonlinear functions of independent and identically distributed (i.i.d.) model errors.

This paper aims to address potential challenges associated with local minimum issues in the objective function of the estimator GCov applied to mixed causal and noncausal models and optimized by algorithms that are routinely used. In particular, we show that these challenges may arise from difficulties in distinguishing between causal and noncausal dynamics, often linked to factors such as an insufficient number of nonlinear autocovariances, inappropriate nonlinear transformations, or a close to Gaussian error density. As a result, our findings indicate that traditional optimization algorithms, like the Broyden-Fletcher Goldfarb-Shanno (BFGS) algorithm, may struggle to converge to the global minimum in this context when their starting points are poorly selected (see Dennis and Schnabel 1996; Fletcher 2000, and Byrd et al. 1995). This difficulty can lead to inaccurate results, underscoring the limitations of conventional optimization methods when applying GCov to processes involving a noncausal component.

To avoid optimization problems caused by a potential local minimum occurrence, we propose combining the estimator GCov with the Simulated Annealing (SA) optimization algorithm. SA is a powerful metaheuristic method designed to converge to the global minimum when the objective function contains numerous local minima. Originally proposed by Kirkpatrick et al. (1983), SA draws inspiration from the solid annealing process to address optimization problems. Over the years, SA has shown remarkable success in solving complex optimization problems in various fields, including computer (VLSI) design, image processing, molecular physics, and chemistry (see, for example, Wong et al. 2012; Carnevali et al. 1987; Jones 1991, and Pannetier et al. 1990). This paper shows that the SA algorithm significantly improves the optimization of the estimator GCov in mixed causal-noncausal autoregressive models, ensuring accurate parameter estimates and correct inference on autoregressive orders.

It is important to note that this paper is focused exclusively on the estimation of causal and noncausal parameters. We do not study inference on estimated parameters nor perform portmanteau-type tests GCov (see Gourieroux and Jasiak 2023; Jasiak and Neyazi 2023), and assume that the models are correctly identified and specified. This paper focuses primarily on the application of the GCov estimator to multivariate models. For comparison, we also present some results on univariate processes to illustrate graphically the objective function of the estimator displayed as a function of a single parameter. In this context, alternative optimization strategies can be employed to achieve a successful convergence of GCov. For example, a grid search strategy over the set of parameter values can be used to find the estimators that minimize the objective function (see Bec et al. 2020 for a grid search approach in the parametric framework). However, applying this alternative methodology in the multivariate framework can be challenging due to the large dimensions of the grid arrangement.

The paper is organized as follows. Section 2 discusses mixed causal and noncausal models and introduces the GCov estimator. Section 3 shows that its objective function may exhibit local minima under some conditions, which adversely affect the results of BFGS optimization. Section 4 suggests the use of SA to solve the problem of local minima and to provide optimal starting values. Section 5 investigates a bivariate series of commodity prices. Section 6 concludes.

2 GCov estimator of mixed causal and noncausal processes

This section describes the causal-noncausal models and defines the GCov estimator.

2.1 Model representation

This section reviews univariate and multivariate mixed causal-noncausal models.

A strictly stationary univariate mixed causal and noncausal process for a zero-mean series $y_t$, where $t=1, 2, \dots$, is given by:

$$\begin{aligned} \phi (L)\varphi (L^{-1})y_t=\eta _t, \end{aligned}$$

(1)

where the backward-looking polynomial, also defined as the causal polynomial, is given by $\phi (L) = 1 - \phi _1 L - \dots - \phi _r L^r$. On the other hand, the forward-looking polynomial, also defined as the noncausal polynomial, is defined as $\varphi (L^{-1}) = 1 - \varphi _1 L^{-1} - \dots - \varphi _s L^{-s}$. Furthermore, $\eta _t$ represents a sequence of random variables i.i.d. with a mean of 0 and a variance of $\sigma ^2$. In (1), both the causal and noncausal polynomials are characterized by roots outside the unit circle:

$$\begin{aligned} \phi (z) \ne 0 \ \ \text {and} \ \ \varphi (z) \ne 0 \ \ \text {for} \ \ |z| \le 1. \end{aligned}$$

If $\varphi \ne 0$ for some $j \in \{1, \dots , s \}$, the process in (1) is defined as purely noncausal if $\phi _1 = \phi _2 = \dots = \phi _r=0$. The conventional causal autoregression is obtained when $\varphi _1 = \varphi _2 = \dots = \varphi _s=0$.

As shown in Lanne and Saikkonen (2011), the mixed causal and noncausal process expressed in (1) has the following alternative model representation (Breidt et al. 1991):

$$\begin{aligned} y_{t}=\sum _{j=1}^{p}\theta _{j}y_{t-j}+\epsilon _{t}, \end{aligned}$$

with $\theta (z) \ne 0$ for $|z|=1$. When $p=r+s$, the autoregressive polynomial can be factored as $\theta (z) = \theta ^+(z) \theta ^-(z)$, where:

$$\begin{aligned} \theta ^+(z)=1 - \theta ^+_1 z - \dots - \theta ^+_r z^r \ne 0 \ \ \ \text {for} \ \ |z| \le 1, \end{aligned}$$

and

$$\begin{aligned} \theta ^-(z)=1 - \theta ^-_{1} z - \dots - \theta ^-_s z^s \ne 0 \ \ \ \text {for} \ \ |z| \ge 1. \end{aligned}$$

This alternative model representation, even if characterized by roots inside the unit circle, is not an explosive process because the error term $\epsilon _t$ is not an innovation with respect to the past of $y_t$, since $\epsilon _t=-(1/\varphi _s)\eta _{t-s}$ (Lanne and Saikkonen 2011).

Due to the presence of the noncausal component, the process in (1) becomes capable of capturing nonlinear dynamics, including local trends (bubbles) and conditional heteroskedasticity (see Breidt et al. 1991; Lanne and Saikkonen 2011; Hencic and Gouriéroux 2015, and Gourieroux and Jasiak 2018).

As shown in Breidt et al. (1991), Lanne and Saikkonen (2011), Gourieroux and Zakoian (2017), mixed causal-noncausal processes defined in (1) admit a unique two-sided strictly stationary solution:

$$\begin{aligned} y_t = \sum _{j=-\infty }^{\infty } \psi _j \eta _{t+j}, \end{aligned}$$

(2)

with $\psi _0$ equal to 1. The two-sided MA representation clarifies that the autoregressive process (1) is mixed, that is, causal-noncausal since the current value of the process $y_t$ is affected by past, present, and future shocks. When the process in (1) is purely causal (resp. noncausal), then $\psi _j = 0$ for all $j > 0$ (resp. $j < 0$) and its current value is affected only by current and past shocks (resp. present and future shocks) (see Breidt et al. 1991 and Lanne and Saikkonen 2011).

Findley (1986) points out that the coefficients of a two-sided moving average representation (including present, past, and future errors) can be distinguished from a one-sided moving average representation (including the past and present errors) only if the error term $\eta _t$ follows a non-Gaussian distribution. The reason is that the Gaussian distributions are entirely characterized by their second-order moments, which display symmetry over time in stationary processes. Therefore, in Gaussian processes, distinguishing between backward and forward representations is not possible (see Giancaterini et al. 2022). As a consequence, any estimator that relies solely on linear second-order properties, such as the OLS, does not possess the capability to discern this feature. Therefore, mixed causal-noncausal processes can always be represented as purely causal AR(p) (resp. purely noncausal) with the same linear sample autocovariance function as the true data-generating process (DGP). In addition, the causal representation of a noncausal process has autoregressive roots equal to the inverses of autoregressive roots of the DGP that lie inside the unit circle. In general, the sample autocovariance functions are identical for mixed causal-noncausal processes and their representations are obtained by replacing the autoregressive coefficients by the coefficients of autoregressive polynomials with roots equal to the inverses of the true ones (see Breidt et al. 1991). However, among all processes that share the same linear sample autocovariance functions as the true DGP, only the correct specification has serially i.i.d. errors. For this reason, in addition to the assumption of non-Gaussianity, the correct identification of the noncausal component also requires serially i.i.d. model errors (Hecq et al. 2016).

In the multivariate level, the autoregressive representation with roots inside and outside the unit circle and the multiplicative specification in (1) do not always overlap. In particular, as underscored by Davis and Song (2020), Swensen (2022), Cubadda et al. (2023) and Gourieroux and Jasiak (2022), the multiplicative representation in (1) does not always exist and covers only a subset of mixed causal-noncausal processes at the multivariate level. This makes the following specification:

$$\begin{aligned} Y_t=\Theta _1 Y_{t-1}- \dots \Theta _p Y_{t-p}+u_t, \end{aligned}$$

(3)

with $|\Theta |\ne 0$ for $|z|=1$, more general compared to the multiplicative representation. Therefore, this paper only considers the specification in (3) at the multivariate level.

Let us assume that the process in (3) is strictly stationary and satisfies the following assumptions:

• Assumption A.1: The roots of det($\Theta (z)$) are of modulus different from 1.

• Assumption A.2: Vectors $u_t, t=1,...,T$ are serially i.i.d., non-Gaussian and square-integrable with zero mean $E(u_t) = 0$ and variance–covariance matrix $V(u_t) = \Sigma _u$;

In addition, we suppose that det($\Theta (z)$) has $n_1$ roots outside and $n_2=n-n_1$ inside the unit circle. As in Gourieroux and Jasiak (2017), we consider the semi-parametric specification of the causal-noncausal model and do not impose any distributional assumptions on the errors, except for serial independence and non-Gaussian distribution in A.2. Like in the univariate framework, the assumptions of i.i.d. and non-Gaussian errors $\{ u_t \}_{t=1}^{T}$, are required to hold for correct identification of the noncausal component of the process with autoregressive roots inside the unit circle (see Davis and Song 2020; Gourieroux and Jasiak 2017).

The existence of a strictly stationary solution of (3), as well as the two-sided moving average representation of Y, is shown in Gourieroux and Jasiak (2017). We review their Representation Theorem for a Vector Autoregressive process of order 1, VAR(1): $Y_t=\Theta Y_{t-1} +u_t$, satisfying A.1 and A.2 where the matrix $\Theta$ is of dimension $n\times n$ and has eigenvalues of modulus different from 1, to set up the notation.

Representation Theorem (Gourieroux and Jasiak 2017): Under Assumptions A.1-A.2, a mixed causal-noncausal n-dimensional VAR (1) (with $n \ge 1$), admits a decomposition of the autoregressive matrix $\Theta$ with an invertible $(n\times n)$ real matrix A of eigenvectors and two square real matrices: $J_{1}$ of dimension ($n_{1}\times n_{1}$) and $J_{2}$ of dimension ($n_{2}\times n_{2}$) containing the eigenvalues of $\Theta$ of modulus strictly less (resp. larger) than 1, and such that:

$$\begin{aligned} Y_{t}= & {} A_{1}Y_{1,t}^{*}+ A_{2} Y_{2,t}^{*}, \end{aligned}$$

(4)

$$\begin{aligned} Y_{1,t}^{*}= & {} J_{1}Y_{1,t-1}^{*}+ u_{1,t}^{*},\ \ \ Y_{2,t}^{*} = J_{2}^{-1}Y_{2,t+1}^{*}-J_{2}^{-1} u_{2,t+1}^{*},\nonumber \\ \end{aligned}$$

(5)

$$\begin{aligned} Y_{1,t}^{*}= & {} A^{1}Y_{t}, \ \ \ Y_{2,t}^{*} = A^{2}Y_{t}, \end{aligned}$$

(6)

$$\begin{aligned} u_{1,t}^{*}= & {} {} A^{1} u_{t}, \ \ \ u_{2,t}^{*} = A^{2} u_{t}, \end{aligned}$$

(7)

where $[A_{1},A_{2} ]=A$ and $[A^{1\prime },A^{2\prime } ]^{\prime }=A^{-1}$.

In equation (5), the processes $Y_{1,t}^*$ and $Y_{2,t}^*$ are the purely causal and purely noncausal components of the process $Y_t$, respectively. Any mixed causal-noncausal VAR(p) model (3), with $p \ge 2$, can be written as mixed causal-noncausal VAR(1) by using the companion form as follows (Gourieroux and Jasiak 2017):

$$\begin{aligned} X_t= \Psi X_{t-1} + \xi _t, \end{aligned}$$

where $X_t=[Y_t, Y_{t-1}, \dots , Y_{t-p+1} ]^{\prime }$, $\xi _t=[u_t, 0, 0, \dots , 0]$, and:

$$\begin{aligned} \Psi =B \begin{bmatrix} J_1 &{} 0\\ 0 &{} J_2 \end{bmatrix}B^{-1}, \end{aligned}$$

with B and J containing the eigenvectors and eigenvalues of matrix $\Psi$, respectively. As a consequence, for $p \ge 2$, we have:

$$\begin{aligned}&X_{t} = B_{1}X_{1,t}^{*}+ B_{2} X_{2,t}^{*}\\ {}&X_{1,t}^{*} = J_{1}X_{1,t-1}^{*}+ \xi _{1,t}^{*}, \ \ \ X_{2,t}^{*} = J_{2}^{-1}X_{2,t+1}^{*}-J_{2}^{-1} \xi _{2,t+1}^{*}\\ {}&X_{1,t}^{*} = B^{1}Y_{t}, \ \ \ \ X_{2,t}^{*} = B^{2}Y_{t}\\ {}&\xi _{1,t}^{*} = B^{1}u_{t}, \ \ \ \ \ \xi _{2,t}^{*} = B^{2}u_{t} \end{aligned}$$

where $[B_{1},B_{2}]=B$ and $[B^{1\prime },B^{2\prime }]^{\prime }=B^{-1}$. Consequently, when $p \ge 2$, the causal and noncausal components are functions of the current and lagged values of $Y_t$, since $X^*_{1,t}=B^1X_t=\sum _{h=0}^{p-1}B^1_h Y_{t-h}$ and $X^*_{2,t}=B^2X_t=\sum _{h=0}^{p-1}B^2_h Y_{t-h}$.

2.2 GCov estimator

Section 2.1 showed that identification of mixed causal-noncausal processes from second-order moments only is not possible. It also noted that among the processes that share the same linear autocovariance function, only the true model has serially i.i.d. errors. Although distinguishing the true model based on the linear second-order moments only is not feasible, the second-order moments and second cross-moments of nonlinear functions of i.i.d. non-Gaussian errors can identify the process (Chan et al. 2006). This concept underlies the semi-parametric estimators GCov introduced by Gourieroux and Jasiak (2017) and Gourieroux and Jasiak (2023) and denoted GCov17 and GCov22, respectively. The estimator GCov22 minimizes a portmanteau-type objective function involving the autocovariances of nonlinear transformations of model errors viewed as functions of model parameters. For example, the GCov22 estimator of the parameter $\theta = vec(\Theta ')$ of the strictly stationary n-dimensional mixed causal-noncausal VAR(1) process with $u_t = Y_t- \Theta Y_{t-1}$ minimizes the following portmanteau statistic:

$$\begin{aligned} {\hat{\theta }}\, =\, \underset{\Theta }{\textrm{argmin}} \!\sum _{h=1}^{H}\! Tr \bigl [ {\hat{\Gamma }}_a(h; \theta ) {\hat{\Gamma }}_a(0; \theta )^{-1}{\hat{\Gamma }}_a(h; \theta )' {\hat{\Gamma }}_a(0; \theta )^{-1} \bigr ], \end{aligned}$$

(8)

where H is the highest selected lag, ${\hat{\Gamma }}_a(h; \theta )$ is the sample autocovariance between $a(u_t)$ and $a(u_{t-h})$, with $a(u_t)= \bigl [ a_1(u_{t})^{\prime }, \dots , a_K(u_t)^{\prime }\bigr ]$, and $a_j(u_t)$ is an element by element function, for $j=1, \dots , K$. K indicates the number of linear and nonlinear transformations included in the estimator GCov22 and Tr denotes the trace of a matrix. The choice of an informative set of transformations ($a_{j}$) depends on the specific series under investigation. Gourieroux and Jasiak (2017) and Gourieroux and Jasiak (2023) explain that this problem is analogous to selecting moments in the Generalized Method of Moments (GMM) estimation or instruments in the Instrumental Variable (IV) estimation. For example, in financial applications that aim to capture the absence of a leverage effect, one can select both linear and quadratic functions. For a bivariate process with $n=2$, we may consider the following set of four functions ($K=4$): $a_1(u_t) = u_{1,t}$, $a_2(u_t) = u_{2,t}$, $a_3(u_t) = u_{1,t}^2$, and $a_4(u_t) = u_{2,t}^2$. This implies that $a_1$ and $a_2$ are linear functions of errors in a causal-noncausal process, while, $a_3$ transforms the error term of the first variable, $u_{1,t}$, squaring it for each $t=1, \dots , T$, where T represents the total number of observations. Similarly, the function $a_4$ emulates the behavior of $a_3$, except that it applies the squaring operation to $u_{2,t}$ for each $t=1, \dots , T$. Alternatively, we can consider the signs of returns and their squares to separate the volatility dynamics from the bounce effect of the bid-ask: $a_1(u_t) = \text {sign}(u_1)$, $a_2(u_t) = \text {sign}(u_2)$, $a_3(u_t) = u_1^2$, and $a_4(u_t) = u_2^2$. It is important to note that if $a(u_t)$ includes only linear transformations of the error term, then ${\hat{\Gamma }}(h)$, with $h=1, \dots , H$, would provide only information on the second-order linear moments of the process, rendering the estimator unable to identify and estimate the correct specification. Therefore, the nonlinear transformations enable us to estimate the true process. Under the regularity conditions given in Gourieroux and Jasiak (2023), the semi-parametric estimator in (8) is consistent and asymptotically normally distributed when the fourth moments of $a(u_t)$ are finite. Additionally, the GCov22 estimator in (8) is semi-parametrically efficient. The matrix on the r.h.s of (8) is diagonalizable, with the sum of its eigenvalues being the sum of the squares of the canonical correlations between $a(u_{t})$ and $a(u_{t-h})$, for $h=1, \dots , H$.

For comparison, we could estimate the parameters of the n-dimensional VAR(1) by the GCov17, which minimizes:

$$\begin{aligned} {\hat{\theta }}= {} \underset{\Theta }{\text {argmin}} \sum _{h=1}^{H} Tr \bigl [ {\hat{\Gamma }}_a (h; \theta ) diag({\hat{\Gamma }}_a(0; \theta ))^{-1} {\hat{\Gamma }}_a(h; \theta )^{\prime } diag({\hat{\Gamma }}_a(0; \theta ))^{-1} \Bigr ], \end{aligned}$$

(9)

where $diag({\hat{\Gamma }}_a(0; \theta ))$ is the matrix containing solely the diagonal elements of ${\hat{\Gamma }}_a(0)$. Therefore, the only difference between (8) and (9) is that Gcov17 takes into account only the diagonal elements of the matrix ${\hat{\Gamma }}_a(0)$. This feature makes GCov17 particularly appealing in the high-dimensional framework, when the matrix ${\hat{\Gamma }}(0)$ is of large dimension, potentially leading to a numerically more stable computation. Like the estimators defined in (8), GCov17 is consistent and is normally distributed asymptotically when the fourth-order moments of $a(u_t)$ are finite. In general, estimator (9) is not semi-parametrically efficient, except when the weights in the objective function are ${\hat{\Gamma }}(0)$, instead of $diag {\hat{\Gamma }}(0)$ and the estimators in (8) and (9) coincide (see Gourieroux and Jasiak 2017).

3 BFGS optimization of Gcov22

This section examines the behavior of the objective function of the GCov22 estimator for different types and numbers K of nonlinear error transformations and illustrates the performance of the BFGS optimization algorithm as implemented in Broyden (1970), Fletcher (1970), Goldfarb (1970), and Shanno (1970).

Our investigation concerns both multivariate and univariate models. As mentioned in Sect. 1, our analysis of univariate models is intended solely to offer a clear visual representation of the objective function in a two-dimensional Cartesian plane. For this purpose, we consider a purely noncausal AR(1) process. In the multivariate framework, we consider the mixed causal-noncausal VAR(1) process.

The results presented focus exclusively on the Gcov22 estimator. This decision is made because both Gcov22 and Gcov17 perform similarly in terms of accuracy in the univariate and multivariate models considered. Results for GCov17 are available upon request.

3.1 The univariate framework

We consider a univariate ($n=1$) purely noncausal autoregressive process of order 1:

$$\begin{aligned} y_t=\theta y_{t+1} + \eta _{t}, \; t=1,\ldots ,T. \end{aligned}$$

(10)

where the autoregressive coefficient $|\theta | <1$ and $\eta _t$ is a strong (i.i.d.) white noise with the t-Student$(\nu$) distribution. This process is a strictly stationary noncausal process and characterized by a root outside the unit circle (Lanne and Saikkonen 2011). As highlighted in Sect. 2, the noncausal process in (10) can be written as a causal process $y_t = 1/\theta y_{t-1} + \epsilon _t$ where $E(\epsilon _t \ y_{t-1}) \ne 0$. In other words, the error process $\epsilon _t$ is not an innovation process, and the coefficient on $y_{t-1}$ is greater than 1 in absolute value. Consequently, a local minimum at $1/\theta$ can emerge, and we aim to investigate this phenomenon in this section.

To display the objective function of the estimator GCov22 of $\theta$ and to analyze the possible existence of local minima, we calculate the values of the objective function in (8). This computation is carried out based on the simulated process given above, using $\theta =(0.66, 0.9)$, $\nu =(4,10)$, $T=500$, and $H=10$. This choice of autoregressive coefficients of the DGP allows us to analyze the objective function when the coefficient is close to the unit circle ($\theta = 0.9$) or farther away from it ($\theta =0.66$). The choice of parameter $\nu$ in the error density is intended to examine cases where the process is well identified ($\nu =4$) and situations where identification issues may arise due to the proximity of the error density to the Gaussian framework ($\nu =10$).

In empirical investigations, we do not have prior knowledge of the most suitable functions $a_j$ and the appropriate value of K for our dataset. Indeed, as mentioned in Sect. 2, the choice depends on the specific process under investigation. Therefore, we explore various combinations of $a_k$ and K:

• T0: $a_{1}(\eta _t)$=$\eta _t$;

• T1: $a_{1}(\eta _t)$=$\eta _t$, $a_{2}(\eta _t)$=$\eta _t^{2}$, $a_{3}(\eta _t)$=$\eta _t^{3}$, $a_{4}(\eta _t)$=$\eta _t^{4}$;

• T2: $a_{1}(\eta _t)$=$\eta _t$, $a_{2}(\eta _t)$=$log(\eta _t^{2})$;

• T3: $a_{1}(\eta _t)$=$sign(\eta _{t})$, $a_{2}(\eta _t)$=$\eta _t^{2}$;

• T4: $a_{1}(\eta _t)$=$sign(\eta _t)$, $a_{2}(\eta _t)$=$log(\eta _t^{2})$.

We consider $H=10$ in (8) since this number of lags can capture the correct dynamics in most cases, as reported in Gourieroux and Jasiak (2017) and Gourieroux and Jasiak (2023).

Fig. 1

BFGS optimization of $\varvec{Gcov22}$ in noncausal AR(1) with $\varvec{\theta =0.66}$, $\varvec{T=500}$ and OLS starting value

Fig. 2

BFGS optimization of $\varvec{Gcov22}$ in noncausal AR(1) with $\varvec{\theta =0.9}$, $\varvec{T=500}$ and OLS starting value

Table 1 Estimated dynamics: univariate framework

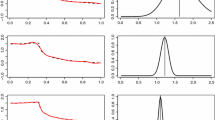
For illustration, the objective function (8) is calculated on a set of the values of the autoregressive coefficients, covering a range of -1 to 5 with a step size of 0.01. For each coefficient within this interval, we calculate and plot the value of the objective function. The objective functions displayed in Figs. 1a, c and 2a, c confirm that when only the linear transformations of the error term (T0) are used, the objective function of GCov22 exhibits two global minima, associated with the true parameter value ($\theta$) and its causal explosive counterpart ($1/\theta$). Consequently, GCov22, in this context, cannot differentiate between the true noncausal and the causal autoregressive processes. The minimum coordinate in the neighborhood of the true parameter value is the maximizer of a Gaussian maximum likelihood function or the OLS estimator of a regression of $y_t$ on its lead or lag.

Next, we consider both linear and nonlinear transformations (T1-T4). The bimodality issue in the objective function of GCov22 is alleviated, but not completely resolved. Figure 1a, c show that when the true autoregressive coefficient is 0.66, the objective function has a global minimum at 0.66 but there can remain a local minimum at the incorrect parameter value $1.5=\theta ^{-1}$. Furthermore, Fig. 2a, c)show that when $\theta =0.9$ is closer to the unit root, then in addition to the global minimum at 0.9 there is a local minimum corresponding to $1.1=\theta ^{-1}$. In the latter case, it is noticeable that the distance between the local and global minima decreases, making the bimodality issue more problematic. These results remain valid, regardless of the specific choices of $a_k$ and K (similar results were obtained for various $a_k$ and K beyond T0-T4, not presented here but available upon request). Whether the problem with the local minimum is related to the choice of $a_j$, K, or a combination of both, it is crucial to recognize that in empirical investigations where the optimal selection of these inputs is unknown, the optimization of the objective function can be challenging in the presence of local minima.

Let us illustrate the performance of the BFGS optimization algorithm under these conditions. The BFGS algorithm is a well-known deterministic optimization technique that approximates the inverse gradient of the objective function to locate the minimum. It starts from the given starting value and iteratively refines this estimate using gradient information and an approximation of the inverse Hessian matrix. We also optimize the objective function related to GCov22 with other commonly used numerical optimization algorithms, such as the Nelder-Mead method, the conjugate gradient method, and BFGS with limited memory. We do not report these findings here, but they are available upon request. In Figs. 1b, d and 2b, d, we present the empirical density function of the estimator GCov22, which has been optimized using the BFGS algorithm. The empirical density is derived from Monte Carlo simulations of the noncausal process in equation (8) with $N=1000$ replications and parameters $\theta =(0.66, 0.9)$, $\nu = (4,10)$, $T=500$, and $H=10$. Specifically, we illustrate scenarios where the starting value of the optimization algorithm corresponds to the local minimum $(0.66^{-1}, 0.9^{-1})$, respectively. Figures 1b, d and 2b, d depict the performance of the BFGS optimization algorithm under these conditions: an erroneous choice of an initial value close to the local minimum may hinder the BFGS optimization algorithm from escaping it and converging towards the global minimum. For results obtained when the true value $\theta =(0.66, 1.5)$ is selected as the initial value, refer to Table 1.

Furthermore, the results indicate that when the BFGS optimizer is applied to GCov22, it performs worse when the coefficient is farther away from the unit circle ($\theta = 0.66$). Table 1 shows that a lower percentage of correctly estimated (and identified) models is achieved for $\theta = 0.9$ compared to $\theta =0.66$. The reason is that when the autoregressive coefficient approaches the unit circle, the distance between the local and global minima decreases, making it more challenging for the optimization algorithm to differentiate between the global minimum and the associated correct coefficient estimator.

The results suggest that if the stationarity restriction on $\theta$ is ignored, local minima issues can arise due to the domain of the estimator GCov22 being divided into two sets within this specific DGP: set 1 with coefficients $\theta < 1$ and set 2 with coefficients $\theta > 1$. As a consequence, if the optimization problem starts in set 2, that is, where a local minimum occurs, it is likely that the numerical optimization algorithm will get trapped in that set and converge to the local minimum instead of the global one. Finally, it should be noted that the results illustrated in Figs. 1, 2 and Table 1 are obtained from simulated length processes $T=500$. For $T=(1000, 1500)$, the results are slightly better and the local minima disappear asymptotically. These results are not reported but are available upon request.

We conclude that careful selection of an appropriate starting value for an optimization algorithm is essential to ensure accurate parameter estimates. This is even more important in multivariate analysis, as we will show in Sect. 3.2. Indeed, the larger number of parameters in multivariate analysis adds a layer of complexity, making the task of achieving convergence towards the global minimum a more intricate challenge.

3.2 The multivariate framework

Let us now investigate the performance of the BFGS-optimized estimator GCov22 in multivariate causal-noncausal models. We consider a 3-dimensional mixed causal-noncausal VAR(1):

$$\begin{aligned} Y_t=\Theta Y_{t-1}+u_t, \end{aligned}$$

(11)

where $u_t$ is serially i.i.d. with a multivariate t-Student distribution characterized by $\nu =4$ degrees of freedom and a diagonal variance-covariance matrix $\Sigma _u$. The autoregressive matrix is $\Theta$, and referring to Representation Theorem, we consider:

$$\begin{aligned} A=\begin{bmatrix} 0.8 &{} 0.7 &{} 1.2\\ 1 &{} 0.9 &{} 0.8\\ 0.6 &{} 0.7 &{} 0.65 \end{bmatrix}, \ \ J=\begin{bmatrix} 0.3 &{} 0 &{} 0\\ 0 &{} 0.5 &{} 0\\ 0 &{} 0 &{} 2.2 \end{bmatrix}, \end{aligned}$$

such that:

$$\begin{aligned} \Theta =AJA^{-1}= \begin{bmatrix} 3.97 &{} -3.73 &{} 1.3\\ 2.29 &{} -2.38 &{} 1.41\\ 1.87 &{}-2.16 &{} 1.40 \end{bmatrix}. \end{aligned}$$

(12)

Hence, the considered process is characterized by two eigenvalues inside the unit circle related to the causal component ($j_1$ and $j_2$) that are collected in matrix $J_1$:

$$\begin{aligned} J_1=\begin{bmatrix} j_1 &{} 0 \\ 0 &{} j_2 \\ \end{bmatrix}= \begin{bmatrix} 0.3 &{} 0 \\ 0 &{} 0.5 \\ \end{bmatrix}, \end{aligned}$$

and an eigenvalue outside the unit circle (related to the noncausal component): $j_3 = 2.2$. Despite the assumption that (11) exhibits an eigenvalue outside the unit circle, this process is not explosive in light of the Representation Theorem presented in Sect. 2. In particular, according to equations (4), (5), and (6), the DGP of process (11) is expressed as the following linear combination of its causal and noncausal components:

$$\begin{aligned} Y_{t}&=A_1 Y_{1,t}^*+A_2 Y_{2,t}^*\\ {}&=A_1 J_1 A^1 Y_{t-1} + A_2 j_3^{-1} A^2 Y_{t+1}+ A_1A^1u_t\\&+A_2 j_3^{-1} A^2 u_{t+1}. \end{aligned}$$

Appendix A displays the path and autocorrelation function of a simulated process $Y_t$.

Next, we explore the performance of the BFGS optimizer of the GCov22 estimator in multivariate VAR(1) processes. We calculate the empirical density function of the estimator of matrix $\Theta$ by implementing a Monte Carlo experiment with $N=1000$ replications of the VAR(1) for $T=500$ observation.

We examine the “worst case scenario” when the OLS estimate of $\Theta$ ($\Theta _{OLS}$) is used as the starting value of the BFGS algorithm for the optimization of GCov22. The OLS estimator of a multivariate causal-noncausal model is inconsistent and $\Theta _{OLS}$ is potentially associated with local minima in the objective function, since they are characterized by eigenvalues $j_1$, $j_2$, and $j_3^{-1}$ (Gourieroux and Jasiak 2017). Then, in the presence of such a local minimum, the algorithm would have difficulty converge to the global minimum.

Fig. 3

Density function of BFGS optimized ${\hat{\Theta }}$, OLS starting value $\varvec{\Theta }_{OLS}$. The empirical density function of BFGS optimized ${\hat{\Theta }}$ estimating the true autoregressive matrix (12), marked with vertical green dashed lines. The starting value for the BFGS optimization algorithm is set at the OLS estimate of the causal counterpart of the matrix (12), that is, $\Theta _{OLS}$, shown with red dashed lines, $T=500$

Table 2 Estimated dynamics: multivariate framework

Fig. 4

Density function of BFGS optimized ${\hat{\Theta }}$: OLS starting value $\varvec{{\tilde{\Theta }}}$. The empirical density function of BFGS optimized ${\hat{\Theta }}$ estimating the true autoregressive matrix (12), marked with vertical green dashed lines. The starting value for the BFGS optimization algorithm is set at the OLS estimate of the noncausal counterpart of the matrix (12), ${\tilde{\Theta }}$, shown with violet dashed lines, $T=500$

Fig. 5

Density function of BFGS optimized ${\hat{\Theta }}$: starting value true $\varvec{\Theta }$ in (12). The empirical density function of BFGS optimized ${\hat{\Theta }}$ estimating the true autoregressive matrix (12), marked with vertical green dashed lines. Here, the matrix in (12) serves a dual purpose as both the population matrix and the starting point for the optimization algorithm

Figure 3 and Table 2 show the results obtained from the nonlinear transformations T1–T4. We do not illustrate the linear transformation T0 since, as shown in the previous sections, it is not capable of capturing the true DGP in mixed causal-noncausal processes. It should be noted that in multivariate processes, the number K increases since we implement the transformations of the errors of each series of components. As a consequence, T1 is now characterized by $K=12$, while all other transformations are characterized by $K=6$. The results show that, like in the univariate framework, the objective function of GCov22 can have local minima at the parameter values of incorrect autoregressive matrices with eigenvalues replaced by their reciprocals. More specifically, Fig. 3 illustrates that the empirical density function of ${\hat{\Theta }}$ is centered on the starting value $\Theta _{OLS}$ of a matrix characterized by the eigenvalues $j_1$, $j_2$, and $j_3^{-1}$ rather than the population matrix $\Theta$ expressed in (12). Then, the BFGS algorithm remains trapped around the starting value. Table 2 summarizes our findings and shows that, as a consequence, the process is predominantly identified erroneously as purely causal by GCov22. The transformation T1 performs better than the other transformations in identifying the true process (Table 2), although the density function of ${\hat{\Theta }}$ still focuses mainly around $\Theta _{OLS}$ rather than on the true autoregressive matrix.

For comparison, Fig. 4 displays the density function of ${\hat{\Theta }}$ when the BFGS algorithm starts at the starting value equal to an autoregressive matrix with all eigenvalues outside the unit circle, i.e, $j_{1}^{-1}$, $j_{2}^{-1}$, and $j_{3}$. To obtain this starting value, we estimate $Y_t=\Theta Y_{t+1}+u_t$ using OLS and then find the inverse of the estimated matrix, denoted by ${\tilde{\Theta }}$. The empirical density function of ${\hat{\Theta }}$ is obtained from a MC experiment with $N=1000$ replications. Using ${\tilde{\Theta }}$ as the starting value makes us mistakenly identify the process as purely noncausal most of the time and produces an empirical density function centered on ${\tilde{\Theta }}$, instead of matrix (12). The BFGS algorithm is again trapped around the inconsistent estimate that serves as the starting value.

Let us now discuss the case when the BFGS algorithm is initiated at the true autoregressive matrix as the starting value. In Fig. 5, the empirical density function of the BFGS optimized GCov22 estimator is shown. The results highlight that in this scenario the conventional BFGS optimization algorithm successfully converges to the global minimum, producing an empirical density function centered on (12). As a result, the model is correctly identified most of the time, regardless of the nonlinear transformations T1-T4 employed (see Table 2).

In the multivariate framework, we also explore autoregressive matrices with eigenvalues close to the unit circle and error distributions close to the Gaussian. Our findings about the GCov22 objective function resemble those of the previous section: higher degrees of freedom in the t-Student error distribution lead to more identification problems and more pronounced local minimum challenges. In addition, when the eigenvalues are near the unit circle, the distance between the local and global minima is reduced, deteriorating the convergence of the optimization algorithms. Since these results resemble those of Sect. 3.1, their presentation is omitted but is available upon request.

The above results extend the findings of the univariate framework as follows: the domain of the objective function of the GCov22 estimator consists of four sets, characterized by the matrices producing specific roots:

• Set 1: Characterized by all those autoregressive matrices that provide eigenvalues inside the unit circle (resp. roots outside the unit circle);

• Set 2: Characterized by all those autoregressive matrices that provide two eigenvalues inside the unit circle and one eigenvalue inside the unit circle;

• Set 3: Characterized by all those autoregressive matrices that provide one eigenvalue inside the unit circle and two eigenvalues outside the unit circle;

• Set 4: Characterized by all those autoregressive matrices that provide eigenvalues outside the unit circle.

Each set contains a matrix that minimizes the value of the objective function based on the autocovariances of linear functions of model errors. However, when nonlinear transformations of errors are considered, there is a single global minimum associated with the true values of the autoregressive matrix (12), and potentially local minima associated with the parameters of incorrect autoregressive matrices. Therefore, in our case, if the optimization algorithm starts within a set, particularly in proximity to a local minimum (Sets 1-3-4), conventional optimization algorithms are likely to become trapped in that set and converge to the local minimum instead of the global one. On the other hand, successful convergence is always achieved when the starting value is selected from the same set as the global minimum (Set 2). Therefore, the choice of the starting point for the optimization algorithm and the optimization algorithm itself are two crucial steps to avoid identification issues, potentially preventing incorrect identification and estimation of the investigated process.

4 Simulated annealing

In the previous section, we stressed the importance of selecting a starting value of the optimization algorithm that belongs to the same set as the global minimum. Indeed, selecting a matrix with $n_1$ and $n_2$ equal to the true orders, as a starting value, helps achieve a successful convergence of the BFGS optimization algorithm. However, in empirical investigations, determining a priori the number of roots that lie within and outside the unit circle of the population matrix can be challenging. Therefore, in this section, we investigate the performance of the SA optimization algorithm (Kirkpatrick et al. 1983; Černy 1985 and Goffe et al. 1994) applied to the optimization of the estimator GCov22. Our particular focus will be on the nonlinear transformation T1, which, as demonstrated in Sect. 3 outperforms T2-T4, in addition to being the most commonly employed nonlinear transformation (see Gourieroux and Jasiak 2022, 2023).

4.1 The algorithm

SA is an optimization method inspired by the annealing process used in metallurgy. In metallurgy, materials are gradually cooled to eliminate imperfections and achieve a more stable state. The algorithm starts at a high temperature ($T^o$) and gradually cools over time to reduce the probability of getting stuck at a local minimum. Therefore, in optimization problems, $T^o$ is a parameter that controls the search space exploration during optimization. When $T^o$ is high, the algorithm is more likely to accept worse solutions than the current one, allowing it to escape local optima and explore new areas of the search space. As $T^o$ decreases, the algorithm is less likely to accept suboptimal solutions and converge toward the global optimum. However, if the cooling rate is too high, the algorithm may not be able to escape local minima (see Corana et al. 1987; Goffe et al. 1992, 1994, and Goffe 1996).

Let us now explain how the SA algorithm works when applied to the estimator GCov22. We consider a mixed causal-noncausal VAR(1) in (11), and we use f to denote the objective function of GCov17 or GCov22. Furthermore, we denote the maximum and minimum temperature values of $T^{o}$ by $T^{o}_{MAX}$ and $T^{o}_{MIN}$, respectively.

To initiate the optimization process, a function evaluation is performed at the randomly selected starting point, denoted $\Theta ^{S}$. Subsequently, a new matrix $\Theta$ ($\Theta ^{\prime }$) is computed. Specifically, it is determined by adjusting the ij-th element of the matrix $\Theta ^{\prime }$ ($\theta ^{\prime }_{ij}$) using the following equation:

$$\begin{aligned} \theta ^{\prime }_{ij} = \theta ^{S}_{ij} + m_{ij} \ \ \ \forall i, j = 1, \dots , n. \end{aligned}$$

(13)

Here, $\theta ^{S}_{ij}$ is the ij-th element of matrix $\Theta _S$, and $m_{ij}$ is randomly selected from a uniform distribution within the interval $[m_{MIN}, m_{MAX]}$. The value $f(\Theta ^{\prime })$ is then calculated and compared with $f(\Theta ^{S})$. If $f(\Theta ^{\prime }) < f(\Theta ^{S})$, $\Theta ^{\prime }$ is accepted and the algorithm goes downhill. In the opposite scenario, when $f(\Theta ^{\prime }) > f(\Theta ^{S})$, the potential acceptance of $\Theta ^{\prime }$ is determined using the Metropolis criterion. According to this criterion, we compute the variable $p^o$ as follows:

$$\begin{aligned} p^o = e^{-\frac{(f(\Theta ^{\prime }) - f(\Theta ^S))}{T^{o}}}, \end{aligned}$$

(14)

we then compare it with $p^{*}$, that is, a number randomly selected from the range [0, 1]. If $p^o < p^{*}$, $\Theta ^{\prime }$ is rejected, and the algorithm remains at the current point in the function. On the contrary, if $p^o > p^{*}$, we accept $\Theta ^{\prime }$ and move downward. Equation (14) illustrates why a lower value of $T^o$ decreases the probability of making an upward move. To find the optimal solution, the procedure is repeated M times for each $T^{o}$, starting from $T^{o}_{MAX}$ and gradually reducing it at a rate of r, for a total of Q times, until it reaches $T^{o}_{MIN}$.

Unlike conventional optimization algorithms, SA can escape local minima (see Corana et al. 1987; Aarts et al. 2005). However, as a drawback, the parameters associated with the SA method, such as $\theta _{MIN}$, $\theta _{MAX}$, $T^{o}_{MAX}$, r, Q, , and M, are typically treated as black-box functions and are dependent upon the objective function to be minimized. In empirical studies, a common approach to investigate whether the global minimum has been found is to repeat the algorithm with a different initial state $\Theta ^{S}$. If the same global minimum is reached, it can be concluded with high confidence that convergence has been achieved. In the cases where a different result is obtained, it may be necessary to modify one or more of the parameters involved in the SA algorithm.

4.2 Performance of BFGS with SA starting values: univariate framework

In this section, we evaluate the performance of the SA algorithm for minimizing the objective function of GCov22 in mixed univariate causal-noncausal models. To this end, we conducted a Monte Carlo experiment to calculate the empirical density functions of ${\hat{\theta }}$, while maintaining the same DGP as specified in (10), that is, $\theta =(0.66, 0.9)$, $\nu =(4,11)$, and $T=500$. The coefficient $\theta$ obtained from SA optimization and known as $\theta _{SA}$, serves as a starting point for the BFGS optimization of the estimator GCov22. This strategy offers two distinct benefits. First, it provides an opportunity to explore the impact of different initial value strategies on reaching the global optimum, thus facilitating comparison with the results presented in Figs. 1, 2 and Table 1. Second, it allows for the refinement of the solution obtained through the SA method. This refinement proves particularly valuable when $\theta _{SA}$ is close to the global minimum, but there is room for improvement in its solution.

Fig. 6

Performance of SA in univariate noncausal process with $\varvec{\theta =0.66}$, $\varvec{\nu =4}$, and $\varvec{T =500}$

As previously mentioned, we begin with an initial temperature of $T^{o}_{MAX}$, and at each of the iterations Q, we allow it to decrease at a rate of r. After Q iterations, it reaches the minimum temperature, denoted $T^{o}_{MIN}$. It is worth noting that, in our approach, the final temperature $T^{o}_{MIN}$ is a deterministic function of $T^{o}_{MAX}$, r, and Q. This is true because $T^{o}_{MIN}$ is obtained by Q reductions at a rate of r from the initial value $T^{o}_{MAX}$, that is, $T^{o}_{MIN} = T^{o}_{MIN}(T^{o}_{MAX}, r, Q)$.

In the literature, it is common to employ a cooling rate of $r=0.85$, as indicated in Goffe et al. (1994) and Corana et al. (1987). However, determining the appropriate values for $T^{o}_{MAX}$ and Q, which later determine $T^{o}_{MIN}$, often requires an empirical approach. Therefore, before conducting our MC experiment, we perform a preliminary analysis of the behavior of DGP under investigation by initially setting $T^{o}_{MAX}$ and Q at high values. This allows us to monitor the performance of the objective function throughout the optimization process. More specifically, in this preliminary analysis, we set $T^{o}_{MAX}=5000$ and $Q=150$. Figure 6a illustrates the behavior of the value of a minimized objective function of GCov22 as a function of the number of iterations Q when $\theta =0.66$ and $\nu =4$. The value of the minimized objective function of GCov22 calculated from approximately 50 iterations fluctuates around an average value of 2.7 without making any improvements to our optimization problem. This suggests that $T^{o}_{MAX}=5000$ is excessively high and results in inefficient time use. Approximately for $Q=50$, corresponding to $T^{o}=1.5$, the value of the minimized value objective function decreases toward the global minimum. These results are further confirmed in Fig. 6b, which shows the behavior of the GCov22 estimator of the parameter $\theta$ as a function of Q. Based on the insights gained from this analysis, we set $T_{MAX}=1.5$ and $Q=100$ in our MC experiment. Furthermore, to effectively explore the search space, we set $M=100$. The choice of a high value for M is crucial for a comprehensive exploration of the search space. The results are summarized in Table 1. The SA algorithm yields a significant improvement in the results compared to Sect. 3.1: ${\hat{\theta }}$ closely approximates the true value and the true dynamic is captured $90\%$ of the time. It should be noted that cases where GCov22 incorrectly identified our process as purely causal can arise from certain replications of our MC experiment when the objective function requires higher values of $T^{o}_{MAX}$, Q, M, or a combination of them. As mentioned previously, these parameters are typically problem-specific, and their selection involves experimentation. However, for practical reasons, we maintain the same values for Q and M in all replications.

We find that improved results are obtained when SA is implemented for the estimation of the simulated DGPs characterized by different autoregressive coefficients and degrees of freedom (see Table 1) of t-Student error distribution.

Fig. 7

Empirical density function of ${\hat{\Theta }}$ with SA starting values. The empirical density function of BFGS optimized Gcov22 with SA starting values and $\Theta$ in (12), as the true parameter matrix. The vertical green lines in the plot indicate the corresponding parameter values

4.3 Performance of BFGS with SA starting values: multivariate framework

In this section, we evaluate the performance of the SA algorithm for optimizing the estimator GCov22 in multivariate mixed causal-noncausal models. As in Sect. 3.2, in each Monte Carlo replication, we simulate the time series and then estimate them by the BFGS algorithm, using the SA-provided starting value. For comparison, we maintain the same Monte Carlo input and autoregressive model specified in Sect. 3.2. In this way, we can explore the impact of different starting value choices on the convergence of BFGS to the global minimum and compare them with the results presented in Figs. 3, 4, 5 and Table 2.

Using the approach employed in Sect. 4.2 on univariate models, we set $T_{MAX}=800$, $Q=200$, and $M=2000$. The results are shown in Fig. 7 and summarized in Table 2. In the multivariate framework, the SA algorithm yields a significant improvement in results compared to Sect. 3.1. The density of the estimator is now centered on the population value (12). Lastly, as in the previous section, it is worth noting that, for practical reasons, we maintain a constant value for $T^{o}_{MAX}$, Q, and M in each replication of the Monte Carlo experiment.

5 Empirical analysis

We conduct an empirical analysis of a bivariate time series consisting of 363 daily observations on the CBOT closing prices of wheat and soybean futures in US Dollars, over the medium term. For this analysis, we use the same data range as Gourieroux and Jasiak (2023), covering the period from October 18, 2016, to March 29, 2018. The dataset was obtained from https://ca.finance.yahoo.com, with the wheat futures represented by the ticker ZW = F and the soybean futures by the ticker ZS = F. Figure 8 shows the demeaned data, while Fig. 9 presents the kernel-smoothed density estimators of the series.

Fig. 8

Empirical investigation: wheat and soybean. The graph shows the demeaned prices of wheat (black line) and soybean (red line) futures from October 18, 2016, to March 29, 2018

Fig. 9

Marginal sample densities of demeaned daily future price series. Marginal sample densities of demeaned daily future price series are non-Gaussian

Table 3 Estimated coefficients of mixed bivariate VAR(2)

Our primary objective is to evaluate the performance of the BFGS optimized estimator GCov22. Additionally, we seek to identify the presence of speculative bubbles in agricultural commodity markets. Detecting such bubbles has significant implications for various stakeholders, including market participants, policymakers, and investors, as it directly impacts decision-making in both the agricultural and financial sectors. It should be noted that the examined series does not exhibit global trends or other widespread and persistent explosive patterns. Instead, they display local trends and spikes, often sharing similar patterns with concurrent spikes. To gain insight into the interactions among these variables and determine whether noncausal components drive these processes, we proceed to estimate a 2-dimensional VAR(p).

Following Gourieroux and Jasiak (2017), we select the value of autoregressive order $p=2$ that eliminates serial autocorrelation from residuals and apply the BFGS optimized GCov22 to the demeaned data. Furthermore, we reject the null hypothesis of the Gaussianity of the residuals of the estimated model.

We use both the OLS estimate of the bivariate process ($\Theta _{OLS}$) and the starting value obtained from the SA as starting points for the BFGS algorithm. The results are presented in Table 3, which indicates that the choice of starting value significantly affects the results. When we use the OLS starting values, the optimized BFGS GCov22 identifies the process as a purely causal VAR(2). However, when the SA starting values are used, we obtain a lower value of the objective function GCov22, and the bivariate process is identified as a mixed causal and noncausal VAR(2) with three roots outside the unit circle and one root inside the unit circle: $j_1=0.972$, $j_2=0.88$, $j_3=0.604$, $j_4=-4.355$ and:

$$\begin{aligned} {\hat{\Theta }}_1= \begin{bmatrix} 0.44 &{} 1.23\\ 3.31 &{} -2.34 \end{bmatrix}, \ \ \ {\hat{\Theta }}_2 = \begin{bmatrix} 0.52 &{} -1.21\\ -3.19 &{} 3.10 \end{bmatrix}. \end{aligned}$$

The associated matrix ${\hat{B}}$ (Sect. 2.1) is:

$$\begin{aligned} {\hat{B}}= \begin{bmatrix} -0.68 &{} -0.45 &{} 0.38 &{} -0.29\\ -0.15 &{} -0.47 &{} 0.34 &{} 0.92\\ -0.70 &{} -0.52 &{} 0.63 &{} 0.07\\ -0.15 &{} -0.54 &{} 0.57 &{} -0.21 \end{bmatrix}. \end{aligned}$$

Since $j_4$ lies outside the unit circle, it implies the simultaneous occurrence of “speculative” bubbles in the two series considered. Furthermore, the negative value of this eigenvalue underscores the fact that these bubbles display fluctuations (see Gourieroux and Zakoian 2017 and Hecq and Voisin 2021).

After computing $B^{-1}$, we obtain a noncausal component of dimension 1 representing a common bubble in commodity prices:

$$\begin{aligned} X^*_{2,t}= 1.54Y_{1,t}-1.21Y_{2,t}+0.78Y_{1,t-1}-0.66Y_{2,t-1} \end{aligned}$$

These findings underscore the importance of combining SA with the BFGS optimization of the GCov22 or another routinely used optimization algorithm. Employing SA to get the starting value is crucial in this case, enabling us to identify a noncausal component of the process, which, in turn, allows us to capture the nonlinear features that define these series.

6 Conclusions

In this paper, we have investigated the performance of the BFGS algorithm for the optimization of the GCov22 estimator in mixed causal-noncausal models. The GCov22 estimator is a semi-parametric method, which does not require any distributional assumptions on the model errors other than serial independence and non-Gaussianity. It minimizes a portmanteau-type criterion based on nonlinear autocovariances, providing consistent estimates and consequently allowing for the identification of the causal and noncausal orders of the mixed VAR.

Our findings highlight the importance of considering an adequate number and type of nonlinear autocovariances in the objective function of the estimator GCov22. When these autocovariances are insufficient or inadequate or when the error density closely resembles the Gaussian distribution, identification issues can arise. This manifests itself in the presence of local minima in the objective function, occurring at parameter values associated with the incorrect causal and noncausal orders. Consequently, the optimization algorithm may converge to a local minimum, leading to inaccurate estimates.

To avoid the optimization problem due to local minima and improve the accuracy of the estimation, we propose the use of the SA optimization algorithm as an alternative to conventional numerical optimization methods. The SA algorithm effectively manages the identification issues caused by local minima, successfully eliminating their effects. By exploring the parameter space more robustly and flexibly, SA provides a reliable solution for obtaining more accurate estimates of the causal and noncausal orders. However, it is worth noting that, in high-dimensional frameworks, Simulated Annealing (SA) may be time-consuming, due to the computational complexity involved in finding the global minimum. For future research in this framework, it would be beneficial to investigate the optimization of GCov22 using more complex optimization algorithms. For example, it would be interesting to explore how Dynamic Mode Decomposition performs in this context (see Tu 2013; Schmid 2010, and Gu et al. 2024). Regardless, one should reestimate the model using several different sets of starting values and compare the minimized values of the objective functions to ensure a correct outcome.

The proposed method is applied to the GCov22 estimator of the causal-noncausal vector autoregressive model of a series of bivariate commodity prices. The results highlight the existence of local minima in this application and the advantage of the SA algorithm in providing reliable results in empirical research.

Appendix

See Figs. 10 and 11.

Fig. 10

Graph of the simulated time series in (11)–(12)

Fig. 11

Autocorrelation function of process generated by (11)–(12)