Maximum likelihood estimation of log-concave densities on tree space

Abstract

Phylogenetic trees are key data objects in biology, and the method of phylogenetic reconstruction has been highly developed. The space of phylogenetic trees is a nonpositively curved metric space. Recently, statistical methods to analyze samples of trees on this space are being developed utilizing this property. Meanwhile, in Euclidean space, the log-concave maximum likelihood method has emerged as a new nonparametric method for probability density estimation. In this paper, we derive a sufficient condition for the existence and uniqueness of the log-concave maximum likelihood estimator on tree space. We also propose an estimation algorithm for one and two dimensions. Since various factors affect the inferred trees, it is difficult to specify the distribution of a sample of trees. The class of log-concave densities is nonparametric, and yet the estimation can be conducted by the maximum likelihood method without selecting hyperparameters. We compare the estimation performance with a previously developed kernel density estimator numerically. In our examples where the true density is log-concave, we demonstrate that our estimator has a smaller integrated squared error when the sample size is large. We also conduct numerical experiments of clustering using the Expectation-Maximization algorithm and compare the results with k-means++ clustering using Fréchet mean.

1 Introduction

Inference of phylogeny is one of the key problems in biology. Phylogenetic trees represent the evolutionary histories of taxa. The methods of phylogenetic reconstruction using current gene data have been highly developed, and it is now possible to reconstruct them easily with various models and inference methods (Felsenstein 2004).

However, due to the uncertainty of inference, incomplete lineage sorting or irregular biological processes such as horizontal transfer, it is usually the case that different gene loci indicate different evolutionary histories (Reid et al. 2014). The classical approach to this problem is finding a consensus tree (Bryant 2003), a single summary tree of multiple trees inferred from different loci, which is constructed by some rules. In 2001, Billera et al. (2001) introduced the space of phylogenetic trees with n leaves, tree space, which is a geodesic metric space with nonpositive curvature. Recent research has shifted to the statistical analysis of a set of trees in such spaces, enabling a geometrical perspective. These efforts include point estimation by Fréchet mean (Bačák 2014a; Sturm 2003), principal component analysis (Nye 2011), outlier detection using a kernel density estimator (Weyenberg et al. 2014, 2017), and construction of confidence sets (Willis 2019).

Since numerous factors affect the inferred phylogenetic trees, the parametric approach to specifying the distribution of inferred trees is difficult, and the risk of misspecifying models is high. In this sense, the nonparametric approach generally specifies fewer constraints in the distribution and might be desirable. The kernel density estimator proposed in Weyenberg et al. (2014, 2017) is designed for this purpose.

In Euclidean space, log-concave density estimation has emerged as a new shape-constrained, nonparametric method of density estimation. Log-concave density is a class of probability densities whose logarithm are concave functions. Compared to classical smoothing approaches such as kernel density estimates, in which we need to specify some hyperparameters such as bandwidths, log-concave density has an advantageous property that the estimation can be done automatically. Concretely, it has been shown that the maximum likelihood estimators exist in both the one-dimensional and multi-dimensional cases and that the calculation of the estimators can be reduced to a N-dimensional convex optimization problem with N sample points (Cule et al. 2010).

In this paper, we show that the maximum likelihood estimator of log-concave density in tree space exists under some conditions and that the estimation can be implemented in the one-dimensional case. Although we do not derive an algorithm for multidimensional cases due to the difficulty of finding the closure of convex hulls, we also show that we can approximately calculate the maximum likelihood estimator in the two-dimensional case.

The remaining sections are organized as follows. In Sect. 2, we review some basic concepts of tree space and define some concepts for convex analysis in Hadamard spaces. Section 3 presents our main result for maximum likelihood estimation in tree space, in one dimension and multiple dimensions. Section 4 explains how to calculate the maximum likelihood estimator in the one-dimensional and two-dimensional cases. Section 5 shows the results of simulation studies. We compare the performance of density estimation with the kernel density estimator. We also compare the simulation results of clustering with a mixture of log-concave densities to the k-means++ approach using the Fréchet mean.

2 Preliminaries

2.1 Phylogenetic trees and tree space

A phylogenetic tree is modeled as a tree with labels only on the leaves. We call a tree with $n+1$ labeled leaves an n-tree. n-trees have one root leaf representing the common ancestor and n leaves representing present taxa. Internal edges are edges that are not directly connected to leaves. In binary n-trees, the number of internal edges is $n-2$. Nonbinary trees have fewer internal edges since they can be obtained by contracting some internal edges of some binary trees. The number of binary n -tree topologies is $(2n-3)!!$(Felsenstein 1978). Note that the edges in different trees are identified if they partition the leaves in the same way. If each internal edge in an n-tree has a positive length, we call it a metric n-tree.

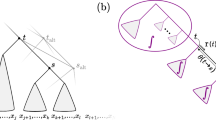
Billera et al. (2001) constructed the space of metric n-trees as follows. First, each binary tree topology is modeled as a positive Euclidean orthant with dimension $n-2$, with each axis corresponding to the length of each internal edge of that topology. These orthants are stuck together on the axes representing the same edges. Nonbinary trees consitute the boundaries of these orthants since they are obtained by contracting some internal edges. In particular, the n-tree without any internal edges is the point located at the center of tree space connected to every orthant. We call this point the origin in this paper. The space of metric n-trees obtained in this way is called tree space and is denoted as ${\mathcal {T}}_n$.

In this paper, we mainly discuss the results in the one-dimensional or two-dimensional case. By dimension, we mean the dimension of each orthant. Therefore, by the p-dimensional tree space, we mean the space ${\mathcal {T}}_{p+2}$. In the one-dimensional tree space, we only have $3!! = 3$ topologies and each orthant representing some topology is a half-line connected to the other two at the origin, the point representing a trifurcating tree (Fig. 1). Two-dimensional tree space ${\mathcal {T}}_4$ has $5!! = 15$ topologies, each orthant being a nonnegative Euclidean plane, and three different orthants are connected to each axis (Fig. 1). It is known that if we represent each axis as a vertex and each orthant as an edge connecting two vertices, then the whole of space ${\mathcal {T}}_4$ can be graphically depicted as a Petersen graph, as shown in Fig. 1. For details, see Billera et al. (2001) or Lubiw et al. (2020), for example.

Fig. 1

Depiction of tree space. (Top): one-dimensional tree space ${\mathcal {T}}_3$. (Center): part of two-dimensional tree space. (Bottom): Petersen graph. Vertices corresponding to axes are indexed from 0 to 9 for convenience

2.2 Geometry of tree space

Tree space can be readily formulated as a metric space. Since it is the union of Euclidean orthants, we can simply define the distance between two points in the same orthant as the usual Euclidean distance. For any two points in distinct orthants, we can set the distance between them as the infimum of the lengths of paths with endpoints in those two points. The infimum is attained since tree space consists of a finite number of orthants, and once a sequence of orthants of a path is decided, there is a unique path with minimum length. The paths which attain the minimum distances are called geodesics, and a metric space with a geodesic between any two points is called a geodesic metric space.

Tree space is also known to be a Hadamard space; i.e., it is a complete metric space with nonpositive curvature. See, for example, Bačák (2014b) for proof.

This property is key to many important results in this space. In Hadamard spaces, the geodesic connecting any two points is guaranteed to be unique. Owen and Provan (2011) has developed an algorithm to find geodesics in tree space in $O(p^4)$ time, where p denotes the dimension of tree space. In tree space, geodesics are piecewise segments through sequences of orthants, and in some cases, they become cone paths, where each geodesic consists of two segments connecting the endpoints and the origin. In particular, in two-dimensional tree space ${\mathcal {T}}_4$, whether a geodesic between two points becomes a cone path depends only on the “angle” between them. See, for example, Lubiw et al. (2020) for a detailed account of this property. The nonpositively curved property also results in the existence and uniqueness of the Fréchet mean. For a given sample $X_1,\ldots ,X_N$ in Hadamard space $({\mathcal {H}},d)$ and weights $w_1,\ldots , w_N > 0$, the Fréchet mean ${\bar{X}}$ is defined as the minimizer of the sum of squared distances:

$$\begin{aligned} {\bar{X}} = \mathop {\mathrm {arg\,min}}\limits _{x\in {\mathcal {H}}}\sum _{i=1}^{ {N}} w_i d(x,X_i)^2. \end{aligned}$$

(1)

It is a generalization of the arithmetic mean since they coincide with uniform weights in Hilbert spaces. It is known that the Fréchet mean can be calculated using the proximal point algorithm (Bačák 2013). See, for example, Bačák (2014b) for proof of results regarding the Fréchet mean in Hadamard spaces.

2.3 Convex sets and concave functions on Hadamard spaces

In this section, we define several concepts of convex sets and concave functions on Hadamard spaces.

First, we define convex sets as in Bačák (2014b). Let $({\mathcal {H}},d)$ be a Hadamard space . For any points $x,y \in {\mathcal {H}}$, we use the notations $\gamma _{x,y}$ or [x, y] to denote the unique geodesic between them. Also, for $\lambda \in [0,1]$, we use the notations $\gamma _{x,y}(\lambda )$ or $(1-\lambda ) x + \lambda y$ to denote the points in the geodesic [x, y] with distance $\lambda d(x,y)$ from x. We say $A\subseteq {\mathcal {H}}$ is convex if for any points $x,y\in A, [x,y] \subseteq A$.

A function $\psi :{\mathcal {H}}\rightarrow [-\infty , \infty ]$ is concave if its hypograph ${{{\,\textrm{hypo}\,}}\psi } = \{(x,\mu ) \in {\mathcal {H}} \times {\mathbb {R}}\mid \mu \le \psi (x)\}$ is convex. Note that a product of Hadamard spaces is also a Hadamard space, and thus, in particular, ${\mathcal {H}}\times {\mathbb {R}}$ is also a Hadamard space.

Given any set S in ${\mathcal {H}}$, the convex hull of S is the smallest convex set in ${\mathcal {H}}$ containing S. This set exists because the intersection of (possibly infinite) convex sets is convex and that ${\mathcal {H}}$ is convex. We denote the convex hull of S as ${{\,\textrm{conv}\,}}S$. In Hadamard spaces, it is known that a convex hull can be written as in the following Lemma.

Lemma 1

(Bačák (2014b), Lemma 2.1.8) For $S\subseteq {\mathcal {H}}$, put $D_0 = S$ and for $k\in {\mathbb {N}}$, recursively define $D_k$ by $D_k = \{x\in {\mathcal {H}} \mid x \in [y,z] \text { for some }y,z\in D_{k-1}\}$. Then,

$$\begin{aligned} {{\,\textrm{conv}\,}}S = {\bigcup _{k=0}^\infty } {D_k} . \end{aligned}$$

(2)

This Lemma indicates that taking geodesics between points an infinite number of times obtains the convex hull. Next, we define an important concept of the concave hull of a function. Given any function $\psi$ on ${\mathcal {H}}$, the concave hull of $\psi$, ${{\,\textrm{conc}\,}}\psi$, is defined as the least concave function minorized by $\psi$. Its existence and uniqueness in Euclidean space is a well-known result; see chapter 5 of Rockafellar (1970) for a detailed account. Here we give the existence and uniqueness in the Hadamard case.

Lemma 2

For any function $\psi :{\mathcal {H}}\rightarrow [-\infty , \infty ]$, the concave hull ${{\,\textrm{conc}\,}}\psi$ exists and is unique. Furthremore, ${{\,\textrm{conc}\,}}\psi$ can be written as follows:

$$\begin{aligned} {{{\,\textrm{conc}\,}}\psi (x) = \{\mu \mid (x,\mu )\in {{\,\textrm{conv}\,}}({{\,\textrm{hypo}\,}}\psi )\} }\end{aligned}$$

(3)

The proof is given in the suplementary material. An important implication of the Lemma 2 is how to derive the concave hull of a function: calculate the convex hull of its hypograph, and take the supremum.

Another condition that is usually assumed with concavity is upper-semicontinuity. A function $\psi :{\mathcal {H}}\rightarrow [-\infty ,\infty ]$ is upper-semicontinuous at x if $\limsup _{y\in {\mathcal {H}}:d(x,y)\rightarrow 0} \psi (y) \le \psi (x)$. If function $\psi$ is upper-semicontinuous at all points $x\in {\mathcal {H}}$, then it is upper-semicontinuous on ${\mathcal {H}}$. It is also equivalent to the hypograph of $\psi$ being closed.

Similar to concave hulls, we can define an upper-semicontinuous hull of a function $\psi$ as the least upper-semicontinuous function minorized by $\psi$. That this function exists follows from the fact that (possibly infinite) intersections of closed sets are closed. Furthermore, it is possible to define the upper-semicontinuous concave hull of a function of $\psi$, as the least upper-semicontinuous concave function minorized by $\psi$. Concretely, this function is derived by taking intersections of the hypographs of all upper-semicontinuous and concave functions minorized by $\psi$. It can also be characterized as the function whose hypograph is ${{\,\textrm{cl}\,}}({{\,\textrm{conv}\,}}{{\,\textrm{hypo}\,}}\psi )$ where ${{\,\textrm{cl}\,}}$ is the closure operator. We denote the upper-semicontinous concave hull of a function $\psi$ as ${\overline{{{\,\textrm{conc}\,}}}}\psi$.

2.4 Log-concave density

A function $f: {\mathcal {H}}\rightarrow [0,\infty ]$ is called log-concave if its logarithm $\log f: {\mathcal {H}}\rightarrow [-\infty ,\infty ]$ is concave. Figure 2 illustrates two example densities on ${\mathcal {T}}_3$: Laplace distribution-like density $f_l(x) \propto \exp (-d(x,x_0))$ and t distribution-like density $f_t(x)\propto (1+d(x,x_0)^2/2)^{-3/2}$. By the form of log-densities, we can see that $f_l$ is an example of a log-concave density while $f_t$ is an example of a density that is not log-concave.

Fig. 2

Illustration of densities $f_l$ and $f_t$ (Top) and log-densities $\log f_l$ and $\log f_l$ (Bottom). In each figure, the right side of the origin corresponds to the orthant $O_1$ that $x_0$ is in. Since these densities have exact same values at the other two other orthants, left side of the origin represents both of these orthants $O_2$ and $O_3$

The class of probability density functions that are log-concave is well-studied in Euclidean spaces. It especially contains some very often used densities such as multivariate normal, exponential, gamma distribution with the shape parameter greater than or equal to 1, and so on. A recent review on this topic can be found in Samworth (2018).

In terms of the estimation of log-concave density in Euclidean spaces, Cule et al. (2010) has shown that for an i.i.d. sample $X_1,\ldots ,X_N (N\ge p+1)$ from a density on p-dimensional Euclidean space ${\mathbb {R}}^p$, the log-concave maximum likelihood estimator exists with probability 1. Here, the log-concave maximum likelihood estimator is the log-concave density f that maximizes the log-likelihood function:

$$\begin{aligned} {l_N(f) = \sum _{i=1}^N \log f(X_i). }\end{aligned}$$

(4)

We outline their key findings about the form of the log-concave maximum likelihood estimator here since a similar argument can be applied in the case of tree space as well.

The authors show that the optimization of the equation (4) can be reformulated into the maximization of the following objective function over log-concave functions, by introducing the Lagrange multiplier term:

$$\begin{aligned} {{\mathcal {L}}_N(f) = \frac{1}{N}\sum _{i=1}^N \log f(X_i) - \int _{{\mathbb {R}}^p} f(x)dx. }\end{aligned}$$

(5)

The maximization of (5) results in a probability density ${\hat{f}}_N$ whose logarithm is a “tent” function: $\log {\hat{f}}_N$ is a piece-wise linear concave function that has its “knots” at some selected sample points and takes finite values only on the convex hull of sample points (Fig. 3). Intuitively, this holds because among any log-concave density f that satisfies $f(X_i) \ge {\hat{f}}_N(X_i)~(i=1,\ldots ,N)$, the “tent” function minimizes the Lagrange term in the equation (5).

Fig. 3

An example of “tent” function on ${\mathbb {R}}$. $X_1,\ldots ,X_5$ are the given sample points

For any $y = (y_1,\ldots ,y_N)^\top \in {\mathbb {R}}^N$, let $\psi _y:{\mathbb {R}}^p \rightarrow [-\infty ,\infty ]$ denote the following function:

$$\begin{aligned} {\psi _y(x) = {\left\{ \begin{array}{ll} y_i &{} \text {if } x=X_i \\ -\infty &{} \text {otherwise} \end{array}\right. }. } \end{aligned}$$

(6)

Then using the terminology of section 2.3, any tent function can be characterized as the concave hull of $\psi _y$ for some suitable $y\in {\mathbb {R}}^N$. Therefore, the log-concave maximum likelihood estimator in Euclidean spaces is included in the following function class:

$$\begin{aligned} {\{\exp ({{\,\textrm{conc}\,}}\psi _y(x)) \mid y\in {\mathbb {R}}^p\}. } \end{aligned}$$

(7)

The problem of finding the log-concave maximum likelihood estimator can now be turned into that of finding a suitable N-dimensional vector y.

2.5 Probability measure on tree space

In this section, we introduce one of the possible constructions of a probability measure on tree space. This construction is due to Willis (2019).

Let $({\mathcal {T}}_{n}, d)$ be tree space. Note that this space consists of $(2n-3)!!$ Euclidean $(n-2)$-dimensional nonnegative orthants. Now, one can write any set A in ${\mathcal {T}}_{n}$ as a union of Euclidean sets, $A = \cup _{i=0}^{(2n-3)!!} A_i$. Here, $A_0$ denotes the set of trees in A that are in the boundary of ${\mathcal {T}}_n$, and $A_i$ denotes the set of trees in A that are in the i-th positive orthant. Let $\nu _B$ be the Lebesgue measure on ${\mathbb {R}}^{n-2}$, and define $\nu$ by $\nu (A) = \sum _{i=1}^{(2n-3)!!} \nu _B(A_i)$. This $\nu$ preserves sigma additivity, and by completion of measures, $\nu$ becomes a complete measure.

In the remaining sections, we consider densities with respect to the measure $\nu$.

3 Existence and uniqueness of maximum likelihood estimator

3.1 One-dimensional case

In this section, we consider the simplest tree space, ${\mathcal {T}}_3$. Let ${\mathcal {F}}_0^{(1)}$ be the set of log-concave probability densities with respect to the base measure $\nu$ on this one-dimensional tree space. The following theorem indicates that maximum likelihood estimation in ${\mathcal {T}}_3$ could be performed in the same manner as in the Euclidean case.

Theorem 3

Let $(X_1, \ldots , X_N)$ be an independent sample from some density on ${\mathcal {T}}_3$, with $N \ge 2$. Then, with probability 1, the maximum likelihood estimator ${\hat{f}}_N$ of f exists and is unique: i.e., ${\hat{f}}_N$ is the unique maximizer in ${\mathcal {F}}_0^{(1)}$ of the log-likelihood function $l_N(f) = \sum _{i=1}^N \log f(X_i)$.

The proof is given in the supplementary material.

Remark 1

Although our main interest is in tree space, it is simple to see that the above result also applies to the space of $K\in {\mathbb {N}}$ half-lines connected at the origin.

3.2 Multidimensional case

In this section, we consider the general p-dimensional tree space, ${\mathcal {T}}_{p+2}$. We let $\bar{{\mathcal {F}}}_0^{(p)}$ be the set of upper-semicontinuous log-concave densities in ${\mathcal {T}}_{p+2}$ and $l_N(f) = \sum _{i=1}^N \log f(X_i)$ denote the log-likelihood function. The maximum likelihood estimator in this case, unlike in the cases of the one-dimensional tree space and Euclidean space, might not even exist. Before deriving a sufficient condition for the existence of the MLE, we first show that when the maximizer exists, its uniqueness can be stated as in the following theorem.

Theorem 4

Let $(X_1, \ldots , X_N)$ be a sample from some density on ${\mathcal {T}}_{p+2}$. Suppose that a maximizer of $l_N(f)$ in $\bar{{\mathcal {F}}}_0^{(p)}$ exists. Then the maximizer is unique $\nu -$almost everywhere.

Proof

Suppose $f_1, f_2\in \bar{{\mathcal {F}}}_0^{(p)}$ both maximize $l_N(f)$. If we put $f(x)=\{f_1(x)f_2(x)\}^{1/2}/\int _{{\mathcal {T}}_{p+2}}\{f_1(z)f_2(z)\}^{1/2}d\nu (z)$, f is log-concave and

$$\begin{aligned} l {_N} (f)&={\frac{1}{2N} \sum _{i=1}^N} \{\log f_1(X_i) + \log f_2(X {_i} )\} \nonumber \\&\quad - \log \int _{{\mathcal {T}}_{p+2}}\{f_1(z)f_2(z)\}^{1/2}d\nu (z) \nonumber \\&\ge l(f_1) - \log \int _{{\mathcal {T}}_{p+2}}\frac{f_1(z)+f_2(z)}{2}d\nu (z) \nonumber \\&= l(f_1). \end{aligned}$$

(8)

Here, the last inequality is the relationship between the arithmetic mean and geometric mean, and equality holds if and only if $f_1(x) = f_2(x)~ \nu \mathrm {-a.e.}$. $\square$

The next theorem provides a sufficient condition for sample points such that the maximum likelihood estimator exists and is unique almost everywhere. For a set S, let ${{\,\textrm{int}\,}}(S)$ denote the interior of the set.

Theorem 5

Let $(X_1, \ldots , X_N)$ be a sample from a density f on ${\mathcal {T}}_{p+2}$, $N\ge p+1$. Let $C_N = {{\,\textrm{conv}\,}}\{X_1, \ldots , X_N\}$, and suppose the following condition holds:

• 1. For each $X_i$, there exists a nonnegative orthant $O_j$ such that $X_i\in O_j$ and ${{\,\textrm{cl}\,}}(C_N)\cap O_j$ is a p-dimensional set: i.e., $\nu ({{\,\textrm{cl}\,}}(C_N)\cap O_j) > 0$.

Then, the maximum likelihood estimator ${\hat{f}}_N$ in $\bar{{\mathcal {F}}}_0^{(p)}$ exists: i.e., ${\hat{f}}_N\in \bar{{\mathcal {F}}}_0^{(p)}$ is a maximizer of the log-likelihood function $l_N(f) = \sum _{i=1}^N \log f(X_i)$. Moreover, it is unique except in some set of $\nu$-measure zero excluding ${{\,\textrm{int}\,}}(C_N)$.

Note that the sufficient condition is a condition that holds with a probability approaching one as N goes to infinity. This can be seen as follows. With probability 1, each $X_i$ is included in at least one nonnegative orthant $O_i$ with a positive probability under the true distribution. For any orthants that have positive probability under the true density, the probability that the orthant contains less than $p+1$ points approaches zero as $N\rightarrow \infty$.

The proof is given in the supplementary material. As in the case of Euclidean spaces, in the proof of Theorem 3 and Theorem 5, it is shown that the maximum likelihood estimator can be characterized as the maximizer of the following function ${\mathcal {L}}_N(f)$ over the class of upper-semicontinuous log-concave functions:

$$\begin{aligned} {{\mathcal {L}}_N(f) = \frac{1}{N}\sum _{i=1}^N \log f(X_i) - \int _{{\mathcal {T}}_{p+2}}f(x)d\nu (x). } \end{aligned}$$

(9)

In addition, as in Euclidean cases, the maximizer of this function ${\mathcal {L}}_N(f)$ has the form $\exp ({\bar{h}}_y)(x)$ for a suitably selected $y\in {\mathbb {R}}^N$, where ${\bar{h}}_y= {\overline{{{\,\textrm{conc}\,}}}} \psi _y(x)$ and $\psi _y: {\mathcal {T}}_{p+2}\rightarrow [-\infty ,\infty ]$ is defined by equation (6). We call this function ${\bar{h}}_y$, the upper-semicontinuous least concave function with ${\bar{h}}_y(X_i)\ge y_i$. As a result, we need to find $y\in {\mathbb {R}}^N$ that maximizes the function $\rho _N: y\mapsto {\mathcal {L}}(\exp ({\bar{h}}_y))$.

Also, note that in one-dimensional case, the concave hull of $\psi _y$ is automatically upper-semicontinuous and ${{\,\textrm{conc}\,}}\psi _y = {\overline{{{\,\textrm{conc}\,}}}}\psi _y$. We denote this concave hull by $h_y = {{\,\textrm{conc}\,}}\psi _y$ and call it the least concave function with $h_y(X_i) \ge y_i$.

The uniqueness of the log-concave maximum likelihood estimator is only assured in $\nu$-almost sure sense outside ${{\,\textrm{int}\,}}(C_n)$ in multidimensional cases. This is because the addition of a new point outside the existing convex hull sometimes does not induce an increase in the measure of the convex hull of the new set of points. Next is an example.

Example 1

(Nonuniqueness) Consider that we have three points $X_1, X_2, X_4 \in {\mathcal {T}}_4$ as depicted in Fig. 4. Then ${{\,\textrm{conv}\,}}\{X_1, X_2, X_4\}$ is the triangle $X_1X_2X_4$. Suppose that we add $X_3$ and consider ${{\,\textrm{conv}\,}}\{X_1, X_2, X_4, X_3\}$. Then this set is the union of triangle $X_1X_2X_4$ and the segment $X_4X_3$, and it is clear that the measure has not increased: i.e., $\nu ({{\,\textrm{conv}\,}}\{X_1, X_2, X_4\}) = \nu ({{\,\textrm{conv}\,}}\{X_1, X_2, X_4, X_3\})$. Suppose that we have obtained $f\in \bar{{\mathcal {F}}}_0^{(p)}$ that satisfies $f(x)>0~(x\in {{\,\textrm{conv}\,}}\{X_1, X_2, X_4\}), f(x)=0~ (x\not \in {{\,\textrm{conv}\,}}\{X_1, X_2, X_4\})$. Then “extending” the support of f to include the segment $X_3X_4$ preserving log-concavity would not change the value of the likelihood, and the extension of f would also be a density. Thus, $\nu$-almost sure uniqueness holds, but strict uniqueness does not hold in this case.

Fig. 4

Illustration of Example 1 and Example 2. The two trees depicted are the topologies that the two orthants represent. Geodesics between them are always cone paths

Cases in which the maximum likelihood estimator does not exist occur when the convex hull has a measure-zero intersection with some orthant.

Example 2

(Nonexistence) Consider that we have three samples $X_1, X_2, X_3 \in {\mathcal {T}}_4$ as depicted in Fig. 4. The geodesics between points in these two trees necessarily are cone paths. It is clear that the assumption in Theorem 5 is not satisfied. Now, assume that the lengths of segments $X_1X_4$ and $X_2X_4$ are the same, and the length of segment $X_3X_4$ is three times that of $X_1X_4$ and $X_2X_4$. Let $\log f$ be an affine-like function with $\log f(X_3) = y+\Delta$ and $\log f(X_2) = \log f(X_1) = y-\Delta /3$. Then $\log f(X_4) = y$ and letting $z(\Delta ) = (y-\Delta /3, y-\Delta /3, y+\Delta )^\top$,

$$\begin{aligned} {\rho _N} ( {z(\Delta } ) {) } = y +\frac{\Delta }{9} - {\int _{C_N} } f(x)dx.\end{aligned}$$

(10)

One can see that as $\Delta$ goes to $+\infty$ the second term linearly goes to $+\infty$ and the last integral term converges to zero. Thus, $\rho _N$ is a diverging monotone increasing function with respect to $\Delta$ and does not attain a maximum. Therefore, the maximum likelihood estimator does not exist in this case.

3.3 Densities that bend at the boundary

Although the nonparametric class of log-concave densities seem to be large enough to model various densities, there are densities that arise narturally which are not log-concave around the boundary. In this section, we focus on the simplest one-dimensional tree space ${\mathcal {T}}_3$, and discuss a way to incorporate densities that are not log-concave at the origin. Let $O_1,O_2,O_3$ represent the three half-lines, and let the restriction of a density $f:{\mathcal {T}}_3\rightarrow {\mathbb {R}}$ to each half-line $O_i$ be $f_i$, which is a function on ${\mathbb {R}}_{\ge 0}$. Denote the exterior derivative at the origin by $\partial f_i / \partial n_i(0)$, defined as:

$$\begin{aligned} \frac{\partial f_i}{\partial n_i}(0) = \lim _{h\rightarrow +0} \frac{f_i(0)-f_i(h)}{h}. \end{aligned}$$

(11)

Nye and White (2014) considered diffusion process on ${\mathcal {T}}_3$ and defined a natural generalization of Gaussian density as a solution to the heat equation. If diffusion starts from the point $x_0\in {\mathbb {R}}_{>0}$ in the orthant $O_1$, the probabilty density $f^{(D)}$ at time t in each orthant can be written as follows:

$$\begin{aligned} \begin{aligned} f {^{(D)}_1}(x {; x_0, t} )&= \phi (x;x_0,t) - \frac{1}{3}\phi (x;-x_0,t) \\ f {^{(D)}_i}(x {; x_0, t} )&= \frac{2}{3}\phi (x;-x_0,t) ~~~~~ (i\in \{2,3\}) \end{aligned} \nonumber \\ \end{aligned}$$

(12)

Here, $\phi (x;\mu ,\sigma ^2)$ denotes the normal density on ${\mathbb {R}}$ with mean $\mu$ and variance $\sigma ^2$.

Density (12) does not have log-concavity since it “bends” at the origin (Fig. 5). In fact, the exterior derivatives are

$$\begin{aligned} \begin{aligned} {\frac{\partial f^{(D)}_1}{\partial n_1}(0; x_0, t) }&= -\frac{4}{3}\phi ^\prime (0;x_0,t), \\ {\frac{\partial f^{(D)}_i}{\partial n_i}(0; x_0, t) }&= \frac{2}{3}\phi ^\prime (0;x_0,t)~~~~~ (i\in \{2,3\}). \end{aligned}\nonumber \\ \end{aligned}$$

(13)

This makes density f to be not log-concave around the origin.

Fig. 5

(Top): Illustration of densities $f^{(D)}(x;x_0,1)$ and $f^{(C)}(x; 1)$. (Bottom): Låog-densities $\log f^{(D)}(x; x_0, 1)$ and $\log f^{(C)}(x; 1)$. $x_0$ is the point in $O_1$ that is one unit away from the origin. The right side of the origin corresponds to $O_1$ and the left side corresponds to both $O_2$ and $O_3$

Another example can be constructed by considering a simple multispecies coalescent process of three lineages from three different species. Suppose the species tree topology corresponds to the orthant $O_1$ and let T denote the length of the internal edge of the species tree. Then, the probability density of gene trees $f^{(C)}$ can be derived as follows (see supplementary material for the detailed derivation):

$$\begin{aligned} \begin{aligned} f {^{(C)}_1}(x {; T} )&= -\frac{1}{6}\exp ({-x-T}) \\&\quad + \frac{1}{2}\exp \left( - {|x-T|} \right) \\ f {^{(C)}_i}(x {; T} )&= \frac{1}{3}\exp ({-T-x}) ~~~~ (i\in \{2,3\}). \end{aligned} \end{aligned}$$

(14)

The exterior derivatives are

$$\begin{aligned} \begin{aligned} {\frac{\partial f^{(C)}_1}{\partial n_1}(0; T) }&= -\frac{2}{3}\exp (-T) ~~~~ \\ {\frac{\partial f^{(C)}_i}{\partial n_i}(0; T) }&= \frac{1}{3}\exp (-T) ~~~~ (i\in \{2,3\}),\\ \end{aligned} \end{aligned}$$

(15)

so the log-concavity does not hold.

In these two examples, densities restricted to each half-line ${\mathbb {R}}_{\ge 0}$ are log-concave. The only non log-concave part is at the origin, where the absolute value of the slope of density differs. Concretely, the following relationship holds:

$$\begin{aligned} \frac{\partial f_1}{\partial n_1}(0) \le 0, ~~~~~\frac{\partial f_1}{\partial n_1}(0) = -2\frac{\partial f_{j}}{\partial n_{j}}(0)~~~~~j\in \{2,3\}. \end{aligned}$$

(16)

We can also see that it satisfies the following Kirchhoff-type condition:

$$\begin{aligned} \sum _{i=1}^3 \frac{\partial f_i}{\partial n_i}(0) = 0. \end{aligned}$$

(17)

These densties that bend at the origin can be incorporated in the model. We relax convexity condition of ${{\,\textrm{hypo}\,}}(\log f)$ to be the following:

• 1. ${{\,\textrm{hypo}\,}}(\log f)\cap O_i\times {\mathbb {R}}$ is convex for all $i\in \{1,2,3\}$

• 2. For $x_1\in O_i$ and $x_2\in O_j$ with $i\ne j$, let $\lambda =d(x_1,0)/d(x_1,x_2)$, and

  $$\begin{aligned} y_0 =&\min \left\{ \frac{2(1-\lambda )\log f(x_1) + \lambda \log f(x_2)}{2-\lambda }, \right. \nonumber \\&\left. \frac{(1-\lambda )\log f(x_1) + 2\lambda \log f(x_2)}{1+\lambda } \right\} . \end{aligned}$$

  (18)

  Then, $(0,y_0)\in {{\,\textrm{hypo}\,}}(\log f)$

We denote by ${\mathcal {G}}_0$ the class of densities which satisfy these two conditions. Any log-concave density f satisfies these two conditions since $y_0 \le (1-\lambda )\log f(x_1) + \lambda \log f(x_2)$. Also, this allows for the bending at the origin to certain extent. In fact, the two densities we considered in this section are included in ${\mathcal {G}}_0$.

We can now exploit similar arguments to the one-dimensional log-concave case in Sect. 3.1 and derive the existence and uniqueness of the maximum likelihood estimator in ${\mathcal {G}}_0$. Note that the resulting estimator does not require Kirchhoff-type condition.

4 Calculation of maximum likelihood estimator in one and two dimensions

Given sample points $(X_1,\ldots ,X_N)\in {\mathcal {T}}_{p+2}$, for the maximization of the function $\rho _N$, we need to be able to calculate ${\bar{h}}_y={\overline{{{\,\textrm{conc}\,}}}}\psi _y$ for a given input vector $y = (y_1,\ldots ,y_N)^\top \in {\mathbb {R}}^N$. In the one-dimensional case, this problem is reduced to finding the convex hull of points $\{(X_1, y_1), \ldots , (X_N, y_N)\}$ in ${\mathcal {T}}_3\times {\mathbb {R}}$. We explain below that this can be reduced to convex hull calculation in ${\mathbb {R}}^2$. In the two-dimensional case, we need to find the closure of the convex hull of points $\{(X_1, y_1), \ldots , (X_N, y_N)\}$ in ${\mathcal {T}}_4\times {\mathbb {R}}$. It is not known if we can obtain such algorithm, but we show below that obtaining an approximate convex hull is possible.

4.1 Calculation of the least concave functions on ${\mathcal {T}}_3$

As discussed in Sect. 2.3, concave hulls can be found by first taking the convex hull of the hypograph and then taking the supremum. In this case, the problem is to find the convex hull $E_N$ of a finite set of sample points in ${\mathcal {T}}_3\times {\mathbb {R}}$.

${\mathcal {T}}_3$ is a space consisting of three half-lines ${\mathbb {R}}_{\ge 0}$ connected at the origin. If all sample points are from one orthant, then the situation is the same as the Euclidean case, so we consider the case that the sample points are from at least two orthants. Let $y_0 = \max \{ (1-\lambda )y_i + \lambda y_j~|~ i,j\in \{1,\ldots ,N\}, \lambda \in [0,1], \gamma _{X_i,X_j}(\lambda ) = 0\}$. Then, $(0,y_0)$ needs to be in the convex hull $E_N$. Furthermore, if we compute the convex hull of sample points in each orthant including $(0,y_0)$ and take their union, this set, say $F_N$, becomes a convex set. Obviously $F_N$ is included in $E_N$, thus by the minimality of convex hulls, this set $F_N$ in fact equals $E_N$. Since $y_0$ can be calculated by taking geodesics of all pairs of sample points, one can calculate $E_N$ easily using the convex hull algorithm in Euclidean space ${\mathbb {R}}^2$.

Similar arguments hold if we allow for the bend at the origin as discussed in the Sect. 3.3. Concretely, we only need to alter the definition of $y_0$ to be

$$\begin{aligned} y_0 =&\max \left\{ \min \left\{ \frac{\lambda y_j + 2(1-\lambda )y_i}{2-\lambda }, \frac{2\lambda y_j + (1-\lambda )y_i}{1+\lambda }\right\} \nonumber \right. \\&\left. ~|~ i < j, \lambda \in [0,1], \gamma _{X_i,X_j}(\lambda ) = 0\right\} . \end{aligned}$$

4.2 Approximation of ${\bar{h}}_y$ on ${\mathcal {T}}_4$

In the two-dimensional case, it is not even known whether the convex hull of a finite number of points is closed. Recently, Lubiw et al. (2020) constructed an algorithm to find the closure of the convex hull of a finite number of points in single-vertex 2D CAT(0) complexes, including two-dimensional tree space ${\mathcal {T}}_4$, utilizing linear programming. Although we cannot transfer the algorithm directly to the product space of ${\mathcal {T}}_4$ and ${\mathbb {R}}$, Lubiw et al. (2020) also showed that by iteratively updating the values at the boundaries, one can construct a sequence of sets that converge to the desired convex hull. With a slight modification to this argument, as we show below, we can also create a similar situation so that by stopping at some iteration number, we can obtain an approximation of the convex hull.

To see this, let $S_0$ be all the sample points $\{(X_i, y_i)\mid X_i\in {\mathcal {T}}_4, y_i\in {\mathbb {R}}\}$. For simplicity, we will only consider the situation where the origin is in the convex hull (if the convex hull of sample points does not contain the origin, then the situation is the same as the Euclidean case). We call a geodesic in the space ${\mathcal {T}}_4 \times {\mathbb {R}}$ a cone path if it crosses the point of the type $\{0, y_j\}$, where 0 denotes the origin in ${\mathcal {T}}_4$: that is, we call a geodesic a cone path when its projection onto ${\mathcal {T}}_4$ is a cone path. Also, for any nonnegative orthant O in ${\mathcal {T}}_4$, define $S_0(O)=S_0\cap (O\times {\mathbb {R}})$, $H_0(O) = {{\,\textrm{conv}\,}}(S_0(O))$ and $H_0 = \cup _{O} H_0(O)$. Following the notation of Lubiw et al. (2020), we define sets $S_k\subseteq {\mathcal {T}}_4\times {\mathbb {R}}~(k=0,1,2,\ldots )$ (which Lubiw et al. (2020) call the k -th skeletons) and $H_k\subseteq {\mathcal {T}}_4\times {\mathbb {R}}~(k=0,1,2,\ldots )$ iteratively as follows.

First, we take geodesics between points in $H_{k-1}$ that are cone paths and find the values at the origin, which can be represented as $(0,y_{k,j})$. Then we find maximum and minimum values of $\{y_{k,j}\}$, and let them be $y_{k1}, y_{k0}$, respectively. We initialize $T_k$ with $S_{k-1}\cup \{(0, y_{k1}), (0, y_{k0})\}$. Although it is practically difficult to find the exact maximum and minimum values, we can use an approximation algorithm. We discuss on this approximation in the supplementary material.

Now for each pair of points in $T_k$, take the geodesic between them, and add all intersection points with the boundaries to $T_k$. Here, by a boundary, we mean a two-dimensional plane formed by an axis on ${\mathcal {T}}_4$ and ${\mathbb {R}}$. Then, for each boundary in ${\mathcal {T}}_4$, take all points that are also in $T_k$, including points at the origin, which are of the form $(0,y_{ki})$. Since each boundary is a two-dimensional plane, these points can be thought of as points in ${\mathbb {R}}^2$, and we take the usual two-dimensional Euclidean convex hull in this space. Then discard any points that are not vertices of this convex hull from $T_k$, and set $S_k = T_k$. Further, let O be any nonnegative orthant in ${\mathcal {T}}_4$ and $S_k(O)$ be the points in $S_k$ that are also in $O\times {\mathbb {R}}$. Define $H_k(O) = {{\,\textrm{conv}\,}}(S_k(O))$, which can be computed easily since $S_k(O)$ can be embedded into a nonnegative orthant in ${\mathbb {R}}^3$, and $H_k = \cup H_k(O)$.

This construction is similar to the two-dimensional CAT(0) case (Lubiw et al. 2020), but the differences are that in this case, we have to determine the maximum and minimum values at the origin first, and instead of preserving only extreme points in a one-dimensional axis, we need here to save all the vertices in the convex hull of points on two-dimensional boundaries.

To validate the first step, we first show the following lemma.

Lemma 6

If $S_{k-1}$ is included in ${{\,\textrm{conv}\,}}(S_0)$, then so is $S_k$.

Proof

$S_{k-1} \subseteq {{\,\textrm{conv}\,}}(S_0)$ indicates $H_{k-1}\subseteq {{\,\textrm{conv}\,}}(S_{0})$, and thus ${{\,\textrm{conv}\,}}(H_{k-1})\subseteq {{\,\textrm{conv}\,}}(S_{0})$. By construction, $S_k \subseteq {{\,\textrm{conv}\,}}(H_{k-1}) \subseteq {{\,\textrm{conv}\,}}(S_{0})$. $\square$

The next theorem ensures that $H_k$ converges to ${{\,\textrm{conv}\,}}(S_0)$.

Theorem 7

Assume $a,b\in H_{k-1}$. Then the geodesic from a to b, $\gamma _{a,b}$, is included in $H_k$. This indicates that $\cup H_k = {{\,\textrm{conv}\,}}(S_0)$.

The proof is given in the supplementary material.

In Lubiw et al. (2020), a similar fact was revealed, and they proceed to reduce the problem of finding the closure of a convex hull to a linear programming problem. However, such a reduction is difficult in our case, given that we do not have prior knowledge about how many vertices ${{\,\textrm{conv}\,}}(S_0)$ would have on each boundary. We will content ourselves here with the approximation algorithm derived from the previous theorem. Note that if we can find maximum and minimum values at the origin exactly in the first step and the sets $S_k$ converge in finite iteration number T, the set $H_T$ is exactly equal to the desired convex hull. Furthermore, $H_T$ is closed in this case, thus function ${\bar{h}}_y$ calculated by this set is the exact least upper-semicontinuous concave function.

4.3 Altering the objective function

Sections 4.1 and 4.2 show that we can calculate the function ${\bar{h}}_y$ for given y in one-dimensional and two-dimensional cases at least approximately. As shown at the beginning of this section, in order to find the maximum likelihood estimator, we need to solve the optimization problem of the form $\max _{y\in {\mathbb {R}}^N} \rho _N(y) = {\mathcal {L}}_N(\exp ({\bar{h}}_y))$. As in the Euclidean case (Cule et al. 2010), the objective function is not a convex function of y, but by properly altering it, we can make this a convex optimization problem. In the d-dimension case, the new objective function $\sigma _N(y)$ is defined as

$$\begin{aligned} \sigma _N (y) = - {\frac{1}{N}} \sum _{i=1}^{N} y_i + \int _{{\mathcal {T}}_{d+2}} \exp (h_y(x))d\nu (x). \end{aligned}$$

(19)

The convexity of ${\bar{h}}_y$ with respect to y can be derived in exactly the same manner as in the Euclidean case (Cule et al. 2010). This ensures that $\sigma _N$ is a convex function of y. Therefore, we can utilize ordinary solvers for convex optimization to calculate MLE.

5 Numerical study

In this section, we give two simulation results. First, we estimate some log-concave distributions in one and two dimensions. We also conduct the estimation of one-dimensional densities that bends at the origin. Secondly, we give an example of clustering with the log-concave mixture model.

For the first simulation, we compare results with the kernel density estimator. The following set of bandwidths selection algorithms are considered:

• 1.  [NN0.2]: Nearest neighbor approach adopted by Weyenberg et al. (2014), where we adaptively set the distance from each center to $m=0.2N$th closest point as the bandwidth.

• 2.  [CV]: Least squares cross validation approach (Rudemo 1982; Bowman 1984).

• 3.  [OPT_NN] Nearest neighbor approach with numerically optimal proportion with respect to the integrated squared error (ISE).

• 4.  [OPT_FIX] Fixed bandwidths selected to numerically optimize ISE.

Note that we use the true density to evaluate and optimize ISE for the last two approaches. Thus, these approaches are infeasible in practice, but they are included as a benchmark. ISE is numerically optimized for each sample, thus these bandwidths are sample dependent as well. NN0.2 and OPT_NN are adaptive methods that use varying bandwidths for each center while CV and OPT_FIX use fixed bandwidths for all centers.

5.1 Estimation of one-dimensional log-concave densities

For one-dimensional examples, we consider the following two types of log-concave densities, using $O_i~(i=1,2,3)$ to denote the three orthants in ${\mathcal {T}}_3$.

Case 1.:

Normal-like density $f_1$ with mean equal to the point in $O_1$ that is 1 unit from the origin, $x_0$: i.e., for a point $x\in {\mathcal {T}}_3$, $f_1(x) \propto \exp (-d(x,x_0)^2/2)$.

Case 2.:

Exponential-like density $f_2$, defined as follows: Let the support of the density be ${{\,\textrm{supp}\,}}(f_2) = \{x\in O_1\mid d(x,0)\le 1\}\cup O_2\cup O_3$, and for $x\in {{\,\textrm{supp}\,}}(f_2)$,

$$\begin{aligned} f_2(x) \propto \exp (-d(x,x_0)). \end{aligned}$$

(20)

Because the density function in orthants $O_2$ and $O_3$ are identical, the generation of samples from these distributions can be implemented using ordinary sampling techniques in ${\mathbb {R}}$. We generated 100 samples each for sample size 100, 200, 300, 500, and 1000 from the true density and calculated ISE. The average ISE versus sample size is reported in Fig. 6.

Fig. 6

Average ISE for sample sizes 100, 200, 300, 500, and 1000 in case 1 ( Top ) and case 2 ( Bottom ). LCMLE denotes log-concave MLE, and KDE denotes kernel density estimator

Our simulation results show that in case 1, our log-concave MLE is comparable to kernel density estimator with optimized bandwidths (OPT_NN, OPT_FIX) and dominates practical bandwidth selection approaches. In case 2, our log-conave MLE performs better than any kernel density estimator . This could be due to the density used for case 2 does not have the whole space as support; Log-concave MLE restricts its support to the convex hull of sample points, thus they can be considered better at detecting the shape of the support as long as it is convex.

5.2 Estimation of two-dimensional normal-like densities

We denote each orthant of ${\mathcal {T}}_4$ by the indices of the axes at the boundary as in Fig. 1. For instance, the orthant with axes 0 and 1 is denoted by $\{0,1\}$. We consider densities of the following types:

Case 3.:

Positive truncated multivariate normal density $f_3$ with mean 0 and variance I, supported on all orthants in ${\mathcal {T}}_4$:

$$\begin{aligned} f_3(x) \propto \exp (-d(x,0)^2/2).\end{aligned}$$

(21)

Case 4.:

Positive truncated multivariate normal density $f_4$ with mean 0 and variance I, supported on orthants $\{0,1\}, \{1,6\}, \{6,8\}, \{3,8\}, \{3,4\}, \{0,4\}$: For x in one of the above orthants,

$$\begin{aligned} f_4(x) \propto \exp (-d(x,0)^2/2). \end{aligned}$$

(22)

Also, because of the nonpositive curvature property of tree space, we have that these densities are log-concave.

Generation of samples from these distributions can be implemented using sampling from positive truncated two-dimensional normal density. We generated 100 samples each for sample size 100, 200, 300, 500 and 1000 from the true density and calculated MLE and the average ISE. The estimation results are illustrated in Fig. 7.

Fig. 7

(Top) average ISE in case 3. (Bottom) average ISE in case 4

In case 3, the kernel density estimator performs better in small samples, but with large number samples, log-concave MLE outperforms the kernel density estimator. This result is similar to the Euclidean case (Cule et al. 2010). On the other hand, in case 4, log-concave MLE dominates the kernel density estimator. This is again because while log-concave MLE can effectively approximate the support of the true density with enough data, the kernel density estimator cannot.

5.3 Estimation of one-dimensional densities that bend at the origin

As one-dimensional densities that bend at the origin, we take two densities we considered in the Sect. 3.3. Concretely, we consider the following two densities:

Case 5.:

Normal density constructed by Brownian motion $f_5$ at time 5 and starting position equal to the point in $O_1$ that is 1 unit away from the origin:

$$\begin{aligned} f_{5,1}(x)&= \phi (x;1,5) - \frac{1}{3}\phi (x;-1,5) \end{aligned}$$

(23)

$$\begin{aligned} f_{5,j}(x)&= \frac{2}{3}\phi (x;-1,5) ~~~~~ (j\in \{2,3\}) \end{aligned}$$

(24)

Case 6.:

Density of coalescent time (equation (14)) $f_6$ with $T=1$: i.e., for a point $x\in {\mathcal {T}}_3$,

$$\begin{aligned} f_{6,1}(x) =&-\frac{1}{6}\exp (-x-1) + \frac{1}{2}\exp \{ - {|x-1|} )\} \end{aligned}$$

(25)

$$\begin{aligned} f_{6,j}(x) =&\frac{1}{3}\exp (-x-1) ~~~~~j\in \{2,3\} \end{aligned}$$

(26)

As in the previous experiment with one-dimensional log-concave density, generation of samples are simple. We generated 100 samples each for sample size 100, 200, 300, 500 and 1000 from the true density and calculated MLE and the average ISE. The estimation results are illustrated in Fig. 8.

Fig. 8

Average ISE for sample sizes 100, 200, 300, 500, and 1000 in case 5 (left) and case 6 (right). LCMLE with bend denotes MLE in ${\mathcal {G}}_0$, and KDE denotes kernel density estimator

The maximum likelihood estimator in ${\mathcal {G}}_0$ again performs comparable to the kernel density estimator with the optimized bandwidths while it performs better than any practical approaches in almost all sample sizes.

5.4 Clustering example

In this section, we consider the problem of clustering in the space ${\mathcal {T}}_4$. Let $x_1, x_2, x_3$ denote points in the orthants $\{0,1\}, \{2,3\}, \{5,8\}$ located at coordinates $\{4,4\}, \{1,1\}, \{1,1\}$ respectively. We consider three normal-like densities on ${\mathcal {T}}_4$, $g_1, g_2$ and $g_3$, defined as follows:

$$\begin{aligned} g_1(x)&\propto \exp (-d(x,x_1)^2/16), \end{aligned}$$

(27)

$$\begin{aligned} g_2(x)&\propto \exp (-8d(x,x_2)^2), \end{aligned}$$

(28)

$$\begin{aligned} g_3(x)&\propto \exp (-8d(x,x_3)^2), \end{aligned}$$

(29)

Note that $g_1, g_2, g_3$ differ in variance as well as mean.

Generation of samples from each component can be implemented in the following way. First, we divide the space ${\mathcal {T}}_4$ into two: One is the space of points whose geodesic to the center $x_i$ of the component is a cone path, and the other is that with the opposite property. The probability of each space can be easily computed using cumulative distribution function of normal distribution on ${\mathbb {R}}^2$. Because the density only depends on the distance from the origin in the former space, the sampling from this space can be reduced to sampling from some one-dimensional density. The sampling from the latter space is possible utilizing sampling from normal density on ${\mathbb {R}}^2$, because geodesics in this case can be embedded into ${\mathbb {R}}^2$.

We generated a sample of size 200 from the mixture of $g_i$, $f=\sum _{i=1}^3 \pi _i g_i$ with proportions $\pi _1=0.4, \pi _2 = 0.3, \pi _3 = 0.3$, and we attempted to cluster these points using log-concave MLE.

As in the Gaussian mixture in Euclidean space, we can construct an Expectation-Maximization algorithm (EM algorithm) to solve the clustering problem. We will assume that we know the number of clusters to be $K=3$. We model the density in the following equation:

$$\begin{aligned} {\hat{f}}=\sum _{i=1}^3 {\hat{\pi }}{_i }{\hat{g}}{_i } \end{aligned}$$

(30)

where ${\hat{g}}_i$ is assumed to be log-concave. Cule et al. (2010) explained the EM algorithm applied to the log-concave mixture model, and we adopt their framework here.

To compare the results with other methods, we use the k-means++ algorithm (Vassilvitskii and Arthur 2006) applied to this space as an alternative method. Concretely, we implemented the k-means++ algorithm with the Fréchet mean instead of the usual arithmetic mean. It is simple to see that the sum of squared distances from the cluster centers strictly decreases at each iteration of the k-means++ or k-means algorithm (MacQueen 1967). Thus the algorithm terminates within a finite number of steps. Fréchet mean is computed using the proximal point algorithm developed in Bačák (2013).

The results of clustering are shown using the Petersen graph in Fig. 9. We see from these results that in this case, the clusters estimated by the log-concave mixture estimate are more representative of the true density. This is a natural result, as the true density is indeed log-concave, and the mixed normal densities have different variances.

Fig. 9

Clustered points displayed in the Petersen graph (Fig. 1) with labels. (Left): data points with markers indicating the true clusters to which they belong. (Center): clustering results using the log-concave mixture (97% accuracy). (Right): clustering results using k-means++ (57 % accuracy). Note that closeness in this graph does not necessarily mean closeness in ${\mathcal {T}}_4$

6 Conclusion

In this paper, we showed that the maximum likelihood estimator within the class of log-concave density in tree space exists under certain conditions. In one dimension, the maximum likelihood estimator exists with probability one and is unique, which is the same result as in the Euclidean case. In multiple-dimension, there are conditions under which the MLE does not exist. However, if we restrict our attention to a particular situation, we have shown that the MLE exists and is unique $\nu$-almost surely. Also, we have presented an algorithm to calculate the MLE exactly in the one-dimensional case and approximately in the two-dimensional case. We compared the results with the previously developed kernel density estimator and confirmed that our estimator dominates in well-modeled cases with a large enough sample size.

The method derived here is promising in that it gives a new nonparametric approach to density estimation on tree space. As we saw in a two-dimensional example, it is also able to respect the support of the sample distribution when it is convex, which might affect the estimation accuracy considerably in some situations. Unlike kernel density estimates, we do not need either the determination of smoothing parameters or the calculation of any (approximate) normalizing constant. Although the computation is much slower than kernel density estimates, the accuracy of density estimation can be expected to be high when the log-concavity assumption is not far away from the properties of the true density. The developed method gives an intermediate choice between fully unconstrained, nonparametric approaches, which have difficulties improving accuracy and estimation, and parametric approaches, for which it is difficult to specify the correct models for tree space.

We also note that with a slight modification to the statements, the main theoretical results on the existence and the uniqueness of the log-concave maximum likelihood estimator (Theorem 4 and the existence part of Theorem 5) holds in CAT(0) orthant spaces defined by Miller et al. (2015), or locally compact CAT(0) polyhedral complexes.

For future research, it is important to derive some theoretical properties of the estimator on tree space. In Euclidean space, log-concave MLE is known to be strictly consistent, and even if the model is misspecified, it converges to the “log-concave projection” of the true density (the log-concave density that minimizes Kullback–Leibler divergence from the true density). It is crucial to investigate whether these properties hold on tree space as well. Also, It is of interest whether we can introduce different constraints on the density in order to include other types of densities on this space, or to lessen the computational load. The density that bend at the boundary, which we considered only in the one-dimensional case, is a candidate class for this purpose. Finally, further simulation studies in both well-modeled and misspecified cases are necessary for practical purposes.

As tree space is constructed for modeling the space of phylogenetic trees, one immediate interest of further research is the applicability to biological data and problems. As we only have (approximate) algorithms for one and two dimensions, corresponding to the case where a maximum of four taxa are present, the applicability seems to be limited for now. However, it might be possible to seek lower-dimensional representations of large trees, for example, by grouping some taxa when they are irrelevant in terms of the inconsistency of multiple trees. It is of interest how well our method with these modifications performs compared to the existing methods with the biological data. Another possible way to utilize these lower-dimensional estimation results in large trees is to combine it with tree-construction methods based on subtrees, in particular quartets and rooted triples. Further careful assessment of the log-concavity assumption about the data distribution is also of interest. Furthermore, an attempt to improve computational efficiency is called for, as our method currently is not suited for use with large datasets.

Appendices

Appendix A: Proofs

In this section, we give some proofs of the results stated in the main text.

1.1 A.1 Proof of Lemma 2

Proof of Lemma

Let $\psi$ be an arbitrary function on ${\mathcal {H}}$, and define a function $g(x) = \sup \{\mu \mid (x,\mu ) \in {{\,\textrm{conv}\,}}({{\,\textrm{hypo}\,}}\psi )\}$. Here, we define $\sup \emptyset = -\infty$. We show below that this g is the desired concave hull. We first show that g is concave. For any points $x,y\in {\mathcal {H}}$, if $\alpha < g(x)$ and $\beta < g(y)$, there exist $\varepsilon >0$ such that $\alpha +\varepsilon < g(x)$ and $\beta +\varepsilon < g(y)$. Then, $((1-\lambda )x + \lambda y, (1-\lambda )\alpha + \lambda \beta + \varepsilon ) \in {{\,\textrm{conv}\,}}({{\,\textrm{hypo}\,}}\psi )$ for any $\lambda \in (0,1)$. This leads to $g((1-\lambda )x + \lambda y) > (1-\lambda )\alpha + \lambda \beta$, thus showing that g is indeed concave. Also, by definition, g is minorized by $\psi$. The minimality of g follows from the minimality of a convex hull of sets. The uniqueness is obvious from the minimality. $\square$

1.2 A.2 Proofs of Theorem 3 and Theorem 5

Before proving Theorem 3 and Theorem 5, we first derive some Lemmas related to the convex analysis in Hadamard spaces. Then, we give the proof of Theorem 5, the existence of the maximum likelihood estimator in multi-dimensional cases. The proof of Theorem 3, the existence and uniqueness of the maximum likelihood estimator, follows similar arguments to the multi-dimensional cases (the proof of Theorem 5 and Theorem 4). Thus we only note the differences we need to consider.

1.2.1 A.2.1 Lemmas

First, we prepare some Lemmas. Let $({\mathcal {H}},d)$ be a Hadamard space and for $i=1,2,\ldots ,N$, $(X_i, y_i)\in {\mathcal {H}}\times {\mathbb {R}}$. Let $D_0 = \{X_1, \ldots , X_N\}$, and $C_N = {{\,\textrm{conv}\,}}(X_1,\ldots ,X_N)$. Lemma 1 suggests that this convex hull can be obtained by repeatedly taking geodesics starting from the set $D_0$. Concretely, $C_N = \cup _{k=0}^\infty D_k$, where $D_k$ consists of all points on the geodesics between points in $D_{k-1}$. We first show the boundedness of this convex hull.

Lemma 8

Let $X_1, \ldots , X_N \in {\mathcal {H}}$. Then $C_N = {{\,\textrm{conv}\,}}\{X_1, \ldots , X_N\}$ is a bounded set.

Proof of Lemma

This is proved using the nonpositive curvature property. By Lemma 1, $C_N = \cup _{k=0}^\infty D_k$, where $D_0 = \{X_1, \ldots , X_N\}$ and $D_k$ consists of all points that are on some geodesic with endpoints in $D_{k-1}$. Let $R = \max _{j=2,\ldots ,N}d(X_1, X_j)$. We can recursively show that for any points $x_k \in D_k$, $d(X_1, x_k) \le R$. To see this, first note that at $k=0$, the statement holds. Assuming that the statement holds at k, for any points $x_{k+1} \in D_{k+1}$, there exist $a_{k1}, a_{k2} \in D_k$ and $0\le \lambda \le 1$ such that $x_{k+1} = \lambda a_{k1} + (1-\lambda ) a_{k2}$. Then by CAT(0) inequality, $d(X_1, x_{k+1}) \le \max _{j=1,2} d(X_1, a_{kj}) \le R$. This shows the boundedness of $C_N$. $\square$

We say that ${\mathcal {H}}$ has the geodesic extension property if any geodesic between two points in ${\mathcal {H}}$ can be extended to a geodesic line. Now, we can show the following Lemma.

Lemma 9

Suppose ${\mathcal {H}}$ has the geodesic extension property. Then, any upper-semicontinuous concave function $\psi$ on ${\mathcal {H}}$ that is bounded in the domain S is continuous on ${{\,\textrm{int}\,}}(S)$.

Proof

Take $x\in {{\,\textrm{int}\,}}(S)$. Then we can take $\varepsilon _1 > 0$ such that the closed ball ${\bar{B}}_{\varepsilon _1}(x) = \{ y \in {\mathcal {H}} \mid d(x,y)\le \varepsilon _1\}$ is included in ${{\,\textrm{int}\,}}(S)$. Now, take $\varepsilon _2>0$ to satisfy $\varepsilon _2 < \varepsilon _1$. For any point ${\tilde{y}}\in {\bar{B}}_{\varepsilon _2}(x)$, by the geodesic extension property, there exists $y\in {{\,\textrm{int}\,}}(S)$ such that $d(x,y) = \varepsilon _1$ and for some $0<\lambda < 1$, $(1-\lambda )x + \lambda y = {\tilde{y}}$. Note that this $\lambda$ satisfies $\lambda \le \varepsilon _2 / \varepsilon _1$. Because of concavity,

$$\begin{aligned} {\psi ({\tilde{y}}) }&{\ge \psi (x) - \lambda (\psi (x) - \psi (y)) }\nonumber \\&{\ge \psi (x) - \frac{\varepsilon _2}{\varepsilon _1}|\psi (x)-\psi (y)| }\end{aligned}$$

(A1)

This expression together with the boundedness of $\psi$ in S implies the lower-semicontinuity : $\liminf _{{\tilde{y}}\rightarrow x}\psi ({\tilde{y}}) \ge \psi (x)$. $\square$

Now, denote by $\Delta ^{N-1}$ the $(N-1)$ -dimensional simplex in ${\mathbb {R}}^N$:

$$\begin{aligned} \Delta {^{N-1} } = \left\{ \lambda = (\lambda _1,\ldots ,\lambda {_N} )\in {\mathbb {R}} {^N } \right. \nonumber \\ \left. | \lambda _i\ge 0, \sum _{i=1} {^N } \lambda _i = 1\right\} \end{aligned}$$

(A2)

For $\lambda \in \Delta ^{N-1}$ and $k=0,1,\ldots$, define sets $S_{\lambda , k}$ as follows:

$$\begin{aligned} \begin{aligned} S_{\lambda ,0}&= {\left\{ \begin{array}{ll} \{X_i\} &{} \text {if }\lambda _i = 1, \lambda _j = 0 ~~(\forall j\ne i) \\ \emptyset &{} \text {otherwise} \end{array}\right. } \\ S {_{\lambda , k} }&= \{ x\in D {_k} \mid \exists x_1\in S {_{\lambda _1, k-1}} , \exists x_2\in S {_{\lambda _2, k-1}} , \nonumber \\&\quad 0 \le \exists {\theta } \le 1,\gamma _{x_1,x_2}( {\theta } ) = x, \\&\quad (1- {\theta } )\lambda _1 + {\theta } \lambda _2 = \lambda \}~~~~~~~~(l= 1,2,\ldots ). \end{aligned} \end{aligned}$$

Let $S_{\lambda } = \cup _{l=0}^\infty S_{\lambda , l}$. Informally, $S_\lambda$ is the set of points which can be generated with cumulated coefficient of convex combination $\lambda$. Lemma 1 indicates that for any point $x\in C_N$, at least one $\lambda \in \Delta ^{N-1}$ exists such that $x\in S_{\lambda }$. This also implies that ${{\,\textrm{conv}\,}}(\{X_i,y_i\}_{i=1}^N)$ includes the point $(x, \lambda ^\top y)$.

Let $y=(y_1,\ldots ,y_N)$ and define $\psi _y(x)$ by the equation (6). å Let ${\bar{h}}_y$ denote the upper-semicontinuous concave hull of $\psi _y$. Following two Lemmas show some properties of this function.

Lemma 10

${\bar{h}}_y(x)$ is continuous with respect to $y = (y_1, \ldots , y_N)$.

Proof

For any fixed value $x\in {\mathcal {H}}$, ${\bar{h}}_{y+\delta }(x)$ cannot deviate from ${\bar{h}}_y(x)$ by more than $\Vert \delta \Vert _{2}$.

In order to see this, first, assume ${\bar{h}}_{y+\delta }(x)\le {\bar{h}}_y(x)$. By construction, the hypograph of ${\bar{h}}_y$ is given by

$$\begin{aligned} {{\,\textrm{hypo}\,}}{\bar{h}}_y = {{\,\textrm{cl}\,}}({{\,\textrm{conv}\,}}({{\,\textrm{hypo}\,}}{\psi } _y)) \end{aligned}$$

(A3)

Let $\mu ={\bar{h}}_y(x)$. Equation (A3) indicates that there exists $\{(x_i, \mu _i)\}_{i=1}^\infty \subseteq {{\,\textrm{conv}\,}}({{\,\textrm{hypo}\,}}\psi _y)$ such that the sequence $\{(x_i, \mu _i)\}_{i=1}^\infty$ converges to $(x, \mu )$. Furthermore, by Lemma 1, there exists $\lambda ^{(i)}\in \Delta ^{N-1}$ for each $(x_i, \mu _i)$ such that $x_i\in S_{\lambda ^{(i)}}$ and $\mu _i \le (\lambda ^{(i)})^\top y$. This implies that $(x_i, (\lambda ^{(i)})^\top (y+\delta ))\in {{\,\textrm{hypo}\,}}({\bar{h}}_{y+\delta })$, $\mu _i - \Vert \delta \Vert _{2} \le (\lambda ^{(i)})^\top (y+\delta )$, and thus $(x_i, \mu _i - \Vert \delta \Vert _{2}) \in {{\,\textrm{hypo}\,}}({\bar{h}}_{y+\delta })$. Now, the sequence of points $\{(x_i, \mu _i - \Vert \delta \Vert _{2})\}_{i=1}^\infty$ converges to $(x, \mu -\delta )$, and this points is included in ${{\,\textrm{hypo}\,}}({\bar{h}}_{y+\delta })$ by the upper-semicontinuity. This shows that ${\bar{h}}_{y+\delta }(x)\ge \mu -\Vert \delta \Vert _{2}$ and consequently, ${\bar{h}}_y(x) - {\bar{h}}_{y+\delta }(x) \le \Vert \delta \Vert _2$.

If ${\bar{h}}_{y+\delta }(x)>{\bar{h}}_y(x)$, let $\mu =h_{y+\delta }(x)$, and by interchanging the roles of ${\bar{h}}_y$ and ${\bar{h}}_{y+\delta }$ in the above argument, we can show ${\bar{h}}_{y+\delta }(x) - {\bar{h}}_{y}(x) \le \Vert \delta \Vert _2$. $\square$

We define ${{\,\textrm{dom}\,}}{\bar{h}}_y {:}{=}\{ x\in {\mathcal {H}}\mid {\bar{h}}_y(x) > -\infty \}$ to denote the effective domain of the concave function ${\bar{h}}_y$.

Lemma 11

${{\,\textrm{dom}\,}}{\bar{h}}_y = {{\,\textrm{cl}\,}}(C_N)$.

Proof

For any upper-semicontinuous concave function $\psi$ satisfying $\psi (X_i)\ge y_i$, let the restriction of $\psi$ to ${{\,\textrm{cl}\,}}(C_N)$ be $\psi _{{{\,\textrm{cl}\,}}(C_N)}$. Then ${{\,\textrm{hypo}\,}}\psi _{{{\,\textrm{cl}\,}}(C_N)} = {{\,\textrm{hypo}\,}}\psi \cap \{(x,\mu )\mid x\in {{\,\textrm{cl}\,}}(C_N), \mu \in {\mathbb {R}}\}$ is closed. This means that $\psi _{{{\,\textrm{cl}\,}}(C_N)}$ is upper-semicontinuous. Furthermore, since $X_i\in C_N$, $\psi _{{{\,\textrm{cl}\,}}(C_N)}(X_i) = \psi (X_i)\ge y_i$. With the minimality of ${\bar{h}}_y$, this implies that ${{\,\textrm{dom}\,}}{\bar{h}}_y\subseteq {{\,\textrm{cl}\,}}(C_N)$.

On the other hand, take any $x\in {{\,\textrm{cl}\,}}(C_N)$. Then there exists a sequence $\{x_i\}_{i=1}^\infty \subseteq C_N$ such that $x = \lim _{i\rightarrow \infty } x_i$. By the concavity of ${\bar{h}}_y$, ${\bar{h}}_y(x_i)\ge \min _{j=1,2,\ldots ,N} y_j$ for all $i=1,2,\ldots$. By the upper-semicontinuity, $\min _{j=1,2,\ldots ,N} y_j \le \limsup _{i\rightarrow \infty } {\bar{h}}_y(x_i)\le {\bar{h}}_y(x)$. This shows that $x\in {{\,\textrm{dom}\,}}{\bar{h}}_y$, and consequently, ${{\,\textrm{cl}\,}}(C_N)\subseteq {{\,\textrm{dom}\,}}{\bar{h}}_y$. $\square$

1.2.2 A.2.2 Proof of Theorem 5

Proof of theorem

The proof is essentially a modification of the proof of Theorem 1 from Cule et al. (2010).

By Lemma 1, $C_N = \cup _{k=0}^\infty D_k$, where $D_k$ denotes the set defined in the proof of the previous Lemma. Let $\bar{{\mathcal {F}}}^{(p)}$ be the set of upper-semicontinuous log-concave functions on ${\mathcal {T}}_{p+2}$, and consider the maximization of the function ${\mathcal {L}}_N(f) = N^{-1}\sum _{i=1}^N \log f(X_i) - \int _{{\mathcal {T}}_{p+2}}f(x)d\nu (x)$ over $\bar{{\mathcal {F}}}^{(p)}$.

First, we can show that for any $g\in \bar{{\mathcal {F}}}^{(p)}$, there exists $f\in \bar{{\mathcal {F}}}^{(p)}$ such that ${\mathcal {L}}_N(f)\ge {\mathcal {L}}_N(g)$ with

$$\begin{aligned} f(x) > 0~(x\in {{\,\textrm{cl}\,}}(C {_N} )), ~~f(x) = 0~(x\not \in {{\,\textrm{cl}\,}}(C {_N} )). \end{aligned}$$

(A4)

First, assume $g(x)=0$ for some $x\in C_N$. Lemma 1 suggests that there exists $k\in {\mathbb {N}}$ such that $x\in D_k$. If $k=1$, we have for some i, $g(X_i)=0$, implying ${\mathcal {L}}_N(g) = -\infty$. Otherwise, take minimum such k, then one can take some $x_{1, k-1}, x_{2, k-1} \in D_{k-1}$ and $\lambda \in (0,1)$ such that $x = (1-\lambda )x_{1,k-1} + \lambda x_{2,k-1}$. By concavity, $-\infty = \log g(x) \ge (1-\lambda )\log g(x_{1, k-1})+ \lambda \log g( x_{2, k-1})$. This leads to that at least one of $g(x_{1,k-1})$ and $g(x_{1,k-2})$ must be zero. Repeating this process, we can show that there exists $i\in \{1,\ldots , N\}$ such that $g(X_i) = 0$, resulting again in ${\mathcal {L}}_N(g) = -\infty$. Therefore, if for some $x\in C_N, g(x) = 0$, then any f with (A4) satisfies ${\mathcal {L}}_N(f) \ge \psi (g)$. If $g(x)=0$ for some $x\in {{\,\textrm{cl}\,}}(C_N)\backslash C_N$, then one can take a sequence $\{x_j\}\in C_N$ such that $x_j$ converges to x. The upper-semicontinuity implies that $\limsup _{j\rightarrow \infty } g(x_j)\le g(x) = 0$. Then for all $\varepsilon >0$, there exists j such that $g(x_j)<\varepsilon$. This with the previous argument leads to that $\min _{i=1,\ldots ,N}g(X_i) < \varepsilon$. Since $\varepsilon$ can be taken arbitrarily small, $\min _{i=1,\ldots ,N}g(X_i) = 0$, which leads again to ${\mathcal {L}}_N(g) = -\infty$. On the other hand, because ${{\,\textrm{cl}\,}}(C_N)$ is bounded by Lemma 8, if we take $f\in {\mathcal {F}}$ to be finitely positive and upper-semicontinuous on ${{\,\textrm{cl}\,}}(C_N)$ and 0 elsewhere, f becomes upper-semicontinuous on ${{\,\textrm{dom}\,}}f$ and ${\mathcal {L}}_N(f) > -\infty$. Thus, we can strictly restrict our attention to f such that $f(x)>0$ for all $x\in {{\,\textrm{cl}\,}}(C_N)$.

Now, assume that $g(x) > 0$ for some $x\not \in {{\,\textrm{cl}\,}}(C_N)$. Then by letting f(x) be the restriction of g(x) to ${{\,\textrm{cl}\,}}(C_N)$, it is easy to see that f satisfies (A4), log-concavity, and upper-semicontinuity. Furthermore, ${\mathcal {L}}_N(f) \ge {\mathcal {L}}_N(g)$, and the inequality becomes the strict one if $\nu (\{x\mid x\in {{\,\textrm{dom}\,}}g, x\not \in {{\,\textrm{cl}\,}}(C_N) \}) > 0$. This means that we can strictly restrict attention to the density that satisfies (A4), or the ones that satisfy them except for some set of $\nu -$measure zero excluding ${{\,\textrm{cl}\,}}(C_N)$.

Secondly, we can show that for any upper-semicontinous function g, there exists f which has its logarithm in the form ${\bar{h}}_y$ such that ${\mathcal {L}}_N(f)\ge {\mathcal {L}}_N(g)$. This is achieved if we put $y_i = \log g(X_i)$, $y=(y_1,\ldots ,y_N)$ and $f=\exp ({\bar{h}}_y)$. Note that by Lemma 11, ${{\,\textrm{dom}\,}}{\bar{h}}_y = {{\,\textrm{cl}\,}}(C_N)$. Also, by Lemma 9, ${\bar{h}}_y$ is continuous relative to ${{\,\textrm{int}\,}}(C_N)$. Because of continuity, if $g(x)\ne \exp ({\bar{h}}_y)(x)$ at some $x\in {{\,\textrm{int}\,}}(C_N)$, ${\mathcal {L}}_N(\exp ({\bar{h}}_y))>{\mathcal {L}}_N(g)$. This shows that a maximizer of ${\mathcal {L}}_N$, if it exists, has to take the form ${\mathcal {L}}_N(\exp ({\bar{h}}_y))$ in ${{\,\textrm{int}\,}}(C_N)$.

Next, we can also show that we can restrict attention to the case $f\in \bar{{\mathcal {F}}}_0^{(p)}$. For any upper-semicontinous function g, without loss of generality, assume $0<\int _{{\mathcal {T}}_{p+2}} g(x) = c < \infty$. By setting $f=g/c$, $f\in {\bar{{\mathcal {F}}}_0}^{(p)}$, and

$$\begin{aligned} {{\mathcal {L}}_N} (f)&= {\frac{1}{N}} \sum _{i=1} {^N } \log f(X_i) - \int _{T_{p+2}}f(x)d\nu (x) \nonumber \\&= {\frac{1}{N}} \sum _{i=1} {^N } \log g(X_i) -\log c - 1 \nonumber \\&= {{\mathcal {L}}_N} (g) + c -\log c -1 \nonumber \\&\ge {{\mathcal {L}}_N} (g). \end{aligned}$$

(A5)

Equality is attained only when $c=1$.

For the existence of a maximizer of $l_N(f)$, it only remains to show that ${\mathcal {L}}_N$ has a maximizer of the form $f = \exp ({\bar{h}}_y)\in \bar{{\mathcal {F}}}_0^{(p)}$

This is seen as follows. For an arbitrary function $f=\exp ({\bar{h}}_y)$, let $X_{\max } = \mathop {\mathrm {arg\,max}}\limits _{X_i} g(X_i)$ and $O_{\max }$ be one of the nonnegative orthants of ${\mathcal {T}}_{p+2}$ which $X_{\max }$ belongs to. Then by assumption, we can take $O_{\max }$ suitably such that $\nu ({{\,\textrm{cl}\,}}(C_N)\cap O_{\max }) {=}{:}V > 0$. Now, put $M={\bar{h}}_y(X_{\max })$ and $m=\min _{x\in O_{\max }}{\bar{h}}_y(x)$. For sufficiently large M, $M-1>m$. Then by setting $\lambda =1/(M-m)$, the concavity ${\bar{h}}_y(\lambda x + (1-\lambda )X_{\max }) \ge \lambda {\bar{h}}_y(x) + (1-\lambda ) {\bar{h}}_y(x)$ indicates

$$\begin{aligned}&{\bar{h}}{_y} \left( \frac{1}{M-m}x + \frac{M-m-1}{M-m}X_{\max }\right) \\&\qquad \ge \frac{m}{M-m} + \frac{(M-m-1)M}{(M-m)} \\&\qquad = M-1. \end{aligned}$$

This in turn indicates $\nu (\{x\mid {\bar{h}}_y(x) \ge M-1\})\ge V/(M-m)^p$, and thus $1 = \int _{{\mathcal {T}}_{p+2}} \exp ({\bar{h}}_y(x))d\nu (x) \ge V(\exp (M-1))/(M-m)^p$. Therefore,

$$\begin{aligned} M - m&\ge V^{\frac{1}{p}}(\exp (M-1))^{\frac{1}{p}} \nonumber \\ \therefore m&\le M - V^{\frac{1}{p}}\exp \left( \frac{M-1}{p}\right) . \end{aligned}$$

(A6)

This leads to the following inequality:

$$\begin{aligned} {{\mathcal {L}}_N} (\exp ( {\bar{h}}{_y} ))&= {\frac{1}{N}} \sum _{i=1} {^N }{\bar{h}}{_y} (X_i) - 1 \nonumber \\&\le {\frac{N-1}{N} } M + {\frac{M}{N} } - {\frac{V^{\frac{1}{p}}}{N}} \exp \left( \frac{M-1}{p}\right) {-1 } \nonumber \\&= M - {\frac{V^{\frac{1}{p}}}{N}} \exp \left( \frac{M-1}{p}\right) {-1 } \end{aligned}$$

(A7)

This inequality shows that as M goes to infinity, ${\mathcal {L}}_N$ goes to $-\infty$. On the other hand, because ${\bar{h}}_y$ is continuous with respect to y, as shown in Lemma 10, ${\mathcal {L}}_N(\exp ({\bar{h}}_y)) = N^{-1}\sum _{i=1}^N {\bar{h}}_y(X_i) - \int _{{\mathcal {T}}_{p+2}} \exp ({\bar{h}}_y)(x)dx$ is also continuous. Thus, for any $s<M$, there exists $u{:}{=}\max _{y\in [s, M]^N} {\mathcal {L}}_N(\exp ({\bar{h}}_y))$. This shows the existence of the maximizer of ${\mathcal {L}}_N(f)$, and thus $l_N(f)$.

The uniqueness of the maximizer in the $\nu$-almost sure sense is guaranteed by Theorem 4. Moreover, by the previous argument, the maximizer needs to be the form $\exp ({\bar{h}}_y)$ for some $y\in {\mathbb {R}}^N$, in ${{\,\textrm{int}\,}}(C_N)$. Since ${\bar{h}}_y$ is continuous in ${{\,\textrm{int}\,}}(C_N)$, the strict uniqueness in ${{\,\textrm{int}\,}}(C_N)$ holds. $\square$

1.2.3 A.2.3 Proof of Theorem 3

Proof

The proof goes in a similar way as in the proof of Theorem 5. Here, we note several properties specific to the one-dimensional case, which is necessary for the proof.

• $C_N = {{\,\textrm{conv}\,}}(X_1, \ldots , X_N)$ is a closed bounded set. This, in particular, implies ${{\,\textrm{cl}\,}}(C_N) = C_N$. Thus the domain of the maximizer can be restricted to exactly $C_N$.

• The logarithm of the maximizer can always be written in the form $h_y$, the least concave function with $h_y(X_i)\ge y_i$. $h_y$ is continuous on $C_N$.

• Because f is absolutely continuous with respect to $\nu$, with probability 1, $C_N$ is not merely a point, but constitutes an interval. This is essentially a substitute for the sufficient condition 1. we considered in the multi-dimensional case. We can easily see that this condition is sufficient for showing that the maximizer of ${\mathcal {L}}_N$ exists in the set of densities of the form $\exp (h_y)$.

• The strict uniqueness follows from the following two observations: $h_y$ is continuous on $C_N$, and the extension of the domain always provokes the increase in the measure.

$\square$

1.3 A.3 Proof of Theorem 7

Proof

If $\gamma _{a,b}$ is a cone path, let $(0, y_{0ab})$ be the point at which the geodesic crosses the origin. By construction, $S_k$ includes points $(0, y_{k1})$ and $(0, y_{k0})$ such that $y_{k0}\le y_{0ab} \le y_{k1}$. Therefore, $H_k$ includes $(0, y_{0ab})$, and thus all points of $\gamma _{a,b}$ are included in $H_k$.

Fig. 10

(Top): Embeddings of three connected orthants to the Euclidean space ${\mathbb {R}}^2$. (Center): An illustration that the path $\gamma _{ab}$ goes under the segment $r_1r_2$. The three blue points are included in the blue plane. (Bottom): Central figure seen from the direction of y-axis. (Color figure online)

If $\gamma _{a,b}$ is not a cone path, then the simplest case is that a, b are in the same orthant. In such a case, by construction, $\gamma _{a,b}\subseteq H_{k-1}$ as well. Thus, in particular, $\gamma _{a,b}\subseteq H_{k}$. Otherwise, let $a=(a_x,a_y), a_x\in {\mathcal {T}}_4, a_y\in {\mathbb {R}}$, and $b=(b_x,b_y), b_x\in {\mathcal {T}}_4, b_y\in {\mathbb {R}}$. We can take two nonnegative orthants $O_a, O_b\in {\mathcal {T}}_4$ to which $a_x$ and $b_x$ belong in such a manner that $O_a$ and $O_b$ are connected with at most one another orthant between them. Here, note that three connected orthants can be embedded in a part of ${\mathbb {R}}^2$ in the manner shown on the top of Fig. 10. Now, we can take $x_{a1}, x_{a2}, x_{a3} \in S_{k-1}(O_a)$ having the following property: the triangle $x_{a1}x_{a2}x_{a3}$ includes the points of the form $(a_x,y_{aa})$ with $y_{aa}\ge a_y$. These points are the ones that form the triangle “over” point p. In the same way, we can take $x_{b1}, x_{b2}, x_{b3}\in S_{k-1}(O_q)$ having the property that the triangle $x_{b1}x_{b2}x_{b3}$ includes the points of the form $(b_x,y_{bb})$ with $y_{bb}\ge b_y$. The case when the triangles exactly include a and b are drawn in Fig. 10. Let the intersection points of $\gamma _{ab}$ with one of the boundaries, say B, be $r=(x_r, y_r)$. Also, in the Euclidean embedding of $O_a$, $O_b$, and B, as in Fig. 10, let $-B$ denote the axis in the direction opposite to B (Fig. 10). Recall that a “boundary” here means the Euclidean plane an axis in ${\mathcal {T}}_4$ makes in the space ${\mathcal {T}}_4\times {\mathbb {R}}$. Consider embedded space ${\mathbb {R}}^3$ which includes $O_a$ and $O_b$. If we allow paths to cross the part of the Euclidean space in which no orthants are embedded (the hatched region in Fig. 10), it is easy to see from Euclidean geometry that we can find two straight lines between points in $\{x_{a1},x_{a2},x_{a3}\}$ and $\{x_{b1},x_{b2},x_{b3}\}$, say $\gamma _1$ and $\gamma _2$, such that the line segment between the intersection points of $\gamma _1$ and $\gamma _2$ with B or $-B$, say $r_1 = (x_{r1}, y_{r1})$ and $r_2 = (x_{r2}, y_{r2})$, includes a point of the form $(x_r, y_r^\prime )$ with $y_r^\prime \ge y_r$. If both $r_1$ and $r_2$ lie in B, then we just showed that $(x_r, y_r^\prime ) \in H_{l}$. If $r_1$ or $r_2$ does not lie in B, say $r_1$ does not, then we still find that the segment from $r_1$ to $r_2$ goes “under” $(0,y_{k1})$, since if we let $(0,y_{r_1r_2})$ be the origin point included in the segment $r_1r_2$, then this point is included in some cone path between a point in the triangle $x_{a1}x_{a2}x_{a3}$ and a point in the triangle $x_{b1}x_{b2}x_{b3}$. Thus, the segment from $(0,y_{k1})$ to $r_2$ goes “over” $(x_r, y_r^\prime )$: i.e., the segment includes a point of the form $(x_r, y_r^{\prime \prime })$ with $y_r^{\prime \prime }\ge y_r^\prime \ge y_r$. Thus in summary, by setting either ${\tilde{y}}_r=y_r^\prime$ or ${\tilde{y}}_r=y_r^{\prime \prime }$, we are able to find a point $(x_r, {\tilde{y}}_r)\in H_k$ such that ${\tilde{y}}_r\ge y_r$. A similar argument leads to that we can find a point $(x_r, {\hat{y}}_r)\in H_k$ such that ${\hat{y}}_r\le y_r$. This indicates $r=(x_r,y_r)\in {H}_l$, and consequently, the whole $\gamma _{ab}$. $\square$

Appendix B: Derivation of distribution of 3-trees under multispecies coalescent

In this section, we derive one example density given in the equation (14) of the main text which “bends” at the origin. The example is constructed by a simple multispecies coalescent process from three lineages each drawn from different three species.

Example 3

Consider the species tree drawn on the left of Fig. 11, and that three lineages are drawn from three species. In a neutral coalescent process (Kingman 1982) with L lineages, the distribution of time that takes for any two lineages to coalesce is given by simple exponential distribution:

$$\begin{aligned} p(t) = \left( {\begin{array}{c}L\\ 2\end{array}}\right) \exp \left( {- \left( {\begin{array}{c}L\\ 2\end{array}}\right) t}\right) {. } \end{aligned}$$

(B8)

In a multispecies coalescent (Rannala and Yang 2003), one assume that the two lineages coalesce only after the corresponding two species coalesce. Let T be the time where exactly two clades of species exist as shown in the Fig. 11. We can write the distribution of the length of internal edges by

$$\begin{aligned} \begin{aligned} f_1(x) =&-\frac{1}{6}\exp ({-x-T}) + \\&\frac{1}{2}\exp \left( { - {|x-T|} }\right) \\ f_i(x) =&\frac{1}{3}\exp ({-T-x}) ~~~~ (i\in \{2,3\}), \end{aligned} \end{aligned}$$

(B9)

where i denotes an index of orthant. We derive this equation (B9) in the following.

Fig. 11

An example of how three lineages inside a species tree coalesce. T represents the length of internal edge in the species tree. $\tau$ represents the time between the first coalescence of the species and the first coalescence of lineages

In order to consider the distribution on tree space, we need to consider the distribution of gene tree topology and the internal edge length given species tree. Algorithms for calculating gene tree topology given specific species trees have been considered in general dimension (Degnan and Salter 2005; Wu 2012), but the direct calculation is also available in small trees (e.g. Takahata and Nei 1985; Pamilo and Nei 1988). In the case of simplest case of 3-trees, denote by $u_1$ the topology of the species tree and by $u_2, u_3$ the rest of the topologies. Then the distribution of gene tree topology $U_g$ is given by:

$$\begin{aligned} \begin{aligned} P\left( U_g = u_1\right)&= 1-\frac{2}{3}e^{-T}, \\ P\left( U_g = u_j\right)&= \frac{1}{3}e^{-T} ~~~~~~~ (j=2,3), \end{aligned} \end{aligned}$$

(B10)

where T denotes the length of the internal edge of the species tree.

Given $U_g$, the distribution of the internal edge length can be derived in the following manner. First, consider the cases where $U_g \ne u_1$. In these cases, the distribution of the internal edge length is the same as the distribution of the coalescence time of two lineages. Standard coalescent theory implies that the density of the internal edge length is given by

$$\begin{aligned} f(x {\mid } U_g = u_j) = \exp ({-x}). \end{aligned}$$

(B11)

Next, we consider the case $U_g = u_1$. Let $\tau$ denote the time of the first coalescence of any two lineages after the first coalescence of the species tree coalescence (Figure 11 ). Thus, the value of $\tau$ being close to zero means that the two gene lineages coalesce right after the species tree coalesces, and the value of $\tau$ larger than T means that two gene lineages coalesce after whole three species coalesced in the species tree.

Multispecies coalescent assumes that the coalescence is neutral. In terms of $\tau$, this can be written as

$$\begin{aligned} P(U_g = u_1\mid \tau ) = {\left\{ \begin{array}{ll} 1 &{} \text {if } \tau \le T \\ \frac{1}{3} &{} \text {otherwise} \end{array}\right. } . \end{aligned}$$

(B12)

When $\tau \le T$, the density of $\tau$ is $\exp ({-\tau })$. This, combined with the equation (B12), implies that the conditional density of $\tau$ given $U_g=u_1$ for $\tau \le T$ is given by

$$\begin{aligned} f(\tau \mid U_g&= u_1) = \frac{1}{1 - (2/3)\exp (-T)}\exp (-\tau ) \nonumber \\&~~~~~~~~~~~~~~ \text {if } \tau \le T. \end{aligned}$$

(B13)

We can now calculate the density of the internal edge length x given $U_g = u_1$ as follows:

$$\begin{aligned}&f(x\mid U_g = u_1) \nonumber \\ =&\int _0^T f(x\mid U_g=u_1, \tau ) f(\tau \mid U_g=u_1)d\tau \nonumber \\&+ \int _T^\infty f(x\mid U_g=u_1, \tau ) f(\tau \mid U_g=u_1)d\tau \nonumber \\ =&\left( 1-\frac{2}{3}\exp (-T)\right) ^{-1} {\times } \nonumber \\&\int _0^T \exp (-(x-(T-\tau ))) \mathbbm {1}(x\ge T-\tau ) \exp (-\tau )d\tau \nonumber \\&+ \int _T^\infty \exp (-x) f(\tau \mid U_g = u_1)d\tau \nonumber \\ =&\left( 1-\frac{2}{3}\exp (-T)\right) ^{-1} {\times }\nonumber \\&\int _{\max \{0, T-x\}}^T \exp (- x + T) \exp (-2\tau )d\tau \nonumber \\&+ \exp (-x)\left\{ 1 - \int _{0}^T f(\tau \mid U_g = u_1)d\tau \right\} \nonumber \\ =&\left( 1-\frac{2}{3}\exp (-T)\right) ^{-1} {\times }\nonumber \\&\left\{ -\frac{1}{2}\exp (-x+T)\left[ \exp (-2\tau ) \right] _{\max \{0, T-x\}}^T \right\} \nonumber \\&+ \frac{\exp (-T)}{3}\left( 1-\frac{2}{3}\exp (-T)\right) ^{-1} \exp (-x) \nonumber \\ =&\left( 1-\frac{2}{3}\exp (-T)\right) ^{-1} {\times } \nonumber \\&\left[ -\frac{1}{6}\exp (-x-T) + \frac{1}{2}\exp ( {-|x-T|} )\right] {. } \end{aligned}$$

(B14)

Equations (B14), (B10) leads to the equation (B9).

This density is illustrated in in Fig. 5 in the main text for the case $T=1$. We can clearly see that it is not log-concave. In fact, the exterior derivative is

$$\begin{aligned} \begin{aligned} \frac{\partial f_1}{\partial n_1}(0)&= -\frac{2}{3}\exp (-T) ~~~~ \\ \frac{\partial f_i}{\partial n_i}(0)&= \frac{1}{3}\exp (-T) ~~~~ (i\in \{2,3\}).\\ \end{aligned} \end{aligned}$$

(B15)

Appendix C: Bounds for maximum and minimum values at the origin generated by geodesics in $H_{k-1}$

As mentioned in the main text, finding the maximum and minimum values at the origin in the first step of this approximation algorithm is not a simple optimization problem. For example, the problem of finding the maximum value at the origin among all geodesics between points in two specific orthants, say $O_1$ and $O_2$, can be written in the following way: given points $\{x_i, y_i\}\in O_1\times {\mathbb {R}}$ and $\{z_j, w_j\}\in O_2\times {\mathbb {R}}$,

$$\begin{aligned} \begin{aligned} \max _{{\theta _i}, {\lambda _j}}&~~~ \frac{\Vert \sum _i \theta _i x_i\Vert \sum _{j} \lambda _j w_j + \Vert \sum _j \lambda _j z_j\Vert \sum _i\theta _i y_i}{\Vert \sum _i \theta _i x_i\Vert + \Vert \sum _j \lambda _j z_j\Vert } \\ \text {s.t.}&~~~ \sum _{i}\theta _i = 1 \\&~~~ \sum _j \lambda _j = 1 \\&~~~ 1\ge \theta _i, \lambda _j \ge 0 \\&~~~ \text {the geodesic between } \sum _{i}\theta _ix_i\text { and }\sum _j\lambda _j z_j \\&~~~~~~~~~~\text { is a cone path.} \end{aligned} \end{aligned}$$

(C16)

Although the last nonconvex constraint can be removed when we are considering some combinations of two orthants, the objective function is also nonconvex. The next is an example that shows nonconvexity in a very simple case.

Example 4

Consider two orthants $O_1$ and $O_2$ separated by two other orthants so that the geodesic between points in two orthants are necessarily cone paths. We assume that we have two points in each orthant, say $x_1\in O_1, x_2\in O_1, z_1\in O_2, z_2\in O_2$, with the coordinates at each orthant being (0, 1), (1, 0), (0, 1), (1, 0) respectively. We consider the problem (C16) with four points $(x_1,1), (x_2, 1), (z_1, -1), (z_2, -1)$ (Fig. 12).

Fig. 12

Points used in Example 4. (Top): Four points $x_1, x_2, z_1, z_2$. (Center): The optimal cone paths with $(\lambda , \theta ) = (0.5, 1), (0.5,0)$. (Bottom): The cone path when $(\lambda , \theta ) = (0.5, 0.5)$

Then the optimization problem to solve is

$$\begin{aligned} \begin{aligned} \max _{\theta , \lambda }&~~~ f(\theta , \lambda ) = \frac{-\sqrt{\theta ^2 + (1-\theta )^2} + \sqrt{\lambda ^2 + (1-\lambda )^2}}{\sqrt{\theta ^2 + (1-\theta )^2} + \sqrt{\lambda ^2 + (1-\lambda )^2}} \\ \text {s.t.}&~~~ 1 \ge \theta , \lambda \ge 0 \end{aligned}\nonumber \\ \end{aligned}$$

(C17)

The optimal solutions to this problem are $(\lambda , \theta ) = (0.5, 1)$ and $(\lambda , \theta ) = (0.5, 0)$. Moreover, $(\lambda , \theta ) = (0.5, 0.5)$ is a saddle point, and the second derivatives are

$$\begin{aligned} {\frac{\partial ^2 f}{\partial \theta ^2}} \mid {_{\theta =0.5, \lambda =0.5} }&= -2, \end{aligned}$$

(C18)

$$\begin{aligned} \frac{\partial ^2 f}{\partial \lambda ^2}\mid {_{\theta =0.5, \lambda =0.5} }&= 2. \end{aligned}$$

(C19)

Thus, the objective function is concave in $\theta$ and convex in $\lambda$ around $(\theta , \lambda )=(0.5, 0.5)$.

As it is computationally intensive to solve this nonconvex optimization problem at each iteration, we replace the maximum (resp. minimum) values at the origin with its lower bound (resp. upper bound), which can be easily computed by linear programming. In the following paragraph, we explain the algorithm to calculate the replacement value.

First, note that in the two-dimensional tree space, there are 15 orthants, each consisting of two axes at a right angle, and each axis is connected to two other orthants. Thus, there are $15\times 4 = 60$ combinations of three orthants connected sequentially, as one can see by Figure 1 in the main text. We denote these combinations of orthants as $\{(O_{j1}, O_{j2}, O_{j3})\}_{j=1}^{60}$, where $O_{j1}, O_{j2}, O_{j3}$ are connected in this order.

The top figure of Fig. 10 is a valid representation of orthants $O_{j1}, O_{j2}, O_{j3}$ in the Euclidean space, in the sense that the distance between two points in these orthants is respected if we do not allow the paths to cross the space outside these three orthants, which is the hatched region on the left in the figure. Then, the space $\cup _{i=1}^3 O_{ji} \times {\mathbb {R}}$ constitutes a part of ${\mathbb {R}}^3$, as depicted in the central figure of Fig. 10. For all 60 combinations of these orthants, we embed points of $S_{k-1}$ in ${\mathbb {R}}^3$, calculate the usual three-dimensional convex hull in this space (allowing paths to cross the quadrant which is not used for the embedding), and if the convex hull includes a point of the form $\{(0,y)\}$, where 0 is the origin, then set the maximum and minimum y-values at the origin as $y_{k,j1}$ and $y_{k,j0}$, respectively. Note that the convex hull calculated here includes points outside the embeddings. In practice, we do not need to compute the whole convex hull. Rather, we only need to solve a linear programming problem. In the case of finding maximum values, given Euclidean embeddings $\{(x_{jm}, y_{jm})\}_{m=1}^{N_j}$, the problem is written as follows:

$$\begin{aligned} \begin{aligned} \max _{\{\lambda _m\}_{m=1}^{N_j}}&~~~ \sum _{m=1}^{N_j} \lambda _m y_{jm}, \\ \text {s.t.}&~~~ \sum _{m=1}^{N_j} \lambda _m = 1, \\&~~~1 \ge \lambda _m \ge 0. \end{aligned} \end{aligned}$$

(C20)

Then let the maximum of all $\{y_{k,j1}\}$ and the minimum of all $\{y_{k,j0}\}$ be $y_{k1}^\prime$ and $y_{k0}^\prime$, respectively, and make them replacements for $y_{k1}$ and $y_{k0}$.

Note that $y_{k1}^\prime$ (resp. $y_{k0}^\prime$ ) is a valid lower (resp. upper) bound for $y_{k1}$ (resp. $y_{k0}$ ), since there always exists a cone path geodesic between points in $S_{k-1}$ that crosses $(0,y_{k1}^\prime )$ and $(0,y_{k0}^\prime )$. Also, as we can see from the proof of Theorem 9, this procedure assures that all geodesics between points in $H_{k-1}$ that are not cone paths are always included in $H_k$.