A reliable data-based smoothing parameter selection method for circular kernel estimation

Abstract

A new data-based smoothing parameter for circular kernel density (and its derivatives) estimation is proposed. Following the plug-in ideas, unknown quantities on an optimal smoothing parameter are replaced by suitable estimates. This paper provides a circular version of the well-known Sheather and Jones bandwidths (J R Stat Soc Ser B Stat Methodol 53(3):683–690, 1991. https://doi.org/10.1111/j.2517-6161.1991.tb01857.x), with direct and solve-the-equation plug-in rules. Theoretical support for our developments, related to the asymptotic mean squared error of the estimator of the density, its derivatives, and its functionals, for circular data, are provided. The proposed selectors are compared with previous data-based smoothing parameters for circular kernel density estimation. This paper also contributes to the study of the optimal kernel for circular data. An illustration of the proposed plug-in rules is also shown using real data on the time of car accidents.

1 Introduction

Circular data are observations that can be represented on the unit circumference and where periodicity must be taken into account. Classic examples appear when the goal is to model orientations or a periodic phenomenon with a known period. Several applications of circular data can be found, e.g., in Ley and Verdebout (2018) or SenGupta and Arnold (2022). The complicated features that circular data can exhibit on real data applications lead to several new flexible models in the statistical literature. A recent review of flexible parametric circular distributions can be found in Ameijeiras-Alonso and Crujeiras (2022).

When trying to obtain a flexible fit of the density function, an alternative to parametric models is the kernel density estimation. Kernel density estimation for circular data dates back to Beran (1979) and Hall et al. (1987), while the estimator of the density derivatives was studied by Di Marzio et al. (2011). Additionally, the extension of density (and its derivatives) to the (hyper-)toroidal and (hyper-)spherical cases was considered by Di Marzio et al. (2011) and Klemelä (2000), respectively. It is well-known that, for all these estimators, the choice of the smoothing parameter is crucial when using these kernel methods.

In the usual linear inferential framework, where random variables are supported on the Euclidean space, one can find many approaches for selecting the “best” data-driven bandwidth parameter (see, e.g., Jones et al. 1996, for a discussion on this topic). Due to its good performance, one of the most-employed bandwidth selectors is the plug-in bandwidth proposed by Sheather and Jones (1991). The relevance of this plug-in selector is evident from the impressive number of citations that Sheather and Jones (1991) have received, and although other authors have introduced new bandwidth selectors, none of the proposals outperforms, in general, their plug-in selector.

There exists some literature on smoothing parameter selection for circular data, some of these ideas are based on cross-validation (Hall et al. 1987), rule-of-thumb (Taylor 2008), plug-in (Oliveira et al. 2012; García-Portugués 2013; Tenreiro 2022), or bootstrap (Di Marzio et al. 2011) techniques. But none of the approaches introduced so far presents an outstanding performance with respect to its competitors, as is the case with the proposal by Sheather and Jones (1991) in the linear case. Hence, the goal of this paper is to provide the needed theory to derive an algorithm that replicates the idea of the two-stage direct and solve-the-equation plug-in bandwidth selectors for circular kernel density estimation. In addition, the developed theory can be also employed when estimating the density derivatives.

Regarding the kernel choice, most of the results for circular density estimation fix the kernel to be the von Mises density function. In this paper, we study the asymptotic results for a more general class of kernels. This allow us to obtain the optimal kernels in the circular estimation context.

This paper is organized as follows. Section 2 is devoted to the definition of the circular kernel density derivative estimate. Also, the key function needed to derive the optimal smoothing parameter is introduced in this section. For a general circular kernel, the asymptotic mean integrated squared error and the optimal smoothing parameter of the derivative estimator are derived in Sect. 3. Section 4 is devoted to the estimation of density functionals needed to derive the plug-in rules. In Sect. 5, we discuss the kernel choice. Section 6 provides all the essential details to compute the two-stage direct and solve-the-equation plug-in smoothing selectors. We analysed the performance of the proposed plug-in rules through a simulation study. The summarized conclusions appear in Sect. 7. Section 8 uses a real data example to show the applicability of the proposed selector. Some final remarks are provided in Sect. 9. Section 10 describes the software that implements the proposed smoothing parameters. The complete simulation study showing that the proposed rules provide a competitive smoothing parameter, some additional comments regarding how to use the software, and the proofs of the theoretical results are provided as Supplementary Material.

2 Circular kernel density derivative estimation

Given a circular random sample in angles $\Theta _1, \ldots , \Theta _n \in [-\pi , \pi )$, with an associated density function f, the circular kernel density estimator (see, for example, Oliveira et al. 2012) can be defined as follows:

$$\begin{aligned} {\hat{f}}_\nu (\theta )=\frac{1}{n} \overset{n}{\underset{i=1}{\sum }} K_\nu \left( \theta -\Theta _i\right) , \end{aligned}$$

(1)

where $K_\nu$ is the circular kernel with a smoothing parameter $\nu \in [0, 1]$, representing the mean resultant length. It is worth noting that, in contrast to previous circular literature (Di Marzio et al. 2009, 2011), we use the notation $K_\nu$ instead of $K_\kappa$ since our smoothing parameter focuses on the mean resultant length rather than the concept of “concentration”. This choice allows us to establish a theory that is valid for both types of kernels, whether they depend on concentration, such as the von Mises, or on the mean resultant length, such as the wrapped normal (see Sect. 5 for a formal introduction to these kernels).

The estimator (1) can be easily extended, when the objective is estimating the r-th derivative of f, denoted by $f^{(r)}$. In that case, the estimator of $f^{(r)}$ can be defined as (Di Marzio et al. 2011),

$$\begin{aligned} {\hat{f}}^{(r)}_\nu (\theta )=\frac{1}{n} \overset{n}{\underset{i=1}{\sum }} K^{(r)}_\nu \left( \theta -\Theta _i\right) . \end{aligned}$$

(2)

The first question is which function can be employed as a kernel? In this case, we will assume that $K_\nu$ satisfies assumptions reminiscent of the canonical conditions for the linear kernel ( Wand and Jones 1995, Ch. 2). In particular, a circular kernel $K_\nu$ (reflectively) symmetric about zero and square-integrable in $[-\pi ,\pi )$ would admit the following convergent Fourier series representation (see Mardia and Jupp 1999, Section 4.2),

$$\begin{aligned} K_\nu (\theta ) = \frac{1}{2\pi } \left( 1+ 2\sum _{j=1}^{\infty } \alpha _{K,j}(\nu ) \cos (j\theta ) \right) , \end{aligned}$$

(3)

where only the values of $\alpha _{K,j}(\nu )\in [0,1]$, for $j\in \{1,2,\ldots \}$, depend on the employed kernel and the mean resultant length $\nu$. In Sect. 3, we will impose that Fourier series representation for the kernel $K_\nu$.

Secondly, a crucial element in kernel density estimation is the smoothing parameter. Generally, this parameter is taken as a non-random sequence, depending on the sample size, and then as a fixed value for a sample realization. In this work, we will introduce the function h depending on $\nu$,

$$\begin{aligned} h \equiv h_{K}(\nu )= \frac{\pi ^2}{3}+4 \sum _{j=1}^{\infty } \frac{(-1)^j \alpha _{K,j}(\nu )}{j^2}. \end{aligned}$$

(4)

We denote h as the circular bandwidth and the sequence of numbers $h_{n} \equiv h_{K}(\nu _n)$ must satisfy $\lim _{n\rightarrow \infty } h_{n} =0$. It is important to note that this circular bandwidth is constructed from trigonometric moments, distinguishing it from the concept of “bandwidth” used in scale-family kernels. The distinction arises because circular distributions, such as the von Mises, do not belong to the scale family. In this paper, we aim to derive an explicit expression for the optimal circular bandwidth without imposing assumptions that resemble scalar theory. Specifically, we do not require conditions like $K_g(\theta )=K(\theta /g)/g$ (Tenreiro 2022) or $K_{g_n}(\theta )=\lambda g_n^{-2} K((1-\cos (\theta ))/g_n^2)$, for some constant $\lambda$, when $g_n\rightarrow 0$ (García-Portugués 2013).

3 Asymptotic results

In this section, we establish the results needed for deriving the asymptotic mean integrated squared error (AMISE) and the AMISE-optimal smoothing parameter. Throughout this section, for a given derivative order r, we will employ the following assumptions to derive the asymptotic results.

• (A1) The circular density f is such that its derivative $f^{(r+2)}$ is continuous.

• (A2) For all $\nu$, the kernel $K_\nu$ admits the Fourier series representation (3).

• (A3) For $t\in \{1,2\}$, define the function $R_{K;r,t}$ as:

  $$\begin{aligned}&R_{K;r,t}(\nu ) = \\&\left\{ \begin{array}{ll} (2 \pi )^{-1}\left( 1+2 \sum _{j=1}^{\infty } \alpha _{K,j}^t(\nu ) \right) &{} \text { if } r=0, \\ {\mathfrak {s}} \pi ^{-1} \sum _{j=1}^{\infty } j^{t r} \alpha _{K,j}^t(\nu ) &{} \text { otherwise, } \end{array}\right. \\&{\mathfrak {s}} =\left\{ \begin{array}{ll} -1 &{} \text { if } t=1 \text { and } r \text { modulo } 4 = 1, \\ -1 &{} \text { if } t=1 \text { and } r \text { modulo } 4 = 2, \\ 1 &{} \text { otherwise. } \end{array}\right. \end{aligned}$$

  The smoothing parameter satisfies that $\lim _{n\rightarrow \infty } h_{K}(\nu _n)=0$ and $\lim _{n\rightarrow \infty } n^{-1} R_{K;r,2}(\nu _n)=0$.

As mentioned in Sect. 1, Assumptions (A1) and (A2) are reminiscent of those employed in the standard linear case. For a large class of kernels, including the von Mises or the wrapped normal (see Sect. 5), we will see that Assumption (A3) translates into the standard conditions on the bandwidth, namely, $\lim _{n\rightarrow \infty } h_{n}=0$ and $\lim _{n\rightarrow \infty } n h_{n}^{(2r+1)/2}=\infty$. The result in Theorem 1 (see Section S3 of the Supplementary Material for a formal proof) states the AMISE order of the kernel derivative estimator (2). If we also assume the following two extra conditions, we can derive an explicit expression of the AMISE.

• (E1) $\int _{-\pi }^{\pi } \theta ^4 K_{\nu _n}(\theta ) d\theta =o(h_{n})$, as $n\rightarrow \infty$.

• (E2) $\lim _{n\rightarrow \infty } R_{K;r,2}(\nu _n)=\infty$ and, as $n\rightarrow \infty$, $\int _{-\pi }^{\pi } \theta ^2 (K_{\nu _n}^{(r)}\left( \theta \right) )^2 d\theta = o[R_{K;r,2}(\nu _n)]$.

Theorem 1

Under the Assumptions (A1)–(A3), we have

$$\begin{aligned} \hbox {AMISE}\left[ {\hat{f}}^{(r)}_\nu \right] = O\left( h_{K}^2(\nu _n) \right) +O\left( n^{-1} R_{K;r,2}(\nu _n) \right) . \end{aligned}$$

If we also assume Conditions (E1) and (E2), then the AMISE has the following explicit expression.

$$\begin{aligned} \hbox {AMISE}\left[ {\hat{f}}^{(r)}_\nu \right]&= \frac{1}{4} h_{K}^2(\nu _n) \int _{-\pi }^{\pi } \left( f^{(r+2)} (\theta )\right) ^2 d \theta \nonumber \\&\quad + \frac{1}{n} R_{K;r,2}(\nu _n). \end{aligned}$$

(5)

Theorem 1 states the expression of the AMISE which depend on the sample size n, the derivative of the density function $f^{(r+2)}$, the kernel $K_\nu$, and the mean resultant length $\nu$. The complete expression of the asymptotic mean squared error (AMSE) is provided in Section S3 of the Supplementary Material.

Remark 1

Di Marzio et al. (2009, 2011) also analysed the AMISE of the circular kernel estimation obtaining a similar result as in (5), replacing $h_{K}(\nu _n)$ by $(1-\alpha _{K,2}(\nu _n))/2$. Note that, although not stated in their paper, additional conditions must be imposed to derive their asymptotic results. We further elaborate on this matter in Section S3.1 of the Supplementary Material. In particular, their results hold true assuming Condition (E1). Under this condition, we can approximate $h_{K}(\nu _n)$ by $(1-\alpha _{K,2}(\nu _n))/2$, as n increases. Thus, asymptotically, both results coincide, but the expression provided in this paper will allow us to derive an expression of the optimal smoothing parameter.

The issue, under the general AMISE expression given in (5), is that it is not straightforward to know how to derive an explicit expression of the optimal smoothing parameter, unless a specific kernel, such as the von Mises is chosen (see, e.g., Di Marzio et al. 2011). This problem can be solved when the following extra condition is assumed.

• (E3) As $n\rightarrow \infty$, $R_{K;r,2}(\nu _n)=Q_{K;r,2} h_{n}^{-(2r+1)/2} + o(h_{n}^{-(2r+1)/2})$, where $Q_{K;r,2}$ is a constant only depending on the kernel family and the derivative order r.

Note that under the Condition (E3), the Assumption (A3) simplifies to $\lim _{n\rightarrow \infty } h_{n}=0$ and $\lim _{n\rightarrow \infty } n h_{n}^{(2r+1)/2}=\infty$. Using this last assumption, we can observe the classic variance-bias trade-off, where the bias is reduced if $h_{n}$ is “small” and the variance decreases if $h_{n}$ is “large”. The optimal smoothing parameter with respect to the AMISE criteria can be obtained using the following corollary of Theorem 1, which is a direct consequence of $h_{K}(\nu )>0$ (see Section S3 of the Supplementary Material).

Corollary 1

Consider the Assumptions (A1)–(A3) and (E1)–(E3). Then, for the kernel derivative estimator of order r (see (2)), we have that, asymptotically, the optimal (AMISE) value of $h_{n}$ can be obtained from,

$$\begin{aligned} h_{K; r; \tiny {\hbox {AMISE}}}= \left( \frac{(2r+1) Q_{K;r,2} }{n \int _{-\pi }^{\pi } \left( f^{(r+2)} (\theta ) \right) ^2 d \theta } \right) ^{2/(2r+5)}. \end{aligned}$$

(6)

Under the previous assumptions, the minimal AMISE of ${\hat{f}}^{(r)}_\nu$ is equal to

$$\begin{aligned}&\inf _{0\le \nu <1} \hbox {AMISE}\left[ {\hat{f}}^{(r)}_\nu \right] = \left( \frac{(2r+1) Q_{K;r,2} }{n} \right) ^{4/(2r+5)} \nonumber \\&\times \frac{2r+5}{8r+4} \left( \int _{-\pi }^{\pi } \left( f^{(r+2)} (\theta )\right) ^2 d \theta \right) ^{(2r+1)/(2r+5)}. \end{aligned}$$

(7)

Remark 2

From Corollary 1, it can be observed that the optimal order for circular bandwidth density estimation $h_{K; 0; \tiny {\hbox {AMISE}}}$, which is $O(n^{-2/5})$, does not coincide with the optimal bandwidth order, $O(n^{-1/5})$, as presented in Tenreiro (2022). The reason for this discrepancy, as explained in Sect. 2, is their lack of alignment. However, it is worth noting that, for example, in the case of the von Mises kernel (see Sect. 5.1), when translating this result to the optimal concentration $\kappa$ for density estimation, both theoretical outcomes yield the same asymptotic optimal concentration of order $O(n^{2/5})$.

Remark 3

Note that the AMISE expression in (7) aligns with the one obtained in the linear case ( Wand and Jones 1995, Chapter 2), except for terms related to the kernel. If $K_\ell$ is a scalar kernel with a variance of one, the same AMISE expression in the linear case can be obtained by replacing $Q_{K;r,2}$ in (7) with $\int _{-\infty }^\infty (K_\ell ^{(r)}(x))^2 dx$.

The optimal mean resultant length $\nu$ is the solution to the equation $h_{K}(\nu )=h_{K;r;\tiny {\hbox {AMISE}}}$, see Equation (4). Alternatively, to avoid the infinite sum in (4), one can also obtain the optimal $\nu$ by solving the equation $\alpha _{K,2}(\nu )=1-2h_{K;r;\tiny {\hbox {AMISE}}}$ (see Remark 1).

As usual, when using data-based plug-in smoothing parameters, the main problem with employing the optimal $h_{K;r;\tiny {\hbox {AMISE}}}$ in Corollary 1, is that its value depends on the unknown value of $\int _{-\pi }^{\pi } \left( f^{(r+2)} (\theta ) \right) ^2 d \theta$. A rule-of-thumb smoothing selector can be obtained by replacing f with a simple and standard density function, such as the von Mises density. One can also follow the Ćwik and Koronacki (1997) approach and replace f with a mixture model, such as the mixture of von Mises. Both techniques were already proposed and studied in the circular literature when employing the von Mises density as the kernel $K_\nu$ (see Taylor 2008; Oliveira et al. 2012; García-Portugués 2013). Following Sheather and Jones (1991), an alternative is to estimate density functionals related to $\int _{-\pi }^{\pi } \left( f^{(s)} (\theta ) \right) ^2 d \theta$. In the next section, we study how to obtain a kernel estimator of this last quantity, in the circular context.

4 Estimation of density functionals

As mentioned in the previous section, an issue with using, in practice, the optimal smoothing parameter (6) is its dependence on the unknown quantity $\int _{-\pi }^{\pi } \left( f^{(r+2)} (\theta ) \right) ^2 d \theta$. In this section, we will see how to estimate this last quantity using kernel techniques. For doing so, we first define the functional of the form

$$\begin{aligned} \psi _s= \int _{-\pi }^{\pi } f^{(s)} (\theta ) f (\theta ) d\theta . \end{aligned}$$

Note that under sufficient smoothness assumptions on f (e.g., the needed conditions to apply integration by parts), we obtain that,

$$\begin{aligned} \int _{-\pi }^{\pi } \left( f^{(s)} (\theta ) \right) ^2 d \theta = (-1)^s \psi _{2s}. \end{aligned}$$

(8)

Since $\psi _s ={\mathbb {E}} (f^{(s)} (\Theta ))$, the following estimator can be employed to estimate the unknown quantity $\int _{-\pi }^{\pi } \left( f^{(r+2)} (\theta ) \right) ^2 d \theta$ on the optimal smoothing parameter (6),

$$\begin{aligned} {{\hat{\psi }}}_{s;\rho } = \frac{1}{n} \overset{n}{\underset{i=1}{\sum }} {\hat{f}}^{(s)}_\rho (\Theta _i)= \frac{1}{n^2} \overset{n}{\underset{i=1}{\sum }} \overset{n}{\underset{j=1}{\sum }} L_\rho ^{(s)}\left( \Theta _i-\Theta _j\right) , \end{aligned}$$

(9)

where $L_\rho$ and $\rho$ are a kernel and a mean resultant length parameter. In the following theory, we will assume that $L_\rho$ and $\rho$ may differ from $K_\nu$ and $\nu$. However, it is important to note that, in practice, the same kernel is typically employed for both the density (derivative) and the density functionals estimators. Later on, we will observe that, conversely, $\nu$ and $\rho$ usually take distinct values, and we will delve into how to derive a data-driven value for $\rho$.

Using the estimator (9), a direct plug-in estimator of the smoothing parameter can be obtained from (6), replacing the quantity depending on the true f, by its estimator, in the following way,

$$\begin{aligned} h_{K; r; \tiny {\hbox {PI}}}= \left( \frac{(2r+1) Q_{K;r,2} }{n (-1)^{r+2}{{\hat{\psi }}}_{2r+4; \rho } } \right) ^{2/(2r+5)}. \end{aligned}$$

(10)

The problem with the direct plug-in estimator (10), is that it still depends on a choice of the pilot mean resultant length $\rho$. Below, we establish the asymptotic theory to derive the optimal smoothing parameter of ${{\hat{\psi }}}_{2r+4; \rho }$. For obtaining that result, the following conditions on the pilot parameter are required.

• (A4) The smoothing parameter satisfies that $\lim _{n\rightarrow \infty } h_{L}(\rho _n)=0$ and $\lim _{n\rightarrow \infty } n^{-2} R_{L;s,2}(\rho _n)=0$.

• (A5) $\lim _{n\rightarrow \infty } R_{L;s,1}(\rho _n)=\infty$ and $\lim _{n\rightarrow \infty } n^{-1} R_{L;s,1}(\rho _n)=0$.

Note that when replacing the kernel $K_\nu$ by $L_\rho$, the mean resultant length $\nu _n$ by $\rho _n$, and the order of the derivative r by s, Assumption (A3) implies Condition (A4). Below, we provide the AMSE for the estimator ${{\hat{\psi }}}_{s; \rho }$ (see Section S4 of the Supplementary Material for a formal proof).

Theorem 2

If f satisfies Assumption (A1) (replacing r by s), the kernel $L_\rho$ and $\rho _n$ verifies (A2), (A4) and (A5); then, for an even value of s,

$$\begin{aligned}&\hbox {AMSE}\left[ {{\hat{\psi }}}_{s; \rho } \right] = O\left( n^{-2} R_{L;s,1}^2(\rho _n) \right) + O\left( h_{L}^2 (\rho _n) \right) \nonumber \\&\qquad + O(n^{-2}R_{L;s,2}(\rho _n)) + O(n^{-1}). \end{aligned}$$

(11)

If, in addition, Conditions (E1) and (E2) (using $L_\rho$, instead of $K_\nu$; $\rho _n$, instead $\nu _n$; and $r=s$) are verified, we have

$$\begin{aligned}&\hbox {AMSE}\left[ {{\hat{\psi }}}_{s; \rho } \right] = \left( n^{-1} R_{L;s,1}(\rho _n) + \frac{1}{2} h_{L} (\rho _n) \psi _{s+2} \right) ^2 \nonumber \\&\qquad + 2 n^{-2} \psi _{0} R_{L;s,2}(\rho _n) \nonumber \\&\qquad + 4 n^{-1} \left( \int _{-\pi }^{\pi } \left( f^{(s)} (\theta ) \right) ^2 f (\theta ) d \theta - \psi _{s}^2 \right) . \end{aligned}$$

(12)

As for Corollary 1, in order to derive a simpler expression of the AMSE and the optimal value of ${\mathfrak {h}}_{n} \equiv h_{L} (\rho _n)$, we will assume the following extra conditions:

• (E4) $R_{L;s,1}(\rho _n)=Q_{L;s,1} {\mathfrak {h}}_{n}^{-(s+1)/2} + o({\mathfrak {h}}_{n}^{-(s+1)/2})$, as $n\rightarrow \infty$, where $Q_{L;s,1}$ is a constant only depending on the kernel and the even number s. The sign of $Q_{L;s,1}$ is equal to the sign of $(-1)^{s/2}$.

• (E5) $\int _{-\pi }^{\pi } \theta ^4 L_{\rho _n}(\theta ) d\theta =o({\mathfrak {h}}_{n}^{5/4})$, as $n\rightarrow \infty$.

From the AMSE expression in (12), we can see that the optimal ${\mathfrak {h}}_{n}$ value, in terms of AMSE, will depend on the relation between $R_{L;s,1}(\rho _n)$, $R_{L;s,2}(\rho _n)$, and $h_{L} (\rho _n)$. Conditions (E3) and (E4) help to establish this relation, from which the following corollary is derived (see Section S4 of the Supplementary Material).

Corollary 2

Consider the assumptions of Theorem 2, Conditions (E3; replacing $K_\nu$ by $L_\rho$; using $\rho _n$, instead $\nu _n$; and $r=s$), and (E4). Then, for the kernel estimator of $\psi _s$ (see (9)), we have that, asymptotically, the optimal value, in terms of the AMSE expression, of ${{\mathfrak {h}}}_{n}$ can be obtained from,

$$\begin{aligned} {\mathfrak {h}}_{L; s; \tiny {\hbox {AMSE}}}= \left( -\frac{2 Q_{L;s,1} }{n \psi _{s+2}} \right) ^{2/(s+3)}. \end{aligned}$$

(13)

Under the previous assumptions, if Condition (E5) is also assumed, the minimal AMSE for (9) is of order $O(n^{-\min (5,s+3)/(s+3)})$. If s is an even number greater than 2, the minimal AMSE would be equal to

$$\begin{aligned}&\inf _{0\le \rho <1} \hbox {AMSE}\left[ {{\hat{\psi }}}_{s; \rho } \right] = 2 \psi _{0} Q_{K;r,2} \nonumber \\&\qquad \times \left( -\frac{\psi _{s+2} }{2 Q_{L;s,1}} \right) ^{(2s+1)/(s+3)} n^{-5/(s+3)}. \end{aligned}$$

(14)

If $s=0$, the minimal AMSE is equal to

$$\begin{aligned}&\inf _{0\le \rho <1} \hbox {AMSE}\left[ {{\hat{\psi }}}_{s; \rho } \right] = 4 n^{-1} \nonumber \\&\qquad \times \left( \int _{-\pi }^{\pi } \left( f^{(s)} (\theta ) \right) ^2 f (\theta ) d \theta - \psi _{s}^2 \right) . \end{aligned}$$

(15)

When $s=2$, the minimal AMSE is equal to the sum of the right-hand sides of (14) and (15).

Note that Condition (E5) is only assumed to obtain the same AMSE optimal order as in the linear case. If that condition is not fulfilled, then, when $s>0$, the leading term in the AMSE could be of a larger order (see Section S4 of the Supplementary Material). Another important consideration is that the sign of $\psi _{s+2}$ is the same as that of $(-1)^{s/2+1}$ and, using Condition (E4), it also coincides with the sign of $-Q_{L;s,1}$. Therefore, we always have that ${\mathfrak {h}}_{L; s; \tiny {\hbox {AMSE}}} \ge 0$ in (13).

Using the quantity ${\mathfrak {h}}_{L; 2r+4; \tiny {\hbox {AMSE}}}$ in (13), one can obtain the pilot mean resultant length $\rho$ needed to derive the direct plug-in estimator (10). The issue, as in the linear case, is that ${\mathfrak {h}}_{L; 2r+4; \tiny {\hbox {AMSE}}}$ still depends on the unknown value of the functional $\psi _{2r+6}$. We comment on how to overcome this difficulty in Sect. 6.

5 The kernel choice

Theoretical results in Sects. 3 and 4 provide mathematical support for deriving the optimal smoothing parameter. However, we still did not discuss how to obtain the plug-in mean resultant length parameter $\nu _{r; \tiny {\hbox {AMISE}}}$ from $h_{K; r; \tiny {\hbox {AMISE}}}$. As mentioned in Sect. 3, we must solve the equation $h_{K}(\nu )=h_{K;r;\tiny {\hbox {AMISE}}}$. We also need to obtain the values of $Q_{K;r,1}$ and $Q_{K;r,2}$ in (6) and (13).

In this section, we study what happens when the “most common” circular models are employed as kernels. For doing so, we restrict our attention to the four standard choices of circular densities (see Mardia and Jupp 1999, Section 3.5): cardioid, von Mises, wrapped normal, and wrapped Cauchy. Although all of them satisfy Assumption (A2), the cardioid kernel, $K_{\tiny {\hbox {C}};\nu }(\theta )=(1+2\nu \cos (\theta ))/(2\pi )$, with $|\nu |< 1/2$, does not meet Assumption (A3) and will be hence discarded from the analysis. This can be seen by observing that, for any $\nu$, $h_{K_{\tiny {\hbox {C}}}}(\nu )= \pi ^2/{3}-4 \nu \ge \pi ^2/{3} -2$. The other three circular densities are studied in Sects. 5.1 and 5.2.

Once the behaviour of the standard kernels is studied, a second question to discuss is which is the optimal kernel in the circular context. As in Muller (1984), we study the kernel optimality in terms of the AMISE expression in (7). Fixing f and the sample size n, in Sect. 5.3, we obtain the circular kernel that minimizes the AMISE.

5.1 Von Mises and wrapped normal kernels

First, denote by ${\mathcal {I}}_j$ to the modified Bessel function of the first kind and order j, the density expression of the von Mises (VM) kernel is

$$\begin{aligned} K_{\tiny {\hbox {VM}};\nu }(\theta )&= \frac{\exp \left( \kappa \, \cos (\theta ) \right) }{\left( 2 \pi \ {{\mathcal {I}}}_0(\kappa ) \right) } \\&= \frac{1}{2\pi } \left( 1+ 2\sum _{j=1}^{\infty } \frac{{{\mathcal {I}}}_j(\kappa )}{{{\mathcal {I}}}_0(\kappa )} \cos (j\theta ) \right) , \end{aligned}$$

where $\nu ={{\mathcal {I}}}_1(\kappa )/{{\mathcal {I}}}_0(\kappa )$, being $\kappa \ge 0$. The density expression of the wrapped normal (WN), with a mean resultant length $\nu \in [0,1]$, is

$$\begin{aligned} K_{\tiny {\hbox {WN}};\nu }(\theta ) = \frac{1}{2\pi } \left( 1+ 2\sum _{j=1}^{\infty } \nu ^{j^2} \cos ( j\theta ) \right) . \end{aligned}$$

For both kernels, if $\lim _{n\rightarrow \infty } \nu _n=1$ (equivalently $\lim _{n\rightarrow \infty } \kappa _n=\infty$, for the von Mises kernel), then $\lim _{n\rightarrow \infty } h_{K}(\nu _n)=0$. Even more, it is easy to show that, in that setting, Conditions (E1) and (E2) are satisfied. Thus, as $n\rightarrow \infty$, we obtain the following asymptotic approximations:

$$\begin{aligned} h_{K_{\tiny {\hbox {VM}}}}(\nu _n)&= \frac{1}{2}\left( 1- \frac{{{\mathcal {I}}}_2(\kappa _n)}{{{\mathcal {I}}}_0(\kappa _n)}\right) = \frac{1}{\kappa _n} ,\\ h_{K_{\tiny {\hbox {WN}}}}(\nu _n)&= \frac{1}{2}\left( 1- \nu _n^4 \right) . \end{aligned}$$

From the previous equalities, we can see that $\kappa _n$ or $\nu _n$ are easily derived, after computing the optimal/plug-in value of $h_n$ (see, e.g., (6) or (10)).

$$\begin{aligned} \kappa _n \overset{\tiny {\hbox {VM}}}{=} h_n^{-1} \qquad \hbox {and} \qquad \nu _n \overset{\tiny {\hbox {WN}}}{=} (1-h_n)^{1/4}. \end{aligned}$$

(16)

Again, considering $\lim _{n\rightarrow \infty } \nu _n=1$, it can be seen that Conditions (E3)–(E5) are satisfied for the von Mises and wrapped normal kernels. For both kernels and a non-negative integer number r, the values of the constants in (E3) and (E4) are the following ones:

$$\begin{aligned} Q_{K;r,1}&= (-1)^{r/2} \frac{r!}{2^{r/2} (r/2)! \sqrt{2 \pi }} \, (r \hbox { being even}), \nonumber \\ Q_{K;r,2}&= \frac{(2r)!}{2^{2r+1} r! \pi ^{1/2}}. \end{aligned}$$

(17)

We can see that the AMSE and AMISE results derived in Sects. 3 and 4 can be easily computed in practice from these last quantities. These optimal asymptotic results will coincide for both the von Mises and wrapped normal kernels.

5.2 Wrapped Cauchy kernel

The expression of the wrapped Cauchy kernel, with a mean resultant length $\nu \in [0,1]$, is given by

$$\begin{aligned} K_{\tiny {\hbox {WC}};\nu }(\theta ) = \frac{1}{2\pi } \left( 1+ 2\sum _{j=1}^{\infty } \nu ^j \cos (j\theta ) \right) . \end{aligned}$$

From the density expression, we derive that $h_{K_{\tiny {\hbox {WC}}}}(\nu )=\pi ^2/3+4 \text {Li}_2 (-\nu )$, where $\text {Li}_s$ is the polylogarithm of order s. The last implies $\lim _{n\rightarrow \infty } h_{K_{\tiny {\hbox {WC}}}}(\nu _n)=0$ if $\lim _{n\rightarrow \infty } \nu _n=1$. Also, the expressions of $R_{K_{\tiny {\hbox {WC}}};r,2}(\nu )$ can be obtained in terms of a polylogarithm,

$$\begin{aligned}&R_{K_{\tiny {\hbox {WC}}};r,2}(\nu ) \nonumber \\&\quad =\left\{ \begin{array}{ll} (2 \pi )^{-1}\left( 1+2 \text {Li}_{0} (\nu ^2) \right) &{} \text { if } r=0, \\ \pi ^{-1} \text {Li}_{-2r} (\nu ^2) &{} \text { otherwise, } \end{array} \right. \nonumber \\&\quad = O(h_n^{-(2r+1)}) \text {, as } n\rightarrow \infty . \end{aligned}$$

(18)

If we consider a value of $h_n$ such that $\lim _{n\rightarrow \infty } h_{n}=0$ and $\lim _{n\rightarrow \infty } n h_{n}^{2r+1}=\infty$, Condition (A3) is satisfied. Therefore, from Theorem 1, if f also satisfies Assumption (A1), we obtain the following AMISE for the wrapped Cauchy kernel,

$$\begin{aligned} \hbox {AMISE}\left[ {\hat{f}}^{(r)}_\nu \right] = O\left( h_n^2 \right) +O\left( n^{-1} h_n^{-(2r+1)} \right) . \end{aligned}$$

(19)

The AMISE expression (19) would be minimized if $h_n$ is of order $n^{-1/(2r+3)}$. Using the previous result, we obtain that the AMISE order of the wrapped Cauchy kernel is worse than that obtained with the von Mises or the wrapped normal kernel (see Corollary 1). In particular, its minimal AMISE is equal to

$$\begin{aligned} \inf _{0\le \nu <1} \hbox {AMISE}\left[ {\hat{f}}^{(r)}_\nu \right] = O\left( n^{-2/(2r+3)} \right) . \end{aligned}$$

When searching for an explicit expression of the optimal smoothing parameter, one could be tempted to combine (5) and (18). But note that this cannot be done as Condition (E1) is not verified (see Section S3.1). Thus, the explicit expression of the asymptotic bias cannot be obtained following the steps in Section S3 of the Supplementary Material. This implies that the AMISE does not have a closed expression as given in (5). On the contrary, Tsuruta and Sagae (2017) were able to obtain an optimal smoothing parameter for the wrapped Cauchy kernel from the results by Di Marzio et al. (2009). Nevertheless, it should be noted that Di Marzio et al. (2009) results must not be employed for this kernel as Condition (E1) is not satisfied (see Section S3.1 for further details).

5.3 Wrapped bounded-support kernels

To find the optimal kernels, consider a wrapped kernel $\displaystyle K_{\nu }(\theta ) =\sum _{\ell =-\infty }^{\infty } K_{X; \lambda }(\theta + 2 \, \ell \, \pi )$, whose associated linear density $K_{X; \lambda }$ has bounded support, i.e., $K_{X; \lambda }(x)=0$ if $|x |> \lambda$. Then, $K_{\nu }(\theta ) = K_{X; \lambda }(\theta )$, for all $\theta \in [-\pi ,\pi )$, when $\lambda < \pi$. In that case, $h= \int _{-\lambda }^{\lambda } x^2 K_{X; \lambda }(x) dx$ and $R_{K;r,2}(\nu )=\int _{-\lambda }^{\lambda } (K_{X; \lambda }^{(r)}(x ) )^2 dx$.

Consider the asymptotic case for linear bounded-support kernels, i.e., $\lim _{n\rightarrow \infty } \lambda _n=0$. Fixing the unknown linear density function $f_X$, Muller (1984) gives explicit expressions of the bounded-support kernels minimizing the AMISE when estimating the density function and its derivatives, in the linear case.

Assume now that the wrapped bounded-support kernel satisfies the assumptions of Corollary 1. Except for the values not depending on the kernel, the minimal AMISE of ${\hat{f}}^{(r)}_\nu$ in (7) is equal to the minimal AMISE obtained in the linear case. As a consequence, Theorem 2.4 of Muller (1984) can be employed to see that the optimal kernels in terms of AMISE coincide with the wrapped version of those employed on linear kernel estimation.

The latter means that the optimal kernel for circular density estimation is the wrapped Epanechnikov, whose associated linear density is $K_{X; \lambda }(x)=3(1-(x/\lambda )^2)/(4\lambda )$. When $\lambda < \pi$, the mean resultant length is $\nu =(3\sin (\lambda )-3\lambda \cos (\lambda ))/\lambda ^3$, $h= \lambda ^2/5$, and $R_{K;0,2}(\nu )= 3/(5\lambda )$. Thus, for circular density estimation with the wrapped Epanechnikov, the optimal (AMISE) value of $h_n$ is obtained by taking $Q_{K;0,2}=3/(5\sqrt{5})$ in (6). Regardless of the employed kernel, the minimum achievable AMISE for estimating a circular density function is given by:

$$\begin{aligned}&\inf _{0\le \nu <1} \hbox {AMISE}\left[ {\hat{f}}_\nu \right] = \frac{5}{4} \left( \frac{3}{5 \sqrt{5} n } \right) ^{4/5} \\&\qquad \times \left( \int _{-\pi }^{\pi } \left( f^{(2)} (\theta )\right) ^2 d \theta \right) ^{1/5}. \end{aligned}$$

This is the AMISE obtained with the wrapped Epanechnikov kernel. Note that this optimality is established among kernels that satisfy the conditions outlined in Corollary 1. The optimality of the Epanechnikov kernel for circular density estimation is also established by Tenreiro (2022) when restricting to kernels that satisfy alternative necessary assumptions. For the derivatives of the density, we refer to Muller (1984). There, we can see, e.g., that the wrapped Biweight would be the optimal kernel for the first derivative of f.

6 Plug-in smoothing parameters

In this section, we will study how to implement, in practice, the plug-in smoothing parameter $h_{K; r; \tiny {\hbox {PI}}}$ in (10). As mentioned in Sect. 4, the issue of directly employing (10) is that the AMISE-optimal smoothing parameter for ${{\hat{\psi }}}_{s;\rho }$ will always depend on an unknown value of $\psi _{s+2}$. A way to overcome this difficulty is to provide an l-stage direct plug-in smoothing selector. This procedure consists in estimating $\psi _{s}$ with ${{\hat{\psi }}}_{s+2;\rho }$, in an iterative process, until some point in which we replace $\psi _{2r+2l+4}$ by its value obtained with a simple density (see Sect. 6.1 for more details). An alternative selector can be computed by noting that the smoothing parameter for ${\hat{f}}^{(r)}$ can be obtained as a function of the smoothing parameter for ${{\hat{\psi }}}_{2r+4}$. This allows us to construct a solve-the-equation rule. In Sect. 6.2, we discuss in more detail how this selector is derived.

6.1 Two-stage direct plug-in smoothing selector

The procedure to obtain the l-stage direct plug-in smoothing selector consists in, at stage 0, using a simple rule of thumb to compute the smoothing parameter of ${{\hat{\psi }}}_{2r+4+2l;\rho }$. Once this initial step is achieved, from that estimator of $\psi _{2r+4+2l}$, the following functional estimators are derived in an iterative process (see Algorithm 2 for details).

Two decisions remain from this brief explanation: the number of stages l and which reference density should be employed at stage 0. Regarding the number of stages l, we suggest employing $l=2$ for two reasons. First, $l=2$ is a common choice in the linear case (see, e.g., Wand and Jones 1995, Section 3.6). A second reason was obtained when replicating the simulation study in Sect. 7, with $l=3$. In that case, similar results were achieved with respect to those obtained with $l=2$, with the added inconvenience of the extra computational time. The only scenario in which we would recommend increasing the value of l is when complex multimodal patterns are expected.

As mentioned before, at stage 0, a reference density is needed to compute the smoothing parameter of ${{\hat{\psi }}}_{2r+2l+4;\rho }$. Here, in the same spirit of the original rule of thumb proposed by Taylor (2008), a natural selection would be to replace $\psi _{2r+2l+4}$ in (13) by the quantity obtained when assuming that the true density follows a von Mises. In the circular case, the main pitfall of employing that simple strategy is that a uniform estimation of the density can be obtained even if the true distribution is not uniform. This occurs, for example, when considering distributions with antipodal symmetry (see also Oliveira et al. 2012, for further discussion on this topic). The consequence would be to have a value of ${{\hat{\psi }}}_{2r+2l+4;\rho }$ close to zero, which leads to a “large” value of the smoothing parameter at the next stage ${\mathfrak {h}}_{L; 2r+2l+2; \tiny {\hbox {PI}}}$.

To avoid that last issue, while still having a simple model, one can use as the reference density the following mixture of M von Mises, all having the same concentration parameter $\kappa \ge 0$:

$$\begin{aligned}&f_{\tiny {\hbox {MvM}}}(\theta ;M;\varvec{\mu },\kappa ,\varvec{w}) = \frac{1}{\left( 2 \pi \ {{\mathcal {I}}}_0(\kappa ) \right) } \nonumber \\&\qquad \times \sum _{m=1}^{M} w_m \exp \left( \kappa \, \cos (\theta -\mu _m) \right) , \end{aligned}$$

(20)

where the parameters $\mu _m \in [-\pi ,\pi )$, $w_m \in [0,1]$, for all $m \in \{1,\ldots , M\}$, and with $\sum _{m=1}^{M} w_m=1$. The value of $\psi _{2r+2l+4}$ is calculated from the density (20), replacing its parameters by their maximum likelihood estimates obtained from the sample. An algorithm providing the maximum likelihood estimates for the density (20) was implemented in the R (R Core Team 2022) library movMF by Hornik and Grün (2014). In practice, following Oliveira et al. (2012), the value of M can be chosen, using the Akaike Information Criterion (AIC), by comparing the results obtained with the mixtures (20) of $M=1,\ldots ,M_{\max }$ components.

In Algorithm 2, we summarize the steps that are needed to obtain our proposed two-stage direct plug-in smoothing parameter. There, for simplicity, we use the same kernel for both K and L, and this kernel satisfies Assumptions (A1)–(A5) and the extra Conditions (E1)–(E4).

The uniform distribution belongs to all the reference distributions mentioned before. Thus, in practice, the denominator of (10) or (13) could be equal to zero. If that occurs, we suggest directly returning a value of the mean resultant length $\nu _{ \tiny {\hbox {DPI}}}=0$, which would correspond to the uniform estimation of the density.

Given a finite value of n in (10) or (13), the equation $h_{K}(\nu )=h_{K;r;\tiny {\hbox {PI}}}$, or its approximation $\alpha _{K,2}(\nu )=1-2h_{K;r;\tiny {\hbox {AMISE}}}$, cannot be solved for “large” values of $h_{K;r;\tiny {\hbox {PI}}}$. The reason is that $h_{K}(\nu )$ and $\alpha _{K,2}(\nu )$ are non-negative and bounded for any value of $\nu$. Since a “large” value of $h_{K}(\nu )$ corresponds to $\nu =0$, if the equation $h_{K}(\nu )=h_{K;r;\tiny {\hbox {AMISE}}}$ cannot be solved, we also suggest employing the uniform as the density estimator.

6.2 Solve-the-equation plug-in smoothing selector

An alternative to the previous smoothing selector is the solve-the-equation rule. This rule consists in searching for the smoothing parameter that satisfies

$$\begin{aligned} h_{K; r; \tiny {\hbox {STE}}}= \left( \frac{(2r+1) Q_{K;r,2} }{n (-1)^{r+2}{{\hat{\psi }}}_{2r+4; \rho _{K; r; \tiny {\hbox {STE}}}} } \right) ^{2/(2r+5)}, \end{aligned}$$

(21)

with $h_{K}(\rho _{K; r; \tiny {\hbox {STE}}})=\gamma (h_{K; r; \tiny {\hbox {STE}}})$.

Now, the smoothing parameter for ${{\hat{\psi }}}_{2r+4}$ is a function of the smoothing parameter for ${\hat{f}}^{(r)}$. We suggest taking the function $\gamma$ by looking at the relation between the optimal smoothing parameter of these two estimators,

$$\begin{aligned}&{\mathfrak {h}}_{L; 2r+4; \tiny {\hbox {AMSE}}}= \left( (-1)^{r+1}\frac{2 Q_{L;2r+4,1} }{(2r+1) Q_{K;r,2}} \right) ^{2/(2r+7)} \\&\qquad \times \left( \psi _{2r+4}/\psi _{2r+6} \right) ^{2/(2r+7)} h_{K; r; \tiny {\hbox {AMISE}}}^{(2r+5)/(2r+7)}. \end{aligned}$$

Using a plug-in rule, this last relation suggests taking the following function:

$$\begin{aligned}&\gamma \left( {h} \right) = \left( (-1)^{r+1}\frac{2 Q_{L;2r+4,1} }{(2r+1) Q_{K;r,2}} \right) ^{2/(2r+7)} \nonumber \\&\quad \times \left( {{\hat{\psi }}}_{2r+4;\rho _1}/{{\hat{\psi }}}_{2r+6;\rho _2} \right) ^{2/(2r+7)} h^{(2r+5)/(2r+7)}. \end{aligned}$$

(22)

The two smoothing parameters of the density functional estimators, ${{\hat{\psi }}}_{2r+4}$ and ${{\hat{\psi }}}_{2r+6}$, can be obtained from (13). Those smoothing parameters will depend on some other density functionals, $\psi _{2r+6}$ and $\psi _{2r+8}$. Following Sheather and Jones (1991), we suggest estimating these two new functionals with a rule of thumb. In Algorithm 1, we summarize the steps that are needed to obtain our proposed solve-the-equation plug-in smoothing parameter. Again, for simplicity, we use the same kernel for both K and L, a kernel that satisfies Assumptions (A1)–(A5) and the extra Conditions (E1)–(E4).

Note that two extra functional estimators must be computed in Step 1 of Algorithm 1. For this reason, the obtained smoothing parameter could be considered as a two-stages solve-the-equation plug-in selector. As for the direct rule, the number of stages could be increased to estimate the density functionals. In particular, a rule of thumb can be employed to estimate $\psi _{2r+10}$ or $\psi _{2r+12}$ and then, in an iterative process, the values of $\rho _1$ and $\rho _2$ are obtained (as in Steps 2 and 3 of Algorithm 2). The simulation study in Sect. 7 was carried out under the same conditions, using three (relying on ${{\hat{\psi }}}_{2r+8;\tiny {\hbox {RT}}}$ and ${{\hat{\psi }}}_{2r+10;\tiny {\hbox {RT}}}$) and four (relying on ${{\hat{\psi }}}_{2r+10;\tiny {\hbox {RT}}}$ and ${{\hat{\psi }}}_{2r+12;\tiny {\hbox {RT}}}$) stages. The results in practice were similar to those obtained with Algorithm 1, with the drawback of the extra computational time.

7 Simulation study

In Section S1 of the Supplementary Material, we performed a simulation study to analyse the performance of the direct two-stage plug-in smoothing parameter (see Algorithm 2) and the solve-the-equation plug-in smoothing selector (see Algorithm 1). We focused only on the density estimation case ($r=0$ in (2)), with $K_\nu$ being the von Mises kernel. The reason is that their effectiveness can be compared with other smoothing parameters proposed in the literature. But note that our data-driven smoothing parameters could be employed to estimate any derivative and with other kernels. In particular, in this framework, slightly better results are expected by employing the wrapped Epanechnikov kernel (see Sect. 5.3).

Table 1 Average ISE ($\times 100$) and standard deviations ($\times 100$, in parentheses) computed from 1000 samples of sample size $n=100$ for Models M5–M20 of Oliveira et al. (2012)

A complete report on the results obtained when comparing the proposed smoothing selectors with other data-based smoothing selectors available in the circular literature (see Sect. 1) is provided in Section S1. In the current section, Table 1 presents the results obtained, for $n=100$, using the proposed smoothing selectors and other data-driven rules available in the literature. Table 1 contains the average integrated square error (ISE) computed from 1000 samples of the reference Models M5–M20 that can be found in Oliveira et al. (2012). Models M1–M4 were not included here as they can be well-approximated by a von Mises density. In those cases, as expected, the rule of thumb provides the best results. The full discussion of the obtained results is provided in Section S1. Below, as a summary of our findings, we provide our recommendations. In this summary, in parentheses, we provide the abbreviated names of the analysed smoothing rules. The same notation is used in the tables presenting the simulation results.

• For small sample sizes (say $n=50$), employ the proposed direct plug-in rule with $M_{\max }=1$ ($\nu _{ \tiny {\hbox {DPI}};1}$). The only exception to this recommendation is if there could be evidence of the density function being multimodal and k-fold rotational symmetric. In that case, employ the solve-the-equation plug-in smoothing selector with $M_{\max }=1$ ($\nu _{ \tiny {\hbox {STE}};1}$).

• For moderate sample sizes (say $n=100$ or $n=250$), employ the solve-the-equation plug-in smoothing selector with $M_{\max }=1$ ($\nu _{ \tiny {\hbox {STE}};1}$). The direct plug-in rule with $M_{\max }=1$ ($\nu _{ \tiny {\hbox {DPI}};1}$) is also recommendable if there is evidence of unimodality.

• For large sample sizes (say $n=1000$), employ the Fourier series-based plug-in approach of Tenreiro (2022) $(\nu _{ \tiny {\hbox {PIT}}})$.

8 Real data application

In this section, we revisit the car accident data that can be found in Ameijeiras-Alonso and Crujeiras (2022). This real dataset consists of the time of the day (at a resolution of one minute) at which the car crash happened in El Paso County (Texas, USA) in 2018. A total of 85 observations were recorded on the webpage of the National Highway Traffic Safety Administration of the United States.

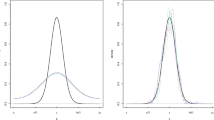
In Ameijeiras-Alonso and Crujeiras (2022), several features of the shape of the distribution are analysed with different inferential tools. The conclusion is that the density is unimodal and (reflectively) asymmetric. More specifically among several parametric models studied by Ameijeiras-Alonso and Crujeiras (2022), the conclusion is that the “best” parametric fitting is achieved by the wrapped skew normal density of Pewsey (2000). A representation of the fitted wrapped skew normal density is provided in Fig. 1 (top, thick solid line).

Fig. 1

Car accident data. Top, rug plot (with tick marks) and density estimation: fitted wrapped skew normal density (thick solid line), histogram (grey rectangles), and kernel density estimator with the von Mises kernel and different smoothing parameters. Smoothing parameters: rule of thumb of Taylor (2008) (RTT, dashed line), proposed direct plug-in rule with $M_{\max }=1$ (DPI; 1; dot-dashed line), proposed solve-the-equation plug-in rule with $M_{\max }=1$ (STE; 1; thin solid line), and plug-in rule of Oliveira et al. (2012) (PIO, dotted line). Bottom (solid line): kernel density derivative estimation, with a von Mises kernel and the proposed two-stage direct plug-in smoothing selector ($M_{\max }=1$). Bottom (dotted lines): estimated location of the modal and antimodal directions

This real dataset constitutes a good example where we would recommend employing the proposed direct plug-in smoothing selector, with $M_{\max }=1$, to estimate the density function as the sample size is “small” ($n=85$) and unimodality cannot be rejected for this sample. In Fig. 1 (top), we show the estimated density function employing this direct plug-in rule (DPI; 1), the proposed solve-the-equation plug-in selector (STE; 1), the rule of thumb of Taylor (2008) (RTT), and the plug-in rule of Oliveira et al. (2012) (PIO). We give the values of the smoothing parameters in Table 2. If we take the wrapped skew normal density as a reference, we can visually see that the closest kernel estimation is provided by the direct plug-in rule. This can be confirmed by computing the ISE (its expression is given in Equation (S1.1) in the Supplementary Material), replacing the “true” f with the fitted wrapped skew normal density. In Table 2, we computed the ISE obtained by different smoothing parameters proposed in the literature (see Section S1). There, we can observe that the “best” fitting (smallest ISE) is obtained with the proposed direct plug-in rule.

Table 2 Value of different smoothing parameters and ISE ($\times 100$) computed from the car accident data, taking the fitted wrapped skew normal density as the reference density f in (S1.1)

Finally, another application of the results derived in this paper can be found when the interest is in the density derivative estimate. As before, we will focus on the results obtained with the direct plug-in rule, with $M_{\max }=1$. In that case, the smoothing parameter for the kernel estimator can be derived with Algorithm 2 (with $r=1$). The obtained estimator, with the von Mises kernel, for the car accident data is plotted in Fig. 1 (bottom). There, one can see that the derivative estimation is positive between 13:29 and 20:25 and it is negative during the remaining times of the day. Thus, if one wants to answer the question of when the peak of car accidents is produced, we see that, according to this estimator, one can find a modal direction at 20:25. The antimodal (valley) direction is achieved at 13:29. This is also remarkable as these values are close to the nonparametric modal (20:18) and antimodal (13:35) estimators by Ameijeiras-Alonso et al. (2019).

9 Concluding remarks

The main contributions of this paper are the new plug-in smoothing parameters for circular kernel density (and its derivatives) estimation. In the past, some papers provided data-driven smoothing parameters for estimating the circular density function, but still, a Sheather and Jones (1991) plug-in rule was missing in the circular literature. This paper fills that gap by providing all the theoretical results needed to derive an l-stage direct and solve-the-equation plug-in smoothing selectors for a general kernel satisfying some assumptions. The needed constants to obtain the optimal smoothing parameter are given for the “most-popular” circular kernels. Besides that, following the optimality criterion of Muller (1984), this paper also discusses kernel choice. The conclusion is that the optimal kernel for circular density estimation is the wrapped Epanechnikov.

An interesting point for future research would be to analyse the asymptotic relative rate of convergence of the smoothing selectors. However, it is worth noting, at least in the linear case (see Jones et al. 1996), that achieving better asymptotics does not always translate to improved performance in real scenarios, especially with small sample sizes. In this paper, we decided to include a simulation study to compare the different proposed selectors. This study confirms that the suggested plug-in rules yield competitive smoothing parameters when compared with other proposals available in the statistical literature, particularly for small or moderate sample sizes.

Although not done in this paper, the presented ideas could be extended to the multivariate toroidal setting, using the product kernel of Di Marzio et al. (2011). In that case, the optimal smoothing parameter could be derived if the same kernel and mean resultant length are employed in all the dimensions. Thus, in principle, one could obtain an explicit expression of the optimal smoothing parameter for the kernel estimators of the density derivative and the density functionals. Then, a similar scheme to that provided in Algorithms 2 or 1 could be employed to obtain a two-stage or a solve-the-equation plug-in rule for the toroidal kernel density (and its derivatives) estimator.

10 Availability

The proposed l-stage direct plug-in rule and the solve-the-equation selector have been added to the R library NPCirc (Oliveira et al. 2014). Given a dataset x, the two-stage plug-in rule, described in Algorithm 2 (with $M_{\max }=5$), for density estimation, can be obtained with the function bw.AA(x, method=‘dpi’). The solve-the-equation smoothing selector, described in Algorithm 1 (with $M_{\max }=1$), for density estimation is computed with bw.AA(x) or bw.AA(x, method=‘ste’). Thus, bw.AA is the circular equivalent of the function bw.SJ of the stats R package.

The kernel density derivative estimate for circular data was also added to the NPCirc package, inside the kern.den.circ function. By default it employs, as the smoothing parameter, the proposed solve-the-equation plug-in selector (with $M_{\max }=1$). A representation of the circular kernel density estimator, using the von Mises kernel and that smoothing parameter, for a sample x could be obtained as follows.

Some other extra possibilities are available by changing the arguments in the functions bw.AA and kern.den.circ. This includes, among others, the kernel $K_\nu$ choice (argument kernel) or the derivative order r (argument deriv.order). More details are provided in Section S2 of the Supplementary Material. There, also some additional examples of how to use the bw.AA function are included.