Detecting and diagnosing prior and likelihood sensitivity with power-scaling

Abstract

Determining the sensitivity of the posterior to perturbations of the prior and likelihood is an important part of the Bayesian workflow. We introduce a practical and computationally efficient sensitivity analysis approach using importance sampling to estimate properties of posteriors resulting from power-scaling the prior or likelihood. On this basis, we suggest a diagnostic that can indicate the presence of prior-data conflict or likelihood noninformativity and discuss limitations to this power-scaling approach. The approach can be easily included in Bayesian workflows with minimal effort by the model builder and we present an implementation in our new R package priorsense. We further demonstrate the workflow on case studies of real data using models varying in complexity from simple linear models to Gaussian process models.

1 Introduction

Bayesian inference is characterised by the derivation of a posterior from a prior and a likelihood. As the posterior is dependent on the specification of these two components, investigating its sensitivity to perturbations of the prior and likelihood is a critical step in the Bayesian workflow (Gelman et al. 2020; Depaoli et al. 2020; Lopes and Tobias 2011). Along with indicating the robustness of an inference in general, such sensitivity is related to issues of prior-data conflict (Evans and Moshonov 2006; Al Labadi and Evans 2017; Reimherr et al. 2021) and likelihood noninformativity (Gelman et al. 2017; Poirier 1998). Historically, sensitivity analysis has been an important topic in Bayesian methods research (e.g. Canavos 1975; Skene et al. 1986; Berger 1990; Berger et al. 1994; Hill and Spall 1994). However, the amount of research on the topic has diminished (Watson and Holmes 2016; Berger et al. 2000) and results from sensitivity analyses are seldom reported in empirical studies employing Bayesian methods (van de Schoot et al. 2017). We suggest that a reason for this is the lack of sensitivity analysis approaches that are easily incorporated into existing modelling workflows.

Fig. 1

Example of our power-scaling sensitivity approach. Here, the prior is power-scaled, and the effect on the posterior is shown. In this case the prior is ${{\,\textrm{normal}\,}}(0, 2.5)$ and the likelihood is equivalent to ${{\,\textrm{normal}\,}}(5, 1)$. Power-scaling the prior by different $\alpha$ values (in this case 0.5 and 2.0) shifts the posterior (shaded for emphasis), indicating prior sensitivity

In this work, we present a sensitivity analysis approach that fits into workflows in which modellers use probabilistic programming languages, such as Stan (Stan Development Team 2021) or PyMC (Salvatier et al. 2016), and employ Markov chain Monte Carlo (MCMC) methods to estimate posteriors via posterior draws (e.g. workflows described in Grinsztajn et al. 2021; Gelman et al. 2020; Schad et al. 2021). The number of active users of such frameworks is currently estimated to be over a hundred thousand (Carpenter 2022). We provide examples with models that are commonly used by this community, but the general principles are not tied to any specific model or prior families. Furthermore, as the approach focuses on MCMC-based workflows, analytical derivations that would rely on conjugate priors or specific model families are not the focus and are not presented here.

A common workflow is to begin with a base model with template or ‘default’ priors, and iteratively build more complex models (Gelman et al. 2020). Recommended template priors, and default priors in higher-level interfaces to Stan and PyMC, such as rstanarm (Goodrich et al. 2020), brms (Bürkner 2017), and bambi (Capretto et al. 2022), are designed to be weakly informative and should work well when the data is highly informative so that the likelihood dominates. However, the presence of prior and likelihood sensitivity should still be checked, as no prior can be universally applicable. Considering the prevalence of default priors, a tool that assists in checking for prior (and likelihood) sensitivity is a valuable contribution to the community.

User-guided sensitivity analysis can be performed by fitting models with different specified perturbations to the prior or likelihood (Spiegelhalter et al. 2003), but this can require substantial amounts of both user and computing time (Pérez et al. 2006; Jacobi et al. 2018). Using more computationally efficient methods can reduce the computation time, but existing methods, while useful in many circumstances, are not always applicable. They are focused on particular types of models (Roos et al. 2021; Hunanyan et al. 2022) or inference mechanisms (Roos et al. 2015), rely on manual specification of perturbations (McCartan 2022), require substantial or technically complex changes to the model code that hinder widespread use (Giordano et al. 2018; Jacobi et al. 2018), or may still require substantial amounts of computation time (Ho 2020; Bornn et al. 2010).

We present a complementary sensitivity analysis approach that aims to

• be computationally efficient;

• be applicable to a wide range of models;

• provide automated diagnostics;

• require minimal changes to existing model code and workflows.

We emphasise that the approach should not be used for repeated tuning of priors until diagnostic warnings no longer appear. Instead, the approach should be considered as a diagnostic to detect accidentally misspecified priors (for example default priors) and unexpected sensitivities or conflicts. The reaction to diagnostic warnings should always involve careful consideration about domain expertise, priors, and model specification.

Our proposed approach uses importance sampling to estimate properties of perturbed posteriors that result from power-scaling (exponentiating by some $\alpha > 0$) the prior or likelihood (see Fig. 1). We use a variant of importance sampling (Pareto smoothed importance sampling; PSIS) that is self-diagnosing and alerts the user when estimates are untrustworthy (Vehtari et al. 2022). We propose a diagnostic, based on the change to the posterior induced by this perturbation, that can indicate the presence of prior-data conflict or likelihood noninformativity. Importantly, as long as the changes to the priors or likelihood induced by power-scaling are not too substantial, the procedure does not require refitting the model, which drastically increases its efficiency. The envisioned workflow is as follows (also see Fig. 2):

Fig. 2

Workflow of our proposed sensitivity analysis approach

• (1) Fit a base model (either a template model or a manually specified model) to data, resulting in a base posterior distribution.

• (2, 3) Estimate properties of perturbed posteriors that result from separately power-scaling the prior and likelihood.

• (4, 5) Evaluate the extent the perturbed posteriors differ from the base posterior numerically and visually.

• (6) Diagnose based on the pattern of prior and likelihood sensitivity.

• (7) Reevaluate the assumptions implied by the base model and potentially modify it (and repeat (1)–(6)).

• (8) Continue with use of the model for its intended purpose.

2 Details of the approach

2.1 Power-scaling perturbations

The proposed sensitivity analysis approach relies on separately perturbing the prior or likelihood through power-scaling (exponentiating by some $\alpha > 0$ close to 1). This power-scaling is a controlled, distribution-agnostic method of modifying a probability distribution. Intuitively, it can be considered to weaken (when $\alpha < 1$) or strengthen (when $\alpha > 1$) the component being power-scaled in relation to the other. Although power-scaling changes the normalising constant, this is not a concern when using Monte Carlo approaches for estimating posteriors via posterior draws. Furthermore, while the posterior can become improper when $\alpha$ approaches 0, this is not an issue as we only consider values close to 1.

For all non-uniform distributions, as $\alpha$ diverges from $1$, the shape of the distribution changes. However, it retains the support of the base distribution (if the density at a point in the base distribution is zero, raising it to any power will still result in zero; likewise any nonzero density will remain nonzero).

The power-scaling approach is not dependent on the form of the distribution family and will work providing that the distribution family is non-uniform (distributions with parameters controlling the support will only be power-scaled with respect to the base support). To provide intuition, we present analytically how power-scaling affects several exponential family distributions commonly used as priors (Fig. 3 and Table 1). For instance, a normal distribution, ${{\,\textrm{normal}\,}}(\theta \mid \mu , \sigma ) \propto \exp {(-\frac{1}{2} (\frac{\theta - \mu }{\sigma })^2)}$, when power-scaled by some $\alpha > 0$ simply scales the $\sigma$ parameter by $\alpha ^{-1/2}$, thus ${{\,\textrm{normal}\,}}(\theta \mid \mu , \sigma )^\alpha \propto {{\,\textrm{normal}\,}}(\theta \mid \mu , \alpha ^{-1/2}\sigma )$.

Power-scaling, while effective, is only able to perturb a distribution in a particular manner. For example, it is not possible to directly shift the location of a distribution via power-scaling, without also changing other aspects. Like most diagnostics, when power-scaling sensitivity analysis does not indicate sensitivity, this only means that it could not detect sensitivity to power-scaling, not that the model is certainly well-behaved or insensitive to other types of perturbations. Nevertheless, power-scaling remains an intuitive perturbation as it mirrors increasing or decreasing the strength of prior beliefs or amount of data.

Fig. 3

The effect of power-scaling on exponential family distributions commonly used as priors. In each case, the resulting distributions can be expressed in the same form as the base distribution with modified parameters. The power-scaling approach is not tied to specific distribution families, and these formulations are provided for intuition

2.2 Power-scaling priors and likelihoods

In the context of prior perturbations, the properties of power-scaling are desirable as slight perturbations from power-scaling result in distributions that likely represent similar implied assumptions to those of the base distribution. A set of slightly perturbed priors can thus be considered a reasonable class of distributions for prior sensitivity analysis (see Berger 1990; Berger et al. 1994).

In order for the sensitivity analysis approach to be independent of the number of parameters in the model, all priors could be power-scaled simultaneously. However, in some cases, certain priors should be excluded from this set or others selectively power-scaled. For example, in hierarchical models, power-scaling both top- and intermediate-level priors can lead to unintended results. To illustrate this, consider two forms of prior, a non-hierarchical prior with two independent parameters $p(\theta ) \, p(\phi )$ and a hierarchical prior of the form $p(\theta \mid \phi ) \, p(\phi )$. In the first case, the appropriate power-scaling for the prior is $p(\phi )^\alpha \, p(\theta )^\alpha$, while in the second, only the top level prior should be power-scaled, that is, $p(\theta \mid \phi ) \, p(\phi )^\alpha$. If the prior $p(\theta \mid \phi )$ is also power-scaled, $\theta$ will be affected by the power-scaling twice, directly and indirectly, perhaps even in opposite directions depending on the parameterisation.

For the likelihood, power-scaling acts as an approximation for decreasing or increasing the number of (conditionally independent) observations, akin to data cloning (Lele et al. 2007) and likelihood weighting (Greco et al. 2008; Agostinelli and Greco 2013). Power-scaling can be performed on the joint likelihood, or the likelihood contribution from a subset of observations or a single observation. High likelihood sensitivity for single observations may indicate those are more influential than others. For hierarchical models, high sensitivity of group-level parameters to power-scaling likelihood contributions of a specific group can indicate that group is an outlier. In models with parameters informed by different subsets of data, such as evidence synthesis models (Presanis et al. 2008), comparing the effects on a shared parameter of power-scaling the likelihood contributions of different data subsets can highlight conflict between the subsets.

Table 1 Forms of power-scaled distributions for common distributions

2.3 Estimating properties of perturbed posteriors

As the normalizing constant for the posterior distribution can rarely be computed analytically in real-world analyses, our approach assumes that the base posterior is approximated using (Markov chain) Monte Carlo draws (workflow step 1, see Fig. 2). These draws are used to estimate properties of the perturbed posteriors via importance sampling (workflow steps 2 and 3, see Fig. 2). Importance sampling is a method to estimate expectations of a target distribution by weighting draws from a proposal distribution (Robert and Casella 2004). After computing these weights, there are several possibilities for evaluating sensitivity. For example, different summaries of perturbed posteriors can be computed directly, or resampled draws can be generated using importance resampling (Rubin 1988).

Importance sampling as a method for efficient sensitivity analysis has been previously described by Berger et al. (1994); Besag et al. (1995); O’Neill (2009); Tsai et al. (2011). However, one limitation of importance sampling is that it can be unreliable when the variance of importance weights is large or infinite. Hence, as described by Berger et al. (1994), relying on importance sampling to estimate a posterior resulting from a perturbed prior or likelihood, without controlling the width of the perturbation class (e.g. through a continuous parameter to control the amount of perturbation, $\alpha$ in our case) is likely to lead to unstable estimates.

To further alleviate issues with importance sampling, we use Pareto smoothed importance sampling (PSIS; Vehtari et al. 2022), which stabilises the importance weights in an efficient, self-diagnosing and trustworthy manner by modelling the upper tail of the importance weights with a generalised Pareto distribution. In cases where PSIS does not perform adequately, weights are adapted with importance weighted moment matching (IWMM; Paananen et al. 2021), which is a generic adaptive importance sampling algorithm that improves the implicit proposal distribution by iterative weighted moment matching. The combination of using a continuous parameter to control the amount of perturbation, along with PSIS and IWMM, allows for a reliable and self-diagnosing method of estimating properties of perturbed posteriors.

2.3.1 Calculating importance weights for power-scaling perturbations

Consider an expectation of a function $h$ of parameters ${\theta }$, which come from a target distribution $f({\theta })$:

$$\begin{aligned} {\mathbb {E}}_f[h({\theta })] = \int h({\theta })f({\theta }) d{\theta }. \end{aligned}$$

(1)

In cases when draws can be generated from the target distribution, the simple Monte Carlo estimate can be calculated from a sequence of $S$ draws from $f({\theta })$:

$$\begin{aligned} {\mathbb {E}}_f[h({\theta })] \approx \frac{1}{S} \sum _{s=1}^Sh({\theta }^{(s)}), \text {where } {\theta }^{(s)} \sim f({\theta }). \end{aligned}$$

(2)

As an alternative to calculating the expectation directly with draws from $f({\theta })$, the importance sampling estimate instead uses draws from a proposal distribution $g({\theta })$ and the ratio between the target and proposal densities, known as the importance weights $w$. The self-normalised importance sampling estimate does not require known normalising constants of the target or proposal. Thus, it is well suited for use in the context of probabilistic programming languages, which do not calculate these:

$$\begin{aligned}{} & {} {\mathbb {E}}_f[h({\theta })] \approx \frac{\sum _{s=1}^S h(\theta ^{(s)}) \frac{f({\theta }^{(s)})}{g({\theta }^{(s)})}}{\sum _{s=1}^S \frac{f({\theta }^{(s)})}{g({\theta }^{(s)})}} = \frac{\sum _{s=1}^S h(\theta ^{(s)}) w^{(s)}}{\sum _{s=1}^S w^{(s)}},\nonumber \\{} & {} \quad \text {where } \theta ^{(s)} \sim g(\theta ). \end{aligned}$$

(3)

In the context of power-scaling perturbations, the proposal distribution is the base posterior and the target distribution is a perturbed posterior resulting from power-scaling. If the proposal and target distributions are expressed as the products of the prior $p(\theta )$ and likelihood $p(y \mid {\theta })$, with one of these components raised to the power of $\alpha$, the importance sampling weights only depend on the density of the component being power-scaled. For prior power-scaling, the importance weights are

$$\begin{aligned} w_{\alpha _\text {pr}}^{(s)}= & {} \frac{p({\theta }^{(s)})^\alpha p(y \mid {\theta }^{(s)})}{p({\theta }^{(s)})p(y \mid {\theta }^{(s)})} \nonumber \\= & {} p({\theta }^{(s)})^{\alpha - 1}. \end{aligned}$$

(4)

Analogously, the importance weights for likelihood power-scaling are

$$\begin{aligned} w_{\alpha _\text {lik}}^{(s)} = p(y \mid {\theta }^{(s)})^{\alpha - 1}. \end{aligned}$$

(5)

As the importance weights are only dependent on the density of the power-scaled component at the location of the proposal draws, they are easy to compute for a range of $\alpha$ values. See Appendix B for practical implementation details about computing the weights.

2.4 Measuring sensitivity

There are different ways to evaluate the effect of power-scaling perturbations on a posterior (workflow steps 4 and 5, see Fig. 2). Here we present two options: first, a method that investigates changes in specific posterior quantities of interest (e.g. mean and standard deviation), and second, a method based on the distances between the base marginal posteriors and the perturbed marginal posteriors. These methods should not be considered competing, but rather allow for different levels of sensitivity analysis, and depending on the context and what the modeller is interested in, one may be more useful than the other. Importantly, the proposed power-scaling approach is not tied to any particular method of evaluating sensitivity. These methods are our suggestions, but once quantities or weighted draws from perturbed posteriors are computed, a multitude of comparisons to the base posterior and other posteriors can be performed.

2.4.1 Quantity-based sensitivity

In some cases it can be most useful to investigate sensitivity of particular quantities of interest. Expectations of interest for a perturbed posterior can be calculated from the base draws and the importance weights using Equation (3). Other quantities that are not expectations (such as the median and quantiles) can be derived from the weighted empirical cumulative distribution function (ECDF). Computed quantities can then be compared based on the specific interests of the modeller, or local sensitivity can be quantified by derivatives with respect to the perturbation parameter $\alpha$.

2.4.2 Distance-based sensitivity

We can investigate the sensitivity of marginal posteriors using a distance-based approach. Here, we follow previous work which has quantified sensitivity based on the distance between the base and perturbed posteriors (O’Hagan 2003; Al Labadi et al. 2021; Kurtek and Bharath 2015). In principle, many different divergence or distance measures can be used, although there may be slight differences in interpretation (see, for example van de Schoot 2019; Cha 2007), however, the cumulative Jensen–Shannon divergence (CJS; Nguyen and Vreeken 2015) has two properties that make it appropriate for our use case. First, its symmetrised form is upper-bounded, like the standard Jensen–Shannon divergence (Lin 1991), which aids interpretation. Second, instead of comparing probability density functions (PDFs) or empirical kernel density estimates, as the standard Jensen–Shannon divergence does, it compares cumulative distribution functions (CDFs) or ECDFs, which can be efficiently estimated from Monte Carlo draws. Although PDFs could be estimated from the draws using kernel density estimation and then the standard Jensen–Shannon distance used, this relies on smoothness assumptions and may require substantially more draws to be accurate, and lead to artefacts otherwise (for further discussion of the benefits of ECDFs, see, for example Säilynoja et al. 2022).

Given two CDFs $P(\theta )$ and $Q(\theta )$,

$$\begin{aligned} {{\,\textrm{CJS}\,}}(P(\theta ) \Vert Q(\theta ))= & {} \int P(\theta )\log _2 \left( \frac{2 P(\theta )}{P(\theta ) + Q(\theta )}\right) \mathop {d\theta } \nonumber \\{} & {} + \frac{1}{2\ln (2)} \int \left( Q(\theta ) - P(\theta )\right) \mathop {d\theta }. \end{aligned}$$

(6)

As a distance measure, we use the symmetrised and metric (square root) version of CJS, normalised with respect to its upper bound, such that it is bounded on the 0 to 1 interval (for further details see Nguyen and Vreeken 2015):

$$\begin{aligned}{} & {} {{\,\textrm{CJS}\,}}_{\text {dist}}(P(\theta ) \Vert Q(\theta )) \nonumber \\{} & {} \quad {=} \sqrt{\frac{{{\,\textrm{CJS}\,}}(P(\theta ) \Vert Q(\theta )) {+} {{\,\textrm{CJS}\,}}(Q(\theta ) \Vert P(\theta ))}{\int \left( P(\theta ) {+} Q(\theta )\right) \mathop {d\theta }}}. \end{aligned}$$

(7)

As ${{\,\textrm{CJS}\,}}$ is not invariant to the sign of the parameter values, ${{\,\textrm{CJS}\,}}(P(\theta )\Vert Q(\theta )) \ne {{\,\textrm{CJS}\,}}(P(-\theta )\Vert Q(-\theta ))$, we use $\max ({{\,\textrm{CJS}\,}}_{\text {dist}}(P(\theta )\Vert Q(\theta )),{{\,\textrm{CJS}\,}}_{\text {dist}}(P(-\theta )\Vert Q(-\theta )))$ to account for this and ensure applicability regardless of possible transformations applied to posterior draws that may change the sign.

In our approach, we compare the ECDFs of the base posterior to the perturbed posteriors. The ECDF of the base posterior is estimated from the base posterior draws, whereas the ECDFs of the perturbed posteriors are estimated by first weighting the base draws with the importance weights. The ECDF is a step-function derived from the draws. In an unweighted ECDF, the heights of each step are all equal to $1/S$, where $S$ is the number of draws. In the weighted ECDF, the heights of the steps are equal to the normalised importance weights of each draw. As described by Nguyen and Vreeken (2015), when using ECDFs, the integrals in Eqs. (6) and (7) reduce to sums, which allows for efficient computation.

Table 2 The interplay between prior sensitivity and likelihood sensitivity can be used to diagnose the cause

2.4.3 Local sensitivity

Both distance-based and quantity-based sensitivity can be evaluated for any $\alpha$ value. It is also possible to obtain an overall estimate of sensitivity at $\alpha = 1$ by differentiation. This follows previous work which defines the local sensitivity as the derivative with respect to the perturbation parameter (Gustafson 2000; Maroufy and Marriott 2015; Sivaganesan 1993; Giordano et al. 2018). For power-scaling, we suggest considering the derivative with respect to $\log _2(\alpha )$ as it captures the symmetry of power-scaling around $\alpha = 1$ and provides values on a natural scale in relation to halving or doubling the log density of the component.

Because of the simplicity of the power-scaling procedure, local sensitivity at $\alpha = 1$ can be computed analytically with importance sampling for certain quantities, such as the mean and variance, without knowing the analytical form of the posterior. This allows for a highly computationally efficient method to probe for sensitivity in common quantities before performing further sensitivity diagnostics. For quantities that are computed as an expectation of some function $h$, the derivative at $\alpha = 1$ can be computed as follows. We denote the power-scaling importance weights as $p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1}$, where $p_{\text {ps}}(\theta ^{(s)})$ is the density of the power-scaled component, which can be either the prior or likelihood depending on the type of scaling. Then

$$\begin{aligned}&\left. \frac{\sum _{s=1}^S h(\theta ^{(s)}) p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1} }{\sum _{s=1}^S p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1}} \frac{\partial }{\partial \log _2(\alpha )}\right| _{\alpha = 1}= \left. \frac{\left( \sum _{s=1}^S \alpha \ln (2) h(\theta ^{(s)}) p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1} \ln (p_{\text {ps}}(\theta ^{(s)}))\right) \left( \sum _{s=1}^S p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1}\right) }{\left( \sum _{s=1}^S p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1}\right) ^2} \right| _{\alpha = 1}\\&\qquad - \left. \frac{\left( \sum _{s=1}^S h(\theta ^{(s)}) p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1}\right) \left( \sum _{s=1}^S \alpha \ln (2) p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1} \ln (p_{\text {ps}}(\theta ^{(s)}))\right) }{\left( \sum _{s=1}^S p_{\text {ps}}(\theta ^{(s)})^{\alpha - 1}\right) ^2} \right| _{\alpha = 1}\\&\quad = \ln (2) \left( \frac{1}{S} \sum _{s=1}^S \ln (p_{\text {ps}}(\theta ^{(s)})) h( \theta ^{(s)}) - \left( \frac{1}{S} \sum _{s=1}^S h(\theta ^{(s)}) \right) \left( \frac{1}{S} \sum _{s=1}^S \ln (p_{\text {ps}}(\theta ^{(s)})) \right) \right) . \end{aligned}$$

Consider for example that we are interested in the sensitivity of the posterior mean of the parameters $\theta$. For power-scaling the prior, the derivative of the mean with respect to $\log _2(\alpha )$ at $\alpha = 1$ is then

$$\begin{aligned} D_{\text {mean}}&= \ln (2) \left( \frac{1}{S} \sum _{s=1}^S \ln (p(\theta ^{(s)})) \theta ^{(s)} \right. \nonumber \\&\quad \left. - \left( \frac{1}{S} \sum _{s=1}^S \theta ^{(s)} \right) \left( \frac{1}{S} \sum _{s=1}^S \ln (p(\theta ^{(s)})) \right) \right) . \end{aligned}$$

(8)

As with quantity-based sensitivity, distance-based sensitivity can also be quantified by taking the corresponding derivative. ${{\,\textrm{CJS}\,}}_{\text {dist}}$ increases from 0 as $\alpha$ diverges from 1 (approximately linearly in log scale) and its derivative is discontinuous at $\alpha = 1$. As a measure of local power-scaling sensitivity, we take the average of the absolute derivatives of the divergence in the negative and positive $\alpha$ directions, with respect to $\log _2(\alpha )$. We approximate this numerically from the ECDFs with finite differences:

$$\begin{aligned}&D = \frac{1}{2}\left( \left| \frac{f(x - \Delta x) - f(x)}{-\Delta x} \right| + \left| \frac{f(x + \Delta x) - f(x)}{\Delta x} \right| \right) \\&D_{{{\,\textrm{CJS}\,}}} =\\&\quad \frac{{{\,\textrm{CJS}\,}}_{\text {dist}}({\hat{P}}_1(\theta ) \Vert {\hat{P}}_{1/(1 + \delta )}(\theta )) + {{\,\textrm{CJS}\,}}_{\text {dist}}({\hat{P}}_1(\theta ) \Vert {\hat{P}}_{1 + \delta }(\theta ))}{2\log _2(1+\delta )}, \end{aligned}$$

where ${\hat{P}}_1(\theta )$ is the ECDF of the base posterior (when $\alpha = 1$), ${\hat{P}}_{1/(1+\delta )}(\theta )$ is the weighted ECDF when $\alpha = 1/(1+\delta )$ and ${\hat{P}}_{1+\delta }(\theta )$ is the weighted ECDF when $\alpha = 1 + \delta$, where $\delta$ is the step size for the finite difference. For implementation we use step size $\delta = 0.01$ following Hunanyan et al. (2022) which worked well in our experiments, but can adjusted if needed (e.g. decreased if the importance sampling estimates are unreliable).

2.4.4 Diagnostic threshold

The diagnostic $D_{{{\,\textrm{CJS}\,}}}$ is a continuous value based on the differences between ECDFs, so it is not tied to specific properties of the posterior and should be generic (Fig. 16 in Appendix A shows pairs of ECDFs all with the same ${{\,\text {CJS}\,}}_{\text {dist}}$). For ease of use, it can be helpful to have a threshold to define when to provide warnings to the user. We found a threshold of $D_{{{\,\textrm{CJS}\,}}} \ge 0.05$ to be a reasonable indication of sensitivity based on our experiments. However, as with many continuous diagnostics, a threshold should be considered as a guide and may be adjusted by the user depending on the context, how concerned a modeller is with sensitivity, or to reflect what constitutes a meaningful change in the specific model.

Distance metrics (and corresponding sensitivity diagnostics) can be calibrated and transformed with respect to perturbing a known distribution, such as a standard normal (e.g. Roos et al. 2015). While we do not transform the value of $D_{{{\,\textrm{CJS}\,}}}$ directly, a comparison with the normal distribution can aid interpretation: For a standard normal, a $D_{{{\,\textrm{CJS}\,}}}$ of 0.05 corresponds to the mean being shifted by more than approximately 0.3 standard deviations, or the standard deviation differing by a factor greater than approximately 0.3, when the power-scaling $\alpha$ is changed by a factor of two.

2.5 Diagnosing sensitivity

Sensitivity can be diagnosed by comparing the amount of exhibited prior and likelihood sensitivity (workflow step 6, see Table 2). When a model is well-behaved, it is expected that there will be likelihood sensitivity, as power-scaling the likelihood is analogous to changing the number of (conditionally independent) observations. In hierarchical models, it is important to recognise that this is analogous to changing the number of observations within each group, rather than the number of groups. As such, in hierarchical models, lack of likelihood sensitivity based on power-scaling does not necessarily indicate that the likelihood is weak overall. As there can be relations between parameters, the pattern of sensitivity for a single parameter should be considered in the context of others. Cases in which the posterior is insensitive to both prior and likelihood power-scaling (i.e. uninformative prior with likelihood noninformativity) will likely be detectable from model fitting issues, and are not further addressed by our approach.

Likelihood domination (the combination of a weakly informative or diffuse prior combined with a well-behaving and informative likelihood) will result in likelihood sensitivity but no prior sensitivity. This indicates that the posterior is mostly reliant on the data and likelihood rather than the prior (see Fig. 4). This is the outcome that default priors aim for, as the prior has little influence on the posterior.

Fig. 4

A weakly informative ${{\,\textrm{normal}\,}}(0, 10)$ prior and a well-behaving ${{\,\textrm{normal}\,}}(5, 1)$ likelihood lead to likelihood domination. This is indicated by little to no prior sensitivity and expected likelihood sensitivity. This is the outcome that many default priors aim for, as the prior has little influence on the posterior. Top row: the prior is power-scaled; bottom row: the likelihood is power-scaled. Note that in the figure the likelihood and posterior densities are almost completely overlapping

In contrast, prior sensitivity can result from two primary causes, both of which are indications that the model may have an issue: 1) prior-data conflict and 2) likelihood noninformativity. In the case of prior-data conflict, the posterior will exhibit both prior and likelihood sensitivity, whereas in the case of likelihood noninformativity (in relation to the prior) there will be some marginal posteriors which are not as sensitive to likelihood power-scaling as they are to prior power-scaling (or not at all sensitive to likelihood power-scaling).

Prior-data conflict (Walter and Augustin 2009; Evans and Moshonov 2006; Nott et al. 2020) can arise due to intentionally or unintentionally informative priors disagreeing with, but not being dominated by, the likelihood. When this is the case, the posterior will be sensitive to power-scaling both the prior and the likelihood, as illustrated in Fig. 5. When prior-data conflict has been detected, the modeller may wish to modify the model by using a less informative prior (e.g., Evans and Jang 2011; Nott et al. 2020) or using heavy-tailed distributions (e.g., Gagnon 2022; O’Hagan and Pericchi 2012).

Fig. 5

Conflict between $t_4(0, 2.5)$ prior and $t_4(5, 1)$ likelihood, results in the posterior (shaded for emphasis) being sensitive to both prior and likelihood power-scaling. Top row: the prior is power-scaled; bottom row: the likelihood is power-scaled

The presence of prior sensitivity but relatively low (or no) likelihood sensitivity is an indication that the likelihood is weakly informative (or noninformative) in relation to the prior. This can occur, for example, when there is complete separation in a logistic regression. The simplest case of complete separation occurs when there are observations of only one class. For example, suppose a researcher is attempting to identify the occurrence rate of a rare event in a new population. Based on previous research, it is believed that the rate is close to 1 out of 1000. The researcher has since collected 100 observations from the new population, all of which are negative. As the data are only of one class, the posterior will then exhibit prior sensitivity as the likelihood is relatively weak. In the case of weakly informative or noninformative likelihood, the choice of prior will have a direct impact on the posterior and is therefore of a greater importance and should be considered carefully. In some cases, the likelihood (or the data) may not be problematic in and of itself, but if the chosen prior is highly informative and dominates the likelihood, the posterior may be relatively insensitive to power-scaling the likelihood. As such, when interpreting sensitivity it is important to consider both the prior and the likelihood and the interplay between them (see related discussion by Gelman et al. 2017).

2.5.1 Sensitivity for parameter combinations and other quantities

As discussed, sensitivity can be evaluated for each marginal distribution separately in a relatively automated manner. This approach may lead to interpretation issues when individual parameters are by definition not informed by the likelihood, or are not readily interpretable. In the case when the likelihood may be informative for a combination of parameters, but not any of the parameters individually, it can be useful to perform a whitening transformation (such as principle component analysis) (Kessy et al. 2018) on the posterior draws and then investigate sensitivity in the compressed parameter space. This can indicate which parameter combinations are sensitive to likelihood perturbations, indicating that they are jointly informed by the likelihood, and which are not.

This whitening approach works when there are few parameters, but as the number of parameters grows, the compressed components can be more difficult to interpret. Instead, in more complex cases, we suggest the modeller focus on target quantities of interest. For example, in the case of Gaussian process regression or models specifically focused on predictions, it can be more useful to investigate the sensitivity of predictive distributions (Paananen et al. 2021, 2019) than posterior distributions of model parameters.

3 Software implementation

Our approach for power-scaling sensitivity analysis is implemented in priorsense (https://github.com/n-kall/priorsense), our new R (R Core Team 2022) package for prior sensitivity diagnostics. The implementation focuses on models fit with Stan (Stan Development Team 2021), but it can be extended to work with other probabilistic programming frameworks that provide similar functionality. The package includes numerical diagnostics and graphical representations of changes in posteriors. These are available for both distance- and quantity-based sensitivity. Further details on the usage and implementation are included in Appendix B.

Fig. 6

Relationship between data separability and sensitivity in the separation simulation. $n_{\text {complete}}$ is the minumum number of observations that need to be removed to result in complete separation. Each point represents the mean over the data realisations for which the $n_{\text {complete}}$ were equal

4 Simulations

Here we present two simulations demonstrating how the diagnostic $D_{{{\,\textrm{CJS}\,}}}$ performs in two scenarios: (a) when the likelihood corresponds to the true model, but the data realisation may weakly inform some parameters, and (b) when the prior is changed to be in increasing conflict with the likelihood. We show that the diagnostic can detect these two cases.

4.1 Separation simulation

We generated 1000 data realisations of $N = 25$ observations, with the following structure:

$$\begin{aligned}{} & {} x_{1,i} \sim {{\,\textrm{uniform}\,}}(-1, 1),\quad x_{2,i} \sim {{\,\textrm{uniform}\,}}(-1, 1),\\{} & {} Y_{i} \sim {{\,\textrm{Bernoulli}\,}}(p_{i}),\quad \log \left( \frac{p_{i}}{1-p_{i}}\right) = x_{1,i} + x_{2,i}. \end{aligned}$$

We then fit a Bernoulli logit model to each realisation as follows:

$$\begin{aligned} Y_{i} \sim {{\,\textrm{Bernoulli}\,}}(p_{i}),\quad \log \left( \frac{p_{i}}{1-p_{i}}\right) = \beta _0 + \sum _{k=1}^2{\beta _k x_{k,i}} \end{aligned}$$

$$\begin{aligned} \beta _0 \sim {{\,\textrm{normal}\,}}(0, 10),\quad \beta _k \sim {{\,\textrm{normal}\,}}(0, 2.5). \end{aligned}$$

The model is correctly specified and matches the data generating process. However, a single realisation of 25 observations may be weakly informative due to complete or near-complete separation.

For each data realisation, we compare the a measure of separation $n_{\text {complete}}$ (Christmann and Rousseeuw 2001), to the power-scaling sensitivity diagnostic $D_{\text {CJS}}$. $n_{\text {complete}}$ is defined as the minimum number of observations that need to be removed to result in complete separation. As shown in Fig. 6, separability induced high sensitivity. When the data is completely or nearly separable, the prior sensitivity is high and when the data is far from completely separable, the prior sensitivity is low.

4.2 Conflict simulation

We generate 100 data realisations of $N = 25$ observations, with the following structure, for $k \in {1,2,3,4}$:

$$\begin{aligned}{} & {} x_{k,i} \sim {{\,\textrm{normal}\,}}(0, 1),\quad y_i \sim {{\,\textrm{normal}\,}}(\mu _i, 1),\quad \mu _i = 0.25 x_{1,i} \\{} & {} \quad + 0.25 x_{2,i} + 0.25 x_{3,i} + 0.25 x_{4,i}. \end{aligned}$$

We then transform each data realisation such that $x_{1,i} \leftarrow x_{1,i}/c$ and $x_{2,i} \leftarrow x_{2,i}/c$, for $c \in \{0.25, 0.5, 1, 2, 4\}$ to change the scale of the $x_1$ and $x_2$ variables and the corresponding coefficients, but not the values of $y$. We then fit the following model to each transformed data set:

$$\begin{aligned} y_i \sim {{\,\textrm{normal}\,}}(\mu _i, 1),\quad \mu _i = \beta _0 + \sum _{k=1}^{4}x_{k,i}\beta _k, \end{aligned}$$

$$\begin{aligned} \beta _0 \sim t_3(0, 2.5),\quad \beta _k \sim {{\,\textrm{normal}\,}}(0, 1). \end{aligned}$$

The model is well specified in the sense that the parameter space of the model includes the parameter value of the data generating process.

As $c$ is increased, the priors on $\beta _1$ and $\beta _2$ will begin to conflict with the likelihood from finite data. We investigate the effect of this increase on the power-scaling sensitivity diagnostic $D_{{{\,\textrm{CJS}\,}}}$ for each regression coefficient.

Fig. 7

Relation between scaling the covariates and the sensitivity. Each point represents the mean of 100 model fits (using different data realisations)

As shown in Fig. 7, the coefficients for the scaled predictors ($\beta _1, \beta _2$) exhibit different degrees of sensitivity depending on the degree of scaling. Prior sensitivity increases as the scaling factor increases, indicating prior-data conflict. Importantly, likelihood sensitivity decreases when $c = 4$, indicating that the prior is beginning to dominate the likelihood. As expected, the other coefficients ($\beta _3, \beta _4$), do not exhibit sensitivity or changes in sensitivity.

5 Case studies

In this section, we show how priorsense can be used in a Bayesian model building workflow to detect and diagnose prior sensitivity in realistic models fit to real data (corresponding data and code are available at https://github.com/n-kall/powerscaling-sensitivity). We present a variety of models and show sensitivity diagnostics for different quantities, including regression coefficients (Sects. 5.1 and 5.2), scale parameters (Sects. 5.1, 5.3, 5.4), model fit (Sect. 5.5), and posterior predictions (Sects. 5.4 and 5.6).

We use the brms package  (Bürkner 2017), which is a high-level R interface to Stan, to specify and fit the simpler regression models and Stan directly for the more complex models. Unless further specified, we use Stan to generate posterior draws using the default settings (4 chains, 2000 iterations per chain, half discarded as warm-up). Convergence diagnostics and effective sample sizes are checked for all model fits (Vehtari et al. 2021), and sampling parameters are adjusted to relieve any identified issues before proceeding with sensitivity analysis. As the quantitative indication of sensitivity, we use $D_{\text {CJS}}$ and the threshold of 0.05 as described in Sect. 2.4, but we also present graphical checks.

5.1 Body fat (linear regression)

This case study shows a situation in which prior-data conflict can be detected by power-scaling sensitivity analysis. This conflict results from choosing priors that are not of appropriate scales for some predictors. For this case study, we use the bodyfat data set (Johnson 1996), which has previously been the focus of variable selection experiments (Pavone et al. 2022; Heinze et al. 2018). The aim of the analysis is to predict an expensive and cumbersome water immersion measurement of body fat percentage from a set of thirteen easier to measure characteristics, including age, height, weight, and circumferences of various body parts.

We begin with a linear regression model to predict body fat percentage from the aforementioned variables. By default, in brms the $\beta _0$ (intercept) and $\sigma$ parameters are given data-derived weakly informative priors, and the regression coefficients are given improper flat priors. Power-scaling will not affect flat priors, so we specify proper priors for the regression coefficients. We specify the same prior for all coefficients, ${{\,\textrm{normal}\,}}(0, 1)$, which does not seem unreasonable based on preliminary prior-predictive checks. We arrive at the following model:

$$\begin{aligned} y_i \sim {{\,\textrm{normal}\,}}(\mu _i, \sigma ),\quad \mu _i = \beta _0 + \sum _{k=1}^{13} \beta _k x_{k,i}, \end{aligned}$$

$$\begin{aligned} \beta _0 \sim t_3(0, 9.2),\quad \beta _k \sim {{\,\textrm{normal}\,}}(0, 1),\quad \sigma \sim t_3^+(0, 9.2). \end{aligned}$$

From the marginal posteriors, there do not appear to be issues, and all estimates are in reasonable ranges (Fig. 17). Power-scaling sensitivity analysis, performed with the powerscale_sensitivity function, however, shows that there is both prior sensitivity and likelihood sensitivity for one of the parameters, $\beta _{\text {wrist}}$ (Table 3). This indicates that there may be prior-data conflict.

Table 3 Sensitivity diagnostic values for the body fat case study

We then check how the ECDF of the posterior is affected by power-scaling of the prior and likelihood. In priorsense, this is done creating a sequence of weighted draws (for a sequence of $\alpha$ values) using powerscale_sequence, and then plotting this sequence with powerscale_plot_ecdf (Fig. 8, left). We see that the posterior is sensitive to both prior and likelihood power-scaling, and that it shifts right (towards zero) as the prior is strengthened, and left (away from zero) as the likelihood is strengthened. This is an indication of prior-data conflict, which can be further seen by plotting the change in quantities using powerscale_plot_quantities (Fig. 9). Prior-data conflict is evident by the ‘X’ shape of the mean plot, as the mean is shifting in opposite directions. As there is prior sensitivity arising from prior-data conflict, which is unexpected and unintentional as our priors were chosen to be weakly informative, we consider modifying the priors. On inspecting the raw data, we see that although the predictor variables are all measured on similar scales, the variances of the variables differ substantially. For example, the variance of wrist circumference is 0.83, while the variance of abdomen is 102.65. This leads to our chosen prior to be unintentionally informative for some of the regression coefficients, including wrist, while being weakly informative for others. To account for this, we refit the model with priors empirically scaled to the data, $\beta _k \sim {{\,\textrm{normal}\,}}(0, 2.5 s_y/s_{x_k})$, where $s_y$ is the standard deviation of $y$ and $s_{x_k}$ is the standard deviation of predictor variable $x_k$. This corresponds to the default priors used for regression models in the rstanarm package (Goodrich et al. 2020), as described in Gelman et al. (2020) and Gabry and Goodrich (200). We refit the model and see that the posterior mean for $\beta _{\text {wrist}}$ changes from $-$1.45 to $-$1.86, indicating that the base prior was indeed unintentionally informative and in conflict with the data, pulling the estimate towards zero. Power-scaling sensitivity analysis on the adjusted model fit shows that there is no longer prior sensitivity, and there is appropriate likelihood sensitivity (Table 3, Fig. 8 right).

This is a clear example of how power-scaling sensitivity analysis can detect and diagnose prior-data conflict. Unintentionally informative priors resulted in the conflict, which could not be detected by only inspecting the posterior estimates of the base model. Once detected and diagnosed, the model could be adjusted and analysis could proceed. It is important to emphasise that the model was modified as the original priors were unintentionally informative. If the original priors had been manually specified based on prior knowledge, it may not have been appropriate to modify the priors after observing the sensitivity, as the precise prior specification would be an inherent part of the model.

Fig. 8

Power-scaling diagnostic plot of marginal ECDFs for posterior $\beta _{\text {wrist}}$ in the body fat case study. (Left) Original prior; There is both prior and likelihood sensitivity, as the ECDFs are not overlapping. (Right) Adjusted prior; There is now no prior sensitivity, as the ECDFs are overlapping, whereas there is still likelihood sensitivity

Fig. 9

Posterior quantities of $\beta _{\text {wrist}}$ as a function of power-scaling for the body fat case study. With this plot, we can compare the effect of prior and likelihood power-scaling on specific quantities. Shown as dashed lines are $\pm 2$ Monte Carlo standard errors (MCSE) of the base posterior quantity, as guides to whether an observed change is meaningful. Top: original prior; The pattern of the change in the mean indicates prior-data conflict, as power-scaling the prior and likelihood have opposite directional effects on the posterior mean. Bottom: adjusted prior; there is no longer prior or likelihood sensitivity for the mean, indicating no prior-data conflict. Likelihood sensitivity for the posterior standard deviation remains, indicating that the likelihood is informative

Table 4 Sensitivity diagnostic values for the bank notes case study

5.2 Banknotes (logistic regression)

This case study is an example of using power-scaling sensitivity analysis to detect and diagnose likelihood noninformativity. We use the banknote data set (Flury and Riedwyl 1988) available from the mclust package (Scrucca et al. 2016), which contains measurements of six properties of 100 genuine ($Y = 0$) and 100 counterfeit ($Y = 1$) Swiss banknotes. We fit a logistic regression on the status of a note based on these measurements. For priors, we use the template priors ${{\,\textrm{normal}\,}}(0, 10)$ for the intercept and ${{\,\textrm{normal}\,}}(0, 2.5/s_{x_k})$ for the regression coefficients, where $s_{x_k}$ is the standard deviation of predictor $k$. The model is then

$$\begin{aligned} Y_{i} \sim {{\,\textrm{Bernoulli}\,}}(p_{i}),\quad \log \left( \frac{p_{i}}{1-p_{i}}\right) = \beta _0 + \sum _{k=1}^6{\beta _k x_{k,i}}, \end{aligned}$$

$$\begin{aligned} \beta _0 \sim {{\,\textrm{normal}\,}}(0, 10),\quad \beta _k \sim {{\,\textrm{normal}\,}}(0, 2.5/s_{x_k}). \end{aligned}$$

Power-scaling sensitivity analysis indicates prior sensitivity for all predictor coefficients (Table 4). Furthermore, most exhibit low likelihood sensitivity, indicating a weak likelihood. In a Bernoulli model, this may arise if the binary outcome is completely separable by the predictors. This can be confirmed using the detectseparation package (Kosmidis and Schumacher 2021), which detects infinite maximum likelihood estimates (caused by separation) in binary outcome regression models without fitting the model. Indeed, according to this method, the data set is completely separable and the prior sensitivity will remain, regardless of choice of prior. As shown in the simulation study in Sect. 4.1, this is not necessarily an indication that the model is misspecified or problematic, but rather the complete separation in the data realisation may be causing issues for estimating the regression coefficients.

5.3 Bacteria treatment (hierarchical logistic regression)

Here, we use the bacteria data set, available from the MASS package (Venables and Ripley 2002) to demonstrate power-scaling sensitivity analysis in hierarchical models. This data has previously been used by Kurtek and Bharath (2015) in a sensitivity analysis comparing posteriors resulting from different priors. We use the same model structure and similar priors and arrive at matching conclusions. Importantly, we show that the problematic prior can be detected from the resulting posterior, without the need to compare to other posteriors (and without the need for multiple fits). The data set contains 220 observations of the effect of a treatment (placebo, drug with low compliance, drug with high compliance) on 50 children (denoted by index $i$) with middle ear infection over 5 time points (weeks, denoted by index$j$). The outcome variable is the presence ($Y = 1$) or absence ($Y = 0$) of the bacteria targeted by the drug. We fit the same generalised linear multilevel model (with group-level intercepts $V_j$), on the data as Kurtek and Bharath (2015), based on an example from Brown and Zhou (2010):

$$\begin{aligned}{} & {} Y_{ij} \sim {{\,\textrm{Bernoulli}\,}}(p_{ij}),\quad \log \left( \frac{p_{ij}}{1-p_{ij}}\right) = \mu + \sum _{k=1}^3{x_{kij}\beta _k + V_i}, \\{} & {} \mu \sim {{\,\textrm{normal}\,}}(0, 10),\quad \beta _k \sim {{\,\textrm{normal}\,}}(0, 10), \\{} & {} V_i \sim {{\,\textrm{normal}\,}}(0, \sigma ),\quad \tau = \frac{1}{\sigma ^2} \sim {{\,\textrm{gamma}\,}}(0.01, 0.01). \end{aligned}$$

We try different priors for the precision hyperparameter $\tau$. We compare the sensitivity of the base model, with prior $\tau \sim {{\,\textrm{gamma}\,}}(0.01, 0.01)$, to the comparison priors. Three of which are considered reasonable, $\tau \sim {{\,\textrm{normal}\,}}^+(0, 10), {{\,\textrm{Cauchy}\,}}^+(0, 100), {{\,\textrm{gamma}\,}}(1, 2)$, and one is considered unreasonable, $\tau \sim {{\,\textrm{gamma}\,}}(9, 0.5)$. These priors are shown in Fig. 10. We fit each model with four chains of 10000 iterations (2000 discarded as warmup) and perform power-scaling sensitivity analysis on each. As discussed in Sect. 2.2, only the top-level parameters in the hierarchical prior are power-scaled (i.e. the prior on $V_i$ is not power-scaled). Posterior quantities and sensitivity diagnostics for all models are shown in Appendix D. It is apparent that the $\tau$ parameter is sensitive to the prior when using the ${{\,\textrm{gamma}\,}}(9, 0.5)$ prior. This indicates that the prior may be inappropriately informative. Although there is no indication of power-scaling sensitivity for the $\mu$ and $\beta$ parameters, comparing the posteriors for the models indicates differences in these parameters for the unreasonable $\tau$ prior compared to the other priors. This is an important observation, and highlights that power-scaling is a local perturbation and may not influence the model strongly enough to change all quantities, yet can indicate the presence of potential issues.

5.4 Motorcycle crash (Gaussian process regression)

Here, we demonstrate power-scaling sensitivity analysis on model without readily interpretable model parameters. We fit a Gaussian process regression to the mcycle data set, also available in the MASS package and show the sensitivity of predictions to perturbations of the prior and likelihood. For a primer on Gaussian process regression, see Seeger (2004).

Fig. 10

Priors for the hyperparameter $\tau$ in the bacteria case study. Priors considered reasonable for this application are shown on the left while priors considered unreasonable are shown on the right

The data set contains 133 measurements of head acceleration at different time points during a simulated motorcycle crash. It is further described by Silverman (1985). We fit a Gaussian process regression to the data, predicting the head acceleration ($y$) from the time ($x$). We use two Gaussian processes; one for the mean and one for the standard deviation of the residuals. The model is

$$\begin{aligned}{} & {} y \sim {{\,\textrm{normal}\,}}(f(x), \exp (g(x))), \\{} & {} f \sim {{\,\textrm{GP}\,}}(0, K_1(x, x^\prime , \rho _f, \sigma _f)),\\{} & {} g \sim {{\,\textrm{GP}\,}}(0, K_2(x, x^\prime , \rho _g, \sigma _g)), \\{} & {} \rho _f \sim {{\,\textrm{normal}\,}}^+(0, 1),\quad \rho _g \sim {{\,\textrm{normal}\,}}^+(0, 1), \\{} & {} \sigma _f \sim {{\,\textrm{normal}\,}}^+(0, 0.05),\quad \sigma _g \sim {{\,\textrm{normal}\,}}^+(0, 0.5). \end{aligned}$$

Table 5 Prior and likelihood sensitivity in the motorcycle crash case study using the original prior

Fig. 11

Sensitivity of posterior predictions to prior and likelihood power-scaling in the motorcycle case study. Shown in the plots are the mean, 50% and 95% credible intervals for the posterior predictions. Top: original prior $\sigma _f \sim {{\,\textrm{normal}\,}}(0, 0.05)$. There is clear prior and likelihood sensitivity in the predictions around 20 ms after the crash. Bottom: alternative prior $\sigma _f \sim {{\,\textrm{normal}\,}}(0, 0.1)$. There is now no prior sensitivity and minimal likelihood sensitivity for the predictions

For $K_1$ and $K_2$ we use Matérn covariance functions with $\nu = 3/2$. These functions are controlled by the $\rho$ and $\sigma$ parameters. The $\rho$ parameters are the length-scales of the processes and define how close two points $x$ and $x^\prime$ must be to influence each other. The $\sigma$ parameters define the standard deviations of the noise. For efficient sampling with Stan, we use Hilbert space approximate Gaussian processes (Solin and Särkkä 2020; Riutort-Mayol et al. 2022). The number of basis functions ($m_f = m_g = 40$) and the proportional extension factor ($c_f = c_g = 1.5$) are adapted such that the posterior length-scale estimates ${\hat{\rho }}_f$ and ${\hat{\rho }}_g$ are above the threshold of that which can be accurately approximated (see Riutort-Mayol et al. 2022). We can then focus on the choice of priors for the length-scale parameters ($\rho _f, \rho _g$) and the marginal standard deviation parameters ($\sigma _f, \sigma _g$). It is known that for a Gaussian process, the $\rho$ and $\sigma$ parameters are not well informed independently (Diggle and Ribeiro 2007), so the sensitivity of the marginals may not be properly representative as there may be prior sensitivity no matter the choice of prior. We first demonstrate the sensitivity of the marginals before proceeding with a focus on the sensitivity of the model predictions, in accordance with Paananen et al. (2021).

As expected, there is prior sensitivity in the marginals (Table 5). The prior and likelihood sensitivity for the parameters is high, which may be an indication of an issue, however it is difficult to determine based on the parameter marginals alone. Instead we follow up by plotting how the predictions are affected by power-scaling. As shown in Fig. 11 (top), the predictions around 20 ms exhibit sensitivity to both prior and likelihood power-scaling. The prediction interval widens as the prior is strengthened ($\alpha > 1$), and narrows as it is weakened ($\alpha < 1$). Likelihood power-scaling has the opposite effect. This indicates potential prior-data conflict from an unintentionally informative prior. Widening the prior on $\sigma _f$ from ${{\,\textrm{normal}\,}}(0, 0.05)$ to ${{\,\textrm{normal}\,}}(0, 0.1)$ alleviates the conflict such that it is no longer apparent in the predictions (Fig. 11, bottom). Plotting the predictions with the raw data indicates a good fit (Fig. 18). However, there remains sensitivity in the parameters, although it is lessened (Table 5). This further demonstrates that depending on the model, prior sensitivity may be present, but is not necessarily an issue. We advise modellers to pay attention to specific quantities and properties of interest, particularly when performing sensitivity analyses on more complex models, rather than focusing on parameters without clear interpretations.

5.5 US Crime (linear regression with shrinkage prior)

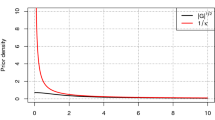
Here, we show how sensitivity can be analysed with respect to model fit. We fit a regression to the UScrime data set, available from the MASS (Venables and Ripley 2002) package, and use a joint prior on the regression coefficients based on a prior on the model fit, Bayesian $R^2$ (Gelman et al. 2019). Such a prior structure can be used to specify a weakly informative prior on the model fit to prevent overfitting (Gelman et al. 2020). We use the R2-D2 prior (Zhang et al. 2022) as implemented in brms and check for sensitivity of the posterior $R^2$ to changes to the prior on $R^2$.

The data has observations from 47 US states in the year 1960. See Clyde et al. (2022) for further details on the data set. We model the crime rate $y$ from 15 predictors $x_k$ using a logNormal observation model. All continuous predictors are log transformed, following Venables and Ripley (2002). We use the brms default weakly informative priors on the intercept $\beta _0$ and residual standard deviation $\sigma$.

Table 6 Power-scaling sensitivity and predictive model performance for prior specifications in the US crime case study

The full model, including the R2-D2 prior is specified as

$$\begin{aligned}{} & {} y_i \sim {{\,\textrm{logNormal}\,}}(\mu _i, \sigma ),\quad \mu _i = \beta _0 + \sum _{k=1}^{15}x_{k,i}\beta _k, \\{} & {} \beta _0 \sim t_3(6.7, 2.5),\quad \sigma \sim t_3^+(0, 2.5),\\{} & {} \beta _k \sim {{\,\textrm{normal}\,}}(0, (\frac{\sigma ^2}{s^2_{x_k}} \phi _k \tau ^2)^{1/2}), \\{} & {} \phi \sim {{\,\textrm{Dirichlet}\,}}(1,\dots ,1),\quad \tau ^2 = \frac{R^2}{1-R^2},\\{} & {} R^2 \sim {{\,\textrm{beta}\,}}(s_1, s_2), \end{aligned}$$

where $s^2_{x_k}$ is the sample variance of predictor $x_k$.

Fig. 12

The priors and corresponding posteriors for the model fit ($R^2$) in the US Crime case study

We contrast two prior specifications, prior 1: $R^2 \sim {{\,\textrm{beta}\,}}(3, 7)$ and prior 2: $R^2 \sim {{\,\textrm{beta}\,}}(0.45, 1.05)$, shown in Fig. 12. The sensitivity analysis indicates that prior 1 may be informative and affecting the posterior. Indeed, the posterior for $R^2$ is lower with prior 1 than prior 2 (Table 6).

To follow up this, we perform leave-one-out cross validation on both models to compare predictive performance using the $\text {elpd}_{\text {loo}}$ metric (Vehtari et al. 2020). The results, also shown in Table 6, indicate that prior 1 leads to lower predictive performance than prior 2, and induces a lower effective number of parameters ($p_\text {loo}$). This further corroborates the results of the sensitivity analysis, and shows that the power-scaling sensitivity diagnostic can be used as an early indication of issues that can influence predictive performance.

5.6 COVID-19 interventions (infections and deaths model)

In this case study, we evaluate the prior and likelihood sensitivity in a model of deaths from the COVID-19 pandemic (Flaxman et al. 2020). The Stan code and data for this model are available from PosteriorDB (Magnusson et al. 2021). We focus on the effects of power-scaling the priors on three parameters of the model: $\tau$, $\phi$ and $\kappa$. Due to the complexity of the model, we separately power-scale each prior to determine their individual effects. We evaluate the sensitivity of predictions (expected number of deaths due to COVID-19) in 14 countries over 100 days.

Fig. 13

Likelihood sensitivity of posterior predictions (expected deaths due to COVID-19) for four countries. Vertical lines indicate the onset of major governmental intervention. The dotted lines indicate the sensitivity threshold of 0.05, above which we consider sensitivity to be present

Fig. 14

Prior sensitivity of posterior predictions (expected deaths due to COVID-19) for four countries. The vertical lines indicate the onset of major governmental intervention. The dotted lines indicate the sensitivity threshold of 0.05, above which we consider sensitivity to be present

For a full description of the model, see Flaxman et al. (2020). The parts of the model which we focus on are as follows. The prior on $\phi$ which partially controls the variance of the negative binomial likelihood of observed daily deaths $D_{t,m}$, modelled from the expected deaths due to the virus $d_{t,m}$ for a given day $t$ and country $m$:

$$\begin{aligned}{} & {} D_{t, m} \sim {{\,\textrm{negBinomial}\,}}(d_{t,m}, d_{t,m} + d_{t,m}^2/\phi ),\\{} & {} \phi \sim {{\,\textrm{normal}\,}}^+(0, 5). \end{aligned}$$

$d_{t,m}$ is a function of $R_{0,m}$ and $c_{1,m} \dots c_{6,m}$ (among other parameters). The prior on $\kappa$ which controls the variance of the baseline reproductive number $R_0$ of the virus for each country $m$:

$$\begin{aligned} R_{0, m} \sim {{\,\textrm{normal}\,}}^+(3.28, \kappa ),\quad \kappa \sim {{\,\textrm{normal}\,}}^+(0, 0.5), \end{aligned}$$

and the prior on $\tau$ which affects the number of seed infections (infections in the six days following the beginning of the seed period, which is defined as the 30 days before a country observes a total of ten or more deaths):

$$\begin{aligned} c_{1,m},\ldots , c_{6, m} \sim {{\,\textrm{exponential}\,}}(1/\tau ),\quad \tau \sim {{\,\textrm{exponential}\,}}(0.03). \end{aligned}$$

Here we focus on a subset of four countries, but results for all 14 countries are presented in Appendix F. The results shown in Fig. 13 indicate that there is likelihood sensitivity throughout the time period, indicating the data is informative, as seen in Fig. 14. Furthermore, there is clear sensitivity to the $\kappa$ prior, and some sensitivity to the $\tau$ prior. This is most pronounced in the predictions of deaths from day 30 to 70, shortly after the first major governmental interventions. Sensitivity is particularly high for the predictions for Germany. Following this up by plotting the sensitivity of predictions on day 50 in Germany (Fig. 15), there is an indication that the prior is in conflict with the data, as the mean is shifted in opposite directions by prior and likelihood scaling.

These results are an indication that the chosen prior on $\kappa$ may be informative and in conflict with the data, and the justification for this prior should be carefully considered. As the prior on $R_0$ for each country is centred around a specific value, 3.28, based on previous literature (Liu et al. 2020), some sensitivity to the prior on $\kappa$ may be expected, however the finding that it may be in conflict with the data is nevertheless important and may warrant further attention. This is an example for how a more complex model can be checked for prior and likelihood sensitivity by selectively perturbing priors and focusing on predictions.

Fig. 15

Prior and likelihood sensitivity of posterior predictions (expected deaths due to COVID-19) for day 50 in Germany. Only the $\kappa$ prior is power-scaled

6 Discussion

We have introduced an approach and corresponding workflow for prior and likelihood sensitivity analysis using power-scaling perturbations of the prior and likelihood. The proposed approach is computationally efficient and applicable to a wide range of models with minor changes to existing model code. This will allow automated prior sensitivity diagnostics for probabilistic programming languages such as Stan and PyMC, and higher-level interfaces like brms, rstanarm and bambi, and make the use of default priors safer as potential problems can be detected and warnings presented to users. The approach can also be used to identify which priors may need more careful specification. The use of PSIS and IWMM ensures that the approach is reliable while being computationally efficient. These properties were demonstrated in several simulated examples and case studies of real data, and our sensitivity analysis workflow easily fits into a larger Bayesian workflow involving model checking and model iteration.

Rather than fixing the power-scaling $\alpha$ values, it could be possible to include the $\alpha$ parameters in the model and place hyperpriors on them. However, this naturally complicates the model by adding additional levels of hierarchy. In addition, the question of sensitivity to the choice of hyperprior would then be raised, which may require further sensitivity analysis, or additional levels of hierarchy, the parameters of which become less and less informed by the data (Goel and DeGroot 1981). Instead, the power-scaling sensitivity approach can be seen as a controlled method for automatically comparing alternative priors, which are interpretable by the modeller.

We have demonstrated checking the presence of sensitivity based on the derivative of the cumulative Jensen–Shannon distance between the base and perturbed priors with respect to the power-scaling factor. While this is a useful diagnostic, power-scaling sensitivity analysis is a general approach with multiple valid variants. Future work could include further developing quantity-based sensitivity to identify meaningful changes in quantities and predictions with respect to power-scaling, and working towards automated guidance on safe model adjustment after sensitivity has been detected and diagnosed.

Other extensions include developing additional perturbations that affect different aspects of distributions. Our sensitivity approach could be applied to other perturbations, however, they may require recomputing likelihood and prior evaluations. An important benefit of the power-scaling approach is that the values required for the importance weights (the evaluations of the prior and likelihood) are already calculated when computing the unnormalized posterior density used in MCMC, so no new computations from the model are required if these are saved. Another potential perturbation that could be done without recomputation is inducing a mean shift via exponential tilting (Siegmund 1976), however this would require draws from the prior.

It is also possible to use the same framework to investigate the influence of individual or groups of observations, by perturbing the likelihood contribution of a single or subset of observations. This would be particularly useful in evidence synthesis models where different data sources are included. The workflow for this should be explored in future work.

Finally, we emphasise that the presence of prior sensitivity or the absence of likelihood sensitivity are not issues in and of themselves. Rather, context and intention of the model builder need to be taken into account. We suggest that the model builder pay particular attention when the pattern of sensitivity is unexpected or surprising, as this may indicate the model is not behaving as anticipated. We again emphasise that the approach should be coupled with thoughtful consideration of the model specification and not be used for repeated tuning of the priors until diagnostic warnings disappear.

Appendices

Appendix

A. Diagnostic threshold

See Fig. 16.

Fig. 16

Pairs of ECDFs of 4000 draws from distributions of the same form with different parameters. ${{\,\textrm{CJS}\,}}_{\text {dist}} \approx 0.05$ between each of the pairs

B. Software implementation

1.1 B.1 Usage

Conducting a power-scaling sensitivity analysis with priorsense can be done as follows: given a fitted model object, powerscale_sensitivity will automatically perform workflow steps 2–5 and return the local sensitivity of each parameter in a model fit (based on numerical derivatives of ${{\,\textrm{CJS}\,}}_\text {dist}$ by default). Follow-up analysis for diagnosing the sensitivity can be performed with powerscale_sequence, which returns an object containing the base posterior draws along with weights corresponding to each perturbed posterior (or optionally resampled posterior draws). This can be plotted to visualise the change in ECDFs, kernel density etimates, or estimated quantities, with respect to the degree of power-scaling. Sensitivity of posterior quantities such as the mean, median or standard deviation can be assessed with the powerscale_derivative (for analytical derivatives) and powerscale_gradients (for numerical derivatives) functions. All functions will provide warnings when estimates derived from PSIS or IWMM may not be trustworthy due to too large differences between the perturbed and base posteriors.

1.2 B.2 Practical implementation details

In this section, we provide more details for a practical implementation of the approach. The importance weights for power-scaling the prior or likelihood rely on density evaluations of the power-scaled component. Thus, the following are required for estimating properties of the perturbed posteriors:

• posterior draws from the base posterior

• (log of) likelihood evaluations at the locations of the posterior draws

• (log of) joint prior evaluations (for the priors to be power-scaled) at the locations of the posterior draws

In R, posterior draws can be accessed from the model fit object directly, while the posterior package (Bürkner et al. 2022) provides convenient functions for working with them. Existing R packages interfacing with Stan already make use of the log likelihood evaluations (e.g. the loo package; Vehtari et al. 2020), and the log prior evaluations can be specified in the model code, for example in the generated quantities block of the Stan code (as shown in Listing 1). In cases where some priors should be excluded from the power-scaling (such as intermediate priors in hierarchical models), only the priors to be power-scaled should be included here. Log prior evaluations can also be stored in an array, allowing for selective power-scaling of subsets of priors.

priorsense uses the loo package for PSIS, while IWMM is currently implemented directly. ${{\,\textrm{CJS}\,}}_\text {dist}$ is also implemented directly, while other divergence measures can be used from philentropy (Drost 2018). Functions from matrixStats (Bengtsson 2020) and spatstat (Baddeley et al. 2015) are used for calculating weighted quantities and weighted ECDFs, respectively. Diagnostics graphics are created using ggplot2 (Wickham 2016).

C. Body fat (linear regression)

See Fig. 17.

Fig. 17

Marginal posteriors for the body fat case study. Points show means, thick and thin lines correspond to 50% and 95% credible intervals

Table 7 Sensitivity diagnostic values for the bacteria case study

D. Bacteria (hierarchical logistic regression)

See Table 7.

E. Motorcycle crash (Gaussian process regression)

See Fig. 18.

Fig. 18

Prediction plot for the adjusted model with the data superimposed. Shown in the plot are the mean, 50% and 95% credible intervals for the posterior predictions. The predictions capture the raw data well, indicating that we have arrived at a reasonable model

F. COVID-19 interventions (infections and deaths model)

See Figs. 19, 20.

Fig. 19

Likelihood sensitivity of posterior predictions (expected deaths due to COVID-19) for a sequence of 100 days, for each country. The vertical line indicates the onset of major governmental intervention. The dotted line indicates the sensitivity threshold of 0.05, above which we consider sensitivity to be present

Fig. 20

Prior sensitivity of posterior predictions (expected deaths due to COVID-19) for a sequence of 100 days, for each country. The vertical lines indicate the onset of major governmental intervention. The dotted lines indicate the sensitivity threshold of 0.05, above which we consider sensitivity to be present