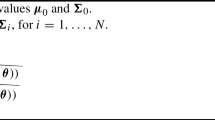Maximum likelihood estimation for discrete latent variable models via evolutionary algorithms

Abstract

We propose an evolutionary optimization method for maximum likelihood and approximate maximum likelihood estimation of discrete latent variable models. The proposal is based on modified versions of the expectation–maximization (EM) and variational EM (VEM) algorithms, which are based on the genetic approach and allow us to accurately explore the parameter space, reducing the chance to be trapped into one of the multiple local maxima of the log-likelihood function. Their performance is examined through an extensive Monte Carlo simulation study where they are employed to estimate latent class, hidden Markov, and stochastic block models and compared with the standard EM and VEM algorithms. We observe a significant increase in the chance to reach global maximum of the target function and a high accuracy of the estimated parameters for each model. Applications focused on the analysis of cross-sectional, longitudinal, and network data are proposed to illustrate and compare the algorithms.

1 Introduction

Discrete latent variable (DLV) models (Bartolucci et al. 2022) have attracted much attention in the statistical literature as these models: (i) ensure a high degree of flexibility to account for complex dependence data structures; (ii) allow performing model-based clustering; (iii) have a likelihood that is generally much simpler to be maximized with respect to models based on latent variables with a continuous distribution. When the likelihood of a DLV model is explicitly computable, maximum likelihood estimation of the model parameters may be performed by the expectation–maximization (EM) algorithm (Baum et al. 1970; Dempster et al. 1977), which is known to converge to a maximum of the target function monotonically. If this approach turns out to be computationally unfeasible, a modified version known as variational expectation–maximization (VEM) algorithm (Jordan et al. 1999; Daudin et al. 2008) may be employed in most cases.

The choice of the initialization rule of these algorithms is crucial in this setting, since a relevant drawback of DLV models is that the model likelihood has generally multiple local maxima, especially when many latent components are assumed and the EM and VEM algorithms may easily be trapped into one of them. Different sets of starting values are usually chosen according to a combination of deterministic and stochastic random rules (Berchtold 2004; Bartolucci et al. 2014; Maruotti and Punzo 2021), and inference is based on the solution corresponding to the largest value of the likelihood at convergence.

An alternative to using different starting values is adopting a suitably modified maximization algorithm to increase the chance of reaching the global maximum of the likelihood. Along this direction, Brusa et al. (2023) illustrate a tempered EM (TEM) algorithm that allows exploring a broader region of the parameter space and outperforms the standard algorithm in avoiding local maxima. In line with this previous work we propose the evolutionary expectation–maximization (EEM) algorithm as an enhancement of the TEM approach, and explore an extension of the VEM algorithm, named evolutionary expectation–maximization (EVEM) algorithm. These are defined following the idea of the evolutionary algorithms (Bäck 1996; Deb 2001; Ashlock 2004) already employed in the finite mixture models (McLachlan and Peel 2000) but never explored with DLV models in general; see, among others, Pernkopf and Bouchaffra (2005), Andrews and McNicholas (2013), and McNicholas et al. (2021). We evaluate the performance of the EEM and EVEM algorithms through Monte Carlo simulation studies conducted using three main classes of DLV models, namely latent class (LC, Goodman 1974), hidden Markov (HM, Bartolucci et al. 2013), and stochastic block (SB, Nowicki and Snijders 2001) models. We compare the proposals with the standard EM and VEM algorithms evaluating: (i) the frequency of convergence to the global maximum; (ii) the average distance from the global maximum; (iii) the accuracy of the estimated parameters; and (iv) the computational time. The algorithms are also compared through applications concerning cross-sectional, longitudinal, and network data analysis. The code implemented for the proposals is written in C++  and is available for the R software (R Core Team 2023) at the following link in the GitHub repository: https://github.com/LB1304/estDLVM.

Overall, the main features of the proposal are that: (i) taking inspiration form the evolutionary approach, a new method, able to explore the parameter space more broadly with respect to the tempered technique, is used to improve the EM algorithm; (ii) an advanced version of the VEM algorithm is implemented; (iii) the proposed methods are tested for DLV models of different complexity. These methods prove to be particularly effective in avoiding local maxima in applications.

The remainder of this paper is organized as follows. In Sect. 2 we outline the assumptions of DLV models and we review the steps of the EM and VEM algorithms. In Sect. 3, after having introduced some features of the evolutionary algorithms, we illustrate the EEM and EVEM algorithms dealing with their specific settings. In Sect. 4 we report and discuss simulation results. In Sect. 5 we use cross-sectional, longitudinal, and network data to estimate LC, HM, and SB models with the proposed algorithms evaluating their performance. In Sect. 6 we summarize findings and offer concluding remarks. Details about the simulation study and the applications results are illustrated in the Appendices and in the Supplementary Material (SM).

2 Notation and maximum likelihood of DLV models

Denoting by ${\varvec{Y}} = (Y_1, \ldots , Y_r)$ the vector of response variables and by ${\varvec{U}} = (U_1, \ldots , U_l)$ the set of discrete latent variables, the conditional distribution of the responses given the latent variables, expressed as $p_{{\varvec{Y}} | {\varvec{U}}}({\varvec{y}} | {\varvec{u}})$, and the distribution of the latent variables, denoted by $p_{{\varvec{U}}}({\varvec{u}})$, characterize a DLV model. The manifest distribution of the response variables is expressed as

$$\begin{aligned} p_{{\varvec{Y}}}({\varvec{y}}) = \sum _{{\varvec{u}}} p_{{\varvec{Y}} | {\varvec{U}}}({\varvec{y}} | {\varvec{u}}) p_{{\varvec{U}}}({\varvec{u}}), \end{aligned}$$

(1)

and the posterior distribution of the latent variables given the responses is computed according to the Bayes’ law as

$$\begin{aligned} p_{{\varvec{U}}|{\varvec{Y}}}({\varvec{u}} | {\varvec{y}}) = \frac{p_{{\varvec{Y}} | {\varvec{U}}}({\varvec{y}} | {\varvec{u}}) p_{{\varvec{U}}}({\varvec{u}})}{p_{{\varvec{Y}}}({\varvec{y}})}; \end{aligned}$$

(2)

see Bartolucci et al. (2022) for a thorough review of DLV models.

The EM algorithm maximizes the observed-data log-likelihood $\ell ({\varvec{\theta }})=\log p_{{\varvec{Y}}}({\varvec{y}})$ with respect to the model parameters collected in the vector ${\varvec{\theta }}$, relying on the complete-data log-likelihood $\ell ^*({\varvec{\theta }})$, which can be written as

$$\begin{aligned} \ell ^*({\varvec{\theta }}) = \log p_{{\varvec{Y}}, {\varvec{U}}}({\varvec{y}}, {\varvec{u}}) = \log p_{{\varvec{Y}} | {\varvec{U}}}({\varvec{y}} | {\varvec{u}}) + \log p_{{\varvec{U}}}({\varvec{u}}). \end{aligned}$$

Once the model parameters have been initialized, the algorithm alternates two coupled steps: (i) an expectation step (E), where the conditional expected value of $\ell ^*({\varvec{\theta }})$ is computed given the value of the parameters at the previous step and the observed data and (ii) a maximization step (M), where the parameters are updated by maximizing the expected value of $\ell ^*({\varvec{\theta }})$. In particular, the E-step relies on the posterior distribution $p_{{\varvec{U}}|{\varvec{Y}}}({\varvec{u}} | {\varvec{y}})$. Note that, for certain models, such as the HM model, computation of $p_{{\varvec{Y}}}({\varvec{y}})$ through the sum in (1), and consequently of the log-likelihood and the posterior distribution defined in (2), is infeasible and suitable recursions are necessary (Baum et al. 1970; Welch 2003). For other DLV models with a complex latent structure, such as the SB model, computation of $p_{{\varvec{Y}}}({\varvec{y}})$ is infeasible and then maximum likelihood estimates cannot be obtained. In these cases, the VEM algorithm (Jordan et al. 1999) is an efficient alternative to the EM algorithm. It relies on the following lower bound of the observed-data log-likelihood function:

$$\begin{aligned} {\mathcal {J}}({\varvec{\theta }}, {\varvec{\tau }}) = \log p_{{\varvec{Y}}}({\varvec{y}}) - \text {KL} \left[ q_{{\varvec{U}}}({\varvec{u}})\ ||\ p_{{\varvec{U}} | {\varvec{Y}}}({\varvec{u}} | {\varvec{y}})\right] , \end{aligned}$$

where ${\varvec{\tau }}$ collects the variational parameters and $\text {KL}[\cdot || \cdot ]$ denotes the Kullback–Leibler divergence (Kullback and Leibler 1951) measuring the (non-symmetric) distance between the intractable posterior distribution $p_{{\varvec{U}} | {\varvec{Y}}}({\varvec{u}} | {\varvec{y}})$ and a suitable approximation $q_{{\varvec{U}}}({\varvec{u}})$. The VEM algorithm then alternates the following two steps: (i) a variational expectation step (VE), where ${\mathcal {J}}({\varvec{\theta }}, {\varvec{\tau }})$ is maximized with respect to ${\varvec{\tau }}$, thus finding the best approximation $q_{{\varvec{U}}}({\varvec{u}})$ for the conditional distribution and (ii) a maximization step (M), where ${\mathcal {J}}({\varvec{\theta }}, {\varvec{\tau }})$ is maximized with respect to ${\varvec{\theta }}$, thus updating the model parameters as in the EM algorithm.

Concerning the choice of the starting values for both the EM and VEM algorithms, the general advice is using a combination of deterministic and random rules in order to limit the problem of the likelihood multimodality (Bartolucci et al. 2013). The global maximum is then taken as the solution corresponding to the largest value of log-likelihood at convergence. This approach, implemented to explore the parameter space, has some drawbacks since, even with many different sets of starting values, reaching the global maximum may be unfeasible and the resulting computational time can be extremely high.

Rather than relying on multiple sets of starting values, the aforementioned TEM algorithm (Brusa et al. 2023) employs a parameter, known as temperature, to re-scale the conditional expected value of $\ell ^*({\varvec{\theta }})$ computed in the E-step and hence controls the prominence of all maxima. By alternating high temperatures, which ensure an adequate exploration of the parameter space, and low temperatures, which secure a precise optimization in a local region of the parameter space, the procedure is gradually attracted towards the global maximum, escaping local sub-optimal solutions. Despite a significant increase in the chance to reach the global maximum, a main limitation of the TEM algorithm is the required choice of the temperature sequence, also known as tempering profile. Two possibilities are illustrated in Brusa et al. (2023), both relying on some tempering constants: a monotonically decreasing exponential profile and a non-monotonic profile with oscillations of gradually smaller amplitude. None of these constants has a straightforward interpretation, and the effect of a change in their values on the performance of the TEM algorithm may be unpredictable. Therefore, a drawback of this approach is that a grid search is required for an optimal tuning, resulting in a time and resources demanding procedure.

2.1 Three classes of discrete latent variable models

The LC model (Lazarsfeld and Henry 1968; Goodman 1974; Lindsay et al. 1991) is employed in the context of cross-sectional data and it considers s categorical response variables for n individuals. These variables are relabelled as $Y_{ij}$, $i=1,\ldots ,n$, $j=1,\ldots ,s$, and have c categories. Individual-specific latent variables $U_i$ with k support points are assumed and identify k latent classes in the population. The model parameters are the class weights $\pi _u=p(U_i=u)$, $u = 1, \ldots , k$, and the conditional response probabilities $\phi _{jy|u}=p(Y_{ij}=y|U_i=u)$, $j = 1, \ldots , s$, $u = 1, \ldots , k$, $y = 0, \ldots , c-1$. For this model, $p_{{\varvec{Y}}}({\varvec{y}})$ may be directly computed by (1) and simple steps of the EM algorithm may be implemented to maximize $\ell ({\varvec{\theta }})$.

The HM model (Bartolucci et al. 2013; Zucchini et al. 2016) considers response variables observed at T time occasions, with response variables relabelled as $Y_{ijt}$, $i=1,\ldots ,n$, $j=1,\ldots ,s$, $t=1,\ldots ,T$, and relies on individual-specific latent processes ${\varvec{U}}_i=(U_{i1},\ldots ,U_{iT})'$, usually assumed as a first-order Markov chain, with k latent states. The corresponding model parameters are the initial probabilities $\pi _u=p(U_{i1}=u)$, $u = 1, \ldots , k$, the transition probabilities $\pi _{u|{\bar{u}}}^{(t)}=p(U_{it}=u|U_{i,t-1}={\bar{u}})$, $t = 2, \ldots , T$, ${\bar{u}}, u = 1, \ldots , k$. When categorical response variables with c categories are considered (the corresponding model is denoted by HMcat in the following) the parameters include the conditional response probabilities $\phi _{jy|u}=p(Y_{ijt}=y|U_{it}=u)$, $t = 1, \ldots , T$, ${\bar{u}}, u = 1, \ldots , k$, $y=0,\ldots ,c-1,$ whereas, when continuous response variables are analyzed (HMcont in the following), state specific mean vectors ${\varvec{\mu }}_u$ ($u = 1, \ldots , k$) and a variance-covariance matrix ${\varvec{\Sigma }}$ of dimension $r \times r$ are estimated under the assumption of conditional Gaussian distribution of the responses (Pennoni et al. 2022). Another important aspect of the HM model is that it allows performing a dynamic clustering where units may move between clusters across time through local and global decoding (Viterbi 1967).

The SB model deals with network data, typically encoded in graphs (Holland et al. 1983; Snijders and Nowicki 1997; Nowicki and Snijders 2001) and the set of response variables corresponds to the adjacency matrix ${\varvec{Y}}$ of dimension $n \times n$ with elements $Y_{ij}$, such that $Y_{ij} = 1$ if there exists an edge connecting nodes i and j and $Y_{ij} = 0$ otherwise. Similarly to the LC model, individual-specific latent variables $U_i$ with k support points identifying the latent blocks are conceived. The model parameters are the group weights $\pi _u$, $u = 1, \ldots , k$, and the connection probabilities $\beta _{uv}$, $u, v = 1, \ldots , k$, between nodes of the graph.

3 Evolutionary EM and VEM algorithms

In this section we first introduce the main rationale under the evolutionary algorithms and then provide a comprehensively description the proposed algorithms.

3.1 Preliminaries

Evolutionary algorithms represent a class of computational methods commonly employed to solve complex optimization problems for continuous and discrete functions; see, among others, Bäck (1996), Deb (2001), and Ashlock (2004). For a related $\textsf {R}$ package, see Scrucca (2013). Individuals of a certain population become more eligible for a specific context through an iterative procedure that mimics the basic principles of the Darwinian theory of evolution. Potential solutions for the optimization problem at issue play the role of individuals in the population, and their evolution is aimed at gradually improving the result of the optimization procedure. Once an initial population has been defined, evolutionary algorithms are based on the following three steps:

(i):

selection is performed according to an estimated score assigned to each individual through a fitness function, and aims at favoring the most eligible candidate solutions;

(ii):

crossover produces a new generation of individuals (offspring) from the previous one (parents);

(iii):

mutation introduces random variations to the individuals in the population.

This algorithm is successfully employed for unsupervised clustering to determine suitable partitions of the points into clusters; see Hruschka et al. (2009), among others. It is also used for the estimation of Gaussian finite mixture models, see Pernkopf and Bouchaffra (2005), Andrews and McNicholas (2013) and McNicholas et al. (2021) among others, and for Gaussian parsimonious clustering models (Kampo 2021).

3.2 Steps of the EEM and EVEM algorithms

In the context of DLV models, the EEM and EVEM algorithms deal with populations in which each individual is associated with a different array containing the posterior probabilities of the latent states for each response configuration and, in the case of longitudinal data, also for each time occasion. In this respect, our proposal follows McNicholas et al. (2021), and differs from that in Pernkopf and Bouchaffra (2005) where the evolution of the parameter space is considered, and crossover and mutation are performed on the model parameters. It is worth mentioning that, as we will show in the following, the structure of the algorithms can be adapted to estimate many different DLV models with minor changes.

Hereafter we denote by letter P the evolving population and by $N_P$ and $N_O$ the number of parents (individuals before crossover) and offspring (individuals after crossover), respectively. The pseudo-code of the two algorithms is presented in Algorithm 1.

Algorithm 1

General scheme of the EEM and EVEM algorithms

In the following, we detail the steps of the EEM algorithm; the EVEM follows the same overall structure illustrated below, except that in steps 1 and 3, the VEM approach is employed in place of the EM algorithm.

Once the initial population $P_0$ is initialized with $N_P$ individuals, the algorithm alternates the following procedures until convergence:

• 1. Update. Population $P_0$ is updated by performing R cycles of the EM algorithm with random initialization on each individual; $P_1$ denotes the resulting updated population. The value of R should be kept sufficiently small to reduce the computational time. Convergence is checked on the basis of the relative change in the log-likelihood of two consecutive steps; if this condition is fulfilled, the EM algorithm is interrupted without performing the remaining cycles. In implementing the algorithm, specificities of each model are limited to this step, as well as to step 3 illustrated below.

• 2. Crossover. Individuals from population $P_1$ are recombined to obtain the $N_O$ offspring of new population denoted by $P_2$. Parents are randomly selected among the individuals of population $P_1$, the same row of the posterior probabilities array is randomly chosen from the two corresponding arrays, which are swapped from that line to the end. This operator is usually known as single-point crossover; see Bäck (1996) and Michalewicz and Fogel (2000) for additional details. This operation is repeated for every time occasion when the HM model is estimated. Note that the same pair of parents could be selected multiple times; this surely happens if $N_P(N_P-1)/2 < N_O$.

• 3. Update. Population $P_2$ is updated through R steps of the EM algorithm on each offspring, generating the updated population $P_3$. This procedure is identical to the previous update performed at step 1.

• 4. Selection. The selection strategy employs the complete data log-likelihood as a fitness function (see Sect. 3.1), and is performed by adapting the proposal in Bäck et al. (1996) to the context of DLV models. In this case, members from populations $P_1$ and $P_3$ are considered jointly and the $N_P$ individuals with the highest fitness value are selected for the next generation, denoted by $P_4$. This elitist approach allows us to retain the property of monotonic convergence of the EM algorithm to the maximum of the log-likelihood.

• 5. Mutation. Differently from the crossover operator, mutation introduces variations with respect to a single individual at a time. More specifically, given a row of the corresponding array, selected with a certain probability denoted by $p_m$, the mutation operator swaps the highest value with a random one; that is, it changes the latent component to which a subject is assigned. To preserve the elitism of the algorithm, the best individual of the current population is always retained for the next generation, denoted by $P_5$.

To check the convergence of both EEM and EVEM algorithms, the best solution of population $P_4$ is selected at each step, considering both the relative difference in terms of the log-likelihood of two consecutive steps and the difference between the corresponding parameter vectors. The algorithms are stopped when:

$$\begin{aligned} \frac{\ell ({\varvec{\theta }}^{(h)}) - \ell ({\varvec{\theta }}^{(h-1)})}{|\ell ({\varvec{\theta }}^{(h)})|}< \varepsilon _1 \quad {\text {and}} \quad \max _s |\theta ^{(h)}_s - \theta ^{(h-1)}_s| < \varepsilon _2, \end{aligned}$$

where ${\varvec{\theta }}^{(h)}$ is the vector of parameter estimates corresponding to the best candidate solution at the h-th iteration, and $\varepsilon _1$, $\varepsilon _2$ are suitable tolerance levels (both are set equal to $10^{-8}$ in the following simulation study). After convergence, the vector $\hat{{\varvec{\theta }}}$ corresponding to the highest log-likelihood is taken as an estimate of the model parameters among $\hat{{\varvec{\theta }}}_0, \ldots , \hat{{\varvec{\theta }}}_{N_P}$.

The proposed algorithms respond to the need to explore the entire parameter space; therefore, a random initialization of the population is the most suitable choice, and more elaborated initializations, such as k-means or k-modes algorithms, are neither necessary nor appropriate. Model parameters are then randomly drawn and used to compute the array of the estimated posterior probabilities. The process is repeated for each of the $N_P$ individuals of the initial population.

4 Simulation study

We show the simulation experiments carried out to evaluate the quality of the EEM and EVEM algorithms. The simulation study is designed providing specific settings for each DLV model illustrated in Sect. 2.1. A total of 22 different scenarios, listed in Table 4 in Appendix A, are considered according to the following simulation setup: sample size $n = 500, 1000$, number of response variables $r = 6, 12$, and of categories $c = 3, 6$, number of time occasions $T = 5, 10$, and number of latent components $k = 3, 6$. With respect to the SB model we consider two different behaviors defined as assortative, with high intra-group and low inter-groups connection probabilities, and disassortative, with low intra-group and high inter-groups connection probabilities.

For each scenario, we randomly draw 50 samples and we estimate 100 times the corresponding model using both the true number of latent components (k, for a correctly specified model) and a wrong number of latent components ($k+1$, for a misspecified model). In this way, we can evaluate the performance of the algorithms in situations where the true model generating the data is unknown. This circumstance is common in practical applications and can lead to errors in the specification of the latent structures.

The performance of the proposed algorithms is compared with that of the standard EM and VEM algorithms initialized with random starting values using the following relevant criteria: frequency of convergence to the global maximum, average distance from the global maximum, and accuracy of the estimated parameters. In the SM we also assess the performance of the proposals in term of computational time, showing that the proposed algorithms are generally slower with respect to the EM and VEM algorithms.

4.1 Evaluating the achievement of the optimum

We let ${{\hat{\ell }}}_{MAX}$ be the highest log-likelihood value and ${{\hat{\ell }}}$ a generic value of the log-likelihood function at convergence. We assume that the global optimum is reached when

$$\begin{aligned} \frac{ {{\hat{\ell }}}_{MAX} - {{\hat{\ell }}} }{ |{{\hat{\ell }}}_{MAX}| } < {\tilde{\varepsilon }}, \end{aligned}$$

where ${\tilde{\varepsilon }}$ is a suitable threshold, fixed at $10^{-4}$ in the simulation study.

Figure 1 depicts the percentages of global maxima reached by the EEM and EVEM compared to the EM and VEM algorithms for each class of models estimated with a correctly specified latent structure. The proposed algorithms outperform the standard ones under all the simulated scenarios, thus revealing their superior performance to avoid local maxima. The improvement is especially evident in the most complex scenarios, namely those with many latent components and those related to the SB models (see Table 4 in Appendix A for details of each scenario).

Fig. 1

Percentages of global maxima obtained using EM or VEM algorithms (in ) and EEM or EVEM algorithms (in ) under the simulated scenarios (see Table 4 in Appendix A) for the LC, HMcat, HMcont, and SB models with correctly specified latent structure (estimated with k latent components)

Fig. 2

Percentages of global maxima obtained using EM or EVEM algorithms (in ) and EEM or EVEM algorithms (in ) under the simulated scenarios (see Table 4 in Appendix A) for the LC, HMcat, HMcont, and SB models with misspecified latent structure (estimated with $k+1$ latent components)

Figure 2 shows percentages of global maxima obtained when the models are estimating with a misspecified latent structure. In this case, in each simulated scenario, the performance of the proposed evolutionary approach is much superior to that of the EM and VEM algorithms. For example, in Setting C of the LC model the average percentage increases from 16% with the EM algorithm to 93% with the EEM algorithm. In Setting A of the HMcont model this percentage reaches only 33% when the EM algorithm is employed, and is much higher (83%) with the EEM algorithm. Considering the LC and HM models estimated with many latent components, both the EM and EEM show poor performance in reaching the global optimum; for example, the percentage is equal to 2% and 9%, respectively for scenario F referred to the HMcat model. In these cases, however, a second fundamental property of the EEM algorithm emerges, namely its ability to improve the value of the found global maximum, in addition to increasing the chance of reaching it. In particular, focusing again on scenario F for the HMcat model, the EM algorithm is unable to detect the global maximum in 30 samples (out of 50), while the EEM algorithm always reaches the optimum.

4.2 Evaluating the average distance from the global maximum

We compute the normalized average distance of the 100 log-likelihood values ${{\hat{\ell }}}_1, \ldots , {{\hat{\ell }}}_{100}$ from the global maximum ${{\hat{\ell }}}_{MAX}$ for each simulated scenario considering the following simple measure

$$\begin{aligned} d_{gm} = \frac{1}{100} \sum _{s=1}^{100} \frac{ {{\hat{\ell }}}_{MAX} - {{\hat{\ell }}}_s }{ |{{\hat{\ell }}}_{MAX}| }. \end{aligned}$$

(3)

Table 5 in Appendix B presents the results depicting the normalized average distance in (3) for each scenario under correctly and misspecified latent structures. The proposed EEM and EVEM algorithms perform much better than the standard ones, always showing significantly lower values. Regarding the correctly specified LC model, and specifically considering scenario D, the average distance is $4.7\cdot 10^{-7}$ with the EM algorithm and decreases to $2.5\cdot 10^{-18}$ with the EEM. Note that the reported distance values are negligible (of the order of $10^{-16}$ or smaller), highlighting that the global maximum is reached for all 50 samples and 100 starting values of each sample. The slightest improvement is obtained under scenario F for the HMcat model with misspecified latent structure, showing values equal to $1.2\cdot 10^{-3}$ and $6.8\cdot 10^{-4}$ for EM and EEM, respectively. This measure shows that the proposed algorithms never provide values significantly distant from the global maximum.

4.3 Evaluating the accuracy of the estimated parameters

Considering correctly specified models we also assess the quality of the proposals in terms of root mean square error (RMSE) of the parameter estimates defined as

$$\begin{aligned} \text {RMSE} = \sqrt{\frac{1}{M}\sum _{m=1}^{M} ({\hat{\theta }}_m -\theta _m)^2}, \end{aligned}$$

where M denotes the number of free parameters. Results are presented in Table 6 in Appendix C, showing that the evolutionary algorithms provide more accurate estimates of the model parameters. In particular, they show major improvements when used for estimating the HMcont and SB models.

5 Applications

In the following we show the performance of the algorithms to estimate DLV models with cross-sectional, longitudinal, and network data. Each model is estimated 500 times for every data set using both the proposed algorithms and their standard counterparts. Model selection is performed by choosing between a number of components ranging from 1 to 8 and considering the Bayesian information criterion (BIC, Schwarz 1978) or the integrated classification likelihood criterion (ICL, Biernacki et al. 2000). In the next subsections, we illustrate the data and the results of each application.

5.1 Latent class model: drinking behavior in young adults

We consider cross-sectional data coming from a national representative survey conducted in 2014 about alcohol behavior of $n=250$ high school seniors in the United States. The following six variables ($r=6$), measuring lifetime, past-year, and past-month alcohol use and drunkenness based on a seven point scale ($c=7$) are considered. The data set is a portion of the survey described in Johnston et al. (2017) and data are freely available at the following link: https://www.icpsr.umich.edu/web/NAHDAP/studies/36263/datadocumentationhttps://www.icpsr.umich.edu/web/NAHDAP/studies/36263/datadocumentation. An LC model was proposed for the analysis of similar data, related to the year 2004, in Lanza et al. (2007) to discover sub-populations with similar drinking behavior (see also Collins and Lanza 2010).

Fig. 3

Estimated weights (${\hat{\pi }}_k$) and conditional response probabilities (${\hat{\phi }}_{jy|u}$) for the LC model with $k=3$ latent classes for the data on alcohol behavior; categories are referred to occasions of alcohol consumption coded as follows: 1 = 0, 2 = 1–2, 3 = 3–5, 4 = 6–9, 5 = 10–19, 6 = 20–39, 7 = 40 or more

The BIC suggests selecting three latent classes. The results of the log-likelihood values at convergence are shown in Figure 1a in the SM. The global maximum is almost always obtained with the EEM algorithm and all log-likelihood values are equal or very close to that global optimum. On the other hand, with the standard EM algorithm, the global maximum is not the most frequent mode, and shallow values are sometimes reached. In more detail, the frequency of global maximum, computed as shown in Sect. 4.1, is equal to 96.4% with the EEM algorithm and 9.4% with the standard EM algorithm.

The estimated conditional response probabilities are depicted in Fig. 3 and they show that the three subpopulations of young people are defined according to increasing levels of alcohol consumption. The 1st class, the largest with about 49% of the scholars, is mainly related to young people who do not drink alcohol or drink few. They exhibit a high probability of never having drunk alcohol (0.64) and an even higher chance of never having consumed alcohol in the past month (0.96). Furthermore, individuals in this class have a probability of 0.90 of never having been drunk and a probability almost equal to one of being drunk in the past year. The 2nd latent class comprises approximately 35% of the subjects. They are moderate drinkers who have consumed alcohol two times or less in the last month with a probability of 0.84. Instances of being drunk are even less frequent: the probability of this occurring 1 or 2 times in the past year is 0.57, while the probability of never being drunk in the last month is 0.72. Finally, the 3rd latent class encompasses 15% of young people identified as heavy drinkers, showing a probability equal to 0.81 of having been drunk at least 40 times in their lifetime.

5.2 Hidden Markov model with categorical responses: criminal histories

We analyze longitudinal data simulated according to the official criminal histories of a cohort of $n=10,000$ individuals born in 1953 in England and Wales during six age bands ($T=6$) of five years in length, from the age of criminal responsibility (10 years) until the end of 1993. Data are available in the R package LMest (Bartolucci et al. 2017). Four binary response variables ($r=4$, $c=2$) indicate whether or not a subject has committed a particular offense among the following typologies: violence against the person, sexual offenses, theft and handling of stolen goods, and drug offenses (see Development and Directorate 1998). As proposed in Bartolucci et al. (2007) and Pennoni (2014), an HMcat model may be used to determine trajectories of criminal behavior over time.

Table 1 Estimated initial probabilities (${{\hat{\pi }}}_u$) and conditional response probabilities (${{\hat{\phi }}}_{j1|u}$) of the HMcat model with $k=3$ latent states for the criminal data. Reported values are referred to the probabilities of commiting the four types of crime

Fig. 4

State transition diagram (${\hat{\pi }}_{u|{\bar{u}}}$) of the HMcat model with $k=3$ latent states for the criminal data

According to the BIC index, a number of latent states equal to three is selected. Results are reported in Figure 1b in the SM. Employing the EEM algorithm the global optimum is reached steadily on around 97.2% of the time. On the other hand, using the EM algorithm, the global optimum is reached only in 8.6% of times and the most frequent local maximum, which is far smaller than the global one, is obtained around 60% of the time.

Table 2 Estimated initial probabilities (${{\hat{\pi }}}_u$) and averages (${{\hat{\mu }}}_{j|u}$) across latent states of the HMcont model with $k = 6$ states for the energy consumption data. The last column reports the sum of the estimated averages for each latent state

The estimated initial and conditional probabilities are summarized in Table 1 and allow us to identify different criminal behaviors. At the initial time, the majority of individuals (96%) fall into the 1st latent state, which characterizes subjects not committing crimes. The 2nd latent state, representing only 2% of the population describes individuals with an evident prevalence of theft and handling of stolen goods since the estimated conditional probability is equal to 0.63 and of violence against the person (0.12). The 3rd latent state represents individuals committing all crimes with a prevalence of violence against the person and drug offenses (0.17 and 0.10, respectively). The estimated transition probabilities of the Markov chain are depicted in Fig. 4. It is interesting to note that 22% of criminals tend to reduce crimes over time and transit from the 3rd to the 2nd state, and 43% of individuals are becoming nonoffenders, switching from the 3rd to the 1st latent state.

5.3 Hidden Markov model with continuous responses: energy consumption across countries

We use the HMcont model to study per capita energy consumption over the years 1990–2020 in 71 countries considering the following sources: coal, natural gas, hydroelectric, nuclear, oil, solar, and wind. Data are stored by the public repository freely available at the link https://github.com/owid/energy-data (Ritchie et al. 2022). A Box–Cox transformation (Box and Cox 1964) is applied to all the variables before estimating an HMcont model to fulfill the assumption of conditional Gaussian distribution of the response variables. When estimating the HMcont model for an increasing number of latent states, the BIC index always decreases until a certain large value of k. This tendency is frequently observed with large data and heuristic approaches are applied to reach a good compromise between fit and parsimony. For the data at hand we choose $k=6$ and we notice that the EEM algorithm ensures convergence to the global maximum, corresponding to a log-likelihood value equal to $-7,346.16$ (see Figure 1c in the SM). The EM algorithm never detects such a maximum, providing $-7,358.35$ as the highest value at convergence.

Table 2 reports the estimated conditional means of the response variables given the latent state and the last column shows the sum of the estimated averages. The first two subpopulations refer to countries with reduced energy consumption, relying on fossil fuel sources, especially coal and oil. Their usage of renewable energy is extremely limited. The 3rd group is characterized by countries with a relatively balanced energy mix among different sources. While fossil fuels, particularly gas and oil, dominate their energy profile, there is also a significant use of renewable sources. Countries in the 4th and 5th groups show high energy consumption and they differ significantly in hydroelectric and nuclear energy use, respectively. Finally, countries allocated to the 6th group are major producers of oil and gas and stand out with extremely high overall energy consumption.

The highest transition probabilities, shown in Fig. 5, occur towards the 3rd latent state and reflect, on the one hand, the economic growth of emerging countries. We notice high persistence in each state. With this model, countries are dynamically clustered into six groups according to the posterior probabilities through the local decoding (see Sect. 2.1). Results are not reported here, but we notice that China, Iran, Brazil, and Mexico are switching from the 1st and 2nd state to the 3rd. Japan transits from the 5th state to the 3rd, showing a decrease in energy consumption likely due to the decision to phase out nuclear energy in 2013. The United Arab Emirates also transits from the 6th state to the 3rd, possibly due to the reduced oil reserve.

Fig. 5

State transition diagram of the averaged transition probabilities ${\hat{\pi }}_{u|{\bar{u}}}^{(t)}$ of the HMcont model with $k=6$ latent states for the energy consumption data

5.4 Stochastic block model: links between members of a karate club

We analyze network data concerning $n=34$ members of a university-based karate club in the United States during the 1970s (Zachary 1977). After a dispute between the president and the instructor over the price of karate lessons, the club experienced a significant division, forming opposing factions and eventually leading to the emergence of two distinct clubs. Relationships among members are stored as a $34 \times 34$ adjacency matrix and are available in the R package igraphdata (Csardi and Nepusz 2006). By estimating an SB model, we cluster the club members into different groups, according to their friendship relations. An SB model with 6 latent blocks is selected according to the ICL criterion. As shown in Figure 1d in the SM, the EVEM algorithm consistently converges to a log-likelihood value equal to $-277.91$. When the model is estimated with the EM algorithm, its highest value is $-316.46$.

Fig. 6

Graph visualization with nodes referred to the karate club data colored by estimated partition of the SB model with $k=6$ latent blocks

Table 3 Estimated connection probabilities of the SB model with $k=6$ latent blocks for the karate club data

Figure 6 depicts the network with nodes colored according to the estimated partition. The connection probabilities are instead summarized in Table 3, showing that the model effectively identifies the two opposing factions that emerge within the network. The faction led by the president (denoted by A) consists of 2 latent blocks, in the following referred to as Aa and Ab. Block Aa (depicted in blue) contains only the president and another individual; they are characterized by a high number of interactions with other members (17 and 12, respectively). Block Ab (pictured in red) is larger, comprising 16 individuals; these are marked by a limited number of interactions with other members (at most 6). Being part of the same faction, the estimated connection probability between these two blocks is quite high (0.75). On the other hand, the faction led by the instructor (denoted by H) is constituted by the remaining 4 latent blocks, in the following referred to as Ha, Hb, Hc, and Hd. Block Ha (represented in violet) solely contains the instructor; as leader of the faction, he presents many interactions with other subjects (16). The other three blocks of this faction (Hb, Hc, and Hd depicted in yellow, pink, and green, respectively) exhibit a strong link with the instructor’s block, as highlighted by the estimated connection probabilities, equal to 1.00, 0.81, and 1.00, respectively. These three groups differ in terms of the number and type of interactions: individuals allocated to latent block Hb are characterized by a higher number of interactions with respect to blocks Hc (having only intra-group links, beyond relations with the instructor) and Hd (having only inter-groups links). Notably, the connection probabilities between blocks belonging to different factions are generally very low, with a maximum of 0.17 and there is no connection at all between president and instructor.

6 Conclusions

In this paper we introduce the evolutionary expectation–maximization (EEM) and the evolutionary variational expectation–maximization (EVEM) algorithms to tackle the local maxima problem in estimating discrete latent variable (DLV) models based on maximum likelihood and approximate maximum likelihood approaches. Along with other evolutionary algorithms, the proposed algorithms rely on an iterative procedure that accounts for multiple possible solutions at each step using suitable criteria to evaluate their performance. Employing evolutionary operators, such as crossover and mutation, facilitates broad exploration of the parameter space, avoiding local maxima and converging closer to the global maximum. The behavior of the EEM and EVEM algorithms is controlled by a set of constants having a simple interpretation. We perform an extensive Monte Carlo simulation study to compare the performance of the EEM and EVEM algorithms with the expectation–maximization (EM) and variational expectation–maximization (VEM) algorithms. Simulation results show the superior performance of the two proposals under each scenario designed for the latent class, hidden Markov, and stochastic block models. The applications conducted using cross-sectional, longitudinal, and network data confirm that the EEM and EVEM algorithms outperforms their counterparts.

In light of the current results these new algorithms could also be applied for estimating more complex DLV models including covariates, missing values, and dropout. Moreover the EVEM may be extended to estimate different versions of the SBM, for example, accounting for directed networks. Future research can address the choice of different evolutionary operators; for example crossover and mutation may be performed on model parameters directly. Similarly, the EEM and EVEM algorithms would benefit from an automatic update of its constants. Along this line high values of $N_O$ (number of offspring) and $p_m$ (probability of mutation) may be employed in the first steps to encourage exploration of the parameter space, and gradually decreased after some iterations to reduce the computational time. Moreover the algorithms could be used to select the number of latent components. To this aim the evolutionary selection step may be updated to use an information criterion as fitness function instead of the log-likelihood function.

Table 4 Simulated designs for LC, HMcat, HMcont, and SB models varying: sample size (n), number of response variables (r), categories (c), time occasions (T), and latent states (k). For the SB model the design also specifies whether intra-group probabilities ($\beta _{uu}$) are higher or lower than inter-groups probabilities ($\beta _{uv}$, $u\ne v$)

Overall, the EEM and EVEM algorithms offer an improved solution for parameter estimation in DLV models, addressing the drawbacks of existing algorithms and providing effective and versatile approaches. Their main limitation is related to the computational complexity: they involve multiple iterations and evaluations of potential solutions, and therefore could be enhanced by a parallel implementation to reduce the computational time. Models presented in this paper have the peculiarity to achieve a considerable dimension reduction. However, an aspect of research that also needs to be addressed in the future is the scalability of the estimation algorithms in order to handle also the analysis of a variety of new data of also large dimension.

Appendices

Appendices

Appendix A details the scenarios of the simulations presented in Sect. 4. Appendices B and C provide additional simulation results. The SM contains further results concerning the simulation study and the applications.

Appendix A: Description of the simulation design

We provide additional details about the simulation studies presented in Sect. 4. Table 4 describes the settings of the simulated scenarios for the latent class (LC), hidden Markov with categorical response variables (HMcat), hidden Markov with continuous response variables (HMcont), and stochastic block (SB) models.

Table 5 Normalized average distance from the global maximum computed as the average over 50 samples and 100 starting values (see Sect. 4) with the EM or VEM algorithms (in ) and EEM or EVEM algorithms (in ) under the simulated scenarios presented in Table 4 of Appendix A for the LC, HMcat, HMcont, and SB models with correctly specified (top panel) and misspecified (bottom panel) latent structures. Values are expressed in scientific notation and the colored bars show the value obtained with the EEM or EVEM algorithm as a proportion of the corresponding ones computed with the standard counterparts

Regarding the values set for the parameters of each model, the following general rules are considered:

• Weights or initial probabilities $\pi _u$ are randomly selected from a uniform distribution from 0 to 1 and suitably normalized.

• The transition probabilities for the HM models are designed to favor persistence so that the chance of remaining in a given latent component is always higher than that of switching to another one. In particular, when $k=3$ and $k=6$ we set, for $t=2,\ldots ,T$, the following two matrices of transition probabilities:

  $$\begin{aligned} {\varvec{\Pi }}= & {} \begin{bmatrix} 0.80 &{} 0.15 &{} 0.05 \\ 0.10 &{} 0.80 &{} 0.10 \\ 0.05 &{} 0.15 &{} 0.80 \end{bmatrix} \quad \text {and} \quad \\ {\varvec{\Pi }}= & {} \begin{bmatrix} 0.85 &{} 0.10 &{} 0.05 &{} 0.00 &{} 0.00 &{} 0.00 \\ 0.10 &{} 0.75 &{} 0.10 &{} 0.05 &{} 0.00 &{} 0.00 \\ 0.05 &{} 0.10 &{} 0.70 &{} 0.10 &{} 0.05 &{} 0.00 \\ 0.00 &{} 0.05 &{} 0.10 &{} 0.70 &{} 0.10 &{} 0.05 \\ 0.00 &{} 0.00 &{} 0.05 &{} 0.10 &{} 0.75 &{} 0.10 \\ 0.00 &{} 0.00 &{} 0.00 &{} 0.05 &{} 0.10 &{} 0.85 \end{bmatrix}. \end{aligned}$$

• For the HMcat model we set (for $j = 1, \ldots , s$) the following values for the matrix of the conditional response probabilities:

  $$\begin{aligned} {\varvec{\Phi }}&= \begin{bmatrix} 0.80 &{} 0.10 &{} 0.05 \\ 0.15 &{} 0.80 &{} 0.15 \\ 0.05 &{} 0.10 &{} 0.80 \end{bmatrix} \quad (c = 3, k = 3),\\ {\varvec{\Phi }}&= \begin{bmatrix} 0.70 &{} 0.00 &{} 0.00 \\ 0.15 &{} 0.10 &{} 0.00 \\ 0.10 &{} 0.40 &{} 0.05 \\ 0.05 &{} 0.40 &{} 0.10 \\ 0.00 &{} 0.10 &{} 0.15 \\ 0.00 &{} 0.00 &{} 0.70 \end{bmatrix} \quad (c = 6, k = 3), \\ {\varvec{\Phi }}&= \begin{bmatrix} 0.95 &{} 0.65 &{} 0.30 &{} 0.20 &{} 0.10 &{} 0.00 \\ 0.05 &{} 0.25 &{} 0.50 &{} 0.50 &{} 0.25 &{} 0.05 \\ 0.00 &{} 0.10 &{} 0.20 &{} 0.30 &{} 0.65 &{} 0.95 \end{bmatrix} \\&\quad (c = 3, k = 6). \end{aligned}$$

• For the HMcont model the following conditional means are considered for each response variable: ${\varvec{\mu }} = [-2, 0, 2]'$ and ${\varvec{\mu }} = [-5, -3, -1, 1, 3, 5]'$ under the scenarios with $k=3$ and $k= 6$, respectively. The variance-covariance matrix ${\varvec{\Sigma }}$ is assumed with all variances equal to 1 and covariances equal to 0.

• For the SB model the connection probabilities are set considering two different scenarios: (i) assortative case, characterized by high intra-group and low inter-groups connection probabilities $\beta _{uu} = 0.7 > \beta _{uv} = 0.3$; (ii) disassortative case, characterized by low intra-group and high inter-groups connection probabilities $\beta _{uu} = 0.3 < \beta _{uv} = 0.7$.

Appendix B: Results for the average distance from the global maximum

See Table 5.

Appendix C: Results for the accuracy of the estimated parameters

See Table 6.

Table 6 Root mean squared error of the estimated model parameters computed as the average over 50 samples and 100 starting values (see Sect. 4) with respect to the true model parameters, using EM or VEM algorithm (in ) and EEM or EVEM algorithm (in ) under the simulated scenarios presented in Table 4 in Appendix A for the LC, HMcat, HMcont, and SB models with a correctly specified latent structure. Values are expressed in scientific notation and the colored bars show the value obtained with the EEM or EVEM algorithm as the proportion of the corresponding ones computed with the standard counterparts