Penalized model-based clustering of complex functional data

Abstract

High dimensional data, large-scale data, imaging and manifold data are all fostering new frontiers of statistics. These type of data are commonly considered in Functional Data Analysis where they are viewed as infinite-dimensional random vectors in a functional space. The rapid development of new technologies has generated a flow of complex data that have led to the development of new modeling strategies by scientists. In this paper, we basically deal with the problem of clustering a set of complex functional data into homogeneous groups. Working in a mixture model-based framework, we develop a flexible clustering technique achieving dimensionality reduction schemes through an $L_1$ penalization. The proposed procedure results in an integrated modelling approach where shrinkage techniques are applied to enable sparse solutions in both the means and the covariance matrices of the mixture components, while preserving the underlying clustering structure. This leads to an entirely data-driven methodology suitable for simultaneous dimensionality reduction and clustering. The proposed methodology is evaluated through a Monte Carlo simulation study and an empirical analysis of real-world datasets showing different degrees of complexity.

1 Introduction

With the rapid growth of modern technology, many studies have been conducted to analyse increasingly complex and high dimensional data such as 3D images generated by medical scanners, satellite remote sensing and many others from digital sensors. The analysis of these data poses new challenging problems and requires the development of novel statistical models which can be framed within the new research areas of next-generation functional data analysis (Müller 2016) and object oriented data analysis (Marron and Dryden 2022).

A large amount of complex and high dimensional data are represented by functions or higher dimensional surfaces defined on a compact domain, or by 3D images of anatomical objects with complex shapes. Because of the high dimensionality and the lack of vector space properties, the statistical modelling of these data objects is highly challenging and requires delicate extensions of standard statistical tools.

A challenging data analysis task that motivates our research originates from the problem of clustering a set of complex functional data into homogeneous groups. Over the past decade, there have been rapid advances and substantial developments in this research field for one-dimensional functional data. Compared with traditional multivariate data analysis, the difficulties of clustering such data mainly arise from the infinite dimensionality of the input space, the lack of a definition for the probability density of a functional random variable, the choice of a suitable metric and the possible dependence existing among the functions. An up-to-date review and a comprehensive taxonomy of clustering methods of functional data is provided by Zhang and Parnell (2023). For one-dimensional functions, further surveys on functional clustering can also be found in Jacques and Preda (2014a) and Chamroukhi and Nguyen (2019).

Popular approaches have successfully extended classical clustering concepts by first approximating functional data in a finite dimensional space, and then applying traditional clustering tools on the basis expansion coefficients, thus performing a two-steps approach. By extending the notion of asymptotically perfect classification (Delaigle and Hall 2012) in a functional data clustering problem, Delaigle et al. (2019) have proved theoretically that, appropriately projecting the data on a carefully reduced space, it is possible to cluster the observations asymptotically perfectly in a two-population example. In more general examples, B-splines coefficients have been used as features to feed k-means, partition around medoids or self-organizing maps algorithms—see, Abraham et al. (2003), Ignaccolo et al. (2008) and Rossi et al. (2004). Similar methods, based on wavelet and Fourier coefficients, were also considered by Antoniadis et al. (2013), Mets et al. (2016) and Serban and Wasserman (2005). To avoid relying on a pre-specified set of basis functions, one could also employ data adaptive basis functions, as those obtained from the covariance function of the functional data. In this case, functional principal component (FPC) scores (Ramsay and Silverman 2005), could be used as feature vectors for k-means or other algorithms—see e.g. Peng and Müller (2008). In Pulido et al. (2023) dimensionality reduction is achieved by applying epigraph and hypograph indexes to the original curves and to their first and/or second derivatives.

While reducing the dimensionality of data and clustering functions based on expansion coefficients resulting from PCA or similar techniques is a common approach, it has several drawbacks. For instance, the resulting clustering is not sparse in features because the expansion coefficients depend on the full set of information in the data. Additionally, there is no guarantee that the expansion coefficients capture the signal one aims to detect via clustering. For example, in the case of functional principal component analysis (FPCA), the FPC scores with the largest eigenvalues do not necessarily provide the best separation between subgroups.

The model-based clustering (Bouveyron et al. 2019), where finite mixture of Gaussian distributions have been largely employed, has been studied extensively in recent years. In an infinite, or high-dimensional setting, however, problems arise because the covariance matrices, $\varvec{\Sigma }_k$, of the involved Gaussian distributions cannot be estimated directly from the available data. To address this issue, proposals still rely on dimensionality reduction approaches, which assume that observations lie in a low-dimensional latent factor space and that the covariance matrices, $\varvec{\Sigma }_k$, now are of low rank. In the pioneering work by James and Sugar (2003) clustering models based on Gaussian mixture distributions are applied to the natural cubic spline basis coefficients. Similarly, other authors have applied the idea of Gaussian mixture modelling (GMM) to group-specific functional expansion coefficients as in Bouveyron and Jacques (2011), or FPCs as Jacques and Preda (2013, 2014b), or wavelets coefficients as Giacofci et al. (2013), or linear discriminant scores as Bouveyron et al. (2015). Another effective way to improve clustering is by inducing sparsity in the expansion coefficients, which can be particularly useful in addressing high-dimensional problems that may persist even after applying dimensionality reduction techniques. The idea of sparse clustering for functional data was first proposed in a non-model-based approach by Floriello and Vitelli (2017), using penalized weights of a weighted $L_2$ distance in k-means. Later, this idea was extended by Cremona and Chiaromonte (2023) to locally cluster curves and identify shared portions of curves, known as functional motifs.

Model-based clustering also offers a method to introduce sparsity by maximizing the log likelihood subject to a penalty that allows for the selection of the most relevant features, which can improve the interpretability of the clustering results. In our study, we also use a GMM approach to cluster objects of interest, and reduce the dimensionality of the data prior to clustering. Then, to perform feature selection with the expansion coefficients, we follow the approach presented in Zhou et al. (2009) and maximize the log likelihood subject to an $\hbox {L}_1$-penalty function that promotes sparsity in both the means, $\varvec{\mu }_k$, and covariance matrices, $\varvec{\Sigma }_k$, of the Gaussian distributions. The procedure, implemented within the classical Expectation Maximization (EM) algorithm (Dempster et al. 1977), favours an adaptive regularization that preserves the dominant local features of the objects and, at the same time, allows to look for directions in the space of projection coefficients that are the most useful in separating the underlying groups.

This approach may offer several advantages. First, by using expansion coefficients, we obtain an intuitive representation of the data in different domains, depending on the dimensionality reduction technique employed. This facilitates subsequent analyses, such as filtering, smoothing, and pattern detection. Second, by favouring sparse structures, we can retain only the most important local features of the objects, allowing for effective comparison and summarization of complex functional data across different groups or regions of the domain. Third, working with expansion coefficients can make the analyses more computationally efficient, allowing us to leverage existing tools and methodologies from multivariate analysis and the analysis of stochastic processes.

Another recent approach in the framework of Gaussian mixture model (GMM), which differs from the references cited above, is proposed by Centofanti et al. (2023). Their aim is to classify a sample of curves into homogeneous groups while jointly detecting the most informative portions of the domain in which the functions are observed. Extending the approach introduced by James and Sugar (2003), the log-likelihood is penalized using both a functional adaptive pairwise fusion penalty and a roughness penalty. The adaptive pairwise fusion penalty aids in identifying the non-informative portion of the domain by shrinking the means of separated clusters toward common values, while the roughness penalty enhances interpretability by imposing some degree of smoothing to the estimated cluster means. To prevent overparametrization, the authors assume that the cluster covariances are equal across all clusters, thereby implicitly assuming that the clusters are differentiated only by their mean functions. Since this approach differs substantially from our proposal, in the remainder of the paper we provide comparisons for both simulated and benchmark datasets by considering also other model-based state-of-art clustering methods.

To provide evidence of the flexibility of our proposal, we also introduce the following two diverse applications.

Functional zoning for air quality monitoring European and Italian directives (Dir. 96/62/EC and D. Lgs. 351/99 art. 6) require Italian regions to classify land zones in connection to air quality status. In fact, in order to improve or preserve air quality conditions, policy makers define recovery, action or maintenance plans for the different areas. By using $\hbox {PM}_{10}$ time series obtained by integrating data observed at monitoring stations and data provided by a deterministic air quality model on a regular grid (1763 points) defined over Piemonte region (Italy), we seek to classify the Piemonte region in zones featured by different levels of atmospheric pollution. The problem was previously considered in Ignaccolo et al. (2013) where clustering was performed by using at the second step the PAM algorithm over the projection coefficients recovered at the first step. Because the PAM algorithm was inadequate to model the spatial dependence existing among the functions, we show how the combination of functional data analysis (FDA) and spatial statistics can resolve this inadequacy within the framework of our regularized GMM.

Mandibular shape changes Functional data can also have a more complex domain and here we consider the case in which continuous data observed over a manifold in $\mathcal {R}^3$ can be approximated by using finite elements analysis. In particular, we consider a dataset which consists of Computed Tomography (CT) images processed to obtain 3D surface meshes of the human mandible. For the statistical analysis, we consider the displacement length as a functional variable. Understanding the morphological changes of the mandible is important for orthodontic treatment planning. To decide on a proper treatment plan, the events of growth and development must be correlated with the maturational level of individuals. In particular, the biological question of interest is to understand when and where there exist localized differences between the maturational levels. In practice, it is common to define these maturational stages by binning the subjects into age categories defined a priori (see, for example, Chung et al. 2015; Fontanella et al. 2019b and references therein). A limitation of this approach is that, since there is considerable variation in the age, grouping the subjects by chronological age may not reflect developmental stage sufficiently and accurately. To this purpose, we propose here to define the maturational levels by clustering the individuals by local shape similarity. In the following we thus show how our approach can be used also for clustering surface data.

To summarize, our paper makes contributions with respect to the following points:

• We evaluate the performance of our $\hbox {L}_1$-penalty approach, here referred to as PFC-$\hbox {L}_1$, in a functional data setting. For PFC-$\hbox {L}_1$, we suggest an entirely data-driven strategy for model specification, estimation and selection. We conduct an extensive simulation study that considers various degrees of complexity and different basis functions. To facilitate comparison with a number of competitors, an experimental study is also carried out for one-dimensional functions, both for synthetic data and for benchmark datasets. The results demonstrate that the PFC-$\hbox {L}_1$ approach is a promising method for clustering functional data and performs similarly to, or better than, other competitors in various scenarios.

• We address the challenging problem of clustering spatially dependent functional data. Clustering this type of data is a complex problem that requires careful consideration of the dependence structure of the data and the computational challenges of high-dimensional data. Compared to the case of clustering independent functions, the literature on clustering spatially dependent functional data is not as rich (see Sect. 5), particularly in the framework of model-based clustering. To address this gap, we propose within the EM algorithm a reduced rank weighted multinomial logistic regression model that generalizes some of the approaches found in the literature. This is achieved by modeling spatial dependence of the prior mixing probabilities through a generalized covariance function whose parametrization leads to a thin-plate spline solution.

• We further address the problem of working with functional data with more complex domains such as surface mesh data. Determining the similarity between these data is a fundamental task in shape-based recognition, retrieval, classification, and clustering. One common approach is to use global and/or local features depending on surface information of 3D objects (Shilane and Funkhouser 2007). Once the objects are represented using these descriptors, standard algorithms can be used for clustering. The use of many local shape descriptors dramatically increases the size of the feature vector and this leads to investigate methods for selecting a small subset of shape descriptors to be used for clustering. In contrast with this approach, we use finite element analysis techniques to represent the object in a lower-dimensional space using data adaptive Laplace-Beltrami eigenfunctions in the framework of heat kernel regression. We show that this approach allows for model-based sparse clustering of 3D objects while making inferences on functional data observed on a compact manifold. By reducing the dimensionality of the data, our approach can handle high-dimensional surface mesh data and overcome the computational challenges of clustering in this setting.

The rest of the manuscript is organised as follows. Section 2 introduces a parametrization in which a functional object is modelled hierarchically by a low-dimensional latent random process. This is then followed by the description of the considered GMM. In Sect. 3 we consider the issues associated with: (i) model specification, where we discuss the choice of the basis functions that map the vector of expansion coefficients to the random object of interest; (ii) model fit, where we describe the EM algorithm (Dempster et al. 1977) as a method for parameter estimation; (iii) model selection, where we discuss the use of information criteria used to select the number of clusters; and (iv) implementation, where we propose a possible data-driven procedure to define the dimension of the subspace where data are represented. Section 4 discusses results from an intensive simulation study where different scenarios are considered to assess the performance of the proposed clustering algorithm. Also it shows results on benchmark datasets, whereas results for the two real case studies, with spatially dependent functions, and surface data are shown in Sects. 5 and 6. Section 7 concludes the paper with a discussion on further developments.

2 Penalized model-based functional clustering

Let $\mathcal {Y}= \{Y(\varvec{t}), \varvec{t} \in \mathcal {T}\}$ be a functional random variable represented by the following measurement equation

$$\begin{aligned} Y(\varvec{t}) = X(\varvec{t}) + \epsilon (\varvec{t}), \end{aligned}$$

(1)

where $\mathcal {X}= \{ X(\varvec{t}), \varvec{t} \in \mathcal {T}\}$ represents an unobservable functional random variable of interest taking values in $L^2\big (\mathcal {T}\bigr )$, with $\mathcal {T} \subset \mathcal {R}^d$, and $\epsilon (\varvec{t})$ is an uncorrelated measurement error, with zero mean, variance $\sigma _\epsilon ^2$ and independent of $X(\varvec{t})$. A hierarchical representation of $Y(\varvec{t})$ assumes that the true process $X(\varvec{t})$ admits the following basis expansion

$$\begin{aligned} X(\varvec{t})= & {} \sum _{j=1}^p \beta _{j} \ \phi _{j}(\varvec{t}) + \eta (\varvec{t}) \nonumber \\= & {} \varvec{\phi }(\varvec{t})' \varvec{\beta } + \eta (\varvec{t}) \end{aligned}$$

(2)

where $\varvec{\phi }(\varvec{t})= (\phi _{1}(\varvec{t}) \ldots \phi _{p}(\varvec{t}) )'$ is a p-dimensional expansion vector that maps the low-dimensional random vector, $\varvec{\beta } = (\beta _1 \ldots \beta _p)'$, to the true object of interest, and p is the number of basis functions which is usually assumed to be fixed and known. The residual error term, $\eta (\varvec{t})$, accounts for possible differences between $X(\varvec{t})$ and its low-dimensional representation, $\varvec{\phi }(\varvec{t})' \varvec{\beta }$. Typically, as p increases, the residual structure $X(\varvec{t}) - \varvec{\phi }(\varvec{t})' \varvec{\beta }$ will tend to have smaller scale dependence until it degenerates to have zero variance. In such specific case $X(\varvec{t})$ is completely reconstructed through a truncated expansion and the difference with $Y(\varvec{t})$ is thus represented only by the measurement error $\epsilon (\varvec{t})$.

With the goal of clustering n objects into K homogeneous clusters, we consider the set of true (latent) objects $\bigl \{\textbf{x}_1, \textbf{x}_2, \ldots , \textbf{x}_n \bigr \}$, each considered as a realization of the functional random variable $\mathcal {X}$, and use the projection vectors $\varvec{\beta }_i, \ i=1, \ldots ,n,$ as the data of a GMM.

To this end, we assume that it exists an unobservable grouping variable $\textbf{Z}=(Z_1,...,Z_K) \in [0,1]^K$ indicating the cluster membership: $z_{k,i}=1$ if $\textbf{x}_i$ belongs to cluster k and 0 otherwise. By following a model-based clustering approach, we denote with $\pi _k$ the (a priori) probabilities of belonging to a group,

$$\begin{aligned} \pi _k=p(Z_k=1), \qquad k=1,\ldots ,K, \end{aligned}$$

such that $\sum _{k=1}^K \pi _k=1$ and $\pi _k>0$ for each k, and we assume that, conditionally on $\textbf{Z}$, the random vector $\varvec{\beta }$ follows a multivariate Gaussian distribution, that is for each cluster

$$\begin{aligned} \varvec{\beta }|(Z_k=1) =\varvec{\beta }_k \sim \mathcal {N}(\varvec{\mu }_k,\varvec{\Sigma }_k) \end{aligned}$$

where $\varvec{\mu }_k = (\mu _{1,k}, \ldots , \mu _{p,k})^T$ and $\varvec{\Sigma }_k$ are respectively the mean vector and the covariance matrix of the kth group. Then the marginal distribution of $\varvec{\beta }$ can be written as a finite mixture with mixing proportions $\pi _k$ as

$$\begin{aligned} p(\varvec{\beta }) = \sum _{k=1}^K \pi _k f(\varvec{\beta }_k; \varvec{\mu }_k,\varvec{\Sigma }_k) \end{aligned}$$

where f is the multivariate Gaussian density function. It is then possible to write the log-likelihood function as

$$\begin{aligned} l(\varvec{\theta };\varvec{\beta })=\sum _{i=1}^n log \sum _{k=1}^K \pi _k f(\varvec{\beta }_i;\varvec{\mu }_k,\varvec{\Sigma }_k), \end{aligned}$$

where $\varvec{\theta } = \lbrace \pi _1, \ldots , \pi _K; \varvec{\mu }_1, \ldots , \varvec{\mu }_K;\varvec{\Sigma }_1, \ldots , \varvec{\Sigma }_K \rbrace$ is the vector of parameters to be estimated and $\varvec{\beta }_i =(\beta _{1,i}, \ldots , \beta _{p,i})^T$ is the vector of projection coefficients of the ith object.

In this modeling framework, we consider a very general situation without introducing any kind of constraints neither for cluster means nor for covariance matrices, that are allowed to be different in each cluster. The possible overparametrization which might follow from this model flexibility is treated by introducing two penalties that allow regularized parameter estimation as in Zhou et al. (2009). Given the projection coefficients $\varvec{\beta }_i$, and conditional on the number of groups K, the proposed penalized log-likelihood function is given by

$$\begin{aligned} l_P(\varvec{\theta };\varvec{\beta })= & {} \sum _{i=1}^{n}log \left[ \sum _{k=1}^{K}\pi _k f(\varvec{\beta }_i;\varvec{\mu }_k,\varvec{\Sigma }_k)\right] \nonumber \\{} & {} -\lambda _1\sum _{k=1}^{K} \sum _{j=1}^{p}|\mu _{k,j}|-\lambda _{2}\sum _{k=1}^{K}\sum _{j,l}^{p}|W_{k;j,l}|, \end{aligned}$$

(3)

where $\lambda _1>0$ and $\lambda _2>0$ are tuning parameters to be suitably chosen, $\mu _{k,j}$ are cluster mean elements and $W_{k;j,l}$ are entries of the group precision matrix $\textbf{W}_k=\varvec{\Sigma }_{k}^{-1}$. Note that the penalty terms contain sums of absolute values and so they are of $L_1$ (or LASSO) type; this motivates the name Penalized model-based Functional Clustering (PFC-$\hbox {L}_1$). The penalty term on the cluster mean vectors allows for basis functions selection; when the jth term in the expansion is not useful in separating groups it is because it shows a common mean across groups. On the other hand, the second part of the penalty imposes a shrinkage on the elements $W_{k;j,l}$, thus avoiding possible singularity problems and facilitating the estimation of large and sparse covariance matrices.

3 Modeling and inference

In this section we show how some standard methods for model fitting and identification can be used in the framework of the PFC-$\hbox {L}_1$ procedure.

3.1 Model specification and estimation of the latent process X

Equations (1) and (2) provide a reduced-rank random effects parametrization of a functional measurement $Y(\varvec{t})$. In this context, an important part of model specification refers to the choice of the form of the expansion vector, $\varvec{\phi }(\varvec{t})$. In general, there is a long tradition of using orthogonal basis functions with typical examples provided by Fourier, orthogonal polynomials (e.g., Hermite polynomials), certain wavelets, or eigenvectors from specified covariance matrices. However, although there are some computational advantages to choosing orthogonal basis functions when constructing $\varvec{\phi }(\varvec{t})$, there is no requirement to do so. In fact, there are many other examples for nonorthogonal basis functions, including wavelets, radial basis functions, spline functions, and kernel functions. In this paper, we do not rely on a specific form of the basis functions $\phi _{j}(\varvec{t})$. The choice of preferring one approach over the others is somewhat subjective, although there can be advantages and disadvantages to each, depending on the problem at hand. The effect of using different basis functions in the proposed clustering procedure will be assessed here by means of a simulation study described in Sect. 4.

Given a specific basis of functions and denoting with $\varvec{\Phi }_p$ the expansion matrix collecting all the p chosen basis functions $\varvec{\phi }_j(\cdot )$, the p-dimensional vector of expansion coefficients for the ith object can be estimated by applying standard least squares

$$\begin{aligned} \hat{\varvec{\beta }}_i =(\varvec{\Phi }_p'\varvec{\Phi }_p)^{-1}\varvec{\Phi }_p'\varvec{y}_i, \quad i=1, 2, \ldots , n, \end{aligned}$$

(4)

so that the smooth process $X(\varvec{t})$ is estimated by

$$\begin{aligned} \hat{X}(\varvec{t}) = \varvec{\phi }(\varvec{t})' \hat{\varvec{\beta }} \end{aligned}$$

where $\hat{\varvec{\beta }}$ collects all $\hat{\varvec{\beta }}_i$.

3.2 Model parameter estimation

The problem of estimating the parameters in a finite mixture has been studied extensively in the literature. Direct optimization of the likelihood function given in Eq. (3) can be quite complicated because the objective function is nonconvex and the optimization problem is of rather high dimensionality. Since Z is not given, the maximization of log-likelihood can be efficiently carried out using the Expectation-Maximization (EM) algorithm (Dempster et al. 1977). In this case, the dth iteration of the E-step provides the expected conditional complete log-likelihood

$$\begin{aligned} Q_{P}(\varvec{\theta };\varvec{\theta }^{(d)})= & {} \mathbb {E}_{Z|\hat{\varvec{\beta }},\varvec{\theta }^{(d)} }( l(\varvec{\theta }, \hat{\varvec{\beta }}, Z))\nonumber \\= & {} \sum _{k=1}^{K}\sum _{i=1}^{n}\tau _{k,i}^{(d)}[\log \pi _{k}+\log f(\hat{\varvec{\beta }}_i;\varvec{\mu }_k,\varvec{\Sigma }_k)]\nonumber \\{} & {} -\lambda _1\sum _{k=1}^{K} \sum _{j=1}^{p}|\mu _{k,j}|-\lambda _{2}\sum _{k=1}^{K}\sum _{j,l}^{p}|W_{k;j,l}|, \qquad \end{aligned}$$

(5)

where

$$\begin{aligned} \widehat{\tau }_{k,i}^{(d)}=\frac{\widehat{\pi }_{k}^{(d)} f(\hat{\varvec{\beta }}_i;\widehat{\varvec{\mu }}_k^{(d)},\widehat{\varvec{\Sigma }}_k^{(d)})}{\sum _{k=1}^{K} \widehat{\pi }_{k}^{(d)}f(\hat{\varvec{\beta }}_i;\widehat{\varvec{\mu }}_k^{(d)},\widehat{\varvec{\Sigma }}_k^{(d)})} \end{aligned}$$

(6)

is the posterior probability that an object i, summarised here by $\hat{\varvec{\beta }}_i$, belongs to the kth group. The M-step then maximizes the function $Q_P$ in order to update the estimate of $\varvec{\theta }$. By setting to zero the first derivates of $Q_P$ w.r.t. $\pi _k$ we obtain

$$\begin{aligned} \widehat{\pi }_{k}^{(d+1)}=\sum _{i=1}^{n}\frac{\tau _{k,i}^{(d)}}{n}. \end{aligned}$$

(7)

Then, for the mean vectors, given j and k, the EM algorithm leads to the following updating formulas for $\mu _{j,k}$ (Zhou et al. 2009)

$$\begin{aligned} {\left\{ \begin{array}{ll} \widehat{\mu }_{j,k}^{(d+1)}=0 \quad \text {if} \quad \left| \sum _{i=1}^{n}\tau _{k,i}^{(d)}\left( \sum _{l=1,l\ne j}^{p}(\hat{{\beta }}_{l,i}-\widetilde{\mu }_{l,k}^{(d+1)})W_{k;j,l}+\hat{{\beta }}_{j,i}W_{k;j,j}\right) \right| \le \lambda _{1}\\ \\ \widehat{\mu }_{j,k}^{(d+1)}=\left[ \Bigl (H-\lambda _1\text {sign}(H) \Bigr )/\sum _{i=1}^{n} \tau _{k,i}^{(d)} \right] W_{k;j,j}^{-1} \quad \text {otherwise}, \\ \end{array}\right. } \end{aligned}$$

(8)

where $H=\sum _{i=1}^{n}\tau _{k,i}^{(d)}(\hat{\varvec{\beta }}_i' \textbf{W}_{k;. j})-\left( \sum _{i=1}^{n} \tau _{k,i}^{(d)}\right) \left( \widetilde{\varvec{\mu }}_{k}^{(d+1)'}\right. \left. \textbf{W}_{k;. j}-\widetilde{\mu }_{k,j}^{(d)} W_{k;j,j}\right)$, $\textbf{W}_{k;. j} = (W_{k;1,j},\ldots , W_{k;p,j})'$, and $\widetilde{\varvec{\mu }}_{k}^{(d+1)}= \sum _{i=1}^n \tau _{k,i}^{(d+1)} \hat{\varvec{\beta }}_i / \sum _{i=1}^n \tau _{k,i}^{(d+1)}$.

Finally, for the elements of the precision matrices $\textbf{W}_k=\varvec{\Sigma }_{k}^{-1}$, to maximize $Q_p$ we maximize

$$\begin{aligned}&\frac{1}{2} \sum _{k=1}^{K} \sum _{i=1}^{n} \tau _{k,i}^{(d)} \log \text {det}\left( \textbf{W}_{k}\right) \nonumber \\&\qquad -\frac{1}{2} \sum _{k=1}^{K} \sum _{i=1}^{n} \tau _{k,i}^{(d)}\left( \hat{\varvec{\beta }}_{i}-\varvec{\mu }_{k}\right) ' \textbf{W}_{k}\left( \hat{\varvec{\beta }}_{i}-\varvec{\mu }_{k}\right) \nonumber \\&\qquad -\lambda _{2} \sum _{k=1}^{K}\sum _{j,l}^{p}|W_{k;j,l}| \nonumber \\&\quad = \sum _{k=1}^{K}\left( \frac{\sum _{i=1}^{n} \tau _{k,i}^{(d)}}{2} \log \text {det}\left( \textbf{W}_{k}\right) \right. \nonumber \\&\qquad \left. -\frac{\sum _{i=1}^{n} \tau _{k,i}^{(d)}}{2} \text {tr}\left( \tilde{\textbf{S}}_{k} \textbf{W}_{k}\right) -\lambda _{2} \sum _{j,l}^{p}|W_{k;j,l}| \right) , \end{aligned}$$

(9)

where $\tilde{\textbf{S}}_{k}$ is the empirical covariance matrix in each cluster

$$\begin{aligned} \tilde{\textbf{S}}_{k} =\frac{\sum _{i=1}^{n}\tau _{k,i}^{(d)}(\hat{\varvec{\beta }}_{i}-\varvec{\mu }_{k})' (\hat{\varvec{\beta }}_{i}-\varvec{\mu }_{k})}{\sum _{i=1}^{n}\tau _{k,i}^{(d)}}. \end{aligned}$$

As shown by Zhou et al. (2009), these equations are at the base of the “graphical lasso” (GLASSO) algorithm (Friedman et al. 2008) such that the estimates of $\widehat{W}_{k;j,l}^{(d+1)}$ can be obtained by using the R package glasso ( Friedman et al. 2019). For the more restricted cases of common and diagonal covariance matrices the solutions can be adapted from those in Pan and Shen (2007) and Zhou et al. (2009).

3.3 Model selection

Thus far, we have treated the number of clusters K and the tuning parameters $\lambda _1$ and $\lambda _2$ as fixed. In practice, the choice is critical in determining the performance of our clustering procedure. A commonly used strategy to choose these parameters is to find the best combination of values for $(K,\lambda _1,\lambda _2)$ using a cross-validation procedure (CV). Despite its general applicability and competitive performance, a major drawback of CV is the intensive computation it requires. To overcome this problem, we first determine candidate values of $\lambda _1$, $\lambda _2$ and K from a discrete three-dimensional grid and then we evaluate the choice of the triplet $(K,\lambda _1,\lambda _2)$ relying on likelihood-based measures of model fit that include a penalty for model complexity. In particular, we consider the Bayesian Information Criterion (BIC)

$$\begin{aligned} BIC(K, \lambda _1, \lambda _2)=l(\hat{\varvec{\theta }}_K; \hat{\varvec{\beta }}|K, \lambda _1, \lambda _2)-\frac{M}{2}\log (n), \end{aligned}$$

and the Integrated Classification Likelihood (ICL) index (Baudry 2015)

$$\begin{aligned} ICL(K, \lambda _1, \lambda _2)= & {} BIC(K, \lambda _1, \lambda _2)\\{} & {} + \sum _{k=1}^K\sum _{i=1}^n \hat{T}_{k,i} \log (\hat{T}_{k,i}) \end{aligned}$$

where $\hat{\varvec{z}}$ are the MLE allocations/membership corresponding to the estimated parameters, $l(\hat{\varvec{\theta }}_K)$ is the value of the maximized log-likelihood objective function with parameters $\hat{\varvec{\theta }}_K$ estimated under the assumption of a model with K components, M is the number of parameters under the assumption of K groups and $\widehat{\tau }_{k,i}$ is the estimated posterior probability that an object i belongs to the kth group. The key difference between BIC and ICL is that the latter includes an additional term (the estimated mean entropy) that penalises clustering configurations exhibiting overlapping groups: low entropy solutions with well-separated groups are preferred to configurations that give the best match with regard to the distributional assumptions.

One difficulty in using the above criteria is that it is not always clear what is M in a penalized model. In our case we set

$$\begin{aligned} M= \sum _{k=1}^{K} \sum _{j=1}^{p} I \Bigl (\hat{\mu }_{k,j} \ne 0\Bigr ) \!+\! \sum _{k=1}^K \sum _{i \le j} I\Bigl ( \widehat{{\Sigma }}_{k;j,l} \ne 0\Bigr )\!+\! (K-1) \end{aligned}$$

where $I(\cdot )$ is the indicator function which applies to the (sparse) likelihood estimate of $\varvec{\mu }_{k}$ and $\varvec{\Sigma }_k$. In practice, we set the degrees of freedom M as the number of nonzero entries in both the means and the upper half of the covariance matrices plus the number of parameters for the mixing proportions.

3.4 Implementation of PFC-$\hbox {L}_1$

In order to implement the PFC-$\hbox {L}_1$ algorithm, the first step is to specify the number of basis functions, p, in the expansion of Eq. (2), to recover the true smooth process $X(\varvec{t})$. There are two cases to consider. If the data are observed without a measurement noise, a possibility is to choose p big enough to interpolate exactly $\textbf{x}_i$. On the other hand, by choosing $p < T$, where T is the number of evaluation points, the expansion will be a smoothed version of the original data $Y(\varvec{t})$ and this choice of p appears thus suitable in the presence of a measurement noise $\epsilon (\varvec{t})$. A useful assumption for us is to assume that the noise variance is homoscedastic and constant across the objects. In this case, the presence of the measurement noise can be detected through several methods and some of them have been compared in Ippoliti et al. (2005) in the context of image analysis. One possibility, for example, is to estimate the variance $\sigma _\epsilon ^2$ by the median absolute deviations (MAD) of the wavelet coefficients obtained for each random object $\mathcal {Y}$ (Donoho et al. 1995) or, alternatively, following a geostatistical approach, by considering the behaviour of the variogram of the data near the origin—i.e., treating $\epsilon (\varvec{t})$ as nugget effect (Huang and Cressie 2000). Both these methods can be used for one-dimensional functional data and surface data. If there is evidence of a measurement noise, the model assumptions under equations (1) and (2) suggest to choose p as the value for which the corresponding estimated correlation matrix of the noise, $\hat{\varvec{R}}_\epsilon (p)$, as a function of p, becomes spherical. In practice, considering the observed objects $\bigl \{\textbf{y}_1, \textbf{y}_2, \ldots , \textbf{y}_n \bigr \}$, where $\textbf{y}_i = (y_{i1} \ldots y_{iT})'$ is defined over a discrete domain with T points, the correlation matrix of the noise is estimated as

$$\begin{aligned} \hat{\varvec{R}}_\epsilon (p)= diag(\hat{\varvec{\Sigma }}_\epsilon (p)^{-1/2})\, \hat{\varvec{\Sigma }}_\epsilon (p) \, diag(\hat{\varvec{\Sigma }}_\epsilon (p)^{-1/2}) \end{aligned}$$

where $\hat{\varvec{\Sigma }}_\epsilon (p) = \frac{1}{n-1}\sum _{i=1}^{n} (\textbf{e}_i- \overline{\textbf{e}_i})(\textbf{e}_i- \overline{\textbf{e}_i})'$ is the covariance matrix, $\textbf{e}_i= \textbf{y}_i -\hat{\textbf{y}}_i$ and $\hat{\textbf{y}}_i = \varvec{\Phi }_p \hat{\varvec{\beta }}_i$. By evaluating the Frobenius norm

$$\begin{aligned} F(p)=||\hat{\varvec{R}}_\epsilon (p)-\varvec{I}||_F, \end{aligned}$$

(10)

we consider a distance from the assumption of sphericity such that we choose the value of p, say $p_0$, for which F(p) is minimized. We note that this is a specific case of the Procrustes size-and-shape distance used by Dryden et al. (2009).

To give a flavour of the performance of the proposed procedure, Fig. 1 shows the results of choosing $p_0$ for the representation of a set of 200 one-dimensional functions generated by using equations (1) and (2) with 25 Fourier basis functions and an additive measurement noise with $\sigma _{\epsilon }^2= 1$. By working with the same family of basis functions, the minimum in Fig. 1 clearly suggests a choice of $p_0=25$. Note that these results refer to the first scenario of the simulation setting described in Sect. 4.1.

Fig. 1

The F(p) function at different values of number of basis functions p ($p_0=25$ is chosen at the minimum)

To sum up, the proposed PFC-$\hbox {L}_1$ algorithm thus follows the steps delineated below:

Algorithm 1

PFC-L$_1$ algorithm

4 Simulation results and benchmark data

An initial assessment of the methodology proposed for clustering functional data is performed by means of a simulation study performed in R (R Core Team 2023). To compare our procedure with other approaches, the simulations are carried out for one-dimensional functions.

Section 4.1 of this study aims to first ensure the appropriate identification of the features of the generating mixture model. To this end, we provide an illustration of the behavior of the penalized functional clustering method PFC-$\hbox {L}_1$ under different scenarios that correspond to various sources of variability. Additionally, in Sect. 4.2, we compare PFC-$\hbox {L}_1$ with existing methods in the literature through experiments where the stochastic part of the functions is simulated using Wiener processes. Finally, we conclude the section by discussing the performance of PFC-$\hbox {L}_1$ on benchmark datasets.

Given that labels are known both in simulations and benchmark datasets, performances are evaluated in terms of clustering accuracy, that is the percentage of correctly classified functions.

4.1 Simulation 1: functional clustering and discriminant basis function retrieval

The selection of cluster-relevant discriminant basis functions appears an important and challenging issue within functional clustering. Since the inclusion of unnecessary components might mask the cluster structure, the aim of this simulation is twofold: (i) show that the $L_1$ penalization on the set of the expansion coefficients of Eq. (2) favours an adaptive regularization that removes noise while preserving dominant local features, accommodating for possible heterogeneity along the domain of the curves; (ii) investigate how different sources of variability affect the clustering performance of PFC-$\hbox {L}_1$, measured as clustering accuracy.

In the following scenarios, the statistical analysis is illustrated for data simulated by means of a finite mixture of specific distributions. In particular, based on Eqs. (1) and (2), the curves are simulated (except for scenario E) using a combination of $p=25$ Fourier basis functions defined over a one-dimensional regular grid with 100 discrete points (i.e. $\mathcal {T} =\{0, 1, \ldots , 99 \}$). Cluster-relevant basis functions are defined as those with specific frequency content (from 1 to 12 Hz) and for which the corresponding expansion coefficients appear “significantly” larger than others and particularly relevant for discriminating between groups. In all cases, the measurement noise is considered as independent with mean zero and variance $\sigma _\epsilon ^2=1$, and the estimate of the latent/true function X(t) follows the procedure described in Sect. 3.1 using the MAD estimator for $\sigma _\epsilon ^2$. The estimate of the number of groups K is performed using both the BIC and the ICL indices.

To generate distinct patterns across the domain and define the axes of group separability, we specify the distributions of the expansion coefficients according to five scenarios. Firstly, coefficient vectors are drawn from Normal distributions with isotropic, diagonal, and non-diagonal covariance matrices (scenarios A, B, and C). Secondly, to assess the performance of PFC-$\hbox {L}_1$ under non-Gaussian assumptions, coefficient vectors are drawn from Skew Normal distributions (scenario D). Finally, to examine the effect of the choice of basis functions on classification, we generate functions using a wavelet basis and reconstruct them using Fourier basis functions (scenario E). Specifically:

• (1) Scenario A considers a mixture of four ($K=4$) multivariate Gaussian distributions with isotropic covariance matrices, i.e.

  $$\begin{aligned} \varvec{\beta }_k \sim \mathcal {N}(\varvec{\mu }_k; \textbf{I}_k), \ \ k=1, \ldots ,4. \end{aligned}$$

  With the exclusion of 3 entries per group, the means $\varvec{\mu }_k$ are all zero mean vectors. The amplitude of the non-zero expansion coefficients identify the cluster-relevant variables and, at the same time, highlight the dominant frequency contents of the sine and cosine functions per each group. The number (n) of simulated curves is 200, with 50 functions per group.

• (2) Scenario B considers a mixture of two ($K=2$) multivariate Gaussian distributions with diagonal covariance matrices, $\varvec{\Sigma }_k$, i.e.

  $$\begin{aligned}{} & {} \varvec{\beta }_k \sim \mathcal {N}(\varvec{\mu }_k; \varvec{\Sigma }_k) \; \text {with} \\{} & {} \varvec{\Sigma }_k=diag\{\sigma _{j,k}^2\}, \sigma _{j,k}^2\sim U(1,3), \ \ j=1, \ldots , 25, \ k=1, 2. \end{aligned}$$

  As in the previous scenario, with the exclusion of 3 entries per group, the means $\varvec{\mu }_k$ are all zero mean vectors. However, differently from scenario A, the expansion coefficients for the two groups are defined at the same frequencies such that the difference is only in their amplitude. The number (n) of simulated curves is 200, with 100 functions per group.

• (3) Scenario C considers a mixture of two ($K=2$) multivariate Gaussian distributions with non-diagonal covariance matrices, i.e.

  $$\begin{aligned} \varvec{\beta }_k \sim \mathcal {N}(\varvec{\mu }_k; \varvec{\Sigma }_k), \ k=1, 2. \end{aligned}$$

  In this case, apart from 5 entries per group, the means $\varvec{\mu }_k$ are all zero mean vectors and the covariance matrices are sparse. The expansion coefficients of the two groups are specified at the same frequencies and the group covariance matrices are obtained by rescaling a given correlation matrix by a diagonal matrix of standard deviations drawn from a Uniform distribution with interval [1, 3]. The covariance matrices result sparse with maximum correlations of 0.6 between coefficients. The number (n) of simulated curves is 200, with 100 functions per group.

• (4) Scenario D considers a mixture of four ($K=4$) multivariate Skew Normal distributions, i.e.

  $$\begin{aligned} \varvec{\beta }_k \sim \mathcal{S}\mathcal{N}(\varvec{\mu }_k; \textbf{I}_k;\alpha _k) \; \text {with} \ \alpha _k \sim \mathcal {U}(-4; 4),\ \ k=1, \ldots ,4. \end{aligned}$$

  with the exclusion of 3 entries per group, the location parameters $\varvec{\mu }_k$ are all zero vectors. The amplitude of the non-zero expansion coefficients identify the cluster-relevant variables and, at the same time, highlight the dominant frequency contents of the sine and cosine functions per each group. Note that here, differently from Scenario A, the parameters $(\varvec{\mu }_k; \textbf{I}_k)$ are not the mean and the covariance in each cluster, while the vector parameter $\alpha _k$ regulates the skewness of the distribution in each cluster (see, for example, Azzalini and Capitanio 1999 for more details). The number (n) of simulated curves is 200, with 50 functions per group.

• (5) Scenario E considers a mixture of four ($K=4$) multivariate Gaussian distributions with spheric covariance matrices, i.e.

  $$\begin{aligned} \varvec{\beta }_k \sim \mathcal {N}(\varvec{\mu }_k; \textbf{I}_k), \ \ k=1, \ldots ,4. \end{aligned}$$

  Here the main difference from the previous scenarios is that the functions are generated from a series of $p=128$ Daubechies extremal phase wavelets basis functions (Daubechies 1999) but reconstructed using Fourier basis functions.

In the following we provide a brief summary of the results of the simulations. More details, including the complete set of associated figures, can be found in the Supplementary Material. The comments refer to estimates averaged over 100 replicated functional datasets, each consisting of 200 curves recontructed using Fourier basis functions. The performance of the PFC-$\hbox {L}_1$ method is satisfactory in general; moreover the strategy based on F(p) illustrated in Sect. 3.4 shows an high level of accuracy in selecting the number of basis functions for the first four scenarios. Furthermore, the number of clusters is estimated correctly and both the BIC and the ICL indices appear to be robust estimators of K considering the different types of complexity of the generated data. In all the proposed scenarios the results provided by BIC and ICL are very similar.

Considering scenarios A and B, results show that the PFC-$\hbox {L}_1$ procedure is able to correctly retrieve the cluster-discriminant basis functions (i.e. the correct sparseness structure) and the number of groups. The level of accuracy of the identified groups is very high being $100 \%$ for A and $97 \%$ for B. For the second and third scenarios it seems to be slightly more difficult to retrieve the discriminant basis functions as some coefficients fixed at zero in the simulation are included in the model (see Figures 5 and 7 in the Supplementary Material). There is the hint that the retrieval of the correct structure becomes more difficult when the expansion coefficients are correlated. However, also for these scenarios the number of clusters is always correctly identified. For the third and fourth scenarios the level of accuracy remains significantly high being $86 \%$ on average for scenario C and $100\%$ for scenario D. Finally, regarding the scenario E, the simulation suggests that using Fourier basis functions requires a smaller number ($p_0=35$) of functions compared with the number of wavelets ($p=128$) used to generate the data. Also, Figure 11 in the Supplementary Material shows that it is difficult to obtain a sparse structure in the mean component under this scenario. The number of estimated clusters is correctly estimated at $96\%$ with only a $4\%$ associated to a value of $K=3$. The quality of the estimated clusters remains very good as the clustering procedure gives a $99\%$ of accuracy.

4.2 Simulation 2: a comparison with other approaches

To evaluate the performance of PFC-$\hbox {L}_1$ and compare it with other existing clustering methods, we conduct an experiment where groups of functions are generated using one of the three different models defined in the simulation design proposed in Aguilera et al. (2021) for homogeneity tests. This simulation design has also been discussed (Górecki and Smaga 2015).

In particular, the generating model assumes the following decomposition

$$\begin{aligned} y_{k}(t) = \mu _{k}(t) + \zeta (t), \quad k=1,\ldots ,K, \end{aligned}$$

where $\mu _{k}(t)$ is the mean function of the kth group and $\zeta (t)$ is a Wiener process with mean zero and covariance function $C_\zeta (s,t)=\sigma ^2 min(s,t)$, with $(s,t) \in [0,1]$. Note that the groups only differ in terms of the means function $\mu _{k}(t)$. Since the eigenfunctions and the eigenvalues of the Wiener process are known, the truncated Karhunen–Loève expansion can be used to generate realisations of $\zeta (t)$ as follows

$$\begin{aligned} \zeta (t) \simeq \sum _{j=1}^{q} \sqrt{\xi _j} \ \psi _j(t) \ Z_j \end{aligned}$$

where $\xi _j = \frac{\sigma ^2}{\left( j-\frac{1}{2}\right) ^2 \pi ^2}$ and $\psi _j(t)= \sqrt{2} \sin \left( \left( j-\frac{1}{2}\right) \pi t\right)$ are, respectively, the eigenvalues and the eigenfunctions of the covariance operator $C_\zeta (s,t)$, while $Z_j$ are independent Gaussian random variables $\mathcal {N}(0,1)$. In order to differentiate the groups, the mean functions are defined as $\mu _k(t)=0.025 \ k \ |sin(4\pi t)|, \;$ with $k=1,2,3$. This parametrization for the mean corresponds to model M3 in Aguilera et al. (2021), which is the most challenging scenario considered in their simulation experiment. Also, as in Aguilera et al. (2021), we set the truncation parameter at $q=20$ and consider 5 values for $\sigma$, namely $\sigma \in (0.02, 0.05, 0.10, 0.20, 0.40)$. Finally, to evaluate the robustness of the procedure in a non-Gaussian scenario, we compute the exponential of the error terms $\zeta (t)$, suitably centered.

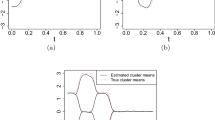
Overall, 10 different parameterizations are considered in this simulation study providing two scenarios considering Gaussian and non-Gaussian processes, and 5 different values for the dispersion parameter $\sigma$. For 51 equally spaced points in the interval [0, 1], and for $K=3$, examples of two simulated datasets, obtained with $\sigma =0.02$ and $\sigma =0.10$, and for Gaussian and non-Gaussian errors, are shown in Fig. 2 − other plots can be found in the Supplementary Material. As can be observed, the identification of the three clusters becomes more challenging for larger values of $\sigma$ and in the case of Gaussianity, where the differences between mean functions become smaller relative to the variability of the data.

The following comments refer to estimates of the accuracy index averaged over 100 replicated functional datasets, each containing $n=75$ curves divided into $K=3$ groups, each consisting of 25 curves.

As competing algorithms for PFC-$\hbox {L}_1$, we consider several methods implemented in R packages. Specifically, we compare PFC-$\hbox {L}_1$ with FunHDDC proposed by Bouveyron and Jacques (2011), Curvclust by Giacofci et al. (2013), and FunFEM by Bouveyron et al. (2015), which are implemented in the homonymous R packages (Schmutz et al. 2021; Giacofci et al. 2012; Bouveyron 2021). Additionally, we evaluate the performance of the most recent method SaS-Funclust by Centofanti et al. (2023), which is implemented in the R package sasfunclust (Centofanti et al. 2021). Finally, we implement Fclust by James and Sugar (2003) using the sasfunclust package without penalties.

Figure 3 shows the average clustering accuracy as a function of the dispersion parameter $\sigma$ (in logarithmic scale) for the considered models in the two cases of Gaussian and non Gaussian errors. As can be observed, possible differences in the clustering results among the different procedures become more apparent for the first two values of $\sigma$. As expected, as $\sigma$ increases, it becomes more challenging to retrieve the true clusters, and all methods perform similarly, resulting in small values for the accuracy index. Under Gaussianity assumptions, results show that PFC-$\hbox {L}_1$ has the best performance, followed by SaS-Funclust and Fclust, whose accuracy values are similar. Our results also suggest that, for small values of $\sigma$, FunFEM—with default values - has the worst performance among the methods evaluated. Finally, we also notice that the task of accurately clustering the functions is less challenging in the non-Gaussian case, and all methods achieve higher accuracy values. This may be due to the lower level of variability in the data (see Fig. 2). In this scenario, all the methods perform similarly well, with slight preferences for SaS-Funclust and Fclust. In general, FunFEM and Curvclust perform the worst among the methods evaluated.

Fig. 2

Simulated curves with Gaussian (first row) and not Gaussian (second row) error functions, with dispersion parameter  $\sigma =0.02$ (left) and $\sigma =0.10$ (right) (Note that the value interval is larger for larger $\sigma$)

Fig. 3

Average Clustering Accuracy as a function of $\sigma$ in logarithmic scale in the Gaussian error (left) and not Gaussian error case (right)

4.3 Results from benchmark datasets

In this section, we also briefly compare the performance of PFC-$\hbox {L}_1$ with other existing clustering algorithms by considering three well-known benchmark data sets, namely the electrocardiogram (ECG), the Face and the Wafer dataset.¹

The ECG dataset comprises a set of 200 electrocardiograms from 2 groups of patients, myocardial infarction and healthy, sampled at 96 time instants in time, while the Face dataset consists of 112 outlines of face sampled at 350 discrete points for four groups. Finally, the Wafer data collects 7174 curves sampled from 2 groups at 152 instants of time collection of in-line process control measurements recorded from various sensors during the processing of silicon wafers for semiconductor fabrication.

These data were previously used to compare the performance of several functional clustering models in Bouveyron et al. (2015), with $p=20$ cubic spline basis functions. The results in their Table 5 show that the FunFEM model, compared with other clustering techniques, achieved the best performance in terms of accuracy (according to known labels) in two out of the three datasets considered. Table 1 reports their clustering accuracy results updated with ours obtained by using PFC-$\hbox {L}_1$ (and the BIC index for model selection) and with results of SaS-Funclust by Centofanti et al. (2023). As it can be noticed, PFC-$\hbox {L}_1$ is the second best for the ECG data, and stands apart from the others together with the best SaS-Funclust in the Face case. For the Wafer data PFC-$\hbox {L}_1$ is reasonably close to FunFEM and comparable (or slightly better) with the others. Actually, PFC-$\hbox {L}_1$ behaves well in all three cases showing a sort of robustness with respect to the case study.

Table 1 Clustering accuracies on the ECG, Face and Wafer data set for other state of the arts models as shown in Table 5 of Bouveyron et al. (2015), augmented with  SaS-Funclust by Centofanti et al. (2023) and the selected PFC-$\hbox {L}_1$ results in the last line.

5 Functional zoning for air quality monitoring

In this section we still focus on one-dimensional functional data but now consider the more complicated case of working with spatially indexed functional data. In this case, the curves $Y(\textbf{s},t)$ show a spatial component $\textbf{s} \in \mathcal {R}^2$ that represents the locations in a given region of interest, while t represents the continuous parameter of the functional data (time in our case).

The literature on clustering spatially dependent functions is not as extensive as for the case of independent functions, as it can be also seen in Sect. 6 of the updated review by Zhang and Parnell (2023). Proposals in the frameworks of hierarchical and dynamic clustering approaches, where the similarity between pairs of curves is based on the use of the variogram function, are given by Giraldo et al. (2012), Romano et al. (2012) and Romano et al. (2017). Other approaches based on the use of spatial heterogeneity measures and spatial partitioning methods were also proposed by Dabo-Niang et al. (2010) and Secchi et al. (2013), respectively. Proposals in a model-based framework, instead, can be found in Jiang and Serban (2012), where spatial dependence is introduced by assuming a Gibbs distribution for the cluster membership variable Z, and Vandewalle et al. (2021), as well as Wu and Li (2022), where a multinomial logistic regression model for $\pi _k$, with longitude and latitude coordinates included as regressors, is used to account for the spatial information. Also Liang et al. (2021) model cluster membership but by means of a locally dependent Markov Random Field to account for spatial dependence. In this paper, we consider a multinomial logistic regression model too and extend this approach by properly modelling the spatial dependence of the mixing coefficients of the GMM model.

We consider the problem of functional zoning introduced in Sect. 1 and use daily $\hbox {PM}_{10}$ time series as in Ignaccolo et al. (2013). In particular, the data refer to calibrated output of a three-dimensional deterministic modeling system (Chemistry Transport Model Flexible Air Quality Regional Model) implemented by the environmental agency ARPA Piemonte (Italy). The calibration is obtained by “assimilating” data observed at monitoring stations through a spatial kriging for each day, where the output of the deterministic model plays as a covariate in the external drift. The “krigged” $\hbox {PM}_{10}$ concentrations are available on a regular grid with resolution 4km $\times$ 4km covering a surface of $220 \times 284$ km$^2$. Overall, there are $n=1763$ sampled curves available (one for each knot of the grid), each with $T=365$ temporal observations.

Since the time series show some periodicities, we use Fourier basis functions to obtain our smoothed curves. The MAD estimator, providing an estimate of $\widehat{\sigma }_\epsilon$ equal to 6.02, gives evidence of the presence of measurement noise. As shown in Fig. 4, it follows that 200 basis functions are necessary to minimize the Frobenius norm F(p) and to improve the signal-to-noise ratio.

Fig. 4

The F(p) function at different values of number of basis functions p. The Frobenius norm is minimized by using  $p_0=200$ Fourier basis functions

Because the spatial dependence of the smoothed curves cannot be neglected in partitioning the Piemonte region in spatially homogeneous zones, the second step of the algorithm outlined at the end of Sect. 3 is adjusted by introducing spatially varying mixing coefficients in the GMM model.

As in Vandewalle et al. (2021), we model the spatial dependence of the curves by modelling the distribution of the weights such that observations corresponding to nearby locations are more likely to have similar allocation probabilities than observations that are far apart in space. In particular, we denote the mixing proportions as $\pi _k(\textbf{s}), \ \textbf{s}=(s_1, s_2) \in \mathcal {R}^2$ and, considering the Kth group as a baseline, we also define the log-odds $\gamma _k(\textbf{s}_i) = \log \bigl (\pi _k(\textbf{s}_i) / \pi _K(\textbf{s}_i)\bigr )$, for $i=1, \ldots , n$ and $k=1, \ldots , K-1$. Considering a multinomial logit model, we thus assume that the log-odds at each site follow a linear model

$$\begin{aligned} \gamma _k(\textbf{s}_i | \varvec{\omega }_{k})= \sum _{l=1}^L \omega _{l,k} \ \varvec{\psi }_{l}(\textbf{s}_i), \end{aligned}$$

(11)

where $\varvec{\psi }_{l}$ are basis functions lying in a L-dimensional vector space of functions $\varvec{\mathcal {P}}$ specifying how the process can vary spatially, $\varvec{\omega }_k=\bigl (\omega _{1,k}, \ldots , \omega _{L,k} \bigr )$ are model regression coefficients and $L \le n$. Estimation of the parameters of this model can be carried out by maximum likelihood thus obtaining

$$\begin{aligned} \widehat{\varvec{\omega }}_k^{(d+1)} = \underset{\varvec{\vartheta }_k}{arg \ max} \sum _{i=1}^n\sum _{k=1}^K \hat{\tau }_{k,i}^{(d)}(\textbf{s}_i) \log \bigl (\pi _k(\textbf{s}_i | \varvec{\omega }_{k})\bigr ) \end{aligned}$$

where $\hat{\tau }_{k,i}^{(d)}(\textbf{s}_i)$ are the estimated posterior probabilities computed as in (6) but with the spatially varying mixing coefficients $\hat{\pi }_k(\textbf{s}_i| \varvec{\omega }_{k})$.

To provide more details about the spatial structure of the log-odds $\gamma _k(\textbf{s}_i)$, we note that Eq. (11) represents a truncated expansion of the spatial process $\varvec{\gamma }_k= \bigl (\gamma _k(\textbf{s}_1), \ldots , \gamma _k(\textbf{s}_n) \bigr )$. This can be done as a result of the Karhunen-Loéve (KL) theorem (Adler 2010), which establishes that $\gamma _k(\textbf{s})$ admits a decomposition $\gamma _k(\textbf{s})=\sum _{l=1}^\infty \omega _{l,k} \ \varvec{\psi }_{l}(\textbf{s})$, where $\omega _{l,k}$ are pairwise uncorrelated random variables and the $\varvec{\psi }_{l}(\textbf{s})$ are pairwise orthogonal basis functions in the domain of $\gamma _k(\textbf{s})$. In practice, the prediction of $\gamma _k(\textbf{s})$ is typically the truncated KL expansion based on the property that given any orthonormal basis functions $\varvec{\psi }_{l}(\textbf{s})$, we can choose a large integer L, so that $\gamma _k(\textbf{s})$ can be approximated by the finite weighted sum of basis functions. In this paper, to specify the basis functions in Eq. (11), we define the matrices

$$\begin{aligned} \varvec{\Pi }=\left( \begin{array}{cc} \varvec{V} &{} \textbf{U} \\ \textbf{U}' &{} \textbf{0} \\ \end{array}\right) \quad \text {and } \quad \varvec{\Pi }^{-1}=\left( \begin{array}{cc} \textbf{B} &{} \textbf{R} \\ \textbf{R}' &{} \textbf{C} \\ \end{array}\right) \end{aligned}$$

and assume that $\textbf{U}$ is the $(n \times 3)$ design matrix containing the coordinates of the sites, i.e. the ith row is $\varvec{u}_{i}(\textbf{s}_i)= ( 1 \ s_{1i} \ s_{2i} ), \ i=1, \ldots , n$, and $\varvec{V}$ is the Generalized covariance (variogram) matrix with elements $v(\textbf{s}_i,\textbf{s}_j)=\frac{1}{8\pi }\Vert \textbf{s}_i - \textbf{s}_j\Vert ^2 \log \Vert \textbf{s}_i - \textbf{s}_j\Vert$ (Chilès and Delfiner 2012). Then, the basis functions $\varvec{\psi }_{l}(\textbf{s}_i)$ are defined as the eigenvectors of the spectral decomposition of $\textbf{B}=\varvec{\Psi } \varvec{\Xi } \varvec{\Psi }'$, where $\varvec{\Psi }= \bigl (\varvec{\mathcal {\varvec{\psi }}}_1, \ldots , \varvec{\varvec{\psi }}_n \bigr )$, $\varvec{\varvec{\psi }}_l= \Bigl (\varvec{\psi }_{l}(\textbf{s}_1), \ldots , \varvec{\psi }_{l}(\textbf{s}_n) \Bigr )'$ and $\varvec{\Xi }=diag(\xi _1, \ldots , \xi _n)$. Since for this choice of $\textbf{U}$ and $\textbf{V}$, $\textbf{B}\textbf{U}=\varvec{0}$ and $\varvec{\mathcal {P}}_0=span(1,s_{1i}, s_{2i})$ is a vector space of functions called the null space, which forms a subspace of $\varvec{\mathcal {P}}$, it follows that the first three eigenvalues are equal to zero, and writing them in non-decreasing order we thus have $0 = \xi _1 = \xi _2 = \xi _3 < \xi _4 \le \xi _5 \le \ldots \le \xi _n$. Under these assumptions, it follows that Eq. (11) can be rewritten as

$$\begin{aligned} \gamma _k(\textbf{s}_i | \varvec{\omega }_{k})= & {} \omega _{0,k} + \omega _{1,k} \ s_{1i} + \omega _{2,k} \ s_{2i} + \sum _{l=3}^L \omega _{l,k} \ \varvec{\psi }_{l}(\textbf{s}_i)\nonumber \\= & {} \sum _{l=0}^L \omega _{l,k} \ \varvec{\psi }_{l}(\textbf{s}_i), \end{aligned}$$

(12)

where $\varvec{\psi }_{0}(\textbf{s}_i)=1$, $\varvec{\psi }_{1}(\textbf{s}_i)=s_{1i}$, $\varvec{\psi }_{2}(\textbf{s}_i)=s_{2i}$ and $L \le n$. Furthermore, because the eigenfunctions are estimated through a spectral decomposition of $\textbf{B}$, the $\varvec{\psi }_{l}(\textbf{s}_i)$ have been sometime denoted in the past as principal functions. Similar approaches, in fact, can be found, for example, in Mardia et al. (1998) in the field of spatio-temporal statistics and then in Kent et al. (2001), Fontanella et al. (2019a) and Fontanella et al. (2019b) for applications in shape analysis. It also turns out that under this model parametrization, the $\varvec{\psi }_{l}(\textbf{s}_i)$ is also an interpolating thin-plate spline which, subject to the constraints $\varvec{\psi }_{l}(\textbf{s}) \equiv \varvec{\psi }_{l}(\textbf{s}_i)$ for any $\textbf{s} \in \{ \textbf{s}_1, \ldots , \textbf{s}_n\}$, minimises the penalty (Mardia et al. 1996)

$$\begin{aligned} J(\varvec{\psi }_l)= \int \left[ \left( \frac{\partial ^2 \ \varvec{\psi }_l}{\partial s_1^2} \right) ^2 + 2 \left( \frac{\partial ^2 \ \varvec{\psi }_l}{\partial s_1\partial s_2} \right) ^2 + \left( \frac{\partial ^2 \ \varvec{\psi }_l}{\partial s_2^2} \right) ^2 \right] d \textbf{s} \end{aligned}$$

where the integral is over $\mathcal {R}^2$. It thus follows that, given the relationship between thin-plate splines and the kriging interpolator, for any new site $\textbf{s}_0 \notin \{ \textbf{s}_1, \ldots , \textbf{s}_n\}$, the spatial process of the log-odds can be predicted as

$$\begin{aligned} \gamma _k(\textbf{s}_0 | \varvec{\omega }_{k})= & {} \omega _{0,k} + \omega _{1,k} \ s_{10} + \omega _{2,k} \ s_{20} \nonumber \\{} & {} + \sum _{l=3}^L \omega _{l,k} \ \varvec{\psi }_{l}(\textbf{s}_0) \end{aligned}$$

(13)

where the eigenfunctions $\varvec{\varvec{\psi }}_l$ are predicted by kriging through

$$\begin{aligned} \varvec{\psi }_{l}(\textbf{s}_0) = \left[ \textbf{B} \ \textbf{v}_0(\textbf{s}_i,\textbf{s}_0)+\textbf{R} \ \varvec{u}(\textbf{s}_0)\right] ~ ' \varvec{\varvec{\psi }}_l \qquad \text {for} \qquad l \ge 3, \end{aligned}$$

with $\textbf{v}_0(\textbf{s}_i,\textbf{s}_0)= \bigl (v(\textbf{s}_0,\textbf{s}_1) \ \ldots \ v(\textbf{s}_0,\textbf{s}_n) \bigr )'$ and $\varvec{u}(\textbf{s}_0)= (1 \ s_{10} \ s_{20})$.

Fig. 5

Spatial maps of the basis function  ${\varvec{\psi }}_l, \ l=1, \ldots , 18$ used to model the spatial variability of the log-odds as in Eq.  (12)

In our case, the vector $\varvec{\gamma }_k$ is thus treated as an intrinsic spatial process with variogram function as specified above. This is different from Vandewalle et al. (2021) where the spatial variability of the log-odds is only modelled through a linear spatial trend surface. Furthermore, our principal functions have some advantages over polynomials in general. First they grow less quickly than polynomials outside the domain of the data and so are more stable for extrapolation. Second, they allow more structures at locations with more data around them, and are also automatically adaptive to data locations, so that they can represent more detailed behaviour where the sites are most dense. Finally, since the basis functions are given in a decreasing order in terms of their degrees of smoothness, the spatial process can be parsimoniously represented by using only a limited number, $L \le n$ of basis functions. For our case study, we have chosen $L=18$ basis functions which, in practice, explain about the $90 \%$ of the spatial variability. To provide an example of their spatial structure, the panels in Fig. 5 provide the spatial maps of $\varvec{{\psi }}_l, \ l=1, \ldots , 18$ which, as expected, show a decreasing order of smoothness. Note that the first basis function $\varvec{\psi }_0(s)$ is not reported as it is constant equal to one overall the domain of interest.

Fig. 6

Left: Functional zoning of Piemonte with three clusters. Right: Spatial distribution of the estimated prior probabilities $\hat{\pi }_k(\varvec{s})$ for each cluster

Fig. 7

Smooth estimated mean functions in each cluster

Using $L=18$ and evaluating M (see Sect. 3.3) with the last term equal to $L(K-1)$ to consider all the parameters of the spatially varying mixing proportions, the BIC suggests a model with $K=3$ spatial clusters whose spatial representation in given in Fig. 6. Figure 7, instead, shows the patterns of the estimated shrinked cluster-mean functions; this representation gives some insights on how actually the clusters differ. In particular, it emerges a less polluted area which roughly overlaps with the Alps belt and piedmont territory (green cluster) while the plain area is divided in two zones: the first one in red around Turin metropolitan area (white dot in Fig. 6) moving towards Lombardy, while the second in blue overlaps with the province of Alessandria. Those findings partially confirms the ones reported by Ignaccolo et al. (2013), however it seems that by modeling the spatial correlation in the data it is possible to isolate an area in the south west of the region (blue cluster). This last insight seems in line with the results reported independently by Gamerman et al. (2022) regarding $\text {PM}_{10}$ concentration. As expected, by estimating an increased number of clusters, it is possible to show maps featuring more spatial details (see Fig. 8). Although sub-optimal in terms of information criteria, solutions with 4 and 5 clusters show a more specific descriptive analysis of the spatial distribution of $\hbox {PM}_{10}$. In particular, the western and southermost parts of Cuneo are now split from the Po valley while, in the north, a cluster represented by piedmont municipalities (cluster 2, Fig. 8 right) clearly separates the region bordered by the mountains (cluster 5) from the main road networks leading toward Milan (cluster 1).

Fig. 8

Functional zoning with $K=4$ and $K=5$

Note that an advantage of our proposal is that, given $\hat{\theta }$ estimated by the EM-algorithm and the associated final clustering partition, it is possible to obtain optimal predictions of the clustering membership of a new functional observation in $\varvec{s}_0$. In fact, by interpolating the eigenvectors at a new site $\varvec{s}_0$ by kriging, predictions of ${\hat{\pi }}(\varvec{s}_0)$ can be obtained by using Eq. (13). This motivates the alternative name principal kriging function for $\varvec{\psi }_{l}(\textbf{s}_i)$. Finally, by means of Eq. (6), it is also possible to get an estimate of ${\hat{\tau }}_{k,0}={\hat{P}}(Z_0=k|\varvec{s}_0)$.

6 Mandibular shape changes

Further challenging data analysis tasks that motivate our research refer to data that appear on non-Euclidean manifolds. Current strategies use surface or shape descriptors as features in a clustering algorithm, or consider appropriate distances between shapes such as the geodesic one (see Srivastava and Klassen 2016; Marron and Dryden 2022). Here we consider the problem introduced in Sect. 1 and that deals with the study of the dynamic mandibular changes from childhood to adulthood. This problem has been extensively described in the literature in 2D (see, for example, Enlow and Hans 1997; Franchi et al. 2001), but how and when each region of the mandible develops in 3D from childhood to adulthood is not fully understood yet. Hence, one might be interested to determine whether sudden changes occur and where these are located in time.

As a case study, we consider the shape of registered human mandibles for a group of $n=77$ subjects with ages between 0 and 19 years. The objects have identical mesh topology so that they have an anatomical correspondence across different mesh vertices and there are no global size differences across subjects—see Chung et al. (2015) for details on the registration of the mandible surfaces. To evaluate the shape changes we consider the length of the displacement vector defined at each point $\varvec{t}$, as a functional random variable $\textbf{Y}(\varvec{t})$ with $\varvec{t}$ varying on a compact manifold $\mathcal {M} \subset \mathcal {R}^3$, taking values in $\mathcal {L}^2(\mathcal {M})$. The displacement vector is a vector map defined at each position that matches an anatomically corresponding point onto another object. Hence, the displacement length has a biological interpretation since it provides a measure of local shape variation. $\mathcal {M}$ is a known manifold that in this case study is specified by a reference mandible (template) and formed by triangle meshes with 4326 triangles and $T=2165$ vertices.

The displacement length $\textbf{Y}(\varvec{t})$ can be represented through the Eqs. (1) and (2) where the set of basis functions in $\varvec{\Phi }_p$ are now associated with the mesh. In some cases, the fit of the surface can be obtained by using basis functions that are piece-wise polynomials and that represent elegant generalizations of univariate B-splines to planar and curved domains with fully irregular knot configuration. Applications in this context can be found, for example, in Hou et al. (2017), Sangalli et al. (2013) or Sangalli (2020). Here, we do not follow this approach as they either involve an optimization-driven knot selection for spline construction or add further penalization components to the estimation process. Here, instead, following Rosenberg (1997) and Seo et al. (2010), we use a heat kernel regression approach where the $\varvec{\phi }_j$ are the eigenfunctions of the Laplace-Beltrami (LB) operator, denoted with $\varvec{\triangle }$, which solves the equation

$$\begin{aligned} \varvec{\triangle } \ \varvec{\phi }_j = d_j \ \varvec{\phi }_j \end{aligned}$$

over the manifold $\mathcal {M}$, where $0=d_1 < d_2 \le d_3 \le \ldots$ are ordered eigenvalues of $\varvec{\phi }_1, \varvec{\phi }_2, \varvec{\phi }_3, \ldots$. These eigenfunctions form an orthonormal basis in $\mathcal {L}^2(\mathcal {M})$ and can be ordered in terms of their degrees of smoothness with higher order functions corresponding to larger-scale features and lower-order ones corresponding to smaller-scale details. Furthermore, unlike spline-based functions, we do not need to be concerned about the allocation of the basis functions, but we can simply select the number of functions, which links to a specific resolution.

Using the eigenfunctions, the heat kernel is written as

$$\begin{aligned} K_\delta (\varvec{t}, \varvec{t}') = \sum _{j=1}^\infty e^{- d_j \delta } {\phi }_j(\varvec{t}) \ {\phi }_j(\varvec{t}') \end{aligned}$$

where $\delta$ is the bandwidth of the kernel (Rosenberg 1997). Since the closed form expression for the eigenfunctions of the LB-operator on an arbitrary curved surface is unknown, the eigenfunctions are estimated numerically by discretizing the the operator by using the Cotan formulation (Chung and Taylor 2004). This leads to solve a generalized eigenvalue problem

$$\begin{aligned} \textbf{P} \ \varvec{\phi }_j = d_j \ \textbf{H} \ \varvec{\phi }_j \end{aligned}$$

where $\textbf{P}$ and $\textbf{H}$ are the stiffness and the mass matrices in a Finite Element system (these matrices are sparse and can be used without consuming large amount of memory).

In practice, to find the eigenfunctions $\varvec{\phi }_j$, we solve the generalized eigenvalues problem over the reference $\mathcal {M}$ obtained as the average of all 77 configurations (Chung et al. 2015). By setting $\delta =0$ and convolving the heat kernel with the surface values $Y(\varvec{t})$ from the heat kernel regression we obtain

$$\begin{aligned} \hat{X}(\varvec{t}) = \sum _{j=1}^{p} {\phi }_j(\varvec{t}) \hat{\beta }_{j} \end{aligned}$$

where the expansion coefficients are obtained through Eq. (4). Note that, for the statistical analysis, we have used $p_0=500$ basis functions for 2165 vertices. The coefficients $\hat{\varvec{\beta }}_i,$ $i=1, \ldots , n,$ are then used in the PFC-$\hbox {L}_1$ algorithm to identify the maturational stages of the individuals through a clustering procedure based on shape similarity. The results of the clustering are reported in Fig. 9 which shows that the estimated maturational levels (groups) do correlate with the age of the individuals. However, there exist some overlaps among the 4 groups, especially between the second and the third, suggesting that, because of the variation in the age at which children reach puberty, chronological age may not reflect accurately the developmental stages. Hence, to further analyse the local shape changes of the mandible, instead of grouping the subjects into age categories defined a priori (see Chung et al. 2015, and Fontanella et al. 2019b), we compare the mean displacement differences between the identified groups.

Fig. 9

Groups reflecting stages of development of the human mandible based on shape similarity. The 77 subjects are binned into four categories for which we show the age distribution of the individuals. The number of subjects per group is: 8, 40, 23 and 6

Fig. 10

Pairwise local differences between the mean displacements of groups 1 and 2. The differences are displayed by arrows and colors indicate their lengths in mm. Longer arrows imply larger mean displacement. The arrows have been blown up by a factor of 5 for clarity. On the right, regions of significant changes between the two groups are coloured in black and correspond to point-wise confidence intervals which do not include zero

For illustrative purposes, Fig. 10 provides a 3D representation of the reference mandible that is used to show the results of the statistical analysis. Viewed from the side, each half of the mandible is L-shaped. Starting from the left, we find the posterior border of the ramus which is straight (vertical) and continuous with the inferior border of the body of the bone. At the superior aspect of each ramus we also find the coronoid and condylar processes. At its junction with the posterior border is the angle of the mandible which is important for the attachment of the Masseter and the Pterygoideus muscles. Moving toward the right, we then find the “menton” (the point of the chin) which is the most inferior part of the mandibular symphysis. This ridge, which sometimes presents a centrally depressed area, represents the median line of the external surface of the mandible. The first two pictures of Fig. 10 show different views of the differences between groups 1 and 2 as a result of an heat kernel regression of the displacement length obtained using 500 basis functions. In particular, they display the group mean vector difference on top of its length as quivers. The arrows show the direction of the shape changes with their length being representative of mean displacement differences and with colors indicating the variation in millimetres. Being in a regression framework, it is relatively easy to use bootstrap (Efron and Tibshirani 1993) to perform marginal inference for single locations on the surface for any hypotheses of interest. To this purpose, the third picture of Fig. 10 shows the regions of significant changes as measured by mean displacement differences between the two groups. The regions correspond to point-wise $95 \%$ confidence intervals computed by resampling the residuals for updating the predictions of the functional variable. In particular, the regions in black correspond to point-wise confidence intervals which do not include zero. Similar graphical comparisons for other group mean shapes can be seen in Sect. 2 of the Supplementary Material. As a whole, we notice that the condyle shows active morphological changes, elongating predominantly posteriorly and superiorly along with the lengthening of the ramus. During the first years the changes are especially visible at the alveolar border, at the distal and superior surfaces of the ramus, at the condyle, along the lower border of the mandible and on its lateral surfaces. The ramus height, in particular, clearly increases vertically, and the two sides of the ramus diverge outward to increase the inter-ramus distance. The mandibular body also elongates and the chin protrudes distinctively over time confirming the expected vertical and sagittal changes in the mandible (Enlow and Hans 1997). In general, year by year, the mandibular changes become more selective.

7 Discussion

In recent years, model-based clustering has become a powerful tool for performing functional cluster analysis, due to its ability to handle high-dimensional and complex data. However, despite the recent advances, there still exist several challenging statistical issues that need to be addressed. One of these issues is how to achieve a dimensional reduction able to optimize clustering performance and to this end we maximize the log likelihood subject to a penalty that promotes sparsity in the features. This is a crucial problem, as it can help reduce the dimensionality of the feature space and improve the interpretability of the clustering results. However, the choice of the penalty function and the selection of the tuning parameters can be difficult, as they can affect the sparsity and accuracy of the clustering model.

In this paper, we obtain dimensionality reduction of the data prior to clustering, in order to reduce the complexity of the feature space. Then, to induce sparsity structures within the expansion coefficients, we follow the approach presented in Zhou et al. (2009) where the log likelihood is maximized subject to an $\hbox {L}_1$-penalty function applied to the parameters of the Gaussian distributions of the mixture.

Both simulation studies and the analysis of real data suggest that the PFC-$\hbox {L}_1$ procedure is worth considering for clustering complex objects. In particular, experiments on one-dimensional functions demonstrate that the PFC-L1 procedure is robust to distributional assumptions and, compared with other competing methods, performs similarly, if not better, in terms of accuracy. Moreover, the simplicity and flexibility of the PFC-L1 procedure make it an attractive option for functional clustering, and its versatility has been demonstrated by its ability to cluster complex objects, including spatially correlated functions and surface mesh data.

For spatially dependent functions, we have proposed a simple and straightforward parametrization of the multinomial logit model that does not require the estimation of spatial covariance parameters. However, there are other solutions that can be used to model spatial dependence in functional data, including the use of different basis functions. For example, Cressie and Johannesson (2008) proposed the use of bisquare basis functions, which can capture both smooth and abrupt changes in the spatial dependence structure. Alternatively, Gamerman et al. (2022) proposed the use of univariate and multivariate Gaussian processes in a Bayesian setting, which can provide a flexible approach to modeling spatial dependence in functional data. Overall, the choice of method for modeling spatial dependence in model-based clustering for functional data is an important and challenging problem that requires careful consideration and further investigation.

For surface mesh data, dimensionality reduction can be achieved by relying on the heat kernel smoothing approach and the eigenfunctions of the Laplace-Beltrami (LB) operator. The eigenfunctions of the LB-operator provide a natural basis for representing the surface geometry, and can be used to obtain a low-dimensional representation of complex data. The expansion coefficients obtained using a standard regression framework can then be used for clustering the objects, enabling accurate and reliable clustering of high-dimensional surfaces. Furthermore, this approach allows for subsequent analysis and inference. Overall, the use of heat kernel smoothing and the eigenfunctions of the LB-operator provides a powerful and effective approach to dimensionality reduction for surface mesh data, and can be combined with various clustering algorithms to enable accurate and reliable clustering of complex and high-dimensional surfaces.

There still exist several challenging statistical issues that need to be addressed in future works. For example, an important issue in functional clustering is determining the appropriate number of clusters (K) and penalization parameters. In this work, model selection and validation procedures were performed using two information criteria, BIC and ICL, with reliable results demonstrated under the proposed simulation designs. An alternative approach would be to use a non-parametric Bayesian approach with a Dirichlet process prior (Ferguson 1973) over mixture components, which has the advantage of automatically selecting the number of clusters during the clustering procedure within a suitable Markov chain Monte Carlo (MCMC) algorithm (see also White and Gelfand 2021, and Margaritella et al. 2021). Stochastic Search Variable Selection (SSVS) priors (George and McCulloch 1993) for variable selection could also be included in the model, allowing for simultaneous identification of cluster-relevant variables and estimation of the number of mixture components. This approach could provide a unified procedure for estimating both the model parameters and the free-noise process $X(\varvec{t})$, which naturally incorporates uncertainty into the posterior inference. The hierarchical structure of the process provided by Eqs. (1) and (2) is consistent with a Bayesian formulation of the model, and further investigation in this direction will be a topic for future research.