Unlabelled landmark matching via Bayesian data selection, and application to cell matching across imaging modalities

Abstract

We consider the problem of landmark matching between two unlabelled point sets, in particular where the number of points in each cloud may differ, and where points in each cloud may not have a corresponding match. We invoke a Bayesian framework to identify the transformation of coordinates that maps one cloud to the other, alongside correspondence of the points. This problem necessitates a novel methodology for Bayesian data selection, simultaneous inference of model parameters, and selection of the data which leads to the best fit of the model to the majority of the data. We apply this to a problem in developmental biology where the landmarks correspond to segmented cell centres, where potential death or division of cells can lead to discrepancies between the point-sets from each image. We validate the efficacy of our approach using in silico tests and a microinjected fluorescent marker experiment. Subsequently we apply our approach to the matching of cells between real time imaging and immunostaining experiments, facilitating the combination of single-cell data between imaging modalities. Furthermore our approach to Bayesian data selection is broadly applicable across data science, and has the potential to change the way we think about fitting models to data.

1 Introduction

Understanding early mammalian development is key to the advancement of in vitro fertilisation (IVF) techniques and improved understanding of early cell specification within mammals. Within developmental biology there have been significant advances in experimental techniques, including the ability to culture preimplantation embryos ex vivo and monitor their development through periodic 3D imaging, known as real time imaging (RTI) (Abe and Fujimori 2013; Grabarek and Plusa 2012; Plusa 2008). In conjunction with the generation of mouse reporter lines, such as the H2b:GFP line, we are able to visualise the development of the murine embryo and monitor the behaviour of individual cells (Hadjantonakis and Papaioannou 2004). One of the highly disputed questions regarding the development of the preimplantation embryo, is the effect of cell history and changes in embryo architecture on cell lineage specification (Płusa and Piliszek 2020; Fischer 2020; Forsyth 2021).

After RTI experiments, embryos can be fixed to halt their development and stained for proteins of interest via immunostaining. The cells’ respective fates can then be inferred from their protein expression profiles. In order to interrogate the relationship between cell history and cell specification it is crucial to link historical information (gained from RTI experiments) with protein expression (quantified from immunostaining) at the single cell level. However, the cell-to-cell matching across these two imaging modalities is non-trivial due to the random re-orientation of the embryo during staining and potential deformation during the fixation process.

Coordinates of cell centres can be extracted from the final frame of the RTI experiment, using the H2b:GFP signal, and from the immunostained image, using the nuclear stain. The formulation of this problem as a collection of two point sets to be registered is analogous to point-set registration problems where sets of noisily observed points are to be registered, or ‘matched’ where the correspondence of points can be partially or entirely unknown a priori. Point-set registration problems appear in a broad range of applications reliant on accurate alignment or registration of landmarks including the comparison of evolutionary protein structures (Dryden 2007; Challis and Schmidler 2012; Rodriguez and Schmidler 2014; Fallaize et al. 2020), and medical image assessments (Gutierrez-Becker 2017; Ramalhinho 2021).

It is most common for point/landmark registration to be approached using variational techniques (Gutierrez-Becker 2017; Kent et al. 2004), but these approaches lack comprehensive description of the uncertainty associated with the identified registration. A well known and extensively used example is the Procrustes algorithm that aligns two point sets through optimisation of the scaling, translation and rotation of the point sets. However, the Procrustes algorithm is dependent on a known matching of points and therefore must be combined with other methods to infer the matching of the points which can be variational or probabilistic (Hurley and Cattell 1962; Gower 1975; Dryden and Mardia 2016). Another variational algorithm is the iterative closest point (ICP) method, this approach iterates over potential matchings of points and then performs a rigid transformation between the point sets, aiming to minimise an energy function describing the mismatch of the points (Besl and McKay 1992). However, the ICP method can be highly sensitive to outliers or non-corresponding points. An alternative approach, the robust point matching (RPM) approach was developed by Gold et al. in an attempt to improve this (Gold 1998). The RPM algorithm however can still prove to be highly dependent on the initialisation of the optimiser in complex problems and often requires additional information in more complex registration problems (Gold 1998).

There have been some probabilistic approaches developed, which work to identify not only the correct matching of points but also the relative uncertainty of the matching (Dryden 2007; Green and Mardia 2006; Challis and Schmidler 2012; Rodriguez and Schmidler 2014; Fallaize et al. 2020). Myronenko et al. developed the Coherent Point Drift (CPD) algorithm which models the points in one point-set as the centroids of a Gaussian mixture model and then interprets the optimal matching of the points across the point sets to be the maximum of the Gaussian mixture posterior (Myronenko et al. 2006; Myronenko and Song 2010). This method allows for non-rigid transformations between point sets as does the large deformation diffeomorphic metric matching (LDDMM) method (Younes 2009; Joshi and Miller 2000). The LDDMM uses a curve to describe diffeomorphic mapping of individual landmarks between the target and template point clouds (Younes 2009; Joshi and Miller 2000). A Bayesian approach of shape matching via a non-linear deformation is also presented in Cotter (2013), where the geodesic map which takes one shape to the other is inferred. Other probabilistic approaches use affine transformations where point-sets are matched to hidden point sets described by Poisson processes, which allows the subsequent inference of point matching (Green and Mardia 2006; Hu et al. 2019; Fallaize et al. 2020).

Ultimately the quality of the identified matching is dependent on the quality of the point sets as well as the approach. If there are points without matches, these can bias the registration and potentially prevent the identification of the correct matching. Fallaize et al. and Hu et al. account for non-corresponding points through the introduction of gap penalties for points without identified matches and Gold et al. uses the ‘softassign’ method to describe the matching of cells where non-corresponding cells were present (Fallaize et al. 2020; Hu et al. 2019; Gold 1998).

In this work we invoke the Bayesian framework in order to find likely cell matchings, as well as quantify the uncertainty in those matchings. Our biological example has additional difficulties, since the landmarks are unlabelled, and the assumption that all landmarks exist in both point-sets does not hold. This discrepancy in landmarks can occur due to cell death or division between the time that the RTI experiment was stopped and fixation, or due to inaccurate segmentation of cell centres. One approach would be to manually clean the data and select only cells with guaranteed matches in the corresponding image, however this is highly subjective with potential for significant errors as we do not know a priori which cells to eliminate from the registration.

There has been some work on data selection with regards to single and multi-source data acquisition (Rahm and Do 2000), and data ‘re-weighting’ in a Bayesian context (Wang et al. 2017) which has similarities with Bayesian model selection (Ando 2010) and outlier detection (Aggarwal 2017). In this work, we introduce a novel approach to Hierarchical Bayesian data selection within this point registration problem (Cotter 2022). This approach limits the effect that cells which do not appear in both images have on the inference. This is implemented through the introduction of parameters which describe our belief in the fidelity of each observation in the data rather than the binary inclusion/exclusion of the points within the matching (Fallaize et al. 2020; Challis and Schmidler 2012; Rodriguez and Schmidler 2014). The values of these fidelity parameters are jointly inferred alongside the model parameters describing the transformation and correspondence of the landmarks.

We implement Markov chain Monte Carlo (MCMC) methods to explore the complex distribution on the model and fidelity parameters. The posterior is frequently highly multimodal, preventing complete exploration of the parameter state space due to ‘trapping’ in local minima. We therefore implement tempering of the likelihood to optimise our sampling and minimise trapping.

Fig. 1

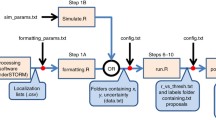
Experimental design with examples of two-dimensional slices from images. Spot detection using IMARIS (BitPlane) from final frames of RTI (using H2b:GFP signal) and immunostained image (Hoechst). Cell matching via observation operator $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$. Experimental protocols for embryo collection, visualisation and staining can be found in Sections (S1.1–S1.4)

Although the introduction of data selection is primarily introduced to facilitate landmark registration within our specific biological example, it is clear that this framework could be expanded to a very broad range of inferential problems, with potential for wide-ranging impact in many applications of data science.

In Sect. 2 we introduce the transformation model, including the description of a 3D affine transformation and a non-linear deformation, and a method of describing landmark correspondence within the model. In Sect. 3 we introduce the concept of Bayesian data selection and its implementation. In Sect. 4 we describe the construction of the posterior distributions that we wish to characterise. We then go on to describe the MCMC implementation in Sect. 5. In Sect. 6 we firstly present several in silico test problems demonstrating the efficacy of our approach. We then perform inference on embryos with microinjected fluorescent cells which enable us to identify a subset of the cells in both images for validation on a real data set. Finally we demonstrate the applicability of our approach on a problem in which we wish to match cells from the final frame of an RTI experiment with corresponding immunostained images, with the additional challenge of embryo matching. We conclude with a discussion in Sect. 7.

2 Landmark matching

In order to better understand mammalian development, spatiotemporal information from RTI experiments must be linked with protein expression which is inferred from secondary immunostaining images. To link these two data sets, cell centres are extracted from the final frame of the RTI study and the immunostained image and matched, Fig. 1. Previously, attempts have been made to manually match the cells between images, however this is non-trivial due to the manipulation of the embryos during staining and can lead to low confidence matchings of cells between images.

We can generalise this problem to the matching of two unlabelled point clouds:

$$\begin{aligned} {\textbf {Y}}^1 \in \mathbb {R}^{d \times n_1}, \qquad {\textbf {Y}}^2 \in \mathbb {R}^{d \times n_2}, \end{aligned}$$

(1)

where $d \in \mathbb {N}$ is the dimension of the observation space, in our application $d=3$, and the number of points in ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$ is $n_1$, $n_2$ respectively where we assume $n_1\le n_2$. In the context of cell matching, potential differences in $n_1$ and $n_2$ may arise from cell death or division after the completion of the RTI prior to fixation of the embryos, or due to segmentation errors. ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$ are pre-processed such that the average coordinate in each cloud is shifted to (0, 0, 0), and re-scaled through division by the minimum cell-to-cell Euclidean distance.

The two point clouds can be considered to be noisily transformed versions of each other, with labels subject to a random permutation, along with the potential addition or subtraction of points in both clouds. The transformation of ${\textbf {Y}}^2$ to ${\textbf {Y}}^1$ can be described by the composition of a non-linear deformation, an affine transformation and a permutation of labels, described by an observation operator $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$ with parameters $\varvec{\theta }$.

2.1 Non-linear deformations via geodesic motion

Deformation to the embryo can occur due to continued growth of the embryo prior to fixation or manipulation of the embryo during immunostaining. Therefore we include an explicit description of a non-linear deformation within $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$ in addition to an affine transformation.

The non-linear deformation to the point-set is modelled as a geodesic transformation resulting from the application of an initial momentum, ${\textbf {p}}_0 \in \mathbb {R}^{d\times n_2}$ to ${\textbf {Y}}^2$ where ${\textbf {q}}_0 \in \mathbb {R}^{d \times n_2}$ is the initial position of the points in ${\textbf {Y}}^2$ (Bock and Cotter 2021; Younes 2019). The deformed points, ${\textbf {q}}_1$, are evaluated using:

$$\begin{aligned} \frac{d \varvec{p}_t^j}{d t}= & {} \left( -\sum _{i=1}^{n_2} \frac{(\varvec{q}_t^i-\varvec{q}_t^j)}{\sigma _K^2} \exp \left( -\frac{\Vert \varvec{q}_t^i - \varvec{q}_t^j \Vert _2^2}{2 \sigma _K^2} \right) \varvec{p}_t^i \right) ^\top \cdot \varvec{p}_t^j, \end{aligned}$$

(2a)

$$\begin{aligned} \frac{d \varvec{q}_t^j}{dt}= & {} \sum _{i=1}^{n_2} \exp \left( -\frac{\Vert \varvec{q}_t^i - \varvec{q}_t^j \Vert _2^2}{2 \sigma _K^2} \right) \varvec{p}_t^i , \end{aligned}$$

(2b)

over the time interval $t=[0,1]$, where $\varvec{q}^j_t {\in \mathbb {R}^{d \times 1}}$ is the position of the $j^{th}$ point at time t and $\varvec{p}^j_t{\in \mathbb {R}^{d \times 1}}$ is the momentum of the $j^{th}$ point at time t, details given in “Appendix A”.

The application of the geodesic flow is computationally expensive due to the solving of $2n_2$ differential equations. We envisage that for smaller embryos, deformation is minimal, in which case we set ${\textbf {p}}_{0}$ to be a matrix of zeros. However for larger embryos, it may not be possible to accurately match cells without the addition of inference of a non-linear transformation between ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$.

2.2 Affine transformation

Our observation operator, $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$, also incorporates a three dimensional affine transformation to account for shear scaling, rotation and translation of points.

The affine transformation matrix ${\textbf {A}}(\varvec{\theta })$ is $d \times d$ and applies the shear scaling and rotation. We define ${\textbf {A}}(\varvec{\theta })={\textbf {R}}_1 {\textbf {S}} {\textbf {R}}_2$ where an initial rotation is applied through ${\textbf {R}}_1(\phi _1^x, \phi _1^y, \phi _1^z)$, a scaling performed in the new rotated axis through ${\textbf {S}}(s_1, s_2, s_3)$ and then a final second rotation through ${\textbf {R}}_2(\phi _2^x, \phi _2^y, \phi _2^z)$, where ${\textbf {R}}_1, {\textbf {S}},$ and ${\textbf {R}}_2$ are all $d \times d$ matrices given in “Appendix B”.

Parameters $\varvec{\phi }$ are Euler angles, and $\varvec{s}$ are scaling parameters in each of the axes. We chose to define ${\textbf {A}}(\varvec{\theta })$ using two rotations and a scale matrix which results in a shear scaling and rotation of points, described in Glassner (2013), as it allows us to better define our prior distributions on the parameters used to generate ${\textbf {A}}(\varvec{\theta })$. To account for translation we introduce the $d \times 1$ vector $\varvec{b}(b_1, b_2, b_3)$ where $b_\cdot$ are the translation parameters in the three axes x, y and z.

The affine transformation is applied to the deformed points to give

$$\begin{aligned} \mathcal {F} (\varvec{\theta };{\textbf {Y}}^2)={\textbf {A}}(\varvec{\theta }){\mathcal {D}}(\varvec{\theta };{\textbf {Y}}^2) + \varvec{b}(\varvec{\theta })\varvec{1}_{n_2}^\top , \end{aligned}$$

(3)

where $\varvec{1}_{n_2} \in \mathbb {R}^{n_2}$ is a column vector of ones and $\mathcal {D}(\varvec{\theta };{\textbf {Y}}^2) {= {\textbf {Y}}^2}$ when no deformation is applied.

2.3 Permutation of labels

Our overall aim is to find the labelling of points in order to match cells across images. We introduce a permutation vector as a method of describing the matching of cells from ${\textbf {Y}}^1$ in ${\textbf {Y}}^2$. The permutation vector $\varvec{P}\in \mathbb {N}^{n_2}$ contains each of the numbers $\{1,\ldots ,n_2\}$ exactly once, and describes the ordering of cells in ${\textbf {Y}}^2$ in order to match them with cells in ${\textbf {Y}}^1$. Note that in the case that $n_1<n_2$, the cell numbers in the $n_2-n_1$ last entries of the permutation vector are assumed not to have a corresponding match in ${\textbf {Y}}^1$, and as such are not required for the calculation of the likelihood.

Our aim is to compare the positions of points in ${\textbf {Y}}^1$ with their corresponding matches, as given by $\varvec{P}$, in the transformed cell centres in ${\textbf {Y}}^2$. As such, we define the matrix ${\textbf {M}}_P \in {\{0,1\}}^{n_2 \times n_1}$

$$\begin{aligned} {\textbf {M}}_P = \begin{pmatrix} e_{P_1}&e_{P_2}&\ldots&e_{P_{n_1}} \end{pmatrix}, \end{aligned}$$

where $e_i \in \mathbb {R}^{n_2 \times 1}$ are the standard canonical basis column vectors for $\mathbb {R}^{n_2}$. The permutation matrix ${\textbf {M}}_P$ relates to the permutation vector $\varvec{P}$ via ${\textbf {M}}_P(P_i,i)=1$ and ${\textbf {M}}_P(j\ne P_i,i)=0$, where we define $P_i$ is the $i^{th}$ entry of $\varvec{P}$. Post multiplication of the transformed ${\textbf {Y}}^2$ coordinates by ${\textbf {M}}_P$ gives us a matrix of the new cell center positions ordered according to $\varvec{P}$.

2.4 The observation operator

We define our observation operator $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2):(\Theta \times \mathbb {R}^{{d} \times n_2}) \rightarrow \mathbb {R}^{{d} \times n_1}$, which takes the cell center coordinates of ${\textbf {Y}}^2$, applies a non-linear transformation (if being applied), an affine transformation, and then reorders the subset of the cells which we aim to match to ${\textbf {Y}}^1$ according to the permutation vector $\varvec{P}$. Therefore we arrive at

$$\begin{aligned} \mathcal {G}(\varvec{\theta };{\textbf {Y}}^2) = \left( {\textbf {A}}(\varvec{\theta }){\mathcal {D}}(\varvec{\theta };{\textbf {Y}}^2) + \varvec{b}(\varvec{\theta }) \varvec{1}_{n_2}^\top \right) {\textbf {M}}_P(\varvec{\theta }). \end{aligned}$$

(4)

3 Hierarchical Bayesian data selection

The observation operator $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$ describes the transformation and permutation of points in ${\textbf {Y}}^2$ to match ${\textbf {Y}}^1$, but assumes that all cells in ${\textbf {Y}}^1$ have a corresponding match in $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$. This assumption does not always hold, since cells can divide or undergo apoptosis in between the RTI experiment and fixation, or may be too faint for accurate segmentation, resulting in the presence of cells within one or both of the point clouds with no corresponding match. We cannot know which cells do not have a match a priori, and therefore we aim to infer this information, thereby conducting what we will refer to as Hierarchical Bayesian data selection (Cotter 2022). This refers to any approach where additional parameters are introduced into the inference which dictate the sensitivity of the posterior to a given observation, where the values of these parameters are themselves inferred from data, jointly with the model parameters.

3.1 Data fidelity

The likelihood function is ordinarily a function $f_L$ of the mismatch between each observation and the observation operator at a given value of the model parameters such that

$$\begin{aligned} L({{\textbf {Y}}^1,{\textbf {Y}}^2}|\varvec{\theta }) {=} f_L(\varvec{Y}^1_1 {-} [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_1, \ldots , \varvec{Y}^1_n - [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_n),\nonumber \\ \end{aligned}$$

(5)

where $\varvec{Y}^1_i$ is the $i^{th}$ column of ${\textbf {Y}}^1$ and $[\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_i$ is the $i^{th}$ column of the transformed ${\textbf {Y}}^2$. In ordinary Bayesian inference the likelihood is sensitive to each of the data-model mismatches $\varvec{Y}^1_i - [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_i$, which causes issues when the data is corrupted, or where the model does not adequately describe the entirety of the data.

We now aim to infer which of these data can be well-matched to the model, we introduce fidelity parameters $\gamma _i \in {(0,1)}$ for each observation (in our case a cell center from ${\textbf {Y}}^1$), that controls the relative contribution of that observation to the likelihood.

These $\gamma _i$ are effectively inverse annealing temperatures for each observation, with high temperatures (where $\gamma _i\ll 1$) resulting in a likelihood which is not sensitive to the data-model mismatch for this observation. This approach limits the effect on the posterior of spurious data through a likelihood which takes into account the fidelity of each observation, given by:

$$\begin{aligned} L_{\varvec{\gamma }}({\textbf {Y}}^1,{\textbf {Y}}^2|\varvec{\theta }, \varvec{\gamma }= & {} [\gamma _1, \ldots , \gamma _n]) \nonumber \\= & {} f_L(\gamma _1(\varvec{Y}^1_1 - [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_1), \ldots ,\nonumber \\{} & {} \gamma _n (\varvec{Y}^1_n - [\mathcal {G} (\varvec{\theta };{\textbf {Y}}^2)]_n)). \end{aligned}$$

(6)

For each point in ${\textbf {Y}}^1$, $\gamma _i$ represents our belief that this cell in ${\textbf {Y}}^1$ has a match in ${\textbf {Y}}^2$. A value of $\gamma _i=0$ corresponds to a likelihood which is independent of the data-model mismatch of the $i^{th}$ observation, and $\gamma _i=1$ corresponds to a likelihood which is dependent on the $i^{th}$ cell’s mismatch.

The inclusion of the fidelity parameters works to prevent the fitting of the model to the entire set of points for which a subset may not be adequately described by that model. Without appropriate data selection in the landmark matching problem, there are no guarantees that the transformation and permutation that leads to the lowest overall least squares fit corresponds with the correct matching.

Table 1 Prior distributions. $S_{n_2}$ denotes the symmetric group of all possible permutations of $\{1, \ldots , n_2\}$

4 Bayesian cell matching

The matching of cells between images can be considered as an inverse problem where we wish to identify a transformation of ${\textbf {Y}}^2$ in order to identify the correct matching, $\varvec{P}$, of the cells. The inverse problem of cell matching is complex with potentially correlated parameters across the components of the model, leading to potentially multimodal posterior distributions.

Bayes’ theorem is a fundamental property of sets and measures that forms the basis of a probabilistic framework for inverse problems, involving the combination of prior knowledge, observations, and models. Within this study we aim to characterise two posterior probability densities, $\pi (\varvec{\theta }|{{\textbf {Y}}^1,} {\textbf {Y}}^2)$ and $\pi (\varvec{\theta }, {\varvec{\gamma }}|{{\textbf {Y}}^1,} {\textbf {Y}}^2)$. Where the first posterior density is the original posterior on the model parameters $\varvec{\theta }$ conditioned on the data ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$, and the second posterior includes data selection via the fidelity parameters $\varvec{\gamma }$. We first define the posterior distribution without data selection which by Bayes’ theorem is given by:

$$\begin{aligned} \pi (\varvec{\theta }|{{\textbf {Y}}^1, {\textbf {Y}}^2}) \propto \pi _0(\varvec{\theta }) \; L({{\textbf {Y}}^1, {\textbf {Y}}^2}|\varvec{\theta }), \end{aligned}$$

(7)

where $\pi _0(\varvec{\theta })$ is the prior density and $L({{\textbf {Y}}^1, {\textbf {Y}}^2}|\varvec{\theta })$ is the likelihood of the observations given $\varvec{\theta }$.

4.1 The likelihood

We assume that the observations of the cell centers are subject to mean-zero i.i.d. Gaussian noise, such that:

$$\begin{aligned} \varvec{Y}^1_i=[\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_i + \eta _i, \qquad \eta _i \sim \mathcal {N}(0,\varvec{\Sigma }), \end{aligned}$$

(8)

where $\eta _i$ the combined observational noise of $\varvec{Y}^1_i$ and the transformation and $\varvec{\Sigma }$ is the $3 \times 3$ unknown noise covariance matrix combining the effects of the observational noise and transformation. Therefore the likelihood is given by:

$$\begin{aligned} L({\textbf {Y}}^1, {\textbf {Y}}^2|\varvec{\theta },\varvec{\Sigma }) \propto \prod _{i=1}^{n_1} \exp \left( -\frac{1}{2} \left\| \varvec{Y}^1_i - [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_i\right\| _{\varvec{\Sigma }} ^2\right) , \nonumber \\ \end{aligned}$$

(9)

where, $\Vert \varvec{x}\Vert ^2_{\varvec{\Sigma }} = \varvec{x}^\top \varvec{\Sigma }^{-1} \varvec{x}$, is the covariance-weighted norm.

4.2 Priors

We choose mean zero priors on the affine transformation parameters introduced in Sect. 2.2 and deformation momenta as shown in Table 1, and a uniform prior on label permutations.

We define priors directly on the angular and scale parameters that generate the affine matrix, this allows us to choose priors which are more intuitive and results in an implied prior on each of the affine matrix components. We choose relatively restrictive priors on the deformation momenta, $\varvec{p_0}^i$ in order to prevent large deformations of points which could mimic affine-like transformations or result in the severe alteration of the topography of the point set.

4.3 Hierarchical Bayes posterior

The noise covariance $\varvec{\Sigma }$ within the likelihood is unknown a priori and so we use a hierarchical Bayes approach to infer its value alongside the model parameters. We choose the Inverse-Wishart distribution as a prior on $\varvec{\Sigma }$ which is conjugate to the Gaussian likelihood, enabling marginalisation of $\varvec{\Sigma }$ (Alvarez 2014; Liu 2016). This distribution has two parameters, the degrees of freedom $\nu >d-1$, and the positive definite symmetric scale matrix $\varvec{\Psi } \in \mathbb {R}^{d \times d}$. The Inverse-Wishart distribution has a mean given by

$$\begin{aligned} \mathbb {E}(\varvec{\Sigma })=\frac{\varvec{\Psi }}{\nu -d-1}, \end{aligned}$$

(10)

when $\nu >d+1$, and variance of the diagonal terms given by

$$\begin{aligned} \text {Var}(\Sigma _{ii}) =\frac{2\Psi _{ii}^2}{(\nu -d-1)^2(\nu -d-3)}, \end{aligned}$$

(11)

when $\nu >d+3$. The inverse Wishart distribution can be a problematic choice as a prior due to the potential for biasing towards large variances, and the issue of controlling the uncertainty of all parameters through a single parameter. However we choose $\nu$ and $\varvec{\Psi } \propto {\textbf {I}}_3$ to achieve $\mathbb {E}(\varvec{\Sigma })= 0.01{\textbf {I}}_3$ and $\text {Var}(\Sigma _{i,i})=0.2^2$, as opposed to the commonly used $\Psi ={\textbf {I}}_d$ and $\nu =d+1$, giving us $\nu =6.0050$ and $\Psi =0.0201 \; {\textbf {I}}_3$. This choice makes our prior on $\varvec{\Sigma }$ more informative and scaled about smaller values of the variance.

This selection of hyperparameters could therefore potentially lead to an under estimate of the covariance but it can be argued that we want to encourage these smaller variances as opposed to encouraging large mismatches through our conjugate prior on $\varvec{\Sigma }$ (Schuurman 2016). Alternative approaches include methods such as the extended onion method (Ghosh and Henderson 2003; Lewandowski 2009) or generating random covariance matrices using partial correlations with regular vines (Joe 2006; Lewandowski 2009). These different methods no longer preserve conjugacy but can help mitigate some of the issues with the inverse Wishart priors.

By choosing the conjugate inverse Wishart prior on $\varvec{\Sigma }$ we can define the posterior, without data selection as:

$$\begin{aligned} \pi (\varvec{\theta }, \varvec{\Sigma } | {\textbf {Y}}^1, {\textbf {Y}}^2) \propto L({\textbf {Y}}^1, {\textbf {Y}}^2 |\varvec{\theta }, \varvec{\Sigma }) \pi _0(\varvec{\theta }) \pi _0(\varvec{\Sigma }), \end{aligned}$$

(12)

which can be marginalised by integrating over all $\varvec{\Sigma }$ in the support of the prior, denoted by $\Omega$, to give the target density:

$$\begin{aligned} \pi (\varvec{\theta } | {\textbf {Y}}^1, {\textbf {Y}}^2){} & {} \propto \pi _0(\varvec{\theta }) \int _\Omega L({\textbf {Y}}^1, {\textbf {Y}}^2 |\varvec{\theta }, \varvec{\Sigma }) \pi _0(\varvec{\Sigma }) \; d\varvec{\Sigma }, \end{aligned}$$

(13a)

$$\begin{aligned}{} & {} \propto \pi _0(\varvec{\theta }) \int _\Omega \prod _{i=1}^{n_1} \exp \nonumber \\{} & {} \quad \left( -\frac{1}{2} \left\| \varvec{Y}^1_i - [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_i\right\| _\Sigma ^2\right) \mathcal {W}^{-1}(\varvec{\Sigma }) \; d\varvec{\Sigma },\nonumber \\ \end{aligned}$$

(13b)

$$\begin{aligned}{} & {} \propto \pi _0(\varvec{\theta }) \; {\text {det}}\left( \varvec{\Psi } + ({\textbf {Y}}^1 - \mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)) \right. \nonumber \\{} & {} \quad \left. ({\textbf {Y}}^1 - \mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)) ^\top \right) ^{\frac{-\nu + n_1}{2}}, \end{aligned}$$

(13c)

$$\begin{aligned}{} & {} {\propto \pi _0(\varvec{\theta }) \; L^{(\Sigma )}({{\textbf {Y}}^1}, {\textbf {Y}}^2|\varvec{\theta })}, \end{aligned}$$

(13d)

where $L^{(\Sigma )}({\textbf {Y}}^1, {\textbf {Y}}^2|\varvec{\theta })$ is the likelihood function with $\varvec{\Sigma }$ integrated out up to a constant of proportionality, equal to $\text {det}\left( \varvec{\Psi } + {\textbf {X}} {\textbf {X}}^\top \right) ^{\frac{-\nu + n_1}{2}}$ given that ${\textbf {X}}={\textbf {Y}}^1-\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$ and $\pi _0(\varvec{\theta })$ is the prior density on the model parameters.

4.4 Introducing data selection into the posterior

In the previous sections we formulated the target distribution, Eq. 13d, where we do not include data selection. We now modify our target distribution to include data selection via the introduction of the fidelity parameters $\varvec{\gamma }$.

We write the data selection posterior distribution as

$$\begin{aligned} \pi (\varvec{\theta }, \varvec{\gamma } | {\textbf {Y}}^1, {\textbf {Y}}^2) \propto \pi _0(\varvec{\theta }) \; \pi _0(\varvec{\gamma }) \; {\frac{1}{Z(\varvec{\gamma })}} \; {L^{(\Sigma )}_{\varvec{\gamma }}({\textbf {Y}}^1,{\textbf {Y}}^2|\varvec{\theta }, \varvec{\gamma })}, \nonumber \\ \end{aligned}$$

(14)

where $L^{(\Sigma )}_{\varvec{\gamma }}({\textbf {Y}}^1,{\textbf {Y}}^2|\varvec{\theta }, \varvec{\gamma }) = \text {det}\left( \varvec{\Psi } + {\textbf {X}}_\gamma {\textbf {X}}_\gamma ^\top \right) ^{\frac{-\nu + n_1}{2}}$ is the likelihood function including data selection with ${\textbf {X}}_\gamma = {\textbf {X}} \; \text {diag}(\varvec{\gamma })$, and $\varvec{\Sigma }$ has been integrated out as in Eqs. 13a to 13d. As the likelihood is now dependent on the fidelity parameters which change during sampling, we have to include a normalisation factor $Z(\varvec{\gamma })$ which is given by

$$\begin{aligned} {Z(\varvec{\gamma })} \propto \prod _{i=1}^{n_1} \gamma _i^{-d}, \end{aligned}$$

(15)

as derived in “Appendix C”.

We choose a beta prior $\text {Beta}(\alpha _\gamma ,\beta _\gamma )$ on each $\gamma _i$, with $\alpha _\gamma =2$ and $\beta _\gamma =2$ such that $\mathbb {E}(\gamma _i)=0.5$ and $\text {Var}(\gamma _i)=0.05$.

We now have two target distributions, one for tests where we do not include data selection given in Eq. 13d and one when we include data selection given by Eq. 14. We define both these target distributions such that we can assess the performance of our point registration without and with data selection.

5 MCMC methodology

Both of the posterior distributions in Eqs. 13d and 14 are highly complex and multimodal on high dimensional spaces, involving a mixture of continuous and discrete variables. In order to generate samples from the posterior distributions, we implement MCMC, a commonly used approach to sample from complex probability distributions. As our model and data selection approach is inherently modular (transformation, permutation and fidelity modules), we use a Random Walk Metropolis-within-Gibbs approach (Tierney 1994). By using a Metropolis-within-Gibbs approach we are able to tune the random walk proposal variances for the spatial transformation parameters and fidelity parameters separately therefore promoting efficient exploration of the state spaces.

Standard random walk proposals are made on the non-bounded continuous random variables including the momenta, scale parameters and translation parameters using

$$\begin{aligned} \varvec{\theta }'=\varvec{\theta }+\beta \varvec{\xi }, \; \; \; \; \varvec{\xi } \propto \mathcal {N}(0,{\textbf {C}}), \end{aligned}$$

(16)

where $\varvec{\theta }'$ is the proposal, $\varvec{\theta }$ the current parameters and $\beta$ is the step-size of the proposals on the transformation parameters, and tuned so that we achieve the optimum 23.4% acceptance rate within each Gibbs module (Gelman 1997). ${\textbf {C}}$ is the proposal covariance matrix and chosen to be the diagonal matrix of prior variances, to help with different scales of parameter values.

5.1 Proposals on periodic continuous random variables

The six angles in the affine transformation, $\phi _{1,2}^{x,y,z}$ ($\varvec{\phi }$), are defined on a bounded state space, $[-\pi ,+\pi ]$, and are periodic due to the equivalence of a rotation by $-\pi$ radians and $+\pi$ radians. Sampling on the rotation matrices using Euler angles can be challenging and several approaches and statistical packages have been developed to ensure uniform exploration of the rotation matrices (Habeck 2009; Stanfill 2014). In order to facilitate the intuitive choice of prior distributions on the affine transformation parameters, we generate proposals on $\varvec{\phi }$ using

$$\begin{aligned} \varvec{\phi }'=\mod (\varvec{\phi } + \varvec{\omega },2\pi ), \; \; \varvec{\omega } \sim \mathcal{T}\mathcal{N} \left( 0,\beta \sigma _{c} {{\textbf {I}}_6},-\pi ,\pi \right) ,\nonumber \\ \end{aligned}$$

(17)

where $\varvec{\phi }'$ is an array of proposed angles, $\varvec{\phi }$ the current angle values and $\mathcal{T}\mathcal{N} \left( 0,\beta \sigma _{c} {{\textbf {I}}_6},-\pi ,\pi \right)$ is a mean-zero truncated normal distribution with a standard deviation $\beta \sigma _c$ and lower and upper bounds $-\pi$ and $+\pi$ respectively. Here, rather than using the variance of the uniform prior imposed on $\varvec{\phi }$, we use the prior circular variance $\sigma _c$ calculated using the MATLAB toolbox presented in Berens (2009) which helps account for the periodicity of the domain.

5.2 Proposals on bounded continuous random variables

The fidelity parameters are defined on bounded state spaces (0, 1). In order to facilitate efficient proposals on these parameters we transform them onto an unbounded domain using the map $\mathcal {T}(\varvec{\gamma })$ onto the transformed parameters

$$\begin{aligned} \varvec{\theta }_\gamma = \mathcal {T}(\varvec{\gamma }) = \log \left( \frac{1}{\varvec{\gamma } } -1 \right) . \end{aligned}$$

(18)

After the transformation onto an unbounded domain, we perform standard random walk proposals on $\varvec{\theta }_\gamma$ using

$$\begin{aligned} \varvec{\theta }_\gamma '=\varvec{\theta }_\gamma +\beta _\gamma \varvec{\xi }, \; \; \; \; \varvec{\xi } \propto \mathcal {N}(0,\sigma _\gamma {\textbf {I}}_{n_1}), \end{aligned}$$

(19)

where the proposal variance $\sigma _\gamma$ is the prior variance on the transformed fidelity parameters calculated analytically using samples from the prior on $\varvec{\gamma }$ and $\beta _\gamma$ is the step-size for sampling on the transformed fidelity parameters.

We then use the inverse map $\mathcal {T}^{-1}$ to map the proposals back to the bounded fidelity domain using

$$\begin{aligned} \mathcal {T}^{-1}(\varvec{\theta }_\gamma ) = \frac{1}{\exp (\varvec{\theta }_\gamma ) + 1}. \end{aligned}$$

(20)

By making proposals on the transformed parameters, we have transformed the likelihood and therefore the posterior, we can correct for this to find the target density on $\varvec{\theta }_\gamma$ as

$$\begin{aligned} \tilde{\pi }(\varvec{\theta },\varvec{\theta }_\gamma |{\textbf {Y}}^1, {\textbf {Y}}^2)&= \pi (\varvec{\theta },\mathcal {T}^{-1}(\varvec{\theta }_\gamma )|{\textbf {Y}}^1, {\textbf {Y}}^2) \cdot | \text {det}\left( D_{\mathcal {T}^{-1}}\right) |, \end{aligned}$$

(21a)

$$\begin{aligned}&= \pi (\varvec{\theta }, \mathcal {T}^{-1}(\varvec{\theta }_\gamma )|{\textbf {Y}}^1,{\textbf {Y}}^2) \nonumber \\&\cdot \prod _{i=1}^{n_1} \frac{\exp (\theta _{\gamma , i})}{(\exp (\theta _{\gamma , i})+1)^2} , \end{aligned}$$

(21b)

where $D_{\mathcal {T}^{-1}}$ is the Jacobian of $\mathcal {T}^{-1}$ and $\theta _{\gamma ,i}$ is the $i^{th}$ transformed fidelity parameter.

5.3 Proposals on the permutation vector

MCMC techniques are predominantly designed for continuous problems, rather than for discrete problems such as permutation sampling (Zanella 2019). In order to explore different permutation vectors, we use a proposal distribution that is uniform on a set of permutations which are one switch of labels different from the current state. When at an initial permutation vector $\varvec{P}$ we propose the swapping of two cell labels $i\ne j$ to generate $\varvec{P}'$. This proposal is uninformed and symmetric about $\varvec{P}$, therefore giving the same acceptance probability as a standard random-walk on continuous random variables.

5.4 Multimodality and tempering

We assume that the parameter state space is dominated by a single best-fit mode, corresponding to the correct matching of points. However, the state-space is likely to be multimodal and difficult to sample from due to its complexity and the level of correlation between components of the model. To facilitate better exploration of the parameter space and avoid trapping in local minima, we implement likelihood-tempering, as described in Marinari and Parisi (1992). During early iterations improved mixing is promoted through a high temperature T, within the acceptance ratio given by:

$$\begin{aligned} \alpha= & {} \min \left( 1, \frac{\pi _0({\varvec{\theta }'})}{\pi _0({\varvec{\theta }})} \exp \left( \frac{1}{T} (\log (L_{\varvec{\gamma }}^{(\Sigma )}({\textbf {Y}}^1,{\textbf {Y}}^2|\varvec{\theta }',\varvec{\gamma }')) \right. \right. \nonumber \\{} & {} \left. \left. - \log (L_{\varvec{\gamma }}^{(\Sigma )}({\textbf {Y}}^1, {\textbf {Y}}^2|\varvec{\theta },\varvec{\gamma })))\right) {C_\gamma } \right) , \end{aligned}$$

(22)

where

$$\begin{aligned} C\gamma = \prod _{i=1}^{n_1} \exp \left( \theta '_{\gamma , i} - \theta _{\gamma ,i}\right) \left( \frac{\exp (\theta _{\gamma ,i})+1}{\exp (\theta '_{\gamma , i})+1} \right) ^2, \end{aligned}$$

as defined in Eq. 21b and $\varvec{\theta }$ and $\varvec{\theta }'$ are the current and proposed model parameters.

The temperature $T>0$ is gradually reduced until $T=1$ via an exponential cooling schedule along with corrections to the step-size parameters $\beta$ and $\beta _\gamma$ to help account for the change in the posterior when the likelihood is tempered. Selection of the start temperature $T_0$, the cooling rate of the system and the adjustment to the step-size are crucial to the successful and efficient identification of the dominant mode, details given in “Appendix D”.

By the point at which we sample at $T=1$ we assume that we have explored the entire state space sufficiently, facilitated by tempering, and come to reside in a mode with probability approximately proportional to its probability mass. Chains are unlikely to switch modes once the temperature has cooled, but then we are able to explore the local mode. The multimodality of the target distributions necessitates the use of multiple chains. Once $T=1$, the temperature is fixed and subsequent samples from the posterior recorded.

5.5 Interpretation of results

To interpret the results of our sampling on the permutation vector, we record the number of times each cell in ${\textbf {Y}}^1$ matches with each cell in ${\textbf {Y}}^2$ during sampling at $T=1$. The number of matches is recorded using a matrix ${{\textbf {M}}_{\text {counts}}} \in \mathbb {R}^{n_1 \times n_2}$. The matrix is then normalised so that the entries represent the proportion of samples in each matching, which can be visualised using probability heatmaps.

In order to calculate the most likely matching (MLM) of the cells in ${\textbf {Y}}^1$, we solve the linear assignment problem using the matchpairs MATLAB function (Duff and Koster 2001)

$$\begin{aligned} \varvec{P}_{\text {MLM}} = {{\,\mathrm{arg\,min}\,}}_{\varvec{P}\in S_{n_2}} \sum _{i=1}^{n_1} {1-{\textbf {M}}_{\text {counts}}(i,P_i)}{.} \end{aligned}$$

(23)

From this we can describe the MLM of a given chain, and compare this to the ground truth permutation vector for the in silico tests. In tests using real data where the true matching is unknown, this MLM would be representative of the inferred matching of points for subsequent analyses.

To assess the accuracy of the spatial matching of the points, we evaluate and store thinned samples of the cell-to-match distances for each cell i in ${\textbf {Y}}^1$ given by

$$\begin{aligned} {\Delta }_i=\Vert Y^1_i - [\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)]_i \Vert _2, \end{aligned}$$

(24)

during sampling at $T=1$. These values are then used to evaluate the median and root-mean-squared-error (RMSE) of the cell-to-match distances for each chain, thereby giving an indication of the spatial quality of the matchings.

To allow us to visualise the inferred spatial matching, and compare fidelity parameters of matches, we also calculate the MAP estimates on the transformation and fidelity parameters, conditioned on the MLM. During non-tempered sampling (at $T=1$) the minimum value of the negative log of the posterior (with $\varvec{\Sigma }$ marginalised out) is stored, along with corresponding $\varvec{\theta }$ and $\varvec{\gamma }$ parameter values. This gives us an estimate of the the deepest mode within the explored state space.

Fig. 2

a Example normalised probability heatmap of matches for the 15-cell problem with corresponding MAP estimates (conditioned on MLM) on $\varvec{\gamma }$. b Corresponding spatial matching of ${\textbf {Y}}^1$ and $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$ using MAP estimates (conditioned on the MLM) of the transformation parameters

To estimate the MAPs of model parameters conditioned on the MLM, we use the inbuilt fmincon optimiser in MATLAB, using starting positions of the parameters as those identified at the minimum negative log of the posterior.

The permutation vector is not changed from the MLM during optimisation as optimisation over the discrete permutation vector state space would have been computationally expensive and likely unnecessary due to the low acceptance of new permutation vectors during sampling at $T=1$. The maximum number of iterations and evaluations of the function were set to $10^6$. These values of $\varvec{\theta }$ and $\varvec{\gamma }$ are then used to generate spatial matching figures and displayed alongside permutation heatmaps.

6 Results

We first constructed several in silico tests which were designed to mimic real cell matching problems. The in silico test problems used real cell centre coordinates segmented from images of fixed embryos for ${\textbf {Y}}^2$. We chose to use embryos from four key stages within the mammalian preimplantation period with; 8, 15, 33 and 62 cells respectively, see S1.1–S1.3 for details. ${\textbf {Y}}^1$ was then generated by applying the observation operator with known values of the model parameters to ${\textbf {Y}}^2$, parameters given in Section S3, and adding i.i.d. mean zero Gaussian noise. The permutation was chosen to be the identity to make it simpler to visualise a correct matching.

All test problems were evaluated through 8 independent Markov chains, on a machine with specification outlined in S2. Initial positions of chains were randomly chosen as draws from the parameter priors, and a random initial permutation vector chosen. A minimum of $7\times 10^6$ tempered samples were performed (unless stated otherwise) and a further $10^6$ samples at $T=1$, where thinned chains were used to characterise the posterior. The average acceptance ratio $\bar{\alpha }$ was evaluated every 2000 iterations, and the step-sizes adjusted accordingly to ensure efficient sampling.

Fig. 3

Marginal posteriors of a affine matrix entries ($A_1$-$A_9$) and the translation vector components ($b_1$-$b_3$). b Fidelity parameters for the 15-cell in silico example. Grey and black dashed lines are the prior and maximum possible posterior on $\varvec{\gamma }$ respectively where $d=3$ is the dimension of each observation

6.1 In silico cell matching

For the first test, we generated problems where a known random affine transformation was applied to the original ${\textbf {Y}}^2$ coordinates in order to generate ${\textbf {Y}}^1$, parameters given in Section S3. Additive noise of the form $\mathcal {N}(0,0.01^2{\textbf {I}}_3)$ was then added to each point.

We performed sampling on the affine transformation parameters, the permutation vector along with fidelity parameters and disregarded non-linear deformation. All chains for the 8-, 15-, 33- and 62-cell tests converged to a posterior distribution highly concentrated on the correct matching of points as can be seen in the example permutation probability heatmap in Fig. 2a.

In order to spatially map ${\textbf {Y}}^2$ back on to ${\textbf {Y}}^1$ and visualise the matching, we calculated the MAP estimates on the transformation parameters, conditioned on the MLM and plotted ${\textbf {Y}}^1$ and $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$, Fig. 2b.

Example marginal posteriors of the affine matrix entries $A_1$–$A_9$, the translation vector components $b_1$–$b_3$ and fidelity parameters $\varvec{\gamma }$ are shown in Fig. 3a, b. We present the marginal posteriors on the affine matrix entries ($A_1$–$A_9$) rather than the marginal posteriors of the affine transformation parameters ($\phi ^{x,y,z}_{1,2}, s_{1,2,3}$), as in cases where there are low levels of shear scaling within the transformation, there is degeneracy in the construction of the affine matrix.

The fidelity parameter posteriors for all cells, in all tests, lie close to the maximum possible fidelity posterior (the fidelity posterior arising when the model and data are exactly equal), indicating excellent evidence for inclusion of all observations in this example. The noisiness of the fidelity parameter histograms is likely due to high correlations with the model parameters, causing slower convergence.

We also estimated the MAPs of the fidelity parameters conditioned on the MLM and found the fidelity parameter estimates to be close to the maximum possible posterior mode value for all matches.

Fig. 4

Typical average acceptance ratio ($\bar{\alpha }$) plots for permutation, transformation and fidelity modules (subscript P, t, and f respectively) during tempering

Average acceptance ratios were typically stable during tempering until the average acceptance ratio of the permutation sampling, $\bar{\alpha _P}$, decreased rapidly, Fig. 4. Here the average acceptance ratio of the transformation sampling, $\bar{\alpha _t}$ fluctuated and the step size $\beta$ adjusted to ensure $\bar{\alpha _t}$ was within $23.4\pm 10\%$. $\bar{\alpha _P}$ was close to zero during sampling at $T=1$ for all successful chains, most likely due to the chains being within the mode containing the global minimum whereby any proposed move in the permutation vector was unlikely to be accepted. The average acceptance ratio for the fidelity sampling $\bar{\alpha _f}$ appeared more stable than $\bar{\alpha _t}$ but we continued to adjust $\beta _\gamma$ whenever the acceptance rate was not within tolerance limits.

6.2 Data selection in presence of non-corresponding cells

The assumption that every cell in ${\textbf {Y}}^2$ has a corresponding match in ${\textbf {Y}}^1$ does not always hold, as discussed in Sect. 3, motivating the introduction of fidelity parameters to facilitate the selection of data within the point sets. If there is sufficient evidence that a match can not be described by the current model, the fidelity parameter posterior will have a small mean, dramatically reducing the impact of that observation on the likelihood.

To investigate the effectiveness of Bayesian data selection in an in silico setting, we simulated two test problems based on the 33- and 62-cell embryos. As before, we applied a random affine transformation, parameter values given in Section S3, and added noise of the form $\mathcal {N}(0,0.01^2{\textbf {I}}_3)$ to each point. To introduce cells without corresponding matches whilst maintaining $n_1=n_2$, we removed the first $n_r$ cells from ${\textbf {Y}}^1$ and the last $n_r$ cells from ${\textbf {Y}}^2$, resulting in $n_r$ cells in ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$ without corresponding matches. We first generated two problems where $n_r=3$, and 6 for the 33- and 62-cell data sets respectively. We chose to model these two stages as cells divide asynchronously at this stage in development, making the presence of points without associated matches more likely. For now we neglect the non-linear deformation.

Within these simulations we were aiming to sample from the target distribution given in Eq. 13d when we were not including data selection and Eq. 14 when we were including data selection.

Fig. 5

Comparison of matching for 33-cell test with $n_r$ cells without corresponding matches. a Example of a permutation heatmap when data selection was included, with associated MAP estimates of $\varvec{\gamma }$, conditioned on MLM. b Corresponding heatmap when data selection was not included, with two incorrect matches (pink arrows). c, d Spatial matching of points for example with and without data selection respectively

All chains for the 33-cell tests when we included data selection converged to distributions which were highly concentrated on the correct permutation vector, with reductions in the final $n_r$ fidelity parameter posterior distributions, Fig. 5a. The MLM identified was the expected permutation vector with the final non-corresponding $n_r$ cells in ${\textbf {Y}}^1$ matching to cells without corresponding matches in ${\textbf {Y}}^2$.

We then compared these results with examples where we did not include data selection. All 8 chains in the 33-cell example were concentrated about an MLM with 2 incorrect matches, Fig. 5b.

We compared the median and RMSE cell-to-match distances with and without data selection, see Table 2. It was evident that at a small cost to the RMSE, we were able to reduce the median cell-to-match distance, thereby facilitating a better, more accurate matching for the majority of cells with definitive matches, as can be seen in Fig. 5c, d and “Appendix E”. Without data selection, the matching identified is the effective result of minimising the RMSE of the cell-to-match distances for all cells, including those without corresponding matches. When using data selection, there are some matchings where the two cells are very far apart, but have very low fidelity, and as such are not heavily penalised in the potential. This leads to a higher RMSE than the examples with data selection, where the posterior concentrates on regions which have as good a match as possible over all cells. However, because these problematic matchings have been tuned out by the fidelity parameters in the data selection case, the matches with high fidelity have much lower distance between cells, and we see this in the much reduced median distance. This effect can be seen clearly in Fig. 5, where with data selection we can see a large number of very high quality matches in (c), but with a few outliers, in comparison with the results without data selection in (d), where none of the matches are of high quality, since the two point sets are inconsistent, leading to incorrect matches.

Table 2 Example of median and RMSE cell-to-match distances corresponding to the chains with the minimum values of the negative log of the posterior

Larger problems with more densely packed points could result in an increased number of incorrect matchings, as we found in the 62-cell example with $n_r=6$. When we included data selection, we were able to retrieve an MLM equal to the correct matching in all chains with non-committal matching for cells with non-corresponding matches, Fig. 6a, b.

There were between 12 and 50 incorrect matches in the MLM when data selection was not included, and the distribution appeared less concentrated on the correct permutation vector in all chains, Fig. 6c and “Appendix E”. This variability in the number of errors is indicative of a posterior that is much more difficult to explore, leading to local trapping. In this instance, Bayesian data selection helped us not only identify suitable data to be registered between ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$, but also to smooth the posterior making it easier to explore.

Fig. 6

Example of the 62-cell test with $n_r=6$ non-corresponding cells. a Permutation heatmap when data-selection is included. b Inset of region where cells have no corresponding matches and reduced $\varvec{\gamma }$. c Example permutation heatmap when data selection is not included, 14 incorrect matches in the MLM

In the 62-cell test problem we observed an increase in the RMSE of cell-to-match distances when data selection was included, but improvement in the median cell-to-match distance, indicative of an improved matching of the majority of cells, see Tables 2 and “Appendix E”. We conducted a test with larger values for $n_r$ with even more stark differences in success, see “Appendix F”.

6.3 Non-linear deformations

We next sought to incorporate non-linear deformation within the data. We generated a test problem based on the 33-cell data set where we assigned non-zero momenta, drawn from the prior, to 18 points where the x coordinates of ${\textbf {Y}}^2$ were less than 0 after the pre-processing of ${\textbf {Y}}^2$. These points were then deformed explicitly through Eqs. 2a and 2b to simulate a deformation that has occurred in one region of the embryo, rather than a global deformation. The points were then subject to an affine transformation, all parameters given in Section S3. Noise of the form $\mathcal {N}(0,0.01^2{\textbf {I}}_3)$ was then added. We designed four tests covering all combinations of inclusion of deformation in the observation operator and/or data selection.

When neglecting non-linear deformation and data selection, referred to as test (a), we found that all chains had the same MLM with two incorrect matches, see “Appendix G”. Although the number of errors in this particular example is low, when we tried another test problem with the initial momenta scaled by a factor of 1.1, we found three unique MLMs with up to 31 incorrect matches. Without data selection and the inclusion of the non-linear deformation, even small increases in problem difficulty can lead to large numbers of incorrect matches.

Next we included non-linear deformation within $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$, and neglected data selection, test (b). The posterior here is higher dimensional and more complex, leading to potentially poor mixing. We therefore increased the minimum number of tempered samples to $10\times 10^6$ which enforced a slower cooling within the tempering regime. We only found one out of eight chains that converged to the correct permutation vector, see “Appendix G”. This supports our initial belief that this higher-dimensional state space is more difficult to explore and has a higher likelihood of chain trapping within local minima. Additionally, without the fidelity parameters to assist in interpretation of the results, the identification of good matches is ambiguous within this test and therefore the interpretation of the results is limited to the assessment of the negative log of the posterior or cell to match distances.

We then included data selection and non-linear deformation within $\mathcal {G}(\varvec{\theta };{\textbf {Y}}^2)$, test (c). We increased the number of tempered samples to $10\times 10^6$ to account for the increased dimensionality of the state space. There was evidence of a highly multi-modal state space, as in test (b), as we identified five unique MLMs with between 0 and 9 incorrect matches. However, we did identify three chains out of the eight chains that converged to the correct permutation vector, see “Appendix G”. This increase in chain success could be indicative of a smoothing effect of the fidelity parameters, making the multi-modal distribution somewhat easier to explore and reducing the likelihood of chain trapping. This test however has the additional difficulty that the prior on the momenta must be carefully balanced with the prior on the fidelity parameters.

We are most interested in the identification of cell matchings where we are confident in the identified matching, i.e. not necessarily identifying all cells’ matches. We therefore neglected non-linear deformation but included data selection, test (d). Due to the reduced dimensionality, compared to tests (b) and (c), we reduced the minimum number of tempered samples back to $7\times 10^6$. We found that the 8 chains identified 2 unique MLMs with either 5 or 6 incorrect matches. The cells with incorrect matches were associated with reduced fidelity parameter posterior means ($\gamma _i<0.15$) and corresponded to cells which were explicitly deformed in the generation of the test problem. Two cells that were not deformed explicitly did have reduced posterior means of their fidelity parameters, but this is due to the interaction of points and their mutual repulsion via $\sigma _K$ in Eqs. 2a and 2b. We identified consistent matching for cells with MAP estimates of fidelity parameters (conditioned on the MLM) greater than 0.5 which corresponded with cells from the un-deformed region, see Fig. 7.

Fig. 7

Permutation heatmap for the non-linear deformation test (d). Cells ordered vertically according to the ordering of the MAP estimates of the fidelity parameters conditioned on the MLM. Un-deformed cells highlighted with cyan box

We compared the median and RMSE cell-to-match distances for test (d) with the previous tests and found that all chains in test (d) had higher distances. However, when we considered only the un-deformed cells, we found that the median cell-to-match distances were reduced, indicating a successful matching of this subset of un-deformed cells, see “Appendix G”.

We also trialled the more difficult test where the initial momentum was scaled by a factor of 1.1, and sampled only on the affine transformation, permutation vector and fidelity parameters. The 8 chains identified one unique MLM, and all cells that were subject to an initial deformation had low posterior means of their fidelity parameters (<0.15) indicating the successful reduction of their contribution to the likelihood. As for the previous example, we observed reduction of the median cell-to-match distance for the un-deformed cells, with correct matchings, again suggesting a good matching for the subset of un-deformed cells.

A final key point regarding the benefit of including data selection rather than complex non-linear deformation models is the significant improvement in run-time, due to the cost of solving the ODEs given in Eqs. 2a–2b. Tests (b) and (c) that included the deformation took approximately 30 hours to run, and suffered from slow mixing due to additional dimensionality, correlation between parameters and complexity of the posterior. On the other hand, test (d) took approximately one hour and converged to consistent MLMs therefore making it a far more feasible approach to match subsets of cells accurately within reasonable time frames.

6.4 Validation of cell matching for fixed embryos using reference markers

Next we devised a simple biological test problem where we introduced reference markers within the embryo via microinjection. We collected embryos at the 8-cell stage and then microinjected a single cell with H2b-mCherry, a fluorescent protein. Embryos were then subject to 24 h ex vivo culture and then fixed and stained with Hoechst to facilitate nuclear segmentation. See Sects. S1.1–S1.3, S1.5, Al-Anbaki (2017) and Plusa (2005) for full protocols.

We selected one embryo where four mCherry positive cells were identified and used as reference markers. The embryo was imaged and then moved randomly using a pipette before a second image of the embryo was taken, Fig. 8a, b. Cell centres were approximated through segmentation of the nuclei in both images, see Section S1.3.

Fig. 8

a The first confocal image of the embryo prior to movement on the imaging stage- reference cells marked with arrows b Second image of embryo after random reorientation. Scale bar equal to 20$\mu m$. c Example permutation heatmap with four known mCherry reference markers, ordered by MAP estimates of the fidelity parameters and most likely cell matches in ${\textbf {Y}}^2$. Highlighted rows/columns indicate the successful matching of the four reference marker (RFP positive) cells

We performed inference including data selection, neglecting non-linear deformations, and initiated 8 chains randomly using draws from the priors. A minimum of $7 \times 10^6$ tempered iterations were conducted, and a further $10^6$ iterations at $T=1$.

All eight chains were found to have the same MLM and had good spatial matching between the two point sets, with an average median cell-to-match distance equal to 0.0400 units across the 8 chains. We noticed that 6 cells had reduced fidelity posterior means in this example, Fig. 8c, but not so low as to indicate poor overall matching. We were able to confirm this by ordering the cells in the permutation heatmap such that the cells in ${\textbf {Y}}^1$ were ordered according to the MAP estimates (conditioned on the MLM) of the fidelity parameters, and then the order of ${\textbf {Y}}^2$ changed according to the maximum match probability for each cell in ${\textbf {Y}}^1$. The resulting heatmap was a diagonal matrix and we were able to show that the reference cells in ${\textbf {Y}}^1$ corresponded to the reference (RFP positive) cells in ${\textbf {Y}}^2$, Fig. 8c.

6.5 Matching of cells and embryos across imaging modalities

Finally, we wanted to trial matching cells between the final frame of a RTI experiment and an immunostained image. H2b:GFP embryos were chosen to facilitate the segmentation of cell centres from the movie, and were subject to ex vivo culture. Prior to removal of the embryos from the confocal microscope, they were imaged a final time using a z-axis resolution of 1$\mu$m to increase the accuracy of the extracted cell centres. Embryos were then fixed to halt development and stained using Hoechst to enable visualisation of the nuclei for segmentation. Details of experimental protocol given in Sections S1.1–S1.4.

We chose a group of four embryos (embryos 1–4) that were co-cultured and successfully stained (embryos A-D). Due to the co-culture of the embryos, the embryo matching was unknown a priori, Fig. 9. Embryos 1–4 had 39, 22, 37 and 28 cells respectively, and embryos A–D had 39, 23, 27 and 40 cells respectively. Each embryo combination was attempted (8 chains for each combination) using data selection and excluding the non-linear deformation. We ran a minimum of $7\times 10^6$ tempered iterations and a further $10^6$ iterations at $T=1$.

Fig. 9

Representative 2D slices from RTI study and immunostaining, confocal image. Embryos 1-4 from the final frame of the RTI, with cell nuclei visualisation via the green fluorescent channel (H2b:GFP signal). Corresponding immunostained, confocal image, embryos A-D with nuclei visualisation via Hoechst staining

We identified one unique MLM for the embryo pairings 2B and 4C, with the other embryo combinations (2A, 2C, 2D, 4A, 4B, 4D) displaying at least 5 unique MLMs, see Table 3. The identification of one unique MLM for embryo parings 2B and 4C suggests that we had found the dominating mode of the posterior distribution which we assume to represent the correct matching of the cells within the correct embryo pairing.

We identified 2 unique MLMs for the embryo pairing 1A, with seven out of eight chains sharing one of the unique MLMs, and the remaining chain converging to a different permutation vector. The other embryo pairings for embryo 1 (1B, 1C, 1D) all had more than 5 unique MLMs across the eight chains and typically had more diffuse permutation heatmaps, Fig. 10.

Table 3 Number of unique MLMs identified for each embryo combination, out of 8 chains

Due to the increase in embryo size (and therefore the number of points), the state space describing the matching of the cells in embryo 1 was likely to be more difficult to explore. We therefore tried running the matching between embryo 1 and A with a slower cooling rate by increasing the number of tempered samples to $15\times 10^6$. In this test, all chains converged to the same permutation vector which was the same permutation vector identified in 7 out of 8 chains previously, see Fig. 11a. This suggests that the one chain that converged to a different permutation vector in the shorter run was simply trapped in a local minimum due to the complexity of the state space.

We did notice that two cells in embryo 1 had reduced fidelity parameters in all chains, Fig. 11a. Upon closer inspection we identified the corresponding points of these cells and found they were in different regions of the embryo, Fig. 11b, suggesting that there were some segmentation errors within this dataset. This highlights the strength of the data selection approach as its inclusion has not only allowed us to identify the matching despite the non-corresponding cells, but also allows us to go back to the biological images and potentially re-segment the images more accurately.

Fig. 10

Example permutation heatmaps for embryo 1 and 3 with embryos A, B, C and D. Heatmaps ordered according to the MAP estimate of $\varvec{\gamma }$ conditioned on the MLM and then the corresponding maximum match in ${\textbf {Y}}^2$. More diffuse permutation heatmaps for embryo pairings 1B, 1C, 1D and 3A-D suggesting poor matching of these embryo combinations

Fig. 11

a Example permutation heatmap for the matching of embryo 1 with embryo A after performing sampling at $T=1$ for $15\times 10^6$ iterations. Two cells with significantly reduced fidelity parameter MAP estimates conditioned on the MLM highlighted in pink box. b Spatial mapping of ${\textbf {Y}}^2$ onto ${\textbf {Y}}^1$ using the MAP estimates (conditioned on the MLM) of the affine transformation parameters, low fidelity cells marked in pink. Cells with low fidelity parameters found in regions deep in the embryo and in the extremes of the z-axis where segmentation errors are more likely to occur

By deduction we could infer that embryo 3 should match with embryo D. However this was not as clear when considering the identification of unique MLMs. We trialled each embryo pairing (3A, 3B, 3C, and 3D), but found at least 6 unique MLMs for each pairing, suggesting that there is no clear matching for embryo 3. We tried running the assumed embryo pairing, 3D, with a slower cooling rate, as performed for the embryo pairing 1A, however we still identified 6 unique MLMs leading us to believe that embryo 3 is potentially a low quality data set. The permutation heatmaps were typically more diffuse for all embryo combinations, again suggesting that we were unable to identify a single global minimum indicative of the true cell matching, see Fig. 10. We referred back to the biological data and noticed that several cells in both the final frame of the movie and the stained image were undergoing cell division which could have caused differences in cell position and number that our algorithm was unable to account for.

However, it is important to highlight the fact that this result is not discouraging as we were able to robustly identify what embryos had point sets that were of sufficient quality to enable the matching of the majority of cells using our approach which is not possible when attempting matching manually.

To extend our analysis past the MLMs, we recorded the cell-to-match distances during sampling at $T=1$ and then compared the median and RMSE distances from the chain that converged to the minimum negative log of the posterior for each embryo pairing, see Table 4. By considering the median cell-to-match distance, we were able to clearly support the three identified embryo matchings; embryo 1, 2 and 4 with A, B and C respectively and we could clearly identify the low quality matches identified for embryo 3 which consistently had larger RMSE and median cell to match distances.

The identified embryo pairings did not always correspond to the lowest RMSE distances. For instance, the pairing of embryo 1 with embryo A had the largest RMSE distance, despite having the overall minimum median cell-to-match distance. This is a result of cells 5 and 19 in ${\textbf {Y}}^1$ being matched with cells 14 and 31 in ${\textbf {Y}}^2$ which were clearly in different regions of the embryo, and therefore had large cell to match distances. With data selection, the effect of these outliers can be minimised, reducing the median distance but increasing the overall RMSE.

To help us evaluate the impact of the data selection within this test, we performed the cell matching for each of the well-identified embryo matches (embryo pairs 1A, 2B and 4C) without data selection. All 8 chains for embryo pairings 2A and 4C identified the same MLM as with data selection, as we would hope for high quality data. However, when we tried to match embryo 1 with embryo A without data selection, we identified 2 MLMs with large numbers of differences when compared to the MLM identified previously with data selection. One chain had 39 differences and the remaining seven chains had 11 differences indicating the identification of completely different MLMs. This highlights our need to include the data selection framework, to ensure the accurate matching where there are cells without corresponding matches. Furthermore, the inclusion of data selection facilitates further inference and interpretation of the confidence of the matches presented within the MLM, and enables better mixing of the Markov chains due to its smoothing properties.

7 Discussion

In this work we presented a solution to an unlabelled landmark registration problem by introducing a novel Bayesian data selection approach to account for non-corresponding cells. We included non-linear deformation, 3D affine transformation and description of the matching of cells via a permutation matrix within the registration model. By using MCMC and tempering of the likelihood, we were able to explore the complex, multimodal posterior and identify most likely matchings of two point-sets. To demonstrate the efficacy of the approach, we constructed a series of in silico problems, and used real data from biological imaging experiments. We were able to determine the matching of cells between the final frame of a RTI experiment and corresponding immunostained images, even when the embryo correspondence was originally unknown due to co-culture of the embryos.

Table 4 Median and RMSE cell-to-match distances for each embryo combination, given in arbitrary units corresponding to the chain that converged to the minimum negative log of the posterior density

Our development of an approach to match single cells between imaging modalities enables the combination of historical cell data extracted from RTI studies, with protein expression at the single cell level. Previously this has been approached manually, resulting in potentially subjective conclusions relating cell behaviour and protein expression. By enabling this joint assessment of spatio-temporal information at the single cell level using our approach, we can begin to investigate the importance of cell history during cell lineage specification within the mammalian preimplantation period.

Existing landmark registration approaches are predominantly framed as optimisation problems, and therefore provide no measure of uncertainty in the identified matching of points (Kent et al. 2004). Some of these approaches also rely on some partial labelling of matches and additional information relating the points such as the properties of the landmarks (Kent et al. 2004; Dryden 2007; Green and Mardia 2006). In contrast our approach is based solely on the geometrical coordinates of the landmarks.

The development of the data selection aspect of this approach was crucial to the accurate registration in the real-world problem due to the presence of cells without corresponding matches in either image. We demonstrated that without the incorporation of the data selection framework, the accuracy of identified cell matchings was reduced, especially in larger embryos where the number of cells without corresponding matches was potentially increased. We also demonstrated that the inclusion of data selection facilitated better mixing of the MCMC chains by reducing the roughness of the state space, thus improving chain convergence and improving the robustness of the approach. More sophisticated MCMC methods that are known to be more efficient in multimodal targets, such as parallel tempering, could be used to further improve mixing and reduce computational complexity. Choosing conjugate priors for the fidelity terms could also reduce the dimensionality of the problem, and further improve mixing (Cotter 2022).

The idea of Bayesian data selection, in which parameters which govern the effect of an observation on the posterior are inferred alongside the model parameters, is extremely general, with great potential to be applicable to a very broad class of inferential problems in statistics and data science. Data cleaning is a subjective and laborious task which is often undertaken by hand, the results of which can have a profound impact on the outputs of the inference, and this approach automates that process in a way which is consistent and free from user-bias. In future work we plan to explore these ideas in more depth, and apply them to a range of disparate application areas.

Appendices

Appendix A: Description of the non-linear geodesic deformation

During fixation of the embryo and immunostaining, the embryo structure can undergo some deformation due to partial collapse or through mechanical damage which is subsequently reflected in the coordinates of the cell centres. Providing the level of the deformation is relatively small and does not affect the outcome of the intended analyses, the data can still be used. However, the transformation between the two point sets can no longer be described via an affine transformation only as the deformation can often be localised within the embryo and non-linear. We therefore include the description of a non-linear deformation to ${\textbf {Y}}^2$ using the approach introduced in Cotter (2013).

The displacement to the cells is applied through a flow field $u_t$, which can be evaluated at the current position of the landmarks ${\textbf {q}}_0={\textbf {Y}}^2$. The flow field advects the landmarks over the time interval $t \in [0,1]$. The flow field is chosen to be a geodesic which minimises the energy of the deformation given by

$$\begin{aligned} \frac{1}{2}\int _0^1 \Vert u_t\Vert ^2_V\, \textrm{d}t, \end{aligned}$$

which is uniquely determined by the initial momenta $\varvec{p}^j_t$ at $t=0$ at each landmark with coordinate $\varvec{q}^j_t$. Here V is a reproducing kernel Hilbert space (Younes 2019) with norm $\Vert \cdot \Vert _V$, and with kernel ${\textbf {K}}_V$, which we assume to be Gaussian:

$$\begin{aligned} {\textbf {K}}_V(\textbf{x},\textbf{y}) = \exp \left( -\frac{\Vert \textbf{x} - \textbf{y}\Vert ^2_2}{2\sigma _K^2} \right) . \end{aligned}$$

The geodesic deformation is then given by the solution of the following differential equations

$$\begin{aligned} \frac{d {\varvec{p}}_t^j}{d t}&= - \nabla (u_t({\varvec{q}}^j_t))^\top \cdot {\varvec{p}}_t^j, \end{aligned}$$

(25a)

$$\begin{aligned} \frac{d {\varvec{q}}_t^j}{dt}&= u_t({\varvec{q}}^j_t), \end{aligned}$$

(25b)

over the time interval [0, 1], where $\varvec{q}_t^j$ and $\varvec{p}_t^j$ are the initial position and momentum of the $j^{th}$ cell respectively, at time t in three dimensions. We define $u_t$ at ${\varvec{q}}^j_t$ as

$$\begin{aligned} u_t({\varvec{q}}_t^j)= \sum _{i=1}^{n_2} {\textbf {K}}_V({\varvec{q}}^i_t,{\varvec{q}}^j_t) {\varvec{p}}_t^i,= \sum _{i=1}^{n_2} \exp \left( -\frac{\Vert {\varvec{q}}_t^i - {\varvec{q}}_t^j \Vert ^2_2}{2 \sigma _K^2} \right) {\varvec{p}}_t^i, \nonumber \\ \end{aligned}$$

(26)

where $\sigma _K$ describes the variance of the kernel. As the data is pre-processed to ensure a minimum cell-to-cell distance of one, we found that $\sigma _K=1$ was a sensible value to use. Using Eqs. 26, 25a and 25b can be re-written as

$$\begin{aligned} \frac{d {\varvec{p}}_t^j}{d t}&= \left( -\sum _{i=1}^{n_2} \frac{({\varvec{q}}_t^i-{\varvec{q}}_t^j)}{\sigma _K^2} \exp \left( -\frac{\Vert {\varvec{q}}_t^i - {\varvec{q}}_t^j \Vert _2^2}{2 \sigma _K^2} \right) {\varvec{p}}_t^i \right) ^\top \cdot {\varvec{p}}_t^j, \end{aligned}$$

(27a)

$$\begin{aligned} \frac{d {\varvec{q}}_t^j}{dt}&= \sum _{i=1}^{n_2} \exp \left( -\frac{\Vert {\varvec{q}}_t^i - {\varvec{q}}_t^j \Vert _2^2}{2 \sigma _K^2} \right) {\varvec{p}}_t^i. \end{aligned}$$

(27b)

The deformation is applied to ${\textbf {q}}_0={\textbf {Y}}^2$, the original positions of the cell points prior to deformation, through ${\textbf {p}}_0$ and Eqs. 27a and 27b solved over $t=[0,1]$ to give ${\mathcal {D}}(\varvec{\theta };{\textbf {Y}}^2)$, the deformed ${\textbf {Y}}^2$ coordinates at time $t=1$.

Appendix B: Affine transformation in three dimensions

To apply an affine transformation to three dimensional points we define the matrix ${\textbf {A}}(\varvec{\theta })$ as a combination of two rotation matrices ${\textbf {R}}_1(\phi _1^x, \phi _1^y, \phi _1^z)$, ${\textbf {R}}_2(\phi _2^x, \phi _2^y, \phi _2^z)$, and a scaling matrix ${\textbf {S}}(s_1, s_2, s_3)$

$$\begin{aligned} {\textbf {R}}_1(\varvec{\theta })= & {} \begin{bmatrix} \cos ({\phi _1^z}) &{} \sin ({\phi _1^z}) &{} 0\\ -\sin ({\phi _1^z}) &{} \cos ({\phi _1^z}) &{} 0\\ 0 &{}0 &{}1 \end{bmatrix} \begin{bmatrix} \cos ({\phi _1^y}) &{}0&{} -\sin ({\phi _1^y}) \\ 0&{}1&{}0\\ \sin ({\phi _1^y}) &{}0&{} \cos ({\phi _1^y})\\ \end{bmatrix}\nonumber \\{} & {} \begin{bmatrix} 1&{}0&{}0\\ 0&{} \cos ({\phi _1^x}) &{} \sin ({\phi _1^x}) \\ 0&{}-\sin ({\phi _1^x}) &{} \cos ({\phi _1^x}) \\ \end{bmatrix},\end{aligned}$$

(28)

$$\begin{aligned} {\textbf {S}}= & {} \begin{bmatrix} s_1+1 &{}0 &{}0\\ 0 &{} s_2+1 &{} 0\\ 0&{} 0&{} s_3+1 \end{bmatrix},\end{aligned}$$

(29)

$$\begin{aligned} {\textbf {R}}_2(\varvec{\theta })= & {} \begin{bmatrix} \cos ({\phi _2^z}) &{} \sin ({\phi _2^z}) &{} 0\\ -\sin ({\phi _2^z}) &{} \cos ({\phi _2^z}) &{} 0\\ 0 &{}0 &{}1 \end{bmatrix} \begin{bmatrix} \cos ({\phi _2^y}) &{}0&{} -\sin ({\phi _2^y}) \\ 0&{}1&{}0\\ \sin ({\phi _2^y}) &{}0&{} \cos ({\phi _2^y})\\ \end{bmatrix}\nonumber \\{} & {} `\begin{bmatrix} 1&{}0&{}0\\ 0&{} \cos ({\phi _2^x}) &{} \sin ({\phi _2^x}) \\ 0&{}-\sin ({\phi _2^x}) &{} \cos ({\phi _2^x}) \\ \end{bmatrix}, \end{aligned}$$

(30)

where ${\textbf {A}}(\varvec{\theta })={\textbf {R}}_1 {\textbf {S}} {\textbf {R}}_2$, $\varvec{\phi }$ are Euler angles, and $\varvec{s}$ are the scaling coefficients. We describe the affine transformation matrix by applying two rotational matrices and a scaling matrix to achieve a shear scaling and rotation of the points as in Glassner (2013). This enables us to set more intuitive priors on each of the affine transformation parameters.

The affine transformation is applied as

$$\begin{aligned} {\mathcal {F}} (\varvec{\theta };{\textbf {Y}}^2)=A(\varvec{\theta }){\mathcal {D}}(\varvec{\theta };{\textbf {Y}}^2) + \varvec{b}(\varvec{\theta })\varvec{1}_{n_2}^\top , \end{aligned}$$

(31)

where $\varvec{b}(\varvec{\theta }) \in \mathbb {R}^{3}$ is a column vector of the translation parameters $b_1, b_2, b_3$ and $\varvec{1}_{n_2} \in \mathbb {R}^{n_2}$ is a column vector of ones. When non-linear deformation is not included within the transformation model ${\mathcal {D}}(\varvec{\theta };{\textbf {Y}}^2)={\textbf {Y}}^2$.

Appendix C: Calculating the ${\gamma }$-dependent normalisation to the posterior density

The normalisation factor of the posterior distribution when we include data selection, is no longer constant when we include data selection, instead it is dependent on $\varvec{\gamma }$ as

$$\begin{aligned} Z (\varvec{\gamma })= \int \det \left( \varvec{\Psi } + ({\textbf {X}}_\gamma )({\textbf {X}}_\gamma )^\top \right) ^{-\frac{\nu + n_1}{2}} d{\textbf {X}}, \end{aligned}$$

(32)

where ${\textbf {X}}_\gamma = {\textbf {X}} \; \text {diag}(\varvec{\gamma })$. We can directly calculate the $\varvec{\gamma }$-dependent normalisation by considering the substitution ${\textbf {Y}}={\textbf {X}}_\gamma$, equivalent to $y_{ij}=\gamma _i x_{ij}$. Given that $d{\textbf {X}} = \frac{d{\textbf {Y}}}{|{\text {det}}(D_J)|}$, where $D_J$ is the Jacobian of the transformation from ${\textbf {X}}$ to ${\textbf {Y}}$, given by

$$\begin{aligned} D_J = \begin{pmatrix} \gamma _1 {\textbf {I}}_3 &{} &{} \\ &{} \ddots &{} \\ &{}&{} \gamma _{n_1} {\textbf {I}}_3 \end{pmatrix} \end{aligned}$$

(33)

and the absolute value of the determinant given by

$$\begin{aligned} |\det (D_J)|= \prod _{i=1}^{n_1} \gamma _i^d. \end{aligned}$$

(34)

From this we can re-write $d{\textbf {X}}$ and write $Z(\varvec{\gamma })$ as a combination of a $\varvec{\gamma }$ dependent function multiplied by some constant

$$\begin{aligned} {Z (\varvec{\gamma })}&= \left( \prod _{i=1}^{n_1} \gamma _i^{-d} \right) \int \left| \Psi + {\textbf {Y}}{\textbf {Y}}^\top \right| ^{-\frac{\nu + n_1}{2}} d{\textbf {Y}}, \end{aligned}$$

(35a)

$$\begin{aligned}&= \left( \prod _{i=1}^{n_1} \gamma _i^{-d} \right) \frac{\pi ^{d n_1/2} \Gamma _d(\frac{\nu }{2})}{|\Psi |^{\nu /2} \Gamma _d(\frac{\nu +n_1}{2})}, \end{aligned}$$

(35b)

where $\Gamma _d(\cdot )$ is the gamma-function. By dropping the constant terms in $Z (\varvec{\gamma })$ and retaining only the factor dependent on $\varvec{\gamma }$, we re-write the posterior as

$$\begin{aligned} \pi (\varvec{\theta }, \varvec{\gamma } | {\textbf {Y}}^1, {\textbf {Y}}^2) \propto \pi _0(\varvec{\theta }) \pi _0(\varvec{\gamma }) \left( \prod _{i=1}^{n_1} \gamma _i^{d} \right) \left| \varvec{\Psi } + {{\textbf {X}}_\gamma {\textbf {X}}_\gamma }^\top \right| ^{\frac{-\nu + n_1}{2}}.\nonumber \\ \end{aligned}$$

(36)

Appendix D: Selection of the start temperature and cooling rate

The start temperature $T_0$, and the cooling rate $t_c$ of the tempering schedule, must be chosen carefully. If $T_0$ is too low, then the chain will not be able to explore the state space freely, and become trapped in a local minima early in the simulation. Alternatively, if $T_0$ is initiated too high, sampling is inefficient with too many samples obtained from the priors in early iterations of the tempering regime.

To inform our selection of $T_0$ appropriately, we first sample randomly from the priors on $\varvec{\theta }$ and $\varvec{\gamma }$ and propose random $\varvec{P}$ vectors. We then calculate the negative log of the likelihood marginalised over $\varvec{\Sigma }$, for each combination. We then calculate $T_0$ as

$$\begin{aligned} T_0 = \frac{{p}_{95}-{p}_{5}}{\log {(1+\tau )}}, \end{aligned}$$

(37)

where $\tau =0.01$, a user defined tolerance to govern how high a start temperature should be set and $p_{95}$ and $p_{5}$ the $95^{th}$ and $5^{th}$ percentiles of the negative log of the marginalised likelihood values. We then set the cooling rate to equal

$$\begin{aligned} t_c=T_0^{-f_c/N} \end{aligned}$$

(38)

where $f_c=2000$ is the minimum number of iterations performed at one temperature, and N is the original, user-defined minimum number of tempered iterations of the algorithm. We choose $f_c$ to ensure accurate calculation of acceptance rates between temperature changes and enable the system to equilibriate between each decrease in temperature. The temperature is decreased as

$$\begin{aligned} T'=T t_c, \end{aligned}$$

(39)

using an exponential multiplicative cooling regime as proposed in Kirkpatrick et al. (1983).

Table 5 Summary of the number of incorrect matches in the MLM, median and RMSE cell-to-match distances ($\Delta$) for each chain, for test problems in Sect. 6.2 and “Appendix F” when data selection was included

Table 6 Summary of the number of incorrect matches in the MLM, median and RMSE cell-to-match distances (d) for each chain, for each test problem in Sect. 6.2 and “Appendix F” when data selection was not included

The temperature is reduced every $f_c$ iterations until $T=1$, where we then perform $N_{T=1}$ samples at $T=1$, the assumed un-tempered posterior distribution. It is crucial that the reduction of T is sufficiently slow, otherwise it is likely that the chain will become trapped in some local minima of the state space. We therefore impose the condition that T is only decreased when the acceptance rate of proposals on the model transformation parameters is 23.4$\pm 10\%$ to ensure that we are sampling efficiently at any given instance of the tempered posterior, before progressing to a different temperature.

The step-sizes of the random walks are also adjusted when the temperature is reduced. $\beta$ and $\beta _\gamma$ are reduced by a factor $(1-\sqrt{t_c})$, to account for changes in the target distribution density. To further improve the random walk the step-sizes are initialised with values dependent on the number of parameters within the Gibbs module. $\beta$ is initialised with a value $\frac{2.38^2}{12+3n_2}$ when the affine and deformation transformations are included, if affine only, $\beta$ is initiated as $\frac{2.38^2}{12}$. $\beta _\gamma$ is initiated with a value of $\frac{2.38^2}{n_1}$.

Appendix E: Statistics of in silico tests with non-corresponding cells

See Tables 5 and 6.

Fig. 12

Example of permutation heatmaps for the test-problems included in Sect. 6.2, where $n_r=6,12$ cells were removed from the 33-cell and 62-cell datasets respectively. a, b Example permutation heatmaps for the 32 and 62-cell problems when data selection is included. c, d Example permutation heatmaps when data selection is not included for the two tests, MLMs found to have 21 and 37 incorrect matches for these particular examples

Appendix F: Fidelity parameter test with higher $n_r$

To further investigate the effect of the fidelity parameters (in addition to tests in Sect. 6.2), we designed a more challenging test. We instead removed $n_r=6$ and 12 cells from ${\textbf {Y}}^1$ and ${\textbf {Y}}^2$ for the 33- and 62-cell examples respectively.

When data selection was included for the 33-cell test, 6 out of 8 chains sampled from distributions highly concentrated about the correct permutation vector for the first ($n_1-n_r$) cells. The two chains that did not converge to the correct permutation vector converged to a permutation vector that had 21 incorrect matches. All chains in the 62-cell test converged to the correct permutation vector and the final $n_r$ cells had reduced posterior means of the fidelity parameters and exhibited non-committal matching in the permutation probability heatmap, Fig. 12a, b.

When we attempted to identify the matching of the points without data selection, matching success was reduced with increased numbers of incorrect matches in the MLMs, see Fig. 12c, d, and increased median cell-to-match distances, see Appendix E.

Table 7 Summary statistics for all chains from the non-linear deformation testing in Sect. 6.3

Appendix G: Statistics of synthetic tests with non-linear deformation included in Sect. 6.3

See Table 7.