Wavelet Monte Carlo: a principle for sampling from complex distributions

Abstract

We present Wavelet Monte Carlo (WMC), a new method for generating independent samples from complex target distributions. The methodology is based on wavelet decomposition of the difference between the target density and a user-specified initial density, and exploits both wavelet theory and survival analysis. In practice, WMC can process only a finite range of wavelet scales. We prove that the resulting $L_1$ approximation error converges to zero geometrically as the scale range tends to $(-\infty ,+\infty )$. This provides a principled approach to trading off accuracy against computational efficiency. We offer practical suggestions for addressing some issues of implementation, but further development is needed for a computationally efficient methodology. We illustrate the methodology in one- and two-dimensional examples, and discuss challenges and opportunities for application in higher dimensions.

1 Introduction

Accurately and efficiently calculating functionals of probability distributions is central to the majority of statistical applications. Such calculations, particularly in a Bayesian context, can be intractable, requiring integration over complex and high-dimensional distributions. To address this problem, a variety of methods have been developed, such as Importance Sampling, Rejection Sampling, and Markov Chain Monte Carlo (MCMC); see for example Robert and Casella (2004). These methods, collectively known as Monte-Carlo methods of integration, produce either independent or dependent samples from a distribution of interest. Under regularity conditions specific to each method, theoretical quantities of interest are then approximated by averages over the sampled points. We henceforth refer to a distribution of interest as the target distribution, and sampled values as particles.

Methods of Monte-Carlo integration each have their advantages and disadvantages in terms of accuracy, computational efficiency and human demands. All methods benefit from a good initial sampling distribution that well-approximates the target distribution, but such a sampling distribution may be elusive especially when the target is irregular: perhaps multimodal with intricate, convoluted or concentrated density contours. Such problems are exacerbated in high dimensions, but can be challenging even in low-dimensional settings. Large sample sizes or run lengths may be required to compensate for a poor initial sampling distribution, but even then may produce misleading results, in particular when regions of the target are under-represented or entirely missed by the generated samples.

Here we present a new method of Monte-Carlo integration: Wavelet Monte Carlo (WMC)¹, first introduced by one of us in Cironis (2019). Our WMC methodology is built upon a novel combination of the theories of wavelet decomposition and survival analysis. Particles are independently sampled from the initial distribution and then undergo a sequence of transitions based on a wavelet approximation to the difference between the initial and target distributions. The resulting set of particles is an independent sample approximately from the target. For computational efficiency, the level of this approximation can be explicitly controlled by the user, and can be sequentially improved using particles generated in previous runs. WMC has potential for parallel implementation on computer arrays.

Like other Monte-Carlo samplers, WMC benefits from a well-located initial sampling distribution but, unlike some, it does not rely on ad hoc or bespoke methods to accommodate awkward or unusual features of the target distribution. Rather, it relies only on wavelet approximations, these being well-defined as a consequence of the multiresolution analysis of wavelet decomposition (Meyer 1992).

Wavelets are functions that resemble wave-like oscillations. Subject to regularity conditions, a function of interest may be decomposed into a linear combination of location- and scale-adjusted wavelets. Efficient algorithms for this decomposition have led to their widespread use in applications of signal processing and image analysis; see for example Percival and Walden (2000), Nason (2008). From a probabilistic point of view, wavelets have been used in density estimation and statistical modelling (Donoho et al. 1996; Kerkyacharian and Picard 1992; Percival and Walden 2000). However, to our knowledge, wavelets have not previously been used in random-variate-generation algorithms.

For ease of exposition, we present the theory and methods of WMC mainly in the context of one-dimensional target distributions. In Sect. 2, before describing our methodology in detail, we review relevant elements of the extensive mathematical theory of wavelets. In Sect. 3 we introduce WMC and present a preliminary algorithm, preconditioned WMC (pWMC). In Sect. 4, to remove an awkward and restrictive precondition of pWMC, we present a modified and multistage algorithm, n-step WMC (nWMC). Section 5 presents our final algorithm, survival WMC (sWMC), which finesses nWMC into a simple recursive algorithm by appeal to the theory of survival analysis. We extend the methodology to multiple dimensions in Sect. 6. Sections 7 and 8 discuss practical issues and present some simple low-dimensional examples. Section 9 contains some concluding remarks, and the Appendix contains proofs of assertions made in the main body of the paper.

Our aim is to present only the concepts, theory and basic algorithms of WMC. Further work is required to develop the method to compete with other established methods of Monte-Carlo integration in terms of applicability, computational efficiency and ease of use.

2 Wavelet theory

Wavelet theory is extensive, developed primarily to approximate signals and images. In this section we present only those elements of the theory relevant to our methodology. There are many texts which present the theory more comprehensively; see for example Daubechies (1992), Meyer (1992) and Mallat (2009).

We first introduce the notion of a mother wavelet $\psi$, a function on the real line $\mathbb {R}$. The simplest example of a mother wavelet is the Haar wavelet

$$\begin{aligned} \psi ^\text {Haar}(x):= {\left\{ \begin{array}{ll} -1, &{} 0 \leqslant x< \tfrac{1}{2} \\ \quad 1, &{} \tfrac{1}{2} \leqslant x < 1 \\ \quad 0, &{} \text {otherwise}, \end{array}\right. } \end{aligned}$$

(1)

which has compact support and its integral over the real line is zero. We require mother wavelets $\psi$ to have the following properties.

• (i) The support of $\psi = [0,a]$, where $\psi (0) = \psi (a) = 0$, $a>1$, and $a \in \mathbb {Z}$, where $\mathbb {Z}$ denotes the set of all integers.

• (ii) $\psi$ has a number $r_\psi \ge 1$ of vanishing moments. That is,

  $$\begin{aligned} \int x^{k} \psi (x) {\text {d}}\!{x}&= 0, \qquad 0\le k \le r_\psi -1. \end{aligned}$$

  (2)

  Here and below, unless otherwise stated, integration is understood to be over $\mathbb {R}$.

• (iii) $\psi$ and its first $r_\psi$ derivatives exist, are continuous and bounded. That is, there exists a constant $C_\psi < \infty$ such that for all $x\in \mathbb {R}$

  $$\begin{aligned} |\psi ^{(k)}(x) |&\le C_\psi , \qquad 0\le k\le r_\psi , \end{aligned}$$

  (3)

  where $\psi ^{(k)}(x)$ denotes the $k^{\text {th}}$ derivative of $\psi$ at x.

• (iv) Translated and dilated wavelets $\psi _{ji}$, defined as

  $$\begin{aligned} \psi _{ji}(x) := 2^{j/2}\psi (2^jx-i), \;\; j\in \mathbb {Z},\; i\in \mathbb {Z} \end{aligned}$$

  (4)

  are orthonormal, that is

  $$\begin{aligned} \int \psi _{ji}(x)\psi _{\ell k}(x) {\text {d}}\!{x}&= {\left\{ \begin{array}{ll} 1, &{} i=k, j=\ell \\ 0, &{} \text {otherwise}. \end{array}\right. } \end{aligned}$$

These conditions are slightly more restrictive than those generally given. Specifically, it is not generally assumed that wavelet $\psi$ has compact support, as we assume in condition (i) above. Instead, condition (i) is generally replaced by one of fast-decay in $\psi$.

It is easily verified that the Haar wavelet (1) satisfies conditions (ii)–(iv) with ${r_\psi =1}$, but not condition (i) which is needed for the proofs in Appendix A.1. Many other wavelet systems satisfying all four conditions have been developed, in particular the compactly supported wavelet family of Daubechies (1988) which have ${r_\psi \ge 1}$ with minimum support length given $r_\psi$ and which we exploit in Sect. 8. See also Daubechies (1992), Meyer (1992) and Mallat (2009) for discussion of other systems, including those that relax the orthonormality condition (iv).

Conditions (i)–(iv) are a special case of those given by Meyer (1992), p.72, which admit the Haar wavelet. Meyer (1992) shows that the collection of functions

$$\begin{aligned} B&= \left\{ \psi _{ji};\, j\in \mathbb {Z},\,i\in \mathbb {Z}\right\} \end{aligned}$$

(5)

forms an orthonormal basis for $L_2(\mathbb {R})$, the space of square-integrable functions on $\mathbb {R}$. That is, any function $h\in L_2(\mathbb {R})$ can be expressed as a homogeneous wavelet expansion:

$$\begin{aligned} h(x)&= \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \tilde{h}_{j i} \psi _{j i}(x), \end{aligned}$$

(6)

where $\tilde{h}_{ji}$ is the coefficient of wavelet $\psi _{ji}$ given by

$$\begin{aligned} \tilde{h}_{ji}&= \int h(x)\psi _{ji}(x) {\text {d}}\!{x}, \qquad j\in \mathbb {Z},\; i\in \mathbb {Z}. \end{aligned}$$

(7)

Moreover with the same conditions, for suitably large $r_\psi$, decomposition (6) holds also for functions h in the more general homogeneous Triebel-Lizorkin and Besov spaces, $\dot{F}^s_{p,q}(\mathbb {R}_n)$ and $\dot{B}^s_{p,q}(\mathbb {R}_n)$, as shown in Proposition 4.2 of Kyriazis (2003). The definitions of these spaces are quite technical; see for example Triebel (1983). Of particular concern here is the homogeneous Besov space $\dot{B}^0_{1,1}(\mathbb {R})$. Informally, all functions $h \in \dot{B}^0_{1,1}(\mathbb {R})$ are integrable in absolute value over $\mathbb {R}$ and have roughness that decays over increasingly large intervals. Proposition 4.2 of Kyriazis (2003) shows that the norm of $h \in \dot{B}^0_{1,1}(\mathbb {R})$ has the equivalence

$$\begin{aligned} \Vert h\Vert _{\dot{B}^0_{1,1}}&\approx \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} 2^{-j/2} |\tilde{h}_{ji}|\; <\infty . \end{aligned}$$

(8)

For the methodology we describe below, in addition to the conditions (i)–(iv), we require (8) to hold, as we demonstrate in Sect. 3.3 and illustrate in Sect. 3.4. That is, we require functions h of interest to belong to $\dot{B}^0_{1,1}(\mathbb {R})$.

We use the homogeneous wavelet expansion (6) exclusively, rather than the more commonly encountered decomposition which additionally involves translations and dilations of a father wavelet $\phi$ (see for example Meyer (1992), Daubechies (1992), Mallat (2009)). Note that here the finest levels of detail in h are provided by $j \gg 0$, while the coarsest are provided by $j\ll 0$. Some authors adopt the opposite convention wherein j is replaced by $-j$.

The principal practical purpose of wavelet theory is to produce optimal approximations to a function h of interest, for efficient representation of sounds and images, etc. For given $j_1\in \mathbb {Z}$, omitting the finest levels of detail $j>j_1$ in equation (6) gives

$$\begin{aligned} \hat{h}_{j_1}(x)&= \sum _{j\le j_1} \sum _{i\in \mathbb {Z}} \tilde{h}_{j i} \psi _{j i}(x). \end{aligned}$$

(9)

The set of approximations $\{\hat{h}_{j_1}, \, j_1\in \mathbb {Z}\}$ is termed a multi-resolution analysis (MRA) of h. Regularity conditions (i)–(iv) ensure that $\hat{h}_{j_1}$ converges geometrically in $L_2$-norm to h at rate $r_\psi$ as $j_1 \rightarrow \infty$ (Meyer 1992; Daubechies 1992). For practical implementation of the methodology we develop below, we work with approximations that omit both finest and coarsest levels of decomposition (6):

$$\begin{aligned} \hat{h}_{j_0,j_1}(x)&= \sum _{j=j_0}^{j_1} \sum _{i\in \mathbb {Z}} \tilde{h}_{j i} \psi _{j i}(x). \end{aligned}$$

(10)

For such an approximation to converge geometrically to h we require further regularity conditions, similar to those above, but where the roles of h and $\psi$ are partially interchanged:

• (v) h has a single vanishing moment

  $$\begin{aligned} \int h(x) {\text {d}}\!{x}&= 0. \end{aligned}$$

  (11)

• (vi) h has rapid decay: that is, there exist real-valued constants $C_h<\infty$ and $s_h>1$ such that for all $x\in \mathbb {R}$

  $$\begin{aligned} |h^{(k)}(x) |&\le C_h \left( 1+|x |\right) ^{-s_h}, \;\; k\in \{0,1\}. \end{aligned}$$

  (12)

We show in Corollary 5 of Appendix A.1, subject to regularity conditions (i)–(vi), that $\hat{h}_{j_0,j_1}$ converges geometrically to h in $L_1$ norm at rate $2^{-r_\psi }$ with increasing $j_1$ and at rate $2^{-(1-s_h^{-1})}$ with decreasing $j_0$.

3 Wavelet Monte Carlo-preliminaries

In this section we prepare the groundwork for WMC, and present a preliminary algorithm which, for reasons that will become clear, we call pre-conditioned WMC, or pWMC for short.

For any real value z, let $z^+$ and $z^-$ denote its positive and negative parts

$$\begin{aligned} z^+ = {\left\{ \begin{array}{ll} z, &{} z\ge 0 \\ 0, &{} z< 0, \end{array}\right. } \qquad z^- = {\left\{ \begin{array}{ll} 0, &{} z\ge 0 \\ -z, &{} z < 0, \end{array}\right. } \end{aligned}$$

(13)

whence

$$\begin{aligned} z = z^+ - z^-, \qquad |z|= z^+ + z^-. \end{aligned}$$

(14)

Define

$$\begin{aligned} A_0&:= \int \psi ^+(x) {\text {d}}\!{x} = \int \psi ^-(x) {\text {d}}\!{x} \end{aligned}$$

where the right-hand equality follows from (2),(14). Also define

$$\begin{aligned} A_j&:= \int \psi _{ji}^+(x) {\text {d}}\!{x} = \int \psi _{ji}^-(x) {\text {d}}\!{x} = 2^{-j/2}A_0, \end{aligned}$$

(15)

where the right-hand equality follows from (4).

Let $g_0$ be an initial unnormalised density from which independent samples can be easily generated. Let $g_1$ be an unnormalised target density from which we would like to obtain independently sampled particles. For now, we assume the normalising constant $c_g$ of $g_0$ is equal that of $g_1$: that is, $\int g_0(x){\text {d}}\!{x} = \int g_1(x){\text {d}}\!{x} = c_g$. In Sect. 7.1, we propose a method for estimating the ratio: $\int g_1(x){\text {d}}\!{x}/\int g_0(x){\text {d}}\!{x}$ and adjusting $g_0$ accordingly.

In our preliminary algorithm pWMC, and in each of the algorithms presented subsequently, h will be taken as the difference between the unnormalised target and initial densities

$$\begin{aligned} h(x) = g_1(x) - g_0(x). \end{aligned}$$

(16)

Assuming that h satisfies conditions (i)–(vi) of Sect. 2, which ensure that expansion (6) holds, each run of pWMC will independently generate a particle $y \in \mathbb {R}$ from the target distribution $g_1$. Note that condition (v) implies that the normalising constants of $g_0$ and $g_1$ are equal. If they are not, they can be adjusted as noted above. Condition (vi) is unlikely to be of practical consequence since it holds even for differences between heavy-tailed densities such as scale- and location-shifted $t_3$ distributions, and pathological behaviour in the tails of $g_0$ or $g_1$ would be unusual.

Central to pWMC is the move mass function H, defined as

$$\begin{aligned} H(x)&:= \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \left[ \tilde{h}_{j i} \psi _{j i}(x)\right] ^{-}, \end{aligned}$$

(17)

which is assumed to satisfy the following precondition (for which pWMC is named):

$$\begin{aligned} H(x)&\le g_0(x), \qquad \text {for all~}x\in \mathbb {R}. \end{aligned}$$

(18)

3.1 The pWMC algorithm

Here we present the algorithm for pWMC. We discuss it in Sect. 3.3.

   Step p0::

Sample a real value $x \in \mathbb {R}$ with probability density

$$\begin{aligned} p_0(x)&= g_0(x)/c_g. \end{aligned}$$

(19)

   Step p1::

With conditional probability

$$\begin{aligned} p_1(\text {Stay}\mid x)&= 1-\frac{H(x)}{g_0(x)}, \end{aligned}$$

(20)

set $y=x$ then stop and return the value y. Otherwise, continue.

   Step p2::

Sample a pair of integers $(j,i)\in \mathbb {Z}^2$ with conditional probability

$$\begin{aligned} p_2(j, i\mid x)&= \frac{\left[ \tilde{h}_{j i} \psi _{j i}(x)\right] ^-}{H(x)}. \end{aligned}$$

(21)

   Step p3::

Sample $y \in \mathbb {R}$ with conditional probability density

$$\begin{aligned} p_3(y\mid j,i):= {\left\{ \begin{array}{ll} \psi _{j i}^+(y)/A_j, &{} \tilde{h}_{j i} \ge 0 \\ \psi _{j i}^-(y)/A_j, &{} \tilde{h}_{j i} < 0, \end{array}\right. } \end{aligned}$$

(22)

then stop and return the value y.

3.2 Proof of principle of pWMC

Lemma 1

The particle delivered by one run of the pWMC algorithm has the target density, $g_1/c_g$, provided that regularity conditions (i)–(vi) and precondition (18) all hold.

Proof

Let q(x, y) denote the joint probability density of sampling a value x at Step p0 then returning a value y at either Step p1 or Step p3. A returned value of $y\ne x$ can only be generated at Step p3. So, for $y\ne x$, marginalising over the events of Steps p1 and p2, noting that progression to Steps p2 and p3 implies $H(x)>0$ a.s., we have by construction from (19)–(22):

$$\begin{aligned} q(x,y)&= p_0(x) (1-p_1(\text {Stay}\mid x)) \nonumber \\&\qquad \times \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} p_2(j, i\mid x)p_3(y\mid j,i) \nonumber \\&= \frac{g_0(x)}{c_g} \frac{H(x)}{g_0(x)} \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \frac{\left[ \tilde{h}_{j i} \psi _{j i}(x)\right] ^-}{H(x)} \frac{\psi _{j i}^{\tilde{s}_{j i}} (y)}{A_j} \nonumber \\&= \frac{1}{c_g} \sum _{j\in \mathbb {Z}} \frac{1}{A_j} \sum _{i\in \mathbb {Z}} \left\{ \tilde{h}_{j i}^+\psi _{j i}^-(x)\psi _{j i}^+(y) \right. \nonumber \\&\quad + \left. \tilde{h}_{j i}^-\psi _{j i}^+(x)\psi _{j i}^-(y) \right\} , \end{aligned}$$

(23)

where $\tilde{s}_{j i} = \text {sign}(\tilde{h}_{j i})$. Let $p_1(y)$ denote the marginal probability density of returning the value y from the pWMC algorithm. The Kolmogorov Forward Equation gives the update:

$$\begin{aligned} p_1(y)&= p_0(y) + \int q(x,y) - q(y,x) {\text {d}}\!{x} \\&= \frac{g_0(y)}{c_g} + \int \sum _{j\in \mathbb {Z}} \frac{1}{c_gA_j} \sum _{i\in \mathbb {Z}} \left\{ \tilde{h}_{j i}^+\psi _{j i}^-(x)\psi _{j i}^+(y) \right. \\&\qquad \qquad \qquad + \tilde{h}_{j i}^-\psi _{j i}^+(x)\psi _{j i}^-(y) \\&\qquad \qquad \qquad - \tilde{h}_{j i}^+\psi _{j i}^-(y)\psi _{j i}^+(x) \\&\qquad \qquad \qquad - \left. \tilde{h}_{j i}^-\psi _{j i}^+(y)\psi _{j i}^-(x) \right\} {\text {d}}\!{x} \\&= \frac{g_0(y)}{c_g} + \frac{1}{c_g} \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \left\{ \tilde{h}_{j i}^+\psi _{j i}^+(y) + \tilde{h}_{j i}^-\psi _{j i}^-(y)\right. \\&\qquad \qquad \qquad -\left. \tilde{h}_{j i}^+\psi _{j i}^-(y) - \tilde{h}_{j i}^-\psi _{j i}^+(y) \right\} \end{aligned}$$

using (15), where we have used Fubini’s Theorem to switch the order of integration and summations, since $\int |q(x,y) - q(y,x)|{\text {d}}\!{x} < \infty$, as shown in Appendix A.2. Hence,

$$\begin{aligned} p_1(y)&= \frac{g_0(y)}{c_g} + \frac{1}{c_g} \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} (\tilde{h}_{j i}^+ - \tilde{h}_{j i}^-)(\psi _{j i}^+(y) - \psi _{j i}^-(y)) \\&= \frac{g_0(y)}{c_g} + \frac{1}{c_g} \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \tilde{h}_{j i} \psi _{j i}(y) \\&= \frac{g_0(y)}{c_g} + \frac{h(y)}{c_g} \qquad =\qquad \frac{1}{c_g}g_1(y), \end{aligned}$$

using (6),(13),(16), where (6) follows from regularity conditions (i)–(vi), as discussed in Sect. 2. $\square$

3.3 Remarks on pWMC

Lemma 1 shows that the pWMC algorithm produces a particle from the target distribution $g_1/c_g$. Repeating the algorithm L times produces L independent particles from $g_1$.

The intuition behind the pWMC algorithm is as follows. Function h in (16) is proportional to the difference between the target density $g_1/c_g$ and the initially sampled density $g_0/c_g$. At the initial particle position x, this difference may be decomposed into contributions, positive and negative, from each term in wavelet expansion (6). Now consider each contribution $\tilde{h}_{j i} \psi _{j i}(x)$ at x in isolation of all others. A negative-valued contribution suggests that $g_0(x)$ over-represents $g_1(x)$, while a positive-valued contribution suggests $g_0(x)$ under-represents $g_1(x)$. At an “over-represented" position x, the particle will transition with probability $p_2(j, i{\mid } x)p_3(y{\mid } j,i)$ to an “under-represented" position y elsewhere. We call $\psi _{ji}$ the vehicle of this transition. At an “under-represented" position x, the particle will not move, so $y=x$. This is illustrated in Fig. 1. Thus, considering all contributions collectively, in regions of net over-representation ($h(x) < 0$) particle transitions away from x to elsewhere will occur more frequently than transitions to x from elsewhere, while in regions of net under-representation ($h(x) > 0$) the converse is true.

Fig. 1

The intuition underlying the pWMC algorithm. The jagged line is the Daubechies wavelet $\psi _{00}$ with $r_\psi =2$ vanishing moments at scale $j=0$ and location $i=0$. Suppose vehicle $\psi _{00}$ has been selected for transition. The arrows illustrate two particles moving from “over-" to “under-represented" regions. Particle “A" moves if wavelet coefficient $\tilde{h}_{00}>0$, otherwise it does not move. Particle “B" moves if $\tilde{h}_{00}<0$, otherwise it does not move. Thus, since $\int \psi _{00}^+(x) {\text {d}}\!{x} = \int \psi _{00}^-(x) {\text {d}}\!{x}$, over- and under-representations are neutralised

Note that, with probability $p_1(\text {Stay}\mid x)$, a particle at x is not moved and the value $y=x$ is returned. Precondition (18) ensures that $p_1(\text {Stay}\mid x) \geqslant 0$. Integrating (18) over $x \in \mathbb {R}$, using (17) and Tonelli’s Theorem to exchange the order of integration and summations of the non-negative integrand, gives

$$\begin{aligned} \int H(x) {\text {d}}\!{x}&= \int \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \left[ \tilde{h}_{j i} \psi _{j i}(x)\right] ^{-} {\text {d}}\!{x} \nonumber \\&= \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \tilde{h}_{j i}^- \int \psi _{j i}^+(x) {\text {d}}\!{x} + \tilde{h}_{j i}^+ \int \psi _{j i}^-(x) {\text {d}}\!{x} \nonumber \\&= \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} |\tilde{h}_{j i} |A_j = A_0 \sum _{j\in \mathbb {Z}} 2^{-j/2} \sum _{i\in \mathbb {Z}} |\tilde{h}_{j i}| \nonumber \\&\le \int g_0(x) {\text {d}}\!{x} = c_g < \infty , \end{aligned}$$

(24)

using (14),(15). Hence, implicit in precondition (18) is the requirement that

$$\begin{aligned} \sum _{j\in \mathbb {Z}} 2^{-j/2} \sum _{i\in \mathbb {Z}} |\tilde{h}_{j i}|< \infty . \end{aligned}$$

(25)

This is the homogeneous Besov space norm $\Vert h\Vert _{\dot{B}^0_{1,1}}$ given in (8). Whether the requirement (25) is satisfied depends on both the wavelet family $\psi (x)$ and the difference function h(x). The following simple example illustrates failure of this requirement.

3.4 A pathological example

Suppose that $\psi$ is the Haar wavelet (1) (ignoring for the time being that it violates condition (i) of Sect. 2). Suppose also that $h(x) = \,\mathbb {I}\!\left[ 0\leqslant x< 1\right] - \,\mathbb {I}\!\left[ -1 \leqslant x < 0\right]$, where $\,\mathbb {I}\!\left[ \cdot \right]$ is the indicator function, taking the value 1 when its argument is true and 0 otherwise. Then it can be shown that

$$\begin{aligned} \tilde{h}_{j i}&= {\left\{ \begin{array}{ll} -2^{j/2}, &{} j<0,\; i\in \{-1,0\}\\ 0, &{} \text {otherwise.} \end{array}\right. } \end{aligned}$$

Substituting this into precondition (25) gives

$$\begin{aligned} \sum _{j\in \mathbb {Z}} 2^{-j/2} \sum _{i\in \mathbb {Z}} |\tilde{h}_{j i}|&= \mathop \sum \limits _{{j<0}} 2^{-j/2} (2^{j/2} + 2^{j/2}) \\&= 2\mathop \sum \limits _{{j<0}}1 = \infty , \end{aligned}$$

which violates the precondition.

This example was constructed so that the total probability on the positive x-axis differs between distributions $g_1/c_g$ and $g_0/c_g$. Consequently, for the algorithm to succeed in delivering a particle sampled from $g_1$, there needs to be a positive probability that the value y sampled in Step p3 of pWMC lies on the opposite side of the origin to the value x sampled in Step p0. However, there exists no translated and dilated Haar wavelet $\psi ^\text {Haar}_{ji}(x)$ whose support straddles the origin. Thus the system in this example provides no vehicle for transiting $x \rightarrow y$ across the origin, and therefore no way in which the target distribution can be realised. This manifests itself in the failure of precondition (25). In the multivariate generalisation of pWMC (see Sect. 6), the Haar system would provide no mechanism for transiting between the negative and positive domains of any coordinate axis.

4 Discrete-time WMC

In general, precondition (18) will be difficult to verify analytically. Violation of this precondition for any x would lead to a negative probability $p_1(\text {Stay}\mid x)$ in (20). One approach would be simply to ignore the problem and hope that no such x would be encountered while running the algorithm. However, this would not guarantee that the value y produced is a particle from the target density, $g_1/c_g$. An alternative, multistage, approach might be considered, at each stage applying pWMC to initial and target distributions that differ only slightly, incrementally progressing from $g_0/c_g$ to $g_1/c_g$. For such an approach, a precondition of the form of (18) would still be required, but would be weaker due to the smaller difference function h encountered at each stage. We present such an algorithm now with n stages, but with an adjusted initial and final distribution that removes completely the need for such a precondition. We term this algorithm n-step WMC, or nWMC for short.

For nWMC, we require that h belongs to the homogeneous Besov space $\dot{B}^0_{1,1}$ so (8) holds. We introduce an artificial time axis $t\in [0,1]$; an adjustment constant $\delta \in (0,1]$; and define $g_{t,\delta }$ to be a density located between an initial density $g_{0,\delta }$ and a target density $g_{1,\delta }$:

$$\begin{aligned} g_{t,\delta }(x)&:= g_0(x) + t h(x) + \delta H(x), \;\;\; x\in \mathbb {R}, \end{aligned}$$

(26)

where H is given by (17). It is easily verified using (16) that $g_{t,\delta }(x)$ linearly interpolates between ${g_{0,\delta }(x)=g_0(x)+ \delta H(x)}$ and ${g_{1,\delta }(x)=g_1(x)+ \delta H(x)}$, from which it is clear that our original initial and target densities are adjusted by $\delta H(x)$. For all $t\in [0,1]$, the normalising constant $\int g_{t,\delta }(x){\text {d}}\!{x}$ is given by

$$\begin{aligned} c_\delta&= \int g_0(x) {\text {d}}\!{x} + t\int h(x){\text {d}}\!{x} + \delta \int H(x) {\text {d}}\!{x} \\&= c_g + \delta A_0 \sum _{j\in \mathbb {Z}} 2^{-j/2} \sum _{i\in \mathbb {Z}} |\tilde{h}_{j i}|, \end{aligned}$$

using (24) and $\int h(x) {\text {d}}\!{x} = 0$. Note that our assertion of (8) ensures that $c_\delta$ is finite, which is critical to the validity of nWMC.

We partition the half-open time-interval (0, 1] into $n =1/\delta$ intervals of length ${\delta >0}$ indexed by $k=1,\dots ,n$. Thus the kth time-interval is the half-open interval ${((k-1)\delta ,\,k\delta ]}$. For each time-interval k, we will run pWMC taking the initial density as $g_{(k-1)\delta ,\,\delta }$ and the target density as $g_{k\delta ,\,\delta }$. Thus the normalising constant $c_g$ will become $c_\delta$, and the difference h(x) between the initial and target densities will become $g_{k\delta ,\,\delta }(x) - g_{(k-1)\delta ,\,\delta } = h(x)\delta$. Accordingly, $\tilde{h}_{j i}$ given by (7) will become $\tilde{h}_{j i}\delta$ and H given by (17) will become $H\delta$.

The nWMC algorithm starts by generating a single particle at location $x_0$ from distribution $g_{0,\delta }/c_\delta$. (The practicality of this is not our concern, as nWMC is merely a staging post en route to our final algorithm in Sect. 5.) This particle is then input to Step p1 of pWMC (adapted for $k=1$ as described above), and output to location $x_1$ from Steps p1 or p3. The particle now at $x_1$ is then re-input to Step p1 of pWMC (adapted for $k=2$) and re-output to location $x_2$ from Steps p1 or p3. This process is repeated for each time-interval $k=1,\dots ,n$, producing a sequence of particle locations $x_1,\dots ,x_n$, not necessarily all distinct.

4.1 Proof of principle of nWMC

Lemma 2

Provided that h belongs to the homogeneous Besov space $\dot{B}^0_{1,1}$ and the regularity conditions (i)–(vi) of Sect. 2 all hold, a particle delivered by one run of the nWMC algorithm will have density $g_{1,\delta }/c_\delta$.

Proof

We first show that nWMC does not require a precondition of the form of (18). With the above adaptations for time-interval k, precondition (18) becomes

$$\begin{aligned}&\delta H(x) \le g_{(k-1)\delta }(x) \nonumber \\&= g_0(x) + (k-1)\delta h(x) + \delta H(x) \nonumber \\&= (1{-}(k{-}1)\delta )g_{0,\delta }(x) {+} (k{-}1)\delta g_{1,\delta }(x) {+} \delta H(x), \end{aligned}$$

(27)

for all $x \in \mathbb {R}$, using (26), where $1\le k \le n$. But (27) is necessarily true for all $x \in \mathbb {R}$ since $g_{0,\delta }$ and $g_{1,\delta }$ are non-negative. Thus nWMC requires no precondition of the form of (18).

We complete the proof with the following inductive argument, noting that $h\in \dot{B}^0_{1,1}$ implies that $c_\delta < \infty$, as discussed above.

Assertion::

At time $t\in \{0,\delta ,\dots ,n\delta =1\}$, an nWMC particle has marginal density $g_{t,\delta }/c_\delta$.

Base case::

The particle generated at time $t=0$ has density $g_{0,\delta }/c_\delta$. Thus the assertion holds trivially for $t=0$.

Induction step::

Suppose the assertion holds for a given $t\in \{0,\delta ,\dots ,(n-1)\delta \}$. Then, on input to Step p1 of the application of pWMC to time-interval $(t,t+\delta ]$, the particle will have marginal density $g_{t,\delta }/c_\delta$. By Lemma 1, the particle output from Steps p1–p3 of this application of pWMC will have the marginal density of its target density, $g_{t+\delta ,\delta }/c_\delta$. Hence, the assertion is also true at time $t+\delta$.

Conclusion::

The base case shows that the assertion is true at $t=0$. Therefore, by induction, the assertion is true for all times $t\in \{0,\delta ,\dots ,n\delta =1\}$.

$\square$

4.2 Remarks on nWMC

An nWMC particle may or may not be moved in a given time-interval k. The foregoing provides a complete and exact description of nWMC, but greater computational efficiency might be found by eliding multiple steps together, as we now describe.

Conditional on being at location x at the start of time-interval k, let $\pi _k(x)$ denote the probability that the particle is somewhere else at the end of that time-interval. From Step p1 of pWMC adapted for time-interval k as described above, the probability of moving in time-interval k, i.e. of not stopping at x, is

$$\begin{aligned} \pi _{k}(x)&= \frac{\delta H(x)}{g_{k\delta }(x)}. \end{aligned}$$

(28)

Let $p_{k\ell }(x)$ denote the conditional probability that this particle survives at x until the start of time-interval $\ell$ whereupon it moves elsewhere, or until time 1, whichever is the sooner. Then, for $1\le k < n$, we have for $\ell \in \{k,\dots ,n\}$,

$$\begin{aligned} p_{k\ell }(x)&= {\left\{ \begin{array}{ll} \pi _\ell (x) \prod _{m=k}^{\ell -1} (1-\pi _m(x)), &{}\ell < n, \\ \prod _{m=k}^n (1-\pi _m(x)), &{} \ell =n, \end{array}\right. } \end{aligned}$$

(29)

where the product $\prod _{m=k}^{\ell -1}$ is understood to take the value 1 when $k=\ell$.

The following implementation of nWMC elides all ‘non-move’ steps into a single step, where the notation “set $u\Leftarrow v$" means “put the value of v into variable u".

4.3 The nWMC algorithm

Here we present the algorithm for nWMC, as motivated above.

   Step n0::

Sample a real value $x_0 \in \mathbb {R}$ with probability density

$$\begin{aligned} p_0(x_0)&= g_{0,\delta }(x_0)/c_\delta . \end{aligned}$$

(30)

Set $x\Leftarrow x_0$ and $k\Leftarrow 0$.

   Step n1::

Set $k \Leftarrow k+1$. Sample an integer $\ell \in \{k,\dots ,n\}$ with conditional probability $p_{k\ell }$ given in (29). If $\ell = n$, stop and return the value x. Otherwise, set $k \Leftarrow \ell +1$ and continue.

   Step n2::

Sample a pair of integers $(j,i)\in \mathbb {Z}^2$ with probability $p_2(j, i\mid x)$ given by (21).

   Step n3::

Sample a new value $x \in \mathbb {R}$ with probability density $p_3(x\mid j,i)$ given by (22), then return to Step n1.

Note that Steps n2–n3 above are essentially identical to Steps p2–p3 of pWMC.

In summary a run of the nWMC algorithm, as just described, first produces a particle at a location $x_0$ sampled from the initial distribution $g_{0,\delta }$ at time $t=0$. The particle may then jump to a new location $x_t$ at any number of subsequent times t, $0<t\le 1$. The computational efficiency of the algorithm clearly depends on the number of jumps, which will be small only if $\pi _k(x)$ given in (28) is generally small.

Lemma 2 shows that nWMC delivers a particle $x_1$ at time $t=1$ with marginal density $g_{1,\delta }/c_\delta$, where from (26) we have $g_{1,\delta } = g_1 + \delta H$. This only approximates the desired target $g_1/c_g$, the approximation error being proportional to $\delta$. This error will be small for $\delta$ close to zero, but the number of time-intervals $n=1/\delta$ will then be large. The computational demands of nWMC for large n would be burdensome, but we now adapt it to produce an algorithm, for arbitrarily large n, that is simple, practical and accurate.

5 Continuous-time WMC

For a particle at location x at a time $t=k\delta$, where $0\le k < n$, the probability $\pi _k(x)$ of moving away from x in the $(k+1)$th time-interval of nWMC is

$$\begin{aligned} \pi _{t/\delta }(x)&= \frac{\delta H(x)}{g_{t,\delta }(x)} \nonumber \\&= \frac{\delta H(x)}{g_{0,\delta }(x) + t h(x) + \delta H(x)} \nonumber \\&= \frac{\delta H(x)}{g_{0,\delta }(x) + t h(x)} + \mathcal {O}(\delta ), \end{aligned}$$

(31)

from (26),(28). Note that $g_{0,\delta }(x) + t h(x)$ is a linear time-interpolation between $g_{0,\delta }(x)$ and $g_{1,\delta }(x)$, as already noted in connection with (26), and $g_{0,\delta }$ and $g_{1,\delta }$ are both strictly positive by construction, so the denominator of (31) is necessarily strictly positive.

As $\delta \rightarrow 0$, the initial density $g_{0,\delta } \rightarrow g_0$; the target density $g_{1,\delta } \rightarrow g_1$; and the number of intervals $n=1/\delta \rightarrow \infty$. Then the length of time that the particle remains at a location x can be characterised as a continuous-time survival process with a position-dependent hazard rate at time t of $\lambda _t(x)=\lim _{\delta \rightarrow 0} \pi _{t/\delta }(x)/\delta$. From (31), for $t\in [0,1)$, this is

$$\begin{aligned} \lambda _t(x)&= \frac{H(x)}{g_0(x) + t h(x)}. \end{aligned}$$

(32)

Suppose the particle arrives at location x at a time $s\in [0,1)$. Let t be the subsequent time at which the particle departs from x. From (32), if $g_0(x)=0$ and $t=0$ or if $g_0(x) = g_1(x) = 0$, then departure is immediate: $t=s$. Otherwise, let $F(t\mid x,s)$ denote the conditional cumulative distribution function (CDF) of departure-time t given s and x. From the theory of survival analysis (see, for example, Cox and Oakes (1984)), for $s <t\le 1$

$$\begin{aligned} F(t\mid x,s)&= 1 - \exp \left\{ -\int _s^t\lambda _u(x) du\right\} \nonumber \\&= 1-\exp \left\{ -\int _s^t \frac{H(x)}{g_0(x) + u h(x)} du\right\} \nonumber \\&= {\left\{ \begin{array}{ll} 1 {-} \left( \frac{ g_0(x) + s h(x) }{ g_0(x) + t h(x) }\right) ^{\frac{H(x)}{h(x)}}, &{} h(x) {\ne } 0, \\ 1 {-} \exp \left\{ {-}(t{-}s)\frac{H(x)}{g_0(x)}\right\} , &{} h(x) {=} 0. \end{array}\right. } \end{aligned}$$

(33)

Thus, the probability of not departing from x by time $t=1$ is, from (33),

$$\begin{aligned} p(t > 1\mid x,s)&= {\left\{ \begin{array}{ll} \left( \frac{ g_0(x) + s h(x) }{ g_0(x) + h(x) }\right) ^{\frac{H(x)}{h(x)}}, &{} h(x) {\ne } 0, \\ \exp \left\{ {-}(1{-}s)\frac{H(x)}{g_0(x)}\right\} , &{} h(x) {=} 0. \end{array}\right. } \end{aligned}$$

(34)

We note in passing that the first case of (33) is the CDF of a scale-location-shifted generalised Pareto distribution, and the second case is the CDF of a location-shifted exponential distribution. In either case, sampling the time t of departure from x is straightforward using the inverse-CDF method, as follows. Sample a random variate u from the Standard Uniform distribution. Then set

$$\begin{aligned} t&= {\left\{ \begin{array}{ll} s {+} \left( \frac{g_0(x)}{h(x)} {+} s\right) \left( (1{-}u)^{{-}\frac{h(x)}{H(x)}}{-}1\right) , &{} h(x) {\ne } 0 \\ s {-} \log (u)\frac{g_0(x)}{H(x)}, &{} h(x){=}0. \end{array}\right. } \end{aligned}$$

(35)

If the sampled t is greater than 1, the particle does not move from x.

We can now implement the continuous-time survival-time version of nWMC which we call survival WMC(sWMC). The major difference between nWMC and sWMC is in Step s1.

5.1 The sWMC algorithm

   Step s0::

Sample a real value $x_0 \in \mathbb {R}$ with probability density

$$\begin{aligned} p_0(x_0)&= g_0(x_0)/c_g. \end{aligned}$$

(36)

Set $x\Leftarrow x_0$ and $t\Leftarrow 0$.

   Step s1::

If $g_0(x)=0$ and $t=0$ or if $g_0(x) = g_1(x) = 0$, then departure from x is immediate: go to Step s2. Otherwise, set $s \Leftarrow t$; sample u from the Standard Uniform distribution; then set t as in (35). If $t \ge 1$, stop and return the value x. Otherwise, continue.

   Step s2::

Sample a pair of integers $(j,i)\in \mathbb {Z}^2$ with probability $p_2(j, i\mid x)$ given by (21).

   Step s3::

Sample a new value $x \in \mathbb {R}$ with probability density $p_3(x\mid j,i)$ given by (22), then return to Step s1.

Note that Steps s2–s3 above are essentially identical to Steps p2–p3 of pWMC and to Steps n2–n3 of nWMC.

In summary, a run of sWMC first produces a particle at a location $x_0$ sampled from the initial density $g_0/c_g$ at time $t=0$. The particle may then jump to a new location $x_t$ at any number of subsequent times t, $0<t\le 1$. The computational efficiency of the algorithm clearly depends on the number of jumps, which will be small only if $\lambda _t(x)$ given in (32) is generally small.

As discussed at the end of Sect. 4.3, Lemma 2 shows that nWMC delivers a particle $x_1$ at time $t=1$ with marginal density $(g_1 + \delta H)/c_\delta$. Since sWMC is the continuous limit of nWMC and $g_{t,\delta }(x)/c_\delta \rightarrow g_t(x)/c_g$ as $\delta \rightarrow 0$ for all $x\in \mathbb {R}$, it follows that sWMC delivers a particle $x_1$ at time $t=1$ with marginal density $g_1/c_g$, the original target density.

6 Multiple dimensions

As noted above, the set of wavelets B given in (5) forms an orthonormal basis for $L_2(\mathbb {R})$. Therefore, an orthonormal basis for the d-dimensional space $L_2(\mathbb {R}^d)$ is given by the d-fold Cartesian product of B with itself, $B^d$. Accordingly, our d-dimensional generalisation of the homogeneous wavelet expansion (6) is

$$\begin{aligned} h(\textbf{x})&= \sum _{\textbf{j}\in \mathbb {Z}^d} \sum _{\textbf{i}\in \mathbb {Z}^d} \tilde{h}_{\textbf{j} \textbf{i}} \psi _{\textbf{j} \textbf{i}}(\textbf{x}), \end{aligned}$$

(37)

where ${\textbf{x} = (x_1,\dots ,x_d) \in \mathbb {R}^d}$, ${\textbf{j} = (j_1,\dots ,j_d) \in \mathbb {Z}^d}$, ${\textbf{i} = (i_1,\dots ,i_d) \in \mathbb {Z}^d}$. Here the multivariate wavelet $\psi _{\textbf{j} \textbf{i}}$ is simply the product of univariate wavelets $\psi _{j_1 i_1}, \dots , \psi _{j_d i_d}$:

$$\begin{aligned} \psi _{\textbf{j} \textbf{i}}(\textbf{x})&= \prod _{k=1}^d \psi _{j_k i_k}(x_k), \qquad \textbf{j}\in \mathbb {Z}^d,\, \textbf{i}\in \mathbb {Z}^d; \end{aligned}$$

(38)

and $\tilde{h}_{\textbf{j} \textbf{i}}$ is the coefficient of wavelet $\psi _{\textbf{j} \textbf{i}}$, given by

$$\begin{aligned} \tilde{h}_{\textbf{j} \textbf{i}}&= \int _{\mathbb {R}^d} h(\textbf{x}) \psi _{\textbf{j} \textbf{i}}(\textbf{x}) {\text {d}}\!{\textbf{x}}. \end{aligned}$$

(39)

Note that expansion (37) involves products of wavelets (38) at different scales in different dimensions, unlike the more usual d-dimensional wavelet expansion given for example in Meyer (1992), which additionally involves father wavelets.

Let $g_0(\textbf{x})$ and $g_1(\textbf{x})$ denote the multivariate initial and target densities at location $\textbf{x}$. Let ${h(\textbf{x})= g_1(\textbf{x})-g_0(\textbf{x})}$ denote the difference function, generalising (16). Then the d-dimensional version of sWMC is exactly as described in Sect. 5.1, replacing functions $g_0,g_1,h$ and the univariate quantities $x_0,x,j,i,\psi _{ji},\tilde{h}_{ji},H,A_j$ used and referenced therein in equations (17),(21),(22),(35) with their d-dimensional counterparts, which for $A_j$ is $\prod _{k=1}^d A_{j_k}$.

7 Practical considerations

In this section we discuss several practical issues confronted when running sWMC. For ease of exposition, we return to the univariate setting for most of this discussion, but include some brief comments on the multivariate setting at the end.

Applications of Monte-Carlo methods typically generate large sample sizes, sometimes dependently, as in MCMC. However, there are potential advantages for methods such as WMC that generate independent samples, in terms of both statistical and computational efficiency. In particular, they allow parallel and distributed implementation on multiple independent processors. Below, we use the notation $S_L = {\{x^{[\ell ]},\;\ell =1,\dots ,L\}}$ to denote a sample of L particles independently drawn from the same distribution.

7.1 Estimating the normalising-constant ratio

Suppose the normalising constants $c_{g_0}=\int g_0(x){\text {d}}\!{x}$ and $c_{g_1}=\int g_1(x){\text {d}}\!{x}$ are unknown or unequal. We can estimate the ratio $\rho = c_{g_0}/c_{g_1}$ as follows. Let $p_{\text {dom}}$ denote a convenient probability density which dominates both $g_0$ and $g_1$. Draw a sample $S_L$ from $p_{\text {dom}}$, then estimate $\rho$ as follows:

$$\begin{aligned} \hat{\rho }_L&= \frac{ \sum _{\ell =1}^L \frac{g_1(x^{[\ell ]})}{p_{\text {dom}}(x^{[\ell ]})} }{ \sum _{\ell =1}^L \frac{g_0(x^{[\ell ]})}{p_{\text {dom}}(x^{[\ell ]})} }. \end{aligned}$$

(40)

Using $\hat{\rho }_L$, we can adjust $g_0$ to produce an unnormalised density $\tilde{g}_0$ for which $c_{\tilde{g}_0} = c_{g_1}$ for use in WMC, thus

$$\begin{aligned} \tilde{g}_0(x)&= \hat{\rho }_L \,g_0(x). \end{aligned}$$

(41)

7.2 Estimating wavelet coefficients

Methods of Monte-Carlo integration replace explicit computation of integrals on a target distribution with averages over particles sampled from that distribution. sWMC is one such method, but its implementation involves calculation of many wavelet coefficients $\tilde{h}_{ji}$, each of which is itself an integral (7), typically not of closed form. This feature would seem self defeating, but we now show that it is sufficient, for each particle, to replace each $\tilde{h}_{ji}$ encountered in the algorithm with an independent unbiased estimate of it. From regularity condition (i) of Sect. 2, the mother wavelet $\psi$ has support [0, a] for some integer $a>1$ so, from (4), the support of $\psi _{j i}$ is $[2^{-j}i,\,2^{-j}(i+a)]$. A simple unbiased estimate of $\tilde{h}_{ji}$ is obtained by averaging the value of $h(u)\psi _{ji}(u)$ obtained from $N\ge 1$ values of u sampled independently from the Uniform distribution with the same support as $\psi _{j i}$.

Let $\tilde{h}_{jiN}^{[\ell ]}$ denote such an unbiased independent estimate of $\tilde{h}_{ji}$ for particle $\ell$. For each particle $\ell \in \{1,\dots ,L\}$, replacing each $\tilde{h}_{ji}$ encountered in running sWMC by its estimate leads to approximating h by an empirical version of equation (6):

$$\begin{aligned} \bar{h}_{LN}(x)&= L^{-1}\sum _{\ell =1}^L \sum _{j\in \mathbb {Z}} \sum _{i\in \mathbb {Z}} \tilde{h}_{jiN}^{[\ell ]} \psi _{j i}(x), \qquad x\in \mathbb {R}, \end{aligned}$$

(42)

which is unbiased for $\tilde{h}_{ji}$ with variance proportional to $L^{-1}N^{-1}$. However, inaccurate estimates of $\tilde{h}_{ji}$ will likely increase the number of jumps at Step s3 of sWMC.

7.3 Range of scales j

As described in Sect. 5.1, the sWMC algorithm assumes an unbounded range of scales j. However, for practical computation, we must restrict scales j to a finite range $[j_0,j_1]$, as in (10). As noted above, the support of $\psi _{j i}$ is $[2^{-j}i,\,2^{-j}(i+a))$. At any given location x and scale j, there are therefore exactly a wavelets supported at x: $\{\psi _{j i}:\; 2^jx-a < i \le 2^jx\}$, and Step s2 of sWMC requires a coefficient $\tilde{h}_{ji}$ to be calculated for each of these wavelets. Consequently, for a particle arriving at x, the total number of wavelet coefficients to be calculated is $(j_1-j_0+1)a$, which will need to be repeated after every jump (Step s3 of sWMC).

With the regularity conditions (i)–(vi) of Sect. 2, Lemma 3 of Appendix A.1 shows that omitting scales $j>j_1$ produces an $L_1$ error in the wavelet approximation (10) of h proportional to $2^{-r_\psi j_1}$. So choosing a wavelet family with compact support and large $r_\psi$ would ensure rapid convergence to h as $j_1\rightarrow \infty$. However, orthogonal wavelets with $r_\psi$ vanishing moments have support length $a \ge 2r_\psi -1$ (Mallat 2009), so increasing $r_\psi$ will proportionately increase the amount of computation in sWMC. A computationally efficient choice of wavelet family $\psi$ and upper scale-range limit $j_1$ will depend on the magnitude of fine-scale details in h, and would need to be decided on a case-by-case basis, possibly by trial and error. Setting the finest level $j_1$ too low could result in blurring some fine-scale details of the target distribution.

Lemma 3 of Appendix A.1 shows that omitting scales $j<j_0$ produces an $L_1$ error in the wavelet approximation $\hat{h}_{j_0,j_1}$ of h in (10) proportional to $2^{-j_0(1-s_h^{-1})}$. Thus, unfortunately, the rate of convergence to h as $j_0\rightarrow -\infty$ depends on the rate of decay $s_h$ in the tails of h, and not on the choice of wavelet family $\psi$ with $r_\psi$ vanishing moments, which is under the control of the user. Wavelets in WMC act as vehicles that transition particles from one location to another, but each wavelet $\tilde{h}_{ji}$ can only perform such a transition within its support. To reduce the average number of jumps per particle, the coarsest resolution level $j_0$ should be chosen to ensure that a particle will generally be able to move from its initial location to all regions of high target density in a single jump. Running sWMC restricting $j\in [j_0,j_1]$ will produce a particle with output density $g_0 + \hat{h}_{j_0,j_1}$. Setting the coarsest level $j_0$ too high could miss some coarse-scale features of the target distribution and could potentially lead to negative values of this theoretical output density at certain locations, which would clearly invalidate regularity condition (vi) of Sect. 2. If such a problem is suspected or detected, sWMC should be rerun with a reduced setting of $j_0$.

As a rule of thumb, the more irregular or complex the target, the wider should be the range $[j_0,j_1]$. To improve the approximation to target $g_1$ of the particle output density $g_0 + \hat{h}_{j_0,j_1}$ from a run of sWMC, the particle’s location can be input to Step s1 of a second run of sWMC, this time restricting $j\in [j_1+1,\,j_1^\star ]$, where $j_1^\star >j_1$. The particle will then on output have density $g_0 + \hat{h}_{j_0,j_1^\star }$. Inputting the particle to a third run of sWMC, this time restricting $j\in [j_0^\star ,\,j_0-1]$, where $j_0^\star <j_0$, will produce a particle output density of $g_0 + \hat{h}_{j_0^\star ,j_1^\star }$. Repeating this process in parallel on an entire particle-set $S_L$ provides a multistage version of sWMC which will improve the approximation to $g_1$ at each stage. Such an algorithm could be useful in determining iteratively an adequate range for scale j.

7.4 Multivariate practical considerations

All of the practical considerations discussed above apply equally in the multivariate setting, replacing the univariate quantities $x_0,x,j,i,\psi _{ji},\tilde{h}_{ji},H,A_j$ with their d-dimensional counterparts, as described in Sect. 6. In particular, an unbiased estimate of multivariate wavelet coefficient $\tilde{h}_{\textbf{j} \textbf{i}}$ can be obtained by averaging $h(\textbf{u})\psi _\textrm{ji}(\textbf{u})$ over N values of $\textbf{u}$ sampled independently from the d-dimensional Uniform distribution whose support is that of $\psi _\textrm{ji}$. The total number of wavelet coefficients $\tilde{h}_{\textbf{j} \textbf{i}}$ to be calculated for each particle, initially and after each jump, will be $(j_1-j_0+1)^d a^d$.

8 Examples

This paper is essentially a proof-of-concept of sWMC. However, as a limited exploration of the strengths and weaknesses of the method, we compare its performance in 1- and 2-dimensional examples with three well-established Monte-Carlo samplers: Rejection Sampling (von Neumann 1951); Importance Sampling (Kahn and Harris 1951); and the Random Walk Metropolis algorithm (Metropolis et al. 1953). Each of these methods involves an initial sampling distribution $g_0$ and a target distribution $g_1$. Let $w(\textbf{x}) = g_1(\textbf{x})/g_0(\textbf{x})$.

To be practically useful, a method should be highly computationally efficient. For each Monte-Carlo sampler, we define its computational efficiency as

$$\begin{aligned} \mathcal{E}&= p_\text {keep} \times \text {{ESS}}/\bar{n}_\text {eval}, \end{aligned}$$

(43)

where $p_\text {keep}$ is the proportion of generated particles that are retained, ESS is the effective sample size per retained particle (which compares the informational content of a sample of retained particles with that of an equal-sized i.i.d. sample from the target), and $\bar{n}_\text {eval}$ is the average number of calls to the function $g_1$ per particle. Our focus on $\bar{n}_\text {eval}$ rather than CPU time per se is motivated with applications to computationally expensive targets in mind, although the toy examples presented below are not of this nature.

For each Monte-Carlo sampler, we also compute its discrepancy. For this, we first construct a finite mesh $\mathcal{M}$ covering the main support of the target distribution, and for each cell $k \in \mathcal{M}$ compare the observed proportion of samples $o_k$ falling into that cell with its expected value $e_k$ under the target distribution, where both $o_k$ and $e_k$ are normalised over the mesh. The simple form of the target distributions in the examples below allows $e_k$ to be calculated exactly. We then compute discrepancy as:

(44)

We compare and contrast the following four Monte-Carlo samplers:

• Wavelet Monte Carlo (sWMC) As described above, all samples are retained and are independent, so $p_\text {keep}=1$ and ${\textsc {ESS}}=1$. Thus $\mathcal{E} = 1/\bar{n}_\text {eval}$. The number of target evaluations for a particle is related to its number of its jumps en route, the number of wavelet coefficients that must be computed before each jump, and the method of computing them. In the examples below, we evaluate wavelet coefficients numerically on a fine grid, but gain a substantial reduction in this overhead by caching and reusing coefficients previously computed during the run.

• Rejection Sampling (RS) assumes the existence of a finite upper bound M on $w(\textbf{x})$. Independently sampled proposed particles $\textbf{x}$ from $g_0/c_g$ are retained as samples from the target with probability $a = w(\textbf{x})/M$ and discarded with probability $1-a$. Here $p_\text {keep}=1/M$; ESS$=1$; and $\bar{n}_\text {eval}=1$. Thus $\mathcal{E} = 1/M$.

• Importance Sampling (IS) requires the variance $\text {Var}_{g_0}[w]$ of $w(\textbf{x})$ under $g_0(\textbf{x})$ to be finite. Independently sampled particles $\textbf{x}$ from $g_0/c_g$ are retained as weighted samples from the target with weight $w(\textbf{x})$. Here $p_\text {keep}=1$; ESS is estimated as $1/\text {E}_{g_0}[w^2(\textbf{x})]$; and $\bar{n}_\text {eval}=1$. Thus $\mathcal{E} = 1/\text {E}_{g_0}[w^2(\textbf{x})]$.

• Random-walk Metropolis (RWM) From an initial point $\textbf{x}^{[1]}$ sampled from $g_0$, subsequent particles $\textbf{x}^{[i]}$, $i>1$, are generated by first sampling a particle $\textbf{y}$ from a symmetric proposal distribution $q^{\text {prop}}$ centered at $\textbf{x}^{[i-1]}$, then assigning to $\textbf{x}^{[i]}$ either the value $\textbf{y}$ with probability $\alpha$ or the value $\textbf{x}^{[i-1]}$ with probability $1-\alpha$, where $\alpha =\min (1,g_1(\textbf{y})/g_1(\textbf{x}^{[i-1]}))$. After discarding particles generated during the burn-in of the Markov chain, all particles are retained as autocorrelated samples from the target. Here $p_\text {keep}$ is therefore the proportion of the chain remaining after discarding the burn-in; $\bar{n}_\text {eval}=1$; and we estimate ESS using the Mahalanobis step-distance measure of Sherlock and Roberts (2009).

8.1 Example 1

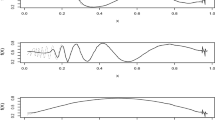
To lower the computational cost of the algorithm, one would ideally choose a convenient initial distribution $g_0/c_g$ that is similar to the target $g_1/c_g$. However, the final result of a run of sWMC should change little if the chosen initial distribution is far from the target in location, spread and shape. This is demonstrated in Fig. 2, where the initial univariate Normal distribution $g_0$ has extremely low probability within the main mass of the target mixture $g_1$ of Normal, Exponential and Uniform densities. Daubechies wavelets $\psi$ with 4 vanishing moments were used, setting the scale-range $[j_0,j_1]$ to $[-7,12]$. Numerical integration was used to calculate wavelet coefficients. An average of 7.4 jumps per particle was recorded. We see that sWMC has recovered the target distribution well despite its multimodality, with no tendency to get stuck in local modes.

Fig. 2

A one-dimensional example where the initial density $g_0$, shown with a broken line, is the Normal distribution $N(-2,2^2)$ and the target density $g_1$, shown with a solid line, is a weighted mixture of Normal, Uniform and shifted-Exponential distributions: $N(-20, 0.5^2)$ with weight 1/8; U(25, 26) with weight 1/8; $N(30, 9^2)$ with weight 1/4; U(40, 41) with weight 1/4; and $\text { {Expon}}(0.2)$ with origin at 43 and weight 1/4. The shaded histogram is of $L=100\,000$ independent particles generated by sWMC

In this example, the regularity conditions for RS and IS are not met as $g_0$ does not dominate the tails of $g_1$. Thus $M=\infty$ and $\text {Var}_{g_0}[w]=\infty$, implying in (43) that numerical efficiency $\mathcal{E}_{\texttt {RS}}=\mathcal{E}_{\texttt {IS}}=0$. This might seem an easy win for sWMC but perhaps not a fair comparison as practitioners of RS and IS would avoid using this $g_0$ in this example. To address this point, for sWMC, RS and IS, we performed a single simulation of $L=100\,000$ iterations progressing through a sequence of five initial distributions $g_0$ of 20 000 iterations each, using $t_5$-distributions located at $-$2.0 with increasing scale from 5.0 to 80.0 (sd 6.45 to $-$103.3). For RWM, we set $x^{[1]}=-2$ and used the same sequence of $t_5$-distributions as proposal distributions $q^{\text {prop}}$, centering them at the current point $x^{[i-1]}$ instead of at $-2$. For sWMC, we used Daubechies wavelets² $\psi$ with $r_\psi =4$ vanishing moments and scale-range $[j_0,j_1]=[-9,12]$, and at each scale we estimated the normalising-constant ratio $\hat{\rho }_L$ (40) from $L=20\,000$ samples drawn from a $p_{\text {dom}}$ which comprised an equally weighted mixture of the five initial distributions $g_0$. For RS, the upper bound M was determined theoretically; this would not generally be an option for more complex targets. The discrepancy mesh $\mathcal{M}$ in (44) covered the interval $(-25, 55)$ with cell width 0.5. The results are reported in Tables 1 and 2.

Table 1 Example 1: Monte-Carlo sampler efficiency calculations (43) for a sequence of scalings of the initial/proposal $t_5$ distribution

Table 2 Example 1: Monte-Carlo sampler discrepancy calculations (44) for a sequence of scalings of the initial/proposal $t_5$ distribution

Table 1 shows that optimal efficiency $\mathcal{E}$ is obtained for each sampler with an initial distribution (or proposal distribution) scaling of $\approx$40.0. For $\texttt {sWMC}$, efficiency is progressively aided by the caching of wavelet coefficient as they are calculated. The efficiency of RS is abetted by the pre-calculation of an exact upper bound M on w(x) at each stage; in general this would not be practical and a much larger M might be adopted, implying smaller $\mathcal{E}$. These efficiency calculations appear to suggest that sWMC is the least desirable of these methods. However, the discrepancy calculations $\mathcal{D}$ in Table 2 tell a different story. Theoretically, RS delivers samples exactly from the target $g_1$, provided M is suitably large; (iterations 1–20 000 were skipped to avoid an excessive run time due to their extremely large value of M, see Supplementary Table 5). Although $\mathcal{D}$ is more discrepant for sWMC than RS, we see that RWM and IS can be much worse depending on scaling, due to poor mixing of RWM and the large standard deviation in weights w for IS (see Supplementary Table 5). Supplementary Figs. 4–7 show, for sWMC and RS, excellent fits of simulated particles to the target distribution, but for IS the fit is rough with a spurious peak, while for RWM the heights of the sharp peaks in the target distribution are poorly estimated.

Supplementary Table 5 gives the mean number of particle moves at each stage of the sWMC simulation, showing that the number of moves increased in the mid-scale range. Supplementary Fig. 8 shows the position–time tracks of eight particles from the mid-scale of the simulation. Some of these particles moved only a few times, while others moved many times, sometimes briefly visiting far-off places. Supplementary Table 5 also shows that the estimated normalising-constant ratio $\hat{\rho }_L$ (40) remained close to its true value, in this example $\rho = 1.0$. Further simulations revealed that setting $\hat{\rho }_L = 1.0$ had little effect on the results (not shown).

8.2 Example 2

A two-dimensional application of sWMC is illustrated in Fig. 3, where the target distribution is a mixture of four bivariate Normals, one being highly concentrated, scattered within the main support of the initial bivariate Normal. Daubechies wavelets $\psi$ with 3 vanishing moments were used, setting the scale-range $[j_0,j_1]$ to $[-2,4]$. Numerical integration was used to calculate wavelet coefficients. Again we see that sWMC has recovered the target distribution well. Around the point (-2,3), the black (particle) contours are more spread out than the red (target) contours; this is due to the smoothing effect of the kernel-density estimate of the particles around this highly concentrated point of the target.

Fig. 3

A two-dimensional example where the initial density $g_0$, shown with dotted contours, is a bivariate Normal distribution $N \left( \left[ \begin{array}{c} 3 \\ 0 \end{array} \right] , 4^2 \left[ \begin{array}{cc} 1 &{} 0 \\ 0 &{} 1 \end{array} \right] \right)$ and the target density $g_1$, shown with broken contours, is an equally weighted mixture of four bivariate Normal distributions $N \left( \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] , \left[ \begin{array}{cc} 2 &{} 2 \\ 2 &{} 3 \end{array} \right] \right) ,\! N\left( \left[ \begin{array}{c} 4 \\ 4 \end{array}\right] , \left[ \begin{array}{cc} 7 &{} 2 \\ 2 &{} 3 \end{array}\right] \right) ,\! N\left( \left[ \begin{array}{c} -2 \\ 3 \end{array}\right] , \left[ \begin{array}{cc} .004 &{} .001 \\ .001 &{} .003 \end{array}\right] \right) , N\left( \left[ \begin{array}{c} 5 \\ -5 \end{array}\right] , \left[ \begin{array}{cc} 6 &{} 2 \\ 2 &{} 3 \end{array}\right] \right) .$ The solid contours are those of a kernel density estimate based on 10 000 independent particles generated by sWMC

Tables 3 and 4 compare the performance of sWMC with that of RS, IS and RWM, for different scalings of the initial distribution. Preliminary runs suggested setting the burn-in for RWM to zero. Scale 4 corresponds to the initial distribution of Fig. 3, for which we see in Table 3 that sWMC is less efficient than the other methods, but in Table 4 that it also has low discrepancy D. However, the discrepancy statistic does not tell the whole story. Supplementary Fig. 11 shows that both sWMC and RS recover the target well, but there are serious problems with the IS and RWM solutions; both miss the concentrated target peak at (-2,3). At scale 2, a similar picture emerges (Supplementary Fig. 10). At scale 1, we find that sWMC has not performed well but IS and RWM have performed much worse, the latter due to slow mixing (Supplementary Fig. 9), while RS was not performed at all due to its long predicted run time ($\approx$ 85 000 $\times$ that for scale 2, see Supplementary Table 6). Compared to scale 4, at scale 6 the performance of sWMC has deteriorated, while that of IS and RWM has improved (Supplementary Fig. 12).

Table 3 Example 2: Monte-Carlo sampler efficiency calculations (43) for scalings of the initial/proposal bivariate normal distribution

Table 4 Example 2: Monte-Carlo sampler discrepancy calculations (44) for scalings of the initial/proposal bivariate normal distribution

8.3 Summarising results

Examples 1 and 2 provide a snapshot of how the methodology might perform in practice in comparison to other Monte Carlo methods. In particular we see that sWMC can provide good precision with low-dimensional but highly irregular targets. Unlike RS, IS and RWM, we found that sWMC was better able to cope with under-dispersed initial distributions relative to the target, while the other methods performed better when over-dispersed. These examples also illustrate that sWMC can provide reasonable efficiency when measured in terms of numbers of target-function evaluations, which is appropriate when such evaluations are computationally burdensome. Clearly, the target functions in these examples are easily evaluated, and in terms of CPU-time there are relatively large overheads in running sWMC. For example, in the mid-scale range of Table 1, the CPU-time of sWMC was $7~\times$ that of RS and $280~\times$ that of RWM.

These examples are intended only to illustrate the behaviour of sWMC. They do not provide thorough comparisons with other methods, each of which could benefit from tailored or adaptive initial/proposal distributions depending on the form of target distribution. Any method, including sWMC, will benefit from an initial distribution that is close to the target. Other methods might be more appropriate; indeed, in each of the toy examples presented above, the target distribution can be simulated directly!

9 Conclusions

We have presented here the theory and methodology of WMC, a new method for Monte-Carlo integration which independently samples particles from a potentially complex target distribution. Independence of the particles opens the possibility of implementation on parallel computing arrays, for computational speed. For computational efficiency, the user can control the accuracy of approximation to the target distribution through the settings of the coarsest and finest scales $j_0$ and $j_1$. As discussed in Sect. 7, the choice of wavelet family $\psi$, with its attendant number of zero moments $r_\psi$, controls inaccuracy due to omitting scales finer than $j_1$, but this has no effect on inaccuracy due to omitting scales coarser than $j_0$, which depends on the differential tail decay-rate $s_h$ between the initial and target densities, $g_0$ and $g_1$. As discussed in Sect. 7, sWMC can be run to sequentially improve approximations in previously obtained sWMC particles.

Our emphasis in this paper has been on developing the theory and methodology of sWMC. The computational efficiency of sWMC will depend heavily on the number of wavelet coefficients to be calculated before each jump and on the expected number of jumps, which in turn depend on the choice of mother wavelet $\psi$, the scale range $[j_0,j_1]$, the initial distribution $g_0$, the method of evaluating wavelet coefficients; and the number of dimensions d. The number of jumps will be reduced substantially if an initial distribution is chosen to be close to the target, but in general this will be infeasible. As suggested in Sect. 7, wavelet coefficients may be estimated rather than directly calculated, with potential computational savings. Inaccurate estimates may however increase the number of jumps. Much remains to be done to explore the impact of these factors on computational efficiency and accuracy in different settings. New methods for accurate and computationally efficient evaluation of wavelet coefficients could hugely improve the practicality of sWMC.

The number of wavelet coefficients increases exponentially with the number of dimensions d, as shown at the end of Sect. 7. The ‘curse of dimensionality’ is common to most if not all methods of Monte Carlo integration, and is unavoidable unless the target distribution has a structure that is decomposable in some way, as in the case of graphical models (see, for example, Jordan (2004)). Further development of sWMC would be required to exploit such target-distribution decomposability.