Abstract
Stochastic gradient Markov chain Monte Carlo (SGMCMC) is a popular class of algorithms for scalable Bayesian inference. However, these algorithms include hyperparameters such as step size or batch size that influence the accuracy of estimators based on the obtained posterior samples. As a result, these hyperparameters must be tuned by the practitioner and currently no principled and automated way to tune them exists. Standard Markov chain Monte Carlo tuning methods based on acceptance rates cannot be used for SGMCMC, thus requiring alternative tools and diagnostics. We propose a novel bandit-based algorithm that tunes the SGMCMC hyperparameters by minimizing the Stein discrepancy between the true posterior and its Monte Carlo approximation. We provide theoretical results supporting this approach and assess various Stein-based discrepancies. We support our results with experiments on both simulated and real datasets, and find that this method is practical for a wide range of applications.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Most MCMC algorithms contain user-controlled hyperparameters which need to be carefully selected to ensure that the MCMC algorithm explores the posterior distribution efficiently. Optimal tuning rates for many popular MCMC algorithms such the random-walk (Gelman et al. 1997) or Metropolis-adjusted Langevin algorithms (Roberts and Rosenthal 1998) rely on setting the tuning parameters according to the Metropolis-Hastings acceptance rate. Using metrics such as the acceptance rate, hyperparameters can be optimized on-the-fly within the MCMC algorithm using adaptive MCMC (Andrieu and Thoms 2008; Vihola 2012). However, in the context of stochastic gradient MCMC (SGMCMC), there is no acceptance rate to tune against and the trade-off between bias and variance for a fixed computation budget means that tuning approaches designed for target invariant MCMC algorithms are not applicable.
1.1 Related work
Previous adaptive SGMCMC algorithms have focused on embedding ideas from the optimization literature within the SGMCMC framework, e.g. gradient preconditioning (Li et al. 2016), RMSprop (Chen et al. 2016) and Adam (Kim et al 2020). However, all of these algorithms still rely on hyperparameters such as learning rates and subsample sizes which need to be optimized. To the best of our knowledge, no principled approach has been developed to optimize the SGMCMC hyperparameters. In practice, users often use a trial-and-error approach and run multiple short chains with different hyperparameter configurations and select the hyperparameter setting which minimizes a metric of choice, such as the kernel Stein discrepancy (Nemeth and Fearnhead 2020) or cross-validation (Izmailov et al. 2021). However, this laborious approach is inefficient and not guaranteed to produce the best hyperparameter configuration.
1.2 Contribution
In this paper we propose a principled adaptive SGMCMC scheme that allows users to tune the hyperparameters, e.g. step-sizes h (also known as the learning rate) and data subsample size n. Our approach provides an automated trade-off between bias and variance in the posterior approximation for a given computational time budget. Our adaptive scheme uses a multi-armed bandit algorithm to select SGMCMC hyperparameters which minimize the Stein discrepancy between the approximate and true posterior distributions. The approach only requires a user-defined computational budget as well as unbiased estimates of the gradients of the log-posterior, which are already available to us via the stochastic gradient MCMC algorithm. A second contribution in this paper is a rigorous assessment of existing tuning methods for SGMCMC, which to our knowledge is not present in the literature.
2 Background
2.1 Stochastic Gradient Langevin Algorithm
We are interested in sampling from a target density \(\pi (\varvec{\theta })\), where for some parameters of interest \(\varvec{\theta }\in {\mathbb {R}}^d\) the unnormalized density is of the form \(\pi (\varvec{\theta }) \propto \exp \{ -U(\varvec{\theta })\}\). We assume that the potential function \(U(\varvec{\theta })\) is continuous and differentiable almost everywhere. If we have independent data, \(y_1,\ldots ,y_N\) then \(\pi (\varvec{\theta }) \propto p(\varvec{\theta }) \prod _{i=1}^N f(y_i \mid \varvec{\theta })\) is the posterior density, where \(p(\varvec{\theta })\) is the prior density and \(f(y_i\mid \varvec{\theta })\) is the likelihood for the ith observation. In this setting, we can define \(U(\varvec{\theta })=\sum _{i=1}^N U_i(\varvec{\theta })\), where \(U_i(\varvec{\theta })= - \log f(y_i \mid \varvec{\theta })-(1/N)\log p(\varvec{\theta })\).
We can sample from \(\pi (\varvec{\theta })\) by simulating a stochastic process that has \(\pi \) as its stationary distribution. Under mild regularity conditions, the Langevin diffusion (Roberts and Tweedie 1996; Pillai et al. 2012) has \(\pi \) as its stationary distribution, however, in practice it is not possible to simulate the Langevin diffusion exactly in continuous time and instead we sample from a discretized version. That is, for a small time-interval \(h>0\), the Langevin diffusion has approximate dynamics given by
where \(\varvec{\xi }_k\) is a vector of d independent standard Gaussian random variables. In the large data setting, we replace \(\nabla U(\varvec{\theta })\) with an unbiased estimate \(\nabla {\tilde{U}}(\varvec{\theta }) = \frac{N}{n} \sum _{i \in {\mathcal {S}}_n} \nabla U_i(\varvec{\theta })\), calculated using a subsample of the data of size \(n<<N\), where \({\mathcal {S}}_n\) is a random sample, without replacement, from \(\{1,\ldots ,N\}\). This algorithm is known as the stochastic gradient Langevin dynamics (SGLD, Welling and Teh 2011).
In this paper we present our adaptive stochastic gradient MCMC scheme in the context of the SGLD algorithm for simplicity of exposition. However, our proposed approach is readily generalizable to all other stochastic gradient MCMC methods, e.g. stochastic gradient Hamiltonian Monte Carlo (Chen et al. 2014). Details of the general class of stochastic gradient MCMC methods presented under the complete recipe framework are given in Ma et al. (2015). See Sect. C of the Supplementary Material for a summary of the SGMCMC algorithms used in this paper.
2.2 Stein discrepancy
We define \({\tilde{\pi }}\) as the empirical distribution generated by the stochastic gradient MCMC algorithm (1). We can define a measure of how well this distribution approximates our target distribution of interest, \(\pi \), by defining a discrepancy metric between the two distributions. Following Gorham and Mackey (2015) we consider the Stein discrepancy
where \(\phi : {\mathbb {R}}^d \rightarrow {\mathbb {R}}^d\) is any smooth function in the Stein set \({\mathcal {F}}\) which satisfies Stein’s identity \(\mathbb {E}_{{\pi }} \left[ {{\mathcal {A}}_{\pi }\phi (\varvec{\theta })}\right] =0\) for all \(\phi \in {\mathcal {F}}\).
2.2.1 Kernel Stein discrepancy
To obtain an analytic form of the Stein discrepancy, Liu et al. (2016) and Chwialkowski et al. (2016) introduced the kernelized Stein discrepancy (KSD) where \({\mathcal {F}}\) is the unit ball of a d-dimensional reproducing kernel Hilbert space. The KSD has the closed form solution
where
The kernel k must be positive definite, which is a condition satisfied by most popular kernels, including the Gaussian and Matérn kernels. Gorham and Mackey (2017) recommend using the inverse multi-quadric kernel, \(k(\varvec{\theta },\varvec{\theta }^\prime ) = (c^2 + ||\varvec{\theta }-\varvec{\theta }^\prime ||_2^2)^\beta \), which they prove detects non-convergence when \(c>0\) and \(\beta \in (-1,0)\).
2.2.2 Finite set Stein discrepancy
KSD is a natural discrepancy measure for stochastic gradient MCMC algorithms as \(\pi (\varvec{\theta })\) is only required up to a normalization constant and the gradients of the log-posterior density are readily available. The drawback of KSD is that the computational cost is quadratic in the number of samples. Linear versions of the KSD (Liu et al. 2016) are an order of magnitude faster, but the computational advantage is outweighed by a significant decrease in the accuracy of the Stein estimator.
Jitkrittum et al. (2017) propose a linear-time Stein discrepancy, the Finite Set Stein Discrepancy (FSSD), which utilizes the Stein witness function \(g(\varvec{\theta }^\prime ):=\mathbb {E}_{{\varvec{\theta }\sim {\tilde{\pi }}}} \left[ {-\nabla _{\varvec{\theta }}U(\varvec{\theta })^{\top } k(\varvec{\theta },\varvec{\theta }^\prime ) + \nabla _{\varvec{\theta }}^{\top } k(\varvec{\theta },\varvec{\theta }^\prime )}\right] \). The function g can be thought of as witnessing the differences between \({\tilde{\pi }}\) and \(\pi \), where a discrepancy in the region around \(\varvec{\theta }\) is indicated by large \(|g(\varvec{\theta }) |\). The Stein discrepancy is essentially then measured via the flatness of g, where the measure of flatness can be computed in linear time. The key to FSSD is to use real analytic kernels k, e.g, Gaussian kernel, which results in \(g_1,\ldots ,g_d\) also having a real analytic form. If \(g_i \ne 0\) then this implies almost surely that \(g_i({\textbf{v}}_1),\ldots ,g_i({\textbf{v}}_J)\) are not zero for a finite set of test locations \(V=\{{\textbf{v}}_1,\ldots ,{\textbf{v}}_J\}\). Under the same assumptions as KSD, FSSD is defined as,
Theorem 1 of Jitkrittum et al. (2017) guarantees that \(\textrm{FSSD}^2=0\) if and only if \({\tilde{\pi }}=\pi \) for any choice of test locations \(\{{\textbf{v}}\}_{j=1}^J\). However, some test locations will result in an improved test power for finite samples and so, following Jitkrittum et al. (2017), we optimize the test locations by first sampling them from a Gaussian fit to the posterior samples and then use gradient ascent so that they maximise the FSSD.
3 Hyperparameter learning
In this section we introduce an automated and generally-applicable approach to learning the user-controlled parameters of a stochastic gradient MCMC algorithm, which throughout we will refer to as hyperparameters. For example, in the case of SGLD, this would be the stepsize parameter h and batch size n, or in the case of stochastic gradient Hamiltonian Monte Carlo, this would also include the number of leap frog steps. Our adaptive scheme relies on multi-armed bandits (Slivkins 2019) to identify the optimal setting for the hyperparameters such that, for a given time budget, the selected parameters minimize the Stein discrepancy, and therefore maximize the accuracy of the posterior approximation. Our proposed approach, the Multi-Armed MCMC Bandit Algorithm (MAMBA), works by sequentially identifying and pruning, i.e. removing, poor hyperparameter configurations in a principled, automatic and online setting to speed-up hyperparameter learning. The MAMBA algorithm can be used within any stochastic gradient MCMC algorithm and only requires the user to specify the training budget and the number of hyperparameter sets.
3.1 Multi-armed bandits with successive halving
Multi-armed bandits are a class of algorithms for sequential decision-making that iteratively select actions from a set of possible decisions. These algorithms can be split into two categories: 1) best arm identification in which the goal is to identify the action with the highest average reward, and 2) exploration vs. exploitation, where the goal is to maximize the cumulative reward over time (Bubeck and Cesa-Bianchi 2012). In the best-arm identification setting, an action, aka arm, is selected and produces a reward, where the reward is drawn from a fixed probability distribution corresponding to the chosen arm. At the end of the exploration phase, a single arm is chosen which maximizes the expected reward. This differs from the typical multi-armed bandit setting where the strategy for selecting arms is based on minimizing cumulative regret (Lattimore and Szepesvári 2020).
The successive halving algorithm (Karnin et al. 2013; Jamieson and Talwalkar 2016) is a multi-armed bandit algorithm based on best arm identification. Successive halving learns the best hyperparameter settings, i.e. the best arm, using a principled early-stopping criterion to identify the best arm within a set level of confidence, or for a fixed computational budget. In this paper, we consider the fixed computational budget setting, where the algorithm proceeds as follows: 1) uniformly allocate a computational budget to a set of arms, 2) evaluate the performance of all arms against a chosen metric, 3) promote the best \(1/\eta \) of arms to the next stage, where typically \(\eta =2 \ \text {or} \ 3\), and prune the remaining arms from the set. The process is repeated until only one arm remains. As the total computational budget is fixed, pruning the least promising arms allows the algorithm to allocate exponentially more computational resource to the most promising hyperparameter sets.
3.2 Tuning stochastic gradients with a multi-armed MCMC bandit algorithm (MAMBA)
We describe our proposed algorithm, MAMBA, to tune the hyperparameters of a generic stochastic gradient MCMC algorithm. For ease of exposition, we present MAMBA in the context of the SGLD algorithm (1), where a user tunes the step size h and batch size n. Details on other SGMCMC algorithms can be found in Appendix C. We present MAMBA as the following three stage process:
3.2.1 Initialize
In our multi-armed bandit setting we assume M possible stochastic gradient MCMC hyperparameter configurations, which we refer to as arms. Each arm s in the initial set \(S_0 = \{1,\ldots ,M\}\) represents a hyperparameter tuple \(\phi _s=(h_s,n_s)\). The hyperparameters in the initial set are chosen from a uniform grid.
3.2.2 Evaluate and prune
At each iteration of MAMBA, \(i = 0, 1, \ldots \), each arm s is selected from the set \(S_i\) and the \(s^\text {th}\) SGLD algorithm is run for \(r_i\) seconds using the hyperparameter configuration \(\phi _s\). Each arm is associated with a reward \(\nu _s\) that measures the quality of the posterior approximation. We use the negative Stein discrepancy as the reward function that we aim to maximize. Specifically, we calculate the Stein discrepancy from the SGMCMC output using KSD (3) or FSSD (4), i.e. \(\nu _s = -\textrm{KSD}({\tilde{\pi }}_{s},\pi )\) or \(\nu _s = -\textrm{FSSD}({\tilde{\pi }}_{s},\pi )\). Without loss of generality, we can order the set of arms \(S_i\) by their rewards, i.e. \(\nu _1 \ge \nu _2 \ge \ldots \ge \nu _{M}\), where \(\nu _1\) is the arm with the optimal reward at each iteration of MAMBA. The top \(100/\eta \%\) of arms in \(S_i\) with the highest rewards are retained to produce the set \(S_{i+1}\). The remaining arms are pruned from the set and not evaluated again at future iterations.
3.2.3 Reallocate time
Computation time allocated to the pruned samplers is reallocated to the remaining samplers, \(r_{i+1} = \eta r_i\). As a result, by iteration i, each of the remaining SGLD samplers has run for a time budget of \(R = r_0 + \eta r_0 + \eta ^2r_0 +... + \eta ^{i-1}r_0\) seconds, where \(r_0\) is the time budget for the first MAMBA iteration. This process is repeated for a total of \( \lfloor \log _{\eta }M\rfloor \) MAMBA iterations. We use a \(\log _\eta \) base as we are dividing the number of arms by \(\eta \) at every iteration. Furthermore, we use a floor function for the cases where the initial number of arms M is not a power of \(\eta \). The MAMBA algorithm is summarized in Algorithm 1.

3.2.4 Algorithmic guarantees
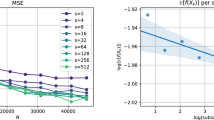
It is possible that MAMBA will eliminate the optimal hyperparameter set during one of the arm-pruning phases. Through examination of the \(1-1/2\eta \) quantile, we can derive a bound on the probability that MAMBA will incorrectly prune the best hyperparameter configuration (see Theorem 1). Using this result, we are also able to bound the maximum computational budget required for MAMBA to identify the optimal hyperparameters.
Definition 1
Let \(s \in \{2,\ldots ,M\}\) be an arm with reward \(\nu _s\), then we define the suboptimality gap between \(\nu _s\) and the optimal reward \(\nu _1\) as \(\alpha _s:= \nu _1 - \nu _s\), and we define \(H_2:= \max _{s \ne 1} s/\alpha _s^2\) as the complexity measure, see Audibert et al. (2010) for details.
Theorem 1
i) MAMBA correctly identifies the best hyperparameter configuration for a stochastic gradient MCMC algorithm with probability at least
where \(\sigma ^2_{\textrm{KSD}} = \max _{s \in S}\textrm{Var}_{{\tilde{\pi }}_{s}}(\mathbb {E}_{{{\tilde{\pi }}_{s}}} \left[ {k_\pi (\varvec{\theta },\varvec{\theta }')}\right] )\).
ii) For a probability of at least \(1-\delta \) that MAMBA will successively identify the optimal hyperparameter set, MAMBA requires a computational budget of
A proof of Theorem 1 is given in Appendix A and builds on the existing work of Karnin et al. (2013) for fixed-time best-arm identification bandits. Theorem 1 highlights the contribution of KSD variance in identifying the optimal arm. In particular, the total computation budget depends on the arm with the largest KSD variance.
3.3 Practical guidance for using MAMBA
3.3.1 Choice of budget
There is flexibility in the choice of budget in MAMBA. We advocate for the use of a compute time budget for fast but biased sampling algorithms like SGMCMC because it allows users to view these algorithms as a trade-off between statistical accuracy and runtime. The goal is then to identify the hyperparameters that produce the best Monte Carlo estimates under a given time constraint. A compute time budget allows users to optimise the batch size in a principled way and ties the hyperparameter optimisation to the available hardware and software, such as whether or not the model was implemented using vectorisation.
Alternative choices for the budget could be based on the total number of iterations or the total number of gradient evaluations. The former would be helpful for storage constraints but has no natural mechanism for tuning the batch size. The total number of gradient evaluations would allow for batch size tuning but is less closely linked to the available hardware and software, and would not take into account implementation decisions such as vectorising the gradient estimator.
3.3.2 Estimating KSD/FSSD
Calculating KSD/FSSD using (3) or (4) requires the gradients of the log-posterior and the SGMCMC samples. Typically, one would calculate the KSD/FSSD using fullbatch gradients (i.e. using the entire dataset) on the full chain of samples. However, as we only use SGMCMC when the dataset is large, this would be a computationally expensive approach. Two natural solutions are to i) use stochastic gradients (Gorham et al. 2020), calculated through subsampling, or ii) use a thinned chain of samples. We investigate both options in terms of KSD/FSSD accuracy in Appendix 3.4.2. We find that using the stochastic KSD/FSSD produces results similar to the fullbatch KSD/FSSD. However, calculating the KSD/FSSD for a large number of high dimensional samples is computationally expensive, so for our experimental study in Sect. 4 we use fullbatch gradients with thinned samples. This leads to lower variance KSD/FSSD estimates at a reasonable computational cost. Note that fullbatch gradients are only used for MAMBA iterations and not SGMCMC iterations. We find that this does not significantly increase the overall computational cost as for each iteration of MAMBA there are thousands of SGMCMC iterations.
3.3.3 Alternative metrics
Stein-based discrepancies are a natural metric to assess the quality of the posterior approximation as they only require the SGMCMC samples and log-posterior gradients. However, alternative metrics to tune SGMCMC can readily be applied within the MAMBA framework. For example, there is currently significant interest in understanding uncertainty in neural networks via metrics such as expected calibration error (ECE), maximum calibration error (MCE, Guo et al. 2017), and out-of-distribution (OOD) tests (Lakshminarayanan et al. 2017). These metrics have the advantage that they are more scalable to very high dimensional problems, compared to the KSD (Gong et al. 2020). As a result, although KSD is a sensible choice when aiming for posterior accuracy, alternative metrics may be more appropriate for some problems, for example, in the case of very high-dimensional deep neural networks.
3.4 Tuning methods
3.4.1 Grid search and heuristic method
We test the efficacy of MAMBA on a simpler grid search approach. For the grid search method we run the sampler using the training data, and calculate the RMSE/log-loss/accuracy on the test dataset. To have a fair comparison to MAMBA (see Sect. 3.4.2), we always start the sampler from the maximum a posteriori estimate (the MAP, found using optimization). As a result we need to add noise around this MAP or else the grid search tuning method will recommend the smallest step size available which results in the sampler not moving away from the starting point. This happens because the MAP has the smallest RMSE/ log-loss (or highest accuracy). To fix this we add Gaussian noise to the MAP, and report the scale of the noise for each model in Sect. B.
The heuristic method fixes the step size to be inversely proportional to the dataset size, i.e. \(h=\frac{1}{N}\) (Brosse et al. 2018). For both the grid search and heuristic approaches, we use a \(10\%\) batch size throughout.
3.4.2 MAMBA
We investigate the tradeoffs involved in estimating the KSD from samples in MAMBA. We can estimate this using the stochastic gradients estimated in the SGMCMC algorithm. However we can also calculate the fullbatch gradients and use these to estimate the KSD. Although the latter option is too computationally expensive in the big data setting, we can also thin the samples to estimate the KSD which may result in the fullbatch gradients being computationally tractable.
In Fig. 1 we estimate the KSD of samples using the logistic regression model over a grid of step sizes. We run SGLD for the three models for 1 s and with a batch size of \(1\%\). We estimate the KSD in 4 ways: fullbatch using all the samples, fullbatch using thinned samples (thin by a factor of 5), stochastic gradients using all samples, and stochastic gradients using thinned samples. In Fig. 2 we do the same but varying the batch size (and keeping the step size fixed to \(h = 10^{-4.5}\). We can see that the KSD estimated using stochastic gradients and unthinned samples follows the fullbatch KSD well. However as calculating the KSD for many high dimensional samples is computationally expensive, we opt for using thinned fullbatch gradients in all our experiments.
4 Experimental study
In this section we illustrate MAMBA (Algorithm 1) on three different models and compare it to alternative tuning methods. We use three core tuning methods for all three models: i) MAMBA-KSD, ii) grid search with log-loss as metric, and iii) the heuristic approach. For the logistic regression model only, we also try two alternative tuning methods: iv) MAMBA-FSSD and v) grid search-KSD. We show in Table 4 an overview of the tuning methods used in these experiments.
The initial arms in MAMBA are set as an equally spaced grid over batch sizes and step sizes (and number of leapfrog steps for SGHMC). The heuristic method fixes the step size to be inversely proportional to the dataset size, i.e. \(h=\frac{1}{N}\) (Brosse et al. 2018). For both the grid search and heuristic approaches, we use a \(10\%\) batch size throughout.
Note that only the tuning methods that use KSD/FSSD are able to estimate both step size and batch size. This is because the log-loss metric used for grid search is not particularly sensitive to the choice of batch size, and over a range of batch sizes the log-loss produces similar values. In contrast, KSD and FSSD measure the quality of the posterior samples and their approximation accuracy to the posterior, which is strongly affected by the batch size as well as the available computational budget.
Full details of the experiments can be found in Appendix B. Experiments were conducted using the Python package SGMCMCJax (Coullon and Nemeth 2022) and code to replicate the experiments can be found at https://github.com/jeremiecoullon/SGMCMC_bandit_tuning. All experiments were carried out on a laptop CPU (MacBook Pro 1.4 GHz Quad-Core Intel Core i5). For each example, the figures show results over a short number of tuning iterations and tables give results for longer runs.
4.1 Logistic regression
We consider logistic regression on a simulated dataset with 10 dimensions and 1 million data points (details of the model and prior are in Appendix B.1). We sample from the posterior using six samplers: SGLD, SGLD with control variates (SGLD-CV, Baker et al. 2019), stochastic gradient Hamiltonian Monte Carlo (SGHMC, Chen et al. 2014), SGHMC-CV, stochastic gradient Nosé Hoover Thermostats (SGNHT), and SGNHT-CV (Ding et al. 2014a).
We recall that we tune each samplers’ hyperparameters using i) MAMBA-KSD, ii) grid search with log-loss, and iii) the heuristic approach. In this section, we also run MAMBA using FSSD as the metric, as well as grid search with KSD as the metric, to assess the practicality of these approaches.
For MAMBA, we set \(R=1sec\) (i.e.: the run time of the longest sampler). We point out that this time budget is small compared to what would be used by most practitioners. However, this example illustrates the MAMBA methodology and compares it against a full MCMC algorithm which provides us with “ground-truth” posterior samples. To calculate the KSD/FSSD efficiently, we thin the samples and use fullbatch gradients.
Applying the grid search approach with KSD as the metric: we thin the samples and use fullbatch gradients as we have done with KSD and FSSD. To allow a close comparison to MAMBA-KSD, we choose a time budget rather than number of iterations and we tune the batch size as well as the step size. The objective of this experiment is to see how grid search would work with a metric that can capture whether the samples are from the correct distribution. We choose 1sec as the time budget, which is the same amount of time that the final sampler will have run for in MAMBA-KSD. So, in the best arm in MAMBA-KSD, as well as for all the combinations of gridsearch-KSD, the sampler will have run for 1sec before the final KSD is computed. We discuss these results below and present them in Table 6 in the appendix.
In Fig. 3, we plot the KSD calculated from the posterior samples for each of the tuning methods. We calculated the KSD curves for ten independent runs and plotted the mean curve along with a confidence interval (two standard deviations). The optimal hyperparameters given by each method can be found in Table 5 of Appendix B.1. Our results from Fig. 3 show that optimizing the hyperparameters with MAMBA, using either KSD or FSSD, produces samples that have the lowest KSD out of all but one of the six samplers. For the SGNHT sampler, the heuristic approach gives the lowest KSD, however, as shown in Table 5 in Appendix B.1, MAMBA-FSSD finds an optimal step size of \(h=N^{-1}\), which coincides with step size given by the heuristic approach. Therefore, the difference in KSD from these two methods is a result of the batch size, which when taking into account computation time, MAMBA-FSSD finds \(1\%\) to be optimal, whereas the heuristic method does not learn the batch size and this is fixed at \(10\%\). Ignoring computation time, a larger batch size is expected to produce a better posterior approximation. However, it is interesting to note that for the five out of six samplers where MAMBA performs the best in terms of KSD, MAMBA chooses an optimal batch size of \(1\%\).
For this simulated data example with only 1 million samples we can compare the posterior accuracy of the SGMCMC algorithms against the ground-truth using NumPyro’s (Bingham et al. 2018; Phan et al. 2019) implementation of NUTS (Hoffman and Gelman 2014) on the full dataset for 20K iterations (after a burn-in of 1K iterations). We then calculate the relative error in the posterior standard deviation for each sampler: \(\xi ({\hat{\sigma }}):= \Vert {\hat{\sigma }}-\sigma _{\text {NUTS}}\Vert _2 / \Vert \sigma _{\text {NUTS}}\Vert _2\). The results are given in Table 1 and further results including predictive accuracy on a test dataset and the number of samples obtained within the time budget are given in Table 6 of Appendix B.1. We tested each sampler by running each sampler for 10 s.
We find that the MAMBA-optimized samplers perform among the best in terms of KSD. As a result, the Monte Carlo estimates of the posterior standard deviations generally perform well. As described above we also run grid search with KSD as a metric and tune the step size as well as the batch size. We find that although grid search with KSD gives results that are comparable to MAMBA-KSD, the running time for this tuning method is slower than MAMBA-KSD. Indeed grid search with KSD ranged from 1.2 to 2.2 times slower than MAMBA-KSD. As a result, we will not use this method for the models in the next sections, as this computational cost would only increase.
Furthermore, when tuning SGHMC and SGHMC-CV, we tune three hyperparameters using MAMBA (step size, batch size, and number of leapfrog steps), and two hyperparameters using grid-search (step size and number of leapfrog steps). We find that although MAMBA is tuning more hyperparameters, the method finds optimal hyperparameters with approximately 3x speedup. As grid search scales poorly with dimension, we expect this gap to widen when tuning more hyperparameters.
4.2 Probabilistic matrix factorization
We consider the probabilistic matrix factorization model (Salakhutdinov and Mnih 2008) on the MovieLens datasetFootnote 1 (Harper and Konstan 2015), which contains 100K ratings for 1682 movies from 943 users (see Appendix B.2.1 for model details). We optimize the hyperparameters for six samplers: SGLD, SGLD-CV, SGHMC, SGHMC-CV, SGNHT, and SGNHT-CV.
To tune these samplers we use a similar setup as for logistic regression and use (i) MAMBA-KSD, (ii) grid search with log-loss, and (iii) the heuristic approach. Details are given in Appendix B.2.
From Fig. 4 we can see that the samplers tuned using MAMBA tend to outperform the ones tuned with the other two methods. We also test the quality of the posterior samples against NumPyro’s (Phan et al. 2019; Bingham et al. 2018) implementation of NUTS (Hoffman and Gelman 2014), which produces 10K samples with 1K samples as burn-in. This state of the art sampler obtains high quality samples but is significantly more computationally expensive, taking around six hours on a laptop CPU. We estimate the posterior standard deviations using these samples and treat them as the ground-truth. We run each SGMCMC sampler for 20 s, and estimate the standard deviation after removing the burn-in. We estimate the posterior standard deviation for each sampler and show the relative errors and KSD in Table 2 (further results are given in Table 8 in Appendix B.2). We find that MAMBA consistently identifies hyperparameters that give the lowest KSD, but that for some samplers the heuristic approach gives a lower error on the estimated standard deviation. This could be due to the random realisation of the SGMCMC chain; however, while accuracy in standard deviation is fast to compute, as a metric it is not as useful as KSD, which measures the quality of the full distribution and not just the accuracy of the second moment.
Moreover, as in the case of logistic regression in the previous section, we find that tuning SGHMC and SGHMC-CV using MAMBA-KSD is faster than grid-search using log-loss (approximately 2x faster). This confirms our expectation that when tuning many hyperparameters MAMBA scales better than grid search.
4.3 Bayesian neural network
In this section we consider a feedforward Bayesian neural network with two hidden layers on the MNIST dataset (LeCun and Cortes 2010) (see Appendix B.3.1 for details). Here we tune six samplers: SGLD, SGLD-CV, SGHMC, SGHMC-CV, SGNHT, and SGNHT-CV.
For this example, as with the previous two examples, we tune these samplers using i) MAMBA-KSD, ii) grid search with log-loss, and iii) the heuristic approach. However, we validate the accuracy of the various tuning approaches against expected calibration error (ECE) and maximum calibration error (MCE) plotted in Fig. 5. We find that the samplers tuned using MAMBA tend to outperform the other approaches in terms of ECE. We assess the performance of the MAMBA-optimized samplers over a longer time budget and run the samplers for 300 s starting from the maximum aposteriori value. We then remove the visible burn-in and calculate the ECE and MCE to compare the quality of the posterior samples. We report the results in Table 3, where ECE and MCE are reported as percentages (lower is better).
Overall, the results in Table 3 show that MAMBA-optimized samplers tend to perform best in terms of KSD and when not the best they produce results which are very close to the best performing method. For all samplers, MAMBA finds an optimal batch size of \(1\%\), which is ten times smaller than the batch size of the other methods and therefore results in a faster and highly accurate algorithm. For SGNHT, both MAMBA and grid search found a step size that was slightly too large (\(\log _{10}(h)=-4.5\) and \(\log _{10}(h)=-4\) respectively) which caused the sampler to lose stability for longer chains. In contrast, the sampler tuned using the heuristic method is the only one that remained stable. As a result we re-ran these two tuning methods for a grid with smaller step sizes: \(\{-5., -5.5, -6., -6.5, -7., -7.5\}\). This smaller grid allowed the two tuning algorithms to find a stable step size (\(\log _{10}(h)=-5\) for both methods), and so this slight decrease in step size was enough to make the sampler stable. We note that there exists samplers with more stable numerical methods such as the BADODAB sampler which solves the same diffusion as SGNHT but with a more stable splitting method (Leimkuhkler and Xiaocheng 2016). Such samplers might be easier to tune with MAMBA or grid search.
Finally, tuning SGHMC and SGHMC-CV using MAMBA is faster than using grid-search (as is the case with the models in the previous two sections): in this case the speedup is 4x–6x faster. This confirms our expectation that when tuning many hyperparameters MAMBA scales better than grid search.
5 Discussion and future work
5.1 Final remarks
In this paper we have proposed a multi-armed bandit approach to estimate the hyperparameters for any stochastic gradient MCMC algorithm. Our approach optimizes the hyperparameters to produce posterior samples which accurately approximate the posterior distribution within a fixed time budget. We use Stein-based discrepancies as natural metrics to assess the quality of the posterior approximation.
The generality of the MAMBA algorithm means that alternative metrics, such as predictive accuracy, can easily be employed within MAMBA as an alternative to a Stein-based metric. We have also compared MAMBA with a grid search approach using the KSD and have found that although the results are comparable, MAMBA finds these optimal hyperparameters much faster than grid search.
When tuning SGHMC and SGHMC-CV (for all three models), we tune three hyperparameters using MAMBA (step size, batch size, and number of leapfrog steps), and two hyperparameters using gridsearch (step size and number of leapfrog steps). We find that although MAMBA is tuning more hyperparameters, the method finds optimal hyperparameters with a speedup ranging from 2x to 6x compared to gridsearch. This illustrates how, as we increase the number of hyperparameters to tune, the speed gains between the methods widens.
Whilst not explored in this paper, it is possible to apply MAMBA beyond the stochastic gradient MCMC setting and directly apply MAMBA to standard MCMC algorithms, such as Hamiltonian Monte Carlo, to estimate the MCMC hyperparameters. A variety of metrics including KSD and absolute difference between the average and optimal acceptance rate could be used in this context. However, existing algorithms like adaptive MCMC (Andrieu and Thoms 2008; Vihola 2012) may be more efficient for standard MCMC because the computational budget that makes MAMBA useful for tuning batch sizes in SGMCMC is less necessary when there is no inherent bias-variance trade-off.
Finally, in this paper we performed a systematic study of different SGMCMC tuning methods for various models and samplers, which to our knowledge is the first rigorous comparison of these methods. While these alternative approaches can work well they are only able to tune the step size parameter, and unlike MAMBA, they do not tune the batch size or other SGMCMC hyperparameters, such as the number of leap frog steps.
5.2 Future work
A limitation of this method is that computing the KSD can be expensive when there are many posterior samples. One solution we explored in this paper is to use the FSSD as a linear-time metric. In the case of KSD, we significantly lowered the cost of this by thinning the Markov chain, but the KSD remains an expensive metric to compute. The KSD also suffers from the curse of dimensionality (Gong et al. 2020), though our results show that the KSD gave good results even for our two high-dimensional problems. As a result, further work in this area should explore alternative discrepancy metrics which are both scalable in sample size and dimension. For example, scalable alternatives to KSD, such as sliced KSD (Gong et al. 2020), could be appropriate for very high-dimensional problems.
6 Supplementary information
The supplementary material for this article is available online. It contains a proof of Theorem 1, further details of experiment settings and details of the various SGMCMC algorithms considered.
References
Andrieu, C., Thoms, J.: A tutorial on adaptive MCMC. Stat. Comput. 18(4), 343–373 (2008)
Audibert, J.Y., Bubeck, S., Munos, R.: Best arm identification in multi-armed bandits. In: COLT, pp. 41–53 (2010)
Baker, J., Fearnhead, P., Fox, E.B., et al.: Control variates for stochastic gradient MCMC. Stat. Comput. 29(3), 599–615 (2019)
Bingham, E., Chen, J.P., Jankowiak, M.: et al. Pyro: Deep Universal Probabilistic Programming. arXiv preprint arXiv:1810.09538 (2018)
Brosse, N., Durmus, A., Moulines, É.: The promises and pitfalls of stochastic gradient Langevin dynamics. In: Advances in Neural Information Processing Systems, pp. 8278–8288 (2018)
Bubeck, S., Cesa-Bianchi, N.: Regret analysis of stochastic and nonstochastic multi-armed bandit problems (2012) arXiv preprint arXiv:1204.5721
Chen, C., Carlson, D., Gan, Z., et al. Bridging the gap between stochastic gradient MCMC and stochastic optimization. In: Artificial Intelligence and Statistics, pp. 1051–1060 (2016)
Chen, T., Fox, E., Guestrin, C.: Stochastic gradient Hamiltonian Monte Carlo. In: International Conference on Machine Learning, pp. 1683–1691 (2014)
Chwialkowski, K., Strathmann, H., Gretton, A.: A kernel test of goodness of fit. In: International Conference on Machine Learning, pp. 2606–2615 (2016)
Coullon, J., Nemeth, C.: SGMCMCJax: a lightweight JAX library for stochastic gradient Markov chain Monte Carlo algorithms. J. Open Source Softw. 7(72), 4113 (2022)
Ding, N., Fang, Y., Babbush, R.: et al Bayesian sampling using stochastic gradient thermostats. In: Advances in Neural Information Processing Systems, pp. 3203–3211 (2014a)
Ding, N., Fang, Y., Babbush, R., et al Bayesian sampling using stochastic gradient thermostats. In: Ghahramani Z, Welling M, Cortes C, et al (eds.) Advances in Neural Information Processing Systems, vol. 27. Curran Associates, Inc (2014b) https://proceedings.neurips.cc/paper/2014/file/21fe5b8ba755eeaece7a450849876228-Paper.pdf
Gelman, A., Gilks, W.R., Roberts, G.O.: Weak convergence and optimal scaling of random walk metropolis algorithms. Ann. Appl. Probab. 7(1), 110–120 (1997)
Gong, W., Li, Y., Hernández-Lobato, J.M.: Sliced kernelized Stein discrepancy. CoRR abs/2006.16531. (2020) https://arxiv.org/abs/2006.16531
Gorham, J., Mackey, L.: Measuring sample quality with Stein’s method. In: Advances in Neural Information Processing Systems, pp. 226–234 (2015)
Gorham, J., Mackey, L.: Measuring sample quality with kernels. In: Proceedings of the 34th International Conference on Machine Learning-Volume 70, JMLR. org, pp. 1292–1301 (2017)
Gorham, J., Raj, A., Mackey, L.: Stochastic Stein discrepancies. (2020) arXiv preprint arXiv:2007.02857
Guo, C., Pleiss, G., Sun, Y., et al. On calibration of modern neural networks. In: Precup, D., Teh, Y.W. (eds) Proceedings of the 34th International Conference on Machine Learning, Proceedings of Machine Learning Research, vol 70. pp. 1321–1330 (2017) http://proceedings.mlr.press/v70/guo17a.html
Harper, F.M., Konstan, J.A.: The movielens datasets: history and context 5(4). (2015) https://doi.org/10.1145/2827872
Hoffman, M.D., Gelman, A.: The no-U-turn sampler: adaptively setting path lengths in Hamiltonian Monte Carlo. J. Mach. Learn. Res. 15(1), 1593–1623 (2014)
Izmailov, P., Vikram, S., Hoffman, M.D., et al.: What are bayesian neural network posteriors really like? (2021) arXiv preprint arXiv:2104.14421
Jamieson, K., Talwalkar, A.: Non-stochastic best arm identification and hyperparameter optimization. In: Artificial Intelligence and Statistics, pp. 240–248 (2016)
Jitkrittum, W., Xu, W., Szabó, Z., et al. A linear-time kernel goodness-of-fit test. (2017) arXiv preprint arXiv:1705.07673
Karnin, Z., Koren, T., Somekh, O.: Almost optimal exploration in multi-armed bandits. In: International Conference on Machine Learning, pp. 1238–1246 (2013)
Kim, S., Song, Q., Liang, F.: Stochastic gradient langevin dynamics algorithms with adaptive drifts. (2020) arXiv preprint arXiv:2009.09535
Lakshminarayanan, B., Pritzel, A., Blundell, C.: Simple and scalable predictive uncertainty estimation using deep ensembles. In: Guyon, I., Luxburg, U.V., Bengio, S., et al (eds) Advances in Neural Information Processing Systems, vol 30. Curran Associates, Inc., (2017) https://proceedings.neurips.cc/paper/2017/file/9ef2ed4b7fd2c810847ffa5fa85bce38-Paper.pdf
Lattimore, T., Szepesvári, C.: Bandit Algorithms. Cambridge University Press, Cambridge (2020)
LeCun, Y., Cortes, C.: MNIST handwritten digit database (2010). http://yann.lecun.com/exdb/mnist/
Leimkuhkler, B., Xiaocheng, S.: Adaptive thermostats for noisy gradient systems. SIAM J. Sci. Comput. 38(2), A712–A736 (2016)
Li, C., Chen, C., Carlson, D., et al. Preconditioned stochastic gradient Langevin dynamics for deep neural networks. In: Proceedings of the AAAI Conference on Artificial Intelligence (2016)
Liu, Q., Lee, J., Jordan, M.: A kernelized stein discrepancy for goodness-of-fit tests. In: International Conference on Machine Learning, pp. 276–284 (2016)
Ma, Y.A., Chen, T., Fox, E.: A complete recipe for stochastic gradient MCMC. In: Advances in Neural Information Processing Systems, pp. 2917–2925 (2015)
Nemeth, C., Fearnhead, P.: Stochastic gradient Markov chain Monte Carlo. J. Am. Stat. Assoc., pp. 1–18 (2020)
Phan, D., Pradhan, N., Jankowiak, M.: Composable effects for flexible and accelerated probabilistic programming in numpyro. (2019) arXiv preprint arXiv:1912.11554
Pillai, N.S., Stuart, A.M., Thiéry, A.H., et al.: Optimal scaling and diffusion limits for the Langevin algorithm in high dimensions. Ann. Appl. Probab. 22(6), 2320–2356 (2012)
Roberts, G.O., Rosenthal, J.S.: Optimal scaling of discrete approximations to Langevin diffusions. J. R. Stat. Soc.: Ser. B (Stat. Methodol.) 60(1), 255–268 (1998)
Roberts, G.O., Tweedie, R.L.: Exponential convergence of Langevin distributions and their discrete approximations. Bernoulli 2(4), 341–363 (1996)
Salakhutdinov, R., Mnih, A.: Bayesian probabilistic matrix factorization using Markov chain Monte Carlo. In: Proceedings of the 25th International Conference on Machine Learning, ACM, pp. 880–887 (2008)
Serfling, R.J.: Approximation Theorems of Mathematical Statistics, vol. 162. Wiley, London (2009)
Slivkins, A.: Introduction to multi-armed bandits (2019). arXiv preprint arXiv:1904.07272
Vihola, M.: Robust adaptive Metropolis algorithm with coerced acceptance rate. Stat. Comput. 22(5), 997–1008 (2012)
Welling, M., Teh, Y.W.: Bayesian learning via stochastic gradient Langevin dynamics. In: Proceedings of the 28th International Conference on Machine Learning (ICML), pp. 681–688 (2011)
Acknowledgements
We thank Henry Moss for helpful discussions about bandit algorithms.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflicts of interest
The authors have no conflicts of interest to disclose. LFS acknowledges financial support from the Queensland University of Technology Centre for Data Science. JC was supported by EPSRC grant EP/S00159X/1 and CN acknowledges the support of EPSRC grants EP/R01860X/1, EP/S00159X/1 and EP/V022636/1.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Appendices
Appendix A: Proof of Theorem 1
Lemma 1
Assume \(\{\varvec{\theta }_i\}_{i=1}^P\) are P samples from \({\tilde{\pi }}\) and \(k(\varvec{\theta }, \varvec{\theta }')\) is a positive definite kernel in the Stein class of \({\tilde{\pi }}\) and \(\pi \). If \(\mathbb {E}_{{{\tilde{\pi }}}} \left[ {k_\pi (\varvec{\theta },\varvec{\theta }')^2}\right] < \infty \), and \({\tilde{\pi }} \ne \pi \), then for a Monte Carlo approximation of the kernel Stein discrepancy (3), we have
where \(\sigma ^2 = \textrm{Var}_{{\tilde{\pi }}}(\mathbb {E}_{{{\tilde{\pi }}}} \left[ {k_\pi (\varvec{\theta },\varvec{\theta }')}\right] )\).
This lemma follows directly from Sects. 5.5.1 and 5.5.2 of Serfling (2009).
Lemma 2
Let s be an arm from the set of arms \(S_i=\{1,2,\ldots \}\) at iteration i of the MAMBA algorithm. We let \(s=1\) be the optimal arm with expected reward \({\bar{\nu }}_1\) and we assume that the optimal arms was not eliminated at iteration \(i-1\) of the MAMBA algorithm. We then have for any arm \(s \in S_i\) with estimated reward \({\hat{\nu }}_s\),
Proof
Using the CLT result from Lemma 1 we assume that \({\hat{\nu }}_s\) is an unbiased estimate of the reward for arm s with sub-Gaussian proxy \(\sigma _s^2\), then by the Hoeffding inequality we have
where \(\alpha _s:= {\bar{\nu }}_1 - {\bar{\nu }}_s\) and therefore \(P\left( {\hat{\nu }}_s-{\bar{\nu }}_s \ge \alpha _s\right) = P({\bar{\nu }}_1 < {\hat{\nu }}_s)\) and the lemma follows. \(\square \)
Lemma 3
The probability that the best arm is eliminated at iteration i of MAMBA (Algorithm 1) is at most
where \(s_i=M/\eta ^{i+1}\).
Proof
This result follows a similar process to Lemma 4.3 from Karnin et al. (2013) but for a general \(\eta \). If the best arm is removed at iteration i, then there must be at least \((1-1/\eta )\) arms in \(S_i\) (i.e. \(\frac{1}{\eta }|S_i|=M/\eta ^{i+1}\)) with empirical reward larger than that of the best arm (i.e. a KSD score lower than the arm with the best possible KSD score). If we let \(S_i'\) be the set of arms in \(S_i\), excluding the \(|S_i|/2\eta =M/2\eta ^{i+1}\) arms with largest reward, then the empirical reward for at least \(|S_i'|/(2\eta -1)=M/2\eta ^{i+1}\) arms in \(|S_i'|\) must be greater than the best arm at iteration i.
Let \(N_i\) be the number of arms in \(S_i'\) with empirical reward greater than the reward of the optimal arm, then by Lemma 2 we have,
where \(\sigma ^2=\max _{s\in S_i'}\sigma _s^2\) and the final inequality follows from the fact that there are at least \(s_i-1\) arms that are not in \(S_i'\) with reward greater than any arm in \(S_i'\). Applying Markov’s inequality we can obtain,
\(\square \)
Using Lemmas 2 and 3 we can now prove Theorem 1.
Proof
The algorithm cannot exceed the budget of T (in our case T is given in seconds). If the best arm survives then the algorithm succeeds as all other arms must be eliminated after \(\log _\eta M\) iterations. Finally, using Lemma 3 and a union bound, the best arm is eliminated in one of the \(\log _\eta M\) iterations of the algorithm with probability at most
This result completes the proof of Theorem 1. \(\square \)
Appendix B: Details of Experiments
We use the SGMCMC samplers in the package SGMCMCJax for the experiments, and we use NumPyro for the NUTS sampler (Bingham et al. 2018; Phan et al. 2019).
We present in table 4 an overview of the tuning methods used in these experiments. We use three core tuning methods for all three models: i) MAMBA-KSD, ii) grid search with log-loss as metric, and iii) the heuristic approach. For the logistic regression example only, we also try two alternative tuning methods: iv) MAMBA-FSSD and v) grid search-KSD.
1.1 B.1 Logistic regression
1.1.1 B.1.1 Model
Consider a binary regression model where \({\textbf{y}}=\{y_i\}_{i=1}^N\) is a vector of N binary responses and \({\textbf{X}}\) is a \(N \times d\) matrix of covariates. If \(\varvec{\theta }\) is a \(d-\)dimensional vector of model parameters, then the likelihood function for the logistic regression model is,
where \({\textbf{x}}_i\) is a \(d-\)dimensional vector for the ith observation. The prior distribution for \(\varvec{\theta }\) is a zero-mean Gaussian with covariance matrix \(\varvec{\Sigma }_{\varvec{\theta }}=10{\textbf{I}}_d\), where \({\textbf{I}}_d\) is a \(d \times d\) identity matrix.
1.1.2 B.1.2 Grid search
For grid search we choose the step size using 14 equally spaced step sizes (on a \(log_{10}\) scale) that result in the best log-loss on a test dataset: \(\{-1., -1.5, -2., -2.5, -3., -3.5, -4., -4.5, -5., -5.5, -6., -6.5, -7, -7.5\}\). To tune SGHMC we use the same step size grid with two leapfrog values: 5 and 10. We fix the batch size ratio to be \(10\%\) for the grid search tuning method as well as the baseline.
We start from the MAP with Gaussian noise (scale: \(\sigma =0.2\)) and run the samplers for 5, 000 for each grid point.
1.1.3 B.1.3 MAMBA
We use the same grid for step sizes as grid search and use a grid of four batch sizes: \(100\%\), \(10\%\), \(1\%\), and \(0.1\%\). To calculate the KSD and FSSD we thin the samples by 10 and calculate the fullbatch gradients. For FSSD-opt we samples 10 test locations from a Gaussian fit to the samples and optimize them using Adam.
1.1.4 B.1.4 Results
Table 5 gives the hyperparameters used to produce the runs in Table 1.
1.2 B.2 Probabilistic matrix factorization
1.2.1 B.2.1 Model
In this example, we will consider the MovieLens datasetFootnote 2 (Harper and Konstan 2015) which contains 100,000 ratings (taking values \(\{1,2,3,4,5\}\)) of 1682 movies by 943 users, where each user has provided at least 20 ratings. The data are already split into 5 training and test sets (\(80\%/20\%\) split) for a 5-fold cross-validation experiment. Let \({\textbf{R}} \in {\mathbb {R}}^{N \times M}\) be a matrix of observed ratings for N users and M movies where \(R_{ij}\) is the rating user i gave to movie j. We introduce matrices \({\textbf{U}}\) and \({\textbf{V}}\) for users and movies respectively, where \({\textbf{U}}_i \in {\mathbb {R}}^d\) and \({\textbf{V}}_j \in {\mathbb {R}}^d\) are \(d-\)dimensional latent feature vectors for user i and movie j. The likelihood for the rating matrix is
where \(I_{ij}\) is an indicator variable which equals 1 if user i gave a rating for movie j. The prior distributions for the users and movies are
with prior distributions on the hyperparameters (where \({\textbf{W}}= {\textbf{U}}\) or \({\textbf{V}}\)) given by,
The parameters of interest in our model are then \(\varvec{\theta }=({\textbf{U}},\mathbf {\mu }_{{\textbf{U}}},\Lambda _{{\textbf{U}}},{\textbf{V}},\mathbf {\mu }_{{\textbf{V}}}, \Lambda _{{\textbf{V}}})\) and the hyperparameters for the experiments are \(\varvec{\tau }=(\alpha ,\mu _0,a_0,b_0)=(3,0,4,5)\). We are free to choose the size of the latent dimension and for these experiments we set \(d=20\).
1.2.2 B.2.2 Grid search
To run grid search we use a grid of 12 step sizes in grid search (on a \(\log _{10}\) scale): \(\{-2., -2.5, -3., -3.5, -4., -4.5, -5., -5.5, -6., -6.5, -7, -7.5\}\). For SGHMC we also try two values of leapfrog steps: 5 and 10.
We start from the MAP with Gaussian noise (scale: \(\sigma =1\)) and run 2, 000 iteration per grid point.
1.2.3 B.2.3 MAMBA
We use a time budget of \(R=10sec\) (time of longest running sampler), and the same step size grid as for gridsearch: \(\{-2., -2.5, -3, -3.5, -4, -4.5, -5, -5.5, -6, -6.5, -7, -7.5 \}\). We also use a grid for batch sizes: \(100\%, 10\%, 1\%\). For SGHMC we try two values of leapfrog steps: 5 and 10.
1.2.4 B.2.4 Results
We show in Table 7 the hyperparameters for the runs in Table 2.
1.3 B.3 Neural network
1.3.1 B.3.1 Model
We consider the problem of multi-class classification on the popular MNIST datasetFootnote 3 (LeCun and Cortes 2010). The MNIST dataset consists of a collection of images of handwritten digits from zero to nine, where each image is represented as \(28 \times 28\) pixels. We model the data using a two layer Bayesian neural network with 100 hidden variables (using the same setup as Chen et al. (2014)). We fit the neural network to a training dataset containing 60, 000 images and the goal is to classify new images as belonging to one of the ten categories. The test set contains 10, 000 handwritten images, with corresponding labels. Let \(y_i\) be the image label taking values \(y_i \in \{0,1,2,3,4,5,6,7,8,9\}\) and \({\textbf{x}}_i\) is the vector of pixels which has been flattened from a \(28 \times 28\) image to a one-dimensional vector of length 784. If there are N training images, then \({\textbf{X}}\) is a \(N \times 784\) matrix representing the full dataset of pixels. We model the data as categorical variables with the probability mass function,
where \(\beta _k(\varvec{\theta }, {\textbf{x}}_i)\) is the kth element of \(\beta (\varvec{\theta }, {\textbf{x}}_i) = \sigma \left( \sigma \left( \textbf{x}_i^\top B + b \right) A + a \right) \) and \(\sigma ({\textbf{x}}_i)=\exp {({\textbf{x}}_i)}/(\sum _{j=1}^N\exp {({\textbf{x}}_i)})\) is the softmax function, a generalization of the logistic link function. The parameters \(\varvec{\theta }= (A, B, a, b)\) will be estimated using SGMCMC, where A, B, a and b are matrices of dimension: \(100 \times 10\), \(784 \times 100\), \(1 \times 10\) and \(1 \times 100\), respectively. We set normal priors for each element of these parameters
\( j = 1,\dots ,784; \quad k = 1,\dots ,100; \quad l = 1,\dots ,10;\).
1.3.2 B.3.2 Grid search
We use the same grid as for PMF: \(\{-2., -2.5, -3., -3.5, -4, -4.5, -5, -5.5, -6, -6.5, -7., -7.5\}\). For SGHMC we also try two values of leapfrog steps: 5 and 10.
We start from the MAP with Gaussian noise (scale: \(\sigma =1\)) and run 1, 000 iteration per grid point.
1.3.3 B.3.3 MAMBA
We use a time budget of \(R=10sec\) (time of longest running sampler), and the same step size grid as for gridsearch: \(\{-2, -2.5, -3, -3.5, -4., -4.5, -5, -5.5, -6, -6.5, -7, -7.5\}\). We also use a grid for batch sizes: \(100\%, 10\%, 1\%\). For SGHMC we try two values of leapfrog steps: 5 and 10.
1.3.4 B.3.4 Results
We show in Table 9 the hyperparameters for the runs in Table 3.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Coullon, J., South, L. & Nemeth, C. Efficient and generalizable tuning strategies for stochastic gradient MCMC. Stat Comput 33, 66 (2023). https://doi.org/10.1007/s11222-023-10233-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-023-10233-3