Truncated Poisson–Dirichlet approximation for Dirichlet process hierarchical models

Abstract

The Dirichlet process was introduced by Ferguson in 1973 to use with Bayesian nonparametric inference problems. A lot of work has been done based on the Dirichlet process, making it the most fundamental prior in Bayesian nonparametric statistics. Since the construction of Dirichlet process involves an infinite number of random variables, simulation-based methods are hard to implement, and various finite approximations for the Dirichlet process have been proposed to solve this problem. In this paper, we construct a new random probability measure called the truncated Poisson–Dirichlet process. It sorts the components of a Dirichlet process in descending order according to their random weights, then makes a truncation to obtain a finite approximation for the distribution of the Dirichlet process. Since the approximation is based on a decreasing sequence of random weights, it has a lower truncation error comparing to the existing methods using stick-breaking process. Then we develop a blocked Gibbs sampler based on Hamiltonian Monte Carlo method to explore the posterior of the truncated Poisson–Dirichlet process. This method is illustrated by the normal mean mixture model and Caron–Fox network model. Numerical implementations are provided to demonstrate the effectiveness and performance of our algorithm.

1 Introduction

The Dirichlet process is a class of random probability measures; it was introduced by Ferguson (1973) to solve nonparametric inference problems from a Bayesian point of view. Since then, much research has been done based on the Dirichlet process, making its distribution a most fundamental prior in Bayesian nonparametric statistics. In the original work of Ferguson (1973), the Dirichlet process was defined by requiring its finite-dimensional marginal distribution to be a Dirichlet distribution. An equivalent representation based on the normalised jumps of a gamma process can also be found in the same work. Later on, Sethuraman (1994) gave a constructive definition for Dirichlet process using the stick-breaking method. A more general class of random probability measures called the stick-breaking priors was studied by Ishwaran and James (2001), and the blocked Gibbs sampler for the posterior of the corresponding Bayesian hierarchical models was also developed. We refer to Yamato (2020) for a summary of different construction methods and properties of the Dirichlet process.

Due to the infinite-dimensional support of the Dirichlet process, both the stick-breaking representation and the gamma process representation involve an infinite number of random variables. This is desirable in Bayesian nonparametric statistics as it makes the prior rich enough to incorporate any given information. However, with an infinite number of random variables, it is difficult to apply simulation-based methods for posterior inference. In the existing literature, there are two approaches to work with infinite-dimensional priors, namely marginalisation and truncation.

The marginalisation approach was introduced by Escobar (1994), it marginalises the distribution of the Dirichlet process via the Blackwell–MacQueen Pólya urn scheme (Blackwell and MacQueen 1973) and leads to a powerful Markov chain Monte Carlo method. This approach is widely used in Dirichlet process hierarchical models. However, it suffers from the side effect of, taking the nonparametric hierarchical model as an example, making inference based only on the latent variables. See Ishwaran and James (2001) for a further discussion about its limitations.

The truncation approach replaces the infinite-dimensional prior with a finite-dimensional approximation. An initial study of a finite approximation of the Dirichlet process is Muliere and Tardella (1998). Using a random stopping rule, they designed an approximation method for Dirichlet process that is able to control the truncation error a priori. Ishwaran and Zarepour (2000) proposed the weak limit representation and almost sure truncation for Dirichlet process, and developed a blocked Gibbs sampler for the posterior of the corresponding hierarchical models. Ishwaran and James (2001) studied the finite approximation of the stick-breaking priors. These methods have been built based on the stick-breaking representation of Dirichlet process. On the other hand, Zarepour and Al Labadi (2012) and Argiento et al. (2016) used the gamma process representation to develop the approximation; they also analysed the truncation error of this method. A comprehensive investigation and characterisation of different truncation methods can be found in Campbell et al. (2019).

The goal of this work is to propose a new class of random probability measures called the truncated Poisson–Dirichlet process, and use it to approximate the distribution of the Dirichlet process. The name that we have chosen for the random probability measure is inspired by the work of Kingman (1975), who showed that the ranked random weights of a Dirichlet process follow the Poisson–Dirichlet distribution. Our random probability measure takes the advantage of the Poisson–Dirichlet distribution in the way that it is based on a decreasing sequence of random weights, thus leading to a lower truncation error comparing to other methods. Moreover, we group together the smaller random weights into a single term and leave it in the truncated Poisson–Dirichlet process. This differs from the existing literature where the smaller random weights are usually removed. The motivation of this construction arises from a variation of the Caron–Fox network model (Caron and Fox 2017, see also Williamson 2016) where the focus is given to the most popular nodes. We will briefly explain the application of the truncated Poisson–Dirichlet process in such models.

Then we develop a posterior sampling algorithm for the truncated Poisson–Dirichlet process. To demonstrate the usage of the algorithm, we fit the truncated Poisson–Dirichlet process into the normal mean mixture model and Caron–Fox network model, then design the posterior inference method for these models. Numerical illustrations are provided based on simulated and real-world data sets.

The paper is organised as follows. Section 2 reviews the basic properties of the Dirichlet process. Section 3 summarises some of the common approximations for the Dirichlet process. Section 4 constructs the truncated Poisson–Dirichlet process and provides a simulation algorithm for such a process. We also analyse the truncation error in this section. Section 5 develops the posterior sampling algorithm. Section 6 illustrates the application of our method in the normal mean mixture model and Caron–Fox network model. Section 7 provides the numerical illustrations. Section 8 sets out some topics for future study.

2 Construction of the Dirichlet process

In this section, we review the construction and basic properties of the Dirichlet process. Let $\alpha >0$ be the concentration parameter and H be the reference distribution, a probability measure $\mathcal {P}=\text {DP}(\alpha H)$ is called a Dirichlet process if for each measurable partition $(B_1, \dots , B_k)$ of the sample space, the distribution

$$\begin{aligned} (\mathcal {P}(B_1), \dots , \mathcal {P}(B_k)) \sim \text {Dir}(\alpha H(B_1), \dots , \alpha H(B_k)) , \end{aligned}$$

where $\text {Dir}(\dots )$ denotes the Dirichlet distribution.

In Bayesian nonparametric statistics, it is more common to use different representations of the Dirichlet process. There are two well-known representations in literature, namely the stick-breaking representation and the gamma process representation.

The stick-breaking representation was introduced by Sethuraman (1994) as a constructive definition of the Dirichlet process, they showed that a Dirichlet process can be represented as

$$\begin{aligned} \tilde{\mathcal {P}}_{\infty }(.)=\sum _{i=1}^{\infty } \tilde{p}_i\delta _{K_i}(.) , \end{aligned}$$

(1)

where $\delta _{K_i}(.)$ denotes a point mass at $K_i$, and $K_i$ are independent and identically distributed random variables with distribution H. The variables $\{\tilde{p}_i\}_{i=1}^{\infty }$ are random weights independent of $K_i$, such that $0<\tilde{p}_i<1$ and $\sum _{i=1}^{\infty } \tilde{p}_i=1$ almost surely. They are constructed by the stick-breaking method:

$$\begin{aligned} \tilde{p}_1=V_1 ~~\text {and}~~ \tilde{p}_i=(1-V_1)\dots (1-V_{i-1})V_i , \end{aligned}$$

(2)

for $i=2, 3, \dots$, where $V_i$ are independent $\text {Beta}(1, \alpha )$ random variables for $\alpha >0$. Throughout this paper, we will use the tilde notation to emphasise that the sequence $\{\tilde{p}_i\}_{i=1}^{\infty }$ is presented in its original order. The subscript of infinity in $\tilde{\mathcal {P}}_{\infty }$ means the expression involves infinite terms, it will be replaced by a finite number if we apply a truncation. Notice that the sequence of random weights $(\tilde{p}_1, \tilde{p}_2, \dots )$ follows a GEM distribution with parameter $\alpha$.

The Dirichlet process can also be represented by the jumps of a gamma process. Consider a gamma process $\tau _{\alpha }$ with Lévy measure $v(dw)=w^{-1}e^{-w}\mathbb {1}_{(0, \infty )}(w)dw$ at time $\alpha$, then $\tau _{\alpha }$ has the Lévy–Khintchine representation

$$\begin{aligned} \begin{aligned}&\mathbb {E}(\exp (-\beta \tau _{\alpha })) \\&\quad =\exp \biggl ( -\alpha \int _{0}^{\infty }(1-e^{-\beta w}) w^{-1}e^{-w}dw \biggr ) . \end{aligned} \end{aligned}$$

Let $\{J_i\}_{i=1}^{\infty }$ be the ranked jumps of $\tau _{\alpha }$ such that $J_1>J_2>\dots$ and $\tau _{\alpha }=\sum _{i=1}^{\infty }J_i$, and let the sequence $\{p_i\}_{i=1}^{\infty }$ be defined as $p_i:=J_i/\tau _{\alpha }$ for $i=1, 2, \dots$, it follows immediately that $p_i>0$ and $\sum _{i=1}^{\infty }p_i=1$ with probability 1. Ferguson (1973) showed that the random probability measure

$$\begin{aligned} \mathcal {P}_{\infty }(.)=\sum _{i=1}^{\infty } p_i\delta _{K_i}(.)=\sum _{i=1}^{\infty } \frac{J_i}{\sum _{j=1}^{\infty }J_j}\delta _{K_i}(.) , \end{aligned}$$

(3)

is a Dirichlet process with concentration parameter $\alpha$ and reference distribution H. Since $J_1>J_2>\dots$, the random weights $\{p_i\}_{i=1}^{\infty }$ are decreasing, this differs from stick-breaking representation (1). Moreover, the sequence of random weights $(p_1, p_2, \dots )$ follows a Poisson–Dirichlet distribution with parameter $\alpha$.

The gamma process representation (3) has an equivalent expression which is known as the Ferguson–Klass representation (Ferguson and Klass 1972):

$$\begin{aligned} \mathcal {P}_{\infty }(.)=\sum _{i=1}^{\infty } \frac{\text {N}^{-1}(\Gamma _i)}{\sum _{j=1}^{\infty }\text {N}^{-1}(\Gamma _j)}\delta _{K_i}(.) , \end{aligned}$$

where $\Gamma _i=E_1+\dots +E_i$, $E_i\sim \text {Exp}(1)$ are i.i.d. exponential random variables, and $N^{-1}(x)$ is the inverse of the tail distribution of $\alpha v(dw)$, i.e.,

$$\begin{aligned} N(x) = \alpha \int _{x}^{\infty }w^{-1}e^{-w}dw, ~~\text {for}~~ x>0 . \end{aligned}$$

In spite of the elegant expression, the inverse function $N^{-1}(x)$ is analytically intractable and an approximate evaluation is needed, see Wolpert and Ickstadt (1998) for more details.

Since the random variables $K_i$ are independent and identically distributed, the difference between the representations (1) and (3) hinges on the orderings of their random weights. McCloskey (1965) (see also Perman et al. 1992; Pitman 1996a) showed that the random weights of the stick-breaking representation are a size-biased permutation of that of the gamma process representation, meaning that $\{\tilde{p}_i\}_{i=1}^{\infty }$ is the same sequence as $\{p_i\}_{i=1}^{\infty }$ but presented in a random order $(p_{\sigma _1}, p_{\sigma _2}, \dots )$, where $\mathbb {P}(\sigma _1=i)=p_i$, and for k distinct $i_1, \dots , i_k$,

$$\begin{aligned} \begin{aligned}&\mathbb {P}(\sigma _k=i_k \mid \sigma _1=i_1, \dots , \sigma _{k-1}=i_{k-1}) \\&\quad =\frac{p_{i_k}}{1-(p_{i_1}+\dots +p_{i_{k-1}})} . \end{aligned} \end{aligned}$$

An index i with a bigger ‘size’ $p_i$ tends to appear earlier in the permutation, hence the name ‘size-biased permutation’. On the other hand, we revert to $\{p_i\}_{i=1}^{\infty }$ by sorting $\{\tilde{p}_i\}_{i=1}^{\infty }$ in descending order. Note that these are exactly the connections between the GEM and Poisson–Dirichlet distributions.

Although both $\tilde{\mathcal {P}}_{\infty }$ and $\mathcal {P}_{\infty }$ are Dirichlet processes, they will lead to different approximation methods. In the next section, we review some of the common approximations for Dirichlet process in literature.

3 Approximation for the Dirichlet process

As we saw in the previous section, the construction of the Dirichlet process involves an infinite number of random variables, and this may cause some difficulties in the simulation of Dirichlet process based models. To avoid this problem, various random probability measures have been proposed whose distributions approximate the Dirichlet process. These random probability measures can be understood as truncated versions of the Dirichlet process. In this section, we review some of the approximation methods in literature.

The most straightforward approximation is to truncate the stick-breaking representation (1) at a positive integer N. To guarantee that the truncation leads to a well-defined probability measure, we set $V_N=1$ in (2), then we have obtained the almost sure truncation of Dirichlet process:

$$\begin{aligned} \tilde{\mathcal {P}}_N(.)=\sum _{i=1}^{N} \tilde{p}_i\delta _{K_i}(.) . \end{aligned}$$

(4)

Using $\tilde{\mathcal {P}}_N$ as the prior, Ishwaran and Zarepour (2000) constructed a Bayesian semiparametric model and developed a blocked Gibbs sampler for posterior inference. The sampling algorithm is based on the results of Connor and Mosimann (1969), who showed that the posterior of $\tilde{\mathcal {P}}_N$ is a generalised Dirichlet distribution, it follows that the prior is conjugate for multinomial sampling. Therefore, we are able to sample from the posterior efficiently, and this is an advantage of the almost sure truncation. A generalisation of this model based on the stick-breaking prior can be found in Ishwaran and James (2001).

It remains to choose an adequate truncation level N. A larger N makes the approximation more accurate, but it also brings more terms into the prior, and eventually into the posterior sampling algorithm. To this end, Muliere and Tardella (1998) proposed a random stopping rule for $\tilde{\mathcal {P}}_N$ which controls the approximation error a priori, Ishwaran and Zarepour (2000) derived an explicit result for the approximation error, and Griffin (2016) introduced an adaptive truncation method which allows the truncation level to be decided by the algorithm and so can avoid large errors in approximating the posterior.

Alternatively, the approximation can be obtained from the gamma process representation (3). Since the infinite sum appears in both the numerator and denominator of (3), a truncation should also be applied to both of them, such that the resulting random probability measure involves only a finite number of random variables. Zarepour and Al Labadi (2012) considered the following approximation for $\mathcal {P}_{\infty }$:

$$\begin{aligned} \mathcal {P}_{N}^{\text {ZA}}(.) = \sum _{i=1}^{N} \frac{J_i}{\sum _{j=1}^{N}J_j}\delta _{K_i}(.) , \end{aligned}$$

which truncates both the numerator and denominator of (3) at the first N terms. The construction guarantees that $\mathcal {P}_{N}^{\text {ZA}}$ is a valid probability measure. Moreover, it only involves the largest N jumps of the underlying gamma process; hence it is possible to sample from this random probability measure and use it in simulation. Zarepour and Al Labadi (2012) used a gamma distribution $\text {Ga}(\alpha /N,1)$ to approximate the Lévy measure of the gamma process, then sampled from the jumps via the inverse transform method. Al Labadi and Zarepour (2014) generalised this idea to the two-parameter Poisson–Dirichlet process and normalised inverse-Gaussian process.

The truncation can also be made to the Lévy measure v(dw) of the underlying gamma process. Recall that a gamma process has infinite activity because its Lévy measure integrates to infinity, i.e., $\int _{0}^{\infty }w^{-1}e^{-w}dw=\infty$. By truncating the Lévy measure from below, we obtain an underlying process with finite activity. Argiento et al. (2016) considered the truncated Lévy measure

$$\begin{aligned} \rho _{\epsilon }(dw)=w^{-1}e^{-w}\mathbb {1}_{(\epsilon , \infty )}(w)dw, ~~\text {for}~~ \epsilon >0 , \end{aligned}$$

and constructed the random probability measure:

$$\begin{aligned} \tilde{\mathcal {P}}^{\text {ABG}}_{\epsilon }(.)=\sum _{i=0}^{N_{\epsilon }}\frac{\tilde{J}_i}{\sum _{j=0}^{N_{\epsilon }}\tilde{J}_j}\delta _{K_i}(.) , \end{aligned}$$

where $\{\tilde{J}_i\}_{i=0}^{N_{\epsilon }}$ are i.i.d. jumps from the density $\rho _{\epsilon }(dw)/(\int _{\epsilon }^{\infty }\rho _{\epsilon }(dw))$, and $N_{\epsilon } \sim \text {Pois}(\int _{\epsilon }^{\infty }\rho _{\epsilon }(dw))$ denotes the total number of jumps, which is almost surely finite. As $\epsilon \rightarrow 0$, $\tilde{\mathcal {P}}^{\text {ABG}}_{\epsilon }$ converges to the Dirichlet process in distribution; hence it provides a finite approximation for the Dirichlet process. The aim of Argiento et al. (2016) was to approximate the normalised generalised gamma (NGG) process, and the approximation for Dirichlet process can be viewed as a special case of their results.

In Bayesian nonparametric statistics, it is possible to use the Dirichlet process prior in its original form but apply a truncation to the posterior instead. Ferguson (1973) showed that the posterior of a Dirichlet process is again a Dirichlet process with an extra point mass for each observation, this property implies a sampling algorithm for the posterior distribution which is known as the ‘Chinese restaurant process’ (see Pitman 2006). Since the posterior of a Dirichlet process still involves infinite terms, Gelfand and Kottas (2002) suggested to apply the truncation directly to the posterior. A generalisation of this approach for the Pitman–Yor process prior can be found in Ishwaran and James (2001), whose posterior was given by Pitman (1996b). More recently, James et al. (2009) derived a general result about the posterior of the normalised random measure with independent increment (NRMI), and Barrios et al. (2013) studied the truncation method for the posterior of the NRMIs. This approach has the advantage of using the prior in its original form, while the truncation method for posterior is similar to what we have introduced above. For example, the random stopping rule $N_{\epsilon }:=\inf \{ i\in \mathbb {N} \mid J_{i+1}/\sum _{j=1}^{i}J_j<\epsilon \}$ can be used to truncate the posterior of a Dirichlet process. This machinery stops sampling when the relative size of the newly sampled jump is small enough, thus involving a finite number of random variables. Argiento et al. (2010) provided an upper bound for the ignored jump sizes in this method.

As we have seen above, a lot of effort has been devoted to dealing with the problem of infinite random variables in the Dirichlet process. In this paper, we provide a new solution to this problem. Our method is inspired by the following observation. Let $\{J_i\}_{i=1}^{\infty }$ be the jumps of a gamma process $\tau _{\alpha }$ sorted in descending order. Conditioning on the largest N jumps $J_1, \dots , J_N$, the sum of the smaller jumps $\tau _{\alpha }^{N-}:=\sum _{i=N+1}^{\infty }J_i$ is a truncated gamma process, and it admits the Lévy–Khintchine representation

$$\begin{aligned} \begin{aligned}&\mathbb {E}\left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) \\&\quad =\exp \biggl ( -\alpha \int _{0}^{J_N}(1-e^{-\beta w})w^{-1}e^{-w}dw \biggr ) . \end{aligned} \end{aligned}$$

We view the right hand side of the equation as the Laplace transform of $\tau _{\alpha }^{N-}$, then derive the density of $\tau _{\alpha }^{N-}$ by inverting this Laplace transform. In the meanwhile, the exact simulation algorithm for a truncated gamma process has been well-studied in literature. Since a truncated gamma process can be viewed as an exponentially tilted Dickman process, we can sample from a Dickman process and use rejection sampling to include the exponential tilt. For the exact simulation algorithm of the Dickman process, see Devroye and Fawzi (2010), Fill and Huber (2010), Chi (2012) and Cloud and Huber (2017). More recently, Dassios et al. (2019) designed an exact simulation algorithm that samples from the truncated gamma process directly. Using these results, we provide a new approximation for the Dirichlet process. We will split the random weights of $\mathcal {P}_{\infty }$ (see Eq. 3) into two parts:

• i. the largest N random weights,

  $$\begin{aligned} p_1:=\frac{J_1}{\sum _{j=1}^{\infty }J_j}, ~~ \dots , ~~ p_N:=\frac{J_N}{\sum _{j=1}^{\infty }J_j} ; \end{aligned}$$

  (5)

• ii. the sum of the smaller random weights,

  $$\begin{aligned} r:=\sum _{i=N+1}^{\infty }p_i=\frac{\sum _{i=N+1}^{\infty }J_i}{\sum _{j=1}^{\infty }J_j} . \end{aligned}$$

  (6)

This is a straightforward truncation for the gamma process representation (3), without changing the total mass or Lévy measure. Moreover, we reserve the term $(\sum _{j=N+1}^{\infty }J_j)/(\sum _{J=1}^{\infty }J_j)$ of the random probability measure and explain it as an indicator for the proportion of the sample space not belonging to the largest N random weights. Therefore, our method can be explained as a rearrangement of the random weights according to their importance.

If we need a motivation, apart from the approximation for Dirichlet process, for our truncation method, the recent research Caron and Fox (2017) and Williamson (2016) about network model should be mentioned. Next, we briefly introduce their models with some simplifications. Let $\tilde{\mathcal {P}}_{\infty }$ be a Dirichlet process, and let G be a sample of $\tilde{\mathcal {P}}_{\infty }$, then G has the format $\sum _{i=1}^{\infty }\tilde{p}_i\delta _{K_i}(.)$. We denote by $K_i$ the index, or identifier, of a node in the network, and $\tilde{p}_i$ the relative popularity of this node. We also use the notation (s, r) for the links in the network, where s is the index of the sending node, and r is the index of the receiving node. Assume that each link chooses its origin and destination according to G independently, then a network model containing n links can be summarised as

$$\begin{aligned} \begin{aligned}&G \sim \tilde{\mathcal {P}}_{\infty } \\&s_j, r_j {\mathop {\sim }\limits ^{\text {i.i.d.}}} G, ~~ j=1, \dots , n. \end{aligned} \end{aligned}$$

(7)

In other words, each link in the network is a sample of the product measure $G\times G$, and the Dirichlet process $\tilde{\mathcal {P}}_{\infty }$ can be viewed as a prior for the relative popularities of the nodes. A node with a higher relative popularity is more likely to send or receive a link, hence more active in the network. Williamson (2016) derived the explicit predictive distribution for this model using a two-dimensional version of the Pólya urn scheme.

A more general network model was considered by Caron and Fox (2017), where the popularity of the nodes are modelled by the jump sizes of a gamma process. Let $\{\tilde{J}_i\}_{i=1}^{\infty }$ be the jumps of a gamma process $\tau _{\alpha }$ without ordering, and let each node $K_i$ have the popularity $\tilde{J}_i$. Assume that the links choose their origins and destinations according to $\sum _{i=1}^{\infty }(\tilde{J}_i/\tau _{\alpha })\delta _{K_i}(.)$, which is clearly a sample of the Dirichlet process. Moreover, assume that the total number of links follows a Poisson distribution with mean $\tau _{\alpha }^2$. Then the Caron–Fox network model can be written as

$$\begin{aligned} \begin{aligned}&G \sim \tilde{\mathcal {P}}_{\infty } \\&M \sim \text {Poisson} ( \tau _{\alpha }^2 ) \\&s_j, r_j {\mathop {\sim }\limits ^{\text {i.i.d.}}} G=\sum _{i=1}^{\infty }\frac{\tilde{J}_i}{\tau _{\alpha }} \delta _{K_i}(.) , ~~ j=1, \dots , M. \end{aligned} \end{aligned}$$

(8)

Conditioning on the total number of links M, model (8) reverts to model (7). However, the Poisson assumption is useful in the analysis of some real-world networks where each link has an associated count.

Next, Caron and Fox (2017) suggested to split the nodes into the following two clusters: (i) the nodes with at least one link, (ii) the nodes without any link. Then they proposed a method that estimates the popularity parameter $\tilde{J}_i$ of each node in the former cluster, and the total popularity parameter of the nodes in the latter cluster. We emphasise that this method estimates the actual popularity parameters $\tilde{J}_i$, not only their relative weights $\tilde{J}_i/\tau _{\alpha }$. Hence, the model prior must be built based on the jumps of a gamma process, rather than the stick-breaking random weights $\tilde{p}_i$.

Inspired by the novel works of Caron and Fox (2017) and Williamson (2016), we want to design a prior that deals with the ‘network with key nodes’ scenario, meaning that we want to focus on the nodes with the highest popularity parameters. Think about a network where a small proportion of nodes occupy the majority of links, while most of the nodes have very few links. An example of this scenario is the social network, where a few top users enjoy the majority of followers, while most of the users have very few followers. It is natural for us to focus on the most popular users. On the other hand, there are many practical applications where only the most popular nodes are relevant. For example, in the ‘who to follow suggestions’ function on a social network, we only expect the most popular users to appear, and an estimation for all the users would be unnecessary and too costly. As a result, we will not estimate the popularity parameters of all the nodes, but only the most popular ones. For this purpose, we sort all the popularity parameters $\{\tilde{J}_i\}_{i=1}^{\infty }$ in descending order and focus on the largest N terms, namely $J_1, \dots , J_N$. The smaller popularity parameters are grouped together in terms of $\sum _{i=N+1}^{\infty }J_i$. Given the observations from the network, we would like to estimate $(J_1, \dots , J_N, \sum _{i=N+1}^{\infty }J_i)$. This can be done if we replace the prior of model (8) by a random probability measure with random weights in terms of (5) and (6), and that is exactly the truncated Poisson–Dirichlet process.

4 The truncated Poisson–Dirichlet process

From the previous section, we know that it is a common trick to avoid the infinite number of random variables in Dirichlet process by ignoring the smaller random weights. In this section, we construct a new random probability measure called the truncated Poisson–Dirichlet process. This random probability measure provides a finite approximation for the distribution of Dirichlet process using the random weights in terms of (5) and (6).

Definition 1

(Truncated Poisson–Dirichlet process) For a positive integer N, a truncated Poisson–Dirichlet process is defined as

$$\begin{aligned} \mathcal {P}_N(.) = \sum _{i=1}^{N}p_i\delta _{K_i}(.)+r\delta _{K_{N+1}}(.) , \end{aligned}$$

with

$$\begin{aligned} p_i:=\frac{J_i}{\sum _{j=1}^{\infty }J_j} , ~~\text {for}~~ i=1, \dots , N , \end{aligned}$$

and

$$\begin{aligned} r:=\frac{\sum _{i=N+1}^{\infty }J_i}{\sum _{j=1}^{\infty }J_j} , \end{aligned}$$

where $\{J_i\}_{i=1}^{\infty }$ denotes the ranked jumps of a gamma process $\tau _{\alpha }$, such that $J_1>J_2>\cdots$ and $\tau _{\alpha }=\sum _{i=1}^{\infty }J_i \sim \text {Ga}(\alpha , 1)$, $\alpha >0$; $K_1, \dots , K_N, K_{N+1}$ are i.i.d. random variables with distribution H, and $\delta _{K_i}(.)$ is a point mass at $K_i$.

When $N\rightarrow \infty$, $\mathcal {P}_N$ converges to $\mathcal {P}_{\infty }$ almost surely. Thus, it provides a finite approximation for the distribution of the Dirichlet process. The truncated Poisson–Dirichlet process still involves an infinite sum, but conditioning on $J_1, \dots , J_N$, the sum of smaller jumps $\sum _{i=N+1}^{\infty }J_i$ is a truncated gamma process. To derive its density, we first prepare the following lemma.

Lemma 1

(Density of a truncated gamma process) Let $Z_{\alpha , \mu }$ be a truncated gamma process with the Lévy–Khintchine representation

$$\begin{aligned} \begin{aligned}&\mathbb {E}(\exp (-\beta Z_{\alpha , \mu })) \\&\quad =\exp \biggl ( -\alpha \int _{0}^{1}(1-e^{-\beta w}) w^{-1}e^{-\mu w}dw \biggr ) , \end{aligned} \end{aligned}$$

and let $g_{Z}(z; \alpha , \mu )$ be the density of $Z_{\alpha , \mu }$, then

$$\begin{aligned} g_{Z}(z; \alpha , \mu )=\sum _{i=0}^{n-1}\frac{(-\alpha )^i}{i!} L_i(z) \end{aligned}$$

for $n-1<z\le n$, $n=1, 2, \dots$, where $L_i(t)$ is defined recursively as follows:

$$\begin{aligned} L_0(z)=e^{\alpha \Gamma (0, \mu )} \frac{\mu ^{\alpha }}{\Gamma (\alpha )}z^{\alpha -1}e^{-\mu z} , ~~\text {for}~~ z>0 , \end{aligned}$$

and

$$\begin{aligned} L_{i+1}(z)=\int _{1}^{z-i} L_i(z-s)s^{-1}e^{-\mu s}ds , ~~\text {for}~~ z>i+1 . \end{aligned}$$

Proof

The density of $Z_{\alpha , \mu }$ can be derived via inverse Laplace transform, we have

$$\begin{aligned} \begin{aligned}&g_{Z}(z; \alpha , \mu )\\&\quad =\mathcal {L}^{-1} \{ \mathbb {E}(\exp (-\beta Z_{\alpha , \mu })) \} \\&\quad =\mathcal {L}^{-1} \biggl \{ \exp \biggl ( -\alpha \int _{0}^{1}(1-e^{-\beta w}) w^{-1}e^{-\mu w}dw \biggr ) \biggr \} \\&\quad =\mathcal {L}^{-1} \biggl \{ \exp \biggl ( -\alpha \int _{0}^{\infty }(1-e^{-\beta w}) w^{-1}e^{-\mu w}dw \biggr ) \biggr . \\&\qquad \biggl . \times \exp \biggl ( \alpha \int _{1}^{\infty }(1-e^{-\beta w}) w^{-1}e^{-\mu w}dw \biggr ) \biggr \} \\&\quad =\mathcal {L}^{-1} \biggl \{ (1+\beta /\mu )^{-\alpha } \exp \biggl ( \alpha \int _{1}^{\infty } w^{-1}e^{-\mu w}dw \biggr ) \biggr . \\&\qquad \biggl . \times \exp \biggl ( -\alpha \int _{1}^{\infty }e^{-\beta w} w^{-1}e^{-\mu w}dw \biggr ) \biggr \} \\&\quad =\mathcal {L}^{-1} \biggl \{ (1+\beta /\mu )^{-\alpha } e^{\alpha \Gamma (0, \mu )} \biggr . \\&\qquad \biggl . \times \sum _{k=0}^{\infty }\frac{(-\alpha )^k}{k!}\left( \int _{1}^{\infty }e^{-\beta w} w^{-1}e^{-\mu w}dw \right) ^k \biggr \} , \end{aligned} \end{aligned}$$

(9)

where $\Gamma (0, \mu )$ is the exponential integral

$$\begin{aligned} \Gamma (0, \mu )=\int _{\mu }^{\infty }w^{-1}e^{-w}dw . \end{aligned}$$

From the Laplace transform of a gamma random variable, we know

$$\begin{aligned} \mathcal {L}^{-1} \biggl \{ \frac{e^{\alpha \Gamma (0, \mu )}}{(1+\beta /\mu )^{\alpha }} \biggr \} = e^{\alpha \Gamma (0, \mu )} \frac{\mu ^{\alpha }}{\Gamma (\alpha )}z^{\alpha -1}e^{-\mu z} , \end{aligned}$$

denote this function by $L_0(z)$, then the last line of (9) can be inverted by convolution. $\square$

Fig. 1

Density of the truncated gamma process and the numerical inverse Laplace transform results

To illustrate the result of Lemma 1, we plot the density $g_{Z}(z; \alpha , \mu )$ with different values of $\alpha$ and $\mu$ in Fig. 1. We also apply the CME method (see Horváth et al. 2020) to invert the Laplace transform of $Z_{\alpha , \mu }$ numerically at some fixed points, and plot the results as stars. From the figure we can see that both methods produce similar results.

Now we can use Lemma 1 to derive the conditional density of $\sum _{i=N+1}^{\infty }J_i$ given $J_1, \dots , J_N$.

Corollary 2

Let $\{J_i\}_{i=1}^{\infty }$ be the ranked jumps of a gamma process $\tau _{\alpha }$. Denote by $\tau _{\alpha }^{N-}:=\sum _{i=N+1}^{\infty }J_i$ the sum of the smaller jumps, then $\tau _{\alpha }^{N-}$ has the conditional Lévy–Khintchine representation

$$\begin{aligned} \begin{aligned}&\mathbb {E} \left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) \\&\quad = \exp \biggl ( -\alpha \int _{0}^{J_N}(1-e^{-\beta w}) w^{-1}e^{-w}dw \biggr ) . \end{aligned} \end{aligned}$$

It follows that the conditional density of $\tau _{\alpha }^{N-}$, given $J_1, \dots ,J_N$, is

$$\begin{aligned} f_{\alpha , J_N}(w)dw = J_N^{-1} g_{Z} \biggl ( w J_N^{-1}; \alpha , J_N \biggr ) dw , \end{aligned}$$

where $g_Z(z; \alpha , \mu )$ is provided in Lemma 1.

Proof

The Lévy–Khintchine representation of $\tau _{\alpha }^{N-}$ follows from the basic properties of Poisson random measure, see Kyprianou (2006). It can be written as

$$\begin{aligned} \begin{aligned}&\mathbb {E} \left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) \\&\quad =\exp \biggl ( -\alpha \int _{0}^{1}(1-e^{-\beta J_N w}) w^{-1}e^{-J_N w}dw \biggr ) , \end{aligned} \end{aligned}$$

then the conditional density of $\tau _{\alpha }^{N-}$ is a direct consequence of Lemma 1. $\square$

Then we can derive the joint density of the jump sizes of the gamma process used in Definition 1.

Theorem 3

Let $\{J_i\}_{i=1}^{\infty }$ be the ranked jumps of a gamma process $\tau _{\alpha }$ with Lévy measure $w^{-1}e^{-w}\mathbb {1}_{(0, \infty )}(w)dw$ at time $\alpha$. Denote by $R_k:=J_{k+1}/J_k$ the ratio between the $(k+1)$-th and k-th largest jumps, and set $\tau _{\alpha }^{N-}:=\sum _{i=N+1}^{\infty }J_i$, then the joint density of the random vector $(J_1, R_1, \dots , R_{N-1}, \tau _{\alpha }^{N-})$ is

$$\begin{aligned} \begin{aligned}&\mathbb {P} ( J_1\in dx_1, R_1\in dr_1, \dots , R_{N-1}\in dr_{N-1}, \tau _{\alpha }^{N-} \in dy) \\&\quad =\exp \biggl ( -\alpha \int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-1}e^{-w}dw \biggr ) \\&\qquad \times \frac{\alpha ^N}{x_1r_1\dots r_{N-1}} e^{-x_1(1+r_1+r_1r_2+\dots +r_1r_2\dots r_{N-1})} \\&\qquad \times f_{\alpha , x_1r_1\dots r_{N-1}}(y)dydr_{N-1}\dots dr_1dx_1 , \end{aligned} \end{aligned}$$

where $x_1\in (0,\infty )$, $r_k\in (0,1)$ for $k=1, \dots , N-1$, $y\in (0,\infty )$, and $f_{\alpha , x_1r_1\dots r_{N-1}}(y)$ is the density of a truncated gamma process with the Lévy measure $w^{-1}e^{-w}\mathbb {1}_{(0, x_1r_1\dots r_{N-1})}(w)dw$ at time $\alpha$.

Proof

The joint density of the largest N jumps of a gamma process follows from the basic properties of Poisson random measure (see Kyprianou 2006):

$$\begin{aligned} \begin{aligned}&\mathbb {P}(J_1\in dx_1, \dots , J_N\in dx_N) \\&\quad =\exp \biggl ( -\alpha \int _{x_N}^{\infty } w^{-1}e^{-w}dw \biggr ) \\&\qquad \times \frac{\alpha ^N}{x_1\dots x_N} e^{-(x_1+\dots +x_N)} dx_N\dots dx_1 , \end{aligned} \end{aligned}$$

where $x_1>x_2>\dots>x_N>0$. Then the joint density of $(J_1, R_1, \dots , R_{N-1})$ can be obtained by changing the variables with $x_k=x_1\prod _{i=1}^{k-1}r_i$, for $k=2, \dots , N$. The conditional density of $\sum _{i=N+1}^{\infty }J_i$ is given by Corollary 2, and this completes the proof. $\square$

Next, we provide a simulation algorithm for the random vector $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$. The algorithm consists two stages; we first applied the rejection method introduced by Rosiński (2001) (see also Godsill and Kı ndap 2022; Imai and Kawai 2013) to sample from the largest N jumps $(J_1, \dots , J_N)$ of the gamma process, then use the exact simulation algorithm for truncated gamma process in Dassios et al. (2019) to simulate the sum of smaller jumps $\tau _{\alpha }^{N-}$. We refer to Algorithm 3.2 of Dassios et al. (2019) as AlgorithmTG(t, $\mu$), and attach the full steps in Appendix A.

Table 1 Sample averages of the largest 5 jumps of a gamma process, the sample size is $10^4$ and CPU is at 2.80 GHz

Proof of Algorithm 1

We apply the rejection method to sample from $(J_1, \dots , J_N)$. This method uses a dominating point process $X_{\alpha }$ with Lévy measure $v_0(dw):=w^{-1}(1+w)^{-1}dw$ at time $\alpha$. Since $v_0(dw)$ has the tail probability $\int _{x}^{\infty }v_0(dw)=\alpha \ln (x^{-1}+1)$, which can be inverted explicitly, we sample from the ranked jumps of $X_{\alpha }$ via Step 4. The ith largest jump of $X_{\alpha }$ is accepted with probability $(1+x_i)\exp (-x_i)$. We refer to in Rosiński (2001), Godsill and Kı ndap (2022) and Imai and Kawai (2013) for more details.

Conditioning on $(J_1, \dots , J_N)$, the Lévy–Khintchine representation of $\tau _{\alpha }^{N-}$ is (see the proof of Corollary 2):

$$\begin{aligned} \begin{aligned}&\mathbb {E} \left( \exp (-\beta \tau _{\alpha }^{N-}) \mid J_1, \dots , J_N \right) \\&\quad = \exp \biggl ( -\alpha \int _{0}^{1}(1-e^{-\beta J_N w})w^{-1}e^{-J_N w}dw \biggr ) , \end{aligned} \end{aligned}$$

it follows that $\tau _{\alpha }^{N-}{\mathop {=}\limits ^{d}}J_N \times Z_{\alpha , J_N}$, where $Z_{t, \mu }$ denotes a truncated gamma process with Lévy measure $w^{-1}e^{-\mu w}\mathbb {1}_{\{ 0<w<1 \}}dw$ at time t, and the exact simulation algorithm for $Z_{t, \mu }$ can be found in Appendix A, see Dassios et al. (2019) for a further discussion. $\square$

We present the numerical results of Algorithm 1 with $N=5$ and various values for $\alpha$ in Table 1. We also use the Hamiltonian Monte Carlo method (Neal 2011, to be introduced in Sect. 5) to sample from the joint density given in Theorem 3. From the table we can see that Algorithm 1 simulates the jumps of the gamma process exactly, and it is very efficient. In fact, Rosiński (2001) gave that the average number of rejected jumps of the dominating process $X_{\alpha }$ is $\alpha \gamma$, where $\gamma$ is the Euler Mascheroni constant. Therefore, to sample from the largest N jumps of the gamma process, we only need to generate $(N+\alpha \gamma )$ number of exponential and uniform random variables respectively in average. Moreover, Algorithm 1 simulates the jumps in succession, thus it is very easy to include a random stopping rule. For example, to apply the random truncation level $N_{\epsilon }$ introduced in Sect. 3, we only need to replace the fixed truncation level N by $N_{\epsilon }$ in the algorithm.

To close this section, we analyse the truncation error of the truncated Poisson–Dirichlet process. From Definition 1, we can see that the truncation error is revealed by the tail probability of the Poisson–Dirichlet process. Let $\{p_i\}_{i=1}^{\infty }$ be the random weights of a Poisson–Dirichlet process, we are interested in the tail probability defined as

$$\begin{aligned} \begin{aligned} r=&\sum _{i=N+1}^{\infty }p_i = \frac{\sum _{i=N+1}^{\infty }J_i}{\sum _{j=1}^{\infty }J_j} \\ =&\frac{\sum _{i=N+1}^{\infty }J_i}{J_1+\dots +J_N+\sum _{j=N+1}^{\infty }J_j} . \end{aligned} \end{aligned}$$

Conditioning on $J_1, \dots , J_N$, we can express the tail probability in terms of

$$\begin{aligned} \begin{aligned}&\{ r=y \mid J_1, \dots , J_N \} \\&\quad =\biggl \{ \sum _{i=N+1}^{\infty }J_i=\frac{y}{1-y}(J_1+\dots +J_N) \mid J_1, \dots , J_N \biggr \} . \end{aligned} \end{aligned}$$

Since the densities of $J_1, \dots , J_N$ and $\sum _{i=N+1}^{\infty }J_i$ have been given in Theorem 3 and Corollary 2, we can integrate out the condition to derive the explicit distribution of r. However, the integral is too complicated to calculate, and we will provide some numerical results for the tail probability instead, see Fig. 2.

Fig. 2

Comparison between the tail probabilities of the Dirichlet and Poisson–Dirichlet processes

We compare the numerical results to the truncation error of the almost sure truncation, for which an explicit result can be found in Ishwaran and Zarepour (2000) (see also Ishwaran and James 2001). Let $\{\tilde{p}_i\}_{i=1}^{\infty }$ be the random weights of a Dirichlet process defined as (2), for each non-negative integer N and each positive integer r, they showed that

$$\begin{aligned} \mathbb {E} \biggl ( \biggl ( \sum _{i=N+1}^{\infty }\tilde{p}_i \biggr )^r \biggr ) = \biggl ( \frac{\alpha }{\alpha +r} \biggr )^N , \end{aligned}$$

(10)

and

$$\begin{aligned} \mathbb {E} \biggl ( \sum _{i=N+1}^{\infty }\tilde{p}_i^r \biggr ) = \biggl ( \frac{\alpha }{\alpha +r} \biggr )^N \frac{\Gamma (r)\Gamma (\alpha +1)}{\Gamma (\alpha +r)} . \end{aligned}$$

(11)

These results provide an upper bound for the tail probability of the Poisson–Dirichlet process. It is clear from the definition that $\sum _{i=1}^{N}p_i \ge \sum _{i=1}^{N}\tilde{p}_i$ almost surely for any fixed N, then $\sum _{i=N+1}^{\infty }p_i \le \sum _{i=N+1}^{\infty }\tilde{p}_i$, and $(\sum _{i=N+1}^{\infty }p_i)^r \le (\sum _{i=N+1}^{\infty }\tilde{p}_i)^r$. Combine this with (10), we have that

$$\begin{aligned} \mathbb {E} \biggl ( \biggl ( \sum _{i=N+1}^{\infty }p_i \biggr )^r \biggr ) \le \biggl ( \frac{\alpha }{\alpha +r} \biggr )^N . \end{aligned}$$

Moreover, since $p_1>p_2>\cdots$, the sequence $\{p_i^r\}_{i=1}^{\infty }$ is decreasing, i.e., $p_1^r> p_2^r > \cdots$, it follows that $\sum _{i=1}^{N}p_i^r \ge \sum _{i=1}^{N}\tilde{p}_i^r$. On the other hand, the event $\{\sum _{i=1}^{\infty }p_i^r = \sum _{i=1}^{\infty }\tilde{p}_i^r\}$ must be true, then we deduce that $\sum _{i=N+1}^{\infty }p_i^r \le \sum _{i=N+1}^{\infty }\tilde{p}_i^r$. Combining this with (11), we get

$$\begin{aligned} \mathbb {E} \biggl ( \sum _{i=N+1}^{\infty }p_i^r \biggr ) \le \biggl ( \frac{\alpha }{\alpha +r} \biggr )^N \frac{\Gamma (r)\Gamma (\alpha +1)}{\Gamma (\alpha +r)} . \end{aligned}$$

In Fig. 2, we plot the sample average of the tail probability of the Poisson–Dirichlet process, as well as the explicit tail probability of the Dirichlet process. The figure shows that we can use the truncated Poisson–Dirichlet process with values of $\alpha$ up to 10 and still have a reasonable truncation error if the truncation level is high enough, for example $N=50$. Also, the figure implies a smaller truncation error arising from the truncated Poisson–Dirichlet process, comparing to the almost sure truncation.

5 Posterior of the truncated Poisson–Dirichlet process

In this section, we develop the posterior sampling algorithm for the truncated Poisson–Dirichlet process. We first work out the posterior, which follows from the Bayes’ Theorem.

Proposition 4

For a sequence of i.i.d. observations ${\textbf {X}}=(X_1, \dots , X_n)$ from a truncated Poisson–Dirichlet process P with concentration parameter $\alpha$, if $n_j=\text {card}\{X_i=K_j\}$ is the number of $X_i$s which equal $K_j$, for $j=1, \dots , N+1$, then the posterior is proportional to

$$\begin{aligned} \begin{aligned}&\pi (P, \alpha \mid {\textbf {X}}) \\&\quad \propto \frac{x_1^{n_1+n_2+\dots +n_N}r_1^{n_2+\dots +n_N} \dots r_{N-1}^{n_N}y^{n_{N+1}}}{(\Sigma +y)^n} \\&\quad \times \mathbb {P}(J_1\in dx_1, R_1\in dr_1, \dots , \\&\quad R_{N-1}\in dr_{N-1}, \tau _{\alpha }^{N-}\in dy) \pi (\alpha ) , \end{aligned} \end{aligned}$$

(12)

where $n=\sum _{j=1}^{N+1}n_j$ is the total number of observations, $\Sigma :=x_1(1+r_1+\dots +r_1r_2\dots r_{N-1})$ denotes the sum of the largest N jumps of the prior, the joint density of $(J_1, R_1, \dots , R_{N-1}, \tau _{\alpha }^{N-})$ is given in Theorem 3, and $\pi (\alpha )$ denotes the prior of the hyperparameter $\alpha$.

Proof

Conditioning on the truncated Poisson–Dirichlet process prior, the likelihood function follows a multinomial distribution,

$$\begin{aligned} \begin{aligned}&\mathbb {P}({\textbf {K}} \mid P, \alpha ) \\&\quad = \biggl ( \frac{x_1}{\Sigma +y} \biggr )^{n_1} \biggl ( \frac{x_1r_1}{\Sigma +y} \biggr )^{n_2} \dots \\&\qquad \times \biggl ( \frac{x_1r_1r_2\dots r_{N-1}}{\Sigma +y} \biggr )^{n_N} \biggl ( \frac{y}{\Sigma +y} \biggr )^{n_{N+1}} ; \end{aligned} \end{aligned}$$

then the proposition is a direct consequence of Bayes’ Theorem. $\square$

To sample from the conditional distribution (12), one way is to sample from $\pi (P \mid {\textbf {K}}, \alpha )$ for a fixed $\alpha$, then update $\alpha$ according to the conditional density $\pi (\alpha \mid P)$ with conjugate sampling or a Metropolis step. This approach was taken for the almost sure truncation of the Dirichlet process, see Ishwaran and Zarepour (2000). If we choose the same approach for the truncated Poisson–Dirichlet process, we can sample from (12) for a fixed $\alpha$ by rejection sampling. The joint density of $(J_1, R_1, \dots , R_{N-1}, \tau _{\alpha }^{N-})$ is taken to be the envelope because its exact simulation algorithm has been developed in Theorem 1. However, this method might be inefficient because the ratio between the target density and envelope is maximised at

$$\begin{aligned} \begin{aligned}&\left( \frac{x_1}{\Sigma +y} \right) ^{n_1} \left( \frac{x_1r_1}{\Sigma +y} \right) ^{n_2} \dots \\&\qquad \times \left( \frac{x_1r_1r_2\dots r_{N-1}}{\Sigma +y} \right) ^{n_N} \left( \frac{y}{\Sigma +y} \right) ^{n_{N+1}} \\&\quad \le \left( \frac{n_1}{n} \right) ^{n_1} \left( \frac{n_2}{n} \right) ^{n_2} \dots \left( \frac{n_N}{n} \right) ^{n_N} \left( \frac{n_{N+1}}{n} \right) ^{n_{N+1}} , \end{aligned} \end{aligned}$$

when n is large, the acceptance rate could be low, and a lot of iterations are needed until a candidate is accepted.

For an efficient exploration of $\pi (P, \alpha \mid {\textbf {K}} )$, we use the Hamiltonian Monte Carlo method (see Neal 2011, see also Caron and Fox 2017 Section 7.2 for a similar application in posterior sampling) within the Gibbs sampler to update $(x_1, r_1, \dots , r_{N-1})$. The HMC method updates the variables according to the gradient of the log-posterior, hence leading to a higher acceptance rate than the rejection sampling method described above. For the update of the remaining mass y and hyperparameter $\alpha$, we apply a rejection sampling step. This step makes use of the exact simulation algorithm for truncated gamma process, see Appendix A. In conclusion, the sampling algorithm for (12) is given as follows.

Step 1 update $(x_1, r_1, \dots , r_{N-1})$ given the rest using the HMC method;

Step 2 update the remaining mass y and hyperparameter $\alpha$ given the rest by rejection sampling.

To facilitate the HMC method, we express the posterior in terms of unconstrained variables. Since $x_1\in (0, \infty )$ and $r_i\in (0, 1)$, we define

$$\begin{aligned} X:=\log (x_1) ~~\text {and}~~ R_i:=\tan (\pi (r_i-0.5)) , \end{aligned}$$

(13)

for $i=1, \dots , N-1$, such that both X and $R_i$ are unconstrained. Then we rewrite the posterior as

$$\begin{aligned}&\pi (X, R_1, \dots , R_{n-1} \mid y, \alpha , {\textbf {K}}) \\&\quad \propto (e^X)^{n_1+n_2+\dots +n_N} \\&\quad \times \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_1) \biggr )^{n_2+\dots +n_N} \dots \\&\quad \times \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_{N-1}) \biggr )^{n_N} (\Sigma +y)^{-n} \\&\quad \times \exp \biggl ( -\alpha \int _{\Pi }^{\infty } w^{-1}e^{-w}dw \biggr ) \frac{1}{\Pi } e^{-\Sigma } f_{\alpha , \Pi }(y) \\&\quad \times e^X \biggl ( \frac{1}{\pi }\frac{1}{1+R_1^2} \biggr )\dots \biggl ( \frac{1}{\pi }\frac{1}{1+R_{N-1}^2} \biggr ) \\&\quad \times dR_{N-1}\dots dR_1dX , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \Pi :=&\, e^{X} \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_1) \biggr ) \times \dots \\&\times \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_{N-1}) \biggr ) , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \Sigma :=&\, e^{X} \biggl [ 1+ \left( \frac{1}{2}+\frac{1}{\pi }\arctan (R_1) \right) +\cdots \biggr . \\&\quad \biggl . +\left( \frac{1}{2}+\frac{1}{\pi }\arctan (R_1) \right) \times \cdots \\&\quad \times \left( \frac{1}{2}+\frac{1}{\pi }\arctan (R_{N-1}) \right) \biggr ] . \end{aligned} \end{aligned}$$

And the log-posterior is given by

$$\begin{aligned} \begin{aligned}&\log (\pi (X, R_1, \dots , R_{n-1} \mid y, \alpha , {\textbf {K}})) \\&\quad =C+(n_1+n_2+\dots +n_N)X \\&\qquad +(n_2+\dots +n_N)\log \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_1) \biggr ) +\dots \\&\qquad +n_N\log \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_{N-1}) \biggr ) \\&\qquad -n\log (\Sigma +y) \\&\qquad -\alpha \int _{\Pi }^{\infty } w^{-1}e^{-w}dw-\log (\Pi )-\Sigma \\&\qquad +\log (f_{\alpha , \Pi }(y))+X \\&\qquad +\log \biggl ( \frac{1}{\pi }\frac{1}{1+R_1^2} \biggr ) +\dots +\log \biggl ( \frac{1}{\pi }\frac{1}{1+R_{N-1}^2} \biggr ) , \end{aligned} \end{aligned}$$

where C is a scaling constant independent of $X, R_1, \dots , R_{N-1}$.

Next, we need to calculate the gradient of the log-posterior. The calculation is straightforward except for the derivative of $\log (f_{\alpha , \Pi }(y))$ with respect to X and $R_i$. To this end, we first calculate the derivative of a truncated gamma density $f_{\alpha , x}(y)$ as follows.

When $0<y\le x$, the ratio $0<y/x\le 1$. From Lemma 1 and Corollary 2 we know the density involves only one term, that is,

$$\begin{aligned} f_{\alpha , x}(y) = \frac{1}{x} g_{Z} \left( \frac{y}{x}; \alpha , x \right) = e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )} y^{\alpha -1}e^{-y} , \end{aligned}$$

then the derivative is

$$\begin{aligned} \begin{aligned} \frac{d}{dx}f_{\alpha , x}(y) =&-\alpha x^{-1}e^{-x} e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )} y^{\alpha -1}e^{-y} \\ =&-\alpha x^{-1}e^{-x}f_{\alpha , x}(y) . \end{aligned} \end{aligned}$$

Next, we consider the range $x<y\le 2x$. In this case, $1<y/x\le 2$, and the density involves two terms,

$$\begin{aligned} \begin{aligned}&f_{\alpha , x}(y) \\&\quad = e^{\alpha \Gamma (0, x)} \frac{1}{\Gamma (\alpha )}y^{\alpha -1}e^{-y} \\&\qquad -\alpha \int _{1}^{y/x} e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )}(y-xs)^{\alpha -1}e^{-y}s^{-1}ds , \end{aligned} \end{aligned}$$

then the derivative is

$$\begin{aligned} \begin{aligned}&\frac{d}{dx}f_{\alpha , x}(y) \\&\quad =-\alpha x^{-1}e^{-x} \biggl ( e^{\alpha \Gamma (0, x)} \frac{1}{\Gamma (\alpha )}y^{\alpha -1}e^{-y} \\&\qquad -\alpha \int _{1}^{y/x} e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )}(y-xs)^{\alpha -1}e^{-y}s^{-1}ds \biggr ) \\&\qquad +\alpha e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )}e^{-y}x^{-1}(y-x)^{\alpha -1} . \end{aligned} \end{aligned}$$

The first term of this derivative can be written as $-\alpha x^{-1}e^{-x}f_{\alpha , x}(y)$, while for the second term, we have

$$\begin{aligned} \begin{aligned}&\alpha e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )}e^{-y}x^{-1}(y-x)^{\alpha -1} \\&\quad = \alpha x^{-1}e^{-x} e^{\alpha \Gamma (0, x)}\frac{1}{\Gamma (\alpha )} (y-x)^{\alpha -1}e^{-(y-x)} \\&\quad = \alpha x^{-1}e^{-x} f_{\alpha , x}(y-x) \mathbb {1}_{\{ y>x \}} . \end{aligned} \end{aligned}$$

Thus, the derivative is given by

$$\begin{aligned} \begin{aligned}&\frac{d}{dx}f_{\alpha , x}(y) \\&\quad = -\alpha x^{-1}e^{-x} \left( f_{\alpha , x}(y)-f_{\alpha , x}(y-x) \mathbb {1}_{\{ y>x \}} \right) . \end{aligned} \end{aligned}$$

(14)

In general, it can be shown by induction that the derivative has the format (14) for any $(k-1)x<y\le kx$, $k=1, 2, \dots$. However, the calculation is quite complicated, so we provide an inverse Laplace transform method towards this result. From Lemma 1 and Corollary 2 we can see that in each subinterval $(k-1)x<y\le kx$, the functions $f_{\alpha , x}(y)$ and $\frac{d}{dx}f_{\alpha , x}(y)$ are continuous in y and x, we then have for each subinterval that

$$\begin{aligned} \begin{aligned}&\mathcal {L}^{-1} \biggl \{ \int _{0}^{\infty }e^{-\beta y}\frac{d}{dx}f_{\alpha , x}(y)dy \biggr \} \mathbb {1}_{\{ (k-1)x<y\le kx \}} \\&\quad = \mathcal {L}^{-1} \biggl \{ \frac{d}{dx}\int _{0}^{\infty }e^{-\beta y}f_{\alpha , x}(y)dy \biggr \} \mathbb {1}_{\{ (k-1)x<y\le kx \}} \\&\quad = \mathcal {L}^{-1} \biggl \{ -\alpha x^{-1}e^{-x} (1-e^{-\beta x}) \biggr . \\&\qquad \times \biggl . \exp \biggl ( -\alpha \int _{0}^{x}(1-e^{-\beta w}) w^{-1}e^{-w}dw \biggr ) \biggr \} \\ {}&\qquad \times \mathbb {1}_{\{ (k-1)x<y\le kx \}} \\&\quad = -\alpha x^{-1}e^{-x} \left( f_{\alpha , x}(y)-f_{\alpha , x}(y-x) \mathbb {1}_{\{ y>x \}} \right) \\&\qquad \times \mathbb {1}_{\{ (k-1)x<y\le kx \}} . \end{aligned} \end{aligned}$$

Then the derivative of $\log (f_{\alpha , x}(y))$ is

$$\begin{aligned} \begin{aligned}&\frac{d}{dx}\log (f_{\alpha , x}(y)) \\&\quad = -\alpha x^{-1}e^{-x} \biggl ( 1-\frac{f_{\alpha , x}(y-x) \mathbb {1}_{\{ y>x \}}}{f_{\alpha , x}(y)} \biggr ) , \end{aligned} \end{aligned}$$

and this enables us to calculate the derivative of $\log (f_{\alpha , \Pi }(y))$ with respect to X and $R_i$,

$$\begin{aligned} \begin{aligned}&\frac{d}{dX}\log (f_{\alpha , \Pi }(y)) \\&\quad = -\alpha e^{-\Pi } \biggl ( 1-\frac{f_{\alpha , \Pi }(y-\Pi ) \mathbb {1}_{\{ y>\Pi \}}}{f_{\alpha , \Pi }(y)} \biggr ) , \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned}&\frac{d}{dR_i}\log (f_{\alpha , \Pi }(y)) \\&\quad = -\alpha e^{-\Pi } \biggl ( 1-\frac{f_{\alpha , \Pi }(y-\Pi ) \mathbb {1}_{\{ y>\Pi \}}}{f_{\alpha , \Pi }(y)} \biggr ) \\&\qquad \times \frac{1}{\pi (1+R_i^2)} \biggl ( \frac{1}{2}+\frac{1}{\pi }\arctan (R_i) \biggr )^{-1} . \end{aligned} \end{aligned}$$

Now we are ready to use the HMC method to update the variables $(X, R_1, \dots , R_{N-1})$. Let $L\ge 1$ be the number of leapfrog steps and $\epsilon >0$ be the step size. For a concise presentation of the algorithm steps, we denote by $W_{1:N}:=(X, R_1, \dots , R_{N-1})$ the variables, and $D(W_{1:N}):=D(X, R_1, \dots , R_{N-1})=\nabla \log (\pi (X, R_1, \dots , R_{n-1} \mid y,\alpha , {\textbf {K}}))$ the gradient of the log-posterior. The HMC method samples the momentum variables $p\sim \mathcal {N}(0, I_N)$, then simulate L steps of the Hamiltonian via the following steps:

$$\begin{aligned}{} & {} \tilde{p}^{(0)} \leftarrow p + (\epsilon /2) D(W_{1:N}) , \\{} & {} \tilde{W}^{(0)}_{1:N} \leftarrow W_{1:N} ; \end{aligned}$$

and for $l=1, \dots , L-1$,

$$\begin{aligned}{} & {} \tilde{W}^{(l)}_{1:N} \leftarrow \tilde{W}^{(l-1)}_{1:N} + \epsilon \tilde{p}^{(l-1)} , \\{} & {} \tilde{p}^{(l)} \leftarrow \tilde{p}^{(l-1)} + \epsilon D(\tilde{W}^{(l)}_{1:N}) ; \end{aligned}$$

finally, set

$$\begin{aligned}{} & {} \tilde{W}_{1:N} \leftarrow \tilde{W}^{(L-1)}_{1:N} + \epsilon \tilde{p}^{(L-1)}, \\{} & {} \tilde{p} \leftarrow -\biggl \{ \tilde{p}^{(L-1)} + (\epsilon /2) D(\tilde{W}_{1:N}) \biggr \} . \end{aligned}$$

The proposal $\tilde{W}_{1:N}=(\tilde{X}, \tilde{R}_1, \dots , \tilde{R}_{N-1})$ is accepted if

$$\begin{aligned} U[0, 1] \le \frac{\pi (\tilde{W}_{1:N} \mid y, \alpha , {\textbf {K}})}{\pi (W_{1:N} \mid y, \alpha , {\textbf {K}})} \exp \biggl ( -\frac{1}{2}\sum _{i=1}^{N}(\tilde{p_i}^2-p_i^2) \biggr ) . \end{aligned}$$

We then output $(x_1, r_1, \dots , r_{N-1})$ using the inverse transform of (13), and Step 1 is completed.

For Step 2, we need to update the remaining mass y and the hyperparameter $\alpha$. We will use the acceptance–rejection method to sample from the conditional density of y and $\alpha$:

$$\begin{aligned} \begin{aligned}&\pi (y, \alpha \mid x_1, r_1, \dots , r_{N-1}, {\textbf {K}}) \\&\quad =C\frac{y^{n_{N+1}}}{(\Sigma +y)^n} \exp \biggl ( -\alpha \int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-1}e^{-w}dw \biggr ) \\&\qquad \times \alpha ^N f_{\alpha , x_1r_1\dots r_{N-1}}(y) \pi (\alpha ) \\&\quad =C'\frac{y^{n_{N+1}}}{(\Sigma +y)^n} \\&\qquad \times \exp \biggl ( -\alpha \biggl ( \nu _2+\int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-1}e^{-w}dw \biggr ) \biggr ) \\&\qquad \times \alpha ^{N+\nu _1-1} f_{\alpha , x_1r_1\dots r_{N-1}}(y) , \end{aligned} \end{aligned}$$

where $\alpha , y \in (0, \infty )$, C and $C'$ are scaling constants, and $\pi (\alpha ) \sim \text {Ga}(\nu _1, \nu _2)$ is the prior for $\alpha$. Conditioning on $\alpha$ and $(x_1, r_1, \dots , r_{N-1})$, we can sample from the truncated gamma density $f_{\alpha , x_1r_1\dots r_{N-1}}(y)$ using the exact simulation algorithm in Appendix A. Thus, we choose the envelope

$$\begin{aligned} \begin{aligned}&C'' \alpha ^{N+\nu _1-1} \\&\quad \times \exp \biggl ( -\alpha \biggl ( \nu _2+\int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-1}e^{-w}dw \biggr ) \biggr ) \\&\quad \times f_{\alpha , x_1r_1\dots r_{N-1}}(y) , \end{aligned} \end{aligned}$$

where $C''$ is a scaling constant. To sample from the envelope, we first simulate a gamma random number

$$\begin{aligned} \tilde{\alpha } \sim \text {Ga} \biggl ( N+\nu _1, \nu _2+\int _{x_1r_1\dots r_{N-1}}^{\infty } w^{-1}e^{-w}dw \biggr ) , \end{aligned}$$

then sample from $f_{\tilde{\alpha }, x_1r_1\dots r_{N-1}}(\tilde{y})$. The ratio between the target density and the envelope is maximised at

$$\begin{aligned} \frac{C'}{C''}\frac{y^{n_{N+1}}}{(\Sigma +y)^n}\le \frac{C'}{C''}\frac{n_{N+1}^{n_{N+1}}}{n^n}\frac{(n-n_{N+1})^{n-n_{N+1}}}{(\Sigma )^{n-n_{N+1}}} , \end{aligned}$$

thus, the candidates $\tilde{\alpha }$ and $\tilde{y}$ are accepted if

$$\begin{aligned} \begin{aligned}&U[0, 1] \\&\quad \le \biggl ( \frac{n}{n_{N+1}}\frac{\tilde{y}}{\Sigma +\tilde{y}} \biggr )^{n_{N+1}} \biggl ( \frac{n}{n-n_{N+1}}\frac{\Sigma }{\Sigma +\tilde{y}} \biggr )^{n-n_{N+1}} , \end{aligned} \end{aligned}$$

and this completes Step 2.

The quantity $\tilde{y}/(\Sigma +\tilde{y})$ on the right hand side of the inequality above represents the tail probability of a truncated Poisson–Dirichlet process, and $n_{N+1}$ stands for the number of latent variables in this cluster. When the truncation level N is large enough, we expect both quantities to be small, and the acceptance rate should be high. If the truncation level N is not large enough, these quantities could be larger. But since the envelope sampling algorithm is very efficient, the acceptance–rejection method may still be feasible. In more extreme cases, we could include y and $\alpha$ in the HMC sampler. To this end, we include $Y:=\log (y)$ and $A:=\log (\alpha )$ in (13) to obtain unconstrained variables.

Finally, we output the accepted candidates of $(x_1, r_1, \dots , r_{N-1}, y)$ and $\alpha$. The posterior jump sizes of the gamma process are derived from $J_1=x_1, ~~ J_2=x_1r_1, ~~ \dots , ~~ J_N=x_1r_1\dots r_{N-1}$, and the posterior random weights are given by

$$\begin{aligned} p_1 = \frac{J_1}{\Sigma +y},~~ \dots , ~~ p_N = \frac{J_N}{\Sigma +y}, ~~ r=\frac{y}{\Sigma +y} , \end{aligned}$$

where $\Sigma =J_1+\dots +J_N$.

From the output we can see that the truncated Poisson–Dirichlet process differs from the almost sure truncation (4) in the following two aspects. First, we include the largest N random weights in the posterior inference, while the almost sure truncation is based on arbitrary N random weights. The largest random weights would be helpful if we want to focus on the most important components in the model. Second, our method is targetted at the jump sizes of the underlying gamma process, which are not available in the almost sure truncation. The jump sizes are critical to some researches, for example the Caron–Fox network model, and the truncated Poisson–Dirichlet process should be used in this case.

6 Models based on truncated Poisson–Dirichlet process

In this section, we consider two models based on the truncated Poisson–Dirichlet process, and discuss their posterior inference method.

Consider a Bayesian nonparametric hierarchical model of the format

$$\begin{aligned} \begin{aligned}&(X_i \mid Y_i) \sim \pi (X_i \mid Y_i), ~~ i=1, \dots , n ,\\&(Y_i \mid P) \sim P ,\\&P \sim \mathcal {P} . \end{aligned} \end{aligned}$$

(15)

In this model, $X_1, \dots , X_n$ represent the observations, they are assumed to be independent conditionally on the latent variables $Y_1, \dots , Y_n$. The latent variables $Y_i$ are independent and identically distributed according to P, and P is a sample of the random probability measure $\mathcal {P}$. We refer to $\mathcal {P}$ as the model prior.

If we use a Dirichlet process for $\mathcal {P}$, (15) reverts to a Dirichlet process hierarchical model. Since the Dirichlet process prior is conjugate to multinomial sampling, the model posterior can be obtained by integrating over P and exploiting the Pólya urn scheme. This approach leads to a marginalised version of the Bayesian nonparametric hierarchical model:

$$\begin{aligned} \begin{aligned}&(X_i \mid Y_i) \sim \pi (X_i \mid Y_i), ~~ i=1, \dots , n ,\\&(Y_1, \dots , Y_n) \sim \pi _{\infty }(Y_1, \dots , Y_n) ,\\&\pi _{\infty }(dY_1, \dots , dY_n) \sim H(dY_1)\prod _{i=2}^{n} \biggl \{ \frac{\alpha }{\alpha +i-1}H(dY_i) \biggr . \\&\quad \biggl . +\frac{1}{\alpha +i-1}\sum _{j=1}^{i-1}\delta _{Y_j}(dY_i) \biggr \} , \end{aligned} \end{aligned}$$

where $\pi _{\infty }(dY_1, \dots , dY_n)$ denotes the distribution of a Pólya urn scheme.

The marginalisation method is widely used in Bayesian nonparametric statistics as it can be implemented easily. However, since the Dirichlet process prior is integrated out by marginalisation, this approach has the side effect of making inference based on the latent variables $Y_1, \dots , Y_n$ only. To combat this problem, Ishwaran and Zarepour (2000) (see also Ishwaran and James 2002) replaced $\mathcal {P}$ by the almost sure truncation $\tilde{\mathcal {P}}_N$ (see Eq. 4). This leads to an approximation for the Dirichlet process hierarchical model which is almost indistinguishable from its limit when N is large enough. Moreover, a direct inference for $\tilde{\mathcal {P}}_N$ can be obtained using this method.

Following this idea, we provide a new approximation for model (15). Our method is to replace the Dirichlet process prior $\mathcal {P}$ by a truncated Poisson–Dirichlet process $\mathcal {P}_N$. To facilitate the posterior sampling algorithm, we recast the model completely in terms of random variables, then model (15) is approximated by

$$\begin{aligned} \begin{aligned}&(X_i \mid {\textbf {Z}}, {\textbf {K}}) \sim \pi (X_i \mid Z_{K_i}), ~~ i=1, \dots , n ,\\&(K_i \mid P) \sim \sum _{i=1}^{N}p_i\delta _{i}(.)+r\delta _{N+1}(.) ,\\&P \sim \mathcal {P}_N , \\&{\textbf {Z}} \sim \pi ({\textbf {Z}}) , \end{aligned} \end{aligned}$$

(16)

where ${\textbf {K}}=(K_1, \dots , K_n)$ are the classifiers that relate the random variables ${\textbf {Z}}=(Z_1, \dots , Z_n)$ to the latent variables $Y_i$, i.e., $Y_i=Z_{K_i}$. We will devise a blocked Gibbs sampler to explore the posterior distribution of model (16), denoted by $\pi (P, {\textbf {Z}}, {\textbf {K}} \mid {\textbf {X}})$. The sampler draws iteratively from the conditional distributions $\pi (P, {\textbf {Z}} \mid {\textbf {K}}, {\textbf {X}})$ and $\pi ({\textbf {K}} \mid P, {\textbf {Z}}, {\textbf {X}})$, thus producing the posterior values $(P^{(b)}, {\textbf {Z}}^{(b)}, {\textbf {K}}^{(b)})$.

Next, we use the normal mean mixture model to illustrate the posterior sampling algorithm. These models are in the format of (15) with $(X_i \mid Y_i) \sim \mathcal {N}(Y_i, \sigma _X)$, where $\sigma _X$ denotes the variance. In the clustering problems, $\sigma _X$ is assumed to be a known constant; while in the predictive density estimation problems, $\sigma _X$ is a parameter that needs to be estimated. For now we assume that $\sigma _X$ is known; this condition will be released to obtain a Bayesian semiparametric hierarchical model later. Using the approximation (16), we express the normal mean mixture model as

$$\begin{aligned} \begin{aligned}&(X_i \mid {\textbf {Z}}, {\textbf {K}} ) \sim \mathcal {N}(Z_{K_i}, \sigma _X) , ~~ i=1, \dots , n ,\\&(K_i \mid P) \sim \sum _{i=1}^{N}p_i\delta _{i}(.)+r\delta _{N+1}(.) , \\&(Z_k \mid \theta , \sigma _Z) \sim \mathcal {N}(\theta , \sigma _Z) , \\&(\theta \mid \sigma _{\theta }) \sim \mathcal {N}(0, \sigma _{\theta }) , \\&(\sigma _Z^{-1} \mid \tau _1, \tau _2) \sim \text {Ga}(\tau _1, \tau _2) , \\&(\alpha \mid \nu _1, \nu _2) \sim \text {Ga}(\nu _1, \nu _2) , \end{aligned} \end{aligned}$$

(17)

where P is a sample of the truncated Poisson–Dirichlet process $\mathcal {P}_N$.

In model (17), we use hyperparameters $\theta$ and $\sigma _Z$ for the distribution of $Z_k$, and choose normal and inverse gamma priors for these hyperparameters respectively. Since the priors are conjugate, the hyperparameters can be updated easily. To obtain noninformative priors, we choose a large value for $\sigma _{\theta }$, i.e., $\sigma _{\theta }=1000$, and use small values for $\tau _1$ and $\tau _2$, i.e., $\tau _1=\tau _2=0.001$. Note that $\alpha$ is directly related to the number of distinct clusters. A large $\alpha$ encourages the mass to spread among distinct $K_i$ values, while a small $\alpha$ means the mass will concentrate on a few clusters. We choose a gamma prior for $\alpha$ due to its flexibility, as we can manipulate the number of distinct clusters by adjusting the hyperparameters $\nu _1$ and $\nu _2$. More importantly, the gamma prior will simplify the update procedure for $\alpha$ in the posterior sampling algorithm.

Next, we design a Gibbs sampling scheme for the posterior of (17). To implement the blocked Gibbs sampler, we need to draw from the following conditional distributions iteratively:

$$\begin{aligned}{} & {} (P, \alpha \mid {\textbf {K}} ) , \end{aligned}$$

(18)

$$\begin{aligned}{} & {} ({\textbf {Z}} \mid {\textbf {K}}, \theta , \sigma _Z, {\textbf {X}} ) , \end{aligned}$$

(19)

$$\begin{aligned}{} & {} ({\textbf {K}} \mid P, {\textbf {Z}}, {\textbf {X}}) , \end{aligned}$$

(20)

$$\begin{aligned}{} & {} (\theta \mid {\textbf {Z}}, \sigma _Z) , \end{aligned}$$

(21)

$$\begin{aligned}{} & {} (\sigma _Z \mid {\textbf {Z}}, \theta ) . \end{aligned}$$

(22)

The first step (18) samples from the posterior of the truncated Poisson–Dirichlet process, then updates the concentration parameter. This can be done using the algorithm introduced in Sect. 5. To sample from (19), (20), (21) and (22), we follow the standard procedure in literature. The means ${\textbf {Z}}$ can be updated using the conditional density

$$\begin{aligned} \begin{aligned}&f({\textbf {Z}} \mid {\textbf {K}}, \theta , \sigma _Z, {\textbf {X}} ) \\&\quad \propto \biggl \{ \prod _{j=1}^{m}f(Z_{K_j^*} \mid \theta , \sigma _Z) \prod _{\{ i: K_i=K_j^* \}} f(X_i \mid Z_{K_j^*}) \biggr \} \\&\qquad \times f(Z^K \mid \theta , \sigma _Z) , \end{aligned} \end{aligned}$$

where $\{ K_1^*, \dots , K_m^* \}$ denote the m unique values in the set ${\textbf {K}}$. For each element of $\left\{ K_1^*, \dots , K_m^* \right\}$, we sample from $Z_{K_j^*}$ according to

$$\begin{aligned} (Z_{K_j^*} \mid {\textbf {K}}, \theta , \sigma _Z, {\textbf {X}}) \sim \mathcal {N}(\theta _j^*, \sigma _{Z_j}^*) , \end{aligned}$$

where $\theta _j^*=\sigma _{Z_j}^*(\theta /\sigma _Z+\sum _{\{i: K_i=K_j^*\}}X_i/\sigma _X)$, $\sigma _{Z_j}^*=(n_j/\sigma _X+1/\sigma _Z)^{-1}$, and $n_j$ is the number of times $K_j^*$ occurs in ${\textbf {K}}$. Also, for each $j\in {\textbf {K}}-\{ K_1^*, \dots , K_m^* \}$, we sample from $Z_j\sim \mathcal {N}(\theta , \sigma _{Z})$ independently.

The conditional distribution for ${\textbf {K}}$ is given by

$$\begin{aligned} (K_j \mid P, {\textbf {Z}}, {\textbf {X}}) \sim \sum _{i=1}^{N} p_{i, j}^* \delta _{i}(.)+r_{j}^* \delta _{N+1}(.) , \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&(p_{1, j}^*, \dots , p_{N, j}^*, r_{j}^*) \\&\quad \propto \biggl ( p_1\exp \biggl ( \frac{-1}{2\sigma _X}(X_j-Z_1)^2 \biggr ), \dots , \biggr . \\&\qquad p_N\exp \biggl ( \frac{-1}{2\sigma _X}(X_j-Z_N)^2 \biggr ) , \\&\qquad \biggl . r\exp \biggl ( \frac{-1}{2\sigma _X}(X_j-Z_{N+1})^2 \biggr ) \biggr ) . \end{aligned} \end{aligned}$$

The conditional distribution of $\theta$ and $\sigma _Z$ are conjugate. We sample from $\theta$ according to $(\theta \mid {\textbf {Z}}, \sigma _Z) \sim \mathcal {N}(\theta ^*, \sigma _{\theta }^*)$, where

$$\begin{aligned} \theta ^*=\frac{\sigma _{\theta }^*}{\sigma _Z}\sum _{i=1}^{N+1}Z_i ~~\text {and}~~ \sigma _{\theta }^*=(N/\sigma _Z+1/\sigma _{\theta })^{-1} . \end{aligned}$$

And for the conditional distribution of $\sigma _Z$, we sample from

$$\begin{aligned} (\sigma _Z^{-1} \mid {\textbf {Z}}, \theta ) \sim \text {Ga} \biggl ( \tau _1+N/2, \tau _2+\sum _{i=1}^{N+1}(Z_i-\theta )^2/2 \biggr ) . \end{aligned}$$

These steps are taken from Ishwaran and James (2002) and Ishwaran and Zarepour (2000), they complete all the steps of the blocked Gibbs sampler and enables us to sample from the posterior of model (17).

The blocked Gibbs sampler can be extended to estimate the variance of the underlying normal distribution. By viewing the variance $\sigma _X$ as an unknown parameter, we get a Bayesian semiparametric hierarchical model where $(X_i \mid Y_i, \sigma _X) \sim \mathcal {N}(Y_i, \sigma _X)$. We choose an inverse gamma prior for $\sigma _X$:

$$\begin{aligned} \sigma _X^{-1} \sim \text {Ga}(\gamma _1, \gamma _2) \end{aligned}$$

(23)

with $\gamma _1=\gamma _2=0.001$, such that the prior is noninformative. Then $\sigma _X$ can be updated by conjugation

$$\begin{aligned} \begin{aligned}&(\sigma _X^{-1} \mid {\textbf {X}}, {\textbf {Z}}, {\textbf {K}}) \\&\quad \sim \text {Ga} \biggl ( \gamma _1+n/2, \gamma _2+\sum _{i=1}^{n}(X_i-Z_{K_i})^2/2 \biggr ) . \end{aligned} \end{aligned}$$

(24)

We add an extra step (24) into the blocked Gibbs sampler, and use the updated value of $\sigma _X$ in other steps. This gives us a sampler for the normal mean mixture model with an unknown variance.

The normal mean mixture model demonstrates the feasibility of the truncated Poisson–Dirichlet process in clustering and predictive density estimation problems. However, these problems can also be solved using the almost sure truncation, and it still remains to justify the novelty of our method. To this end, we provide an application of the truncated Poisson–Dirichlet process in the Caron–Fox network model.

As discussed in Sect. 3, the construction of the truncated Poisson–Dirichlet process is partially motivated by the ‘network with key nodes’, meaning that we want to estimate the largest N popularity parameters in the network. The two-dimensional Pólya urn scheme in Williamson (2016) is not applicable in this problem because the popularity parameters are integrated out by marginalisation; while the method in Caron and Fox (2017) hinges on the estimation of the popularity parameters of all the nodes with at least one link. To our best knowledge, no literature has focused on the most popular nodes in a Caron–Fox network model. We replace the Dirichlet process prior in model (7) by a truncated Poisson–Dirichlet process $\mathcal {P}_{N}$ and consider the network model

$$\begin{aligned} \begin{aligned}&G \sim \mathcal {P}_{N} \\&s_j, r_j {\mathop {\sim }\limits ^{\text {i.i.d.}}} G=\sum _{i=1}^{N}\frac{J_i}{\tau _{\alpha }}\delta _{i}(.) +\frac{\tau _{\alpha }^{N-}}{\tau _{\alpha }}\delta _{N+1}(.) , \end{aligned} \end{aligned}$$

(25)

for $j=1, \dots , n$, where $\{J_i\}_{i=1}^{\infty }$ are the ranked jumps of a gamma process $\tau _{\alpha }$, they denote the popularity parameters of the nodes in the network; and $\tau _{\alpha }^{N-}=\sum _{i=N+1}^{\infty }J_i$ is the total popularity parameter of the less popular nodes.

Next, we discuss the posterior inference procedure for model (25). For a set of observations from the network, we need to count the number of links of all the nodes and find out the largest N values, namely $n_1, \dots , n_{N}$; they are explained as the number of links of the N nodes with the highest popularity parameters. The other links are grouped together in terms of $n_{N+1}:=\sum _{i=N+1}^{\infty }n_i$ and understood as the total number of links of the less popular nodes. Then we input the data $\{n_1, \dots , n_{N}, n_{N+1} \}$ into the posterior of model (25), which is given in Proposition 4, and use the algorithm in Sect. 5 to sample from it. Note that we will only output the jump sizes $J_1, \dots , J_n, , \tau _{\alpha }^{N-}$ in this case.

We emphasise that this method estimates the actual popularity parameters $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$, not only their weights, and this makes the model more flexible. For example, to include the Poisson assumption about the total number of links, we only need to multiply the posterior distribution (12) by a Poisson probability mass function. See Caron and Fox (2017) for a further discussion on the choice of the prior for $\alpha$, as well as the applications of the posterior inference results.

7 Numerical implementations

In this section, we present some numerical results for the models introduced in Sect. 6. We first study the normal mean mixture model with a known variance. Consider a mixture of three normal distributions whose means are $\{-3, 1, 2\}$ with equal probabilities and variance $\sigma _X=1$, we simulate $n=45$ observations from the model, then run the blocked Gibbs sampler and record the posterior mean values. We use the truncation level $N=45$ for the truncated Poisson–Dirichlet process prior, and choose a $\text {Ga}(2, 2)$ prior for $\alpha$. In the HMC step, we use the leapfrog steps $L=10$ and the step size $\epsilon =0.25$. The numerical results are presented in Fig. 3.

Fig. 3

Posterior mean values based on 45 observations, each observation $X_i$ is sampled from a normal mean mixture model with mean $\{-3, 1, 2\}$ with equal probabilities and variance $\sigma _X=1$. Values for $X_i$ and true values for $\mu _X$ are denoted by green cross and red plus respectively. The plot is based on 4500 sampled values following an initial 2500 iteration burn-in using the blocked Gibbs sampler

The outcome of the blocked Gibbs sampler can be used to estimate the predictive density for a new observation $X_{n+1}$. We denote by $f(X_{n+1} \mid {\textbf {X}})$ the predictive density for $X_{n+1}$ conditioning on the current observations ${\textbf {X}}=(X_1, \dots , X_n)$, and $Y_{n+1}$ the latent variable of this new observation, then

$$\begin{aligned} \begin{aligned}&f(X_{n+1} \mid {\textbf {X}}) \\&\quad = \int \mathcal {N}(X_{n+1} \mid Y_{n+1}, \sigma _X)d\pi (Y_{n+1},\sigma _X \mid {\textbf {X}}) \\&\quad = \iint \mathcal {N}(X_{n+1} \mid Y_{n+1}, \sigma _X) \\&\qquad \times d\pi (Y_{n+1} \mid P)d\pi (P, \sigma _X \mid {\textbf {X}}) . \end{aligned} \end{aligned}$$

Since we have used a truncated Poisson–Dirichlet process prior, the probability measure P has the format $P(.)=\sum _{i=1}^{N}p_i\delta _{Z_i}(.)+r\delta _{Z_{N+1}}(.)$, and the inner integral can be expressed as

$$\begin{aligned} \begin{aligned}&\int \mathcal {N}(X_{n+1} \mid Y_{n+1}, \sigma _X)d\pi (Y_{n+1} \mid P) \\&\quad =\sum _{i=1}^{N}p_i\mathcal {N}(X_{n+1} \mid Z_i, \sigma _X) \\&\qquad +r\mathcal {N}(X_{n+1} \mid Z_{N+1}, \sigma _X) . \end{aligned} \end{aligned}$$

(26)

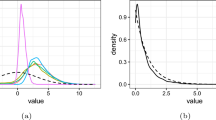
Thus, the predictive density $f(X_{n+1} \mid {\textbf {X}})$ can be estimated by averaging (26) over the posterior values from different iterations. In Fig. 4, we randomly select fifty iterations and use their posterior values to evaluate (26). From the figure we can see that the posterior induces two modes for the model, but it cannot distinguish between the two modes 1 and 2 which are close to each other.

Fig. 4

Fifty randomly selected predictive densities of the format (26). The true values for $X_i$ are presented by the histogram. The plot is based on 4500 sampled values following an initial 2500 iteration burn-in using the blocked Gibbs sampler

Fig. 5

Proportions of the number of distinct values in ${\textbf {K}}^{(b)}$, $b=1, \dots , 4500$. $N=45$

Fig. 6

Proportions of the number of distinct values in ${\textbf {K}}^{(b)}$, $b=1, \dots , 4500$. $N=250$

The performance of the blocked Gibbs sampler can also be seen from the clustering of observations, which is revealed by the number of distinct values in ${\textbf {K}}^{(b)}$. We count the number of distinct values from each iteration and record their proportions in Fig. 5. The figure shows that the posterior distribution has at least two clusters, and it is unlikely to have more than ten clusters. Then we re-run the blocked Gibbs sampler with a higher truncation level $N=250$ for the truncated Poisson–Dirichlet process prior, and count the number of distinct values in ${\textbf {K}}^{(b)}$ again. From Fig. 6 we can see that the proportions are similar as before, although the posterior distribution has at most eight clusters in this case.

Fig. 7

Posterior mean values (km/sec. * 0.001) of the galaxy velocities data. The observations $X_i$ are denoted by green cross. The plot is based on 2500 sampled values following an initial 2500 iteration burn-in using the blocked Gibbs sampler with $N=82$ and $\alpha \sim \text {Ga}(2, 4)$

Fig. 8

Twenty-five randomly selected predictive densities of the format (26). The densities are evaluated over the same partition

For real-world data sets, we also need to estimate the variance $\sigma _X$, and this leads us to the normal mean mixture model with an unknown variance. Next, we provide an illustration based on the galaxy velocities data in Roeder (1990). The data contains the relative velocities of 82 galaxies from six well-separated conic sections of space. Escobar and West (1995) analysed the data using a Dirichlet process mixture model, while Ishwaran and Zarepour (2000) replaced the Dirichlet process by the almost sure truncation (see Eq. 4). We reanalyse the data using the normal mean mixture model (17) with an unknown variance, and record the posterior mean values in Fig. 7. Then we estimate the predictive density (26) using the outcome of the blocked Gibbs sampler and present the numerical results in Fig. 8. We can see that there seems to be six distinct modes in the predictive density. This finding is in line with the results of Escobar and West (1995) and Ishwaran and Zarepour (2000).

We provide another illustration for the normal mean mixture model with unknown variance using the Mexican stamp thickness data. The 1872–1874 Hidalgo postage stamps of Mexico were printed on handmade paper, and their thickness varies considerably. Izenman and Sommer (1988) tested the number of modes in thickness by analyzing 485 thickness data and concluded that there were seven modes, namely 0.072, 0.080, 0.090, 0.100, 0.110, 0.120 and 0.130 mm. Ishwaran and James (2002) used a normal mean mixture model with the almost sure truncation of Dirichlet process to estimate the predictive density. We revisit the data using model (17) with an unknown variance, and record the numerical results in Figs. 9 and 10. From the figures we can recognise seven distinct modes in the predictive density, and the values of the modes are similar to the results of Izenman and Sommer (1988).

Fig. 9

Posterior mean values (mm * 100) of the stamp thickness data. The observations $X_i$ are denoted by green cross. The plot is based on 2500 sampled values following an initial 2500 iteration burn-in using the blocked Gibbs sampler with $N=150$ and $\alpha \sim \text {Ga}(2, 2)$

Fig. 10

Fifty randomly selected predictive densities of the format (26). The densities are evaluated over the same partition

Next, we provide an numerical implementation for the Caron–Fox network model. We first generate simulated observations from model (25). Using the algorithm introduced in Sect. 4, we draw a sample G from the model prior $\mathcal {P}_{N}$. Then we choose the origins and destinations for the links according to G. Since each link involves two nodes, we need to draw 2n independent samples from G. We record the simulated observations in Fig. 11. Note that the number in each box denotes the amount of links with the same origin and destination. Then we apply the posterior sampling algorithm to estimate the popularity parameters of the nodes. The numerical results are presented in Fig. 12. The figure shows that our method recovers the popularity parameters of the prior very well.

Fig. 11

Simulated observation of 6000 links, each link is sampled from the truncated Poisson–Dirichlet process network model (25) with truncation level $N=10$ and concentration parameter $\alpha =5$

Fig. 12

Posterior values of the popularity parameters. The true values of $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$ are denoted by green cross. The plot is based on 2500 sampled values following an initial 2500 iteration burn-in using the blocked Gibbs sampler with $N=10$ and $\alpha \sim \text {Ga}(0.001, 0.001)$

Table 2 Complexity of the posterior sampling algorithm based on different priors, AST and TPD stand for the almost sure truncation and truncated Poisson–Dirichlet process respectively, CPU is at 2.80 GHz

Finally, we investigate the complexity of our posterior sampling algorithm, and compare it to complexity of the blocked Gibbs sampler based on almost sure truncation, which can be found in Ishwaran and Zarepour (2000). Here we explain the complexity as the total number of random variables generated by the algorithm, which contributes to the majority of the computation time. For the normal mean mixture model, our posterior sampler differs from the almost sure truncation method only in step (18), hence we only record the complexity of this step. While for the network model, the almost sure truncation is not applicable. In Table 2, we present the complexities of different algorithms. From the table we can see that our sampler generates more random variables than the almost sure truncation method. In fact, the truncated Poisson–Dirichlet process is not expected to outperform the existing methods based on the almost sure truncation. The purpose of our method is to include the actual jump sizes $(J_1, \dots , J_N, \tau _{\alpha }^{N-})$ into estimation, and that requires more computation.

8 Discussion

In this research, we construct a new random probability measure called the truncated Poisson–Dirichlet process, and use it to approximate the distribution of the Dirichlet process. Then we develop a posterior inference method for the truncated Poisson–Dirichlet process, and illustrate its usage in the normal mean mixture model and Caron–Fox network model.

There are several topics worth a further study. First, our truncation method can be easily extended to the posterior of a Dirichlet process. This means the standard Dirichlet process can be used as the prior, and the posterior will be truncated instead. A similar idea in literature was mentioned in Sect. 3. Another topic is to generalise our truncation method to the Pitman-Yor process and generalised gamma process, this will make use of the algorithms introduced by Dassios and Zhang (2021) and Dassios et al. (2020). Moreover, we will investigate the application of our method in the analysis of real-world network data sets, where the generalised gamma process will be considered. Finally, the truncated Poisson–Dirichlet process seems appropriate for the Bayesian nonparametric Plackett–Luce model (see Caron and Teh 2012; Caron et al. 2014), and we will study it in a future work.

Appendix A: Simulation of truncated gamma process

In this appendix, we attach Algorithm 3.2 of Dassios et al. (2019). This algorithm exactly samples from a truncated gamma process $Z_{t, \mu }$ with Lévy–Khintchine representation

$$\begin{aligned}&\mathbb {E}(\exp (-\beta Z_{t, \mu })) \\&\quad =\exp \biggl ( -t\int _{0}^{1}(1-e^{-\beta w})w^{-1}e^{-\mu w}dw \biggr ) . \end{aligned}$$