Fast and universal estimation of latent variable models using extended variational approximations

Abstract

Generalized linear latent variable models (GLLVMs) are a class of methods for analyzing multi-response data which has gained considerable popularity in recent years, e.g., in the analysis of multivariate abundance data in ecology. One of the main features of GLLVMs is their capacity to handle a variety of responses types, such as (overdispersed) counts, binomial and (semi-)continuous responses, and proportions data. On the other hand, the inclusion of unobserved latent variables poses a major computational challenge, as the resulting marginal likelihood function involves an intractable integral for non-normally distributed responses. This has spurred research into a number of approximation methods to overcome this integral, with a recent and particularly computationally scalable one being that of variational approximations (VA). However, research into the use of VA for GLLVMs has been hampered by the fact that fully closed-form variational lower bounds have only been obtained for certain combinations of response distributions and link functions. In this article, we propose an extended variational approximations (EVA) approach which widens the set of VA-applicable GLLVMs dramatically. EVA draws inspiration from the underlying idea behind the Laplace approximation: by replacing the complete-data likelihood function with its second order Taylor approximation about the mean of the variational distribution, we can obtain a fully closed-form approximation to the marginal likelihood of the GLLVM for any response type and link function. Through simulation studies and an application to a species community of testate amoebae, we demonstrate how EVA results in a “universal” approach to fitting GLLVMs, which remains competitive in terms of estimation and inferential performance relative to both standard VA (where any intractable integrals are either overcome through reparametrization or quadrature) and a Laplace approximation approach, while being computationally more scalable than both methods in practice.

1 Introduction

In many scientific disciplines, there is a growing need to process and analyze multi-response or multivariate data, with a crucial element being the need to take into account the underlying structural relationships between the response variables themselves. A prime example of this comes from community ecology, where researchers analyze multivariate abundance data to establish relationships between interacting plant and animal species and the various processes driving their joint distributions (Warton et al. 2015, 2016; Nabe-Nielsen et al. 2017; Ovaskainen et al. 2017; Ovaskainen and Abrego 2020; Wagner et al. 2020). Multivariate data can naturally be represented as an $n \times m$ matrix $\varvec{Y}$, where element $y_{ij}$ denotes the observation of response $j=1,\dots ,m$ recorded at observational unit $i=1,\dots ,n$. The types of responses can vary widely, for instance in ecology we may record binary ’presence/absence’ responses, overdispersed (and occasionally underdispersed) counts, semi-continuous data, e.g., biomass which is non-negative and has a spike at zero, and proportions data between zero and one. With such a variety of response types, it is important that a statistical modeling approach be able to handle these, and account for their associated mean-variance relationships. Discrete and semi-continuous responses usually have variances that are strongly related to their mean, e.g., the variance is a quadratic or power function of the mean. Ignoring this relationship can yield to misleading inferential results and confounding location and dispersion effects in ordination (Warton and Hui 2017).

Over the past two decades, generalized linear latent variable models (GLLVMs, Skrondal and Rabe-Hesketh 2004) have emerged as a powerful class of methods for analyzing multivariate data capable of handling the aforementioned variety of response types through an appropriate distributional assumption (Warton et al. 2015; Ovaskainen and Abrego 2020). In GLLVMs, the mean response is modeled as a function of a set of underlying latent variable values or scores $\varvec{u}_i = (u_{i1}, \dots , u_{ip})^\intercal$, along with any measured predictors as appropriate. By including only a small number $p \ll m$ of latent variables, GLLVMs offer a parsimonious way of modeling between-response correlations, which are not accounted for by the predictors, through rank-reduction. Furthermore, the latent variables themselves may posses some interpretation, e.g., as unobserved measure of traits such as a person’s intelligence or anxiety in psychology (Moustaki and Knott 2000), and as a set ordination axes describing different sites by their species composition in ecology (Hui et al. 2015; Damgaard et al. 2020; van der Veen et al. 2021).

Although it is a powerful approach, in practice fitting GLLVMs remains a computationally burdensome task. Focusing on likelihood-based estimation, the missing latent variables need to be integrated out, and this results in a marginal likelihood function which lacks a tractable solution except in special cases such as normally distributed responses with the identity link function. This computational challenge has spurred research into several approximation schemes to overcome the integral, with popular ones being variations of the Expectation-Maximization algorithm (Wei and Tanner 1990), Laplace approximations (LA) and quadrature methods (Huber et al. 2004; Bianconcini and Cagnone 2012; Niku et al. 2017), and more recently variational approximations (VA, Hui et al. 2017; Niku et al. 2019a; Zeng et al. 2021) which we focus on in this article. For fitting GLLVMs, VA has been shown to be computationally more efficient and scalable than LA and quadrature, and in some situations can also be more stable (Niku et al. 2019a). On the other hand, unlike LA and other approaches such as Bayesian Markov Chain Monte Carlo (MCMC) sampling, the application of VA to GLLVMs has been hampered by its relative lack of generalizability. That is, although VA can in principle be applied to any type of GLLVMs (and mathematically, VA does not require a fully closed-formed approximation), the resulting approximation may nevertheless be of little practical use. That is, for computational efficiency we desire a fully or very close to fully closed-form approximation to the marginal likelihood for as many forms of GLLVMs as possible. As an example, consider the case of Bernoulli distributed responses. We require using a probit link function in order to obtain a fully closed-form variational lower bound, otherwise for the canonical logit or other links such as complementary log-log link, additional approximations may need to be taken (Ormerod and Wand 2012; Hui et al. 2017). For other response types such as GLLVMs with the Tweedie distribution, no attempt has been made to apply VA (at least to our knowledge) because little simplifications can be made that facilitate a closed-form and thus a computationally scalable approximation.

To address the above issue, we propose an extended variational approximation (EVA) that allows for fast and practically universal fitting of GLLVMs. EVA is inspired by the underlying idea of LA: by replacing the complete-data log-likelihood function with a second-order Taylor series expansion about the mean of the variational distribution, we can obtain a closed-form variational lower bound of the marginal log-likelihood for any combination of response type and link function. We demonstrate how this approach allows VA to be applied to many more types of GLLVMs which are commonly used in community ecology (say), thus greatly extending its practical applicability. Furthermore, as with the standard VA method, we can adapt well-known tools to perform statistical inference with EVA, such as using the observed information matrix for constructing confidence intervals and hypothesis tests, model selection and residual analysis techniques, and ordination and prediction coupled with associated uncertainty quantification. An extensive simulation study and an application to data set of testate amoebae counts recorded at peatland sites across Finland demonstrates how EVA leads to a general approach for fitting GLLVMs. Furthermore, these studies show that EVA is competitive both in estimation and inferential performance, when compared to standard VA (where intractable integrals are either overcome through reparametrization or quadrature) and LA approaches. Additionally, EVA is typically more computationally scalable than LA.

The rest of this article is structured as follows: Sect. 2 provides an overview of GLLVM and the standard VA approach. Section 3 introduces the extended variational approximation (EVA) approach. Section 4 presents derivations of the approximated log-likelihoods using EVA for several commonly applied types of GLLVMs. Section 5 demonstrates the competitive performance as well as computational efficiency of EVA through a set of distinct numerical studies, while Sect. 6 illustrates an application of EVA to a data set of testate amoebae counts across Finland. Finally, potential avenues of future research for EVA are discussed in Sect. 7.

2 Generalized linear latent variable models

Let $\mu _{ij} = \text {E}(y_{ij} | \varvec{u}_i)$ denote the conditional mean for response $j = 1, \dots , m$ at observational unit $i =1{,} \dots , n$, given the vector of latent variables $\varvec{u}_i$. We assume that n observational units are independent of each other. The GLLVM is characterized by the mean model

$$\begin{aligned} g(\mu _{ij}) = \eta _{ij}=\alpha _i + \beta _{0j} + \varvec{x}^\intercal _i\varvec{\beta }_j + \varvec{u}^\intercal _i\varvec{\lambda }_j, \end{aligned}$$

(1)

where $g(\cdot )$ is a known link function, ${\varvec{x}_i}=(x_{i1},\dots ,x_{iq})^\intercal$ denotes a q-vector of the observed predictors for unit i, and ${\varvec{\beta }_j}=(\beta _{j1},\dots ,\beta _{jq})^\intercal$ are the corresponding response-specific regression coefficients. As an aside, note that $\mu _{ij}$ is defined conditionally on $\varvec{x}_i$ as well as on $\varvec{u}_i$, although for ease of notation the former is suppressed. Next, $\beta _{0j}$ denotes the response-specific intercept, while $\alpha _i$ is an optional unit-specific parameter that can be treated either as a fixed or random effect. In ecology, Warton et al. (2015) among others suggested including $\alpha _i$ to account for known differences in sampling intensity (say) across sites. If needed, model selection tools can also be used to decide if $\alpha _i$ should be treated as fixed or random effect (Warton et al. 2015; Niku et al. 2019a). The p-vector ${\varvec{\lambda }_j}=(\lambda _{j1},\dots ,\lambda _{jp})^\intercal$ denotes a set of response-specific loadings which quantify the relationship between the mean response and the latent variables.

Turning to the latent variables, in (1), it is common to assume that the $\varvec{u}_i$’s are independent vectors from a standard multivariate normal distribution, $\varvec{u}_i \sim N_p(\varvec{0}, \varvec{I}_p)$, where $\varvec{I}_p$ denotes a $p\times p$ identity matrix. Here the zero mean fixes the location and the unit variance fixes the scale of latent variables to ensure parameter identifiability (Chapter 5, Skrondal and Rabe-Hesketh 2004). Furthermore, if we consider the $m \times p$ loading matrix formed by stacking the $\varvec{\lambda }_j$’s as row vectors, which we denote as $\varvec{\varLambda }= {[\varvec{\lambda }_1 \dots \varvec{\lambda }_m]^\intercal }$, then to ensure that the parameters are identifiable it is common to constrain the upper triangular component of $\varvec{\varLambda }$ to zero and the diagonal elements to be positive. This ensures that the loading matrix is not rotation invariant (Niku et al. 2017). Note such constraints do not restrict the flexibility of the GLLVM: specifically, the latent variable component $\varvec{u}^\intercal _i {\varvec{\lambda }_j}$ in equation (1) accounts for any residual correlation not accounted for by the covariates $\varvec{x}_i$, such that the residual $m \times m$ covariance matrix on the linear predictor scale is given by $\varvec{\varSigma }= \varvec{\varLambda }\varvec{\varLambda }^\intercal$. We thus see that GLLVM models the covariance between the responses via rank-reduction, and the choice of the number of latent variables p can vary depending on the aim of the GLLVM, e.g., Warton et al. (2015) considered $p = 1,2,3$ for the purposes of ordination, while Tobler et al. (2019) suggested larger values if the goal is to make inference on the $\varvec{\beta }_j$’s while accounting for residual correlation between species.

To complete the formulation of GLLVMs, we assume that the responses $(y_{i1}, \dots , y_{im})^\intercal$ are conditionally independent given the vector of latent variables $\varvec{u}_i$. Specifically, let $\varvec{\varPsi }= (\varvec{\alpha }^\intercal , \varvec{\phi }^\intercal , \varvec{\beta }_0^\intercal ,\varvec{\beta }_1^\intercal , \ldots , \varvec{\beta }_m^\intercal , {{\,\textrm{vec}\,}}(\varvec{\varLambda })^\intercal )^\intercal$ denote the vector of all model parameters in the GLLVM, where $\varvec{\alpha }= (\alpha _1, \dots , \alpha _n)^\intercal$, $\varvec{\beta }_0 = (\beta _{01}, \dots , \beta _{0\,m})^\intercal$, and $\varvec{\phi }= (\phi _1, \ldots , \phi _m)^\intercal$ denotes a vector of nuisance parameters which are also used to characterize the conditional distribution of the responses. These may be known a-priori or may need to be estimated. Let $\varvec{u} = (\varvec{u}_1^\intercal , \dots , \varvec{u}_n^\intercal )^\intercal$ denote the full np-vector of the latent variables. Then the complete-data likelihood function for a GLLVM is defined as

$$\begin{aligned} L(\varvec{\varPsi }; \varvec{u})&= \prod _{i=1}^{n}\left( \prod _{j=1}^{m}f(y_{ij}|\varvec{u}_i, \varvec{\varPsi })\right) f(\varvec{u}_i) \nonumber \\&= f(\varvec{y}|\varvec{u}, \varvec{\varPsi })f(\varvec{u}), \end{aligned}$$

(2)

where $f(y_{ij}| \varvec{u}_i, \varvec{\varPsi })$ denotes the conditional distribution of $y_{ij}$ and $f(\varvec{u}_i) = N_p(\varvec{0}, \varvec{I}_p)$. As discussed previously, one of the main strengths of GLLVM is the capacity to handle a wide variety of response types, and this is done by selecting an appropriate form for $f(y_{ij}| \varvec{u}_i, \varvec{\varPsi })$; see Sect. 4 for some examples of particular relevance in ecology. Also, while we have assumed that all the $y_{ij}$’s follow the same distributional form, this need not be the case and the developments of EVA below can be straightforwardly extended to the case where the m responses are of different types (e.g., Sammel et al. 1997).

Based on (2), we obtain the marginal likelihood function by integrating over the random latent variables $L(\varvec{\varPsi }) = \int f(\varvec{y}|\varvec{u}, \varvec{\varPsi })f(\varvec{u}){\textrm{d}\varvec{u}}$. Maximum likelihood estimates are then calculated as $\arg \max _{\varvec{\varPsi }} \log L(\varvec{\varPsi })$. However, optimizing the marginal likelihood function presents a major computational challenge, as the integral does not possess a closed form except for special cases such as when the $y_{ij}$’s are normally distributed and $g(\cdot )$ is set to the identity link. To overcome this, a variety of approximation approaches have been proposed as reviewed in Sect. 1. One of the most recent approaches, which we focus on in this article, is that of variational approximations.

2.1 Variational approximations

Variational approximations (VA) refers to a general class of methods that originated in the machine learning literature, and were subsequently popularized in statistics by Ormerod and Wand (2010) and Blei et al. (2017) among others. Most of the research into VA has been that of variational Bayes, i.e., approximating the joint posterior distribution of all parameters. However, in this article we focus on likelihood-based estimation and approximations of the marginal log-likelihood function instead. VA was proposed for likelihood-based estimation of generalized linear mixed models initially by Ormerod and Wand (2012), and has since been studied and applied in various mixed models settings (Siew and Nott 2014; Lee and Wand 2016; Nolan et al. 2020) and semiparametric regression including generalized additive models (Luts et al. 2014; Hui et al. 2018b). For GLLVM specifically, VA was first proposed by Hui et al. (2017), and has since been further studied by Niku et al. (2019a), van der Veen et al. (2021), and Zeng et al. (2021), among others. Note however that many of these developments have focused on a limited number of response types and link functions.

The primary aim of variational approximation is to develop a so-called variational lower bound to the marginal log-likelihood function, also known as the VA log-likelihood function. In the context of GLLVMs, this is developed as

$$\begin{aligned} \log L(\varvec{\varPsi })&= \log \left( \int f(\varvec{y}|\varvec{u}, \varvec{\varPsi })f(\varvec{u})\,{\textrm{d}\varvec{u}}\right) \nonumber \\&\ge \int q(\varvec{u})\log \left\{ \frac{f(\varvec{y}|\varvec{u}, \varvec{\varPsi })f(\varvec{u})}{q(\varvec{u})} \right\} {\textrm{d}\varvec{u}} \nonumber \\&\triangleq \underline{\ell }(\varvec{\varPsi }| q), \end{aligned}$$

(3)

where $q(\varvec{u})$ denotes the density of the assumed variational distribution of the latent variables $\varvec{u}$, and equality holds if and only if $q(\varvec{u}) = f(\varvec{u} | \varvec{y}, \varvec{\varPsi })$, i.e., the conditional distribution of the latent variables given the data. We refer readers to Ormerod and Wand (2010) and references therein for a more detailed explanation of (3). In general, $\underline{\ell }(\varvec{\varPsi }| q)$ does not posses a tractable form, and so in VA we typically further assume that the variational distribution belongs to some parametric family of distributions $\{q(\varvec{u} | \varvec{\xi }): \varvec{\xi }\in \varvec{\varXi }\}$ for a set of variational parameters $\varvec{\xi }$. For GLLVMs in particular, and given the form of the complete-data likelihood function in (2), Hui et al. (2017) among others employed a mean-field assumption and set $q(\varvec{u} | \varvec{\xi }) = \prod _{i=1}^n q_i(\varvec{u}_i | \varvec{\xi }_i)$ where $q_i(\varvec{u}_i | \varvec{\xi }_i) = N_p(\varvec{a}_i, \varvec{A}_i)$. That is, the variational distribution of the latent variables for unit i is assumed to be multivariate normal distribution with mean vector $\varvec{a}_i$ and covariance matrix $\varvec{A}_i$. Hui et al. (2017) in fact showed that this choice of $q(\cdot )$ was optimal in a Kullback–Leibler divergence sense, among the family of multivariate normal distributions; see also Wang and Blei (2019) for more details on the choice of optimal variational distributions. Applying this form of the variational distribution to (3), we obtain

$$\begin{aligned} \underline{\ell }(\varvec{\varPsi }, \varvec{\xi }| q)&= \int q(\varvec{u} | \varvec{\xi })\log f(\varvec{y} | \varvec{u}, \varvec{\varPsi })\, {\textrm{d}\varvec{u}} \nonumber \\&\quad + \int q(\varvec{u} | \varvec{\xi })\log \left\{ \frac{f(\varvec{u})}{q(\varvec{u} | \varvec{\xi })}\right\} {\textrm{d}\varvec{u}} \nonumber \\&= \int q(\varvec{u} | \varvec{\xi })\log f(\varvec{y} | \varvec{u}, \varvec{\varPsi })\,{\textrm{d}\varvec{u}} \nonumber \\&\quad + \frac{1}{2} \sum _{i=1}^n \big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\big \}, \end{aligned}$$

(4)

where the last line follows from well-known formulas relating to the entropy of a multivariate normal distribution, and constants with respect to the model and variational parameters are omitted. By treating (4) as the new objective function and solving

$$\begin{aligned} (\hat{\varvec{\varPsi }}, \hat{\varvec{\xi }}) = \underset{\varvec{\varPsi }, \varvec{\xi }}{{{\,\textrm{argmax}\,}}\ }\ \, \underline{\ell }(\varvec{\varPsi }, \varvec{\xi }| q), \end{aligned}$$

we obtain VA estimates of both the model parameters $\varvec{\hat{\varPsi }}$ and the variational parameters $\varvec{\hat{\xi }}$. Indeed, once the GLLVM is fitted using VA, the estimated variational distributional distributions $\hat{q}_i(\varvec{u}_i) = N_p({\varvec{\hat{a}}}_i, {\varvec{{\hat{A}}}_i)}$ are then an approximation of $f(\varvec{u} | \varvec{y}, \varvec{\varPsi })$.

As an approach, VA (and variational Bayes) has been shown in many contexts to provide a strong balance between estimation accuracy and computational efficiency/scalability; see Ormerod and Wand (2010) and Niku et al. (2019a) among many others for a variety of simulations, as well as the asymptotic theory of Hall et al. (2011) and Wang and Blei (2019) and references therein. On the other hand, to facilitate this computational efficiency, we ideally require a closed-form expression for the first term on the right hand side of (4). In general though, this is not guaranteed, and so the development of VA for GLLVMs has so far been limited to selected response distributions and/or link functions, restricting the wider applicability of the approach.

3 Extended variational approximations

As reviewed above, one drawback of the standard VA approach for GLLVMs is that the exact formulation of the variational lower bound in (4) depends heavily on the assumed distribution for the responses $f(y_{ij}{|} \varvec{u}_i, \varvec{\varPsi })$ and the associated link function $g(\cdot )$. A fully tractable form is not always available, even with some of the more popular response-link combinations. A prime example is the case of Bernoulli distributed responses, where the probit link function is known to lead to fully closed-form variational lower bound, but the canonical logit link or the complementary log-log link do not (and has led to various additional approximations being made, e.g., Blei and Lafferty 2007; Hui et al. 2018b). Another example is GLLVM with Tweedie distributed responses, where to our knowledge VA does not lead to a fully-closed form approximation with the commonly-used log link function. This means alternate approaches such as LA have to be used instead in such settings (Niku et al. 2017).

To overcome the above issues and further broaden the applicability of VA as computationally efficient approach to fitting GLLVMs, we propose an approach called extended variational approximation or EVA. The method is similar that of delta method variational inference as proposed by Wang and Blei (2013), although to our knowledge this article is the first to apply it for GLLVMs. The idea of EVA is similar to and indeed inspired by that of the LA. Specifically, we replace the complete-data log-likelihood function $\log L(\varvec{\varPsi };\varvec{u})$ by its second-order Taylor expansion with respect to the latent variables $\varvec{u}$. In the case of GLLVMs, because the latent variables are assumed to be normally distributed, then we need only perform the expansion on the log-density of the responses $\log f(\varvec{y} | \varvec{u}, \varvec{\varPsi })$. Importantly, in EVA this expansion is taken around the mean of the variational distribution, i.e., $\varvec{a} = (\varvec{a}_1^\intercal , \ldots , \varvec{a}_n^\intercal )^\intercal$, which serves as a natural center point of the approximation.

$$\begin{aligned}&\log f(\varvec{y}|\varvec{u}, \varvec{\varPsi }) \\&\quad \approx \log f(\varvec{y}|\varvec{a}, \varvec{\varPsi }) + (\varvec{u} - \varvec{a})^\intercal \, \frac{\partial \log f(\varvec{y}|\varvec{u}, \varvec{\varPsi })}{\partial \varvec{u}}\bigg |_{\varvec{u} = \varvec{a}} \\&\quad + \frac{1}{2}(\varvec{u} - \varvec{a})^\intercal \varvec{H}(\varvec{a},\varvec{\varPsi }) (\varvec{u} - \varvec{a}), \end{aligned}$$

where $\varvec{H}(\varvec{a},\varvec{\varPsi }) = \partial ^2 \log f(\varvec{y}|\varvec{u}, \varvec{\varPsi })/\partial \varvec{u} \partial \varvec{u}^\intercal \big |_{\varvec{u} = \varvec{a}}$. By substituting the above expansion into (4) and noting that $\int (\varvec{u} - \varvec{a})^\intercal \, \partial \log f(\varvec{y}|\varvec{u}, \varvec{\varPsi })/\partial \varvec{u} \big |_{\varvec{u} = \varvec{a}} q(\varvec{u} | \varvec{\xi }) \, d \varvec{u} = \varvec{0}$ as

$E_{q(\varvec{u})}(\varvec{u})=\varvec{a}$, we obtain the EVA log-likelihood for GLLVMs,

$$\begin{aligned}&\underline{\ell }(\varvec{\varPsi }, \varvec{\xi }) \nonumber \\&\quad \approx \int \Big \{ \log f(\varvec{y}|\varvec{a}, \varvec{\varPsi }) + (\varvec{u} - \varvec{a})^\intercal \, \frac{\partial \log f(\varvec{y}|\varvec{u}, \varvec{\varPsi })}{\partial \varvec{u}}\bigg |_{\varvec{u} = \varvec{a}} \nonumber \\&\qquad +\frac{1}{2}(\varvec{u} - \varvec{a})^\intercal \,\varvec{H}(\varvec{a},\varvec{\varPsi })\,(\varvec{u} - \varvec{a}) \Big \}\, q(\varvec{u} | \varvec{\xi }) {\textrm{d}\varvec{u}} \nonumber \\&\qquad + \frac{1}{2} \sum _{i=1}^n \big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\big \} \nonumber \\&\quad = \sum _{i=1}^n \bigg \{\sum _{j=1}^m \log f(y_{ij} | \varvec{a}_i, \varvec{\varPsi }) + \frac{1}{2}{{\,\textrm{Tr}\,}}(\varvec{H}_i(\varvec{a}_i,\varvec{\varPsi }) \varvec{A}_i)\bigg \} \nonumber \\&\qquad + \frac{1}{2} \sum _{i=1}^n \big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\big \} \nonumber \\&\quad \triangleq \ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi }), \end{aligned}$$

(5)

where

$$\begin{aligned} \varvec{H}_i(\varvec{a}_i,\varvec{\varPsi }) = \partial ^2 \sum _{j=1}^m \log f(y_{ij} | \varvec{u}_i, \varvec{\varPsi })/\partial \varvec{u}_i \partial \varvec{u}_i^\intercal \big |_{\varvec{u}_i = \varvec{a}_i}. \end{aligned}$$

Likelihood-based EVA estimates for both model and variational parameters are obtained by maximizing (5), $(\varvec{\hat{\varPsi }}_\text {EVA}, \varvec{\hat{\xi }}_\text {EVA}) = \underset{\varvec{\varPsi }, \varvec{\xi }}{{{\,\text {argmax}\,}}}\ \, \ell _\text {EVA}(\varvec{\varPsi }, \varvec{\xi })$. Importantly, there are no integrals in $\ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi })$, meaning its maximization can be done using generic optimization approaches (say). This allows EVA to be applied to all response types and link functions of GLLVMs (assuming an appropriate form for the conditional distribution of the former), and in Sect. 4 we will provide some examples of applying EVA to common types of GLLVMs seen in ecology among other disciplines. At the same time, EVA inherits the computational efficiency and scalability of the standard VA approach, as will be seen in the simulation studies in Sect. 5.

3.1 Inference and ordination

Similar to the standard VA method for GLLVMs (e.g., Hui et al. 2017), we can adapt many of the existing likelihood-based approaches to statistical inference for EVA. We discuss some of these in this section.

First, after fitting we can calculate approximate standard errors for the estimates of the model parameters based on the observed information matrix. That is, we first calculate

$$\begin{aligned} \varvec{I}(\varvec{\hat{\varPsi }}_\text {EVA}, \varvec{\hat{\xi }}_\text {EVA}) = -\frac{\partial ^2 \ell _{\text {EVA}}(\varvec{\varPsi },\varvec{\xi })}{\partial (\varvec{\varPsi },\varvec{\xi }) \partial (\varvec{\varPsi },\varvec{\xi })^T}\Bigg |_{\varvec{\varPsi }=\varvec{\hat{\varPsi }}_\text {EVA},\,\varvec{\xi }=\varvec{\hat{\xi }}_\text {EVA}}. \end{aligned}$$

Then the relevant sub-block of $\varvec{I}(\varvec{\hat{\varPsi }}_\text {EVA}, \varvec{\hat{\xi }}_\text {EVA})^{-1}$ corresponding to the model parameters, denoted here as $\varvec{I}(\varvec{\hat{\varPsi }}_\text {EVA}, \varvec{\hat{\xi }}_\text {EVA})^{-1}_{\varvec{\varPsi }}$, leads to approximate standard errors for $\varvec{\hat{\varPsi }}_\text {EVA}$. Wald-based confidence intervals and corresponding hypothesis tests for the model parameters can then be constructed. Alternatively, likelihood-ratio tests and corresponding confidence intervals can also be developed based on the (maximized value of the) EVA log-likelihood $\ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi })$.

One very popular application of GLLVMs, particularly in ecology, is that of model-based ordination. Briefly, ordination refers to a class of dimension-reduction methods which aim to visualize the main patterns between different sites in terms of their species composition on a low-dimensional space, e.g., in the form of a scatterplot (Legendre and Legendre 2012). For EVA, we can use the estimated mean vectors of the variational distribution, $\varvec{\hat{a}}_i$, $i=1,\dots ,n$, as point predictions of the latent variables $\varvec{u}_i$, and these can be plotted as a means of model-based unconstrained or residual ordination (Warton et al. 2015; van der Veen et al. 2021). Similar to Hui et al. (2017), $\varvec{\hat{a}}_i$ from EVA can be regarded as variational version of the empirical Bayes predictor and maximum a-posteriori predictor (MAP) of the latent variable. A biplot can also be constructed by including the estimated (and scaled) loadings $\varvec{\hat{\lambda }}_j$, $j=1,\ldots ,m$, on the same ordination plot. Next, regarding uncertainty quantification, note that the estimated covariance matrices ${\varvec{{\hat{A}}_i}}$, $i=1,\ldots ,n$, provide an estimate of the posterior covariance of the latent variables, and can be thus used to obtain prediction regions for the latent variables. However, these tend to underestimate the true covariance as they fail to account for the uncertainty of the estimated parameters (Booth and Hobert 1998; Zheng and Cadigan 2021). To overcome this, we can develop a variational analogue of conditional mean squared errors of prediction (CMSEP, Booth and Hobert 1998). Specifically, we can approximate the CMSEP as

$$\begin{aligned} CMSEP(\varvec{\hat{a}}_i;\varvec{\varPsi },\varvec{y}_i)&= \text{ E }\left\{ (\varvec{\hat{a}}_i - \varvec{u}_i)(\varvec{\hat{a}}_i - \varvec{u}_i)^\intercal |\varvec{y}_i \right\} \\ {}&\approx {\varvec{{\hat{A}}}}_i + \varvec{\hat{Q}} \, \varvec{I}(\varvec{\hat{\varPsi }}_\text {EVA}, \varvec{\hat{\xi }}_\text {EVA})^{-1}_{\varvec{\varPsi }}\, \varvec{\hat{Q}}^\intercal \end{aligned}$$

where $\varvec{\hat{Q}} = \varvec{Q}(\varvec{\hat{\varPsi }}_\text {EVA}, \varvec{\hat{\xi }}_\text {EVA})$ and

$$\begin{aligned} \varvec{Q}(\varvec{\varPsi }, \varvec{\xi }) = \left( \frac{\partial ^2 \ell _{\textrm{EVA}}(\varvec{ \varPsi },\varvec{\xi })}{ \partial \varvec{a}_i\partial \varvec{a}_i^\intercal }\right) ^{-1} \left( \frac{\partial ^2 \ell _{\textrm{EVA}}(\varvec{ \varPsi },\varvec{\xi })}{\partial \varvec{a}_i \partial \varvec{\varPsi }^\intercal } \right) . \end{aligned}$$

Prediction regions can then be constructed for the latent variables using $CMSEP(\varvec{{\hat{a}}}_i;\varvec{\varPsi },\varvec{y}_i)$ as the approximate standard error. Another option for obtaining the prediction regions would be to apply bootstrap procedures, as illustrated in Dang and Maestrini (2021).

Finally, using the EVA estimates we can also perform residual analysis to assess whether there are major violations in the assumptions underlying the GLLVM, in much the same way as with other common regression models. For instance, we can calculate Dunn-Smyth residuals (Dunn and Smyth 1996) to construct residual diagnostic plots such as residual versus fitted values and normal quantile-quantile plots, where these residuals are defined as $r_{q,ij} = \varvec{\varPhi }^{-1}(c_{ij})$, with $c_{ij} = z_{ij}F_{ij}(y_{ij})+(1-z_{ij})F^{-}_{ij}(y_{ij})$, and $F_{ij}$ denoting the cumulative distribution function of the response variable, $F^{-}_{ij}$ denoting the limit as $F_{ij}$ is approached from the negative side, and $z_{ij}$ denoting a random variable generated from the standard uniform distribution. If the underlying assumptions of the GLLVM are reasonably well satisfied, then the Dunn-Smyth residuals should follow a standard normal distribution.

The above describes only some of the various statistical inferences and applications that a practitioner may wish to draw from a GLLVM. There are many others possible, e.g., model selection using information criteria or regularization methods (Hui et al. 2018a; van der Veen et al. 2021), and the main point we wish to highlight is that all of these tools are adaptable to the setting where EVA is used to fit GLLVMs. Indeed, by adapting such tools and studying their theoretical properties in avenues of future research, it will further strengthen the universality of EVA as an approach to estimation and inference for GLLVMs.

We conclude this section with a short note regarding computation. We implemented EVA using a combination of $\textsf{R}$ and in C++ via the package $\textsf{TMB}$ (Kristensen et al. 2016). That is, the (negative) EVA log-likelihood for the relevant GLLVM was first written in C++, after which it is compiled by $\textsf{TMB}$, which employs automatic differentiation, to produce $\textsf{R}$ functions to calculate the negative log-likelihood, the score, and potentially the Hessian matrix. We then pass these to a generic optimization procedure such as $\textsf{optim}$ to optimize the EVA log-likelihood and calculate the observed information matrix. The CMSEP can be calculated in a similar manner. The full implementation of EVA is available as part of the package $\textsf{gllvm}$ (Niku et al. 2019b, 2021). As starting values for EVA, we use the proposal in Section 3.2 in Niku et al. (2019a).

4 EVA for some common types of GLLVMs

In this section, we present specific forms of the EVA log-likelihood for combinations of response distributions and link functions commonly used with GLLVMs, especially in the context of community ecology. We begin by formulating the EVA log-likelihoods where the responses $y_{ij}$ are assumed to come from the one-parameter exponential family of distributions. All proofs are provided in “Appendix A”.

Theorem 1

For the GLLVM with mean model given by (1), let the conditional distribution of the responses be part of the exponential family,

$f(y_{ij}|\varvec{u}_i, \varvec{\varPsi }) = \exp \left\{ h_j(y_{ij})b_j(\mu _{ij}) - c_j(\mu _{ij}) + d_j(y_{ij}) \right\}$ for known functions $h_j(\cdot )$, $b_j(\cdot ), c_j(\cdot )$ and $d_j(\cdot )$. If $b_j(\cdot )$ and $c_j(\cdot )$ as well as the link function $g(\cdot )$ are at least twice continuously differentiable with $g'(\mu _{ij})\ne 0$, then the EVA log-likelihood in (5) takes the closed-form

$$\begin{aligned}&\ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi }) = \sum _{i=1}^n \sum _{j=1}^m \log f(y_{ij} | \varvec{a}_i, \varvec{\varPsi }) \\&\quad + \frac{1}{2} \sum _{i=1}^n \Big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\Big \} \\&\quad + \frac{1}{2}\sum _{i=1}^n \sum _{j=1}^m \left\{ \frac{h_j(y_{ij})b_j''({\tilde{\mu }}_{ij})-c_j''({\tilde{\mu }}_{ij})}{(g'({\tilde{\mu }}_{ij}))^2}\varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j\right\} \\&\quad - \frac{1}{2}\sum _{i=1}^n \sum _{j=1}^m\left\{ \frac{h_j(y_{ij})b_j'({\tilde{\mu }}_{ij})-c_j'({\tilde{\mu }}_{ij})}{\big (g'({\tilde{\mu }}_{ij}) \big )^3/g''({\tilde{\mu }}_{ij})} \varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j\right\} , \end{aligned}$$

where ${\tilde{\mu }}_{ij} = g^{-1}({\tilde{\eta }}_{ij}) = g^{-1}( \alpha _i + \beta _{0j} + \varvec{x}^\intercal _i\varvec{\beta }_j + \varvec{a}^\intercal _i\varvec{\lambda }_j)$.

When the canonical link is used, the last two terms in the EVA log-likelihood can be further simplified as follows.

Corollary 1

If the link function is taken to be the canonical link function, i.e., $g \equiv b$, then the EVA log-likelihood reduces to

$$\begin{aligned} \ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi })&= \sum _{i=1}^n \sum _{j=1}^m \log f(y_{ij} | \varvec{a}_i, \varvec{\varPsi }) \\&\quad + \frac{1}{2} \sum _{i=1}^n \Big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\Big \} \\&\quad + \frac{1}{2}\sum _{i=1}^n \sum _{j=1}^m \left\{ \frac{b_j''({\tilde{\mu }}_{ij})c_j'({\tilde{\mu }}_{ij}) - b_j'({\tilde{\mu }}_{ij})c_j''({\tilde{\mu }}_{ij})}{(b_j'({\tilde{\mu }}_{ij}))^3} \varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j \right\} . \end{aligned}$$

From Theorem 1, we see that EVA shares the same term $\log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)$ as the standard VA log-likelihood for GLLVMs (Hui et al. 2017; Niku et al. 2019a), but also involves computation of a Hessian term based on the conditional distribution of the response (Huber et al. 2004). As can be seen from Theorem 1 and Corollary 1, this Hessian term reduces to a sum of nm scalar terms for responses with conditional distributions part of the exponential family. Calculation of this sum, together with the terms $\log \det (\varvec{A}_i)$, constitute the leading factors for the (asymptotic) computational complexity of the evaluation of $\ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi })$, meaning the EVA log-likelihood has complexity of order $O(np^3 + nmp^2)$.

4.1 Overdispersed counts

Multivariate count data are one of the most common applications for GLLVMs, with a starting choice often being to assume that counts follow a Poisson distribution with the canonical log link. However, in many settings such as community ecology and microbiome data analysis, the Poisson model is often inappropriate due to the prevalence of overdispersion. Therefore, a popular alternative is to consider negative binomial GLLVMs with the log link, where

$$\begin{aligned} f(y_{ij}|\varvec{u}_i, \varvec{\varPsi }) = \frac{\varGamma (y_{ij}+\phi _j^{-1})}{\varGamma (\phi _j^{-1})y_{ij}!} \frac{\left\{ \phi _j\mu _{ij}\right\} ^{y_{ij}}}{\left\{ \phi _j\mu _{ij}+1\right\} ^{y_{ij}+\phi _j^{-1}}} \end{aligned}$$

and $\phi _j > 0$ is the response-specific overdispersion parameter. The mean-variance relationship is quadratic in form, ${{\,\textrm{Var}\,}}(y_{ij}) = \mu _{ij} + \phi _j\mu _{ij}^2$, making it suitable for handling some degree of overdispersion.

Previously, Hui et al. (2017) considered negative binomial GLLVMs using the standard VA approach, but had to reparametrize the negative binomial distribution as a Poisson-Gamma mixture in order to derive closed-form variational lower bound (see also Zeng et al. 2021). With EVA however this is not necessary, and we can explicitly use the form presented above as follows. For fixed $\phi _j$, the negative binomial distribution is part of the exponential family. Therefore we can apply Theorem 1 to straightforwardly show that EVA log-likelihood takes the following closed form for negative binomial GLLVMs:

$$\begin{aligned} \ell _{\textrm{EVA}}(\varvec{\varPsi }, \varvec{\xi })&= \sum _{i=1}^n\sum _{j=1}^m \bigg \{ \log \varGamma \left( y_{ij}+\frac{1}{\phi _j}\right) - \log \varGamma \left( \frac{1}{\phi _j}\right) \\&\quad - \frac{1}{\phi _j}\log (\phi _j) + y_{ij}{\tilde{\eta }}_{ij} - \left( y_{ij}+\frac{1}{\phi _j}\right) \log \left( {\tilde{\mu }}_{ij} + \frac{1}{\phi _j}\right) \bigg \} \\&\quad - \sum _{i=1}^n\sum _{j=1}^m \left\{ \frac{\tilde{\mu _{ij}}(1+\phi _j y_{ij})}{2(1+\phi _j{\tilde{\mu }}_{ij})^2} \varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j \right\} \\&\quad + \frac{1}{2} \sum _{i=1}^n \Big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\Big \}, \end{aligned}$$

where ${\tilde{\mu }}_{ij}= \exp ({\tilde{\eta }}_{ij}) = \exp (\alpha _i + \beta _{0j} + \varvec{x}^\intercal _i\varvec{\beta }_j + \varvec{a}^\intercal _i\varvec{\lambda }_j)$. In practice, the dispersion parameters $\phi _j$ are estimated as a part of the modeling process.

4.2 Binary responses

For binary responses, e.g., presence-absence data in ecology, we can assume that $y_{ij}$ follows a Bernoulli distribution, i.e., $f(y_{ij}|\varvec{u}_i, \varvec{\varPsi }) = \mu _{ij}^{y_{ij}} \{1-\mu _{ij}\}^{1-y_{ij}}$. The Bernoulli distribution belongs to the exponential family meaning we can apply Theorem 1 to obtain the EVA log-likelihood irrespective of the link function assumed. Below, we discuss two of the most commonly used links used.

Bernoulli GLLVMs with the canonical logit link, $\textrm{logit}(\mu _{ij}) = \log \{\mu _{ij}/(1-\mu _{ij})\} = \eta _{ij}$, presents a good example of a situation where the standard VA approach fails to provide a fully closed-form approximation of the log-likelihood function. Further approximations are required in order to produce a tractable form (e.g., Blei and Lafferty 2007; Hui et al. 2018b). By contrast, for EVA we can directly apply Corollary 1 and obtain the following closed-form EVA log-likelihood function for binary GLLVMs with the logit link:

$$\begin{aligned} \ell _{EVA}(\varvec{\varPsi }, \varvec{\xi })&= \sum _{i=1}^n\sum _{j=1}^m \big [y_{ij} {\tilde{\eta }}_{ij} - \log \{1+\exp ({{\tilde{\eta }}_{ij})}\}\big ] \\&\quad -\sum _{i=1}^n\sum _{j=1}^m \left\{ \frac{\exp ({\tilde{\eta }}_{ij})}{2\{1+\exp ({\tilde{\eta }}_{ij})\}^2} \, \varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j \right\} \\&\quad + \frac{1}{2} \sum _{i=1}^n \left\{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\right\} , \end{aligned}$$

where ${\tilde{\eta }}_{ij} = \alpha _i + \beta _{0j} + \varvec{x}^\intercal _i\varvec{\beta }_j + \varvec{a}^\intercal _i\varvec{\lambda }_j$.

On the other hand, to circumvent the above issues with using the logit link, Ormerod and Wand (2010) instead considered binary GLLVMs using the probit link $\varPhi ^{-1}(\mu _{ij}) = \eta _{ij}$, where $\varPhi$ is the cumulative distribution function of the standard normal distribution. Ormerod and Wand (2010) and Hui et al. (2017) showed that standard VA in conjunction with using the probit link can yield a fully-closed form approximation based on augmenting the complete-data likelihood function with an intermediate standard normal random variable and employing the dichotomization trick. By contrast, with EVA binary GLLVMs using the probit link function also follow directly from applying Theorem 1. This leads to the following closed-form EVA log-likelihood function:

$$\begin{aligned}&\ell _{EVA}(\varvec{\varPsi }, \varvec{\xi }) \\&= \sum _{i=1}^n\sum _{j=1}^m \Big \{(y_{ij} \log \big ({\tilde{\mu }}_{ij}\big ) + (1-y_{ij})\log \big (1-{\tilde{\mu }}_{ij}\big )\Big \} \\&\quad + \frac{1}{2}\sum _{i=1}^n\sum _{j=1}^m\phi ({\tilde{\eta }}_{ij})^2 \left( \frac{2{\tilde{\mu }}_{ij}y_{ij}-y_{ij}-{\tilde{\mu }}_{ij}^2}{{\tilde{\mu }}_{ij}^2(1-{\tilde{\mu }}_{ij})^2}\right) \varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j \\&\quad + \frac{1}{2}\sum _{i=1}^n\sum _{j=1}^m \phi '({\tilde{\eta }}_{ij})\left( \frac{y_{ij}-{\tilde{\mu }}_{ij}}{{\tilde{\mu }}_{ij}(1-{\tilde{\mu }}_{ij})}\right) \varvec{\lambda }_j^\intercal \varvec{A}_i \varvec{\lambda }_j \\&\quad + \frac{1}{2} \sum _{i=1}^n \Big \{ \log \det (\varvec{A}_i) - \varvec{a}_i^\intercal \varvec{a}_i - {{\,\textrm{Tr}\,}}(\varvec{A}_i)\Big \}, \end{aligned}$$

where $\phi ({\tilde{\eta }}_{ij})$ and $\phi '({\tilde{\eta }}_{ij})$ denote the density function of the standard normal distribution and its first derivative, respectively, evaluated at ${\tilde{\eta }}_{ij} = \alpha _i + \beta _{0j} + \varvec{x}^\intercal _i\varvec{\beta }_j + \varvec{a}^\intercal _i\varvec{\lambda }_j$.

The above results extend straightforwardly to the case of binomial responses with more than one trial. Also, using Theorem 1 EVA can be easily adapted to other link functions such as the complementary log-log link.

4.3 Semi-continuous responses

One type of semi-continuous responses frequently encountered in community ecology is biomass. Based on recording the total weight of a species at a site, biomass data are non-negative and continuous, usually with a large spike at zero as many species may only be detected at a small number of sites. To model such responses, the Tweedie distribution is often used (Foster and Bravington 2013) which, for a power parameter $1<\nu <2$, can also be parameterized as a compound Poisson-Gamma distribution. Its log-density can be written piecewise as follows:

$$\begin{aligned} \log f(y_{ij}|{\varvec{u}_i}, \varvec{\varPsi }) = -\frac{\mu _{ij}^{2-\nu }}{\phi _j(2-\nu )}, \end{aligned}$$

when $y_{ij} = 0$, and

$$\begin{aligned}&\log f(y_{ij}|{\varvec{u}_i}, \varvec{\varPsi }) \\&\quad = \log W(y_{ij}, \phi _j, \nu ) + \frac{1}{\phi _j} \left( \frac{y_{ij}\mu _{ij}^{1-\nu }}{1-\nu } - \frac{\mu _{ij}^{2-\nu }}{2-\nu }\right) \\&\quad - \log (y_{ij}), \end{aligned}$$

when $y_{ij} > 0$. Here, $W(y_{ij}, \phi _j, \nu )$ is a generalized Bessel function whose evaluation involves an infinite sum and needs to be evaluated numerically, for example using the method described in Dunn and Smyth (2005). The Tweedie distribution admits a power-form mean-variance relationship that is appropriate for biomass data, i.e., ${{\,\textrm{Var}\,}}(y_{ij}|\varvec{u}_i, \varvec{\varPsi }) = \phi _j \mu _{ij}^{\nu }$, where $\phi _j > 0$ is a response-specific dispersion parameter, and the power parameter is also usually assumed to be common across responses (Foster and Bravington 2013). A log link function is commonly used with the Tweedie distribution.

To our knowledge, applying standard VA to Tweedie GLLVMs produces no closed-form approximation to the marginal log-likelihood, and as a result limited implementation has taken place, with practitioners instead relying on other approaches such as the LA. By contrast, it is straightforward to apply EVA to the Tweedie GLLVMs with the log link: the second order derivative of $\log f(y_{ij}|\varvec{u}_i, \varvec{\varPsi })$ with respect to $\varvec{u}_i$ is straightforward to calculate, after which we can substitute these into (5) to produce a closed-form EVA log-likelihood function. We provide details of these derivations in “Appendix A”.

4.4 Proportions data

Finally, we consider proportion or percentage data lying in the open unit interval (0, 1). In the context of ecology, these responses may represent the percent cover of plant species at a site (Damgaard and Irvine 2019). Another example comes from social statistics, where we may consider the proportion of household income that is spent on food (Ferrari and Cribari-Neto 2004). A common choice for analyzing such multivariate proportions data is to use a beta distributed GLLVM, where the log-density of the beta distribution conditional on the latent variables is written as

$$\begin{aligned}&\log f(y_{ij}|{\varvec{u}_i}, \varvec{\varPsi }) \\&\quad = \log \varGamma (\phi _j) - \log \varGamma (\mu _{ij}\phi _j) - \log \varGamma \big \{(1-\mu _{ij})\phi _j\big \} \, + \\&\quad (\mu _{ij}\phi _j-1)\log (y_{ij}) + \big \{(1-\mu _{ij})\phi _j-1\big \}\log (1-y_{ij}), \end{aligned}$$

with $\phi _j > 0$ denoting a response-specific dispersion parameter, and the corresponding mean-variance relationship given by ${{\,\textrm{Var}\,}}(y_{ij}|\varvec{u}_i, \varvec{\varPsi }) = \mu _{ij}(1-\mu _{ij})/(1+\phi _j)$.

As is the case with the Tweedie distribution, implementing the standard VA approach to a beta GLLVM fails to admit a closed-form approximation to the marginal log-likelihood. On the other hand, and if we assume the logit link function (say), then EVA can be straightforwardly applied by calculating the second order derivative of $\log f(y_{ij}|\varvec{u}_i, \varvec{\varPsi })$ with respect to $\varvec{u}_i$, and substituting it into (5) to produce a closed-form EVA log-likelihood function; see “Appendix A” for details.

We conclude this section by pointing out that the above only covers a select set of response distributions and link functions which may be used as part of fitting GLLVMs to multivariate data, motivated strongly by applications in community ecology. Importantly, it serves to demonstrate that EVA offers a potentially more universal approach to variational estimation and inference for GLLVMs, and future computational research will look to expand the implementation of EVA even more, e.g., zero-inflated and hurdle type distributions, and cases where the m responses are of different types.

5 Simulation studies

We conduct an extensive simulation study to evaluate the performance and computational efficiency of EVA for estimation and inference in GLLVMs, compared to other likelihood-based methods. In particular, we compared EVA against the standard VA method (when this is available) and the LA method, both of which are already available in the package $\textsf{gllvm}$ (Niku et al. 2019b). Additionally, for some of the simulation settings we included a version of VA which employs Gauss-Hermite quadrature (Davis and Rabinowitz 2007) to overcome any intractable integrals, which we denote as VA-GH, and an alternative Bayesian MCMC sampling approach based on the R package boral (Hui 2016). The simulation setups below were adapted from those previously proposed by Niku et al. (2019a).

Two main simulation settings were considered, with the intention of covering both the scenarios where $m \ll n$, i.e., when the number of sites is much larger than the number of species, and those where $m \gg n$, i.e., when the number of species is much larger than the number of sites. In the first setting, we generated multivariate data with four possible response types (overdispersed counts, binary, semi-continuous, and proportional data) based on GLLVMs fitted to the testate amoebae data (Daza Secco et al. 2018) considered in Sect. 6. The true GLLVMs included two environmental predictors from the testate amoebae data, and we simulated multivariate data such that the number of observational units n increased incrementally while the number of responses m remain fixed (consistent with the ratio m/n being relatively small in this dataset). More details and results of this setting are presented in Sects. 5.1 and 5.2 below.

In the second simulation setting, we generated multivariate data again with the above four possible response types, but this time based on GLLVMs fitted to a dataset containing species of birds recorded across Borneo (Cleary et al. 2005). Unlike in the first simulation setting, here we increased the number of responses m while keeping the number of observational units n fixed; this was consistent with the original data itself, where the ratio m/n was relatively large. We provide details of the simulation design as well the results in “Appendix B”, and include an overall summary of the results in Sect. 5.1 below.

To assess performance, all methods were compared in terms of: (1) the empirical bias and the empirical root mean squared error (RMSE) of the regression coefficients and the dispersion parameters (if appropriate), where the averaging is across both the number of simulated datasets as well as across the m responses; (2) the corresponding empirical coverage probability of $95\%$ Wald confidence interval (CI), again averaged across both the number of simulated datasets as well as across the m responses; (3) the Procrustes error between the predicted and true $n \times p$ matrices of latent variables, and similarly between the estimated and true $m \times p$ loading matrices. The Procrustes error is a commonly used measure of evaluating the accuracy of ordinations (Peres-Neto and Jackson 2001; 4) average computation time in seconds. All of the compared likelihood-based methods used similar stating values, and were implemented in a similar fashion via the TMB package.

5.1 Setting 1

Multivariate data were simulated from GLLVMs fitted to the testate amoebae data detailed in Sect. 6 as follows. The original testate amoebae data consisted of count records of $m = 48$ species at $n = 263$ sites across Finland. All GLLVMs fitted to the data included $q = 2$ environmental covariates (water pH and temperature) and $p = 2$ latent variables. No row effects $\alpha _i$ were included. Using the parameter estimates from these GLLVMs as the true parameter values, we then simulated datasets with differing numbers of observational units n while keeping the number of responses fixed to the original size, i.e., $m = 48$. This was accomplished by randomly subsampling rows from the original data and the predicted matrix latent variables. We varied the number of units as $n=50, 120, 190$ and 260, noting that the full dataset contained 263 sites. We simulated 1000 datasets for each value of n.

Datasets with four possible response types were generated, following Sects. 4.1, 4.2, 4.3, 4.4.

• 1. Overdispersed counts simulated from a negative binomial GLLVM with log link function fitted to the original testate amoebae data using the standard VA approach. For each simulated dataset, we then compared negative binomial GLLVMs fitted using EVA to those fitted using standard VA, LA, VA-GH and MCMC. For VA-GH, we used either 5 or 9 quadrature points. For MCMC, we used the default values from the boral package.

• 2. Binary responses simulated from Bernoulli GLLVMs fitted to a presence-absence version of the original testate amoebae data (formed by setting all positive counts to one). These binary GLLVMs used either a probit link (fitted using the standard VA approach) or the logit link (fitted using the LA approach). For each simulated dataset, we then compared binary GLLVMs fitted using EVA to those fitted with standard VA or LA. Standard VA was excluded from the simulations involving a logit link binary GLLVM, as per the discussion in Sect. 4.2. In place of VA, comparisons involving the logit link used VA-GH with either 5 or 9 quadrature points.

• 3. Semi-continuous responses simulated from a Tweedie GLLVM with log link fitted to the original testate amoebae count data (after square root transform of the counts), using the LA approach. For each simulated dataset, we then compared Tweedie GLLVMs fitted using EVA to those fitted using LA. Standard VA was again excluded this setting, as per the discussion in Sect. 4.3.

• 4. Proportions data simulated from a beta GLLVM using the logit link. As true parameter values for this true model, we used the parameters of the binary GLLVM with logit link fitted to the presence-absence version of the original testate amoebae data discussed above. Additionally, the true values of the response-specific dispersion parameters $\phi _j$ were drawn independently from the uniform distribution $\text {Unif}(1,3)$. For each simulated dataset, we then compared beta GLLVMs fitted using EVA to those fitted using LA. Standard VA was again excluded this setting, as per the discussion in Sect. 4.4.

5.2 Simulation results

We discuss simulation results for each of the four response types separately, purposefully placing greater emphasis on the cases of negative binomial responses and binary responses using the logit link seeing as they are possibly the two commonly applied version of GLLVMs in community ecology (Warton et al. 2015; Stoklosa et al. 2022), and also since these were the two settings where we compared the largest number of methods for estimating GLLVMs.

First, for multivariate overdispersed counts, we observed that EVA and VA were clearly the fastest among the six methods (Fig. 1a), with MCMC understandably taking by far the longest to finish, on average. Interestingly, LA took around the same time as VA-GH using five quadrature points. Turning to mean empirical bias and RMSE for the regression coefficients of pH (Fig. 2a,b), we observe that EVA, LA and VA-GH tended to perform more similarly to each other. However, it must be noted that on two of the smallest sample sizes, there was unsurprisingly a large of uncertainty in the estimates of the mean biases, as can be seen from the sizes of the error bars representing empirical standard errors. The differences in biases and RMSE appear to even out across all of the methods as sample size increased. Finally, there was relatively little difference between the six methods compared in terms of empirical coverage probability for the effect of pH (Fig. 2c), although MCMC tended to be more conservative than its likelihood-based counterparts. The full results including those for the response-specific intercepts $\beta _{0j}$ and dispersion parameters $\phi _j$ can be found in “Appendix B”, noting in the main text we focused on presenting the performance of the coefficients relating to one of the two environmental predictors, namely pH. In practice, the environmental effects are generally of most interest. As shown in the tables in “Appendix B.1”, the overall trends observed for the regression coefficients above also carry over to the Procrustes error of the loadings and predicted latent values.

Next, for the binary GLLVM with logit link, the computation times are presented in Fig. 1b. Again, EVA was clearly the fastest of all the methods. LA exhibited large variability in its computation times, but was generally on par with or slightly faster than VA-GH with five quadrature points. In terms of empirical bias and RMSE, EVA generally performed much closer to VA-GH than LA, the latter of which seemed to struggle on all but the largest sample size (Fig. 3a, 3b). Figure 3c presents the empirical coverage probabilities for the coefficients of pH, indicating that both EVA and LA tended to undercover a small amount. Similar trends could be drawn from the comparisons of EVA, LA and VA in the binary probit link case, with EVA and VA performing fairly evenly across all metrics and sample sizes, while LA exhibited higher errors for small sample sizes. For the complete summaries for both the logit and probit cases, we refer to the corresponding tables in “Appendix B.1”.

Finally, turning to semi-continuous data with Tweedie GLLVMs and proportions data with beta GLLVMs, noting that standard VA is again not available for these two response types, the performance of EVA and LA in both cases were fairly similar across all metrics and across the four values of n considered (see the corresponding tables in “Appendix B.1”). EVA was substantially faster and scaled computationally better than LA.

Overall, the results from simulation setting 1 demonstrate that in terms of estimation and inferential accuracy, the performance of EVA for GLLVMs was competitive or better than that of LA, and was similar to that of standard VA or VA coupled with Gauss-Hermite for larger number of observational units n. EVA was the most computationally efficient method of all the ones compared, in pretty much every situation. Given its more universal applicability, this suggests that EVA may be the most suitable choice in scenarios particularly when standard VA (or MCMC sampling) cannot be applied due to computational burden.

Fig. 1

Computation times from the testate amoebae data based simulation studies involving: a) negative binomial GLLVMs, and b) binary logit link GLLVMs, with a fix number of species ($m=48$). Here, ’GH5’ and ’GH9’ stand for the VA-GH method with 5 and 9 quadrature points, respectively

Fig. 2

Results from the testate amoebae data based simulation study involving the negative binomial GLLVMs with a fix number of species ($m=48$): a) the mean biases, b) RMSEs, and c) CI coverages for estimates of the effects of pH. The error bars denote the empirical standard error. Here, ’GH5’ and ’GH9’ stand for the VA-GH method with 5 and 9 quadrature points, respectively. A trimming factor of $2\%$ was used in the calculation of the biases and RMSEs

Fig. 3

Results from the testate amoebae data based simulation study involving the binary logit GLLVMs with a fix number of species ($m=48$): a) the mean biases, b) RMSEs, and c) CI coverages for estimates of the effects of pH. The error bars denote the empirical standard error. Here, ’GH5’ and ’GH9’ stand for the VA-GH method with 5 and 9 quadrature points, respectively. A trimming factor of $2\%$ was used in the calculation of the biases and RMSEs

Results from simulation setting 2, which are provided as part of “Appendix B”, are largely consistent with these conclusions, with the only one notable difference being that, with fixed n and increasing number of responses m, the differences in computational times between the three methods are even more dramatic, with both EVA and standard VA gaining even greater computational efficiency compared to LA.

6 Application to testate amoebae data

We illustrate an application of EVA by using it to fit a negative binomial GLLVM (using the log link function) to a multivariate abundance dataset of testate amoebae available from Daza Secco et al. (2018). The data consisted of counts from $m=48$ testate amoebae species measured on $n = 248$ peatland sites spread throughout Finland. In addition to water pH and temperature, the dataset also contained a factor variable on the type of land use for each site (forestry, natural and restored). Note we used this dataset previously as the basis for simulation setting 1 in Sect. 5.1.

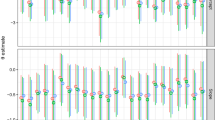
We began by fitting a negative binomial GLLVM using EVA assuming $p = 2$ latent variables, with no covariates or row effects included, as a means of model-based unconstrained ordination. In unconstrained ordination the effects of environmental covariates are carried out by the latent variables, leading to distinct clusters when the scores are plotted. Thus, the aim here was to assess whether the sites tended to cluster according to land usage, as based on their predicted latent variable scores i.e., the ${\varvec{{\hat{a}}}_i}$’s. For comparison, we also fitted the same GLLVM using standard VA to assess if inferences drawn between the two methods of estimation differed. The top row of Fig. 4 presents the resulting unconstrained ordination plots using both standard VA (left panel) and EVA (right panel). The ordinations of the sites given by the two methods matched each other well, and there is evidence that the sites are clustered according to their land use type. On the other hand, there was much less uncertainty in the prediction regions resulting from standard VA compared to EVA.

Fig. 4

Model-based unconstrained ordination (top row) and residual ordination (bottom row) of the sites in the testate amoebae data, along with 95% CMSEP-based prediction regions. The ordinations are constructed based on fitting negative binomial GLLVMs using standard VA (left column) and EVA (right column), where in the top row no covariates are included while in the bottom row the covariates water pH, temperature, and land use were included. The sites are colored and marked according to their type of land use

Based on the above unconstrained ordination results, we proceeded to fit a negative binomial GLLVM but this time including water pH, temperature, and land use type (as a factor with dummy variables) as covariates. The resulting residual ordination plots, which may be interpreted as a visualization of residual covariation between species after accounting for the measured covariates, are presented in the bottom row of Fig. 4. Not surprisingly, after controlling for the land use, the sites exhibit a much more random pattern (using both EVA and standard VA), and on the whole are more closely clustered together compared to the unconstrained ordination plot. The prediction regions produced by EVA are again noticeably bigger than those produced by standard VA.

By examining the definition of CMSEP in Sect. 3.1, one may hypothesize that the larger prediction regions resulting from EVA may be at least partially a consequence of the elements of the estimated variational covariance matrices $\varvec{{\hat{A}}}_i$ being larger. In “Appendix C”, we provide some results which substantiate this idea, namely the traces of the variational covariance matrices from EVA are often greater than those produced by standard VA. These larger traces and larger predictions regions as a whole are not overly surprising, since EVA uses a Taylor approximation rather than the exact form of conditional distribution of the responses.

On the other hand, when we examine the amount of covariation within and between species that is explained by the covariates, as quantified by calculating the relative change in the trace of the estimated residual covariance matrix $\varvec{\hat{\varSigma }} = \varvec{\hat{\varLambda }} \varvec{\hat{\varLambda }}^\intercal$, we observe that, according to GLLVMs fitted using EVA, water pH and temperature together explain only $15.5 \%$ of the covariation in the model, but when land usage was also included this rose to $39.9 \%$. For models fitted using standard VA, these percentages were $15.8 \%$ and $38.7 \%$, respectively. The fact that these percentages were very similar between models fitted using EVA and models fitted using standard VA offers some reassurance of the inferences and conclusions obtained by the former. This result is further supported when we examine plots of the estimated regression coefficients and corresponding 95% Wald intervals from both fits. These plots for pH, temperature and land usage are presented in “Appendix C”, from which we see that the conclusions produced by EVA and VA are practically an exact match, with the list of covariate effects deemed statistically significant differing by only a handful of coefficients.

7 Discussion

In this article, we have proposed extended variational approximations (EVA) for fast and universal fitting of GLLVMs. EVA builds on the ongoing research into variational approximations for GLLVMs, but broadens it to allow for any combination of (parametric) response distribution and link function to be used. Based on extensive simulation studies, the performance accuracy of EVA lies somewhere between the standard method of VA (and VA using Gauss-Hermite quadrature) and the more established method of Laplace approximation (LA). This, combined with its computational efficiency and scalability suggests that EVA presents an exciting and fruitful avenue of further research into computationally efficient estimation and inference for GLLVMs as a whole. Indeed, the EVA approach is potentially more straightforward to derive and implement for more advanced types of GLLVMs such as those involving temporally or spatially dependent latent variables (Ovaskainen et al. 2017), detection probabilities (Tobler et al. 2019), and GLLVMs coupled with sparse regularization penalties for variable selection (Hui et al. 2018a). One particularly important avenue of future use for EVA is as a computationally efficient way to fit mixed-response GLLVMs, when the columns of $\varvec{Y}$ correspond to different types of response variables, and research is currently being done to implement this as part of the gllvm package.

Another interesting topic for future research is the application of EVA to high-dimensional data settings using, for example, parallel computation techniques along the lines of Tran et al. (2016) or stochastic inference and mini-batching as reviewed in Zhang et al. (2018). The form of EVA (and VA) for the common GLLVMs should readily allow the application of mini-batching in terms of the observational units (subindex i). Moreover, procedures could also be developed for mini-batching the subindex j in a way that respects the inter-response correlation structures inherent in abundace data, leading into a doubly stochastic variational inference framework for GLLVMs.

From a theoretical standpoint, the development of EVA leaves considerable avenues for modifications and generalizations, most notably the exact use of the Taylor approximation for the conditional distribution of the response, $\log f(\varvec{y} | \varvec{u}, \varvec{\varPsi })$. For instance, Wang and Blei (2013) previously explored a variant where the Taylor approximation is taken to be the point which maximizes $\log f(\varvec{y} | \varvec{u}, \varvec{\varPsi })$ with respect to the latent variables $\varvec{u}$. This choice leads to yet another method which the authors called Laplace variational inference. Yet another choice is to center the Taylor approximation around the mean of the variational distribution from the previous iterative step of the optimization algorithm, although according to the authors this approach often did not lead to desirable results in terms of model convergence. Notice that none of these methods rely on a unique mode of the likelihood: we simply expand around a point that facilitates convenient computation. To our knowledge, Laplace variational inference has not been considered for GLLVMs, and its performance in comparison to EVA as well as its large sample behavior will be left as an avenue for future research. In addition, the effect of using higher order Taylor expansions could be explored, along with developing general large sample properties for EVA for GLLVMs. Finally, the fact that in EVA we underestimate the latent variable posterior covariances even more than in standard VA requires careful consideration. The potential use of bootstrap-based methods to overcome this issue, as suggested in Dang and Maestrini (2021), will be considered in future.