A non-stationary model for spatially dependent circular response data based on wrapped Gaussian processes

Abstract

Circular data can be found across many areas of science, for instance meteorology (e.g., wind directions), ecology (e.g., animal movement directions), or medicine (e.g., seasonality in disease onset). The special nature of these data means that conventional methods for non-periodic data are no longer valid. In this paper, we consider wrapped Gaussian processes and introduce a spatial model for circular data that allow for non-stationarity in the mean and the covariance structure of Gaussian random fields. We use the empirical equivalence between Gaussian random fields and Gaussian Markov random fields which allows us to considerably reduce computational complexity by exploiting the sparseness of the precision matrix of the associated Gaussian Markov random field. Furthermore, we develop tunable priors, inspired by the penalized complexity prior framework, that shrink the model toward a less flexible base model with stationary mean and covariance function. Posterior estimation is done via Markov chain Monte Carlo simulation. The performance of the model is evaluated in a simulation study. Finally, the model is applied to analyzing wind directions in Germany.

1 Introduction

Advances in geographical information and global positioning systems have generated a large amount of spatial data and, as a consequence, have increased the need for spatial models that accurately describe it (Cressie 1993; Banerjee et al. 2014). In this context, one often aims to develop a statistical model in continuous space based on a limited number of monitoring stations. Gaussian random fields (GRFs) have proven quite helpful in fulfilling this purpose, but are vulnerable to “the big-n problem,” i.e., GRFs can become computationally infeasible since the cost of factorizations is in general cubic in the number of observations n. This renders GRFs infeasible for larger spatial datasets.

Due to the circular geometry of the sample space, environmental and geophysical processes such as surface winds or waves require the reassessment of typical spatial models for non-periodic data. Statistical literature on circular data spans as far back as the 1970’s (Fisher 1995; Mardia 2014), but it was only in the early 2010’s that spatial modeling of circular data really took off. Traditional models for circular data employ the von Mises distribution, but Jona-Lasinio et al. (2012) and Wang and Gelfand (2014) highlight the advantages of the wrapped and projected Gaussian distributions in space and space-time settings. More recent work has continued exploring these advantages (Nuñez-Antonio et al. 2015; Mastrantonio et al. 2016a, b; Alegria et al. 2016). Nonetheless, today circular data models are still behind on the latest advances in spatial statistics. In particular, models developed so far typically assume stationarity in the mean and the covariance of the modeled field.

There is comprehensive literature on how to model the spatial variation in the mean of the response when the response is non-periodic. The fundamental issue for circular responses relates to the fact that including a linear covariate in the mean might induce a circular likelihood for the regression coefficients that has infinitely many maxima, since this model essentially wraps the line infinitely many times around the circle (Fisher and Lee 1992). The typical solution is to use a link function for fixed effects with co-domain H, where H is an interval in $\mathbb {R}$ of length equal to the circular variable’s period of $2\pi$. Typically, the inverse tangent link function $\text{ atan }(\cdot )$ is recommended, which requires additional shifting and rescaling.

When it comes to non-stationarity in the covariance, many spatial data can be well approximated in space by a GRF, but the covariance structure is distinctly non-stationary, i.e., it has a spatially varying dependence structure (Fuentes 2001; Schmidt and O’Hagan 2003). However, non-stationarity in the covariance function is often not accounted for. This is in great part due to the substantial increase in computation time associated with non-stationary covariances, but also because of issues in prior selection. Concretely, the complex likelihood structure induced by the non-stationary covariance makes it harder to understand how priors affect the physical properties of the resulting spatial field (Fuglstad et al. 2015; Marques et al. 2020; Bolin and Kirchner 2020). Consequently, in order to take full advantage of the flexibility that non-stationarity in the covariance allows, there has been a call for better parameterization and prior elicitation of these models (e.g., Fuglstad et al. 2018).

Several methods have been proposed to improve the GRF’s computational bottlenecks. A common approach is to define an approximation of a GRF on a spatial domain $\mathcal {S}$ through a basis expansion with M nodes. By choosing $M < n$, one can reduce the computational burden of GRFs (Banerjee et al. 2008; Cressie and Johannesson 2008), but such low-rank approximations can remove fine-scale variations of the process (Banerjee et al. 2008). Consequently, methods that explore the sparsity of the covariance matrix $\varvec{\varSigma }$ of the GRF, or its precision matrix $\varvec{Q} = \varvec{\varSigma }^{-1}$, have been favored. For the latter, n can be larger than M, since the reduction in computational complexity is achieved through the sparsity of the precision matrix (Datta et al. 2016; Lindgren et al. 2011). In particular, Lindgren et al. (2011) focused on the sparsity of $\varvec{Q}$ by exploring the empirical equivalence between a GRF and the computationally more convenient Gaussian Markov random fields (GMRFs) via a stochastic partial differential equation (SPDE). Bolin and Kirchner (2020) extended this work and introduced the rational SPDE-approach, which additionally allows one to flexibly estimate the smoothness parameter of the GRF. Compared to covariance-based models, the SPDE-approach can more easily be generalized to non-stationary GRFs (Ingebrigtsen et al. 2015; Fuglstad et al. 2015), anisotropic GRFs (Fuglstad et al. 2015), non-separable covariance functions, or general domains such as the sphere (Lindgren et al. 2011).

In this paper, we combine the wrapped Gaussian distribution with the SPDE-approach and create a wrapped Gaussian spatial model, referred to in short as the wrapped-SPDE model. The resulting approach allows us to deal with spatially observed circular data in a computationally more efficient way than ordinary kriging and, simultaneously, it grants us a more approachable way of including non-stationarity in the covariance of the circular response. To avoid using a link function for the fixed effects while still guaranteeing a co-domain for these effects of length equal to $2\pi$, we use a penalized complexity (PC) prior for the parameters of the mean (Klein and Kneib 2016; Simpson et al. 2017). These priors allow for user-defined scaling and at the same time prevent overfitting. As we are also interested in preventing overfitting in the covariance, we additionally build a PC-prior for the non-stationary component of the covariance. The final prior structure shrinks the relevant parameters toward a base model with stationary mean and covariance. Fuglstad et al. (2018) derive a very similar PC-prior to penalize non-stationarity in the covariance of GRFs. However, they shrink the model toward a pre-estimated stationary GRF and combine the PC-prior with a g-prior (Zellner 1986). In this paper, we do not shrink toward a pre-estimated field, but estimate the stationary and non-stationary components simultaneously, and avoid the additional use of a g-prior. Moreover, there are currently no in-depth studies on how to set up PC-priors in this context and, consequently, we also contribute to the literature by developing general guidelines on how to set these up.

The remainder of the paper is organized as follows. Section 2 introduces the wrapped-SPDE model, as well as the PC-priors developed. In Sect. 3, posterior estimation is discussed, with a focus on the sampling scheme for MCMC and the derivation of full conditionals. The performance of the wrapped-SPDE model is investigated in a simulation study in Sect. 4, with a strong focus on the performance of the PC-priors considered. In Sect. 5, we use our model to estimate wind directions in Germany, while Sect. 6 presents conclusions and some discussions on potential extensions.

2 Non-stationary wrapped Gaussian spatial responses

In this section, we present the fundamental components of the non-stationary wrapped-SPDE model. We start by introducing Gaussian spatial processes in Sect. 2.1, followed by a short introduction to wrapped Gaussian spatial processes in Sect. 2.2. After that, in Sects. 2.3 and 2.4, we introduce the key components of the non-stationary model for the mean. In Sect. 2.5, we introduce the computationally efficient SPDE-approach. Finally, Sects. 2.6 and 2.7 introduce the key components of the non-stationarity model for the covariance.

2.1 Gaussian spatial processes

Let $\varvec{s}$ denote a spatial index variable representing the location of an observation $Y(\varvec{s})$ within a spatial domain $\mathcal {S} \subset \mathbb {R}^2$. Observations that are “close” in space tend to exhibit some dependence. One of the crucial tasks in spatial statistics is to account for such dependencies and to identify suitable spatial dependence structures that allow for spatial interpolation to sites where no observations are available.

The most common random object for representing continuously indexed spatial effects are Gaussian random fields (GRFs). A spatial process $\lbrace \gamma (\varvec{s}): \varvec{s} \in \mathcal {S} \rbrace$ is a continuously indexed GRF if all finite-dimensional distributions of the process are Gaussian, i.e., for all $n \in \mathbb {N}$ and all $\varvec{s}_1, \dots , \varvec{s}_n \in \mathcal {S}$, the vector $(\gamma (\varvec{s}_1), \dots , \gamma (\varvec{s}_n))^{T}$ is multivariate Gaussian distributed. This GRF is generally described by a mean function $\mu (\varvec{s})$ and a positive definite covariance function $C(\varvec{s}, \varvec{s}')$, $\varvec{s}, \varvec{s}' \in \mathcal {S}$.

The spatial covariance function of a GRF is

• Stationary (as opposed to non-stationary), if it is only a function of the relative position of two locations, i.e., $C(\varvec{s},\, \varvec{s}') = C( \varvec{s} - \varvec{s}')$, $\varvec{s}, \varvec{s}' \in \mathcal {S}$.

• Isotropic (as opposed to anisotropic), if it only depends on the Euclidean distance between the locations, i.e., $C( \varvec{s},\, \varvec{s}') = C( \vert \vert \varvec{s} - \varvec{s}' \vert \vert )$, $\varvec{s}, \varvec{s}' \in \mathcal {S}$.

One of the most popular covariance functions in geostatistical modeling is the Matérn covariance

$$\begin{aligned} C(\varvec{s},\varvec{s}') = \frac{\sigma ^2}{2^{\nu -1} \Gamma (\nu )} (\kappa \Vert \varvec{s} - \varvec{s}' \Vert )^{\nu } K_\nu (\kappa \Vert \varvec{s} - \varvec{s}' \Vert ). \end{aligned}$$

(1)

The parameter $\sigma ^2 > 0$ is the marginal variance of the spatial field, and $\kappa >0$ is a scaling parameter related to the range of spatial dependence $\rho$. The range is formally defined as the distance at which the spatial dependency between two locations falls to 0.05. Furthermore, $\nu > 0$ is the smoothness parameter of the GRF and $K_\nu$ is a modified Bessel function of the second kind and order $\nu$.

It has been argued that the Matérn family of covariance functions is broad enough to cover the most commonly used models in spatial statistics (Stein 2012). For example, it includes the exponential covariance function as a special case for $\nu = \frac{1}{2}$ and the Gaussian covariance function as the limiting case for $\nu \rightarrow \infty$.

2.2 Wrapped Gaussian spatial processes

To construct distributions for circular data, we can rely on the construction principle of wrapping the distribution of a random variable $Y \in \mathbb {R}$ defined on the real line around the unit circle to make its domain adhere to the interval $[0,2\pi ]$ (Breitenberger 1963). The result is a circular—or wrapped—random variable $X \in [0,2\pi )$. The relation between X and Y can be made more explicit as

$$\begin{aligned} X = Y \, \mod 2\pi \in [0, 2\pi ), \end{aligned}$$

(2)

i.e., X is the wrapped version of Y of period $2\pi$. This expression can be inverted by introducing the winding number, $K \in \mathbb {Z}$, measuring the number of “turns” Y has be wrapped around the unit circle.Let $\varvec{\vartheta }$ be the vector of all model parameters. Then, the unwrapped variable Y can be expressed as $Y = X + 2 \pi K$. If we denote by $f_y(\cdot )$ the probability density function of the random linear variable $Y\in \mathbb {R}$, the probability density function of X is given by

$$\begin{aligned} f_X(x) = \sum _{k = - \infty }^{ \infty } f_y( x + 2 \pi k \vert \varvec{\vartheta }), \end{aligned}$$

(3)

where $x \in [0, 2\pi )$ and $k \in \mathbb {Z} \equiv \lbrace 0, \pm 1, \pm 2, \cdots \rbrace$. Intuitively, expression (3) takes $f_y ( \cdot \vert \varvec{\vartheta })$ and wraps it around the unit circle. If we assume Y is Gaussian distributed, then X is wrapped Gaussian distributed. Similarly to a Gaussian distribution, the wrapped Gaussian distribution is unimodal and symmetric.

We can now rely on the unwrapped variable for building a regression model for a continuous variable on $\mathbb {R}$ which is then transferred to the directional scenarios via (2). Jona-Lasinio et al. (2012) first showed that, with a few steps, this approach can be extended to the context of spatial data. Let $\beta _0$ be the intercept of the model. For every $\varvec{s} \in \mathcal {S}$, a linear GRF model is of the form $Y(\varvec{s}) = \beta _0 + \gamma (\varvec{s})$, where $\gamma (\varvec{s})$ is a zero-mean GRF. For the wrapped GRF, similarly to the beginning of this section, we introduce a latent vector $K(\varvec{s})$. We can then write $X(\varvec{s}) = \beta _0 + \gamma (\varvec{s}) + 2 \pi K(\varvec{s})$ with a similar interpretation for $K(\varvec{s})$ as before.

In order to account for additional variability in the model at a small spatial scale (sometimes called microscale, Cressie 1988), we include a nugget effect in our model such that

$$\begin{aligned} X(\varvec{s}_i) = \beta _0 + \gamma (\varvec{s}_i) + \varepsilon _i + 2 \pi K(\varvec{s}_i), \end{aligned}$$

where $\varepsilon _i \sim N(0, \sigma ^2_\varepsilon )$ are the independently and identically distributed nugget terms, with $i = 1, \ldots , n$, where n is the sample size. Some authors interpret the nugget as a measurement error (e.g., Banerjee et al. 2003), and while a measurement error could also be captured by the nugget (Cressie 1988), in the context of our application in Sect. 5, interpreting it as small scale variation is more appropriate.

2.3 Non-stationarity in the mean

Let $\varvec{z}(\varvec{s}_i)$ represent a vector of B spatially indexed covariates evaluated at location $\varvec{s}_i \in \mathcal {S}$ with associated coefficient vector $\varvec{\beta } = ( \beta _1, \ldots , \beta _B)'$. A wrapped Gaussian spatial model that allows for non-stationary in the mean is given by

$$\begin{aligned} X(\varvec{s}_i)&= \beta _0 + \varvec{z}(\varvec{s}_i)' \varvec{\beta } \nonumber \\ {}&\quad \ + \gamma (\varvec{s}_i) + 2 \pi K(\varvec{s}_i) + \varepsilon _i ,\ \mathrm {for}\ i=1, \ldots ,n, \end{aligned}$$

(4)

where $\gamma (\varvec{s}_i)$ is a zero-mean GRF, $\varepsilon _i$ is a nugget term, and n is the sample size.

Unlike suggested in earlier approaches (e.g., Fisher and Lee 1992; Jona-Lasinio et al. 2012), we do not include a link function for the fixed effects when using non-periodic covariates. Crucially, in model (4) the periodicity of the response is accounted for by the winding number $K(\varvec{s})$. Previously, the winding number $K(\varvec{s})$ has been used to govern the behavior of a non-periodic Gaussian process (e.g., Jona-Lasinio et al. 2012). In the same way, it is also able to govern the behavior of the combination of GRF and fixed effects. Therefore, the fixed effects do not require an additional link function. Moreover, in a Bayesian framework, one can use prior information that enforces the length of the fixed effects— excluding $\beta _0$—to be approximately $2\pi$. This avoids the identification issues identified in Fisher and Lee (1992) and referred to in the introduction to this paper, and it can achieve by using a PC-prior for the fixed effects, which we introduce in detail in the next section.

2.4 Penalized complexity prior for non-stationarity in the mean

In this section, we introduce a prior for the non-stationary component of the mean, inspired by Klein and Kneib (2016) and the PC-prior framework from Simpson et al. (2017). PC-priors conceptualize a model component as a flexible extension of a base model and construct a prior that penalizes deviations from this base model. The less flexible state is favored until the data provide evidence against it. In our model, the base model assumes a stationary mean, i.e., $\varvec{\beta } = 0$, and the more complex alternative allows for non-stationarity, i.e., $\varvec{\beta } \ne 0$. An in-depth introduction to PC-priors can be found in Simpson et al. (2017), and its four guiding principles are listed in Appendix B.

In the context of circular response data, the prior $\beta _0 \sim N(0, 10)$ represents a diffuse prior for the intercept. Furthermore, we let $\varvec{\beta } \vert \xi ^2 \sim N(\varvec{0}, \xi ^2 \varvec{I})$. One can show that if the base model is such that $\xi ^2 \rightarrow 0$ and the prior is constructed according to the PC-prior principles, then $\xi ^2$ has a Weibull prior with shape $\frac{1}{2}$ and scale $\lambda$, i.e., $\xi ^2 \sim \text {Weibull}(\frac{1}{2}, \lambda )$ (see Klein and Kneib 2016, for a detailed derivation).

We elicit $\lambda$ with a user-defined scaling approach based on the probability statement

$$\begin{aligned} P( \mid \varvec{z}(\varvec{s})'\varvec{\beta } \mid \le \, c ,\; \forall \, \varvec{s} \in \mathcal {S}) \ge 1 - \alpha , \end{aligned}$$

(5)

where the parameters $\alpha \in (0, 1)$ and $c > 0$ are chosen by the user. Then, the marginal density of $\varvec{z}(\varvec{s})' \varvec{\beta }$ can be obtained by integrating $\xi ^2$ out. Namely,

$$\begin{aligned} p( \varvec{z}(\varvec{s})' \varvec{\beta })&= \int _0^\infty p(\varvec{z}(\varvec{s})' \varvec{\beta }, \xi ^2) \mathrm{d} \xi ^2 \\&= \int _0^\infty p(\varvec{z}(\varvec{s})' \varvec{\beta } \vert \xi ^2) p(\xi ^2) \mathrm{d} \xi ^2, \end{aligned}$$

where $\varvec{z}(\varvec{s})' \varvec{\beta } \vert \xi ^2 \sim N(0, \xi ^2\, \varvec{z}(\varvec{s})' \varvec{z}(\varvec{s}))$.

Applying the Bonferroni inequality to (5), $\lambda$ can be chosen such that

$$\begin{aligned} \sum _{i = 1}^n \left( 1 - \int _{-c}^{c} \int _0^\infty p_{ \varvec{z}_i' \varvec{\beta } } (u \vert \xi ^2) p(\xi ^2) \mathrm{d} \xi ^2 \mathrm{d} u \right) = \alpha \end{aligned}$$

(6)

is satisfied and can be solved numerically. Depending on the number of observations, it can become quite computationally expensive to compute the double integral n times. Consequently, we instead use a simulation-based method which finds the $\lambda$ that satisfies

$$\begin{aligned} P\left( \text {max}_{\varvec{s} \in \mathcal {S}} \mid \varvec{z}(\varvec{s})'\varvec{\beta } \mid \le \, c \right) \ge 1 - \alpha , \end{aligned}$$

(7)

i.e., we model the probability that the maximum norm of the non-stationary effect in the mean of the response is smaller than a pre-specified level and determine the distribution of the maximum based on simulations from the prior $p(\varvec{z}(\varvec{s})' \varvec{\beta }\vert \xi ^2)$. Computationally, this option is much cheaper, as it does not require solving any integrals.

In Fuglstad et al. (2015c), the authors instead consider $\varvec{\beta } \vert \xi ^2 \sim N(\varvec{0}, \xi ^2 \varvec{S})$, where $\varvec{S}$ is the Gram matrix, following the idea of g-priors. This is done so that the resulting prior is invariant to the scaling of covariates and is able to handle linear dependencies between the covariates in a reasonable way. However, we argue that our choice of $\lambda$ in (7) explicitly takes into account the scale of covariates and the interactions between them, and using a g-prior for this purpose is not necessary, as it would instead lead to $\varvec{z}(\varvec{s})' \varvec{\beta } \vert \xi ^2 \sim N(0, \xi ^2\, \varvec{z}(\varvec{s})' (\varvec{z}(\varvec{s})' \varvec{z}(\varvec{s}))^{-1} \varvec{z}(\varvec{s}))$, for $g=1$.

By design, the choice of c and $\alpha$ is ad hoc and problem-specific. These parameters should be chosen according to the prior knowledge of the user to induce a user-defined amount of scaling. With a focus on structured additive models, Klein and Kneib (2016) use $c = 3$ and argue that with the most common link functions, such as the log-link, there is no more variability in the desired parameter if the predictor exceeds a range from − 3 to 3. For circular data, adequate values for the parameter c are also linked to the size of the winding number since wrapping the latent scale around the unit circle leads to very different scales of effects. In our data analyses and simulations, the variability of the responses is not large enough to make this a problem of practical concern such that we rely on a bound c that is half of the circular variable period of $2\pi$, i.e., $c = \pi \approx 3$. In Sect. 4, we investigate the performance of the PC-prior using this bound.

2.5 The stochastic partial differential equation approach

In Lindgren et al. (2011), an SPDE provides an explicit link between a GRF and a GMRF. The approach links discretized models to a well-defined continuous domain model—the Matérn SPDE. At the same time, the Markov property makes the precision matrix of the corresponding GMRF sparse.

Concretely, a Matérn GRF $\gamma (\varvec{s})$ solves the SPDE

$$\begin{aligned} (\kappa ^2 - \varDelta )^{ \alpha _\nu /2} ( \tau \, \gamma (\varvec{s})) = \mathcal {W}(\varvec{s}), \,\, \varvec{s} \in \mathbb {R}^2, \,\, \alpha _\nu = \nu + 1, \,\, \nu > 0, \end{aligned}$$

(8)

where $\varDelta$ is the Laplacian, $\mathcal {W}$ is a Gaussian spatial white noise innovation process, and $\tau > 0$ is a precision parameter. The stationary solution, $\gamma (\varvec{s})$, of the resulting SPDE on $\mathbb {R}^2$ is a stationary GRF with Matérn covariance function.

The GMRF approximation is obtained by discretizing the domain of the SPDE using the finite elements method (FEM) (see Ern and Guermond 2013, for an example). We consider a triangulated finite elements mesh with M nodes and, based on this, build piecewise linear basis functions $\psi _m(\cdot )$, $m = 1, \ldots , M$, which are subsequently used to expand the GRF

$$\begin{aligned} \gamma (\varvec{s}) = \sum ^M_{m=1} \psi _m(\varvec{s}) \gamma _m, \end{aligned}$$

(9)

where the joint distribution of the weight vector $\varvec{\gamma } = (\gamma _1, \ldots , \gamma _M)'$ is normally distributed with mean zero and sparse precision matrix $\varvec{Q}$, such that $\varvec{\gamma } \sim N(\varvec{0}, \varvec{Q}^{-1}).$

For interpretation purposes, the marginal variance $\sigma ^2$ and the range parameter $\rho$ can be derived from $\tau$ and $\kappa$. Specifically,

$$\begin{aligned} \sigma ^2 = \frac{\Gamma (\nu )}{\Gamma (\alpha _\nu ) 4 \pi \kappa ^{2 \nu } \tau ^2}, \end{aligned}$$

(10)

and, by defining the range as the distance at which the spatial correlation falls to 0.05 (Lindgren et al. 2011), we get the expression

$$\begin{aligned} \rho = \frac{\sqrt{8 \nu }}{\kappa }. \end{aligned}$$

(11)

Thus, $\kappa$ affects both the marginal variance and the range of the GRF. This often leads to difficulties when eliciting priors. We return to this issue in Sect. 2.7.

The SPDE-approach was originally limited to the case $\alpha _\nu \in \mathbb {N}$. This made the approach less flexible than traditional models for two dimensional spatial data where $\alpha _\nu \in [1, \infty )$. However, recent work by Bolin and Kirchner (2020) extends the SPDE-approach to allow for any fractional power satisfying $\alpha _\nu > 1$. For fractional values of below 1, one can use Markov approximations based on spectral densities, but these are thus far only derived for stationary GRFs. Nonetheless, the precision of the GMRF only has an explicit expression as a function of $\kappa$ and $\tau$ for $\nu =1$ ($\alpha _\nu = 2$) and, therefore, unless stated otherwise, we assume $\nu = 1$. More details are provided in Appendix A.

2.6 Wrapped Gaussian spatial processes with non-stationary covariance

Typically, spatial regression models assume the GRF to be stationary. However, in most settings, the intricacy of the spatial structure justifies the use of a more flexible model. The SPDE-approach allows us to easily model non-stationarity in the second-order structure of the GRF. One way to achieve this is by letting the parameters of the SPDE be spatially varying functions. This can be done, e.g., through spatially varying covariate information.

To introduce non-stationarity in the marginal variance and range of the GRF, we only need to make $\kappa$ dependent on covariates (see (10) and (11); for the sake of simplicity, in this paper $\tau$ is kept constant). Concretely, we consider

$$\begin{aligned} \log (\tau ) = \theta ^\tau _0 \text{ and } \log (\kappa (\varvec{s})) = \theta ^\kappa _0 + \varvec{z}^\kappa (\varvec{s})'\varvec{\theta }^\kappa _z, \end{aligned}$$

(12)

where ${\varvec{\theta }^{\kappa }} = (\theta _0^\kappa , {\varvec{\theta }^\kappa _z}')'$ and $\theta ^\tau _0$ are the model’s hyperparameters and $\varvec{z}^\kappa (\varvec{s})$ is a matrix of $B_\kappa$ relevant covariates. For conciseness of notation, when needed we use ${\varvec{\theta }} = (\theta ^\tau _0, {\varvec{\theta }^\kappa }')'$. The parameters $\theta ^\kappa _0$ and $\theta ^\tau _0$ represent the stationary covariance specification of the model. We do not solve the parameterization issue that leads $\kappa (\varvec{s})$ to affect both the marginal variance and range of the GRF, but instead try to improve predictions by having more adequate prior elicitation in the non-stationary components of the covariance function.

We assume $\kappa (\varvec{s})$ to be smooth over the domain of interest since, with slowly varying $\kappa (\varvec{s})$, the appealing local interpretation of the SPDE as a Matérn GRF remains unchanged, whereas the actual form of the non-stationary correlation function achieved is unknown. In this context, it is still possible to obtain a specification of $\kappa (\varvec{s})$ as a function of the range $\rho (\varvec{s})$ and marginal variance $\sigma ^2(\varvec{s})$ via the nominal approximations

$$\begin{aligned} \rho (\varvec{s}) \approx \frac{\sqrt{8 \nu }}{\kappa (\varvec{s})} \end{aligned}$$

(13)

and

$$\begin{aligned} \sigma ^2(\varvec{s}) \approx \frac{\Gamma (\nu )}{\Gamma (\alpha _\nu ) 4 \pi \kappa (\varvec{s})^{2 \nu } \tau ^2}. \end{aligned}$$

(14)

These approximations are valid for $a< \kappa < b$, $a, b \in \mathbb {R}$, where the range is large enough compared to mesh resolution and small enough to avoid boundary effects. We use the above described method to include non-stationarity in the covariance of our model. Concretely, we combine (4) with the spatially varying specification of $\kappa (\varvec{s})$ in (12). Mastrantonio et al. (2016b) account for non-stationarity in the covariance function of a GRF by using categorical variables in an ANOVA-type model. Here, we are more flexible and only restrict covariates in the covariance function to be smooth.

2.7 Penalized complexity prior for non-stationarity in the covariance

In this section, we show how to use PC-priors to penalize non-stationarity in the covariance of the circular response. We will favor a model with a stationary covariance function unless the data indicate that there is non-stationarity that can be expressed by the covariates included in Equation (12).

Consider uniform priors for $\theta ^\tau _0$ and $\theta _0^\kappa$ that guarantee the marginal variance is between $[0.01, (2\pi )^2]$ and the spatial range is between [0.01, 1] for $\mathcal {S} \subseteq [0, 1] \times [0,1]$. Concretely,

$$\begin{aligned} \theta ^\tau _0 \sim U(-10, 3) \quad \ \text {and} \ \quad \theta ^\kappa _0 \sim U(1, 6). \end{aligned}$$

Let $\varvec{\theta }_z^\kappa \vert \zeta ^2 \sim N(\varvec{0}, \zeta ^2 \varvec{I})$. Similarly to Sect. 2.4, $\zeta ^2 \sim \text {Weibull}(\frac{1}{2}, \lambda )$ (Klein and Kneib 2016; Simpson et al. 2017).

We elicit $\lambda$ with a user-defined scaling approach based on the probability statement

$$\begin{aligned} P( \mid \varvec{z}^\kappa (\varvec{s})'\varvec{\theta }^\kappa _z \mid \le \, c ,\; \forall \, \varvec{s} \in \mathcal {S}) \ge 1 - \alpha , \end{aligned}$$

(15)

where the parameters $\alpha \in (0, 1)$ and $c > 0$ are chosen by the user.

The derivation is identical to the one for the PC-prior for fixed effects elicited in Sect. 2.4, and thus, we present only the main steps. Essentially, we get $\varvec{z}^\kappa (\varvec{s})' \varvec{\theta }_z^\kappa \vert \zeta ^2 \sim N(0, \zeta ^2\, \varvec{z}^\kappa (\varvec{s})' \varvec{z}^\kappa (\varvec{s}))$ and, once again, use a simulation-based method to obtain the $\lambda$ that satisfies

$$\begin{aligned} P\left( \text {max}_{\varvec{s} \in \mathcal {S}} \mid \varvec{z}^\kappa (\varvec{s})'\varvec{\theta }^\kappa _z \mid \le \, c \right) \ge 1 - \alpha , \end{aligned}$$

(16)

i.e., we model the probability that the maximum norm of the non-stationary effect is smaller than a pre-specified level and determine the distribution of the maximum based on simulations from the prior $p(\varvec{z}^\kappa (\varvec{s})' \varvec{\theta }_z^\kappa \vert \zeta ^2)$.

In practical terms, if we consider (13) and a spatial domain $\mathcal {S} \subseteq [0, 1] \times [0,1]$—by equivalently re-sizing the domain, it is possible to restrict the values $\kappa (\varvec{s})$ can take. Throughout this paper, we consider $\rho (\varvec{s}) \in [0.01, 1]$ and, based on (13), we set a bound

$$\begin{aligned} c = \left\lfloor 0.5\left| \log (\sqrt{8 \nu }) - \log \left( \frac{\sqrt{8 \nu }}{0.01}\right) \right| \right\rfloor \, \text{ and } \text{ a } \text{ given } \alpha . \end{aligned}$$

(17)

In Sect. 4, we investigate the performance of these settings for the PC-prior.

2.8 The full hierarchical model

Consider the linear predictor $\eta (\varvec{s}) = \beta _0 + \varvec{z}(\varvec{s})' \varvec{\beta } + \gamma (\varvec{s})$. The resulting mean and covariance non-stationary wrapped Gaussian spatial response model has the following hierarchical structure:

$$\begin{aligned} X(\varvec{s}_i)&= \eta (\varvec{s}_i) + 2 \pi K(\varvec{s}_i) + \varepsilon _i = \beta _0 + \varvec{z}(\varvec{s}_i)' \varvec{\beta } \\ {}&\ \quad + \gamma (\varvec{s}_i) + 2 \pi K(\varvec{s}_i) + \varepsilon _i,\; \ \text{ for }\ i=1, \ldots , n \\ \beta _0&\sim N(0, 10) , \varvec{\beta } \vert \xi ^2 \sim N(0, \xi ^2 \varvec{I}), \varvec{\gamma } \vert \varvec{\theta } \sim N(\varvec{0}, \varvec{Q}^{-1}(\varvec{\theta })) \\ \theta _0^\tau&\sim U(-10, 3) , \theta _0^\kappa \sim U(1, 6) , \varvec{\theta }^\kappa _z \vert \zeta ^2 \sim N(\varvec{0}, \zeta ^2 \varvec{I}) \\ \xi ^2&\sim PC\left( c=\pi , \alpha \right) , \zeta ^2 \sim PC\left( c=2, \alpha \right) \\ \varvec{\varepsilon } \vert \sigma ^2_\varepsilon&\sim N(\varvec{0}, \sigma ^2_\varepsilon \varvec{I}) , \sigma ^2_\varepsilon \sim IG (0.001, 0.001)\\ p(K(\varvec{s}))&= {\left\{ \begin{array}{ll} \frac{1}{3},&{}{} \text{ if } \quad K(\varvec{s}) \in \lbrace -1, 0, 1 \rbrace \\ 0, &{}{} \text{ otherwise } \end{array}\right. } \end{aligned}$$

For $\sigma ^2_{\varepsilon }$, we specify an inverse gamma distribution with shape a and scale b such that $IG(a = 0.001, b = 0.001)$. Cases $a = b$ with this value approaching zero are widely used as a weakly informative choice for $\sigma ^2_{\varepsilon }$ (see Section 4.4 of Fahrmeir et al. 2013). Alternative settings, such as strong shrinkage toward zero with $a=1$ and $b=0.005$, were also tested, leading to no improvement in the simulation study results in Sect. 4.

Clearly, $\sum _{k= -\infty }^\infty p(K(\varvec{s}) = k) = 1$. However, implementing this prior is challenging because k has an infinite domain and a non-standard prior. However, while it is difficult to sample over all integers $\mathbb {Z}$ in (3), Mardia et al. (2000) showed that the density can be well approximated by restricting each $K(\varvec{s})$ to the support $\lbrace -1, 0, 1 \rbrace$. This explains our choice of prior for $K(\varvec{s})$, which is identical to the one in Jona Lasinio et al. (2020).

The bound $c=2$ in $\text {PC}\left( c=2, \alpha \right)$ results from (17) for $\nu = 1$ (see Sect. 2.5).

3 Posterior evaluation

We develop a fully Bayesian approach using Markov Chain Monte Carlo (MCMC) simulations for estimating the full vector of model parameters, which is denoted $\varvec{\vartheta } = (\beta _0, \varvec{\beta }', \varvec{\gamma }', \sigma _\epsilon ^2, \varvec{\theta }'$, $\xi ^2$, $\zeta ^2, \varvec{K}')'$ where $\varvec{K} {= }(K(\varvec{s}_1), \ldots , K(\varvec{s}_n))'$. Compared to integrated nested Laplace approximations (INLA, Rue et al. 2009), the method typically used for the SPDE-approach, our approach allows us to flexibly work with posteriors of hyperparameters that are typically far from Gaussian. This is particularly relevant when the covariance function is non-stationary (Fuglstad et al. 2015c).

To perform posterior estimation for the full vector of model parameters $\varvec{\vartheta }$, we separate $\varvec{\vartheta }$ into smaller blocks. Of particular relevance is the separation between variables for which we know the corresponding full conditional distributions, and those for which the full conditional distribution is not analytically available. We will use a Gibbs sampler (Gelfand 2000) for the former and derive the corresponding posterior distributions in Sect. 3.1. For the latter, we use Metropolis Hastings (MH, Metropolis et al. 1953) steps, which are explained in more detail in Sect. 3.2. In Appendix C, a summary of the sampler’s structure can be found.

3.1 Posterior distributions for Gibbs sampler

The full conditionals for $\beta _0$, $\varvec{\beta }$, $\varvec{\gamma }$, and $\sigma _\varepsilon ^2$ are available in closed-form, and we use a Gibbs sampler to sample them. In what follows, recall the hierarchical model structure and all model parameters introduced in Sect. 2.8.

For all parameters that have Gaussian distributed priors, we can use the properties of the product of two Gaussian densities to derive their posterior distribution, since the likelihood is also Gaussian (see Supplement A of Fahrmeir et al. 2013).

Consider the matrix of covariate evaluations $\varvec{Z} = (\varvec{z}(\varvec{s}_1), \ldots , \varvec{z}(\varvec{s}_n))$ and the matrix $\tilde{\varvec{Z}} = (\varvec{1}, \varvec{Z}')'$, as well as the normally distributed priors $\beta _0 \sim N(\mu _{\beta _0}, \sigma ^2_{\beta _0})$ and $\varvec{\beta } \sim N(\mu _{\varvec{\beta }}, \sigma ^2_{\varvec{\beta }} \varvec{I})$. Recall the basis functions in Equation (9). Here, we further define $\varvec{\psi }(\varvec{s}) = (\psi _1(\varvec{s}), \ldots , \psi _M(\varvec{s}))'$ and $\varvec{\psi } = (\varvec{\psi }(\varvec{s}_1), \ldots , \varvec{\psi }(\varvec{s}_n))'$. Recall also the linear predictor $\varvec{\eta } = (\eta (\varvec{s}_1), \ldots , \eta (\varvec{s}_n))'$, which was first introduced in Sect. 2.8.

According to the rules of the product of two normal distributions, the posterior distribution of $(\beta _0, \varvec{\beta }')'$ is

$$\begin{aligned} (\beta _0, \varvec{\beta }')' \vert \cdot \sim \mathcal {N} \left( (\varvec{E} + \varvec{F})^{-1}(\varvec{E}\varvec{e} + \varvec{F}\varvec{f}), (\varvec{E} + \varvec{F})^{-1} \right) \end{aligned}$$

(18)

with $(B + 1)\times (B + 1)$ matrices $\varvec{E} = \frac{1}{\sigma ^2_\varepsilon } \tilde{\varvec{Z}}\tilde{\varvec{Z}}'$ and $\varvec{F} = \text {diag}\left( \sigma ^2_{\beta _0}, {\varvec{\sigma }^2_{\varvec{\beta }}}' \right) ^{-1}$, where $\text {diag}$ denotes a diagonal matrix. Moreover, we have ($B+1$)-dimensional vectors $\varvec{e} = \tilde{\varvec{Z}}(\tilde{\varvec{Z}}'\tilde{\varvec{Z}})^{-1}(\varvec{X} - 2\pi \varvec{K} - \varvec{\psi }\varvec{\gamma })$ and $\varvec{f} = (\mu _{\beta _0}, \varvec{\mu _\beta } ')'$, where $\varvec{X} - 2\pi \varvec{K} = (X(\varvec{s}_1) + 2\pi K(\varvec{s}_1), \ldots , X(\varvec{s}_n) + 2\pi K(\varvec{s}_n))'$ and $X(\cdot )$ and $K(\cdot )$ are as defined in Sect. 2.2.

The posterior $\varvec{\gamma }\vert \cdot$ follows the same structure as (18)

$$\begin{aligned} \varvec{\gamma } \vert \cdot \sim {N} \left( (\tilde{\varvec{E}} + \tilde{\varvec{F}})^{-1}(\tilde{\varvec{E}} \tilde{\varvec{e}} + \tilde{\varvec{F}}\tilde{\varvec{f}}), (\tilde{\varvec{E}} + \tilde{\varvec{F}})^{-1} \right) . \end{aligned}$$

(19)

with $M \times M$ matrices $\tilde{\varvec{E}} = \frac{1}{\sigma ^2_\varepsilon } \varvec{\psi }' \varvec{\psi }$ and $\tilde{\varvec{F}} = \varvec{Q}^{-1}_{\varvec{\gamma }}$ and $M-$dimensional vectors $\tilde{\varvec{e}} = \varvec{\psi }' (\varvec{\psi }\varvec{\psi }')^{-1}(\varvec{X} - 2\pi \varvec{K} - \beta _0\varvec{1} - \varvec{Z}'\varvec{\beta })$ and $\tilde{\varvec{f}} = \varvec{0}$.

In the case of $\sigma _\epsilon ^2$, the prior is inverse gamma distributed IG(0.001, 0.001) (see Sect. 2.8), which combined with the normally distributed response leads to the posterior distribution (see p. 229 of Fahrmeir et al. 2013)

$$\begin{aligned} \begin{aligned}&\sigma _\varepsilon ^2 \vert \cdot \sim IG\bigg ( 0.001 + \frac{n}{2}, 0.001 + \frac{1}{2}(\varvec{X} - 2\pi \varvec{K} - \varvec{\eta })' (\varvec{X} - 2\pi \varvec{K} - \varvec{\eta })\bigg ). \end{aligned} \end{aligned}$$

3.2 Posterior estimation for MH steps

We now turn to parameters $\varvec{\theta }$, $\xi ^2$, $\zeta ^2$, and $K(\varvec{s})$, which are sampled with MH steps.

To sample $\varvec{\theta }$, $\xi ^2$, $\zeta ^2$, we use the robust adaptive MH method from Vihola (2012) with Student’s t-distributed proposal densities. This algorithm estimates the shape of the target distribution and simultaneously coerces the acceptance rate. We target an acceptance rate of $23.4\%$, which is the standard for multidimensional domains (Gelman et al. 1997). More details are provided in Appendix C.

The identification issues associated with the covariance parameters of GRFs are well-known (Zhang 2004; Tang 2019). This is no exception here, and since the parameters in $\varvec{\theta }$ are highly correlated, we sample them in one MH block.

Values of the variance parameters $\xi ^2$ and $\zeta ^2$ smaller than zero will cause invalid proposals—this is possible here since we use Student’s t-distributed proposal densities. We overcome this problem, in the specific case of $\xi ^2$ and $\zeta ^2$, by approximating the log-full conditional $\log (p(\log (\xi ^2) \vert \cdot ))$ and $\log (p(\log (\zeta ^2) \vert \cdot ))$, rather than the log-full conditional $\log (p(\xi ^2 \vert \cdot ))$ and $\log (p(\zeta ^2 \vert \cdot ))$, respectively. The detailed derivation is provided in Appendix C.

The latent variable $K(\varvec{s})$ is updated on each iteration, for each location, with a MH step. On each MCMC step t, given the current value $K_{t}(\varvec{s})$, $t = 1, \ldots , T$, the proposal is selected from the set $\lbrace K_{t}(\varvec{s}) - 1, K_{t}(\varvec{s}), K_{t}(\varvec{s}) + 1 \rbrace$, where each element has probability of $\frac{1}{3}$ of being selected. Given the prior for $K(\varvec{s})$ chosen in Sect. 2.8, one should set a starting value $K_0(\varvec{s}) = 0$, for all $\varvec{s}$.

4 Simulation study

The main objective of this simulation study is to investigate the performance of the priors for the non-stationary components of the mean and the covariance of the circular response. Concretely, we compare different priors for $\xi ^2$ and $\zeta ^2$, introduced in Sect. 2.4 and Sect. 2.7, respectively.

4.1 Scenarios

We consider 4 scenarios:

Scenario 1::

The data have a non-stationary mean and stationary covariance. The estimated model follows the same assumptions.

Scenario 2::

The data have a non-stationary mean and stationary covariance. The estimated model allows for non-stationarity in the covariance, i.e., we test for overfitting.

Scenario 3::

The data have a non-stationary mean and covariance. The estimated model follows the same assumptions.

Scenario 4::

The data have a non-stationary mean and covariance. The estimated model allows for non-stationarity in the mean, but not the covariance.

4.2 General settings

Let $\mathcal {S} \subseteq [0, 1] \times [0,1]$ and $\nu = 1$. We consider the wrapped-SPDE model with

$$\begin{aligned} X(\varvec{s}_i) = \beta _0 + z(\varvec{s}_i)'\beta + \gamma (\varvec{s}_i) + 2 \pi K(\varvec{s}_i) + \varepsilon _i, \end{aligned}$$

(20)

with $\varvec{s}_i \in \mathcal {S}$, $i = 1, \ldots , n$, and where non-stationarity in the covariance follows

$$\begin{aligned} \log (\tau ) = \theta ^\tau _0 \text{ and } \log (\kappa (\varvec{s}_i)) = \theta ^\kappa _0 + z^\kappa (\varvec{s}_i)'\theta ^\kappa _z. \end{aligned}$$

(21)

The datasets are generated with $(\beta _0, \beta ) = (1.05\pi , 0.6)$, $\sigma _\varepsilon ^2 = 0.1$, $K(\varvec{s}) = 0 \,\forall \varvec{s}$, and $z(\varvec{s}) = 2\sin (2 \pi s_1) \sin (4 \pi s_2)$. Moreover, $\theta ^\tau _0 = -3.08$, $\theta ^\kappa _0 = 2.17$. When the covariance is stationary $\theta ^\kappa _z = 0$, and when it is non-stationary $\theta ^\kappa _z = 1$ and $z^\kappa (\varvec{s}) = 0.5 + \cos (4 \pi s_2) \sin (2 \pi s_1)$.

We consider samples sizes $n \in \lbrace 200, 600, 1000 \rbrace$. The finite elements mesh used throughout this section has $M = 866$ mesh nodes, and it can be found in Appendix E.

Inference is performed with MCMC (see Sects. 2.8 and 3). We use one chain with 15,000 samples, burn-in of 7,000, and thinning factor of 8. Starting values for all parameters are random realizations of a standard normal distribution, except for $\beta$ and $\theta ^\kappa _z$, which start at 0.01 (close to zero following an assumption of stationarity), and $K(\varvec{s})$ which starts at 0 for all $\varvec{s}$.

For each scenario, $N = 100$ replications are used to compute the logarithm of the mean squared errors (log-MSEs) of the considered parameters.

The model is implemented in R (R Core Team 2019) using key functions from R-INLA for mesh generation and construction of precision matrices (Lindgren and Rue 2015). The code is available in the supplementary material to this paper.

4.3 Prior competitors

The first three principles of PC-priors, shown in Appendix B, give rise to the Weibull prior for the variance parameter (see Klein et al. 2015). The fourth—and final—principle of user-defined scaling can also be applied to other prior structures, such as inverse gamma priors and proper uniform priors for standard deviations (Gelman 2005, 2006; Hodges 2019).

For an inverse gamma prior with shape parameter $a = 1$ and scale b small, $\varvec{z}(\varvec{s})'\varvec{\beta }$ and $\varvec{z}^\kappa (\varvec{s})' \varvec{\theta }^\kappa _z$ marginally follow a t-distribution and user-defined scaling is possible (Klein and Kneib 2016). Fixing $a = 1$ implies heavy tails in the marginal t-distribution (Klein and Kneib 2016) while the corresponding value for b is then determined from the scaling criterion. We refer to this prior as $IG(\alpha )$, where $\alpha$ is then defined similarly to the PC-prior (see Sect. 2.4 and Sect. 2.7).

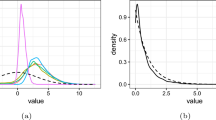
However, user-defined scaling is not generally possible for the inverse gamma distribution. Concretely, in the case of an inverse gamma prior IG(a, b) with $a = b$ small, there are certain ranges of the threshold c and the probability level $\alpha$ for which there is no solution to (6) with respect to b (similarly for $\zeta ^2$). Indeed, by enforcing a small shape parameter a, we implicitly reduce the prior’s ability to shrink toward zero, as we no longer can concentrate as much probability mass close to zero, compared to higher values of a. This can also be observed in Fig. 1 where, for essentially the same scale parameter, a higher shape parameter concentrates most of the mass at zero.

Fig. 1

Densities for PC-priors and inverse gamma priors for different shape parameters

The principle of user-defined scaling can also be applied to the half-Cauchy distribution. The half-Cauchy distribution is usually applied to the standard deviation. The half-Cauchy prior $\xi \sim HC(0, \lambda ^2)$ (similarly for $\zeta$) with location parameter 0, scale parameter $\lambda$, and density proportional to $(1 + (\xi /\lambda )^2)^{-1}$, implies a generalized beta prime distribution with density

$$\begin{aligned} p(\xi ^2) = \frac{1}{\pi \lambda ^2} \left( 1 + \frac{\xi ^2}{\lambda ^2} \right) ^{-1} \left( \frac{\xi ^2}{\lambda ^2} \right) ^{-1/2} \end{aligned}$$

where the three shape parameters are given by 1/2, 1/2, and 1, while the scale parameter corresponds to $\lambda ^2$. This prior is referred to as $HC(\alpha )$. By using a simulation-based technique to choose $\lambda$ in (7) (or (16)), we avoid some of the numerical issues typically experienced for large numbers of observations or small values of $\alpha .$

Finally, we consider a proper uniform prior U(0, b) for $\xi ^2$ where b should be chosen by the user.

The complete list of priors used is presented in Table 1.

Table 1 Prior competitors in the simulation study. The same priors are used for $\xi ^2$ and $\zeta ^2$. The table is based on Table 1 from Klein and Kneib (2016)

In the case of the half-Cauchy prior, we only evaluate its performance for $\theta ^{\kappa }_z$, and not for $\beta$. The reason for this becomes clear in the sections that follow, where $\beta$ is generally quite robust to different prior specifications. Finally, one could also consider other priors for which user-defined scaling is available, such as the half-normal. However, these results do not add additional information, and we refrain from presenting them.

4.4 Results

Scenario 1: :

The results in Fig. 2 show that all priors perform reasonably and similarly well. Thus, there is no evidence that a PC-prior that allows the fixed effects to be in an interval of length no larger than $2\pi$ improves results.

Scenario 2: :

In Fig. 3, the results for $\beta$ are identical to the ones in Scenario 1, where using a PC-prior for covariate effects in the mean does not improve results. However, in Fig. 4, when considering non-stationarity in the covariance function, the log-MSE changes noticeably for different prior elicitations. The inverse gamma prior with strong shrinkage toward zero, i.e., $IG(a=1, b=0.005)$, has the best performance, followed by the scaled inverse gamma and PC-priors with $\alpha = 0.01$. Less informative priors allow for less shrinkage, thus are also less able to prevent overfitting.

Scenario 3: :

Once more, the PC-prior for the fixed effects does not seem to accrue any improvements in terms of the log-MSE compared to its competitors. However, compared to the previous scenarios, the log-MSE of $\beta$ increases considerably, indicating that there is more difficulty identifying fixed effects when the covariance is also non-stationary. This is a known fact for single replicate GRF models (Fuglstad et al. 2015). When it comes to the priors for non-stationarity in the covariance function, we get quite distinct behaviors between priors. In comparison with Scenario 2, the inverse gamma prior with strong shrinkage now performs the worst by not being able to capture the positive $\theta ^\kappa _z$. The uniform prior performs distinctively well, despite the high variance for small sample sizes. Finally, the PC-prior also demonstrates its flexibility, by having its best performance for $\alpha = 0.5$ and reaching a plateau after that (Figs. 5, 6).

Scenario 4: :

As it can be observed in Fig. 7, when it comes to mean, none of the priors stands out. However, this scenario has the highest values for the log-MSE out of all the models considered. This is not surprising, as this is the only model for which the estimated model is less flexible than what the data generation process.

Fig. 2

Log-MSE of $\beta$ in Scenario 1. The columns represent different samples sizes n

Fig. 3

Log-MSE of $\beta$ in Scenario 2. The columns represent different samples sizes n, and the rows represent different priors for $\xi ^2$

Fig. 4

Log-MSE of $\theta ^\kappa _z$ in Scenario 2. The columns represent different samples sizes n, and the rows represent different priors for $\zeta ^2$

Fig. 5

Log-MSE of $\beta$ in Scenario 3. The columns represent different samples sizes n, and the rows represent different priors for $\xi ^2$

Fig. 6

Log-MSE of $\theta ^\kappa _z$ in Scenario 3. The columns represent different samples sizes n, and the rows represent different priors for $\zeta ^2$

Fig. 7

Log-MSE of $\beta$ in Scenario 4. The columns represent different samples sizes n, and the rows represent different priors for $\xi ^2$

4.5 Main conclusions

When it comes to non-stationarity in the mean, all priors lead to satisfying, nearly identical, results. Thus, there is no evidence to believe that a PC-prior for the fixed effects in a wrapped-SPDE model, i.e., restricting the fixed effects to an interval of length of about $2\pi$, is beneficial.

When it comes to non-stationarity in the covariance, results from Scenario 2 and Scenario 3 demonstrate that a PC-prior with $\alpha = 0.3$ is able to both control for overfitting and capture nonzero values of the non-stationary components of the covariance function.

The log-MSE for $\theta ^\kappa _z$ is always considerably higher than for $\beta$. Thus, the fixed effects are considerably easier to estimate—even for circular responses, than the covariance effects. However, fixed effects become more difficult to identify when there is also non-stationarity in the covariance.

5 Application to wind directions in Germany

Wind directions are measured in radians in the interval $[0, 2 \pi )$ and indicate where the wind blows from at a given location. In Germany, wind directions are characterized by predominant westerly winds, coming from the Atlantic Ocean. On the eastern side, wind is generated in the Caucasus, entering Germany through Poland and the Czech Republic. The two wind currents typically clash in northern Germany.

Given the periodic nature of these data, in this section we evaluate the performance of the wrapped-SPDE model when studying wind directions in Germany. We compare the ability of a fully stationary spatial model—stationary mean and covariance, to describe wind directions, in comparison with the fully non-stationary spatial model we developed in this paper, non-stationary mean and covariance.

5.1 Data

German wind data are publicly available on the website of the German weather service Deustcher Wetterdienst (DWD). These data are collected every 10 min at the 263 DWD weather stations. Other weather variables, such as wind speed, air humidity, temperature, and altitude, can be found on the DWD website.

The wrapped Gaussian distribution is unimodal, and consequently, we need to avoid situations in which over a large region, at a given time, a storm is rotating or two different weather systems are meeting (Jona-Lasinio et al. 2012; Mastrantonio et al. 2016b). Given this, and in order to cover a wide range of behavior of wind directions in Germany, we study two different periods of 10 days and calculate the corresponding (circular) average wind direction for each location based on the 10-minute data. The two periods are:

• Stormy weather period: from September 23 to October 2, 2019.

• Calm weather period: from April 1 to April 10, 2019.

Fig. 8

Stormy weather period. On the left: circular average of the 10-minute data over 10 days. On the right: circular histogram of the corresponding observed wind directions

Fig. 9

Calm weather period. On the left: circular average of the 10-minute data over 10 days. On the right: circular histogram of the corresponding observed wind directions

The two full datasets are represented in Figs. 8 and 9. During a storm, wind directions are quite similar throughout the domain. During a calm weather period, one should expect more “flips” in the direction of the wind. This matches our examples, where in Fig. 8 an easterly wind storm covers the whole domain, while in Fig. 9 wind currents seem to clash in the south, creating many changes in direction.

5.2 Model specifications and selection criterion

The data are analyzed as follows. We randomly select a holdout set of data consisting of $20\%$ of the locations and use the remaining $80\%$ as training data. We fit the training data with a

• 1. Fully stationary model: $\varvec{z}(\varvec{s}) = \varvec{z^\kappa }(\varvec{s}) = \varvec{0}$.

• 2. Fully non-stationary model: $\varvec{z}(\varvec{s}) \ne \varvec{0}$ and $\varvec{z}^\kappa (\varvec{s}) \ne \varvec{0}$.

Model performance is evaluated using the circular continuous ranked probability score (Grimit et al. 2006),

$$\begin{aligned} \text{ CRPS }(P, X) = E_F \lbrace \alpha _{{\mathrm{CRPS}}}(x, X) \rbrace - \frac{1}{2} E_F \lbrace \alpha _{{\mathrm{CRPS}}}(x, x^*) \rbrace , \end{aligned}$$

where $\alpha _{{\mathrm{CRPS}}}$ represents the cosine distance, P is a forecast distribution on the circle, x and $x^*$ are independent copies of a circular random variable with distribution P and X is the verifying direction. This criterion is negatively oriented, and it is expressed in units of angular distance, with a maximum allowed of $\pi$. We use the implementation from R-CircSpaceTime (Jona Lasinio et al. 2020) and evaluate it for the test data.

Fig. 10

Posterior predictive mean (left) and standard deviation (right) for each test location during a calm weather period for the fully stationary and non-stationary models. The black arrows represent the true wind directions (left) and the corresponding standard deviation of zero (right)

The covariates considered for $\varvec{z}(\varvec{s})$ are maximum wind speed, average air humidity, and temperature at 10 ms height. For $\varvec{z^\kappa }(\varvec{s})$, we consider altitude and latitude. We additionally applied a tensor-product spline to the altitude covariate to ensure a smoothed density surface. It is important to avoid having the same set of covariates in the mean and covariance, in order to reduce potential confounding between the first- and the second-order structure. The covariates are chosen according to the overall model fit, measured by CRPS. The mesh used can be found in Appendix E.

We use the prior hierarchy from Sect. 2.8. We let each model run long enough such that the potential reduction factor, $\hat{\text {R}}$, for all parameters is stable and below 1.2 (Gelman et al. 1992). We use 30,000 samples, with a burn-in of 10,000, and thinning factor of 10.

5.3 Results

Table 2 shows the CRPS for the test data in both periods. Wind directions are easy to predict during the stormy weather period, as these are quite systematic throughout the domain. Thus, both the fully stationary and non-stationary models perform quite well and achieve a CRPS of 0.03. All the parameters in $\varvec{\beta }$ are significant, while the parameters in $\varvec{\theta }^\kappa _z$ are all insignificant. This suggests that the PC-prior for the mean could potentially have lower $\alpha$ such that it provides more shrinkage.

In a period of calm weather, in which there are shifts in the direction of the wind, the CRPS is generally higher than for a stormy weather period. By including covariates in mean and covariance, we are more able to account for these shifts in the direction of wind. All parameters in $\varvec{\beta }$ and $\varvec{\theta }^\kappa _z$ are significant. The CRPS for the fully non-stationary model is considerably lower than for the fully stationary model. As shown in Table 2, the largest improvements in CRPS occur in southern Germany (northing smaller than 0.5). Figure 10 shows the posterior predictive circular mean and standard deviation of the response on the test locations. The fully stationary model is able to capture the behavior in the north of Germany, but in the area where both wind currents clash in the south, adding covariate information considerably improves mean predictions. Moreover, in the north the prediction uncertainty is lower under the non-stationary model and in the south the prediction uncertainty is similar for both models.. The implied non-stationarity in the mean and covariance during the calm weather period is shown in Fig. 11. The figure shows the average range and fixed effects $\beta _0 + \varvec{z}(\varvec{s})'\varvec{\beta }$. The former is evaluated on the mesh nodes inside the domain (Germany), while the later on the training data locations. Details on the posterior distribution of $K(\varvec{s})$ are provided in Appendix F.

Table 2 CRPS of the test data during the storm and calm weather periods and for the two models considered

Fig. 11

Average spatial range and fixed effects $\beta _0 + \varvec{z}(\varvec{s})'\varvec{\beta }$ based on training data for the calm weather period. For the range, the locations represent the mesh nodes inside the domain (Germany)

5.4 Implications and relevance

Considering orographic and meteorological factors when modeling wind directions can considerably facilitate the prediction of wind shifts and wind behavior in general. By building a model that flexibly allows the user to include covariates in the mean and the covariance of the response model, we are able to considerably improve predictions. Such interpolation properties for wind directions could serve as an input for other modeling tasks in the analysis of climate variables, which, in combination with the use of sparse spatial precision matrices, would have great potential in the generation of efficient models for large-scale datasets for meteorological data.

6 Discussion

The derivation of spatial models for circular data can present several challenges. In this paper, we cover an important gap in the literature of spatial wrapped Gaussian models by developing a method that allows for the flexible inclusion of covariates in the mean and covariance, while only restricting the covariates in the covariance to be a smooth function of space.

In order to prevent overfitting, as well as to crucially improve the estimation of parameters associated with the non-stationary component of the covariance, we develop PC-priors for the mean and covariance of the wrapped-SPDE model. The PC-prior for the mean allows the fixed effects to be in an interval of length no larger than $2\pi$, i.e., the period of the circular response. Finally, by exploring the Markov property in GMRFs, the wrapped-SPDE model is feasible for large spatial datasets, as well as for large-scale simulation studies.

In a simulation study, we show that a PC-prior penalizing non-stationarity in the covariance function prevents overfitting and, in general, improves estimation. However, the non-stationary component of the mean is not sensitive to prior elicitation and, thus, does not seem to benefit from the developed PC-prior.

The model introduced can be improved in several ways. The wrapped Gaussian distribution is symmetric and unimodal. More flexible distributions should be considered. Possible alternatives are the wrapped skew Gaussian distribution (Mastrantonio et al. 2016a), mixture models (Ameijeiras-Alonso et al. 2019; Ranalli et al. 2018), or the projected Gaussian distribution (Wang and Gelfand 2013; Wikle et al. 2001). Furthermore, the winding number $K(\varvec{s})$ is an essential key to our model and it is reasonable to assume that it is spatially correlated. However, the fact that $K(\varvec{s})$ should be an integer complicates the modeling. To add to this, having two spatial fields in the model potentially additively might lead to identification issues. Nonetheless, results showed that once we allow enough flexibility/non-stationarity in the unwrapped model, the current version of $K(\varvec{s})$ performs well enough. Finally, in future work, the present model should be extended to space-time settings.