Variational inference and sparsity in high-dimensional deep Gaussian mixture models

Abstract

Gaussian mixture models are a popular tool for model-based clustering, and mixtures of factor analyzers are Gaussian mixture models having parsimonious factor covariance structure for mixture components. There are several recent extensions of mixture of factor analyzers to deep mixtures, where the Gaussian model for the latent factors is replaced by a mixture of factor analyzers. This construction can be iterated to obtain a model with many layers. These deep models are challenging to fit, and we consider Bayesian inference using sparsity priors to further regularize the estimation. A scalable natural gradient variational inference algorithm is developed for fitting the model, and we suggest computationally efficient approaches to the architecture choice using overfitted mixtures where unnecessary components drop out in the estimation. In a number of simulated and two real examples, we demonstrate the versatility of our approach for high-dimensional problems, and demonstrate that the use of sparsity inducing priors can be helpful for obtaining improved clustering results.

1 Introduction

Exploratory data analysis tools such as cluster analysis need to be increasingly flexible to deal with the greater complexity of datasets arising in modern applications. For high-dimensional data, there has been much recent interest in deep clustering methods based on latent variable models with multiple layers. Our work considers deep Gaussian mixture models for clustering, and in particular a deep mixture of factor analyzers (DMFA) model recently introduced by Viroli and McLachlan (2019). The DMFA model is highly parametrized, and to make the estimation tractable Viroli and McLachlan (2019) consider a variety of constraints on model parameters which enable them to obtain promising results. The objective of the current work is to consider a Bayesian approach to estimation of the DMFA model which uses sparsity-inducing priors to further regularize the estimation. We use the horseshoe prior of Carvalho and Polson (2010), and demonstrate in a number of problems that the use of sparsity-inducing priors is helpful. This is particularly true in clustering problems which are high-dimensional and involve a large number of noise features. A computationally efficient natural gradient variational inference scheme is developed, which is scalable to high-dimensions and large datasets. A difficult problem in the application of the DMFA model is the choice of architecture, i.e., determining the number of layers and the dimension of each layer, since trying many different architectures is computationally burdensome. We discuss useful heuristics for choosing good models and selecting the number of clusters in a computationally thrifty way, using overfitted mixtures (Rousseau and Mengersen 2011) with suitable priors on the mixing weights.

There are several suggested methods in the literature for constructing deep versions of Gaussian mixture models (GMM)s involving multiple layers of latent variables. One of the earliest is the mixture of mixtures model of Li (2005). Li (2005) considers modeling non-Gaussian components in mixture models using a mixture of Gaussians, resulting in a mixture of mixtures structure. The model is not identifiable through the likelihood, and Li (2005) suggests several ways to address this issue, as well as methods for choosing the number of components for each cluster. Malsiner-Walli et al. (2017) identify the model through the prior in a Bayesian approach, and consider Bayesian methods for model choice. Another deep mixture architecture is suggested in van den Oord and Schrauwen (2014). The authors consider a network with linear transformations at different layers, and the random sampling of a path through the layers. Each path defines a mixture component by applying the corresponding sequence of transformations to a standard normal random vector. Their approach allows a large number of mixture components, but without an explosion of the number of parameters due to the way parameters are shared between components. Chandra et al. (2020) propose a latent factor mixture model with sparsity inducing priors on the factor loading matrices suitable for problems where the number of features exceeds the number of observations, a setting which is not considered here.

The model of Viroli and McLachlan (2019) considered here is a multi-layered extension of the mixture of factor analyzers (MFA) model (Ghahramani and Hinton 1997; McLachlan et al. 2003). The MFA model is a GMM in which component covariance matrices have a parsimonious factor structure, making this model suitable for high-dimensional data. The factor covariance structure can be interpreted as explaining dependence in terms of a low-dimensional latent Gaussian variable. Extending the MFA model to a deep model with multiple layers has two main advantages. First, non-Gaussian clusters can be obtained and second, it enables the fitting of GMMs with a large number of components, which is particularly relevant for high-dimensional data and cases when the number of true clusters is large. Tang et al. (2012) were the first to consider a deep MFA model, where a mixture of factor analyzers model is used as a prior for the latent factors instead of a Gaussian distribution. Applying this idea recursively leads to deep models with many layers. Their architecture splits components into several subcomponents at the next layer in a tree-type structure. Yang et al. (2017) consider a two-layer version of the model of Tang et al. (2012) incorporating a common factor loading matrix at the first level and some other restrictions on the parametrization. Fuchs et al. (2022) extend the model of Viroli and McLachlan (2019) to mixed data.

The model of Viroli and McLachlan (2019) combines some elements of the models of Tang et al. (2012) and van den Oord and Schrauwen (2014). Similar to Tang et al. (2012), an MFA prior is considered for the factors in an MFA model and multiple layers can be stacked together. However, similar to the model of van den Oord and Schrauwen (2014), their architecture has parameters for Gaussian component distributions with factor structure arranged in a network, with each Gaussian mixture component corresponding to a path through the network. Parameter sharing between components and the factor structure makes the model parsimonious. Viroli and McLachlan (2019) consider restrictions on the dimensionality of the factors at different layers and other model parameters to help identify the model. A stochastic EM algorithm is used for estimation, and they report improved performance compared to greedy layerwise fitting algorithms. For choosing the network architecture, they fit a large number of different architectures and use the Akaike Information Criterion (AIC) or Bayesian Information Criterion (BIC) to choose the final model. Selosse et al. (2020) report that even with the identification restrictions suggested in Viroli and McLachlan (2019), it can be very challenging to fit the DMFA model. The likelihood surface has a large number of local modes, and it can be hard to find good modes, possibly because the estimation of a large number of latent variables is difficult. This is one motivation for the sparsity priors we introduce here. While sparse Bayesian approaches have been considered before for both factor models (see, e.g., Carvalho et al. 2008; Bhattacharya and Dunson 2011; Ročková and George 2016; Hahn et al. 2018, among many others) and the MFA model (Ghahramani and Beal 2000), they have not been considered for the DMFA model.

The structure of the paper is as follows. In Sect. 2 we introduce the DMFA model of Viroli and McLachlan (2019) and our Bayesian treatment making appropriate prior choices. Section 3 describes our scalable natural gradient variational inference method, and the approach to choice of the model architecture. Section 4 illustrates the good performance of our method for simulated data in a number of scenarios and compares our method to several alternative methods from the literature for simulated and benchmark datasets considered in Viroli and McLachlan (2019). Although it remains challenging to fit complex latent variable models such as the DMFA, we find that in many situations which are well suited to sparsity our approach is helpful for producing better clusterings. Sections 5 and 6 consider two real high-dimensional examples on gene expression data and taxi networks illustrating the potential of our Bayesian treatment of DMFA models. Section 7 gives some concluding discussion.

2 Bayesian deep mixture of factor analyzers

This section describes our Bayesian DMFA model. We consider a conventional MFA model first in Sect. 2.1, and then the deep extension of this by Viroli and McLachlan (2019) in Sect. 2.2. The priors used for Bayesian inference are discussed in Sect. 2.3.

2.1 MFA model

In what follows we write ${{\,\mathrm{\mathcal {N}}\,}}(\mu ,\Sigma )$ for the normal distribution with mean vector $\mu$ and covariance matrix $\Sigma$, and $\phi (y;\mu ,\Sigma )$ for the corresponding density function. Suppose $y_i=(y_{i1},\dots , y_{id})^\top$, $i=1,\dots , n$ are independent identically distributed observations of dimension d. An MFA model for $y_i$ assumes a density of the form

$$\begin{aligned}&\sum _{k=1}^K w_k \phi (y_i;\mu _k,B_kB_k^\top +\delta _k), \end{aligned}$$

(1)

where $w_k>0$ are mixing weights, $k=1,\dots , K$, with $\sum _{k=1}^K w_k=1$; $\mu _k=(\mu _{k1},\dots , \mu _{kd})^\top$ are component mean vectors; and $B_kB_k^\top +\delta _k$, $k=1,\dots , K$, are component specific covariance matrices with $B_k$ $d\times D$ matrices, $D\ll d$, and $\delta _k$ are $d\times d$ diagonal matrices with diagonal entries $(\delta _{k1},\dots , \delta _{kd})^\top$. The model (1) has a generative representation in terms of D-dimensional latent Gaussian random vectors, $z_i\sim {{\,\mathrm{\mathcal {N}}\,}}(0,I)$, $i=1,\dots , n$. Suppose that $y_i$ is generated with probability $w_k$ as

$$\begin{aligned} y_i&=\mu _k+B_k z_i+\epsilon _{ik}, \end{aligned}$$

(2)

where $\epsilon _{ik}\sim {{\,\mathrm{\mathcal {N}}\,}}(0,\delta _k)$. Under this generative model, $y_i$ has density (1). The latent variables $z_i$ are called factors, and the matrices $B_k$ are called factor loadings or factor loading matrices. In ordinary factor analysis (Bartholomew et al. 2011), which corresponds to $K=1$, restrictions on the factor loading matrices are made to ensure identifiability, and similar restrictions are needed in the MFA model. Common restrictions are lower-triangular structure with positive diagonal elements, or orthogonality of the columns of the factor loading matrix. With continuous shrinkage sparsity-inducing priors and careful initialization of the variational optimization algorithm, we did not find imposing an identifiability restriction such as a lower-triangular structure on the factor loading matrices to be necessary in our applications later. Identifiability issues for sparse factor models with point mass mixture priors have been considered recently in Frühwirth-Schnatter and Lopes (2018).

The MFA model is well suited to analyzing high-dimensional data, because the modeling of dependence in terms of low-dimensional latent factors results in a parsimonious model. The idea of deep versions of the MFA model is to replace the Gaussian assumption $z_i\sim {{\,\mathrm{\mathcal {N}}\,}}(0,I)$ with the assumption that the $z_i$’s themselves follow an MFA model. This idea can be applied recursively, to define a deep model with many layers.

2.2 DMFA model

Suppose once again that $y_i$, $i=1,\dots , n$, are independent and identically distributed observations of dimension $D^{(0)}=d$, and define $y_i=z_i^{(0)}$. We consider a hierarchical model in which latent variables $z_i^{(l)}$, at layer $l=1,\dots , L$ are generated according to the following generative process. Let $K^{(l)}$ denote the number of mixture components at layer l. Then, with probability $w_k^{(l)}$, $k=1,\dots , K^{(l)}$, $\sum _k w_k^{(l)}=1$, $z_i^{(l-1)}$ is generated as

$$\begin{aligned} z_i^{(l-1)}&= \mu _k^{(l)}+B_k^{(l)}z_i^{(l)}+\epsilon _{ik}^{(l)}, \end{aligned}$$

(3)

where $\epsilon _{ik}^{(l)}\sim {{\,\mathrm{\mathcal {N}}\,}}(0,\delta _k^{(l)})$, $\mu _k^{(l)}$ is a $D^{(l-1)}$-vector, $B_k^{(l)}$ is a $D^{(l-1)}\times D^{(l)}$ factor loading matrix, $\delta _k^{(l)}={\text{ diag }}(\delta _{k1}^{(l)},\dots , \delta _{kD^{(l-1)}}^{(l)})$ is a $D^{(l-1)}\times D^{(l-1)}$ diagonal matrix with diagonal elements $\delta _{kj}^{(l)}>0$ and $z_i^{(L)}\sim {{\,\mathrm{\mathcal {N}}\,}}(0,I_{D^{(L)}})$. Eq. (3) is the same as the generative model (2) for $z_i^{(l-1)}$, except that we have replaced the Gaussian assumption for the factors appearing on the right-hand side with a recursive modeling using the MFA model. Similar to the MFA each successive layer in the deep model performs some type of dimension reduction, so $D^{(l+1)}\ll D^{(l)}$ for $l=0,\dots ,L$. It is always recommended to use the Anderson–Rubin condition $D^{(l+1)}\le \frac{D^{(l)}-1}{2}$ for $l=0,\dots ,L$ in the construction of the model, which is further discussed in Sect. 3.7. Write $\text {vec}(B_k^{(l)})$ for the vectorization of $B_k^{(l)}$, the vector obtained by stacking the elements of $B_k^{(l)}$ into a vector columnwise. Write

$$\begin{aligned} \begin{aligned} z^{(l)}&= \left( {z_1^{(l)}}^\top , \dots , {z_n^{(l)}}^\top \right) ^\top , \\ \mu ^{(l)}&= \left( {\mu _1^{(l)}}^\top ,\dots , {\mu _{K^{(l)}}^{(l)}}^\top \right) ^\top , \\ B^{(l)}&=\left( {\text {vec}\left( B_1^{(l)}\right) }^\top ,\dots , {\text {vec}\left( B_{K^{(l)}}^{(l)}\right) }^\top \right) ^\top , \\ \delta ^{(l)}&=\left( {\delta _1^{(l)}}^\top ,\dots , {\delta _{K^{(l)}}^{(l)}}^\top \right) ^\top \\ w^{(l)}&=\left( w_1^{(l)},\dots , w_{K^{(l)}}^{(l)}\right) ^\top , \end{aligned} \qquad \begin{aligned} z&= \left( {z^{(1)}}^\top ,\dots , {z^{(L)}}^\top \right) ^\top , \\ \mu&=\left( {\mu ^{(1)}}^\top ,\dots , {\mu ^{(L)}}^\top \right) ^\top , \\ B&=\left( {B^{(1)}}^\top ,\dots , {B^{(L)}}^\top \right) ^\top , \\ \delta&=\left( {\delta ^{(1)}}^\top ,\dots , {\delta ^{(L)}}^\top \right) ^\top , \\ w&=\left( {w^{(1)}}^\top ,\dots , {w^{(L)}}^\top \right) ^\top . \end{aligned} \end{aligned}$$

In (3), we also denote $\gamma _{ik}^{(l)}=1$ if $z_i^{(l-1)}$ is generated from the k-th component model with probability $w_k^{(l)}$, $\gamma _{ik}^{(l)}=0$ otherwise, and

$$\begin{aligned}&\gamma =\left( {\gamma ^{(1)}}^\top ,\dots , {\gamma ^{(L)}}^\top \right) ^\top , \;\;\; \gamma ^{(l)}\\&=\left( {\gamma _1^{(l)}}^\top ,\dots , {\gamma _n^{(l)}}^\top \right) ^\top ,\;\;\;\gamma _i^{(l)}\\&=\left( \gamma _{i1}^{(l)},\dots , \gamma _{iK^{(l)}}^{(l)}\right) ^\top . \end{aligned}$$

Viroli and McLachlan (2019) observe that their DMFA model is just a Gaussian mixture model with $\prod _{l=1}^L K^{(l)}$ components. The components correspond to “paths” through the factor mixture components at the different levels. Write $k_l\in \{1,\dots , K^{(l)}\}$ for the index of a factor mixture component at level l. Let $k=(k_1,\dots , k_L)^\top$ index a path. Let $w(k)=\prod _{l=1}^L w_{k_l}^{(l)}$,

$$\begin{aligned} \mu (k)= & {} \mu _{k_1}^{(1)}+\sum _{l=2}^L\left( \prod _{m=1}^{l-1}B_{k_m}^{(m)}\right) \mu _{k_l}^{(l)} \;\; \text{ and } \;\; \\ \Sigma (k)= & {} \delta _{k_1}^{(1)}+\sum _{l=2}^L \left( \prod _{m=1}^{l-1} B_{k_m}^{(m)}\right) \delta _{k_l}^{(l)}\left( \prod _{m=1}^{l-1}B_{k_m}^{(m)}\right) ^\top . \end{aligned}$$

Then, the DMFA model corresponds to the Gaussian mixture density

$$\begin{aligned} \sum _{k} w(k) \phi (y;\mu (k),\Sigma (k)). \end{aligned}$$

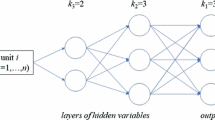
The DMFA allows expressive modeling through a large number of mixture components, but due to the parameter sharing and the factor structure the model remains parsimonious. An example of a DMFA architecture is given in Fig. 1.

Fig. 1

Example of a DMFA architecture with $L=2$ layers. The latent input variables $z_i^{(2)}$ are fed through a fully connected network with $L=2$ layers, with $K^{(1)}=4$ and $K^{(2)}=3$ components, respectively. A possible path through the network is marked in orange. Each component of the network corresponds to a factor analyzer (FA), which transforms the input variable by $z_i^{(l-1)} = \mu _k^{(l)}+B_k^{(l)}z_i^{(l)}+\epsilon _{ik}^{(l)}, l=1,2, k=1,\dots ,K^{(l)}$. This way each layer can be viewed as a MFA

2.3 Prior distributions

For our priors on component mean parameters at each layer, we use heavy-tailed Cauchy priors, and for standard deviations, half-Cauchy priors. These thick-tailed priors tend to be dominated by likelihood information in the event of any conflict with the data. For component factor loading matrices, we use sparsity-inducing horseshoe priors. Sparse structure in factor loading matrices is motivated by the common situation in which dependence can be explained through latent factors, where each one influences only a small subset of components. The horseshoe priors are thus a reasonable choice even though other choices would be possible (see, e.g., the discussion of Bhattacharya and Dunson 2011).

Malsiner-Walli et al. (2017) consider a Bayesian approach to the mixture of mixtures model, which is a kind of DGMM, and give an interesting discussion of prior choice in that context. They observe that in the mixture of mixtures, the mixture at the higher level groups together the lower level clusters to accommodate non-Gaussianity, and their prior choices are constructed with this in mind. Unfortunately, the intuition behind their priors does not hold for the model considered here, since the network architecture of Viroli and McLachlan (2019) does not possess the nested structure of the mixture of mixtures, which is crucial to the prior construction in Malsiner-Walli et al. (2017).

Selecting marginally independent priors, which do not share information across layers and components, is handy for our variational inference approach as it allows us to write down the mean field approximation in closed form as explained further in Sect. 3.2.

A precise description of the priors will be given now. Denote the the complete vector of parameters by $\vartheta = (\mu ^\top ,B^\top ,z^\top ,w^\top ,\delta ^\top ,\gamma ^\top )^\top .$ First, we assume independence between $\mu$, B, z, $\delta$ and w in their prior distribution. For the marginal prior distribution for $\mu$, we furthermore assume independence between all components, and the marginal prior density for $\mu _{kj}^{(l)}$ is assumed to be a Cauchy density, ${{\,\mathrm{\mathcal {C}}\,}}(0,G^{(l)})$, where $G^{(l)}$ is a known hyperparameter possibly depending on l, $l=1,\dots , L$.

This Cauchy prior can be represented hierarchically as a mixture of a univariate Gaussian and inverse gamma distribution, i.e.,

$$\begin{aligned}&\mu _{kj}^{(l)}|g_{kj}^{(l)}\sim {{\,\mathrm{\mathcal {N}}\,}}(0,G^{(l)}g_{kj}^{(l)}),\;\;\;g_{kj}^{(l)}\sim {{\,\mathrm{\mathcal{I}\mathcal{G}}\,}}\left( \frac{1}{2},\frac{1}{2}\right) , \end{aligned}$$

and we write

$$\begin{aligned}&g=\left( {g^{(1)}}^\top ,\dots , {g^{(L)}}^\top \right) ^\top ,\;\;\;g^{(l)}=\left( {g_1^{(l)}}^\top ,\dots , {g_{K^{(l)}}^{(l)}}^\top \right) ^\top ,\\&g_k^{(l)}=\left( g_{k1}^{(l)},\dots , g_{kD^{(l-1)}}^{(l)}\right) ^\top . \end{aligned}$$

We augment the model to include the parameters g in this hierarchical representation.

For the prior on B, we assume elements are independently distributed a priori with a horseshoe prior (Carvalho and Polson 2010),

$$\begin{aligned}&\text {vec}\left( B_k^{(l)}\right) _j \sim {{\,\mathrm{\mathcal {N}}\,}}\left( 0,\tau _k^{(l)}/h_{kj}^{(l)}\right) ,\; \tau _{k}^{(l)}\sim {{\,\mathrm{\mathcal{I}\mathcal{G}}\,}}\left( \frac{1}{2},\frac{1}{\xi _k^{(l)}}\right) ,\;\\&\xi _k^{(l)}\sim {{\,\mathrm{\mathcal{I}\mathcal{G}}\,}}\left( \frac{1}{2},\frac{1}{(\nu ^{(l)})^2}\right) ,\\&h_{kj}^{(l)}\sim {{\,\mathrm{\mathcal {G}}\,}}\left( \frac{1}{2},c_{kj}^{(l)}\right) ,\;c_{kj}^{(l)}\sim {{\,\mathrm{\mathcal {G}}\,}}\left( \frac{1}{2},1\right) , \end{aligned}$$

where ${{\,\mathrm{\mathcal {G}}\,}}(a,b)$ denotes a gamma distribution with shape a and scale parameter b and we write

$$\begin{aligned}&\begin{aligned} h&=\left( {h^{(1)}}^\top ,\dots , {h^{(L)}}^\top \right) ^\top , \\ c&=\left( {c^{(1)}}^\top ,\dots , {c^{(L)}}^\top \right) ^\top , \end{aligned}&\begin{aligned} h^{(l)}&=\left( {h_1^{(l)}}^\top ,\dots , {h_{K^{(l)}}^{(l)}}^\top \right) ^\top , \\ c^{(l)}&=\left( {c_1^{(l)}}^\top ,\dots , {c_{K^{(l)}}^{(l)}}^\top \right) ^\top , \end{aligned}\\&\begin{aligned} h_k^{(l)}&=\left( h_{k1}^{(l)},\dots , h_{k\kappa ^{(l)}}^{(l)}\right) ^\top , \\ c_k^{(l)}&=\left( c_{k1}^{(l)},\dots , c_{k\kappa ^{(l)}}^{(l)}\right) ^\top , \end{aligned}\\&\begin{aligned} \tau&=\left( {\tau ^{(1)}}^\top ,\dots , {\tau ^{(L)}}^\top \right) ^\top , \\ \xi&=\left( {\xi ^{(1)}}^\top ,\dots , {\xi ^{(L)}}^\top \right) ^\top , \end{aligned}&\begin{aligned} \tau ^{(l)}&=\left( {\tau _1^{(l)}}^\top ,\dots , {\tau _{K^{(l)}}^{(l)}}^\top \right) ^\top , \\ \xi ^{(l)}&=\left( {\xi _1^{(l)}}^\top ,\dots , {\xi _{K^{(l)}}^{(l)}}^\top \right) ^\top , \end{aligned} \end{aligned}$$

where $\kappa ^{(l)}=D^{(l-1)} D^{(l)}$ and $\nu =({\nu ^{(1)}}^\top ,\dots , {\nu ^{(L)}}^\top )^\top \in \mathbb {R}^{L}$ are scale parameters assumed to be known. We augment the model to include the parameters $h,c,\tau ,\xi$ in the hierarchical representation.

For $\delta$, we assume all elements are independent in the prior with $\sqrt{\delta _{kj}^{(l)}}$ being half-Cauchy distributed, $\sqrt{\delta _{kj}^{(l)}}\sim {{\,\mathrm{\mathcal{H}\mathcal{C}}\,}}(A^{(l)})$, where the scale parameter $A^{(l)}$ is known and possibly depending on l, $l=1,\dots , L$. This prior can also be expressed hierarchically,

$$\begin{aligned}&\delta _{kj}^{(l)}|\psi _{kj}^{(l)}\sim {{\,\mathrm{\mathcal{I}\mathcal{G}}\,}}\left( \frac{1}{2},\frac{1}{\psi _{kj}^{(l)}}\right) \;\;\; \psi _{kj}^{(l)}\sim {{\,\mathrm{\mathcal{I}\mathcal{G}}\,}}\left( \frac{1}{2},\frac{1}{{A^{(l)}}^2}\right) , \end{aligned}$$

and we write

$$\begin{aligned}&\psi =\left( {\psi ^{(1)}}^\top ,\dots , {\psi ^{(L)}}^\top \right) ^\top ,\;\;\;\psi ^{(l)}=\left( {\psi _1^{(l)}}^\top ,\dots , {\psi _{K^{(l)}}^{(l)}}^\top \right) ^\top ,\\&\psi _k^{(l)}=\left( \psi _{k1}^{(l)},\dots , \psi _{kD^{(l-1)}}^{(l)}\right) ^\top . \end{aligned}$$

Once again, we can augment the original model to include $\psi$ and we do so.

The prior on w assumes independence between $w^{(l)}$, $l=1,\dots , L$, and the marginal prior for $w^{(l)}$ is Dirichlet, $w^{(t)} \sim Dir(\rho _{l}^{(t)},\ldots ,\rho _{k^{(t)}}^{(l)}$. The full set of unknowns in the model is $\lbrace \mu , B, z, w, \delta ,\gamma ,\psi ,g,h,c,\tau ,\xi \rbrace$ and we denote the corresponding vector of unknowns by

$$\begin{aligned} \theta&= \left( \mu ^\top ,\text {vec}(B)^\top ,z^\top ,w^\top ,\delta ^\top ,\gamma ^\top ,\psi ^\top ,g^\top ,h^\top ,c^\top ,\tau ^\top ,\xi ^\top \right) ^\top . \end{aligned}$$

A graphical representation of the model is given in Fig. 2.

Fig. 2

Graphical representation of all parameter dependencies for the Bayesian DMFA with sparsity priors for one layer $l=1,\dots ,L$. Latent variables are in circles, while hyperparameters are not. The parameters $\mu ^{(l)},B^{(l)},\delta ^{(l)}$ and $w^{(l)}$ act as MFA transformation on $z^{(l)}$. We observe $y=z^{(0)}$ and $z^{(L)}$ follows a low-dimensional standard Gaussian distribution

3 Variational inference for the Bayesian DMFA

Next we review basic ideas of variational inference and introduce a scalable variational inference method for the DMFA model.

3.1 Variational inference

Variational inference (VI) approximates a posterior density $p(\theta |y)$ by assuming a form $q_\lambda (\theta )$ for it and then minimizing some measure of closeness to $p(\theta |y)$. Here, $\lambda$ denotes variational parameters to be optimized, such as the mean and covariance matrix parameters in a multivariate Gaussian approximation. If the measure of closeness adopted is the Kullback–Leibler divergence, the optimal approximation maximizes the evidence lower bound (ELBO)

$$\begin{aligned} \mathcal {L}(\lambda )=\int q_{\lambda }(\theta )\log \left\{ \frac{p(y,\theta )}{q_{\lambda }(\theta )}\right\} d\theta \,, \end{aligned}$$

(4)

with respect to $\lambda$. Eq. (4) is an expectation with respect to $q_\lambda (\theta )$,

$$\begin{aligned} \mathcal {L}(\lambda )={\mathbb {E}}_{q_\lambda }\left\{ \log (h(\theta ))-\log (q_{\lambda }(\theta ))\right\} ,\, \end{aligned}$$

(5)

where $h(\theta )=p(y|\theta )p(\theta )$ and this observation enables an unbiased Monte Carlo estimation of the gradient of $\mathcal {L}(\lambda )$ after differentiating under the integral sign. This is often used with stochastic gradient ascent methods to optimize the ELBO, see Blei et al. (2017) for further background on VI methods. For some models and appropriate forms for $q_\lambda (\theta )$, ${\mathcal {L}}(\lambda )$ can be expressed analytically, and this is the case for our proposed VI method for the DFMA model. In this case, finding the optimal value $\lambda ^*$ does not require Monte Carlo sampling from the approximation to implement the variational optimization (see, e.g., Honkela et al. 2008), although the use of subsampling to deal with large datasets may still require the use of stochastic optimization.

3.2 Mean field variational approximation for DMFA

Choosing the form of $q_\lambda (\theta )$ requires balancing flexibility and computational tractability. Here, we consider the factorized form

$$\begin{aligned} q_\lambda (\theta )&= q(\mu )q(\text{ vec }(B))q(z)q(w)q(\delta )q(\gamma )q(\psi )\nonumber \\ {}&\quad \times q(g)q(h)q(c)q(\tau )q(\xi ) \end{aligned}$$

(6)

and each factor in Eq. (6) will also be fully factorized. For the DMFA model, the existence of conditional conjugacy through our prior choices means that the parametric form of the factors follows from the factorization assumptions made. We can give an explicit expression for the ELBO (see the Web Appendix A.2 for details) and use numerical optimization techniques to find the optimal variational parameter $\lambda ^*$. It is possible to consider less restrictive factorization assumptions than we have, retaining some of the dependence structure, while at the same time retaining the closed form for the lower bound. A fully factorized approximation has been used to reduce the number of variational parameters to optimize. For the fully factorized approximation, $\lambda$ has dimension

$$\begin{aligned} \sum _{l=1}^L K^{(l)}\left( 8D^{(l-1)}+6D^{(l)}D^{(l-1)}+2n+5\right) +2nD^{(l)}. \end{aligned}$$

3.3 Optimization for large datasets

Optimization of the lower bound (5) with respect to the high-dimensional vector of variational parameters is difficult. One problem is that the number of variational parameters grows with the sample size. This occurs because we need to approximate posterior distributions of observation specific latent variables $z_i^{(l)}$ and $\gamma _i^{(l)}$, $i=1,\dots , n$, $l=1,\dots , L$. To address this issue, we adapt the idea of stochastic VI by Hoffman et al. (2013) as follows. We split $\theta$ into so-called “global” and “local” parameters, $\theta =(\beta ^\top ,\zeta ^\top )^\top$, where

$$\begin{aligned} \beta =\left( \mu ^\top ,B^\top ,w^\top ,\delta ^\top ,\psi ^\top ,g^\top ,h^\top ,c^\top ,\tau ^\top ,\xi ^\top \right) ^\top , \end{aligned}$$

and $\zeta =(z^\top ,\gamma ^\top )^\top$ denote the “global” and “local” parameters of $\theta$, respectively.

We can similarly partition the variational parameters $\lambda$ into global and local components, $\lambda =(\lambda _G^\top ,\lambda _L^\top )^\top$, where $\lambda _G$ and $\lambda _L$ are the variational parameters appearing in the variational posterior factors involving elements of $\beta$ and $\zeta$, respectively. Write the lower bound ${\mathcal {L}}(\lambda )$ as ${\mathcal {L}}(\lambda _G,\lambda _L)$. Write $M(\lambda _G)$ for the value of $\lambda _L$ optimizing the lower bound with fixed global parameter $\lambda _G$. When optimizing ${\mathcal {L}}(\lambda )$, the optimal value of $\lambda _G$ maximizes

$$\begin{aligned} \overline{\mathcal {L}}(\lambda _G)&= {\mathcal {L}}(\lambda _G,M(\lambda _G)). \end{aligned}$$

Next, differentiate $\overline{\mathcal {L}}(\lambda _G)$ to obtain

$$\begin{aligned} \nabla _{\lambda _G} \overline{\mathcal {L}}(\lambda _G)&= \nabla _{\lambda _G}{\mathcal {L}}(\lambda _G,M(\lambda _G))\nonumber \\&\quad + \nabla _{\lambda _G}M(\lambda _G)^\top \nabla _M {\mathcal {L}}(\lambda _G,M(\lambda _G)) \nonumber \\&= \nabla _{\lambda _G}{\mathcal {L}}(\lambda _G,M(\lambda _G)). \end{aligned}$$

(7)

The last line follows from $\nabla _M {\mathcal {L}}(\lambda _G,M(\lambda _G))=0$, since $M(\lambda _G)$ gives the optimal local variational parameter values for fixed $\lambda _G$. Eq. (7) says that the gradient $\nabla _{\lambda _G} \overline{\mathcal {L}}(\lambda _G)$ can be computed by first optimizing to find $M(\lambda _G)$, and then computing the gradient of ${\mathcal {L}}(\lambda )$ with respect to $\lambda _G$ with $\lambda _L$ fixed at $M(\lambda _G)$.

We optimize $\overline{\mathcal {L}}(\lambda _G)$ using stochastic gradient ascent methods, which iteratively update an initial value $\lambda _G^{(1)}$ for $\lambda _G$ for $t\ge 1$ by the iteration

$$\begin{aligned} \lambda _G^{(t+1)}=\lambda _G^{(t)}+a_t\circ \widehat{\nabla _{\lambda _G} \overline{\mathcal {L}}}(\lambda _G^{(t)}), \end{aligned}$$

where $a_t$ is a vector-valued step size sequence, $\circ$ denotes elementwise multiplication, and $\widehat{\nabla _{\lambda _G} \overline{\mathcal {L}}}(\lambda _G^{(t)})$ is an unbiased estimate of the gradient of $\nabla _{\lambda _G} \overline{\mathcal {L}}(\lambda _G)$ at $\lambda _G^{(t)}$. An unbiased estimator of (7) is constructed by randomly sampling a mini-batch of the data. This enables us to avoid dealing with all local variational parameters at once, lowering the dimension of any optimization. Let A be a subset of $\{1,\dots , n\}$ chosen uniformly at random without replacement inducing the set of indices of a data mini-batch. Then, in view of (7), an unbiased estimate $\widehat{\nabla _{\lambda _G}\overline{\mathcal {L}}}(\lambda _G)$ of ${\nabla _{\lambda _G}}\overline{\mathcal {L}}(\lambda _G)$ can be obtained by

$$\begin{aligned} \widehat{\nabla _{\lambda _G}\overline{\mathcal {L}}}(\lambda _G)&= \nabla _{\lambda _G}\mathcal {L}^F(\lambda _G)+\frac{n}{|A|}\sum _{i\in A} \nabla _{\lambda _G} \mathcal {L}^i(\lambda _G,M(\lambda _G)), \end{aligned}$$

where |A| is the cardinality of A, and we have written ${\mathcal {L}}(\lambda )={\mathcal {L}}^F(\lambda _G)+\sum _{i=1}^n {\mathcal {L}}^i(\lambda )$, where ${\mathcal {L}}^i(\lambda )$ is the contribution to ${\mathcal {L}}(\lambda )$ of all terms involving the local parameter for the ith observation and ${\mathcal {L}}^F(\lambda _G)$ is the remainder. For this estimate, computation of all components of $M(\lambda _G)$ is not required, since only the optimal local variational parameters for the mini-batch are needed.

To optimize $\lambda _G$, we use the natural gradient (Amari 1998) rather than the ordinary gradient. The natural gradient uses an update which respects the meaning of the variational parameters in terms of the underlying distributions they index. Additionally, the use of natural gradients drastically reduces the number of iterations in which updates of components of $\lambda _G$ are pushed out of their respective parameter spaces. For example, the elements of $\lambda _G$, which correspond to variance parameters, have to be strictly positive. In the rare cases where a component update does not respect the constraints, we set the component to a small positive value. The natural gradient is given by $I_F(\lambda _G)^{-1} \widehat{\nabla _{\lambda _G}\overline{\mathcal {L}}}(\lambda _G)$, where $I_F(\lambda _G)=\text {Cov}(\nabla _{\lambda _G} q_{\lambda _G}(\beta ))$, where $q_{\lambda _G}(\beta )$ is the $\beta$ marginal of $q_\lambda (\theta )$. Because of the factorization of the variational posterior into independent components, it suffices to compute the submatrices of $I_F(\lambda _G)$ corresponding to each factor separately. For the Bayesian DMFA, $I_F(\lambda _G)^{-1}$ is available in closed form.

3.4 Algorithm

The complete algorithm can be divided into two nested steps iterating over the local and global parameters, respectively. First, an update of the global parameters is considered using a stochastic natural gradient ascent step for optimizing $\overline{\mathcal {L}}(\lambda _G)$, with the adaptive stepsize choice proposed in Ranganath et al. (2013). For estimating the gradient in this step, the optimal local parameters $M(\lambda _G)$ for the current $\lambda _G$ need to be identified for observations in a mini-batch. In theory, this can be done numerically by a gradient ascent algorithm. But this leads to a long run time, because one has to run this local gradient ascent until convergence for each step of the global stochastic gradient ascent. In our experience, it is not necessary to calculate $M(\lambda _G)$ exactly, and it suffices to use an estimate, which helps to decrease the run time of the algorithm. A natural approximate estimator for $M(\lambda _G)$ can be constructed in the following way. Start by estimating the most likely path $\gamma _i$ using the clustering approach described in Sect. 3.6, while setting $\beta$ to the current variational posterior mean estimate for the global parameters. The local variational parameters appearing in the factor $q\left( z_{ij}^{(l)}\right)$ are then estimated layerwise starting with $l=1$ by setting this density proportionally to $\exp \left( E\left( \log p\left( z_{ij}^{(l)}\vert z_{i}^{(l-1)},\gamma _i,\beta \right) \right) \right)$, where the expectation is with respect to $q\left( z_{ij}^{(l-1)}\right)$, and which has a closed form Gaussian expression. In layer 1, $z_i^{(0)}=y_i$. The above approximation is motivated by the mean field update for $q(z_{ij})$, which is proportional to the exponential of the expected log full conditional for $z_{ij}^{(l)}$. However, the usual mean field update to do the local optimization would require iteration, which is why we use the fast layerwise approximation. The complete algorithm, details of the local optimization step and explicit expressions for the conditional $p(z_{ij}^{(l)}\vert z_i^{(l-1)},\gamma _i,\beta )$ are given in the Web Appendix B.2. We calculate all gradients using the automatic differentiation of the Python package PyTorch (Paszke et al. 2017).

Due to the large number of local modes of the likelihood and the high-dimensionality of the parameter vector, convergence of the DMFA model can be challenging (Selosse et al. 2020). Convergence to a global optimum is not guaranteed and often only a local optimum is found. We recommend running the algorithm several times, selecting the run reaching the highest ELBO. The starting position $\lambda _G^{(0)}$ has huge impact on the convergence of the algorithm and aim at selecting it in a meaningful way, such that $\lambda _G^{(0)}$ is closer to a good mode than a random initialization would be. Details on our choice for $\lambda _G^{(0)}$ can be found in Web Appendix B.1.

3.5 Hyperparameter choices

For all experiments, we set the hyperparameters $G^{(l)}=2,\nu ^{(l)}=1$ and $A^{(l)}=2.5$. The hyperparameter $\rho _k^{(l)}$ is set either to 1 if the number of clusters desired and therefore the number of components in the respective layer is known, or to 0.5 if the number of components is unknown, see Sect. 3.7 for further discussion. In our experiments, the size of the mini-batch is set to $5\%$ of the data size, but not less then 1 or larger then 1024. This way the number of variational parameters which need to be updated at every step remains bounded regardless of the sample size n. We found these hyperparameter choices to work well in all the diverse scenarios considered in Sects. 4, 5 and 6 and therefore consider them as a default. However, if additional prior information is available, selecting different hyperparameters might be more suitable. For example, if the dependence structure between features is complex, it may be helpful to consider non-sparse factor loadings at the first layer, with higher levels of shrinkage in the prior at deeper layers where an elaborate modeling of dependence structure for the latent variables may be difficult to sustain. This can be achieved by setting $\nu ^{(1)}$ to a large value, for example, $\nu ^{(1)}=10^5$ and $\nu ^{(l)}=1$ for $l>1$.

3.6 Clustering with DMFA

The algorithm described in the previous section returns optimal variational parameters $\lambda _G$ for the global parameters $\beta$. A canonical point estimator for $\beta$ is then given by the mode of $q_\lambda (\theta )$. Following Viroli and McLachlan (2019), we consider only the first layer $l=1$ of the model for clustering. Specifically, the cluster of data point y is given by

$$\begin{aligned} {\mathop {{{\,\mathrm{{arg\,max}}\,}}}\limits _{k=1,\dots , K^{(1)}}} w_k^{(1)} p(y\vert \beta ,\gamma ^{(1)}_k=1). \end{aligned}$$

By integration over the local parameters for y, $p(y \vert \beta ,\gamma ^{(1)}_k=1)$ can be written as a mixture of $\prod _{r=2}^L K^{(r)}$ Gaussians of dimension $D^{(0)}$ for $k=1,\dots , K^{(1)}$. This way the parameters of the bottom layers $l=2,\dots ,L$ can be viewed as defining a density approximation to the different clusters and the overall model can be interpreted as a mixture of Gaussian mixtures. Alternatively, the DMFA can be viewed as a GMM with $\prod _{l=1}^LK^{(l)}$ components, where each component corresponds to a path through the model. By considering each of these Gaussian components as a separate cluster, the DMFA can be used to find a very large number of Gaussian clusters. However, Selosse et al. (2020) note that some of these “global” Gaussian components might be empty, even when there are data points assigned to every component in each layer. We investigate the idea of using the DMFA to fit a large-scale GMM further in Sect. 6.

3.7 Model architecture and model selection

So far it has been assumed that the number of layers L, the number of components in each layer $K^{(l)}$ and the dimensions of each layer $D^{(l)}$, $l=1,\dots L$, are known. As this is usually not the case in practice, we now discuss how to choose a suitable architecture.

If the number of mixture components $K^{(l)}$ in a layer is unknown, we initialize the model with a relatively large number of components, and set the Dirichlet prior hyperparameters on the component weights to $\rho _1^{(l)}=\dots =\rho _{K}^{(l)}=0.5$. A large $K^{(l)}$ corresponds to an overfitted mixture, and for ordinary Gaussian mixtures unnecessary components will drop out under suitable conditions (Rousseau and Mengersen 2011). A VI method for mixture models considering overfitted mixtures for model choice is discussed in McGrory and Titterington (2007). The results of Rousseau and Mengersen (2011) do not apply directly to deep mixtures because of the way parameters are shared between components, but we find that this method for choosing components is useful in practice. Our experiments show that in the case of deep Gaussian mixtures, the variational posterior concentrates around a small subset of components with high impact, while setting the weights for other components close to zero. Therefore, we remove all components with weights smaller than a threshold, set to be 0.01 in simulations.

The choice of the number of layers L and the dimensions D is a classical model selection problem, where the model m is chosen out of a finite set of proposed models in the model space $\mathcal {M}$. We assume a uniform prior on the model space $p(m)\propto 1$ for each $m\in \mathcal {M}$. Hence, the model can be selected by

$$\begin{aligned} {\hat{m}}= & {} {\mathop {{{\,\mathrm{{arg\,max}}\,}}}\limits _{m\in \mathcal {M}}}p(m|y)= {\mathop {{{\,\mathrm{{arg\,max}}\,}}}\limits _{m\in \mathcal {M}}}p(m)\int p(y\vert \theta ,m)p(\theta \vert m)d\theta \\= & {} {\mathop {{{\,\mathrm{{arg\,max}}\,}}}\limits _{m\in \mathcal {M}}} p(y|m). \end{aligned}$$

Denoting the ELBO for the architecture m with variational parameters $\lambda _m$ by $\mathcal {L}(\lambda _m \vert m)$, this is a lower bound for $\log p(y|m)$, which is tight if the variational posterior approximation is exact. Hence, we choose the selected model by ${\hat{m}}={\mathop {{{\,\mathrm{{arg\,max}}\,}}}\limits _{m\in \mathcal {M}}} \mathcal {L}(\lambda _m^* \vert m),$ where $\lambda _m^*$ denotes the optimal variational parameter value $\lambda _m$ for model m. Since it is computationally expensive to run the VI algorithm until convergence for all models $m\in \mathcal {M}$, a naive approach would be to estimate $\mathcal {L}(\lambda _m^* \vert m)$ via $\mathcal {L}(\lambda _m^{(T)}\vert m)$ after running the algorithm for T steps, where $\lambda _m^{(t)}$ is the value for $\lambda _m$ at iteration t.

In our experiments, we estimated $\mathcal {L}(\lambda _m^*\vert m)$ as the mean over the last $5\%$ of 250 iterations, i.e., ${\hat{m}}={\mathop {{{\,\mathrm{{arg\,max}}\,}}}\limits _{m\in \mathcal {M}}} \sum _{t=238}^{250} \mathcal {L}(\lambda _m^{(t)}\vert m).$ This calculation can be parallelized by running the algorithm for each model m on a different machine and only involves evaluations of the ELBO, which does not induce additional computational burden as the ELBO needs to be calculated for fitting the model. For the dimensions, we test all possible choices fulfilling the Anderson–Rubin condition $D^{(l+1)}\le \frac{D^{(l)}-1}{2}$ for $l=0,\dots ,L$, which is a necessary condition for model identifiability (Frühwirth-Schnatter and Lopes 2018). Additionally, this condition gives an upper bound for the number of layers. A model with L layers must have at least dimension $D^{(0)}=2^{L+1}-1$. However, in our experiments, we consider only models with $L=2$ or $L=3$ layers, because in our experience architectures with few layers and a rapid decrease in dimension outperform architectures with many deep layers. Once an architecture is chosen based on short runs, the fitting algorithm is fully run to convergence for the optimal choice.

The only input for the complete model selection procedure is the number of components for each layer. Having the initialized number of components as an input and selecting the remaining architecture parameters based on this selection can be motivated by the common situation where at least a rough estimate on the expected number of clusters can be given, while there is no prior information on the architecture parameters D and L available.

4 Benchmarking using simulated and real data

To demonstrate the advantages of our Bayesian DMFA with respect to clustering high-dimensional non-Gaussian data, computational efficiency of model selection, accommodating sparse structure and scalability to large datasets, we experiment on several simulated and publicly available benchmark examples.

4.1 Design of numerical experiments

First we consider two simulated datasets where our Bayesian approach with sparsity-inducing priors is able to outperform the maximum likelihood method considered in Viroli and McLachlan (2019). The data generating process for the first dataset scenario S1 is a GMM with many noisy (uninformative) features and sparse covariance matrices. Here, sparsity priors are helpful because there are many noise features. The data in scenario S2 has a similar structure to the real data from the application presented in Sect. 5 having unbalanced non-Gaussian clusters. Here, the true generative model has highly unbalanced group sizes, and the regularization that our priors provide is useful in this setting for stabilizing the estimation.

Five real datasets considered in Viroli and McLachlan (2019) are tested as well, and our method shows similar performance to theirs for these examples. However, we compare our method, which we will label VIdmfa, not only to the approach of Viroli and McLachlan (2019) (EMdgmm) but to several other benchmark methods, including a GMM based on the EM algorithm (EMgmm) and Bayesian VI approach by McGrory and Titterington (2007) (VIgmm), a skew-normal mixture (SNmm), a skew-t mixture (STmm), k-means (kmeans), partition around metroids (PAM), hierarchical clustering with Ward distance (Hclust), a factor mixture analyzer (FMA) and a mixture of factor analyzer (MFA). In the Web Appendix B, we give more details on all benchmark methods. To measure how close a set of clusters is to the ground truth labels, we consider three popular performance measures (e.g., Vinh et al. (2010)). These are the misclassification rate (MR), the adjusted rand index (ARI) and the adjusted mutual information (AMI). We refer to the Web Appendix C for details on tuning of benchmark methods as well as measures of performance and focus on the main results in the following.

4.2 Datasets

Below we describe the two simulated scenarios S1 and S2 involving sparsity, as well as the five real datasets used in Viroli and McLachlan (2019).

Scenario S1: Sparse location scale mixture. Datasets with $D^{(0)}=30$ features are drawn from a mixture of high-dimensional Gaussian distributions with sparse covariance structure. The first 15 of the features yield information on the clusters and are obtained from a mixture of $K=5$ Gaussian distributions with different means $\mu _k$ and covariances $\Sigma _k$. The mean for component $k=1,\ldots ,5$ has entries

$$\begin{aligned} (\mu _k)_j= {\left\{ \begin{array}{ll} -1 &{} \text{ if }\, k\, \text{ divides }\, j \\ 1 &{} \text{ otherwise, } \end{array}\right. } \end{aligned}$$

for $j=1,\dots ,15$. The covariance matrices $\Sigma _k$ are drawn independently based on the Cholesky factors via the function make_sparse_spd_matrix from the Python package scikit-learn (Pedregosa et al. 2011). An entry of the Cholesky factors of $\Sigma _k$ is set to zero with a probability $\alpha =0.95$ and all nonzero entries are assumed to be in the interval [0.4, 0.7]. The 15 noise (irrelevant) features are drawn independently from an ${{\,\mathrm{\mathcal {N}}\,}}(0,1)$ distribution. The number of elements in each cluster is discrete uniformly distributed as ${{\,\mathrm{\mathcal {U}}\,}}\lbrace 50,200\rbrace$ leading to datasets of sizes $n\in [250,1000]$. This clustering task is not as easy as it might first appear, since only half of the features contain any information on the class-labels.

Scenario S2: Cyclic data: We follow Yeung et al. (2001) and generate synthetic data modeling a sinusoidal cyclic behavior of gene expressions over time. We simulate $n=235$ genes under $D^{(0)}=24$ experiments in $K=10$ classes. Two genes belong to the same class if they have similar phase shifts. Each element of the data matrix $y_{ij}$ with $i=1,\dots ,n$ and $j=1,\dots ,D^{(0)}$ is simulated as

$$\begin{aligned} y_{ij}=\delta _j+\lambda _j\left[ \alpha _i+\beta _i\sin \left( \frac{2\pi j}{8}-\omega _k+\epsilon _{ij}\right) \right] , \end{aligned}$$

where $\alpha _i\sim {{\,\mathrm{\mathcal {N}}\,}}(0,1)$ represents the average expression level of gene i, $\beta _i\sim \mathcal {N}(3,0.5)$ is the amplitude control of gene i, $\lambda _j\sim \mathcal {N}(3,0.5)$ models the amplitude control of condition j, while the additive experimental error $\delta _j$ and the idiosyncratic noise $\epsilon _{ij}$ are drawn independently from $\mathcal {N}(0,1)$ distributions. The different classes are represented by $\omega _k$, $k=1,\ldots ,K$, which are assumed to be uniformly distributed in $[0,2\pi ]$, such that $\omega _k\sim {{\,\mathrm{\mathcal {U}}\,}}(0,2\pi )$. The sizes of the classes are generated according to Zipf’s law, meaning that gene i is in class k with probability proportional to $k^{-1}$. Each observation vector $y_i=(y_{i1},\ldots ,y_{i D^{(0)}})^\top$ is individually standardized to have zero mean and unit variance. Recovering the class labels from the data can be difficult, because the classes are very unbalanced and some classes are very small. On average, only eight observations belong to cluster $k=10$. Furthermore, it is hard to distinguish between classes k and $k'$ if $\omega _k$ is close to $\omega _{k'}$.

Wine data: The dataset from the R-package whitening (Strimmer et al. 2020) describes 27 properties of 178 samples of wine from three grape varieties (59 Barolo; 71 Grignolino; 48 Barbera) as reported in Forina et al. (1986).

Olive data: The dataset from the R-package cepp (Dayal 2016) contains percentage composition of eight fatty acids found by lipid fraction of 572 Italian olive oils from three regions (323 Southern Italy; 98 Sardinia; 151 Northern Italy), see Forina et al. (1983).

Ecoli data: This dataset from (Dua and Graff 2017) describes the amino acid sequences of 336 proteins using seven features provided by Horton and Nakai (1996). The class is the localization site (143 cytoplasm; 77 inner membrane without signal sequence; 52 perisplasm; 35 inner membrane, uncleavable signal sequence; 20 outer membrane; five outer membrane lipoprotein; two inner membrane lipoprotein; two inner membrane; cleavable signal sequence).

Vehicle data: This dataset from the R-package mlbench (Leisch and Dimitriadou 2010) describes the silhouette of one of four types of vehicles, using a set of 19 features extracted from the silhouette. It consists of 846 observations (218 double decker bus; 199 Chevrolet van; 217 Saab 9000; 212 Opel manta 400).

Satellite data: This dataset from (Dua and Graff 2017) consists of four digital images of the same scene in different spectral bands structured into a $3\times 3$ square of pixels defining the neighborhood structure. There are 36 pixels which define the features. We use all 6435 scenes (1533 red soil; 703 cotton crop; 1358 gray soil; 626 damp gray soil; 707 soil with vegetation stubble; 1508 very damp gray soil) as observations.

All real datasets are mean-centered and componentwise scaled to have unit variance.

4.3 Results

To compare the overall clustering performance, we assume in a first step that the true number of clusters is known and fixed for all methods. Data-driven choice of the number of clusters is considered later. For Scenarios S1 and S2, $R=100$ datasets were independently generated. Boxplots of the ARI, AMI and MR across replicates are presented in Fig. 3 for S1 and S2. Our method outperforms other approaches in both simulated scenarios. Even though the data generating process in Scenario S1 is a GMM, VIdmfa outperforms the classical GMM. One reason for this is that the data simulated in S1 is relatively noisy, and all information regarding the clusters is contained in a subspace smaller than the number of features. This is not only an assumption for VIdmfa, but also for FMA and MFA. However, compared to the latter two, VIdmfa is able to better recover the sparsity of the covariance matrices due to the shrinkage prior as Fig. 4 demonstrates. The clusters derived by VIdmfa are Gaussian in this scenario, because only one component was assigned positive weight in the deeper layer.

The data generating process of Scenario S2 is non-Gaussian and so are the clusters derived by VIdmfa, due to the fact that the deeper layer might have multiple components. The performance on the real data examples is summarized in Table 1. Here, our approach is competitive with the other methods considered, but does not outperform the EMdgmm approach. On these low-dimensional example datasets, EMdgmm converges substantially faster compared to VBdmfa, but on large-scale datasets, such as the taxi data considered in Sect. 6, the EMdgmm implementation without mini-batching in the deepgmm package is not feasible anymore, and VBdmfa is a good alternative.

Fig. 3

Scenario S1 (a) and Scenario S2 (b). Boxplots summarize row-wise the MR, ARI across 100 replications. Here, we present only the best performing methods to make the plots more informative. A plot containing all benchmark methods and runs outside the interquartile range can be found in the Web Appendix C.3

Fig. 4

Scenario S1. Heat maps of the true, the empirical and the estimated covariance matrices for each of the 5 clusters. For the calculation of the empirical covariance matrices, the true labels of the data points were used, which are not available in practice

Table 1 The MR, ARI and AMI for the real datasets rounded to three decimals are given and the best result is marked in each column. Following Viroli and McLachlan (2019), we select the best of 10 runs according to BIC for all benchmark methods. For our VIdmfa, the best out of 10 runs is selected according to the highest ELBO

Fig. 5

Scenario S1 (a, b) and Scenario S2 (c, d). The average AMI (a, c) and ARI (b, d) across 10 independent replicates for different choices on the initial number of clusters $K=2,\dots ,16$. The x-axis denotes the initialized number of clusters and the y-axis the average AMI/ARI. The optimal number of clusters for each dataset is denoted by the dashed line

The assumption that the number of clusters is known is an artificial one. Clustering is often the starting point of the data investigation process and used to discover structure in the data. Selecting the number of clusters in those settings is sometimes a difficult task. In Bayesian mixture modeling, this difficulty can be overcome by initializing the model with a relatively large number of components and using a shrinkage prior on the component weights, so that unnecessary components empty out (Rousseau and Mengersen 2011). This is also the idea of our model selection process described in Sect. 3.7. To indicate that this is also a valid approach for VIdmfa, we fit both Scenarios S1, S2 for different choices of $K^{(0)}$ ranging from 2 to 16 and compare the average ARI and AMI over 10 independent replicates. The results can be found in Fig. 5. This suggests that our method is able to find the general structure of the data even when $K^{(0)}$ is larger than necessary, but the best results are derived when the model is initialized with the correct number of components. We have found it useful to fit the model with a potentially large number of components and then to refit the model with the number of components selected. This observation justifies our approach to selecting the number of components for the deeper layers discussed in Sect. 3.7. In both real data examples, the optimal model architecture is unknown and VIdmfa selects a reasonable model.

5 Application to gene expression data

In microarray experiments, levels of gene expression for a large number of genes are measured under different experimental conditions. In this example, we consider a time course experiment where the data can be represented by a real-valued expression matrix $\lbrace m_{ij}$, $1\le i\le n$, $1\le j\le D\rbrace$, where $m_{ij}$ is the expression level of gene i at time j. We will consider rows of this matrix to be observations, so that we are clustering the genes according to the time series of their expression values.

Our model is well suited to the analysis of gene expression datasets. In many time course microarray experiments, both the number of genes and times is large, and our VIdmfa method scales well with both the sample size and dimension. If the time series expression profiles are smooth, their dependence may be well represented using low-rank factor structure. Our VIdmfa method also provides a computationally efficient mechanism for the choice of the number of mixture components. In the simulated Scenario S2 of Sect. 4, VIdmfa is able to detect unbalanced and comparable small clusters, which is the main advantage of our VIdmfa approach in comparison with the benchmark methods on this simulated gene expression dataset and a similar behavior is expected in real data applications.

As an example, we consider the Yeast dataset from Yeung et al. (2001), originally considered in Cho et al. (1998). This dataset has been analyzed by many previous authors (Medvedovic and Sivaganesan 2002; Tamayo et al. 1999; Lukashin and Fuchs 2001) and contains $n=384$ genes over two cell cycles ($D=17$ time points) whose expression levels peak at different phases of the cell cycle. The goal is to cluster the genes according to those peaks and the structure is similar to the simulated cyclic data in Scenario S2 from Sect. 4. The genes were assigned to five cell cycle phases by Cho et al. (1998), but there are other cluster assignments with more groups available (Medvedovic and Sivaganesan 2002; Lukashin and Fuchs 2001). Hence, the optimal number of clusters for this dataset is unknown and we aim to illustrate that our VIdmfa is able to select the number of clusters meaningfully. Also, the gene expression levels change relatively quickly between time points in this dataset, suggesting a sparse correlation structure. VIdmfa is well suited for this scenario due to the sparsity inducing priors.

As in Scenario S2 and following Yeung et al. (2001), we individually scale each gene to have zero mean and unit variance. The simulation study in Sect. 4 suggests that VIdmfa can be initialized with a large number of potential components when the number of clusters is unknown, since the unnecessary components empty out. When initialized with $K^{(0)}=\lfloor \sqrt{n}\rfloor =19$ potential components, the model selection process described in Sect. 3.7 selects a model with $L=2$ layers with dimensions $D^{(1)}=4, D^{(2)}=1$ and $K^{(2)}=1$ components in the second layer. VIdmfa returns twelve clusters as shown in Fig. 6. While some of the clusters are small, others are large and match well with the clusters proposed in Cho et al. (1998). For example, cluster eleven corresponds to their largest cluster. Comparisons to other kinds of information would be needed to decide if all of the twelve clusters are useful here, or if some of the clusters should be merged. For example, clusters two and twelve peak at similar phases of the cell cycle and could possibly be merged, while cluster nine does not seem to have a similar cluster and could be kept even though it contains only $n_9=6$ genes. An investigation of the fitted DMFA suggests that the clusters differ mainly by their means, while the covariance matrices have high sparsity, which matches with our expectation of (distant) time points being only weakly correlated.

Fig. 6

Yeast data. VIdmfa selects twelve clusters, when initialized with $K^{(0)}=19$. For each cluster the cluster mean (bold line), as well as minimum and maximum (dotted lines) on the normalized expression patterns are presented and n denotes the number of elements in the respective cluster. The x-axis denotes the time and the y-axis labels the normalized gene expression

6 Application to taxi trajectories

In this section, we consider a complex high-dimensional clustering problem for taxi trajectories. We use the publicly available data-set of Moreira-Matias et al. (2013) consisting of all busy trajectories from 01/07/2013 to 30/06/2014 performed by 442 taxis running in the city of Porto. Each taxi reports its coordinates at 15 second intervals. The dataset is large in dimension and sample size, with an approximate average of 50 coordinates per trajectory and 1.7 million observations in total. Understanding this dataset is a difficult task. Kucukelbir et al. (2017) propose a subspace clustering, where they project the data into an eleven-dimensional subspace using an extension on probabilistic principal component analysis in a first step and then use a GMM with 30 components to cluster the lower-dimensional data in a second step. This approach is successful in finding hidden structures in the data like busy roads and frequently taken paths. We will illustrate that VIdgmm is a good alternative because it does not require a separate dimension reduction step and is able to fit a GMM with a much larger number of components. Also VIdgmm scales well with the sample size, due to the sub-sampling approach described in Sect. 3.3.

In our analysis, we focus on the paths of the trajectories ignoring the temporal dependencies and interpolate the data accordingly. Each trajectory $f_i$ can be viewed as a mapping $f_i(t): \{t_0,\cdots ,t_{T_i}\} \rightarrow \mathbb {R}^2$ of $T_i+1$ equally spaced time points onto coordinate pairs $(x_{i,t_h},y_{i,t_h})$ for $h=0,\cdots ,T_i$ with 50 time-points on average. We consider the interpolation $\tilde{f_i}: [0,1]\rightarrow \mathbb {R}^2$, where

$$\begin{aligned}&\tilde{f_i}(t)=\sum _{h=0}^{T_i-1}\mathcal {I}{\left\{ \frac{L_{i,h}}{L_{i,T_i}}\le t\le \frac{L_{i,h+1}}{L_{i,T_i}}\right\} }(t)\\&\quad \left[ \left( 1-\frac{t-\frac{L_{i,h}}{L_{i,T_i}}}{\frac{L_{i,h+1}}{L_{i,T_i}}-\frac{L_{i,h}}{L_{i,T_i}}}\right) f_i(t_h)+\frac{t-\frac{L_{i,h}}{L_{i,T_i}}}{\frac{L_{i,h+1}}{L_{i,T_i}}-\frac{L_{i,h}}{L_{i,T_i}}}f_i(t_{h+1})\right] , \end{aligned}$$

and $L_{i,h}=\sum _{s=0}^{h-1}\vert \vert f_i(t_s)-f_i(t_{s+1})\vert \vert$ is the length of the trajectory up to time-point $t_h$. This interpolation is time independent in the sense that $d(\tilde{f_i}(t),\tilde{f_i}(t+\delta ))$ is linear in t for all $\delta >0$, where $d_i(\cdot ,\cdot )$ denotes the distance between two points along a linear interpolation of the trajectory $f_i$. This way two trajectories $f_i$ and $f_{i'}$ with the same path, i.e., the same image in $\mathbb {R}^2$, have similar interpolations $\tilde{f_i}\approx \tilde{f_{i'}}$ even when the taxi on one trajectory was much slower than the taxi on the other trajectory. Additionally, we consider a tour and its time reversal as equivalent, and therefore change an observation to its time reversal if the origin point after reordering is closer to the city center. We use a discretization of $\tilde{f_i}(t)$ at 50 equally spaced points $t=0,\frac{1}{49},\frac{2}{49},\dots ,1$ as feature inputs for our clustering algorithm leading to data points in $\mathbb {R}^{100}$. To avoid numerical errors, all coordinates are centered around the city center and scaled to have unit variance.

The architecture chosen has $L=2$ layers with ten components in both layers. The dimensions are set to $D^{(1)}=5$ and $D^{(2)}=2$. This model is equivalent to a 100-dimensional GMM with 100 components. We consider each of these Gaussian components as a separate cluster. In fact, each observation can be matched to one path $k=(k_1,k_2)$ through the model, building Gaussian clusters. This idea of linking the different paths to the clusters leads to a natural hierarchical clustering, where the clusters are built layer-wise. First, the observations are divided into $K^{(1)}=10$ large main-clusters based on the components of the first layer, where an observation is in cluster $k_1$ if and only if $\gamma _{ik_1}^{(1)}=1$. Those clusters are then divided further into $K^{(2)}=10$ sub-clusters. An observation of the main cluster $k_1$ is in sub-cluster $k_2$ if $\gamma _{ik_{1}}^{(1)}=1$ and $\gamma _{ik_{2}}^{(2)}=1$, leading to a potential of $K^{(1)}\times K^{(2)}=100$ clusters in total. A graphical representation of this idea based on our fitted DGMM can be found in Fig. 7.

Fig. 7

Taxi data. The nested clustering for 10000 randomly selected trajectories is shown. There are ten non-empty components in the first layer and nine non-empty components in the second layer, corresponding to a GMM with 90 components shown in the first row. These clusters can be divided into ten subsets (second row) containing up to nine clusters each. The ten subsets are shown in the second row. Note, that many trajectories connect to endpoints outside the shown region. The map was taken from OpenStreetMap

Even though this hierarchical representation has no very clear interpretation for all clusters, it might be used as a starting point for further exploration. City planners and urban decision makers could be interested in a comparison between start and end points of trajectories in the various clusters to further evaluate the need of connections, for example, via public transport, between different regions of the city. Here, the nested structure of the clusters might be helpful, when scanning the clusters for interesting patterns. The 10 large main clusters based on the first layer give a broad overview, while the sub-clusters allow for a more nuanced analysis. An example is given in Fig. 8.

Fig. 8

Taxi data. VIdmfa detects two clusters consisting of short trajectories connected to the harbor and seaside. Both clusters belong to the same main cluster 6. Cluster (6, 3) connects to a larger region on the west side of the city outside the center with the taxis passing through smaller streets, while cluster (6, 5) connects to the city center. Here, the Taxis pass through one of three parallels. The dots denote starting and end points of the trajectories

7 Conclusion and discussion

In this paper, we introduced a new method for high-dimensional clustering. The method uses sparsity-inducing priors to regularize the estimation of the DMFA model of Viroli and McLachlan (2019), and uses variational inference methods for computation to achieve scalability to large datasets. We consider the use of overfitted mixtures and ELBO values from short runs to choose a suitable architecture in a computationally thrifty way.

As noted recently by Selosse et al. (2020) deep latent variable models like the DMFA are challenging to fit. It is difficult to estimate large numbers of latent variables, and there are many local modes in the likelihood function. While our sparsity priors are helpful in some cases for obtaining improved clustering and making the estimation more reliable, there is much more work to be done in understanding and robustifying the training of these models. The way that parameters for mixture components at different layers are combined by considering all paths through the network allows a large number of mixture components without a large number of parameters, but this feature may also result in probability mass being put in regions where there is no data. It is also not easy to interpret how the deeper layers of these models assist in explaining variation. A deeper understanding of these issues could lead to further improved architectures and interesting new applications in high-dimensional density estimation and regression.