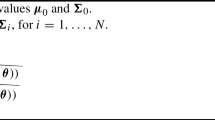Abstract
Double hierarchical generalized linear models (DHGLM) are a family of models that are flexible enough as to model hierarchically the mean and scale parameters. In a Bayesian framework, fitting highly parameterized hierarchical models is challenging when this problem is addressed using typical Markov chain Monte Carlo (MCMC) methods due to the potential high correlation between different parameters and effects in the model. The integrated nested Laplace approximation (INLA) could be considered instead to avoid dealing with these problems. However, DHGLM do not fit within the latent Gaussian Markov random field (GMRF) models that INLA can fit. In this paper, we show how to fit DHGLM with INLA by combining INLA and importance sampling (IS) algorithms. In particular, we will illustrate how to split DHGLM into submodels that can be fitted with INLA so that the remainder of the parameters are fit using adaptive multiple IS (AMIS) with the aid of the graphical representation of the hierarchical model. This is illustrated using a simulation study on three different types of models and two real data examples.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Double hierarchical generalized linear models (DHGLM, Lee and Nelder 2006) provide a unique approach to modeling highly structured datasets allowing for additional flexibility, particularly when modeling the dispersion parameters. The class of DHGLM encompasses a large variety of models such as standard generalized linear models (GLM), mixed effects models, random coefficient models, semi-parametric models and many others. A typical DHGLM includes a linear mixed-effects term to model the mean as well as several terms to model the scale parameters of the likelihood and/or random effects present in the model.
Estimation of DHGLM can be approached in different ways. Lee and Nelder (2006) propose the use of the H-likelihood for model fitting and Rönnegård et al. (2010) use penalized quasi-likelihood. Bayesian inference on DHGLM allows us to estimate the different effects and parameters in the model and estimate their uncertainty by means of the joint posterior distribution.
Because of the different structured terms and effects in a DHGLM, model fitting can become a daunting task. Popular methods such as Markov chain Monte Carlo (MCMC) could take a long time and many simulations to converge. The integrated nested Laplace approximation (INLA, Rue et al. 2009) approach is an appealing option because of its short computation time. However, DHGLM are a class of models that are not currently implemented in the R-INLA package for the R programming language.
In order to fit models that cannot be currently implemented in INLA, given their specific structure, there have been some developments to combine INLA with other methods such as Markov chain Monte Carlo (MCMC) methods (Gómez-Rubio and Rue 2018; Gómez-Rubio 2020). Berild et al. (2021) replace MCMC methods by importance sampling (IS) and adaptive multiple IS (AMIS) to achieve model fitting in a fraction of INLA within MCMC.
In this work, we propose fitting DHGLM with the use of the AMIS-INLA approach (Berild et al. 2021). We show how this class of models can be fitted in this way, providing specific details for the implementation of the algorithms in the cases where variables following Gaussian, Poisson and negative binomial distributions are modelled. Lee and Noh (2012) describe ways of modeling the variance of the random effects for DHGLM. We have focused on modeling the precision instead, but the approach presented here can also be used to model the variance or standard deviation when needed.
This paper is structured as follows. Section 2 describes DHGLM. Section 3 summarizes the integrated nested Laplace approximation for Bayesian inference. Section 4 describes model fitting combining AMIS and INLA, and Sect. 5 includes a simulation study to assess the behavior of our proposed methodology. Section 6 illustrates the usefulness of the proposed method by applying them to two real data examples. Finally, Sect. 7 provides a discussion and summary of our results.
2 Double Hierarchical generalized linear models
Suppose \(Y_{i}\), for \(i=1, \dots , n\) are random variables following a distribution from the exponential family (McCullagh and Nelder 1989). That is, their probability distribution function can be written as:
where \(y_{i}\) is the observation corresponding to the variable \(Y_{i}\), \(\theta _{i}\) is a vector of parameters, \(\phi _{i}\) is a known positive constant value labeled as the scale or dispersion parameter, and b(.) and c(.) are given known functions.
It is known that \({\text {E}}[Y_{i}]= \mu _{i} = b^{\prime }(\theta _{i})\) and that \(\text {Var}[Y_{i}]=\theta _{i}V(\mu _{i})\), with \(V(\mu _{i})=b^{\prime \prime }(\theta _{i})\) being a variance function. Different forms for \(\phi _{i}\) and \(V(\mu _{i})\) for some known distributions are included in Table 1, where \(\sigma ^{2}\) is the variance parameter for the normal distribution, \(n_{i}\) is the number of observations on each trial of the binomial distribution and k the dispersion parameter or size of the negative binomial distribution.
For example, for a variable \(Y_{i}\) having a negative binomial distribution, its probability mass function can be specified as:
where \(p_{i}\) is the probability of success on a Bernoulli trial and \(y_{i}\) would represent the number of failures before the k-th success occurs. The mean is \({\text {E}}[Y_i]= \mu _i= k \left( \frac{1-p_{i}}{p_{i}}\right) \) and the variance is \({\text {V}ar}[Y_i]=k \left( \frac{1-p_{i}}{p_{i}^{2}}\right) =\mu _i+k^{-1}\mu _i^{2}\). If the parameter k is considered fixed, this distribution belongs to the exponential family (see Agresti 2002).
A generalized linear model (GLM) (McCullagh and Nelder 1989) is defined when a regression model is specified for the mean via a link function g(.), obtaining a linear predictor for the i-th observation, so that:
where \(\varvec{X}_{i}\) is a vector of explanatory variables and \(\varvec{\beta }\) is a vector of unknown regression parameters to be estimated.
GLM were further extended by Lee and Nelder (2006) by proposing the DHGLM, which are specified given a set of two random effects \((\varvec{u}^{(\varvec{\mu })},\varvec{u}^{(\varvec{\phi })})\), so that the conditional mean and variance of the response variables \(Y_i\) are \(\text {E}[Y_{i} \mid \varvec{u}^{(\varvec{\mu })},\varvec{u}^{(\varvec{\phi })}]=\mu _i\) and \(\text {Var}[Y_{i} \mid \varvec{u}^{(\varvec{\mu })},\varvec{u}^{(\varvec{\phi })}]=\phi _{i}V(\mu _i)\), respectively, for \(i=1, \dots , n\). The random effects depend on the variance (or precision) parameters \(\varvec{\lambda }\) and \(\varvec{\alpha }\), i.e., \((\varvec{u}^{(\varvec{\mu })}(\varvec{\lambda }),\varvec{u}^{(\varvec{\phi })}(\varvec{\alpha }))\). Here, regression models for the mean, for the dispersion parameters and for the parameters of the random effects are specified, so that:
where \(\varvec{X}_{i}^{\top (.)}\) is the i-th row of the design matrix \(\varvec{X}^{(.)}\) for \(\varvec{\mu }, \varvec{\lambda }, \varvec{\phi }\) and \(\varvec{\alpha }\), \(\varvec{Z}_{i}^{\top (.)}\) is the i-th row of the design matrix \(\varvec{Z}^{(.)}\) for \(\varvec{\mu }, \varvec{\phi }\), and \(\varvec{\beta }^{(.)}\) is a vector of unknown coefficients to be estimated for \(\varvec{\mu }, \varvec{\lambda }, \varvec{\phi }\) and \(\varvec{\alpha }\), respectively.
As we have previously mentioned, estimation of this model can be done by using the H-likelihood proposed by Lee and Nelder (2006) and also penalized quasi-likelihood proposed by Rönnegård et al. (2010). Bayesian methods have been widely employed to fit highly parameterized hierarchical models in the context of DHGLM (see, for example, Bonner et al. 2021, and the references therein). In Cepeda-Cuervo et al. (2018) and Morales-Otero and Núñez-Antón (2021), the authors use MCMC methods to fit generalized overdispersion models, where regression structures depending on some covariates are specified both for the mean and for the dispersion parameters.
3 Integrated nested Laplace approximation
The integrated nested Laplace approximation (INLA) was first proposed by Rue et al. (2009) to provide fast approximate Bayesian inference for latent Gaussian Markov random field (GMRF) models. Given a set of n observed variables \(\mathbf {Y} = (Y_1, \ldots , Y_n)\), usually with a distribution from the exponential family, the density of \(Y_i,\ i=1,\ldots ,n\) may depend on some hyperparameters \(\varvec{\theta _1}\). In addition, the mean of \(Y_i\), \({\text {E}}[Y_i]\), will be linked to a linear predictor \(\eta _i\) on the covariates using a convenient link function \(g(\cdot )\) so that \(g[{\text {E}}(Y_i)] = \eta _i\).
The linear predictor may include different terms, as fixed and/or random effects, so that the distribution of all these terms is a GMRF with zero mean and precision matrix \(Q(\varvec{\theta _2})\), that may depend on some other hyperparameters \(\varvec{\theta _2}\). To simplify notation, we will often use \(\varvec{\theta } = (\varvec{\theta _1}, \varvec{\theta _2})\) to refer to the vector of hyperparameters. In addition, the vector of latent effects will be denoted by \(\varvec{\kappa }\).
In a Bayesian framework, the aim is to compute the posterior distribution of the latent effects and hyperparameters, \(\pi (\varvec{\kappa }, \varvec{\theta }\mid {\mathcal {D}})\), to make inference about them. Here, \({\mathcal {D}}\) represents the available data, which will include the observed response \(\mathbf {y} = (y_1,\ldots ,y_n)\) and, possibly, other covariates required to define the fixed and random effects in the latent GMRF. Using Bayes’ rule, this joint posterior distribution can be written as:
Here, \(L(\varvec{\kappa }, \varvec{\theta }\mid {\mathcal {D}})\) represents the likelihood of the data, while \(\pi (\varvec{\kappa }, \varvec{\theta })\) is the joint prior distribution of the latent effects and hyperparameters. This is often expressed as \(\pi (\varvec{\kappa }, \varvec{\theta }) = \pi (\varvec{\kappa }\mid \varvec{\theta }) \pi (\varvec{\theta })\). Note that \(\pi (\varvec{\kappa }\mid \varvec{\theta }) \) is a GMRF and \(\pi (\varvec{\theta })\) is often defined as the product of univariate distributions as hyperparameters are considered to be independent a priori.
The joint posterior distribution \(\pi (\varvec{\kappa }, \varvec{\theta }\mid {\mathcal {D}})\) is often highly multivariate and difficult to estimate. For this reason, Rue et al. (2009) focus on estimating the marginal posterior distributions of the latent effects and hyperparameters. In this way, approximations \({\tilde{\pi }}(\kappa _j \mid {\mathcal {D}})\) and \({\tilde{\pi }}(\theta _l \mid {\mathcal {D}})\) to \(\pi (\kappa _j \mid {\mathcal {D}})\) and \(\pi (\theta _l \mid {\mathcal {D}})\), respectively, are obtained.
In addition, INLA can be used to obtain an approximation to the marginal likelihood of the model, \(\pi ({\mathcal {D}})\), which is often difficult to compute. Other important quantities for model selection and model choice are available in the R-INLA package that implements the INLA method (Gómez-Rubio 2020).
As discussed in the next section, INLA cannot fit DHGLM directly, but INLA can be embedded into the model fitting process to be able to easily fit these models.
4 Model fitting
DHGLM do not fall into the class of models that INLA can fit due to their particular structure, which includes different hierarchies on the mean and scale parameters. However, as explained below, DHGLM can be expressed as conditional latent GMRF models after conditioning on some model parameters. This idea of fitting conditional models with INLA has been exploited by several authors (see, for example, Gómez-Rubio and Rue 2018) to increase the number of models that can be fit with INLA.
In particular, the vector of hyperparameters \(\varvec{\theta }\) can be decomposed into two sets of parameters \(\varvec{\theta }_c\) and \(\varvec{\theta }_{-c}\), so that the model, conditional on \(\varvec{\theta }_c\), can be fit with INLA. The posterior distribution of \(\varvec{\theta }_c\) can then be expressed as
Here, \(\pi (\varvec{\theta }_c)\) is the prior on \(\varvec{\theta }_c\), which is known, and \(\pi ({\mathcal {D}} \mid \varvec{\theta }_c)\) is the conditional (on \(\varvec{\theta }_c\)) marginal likelihood, as this is obtained after integrating out all the other hyperparameters and latent effects. This quantity can be easily obtained with INLA, so that the posterior distribution of \(\pi (\varvec{\theta }_c \mid {\mathcal {D}})\) can be estimated.
Regarding the other hyperparameters \(\varvec{\theta }_{-c}\) and the latent effects, their marginal posterior distributions can be obtained by noting that
The conditional posterior marginal \(\pi (\cdot \mid \varvec{\theta }_c, {\mathcal {D}})\) is provided by INLA when fitting the model (after conditioning on \(\varvec{\theta }_c\)).
In practice, an approximation to \(\pi (\cdot \mid {\mathcal {D}})\) is obtained by weighing the posterior conditional marginals, that is,
Here, M represents a number of ensembles of values of \(\varvec{\theta }_c^{(m)}\), \(\{\varvec{\theta }_c^{(m)}\}_{m=1}^M\), which is used for numerical integration. In addition, \(w_m\) are weights that can be computed in different ways, depending on how the values of \(\varvec{\theta }_c\) have been obtained.
In this regard, Gómez-Rubio and Rue (2018) use the Metropolis-Hastings algorithm to estimate the distribution of \(\varvec{\theta }_c\), and also use the resulting values to estimate the remainder of the latent effects and hyperparameters. This algorithm requires fitting a model with INLA at each iteration of the Metropolis-Hastings algorithm, which makes it less appealing in practice. Moreover, the average of the posterior conditional marginal distributions is computed by using the corresponding weights \(w_m=1/M,\ m=1,\ldots ,M\).
Similarly, Berild et al. (2021) use the importance sampling (IS) algorithm instead, which can be run in parallel and provides reduced computing times. In this particular case, samples of \(\varvec{\theta }_c\) are obtained using an importance distribution \(s(\cdot )\) to obtain \(\{\varvec{\theta }_c^{(m)}\}_{m=1}^M\). For each value \(\varvec{\theta }_c^{(m)}\), a conditional model is fit with INLA so that integration weights \(w_m\) are obtained as follows:
Weights are re-scaled so that they sum up to one. Furthermore, Berild et al. (2021) describe the use of the adaptive multiple importance sampling (AMIS, Corneut et al. 2012) algorithm that provides a more robust sampling method that updates the importance distribution \(s(\cdot )\).
Regarding model fitting of DHGLM with INLA, we can use IS and AMIS with INLA by conditioning on some of the model hyperparameters or latent effects. These will depend on the way in which the DHGLM is defined. Both Gómez-Rubio and Rue (2018) and Berild et al. (2021) discuss different approaches on how to best select the parameters in \(\varvec{\theta }_c\). In the simplest cases, the choice of \(\varvec{\theta }_c\) will be clear as just a few parameters will need to be fixed to obtain a conditional latent GMRF model. For highly structured models, it may happen that, after conditioning on some hyperparameters or latent effects, two or more conditionally independent submodels appear (see, for example, Lázaro et al. 2020). These submodels can be fit independently with INLA. All the different cases are illustrated in Sect. 5, where different simulations studies are developed in detail on different types of models.
However, in order to provide a more general approach to the choice of \(\varvec{\theta }_c\), we propose the use of a graphical representation of the model. This graphical model encodes conditional independence relationships among the model parameters, so that its structure can be exploited to be able to select the best possible choice of the parameters to be included in \(\varvec{\theta }_c\) (see, for example, Cowell et al. 1999). See Sect. 5.4 for more details and a thorough discussion about this graphical representation using the examples in the simulation study conducted in Sect. 5.
Regarding the sampling distribution for \(\varvec{\theta }_c\), Berild et al. (2021) suggest choosing a multivariate Gaussian distribution or a multivariate t distribution with a small number of degrees of freedom for continuous variables. Note that some of the variables in \(\varvec{\theta }_c\) may need to be rescaled (e.g., a precision will be sampled in the log scale). Hence, the mean and precision of these distributions are updated at each adaptive step. For discrete variables, the choice is not so clear. When the variables are dichotomous, Berild et al. (2021) suggest using a binomial distribution for each of them, so that the probabilities depend on some fixed effects (which are the parameters updated after each adaptive step).
The choice of the parameters of the sampling distribution is crucial to obtain a good performance of the proposed methodology. The initial parameters of the distribution could be based on summary statistics of the observed data as rough estimates. For example, for continuous data, when the sampling distribution is a multivariate normal, the mean can be set to the sample mean of the observed data and the precision can be diagonal with small values in the diagonal. Here, small must be put into context according to the scale of the parameters. Too large values of the precision will imply that the parameter space is not conveniently explored, while too small values will imply that samples with a very small posterior density will be sampled too often. In both cases, bad estimates will be obtained at the adaptive steps that can result in the algorithm requiring more steps to produce reliable estimates. This issue is thoroughly discussed in the simulation study in Sect. 5 and the examples in Sect. 6.
In addition, as a general guidance, the conditional model can be fit with INLA given the set of possible values for the mean of the sampling distribution before running AMIS with INLA. Different sets of values can be tested and the marginal likelihoods compared. The one with the highest value of the marginal likelihood may be a better candidate as it improves model fitting. This will help to be able to choose an initial sampling distribution whose mode is close to the posterior mode of \(\varvec{\theta }_c\), so that less adaptive steps (and, hence, simulations) are required to obtain good estimates.
Another way of assessing the performance of IS with INLA is to compute the effective sample size and conduct graphical diagnostics, as discussed in Berild et al. (2021). The effective sample size can be estimated as
Note that this effective sample size will be the same for all the components of \(\varvec{\theta }_c\) as it is only based on the weights and not on the sampled values.
Graphical diagnostics can be produced for each variable in \(\varvec{\theta }_c\) by re-ordering the sampled values in ascending order and comparing the estimated cumulative probability (i.e., the cumulative sum of the re-ordered weights) with the empirical cumulative probabilities \(1/M, \ldots , M/M\), respectively. A straight line means that the estimated posterior marginal of that parameter is reliable.
Monitoring the convergence of the algorithm could be conducted in a number of ways. First of all, the effective sample size could be computed and the algorithm can be stopped once the desired sample size has been achieved. The conditional marginal likelihood fitted at the mean of the sampling distribution after each adaptive step could also be monitored to assess whether it keeps increasing or approaches a certain value (at this point the algorithm can be stopped). It is worth noting that more samples could be obtained when needed by simply resuming the simulations using updated estimates of the parameters of the sampling distribution.
5 Simulation study
In this section, we develop three different simulation studies to illustrate model fitting of hierarchical models with different structures. In Sect. 5.1, we fit a Poisson log-linear model with random effects, in which the log-precision of the random effects is modeled using a linear term; in Sect. 5.2, we fit a negative binomial model in which the log-size parameter is modeled using a linear term; and in Sect. 5.3, we fit a Gaussian model to grouped data in which the log-precision of each group is modeled using a linear mixed-effects model. In all cases, models are fit using MCMC and AMIS with INLA. IS with INLA has not been considered because Berild et al. (2021) show that in general, AMIS-INLA has a better performance than IS with INLA.
The aim of these simulation studies is twofold. On the one hand, we would like to illustrate the way in which IS and AMIS with INLA can be implemented and how the conditioning effects \(\varvec{\theta }_c\) can be chosen. On the other hand, it is important to compare the results obtained with these methods to a gold standard. In our case, we have fitted the models using Markov chain Monte Carlo (Brooks et al. 2011) using the JAGS software via the R-package rjags (Plummer 2021).
Figure 1 shows the representation of these models as graphical models. In addition to the different elements of the model, the conditioning parameters have been highlighted (using a red dotted box) to illustrate which parameters are estimated using AMIS. The marginals of all the other parameters are obtained by averaging the conditional marginals resulting after fitting the conditional models with INLA. Nodes in a shaded solid circle represent the observed data, nodes in a white solid circle represent model effects, and parameters and nodes in a dotted white circle represent deterministic nodes (i.e., their values are fully determined by the values at their parent nodes).
Graphical representation of the models fit in the simulation study in Sect. 5: Poisson model with random effects (a), negative binomial model with regression on the log-sizes (b) and Gaussian model with regression model on the likelihood log-precisions (c). Nodes in a shaded solid circle represent the observed data, nodes in a white solid circle represent model effects, and parameters and nodes in a dotted white circle represent deterministic nodes (i.e., their values are fully determined by the values at their parent nodes). Parameters fit with AMIS with INLA are in a red dotted box, whereas the conditional model fit with INLA is in a blue dotted box
When implementing AMIS, the importance distribution \(s(\cdot )\) is assumed as a multivariate Gaussian in all examples. Note that this means that some parameters may be transformed so that simulations are feasible. For example, precisions will be sampled in the log-scale, so that samples from the log-precision are obtained. In all cases, we have computed results using a very vague distribution (with zero mean and large precision) and another distribution based on a rough estimate of the parameters of the sampling distribution from the observed data. This should reduce the number of iterations required to obtain a reliable model fitting. In all cases, the estimates from AMIS with INLA are compared with MCMC estimates.
In all the examples presented below, the same number of simulations has been used. When fitting the model using AMIS with INLA, 5000 iterations have been used in the initial step, followed by ten new adaptive steps with 1000 simulations each. For MCMC, a burn-in of 10,000 simulations is used, plus 100,000 simulations of which only one in 100 is retained, leading to a final number of 1000 samples. In addition, in the Gaussian example in Sect. 5.3, different scenarios have been tested (see below for details). Finally, simulations have been carried out on a Linux Ubuntu 18.2 cluster using 60 cores Intel(R) Xeon(R) CPU E5-2683 v4 @ 2.10GHz.
5.1 Poisson model with random effects with different precisions
The first simulation study is based on a Poisson log-linear model with fixed and random effects, so that the precision of the random effects is modeled using a linear term with covariates. In particular, the model is
Note that the Gaussian distribution \(N(\cdot ,\cdot )\) is defined in terms of the mean and precision so that \(\tau _i\) represents the precision of the Gaussian distribution of the random effects. A Poisson distribution with random effects is often used to model overdispersed data (Quintero-Sarmiento et al. 2012).
This model can be expressed as a latent GMRF by conditioning on \(\varvec{\theta }_c = \varvec{\gamma }= (\gamma _0, \gamma _1)\), resulting in a Poisson model with random effects with different precisions. This is illustrated in the graphical representation of the model in Fig. 1a. Hence, this model will be fitted using AMIS with INLA and values of \(\varvec{\gamma }\) will be obtained by simulation. Estimates of the posterior distribution can be obtained by using importance weights and the posterior marginals of \(\beta _0\) and \(\beta _1\) will be obtained by weighting their conditional marginals.
For the simulated data, we have used \(n=1000\), \(\beta _0=1\), \(\beta _1 = 0.25\), \(\gamma _0 = 0\) and \(\gamma _1 = 0.5\). Covariate \(x_i\) has been simulated using a uniform distribution between 0 and 1, and covariate \(z_i\) has been simulated using a standard Gaussian distribution. Once these values have been set, the observed value \(y_i\) has been obtained by sampling from a Poisson distribution with the resulting mean \(\mu _i\).
The sampling distribution for \(\varvec{\gamma }\) is a bivariate Gaussian distribution. The initial value of the mean is vector (0, 0) and the initial value of the variance matrix is a diagonal matrix with entries equal to 5 in the diagonal. This choice provides ample initial variability to explore the parametric space of \(\varvec{\gamma }\) conveniently so that accurate estimates are obtained at the adaptive and final steps of AMIS with INLA.
Table 2 summarizes the estimates using the different methods, and Fig. 2 shows the posterior marginal estimates obtained with both methods. Here, the dashed vertical lines represent the true values of the parameters specified for the simulated data. As can be seen, the estimates obtained with AMIS with INLA and MCMC are very similar. The effective sample size \(n_e\) obtained with AMIS with INLA in this case is 9900.914.
5.2 Negative binomial with different sample sizes
The negative binomial distribution is also used to model overdispersed count data. In this simulation study, the logarithm of the size parameter \(k_i\) of the negative binomial distribution depends on a linear term with covariates, which in turns makes the probability to be different across observations. In particular, the model is as follows:
Similarly, as in the previous example, this model can be expressed as a latent GMRF by conditioning on \(\varvec{\theta }_c = \varvec{\gamma }= (\gamma _0, \gamma _1)\), resulting in a negative binomial model with different sizes. This is illustrated in the graphical representation of the model in Fig. 1b. When fitting the model with AMIS with INLA, values of \(\varvec{\gamma }\) will be obtained by simulation and their estimates will be computed using the importance weights. The posterior marginals of \(\beta _0\) and \(\beta _1\) will be obtained by weighting their conditional marginals.
For our study, \(n=500\) observations have been simulated. Covariate \(x_i\) is simulated from a uniform between 10 and 20, and covariate \(z_i\) has been simulated from a uniform between 0 and 20. Values of \(z_i\) have then been standardized before simulating the data. Regarding the model parameters, we have used \(\beta _0=1\), \(\beta _1 = 0.25\), \(\gamma _0 = 0\) and \(\gamma _1 = 5\). Once the mean and size of the negative binomial have been computed, the values of the response variable have been sampled using a negative binomial distribution.
Likewise, as in the previous simulation study, the sampling distribution for \(\varvec{\gamma }\) is a bivariate Gaussian distribution. The initial value of the mean is vector (0, 0), and the initial value of the variance matrix is a diagonal matrix with entries equal to 5 in the diagonal. This a convenient choice for this example as well, and it provides good estimates of the model parameters (see below).
Table 3 summarizes the estimates using the different methods, and Fig. 3 shows the posterior marginal estimates obtained with both methods. As can be seen, the estimates obtained with AMIS with INLA and MCMC are very similar. The effective sample size \(n_e\) obtained with AMIS with INLA in this case is 9737.075.
5.3 Gaussian model with different scale parameters
In the last simulation study, we have considered the case of grouped Gaussian data so that each group has a different precision and the log-precision is modeled on a mixed-effects model. In particular, we consider the model:
Here, p represents the number of groups and \(n_i\) the number of observations in group i. The values of the parameters used in the simulations are \(\beta _0 = 1\), \(\beta _1 = 0.25\), \(\gamma _0 = 0\), \(\gamma _1 = 5\) and \(\tau _u = 1\). The total number of observations is 2500, which corresponds to \(p = 5\) groups and \(n_i = 500,\ i=1,\ldots , p\). Furthermore, values of covariate \(x_{ij}\) have been simulated from a uniform distribution between 0 and 1, while values of covariate \(z_i\) have been obtained by sampling from a uniform distribution in the interval (-1, 1).
This model is a bit more complex because the log-precision depends on both fixed and random effects. Hence, conditioning on \(\varvec{\gamma }\) alone will not suffice to make this model a latent GMRF. It would be possible to condition on \(\varvec{\gamma }\) and \(\mathbf {u} = (u_i,\ldots , u_p)\) but then the dimension of the parametric space may be difficult to handle by AMIS (in particular, when the value of the number of groups p is large). Furthermore, estimating the random effects \(u_i\) using importance sampling may be difficult, and we prefer INLA to perform this task.
Instead, conditioning will be on \(\varvec{\theta }_c = \varvec{\tau }=(\tau _1,\ldots ,\tau _p)\), which will split the main model into two independent submodels with response variables \(\mathbf {y}\) and \(\log (\varvec{\tau })\), as shown in Fig. 1c. These two submodels can be fit independently, and the resulting log-marginal likelihood will be the sum of the corresponding values from the two submodels, which can be then used to compute the weights.
Note that, in this particular case, nodes \(\tau _1,\ldots ,\tau _p\) are not stochastic nodes as they are fully determined by \(\varvec{\gamma }\), \(z_i\) and \(u_i\). For this reason, there is no prior for them. In order to ease the computations, and without loss of generality, we set \(\pi (\tau _i) = 1,\ i=1,\ldots ,p\), which will not have any effect on the computation of the marginal likelihood.
It is worth mentioning that among the three different examples provided in the simulation study, this one is an actual DHGLM as defined in Lee and Nelder (2006) because it includes random effects when modeling \(\log (\tau _i)\). In order to explore convergence of the AMIS algorithm, we have repeated the analysis using different sets of initial values for the parameters of the importance distribution and number of samples (see below). This will allow us to explore how the adaptive procedure in the AMIS algorithm behaves and to assess the resulting estimates precision. These scenarios are:
-
1.
Initial step of 5000 iterations, ten new adaptive steps with 1000 simulations each, vague initial parameters for the sampling distribution (AMIS-INLA1).
-
2.
Initial step of 5000 iterations, ten new adaptive steps with 1000 simulations each, parameters informed from the data for the sampling distribution (AMIS-INLA2).
-
3.
Initial step of 1000 iterations, ten new adaptive steps with 1000 simulations each, vague initial parameters for the sampling distribution (AMIS-INLA3).
-
4.
Initial step of 1000 iterations, ten new adaptive steps with 1000 simulations each, parameters informed from the data for the sampling distribution (AMIS-INLA4).
-
5.
Initial step of 5000 iterations, ten new adaptive steps with 1000 simulations each, vague initial parameters and large variance for the sampling distribution (AMIS-INLA5).
-
6.
Initial step of 5000 iterations, ten new adaptive steps with 5000 simulations each, parameters informed from the data for the sampling distribution (AMIS-INLA6).
In all the scenarios described above, the sampling distribution is a multivariate normal distribution for \((\log (\tau _1), \ldots ,\log (\tau _p))\). Vague initial parameters refers to using a mean of 0 and a variance matrix that is diagonal with all entries equal to 5. Using a sampling distribution with parameters informed from the data refers to computing the sample variance of each group and computing the parameters of the sampling distribution from them. In particular, the mean is the log of the vector of sample variances and the variance matrix is diagonal with entries the variance of the log-sample variances divided by their corresponding values of \(n_i\). If the scenario indicated that a larger variance for the sampling distribution has been used, these values are multiplied by 10. In all cases, these are initial values of the parameters of the sampling distribution, and they will be updated at each adaptive step.
Table 4 summarizes the results of the estimation of the Gaussian model with the MCMC method. Similarly, Table 5 includes the results of the estimation of the Gaussian model with the AMIS-INLA method, where different scenarios are considered. Furthermore, Fig. 4 presents the estimates of the posterior marginal distributions for the parameters obtained with MCMC, as well as for the different settings of the AMIS-INLA algorithm.
Estimation is good for all model parameters for most scenarios, with point estimates close to that of MCMC in most cases. However, estimates of \(\tau _u\) do not seem to be good as AMIS with INLA tends to underestimate this parameter for scenario 3. The effective sample sizes of AMIS with INLA range from 5.12 (scenario 3, based on 11,000 simulations) to 10444.68 (scenario 2, 15,000 total simulations) and 51,536.74 (scenario 6, based on a total of 55,000 simulations). Hence, scenario 3 is likely to produce poor estimates due to its low effective sample size.
It is worth noting that the estimation of the posterior marginal of \(\tau _u\) has been conducted by first averaging the posterior marginal of \(\log (\tau _u)\) (the internal scale of this parameter in INLA) and then transforming the resulting marginal to obtain that of \(\tau _u\). The reason is that INLA estimates of the posterior marginal of \(\tau _u\) were not reliable.
5.4 Summary of results
The simulation studies conducted above illustrate the use of AMIS with INLA to fit DHGLM. This approach will allow a flexible definition of the models using the R-INLA package as well as efficient model fitting. Given that AMIS can be run in parallel, DHGLM could be fit in a short time provided a computer with a large number of CPUs is available (which is not uncommon these days).
Regarding the selection of the parameters in \(\varvec{\theta }_c\), we have provided new guidelines not discussed in Gómez-Rubio and Rue (2018) or Berild et al. (2021) by using the graphical representation of the models in Fig. 1. By inspecting the graphical model, it is easier to find the parameters to condition on, so that the resulting model is a latent GMRF (see Poisson and negative binomial models). Furthermore, for highly structured models, it is possible to split the model into more than one submodel (that are latent GMRF) by conditioning on a small sample of hyperparameters, as is the case of the Gaussian model with different scale parameters.
The parameters in \(\varvec{\theta }_c\) have been included in a red dotted box, which has been labeled AMIS as this is the method used to estimate the posterior distribution of these parameters. Similarly, the conditional latent GMRF has been included in a blue dotted line, which has been labelled as INLA because this is the method used to estimate the posterior marginals of the parameters in this conditional model.
In a nutshell, the parameters in \(\varvec{\theta }_c\) should be taken so that their dimension is as low as possible, preferable as part of coefficients of fixed effects or precisions of random effects, and so that they split the main model into one or more submodels that are easy to fit with INLA. Choosing the random effects themselves as part of \(\varvec{\theta }_c\) should be avoided as it is difficult to sample efficiently using AMIS and their dimension is likely to increase with the size of the data.
6 Examples
In this section, we illustrate model fitting of DHGLM with AMIS-INLA using two real datasets. Section 6.1 describes a Poisson model with random effects with a hierarchical structure on the precision and also a negative binomial model with a hierarchical structure on the size parameter to analyze infant mortality in Colombia. Section 6.2 fits a model with subject-level random slopes and precisions to participants in a sleep deprivation study.
6.1 Infant mortality in Colombia
The infant mortality data in Colombia that we analyze here has been studied in previous works (see, for example, Quintero-Sarmiento et al. 2012; Cepeda-Cuervo et al. 2018; Morales-Otero and Núñez-Antón 2021). The variables available in this dataset are given for each of the \(n=32\) departments or regions of Colombia: the number of children under one year of age who died in year 2005 (ND), the total number of births in the same year (NB), an index that represents the percentage of people with their basic needs not satisfactorily attended for year 2005 (IBN) and the observed mortality rates, computed as the number of children under one year of age who died in 2005 per 1000 born alive (Rates).
It has been shown in previous works (e.g., Quintero-Sarmiento et al. 2012) that these data presents overdispersion when fitting a Poisson regression model for the mortality rates, a phenomenon that arises when the real variance of the data is larger than the one specified in the model. Additionally, there have been findings of the evidence that there is spatial autocorrelation present in the data (Cepeda-Cuervo et al. 2018). Therefore, these are issues that need to be taken into account if we wish to specify regression models for this data.
The first model considered is the generalized spatial conditional normal Poisson (Cepeda-Cuervo et al. 2018), which is able to accommodate overdispersion and to explain spatial dependence. This model assumes that the variable representing the number of deaths in each region (\(\text {ND}_{i}\)), conditioned on the set of values it takes in the neighboring regions without including region i itself (\(\text {ND}_{\sim i}\)) and on a set of normally distributed random effects \(u_{i} \sim N(0,\tau _{i})\) follows a Poisson distribution, that is \((\text {ND}_i \mid \text {ND}_{\sim i}, u_i) \sim \text {Poi}(\mu _i)\) for \(i=1, \dots , n\).
This model allows the dispersion parameter to vary according to explanatory variables or any other terms by specifying a regression model for the variance of the random effect. It is also able to explain the spatial association which may be present in the data by including the spatial lag of the rates in the regression model for the mean or in the model for the dispersion as well (see Cepeda-Cuervo et al. 2018; Morales-Otero and Núñez-Antón 2021).
The connection with DHGLM appears here because we can model the log-precisions using a linear predictor on IBN so that \(\log (\tau _i) = \gamma _{0} + \gamma _{1}\text {IBN}_{i}, i=1,\ldots , n\). It is worth mentioning that in this particular case, the precisions are univocally determined by the linear predictor.
Following the example from Morales-Otero and Núñez-Antón (2021), we have specified the following model:
where \(\mathbf {W}_{i}\) is the i-th row of a row-standardized spatial neighborhood matrix \(\mathbf {W}\). Adjacency here is defined so that two regions are neighbors if they share at least one point of their boundaries. Therefore, \(\mathbf {W}_{i}\mathbf {Rates}\) is the spatial lag of the observed mortality rates, which in this case represents the average of \(\mathbf {Rates}\) at the neighbors.
In the implementation of AMIS with INLA, we have taken \(\varvec{\theta }_c = \varvec{\gamma }= (\gamma _0, \gamma _1)\). The sampling distribution is a bivariate Gaussian with vector mean (0, 0) and the variance matrix is a diagonal matrix with entries equal to 5. In this case, 5000 simulations were initially run, followed by ten adaptive steps with 1000 simulations each.
Results of the estimation of this model are shown in Table 6 and Fig. 5. As can be seen, AMIS-INLA and MCMC produce close results. The effective sample size of AMIS with INLA is 9263.002.
The negative binomial model could be another option to consider in order to fit the infant mortality data described here. Therefore, we have specified the generalized spatial conditional negative binomial model (Cepeda-Cuervo et al. 2018), where it is assumed that \((\text {ND}_i \mid \text {ND}_{\sim i}) \sim \text {NB}(\mu _i, \text {k}_i)\), with \(\mu _{i}\) being the conditional mean and \(\text {k}_{i}\) the size parameter of a negative binomial distribution. For this model, we can specify regression structures both for the mean and dispersion parameters, which can include the spatial lag of the rates and explanatory variables as well.
In particular, we have fitted the following model:
In order to fit this model with AMIS with INLA, we have also taken \(\varvec{\theta }_c = \varvec{\gamma }= (\gamma _0, \gamma _1)\). Conditional on \(\varvec{\theta }_c\), the resulting model is a negative binomial with different known sizes, which is easy to fit with INLA. Sampling has been done as with the Poisson distribution.
Table 7 and Fig. 6 display the results of the estimation of this model, which show that AMIS with INLA provides very similar results to MCMC. The effective sample size of AMIS with INLA is 9717.207 now.
6.2 Sleep deprivation study
Belenky et al. (2003) conducted an experiment to measure the effect of sleep deprivation on reaction time on a number of subjects. A subset of this dataset is included in the R package lme4 (Bates et al. 2015), and it includes observations for the most sleep-deprived group for the first 10 days of the study. This dataset has been analyzed by different authors (see, for example, Gómez-Rubio 2020) using linear mixed-effects with random slopes as the number of days under sleep deprivation seems to have a different effect on the different subjects.
Variability of the reaction times among subjects is not uniform, with some subjects having a broader range of values than others. In addition, the increase in reaction times with time will vary from subject to subject (see plot in Supplementary materials). For this reason, we have fitted a model with random slopes per subject in which the within-in subject precision of the measurements is different using a DHGLM.
In particular, we have fitted the following model:
Here, \(p = 18\) is the number of subjects and \(n_i=10,\ i=1,\ldots , p\) given that all subjects have the same number of measurements in the dataset. Covariate \(\text {day}_{ij}\) is the number of the days since the beginning of the sleep deprivation experiment. Note that \(\beta _i, i=1,\ldots ,p\) refers to random coefficients to allow for different per-subject slopes. It should be emphasized that this model is similar to the one in Sect. 5.3 and that it will be fitted in a similar way, i.e., by sampling from \((\log (\tau _1), \ldots , \log (\tau _p))\). Note that the dimension of the parametric space is 18, which may be large for algorithms such as IS and AMIS. A graphical representation of this model is available in Fig. 7.
In order to select the parameters of the importance distribution, we have proposed different approaches. Initially, we assumed a multivariate normal distribution with zero mean and a diagonal precision matrix with entries equal to 5 along the diagonal. This provided a vague starting sampling distribution for the log-precisions that after a few adaptation steps may get close to the actual posterior distribution. Unfortunately, this provided very poor estimates, and the results were discarded.
We noticed that importance sampling may not be efficient if the mean of the importance distribution is far from the posterior modes and also when its variance is too large. For this reason, we propose to use the data to obtain some rough estimates of the posterior mean and precisions based on \(S^2_i\), the sample variance computed using measurements from subject i. Then, the mean of the importance distribution is \((\log (1 / S^2_1), \ldots , \log (1 / S^2_p))\) and the variance is diagonal with entries \(0.05 \cdot (\log (1 / S^2_1), \ldots , \log (1 / S^2_p))\). In principle, this should provide a starting sampling distribution which is close to the posterior modes and with a variance in the scale of the posterior variances that allows for short jumps during the adaptive steps.
However, we noticed that we could obtain better initial parameters by performing permutations of the values of \((\log (1 / S^2_1), \ldots , \log (1 / S^2_p))\), fitting the conditional model and checking the values of the conditional marginal likelihood, so that the permutation with the highest value is used to set the parameters of the initial sampling distribution. This simple prior step produced means of the sampling distribution that were very close to the posterior mode of \((\log (\tau _1), \ldots , \log (\tau _p))\). In particular, 500 random permutations were tested prior to running AMIS with INLA.
For all the models fitted in this example, AMIS with INLA has been run using an initial adaptive step based on 1000 simulations followed by 20 adaptive steps with 1000 simulations each. MCMC is based on 10000 burn-in simulations followed by 100000 simulations, of which only 1 in 100 has been kept, so that inference is based on 1000 samples.
Results of the estimation of this model are provided in Table 8 and the densities of the posterior estimations for the parameters are shown in Fig. 8. The effective sample size of AMIS with INLA in this case is 2.015619, which is small but seems to provide good estimates of the marginals of the model parameters. It is worth mentioning that we have computed the effective sample size after each adaptive step and that it reached the value 81.14083 after 12 adaptation steps. AMIS with INLA could be stopped after a certain effective sample size has been achieved. It is worth noting that the estimates of \(\log (\tau _i)\) did not change considerably in the last adaptive steps.
7 Discussion
Double hierarchical models present a particular structure that models both the mean and scale parameter of different hierarchical models with likelihood within the exponential family. Hence, inference on these models can be difficult due to the different levels and effects in the model hierarchy. We have illustrated how the integrated nested Laplace approximation can be used to fit these models by using importance sampling and adaptive multiple importance sampling.
In practice, this allows INLA to integrate most of the latent effects and hyperparameters out so that a small subset of them is estimated using importance sampling. Given that IS can be easily parallelized, this provides an approach that is computationally competitive and computing times can be close to the ones provided by INLA.
We have illustrated model fitting of DHGLM by conducting three different simulation studies and the analysis of two real datasets. In all cases, conducting an adaptive multiple importance sampling provided good estimates of the model effects and hyperparameters that were similar to those obtained with Markov chain Monte Carlo methods.
Although we have discussed examples with Gaussian, Poisson and negative binomial data, the approach presented here can be applied to any of the distributions in the exponential family and, more generally, to other likelihood distributions that can be used together with the R-INLA software. Any model that can be expressed as a latent GMRF by conditioning on a (small) subset of latent effects or hyperparameters is susceptible to be fitted with IS/AMIS with INLA.
Finally, the R code used to develop the simulation study and the examples is available from https://github.com/becarioprecario/DHGLM-INLA. The data for the infant mortality in Colombia in Sect. 6 have been replaced by a simulated dataset due to confidentiality constrains.
Code availability
The code for the AMIS with INLA algorithm has been obtained from an early version of the code described in Berild et al. (2021) available from https://github.com/berild/inla-mc.
References
Agresti, A.: Categorical Data Analysis, 2nd edn. Wiley, Hoboken, NJ (2002)
Bates, D., Mächler, M., Bolker, B., Walker, S.: Fitting linear mixed-effects models using lme4. J. Stat. Softw. 67(1), 1–48 (2015). https://doi.org/10.18637/jss.v067.i01
Belenky, G., Wesensten, N.J., Thorne, D.R., Thomas, M.L., Sing, H.C., Redmond, D.P., Russo, M.B., Balkin, T.J.: Patterns of performance degradation and restoration during sleep restriction and subsequent recovery: a sleep dose-response study. J. Sleep Res. 12(1), 1–12 (2003). https://doi.org/10.1046/j.1365-2869.2003.00337.x
Berild, M.O., Martino, S., Gómez-Rubio, V., Rue, H.: Importance sampling with the integrated nested Laplace approximation. (2021) arXiv:2103.02721 [stat.CO]
Bonner, S., Kim, H.N., Westneat, D., Mutzel, A., Wright, J., Schofield, M.: dalmatian: A package for fitting double hierarchical linear models in r via jags and nimble. J. Stat. Softw. 100(10), 1–25 (2021). https://doi.org/10.18637/jss.v100.i10
Brooks, S., Gelman, A., Jones, G.L., Meng, X.L.: Handbook of Markov Chain Monte Carlo. Chapman & Hall/CRC Press, Boca Raton, FL (2011)
Cepeda-Cuervo, E., Córdoba, M., Núñez-Antón, V.: Conditional overdispersed models: application to count area data. Stat. Methods Med. Res. 27, 2964–2988 (2018). https://doi.org/10.1177/0962280217689968
Corneut, J.M., Marin, J.M., Mira, A., Robert, C.P.: Adaptive multiple importance sampling. Scand. J. Stat. 39(4), 798–812 (2012). https://doi.org/10.1111/j.1467-9469.2011.00756.x
Cowell, R.G., Dawid, A.P., Lauritzen, S.L., Spiegelhalter, D.J.: Probabilistic Networks and Expert Systems. Springer, New York (1999)
Gómez-Rubio, V.: Bayesian Inference with INLA. Chapman and Hall/CRC Press, Boca Raton, FL (2020)
Gómez-Rubio, V., Rue, H.: Markov chain Monte Carlo with the integrated nested Laplace approximation. Stat. Comput. 28(5), 1033–1051 (2018). https://doi.org/10.1007/s11222-017-9778-y
Lázaro, E., Armero, C., Gómez-Rubio, V.: Approximate Bayesian inference for mixture cure models. TEST 29, 750–767 (2020). https://doi.org/10.1007/s11749-019-00679-x
Lee, Y., Nelder, J.A.: Double hierarchical generalized linear models (with discussion). Appl. Stat. 55(2), 139–185 (2006). https://doi.org/10.1111/j.1467-9876.2006.00538.x
Lee, Y., Noh, M.: Modelling random effect variance with double hierarchical generalized linear models. Stat. Modell. 12(6), 487–502 (2012). https://doi.org/10.1177/1471082X12460132
McCullagh, P., Nelder, J.A.: Generalized Linear Models, 2nd edn. Chapman and Hall, London (1989)
Morales-Otero, M., Núñez-Antón, V.: Comparing Bayesian conditional overdispersion and the Besag-York-Mollié models: Application to infant mortality rates. Mathematics 9(3), 282 (2021). https://doi.org/10.3390/math9030282
Plummer, M.: rjags: Bayesian Graphical Models using MCMC. R package version 4-12 (2021)
Quintero-Sarmiento, A., Cepeda-Cuervo, E., Núñez-Antón, V.: Estimating infant mortality in colombia: some overdispersion modelling approaches. J. Appl. Stat. 39(5), 1011–1036 (2012). https://doi.org/10.1080/02664763.2011.634395
Rönnegård, L., Felleki, M., Fikse, F., Mulder, H.A., Strandberg, E.: Genetic heterogeneity of residual variance - estimation of variance components using double hierarchical generalized linear models. Genet. 42(1), 8 (2010). https://doi.org/10.1186/1297-9686-42-8
Rue, H., Martino, S., Chopin, N.: Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B 71(2), 319–392 (2009). https://doi.org/10.1111/j.1467-9868.2008.00700.x
Funding
V. Nú\(\tilde{n}\)ez-Antón and M. Morales-Otero’s research has been funded by Ministerio de Ciencia e Innovación (MCIN, Spain), Agencia Estatal de Investigación (AEI/10.13039/501100011033/) and Fondo Europeo de Desarrollo Regional (FEDER) “Una manera de hacer Europa” under the I+D+i research grant PID2020-112951GB-I00 and by Ministerio de Economía y Competitividad (Spain), Agencia Estatal de Investigación (AEI), and the European Regional Development Fund (ERDF), under research grant MTM2016-74931-P (AEI/ERDF, EU). In addition, V. Nú\(\tilde{n}\)ez-Antón’s research has also been funded by the Department of Education of the Basque Government (UPV/EHU Econometrics Research Group) under research grants IT-1359-19 and IT-1508-22, and by the National Agency for Research and Development - ANID/PCI/REDES190111. V. Gómez-Rubio has been supported by grants SBPLY/17/ 180501/000491 and SBPLY/21/180501/000241, funded by Consejería de Educación, Cultura y Deportes (JCCM, Spain) and FEDER, grant PID2019-106341GB-I00, funded by Ministerio de Ciencia e Innovación (Spain) and a group support grant from Universidad de Castilla-La Mancha (Spain).
Author information
Authors and Affiliations
Contributions
All authors declare no financial or non-financial interests directly or indirectly related to this work. All authors declare that they have equally contributed to this work.
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Supplementary information
Supplementary material including additional results has been included in an accompanying document. The file includes graphical diagnostics for all of the fitted models, a summary of computation times for model fitting and an additional DHGLM fit to the sleep study that considers a shared slope for all participants. (pdf 2,460KB)
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Morales-Otero, M., Gómez-Rubio, V. & Núñez-Antón, V. Fitting double hierarchical models with the integrated nested Laplace approximation. Stat Comput 32, 62 (2022). https://doi.org/10.1007/s11222-022-10122-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-022-10122-1