Abstract
The junction-tree representation provides an attractive structural property for organising a decomposable graph. In this study, we present two novel stochastic algorithms, referred to as the junction-tree expander and junction-tree collapser, for sequential sampling of junction trees for decomposable graphs. We show that recursive application of the junction-tree expander, which expands incrementally the underlying graph with one vertex at a time, has full support on the space of junction trees for any given number of underlying vertices. On the other hand, the junction-tree collapser provides a complementary operation for removing vertices in the underlying decomposable graph of a junction tree, while maintaining the junction tree property. A direct application of the proposed algorithms is demonstrated in the setting of sequential Monte Carlo methods, designed for sampling from distributions on spaces of decomposable graphs. Numerical studies illustrate the utility of the proposed algorithms for combinatorial computations on decomposable graphs and junction trees. All the methods proposed in the paper are implemented in the Python library trilearn.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Decomposable graphs, sometimes also called triangulated or chordal graphs, are characterized by the property that every cycle of length more than three has an edge (or chord) joining two nonconsecutive vertices (Lauritzen 1996). Another characteristic property is that these graphs can be recursively decomposed into smaller graphs, called cliques, where every pair of vertices are connected by an edge. In this paper we rely on the fact that a graph is decomposable if and only if its cliques can be arranged into a so-called junction tree. Figure 1 shows an example of a decomposable graph along with one of its junction tree representations. Decomposable graphs and their junction-tree representations as auxiliary data structure have been used in various contexts; examples include computational geometry, estimation of large-scale random graph models with local dependence, statistical inference (such as sparse covariance- and concentration-matrix computation), contingency-table analysis, probabilistic graphical models, and message passing; see e.g. (Eppstein 2009; Lauritzen 1996; Pearl 1997).
This work is mainly driven by application of decomposability to probabilistic graphical models for representing conditional independence relations. From a statistical point of view, learning the underlying graph structure based on observed data in such models is particularly convenient since the graph likelihood has a closed form. However, the complexity of the graph space makes estimators such as the maximum likelihood graph estimates intractable, which has lead to an increasing interest in Bayesian methods, in particular in Monte Carlo methods for sampling-based approximations of the graph posterior.
The available methods are based on Markov chain Monte Carlo (MCMC) schemes (Tierney 1994), especially variations of the Metropolis–Hastings algorithm (Hastings 1970; Metropolis et al. 1953), where new graphs are proposed by means of random single-edge perturbations, and the set of possible moves generated by subjecting a given graph to such perturbations defines a neighborhood in the decomposable-graph space; see e.g. (Frydenberg and Lauritzen 1989; Giudici and Green 1999; Green and Thomas 2013; Thomas and Green 2009a). However, since the only vertices that may be connected by an edge in a (connected) decomposable graph while maintaining decomposability are those that already have a neighbour in common and the removable edges are necessarily contained in exactly one clique, operations on the edge set are inherently local. As a consequence, an MCMC sampler based on such moves will most likely suffer from mixing problems (Giudici and Green 1999; Green and Thomas 2013).
Green and Thomas (2013) showed that edge moves on decomposable graph space can sometimes be designed more easily if one operates on the extended junction-tree space. While this approach is mainly computationally motivated, it is feasible also from a statistical point of view; indeed, a given distribution on the space of decomposable graphs can always be embedded into an extended version defined on the space of junction trees in such a way that the push-forward distribution of the extended distribution with respect to the underlying graph equals the given distribution on the decomposable-graph space. Thus, by running an MCMC sampler producing a trajectory of junction trees targeting the extended distribution, an MCMC trajectory targeting the original distribution is obtained as a by-product by simply extracting the underlying graphs of the trees in the former sequence.
Against this background, it is desirable to explore alternative ways of simulating decomposable graphs. In the present paper we take a different approach than the above, which instead of altering the edge set of a graph with a fixed set of vertices, builds new graphs incrementally, starting from the empty graph and adding vertices one by one. More specifically, we present two novel stochastic algorithms operating on junction-tree structures: the junction-tree expander (JTE, or the Christmas-tree algorithm) and the junction-tree collapser (JTC). The JTE (JTC) expands (collapses) a junction tree by randomly adding (removing) one vertex to (from) the underlying decomposable graph. As we shall see, the JTE and JTC have two theoretical properties that are of fundamental importance in Monte Carlo simulation. First, the transition probabilities of the induced Markov kernels are available in a closed form and can be computed efficiently; second, the JTE algorithm is able to generate, with positive probability, when applied sequentially, all junction trees with a given number of vertices in its underlying graph.
In order to illustrate their application potential, we employ jointly the JTE and the JTC to construct a sequential Monte Carlo (SMC) sampler (Del Moral et al. 2006), sampling from more or less arbitrary distributions defined on spaces of decomposable graphs. In this construction, which relies on the above-mentioned junction-tree embedding proposed by Green and Thomas (2013), the JTC is used to extend the target distribution to a path space of junction trees of increasing dimension, whereas the JTE is used to generating proposals on this new space.
Using the SMC approach, we are able to provide unbiased estimates of the numbers of decomposable graphs and junction trees for any given number of vertices. This importance-sampling approach to the combinatorics of decomposable graphs and junction trees is the first of its kind. In the follow-up paper (Olsson et al. 2019), we cast further such an SMC sampler into the framework of particle Gibbs samplers (Andrieu et al. 2010). The resulting MCMC algorithm, which relies heavily on on the JTE and JTC derived in the present paper, allows for global MCMC moves across the decomposable-graph space and, consequently, weakly correlated samples and fast mixing.
The JTE is related to other existing approaches of generating junction trees. For instance, the algorithm presented in Markenzon et al. (2008) has similarities to ours in the sense that it expands the underlying graph incrementally in each step of the algorithm. However, unlike our proposed JTE, this algorithm is restricted to connected decomposable graphs and transition probabilities are not directly provided. A completely different strategy for decomposable-graph sampling based on tree-dependent bipartiet graphs is presented in Elmasri (2017a, 2017b). A recent MCMC algorithm for joint sampling of general undirected graphs and corresponding concentration matrices in Gaussian graphical models is presented in van den Boom et al. (2022).
The rest of this paper is structured as follows. Sect. 2 introduces notational conventions and a short background on decomposable graphs and junction trees. For a more detailed presentation, the reader is referred to e.g. (Blair and Peyton 1993) or (Lauritzen 1996). Sect. 3 and Sect. 4 present the JTE and the JTC , respectively, along with their corresponding transition probabilities. Sect. 5 provides a novel factorisation of the number of junction trees of a decomposable graph and demonstrates its computational advantage. The application of the JTE and the JTC in the framework of SMC sampling is found in Sect. 6 and Sect. 7 contains our numerical study. Appendix A contains detailed algorithm descriptions along with the proofs of lemmas and theorems stated in the paper, whereas Appendix B provides an algorithm, originally presented in (Thomas and Green 2009b), for randomly connecting a forest into a tree.
Finally, we remark that the code used for generating the examples in the paper is contained in the Python library trilearn available at https://github.com/felixleopoldo/trilearn. The junction-tree expander is also available through Benchpress (Rios et al. 2021), a recent software that enables execution and seamless comparison between state-of-the-art structure learning algorithms. The junction-tree expander is implemented as a module in Benchpress to simulate graphs underlying data for benchmarking.
2 Preliminaries
2.1 Notational convention
For any finite set \(a\), we denote its power set by \(\varvec{\wp }(a)\). The uniform distribution over the elements in \(a\) is denoted by  . We assume that all random variables are well defined on a common probability space \((\Omega , \mathcal {F}, \mathbb {P})\).Abusing notation, we will always use the same notation for a random variable and a realisation of the same. Further, we will use the same notation for a distribution and its corresponding probability density function. For an arbitrary space \({\mathsf {X}}\), the support of a nonnegative function h defined on \({\mathsf {X}}\) is denoted by
. We assume that all random variables are well defined on a common probability space \((\Omega , \mathcal {F}, \mathbb {P})\).Abusing notation, we will always use the same notation for a random variable and a realisation of the same. Further, we will use the same notation for a distribution and its corresponding probability density function. For an arbitrary space \({\mathsf {X}}\), the support of a nonnegative function h defined on \({\mathsf {X}}\) is denoted by  . For all sequences \((a_j)_{j = 1}^\ell \), we apply the convention
. For all sequences \((a_j)_{j = 1}^\ell \), we apply the convention  . Moreover, for all sequences \((a_j)_{j = 1}^\ell \) of sets and all nonempty sets \(b\), we set
. Moreover, for all sequences \((a_j)_{j = 1}^\ell \) of sets and all nonempty sets \(b\), we set  . We denote by \({\mathbb {N}}\) the set of natural numbers \(\{1,2,\dots \}\) and by \({\mathbb {N}}_{p}\) the set \(\{1,\dots ,p\}\) for some \(p\in {\mathbb {N}}\).
. We denote by \({\mathbb {N}}\) the set of natural numbers \(\{1,2,\dots \}\) and by \({\mathbb {N}}_{p}\) the set \(\{1,\dots ,p\}\) for some \(p\in {\mathbb {N}}\).
The notation, \(\mathsf {pr}(\{ w_\ell \}_{\ell = 1}^N)\) is used to denote the categorical distribution induced by a set \(\{ w_\ell \}_{\ell = 1}^N\) of positive (possibly unnormalised) numbers. More specifically, writing \(x \sim \mathsf {pr}(\{ w_\ell \}_{\ell = 1}^N)\) means that the random variable x takes on the value  with probability \(\textstyle w_\ell / \sum _{\ell ' = 1}^Nw_{\ell '}\).
with probability \(\textstyle w_\ell / \sum _{\ell ' = 1}^Nw_{\ell '}\).
2.2 Graph theory
A pair  of a vertex set
of a vertex set  and an edge set
and an edge set  , where
, where  is a set of unordered pairs
is a set of unordered pairs  such that
such that  , is called an undirected graph. Two vertices
, is called an undirected graph. Two vertices  and \({y'}\) in
and \({y'}\) in  are adjacent if they are directly connected by an edge, i.e.,
are adjacent if they are directly connected by an edge, i.e.,  belongs to
belongs to  . The neighbors
. The neighbors  of a vertex
of a vertex  is the set of vertices in
is the set of vertices in  adjacent to
adjacent to  . A sequence
. A sequence  of distinct vertices is called an
of distinct vertices is called an  -
- -path, denoted by
-path, denoted by  , if for all \(j\in \{2, \ldots , \ell \}\),
, if for all \(j\in \{2, \ldots , \ell \}\),  belongs to
belongs to  . Two vertices
. Two vertices  and \({y'}\) are said to be connected if there exists an
and \({y'}\) are said to be connected if there exists an  -
- -path. Moreover, a graph is said to be connected if all pairs of vertices are connected. A graph is called a tree if there is a unique path between any pair of vertices in the graph. A connectivity component of a graph is a subset of vertices that are pairwise connected. A graph is a forest if all connectivity components induce distinct trees. Further, two graphs are said to be isomorphic if they have the same number of vertices and equivalent edge sets when disregarding the labels of the vertices.
-path. Moreover, a graph is said to be connected if all pairs of vertices are connected. A graph is called a tree if there is a unique path between any pair of vertices in the graph. A connectivity component of a graph is a subset of vertices that are pairwise connected. A graph is a forest if all connectivity components induce distinct trees. Further, two graphs are said to be isomorphic if they have the same number of vertices and equivalent edge sets when disregarding the labels of the vertices.
Now, consider a general graph  which we call
which we call  . The order and the size of
. The order and the size of  refer to the number of vertices
refer to the number of vertices  and the number of edges
and the number of edges  , respectively. Let \(a\), \(b\), and \(s\) be subsets of
, respectively. Let \(a\), \(b\), and \(s\) be subsets of  ; then the set \(s\) separates \(a\) from \(b\) if for all
; then the set \(s\) separates \(a\) from \(b\) if for all  and \({y'}\in b\), all paths
and \({y'}\in b\), all paths  intersect \(s\). We denote this by
intersect \(s\). We denote this by  . The graph
. The graph  is complete if all vertices are adjacent to each other. A graph
is complete if all vertices are adjacent to each other. A graph  is a subgraph of
is a subgraph of  if
if  and
and  . A subtree is a connected subgraph of a tree. For
. A subtree is a connected subgraph of a tree. For  , the induced subgraph
, the induced subgraph  is the subgraph of
is the subgraph of  with vertices
with vertices  and edge set
and edge set  given by the set of edges in
given by the set of edges in  having both endpoints in
having both endpoints in  . A subset of
. A subset of  is a complete set if it induces a complete subgraph. A complete subgraph is called a clique if it is not an induced subgraph of any other complete subgraph.
is a complete set if it induces a complete subgraph. A complete subgraph is called a clique if it is not an induced subgraph of any other complete subgraph.
The primer interest of this paper regards decomposable graphs and the junction-tree representation.
Definition 1
A graph  is decomposable if its cliques can be arranged in a so-called junction tree, i.e. a tree whose nodes are the cliques in
is decomposable if its cliques can be arranged in a so-called junction tree, i.e. a tree whose nodes are the cliques in  , and where for any pair of cliques
, and where for any pair of cliques  and
and  in
in  , the intersection
, the intersection  is contained in each of the cliques on the unique path
is contained in each of the cliques on the unique path  .
.
Note that a decomposable graph may have many junction-tree representations (referred to as a junction tree for the specific graph) whereas for any specific junction tree, the underlying graph is uniquely determined. For clarity, from now on we follow Green and Thomas (2013) and reserve the terms vertices and edges for the elements of  . Vertices and edges of junctions trees will be referred to as nodes and links, respectively. Each link \((a, b)\) in a junction tree is associated with the intersection \(a\cap b\), which is referred to as a separator and denoted by \(s_{a,b}\). Note that, the empty set is also a valid separator and could separate any pair of cliques that belong to distinct connected components. The set of distinct separators in a junction tree with graph
. Vertices and edges of junctions trees will be referred to as nodes and links, respectively. Each link \((a, b)\) in a junction tree is associated with the intersection \(a\cap b\), which is referred to as a separator and denoted by \(s_{a,b}\). Note that, the empty set is also a valid separator and could separate any pair of cliques that belong to distinct connected components. The set of distinct separators in a junction tree with graph  is denoted by
is denoted by  . Since all junction-tree representations of a specific decomposable graph have the same set of separators, we may talk about the separators of a decomposable graph. In the following we consider a fixed sequence
. Since all junction-tree representations of a specific decomposable graph have the same set of separators, we may talk about the separators of a decomposable graph. In the following we consider a fixed sequence  of vertices and denote by
of vertices and denote by  the space of decomposable graphs with vertex set
the space of decomposable graphs with vertex set  . The space of junction-tree representations for graphs in
. The space of junction-tree representations for graphs in  is analogously denoted by
is analogously denoted by  . The graph corresponding to a junction tree
. The graph corresponding to a junction tree  is denoted by
is denoted by  . We let
. We let  denote the subtree induced by the nodes of a junction tree
denote the subtree induced by the nodes of a junction tree  containing the separator \(s\) and let
containing the separator \(s\) and let  denote the forest obtained by deleting, in
denote the forest obtained by deleting, in  , the links associated with \(s\).
, the links associated with \(s\).
3 Expanding and collapsing junction trees
At the highest level, the JTE can be described in a few main steps illustrated in Fig. 3. In the first step, the algorithm starts by drawing, at random, a subtree  of the given tree
of the given tree  (see Step 1 in Fig. 3). In the second step, a new vertex
(see Step 1 in Fig. 3). In the second step, a new vertex  is connected to a random subset of each of the cliques in
is connected to a random subset of each of the cliques in  to form a new subtree
to form a new subtree  , which is isomorphic to
, which is isomorphic to  . The edges in
. The edges in  are then removed and each of the nodes in
are then removed and each of the nodes in  are connected to the nodes in
are connected to the nodes in  to which they stem from, while maintaining the junction tree property (see Step 2-4 in Fig. 3). On the other hand, the JTC starts by selecting the unique subtree
to which they stem from, while maintaining the junction tree property (see Step 2-4 in Fig. 3). On the other hand, the JTC starts by selecting the unique subtree  induced by a given vertex \({y'}\) (see Step 4 in Fig. 3). The second step amounts to drawing, for each clique
induced by a given vertex \({y'}\) (see Step 4 in Fig. 3). The second step amounts to drawing, for each clique  in
in  , a neighboring clique
, a neighboring clique  not containing \({y'}\), for which
not containing \({y'}\), for which  is substituted while maintaining the junction tree property (see Step 3-1 in Fig. 3). The two algorithms are complementary in the sense that the output obtained by subjecting a given tree
is substituted while maintaining the junction tree property (see Step 3-1 in Fig. 3). The two algorithms are complementary in the sense that the output obtained by subjecting a given tree  to either the JTE followed by the JTC, or, vice versa, the JTC followed by the JTE, coincides with
to either the JTE followed by the JTC, or, vice versa, the JTC followed by the JTE, coincides with  with positive probability.
with positive probability.
3.1 Sampling subtrees
Before presenting our main algorithm for expanding junction trees, we present one of its crucial subroutines: an algorithm for random sampling of subtrees of a given, arbitrary tree. It takes two tuning parameters, \((\alpha , \beta ) \in (0,1)^2\), which together control the number of vertices in the subtree. The algorithm either, with probability \(1-\beta \), returns the empty tree or a breadth first tree traversal is performed, where new nodes are visited with probability \(\alpha \). Thus, the parameter \(\alpha \) controls the number of vertices in the subgraph given that it is nonempty. We call this algorithm the stochastic breath-first tree traversal and provide an outline below. Full details are given in Algorithm 3 in Appendix A.
Stochastic breadth-first tree traversal
Let  be a tree.
be a tree.
- Step 1. :
-
Perform a Bernoulli trial that with probability \(\beta \) determines if the subtree
 will be nonempty.
will be nonempty.
If the empty tree was sampled, return it. Otherwise, proceed according to the following steps.
- Step 2. :
-
Sample a node uniformly at random from
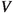 and add it to a list \( a\).
and add it to a list \( a\). - Step 3. :
-
Remove the first item, say
 , from \(a\) and add it to the set
, from \(a\) and add it to the set  .
. - Step 4. :
-
Add independently each of the non-visited neighbors of
 to the end of \(a\) with probability \(\alpha \).
to the end of \(a\) with probability \(\alpha \). - Step 5. :
-
If \(a\) is not empty, go to Step 2.
- Step 6. :
-
Return the induced subtree
 .
.
The probability of extracting the induced subtree  from
from  by following the above steps is given by
by following the above steps is given by

where  is the number of components in the forest
is the number of components in the forest  . The factor
. The factor  stems from the fact that any vertex in
stems from the fact that any vertex in  is a valid starting vertex in the breadth-first traversal-like procedure and the probability of extracting a certain subtree is equal for each choice.
is a valid starting vertex in the breadth-first traversal-like procedure and the probability of extracting a certain subtree is equal for each choice.
3.2 Expanding junction trees
In this section we present the main contribution of this paper, namely an algorithm for expanding randomly a given junction tree  , \(m\in {\mathbb {N}}\), into a new junction tree
, \(m\in {\mathbb {N}}\), into a new junction tree  such that
such that  is the induced subgraph of
is the induced subgraph of  . This operation defines a Markov transition kernel
. This operation defines a Markov transition kernel  , whose expression is derived at the end of this section. The full procedure, which in the following will be referred to as the junction-tree expander, is given below. Further details of these steps are provided in Algorithm 4 in Appendix A.
, whose expression is derived at the end of this section. The full procedure, which in the following will be referred to as the junction-tree expander, is given below. Further details of these steps are provided in Algorithm 4 in Appendix A.
Junction tree expander
Let  be a junction tree in
be a junction tree in  .
.
- Step 1. :
-
Sample a random subtree
 of
of  .
.
If  is empty, proceed as follows:
is empty, proceed as follows:
- Step 2. :
-
Create a new node containing merely the vertex
 and connect it to an arbitrary node in
and connect it to an arbitrary node in 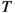 .
. - Step 3. :
-
Cut the new tree at the empty separator to obtain a forest.
- Step 4. :
-
Randomly reconnect the forest into a tree (see Appendix B).
If  is non-empty, enumerate the nodes in
is non-empty, enumerate the nodes in  as
as  , and let, for each
, and let, for each  ,
,  be defined as the union of the separators associated with
be defined as the union of the separators associated with  in
in  . Proceed as follows:
. Proceed as follows:
- Step 2\(^*\).:
-
For each node
 , draw uniformly at random a (possibly empty) subset
, draw uniformly at random a (possibly empty) subset  of
of  to create a new unique node
to create a new unique node  , consisting of
, consisting of  and the vertex
and the vertex 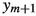 . Note that for
. Note that for  to be unique,
to be unique,  has to be non-empty if any separator associated with
has to be non-empty if any separator associated with 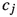 in
in  equals
equals  . If
. If  was engulfed in
was engulfed in  (i.e.
(i.e.  ), simply delete
), simply delete  .
. - Step 3\(^*\).:
-
To the nodes in
 , assign links which replicate the structure of
, assign links which replicate the structure of  . Then remove the links in
. Then remove the links in  and connect by a link each
and connect by a link each  to its corresponding new node
to its corresponding new node  .
. - Step 4\(^*\).:
-
For each node
 , the neighbors whose links can be moved to
, the neighbors whose links can be moved to  while maintaining an equivalent junction tree, are distributed uniformly between
while maintaining an equivalent junction tree, are distributed uniformly between  and
and  . The set of neighbors of
. The set of neighbors of  is denoted by
is denoted by  .
.
When using the subtree sampler provided in Algorithm 3 at Step 1, the parameters \(\alpha \) and \(\beta \) have clear impacts on the sparsity of the outcome  of the JTE; more specifically, since each node in the selected subtree will give rise to a new node in
of the JTE; more specifically, since each node in the selected subtree will give rise to a new node in  , \(\alpha \) controls the number of nodes containing the new vertex
, \(\alpha \) controls the number of nodes containing the new vertex  . The parameter \(\beta \) is simply interpreted as the probability of
. The parameter \(\beta \) is simply interpreted as the probability of  being connected to some vertex in
being connected to some vertex in  .
.
Example 1
We illustrate two possible scenarios for how the junction tree in Fig. 1 with underlying vertex set  could be expanded by the vertex 10. Figure 2 shows the possible scenario where the subtree picked at Step 1 is empty. Figure 3 demonstrates the possible scenario where the subtree sampled at Step 1 contains the nodes
could be expanded by the vertex 10. Figure 2 shows the possible scenario where the subtree picked at Step 1 is empty. Figure 3 demonstrates the possible scenario where the subtree sampled at Step 1 contains the nodes  ,
,  , and
, and  , colored in blue. The new nodes, colored in red, are \(d_{1}^+=\{3,4,10\}\), \(d_{2}^+=\{4,5,10\}\), and \(d_{3}^+=\{5,6,10\}\), built from the sets \(z_{1}=\{4\}\), \(z_{2}=\{4,5\}\), \(z_{3}=\{5\}\) and \(q_{1}=\{3\}\), \(q_{2}=\emptyset \), \(q_{3}=\{6\}\). The sets of moved neighbors are \(n_{1}=\emptyset \), \(n_{2}=\emptyset \) and \(n_{3}=\{\{5,6,9\}\}\). The resulting underlying graphs for these two examples are shown in Fig. 4.
, colored in blue. The new nodes, colored in red, are \(d_{1}^+=\{3,4,10\}\), \(d_{2}^+=\{4,5,10\}\), and \(d_{3}^+=\{5,6,10\}\), built from the sets \(z_{1}=\{4\}\), \(z_{2}=\{4,5\}\), \(z_{3}=\{5\}\) and \(q_{1}=\{3\}\), \(q_{2}=\emptyset \), \(q_{3}=\{6\}\). The sets of moved neighbors are \(n_{1}=\emptyset \), \(n_{2}=\emptyset \) and \(n_{3}=\{\{5,6,9\}\}\). The resulting underlying graphs for these two examples are shown in Fig. 4.
Note that in this example,  is a leaf node in the resulting tree, making it look like decoration in a Christmas tree.
is a leaf node in the resulting tree, making it look like decoration in a Christmas tree.
A possible expansion of the junction tree in Fig. 1, where the empty subtree is drawn at Step 1
A possible outcome of the JTE where a non-empty subtree was drawn in the expansion of the junction tree in Fig. 1
Two decomposable graphs resulting from expanding the graph in Fig. 1 by the vertex 10
Example 2
Figure 5 should be read in chunks of two rows (except for the first row) and shows the junction trees, the corresponding decomposable graphs and the subgraphs generated by the JTE for \(m\in \{1,\dots ,5\}.\) The left column shows the expansion of the junction trees and the right column shows the underlying decomposable graphs. Subtrees are colored in blue and the new nodes are colored in red. Unaffected nodes are black. Vertices in the underlying graphs are colored analogously. For example, the subtree  selected in the generation of
selected in the generation of  on Row 5 is found on Row 4. The underlying nodes in
on Row 5 is found on Row 4. The underlying nodes in  for creating
for creating  are also found on Row 4, and so on. Note that the subtree
are also found on Row 4, and so on. Note that the subtree  used in the creation of
used in the creation of  , is the empty tree, thus
, is the empty tree, thus  is black. The tuning parameters of the junction tree expander are set to \(\alpha =0.3\) and \(\beta =0.9\).
is black. The tuning parameters of the junction tree expander are set to \(\alpha =0.3\) and \(\beta =0.9\).
The main reason for operating on junction trees as opposed to decomposable graphs directly is computational tractability. Next we provide explicit expressions of the transition kernel  of the JTE, for any given \(m\in {\mathbb {N}}\).
of the JTE, for any given \(m\in {\mathbb {N}}\).
For  and
and  generated by the JTE, let
generated by the JTE, let  denote the set of possible subtrees bridging
denote the set of possible subtrees bridging  and
and  through the first step of the JTE. This set contains, depending on
through the first step of the JTE. This set contains, depending on  and
and  , either one unique or two different trees, whose explicit forms are provided by Proposition 1.
, either one unique or two different trees, whose explicit forms are provided by Proposition 1.
Proposition 1
Let \(m \in {\mathbb {N}}\),  , and
, and  be generated by the JTE. If the subtree of
be generated by the JTE. If the subtree of  induced by the nodes containing the vertex
induced by the nodes containing the vertex  has a single node
has a single node  with exactly two neighbors
with exactly two neighbors  and
and  such that
such that  , then
, then  ; otherwise,
; otherwise,  (a single tree), where
(a single tree), where  and
and  . Here
. Here  and
and  denote new nodes in
denote new nodes in  and
and  and
and  are the corresponding nodes in
are the corresponding nodes in  . The sets \( r_{j}\) and \( r_{k}\) may be empty.
. The sets \( r_{j}\) and \( r_{k}\) may be empty.
From a computational point of view, Proposition 1 is crucial since it guarantees a tractable expression of  . Before we state this expression we introduce some further notation. We let
. Before we state this expression we introduce some further notation. We let  denote the number of possible ways that
denote the number of possible ways that  , the tree obtained by cutting
, the tree obtained by cutting  at the separator \(s\), can be connected to form a tree; this number is described in more detail in Theorem 5. Now, the transition probability of the JTE takes the following form
at the separator \(s\), can be connected to form a tree; this number is described in more detail in Theorem 5. Now, the transition probability of the JTE takes the following form

where  is understood as the probability that the JTE generates
is understood as the probability that the JTE generates  with
with  as input given that
as input given that  was drawn at Step 1. We stress again that the sum in (3.1) has either one or two terms and it is thus easily computed. The conditional probability
was drawn at Step 1. We stress again that the sum in (3.1) has either one or two terms and it is thus easily computed. The conditional probability  takes two different forms depending on whether
takes two different forms depending on whether  is empty or not. If
is empty or not. If  is empty, since
is empty, since  is randomised at \(\emptyset \), all the
is randomised at \(\emptyset \), all the  obtainable equivalent junction trees have equal probability. Otherwise, in case of
obtainable equivalent junction trees have equal probability. Otherwise, in case of  non-empty, the probability of the subsets \(q_{j}\) are calculated according to the uniform subset distributions in Step 2\(^*\). Observe that, given
non-empty, the probability of the subsets \(q_{j}\) are calculated according to the uniform subset distributions in Step 2\(^*\). Observe that, given  and
and  , the resulting tree
, the resulting tree  is completely determined by
is completely determined by  and
and  . Since the pairs
. Since the pairs  are drawn conditionally independently given
are drawn conditionally independently given  and
and  we obtain
we obtain

We examine the probabilities in (3.2) in the case where  is nonempty. Since for each \(j\), the existence of a node
is nonempty. Since for each \(j\), the existence of a node  such that
such that  forces \(q_{j}\) to be nonempty, it holds that
forces \(q_{j}\) to be nonempty, it holds that

Conditionally upon  ,
,  , and \(q_{j}\), the probability of each neighbor set \(n_{j}\) at Step \(4^*\) follows straightforwardly; indeed, the distribution of \(n_{j}\) takes two different forms depending on whether
, and \(q_{j}\), the probability of each neighbor set \(n_{j}\) at Step \(4^*\) follows straightforwardly; indeed, the distribution of \(n_{j}\) takes two different forms depending on whether  was engulfed into
was engulfed into  (i.e.
(i.e.  ) or not. If so, all of the neighbors of
) or not. If so, all of the neighbors of  are moved to
are moved to  with probability 1. Otherwise, it has equal probability over all subsets of
with probability 1. Otherwise, it has equal probability over all subsets of  giving
giving

Observe that the simplicity of (3.1) is appealing from a computational point of view. In particular, as shown in Sect. 7, when  is used as a proposal kernel in an SMC algorithm, fast computation of the transition probability is crucial, especially as the graph space increases.
is used as a proposal kernel in an SMC algorithm, fast computation of the transition probability is crucial, especially as the graph space increases.
An important property of the JTE is that for any \(m\in {\mathbb {N}}\) and  , a tree
, a tree  generated by the JTE is also a junction tree. In addition,
generated by the JTE is also a junction tree. In addition,  is an induced subgraph of
is an induced subgraph of  , having one additional vertex.
, having one additional vertex.
Theorem 1
For any \(m \in {\mathbb {N}}\) and  it holds that
it holds that
-
(i)
 ,
, -
(ii)
 for all
for all  .
.
The following theorem states that for any \(m\in {\mathbb {N}}\), all junction trees in  can be generated with positive probability using recursive application of the JTE. More specifically, we may define the marginal probability
can be generated with positive probability using recursive application of the JTE. More specifically, we may define the marginal probability  for any
for any  where
where  and state the following theorem.
and state the following theorem.
Theorem 2
For any ordering of vertices  , \(m \in {\mathbb {N}}\), it holds that
, \(m \in {\mathbb {N}}\), it holds that

For comparison, the algorithm for sequential a sampling of junction trees presented by Markenzon et al. (2008) corresponds to recursive application of a special case of the JTE, where \(\alpha =0\), \(\beta =1\), and where Step 4 is omitted. Note that Theorem 2 does not hold under such assumptions since the algorithm is forced to operate on a restricted space of junction trees for connected decomposable graphs. Markenzon et al. (2008) also proposes a final step that merges neighboring cliques an unspecified number of times in order to increase the number of edges in the underlying graphs. While this step has the intended effect on the graphs, the space is still restricted and calculating the transition probabilities becomes intractable in general.
4 Collapsing junction trees
In this section, we present the junction-tree collapser, a reversed version of the JTE, introduced in the previous section. The idea is to collapse a junction tree  into a new tree
into a new tree  by removing
by removing  from the underlying graph in such a way that
from the underlying graph in such a way that  . As will be proved in this section, this procedure defines a Markov kernel
. As will be proved in this section, this procedure defines a Markov kernel  .
.
Next follows a description of the different suboperations in the sampling procedure for  . The details of the steps are given in Algorithm 5 in Appendix A.
. The details of the steps are given in Algorithm 5 in Appendix A.
Junction tree collapser
Let  be a junction tree in
be a junction tree in  . Similarly to the JTE, the JTC takes two different forms depending on whether
. Similarly to the JTE, the JTC takes two different forms depending on whether  is present as a node in
is present as a node in  or not.
or not.
If  is a node in
is a node in  proceed as follows:
proceed as follows:
- Step 1. :
-
Remove
 and it incident links to obtain a forest, possibly containing only one tree.
and it incident links to obtain a forest, possibly containing only one tree. - Step 2. :
-
Randomly connect the forest into a tree.
If  is not a node in
is not a node in  proceed as follows:
proceed as follows:
- Step 1\(^*\).:
-
Let
 be the subtree of
be the subtree of  induced by the nodes containing the vertex
induced by the nodes containing the vertex  and enumerate the nodes in
and enumerate the nodes in  by
by  .
. - Step 2\(^*\).:
-
For all
 , draw at random
, draw at random  from \(M_{j}\), the set of neighbors of
from \(M_{j}\), the set of neighbors of  in
in  having the associated separator
having the associated separator  . If no such neighbor exists, let
. If no such neighbor exists, let  .
. - Step 3\(^*\).:
-
Replace each node
 by the corresponding node
by the corresponding node  in the sense that
in the sense that  is assigned all former neighbors of
is assigned all former neighbors of  .
.
The next example illustrates a reversed version of Example 1.
Example 3
Consider collapsing the junction tree in the bottom right panel of Fig. 3 by the vertex 10. The induced subgraph  , having the nodes
, having the nodes  , and
, and  is colored in red in the same subfigure. Further we see that \(M_{1}=\emptyset \) implies that
is colored in red in the same subfigure. Further we see that \(M_{1}=\emptyset \) implies that  and \(M_{2}=\{\{1,4,5\}\}\) implies
and \(M_{2}=\{\{1,4,5\}\}\) implies  . By drawing
. By drawing  from \(M_{3}=\{\{2,5,6\}, \{5,6,9\}\}\), the junction tree in the top left panel of Fig. 3 is obtained.
from \(M_{3}=\{\{2,5,6\}, \{5,6,9\}\}\), the junction tree in the top left panel of Fig. 3 is obtained.
The induced transition probability of collapsing  into a tree
into a tree  has the form
has the form

where, as before,  is the set of nodes in
is the set of nodes in  containing
containing  . The max operation is needed in order to make the expression well defined even when \(M_{j}\) is empty.
. The max operation is needed in order to make the expression well defined even when \(M_{j}\) is empty.
The JTC is a reversed version of the JTE in the sense that for all \(m\in {\mathbb {N}}\), a junction tree  , generated by the JTC from a junction tree
, generated by the JTC from a junction tree  , can be used as input to the JTE to generate
, can be used as input to the JTE to generate  . This property is formulated in the next theorem.
. This property is formulated in the next theorem.
Theorem 3
For all \(m \in {\mathbb {N}}\) and  ,
,
-
(i)
 ,
, -
(ii)
 ,
, -
(iii)
 for any
for any 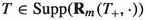 .
.
Theorem 3 proves to be crucial in the SMC context described in Sect. 6 and in particular in the refreshment step of the particle Gibbs sampler detailed in Olsson et al. (2019).
5 Counting the number of junction trees for an expanded decomposable graph
Thomas and Green (2009b) provide an expression for counting the number of equivalent junction trees of a given decomposable graph. In this section we derive a factorisation of the same expression which shows to alleviate the computational burden when calculated for expanded graphs. For sake of completeness, we restate three theorems from (Thomas and Green 2009b). The first counts the number of ways a forest can be reconnected into a tree and was first established in Moon (1967).
Theorem 4
(Moon (1967)) The number of distinct ways that a forest of order \(m\) comprising q subtrees of orders \(r_1,\dots ,r_q\) can be connected into a single tree by adding \(q-1\) edges is
For a given junction tree  , let \(t_{s}\) denote the order of the subtree
, let \(t_{s}\) denote the order of the subtree  induced by the separator \(s\). Now, let \(m_s\) be the number of links associated with \(s\) and let \(f_1,\dots ,f_{m_s+1}\) be the orders of the tree components in
induced by the separator \(s\). Now, let \(m_s\) be the number of links associated with \(s\) and let \(f_1,\dots ,f_{m_s+1}\) be the orders of the tree components in  . Then, by Theorem 4 the following is obtained.
. Then, by Theorem 4 the following is obtained.
Theorem 5
(Thomas and Green (2009b)) The number of ways that the components of  , where \(s\) is a separator in a graph
, where \(s\) is a separator in a graph  with junction tree
with junction tree  , can be connected into a single tree by adding the appropriate number of links is given by
, can be connected into a single tree by adding the appropriate number of links is given by

Theorem 6
(Thomas and Green (2009b)) The number of junction trees for a decomposable graph  is given by
is given by

In the sequential sampling context considered in this paper it is useful to exploit that any decomposable graph  can be regarded as an expansion of another decomposable graph
can be regarded as an expansion of another decomposable graph  , in the sense that
, in the sense that  is obtained by expanding
is obtained by expanding  with the vertex
with the vertex  . This follows for example by induction using (Lauritzen 1996, Corollary 2.8).
. This follows for example by induction using (Lauritzen 1996, Corollary 2.8).
The key insight when calculating  is that when a vertex is added to
is that when a vertex is added to  , not all separators will necessarily be affected. This implies that
, not all separators will necessarily be affected. This implies that  for some separators.
for some separators.
Theorem 7
Let  be an expansion of some graph
be an expansion of some graph  by the extra vertex
by the extra vertex  . Let
. Let  be the set of unique separators created (note that
be the set of unique separators created (note that  might be non-empty) by the expansion. Then
might be non-empty) by the expansion. Then

where  is the set of separators in
is the set of separators in  contained in some separator in \(S^\star \).
contained in some separator in \(S^\star \).
The potential computational gain obtained by using the factorisation in Theorem 7 is illustrated by the following example.
Example 4
Let  be an expansion of a graph
be an expansion of a graph  in the sense that
in the sense that  is connected to every vertex in one of the cliques in
is connected to every vertex in one of the cliques in  . Then, since the set of separators is the same in the two graphs, it holds that
. Then, since the set of separators is the same in the two graphs, it holds that 
6 Applications to sequential Monte Carlo sampling
Sequential Monte Carlo (SMC) methods (Chopin and Papaspiliopoulos 2020) are a class of simulation-based algorithms that offers a principled way of sampling online from very general sequences of distributions, known up to normalising constants only, by propagating recursively a population of random draws, so-called particles, with associated importance weights. The particles evolve randomly and iteratively through selection and mutation. In the selection step, the particles are duplicated or eliminated depending on their importance, while the mutation operation disseminates randomly the particles in the state space and assigns new importance weights to the same for further selection at the next iteration. SMC methods have been particularly successful when it comes to online approximation of state posteriors in general state-space hidden Markov models (Arulampalam et al. 2002).
In this section we demonstrate how the JTE and the JTC can be cast into the framework of SMC methods—or, more precisely, the SMC samplers proposed in Del Moral et al. (2006)—in order to sample from a sequence  of probability distributions, where each
of probability distributions, where each  is a distribution on
is a distribution on  . For every m we assume that
. For every m we assume that  is known only up to a normalising constant, i.e.,
is known only up to a normalising constant, i.e.,  , where
, where  is a tractable, unnormalised function. Following (Del Moral et al. 2006), we introduce path spaces
is a tractable, unnormalised function. Following (Del Moral et al. 2006), we introduce path spaces  and let
and let

be extended target distributions. Importantly, each target  is the marginal of \({\bar{\eta }}_{m}\) with respect to the mth component. In many applications, the aim is to sample from a given distribution \(\pi \) on some junction-tree space
is the marginal of \({\bar{\eta }}_{m}\) with respect to the mth component. In many applications, the aim is to sample from a given distribution \(\pi \) on some junction-tree space  induced by n vertices, and in this case one may let
induced by n vertices, and in this case one may let  and
and  be the marginals of \(\pi \) (if these are known up to normalising constants), serving to guide the distribution flow towards the target \(\pi \).
be the marginals of \(\pi \) (if these are known up to normalising constants), serving to guide the distribution flow towards the target \(\pi \).
Now, introduce, for all m, proposal distributions

Since Theorem 3 implies that  for all \(\ell \in \{1,\dots ,m-1\}\), it is readily checked that \( {\text {Supp}}({\bar{\eta }}_{m}) \subseteq {\text {Supp}}({\bar{\rho }}_m)\). This property, along with Theorems 1 and 2, allows the extended target distributions (6.1) to be sampled by means of an importance-sampling procedure, where independent tree paths \(\tau _{1:m}^{i} = (\tau _{1}^{i},\ldots ,\tau _{m}^{i})\) generated sequentially using the JTE, are assigned importance weights
for all \(\ell \in \{1,\dots ,m-1\}\), it is readily checked that \( {\text {Supp}}({\bar{\eta }}_{m}) \subseteq {\text {Supp}}({\bar{\rho }}_m)\). This property, along with Theorems 1 and 2, allows the extended target distributions (6.1) to be sampled by means of an importance-sampling procedure, where independent tree paths \(\tau _{1:m}^{i} = (\tau _{1}^{i},\ldots ,\tau _{m}^{i})\) generated sequentially using the JTE, are assigned importance weights

Here N is the Monte Carlo sample size. Thanks to the Markovian structure of the proposal (6.2) and the multiplicative structure of the weights (6.3), this procedure can be implemented sequentially by applying recursively the update described in Algorithm 1. This yields a sequence \((\tau _{m}^{i}, \omega _{m}^{i})_{i = 1}^N\), \(m \in {\mathbb {N}}\), of weighted samples, where, since  is the marginal of \({\bar{\eta }}_{m}\) with respect to the last component, \(\sum _{i = 1}^N \omega _{m}^{i} h(\tau _{m}^{i}) / \Omega _{m}^N\), with
is the marginal of \({\bar{\eta }}_{m}\) with respect to the last component, \(\sum _{i = 1}^N \omega _{m}^{i} h(\tau _{m}^{i}) / \Omega _{m}^N\), with  , is a strongly consistent self-normalised estimator of the expectation
, is a strongly consistent self-normalised estimator of the expectation  of any real-valued test function h under
of any real-valued test function h under  . In the SMC literature, the draws \((\tau _{m}^{i})_{i = 1}^N\) are typically referred to as particles.
. In the SMC literature, the draws \((\tau _{m}^{i})_{i = 1}^N\) are typically referred to as particles.

Even though this sequential importance sampling procedure, which is described in Algorithm 1, appears appealing at a first sight, the multiplicative weight updating formula (6.3) (Line 3 in Algorithm 1) is problematic in the sense that it will, inevitably, lead to severe weight skewness and, consequently, high Monte Carlo variance. In fact, it can be shown that updating the weights in this naive manner leads to a Monte Carlo variance that increases geometrically fast with m; see e.g. (Cappé et al. 2005, Chapter 7.3) for a discussion. Needless to say, this is impractical for most applications
In order to cope with the weight-degeneracy problem, Gordon et al. (1993) proposed furnishing the previous sequential importance sampling algorithm with a selection step, in which the particles are resampled, with replacement, in proportion to their importance weights. Upon selection, all particles are assigned the unit weight, and the particles and importance weights are then updated as in Algorithm 1. Such selection is a key ingredient in SMC methods, and it can be shown mathematically that the resulting sequential importance sampling with resampling algorithm, which is given in Algorithm 2, is indeed numerically stable Chopin and Papaspiliopoulos (2020), Del Moral (2004).

In standard self-normalised importance sampling, the average weight provides an unbiased estimator of the normalising constant of the target. However, when the particles are resampled systematically, as in Algorithm 2, this simple estimator is no longer valid. Instead, it is possible to show that for every m, the estimator

with  , is an unbiased estimator of \(\gamma _m(h)\) for any real-valued test function h. In particular,
, is an unbiased estimator of \(\gamma _m(h)\) for any real-valued test function h. In particular,

provides an unbiased estimator of the normalising constant  of
of  . This estimator will be illustrated in the next section.
. This estimator will be illustrated in the next section.
7 Numerical study
We demonstrate two applications of Algorithm 2 for estimating the cardinalities  and
and  of the spaces of decomposable graphs and junction trees, respectively.
of the spaces of decomposable graphs and junction trees, respectively.
7.1 Estimating 
Wormald (1985) provides an exact expression for  and evaluates the same for \(m\le 13\). In the same reference, the author also establishes the asymptotic expression
and evaluates the same for \(m\le 13\). In the same reference, the author also establishes the asymptotic expression  . Another exact algorithm that calculates
. Another exact algorithm that calculates  for \(m\le 10\) is proposed in Kawahara et al. (2018).
for \(m\le 10\) is proposed in Kawahara et al. (2018).
In this study we will use Algorithm 2 for estimating  , \(m \in {\mathbb {N}}\), on the basis of the target probability distributions
, \(m \in {\mathbb {N}}\), on the basis of the target probability distributions

Note that the normalising constant  of
of  equals
equals  .; indeed,
.; indeed,

With this formulation, unbiased estimates of  , \(m \in {\mathbb {N}}\), can be obtained directly using (6.4). Note that in this setting Line 4 of Algorithm 2 reduces to
, \(m \in {\mathbb {N}}\), can be obtained directly using (6.4). Note that in this setting Line 4 of Algorithm 2 reduces to

where  ,
,  , for which, as demonstrated by Example 4, the computational burden can be substantially reduced using the factorisation (5.1) since
, for which, as demonstrated by Example 4, the computational burden can be substantially reduced using the factorisation (5.1) since  .
.
Table 1 shows means and standard errors based on 10 estimates  of
of  for
for  . The upper panel of the table shows
. The upper panel of the table shows  while the lower panel shows
while the lower panel shows  , i.e. estimates of the fraction of undirected graphs that are decomposable. For \(m\le 13\) the exact enumerations are given in the second column. We ran the SMC sampler with tuning parameters \(\alpha =0.5\), \(\beta =0.5\) and the number of particles was set to \(N=10000\). Figure 6 displays the asymptotic behavior of
, i.e. estimates of the fraction of undirected graphs that are decomposable. For \(m\le 13\) the exact enumerations are given in the second column. We ran the SMC sampler with tuning parameters \(\alpha =0.5\), \(\beta =0.5\) and the number of particles was set to \(N=10000\). Figure 6 displays the asymptotic behavior of  and
and  for \(m\le 50\), along with the exact values for \(m\le 13\), justifying a concordance with the exact results. Each of the 10 estimates took about 10 minutes to calculate.
for \(m\le 50\), along with the exact values for \(m\le 13\), justifying a concordance with the exact results. Each of the 10 estimates took about 10 minutes to calculate.
Finally, we also explored other parameterisations for \(\alpha \) and \(\beta \) and found that, in this case, the estimates seem to be less accurate in terms of standard error when using high values of \(\alpha \) about 0.9 and low values of \(\beta \) about 0.3. However, for \(\alpha \) and \(\beta \) about 0.3 and 0.9, respectively, the performance of the estimator was similar to that for the parameterisaion \(\alpha =\beta = 0.5\) considered above.
7.2 Estimating 
As far as we know there is no method available in the literature for efficiently calculating  . However, for \(m\le 5\) it is computationally tractable to first find all the 822 graphs
. However, for \(m\le 5\) it is computationally tractable to first find all the 822 graphs  by Monte Carlo sampling and then evaluate \(\mu \) for each of them.
by Monte Carlo sampling and then evaluate \(\mu \) for each of them.
As in Sect. 7.1 we find an unbiased estimator of  by constructing target distributions
by constructing target distributions

so that the normalising constant  equals
equals  , and then use (6.4). Note that with this setting the first factor in Line 4 in Algorithm 2 simplifies as
, and then use (6.4). Note that with this setting the first factor in Line 4 in Algorithm 2 simplifies as

for all  ,
,  .
.
The third and fourth columns of the upper panel in Table 2 show estimated means and standard deviations of  for \(m\le 15 \) based on 10 replicates. The true values for are shown in the first column for \(m\le 5\). The lower panel of Table 2 displays estimates of the number of junction trees per decomposable graph,
for \(m\le 15 \) based on 10 replicates. The true values for are shown in the first column for \(m\le 5\). The lower panel of Table 2 displays estimates of the number of junction trees per decomposable graph,  , for different numbers of vertices. True numbers as are shown in the first column, and estimated means and standard deviations of
, for different numbers of vertices. True numbers as are shown in the first column, and estimated means and standard deviations of  are shown in the third and fourth columns. Interestingly, Figure 7 indicates an exponential growth rate of the estimated junction trees per decomposable graph for \(p\le 50\). Each of the 10 estimates took about 6 minutes to compute.
are shown in the third and fourth columns. Interestingly, Figure 7 indicates an exponential growth rate of the estimated junction trees per decomposable graph for \(p\le 50\). Each of the 10 estimates took about 6 minutes to compute.
8 Discussion
In this paper we have presented the JTE and the JTC for stochastically generating and collapsing junction trees for decomposable graphs in a vertex-by-vertex fashion. The Markovian nature of these procedures enables the development of sophisticated sampling technology such as SMC and particle MCMC methods; see (Olsson et al. 2019).
Several MCMC methods for approximating distributions on the space of decomposable graphs have been proposed in the literature. Still, in most of these methods, an MCMC chain of graphs (or junction trees) is evolved by means of locally limited random perturbations, leading generally to bad mixing (Giudici and Green 1999; Green and Thomas 2013). The main benefit of casting the JTE and JTC procedures into the particle Gibbs framework is a substantial improvement of the mixing properties of the resulting MCMC chain; this improvement is possible since the JTE procedure allows the produced chain of junction trees to make long-range, global transitions across the state space.
The appealing properties of our approach do not come without a certain price. For instance, relying on the junction-tree representation when sampling from a given decomposable-graph distribution imposes an additional computational burden associated with calculating the number of possible junction-tree representations of each of the sampled graphs. In the present paper, we have been able to alleviate this burden by means of the factorisation property derived in Theorem 7, allowing for faster dynamic updates. Another factor that is challenging when using the SMC procedure in Algorithm 2 for sampling distributions over spaces of decomposable graphs with a very large number p of vertices stems from the well-known particle-path degeneracy phenomenon; see (Jacob et al. 2015; Koskela et al. 2020). More specifically, since the graphs propagated by Algorithm 2 are resampled systematically, many of them will, eventually, as the number of SMC iterations increases, have parts of their underlying graph in common. This may lead to high variance when p is large compared to the sample size N, and the \({\mathcal {O}}(N)\) bound on the resampling-induced particle-path coalescing time obtained recently in Koskela et al. (2020) suggests that p and \(N\) should be of at least the same order in order to keep the Monte Carlo error under control. In the particle Gibbs approach developed in Olsson et al. (2019) the particle-path degeneracy phenomenon is handled by means of an additional JTC-based backward-sampling operation.
As an alternative approach to the JTE, which incrementally constructs a junction tree by adding one vertex at a time to the underlying graph, one may suggest a method that operates directly on the space of decomposable graphs. The main difficulty arising when designing such a scheme is to express the transition probabilities in a tractable form while maintaining the ability to generate any decomposable graph with a given number of vertices, qualities possessed by the methods that we propose.
Finally, we expect that tailored data structures for the junction tree implementation which respect the sequential nature of the algorithms could greatly increase the computational speed. For instance, when propagating the particles in Algorithm 2, the junction trees are not altered but rather copied and expanded (since several trees must be able to stem from the same ancestor); thus, to use persistent data structures— which are widely used in functional programming to avoid the copying of data—in the SMC context of the present paper is an interesting line of research.
References
Andrieu, C., Doucet, A., Holenstein, R.: Particle Markov chain Monte Carlo methods. J. R. Stat. Soc.: Ser. B (Statistical Methodology) 72(3), 269–342 (2010)
Arulampalam, M.S., Maskell, S., Gordon, N., Clapp, T.: A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking. IEEE Trans. Signal Process. 50(2), 174–188 (2002)
Blair, J.R., Peyton, B.: An introduction to chordal graphs and clique trees. In: George, A., Gilbert, J.R., Liu, J.W. (Eds.), Graph Theory and Sparse Matrix Computation, volume 56 of The IMA Volumes in Mathematics and its Applications, pages 1–29. Springer New York (1993). ISBN 978-1-4613-8371-0. https://doi.org/10.1007/978-1-4613-8369-7_1
Cappé, O., Moulines, E., Rydén, T.: Inference in hidden Markov models. Springer, New York (2005)
Chopin, N., Papaspiliopoulos, O., et al.: An introduction to sequential Monte Carlo. Springer, Switzerland (2020)
Del Moral, P.: Feynman-Kac formulae: genealogical and interacting particle systems with applications, vol. 88. Springer, Switzerland (2004)
Del Moral, P., Doucet, A., Jasra, A.: Sequential Monte Carlo samplers. J. R. Stat. Soc. Series B (Statistical Methodology) 68(3), 411–436 (2006). ISSN 13697412, 14679868. URL http://www.jstor.org/stable/3879283
Elmasri, M.: On decomposable random graphs. ArXiv e-prints, (2017)
Elmasri, M.: Sub-clustering in decomposable graphs and size-varying junction trees. ArXiv e-prints, (2017)
Eppstein, D.: Graph-theoretic solutions to computational geometry problems. In: International Workshop on Graph-Theoretic Concepts in Computer Science, pages 1–16. Springer (2009)
Frydenberg, M., Lauritzen, S.L.: Decomposition of maximum likelihood in mixed graphical interaction models. Biom. 76(3), 539–555 (1989)
Giudici, P., Green, P.J.: Decomposable graphical Gaussian model determination. Biom. 86(4), 785–801 (1999)
Gordon, N.J., Salmond, D.J., Smith, A.F.: Novel approach to nonlinear/non-Gaussian Bayesian state estimation. In: IEE Proceedings F (Radar and Signal Processing), volume 140, pages 107–113. IET (1993)
Green, P.J., Thomas, A.: Sampling decomposable graphs using a Markov chain on junction trees. Biom. 100(1), 91–110 (2013)
Hastings, W.K.: Monte Carlo sampling methods using Markov chains and their applications. Biom. 57(1), 97–109 (1970). ISSN 00063444. URL http://www.jstor.org/stable/2334940
Jacob, P.E., Murray, L.M., Rubenthaler, S.: Path storage in the particle filter. Stat. Comput. 25(2), 487–496 (2015)
Kawahara, J., Saitoh, T., Suzuki, H., Yoshinaka, R.: Enumerating all subgraphs without forbidden induced subgraphs via multivalued decision diagrams. arXiv preprintarXiv:1804.03822, (2018)
Koskela, J., Jenkins, P.A., Johansen, A.M., Spano, D.: Asymptotic genealogies of interacting particle systems with an application to sequential Monte Carlo. Ann. Stat. 48(1), 560–583 (2020)
Lauritzen, S.L.: Graphical Models. Oxford University Press, United Kingdom (1996). ISBN 0-19-852219-3
Markenzon, L., Vernet, O., Araujo, L.: Two methods for the generation of chordal graphs. Ann. Oper. Res. 157(1), 47–60 (2008). https://doi.org/10.1007/s10479-007-0190-4. (ISSN 0254-5330)
Metropolis, N., Rosenbluth, A.W., Rosenbluth, M.N., Teller, A.H., Teller, E.: Equation of state calculations by fast computing machines. J. Chem. hys. 21(6), 1087–1092 (1953). https://doi.org/10.1063/1.1699114. URL http://scitation.aip.org/content/aip/journal/jcp/21/6/10.1063/1.1699114
Moon, J.: Enumerating labelled trees. Graph Theory and Theoretical Physics, 261271, (1967)
Olsson, J., Pavlenko, T., Rios, F.L.: Bayesian learning of weakly structural Markov graph laws using sequential Monte Carlo methods. Electron. J. Statist. 13(2), 2865–2897 (2019)
Pearl, J.: Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference. Representation and Reasoning Series. Morgan Kaufmann, (1997). ISBN 9781558604797
Rios F.L.,Moffa G., Benchpress J.K.: A scalable and versatile workflow for benchmarking structure learning algorithms for graphical models. arXiv:2107.03863, (2021)
Thomas, A., Green, P.J.: Enumerating the decomposable neighbours of a decomposable graph under a simple perturbation scheme. Comput. stat. & data anal. 53(4), 1232–1238 (02 2009). https://doi.org/10.1016/j.csda.2008.10.029. URL http://www.ncbi.nlm.nih.gov/pmc/articles/PMC2680312/
Thomas, A., Green, P.J.: Enumerating the junction trees of a decomposable graph. J. Comput. Graph. Stat. 18(4), 930–940 (2009). https://doi.org/10.1198/jcgs.2009.07129
Tierney, L.: Markov chains for exploring posterior distributions. the Annals of Statistics, 1701–1728 (1994)
van den Boom, W., Jasra, A., De Iorio, M., Beskos, A., Eriksson, J.G.: Unbiased approximation of posteriors via coupled particle Markov chain Monte Carlo. Stat. Comput. 32(3), 36 (2022)
Wormald, N.C.: Counting labelled chordal graphs. Graphs and Combinatorics 1(1), 193–200 (1985). (ISSN 0911-0119)
Acknowledgements
We are grateful to the editor and the two reviewers for their valuable comments and helpful suggestions, which have improved the paper significantly. Tatjana Pavlenko’s work has been supported by the AI4Research Grant, Uppsala University. J. Olsson gratefully acknowledges support by the Swedish Research Council, Grant 2018-05230. We are also thankful to Jim Holmström for sharing his Python knowledge with us.
Funding
Open access funding provided by Royal Institute of Technology.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A
1.1 Stochastic breath-first tree traversal
Algorithm 3 provides the detailed steps in the stochastic breath-first tree traversal algorithm outlined in Sect. 3.1. The function push_back adds a new element to the end of a list and the function pop_front returns and removes the first element of a list.

1.2 Junction-tree expander (detailed steps)
Below follows a more detailed description of the JTE. The full algorithm is given in Algorithm 4.

1.2.1 Step 1: Subtree simulation
In this step, a random subtree  of
of  is sampled from
is sampled from  (Line 1). After this, a new tree
(Line 1). After this, a new tree  is initiated as a copy of
is initiated as a copy of  (Line 2), and all the manipulations described below refers to
(Line 2), and all the manipulations described below refers to  . Depending on whether
. Depending on whether  is empty or not, the algorithm proceeds in two substantially different ways.
is empty or not, the algorithm proceeds in two substantially different ways.
1.2.2 Step 2: Node creation
If  is empty, the new vertex
is empty, the new vertex  is added as a node
is added as a node  in its own and connected to one arbitrary existing node.
in its own and connected to one arbitrary existing node.
1.2.3 Step 3 and 4: Randomising the tree
The tree is then cut at each link associated with the empty separator and reconstructed, a process we call randomisation at the separator \(\emptyset \) (Lines 4–6); see Appendix B or (Thomas and Green 2009b) for details. The randomisation step might seem superfluous at a first glance; however, it turns out to be needed in order to ensure that every junction tree has, as stated in Theorem 2, a positive probability of being produced by iterative application of the algorithm.
1.2.4 Step 2\(^*\): Node creation
If  is nonempty, the idea is to replicate its structure so that at the end of the algorithm, a subtree
is nonempty, the idea is to replicate its structure so that at the end of the algorithm, a subtree  of
of  has been created where every node contains
has been created where every node contains  . More specifically, for each node
. More specifically, for each node  ,
,  , in
, in  , a new node
, a new node  is created by connecting
is created by connecting  to a subset of
to a subset of  while ensuring that the decomposability of
while ensuring that the decomposability of  is still maintained. If
is still maintained. If  has more than one node, it is, for each j, in order to avoid that a 4-cycle is formed in
has more than one node, it is, for each j, in order to avoid that a 4-cycle is formed in  , necessary to connect
, necessary to connect  to all vertices in
to all vertices in  . For the rest of the vertices in
. For the rest of the vertices in  , a subset \(q_{j}\) is sampled uniformly at random, and
, a subset \(q_{j}\) is sampled uniformly at random, and  is formed as the union of \(q_{j}\), \(z_{j}\), and
is formed as the union of \(q_{j}\), \(z_{j}\), and  (Lines 11–16). In the case where \(z_{j}\) is identical to one of the separators
(Lines 11–16). In the case where \(z_{j}\) is identical to one of the separators  ,
,  , it is necessary that \(q_{j}\) is nonempty in order to prevent the new node from being engulfed by some of its neighbors in
, it is necessary that \(q_{j}\) is nonempty in order to prevent the new node from being engulfed by some of its neighbors in  (Line 15). In the case where
(Line 15). In the case where  is connected to every vertex in
is connected to every vertex in  ,
,  is replaced by
is replaced by  (Lines 17–19).
(Lines 17–19).
1.2.5 Step 3\(^*\): Structure replication
Having created the new nodes  , links will be added between
, links will be added between  and
and  whenever there is a link between
whenever there is a link between  and
and  in
in  (Line 22). In this case, the link between
(Line 22). In this case, the link between  and
and  is removed (Line 21) in order to avoid a 4-cycle to be formed on Line 28. By this measure,
is removed (Line 21) in order to avoid a 4-cycle to be formed on Line 28. By this measure,  replicates the structure of
replicates the structure of  . In order to connect
. In order to connect  into a tree, links are added between each pair of nodes
into a tree, links are added between each pair of nodes  and
and  (Line 28).
(Line 28).
1.2.6 Step 4\(^*\): Neighbor relocation
Finally, we observe that for all  , any potential neighbor
, any potential neighbor  such that
such that  can be moved to be a neighbor of
can be moved to be a neighbor of  instead while maintaining the junction tree property (Lines 31–32). In the special case where the node
instead while maintaining the junction tree property (Lines 31–32). In the special case where the node  is substituted by
is substituted by  , all the neighbors of
, all the neighbors of  will simply be neighbors of
will simply be neighbors of  instead (Line 25).
instead (Line 25).
1.3 Junction-tree collapser (detailed steps)
Below follows some more detailed description of the JTC. The full algorithm is given in Algorithm 5.

Similarly to the JTE, the JTC takes two different forms depending on whether  is present as a node in
is present as a node in  or not. Specifically, if
or not. Specifically, if  , then
, then  is removed from
is removed from  and the resulting forest is reconnected uniformly at random (Lines 2–4 in Algorithm 5).
and the resulting forest is reconnected uniformly at random (Lines 2–4 in Algorithm 5).
Otherwise, if  we denote by
we denote by  the nodes in the subtree
the nodes in the subtree  induced by the nodes containing the vertex
induced by the nodes containing the vertex  . The aim is now to identify the nodes that can serve as a subtree in Algorithm 4 to produce
. The aim is now to identify the nodes that can serve as a subtree in Algorithm 4 to produce  . Since each node in the subtree sampled initially in Algorithm 4 will give rise to a new node, it is enough to determine, for each
. Since each node in the subtree sampled initially in Algorithm 4 will give rise to a new node, it is enough to determine, for each  , the node
, the node  that can be used for producing
that can be used for producing  (reversing Lines 10–19 in Algorithm 4). For each \(j\), we define a set of candidate nodes
(reversing Lines 10–19 in Algorithm 4). For each \(j\), we define a set of candidate nodes  . If \(M_{j}=\emptyset \), we let
. If \(M_{j}=\emptyset \), we let  (Line 11 in Algorithm 5). Otherwise,
(Line 11 in Algorithm 5). Otherwise,  is drawn at random from the uniform distribution over \(M_{j}\) (Line 13). In either case, the edges incident to
is drawn at random from the uniform distribution over \(M_{j}\) (Line 13). In either case, the edges incident to  are moved to
are moved to  (Line 14).
(Line 14).
1.4 Proofs and lemmas
Lemma 1
Let  be a tree where each node is a subset of some finite set. Then
be a tree where each node is a subset of some finite set. Then  satisfies the junction tree property if and only if for any path
satisfies the junction tree property if and only if for any path  in
in  it holds that
it holds that

Proof
The statement of the lemma follows by noting that

which implies that

\(\square \)
Proof of Theorem 1
We prove this theorem by taking a generative perspective in the sense that we rely on the sampling procedure of  given by Algorithm 4. We also adopt the same notation as in Algorithm 4.
given by Algorithm 4. We also adopt the same notation as in Algorithm 4.
In order to prove (i) we assume that  is generated by Algorithm 4 with input
is generated by Algorithm 4 with input  and show that
and show that  by going through the algorithm in a step-by-step fashion. At Line 1 a subtree
by going through the algorithm in a step-by-step fashion. At Line 1 a subtree  is drawn. We treat the cases
is drawn. We treat the cases  and
and  separately.
separately.
First, assume that  . Since the node
. Since the node  does not intersect any other node in
does not intersect any other node in  , it can be connected to an arbitrary node with separator \(\emptyset \) without violating the junction tree property (Line 4). In addition, Thomas and Green (2009a) show that randomising a tree at a given separator preserves the junction tree property (Line 6).
, it can be connected to an arbitrary node with separator \(\emptyset \) without violating the junction tree property (Line 4). In addition, Thomas and Green (2009a) show that randomising a tree at a given separator preserves the junction tree property (Line 6).
For  , we first show that
, we first show that  produced on Lines 9–28 is a tree that satisfies the junction tree property. Indeed,
produced on Lines 9–28 is a tree that satisfies the junction tree property. Indeed,  is a tree since the subtrees produced up to Line 25 are all reconnected through the same tree
is a tree since the subtrees produced up to Line 25 are all reconnected through the same tree  by the operations on Lines 26–28. To ensure the junction tree property of
by the operations on Lines 26–28. To ensure the junction tree property of  , consider a general path
, consider a general path

passing through  in
in  , where \((a_j)_{j=1}^{{\ell _1}}\) and \( (b_j)_{j=1}^{{\ell _2}}\) are nonempty sequences of nodes which also belong to
, where \((a_j)_{j=1}^{{\ell _1}}\) and \( (b_j)_{j=1}^{{\ell _2}}\) are nonempty sequences of nodes which also belong to  .
.
The fact that  is the
is the  -
- path in
path in  implies that
implies that 
is the  path in
path in  , since, by construction (Lines 20–22),
, since, by construction (Lines 20–22),  if and only if
if and only if  . Thus,
. Thus,

is the \(a\)-\(b\) path in  . The junction tree property of
. The junction tree property of  ensures that \(a\cap b\subset I_{a\sim b}\), where
ensures that \(a\cap b\subset I_{a\sim b}\), where

Now, consider the intersection

of the nodes in \(a\sim b\) in  . For \({\ell _2}=1\), it holds that
. For \({\ell _2}=1\), it holds that  , corresponding to the case where
, corresponding to the case where  is engulfed into
is engulfed into  . For \({\ell _2}\ge 2\), the junction tree property in
. For \({\ell _2}\ge 2\), the junction tree property in  ensures via Lemma 1 that
ensures via Lemma 1 that

It hence holds that \(a\cap b\subset I_{a\sim b} \subset I^+_{a\sim b}\).
Now, consider the final version of  obtained after the relocation step on Lines 29–32. Let
obtained after the relocation step on Lines 29–32. Let  and let
and let  be the subtree of
be the subtree of  induced by the nodes containing the separator
induced by the nodes containing the separator  . In addition to
. In addition to  and
and  , it is clear that
, it is clear that  is also a node in
is also a node in  since
since  . Now the fact that
. Now the fact that  also implies that the tree obtained by letting
also implies that the tree obtained by letting  be a neighbor of
be a neighbor of  instead of
instead of  also satisfies the junction tree property by Thomas and Green (2009b).
also satisfies the junction tree property by Thomas and Green (2009b).
Finally, (ii) follows directly since the only new vertex added to  in order to get
in order to get  is
is  and no edges have been removed between the vertices
and no edges have been removed between the vertices  . \(\square \)
. \(\square \)
Proof of Theorem 2
In this proof we use the property (ii) of  provided by Theorem 3 and proved independently below.
provided by Theorem 3 and proved independently below.
The space containing the trivial junction tree is  . We proceed by induction over the number of vertices. For the base case \(m= 2\),
. We proceed by induction over the number of vertices. For the base case \(m= 2\),  , where
, where  is the unique tree constructed from
is the unique tree constructed from  via the subtree
via the subtree  and
and  is the unique tree constructed from
is the unique tree constructed from  via the subtree \((\emptyset ,\emptyset )\).
via the subtree \((\emptyset ,\emptyset )\).
For \(m \ge 3\), assume inductively that  and let
and let  be an arbitrary junction tree. It suffice to show that there exists a junction tree
be an arbitrary junction tree. It suffice to show that there exists a junction tree  such that
such that  since then
since then  . But this follows directly by drawing any
. But this follows directly by drawing any  since
since  (by (ii) in Theorem 3), meaning that
(by (ii) in Theorem 3), meaning that  . Thus, every junction tree in
. Thus, every junction tree in  can be constructed, and we conclude the proof by induction. \(\square \)
can be constructed, and we conclude the proof by induction. \(\square \)
Proof of Proposition 1
In this proof, we take a generative perspective in the sense that we rely on the sampling procedure given by Algorithm 4 and regard  as an expansion of
as an expansion of  . We further adopt the same notation as in Algorithm 4 when possible.
. We further adopt the same notation as in Algorithm 4 when possible.
Let  be the set of nodes in
be the set of nodes in  containing the vertex
containing the vertex  . The induced subgraph
. The induced subgraph  will necessarily be a subtree of
will necessarily be a subtree of  (see e.g. Blair and Peyton (1993)), which we denote by
(see e.g. Blair and Peyton (1993)), which we denote by  . For each
. For each  , we define a set
, we define a set  , which we interpret as the candidate nodes in
, which we interpret as the candidate nodes in  from which each
from which each  could potentially have emerged. We distinguish between two main situations for
could potentially have emerged. We distinguish between two main situations for  depending on
depending on  .
.
For  ,
,
-
If \(|M_{1}| = 0\), then
 so that
so that  due to Lines 17–19.
due to Lines 17–19. -
If \(|M_{1}| = 1\), then clearly
 , where
, where  due to Lines 26–28.
due to Lines 26–28. -
If \(|M_{1}| \ge 2\), consider the enumeration
 . The set
. The set  is clearly non-empty, thus we can assume that
is clearly non-empty, thus we can assume that  . Note that, since \(M_{1}\) consists of more than one element, all nodes in
. Note that, since \(M_{1}\) consists of more than one element, all nodes in  are former neighbors of
are former neighbors of  by Lines 29–32. Thus, every node in
by Lines 29–32. Thus, every node in  are neighbors of
are neighbors of  in
in  . This implies that for \(|M_{1}|=2\), the subtree could also be
. This implies that for \(|M_{1}|=2\), the subtree could also be  since the
since the  could be moved at Lines 29–32. Thus
could be moved at Lines 29–32. Thus  . For \(|M_{1}| \ge 3\),
. For \(|M_{1}| \ge 3\),  is necessarily the unique subtree in
is necessarily the unique subtree in  since if there would exist another subtree
since if there would exist another subtree  , both
, both  and
and  would have
would have  as neighbor in
as neighbor in  , which would form a cycle.
, which would form a cycle.
For  , by construction, for each link
, by construction, for each link  , where
, where  and
and  we can associate a link
we can associate a link  , where
, where  and
and  are emerging nodes in
are emerging nodes in  and \( r_{j}\) and \( r_{k}\) may be empty sets. Thus we can form the subtree
and \( r_{j}\) and \( r_{k}\) may be empty sets. Thus we can form the subtree  which we regard as the subtree in Algorithm 4 (Line 1), where
which we regard as the subtree in Algorithm 4 (Line 1), where  and
and  . Now, suppose that there exists another subtree
. Now, suppose that there exists another subtree  , isomorphic to
, isomorphic to  , where
, where  ,
,  for some \(j\) and
for some \(j\) and  . Enumerate the nodes such that
. Enumerate the nodes such that  and let for simplicity
and let for simplicity  . Then, since the neighbors of
. Then, since the neighbors of  except for
except for  are neighbors of
are neighbors of  in
in  , the link
, the link  would be present in
would be present in  . Also the link
. Also the link  is present in
is present in  since
since  is a subtree of
is a subtree of  . Similarly, since
. Similarly, since  is a subtree of
is a subtree of  , the link
, the link  would also be present in
would also be present in  . Thus we would have a 3-cycle in
. Thus we would have a 3-cycle in  which contradicts the assumption of
which contradicts the assumption of  being a tree. Thus
being a tree. Thus  . \(\square \)
. \(\square \)
Proof of Theorem 3
We prove this theorem by taking a generative perspective in the sense that we rely on the sampling procedures of  and
and  given by Algorithm 4 and 5 respectively. We also adopt the same notation as in these algorithms. To show (i) and (ii) we distinguish between the cases
given by Algorithm 4 and 5 respectively. We also adopt the same notation as in these algorithms. To show (i) and (ii) we distinguish between the cases  and
and  . For both cases, we let
. For both cases, we let  . We prove (i) by following the steps in Algorithm 5 with input
. We prove (i) by following the steps in Algorithm 5 with input  . For (ii), we show that
. For (ii), we show that  could be obtained by Algorithm 4 with input
could be obtained by Algorithm 4 with input  .
.
If  , then no other node in
, then no other node in  will contain the vertex
will contain the vertex  which in turn implies that each neighbor in
which in turn implies that each neighbor in  will have \(\emptyset \) as associated separator. Removing one node from a tree will always result in a forest possibly containing only one tree. Thus the removal of
will have \(\emptyset \) as associated separator. Removing one node from a tree will always result in a forest possibly containing only one tree. Thus the removal of  from
from  on Line 3 will result in a forest. Since
on Line 3 will result in a forest. Since  is not contained in any of the trees in the forest, these will all trivially satisfy the junction tree property and the connection of
is not contained in any of the trees in the forest, these will all trivially satisfy the junction tree property and the connection of  into a tree by Line 4 will give a random junction tree for
into a tree by Line 4 will give a random junction tree for  , which proves (i) in this case. For the (ii) part, we simply observe that
, which proves (i) in this case. For the (ii) part, we simply observe that  can be constructed from
can be constructed from  by first drawing the empty subtree on Line 1 and then obtaining
by first drawing the empty subtree on Line 1 and then obtaining  at the randomization on Line 6 in Algorithm 4.
at the randomization on Line 6 in Algorithm 4.
Now, assume that  . We proceed by showing (i), i.e. that
. We proceed by showing (i), i.e. that  . We first show that
. We first show that  is a tree. Since for every
is a tree. Since for every  , all elements in
, all elements in  are set to be neighbors of
are set to be neighbors of  in
in  , for all
, for all  it follows that
it follows that

Hence, since  is a subtree of
is a subtree of  ,
,  is a tree, where
is a tree, where  and
and  . Further, since elements of
. Further, since elements of  are not mutual neighbors, and parts of distinct subtrees of
are not mutual neighbors, and parts of distinct subtrees of  ,
,  is a subtree of
is a subtree of  . As a consequence, we may assume that an arbitrary path (of length at least 2) in
. As a consequence, we may assume that an arbitrary path (of length at least 2) in  is of form
is of form

where \({\ell _1}\ge 0\), \({\ell _2}\ge 0\), \({\ell _3}\ge 0\) and  . Let \(a\) and \(b\) be the first and last element in this path, respectively. Let the intersection \(I_{a\sim b}\) be defined by (A.1). We must prove that \(a\cap b\subset I_{a\sim b}\). We know that in
. Let \(a\) and \(b\) be the first and last element in this path, respectively. Let the intersection \(I_{a\sim b}\) be defined by (A.1). We must prove that \(a\cap b\subset I_{a\sim b}\). We know that in  , the node \(a_{{\ell _1}}\) was connected to either
, the node \(a_{{\ell _1}}\) was connected to either  (in which case
(in which case  ) or to
) or to  and \(b_1\) was connected to either
and \(b_1\) was connected to either  (in which case
(in which case  ) or to
) or to  . First, assume that \(a_{{\ell _1}}\) was connected to
. First, assume that \(a_{{\ell _1}}\) was connected to  and \(b_1\) was connected to
and \(b_1\) was connected to  , then the \(a\)-\(b\) path in
, then the \(a\)-\(b\) path in  is of form
is of form

Let

We know that, since  is a junction tree, \(a\cap b\subset I_{a\sim b}^+\). Moreover, by Lemma 1 it holds that
is a junction tree, \(a\cap b\subset I_{a\sim b}^+\). Moreover, by Lemma 1 it holds that  . But,
. But,  and
and  , thus \(I_{a\sim b}=I_{a\sim b}^+\) so that \(a\cap b\subset I_{a\sim b}\). Now, note that
, thus \(I_{a\sim b}=I_{a\sim b}^+\) so that \(a\cap b\subset I_{a\sim b}\). Now, note that  , so that adding
, so that adding  and
and  to the path does not change anything, thus the junction tree property also holds in the case where \(a_{{\ell _1}}\) was connected to
to the path does not change anything, thus the junction tree property also holds in the case where \(a_{{\ell _1}}\) was connected to  or \(b_1\) was connected to
or \(b_1\) was connected to  .
.
To show (ii) in this case, observe that  can be expanded to
can be expanded to  by first drawing the subtree
by first drawing the subtree  on Line 1. Then, by identifying
on Line 1. Then, by identifying  and
and  , there is a positive probability for obtaining \(q_{j}=d_{j} \setminus z_{j}\) for
, there is a positive probability for obtaining \(q_{j}=d_{j} \setminus z_{j}\) for  at Lines 13–15 (Algorithm 4). The neighbors of
at Lines 13–15 (Algorithm 4). The neighbors of  for the resulting tree can now be set to be identical to that in
for the resulting tree can now be set to be identical to that in  by letting
by letting  on Line 3.
on Line 3.
To show (iii) we simply observe that the only vertex removed from  compared to
compared to  is
is  so that
so that  . \(\square \)
. \(\square \)
Proof of Theorem 7
To reduce some notation we define  and
and  . Consider the partitions of the separator sets
. Consider the partitions of the separator sets  and
and  . In order to show that the factorisation holds it is enough to establish that
. In order to show that the factorisation holds it is enough to establish that
-
1.
 ,
, -
2.
 for \(s\in {A^{{\mathsf {c}}}}\),
for \(s\in {A^{{\mathsf {c}}}}\),
where  and
and  are arbitrary junction tree representations of the graphs
are arbitrary junction tree representations of the graphs  and
and  respectively. Note that, showing (1) is equivalent to showing that \({A^{{\mathsf {c}}}_{+}}={A^{{\mathsf {c}}}}\).
respectively. Note that, showing (1) is equivalent to showing that \({A^{{\mathsf {c}}}_{+}}={A^{{\mathsf {c}}}}\).
First let \(s\in {A^{{\mathsf {c}}}_{+}}\). It suffice to show that  since then it follows that \(s\in {A^{{\mathsf {c}}}}\). But since \(s\) is in
since then it follows that \(s\in {A^{{\mathsf {c}}}}\). But since \(s\) is in  and was not created by the expansion (\(s\notin S^\star \)), it has to come from
and was not created by the expansion (\(s\notin S^\star \)), it has to come from  , i.e.
, i.e.  . It follows that \({A^{{\mathsf {c}}}_{+}}\subseteq {A^{{\mathsf {c}}}}\).
. It follows that \({A^{{\mathsf {c}}}_{+}}\subseteq {A^{{\mathsf {c}}}}\).
For the other inclusion, let \(s\in {A^{{\mathsf {c}}}}\). It suffices to show that  since then it follows that \(s\in {A^{{\mathsf {c}}}_{+}}\). But if
since then it follows that \(s\in {A^{{\mathsf {c}}}_{+}}\). But if  and \(s\) is not subset of any separator in
and \(s\) is not subset of any separator in  , it cannot have been removed by the expansion meaning that
, it cannot have been removed by the expansion meaning that  . Thus, \({A^{{\mathsf {c}}}} \subseteq {A^{{\mathsf {c}}}_{+}}\). It follows that \({A^{{\mathsf {c}}}}={A^{{\mathsf {c}}}_{+}}\).
. Thus, \({A^{{\mathsf {c}}}} \subseteq {A^{{\mathsf {c}}}_{+}}\). It follows that \({A^{{\mathsf {c}}}}={A^{{\mathsf {c}}}_{+}}\).
To show 2, let \(s\in {A^{{\mathsf {c}}}}\) and consider the tree  spanned by the nodes in
spanned by the nodes in  associated with separators which are subsets of \(s\). Assume that the tree
associated with separators which are subsets of \(s\). Assume that the tree  , spanned by the nodes in
, spanned by the nodes in  associated with separators which are subsets of \(s\), is different from
associated with separators which are subsets of \(s\), is different from  . This could only occur in two ways: (i) some new separator \(s^\star \) that contains \(s\) has been created or (ii) some separator containing \(s\) has been removed. However, (i) cannot happen since then \(s^\star \) would be a new separator in \(S^\star \) that would also contain \(s\) which was not true by assumption. Thus, (ii) must hold. But the only way a separator \(s'\) of
. This could only occur in two ways: (i) some new separator \(s^\star \) that contains \(s\) has been created or (ii) some separator containing \(s\) has been removed. However, (i) cannot happen since then \(s^\star \) would be a new separator in \(S^\star \) that would also contain \(s\) which was not true by assumption. Thus, (ii) must hold. But the only way a separator \(s'\) of  can be removed is if a new separator
can be removed is if a new separator  also is created. But then
also is created. But then  would be a new separator in \(S^\star \) containing \(s\), leading to a contradiction. This implies that
would be a new separator in \(S^\star \) containing \(s\), leading to a contradiction. This implies that  . \(\square \)
. \(\square \)
Appendix B
Randomize junction tree at separator
(Thomas and Green (2009b)) Given any particular junction tree representation  , we can choose uniformly at random from the set of equivalent junction trees by applying the following algorithm to the forests
, we can choose uniformly at random from the set of equivalent junction trees by applying the following algorithm to the forests  defined by the distinct separators \(s\) in
defined by the distinct separators \(s\) in  . Following the notation in Theorem 4, \(r_i\) refers to the size of subtree i.
. Following the notation in Theorem 4, \(r_i\) refers to the size of subtree i.
- Step 1.:
-
Label each vertex of the forest \(\{i,j\}\) where \(1\le i \le q\) and \(1\le j \le r_i\), so that the first index indicates the subtree the vertex belongs to and the second reflects some ordering within the subtree. The ordering of the subtrees and of vertices within subtrees are arbitrary.
- Step 2.:
-
Construct a list v containing \(q-2\) vertices each chosen uniformly at random with replacement from the set of all p vertices.
- Step 3.:
-
Construct a set w containing q vertices, one chosen uniformly at random from each subtree.
- Step 4.:
-
Find in w the vertex x with the largest first index that does not appear as a first index of any vertex in v. Because the length of v is 2 less than the size of w, there must always be at least two such vertices.
- Step 5.:
-
Connect x to y, the vertex at the head of the list v.
- Step 6.:
-
Remove x from the set w, and delete y from the head of the list v.
- Step 7.:
-
Repeat from step 4 until v is empty. At this point w contains two vertices. Connect them.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Olsson, J., Pavlenko, T. & Rios, F.L. Sequential sampling of junction trees for decomposable graphs. Stat Comput 32, 80 (2022). https://doi.org/10.1007/s11222-022-10113-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-022-10113-2




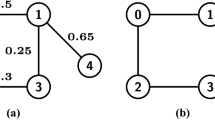
 will be nonempty.
will be nonempty. and add it to a list
and add it to a list  , from
, from  .
. to the end of
to the end of  .
. of
of  .
. and connect it to an arbitrary node in
and connect it to an arbitrary node in 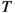 .
. , draw uniformly at random a (possibly empty) subset
, draw uniformly at random a (possibly empty) subset  of
of  to create a new unique node
to create a new unique node  , consisting of
, consisting of  and the vertex
and the vertex 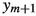 . Note that for
. Note that for  to be unique,
to be unique,  has to be non-empty if any separator associated with
has to be non-empty if any separator associated with 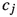 in
in  equals
equals  . If
. If  was engulfed in
was engulfed in  (i.e.
(i.e.  ), simply delete
), simply delete  .
. , assign links which replicate the structure of
, assign links which replicate the structure of  . Then remove the links in
. Then remove the links in  and connect by a link each
and connect by a link each  to its corresponding new node
to its corresponding new node  .
. , the neighbors whose links can be moved to
, the neighbors whose links can be moved to  while maintaining an equivalent junction tree, are distributed uniformly between
while maintaining an equivalent junction tree, are distributed uniformly between  and
and  . The set of neighbors of
. The set of neighbors of  is denoted by
is denoted by  .
.




 ,
, for all
for all  .
. and it incident links to obtain a forest, possibly containing only one tree.
and it incident links to obtain a forest, possibly containing only one tree. be the subtree of
be the subtree of  induced by the nodes containing the vertex
induced by the nodes containing the vertex  and enumerate the nodes in
and enumerate the nodes in  by
by  .
. , draw at random
, draw at random  from
from  in
in  having the associated separator
having the associated separator  . If no such neighbor exists, let
. If no such neighbor exists, let  .
. by the corresponding node
by the corresponding node  in the sense that
in the sense that  is assigned all former neighbors of
is assigned all former neighbors of  .
. ,
, ,
, for any
for any 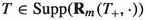 .
.



 so that
so that  due to Lines 17–19.
due to Lines 17–19. , where
, where  due to Lines 26–28.
due to Lines 26–28. . The set
. The set  is clearly non-empty, thus we can assume that
is clearly non-empty, thus we can assume that  . Note that, since
. Note that, since 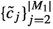 are former neighbors of
are former neighbors of  by Lines 29–32. Thus, every node in
by Lines 29–32. Thus, every node in  are neighbors of
are neighbors of  in
in  . This implies that for
. This implies that for  since the
since the  could be moved at Lines 29–32. Thus
could be moved at Lines 29–32. Thus  . For
. For  is necessarily the unique subtree in
is necessarily the unique subtree in  since if there would exist another subtree
since if there would exist another subtree  , both
, both  and
and  would have
would have  as neighbor in
as neighbor in  , which would form a cycle.
, which would form a cycle. ,
, for
for