Abstract
This article studies M-type estimators for fitting robust additive models in the presence of anomalous data. The components in the additive model are allowed to have different degrees of smoothness. We introduce a new class of wavelet-based robust M-type estimators for performing simultaneous additive component estimation and variable selection in such inhomogeneous additive models. Each additive component is approximated by a truncated series expansion of wavelet bases, making it feasible to apply the method to nonequispaced data and sample sizes that are not necessarily a power of 2. Sparsity of the additive components together with sparsity of the wavelet coefficients within each component (group), results into a bi-level group variable selection problem. In this framework, we discuss robust estimation and variable selection. A two-stage computational algorithm, consisting of a fast accelerated proximal gradient algorithm of coordinate descend type, and thresholding, is proposed. When using nonconvex redescending loss functions, and appropriate nonconvex penalty functions at the group level, we establish optimal convergence rates of the estimates. We prove variable selection consistency under a weak compatibility condition for sparse additive models. The theoretical results are complemented with some simulations and real data analysis, as well as a comparison to other existing methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Additive regression models have turned out to be useful statistical tools in the analysis of high-dimensional data. The attraction of such models is that the additive components can be estimated with the same optimal convergence rate as a one-dimensional nonparametric regression. However, this optimal property holds only when all the additive components share the same degree of “homogeneous” smoothness but it is not anymore true when they have different degrees of smoothness such as, for example, the “inhomogeneous” smoothness described by their appartenance to Besov spaces. While several wavelet-based methods have been developed in the recent literature for performing simultaneous parameter estimation and variable selection in such “inhomogeneous” additive models, these are mainly derived as penalized regression estimators using an unbounded loss function. In practice, however, some extreme observations may occur, and estimation using an unbounded loss function suffers from a lack of robustness, meaning that the estimated functions can be distorted by the outliers. Both the nonparametric function estimates themselves and the choice of the penalization parameters associated with them are affected.
To address these issues, we propose a new class of wavelet-based robust M-type estimators for performing simultaneous additive component estimation and variable selection in such sparse “inhomogeneous” additive models. The additive components are approximated by truncated series expansions of wavelet bases. Such an approximation allows the methodology to be applied to nonequispaced data with sample size not necessarily a power of 2, as it is often the case in practice. With this approximation, the problem of component estimation and selection becomes that of consistent bi-level group variable selection with sparsity of the wavelet coefficients within each group, induced by smoothness of the corresponding components, and sparsity that may appear at the group level by sparsity of the additive model components. A two-stage computational procedure based on a fast accelerated proximal gradient (APG) algorithm, of coordinate descent type and followed by thresholding is proposed and implemented for computing the estimates. It produces robust parameter estimators if nonconvex redescending loss functions are applied. We establish optimal convergence rates for the estimated components and show the variable selection consistency. Our simulation studies and the real data analysis demonstrate satisfactory finite sample performance of the proposed estimators under different irregular settings.
More precisely, consider a general regression model, where a response variable \(Y \in {\mathbb {R}}\) is related to a vector \({\mathbf {X}}=\left( X^{1}, \ldots , X^{p}\right) ^{\mathrm {T}}\) \(\in {\mathbb {R}}^{p}\) of explanatory variables through the following nonparametric regression model:
The error \(\varepsilon \) is assumed to be independent of \({\mathbf {X}}\) with a symmetric distribution whose scale equals 1, so the scale parameter \(\sigma _{0}\) is identifiable. Hence, when first moments exists, we have the usual regression representation that \({\mathbb {E}}(Y \mid {\mathbf {X}})=f({\mathbf {X}}),\) and when second moments exists, we have \(\sigma _0^{2}={{{\mathbb {E}}}}\left( (Y-f({\mathbf {X}}))^{2}\right) \) for the variance. Standard estimators for f can thus be derived relying on local estimates of the conditional mean. It is easy to see that such procedures can be seriously affected either by a small proportion of outliers in the response variable, or when the distribution of \(Y \mid {\mathbf {X}}\) has heavy tails. Note, however, that even when \(\varepsilon \) does not have a finite first moment, the function \(f({\mathbf {X}})\) can still be interpreted as a location parameter for the distribution of \(Y \mid {\mathbf {X}}\). In this case, local robust estimators can be used to estimate the regression function as, for example, the local M-estimators proposed in Boente and Fraiman (1989) and the local medians studied in Welsh (1996).
Unfortunately both robust and non-robust nonparametric regression estimators are affected by the curse of dimensionality, which is caused by the fact that the expected number of observations in local neighborhoods decreases exponentially as a function of p, the number of covariates. This results in regression estimators with a very slow convergence rate. Stone (1985) showed that additive models can avoid these problems and produce nonparametric multiple regression estimators with a univariate rate of convergence.
In this work, we therefore adopt a classical setup and consider an additive model for i.i.d. responses \(Y_i \in {\mathbb {R}}\), \(i=1,\ldots ,n\) and corresponding input covariate vectors \({\varvec{X}}_i=(X^1_i,\ldots ,X^p_i) \in {\mathbb {R}}^p\), \(i=1,\ldots ,n\) of the form
where \(\mu \in {\mathbb {R}}\) is an overall mean parameter, each \(f_{j}\) is a univariate function, the error vector \({\varvec{\varepsilon }}=(\varepsilon _1, \ldots , \varepsilon _n)^T\) has mean the zero vector and is independent of the covariates. Such a model retains the ease of interpretation of linear regression models, where each component \(f_j\) can be thought as the effect of the jth covariate on the center of the conditional distribution of Y. We will have at our disposal observations \((y_i, {\varvec{x}}_i), i=1, \ldots , n\), from model (1). The components \(X_i^j\) are random variables drawn from the jth marginal distribution of the covariate vector \({\varvec{X}}\). The covariate vector \({\varvec{X}}\) is assumed to have a compactly supported continuous distribution such that the marginal density functions \(f_{X^j}\) (possibly different for different j) satisfy certain conditions (essentially no flat parts in the density, or ‘no holes’ in the design). Adopting the stance taken by many others, we will also assume \({{{\mathbb {E}}}}(f_j(X^j))=0\) and that \(\sum _{i=1}^n f_{j}(x^j_i)=0\) to ensure unique identification (both theoretical and empirical) of the additive components and proceed to the estimation of ‘parameters’ of the regression model (1). We will suppose that some of the additive components are zero and will address the problem of distinguishing the nonzero components from the zero components and estimating the nonzero ones. We allow the possibility that p in model (1) increases as n increases. To achieve model selection consistency under simple assumptions that are easy to interpret, we will assume that the number of nonzero components is fixed and independent of n.
A comment on notation: here and throughout, when indexing over the n samples we use subscripts, and when indexing over the p dimensions we use superscripts, so that, e.g., \(x^j_i\) denotes the jth component of the ith input point. (Exceptions will occasionally be made, but the role of the index should be clear from the context).
When the additive model is high-dimensional, that is when p is large, a natural goal is to induce sparsity in the component functions, so that only a few select dimensions of the input space are used in the fitted additive model. The literature on estimation in nonparametric additive models (and by now, sparse additive models) is vast, especially when the additive components are smooth and well approximated by splines. For a nice review, the reader is referred to Amato et al. (2016) and the important list of references there.
In the following, we examine a method for estimating additive models wherein each component is fit in a way that is locally adaptive to the underlying inhomogeneous smoothness along its associated dimension of the input space. A second task in our work will be to perform variable selection. Both estimation and variable selection are done using appropriate robust wavelet procedures adapted to nonregular designs. More precisely, we use wavelet decompositions but do not impose that the sample size n is a power of two, nor do we restrict to equidistant design.
An initial motivation for our approach are the wavelet procedures developed recently in Amato et al. (2017) to estimate both the linear and the nonlinear components in semi-parametric partially additive regression models with unknown nonparametric additive component functions, sparsely represented in the wavelet domain, and unobservable Gaussian distributed random errors.
Inspired by the penalized versions of high-dimensional robust regression estimators with highly nonconvex loss functions developed recently in Amato et al. (2021), we address robust estimation, meaning that our procedures remain valid even when there are aberrant observations of the response variable, called vertical outliers. The key difference with Amato et al. (2017) is that here we propose a robust wavelet-based procedure. The key difference with Amato et al. (2021) is that we are in the context of additive models here, with several univariate (nonlinear, unknown) function effects to be estimated in a robust fashion, including the selection of the sparse additive components. Note, however, that establishing robustness results, similar to those in Avella-Medina (2017), Avella-Medina and Ronchetti (2017), or Gijbels and Vrinssen (2019), based on a study of a theoretical influence function is a research subject on its own and it is not considered here. Bianco and Boente (1998) considered robust estimators for additive models with sufficiently smooth additive components using kernel-based regression, which are a robust version of those defined in Baek and Wehrly (1993). Croux et al. (2011) provide a robust fit for generalized additive models with nuisance parameters using penalized splines. Wong et al. (2014) consider robust fits based on penalized splines M-type estimators. Robust estimators for additive models using back-fitting were studied by Boente et al. (2017), Boente and Martinez (2017) considered a robust method based on the marginal integration with a robust local polynomial fitting and derived its asymptotic properties. Outlier resistant fits for location, scale, and shape generalized additive models with smooth components, that extend the above to the more general setting of GAMLSS has been considered recently in Aeberhard et al. (2020), but no theoretical support is provided for their method. Most of the above papers do not address the variable selection problem when the models are sparse.
The remainder of our paper is organized as follows. We describe our estimation procedures in Sect. 2 and present the asymptotic properties of our estimators in Sect. 3. The numerical implementation is described in Sect. 4. Simulation results and an applications in Sect. 5 illustrate finite sample performance of our estimation and variable selection procedures. Section 6 includes concluding remarks.
The R codes and their description implementing the methods in the paper together with the driver scripts for simulations, plots, and the analysis of real examples are made available in a compressed archive as supplementary material.
2 Robust M-type group estimation and variable selection in nonparametric additive models
More recent work on additive models has focused on high-dimensional, robust or not, nonparametric estimation, where the natural goal is to induce sparsity in the component functions, so that only a few select dimensions of the input space are used in the fitted additive model. Most contributions are primarily based on fitting splines for component functions and aim in achieving sparsity through a group lasso type penalty. The problem of variable selection and estimation in such models becomes that of selecting and estimating a set of grouped variables in a high-dimensional linear model.
Approximating the component functions by their truncated expansions in spline bases and using appropriate penalties is arguably the most common formulation for fitting additive models by P-splines or B-splines (see e.g., Eilers and Marx (1996), Antoniadis et al. (2012a), Antoniadis et al. (2012b), Antoniadis et al. (2014)), and it is the standard in several R statistical packages. The beauty of P-splines or B-splines lies in their simplicity. However, with this simplicity comes serious limitations, in terms of their ability to adapt to varying local levels of smoothness.
This is the reason, hereafter, to consider a robust M-type penalized group estimation and variable selection methodology based on a wavelet representation of each component in additive models with component functions that display locally heterogeneous degrees of smoothness.
Let us consider a nonparametric additive model represented by (1) with additive components that present a wide range of irregular effects. Suppose, without any loss of generality, that each marginal component \(X^j\), \(j=1, \dots , p\) , of the covariate vector \({\mathbf {X}}\) takes values in [0, 1]. To capture key characteristics of variations and of inhomogeneity in each \(f_j\), \(j=1, \dots , p\), and to exploit their sparse wavelet coefficients representations, we will assume that \(f_j\) belong to the (inhomogeneous) Besov space on the unit interval \(\mathcal B^t_{\kappa ,\omega }([0,1])\) with \(t+1/\kappa -1/2>0\) (this condition ensures in particular that evaluation of \(f_j\) at a given point makes sense). The space \({\mathcal {B}}^t_{\kappa ,\omega }([0,1])\) consists of functions that have a specific degree of smoothness in their derivatives. The parameter \(\kappa \) can be viewed as a degree of function’s inhomogeneity while t is a measure of its smoothness. Roughly speaking, the (not necessarily integer) parameter t indicates the number of function’s (fractional) derivatives, where their existence is required in an \(L^{\kappa }\)-sense; the additional parameter \(\omega \) is secondary in its role, allowing for additional fine tuning of the definition of the space (e.g., see Donoho and Johnstone (1998)).
In analogy with splines basis expansions of smooth functions defined on [0, 1], we will approximate the nonparametric additive components using wavelet bases (Antoniadis and Fan 2001). More precisely, for each \(f_j\), we may use its truncated expansion on wavelet basis functions \(\{ W_{ \ell }^{(j)} \}_\ell \):
where \(K_j\) is an appropriate truncation index allowed to increase to infinity with n. A function \(f_j\) within some Besov ball can be well approximated by the above expansion and its estimation is equivalent to estimation of the wavelet coefficient vector \({\varvec{\gamma }}^{(j)}= (\gamma _{1}^{(j)},\dots , \gamma _{K_j}^{(j)})^T\). Similarly to the spline case, as alluded to in Antoniadis and Fan (2001) we can also define the regression design matrices containing wavelet basis functions evaluated at the samples of the corresponding predictors as in Amato et al. (2017):
Given the constraints imposed by identifiability restriction \({{{\mathbb {E}}}}(f_j(X^j))=0\), \(1 \le j \le p\), we may also center the wavelet basis functions by
for \(i=1, \dots , n\), \(j=1, \dots , p\) and \(k=1, \dots , K_j\). Without causing any confusion, to simplify notation, we still denote by \({\mathbf {W}}^{(j)}\) the centered matrices \({\varvec{{\tilde{W}}}}^{(j)}\) in the sequel, so the rows of the matrices \({\mathbf {W}}^{(j)}\) consists now of values of the centered wavelet basis functions at the ith observation of the jth covariate. Adopting a vector-matrix form of the irregular additive model (1), and since the covariate vector is assumed to be independent of the errors, conditionally on the \(\mathbf {X_i}\), \(i=1, \dots , n\), we get the following approximation of the additive model:
where \({\mathbf {Y}}=(Y_1, \dots ,Y_n)^T\), \({\varvec{\beta }}_0\) the n-dimensional constant vector with components \(\mu \) and \(\varvec{\epsilon }=(\epsilon _1,\dots , \epsilon _n)^T\). To simplify notation we will suppose that for all \(j=1,\dots , p\) the truncation index is the same, i.e. \( K_1 = K_2 = \cdots = K_p= K \) for the univariate approximations of the irregular additive components.
Let \({\mathbf {W}} = \left[ {\mathbf {W}}^{(1)} \ldots {\mathbf {W}}^{(p)} \right] \) be the \(n \times (Kp)\) matrix obtained by stacking block-wise the matrices \( {\mathbf {W}}^{(j)}\), \(j=1,\dots , p\) and let \({\varvec{\gamma }}= ({\varvec{\gamma }}^{(1)^T}, \dots , {\varvec{\gamma }}^{(p)^T})^T\) be the long (Kp)-dimensional column vector of centered wavelet coefficients. With such notation, the corresponding high-dimensional linear model becomes
and the estimation and variable selection task of the various components in the “irregular” AM is totally similar to the one developed for the group Lasso based on a spline representation of each component in additive models. With the above notation, the sparsity assumption on the additive model (1) translates to the following group sparsity condition of the model: there exists \(S \subseteq \{1, \cdots , p\}\), independent of n, such that \({\varvec{\gamma }}^{(j)} = {\mathbf {0}}\) for all \(j \notin S\).
In the traditional variable selection setting with all \(K_j=1\), a considerable amount of research has been done. Popular methods are the least absolute shrinkage and selection operator (Lasso; Tibshirani 1996), least angle regression (LARS; Efron et al. 2004), and the nonnegative garrote (Breiman 1995). All three methods have been adjusted by Yuan and Lin (2006) and Zou (2006) to handle grouped variables. Breheny and Huang (2009) follow a different philosophy and introduced a penalized regression framework for bi-level variable selection with grouped variables, i.e., their method first selects the important groups of variables and then the important variables within those groups. Amato et al. (2017) investigated a general penalized estimators framework using convex loss functions and concave \(\ell _2\)-norm penalties for the partially linear model with grouped covariates. Nevertheless, none of these contributions consider the problem of outlying data points. To tackle the estimation and variable selection problem for heavy-tailed or contaminated random errors in the high-dimensional linear model (2), few robust penalized approaches have been recently studied. Chen et al. (2010) apply a more robust version of the groupwise lasso based on a convex combination of \(L^1\) and \(L^2\) loss functions. Alfons et al. (2016) consider an extension of LARS to grouped variables and propose a robustification of their groupwise LARS procedure that aims to reduce the influence of outliers. However, the above robust methods all require the loss function to be convex. It is well known that the convex loss functions do not downweight the very large residuals due to their convexity. Amato et al. (2021) showed that redescending M-estimators with nonconvex loss function possess certain optimal robustness properties. Inspired by their approach, we now propose a novel high-dimensional bi-level variable selection method through a two-stage penalized M-estimator framework: penalized M-estimation with a redescending loss function and a concave \(\ell _2\)-norm penalty achieving the consistent group selection at the first stage, and a post-hard-thresholding operator to achieve the within-group sparsity at the second stage. Our perspective at the first stage is different from Amato et al. (2021) since we allow the loss function to be nonconvex and thus it is more general. In addition, our proposed two-stage framework is able to separate the groups selection and the individual variables selection efficiently, since the post-hard-thresholding operator at the second stage nearly poses no additional computational burden to the first stage.
The two-step M-estimation approach for bi-level variable selection. To perform an efficient bi-level variable selection with potential robustness for the existence of possible data contamination or heavy-tailed error distribution in model (2), we propose the following two-stage penalized M-estimator framework. In the first step, we perform penalized M-estimation with a group concave penalty achieving the between-group sparsity, an appropriate reduction of the dimension in the model and an initial estimator of the retained nonparametric components:
where \( {\mathcal {L}}_n\) is an empirical loss function, to be defined more precisely later on, which encourages a robust solution and \(p_\xi \) is a suitable penalty function with a tuning parameter \(\xi =\lambda \sqrt{K}\), which encourages the group sparsity in the solution. In the second step, we apply a multivariate hard-thresholding operator \({\varvec{\Theta }} (\cdot ,\nu )\) on \({\hat{{\varvec{\gamma }}}}\):
where “\(\cdot \)” and “\(\ge \)” in (4) are applied componentwise and \(\nu \) is a thresholding parameter.
Inspired by the theory on high-dimensional robust estimators developed recently by Amato et al. (2021), we give some sufficient conditions under which optima of regularized robust M-estimators with separable penalties are statistically consistent, even in the presence of heavy-tailed errors and outlier contamination. The conditions involve a bound on the derivatives of the robust loss functions, as well as restricted strong convexity of it in a neighborhood of constant radius about the true parameter vector \({\varvec{\gamma }}^*\), and the conclusions are given in terms of the tails of the error distribution. The ambient dimension p will be allowed to tend to infinity when the number of observations n tends to infinity, but the true sparsity index \(k^*:=|S|\) remains fixed. We will assume that n and \(p_n\) are such that \(n \ge c_0 \log p_n\), for a sufficiently large constant \(c_0\). By known information-theoretic results of Loh and Wainwright (2015), this type of lower bound is required for any method to recover the support of a \(k^*\)-sparse signal, hence is not a restriction.
We include the side condition \(\Vert {\varvec{\gamma }}\Vert _1 \le R\) in the group penalization step in order to guarantee the existence of local/global optima, for the case where the loss or regularizer may be nonconvex. In real applications, we can choose R to be a sufficiently large number such that the vector \({\varvec{\gamma }}^\star \) of wavelet coefficients approximating the true sum of additive components satisfies \(\Vert {\varvec{\gamma }}^*\Vert _1 \le R\) and is therefore feasible for the optimization. Note also that we have dropped \({\varvec{\beta }}_0\) in the argument of \( {\mathcal {L}}_n\), because if the response \({\mathbf {Y}}\) is not centered, the intercept may be efficiently estimated by the empirical median or mean of the observations with \(\sqrt{n}\)-consistency. So, given the identifying restriction of the additive components, there is not any loss of generality to assume that the additive regression model has zero intercept.
Denote by \({\varvec{w}}_i^T={\mathbf {W}}_i^T\) the ith row of the wavelet design matrix and let \(\ell : {\mathbb {R}}\mapsto {\mathbb {R}}^+ \) denote a (robust) loss function, defined on each observation pair (\({\varvec{w}}_i, y_i\)). The corresponding empirical loss function \({\mathcal {L}}_n\) in (3) is then given by \( \frac{1}{n} \sum _{i=1}^{n}\ell (y_i - {\varvec{w}}_i^T{\varvec{\gamma }})\) and equation (3) rewrites as
To address cases where both loss function and penalty are nonconvex, we will rely on Amato et al. (2021) results when necessary. The loss functions that we will adopt in this paper include Tukey’s biweight and Welsh loss (see also Appendix 1 of Amato et al. (2021)) of which we recall the definitions:
-
Tukey’s biweight loss
$$\begin{aligned} \ell _M(u) = \left\{ \begin{array}{cl} 1 - \bigl (1 - (u/M )^2 \bigr )^3 &{} \text{ if } {|{u}|} \le M \\ 1 &{} \text{ if } {|{u}|} > M \end{array} \right. \;, \end{aligned}$$with a \(M=4.685\).
-
Welsh Loss
$$\begin{aligned} \ell _M(u)= 1 - \exp \bigl ( (\frac{u}{M})^2\ \bigr ) \end{aligned}$$with a \(M=2.11\).
The above-mentioned values of the tuning parameter M yield 95% efficiency under strictly parametric linear regression models.
The above loss functions are indexed by the so-called robustness tuning constant M which regulates the trade-off between, on the one hand, the loss of estimation efficiency in the ideal case that the data exactly come from the assumed model with normally distributed errors, and, on the other hand, the maximum bias induced by some contamination whenever the data do not come from the assumed model. The choice of M is typically made before fitting the model to data by targeting a certain loss of estimation efficiency of the robust estimator relative to the maximum likelihood estimator at the assumed model. As, correctly noted by a referee, for Gaussian errors, such estimation efficiency is thought in terms of unpenalized parametric fits, comparing asymptotic covariances of regression coefficients and is meaningful if robust fits achieve the same degree of smoothness for all components. This is discussed in Aeberhard et al. (2020) where the authors propose an alternative way to assess the “efficiency vs. robustness” trade-off with penalized nonparametric fits. Their approach starts by considering a grid of plausible M values. For each grid value of M, a robust model is fitted based on the data sample. This fitted model is used to generate bootstrap samples, and subsequently for evaluating the bootstrap-based likelihood, from which then the sum of robustness weights is obtained. The tuning parameter M is then selected targeting a median downweighting proportion, e.g., 0.95. For more details, the interested reader is referred to Aeberhard et al. (2020). Let us mention that some experimental runs on one of our simulated examples with the procedure advocated by Aeberhard et al. (2020) led in choosing an optimal constant \(M=5.1\) for Tukey’s biweight loss, but with no significantly better fits than those obtained when using the value \(M=4.685\). Since the resulting gain in MSE was not significant in these runs, and since, under our setting, such a tuning parameter selection procedure is computationally expensive, we therefore will follow Croux et al. (2011) and Wong et al. (2014) and resort to somewhat default values for M taken from strictly parametric cases, considering this parameter simply as a downweighting threshold.
Although third derivatives do not always exist for the above loss functions, a unifying property is that the derivative \(\ell '\) is bounded and odd in each case, so they can mitigate the effect of larger residuals which turns out to be an important property for robustness of the resulting estimators. Note in particular (see Amato et al. (2021)) that Tukey’s biweight loss produces redescending M-estimators while Welsh’s loss produce weakly redescending M-estimators.
Adopting the above losses, the loss function \({\mathcal {L}}_{n}\) in (5) satisfies
where \(\nabla h\) denotes the gradient or subgradient of a function h. The condition (6) ensures that \({\varvec{\gamma }}^*\) is a stationary point. Indeed, when the design is deterministic, we have
since the errors in (1) are mean zero i.i.d random variables and the influence function \(\ell '\) is odd. When the design is random then
since \(\epsilon _i\) and \({\varvec{W}}_i\) are stochastically independent and \(\epsilon _i\) are zero mean i.i.d. Therefore, the condition (6) is always satisfied.
The performance of group regularized M-estimators in expression (5) not only depends on the robust loss \(\ell \) used but also on the penalty \(p_\lambda \) and the corresponding regularization parameter \(\lambda \). To select a good penalty function, that is able to generate sparse solutions between groups, we require the penalty function \(p_\lambda \) in (5) to satisfy amenable properties listed and discussed in Amato et al. (2021), whose properties are recalled below.
Assumption 1
(Amenable penalties) \(p_\lambda : {\mathbb {R}}\mapsto {\mathbb {R}}\) is a scalar function that satisfies the following conditions:
-
(i)
For any fixed \(t \in {\mathbb {R}}^+\), the function \(\lambda \mapsto p_\lambda (t)\) is nondecreasing on \({\mathbb {R}}^+\).
-
(ii)
There exists a scalar function \(g:{\mathbb {R}}^+ \mapsto {\mathbb {R}}^+\) such that for any \(r \in [1, \infty )\), \(\frac{p_{r\lambda }(t)}{p_\lambda (t)} \le g(r)\) for all \(t,\lambda \in {\mathbb {R}}^+\).
In addition:
-
(iii)
The function \(t \mapsto p_\lambda (t)\) is symmetric around zero and \(p_\lambda (0) = 0\), given any fixed \(\lambda \in {\mathbb {R}}^+\).
-
(iv)
The function \(t \mapsto p_\lambda (t)\) is nondecreasing on \({\mathbb {R}}^+\), given any fixed \(\lambda \in {\mathbb {R}}^+\).
-
(v)
The function \(t \mapsto \frac{p_\lambda (t)}{t}\) is nonincreasing on \({\mathbb {R}}^+\), given any fixed \(\lambda \in {\mathbb {R}}^+\).
-
(vi)
The function \(t \mapsto p_\lambda (t)\) is differentiable for \(t \ne 0\), given any fixed \(\lambda \in {\mathbb {R}}^+\).
-
(vii)
\(\lim _{t \rightarrow 0^+} p'_\lambda (t) = \lambda \), given any fixed \(\lambda \in {\mathbb {R}}^+\).
-
(viii)
There exists \(\mu > 0\) such that the function \(t \mapsto p_\lambda (t) + \frac{\mu }{2} t^2\) is convex, given any fixed \(\lambda \in {\mathbb {R}}^+\).
-
(ix)
There exists \(\xi \in (0, \infty )\) such that \(p_\lambda '(t) = 0\) for all \(t \ge \xi \lambda \), given any fixed \(\lambda \in {\mathbb {R}}^+\).
The properties above are related to the penalty functions studied in Loh and Wainwright (2015) and Amato et al. (2021). If \(p_\lambda \) satisfies conditions (i)-(viii) of Assumption 1, we say that \(p_\lambda \) is \(\mu \)-amenable. If \(p_\lambda \) also satisfies condition (ix), we say that \(p_\lambda \) is \((\mu , \xi )\)-amenable (see Loh and Wainwright (2015)). In particular, if \(p_\lambda \) is \(\mu \)-amenable, then \(q_\lambda (t) := \lambda |t| - p_\lambda (t)\) is everywhere differentiable. Defining the vector version \(q_\lambda ({\varvec{\gamma }}):=\sum _{j=1}^{p} q_\lambda (\Vert {\varvec{\gamma }}^{(j)}\Vert _2)\) accordingly, it is easy to see that there exists \(\mu >0\) such that \(\frac{\mu }{2}\Vert {\varvec{\gamma }}\Vert _2^2 - q_\lambda ({\varvec{\gamma }})\) is convex. This property is important for both computational implementation and theoretical investigation of the group selection properties. Examples of amenable regularizers are the smoothly clipped absolute deviation (SCAD) penalty (see Antoniadis and Fan (2001)), the minimax concave penalty (MCP) (see Zhang (2010)) and the standard \(\ell _1\)-penalty. The SCAD penalty with fixed parameter \(a>2\) is \((\mu , \xi )\)-amenable, with \(\mu = \frac{1}{a-1}\) and \(\xi = a\). The MCP regularizer is \((\mu , \xi )\)-amenable, with \(\mu = \frac{1}{\gamma }\) and \(\xi = \gamma \). The \(\ell _1\)-penalty \(p_\lambda (t) = \lambda |t|\) is an example of a regularizer that is 0-amenable, but not \((0, \xi )\)-amenable, for any \(\xi < \infty \).
3 Main statistical results
This section presents our results on the asymptotic properties for the proposed two-step penalized M-estimators defined in steps 1 and 2 of Sect. 2. On the one hand, we show a general non-asymptotic bound of the estimation error for the difference between the coefficients \({{\varvec{\gamma }}}^*\) in the true wavelet approximation of the nonparametric additive components and their estimation \({\hat{{\varvec{\gamma }}}}\) with an optimal rate of convergence under certain mild conditions. On the other hand, we show that the estimator \({\hat{{\varvec{\gamma }}}}\) selects with high probability the correct group support and thus displays good group-level properties. We also show that those nice statistical properties of \({\hat{{\varvec{\gamma }}}}\) can be carried over during the hard-thresholding stage. Appropriate conditions on the distribution of the covariate vector \({\varvec{X}}\) and the conditional wavelet-based design matrix lead to asymptotically consistent estimators of the nonparametric additive components.
Following the theory on high-dimensional penalized robust estimators studied recently by Amato et al. (2021), we give some sufficient conditions under which optima of regularized robust M-estimators with group separable penalties are statistically consistent, even in the presence of heavy-tailed errors and outlier contamination. The conditions involve a bound on the derivatives of the robust loss functions, as well as restricted strong convexity of it in a neighborhood of constant radius about the true parameter vector \({\varvec{\gamma }}^*\), and the conclusions are given in terms of the tails of the error distribution.
The restricted strong convexity (RSC) requirement of the loss functions is an important requirement. Denote \({{\widehat{{\varvec{\Delta }}}}}={{\widehat{{\varvec{\gamma }}}}_{\lambda _n}}- {{\varvec{\gamma }}^*}\) the difference between an optimal solution \({\widehat{{\varvec{\gamma }}}}_{\lambda _n}\) and the true parameter, and consider the loss difference \({\mathcal {L}}_{n}({{\widehat{{\varvec{\gamma }}}}_{\lambda _n}})- {\mathcal {L}}_{n}({\varvec{\gamma }}^*)\). In the classical setting, under fairly mild conditions, one expects that the loss difference should converge to zero as the sample size n increases. It is important to note, however, that such convergence on its own is not sufficient to guarantee that \({{\widehat{{\varvec{\gamma }}}}_{\lambda _n}}\) and \({{\varvec{\gamma }}^*}\) are close or, equivalently, that \({\varvec{\Delta }}_n\) is small. Rather, the closeness depends on the curvature of the loss function. The standard way to ensure that a function is “not too flat” is via the notion of strong convexity. However restricted strong convexity traditionally involves a global condition on the behavior of the loss function. Due to the highly nonconvex behavior of the robust regression functions that we are using (Tukey’s biweight or Welsh losses), we will assume only a local condition of restricted strong convexity.
Assumption 2
(Local RSC condition) There exist \(\alpha \), \(\tau >0\) and a radius \(r>0\) such that the loss function \({\mathcal {L}}_{n}\) in (3) satisfies
for all \({\varvec{\gamma }}_1\), \({\varvec{\gamma }}_2 \in {\mathbb {R}}^{Kp}\) such that \(\Vert {\varvec{\gamma }}_j-{\varvec{\gamma }}^*\Vert _2\le r\) for \(j=1, 2\).
Note that the RSC assumption is only imposed on \({\mathcal {L}}_{n}\) inside a ball of radius r centered at \({\varvec{\gamma }}^*\). Thus the loss functions used for robust regression can be wildly nonconvex while away from the origin. The ball of radius r essentially specifies a local region around \({\varvec{\gamma }}^*\), say the local RSC region, in which stationary points of program (3) are well-behaved.
Remark 1
Recall that \({\tilde{{\varvec{\gamma }}}}\) is a stationary point of the optimization in (3) if
for all feasible \({\varvec{\gamma }}\) in a neighbor of \({\tilde{{\varvec{\gamma }}}}\), where \(p_{\lambda }({\varvec{\gamma }})=\sum _{j=1}^{p} p_{\lambda \sqrt{K}}(\Vert {\varvec{\gamma }}^{(j)}\Vert _2 )\). Note that stationary points include both the interior local maxima as well as all local and global minima. It is easy to see that the estimation consistency result also holds for the stationary points in the optimization problem (5). Hence Theorem 1 stated below guarantees that all stationary points within the ball of radius r centered at \({\varvec{\gamma }}^*\) have local statistical consistency at an optimal rate. To simplify the notation, \({\hat{{\varvec{\gamma }}}}\) denotes the stationary points of the optimization problem (5).
We will use some extra notation. Denote the index set of coefficients in group j by \(I_j \subseteq \{1,2, \cdots , pK\}\). Then \(I_S:=\bigcup _{j \in S} I_j\) includes all indexes of coefficients in the important groups. Let \(s=|I_S|\). We can now state the following Theorem of Amato et al. (2021) (see also Loh (2017)) which guarantees that stationary points within the local region where the loss function satisfies restricted strong convexity are statistically consistent.
Theorem 1
Suppose \({{\mathcal {L}}}_n\) satisfies the local RSC assumption 2 with \({\varvec{\gamma }}_2 = {\varvec{\gamma }}^*\) and the penalty \(p_\lambda \) is \(\mu \)-amenable, with \(\frac{3}{4} \mu < \alpha \). Suppose \(n \ge C r^2 \cdot s \log (Kp)\) for some constant \(C>0\) and a radius \(r>0\), that \(\Vert {\varvec{\gamma }}^*\Vert _1 \le R \) and let
A stationary point \({\tilde{{\varvec{\gamma }}}}\) of the objective function in (3) such that \(\Vert {\tilde{{\varvec{\gamma }}}}- {\varvec{\gamma }}^*\Vert _2 \le r\) exists and satisfies the bounds
Note that the statement of Theorem 1 is entirely deterministic and the distributional properties of the covariates, the wavelet basis and the error terms come into play when verifying that the assumptions hold with high probability under a prescribed sample size scaling. In particular, in Theorem 1, when r is chosen to be a constant and \(\frac{s \log (Kp)}{n} = o(1)\) as is the case in the robust regression settings that we are interested in, one can choose \(\lambda ={\mathcal {O}}\left( \sqrt{\frac{\log (Kp)}{n}} \right) \) such that \(\Vert {\hat{{\varvec{\gamma }}}}-{\varvec{\gamma }}^*\Vert _2={\mathcal {O}}_p \left( \sqrt{\frac{ s\log (Kp)}{n}} \right) \) and \(\Vert {\hat{{\varvec{\gamma }}}}-{\varvec{\gamma }}^*\Vert _1={\mathcal {O}}_p \left( s\sqrt{\frac{\log (Kp)}{n}} \right) \). Hence, all stationary points within the constant-radius region are actually guaranteed to fall within a shrinking ball of radius \({{\mathcal {O}}}\left( \sqrt{\frac{s \log (Kp)}{n}}\right) \) centered around \({\varvec{\gamma }}^*\).
When the design is deterministic or more generally conditionally on the covariates vector \({\mathbf {X}}\), using sufficiently regular compactly supported wavelets bases, Proposition 7.1 of Chesneau et al. (2015) implies that \(\Vert n^{-1} \sum {\varvec{w}}_i\Vert _\infty \) \(\le D \sqrt{ \log {(Kp)} n^{-1}}\) for some constant D which depends on the wavelet basis used for regression and the bounds of the compactly supported density of \({\mathbf {X}}\). Moreover, as stated before, the residual function \(\ell \) for the robust loss functions adopted here, has a bounded derivative and is such that \(|\ell ''(u)| < B\) for some constant \(B>0\), and for all \(u\in {\mathbb {R}}\) where \(\ell ''(u)\) exists. Therefore, the influence function \(\ell '\) is Lipschitz. Given the above, it is then easy to see that one may find a sufficiently large constant \(\kappa _1>0\) such that the loss function \({{\mathcal {L}}}_n\) satisfies the bound
We have already seen that under our assumptions condition (6) is always satisfied. Therefore, the gradient bound (7) is established under fairly mild assumptions. When the errors \(\epsilon _i\) are drawn from a sub-Gaussian distribution with an appropriate bound on its variance, or when the errors have a contaminated mean-zero finite variance distribution with an appropriate bound on the fraction of outliers the local RSC condition for the loss functions holds as soon as \( n > C \, \log (Kp)\).
Regarding the consistency properties of the group penalized M-estimators considered, suppose that \(I_S\) is given in advance, and define the group-level local oracle estimator as
Let \({\hat{{\varvec{\gamma }}}}^{\hbox { oracle}} := ( {\hat{{\varvec{\gamma }}}}_{I_S}, {{\mathbf {0}}}_{I_S^c})\). The next theorem, a restatement of Theorem 2 and Corollary 1 of Loh (2017), shows that when a penalty \(p_{\lambda }\) is \((\mu , \xi )\)-amenable (such as SCAD or MCP, for example) and conditions in Theorem 1 are satisfied, the stationary point from (5) within the local neighborhood of \({\varvec{\gamma }}^*\) agrees with the group oracle estimator in (8). For its proof, we refer the reader to the arguments provided in that paper. Denote by \({\varvec{\gamma }}^{*G}_{\min }\) the minimum group strength of \({\varvec{\gamma }}^*\), i.e. \({\varvec{\gamma }}^{*G}_{\min }:= \min _{j \in S} \Vert {\varvec{\gamma }}^*_j\Vert _2\). We have:
Theorem 2
Suppose a penalty \(p_{\lambda }\) is \((\mu , \delta )\)-amenable and conditions in Theorem 1 hold. Suppose in addition \(\Vert {\varvec{\gamma }}^*\Vert _1 \le \frac{R}{2}\) for some \(R > \frac{24 K \lambda s}{4\alpha - 3\mu }\), \({\varvec{\gamma }}^{*G}_{\min } \ge C_1\sqrt{\frac{s\log s}{n}} + \xi \lambda \), \(n \ge C_0 s \log (Kp) \) and \(s^2\log s ={{\mathcal {O}}}(\log (Kp))\). Let \({\hat{{\varvec{\gamma }}}}\) be a stationary point of program (5) in the local RSC region. Then \({\hat{{\varvec{\gamma }}}}\) satisfies \( \hbox {supp}({\hat{{\varvec{\gamma }}}})\subseteq I_S \) (where \( \hbox {supp}({\hat{{\varvec{\gamma }}}})\) denotes the index set supporting \({\hat{{\varvec{\gamma }}}}\)) and \({\hat{{\varvec{\gamma }}}}_{I_S} = {\hat{{\varvec{\gamma }}}}_{I_S}^{\hbox { oracle}}\).
Let \(I_0=\{m:\gamma _m^*\ne 0, 1 \le m \le pK\}\) and thus \(I_0 \subseteq I_S\). Define \({\varvec{\gamma }}^{*{I_0}}_{\min }:= \min _{m \in I_0} |\gamma _m^*|\) as the minimum individual signal strength on \({\varvec{\gamma }}^*\). We are now ready to establish statistical properties of the multivariate hard-thresholding estimator \({\vec {\Theta }}({\hat{{\vec {\gamma }}}},\nu )\) at the second step of our proposed estimation framework. The following theorem ensures that when the condition of minimum individual signal strength is satisfied and since the additive components have sparse wavelet basis expansions there exist some thresholds \(\nu \) that are able to filter out those nonimportant coefficients within the selected important groups, and thus the thresholding stage will indeed perform bi-level variable selection consistently.
Theorem 3
Suppose conditions of Theorem 1 hold and in addition that the individual strength \({\varvec{\gamma }}^{*{I_0}}_{\min } \ge C \sqrt{\frac{s \log s}{n}} + \nu \) and \(\nu > C \sqrt{\frac{s \log s}{n}} \) for some constant \(C>0\). There exists a constant C such that the hard-thresholding estimator \({\vec {\Theta }}({\hat{{\vec {\gamma }}}},\nu )\) satisfies \(\Vert {\vec {\Theta }}({\hat{{\vec {\gamma }}}},\nu ) - {\vec {\gamma }}^*\Vert _2 \le C \sqrt{\frac{s \log s}{n}}\).
Proof
By the condition that \({\varvec{\gamma }}^{*{I_0}}_{\min } \ge C \sqrt{\frac{s \log s}{n}} + \nu \), we have
for all \(j \in I_0\), where the third inequality follows from Theorem 1 and the properties of \({\hat{{\varvec{\gamma }}}}_{I_S}\) in Theorem 2. For \(j \in I_S - I_0\),
where the second inequality follows from Theorem 1 and the properties of \({\hat{{\varvec{\gamma }}}}_{I_S}\) in Theorem 2 and the last inequality follows from the condition in Theorem 3. Recall \({\hat{{\varvec{\gamma }}}}^{\hbox { oracle}} = ({\hat{{\varvec{\gamma }}}}^{\hbox { oracle}}_{I_S}, {{\mathbf {0}}}_{I_S^c})\). By Theorem 2 we have \({\hat{{\varvec{\gamma }}}} = {\hat{{\varvec{\gamma }}}}^{\hbox { oracle}}\). With (9) and (10) and the definition of the thresholding operator with threshold \(\nu \), the result follows. \(\square \)
Regarding now the estimation of the nonzero additive components of the sparse additive model (1), and given the realizations \(x_i^j\) of the components of the sample of the covariate vectors \({\varvec{X}}_i\), \(i=1, \dots , n\), we will use the following notation. For \(j =1, \dots , p\), let \(f^o_j\) be the true centered components defined by
and \({\mathbf {f}}^o_j = (f^o_j(x_1^j), f^o_j(x_2^j) \dots , f^o_j(x_n^j))^T\) the corresponding vector of conditional values. Denote by \(f^*_{nj}\) the truncated wavelet expansion of \(f_j^o\) onto the centered wavelet basis
and \({\mathbf {f}}^*_{nj} = (f^*_{nj}(x_1^j), f^*_{nj}(x_2^j), \dots , f^*_{nj}(x_n^j))^T = {\varvec{W}}^{(j)} {\varvec{\gamma }}^{*(j)}\) using our matrix notation, with the adopted convention that \({\varvec{W}}^{(j)}\) is indeed \({\tilde{{\varvec{W}}}}^{(j)}\). Finally, let
and \(\hat{{\mathbf {f}}}_{nj} = ({\hat{f}}_{nj}(x_1^j),{\hat{f}}_{nj}(x_2^j), \dots , {\hat{f}}_{nj}(x_n^j))^T = {\varvec{W}}^{(j)} {\hat{{\varvec{\gamma }}}}^{(j)}\). The following assumptions, summarize several conditions already stated in previous sections.
Assumption 3
(Components and design) Regarding the covariates each marginal component \(X^j\), \(j=1, \dots , p\), of the covariate vector \({\mathbf {X}}\) has a continuous density with a compact support strictly included in [0, 1]. Regarding the additive components, we assume
-
(i) For each \(j=1, \dots , p\), the additive components \(f_j\) belong to the (inhomogeneous) Besov space on the unit interval \({\mathcal {B}}^t_{\kappa ,\omega }([0,1])\) with \(t+1/\kappa -1/2>0\).
-
(ii) The mother wavelet \(\psi \), defining the wavelet approximation has q null moments and q continuous derivatives where \(q > \max (1, \omega )\).
We may now state the following result, regarding the asymptotic properties of the estimators of the nonzero additive components.
Theorem 4
Suppose conditions of Theorem 3 hold together with the conditions in Assumption 3. Then, for sufficiently large \(K_n\) such that \(K_n \ge c (\frac{n}{\log n})^{1/(2t+1)}\), for \(j \in S\), we have
so that, for the nonzero components in the sparse additive model, \( \hat{{\mathbf {f}}}_{nj}\) inherits the asymptotic mean squared error properties of the hard-thresholded estimator in Theorem 3.
Proof
Note first that by the triangle inequality we have
Regarding the approximation part \(\frac{2}{n} \Vert {\mathbf {f}}^o_j - {\mathbf {f}}^*_{nj} \Vert _2^2 \), as it is traditional in the wavelet estimation literature, using the assertion (i) in Assumption 3 and the regularity stated in assertion (ii) for the mother wavelet \(\psi \) used in the wavelet expansion, one may use for example the approximation part in Theorem 5.1 of Chesneau et al. (2015), to see that, for \(K_n = {\mathcal {O}} (\frac{n}{\log n})^{1/(2t+1)}\) we have
By the adopted notation, the error part \(\frac{1}{n} \Vert {\mathbf {f}}^*_{nj} - \hat{{\mathbf {f}}}_{nj} \Vert _2^2\) in (11) may be also written as \( \frac{1}{n} \Vert {\varvec{W}}^{(j)} ({\varvec{\gamma }}^{*(j)} -{\hat{{\varvec{\gamma }}}}^{(j)})\Vert ^2\). By arguments similar to Proposition 10.3 of Härdle et al. (1998), the largest eigenvalue of each semi-positive definite wavelet matrix \(\frac{1}{n} {\varvec{W}}^{(j)T} {\varvec{W}}^{(j)}\), \(j \in S\), is bounded above. Since \(k^*=|S|\) is finite and fixed, and since the conditions of Theorem 3 hold, by the mean squared error properties of the hard-thresholded estimator in Theorem 3 we have
Combining the above upper bound with the one stated in (12) leads to the desired result.\(\square \)
4 Algorithms for numerical implementation
We describe here a two-step algorithm for computing the proposed two-stage M-estimator, which, for fixed \(\lambda \), is guaranteed to converge to a stationary point in problem (5) within the local region where the RSC condition holds, even when the M-estimator is nonconvex, since we allow both loss function \({\mathcal {L}}_{n}\) and penalty \(p_\lambda \) to be nonconvex. We also discuss the tuning parameters selection for both \(\lambda \) and \(\nu \).
To obtain the corresponding stationary point, we use the composite gradient descend algorithm (Nesterov 2007). Recall that \(q_\lambda ({\varvec{\gamma }}) = \sum _{j=1}^p \sqrt{K}\lambda \Vert {\varvec{\gamma }}^{(j)}\Vert _2 \) \(- \sum _{j=1}^{p} p_{\sqrt{K}\lambda } (\Vert {\varvec{\gamma }}^{(j)}\Vert _2 )\) and using \(\bar{{\mathcal {L}}}_{n}({\varvec{\gamma }})={\mathcal {L}}_{n}({\varvec{\gamma }})-q_\lambda ({\varvec{\gamma }})\), we can rewrite the optimization problem as
Then the composite gradient iterates are given by
where \(\eta \) is the step-size parameter for the update and can be determined by the backtracking line search method described in Nesterov (2007).
Defining the group soft-thresholding operator denoted by \(S_{\sqrt{K} \lambda / \eta }(\cdot )\) as
a simple calculation shows that the iterates (13) take the form
We then adopt the following two-step procedure discussed in Amato et al. (2021) to guarantee the convergence to a stationary point for the nonconvex optimization problem in (5).
-
Step 1 Run the composite gradient descent using a Huber loss function with convex group Lasso penalty to get an initial estimator.
-
Step 2 Run the composite gradient descent on the program (5) at the Group Penalization Stage using the initial estimator from Step 1.
As to the tuning parameters selection, the optimal values of tuning parameters \(\lambda \) and \(\nu \) by optimization of the empirical robust-loss-based prediction error on a two-dimensional grid whose sides range is motivated by the conditions of Theorem 2 and Theorem 3.
Remark 2
The numerical algorithms described in this section could also be supplemented by a numerical implementation of the empirical estimate of the influence function (sensitivity curves) for the estimators of the paper, following the approach described in Boente et al. (2017). However, a fundamental issue is the computational time to evaluate the sensitivity surfaces. For example, to get the four estimates from a single simulation run with 400 data points and 5 covariables requires about 100 seconds. Estimating the influence function requires estimating solutions of all methods on a grid of dimension \(p+1\), with p being the number of components. It is obvious that the computational time required is too high. Summarizing, empirical estimation is technically feasible, provided that a small number of additive components is considered, a coarse evaluation grid is used and each run is executed on a machine with a high number of processors.
5 Simulation study and analysis of real data
This section reports the results from a simulation study and real data analysis that are designed to assess the practical performance of our two-stage M-estimation method.
5.1 Simulation study
Throughout this subsection we will assume without any loss of generality that our model does not contain an intercept and we assess the performance of robust estimators by considering different types of loss functions, namely Tukey’s biweight and Welsh’s, and the MCP penalty function, since SCAD is a particular case of MCP, through our simulation examples. The data are generated from the following model
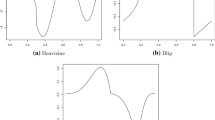
Since we are interested on the robustness in presence of vertical outliers, nonequispaced design sample points \(x^j_i\), \(i=1, \dots , n\), are generated once for all from p independent uniform distributions on [0, 1], i.e., the design matrix is fixed over all simulations. Without any loss of generality the additive components \(f_j\), \(j=1, \ldots , p\), evaluated at their respective design points are centered and have empirical norm \(\left\| f_{j}\right\| _{n}=1\). In the simulations, \(p=5\) and the number of nonzero components |S| is equal to 3. The chosen additive components are displayed in Fig. 1. The number of covariates \(p=5\) is reasonable and allows to explore eventual computational or conceptual weaknesses of certain estimators in higher dimensions. The wavelets used in our simulations are the least asymmetric Daubechies wavelets with 5 vanishing moments, and the number of bases K chosen to approximate each component is \(K=\lfloor \log _2(n) -2 \rfloor \), leading to wavelet design matrices of size \(n \times (Kp)\). We note that, as long as Kp remains less than n (a condition due to the fact that most of the methods used in our paper require an initial (standard) robust regression estimator, which when \(Kp > n\) becomes impossible), our results are not sensitive to these choices. A more important issue is the automatic selection of the tuning parameters.
Several combinations of the loss functions (Tukey’s biweight or Welsh’s), of the penalty functions (SCAD or MCP), of the errors distribution (Gaussian mixture with a given proportion of outliers or Gaussian) for a sample sizes \(n=400\) are considered. Without causing any confusion, let \({\hat{f}}_j\) be any estimator of \(f_j\). Its performance on both parameter estimation and variable selection are evaluated by the following indicators:
-
Root Mean Square Error (RMSE\(_j\)), aimed at evaluating a component-wise accuracy. It is computed for each component as
$$\begin{aligned} \mathrm {RMSE}_j= \sqrt{ \frac{1}{n} \sum _{i=1}^{n} ({\hat{f}}_j(x^j_i) - f_j(x^j_i))^2 },\ j=1,\ldots ,p, \end{aligned}$$at the nonequispaced design points \(x^j_i\);
-
Number of selected variables (NS). It is aimed at evaluating capability of the methods in preserving sparsity of the models:
$$\begin{aligned} \mathrm {NS}:=|{{\hat{S}}}|,\ {{\hat{S}}}=\{j: {{\hat{f}}}_{j} \not = 0\} \end{aligned}$$ -
False-positive rates (FPR) for additive components selection, the percent of selected components which are actually unimportant, defined as
$$\begin{aligned} \mathrm {FPR}:= |{{\hat{S}}}^p|/|S^c| \times 100 \%,\ {{\hat{S}}}^p:=\{j: {{\hat{f}}}_{j}\ne 0 \ \mathrm {and} \ f_j=0\} \end{aligned}$$ -
False-negative rates (FNR) for additive components selection, the percent of non-selected components which are actually important, defined as
$$\begin{aligned} \mathrm {FNR}:= |{{\hat{S}}}^n|/ |S| \times 100 \%,\ {{\hat{S}}}^n:=\{j: {{\hat{f}}}_{j} = 0 \ \mathrm {and} \ f_j\ne 0\} \end{aligned}$$
For each of the above experimental factor combinations, 100 simulated data sets \({\mathbf {Y}}^h \in {\mathbb {R}}^n\), \(h=1,\dots , 100\) are generated according to model (14), where \(\epsilon _i\)’s are i.i.d. noise variables. We set \(\sigma ^{2}\) in the generation of the responses so that the signal-to-noise ratio (SNR) was \(\left\| f_{j}\right\| _{n}^{2} / \sigma ^{2}=4\), \(j=1, \dots , p\). We considered two possible distributions for the errors \(\epsilon _i\) : a mean zero normal distribution with standard deviation \(\sigma \) and a mixture distribution of Gaussians, \((1-\alpha ) {\mathcal {N}}(0,\sigma ) + \alpha {\mathcal {N}}(0,6\sigma )\), with \(\alpha =0.1\) where \(\alpha \) denotes the mixture parameter. The first possibility, scenario 1, corresponds to the classical scenario of normal errors without outliers and is used to illustrate the loss of efficiency incurred by using a robust estimator when it may not be needed. The second possibility, scenario 2, considers a model whose observations can be contaminated by light-tail vertical outliers. As suggested by a referee, we complemented the simulations with two similar scenarios but with an equidistant deterministic design of size a power of 2 (homogeneous setup) allowing us to also consider the robust RAMlet nonlinear back-fitting wavelet-based estimator of additive models developed in Sardy and Tseng (2004), in addition to the alternatives used in scenarios 1 and 2. Table 1 collects the different elements in the simulation models and the different settings.
In each scenario, the additive model has \(p=5\) components, of which 3 are nonzero components. See Fig. 1. Furthermore, in each simulation model the average SNR is 4, and we report on results for 100 simulations.
For each simulated data set \({\mathbf {Y}}^h\), we have applied each of the methods considered in this paper. For estimation by the group penalized regression bi-level variable selection procedure GRPREG of Breheny and Huang (2009), the tuning parameter is chosen by performing a fivefold cross-validation over a grid of values for the regularization parameter lambda and the optimal one is determined using a Bayesian information criterion (BIC). Concerning the robust group-wise LARS procedure of Alfons et al. (2016) the final models are obtained by fitting MM-regression along the respective sequence of predictor groups, and choosing the respective optimal model via BIC using a residual scale estimate from the initial S-estimator. Furthermore, note that the loss function \(\rho \) for MM-regression in GLARS is chosen to be Tukey’s bisquare function tuned towards \(95 \%\) efficiency, and recall this is tailored to the strict parametric, normal case. We noticed that the estimates produced by the GLARS procedure were quite wiggly, so we slightly smoothed them with P-splines with a relatively large number of knots, in order to introduce some extra bias. For our BIWEIGHT and WELSH procedures, a sequence of MM-regression model fits are evaluated along a supplied grid of lambda values and the optimal parameter is chosen via optimization of a robust BIC version. By default, the second step thresholding parameter \(\nu \) is chosen by a minimax threshold rule. For the deterministic equidistant design case, the smoothing parameter of the RAMlet wavelet-based estimator is based on a practical automatic rule for choosing the smoothing parameters automatically, namely the sparsity information criterion SLIC developed in Sardy (2009).
5.2 Simulation scenario 1
Figure 2 displays a typical simulation data set in scenario 1. The display allows to realize the amount of noise added in each of the additive components.
Tables 2 and 3 summarize the results of the simulations.
Finally, boxplots of the fitted simulated additive model RMSEs for each estimate obtained by the four methods for scenario 1 are presented in Fig. 3.
5.3 Simulation scenario 2
A typical simulated data set in scenario 2 is depicted in Fig. 4. Note the presence of several outliers when comparing the display with the one in Fig. 2.
The results of the simulations are summarized in Tables 4 and 5.
Boxplots of the fitted simulated additive model RMSEs of each estimate obtained by the four methods for scenario 2 are presented in Fig. 5.
5.4 Simulation scenario 3
Figure 6 displays a typical simulation data set in scenario 3. The display allows to realize the amount of noise added in each of the additive components.
Tables 6 and 7 summarize the results of the simulations.
Finally, Fig. 7 shows the boxplots of the fitted simulated additive model RMSEs for each estimate obtained by the five methods, for scenario 3.
5.5 Simulation scenario 4
Figure 8 displays a typical simulation data set in scenario 4. The display allows to realize the amount of noise added in each of the additive components.
Tables 8 and 9 summarize the results of the simulations.
Finally, boxplots of the fitted simulated additive model RMSEs for each estimate obtained by the five methods for scenario 4 are presented in Fig. 9.
5.6 Results
We now discuss the simulation results of various robust model selection criteria in terms of both model selection and prediction accuracy for each simulation scenario. Tables 2, 3, 4 and 5 show the accuracy measures RMSE\(_j\) for the additive components and the performance indicators NS, FPR and FNR for the simulation examples with a random design of Sect. 5, while Tables 6, 7, 8 and 9 show similar measures for the simulation examples with a deterministic equidistant design of Sect. 5. Reported values are the averages over the 100 different realizations; standard deviation is shown in parentheses in all tables. Figures 3, 5, 7 and 9 display boxplots of the global RMSE for the fitted additive model by each method.
In scenario 1, from the perspective of variable selection, when considering the performance indicators NS, \(\text {FPR}\) and \(\text {FNR}\), all methods tend to identify the three significant components correctly. Note however that the bi-level GRPREG procedure selects sometimes one or more noise variables compared to the other methods which never select insignificant components. From the prediction point of view, as shown in Table 2 or the boxplots (Fig. 3), all methods maintain satisfactory RMSE. Confirming the results in Alfons et al. (2016), GLARS performs very well and successfully selects relevant components. Note that in the standard normal case both two-step robust procedures display a comparable (better for BIWEIGHT) global RMSE, even if they are essentially designed to handle vertical outliers.
In the case of vertically contaminated data, the non-robust procedures GRPREG has an almost doubled RMSE when compared to the averages in scenario 1 while GLARS, BIWEIGHT and WELSH lead to RMSE averages slightly larger to those in scenario 1. Among the robust procedures, Tukey’s BIWEIGHT is slightly better than GLARS and WESLH, but the three methods remain competitive. Regarding the variable selection properties GLARS, BIWEIGHT, and WELSH select the significant variables correctly while GRPREG sometimes selects some noise variables.
Regarding the homogeneous scenarios 3 and 4, the above conclusions drawn from simulation scenarios 1 and 2 remain mainly true for the methods applied there. In the non-contaminated case, the RAMlet procedure presents a predictive performance that it is slightly worse than BIWEIGHT and WELSH due probably to the fact that it is not designed to perform variable selection (few wavelet coefficients for the noise components are not thresholded). One may also note the several outlying predictions for GLARS in scenario 3, with also rarely selecting some noisy variables, indicating probably that the number of maximum iterations required for convergence of this method should be set to a larger value than the actual one used for realizing the simulation fits, but at a cost of even a larger CPU time. Quite surprisingly, the robust procedures BIWEIGHT, WELSH and RAMlet seem to be quite efficient even in the non-contaminated case. For vertical contaminated data (scenario 4) GLARS and RAMlet robust procedures display a comparable RMSE, but again BIWEIGHT AND WELSH display a better global RMSE.
5.7 Real data examples
5.7.1 Air quality data
We analyze a real data set available in R, namely the airquality data set, which has also been analyzed with a robust backfitting procedure in Boente et al. (2017). As noted by the referees, the effects of the covariates are essentially smooth and could be treated with splines, but we retain the example since we can compare our results with those of Boente et al. (2017). We have fitted data with each of the four procedures already used in the simulations, the robust backfitting of Boente et al. (2017) as implemented in the R-package RBF and a classical fit using the gam function of the R-package mgcv. The data set contains 153 daily air quality measurements in the New York region between May and September 1973. The interest is in explaining mean Ozone concentration (“\(O_{3}\)”,measured in ppb) as a function of three potential explanatory variables: temperature (“Temp”, in degrees Fahrenheit), wind speed (“Wind”, in mph) and solar radiance measured in the frequency band \(4000-7700\) (“Solar.R” in Langleys). Mimicking Boente et al. (2017) in our analysis, we only consider the 111 cases that do not contain missing observations. Simple visual exploration of the data (see Fig. 10) indicates that the relationship between ozone and the other variables does not appear to be linear, so we consider fitting an additive model of the form
where the errors \(\varepsilon \) are assumed to be independent, homoscedastic and with location parameter 0.
The tuning parameters for each of the methods were chosen in the same way as in our simulations. Figure 11 shows the estimated regression components for each explanatory variable, for the estimators. Although the shape of the estimated additive components are similar, some important differences in their pattern can be highlighted. Note first that the shape of the effect of the temperature, justifies the use of wavelets at least for this function. On the other hand, the gam and the RBF estimators appear to magnify the effect of the covariates on the additive components Wind and Temp of the regression function. The BIWEIGHT robust estimator suggests covariate effects that are more moderate.
We can use the residuals obtained with Tukey’s biweight two-step estimator to explore the presence of potential outliers in the data. A rough comparison of the residuals from a classical fit with a robust one, indicates 5 clear outliers (observations 23, 34, 53, 68 and 77).
5.7.2 Blue sharks data
In a second real example, we compare the performance of the robust fitting and variable selection procedures described in our paper with a nonparametric nonnegative garrote variable selection method proposed in Cantoni et al. (2011) on a real data set from the U.S. National Marine Fisheries Service Pelagic Observer Program.Footnote 1 There are six covariates in this example, and the particular interest here is to see how the proposed and existing methods perform with respect to variable selection, and how this is possibly impacted by outliers. The authors of the above cited paper have been utilizing these data to analyze catches of the most commonly caught shark, the blue shark (Prionace glauca), in the main areas where they are caught in the northwest Atlantic, using a nonparametric additive model for the blue shark counts. The blue shark data set corresponds to 91 observed blue shark counts and the interest is in explaining the bluesharks counts as a function of six potentially explanatory variables using a model
where the covariates considered are day of the year (DOFY), number of light stick used (NLIGHTST), soak duration (amount of time from the midpoint of the gear setting to the midpoint of the gear hauling, SOAKTIME), hook depth as measured by the average of the minimum and the maximum of the hook depth (AVGHKDEP), ocean depth (OCEAND), surface water temperature (TEMP) and the total number of hooks (TOTHOOKS) and the errors terms are assumed to be independent of the covariates, homoscedastic and with location parameter 0. Note that the total number of hooks measures the effort and is introduced as an offset to standardize the catch data as it is usual in fisheries science. Cantoni et al. (2011), using their nonnegative garrotte spline-based nonparametric procedure, identify the variables that can be removed from the final model: SOAKTIME and NLIGHTST with an importance of AVGHKDEP that is borderline. The other variates TEMP, OCEAND and DOFY are found to have a nonzero effect. In particular, the day of the year has a complicated functional form, the ocean depth is likely a linear effect and the surface water temperature could be well be approximated by a cubic term. The nonparametric nonnegative garrote model fitted to these data is referred as a GAM model in the plots in Fig. 12.
We have also fitted these data with some of the procedures already used in our simulations. GLARS and BIWEIGHT are based on the least asymmetric Daubechies wavelets with nine vanishing moments,with a number of bases \(K=7\), leading to wavelet design matrices of size \(91 \times 42\). The tuning parameters for each of the methods were chosen in the same way as in our simulations. RBF has been applied using optimal bandwidths for the kernel windows.
The top panel in Fig. 12 displays the estimated regression components for each explanatory variable. As it may be seen, NLIGHTST, SOAKTIME, and AVGHKDEP are not selected by most of the methods agreeing with the findings in Cantoni et al. (2011). NLIGHTST is selected as active by the GRPREG procedure, and is borderline with RBF. The shape of the estimated additive components are quite similar with some extra curvature for OCEAND regarding BIWEIGHT and GRPREG. The nonparametric methodologies considered in the above analysis is therefore a welcome alternative to the nonnegative garrote spline-based analysis performed in Cantoni et al. (2011).
We believe, that the dataset does not contain any vertical outliers affecting the results. To appreciate the behavior of the above procedures in presence of vertical outliers, we artificially replaced some observations by ten vertical outlying observations, and applied again the previous procedures to this new dataset. The results are displayed in the bottom panel of Fig. 12. The outliers are indicated by red circles in the plots. Most of the methods seem to be robust to vertical outliers, with the exception of GRPREG (which is not designed to be robust). Note, however, the tendency of GLARS to eliminate the variable DOFY and to produce an estimate for the variable OCEAND that is very oscillatory.
6 Conclusions
This paper introduces a wavelet-based method for nonparametric estimation and variable selection of nonlinear additive regression models observed on nonequispaced designs with samples that are not power of 2, and with underlying additive components that are of possibly inhomogeneous smoothness. The estimators are based on a orthonormal periodic wavelet basis expansions of the components and are obtained using a two-stage penalized M-estimation framework for high-dimensional bi-level variable selection: penalized M-estimation with a concave \(\ell _2\)-norm penalty achieving the consistent variable selection at the first stage, and a post-hard-thresholding operator to achieve the wavelet basis coefficients sparsity at the second stage.
We provide convergence rates and optimal choices for the tuning parameters for the algorithm implementation. The proposed estimators offer automatic variable selection, and are completely data driven with only a few parameters of choice by the user (i.e. penalty \(\lambda _n\), threshold \(\nu _n\), multi-resolution index K(n) and wavelet filter). Our framework is computationally efficient, relatively easy to implement and is able to find a well-behaved local stationary point when a consistent initialization such as group MCP is used. A simulation study shows satisfactory finite sample performances of the estimators under different design settings, which is consistent with our theoretical findings.
In terms of some of the drawbacks, we can mention that in those design regions were the number of observed samples is small it is possible to obtain abnormally large wavelet regression coefficients (estimation bias); also as a result of the use of periodic wavelets, some problems may arise at the boundaries of the support for each additive component function. Nonetheless, we believe that these drawbacks could be partially avoided using the boundary correction procedures advocated in the univariate case by Amato et al. (2020).
References
Aeberhard, W.H., Cantoni, E., Marra, G., Radice, R.: Robust fitting and smoothing parameter selection for generalized additive models for location, scale and shape (2020). To appear in Statistics and Computing
Alfons, A., Croux, C., Gelper, S.: Robust groupwise least angle regression. Comput. Stat. Data Anal. 33, 421–435 (2016)
Amato, U., Antoniadis, A., De Feis, I., Goude, Y.: Estimation and group variable selection for additive partial linear models with wavelets and splines. S. Afr. Stat. J. 51, 235–272 (2017)
Amato, U., Antoniadis, A., De Feiss, I.: Additive model selection. Stat. Methods Appl. 25(4), 519–564 (2016)
Amato, U., Antoniadis, A., De Feiss, I.: Flexible, boundary adapted, nonparametric methods for the estimation of univariate piecewise-smooth functions. Stat. Surv. 14, 32–70 (2020)
Amato, U., Antoniadis, A., Feis, I.D., Gijbels, I.: Penalised robust estimators for sparse and high-dimensional linear models. Stat. Methods Appl. 3, 1–48 (2021)
Antoniadis, A., Fan, J.: Regularization of wavelet approximations. J. Am. Stat. Assoc. 96(455), 939–967 (2001)
Antoniadis, A., Gijbels, I., Lambert-Lacroix, S.: Penalized estimation in additive varying coefficient models using grouped regularization. Stat. Pap. 55, 727–750 (2014)
Antoniadis, A., Gijbels, I., Verhasselt, A.: Variable selection in additive models using p-splines. Technometrics 54(4), 425–438 (2012)
Antoniadis, A., Gijbels, I., Verhasselt, A.: Variable selection in varying-coefficient models using p-splines. J. Comput. Graph. Stat. 21(3), 638–661 (2012)
Avella-Medina, M.: Influence functions for penalized M-estimators. Bernoulli 23(4B), 3178–3196 (2017)
Avella-Medina, M., Ronchetti, E.: Robust and consistent variable selection in high-dimensional generalized linear models. Biometrika 105(1), 31–44 (2017)
Baek, J., Wehrly, T.: Kernel estimation for additive models under dependence. Stoch. Process. Appl. 47, 95–112 (1993)
Bianco, A., Boente, G.: Robust kernel estimators for additive models with dependent observations. Can. J. Stat. 6, 239–255 (1998)
Boente, G., Fraiman, R.: Robust nonparametric regression estimation. J. Multivar. Anal. 29, 180–198 (1989)
Boente, G., Martinez, A.: Marginal integration m-estimators for additive models. TEST 26(2), 231–260 (2017)
Boente, G., Martinez, A., Salibián-Barrera, M.: Robust estimators for additive models using backfitting. J. Nonparametr. Stat. 29(4), 744–767 (2017)
Breheny, P., Huang, J.: Penalized methods for bi-level variable selection. Stat. Interface 2(3), 369 (2009)
Breiman, L.: Better subset regression using the nonnegative garrote. Technometrics 37(4), 373–384 (1995)
Cantoni, E., Flemming, J.M., Ronchetti, E.: Variable selection in additive models by non-negative garrote. Stat. Model. 11(3), 237–252 (2011)
Chen, X., Wang, Z., McKeown, M.: Fmri group studies of brain connectivity via a group robust lasso. In: 2010 IEEE International Conference on Image Processing, pp. 589—592. Hong Kong (2010)
Chesneau, C., Fadili, J., Maillot, B.: Adaptive estimation of an additive regression function from weakly dependent data. J. Multivar. Anal. 133, 77–94 (2015)
Croux, C., Gijbels, I., Prosdocimi, I.: Robust estimation of mean and dispersion functions in extended generalized additive models. Biometrics 68, 31–44 (2011)
Donoho, D.L., Johnstone, I.M.: Minimax estimation via wavelet shrinkage. Ann. Stat. 26(3), 879–921 (1998)
Efron, B., Hastie, T., Johnstone, I., Tibshirani, R.: Least angle regression. Ann. Stat. 32(2), 407–499 (2004)
Eilers, P., Marx, B.: Flexible smoothing with b-splines and penalties. Stat. Sci. 11, 89–121 (1996)
Gijbels, I., Vrinssen, I.: Robust estimation and variable selection in heteroscedastic linear regression. Statistics 53(3), 489–532 (2019)
Härdle, W., Kerkyacharian, G., Picard, D., Tsybakov, A.: Wavelet, Approximation and Statistical Applications. Lectures Notes in Statistics, vol. 129. Springer-Verlag, New York (1998)
Loh, P.L.: Statistical consistency and asymptotic normality for high-dimensional robust \( m \)-estimators. Ann. Stat. 45(2), 866–896 (2017)
Loh, P.L., Wainwright, M.J.: Regularized m-estimators with nonconvexity: statistical and algorithmic theory for local optima. J. Mach. Learn. Res. 16, 559–616 (2015)
Nesterov, Y.: Gradient methods for minimizing composite objective function. Discussion Paper 2007076, Center for Operations Research and Econometrics (CORE). Université Catholique de Louvain (2007)
Sardy, S.: Adaptive posterior mode estimation of a sparse sequence for model selection. Scand. J. Stat. 36(4), 577–601 (2009)
Sardy, S., Tseng, P.: AMlet, RAMlet, GAMlet: Auto- matic nonlinear fitting of additive models, robust and generalized, with wavelets. J. Comput. Graph. Stat. 13, 283–309 (2004)
Stone, C.: Additive regression and other nonparametric models. Ann. Stat. 13, 689–705 (1985)
Tibshirani, R.: Regression shrinkage and selection via the lasso. J. R. Statist. Soc. Ser. B 58(1), 267–288 (1996)
Welsh, A.: Robust estimation of smooth regression and spread functions and their derivatives. Stat. Sin. 6, 347–366 (1996)
Wong, R.K.W., Yao, F., Lee, T.C.M.: Robust estimation for generalized additive models. J. Comput. Graph. Stat. 23, 270–289 (2014)
Yuan, M., Lin, Y.: Model selection and estimation in regression with grouped variables. J. R. Stat. Soc. B 68(1), 49–67 (2006)
Zhang, C.H.: Nearly unbiased variable selection under minimax concave penalty. Ann. Stat. 38(2), 894–942 (2010)
Zou, H.: The adaptive lasso and its oracle properties. J. Am. Stat. Assoc. 101(476), 1418–1429 (2006)
Acknowledgements
We thank the associate editor and the two anonymous referees for their detailed and constructive comments on an earlier version of the article that substantially improved it. We thank Sylvain Sardy for providing the R-codes implementing the RAMlet related procedures and Eva Cantoni for providing us the nonnegative garrote R-codes and the bluesharks data set. We also thank Andreas Alfons for his help with using GLARS. Part of this work was completed while A. Antoniadis and I. Gijbels were visiting the Istituto per le Applicazioni del Calcolo “M. Picone”, National Research Council, Naples, Italy. I. De Feis acknowledges the INdAM-GNCS 2020 Project ‘Costruzione di metodi numerico/statistici basati su tecniche multiscala per il trattamento di segnali e immagini ad alta dimensionalità’. I. Gijbels gratefully acknowledges financial support from the C16/20/002 project of the Research Fund KU Leuven, Belgium.
Funding
The work presented in this paper has received funding from the ECSEL Joint Undertaking (JU) under grant agreement No. 826589, the MADEin4 project. The JU receives support from the European Unions Horizon 2020 research and innovation programme and Netherlands, Belgium, Germany, France, Italy, Austria, Hungary, Romania, Sweden and Israel.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Amato, U., Antoniadis, A., Feis, I.D. et al. Wavelet-based robust estimation and variable selection in nonparametric additive models. Stat Comput 32, 11 (2022). https://doi.org/10.1007/s11222-021-10065-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11222-021-10065-z
Keywords
- Additive regression
- Contamination
- M-estimation
- Nonconvex penalties
- Variable selection
- Wavelet thresholding