Multiscale stick-breaking mixture models

Abstract

Bayesian nonparametric density estimation is dominated by single-scale methods, typically exploiting mixture model specifications, exception made for Pólya trees prior and allied approaches. In this paper we focus on developing a novel family of multiscale stick-breaking mixture models that inherits some of the advantages of both single-scale nonparametric mixtures and Pólya trees. Our proposal is based on a mixture specification exploiting an infinitely deep binary tree of random weights that grows according to a multiscale generalization of a large class of stick-breaking processes; this multiscale stick-breaking is paired with specific stochastic processes generating sequences of parameters that induce stochastically ordered kernel functions. Properties of this family of multiscale stick-breaking mixtures are described. Focusing on a Gaussian specification, a Markov Chain Monte Carlo algorithm for posterior computation is introduced. The performance of the method is illustrated analyzing both synthetic and real datasets consistently showing competitive results both in scenarios favoring single-scale and multiscale methods. The results suggest that the method is well suited to estimate densities with varying degree of smoothness and local features.

1 Introduction

Nonparametric models have well-known advantages for their weak set of assumptions and great flexibility in a variety of situations. In particular, Bayesian nonparametrics (BNP) has received abundant attention in the last decades and it is nowadays a well-established modeling option in the data scientist’s toolbox. If standard parametric Bayesian inference focuses on the posterior distribution obtained by defining suitable prior distributions over a finite dimensional parametric space $\varXi$ with $\xi \in \varXi$ typically characterizing a specific parametric distribution $G_\xi$ for data $y = (y_1, \dots , y_n)$, in BNP one defines prior distributions on infinite-dimensional probability spaces flexibly characterizing the data distribution G. Under these settings, only minor assumptions are made on G making the whole inferential procedure more robust.

The cornerstone of the discipline is the Dirichlet process (DP) introduced by Ferguson (1973). The DP is a stochastic process that defines a prior on the space of distribution functions; several generalizations of the DP have been proposed such as the Pitman–Yor (PY) process (Perman et al. 1992; Pitman and Yor 1997), the normalized random measures with independent increments (NRMI) (Regazzini et al. 2003; Nieto-Barajas et al. 2004; James et al. 2006, 2009) and, more in general, the Gibbs-type priors (Gnedin and Pitman 2006). Realizations from these priors, however, are almost surely discrete probability functions, and thus, they do not admit a density with respect to the Lebesgue measure. As a remedy to this characteristic, the DP and allied priors can be used as prior distributions for the mixing measure of a mixture model. The first and most useful example of this is the DP mixture (DPM) of Gaussian kernels (Lo 1984; Escobar and West 1995).

Fig. 1

Binary tree with mixture weights $\pi _{s,h}$ and kernel’s parameters $\theta _{s,h}$ at each node (s, h), where s is the scale level and h is the index within the scale

Pólya trees (PT) (Lavine 1992a, b; Mauldin et al. 1992) are alternative formulations whose draws implicitly admit densities with respect to the Lebesgue measure. PT, on the surface, are also particularly appealing in providing a multiscale structure and thus in characterizing possible abrupt local changes on the density. In practice, however, this construction tends to produce highly spiky density estimates even when the true density is smooth. To circumvent this lack of smoothness Wong and Ma (2010) modify the PT construction adding an optional stopping mechanism in the PT construction; more recently Cipolli and Hanson (2017) proposed a smoothed version of the PT. Canale and Dunson (2016) consider a related multiscale mixture model based on Bernstein polynomials but are confined to model continuous densities on (0, 1).

Consistently with these contributions, in this paper we introduce a general class of multiscale stick-breaking processes with support on the space of discrete probability mass functions suitable as mixing measure in multiscale mixture of continuous kernels. We will show that the induced multiscale mixture of kernels provides a compromise between the DPM and the PT able to adapt both to smooth or spiky densities while showing excellent performance when the underlying density presents different local smoothness levels.

The method generalizes Canale and Dunson (2016) in two directions. First, a more general multiscale stick-breaking process inspired by the PY process is introduced. This generalization provides a high degree of flexibility and exhibits only mild dependence from the specific prior parameters, consistently with successful applications of the PY process. Second, a multiscale base measure generating kernel densities that are stochastically ordered and defined on a general sample space is introduced. These two elements induce a class of prior for continuous densities that successfully adapts to the actual degree of smoothness of the true data generating distribution showing competitive performance with respect to state-of-the-art competitors.

The remainder of the paper is organized as follows: In the next section we introduce our multiscale stick-breaking prior and describe some of its basic properties. Section 3 describes a Gibbs sampling algorithm for posterior computation. Section 4 illustrates the performance of the methods through the analysis of several synthetic and real datasets. Section 5 concludes the paper.

2 Multiscale stick-breaking mixture

Let $y \in \mathcal {Y} \subset \mathbb {R}$, be a random variable with unknown density f. We assume for f the following multiscale construction

$$\begin{aligned} f(y)= \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h} \mathcal {K}(y;{\theta }_{s,h}), \end{aligned}$$

(1)

where $\mathcal K(\cdot ; \theta )$ is a kernel function parameterized by $\theta \in \varTheta$ and $\{ \pi _{s,h}\}$ and $\{{\theta }_{s,h}\}$ are unknown sequences of positive weights summing to one and parameters belonging to $\varTheta$, respectively. We will refer to this model with the term multiscale mixture (MSM) of kernel densities. This construction can be represented with an infinitely deep binary tree in which each node is indexed by a scale s and an index $h = 1, \dots , 2^s$ and where each of these nodes is characterized by the pair $(\pi _{s,h}, \theta _{s,h})$. A cartoon of a truncation of this binary tree is reported in Fig. 1.

Model (1) can be equivalently written as

$$\begin{aligned} f(y)= \int \mathcal {K}(y;{\theta }) dP(\theta ), \quad P = \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h} \updelta _{\theta _{s,h}}, \end{aligned}$$

(2)

where $\updelta _x$ is the Dirac delta function. Thus, a prior distribution for the multiscale mixture (1) is obtained by specifying suitable stochastic processes for the random mixing measure P or, equivalently, for the random sequences $\{\pi _{s,h}\}$ and $\{\theta _{s,h}\}$. These characterizations are separately carefully described in the next sections.

Approximations of the mixture model (1) can be obtained fixing an upper bound $s^\mathtt{max}$ for the depth of the tree. This truncation is obtained consistently with Ishwaran and James (2001) for the standard single-scale mixture model and Canale and Dunson (2016) for the multiscale mixture of Bernstein polynomial model. Such a truncation can be applied both if one considers not scientifically relevant higher levels of resolution or to reduce the computational burden.

2.1 Multiscale mixture weights

We first focus on the sequence of mixture weights $\{\pi _{s,h}\}$. We introduce independent random variables $S_{s,h}$ and $R_{s,h}$ taking values in (0, 1) and describing the probability of taking a given path in the binary tree reported in Fig. 1. Specifically, $S_{s,h}$ denotes the probability of stopping at node h of scale s while $R_{s,h}$ denotes the probability of taking the right path from scale s to scale $s+1$ conditionally on not stopping in node h of that scale. The weights are then defined as

$$\begin{aligned} \pi _{s,h} = S_{s,h} \prod _{r<s} (1-S_{r,\lceil h2^{r-s} \rceil }) T_{shr}, \end{aligned}$$

(3)

where $T_{shr} = R_{r, \lceil h2^{r-s} \rceil }$, if $(r+1,\lceil h2^{r-s+1} \rceil )$ is the right daughter of node $(r,\lceil h2^{r-s} \rceil$, and $T_{shr} = 1-R_{r, \lceil h2^{r-s} \rceil }$, otherwise. This construction is reminiscent of the stick-breaking process (Sethuraman 1994; Ishwaran and James 2001) and can be described by the following metaphor: Take a stick of length one and break it according to the law of $S_{0,1}$; the remainder of the stick is then randomly split into two parts according to the law of $R_{0,1}$; at general node (s, h) the remainder of the stick, conditionally on the previous breaks, is broken according to $S_{s,h}$ and then split according to $R_{s,h}$.

Different distributions for $S_{s,h}$ and $R_{s,h}$ lead to different characteristics for the tree of weights. Inspired by the general stick-breaking prior construction of Ishwaran and James (2001) we can set

$$\begin{aligned} S_{s,h} \sim \text{ Be }(a_{s}, b_{s}), \quad R_{s,h} \sim \text{ Be }(c_{s}, c_{s}) \end{aligned}$$

(4)

where $\text {Be}(\alpha , \beta )$ denotes a Beta random variable with parameters $\alpha$ and $\beta$. This construction leads to a proper sequence of weights as formalized in the next Lemma. Its proof is reported in the Appendix.

Lemma 1

Let $\pi _{s,h}$ be an infinite sequence of weights defined by (3) and (4). Then,

$$\begin{aligned} \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h} = 1 \end{aligned}$$

(5)

almost surely.

The above construction is a flexible generalization of Canale and Dunson (2016) that, mimicking the DP and its stick-breaking representation, fixed $a_{s} = 1$, $b_{s} = \alpha > 0$, and $c_{s} = \beta > 0$ for each scale s. While being way more flexible, the specification in (4) has different parameters for each scale and its elicitation may be cumbersome in practice. To avoid these complications while keeping an increasing degree of flexibility through a specific scale dependence for the distribution of the random weights, we consider $\delta \in [0,1)$ and $\alpha > -\delta$ and let

$$\begin{aligned} S_{s,h} \sim \text{ Be }(1-\delta , \alpha + \delta (s+1) ), \quad R_{s,h} \sim \text{ Be }(\beta , \beta ). \end{aligned}$$

(6)

This specification is reminiscent of the PY process, a model which stands out for being a good compromise between modeling flexibility, and mathematical and computational tractability (De Blasi et al. 2015). Following Lemma 1 this construction also leads to a proper sequence of weights.

The $\delta$ parameter introduced in (6) allows for a greater degree of flexibility in describing how the random probability weights are allocated to the nodes. To see this, consider the expectation of $\pi _{s,h}$, i.e.,

$$\begin{aligned} \mathbb {E}(\pi _{s,h})= & {} \mathbb {E}\bigg \{ S_s \prod _{l=0}^{s-1} (1-S_l) \prod _{l=1}^s T_l \bigg \} \\= & {} \bigg ( \frac{ 1-\delta }{ \alpha +1 } \bigg ) \bigg ( \frac{1}{2} \bigg )^s \prod _{l=1}^s \bigg (\frac{ \alpha +\delta l }{ \alpha +\delta l + 1 } \bigg ), \end{aligned}$$

where we discard the h subscript on $S_l \sim \text{ Be }(1-\delta , \alpha + \delta (l +1))$ and $T_l \sim \text{ Be }(\beta ,\beta )$ for ease in notation. This does not impact the calculation because any path taken up to scale s has the same probability a priori and the distribution of the random variables in (6) depends on the scale s only. The expected values of the random weights can be used to calculate the expected scale at which an observation falls, a measure of the expected resolution level, defined by $\mathbb {E}(\tilde{S}) = \sum _{s=0}^\infty s \mathbb {E}(\pi _{s,h})$. The latter simplifies to $\alpha$ when $\delta = 0$ but can be easily obtained numerically for $\delta > 0$.

Fig. 2

Prior total weight $\pi _s = \sum _{h<2^s} \pi _{s,h}$ as a function of s and for $\delta$ equal to 0 (—), 0.25 ($- -$), 0.5 ($\cdots \cdot$), and 0.9 ($\cdot - \cdot -$); $\alpha =1$ (left) and $\alpha = 5$ (right)

To better understand the role of $\delta$, Fig. 2 reports the total expected weight of scale s, defined as the expectation of $\pi _s = \sum _{h} \pi _{s,h}$, for different values of $\delta$ and $\alpha$. It is clear that increasing values of $\delta$ make the first levels of the tree less probable a priori, thus favoring a deeper tree. Note that this characteristic has to be interpreted more in terms of prior robustness rather than favoring rougher densities as the prior mass is more spread through the whole tree allowing the posterior to concentrate on a tree of suitable depth. This interpretation is consistent with the role of the discount parameter of the PY process that controls how much prior probability is concentrated around the prior expected value of the number of occupied clusters and thus inducing a posterior distribution that is more robust to the prior specification. See De Blasi et al. (2015) for a related discussion. We will show in Sect. 4.1 that this conjecture is empirically confirmed via simulations. Note that despite one should be tempted to assume $\delta$ close to one, our experience suggests that values between 0.2 and 0.5 are already sufficient to relieve the prior effect. In any case, it must be kept in mind that arbitrarily increasing $\delta$ without controlling for $\alpha$ may lead to an unnecessary—and harmful—model complexity.

2.2 Multiscale kernel’s parameters

We now discuss the stochastic process for the sequence $\{\theta _{s,h}\}$. For $\mathcal{Y} = (0,1)$, Canale and Dunson (2016) assume that $\mathcal K(\cdot ;\theta _{s,h})$ is a Beta($h, 2^s-h+1$) density so that $\theta _{s,h}$ is identified by the pair $(h, 2^s-h+1)$, a fixed set of parameters. This construction is implicitly inducing a mixture of Bernstein polynomials (Petrone 1999a, b) for each scale s and the randomness is totally driven by the sequence of mixture weights. Here, instead, we will consider the broader case where $\theta _{s,h}$ are unknown parameters and where $\mathcal{K}(\cdot ; \theta )$ is a location-scale kernel defined on a general space $\mathcal Y$. Under this specification, we partition the kernel’s parameter space into a location and scale part letting $\varTheta = \varTheta _{\mu } \times \varTheta _{\omega }$ so that, consistently with Fig. 1, each node of the binary tree is parameterized by the tuple $\{ \pi _{s,h}, \mu _{s,h}, \omega _{s,h}, \}.$

2.2.1 Location parameters

We first focus on defining a suitable sequence of locations $\{\mu _{s,h}\}$ that, consistently with the dyadic partition induced by the binary tree structure, uniformly covers the space $\varTheta _{\mu }$. To this end, for any scale s we introduce a partition of $\varTheta _{\mu }$ by letting

$$\begin{aligned} \varTheta _{\mu } = \bigcup _{h=1}^{2^s} \varTheta _{\mu ;s,h} , \end{aligned}$$

(7)

such that for two neighboring scales s and $s+1$,

$$\begin{aligned} \varTheta _{\mu ;s,h} = \varTheta _{\mu ;s+1,2h-1} \cup \varTheta _{\mu ;s+1,2h}. \end{aligned}$$

(8)

Let $G_{0}$ be a base probability measure defined on $\varTheta _{\mu }$ and use it both to define $\varTheta _{\mu ;s,h}$ and to generate the multiscale locations $\mu _{s,h}$. Specifically, we set

$$\begin{aligned} \varTheta _{\mu ;s,h} = \big [q_{\frac{h-1}{2^s}}, q_{\frac{h}{2^s}}\big ], \end{aligned}$$

(9)

where $q_{r}$ is the r-level quantile of the density of $G_0$. Then, random $\mu _{s,h}$ are sampled proportionally to the density of $G_{0}$ truncated in $\varTheta _{\mu ;s,h}$. While preserving the covering of $\varTheta _{\mu }$ this construction allows for straightforward prior elicitation similarly to what is done for the DP or the PY process. The next lemma, whose proof is reported in the Appendix, shows that a priori the random probability measure on $\varTheta _\mu$ defined by

$$\begin{aligned} G = \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h} \updelta _{\mu _{s,h}} \end{aligned}$$

(10)

is centered around $G_0.$

Lemma 2

Let $G_{0}$ be a base probability measure defined on $\varTheta _{\mu }$. Introduce a dyadic recursive partition of $\varTheta _{\mu }$ defined by (7), (8), and (9) and $G_0$. If G is the discrete measure (10) and each $\mu _{s,h}$ is randomly sampled proportionally to $G_0$ truncated in $\varTheta _{\mu ;s,h}$, then, for any set $A \subseteq \varTheta _{\mu }$,

$$\begin{aligned} \mathbb {E}[G(A)] = G_{0}(A). \end{aligned}$$

Note that equation (10) is similar, in spirit, to the approximate PT (APT) prior of Cipolli and Hanson (2017) and in particular to their equation (3). The difference, however, is twofold. First, our weights come from a multiscale stick-breaking process while those of APT are the result of the PT recursive partitioning. The second, more evident, difference lies on how the Dirac’s delta masses are placed. While equation (3) of Cipolli and Hanson (2017) places these on the center of the intervals $\varTheta _{\mu ; s,h}$, in our construction the masses are randomly placed inside $\varTheta _{\mu ; s,h}$. Hence, while the learning in APT model is totally driven by the random weights, our approach also allows for an update of the values $\mu _{s,h}$ a posteriori.

2.2.2 Scale parameters

We now focus on describing the sequence of scale parameters $\{\omega _{s,h}\}.$ Consistently with our multiscale setup, the scale parameters need to be ordered with respect to the scale levels of the binary tree in order to induce more concentrated kernels for increasing values of s, on average. In general the direction of the ordering depends on the actual role of the scale parameters in the specific kernel $\mathcal{K}(\cdot ; \theta )$. For instance, for scale parameters proportional to the variances—respectively, precisions—a decreasing—respectively, increasing—sequence needs to be specified. Assuming that $\omega _{s,h}$ are proportional to the variances of the kernels, we induce a stochastic ordering of the $\omega _{s,h}$’s at different scales s in the following way. Let $H_0$ be a base probability measure defined on $\varTheta _{\omega }$ with first moment $\mathbb {E}_{H_0}(\omega ) = \omega _0$ and variance $\mathbb {V}_{H_0}(\omega ) = \gamma _0$ both finite. Then, let

$$\begin{aligned} \omega _{s,h} = c(s) W_{s,h}, \quad W_{s,h} {\mathop {\sim }\limits ^{iid}} H_0, \end{aligned}$$

(11)

where c(s) is a monotone decreasing deterministic function of s. Under this definition the sequence of $\{\omega _{s,h}\}$ is stochastically decreasing and

$$\begin{aligned} \mathbb {E}_{H_0}(\omega _{s+1,h}) \le \mathbb {E}_{H_0}(\omega _{s,h}) , \quad \mathbb {V}_{H_0}(\omega _{s+1,h}) \le \mathbb {V}_{H_0}(\omega _{s,h}). \end{aligned}$$

Consistently with our multiscale construction, the first inequality reflects the fact that from scale s to scale $s+1$ we expect more concentrated kernels in equation (2). The second inequality, in addition, implies that the prior uncertainty about $\omega$ scales as well.

In the next section we discuss a specification of this construction by means of Gaussian kernels and suitable choices for $G_0$, $H_0$, and $c(\cdot )$.

2.3 Multiscale mixture of Gaussians

Although several choices for the kernel $\mathcal K(\cdot ; \theta )$ can be made, the Gaussian one is probably the most natural when $\mathcal{Y} = \mathbb {R}$. Hence, we specify the model described in previous sections assuming $\mathcal{K}(\cdot ; \theta ) = \phi (\cdot ; \mu , \omega )$ where $\phi (\cdot ; \mu , \omega )$ is a Gaussian density with mean $\mu \in \mathbb {R}$ and variance $\omega >0$. Under this specification e Equation (1) becomes a MSM of Gaussian densities, i.e.,

$$\begin{aligned} f(y)= \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h} \phi (y;\mu _{s,h},\omega _{s,h}). \end{aligned}$$

A pragmatic choice for the base measures consists in choosing conjugate priors. Specifically we let $G_0$ be a Gaussian distribution with mean $\mu _0$ and variance $\kappa _0$. Similarly, we restrict to the inverse-gamma family of distributions the choice for $H_0$. Following (11), we let $W_{s,h} {\mathop {\sim }\limits ^{iid}} \text{ IGa }(k, \lambda ),$ leading to $\mathbb {E}(W_{s,h})= \lambda /(k-1)$ and $\mathbb {E}(\omega _{s,h})= c(s) \lambda /(k-1)$. A natural choice for the function $c(\cdot )$ is $c(s)=2^{-s}$, which is equivalent to let $\omega _{s,h} \sim \text{ IGa }(k, 2^{-s}\lambda ).$

Consistently with the discussion at the end of Sect. 2.2.1, this final specification is reminiscent of the smoothed approximate Pólya tree (SAPT) of Cipolli and Hanson (2017). In both specifications, indeed, the variances of each Gaussian mixture component are the result of a deterministic scale-decreasing component—represented by the function c(s) here and by the parameter $d_k$ in SAPT—and a random quantity. The latter, while being controlled by a single parameter in the SAPT model, is component specific in the proposed formulation thus allowing for local learning of the values of each scale parameter.

2.4 Multiscale mixture of other kernels

Henceforth, we will focus on the Gaussian kernel specification discussed in the previous section which is undoubtedly the most convenient choice when $\mathcal{Y} = \mathbb {R}$. In this section, however, we want to stress the generality of our approach and to briefly discuss how other kernels can be used if data do not lie in $\mathbb {R}$.

For bounded data, e.g., $\mathcal{Y }= (0,1)$, one can choose a uniform kernel parameterized as

with $\theta = (\mu , \omega )$ and elicit $G_0$ to be a uniform distribution over (0,1) and $H_0$ satisfying the moment conditions discussed in Sect. 2.2.2. Our experience, however, suggests that the multiscale mixture of Bernstein polynomial of Canale and Dunson (2016) is already very competitive in estimating the density over bounded domains and the more general approach described here may lead to minor improvements only for small sample sizes.

Differently, for a count-valued random variable, i.e., $\mathcal{Y} = \mathbb {N}$, our contribution may be of substantial help. In this case one can specify the kernels to be rounded Gaussians following the approach of Canale and Dunson (2011) and choose $G_0$, $H_0$, and $c(\cdot )$ consistently with Sect. 2.3.

3 Posterior computation

In this section we introduce a Markov Chain Monte Carlo (MCMC) algorithm to perform posterior inference under the model introduced in the previous section. In the general settings, the algorithm consists of three steps: (i) Allocate each observation to a multiscale cluster conditionally on the current values of $\{ \pi _{s,h} \}$ and $\{ \theta _{s,h} \}$; (ii) update $\{ \pi _{s,h} \}$ conditionally on the cluster allocations; (iii) update $\{ \theta _{s,h} \}$ conditionally on the cluster allocations.

In this section we focus on the multiscale mixture of Gaussian and related prior elicitation discussed in Sect. 2.3 but steps (i) and (ii) also apply for a general kernel.

Suppose subject i is assigned to node $(s_i,h_i)$, with $s_i$ the scale and $h_i$ the node within scale. Conditionally on the values of the parameters, the posterior probability of subject i belonging to node (s, h) is simply

$$\begin{aligned} \mathbb {P}(s_i = s, h_i=h | y_i, \pi _{s,h})\propto & {} \pi _{s,h} \mathcal{K}(y; \theta _{s,h}). \end{aligned}$$

Consider the total mass assigned at scale s, defined as $\pi _s = \sum _{h=1}^{2^s} \pi _{s,h}$, and let $\bar{\pi }_{s,h} = \pi _{s,h}/\pi _{s}$. Under this notation, we can rewrite the likelihood for the ith observation as

$$\begin{aligned} f(y_i) = \sum _{s=0}^\infty \pi _{s} \sum _{h=1}^{2^s} \bar{\pi }_{s,h} \mathcal{K}(y_i; \theta _{s,h}). \end{aligned}$$

Following Kalli et al. (2011), we introduce the auxiliary random variables $u_i | y_i, s_i \sim \text{ Unif }(0, \pi _{s_i}),$ and consider the joint density

where is the indicator function that returns 1 if $x \in A$. Then, we can update the scale $s_i$ and the node $h_i$ using

Conditionally on cluster allocations, the update of the weights is obtained applying (3) to the updated values of $S_{s,h}$ and $R_{s,h}$ obtained sampling from

$$\begin{aligned} S_{s,h}&\sim \text{ Be }(1-\delta + n_{s,h}, \alpha + \delta (s+1) + v_{s,h} - n_{s,h}), \\ R_{s,h}&\sim \text{ Be }(\beta +r_{s,h}, \beta + v_{s,h} - n_{s,h} - r_{s,h} ), \end{aligned}$$

where $v_{s,h}$ is the number of subjects passing through node (s, h), $n_{s,h}$ is the number of subjects stopping at node (s, h), and $r_{s,h}$ is the number of subjects that continue to the right after passing through node (s, h).

Conditionally on cluster allocation, the update of locations and scale parameters follows from usual conjugate analysis arguments. Specifically the location parameters are sampled from

$$\begin{aligned} \mu _{s,h} \sim \text {N}_{\varTheta _{\mu ;s,h}} \biggl ( \frac{ \mu _0\omega _{s,h}+ n_{s,h} \bar{y}_{s,h}\kappa _0}{ n_{s,h}\kappa _0 + \omega _{s,h}}, \frac{\omega _{s,h}\kappa _0}{ n_{s,h}\kappa _0 + \omega _{s,h}} \biggl ), \end{aligned}$$

where $\bar{y}_{s,h}$ is the sample mean of the observations assigned to node (s, h), and $N_A(m,v)$ denotes a Gaussian distribution with mean parameter m and variance parameter v truncated in the set A. The scale parameters are sampled from

$$\begin{aligned} \omega _{s,h} \sim \text{ IGa }\biggl (k +\frac{n_{s,h}}{2}, \frac{\lambda }{2^s} + \frac{\sum _{i: s_i = s, h_i = h}(y_i-\mu _{s,h})^2}{2}\biggl ). \end{aligned}$$

4 Illustrations

In this section we discuss the performance of the proposed MSM of Gaussian densities through the analysis of different synthetic and real datasets. Specifically, we investigate the role of the $\delta$ parameter in the next section and compare the method with alternative approaches in Sect. 4.2. Finally, in Sects. 4.3 and 4.4 the method and one possible extension of it are used to analyze two different astronomical datasets. The analysis of a third dataset is postponed to the Supplementary Material.

4.1 The role of $\delta$

As already discussed in the previous sections, the $\delta$ parameter allows for a greater degree of flexibility in the prior specification. In this section we want to empirically assess its role a posteriori. To this end we generate 100 samples of size $n=50$ from three different densities and run the Gibbs sampling algorithm described in Sect. 3 to get an estimate of the posterior mean density for different values of the $\alpha$ and $\delta$ parameters.

Fig. 3

Posterior scale as a function of $\delta$ for different values of $\mathbb {E}(\tilde{S})$. Continuous line: $\mathbb {E}(\tilde{S})=1$; dashed line: $\mathbb {E}(\tilde{S})=3$; dotted line: $\mathbb {E}(\tilde{S})=5$; first plot: standard normal distribution. Second plot: mixture of two Gaussians (see text). Third plot: mixture of three Gaussians (see text). Sample size is equal to 50

Data are generated from a finite mixture of Gaussian densities $f(y) = \sum _{k=1}^K \pi _{k} \phi (y;\mu _k,\omega _k)$ with an increasing level of local variability. Specifically, the first density is the standard normal distribution, the second density is a mixture of two components with $\mu _1=-\mu _2 = 0.935$, $\omega _1=\omega _2=1/8$, and $\pi _1=\pi _2=1/2$, while the last density has three components and parameters equal to $\mu _1=0$, $\mu _2=1.392$, $\mu _3=-1.392$, $\omega _1=\omega _2=\omega _3=1/32$, $\pi _1=1/2,\pi _2=\pi _3=1/3$.

We considered $\delta$ equal to 0, 0.25,  and 0.5 and numerically obtain the values of $\alpha$ in order to match a fixed prior expectation for the scale of the density. We considered three values for the prior expected scale that are consistent with the densities of the data generating processes. Specifically we assume $\mathbb {E}(\tilde{S}) = 1, 3$ and 5. The related parameters are summarized in Table 1.

Table 1 Values of $\alpha$ parameters for given $\delta$ and expected scales $\mathbb {E}(\tilde{S})$

We run the Gibbs sampler described in Sect. 3 for 1000 iterations with a burn in of 200. Visual inspections of the trace plots of the posterior mean density on a grid of domain points suggest no lack of convergence.

Figure 3 reports the values of the average (over the 100 replicates) of the posterior mean scale as a function of the discount parameter $\delta$. Each dot corresponds to a specific configuration of the $\alpha$ and $\delta$ parameters and configurations with the same prior mean scale are connected. For $\delta =0$ the prior choice drives the behavior of the posterior, i.e., on average lower posterior mean is obtained when the prior mean scale is equal to 1 while a higher posterior mean is obtained when the prior mean is equal to 5. This prior dependence is less evident for increasing values of $\delta$. Indeed regardless the prior specification, when the value of $\delta$ increases, the posterior mean stabilizes in a neighborhood of a specific value. This behavior is consistent with what happens for the posterior mean number of clusters for a PY process mixture model (see De Blasi et al. 2015; Canale and Prünster 2017, for related discussions).

Note that in addition to this prior robustness on the posterior mean scale—that is related to the actual degree of smoothness of the posterior mean density—we also observe an increasing precision of the density estimates in terms of $L_1$ distance of the posterior mean density and the true density. See the Supplementary Materials for additional details.

The same simulation experiment was carried out also for datasets with sample size equal to 250. The qualitative results are similar but less striking as the different posterior mean scales are closer for small values of $\delta$. This is expected and reflects the informative gain related to a bigger sample size. Additional details and plots are reported in the Supplementary Materials.

4.2 Comparison with alternative methods

In this section we assess the performance of the proposed method and compare it with available alternatives, namely a location-scale DPM of Gaussians, the hierarchical infinite mixture (HIM) model of Griffin (2010) and, for its close relations with our method, a SAPT.

Fig. 4

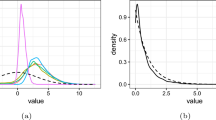
Posterior mean densities (bright thin lines) for 100 independent samples (sample size $n=100$) and true densities generating the data (thick darker lines). Rows reports the results for the four scenarios. The results for MSM, HIM, DPM, and SAPT are reported in the first, second, third and fourth columns, respectively. This figure appears in color in the electronic version of the paper

Synthetic data are simulated from different scenarios corresponding to varying degrees of global and local smoothness. As benchmark scenarios we used the densities reported in Marron and Wand (1992), which provide a commonly used set of different densities in many density estimation exercises. For sake of brevity we report here the results for four scenarios (the results for all the densities of Marron and Wand (1992) are reported in the Supplementary Materials) corresponding to a smooth unimodal skew density (S1), a smooth bimodal density (S2), and two densities with sharp local variability (S3 and S4), more details are reported in the Supplementary Materials. These densities are plotted with a thick dark line in Fig. 4. Obviously, we expect the DPM and the SAPT to perform better in Scenarios 1–2 and 3–4, respectively—the former not having any multiscale structure and the latter presenting different local smoothness levels. The HIM is expected to be uniformly competitive since it is a model that enriches the standard DPM with a tailored hierarchical structure that allows to adapt to the actual smoothness of the unknown density. For each scenario we generate 100 samples of sizes $n=100$ and $n=500$. Before fitting each model, data are standardized to have mean zero and variance one. For the DPM we used the marginal Pólya urn sampler implemented in the R package DPpackage (Jara et al. 2011), for HIM we use the MATLAB routines in Jim Griffin’s home page, while for SAPT we used the Gibbs sampler described in Cipolli and Hanson (2017) and implemented in set of R functions gently provided by the authors—that we thank warmly. The performance of the competing methods are evaluated in terms of $L_1$ distance and Kullback–Leibler (KL) divergence of the posterior mean densities from the true density evaluated on a grid of points.

Table 2 Mean and standard deviation ($\times 10^3$) of the $L_1$ distance and KL divergence between the estimated posterior density and the true data generating density over 100 simulations

For our MSM we set $G_0$ to be the standard normal distribution and $\lambda = k = 2^6$ for the inverse-gamma distribution $H_0$. This choice for $\lambda$ and k leads to a high variance for the scale parameters reflecting mild prior information about these quantities. The maximum depth for the tree was set to $s^\mathtt{max}=6$. Consistently with the discussion on $\delta$ of the previous sections, we assumed $\delta =0.5$. The value of $\alpha$ has been obtained numerically in order to match $\mathbb {E}(\tilde{S})=2$. Finally, we set $\beta =1.$ For the SAPT model we followed the specification presented in Cipolli and Hanson (2017) and additionally let $c \sim \text {Ga}(1, 1)$. The tree was grown up to $J = 6$ levels, consistently with the truncation induced in the multiscale stick-breaking. For the DPM the model specification is

$$\begin{aligned} f(\cdot ) = \int \phi (\cdot ;\mu ,\omega ) d F(\cdot ; \mu , \omega ), \quad F \sim DP(\alpha , F_0), \end{aligned}$$

with $F_0 = \text{ N }(m_1, \omega /\kappa ) \times \text{ IGa }(\nu _1,\psi _1)$ and additional hyperpriors

$$\begin{aligned}&m_1 \sim \text{ N }(m_2,s_2), \quad \kappa \sim \text{ Ga }(\tau _1/2,\tau _2/2), \\&\psi _1 \sim \text{ IGa }(\nu _2, \psi _2), \quad \alpha \sim \text{ Ga }(a_0,b_0), \end{aligned}$$

with values of the parameters equal to $a_0=b_0=1,m_2=0, s_2=1,\nu _1=\nu _2=3, \psi _2=rs_2^2, r=0.1, \tau _1=2, \tau _2=200$ as suggested in Cipolli and Hanson (2017). For HIM we follows the guidelines discussed in Griffin (2010). All prior specifications are broadly comparable looking at the induced prior predictive distributions. Each MCMC algorithm was run for 1000 iterations with a burn-in period of 200.

We want to stress that we are not endowing our MSM with any hyperprior distribution. Conversely we try to favor each competing method adding different layers of hyperprior distributions in order to relieve the effects of specific prior choices on their performance. Our goal here is to show that the proposed multiscale approach, even in its basic specification, provides a competitive alternative to state-of-the-art approaches.

Table 2 reports the results of the simulations study. Overall the performance of all the four methods is comparable. For $n=100$ our MSM of Gaussian performs slightly better—on average—both in terms of $L_1$ distance and KL divergence with respect to DPM and SAPT, and has comparable performance to HIM. The lower values of $L_1$ distance and KL divergence attained by our MSM are also often coupled with less Monte Carlo variability. For the higher sample size of $n=500$, all the methods improve in terms of precision with our MSM always performing slightly better than DPM and SAPT and with a substantial improvement of HIM over all the methods. These results show that both our MSM approach and HIM are able to adapt to the actual smoothness of the density. The performance of our MSM make it a serious competitor of standard methods not only in the situations where a multiscale structure is expected, but also when the density of the data is reasonably smooth.

Figure 4 gives additional insights on the results summarized in Table 2. Each subplot of Fig. 4 depicts, with thin bright lines, the posterior mean densities for each simulated datasets (of size $n=100$) with different subplots in the same row denoting the four different competing methods. While the performance in terms of $L_1$ distance and Kullback–Leibler divergence reported in Table 2 is most of the time comparable among methods, it is evident that for some specific datasets, the DPM estimates are a unimodal density, oversmoothing the true underlying density—see the second, third and fourth lines. On the other side, the SAPT estimates avoid this oversmoothing but exhibit a very high variability with different datasets leading to estimates with prominent differences. The estimates obtained with MSM and HIM, instead, provide a better compromise between bias and variance, resulting in better posterior estimates that are smooth but also able to capture, abrupt local changes in the density—if present. Qualitatively similar results are also noticeable for the datasets with sample size $n=500$. See the Supplementary Materials for details.

4.3 Roeder’s galaxy speed data

As benchmark dataset to assess the performance of our method we use the famous Galaxy velocity dataset of Roeder (1990) reporting the velocity of 82 galaxies sampled from 6 conic sections of the Corona Borealis. Our goal here is to achieve comparable results in terms of goodness of fit with respect to standard methods that already showed to provide meaningful results—namely the DPM and allied models—as we do not expect a prominent multiscale structure.

Fig. 5

Galaxy velocity data histogram and posterior mean density with 95% posterior credible bands for the multiscale mixture of Gaussian model

Fig. 6

Sloan Digital Sky Survey data, $U-R$ color distributions, grouped with respect to luminosity and density. Black line: posterior mean densities; shaded areas: 0.95 posterior credible bands. Group size reported in each upper left corner

We used the same prior specification of the previous section but used a more conservative truncation of the binary trees, namely ${s^\mathtt{max}} = 8$. We compared the three methods using the log-pseudo marginal likelihood (Gelfand and Dey 1994), a cross-validated predictive measure of fit obtained as the sum of the log-conditional predictive ordinates, $\log (\text{ CPO}_i)$ where

$$\begin{aligned} \text {CPO}_i = \int _{\varTheta } f(y_i|\varvec{\theta }) d \varPi (\varvec{\theta }\mid \varvec{y}_{-i}) d\varvec{\theta }, \end{aligned}$$

$f(\cdot ; \theta )$ is the model density, and $\varPi (\cdot \mid \varvec{y}_{-i})$ is the parameters’ posterior probability conditioned on the whole vector of observation excluding $y_i$. A larger value of log-pseudo marginal likelihood (LPML) indicates a better predictive performance. Figure 5 depicts the posterior mean density along with the histogram of the raw data and 95% credible bands. As expected the method has a comparable performance with respect to state-of-the-art competitors and achieve a LPML value of $-217$, comparable to that of the DPM ($-212$), SAPT ($-215$), and HIM ($-199$).

4.4 Sloan Digital Sky Survey data

We consider a second astronomical dataset consisting of $n=24\,312$ galaxies, drawn from the Sloan Digital Sky Survey first data release (see Cimatti et al. 2019, for details). The galaxies are partitioned into 25 different groups (Balogh et al. 2004), by combining the separation in 5 groups for different luminosity and in 5 groups by different density—the latter being a physical characteristic of the galaxy that does not need to be confused with a probability density function. Group sizes vary and range from 158 to 2515. The exact group sizes $n_g$ are reported in Fig. 6.

Our goal here is twofold. From the astronomical point of view, considering this partition of the data as fixed, we want to estimate the probability density function of the difference of ultraviolet and red filters ($U-R$ color) for each group. In addition, we use this example to show the flexibility of the proposed approach in dealing with complex situations proposing a modification of the mixture model discussed in Sect. 2.3. Specifically, for each group $g = 1, \dots , 25$, we assume the multiscale mixture

$$\begin{aligned} f_{g}(y)= \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h}^{(g)} \phi (y;\mu _{s,h},\omega _{s,h}), \end{aligned}$$

(12)

where each set of weights $\pi _{s,h}^{(g)}$ is assumed to be generated independently according to the multiscale stick-breaking process introduced in Sect. 2.1 and each group-specific density $f_{g}$ shares a common set of kernel’s parameters. The idea of a shared-kernel model accounts for the existence of common latent information shared between groups and allows for borrowing of information in learning the values of the kernel’s parameters. See Lock and Dunson (2015) for a related approach.

Posterior sampling under the extension (12) can be performed following the details of Sect. 3 and considering the update of each group specific set of weights independently by simulating

$$\begin{aligned} S^{(g)}_{s,h}&\sim \text{ Be }(1-\delta + n^{(g)}_{s,h}, \alpha + \delta (s+1) + v^{(g)}_{s,h} - n^{(g)}_{s,h}) \\ R^{(g)}_{s,h}&\sim \text{ Be }(\beta +r^{(g)}_{s,h}, \beta + v^{(g)}_{s,h} - n_{s,h} - r^{(g)}_{s,h} ), \end{aligned}$$

where $v^{(g)}_{s,h}$, $n^{(g)}_{s,h}$, and $r^{(g)}_{s,h}$ are defined consistently to $v_{s,h}$, $n_{s,h}$, and $r_{s,h}$ of Sect. 3 but considering only the subjects preassigned to group g.

Assuming the same prior specification of the previous sections with ${ s^\mathtt{max}}=4$ we run 1000 iterations of a Gibbs sampler with a burn-in period of 200. Figure 6 reports, for each group, the estimated posterior mean density along with 95% credible bands. Many estimated densities show a clear bimodality which previous studies justified with the presence of two subpopulations of galaxies: a blue and red population (Balogh et al. 2004; Canale et al. 2019). Note that our characterization of the posterior uncertainty, visualized by means of pointwise posterior credible bands, is smaller than that obtained in Canale et al. (2019) where a dependent Dirichlet process, as defined in Lijoi et al. (2014), was assumed. The different estimated densities clearly show different levels of global and local variability that our model is able to capture.

5 Discussion

We introduced a family of multiscale stick-breaking mixture models for Bayesian nonparametric density estimation. This class of models is made of two building blocks: a flexible multiscale stick-breaking process inspired by the PY literature and a stochastic process that generates a dictionary of stochastically ordered kernel densities. We showed that the $\delta$ parameter of the multiscale stick-breaking process—related to the discount parameter of the PY—makes the prior flexible and robust. Specifically, it allows the method to achieve results comparable to those obtainable by more basic models endowed with an additional degree of hyperpriors—thus relieving the computational burden. The comparison with standard Bayesian nonparametric competitors showed, on average, superior performance in terms of finding the right smoothness of the unknown density.

Multivariate extensions of this approach are possible but not straightforward. One possibility is to introduce a suitable mechanism to define the dyadic splitting of the p-dimensional location parameter space, for example exploiting the concept of tolerance regions in place of the univariate quantiles adopted in (9). A different solution may be build upon a modification of the multiscale tree of Fig. 1 where each node is split into $2^p$ nodes. Consistently with this, at the sth scale, $2^{ps}$ location parameters may be sampled under the constraints induced by the partition obtained taking p dyadic splits for each marginal coordinate similarly to (9) and then taking their Cartesian product. This construction is reminiscent of the approach of Jara et al. (2009) for the multivariate Pólya tree. Clearly with the latter approach also the multiscale stick-breaking needs to be reformulated accordingly. Nonetheless, the univariate model described is amenable to extensions and generalizations to more complex settings involving hierarchical structures or covariates as illustrated through the analysis of the Sloan Digital Sky Survey data.

Appendix

Proof

(Lemma 1) Let $\pi _s = \sum _{h=1}^{2^s} \pi _{s,h}$. For finite integer S, let $\varDelta _S = 1 - \sum _{s=0}^S \pi _s$ which is equivalent to

$$\begin{aligned} \varDelta _S&= \sum _{h=1}^{2^S} \varDelta _{S,h}\\&= \sum _{h=1}^{2^S} \left\{ (1 - S_{S,h} ) \prod _{r<S} (1-S_{r,\lceil h2^{r-s} \rceil }) T_{Shr},\right\} . \end{aligned}$$

To establish the result, it is sufficient to show that the limit of each $\varDelta _{Sh}$ for $S\rightarrow \infty$ is 0 a.s. Note that each $\varDelta _{S,h}$ has the same distribution of

$$\begin{aligned} \prod _{s=1}^S (1-S_s) T_{s-1}, \end{aligned}$$

with $S_s \sim \text{ Be }(a_s, b_s)$ independent of $T_s \sim \text{ Be }(c_s, c_s)$. Using Jensen’s inequality

$$\begin{aligned} \mathbb {E}[\log \{(1-S_s)T_{s-1}\}] \le&\log \{(1-\mathbb {E}[S_s])\mathbb {E}[T_{s-1}]\}\\ =&\log \left( \frac{a_s}{2(a_s + b_s)}\right) < 0, \end{aligned}$$

and therefore

$$\begin{aligned} \sum _{s=0}^\infty \mathbb {E}[\log \{(1-S_s)T_{s-1}\}] = -\infty . \end{aligned}$$

Now use Lemma 1 of Ishwaran and James (2001) to obtain the result. $\square$

Proof

(Lemma 2)

$$\begin{aligned}&\mathbb {E}[G(A)] \\&\quad = \mathbb {E}\left[ \sum _{s=0}^\infty \sum _{h=1}^{2^s} \pi _{s,h} \delta _{\mu _{s,h}} (A) \right] \\&\quad = \sum _{s=0}^\infty \sum _{h=1}^{2^s} \mathbb {E}\left[ \pi _{s,h}\right] G_0\left( A \cap \varTheta _{\mu ;s,h} \right) 2^s \\&\quad = \sum _{s=0}^\infty \sum _{h=1}^{2^s} \frac{\left( 1-\delta \right) \prod _{j=0}^{s-1} \left( \alpha +\delta (j +1)\right) }{\prod _{j=0}^s \left( \alpha +\delta j + 1 \right) } G_0\left( A \cap \varTheta _{\mu ;s,h} \right) \\&\quad = \sum _{s=0}^\infty \frac{\left( 1-\delta \right) \prod _{j=0}^{s-1} \left( \alpha +\delta (j +1)\right) }{\prod _{j=0}^s \left( \alpha +\delta j + 1 \right) } \sum _{h=1}^{2^s} G_0\left( A \cap \varTheta _{\mu ;s,h} \right) \\&\quad = G_0\left( A\right) \sum _{s=0}^\infty \frac{\left( 1-\delta \right) \prod _{j=0}^{s-1} \left( \alpha +\delta (j +1)\right) }{\prod _{j=0}^s \left( \alpha +\delta j + 1 \right) } \\&\quad = G_0\left( A\right) \end{aligned}$$

$\square$