Parallel sequential Monte Carlo for stochastic gradient-free nonconvex optimization

Abstract

We introduce and analyze a parallel sequential Monte Carlo methodology for the numerical solution of optimization problems that involve the minimization of a cost function that consists of the sum of many individual components. The proposed scheme is a stochastic zeroth-order optimization algorithm which demands only the capability to evaluate small subsets of components of the cost function. It can be depicted as a bank of samplers that generate particle approximations of several sequences of probability measures. These measures are constructed in such a way that they have associated probability density functions whose global maxima coincide with the global minima of the original cost function. The algorithm selects the best performing sampler and uses it to approximate a global minimum of the cost function. We prove analytically that the resulting estimator converges to a global minimum of the cost function almost surely and provide explicit convergence rates in terms of the number of generated Monte Carlo samples and the dimension of the search space. We show, by way of numerical examples, that the algorithm can tackle cost functions with multiple minima or with broad “flat” regions which are hard to minimize using gradient-based techniques.

1 Introduction

In signal processing and machine learning, optimization problems of the form

$$\begin{aligned} \min _{\theta \in \varTheta } f(\theta ) = \sum _{i=1}^n f_i(\theta ), \end{aligned}$$

(1.1)

where $\varTheta \subset {\mathbb R}^d$ is the d-dimensional compact search space, have attracted significant attention in recent years for problems where n is very large. Such problems often arise in big data settings, e.g., when one needs to estimate parameters given a large number of observations (Bottou et al. 2018).

Because of their efficiency, the optimization community has focused mainly on stochastic gradient-based methods (Robbins and Monro 1951; Duchi et al. 2011; Kingma and Ba 2014) (see Bottou et al. (2018) for a recent review of the field) where an estimate of the gradient is obtained using a randomly selected subsample of the gradients of the component functions [the $f_i$’s in Eq. (1.1)] at each iteration. The resulting estimate is then used to perform a stochastic descent step. The majority of these stochastic gradient methods construct the subsamples using sampling with replacement to obtain unbiased estimates of the gradient. The latter can then be seen as a noisy gradient estimate with additive, zero-mean noise. In practice, however, there are schemes that subsample the data set without replacement (hence producing biased gradient estimators) and it has been argued that such methods can attain better numerical performance (Gürbüzbalaban et al. 2015; Shamir 2016).

The gradient information may not be always available, however, due to different reasons. For example, in an engineering application, the system to be optimized might be a black-box, e.g., a piece of closed software code with free parameters, which can be evaluated but cannot be differentiated (Nesterov and Spokoiny 2011). In these cases, one needs to use a gradient-free optimization scheme, meaning that the scheme must rely only on function evaluations, rather than any sort of actual gradient information. Classical gradient-free optimization methods have attracted significant interest over the past decades (Appel et al. 2004; Spall 2005; Mariño and Míguez 2007; Conn et al. 2009). These methods proceed either by a random search [which is based on evaluating the cost function at random points and update the parameter whenever a descent in the function evaluation is achieved (Spall 2005)], or by constructing a numerical (finite-difference type) approximation of the gradient that can be used to take a descent step (Nesterov and Spokoiny 2011).

Such methods are not applicable, however, if one can only obtain noisy function evaluations or one can only evaluate certain subsets of component functions in a problem like (1.1). In this case, since the function evaluations are not exact, direct random search methods cannot be used reliably and it is only recently that some authors have described how to compute finite-difference approximations of the gradient (Wibisono et al. 2012; Ghadimi and Lan 2013; Chen and Wild 2015; Bach and Perchet 2016). Also in recent years, evolutionary methods, based on the mutation, recombination and selection of samples, have been suggested for the approximation of gradients. The resulting optimization algorithms, termed evolutionary strategies (ES) have been applied within reinforcement learning schemes (Salimans et al. 2017; Wierstra et al. 2014; Hansen and Ostermeier 2001; Morse and Stanley 2016).

However, when the cost function has multiple minima or has some regions where the gradient vanishes, gradient-based methods may suffer from poor numerical performance. In particular, the optimizer can get stuck in a local minimum easily, due to its reliance on gradient approximations. Moreover, when the gradient contains little information about any minimum (e.g., in flat regions), gradient-free stochastic optimizers (as well as perfect gradient schemes) can suffer from slow convergence.

Model-based random-search methods (Hu et al. 2012), which use probabilistic models of various types in order to speed up the search procedure, have been investigated in order to address problems where gradients cannot be approximated or simply turn out ineffective. The latter include classical algorithms such as simulated annealing (SA) (Kirkpatrick et al. 1983), Monte Carlo expectation maximization (EM) (Robert and Casella 2004) and other Markov chain Monte Carlo (MCMC) based methods (Pereyra et al. 2015). The class of model-based random search schemes also encompasses sequential Monte Carlo (SMC) techniques, e.g., SMC implementations of SA (Zhou and Chen 2013) and several optimization algorithms that mimic standard particle filters (Zhou et al. 2013; Liu et al. 2016). Let us note that most of the latter MCMC- and SMC-based procedures can be cast within the class of SMC samplers described in Del Moral et al. (2006), albeit with a target distribution which is sometimes implicitly defined in order to satisfy certain properties related to the objective function (Zhou et al. 2013). Nevertheless, these optimization techniques are generally designed to be used in problems where the objective function can be evaluated exactly and their extension to stochastic optimization is not straightforward, neither from the point of view of practical performance nor in terms of theoretical convergence guarantees.

Some authors have also explored the duality between optimization and probability theory, in a way that potentially enables the use of general computational inference algorithms for solving optimization problems. While in model-based optimization the emphasis is put on the algorithms (e.g., how to use MCMC methods in Pereyra et al. (2015) or particle filters in Liu et al. (2016), for optimization), in this line of research the emphasis is in converting the optimization problem into an equivalent inference problem, which can then be tackled with any suitable inference algorithm. A rigorous mathematical treatment of the topic can be found in Del Moral and Doisy (1999), while Ikonen et al. (2005) and Míguez et al. (2013) address the problem from a methodological viewpoint. Again, these contributions deal with problems where the objective function can be computed deterministically and exactly, though.

The stochastic setting, where it is only possible to compute noisy evaluations of $f(\theta )$, is harder and the bibliography is limited in comparison with the deterministic setup. The recent survey in Homem-de Mello and Bayraksan (2014) covers various gradient-based Monte Carlo procedures, however it addresses a different class of stochastic optimizaton problems where the cost function itself is defined as an expectation, rather than a finite-sum as in (1.1). Existing model-based random methods for stochastic optimization include MCMC-based samplers which target a probability density function (pdf) matched to the objective function in (1.1) (meaning that the maxima of the pdf coincide with the minima of $f(\theta )$) (Welling and Teh 2011; Chen et al. 2016). Such schemes, however, also rely on the computation of noisy gradients. Other MCMC-based methods (see, e.g., Alquier et al. (2016) which employs noisy Metropolis steps) do not require gradients, yet these techniques have been primarily designed and investigated as sampling algorithms, rather than optimization methods. Similarly, an adaptive importance sampler for a target pdf matched to $f(\theta )$ is reported in Akyildiz et al. (2017). This method uses subsampling to compute noisy weights, but the technique lacks any theoretical guarantees and does not address the problem optimization directly either. A particle filtering algorithm for stochastic global optimization has been proposed by Stinis (2012). The method is intuitive, simple to implement and has been shown to work efficiently in some simple examples, however the contribution of Stinis (2012) is strictly methodological: There is no analysis of performance and no theoretical guarantees.

In this paper, we propose a parallel sequential Monte Carlo optimizer (PSMCO) to minimize cost functions with the finite-sum structure of problem (1.1). The PSMCO is a zeroth-order stochastic optimization algorithm, in the sense that it only uses evaluations of small batches of individual components $f_i(\theta )$ in (1.1). In particular, it does not require the computation or approximation of gradients. The proposed scheme proceeds by constructing parallel samplers, each of which aims at minimizing the same cost function $f(\theta )$. Each sampler performs subsampling without replacement to obtain its mini-batches of individual components and processes each component only once. Using these mini-batches, the PSMCO constructs potential functions, propagates samples via a jittering scheme (Crisan and Miguez 2018) and selects samples by applying a weighting-resampling procedure. The communication between parallel samplers is only necessary when a joint estimate of the minimum is required. In this case, the best performing sampler is selected and the minimum is estimated.

We analytically prove that the estimate provided by each sampler converges almost surely to a global minimum of the cost function and provide explicit convergence rates in terms of the number of Monte Carlo samples generated by the algorithm. This type of analysis goes beyond standard results for particle filters: It tackles the problem of stochastic optimization directly and it yields stronger theoretical guarantees compared to other stochastic optimization methods in the literature. In particular, we obtain error bounds for the solution of problem (1.1) that hold almost surely (a.s.) and vanish at a rate $\mathcal {O}\left( N^{-\frac{1}{2(d+1)}} \right)$, where N is the number of Monte Carlo samples and d is the dimension of the search space $\varTheta$. This is in contrast to the usual results for random search methods in the literature, which are purely asymptotic and do not provide any rates (Appel et al. 2004; Miguez 2010; Hu et al. 2012; Zhou and Chen 2013; Zhou et al. 2013). Let us also remark the difference between the proposed scheme and the SMC-based schemes in Míguez et al. (2013) where the authors partitioned the parameter vector and modeled it as a dynamical system, an approach that cannot be used in the more general setup of (1.1) because each individual function $f_i$ depends on the complete vector $\theta$. The PSMCO algorithm, in turn, is explicitly designed to provide an estimate of the full parameter $\theta$ at each iteration.

The main contribution of this paper includes the theoretical analysis of the proposed PSMCO scheme and its numerical demonstration on three problems where classical stochastic optimization methods (especially gradient-based algorithms) struggle to perform. The paper is organized as follows. After a brief survey of the relevant notation (below), we lay out the relationship between Bayesian inference and optimization in Sect. 2. Then, we develop a sequential Monte Carlo scheme in Sect. 3. In Sect. 4, we analyze this scheme and investigate its theoretical properties. We present some numerical results in Sect. 5 and make some concluding remarks in Sect. 6.

1.1 Notation

For $n\in {\mathbb N}$, we denote $[n] = \{1,\ldots ,n\}$. The space of bounded functions on the parameter space $\varTheta \subset {\mathbb R}^d$ is denoted as $B(\varTheta )$. The set of continuous and bounded real functions on $\varTheta$ is denoted $\mathsf {C}_b(\varTheta )$. The family of Borel subsets of $\varTheta$ is denoted with ${{\mathcal {B}}}(\varTheta )$. The set of probability measures on the measurable space $(\varTheta ,{{\mathcal {B}}}(\varTheta ))$ is denoted ${{\mathcal {P}}}(\varTheta )$. Given $\varphi \in B(\varTheta )$ and $\pi \in {{\mathcal {P}}}(\varTheta )$, the integral of $\varphi$ with respect to (w.r.t.) $\pi$ is written as

$$\begin{aligned} (\varphi ,\pi ) = \int _\varTheta \varphi (\theta ) \pi (\text{ d }\theta ). \end{aligned}$$

Given a Markov kernel $\kappa :{{\mathcal {B}}}(\varTheta ) \times \varTheta \mapsto [0,1]$, we denote $\kappa \pi ({\mathrm {d}}\theta ) = \int \kappa (\text{ d }\theta | \theta ') \pi (\text{ d }\theta ')$. If $\varphi \in B(\varTheta )$, then $\Vert \varphi \Vert _\infty = \sup _{\theta \in \varTheta } |\varphi (\theta )| < \infty$.

Let $\alpha = (\alpha _1,\ldots ,\alpha _{d}) \in {\mathbb N}^* \times \cdots \times {\mathbb N}^*$, where ${\mathbb N}^* = {\mathbb N}\cup \{0\}$, be a multi-index. We define the partial derivative operator ${{\mathsf {D}}}^\alpha$ as

$$\begin{aligned} {{\mathsf {D}}}^\alpha h = \frac{\partial ^{\alpha _1} \cdots \partial ^{\alpha _d} h}{\partial \theta _1^{\alpha _1} \cdots \partial \theta _d^{\alpha _d}} \end{aligned}$$

for a sufficiently differentiable function $h:{\mathbb R}^d \rightarrow {\mathbb R}$. We use $|\alpha | = \sum _{i=1}^d \alpha _i$ to denote the order of the derivative. Finally, the notation $\lfloor x \rfloor$ indicates the floor function for a real number x, which returns the biggest integer $k \le x$.

2 Stochastic optimization as inference

In this section, we describe how to construct a sequence of probability distributions that can be linked to the solution of problem (1.1). Let $\pi _0\in {{\mathcal {P}}}(\varTheta )$ be the initial element of the sequence. We construct the rest of the sequence recursively as

$$\begin{aligned} \pi _t(\text{ d }\theta ) = \pi _{t-1}({\mathrm {d}}\theta ) \frac{G_t(\theta )}{\int _\varTheta G_t(\theta ) \pi _{t-1}({\mathrm {d}}\theta )}, \quad \text {for } t\ge 1, \end{aligned}$$

(2.1)

where the maps $G_t:\varTheta \mapsto {\mathbb R}_+$ are termed potential functions (Del Moral 2004). The key idea is to associate these potentials $(G_t)_{t\ge 1}$ with mini-batches of individual components of the cost function (subsets of the $f_i$’s) in order to construct a sequence of measures $\pi _0,\pi _1,\ldots ,\pi _T$ such that (for a prescribed value of T) the global maxima of the density of $\pi _T$ match the global minima of $f(\theta )$. We remark that the measures $\pi _1,\ldots ,\pi _T$ are all absolutely continuous w.r.t $\pi _0$ if the potential functions $G_t$, $t = 1,\ldots ,T$, are bounded.

To construct the potentials, we use mini-batches consisting of K individual functions $f_i$ for each iteration t. To be specific, we randomly select subsets of indices ${{\mathcal {I}}}_t, t = 1,\ldots ,T$, by drawing uniformly from $\{1,\ldots ,n\}$ without replacement. Each subset has $|{{\mathcal {I}}}_t| = K$ elements, in such a way that we obtain T subsets satisfying $\bigcup _{i=1}^T {{\mathcal {I}}}_t = [n]$ and ${{\mathcal {I}}}_i \cap {{\mathcal {I}}}_j = \emptyset$ when $i\ne j$. Finally, we define the potential functions $(G_t)_{t\ge 1}$ as

$$\begin{aligned} G_t(\theta ) = \exp \left( -\sum _{i \in {{\mathcal {I}}}_t} f_i(\theta )\right) , \quad \quad t = 1,\ldots ,T. \end{aligned}$$

(2.2)

In the sequel, we provide a result that establishes a precise connection between the optimization problem in (1.1) and the sequence of probability measures defined in (2.1), provided that Assumption 1 below is satisfied.

Assumption 1

The functions in the sequence $(G_t)_{t\ge 1}$ are positive and bounded, i.e.,

$$\begin{aligned} G_t(\theta ) > 0 \quad \forall \theta \in \varTheta \quad \text {and} \quad G_t\in B(\varTheta ). \end{aligned}$$

Next, we show the relationship between the minima of $f(\theta )$ and the maxima of $\frac{{\mathrm {d}}\pi _T}{{\mathrm {d}}\pi _0}$.

Proposition 1

Assume that the potentials are selected as in (2.2) for $1\le t \le T$, with ${{\mathcal {I}}}_i \cap {{\mathcal {I}}}_j = \emptyset$ and $\bigcup _i {{\mathcal {I}}}_i = [n]$. Let $\pi _T$ be the T-th probability measure constructed by means of recursion (2.1). If Assumption 1 holds and $\pi _0\in {{\mathcal {P}}}(\varTheta )$, then

$$\begin{aligned} \mathop {\mathrm{argmax}}\limits _{\theta \in \varTheta } \frac{{\mathrm {d}}\pi _T}{{\mathrm {d}}\pi _0}(\theta ) = \mathop {\mathrm{argmin}}\limits _{\theta \in \varTheta } \sum _{i=1}^n f_i(\theta ), \end{aligned}$$

where $\frac{{\mathrm {d}}\pi _T}{{\mathrm {d}}\pi _0}(\theta ):\varTheta \rightarrow {\mathbb R}_+$ denotes the Radon–Nikodym derivative of $\pi _T$ w.r.t. the prior measure $\pi _0$.

Proof

See Appendix A.1. $\square$

For conciseness, we abuse the notation and use $\pi (\theta )$, $\theta \in \varTheta$, to indicate the pdf associated to a probability measure $\pi ({\mathrm {d}}\theta )$. The two objects are distinguished clearly by the context (e.g., for an integral $(\varphi ,\pi )$, $\pi$ necessarily is a measure) but also by their arguments. The probability measure $\pi (\cdot )$ takes arguments ${\mathrm {d}}\theta$ or $A \in {{\mathcal {B}}}(\varTheta )$, while the pdf $\pi (\theta )$ is a function $\varTheta \rightarrow [0,\infty )$.

Remark 1

Notice that when $\pi _0$ is a uniform probability measure on $\varTheta$, we simply have

$$\begin{aligned} \pi _T(\theta ) \propto \exp \left( -\sum _{i=1}^n f_i(\theta )\right) , \quad \theta \in \varTheta . \end{aligned}$$

where $\pi _T(\theta )$ denotes the pdf (w.r.t. Lebesgue measure) of the measure $\pi _T({\mathrm {d}}\theta )$. $\square$

Remark 2

Moreover, if we choose

$$\begin{aligned} \pi _0(\theta ) \propto \exp \left( -f_1(\theta )\right) \end{aligned}$$

(2.3)

and select index subsets such that $\bigcup _{t=1}^T {{\mathcal {I}}}_t = \{2,\ldots ,n\}$ then we also obtain

$$\begin{aligned} \pi _{T}(\theta ) \propto \exp \left( -\sum _{i=1}^n f_i(\theta )\right) , \quad \quad \text {for } \theta \in \varTheta . \end{aligned}$$

When a Monte Carlo is scheme used to realize recursion (2.1), the use of a prior of the form (2.3) requires the ability to sample from it. $\square$

In summary, if we can construct the sequence described by (2.1), then we can replace the minimization problem of $f(\theta )$ in (1.1) by the maximization of a pdf. This relationship was exploited in a Gaussian setting in Akyildiz et al. (2018), i.e., the special case of a Gaussian prior $\pi _0$ and log-quadratic potentials $(G_t)_{t\ge 1}$ (Gaussian likelihoods), which makes it possible to implement recursion (2.1) analytically. The solution of this special case can be shown to match a well-known stochastic optimization algorithm, called the incremental proximal method (Bertsekas 2011), with a variable-metric. However, for general priors and potentials, it is not possible to analytically construct (2.1) and maximize $\pi _T(\theta )$. For this reason, we propose a simulation method to approximate the recursion (2.1) and solve $\mathop {\mathrm{argmax}}\limits _{\theta \in \varTheta } \frac{{\mathrm {d}}\pi _T}{{\mathrm {d}}\pi _0}(\theta )$.

3 The algorithm

In this section, we first describe a sampler to simulate from the distributions defined by recursion (2.1). We then describe an algorithm which runs these samplers in parallel. The parallelization here is not primarily motivated by the computational gain (although it can be substantial). We have empirically found that non-interacting parallel samplers are able to keep track of multiple minima better than a single “big” sampler. For this reason, we will not focus on demonstrating computational gains in the experimental section. Rather, we will discuss what parallelization brings in terms of providing better estimates.

We consider M workers (corresponding to M samplers). Specifically, each worker sees a different configuration of the dataset, i.e., the m-th worker constructs a distinct sequence of index sets $({{\mathcal {I}}}_t^{(m)})_{t\ge 1}$ which determine the mini-batches sampled from the full set of individual components. Having obtained different mini-batches which are randomly constructed, each worker then constructs different potentials $(G_t^{(m)})_{t\ge 1}$, where $G_t^{(m)}(\cdot ) = \exp \left\{ -\sum _{i\in {{\mathcal {I}}}_t} f_i(\cdot ) \right\}$, as described in the previous section.

The m-th worker, therefore, aims at estimating a specific sequence of probability measures $\pi _t^{(m)}$, for $m \in \{1,\ldots ,M\}$. We denote the particle approximation of the posterior $\pi _t^{(m)}$ at time t as

$$\begin{aligned} \pi _t^{(m),N}({\mathrm {d}}\theta ) = \frac{1}{N} \sum _{i=1}^N \delta _{\theta ^{(i,m)}}({\mathrm {d}}\theta ), \end{aligned}$$

where $\delta _{\theta '}({\mathrm {d}}\theta )$ is the unit delta measure located at $\theta ' \in \varTheta$. Overall, the algorithm retains M probability distributions. Note that these distributions are different for each $t<T$, as they depend on different potentials, but $\pi _T^{(m)}=\pi _T$ for all workers because $\bigcup _{t=1}^T {{\mathcal {I}}}_t^{(m)} = [n]$ for every m.

One iteration of the algorithm on a local worker m can be described as follows. Assume the worker has computed the probability measure $\pi _{t-1}^{(m),N}$ using the particle system $\{\theta _{t-1}^{(m,i)}\}_{i=1}^N$. First, we use a jittering kernel $\kappa ({\mathrm {d}}\theta | \theta _{t-1})$ (a Markov kernel on $\varTheta$) to modify the particles (Crisan and Miguez 2018) (see Sect. 3.1 for the precise definition of $\kappa (\cdot |\cdot )$). The idea is to jitter a subset of the particles in order to modify and propagate them into better regions of $\varTheta$ with higher probability density and lower cost. The particles are jittered by sampling,

$$\begin{aligned} \hat{\theta }_t^{(i,m)} \sim \kappa (\cdot | \theta _{t-1}^{(i,m)}) \quad \text {for } i = 1,\ldots ,N. \end{aligned}$$

Note that the jittering kernel may be designed so that it only modifies a subset of particles (again, see Sect. 3.1 for details). Next, we compute weights for the new set of particles $\{\hat{\theta }_t^{(i,m)}\}_{i=1}^N$ according to the t-th potential, namely

$$\begin{aligned} w_t^{(i,m)} = \frac{G_t^{(m)}(\hat{\theta }_t^{(i,m)})}{\sum _{i=1}^N G_t^{(m)}(\hat{\theta }_t^{(i,m)})} \quad \text {for} \quad i = 1,\ldots ,N. \end{aligned}$$

Remark 3

The particle weights can be made proportional to the potentials alone, i.e., $w_t^{(i,m)} \propto G_t^{(m)}({\hat{\theta }}_t^{(i,m)})$, as long as the jittering kernels satisfy Assumption 2 in Sect. 3.1. Under mild assumptions, Algorithm 1 converges with standard error rates $\mathcal {O}(N^{-\frac{1}{2}})$, as proved in Sect. 4.

After obtaining weights, each worker performs a resampling step where for $i = 1,\ldots ,N$, we set $\theta _t^{(i,m)} = \hat{\theta }_t^{(i,k)}$ for $k \in \{1,\ldots ,N\}$ with probability $w_t^{(i,m)}$. The procedure just described corresponds to a simple multinomial resampling scheme, but other standard methods can be applied as well (Douc et al. 2005). We denote the resulting probability measure constructed at the t-th iteration of the m-th worker as

$$\begin{aligned} \pi _t^{(m),N}(\text{ d }\theta ) = \frac{1}{N} \sum _{i=1}^N \delta _{{\theta }_t^{(i,m)}}(\text{ d }\theta ). \end{aligned}$$

The full procedure for the m-th worker is outlined in Algorithm 1. In Sect. 3.1, we elaborate on the selection of the jittering kernels and in Sect. 3.2, we detail the scheme for estimating a global minimum of $f(\theta )$ from the set of random measures $\{\pi _t^{(m),N}\}_{m=1}^M$.

3.1 Jittering kernel

The jittering kernel constitutes one of the key design choices of the proposed algorithm. Following Crisan and Miguez (2018), we put the following assumption on the kernel $\kappa$.

Assumption 2

The Markov kernel $\kappa$ satisfies

$$\begin{aligned} \sup _{\theta ' \in \varTheta } \int _\varTheta |\varphi (\theta ) - \varphi (\theta ')| \kappa (\text{ d }\theta |\theta ') \le \frac{c_\kappa \Vert \varphi \Vert _\infty }{\sqrt{N}} \end{aligned}$$

for any $\varphi \in B(\varTheta )$ and some constant $c_\kappa < \infty$ independent of N.

In this paper, we use kernels of form

$$\begin{aligned} \kappa (\text{ d }\theta | \theta ') = (1 - \epsilon _N) \delta _{\theta '}(\text{ d }\theta ) + \epsilon _N \tau (\text{ d }\theta | \theta '), \end{aligned}$$

(3.1)

where $\epsilon _N \le \frac{1}{\sqrt{N}}$, which satisfy Assumption 2 (Crisan and Miguez 2018). The kernel $\tau$ can be rather simple, such as a multivariate Gaussian or multivariate-t distribution centered around $\theta ' \in \varTheta$. Other choices of $\tau$ are possible as well.

Remark 4

The design of the kernel as a centered Gaussian or a multivariate-t distribution around $\theta '$ may not guarantee the propagation of samples into better (lower cost) regions. In this case, the weighting-and-resampling procedure naturally tends to keep and replicate the particles that attain a lower cost. However, the jittering kernel can also be designed to accelerate the optimization process. In particular, our setup allows for the use of gradient estimators [such as finite-difference schemes (Nesterov and Spokoiny 2011) or nudging steps (Akyildiz and Míguez 2020)] in the jittering kernel to accelerate the propagation of samples into lower-cost regions.

3.2 Estimating the global minima of $f(\theta )$

In order to estimate the global minima of $f(\theta )$, we first assess the performance of the samplers run by each worker. A typical performance measure is the marginal likelihood estimate resulting from $\pi _t^{(m),N}$. After choosing the worker which has attained the highest marginal likelihood (say the $m_0$-th worker), we estimate a minimum of $f(\theta )$ by selecting the particle $\theta _t^{(i,m)}$ that yields the highest density $\pi _t^{(m_0)}(\theta _t^{(i,m_0)})$.

To be precise, let us start by denoting the incremental marginal likelihood associated to $\pi _t^{(m)}$ and its estimate $\pi _t^{(m),N}$ as $Z_{1:t}^{(m)}$ and $Z_{1:t}^{(m),N}$, respectively. They can be explicitly obtained by first computing

$$\begin{aligned} Z_{t}^{(m)}&= \int G_t^{(m)}(\theta ) \hat{\pi }^{(m)}_t(\text{ d }\theta )\\&\approx \frac{1}{N} \sum _{i = 1}^N G_t^{(m)}(\hat{\theta }_t^{(i,m)}) := Z_t^{(m),N} \end{aligned}$$

and then updating the running products

$$\begin{aligned} Z_{1:t}^{(m)} = Z_t^{(m)} Z_{1:t-1}^{(m)} = \prod _{k=1}^t Z_k^{(m)} \end{aligned}$$

and

$$\begin{aligned} Z_{1:t}^{(m),N} = Z_t^{(m),N} Z_{1:t-1}^{(m),N} = \prod _{k=1}^t Z_k^{(m),N}. \end{aligned}$$

The quantity $Z_{1:t}^{(m)}$ is a local performance index that keeps track of the “quality” of the m-th particle system $\{\theta _t^{(i,m)}\}_{i=1}^N$ (Elvira et al. 2017) and, hence, we use $\{Z_{1:t}^{(m),N}\}_{m=1}^M$ to determine the best performing worker¹. Given the index of the best performing sampler, which is given by

$$\begin{aligned} m_t^\star = \mathop {\mathrm{argmax}}\limits _{m\in \{1,\ldots ,M\}} Z_{1:t}^{(m),N}, \end{aligned}$$

we obtain a maximum-a-posteriori (MAP) estimator,

$$\begin{aligned} \theta _t^{\star ,N} = \mathop {\mathrm{argmax}}\limits _{i\in \{1,\ldots ,N\}} \mathsf {p}_t^{(m_t^\star ),N}(\theta ^{(i,m_t^\star )}), \end{aligned}$$

(3.2)

where $\mathsf {p}_t^{(m_t^\star ),N}(\theta )$ is the kernel density estimator (Silverman 1998; Wand and Jones 1994) described in Remark 5. Note that we do not construct the entire density estimator and maximize it. Since this operation is performed locally on the particles from the best performing sampler, it involves $\mathcal {O}(N^2)$ operations, where N is the number of particles on a single worker, which is much smaller than the total number MN. The full procedure is outlined in Algorithm 2.

Remark 5

Let ${{\mathsf {k}}}:\varTheta \rightarrow (0,\infty )$ be a bounded pdf with zero mean and finite second-order moment, i.e., we have $\int _\varTheta \Vert \theta \Vert _2^2 {{\mathsf {k}}}(\theta ) {\mathrm {d}}\theta < \infty$. We can use the particle system $\{\theta _t^{(i,m)}\}_{i=1}^N$ and the pdf ${{\mathsf {k}}}(\cdot )$ to construct the kernel density estimator (KDE) of $\pi _t^{(m)}(\theta )$ as

$$\begin{aligned} \mathsf {p}_t^{(m),N}(\theta )&= \frac{1}{N}\sum _{i=1}^N {{\mathsf {k}}}(\theta - \theta _t^{(i,m)})\nonumber \\&= (k^\theta ,\pi _t^{(m),N}), \end{aligned}$$

(3.3)

where ${{\mathsf {k}}}^\theta (\theta ') = {{\mathsf {k}}}(\theta - \theta ')$. Note that $\mathsf {p}_t^{(m),N}(\theta )$ is not a standard KDE because the particles $\{\theta _t^{(i,m)}\}_{i=1}^N$ are not i.i.d. samples from $\pi _t^{(m)}(\theta )$. Equation (3.3), however, suggests that the estimator, $\mathsf {p}_t^{(m),N}(\theta )$ converges when the approximate measure $\pi _t^{(m),N}$ does. See Crisan and Míguez (2014) for an analysis of particle KDE’s. $\square$

4 Analysis

In this section, we provide some basic theoretical guarantees for Algorithm 2. In particular, we prove results regarding a sampler on a single worker m. To ease the notation, we skip the superscript ${}^{(m)}$ in the rest of this section and simply note that results presented below hold for every $m\in \{1,\ldots ,M\}$. All proofs are deferred to the Appendix.

When constrained to a single worker m, the approximation $\pi _t^{N}$ is provably convergent. In particular, we have the following results that hold for every worker $m = 1,\ldots ,M$.

Theorem 1

If the sequence $(G_t)_{t\ge 1}$ satisfies Assumption 1 and the jittering kernels satisfy Assumption 2, then, for any $\varphi \in B(\varTheta )$, we have

$$\begin{aligned} \left\| \left( \varphi ,\pi _t\right) - \left( \varphi ,\pi _t^{N}\right) \right\| _p \le \frac{c_{t,p} \Vert \varphi \Vert _\infty }{\sqrt{N}} \end{aligned}$$

for every $t = 1,\ldots ,T$ and for any $p\ge 1$, where $c_{t,p} > 0$ is a constant independent of N.

Proof

See Appendix A.2.$\square$

Theorem 1 states that the samplers on local workers converge to their correct probability measures (for each m) with rate $\mathcal {O}(1/\sqrt{N})$, which is standard for Monte Carlo methods. Next we provide an upper bound for the random error $| (\varphi ,\pi _t) - (\varphi ,\pi _t^N) |$.

Corollary 1

Under the assumptions of Theorem 1, for every $\varphi \in B(\varTheta )$, we have

$$\begin{aligned} \left| (\varphi ,\pi _t^{N}) - (\varphi ,\pi _t)\right| \le \frac{U_{t,\delta }}{N^{\frac{1}{2}-\delta }}, \quad \text{ and } \quad 1 \le t \le T, \end{aligned}$$

where $U_{t,\delta }$ is an a.s. finite random variable and $0< \delta < \frac{1}{2}$ is an arbitrary constant independent of N. In particular,

$$\begin{aligned} \lim _{N\rightarrow \infty } (\varphi ,\pi _t^{N}) = (\varphi ,\pi _t) \quad \quad \text {a.s.} \end{aligned}$$

(4.1)

for any $\varphi \in B(\varTheta )$.

Proof

See Appendix A.3. $\square$

This result ensures that the random error made by the estimators vanishes as $N\rightarrow \infty$. Moreover, it provides us with a rate $\mathcal {O}(1/\sqrt{N})$ since the constant $\delta > 0$ can be chosen arbitrarily small.

These results are important because they enable us to analyze the properties of the kernel density estimators constructed using the samples at each worker. In order to be able to do so, we need to impose regularity conditions on the sequence of densities $\pi _t(\theta )$ and the kernels we use to approximate them.

Assumption 3

For every $\theta \in \varTheta$, the derivatives ${{\mathsf {D}}}^\alpha \pi _t(\theta )$ exist and they are Lipschitz continuous, i.e., there is a constant $L_{\alpha ,t} > 0$ such that

$$\begin{aligned} | {{\mathsf {D}}}^\alpha \pi _t(\theta ) - {{\mathsf {D}}}^\alpha \pi _t(\theta ')| \le L_{\alpha ,t} \Vert \theta - \theta '\Vert \end{aligned}$$

for all $\theta ,\theta ' \in \varTheta$, $t = 1,\ldots ,T$ and for all $\alpha = (\alpha _1,\ldots ,\alpha _d) \in \{0,1\}^d$.

Note that for $\alpha = (0,\ldots ,0)$ it is not hard to relate Assumption 3 directly to the cost function as we do in the following proposition.

Proposition 2

Assume that we define the incremental cost functions

$$\begin{aligned} F_t(\theta ) = \sum _{i \in \bigcup _{k=1}^t {{\mathcal {I}}}_k} f_i(\theta ) \end{aligned}$$

and there exists some $\ell _t$ such that

$$\begin{aligned} |F_t(\theta ) - F_t(\theta ')| \le \ell _t \Vert \theta - \theta '\Vert , \end{aligned}$$

i.e., $F_t$ is Lipschitz. Assume there exists $F^\star _t = \min _{\theta \in \varTheta } F_t(\theta )$ such that $|F^\star _t| < \infty$ and recall that $\pi _t(\theta ) \propto \exp (-F_t(\theta ))$. Then we have the following inequality,

$$\begin{aligned} |\pi _t(\theta ) - \pi _t(\theta ')| \le \frac{\ell _t \exp (-F_t^\star )}{Z_{\pi _t}} \Vert \theta - \theta '\Vert _2 \end{aligned}$$

where $Z_{\pi _t} = \int _\varTheta \exp (-F_t(\theta )) {\mathrm {d}}\theta$.

Proof

See Appendix A.4. $\square$

Next, we state assumptions on the kernel ${{\mathsf {k}}}$. We first note that the kernels in practice are defined with a bandwidth parameter $h\in {\mathbb R}_+$. In particular, given a kernel ${{\mathsf {k}}}$, we can define scaled kernels ${{\mathsf {k}}}_h$ as

$$\begin{aligned} {{\mathsf {k}}}_h(\theta ) = h^{-d} {{\mathsf {k}}}(h^{-1} \theta ), \quad \quad h > 0, \end{aligned}$$

where, we recall, d is the dimension of the parameter vector $\theta$. Hence, given ${{\mathsf {k}}}$ we define a family of kernels $\{{{\mathsf {k}}}_h, h\in {\mathbb R}_+\}$.

Assumption 4

The kernel ${{\mathsf {k}}}:\varTheta \rightarrow (0,\infty )$ is a zero-mean bounded pdf, i.e., ${{\mathsf {k}}}(\theta ) \ge 0$$\forall \theta \in \varTheta$ and $\int {{\mathsf {k}}}(\theta ) {\mathrm {d}}\theta = 1$. The second moment of this density is bounded, i.e., $\int _\varTheta \Vert \theta \Vert ^2 {{\mathsf {k}}}(\theta ) {\mathrm {d}}\theta < \infty$. Finally, ${{\mathsf {D}}}^\alpha {{\mathsf {k}}}\in {{\mathsf {C}}}_b(\varTheta )$, i.e., $\Vert {{\mathsf {D}}}^\alpha {{\mathsf {k}}}\Vert _\infty$$<~\infty$ for any $\alpha \in \{0,1\}^d$.

Remark 6

We note that Assumption 4 implies that ${{\mathsf {D}}}^\alpha {{\mathsf {k}}}_h \in {{\mathsf {C}}}_b(\varTheta )$ and we have $\Vert {{\mathsf {D}}}^\alpha {{\mathsf {k}}}_h\Vert _\infty = \frac{1}{h^{d + |\alpha |}} \Vert {{\mathsf {D}}}^\alpha {{\mathsf {k}}}\Vert _\infty$ for any $h > 0$ and $\alpha \in \{0,1\}^d$. $\square$

We denote the kernel density estimator defined using a scaled kernel ${{\mathsf {k}}}_h$ and the empirical measure $\pi _t^N$ as ${{\mathsf {p}}}_t^{h,N}(\theta )$. In particular, given a normalized kernel (a pdf) ${{\mathsf {k}}}:\varTheta \rightarrow (0,\infty )$, satisfying the assumptions in Assumption 4, we can construct the KDE

$$\begin{aligned} \mathsf {p}_t^{h,N}(\theta )&= ({{\mathsf {k}}}^{\theta }_h,\pi _t^{N}). \end{aligned}$$

where ${{\mathsf {k}}}_h^\theta (\theta ') = {{\mathsf {k}}}_h(\theta - \theta ')$ (see Remark 5). Now, we are ready to state the main results regarding the kernel density estimators, adapted from Crisan and Míguez (2014).

Theorem 2

Choose

$$\begin{aligned} h = \left\lfloor {N^{\frac{1}{2 (d + 1)}}}\right\rfloor ^{-1} \end{aligned}$$

(4.2)

and denote ${{\mathsf {p}}}_t^N(\theta ) = {{\mathsf {p}}}_t^{h,N}(\theta )$ (since $h = h(N)$). If Assumptions 1, 2, 3 and 4 hold, and $\varTheta$ is compact, then

$$\begin{aligned} \sup _{\theta \in \varTheta } | {{\mathsf {p}}}_t^N(\theta ) - \pi _t(\theta )| \le \frac{V_\varepsilon }{N^{\frac{1-\varepsilon }{2 (d + 1)}}} \end{aligned}$$

(4.3)

where $V_\varepsilon \ge 0$ is an a.s. finite random variable and $0< \varepsilon < 1$ is a constant, both of which are independent of N and $\theta$. In particular,

$$\begin{aligned} \lim _{N\rightarrow \infty } \sup _{\theta \in \varTheta } | {{\mathsf {p}}}_t^N(\theta ) - \pi _t(\theta )| = 0 \quad \quad \text {a.s.} \end{aligned}$$

(4.4)

Proof

It follows from the proof of Theorem 4.2 and Corollary 4.1 in Crisan and Míguez (2014). See Appendix A.5 for an outline. $\square$

This theorem is a uniform convergence result, i.e., it holds uniformly in a compact parameter space $\varTheta$. We note that Theorem 2 specifies the dependence of the bandwidth h on the number of Monte Carlo samples N for convergence to be attained at that rate. Based on this result, we can relate the empirical maxima to the true maxima.

Theorem 3

Let $\theta _t^{\star ,N} \in \mathop {\mathrm{argmax}}\limits _{i\in \{1,\ldots ,N\}} {{\mathsf {p}}}_t^{N}(\theta _t^{(i)})$ be an estimate of a global maximum of $\pi _t$ and let $\theta _t^{\star } \in \mathop {\mathrm{argmax}}\limits _{\theta \in \varTheta } \pi _t(\theta )$ be an actual global maximum. If $\varTheta$ is compact, $\pi _t$ is continuous at $\theta _t^\star$ and Assumptions 1, 2, 3 and 4 hold, then for N sufficiently large

$$\begin{aligned} \pi _t(\theta _t^\star ) - \pi _t(\theta _t^{\star ,N}) \le \frac{W_{t,d,\varepsilon }}{N^{\frac{1-\varepsilon }{2 (d + 1)}}}, \quad 1 \le t \le T, \end{aligned}$$

where $\varepsilon \in (0,1)$ is an arbitrarily small constant and $W_{t,d,\varepsilon }$ is an a.s. finite random variable, both independent of N.

Proof

See Appendix A.6. $\square$

Remark 7

By choosing $t=T$, Theorem 3 provides a convergence rate for the MAP estimator $\theta _T^\star$, which is also the approximate solution of problem (1.1). $\square$

Theorem 3 also yields a convergence rate for the error $f(\theta _T^{\star ,N}) - f(\theta ^\star )$, where $f(\cdot )$ is the original cost function in problem (1.1), provided that the prior is chosen so that $\pi _T(\theta ) \propto \exp (-f(\theta ))$ (see Remark 1).

Corollary 2

Choose any

$$\begin{aligned} \theta ^\star \in \mathop {\mathrm{argmin}}\limits _{\theta \in \varTheta } f(\theta ) \quad \text{ and } \quad \theta _T^{\star ,N} \in \mathop {\mathrm{argmax}}\limits _{i\in \{1,\ldots ,N\}} {{\mathsf {p}}}_T^{N}(\theta _T^{(i)}). \end{aligned}$$

Under the same assumptions as in Theorem 3, if $\Vert f \Vert _\infty <\infty$ then we have

$$\begin{aligned} 0 \le f(\theta _T^{\star ,N}) - f(\theta ^\star ) \le \frac{\tilde{W}_{T,d,\varepsilon }}{N^{\frac{1-\varepsilon }{2 (d + 1)}}}, \end{aligned}$$

where $\tilde{W}_{T,d,\varepsilon }$ is an a.s. finite random variable.

Proof

See Appendix A.7. $\square$

Finally, we obtain a convergence rate for the expected error.

Corollary 3

Choose any

$$\begin{aligned} \theta ^\star \in \mathop {\mathrm{argmin}}\limits _{\theta \in \varTheta } f(\theta ) \quad \text{ and } \quad \theta _T^{\star ,N} \in \mathop {\mathrm{argmax}}\limits _{i\in \{1,\ldots ,N\}} {{\mathsf {p}}}_T^{N}(\theta _T^{(i)}). \end{aligned}$$

Under the same assumptions as in Theorem 3, if $\Vert f \Vert _\infty <\infty$ then we have

$$\begin{aligned} 0 \le {\mathbb E}[f(\theta _T^{\star ,N})] - f(\theta ^\star ) \le \frac{C_{T,d,\varepsilon }}{N^{\frac{1-\varepsilon }{2 (d + 1)}}}, \end{aligned}$$

where $C_{T,d,\varepsilon } = {\mathbb E}[\tilde{W}_{T,d,\varepsilon }] < \infty$ is a constant independent of N.

Proof

The proof follows from Corollary 2, since $\tilde{W}_{T,d,\varepsilon }$ is an a.s. finite random variable. $\square$

4.1 Discussion

Theorem 3 and Corollaries 2 and 3 go beyond standard results on the convergence of SMC methods. While the latter refer to the approximation of integrals (in the vein of Theorem 1 and Corollary 1), Corollaries 2 and 3 directly address the convergence of the sequence of optimizers $\theta _T^{\star ,N}$ and state that the proposed algorithm yields, with probability 1, an asymptotically optimal solution to problem (1.1) even if $f(\theta )$ is non-convex and presents multiple local and/or global minima. These results also provide explicit convergence rates that depend on the computational cost (the number of particles N) and the dimension d of the search space.

Note that the analyses available in the literature for most Monte Carlo optimization algorithms are purely asymptotical (see Appel et al. 2004; Ikonen et al. 2005; Miguez 2010; Hu et al. 2012; Zhou et al. 2013, i.e., they do not provide explicit convergence rates. Moreover, they often rely on restrictive assumptions. For example, Hu et al. (2012) and Zhou et al. (2013) require that the objective function present a unique global minimum. More detailed analyses are carried out by Zhou and Chen (2013) and Míguez et al. (2013). However, the former falls short of providing explicit error rates for the sequence of optimizers (bounds are given for the total variation distance between the Boltzmann distributions and their SMC approximations in a SA scheme) and the latter relies on a sequential decomposition of the cost function that is not satisfied by $f(\theta )$ in problem (1.1). Moreover, all the analytical results in these papers (Appel et al. 2004; Ikonen et al. 2005; Miguez 2010; Hu et al. 2012; Zhou et al. 2013; Zhou and Chen 2013; Míguez et al. 2013) are obtained for deterministic optimization problems where the objective function can be evaluated exactly, while Theorem 3 and Corollaries 2 and 3 hold for a more general stochastic optimization framework where $f(\theta )$ can only be estimated using mini-batches of data.

5 Numerical results

In this section, we show numerical results for three optimization problems which are hard to solve with conventional methods. In the first example, we focus on minimizing a function with multiple global minima. The aim of this experiment is to show that, when the cost function has several global minima, the PSMCO algorithm can successfully populate with Monte Carlo samples the regions of $\varTheta$ that contain these minima. In the second example, we tackle the minimization of a challenging cost function, with broad flat regions, for which standard stochastic gradient optimizers struggle. The third example involves a non-convex, non-smooth cost function and we use it to compare the proposed PSMCO scheme with a similar SMC-based optimization method proposed in Stinis (2012).

5.1 Minimization of a function with multiple global minima

Fig. 1

An illustration of the performance of the proposed algorithm for a cost function with four global minima. a The plot of $\pi _T(\theta ) \propto \exp (-f(\theta ))$. The blue regions indicate low values. It can be seen that there are four global maxima. b Samples drawn by the PSMCO at a single time instant. c The plot of the samples together with the actual cost function $f(\theta )$

In this experiment, we tackle the problem

$$\begin{aligned} \min _{\theta \in {\mathbb R}^2} f(\theta ), \text { where } \quad f (\theta ) = \sum _{i=1}^n f_i(\theta ) \end{aligned}$$

and

$$\begin{aligned} f_i(\theta ) = -\frac{1}{\lambda } \log \left( \sum _{k=1}^4 {{\mathcal {N}}}(\theta ;m_{i,k}, R)\right) , \end{aligned}$$

with $\lambda = 10$ and $R = r I_2$, with $I_2$ denoting the $2 \times 2$ identity matrix and $r = 0.2$. We choose the means $m_{i,k}$ randomly, namely $m_{i,k} \sim {{\mathcal {N}}}(m_{i,k}; m_k, \sigma ^2)$ where,

$$\begin{aligned}&m_1 = [4,4]^\top , \quad m_2 = [-4,-4]^\top ,\\&m_3 = [-4,4]^\top , \quad m_4 = [4,-4]^\top , \end{aligned}$$

and $\sigma ^2 = 0.5$. This selection results in a cost function with four global minima. Such functions arise in many machine learning problems, see, e.g., Mei et al. (2018). In this experiment, we have chosen $n = 1,000$. Although a small number for stochastic optimization problems, we note that each $f_i(\theta )$ represents a mini-batch in this scenario and we set $K= 1$ in the PSMCO algorithm.

In order to run the algorithm, we choose a uniform prior measure $\pi _0(\theta ) = \mathcal {U}([-a,a]\times [-a,a])$ with $a = 50$. It follows from Proposition 1 that the pdf that matches the cost function $f(\theta )$ can be written as

$$\begin{aligned} \pi _T(\theta ) \propto \exp (-f(\theta )), \end{aligned}$$

and it has four global maxima. This pdf is displayed in Fig. 1a. We run $M = 100$ samplers, with $N = 50$ particles each, yielding a total number of $MN = 5,000$ particles. We choose a Gaussian jittering scheme; specifically, the jittering kernel is defined as

$$\begin{aligned} \kappa (\text{ d }\theta | \theta ') = (1 - \epsilon _N) \delta _{\theta '}(\text{ d }\theta ) + \epsilon _N {{\mathcal {N}}}(\theta ; \theta ',\sigma ^2_j){\mathrm {d}}\theta , \end{aligned}$$

(5.1)

where $\epsilon _N = 1/\sqrt{N}$ and $\sigma _j^2 = 0.5$.

Some illustrative results can be seen from Fig. 1. To be specific, we have run independent samplers and plot all samples for this experiment (instead of estimating a minimum with the best performing sampler). From Fig. 1b, it can be seen that the algorithm populates the regions surrounding all maxima with samples. Finally, Fig. 1c shows the location of the samples relative to the actual cost function $f(\theta )$. These plots illustrate how the algorithm “locates” multiple, distinct global maxima with independent samplers. Note different samplers can converge to different global maxima in practice—which is in agreement with the analysis provided in Sect. 4.

Fig. 2

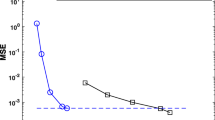
a The cost function and a snapshot of samples from the 50th iteration of the PSMCO, PSGD with bad initialization (blue dot on the yellow area) and PSGD with good initialization (black dots on the blue area). b Performance of each algorithm: it can be seen that PSMCO first converges to the wide region with low values (blue region) and then jumps to the minimum. This is because the marginal likelihood estimate of the sampler close to the minimum dominates after a while. There is effectively full communication among samplers only to determine the minimizer

5.2 Minimization of the sigmoid function

In this experiment, we address the problem,

$$\begin{aligned} \min _{\theta \in {\mathbb R}^2} f(\theta ) := \sum _{i=1}^n (y_i - g_i(\theta ))^2, \end{aligned}$$

(5.2)

where

$$\begin{aligned} \quad g_i(\theta )= \frac{1}{1 + \exp (-\theta _1 - \theta _2 x_i)}, \end{aligned}$$

with $x_i\in {\mathbb R}$, $f_i(\theta ) = (y_i - g_i(\theta ))^2$ and $\theta = [\theta _1,\theta _2]^\top$. The function $g_i$ is called as the sigmoid function. Cost functions of the form in eq. (5.2) are widely used in nonlinear regression with neural networks in machine learning (Bishop 2006).

In this experiment, we have $n = 100,000$. We choose $M = 25$ and $MN = 1,000$, leading to $N=40$ particles for every sampler. The mini-batch size is $K = 100$. The jittering kernel $\kappa$ is defined in the same way as in (5.1), where the Gaussian pdf has a variance chosen as the ratio of the dataset size L to the mini-batch size K, i.e., $\sigma _j^2 = {n}/{K}$, which yields a rather large variance²$\sigma _j^2 = 1000$. To compute the maximum as described in Eq. (3.2), we use a Gaussian kernel density with bandwidth $h = \lfloor {N^{\frac{1}{6}}}\rfloor ^{-1}$.

In Fig. 2, we compare the PSMCO algorithm with a parallel stochastic gradient descent (PSGD) scheme (Zinkevich et al. 2010) using M optimizers. We note that, given a particular realization³ of $(x_i)_{i=1}^n$, searching for a minimum of $f(\theta )$ may be a hard task. Figure 2a shows one such case, where the cost function has broad flat regions which make it difficult to find its maxima using gradient-based methods unless their initialization is sufficiently good. Accordingly, we have run two instances of PSGD with “bad” and “good” initializations.

The bad initial point for PSGD can be seen from Fig 2a, at $[-190,0]^\top$ (the blue dot). We initialize M parallel SGD optimizers around $[-190,0]^\top$, each with a small zero-mean Gaussian perturbation with variance $10^{-8}$. This is a poor initialization because gradients are nearly zero in this region (yellow area in Fig. 2a). We refer to the PSGD algorithm starting from this point as PSGD with B/I, which refers to bad initialization. We also initialize the PSMCO from this region, with Gaussian perturbations around $[-190,0]^\top$, with the same small variance $\sigma _\text {init}^2 = 10^{-8}$.

The “good” initialization for the PSGD is selected from a better region, namely around the point $[0,-100]^\top$, where gradient values actually contain useful information about the minimum. We refer to the PSGD algorithm starting from this point as PSGD with G/I.

The results can be seen in Fig. 2b. We observe that the PSGD with good initialization (G/I) moves towards a better region, however, it gets stuck because the gradient becomes nearly zero. On the other hand, PSGD with B/I is unable to move at all, since it is initialized in a region where all gradients are negligible (which is true even for the mini-batch observations). The PSMCO method, on the other hand, searches the space effectively to find the global minimum, as depicted in Fig. 2b.

5.3 Constrained nonsmooth nonconvex optimization

In this section, we compare the proposed PSMCO scheme to the method of Stinis (2012), labeled here as ‘particle filtering for stochastic global optimization’ (PFSGO), and the stochastic evolution strategies (SES) algorithm in Salimans et al. (2017) for a high-dimensional non-smooth and non-convex optimization problem. In particular, we apply this algorithms to numerically solve the problem

$$\begin{aligned} \min _{\theta \in \varTheta } \frac{1}{2} \Vert y - X^\top \theta \Vert ^2 + \frac{\rho }{2} \sum _{i=1}^d P_{\lambda ,\gamma }(\theta _i), \end{aligned}$$

(5.3)

where $y \in {\mathbb R}^n$, $X \in {\mathbb R}^{d\times n}$, $\varTheta = [-5,5]^d$, the dimension d is set to different values (see below), and $P_{\lambda ,\gamma }:{\mathbb R}\mapsto {\mathbb R}$ is given by

$$\begin{aligned} P_{\lambda ,\gamma }(x) = \left\{ \begin{aligned}&\lambda |x|&~\text {if} ~|x|\le \lambda ,\\&\tfrac{2\gamma \lambda |x|-x^2-\lambda ^2}{2(\gamma -1)}&~\text {if}~ \lambda<|x|<\gamma \lambda ,\\&\tfrac{\lambda ^2(\gamma +1)}{2}&~\text {if} ~|x|\ge \gamma \lambda , \end{aligned} \right. \end{aligned}$$

where $\lambda > 2$ and $\gamma > 0$. This problem formulation is useful for variable selection, see, e.g., Fan and Li (2001) or Lan and Yang (2019). It is easy to see that problem (5.3) can be written as

$$\begin{aligned} \min _{\theta \in \varTheta } \frac{1}{2} \sum _{i=1}^n (y_i - x_i^\top \theta )^2 + \frac{\rho }{2} \sum _{i=1}^d P_{\lambda ,\gamma }(\theta _i), \end{aligned}$$

(5.4)

where $y_i \in {\mathbb R}$, and $x_i \in {\mathbb R}^d$. This, in turn, makes the problem an instance of (1.1), with

$$\begin{aligned} f_i(\theta ) = \frac{1}{2} (y_i - x_i^\top \theta )^2 + \frac{{\tilde{\rho }}}{2} \sum _{i=1}^d P_{\lambda ,\gamma }(\theta _i), \end{aligned}$$

and $\tilde{\rho } = \rho /n$.

In this problem, we also test the single-worker version of the proposed optimization scheme. We refer to this algorithm simply as SMCO and it is obtained as the particular case of PSMCO with $M=1$. We use the usual jittering kernel of the form (3.1)

$$\begin{aligned} \kappa (\text{ d }\theta | \theta ') = (1 - \epsilon _N) \delta _{\theta '}(\text{ d }\theta ) + \epsilon _N \tau (\text{ d }\theta | \theta '), \end{aligned}$$

where $\tau$ is a Gaussian kernel with covariance $C = \sigma ^2 I_d$ for both methods. We also use the same Gaussian transition kernel for the PFSGO. Let us remark, though, that (unlike SMCO and PSMCO) the PFSGO scheme modifies all particles at every iteration, i.e., it uses $\tau (\cdot | \theta ')$ instead of $\kappa (\cdot |\theta ')$ for sampling. The SES scheme also uses $\tau$ in order to estimate the gradients.

We choose $\sigma ^2 = 10^{-2}$ and $N = 100$. The mini-batch size is taken as $K = 1$ and the number of components is $n = 1,000$. For the PSMCO, we chose $M = 5$, so it essentially runs 5 samplers with 20 particles each while the SMCO scheme runs a single sampler with $N=100$ particles. For the regularization parameters, we choose $\tilde{\rho } = 1, \lambda = 10^{-3}$, and $\gamma = 2.01$. For the SES, we choose a small step size of $\alpha = 10^{-7}$ as larger values cause it to diverge. We simulate the data using a sparse parameter $\theta ^\star$, where only three values are nonzero. We simulate the entries of the matrix X as i.i.d. variates from ${{\mathcal {N}}}(0,1)$ and compute $y = X^\top \theta ^\star$. In order to compute the error for an iterate $\theta _k$ produced by any method, we compute

$$\begin{aligned} \mathsf {NMSE}(k) = \frac{\Vert \theta _k - \theta ^\star \Vert ^2}{\Vert \theta ^\star \Vert ^2}. \end{aligned}$$

The results can be seen in Fig. 3. We also plot the 0.5$\sigma$ curves around the error curves which are averaged over 1, 000 Monte Carlo runs. It can be seen that, for this particular example, the SMCO performs the best, while the PSMCO still outperforms the PFSGO. The SES basically is very slow due to the inefficiency of the gradient estimators for this problem.

Fig. 3

Comparison of algorithms for problem (5.4) with $d = 10$, $N = 100$, and $n = 1,000$. It can be seen that the SMCO is the most efficient method for this problem and the PSMCO ($M = 5$) is the second best. Although PFSGO converges faster, the steady error that it attains is higher. The results are averaged over 1, 000 Monte Carlo runs

Fig. 4

Comparison of algorithms for problem (5.4), with $d = 30$, $N = 1,000$, and $n = 10,000$ –only for the PSMCO ($M = 25$) and PFSGO schemes. The results are averaged over 1, 000 Monte Carlo runs

To gain further insight, we also compare PSMCO ($M = 25$) and the PFSGO on a problem that is higher-dimensional, namely $d = 30$, and with more data points, $n = 10,000$. We set $\sigma ^2 = 10^{-3}$ and leaving other parameters same as in the example with $d = 10$.

Figure 4 displays the results for this example. It can be seen that again the PSMCO algorithm converges to a point which has lower NMSE than the PFSGO. We believe that this is mainly due to the difference in the transition kernels. The PFSGO uses a full transition kernel where every particle is modified whereas jittering enables us to induce slower and more careful changes and also gives us a chance to keep a particle unmodified if it is in a good location.

6 Conclusions

We have proposed a parallel sequential Monte Carlo optimization algorithm which does not require the computation (either exact or approximate) of gradients and, therefore, can be applied to the minimization of challenging cost functions, e.g., with multiple global minima or with broad “flat” regions. The proposed method uses jittering kernels to propagate samples (Crisan and Miguez 2018) and particle kernel density estimators to find the minima (Crisan and Míguez 2014), within a stochastic optimization setup. We have provided a detailed analysis of the proposed scheme. In particular, we have proved that it yields asymptotically optimal solutions to the stochastic optimization problem (1.1) (as the number of samples N is increased) and we have computed explicit convergence rates for the resulting optimizers that depend on N and the dimension of the search space, d. These results are new and improve on classical asymptotic analyses for Monte Carlo optimization methods, which typically lack convergence rates.

From a practical perspective, we argue that the parallel setting where each sampler uses a different configuration of the same dataset can be useful to improve the practical behaviour of the algorithm. To illustrate this point, we have studied the numerical performance of the PSMCO algorithm in scenarios where gradient-based methods struggle to converge. In this work, we have focused on challenging but relatively low-dimensional cost functions. We leave the potential applications of our scheme to high-dimensional optimization problems as a future work. Also the design of an interacting extension of our method similar to particle islands (Vergé et al. 2015) can be potentially useful in more challenging settings.

Appendix

1.1 Proof of Proposition 1

We prove this result by induction. For $t = 1$, let

$$\begin{aligned} \pi _1({\mathrm {d}}\theta ) = \pi _0({\mathrm {d}}\theta ) \frac{G_1(\theta )}{\int _\varTheta G_1(\theta ) \pi _0({\mathrm {d}}\theta )} = \pi _0({\mathrm {d}}\theta ) \frac{G_1(\theta )}{(G_1,\pi _0)}. \end{aligned}$$

Since $G_1 \in B(\varTheta )$ it follows that

$$\begin{aligned} \sup _{\theta \in \varTheta } \left| \frac{G_1(\theta )}{(G_1,\pi _0)}\right| = \frac{\sup _{\theta \in \varTheta } G_1(\theta )}{(G_1,\pi _0)} < \infty \end{aligned}$$

because of Assumption 1. Hence $\pi _1 \ll \pi _0$ is a proper measure. Assume next, as an induction hypothesis, that $\pi _{T-1} \ll \pi _0$. Then

$$\begin{aligned} \pi _T({\mathrm {d}}\theta ) = \pi _{T-1}({\mathrm {d}}\theta ) \frac{G_T(\theta )}{(G_T,\pi _{T-1})} \end{aligned}$$

and Assumption 1 implies (again) that

$$\begin{aligned} \frac{\sup _{\theta \in \varTheta } G_T(\theta )}{(G_T,\pi _{T-1})} < \infty , \end{aligned}$$

hence $\pi _T$ is proper and $\pi _T \ll \pi _0$. Therefore, the Radon-Nikodym derivative of the final measure $\pi _T$ w.r.t. the prior $\pi _0$ is

$$\begin{aligned} \frac{{\mathrm {d}}\pi _T}{{\mathrm {d}}\pi _0}(\theta ) \propto \prod _{t=1}^T G_t(\theta ) = \exp \left( -\sum _{i=1}^n f_i(\theta )\right) . \end{aligned}$$

From here, it readily follows that maximizing this Radon-Nikodym derivative is equivalent to solving problem (1.1). $\square$

1.2 Proof of Theorem 1

We proceed by an induction argument. At time $t = 0$, the bound

$$\begin{aligned} \Vert (\varphi ,\pi _0^N) - (\varphi ,\pi _0) \Vert _p \le \frac{c_{0,p} \Vert \varphi \Vert _\infty }{\sqrt{N}} \end{aligned}$$

is a straightforward consequence of the Marcinkiewicz–Zygmund inequality (Shiryaev 1996) because the particles $\{\theta _0^{(i)}\}_{i=1}^N$ are i.i.d samples from $\pi _0$.

Assume now that, after iteration $t-1$, we have a particle set $\{{\theta }_{t-1}^{(i)}\}_{i=1}^N$ and the empirical measure $\pi ^N_{t-1}(\text{ d }\theta _{t-1}) = \frac{1}{N} \sum _{i=1}^N \delta _{\theta _{t-1}^{(i)}} (\text{ d }\theta _{t-1})$, which satisfies

$$\begin{aligned} \left\| (\varphi ,\pi _{t-1}) - (\varphi ,\pi _{t-1}^N)\right\| _p \le \frac{c_{t-1,p} \Vert \varphi \Vert _\infty }{\sqrt{N}}. \end{aligned}$$

(A.1)

We first analyze the error in the jittering step. To this end, we construct the jittered random measure

$$\begin{aligned} \hat{\pi }^N_t({\mathrm {d}}\theta ) = \frac{1}{N} \sum _{i=1}^N \delta _{\hat{\theta }_t^{(i)}}({\mathrm {d}}\theta ) \end{aligned}$$

and iterate the triangle inequality to obtain

$$\begin{aligned}&\Vert (\varphi ,\pi _{t-1}) - (\varphi ,\hat{\pi }_t^N)\Vert _p \le \Vert (\varphi ,\pi _{t-1}) - (\varphi ,\pi ^N_{t-1})\Vert _p \nonumber \\&\quad +\Vert (\varphi ,\pi _{t-1}^N) - (\varphi ,\kappa {\pi }_{t-1}^N)\Vert _p \nonumber \\&\quad + \Vert (\varphi ,\kappa \pi _{t-1}^N) - (\varphi ,\hat{\pi }_t^N)\Vert _p, \end{aligned}$$

(A.2)

where

$$\begin{aligned} \kappa \pi _{t-1}^N = \int \kappa (\text{ d }\theta |\theta _{t-1}) \pi _{t-1}^N(\text{ d }\theta _{t-1}) = \frac{1}{N} \sum _{i=1}^N \kappa (\text{ d }\theta |{\theta _{t-1}^{(i)}}). \end{aligned}$$

The first term on the right-hand side (rhs) of (A.2) is bounded by the induction hypothesis (A.1). For the second term, we note that,

$$\begin{aligned}&\left| (\varphi ,\pi _{t-1}^N) - (\varphi ,\kappa {\pi }_{t-1}^N)\right| \nonumber \\&\quad = \left| \frac{1}{N} \sum _{i=1}^N \varphi (\theta _{t-1}^{(i)}) - \frac{1}{N} \sum _{i=1}^N \int \varphi (\theta ) \kappa (\text{ d }\theta |{\theta _{t-1}^{(i)}}) \right| \nonumber \\&\quad = \left| \frac{1}{N} \sum _{i=1}^N \int \left( \varphi (\theta _{t-1}^{(i)}) - \varphi (\theta )\right) \kappa (\text{ d }\theta |{\theta _{t-1}^{(i)}}) \right| \nonumber \\&\quad \le \frac{1}{N} \sum _{i=1}^N \int \left| \varphi (\theta _{t-1}^{(i)}) - \varphi (\theta ) \right| \kappa (\text{ d }\theta |{\theta _{t-1}^{(i)}})\nonumber \\&\quad \le \frac{c_\kappa \Vert \varphi \Vert _\infty }{\sqrt{N}}, \end{aligned}$$

(A.3)

where the last inequality follows from Assumption 2. The upper bound in (A.3) is deterministic, so the inequality readily implies that

$$\begin{aligned} \Vert (\varphi ,\pi _{t-1}^N) - (\varphi ,\kappa \pi _{t-1}^N)\Vert _p \le \frac{c_\kappa \Vert \varphi \Vert _\infty }{\sqrt{N}}. \end{aligned}$$

(A.4)

For the last term on the right-hand side of (A.2), we let ${{\mathcal {F}}}_{t-1}$ be the $\sigma$-algebra generated by the random sequence $\{\theta _{0:t-1}^{(i)},\hat{\theta }_{1:t-1}^{(i)}\}_{i=1}^N$. Let us first note that

$$\begin{aligned} {\mathbb E}\left[ (\varphi ,\hat{\pi }_t) | {{\mathcal {F}}}_{t-1}\right]&= \frac{1}{N} \sum _{i=1}^N {\mathbb E}\left[ \varphi (\hat{\theta }_t^{(i)}) | {{\mathcal {F}}}_{t-1} \right] \\&= \frac{1}{N}\sum _{i=1}^N \int \varphi (\theta ) \kappa ({\mathrm {d}}\theta |\theta _{t-1}^{(i)}) = (\varphi ,\kappa \pi _{t-1}^N). \end{aligned}$$

Therefore, the difference $(\varphi ,\hat{\pi }_t^N) -(\varphi ,\kappa \pi _{t-1}^N)$ takes the form

$$\begin{aligned} (\varphi ,\hat{\pi }_t^N) - (\varphi ,\kappa \pi _{t-1}^N) = \frac{1}{N} \sum _{i=1}^N S^{(i)}, \end{aligned}$$

where $S^{(i)} = \varphi (\hat{\theta }_t^{(i)}) - {\mathbb E}[\varphi (\hat{\theta }_t^{(i)})|{{\mathcal {F}}}_{t-1}]$, $i = 1,\ldots ,N$, are zero-mean and conditionally independent random variables, with $|S^{(i)}| \le 2 \Vert \varphi \Vert _\infty$. Then, we readily obtain the bound

$$\begin{aligned} {\mathbb E}\left[ \left. \left| (\varphi ,\hat{\pi }_t^N) - (\varphi ,\kappa \pi _{t-1}^N)\right| ^p \right| {{\mathcal {F}}}_{t-1}\right]&= \frac{1}{N^p} {\mathbb E}\left[ \left. \left| \sum _{i=1}^N S^{(i)}\right| ^p\right| {{\mathcal {F}}}_{t-1}\right] \nonumber \\&\le \frac{B_{t,p} N^{\frac{p}{2}}\Vert \varphi \Vert _\infty ^p}{N^p}. \end{aligned}$$

(A.5)

where the relation (A.5) follows from the Marcinkiewicz–Zygmund inequality (Shiryaev 1996) and $B_{t,p} < \infty$ is some constant independent of N. Taking unconditional expectations on both sides of (A.5) and then computing $(\cdot )^\frac{1}{p}$ yields

$$\begin{aligned} \Vert (\varphi ,\hat{\pi }_t^N) - (\varphi ,\kappa \pi _{t-1}^N)\Vert _p \le \frac{\hat{c}_{t,p} \Vert \varphi \Vert _\infty }{\sqrt{N}}. \end{aligned}$$

(A.6)

where $\hat{c}_{t,p} = B_{t,p}^{\frac{1}{p}}$ is a finite constant independent of N. Therefore, taking together (A.1), (A.4) and (A.6) we have established that

$$\begin{aligned} \Vert (\varphi ,\pi _{t-1}) - (\varphi ,\hat{\pi }_t^N)\Vert _p \le&\frac{c_{1,t,p} \Vert \varphi \Vert _\infty }{\sqrt{N}}, \end{aligned}$$

(A.7)

where $c_{1,t,p} = c_{t-1,p} + c_\kappa + \hat{c}_{t,p} < \infty$ is a finite constant independent of N.

Next, we have to bound the error after the weighting step. We recall that

$$\begin{aligned} \pi _t(\text{ d }\theta ) = \pi _{t-1}(\text{ d }\theta ) \frac{G_t(\theta )}{(G_t,\pi _{t-1})} \end{aligned}$$

and define

$$\begin{aligned} \tilde{\pi }_t^N(\text{ d }\theta ) = \hat{\pi }^N_{t}(\text{ d }\theta ) \frac{G_t(\theta )}{(G_t,\hat{\pi }^N_{t})} \end{aligned}$$

where $\tilde{\pi }_t^N$ denotes the weighted measure. We first note that

$$\begin{aligned}&|(\varphi ,\pi _t) - (\varphi ,\tilde{\pi }_t^N)| = \left| \frac{(\varphi G_t, \pi _{t-1})}{(G_t,\pi _{t-1})} - \frac{(\varphi G_t, \hat{\pi }_t^N)}{(G_t,\hat{\pi }_t^N)} \pm \frac{(\varphi G_t, \hat{\pi }^N_t)}{(G_t,\pi _{t-1})} \right| \nonumber \\&\le \frac{\left| (\varphi G_t, \pi _{t-1}) - (\varphi G_t, \hat{\pi }_t^N)\right| + \Vert \varphi \Vert _\infty |(G_t,\hat{\pi }_t^N) - (G_t,\pi _{t-1})|}{(G_t,\pi _{t-1})}. \end{aligned}$$

(A.8)

Using Minkowski’s inequality together with (A.7) and (A.8) yields

$$\begin{aligned} \Vert (\varphi ,\pi _t) - (\varphi ,\tilde{\pi }_t^N)\Vert _p&\le \frac{c_{1,t,p} \Vert \varphi G_t\Vert _\infty + c_{1,t,p} \Vert \varphi \Vert _\infty \Vert G_t\Vert _\infty }{(G_t,\pi _{t-1})\sqrt{N}}, \\&\le \frac{2 c_{1,t,p} \Vert \varphi \Vert _\infty \Vert G_t\Vert _\infty }{(G_t,\pi _{t-1})\sqrt{N}} \end{aligned}$$

where the second inequality follows from $\Vert \varphi G_t \Vert _\infty \le \Vert \varphi \Vert _\infty \Vert G_t\Vert _\infty$. More concisely, we have

$$\begin{aligned} \Vert (\varphi ,\pi _t) - (\varphi ,\tilde{\pi }_t^N)\Vert _p \le \frac{c_{2,t,p} \Vert \varphi \Vert _\infty }{\sqrt{N}} \end{aligned}$$

(A.9)

where the constant

$$\begin{aligned} c_{2,t,p} = \frac{2 c_{1,t,p} \Vert G_t\Vert _\infty }{(G_t,\pi _{t-1})} < \infty \end{aligned}$$

is independent of N. Note that the assumptions on $(G_t)_{t\ge 1}$ imply that $(G_t,\pi _{t-1}) > 0$.

Finally, we bound the resampling step. Note that the resampling step consists of drawing N i.i.d samples from $\tilde{\pi }_t^N$, i.e., $\theta _t^{(i)} \sim \tilde{\pi }_t^N$ i.i.d for $i = 1, \ldots ,N$, and then constructing

$$\begin{aligned} \pi ^N_t(\text{ d }\theta ) = \frac{1}{N} \sum _{i=1}^N \delta _{\theta _t^{(i)}}(\text{ d }\theta ). \end{aligned}$$

Since samples are i.i.d, as in the base case, we have,

$$\begin{aligned} \Vert (\varphi ,\tilde{\pi }_t^N) - (\varphi ,\pi _t^N)\Vert _p \le \frac{\tilde{c}_p \Vert \varphi \Vert _\infty }{\sqrt{N}}, \end{aligned}$$

(A.10)

for some constant $\tilde{c}_p < \infty$ independent of N. Now combining (A.9) and (A.10), we have the desired result,

$$\begin{aligned} \Vert (\varphi ,\pi _t) - (\varphi ,\pi _t^N)\Vert _p \le \frac{c_t \Vert \varphi \Vert _\infty }{\sqrt{N}} \end{aligned}$$

where $c_t = c_{2,t,p} + \tilde{c}_p$ is a finite constant independent of N. $\square$

1.3 Proof of Corollary 1

From Theorem 1, we obtain

$$\begin{aligned} \Vert (\varphi ,\pi _t) - (\varphi ,\pi _t^N)\Vert _p \le \frac{c_t \Vert \varphi \Vert _\infty }{\sqrt{N}}, \end{aligned}$$

where $c_t < \infty$ is a constant independent of N. Let us choose $p\ge 4$ and $0< \epsilon < 1$. We construct the nonnegative random variable

$$\begin{aligned} U_{t,\epsilon }^{p} = \sum _{N=1}^\infty N^{\frac{p}{2} - 1 - \epsilon } |(\varphi ,\pi _t) - (\varphi ,\pi _t^N)|^p. \end{aligned}$$

and use Fatou’s lemma to obtain

$$\begin{aligned} {\mathbb E}[U_{t,\epsilon }^{p}]&\le \sum _{N=1}^\infty N^{\frac{p}{2} - 1 - \epsilon } {\mathbb E}\left[ \left| (\varphi ,\pi _t) - (\varphi ,\pi ^N_t)\right| ^p \right] ,\nonumber \\&\le c^p \Vert \varphi \Vert _\infty ^p \sum _{N=1}^\infty N^{- 1 - \epsilon } < \infty , \end{aligned}$$

(A.11)

where the second inequality follows from Theorem 1. The relationship (A.11) implies that the r.v. $U^p_{t,\epsilon }$ is a.s. finite.

Finally, since (trivially) $N^{\frac{p}{2} - 1 - \epsilon } |(\varphi ,\pi _t) - (\varphi ,\pi _t^N)|^p \le U_{t,\epsilon }^{p}$, we have

$$\begin{aligned} |(\varphi ,\pi _t) - (\varphi ,\pi _t^N)| \le \frac{U_{t,\delta }}{N^{\frac{1}{2} - \delta }}, \end{aligned}$$

(A.12)

where $\delta = \frac{1 + \epsilon }{p}$ and $U_{t,\delta } = (U_{t,\epsilon }^{p})^{\frac{1}{p}}$. Since $p\ge 4$ and $0< \epsilon < 1$, it follows that $0< \delta < \frac{1}{2}$. The almost sure convergence follows from (A.12). Taking $N\rightarrow \infty$ yields

$$\begin{aligned} \lim _{N\rightarrow \infty } |(\varphi ,\pi _t) - (\varphi ,\pi _t^N)| = 0 \quad \quad \text {a.s.} \end{aligned}$$

$\square$

1.4 Proof of Proposition 2

Recall the assumption

$$\begin{aligned} |F_t(\theta ) - F_t(\theta ')| \le \ell _t \Vert \theta -\theta '\Vert . \end{aligned}$$

We write $F_t^\star = \min _{\theta \in \varTheta } F_t(\theta )$, which is assumed to be finite, but not necessarily nonnegative. We first prove that $\exp (-F_t(\theta ))$ is also Lipschitz continuous. Note that we trivially have $\exp (-F_t(\theta )) \le \exp (-F^\star _t)$ for all $\theta$ since $F_t(\theta ) \ge F_t^\star$ for all $\theta$. Now consider any $(\theta ,\theta ') \in \varTheta \times \varTheta$. We first consider the case where $F_t(\theta ) \le F_t(\theta ')$. We obtain

$$\begin{aligned} 0 < e^{-F_t(\theta )} - e^{-F_t(\theta ')}&= e^{-F_t(\theta )} \left( 1 - e^{F_t(\theta ) - F_t(\theta ')}\right) ,\nonumber \\&\le e^{-F_t(\theta )} \left( 1 - (1 + F_t(\theta ) - F_t(\theta '))\right) , \end{aligned}$$

(A.13)

where we have used the inequality $e^a \ge 1 + a$. Therefore, we readily obtain from (A.13)

$$\begin{aligned} 0< e^{-F_t(\theta )} - e^{-F_t(\theta ')}&\le e^{-F_t(\theta )} \left( F_t(\theta ') - F_t(\theta )\right) ,\nonumber \\&\le e^{-F_t^\star } \left( F_t(\theta ') - F_t(\theta )\right) \end{aligned}$$

(A.14)

$$\begin{aligned}&= e^{-F_t^\star } |F_t(\theta ') - F_t(\theta )|, \end{aligned}$$

(A.15)

since $F_t(\theta ) \le F_t(\theta ')$. Next, assume otherwise, i.e., $F_t(\theta ) \ge F_t(\theta ')$. In this case, we can also show using the same line of reasoning that

$$\begin{aligned} e^{-F_t(\theta ')} - e^{-F_t(\theta )}&\le e^{-F_t^\star } \left( F_t(\theta ) - F_t(\theta ')\right) \end{aligned}$$

(A.16)

$$\begin{aligned}&= e^{-F_t^\star } |F_t(\theta ') - F_t(\theta )|, \end{aligned}$$

(A.17)

since $F_t(\theta ) \ge F_t(\theta ')$. Therefore, we can conclude (combining (A.15) and (A.16)) that

$$\begin{aligned} |e^{-F_t(\theta )} - e^{-F_t(\theta ')}| \le e^{-F_t^\star } |F_t(\theta ') - F_t(\theta )| \le e^{-F_t^\star } \ell _t \Vert \theta - \theta '\Vert , \end{aligned}$$

where the last inequality holds because $F_t$ is Lipschitz. Finally recall that

$$\begin{aligned} \pi _t(\theta ) = \frac{e^{-F_t(\theta )}}{Z_{\pi _t}}, \end{aligned}$$

where we denote $Z_{\pi _t} = \int _\varTheta e^{-F_t(\theta )}{\mathrm {d}}\theta$. We straightforwardly obtain

$$\begin{aligned} |\pi _t(\theta ) - \pi _t(\theta ')| \le \frac{1}{Z_{\pi _t}} e^{-F_t^\star } \ell _t \Vert \theta - \theta '\Vert . \end{aligned}$$

$\square$

1.5 Proof of Theorem 2

Using the proof of Theorem 4.2 and Corollary 4.1 in Crisan and Míguez (2014), we obtain

$$\begin{aligned} \sup _{\theta \in \varTheta } | {{\mathsf {p}}}_t^N(\theta ) - \pi _t(\theta )| \le \frac{V_{1,\varepsilon }}{\left\lfloor {N^{\frac{1}{2 (d + 1)}}}\right\rfloor ^{1-\varepsilon }}, \end{aligned}$$

where $V_{1,\varepsilon }$ is an a.s. finite random variable. Noting that

$$\begin{aligned} \sup _{a \ge 1} \frac{a}{\left\lfloor a \right\rfloor } = 2, \end{aligned}$$

we obtain

$$\begin{aligned} \sup _{\theta \in \varTheta } | {{\mathsf {p}}}_t^N(\theta ) - \pi _t(\theta )| \le \frac{V_\varepsilon }{N^{\frac{1-\varepsilon }{2 (d + 1)}}}, \end{aligned}$$

where $V_\varepsilon = 2 V_{1,\varepsilon }$ is an almost surely finite random variable. $\square$

1.6 Proof of Theorem 3

Recall that $\pi _t(\theta )$ is a probability density w.r.t. the Lebesgue measure. Choose $\theta _t^\star \in \arg \max _{\theta \in \varTheta } \pi _t(\theta )$ and construct the ball

$$\begin{aligned} B_{t,n}^\star := B\left( \theta _t^\star , \frac{1}{n} \right) \subset \varTheta \end{aligned}$$

where $n \ge 1$ is a positive integer. We assume, without loss of generality, that $B_{t,1}^\star \subseteq \varTheta$ and denote

$$\begin{aligned} \pi _t(B_{t,n}^\star ) = \int _{B_{t,n}^\star } \pi _t(\theta ) {\mathrm {d}}\theta \quad \text{ and } \quad \pi _t^N(B_{t,n}^\star ) = \int _{B_{t,n}^\star } \pi _t^N({\mathrm {d}}\theta ). \end{aligned}$$

Also recall that the grid of points generated by the SMC sampler at time t is $\{ \theta _t^{(i)} \}_{1 \le i \le N} \subset \varTheta$ and the estimate of $\theta _t^\star$ obtained from the grid is denoted

$$\begin{aligned} \theta _t^{\star ,N} \in \arg \max _{\theta \in \{ \theta _t^{(i)} \}_{1 \le i \le N} } {\textsf {p}}_t^N(\theta ), \end{aligned}$$

(A.18)

where ${\textsf {p}}_t^N(\theta )$ is the kernel density estimator of $\pi _t$. Our argument to prove Theorem 3 proceeds in two steps:

• 1. We show that, for any given $n \ge 1$, one can a.s. find N sufficiently large to ensure that $\{ \theta _t^{(i)} \}_{1 \le i \le N} \cap B_{t,n}^\star \ne \emptyset$, i.e., that there are points of the grid contained in the ball $B_{t,n}^\star$. Moreover, we deduce an inequality that relates the radius $n^{-1}$ of the ball $B_{t,n}^\star$ with the number of necessary particles N.

• 2. From the existence of at least one particle $\theta _t^{(i)}$ inside $B_{t,n}^\star$ and the assumption that $\pi _t(\theta )$ is Lipschitz, we deduce bounds for the differences $|\pi _t(\theta _t^\star )-\pi _t(\theta _t^{(i)})|$ and $|\pi _t(\theta _t^{\star ,N})-\pi _t(\theta _t^{(i)})|$, and, as a consequence, for the approximation error $|\pi _t(\theta _t^{\star ,N})-\pi _t(\theta _t^\star )|$.

1.6.1 The ball $B_{t,n}^\star$ is a.s. non-empty

Since $\pi _t(\theta )$ is assumed continuous at every $\theta _t^\star \in \arg \max _{\theta \in \varTheta }$$\pi _t(\theta )$, we have $\pi _t(B_{t,n}^\star )>0$. Therefore, for every $n<\infty$, Theorem 2 ensures that there exists $N_n$ (a.s. finite) such that for all $N \ge N_n$,

$$\begin{aligned} \left| \pi _t^N(B_{t,n}^\star ) - \pi _t(B_{t,n}^\star ) \right|< \frac{ U_{t,\delta } }{ N^{\frac{1}{2}-\delta } } < \frac{ \pi _t(B_{t,n}^\star )}{2}, \end{aligned}$$

(A.19)

where $U_{t,\delta }$ is an a.s. finite random variable and $\delta \in (0,\frac{1}{2})$ is an arbitrarily small constant (both independent of N). Moreover, the second inequality in (A.19) implies that

$$\begin{aligned} \pi _t^N(B_{t,n}^\star )> \frac{\pi _t(B_{t,n}^\star )}{2} > 0. \end{aligned}$$

(A.20)

Therefore, for all $N>N_n$ there exists at least one integer $i_b \in \{1, \ldots , N\}$ such that $\theta _t^{(i_b)} \in B_{t,n}^\star$.

To be specific, since $\pi _t(\theta )$ is a density w.r.t. the Lebesgue measure, we can readily find a lower bound for the integral $\pi _t(B_{t,n}^\star )$, namely

$$\begin{aligned} \frac{\pi _t(B_{t,n}^\star )}{2}> \frac{1}{2} \text {Leb}\left( B_{t,n}^\star \right) \times \inf _{\theta \in B_{t,n}^\star } \pi _t(\theta ) > c_{t,d} n^{-d} \end{aligned}$$

where $\text {Leb}(B_{t,n}^\star ) = \frac{\pi ^{\frac{d}{2}}}{\varGamma \left( \frac{d}{2}+1 \right) n^d}$ is the Lebesgue measure of the d-dimensional ball with radius $n^{-1}$, $\varGamma (\cdot )$ is Euler’s gamma function and

$$\begin{aligned} c_{t,d} := \frac{\pi ^{\frac{d}{2}}}{2 \varGamma \left( \frac{d}{2}+1 \right) n^d} \times \inf _{\theta \in B_{t,1}^\star } \pi _t(\theta ) > 0. \end{aligned}$$

Therefore, for any given $n<\infty$, if we choose N such that $0< \frac{ U_{t,\delta } }{ N^{\frac{1}{2}-\delta } } < c_{t,d}n^{-d}$, i.e.,

$$\begin{aligned} N \ge N_n := \left( \frac{ U_{t,\delta } }{ c_{t,d} } \right) ^{\frac{2}{1-2\delta }} n^{\frac{2d}{1-2\delta }} \end{aligned}$$

(A.21)

then the inequalities (A.19) and (A.20) hold a.s. (note that $N_n<\infty$ a.s. because $n<\infty$ and $U_{t,\delta }<\infty$ a.s.).

1.6.2 Error bounds

Choose $i_b \in \{1, \ldots , N\}$ such that $\theta _t^{(i_b)} \in B_{t,n}^\star$. Such index exists a.s. whenever N satisfies the inequality (A.21). Let us recall the construction of the estimate $\theta _t^{\star ,N}$ from expression (A.18) and denote

$$\begin{aligned} {\hat{\theta }}_t^{\star ,N} \in \arg \max _{\theta \in \varTheta } {\textsf {p}}_t^N(\theta ). \end{aligned}$$

Let $L_t<\infty$ be the Lipschitz constant of the pdf $\pi _t(\theta )$. Since $\theta _t^{(i_b)} \in B_{t,n}^\star$, we readily obtain the upper bound

$$\begin{aligned} \pi _t(\theta _t^\star ) - \pi _t(\theta _t^{(i_b)}) < L_t n^{-1} \end{aligned}$$

and, therefore,

$$\begin{aligned} \pi _t(\theta _t^\star ) - L_t n^{-1} < \pi _t(\theta _t^{(i_b)}). \end{aligned}$$

(A.22)

However, using Theorem 2 we obtain

$$\begin{aligned} \left| \pi _t(\theta _t^{(i_b)}) - {\textsf {p}}_t^N(\theta _t^{(i_b)}) \right| < \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} }, \end{aligned}$$

(A.23)

where $\varepsilon \in (0,1)$ is an arbitrarily small constant and $V_{t,\varepsilon }$ is an a.s. finite random variable, both independent of N. Combining (A.22) and (A.23) yields

$$\begin{aligned} {\textsf {p}}_t^N(\theta _t^{(i_b)})> \pi _t(\theta _t^{(i_b)}) - \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} } > \pi _t(\theta _t^\star ) - L_t n^{-1} - \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} } \end{aligned}$$

and, as a consequence,

$$\begin{aligned} {\textsf {p}}_t^N(\theta _t^{\star ,N}) \ge {\textsf {p}}_t^N(\theta _t^{(i_b)}) > \pi _t(\theta _t^\star ) - L_t n^{-1} - \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} }. \nonumber \\ \end{aligned}$$

(A.24)

Moreover, using Theorem 2 again, we find that

$$\begin{aligned} \left| \pi _t({\hat{\theta }}_t^{\star ,N}) - {\textsf {p}}_t^N({\hat{\theta }}_t^{\star ,N}) \right| < \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} }, \end{aligned}$$

(A.25)

with the same constant $\varepsilon \in (0,1)$ and a.s. finite random variable $V_{t,\varepsilon }$ as in (A.24). Since $\pi _t({\hat{\theta }}_t^{\star ,N}) \le \pi _t(\theta _t^\star )$, the inequality (A.25) implies that

$$\begin{aligned} {\textsf {p}}_t^N({\hat{\theta }}_t^{\star ,N}) < \pi _t(\theta _t^\star ) + \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} } \end{aligned}$$

and, since ${\textsf {p}}_t^N(\theta _t^{\star ,N}) \le {\textsf {p}}_t^N({\hat{\theta }}_t^{\star ,N})$, we arrive at

$$\begin{aligned} {\textsf {p}}_t^N(\theta _t^{\star ,N}) < \pi _t(\theta _t^\star ) + \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} }. \end{aligned}$$

(A.26)

Taking the inequalities (A.24) and (A.26) together, we readily obtain the uniform bound (for $\theta \in \varTheta$)

$$\begin{aligned} \left| \pi _t(\theta _t^\star ) - {\textsf {p}}_t^N(\theta _t^{\star ,N}) \right| < \frac{ V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} } + L_t n^{-1} \end{aligned}$$

(A.27)

and a simple triangle inequality then yields

$$\begin{aligned} \left| \pi _t(\theta _t^{\star ,N}) - \pi _t(\theta _t^\star ) \right|\le & {} \left| \pi _t(\theta _t^{\star ,N}) - {\textsf {p}}_t^N(\theta _t^{\star ,N}) \right| \nonumber \\&+ \left| {\textsf {p}}_t^N(\theta _t^{\star ,N}) - \pi _t(\theta _t^\star ) \right| \nonumber \\< & {} \frac{ 2V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} } + L_t n^{-1}, \end{aligned}$$

(A.28)

where the second inequality follows from (A.27) and yet another application of Theorem 2.

The inequality (A.28) holds for any pair of integers (N, n) that satisfies the relationship (A.21). For any given N, sufficiently large for

$$\begin{aligned} n_N := \sup \left\{ m \in \mathbb {N}: m^{-1} > \left( \frac{ U_{t,\delta } }{ c_{t,d} } \right) ^{\frac{1}{d}} \frac{1}{N^{\frac{1 - 2\delta }{2d}}} \right\} \end{aligned}$$

to be well defined, the pair consisting of N and $n=n_N$ satisfies (A.21), while

$$\begin{aligned} n_N^{-1} \le 2 \left( \frac{ U_{t,\delta } }{ c_{t,d} } \right) ^{\frac{1}{d}} \frac{1}{N^{\frac{1 - 2\delta }{2d}}}. \end{aligned}$$

(A.29)

Hence, if we substitute $n=n_N$ in the inequality (A.28) and then apply the inequality (A.29) we arrive at

$$\begin{aligned} \left| \pi _t(\theta _t^{\star ,N}) - \pi _t(\theta _t^\star ) \right| < \frac{ 2V_{t,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} } + 2 \left( \frac{ U_{t,\delta } }{ c_{t,d} } \right) ^{\frac{1}{d}} \frac{ L_t }{ N^{\frac{1 - 2\delta }{2d}} }, \end{aligned}$$

(A.30)

where $V_{t,\varepsilon }$ and $U_{t,\delta }$ are a.s. finite, and $L_t$ and $c_{t,d}$ are finite. The constants $\varepsilon \in (0,1)$ and $\delta \in (0,1/2)$ can be chosen arbitrarily small. Hence, if we let $0<\delta = \varepsilon / 2<\frac{1}{2}$, the r.h.s. of (A.30) can be upper bounded, which results in the bound

$$\begin{aligned} \left| \pi _t(\theta _t^{\star ,N}) - \pi _t(\theta _t^\star ) \right| < \frac{ W_{t,d,\varepsilon } }{ N^{\frac{1-\varepsilon }{2(d+1)}} }, \end{aligned}$$

where

$$\begin{aligned} W_{t,d,\varepsilon } = 2\left[ V_{t,\varepsilon } + \left( \frac{ U_{t,\delta (\varepsilon )} }{ c_{t,d} } \right) ^{\frac{1}{d}} L_t \right] < \infty \quad \text{ a.s. } \end{aligned}$$

1.7 Proof of Corollary 2

Recall that

$$\begin{aligned} \Vert f\Vert _\infty = \sup _{\theta \in \varTheta } |f(\theta )| < \infty . \end{aligned}$$

Note that Theorem 3 implies that

$$\begin{aligned} 0 \le e^{-f(\theta ^\star )} - e^{- f(\theta _T^{\star ,N})} \le \frac{W_{T,d,\varepsilon } Z_{\pi _T}}{N^\frac{1}{2(d+1)}}, \end{aligned}$$

(A.31)

where $Z_{\pi _T}$ is the normalizing constant of $\pi _T$. Next, we lower bound the left-hand side of (A.31) as

$$\begin{aligned} e^{-f(\theta ^\star )} - e^{- f(\theta _T^{\star ,N})}&= e^{- f(\theta _T^{\star ,N})} \left( e^{f(\theta _T^{\star ,N}) - f(\theta ^\star )} - 1\right) \nonumber \\&\ge e^{-\Vert f\Vert _\infty } (f(\theta _T^{\star ,N}) - f(\theta ^\star )) \end{aligned}$$

(A.32)

where the last inequality follows from the relationships

$$\begin{aligned} e^{-f(\theta _T^{\star ,N})} \ge e^{-\Vert f\Vert _\infty } \end{aligned}$$

(since $f(\theta _T^{\star ,N}) \le \Vert f\Vert _\infty$) and $e^a \ge a + 1$ for $a \in {\mathbb R}$. Combining (A.31) and (A.32), we obtain

$$\begin{aligned} f(\theta _T^{\star ,N}) - f(\theta ^\star ) \le \frac{\tilde{W}_{T,d,\varepsilon }}{{N^\frac{1}{2(d+1)}}} \end{aligned}$$

where

$$\begin{aligned} \tilde{W}_{T,d,\varepsilon } = Z_{\pi _T} W_{T,d,\varepsilon } e^{\Vert f\Vert _\infty } \end{aligned}$$

is a.s. finite.