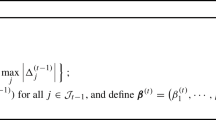1 Introduction

The future remains unknown, yet we have witnessed considerably improved predictions owing to advances in statistical and machine learning over the last two decades. Numerous procedures, such as support vector machines, random forests, and tree boosting, deliver accurate point predictions of conditional means. However, in many applications, a mean prediction is not good enough. Full predictive distributions, also known as probabilistic forecasts, are required in applications where an assessment of the associated uncertainty is essential, for example in models of future disease progression (Küffner et al. 2015), electricity demand (Cabrera and Schulz 2017), stock asset returns (Mitrodima and Griffin 2017), and counterfactual distributions (Chernozhukov et al. 2013). In these applications, the prediction “takes the form of a predictive probability distribution over future quantities or events of interest” (Gneiting and Katzfuss 2014). Here, I present a novel generic boosting approach to the estimation of full predictive distributions under mild assumptions.

Apart from completely model-free procedures (such as kernel smoothing, Li and Racine 2008), four main approaches of obtaining predictive distributions exist. (1) Flexible parametric models for conditional density functions rely on a strict parametric model of the response distribution those parameters might be linked to predictor variables in complex ways, for example, in generalized additive models for location, scale, and shape (GAMLSS, Rigby and Stasinopoulos 2005) and in heteroscedastic Bayesian additive regression tree ensembles (Pratola et al. 2017). (2) Quantile regression models for conditional quantiles of interest can be modelled in a linear or nonlinear additive form (Koenker 2005); more complex relationships can be estimated by quantile regression forests (Meinshausen 2006; Athey et al. 2019). (3) Distribution regression and transformation models potentially allow response-varying (or time-varying) effects (Foresi and Peracchi 1995; Rothe and Wied 2013; Chernozhukov et al. 2013; Wu and Tian 2013; Leorato and Peracchi 2015) in models for conditional distribution functions on the probit, logit, or complementary log–log scale. (4) Hazard regression (Kooperberg et al. 1995) aims at estimating conditional nonproportional hazard functions directly.

Boosting, and especially the statistical view on boosting (Friedman et al. 2000; Bühlmann and Hothorn 2007), have already proved helpful in these four different approaches. Mayr et al. (2012) developed boosting for GAMLSS, conditional quantile boosting was introduced by Fenske et al. (2011), and nonproportional hazard boosting was recently introduced by Lee and Chen (2018). Distribution regression is a special case of conditional transformation models (Hothorn et al. 2014). What is interesting about conditional transformation models is that very simple models, such as the linear proportional odds and hazards models, and essentially unstructured models for conditional distribution functions can be understood in a unified theoretical framework (Hothorn et al. 2018). The same level of generality is, however, lacking from an algorithmic perspective. The boosting algorithm introduced by Hothorn et al. (2014) is limited to additive models and explicitly excludes tree-based interaction models. Furthermore, the target function is approximate and applicable to responses observed without censoring or truncation only. The aim of this work is to establish a general computational framework that allows specification, estimation, evaluation, and comparison in a cascade of models starting with very simple linear models and ending with essentially unstructured models for conditional distribution functions for arbitrary response variables.

Section 2 gives a dense introduction to transformation models. An elaborate description and connections to well-established models can be found in Hothorn et al. (2014) and Hothorn et al. (2018). Sections 3 and 4 develop two boosting algorithms for complex and simple transformation models based on a generic form of the likelihood (technical details regarding the definition of the likelihood for all types of response variables, including random censoring and truncation, are discussed by Hothorn et al. 2018). Empirical evaluations are presented in Sect. 5.

2 Transformation models

Let \(Y\) denote a univariate and at least ordered response variable on a measurable space \(({\varXi }, {\mathfrak {C}})\) and \(\varvec{X}\in \chi \) a set of predictor variables with joint distribution \((Y, \varvec{X}) \sim {\mathbb {P}}_{Y, \varvec{X}}\). Based on random samples from \({\mathbb {P}}_{Y, \varvec{X}}\), the goal is to estimate the conditional distribution \({\mathbb {P}}_{Y\mid \varvec{X}= \varvec{x}}\) of a response given predictors. For each conditional cumulative distribution function \(F_{Y\mid \varvec{X}= \varvec{x}}(y) = {\mathbb {P}}_{Y\mid \varvec{X}= \varvec{x}}(\{\upsilon \in {\varXi }\mid \upsilon < y\})\), a unique conditional transformation function \(h: {\varXi }\times \chi \rightarrow {\mathbb {R}}\) exists such that \(F_{Y\mid \varvec{X}= \varvec{x}}(y) = F_Z(h(y\mid \varvec{x}))\), assuming \(F_Z: {\mathbb {R}}\rightarrow [0, 1]\) is an a priori given cumulative distribution function of an absolutely continuous random variable \(Z\) with log-concave density \(f_Z\) (Hothorn et al. 2018). The conditional transformation function \(h\) is monotonic in \(y\)

(1)

Starting with Box and Cox (1964), shift transformation functions based on the decomposition \(h(y\mid \varvec{x}) = h_Y(y) - \beta (\varvec{x})\) featuring a baseline transformation function \(h_Y: {\varXi }\rightarrow {\mathbb {R}}\) and a shift term \(\beta : \chi \rightarrow {\mathbb {R}}\) have been studied intensively. The proportional hazards (with \(F_Z(z) = 1 - \exp (-\exp (z))\)) and proportional odds (with \(F_Z(z) = \text {expit}(z)\)) models are the most well-known representatives of this class of shift transformation models (STM, often also referred to as linear or nonlinear transformation models, depending on the functional form of \(\beta (\varvec{x})\)). Boosting procedures that allow flexible estimation of \(\beta (\varvec{x})\) have been studied for proportional hazards models under right censoring (Ridgeway 1999; Schmid and Hothorn 2008; Lu and Li 2008; Yue et al. 2017) and proportional odds models have been studied for ordered responses (Schmid et al. 2011). A comparison of prominent and less prominent members of this model class is given in Hothorn et al. (2018).

Structured additive transformation functions that allow interactions between the two arguments \(y\) and \(\varvec{x}\) of the form \(h(y\mid \varvec{x}) = \sum _{j = 1}^J h_j(y\mid \varvec{x})\) lead to conditional transformation models (CTM, Hothorn et al. 2014). The J partial transformation functions \(h_j\) allow formulation of problem-specific effects of the predictors \(\varvec{x}\), such as linear, nonlinear, spatio-temporal, or other model terms. Distribution regression models featuring response-varying effects are an important special case of this model class. When \(\varvec{x}= (x_1, \dots , x_J) \in {\mathbb {R}}^J\), a distribution regression model is characterized by partial transformation functions \(h_j(y\mid x_j) = \beta _j(y) x_j\) and corresponding interpretable response-varying effects \(\beta _j: {\varXi }\rightarrow {\mathbb {R}}\). The analogon of an additive model features partial transformation functions \(h_j(y\mid x_j)\), i.e. bivariate smooth functions of both \(y\) and \(x_j\). These bivariate terms are more complex than the one-dimensional coefficient functions \(\beta _j(y)\) but can still be visualized and interpreted. If \(x_j\) is more complex, for example, if it describes a spatial location, \(h_j(y\mid x_j)\) might be a spatially smooth term that captures unexplained spatial heterogeneity (Hothorn et al. 2014).

Models with transformation function \(h(y\mid \varvec{x}) = \sum _{j = 1}^J h_j(y\mid x_j)\) and potential applications are discussed in Hothorn et al. (2014) and Hothorn et al. (2018). The standard estimation of maximizing the continuously ranked probability score over a discrete grid covering \({\varXi }\) (Foresi and Peracchi 1995; Chernozhukov et al. 2013; Hothorn et al. 2014), potentially with inverse probability of censoring weight adjustment for right censoring (Möst and Hothorn 2015; Garcia et al. 2019), does not allow essentially unstructured transformation functions \(h(y\mid \varvec{x})\), including higher-order interactions, and thus relaxation of the additivity assumption on the scale of the transformation function \(h\). Furthermore, it is computationally inefficient (because the data have to be expanded) and is unable to handle censoring or truncation directly.

This paper addresses these issues by introducing computationally efficient boosted likelihood estimation for unstructured or structured additive conditional transformation functions (Sect. 3) and shift transformation functions (Sect. 4) under all forms of random censoring and truncation for at least ordered responses based on potentially correlated observations.

3 Boosting the likelihood of conditional transformation models

In the following, the conditional transformation function \(h(y\mid \varvec{x}) = \varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x})\) is parameterized in terms of basis functions \(\varvec{a}: {\varXi }\rightarrow {\mathbb {R}}^P\) of the response and a conditional parameter function \(\varvec{\vartheta }: \chi \rightarrow {\mathbb {R}}^P\); the latter function will be estimated.

3.1 Definition of the likelihood

The parameterisation of \(h\) implies a conditional cumulative distribution function \({\mathbb {P}}(Y\le y\mid \varvec{X}= \varvec{x}) = F_Z(\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x}))\) and thus a conditional density

$$\begin{aligned} f_Y(y\mid \varvec{\vartheta }(\varvec{x}))= & {} \frac{\partial F_Z(\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x}))}{\partial y} \\= & {} f_Z(\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x})) \varvec{a}^\prime (y)^\top \varvec{\vartheta }(\varvec{x}) \end{aligned}$$

when \(y\in {\mathbb {R}}\) comes from an absolutely continuous distribution (\(\varvec{a}^\prime \) is the derivative of \(\varvec{a}\)). For discrete \(y\in {\varXi }= \{y_1, y_2, \dots \}\), the density function is

$$\begin{aligned}&f_Y(y_k \mid \varvec{\vartheta }(\varvec{x})) \\&\quad = \left\{ \begin{array}{ll} F_Z(\varvec{a}(y_k)^\top \varvec{\vartheta }(\varvec{x})) &{} k = 1 \\ F_Z(\varvec{a}(y_k)^\top \varvec{\vartheta }(\varvec{x})) - F_Z(\varvec{a}(y_{k - 1})^\top \varvec{\vartheta }(\varvec{x})) &{} k > 1. \end{array} \right. \end{aligned}$$

There are also other forms of the density, for example, in mixed discrete-continuous distributions. The population optimizer for the conditional parameter function \(\varvec{\vartheta }\) is

$$\begin{aligned}&\varvec{\vartheta }:= \mathop {\mathrm{arg\,max}}\limits _{\varvec{\vartheta }: \chi \rightarrow {\mathbb {R}}^P} \int \log \{f_Y[y\mid \varvec{\vartheta }(\varvec{x})]\} \, d {\mathbb {P}}_{Y, \varvec{X}}(y, \varvec{x}) \\&\qquad \text { st. }~(1). \end{aligned}$$

Based on N independent observations \((y_i, \varvec{x}_i), i = 1, \dots , N\) from \({\mathbb {P}}_{Y, \varvec{X}}\), empirical risk minimization with negative log-likelihood loss

$$\begin{aligned} {\hat{\varvec{\vartheta }}}_N = \mathop {\mathrm{arg\,max}}\limits _{\varvec{\vartheta }: \chi \rightarrow {\mathbb {R}}^P} \sum _{i = 1}^N \ell _i(\varvec{\vartheta }(\varvec{x}_i)) \quad \text { st.}~(1) \end{aligned}$$

can be applied to estimate the conditional parameter function \(\varvec{\vartheta }\). The log-likelihood contribution \(\ell _i: {\mathbb {R}}^P\rightarrow {\mathbb {R}}\) for the \(i\hbox {th}\) observation is given by

$$\begin{aligned}&\ell _i(\varvec{\vartheta }(\varvec{x}_i)) \nonumber \\&\quad = \left\{ \begin{array}{ll} \log \{f_Y[y_i \mid \varvec{\vartheta }(\varvec{x}_i)]\} &{} y_i \in {\varXi }\\ \log \left\{ \int _{y_i} f_Y[y\mid \varvec{\vartheta }(\varvec{x}_i)] \, d\mu (y) \right\} &{} y_i \in {\mathfrak {C}}\setminus {\varXi }, \end{array} \right. \end{aligned}$$
(2)

where the first case corresponds to an observation \(y_i\) from an absolutely continuous or ordered response and the second case corresponds to the situation where a set or interval was observed (for example, for a left-, right-, or interval-censored observation \(y_i\)). Integration is with respect to the measure \(\mu \) dominating \({\mathbb {P}}_{Y\mid \varvec{X}= \varvec{x}}\). Details on the likelihood function for models parameterized by \(\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x})\), including gradients (denoted \(\varvec{u}_i\) in Algorithm 1) and Hessians under censoring and truncation, are given in Hothorn et al. (2018).

3.2 Boosting the likelihood

The proposed boosting Algorithm 1 outputs a model of the form

$$\begin{aligned} \varvec{\vartheta }(\varvec{x}) = \varvec{\vartheta }^{[0]}(\varvec{x}) + \sum _{b = 1}^B {\varvec{\Gamma }}^{[b]} \varvec{b}_{j(b)}(\varvec{x}), \end{aligned}$$
(3)

with offset term \(\varvec{\vartheta }^{[0]}(\varvec{x})\) and \(j = 1, \dots , J\) a priori defined basis functions \(\varvec{b}_j: \chi \rightarrow {\mathbb {R}}^{P_j}\) of the predictor variables. The function j(b) returns the index of the basis function \(\varvec{b}_j\) which was selected in the bth iteration of the algorithm. Each basis may be equipped with an explicit penalty function \(\text {Pen}_j\). The corresponding penalty parameter \(\lambda _j\) is chosen such that the degrees of freedom are the same for all J basis functions to facilitate unbiased model selection (Hofner et al. 2011). The number of terms B, selected basis functions j(b), and corresponding coefficient matrices \({\varvec{\Gamma }}^{[b]} \in {\mathbb {R}}^{P\times P_{j(b)}}\) are unknowns and are estimated from data. The basis functions \(\varvec{b}_j\) may feature unknown parameters. With relatively deep regression trees \(\varvec{b}_j\) (where the tree structure is estimated from the data in every boosting iteration and \({\varvec{\Gamma }}\) are the parameters in each terminal node), model (3) is the sum of B trees and as such is potentially highly unstructured. Similar to GAMLSS-boosting (Mayr et al. 2012), a parameter vector \(\varvec{\vartheta }\) is modelled instead of a scalar predictor function. The main difference is that all dimensions of the parameter vector \(\varvec{\vartheta }\) are updated simultaneously whereas each dimension is assigned its own predictor function in GAMLSS-boosting.

figure a

Algorithm 1 is essentially a multivariate version of \(L_2\) boosting (Bühlmann and Yu 2003) using the negative transformation log-likelihood (2) as loss function. This choice makes the algorithm agnostic with respect to the scale of the response variable and potential censoring or truncation. The default offset is the unconditional maximum-likelihood estimator \(\varvec{\vartheta }^{[0]}(\varvec{x}_i) \equiv {\hat{\varvec{\vartheta }}}_\text {ML}\) for \(i = 1, \dots , N\) that maximizes \(\sum _{i = 1}^N \ell _i(\varvec{\vartheta })\). The algorithm is also applicable to the high-dimensional setting where the number of predictor variables exceeds the number of observations N. The number of boosting iterations \(b_\text {stop}\) is a tuning parameter that has to be chosen by the out-of-sample log-likelihood for a validation sample \(i = N + 1, \dots , N + {\tilde{N}}\)

$$\begin{aligned} {\hat{B}} = {\hat{b}}_\text {stop} = \mathop {\mathrm{arg\,max}}\limits _{b = 0, 1, \dots } \sum _{i = N + 1}^{N + {\tilde{N}}} \ell _i(\varvec{\vartheta }^{[b]}(\varvec{x}_i)). \end{aligned}$$

Model choice, for example using cross-validation, subsampling, or the bootstrap, can also be implemented conveniently by comparing this out-of-sample log-likelihood of different candidate models.

An additional advantage of this algorithm over boosted continuously ranked probability scores (“CTM-CRPS-boosting”, Hothorn et al. 2014) is that computations of tensor products in \(\varvec{a}(y)^\top \otimes \varvec{b}_j(\varvec{x})^\top \text {vec}({\varvec{\Gamma }}) = \varvec{a}(y)^\top {\varvec{\Gamma }}\varvec{b}_j(\varvec{x})\) are never explicitly required because the linear array model formulation (i.e. the right-hand side of the equation, see Currie et al. 2006, formula 2.5) formula 2.5 is implemented by Algorithm 1. This allows estimation of potentially highly unstructured models by choosing relatively deep multivariate regression trees as basis functions \(\varvec{b}\). Moreover, the algorithm does not require expansion of the data set (to size sample size \(N^2\), in the worst case).

3.3 Model interpretation

The partial transformation functions \(h_j\) can be obtained from the boosted model (3)

$$\begin{aligned} h_j(y\mid \varvec{x})= & {} \varvec{a}(y)^\top \left( \sum _{b: j(b) = j} {\varvec{\Gamma }}^{(b)} \varvec{b}_{j(b)}(\varvec{x})\right) \\= & {} \varvec{a}(y)^\top \varvec{\vartheta }_j(\varvec{x}). \end{aligned}$$

The choice \(\varvec{b}_j(\varvec{x}) = x_j\) results in the distribution regression model \(F_{Y\mid \varvec{X}= \varvec{x}}(y) = F_Z(h_Y(y) - \varvec{x}^\top \varvec{\beta }(y))\) with partial transformation functions \(h_j(y\mid x_j) = x_j \beta _j(y) = x_j \varvec{a}(y)^\top \varvec{\vartheta }_j\) and corresponding response-varying effects \(\beta _j(y) = \varvec{a}(y)^\top \varvec{\vartheta }_j\). Thus, this boosting procedure can also be used to estimate Cox models with time-varying effects under all forms of random censoring and truncation. Nonlinear effects can be implemented by a B-spline basis \(\varvec{b}_j(\varvec{x}) = \varvec{b}_j(x_j)\), and more complex bases allow specification of terms that capture spatio-temporal correlations or other forms of unexplained heterogeneity (Kneib et al. 2009; Hofner et al. 2011). A collection of commonly used basis functions \(\varvec{b}\), along with corresponding penalty functions and interpretable model terms, is reviewed in Mayr and Hofner (2018). Specific choices of basis functions underlying the empirical results presented in Sect. 5 are discussed in detail in Hothorn (2019).

4 Boosting the likelihood of shift transformation models

A comparison of conditional transformation models that allow interactions of \(y\) and \(\varvec{x}\) in the transformation function \(h\) with shift transformation models in which these terms are absent can help to identify situations where the simpler models perform as good as or even better than the more complex models. Likelihood boosting for shift transformation models of the form \(h(y\mid \varvec{x}) = \varvec{a}(y)^\top \varvec{\vartheta }- \beta (\varvec{x})\) is presented as Algorithm (2).

figure b

The procedure outputs a model

$$\begin{aligned} \beta (\varvec{x}) = \beta ^{[0]}(\varvec{x}) +\sum _{b = 1}^B {\varvec{\Gamma }}{^{[b]}} \varvec{b}_{j(b)}(\varvec{x}), \end{aligned}$$

with univariate shift function \(\beta (\varvec{x}) \in {\mathbb {R}}\), i.e. with \(\varvec{\gamma }^\top = {\varvec{\Gamma }}\in {\mathbb {R}}^{1 \times P_j}\). In contrast to conditional transformation models, the model term \(\beta (\varvec{x})\) does not depend on \(y\) and thus shift transformation models are easier to interpret. \(L_2\) boosting in this setup is performed based on log-likelihood contributions \(\ell _i(\varvec{\vartheta }, \beta (\varvec{x}_i))\) for \(\ell _i: {\mathbb {R}}^{P+ 1} \rightarrow {\mathbb {R}}\) from densities

$$\begin{aligned} f_Y(y\mid \varvec{\vartheta }, \beta (\varvec{x}))= & {} \frac{\partial F_Z(\varvec{a}(y)^\top \varvec{\vartheta }- \beta (\varvec{x}))}{\partial y} \\= & {} f_Z(\varvec{a}(y)^\top \varvec{\vartheta }- \beta (\varvec{x})) \varvec{a}^\prime (y)^\top \varvec{\vartheta }\end{aligned}$$

for the absolutely continuous case and

$$\begin{aligned}&f_Y(y_k \mid \varvec{\vartheta }, \beta (\varvec{x})) \\&\quad = \left\{ \begin{array}{ll} F_Z(\varvec{a}(y_k)^\top \varvec{\vartheta }- \beta (\varvec{x})) &{} k = 1 \\ F_Z(\varvec{a}(y_k)^\top \varvec{\vartheta }- \beta (\varvec{x})) - F_Z(\varvec{a}(y_{k - 1})^\top \varvec{\vartheta }- \beta (\varvec{x})) &{} k > 1 \end{array} \right. \end{aligned}$$

for the discrete case. The core idea is to update the nuisance parameter \(\varvec{\vartheta }\) before computing the gradients in every boosting iteration (following Schmid and Hothorn 2008). For discrete proportional odds models, Algorithm (2) is equivalent to the procedure proposed by Schmid et al. (2011). The ability to handle censoring and truncation in the likelihood allows proportional hazards models with potentially very flexible log-hazard ratios \(\beta (\varvec{x})\) to be fitted to randomly censored (including left- and interval-censoring) or truncated responses.

5 Empirical evaluation

The rationale for the empirical evaluation of Algorithms 1 and 2 was to demonstrate that interpretable transformation models can be estimated for applications where information about predictive distribution matters (Sect. 5.1) and to investigate the robustness of boosted transformation models under model misspecification (Sect. 5.2).

Table 1 Applications. Eight prediction problems with continuous, ordered categorical (number of categories in parentheses), or right-censored response (per cent censored in parentheses)
Full size table
Table 2 Applications. Median out-of-sample log-likelihoods (centered by out-of-sample log-likelihoods of the corresponding unconditional model) from 100 subsampled divisions into learning and test samples
Full size table

5.1 Applications

Eight life science applications in which estimation of a predictive distribution is of special interest are listed in Table 1. Four applications are described by a continuous response, two feature an ordered categorical response, and two feature a right-censored response. Except for the Beetle Extinction Risk application, which requires a discrete basis \(\varvec{a}\), a Bernstein basis \(\varvec{a}\) of order \(M = 6\) (for technical details see Hothorn et al. 2018) was used to parameterize the transformation functions. Conditional transformation models (Algorithm 1) with nonlinear (N, using B-splines), linear (L), and tree-based (T, of depth two and thus allowing only two-way interactions) basis functions \(\varvec{b}\) as well as shift transformation models (Algorithm 2) using the same bases were evaluated. The performance of these boosted transformation models was compared to the performance of transformation trees and transformation forests (Hothorn and Zeileis 2017). The latter two procedures estimate conditional transformation models of the form \(F_Z(\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x}))\), where \(\varvec{\vartheta }(\varvec{x})\) is obtained either from a single tree (transformation trees) or from a nonlinear interaction function (transformation forest). I hypothesized a priori that transformation trees should perform worst across all applications because this method corresponds to the most simple (but easily interpretable) model. Also, I expected transformation forests to outperform transformation trees and to perform only slightly worse than the best performing boosting procedure because of the high adaptivity of the underlying random forest procedure. My motivation for this experiment was the hope that I would be able to find a simple and interpretable transformation model that outperforms the most complex transformation forests by means of either Algorithm 1 or 2.

Subsampling (with \(n = 3/4 N\) observations in the learning and \({\tilde{n}} = 1/4 N\) observations in the validation sample) was performed 100 times. Performance of the competitors was assessed by the out-of-sample log-likelihood centered by the out-of-sample log-likelihood of the unconditional transformation model \(F_Z(\varvec{a}(y)^\top {\hat{\varvec{\vartheta }}}_\text {ML})\). For a learning sample of size n and a validation sample \(i = n + 1, \dots , {\tilde{n}}\), the centered out-of-sample log-likelihood is given by

$$\begin{aligned} {\tilde{n}}^{-1} \sum _{i = n + 1}^{n + {\tilde{n}}} \ell _i\left( \varvec{\vartheta }^{[{\hat{b}}_\text {stop}]}(\varvec{x}_i)\right) - {\tilde{n}}^{-1} \sum _{i = n + 1}^{n + {\tilde{n}}} \ell _i({\hat{\varvec{\vartheta }}}_\text {ML}). \end{aligned}$$

Values close to zero indicate that the conditional model did not outperform the unconditional model.

The results presented in Table 2 demonstrate that the best-performing method was always a boosted transformation model. Transformation forests performed only slightly worse than the top model for the Beetle Extinction Risk, Birth Weight Prediction, Body Fat Mass, and Childhood Malnutrition applications. In the remaining four applications, the best boosting procedure outperformed transformation forests substantially. Nonlinear conditional transformation models (N \(\varvec{\vartheta }(\varvec{x})\)) performed best twice, as did tree-based shift transformation models (T \(\beta (\varvec{x})\)). Each of the remaining models ranked at the top once. Transformation trees outperformed transformation forests for two applications (Head Cirumference and PRO-ACT ALSFRS) but never performed better than any of the boosted transformation models.

Graphical representations of the distributions of out-of-sample log-likelihoods along with the exact model and algorithm specification and corresponding software implementation are presented for all eight applications in Hothorn (2019).

5.2 Artificial data-generating processes

The response \(Y\) was generated conditionally on two groups and one numeric predictor variable \(x \in [0, 1]\) following a transformation model of the form

$$\begin{aligned} {\mathbb {P}}(Y\le y\mid \text {Group}, x) = {\varPhi }(h(y\mid \text {Group}, x)), \end{aligned}$$

where the conditional transformation function \(h(y\mid \text {Group}, x) = {\varPhi }^{-1}({\mathbb {P}}(Y\le y\mid \text {Group}, x))\) for four data-generating processes (DGPs) is given in Table 3. The model labelled “Linear \(\beta (\varvec{x})\)” is a shift transformation model with a main effect of group, a linear main effect of x, and a corresponding linear interaction effect. The linear main and interaction effects of x are replaced by nonlinear effects (a scaled \(\sin \) function) of x in the shift transformation model “Nonlinear \(\beta (\varvec{x})\)”. The extension to response-varying main and interaction effects defines the distribution regression model “Linear \(\varvec{\vartheta }(\varvec{x})\)” and the conditional transformation model “Nonlinear \(\varvec{\vartheta }(\varvec{x})\)”. The coefficients of the terms introduced in Table 3 are given in Table 4. Details of the implementation of these DGPs are explained in Hothorn (2019). The conditional densities associated with the four DGPs are shown in Fig. 1.

Table 3 Artificial data-generating processes (DGPs). Description of four simulation models
Full size table
Table 4 Artificial data-generating Processes (DGPs). Coefficients of baseline transformation \(h_Y\) and response-varying effects \(\beta _1, \beta _2\), and \(\beta _3\)
Full size table
Fig. 1
figure 1

Artificial Data-generating Processes (DGPs). Conditional densities given two groups (left and right panel) and \(x \in [0, 1]\) (gray color coding) for four different data-generating processes

Full size image

Models were evaluated by out-of-sample log-likelihoods centered by the out-of-sample log-likelihood of the true DGP (for test samples of size \({\tilde{N}} = 2000\))

$$\begin{aligned} {\tilde{N}}^{-1} \sum _{i = N + 1}^{N + {\tilde{N}}} \ell _i\left( \varvec{\vartheta }^{[{\hat{b}}_\text {stop}]}(\varvec{x}_i)\right) - {\tilde{N}}^{-1} \sum _{i = N + 1}^{N + {\tilde{N}}} \ell _i(\varvec{\vartheta }_\text {True}), \end{aligned}$$

where \(\varvec{\vartheta }_\text {True}\) is as given in Tables 3 and 4.

In Part A of this simulation, nonlinear (N, using B-splines), linear (L), and tree-based (T, of depth six, which allows higher-order interactions) basis functions \(\varvec{b}\) for shift transformation models, i.e. models for \(\beta (\varvec{x})\), and for conditional transformation models, i.e. models for \(\varvec{\vartheta }(\varvec{x})\), were evaluated for sample sizes \(N = 75, 150, 300\) under correctly specified models; this means that models were fitted using the correct distribution function \(F_Z= {\varPhi }\), the correct order \(M = 6\) of \(\varvec{a}\), no uninformative predictor variables, and the correct basis functions. Both the linear and nonlinear models were fitted with basis functions representing a main effect of group, a main effect of x, and a corresponding interaction effect, whereas trees had to learn this structure from the data. In Part B, these models were evaluated under model misspecification, i.e. using the incorrect distribution function \(F_Z= \text {expit}\) (standard logistic distribution) or \(F_Z= \text {MEV}\) (standard minimum extreme value distribution), a too large dimension of the Bernstein basis \(\varvec{a}\) (\(M = 12\)), or \(J^+ = 5, 25\) additional uninformative uniform predictor variables. The same “correct” basis functions as in Part A were used in Part B. I hypothesized a priori that models exactly matching the DGP would perform best and that tree-based boosting would outperform boosting with linear basis functions in nonlinear problems. Under misspecification, I expected the performance of all models to decrease, but this general ranking to persist.

The results for Part A presented in the top three rows of Table 5 show that the model corresponding to the underlying DGP was associated with the largest median out-of-sample log-likelihood. For linear DGPs, the performance of boosted models with nonlinear basis functions was only slightly inferior to the performance of boosted models with linear basis functions, while tree-based boosting performed substantially worse in this situation. By contrast, the signal in nonlinear DGPs was captured relatively well by tree-based boosting, whereas linear basis functions were not able to recover this signal. This shows that tree-based boosting was able to adapt to the underlying nonlinear interaction signal in the two nonlinear simulation models “Nonlinear \(\beta (\varvec{x})\)” and “Nonlinear \(\varvec{\vartheta }(\varvec{x})\)”.

The out-of-sample log-likelihoods for misspecified models presented in Table 5, Part B for \(F_Z= {\varPhi }\), follow this general pattern in that the model corresponding to the DGP performed best and tree-based boosting outperformed boosting with linear basis functions on nonlinear problems. In only two cases, which were characterized by small samples, did a linear model for \(\varvec{\vartheta }(\varvec{x})\) outperform a true linear model for \(\beta (\varvec{x})\) or vice versa. More frequently, the too complex nonlinear model for \(\varvec{\vartheta }(\varvec{x})\) outperformed the nonlinear model for \(\beta (\varvec{x})\) slightly. Overall, Algorithms 1 and 2 seemed to be robust against overly complex basis functions \(\varvec{a}\) and additional noninformative predictor variables.

This was also true under a misspecified distribution function \(F_Z= \text {expit}\) for linear shift transformation models “Linear \(\beta (\varvec{x})\)”. More severe deviations occurred when an incorrect \(F_Z= \text {expit}\) was used for model specification in Algorithms 1 and 2 under the nonlinear shift transformation model “Nonlinear \(\beta (\varvec{x})\)”, distribution regression model “Linear \(\varvec{\vartheta }(\varvec{x})\)”, and conditional transformation model “Nonlinear \(\varvec{\vartheta }(\varvec{x})\)”. The absolute differences in the corresponding out-of-sample log-likelihoods were, however, marginal in most of these cases.

When the asymmetric standard minimum value distribution was used (\(F_Z= \text {MEV}\)), the distortions were more pronounced. The general pattern observed for \(F_Z= \text {expit}\) was the same, but the centered out-of-sample log-likelihoods seemed in general smaller in this setup. Visualizations of the distributions underlying the figures in Table 5 are presented in Hothorn (2019).

6 Discussion

Models defined in terms of simple linear transformation functions up to models featuring unstructured complex transformation functions can be specified, estimated, evaluated, and compared in the unified computational framework of Algorithms 1 and 2. Data analysts are no longer limited in their freedom to define and estimate transformation models, because the strong ties between models of a certain complexity and a tailored estimation procedure (such as CTM-CPRS-boosting for additive or transformation forests for interaction models) can be cut with the boosting algorithms presented here.

For model specification, the choice of \(F_Z\) is important in simple shift transformation models because it affects the interpretation of model parameters (log-odds ratios vs. log-hazard ratios, for example). In more complex models, a direct interpretation of parameters is hardly possible, and the estimated conditional distribution functions are insensitive to the choice of \(F_Z\) (Hothorn et al. 2018). However, one could use Algorithm 1 to estimate an unstructured log-hazard function \(\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x}) + \log (\varvec{a}^\prime (y)^\top \varvec{\vartheta }(\varvec{x}))\) in the model \({\mathbb {P}}(Y\le y\mid \varvec{X}= \varvec{x}) = 1 - \exp (-\exp (\varvec{a}(y)^\top \varvec{\vartheta }(\varvec{x}))\), with \(\varvec{\vartheta }(\varvec{x})\) being, for example, the sum of B deep trees. The log-likelihood risk function employed here, which is also able to handle time-varying covariates through appropriate truncation, avoids the technical obstacles reported by Lee and Chen (2018) when defining an appropriate nonparametric risk function for boosting in a class of models for conditional log-hazard functions.

Table 5 Artificial data-generating processes (DGPs). Median out-of-sample log-likelihoods (centered by out-of-sample log-likelihoods of the true model) based on 100 simulation runs of varying sample sizes \(N = 75, 150, 300\), number of additional noninformative predictor variables \(J^+ = 0, 5, 25\), choices of \(F_Z\) (\({\varPhi }= \) standard normal, \(\text {expit} = \) standard logistic, and \(\text {MEV} = \) standard minimum extreme value), and choices of the Bernstein polynomial order \(M = 6, 12\) for four different DGPs and Boosting CTM Likelihoods (parameter \(\varvec{\vartheta }(\varvec{x})\)) with nonlinear (N), linear (L), and tree-based (T, depth two) basis functions \(\varvec{b}\) as well as Boosting STM Likelihoods (parameter \(\beta (\varvec{x})\)) with the same basis functions
Full size table

In contrast to quantile regression, where separate models for each quantile are fitted, likelihood boosting for transformation models estimates conditional distribution functions simultaneously for all quantiles. It is interesting to note that a recently suggested Bayesian approach to simultaneous linear quantile regression (Yang and Tokdar 2017) maximizes a log-likelihood obtained from a numerical inversion of the quantile function instead of using the traditional check risk minimization. In light of this approach, it seems computationally attractive to model the distribution function in the distribution regression model \(F_{Y\mid \varvec{X}= \varvec{x}}(y\mid \varvec{X}= \varvec{x}) = F_Z(h_Y(y) - \varvec{x}^\top \varvec{\beta }(y))\) rather than the quantile function in a quantile regression model \(Q_{Y\mid \varvec{X}= \varvec{x}}(\tau \mid \varvec{X}= \varvec{x}) = \alpha (\tau ) + \varvec{x}^\top \varvec{\delta }(\tau )\) of the same complexity (\(\tau \in [0, 1]\); \(\alpha \) and \(\varvec{\delta }\) being the probability-varying intercept and coefficient functions, respectively). Bayesian inference for the corresponding model parameters in conditional transformation models is, however, still under development (Mitrodima and Griffin 2017).

6.1 Computational details

A reference implementation of transformation boosting machines (Algorithms 1 and 2) is available in the tbm package (Hothorn 2019). Analyses of all applications and simulation results can be reproduced in the dynamic document Hothorn (2019). All computations were performed using R version 3.5.2 (R Core Team 2018).