Efficient sampling of conditioned Markov jump processes

Abstract

We consider the task of generating draws from a Markov jump process (MJP) between two time points at which the process is known. Resulting draws are typically termed bridges, and the generation of such bridges plays a key role in simulation-based inference algorithms for MJPs. The problem is challenging due to the intractability of the conditioned process, necessitating the use of computationally intensive methods such as weighted resampling or Markov chain Monte Carlo. An efficient implementation of such schemes requires an approximation of the intractable conditioned hazard/propensity function that is both cheap and accurate. In this paper, we review some existing approaches to this problem before outlining our novel contribution. Essentially, we leverage the tractability of a Gaussian approximation of the MJP and suggest a computationally efficient implementation of the resulting conditioned hazard approximation. We compare and contrast our approach with existing methods using three examples.

1 Introduction

Markov jump processes (MJPs) can be used to model a wide range of discrete-valued, continuous-time processes. Our focus here is on the MJP representation of a reaction network, which has been ubiquitously applied in areas such as epidemiology (Fuchs 2013; Lin and Ludkovski 2013; McKinley et al. 2014), population ecology (Matis et al. 2007; Boys et al. 2008) and systems biology (Wilkinson 2009, 2018; Sherlock et al. 2014). Whilst exact, forward simulation of this class of MJP is straightforward (Gillespie 1977), the reverse problem of performing fully Bayesian inference for the parameters governing the MJP given partial and/or noisy observations is made challenging by the intractability of the observed data likelihood. Simulation-based approaches to inference typically involve “filling in” event times and types between the observation times. A key repeated step in many inference mechanisms starts with a sample of possible states at one observation time and, for each element of the sample, creates a trajectory starting with the sample value and ending at the time of the next observation with a value that is consistent with the next observation. The resulting conditioned samples are typically referred to as bridges, and ideally, the bridge should be a draw from the exact distribution of the path given the initial condition and the observation. However, except for a few simple cases, exact simulation of MJP bridges is infeasible, necessitating approximate bridge constructs that can be used as a proposal mechanism inside a weighted resampling and/or Markov chain Monte Carlo (MCMC) scheme.

The focus of this paper is the development of an approximate bridge construct that is both accurate and computationally efficient. Our contribution can be applied in a generic observation regime that allows for discrete, partial and noisy measurements of the MJP, and is particularly effective compared to competitors in the most difficult regime where the observations are sparse in time and the observation variance is small. Many bridge constructs have been proposed for partially observed stochastic differential equations [SDEs, e.g. Delyon and Hu (2006), Bladt and Sørensen (2014), Bladt et al. (2016), Schauer et al. (2017) and Whitaker et al. (2017)], but the literature on bridges for MJPs is relatively sparse. Recent progress involves an approximation of the instantaneous rate or hazard function governing the conditioned process. For example, Boys et al. (2008) linearly interpolate the hazard between observation times but require full and error-free observation of the system of interest. Fearnhead (2008) recognises that the conditioned hazard requires the intractable transition probability mass function of the MJP. This is then directly approximated by substituting the transition density associated with the coarsest possible discretisation of a spatially continuous approximation of the MJP, the chemical Langevin equation (Gillespie 2000). Golightly and Wilkinson (2015) derive a conditioned hazard by approximating the expected number of events between observations, given the observations themselves. Unfortunately, the latter two approaches typically perform poorly when the behaviour of the conditioned process is nonlinear.

We take the approach of Fearnhead (2008) as a starting point and replace the intractable MJP transition probability with the transition density governing the linear noise approximation (LNA) (Kurtz 1970; Elf and Ehrenberg 2003; Komorowski et al. 2009; Schnoerr et al. 2017). Whilst the LNA has been used as an inferential model (see e.g. Ruttor and Opper (2009) and Ruttor et al. (2010) for a maximum likelihood approach and Stathopoulos and Girolami (2013) and Fearnhead et al. (2014) for an MCMC approach), we believe that this is the first attempt to use the LNA to develop a bridge construct for simulation of conditioned MJPs. We find that the LNA offers superior accuracy over a single step of the CLE (which must be discretised in practice), at the expense of computational efficiency. Notably, the LNA solution requires, for each event time in each trajectory, integrating forwards until the next event time a system of ordinary differential equations (ODEs) whose dimension is quadratic in the number of MJP components. We therefore leverage the linear Gaussian structure of the LNA to derive a bridge construct that only requires a single full integration of the LNA ODEs, irrespective of the number of transition events on each bridge or the number of bridges required. We compare the resulting novel construct to several existing approaches using three examples of increasing complexity. In the final, real data application, we demonstrate use of the construct within a pseudo-marginal Metropolis–Hastings scheme, for performing fully Bayesian inference for the parameters governing an epidemic model.

The remainder of this paper is organised as follows. In Sect. 2, we define a Markov jump process as a probabilistic description of a reaction network. We consider the task of sampling conditioned jump processes in Sect. 3 and review two existing approaches. Our novel contribution is presented in Sect. 4 and illustrated in Sect. 5. Conclusions are drawn in Sect. 6.

2 Reaction networks

Consider a reaction network involving u species $\mathcal {X}_1, \mathcal {X}_2, \ldots ,\mathcal {X}_u$ and v reactions $\mathcal {R}_1,\mathcal {R}_2,\ldots ,\mathcal {R}_v$ such that reaction $\mathcal {R}_i$ is written as

$$\begin{aligned} \sum _{j=1}^{u}a_{ij}\mathcal {X}_j \longrightarrow \sum _{j=1}^{u}b_{ij}\mathcal {X}_j, \quad i=1,\ldots ,v \end{aligned}$$

where $a_{ij}$ denotes the number of molecules of $\mathcal {X}_j$ consumed by reaction $\mathcal {R}_i$ and $b_{ij}$ denotes the number of molecules of $\mathcal {X}_j$ produced by reaction $\mathcal {R}_i$. Let $X_{j,t}$ denote the (discrete) number of species $\mathcal {X}_j$ at time t, and let $X_t$ be the u-vector $X_t = (X_{1,t},X_{2,t}, \ldots , X_{u,t})'$. The effect of a particular reaction is to change the system state $X_t$ abruptly and discretely. Hence, if the ith reaction occurs at time t, the new state becomes

$$\begin{aligned} X_t=X_{t-}+S^{i} \end{aligned}$$

where $S^i=(b_{i1}-a_{i1},\ldots ,b_{iu}-a_{iu})'$ is the ith column of the $u\times v$ stoichiometry matrix S. The time evolution of $X_t$ is therefore most naturally described by a continuous-time, discrete-valued Markov process defined in the following section.

2.1 Markov jump processes

We model the time evolution of $X_t$ via a Markov jump process (MJP), so that the state of the system at time t is

$$\begin{aligned} X_t=x_0+\sum _{i}S^{i}R_{i,t} \end{aligned}$$

where $x_0$ is the initial system state and $R_{i,t}$ denotes the number of times that the ith reaction occurs by time t. The process $R_{i,t}$ is a counting process with intensity $h_i(x_t)$, known in this setting as the reaction hazard, which depends on the current state of the system $x_t$. Explicitly, we have that

$$\begin{aligned} R_{i,t}=Y_i\left( \int _{0}^{t}h_i(x_s)\mathrm{d}s \right) \end{aligned}$$

where the $Y_i$, $i=1,\ldots ,v$ are independent, unit rate Poisson processes (see e.g. Kurtz (1972) or Wilkinson (2018) for further details of this representation). The hazard function is given by $h(x_t)=(h_1(x_t),\ldots , h_v(x_t))'$. Under the standard assumption of mass-action kinetics, $h_i$ is proportional to a product of binomial coefficients. That is

$$\begin{aligned} h_i(x_t) = c_i\prod _{j=1}^u \left( {\begin{array}{c}x_{j,t}\\ a_{ij}\end{array}}\right) \end{aligned}$$

where $c_i$ is the rate constant associated with reaction $\mathcal {R}_i$ and $c=(c_1,c_2,\ldots ,c_v)'$ is a vector of rate constants. Since in this article, except in Sect. 5.3 the rate constants are assumed to be a known fixed quantities, we drop them from the notation where possible.

Given a value of the initial system state $x_0$, exact realisations of the MJP can be generated via Gillespie’s direct method (Gillespie 1977), given by Algorithm 1.

3 Sampling conditioned MJPs

Denote by $\varvec{X}=\{X_{s}\,|\, 0< s \le T\}$ the MJP sample path over the interval (0, T]. Complete information on an observed sample path $\varvec{x}$ corresponds to all reaction times and types. To this end, let $n_{r}$ denote the total number of reaction events; reaction times (assumed to be in increasing order) and types are denoted by $(t_{i},\nu _{i})$, $i=1,\ldots ,n_{r}$, $\nu _{i}\in \{1,\ldots ,v\}$, and we take $t_{0}=0$ and $t_{n_{r}+1}=T$.

Suppose that the initial state $x_{0}$ is a known fixed value and that (a subset of components of) the process is observed at time T subject to Gaussian error, giving a single observation $y_{T}$ on the random variable

$$\begin{aligned} Y_{T}=P'x_{T}+\varepsilon _{T}\,,\qquad \varepsilon _{T}\sim \text {N}\left( 0,\varSigma \right) . \end{aligned}$$

(1)

Here $Y_{T}$ is a length-d vector, P is a constant matrix of dimension $u\times d$, and $\varepsilon _{T}$ is a length-d Gaussian random vector. The role of the matrix P is to provide a flexible set-up allowing for various observation scenarios. For example, taking P to be the $u\times u$ identity matrix corresponds to the case of observing all components of $X_t$ (subject to error). We denote the density linking $Y_{T}$ and $X_{T}$ as $p(y_{T}|x_{T})$.

We consider the task of generating trajectories from $p(\varvec{x}|x_{0},y_{T})$ given by

$$\begin{aligned} p(\varvec{x}|x_{0},y_{T})&= \frac{p(y_{T}|x_{T})p(\varvec{x}|x_{0})}{p(y_{T}|x_{0})}\nonumber \\&\propto p(y_{T}|x_{T})p(\varvec{x}|x_{0}) \end{aligned}$$

(2)

Here, $p(\varvec{x}|x_{0})$ is the complete data likelihood (Wilkinson 2018) which takes the form

$$\begin{aligned} p(\varvec{x}|x_{0})=\left\{ \prod _{i=1}^{n_{r}}h_{\nu _{i}}\left( x_{t_{i-1}} \right) \right\} \exp \left\{ -\int _{0}^{T}h_{0}\left( x_t\right) \mathrm{d}t\right\} \end{aligned}$$

where $h_0$ is as defined in line 2 of Algorithm 1. Although $p(\varvec{x}|x_{0},y_{T})$ will typically be intractable, generating draws from $p(\varvec{x}|x_{0})$ is straightforward via Gillespie’s direct method (Algorithm 1). This immediately suggests drawing samples from (2) using a numerical scheme such as weighted resampling. However, as discussed in Golightly and Wilkinson (2015), drawing unconditioned trajectories from $p(\varvec{x}|x_{0})$ and weighting by $p(y_{T}|x_{T})$ is likely to lead to highly variable weights, unless the level of intrinsic stochasticity of $X_t$ is outweighed by the variance of the observation process. Our umbrella aim, therefore, is to find an approximating MJP whose dynamics remain tractable under conditioning on $y_T$. The resulting construct can then be used to generate proposed trajectories within the weighted resampling scheme. We will show that this is possible via the derivation of an approximate conditioned hazard function, $\tilde{h}(x_t|y_T)$, $t\in (0,T]$, that can be used in place of $h(x_t)$ in Algorithm 1. The form for $\tilde{h}(x_t|y_T)$ that we initially derive depends explicitly on t, so that sampling events might not be straightforward; however, the time dependence is sufficiently small that it can be ignored and the resulting bridge mechanism, which has a constant rate between events, still leads to efficient proposals.

3.1 Weighted resampling

Let $q(\varvec{x}|x_{0},y_{T})$ denote the complete data likelihood for a sample path $\varvec{x}$ drawn from an approximate jump process with hazard function $\tilde{h}(x_{t}|y_{T})$. The importance weight associated with $\varvec{x}$ is given by

$$\begin{aligned} w\left( \varvec{x}\right) = p(y_{T}|x_{T})\frac{\mathrm{d}\mathbb {P}}{\mathrm{d}\mathbb {Q}}\left( \varvec{x}\right) \end{aligned}$$

where $\frac{\mathrm{d}\mathbb {P}}{\mathrm{d}\mathbb {Q}}$ is the Radon–Nikodym derivative of the true Markov jump process ($\mathbb {P}$) with respect to the approximating process ($\mathbb {Q}$) and can be derived in an entirely rigorous way (Brémaud 1981). An informal approach is provided by Wilkinson (2018), giving the Radon–Nikodym derivative as the likelihood ratio

$$\begin{aligned} \frac{\mathrm{d}\mathbb {P}}{\mathrm{d}\mathbb {Q}}\left( \varvec{x}\right)&= p(y_{T}|x_{T})\left\{ \prod _{i=1}^{n_{r}}\frac{h_{\nu _{i}}\left( x_{t_{i-1}}\right) }{\tilde{h}_{\nu _{i}}\left( x_{t_{i-1}}|y_{T}\right) }\right\} \\&\quad \times \exp \left\{ -\int _{0}^{T}\left[ h_{0}\left( x_t\right) -\tilde{h}_{0}\left( x_t|y_{T}\right) \right] dt\right\} \end{aligned}$$

where $h_0(x_t)=\sum _{i=1}^{v}h_i(x_t)$ and $\tilde{h}_{0}(x_t|y_{T})$ is defined analogously. As noted above, the explicit dependence of $\tilde{h}$ on t is ignored so that both $h_0$ and $\tilde{h}_0$ are piece-wise constant (between reaction events). Hence, in practice, we evaluate the weight using

$$\begin{aligned} w\left( \varvec{x}\right)&= p(y_{T}|x_{T})\left\{ \prod _{i=1}^{n_{r}}\frac{h_{\nu _{i}}\left( x_{t_{i-1}}\right) }{\tilde{h}_{\nu _{i}}\left( x_{t_{i-1}}|y_{T}\right) }\right\} \nonumber \\&\quad \times \exp \left\{ -\sum _{i=0}^{n_{r}}\left[ h_{0}\left( x_{t_{i}}\right) -\tilde{h}_{0}\left( x_{t_{i}}|y_{T}\right) \right] \varDelta t_{i}\right\} \end{aligned}$$

(3)

where $\varDelta t_{i}=t_{i+1}-t_{i}$.

The general weighted resampling algorithm is given by Algorithm 2. It is straightforward to show that the average unnormalised weight gives an unbiased estimator of the transition density $p(y_{T}|x_{0})$. This estimator is given by

$$\begin{aligned} \hat{p}(y_{T}|x_0) = \frac{1}{N}\sum _{j=1}^{N}p(y_{T}|X_{T}^j)\frac{p( \varvec{X}^{j}|x_{0})}{q(\varvec{X}^{j}|x_{0},y_{T})} \end{aligned}$$

(4)

where $\varvec{X}^{j}$ is an independent draw from $q(\cdot |x_{0},y_{T})$. In the case of an unknown initial value $X_0$ with density $p(x_0)$, Algorithm 2 can be initialised with a sample of size N from $p(x_0)$ in which case (4) can be used to estimate $p(y_T)$.

It remains for us to find a suitable form of $\tilde{h}(x_{t}|y_{T})$. In what follows, we review two existing methods before presenting a novel, alternative approach. Comparisons are made in Sect. 5.

3.2 Golightly and Wilkinson approach

The approach of Golightly and Wilkinson (2015) is based on a (linear) Gaussian approximation of the number of reaction events in the time between the current event time and the next observation time. Suppose we have simulated as far as time t and let $\varDelta R_{t}$ denote the number of reaction events over the time $T-t=\varDelta t$. Golightly and Wilkinson (2015) approximate $\varDelta R_{t}$ by assuming a constant reaction hazard over the whole non-infinitesimal time interval, $\varDelta t$. A Gaussian approximation to the corresponding Poisson distribution then gives

$$\begin{aligned} \varDelta R_{t}\sim \text {N}\left( h(x_t)\varDelta t\,,\,H(x_t)\varDelta t\right) \end{aligned}$$

where $H(x_t)=\text {diag}\{h(x_t)\}$. Under the Gaussian observation regime given by (1), it should be clear that the joint distribution of $\varDelta R_{t}$ and $Y_{T}$ can then be approximated by

$$\begin{aligned}&\begin{pmatrix} \varDelta R_{t} \\ Y_{T} \end{pmatrix} \sim \text {N}\left\{ \begin{pmatrix} h(x_t)\varDelta t \\ P'\left( x_{t}+S\,h(x_t)\varDelta t\right) \end{pmatrix}\,,\, \right. \\&\qquad \left. \begin{pmatrix} H(x_t)\varDelta t &{} H(x_t)S'P\varDelta t\\ P'S\,H(x_t)\varDelta t &{} P'S\,H(x_t)S'P\varDelta t +\varSigma \end{pmatrix}\right\} . \end{aligned}$$

Taking the expectation of $(\varDelta R_{t}|Y_{T}=y_{T})$ and dividing by $\varDelta t$ gives an approximate conditioned hazard as

$$\begin{aligned} \tilde{h}(x_t|y_{T})&=h(x_t) \nonumber \\&\quad +H(x_t)S'P\left( P'S\,H(x_t)S'P\varDelta t +\varSigma \right) ^{-1}\nonumber \\&\quad \times \left( y_{T}-P'\left[ x_{t}+S\,h(x_t)\varDelta t\right] \right) . \end{aligned}$$

(5)

By ignoring the explicit time dependence of $\tilde{h}(x_t|y_{T})$ (i.e. after each most recent event, until the next event, fixing $\varDelta t$ to its value at the most recent event), we can use (5), suitably truncated to ensure positivity, in Algorithm 1 to give trajectories $\varvec{x}^i$, $i=1,\ldots ,N$, to be used in Algorithm 2. Whilst use of (5) has been shown to work well in several applications, assumptions of normality of $\varDelta R_t$ and that the hazard is constant over a time interval of length $\varDelta t$ are often unreasonable, as we will show.

3.3 Fearnhead approach

As noted by Fearnhead (2008) [see also Ruttor and Opper (2009)], an expression for the intractable conditioned hazard can be derived exactly. Consider again an interval [0, T] and suppose that we have simulated as far as time $t\in [0,T]$. For reaction $\mathcal {R}_i$, let $x'=x_{t}+S^{i}$. Recall that $S^{i}$ denotes the ith column of the stoichiometry matrix so that $x'$ is the state of the MJP after a single occurrence of $\mathcal {R}_i$. The conditioned hazard of $\mathcal {R}_i$ satisfies

$$\begin{aligned} h_{i}(x_t|y_T)&=\lim _{\delta t\rightarrow 0}\frac{Pr(X_{t+\delta t}=x'|X_{t}=x_{t},y_{T})}{\delta t} \nonumber \\&=h_{i}(x_t)\lim _{\delta t\rightarrow 0}\frac{p(y_{T}|X_{t+\delta t}=x')}{p(y_{T}|X_{t}=x_t)} \nonumber \\&=h_{i}(x_t)\frac{p(y_{T}|X_{t}=x')}{p(y_{T}|X_{t}=x_t)}. \end{aligned}$$

(6)

In practice, the intractable transition density $p(y_{T}|x_{t})$ must be replaced by a suitable approximation. Golightly and Kypraios (2017) (see also Fearnhead (2008) for the case of no measurement error) used the transition density governing the (discretised) chemical Langevin equation (CLE). The CLE (Gillespie 1992, 2000) is an Itô stochastic differential equation (SDE) that has the same infinitesimal mean and variance as the MJP. It is written as

$$\begin{aligned} \mathrm{d}X_t = S\,h(X_t)\mathrm{d}t + \sqrt{S{\text {diag}}\{h(X_t)\}S'}\,\mathrm{d}W_t, \end{aligned}$$

(7)

where $W_t$ is a u-vector of standard Brownian motion and $\sqrt{S{\text {diag}}\{h(X_t)\}S'}$ is a $u\times u$ matrix B such that $BB'=S{\text {diag}}\{h(X_t)\}S'$. Since the CLE can rarely be solved analytically, it is common to work with a discretisation such as the Euler–Maruyama discretisation:

$$\begin{aligned} X_{t+\delta t}-X_{t} = S\,h(X_t)\delta t + \sqrt{S{\text {diag}}\{h(X_t)\}S'\delta t}\,Z \end{aligned}$$

(8)

where Z is a standard multivariate Gaussian random variable. Combining (8) with the observation model (1) gives an approximate conditioned hazard as

$$\begin{aligned} \tilde{h}_{i}(x_t|y_T)=h_{i}(x_t)\frac{p_{\text {cle}}(y_{T}| X_{t}=x')}{p_{\text {cle}}(y_{T}|X_{t}=x_t)} \end{aligned}$$

(9)

where

$$\begin{aligned} p_{\text {cle}}(y_{T}|X_{t}=x_t)&=N\left( y_T; P'(x_t+S\,h(x_t)\varDelta t)\,,\right. \\&\quad \left. \,P'S\,H(x_t)S'P\varDelta t+\varSigma \right) \end{aligned}$$

with $p_{\text {cle}}(y_{T}|X_{t}=x')$ defined similarly. As with the approach of Golightly and Wilkinson (2015), the remaining time $\varDelta t$ until the observation is treated as a single discretisation. However, unless $\varDelta t=T-t$ is very small, $p_{\text {cle}}$ is unlikely to achieve a reasonable approximation of the transition probability under the jump process. In what follows, therefore, we seek an approximation that is both accurate and computationally inexpensive.

4 Improved constructs

We take (6) as a starting point and replace $p(y_{T}|X_{t}=x')$ and $p(y_{T}|X_{t}=x_t)$ using the linear noise approximation (LNA) (Kurtz 1970; Elf and Ehrenberg 2003; Komorowski et al. 2009; Schnoerr et al. 2017). We first describe the LNA and then consider two constructions for bridges from a known initial condition, $x_0$, to a potentially noisy observation $Y_T$, based on different implementations of the LNA. The first is expected to be more accurate as the approximate hazard is recalculated after every event by re-integrating a set of ODEs from the event time to the observation time both from the current value and once for each possible next reaction. The second is more computationally efficient as the recalculation is based on a single, initial integration of a set of ODEs from time 0 to time T.

4.1 Linear noise approximation

For notational simplicity, we rewrite the CLE in (7) as

$$\begin{aligned} \mathrm{d}X_t = \alpha (X_t)\mathrm{d}t + \sqrt{\beta (X_t)}\,\mathrm{d}W_t \end{aligned}$$

(10)

where

$$\begin{aligned} \alpha (X_t)= S\,h(X_t),\qquad \beta (X_t)=S\,\text {diag}\{h(X_t)\}S' \end{aligned}$$

and derive the LNA by directly approximating (10). The basic idea behind construction of the LNA is to adopt the partition $X_t=z_t+M_t$ where the deterministic process $z_t$ satisfies an ordinary differential equation

$$\begin{aligned} \frac{\mathrm{d}z_{t}}{\mathrm{d}t}=\alpha (z_{t}) \end{aligned}$$

(11)

and the residual stochastic process $M_t$ can be well approximated under the assumption that residual stochastic fluctuations are “small” relative to the deterministic process. Taking the first two terms in the Taylor expansion of $\alpha (X_t)$ and the first term in the Taylor expansion of $\beta (X_t)$ gives an SDE satisfied by an approximate residual process $\tilde{M}_t$ of the form

$$\begin{aligned} \mathrm{d}\tilde{M}_t = F_t\tilde{M}_t\,\mathrm{d}t + \sqrt{\beta (z_t)}\,\mathrm{d}W_t, \end{aligned}$$

(12)

where $F_t$ is the Jacobian matrix with (i, j)th element $(F_t)_{i,j}=\partial \alpha _i(z_t)/\partial z_{j,t}$. The SDE in (12) can be solved by first defining the $u\times u$ fundamental matrix $G_t$ as the solution of

$$\begin{aligned} \frac{\mathrm{d}G_{t}}{\mathrm{d}t}=F_tG_t,\qquad G_0=I_u, \end{aligned}$$

(13)

where $I_u$ is the $u\times u$ identity matrix. Under the assumption of a fixed or Gaussian initial condition, $\tilde{M}_0\sim N(m_{0},V_{0})$, it can be shown that (see e.g. Fearnhead et al. 2014)

$$\begin{aligned} \tilde{M}_t|\tilde{M}_0=m_0\sim N(G_t m_0,G_t\psi _t G_t') \end{aligned}$$

where $\psi _t$ satisfies

$$\begin{aligned} \frac{\mathrm{d}\psi _{t}}{\mathrm{d}t}=G_t^{-1}\beta (z_t,c)\left( G_t^{-1}\right) '. \end{aligned}$$

(14)

It is convenient here to write $V_t=G_t\psi _t G_t'$, and it is straightforward to show that $V_t$ satisfies

$$\begin{aligned} \frac{\mathrm{d}V_{t}}{\mathrm{d}t}=V_t F_t'+\beta (z_t,c)+F_t V_t. \end{aligned}$$

(15)

In practice, if $x_0$ is a known fixed value, then we may take $z_0=x_0$, $m_0=0_u$ (the u-vector of zeros) and $V_0=0_{u\times u}$ (the $u\times u$ zero matrix). Solving (11) and (15) gives the approximating distribution of $X_t$ as

$$\begin{aligned} X_t|X_0=x_0 \sim N(z_t,V_t). \end{aligned}$$

In this case, the ODE system governing the fundamental matrix $G_t$ need not be solved.

4.2 LNA bridge with restart

Now, consider again the problem of approximating the MJP transition probability $p(y_{T}|X_{t}=x_t)$. Given a value $x_t$ at time $t\in [0,T)$, the ODE system given by (11) and (15) can be re-integrated over the time interval (t, T] to give output denoted by $z_{T|t}$ and $V_{T|t}$. Similarly, the initial conditions are denoted $z_{t|t}=x_t$ and $V_{t|t}=0_{u\times u}$. We refer to use of the LNA in this way as the LNA with restart (LNAR). The approximation to $p(y_{T}|X_{t}=x_t)$ is given by

$$\begin{aligned} p_{\text {lnar}}(y_{T}|X_{t}=x_t)=N\left( y_T; P'z_{T|t}\,,\,P'V_{T|t}P+\varSigma \right) . \end{aligned}$$

Likewise, $p_{\text {lnar}}(y_{T}|X_{t}=x')$ can be obtained by initialising (11) with $z_{t|t}=x'$ and integrating again. Hence, the approximate conditioned hazard is given by

$$\begin{aligned} \tilde{h}_{i}(x_t|y_T)=h_{i}(x_t)\frac{p_{\text {lnar}} (y_{T}|X_{t}=x')}{p_{\text {lnar}}(y_{T}|X_{t}=x_t)} \end{aligned}$$

(16)

Whilst use of the LNA in this way is likely to give an accurate approximation to the intractable transition probability (especially as t approaches T), the conditioned hazard in (6) must be calculated for $x_t$ and for each $x'$ obtained after the v possible transitions of the process. Consequently, the ODE system given by (11) and (15) must be solved at each event time for each of the $v+1$ possible states. Since the LNA ODEs are rarely tractable (necessitating the use of a numerical solver), this approach is likely to be prohibitively expensive, computationally. In the next section, we outline a novel strategy for reducing the cost associated with integrating the LNA ODE system, that only requires one full integration.

4.3 LNA bridge without restart

Consider the solution of the ODE system given by (11), (13) and (14) over the interval (0, T] with respective initial conditions $Z_0=x_0$, $G_0=I_u$ and $\psi _0=0_{u\times u}$. Although in practice a numerical solver must be used, we assume that the solution can be obtained over a sufficiently fine time grid to allow reasonable approximation to the ODE solution at an arbitrary time $t\in (0,T]$, denoted by $z_t$, $G_t$ and $\psi _t$.

Given a value $x_t$ at time $t\in [0,T)$, the LNA (without restart) approximates the intractable transition probability under the MJP by

$$\begin{aligned} p_{\text {lna}}(y_{T}|X_{t}=x_t)&=N\left( y_T; P'[z_{T}+G_{T|t}(x_t-z_t)]\,,\right. \\&\quad \left. \,P'[G_{T|t}\psi _{T|t}G_{T|t}']P+\varSigma \right) \end{aligned}$$

where $G_{T|t}$ and $\psi _{T|t}$ are the solutions of (13) and (14) integrated over (t, T] with initial conditions $G_{t|t}=I_{u}$ and $\psi _{t|t}=0_{u\times u}$. Crucially, the ODE system satisfied by $z_t$ is not re-integrated (and hence the residual term at time t is $\tilde{M}_t=x_t-z_t$). Moreover, $G_{T|t}$ and $\psi _{T|t}$ can be obtained without further integration. We have that

$$\begin{aligned} \text {E}(\tilde{M}_T|\tilde{M}_0 = m_0)&=G_T m_0 \\&= G_{T|t}\text {E}(\tilde{M}_t|\tilde{M}_0 = m_0)\\&=G_{T|t}G_t m_0, \end{aligned}$$

and therefore, the first identity we require is

$$\begin{aligned} G_{T|t}=G_{T}G_{t}^{-1}. \end{aligned}$$

(17)

Similarly,

$$\begin{aligned} \text {Var}(\tilde{M}_T|\tilde{M}_0=m_0)&= G_T \psi _T G_T\\&=G_{T|t}\text {Var}(\tilde{M}_t|\tilde{M}_0=m_0)G_{T|t}'\\&\quad +G_{T|t}\psi _{T|t}G_{T|t}'\\&=G_T\psi _t G_T' + G_{T|t}\psi _{T|t}G_{T|t}'\\&=G_T \psi _t G_T' +G_T G_t^{-1}\psi _{T|t}(G_t')^{-1}G_T' \end{aligned}$$

where we have used (17) to obtain the last line. The second identity we require is therefore

$$\begin{aligned} \psi _{T|t}=G_{t}(\psi _{T}-\psi _{t})G_{t}'. \end{aligned}$$

(18)

Hence, given $z_t$, $G_t$ and $\psi _t$ for $t\in (0,T]$, $p_{\text {lna}}(y_{T}|X_{t}=x_t,c)$ is easily evaluated via repeated application of (17) and (18). Additionally obtaining $p_{\text {lna}}(y_{T}|X_{t}=x')$ is straightforward by replacing the residual $x_t-z_t$ with $x'-z_t$. Hence, only one full integration of (11), (13) and (14) over (0, T] is required, giving a computationally efficient construct. The conditioned hazard takes the form

$$\begin{aligned} \tilde{h}_{i}(x_t,c|y_T)=h_{i}(x_t)\frac{p_{\text {lna}} (y_{T}|X_{t}=x')}{p_{\text {lna}}(y_{T}|X_{t}=x_t)} \end{aligned}$$

(19)

In Sect. 6, we describe how in the case of unknown $X_0$ it is possible to make further computational savings, using this technique.

The accuracy of $p_{\text {lna}}$ (and therefore the accuracy of the resulting conditioned hazard) is likely to depend on T, the length of the inter-observation period over which a realisation of the conditioned process is required. For example, the residual process $\tilde{M}_t$ will approximate the true (intractable) residual process increasingly poorly if $z_t$ and $X_t$ diverge significantly as t increases. We investigate the effect of inter-observation time in the next section.

5 Applications

In order to examine the empirical performance of the methods proposed in Sect. 4, we consider three examples of increasing complexity. These are a simple (and tractable) death model, the stochastic Lotka–Volterra model examined by Boys et al. (2008) among others and a susceptible-infected-removed (SIR) epidemic model. For the last of these, we use the best-performing LNA-based construct to drive a pseudo-marginal Metropolis–Hastings (PMMH) scheme to perform fully Bayesian inference for the rate constants c. Using real data consisting of susceptibles and infectives during the well-studied Eyam plague (Raggett 1982), we compare bridge-based PMMH with a standard implementation (using blind forward simulation) and a recently proposed scheme based on the alive particle filter (Drovandi et al. 2016). All algorithms are coded in R and were run on a desktop computer with an Intel Core i7-4770 processor at 3.40 GHz.

5.1 Death model

We consider a single reaction, governing a single specie $\mathcal {X}$, of the form

$$\begin{aligned} \mathcal {R}_{1}:\,\mathcal {X} \longrightarrow \emptyset \end{aligned}$$

with associated hazard function

$$\begin{aligned} h(x_t) = c\,x_{t} \end{aligned}$$

where $x_t$ denotes the state of the system at time t.

Under the assumption of an error-free observation scenario, the conditioned hazard of Golightly and Wilkinson (2015), given by (5), takes the form

$$\begin{aligned} \tilde{h}(x_t|y_{T})=\frac{x_T-x_t}{\varDelta t} \end{aligned}$$

and recall that $\varDelta t=T-t$.

The CLE is given by

$$\begin{aligned} \mathrm{d}X_{t}=-c\,X_{t}\,\mathrm{d}t + \sqrt{c\,X_{t}}\,\mathrm{d}W_{t}. \end{aligned}$$

Although the CLE is tractable in this special case (Cox et al. 1985), for reaction networks of reasonable size and complexity, the CLE will be intractable. We therefore implement the approach of Fearnhead (2008) by taking the conditioned hazard as in (9) where $p_{\text {cle}}$ is based on a single time step numerical approximation of the CLE. The Euler-Maruyama approximation gives

$$\begin{aligned} p_{\text {cle}}(x_T|x_t)=N\left( x_t\,;\, x_{t}-c\,x_{t}\,\varDelta t\,,\,c\,x_{t}\,\varDelta t\right) . \end{aligned}$$

The ODE system characterising the LNA (equations (11), (13) and (14)) with respective initial conditions $z_0=x_0$, $G_0=I_u$ and $\psi _0=0_{u\times u}$ can be solved analytically to give

$$\begin{aligned} z_t=x_0\mathrm{e}^{-c\, t},\qquad G_t=\mathrm{e}^{-c\, t},\qquad \psi _t= x_0 \left( \mathrm{e}^{c\, t}-1\right) . \end{aligned}$$

Hence, for the LNA with restart, we have that

$$\begin{aligned} p_{\text {lnar}}(x_{T}|x_t)=N\left\{ x_T\,;\, x_t \mathrm{e}^{-c\, \varDelta t}\,,\,x_t \mathrm{e}^{-c\, \varDelta t}\left( 1-\mathrm{e}^{-c\, \varDelta t}\right) \right\} . \end{aligned}$$

For the LNA without restart, we obtain

$$\begin{aligned} p_{\text {lna}}(x_{T}|x_t)=N\left\{ x_T\,;\, x_t \mathrm{e}^{-c\, \varDelta t} \,,\,x_0 \mathrm{e}^{-c\, T}\left( 1-\mathrm{e}^{-c\, \varDelta t}\right) \right\} . \end{aligned}$$

Table 1 Death model

In what follows, we took $c=0.5$ and $x_{0}=50$ to be fixed. The end-point $x_T$ was chosen as either the median, lower 1% or upper 99% quantile of the forward process $X_{T}|X_{0}=50$. We adopt the notation that $x_{T,(\alpha )}$ is the $\alpha \%$ quantile of $X_{T}|X_{0}=50$. Hence, we took the end-point $x_T \in \{x_{T,(1)},x_{T,(50)},x_{T,(99)}\}$. To assess the performance of the proposed approach as an observation is made with increasing time sparsity, we took $T\in \{0.5,1,2\}$. We applied weighted resampling (Algorithm 2) with five different hazard functions. These were: the unconditioned ‘blind’ hazard function, the conditioned hazard of Golightly/Wilkinson given by (5) and the Fearnhead approach based on the CLE (9), LNA with restart (16) and LNA without restart (19). The resulting algorithms are designated as blind, GW, F-CLE, F-LNAR and F-LNA. Each was run $m=5000$ times with $N=10$ samples to give a set of 5000 estimates of the transition probability $\pi (x_{t}|x_{0})$, and we denote this set by $\widehat{\pi }^{1:m}(x_{t}|x_{0})$. To compare the algorithms, we report the effective sample size

$$\begin{aligned} \text {ESS}(\widehat{\pi }^{1:m}) =\frac{\left( \sum _{i=1}^{m} \widehat{\pi }^{i}\right) ^{2}}{\sum _{i=1}^{m}\left( \widehat{\pi }^{i} \right) ^{2}} \end{aligned}$$

and relative mean-squared error $\text {ReMSE}(\widehat{\pi }^{1:m})$ given by

$$\begin{aligned} \text {ReMSE}(\widehat{\pi }^{1:m})=\frac{1}{m}\sum _{i=1}^{m} \frac{\left[ \widehat{\pi }^{i}(x_{t}|x_{0})-\pi (x_{t}|x_{0})\right] ^{2}}{\pi (x_{t}|x_{0})} \end{aligned}$$

where $\pi (x_{t}|x_{0})$ can be obtained analytically [e.g. Bailey (1964)] as

$$\begin{aligned} \pi (x_{t}|x_{0})=\begin{pmatrix} x_0 \\ x_t \end{pmatrix} \mathrm{e}^{-c\,t\, x_t}\left( 1-\mathrm{e}^{-c\,t}\right) ^{x_0-x_t}. \end{aligned}$$

The results are summarised in Table 1. Whilst the blind approach gives broadly comparable performance to the conditioned approaches when $x_T=x_{T,(50)}$, its performance deteriorates significantly when the end point is taken to be a value in the tails of $X_t | X_0 = 50$. This is due to the blind approach struggling to generate trajectories that are highly unlikely to hit the neighbourhood of the end point. For the CH approach, we see a decrease in ESS and an increase in ReMSE as T increases, due to the linear form being unable to adequately describe the exponential like decay exhibited by the true conditioned process. Whilst the F-CLE approach performs well when $x_T=x_{T,(50)}$ and $x_T=x_{T,(99)}$, it is unable to match the performance of the LNA-based methods across all scenarios. The effect of not restarting the LNA (i.e. by re-integrating the LNA ODEs after each value of the jump process is generated) appears to be minimal here, with both F-LNAR and F-LNA giving comparable ESS and ReMSE values.

5.2 Lotka–Volterra

We consider here a Lotka–Volterra model of prey ($\mathcal {X}_1$) and predator ($\mathcal {X}_2$) interaction comprising three reactions of the form

$$\begin{aligned}&\mathcal {R}_1:\quad \mathcal {X}_{1} \xrightarrow {c_{1}} 2\mathcal {X}_{1}\\&\mathcal {R}_2:\quad \mathcal {X}_{1}+\mathcal {X}_{2} \xrightarrow {c_{2}} 2\mathcal {X}_{2}\\&\mathcal {R}_3:\quad \mathcal {X}_{2} \xrightarrow {c_{3}} \emptyset . \end{aligned}$$

The stoichiometry matrix is given by

$$\begin{aligned} S = \left( \begin{array}{rrr} 1 &{} -1 &{} 0\\ 0 &{} 1 &{} -1 \end{array}\right) , \end{aligned}$$

and the associated hazard function is

$$\begin{aligned} h(x_t) = (c_{1}x_{1,t}, c_{2}x_{1,t}x_{2,t}, c_{3}x_{2,t})'. \end{aligned}$$

The conditioned hazard described in Sect. 3.2 and given by (5) can then be obtained.

The CLE for the Lotka–Volterra model is given by

$$\begin{aligned}&\mathrm{d}\begin{pmatrix}X_{1}\\ X_{2}\end{pmatrix}= \begin{pmatrix} c_{1}X_{1}-c_{2}X_{1}X_{2} \\ c_{2}X_{1}X_{2}-c_{3}X_{2} \end{pmatrix}\,\mathrm{d}t\nonumber \\&\qquad + \begin{pmatrix}c_{1}X_{1}+c_{2}X_{1}X_{2} &{}\quad -c_{2}X_{1}X_{2} \\ -c_{2}X_{1}X_{2} &{}\quad c_{2}X_{1}X_{2}+c_{3}X_{2} \end{pmatrix}^{1/2}\,\mathrm{d} \begin{pmatrix}W_{1}\\ W_{2}\end{pmatrix} \end{aligned}$$

(20)

after suppressing dependence on t. It is then straightforward to obtain the Euler-Maruyama approximation of the CLE, for use in the conditioned hazard described in Sect. 3.3 and given by (9).

For the linear noise approximation, the Jacobian matrix $F_t$ is given by

$$\begin{aligned} F_{t} = \left( \begin{array}{ll} c_{1}-c_{2}z_{2,t} &{}\quad -c_{2}z_{1,t} \\ c_{2}z_{2,t} &{}\quad c_{2}z_{1,t}-c_{3} \end{array}\right) . \end{aligned}$$

Unfortunately, the ODEs characterising the LNA solution, given by (11), (13) and (14), are intractable, necessitating the use of a numerical solver. In what follows, we use the deSolve package in R, with the default LSODA integrator (Petzold 1983).

Our initial experiments used the following settings. Following Boys et al. (2008) among others, we imposed the parameter values $c=(c_1,c_2,c_3)'=(0.5,0.0025, 0.3)'$ and let $x_0=(50,50)'$. We assumed an observation model of the form (1) and took $\varSigma =\sigma ^2 I_{2}$ with $\sigma =5$ representing low measurement error (since typical simulations of $X_{1,t}$ and $X_{2,t}$ are around two orders of magnitude larger than $\sigma$). We generated a number of challenging scenarios by taking $y_T$ as the pair of 1%, 50% or 99% marginal quantiles of $Y_T|X_0=(50,50)'$ for $T\in \{1,2,3,4\}$. These quantiles are denoted by $y_{T,(1)}$, $y_{T,(50)}$ and $y_{T,(99)}$, respectively, and are shown in Table 2.

Table 2 Lotka–Volterra model

Fig. 1

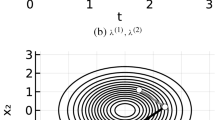
Lotka–Volterra model. Mean and two standard deviation intervals for the true conditioned process $X_{t}|x_0,y_T$ (solid lines) and various bridge constructs (dashed lines) using $y_T=y_{T,(99)}$, $T=4$ and $\sigma =5$. The upper lines correspond to the prey component, and the lower lines correspond to the predator component

Fig. 2

Lotka–Volterra model. Effective sample size (ESS, top row), log (base 10) computing time in seconds (CPU, middle row) and log (base 10) effective sample size per second (ESS/s, bottom row) based on the output of the weighted resampling algorithm with $N=5000$ and $y_T\in \{y_{T,(1)},y_{T,(50)},y_{T,(99)}\}$, $T=1,2,3,4$. Dotted lines: CH. Dashed lines: F-LNAR. Solid lines: F-LNA

Figure 1 compares summaries (mean plus and minus two standard deviations) of each competing bridge process with the same summaries of the true conditioned process (obtained via simulation), for the extreme case of $T=4$ and $y_T=y_{T,(99)}$. Plainly, the blind forward simulation approach and CLE-based Fearnhead approach (F-CLE) are unable to match the dynamics of the true conditioned process. Moreover, we found that these bridges gave very small effective sample sizes for $T\ge 2$ and we therefore omit these results from the following analysis.

We report results based on weighted resampling using $N=5000$ with three different hazard functions: the Golightly/Wilkinson approach (CH) and the Fearnhead approach based on the LNA with and without restart (F-LNAR and F-LNA, respectively). For the latter (F-LNA), we integrated the LNA once in total. Figure 2 shows, for each value of $y_T$ in Table 2, effective sample size (ESS), log (base 10) CPU time and log (base 10) ESS per second. Note that for this example, ESS is calculated as

$$\begin{aligned} \text {ESS}(\tilde{w}^{1:N}) =\frac{\left( \sum _{i=1}^{N}\tilde{w}^{i} \right) ^{2}}{\sum _{i=1}^{N}\left( \tilde{w}^{i}\right) ^{2}} \end{aligned}$$

where $\tilde{w}^{1:N}$ denotes the unnormalised weights generated by the weighted resampling algorithm. We see that although CH is computationally inexpensive, ESS decreases as T increases, as it is unable to match the nonlinear dynamics of the true conditioned process. In contrast, although more computationally expensive, F-LNAR and F-LNA maintain high ESS values as T is increased. Consequently, in terms of ESS per second, CH is outperformed by F-LNAR for $T\ge 3$ and F-LNA for $T\ge 2$. Due to not having to restart the LNA ODEs after each simulated value of the jump process, F-LNA is around an order of magnitude faster than F-LNAR in terms of CPU time, with the difference increasing as T is increased. Given then the comparable ESS values obtained for F-LNAR and F-LNA, we see that in terms of ESS/s, F-LNA outperforms F-LNAR by at least an order of magnitude in all cases and outperforms CH by 1-2 orders of magnitude when $T=4$.

Table 3 Lotka–Volterra model

Fig. 3

Lotka–Volterra model. Effective sample size (ESS, left panel), log (base 10) computing time in seconds (CPU, middle panel) and log (base 10) effective sample size per second (ESS/s, right panel) based on the output of the weighted resampling algorithm with $N=5000$ and $y_T=y_{T,(50)}$, $T=1,2,3,4$. Dotted lines: $x_0=(10,10)'$ and $\sigma =1$. Dashed lines: $x_0=(25,25)'$ and $\sigma =2.5$. Solid lines: $x_0=(50,50)'$ and $\sigma =5$

The LNA is known to break down as an inferential model in situations involving low counts of the MJP components (Schnoerr et al. 2017). Therefore, to investigate the performance of the use of the LNA in constructing an approximate conditioned hazard in low-count scenarios, we additionally considered an initial condition with $x_{1,0}=x_{2,0}\in \{10,25,50\}$ and took $y_T$ as the median of $Y_T|X_0=x_0$ for $T\in \{1,2,3,4\}$. To fix the relative effect of the measurement error, we took $\sigma =1$ for the case $x_0=(10,10)'$ and scaled $\sigma$ in proportion to the components of $x_0$ for the remaining scenarios. The resulting values of $y_T$ can be found in Table 3. We report results based on weighted resampling using $N=5000$ and F-LNA in Fig. 3. We see that when the initial condition is decreased from $x_0=(50,50)'$ to $x_0=(10,10)'$, ESS decreases by a factor of around 1.6 (4906 vs 2998) when $T=1$ and 2.5 (4562 vs 1853) when $T=4$. Nevertheless, computational cost decreases as $x_0$ decreases (and in turn, the expected number of reaction events in the observation window decreases). Hence, there is little difference in overall efficiency (ESS/s) across the three scenarios.

5.3 SIR model

5.3.1 Model and data

The susceptible–infected–removed (SIR) epidemic model has two species (susceptibles $\mathcal {X}_{1}$ and infectives $\mathcal {X}_{2}$) and two reaction channels (infection of a susceptible and removal of an infective):

$$\begin{aligned} \mathcal {R}_1:\quad \mathcal {X}_{1}+\mathcal {X}_{2}&\xrightarrow {c_1} 2\mathcal {X}_{2}\\ \mathcal {R}_2:\quad \mathcal {X}_{2}&\xrightarrow {c_2} \emptyset . \end{aligned}$$

The vector of rate constants is $c=(c_1,c_2)'$, and the stoichiometry matrix is given by

$$\begin{aligned} S = \left( \begin{array}{rr} -1 &{}\quad 0\\ 1 &{}\quad -1 \end{array}\right) . \end{aligned}$$

The hazard function is given by $h(x_t) = (c_1 x_{1,t}x_{2,t}, c_2 x_{2,t})'$. For the linear noise approximation, the Jacobian matrix $F_t$ is given by

$$\begin{aligned} F_{t} = \left( \begin{array}{ll} -c_1 z_{2} &{}\quad -c_1 z_{1} \\ c_1 z_{2} &{}\quad c_1 z_{1}-c_2 \end{array}\right) . \end{aligned}$$

The ODEs characterising the LNA solution, given by (11), (13) and (14) are intractable. As in Sect. 5.2, we use the deSolve package in R whenever a numerical solution is required.

We consider data consisting of eight observations on susceptible and infectives during the outbreak of plague in the village of Eyam, England. The data are taken over a four-month period from June 18th 1666 and are presented here in Table 4. Note that the infective population is estimated from a list of deaths, and by assuming a fixed illness length (Raggett 1982).

Table 4 Eyam plague data

5.3.2 Pseudo-marginal Metropolis–Hastings

Let $\varvec{y}=\{y_{t_i}\}$, $i=1,\ldots ,8$ denote the observations at times $0=t_1<\cdots < t_8 = 4$. The latent Markov jump process over the time interval $(t_i,t_{i+1}]$ is denoted by $\varvec{X}_{(t_i,t_{i+1}]}=\{X_{s}\,|\, t_i< s \le t_{i+1}\}$. Under the assumption of no measurement error, we have that $X_{t_i}=y_{t_{i}}$, $i=1,\ldots ,8$. Upon ascribing a prior density p(c) to the rate constants c, Bayesian inference may proceed via the marginal parameter posterior

$$\begin{aligned} p(c|\varvec{y})\propto p(c)p(\varvec{y}|c) \end{aligned}$$

(21)

where

$$\begin{aligned} p(\varvec{y}|c)=\prod _{i=1}^{7}p(y_{t_{i+1}}|y_{t_{i}},c) \end{aligned}$$

(22)

is the observed data likelihood. Although $p(\varvec{y}|c)$ is intractable, we note that each term in (22) can be seen as the normalising constant of

$$\begin{aligned} p(\varvec{x}_{(t_i,t_{i+1}]}|x_{t_i},y_{t_{i+1}},c)\propto p(y_{t_{i+1}}|x_{t_{i+1}})p(\varvec{x}_{(t_i,t_{i+1}]}|x_{t_i},c) \end{aligned}$$

where $p(y_{t_{i+1}}|x_{t_{i+1}})$ takes the value 1 if $x_{t_{i+1}}=y_{t_{i+1}}$ and 0 otherwise. Hence, running steps 1(a) and (b) of Algorithm 2 with $x_0$ and $y_T$ replaced by $x_{t_i}$ and $y_{t_{i+1}}$, respectively, can be used to unbiasedly estimate $p(y_{t_{i+1}}|y_{t_{i}},c)$. No resampling is required, since only those trajectories that coincide with the observation $y_{t_{i+1}}$ will have nonzero weight. By analogy with Eq. (4), and allowing explicit dependence on c, we have the unbiased estimator

$$\begin{aligned}&\hat{p}(y_{t_{i+1}}|y_{t_{i}},c)\nonumber \\&\quad =\frac{1}{N}\sum _{j=1}^{N}p(y_{t_{i+1}}|X_{t_{i+1}}^j) \frac{p(\varvec{X}_{(t_i,t_{i+1}]}^{j}|x_{t_i},c)}{q(\varvec{X}_{(t_i,t_{i+1}]}^{j}|x_{t_i},y_{t_{i+1}},c)} \end{aligned}$$

(23)

where $\varvec{X}_{(t_i,t_{i+1}]}^{j}$ is an independent draw from $q(\cdot |x_{t_i},y_{t_{i+1}},c)$. Then, multiplying the $\hat{p}(y_{t_{i+1}}|y_{t_{i}},c)$, $i=1,\ldots ,7$, gives an unbiased estimator of the observed data likelihood $p(\varvec{y}|c)$.

An alternative unbiased estimator of the observed data likelihood can be found by using (a special case of) the alive particle filter (Del Moral et al. 2015). Essentially, forward draws are repeatedly generated from $p(\cdot |x_{t_i},c)$ (via Gillespie’s direct method) until $N+1$ trajectories that match the observation are obtained. Let $n_i$ denote the number of simulations required to generate $N+1$ matches with $y_{t_{i+1}}$. The estimator is then given by

$$\begin{aligned} \hat{p}(y_{t_{i+1}}|y_{t_{i}},c)= \frac{N}{n_i - 1}. \end{aligned}$$

(24)

Fig. 4

SIR model. Marginal posterior densities based on the output of F-LNA

Fig. 5

SIR model. Mean and two standard deviation intervals for the true conditioned process $X_{t}|x_0,y_{0.5},c$ over the first observation interval, with $c=(0.02,3.2)'$

Let $U\sim p(\cdot |c)$ denote the flattened vector of all random variables required to generate the estimator of observed data likelihood, which we denote by $\hat{p}_{U}(\varvec{y}|c)$. The pseudo-marginal Metropolis–Hastings (PMMH) scheme is an MH scheme that targets the joint density

$$\begin{aligned} p(c,u)\propto p(c)\hat{p}_{u}(\varvec{y}|c)p(u|c) \end{aligned}$$

for which it is easily checked that

$$\begin{aligned} \int p(c,u)\, \mathrm{d}u&\propto p(c)\int \hat{p}_{u}(\varvec{y}|c)p(u|c)\,\mathrm{d}u\\&\propto p(c)p(\varvec{y}|c) \end{aligned}$$

where the last line follows from the unbiasedness property of $\hat{p}_{U}(\varvec{y}|c)$. Hence, we see that the target posterior $p(c|\varvec{y})$ is a marginal of the joint density p(c, u). Now, running an MH scheme with a proposal density of the form $q(c^*|c)p(u^*|c^*)$ gives the acceptance probability

$$\begin{aligned} \text {min}\left\{ 1, \frac{p(c^*)\hat{p}_{u^*}(\varvec{y}|c^*)}{p(c)\hat{p}_{u}(\varvec{y}|c)}\times \frac{q(c|c^*)}{q(c^*|c)}\right\} . \end{aligned}$$

Practical advice for choosing N to balance mixing performance and computational cost can found in Doucet et al. (2015) and Sherlock et al. (2015). The variance of the log posterior (denoted $\sigma ^{2}_{N}$, computed with N samples) at a central value of c (e.g. the estimated posterior median) should be around 2. In what follows, we use a random walk on $\log c$ as the parameter proposal. The innovation variance is taken to be the marginal posterior variance of $\log c$ estimated from a pilot run and further scaled to give an acceptance rate of around 0.2–0.3. We followed Ho et al. (2018) by adopting independent $N(0,100^2)$ priors for $\log c_i$, $i=1,2$.

Although we do not pursue it here, the case of nonzero measurement error is easily accommodated by iteratively running Algorithm 2 in full, for each observation time $t_i$, $i=1,\ldots ,7$. At time $t_i$, $y_T$ is replaced by $y_{t_{i+1}}$ and $x_0$ is replaced by $x_{t_i}^j$. At time $t_1$, $x_0$ can be replaced by a draw from a prior density $p(x_{t_1})$ placed on the unobserved initial value. The product (across time) of the average unnormalised weight can be shown to give an unbiased estimator of the observed data likelihood (Del Moral 2004; Pitt et al. 2012). We refer the reader to Golightly and Wilkinson (2015) and the references therein for further details of the resulting Metropolis–Hastings scheme.

5.3.3 Results

We ran PMMH using the observed data likelihood estimator based on (23), with trajectories drawn using either forward simulation or the Fearnhead approach based on the LNA (without restart). We designate the former as “Blind” and the latter as “F-LNA”. Additionally, we ran PMMH using the observed data likelihood estimator based on (24). We designate this scheme as “Alive”.

We ran each scheme for $10^4$ iterations. For Alive, we followed Drovandi and McCutchan (2016) by terminating any likelihood calculation that exceeded 100,000 forward simulations, and rejecting the corresponding move. Marginal posterior densities can be found in Fig. 4 and are consistent with the posterior summaries reported by Ho et al. (2018). Figure 5 summarises the posterior distribution of $X_{t}|x_0,y_{0.5},c$, where c is fixed at the estimated posterior mean. We note the nonlinear behaviour of the conditioned process over this time interval, with similar nonlinear dynamics observed for other intervals (not reported). Table 5 summarises the computational and statistical performance of the competing inference schemes. We measure statistical efficiency by calculating minimum (over each parameter chain) effective sample size per second (mESS/s). As is appropriate for MCMC output, we use

$$\begin{aligned} \text {ESS}=\frac{n_{\text {iters}}}{1+2\sum _{k=1}^{\infty }\alpha _k} \end{aligned}$$

where $\alpha _k$ is the autocorrelation function for the series at lag k and $n_{\text {iters}}$ is the number of iterations in the main monitoring run. Inspection of Table 5 reveals that although use of the alive particle filter only requires $N=8$ (compared to $N=5000$ and $N=100$ for Blind and F-LNA, respectively), it exhibits the largest CPU time. We found that for parameter values in the tails of the posterior, Alive would often require many thousands of forward simulations to obtain $N=8$ matches. Consequently, Alive is outperformed by Blind by a factor of 2 in terms of overall efficiency. Use of the LNA-driven bridge (without restart) gives a further improvement over Blind of a factor of 2.

6 Discussion

Performing efficient sampling of a Markov jump process (MJP) between a known value and a potentially partial or noisy observation is a key requirement of simulation-based approaches to parameter inference. Generating end-point conditioned trajectories, known as bridges, is challenging due to the intractability of the probability function governing the conditioned process. Approximating the hazard function associated with the conditioned process (that is, the conditioned hazard), and correcting draws obtained via this hazard function using weighted resampling or Markov chain Monte Carlo offers a viable solution to the problem. Recent approaches in this direction (Fearnhead 2008; Golightly and Wilkinson 2015) give approximate hazard functions that utilise a Gaussian approximation of the MJP. For example, Golightly and Wilkinson (2015) approximate the number of reactions between observation times as Gaussian. Fearnhead (2008) recognises that the conditioned hazard can be written in terms of the intractable transition probability associated with the MJP. The transition probability is replaced with a Gaussian transition density obtained from the Euler–Maruyama approximation of the chemical Langevin equation. In both approaches, the remaining time until the next observation is treated as a single discretisation. Consequently, the accuracy of the resulting bridges deteriorates as the inter-observation time increases.

Starting with the form of the conditioned hazard function, we have proposed a novel bridge construct by replacing the intractable MJP transition probability with the transition density governing the linear noise approximation (LNA). Whilst our approach also involves a Gaussian approximation, we find that the tractability of the LNA can be exploited to give an accurate bridge construct. Essentially, the LNA solution can be re-integrated over each observation window to maintain accuracy. The cost of ‘restarting’ the LNA in this way is likely to preclude its practical use. We have therefore further proposed an implementation, which only requires a single full integration of the ordinary differential equation system governing the LNA. Our experiments demonstrated superior performance of the LNA-based bridge over existing constructs, especially in data-sparse scenarios. Whilst the LNA is known to give a poor approximation of the MJP in low-count scenarios (Schnoerr et al. 2017), we note that its role here is in the approximation of transition densities over ever diminishing time intervals. Moreover, the resulting approximate conditioned hazard function is corrected for via a weighted resampling scheme. Consequently, we find that use of the LNA in this way is relatively robust to situations involving low counts. Using a real data application, we further demonstrated the potential of the proposed methodology in allowing efficient parameter inference.

Table 5 SIR model

When the dimension of the statespace is finite, then the transition probability from a known state at time 0 to a known state at time T can be calculated exactly and efficiently via the action of a matrix exponential on a vector (e.g. Sidje and Stewart 1999), giving the likelihood directly; alternatively, the uniformisation method of Rao and Teh (2013) may be used for Bayesian inference. The recent article Georgoulas et al. (2017) extends the standard finite-statespace matrix-exponential method to an infinite statespace pseudo-marginal MCMC algorithm which uses random truncation (e.g. Glynn and Rhee 2014) to produce a realisation from an unbiased estimator of the likelihood when the observations are exact. In contrast to the algorithms which we have investigated, which simulate paths for the process and whose performance improves as the observation noise increases, any extension to the algorithm of Georgoulas et al. (2017) that allows for observation error would reduce the efficiency of the algorithm. This suggests the possibility that for small enough observation noise an extension to the algorithm in Georgoulas et al. (2017) might be more efficient than our non-restarting bridge. Investigations into the relative efficiencies of such algorithms are ongoing.

This article has focused on bridges from a known initial condition. When the initial condition is unknown, such as typically arises in a particle filter-based analysis, a sample from the distribution of the initial state, $\{x_0^{1},\ldots ,x_0^N\}$, is available and a separate bridge to the observation is required from each element of the sample. In this case, two different implementations of the LNA bridge without restarting are possible. In the first implementation, trajectories $\varvec{X}^i|x_0^i,y_T$ are generated using one full integration of (11), (13) and (14) over (0, T] for each$x_0^i$. That is, each trajectory has (11) initialised at $x_0^i$. In the second implementation, (11), (13) and (14) are integrated just once, irrespective of the number of required trajectories. This can be achieved by initialising (11) at some plausible value e.g. $E(X_0)$. Although the second implementation will be more computationally efficient than the first, some loss of accuracy is expected, especially when the uncertainty in $X_0$ is large. A single integral, however, may well be adequate in the cases which are the focus of this article: where the observation noise is small. Investigating the efficiency of the bridge construct in this scenario, as well as in multi-scale settings (see e.g. Thomas et al. 2014) where some reactions regularly occur more frequently than others, remains the subject of ongoing research.