A constrained regression model for an ordinal response with ordinal predictors

Abstract

A regression model is proposed for the analysis of an ordinal response variable depending on a set of multiple covariates containing ordinal and potentially other variables. The proportional odds model (McCullagh in J R Stat Soc Ser B (Methodol) 109–142, 1980) is used for the ordinal response, and constrained maximum likelihood estimation is used to account for the ordinality of covariates. Ordinal predictors are coded by dummy variables. The parameters associated with the categories of the ordinal predictor(s) are constrained, enforcing them to be monotonic (isotonic or antitonic). A decision rule is introduced for classifying the ordinal predictors’ monotonicity directions, also providing information whether observations are compatible with both or no monotonicity direction. In addition, a monotonicity test for the parameters of any ordinal predictor is proposed. The monotonicity constrained model is proposed together with five estimation methods and compared to the unconstrained one based on simulations. The model is applied to real data explaining a 10-points Likert scale quality of life self-assessment variable by ordinal and other predictors.

1 Introduction

In many situations where regression models are suitable, the relationship between ordinal responses and ordinal predictors is of interest. However, statistical modelling for this type of relationship has called little attention. Even the literature for ordinal predictors with any other type of scale of the response variable is scarce (see, for example, Tutz and Gertheiss 2014 and Rufibach 2010).

In order to account for an ordinal response variable, proportional odds cumulative logit models (McCullagh 1980) are used here in the presence of multiple predictors allowing for different measurement scales. We pay special attention to the treatment of ordinal scale predictors. Their parameter estimates are restricted to be monotonic through constrained maximum likelihood estimation (CMLE). To begin with, consider for simplicity one ordinal response variable y with k categories and one ordinal predictor x with p categories. The corresponding model for this setup is

$$\begin{aligned} \text {logit}[P(y_{i}\le j|x_i)] = \alpha _j + \sum _{h=2}^p \beta _h x_{i,h}, \end{aligned}$$

(1)

$j = 1,\ldots , k-1$. $\alpha _j$ and $\beta _h$ for $h=2,\ldots p$ are real parameters. The observations are $(\mathbf {x}_i,y_i),\ i=1,\ldots ,n$. The vector $\mathbf {x}_i$ contains the $x_{i,h}$, which are dummy variables defined as $x_{i,h}=1$ if $x_i$ falls in the h-th category of the ordinal predictor and 0 otherwise, with $h=2,\ldots , p$. Category number 1 is treated as the baseline category with $\beta _1=0$; therefore, the dummy variable $x_{i,1}=1-\sum _{h=2}^p x_{i,h}$ is omitted and the sum in model (1) starts at $h=2$. Monotonicity on $\{\beta _h\}$ is obtained by using CMLE. The general model is defined in Sect. 2, which allows for multiple ordinal predictors and other covariates of different measurement scales.

The monotonic effects approach to the ordinal predictors treatment is conceived here as an intermediate point between two general and common approaches within the context of regression analysis on observed variables. One of these common approaches corresponds to an unconstrained version of (1), treating the ordinal predictor as if it were nominal. This ignores the ordinal information. The other common approach treats an ordinal predictor as if it were of interval scale, replacing it by a single transformed variable after applying some scoring method, f. More formally,

$$\begin{aligned} \text {logit}[P(y_{i}\le j|x_i)] = \alpha _j + \beta \tilde{x}_{i}, \end{aligned}$$

(2)

with $\tilde{x}=f(x)$. This treats f(x) as interval scaled. Numerous data-based methods for scaling of ordinal variables have been proposed in the literature, on top of using plain equidistant Likert scaling (see, e.g., Bross 1958; Harter 1961; Tukey 1962; Hensler and Stipak 1979; Brockett 1981; Casacci and Pareto 2015), but ultimately in most situations the data do not carry conclusive information about the appropriateness of any scaling f.

The intermediate approach proposed here is defined to achieve a set of linear estimates described by multiple magnitudes, as in the nominal scale approach, but allowing one direction only, as in the interval scale approach. The latter is attained by restricting the effects of model (1) to be monotonic in either direction. The monotonicity assumption should not necessarily be taken for granted in regression with ordinal predictor and response. But it has a special status, similarly to linearity between interval-scaled variables. According to Stevens (1946) the interval scale is defined by the equality in the meaning of differences between values regardless of the location of these differences on the measurement range. A linear relationship between interval-scaled variables means that the impact of a change in the predictor on the response is proportional to the meaning of the change of measurement at all locations of the measurement scale. For the ordinal measurement scale, only the order of measured values is meaningful. In this case, monotonic relationships are those that imply that a change in the predictor of the same meaning (i.e., changing to a value that is higher, or lower, respectively) at all locations of the measurement scale has an effect of the same meaning on the response.

Some other regression models for ordinal predictors are also based on the monotonic effects assumption. However, models for ordinal responses have not been explicitly discussed in this context. Tutz and Gertheiss (2014) used penalisation methods for modelling rating scales as predictors, and an active set algorithm was proposed by Rufibach (2010) to incorporate ordinal predictors in some regression models considering the response variable to be continuous, binary, or represent censored survival times, and assuming isotonic effects of the ordinal predictors’ categories. Another related method is isotonic regression, mostly applied to continuous data (see, for example, Barlow and Brunk 1972; Dykstra and Robertson 1982; Stout 2015). In a broader context, there are some other types of statistical models that deal with ordinal data, such as those in item response theory (IRT) (e.g., Tutz 1990; Bacci et al. 2014), latent class models (e.g., Moustaki 2000, 2003; Vasdekis et al. 2012), nonlinear principal components analysis (NLPCA) (e.g., De Leeuw and Mair 2009; Linting and van der Kooij 2012; Mori et al. 2016), and nonlinear canonical correlation analysis (NLCCA) (e.g., Mardia et al. 1979; De Leeuw and Mair 2009). However, their settings are somewhat different compared to the one corresponding to modelling an ordinal response with ordinal predictors (and others) in classical regression. For instance, unlike IRT models and latent class models, classical regression models do not assume latent variables; and in contrast to NLPCA and NLCCA, classical regression models are not used as a dimensionality reduction technique and need a single dependent variable, respectively.

The monotonicity constrained regression model discussed here can be used for several purposes. When the unconstrained parameter estimates associated with the ordinal predictor are monotonic, then clearly there is no need of a constrained model. However, when these unconstrained estimates are non-monotonic, then there are some reasons why the constrained model could be useful. It is often of interest to compare unconstrained and constrained fits in order to decide whether there is evidence for non-monotonic relationship. In case that the unconstrained version does not provide a clearly better fit, the monotonic fit may be superior regarding interpretability, and may also lead to a smaller mean square error, as will be shown by simulations and a real data application.

In Sect. 2, the proposed model is developed in detail to obtain both constrained parameter estimates for multiple ordinal predictors and unconstrained estimates for other types of covariates. As the monotonic estimates can be either increasing (isotonic) or decreasing (antitonic), it is necessary to specify this relation while defining the constraints. Also, investigating possible directions of monotonicity for all ordinal predictors is of interest in its own right. Therefore, a monotonicity direction classification (MDC) procedure is introduced in Sect. 3 that determines the best possible combination of isotonic and/or antitonic associations as a way of assisting the estimation method of the constrained model introduced in Sect. 2. In Sect. 4, a monotonicity test is proposed as a complementary tool to assess the validity of the monotonicity assumption of each ordinal predictor. Both the MDC procedure and the monotonicity test provide statistical evidence on the validity of the monotonicity assumption. This can be incorporated in the estimation procedure; Sect. 5 presents four approaches, one based on the monotonicity test and three based on the MDC procedure. On the other hand, the same procedures may also detect that the data are consistent with zero influence of a variable, in which case the variable may be dropped, this is treated in Sect. 5.3. Simulations are presented in Sect. 6 comparing the mean square error and standard error between the constrained and unconstrained approaches. Finally, the proposed model is applied to real data from the Chilean National Socio-Economic Characterisation in Sect. 7. A quality of life self-assessment variable using a 10-points Likert scale is analysed considering ordinal and other predictors.

2 Proportional odds with monotonicity constraints

For an ordinal response variable y with k categories, let $y_i$ be the response category for subject i. The model of proportional odds is

$$\begin{aligned} \text {logit}[P(y_{i}\le j | \mathbf {x}_i)]=\alpha _j+\varvec{\beta }'\mathbf {x}_i, \end{aligned}$$

(3)

$j=1,\ldots , k-1,\ i=1,\ldots ,n.$ A part of the elements of $\varvec{\beta }$ corresponds to those effects associated with ordinal predictors categories in $\mathbf {x}$, for which their parameter estimates are constrained to account for monotonicity as explained later.

When this model has one or more of both ordinal and non-ordinal predictors, it can be represented as

$$\begin{aligned} \text {logit}[P(y_{i}\le j | \mathbf {x}_i)]=\alpha _j+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s} \beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}, \end{aligned}$$

(4)

where $\mathbf {x}_i$ is a vector with $v-t+\sum _{s=1}^{t}p_s$ elements representing a set of t ordinal predictors (OP) and their $\sum _{s=1}^t p_s$ categories together with v non-ordinal predictors for the i-th observation. Each ordinal predictor is denoted by the subindex s, with $s=1,\ldots ,t$, and contributes $p_s-1$ dummy variables to the model representing its ordinal categories $\{1,\ldots ,p_s\}$ assuming the first one as the baseline category, thus $\beta _{s,1}=0$. Note that differences between the regression parameters belonging to the ordinal categories are independent of the baseline category. We later use confidence intervals (CIs) for these parameters, the widths of which can depend on the baseline category. For ordinal variables, the beginning or end point of the scale seems natural choices. Each dummy variable is defined as $x_{i,s,h_s}=1$ if the i-th observation falls in the category $h_s$ of the ordinal predictor s and 0 otherwise, with $h_s=1,\ldots ,p_s$. Therefore, $\mathbf {x}_i'=(x_{i,1,2},\ldots ,x_{i,1,p_1},x_{i,2,2},\ldots ,x_{i,2,p_2},\ldots , x_{i,t,2},\ldots ,x_{i,t,p_t},x_{i,1},\ldots ,x_{i,v})$, where those variables with three indexes correspond to the observation of an ordinal predictor category and those with two are observations of other types of covariates.

2.1 Likelihood model fitting

Define $\pi _j(\mathbf {x}_i)=P(y_{i}=j|\mathbf {x}_i)$, the probability of the response of subject i to fall in category j, and let $y_{i1},\ldots , y_{ik}$ be the binary indicators of the response for subject i, where $y_{ij}=1$ if its response falls in category j and 0 otherwise. Therefore, for independent observations, the likelihood function is based on the product of the multinomial mass functions for the n subjects:

$$\begin{aligned}&L(\{\alpha _j\},\varvec{\beta })\nonumber \\&\quad =\prod _{i=1}^n\Bigg \{\prod _{j=1}^k\pi _j(\mathbf {x}_i)^{y_{ij}}\Bigg \} \nonumber \\&\quad =\prod _{i=1}^n\Bigg \{\prod _{j=1}^k P(y_{i}=j|\mathbf {x}_i)^{y_{ij}}\Bigg \} \nonumber \\&\quad =\prod _{i=1}^n\Bigg \{\prod _{j=1}^k [P(y_{i}\le j|\mathbf {x}_i)-P(y_{i}\le j-1|\mathbf {x}_i)]^{y_{ij}}\Bigg \}\nonumber \\&\quad =\prod _{i=1}^n\left\{ \prod _{j=1}^k \left[ \frac{e^{\alpha _j+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}}{1+e^{\alpha _j+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}} \right. \right. \nonumber \\&\left. \left. \qquad -\frac{e^{\alpha _{j-1}+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}}{1+e^{\alpha _{j-1}+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}}\right] ^{y_{ij}}\right\} . \end{aligned}$$

(5)

Hence,

$$\begin{aligned} \pi _j(\mathbf {x}_i)&=\frac{e^{\alpha _j+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}}{1+e^{\alpha _j+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}} \nonumber \\&\quad -\frac{e^{\alpha _{j-1}+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}}{1+e^{\alpha _{j-1}+\sum _{s=1}^{t}\sum _{h_s=2}^{p_s}\beta _{s,h_s}x_{i,s,h_s}+\sum _{u=1}^{v}\beta _{u}x_{i,u}}}, \end{aligned}$$

(6)

and the log-likelihood function for the model is

$$\begin{aligned}&\ell (\{\alpha _j\},\varvec{\beta })=\sum _{i=1}^n\sum _{j=1}^k{y_{ij}} \log \pi _j(\mathbf {x}_i). \end{aligned}$$

(7)

As we are interested in a constrained version of this model with the aim of getting monotonic increasing/ decreasing effects, it is necessary to define the set of constraints to be applied on the t sets of $p_s$ coefficients. The isotonic constraints are

$$\begin{aligned} 0\le \beta _{s,2}\le \cdots \le \beta _{s,p_s}, \quad \forall s \in \mathcal {I}, \end{aligned}$$

(8)

where $\mathcal {I}\subseteq \mathcal {S}$, with $\mathcal {S}=\{1,2,\ldots ,t\}$, and $\beta _{s,1}=0$. The antitonic constraints are

$$\begin{aligned} 0\ge \beta _{s,2}\ge \cdots \ge \beta _{s,p_s}, \quad \forall s \in \mathcal {A}, \end{aligned}$$

(9)

where $\mathcal {A}\subseteq \mathcal {S}$, and $\beta _{s,1}=0$. An estimation method based on a monotonicity direction classification (MDC) procedure will be discussed in Sect. 3, allocating the ordinal predictors in either of these two subsets, achieving $\mathcal {I}\cup \mathcal {A}= \mathcal {S}$.

These constraints can be expressed in matrix form as $\mathbf {C}\varvec{\beta }_{(ord)}\ge \mathbf {0}$. The vector $\varvec{\beta }_{(ord)}$ is part of the vector $\varvec{\beta }$. The latter contains all the parameters associated with the t ordinal predictors and their $p_s-1$ categories together with the v non-ordinal predictors, $\varvec{\beta }'=\left( \varvec{\beta }_{(ord)}',\varvec{\beta }_{(nonord)}'\right)$, with $\varvec{\beta }_{(ord)}'=(\varvec{\beta }_1',\ldots ,\varvec{\beta }_t')$ with $s=1,\ldots ,t,$ and $\varvec{\beta }_{(nonord)}'=(\beta _1,\ldots ,\beta _v)$ with $u=1,\ldots ,v$, where each vector $\varvec{\beta }_s'=(\beta _{s,2},\ldots ,\beta _{s,p_s})$ with $h_s=2,\ldots ,p_s$. The matrix $\mathbf {C}$ is a square block diagonal matrix of $\sum _{s=1}^{t}(p_s-1)$ dimensions composed of t square submatrices $\mathbf {C}_s$ in its diagonal structure and zeros in its off-diagonal blocks as follows:

$$\begin{aligned} \mathbf {C}=\left[ \begin{array}{ccccc} \mathbf {C}_{1}&{}\mathbf {0}&{}\cdots &{}\mathbf {0}\\ \mathbf {0}&{}\mathbf {C}_{2}&{}\mathbf {0} &{}\mathbf {0}\\ \mathbf {0}&{} \cdots &{} \ddots &{}\mathbf {0}\\ \mathbf {0}&{} \cdots &{} \cdots &{}\mathbf {C}_{t}\\ \end{array}\right] , \text { with } s=1,\ldots ,t, \end{aligned}$$

where

$$\begin{aligned} \mathbf {C}_s= & {} \left[ \begin{array}{cccc} 1&{}0&{} \cdots &{}0\\ -1&{}1&{} 0 &{}0\\ 0 &{}\ddots &{}\ddots &{} 0\\ 0&{}\cdots &{}-1&{}1\\ \end{array}\right] \quad \forall s \in \mathcal {I},\\ \mathbf {C}_s= & {} \left[ \begin{array}{cccc} -1&{}0&{}\cdots &{}0\\ 1&{}-1&{} 0 &{}0\\ 0 &{}\ddots &{}\ddots &{} 0 \\ 0&{}\cdots &{}1&{}-1\\ \end{array}\right] \quad \forall s \in \mathcal {A}, \end{aligned}$$

and each square submatrix $\mathbf {C}_s$ has $p_s-1$ dimensions.

Then, the maximisation problem is

$$\begin{aligned} \text {maximise }&\ell (\{\alpha _j\},\varvec{\beta }) \nonumber \\ \text {subject to }&\mathbf {C}\varvec{\beta }_{(ord)}\ge \mathbf {0}, \end{aligned}$$

(10)

where $\mathbf {0}$ is a vector of $\sum _{s=1}^{t}(p_s-1)$ elements. Now, (10) can be expressed as the Lagrangian

$$\begin{aligned} \mathcal {L}(\{\alpha _j\},\varvec{\beta },\varvec{\lambda })&=\ell (\{\alpha _j\},\varvec{\beta })-\varvec{\lambda }' \mathbf {C}\varvec{\beta }_{(ord)}, \end{aligned}$$

(11)

where $\varvec{\lambda }$ is the vector of $\sum _{s=1}^t(p_s-1)$ Lagrange multipliers denoted by $\lambda _{s,h_s}$.

The set of equations to be solved is obtained by differentiating $\mathcal {L}(\{\alpha _j\},\varvec{\beta },\varvec{\lambda })$ with respect to its parameters and equating the derivatives to zero. In order to solve this in R (R Core Team 2018), the package maxLik (Henningsen and Toomet 2011) offers the maxLik function which refers to constrOptim2. This function uses an adaptive barrier algorithm to find the optimal solution of a function subject to linear inequality constraints such as in (10) (Lange 2010).

3 Monotonicity direction classification

Under the monotonicity assumption for all OPs, an important decision to be made is whether each ordinal predictor’s set of effects (also referred to as pattern), is either isotonic, namely $s\in \mathcal {I}$, or antitonic, $s\in \mathcal {A}$. Also outside the context of parameter estimation, it may be of interest whether a predictor is connected to the response in an isotonic or antitonic way, or potentially whether monotonicity may not hold or whether both directions are compatible with the data.

One possible way to deal with this decision is to just maximise the likelihood, i.e., to fit $2^{t}$ models, one for each possible combination of monotonicity directions for the t ordinal predictors, and then choose the one with the highest likelihood. However, as the number of ordinal predictors t increases, the number of possible combinations of monotonicity directions becomes greater, which could lead to a considerable number of models to be fitted, each involving a large number of covariates.

Another possible estimation method uses a monotonicity direction classifier to find the monotonicity direction for each ordinal predictor and then fits only one model. This will be based on CIs for the parameters and on checking which monotonicity direction is compatible with these. This may miss the best model, but in some situations it may be desirable to take into account fewer than $2^t$ but more than a single model.

The two approaches are put together in a three steps monotonicity direction classification (MDC) procedure exploiting their best features. Each of the first two steps uses a decision rule with different confidence levels for the CIs, and the last step applies the multiple models fitting process described above over those patterns with no single monotonicity direction established in the previous steps. Before describing its steps, consider some remarks and definitions.

The parameters’ CIs from an unconstrained model are the main input for the decision rule proposed here. It is possible to compute the CI defined in Eq. (12) for the parameters of an unconstrained version of model (4) (Agresti 2010). Denote $SE_{\hat{\beta }}$ as the standard error of the parameter estimate $\hat{\beta }$, then an approximate confidence interval for $\beta$ with a $100(1-\tilde{\alpha })\%$ confidence level is

$$\begin{aligned} \hat{\beta }\pm z_{\tilde{\alpha }/2}(SE_{\hat{\beta }}), \end{aligned}$$

(12)

where $z_{\tilde{\alpha }/2}$ denotes the standard normal percentile with probability $\tilde{\alpha }/2$. The values for $\hat{\beta }$ and $SE_{\hat{\beta }}$ are obtained by fitting the proportional odds model (McCullagh 1980) over the unconstrained model (4). The R function vglm of the package VGAM was used here (Yee 2018).

The first two steps of the MDC procedure provide four possible outcomes for each pattern of unconstrained parameter estimates associated with an ordinal predictor’s categories: ‘isotonic’, ‘antitonic’, ‘both’, and ‘none’. The first two correspond to a classification of monotonicity direction, whereas the remaining two to the case where a single direction is not found because either both directions of monotonicity are possible or the parameter estimates’ pattern is not compatible with monotonicity, respectively. The idea is that the intersections of all CIs for the parameters of a single ordinal predictor together will either allow for isotonic but not antitonic parameters, or for antitonic but not isotonic parameters, or for both, or for neither. Formally, the MDC of the parameter estimates’ pattern is defined as

$$\begin{aligned} d_{s,\tilde{c}} = {\left\{ \begin{array}{ll} \text {isotonic} &{}\quad \text {if }\mathcal {D}_{s,\tilde{c}}= \{0,1\} \text { or }\mathcal {D}_{s,\tilde{c}}= \{1\}\\ \text {antitonic} &{}\quad \text {if }\mathcal {D}_{s,\tilde{c}}=\{-1,0\} \text { or }\mathcal {D}_{s,\tilde{c}}= \{-1\}\\ \text {both} &{}\quad \text {if }\mathcal {D}_{s,\tilde{c}}=\{0\}\\ \text {none} &{}\quad \text {if }\mathcal {D}_{s,\tilde{c}}\supseteq \{-1,1\}, \end{array}\right. } \end{aligned}$$

(13)

where $\mathcal {D}_{s,\tilde{c}}=\{d_{s,h_s,h_s',\tilde{c}}\}$ is defined as the set of distinct values resulting from (14) for the ordinal predictor s considering confidence intervals with a $100\tilde{c}\%$ confidence level, and

$$\begin{aligned} d_{s,h_s,h_s',\tilde{c}} = {\left\{ \begin{array}{ll} 1 &{}\quad \text {if }\tilde{L}_{s,h_s,\tilde{c}}\ge \tilde{U}_{s,h_s',\tilde{c}}\\ -1 &{}\quad \text {if }\tilde{U}_{s,h_s,\tilde{c}}\le \tilde{L}_{s,h_s',\tilde{c}}\\ 0 &{}\quad \text {otherwise,} \\ \end{array}\right. } \end{aligned}$$

(14)

$\forall h_s'<h_s$ and $h_s \in \{2,3,\ldots ,p_s\}$, where $\tilde{U}_{s,h_s,\tilde{c}}$ is the confidence interval’s upper bound of the parameter $\beta _{s,h_s}$ associated with the category $h_s$ of the ordinal predictor s given a $100\tilde{c}\%$ confidence level, and $\tilde{L}_{s,h_s,\tilde{c}}$ is its corresponding lower bound. Note that, by definition, the first category of all ordinal predictors is set to zero, so $\tilde{L}_{s,1,\tilde{c}}=\tilde{U}_{s,1,\tilde{c}}=0$, $\forall s$. (14) yields 1 when the CI of the parameter $\beta _{s,h_s}$ is fully above the one of $\beta _{s,h_s'}$, and consequently, their CIs only allow an isotonic pattern; -1 when it is fully below pointing to an antitonic pattern; and 0 when there exists an overlap, meaning that both monotonicity directions are still possible.

Each result of (14), denoted as $d_{s,h_s,h_s',\tilde{c}}$, can be understood as an indicator of the relative position of the confidence interval of the parameter $\beta _{s,h_s}$ compared to the one of $\beta _{s,h_s'}$, $\forall h_s'<h_s$ and $h_s \in \{2,3,\ldots ,p_s\}$, belonging to the same ordinal predictor s and given a $100\tilde{c}\%$ confidence level. As this is a pairwise comparison, there exist $p_s(p_s-1)/2$ indicators for each ordinal predictor s. Equation (13) uses these indicators to classify the monotonicity direction of an ordinal predictor as a whole at a particular $\tilde{c}$.

As an illustration, Fig. 1 shows some arbitrary patterns representing a particular example for each one of the possible results of (13). For instance, OP 1 is classified as ‘isotonic’ because all but one of the results of (14) are 1, where the only different is $d_{1,4,3,0.95}=0$, and therefore $\mathcal {D}_{1,0.95}=\{0,1\}$. The monotonicity direction of OP 2 is clear also, for which the results of (14) are $-1$ except for $d_{2,4,3,0.95}=0$, with which (13) classifies this OP as ‘antitonic’. All the individual confidence intervals of OP 3 jointly overlap and contain zero. Therefore, $d_{3,h_3,h_3',0.95}=0$$\forall h_3'<h_3$ and thus $\mathcal {D}_{3,0.95}=\{0\}$, classifying OP 3 as ‘both’. Finally, each individual confidence interval associated with the OP 4 is either fully above or fully below the ones of previous categories belonging to the same ordinal predictor. In particular, $\mathcal {D}_{4,0.95}=\{-1,1\}$ because, for example, $d_{4,2,1,0.95}=1$ and $d_{4,3,2,0.95}=-1$, which (13) classifies as ‘none’.

Fig. 1

Illustration of particular examples for each possible monotonicity direction classification

The three steps MDC procedure has the following structure:

• Step 1 Set $\tilde{c}$ at a relatively high $100\tilde{c}\%$ confidence level, say 0.99, 0.95 or 0.90, and apply the MDC (13) to assign the subindexes s either to the set $\mathcal {I}$ or $\mathcal {A}$ defined in Sect. 2.1. Therefore, $\mathcal {I}_1=\{s : d_{s,\tilde{c}}=\text {isotonic}\}$ and $\mathcal {A}_1=\{s : d_{s,\tilde{c}}=\text {antitonic}\}$, where $\mathcal {I}_1$ and $\mathcal {A}_1$ denote the isotonic and antitonic sets resulting from the step 1 respectively. In addition, define $\mathcal {B}_1=\{s : d_{s,\tilde{c}}=\text {both}\}$ and $\mathcal {N}_1=\{s : d_{s,\tilde{c}}=\text {none}\}$. If $(\mathcal {I}_1 \cup \mathcal {A}_1)= \mathcal {S}$, then all the ordinal predictors’ monotonicity directions have been decided, and there is no need to continue with the MDC procedure. Otherwise, the following step is used for the remaining cases only, $(\mathcal {B}_1 \cup \mathcal {N}_1)$.

• Step 2 Consider the set of ordinal predictors $\{s:s\in (\mathcal {B}_1 \cup \mathcal {N}_1)\}$ and apply the MDC (13) in an iterative manner while varying the confidence level $100\tilde{c}\%$. A decrease/increase of $\tilde{c}$ reduces/enlarges the range of the CIs of the parameter $\beta _{s,h_s}$$\forall s\in (\mathcal {B}_1\cup \mathcal {N}_1)$ and $h_s\in \{2,3,\ldots ,p_s\}$. These changes in $\tilde{c}$ produce different effects on the classification depending on whether $s\in \mathcal {B}_1$ or $s\in \mathcal {N}_1$, which must be used as follows:

  • (a) For each $s\in \mathcal {B}_1$, the second step is to gradually decrease $\tilde{c}$ while applying the decision rule (13) using a new confidence level $\tilde{c}_s'$ instead of $\tilde{c}$, obtaining $d_{s,\tilde{c}_s'}$. The level of $\tilde{c}_s'$ must be gradually decreased until either a pre-specified minimum confidence level referred to as tolerance level $\tilde{c}_s'^{*}$ is reached, with $0<\tilde{c}_s'^{*}<\tilde{c}$, or the ordinal predictor s is classified as either isotonic or antitonic by $d_{s,\tilde{c}_s'}$.

  • (b) Conversely, for each $s\in \mathcal {N}_1$, gradually increase $\tilde{c}$ while applying MDC (13) using a new confidence level $\tilde{c}_s''$ obtaining $d_{s,\tilde{c}_s''}$. The level of $\tilde{c}_s''$ must be gradually increased until either a pre-specified maximum confidence level referred to as tolerance level $\tilde{c}_s''^{*}$ is reached, with $\tilde{c}<\tilde{c}_s''^{*}<1$, or the ordinal predictor s is classified as either isotonic or antitonic by $d_{s,\tilde{c}_s''}$.

  Finally, $\mathcal {I}_2=\mathcal {I}_1\cup \{s : d_{s,\tilde{c}_s'}=\text {isotonic or }d_{s,\tilde{c}_s''}=\text {isotonic}\}$ and $\mathcal {A}_2=\mathcal {A}_1\cup \{s : d_{s,\tilde{c}_s'}=\text {antitonic}$ or $d_{s,\tilde{c}_s''}=\text {antitonic}\}$, where the subindex of $\mathcal {I}_2$ and $\mathcal {A}_2$ denotes results from the second step. After completing the second step, if $(\mathcal {I}_2 \cup \mathcal {A}_2)=\mathcal {S}$, then it is not necessary to continue with step 3 and the MDC procedure ends. If $(\mathcal {I}_2 \cup \mathcal {A}_2)\subset \mathcal {S}$, then the third and final step must be carried out.

• Step 3 Fit $2^{\#\{s:s\notin (\mathcal {I}_2\cup \mathcal {A}_2)\}}$ models accounting for possible combinations of monotonicity directions of the ordinal predictors that were not classified as ‘isotonic’ or ‘antitonic’, i.e., those in the set $\{s:s\notin (\mathcal {I}_2\cup \mathcal {A}_2)\}$, and choose the best model based on some optimality criterion, such as the maximum likelihood as used here.

In general, the MDC procedure describes two levels of decision. The first one is provided by step 1, where a confidence level is applied to all ordinal predictors by the use of a single parameter $\tilde{c}$. The second one is in step 2, where each ordinal predictor $s\in (\mathcal {B}_1 \cup \mathcal {N}_1)$ is classified based on its own confidence level. Step 2 allows to classify predictors that were not classified based on the fixed initial confidence level.

In step 2, classifying more parameter estimates’ patterns with $s\in \mathcal {B}_1$ as either isotonic or antitonic requires a gradual reduction of the confidence level. The tolerance levels $\tilde{c}_s'^{*}$ and $\tilde{c}_s''^{*}$ determine the leeway allowed for the confidence levels in order to enforce a decision. The choice of these may depend on the number of ordinal variables; if the number is small, running step 3 may not be seen as a big computational problem, and it may not be necessary to enforce many decisions in step 2. The tolerance level $\tilde{c}_s'^{*}$ should not be too low, less than 0.8, say, because it is not desirable to make decisions based on a low probability of occurrence.

For those $s\in \mathcal {N}_1$ in step 2, the researcher does not face such a trade-off, because greater confidence levels could increase (not decrease) the number of new isotonic or antitonic classifications for those $s\in \mathcal {N}_1$.

It is important to reduce (or increase) the confidence level in step 2 in a gradual manner, by 0.01 or 0.005, say, for each iteration. If the chosen intervals in the sequence of confidence levels to be assessed are too thick without assessing intermediate levels, then, for an ordinal predictor $s\in \mathcal {B}_1$, it is possible to switch its classification from ‘both’ to ‘none’ instead of updating it from ‘both’ to either ‘isotonic’ or ‘antitonic’. Conversely, the class of an ordinal predictor $s\in \mathcal {N}_1$ could change from ‘none’ to ‘both’. The thinner the intervals in the sequence of confidence levels to be assessed are, the less likely it is to switch from ‘both’ to ‘none’ or ‘none’ to ‘both’. However, in some specific cases, there still is a probability of having such an undesired class change.

The researcher may also be interested in exploring other monotonicity directions rather than those resulting from the MDC procedure proposed here, although the maximum likelihood attained by the MDC procedure would not be reached. In this case, the correspondence of each ordinal predictor s to either $\mathcal {I}$ or $\mathcal {A}$ should simply be enforced when constructing $\mathbf {C}$, the matrix of constraints, as described in Sect. 2.1.

In order to illustrate the MDC procedure, we consider a particular example of model (4) with four ordinal predictors only ($t=4$ and $v=0$), where $p_1=3$, $p_2=4$, $p_3=5$, $p_4=6$, and $k=4$, i.e., $j=1,2,3$. The parameters are chosen to be $\alpha _1=-1$, $\alpha _2=-0.5$, and $\alpha _3=-0.1$; and

$$\begin{aligned} \varvec{\beta }_1'&=(1.0,1.5),\\ \varvec{\beta }_2'&=(0.1,0.2,0.25),\\ \varvec{\beta }_3'&=(-0.02,-0.04,-0.041,-0.05), \text { and}\\ \varvec{\beta }_4'&=(-0.2,-0.3,-0.31,-0.35,-0.36). \end{aligned}$$

These parameters represent a situation in which all covariates are monotonic, with the elements of $\varvec{\beta }_1'$ and $\varvec{\beta }_2'$ being isotonic, and those of $\varvec{\beta }_3'$ and $\varvec{\beta }_4'$ antitonic patterns. Given monotonicity, the higher the distances between adjacent parameters are, the clearer the monotonicity direction is. In this illustration, these distances were chosen to make the monotonicity direction clear for the first ordinal predictor only and less clear for the remaining ones, $s=3$ being the most unclear and challenging case because all of its parameters show little distance between adjacent categories and consequently from zero.

The 2000 simulated observations of the ordinal predictors were obtained from the population distributions shown in Fig. 2.

Fig. 2

Distributions of simulated ordinal predictors

Using this simulated data set, an unconstrained version of the model was fitted to obtain the parameter estimates and their standard errors, with which a confidence interval can be computed for any level of $\tilde{\alpha }$ using Eq. (12).

For the first step of the MDC procedure, the confidence level was set at a high $\tilde{c}=0.99$. The resulting confidence intervals allowed to classify the first and second OP as ‘isotonic’, $\mathcal {I}_1=\{1,2\}$, and the remaining two patterns of parameter estimates as ‘both’, $\mathcal {B}_1=\{3,4\}$. Figure 3 shows that the latter two ordinal predictors allowed both directions of monotonicity, which is the reason why they were not classified as ‘antitonic’. The second step was applied over each ordinal predictor $s \in \mathcal {B}_1=\{3,4\}$ using the same tolerance level, $\tilde{c}_3'^{*}=\tilde{c}_4'^{*}=0.8$. For $s=3$, it was not possible to classify its pattern as ‘antitonic’ before reaching the tolerance level. Therefore, it remained as ‘both’. For $s=4$, the procedure was applied until reaching $\tilde{c}_s'=0.96$, where the fourth OP was classified as ‘antitonic’. Now, $\mathcal {I}_2=\{1,2\}$ and $\mathcal {A}_2=\{4\}$. As no monotonicity direction was identified for the third OP, two models were fitted in step 3 of the MDC procedure, one treating the third OP as ‘isotonic’ and the other one as ‘antitonic’. Finally, the model with the highest log-likelihood was selected as the final one.

Fig. 3

Parameters of ordinal predictors’ categories and their unconstrained estimates with 99% confidence intervals

The procedure successfully classified the ordinal predictors $s=1,2,3,4$ as ‘isotonic’, ‘isotonic’, ‘antitonic’, and ‘antitonic’, respectively, despite the fact that the unconstrained parameter estimates of the last three are not monotonic. Furthermore, it reduced the number of possible models to be fitted from 17 (the unconstrained model and 16 constrained models) to 3 (the unconstrained and two models in step 3) while making decisions based on individual confidence levels of 96% or greater.

As shown in Fig. 3, it is not easy to classify cases like $s=3$ where all the parameter estimates are close to zero and their confidence intervals are big enough to make the monotonicity direction classification infeasible for any reasonable tolerance level. In this case, the tolerance level would have needed to be set at $\tilde{c}_3'^{*}\le 0.53$ had we wanted the MDC procedure to classify the third ordinal predictor as either ‘isotonic’ or ‘antitonic’. In fact, when doing so, the MDC makes a mistake and classifies it as ‘isotonic’. This relationship between low tolerance levels and misclassification is the main reason why the procedure needs to start with a relatively high confidence level $\tilde{c}_s$ and then gradually decrease it until reaching a reasonable tolerance level if necessary.

In cases like $s=3$, one option is to remove this variable from the model because all of the CIs associated with it contain zero even if we choose a tolerance level lower than 0.80, which we consider too low. Removing this variable would have allowed us to fit just two models (the unconstrained and one constrained) instead of three in the whole procedure. However, removing variables may not be good if the aim is to obtain a model with optimal predictive power.

4 A monotonicity test

The MDC procedure assists the decision on the choice of an appropriate monotonicity direction assumption for each OP when fitting model (4), but it is not a formal monotonicity test. It relies on the analysis of multiple pairwise comparisons of confidence intervals with flexibly chosen confidence levels without caring about the simultaneous error probability.

When analysing the monotonicity assumption on the parameters associated with an OP s, the Bonferroni correction method can be used to construct a formal monotonicity test for an OP. The Bonferroni correction method allows to compute a set of confidence intervals achieving at least a $100(1 - \alpha _s^*)\%$ confidence level simultaneously (see Miller 1981, p. 67, and Bonferroni 1936), which is the probability that all the parameters are captured by the confidence intervals simultaneously. For a given ordinal predictor s and a pre-specified $\alpha _s^*$, if each one of the $p_s-1$ confidence intervals is built with a $100(1-\alpha _s^* /(p_s-1))\%$ confidence level, then the simultaneous confidence level will be at least $100(1-\alpha _s^*)\%$.

The null hypothesis ‘$H_0:$ The parameters $\{\beta _{s,h_s}: h_s=1,2,\ldots ,p_s\}$ are either isotonic or antitonic’ ($0\le \beta _{s,2}\le \beta _{s,3} \cdots \le \beta _{s,p_s}$ (isotonic) and $0\ge \beta _{s,2}\ge \beta _{s,3} \cdots \ge \beta _{s,p_s}$ (antitonic)) is tested against the alternative ‘$H_1:$ The parameters $\{\beta _{s,h_s}: h_s=1,2,\ldots ,p_s\}$ are neither fully isotonic nor fully antitonic’ for a given OP s, and setting $\beta _{s,1}=0$ as in previous sections.

For a given ordinal predictor s, and taking advantage of the ordinal information provided by its categories, it is then checked whether all the confidence intervals simultaneously are compatible with monotonicity.

In order to identify whether there are pairs of confidence intervals of $\beta _{s,h_s}$ that are incompatible with monotonicity, a slight modification of Eqs. (13) and (14) is used. Now, instead of the confidence level $\tilde{c}$, those equations use $\tilde{b}=1-\alpha _s^*/(p_s-1)$. Therefore, the monotonicity test for an ordinal predictor s is

$$\begin{aligned} T_{s,\tilde{b}} = {\left\{ \begin{array}{ll} {\textit{reject }}H_0 &{}\quad \text {if }\mathcal {D}_{s,\tilde{b}}\supseteq \{-1,1\} \\ {\textit{not reject }}H_0 &{}\quad \text {otherwise} \end{array}\right. } \end{aligned}$$

(15)

where $\mathcal {D}_{s,\tilde{b}}=\{d_{s,h_s,h_s',\tilde{b}}\}$ is defined as the set of distinct values resulting from using Eq. (14) for the ordinal predictor s considering each confidence interval with a $100\tilde{b}\%$ confidence level (instead of $100\tilde{c}\%$) in order to achieve a simultaneous confidence level of at least $100(1-\alpha _s^*)\%$ for the parameters associated with the OP s.

If $T_{s,\tilde{b}}={\textit{reject }}H_0$, then the parameters associated with the ordinal predictor s are not compatible with the monotonicity assumption with a simultaneous confidence level of at least $100(1-\alpha _s^*)\%$.

When applying this monotonicity test to the four OPs of the illustration discussed in Sect. 3 and using a pre-specified $\alpha _s^*=0.05$, all the OPs were found to be compatible with the monotonicity assumption.

For a given pre-determined significance level of $\alpha _s^*$ (say 0.1, 0.05 or 0.01), the Bonferroni correction will often be very conservative, and it will be the more conservative the higher the number of ordinal categories involved in the monotonicity test is. A higher $p_s$ implies larger ranges of the intervals, making the test more likely to not reject $H_0$.

In order to show some results for the monotonicity test with OPs for which their association with the response variable is truly non-monotonic, consider a setting for model (4) with two OPs only ($t=2$ and $v=0$), where $p_1=4$, $p_2=5$, and $k=4$, i.e., $j=1,2,3$. The parameters for the intercepts are $\alpha _1=-1$, $\alpha _2=-0.5$, and $\alpha _3=-0.1$; and the true sets of parameters of the OPs 1 and 2 represent non-monotonic associations, being $\varvec{\beta }_1'=(0.4,1.7,0.8)$ and $\varvec{\beta }_2'=(-0.25,-0.7,-0.05,0.40)$. The distributions among categories of OPs 1 and 2 are the same as the ones shown in Fig. 2 for OPs 2 and 3 correspondingly, and the number of observations is 2000.

Fig. 4

True parameter patterns simulating non-monotonicity with different rejection rates of the monotonicity test

After fitting the new unconstrained model on 1000 simulated data sets and testing for monotonicity, the null hypothesis was rejected in 84.9% of the data sets for the OP 1 and in 84.5% for the second OP, in both cases with $\alpha ^*_s=0.05$. Figure 4 shows the patterns of these non-monotonic OPs together with additional patterns with which rejection rates of around 5% are obtained (4.5% and 5.5% respectively).

5 Dropping constraints and variable selection

5.1 Dropping monotonicity constraints using the monotonicity test

The MDC procedure described in Sect. 3 implies that the parameter estimates of all OPs are restricted to be monotonic. However, the researcher may want to drop monotonicity constraints on OPs in case that there is clear evidence against monotonicity.

The monotonicity test proposed in Sect. 4 can be used as a complementary tool to the MDC procedure in order to assist the estimation process. If the researcher is open to the possibility of not imposing the monotonicity constraints on some OPs, then he/she could first test monotonicity on each one of them, then drop the monotonicity constraints on those OPs for which the null hypothesis was rejected, and finally perform the MDC procedure imposing monotonicity constraints on all the remaining OPs. Under this scenario, in case that monotonicity is rejected for an OP, it would be more prudent to fit unconstrained estimates on the parameters associated with it. Therefore, such an OP should not be part of $\mathcal {S}$, the set of OPs to be constrained, but rather part of the non-ordinal predictors, considering it at the nominal scale level.

5.2 Dropping monotonicity constraints using the MDC procedure

When dropping the monotonicity constraint for some of the OPs is considered as a feasible option, then not only the approach introduced in Sect. 5.1 could be used, but also three alternative ones that are proposed in this section. As in the previous section, consider the case where the researcher might also want to explore whether the monotonicity assumption holds for all of the OPs or for a subset of them, but now using a less conservative (i.e., dropping constraints more easily) approach than the one based on the monotonicity test. We propose three additional methods. Two of them are based on the first and second steps of the MDC procedure correspondingly (‘CMLE MDC S1’ and ‘CMLE MDC S2’), and another one is based on a slight modification of the MDC procedure (‘CMLE filtered’).

5.2.1 CMLE MDC S1

Both monotonicity constraints and monotonicity directions are established using the first step of the MDC procedure. Once it determines $\mathcal {I}_1$ and $\mathcal {A}_1$, the monotonicity constraints are dropped for the remaining ordinal predictors $\{s : s \notin (\mathcal {I}_1 \cup \mathcal {A}_1)\}$, namely $\{s : s \in (\mathcal {B}_1 \cup \mathcal {N}_1)\}$. Therefore, there is no need of executing further steps.

The model is fitted imposing monotonicity constraints on ordinal predictors $\{s : s \in (\mathcal {I}_1 \cup \mathcal {A}_1)\}$ using their corresponding monotonicity directions, which requires to consider the ordinal predictors $\{s : s \in (\mathcal {B}_1 \cup \mathcal {N}_1)\}$ as nominal scaled variables.

This method is the least conservative one because it assumes that if a monotonic pattern is not established without adjustment of the confidence level $100\tilde{c}\%$, then the monotonicity constraint has to be dropped.

5.2.2 CMLE MDC S2

This method follows the same structure as the previous one but executing the MDC procedure until the end of its second step. Therefore, the third step is not executed and the model is fitted imposing monotonicity constraints on ordinal predictors $\{s : s \in (\mathcal {I}_2 \cup \mathcal {A}_2)\}$ only, using their corresponding monotonicity directions according to $\mathcal {I}_2$ and $\mathcal {A}_2$, and assuming the ordinal predictors $\{s : s \notin (\mathcal {I}_2 \cup \mathcal {A}_2)\}$ as nominal scaled variables.

5.2.3 CMLE filtered

An adjusted version of the MDC procedure described in Sect. 3 allows to drop the monotonicity assumption for some OPs. There are only two adjustments, one in step 2.b and the other one in step 3. The first one is to set $\tilde{c}_s''^{*}=\tilde{c}$, i.e., the tolerance level for each OP $s\in \mathcal {N}_1$ is set to be the same as the confidence level chosen in step 1. Therefore, the second step is not performed on any ordinal predictor $s\in \mathcal {N}_1$. The second modification is to apply step 3 over the possible combinations of monotonicity directions of the ordinal predictors that were classified as ‘both’ by the end of step 2, i.e., the number of models to be fitted is now $2^{\#\{s : d_{s,\tilde{c}_s'}=\text {both}\}}$ instead of $2^{\#\{s:s\notin (\mathcal {I}_2\cup \mathcal {A}_2)\}}$. This implies that $\mathcal {S}$, the set of OPs to be constrained, must be updated excluding each ordinal predictor $s\in \mathcal {N}_1$ from the set of monotonicity constraints. Finally, the model should be fitted considering these OPs as nominal scaled variables.

These adjustments are equivalent to considering the first step of the MDC procedure as a filter of OPs to be constrained, where those that are classified as ‘none’ by the end of this step are removed from $\mathcal {S}$ and excluded from steps 2 and 3.

5.3 Using the MDC procedure for variable selection

The parameter estimates’ patterns classified as ‘both’ at the end of the second step of the MDC procedure are also of interest. ‘Both’ refer to an ordinal predictor for which all of the parameters associated with its categories have CIs containing zero. Therefore, if this is true even for the CIs evaluated at the tolerance level, an option is to remove such an ordinal predictor from the model of interest and apply the MDC procedure again using the new model. If more than one OP is classified as ‘both’ and there is appetite to drop such variables, then it is advisable to do it in a stepwise fashion such as backward elimination, while checking the results of the MDC procedure in each step, because dropping an OP could affect the monotonicity direction classification of another OP. We will not investigate this in detail here, assuming that the data are rich enough so that variable selection is not required.

The methods ‘CMLE MDC S1’ and ‘CMLE MDC S2’ do not use step 3 at all. The methods ‘CMLE filtered’ and the one described in Sect. 5.3, i.e., dropping monotonicity constraints for those ordinal predictors $s\in \mathcal {N}_1$ and dropping ordinal predictors $\{s : d_{s,\tilde{c}_s'^{*}}=\text {both}\}$, reduce the number of models to be fitted in step 3. If these last two methods are used simultaneously, then step 3 is avoided.

6 Simulations

Model (4) with two ordinal and two interval scale predictors,

$$\begin{aligned} \text {logit}[P(y_{i}\le j | \mathbf {x}_i)]&=\alpha _j+\sum _{h_1=2}^{4}\beta _{1,h_1}x_{i,1,h_1} \nonumber \\&\quad +\sum _{h_2=2}^{6}\beta _{2,h_2}x_{i,2,h_2}+\beta _{1}x_{i,1}+\beta _{2}x_{i,2}, \end{aligned}$$

(16)

where $k=5$, i.e., $j=1,2,3,4$, was fitted for 1000 data sets simulated as described in Sect. 3 using the following parameters: for the intercepts $\alpha _1=-1.4$, $\alpha _2=-0.4$, $\alpha _3=0.3$, and $\alpha _4=1.1$; for the ordinal predictors’ categories $\varvec{\beta }_1'=(0.3,1.0,1.005)$, and $\varvec{\beta }_2'=(-0.2,-1.5,-1.55,-2.4,-2.41)$; and for the interval scale predictors $\beta _1=-0.15$ and $\beta _2=0.25$. The parameters vectors $\varvec{\beta }_1$ and $\varvec{\beta }_2$ were chosen to represent isotonic and antitonic patterns respectively. Several sample sizes were considered: $n=50, 100, 500, 1000, 5000$. The ordinal predictors were drawn from the population distributions used in Sect. 3 of those covariates with the same number of ordinal categories, 4 and 6. The interval scale covariates $x_1$ and $x_2$ were randomly generated from normal distributions, N(0, 1) and N(5, 4) correspondingly.

For each one of the 1000 data sets and for every sample size, model (16) was fitted following different approaches:

• 1. UMLE (unconstrained MLE).

• 2. CMLE: constrained MLE based on the MDC procedure with $\tilde{c}=0.90$ in step 1, $\tilde{c}_s'^{*}=0.85$ and $\tilde{c}_s''^{*}=0.999$ for $s=1,2$ in step 2, with versions using some or all of the steps of the MDC procedure:

  • a) MDC S1 as described in Sect. 5.2.1,

  • b) MDC S2 as described in Sect. 5.2.2,

  • c) MDC S3 as described in Sect. 3, imposing monotonicity constraints on all OPs.

• 3. CMLE Bonferroni: dropping monotonicity constraints on those ordinal predictors for which the null hypothesis of monotonicity was rejected as described in Sect. 5.1, using $\alpha _s^*=0.05$, for $s=1,2$.

• 4. CMLE filtered as described in Sect. 5.2.3, $\tilde{c}=0.90$.

Table 1 Classification of monotonicity direction of 2 OPs based on five methods with 1000 simulated data sets, different sample sizes and independent covariates (%)

Table 1 shows the resulting classification of the monotonicity direction for each OP according to the five constrained estimation methods discussed here. After fitting the UMLEs, the MDC procedure was performed as part of the constrained approaches. Its first, second, and third steps (‘MDC S1’, ‘MDC S2’, and ‘MDC S3’ in Table 1) correctly classified OPs 1 and 2 in nearly 100% of the cases when the sample size was at least 500. For smaller sample sizes, ‘CMLE MDC S2’ showed some better results than ‘CMLE MDC S1’ as expected, and the third step allowed to finally classify OP 1 as ‘isotonic’ in 69.2% of the cases when $n=50$, which rapidly increased to 92.9% when $n=100$ and improved even more for larger sample sizes. Regarding OP 2, better results were obtained even with small sample sizes.

‘CMLE Bonferroni’ performed in exactly the same way as ‘CMLE MDC S3’ because the null hypothesis of monotonicity was not rejected in 100% of the data sets for both OPs with $\alpha _s^*=0.05$ and for any sample size. Therefore, the monotonicity constraints were not dropped. A rejection rate of approximately 5% would have been obtained for each OP if, for instance, $\varvec{\beta }_1'=(0.3,1.8,1.005)$ and $\varvec{\beta }_2'=(-0.2,-1.5,-0.17,-2.4,-2.41)$ have been used as the true parameter patterns instead of the original ones for this simulation, $\varvec{\beta }_1'=(0.3,1.0,1.005)$ and $\varvec{\beta }_2'=(-0.2,-1.5,$$-1.55,-2.4,$$-2.41)$ when $n=500$.

The results of ‘CMLE filtered’ were similar to the ones of both ‘CMLE MDC S3’ and ‘CMLE Bonferroni’. The monotonicity constraints were dropped in at most 1.9% of the cases, which hardly affected the final monotonicity direction classification.

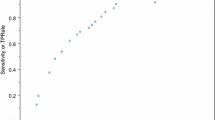
In general, smaller sample sizes provide less information to any method, increasing the misclassification rate of the monotonicity direction. However, given a monotonic association, when the value of the parameter estimate associated with the last category is further away from zero, there is less probability of misclassification irrespective of the sample size. This is the case for OP 2 (see Fig. 5 as an example when $n=500$), which was correctly classified in more than 90% of the cases by every method, even when the sample size was as small as 50.

Consider one of the 1000 data sets as an example to illustrate the case of imposing monotonicity constraints. As shown in Fig. 5, some unconstrained parameter estimates are incompatible with the monotonicity assumptions. Despite the fact that the OP 1 is assumed to be isotonic, the UMLE yields $\hat{\beta }_{1,2}<0$ and $\hat{\beta }_{1,3}>\hat{\beta }_{1,4}$. Similar violations occur with the second ordinal predictor (antitonic), with $\hat{\beta }_{2,3}<\hat{\beta }_{2,4}$. By contrast, the results of the CMLEs imposed monotonicity constraints, with the estimate for $\beta _{1,2}$ being greater than zero, the estimate for $\beta _{1,4}$ being slightly greater than the one for $\beta _{1,3}$, and where the estimate for $\beta _{2,4}$ was slightly lesser than the one for $\beta _{2,3}$. The monotonicity directions were established in the first step of the MDC procedure; therefore, the methods ‘CMLE MDC S1’, ‘CMLE MDC S2’, and ‘CMLE MDC S3’ provided the same result. Similarly, the first step of the MDC procedure did not classify OPs 1 or 2 as ‘none’, and the monotonicity test did not reject the null hypothesis of monotonicity for any of these two OPs; therefore ,‘CMLE Bonferroni’ and ‘CMLE filtered’ are not shown.

Fig. 5

An example of unconstrained MLE and constrained MLE for a particular data set from simulations with 2 independent OPs and $n=500$

In this particular example, the CMLEs for the parameter estimates associated with both intercepts and interval scale covariates were hardly affected by the monotonicity assumption when comparing the CMLE to the UMLE.

Regardless of the sample size, imposing monotonicity constraints reduces the parameter space, which affects the distribution of the parameter estimates when they are active. As an illustration, Fig. 6 uses boxplots to visualise the distribution of each parameter estimate resulting from several methods together with the true parameters used in the data generation process for the 1000 simulation iterations with $n=100$.

Fig. 6

Unconstrained MLE, different methods with constrained MLE and true parameters used for 1000 simulated data sets with 2 independent OPs, example for $n=100$

The effect of the monotonicity constraints is depicted by the range of values that the parameter estimates take for an OP in some of the constrained approaches, which differs from the one of the UMLEs in two aspects. First, when the parameter estimates are correctly constrained, they are compatible with their monotonicity direction, i.e., they take positive values for the isotonic case and negative for the antitonic one. This is why the boxes of some constrained approaches seem to be truncated at zero for $\beta _{1,2}$ and $\beta _{2,2}$. The second difference is a generalisation of the first one as any constrained parameter estimate is greater/lower than the one of the preceding category rather than greater/lower than zero only. Hence, the lower extremes of their boxplots show shorter whiskers than the ones of the UMLE when there is an isotonic relationship, and the same effect occurs for the upper whiskers when the relationship is antitonic.

The results of ‘CMLE MDC S1’ are the closest to the ones of the unconstrained method. This is due to the fact that ‘CMLE MDC S1’ drops the monotonicity constraints more frequently than any other constrained method. Conversely, ‘CMLE MDC S3’ is the furthest because it does not drop constraints. Other constrained methods are in between these two. The approaches ‘CMLE MDC S3’ and ‘CMLE Bonferroni’ delivered the same results because the monotonicity tests did not reject monotonicity for any OP. Compared to other constrained approaches, the results of ‘CMLE filtered’ are slightly different because there are 18 cases where the OP 2 was considered as non-monotonic and 3 for OP 1, for which the monotonicity constraints were not imposed. Unconstrained cases together with misclassification of the monotonicity direction are the reason why there are some negative values for the estimates of OP 1 and positive values for the ones of OP 2 in the constrained approaches.

Mean square error (MSE) and the standard error (SE) of the parameter estimates are shown in Table 2, averaged over all parameters belonging to an OP. The values for the constrained methods are given relative to the values for UMLE.

Table 2 Average of the MSEs and average of the SEs associated with the categories of each OP when using UMLE ($\text {MSE}_\text {UMLE}$ and $\text {SE}_\text {UMLE}$)

Fig. 7

Mean square error for unconstrained and constrained MLEs and its decomposition, example for $n=100$

The constrained methods lead to a lower MSE than UMLE irrespective of the sample size. The MSE ratio of the constrained methods with UMLE is higher for both the smallest and largest sample sizes than for the intermediate ones. For the largest sample size and given truly monotonic ordinal predictors as in this simulation, the constrained methods provide results close to UMLE, because the UMLE reveals the true monotonic patterns for large enough n. For the smallest sample size, the MSE results of the constrained methods are fairly close to UMLE because the variability of their parameter estimates is affected by a considerable misclassification rate when imposing monotonicity constraints.

Table 3 Classification of monotonicity direction of 2 OPs based on five methods with 1000 simulated data sets, different sample sizes and correlated covariates (%)

Table 4 Average of the MSEs and average of the SEs associated with the categories of each OP when using UMLE ($\text {MSE}_\text {UMLE}$ and $\text {SE}_\text {UMLE}$)

As an example of the analysis of the MSE, consider the results for $n=100$ shown in Fig. 7. The total MSE is notably smaller for the constrained approaches. On average, the ‘CMLE MDC S1’ shows a 10.2% smaller MSE compared to the MSE of UMLE for the intercepts , 10.7% smaller for the first ordinal predictor, and 11.2% smaller for the second. The corresponding figures for ‘CMLE MDS S3’ are 24.2%, 24.6%, and 24.9%, and for ‘CMLE filtered’ are 22.9%, 24.1%, and 24.6%.

The performance of ‘CMLE Bonferroni’ is almost identical to ‘CMLE MDC S3’. The results of ‘CMLE MDC S2’ lie between those of ‘CMLE MDC S1’ and ‘CMLE MDC S3’. These are not shown in Fig. 7 and later.

Despite the fact that the squared bias makes a markedly small contribution to the total MSE (lighter colours in Fig. 7), it is clearly higher for some constrained parameter estimates, specially for those of OP 2. Its sixth category produced the highest squared bias, which represents from 3.9% of its total MSE for ‘CMLE MDC S1’ up to 10.0% for ‘CMLE filtered’. The squared bias of the constrained approaches associated with the remaining categories of OP 2 together with the first OP and the intercepts represent, on average, between 1.4 and 3.4% of the MSE depending on the constrained method (‘CMLE MDC S1’ being the smallest and both ‘CMLE MDC S3’ and ‘CMLE Bonferroni’ the largest). Consequently, the MSEs are dominated by variances, which are considerably lower than the ones of the UMLE not only for the parameters associated with the ordinal predictor categories, but also for the intercepts.

The simulation was repeated with dependence among covariates. In order to simulate the predictors, we generated a set of four variables from a multivariate normal distribution with means equal to zero and unit variances for the two ordinal variables and the same means and variances that were used in the setting with independent covariates for the two interval scale variables. The correlation structure was set allowing different magnitudes and directions as follows:

$$\begin{aligned} \rho =\left[ \begin{array}{cccc} 1 &{} -0.3 &{} 0.6 &{} 0.7\\ -0.3 &{} 1 &{} -0.5 &{} -0.2\\ 0.6 &{} -0.5 &{} 1 &{} 0.2\\ 0.7 &{} -0.2 &{} 0.2 &{} 1\\ \end{array}\right] . \end{aligned}$$

The categorisation of the ordinal variables resulted from classifying each simulated value within the limits defined by the normal quantiles corresponding to the cumulative probabilities obtained from the marginal distributions that were previously set for those OPs with 4 and 6 categories (see Fig. 2).

The monotonicity direction classification results obtained from the setting with correlated predictors are shown in Table 3. For sample sizes $n=50$ and $n=100$, there is more misclassification for OP 1 in the scenario with correlated covariates. For larger sample sizes ($n\ge 500$), the final results of the setting with correlated covariates are nearly as good as the ones with independent covariates for OP 1. The latter occurs for OP 2 also, but for any of the sample sizes, including the smallest.

Table 4 shows the MSE results with correlated predictors. Compared to the scenario with independent covariates, the MSE of the version with correlated covariates is always higher, regardless of the sample size and method. The MSEs decrease as n increases; the magnitude of the reduction depends on the method and the sample size. For example, for ‘CMLE MDC S3’ and other highly constrained methods, with correlated predictors the ratio $\text {MSE/MSE}_{\text {UMLE}}$ increases for OP 1 when n changes from 50 to 100. Despite the fact that OP 1 is often misclassified by the more restrictive methods such as ‘CMLE MDC S3’, their MSE ratio is still low when $n=50$ because of the high variance of the UMLE, which is amended by the constrained methods.

Table 5 Classification of monotonicity direction of 4 OPs based on five methods with 1000 simulated data sets and independent covariates (%)

In the simulation presented above, no non-monotonic ordinal predictor was included and its results showed that any constrained approach performed better than the unconstrained one in almost every simulated scenario. In order to analyse their performance in presence of non-monotonic OPs, consider another simulation of model (4). This time we use an ordinal response with four categories, i.e., $k=4$ and $j=1,2,3$; four ordinal predictors ($t=4$) with $p_1=3$, $p_2=4$, $p_3=5$, and $p_4=6$ categories correspondingly; and one interval scale predictor ($v=1$). Again, several sample sizes were considered: $n=50, 100, 500, 1000, 5000$. The chosen parameters for the intercepts were $\alpha _1=-1.4$, $\alpha _2=-0.1$, and $\alpha _3=1.7$; for OP 1, $\varvec{\beta }_1'=(0.5,1)$; for OP 2, $\varvec{\beta }_2'=(-0.65,-0.70,-1.60)$; for OP 3, $\varvec{\beta }_3'=(0,0,0,0)$; for OP 4, $\varvec{\beta }_4'=(-0.8,-1.6,-0.6,0.6,1.6)$; and for the interval scale predictor $\beta _1=0.3$. The parameters of the OPs 1 to 4 were chosen to be isotonic, antitonic, zero, and non-monotonic correspondingly. For OP 3, all the parameters were set to zero, and therefore, optimally, the monotonicity test should not reject monotonicity and its second step should classify it as ‘both’.

This model was fitted for 1000 simulated data sets and for every sample size. The ordinal predictors were drawn from the population distributions showed in Fig. 2. The interval scale predictor was randomly generated from a normal distribution N(1, 4).

Table 6 Average of the MSEs and average of the SEs associated with the categories of each OP when using UMLE ($\text {MSE}_\text {UMLE}$ and $\text {SE}_\text {UMLE}$)

The MDC procedure was executed with a $90\%$ confidence level in the first step ($\tilde{c}=0.90$) and tolerance levels $\tilde{c}_s'^{*}=0.85$ and $\tilde{c}_s''^{*}=0.999$ for $s=1,2,3,4$ in the second step.

Table 5 shows the results of the MDC for the constrained estimation methods. OPs 1 and 2 follow the same trends as in the earlier simulation. OPs 3 and 4 make the constrained methods differ markedly, mainly because smaller sample sizes do not only increase the probability of misclassification of the monotonicity direction, but also decrease the probability of dropping monotonicity constraints for an OP that is truly non-monotonic, which is the case for OP 4 in this simulation. This also affects the classification of OP 3 with true pattern ‘both’.

For ‘CMLE MDC S1’, OP 3 shows a high percentage of ‘both’ classifications for any sample size, and OP 4 was correctly classified when $n\ge 500$. However, it was constrained to be either ‘isotonic’ or ‘antitonic’ in a total of 50.1% of the data sets when $n=50$, which is relatively high as this method is the least restrictive one. The monotonicity direction classification of ‘CMLE MDC S2’ is hardly affected when $n\ge 1000$, whereas for smaller sample sizes it is between ‘CMLE MDC S1’ and ‘CMLE MDC S3’, reducing ‘both’ for OP 3 and ‘none’ for OP 4. The classification of OPs 3 and 4 by ‘CMLE MDC S3’ is more evenly distributed for small sample sizes, which is not unreasonable for an OP that is set to be ‘both’ and an OP of class ‘none’. However, for larger sample sizes ($n\ge 500$), the classification of OP 3 is more concentrated in ‘antitonic’, whereas OP 4 is highly concentrated in ‘isotonic’, which is due to the fact that an isotonic association dominates throughout the pattern of OP 4. ‘CMLE Bonferroni’ does not impose monotonicity constraints on OP 4 for small sample sizes. Therefore, its performance is almost identical to the one of ‘CMLE MDC S3’ when $n\le 100$. For larger sample sizes, the monotonicity constraints are dropped much more frequently for OP 4, and the classification of OP 3 remains consistent with its definition of ‘both’. The results of ‘CMLE filtered’ are similar to those of ‘CMLE Bonferroni’ for OPs 1, 2 and 3. OP 4 was constrained less frequently, regardless of the sample size.

Fig. 8

Unconstrained MLE, different methods with constrained MLE and true parameters used for 1000 simulated data sets with 4 correlated OPs, example for $n=500$

Based on the results of the average MSE (see Table 6) and given that there is a non-monotonic ordinal predictor, ‘CMLE MDC S3’ is the only method that is occasionally notably worse than UMLE, because it always imposes constraints on an OP that is not monotonic, but for $n=50$ the MSE of the UMLE is still so high that ‘CMLE MDC S3’ is better. The performance of the remaining constrained methods depends on the degree of conservativity when establishing the set of OPs with non-monotonic effects. The less conservative the method, the closer is its MSE to the one of UMLE. The best options are ‘CMLE Bonferroni’ and ‘CMLE filtered’ because they drop constraints for OP 4 and not for other OPs, specially when $n\ge 500$, although they are still good options for smaller sample sizes.

The simulation of the current model using four OPs was done again with dependence among covariates. The OPs and the interval scale predictor were generated from a multivariate normal distribution with the same means and variances as the ones used in the previous simulation scenario. The correlation structure is now:

$$\begin{aligned} \rho =\left[ \begin{array}{ccccc} 1 &{} -0.5 &{} -0.1 &{} 0.3 &{} 0.6\\ -0.5 &{} 1 &{} 0 &{} -0.4 &{} -0.6\\ -0.1 &{} 0 &{} 1 &{} 0.2 &{} 0.1\\ 0.3 &{} -0.4 &{} 0.2 &{} 1 &{} 0.7\\ 0.6 &{} -0.6 &{} 0.1 &{} 0.7 &{} 1\\ \end{array}\right] . \end{aligned}$$

The ordinal categories of the OPs were obtained through categorisation as previously described but using the marginals of OPs according to those shown in Fig. 2.

As an example to visualise the behaviour of the parameter estimates resulting from some selected methods under the simulation scenario with correlated covariates, Fig. 8 shows their boxplots when $n=500$. In general, the constrained methods perform in almost the same way as the unconstrained one for OP 1 and better for OP 2 and 3. As expected, the non-monotonic OP 4 produces more differences for ‘CMLE MDC S3’ than for other constrained methods, which are much closer to the unconstrained results for a non-monotonic OP.

Table 7 Classification of monotonicity direction of 4 OPs based on five methods with 1000 simulated data sets and correlated covariates (%)

Table 8 Average of the MSEs and average of the SEs associated with the categories of each OP when using UMLE ($\text {MSE}_\text {UMLE}$ and $\text {SE}_\text {UMLE}$)

Table 7 shows the MDC results with correlated predictors. Compared to the independent covariates scenario, the general trends remain the same. The results of the largest sample size are hardly affected, whereas the others are somewhat worse. Regarding the MSE (see Table 8), the correlation among covariates increased the MSE in all the methods, specially when $n=50$ and for OP 4 with $n\le 100$. However, the constrained results are better or almost equal to those of the UMLE, except for ‘CMLE MDC S3’ when $n\ge 500$.

This section shows that the constrained methods are better than the UMLE when associations between the OPs and the response are truly monotonic, in which case the more restrictive the better. On the other hand, if there is a truly non-monotonic association, the most restrictive method ‘CMLE MDC S3’ could be bad depending on the sample size (e.g., for $n\ge 500$), whereas the other constrained methods are good options, from which the researcher can choose according to its degree of conservativeness when establishing non-monotonic effects, with ‘CMLE Bonferroni’ and possibly ‘CMLE filtered’ being the more conservative ones. In addition, the constrained methods perform better than the UMLE when $n=50$, despite the fact that their misclassification rate increases as n decreases and that they drop the monotonicity constraints less frequently (or never).

7 Application to quality of life assessment in Chile

As an illustration of the proposed methodology, we analyse the association between a quality of life self-assessment variable (10-point Likert scale) and ordinal and other predictors from a Chilean survey, the National Socio-Economic Characterisation 2013 (CASEN). This survey retrieves information with the aim of characterising the population of people and households. Our analysis is based on 7,374 householders, namely those who live in the capital and have reported the quality of life self-assessment.

The set of covariates was chosen on the basis of previous research in the field (for example, Di Tella et al. 2003; Cheung and Lucas 2014; Boes and Winkelmann 2010). The data set was published by the Ministry of Social Development of Chile and it is available online at: http://observatorio.ministeriodesarrollosocial.gob.cl/casen-multidimensional/casen/basedatos.php. The detailed data preprocessing is described in the electronic supplementary material.

The response variable is a self-assessment of the quality of life (QoL). The question was ‘Considering everything, how satisfied are you with your life at this moment?’. The possible alternatives were: ‘1 Completely Unsatisfied’, ‘2’,$\ldots$, ‘9’, ‘10 Completely Satisfied’.

The model was fitted with ordinal, ratio, and nominal scale covariates. For the ordinal and nominal scale ones, the first category to be mentioned was considered as the baseline. The ordinal covariates are Educational Level (Edu) with categories ‘Not Educated’, ‘Primary’, ‘Secondary’, and ‘Higher’; Income Quintile (Inc) with levels from ‘Q1’ to ‘Q5’ where ‘Q5’ represents the highest income; Health Status (Hea), a health self-assessment reported as ordinal Likert scale from 1 to 7, with 7 being the best possible status; Overcrowding (Ove), which is an index representing the number of people living in the household per bedroom, with categories ‘Not Overcrowded’ for less than 2.5, ‘[2.5,3.5)’, ‘[3.5,5.0)’, and ‘5.0 or more’; and Children (Chi), a grouped version of the number of people under 15 years old living in the household, with categories ‘0’,‘1’, ‘2’, ‘3’, and ‘4 or more’. The ratio scale variable is Age. The nominal scale ones are Activity (Act), with categories ‘Economically Inactive’, ‘Unemployed’, and ‘Employed’; and Sex (‘Male’, ‘Female’). Therefore, the set of ordinal predictors is $\mathcal {S}=\{Edu, Inc,Hea,Ove,Chi\}$.

Each set of parameter estimates associated with the ordinal predictors in $\mathcal {S}$ was classified as either ‘antitonic’ or ‘isotonic’. The interpretation for the relationship between an ordinal predictor and the response variable with ‘antitonic’ pattern is that the further away an ordinal category is from its baseline, the smaller $P(y_i\le j|\mathbf {x}_i)$ is, i.e., the probability of self-assessing QoL in the jth category or smaller. In other words, ‘antitonic’ patterns mean that higher categories of ordinal variables are associated with more probability of self-assessing QoL in a higher part of the scale. The inverse interpretation applies for ‘isotonic’ patterns.

An unconstrained version of model (4) was fitted to obtain the parameter estimates and their standard errors. The unconstrained parameter estimates and their 95% confidence intervals are shown in Fig. 9. The definition of the variables suggests a monotonic association with respect to the response, and the unconstrained results seem to be consistent with the monotonicity assumption for all the OPs. Therefore, the assumption of monotonicity was imposed on all of them and the approach ‘CMLE MDC S3’ was chosen to be the constrained method to compute the CMLEs.

With a 95% individual confidence level ($\tilde{c}=0.95$), the MDC procedure classified the sets of parameters associated with three ordinal variables as ‘antitonic’ in its first step (Income Quintile, Health Status, and Children), whereas Overcrowding was classified as ‘isotonic’ and Educational Level as ‘both’. There was no ordinal predictor classified as ‘none’ by the end of the first step. Therefore, there was no need of making a decision on whether dropping the monotonicity constraints for variables classified as ‘none’. Hence, $\mathcal {A}_1=\{Inc,Hea,Chi\}$, $\mathcal {I}_1=\{Ove\}$, and $\mathcal {B}_1=\{Edu\}$.

Educational Level was the only variable in the MDC procedure’s second step. To perform this step, a tolerance level of 0.9 was set together with steps of 1% when gradually decreasing the confidence level starting from the one analysed in step one, 95%. As a result of this step, Educational Level was classified as ‘antitonic’ with a 92% confidence level for each confidence interval.

There was no need to execute the third step of the MDC procedure because all of the monotonicity directions were established earlier. All the ordinal predictors were finally classified as ‘antitonic’ except for Overcrowding, which was classified as ‘isotonic’. Therefore, only one model was fitted.

We also used the monotonicity test described in Sect. 4 as a complementary assessment of the monotonicity assumptions. Its results were consistent with the MDC procedure, i.e., it did not reject the null hypothesis of monotonicity for any of the OPs with $\alpha ^*=0.05$.

Some of the parameter estimators resulting from UMLE are not in line with the monotonicity assumption. Keeping all the other variables constant, an improvement in the Income Quintile from ‘Q3’ to ‘Q4’, i.e., an increment in the income level, increases the probability of self-assessing QoL in lower categories of the scale, according to the UMLE. The same happens with Health Status, for which changes from ‘2’ to ‘3’, i.e., improving the health status, seemingly increase the probability of reporting a low self-assessment of QoL. These particular unconstrained results are counterintuitive. Therefore, it is reasonable to think that these may have been the result of random variation, and to impose the monotonicity assumption.

In fact, in these cases there is little difference between neighbouring UMLEs, so in terms of the parameter values constrained and unconstrained results are fairly similar, but the proposed methodology can assure the user that monotonicity is compatible with the data.

For the OP Educational Level, the UMLE allows both positive and negative values in all confidence intervals, but after having classified this OP as antitonic, with the baseline parameter fixed at zero and using the CMLE, all further parameters can only be negative.

In general, the UMLEs are compatible with a monotonic association between ordinal predictors and the response variable, but the parameter estimates produce violations of monotonicity. The CMLEs avoid these, and allow for a simpler and more consistent interpretation.

Fig. 9

CMLEs and UMLEs for a model applied on real data with an ordinal response, ordinal predictors, and others. The first category of each ordinal or nominal predictor is assumed as the reference category. Intercept parameter estimates omitted. The 95% confidence intervals correspond to the UMLEs

Given that the sample size is relatively large, the individual confidence intervals are relatively small, which allows the first step of the MDC procedure to classify all but one OP as either isotonic or antitonic. In order to explore a situation with a smaller sample size, we ran the methodology on a random subsample of $n=200$, i.e., 2.7% of the full sample size. All the OPs are classified as ‘antitonic’ by the end of the MDC procedure in the new setting. The only discrepancy is the classification of the monotonicity direction of Overcrowding. This is an appropriate reflection of the bigger uncertainty in classification when using a smaller sample size.

8 Conclusions

We propose a constrained regression model for an ordinal response with ordinal predictors, which can involve other types of predictors. The information provided by the category ordering of the ordinal predictors is used appropriately for ordinal data, rather than ignoring it (assuming categories as nominal) or overstating it as interval-scaled.

Each set of parameters associated with an ordinal predictor’s categories can be enforced to be monotonic in our procedure, which decides automatically whether associations are isotonic or antitonic. The monotonicity direction classification procedure can classify variables not only as isotonic or antitonic, but also as compatible with both monotonicity directions or none, and the researcher may sometimes prefer to leave out variables compatible with both directions and zero parameters, and to drop the monotonicity constraint for variables incompatible with either direction, which can easily be done within the framework presented here.

The MDC relies on the choice of a pre-specified range of confidence levels between $\tilde{c}_s'^{*}$ and $\tilde{c}_s''^{*}$, but the regression model itself does not require a tuning parameter and does deliver monotonic parameter estimates, unlike the penalised version in Tutz and Gertheiss (2014), which pushes parameters in the direction of monotonicity but does not necessarily achieve it.

A monotonicity test is proposed to assess the validity of the monotonicity assumption for an ordinal predictor. This checks whether the set of confidence intervals belonging to the parameters of an ordinal predictor is compatible with monotonicity or not. As this is based on the Bonferroni correction of confidence levels, it can be very conservative, and more powerful tests can probably be developed. This is left to future work.

Five different approaches for the estimation method are proposed depending on whether the researcher wishes to impose monotonicity constraints on all of the OPs. In that case, the MDC procedure is fully applied (‘CMLE MDC S3’). Otherwise, the four remaining approaches differ in the way they identify the subset of OPs on which the monotonicity assumption is not imposed. ‘CMLE MDC S1’ imposes monotonicity constraints only in step 1 of the MDC and gives variables the biggest chance to be classified as either ‘none’ or ‘both’. ‘CMLE MDC S2’ will re-classify some of these variables as monotonic. ‘CMLE MDC S3’ will impose monotonicity on all OPs. ‘CMLE Bonferroni’ uses the monotonicity test for the decision of dropping constraints. ‘CMLE filtered’ will enforce monotonicity except if the MDC gives a strong indication against it. This happens somewhat earlier than under ‘CMLE Bonferroni’. Due to the conservativity of the Bonferroni test, its main use is to provide a test with a guaranteed low type I error probability, whereas the other methods are probably more appropriate for classification in connection with parameter estimation. In practice, the researcher will need to decide whether monotonicity should be always enforced (‘CMLE MDC S3’), whether there is a clear preference to impose monotonicity except if there is a clear indication against it (‘CMLE filtered’ or ‘CMLE Bonferroni’ in case that the significance level needs to be guaranteed), or whether it is fine to drop monotonicity constraints more easily in case of doubt (‘CMLE MDC S1’), possibly together with dropping variables completely that are classified as ‘both’; ‘CMLE MDC S2’ is a compromise that will probably not play much of a role in practice but was analysed here because it adds insight in the overall procedure.

Our approaches offer the researcher alternatives, because we believe that there are various legitimate interests. The researcher may be in the first place interested in the precision of the resulting estimates. However, in many applications, e.g., in the social sciences, the precise numerical values can be of less interest than qualitative statements about the monotonicity of the OPs. Monotonicity may be favoured because of better interpretability in some cases in which OPs are by and large approximately monotonic even if the true parameters show a mild deviation from monotonicity. If sample sizes are low, monotonicity may be favoured because constraints can support both precision and interpretation. However, in this case the researcher cannot expect a strong power to detect non-monotonicity, and there is always the risk that non-monotonic OPs are treated as monotonic, with loss of precision. In some instances, particularly with low sample sizes and a relatively high number of categories of the OPs, the researcher may prefer making decisions about monotonicity based on the meaning of the OPs rather than in a data driven manner.

A further issue is that a large number of categories $p_s$ for an OP will imply that the Bonferroni test is very conservative and a large number of observations may be required to detect moderate deviations from monotonicity. It may be reasonable in such a case to pool some categories and to make statements about monotonicity at lower ‘granularity’ with better power.

For the real data application, ‘CMLE MDC S3’ enabled a consistent interpretation for the ordinal variables’ categories, which would not have been the case for the UMLE.

The approaches of imposing monotonicity constraints on ordinal predictors allowing for both isotonic and antitonic patterns described in Sect. 5 can also be used in situations in which the response variable is non-ordinal. In addition, the MDC procedure itself can be performed on an ordinal predictor in models for responses of any scale of measurement, as well as the monotonicity test. Asymptotic theory for the CMLE is a matter of ongoing research. This would enable us to make inference about the parameters in the fully constrained model. The R package crov was made available at CRAN.