Abstract
We address the approximation of functionals depending on a system of particles, described by stochastic differential equations (SDEs), in the mean-field limit when the number of particles approaches infinity. This problem is equivalent to estimating the weak solution of the limiting McKean–Vlasov SDE. To that end, our approach uses systems with finite numbers of particles and a time-stepping scheme. In this case, there are two discretization parameters: the number of time steps and the number of particles. Based on these two parameters, we consider different variants of the Monte Carlo and Multilevel Monte Carlo (MLMC) methods and show that, in the best case, the optimal work complexity of MLMC, to estimate the functional in one typical setting with an error tolerance of \(\mathrm {TOL}\), is  when using the partitioning estimator and the Milstein time-stepping scheme. We also consider a method that uses the recent Multi-index Monte Carlo method and show an improved work complexity in the same typical setting of
when using the partitioning estimator and the Milstein time-stepping scheme. We also consider a method that uses the recent Multi-index Monte Carlo method and show an improved work complexity in the same typical setting of  . Our numerical experiments are carried out on the so-called Kuramoto model, a system of coupled oscillators.
. Our numerical experiments are carried out on the so-called Kuramoto model, a system of coupled oscillators.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In our setting, a stochastic particle system is a system of coupled d-dimensional stochastic differential equations (SDEs), each modeling the state of a “particle.” Such particle systems are versatile tools that can be used to model the dynamics of various complicated phenomena using relatively simple interactions, e.g., pedestrian dynamics (Helbing and Molnar 1995; Haji-Ali 2012), collective animal behavior (Erban et al. 2016; Erban and Haskovec 2012), interactions between cells (Dobramysl et al. 2016) and in some numerical methods such as ensemble Kalman filters (Pierre Del Moral and Tugaut 2016). One common goal of the simulation of these particle systems is to average some quantity of interest computed on all particles, e.g., the average velocity, average exit time or average number of particles in a specific region.
Under certain conditions, most importantly the exchangeability of particles and sufficient regularity of the SDE coefficients, the stochastic particle system approaches a mean-field limit as the number of particles tends to infinity (Sznitman 1991). Exchangeability of particles refers to the assumption that all permutations of the particles have the same joint distribution. In the mean-field limit, each particle follows a single McKean–Vlasov SDE where the advection and/or diffusion coefficients depend on the distribution of the solution to the SDE (Gärtner 1988). In many cases, the objective is to approximate the expected value of a quantity of interest (QoI) in the mean-field limit as the number of particles tends to infinity, subject to some error tolerance, \(\mathrm {TOL}\). While it is possible to approximate the expectation of these QoIs by estimating the solution to a nonlinear PDE using traditional numerical methods, such methods usually suffer from the curse of dimensionality. Indeed, the cost of these methods is usually of  for some constant \(w>1\) that depends on the particular numerical method. Using sparse numerical methods alleviates the curse of dimensionality but requires increasing regularity as the dimensionality of the state space increases. On the other hand, Monte Carlo methods do not suffer from this curse with respect to the dimensionality of the state space. This work explores different variants and extensions of the Monte Carlo method when the underlying stochastic particle system satisfies certain crucial assumptions. We theoretically show the validity of some of these assumptions in a somewhat general setting, while verifying the other assumptions numerically on a simple stochastic particle system, leaving further theoretical justification to a future work.
for some constant \(w>1\) that depends on the particular numerical method. Using sparse numerical methods alleviates the curse of dimensionality but requires increasing regularity as the dimensionality of the state space increases. On the other hand, Monte Carlo methods do not suffer from this curse with respect to the dimensionality of the state space. This work explores different variants and extensions of the Monte Carlo method when the underlying stochastic particle system satisfies certain crucial assumptions. We theoretically show the validity of some of these assumptions in a somewhat general setting, while verifying the other assumptions numerically on a simple stochastic particle system, leaving further theoretical justification to a future work.
Generally, the SDEs that constitute a stochastic particle system cannot be solved exactly, and their solution must instead be approximated using a time-stepping scheme with a number of time steps, N. This approximation parameter and a finite number of particles, P, are the two approximation parameters that are involved in approximating a finite average of the QoI computed for all particles in the system. Then, to approximate the expectation of this average, we use a Monte Carlo method. In such a method, multiple independent and identical stochastic particle systems, approximated with the same number of time steps, N, are simulated, and the average QoI is computed from each and an overall average is then taken. Using this method, a reduction in the variance of the estimator is achieved by increasing the number of simulations of the stochastic particle system or increasing the number of particles in the system. Section 3.1 presents the Monte Carlo method more precisely in the setting of stochastic particle systems. Particle methods that are not based on Monte Carlo were also discussed in Bossy and Talay (1996, 1997). In these methods, a single simulation of the stochastic particle system is carried out, and only the number of particles is increased to reduce the variance.
As an improvement of Monte Carlo methods, the Multilevel Monte Carlo (MLMC) method was first introduced in Heinrich (2001) for parametric integration and in Giles (2008b) for SDEs; see Giles (2015) and references therein for an overview. MLMC improves the efficiency of the Monte Carlo method when only an approximation, controlled with a single discretization parameter, of the solution to the underlying system can be computed. The basic idea is to reduce the number of required samples on the finest, most accurate but most expensive discretization, by reducing the variability of this approximation with a correlated coarser and cheaper discretization as a control variate. More details are given in Sect. 3.2 for the case of stochastic particle systems. The application of MLMC to particle systems has been investigated in many works (Bujok et al. 2013; Haji-Ali 2012; Rosin et al. 2014). The same concepts have also been applied to nested expectations (Giles 2015). More recently, a particle method applying the MLMC methodology to stochastic particle systems was also introduced in Ricketson (2015) achieving, for a linear system with a diffusion coefficient that is independent of the state variable, a work complexity of  .
.
Recently, the Multi-index Monte Carlo (MIMC) method (Haji-Ali et al. 2015a) was introduced to tackle high-dimensional problems with more than one discretization parameter. MIMC is based on the same concepts as MLMC and improves the efficiency of MLMC even further but requires mixed regularity with respect to the discretization parameters. More details are given in Sect. 3.3 for the case of stochastic particle systems. In that section, we demonstrate the improved work complexity of MIMC compared with the work complexity of MC and MLMC, when applied to a stochastic particle system. More specifically, we show that, when using a naive simulation method for the particle system with quadratic complexity, the optimal work complexity of MIMC is  when using the Milstein time-stepping scheme and
when using the Milstein time-stepping scheme and  when using the Euler–Maruyama time-stepping scheme. Finally, in Sect. 4, we provide numerical verification for the assumptions that are made throughout the current work and the derived rates of the work complexity.
when using the Euler–Maruyama time-stepping scheme. Finally, in Sect. 4, we provide numerical verification for the assumptions that are made throughout the current work and the derived rates of the work complexity.
In what follows, the notation \(a \lesssim b\) means that there exists a constant c that is independent of b such that \(a < cb\).
2 Problem setting
Consider a system of P exchangeable stochastic differential equations (SDEs) where for \(p = 1 \ldots P\), we have the following equation for \(X_{p|P}(t) \in \mathbb {R}^d\)

where  and for some (possibly stochastic) functions,
and for some (possibly stochastic) functions,  and
and  and \(\mathbb P(\mathbb {R}^d)\) is the space of probability measures over \(\mathbb {R}^d\). Moreover,
and \(\mathbb P(\mathbb {R}^d)\) is the space of probability measures over \(\mathbb {R}^d\). Moreover,
where \(\delta \) is the Dirac measure, is called the empirical measure. In this setting,  are mutually independent d-dimensional Wiener processes. If, moreover, \(\{x^0_p\}_{p \ge 1}\) are i.i.d., then under certain conditions on the smoothness and form of
are mutually independent d-dimensional Wiener processes. If, moreover, \(\{x^0_p\}_{p \ge 1}\) are i.i.d., then under certain conditions on the smoothness and form of  and
and  (Sznitman 1991), as \(P \rightarrow \infty \) for any \(p \in \mathbb {N}\), the \(X_{p|\infty }\) stochastic process satisfies
(Sznitman 1991), as \(P \rightarrow \infty \) for any \(p \in \mathbb {N}\), the \(X_{p|\infty }\) stochastic process satisfies

where \(\mu _\infty ^t \in \mathbb P(\mathbb {R}^d)\) is the corresponding mean-field measure. Under some smoothness and boundedness conditions on  and
and  , the measure \(\mu _\infty ^t\) induces a probability density function (pdf), \(\rho _\infty (t, \cdot )\), that is the Radon–Nikodym derivative with respect to the Lebesgue measure. Moreover, \(\rho _\infty \) satisfies the McKean–Vlasov equation
, the measure \(\mu _\infty ^t\) induces a probability density function (pdf), \(\rho _\infty (t, \cdot )\), that is the Radon–Nikodym derivative with respect to the Lebesgue measure. Moreover, \(\rho _\infty \) satisfies the McKean–Vlasov equation

on \(t \in [0, \infty )\) and  with \(\rho _\infty (0, \cdot )\) being the pdf of \(x_p^0\) which is given and is independent of p. Due to (2) and \(x_p^0\) being i.i.d, \(\{X_{p|\infty }\}_p\) are also i.i.d.; hence, unless we want to emphasize the particular path, we drop the p-dependence in \(X_{p|\infty }\) and refer to the random process \(X_\infty \) instead. In any case, we are interested in computing
with \(\rho _\infty (0, \cdot )\) being the pdf of \(x_p^0\) which is given and is independent of p. Due to (2) and \(x_p^0\) being i.i.d, \(\{X_{p|\infty }\}_p\) are also i.i.d.; hence, unless we want to emphasize the particular path, we drop the p-dependence in \(X_{p|\infty }\) and refer to the random process \(X_\infty \) instead. In any case, we are interested in computing  for some given function, \(\psi \), and some final time, \(T < \infty \).
for some given function, \(\psi \), and some final time, \(T < \infty \).
Kuramoto Example
(Fully connected Kuramoto model for synchronized oscillators) Throughout this work, we focus on a simple, one-dimensional example of (1). For \(p = 1, 2,\ldots , P\), we seek \(X_{p|P}(t) \in \mathbb {R}\) that satisfies

where \(\sigma \in \mathbb {R}\) is a constant and \(\{\vartheta _p\}_p\) are i.i.d. and independent from the set of i.i.d. random variables \(\{x_p^0\}_p\) and the Wiener processes  . The limiting SDE as \(P \rightarrow \infty \) is
. The limiting SDE as \(P \rightarrow \infty \) is

Note that in terms of the generic system (1), we have

with \(\vartheta \) a random variable and  is a constant. We are interested in
is a constant. We are interested in

a real number between zero and one that measures the level of synchronization in the system with an infinite number of oscillators (Acebrón et al. 2005); with zero corresponding to total disorder. In this case, we need two estimators: one where we take \(\psi (\cdot ) = \sin (\cdot )\) and the other where we take \(\psi (\cdot ) = \cos (\cdot )\).
While it is computationally efficient to approximate  by solving the McKean–Vlasov PDE, that \(\rho _\infty \) satisfies, when the state dimensionality, d, is small (cf., e.g., Haji-Ali 2012), the cost of a standard full tensor approximation increases exponentially as the dimensionality of the state space increases. On the other hand, using sparse approximation techniques to solve the PDE requires increasing regularity assumptions as the dimensionality of the state space increases. Instead, in this work, we focus on approximating the value of
by solving the McKean–Vlasov PDE, that \(\rho _\infty \) satisfies, when the state dimensionality, d, is small (cf., e.g., Haji-Ali 2012), the cost of a standard full tensor approximation increases exponentially as the dimensionality of the state space increases. On the other hand, using sparse approximation techniques to solve the PDE requires increasing regularity assumptions as the dimensionality of the state space increases. Instead, in this work, we focus on approximating the value of  by simulating the SDE system in (1). Let us now define
by simulating the SDE system in (1). Let us now define

Here, due to exchangeability, \(\{X_{p|P}(T)\}_{p=1}^P\) are identically distributed, but they are not independent since they are taken from the same realization of the particle system. Nevertheless, we have  for any p and P. In this case, with respect to the number of particles, P, the cost of a naive calculation of \(\phi _P\) is
for any p and P. In this case, with respect to the number of particles, P, the cost of a naive calculation of \(\phi _P\) is  due to the cost of evaluating the empirical measure in (1) for every particle in the system. It is possible to take \(\{X_{p|P}\}_{p=1}^P\) in (4) as i.i.d., i.e., for each \(p=1\ldots P\), \(X_{p|P}\) is taken from a different independent realization of the system (1). In this case, the usual law of large numbers applies, but the cost of a naive calculation of \(\phi _P\) is
due to the cost of evaluating the empirical measure in (1) for every particle in the system. It is possible to take \(\{X_{p|P}\}_{p=1}^P\) in (4) as i.i.d., i.e., for each \(p=1\ldots P\), \(X_{p|P}\) is taken from a different independent realization of the system (1). In this case, the usual law of large numbers applies, but the cost of a naive calculation of \(\phi _P\) is  . For this reason, we focus in this work on the former method of taking identically distributed but not independent \(\{X_{p|P}\}_{p=1}^P\).
. For this reason, we focus in this work on the former method of taking identically distributed but not independent \(\{X_{p|P}\}_{p=1}^P\).
Following the setup in Collier et al. (2015), Haji-Ali et al. (2015b), our objective is to build a random estimator, \(\mathcal {A}\), approximating  with minimal work, i.e., we wish to satisfy the constraint
with minimal work, i.e., we wish to satisfy the constraint

for a given error tolerance, \(\mathrm {TOL}\), and a given confidence level determined by \(0<\epsilon \ll 1\). We instead impose the following, more restrictive, two constraints:


for a given tolerance splitting parameter, \(\theta \in (0,1)\), possibly a function of \(\mathrm {TOL}\). To show that these bounds are sufficient note that

imposing (6) yields

then imposing (7) gives (5). Next, we can use Markov inequality and impose  to satisfy (7). However, by assuming (at least asymptotic) normality of the estimator, \(\mathcal {A}\), we can get a less stringent condition on the variance as follows:
to satisfy (7). However, by assuming (at least asymptotic) normality of the estimator, \(\mathcal {A}\), we can get a less stringent condition on the variance as follows:

Here, \(0<C_\epsilon \) is such that \(\Phi (C_\epsilon ) = 1 - \frac{\epsilon }{2}\), where \(\Phi \) is the cumulative distribution function of a standard normal random variable, e.g., \(C_\epsilon \approx 1.96\) for \(\epsilon = 0.05\). The asymptotic normality of the estimator is usually shown using some form of the central limit theorem (CLT) or the Lindeberg–Feller theorem (see, e.g., Collier et al. 2015; Haji-Ali et al. 2015a for CLT results for the MLMC and MIMC estimators and Fig. 3-right).
As previously mentioned, we wish to approximate the values of \(X_\infty \) by using (1) with a finite number of particles, P. For a given number of particles, P, a solution to (1) is not readily available. Instead, we have to discretize the system of SDEs using, for example, the Euler–Maruyama time-stepping scheme with N time steps. For \(n = 0,1, 2, \ldots N-1\),

where \(\varvec{X}_{P}^{n|N} = \{X_{p|P}^{n|N}\}_{p=1}^P\) and  are i.i.d. For the remainder of this work, we use the notation
are i.i.d. For the remainder of this work, we use the notation

At this point, we make the following assumptions:

These assumptions will be verified numerically in Sect. 4. In general, they translate to smoothness and boundedness assumptions on  and \(\psi \). Indeed, in (P1), the weak convergence of the Euler–Maruyama method with respect to the number of time steps is a standard result shown, for example, in Kloeden and Platen (1992) by assuming 4-time differentiability of
and \(\psi \). Indeed, in (P1), the weak convergence of the Euler–Maruyama method with respect to the number of time steps is a standard result shown, for example, in Kloeden and Platen (1992) by assuming 4-time differentiability of  and \(\psi \). Showing that the constant multiplying \(N^{-1}\) is bounded for all P is straightforward by extending the standard proof of weak convergence the Euler–Maruyama method in (Kloeden and Platen 1992, Chapter 14) and assuming boundedness of the derivatives
and \(\psi \). Showing that the constant multiplying \(N^{-1}\) is bounded for all P is straightforward by extending the standard proof of weak convergence the Euler–Maruyama method in (Kloeden and Platen 1992, Chapter 14) and assuming boundedness of the derivatives  and \(\psi \). On the other hand, the weak convergence with respect to the number of particles, i.e.,
and \(\psi \). On the other hand, the weak convergence with respect to the number of particles, i.e.,  , is a consequence of the propagation of chaos which is shown, without a convergence rate, in Sznitman (1991) for \(\psi \) Lipschitz,
, is a consequence of the propagation of chaos which is shown, without a convergence rate, in Sznitman (1991) for \(\psi \) Lipschitz,  constant and
constant and  of the form
of the form

where \(\kappa (t, \cdot , \cdot )\) is Lipschitz. On the other hand, for one-dimensional systems and using the results from Kolokoltsov and Troeva (2015, Theorem 3.2) we can show the weak convergence rate with respect to the number of particles and the convergence rate for the variance of \(\phi _P\) as the following lemma shows. Below, \(C(\mathbb {R})\) is the space of continuous bounded functions and \(C^k(\mathbb {R})\) is the space of continuous bounded functions whose i’th derivative is in \(C(\mathbb {R})\) for \(i=1, \ldots , k\).
Lemma 2.1
(Weak and variance convergence rates w.r.t. number of particles) Consider (1) and (2) with \(d=1\), strictly positive  and
and  as in (9) with \(\kappa (t, x, \cdot ) \in C^{2}(\mathbb {R})\), \(\frac{\partial \kappa (t, x, \cdot )}{\partial x} \in C(\mathbb {R})\) and \(\kappa (t, \cdot , y) \in C^{2}(\mathbb {R})\) where the norms are assumed to be uniform with respect to the arguments, x and y, respectively. If, moreover, \(\psi \in C^{2}(\mathbb {R})\), then
as in (9) with \(\kappa (t, x, \cdot ) \in C^{2}(\mathbb {R})\), \(\frac{\partial \kappa (t, x, \cdot )}{\partial x} \in C(\mathbb {R})\) and \(\kappa (t, \cdot , y) \in C^{2}(\mathbb {R})\) where the norms are assumed to be uniform with respect to the arguments, x and y, respectively. If, moreover, \(\psi \in C^{2}(\mathbb {R})\), then


Proof
The system in this lemma is a special case of the system in Kolokoltsov and Troeva (2015, Theorem 3.2). From there and given the assumptions of the current lemma, (10) immediately follows. Moreover, from the same reference, we can further conclude that

for \(1 \le p\ne q \le P\). Using this, we can show (11) since

and

\(\square \)
From here, the rate of convergence for the variance of \(\phi _P^N\) can be shown by noting that

and noting that  , then showing that the first term is
, then showing that the first term is  because of the weak convergence with respect to the number of time steps.
because of the weak convergence with respect to the number of time steps.
Finally, as mentioned above, with a naive method, the total cost to compute a single sample of \(\phi _{P}^N\) is  . The quadratic power of P can be reduced by using, for example, a multipole algorithm (Carrier et al. 1988; Greengard and Rokhlin 1987). In general, we consider the work required to compute one sample of \(\phi _P^N\) as
. The quadratic power of P can be reduced by using, for example, a multipole algorithm (Carrier et al. 1988; Greengard and Rokhlin 1987). In general, we consider the work required to compute one sample of \(\phi _P^N\) as  for a positive constant, \({{\gamma _{\mathrm {p}}}}\ge 1\).
for a positive constant, \({{\gamma _{\mathrm {p}}}}\ge 1\).
3 Monte Carlo methods
In this section, we study different Monte Carlo methods that can be used to estimate the previous quantity, \(\phi _\infty \). In the following, we use the notation  where, for each q, \(\omega ^{(m)}_{q}\) denotes the m’th sample of the set of underlying random variables that are used in calculating \(X_{q|P}^{N|N}\), i.e., the Wiener path, \(W_{q}\), the initial condition, \(x_q^0\), and any random variables that are used in
where, for each q, \(\omega ^{(m)}_{q}\) denotes the m’th sample of the set of underlying random variables that are used in calculating \(X_{q|P}^{N|N}\), i.e., the Wiener path, \(W_{q}\), the initial condition, \(x_q^0\), and any random variables that are used in  or
or  . Moreover, we sometimes write \(\phi _P^N(\varvec{\omega }_{1:P}^{(m)})\) to emphasize the dependence of the \(m'\)th sample of \(\phi _P^{N}\) on the underlying random variables.
. Moreover, we sometimes write \(\phi _P^N(\varvec{\omega }_{1:P}^{(m)})\) to emphasize the dependence of the \(m'\)th sample of \(\phi _P^{N}\) on the underlying random variables.
3.1 Monte Carlo (MC)
The first estimator that we look at is a Monte Carlo estimator. For a given number of samples, M, number of particles, P, and number of time steps, N, we can write the MC estimator as follows:
Here,

Hence, due to (P1), we must have  and
and  to satisfy (6), and, due to (P2), we must have
to satisfy (6), and, due to (P2), we must have  to satisfy (8). Based on these choices, the total work to compute \(\mathcal A_{\text {MC}}\) is
to satisfy (8). Based on these choices, the total work to compute \(\mathcal A_{\text {MC}}\) is

Kuramoto Example
Using a naive calculation method of \(\phi _{P}^N\) (i.e., \({{\gamma _{\mathrm {p}}}}=2\)) gives a work complexity of  . See also Table 1 for the work complexities for different common values of \({{\gamma _{\mathrm {p}}}}\).
. See also Table 1 for the work complexities for different common values of \({{\gamma _{\mathrm {p}}}}\).
3.2 Multilevel Monte Carlo (MLMC)
For a given \(L \in \mathbb {N}\), define two hierarchies, \(\{N_\ell \}_{\ell =0}^L\) and \(\{P_\ell \}_{\ell =0}^L\), satisfying \(P_{\ell -1} \le P_{\ell }\) and \(N_{\ell -1} \le N_{\ell }\) for all \(\ell \). Then, we can write the MLMC estimator as follows:

where we later choose the function \(\varphi _{P_{\ell -1}}^{N_{\ell -1}}(\cdot )\) such that \(\varphi _{P_{-1}}^{N_{-1}}(\cdot ) = 0\) and  so that
so that  due to the telescopic sum. For MLMC to have better work complexity than that of Monte Carlo, \(\phi _{P_\ell }^{N_\ell }(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) and \(\varphi _{P_{\ell -1}}^{N_{\ell -1}}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) must be correlated for every \(\ell \) and m, so that their difference has a smaller variance than either \(\phi _{P_\ell }^{N_\ell }(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) or \(\varphi _{P_{\ell -1}}^{N_{\ell -1}}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) for all \(\ell > 0\).
due to the telescopic sum. For MLMC to have better work complexity than that of Monte Carlo, \(\phi _{P_\ell }^{N_\ell }(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) and \(\varphi _{P_{\ell -1}}^{N_{\ell -1}}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) must be correlated for every \(\ell \) and m, so that their difference has a smaller variance than either \(\phi _{P_\ell }^{N_\ell }(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) or \(\varphi _{P_{\ell -1}}^{N_{\ell -1}}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) for all \(\ell > 0\).
Given two discretization levels, \(N_\ell \) and \(N_{\ell -1}\), with the same number of particles, P, we can generate a sample of \(\varphi _{P}^{N_{\ell -1}}(\varvec{\omega }_{1:P}^{(\ell ,m)})\) that is correlated with \(\phi _{P}^{N_\ell }(\varvec{\omega }_{1:P}^{(\ell ,m)})\) by taking
That is, we use the same samples of the initial values, \(\{x_{p}^0\}_{p\ge 1}\), the same Wiener paths, \(\{W_p\}_{p=1}^P\), and, in case they are random as in (3), the same samples of the advection and diffusion coefficients,  and
and  , respectively. We can improve the correlation by using an antithetic sampler as detailed in Giles and Szpruch (2014) or by using a higher-order scheme like the Milstein scheme (Giles 2008a). In the Kuramoto example, the Euler–Maruyama and the Milstein schemes are equivalent since the diffusion coefficient is constant.
, respectively. We can improve the correlation by using an antithetic sampler as detailed in Giles and Szpruch (2014) or by using a higher-order scheme like the Milstein scheme (Giles 2008a). In the Kuramoto example, the Euler–Maruyama and the Milstein schemes are equivalent since the diffusion coefficient is constant.
On the other hand, given two different sizes of the particle system, \(P_\ell \) and \(P_{\ell -1}\), with the same discretization level, N, we can generate a sample of \(\varphi _{P_{\ell -1}}^{N}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) that is correlated with \(\phi _{P_\ell }^{N}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\) by taking

In other words, we use the same \(P_{\ell -1}\) sets of random variables out of the total \(P_\ell \) sets of random variables to run an independent simulation of the stochastic system with \(P_{\ell -1}\) particles.
We also consider another estimator that is more correlated with \(\phi _{P_\ell }^{N}(\varvec{\omega }_{1:P_\ell }^{(\ell ,m)})\). The “antithetic” estimator was first independently introduced in Haji-Ali (2012, Chapter 5) and Bujok et al. (2013) and subsequently used in other works on particle systems (Rosin et al. 2014) and nested simulations (Giles 2015). In this work, we call this estimator a “partitioning” estimator to clearly distinguish it from the antithetic estimator in Giles and Szpruch (2014). We assume that \(P_\ell = {{\beta _{\mathrm {p}}}}P_{\ell -1}\) for all \(\ell \) and some positive integer \({{\beta _{\mathrm {p}}}}\) and take

That is, we split the underlying \(P_\ell \) sets of random variables into \({{\beta _{\mathrm {p}}}}\) identically distributed and independent groups, each of size \(P_{\ell -1}\), and independently simulate \({{\beta _{\mathrm {p}}}}\) particle systems, each of size \(P_{\ell -1}\). Finally, for each particle system, we compute the quantity of interest and take the average of the \({{\beta _{\mathrm {p}}}}\) quantities.
In the following subsections, we look at different settings in which either \(P_\ell \) or \(N_\ell \) depends on \(\ell \) while the other parameter is constant for all \(\ell \). We begin by recalling the optimal convergence rates of MLMC when applied to a generic random variable, Y, with a trivial generalization to the case when there are two discretization parameters: one that is a function of the level, \(\ell \), and the other, \({\widetilde{L}}\), that is fixed for all levels.
Theorem 3.1
(Optimal MLMC complexity) Let \(Y_{{\widetilde{L}}, \ell }\) be an approximation of the random variable, Y, for every \(({\widetilde{L}}, \ell ) \in \mathbb {N}^2\). Denote by \(Y^{(\ell , m)}\) a sample of Y and denote its corresponding approximation by \(Y_{{\widetilde{L}}, \ell }^{(\ell , m)}\), where we assume that the samples \(\{Y^{(\ell , m)}\}_{\ell , m}\) are mutually independent. Consider the MLMC estimator
with \(Y_{{\widetilde{L}}, -1}^{\ell , m} = 0\) and for \(\beta , w, \gamma , s, {\widetilde{\beta }}, {\widetilde{w}}, {\widetilde{\gamma }}, {\widetilde{c}} > 0\) where \(s \le 2 w\), and assume the following:
-
1.

-
2.
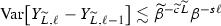
-
3.
\(\mathrm {Work}\left[ Y_{{\widetilde{L}}, \ell } - Y_{{\widetilde{L}}, \ell -1}\right] \lesssim {\widetilde{\beta }}^{{\widetilde{\gamma }} {\widetilde{L}}} \beta ^{\gamma \ell }\).
Then, for any \(\mathrm {TOL}< e^{-1}\), there exist \({\widetilde{L}}, L\) and a sequence of  such that
such that

and

This plot shows, for the Kuramoto example (3), numerical evidence for Assumption (P1) (left) and Assumptions (P2), (MLMC1)–(MLMC3) (right). Here, \(P_{\ell }\) and \(N_{\ell }\) are chosen according to (22). From the right plot, we can confirm that \({{s_{\mathrm {t}}}}=2\) for the Milstein method. We can also deduce that using the \(\overline{\varphi }\) sampler in (13) yields \({{s_{\mathrm {p}}}}=0\) in (MIMC2) (i.e., no variance reduction compared to  ), while using the \(\widehat{\varphi }\) sampler in (14) yields \({{s_{\mathrm {p}}}}=1\) in (MIMC2) (i.e.,
), while using the \(\widehat{\varphi }\) sampler in (14) yields \({{s_{\mathrm {p}}}}=1\) in (MIMC2) (i.e.,  )
)

Proof
The proof can be straightforwardly derived from the proof of Cliffe et al. (2011, Theorem 1), we sketch here the main steps. First, we split constraint (15) to a bias and variance constraints similar to (6) to (8), respectively. Then, since  , given the first assumption of the theorem and imposing the bias constraint yield
, given the first assumption of the theorem and imposing the bias constraint yield  and
and  . The assumptions on the variance and work then give:
. The assumptions on the variance and work then give:

Then

due to mutual independence of \(\{Y^{(\ell , m)}\}_{\ell , m}\). Moreover,
Finally, given L, solving for \(\{M_\ell \}_{\ell =0}^L\) to minimize the work while satisfying the variance constraint gives the desired result. \(\square \)
3.2.1 MLMC hierarchy based on the number of time steps
In this setting, we take  for some \({{\beta _{\mathrm {t}}}}>0\) and \(P_\ell = P_L\) for all \(\ell \), i.e., the number of particles is a constant, \(P_L\), on all levels. We make an extra assumption in this case, namely:
for some \({{\beta _{\mathrm {t}}}}>0\) and \(P_\ell = P_L\) for all \(\ell \), i.e., the number of particles is a constant, \(P_L\), on all levels. We make an extra assumption in this case, namely:

for some constant \({{s_{\mathrm {t}}}}> 0\). The factor  is the usual assumption on the variance convergence of the level difference in MLMC theory (Giles 2008b) and is a standard result for the Euler–Maruyama scheme with \({{s_{\mathrm {t}}}}= 1\) and for the Milstein scheme with \({{s_{\mathrm {t}}}}=2\), (Kloeden and Platen 1992). On the other hand, the factor \(P_L^{-1}\) can be motivated from (P2), which states that the variance of each term in the difference converges at this rate.
is the usual assumption on the variance convergence of the level difference in MLMC theory (Giles 2008b) and is a standard result for the Euler–Maruyama scheme with \({{s_{\mathrm {t}}}}= 1\) and for the Milstein scheme with \({{s_{\mathrm {t}}}}=2\), (Kloeden and Platen 1992). On the other hand, the factor \(P_L^{-1}\) can be motivated from (P2), which states that the variance of each term in the difference converges at this rate.
Due to Theorem 3.1, we can conclude that the work complexity of MLMC is

Kuramoto Example
In this example, using the Milstein time-stepping scheme, we have \({{s_{\mathrm {t}}}}= 2\) (cf. Fig. 1), and a naive calculation method of \(\phi _{P}^N\) (\({{\gamma _{\mathrm {p}}}}=2\)) gives a work complexity of  . See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
. See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
3.2.2 MLMC hierarchy based on the number of particles
In this setting, we take  for some \({{\beta _{\mathrm {p}}}}>0\) and \(N_\ell = N_L\) for all \(\ell \), i.e., we take the number of time steps to be a constant, \(N_L\), on all levels. We make an extra assumption in this case:
for some \({{\beta _{\mathrm {p}}}}>0\) and \(N_\ell = N_L\) for all \(\ell \), i.e., we take the number of time steps to be a constant, \(N_L\), on all levels. We make an extra assumption in this case:

for some constant \({{s_{\mathrm {p}}}}\ge 0\). The factor \({{\beta _{\mathrm {p}}}}^{-{{s_{\mathrm {p}}}}\ell }\) is the usual assumption on the variance convergence of the level difference in MLMC theory (Giles 2008b). On the other hand, the factor \(P_\ell ^{-1}\) can be motivated from (P2), since the variance of each term in the difference is converging at this rate.
Due to Theorem 3.1, we can conclude that the work complexity of MLMC in this case is

Kuramoto Example
Using a naive calculation method of \(\phi _{P}^N\) (\({{\gamma _{\mathrm {p}}}}=2\)), we distinguish between the two samplers:
-
Using the sampler \(\overline{\varphi }\) in (13), we verify numerically that \({{s_{\mathrm {p}}}}= 0\) (cf. Fig. 1). Hence, the work complexity is
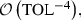 which is the same work complexity as a Monte Carlo estimator. This should be expected since using the “correlated” samples of \(\overline{\varphi }_{P_{\ell -1}}^N\) and \(\phi _{P_\ell }^N\) does not reduce the variance of the difference, as Fig. 1 shows.
which is the same work complexity as a Monte Carlo estimator. This should be expected since using the “correlated” samples of \(\overline{\varphi }_{P_{\ell -1}}^N\) and \(\phi _{P_\ell }^N\) does not reduce the variance of the difference, as Fig. 1 shows. -
Using the partitioning estimator, \(\widehat{\varphi }\), in (14), we verify numerically that \({{s_{\mathrm {p}}}}= 1\) (cf. Fig. 1). Hence, the work complexity is
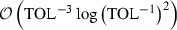 . Here the samples of \(\widehat{\varphi }_{P_{\ell -1}}^N\) have higher correlation to corresponding samples of \(\phi _{P_\ell }^N\), thus reducing the variance of the difference. Still, using MLMC with hierarchies based on the number of times steps (fixing the number of particles) yields better work complexity. See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
. Here the samples of \(\widehat{\varphi }_{P_{\ell -1}}^N\) have higher correlation to corresponding samples of \(\phi _{P_\ell }^N\), thus reducing the variance of the difference. Still, using MLMC with hierarchies based on the number of times steps (fixing the number of particles) yields better work complexity. See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
This figure provides numerical evidence for (MIMC1) (left) and (MIMC2) (right) for the Kuramoto example (3) when using the Milstein scheme for time discretization (yielding \({{s_{\mathrm {t}}}}=2\)) and the partitioning sample of particle systems (yielding \({{s_{\mathrm {p}}}}=1\)). Here, \(P_{\alpha _1}\) and \(N_{\alpha _2}\) are chosen according to (22). When considering a mixed difference (i.e, \({{{\varvec{\alpha }}}}=(i,i)\)), a higher rate of convergence is observed
3.2.3 MLMC hierarchy based on both the number of particles and the number of times steps
In this case, we vary both the number of particles and the number of time steps across MLMC levels. That is, we take  and
and  for all \(\ell \). In this case, a reasonable assumption is
for all \(\ell \). In this case, a reasonable assumption is

The factor \({{\beta _{\mathrm {p}}}}^{-\ell }\) can be motivated from (P2) since the variance of each term in the difference is converged at this rate. On the other hand,  is the larger factor of (MLMC1) and (MLMC2).
is the larger factor of (MLMC1) and (MLMC2).
Due to Theorem 3.1 and defining
we can conclude that the work complexity of MLMC is

Kuramoto Example
We choose \({{\beta _{\mathrm {p}}}}={{\beta _{\mathrm {t}}}}\) and use a naive calculation method of \(\phi _{P}^N\) (yielding \({{\gamma _{\mathrm {p}}}}=2\)) and the partitioning sampler (yielding \({{s_{\mathrm {p}}}}=1\)). Finally, using the Milstein time-stepping scheme, we have \({{s_{\mathrm {t}}}}=2\). Refer to Fig. 1 for numerical verification. Based on these rates, we have, in (19), \(s=2\log ({{\beta _{\mathrm {p}}}}), w=\log ({{\beta _{\mathrm {p}}}})\) and \(\gamma =3\log ({{\beta _{\mathrm {p}}}})\). The MLMC work complexity in this case is  See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
3.3 Multi-index Monte Carlo (MIMC)
Following (Haji-Ali et al. 2015a), for every multi-index \({{{\varvec{\alpha }}}}= (\alpha _1, \alpha _2) \in \mathbb {N}^{2}\), let  and
and  and define the first-order mixed-difference operator in two dimensions as
and define the first-order mixed-difference operator in two dimensions as

with \(\phi _{P_{-1}}^{N}=0\) and \(\phi _{P}^{N_{-1}}=0\). The MIMC estimator is then written for a given \(\mathcal I \subset \mathbb {N}^{2}\) as

At this point, similar to the original work on MIMC (Haji-Ali et al. 2015a), we make the following assumptions on the convergence of \(\varvec{\Delta }\phi _{P_{\alpha _1}}^{N_{\alpha _2}} \), namely

Assumption (MIMC1) is motivated from (P1) by assuming that the mixed first-order difference, \(\varvec{\Delta }\phi _{P_{\alpha _1}}^{N_{\alpha _2}}\), gives a product of the convergence terms instead of a sum. Similarly, (MIMC2) is motivated from (MLMC1) and (MLMC2). To the best of our knowledge, there are currently no proofs of these assumptions for particle systems, but we verify them numerically for (3) in Fig. 2.
In these plots, each marker represents a separate run of the MLMC or MIMC estimators (as detailed in Sects. 3.2.3 and 3.3, respectively) when applied to the Kuramoto example (3). Left the exact errors of the estimators, estimated using a reference approximation that was computed with a very small \(\mathrm {TOL}\). This plot shows that, up to the prescribed 95% confidence level, both methods approximate the quantity of interest to the same required tolerance, \(\mathrm {TOL}\). The upper and lower numbers above the linear line represent the percentage of runs that failed to meet the prescribed tolerance, if any, for both MLMC and MIMC, respectively. Right A PP plot of the CDF of the value of both estimators for certain tolerances, shifted by their mean and scaled by their standard deviation showing that both estimators, when appropriately shifted and scaled, are well approximated by a standard normal random variable
Henceforth, we will assume that \({{\beta _{\mathrm {t}}}}= {{\beta _{\mathrm {p}}}}\) for easier presentation. Following (Haji-Ali et al. 2015a, Lemma 2.1) and recalling the assumption on cost per sample, \( \mathrm {Work}\left[ \varvec{\Delta }\phi _{P_{\alpha _1}}^{N_{\alpha _2}}\right] \lesssim P_{\alpha _1}^{{{\gamma _{\mathrm {p}}}}} N_{\alpha _2}^{} \), then, for every value of \(L\in \mathbb {R}^+\), the optimal set can be written as

and the optimal computational complexity of MIMC is  , where
, where

Maximum discretization level of the number of time steps and the number of particles for both MLMC and MIMC (as detailed in Sects. 3.2.3 and 3.3, respectively) for different tolerances (cf. (22)). Recall that, for a fixed tolerance in MIMC, \(2 \alpha _2 + \alpha _1\) is bounded by a constant (cf. (21))
Kuramoto Example
Here again, we use a naive calculation method of \(\phi _{P}^N\) (yielding \({{\gamma _{\mathrm {p}}}}=2\)) and the partitioning sampler (yielding \({{s_{\mathrm {p}}}}=1\)). Finally, using the Milstein time-stepping scheme, we have \({{s_{\mathrm {t}}}}=2\). Hence, \(\zeta = 0\), \(\mathfrak z=1\) and  See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
See also Table 1 for the work complexities for different common values of \({{s_{\mathrm {t}}}}\) and \({{\gamma _{\mathrm {p}}}}\).
4 Numerical example
In this section, we provide numerical evidence of the assumptions and work complexities that are made in Sect. 3. This section also verifies that the constants of the work complexity (which were not tracked) are not significant for reasonable error tolerances. The results in this section were obtained using the mimclib software library (Haji-Ali 2016) and GNU parallel (Tange 2011).
In the results outlined below, we focus on the Kuramoto example in (3), with the following choices: \(\sigma = 0.4\), \(T=1\), \(x_{p}^0 \sim \mathcal N(0, 0.2)\) and \(\vartheta _p \sim \mathcal U(-0.2, 0.2)\) for all p. We also set
Figure 1 shows the absolute expectation and variance of the level differences for the different MLMC settings that are outlined in Sect. 3.2. These figures verify Assumptions (P1), (P2) and (MLMC1)–(MLMC3) with the values \({{s_{\mathrm {t}}}}=2\) and \({{s_{\mathrm {p}}}}=0\) for the \(\overline{\varphi }\) sampler in (13) or the value \({{s_{\mathrm {p}}}}=1\) for the \(\widehat{\varphi }\) sampler in (14). For the same parameter values, Fig. 2 provides numerical evidence for Assumptions (MIMC1) and (MIMC2) for the \(\widehat{\varphi }\) sampler (14).
Maximum work estimate (left) and running time (in seconds, right) of the samples used in MLMC and MIMC (as detailed in Sects. 3.2.3 and 3.3, respectively) when applied to the Kuramoto example (3). These plots show the single, largest indivisible work unit in MLMC and MIMC which gives an indication of the parallelization scaling of both methods
Work estimate (left) and running time (in seconds, right) of MLMC and MIMC (as detailed in Sects. 3.2.3 and 3.3, respectively) when applied to the Kuramoto example (3). For sufficiently small tolerances, the running time closely follows the predicted theoretical rates (also plotted) and shows the performance improvement of MIMC
We now compare the MLMC method (Giles 2008b) in the setting that is presented in Sect. 3.2.3 and the MIMC method (Haji-Ali et al. 2015a) that is presented in Sect. 3.3. In both methods, we use the Milstein time-stepping scheme and the partitioning sampler, \(\widehat{\varphi }\), in (14). Recall that in this case, we verified numerically that \({{\gamma _{\mathrm {p}}}}=2\), \({{s_{\mathrm {p}}}}=1\) and \({{s_{\mathrm {t}}}}=2\). We also use the MLMC and MIMC algorithms that were outlined in their original work and use an initial 25 samples on each level or multi-index to compute a corresponding variance estimate that is required to compute the optimal number of samples. In the following, we refer to these methods as simply “MLMC” and “MIMC.” We focus on the settings in Sects. 3.2.3 and 3.3 since checking the bias of the estimator in those settings can be done straightforwardly by checking the absolute value of the level differences in MLMC or the multi-index differences in MIMC. On the other hand, checking the bias in the settings outlined in Sects. 3.1, 3.2.1 and 3.2.2 is not as straightforward and determining the number of times steps and/or the number of particles to satisfy a certain error tolerance requires more sophisticated algorithms. This makes a fair numerical comparison with these later settings somewhat difficult.
Figure 3-left shows the exact errors of both MLMC and MIMC for different prescribed tolerances. This plot shows that both methods estimate the quantity of interest up to the same error tolerance; comparing their work complexity is thus fair. On the other hand, Fig. 3-right shows a PP plot, i.e., a plot of the cumulative distribution function (CDF) of the MLMC and MIMC estimators, normalized by their variance and shifted by their mean, versus the CDF of a standard normal distribution. This figure shows that our assumption in Sect. 2 of the asymptotic normality of these estimators is well founded. Figure 4 shows the maximum discretization level for both the number of time steps and the number of particles for MLMC and MIMC (cf. (22)). Recall that, for a fixed tolerance in MIMC, \(2 \alpha _2 + \alpha _1\) is bounded by a constant (cf. (21)). Hence, Fig. 4 shows a direct implication on the results reported in Fig. 5 where we plot the maximum cost of the samples used in both MLMC and MIMC for different tolerances. This cost represents an indivisible unit of simulation for both methods, assuming we treat the simulation of the particle system as a black box. Hence, Fig. 5 shows that MIMC has better parallelization scaling, i.e., even with an infinite number of computation nodes MIMC would still be more efficient than MLMC.
Finally, we show in Fig. 6 the cost estimates of MLMC and MIMC for different tolerances. This figure clearly shows the performance improvement of MIMC over MLMC and shows that the complexity rates that we derived in this work are reasonably accurate.
5 Conclusions
This work has shown both numerically and theoretically under certain assumptions, which could be verified numerically, the improvement of MIMC over MLMC when used to approximate a quantity of interest computed on a particle system as the number of particles goes to infinity. The application to other particle systems (or equivalently other McKean–Vlasov SDEs) is straightforward, and similar improvements are expected. The same machinery was also suggested for approximating nested expectations in Giles (2015), and the analysis here applies to that setting as well. Moreover, the same machinery, i.e., multi-index structure with respect to time steps and number of particles coupled with a partitioning estimator, could be used to create control variates to reduce the computational cost of approximating quantities of interest on stochastic particle systems with a finite number of particles.
Future work includes analyzing the optimal level separation parameters, \({{\beta _{\mathrm {p}}}}\) and \({{\beta _{\mathrm {t}}}}\), and the behavior of the tolerance splitting parameter, \(\theta \). Another direction could be applying the MIMC method to higher-dimensional particle systems such as the crowd model in Haji-Ali (2012). On the theoretical side, the next step is to prove the assumptions that were postulated and verified numerically in this work for certain classes of particle systems, namely:
the second-order convergence with respect to the number of particles of the variance of the partitioning estimator (14) and the convergence rates for mixed differences (MIMC1) and (MIMC2).
References
Acebrón, J.A., Bonilla, L.L., Vicente, C.J.P., Ritort, F., Spigler, R.: The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77(1), 137 (2005)
Bossy, M., Talay, D.: Convergence rate for the approximation of the limit law of weakly interacting particles: application to the Burgers equation. Ann. Appl. Probab. 6(3), 818–861 (1996)
Bossy, M., Talay, D.: A stochastic particle method for the McKean–Vlasov and the Burgers equation. Math. Comput. Am. Math. Soc. 66(217), 157–192 (1997)
Bujok, K., Hambly, B., Reisinger, C.: Multilevel simulation of functionals of Bernoulli random variables with application to basket credit derivatives. Methodol. Comput. Appl. Probab. 73, 1–26 (2013)
Carrier, J., Greengard, L., Rokhlin, V.: A fast adaptive multipole algorithm for particle simulations. SIAM J. Sci. Stat. Comput. 9(4), 669–686 (1988)
Cliffe, K., Giles, M., Scheichl, R., Teckentrup, A.: Multilevel Monte Carlo methods and applications to elliptic PDEs with random coefficients. Comput. Vis. Sci. 14(1), 3–15 (2011)
Collier, N., Haji-Ali, A.-L., Nobile, F., von Schwerin, E., Tempone, R.: A continuation multilevel Monte Carlo algorithm. BIT Numer. Math. 55(2), 399–432 (2015)
Dobramysl, U., Rüdiger, S., Erban, R.: Particle-based multiscale modeling of calcium puff dynamics. Multiscale Model. Simul. 14(3), 997–1016 (2016)
Erban, R., Haskovec, J.: From individual to collective behaviour of coupled velocity jump processes: a locust example. Kinet. Relat. Models 5(4), 817–842 (2012)
Erban, R., Haskovec, J., Sun, Y.: A Cucker–Smale model with noise and delay. SIAM J. Appl. Math. 76(4), 1535–1557 (2016)
Gärtner, J.: On the McKean–Vlasov limit for interacting diffusions. Mathematische Nachrichten 137(1), 197–248 (1988)
Giles, M.B.: Improved multilevel Monte Carlo convergence using the Milstein scheme. In: Keller, A., Heinrich, S., Niederreiter, H. (eds.) Monte Carlo and Quasi-Monte Carlo Methods 2006, pp. 343–358. Springer, Berlin (2008a)
Giles, M.B.: Multilevel Monte Carlo path simulation. Oper. Res. 56(3), 607–617 (2008b)
Giles, M.B.: Multilevel Monte Carlo methods. Acta Numer. 24, 259–328 (2015)
Giles, M.B., Szpruch, L.: Antithetic multilevel Monte Carlo estimation for multi-dimensional SDEs without Lévy area simulation. Ann. Appl. Probab. 24(4), 1585–1620 (2014)
Greengard, L., Rokhlin, V.: A fast algorithm for particle simulations. J. Comput. Phys. 73(2), 325–348 (1987)
Haji-Ali, A.-L.: Pedestrian flow in the mean-field limit. King Abdullah University of Science and Technology (KAUST). http://hdl.handle.net/10754/250912 (2012)
Haji-Ali, A.-L.: mimclib. https://github.com/StochasticNumerics/mimclib (2016)
Haji-Ali, A.-L., Nobile, F., Tempone, R.: Multi-index Monte Carlo: when sparsity meets sampling. Numer. Math. 132, 767–806 (2015a)
Haji-Ali, A.-L., Nobile, F., von Schwerin, E., Tempone, R.: Optimization of mesh hierarchies in multilevel Monte Carlo samplers. Stoch. Partial Differ. Equ. Anal. Comput. 4, 76–112 (2015b)
Heinrich, S.: Multilevel Monte Carlo methods. In: Large-Scale Scientific Computing, vol. 2179 of Lecture Notes in Computer Science. Springer, Berlin, pp. 58–67 (2001)
Helbing, D., Molnar, P.: Social force model for pedestrian dynamics. Phys. Rev. E 51(5), 4282 (1995)
Kloeden, P.E., Platen, E.: Numerical solution of stochastic differential equations. Springer, Berlin (1992). doi:10.1007/978-3-662-12616-5
Kolokoltsov, V., Troeva, M.: On the mean field games with common noise and the Mckean–Vlasov SPDEs. ArXiv preprint arXiv:1506.04594 (2015)
Pierre Del Moral, A.K., Tugaut, J.: On the stability and the uniform propagation of chaos of a class of extended Ensemble Kalman–Bucy filters. SIAM J. Control Optim. 55(1), 119–155 (2016)
Ricketson, L.: A multilevel Monte Carlo method for a class of McKean–Vlasov processes. ArXiv preprint arXiv:1508.02299 (2015)
Rosin, M., Ricketson, L., Dimits, A., Caflisch, R., Cohen, B.: Multilevel Monte Carlo simulation of Coulomb collisions. J. Comput. Phys. 274, 140–157 (2014)
Sznitman, A.-S.: Topics in propagation of chaos. In: Ecole d’été de probabilités de Saint-Flour XIX–1989. Springer, pp. 165–251 (1991)
Tange, O.: GNU parallel—the command-line power tool. login USENIX Mag. 36(1), 42–47 (2011)
Acknowledgements
R. Tempone is a member of the KAUST Strategic Research Initiative, Center for Uncertainty Quantification in Computational Sciences and Engineering. R. Tempone received support from the KAUST CRG3 Award Ref: 2281 and the KAUST CRG4 Award Ref: 2584. The authors would like to thank Lukas Szpruch for the valuable discussions regarding the theoretical foundations of the methods.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Haji-Ali, AL., Tempone, R. Multilevel and Multi-index Monte Carlo methods for the McKean–Vlasov equation. Stat Comput 28, 923–935 (2018). https://doi.org/10.1007/s11222-017-9771-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11222-017-9771-5
Keywords
- Multi-index Monte Carlo
- Multilevel Monte Carlo
- Monte Carlo
- Particle systems
- McKean–Vlasov
- Mean-field
- Stochastic differential equations
- Weak approximation
- Sparse approximation
- Combination technique






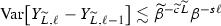

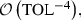 which is the same work complexity as a Monte Carlo estimator. This should be expected since using the “correlated” samples of
which is the same work complexity as a Monte Carlo estimator. This should be expected since using the “correlated” samples of 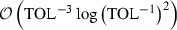 . Here the samples of
. Here the samples of 



