Abstract
A typical problem in optimal design theory is finding an experimental design that is optimal with respect to some criteria in a class of designs. The most popular criteria include the A- and D-criteria. Regular graph designs occur in many optimality results, and if the number of blocks is large enough, an A-optimal (or D-optimal) design is among them (if any exist). To explore the landscape of designs with a large number of blocks, we introduce extensions of regular graph designs. These are constructed by adding the blocks of a balanced incomplete block design repeatedly to the original design. We present the results of an exact computer search for the best regular graph designs and the best extended regular graph designs with up to 20 treatments v, block size \(k \le 10\) and replication r \(\le 10\) and \(r(k-1)-(v-1)\lfloor r(k-1)/(v-1)\rfloor \le 9\).
Similar content being viewed by others
References
Amerine, M.A., Roessler, E.B.: Wines: Their Sensory Evaluation. W. H, Freeman, San Francisco (1979)
Bailey, R.A., Cameron, P.J.: Combinatorics of optimal designs. In: Surveys in Combinatorics 2009, London Mathematical Society Lecture Notes, vol 365, pp 19–73. Cambridge University Press, Cambridge (2009)
Bailey, R.A.: Designs for two-colour microarray experiments. Appl. Stat. 56(4), 365–394 (2007)
Beckenbach, E.F., Bellman, R.: Inequalities, Ergebnisse der Mathematik und ihrer Grenzgebiete. Springer, Berlin (1965)
Best, D.J., Rayner, J.C., Allingham, D.: A statistical test for ranking data from partially balanced incomplete block designs. J. Sensory Stud. 26, 81–84 (2011)
Bose, R.C., Nair, K.R.: Partially balanced incomplete block designs. Sankhya 4, 337–372 (1939)
Bose, R.C., Shimamoto, T.: Classification and analysis of partially balanced incomplete block designs with two associate classes. J. Am. Stat. Soc. 47, 151–184 (1952)
Cheng, C.S.: Optimality of certain asymmetrical experimental designs. Annal Stat. 6, 1239–1261 (1978)
Cheng, C.S.: Maximizing the total number of spanning trees in a graph: Two related problems in graph theory and optimum design theory. J. Comb. Theory 31, 240–248 (1981)
Cheng, C.S.: On the optimality of (M.S)-optimal designs in large systems. Sankhya 54, 117–125 (1992)
Cheng, C.S., Bailey, R.A.: Optimality of some two-associate-class partially balanced incomplete-block designs. Annal Stat. 19(3), 1667–1671 (1991)
Clatworthy, W.H.: Tables of two-associate-class partially balanced designs, NBS Applied Mathematics Series, vol 63. The United States Department of Commerce Publications, National Bureau of Standards (U.S.) (1973)
Cochran, W.G., Cox, G.: Experimental Designs. John Wiley and Sons, New York, NY (1957)
Constantine, G.M.: On the E-optimality of PBIB designs with a small number of blocks. Annal Stat. 10, 1027–1031 (1982)
Constantine, G.M.: On the optimality of block designs. Ann. Inst. Stat. Math. 38, 161–174 (1986)
Gacula, M.C., Singh, J., Bi, J., Altan, S.: Statistical Methods in Food and Consumer Research. Academic Press, New York, NY (2009)
John, J.A., Mitchell, T.J.: Optimal Incomplete Block Designs. ORNL/CSD-8 Available from the National Technical Information Service, The United States Department of Commerce, 5285 Port Royal Road, Springfield, VA (1976)
John, J.A., Wolock, F.W., David, H.A.: Cyclic designs, NBS Applied Mathematics Series, vol 62. The United States Department of Commerce Publications, National Bureau of Standards (U.S.) (1972)
John, J.A.: Reduced group divisible paired comparison designs. Ann. Math. Stat. 38, 1887–1893 (1967)
John, J.A., Mitchell, T.J.: Optimal incomplete block designs. J. R. Stat. Soc. 39B, 39–43 (1977)
John, J.A., Williams, E.R.: Conjectures for optimal block designs. J. R. Stat. Soc. 44B, 221–225 (1982)
Jones, B., Eccleston, J.A.: Exchange and interchange procedures to search for optimal designs. J. R. Stat. Soc. 42, 238–243 (1980)
Kerr, M.K., Churchill, G.A.: Experimental design for gene expression microarrays. Biostatistics 2, 183–201 (2001)
Kiefer, J.: Optimality and Construction of Generalized Youden Designs. A Survey of Statistical Designs and Linear Models, pp. 333–354. North-Holland, Amsterdam (1975)
Kirchhoff, G.: Über die Auflösung der Gleichung, auf welche man bei der Untersuchung der linearen Verteilung galvanischer Ströme geführt wird. Ann. Phys. Chem. 72, 497–508 (1847)
Lockshin, L., Mueller, S., Louviere, J., Francis, L., Osidacz, P.: Development of a new method to measure how consumers choose wine. Aust. N. Z. Wine Ind. J. 24, 81–84 (2011)
Meringer, M.: Fast generation of regular graphs and construction of cages. J. Graph Theory 30, 137–146 (1999)
Morgan, J.P.: Optimal incomplete block designs. J. Am. Stat. Assoc. 102, 655–663 (2007)
Shah, K.R., Sinha, B.K.: Theory of Optimal Designs, Lecture Notes in Statistics, vol 54. Springer, Berlin (1989)
Soicher, L.H.: The DESIGN Package for GAP, Version 1.4. http://designtheory.org/software_design/ (2006)
Takeuchi, K.: On the optimality of certain type of PBIB designs. Rep. Stat. Appl. Res. Union Jpn. Sci. Eng. 8, 140–145 (1961)
Wit, E., Nobile, A., Khanin, R.: Near-optimal designs for dual channel microarray studies. Appl. Stat. 54, 817–830 (2005)
Wolfram Research, I.: Mathematica (2012)
Acknowledgements
The author would like to thank Peter J. Cameron and R. A. Bailey for the many conversations on optimal designs and is extremely grateful to J. P. Morgan for bringing the topic to her attention and the helpful discussions about RGDs and the arising computational difficulties. Joachim Kunert has been an invaluable source of information for preference designs. Parts of the computations were performed using the facilities at the London Research Institute, Cancer Research UK.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix 1: Catalogue of A- and D-best RGDs
There follows a table of the A- and D-best RGDs (except for the case \(v=14\), \(r=5\), \(k=2\), where only the D-best RGD is included). These RGDs also produce optimal BIBD-extended RGDs for large y. We list \(\delta =r(k-1)-\lambda (v-1)\) and the smallest \({\tilde{\lambda }}\) such that a 2-\((v,k,{\tilde{\lambda }})\)-design exists. There exists only one irreducible matrix for \(\delta =2\) or \(\delta =v-1\), and we therefore exclude these cases.
Most designs can be found in either Clatworthy (1973) or John et al. (1972). To follow the convention as in John and Mitchell (1977), we write in the reference column P.XY for a design in Clatworthy (1973) with reference number XY and C.XY for a design in John et al. (1972) with reference number XY. If the design is not in either catalogues but can be found in John and Mitchell (1977) we give the reference number as JM.XY, and if it is cyclic, we give the initial blocks. If the design is the complement of a design in one of the catalogue, we add an (C) to the reference number. All other designs can be found in the appendix. However, some of these designs are possible to construct with known methods, such as the ones in John (1967). A full catalogue of all designs as XML files in external representation format is included in the electronic appendix. For more information on external representation see Soicher (2006).
v | k | r | \({\tilde{\lambda }}\) | \(\delta \) | Reference |
|---|---|---|---|---|---|
6 | 2 | 3 + 5y | 1 | 3 | P.SR6,C.A2 |
6 | 2 | 4 + 5y | 1 | 4 | P.R18,C.A3 |
6 | 2 | 8 + 5y | 1 | 3 | P.R24 |
6 | 2 | 9 + 5y | 1 | 4 | P.R27 |
6 | 3 | 4 + 5y | 2 | 3 | (1,2,4)(1,3,5) |
6 | 3 | 7 + 5y | 2 | 4 | P.R46 |
6 | 3 | 9 + 5y | 2 | 3 | P.R52 |
6 | 4 | 6 + 10y | 6 | 3 | P.SR35 |
6 | 4 | 8 + 10y | 6 | 4 | P.R96 |
7 | 2 | 4 + 6y | 1 | 4 | #1 |
7 | 2 | 10 + 6y | 1 | 4 | JM.1 |
7 | 5 | 10 + 15y | 10 | 4 | #2 |
8 | 2 | 3 + 7y | 1 | 3 | C.A7 |
8 | 2 | 4 + 7y | 1 | 4 | P.SR9,C.A8 |
8 | 2 | 5 + 7y | 1 | 5 | JM.3 |
8 | 2 | 6 + 7y | 1 | 6 | P.R29,C.A10 |
8 | 2 | 10 + 7y | 1 | 3 | (1,2)(1,2)(1,3)(1,4)(1,5)(1,5) |
8 | 3 | 3 + 21y | 6 | 6 | P.R54,C.B3 |
8 | 3 | 6 + 21y | 6 | 5 | JM.4 |
8 | 3 | 9 + 21y | 6 | 4 | P.R58 |
8 | 4 | 4 + 7y | 3 | 5 | C.B6 |
8 | 4 | 6 + 7y | 3 | 4 | P.SR38 |
8 | 4 | 8 + 7y | 3 | 3 | (1,2,3,5)(1,2,3,6) |
8 | 4 | 9 + 7y | 3 | 6 | P.R101 |
8 | 5 | 5 + 35y | 20 | 6 | P.R314,C.B3(C) |
8 | 5 | 10 + 35y | 20 | 5 | JM.4(C) |
8 | 6 | 9 + 21y | 15 | 3 | C.A7(C) |
9 | 2 | 4 + 8y | 1 | 4 | C.A11 |
9 | 2 | 6 + 8y | 1 | 6 | P.R34,C.A13 |
9 | 3 | 3 + 4y | 1 | 6 | P.SR23 |
9 | 3 | 6 + 4y | 1 | 4 | JM.8 |
9 | 3 | 7 + 4y | 1 | 6 | P.R62 |
9 | 3 | 10 + 4y | 1 | 4 | JM.10 |
9 | 4 | 4 + 8y | 3 | 4 | C.B12 |
9 | 5 | 5 + 10y | 5 | 4 | C.B12(C) |
9 | 6 | 6 + 8y | 5 | 6 | P.SR65 |
10 | 2 | 3 + 9y | 1 | 3 | P.T2 |
10 | 2 | 4 + 9y | 1 | 4 | C.A16 |
10 | 2 | 5 + 9y | 1 | 5 | P.SR11,C.A17 |
10 | 2 | 6 + 9y | 1 | 6 | JM.12 |
10 | 2 | 7 + 9y | 1 | 7 | JM.13 |
10 | 2 | 8 + 9y | 1 | 8 | P.R36,C.A20 |
10 | 3 | 3 + 9y | 2 | 6 | JM.14 |
10 | 3 | 6 + 9y | 2 | 3 | P.T12 |
10 | 4 | 4 + 6y | 2 | 3 | P.T33 |
10 | 4 | 8 + 6y | 2 | 6 | JM.15 |
10 | 4 | 10 + 6y | 2 | 3 | P.T37 |
10 | 5 | 6 + 9y | 4 | 6 | JM.16 |
10 | 5 | 8 + 9y | 4 | 5 | JM.17 |
10 | 5 | 10 + 9y | 4 | 6 | JM.19 |
10 | 6 | 6 + 9y | 5 | 3 | P.T60 |
10 | 7 | 7 + 21y | 14 | 6 | JM.14(C) |
11 | 2 | 4 + 10y | 1 | 4 | C.22 |
11 | 2 | 6 + 10y | 1 | 6 | #3 |
11 | 2 | 8 + 10y | 1 | 8 | JM.20 |
11 | 3 | 3 + 15y | 3 | 6 | #4 |
11 | 3 | 9 + 15y | 3 | 8 | JM.21 |
11 | 4 | 8 + 20y | 6 | 4 | C.B25(C) |
11 | 8 | 8 + 40y | 28 | 6 | #4(C) |
12 | 2 | 3 + 11y | 1 | 3 | JM.22 |
12 | 2 | 4 + 11y | 1 | 4 | C.A27 |
12 | 2 | 5 + 11y | 1 | 5 | #5 |
12 | 2 | 6 + 11y | 1 | 6 | P.SR13,C.A29 |
12 | 2 | 7 + 11y | 1 | 7 | JM.24 |
12 | 2 | 8 + 11y | 1 | 8 | P.R38,C.A31 |
12 | 2 | 9 + 11y | 1 | 9 | P.R39,C.A32 |
12 | 3 | 3 + 11y | 2 | 6 | #6 |
12 | 3 | 4 + 11y | 2 | 8 | P.SR26 |
12 | 3 | 7 + 11y | 2 | 3 | JM.25 |
12 | 3 | 9 + 11y | 2 | 7 | JM.27 |
12 | 3 | 10 + 11y | 2 | 9 | P.R78,C.B34 |
12 | 4 | 3 + 11y | 3 | 9 | P.SR41 |
12 | 4 | 5 + 11y | 3 | 4 | C.B37 |
12 | 4 | 6 + 11y | 3 | 7 | JM.28 |
12 | 5 | 5 + 55y | 20 | 9 | P.R145,C.B43 |
12 | 6 | 10 + 11y | 5 | 6 | P.SR71 |
12 | 7 | 7 + 77y | 42 | 9 | P.R176, |
C.B43(C) | |||||
12 | 9 | 9 + 33y | 24 | 6 | #6(C) |
13 | 2 | 4 + 12y | 1 | 4 | C.A35 |
13 | 2 | 6 + 12y | 1 | 6 | #7 |
13 | 2 | 8 + 12y | 1 | 8 | #8 |
13 | 3 | 9 + 6y | 1 | 6 | #9 |
7 13 | 5 | 5 + 15y | 5 | 8 | C.B58 |
14 | 2 | 3 + 13y | 1 | 3 | #10 |
14 | 2 | 4 + 13y | 1 | 4 | #11 |
14 | 2 | 5 + 13y | 1 | 5 | #12 |
14 | 3 | 9 + 39y | 6 | 5 | #13 |
14 | 3 | 15 + 39y | 6 | 4 | #14 |
14 | 6 | 6 + 39y | 15 | 4 | C.B72 |
15 | 2 | 4 + 14y | 1 | 4 | #15 |
15 | 3 | 9 + 28y | 1 | 4 | C.B77 |
16 | 2 | 3 + 15y | 1 | 3 | #16 |
16 | 3 | 9 + 13y | 2 | 3 | #17 |
16 | 4 | 6 + 5y | 1 | 3 | P.R118 |
18 | 2 | 3 + 17y | 1 | 3 | #18 |
18 | 3 | 10 + 17y | 2 | 3 | #19 |
18 | 5 | 5 + 85y | 20 | 3 | #20 |
20 | 2 | 3 + 19y | 1 | 3 | #21 |
Appendix 2: Optimal regular graph designs
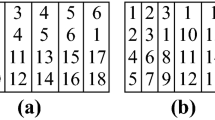
There follows a list of all designs not found in the used reference catalogues. Blocks are represented as k-tuples of treatments in the rows.
\(\underline{\#1\,v=7,\,k=2,\,r=4+6y}\)

\(\underline{\#2\,v=7,\,k=5,\,r=10+15y}\)

\(\underline{\#3\,v=11,\,k=2,\,r=6+10y}\)

\(\underline{\#4\,v=11,\,k=3,\,r=3+15y}\)

\(\underline{\#5\,v=12,\,k=2,\,r=5+11y}\)

\(\underline{\#6\,v=12,\,k=3,\,r=3+11y}\)

\(\underline{\#7\,v=13,\,k=2,\,r=6+12y}\)

\(\underline{\#8\,v=13,\,k=2,\,r=8+12y}\)

\(\underline{\#9\,v=13,\,k=3,\,r=9+6y}\)

\(\underline{\#10\,v=14,\,k=2,\,r=3+13y}\)

\(\underline{\#11\,v=14,\,k=2,\,r=4+13y}\)

\(\underline{\#12\,v=14,\,k=2,\,r=5+13y}\)

\(\underline{\#13\,v=14,\,k=3,\,r=9+39y}\)

\(\underline{\#14\,v=14,\,k=3,\,r=15+39y}\)

\(\underline{\#15\,v=15,\,k=2,\,r=4+14y}\)

\(\underline{\#16\,v=16,\,k=2,\,r=3+15y}\)

\(\underline{\#17\,v=16,\,k=3,\,r=9+13y}\)

\(\underline{\#18\,v=18,\,k=2,\,r=3+17y}\)

\(\underline{\#19\,v=18,\,k=3,\,r=10+17y}\)

\(\underline{\#20,v=18,\,k=5,\,r=5+85y}\)

\(\underline{\#21\,v=20,\,k=2,\,r=3+19y}\)

Rights and permissions
About this article
Cite this article
Cakiroglu, S.A. Optimal regular graph designs. Stat Comput 28, 103–112 (2018). https://doi.org/10.1007/s11222-016-9720-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11222-016-9720-8