Test-driven development with mutation testing – an experimental study

Abstract

Test-driven development (TDD) is a popular design approach used by the developers with testing being the important software development driving factor. On the other hand, mutation testing is considered one of the most effective testing techniques. However, there is not so much research on combining these two techniques together. In this paper, we propose a novel, hybrid approach called TDD+M which combines test-driven development process together with the mutation approach. The aim was to check whether this modified approach allows the developers to write a better quality code. We verify our approach by conducting a controlled experiment and we show that it achieves better results than the sole TDD technique. The experiment involved 22 computer science students split into eight groups. Four groups (TDD+M) were using our approach, the other four (TDD) – a normal TDD process. We performed a cross-experiment by measuring the code coverage and mutation coverage for each combination (code of group X, tests from group Y). The TDD+M tests achieved better coverage on the code from TDD groups than the TDD tests on their own code (53.3% vs. 33.5% statement coverage and 64.9% vs. 37.5% mutation coverage). The TDD+M tests also found more post-release defects in the TDD code than TDD tests in the TDD+M code. The experiment showed that adding mutation into the TDD process allows the developers to provide better, stronger tests and to write a better quality code.

1 Introduction

Test-driven development (TDD) is a common Agile practice introduced by Kent Beck (2002) for software development. According to the recent State of Agile Report (2018), 33% of teams use this technique in their everyday work. On the other hand, mutation testing is considered one of the most effective test techniques Ammann and Offutt (2008). We understand test effectiveness as the ability to detect faults in code. Test thoroughness is usually measured in terms of coverage. Two most popular measures are statement coverage and – in case of mutation testing – mutation coverage (known also as mutation score).

The recent study of Papadakis et al. (2019) gathers the results on the mutation testing effectiveness published in years 1991-2018. In particular, the authors refer to (Ahmed et al. 2016; Chekam et al. 2017; Gligoric et al. 2015; Gopinath et al. 2014; Just et al. 2014; Li et al. 2009; Papadakis et al. 2018; Ramler et al. 2017) reporting the following findings:

• there is a correlation between coverage and test effectiveness;

• both statement and mutation coverage correlate with fault detection, with mutants having higher correlation;

• there is a weak correlation between coverage and number of bug-fixes

• mutation testing provides valuable guidance toward improving the test suites of a safety-critical industrial software system;

• mutation testing finds more faults than prime path, branch and all-uses;

• there is a strong connection between coverage attainment and fault revelation for strong mutation but weak for statement, branch and weak mutation; fault revelation improves significantly at higher coverage;

• mutation coverage and test suite size correlate with fault detection rates, but often the individual (and joint) correlations are weak; test suites of very high mutation coverage levels enjoy significant benefits over those with lower score levels.

In this paper, we investigate the impact of mutation testing on the overall TDD process. To do this, we modified the TDD framework by extending it with the additional step involving mutation testing. Next, we asked eight groups of students to write the same software. Four groups used TDD approach and four others the modified approach with mutation step (TDD+M). Then, by using a cross-testing approach, we compared the effectiveness of tests written in these two TDD frameworks: with and without mutation.

We measure the test effectiveness (and the overall code quality) using statement and mutation coverage. In this context, the study of Papadakis et al. (2019) is important for our research, as it supports the thesis that we can measure effectiveness of test suites in terms of statement and mutation coverage. We also measure the overall code quality by analyzing the number of field defects (that is, found after the release) detected by tests written in one framework on code written by the other one.

The novelty of this paper, comparing to the studies previously cited, is that we do not focus on the coverage criteria themselves, but on the role of mutation in the TDD process: we investigate if mutation testing improves the quality of code developed within the TDD approach. Also, because in our experiment all the teams were independently writing the same software, that is, the code for the same set of requirements, we were able to compare the effectiveness of mutation in a more objective way by performing a cross-experiment with cross-testing. Its concept is similar to the one from defect pooling technique for defect prediction. We use a test suite from one team on the code written by another team. Such an approach allows us to check the effectiveness of the test suite more fairly, because in the cross-experiment the test case design is not biased by the code for which it was written. The tests are executed on code which was not seen by the test designers. We can compare their results with the results of tests written exactly for this code. This way we can compare two test design approaches: without (TDD) and with (TDD+M) mutation involved. We measure the TDD+M tests effectiveness ”itself”, by not considering the code for which it was written.

The goal of our study was to answer the following research questions:

RQ1. Do the tests written with the TDD+M approach give better code coverage than the ones written in a pure TDD approach with no mutation process involved?

RQ2. Are the tests written with the TDD+M approach stronger (more effective) than the ones written using a pure TDD approach?

RQ3. Is the external code quality better when the TDD+M is used than in case of using the TDD approach only?

By ’stronger’ or ’more effective’ tests, we mean tests that have higher probability of detecting faults and that give better coverage in terms of metrics such as statement coverage or mutation coverage (see Section 5.1 for the definition).

To verify RQ1, we use the statement coverage, to verify RQ2 – mutation coverage, and to verify the RQ3 – the number of field defects found by the tests in the code and their defect detection efficiency. The model for comparison should be as simple as possible to give us clear results and to avoid any biases caused by the model complexity. RQ1 seems to be easy to answer: mutation forces the developers to cover their code more thoroughly, so by definition it will give higher coverage. But it is still interesting to measure how much better would their tests be in terms of the statement coverage comparing to tests written without mutation. To answer RQ2 and RQ3, we will use the above-mentioned cross-testing technique.

RQ1 and RQ2 are about internal quality, and RQ3 about external quality (ISO, 2005). Internal software quality is about the design of the software and we express it in terms of the coverage. External quality is the fitness for purpose of the software and we express it in terms of number of field defects, that is – defects detected after the release. Of course, this is a simplified view on quality, because quality is a multi-dimensional concept. However, the mentioned metrics are related with quality and are easy to calculate, so we decided to use them in our study.

The rest of the paper is organized as follows. In Sections 2 and 3, we describe the TDD framework and the mutation technique in more detail. In Section 4, we introduce the TDD+M approach, which combines test-driven approach with mutation testing process. Section 5 describes the experiment we performed to verify if our approach works better than a pure TDD method. Section 7 follows with the summary of our findings and some final conclusions. In the Appendix, we describe in detail the two experiments we performed.

2 Test-driven development

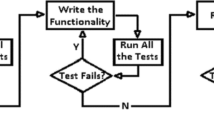
A developer working with the TDD framework writes tests for the code before writing this code. Next, the developer implements a part of the code for which all the tests designed earlier should pass. This iterative approach allows the developer to create the application in small pieces, although even when using TDD, the developers sometimes tend to write quite large test cases (Čaušević et al. 2012; Fucci et al. 2017). In each iteration, some part of the functionality is created, but the main rule holds all the time: before the code is written, the developer has to implement the corresponding tests.

The steps within the TDD approach are as follows:

• 1 Write a test for the functionality to be implemented.

• 2 Run the test (the new test should fail, because there is no code for it) – this step verifies that the tests themselves are written correctly.

• 3 Implement the minimal amount of code so that all the tests pass – this step verifies that the code implements the intended functionality for a given iteration. In case of failures, modify the code until all the tests pass.

• 4 Refactor the code in order to improve its readability and maintainability.

• 5 Return to step 1.

Fig. 1

Test-driven development approach

Refactoring is done, because the code is implemented in a series of many short iterations. In each of them, some small portion of a new functionality is added, so the frequent code changes may easily affect its clean structure. Refactoring can make the code tidy again. The TDD process is presented schematically in Fig. 1.

There is a plethora of the literature on the TDD method, such as the seminal publication is the Kent Beck’s book (Beck, 2002) mentioned earlier. Another interesting source of knowledge on TDD is (Astels, 2003), which is a practical guide to the TDD from the developer’s perspective. Of course, there is also a lot of publications that investigate the impact of the TDD on the final application quality.  Janzen (2005) verifies the TDD approach in practice and in particular evaluate its impact on the internal software quality. They also focus on some pedagogical implications. In (Bhat and Nagappan, 2006) a support of TDD for two different Microsoft company applications (Windows and MSN) is presented. The great number of publications (cf. the references in (Khanam and Ahsan, 2017)) suggests that the method is frequently used and it has de facto become a standard practice for iterative software development.

However, some meta-analyses and surveys show that the TDD impact on different aspects of software development process is inconclusive. In Table 1, we reproduce the results of such a survey from (Pančur and Ciglarič, 2011). The table presents a quick overview of perceived effects on different parameters in several studies.

Table 1 Overview of perceived effects of TDD on different aspects of software development process (after (Pančur and Ciglarič 2011))

Four out of seven studies showed that TDD impacts positively on the productivity, but three others showed the negative effect. For the external quality (probably the most interesting characteristic) four out of 10 studies showed the positive effect, three – negative effect and three – no effect. One study showed the positive effect of TDD on software complexity. Three out of six showed positive effect on code coverage and three others – a negative one.

On the other hand, a more recent study (Munir et al. 2014) seems to come to a different conclusion. It investigates several research studies on TDD taking into account two study quality dimensions: rigor and relevance, which can be either low or high, forming four combinations of these characteristics. The authors conclude: ’We found that studies in the four categories come to different conclusions. In particular, studies with a high rigor and relevance scores show clear results for improvement in external quality, which seem to come with a loss of productivity. At the same time, high rigor and relevance studies only investigate a small set of variables. Other categories contain many studies showing no difference, hence biasing the results negatively for the overall set of primary studies.’

In another survey (Khanam and Ahsan, 2017), the authors examined the impact of TDD on different software parameters, such as: software quality, cost effectiveness, speed of development, test quality, refactoring phenomena and its impact, overall effort required and productivity, maintainability and time required. They conclude that using the TDD improves internal and external quality, but the developers’ productivity tends to reduce as compared to ’test-last development’. The difference in metrics such as: McCabe cyclomatic complexity, LOC, branch coverage are statistically insignificant.

3 Mutation testing

Mutation is typically used as a way to evaluate the adequacy of test suites, to guide the generation of test cases and to support experimentation (Papadakis et al. 2019). In mutation testing process, we introduce some number of small structural changes in code. These changes are called mutations and the code with one or more mutations is called mutant (Ammann and Offutt, 2008). Each mutation represents some simulated defect in a code (Jia and Harman, 2011). This way, mutation testing tries to mimic the common programmers errors, like inverting conditional boundaries in logical statements or making the ’by-one’ mistakes (for example, writing ’if $x>0$’ instead of ’if $x \ge 0$’).

All mutations are defined by the corresponding mutation operators. Mutation operator is a set of syntactic transformation rules defined on the artifact to be tested (usually the source code) (Papadakis et al. 2019). It is crucial that after the mutation the source code can be compiled with no problems. Each mutation operator is designed to introduce a certain type of defect in the code. For example, Arithmetic Operator Replacement changes an arithmetic operation to any other arithmetic operator. During the testing, both original code and all the mutants are tested with the same set of unit tests. When a test gives different result on original and mutated code, we say that this mutation is detected or killed.

Numerous types of mutation operators have been proposed in the literature. A good review of this topic is presented in (Kim et al. 2001). Mutation operators can not only generate simple syntactic mutations (e.g., by changing one relational operator to another), but also mutations that reflect the types of errors characteristic for object-oriented programming (see (Ma et al. 2002)).

Depending on the mutation detection ratio (hereinafter called the mutation coverage or mutation score), we infer directly about the quality of our tests, i.e. the ability of our tests to detect defects. If a given test did not kill any mutant, this may suggest that this test is weak and maybe should be removed from our test suite. On the other hand, if a given test kills many mutants, this may suggest that this test is strong. However, one must be very careful with such analyses. For example, a mutant can be trivial, which means that all or almost all tests are able to kill it. This means that the corresponding mutation is very easy to detect, so it does not bring really any added value to the whole process. The decision about the strength of a given test should be based not only on its own results, but also on the performance of all the tests regarding a given mutant.

Assuming that a given mutant is not equivalent, if no test was able to kill it, this means that our test suite should be enriched (or modified) by a test able to kill this mutant. Adding such a test is usually easy, because we know exactly what kind of defect was introduced in a given mutant and what is its location. This way, by adding new tests, we test our program better. In result, we increase the external quality of our software.

Mutation testing has a long history. The paper of DeMillo, Lipton and Sayward (DeMillo et al. 1978) is generally considered as the seminal reference for mutation testing. Theoretical background of the mutation testing can be found in the Ammann and Offutt’s book (Ammann and Offutt, 2008). The authors also claim that mutation is widely considered a ”high-end” criterion, more effective than most other criteria but also more expensive.

From a theoretical point of view, mutation testing can be considered as a white-box, fault-based testing approach. The possibility of fault injection is itself a fault-based technique, and it clearly suggests that we must be able to operate on the source code to generate mutants. Therefore, mutation testing can be classified as a white-box technique. Mutation testing can be also classified as a syntax-based testing, as the mutation operators operate on strings being the fragments of the source code.

Mutation testing can be performed at all test levels, even at higher levels of testing, like integration testing, acceptance testing or system testing. But in most cases, it is used by developers at the unit testing level. We can mutate all kinds of architectural software logic, like call graphs (integration testing level), architecture design (system testing level) or business requirements specification written in a formal language (acceptance level). The mutation operators must be, of course, defined separately for each level of testing, as there will be a clear difference between the simulation of a defect in a source code and the simulation of a defect in a business requirement specification.

3.1 Mutation testing process

Fig. 2

Mutation testing process

The mutation testing process is presented in Fig. 2. The input data to this process are:

• a source code of the original, unmodified program P called the System Under Test (SUT),

• a test suite T written for P.

The set T can be given beforehand (these may be the unit tests written by the developers) or created/modified ’on the fly’ in each iteration of the mutation process. The first case usually takes place if our intention is to check the quality of the tests. The second one – when we want to guide the creation of a new test case.

Both P and all generated mutants are subject to the test set T. Let M be the set of all generated mutants, $m \in M$ – a particular mutant, and $t \in T$ – a particular test. By P(t) (resp. m(t)) we denote the result of running t on the original program P (resp. on the mutant m). If, for a given $m \in M$, there exists $t \in T$ such that $P(t) \ne m(t)$, we say that m has been killed by t. This means that a given set of tests is able to detect the injected defect represented by m (notice that there is no need to run other tests for this mutant). If, on the other hand, $\forall t\in T m(t)=P(t)$, it means that the given set of tests was not able to detect the fault simulated within m. In this case, a tester should add a new test $t'$ (or modify some test $t' \in T$), so that $m(t') \ne P(t')$. The process is repeated until a desirable mutation coverage is achieved or some other previously defined condition is fulfilled (the most obvious one is out of time).

Let $M_1 \subset M$ be the set of all $m \in M$ such that $\exists t \in T:\ m(t) \ne P(t)$. The ratio $|M_1| / |M|$ of killed mutants to all generated mutants is called the mutation coverage. Usually, it is required that M does not contain equivalent mutants, that is, mutants that are semantically equivalent to P. This may happen during the mutant generation process, but unfortunately the problem of deciding whether a given mutant is equivalent to P is undecidable. There are some heuristics to detect some simple equivalences (for example, when a mutation changes two lines of code whose ordering is not important), but in general it is not possible to detect all of them. Hence, because we can never be sure if some mutants are not equivalent, the mutation coverage metric may be lower than the true mutation coverage (with equivalent mutants eliminated). On the other hand, the redundant mutants can inflate the mutation score (Ammann et al. 2014). Therefore, the mutation score can be disturbed in both ways and should be treated with caution.

It is obvious that the effectiveness of the mutation process depends heavily on the types of mutation operators used. As in the case of mutants, we can introduce the notion of a trivial mutation operator, which generates only trivial mutations. Such an operator is not of much value. We can also define the effectiveness of a mutation operator. Let $M_O \subset M$ be the set of all mutants generated by the mutation operator O and let $M_O' \subset M_O$ be the set of all mutants $m \in M_O$ such that $\forall m \in M_O' \forall t \in T\ m(t) = P(t)$. The effectiveness eff of m can be defined as $eff(m) = |M_O'| / |M_O|$.

In the following considerations, let us assume that we were able to detect equivalent mutants and remove them prior to further analysis. If $eff(m)=0$, a given operator is weak, as all its mutants were killed. If $eff(m)=1$, all mutants generated by O have survived. But, again, one must be very careful with such analyses. It may happen that, for example, all mutations generated by O were introduced in a so-called dead code (that is, a part of the code which for some reasons cannot be executed). In such case $eff(m)=1$, but the mutation operator O cannot be evaluated. This metric can be easily corrected by requiring $M_O$ to be the set of mutants in which the mutated instruction was actually executed.

The operator’s effectiveness is measured in reference to a given program. Maintaining inefficient mutation operators may contribute to the formation of trivial mutants.

4 Test-Driven Development + Mutation Testing

To the best of our knowledge, the subject of mutation testing in context of Agile programming techniques has not been studied so far. In the literature, there are only a few papers related to this topic. One of such works is  (Derezinska and Trzpil, 2015), where the usage of mutation testing is proposed as an enrichment of some software development methodologies. However, the authors consider this problem only speculatively and theoretically, without using any empirical research to examine its effectiveness in practice.

Most of the research that combines TDD and mutation uses mutation coverage only to assess the quality of test cases or to compare test-first vs. test-last approach (cf. (Madeyski, 2010b; Aichernig et al. 2014; Tosun et al. 2018)). As these researchers do not use cross-testing approach, they are not able to evaluate the effectiveness of TDD+M approach in the way we do in this research. They use mutation coverage as the quality metric, while we use the mutation testing directly in the TDD process. In this case, a non-cross-testing setting does not allow us to use mutation coverage as an indicator, because of the obvious bias. The cross-testing approach allows us to do that (see Section 5).

In the literature, one can also find a number of information indicating that some of the software development companies are starting to use mutation testing as an extension to the software development methodologies used so far (Ahmed et al. 2017; Coles et al. 2016; Groce et al. 2015). One of such information can be found on the website of PITest (Kirk, 2018) – a mutation testing system, providing good standard test coverage for Java and JVM. The PIT tool is scalable and integrates well with modern test and build tools like Maven, Ant or Gradle. However, these studies do not report the detailed impact of mutation on test effectiveness.

The TDD methodology can be enriched with the mutation testing process. We call it the TDD+M approach. We modify the TDD practice by adding to the TDD process an additional step of mutation testing, before the code is refactored. This way, the quality and security of software can be significantly improved, as the developers may be aware early about the low quality of their tests. This gives them a chance to improve their unit tests before the next TDD iteration. It is important to remember that applying the TDD+M methodology can allow us to verify correctness and strength of our tests, but it can also be used to better control the correctness of the tested implementation. The TDD+M process is presented in Fig. 3.

Fig. 3

Test-driven development + mutation (TDD+M) process

The additional step – mutation testing – is inserted between the test execution and the code refactoring. After all the tests pass we perform the mutation testing process. It may reveal that although the tests have passed, they may be weak. If they are not able to kill some of the generated mutants, we may add new tests or modify the existing ones, to kill them or we can end the process if we achieved some desirable mutation coverage. Only after this step is finished, we refact the code if necessary and repeat the whole cycle again.

TDD process allows the developer to reduce one of the cognitive biases, the so-called confirmation bias. It is defined as the tendency of people to seek evidence that verifies the hypothesis rather than seeking evidence to falsify it. Due to the confirmation bias, the developers tend to design unit tests so that they confirm the software works as they expect it to work. This phenomenon was confirmed empirically in the context of unit testing and software quality (Calikli and Bener, 2013). TDD forces the developers to write test cases before the whole design and implementation process, allowing to achieve a larger independence from the code, thus reducing the bias.

In the TDD+M approach, mutation testing is an additional step that allows the developer to verify objectively the bias reduction by direct evaluation of the test cases quality. When the software fails during the mutation phase, the developer knows that the designed test cases are weak, because they are not able to detect a potential defect in the code. The test case is modified or a new test case is added so that this particular defect is detected. Test correction is done in the same way as in the original TDD approach. When no test is able to kill the mutant, there is a chance that this is an equivalent mutant. Because the problem of deciding whether a given mutant is equivalent is undecidable in general, the process of checking it must be usually done manually. This is also an opportunity for a developer to understand better their code.

The mutation step ends when a mutation score threshold is achieved. This threshold is set by the developers, and the decision should be based on their experience, historical data, source code, software development lifecycle, risk level taken into account etc. The rules here are the same as with any other white-box coverage criteria, like statement or decision coverage. The threshold can be set up for a particular project or even for a set of iterations in the project. It may be modified when the results clearly show that it may be difficult to achieve it.

The main question in this research study is this: how the TDD+M process influences the strength of the tests and, at the end of the development, the external software quality?

5 Experimental comparison of TDD and TDD+M

As stated in Section 1, the goal of our study is to answer the following research questions:

RQ1. Do the tests written with the TDD+M approach give better code coverage than the ones written in a pure TDD approach with no mutation process involved?

RQ2. Are the tests written with the TDD+M approach stronger (more effective) than the ones written using a pure TDD approach?

RQ3. Is the external code quality better when the TDD+M is used than in case of using the TDD approach only?

In order to test the hypotheses about the TDD+M approach, related to RQs 1-3 we performed a pre-experiment (called later Experiment 0), followed by the controlled experiment. The pre-experiment was done on a small group of eight computer science students split into two groups. The aim was to verify if the TDD+M approach can be applied at all. The proper experiment was then done on a larger group of 22 students. Since we cannot draw any statistically significant conclusions due to a small sample size, the description and results of Experiment 0 are described in Appendix 1, so that it does not disturb the flow of the paper.

5.1 The scope of experiment

The main goal of our experimental study was to verify to what extent the quality of software and tests grows, when using the TDD+M approach.

Using the standard goal template (Basili and Rombach, 1988) we can define the scope as follows:

• Analyze the TDD+M approach

• for the purpose of evaluation

• with respect to effectiveness related to code quality

• from the point of view of researcher

• in the context of computer science students developing the code.

5.2 Context selection

The experiment compares the existing TDD approach with its modified version, TDD+M. The comparison is performed in the context of software quality, expressed in terms of the strength of the tests and the number of defects found.

5.3 Hypotheses

We test the following null vs. alternative hypotheses, related to Research Questions 1–3

• $H^1_0$: TDD+M tests run on all codes (excluding their own code) give equal statement coverage as TDD tests run on all codes (excluding their own code) vs. $H^1_A$ they give different statement coverage,

• $H^2_0$ TDD+M tests run on all codes (excluding their own code) give equal mutation coverage as TDD tests run on all codes (excluding their own code) vs. $H^2_A$, they give different mutation coverage,

• $H^3_0$ TDD+M tests find the same number of defects in code as TDD tests vs. $H^3_A$, they find the different number of defects in code.

The hypotheses, if rejected, are rejected in favor of the alternatives. If the test statistics is in the right tail of the distribution, it means that TDD+M technique provides stronger tests than the ones written using the TDD approach.

5.4 Variables selection

The study of Madeyski (2010a) evaluated the TDD approach with, among others, the MSI (Mutation Score Indicator) defined as the lower bound on the ratio of the number of killed mutants to the total number of non-equivalent mutants. It is lower bound, not the exact value, because of the possible existence of undetectable equivalent mutants. The MSI metric (we call it the ’mutation coverage’) serves as a complement to code coverage in evaluating test thoroughness and effectiveness. The study of Madeyski showed positive effect of the TDD in comparison with the ’test last’ technique.

We follow this approach and we propose a modification of the TDD approach, enriched with the mutation testing step. We evaluate the software quality in terms of the strength of tests expressed in terms of statement coverage and mutation coverage. These are the two main dependent variables. Our main hypothesis is that the developers working with the TDD+M method achieve better code coverage and their tests are stronger than in case when only TDD is used. The third metric used is the total number of defects found.

5.5 Selection of subjects

The experiment involved 22 computer science students, split into eight 2- or 3-member teams. Four groups (numbered 1, 2, 3, 4) were working using the TDD+M approach and the other four (numbered 5, 6, 7, 8) were using the ordinary TDD approach. Initially there were nine groups, but one was removed from the experiment, as during the weekly review it turned out that its members did not follow the TDD approach. Before the experiment, the students were trained in the TDD method. In case of the TDD+M group, the students were also trained in mutation testing.

The groups were selected using a simple random sampling technique. Before the experiment, the participants were asked to self-assess their developing and testing skills. A simple survey contained only two questions:

• 1 How good, according to you, are your developing skills?

• 2 How good, according to you, are your testing skills?

Both answers had to be expressed in a 5-level Likert-like scale (Likert, 1932), where 1 = no skills, 5 = expert skills. The answers (raw data) and their mean values for the teams are presented in Table 2. The TDD+M groups seem to self-assess their developing skills a bit better than the TDD groups, but the relation is opposite regarding the testing skills. Due to the small sample sizes (two or three values) and the scale used (ordinal Likert-like scale, not a ratio scale), we cannot apply the Kruskall-Wallis test to statistically verify the hypothesis about the distributant equality.

Table 2 Team members self-assessment

5.6 Experiment design

The groups had to implement the extended version of the application from Experiment 0 (See Appendix 1). It was a library implementing matrix operations, a library implementing simple geometric computations, web interface for both libraries and a server processing HTTP requests. Last two components were supposed to implement a functionality of the user interface.

The students received only the JavaDoc file, so they had to write code from scratch. This is a technical, but very important step in our experiment. By providing the same interfaces to implement for all groups, we were able to perform the ”cross-testing” procedure described later.

The mutation was performed by the PIT software. All TDD+M groups were using the identical PIT configuration in which all mutation operators were used. The same configuration was used for the TDD groups when checking the mutation coverage. The following, default in PIT, set of mutation operators was used:

• ReturnValsMutator – mutates the return value (for bool variable replaces TRUE with FALSE; for int, byte and short replaces 1 with 0 and 0 with other than 0 value; for long replaces x with $x+1$; for float replaces x with $-(x+1.0)$ if x is not NAN and replaces NAN with 0; for object replaces non-null return values with null and throws a java.lang.RuntimeException if the unmutated method would return null;

• IncrementsMutator – replaces increments with decrements and vice versa, for example i++ is changed to i–;

• MathMutator – replaces binary arithmetic (int or float) operator with another operator;

• NegateConditionalsMutator – replaces operator with its negation: $==$ with $!=$, $<=$ with >, > with $<=$ etc.;

• InvertNegsMutator – inverts negation of integer and floating point numbers, for example i = j+1 will be changed to i = -j+1;

• ConditionalsBoundaryMutator – replaces open bound with closed one and vice versa, for example < with $<=$, $>=$ with > and so on;

• VoidMethodCallMutator – removes method calls to void methods.

The students used the following tech stack for their projects: Java v. 1.8, PIT v. 1.3.0, JUnit v.4.0 and Maven v. 3.5.2. The experiment lasted for three weeks. The teams implemented the application and created the tests using the iterative approach. After this time, a manual process of adjusting the test cases was performed, so that they were able to be run for each team’s software. It required to create 64 pairs (team X tests run on team Y software).

Hence, this experimental design allowed us to execute tests from any group on the code from any group. We were able to measure the performance of the tests: 1) from the TDD+M groups on all codes, 2) from the TDD groups on all codes, 3) from the TDD+M groups on their own code, 4) from the TDD groups on their own code, 5) from the TDD+M tests on the TDD code and 6) from the TDD groups on the TDD+M code. This ’cross-testing’ was performed to assess the tests’ strength in a more objective way, as the tests are assessed by executing them on the code from different groups, that is – on the code which was not the basis for these tests’ design.

5.7 Results

Due to the number of groups, all the applications developed in this experiment were also subject to static analysis performed with the use of the SonarQube application (ver. 6.3). The aim was to verify if the applications are similar in terms of size and complexity. To check this, two metrics were used: lines of code (LOC) and cyclomatic complexity (CC).

The results are presented in Table 3. The metrics were calculated for each file separately. The students received the pre-prepared code with the definitions of interfaces. The total LOC of this pre-prepared code was 284. Last two rows present also the sum and the mean value for all the metrics. A symbol ’(M)’ denotes that a given group worked with the TDD+M approach. A dash symbol means that a given group did not implement a given piece of code.

Table 3 Statistics for the projects

The results from Table 3 show that the biggest program was written by Group 07. Its mean cyclomatic complexity for all the modules is also the biggest one, 13.1. Its two classes, MatrixMath.java and Matrix.java had cyclomatix complexity 38 and 24. This suggests that the code in these classes is unstable, probably has many loops, and its control flow graph is quite complex. For this group, one can expect a large number of mutants. Group 07 is also the one which did not work with the TDD+M, but with the ’normal’ TDD approach.

Group 06 seems to be the best out of all groups, according to the software complexity. Its code is quite small and the complexity is low. However, after a precise analysis it turned out that the reason was the inaccurate and cursory implementation of both tests and classes. Group 06 also used the TDD approach and did not use the mutation testing.

The results suggest that out of all groups that did not use mutation technique, the best one seems to be Group 05. Its mean cyclomatic complexity is 9.4, and the total number of lines of code is 789. In the self-assessment survey (see Table 2), this group did not evaluate itself highly. What may be worrying for Group 05 is a high value of the cyclomatic complexity for classes Matrix.java and MatrixMath.java. They are resp. 48 and 32. These two classess in general have a large cyclomatic complexity due to the fact that they implement most of the computational code.

The manual code analysis of the TDD+M groups allows us to say that the best out of all groups was 01, and the one with the most complex code – 02. However, this is not reflected by the metrics in Table 3, maybe except for the Matrix.java class.

Due to the aim of the experiment and the techniques used (test-driven approach, mutation testing), the code quality should be, to some extent, a side effect of good, strong tests. When tests are executed and the defects found are corrected, this testing process should increase the confidence in the software quality. Hence, even if the metrics show high values for the code complexity (and, in result, a potentially unstable or hard to maintain code), good tests may compensate a danger of the defect insertion.

In Table 4, we present the summary results on statement and mutation coverage for all 56 pairs (X, Y) (meaning: code from Group X, tests from Group Y, $X, Y \in \{1, ..., 8\}$, $X \ne Y$) in the cross-experiment. As we want to assess the quality of tests by running tests on codes from other groups, we do not take into account the results of tests written by group X run on the X’s group code. That is why we exclude from the further considerations all eight pairs (X, Y) in which $X=Y$. Just for the informative purposes, the results for the pairs (X, X) for mutation groups 01M, 02M, 03M, 04M were resp.: 67/70; 21/24; 45/62; 84/90. The results for groups 05, 06, 07, 08 were resp.: 64/82; 31/21; 42/49; 28/25.

The columns in the table correspond to the codes from all eight groups, the rows represent the tests written by these groups. In the top row, the number in the brackets denotes the number of mutants generated for a given group’s code. The numbers in the brackets in the leftmost column denote the number of tests written by a given group. For example, Group 04 wrote 76 tests and for their code 392 mutants were generated.

After the mutants were generated, we had to eliminate the equivalent mutants. The manual analysis detected no such mutants. The reason may be that most of the mutations were related to math or arithmetic operations, where changing the sign, relational operator or arithmetic operator usually cannot introduce equivalence of the expressions under mutation.

Each cell (X, Y) of the table shows the statement coverage and mutation coverage for code from Group X tested with tests from Group Y. For example, the tests from Group 03 executed on code from Group 06 achieved 65% of statement coverage and 83% of mutation coverage. For groups 05, 06, 07, 08, which did not use the mutation testing during the development process, the mutation was performed post factum on the final version of the code.

Last two columns show the mean coverage values for tests executed on all TDD+M (resp. TDD) groups. Similarly, last two rows of the table represent the mean coverage values for a given code and all tests from TDD+M (resp. TDD) groups.

Table 4 Statement/mutation coverage (in %) for all combinations (code from Group X, tests from Group Y)

In Table 5, the mean coverage for both TDD+M and TDD groups is compared. Group id (first column) XY encodes ”X tests on Y code”, where $X, Y \in {M, T, A}$. Symbol M denotes the TDD+M teams, T – TDD teams and A – all teams. The coverage for MA and TA groups is averaged from 28 measurements (4 test suites times 7 groups, excluding the code of the group that wrote the tests). The coverage for MT and TM groups is averaged from 16 measurements (4 test suites from 4 groups times 4 codes from 4 groups). In case of MM and TT, the coverage is averaged from 12 values (excluding tests run on the code written by the same team).

Using our cross-test approach, we can compare different groups using different comparison criteria. Using this, we will now answer to the Research Questions RQ1, RQ2 and RQ3.

5.7.1 Answer to Research Question 1

RQ1. Do the tests written with the TDD+M approach give better code coverage than the ones written in a pure TDD approach with no mutation process involved?

In order to answer the RQ1, we compare MA with TA in terms of statement coverage. The code coverage for MA is higher than for TA (49.3% vs. 31.1%; the difference is 18.2%). This shows that the tests written using the TDD+M approach are stronger, as they achieve better statement coverage. Notice that the difference is significant also when we restrict our measurements to code from TDD groups only. In this case, the difference between MT and TT groups is $53.3\%-30.9\%=22.4\%$ in terms of statement coverage.

5.7.2 Answer to Research Question 2

RQ2. Are the tests written with the TDD+M approach stronger (more effective) than the ones written using a pure TDD approach?

To answer RQ2, we compared MA with TA in terms of mutation coverage. That is, we compare test results of both TDD+M and TDD approaches on all codes, excluding the cases of tests executed on the code for which they were written. The MA group achieved, on average, 63.3% mutation coverage. The TA group achieved only 39.4% mutation coverage, which is 23.9% less than in the MA case. The difference in mutation coverage is significant also when we restrict our measurements to code from TDD groups only and equals $64.9\%-35.2\%=29.7\%$. This shows that mutation analysis may be a powerful tool. When a team does not use it, the tests are much more weaker then the ones written with TDD+M – the probability of detecting a fault will be lower than in case of TDD+M teams.

5.7.3 Statistical analysis for the results on RQ1 and RQ2

We observe the difference both in terms of statement and mutation coverage. Now, we will check whether the obtained results are statistically significant. We perform a statistical analysis to verify if the TDD+M approach allowed the teams to create stronger tests than in case of groups using only the TDD approach.

Table 5 Coverage comparison of TDD+M groups and TDD groups (in %)

We applied the two-tailed, unpaired Student’s t-tests for the coverage values (statement (RQ1) and mutation (RQ2)) of the TDD+M and TDD groups applied to all eight projects to verify if there is a statistically significant difference between the two approaches. As it was mentioned earlier, to avoid the obvious bias, we removed from the analysis all pairs (x, y) where $x=y$ (that is, we excluded the data from the diagonal in Table 4). We have two t-tests: one for statement coverage and the other for mutation coverage. We compare two populations: one ($P_M$) with tests written by the TDD+M groups and the other ($P_T$) with tests written by the TDD groups.

The compared groups are formed by the values from rows 1-4 and 5-8 of Table 4, excluding the diagonal values. So, we have two samples of equal size (28) for the statement coverage and two samples of the same size for the mutation coverage. First, we have to check if the t-test assumptions are fulfilled. These are: 1) homogenity of variances of both populations; 2) normal distribution of the estimator of the mean value.

All four samples are close to the normal distribution (p-values for Shapiro-Wilk normality test for statement coverage: $P_M$ – $p=0.1825$, $P_T$ – $p=0.02$; for mutation coverage: $P_M$ – $p=0.011$, $P_T$ – $p=0.08$. The results are statistically significant for $\alpha =0.01$. Hence, we can use F-test to check the homogenity of variance in the samples. In case of statement coverage – $p=0.94$, in case of mutation coverage – $p=0.45$, so we cannot reject the hypothesis about the equality of variances for both statement coverage population and mutation coverage population. Because the samples follow more or less the normal distribution, the estimators of the mean value will also be normally distributed. As for the power of the t-test in our case, all samples are of size 28. The power of two-sample t-test for $\alpha =0.05$ and effect size 0.8 is 0.836, which is considered reasonable.

The above analysis suggests that we can use t-test to analyze the difference between means of both statement and mutation coverage. The results are shown in Figs 4 and 5, and the detailed results of the t-test are shown in Table 6.

Fig. 4

The difference in statement coverage between TDD+M and TDD groups

Fig. 5

The difference in mutation coverage between TDD+M and TDD groups

Table 6 Results of Student’s t-tests for TDD+M and TDD groups

The t-tests show the statistically significant difference in the coverage achieved by the TDD+M tests and the TDD tests, both in terms of statement and mutation coverage ($p<0.0001$). Cohen’s d for the statement (resp. mutation) coverage is 1.091 (resp. 1.07), which is considered to be between large and very large (Cohen, 1988; Savilowsky, 2009).

The results answer the Research Questions RQ1 and RQ2 positively: the tests written with the TDD+M approach give higher code coverage and achieve better mutation coverage. This means the TDD+M approach allows the developers to write stronger tests in terms of their ability to detect faults.

5.7.4 Answer to Research Question 3

RQ3. Is the external code quality better when the TDD+M is used than in case of using the TDD approach only?

Table 7 presents the number of defects found by the tests for each pair (tests, code). As we can see, the tests from the TDD+M groups were able to detect, on average, 10 (=(0+11+18+11)/4) defects in the code from a TDD group. On the other hand, the tests from the TDD groups were able to detect, on average, only 1.75 defects in the code written by a TDD+M group. The tests from Groups 01, 06 and 08 were not able to detect any defects in any project.

Table 7 Defects found for each pair (tests, code)

This answers RQ3 in terms of the number of field defects: the code written with TDD+M method seems to be of better quality than in case of a pure TDD technique. However, due to small sample sizes (four TDD+M teams vs. four TDD teams) we cannot perform any reasonable statistical test – we can only report the raw results in Table 7.

From Table 3, we know that the total cyclomatic complexity for the TDD+M (resp. TDD) groups was 171 and 174.5 and the average LOC – 750 and 792. This means that the TDD+M and TDD projects are similar in the sense of complexity and size. Taking the LOC metric into account we can say that, on average, the TDD+M tests were able to detect 12.62 defects per KLOC in the TDD+M code, while the TDD tests were able to detect only 2.33 defects per KLOC in the TDD code. This shows that the TDD+M tests seem to be stronger and more effective than the tests written in ’pure’ TDD approach.

The code from Group 05 had 18 defects detected (the 11 defects detected by the tests from Groups 02 and 04 are the proper subsets of the defects detected by the test from Group 03). These results show that the code written with the TDD+M approach seems to be of a better quality than the code written with ’pure’ TDD approach. This answers positively our Research question 3: the external code quality is better when the TDD+M is used than in case of using the TDD approach only.

5.7.5 A note on Defect Detection Efficiency regarding RQ1, RQ2 and RQ3

We can evaluate the strength of the test cases and the code quality with yet another measure. As we have four independent TDD+M test suites for the same set of 4 TDD programs, and four independent TDD test suites for the same set of 4 TDD+M programs, we can compare the test suites written using the TDD and TDD+M approaches in terms of their defect detection ability. We can do this by calculating the ratio of DDE (Defect Detection Efficiency) metric for both approaches, assuming we have only one phase/stage of development. Let $S = {1, 2, ...}$ be the set of all teams (represented by indices) and let $S=T \cup M$, $T \cap M = \emptyset$, where T denotes the teams that used only TDD without mutation and M – the teams that used the TDD+M approach. Let $d_{ij}$, $i, j \in T$ be the number of defects found by the i-th team’s tests on the j-th team’s code. Let $D_j$ be the total number of different defects found in the code of team j. In our case, by manual checking, we know that $D_2=2$, $D_3=5$ and $D_5=18$. No defects were found in other teams, so we assume (for the sake of this analysis) that they are bug-free.

We can now define the metrics $DDE_T$ and $DDE_M$ for the TDD and TDD+M approach. We do it by averaging the defect detection efficiency for all TDD (resp. TDD+M) tests on all buggy codes:

$$\begin{aligned} DDE_T= & {} \frac{1}{|\{j \in M: D_j>0\}|} \times \sum _{j \in M: D_j>0} \frac{1}{|T|} \sum _{i \in T} \frac{d_{ij}}{D_j},\\ DDE_M= & {} \frac{1}{|\{j \in T: D_j>0\}|} \times \sum _{j \in T: D_j>0} \frac{1}{|M|} \sum _{i \in M} \frac{d_{ij}}{D_j}. \end{aligned}$$

Using the data from Table 7, we have:

$$\begin{aligned} DDE_T= & {} \frac{1}{2} \times \left[ \frac{1}{4}\left( 0+0+\frac{2}{2}+0 \right) + \frac{1}{4}\left( \frac{5}{5}+0+0+0\right) \right] = 0.25,\\ DDE_M= & {} 1 \times \frac{1}{4} \left( 0+\frac{11}{18}+\frac{18}{18}+\frac{11}{18} \right) = 0.55. \end{aligned}$$

This analysis answers RQ1 and RQ2 in terms of the test strength measured by the DDE. It may also, indirectly, answer RQ3, when we assume that all detected defects are removed. In such case, we may claim that the test suites with higher DDE contribute better to the overall code quality than the test suites with lower DDE. In our case, the tests written with the TDD+M approach are $\frac{DDE_M}{DDE_T}=\frac{0.55}{0.25}=2.2$ times more effective in detecting defects than test suites written with TDD without mutation.

5.7.6 Learning outcome of the students involved in the experiment

We did not measure the learning outcome of the students that actually used mutation testing as opposed to those that did not. However, during the experiment, the TDD+M students told the experimentator that they were happy with using mutation testing and that the other (TDD) groups ”were even envy” about this fact. Moreover, the TDD+M groups were usually delivering their tasks ca. 1-2 days before the deadline.

6 Threats to validity

6.1 External validity

The experimental outcomes in both experiments might be disturbed due to the fact that the participants were not experts in the professional software development. This refers especially to Experiment 0 described in Appendix 1, as the participants had no experience as developers in professional software houses. On the other hand, almost all participants in the main experiment had been already working in software houses, but did not have a great experience as developers. Some parts of the code were of poor quality (as in case of Group 06).

Although the number of measurements in the experiment was high enough (64 sample data in the cross-experiment) to provide the reliable statistical results, the experiment was performed only on one, small project. The developers were the undergraduate computer science students, not the professional developers. Hence, we cannot generalize that the TDD+M approach will work better in any type of project, involving people with any level of experience. However, the high statistical significance of a difference between TDD and TDD+M approaches may suggest some support for the generalization.

The chosen problem domain (martix operations library) fits well into mutation testing because of many opportunities of creating different mutants. Hence, the obtained results could be influenced in part by just choosing this particular problem to solve. The results may be different for other types of software.

6.2 Internal validity

The students formed two disjoint sets of participants; hence, the reactive or interaction effect of testing was not present (this factor may jeopardize external validity, because a pretest may increase or decrease a subject’s sensitivity or responsiveness to the experimental variable (Willson and Putnam, 1982).

However, in both experiments students were working in teams (pairs or larger groups). This may introduce a new covariate which is not controlled and may have some impact for the observed results. This threat is minimized when we consider the results on the team level, not the individual level.

The code was measured by two simple metrics only: code coverage and mutation coverage. Although it is well known that these factors are correlated with code quality, one must remember that the notion of quality (especially the external quality) is a much more complicated, multi-dimensional concept. Hence, we cannot treat the results as the final evaluation of the external code quality – only as its more or less accurate indicators. We also measured the number of defects, but due to the small number of teams and the defects detected, we cannot conclude definitely about the significant difference in code quality between TDD and TDD+M. We can only compare these two approaches in terms of the raw data and metrics used.

The experiment was a controlled one, performed as the so-called static group comparison. This is a two group design, where one group is exposed to the factor in question (using the mutation testing) and the results are tested while a control group is not exposed to it (using a simple TDD without mutation) and similarly tested in order to compare the effects of including mutation into the TDD process. In such setting, the threats to validity include mainly selection.

Selection of subjects to groups was done randomly, which is a counter-attack against the ’selection of subjects’ factor that jeopardizes internal validity. However, due to the small size of samples (eight teams, each of three or two students), randomization may lead to the well-known Simpson Paradox (Simpson, 1951).

Another possible factor that jeopardizes the internal validity is maturation. If an experiment lasts for a long time, the participants may improve their performance regardless of the impact of mutation testing. However, the students worked on their projects only for three weeks, hence the risk of this threat to validity is rather small.

The disturbance of the results might also be caused by the fact, that some participants did not strictly follow the interface templates delivered to them. Because of the changes in these templates in some cases it was necessary to add some setter or getter for some parameter. This way, the corrected code might cause the generation of one or two additional mutants. However, in all cases those were the trivial mutants and they were always being detected and killed.

For Research Question 3, we could not use any statistical machinery to verify our claims due to small sample size (four data points vs. four other data points). We could only report the results in the raw format.

Some students reported in the self-assessment questionnaire that they had no prior experience in programming or testing (1 on the 1-5 scale). This would mean that they had to learn these skills from scratch before or during the experiment. Since they were the 3rd year undergraduate computer science students, this seems impossible, as they had lectures on programming during the first two year of their studies. They probably misunderstood the meaning of the scale and thought that 1 means ’a little knowledge’ on development or software testing. However, we cannot prove this claim. Nevertheless, all the teams managed to successfully write their code and tests, so it is very unlikely that these students had absolutely no prior experience in programming.

The code of some groups had to be modified by adding some getters and setter, so that we could execute the tests in the cross-experiment (see Appendix 2). This introduces a risk (although not very likely) of the unintentional introduction of some defects.

7 Conclusions

Our experiment shows that using the TDD+M approach is more effective than using only a pure TDD method. The effectiveness is understood here as the ability to write good, effective tests that achieve high code coverage and mutation coverage, and also as the ability to write a good quality code.

The tests written with the TDD+M approach achieve 17% better statement coverage and 23% better mutation coverage than the tests written with the TDD approach. The differences are statistically significant. The cross-testing (TDD+M tests on TDD code and vice versa) also shows the difference: TDD+M tests on TDD code give 22% more statement coverage and 23% mutation coverage than in case of TDD tests on TDD+M code.

The results of the experiment confirm the results from the Experiment 0 (see Appendix 1). They clearly show that the TDD+M approach allows the teams to create stronger tests and – as a side effect – a code with lower number of defects.

Implementing the mutation testing step into the iterative test-driven development process increases confidence in the code quality. The TDD approach is not the only development technique that can be enriched with the mutation testing component. It can be as well implemented as a developer’s practice in any kind of a software development model, like: waterfall, V-model, spiral etc.

In our experiments, the mutation testing allowed the developers to detect incorrect implementation of computations and write code of better quality. The participants of the experiment were 3rd year undergraduate students (junior or less than junior level), which means – regarding the experiment’s results – that the TDD+M approach may be a powerful method in hands of the experienced senior developers in professional software houses.

Appendices

Appendix

Experiment 0

The Experiment 0 was conducted on a group of eight third-year computer science students at the Jagiellonian University, Faculty of Mathematics and Computer Science in Krakow, Poland. All of them were studying the ’software engineering’ track. The experiment itself together with data gathering and data analysis took about one month.

The students were split into two four-person teams. One group (referred to as the TDD group) was working in the plain TDD approach, and the other one (referred to as the TDD+M group) in TDD+M. Before the experiment the students were trained in the TDD method. In case of the second group, the students were also trained in performing the mutation testing.

The TDD group was composed of two developers, one tester and one team leader whose responsibility was to monitor and control the whole development process. The team leader was also responsible for designing the software.

The TDD+M group was working in TDD enriched with the mutation testing activity. The team composition and responsibilities were similar: two developers, one tester and one team leader. Furthermore, the tester was responsible for performing the mutation testing and the team leader was monitoring and controlling the mutation testing process. The tester and team leader were conducting the code reviews based on the mutation testing results.

Both groups were working on the same project. The project was to create a software realizing some simple matrix operations, such as:

• adding two matrices ($M_1+M_2)$;

• subtracting matrices ($M_1 - M_2$);

• matrix transposition $M^T$;

• calculating the inverse $M^{-1}$ of a matrix M.

The maximal size of the matrices was $3 \times 3$.

The project requirements were delivered to the teams as the JavaDoc file. The file contained the application framework in form of the declaration of all needed interfaces, which were then to be implemented by the teams. The teams were told not to modify any interfaces, nor adding the new ones. The reason was to make all unit testing from one group possible to be run on the other team’s code. This cross-testing was performed at the end of the experiment to compare the tests created independently of a code and to see if the tests from the TDD+M group were stronger on the TDD group code than the TDD group tests on the TDD+M group code.

The TDD group went through eight full, short iterations. The TDD+M group did nine full, short iterations. Both groups were continuously working within the prescribed methods.

In order to better evaluate the tests, an additional factor was introduced to the evaluation process. We asked the experienced developer (with over five years of experience in the IT industry) to design test cases based on the same specification that was given to the groups. His tests were then used during the mutation testing process and also to verify if any of the groups was able to achieve better results than the other. These tests were executed at the end of the last iteration of the TDD+M group.

The idea to compare the students with the expert was to check if inexperienced students are able to achieve comparable coverage with their tests as the professional with a large experience in software development. This comparison makes sense only because the students were inexperienced.

2.1 Experiment 0 – results

After all the iterations were finished, we gathered the data and analyzed it. For the TDD+M group we gathered and analyzed the test results from all nine iterations. Next, their tests were replaced by the tests from the TDD group and the additional mutation testing session was performed for the TDD+M code from the last, ninth iteration. This was done to compare the strength of the test suites from both groups. The TDD+M project was also tested with the expert’s test cases.

For the TDD group a mutation testing session was performed for the code from each iteration. As TDD group did not use the mutation, it was conducted post factum in order to compare the groups in terms of the mutation coverage. Similar to the TDD+M group, an additional mutation testing session was performed with their code and tests from the TDD+M group. The experimental setting is shown figuratively in Fig. 6.

Fig. 6

Experiment 0 experimental design

Both projects were composed of two interfaces and two classes implementing them. The data on the project size is presented in Table 8. The students received only the JavaDoc file, so they had to write code from scratch. The TDD+M project had 321 LOC without the tests and 857 with the test cases. The TDD project had, respectively, 216 and 430 LOC. This means that the size of the test suite was, respectively for TDD+M and TDD, 536 and 214 LOC. It is noteworthy that despite the TDD project size was only 70% of the TDD+M project, its test suite was only of 40% size of the TDD+M test suite. Also, when comparing the test suite size to the code size we can see that the TDD+M group had more test code than the application code (the ratio was 1.67), while for the TDD group the size of test code was almost equal to the size of the application code (the ratio was 0.99).

Table 8 Code and test size for both groups in Experiment 0

Regarding the test cases, the TDD group designed the following test cases:

• simple adding of two matrices;

• simple subtraction of two matrices;

• correctness of creating the identity matrix;

• computing the determinant for three cases of $2 \times 2$ matrices;

• testing the setMartixValues function, four cases.

The test cases for matrix multiplication, matrix transposition and multiplication by scalar were defined, but not filled with the test code.

The TDD+M group created more test cases

• simple adding of two matrices (two tests: one on $3 \times 3$ matrices, another one had seven assertions checking the addition for seven matrices in different combinations;

• simple subtraction (as in TDD group);

• multiplication (two tests, in each of them different matrices were used);

• computing the inverted matrix (two tests, including $3 \times 3$ case);

• computing the transposition (one test for $3 \times 3$ matrix);

• computing the determinant (tested with four matrices: $3 \times 3$, two $2 \times 2$ and one $1 \times 1$; one test with four assertions;

• three tests checking the correctness of matrices dimensions (on seven different matrices);

• identity matrix (with a re-use of the two above mentioned tests for checking the matrices dimensions); the test used $2 \times 2$ matrix and a matrix with incorrect dimensions;

• computing the determinant (three assertions on three matrices)

• checking the correctness of the input data (one test with a loop for seven different matrices).

The TDD+M group prepared two sets of seven matrices each, which were used in their tests in different combinations. In a few test cases they also generated the matrices on-line.

In both groups the test cases were able to detect some defects. The tests from the TDD group detected the following ones:

• wrong computation of the determinant;

• matrix analysis methods were vulnerable to the null parameter;

• arithmetic error in computations caused by using int variables instead of double.

There was an interesting issue in the TDD group: the defect of an incorrect type of variables used to test the matrix identity method. Instead of using double the group used int. This defect has occurred twice in two different iterations, and the group has also noticed it twice. In the TDD+M group such a situation did not happen, which is natural, as a properly performed mutation testing eliminates the defects in tests instantly.

The TDD+M group focused on killing all the generated mutants. In this group the following defects were found:

• a problem in throwing an exception;

• wrong output in one function;

• wrong sequence of overriding the values in matrices;

• correction of the test for the identity matrix.

Within 58 commits to the GIT system the TDD+M group focused on killing mutants. The ’wrong output’ defect was detected by the test case itself, with no help of the mutation process. After killing the mutants the group did not find anything else to fix.

The results of Experiment 0, in terms of the coverage metrics, are presented in Tables 9 and 10.

Table 9 TDD group tested with the TDD+M tests

Table 9 presents the results of the mutation testing for the TDD group. The columns represent: iteration number, statement coverage, mutation coverage (post factum), number of tests, number of mutants and number of methods implemented. Last two rows show the results of the mutation tests taken from the TDD+M group and of the testing done by the expert.

The decrease in coverage between iterations 5 and 6 was due to the increase in number of implemented methods (six new methods were added and only one new test was created). The decrease in coverage between iterations 6 and 7 was due to new code (and – as the result – the new mutants), with no increase in number of tests. The final increase in coverage (between two last iterations) was due to five new tests.

For the same number of mutants (104) the mutation testing was performed with the tests provided by the TDD+M group. As we can see, the coverage is much higher than in case of the tests from the TDD group: 86.7% to 60.4% in terms of statement coverage and 75.9% to 64.4% in terms of mutation coverage. Also, the number of tests was higher (16 to 11). Hence, the TDD+M tests increased the statement (resp. mutation) coverage by 26.3% (resp. 11.5%). The expert’s tests achieved a slightly better coverage than in case of the TDD+M group’s tests: 91.4% of statement coverage and 82.3% of mutation coverage.

Table 10 TDD+M group tested with the TDD tests

In Table 10 the analogous results are presented for the TDD+M group. The decrease in coverage between two last iterations is due to adding a new portion of code without adding any new tests.

The methods implementing the interfaces were bigger than in case of the TDD group. The tests from the TDD group were able to achieve only 39.5% of statement and only 40.2% of mutation coverage. This is of 47.2% (resp. 35.7%) less than in case of the TDD+M tests covering the TDD code. The expert’s tests were, again, slightly better than the group’s own tests: they achieved 90.3% (resp. 82.3%) of statement and mutation coverage, which is of 8.9% (resp. 8.8%) more than in case of the TDD+M own tests.

The TDD+M group was able to achieve – on their own code – 81.4% (resp. 73.5%) of statement (resp. mutation) coverage. This is of 21% (resp. 13.1%) more than in case of the TDD group, which achieved only 60.4% (resp. 64.4%) coverage of their code with their own tests. Notice also that the number of mutants was greater in case of the TDD+M group (134 vs. 104), which means that their code was bigger, more complicated and it was more difficult to cover in terms of both coverage criteria. Still, the TDD+M group was able to achieve better coverage than the TDD group.

In Experiment 0 the TDD+M group performed much better than the TDD group, both in terms of the quality of their own tests regarding their own code, and regarding the TDD group’s code. The best results were achieved by the expert. However, notice that even the expert was not able to cover all the statements in this relatively simple code. Some mutants survived. They contained the mutations of the code responsible for matrix multiplication. The reason was that in some cases the results were correct even for the wrong formula (for example, $2 \cdot 2$ = $(-2) \cdot (-2)$, so if the test was to multiply two $1 \times 1$ matrices both equal to [2] and the mutation operator changed multiplication to adding, the test result was false positive).

Detailed results and comments on the main experiment

In Tables 11 – 18 we present a detailed data on the mutation process performed for each group in the experiment described in Section 5. Each table describes the mutation testing results with the group’s own tests and with tests from other groups used on this group’s code. The data is split by modules (so-called ’spacenames’). For each spacename we present the number of classes contained in it, as well as the coverage data in terms of statement coverage (SC) and mutation coverage (MC).

The group labeling in the first column includes the group number and the code being the result of the consecutive iterations. For example, in Table 11 for Group 01 the row Gr1.2 (SC) means the statement coverage data for Group 01 code in the second iteration of their project. The tests from other groups are always taken from the last iteration of their projects. For Groups 05–08, which did not use the mutation process, the mutation was performed in the last iteration, so there is only one (last) version for these groups in their corresponding tables.

The other columns (all except the first one) show the coverage data for given modules. Each coverage data is expressed as a percentage, number of covered statements or killed mutants and the total number of statements or mutants.

Table 11 Group 01 – detailed mutation results

Group 01 (see Table 11) is a TDD+M group. Its tests were almost as strong as tests from the group 04. The average mutation coverage for tests from group 01 in other groups is 66.8%. It is second best result, just after the group 04. According to the self-assessment, the developer’s skills in group 01 were lower than in group 04. The developers had little prior experience in Java language used in all projects. However, the group made up their results by following strictly the TDD+M method, which gave a very good results. It is interesting that despite the group 01 did not pay much attention to the web layer tests, their tests were very strong when applied for the other groups’ code.

Table 12 Group 02 – detailed mutation results

For Group 02 tests (Table 12), in order to assure the compatibility, some setters and getters had to be added. This resulted in an increased number of mutants. For Group 04 it was necessary to comment 11 tests because of the incompatible internal logic of the core.web module. In Group 06 one setter was added, and in Group 01 – two setters for the collections, which increased the total number of generated mutants. Group 02 was the weakest one. Its members did not follow TDD+M or even TDD in first three iterations. TDD+M was used only in the last iteration and almost all tests were also written in this iteration.

Table 13 Group 03 – detailed mutation results

Group 03 (see Table 13) worked following strictly the TDD+M approach. There were no abnormal peaks in the number of mutants and tests. Each iteration was based on the effects of the previous one. At the end, in the final iteration, the group has refactored the code and the tests by removing unnecessary methods and ’empty tests’ which were checking nothing. This way the number of mutants has decreased. When using the tests from Group 04 it was necessary to comment five tests, which resulted in a decrease in the coverage. Tests from Group 06 were suited only for core.Math.Shapes. For other modules most tests had to be commented.

Table 14 Group 04 – detailed mutation results

Group 04 (TDD+M) also followed the TDD+M method (see Table 14). In the final iteration the group achieved 84% statement coverage and 90% mutation coverage. In this iteration the group was able to improve the quality of tests and increase the number of code flows, which generated the larger number of mutants. Group 04 tests are one of the strongest. The average mutation coverage achieved by their tests on the other groups’ code was 67.3%. It is a very good result, which suggests the advantage of the TDD+M approach over the pure TDD. However, the results might also be the consequence of the high (self-assessed) developer’s skills.

Table 15 Group 05 – detailed mutation results

Group 05 (see Table 15) was a TDD group which did not use mutation approach. Its tests had a low compatibility with the code from other groups. Group 05 generated 75 tests and achieved 82% mutation coverage. For the tests from Groups 02 and 04 eleven of them have failed, and in case of Group 03 - eighteen tests have failed. Also, in this case it was needed to add a few getters and setters which increased the number of mutants by six. Group 01 tests achieved better results than on their own code, because Group 05 wrote less code than Group 01 and did not implement some classes and methods, which were left in their abstract form. After some more thorough analysis it turned out that the tests generate a lot of errors, which results in a mass mutant killing. Despite of the low cyclomatic complexity, after the code analysis it can be noticed that it contains a lot of unhandled exceptions, edge cases and the code is not flexible. All these factors result in the fact that the majority of the mutations are not discovered by the failing tests, but by throwing the unhandled exceptions.

Table 16 Group 06 – detailed mutation results

Group 06 (see Table 16) was a TDD group. For the tests from Groups 01, 03 and 08 some getters and setters had to be added, which generated some new mutants.

Table 17 Group 07 – detailed mutation results

Group 07 was a TDD group (see 17). Also, in this case it was needed to add a few getters and setters for greater compatibility with Groups 06 and 01, which increased the number of mutants. Because of the code incompatibility with the tests from Group 04 it was necessary to comment 11 of those.

Table 18 Group 08 – detailed mutation results

Group 08 (see Table 18) was a TDD group. For the tests from Group 01 one setter had to be added.