The Europa Thermal Emission Imaging System (E-THEMIS) Investigation for the Europa Clipper Mission

Abstract

The Europa Thermal Emission Imaging System (E-THEMIS) on the Europa Clipper spacecraft will investigate the temperature and physical properties of Europa using thermal infrared (TIR) images in three wavelength bands centered from 7-14 μm, 14-28 μm and 28-80 μm. E-THEMIS will map >80% of the surface Europa at multiple times of day at a resolution of 8-km per pixel, ∼32% percent of the surface at ≤1 km/pixel resolution, and ∼6% percent at ≤100 m/pixel resolution. The specific objectives of the investigation are to 1) understand the formation of surface features, including sites of recent or current geologic activity, in order to understand regional and global processes and evolution and 2) to identify safe sites for future landed missions. E-THEMIS uses an uncooled microbolometer detector array for the IR focal plane. The E-THEMIS focal plane has 920 cross-track pixels (896 active) and 140 along-track pixels in each of the three spectral bands. The image data are collected at 14-bits per pixel at a frame rate of 60 Hz. The instrument can operate in framing mode, where full frame images are collected, and optionally co-added in time, in each band, or in time-delay-integration (TDI) mode where consecutive rows from each band are offset spatially to remove the spacecraft motion and then summed. In addition, the data in each band can be spatially aggregated from 2 × 2 to 5 × 5 pixels. These modes will be varied throughout each Europa flyby to optimize the data precision while fitting within the E-THEMIS data allocation. The expected temperature precision, measured as the noise equivalent spectral radiance, is 1.2 K at scene temperatures ≥90 K for a TDI of 16 with 4 × 4 pixel coaggregation in Band 2. The absolute accuracy at 90 K is 2−3 K in Band 2. E-THEMIS is an all-reflective, three-mirror anastigmat telescope with a 6.45-cm effective aperture and a speed of f/1.34 cross-track and 1.92 along-track. The mass of instrument Sensor Assembly, mounted on the spacecraft nadir deck, is 11.4 kg, the vault electronics are 1.8 kg, and the two are connected through a 3.1 kg harness. The Sensor volume is 23.7 cm x 31.8 cm x 29.8 cm. E-THEMIS consumes an average operation power of 34.8 W at 28 V. E-THEMIS was developed by Arizona State University with Raytheon Vision Systems developing the microbolometer focal plane assembly and Ball Aerospace developing the electronics. E-THEMIS was integrated, tested, and radiometrically calibrated on the Arizona State University campus in Tempe, AZ.

1 Introduction

The scientific goals of the Europa Thermal Emission Imaging System (E-THEMIS) investigation are to 1) understand the formation of surface features, including sites of recent or current geologic activity, in order to understand regional and global processes and evolution and 2) identify safe sites for future landed missions. The investigation’s goals support the primary Europa Clipper mission goal to understand Europa’s habitability, both present and past, beginning with characterizing the nature of the satellite’s interior ocean and icy shell and understanding its geological history (National Research Council 2003, 2011).

The E-THEMIS investigation will achieve its goals through the acquisition of thermal infrared images in three spectral bands from 7 to 80 μm at multiple times of day and from a wide range of flyby altitudes. The three spectral bands will allow E-THEMIS to accurately determine the temperature of surfaces from ∼70 to >230 K, to identify and map thermal anomalies, to quantify the abundance of sub-pixel blocks, and to identify small-scale active, or recently active, vents and flows. E-THEMIS provides the capability to image Europa in the thermal infrared with high spatial resolution, excellent radiometric precision and accuracy, broad contextual image coverage, and multiple wavelength bands in a high-heritage instrument.

Much of Europa’s surface is disrupted by extensive and mysterious fracture and chaos regions. Active endogenic geologic processes associated with convection in the ocean and extension of the icy crust are likely to be important drivers in the evolution of Europa’s surface, but the details of these processes remain unclear. E-THEMIS will provide temperature data to detect, map, and monitor thermal anomalies to better understand these processes and to constrain Europa’s thermal evolution and history, providing a critical window into our solar system’s history and insights into how planetary systems have formed and evolved. The specific E-THEMIS science objectives are to 1) detect and characterize thermal anomalies on the surface that may be indicative of recent resurfacing or active venting; and 2) determine the regolith particle size, block abundance, and sub-surface layering for landing site assessment and surface process studies. High spatial resolution is required to both identify small regions of recent geologic activity and to accurately determine surface temperatures associated with areas of active venting, which will provide key constraints on heat transport mechanisms.

E-THEMIS utilizes an uncooled microbolometer array, first used for planetary exploration on Arizona State University’s (ASU) Thermal Emission Imaging System (THEMIS) infrared camera, which is still operating at Mars as of February 2024 following its arrival in 2001 on Mars Odyssey (Christensen et al. 2004). Microbolometers have been used on other flight missions, for example the Mercury Radiometer and Thermal Infrared Spectrometer instrument on BepiColombo (Helbert et al. 2013) and the Lunar Compact Infrared Imaging System (Hayne et al. 2020). The microbolometer array used on E-THEMIS is significantly improved from the initial THEMIS implementation, with an array size of 1280 × 1200 elements versus 320 × 240 on THEMIS, a pixel pitch size reduced to 12 μm from 50 μm, and a factor of three improvement in radiometric performance.

2 Science Objectives and Measurement Requirements

2.1 Passive Temperatures

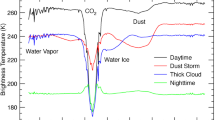
E-THEMIS measures the emitted radiance in three spectral bands and these radiances are converted to brightness temperature – the temperature of a blackbody emitting the measured radiance – in each band. Passive temperatures, i.e. temperatures controlled by solar or other external heating, are determined by surface bolometric albedo (the fraction of incident solar radiation, integrated over all wavelengths, that is reflected and not absorbed by the surface), and surface thermal inertia (Fig. 1). Thermal inertia is a measure of how quickly the surface temperature responds to changes in external forcing such as the day/night insolation cycle, with lower thermal inertias implying a more rapid response. In the MKS system the units for thermal inertia are J m⁻² K⁻¹ s^{- 1/2}, referred to simply as “MKS” henceforth.

Fig. 1

Effects of thermal inertia, albedo, and regolith thickness on diurnal surface temperatures, derived from a 1-dimensional numerical thermal model (Kieffer 2013), for Europa’s rotation period (3.55 days) and heliocentric distance (5.2 AU). A regolith density of 300 kg m⁻³ is assumed in the thin-regolith models (bottom panel)

2.1.1 Spatial Distribution of Temperatures and Thermal Inertia

Ground-based observations of Europa’s thermal emission began in the 1970s. The rotational thermal light curve was found to have high amplitude- the trailing side being nearly a factor of 2 brighter than the leading side at 20 μm (Morrison 1977). This high amplitude is expected for a high-albedo object with a substantial visible lightcurve because absorbed sunlight varies as (1-albedo). This lightcurve was subsequently refined by Blaney et al. (1999) (Fig. 2). The 10 and 20 μm observations of Europa’s rapid cooling in Jupiter eclipse implied a surface layer of very low thermal inertia (Hansen 1973), like the other Galilean satellites, though Europa’s large-amplitude rotational lightcurve, which results in different pre-eclipse and post-eclipse globally-averaged temperatures, has hampered interpretation in Europa’s case.

Fig. 2

The brightness temperature of Europa at 8.7 μm (triangles), 12.5 μm (solid circles), and at 20 μm (squares), from Earth-based radiometry (Blaney et al. 1999). The very low temperatures near longitude zero were measured during Jupiter eclipse

The first spatially resolved temperature measurements of Europa were by the Voyager IRIS instrument, which had very low spatial resolution (900 km) but excellent spectral resolution (Spencer 1987a). Spectra are consistent with combinations of blackbodies with best-fit emissivity of ∼0.9 and are featureless to <1% precision in brightness temperature in the 15−50 micron range. Ground-based spectroscopy shows that emission spectra are also featureless at 9–13 μm (Mills and Brown 2000). While the featureless spectrum prevents compositional inferences from Europa’s thermal IR emission, the near-blackbody emission increases confidence in the determination of surface temperature from the thermal emission.

The first detailed thermal mapping of Europa was accomplished by the PPR instrument on the Galileo spacecraft (Spencer et al. 1999; Rathbun et al. 2010), with the best surface temperature measurements obtained by the PPR shown in Fig. 3 (Rathbun et al. 2010). Differences from simple models are plausibly explained by local variations in surface thermal properties, though there are some puzzling features, including a region of anomalously low thermal inertia closely aligned with the equator on the leading hemisphere (Spencer et al. 1999; Rathbun et al. 2010) (Figs. 3, 4). More recent Earth-based measurements of Europa’s daytime temperatures at 1.3 mm wavelength using Atacama Large Millimeter/submillimeter Array (ALMA) data, with 200 km spatial resolution, when combined with spacecraft-observed albedo maps, provide global maps of a combination of thermal inertia and 1.3 mm emissivity, which may be lower than the emissivity at shorter wavelengths (Trumbo et al. 2018). Observed spatial emission variations seen by ALMA can also be plausibly explained by variations in surface thermophysical properties. Fits to the PPR and ALMA data give albedos of 0.3 to 0.7 and thermal inertias of approximately 50-200 MKS (Rathbun et al. 2014; Trumbo et al. 2018; Daubar et al. 2024, this collection). Due to the low spatial resolution of the available temperature measurements, the derived thermal properties are only indicative of the average properties of the surface at >100 km scales and with limited spatial coverage.

Fig. 3

Surface temperatures on Europa observed by the Galileo PPR (Rathbun et al. 2010), with a spatial resolution of 80–200 km. Top panel shows daytime temperatures from observations on Galileo orbits G7 and E25. Asterisks show the subsolar point for each of the observations. Bottom panel shows nighttime temperatures from observations on Galileo orbits E17 and E25. Each panel has a different temperature color scale (see keys at right). For both panels, local time is given in degrees, with 0 at midnight and 180 at noon

Fig. 4

Thermal inertia derived from fits to Galileo PPR day and night observations, from Rathbun et al. (2010), showing the paucity of existing coverage

The thermal inertias derived from ALMA data are generally higher than those derived from PPR data, which, given the longer wavelength and greater penetration of the ALMA measurements, might indicate differences in thermal properties at near-surface depths (millimeters vs microns). This is consistent with previously mentioned telescopic eclipse observations (Hansen 1973) that found that the top few millimeters of Europa have a low thermal inertia with an underlying layer having a much higher thermal inertia. Molaro et al. (2019) interpreted this as an indication of an actively self-healing regolith.

Thermophysical properties also carry the signature of exogenic processes. The constant alteration of Europa’s trailing hemisphere by radiolysis has made it darker and redder than its leading side (Johnson et al. 1983; McEwen 1986; Nelson et al. 1986; Johnson et al. 1988; Pospieszalska and Johnson 1989; Paranicas et al. 2001, 2002; Carlson et al. 2009; Paranicas 2009; Hand and Carlson 2015; Trumbo et al. 2019). This exogenous darkening results in warmer surface temperatures on the trailing side (Blaney et al. 1999) (Fig. 2).

Thermal inertia is also affected by ice grain size variations, with larger grain sizes producing higher thermal inertias (e.g. Ferrari and Lucas 2016; Mellon et al. 2022). Clark et al. (1983) showed larger ice grain sizes on Europa’s trailing hemisphere, perhaps because higher irradiation and sputtering rates lead to the preferential destruction of small grains (Cassidy et al. 2012). There is some evidence from Galileo PPR data for higher thermal inertia on the trailing side of Europa (Rathbun et al. 2010) (Fig. 4), though coverage is very limited, and ALMA dayside data do not show a strong asymmetry in thermal inertia between the leading and trailing hemisphere (Trumbo et al. 2018).

Radiation can affect thermal inertia in other ways. Mimas and Tethys, two of Saturn’s icy satellites, show evidence of an IR/UV color and thermal anomaly at low latitudes on their leading hemispheres, dubbed PacMen (Howett et al. 2011; Schenk et al. 2011; Howett et al. 2012, 2019, 2020). This sharply defined region is bluer than its surroundings, and ∼15 K cooler during the day and warmer during the night, indicating a higher thermal inertia. It is spatially correlated with the region preferentially bombarded by high-energy elections (Paranicas et al. 2012, 2014; Nordheim et al. 2017). It is hypothesized that these high-energy electrons increase the contact-areas between grains, increasing their thermal conductivity and hence thermal inertia (Howett et al. 2011; Schenk et al. 2011; Schaible et al. 2017). Jupiter’s magnetospheric electrons are higher energy than those in the Saturn system (Nordheim et al. 2017, 2018) and thus it is feasible that similar thermal anomalies are present on Jupiter’s icy satellites, but currently undiscovered. It is possible that the anomalously low nighttime temperatures along Europa’s equator on the leading side (Spencer et al. 1999) (Fig. 3) have an analogous origin, though the sign of the observed anomaly is opposite to that seen at similar locations on Mimas and Tethys.

Recent resurfacing can also produce passive thermal anomalies. Pyroclastic deposits from plume activity may consist of fine particles with potentially low thermal inertia like those observed on the Moon (Hayne et al. 2017; Bennett et al. 2018). The low-albedo pyroclastic deposits surrounding Pele and Babbar Paterae on Io are colder than their surroundings at night, perhaps due to this effect (Rathbun et al. 2004). Conversely, surface deposition of plume gasses could potentially increase thermal inertia by sintering grains together, analogous to the high thermal inertia “Pac Man” anomalies likely due to regolith sintering by electron impact on Mimas, Tethys, and Dione discussed above. High nighttime temperatures in the red outer ring of the Pele pyroclastic deposits on Io (Rathbun et al. 2004) may also be due to this sintering process. The surfaces of recent extrusive deposits such as water flows would also likely have thermophysical properties that are different, perhaps with higher thermal inertia, than older surfaces that are coated with an impact gardened or sputtered regolith.

2.1.2 Vertical Inhomogeneities

Although mid-IR emission originates from the uppermost microns of Europa’s surface, surface temperatures inferred from this emission probe subsurface properties at much greater depths, due to heat exchange between surface and subsurface on various timescales. The depth involved in such heat exchange, the skin depth, given by $d_{s} \ =\ \sqrt{kt/(\rho c)}$, where $k$ is the thermal conductivity, $t$ is the timescale of the temperature changes ($t\ =\ 2/\omega$, where $\omega$ is the rotational angular velocity, for rotational forcing), $\rho$ is the bulk density of the surface, and $c$ is the specific heat capacity. Alternatively, skin depth can be described in terms of thermal inertia $\Gamma \ =\ \sqrt{k\rho c}$: $d_{s} =\ k/\Gamma \ \sqrt{t}$. Table 1 gives typical thermal inertias and skin depths for solid ice at Europa temperatures, and for typical low-thermal-inertia Europa regolith (with thermal conductivity inferred from the observed thermal inertia assuming a density, of 180 kg m⁻², appropriate for water ice with 80% porosity). For comparison, recent spectroscopic analysis (Mishra et al. 2021) has inferred porosities of 0.81–0.97 for Europa’s surface.

Table 1 Thermophysical properties of plausible Europa surface materials

Observations of diurnal variations in typical Europa regolith thus probe to depths of a few centimeters, while the faster temperature changes during Jupiter eclipse are sensitive to the top few millimeters. Seasonal temperature variations probe much deeper. Because of Europa’s low obliquity, about 3°, seasonal effects due to variations in subsolar latitude are difficult to observe on Europa except very close to the poles, where the expected surface temperatures of 30 to 40 K are well below the threshold of ∼70 K at which E-THEMIS can measure temperatures with a precision of less than ±5 K (see Sect. 4.4 and Fig. 39). However, the eccentricity of Jupiter’s orbit causes 20% annual variations in insolation between aphelion and perihelion, perhaps producing a seasonal surface temperature variation that the E-THEMIS investigation can use to constrain regolith properties to depths approaching a meter.

To some extent, variations of thermophysical properties with depth can be determined just from the diurnal temperature curves. Fig. 1, bottom panel, shows a model diurnal curve with low thermal inertia material of two different depths, overlying a higher thermal inertia substrate. The peak temperature occurs closer to noon, and the nighttime cooling rate is reduced, compared to homogeneous models with similar day/night temperature ranges (also shown).

Eclipses, because of their rapid timescales (eclipse ingress takes only 80 seconds for a given point on the surface), probe shallower depths than diurnal insolation variations, and as previously mentioned, eclipses give even lower thermal inertias, 14 ± 4 MKS (Hansen 1973), than diurnal variations, indicating that the uppermost few millimeters of the surface are less consolidated than deeper layers.

2.1.3 Lateral Inhomogeneities

Horizontal variations in temperature within the detector field of view are detectable as variations in brightness temperature with wavelength. Such variations may have several causes, including lateral variations in thermal inertia (e.g. blocks vs. regolith), albedo (e.g., ice vs. non-ice components), or topography.

E-THEMIS will map the distribution of blocks, rocks, or bedrock (referred to as blocks here) exposed at the surface of Europa, if they have higher thermal inertia than the surrounding regolith, even if they are not directly spatially resolved. The approach relies on an interpretation of apparent anisothermality between observations at two thermal infrared wavelengths; it was originally designed and validated at Mars (Christensen 1986b; Nowicki and Christensen 2007; McKeeby et al. 2022), and the Moon (Bandfield et al. 2011). Typical low thermal inertia regolith fines display higher-amplitude diurnal temperature variations compared to blocks, rocks, or bedrock (Fig. 1). A complex natural surface can be modeled with a combination of two materials: high thermal inertia blocks, typically assumed to have the thermal properties of solid ice, and low thermal inertia fines of unknown thermal inertia. In this model, blocks are assumed to be larger than the diurnal skin depth (about 0.9 m for solid ice, Table 1) so that temperature does not depend on block size. While the linear mixing of spatially unresolved materials at two different temperatures results in the linear mixing of radiances, brightness temperatures are wavelength-dependent (Fig. 5). With simultaneous temperature measurements at two distinct wavelengths at multiple times of day, one can deconvolve both the surface area of blocks (vs. fines) and the thermal inertia of the fines.

Fig. 5

left: Model pre-dawn equatorial blackbody radiance vs. wavenumber for a material at 116 K typical of massive blocky material (I = 2200 MKS), 88 K typical of Europa fines (I = 70 MKS), and 50/50 linear mixing of both materials (Albedo = 0.5, latitude = 0). The resulting Planck curve is not equivalent to that of a 116 + 88 = 102 K body. right: apparent brightness temperature versus wavelength for a warm blocky endmember (116 K), a cold regolith-like endmember (102 K), a 50/50 mixture of both, and a 102 K black body. Anisothermality results in a wavelength-dependence of the brightness temperature, which E-THEMIS can detect

Global scans (Sect. 4.2) with E-THEMIS bands 2 and 3 (14−28 and 28−80 μm) will be used to map anisothermality to derive block abundance globally. With an accuracy of 2 K at 90 K, broad regions of high and low block abundance will be identified with an accuracy of ∼10-20% based on the anisothermality observed measured bands 2 and 3 (Fig. 6). Spatial binning will be adjusted to increase the signal-to-noise ratio (SNR) where needed. Correlations with the largest blocks recognized in high resolution visible imagery from the Europa Imaging System will validate the approach in the Europa environment and will further provide constraints on the thermal properties of blocks. In particular, we can determine whether blocks are indeed associated with high thermal inertia values as are terrestrial or Martian clasts (i.e., >1200 MKS (Fergason et al. 2006b; Vasavada et al. 2017), or instead most consistent with lower thermal inertia values (i.e., < 600 MKS) as on 162173 Ryugu and 101955 Bennu (Grott et al. 2019; Okada et al. 2020; Rozitis et al. 2020). In other words, an absence of anisothermality between band 2 and band 3 will also be interpretable in terms of thermophysical block properties, especially when combined with high-resolution image data of the surface.

Fig. 6

Simulated band 2 and band 3 brightness temperature difference versus block abundance

Lateral temperature gradients can be caused by albedo variations as well as thermal inertia variations. Europa shows albedo patterns on all spatial scales, associated with endogenic and impact features, due to variations in surface composition, especially the relative quantities of ice and darker non-ice species (e.g., Carlson et al. 2009). In addition, the volatility of water ice at Europa surface temperatures is likely to cause local thermal segregation of a surface consisting of ice and darker contaminants into cold, bright, ice-rich regions and warmer, darker, ice-poor regions (Spencer 1987b), perhaps at scales below Galileo imaging resolution. Because darker areas will in general be warmer, these albedo variations will also contribute to local anisothermalities inferred from the wavelength dependence of Europa’s thermal emission (Fig. 5).

Surface topography also produces lateral temperature variations. A variety of geological processes compete to both form and erase surface roughness. Processes of ice extrusion, tectonic uplift and faulting, downslope mass wasting, impacts, and sublimation degradation contribute to roughness on a range of scales (Moore et al. 1996, 1999, 2009). While large impacts on Europa are few, they locally produce ejected crushed and fragmented debris, as well as distant secondary craters (Bierhaus et al. 2009). On small scales, physical and chemical weathering break down bedrock ice and blocky fragments to produce an assortment of regolith fines. Micrometeorites continually sand blast the surface (Phillips and Grossman 2007). Energetic particles can break down surface ices and minerals (Carlson et al. 2009). Because the surface of Europa is dominated by water, volatile redistribution may also play a significant role (Spencer 1987a). Sublimation can lead to muting or erasure of existing landforms. On the other hand, differential sublimation may enhance surface roughness. Differential sublimation exploits micro-variations in surface properties and over time may lead to submeter-to-meter scale structures such as sun cups (Hobley et al. 2018; Hand et al. 2020; Hobley et al. 2020; Warren 2022). This process is expected to be particularly efficient in equatorial regions where solar incidence is close to vertical.

Rough surfaces exhibit an array of facets with differing solar illumination and heating, that result in a local distribution of surface temperatures, the emission from which integrates into a single field of view. These facets occur on a range of spatial scales from just smaller than the E-THEMIS resolution (depending on the field of view and altitude) down to the scale of a thermal skin depth (about 2 to 90 cm for loose regolith to solid ice, respectively, Table 1). These facetted surfaces may also lead to thermal emission having a directional quality related to emission and solar phase angles. Generally, sun-facing facets will receive more insolation per unit area and thus be warmer in daytime, though local differences in thermal inertia and albedo will also play a significant role (McKeeby et al. 2022). Depending on the solar phase angle, E-THEMIS’s field of view may see proportionately more of the warmer directly illuminated surfaces (low phase angle) or more of the cooler slant illuminated or shadowed surfaces (high phase angle). The alignment of sun facing facets viewed at low phase angle can enhance the thermal emission above that expected from a smooth surface viewed off normal, especially noticeable for low thermal surfaces found on some airless bodies; this enhancement where viewing the entire planetary disk is commonly referred to as beaming (Smith 1967; Spencer 1990; Rozitis and Green 2011). Examination of the emission phase function (measured emission of the same location and time of day over a range of emission angles), obtained from E-THEMIS global scans will thus constrain surface roughness (Bandfield et al. 2015).

Temperature variations due to roughness will be largest near the terminator, as the slanting sunlight causes the largest temperature variability there (Spencer 1987a; Bandfield et al. 2015). Voyager provided the best constraints to date on the effects of roughness on spectral slope, the variation of brightness temperature with wavelength on Europa (Spencer 1987a; Bandfield et al. 2015) (Fig. 7). Spectral slope depends little on solar incidence angle, unlike the case of Callisto, for instance, suggesting roughness effects on spectral slope are modest on Europa at the coarse spatial scale of the Voyager data.

Fig. 7

Variation in spectral slope (defined as the brightness temperature difference between 20 μm and 40 μm) for disk-resolved Voyager IRIS spectra of Europa, compared to Callisto. Callisto brightness temperature spectra are much steeper near the terminator, likely due to surface roughness effects, whereas Europa slopes show little dependence on incidence angle. Adapted from Spencer (1987b)

2.1.4 Physical Interpretation of Thermal Inertia

The thermal inertia of a planetary regolith is typically interpreted in terms of variations in surface physical structure (e.g., Kieffer et al. 1977; Christensen 1986a; Jakosky 1986; Spencer et al. 1999; Mellon et al. 2000; Rathbun et al. 2010; Hayne et al. 2017). Bedrock, block abundance, and the relative distribution of regolith fines are common components, discussed above (e.g. Christensen 1986b; Nowicki and Christensen 2007). The fine component of a regolith may exhibit a range of thermal-inertia values depending on factors of grain size, grain angularity, composition and mineral properties, the presence of grain cements (e.g. Mellon et al. 2008, 2022).

On airless bodies grain size dominates among these effects, resulting in a discernable range of thermal inertia values for a given bulk density (e.g., Huetter et al. 2008; Ferrari and Lucas 2016; Mellon et al. 2022). Grain angularity also affects bulk density, and the inter-grain spacing on which grain-to-grain radiative heat transfer depends. Composition plays a role in terms of conduction of heat through individual grains and the radiative characteristics of grain surfaces. In addition, natural regolith typically exhibits complex, multi-modal grain-size distributions, reflective of the array of competing regolith formation and evolution processes. However, the smaller grains tend to play a dominant role, in both impeding the radiative coupling between grains, and by infilling of pores between larger fragments to raise the bulk density (Mellon et al. 2022).

The composition of Europa’s surface is dominated by volatile ices (Grundy et al. 1999). Unlike surface comprised of silicate minerals, ice-regolith grains can become cemented over time, a process known as sintering in which ice is transferred through sublimation from grain surfaces to the grain contacts (Hobbs and Mason 1964). Cementing can increase thermal inertia by increasing conduction at grain contacts (e.g., Spencer et al. 1999; Howett et al. 2011; Molaro et al. 2019). In a vacuum radiative and contact conduction components trade off depending on ambient temperature. At typical Europa temperatures contact conduction may dominate heat flow depending on grain size and angularity. Therefore, even a small degree of sintering may play a large role.

2.2 Discrete Endogenic Thermal Anomalies

2.2.1 Geological Context

A thermal anomaly is a region of a planetary body whose temperature is substantially different from the surrounding terrain. The most interesting thermal anomalies are due to endogenic heat sources. In such cases, the temperature variations cannot be explained by passive reradiation of solar energy. The most common endogenic thermal anomalies are associated with volcanic eruptions but can also be formed by other processes (Daubar et al. 2024, this collection). Endogenic thermal anomalies are a clear sign of a young and active surface, making a search for them a high-priority target for Europa Clipper. Among the geologic features identified on Europa’s surface, those associated with possible extrusion of warm ice (such as chaos), near surface deposits of warm ice or liquid water (chaos and domes), and those with tectonic deformation and possible active venting (ridges and bands) are the most likely to be associated with endogenic thermal anomalies (Daubar et al. 2024, this collection). Europa’s young surface age and the expected duration of thermal anomalies makes the presence of thermally detectable endogenic activity somewhere on Europa statistically likely (Hayne et al. 2019).

Existing observations of Europa’s surface temperatures (Fig. 3), primarily from Galileo PPR and ALMA, have been successfully modeled as passively reradiated solar radiation, requiring no endogenic thermal anomalies (Spencer et al. 1999; Rathbun et al. 2010; Trumbo et al. 2018; Rathbun and Spencer 2020) (see Sect. 2.1.1). However, these observations have a low spatial resolution (100-300 km) and limited coverage. Rathbun et al. (2010) determined detection limits for the Galileo PPR search for thermal anomalies and found that only a few percent of Europa was covered with sufficient resolution and SNR to eliminate the possibility of recent liquid water eruptions on the surface (Daubar et al. 2024, this collection).

2.2.2 Comparison to Enceladus

Enceladus was extensively observed by a suite of instruments onboard the Cassini spacecraft during numerous close flybys. Much like Europa, Enceladus likely has liquid water beneath an icy shell (e.g., Waite et al. 2009; Postberg et al. 2011; Thomas et al. 2016). Active venting from warm fractures was discovered by Cassini in the south polar region of Enceladus (Dougherty et al. 2006; Porco et al. 2006; Spencer et al. 2006). The source of venting has been localized to four ridge-bound fractures dubbed “tiger stripes”, which have elevated temperatures (Spencer et al. 2006; Spitale and Porco 2007; Abramov and Spencer 2009). Substantial heat flow, 4−19 GW total (Spencer et al. 2006; Howett et al. 2010; Spencer et al. 2018), emitted primarily at wavelengths beyond 15 μm, was detected from these fractures. Example peak fracture temperatures and emitting fracture widths in regions sampled at high resolution are 9 meters at 197 ± 20 K and 9 meters as inferred from 3-5 μm emission (Goguen et al. 2013), and 214 meters at 167 K (Spencer et al. 2018). Emission is consistent with heating by fractures at temperatures up to 223 K (Abramov and Spencer 2009) or warmer, plausibly maintained by heat supply by injection of water and water vapor from the underlying ocean (Ingersoll and Pankine 2010; Spencer et al. 2018).

Though the formation mechanism of thermal anomalies on Enceladus is still uncertain (Prockter and Patterson 2009), their successful detection bodes well for detection of comparable anomalies on Europa, which has a younger average surface age than Enceladus. Europa’s ubiquitous double ridges are potentially analogous to the warm double ridges that are the active vent sources on Enceladus. The tentative detection of active plumes on Europa by the Hubble Space Telescope (Roth et al. 2014; Sparks et al. 2017; Paganini et al. 2020) makes it plausible that some of these ridges are currently active and likely warm enough for E-THEMIS to detect.

2.2.3 Interpretation

Detections of endogenic hotspots by E-THEMIS may indicate one or more of the following: areas of recent eruptions of liquid water, active venting, shear heating, recent chaos formation, locations where the ice shell is thinner, and subsurface fractures connected directly or indirectly to Europa’s ocean. The specifics of the detected temperature distribution and its spatial extent would provide strong constraints on its mode of formation. Observed emission brightness temperatures (and color temperatures for unresolved sources) directly measure surface temperatures and provide lower limits to subsurface temperatures. Total radiated power can also be measured to constrain formation mechanisms. The improved spatial detailed provided by E-THEMIS’s high spatial resolution (10s of meters near close approach) will aid in interpreting the processes that have produced endogenic thermal anomalies. However, to fully interpret the mode of formation of thermal anomalies, context from other instruments on Europa Clipper is crucial. For example, the Europa Ultraviolet Spectrograph (Europa-UVS) may be able to constrain the origin of possible venting observed by Hubble (Roth et al. 2014), allowing an assessment of correlation with regions of elevated temperatures. The Mass Spectrometer for Planetary Exploration (MASPEX) and Surface Dust Analyzer (SUDA) would allow compositional analyses of the plumes to assess if they originate from the subsurface ocean. EIS would provide geologic context to further constrain the interpretation.

Modeling is also an important tool to interpret E-THEMIS detections. Models of subsurface structures and heat sources can be used to generate surface temperature expressions, which can then be compared to E-THEMIS observations. 2-D models of subsurface temperatures associated with warm fractures (Abramov and Spencer 2009; Nakajima and Ingersoll 2016) can be used to infer fracture temperatures from surface temperatures, and 1-D models of subsurface liquid water or warm ice on the surface (Abramov and Spencer 2009; Abramov et al. 2013; Hayne et al. 2019) can constrain the depth and age of activity such as chaos formation from its surface temperature expression (Abramov and Spencer 2008; Abramov et al. 2013).

To first order, the number, spatial extent, and temperature of detected thermal anomalies would be a proxy for Europa’s current geologic activity in its ice shell, such as formation of fissures or cracks, solid-state convection, and/or cyrovolcanism. As noted above, plume deposits may also exhibit unusual thermophysical properties indicative of recently active regions.

2.3 Conducted Endogenic Heat Flow

Europa’s internal heat budget is dominated by tidal heating, arising in the ice shell and/or the silicate mantle, plus roughly 0.3 TW (equivalent to a globally-averaged heat flux of 10 mW m⁻²) of radiogenic heating (Greenberg et al. 2002). Based on scaling with Io, the maximum expected tidal heating is about 4 TW (130 mW m⁻²) (Greenberg et al. 2002), but the actual value is unknown. A conductive ice shell thickness of 20 km would imply a conductive heat flux of around 30 mWm⁻². If the ice shell is convecting, the same shell thickness would imply a substantially higher heat flux (Barr and Showman 2009; Nimmo and Manga 2009) though the conductive part of the ice shell may be much thinner than this. Europa’s ice shell must transport this heat, either by conduction or (if the shell is sufficiently thick) by convection. Because tidal heating varies spatially, a conductive shell would experience spatial variations in thickness (Ojakangas and Stevenson 1989) and the heating rate could be up to three times higher at the poles than at the equator (Nimmo et al. 2007).

Unlike the thermal signatures of discrete geologically active regions, where heat flow is locally concentrated, conducted heat flow through the ice shell may be broadly distributed and detectable only as a small, spatially uniform, increase in surface temperature. Detection of heat flow at the 100 mW m⁻² level is possible in principle but difficult in practice. At high latitudes, surface temperatures are low enough that endogenic heat could warm the surface sufficiently that the temperature increase could exceed the noise levels of the E-THEMIS instrument (Fig. 8). However, thermal inertia, topographic variations, and particularly bolometric albedo uncertainties can produce temperature variations of comparable magnitude that will likely be difficult to separate from endogenic heat effects (Fig. 8). Obtaining both day and night temperatures will help constrain thermal inertia, and observations by EIS and the Mapping Infrared Spectrometer for Europa (MISE)will independently constrain bolometric albedo, but high precision will be required to separate expected endogenic signatures with any confidence.

Fig. 8

Temperature increases due to endogenic heat between 25 and 150 mW m⁻², compared to E-THEMIS noise levels for bands 2 and 3, assuming 5 × 5 pixel binning and 64 coadds. The blue line shows the temperature uncertainty due to albedo, assuming a bolometric albedo of 0.5 and an optimistic bolometric albedo uncertainty of 0.02, along with the latitude corresponding to that temperature, for a fast-rotator (infinite thermal inertia) model. The figure illustrates that detection of expected levels of endogenic heat with E-THEMIS will require high-latitude observations, and very precise knowledge of bolometric albedo. Other variables including roughness and thermal inertia will further increase uncertainties

2.4 Separation of Contributions to Surface Temperatures

As is clear from the above discussion, multiple factors will influence the spectral radiances that E-THEMIS will observe at Europa. Albedo, thermal inertia, endogenic heat, roughness, and their variations on both large (spatially resolved) and small (spatially unresolved) scales are all important. Fortunately, the richness and diversity of the E-THEMIS and other Clipper data sets should allow disentangling all these effects.

Global mapping of Europa on the inbound and outbound legs of each flyby (see Sect. 5.2) will observe the same terrain at a wide variety of local times. Albedo and thermal inertia have different effects on the diurnal temperature variation (Fig. 1), allowing generation of near-global maps of both quantities at 10 km resolution by fitting models to the observed diurnal variations. Albedo will of course be additionally constrained by visible and near-IR imaging by EIS and MISE, and discrepancies between E-THEMIS and EIS/MISE albedos may reveal regions heated by endogenic heat in addition to absorbed sunlight. In addition, any areas with temperatures higher than the maximum attainable by solar heating at Jupiter (∼175 K during the day, or ∼130 K at night, at the equator) will be unambiguous indicators of endogenic heating.

Additionally, the variation of radiance with wavelength will reveal sub-pixel spatial temperature variations due to small scale lateral variations in albedo, thermal inertia, or topography. Each effect will have different variation with local time or incidence angle. Albedo-related temperature contrasts will be largest during the day (Fig. 1), surface roughness effects will peak near the terminator (Fig. 7), and thermal inertia-related temperature variations will peak during both day and night but will be minimized at intermediate local times (Fig. 1). Variation in thermal emission with viewing angle will further constrain surface roughness. The high (∼30 meter) spatial resolution close approach data will also allow direct spatial separation of many temperature variations that are unresolved in the global maps, revealing for instance correlations with terrain types mapped by EIS that will allow extrapolation of the high-resolution data to the rest of Europa.

2.5 Science Requirements

E-THEMIS’s ability to address the science goals discussed above is formalized in its science requirements. E-THEMIS is the primary science data contributor for two overarching mission goals, achieved in concert with other investigations: 1) the search for endogenic thermal anomalies, and 2) the characterization of (sub)surface thermophysical properties. These two goals are associated with two mission level themes (“Geology” and “Current Activity”) that also includes “Ice Shell and Ocean” and “Composition”. Meeting these goals formally contributes to mission success, and requires E-THEMIS to generate the following products:

• A global thermal imaging dataset that “shall map daytime and nighttime temperatures over ≥80% of the surface at a resolution of ≤ 25 km and with ≤ 2 K accuracy and precision, in order to characterize the thermal state of the ice shell and identify heat flow anomalies, regolith depth, and block abundance”.

• A regional thermal imaging dataset that “shall map daytime or nighttime temperatures of ≥18 geologically distinct sites at a ≤ 250-m pixel scale and with ≤2 K accuracy and precision, in order to characterize the thermophysical properties indicative of erosion and deposition processes at the sub-pixel spatial scale”.

These goals lead to a number of additional requirements that dictated the design of the instrument (as described in this paper), the overall design and operation of the spacecraft, and also the design of the mission plan (i.e., the selected trajectory and pointing of the Europa Clipper spacecraft in the Jovian system). Selected examples of lower-level requirements directly relevant to the operation of the E-THEMIS investigation include:

• For optimal constraints on regolith thermophysical properties, daytime in the above goals is defined to be between 8:30 and 15:30 Local True Solar Time and nighttime between 18:30 and 6:00 Local True Solar Time.

• To minimize the effects of surface roughness and directional emissivity effects on surface temperature determination, the range of acceptable emission angles is <5° for local scale observations acquired during nadir observations around closest approach, and < 70° for global mapping.

• Because both daytime and nighttime temperatures are required to constrain both thermal inertia and endogenic heat sources, at least 50% of the area covered by the global daytime dataset should also be covered by the global nighttime dataset.

• To ensure adequate sampling of Europa’s thermophysical properties at high spatial resolution, at least 15 distinct sites should be observed near closest approach with overlapping daytime and nighttime observations. The acquisition of these overlapping observations requires flybys of the same locations on both the night side and the day side of Europa, and thus will not be completed till late in the primary mission.

• Finally, the design of the trajectory in the Jovian system considers a “planning guideline” (a desired outcome, not a formal requirement) for these day/night crossing points to be well distributed between the anti-Jovian and sub-Jovian hemispheres, with at least 8 crossing points on each hemisphere, in order to avoid a clustering of overlapping observations at the expense of global sampling.

E-THEMIS will also search for and characterize plumes primarily by leveraging limb observations acquired as part of its global scans, in the event that plumes contribute measurable signal at thermal infrared wavelengths. However, no formal requirement or dedicated spacecraft maneuvers will drive this search with E-THEMIS.

2.6 Measurement Requirements

The science requirements were used to develop the radiometric, spectral, and spatial instrument measurement requirements that controlled the design of the E-THEMIS instrument. These requirements led to the choice of the detector and filters and the optical, mechanical, and electronical design.

Radiometric Requirements

The E-THEMIS radiometric requirements are given in terms of precision and accuracy. The radiometric precision is driven by the requirement to identify relative surface temperature anomalies (e.g., Pappalardo et al. 1999). Measured thermal anomalies observed on Enceladus have temperatures of ≥135 K (Spencer et al. 2006; Goguen et al. 2013) and a 5 K thermal anomaly associated with the geologically recent emplacement of water or warm ice can persist for several hundred years (Abramov and Spencer 2008). The surface thermal inertia will be used to determine surface particle sizes to within 10%, requiring a temperature precision of ±3 K for typical night (90 K) and day (130 K) temperatures (Presley and Christensen 1997; Piqueux and Christensen 2009a,b; Kieffer 2013). The absolute accuracy requirements are less stringent, as it is relative differences in surface temperature that will be used to study differences in surface characteristics and identify recent resurfacing. Nonetheless, an absolute accuracy of 3% will provide an absolute temperature accuracy of 4 K at 90 K in Band 3, which is of sufficient quality to accomplish all of the proposed mission objectives (Abramov and Spencer 2008). The E-THEMIS precision requirement is 1 K to confidently detect thermal anomalies that are 2 K warmer than their surroundings. This requirement shall be met for surface temperatures from 90 to >130 K. The E-THEMIS accuracy requirement is 3%.

Spectral Requirements

The E-THEMIS spectral requirements are driven by the requirement to map materials of different temperature and to determine the sub-pixel abundance of warm blocky materials and vents. We have performed analyses to determine the optimal spectral bandwidths required to determine temperatures to ±1 K over the range from 90 to 220 K. The E-THEMIS Band 1 (7−14 μm) was selected to meet this requirement for objects with temperatures >170 K. Band 2 (14−28 μm) was selected to meet the radiometric requirement for 110 to 170 K objects, and Band 3 (28−80 μm) was selected to meet the requirement for 80 to 110 K objects. Note that all bands detect the emitted radiation but the data become noisier at temperatures below the design temperature.

Spatial Resolution Requirements

The individual field of view (IFOV) requirement is determined by the need to resolve the 1 km wide ridges observed in Galileo data (e.g., Pappalardo et al. 1999). In order to resolve a 1 km wide linear or circular feature from 100 km, it is required to have 0.25 km IFOV with a modulation transfer function (MTF) of > 0.3. Separating the optical performance from the spacecraft-motion-induced image smear results in optical IFOV requirement of 0.150 mrad (15 m at 100 km altitude).

3 Instrument Description

3.1 General Description and Overview

The E-THEMIS design is based on the highly successful Mars Odyssey THEMIS instrument, with modifications to improve performance and optimize the instrument for the Europa environment. THEMIS demonstrated that an uncooled, microbolometer-based, multispectral imager can provide excellent radiometric performance (Christensen et al. 2004), achieve excellent science (e.g., Christensen et al. 2005; Hamilton and Christensen 2005; Christensen et al. 2008; Edwards et al. 2009), and meet the Europa Clipper science objectives. The primary improvements from THEMIS that are implemented in E-THEMIS are a larger detector format and smaller pixels, improved radiometric performance, modernized electronics, a significantly more flexible time delay integration implementation (TDI) to optimize data collection throughout the Europa flybys, an expanded telescope field of view (FOV), expanded wavelength range, and significantly higher radiation tolerance.

The major E-THEMIS components are the Sensor Assembly (SA) mounted to the spacecraft nadir deck, the processing and control, or “vault” electronics (VE) that are located in the spacecraft radiation vault, and 3.4-m long cables that provide power, commands, data, and telemetry between the SA and the VE (Fig. 9). The sensor assembly consists of 1) a three-mirror, off-axis, reflective telescope with a 6.45-cm effective entrance pupil diameter; 2) an uncooled microbolometer focal plane module (FPM) that includes the focal plane assembly and electronics; 3) a three-band optical filter assembly; and 4) an internal calibration subsystem (Fig. 10). The E-THEMIS telescope provides a 5.85° cross-track and 0.91° along-track FOV in each of the three spectral bands with bandpasses from 7−14 μm, 14−28 μm, and 28−80 μm, and is located within a monolithic all-aluminum housing that provides mechanical support and radiation shielding. The focal plane has 920 cross track and 140 along track pixels in each spectral band. On-board data processing provides selectable TDI and spatial aggregation to improve the radiometric precision. The functional block diagram (Fig. 11) illustrates the optical and electrical interactions and interfaces between these elements and the spacecraft.

Fig. 9

The E-THEMIS flight instrument. a) Sensor Assembly; b) Vault Electronics

Fig. 10

E-THEMIS Sensor Assembly. a) assembled; b) expanded view showing the major optical, mechanical, and electrical components

Fig. 11

The E-THEMIS functional block diagram showing the functions in the Sensor Assembly on the Nadir Platform and the Vault Electronics in the spacecraft vault and the connections between them and to the spacecraft

3.2 Design

3.2.1 Focal Plane Module

The heart of the E-THEMIS instrument is the FPM that was developed by Raytheon Vision Systems (RVS). The FPM is comprised of the Focal Plane Dewar Assembly (FPDA) and the Focal Plane Electronics (FPE). The FPDA incorporates an uncooled, 1280 × 1200 pixel, 12- μm pitch vanadium oxide microbolometer focal plane and readout integrated circuit (ROIC) installed inside a hermetically-sealed dewar (Fig. 12). The E-THEMIS FPM is a significant advance from the successful Mars Odyssey THEMIS focal plane module (Christensen et al. 2004) with similar pixel construction and materials as the earlier detector. For the Europa mission, E-THEMIS incorporates three significant modifications to the existing tactical version of the RVS focal plane module: 1) repackaging of the FPA in a heavy Tungsten dewar to provide the required radiation shielding, 2) significant modifications to the focal plane electronics, which are located adjacent to the FPDA, to use electronic components that can tolerate the extreme Europa radiation environment, and 3) replacement of the standard Ge window with a chemical vapor deposition (CVD) diamond window with the required optical transmission from 7 μm to >100 μm.

Fig. 12

Flight Focal Plane Module. The assembly is a modified commercial microbolometer with entirely new Focal Plane Electronics built from parts that can survive the Clipper radiation environment, a focal plane dewar machined from heavy Tungsten, a housing design that will survive the launch vibrational environment, and straps to remove excess heat from the assembly

Microbolometers employ thin films that absorb broadband IR radiance, which heats the material and changes its electrical resistance. This resistance change is measured and read out by the ROIC and provides the mechanism for remotely determining the scene temperature. The monolithic detector structure consists of pixels fabricated directly on the silicon ROIC wafer, eliminating wire bonds or other interconnects, and providing high reliability on the signal chain, from photons to the analog signal and then to the 14-bit digital output generated by the ROIC’s Analog to Digital Converter (ADC) (Puschell and Masini 2014; Kennedy et al. 2015). A coarse-level equalization is performed on the raw analog signal data on a pixel-by-pixel basis prior to digitization.

E-THEMIS image data are collected from the FPM at 60 frames per second from 920 cross-track by 140 along-track pixel regions under each of the three filters. This readout rate is slightly slower than the 0.012 sec detector time constant. Each cross-track row contains 12 reference pixels on each side of the array that are insensitive to incoming scene radiance and are used to control the focal plane thermoelectric cooler (TEC), giving a total of 896 active scene pixels per row. Laboratory measurement and radiometric calibration results show that the detector sensitivity extends to >80 μm. The measured NEDT performance of the E-THEMIS Flight FPM is 0.042 ± 0.006 K across all pixels in the array viewing a 300 K scene at f/1.

The sensing elements in a microbolometer can also change temperature due to temperature changes in the array itself. The FPM utilizes a space-heritage Marlow thermoelectric cooler (TEC) to stabilize the microbolometer temperature in order to minimize these temperature changes (e.g., Nugent et al. 2013). The RVS FPM electronics use the 24 reference pixels in real time to control the TEC and remove any temporal detector temperature variations. The use of the TEC and the reference pixels was demonstrated in test to provide ±0.002 K control of the array temperature, meeting the detector stabilization allocation derived from the absolute calibration requirement (Sect. 4.3) and results in an absolute calibration that is limited only by the accuracy of the reference calibration target and the removal of background radiance from the telescope housing.

The FPE receive the 14-bit digital IR signal from the FPA ROIC at 60 frames/sec. The FPE also provide the clock, on-chip calibration terms and bias signals to the FPA ROIC. The FPE use a Xilinx Virtex-5QV FPGA to perform the digital post-processing on the image frames, correcting for gain, offset, and non-uniformity. This includes a two-point responsivity calibration and a fine-level equalization on a pixel-by-pixel basis. A high-speed LVDS serializer is used to transmit the FPE post-processed image data/telemetry (16-bit) to the VE at a rate of 372 Mbps. The FPE uses two 64 MB MRAMs to store the FPGA configuration and four tables of selectable Non-Uniformity Coefficient (NUCs) for each pixel in the array (see Sect. 3.2.5).

3.2.2 Optical/Mechanical Design

E-THEMIS uses a compact three-mirror, off-axis, unobscured reflective telescope with an effective focal length of 10.52 cm and effective entrance pupil diameter of 6.45 cm. It is f/1.34 cross-track and f/1.92 along-track (Table 2). The three telescope mirrors are gold coated, diamond-turned aluminum and mounted in a monolithic aluminum housing and were fabricated by General Dynamics Global Imaging Technologies (now CMM Optic). Single-pixel image quality is diffraction-limited in Bands 2 and 3 and near diffraction-limited for Band 1. The housing has a three-point rigid mounting to the spacecraft nadir deck, with titanium flexures to provide thermal expansion compensation between the aluminum housing and the composite deck. Measurement of temperatures within the telescope housing to ±1 K complies with the allocation from radiometric absolute accuracy without the need for active temperature stabilization.

Table 2 Instrument performance

Like THEMIS, E-THEMIS incorporates a butcher block filter assembly placed in front of the detector, but the E-THEMIS filters had to be mounted outside of the focal plane dewar due to mechanical size of the filter package and the need to minimize changes to the existing focal plane design and dewar for cost and schedule constraints. Bands 1 and 2 were fabricated by the University of Reading and utilize thin-film interference filters on dielectric substrates, with Band 1 using ZnSe and Band 2 using CdTe. The Band 3 filter was fabricated by QMC Instruments and is a metal mesh array type that comprises alternating films of patterned copper and polypropylene built into a single unit. The metal mesh filter element is mounted on a CVD diamond substrate with a polypropylene anti-reflection coating.

The unobscured telescope optical design maximizes the scene radiance throughput and also provides excellent detector radiation shielding because there is no direct path from the entrance aperture to the detector, as can be seen in the cross-sectional ray trace (Fig. 13). Advances in diamond turning technology in the 20 years since THEMIS was built allowed for an improved and significantly more complex optical prescription, which in turn provides a wider field of view and improved optical performance compared with THEMIS. The telescope includes a carbon fiber baffle (Fig. 10) to prevent straylight from entering the telescope. Internal baffling machined into the housing provides additional straylight rejection. E-THEMIS was designed to provide “bolt-together” assembly and optical alignment, with the focal plane assembly, including the filter assembly, attached to the housing with titanium flexures with built-in alignment pins.

Fig. 13

The E-THEMIS Sensor Assembly optical schematic and ray trace

Radiation shielding of the FPM is provided by the thick aluminum housing and augmented by a CuW (outer) and aluminum (inner) shield positioned over the focal plane assembly (Fig. 10). The total shielding mass, above the required structural mass, is ∼4 kg. Graphene heat straps connect the FPE to the telescope housing to provide a conduct heat sink path to the housing and eventually to the nadir deck, thus helping to maintain thermal stability and uniformity during operation.

In-flight calibration utilizes periodic observations of an internal calibration flag and deep space. The internal cal flag is moved in and out of the optical path using a two-position, bi-stable rotary actuator developed by Avior Control Technologies (now Honeybee) (Fig. 14). This actuator provides the required magnetic detent torque to prevent motion during launch. The flag is made of magnesium to minimize mass and inertia and is 0.8 cm x 0.98 cm in area with a weight of ∼5 gm. The calibration surface is coated with high emissivity Z306 paint manufactured by Lord Corp.

Fig. 14

The E-THEMIS calibration flag mechanism/assembly showing the (a) open and (b) closed configurations

3.2.3 Thermal Design

The E-THEMIS sensor assembly is designed to operate within its performance requirements from −7 °C to +35 °C and survive from −30 °C to +45 °C. These temperatures are referenced to the platinum resistance thermistors (PRTs) on the outside of the E-THEMIS housing next to the survival heater that is controlled by the spacecraft. The VE must operate and survive from −20 °C to +50 °C. The primary thermal challenge was the large temperature gradient across the instrument from the spacecraft deck, whose temperature is modeled to vary from −60 °C to 0 °C at Jupiter, to the focal plane assembly, whose electronics consume 35 W of power and generate significant internal heat that results in an operating temperature of up to 65 °C. This thermal gradient is significant for a thermal instrument whose performance is optimized near 10 °C and requires thermal stability of less than ±0.1 °C per minute. The SA meets these requirements using titanium flexures as thermal conductive isolators, reduced radiative coupling to the spacecraft deck, multi-layer thermal insulation (MLI) blankets, a 34 cm² thermal control radiator surface, and spacecraft-controlled Fralock survival heaters. The large thermal mass of the telescope housing, the thermal isolation from the spacecraft, and efficient removal and redistribution of the FPM heat results in uniform temperatures throughout the telescope and cal flag assembly (Fig. 15). Note that the temperature at the survival heater PRT used to define the E-THEMIS operational temperature is ∼30 °C in Fig. 15.

Fig. 15

Example predicted E-THEMIS internal temperatures. The case shown is for a warm Europa flyby condition, with the coldest temperatures (∼0 °C) occurring at the nadir deck and the warmest temperatures (∼65 °C) in the focal plane electronics. The temperature at the survival heater reference PRT used to define the E-THEMIS operational temperature is ∼30 °C

The E-THEMIS internal temperatures are monitored using PRTs. The two thermistors used to measure the cal flag housing are 4-wire PRTS calibrated to an accuracy of ± 0.5 °C, and a precision of ≤0.2 °C (1-sigma) over a temperature range of 0 °C to +55 °C. The telescope cavity, filter assembly components, and sunshade interior use Acktar Fractal Black coating to provide high-emissivity, diffuse radiating surfaces for calibration purposes.

The E-THEMIS thermal model was validated in instrument-level testing in four thermal balance tests to model cold (−60 °C spacecraft deck) and hot (0 °C spacecraft desk) cases. These tests revealed a higher-than-expected heat loss in the Project-provided MLI test blankets, but otherwise confirmed the accuracy of the E-THEMIS thermal model. The performance of the flight blankets and the resulting final size of the radiator opening in the blanket will be determined during spacecraft-level thermal balance testing.

A key element of the E-THEMIS calibration is the thermal stability between observations of the internal cal flag and/or deep space. The design requirement of ±0.1 °C per minute was achieved during instrument thermal vacuum testing after ∼4 hours following instrument turn on from the expected non-operational thermal state. Similar behavior is expected at Europa and will be confirmed during spacecraft-level thermal vacuum testing.

3.2.4 Vault Electronics

The vault electronics (VE; Fig. 9b) perform the processing and control functions and were developed by Ball Aerospace and were delivered to ASU in February 2021. The VE consist of a single, dual-sided 24 × 20 cm board, that is located inside the Europa Clipper radiation-shielded vault and provides: 1) regulated power (+4.9 V, +10.5 V) to the FPE; 2) high-speed LVDS deserializer data interface from FPE; 3) LVDS UART command/telemetry interface to/from FPE; 4) instrument command and control; 5) selectable data summing and aggregation; 6) data formatting; 7) readout of the internal thermistors; and 8) redundant SpaceWire (data/command) interfaces with the spacecraft. The VE accepts and filters 28 V unregulated power from the spacecraft.

The VE uses a Xilinx Virtex-5QV FPGA as the core data processor, with a 64 MB MRAM for FPGA configuration nonvolatile memory. The FPGA processor is firmware-based with no flight software. The FPGA core post-processing engine provides data collection flexibility throughout each Europa flyby in order to comply with bandwidth limitations. The imaging parameters provide the ability to select full-frame or TDI imaging mode, frame/TDI co-adds, delay frames, pixel binning per band, row shift and TDI sets (see Sect. 3.2.6). E-THEMIS imaging commands are stored in the spacecraft sequence engine and issued to the instrument over the SpaceWire interface at the applicable start times. The VE uses 4 GB of DDR2 memory for data post-processing workspace, storage, and packetization/buffering. Redundant SpaceWire interfaces between the VE and the spacecraft support the transfer of the science data, telemetry, and commands.

3.2.5 Non-uniformity Correction

The application of the stored non-uniformity coefficients (NUC) in the FPE are required in order to perform on-board equalization and calibration of the image data as they are acquired in real-time. The goal of these corrections is to equalize the signal response in each pixel and produce uniform images as the scene temperature varies. These corrections are applied in real time during the normal video operation of an infrared camera to produce high quality images. In the case of E-THEMIS, much of this processing will be applied on the ground. However, because the data from different detector rows are summed during TDI and then detector rows and columns are spatially aggregated, it remains important to correct for non-uniformity in the pixel response prior to this aggregation.

There are three steps to this NUC process that are applied to the image data on a pixel-by-pixel basis: 1) Coarse-Level Equalization (CLE) coefficients are applied to the raw analog data as each line of data is read off of the detector and prior to digitization by the ROIC ADC. This initial step is used to equalize the resistance variations for each of the pixels in the detector array so that the raw signal stays within the dynamic range of the ADC; 2) Response Equalization (RE) coefficients are applied to the CLE equalized digital data to equalize the responsivity gain variations for each of the pixels in the detector array; and 3) Fine-Level Equalization (FLE) coefficients are applied to the data to equalize the responsivity offset variations for each of the pixels in the detector array.

The maximum analog gain without signal saturation is dependent on the background radiance, and therefore varies with instrument temperature. In addition, the E-THEMIS analog gains were set as high as possible to provide the best possible digitization and precision at the low Europa scene temperatures. As a result, each set of CLE, RE and FLE NUC terms are only valid over a relatively narrow instrument temperature range that was determined during TVAC testing to be ∼8 ° C. Four sets of NUC tables can be stored in the nonvolatile memory. These tables are computed using firmware within the FPE using observations of a thermally uniform and stable internal calibration flag and an external source. These tables were acquired and stored in memory during TVAC testing at ASU. At the time of the E-THEMIS TVAC testing the spacecraft and E-THEMIS thermal models indicated that the instrument would operate relatively warm (5 to 25 °C). Therefore, NUC tables were stored for instrument temperatures of 7 °C, 15 °C, 23 °C, and 31 °C. After E-THEMIS delivery and installation on the spacecraft, refinements to the spacecraft thermal model indicated that E-THEMIS is likely to operate at temperatures <-5 °C for the coldest Nadir deck case. This is lower than the useable operational range of any of the NUC tables currently stored in the instrument non-volatile memory. Extremely stable instrument and target temperatures, as were used in TVAC, are required to accurately compute the NUC parameters – any non-uniformity in the targets would be built into the NUC coefficients and transferred to the scene observations resulting in calibration errors. Unfortunately, the necessary thermal stability cannot be achieved under ambient conditions, especially for instrument temperatures lower than typical cleanroom dew point temperatures (∼10 °C). It is therefore expected that an in-flight NUC table update will need to be performed once E-THEMIS reaches its Europa operating temperature (see Sect. 5.1). Once an in-flight NUC calibration at these colder temperatures is successfully completed, it will be stored in the warmest NUC table location in non-volatile memory for use during on-orbit operations.

3.2.6 Operational Modes and on-Instrument Data Processing

E-THEMIS has two operational modes: 1) framing and 2) TDI. In framing mode full 920 × 140-pixel images are acquired from each band at 60 Hz, and a selectable (1, 2, 4, 8, 16, 32, 64, or 128) number of successive individual frames can be co-added to create a single output image frame. A frame delay parameter can be used to collect a set of images; for example, a sequence of twenty images with 32-frame summing (i.e., 0.53 sec temporal integration) could be collected every 30 seconds (29.47 sec delay) for 10 minutes using a single command. The TDI mode accumulates the output from a single row under each filter in each frame at 60 Hz and sums rows from successive frames in accumulators. The row used in each successive frame can be offset to compensate for the spacecraft motion. This offset can be adjusted from one to six rows based on the ground velocity. At the slowest flyby ground velocity, the FOV moves a single row between successive frames and the firmware offsets the input row by one from frame to frame, i.e. row 1 from frame 1 is added to row 2 from frame 2, row 3 from frame 3, etc. At higher ground velocities the offset is increased; for example, rows 1, 3, 5, etc. or 1, 4, 7, 10, etc. would be combined as the velocity increased. The number of TDI frames that can be summed can be 8, 16, 32, or 64. Because there are 140 rows under each filter the values for the offset and TDI are interconnected. When the offset is 1 a TDI of 64 can be accommodated. However, when the offset is 3 then TDI can only be 32 in order to fit within the available 140 rows. These imaging parameters will be determined for each predicted flyby geometry and used to design the operational sequence.

An additional TDI option is the number of “sets” of rows that can be collected. In normal operation only a single set of data would be collected, for example with TDI = 32 and offset = 3, then rows 1, 4, 7, 10, …, 94 would be collected into a single set. However, photons are also being collected in rows 2, 3, 5, 6, etc. If the sets parameter is set to 2, then the data from rows 2, 5, 8, 11, …, 95 would also be collected and downlinked. The number of sets can be 1, 2, or 4. The data from each set are transmitted to the ground so this option increases the E-THEMIS data volume, but the additional data provide a mechanism to increase the SNR of the acquired images by fully utilizing all of the available pixels on the detector.

The final on-instrument data processing that can be performed is spatial aggregation through binning of neighboring pixels. The available aggregation values can be from 1 × 1 (no binning) to 5 × 5 pixels. Note that the TDI, offset, and sets parameters are the same for all bands, but the spatial aggregation can be selected separately for each band. This additional complexity was implemented to account for the variation in the wavelength-dependent diffraction blur and the signal-to-noise differences between the bands. A larger aggregation factor will be selected for the longer-wavelength bands and low signal scenes to optimize the use of the data volume allocated to E-THEMIS.

3.2.7 Radiation Modeling and Mitigation

Due to the harsh environment surrounding Jupiter and Europa, the THEMIS design required significant modifications to survive and meet performance requirements during and after exposure to the radiation. The approach to mitigating degradation due to radiation was as follows, 1) quantify radiation tolerance of critical hardware via testing; 2) model the expected dose level for the hardware; and 3) design and fabricate hardware to provide the necessary shielding. Total Integrated Dose (TID) Radiation Lot Acceptance Testing (RLAT) was performed at the Cobham RAD facility to quantify rad-tolerance of the sensitive E-THEMIS hardware, including FPM ROIC, FPE and VE piece parts (including M3GB2812S/CK Hybrid DC-DC Converter and ISL70444SEH Operational Amplifier), and all three optical filters. Additional RLATs were performed by JPL in support of the E-THEMIS material and part selections, including the optical and thermal coatings, adhesives, Gore wire, Amphenol connectors, and many EEE components used across multiple payloads. Extensive radiation modeling was performed to calculate the mission fluences (trapped electron, proton, and solar) and identify the necessary shielding, with adequate margin. The Europa Clipper project required all hardware to be protected by a Radiation Design Factor (RDF) of at least two (e.g., if the RLAT shows the hardware will survive up to 100krad, it must be shielded such that it is not exposed to >50 krad in the mission). This requirement was met using the CuW FPE shield and the heavy Tungsten alloy FPA dewar and shield, with the FPM ROIC shielded to 22 krad and the FPE to 100 krad. The telescope structure and baffles provide shielding for the optical filters to 27 krad and other optical coatings to <400 krad. The intra-instrument harnesses are protected with copper tape overwrap and MLI, shielded to 20 Mrad. The VE assembly is protected with an aluminum housing and the spacecraft Vault structure, shielded to 300 krad.

Single Event Effect (SEE) testing of the FPA was performed at the Texas A&M University (TAMU) Radiation Effects Facility’s K500 beam line. This SEE testing was only applied to the unpackaged RVS FPA (microbolometer and ROIC) and not the FPE. Because heavy ion transients in the microbolometer pixels would not deposit enough thermal energy to generate significant noise, the ROIC SEE tolerance was the focus of these tests. SEE testing was not required for the FPE and VE because they were designed using existing radiation-hardened and SEE-tolerant parts.

3.2.8 Planetary Protection and Contamination Control Approach

In accordance with requirements defined for Europa Clipper in agreement with the NASA Office of Planetary Protection, all payloads and subsystems were required to verify compliance with planetary protection and contamination requirements. These requirements were designed to ensure the integrity of the scientific evidence of this and future missions to Europa, Jupiter, and other planetary bodies, by preventing particulate or micro-organism contamination. All E-THEMIS materials were subject to thorough review; materials required qualification testing and verification assays were used to quantify and evaluate the contamination and bioburden of each subassembly prior to selection or use in the flight instrument. Assembly operations were adjusted to incorporate stringent protocol designed to reduce contamination, including enhancements to cleanroom gowning for personnel, adding in-process cleaning operations for all hardware, upgraded vacuum bakeout and outgassing measurement equipment, and sterilized work surfaces and protocol for regular assays. At delivery to the spacecraft, E-THEMIS was verified to meet all particulate, bioburden, and outgassing requirements with margin.

3.2.9 Flight Instrument Development History

The E-THEMIS investigation was selected in May of 2015 with the Instrument Accommodation Review held in March of 2016 and the System Requirements Review in January 2017. The initial design phase was concluded with the Preliminary Design Review in April 2018 and the Critical Design Review 16 months later in August 2019. The E-THEMIS development included fabrication of engineering model and two flight units of the Vault Electronics and one qualification unit, one engineering model, and two flight units of the Focal Plane Module. In addition, one VE plus FPE simulator were delivered to JPL for use in the spacecraft testbed. One EM and two flight fully aligned telescope assemblies were built, along with one qualification and one flight filter assembly and one EM and two sets of flight harnesses. The major challenges that were overcome in the development were issues related to design, fabrication, and welding of the focal plane dewar assembly, which are made of a heavy Tungsten alloy for shielding in the extreme Europa radiation environment and to incorporate a CVD diamond window to meet the long-wavelength spectral requirements. The intense phase of flight hardware development began in the spring of 2020 just as the lockdowns and disruptions due to COVID were beginning, and this development and the instrument integration and testing at ASU were performed during the COVID phase, adding significant challenges and delays to an already complex instrument development.

E-THEMIS performed vibration and electromagnetic interference (EMI) and electromagnetic compatibility (EMC) testing in January of 2022 and performed extensive thermal vacuum testing and radiometric calibration from February through mid-April 2022. Fig. 16 gives a summary of the key thermal plateaus and cycles used for thermal model validation and the instrument temperatures at which radiometric performance data were collected (see Sect. 4.4). E-THEMIS was delivered to JPL on May 22, 2022, and completed installation, alignment, and electrical checkout on the spacecraft in mid-October 2022. The successful development and delivery of E-THEMIS in the midst of the COVID pandemic was a significant accomplishment by the RVS, Ball, ASU, and JPL teams.

Fig. 16

E-THEMIS planned thermal vacuum testing schedule

4 Instrument Calibration

4.1 Methodology

4.1.1 Optical Performance

The optical performance of E-THEMIS is specified in terms of the modulation transfer function (MTF), the universally used metric for defining the spatial resolution requirements of an optical imaging sensor. The MTF requirement was specified for each band in the along-track (AT) and cross-track (XT) directions and measured during ambient system test. The methodology used to characterize MTF was a well-established technique commonly referred to as a knife edge response (KER) measurement. The KER data were then analytically processed into MTF.

The KER function was obtained by differentiating the Line Spread Function (LSF); a one-dimensional slice through the optical system Point Spread Function (PSF). The Fourier transform of the LSF yields the complex, one dimensional Optical Transfer Function (OTF) of the system. The magnitude of the OTF gives the MTF for the two scanned directions. Each KER scan typically sampled a ±1.36° region in the FOV, with a step size of .00218°. The KER scan data were exported as a series of uncompressed 16-bit images, which were then post-processed to generate the respective KER functions and processed into MTF. The PSF and MTF results are presented in Sect. 4.4.2.

A Test Collimator System (see Sect. 4.2.1) was used for the KER/MTF measurements, as well as FOV, pointing, and focus optimization during instrument integration. A hexapod system, located under the E-THEMIS instrument, was added to the test system to enable the high accuracy (±2 μrad) angular scans needed for the KER measurements. The KER scans were automated and performed along-track and cross-track at three FOV locations in each spectral band, for a total of 18 MTF measurements across the full instrument FOV.

A STOP analysis (Structural Thermal Optical Performance) was performed to quantify the impact of the worst case operational thermal environment on MTF and pointing. The results of the analysis indicated the need for a more thermally isolated and structurally compliant (flexure based) mounting interface between the E-ETHEMIS feet and the deck. The updated mechanical/thermal design was evaluated via STOP analysis thus verifying that the on-orbit MTF and pointing requirements would be met with sufficient margin.

To fully verify the E-THEMIS instrument pointing requirements, the instrument static boresight was characterized using the Test Collimator System in combination with additional metrology equipment. The angular relationship between the instrument boresight, alignment cube, and instrument mounting feet was determined and delivered in a report to the project to facilitate spacecraft integration and alignment. These measurements were repeated before and after vibration thermal vacuum testing to confirm the optical stability.

4.1.2 Calibrated Radiance

The E-THEMIS radiometric performance is determined by the instrument characteristics and the calibration methodology. E-THEMIS will be calibrated in flight using a two-temperature calibration method that utilizes deep space and the internal calibration target to calibrate each pixel in each spectral band. The internal calibration target (“cal flag”) is between the detector/filter assembly and the telescope optics, so observations of the cal flag do not include the telescope. Therefore, the intensity must be adjusted between the external views of space or the target (e.g. Europa) and the internal cal flag to account for attenuation by, and thermal emission from, the optics using their known reflectivity/emissivity and measured temperature. The magnitude of this correction is small because these gold-plated mirrors have very low emissivity (<0.015), and their temperatures will be accurately measured in flight. This same calibration approach is used for THEMIS, but the E-THEMIS has the significant added advantage of being able to routinely view space as a second calibration target.

Based on the tight packaging of the E-THEMIS optical design, the field stop is located at the entrance of the FPA radiation shield (Fig. 13). As a result, the observations of the cal flag and space/target differ significantly, with the external views including both the desired radiance through the telescope as well as the radiance from the telescope housing (“wall”). Fig. 17a shows a schematic optical layout of the instrument, illustrating the different view angles seen by the detector. These include the angular size ($\Theta$) of the radiation shield (shield), telescope (tele), and housing (wall). Converting to the solid angles ($\Omega$) seen by the detector gives $\Omega _{\mathrm{shield}}$, $\Omega _{\mathrm{tele}}$, and $\Omega _{\mathrm{wall}}$. Fig. 17b shows a cross-section through the E-THEMIS mechanical drawing, including representative ray paths in both the along- and cross-track directions. The E-THEMIS optical design results in significantly different view factors in the different directions.

Fig. 17a

Solid angle view factors as seen from the detector. A) schematic representation illustrating the solid angle of the radiation (rad) shield, the housing (wall) and the telescope (tele). When the cal flag is inserted in obscures the view to the telescope and wall

Fig. 17b

Modeled ray traces of the radiance from the telescope (green), housing (blue) and rad shield (red) in cross sections in the along-track and cross-track directions

With these definitions, the measured fluxes ($F$ in W m⁻²) of the target, space, and cal observations are given by:

$$\begin{aligned} F_{\mathrm{target}} ={}& \varepsilon _{\mathrm{shield}} B_{\mathrm{shield}} \Omega _{\mathrm{shield}} + \left ( \varepsilon _{\mathrm{target}} B_{\mathrm{target}} R_{ext} \tau _{\mathrm{optics}} + I_{\mathrm{optics}} \right ) \Omega _{\mathrm{tele}} \\ &{}+ \varepsilon _{\mathrm{wall}} B_{\mathrm{wall}} \Omega _{\mathrm{wall}} \end{aligned}$$

(1a)

$$\begin{aligned} F_{\mathrm{space}} ={}& \varepsilon _{\mathrm{shield}} B_{\mathrm{shield}} \Omega _{\mathrm{shield}} + \left ( \varepsilon _{\mathrm{space}} B_{\mathrm{space}} R_{\mathrm{ext}} \tau _{\mathrm{optics}} + I_{\mathrm{optics}} \right ) \Omega _{\mathrm{tele}} \\ &{} + \varepsilon _{\mathrm{wall}} B_{\mathrm{wall}} \Omega _{\mathrm{wall}} \end{aligned}$$

(1b)

$$\begin{aligned} F_{\mathrm{cal}} ={}& \varepsilon _{\mathrm{shield}} B_{\mathrm{shield}} \Omega _{\mathrm{shield}} + \varepsilon _{\mathrm{cal}} B_{\mathrm{cal}} \Omega _{\mathrm{tele}} + \varepsilon _{\mathrm{cal}} B_{\mathrm{cal}} \Omega _{\mathrm{wall}} \end{aligned}$$

(1c)

where:

F = measured flux (W m⁻²)

B = Planck function intensity (radiance) (W m⁻² sr⁻¹)

$\epsilon =$ emissivity

I = intensity (radiance) including emissivity (W m⁻² sr⁻¹)

R$_{\mathrm{ext}} =$ reflectivity of the external mirror (thermal vacuum testing only)

$\tau _{\mathrm{optics}} =$ total telescope optical throughput

space = space or space simulation target

cal = internal calibration flag

target = external scene (e.g. Europa or thermal vacuum target)

Note that the radiances in Eq. (1a)–(1c) are bandpass averages computed by convolving the filter, window, and detector responses (Sect. 4.3) with the Planck function and integrating across each filter wavelength range.

Assuming that all of the emitted target intensities are isotropic, then:

$$ I_{\mathrm{target}} = \frac{F_{\mathrm{target}}}{\pi} $$

$$ I_{\mathrm{space}} = \frac{F_{\mathrm{space}}}{\pi} $$

$$ I_{\mathrm{cal}} = \frac{F_{\mathrm{cal}}}{\pi} $$

Let:

$$ a= \frac{\varepsilon _{\mathrm{shield}} \Omega _{\mathrm{shield}}}{\pi} $$

$$ b= R_{\mathrm{ext}} \tau _{\mathrm{optics}} $$

$$ c= \frac{\Omega _{\mathrm{tele}}}{\pi} $$

$$ d= \frac{\Omega _{\mathrm{wall}}}{\pi} $$

With these definitions Eq. (1a)–(1c) becomes:

$$\begin{aligned} I_{\mathrm{target}} &= \mathrm{a} B_{\mathrm{shield}} + bc\varepsilon _{\mathrm{target}} B_{\mathrm{target}} + cI_{\mathrm{optics}} +d \varepsilon _{\mathrm{wall}} B_{\mathrm{wall}} \end{aligned}$$

(2a)

$$\begin{aligned} I_{\mathrm{space}} &= \mathrm{a} B_{\mathrm{shield}} +bc \varepsilon _{\mathrm{space}} B_{\mathrm{space}} + cI_{\mathrm{optics}} +d \varepsilon _{\mathrm{wall}} B_{\mathrm{wall}} \end{aligned}$$

(2b)

$$\begin{aligned} I_{\mathrm{cal}} &= \mathrm{a} B_{\mathrm{shield}} + c\varepsilon _{\mathrm{cal}} B_{\mathrm{cal}} + d\varepsilon _{\mathrm{cal}} B_{\mathrm{cal}} \end{aligned}$$

(2c)

The measured signal output from the instrument is a 14-bit integer data number (DN) whose value is a function of the intensity ($I$) reaching the detector. Assuming a linear relationship between input intensity and output DN, which was verified in thermal vacuum testing (Sect. 4.4.4), then the DN is given by:

$$ DN=IRF*I+\mathrm{offset} $$

where IRF is the instrument response function.

Observations of the internal cal target and space can be combined to determine the IRF and offset, giving:

$$\begin{aligned} IRF&= \frac{DN_{\mathrm{cal}} - DN_{\mathrm{space}}}{I_{\mathrm{cal}} - I_{\mathrm{space}}} \\ \end{aligned}$$

(3a)

$$\begin{aligned} \mathrm{offset}&= DN_{\mathrm{space}} - I_{\mathrm{space}} *IRF \end{aligned}$$

(3b)

Finally, the desired quantity, $\epsilon _{\mathrm{\mathit{target}}} B_{\mathrm{\mathit{target}}}$, is given by:

$$ \varepsilon _{\mathrm{target}} B_{\mathrm{target}} = \frac{\frac{DN_{\mathrm{target}} -\mathrm{offset}}{IRF} - \mathrm{a} B_{\mathrm{shield}} - cI_{\mathrm{optics}} -d \varepsilon _{\mathrm{wall}} B_{\mathrm{wall}}}{bc} $$

(4)

In Eq. (4) the following fifteen parameters must be measured, modeled, or derived:

Ωshield, Ωtele, Ωwall	Modeled from raytrace
ϵshield, ϵwall, ϵcal	Derived
Rext	Derived
Tshield, Twall, Tcal	Derived using measured thermistor temperatures
Ioptics	Derived using measured thermistor temperatures and the telescope mirror reflectivity
τoptics
Diamond window transmission	Measured
Filter transmission	Measured
Telescope mirror reflectivity	Measured
Detector response	Measured (5–25 μm); derived (25–100 μm)

The nine derived parameters were determined using a combination of measured values and the comparison of the measured target temperature with that derived from the calibration of the E-THEMIS observations. For example, $\epsilon$_wallB_wall, and other similar terms that depend on both the surface emissivity (e.g., $\epsilon$_wall) and temperature (e.g., T_wall) were initially estimated using emissivity measurements of the surface coatings and the thermistor temperatures from the appropriate locations. These terms were adjusted as necessary until the instrument-derived target temperature matched the measured temperature. These adjustments were necessary due to the difficulty in directly modeling the emission from the complex baffles on the interior of the housing at low emission angles and the potential differences between the temperatures of the radiating housing surfaces and the temperatures measured by thermistors embedded within the housing. The data used for these analyses were acquired in thermal vacuum testing at five different instrument temperatures and eight target temperatures (Sect. 4.2.3). Section 4.4 provides a discussion of the verification of the modeled, measured, and derived instrument parameters and the sensitivity in the E-THEMIS absolute temperature accuracy to uncertainties in their values.

Experience with the THEMIS microbolometer array has shown that the IRF remains constant under normal operating conditions (<1% variation has been seen over the life of the THEMIS mission), but changes may occur to the E-THEMIS IRF over time due to detector degradation from radiation effects in the extreme Europa environment. Observations of space and the cal target at the beginning and end of each flyby will be used to determine the IRF. These observations will be linearly interpolated to determine the IRF throughout the flyby and trended over the mission to monitor any changes in the instrument performance.

The instrument radiance terms in Eq. (4) (e.g., B_shield, B_wall) vary with instrument temperature and are modeled using the eight thermistors mounted throughout the Sensor Assembly housing. Thermal modeling, together with THEMIS flight experience, shows that the housing will only vary by 1-4 K throughout a flyby and will vary linearly in time over 10–20-minute periods. This variation will be accounted for by acquiring ∼2 sec observations of the cal flag at ∼10-minute intervals to verify and adjust, if necessary, the instrument radiances throughout each flyby.

4.2 Pre-Delivery Characterization and Testing

The testing of E-THEMIS prior to delivery to the NASA Jet Propulsion Laboratory (JPL) was done at ASU and consisted of 1) component level characterization; 2) ambient performance testing; 3) environmental testing; and 4) thermal vacuum testing and radiometric performance characterization. E-THEMIS was assembled, tested, and calibrated in the ASU ISO Class 7 (class 10,000) cleanroom in building ISTB4 on the ASU Tempe campus, with Class 6 (1,000) flow benches for component assembly (Christensen et al. 2018). E-THEMIS calibration in both ambient and thermal vacuum conditions was done using test equipment that was calibrated to NIST standards on a routine basis. Bench-level E-THEMIS testing consisted of piece-part and system-level testing of each sub-assembly under ambient conditions, followed by system performance testing that was conducted before and after each environmental test and throughout thermal-vacuum testing. Ambient tests determined the instrument functional performance, the field-of-view definition and alignment, the out-of-field response (encircled energy), the modulation transfer function, and verified the command and data interfaces. The thermal vacuum calibration testing determined the instrument response function in vacuum over the expected range of instrument temperatures, the emissivity and temperature of the internal calibration blackbody and housing, and the radiometric precision and accuracy.

4.2.1 Optical Test Equipment and Facilities – ASU

The Test Collimator System (Fig. 18a–18c) was central to verifying the E-THEMIS flight instrument optical performance requirements which included MTF, pointing, FOV, IFOV and stray light. The f/4, 8” aperture test collimator was used in tandem with a hexapod system to enable very accurate (±2 μrad) angular scans of the knife edge targets, located at the collimator focal plane. The KER scans were performed along-track and cross-track at three FOV locations in each spectral band, for a total of 18 MTF measurements across the full instrument FOV. An assortment of targets located at the collimator image plane were utilized to facilitate the different measurement modes. Knife edge targets were used for the MTF measurements, pinholes for FOV mapping, line sources for verifying IFOV profiles and centroid locations in the FOV with respect to the instrument boresight, and small obscurations for stray light detection.

Fig. 18a

E-THEMIS optical performance collimator test equipment. a) Side view. The arrows represent up/down (elevation) motion of the alignment telescope

Fig. 18b

Top view. The arrows represent left/right (azimuth) motion of the alignment telescope

Fig. 18c

E-THEMIS Test Collimator System

The E-THEMIS integration and alignment onto the spacecraft deck required accurate knowledge of the instrument boresight with respect to the instrument mounting plane, which goes through the feet of the instrument (Fig. 10). The necessary reference data were acquired using a test system that included a calibrated granite surface plate, a digital theodolite and other support optics. Using this test configuration, the angular relationship between the instrument alignment cube and feet (mounting plane) in elevation, azimuth, and yaw, was measured with a precision of 1–2 arc-seconds and a measurement uncertainty of ±5 arc-seconds. The Test Collimator System was then used to transfer the instrument optical boresight to the alignment cube, thus establishing a transformation matrix for the E-THEMIS pointing vector to the spacecraft platform. Finally, the test setup enabled the instrument pointing stability to be accurately verified throughout the environmental test program.

4.2.2 Radiometric Test Equipment and Facilities – ASU

The absolute radiance calibration depends on the knowledge of the cal target’s emissivity and temperature, which was determined in thermal vacuum testing using two blackbody calibration unit (BCU) reference targets (Fig. 19, Christensen et al. 2018) that were placed inside the vacuum chamber (Fig. 20). The absolute temperature of these targets was determined using precision thermistors that were NIST-calibrated to ±0.1 °C. Their emissivities were determined to be 0.9989 ±0.0005 based on the spectral properties of the PT-401 paint and the analysis of a cone blackbody (Bedford 1988; Prokhorov et al. 2009). The temperature of the primary, secondary, and tertiary mirrors was determined using NIST calibration of the flight thermistors mounted to these elements, and the reflectivity was determined using laboratory measurements of witness samples of the gold coatings that were applied to the optical surfaces.

Fig. 19

The E-THEMIS Blackbody Calibration Unit (BCU) targets seen mounted in the ASU thermal vacuum test facility

Fig. 20

The Thermal Vacuum Test Facility in ASU’s School of Earth and Space Exploration that was used for E-THEMIS TVAC testing

Radiometric calibration was performed in ASU’s thermal vacuum infrared calibration facility (Fig. 20). The vacuum chamber has a thermally controlled shroud that can be cooled to liquid nitrogen temperatures to simulate the space background environment, a temperature-controlled enclosure for the SA that was used to simulate the expected in-flight sensor temperatures, and a separate thermal enclosure for the VE that are in the spacecraft vault with different temperature limits (Fig. 21). Thermostatically controlled heaters and liquid-nitrogen-cooled plates provided the capability to cool and heat these enclosures to the required temperatures during thermal balance testing, thermal cycling, and radiometric calibration. The rigidity and complexity of the 3.4-m cables from the sensor to the VE precluded rotating the sensor to view the two external BCU blackbody calibration targets, so the sensor aperture was pointed between the two BCU targets using an external, bare-gold-coated mirror mounted on a vacuum-compatible rotary stage (Fig. 21). The sensor and mounting bracket were fully blanketed with flight-like Multi-Layer Insulation (MLI) thermal blankets to simulate the spacecraft nadir deck thermal configuration. Ground Support Equipment (GSE) controlled the E-THEMIS, enclosures, BCU targets, and rotary stage via cabling through the chamber feedthroughs. More than 60 thermistors mounted throughout the chamber, the enclosures, and the BCU targets provided the thermal data needed for thermal balance modeling and absolute radiometric calibration.

Fig. 21

The E-THEMIS thermal vacuum test equipment. (a) configuration and (b) TV chamber equipment

4.2.3 Pre-Delivery Test Program

Throughout the integration and test phase an Instrument Functional Test (IFT) was performed using the E-THEMIS ambient target and/or the two BCU targets to provide trending of instrument performance. An Instrument Performance Test (IPT) was performed using the ambient and/or BCU targets and provided the baseline radiometric performance assessment for the instrument. These tests were also performed before and after each environmental test; no significant changes in the instrument performance were observed following any environmental test.

E-THEMIS was radiometrically calibrated during thermal vacuum (TVAC) testing at instrument temperatures of 0, 8, 15, 25, and 31 °C to simulate the expected in-flight operating temperature range; the 0 °C was not saved in the non-volatile memory. Calibration tests were performed by viewing the two BCU targets, one set to a temperature of 100 K using liquid nitrogen to provide the best available simulations of the space observations and the second BCU set to temperatures of 100, 125, 180, 150, 180, 210, 240, 270, and 310 K to span the range of target temperatures.

4.3 Radiometric Performance Modeling and Expected Results

The expected E-THEMIS radiometric performance was determined using an instrument model that incorporates the detector response, optical design, detector window and filter transmission, mirror reflectivity, and pixel aggregation. The net instrument throughput ($\tau$) is a function of the measured diamond window and filter transmission ($t$) and the measured/modeled value for the detector response, all of which are a function of wavelength:

$$ \tau = t_{\mathrm{filter}} t_{\mathrm{window}} response_{\mathrm{detector}} $$

Fig. 22 gives the values for each of these parameters.

Fig. 22

The measured and derived E-THEMIS instrument optical properties

The band-integrated radiance ($I$ in W m⁻² sr⁻¹) reaching the detector from a scene at temperature ($T$) is given by the Planck function ($B$) integrated across a E-THEMIS filter bandpass from $\lambda _{1}$ to $\lambda _{2}$:

$$ I= \int _{\lambda 1}^{\lambda 2} B \left ( T, \lambda \right ) \tau \left ( \lambda \right ) d\lambda $$

(5)

The radiance versus scene temperature function was determined for each of the three E-THEMIS filters. Because the internal cal flag observations do not include the telescope, the reflective loss due to the bare gold on each of the three telescope mirrors is modeled separately. The gold reflectivity was measured using witness samples and is 0.985 ±.002 across the E-THEMIS bandpasses, giving an additional intensity loss from external observations of (0.985)$^{3} = 0.956$.

The power ($P$ in $W$) measured at the detector is given by:

$$ P=I A_{\mathrm{detector}} \Omega _{\mathrm{telescope}} $$

(6)

where $A$ is the detector area and $\Omega$ is the solid angle of the telescope.

The standard metric for a thermal instrument performance is the noise equivalent delta temperature (NEDT). An instrument performance model was constructed to model NEDT as a function of scene temperature using the measured NEDT of the detector and the modeled power in each band. The E-THEMIS flight detectors have an average measured NEDT of 0.33 °C measured in an f/1 system ($\Omega =0.66$ sr) at room temperature viewing a 300 K scene. This measured performance is used to determine the detector noise equivalent power (NEP in W), giving an NEP value of 4.95e⁻¹² W. NEP for a microbolometer is constant with scene radiance because the bolometer noise is not a function of photon flux, as it is for photon-limited photovoltaic detectors where the shot noise component of the flux dominates.

The NEDT is given by:

$$ NEDT= \frac{NEP}{\frac{dP}{dT} \sqrt{N_{TDI}} \sqrt{N_{\mathrm{frames}}} \sqrt{N_{\mathrm{bining}}}} $$

(7)

where $dP$/$dT$ is the derivative of power with temperature, computed at the scene temperature of interest ($T_{1}$) and at a small delta temperature ($T_{2}$) using Eq. (6), and is given by:

$$ \frac{dP}{dT} = \frac{\left ( P_{2} - P_{1} \right )}{\left ( T_{2} - T_{1} \right )} $$

$N_{\mathit{TDI}}$ and $N_{\mathit{frames}}$ are the number of TDI integrations and sequential frames respectively that are co-added to produce each image, and $N_{\mathit{binning}}$ is the number of spatial pixels that are subsequently aggregated in the instrument prior to downlink to the Earth. Each of these values can be adjusted by command and used to improve (decrease) the NEDT in each image.

Using this performance model, the expected NEDT values for each band are given in Fig. 23 for the case of no summing (TDI = 1; aggregation = 1 × 1) over the range of expected Europa temperatures. Also shown are the results for representative values of TDI (16 and 128) with the nominal spatial aggregation of 3 × 3, 4 × 4, and 5 × 5 pixels in Bands 1, 2, and 3, respectively. The NEDT required for E-THEMIS to achieve its science goals was set to be 2 K for regional observations and 1 K for global observations for scene temperatures ≥90 K. These differences are due to the assumptions regarding the number of TDI co-adds that would be possible for the regional observations (16) compared to a much higher number (128) that will be accumulated during the Europa global scan observations acquired on each flyby (see Sect. 5.2). As seen in Fig. 23, the expected E-THEMIS NEDT meets these requirements with significant margin. A discussion of the measured NEDT results and the validation of the E-THEMIS instrument model are given in Sect. 4.4.

Fig. 23

The expected (modeled) noise equivalent delta temperature (NEDT). a) TDI of 1 and no spatial aggregation. b) Regional observations: 16 TDI and band-dependent spatial aggregation. c) Global observations: 128 TDI and band-dependent spatial aggregation. Note the change in y-axis scale between panels. The requirements that must be met in at least one band for temperatures ≥90 K for 16 TDI (regional) and 128 TDI (global) observations are also shown, demonstrating that E-THEMIS readily meets these requirements

The expected E-THEMIS absolute accuracy was determined using a calibration model developed and validated on several prior instruments (Christensen et al. 2004, 2018; Edwards et al. 2021). As with OTES (Christensen et al. 2018), the E-THEMIS instrument has an internal calibration target located behind the field stop. The basic calibration approach is given in Eq. (2a)–(2b) for the three observations of the scene (nominally Europa), space, and the cal surface. The internal cal target is similar to that used on THEMIS and has an emissivity of 0.998 ± 0.002 over the E-THEMIS wavelength range and is its temperature is known to ±0.3 °C.

An assessment of the calibration error associated with expected uncertainties in each of the parameters in Eq. (4) was studied using Monte Carlo methods. The critical parameters are the emissivity and temperature of the calibration flag and the instrument housing. For an instrument operating temperature of 10 °C, worst-case uncertainties of +0.0025 in emissivity, +0.5 K in cal flag and housing temperatures, and 1 K in the optics temperature, equates to absolute uncertainties of 1.5 and 1.8 K at 90 K in Bands 2 and 3, respectively, which meet the 2 K requirement in both bands.

4.4 Calibration Results

4.4.1 Pointing and Field of View

As described in Sect. 4.1.1, the methodology used to verify the E-THEMIS instrument on-orbit pointing requirements involved both measurement and STOP analysis. The calculated on-orbit pointing accuracy is shown in Table 3. This is a conservative prediction (model uncertainty factor of 1.5) that includes ground-based measurement uncertainties, measured fixed offsets, 1-G post-launch mechanical release, and the worst case on-orbit thermal predictions that were used in the STOP analysis. The performance margins in elevation, azimuth and yaw have significant margin relative to their required values.

Table 3 On-orbit Pointing Accuracy

The Test Collimator System (Sect. 4.2.1) was used to characterize the E-THEMIS instrument full FOV and pixel level IFOV. For the full FOV verification, a 1-mrad pinhole aperture was scanned across the boundaries between the active imaging area and masked areas of the FPM to map out the along-track and cross-track FOV in each band. The measured FOV (FWHM points) and the corresponding requirements are summarized in Table 4. Table 5 gives the geometric individual fields of view for spatially aggregated pixels in each band.

Table 4 Field of View

Table 5 Geometric IFOV

The IFOV requirement is a geometric definition determined by the physical pixel size and the measured EFL (effective focal length) of the telescope. The single pixel IFOV in radians is then given by:

$$ \mathrm{IFOV} = \tan ^{-1} \left ( \frac{\mathrm{Pixel\, Size}}{\mathrm{efl}} \right ) $$

Using the single microbolometer pixel of 0.0114 mm square (RVS data), and the measured telescope EFL of 105.2 mm ± 0.05 mm, we obtain a single pixel IFOV of 0.1084 mrad.

Knowledge of the as-built instrument diffraction IFOV response, or line spread function, is needed for image modeling. The LSF was measured using a nichrome wire line source target at multiple locations across the E-THEMIS FOV. The line source measurements, unlike the LSF produced by the MTF analysis, were referenced directly to the instrument boresight, thus providing centroid locations for the image model and for cross checking distortion against the optical model. Representative measured response plots are given in Fig. 24a for a single pixel in Band 2. These line source measurements, as well as the LSF results generated as part of the MTF analysis process, correlate well with the E-THEMIS optical models. On the basis of this correlation, the single-pixel point spread function (PSF) was modeled using CodeV optical software for each band and given in Fig. 24b. The shape and FWHM compare well with the measured Band 2 IFOV response shown in Fig. 24a, and the measured LSF profiles correlate well with the modeled PSF’s due to the near diffraction limited performance of the as-built optical system.

Fig. 24a

E Representative measured E-THEMIS line source response for a single pixel measured in the along-track (AT) and cross-track (XT) optical directions. Results are shown for the center pixel of Band 2

Fig. 24b

Modeled PSF for each band measured in the along-track and cross-track optical directions. Results are shown for the center pixel of each filter

4.4.2 Modulation Transfer Function

The measured MTF results for the delivered flight instrument are given in Table 6 and meet the requirements with comfortable margin in all bands. The MTF for Band 1 (Fig. 25) shows that the E-THEMIS flight instrument meets the MTF optical performance requirement with margin. This data set was taken at the center of Band 1 and is representative of the MTF across the full FOV. The Band 2 and 3 MTF results are similar; Band 1 is the shortest wavelength band and therefore the most sensitive to alignment and optical wavefront errors that impact MTF. This is consistent with the Band 2 and 3 data, which show increasing margins with wavelength.

Fig. 25

Measured optical Modulation Transfer Function (MTF) for a single pixel in Band 1 in the center of the filter. The “plus” symbols represent the required E-THEMIS system-level optical performance, which is met with margin

Table 6 Modulation Transfer Function (MTF) results

4.4.3 Instrument Response

Linearity

The instrument response function (IRF) characterizes how the E-THEMIS instrument converts the spectral radiance from the scene and the instrument itself into an output voltage from the focal plane that is digitized as a 14-bit data number (DN). The IRF is computed for each pixel using the assumption that this conversion from radiance to DN, while slightly different for each pixel, is a linear function (Sect. 4.1.2). Fig. 26 shows examples of the measured DN’s in each band as a function of radiance on the detector for a single instrument temperature, together with a linear fit to these data. The incoming radiance has been computed using Eq. (2a)–(2c) with modeled values of the solid angles ($\Omega$) seen by the detector for the housing and telescope using the values for $T_{\mathrm{wall}}$ and $T_{\mathrm{shield}}$ determined from the instrument thermistors and $\epsilon _{\mathrm{wall}}$ and $\epsilon _{\mathrm{shield}}$ determined from a best fit to the TVAC data collected for all five instrument temperatures and the eight blackbody temperatures (Table 7).

Fig. 26

The E-THEMIS Instrument Response Function (IRF) measured in vacuum at a single instrument temperature (−0.4 °C) viewing the BCU-2 target whose temperature varied from 100 K to 310 K. (a) Band 1. (b) Band 2. (c) Band 3. The BCU temperatures have been converted to band-integrated radiance (W m⁻² sr⁻¹)

Table 7 Instrument properties

In the initial analysis Band 3 had a significantly higher than expected departure from linearity (Fig. 26). Several possible causes were investigated, including stray light, optical crosstalk beneath the filter substrates, electrical crosstalk, and a true non-linear detector response. Close attention was given to optical crosstalk between the filters because the microbolometer detector material reflects more than 30% of the incoming radiance at long wavelengths (Fig. 22) and the filter substrates are located outside the detector dewar approximately1-mm from the detector surface, allowing the potential for radiance that passed through one filter (e.g. Band 1 7–14 μm) to be multiply reflected beneath the filters and end up falling as out-of-band radiance on the Band 3 detectors. Analysis confirmed that this effect is >100x smaller than the measured excess Band 3 radiance, and analyses showed that none of the other processes could produce what is observed in Band 3 and only Band 3 (Fig. 26).

In discussions with the Band 3 filter vendor, it was noted that the polypropylene substrate for the copper mesh that provides the primary filter properties has significant absorption in the 5–13 μm region and that some of the out-of-band energy rejection is accomplished via absorption, rather than reflection. This absorbed energy will be re-radiated, approximately half of it upward and out the telescope, but half of it downward toward the detector. Because the substrate is beneath the copper mesh, this energy is no longer limited by the filter bandpass and reaches the detector. As the scene temperature increases the amount of energy absorbed, and re-emitted, by the filter increases, producing the observed higher-than-expected DN signal as the scene temperature increases. This effect is only significant for relatively warm temperatures (>∼200 K) where the peak of the Planck emission is in the 5–13 μm region. However, it is significant at the expected instrument, and therefore cal flag, temperature and must be accounted for in the Band 3 cal flag observations. The effect has been successfully modeled using the measured polypropylene absorption convolved with the Planck radiance from the scene and weighted by the fraction of the energy reaching the detector through the telescope. Only the scene radiance is corrected for in this model because the background radiance remains constant in all observations when the instrument temperature remains constant. Fig. 27 shows the magnitude of the effect as a function of scene temperature, weighted by the solid angle of the telescope seen by the detector. Fig. 28 gives the DN versus radiance for Band 3 before and after the correction has been applied. The magnitude of the correction matches the apparent excess radiance very closely, and after incorporating the filter re-emission, the DNs have the expected linear relation with the total radiance reaching the detector (Fig. 28b). All of the Band 3 results presented in the subsequent sections have been corrected for this scene-dependent filter absorption and re-emission. We note that these metal mesh filters were originally designed for cryogenic applications where re-emission from the filter would be negligible, and that despite this additional calibration complexity the metal mesh filter technology is the best available method for long-wavelength spectral separation.

Fig. 27

The computed Band 3 filter re-emission, weighted by the solid angle of the telescope as seen from the detector, as a function of scene (BCU-2) temperature

Fig. 28

Band 3 instrument response function. a) Band 3 without filter re-emission correction. b) Band 3 with filter re-emission correction

The requirement for linearity was 10% of the maximum signal (DN) in each band. Fig. 29 gives the calculated percent departure from linearity in all three bands, using a more appropriate (and larger) value derived from the percent error relative to the measured DN. The maximum deviation in any band is <1.5%, well below the requirement and within the expected linear performance typical of microbolometer detectors and seen previously in the Mars THEMIS instrument (Christensen et al. 2004).

Fig. 29

Signal linearity specified as a percent deviation of the measured DN from linearity

Instrument response variation with temperature

In addition to demonstrating linearity, the slope of the DN vs. radiance relationship (e.g., Fig. 26) is the instrument response function, measured in DN / (W m⁻² sr⁻¹). The focal plane temperature is held to within ∼0.002 K using the TEC, but this temperature is set to be close to the instrument temperature to minimize the power required by the TEC for temperature control. The microbolometer detector performance is expected to vary with temperature and thus with instrument temperature, and this relationship is shown for each band in Fig. 30 for the five instrument temperatures measured during TVAC testing. E-THEMIS performs best at low temperatures; the current spacecraft and E-THEMIS thermal models indicate that the expected operating temperature at Europa will be in the –10 °C to 0 °C range, which is optimal for instrument performance. The actual operating temperature will remain uncertain, however, until the spacecraft thermal balance testing is completed, and the thermal models are validated. It is important to note that the IRF will be determined directly in flight using observations of space and the internal cal flag, and the TVAC data are only used to characterize the expected instrument performance.

Fig. 30

Instrument response versus instrument temperature

Uniformity

Another key element of the IRF is the uniformity across the detector array in each band. Fig. 31 shows the IRF distribution, with a 1-sigma variation of only 0.3%, 0.4% and 2% in bands 1, 2, and 3 respectively. This narrow distribution of the performance of the ∼125,000 individual detector elements under each filter is typical for the quality of the manufacturing process control in modern microbolometers.

Fig. 31

Instrument response uniformity

4.4.4 Absolute Accuracy

Once each of the terms in Eq. (4) have been determined and the modeling of the Band 3 filter re-emission has been applied, it is possible to combine the space, cal flag, and target observations to solve for the target emitted radiance using Eq. (4). An example of the application of these corrections is shown in Fig. 32 for a set of target (BCU-2) and cal flag observations acquired at an instrument temperature of −0.4 °C. If all of the radiance terms have been correctly accounted for, then the radiance from each view (target and cal flag) should fall on a single linear function. The observed linear behavior is in part due to the fact that the corrections were determined using these data, but as a consistency check the same corrections produce linear results when applied at all instrument and scene temperatures (Fig. 33). The data at each instrument temperature, although having instrument-temperature-dependent differences in the value of the IRF slope, are also represented by linear functions, providing additional confidence in the absolute temperature calibration model and the values of the selected parameters.

Fig. 32

Instrument response function – with cal flag observations (green +). Data were collected at an instrument temperature of 0.4 °C

Fig. 33

Band 2 instrument response function at four instrument temperatures measured in TVAC testing. Each plot represents a different instrument temperature (Tinst). (a) Tinst $=-0.4$ °C. (b) Tinst = 7.6 °C. (c) Tinst = 23.9 °C. (d) Tinst = 31.9 °C

The sensitivity of the scene brightness temperature, $T_{b}$, to the derived calibration parameters can be studied by computing the derivative of $T_{b}$ with each of the key parameters (Table 8). The largest contributor to the uncertainly in the derived radiance is the emissivity of the telescope housing ($\epsilon _{\mathrm{wall}}$). This term cannot be determined directly given the complex geometry of the housing (see Sect. 4.1.2) and $\epsilon _{\mathrm{wall}}$ was determined by varying it to give the best fit to data acquired for all instrument and target temperatures (Table 7). As seen in Table 8, the brightness temperature error is <0.15 K for reasonable errors (±0.005) in the wall emissivity in Bands 2 or 3 at 90 K. These small errors are the (fortunate) result of the fact that Europa will be close to the temperature of the deep space observations used to determine the IRF. Thus, errors in the IRF that result from errors in the knowledge of the warm cal flag observations have a small effect at low temperatures.

Table 8 Brightness temperature (T_b) sensitivity

Signal (DN) errors are also significant, especially at low temperatures, with 1 DN being equivalent to 0.65 K at 90 K in Band 2 (Table 8). The DN can be measured precisely, but as discussed previously, its value is a function of the radiance from the scene and the radiance from the housing. Given the T⁴ dependence of emitted radiance on temperature, a change of 0.1 K in the instrument temperature equates to an absolute temperature error of ∼3 K in Band 2 at a typical Europa nighttime temperature of 90 K. Therefore, it will be essential to remove the effects of thermal drift in the instrument temperatures during each flyby. This removal will be accomplished using the measured housing temperatures, together with periodic observations of the internal cal flag as a proxy the instrument housing temperature. These measured and derived temperatures will then be used to adjust and remove the housing contributions to the measured radiances (Eq. (4)) throughout each flyby.

The derived, absolute brightness temperatures for the data acquired in thermal vacuum are given in Fig. 34a and the differences between these temperatures and the measured BCU temperature are given in Fig. 34b. Inspection of the raw E-THEMIS images showed relatively small (5-15) DN offsets from the image average around the edges of the images that are likely due to emission from the filter housing that has not yet been removed but will be in future improvements to the image processing pipeline software. To avoid these effects, only the DNs from pixels in columns 120 to 800 and rows 20 to 120 in each filter were averaged to produce the brightness temperatures shown in Fig. 34. Only Bands 2 and 3 are intended for use at the low Europa temperatures, so the large temperature errors seen in Band 1 at low temperatures are not relevant. The uncertainties associated with Band 3 filter re-emission likely are a primary contributor to the absolute temperature errors in this band, and these will be addressed in future analyses and observations (see Sect. 5). Band 2 thus provides the most accurate temperatures at the current stage of data analysis. The formal requirement for absolute temperature accuracy is ±2 K for temperature ≥90 K in at least one band. This requirement is currently met in Band 2 for some instrument temperatures but not all (Fig. 34b). It is unlikely that the error is truly a function of instrument temperature and is more likely the result of imperfect correction for the many factors that affect the absolute calibration. Improvements in these corrections will require further analysis and modeling. In the present data processing there are also significant (2–5 K) variations in the calibrated brightness temperature across each of the filters. These differences are likely due in part to thermal effects from the filter bezel; a correction for this effect will also be incorporated in future data processing.

Fig. 34

Brightness temperature accuracy. a) Derived temperature versus measured scene temperature for each band. b) Temperature error versus scene temperature for each band. The ±2 K absolute accuracy requirement for scene temperatures ≥90 K (dashed lines) is met in Band 2 for most instrument temperatures

A critical advantage for the E-THEMIS absolute calibration at the low Europa surface temperatures is the accuracy and stability of the low-temperature, deep space observation. Therefore, the calibration at Europa will be significantly better than the TVAC results because of the ability to observe deep space during the entry and exit phase of each flyby (see Sect. 5.2). The essentially zero radiance from space provides an excellent target to remove the background instrument radiances (Eq. (2a)–(2c)), all of which will be present in the Europa observations, and several are present in the cal flag observations. These radiance terms will be modeled using the measured instrument temperatures and the derived interior surface emissivities, but the ability to directly observe space provides an excellent means to validate and adjust, if necessary, the modeled radiance terms. In addition, deep space is also a perfectly uniform thermal source at the E-THEMIS sensitivity and the observations of space will be used for the initial “flat fielding” (CLE) operation where each pixel is set to the same DN value (see Sect. 3.2.5). This operation was performed for each E-THEMIS image acquired in the TVAC radiometric calibration, but the BCU target used as the “space” observation likely had small (0–1 K) thermal gradients across its surface, as well as small amounts of radiance reflected from the instrument and the chamber walls. These extraneous radiances are small due to the high emissivity of the BCU and the effort to control the BCU internal temperature (Sect. 4.2.2), but when attempting to determine the absolute temperature of a target at 100 K even these small radiance errors can be significant. For example, a BCU emissivity uncertainty of 0.005 (Sect. 4.2.2) reflecting an instrument temperature at 273 K (∼0 °C) results in an excess radiance error that is equivalent to a temperature error of 1.3 K in Band 2 when viewing a 100 K target. This effect will not be present in space. Finally, the space observations will not have the external mirror that had to be used in TVAC, thus removing an additional uncertainty from the calibration process.

In summary, the TVAC absolute temperature uncertainty of 2–3 K in Band 2 for temperatures ≥90 K is close to the 2 K requirement and is likely the worst case limit to the performance at Europa. Work on improving the Band 3 calibration is continuing, and improvements in the data processing algorithms and the ability to directly observe deep space will likely result in absolute temperature accuracy at Europa that is better in all bands than the results achieved to date.

4.4.5 Precision: Noise Equivalent Delta Temperature

The precision of the calibrated brightness temperature is a key performance metric and for some science applications, such as searching for and assessing the distribution of localized warm surfaces associated with endogenic heating, the relative temperature difference (i.e., the precision) can be more significant than the absolute temperature. The standard measure of precision in infrared imagers is the noise equivalent delta temperature (NEDT), which is a function of the detector noise and responsivity performance and the optical design and optical throughput. It can be lowered (i.e., improved) through temporal summing (TDI) and spatial aggregation, with the theoretical improvement set by the square root of the number of temporally and/or spatially summed observations. This improvement only applies to random noise and is therefore limited by the systematic noise of the system.

Fig. 35 gives a histogram of the measured NEDT for all pixels for a target temperature of 125 K in Band 2 for a single frame with no spatial aggregation. These data have a median NEDT of 1.8 °C, which is better than the modeled performance (Sect. 4.3) of 2.6 °C. The performance also shows excellent uniformity across the detector elements. Fig. 36 shows the improvement that is achieved using TDI, increasing from no temporal summing (TDI = 1) to a TDI of 32 for Band 2. The theoretical limit of $n^{0.5}$, where $n$ is the number of observations, is also shown for comparison. As expected, the data do not reach the theoretical limit, but do show significant, and continually improving, reduction in NEDT with increasing $n$. Instrument noise is inherently difficult to measure given that any changes in target and/or instrument temperatures contribute to a change in signal and thus the apparent noise. Therefore, the measured noise represents the upper limit of the true noise performance. Fitting the measured NEDT improvement with increasing $n$ using $n^{x}$ gives a value of $x$ of approximately 0.35; a similar value is obtained for all three bands and at other instrument temperatures. It is expected that higher values of TDI up to 128 are possible in the instrument and will be applied at Europa. Using the value of $x=0.35$ gives a noise reduction factor of 5.5 for a TDI of 128. Under the limitations of schedule during TVAC testing, data sets with the large number of frames needed to assess the performance 128 TDI were not collected under the necessary, highly stable thermal conditions. A similar analysis of spatial aggregation shows that the improvement is very close to the theoretical $n$^0.5 limit.

Fig. 35

Noise equivalent delta temperature (NEDT) in Band 2. Data are for a single frame viewing a 127 K target with no spatial co-aggregation. The standard deviation of the brightness temperature was computed for each pixel using successive temporal frames

Fig. 36

Noise equivalent delta temperature (NEDT) as a function of the number frames combined using TDI. The data were collected at an instrument temperature of 0.4 °C viewing a 127 K target a) The measured results together with theoretical limit of the n^0.5. b) The measured results together with a model assuming that NEDT improves as TDI^0.35

The comparison of the E-THEMIS instrument model predictions (Sect. 4.3) and the measured NEDT is shown in Fig. 37 for a single frame (TDI = 1) and no spatial aggregation. Given the large number of parameters that are required for such a model, and the uncertainties in many of those parameters, the agreement between the model and the actual performance is remarkably good. This agreement also demonstrates that the instrument model is successful in accurately predicting the performance of uncooled microbolometer instruments and can be used to predict the performance of future instruments. The nominal E-THEMIS operation assumes 3 × 3, 4 × 4, and 5 × 5 on-instrument pixel spatial aggregation in Bands 1, 2, and 3, respectively. These values were chosen as a compromise to meet the spatial resolution requirements and to fit within the nominal E-THEMIS data volume allocation. However, point spread functions, including diffraction, are smaller than the size of these spatially aggregated “super pixels”, and lower levels of on-instrument binning will be used whenever the data allocation permits.

Fig. 37

The measured NEDT versus scene temperature in all three bands for a single pixel, single frame with no temporal or spatial aggregation. Also shown are the predicted results (dashed lines) using the E-THEMIS instrument model

Fig. 38 gives the NEDT that is achieved through the combined use of both TDI and spatial aggregation, along with the instrument model predictions for the same conditions, assuming an $n$^0.35 improvement with TDI and $m^{0.5}$ with spatial aggregation, where m is 3, 4, and 5 for Bands 1, 2, and 3 respectively. The use of liquid nitrogen to cool the TVAC targets limited the lowest controlled target temperature to 100 K, so the expected NEDT values at 90 K can only be estimated by fitting and extrapolating the available data (Fig. 38a). The comparison of these fits instrument model is given in Fig. 39b. There is good agreement between the measured performance and the instrument model in Bands 1 and 2, with approximately 1.7x worse performance in Band 3 than the model predicts (Fig. 38b). The E-THEMIS Band 2 NEDT performance at the requirement conditions of 16 TDI and 4 × 4 spatial summing is 1.0 K based on the extrapolated fit to the measured data and 1.3 K using the instrument model (Fig. 38b); both estimates are well below the 2 K requirement for the regional observations (16 TDI) and close to the 1 K requirement for the global (128 TDI) observations. Modeling of a TDI of 128 gives in estimated NEDT of 0.6 K at 90 K, well below the 1 K requirement. The Band 1 performance also matches the model over the temperature range >140 K where it is designed to operate. Additional analysis, modeling, and Engineering Model data collection is on-going to understand the lower-than-expected performance in Band 3.

Fig. 38

E-THEMIS NEDT performance for all three bands at an instrument temperature of 0.4 °C. a) The measured NEDT versus scene temperature for 16 TDI and band-dependent spatial co-aggregation. Also shown is a best-fit model to the data that can be used to extrapolate the performance to lower scene temperatures than could be measured in TVAC. b) Comparison of the best fit to the measured performance and the E-THEMIS instrument model assuming $x=0.35$ (see text). The instrument model matches the performance well in Bands 1 and 2 but predicts ∼1.7x better (lower NEDT) performance in Band 3 than was measured

Fig. 39

E-THEMIS predicted precision (NEDT) performance. The Band 3 modeled NEDT values have been increased by 1.7x to match the measured data. a) The predicted performance for a TDI of 16 with band-dependent spatial summing. b) The predicted performance for a TDI of 128 with band-dependent spatial summing. In both cases the requirement is meet with significant margin in Bands 1 and 2

Fig. 39 summarizes the NEDT results for regional (16 TDI) and global (128 TDI) observations, giving the predicted performance using the E-THEMIS instrument model that has been adjusted to match the measured performance in Band 3 and extrapolated to scene temperatures that are lower than what was measured in TVAC. The mission requirement is for E-THEMIS to meet its performance in at least one band; E-THEMIS meets the requirement with margin in both Bands 2 and 3.

4.4.6 E-THEMIS System Performance

A system-level test of the E-THEMIS performance and the validation of the on-board TDI and spatial summing firmware was achieved using observations from the roof of the ISTB-4 building at ASU. An environmentally controlled and nitrogen-purged enclosure/cart was developed to transport E-THEMIS to the roof and ensure that it maintained its required cleanliness throughout the test. A precision rotatory stage was used to simulate the different angular ground motion rates throughout each Europa flyby, including the global scan (Sect. 5.2). Data were acquired in framing and TDI modes, with a TDI of 1, 4, 8, 16, and 64, line shifts of 1, 2, and 4, and spatial aggregation from 1 × 1 to 5 × 5. The rotary stage was set to the appropriate angular velocity for each line shift and was also set at a rate halfway between the optimal shift to simulate the worst case where the ground velocity is between the available integer line shifts. All acquired images were as expected, thus validating the on-board binning and summing algorithms.

Fig. 40 shows an example of these data for a portion of a single image, acquired in Band 1 with 16 TDI and no spatial aggregation. The Earth’s atmosphere has strong absorptions in the wavelength regions covered by Bands 2 and 3 so these data had limited utility for evaluating the system performance. Analysis of the Band 1 data confirm that E-THEMIS is in excellent focus and matches the expected optical performance. These data also confirm that there are no detectable “ghost” or straylight artifacts resulting from the optical design. Fig. 41 gives a color composite using Band 1 and 2 of nearby team members and the distant horizon. E-THEMIS is focused at infinity, so the human subjects are out of focus, but the horizon is clearly imaged. These data illustrate the strong atmospheric absorption in Band 2; there are spectral color differences in the individuals in the near field between Bands 1 and 2, but virtually no signal from the distant horizon in Band 2. Fig. 42 shows examples of temperature images acquired at 12:40 PM, 4:40 PM, and 6:20 PM (post-sunset), and illustrates the thermophysical information that is contained in thermal infrared images acquired at multiple times of day.

Fig. 40

E-THEMIS Band 1 image from the roof of building ISTB4 on the ASU campus. The data were acquired on a rotating stage to simulate ground velocities at Europa and with a TDI of 16. The image shows the ASU football stadium with the ASU logo and other stadium marking clearly visible in this thermal infrared image

Fig. 41

E-THEMIS color composite image of members of the instrument team, taken during the rooftop calibration test. Team members are out of focus, as the instrument is focused at infinity. Band 1 = cyan, Band 2 = red

Fig. 42

E-THEMIS Band 1 false-color temperature images acquired at local time of 12:40 PM, 4:40 PM, and 6:20 PM (post sunset). The warmest temperatures (red) are approximately 25 °C; the coldest temperatures (blue) are approximately 10 °C. Temperature changes due to varying solar illumination, thermophysical properties of the materials, atmospheric clouds, and path-length-dependent atmospheric absorptions are clearly seen

5 E-THEMIS Instrument Operations

5.1 Cruise Calibrations and Operations

E-THEMIS will be turned on and collect data of space and the internal calibration flag at regular intervals throughout the cruise phase to verify the instrument response and proper in-flight performance. E-THEMIS has four stored versions of the NUC tables that will work properly for instrument temperatures from ∼3 °C to 36 °C. If the flight operational temperature is outside this range, then an in-flight NUC computation will be required. This operation will need to be performed when E-THEMIS is within ∼±5 °C of its expected Europa flyby temperature and the new tables will be generated and stored in memory.

Europa Clipper will reach Jupiter’s orbit using gravitational assist flybys of Mars and Earth. These flybys present excellent calibration opportunities to collect data of extended targets with well known (especially in the case of Mars) surface temperatures and thermal emissivities. Observations of Mars would be particularly useful because of its very well characterized surface properties (e.g., Bandfield 2002; Rogers and Christensen 2003; Fergason et al. 2006a), its thin atmosphere, and the potential for possible simultaneous observations from the Odyssey THEMIS (Christensen et al. 2004), the Mars Reconnaissance Orbiter MCS (McCleese et al. 2007), and the Emirates Mars Mapper EMIRS (Edwards et al. 2021) instruments. As discussed previously there are many calibration parameters in Eq. (4) whose values have been modeled and estimated; observations of well-characterized targets would provide essential validation of these models. In addition, the TVAC data collected during radiometric calibration had a several key limitations that impact the calibrations (Sect. 4.2.3), including a lower limit on target temperature (∼100 K) set by the use of liquid nitrogen to cool the targets, the need for an external pointing mirror to view the TVAC targets, and the potential for reflected energy from the instrument and chamber contributing to the energy from the BCU targets. In-flight observations of Mars or Earth would remove both of these limitations.

5.2 Europa Operations

E-THEMIS will collect Europa data for several hours centered on each flyby. These data will consist of a mixture of TDI and framing observations. Framing mode will be used when the E-THEMIS footprint is moving with an angular ground velocity per 1/60-sec framerate that is significantly less than the E-THEMIS IFOV (0.114 mrad), so that one or more frames can be collected and co-added with less than one-pixel of image smear. TDI mode will be used when the ground velocity is higher than this value. As the ground velocity increases and the motion between frames is greater than a single row, a row-skipping methodology will be incorporated to match the ground motion. At altitudes below 100 km, where the scene moves faster than the six-pixel maximum row skip per frame, framing mode will again be utilized, with the resulting greater data volume, and individual frames will be downlinked and shifted and combined on the ground. All of these parameters are controlled from ground commands and will be adjusted during each flyby to provide the best balance between SNR and image smear at each altitude. Data rates to the spacecraft are kept below the allowable maximum, and total data volume is constrained, by adjusting the spatial aggregation in each band, and the observation cadence. Fig. 43 shows a simulation of data quality obtained during daytime and nighttime nadir-pointed scans from 50 km altitude. Along-track image resolution is limited by smear near close approach, to no better than the product of the detector time constant (about 0.012 sec) and ground track speed (typically ∼4.5 km/sec), i.e. about 55 meters. Fig. 44a shows the geometry of the E-THEMIS footprints in the three bands, during part of the nadir-pointed portion of a representative flyby.

Fig. 43

Idealized simulations of 3-color E-THEMIS images of Europa, combining data from the three bands (Red=Band 3, Green=Band 2, Blue=Band 1). Noise, resolution, and smear are realistic, given expected instrument parameters used for these data sets. A, B: Portions of a nadir scan during daytime (A) or nighttime (B), from 50 km altitude. Black lines are missing data in the Galileo image mosaic (of Conamara chaos) that was translated into plausible ranges of daytime and nighttime temperatures, as input for the simulations. A simulated warm fracture, 10 meters wide at 160 K, has been added to both data sets, but is readily visible only in the nighttime simulation (center left). C: Global image from a joint scan taken during a nighttime approach. Input radiances were modeled using a diurnal thermal model that includes a Europa-like thermal inertia and spatially variable albedo derived from Galileo visible image mosaics. Each of the clusters of four bright lines represents synthetic approximations to the brightness of the four Enceladus tiger stripes, placed at various longitudes at north and south mid-latitudes, showing that Enceladus-level activity is readily detected in the E-THEMIS nighttime global data set. The “tiger stripes” appear blue because their high color temperatures result in relatively stronger emission in Band 1

Fig. 44

Example E-THEMIS footprints on Europa, for two periods during the 31E25 flyby of the Rnd7_T1 tour, illustrated using the ASU JMARS planning/data visualization tool. Footprints are shown every 50 seconds: in reality, data in each band are taken continuously, at 60 Hz, providing contiguous coverage. Red = Band 3, Green = Band 2, Blue = Band 1. A. Nadir scan, shown from 45 minutes before closest approach to closest approach. Scale varies from 1.15 km/pixel at the start, to 4 m/pixel at closest approach, which is at an altitude of 35 km, though smear limits along-track resolution to about 60 meters. The three bands initially cover different areas (right), but generate overlapping coverage during the close approach period (center and left), so that each point along the highest resolution part of the groundtrack swath is observed in all three bands. B. Joint scan, shown from 2.23 to 2.02 hours before close approach, which provides global coverage at a scale of 3.5 km/pixel

As discussed in Sect. 4.4.4, deep space during the entry and exit phase of each flyby will provide an excellent target to remove the background instrument radiances. Space observations will be used for the initial flat fielding of the detector array and combined with the cal flag data to determine the IRF. The measured housing temperatures, together with periodic observations of the internal cal flag, will be used to adjust and remove the housing contributions to the measured radiances throughout each flyby.

The nominal observing plan also includes global, framing-mode observations ∼2 hours before and after closest approach on each flyby when Europa fully fills the cross-track field of view. These data will be acquired by scanning the spacecraft at ∼0.2 mrad/sec over ∼10° of arc to scan all three E-THEMIS filters across Europa (Fig. 44b). The EIS and UVS instruments will also participate in these “joint scans”, building up their own global coverage of Europa. These data will provide ground resolutions at the sub-spacecraft point of ∼4 km per unbinned pixel and ∼8 km with 2 × 2 pixel aggregation. Figure 43c shows a simulation of the spatial resolution and data quality that will be achieved from one of these joint scans. Combining in- and out-bound joint scan data from all flybys will result in excellent coverage of all longitudes on Europa at multiple times of day (Fig. 45) for global thermal inertia, surface roughness, and block abundance modeling. The nighttime data will also provide a sensitive global search for endogenic activity (Fig. 43c) and will allow separation of the endogenic and solar insolation thermal effects.

Fig. 45

Global coverage of Europa in both longitude and local time, for the baseline mission, showing the excellent global time-of-day coverage obtained at most longitudes. Local time is measured in degrees of rotation, starting at midnight. Global data are assumed to be obtained during joint scans obtained at roughly 30,000 km range on approach and departure for each flyby. Each diamond represents the sub-spacecraft point during the approach (suffix “A”) or departure (suffix “D”) leg of the named orbit, and the diagonal line shows longitude and local time away from the sub-spacecraft point, out to 60-degree emission angle. Arbitrary colors are used to distinguish different orbits. Orange and purple background indicates the desired “day” and “night” local times for thermal inertia determination, as specified in the E-THEMIS requirements