The Ionospheric Equivalent Slab Thickness: A Review Supported by a Global Climatological Study Over Two Solar Cycles

Abstract

The ionospheric equivalent slab thickness ($\tau$) is a parameter characterizing both the distribution of the plasma in the ionosphere and the shape of the corresponding vertical electron density profile. It is calculated as the ratio of the vertical total electron content (vTEC) to the ionospheric F2-layer electron density maximum (NmF2). Since its definition dated back in the 60s, a lot of information on the behavior of $\tau$ for different helio-geophysical conditions has been cumulated and the connection with several plasma properties has been also demonstrated. The beginning of the Global Positioning System (GPS) era in the 90s had a strong effect on the studies about $\tau$ because GPS signals allow to obtain the vTEC up to about 20000 km of altitude. Recently, $\tau$ has also found application in many data-assimilation methodologies, especially for the improvement of empirical ionospheric models based on near real-time data. All of these topics are reviewed and discussed in this paper based on the literature published in the last sixty years.

Moreover, to highlight and summarize the main global climatological features of $\tau$, in this work we selected thirty-two ionospheric stations globally distributed and co-located with ground-based Global Navigation Satellite System (GNSS) receivers, for the last two solar cycles. This allowed to collect a dataset of NmF2 and vTEC that represents the largest and most complete ever analyzed for studies concerning $\tau$, which gave the chance to deeply investigate its spatial, diurnal, seasonal, and solar activity variations. The corresponding results are presented and discussed in the light of the existing literature.

1 Introduction

The ionospheric equivalent slab thickness ($\tau$) is an important parameter characterizing the shape of the vertical electron density profile and, as a consequence, the plasma distribution in the dynamical system composed by the ionosphere and plasmasphere. Its definition, in terms of ratio of the vertical total electron content (vTEC) to the ionospheric F2-layer electron density maximum (NmF2), and early corresponding applications, date back to the 60s when the first measurements of vTEC through Faraday rotation or Doppler frequency shift from geostationary satellites became available (Bauer 1960; Garriott 1960; Ross 1960; Roger 1964; Garriott et al. 1965; Taylor 1965; Titheridge 1972). Since then, a bulk of evidences regarding the $\tau$ behavior for different geophysical conditions have been accumulated. In addition to this, the ionospheric equivalent slab thickness found applications in various modeling approaches. Its relation to other important ionospheric parameters, like the plasma scale height and the neutral and plasma temperature, was also investigated. All these matters are reviewed and discussed in this work.

This review is complemented with the most remarkable dataset of $\tau$ compiled so far. Specifically, thirty-two ionosonde stations globally distributed and co-located with ground-based Global Navigation Satellite System (GNSS) receivers, for the last two solar cycles (from 1997 to 2019), allowed to collect a valuable dataset of NmF2 and vTEC to get the main $\tau$ climatological features at equatorial, low, middle, high, and polar cap latitudes for both hemispheres. To perform the climatological analysis, the same methodology and procedures adopted by Pignalberi et al. (2021a) are applied. The analysis is performed for each of the thirty-two ionospheric stations considered in terms of: a) two-dimensional grids of binned medians of measured $\tau$ as a function of the local time (LT) and the month of the year, for three different levels of solar activity; b) boxplots representing the median and dispersion of $\tau$ as a function of the LT, for four months representative of different seasons, and for three different levels of solar activity. In order to highlight the most important characteristics of $\tau$, the paper focuses on selected ionospheric stations representative of specific latitudinal sectors in terms of the Quasi-Dipole (QD, Laundal and Richmond 2017) magnetic latitude. The reader can find the results for all the thirty-two stations in the Supplementary Material.

The paper is organized in three parts:

• Part I (Sect. 2 to 4) pertains the review section. In Sect. 2, the ionospheric equivalent slab thickness is defined and its physical and geometrical meanings are described along with the implications that the different methods applied over the years to measure the vTEC have on it. In the same section, the slab thickness sensitivity to both NmF2 and vTEC is analyzed to highlight the corresponding strengths and weaknesses. Section 3 presents the historical background and a review of the current knowledge on $\tau$. The most relevant past studies on $\tau$ are here described to highlight the corresponding main spatial, diurnal, seasonal, solar and magnetic activities variations. The topics of this section, except the magnetic activity dependence, will be further discussed and deepened in Sect. 6 considering the results of the original climatological analysis reported in Sect. 5. In Sect. 4 a list of theoretical and modeling applications of $\tau$ developed by different authors are reported and discussed;

• Part II includes the climatological analysis based on the new and original $\tau$ dataset (Sect. 5), and the corresponding discussion of the main patterns (Sect. 6). Section 5 first describes both the dataset of thirty-two co-located ionosonde stations and ground-based GNSS receivers used to obtain the $\tau$ time series, and the corresponding data filtering, binning, and statistical analysis. Then, the results of the statistical analysis are presented for five different latitudinal ranges by highlighting the main spatial, diurnal, seasonal, and solar activity variations of $\tau$. Section 6 discusses the results of Sect. 5 in the light of the current knowledge on $\tau$ as outlined in Sect. 3. The most relevant features are here outlined and critically discussed by complementing and expanding the current knowledge on $\tau$;

• Part III aims to bring to light what are the main gaps in the current knowledge on $\tau$ both from a theoretical and modeling point of view, and which future developments (Sect. 7) might be of help to this regard. Conclusive remarks are provided in Sect. 8.

Part I

2 The Ionospheric Equivalent Slab Thickness

2.1 Definition and Calculation

The ionospheric equivalent slab thickness is defined as the ratio of vTEC to NmF2:

$$ \tau = \frac{\mathrm{vTEC}}{\mathit{Nm}\mathrm{F}2}, $$

(1)

where NmF2 is expressed in electrons per $\text{m}^{3}$ ($\text{el/m}^{3}$), and $\mathrm{vTEC}$ is measured in electrons per $\text{m}^{2}$ ($\text{el/m}^{2}$). As a consequence, $\tau$ is expressed in meters (m) and represents the thickness of an ideal ionospheric slab of constant electron density equal to NmF2 with a vTEC value equivalent to that of the entire vertical electron density profile. Figure 1 is a schematic representation of an ionospheric vertical electron density profile with highlighted $\textit{Nm}\text{F}2 = 10^{12}~\text{el/m}^{3}$ (red circle) at F2-layer peak, $\text{vTEC} = 30~\text{TECU}$ ($1~\text{TECU} = 10^{16}~\text{el/m}^{2}$) (green double arrow segment), and $\tau = 3\cdot10^{5}~\text{m} = 300~\text{km}$ (blue shadowed rectangle) as an ideal ionospheric slab with thickness 300 km around the F2-layer peak.

Fig. 1

Schematic representation of an ionospheric vertical electron density profile with highlighted the F2-layer electron density maximum NmF2 (red circle), the vertical total electron content vTEC (green double arrow segment), and the equivalent slab thickness $\tau$ (blue shadowed rectangle)

NmF2 is obtained from the ordinary critical frequency of the F2 ionospheric layer (foF2) through the following relation $\textit{Nm}\text{F}2 = (1.24\cdot10^{10})$ foF2², with foF2 in MHz and NmF2 in $\text{el/m}^{3}$ (e.g., Davies 1990). foF2 is scaled from ionograms recorded by ionosondes either manually by an expert operator or automatically by robust autoscaling software (Galkin and Reinisch 2008; Pezzopane and Scotto 2007). Of course, values validated by an expert operator are more reliable than those output by the autoscaling software. Nevertheless, the manual validation of the ionograms is really demanding and time consuming and, most of all, cannot be performed in real time, which is limiting for Space Weather purposes. This is why since the 80s much work has been done to develop algorithms able to automatically scale the ionograms giving as output the standard ionospheric characteristics and an estimation of the vertical electron density profile (e.g. Reinisch and Huang 1983; Fox and Blundell 1989). Figure 2 shows an example of ionogram recorded at the ionospheric station of Rome ($41.8^{\circ}~\text{N}$, $12.5^{\circ}~\text{E}$; QD Lat. $35.9^{\circ}~\text{N}$) on 07 April 2022 at 19:00 UT and autoscaled by the Autoscala algorithm developed at the Istituto Nazionale di Geofisica e Vulcanologia (Pezzopane et al. 2010; Scotto et al. 2012).

Fig. 2

Ionogram recorded at the ionospheric station of Rome on 07 April 2022 at 19:00 UT and autoscaled by the Autoscala algorithm developed at the Istituto Nazionale di Geofisica e Vulcanologia. In this case, the autoscaling software outputs a correct value for foF2 equal to 8.8 MHz, identified in correspondence of the asymptotical trend (highlighted by the dashed black vertical line) of the F2-layer ordinary ray. The figure shows also the vertical electron density profile obtained by applying the inversion procedure proposed by Scotto (2009) on the identified trace represented in blue. The ionogram has been downloaded from the Electronic Space Weather upper atmosphere database system (eSWua) owned by the Istituto Nazionale di Geofisica e Vulcanologia and managed by the Upper Atmosphere Physics and Radiopropagation group (www.eswua.ingv.it – HF data, version 1.0, https://doi.org/10.13127/eswua/hf)

Figure 2 shows a well-defined ionogram, the F2-layer trace is very clear up to the critical frequency and therefore foF2 (and consequently NmF2) can be easily autoscaled by Autoscala from the vertical asymptote of the trace. Unfortunately, the ionograms are not always like that shown in Fig. 2, and often the F2-layer trace near the critical frequency is not clearly recorded due to multiple reasons: interference, absorption, scattering, multiple reflections, presence of sporadic E layers. In these cases, the autoscaling analysis that follows might be wrong and the output for the foF2 value unreliable (Reinisch et al. 2005; Galkin and Reinisch 2008; Pezzopane and Scotto 2010; Scotto and Pezzopane 2008). Bullett et al. (2010) tested thoroughly the accuracy of the Autoscala software on the ionograms recorded by the Vertical Incidence Pulsed Ionospheric Radar ionosonde and found that, when the ionogram trace is clear, foF2 is automatically scaled with an accuracy of 0.1 MHz for 75% of the dataset and with an accuracy of 0.5 MHz for 99% of the dataset. Instead, when the ionogram trace is noisy or characterized by spread-F phenomena they found that the percentage of the autoscaling accuracy of 0.1 MHz drops to 50% and that of the autoscaling accuracy of 0.5 MHz drops to 94%. Therefore, when carrying out studies based on autoscaled data, one must be sure that these are largely reliable, as on the other hand it will be highlighted in Sect. 5.1.

The methodologies and techniques applied to calibrate vTEC values have evolved over the years and different approaches exist with different performances (Pignalberi et al. 2021b). Before the advent of the Global Positioning System (GPS) era in the 90s, vTEC was retrieved through Faraday rotation or Doppler frequency shift of geostationary satellites radio signals (Garriott et al. 1965; Titheridge 1972). However, Faraday rotation measurements are affected by the assumed hypothesis of a constant magnetic factor along the ray path, and this limits the retrieval of vTEC up to about 2000 km of height (Titheridge 1972; Davies 1990). The current availability of GPS and GNSS satellites have had a deep impact on the vTEC calculation, both for the ever increasing number of GNSS satellites constellations and for the possibility of using different vTEC retrieval techniques based on single-frequency and multi-frequency signals. vTEC retrieved from GNSS signals has the advantage of representing the contribution of the ionosphere-plasmasphere system up to about 20000 km of height. For the purpose of calculating $\tau$, it has to be considered that the seminal works dated back to the 60s–80s were based on vTEC values retrieved through Faraday rotation measurements, while the most recent works are based on vTEC from GNSS signals. As a consequence, when comparing results obtained with different vTEC retrieval techniques, differences are expected because of the plasmaspheric contribution in the range 2000–20000 km of height (Pignalberi et al. 2021a). vTEC values retrieved from dual-frequency GNSS signals, as explained below, are used in the climatological analysis described in Sect. 5.

In recent times, TEC is usually measured by combining GNSS observables on, at least, two different frequencies (e.g., GPS L1 and L2). In fact, the ionospheric effects on GNSS signal propagation include a phase advance and a range delay, being proportional to the slant TEC (sTEC, i.e., the electron density integrated along the ray path connecting a given satellite-receiver couple) according to:

$$ I[ \text{m} ] = 40.3 \frac{\mathrm{sTEC}}{f^{2}}, $$

(2)

in which sTEC is expressed in $\text{el/m}^{2}$, $f$ in Hz, and $I$ is the delay in length unit induced by the ionosphere in the pseudo-range. Given Eq. (2), sTEC can be obtained by calculating the so-called geometry-free linear combination, that is defined as:

$$ L_{12\_\mathrm{arc}} [\text{m}]= L_{4} = L_{1} - L_{2} = I_{1} - I_{2} + c ( t_{1,\mathrm{R}} - t_{2,\mathrm{R}} ) + c ( t_{1,\mathrm{S}} - t_{2,\mathrm{S}} ) + \lambda _{1} N_{1} + \lambda _{2} N_{2} +\varepsilon , $$

(3)

in which subscripts 1 and 2 refer to two different GNSS frequencies (e.g., $L_{1}$ and $L_{2}$ GPS frequencies), respectively, while $\lambda$ refers to the corresponding wavelength, $N$ is the ambiguity on carrier phase measurements, “arc” refers to continuous carrier phase observations (i.e., for which the product $\lambda N$ can be considered constant), $t$ is the frequency-dependent delay due to the receiver (R) and satellite (S), $c$ is the speed of light in vacuum, and $\varepsilon$ is the noise on the carrier phase observation combination in length units.

From (2) and (3), the following can be derived:

$$ L_{\mathrm{arc}} [\mathrm{TECU}]=\mathrm{sTEC}+ B_{\mathrm{R}} + B_{\mathrm{S}} + C_{\mathrm{arc}} + \varepsilon _{L}, $$

(4)

in which $B_{\mathrm{R}} =c ( t_{1,\mathrm{R}} - t_{2,\mathrm{R}} ) \frac{f^{2}}{40.3}$ and $B_{\mathrm{S}} =c ( t_{1,\mathrm{S}} - t_{2,\mathrm{S}} ) \frac{f^{2}}{40.3}$ are the “inter-frequency biases” (IFBs) for carrier phase observables induced by the receiver and the transmitter, respectively, $C_{\mathrm{arc}} = \frac{f^{2}}{40.3} ( \lambda _{1} N_{1} + \lambda _{2} N_{2} )$ is the ambiguity for $L_{4}$, and $\varepsilon _{L} = \frac{f^{2}}{40.3} \varepsilon$ is the carrier phase noise in TECU.

A similar linear combination for the code measurements can be obtained as:

$$ P [ \mathrm{TECU} ] =\mathrm{sTEC}+ b_{\mathrm{R}} + b_{\mathrm{S}} + \varepsilon _{\mathrm{P}}, $$

(5)

where $b_{\mathrm{R}}$ and $b_{\mathrm{S}}$ are the so called “differential code biases” (DCBs), due to the receiver and satellite, and $\varepsilon_{\mathrm{P}}$ is the noise on code measurements. In Eq. (5) there are no ambiguity terms since, differently from phase observables, code measurements are “absolute”, i.e., they do not suffer from cycle ambiguities.

Considering a single arc of observations, by subtracting the two new observables, one for code measurements and the other one for phase measurements, the average difference on a single arc (brackets in Eq. (6)) between carrier phase and code observables can be written:

$$ \langle L_{\mathrm{arc}} - P \rangle _{\mathrm{arc}} = C_{\mathrm{arc}} + B_{\mathrm{R}} + B_{\mathrm{S}} - b_{\mathrm{R}} - b_{\mathrm{S}} - \langle \varepsilon _{\mathrm{P}} \rangle _{\mathrm{arc}}, $$

(6)

in which $\varepsilon _{L}$ can be neglected (Braasch 1996).

By subtracting (6) from (4), the following can be derived:

$$ \tilde{L}_{\mathrm{arc}} =\mathrm{sTEC}+ b_{\mathrm{R}} + b_{\mathrm{S}} + \langle \varepsilon _{\mathrm{P}} \rangle _{\mathrm{arc}}, $$

(7)

being the carrier-phase ionospheric observable “levelled” to the code-delay ionospheric observable. The term $\langle \varepsilon _{\mathrm{P}} \rangle _{\mathrm{arc}}$ is the effect of the noise and the multipath along the arc on carrier-phase observations, as described in Ciraolo et al. (2007).

There are several approaches that can be used to estimate the $b_{\mathrm{R}}, b_{\mathrm{S}}, \langle \varepsilon _{\mathrm{P}} \rangle _{\mathrm{arc}}$ “bias” terms based on different assumptions (e.g., $\langle \varepsilon _{\mathrm{P}} \rangle _{\mathrm{arc}} \approx 0$) estimating the biases for a single station or for multiple stations at once (Seemala and Delay 2010; Conte et al. 2011). One possible approach to estimate sTEC without neglecting $\langle \varepsilon_{\mathrm{P}} \rangle _{\mathrm{arc}}$ consists in estimating a single bias for each arc, instead of separate biases for the receiver and satellites. In this case, Eq. (7) can be written as:

$$ \tilde{L}_{\mathrm{arc}} =\mathrm{sTEC}+ \beta _{\mathrm{arc}}, $$

(8)

in which $\beta_{\mathrm{arc}}$ is the sum of all the errors with non-zero mean. This is the equation defining the TEC calibration, following the method described by Ciraolo et al. (2007). In the specific, sTEC values are mapped as a two-dimensional surface by means of the classical thin shell method as:

$$ \mathrm{sTEC} = \mathrm{vTEC} ( \phi _{1}, \phi _{2} ) \cdot \mathrm{sec} \chi , $$

(9)

where $\mathrm{vTEC} ( \phi _{1}, \phi _{2} )$ is the unknown describing a surface in the reference frame defined by a coordinates couple $( \phi _{1}, \phi _{2} )$ over the thin shell (bi-dimensional), and $\chi$ is the angle formed by the ray-path and the perpendicular to the shell at the ionospheric pierce point (IPP) (Pi et al. 1997; Mannucci et al. 1998). The geometry of the thin shell mapping approach to retrieve vTEC from sTEC is outlined in Fig. 3.

Fig. 3

Thin shell geometry representation. $R_{\mathrm{e}}$ is the radius of the Earth, $\chi$ is the angle formed by ray path and the vertical crossing the ionosphere in the ionospheric pierce point (IPP), $H_{\mathrm{IPP}}$ is the height of the thin shell ionosphere. Red line represents the sTEC while the blue line represents the vTEC

Once defined the functional form of $\mathrm{vTEC} ( \phi _{1}, \phi _{2} )$, Eq. (9) can be solved via the standard least squares method.

2.2 Meaning and Implications for the Ionosphere

$\tau$ is a significant ionospheric parameter because depending on both vTEC and NmF2 observations can provide information on both the topside and bottomside ionosphere, and on how the plasma is distributed between these regions and the overlying plasmasphere. To highlight that, top panels of Fig. 4 represent $\tau$ curves from 100 to 500 km in steps of 100 km for NmF2 and vTEC values usually observed in the ionosphere-plasmasphere system. Top right panel of Fig. 4 is a zoom of the left one for low NmF2 and vTEC values that are usually observed at night or at the solar terminator passage. From its mathematical definition and the observation of Fig. 4 top panels it is clear how $\tau$ is very sensitive to NmF2 or vTEC changes for very low NmF2 and vTEC values, while it is more stable for high NmF2 and vTEC values. At very low NmF2 and vTEC values, a little change in vTEC of the order of few TECUs (i.e., of few $10^{16}~\text{el/m}^{2}$), or a corresponding one in NmF2 of the order of $10^{11}~\text{el/m}^{3}$, allows stepping from a $\tau$ curve to another. For example, at $\textit{Nm}\text{F}2 = 10^{11}~\text{el/m}^{3}$ ($\textit{fo}\text{F}2 \approx 2.8~\text{MHz}$) stepping from 2 to 3 TECU, $\tau$ rises from 200 to 300 km (corresponding curves are identified respectively in orange and green in the top right panel of Fig. 4). On the contrary, at $\textit{Nm}\text{F}2 = 20\cdot10^{11}~\text{el/m}^{3}$ ($\textit{fo}\text{F}2\approx12.7~\text{MHz}$), to obtain the same $\tau$ change, vTEC has to step from 40 to 60 TECU. This fact has a lot of implications when comparing $\tau$ values retrieved by the oldest methodologies based on geostationary satellites data and the newest ones based on GNSS satellites data. In fact, the plasmaspheric contribution between 2000 and 20000 km is of the order of magnitude of units of TECU and, more importantly, during night the plasmaspheric contribution to vTEC is relevant while the ionospheric one is at its minimum. From these considerations, one might expect that most of the differences between the results shown by different authors in the past could be ascribed (especially when vTEC values are low) to the technique applied to retrieve vTEC data for the $\tau$ calculation, and to the errors associated to the vTEC calibration itself. On the contrary, the NmF2 retrieval from ionograms has not changed over the years and the error associated to this kind of remote sensing technique is negligible compared to the one affecting the vTEC retrieval and calibration. Moreover, while the NmF2 is a punctual measure associated to the F2-layer peak, the vTEC is an integral one from the base of the ionosphere (at about 50–60 km of height) to the GNSS satellites height (at about 20000 km of height). As a consequence, the vTEC includes the contribution of the bottomside ionosphere (up to the F2-layer peak height), of the topside ionosphere (from the F2-layer peak height to the plasmasphere) and of the plasmasphere itself. However, the separation in these three regions is a matter of nomenclature because there are continuous exchanges of plasma between them and such fluxes of charged particles are not stationary being dependent on the ongoing helio-geophysical conditions; thus, diurnal, seasonal, geographic, solar and magnetic activity variabilities are found. The only vTEC value cannot describe all these complications, providing only an overview of the ionosphere-plasmasphere system; as a consequence, also the information given by the slab thickness is partial and it is difficult to effectively separate the ionospheric and the plasmaspheric contributions. However, by making simple assumptions on the vertical electron density profile shape, it is possible to infer very useful information from the slab thickness value. According to this, in order to understand the geometrical meaning of the slab thickness, we used a prototype version of the NeQuick model (Nava et al. 2008) in which the $\tau$ value (and hmF2, where hmF2 is the height of the F2-layer peak) can be constrained, to show the effect that changing the $\tau$ value has on the shape of the vertical electron density profile, for fixed vTEC or NmF2 values. In the bottom panels of Fig. 4 the prototype NeQuick model was run for $\tau$ values from 100 to 500 km in steps of 100 km in two different ways: by fixing the NmF2 value at $10^{12}~\text{el/m}^{3}$ ($\approx8.98~\text{MHz}$) and leaving vTEC free; by fixing the vTEC value at 20 TECU and leaving NmF2 free. In both cases, the NeQuick model was run according to the following parameters: $\text{latitude} = 45^{\circ}~\text{N}$, $\text{longitude} = 15^{\circ}~\text{E}$, $\text{month} = \text{April}$, $\text{hour} = 14$ Universal Time (UT), $\textit{hm}\text{F}2 = 300~\text{km}$. From the bottom panels of Fig. 4 it is evident the effect of the slab thickness on the shape of the profile: in a nutshell, small $\tau$ values are representative of “thinner” electron density profiles, while high $\tau$ values are associated to “thicker” profiles, at the F2-layer peak. Therefore, $\tau$ can describe the distribution of the plasma between the lower (bottomside) and the upper (topside) ionosphere by modifying the profile shape.

Fig. 4

(Top left panel) Slab thickness ($\tau$) curves from 100 to 500 km in steps of 100 km as a function of NmF2 ($x$-axis) and vTEC ($y$-axis). (Top right panel) Zoom of the top left panel plot for low values of NmF2 and vTEC. (Bottom left panel) Vertical electron density profiles described by the NeQuick model with fixed $\textit{Nm}\text{F}2 = 10^{12}~\text{el/m}^{3}$ and $\tau$ values from 100 to 500 km in steps of 100 km. (Bottom right panel) Vertical electron density profiles described by the NeQuick model with fixed $\text{vTEC} = 20$ TECU and $\tau$ values from 100 to 500 km in steps of 100 km

The $\tau$ sensitivity to variations of vTEC and NmF2 can also be analytically studied through a two-variables Taylor series expansion around specific vTEC and NmF2 values, as outlined below. From the mathematical theory of two-variables Taylor series expansion, at the first order, a two-variables function can be approximated by:

$$ f(x,y) \approx f(x_{0},y_{0}) + \nabla f(x_{0},y_{0}) \cdot (x - x_{0},y - y_{0}), $$

(10)

with

$$ \nabla f(x_{0},y_{0}) = \biggl( \frac{\partial f(x_{0},y_{0})}{\partial x}, \frac{\partial f(x_{0},y_{0})}{\partial y} \biggr). $$

(11)

In our specific case, the two-variables function is $\tau$, then:

$$ \left \{ \textstyle\begin{array}{l} f(x,y) = \tau (\textit{Nm}\mathrm{F}2,\mathrm{vTEC}) \equiv \frac{\mathrm{vTEC}}{\textit{Nm}\mathrm{F}2} \\ f(x_{0},y_{0}) = \tau _{0} \equiv \frac{\mathrm{vTEC}_{0}}{\textit{Nm}\mathrm{F}2_{0}}. \end{array}\displaystyle \right . $$

(12)

By applying Eqs. (10)–(11) to Eq. (12), we obtain:

$$ \Delta \tau \approx \frac{1}{\textit{Nm}\mathrm{F}2_{0}}\Delta \mathrm{vTEC} - \frac{\mathrm{vTEC}_{0}}{\textit{Nm}\mathrm{F}2_{0}^{2}}\Delta \textit{Nm}\mathrm{F}2, $$

(13)

with

$$ \left \{ \textstyle\begin{array}{l} \Delta \tau = \tau - \tau _{0} \\ \Delta \textit{Nm}\mathrm{F}2 = \textit{Nm}\mathrm{F}2 - \textit{Nm}\mathrm{F}2_{0} \\ \Delta \mathrm{vTEC} = \mathrm{vTEC} - \mathrm{vTEC}_{0}. \end{array}\displaystyle \right . $$

(14)

Equation (13) describes the first-order variations of $\tau$ to variations of both vTEC and NmF2 around the point ($\textit{Nm}\text{F}2_{0},\text{vTEC}_{0}$). In case of only vTEC or NmF2 variations, the corresponding $\tau$ variations are described by Eq. (15):

$$ \left \{ \textstyle\begin{array}{l} \left . \Delta \tau \right \vert _{\Delta \textit{Nm}\mathrm{F}2 = 0} = \frac{\Delta \mathrm{vTEC}}{\textit{Nm}\mathrm{F}2_{0}} \\ \left . \Delta \tau \right \vert _{\Delta \mathrm{vTEC} = 0} = - \frac{\mathrm{vTEC}_{0}}{\textit{Nm}\mathrm{F}2_{0}^{2}}\Delta \textit{Nm}\mathrm{F}2. \end{array}\displaystyle \right . $$

(15)

It is worth noting that Eqs. (13) and (15) are locally valid as a first-order approximation around the point ($\textit{Nm}\text{F}2_{0}, \text{vTEC}_{0}$). Thus, they are useful to estimate $\tau$ variations due to possible measurement errors characterizing either vTEC or NmF2, or both of them.

As a first example, we consider the effect on $\tau$ of an autoscaling error characterizing foF2, with the consequent error in estimating NmF2, and error-free vTEC estimation. Let us consider the two cases in which foF2 is affected by an error of 0.1 MHz and 0.5 MHz, corresponding to an error in NmF2 equal to $1.24\cdot10^{8}~\text{el/m}^{3}$ and $3.1\cdot10^{9}~\text{el/m}^{3}$, respectively (see Sect. 2.1). Focusing on the curve $\tau _{0} = 300~\text{km}$ (see Fig. 4), we calculate $\Delta \tau$ for two limiting cases of high and low $\text{vTEC}_{0}$ and $\textit{Nm}\text{F}2_{0}$ values by using Eq. (15): $\text{vTEC}_{0} = 60$ TECU and $\textit{Nm}\text{F}2_{0} = 2\cdot10^{12}~\text{el/m}^{3}$ (i.e., $\textit{fo}\text{F}2 \approx 12.7~\text{MHz}$), and $\text{vTEC}_{0} = 6$ TECU and $\textit{Nm}\text{F}2_{0} = 2\cdot10^{11}~\text{el/m}^{3}$ (i.e., $\textit{fo}\text{F}2 \approx 4.0~\text{MHz}$).

$$\begin{aligned} &\text{High values} = \left \{ \textstyle\begin{array}{l} \tau _{0} = 300~\text{km} \\ \mathrm{vTEC}_{0} = 60 \cdot 10^{16}~\text{el/m}^{2} \\ \textit{Nm}\mathrm{F}2_{0} = 2 \cdot 10^{12}~\text{el/m}^{3} \end{array}\displaystyle \right . \\ &\quad \Rightarrow\quad \left \{ \textstyle\begin{array}{l} \left . \Delta \tau \right \vert _{\Delta \mathrm{vTEC} = 0,\Delta \textit{Nm}\mathrm{F}2 = 1.24 \cdot 10^{8}~\text{el/m}^{3}} \approx - 0.019~\text{km} \\ \left . \Delta \tau \right \vert _{\Delta \mathrm{vTEC} = 0,\Delta \textit{Nm}\mathrm{F}2 = 3.1 \cdot 10^{9}~\text{el/m}^{3}} \approx - 0.465~\text{km}, \end{array}\displaystyle \right . \end{aligned}$$

(16)

$$\begin{aligned} &\text{Low values} = \left \{ \textstyle\begin{array}{l} \tau _{0} = 300~\text{km} \\ \mathrm{vTEC}_{0} = 6 \cdot 10^{16}~\text{el/m}^{2} \\ \textit{Nm}\mathrm{F}2_{0} = 2 \cdot 10^{11}~\text{el/m}^{3} \end{array}\displaystyle \right . \\ &\quad \Rightarrow\quad \left \{ \textstyle\begin{array}{l} \left . \Delta \tau \right \vert _{\Delta \mathrm{vTEC} = 0,\Delta \textit{Nm}\mathrm{F}2 = 1.24 \cdot 10^{8}~\text{el/m}^{3}} \approx - 0.186~\text{km} \\ \left . \Delta \tau \right \vert _{\Delta \mathrm{vTEC} = 0,\Delta \textit{Nm}\mathrm{F}2 = 3.1 \cdot 10^{9}~\text{el/m}^{3}} \approx - 4.650~\text{km}. \end{array}\displaystyle \right . \end{aligned}$$

(17)

From Eqs. (16)–(17) it is clear how an error in the autoscaling of foF2 of the order of 0.1–0.5 MHz has a little impact on $\tau$ estimation and it has to be considered above all for low values of vTEC and NmF2 and for cases when the autoscaling of foF2 from ionograms is evidently biased. However, even in the worst case scenario here considered, i.e., low values with an foF2 error of 0.5 MHz, the percentage relative error $\Delta \tau/\tau _{0}\cdot 100$ is only 1.55%.

As a second example, we consider the effect on $\tau$ of an error in the vTEC calibration and error-free NmF2 estimation. Let us consider the two cases in which vTEC is affected by an error of 0.5 TECU and 2 TECU. Focusing again on the curve $\tau _{0} = 300~\text{km}$ (see Fig. 4), we calculate $\Delta \tau$ for two limiting cases of high and low $\text{vTEC}_{0}$ and $\textit{Nm}\text{F}2_{0}$ values by using Eq. (15), as done before: $\text{vTEC}_{0} = 60$ TECU and $\textit{Nm}\text{F}2_{0} = 2\cdot10^{12}~\text{el/m}^{3}$ (i.e., $\textit{fo}\text{F}2 \approx 12.7~\text{MHz}$), and $\text{vTEC}_{0} = 6$ TECU and $\textit{Nm}\text{F}2_{0} = 2\cdot10^{11}~\text{el/m}^{3}$ (i.e., $\textit{fo}\text{F}2 \approx 4.0~\text{MHz}$).

$$ \text{High values} = \left \{ \textstyle\begin{array}{l} \tau _{0} = 300~\text{km} \\ \mathrm{vTEC}_{0} = 60 \cdot 10^{16}~\text{el/m}^{2} \\ \textit{Nm}\mathrm{F}2_{0} = 2 \cdot 10^{12}~\text{el/m}^{3} \end{array}\displaystyle \right . \quad\Rightarrow\quad \left \{ \textstyle\begin{array}{l} \left . \Delta \tau \right \vert _{\Delta \textit{Nm}\mathrm{F}2 = 0,\Delta \mathrm{vTEC} = 5 \cdot 10^{15}~\text{el/m}^{2}} \approx 2.5~\text{km} \\ \left . \Delta \tau \right \vert _{\Delta \textit{Nm}\mathrm{F}2 = 0,\Delta \mathrm{vTEC} = 2 \cdot 10^{16}~\text{el/m}^{2}} \approx 10~\text{km}, \end{array}\displaystyle \right . $$

(18)

$$ \text{Low values} = \left \{ \textstyle\begin{array}{l} \tau _{0} = 300~\text{km} \\ \mathrm{vTEC}_{0} = 6 \cdot 10^{16}~\text{el/m}^{2} \\ \textit{Nm}\mathrm{F}2_{0} = 2 \cdot 10^{11}~\text{el/m}^{3} \end{array}\displaystyle \right . \quad\Rightarrow\quad \left \{ \textstyle\begin{array}{l} \left . \Delta \tau \right \vert _{\Delta \textit{Nm}\mathrm{F}2 = 0,\Delta \mathrm{vTEC} = 5 \cdot 10^{15}~\text{el/m}^{2}} \approx 25~\text{km} \\ \left . \Delta \tau \right \vert _{\Delta \textit{Nm}\mathrm{F}2 = 0,\Delta \mathrm{vTEC} = 2 \cdot 10^{16}~\text{el/m}^{2}} \approx 100~\text{km}. \end{array}\displaystyle \right . $$

(19)

In this case, Eqs. (18)–(19) show the very strong impact that an error in the calibration on vTEC has on the $\tau$ estimation, much higher than that associated to NmF2 one. As before, the major impact is when vTEC and NmF2 are low (as during nighttime) with percentage relative error of about 8.3% and 33.3% for $\Delta\text{vTEC}$ equal to 0.5 and 2 TECU, respectively.

These analytical reasonings, along with Fig. 4 results and corresponding discussion, point out the very high sensitivity of $\tau$ to vTEC variations, especially for low vTEC and NmF2 values, which are usual during nighttime. Then, even a relatively small error in the vTEC calibration can produce a quite high misrepresentation of $\tau$. This has also many implications when comparing results obtained from vTEC values obtained from Faraday rotation measurements versus those obtained with modern GNSS ground-based receivers. In fact, the contribution to vTEC of the plasmaspheric region between about 2000 and 20000 km of altitude ranges from tenths to units of TECU, thus producing a relevant underestimation in the $\tau$ prediction when Faraday rotation measurements are used.

3 Historical Background and Current Knowledge on the Slab Thickness

Ionospheric and plasmaspheric processes affect concurrently both the bottomside and topside ionospheric variability making the $\tau$ behavior rather complex. The main diurnal, seasonal, latitudinal, solar and magnetic activities climatological features of $\tau$ have been investigated by many authors. From the wide existing literature, it emerges a very complicated picture that reflects the inherent complexity of this ionospheric parameter and, as a consequence, the need of further studies.

Since $\tau$ depends significantly on the latitude, the most relevant studies here cited are first grouped taking into account the location of the stations used by the authors, and the main diurnal and seasonal features are described. Thereafter, the main results about the $\tau$ variations connected to the solar and magnetic activity are shown.

This Section aims at briefly introducing the main climatological features of $\tau$ as outlined so far by many authors. The topics here presented will be further discussed, complemented, and deepened in Sect. 6 considering the results of the original climatological analysis reported in Sect. 5. The only exception is the magnetic activity dependence which is not faced by Sect. 5: as a consequence, a more detailed picture of this dependence is given in Sect. 3.6.

3.1 Slab Thickness at Low Latitudes

With regard to studies over the equatorial sector, the diurnal variation of $\tau$ over Kodaikanal ($10.1^{\circ}~\text{N}, 77.3^{\circ}~\text{E}$; QD Lat. $2.7^{\circ}~\text{N}$) during the winter of 1966–1967 shows the presence of a pre-sunrise peak with high values visible throughout the day (Das Gupta et al. 1975). Iyer and Rastogi (1978), analysing data again over Kodaikanal during half a solar cycle (1964–1969), found a semi-annual variation of $\tau$ characterized by equinoctial maxima both during daytime and nighttime, with a pre-sunrise peak in winter and summer months for high solar activity. Values greater in summer and winter, unusual summer pre-sunrise peaks along with minima during post-sunrise and sunset hours were found by Kenpankho et al. (2011), who investigated the $\tau$ behavior for medium solar activity over Chumphon ($10.7^{\circ}~\text{N}, 99.4^{\circ}~\text{E}$; QD Lat. $3.1^{\circ}~\text{N}$) for the period 2004–2006. Strong pre-sunrise peaks with a secondary maximum around noon-time hours were observed during all seasons at the Indian equatorial stations of Trivandrum ($8.5^{\circ}~\text{N}, 76.9^{\circ}~\text{E}$; QD Lat. $0.9^{\circ}~\text{N}$) and Waltair ($17.7^{\circ}~\text{N}, 83.3^{\circ}~\text{E}$; QD Lat. $10.8^{\circ}~\text{N}$) for the low solar activity period from March 2004 to February 2005 (Venkatesh et al. 2011).

At low latitudes, the $\tau$ behavior at Hawaii ($19.0^{\circ}~\text{N}, 154.0^{\circ}~\text{W}$; QD Lat. $19.3^{\circ}~\text{N}$) relative to one year of high (1981) and low (1985) solar activity has revealed the occurrence of pronounced pre-sunrise peaks in winter, with daytime yearly mean significantly higher than nighttime ones for high solar activity conditions, while the reverse is true for solar minimum activity (Jayachandran et al. 2004). Likewise, also studies conducted over Nicosia ($35.0^{\circ}~\text{N}, 33.0^{\circ}~\text{E}$; QD Lat. $29.2^{\circ}~\text{N}$) during minimum solar activity (from January 2009 to August 2010) by Haralambous (2011) confirmed the presence of pre-sunrise peaks in winter with a post-sunset increase and mean nighttime values higher than the mean daytime ones for all seasons except for summer. Venkatesh et al. (2011) observed significantly high post-sunset peaks in winter around 22 Local Time (LT) at Delhi ($28.6^{\circ}~\text{N}, 77.2^{\circ}~\text{E}$; QD Lat. $22.9^{\circ}~\text{N}$) for the low solar activity period from March 2004 to February 2005.

A clear latitudinal dependence in the magnetic latitude sector [$0^{\circ}~\text{N--}23^{\circ}~\text{N}$], with $\tau$ decreasing as the latitude increases, was observed for medium solar activity during daytime in winter by Das Gupta et al. (1975) and for all seasons by Venkatesh et al. (2011), who analyzed the hourly behavior of $\tau$ at some equatorial and low-latitude stations.

3.2 Slab Thickness at Middle Latitudes

The complexity of the $\tau$ behavior at Northern and Southern middle latitudes has been highlighted by several works (Bhonsle et al. 1965; Titheridge 1973; Essex 1978; Davies and Liu 1991; Minakoshi and Nishimuta 1994; Spalla and Ciraolo 1994; Goodwin et al. 1995a, 1995b; Breed et al. 1997; Jayachandran et al. 2004; Leitinger et al. 2004; Jin et al. 2007; Kouris et al. 2008, 2009; Stankov and Warnant 2009; Mosert et al. 2013; Huang and Yuan 2015; Sharifi and Farzaneh 2015) which highlighted:

• a) pre-sunrise peaks in all seasons for both low and high solar activity;

• b) post-sunset peaks in winter for low solar activity and in summer for both medium and high solar activity;

• c) the occurrence of pronounced peaks during post-midnight hours;

• d) daytime values smaller than nighttime ones for all seasons for low solar activity, except for summer where the reverse occurs;

• e) daytime values significantly larger in summer than in winter.

Moreover, a more recent analysis conducted by Pignalberi et al. (2021a) over two solar cycles at the middle-latitude stations of Wallops Island ($37.9^{\circ}~\text{N}, 75.5^{\circ}~\text{W}$; QD Lat. $47.8^{\circ}~\text{N}$), Chilton ($51.5^{\circ}~\text{N}, 0.6^{\circ}~\text{W}$; QD Lat. $47.7^{\circ}~\text{N}$), and Roquetes ($40.8^{\circ}~\text{N}, 0.5^{\circ}~\text{E}$; QD Lat. $34.7^{\circ}~\text{N}$) has revealed the presence of:

• a) pre-sunrise peaks in all seasons for low, medium, and high solar activity, which stand out clearly in winter;

• b) post-sunset peaks in winter for low and medium solar activity;

• c) high values for high solar activity for some equinoctial and summer months in the LT sector 19–22;

• d) daytime values markedly smaller than nighttime ones, regardless of solar activity (except in summer);

• e) a higher dispersion of measurements during nighttime and solar terminator hours.

The studies carried out by Gulyaeva et al. (2004), analyzing the $\tau$ behavior for fourteen world-wide stations located at different latitudes from the geomagnetic equator to the North pole for high solar activity, showed that $\tau$ can behave in a really complex manner with latitude; they found a clear decreasing trend of $\tau$ as the latitude increases only in winter during daytime.

3.3 Slab Thickness at High Latitudes

Compared to studies performed at low- and middle-latitude stations, the investigation of the $\tau$ behavior at high and polar cap latitudes are very rare. Jayachandran et al. (2004) found nighttime values higher than daytime ones at Goose Bay ($53.3^{\circ}~\text{N},60.3^{\circ}~\text{W}$; QD Lat. $60.2^{\circ}~\text{N}$) for both solar maximum and minimum conditions; while the occurrence of pronounced post-sunset peaks was observed in winter and equinoctial months for high solar activity. Analysing data over the Antarctica station of Casey ($66.3^{\circ}~\text{S},110.6^{\circ}~\text{E}$; QD Lat. $80.6^{\circ}~\text{S}$) during a period of high solar activity, Yadav and Bhawre (2020) found nighttime values significantly higher than daytime ones, mostly during equinoctial months, and pre-sunrise peaks were clearly detected during summer and equinoctial months.

3.4 Global-Scale Variations of the Slab Thickness as Derived from vTEC Maps

The $\tau$ behavior has been analyzed also by means of vTEC maps derived from ground-based GPS receivers and Constellation Observing System for Meteorology, Ionosphere and Climate (COSMIC) Radio Occultation (RO) measurements (Anthes et al. 2008). To this regard, Guo et al. (2011) calculated $\tau$ maps showing the diurnal variations in the latitudinal range [$60^{\circ}~\text{S},60^{\circ}~\text{N}$] during the low solar activity year 2007. They highlighted the following features:

• a) during nighttime, values are higher than during daytime for non-auroral latitudes in all seasons; an opposite behavior is observed at auroral latitudes in summer;

• b) at high latitudes, higher values are observed in winter with a constant trend of around 350 km during daytime, while a decreasing trend was observed after the pre-sunrise peak for equinoxes;

• c) minimum values around 200 km were noticed in summer during daytime;

• d) for all seasons, the diurnal variation in the Southern hemisphere is smaller than that in the Northern one;

• e) the diurnal variations observed in the winter hemisphere are comparatively greater than those in the summer one;

• f) pre-sunrise peaks at middle latitudes are higher than those observed at equatorial and high latitudes;

• g) peaks near the magnetic equator around mid-noon are observed in all seasons;

• h) post-sunset peaks are observed especially in winter and equinoxes at middle latitudes.

In a next investigation, from the global diurnal maps of $\tau$ reconstructed from Global Ionospheric Map (GIM) TEC and COSMIC RO observations collected during the period from 2006 to 2014, Huang et al. (2016) found:

• a) a depletion in the Equatorial Ionization Anomaly (EIA) region, with a pre-sunrise enhancement observed at all latitudes and the occurrence of a post-sunset enhancement only in some areas at equinoxes for low and high solar activity;

• b) during June solstice, daytime values larger in the Northern hemisphere (summer) than in the Southern hemisphere (winter), while pre-sunrise and post-sunset peaks larger in the winter hemisphere than in the summer one;

• c) particularly large values at high and polar cap latitudes for all seasons and for both minimum and maximum solar activity;

• d) an enhancement at nighttime in the longitude sector $0^{\circ}\text{--}120^{\circ}~\text{E}$ and latitude sector $30^{\circ}\text{--}75^{\circ}~\text{S}$ during the Southern hemisphere summer.

3.5 Solar Activity Dependence

The $\tau$ variability in relation to the solar activity cycle has been also widely studied in order to find possible correlations. With this regard, there exists a large variety of results depending on the latitudinal sector and the location of the considered station. For example, in all seasons, no distinct dependence on the solar activity was observed over Kodaikanal near the magnetic equator (Iyer and Rastogi 1978). On the contrary, over Chumphon, again close to the magnetic equator, a diurnal variation clearly increasing with the solar activity was found (Kenpankho et al. 2011). With regard to low latitudes, a positive correlation with the solar index F10.7 data was found in winter during daytime by Jayachandran et al. (2004) at Hawaii; analogously, at Lunping ($23.0^{\circ}~\text{N},121.9^{\circ}~\text{E}$; QD Lat. $16.3^{\circ}~\text{N}$), positive correlations were observed in all seasons with solar indices EUV (170–190 Å), F10.7, and SSN (solar sunspot number), with the best one associated to the EUV flux (Dabas et al. 1993). Also Chuo (2007) over Chung-Li ($24.9^{\circ}~\text{N}, 121.0^{\circ}~\text{E}$; QD Lat. $18.3^{\circ}~\text{N}$) found a positive correlation with the solar index F10.7. Again, Iyer and Rastogi (1978) report that for low and middle latitudes $\tau$ increases with solar activity. At middle latitudes, a positive correlation over Sagamore Hill ($42^{\circ}~\text{N},288^{\circ}~\text{E}$; QD Lat. $51.3^{\circ}~\text{N}$) was observed for all seasons at noon (Davies and Liu 1991); while, more recently, an increase of $\tau$ with solar activity was observed over Dourbes ($50.1^{\circ}~\text{N}, 4.6^{\circ}~\text{E}$; QD Lat. $45.8^{\circ}~\text{N}$), with variations of up to 24% and 14% in the daytime and nighttime hours respectively (Stankov and Warnant 2009). At high latitude, an increase of $\tau$ with F10.7 was observed at Goose Bay but only for high solar activity (Jayachandran et al. 2004). In a study conducted at Casey, located over the Southern polar cap, positive correlations were found between $\tau$ and solar radiation fluxes X ray (1–8 Å) and EUV (260–340 Å), while a poor correlation was detected with F10.7 (Yadav and Bhawre 2020). Finally, also a significant negative correlation during winter nighttime hours was observed in the Southern hemisphere at Salisbury ($34.8^{\circ}~\text{S},138.6^{\circ}~\text{E}$; QD Lat. $45.6^{\circ}~\text{S}$) during the years 1991–1994 (Breed et al. 1997).

3.6 Magnetic Activity Dependence

The effects of magnetic activity disturbances on $\tau$ is a topic that has received much attention since the first studies dating back to the 60s due to the very important implications that such impulsive and short-time events have on the F2 layer and on the plasma distribution in the ionosphere. Although not strictly connected to the climatological behavior of $\tau$, the magnetic activity dependence is a relevant topic and the most remarkable findings of past studies are here reported.

The difficulties to relate the magnetic activity to corresponding $\tau$ variations is testified by the results shown by different studies: a little daytime effect in summer (Ross 1960); a not clear or a very weak correlation (Taylor 1965; Dabas et al. 1979); no quiet-time and storm-time significant correlation (Fox et al. 1991); conflicting results, with $\tau$ increasing and decreasing according to the season (Bhonsle et al. 1965).

On the contrary, from several studies has emerged that considerable and clear increases of $\tau$ just occur in the course of a geomagnetic storm in all seasons and hours of the day and in both hemispheres. For example, in several cases analyzed by Garriott (1960), a remarkable increase of daytime $\tau$ values was observed during a geomagnetic storm occurred in winter; while during a geomagnetic storm occurred in summer in the northern hemisphere, $\tau$ was observed to increase by 30% (Bauer 1960), and it was seen even to double during the development of a geomagnetic storm occurred in the southern hemisphere in winter (Munro 1962).

By plotting the average $\tau$ value calculated for the period July 1961–October 1964 in three separate daytime intervals against the geomagnetic index $K\text{p}$, Yeh and Flaherty (1966) from $\tau$ observations made at the middle latitude station of Urbana ($40.1^{\circ}~\text{N},88.1^{\circ}~\text{W}$; QD Lat. $50.4^{\circ}~\text{N}$) found a tendency of $\tau$ to increase as the magnetic activity increases. Hibberd and Ross (1967) analyzed storm-time variations of $\Delta\tau/\tau$ (being $\Delta \tau$ the departure of $\tau$ measurements from climatological values) calculated during 18 geomagnetic storms occurred in the period July 1961–June 1962, from the beginning of the sudden storm commencement or when the geomagnetic index $a\text{p} > 39~\text{nT}$. They found a positive correlation as described by the positive $\Delta \tau/\tau$ variations clearly observed up to three days later the storm commencement, with greater values occurring within the first ten hours. Titheridge and Andrews (1967) studied the behavior of $\tau$ at a southern hemisphere middle-latitude station near Auckland ($36.8^{\circ}~\text{S},174.7^{\circ}~\text{E}$; QD Lat. $42.6^{\circ}~\text{S}$) during the geomagnetic storm of 16 June 1965. They observed $\tau$ values above the monthly median level for almost one day ($\approx 06{:}00_{16\text{th}}\text{--}06{:}00_{17\text{th}}$) and some hours after the storm commencement (23:00_15th LT), correspondingly to a clear increase of the $K\text{p}$ index. $\tau$ values below the monthly median value and a slow gradual decrease of $K\text{p}$ were observed in the next 42 hours (06:00_17th–24:00_18th LT). Mendillo et al. (1972) investigated the average storm time and local time variations of $\tau$ from the monthly median during 28 geomagnetic storms occurred in the period December 1967–November 1969 at the middle-latitude station of Hamilton ($42.6^{\circ}~\text{N},70.8^{\circ}~\text{W}$; QD Lat. $51.7^{\circ}~\text{N}$). During such storms, $\tau$ enhanced with peaks clearly observed during the first two days of the storm in the early morning (10:00–12:00 LT) and in the afternoon hours (12:00–15:00 LT). Kerseley and Hajeb-Hosseinieh (1976) found an increasing linear trend between $\tau$ and geomagnetic activity during moderate solar activity levels at the middle-latitude station of Aberystwyth ($52.4^{\circ}~\text{N},4.0^{\circ}~\text{W}$; QD Lat. $49.0^{\circ}~\text{N}$). Balan and Iyer (1978) selected storm periods characterized by $A\text{p}\geq30~\text{nT}$ and studied the departures of $\tau$ from the mean of the 7 days before the sudden storm commencement ($\Delta \tau$) to find whether geomagnetic activity can influence the $\tau$ behavior observed at Hamilton station. They observed positive phase ($\Delta \tau > 0$) and negative phase ($\Delta \tau < 0$) occurring more frequently during daytime and nighttime, respectively. The effect of storm magnitude on $\tau$ was investigated plotting $\Delta \tau$ vs. $A\text{p}$. The results showed that the increase of the geomagnetic activity leads to a clear increase of $\Delta \tau$, while for negative values of $\Delta \tau$ no clear dependence on geomagnetic activity was observed. Chauhan and Gurm (1981) studied the effects of geomagnetic storms on $\tau$ during the solar minimum period of 1975–1976 for two Indian low-latitude stations. At Ahmedabad ($23.0^{\circ}~\text{N},72.6^{\circ}~\text{E}$; QD Lat. $17.0^{\circ}~\text{N}$) station, located near the crest of the EIA, $\tau$ exhibited values above its mean level during two moderate geomagnetic storms. Differently, at Delhi station, far from EIA, the results turned out to be in general inconclusive without any clear dependence on magnetic activity. Huang (1983) considered weak ($A\text{p} < 30~\text{nT}$) and strong ($A\text{p} \geq 30~\text{nT}$) geomagnetic storms occurring during the period March 1977–February 1982 to investigate the geomagnetic storm effects on the variation of $\tau$ at the low-latitude station of Lunping. The results highlighted that, when strong storms occur, two hours after the storm commencement $\tau$ starts to increase reaching its maximum three hours later, and a positive phase around midnight or pre-sunrise hours and a negative phase in daytime are observed until the end of the second storm day. Instead, during weak storms, $\tau$ shows features that are similar to those observed for the strong ones, even though unusual negative phases during pre-storm hours are observed. Jayachandran et al. (2004) investigated the effect of magnetic disturbances on $\tau$ by comparing the mean diurnal variations of $\tau$ for magnetically quiet days ($A\text{p} < 10~\text{nT}$) with the ones obtained for disturbed days. They found a significant enhancement of $\tau$, both in daytime and nighttime hours, at the middle-latitude station of Boulder ($40.0^{\circ}~\text{N},105.3^{\circ}~\text{W}$; QD Lat. $48.3^{\circ}~\text{N}$) and at the high-latitude station of Goose Bay during the years of solar minimum (1985) and solar maximum (1981), respectively. Gulyaeva and Stanislawska (2005) studied the storm-time $\tau$ behavior through spatial maps of $\tau$ during five magnetic storms occurred in the years of minimum (1995–1996) and maximum (2002) of solar activity using data from several stations spread throughout Europe. They performed a super-posed epoch analysis based on an index defined to describe how much the measured map differ from the climatological one. Their study highlighted an enhancement of $\tau$ for more than 2 days from the onset of the storm at solar maximum, while at solar minimum the increase of $\tau$ appears delayed by 12 to 24 hours with respect to the onset of the storm and with a shorter duration. The $\tau$ storm-time behavior was also investigated at the European middle-latitude station of Dourbes by Stankov and Warnant (2009) during two severe geomagnetic storms occurred on 15 July 2000 and on 8 November 2004, both characterized by a Dst geomagnetic index close to $-400~\text{nT}$. For the first storm, during both the main phase ($\approx19{:}30_{15\text{th}}\text{--}23{:}00_{15\text{th}}~\text{UT}$) and the early hours of the recovery phase ($\approx23{:}00_{15\text{th}}~\text{UT--}06{:}00_{16\text{th}}~\text{UT}$), a peak of $\tau$ with a value greater than 600 km was observed. In the second storm, during the main phase ($\approx21{:}00_{7\text{th}}~\text{UT--}06{:}00_{8\text{th}}~\text{UT}$) and the early stages of the recovery phase ($\approx06{:}00_{8\text{th}}~\text{UT--}09{:}00_{8\text{th}}~\text{UT}$), a very significant increase of $\tau$ was observed. A peak of $\tau$ at 650 km, corresponding to 250% above the monthly mean, was found three hours after the beginning of the recovery phase; after that, $\tau$ started to decrease but always with values higher than the quiet reference level for all the storm period. Chuo et al. (2010) found an apparent increase of $\tau$ with respect to its monthly median behavior at Wuhan ($30.6^{\circ}~\text{N},114.4^{\circ}~\text{E}$; QD Lat. $24.5^{\circ}~\text{N}$), a middle-latitude station close to the northern crest of EIA, during the main and recovery phase of a moderate geomagnetic storm (minimum $\textit{Dst} = -238~\text{nT}$) occurred on 22 October 1999. Studies analyzing $\tau$ during storm time at equatorial latitudes are relatively few. In a recent survey, Zhang et al. (2021) defined a disturbance index (DI) based on $\tau$ measurements recorded at Guam ($13.6^{\circ}~\text{N},144.8^{\circ}~\text{E}$; QD Lat. $6.1^{\circ}~\text{N}$) station, located near the magnetic equator ($5.54^{\circ}~\text{N}$ dip latitude), during the years 2012–2017. DI quantitatively describes the effects of geomagnetic storms on $\tau$ variations. The comparison between the storm-time and quiet-time DI diurnal variations leads to the conclusion that geomagnetic storms enhance $\tau$ during most of the storm period except for some cases when they have negative effects around sunrise.

The above mentioned studies highlighted a very cryptic picture with different results depending on location, solar activity level, local time hour, and the level of magnetic disturbance. In fact, from past studies it is difficult to draw a clear and definite pattern of the magnetic activity influence on $\tau$ variations. In the investigation of the $\tau$ variations triggered by magnetic activity disturbances, an issue that has to be taken into account is that it is not always easy to establish the quiet level of $\tau$ to which refer. Moreover, it may not be wholly correct to correlate the time series of $\tau$ with the simultaneous ones of a whatever geomagnetic index or with its daily average (Hibberd and Ross 1967). For example, time lags of one or two hours between magnetic data and $\tau$ time series should also be investigated to see whether better results may be achieved.

4 Main Applications and Models of the Slab Thickness

Over the years, the slab thickness has found application in several fields linked to both the explanation of physical processes and modeling purposes. We review here the most relevant of these applications, although some of them are now outdated.

Several studies have shown that $\tau$ is related to a variety of physical processes:

• a) it allows to estimate the scale height of the ionized constituents through the relationship linking $\tau$ to the neutral vertical scale height $H_{\mathrm{n}} =k_{\mathrm{B}} T_{\mathrm{n}} /m_{\mathrm{i}} g$ (Hargreaves 1992; Rishbeth and Garriott 1969), where $k_{\mathrm{B}}$ is the Boltzmann’s constant, $T_{\mathrm{n}}$ is the neutral temperature, $m_{\mathrm{i}}$ is the ion mass and $g$ is the acceleration due to the gravity field. Specifically, in the simplifying working hypothesis of a single $\alpha$-Chapman layer with constant scale height $H_{\mathrm{n}}$, it can be demonstrated that $\tau = 4.133H_{\mathrm{n}}$ (Wright 1960; Hibberd and Ross 1966; Titheridge 1973). However, like discussed in Pignalberi et al. (2021a), this formula implies the assumption of a constant value of $H_{\mathrm{n}}$ for the whole topside ionosphere, which is a strong assumption, as pointed out by recent studies (e.g., dos Santos Prol et al. 2019; Pignalberi et al. 2020a). Moreover, and more importantly, the $\alpha$-Chapman function represents the F2 layer of the ionosphere only under very strict assumptions unrepresentative of the real ionosphere whose vertical distribution of plasma is driven by the plasma scale height $H_{\mathrm{p}} =k_{\mathrm{B}} T_{\mathrm{p}} /m_{\mathrm{i}} g$ that, in turn, depends on the plasma temperature $T_{\mathrm{p}}$ and other physical quantities (e.g., Pignalberi et al. 2018, 2020a,b);

• b) it is related to the plasma temperature $T_{\mathrm{p}} = (T_{\mathrm{e}} + T_{\mathrm{i}})$ even if it does not seem to be a good indicator of electron ($T_{\mathrm{e}}$) and ion ($T_{\mathrm{i}}$) temperatures (Amayenc et al. 1971; Furman and Prasad 1973; Stankov and Jakowski 2006). Also in this case, albeit a slight dependence of $\tau$ on $T_{\mathrm{p}}$ is not excluded, since the electron density has a certain degree of correlation with the electron temperature, it is too simplistic to reduce the $\tau$ trends to the $T_{\mathrm{p}}$ ones;

• c) it allows to estimate the thermospheric neutral temperatures ($T_{\mathrm{n}}$) through the relationship $\tau = 0.216T_{\mathrm{n}}$ (Titheridge 1973) or $T_{\mathrm{n}} = (\tau + 250)/0.5$ (Jakowski et al. 2017). As above, $T_{\mathrm{n}}$ regulates many chemical reactions that are fundamental for the ionization of the particles constituting the ionosphere and affects the vertical extension of the atmosphere as a whole; then, a slight dependence of $\tau$ on $T_{\mathrm{n}}$ has to be expected. However, no strict correlation between $\tau$ and $T_{\mathrm{n}}$ has been ever demonstrated.

For what concerns modeling applications, the slab thickness found application in several data-assimilation methodologies as the parameter linking vTEC to NmF2 (the vice versa is also possible but not very useful). In fact, its knowledge is of practical interest to predict NmF2 at locations where only vTEC values are known from observations, a condition of easy occurrence given that the number of ground-based GNSS receivers is by far greater than that of ionosondes. For example, Krankowski et al. (2007) used $\tau$ as a factor to convert vTEC maps from GPS observations of the EUREF permanent GNSS network (https://www.epncb.oma.be/) to foF2 values. Specifically, they found $\tau = 310~\text{km}$ as the optimal conversion factor on the basis of the analysis of foF2 observations recorded at five European ionospheric stations from 1996 to 2001 and corresponding vTEC values from co-located GPS receivers. Gerzen et al. (2013) extended this approach to a global scale by reconstructing NmF2 global maps from vTEC global maps. Differently from Krankowski et al. (2007), Gerzen et al. (2013) modeled $\tau$ on the basis of vTEC values given by the Neustrelitz global TEC model (NTCM-GL, Jakowski et al. 2011a) and NmF2 values from the Neustrelitz Peak Density Model (NPDM, Hoque and Jakowski 2011). Modeled $\tau$ values were then used by Jakowski et al. (2011b) to obtain NmF2 maps from vTEC maps given by the NTCM-GL model after the assimilation of vTEC values from ground-based GPS stations of the International GNSS Service (IGS, http://www.igs.org/) network. Froń et al. (2020) were able to provide global maps of $\tau$ by putting together the information given by the IGS network and that of the ionosondes of the Global Ionosphere Radio Observatory (GIRO, Reinisch and Galkin 2011) network. Specifically, GIRO ionosondes data are assimilated by the IRI-based Real-time Assimilative Model (IRTAM, Galkin et al. 2012, 2020) to produce an update of the International Reference Ionosphere (IRI, Bilitza et al. 2017) representation of NmF2; at the same time, vTEC maps are produced through the assimilation of vTEC data from the IGS network (Hernández-Pajares et al. 2009). Finally, by joining the two representations, $\tau$ global maps are produced and delivered through the GAMBIT Explorer software (http://giro.uml.edu/GAMBIT). It is worth highlighting that the sensitivity of $\tau$ with respect to not climatological processes makes it a good candidate for Space Weather monitoring and alerts (Galkin et al. 2022).

$\tau$ is applied also to improve the modeling of the electron density profile shape when ingested by empirical models like NeQuick (Nava et al. 2011). Gulyaeva et al. (2021) explored the possibility to use the center of mass (Hc) of the ionosphere as a proxy for the effective ionospheric shell height (to be used in the conversion of sTEC to vTEC). For this purpose, Hc has been determined from the electron density profiles within the boundaries of $\tau$ in the height range ($\textit{hm}\text{F}2- \tau _{\mathrm{bot}}, \textit{hm}\text{F}2 + \tau_{\mathrm{top}}$) where $\tau_{\mathrm{bot}}$ and $\tau_{\mathrm{top}}$ are the bottomside and topside equivalent slab thickness.

Fox et al. (1991) developed a model describing the $\tau$ climatological behavior for middle latitudes based on NmF2 values recorded by the ionosonde installed at Wallops Island and vTEC data measured at Hamilton using Faraday rotation of signals from geosynchronous satellites, during the period 1965 to 1986. Pignalberi et al. (2021a) compared the output of the Fox et al. (1991) model to actual $\tau$ values recorded at Wallops Islands for the last two solar cycles, highlighting several differences most of which are due to the different methodologies applied to derive vTEC data for the $\tau$ calculation, as discussed in Sect. 2.

Recently, Jakowski and Hoque (2021) developed an empirical global climatological model of $\tau$ which is the only available so far. They modeled $\tau$ based on a dataset of NmF2 values derived from CHAMP (CHAllenging Minisatellite Payload), GRACE (Gravity Recovery And Climate Experiment), and COSMIC/FORMOSAT-3 radio occultation measurements, and vTEC values from vTEC maps generated by CODE (Center for Orbit Determination in Europe) based on IGS data archive. Through a dataset spanning from 2001 to 2018, they described the main spatial, diurnal, seasonal, and solar activity variations in $\tau$ in a very compact way based on 12 coefficients via non-linear least square methods. Jakowski and Hoque (2021) model reproduces the main $\tau$ climatological variations and anomalies but the comparison with $\tau$ values derived by five co-located ionosondes-GNSS receivers at different latitude revealed the very-high variability and dispersion of $\tau$ (particularly for the nighttime and solar terminator hours) which the model can hardly represent. As a consequence, there is still a lot of room for improvement about $\tau$ global empirical modeling to better describe its behavior also under non-equilibrium conditions.

It is of course possible to calculate $\tau$ as a by-product of the NmF2 and vTEC values modeled by IRI and NeQuick (Nava et al. 2008) global models. However, such models are not designed for the $\tau$ calculation and the datasets on which they are based are heavily unbalanced towards the lowest part of the ionosphere. So, the description of the topside part of the ionosphere made by such models needs improvements (Pignalberi et al. 2016, 2018; Pezzopane and Pignalberi 2019).

Part II

5 Global Climatology of the Ionospheric Equivalent Slab Thickness

5.1 vTEC and NmF2 Datasets

Section 3 summarized the most relevant investigations of the $\tau$ behavior performed in the last 60 years, most of which are related to very limited datasets. This happens because it is not easy to get datasets of NmF2 and vTEC measurements that are simultaneously available for a long period of time over a given location (i.e., a specific ionospheric station). As a consequence, the selection criteria of an ionospheric station suitable for studying the behavior of $\tau$ heavily rely on the availability of an operational ionosonde and a co-located GNSS receiver, both of them continuously working for a long period of time to allow for a climatologic study based on a robust statistics.

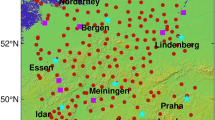
Specifically, in this study, the pairs ionosonde station-GNSS receiver routinely working for at least ten years, so as to cover at least a solar cycle, were selected. When available, we selected exactly co-located ionosonde station-GNSS receiver pairs; however, in some cases this was not possible due to the current spatial distributions of such observational facilities. Anyway, we selected pairs of ionosonde station-GNSS receiver whose distance is well below the ionospheric horizontal correlation distance (Forsythe et al. 2020); the maximum distance between pairs is the one of Jicamarca station (759 km, see Table 1). According to this criterion, we were able to select thirty-two ionospheric stations (i.e., pairs of co-located ionosondes-GNSS receivers) distributed all over the world (see Table 1 and Fig. 5). NmF2 and vTEC data, recorded respectively by co-located ionosondes and GNSS receivers, were used to calculate $\tau$ values during the last two solar cycles, from the beginning of 1997 to the end of 2019. Figure 6 represents the time spanned and yearly percentages of available $\tau$ values for each ionospheric station. As far as we know, the dataset considered in this study is the longest and most complete used so far for a climatological analysis of $\tau$.

Fig. 5

Global map indicating the geographic position of the thirty-two ionosonde stations and GNSS receivers considered in this study. Red circles refer to ionosonde stations, while yellow ones to GNSS receivers. Refers to Table 1 for the identification number (ID) specification

Fig. 6

(Top panel) $\text{F10.7}_{81}$ time series from 1997 to 2019; blue horizontal dashed lines mark the thresholds used to perform the solar activity binning of the dataset. (Bottom panel) Percentages of $\tau$ values available year by year for each ionospheric station

Table 1 List of ionosonde stations and corresponding GNSS ground-based receivers, with the corresponding network of belonging, used in this study. The first column marks the identification number (ID) of each ionospheric station (see Fig. 5). The geographic coordinates of each ionosonde station and GNSS ground-based receiver are reported along with the distance between them in km (last column). The Quasi-Dipole magnetic latitude (Laundal and Richmond 2017) is also reported for each ionosonde station

It is worth noting that most of the selected ionospheric stations are located at Northern middle latitudes (Fig. 5), while for both the equatorial and very high latitudes, there are only a few ionospheric stations satisfying our requirements. Overall, it is almost the same for the Southern hemisphere. This is due to the unevenly distribution of both ionosondes and GNSS receivers between the two hemispheres and to the difficulties in installing and maintaining such instrumentation at equatorial and high latitudes. With the growing number of GNSS receivers installed throughout the world and newly installed ionosondes, over the next few years it will be possible to collect enough data to extend and enlarge this investigation at equatorial and high latitudes.

As mentioned in the Introduction, this investigation represents an extension of a previous work recently published by Pignalberi et al. (2021a) concerning the $\tau$ climatology over three Northern middle-latitudes ionospheric stations. In this study, we applied the same methodology and validation analysis proposed by Pignalberi et al. (2021a). As a consequence, only the essential information about NmF2 and vTEC datasets and corresponding data selection and binning are provided here, the full details and additional information can be found in Sect. 2 of Pignalberi et al. (2021a).

NmF2 data were retrieved from ionograms recorded by DPS Digisondes (Bibl and Reinisch 1978) at the thirty-two ionospheric stations, and autoscaled by the Automatic Real-Time Ionogram Scaler with True height analysis (ARTIST) software (Galkin and Reinisch 2008). Only ionograms characterized by a suitable Confidence Score (C-Score) index were selected (C-Score $\geq75$) so as to guarantee the reliability of the ionogram itself and consequently of the autoscaled NmF2 value. According to the sounding repetition rate of the ionosondes, the NmF2 time series have a time sampling of fifteen minutes (at minutes 0, 15, 30, and 45 of each UT hour).

vTEC data were obtained from daily Receiver INdependent EXchange (RINEX) files, recorded by GNSS ground-based receivers selected as near as possible to the ionosonde stations, through the application of the Ciraolo’s calibration method (Ciraolo et al. 2007). The ionospheric pierce point altitude was set to 350 km, and the minimum elevation angle to $20^{\circ}$. Differently from the NmF2 time series, vTEC ones have a thirty-seconds time sampling. To make the two datasets consistent, a procedure making use of a Gaussian weight was adopted so as to provide the vTEC values actually used for the $\tau$ calculation as weighted mean of vTEC values sampled at a thirty-seconds rate ($\overline{\mathrm{vTEC}}$) in windows fifteen-minutes wide centered at minutes 0, 15, 30, and 45 of each UT hour. The details of this procedure are given in Pignalberi et al. (2019, 2021a).

5.2 Slab Thickness Calculation and Binning

NmF2 and $\overline{\mathrm{vTEC}}$ time series concurrently available were used to get the $\tau$ time series, for each ionospheric station listed in Table 1, through the application of Eq. (1). As a consequence, $\tau$ time series at a fifteen-minutes time interval were obtained for each ionospheric station of Table 1, according to the time span and availability shown in the bottom panel of Fig. 6.

Since our investigation concerns the climatological behavior of $\tau$, we focused on magnetically quiet time periods. Similarly to Pignalberi et al. (2021a), quiet time periods were selected on the basis of the Sym-H (http://isgi.unistra.fr/Documents/References/Iyemori_et_al_2010.pdf) and AE (Rostoker 1972) geomagnetic indices. Further details about the choice of Sym-H and $AE$ geomagnetic indices are provided in the Sect. 2.2 of Pignalberi et al. (2021a). Geomagnetic activity indices, at one-minute interval, were downloaded from the OMNIWeb Data Explorer website (https://spdf.gsfc.nasa.gov/pub/data/omni/high_res_omni/). $\tau$ values actually employed in this survey are those calculated for the following conditions:

$$ -25~\text{nT} \leq \textit{Sym-H} \leq 5~\text{nT}\quad \text{AND}\quad \textit{AE} \leq 300~\text{nT}. $$

The solar activity variation of $\tau$ was investigated by using the $\text{F10.7}_{81}$ solar index, i.e., the 81-day running mean of the daily value of the solar radio flux at 10.7 cm (F10.7) wavelength (Tapping 2013). This index is particularly suitable for a climatological study since it smooths the short-time variability of F10.7.

F10.7 daily data were downloaded from the OMNIWeb Data Explorer website (https://omniweb.gsfc.nasa.gov/form/dx1.html). The solar activity dependence has been studied by binning the $\tau$ time series according to the following three ranges:

• Low solar activity (LSA): $\text{F10.7}_{81} \,{<}\, 80$ s.f.u. (solar flux unit, $1~\text{s.f.u.} \,{=}\, 10^{-22}~\text{Wm}^{-2}\,\text{Hz}^{-1}$);

• Medium solar activity (MSA): $80~\text{s.f.u.} \leq \text{F10.7}_{81} < 120~\text{s.f.u.}$;

• High solar activity (HSA): $\text{F10.7}_{81} \geq 120~\text{s.f.u.}$

The three solar activity ranges were selected to optimize and uniform the data distribution in each of the three considered bins taking into consideration the $\text{F10.7}_{81}$ values characterizing the last two solar cycles (from 1997 to 2019). The $\text{F10.7}_{81}$ time series is represented in the top panel of Fig. 6 along with the chosen thresholds.

For each of the thirty-two ionospheric stations considered, and for each level of solar activity, the diurnal and seasonal $\tau$ variability were investigated by binning data in bins fifteen-minutes wide in LT, for each month of the year. For each bin, the following statistical metrics were calculated:

• 5th percentile, i.e., the lower whisker;

• 25th percentile, i.e., the first quartile;

• 50th percentile, i.e., the second quartile, representative of the median;

• 75th percentile i.e., the third quartile;

• 95th percentile, i.e., the upper whisker.

Note that the median is the more appropriate statistical parameter to be used when dealing with climatological studies because it cuts off the outliers of the distribution. The difference between 75th and 25th percentiles defines the interquartile range (IQR) which provides a measure of the data dispersion around the median value, while the whiskers highlight the tails of the distribution.

5.3 Diurnal, Seasonal, and Solar Activity Variations for Different Latitudinal Sectors

Due to the extension of the analyzed dataset, in this section we present the results relative to selected ionospheric stations (among those listed in Table 1); the reader can find the results relative to all the stations in the Supplementary Material. Information on the Supplementary Material are given in the Appendix. The selected ionospheric stations are those characterized by the greatest amount and completeness of data, and are representative of different geomagnetic latitudinal sectors.

The following latitudinal sectors were identified on the basis of the QD magnetic latitude (Laundal and Richmond 2017) of the ionospheric stations:

• Equator: QD latitude $\in[10^{\circ}~\text{S},10^{\circ}~\text{N}]$;

• Low latitudes: QD latitude $\in(10^{\circ}~\text{S--}30^{\circ}~\text{S}]\cup(10^{\circ}~\text{N--}30^{\circ}~\text{N}]$;

• Middle latitudes: QD latitude $\in(30^{\circ}~\text{S--}55^{\circ}~\text{S}]\cup(30^{\circ}~\text{N--}55^{\circ}~\text{N}]$;

• High latitudes: QD latitude $\in(55^{\circ}~\text{S--}70^{\circ}~\text{S}]\cup(55^{\circ}~\text{N--}70^{\circ}~\text{N}]$;

• Polar cap: QD latitude $\in(70^{\circ}~\text{S--}90^{\circ}~\text{S}]\cup(70^{\circ}~\text{N--}90^{\circ}~\text{N}]$.

For the three different solar activity levels, the results are presented as:

• a) grids of fifteen-minutes binned medians as a function of LT and month of the year. Only bins with at least 10 values are considered statistically significant. Bins poorly populated are represented in white;

• b) boxplots as a function of the LT for March, June, September, and December, that are representative of equinoxes and solstices. It is worth noting that the $y$-width of each box represents the IQR, which means that the boxplots provide useful information about the dispersion of data around the median values.

In addition, for each solar activity level and for each ionospheric station considered in this study, the arithmetic mean of $\tau$ median values was calculated for the LT sectors [$5,8$) (dawn hours), [$8,16$) (daytime hours), [16–21) (dusk hours), and [$21,5$) (nighttime hours) for March, June, September, and December. Corresponding results are provided in the Supplementary Material. The possible dependence of $\tau$ on the solar activity was further investigated examining the daytime and nighttime mean of $\tau$ median values. The most significant cases, i.e., those characterized by an increase or decrease of $\tau$ of at least 20 km when passing from LSA to MSA and from MSA to HSA are shown for the selected latitudinal zones in the Supplementary Material.

5.3.1 Equatorial Sector

The climatological behavior of $\tau$ at equatorial latitudes is investigated through the Jicamarca station that has a percentage of available data (40.4%) much greater than Fortaleza (22.2 %) and Sao Luis (31.8%), and it lies right above the magnetic equator (QD Lat. $0.2^{\circ}~\text{N}$). We remind to the reader that for Jicamarca station the GNSS considered as co-located is at more than 700 km south of the ionosonde. Especially in this geomagnetic sector this could have an impact on the results.

Figure 7 shows the grids of fifteen-minutes binned medians of $\tau$ values measured at Jicamarca for LSA, MSA, and HSA. Figures 8–10 show the corresponding boxplots for March, June, September, and December.

Fig. 7

Grids of fifteen-minutes binned medians of $\tau$ recorded at Jicamarca for low (top panel), medium (middle panel), and high (bottom panel) solar activity, as a function of LT ($x$-axis) and month of the year ($y$-axis). Empty bins are white colored

Fig. 8

Boxplots of fifteen-minutes binned $\tau$ values measured at Jicamarca station as a function of the LT ($x$-axis), for March, June, September, and December, for low solar activity. In each boxplot, the red horizontal line is the median value for that bin; the 25th and 75th percentiles are represented as the lower and upper limits of each box, respectively; the 5th and 95th percentiles are shown as lines extending below and above each box (whiskers), respectively. Green shaded bars at the bottom of each panel represent the number of values falling in that bin

Overall, the main results shown by Fig. 7 are:

• a) the presence in all seasons of higher values around the central hours of the day (10–16 LT) than for nighttime ones (21–03 LT); this feature occurs for each solar activity level, in particular for HSA where the highest values are observed. Moreover, around equinoctial months, for HSA, such high values tend to last until the late afternoon hours;

• b) the presence of significant pre-sunrise peaks independently of both season and solar activity;

• c) the presence of post-sunset peaks around the equinoxes for HSA.

Diurnal median variations shown in boxplots of Figs. 8, 9 and 10 emphasize the presence of two distinct maxima occurring during sunrise and around the midday hours. During daytime hours, minimum and maximum values are observed in December and September, respectively. During nighttime hours, minimum values are observed in December for LSA and MSA, and in June for HSA; while maximum values are detected in June for LSA and in September for MSA and HSA. The average values of medians observed for the four selected months, for both daytime and nighttime hours and for the three levels of solar activity, are shown in Figure SM1 in the Supplementary Material. With regard to the solar activity dependence, a positive correlation is found in September in daytime hours and in all seasons in nighttime hours (Figure SM2 in the Supplementary Material).

Fig. 9

Same as Fig. 8, but for medium solar activity

Fig. 10

Same as Fig. 8, but for high solar activity

5.3.2 Low Latitudes: Main Differences Between Northern and Southern Hemispheres

The results for Ramey (QD Lat. $27.5^{\circ}~\text{N}$) and Learmonth (QD Lat. $32.3^{\circ}~\text{S}$) stations are shown as representative of the low latitudes for the Northern and Southern hemispheres, respectively. The data availability is 28.8% and 35.7% for Ramey and Learmonth, respectively.

Figure 11 shows the grids of fifteen-minutes binned medians of $\tau$ values measured at Ramey and Learmonth stations. Figures 12, 13 and 14 show the corresponding boxplots for March, June, September and December. For an easy seasonal comparison between the two stations, the sequence of the months of Learmonth grids and boxplots is from July to June with respect to Ramey’s one that is from January to December. The same holds for all the other stations located in the Southern hemisphere.

Fig. 11

Same as Fig. 7 but for (left panels) Ramey, and (right panels) Learmonth stations

Fig. 12

Same as Fig. 8, but for (left panels) Ramey and (right panels) Learmonth stations

Fig. 13

Same as Fig. 12 but for medium solar activity

Fig. 14

Same as Fig. 12 but for high solar activity

For LSA the results of Fig. 11 show that the $\tau$ median behavior at Ramey is morphologically similar to that of Learmonth in terms of: pre-sunrise peaks observed in all seasons; values at nighttime and around solar terminator hours larger than daytime ones; an evident increase of values between 8–12 LT in summer. For MSA, Learmonth exhibits daytime values higher than Ramey in summer, and also at nighttime in equinoctial months. Conversely, Ramey values around the morning solar terminator hours in spring and winter are considerably higher than Learmonth ones.

Looking at the boxplots for LSA, pre-sunrise peaks are larger at Learmonth than at Ramey during equinoctial months and summer, while a more defined pre-sunrise peak is observed at Ramey in winter. On the contrary, for MSA and HSA, more evident pre-sunrise peaks are observed at Ramey in equinoctial months and winter, while no pre-sunrise peak is detected in summer. The presence of post-sunset peaks is visible above all at Learmonth in winter, regardless of solar activity. With regard to the main differences between the two sites we can assert that during daytime Learmonth presents values that are systematically higher than those at Ramey and the most significant differences are found in the vernal equinox for LSA and MSA, in summer for MSA and HSA, and in winter for HSA. During nighttime, higher values are found at Ramey in winter, for LSA and MSA. Moreover, in the vernal equinox for HSA, Ramey shows values noticeably higher than those observed at Learmonth. In all the other cases, significantly higher values are observed at Learmonth.

The average values of medians observed at Ramey and Learmonth for both daytime (08:00–16:00 LT) and nighttime (21:00–05:00 LT) hours, and for each level of solar activity, as well as the amount of the most significant variations (at least 20 km), are shown in Fig. 15. Finally, for both sites no significant correlation with solar activity is found.

Fig. 15

Average values of $\tau$ medians observed at Ramey and Learmonth for (left) daytime and (right) nighttime hours, for (top panel) LSA, (middle panel) MSA, and (bottom panel) HSA, for the four selected months; the most significant variations ($\Delta$), positive (when $\tau_{\text{Ramey}} > \tau_{\text{Learmonth}}$) or negative (when $\tau_{\text{Ramey}} < \tau_{\text{Learmonth}}$), are also indicated

5.3.3 Middle Latitudes: Main Differences Between Northern and Southern Hemispheres

Regarding the middle-latitude sector, we selected two pairs of stations at different longitudinal sectors for both hemispheres: the pair Boulder (QD Lat. $48.3^{\circ}~\text{N}$) – Port Stanley (QD Lat. $38.7^{\circ}~\text{S}$) as representative of the American sector; the pair Rome (QD Lat. $35.9^{\circ}~\text{N}$) – Hermanus (QD Lat. $42.5^{\circ}~\text{S}$) as representative of the European-African sector. As already done for low latitudes, the stations with the highest percentage of available data were selected: Boulder (61.9%), Port Stanley (53.2%), Rome (66.2%), and Hermanus (65.9%).

Grids of $\tau$ median values for Boulder (fifteen-minutes wide bins) and Port Stanley (thirty-minutes wide bins) for the three solar activity levels are shown in Fig. 16, while the corresponding boxplots are shown in Figs. 17, 18 and 19. Port Stanley is the only station whose data are binned at thirty-minutes because of its ionosonde time sampling.

Fig. 16

Same as Fig. 7 but for (left panels) Boulder (fifteen-minutes wide bins) and (right panels) Port Stanley (thirty-minutes wide bins)

Fig. 17

Same as Fig. 12 but for Boulder (left panels, fifteen-minutes wide bins) and Port Stanley (right panels, thirty-minutes wide bins)

Fig. 18

Same as Fig. 17 but for medium solar activity

Fig. 19

Same as Fig. 17 but for high solar activity

The results of Fig. 16 show a $\tau$ median behavior at Boulder qualitatively similar to that of Port Stanley. At both sites, and for each solar activity level, in equinoctial and winter months greater values are observed during nighttime and around the solar terminator hours, while a depletion characterizes the daytime hours. Differently, in summer, the central hours of the day are characterized by slightly greater values.

Looking at the boxplots, while post-sunset peaks are clearly visible in winter, the same cannot be said for pre-sunrise peaks. During daytime, values at Boulder are significantly higher than those at Port Stanley independently of solar activity level and season, except in summer for HSA. During nighttime, the situation appears more variegated: for LSA, except for the vernal equinox, higher values are observed at Boulder; for MSA, higher values are observed at Port Stanley for the vernal equinox and at Boulder in winter, while during summer and autumn equinox no significant difference is found; for HSA, except in winter, higher values are observed at Port Stanley. The average values of medians observed at Boulder and Port Stanley for both daytime and nighttime hours and for each solar activity level are reported in Fig. 20, along with their most significant differences (at least 20 km).

Fig. 20

Same as Fig. 15 but for Boulder and Port Stanley; the most significant variations ($\Delta$), positive (when $\tau_{\text{Boulder}} > \tau_{\text{Port Stanley}}$) or negative (when $\tau _{\text{Boulder}} < \tau_{\text{Port Stanley}}$), are also indicated

With regard to the solar activity dependence, a negative correlation is observed in equinoctial months at Boulder for nighttime hours. Port Stanley instead exhibits a positive correlation in summer for daytime hours, while a negative correlation is observed in the autumn equinox for nighttime hours (Figure SM3 in the Supplementary Material).

Grids of $\tau$ median values for Rome and Hermanus, for each solar activity level, are shown in Fig. 21, while the corresponding boxplots are shown in Figs. 22, 23 and 24.

Fig. 21

Same as Fig. 11 but for (left panels) Rome, and (right panels) Hermanus

Fig. 22

Same as Fig. 12 but for Rome and Hermanus

Fig. 23

Same as Fig. 22 but for medium solar activity

Fig. 24

Same as Fig. 22 but for high solar activity

The results of Fig. 21 show that the median behavior observed at Rome is qualitatively comparable to that observed at Hermanus. The climatological features previously described for Boulder and Port Stanley hold also for Rome and Hermanus. This means that, independently of solar activity, greater values occurring during nighttime and around the solar terminator hours in equinoctial and winter months, a decrease of values during daytime hours, and higher values during the central hours of the day in summer, characterize the climatological trend at middle latitudes.

Looking at the boxplots, pre-sunrise and post-sunset peaks are clearly observed only in winter at both sites. With regard to the main differences between the two sites, it can be said that: in daytime hours, apart from the exceptional case observed for HSA in the autumn equinox, whose explanation would require further investigations, higher values are observed in Rome than Hermanus, but with differences not exceeding 33 km; during nighttime hours, except for the summer LSA case, Rome shows values systematically by far higher than Hermanus ones, independently of solar activity. The average values of medians observed at Rome and Hermanus for both daytime and nighttime hours and for each solar activity level are shown in Fig. 25 along with the extent of their most representative variations (at least 20 km).

Fig. 25

Same as Fig. 15 but for Rome and Hermanus; the most significant variations ($\Delta$), positive (when $\tau_{\text{Rome}} > \tau_{\text{Hermanus}}$) or negative (when $\tau_{\text{Rome}} < \tau_{\text{Hermanus}}$), are also indicated

Concerning the solar activity dependence, during daytime hours no clear dependence is observed for both sites, while for nighttime hours a negative correlation is found in equinoctial months for both sites, and in summer for Hermanus (Figure SM4 in the Supplementary Material).

5.3.4 High Latitudes

The Tromso (QD Lat. $66.5^{\circ}~\text{N}$) station, with a data availability of 34.9%, has been selected as representative of the $\tau$ climatological behavior at high latitudes.

Figure 26 shows the grids of fifteen-minutes binned $\tau$ medians measured at Tromso for the three solar activity levels, while the corresponding boxplots are shown in Figs. 27, 28 and 29.

Fig. 26

Same as Fig. 7, but for Tromso

Fig. 27

Same as Fig. 8, but for Tromso

Fig. 28

Same as Fig. 27, but for medium solar activity

Fig. 29

Same as Fig. 27, but for high solar activity

Figure 26 shows that Tromso is characterized by exceptionally high $\tau$ values during nighttime and dawn hours (0–8 LT), occurring mainly at equinoxes and in winter. Except for the summer season, the examination of boxplots also highlights important pre-sunrise peaks more evident for LSA and MSA, while post-sunset peaks are clearly observed only in winter, except for HSA.

In principle, given that Tromso is situated at a very high geographic latitude we would expect a marked seasonal dependence because the intensity of the solar radiation has an important effect on both NmF2 and vTEC. Nevertheless, this is not the case because Tromso median grids offer an overall picture substantially similar to that found at middle latitudes.

During daytime hours, low values are observed in the vernal equinox for LSA and MSA and in the autumn equinox for HSA, while high values are observed in winter for LSA and HSA and in summer for MSA; during nighttime hours, low values are observed in summer, while high values are detected in the vernal equinox.

The average values of medians observed for the four selected months, for both daytime and nighttime hours and for the three levels of solar activity, are shown in Figure SM5 in the Supplementary Material. Finally, no correlation with the solar activity cycle is found.

5.3.5 Polar Cap Sector

For the polar cap sector, the choice is limited to the only Thule (QD Lat. $84.5^{\circ}~\text{N}$) station, characterized by a relatively high percentage of available data (57.8%).

Figure 30 shows the grids of fifteen-minutes binned medians of $\tau$ values measured at Thule for each solar activity level. The corresponding boxplots are shown in Figs. 31, 32 and 33.

Fig. 30

Same as Fig. 7, but for Thule

Fig. 31

Same as Fig. 8, but for Thule

Fig. 32

Same as Fig. 31, but for medium solar activity

Fig. 33

Same as Fig. 31, but for high solar activity

Figure 30 shows that the results obtained for Thule are by far different than those obtained for Tromso, and in general they are very different from those characterizing other latitudes. In fact, in this case, the trend is strongly driven by the intensity of the solar radiation, thus a very strong seasonal dependence is observed for such extremely high latitudes. For LSA and MSA, the highest values are observed mainly in summer, for both daytime and nighttime hours, when the solar radiation is always present, and the lowest values are observed mainly in winter when the solar radiation is practically absent.

Nevertheless, for HSA, the seasonal variability is less marked and a peculiar diurnal variability in February and March is observed. The explanation of these features needs further specific studies.

Due to the extremely high latitude, there are no effects ascribable to the solar terminator passage; as a consequence, distinct pre-sunrise and post-sunset peaks are never observed. This is also supported by boxplots results that show an almost flat diurnal trend for all seasons.

For both daytime and nighttime hours, minimum values are observed in winter for LSA and MSA and in the autumn equinox for HSA. During daytime hours, maximum values are visible in summer, while during nighttime hours they occur in summer for LSA and in the vernal equinox for MSA and HSA. The average values of $\tau$ medians observed for the four selected months, for both daytime and nighttime hours and for the three levels of solar activity, are shown in Figure SM6 in the Supplementary Material. The dependence of $\tau$ with solar activity shows a positive correlation, independently of the season and the hour of the day (Figure SM7 in the Supplementary Material).

6 The Ionospheric Equivalent Slab Thickness Main Patterns

In the present paper, the $\tau$ climatological behavior has been investigated over thirty-two ionospheric stations spread throughout the Northern and Southern hemispheres. Results of Sect. 5 and those shown in the Supplementary Material highlighted very distinct diurnal, seasonal, and solar activity variations for different latitudinal sectors. Some of the outcomes here presented are consistent with the ones achieved in the past by several authors, while others are completely new.

To summarize the main results here presented and discuss them in the light of what is already known from the literature (Sect. 3), in the following the main points concerning the diurnal, seasonal, solar activity, and latitudinal $\tau$ variations will be discussed.

6.1 Diurnal and Seasonal Variations

Results of Sect. 5 highlighted how the diurnal variation of $\tau$ is strongly dependent on latitude and season, so that it is not possible to find a general diurnal trend common to all analyzed stations. However, there are some specific diurnal features shared by many stations over a wide range of latitudes, e.g., daytime/nighttime differences in the $\tau$ magnitude, and the presence of pre-sunrise and post-sunset peaks.

The most remarkable diurnal differences are due to the latitude with three main different behaviors for equatorial, low to high, and polar cap latitudes, respectively. Equatorial stations like Jicamarca (see Sect. 5.3.1) exhibit a diurnal trend characterized by a well-defined pre-sunrise peak and daytime relative maximum values, with slight seasonal variations. Stations in a wide range of latitude from low to high (see Sects. 5.3.2–5.3.4) share a common diurnal pattern characterized by highest values at nighttime and lowest at daytime (with the exception of the summer season), and the presence of pre-sunrise and post-sunset peaks, with local variations induced by seasonal and solar activity dependence. Instead, at polar cap latitudes (see Sect. 5.3.5) the diurnal variation is very faint compared to the seasonal and solar activity ones, and very different compared to other stations.

A remarkable diurnal feature exhibited by $\tau$ at many stations is the presence of pre-sunrise and post-sunset peaks. In this regard, results of Sect. 5 highlighted that:

• at equatorial latitudes, regardless of solar activity, a clear evidence of pre-sunrise peaks and an absence of post-sunset peaks is observed;

• at low latitudes, for LSA, both hemispheres exhibit pre-sunrise peaks in each season, while post-sunset peaks are visible only in the autumn equinox and in winter; for MSA and HSA, pre-sunrise peaks are detected in the Northern hemisphere except in summer, while less distinct pre-sunrise peaks are observed in the Southern hemisphere; post-sunset peaks are detected only in winter in both hemispheres;

• at middle latitudes, pre-sunrise peaks are barely visible at equinoxes, but clearly defined in winter, for different solar activity; regardless of solar activity, post-sunset peaks are found for both hemispheres in winter;

• at high latitudes, for LSA and MSA, pre-sunrise peaks are mostly visible at equinoxes and in winter, while post-sunset peaks only in winter;

• at polar cap latitudes, neither pre-sunrise nor post-sunset peaks are detected, independently of solar activity.

The results for the equatorial latitude station of Jicamarca (QD Lat. $0.2^{\circ}~\text{N}$) are fully in accordance with those achieved by Kenpankho et al. (2011) and Venkatesh et al. (2011) who detected pre-sunrise peaks in all seasons over Chumphon (QD Lat. $3.1^{\circ}~\text{N}$) and Trivandrum (QD Lat. $0.9^{\circ}~\text{N}$), respectively. Likewise, the occurrence of low-latitude pre-sunrise and post-sunset peaks observed in winter at Ramey (QD Lat. $27.5^{\circ}~\text{N}$) and Learmonth (QD Lat. $32.3^{\circ}~\text{S}$) are consistent with the winter pre-sunrise peaks observed over Hawaii (QD Lat. $19.3^{\circ}~\text{N}$) islands (Jayachandran et al. 2004) and equinox/winter pre-sunrise and post-sunset peaks over Nicosia (QD Lat. $29.2^{\circ}~\text{N}$) (Haralambous 2011). At the middle-latitude stations considered in this study, peaks are observed at equinoxes and more clearly in winter with a tendency to be less pronounced as the solar activity increases. These facts agree with the results obtained by several authors (Titheridge 1973; Goodwin et al. 1995a; Mosert et al. 2013; Jayachandran et al. 2004; Pignalberi et al. 2021a). At high latitudes, the results found at Tromso (QD Lat. $66.5^{\circ}~\text{N}$) are in agreement with those of Jayachandran et al. (2004) for Goose Bay (QD Lat. $60.2^{\circ}~\text{N}$) who found pre-sunrise peaks at equinoxes and post-sunset peaks at equinoxes and in winter. A difference between Northern and Southern hemispheres emerges at polar cap latitudes since an absence of pre-sunrise peaks is noted in the Arctic station of Thule (QD Lat. $84.5^{\circ}~\text{N}$), while an occurrence of pre-sunrise peaks was detected by Yadav and Bhawre (2020) at the Antarctic station of Casey (QD Lat. $80.6^{\circ}~\text{S}$).

The physical mechanisms that can concur in the explanation of peaks observed in this investigation are:

• since the equatorial ionosphere is not connected to the plasmasphere by magnetic field lines, there is no plasma replenishment to balance the loss of electrons in the lower ionosphere due to the recombination (Kenpankho et al. 2011); this circumstance could play a role for the observed equatorial pre-sunrise peaks;

• during the early evening hours, the equatorial pre-reversal electric fields produce an upward vertical $\textbf{E}\times \textbf{B}$ drift causing a plasma fountain rising to heights larger than 1200 km at the equator, with accompanying plasma density depletions in the F region (Balan and Bailey 1995; Balan et al. 1997). After the pre-reversal strengthening, the $\textbf{E}\times \textbf{B}$ drift rapidly reverses causing a downward plasma flux which is forced by the neutral winds to move away from equator, thus increasing the topside electron content in the range of magnetic latitude between $10^{\circ}~\text{S}$ and $20^{\circ}~\text{S}$, and between $10^{\circ}~\text{N}$ and $20^{\circ}~\text{N}$. The plasma depletion in the F region created by the pre-reversal strengthening is instead still maintained in the range of magnetic latitude between $30^{\circ}~\text{S}$ and $30^{\circ}~\text{N}$ (Balan et al. 1997). This would explain why at Jicamarca, as well as at Fortaleza (QD Lat. $7.1^{\circ}~\text{S}$), an increasing trend of $\tau$ with a clear peak is practically never observed during post-sunset hours, while at Cachoeira Paulista (QD Lat. $18.8^{\circ}~\text{S}$), just located near the equatorial anomaly crest, an increase of $\tau$ with well-defined peaks is observed especially in the equinoctial and summer months around 20–21 LT (see Supplementary Material). This circumstance is also in agreement with the nighttime phenomenon of the equatorial electron temperature anomaly, occurring predominantly at equinoxes and clearly associated to the deposition of plasma in the range of latitude |$10^{\circ}$|–|$20^{\circ}$| resulting from the sunset electrodynamical processes (Oyama et al. 1997) strictly connected to the existence of strong electric fields over the equatorial latitudes (Modi and Iyer 1989);

• due to the field-aligned plasma flow from the magnetosphere to the ionosphere, large downward fluxes of protons are injected in the topside at pre-sunrise hours, thus lowering the upper transition height, i.e., the height where [$\text{O}^{+}$] is equal to [$\text{H}^{+}$] (Mosert et al. 2013). Evans and Holt (1978) revealed that the duration of such fluxes in the winter hemisphere, in particular during the post-midnight hours, decreases as the solar activity increases. Belehaki et al. (2003) found an increased plasmaspheric content during nighttime. These findings indicate an increase of the topside ionosphere content, thus explaining the presence at the various latitudes of the sharp pre-sunrise and post-sunset peaks observed in the winter season especially for LSA;

• at solar terminator hours, the ionosphere is sunlit differently at different altitudes; then, NmF2 and vTEC manifest a time lag which is well reflected in $\tau$. For example, at sunrise, higher values of $\tau$ mean that NmF2 is low while vTEC is increasing due to the solar radiation impinging from above. The reverse is usually observed at sunset hours;

• changes of the meridional neutral winds direction most pronounced in winter months, and enhanced zonal electric fields, are responsible for the downward movement of the ionosphere. Consequently, the abrupt increase in the loss rate and the corresponding rapid decrease of NmF2 before sunrise, while smaller changes in the topside ionosphere occur, would explain the winter peaks observed at middle latitudes (Titheridge 1973);

• the so called morning overshoot phenomenon, namely, the rapid increase of the electron temperature observed around sunrise (Oyama et al. 1996), which increases the plasma scale height, thus justifying the observed pre-sunrise peaks. Specifically, as observed around the magnetic equator in the range of magnetic latitude between $10^{\circ}~\text{S}$ and $10^{\circ}~\text{N}$ for the period 05:30–06:30 LT, the enhancement of the morning overshoot following the combined action of the downward plasma vertical $\textbf{E}\times \textbf{B}$ drift and neutral winds (Oyama et al. 1996) could play a role in the development of pre-sunrise peaks observed in all seasons at Jicamarca.

A quite common diurnal feature shared by many stations from low to high latitudes is the daytime/nighttime differences in $\tau$ absolute values. Specifically, results of Sect. 5 highlighted how, from low to high latitudes, nighttime values are greater than daytime ones in equinoctial months and even more in winter months, while the reverse is true for summer months.

The highest daytime (10–16 LT) values, regardless of solar activity, are always observed at the magnetic equator (e.g., Jicamarca station), except in winter. Such feature constitutes a second maximum, in addition to the pre-sunrise one, that is not noticed in the other sites under investigation. Instead, the highest nighttime (22–04 LT) values are observed at high latitudes (e.g., Tromso station), especially in winter and equinoctial seasons.

The fact that during daytime hours the largest values are observed near the magnetic equator is also confirmed by Kenpankho et al. (2011) who demonstrate that the slab thickness at Chumphon is much larger than that found at low, middle, and high latitudes.

The two distinct maxima observed during sunrise hours and around the midday at Jicamarca well agree with the results of Venkatesh et al. (2011) who found strong pre-sunrise peaks with a secondary maximum around noon-time hours during all seasons at different Indian equatorial stations. This fact confirms that the maximum around the central hours of the day is a typical feature of the equatorial latitudes. This unusual feature of the equatorial region can be explained in terms of the fountain effect: the equatorial vertical $\mathbf{E}\times \mathbf{B}$ drift during the morning hours is positive (Fejer et al. 1995; Oyama et al. 1996; Balan et al. 1997), which means that the ionospheric plasma is lifted upward. The resulting effect is that while NmF2 does not show any significant increase (Huang 1974), an enhancement of the topside electron content occurs, thus leading to an enhancement of $\tau$ over the magnetic equator (Das Gupta et al. 1975).

The diurnal variations observed at low, middle, and high latitudes, characterized by pre-sunrise and post-sunset peaks and generally higher nighttime values than daytime ones during the equinoxes and winter (while the opposite occurs in summer), are in agreement with the results of other authors (Chuo et al. 2010; Guo et al. 2011; Mosert et al. 2013). The explanation of the diurnal trends can be given regarding them as a superposition of two diurnal curves: a first one which maximizes at noon corresponding to the typical thermospheric variation, and a second one with a double peak at sunrise and at sunset which corresponds to the plasmaspheric variation (Belehaki et al. 2003) which is most prominent in winter and it is due to the lowering of the upper transition height (Mosert et al. 2013). Anyway, it is worth noting that the unusual larger daytime values observed for HSA in the autumn equinox at Hermanus constitute a feature that has no clear explanation.

The extremely high values observed at Tromso for each level of solar activity, and the relatively high values noticed at Thule, for HSA, are in agreement with the outcomes of Huang et al. (2016) who, analyzing global maps of $\tau$ reconstructed from vTEC data obtained from GIM and NmF2 retrieved from COSMIC data, found particularly high values at high and polar cap latitudes for all seasons and for both minimum and maximum solar activity.

The really high values observed at Tromso, in the nighttime and solar terminator hours, could be due to the high-latitude ionospheric trough phenomenon, that is a limited region of depleted plasma density occurring in the ionosphere within the auroral oval or in the polar cap (Rodger et al. 1992; Voiculescu et al. 2016). Troughs were originally considered as phenomena occurring at night during winter (Moffet and Quegan 1983; Rodger et al. 1992). More recent investigations, based on satellite records, have shown that troughs form during all seasons and also during daytime (Aa et al. 2020; Karpachev 2019). Ma et al. (2000) using European Incoherent Scatter Scientific Association (EISCAT) observations showed that high-latitude ionospheric troughs occur in the dawn sector, extending from early morning to pre-noon, but sometimes also in the afternoon and pre-midnight. Winser et al. (1986) again using EISCAT observations found an ionospheric trough characterized by a drop of electron density of 54% on 6 March 1984 right over Tromso. These studies support the idea that the ionospheric trough can play a significant role in causing an enhancement of $\tau$ at high latitudes, as that observed at Tromso.

6.2 Solar Activity Variations

Results of Sect. 5 highlighted how the solar activity affects the $\tau$ magnitude. Except for the very high-latitude station of Thule, no general solar activity trend in $\tau$ can be found, with variations that are function of local time, season, and latitude. The most remarkable variations induced by the solar activity are:

• at equatorial latitudes, for nighttime hours, a positive correlation is observed in all seasons;

• during daytime hours, from equatorial to high-latitude sectors, no significant correlation is observed in both hemispheres, except for rare cases for which a positive correlation is found;

• during nighttime hours, negative correlations are found essentially in equinoctial months for both Northern and Southern middle latitudes;

• at polar cap latitudes, for both daytime and nighttime hours, a positive correlation is observed in all seasons.

This study showed that at equatorial, low, middle, and high latitudes a correlation of $\tau$ with solar activity is practically absent in daytime except for a few cases. The result obtained in the vernal equinox at Jicamarca (QD Lat. $0.2^{\circ}~\text{N}$), for which a positive correlation is observed, is consistent with that of Kenpankho et al. (2011) who, analyzing data over Chumphon (QD Lat. $3.2^{\circ}~\text{N}$), found in equinoctial months a diurnal variation of $\tau$ in the years 2004–2006 clearly increasing for years of higher solar activity.

The absence of any correlation at low latitudes is in contrast with both the positive correlation observed at Hawaii (QD Lat. $19.3^{\circ}~\text{N}$) by Jayachandran et al. (2004) and with the results of Dabas et al. (1993) who, from the examination of data over Lunping (QD Lat. $13.3^{\circ}~\text{N}$), observed a positive correlation between $\tau$ and three different solar indices. However, our results are in accordance with Chuo (2007) who, analyzing data over Chung-Li (QD Lat. $18.3^{\circ}~\text{N}$), found a poor correlation with the solar activity index F10.7.

At middle latitudes, except for the winter case of Port Stanley (QD Lat. $38.7^{\circ}~\text{S}$) for which a positive correlation was noticed, our results are controversial when compared to those of other authors. In fact, the absence of correlation in daytime hours is in sharp contrast with the positive correlation found by Stankov and Warnant (2009) at Dourbes (QD Lat. $45.8^{\circ}~\text{N}$), and by Davies and Liu (1991) at Sagamore Hill (QD Lat. $51.3^{\circ}~\text{N}$). At high latitudes, the lack of any correlation between $\tau$ and solar activity observed at Tromso (QD Lat. $66.5^{\circ}~\text{N}$) is not in accordance with the positive correlation obtained by Jayachandran et al. (2004) at Goose Bay (QD Lat. $60.2^{\circ}~\text{N}$). On the contrary, the results found for Thule (QD Lat. $84.5^{\circ}~\text{N}$) indicate a positive correlation with solar activity in all seasons and match with the observations carried out at the Antarctic station of Casey (QD Lat. $80.6^{\circ}~\text{S}$) for which a positive correlation of $\tau$ was found with each of the three types of solar radiation considered: F10.7, X-ray flux, and EUV flux (Yadav and Bhawre 2020).

The situation is different during nighttime hours when negative correlations are observed at middle latitudes, especially in equinoctial months. Such results are in contrast with those of other authors. For example, both Stankov and Warnant (2009) at Dourbes and Davies and Liu (1991) at Sagamore Hill obtained a positive correlation.

Differently from the Northern hemisphere, in the Southern hemisphere the results found are somewhat consistent with what can be read in the literature. For instance, the results by Breed et al. (1997) agree with ours, even though in our case the negative correlation was found mostly in equinoctial months. The physical mechanism that could explain the observed middle-latitude negative correlations is the following: a lowering of the [$\text{O}^{+}$]–[$\text{H}^{+}$] transition level in the upper F2 region for low solar activity due to large downward fluxes of [$\text{H}^{+}$] from the magnetosphere, occurring generally in winter during post-midnight hours, whose duration decreases as the solar activity increases (Evans and Holt 1978), can increase the topside electron content, which results in higher $\tau$ values at a time of reduced solar activity (Breed et al. 1997).

The circumstances above mentioned tell us that the behavior of $\tau$ for different latitudinal sectors varies in a complicated way in relation to the solar activity cycle, depending on the location of the observing station. An easy classification is then not possible and this topic deserves attention for future studies.

6.3 Latitudinal and Inter-Hemispheric Variations

$\tau$ exhibits large variations with very different diurnal and seasonal patterns as a function of the latitude that show some characteristics features as:

• a decreasing trend of $\tau$ from equatorial to low latitudes is generally observed during daytime hours;

• in the Northern hemisphere, during daytime hours, a tendency of $\tau$ to increase from low to high latitudes is detected for LSA in the vernal equinox, for MSA at both equinoxes, and for HSA in summer; while in winter no significant variations are observed between low and middle latitudes;

• in the Northern hemisphere, during nighttime hours, an increasing trend of $\tau$ from the equator to middle latitudes is observed for LSA in the autumn equinox and in winter, and for MSA in winter.

The decreasing trend of $\tau$ in daytime hours as the latitude increases is deduced comparing the values observed at Jicamarca with those observed at Ramey and Learmonth. A further confirmation comes from the fact that the daytime values of $\tau$ at Jicamarca are almost always higher than those detected at Cachoeira Paulista, a station located near the crest of the equatorial anomaly (see the Supplementary Material).

Our results agree with those by Das Gupta et al. (1975) and Venkatesh et al. (2011). The former, analyzing some low-latitude stations, found that during daytime in winter $\tau$ falls off rapidly as one moves away from the magnetic equator, attaining a minimum value at the stations situated below the crest of the equatorial anomaly; the latter, examining the hourly $\tau$ behavior of some equatorial and low-latitude stations, found $\tau$ values decreasing as the latitude increases, for all seasons.

The observed daytime decreasing latitudinal trend can be explained in terms of the fountain effect: the vertical electrodynamic drift lifts upward the equatorial ionospheric plasma, which diffuses along the magnetic field lines to be deposited at low latitudes. This causes an enhancement of plasma around the crests of the equatorial anomaly and then a reduction of $\tau$, which maximizes around noon when the equatorial anomaly is fully developed (Das Gupta et al. 1975). Anyway, the analysis about the latitudinal variation revealed that $\tau$ can behave in a complex manner and a clear latitudinal signature does not emerge. This circumstance is also confirmed by the studies carried out by Gulyaeva et al. (2004) who, analyzing the $\tau$ behavior at 14 world-wide stations located at different latitudes for high solar activity, observed a clear decreasing trend of $\tau$ as the latitude increases only in winter during daytime.

Another interesting spatial variation is the presence of hemispheric differences, the most remarkable ones are:

• at low latitudes, nighttime and daytime values in the Northern hemisphere are smaller than those in the Southern one;

• at middle latitudes, for both LSA and MSA, during daytime and nighttime hours, Northern values are clearly greater than Southern ones; while no clear pattern emerges for HSA.

The Northern–Southern differences observed at low latitudes by day and night can be explained in terms of changes of the neutral winds pattern between the two hemispheres (Oyama et al. 1996; Balan et al. 1997), which causes large asymmetries in the plasma fountain over all sites for both daytime and nighttime hours (Balan et al. 1997).

At least for daytime hours, the observations of values at the Northern middle latitudes greater than those at the Southern ones for all seasons are consistent with the results of Guo et al. (2011) obtained through the investigation of maps obtained by GPS ground-based receivers and COSMIC radio occultation measurements.

6.4 The Intrinsic Variability of the Slab Thickness

In our analysis we also highlighted the dispersion of $\tau$ values around the medians as represented by the boxes (IQR) and the whiskers in the boxplots shown in Sect. 5, a topic often overlooked by past studies. The investigation of $\tau$ dispersion around median values shed light on its intrinsic variability due to both physical phenomena and to the definition of $\tau$ itself as a function of both a punctual quantity (NmF2) and an integrated one (vTEC).

From our analysis it emerges that:

• a greater dispersion is clearly observed at night and at both dawn and dusk hours. Nevertheless, in some summer cases, at low and middle latitudes, the dispersion characterizing daytime hours is larger, or at most comparable, than that observed during nighttime and solar terminator hours;

• at high latitude, except for summer, a dispersion exceptionally high characterizes the nighttime and solar terminator hours. In particular, for HSA, a large dispersion is visible during daytime in the vernal equinox and winter;

• at polar cap latitudes, except for some cases, no significant difference among nighttime, daytime, and solar terminator hours is observed.

The most relevant fact is the very high dispersion of $\tau$ values at nighttime and for solar terminator hours. The main reason of this behavior lies in the $\tau$ sensitivity to vTEC changes at small NmF2 values, like discussed in Sect. 2 (see Fig. 4). In fact, the nighttime and solar terminator hours are those for which the plasmasphere gives the most relevant contribution to the vTEC (Klimenko et al. 2015), and NmF2 is low. In such circumstances, even small vTEC changes cause large $\tau$ variations thus increasing its corresponding dispersion. Such conditions are even exacerbated at high latitudes, due to the lowest NmF2 values, and produce extremely high $\tau$ values as those recorded at Tromso.

Moreover, part of the dispersion has to be ascribed to the intrinsic day-to-day variability exhibited by both vTEC and NmF2. As a consequence, stations located in regions characterized by large day-to-day ionospheric variations, such as the equatorial and low-latitude regions, as well as the auroral ones, are particularly affected by an increased dispersion of $\tau$ values around the median climatological trend. There is no doubt that this very high intrinsic variability of $\tau$ represents one of the toughest challenges in the $\tau$ modeling.

Part III

7 Current Gaps and Future Developments

In this work, an outstanding dataset of vTEC and NmF2 values has been considered to study the ionospheric equivalent slab thickness over the globe. The variability of $\tau$ in terms of local time, season, and solar activity has been studied with great accuracy at each selected location due to the availability of extremely long and complete time series, spanning almost two solar cycles. Differently, due to the lack of relevant instruments and due to the very strict requirements adopted for the definition of the dataset used, it is difficult to achieve the same level of specification with reference to the geographic coordinates. It would be therefore desirable to increase the knowledge of $\tau$ at low latitudes, for example in the African and Asian longitudinal sectors, with particular focus on the trough and the crests of the EIA, because of the relationship of $\tau$ with the ionosphere plasma scale height. Then, as it has been demonstrated by the very peculiar case of Thule, specific efforts should be devoted to study the behavior of $\tau$ at extremely high latitudes, where the slab thickness patterns are completely different from those at the other latitudes. The ever growing number and distribution of ground-based GNSS stations will allow covering most of the globe in the coming years; however, the lower availability of ionosonde stations compared to GNSS stations, with their uneven spatial distribution, represents a strong limitation for the improvement of the description of the $\tau$ spatial variations. The current distribution of ionosondes (see https://lgdc.uml.edu/common/DIDBFastStationList) is heavily unbalanced towards the Northern hemisphere middle latitudes, with a poor coverage of the low and high latitudes, and, most importantly, of the oceans where only a few island stations are installed. Then, in order to properly describe the $\tau$ spatial variations and for the implementation of a global $\tau$ model based on these observations, a higher number and a more uniform distribution of both ground-based GNSS and ionosonde stations is a requirement to achieve in the near future. A different approach relies on the use of near real-time NmF2 and vTEC global maps to obtain a global representation of $\tau$ (Froń et al. 2020; Galkin et al. 2022); however, the effectiveness of methodologies based on maps is still to be validated. Compared to the robust procedure based on co-located ground-based GNSS and ionosonde stations to obtain $\tau$ (as described in Sect. 5), methodologies based on global maps are possibly prone to misrepresentations due to the inherent smoothing of the mapping procedures, to the uneven distribution of stations used to produce corresponding maps, and to the data-assimilation schemes applied to produce maps (Pignalberi et al. 2021c). This is why a growing number of ionospheric facilities with a more uniform spatial distribution is a key point for a better comprehension of many $\tau$ variations.

As a further step, a deeper analysis should be carried out on the available data to better understand the $\tau$ dependence on solar activity since no clear schemes, common to all locations, have been identified so far. An evident problem in the study of solar activity variations on $\tau$ is the unavailability of time series covering enough solar cycles to properly catch this faint dependence, if any. As evidenced in Sect. 2 and by Pignalberi et al. (2021a), it is not possible to merge the oldest $\tau$ time series based on vTEC from Faraday rotation technique with newest ones based on vTEC from GNSS satellites; as a consequence, time series embracing at most three solar cycles can be obtained from both historical (Faraday rotation, from 60s to 90s) and modern observations (GNSS receivers, from 90s onwards). The shortness of available time series limits the application of spectral time series analyses to highlight solar activity variations around the eleven-year period. Different statistical approaches have to be explored in the future to solve the puzzle of the $\tau$ solar dependence. An attempt should also be made to establish a relationship between $\tau$ and geomagnetic activity, being aware of the intrinsic limitations posed by the scarce availability of case studies. Finally, an assessment about a possible influence on $\tau$ of the Ionospheric Winter Anomaly (Yasyukevich et al. 2018) or the Weddell Sea Anomaly (Chen et al. 2019) could also be envisaged.

In Sect. 4 it has been underlined the importance of the slab thickness parameter because of its relation to several physical processes in the ionosphere, to its capability to contribute to Space Weather monitoring and to ionospheric modeling, including the realization of fast data-ingestion procedures allowing, e.g., the retrieval of foF2 when vTEC is available. As far as future developments are concerned and considering that very few models of slab thickness currently exist, an attempt to build an improved global $\tau$ climatological model is then planned. Due to the geographic distribution of the available data and the remarkable difficulties to be overcome in order to implement a global model, a stepwise approach might be undertaken, with the initial implementation of local (single station) models, followed by the implementation of regional ones (based on multiple stations over a continental or subcontinental area). It is expected that diverse mathematical techniques could be used to accomplish the proposed task, especially in relation to the construction of a global model. Indeed, a classical approach based on Fourier series expansion for time evolution, and functions similar to Spherical Harmonics (Jones and Gallet 1962) to describe the spatial behavior of $\tau$ could be studied. Nevertheless, taking advantage of the newly developed technologies, the utilization of Machine Learning techniques (Yu and Ma 2021) should also be investigated, to go beyond the classical concept of median model and to likely introduce improved forecasting capabilities.

An intriguing and so far poorly explored field of research is the inclusion of a $\tau$ model into an electron density empirical model like NeQuick, even if this might appear as a contradiction because, as it has been pointed out in Sect. 4, empirical models like IRI and NeQuick are already able to provide estimates of $\tau$ as an indirect value obtained from the ratio of vTEC and NmF2. As a first extent, such a $\tau$ model could be used as a reference, or background solution, to provide a “warning” should the electron density model $\tau$ be far from the expected climatological value. As a further step, a procedure to modify NeQuick specific parameters allowing the model to match the expected $\tau$ value could be implemented. This task could be accomplished by taking advantage of the concepts used to develop the data-ingestion techniques based on the use of multiple effective parameters (Nava et al. 2011). It is understood that the implementation of such procedure would require heavy modifications of the NeQuick source code, but it would allow correcting the model $\tau$ a posteriori, keeping the internal consistency of all the parameters values used in the model without modifying its analytical formulation.

8 Conclusive Remarks

In the present paper, first a revision of the literature about the ionospheric equivalent slab thickness has been done and then its climatological behavior has been investigated on the basis of thirty-two ionospheric stations distributed all over the world, for the last two solar cycles, which is the largest and most complete dataset compiled so far. The statistical treatment applied to both NmF2 and vTEC datasets makes the datasets of $\tau$ obtained for the various stations extremely reliable and valuable for the characterization of the $\tau$ behavior at very-large spatial and temporal scales. The climatological analysis highlighted very specific diurnal, seasonal, and solar activity variations depending on the location of the observing station, that were critically discussed in the light of the existing literature.

The extension and completeness of the dataset used in this investigation makes it appropriate for the development of a global empirical climatological model of $\tau$ which, besides representing the main climatological features, would overcome also the limitations characterizing the models developed in the past. For example, the Fox et al. (1991) regional model, being based on the observations of the Faraday rotation of signals from geostationary satellites, provides a relatively large underestimation of $\tau$ measurements, as recently highlighted by Pignalberi et al. (2021a). The Jakowski and Hoque (2021) global model, besides describing the main spatial, diurnal, and seasonal $\tau$ variations, can hardly represent all the variation and dispersion exhibited by $\tau$, particularly during non-equilibrium conditions. Therefore, an empirical climatological global model of $\tau$ based on a very-large dataset derived by co-located ionosondes and ground-based GNSS receivers would be of utmost importance considering that the most important global empirical climatological models of the ionosphere, as NeQuick (Nava et al. 2008) and IRI (Bilitza et al. 2017), do not provide any direct $\tau$ modeling. Moreover, Space Weather applications relying on data-assimilation techniques of either vTEC or NmF2 ionospheric parameters would benefit of a reliable and robust climatological global model of $\tau$.

Appendix: Supplementary Material Description

The statistics shown in Sect. 5 have been calculated for each ionospheric station listed in Table 1, and are available in the Supplementary Material.

Specifically, for each ionospheric station and level of solar activity the Supplementary Material includes:

• a) grids of fifteen-minutes binned counts of measurements on which the median value is calculated;

• b) grids of fifteen-minutes binned medians of measurements;

• c) grids of fifteen-minutes binned IQR values;

• d) boxplots of fifteen minutes binned measurements.

These plots are collected in 32 folders, one for each ionospheric station, with the corresponding station name.

Moreover, the following additional files and figures are also present:

• 1) the README.txt file providing, for each ionospheric station, the information about binning and percentages of available data, with the specification of those rejected after applying the magnetic filtering;

• 2) the Table_tau_mean.xlsx file providing, for the selected ionospheric stations of Sect. 5 and for each level of solar activity, the average values of medians for the LT sectors [$5,8$) (dawn), [$8,16$) (daytime), [16–21) (dusk), and [$21,5$) (nighttime), for March, June, September, and December;

• 3) the Figures SM1–SM7 mentioned in Sect. 5.