Abstract
Interstellar neutrals (ISNs), pick-up ions (PUIs), and energetic neutral atoms (ENAs) are fundamental constituents of the heliosphere and its interaction with the neighboring interstellar medium. Here, we focus on selected aspects of present-day theory and modeling of these particles. In the last decades, progress in the understanding of the role of PUIs and ENAs for the global heliosphere and its interaction with very local interstellar medium is impressive and still growing. The increasing number of measurements allows for verification and continuing development of the theories and model attempts. We present an overview of various model descriptions of the heliosphere and the processes throughout it including the kinetic, fluid, and hybrid solutions. We also discuss topics in which interplay between theory, models, and interpretation of measurements reveals the complexity of the heliosphere and its understanding. They include model-based interpretation of the ISN, PUI, and ENA measurements conducted from the Earth’s vicinity. In addition, we describe selected processes beyond the Earth’s orbit up to the heliosphere boundary regions, where PUIs significantly contribute to the complex system of the global heliosphere and its interaction with the VLISM.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Interstellar neutrals (ISNs), pick-up ions (PUIs), and energetic neutral atoms (ENAs) are fundamental constituents of the heliosphere and its interaction with the neighboring interstellar medium (ISM). Here, we focus on selected aspects of present-day theory and modeling of these particles. However, the accompanying parts of this book greatly complement the material presented here, starting from the historical overview by Zank et al., discussion of ISNs and ENAs observations by Galli et al. and Dialynas et al., and overview of PUI measurements by Zirnstein et al., to list just a few.
Atoms from the local interstellar medium (LISM) enter the heliosphere and interact with the solar environment inside. They are ionized by the solar wind (SW) and the ultraviolet radiation and next are picked up by the ambient magnetic field and propagate outward as PUIs. PUIs are born in the supersonic SW inside the termination shock (TS) and in the heliosheath between the TS and heliopause (HP) due to the charge exchange of the interstellar atoms and SW ions. The PUIs re-neutralized by charge exchange become ENAs, which constitute the so-called globally distributed flux (GDF). The GDF ENAs are just one population of the ENAs present in the heliosphere. Unfortunately, due to the volume limitation for the paper, other ENA populations, like, e.g., planetary ENAs or ribbon ENAs are outside our scope. All three populations of particles, ISNs, PUIs, and ENAs are present throughout the heliosphere. However, their role in the physics of the heliosphere varies with distance to the Sun (Zank 2016). Figure 1 shows the SW—LISM interaction pattern with the TS, HP, and bow shock (BS) according to the MS-FLUKSS model (Pogorelov et al. (2016); see Sect. 3), which is one of several heliosphere concepts, which are extensively described in the accompanying chapter by Kleimann et al.
A general view of the SW-LISM interaction given by the distribution of plasma density (in units of cm−3) in the plane formed by the Sun’s rotation axis and the velocity vector in the LISM unperturbed by the presence of the heliosphere based on the MS-FLUKSS simulation (Zhang and Pogorelov 2016)
A region of the LISM surrounding the Sun that is modified or mediated by heliospheric processes or material is commonly called the very local interstellar medium, VLISM (Zank 2015). Thus, VLISM is the LISM affected by the presence of the heliosphere. Fraternale and Pogorelov (2021) further extended this definition by referring to the LISM modification by the mere presence of the heliosphere, regardless of what physical processes are involved or which LISM properties are affected. This is especially important for the polar and downwind directions. The part of the heliosphere in close vicinity to the Earth is an important region for the study of the heliosphere because the majority of the measurements have been done from Earth’s vicinity. Also, the solar ionizing environment affects the interstellar particles significantly at these distances and cannot be neglected. At distances greater than a few astronomical units (au) from the Sun, the solar influence decreases, PUIs start to contribute substantially to the pressure balance, heat the SW, and slow it down. In the transition region, the SW mixes with the interstellar medium, and the population of PUIs can be subdivided into those transmitted or reflected at the TS and those being created via charge exchange of ISNs inside the inner heliosheath (Zirnstein et al. 2014). They contribute to the ENAs observed from inside the heliosphere next to the ENAs from other sources, like, e.g., those creating the ribbon (McComas et al. 2009).
The ENAs observed are hydrogen ENAs which are the result of charge exchange between SW protons and interstellar H (see chapters by Galli et al. and Dialynas et al.). However, there are also possibilities for the creation of ENAs by interaction with the heavier mass elements, like, e.g., He, Ne, O (see, e.g., Swaczyna and Bzowski (2017) and extensive references on this topic therein). As concluded by Swaczyna and Bzowski (2017) the so-called heavy ENAs could bring information on the global structure of the heliosphere based on the estimated spatial distribution of their fluxes and the energization processes at the TS. However, to successfully observe ENAs of masses greater than hydrogen, a detector with advanced mass resolution capabilities for low intensities is needed.
In the last decades, progress in the understanding of the role of PUIs and ENAs for the global heliosphere and its interaction with VLISM is impressive and still growing. The increasing number of measurements allows for verification and continuing development of the theories and models. We aim to provide a balanced context for these topics and thus we organize the content into the following parts: we start with a brief presentation of the current state of the kinetic model description (Sect. 2). Next, we present the role of PUIs in the MS-FLUKSS model description (Sect. 3). This part is followed with discussions of a fluid model of PUIs at TS (Sect. 4), shock crossing by non-Maxwellian plasma (Sect. 5), and the role of electron impact ionization downstream of the SW TS (Sect. 6). Next, we present heliosphere model solutions proposed by the SHIELD DRIVE Science Center (Sect. 7). In the next part of the chapter, we discuss research fields in which interplay between theory, models, and interpretation of measurements reveals the complexity of the heliosphere and its understanding. In Sect. 8, we discuss topics necessary to interpret ISN, PUI, and ENA measurements conducted from the Earth’s vicinity, where the solar environment significantly modifies fluxes of these interstellar particles. They include ionization rates (Sect. 8.1), ISN and PUI distributions throughout the heliosphere (Sect. 8.2), the secondary population of ISNs (Sect. 8.3), PUIs close to the solar corona (Sect. 8.4), terrestrial ENAs (Sect. 8.5), and inner source PUIs (Sect. 8.6). While in Sect. 9 focuses on processes beyond Earth’s orbit up to the inner heliosheath (IHS), where PUIs significantly contribute to the complex system of the global heliosphere and its interaction with the VLISM. We focus on SW mediation by PUIs (Sect. 9.1), waves due to newborn interstellar PUIs (Sect. 9.2), acceleration of PUIs throughout the heliosphere (Sect. 9.3), and shocks in the IHS (Sect. 9.4). We briefly summarize the chapter in Sect. 10.
2 Kinetic Model Description
The mean free path (mfp) for charge exchange of ISNs is comparable with the size of the heliosphere (Izmodenov et al. 2000) and the ISNs penetrate through the heliopause (HP) reaching the vicinity of the Sun. The ISNs coming from the undisturbed VLISM are called the “primary” component of the ISNs. Their distribution inside the heliosphere is calculated with the use of the Boltzmann equation for the atom distribution function \(f(\mathbf{r},\mathbf{v},t)\) dependent on position \((\mathbf{r})\), velocity \((\mathbf{v})\), and time \((t)\), where \(m\) is the mass of an atom:
The loss term on the right hand side of Equation (1) is due to ionization along the particle trajectory, where \(\beta \) is the ionization rates, \(t\) time, \(r\) distance from the Sun, and \(b\) heliolatitute (more in Sect. 8.1). For H the main contributions to the ionization rate are charge exchange with SW protons and photoionization (see Sect. 8.1).
The force acting on the particle is the Sun’s gravity and, in the case of H, radiation pressure (e.g., Rucinski and Bzowski 1995; Kowalska-Leszczynska et al. 2018):
where \(G\) is the gravitational constant, \(M_{s}\) is the mass of the Sun, and \(\mu \) is the ratio of repulsion from radiation pressure over gravitational attraction \((\mu =|\mathbf{F}_{\mathrm{rad}}|/|\mathbf{F}_{g}|)\). In general, the parameter \(\mu \) depends on time (\(t\)), heliolatitude (\(b\)), and the radial component of the particle velocity (\(v_{r}\)). Due to the low mass of H and the resonant interaction of H with the strong solar Lyman-\(\alpha \) line, the precise determination of \(\mu \) is crucial for the distribution of the ISN H in the vicinity of the Sun (e.g., Rahmanifard et al. 2019; Katushkina et al. 2021b,a; Kowalska-Leszczynska et al. 2022). However, the parameter \(\mu \) is approximately zero for He and O due to their heavier mass compared to H and different line properties (Ruciński 1985).
Under the assumption that the thermal speed of the atom is much less than its bulk flow speed relative to the Sun, the distribution function for the ISNs in VLISM is described by a cold gas approximation (e.g., Fahr 1968a; Blum and Fahr 1970; Holzer 1972; Axford 1972). However, the thermal and bulk flow speeds of atoms in the VLISM are comparable and the gas temperature in the VLISM is an important quantity for the interpretation of the heliospheric observations. Thus, the cold model was extended by Fahr (1971), Thomas (1978), Wu and Judge (1979) to the so-called hot model, in which the source distribution function is assumed as a Maxwell-Boltzmann distribution. The particle trajectories are inferred from solving Kepler’s equation and the moments of the distribution function give number density, velocity, and temperature. The hot model commonly assumes that radiation pressure and losses due to ionization with the solar environment are constant in time. Fahr et al. (1987) and Rucinski and Bzowski (1995) further developed the hot model by including the variations in time for the radiation pressure and ionization losses. Present-day models (e.g., Katushkina et al. 2015; Sokół et al. 2015a) also take into account spatial variations of the ionization losses inside the heliosphere.
The kinetic Equation (1) is a linear partial differential equation that is solved by the method of characteristics. The solution of this equation is
where \(f_{\infty }(\mathbf{r}_{\infty }, \mathbf{v}_{\infty })\) is the velocity distribution function of an ISN atom at the outer boundary. The quantities \(\mathbf{r}_{\infty }, \mathbf{v}_{\infty }\) and \(t_{\infty }\) are the position, velocity, and time when the atom crosses the outer boundary. The integration in the exponential is performed along the atom’s trajectory, which is the characteristic of Equation (1). The velocity distribution function of ISN atoms at the outer boundary can be obtained from the results of the global model of the heliospheric boundary (i.e., Izmodenov and Alexashov 2015, 2020).
2.1 Kinetic Modeling of the Pickup Proton Distribution
The distribution of H PUIs in the heliosphere can be calculated using the plasma and H atom distributions obtained in the frame of the global model of the heliosphere, such as the 3D time-dependent kinetic-MHD model by Izmodenov and Alexashov (2020). The method was developed by Malama et al. (2006) and employed in Chalov et al. (2016) and Baliukin et al. (2020).
The velocity distribution of pickup protons in the SW rest frame is assumed isotropic following theoretical estimates (Vasyliunas and Siscoe 1976) and observations (Gloeckler et al. 1994). The velocity distribution function \(f_{\mathrm{pui}}(t, \mathbf{r}, \mathbf{v})\) is then given by:
where \(\mathbf{v} = \mathbf{V}(\mathbf{r},t) + \mathbf{w}\), \(\mathbf{v}\) and \(\mathbf{V}\) are the velocity of pickup protons and bulk the velocity of the SW plasma in the heliocentric coordinate system, \(\mathbf{w}\) is the velocity of the pickup proton in the SW rest frame, and (\(w\), \(\theta \), \(\varphi \)) are coordinates of \(\mathbf{w}\) in the spherical coordinate system.
The kinetic equation for \(f_{\mathrm{pui}}^{*}(t, \mathbf{r}, w)\) in the general form is (e.g., Isenberg 1987; Chalov et al. 2003):
where \(D(t, \mathbf{r}, w) \) is the velocity diffusion coefficient, but with spatial diffusion neglected. In Equation (5), the source \((S_{+})\) and sink \((S_{-})\) terms are:
Here, \(f_{\mathrm{H}}(t, \mathbf{r}, \mathbf{v}_{\mathrm{H}})\) is the hydrogen velocity distribution function and \(\beta \) is the total ionization rate. In this approach, H atoms experience charge exchange both with SW protons and PUIs, where the effective charge exchange cross section depends on the relative atom-proton velocity (e.g., Lindsay and Stebbings 2005). The production rate of ENAs in Equation (8), \(\nu _{H}\), due to the charge exchange of protons with H atoms, is defined by
For relatively high energies, such as \(|\mathbf{v} - \mathbf{v}_{\mathrm{H}}| \approx v\), the production rate of ENAs can be approximated as \(\nu _{\mathrm{H}} (t, \mathbf{r}, \mathbf{v}) \approx n_{\mathrm{H}}(t, \mathbf{r}) v \sigma _{\mathrm{ex}}(v)\).
The process of velocity (energy) diffusion, which leads to stochastic acceleration of PUIs, is ignored in the approach proposed by Baliukin et al. (2020), i.e. \(D = 0\) is adopted. This corresponds to a quiet SW when the magnetic field fluctuation level is low (Chalov et al. 2003). Nevertheless, the process of velocity (energy) diffusion is connected with effective pitch-angle diffusion, which leads to isotropization of the velocity distribution function, and therefore should be taken into account.
In the case without diffusion, Equation (5) becomes a first-order linear differential equation that can be solved by the method of characteristics. The characteristic is the SW particle trajectory along which the PUI velocity changes:
The solution of Equation (5), \(f_{\mathrm{pui}}^{*}(t, \mathbf{r}, w)\), includes the loss of PUIs due to charge exchange along trajectory. The trajectory of PUIs is reconstructed backward in time from \((t,\mathbf{r}(t), w(t))\) to point \((t_{0}, \mathbf{r}(t_{0}), w(t_{0}))\), which is close to the Sun, where it can be assumed \(f_{\mathrm{pui}}^{*}(t_{0}, \mathbf{r}(t_{0}), w(t_{0})) = 0\).
The kinetic moments of the velocity distribution function of PUIs, the number density, and the temperature, at point \((t, \mathbf{r}) \in \mathbb{R}^{4}\) are the following:
where \(m_{\mathrm{p}}\) is the mass of proton, and \(k_{\mathrm{B}}\) is the Boltzmann constant. The pressure of PUIs is calculated as \(p_{\mathrm{pui}} = n_{\mathrm{pui}} k_{\mathrm{B}} T_{\mathrm{pui}}\).
2.2 Kinetic Model Jump Condition at the TS
The Liouville’s theorem, which states the phase space flow conservation, together with conservation of the first adiabatic invariant (magnetic moment), and assumption of the weak scattering leads to the following condition on the velocity distribution function at the shock (Fahr and Siewert 2011, 2013a):
where
In Equation (12), \(f_{\mathrm{pui},\mathrm{u}}^{*}\) and \(f_{\mathrm{pui},\mathrm{d}}^{*}\) are velocity distribution functions upstream and downstream the TS. The upstream shock-normal angle \(\psi (t, \mathbf{r})\) (between the magnetic field and normal to the shock surface) and the shock compression factor \(s(t, \mathbf{r}) = n_{\mathrm{d}}/n_{\mathrm{u}}\) depend on the position \(\mathbf{r}\) and moment \(t\) of the TS crossing. As observed by Voyager 1 (for TS-2 crossing; see Richardson et al. (2008)) the compression ratio is 2.4. As follows from the jump condition (12) the downstream/upstream ratios for the moments can be obtained:
It should be noted that some PUIs can experience reflections at the shock front due to an abrupt change in the magnetic field. These ions gain energy from their drift motion along the TS in the direction of the induced electric field. The PUIs can also experience the pitch-angle scattering upstream and downstream of the TS, which allows transmitted particles to return to the shock front, so multiple reflections can occur. The process of reflection leads to the anisotropy of the velocity distribution (in the SW rest frame) in the vicinity of the TS, and, therefore, the transport equation for the anisotropic velocity distribution function should be solved (see, e.g., Chalov et al. (2016)).
2.3 Additional Energetic Population of Pickup Protons
An additional energetic PUI population is seen in the form of the energetic “tails” in the velocity distribution (Fisk and Gloeckler 2007). It is produced by the processes such as shock-drift acceleration or reflection from the cross-shock potential (“shock-surfing” mechanism, see also Sect. 9.3). Based on the kinetic model (Sect. 2.1), the velocity distribution function can be calculated everywhere downstream the TS. This distribution is the so-called filled shell \(f_{\mathrm{sh}}^{*}(t, \mathbf{r}, w)\), and its critical velocity \(w_{\mathrm{c}} \approx \sqrt{C(s, \psi )} |\mathbf{V} - \mathbf{V}_{\mathrm{H}}|\), i.e. \(f_{\mathrm{sh}}^{*}(t_{\mathrm{TS}}, \mathbf{r}_{\mathrm{TS}}, w) = 0\) for \(w > w_{\mathrm{c}}\), where \(\mathbf{V}\) is the SW bulk velocity, \(\mathbf{V}_{\mathrm{H}}\) is H atom bulk velocity, \(t_{\mathrm{TS}}\) and \(\mathbf{r}_{\mathrm{TS}} = \mathbf{r}(t_{\mathrm{TS}})\) are the moment and position of a PUI crossing the TS. For \(w \geq w_{\mathrm{c}}\) the power-law distribution \(f_{\mathrm{tail}}^{*}(t_{\mathrm{TS}}, \mathbf{r}_{\mathrm{TS}}, w) \propto w^{- \eta }\) is assumed. If the additional parameter \(\xi \), which is the density fraction of PUIs of the “tail” distribution, is introduced, the velocity distribution function downstream the TS is
where
and \(f_{\mathrm{tail}}(t_{\mathrm{TS}}, \mathbf{r}_{\mathrm{TS}}, w) = 0\) for \(w < w_{\mathrm{c}}\), \(n_{\mathrm{pui},\mathrm{d}}\) is the number density downstream the TS. Equation (15) implies that \(\eta > 3\), otherwise the number density of the PUIs in the “tail” distribution is infinite.
In the IHS, the solution of the kinetic equation (Equation (5)), which can be derived using the method of characteristics, with the boundary condition downstream the TS (Equation (14)) is employed. The first and second terms of this condition can be associated with transmitted and additional energetic populations of PUIs, respectively. This partitioning of PUIs into sub-populations implies the conservation of the total number density, while the pressure balance is not satisfied. By introducing the energetic “tail”, additional energy is injected into the system, so this approach is not completely self-consistent. This additional energy can be “pumped” by the interaction of PUIs with the TS or produced by fluctuations of the heliospheric magnetic field.
The parameters \(\xi \) and \(\eta \), which were artificially introduced in the approach described above, depend on the local TS properties, since the efficiency of acceleration processes depends on the shock-normal angle \(\psi \) and shock compression factor \(s\), in particular. For the specified dependencies of parameters \(\xi \) and \(\eta \) on the position at the TS the velocity distribution function of pickup protons in the heliosphere can be calculated.
Based on the numerical kinetic model and observations of the ENA fluxes from IHS by the IBEX-Hi instrument, Baliukin et al. (2022) characterized the pickup proton distribution and provided estimations on the properties of the energetic pickup proton population downstream of the TS. They have performed the parametric study by varying \(\xi \) and \(\eta \) in different directions (upwind, downwind, flanks, solar poles) and in a wide range of values to minimize the difference between the model results and data. The quantitative estimates for the parameters of the energetic population of pickup protons obtained in their work can be useful for testing and verifying hybrid models that simulate the acceleration of protons at the heliospheric termination shock. The results of the ENA flux simulations based on these estimations are consistent with IBEX-Hi observations and discussed in Sect. 2.5.
2.4 Modeling of the ENA Fluxes
ENAs, which are born in charge exchange between the SW protons and H atoms in the IHS, form the GDF. The directional differential ENA flux in the solar inertial reference frame is the line-of-sight integral:
where
is the survival probability, \(t_{\mathrm{obs}}\) is the moment of observation, \(\mathbf{r}_{\mathrm{obs}}\) is the position of the observer, \(\mathbf{LOS}\) is the unit vector in the line of sight direction, \(\mathbf{v} = v \cdot \mathbf{LOS}\) is the velocity of an ENA, \(m_{\mathrm{H}}\) is the mass of H atom, and \(f = f_{\mathrm{sw}} + f_{\mathrm{pui}}\) is the velocity distribution of protons in the inner heliosheath (the sum of core SW proton distribution, which is assumed to be Maxwellian, and PUI distribution). The integration is performed along the ENA trajectory in the inner heliosheath, with \({\mathrm{d}}s = v {\mathrm{d}}t\) being the differential path length. The values \(s_{\mathrm{TS}}\) and \(s_{\mathrm{HP}}\) correspond to atom intersections of the TS and HP, respectively.
2.5 Kinetic Model Results for ENAs and Comparison with IBEX-Hi Data
For the comparison with modeling results, the data sets of GDF observed by the IBEX-Hi detector during the IBEX mission were used. The data are presented by Schwadron et al. (2014) and available via the public Data Release 8.Footnote 1 To calculate the differential fluxes measured by IBEX-Hi at different energy channels, the energy transmission of IBEX-Hi electrostatic analyzers should be taken into account since it leads to the re-distribution of fluxes between the energy channels and spreading of the observed spectrum. The Compton-Getting and survival probability corrections were applied for the IBEX-Hi data, so in the calculations, both the relative motion of the IBEX-Hi spacecraft and the ionization losses of ENAs in the region of the supersonic SW are not taken into account. The model maps of ENA fluxes were obtained for the lines-of-sight when the sensor views the heliosphere in the ram direction (i.e., in the direction of spacecraft motion), as it was done by Schwadron et al. (2014).
Figure 2 presents the comparison of the IBEX-Hi data at the top five energy channels with the ENA flux maps obtained by Baliukin et al. (2022) based on the time-dependent heliospheric model by Izmodenov and Alexashov (2020). The model fluxes were averaged over 2009 – 2013. The first and third columns present the model results, the second and fourth columns show the measurements. From the comparison of the simulation results with the data the following conclusions can be made:
-
1.
The model reproduces the geometry of the multi-lobe structure seen in the IBEX data. There is a good qualitative agreement between the model results and the observed fluxes.
-
2.
A single structure of enhanced fluxes from the tail region is seen in the IBEX data at low energy channels (∼0.71, 1.1, 1.74 keV). At high energies, this structure “splits” into two parts (to the north and south from the solar equatorial plane). The model results qualitatively reproduce such “splitting” behavior of the lobes. The lines-of-sight within these lobes of enhanced ENA fluxes intersect the regions of the inner heliosheath, where (a) the fast SW, initially emitted from the solar polar coronal holes and propagated to the heliospheric tail, is collimated, and the plasma velocity and temperature are high, and (b) the heliosheath thickness is large.
-
3.
The presence of the low flux areas from the flanks of the heliosphere (so-called Starboard and Port lobes) observed in the IBEX data is also seen in the model results. These low fluxes lobes are located in the vicinity of the solar equatorial plane, where the slow SW dominates and the thickness of the heliosheath is small (McComas et al. 2013; Zirnstein et al. 2016).
-
4.
There are a few differences between the model calculations and the IBEX-Hi data: (a) for quantitative agreement with the data, the model fluxes should be significantly scaled (multiplied by 1.54), which may be an indicator of a lower H number density used in the heliospheric model than it is in reality; (b) the simulated fluxes at ∼0.71 keV energy channel are lower compared to the data. These differences may be induced by several assumptions made by Baliukin et al. (2022), such as (a) the neglect of the velocity (energy) diffusion, (b) the isotropic form of the distribution function throughout the heliosphere, and (c) the weak scattering at the TS.
The Mollweide skymap projections (in ecliptic J2000 coordinates) of the H ENA fluxes as they were observed by IBEX-Hi (by rows). The first and third columns present the model results, the second and fourth columns are the measurements. The maps in the first and second columns are centered at the nose longitude \(255.4^{\circ }\), while the maps in the third and fourth columns – at the tail longitude \(75.4^{\circ }\). The units of fluxes are (cm2 sr s keV)−1. Adapted from Baliukin et al. (2022)
3 PUIs in MS-FLUKSS
A number of one-plasma-fluid models (Baranov and Malama 1993; Pauls et al. 1995; Pogorelov et al. 2006; Heerikhuisen et al. 2006, 2007; Izmodenov et al. 2005, 2009; Opher et al. 2006) take into account the effect of PUIs by assuming that they are in thermal equilibrium with the background plasma. Although this is not correct, the conservation laws of mass, momentum, and energy for the mixture of electrons, ions, and PUIs are satisfied approximately. According to Zank et al. (2014), such approaches are correct only if the heat conduction tensor and the dissipation coefficient due to ion-PUI interaction are zero. This happens when PUIs are coupled with the thermal ions and the scattering time is infinitely small.
Isenberg (1986) shows that the effect of PUIs can be quantified if they are treated as a separate fluid. The time-dependent simulations of the supersonic SW by Usmanov and Goldstein (2006), Usmanov et al. (2012) include PUIs as a separate fluid and also turbulence effects. However, these models still assume instantaneous isotropization, i.e., with PUI described as a filled shell, thus neglecting the nearly-isotropic character of the PUI distribution function when a finite scattering time is included (Zank et al. 2014).
In principle, any PUI fluid model is an approximation of their kinetic behavior (Malama et al. 2006), where it is assumed that PUIs are isotropic away from discontinuities. Recently, Gamayunov et al. (2012) investigate the evolution of the PUI distribution function in a pitch-angle-averaged approximation together with the PUI-generated waves that heat the thermal SW ions. The extension of a 2-fluid SW model developed for the supersonic flows is not straightforward, since the pressure equation for PUIs used in such models is not valid, e.g., across the TS. Instead, some boundary conditions should be developed (Chalov and Fahr 1996; Zank et al. 1996b; Fahr et al. 2000b; Fahr and Chalov 2008; Zank et al. 2010; Fahr et al. 2012; Fahr and Siewert 2013b) since, as revealed when Voyager 1 crossed the TS (Richardson et al. 2008), most of the SW kinetic energy was absorbed by PUI.
Although the SW plasma consists of the thermal SW ions and PUIs, in Multi-Scale Fluid-Kinetic Simulation Suite (MS-FLUKSS) the MHD system is solved in the conservation-law form because this satisfies the shock boundary conditions efficiently. This requires solving the MHD system for the mixture of SW ions and electrons, and PUIs. To separate between the SW ions and PUIs, one can supplement the system with the continuity and pressure equations for PUIs (Pogorelov et al. 2016). The distribution functions of protons, \(f_{\mathrm{p}}\), and PUIs, \(f_{\mathrm{PUI}}\) to calculate the source terms in the MHD system are usually assumed to be Maxwellian. This is not true for PUIs.
Heerikhuisen et al. (2019), DeStefano and Heerikhuisen (2017) studied the effect of the distribution function on the charge exchange source terms considering Lorentzian (kappa) distributions with different \(\kappa \)’s for PUIs. The kappa distribution decreases the contribution of the most probable state while increasing the number of ions in the so-called “energetic tails”. The conclusion derived from DeStefano and Heerikhuisen (2017), DeStefano (2019) is that the dependence of charge-exchange cross-sections (\(\sigma _{\mathrm{ex}}\)) on energy should be preserved when the integration is performed. This becomes crucial for \(\kappa \) approaching the minimum allowed value of 3/2. For \(\kappa \to \infty \), when the distribution function becomes Maxwellian again, the dependence of \(\sigma _{\mathrm{ex}}\) on energy becomes less critical for the integral evaluation. Otherwise, the integrals diverge at \(\kappa =2\) (see also, Scherer et al. (2017, 2019), and Perri et al. this volume). MS-FLUKSS code avoids such divergences by performing the integration more accurately, avoiding exaggeration of the effect of PUIs on the heliosphere (Heerikhuisen et al. 2015). That happens when PUIs are not treated separately from SW protons and a Maxwellian distribution function (with substantially higher temperature) is implied for the ion mixture.
There are essentially three approaches to include PUIs, which form the basis of the MS-FLUKSS models: (1) PUIs are not treated as a separate plasma component, but the conservation of mass, momentum, and energy for the mixture is preserved; (2) an isotropic distribution function for PUIs is chosen; PUIs are assumed to be co-moving with the SW ions, and the continuity and pressure equations are solved to describe the PUI motion; and (3) \(f_{\mathrm{PUI}}\) is assumed isotropic beyond shocks, at which it is intrinsically non-isotropic, and proper boundary conditions describing the PUI transition across the TS, or other shocks, treated kinetically, are applied.
The system describing the plasma mixture (thermal protons, PUIs, and electrons), neutral atom populations, and PUIs is presented below. Subscripts for charge exchange source terms are identified by the letter \(a\), which is a fixed integer for the corresponding population of neutral atoms, \(\mathrm{p}\) for thermal protons, and \(\mathrm{I}\) for pickup protons:
Plasma mixture
Neutrals
Pick-up ions
Here \(p\) is the pressure, \(\rho \) the mass density, \(\mathbf{u}\) the bulk velocity vector, \(\mathbf{B}\) the magnetic field vector, \(e\) the total energy density (includes the magnetic energy), \(p^{*}\) the total pressure of the mixture (including magnetic energy), and \(\mathbf{I}\) is the identity tensor. The source terms \(D\), \(\mathbf{M}\), \(E\), and \(P\) are written out in Pogorelov et al. (2016). The subscript \(\Sigma \) refers to the mixture properties. It is reasonable to assume that there are no pickup electrons. Thus, introducing the number density \(n\), we obtain
which reduces to
Pogorelov et al. (2016) assume a multi-fluid model for H atoms. The system of MHD equations is solved using a Godunov-type method, where the fluxes of mass, momentum, energy and magnetic field are obtained as solutions of an MHD Riemann problem in the linear approximation. The scheme has second order of accuracy in space and time. Both MHD and Euler equations are solved in the framework of MS-FLUKSS (Pogorelov et al. 2008).
Figure 3 shows the plasma density distributions (dimensionless units with the scale of VLISM plasma density) in the meridional plane (the plane formed by the Sun’s rotation axis) for the single-ion-fluid model (left panel) and the case when the PUI and thermal ion fluids behave as co-moving, but distinguishable components (right panel). The HP moves inward towards the Sun and the TS moves outward away from the Sun with the inclusion of PUIs as a distinct component, i.e., the heliosheath width becomes quite significantly narrower when PUIs are treated distinctly from the thermal SW plasma. This result is consistent with that in Malama et al. (2006) and addresses the observation made by Voyager 1 that the HP location was closer than expected (Stone et al. 2013; Burlaga and Ness 2014). In addition, a comparison of MS-FLUKSS simulation based on the model with PUIs governed separately by the continuity and pressure equations and the turbulence model of Breech et al. (2008) with New Horizons (NH) observations is presented in Fig. 4.
Plasma density distributions in the meridional plane (for distances in au) for the single-ion-fluid model (left panel) and for the case when the PUI and thermal ion fluids behave as co-moving, but distinguishable components (right panel). Figure from Pogorelov et al. (2016)
Comparison between MS-FLUKSS simulations of the thermal SW protons and PUIs with measurements along the NH trajectory. The figure is a courtesy of T. Kim (UAH). See more detail in Kim et al. (2018)
4 Two-Fluid Model of PUIs at TS
Voyager 1 and 2 crossed the TS and entered the IHS at 94 and 84 au, respectively. The Voyager 1 crossing of the TS occurred during a data gap, and thus it was incapable of determining its detailed structure. The TS crossing by Voyager 2 returned many surprises and, most importantly, established the importance of non-thermal energetic particles. In contradiction to many predictions from theory and global MHD models, Voyager 2 showed that the thermal gas downstream of the TS is supersonic and much colder than expected. Richardson et al. (2008) suggested that the primary dissipation at the TS is not provided by proton thermal gas, but as was predicted by Zank et al. (1996b) and then studied by Zank et al. (2010), the suprathermal PUIs which preferentially are reflected at the cross-shock electrostatic potential and are capable of getting almost all the heating across the shock.
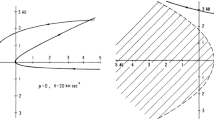
PUIs in the outer heliosphere have the dominant pressure (McComas et al. 2017) and are not equilibrated with the background thermal plasma (Zank et al. 2014). The thermal gas temperature (Richardson et al. 2008) and PUI temperature (Zank et al. 2010) upstream of the TS are about \(0.2\times 10^{6}\) K and \(1.5\times 10^{6}\) K, respectively, leading PUIs to account for the dominant internal energy. Mostafavi et al. (2017b) and Mostafavi et al. (2018) treated PUIs as a separate component and studied the structure of TS by including both collisionless heat flux and viscosity associated with energetic PUIs in their two-fluid model. Figure 5 represents the normalized PUI, thermal gas, and magnetic pressures to thermal gas pressure far upstream of the TS as a function of distance. It shows that the upstream pressure is almost all converted to PUI pressure, and thermal gas is only heated adiabatically. The thermal gas Mach number, and fast magnetosonic Mach number, are greater than 1 downstream of the TS (Fig. 5), meaning that they are insufficient to lead to a supersonic-subsonic transition across the TS. However, the combined thermal gas and PUI Mach number confirmed that the flow changes from supersonic to subsonic through the TS with the inclusion of PUIs. This illustrates that PUIs play a critical role in the dissipation process and smoothing of the TS (Oka et al. 2011; Yang et al. 2015; Mostafavi et al. 2017b,a; Lembège and Yang 2018).
Simulation results of the TS transition with a two-fluid model. a) PUI (blue curve), thermal gas (red curve), magnetic (green curve) pressures normalized to the thermal gas pressure far upstream of the TS. b) The thermal gas Mach number, \(M_{s}=u/a_{g}\), the fast magnetosonic Mach number, and the combined thermal gas and PUI Mach number, through the TS. See more in Mostafavi et al. (2018)
5 Shock Crossing by Non-Maxwellian Plasma
In a collisionless shock, the directed flow energy is converted mainly into the thermal energy of plasma species. At the TS a substantial part of energy goes into the heating of PUIs, while heating of the SW protons is weaker than it would be without PUIs. The shock structure width is much less than the PUI diffusion scale, which makes the particle transport and acceleration more complicated than in the isotropic case. In addition, newly accelerated PUIs can generate waves, which in turn affect acceleration and transport of particles in the shock vicinity, typically a few diffusion lengths of energetic PUI (a few au for the majority of accelerated PUIs). One would have to solve an anisotropic particle transport equation based on pitch-angle diffusion. However, solving the focused transport equation (le Roux et al. 2007; le Roux and Webb 2009; Florinski et al. 2008; Zuo et al. 2011) suitable for this purpose at the entire TS is computationally prohibitive.
While several different approaches have been developed to describe the boundary conditions for PUIs across the TS which describe the energy transfer in this region (Fahr and Chalov 2008; Zank et al. 2010; Fahr et al. 2012; Fahr and Siewert 2013b), Pogorelov et al. (2016) use a simplified, but not exactly justified, assumption that thermal protons experience adiabatic compression. However, more accurate approaches are implemented in Gedalin et al. (2020, 2021a). The extended MHD approach of Zank (2016) provides us with a physics-based width of the shock ramp, but it does not describe the change in the PUI spectrum at shocks. Since the shock transition itself is scatter-free, the fluid approach may miss the physics of relation between the kinetic and MHD scales. Accordingly, the obtained magnetic profiles become monotonic and cannot explain observed overshoots (Mostafavi et al. 2018). In the part of the heliosphere beyond \(\sim 30\) au the fraction of PUIs becomes substantial (Richardson and Stone 2009), so their contribution to the backstreaming ion beams may become dominant. On the other hand, test-particle simulations of Gedalin et al. (2021a) have shown, that backstreaming PUIs is negligible with the magnetic field angles \(\theta _{Bn}> 55^{\circ }\) if the overshoot is absent.
Previous attempts to take into account the ion kinetics at a shock front assumed magnetic moment conservation (Fahr and Chalov 2008; Fahr et al. 2012; Fahr and Siewert 2013b). However, it has been shown that magnetic moment is, in general, not conserved (Terasawa 1979; Gedalin et al. 2020), and such approximation may be satisfied only in the perpendicular regime. Since the distribution function becomes highly anisotropic in the vicinity of shocks, instead of the application of invalid equations, it may be beneficial to use kinetically-derived boundary conditions at the TS, which is of importance for the interpretation of ENA spectra. In the assumption of co-moving thermal and non-thermal ions, this requires a derivation of boundary conditions for the PUI density and pressure behind a shock, which should be accompanied by an appropriate turbulence model to explain SW ion heating by turbulence. Yet another approach may require us to relate the PUI distribution functions in front of and behind shocks, which may go further and treat the waves produced by unstable distributions of PUIs kinetically.
The proper establishment of the boundary conditions on MHD scales requires establishing a relation of the ultimately isotropic distributions to the collisionless ion dynamics within a shock front (Gedalin et al. 2020). The heating of both thermal species is non-adiabatic. The downstream pressure of the mixture is determined by conservation laws for the whole mixture. SW heating is sensitive to the details of the shock front structure, while heating of PUI is not. This made it possible to parametrize the behavior of PUIs across a quasi-perpendicular shock, such as the TS, using a test particle approach and validate those with full particle-in-cell simulations (Gedalin et al. 2021b). This parametrization requires only two parameters: the angle \(\theta _{Bn}\) between the magnetic field direction and the shock normal and magnetic compression (the ratio between the magnetic field magnitude downstream and upstream \(B_{d}/B_{u}\)). The direct tracing of PUIs performed by Gedalin et al. (2021b) shows that the fraction of reflected PUIs may be \(50\%\) larger than that obtained with the cross-shock potential only. It was concluded that, in agreement with observational data, the cross-shock potential is not the only and probably not the main parameter that determines the intensity of PUI reflection, and gyration of ions in the magnetic field should be taken into account. As a result, the downstream temperature of reflected PUIs may be an order of magnitude lower than that predicted in the cross-shock potential estimates by Zank et al. (2010). It was also shown that the overall heating is substantially stronger than the one predicted by magnetic moment conservation (Fahr and Chalov 2008).
Since the behavior of thermal protons across the TS depends on the details of the collisional shock structure, one needs to resort to pressure balance consideration to estimate the separation of energy between the SW protons and PUIs (Gedalin et al. 2021b). On neglecting the kinetic pressure of the SW and electrons in the upstream region and taking into account that the electron heating is much smaller than the SW proton heating (Schwartz et al. 1988), it has been shown that the relative SW heating is much larger than the relative PUI heating, whereas the situation is opposite for the absolute heating. The downstream SW temperature was shown to be strongly dependent on the fraction of PUIs, while the PUI temperature is practically independent of it. Meanwhile, the mean downstream temperature \(T_{\mathrm{d}}= (n_{\mathrm{d, SW}} T_{\mathrm{d, SW}} + n_{\mathrm{d, PUI}} T_{\mathrm{d, PUI}})/ (n_{\mathrm{d, SW}}+n_{\mathrm{d, PUI}})\), varies weakly and remains of the order of \(10^{6}\) K.
Test particle simulations need validation with full particle models. Figure 6 shows typical distributions of quantities in front of and behind a collisionless shock (the TS) for different shock angles, obtained with the particle-in-cell code (Gedalin et al. 2021b). For lower angles, the PUI density increase immediately behind the shock ramp is slightly higher than that of the SW protons and that of the magnetic field, but eventually, it approaches the same value at a distance of the order of 100 ion inertial lengths, \(d_{\mathrm{i}}\). The large increase in the upstream PUI temperature at \(\theta = 60^{\circ }\) is due to backstreaming PUIs, which are not present at larger angles. The ratio of downstream to upstream \(T_{\perp }\) increases slightly with shock angle and shock speed. The relative increase of SW proton temperature is much higher than that of the PUIs, although the downstream PUI temperature is still significantly higher than that of SW protons.
Characteristic distributions of magnetic field, \(B\), the SW and PUI densities, \(n_{\mathrm{SW}}\) and \(n_{\mathrm{PUI}}\), and temperatures, \(T_{\mathrm{SW}}\) and \(T_{\mathrm{PUI}}\), upstream and downstream a collisionless shock for different angles \(\theta \) between the magnetic field direction upstream and the shock normal. Since the distribution functions of SW and PUIs are anisotropic, both parallel and perpendicular temperatures are shown. Figure from Gedalin et al. (2021b)
6 Electron Impact Kinetics Downstream of the Solar Wind Termination Shock
Different plasma fluids, like SW protons, pick-up protons, and electrons can be shock-processed in a fluid-specific way at the SW TS (Fahr and Siewert 2007; Wu et al. 2009; Zank et al. 2010; Fahr and Siewert 2011). SW electrons when passing over the shock might experience extraordinary heating (Chalov and Fahr 2013; Fahr and Siewert 2013b; Fahr and Verscharen 2016). Fahr et al. (2015) have derived a theoretical basis for preferential heating of electrons with respect to ions due to conversion of their overshoot kinetic energies into thermal energies in the downstream bulk frame.
The highly suprathermal electron distribution function contains a substantial portion of keV energetic electrons that can impact ionize neutral VLISM atoms, like H and He, during its passage through the heliosheath. During the last 50 years, it had been taken for granted that VLISM He atoms, due to the complete absence of ionization sources, cross the heliosheath without any interaction with the heliosheath plasma and get ionized only very close to the Sun (Weller and Meier 1981; Möbius et al. 2004; Chalov 2014). H atoms were thought to undergo charge exchange collisions with the heliosheath protons, but in such a negligible manner that the H density over the upwind heliosheath is practically unaffected.
However, the electrons leaving the TS in a downstream direction are strongly energized appearing in pronounced suprathermal distributions (Fahr et al. 2015). The evolution of the SW electron distribution function downstream of the TS can be described under the influence of electron impact ionization of ISN H and He atoms that enter the heliosheath with the interstellar wind from the upwind hemisphere and continue onto the heliotail region. An adequate approach is starting from a kinetic phase-space transport equation in the bulk frame of the heliosheath plasma flow taking into account convective changes, cooling processes, whistler wave-induced energy diffusion, and electron injection into, and removal from velocity-space cells connected with electron impact ionization processes of ISNs.
The phase-space transport equation that describes the evolution of the isotropic electron distribution function \(f_{e}\) along heliosheath flow lines after Fahr and Dutta-Roy (2019) takes into account convective changes (first term), the influence of the change in the magnetic field to the change in \(f_{e}\) due to the conservation of the magnetic moment of the electrons (i.e., magnetic cooling; second term), velocity space diffusion due to non-linear electron-whistler wave interactions (third term), and electron impact ionization (fourth term) in the following form:
Here \(U\) is the plasma bulk velocity. The temporal change of the distribution function \(f_{e}\) due to electron energy losses is caused by electron impact ionization processes with ambient H or He atoms of the VLISM through the heliosheath.
From the kinetic equation, one can ascend to an associated pressure moment of the electron distribution function and arrive at a pressure transport equation describing the evolution of the electron pressure in the bulk-velocity frame of the plasma flow. Assuming that the local electron distribution can be represented by a kappa function with a \(\kappa -\) parameter that varies with the streamline coordinate \(s\), an ordinary differential equation for \(\kappa \) is obtained as a function of \(s\). It turns out that the effect of H and He impact ionizations especially gives its signature to the electron distribution along the extended down-tail region of the heliosheath.
Results show that at the upwind hemisphere of the heliosheath the influences of electron impact ionization are marginal. Downstream it is assumed that the ISN densities are essentially constant. On the downwind side of the heliosheath and down the heliotail this assumption may be questionable. However, this assumption is not bad outside of a circumsolar region of the order of 15 au where the solar ionization reactions produce non-negligible gradients in the neutral atom densities (see Sect. 8.1; Jaeger and Fahr (1998)).
7 SHIELD Modeling of the Heliosphere
Classically, the heliosphere has long been thought to have a long comet-like tail extending for thousands of astronomical units along the direction of interstellar flow (Parker 1961; Baranov et al. 1971; Baranov and Malama 1993; Pauls et al. 1995; Zank et al. 1996c). Opher et al. (2015) and Drake et al. (2015) suggested this might not be the case and that the solar magnetic field in the heliosheath can collimate the SW plasma into two lobes, leading to a shortened heliotail. They showed that the tension of the twisted solar magnetic field can resist the stretching force of the flowing heliosheath plasma, driving the SW ions into two northward and southward columns. When the flow of the interstellar plasma is taken into consideration, these two columns are bent back into lobes. A few hundred astronomical units beyond the TS in the heliotail, reconnected magnetic field lines are present between the two lobes, and mixed VLISM and SW plasma sit on these field lines, giving rise to a shortened heliotail. While other models (Pogorelov et al. 2015; Izmodenov and Alexashov 2015, 2018) have also noted this collimation when using a unipolar solar magnetic field configuration in MHD modeling, these works claim the heliotail to maintain the classical view of a long comet-like structure.
Opher et al. (2017) investigated the effect of magnetic reconnection at the HP. The MHD model suppresses reconnection in the nose region while allowing it in the flanks. This is consistent with recent ideas about reconnection suppression from diamagnetic drifts. The stabilizing effect of diamagnetic drifts is an important kinetic effect missed by MHD models, which can develop at boundaries such as the Earth’s magnetopause or the HP (Swisdak et al. 2003, 2010). The stabilizing influence of these drifts has been extensively documented with SW and magnetospheric data (Phan et al. 2010, 2013). The diamagnetic drift suppresses reconnection when the drift speed is larger than the Alfvén speed in the reconnecting magnetic field. The jump in plasma \(\beta \) (the ratio of the plasma pressure to the magnetic pressure) across the nose of the HP is much greater than in the flanks because the heliosheath \(\beta \) is greater at the nose than in the flanks (Opher et al. 2017). Large-scale reconnection is therefore suppressed in the nose but not at the flanks. The effect of this reconnection results in the twisting of the interstellar magnetic field to the azimuthal direction ahead of the HP. Moreover, the reconnection was used to explain the lack of rotation of the magnetic field observed by Voyager 1 (Burlaga and Ness 2014) and Voyager 2 (Burlaga et al. 2019).
Kornbleuth et al. (2021b) investigated the effect of reconnection at the HP on the heliosphere and the plasma within. They compared the results of two different kinetic-MHD models from the Solar wind with Hydrogen Ion charge Exchange and Large-Scale Dynamics (SHIELD) model (herein referred to as the BU model) and the Moscow model (Izmodenov and Alexashov 2020). Both MHD models treated a single-ion plasma and used a Monte-Carlo approach for modeling ISN H streaming through the heliosphere. Additionally, identical boundary conditions were used for the two models to present a valid comparison. One key difference between the two models was the magnetic reconnection. The BU model allows for magnetic reconnection at the HP, as it was based upon the MHD model used in Opher et al. (2015) and Opher et al. (2017), while the Moscow model does not. The results of the comparison show that the heliosphere is compressed at high latitudes in the BU model relative to the Moscow model due to the increased magnetic pressure from the twisting of the interstellar magnetic field. The results also indicate that while the BU and Moscow models have different tail configurations beyond 300 au from the Sun, both models displayed a split tail in the sense that the solar magnetic field confines the charged solar particles into distinct north and south columns that become lobes (Fig. 7). The different heliotail configurations arise because the BU model allows for reconnection and MHD instabilities (Opher et al. 2021), which are suppressed in the Moscow model, leading to ISM flowing between the two lobes as in Opher et al. (2015).
Meridional slices of plasma conditions within the heliosheath for the BU model (top) and the Moscow model (bottom). Included are color contours and lines of the plasma density [cm−3] (left) and plasma speed [km/s] (middle) with white lines representing the TS (inner) and HP (outer) for each model. Right: Mass flux (\(n_{p}V_{p}\)) through the heliosheath. Black lines represent the magnetic field intensity overlaid on the mass flux. See more in Kornbleuth et al. (2021b)
Moreover, Opher et al. (2020) separated the SW plasma into two ion fluids: thermal SW ions and PUIs created in the supersonic SW. After crossing the TS, the PUIs would be depleted from charge exchange with neutrals originating from the VLISM, which led to a cooling of the heliosheath plasma. The cooler heliosheath led to a shrinking of the heliosphere such that it became smaller and rounder in shape (Fig. 8).
Top left: The density of PUIs (\(\rho _{PUI}\)). Black contours show the temperature at 0.25 MK indicating the HP. Top middle: The density of the SW (\(\rho _{SW}\)). Top right: The density of the single fluid ion (PUIs and SW combined) model (\(\rho \)) from Opher et al. (2015). Bottom: The HP as a 3D surface is shown by the yellow surface defined by the SW density of 0.005 cm−3. The white lines represent the solar magnetic field. The red lines represent the interstellar magnetic field. See more in Opher et al. (2020)
McComas et al. (2013) presented IBEX ENA observations of the heliotail, and found two high latitude lobes of enhanced ENA flux at high energies (∼2 keV), with a deficit of flux in the low latitude tail. McComas et al. (2013) suggested this profile seen at high energies, which was not seen at low energies, could reflect the SW profile from the solar minimum. With fast SW at high latitudes and slow SW at low latitudes in the heliotail, the observed high latitude lobes of ENA flux could reflect the fast SW flowing in the high latitude heliotail. Opher et al. (2015) suggested the confinement of the SW by the solar magnetic field into two high latitude lobes could be a cause for the IBEX heliotail profile at high energies.
Zirnstein et al. (2017) used a time-dependent simulation of the heliosphere with a long tail to model ENA fluxes at IBEX energies. In their ENA model, they partitioned the SW plasma into three distinct populations: thermal SW ions, PUIs transmitted across the TS without reflection, and PUIs reflected and energized at the TS. As per Zank et al. (2010), these three populations were modeled with Maxwellian distributions to approximate the high energy tail of the SW particle distribution. They also included the effect of extinction, which restricts the distance out to which ENAs of particular energy can be observed due to the depletion of parent ions with the same particular energy due to charge exchange. Based on their work, Zirnstein et al. (2017) were able to qualitatively replicate many of the features observed by IBEX, including the high energy tail ENA profile noted by McComas et al. (2013), and concluded that the profile of the SW was the primary driver for the observed ENA structures.
Kornbleuth et al. (2018) employed a similar ENA model to Zirnstein et al. (2017) but used a short-tail heliospheric solution corresponding to Opher et al. (2015) with uniform SW boundary conditions to investigate the effect of collimation of the SW plasma by the solar magnetic field on ENA maps. While they were unable to match the energy dependence of the ENA maps as observed by IBEX, Kornbleuth et al. (2018) qualitatively reproduce the IBEX heliotail observations at high energies with two high latitude lobes of enhanced ENA flux and a deficit of ENA flux in the low latitude tail. They concluded that the confinement of the SW plasma by the solar magnetic field leads to an enhancement of ENA flux.
Kornbleuth et al. (2020) expanded on the work of Kornbleuth et al. (2018) by investigating four distinct heliospheric solutions with varying SW profiles and solar magnetic field intensities. Two of the solutions used a latitudinally-varying SW profile corresponding to yearly-averaged SW conditions from the year 2008 based on interplanetary scintillation observations (Sokół et al. 2015b), which reflected solar minimum conditions. One of these solutions used a solar magnetic field intensity at 1 au corresponding to that observed by OMNI during the same period, while the other solution neglected the solar magnetic field. When solar minimum conditions were used and the solar magnetic field neglected, Kornbleuth et al. (2020) found a significantly reduced ENA flux in the high latitude as compared with the same solution which included the solar magnetic field (Fig. 9). When the solar magnetic field is included, the modeled ENA maps showed good qualitative agreement with the IBEX observations. Moreover, they found that the ENA flux at high latitudes increased with increasing solar magnetic field intensity.
ENA sky map of flux centered on the downwind (tail) direction in units of (cm2 s sr keV)−1. Left: simulated sky maps for the modeled case which includes latitudinally-varying SW without solar magnetic field. Middle: simulated sky maps for the modeled case which includes latitudinally-varying SW and solar magnetic field. Right: IBEX ENA maps from the first five years (2009-2013) of observations with the IBEX Ribbon removed (Schwadron et al. 2014). Simulated sky maps are multiplied by a factor of 1.8. See more in Kornbleuth et al. (2020)
Kornbleuth et al. (2021a) modeled ENA maps using the method of Kornbleuth et al. (2020) from the BU and Moscow MHD models (Kornbleuth et al. 2021b) at IBEX-Hi energies. They found that while the heliotails display differences beyond 300 au, these distances are beyond the cooling length of IBEX-Hi energies. Both MHD models produce a heliotail with heliosheath plasma organized by the solar magnetic field into two distinct high latitude columns, and the two models show qualitative and quantitative agreement with each other in modeled ENA maps. Both models differ quantitatively from IBEX GDF observations from Schwadron et al. (2014) by approximately a factor of 2. To compare with IBEX GDF observations quantitatively, Kornbleuth et al. (2021a) extracted ratios of the ENA flux for the Voyager 1, port lobe, south pole, and south heliotail lobe directions relative to the downwind direction. The downwind direction was selected as a reference point as ENA flux from the downwind direction is only limited by the cooling length and not by heliosheath thickness, for which there is a disagreement between observations and MHD models. The ratios allowed to compare ENA fluxes for different directions without the need to scale ENA fluxes. While there are differences in the ratios between the BU and Moscow models (Fig. 10), Kornbleuth et al. (2021a) found that the differences were largely insufficient to be observed by IBEX considering the estimated \(\sim 20\%\) systematic uncertainty of IBEX-Hi observations (Fuselier et al. 2012). As such, the different heliotail configurations would not be distinguishable at IBEX-Hi energies, and would likely require higher energy observations to probe the shape of the heliotail.
ENA flux spectra for the \(15^{\circ}\times 15^{\circ}\) area centered around the directions of Voyager 1, the port lobe, downwind, the southern pole, and the southern lobe. The black line illustrates to IBEX-Hi data averaged over the years 2009 through 2013. The spectra show qualitative and quantitative agreement between the BU and Moscow models despite different heliotail shapes, but discrepancies remain with respect to the IBEX data. Adapted from Kornbleuth et al. (2021a)
8 Theory and Interpretation of Measurements: Part 1
8.1 Ionization Rates
Sun drives the environment inside the heliosphere through SW outflow, solar EUV radiation, and resonant radiation pressure (e.g., Bzowski et al. 2013b). This ionizing environment influences particles of interstellar origin inside the heliosphere altering their fluxes (see, e.g., Blum and Fahr 1970; Thomas 1978; Ruciński and Fahr 1989; Sokół 2016). The primary ionization process that affects interstellar particles is charge exchange with SW protons; the next is photoionization by solar EUV flux, and the other is impact ionization by SW electrons. The intensity of the ionization processes varies in time in short time scales depending on active region distribution on the solar surface and in long time scales depending on the cycle of solar activity. Moreover, the ionization rates vary with heliographic latitude, especially for charge exchange, which depends on SW (see, e.g., Sokół et al. 2019a) speed and density which vary in latitude during the solar cycle (SC; see, e.g., McComas et al. (2000), Sokół et al. (2013)). These factors need to be accounted for in the model interpretation of measurements.
Among the interstellar atoms observed from the vicinity of the Earth’s orbit, H and O are the most prone to ionization, next is Ne, and the least affected is He. Figure 11 illustrates ionization rates for these four species in the ecliptic plane at 1 au for the last three SCs (22-24) calculated with the Sun-Heliosphere Observation-based Ionization Rates (SHOIR) model (Sokół et al. 2020). The SHOIR model calculates the ionization rates using available SW and solar EUV measurements, including SW variations in latitude, which allows reconstruction of the charge exchange rate variations in latitude after 1985. Figure 11 illustrates charge exchange with SW protons, photoionization, and electron impact ionization rates together with the sum of them all for each species.
Top: time series of SHOIR-calculated ionization rates due to various processes for H, O, Ne, and He in the ecliptic plane at 1 au with Carrington rotation averaged resolution in time for the last three SCs. A total of the rates is presented in red. Bottom: time series of the fraction of the ionization rates due to individual processes to the total ionization rates for a given species. The color code is presented below the bottom panel. See more in Sokół et al. (2020)
Photoionization contributes the most to ionization rates for Ne and He, which follow SC-variations in time with maximum ionization rates during solar maximum and minimum ionization rates during solar minimum. For O, photoionization and charge exchange reactions can contribute equally to the total ionization rates (see Fig. 11). Thus for O, we observed at 1 au variations in time reflecting SC-variations and long-term changes characteristic for the SW temporal variations. For H, the total ionization rates reflect dominantly the SW in-ecliptic variations.
For all species discussed, the SHOIR-calculated total ionization rates show a decrease in time in the last decades, which is due to weakening of the SW flux (e.g., McComas et al. 2008b) and the solar activity, with the last SC (24) weaker than the previous two (22 and 23).
ENAs have been observed inside the heliosphere by several missions (e.g., IBEX, Cassini/INCA). However, before they reach detectors close to the Sun, their fluxes are attenuated by the solar environment, with more attenuation of low-energy ENAs. Thus, to retrieve the ENA flux magnitude in their source regions outside of the TS, a deconvolution of the ionization losses and radiation pressure attenuation is required (e.g., Bzowski 2008). In general, the survival probability of H ENA is calculated by integrating the ionization rate for the ENA exposure to the ionizing factor along its orbit. Calculation of the exposure time in the heliosphere requires solving the equation of motion which takes into account a joint action of solar gravity and resonant radiation pressure by solar Lyman-\(\alpha \) photons (e.g. Bzowski et al. (2013b) with reference therein).
8.2 ISNs and Interstellar PUIs
The solar environment ionizes ISNs inside the heliosphere producing PUIs (Vasyliunas and Siscoe 1976). Sokół et al. (2016) studied the influence of the temporal and spatial variations of ionization rates for the density of ISNs and resulting production rates for PUIs at 1 au as a function of solar activity. The results show that the ISN density and PUI count rates are significantly modulated by variations of ionization rates along the Earth’s orbit, which next affects the determination of the ISN flow direction based on the PUI cone and crescent locations. The bias is the greatest for O+ PUIs (up to a few degrees depending on the phase of solar activity) and the smallest for He+ PUIs. Additionally, Sokół et al. (2016) showed that heliolatitudinal anisotropy of ionization rates produces non-negligible asymmetries in the density distribution for O observed in the ecliptic plane in the downwind hemisphere. As further studied by Sokół et al. (2019b), these anisotropies for ISN and PUI densities along the ecliptic plane are present for all species with the greatest effects for O. It means, that the in-ecliptic observations are affected by the latitudinal structure of the ionization rates in the downwind hemisphere, and thus cannot be neglected in the data interpretation.
Distributions of ISN and PUI densities create large-scale structures throughout the heliosphere. Sokół et al. (2019b) studied those global distributions for H, He, Ne, and O for solar minimum and maximum conditions. A common large-scale feature among all species but H is the elongated enhancement of the density that forms behind the Sun in the direction opposite to the gas inflow, i.e. the focusing cone. According to the model results, the cone can reach as far as the TS distance. The maximum of the ISN density is located for various species at various distances from the Sun; the closest to the Sun for He, next for Ne and O, as illustrated in Fig. 12. Also, the location of the ISN density varies with the phase of solar activity being closer to the Sun during solar minimum and further away from the Sun during solar maximum. This variation is an effect of the solar activity variation of the ionization rates. During solar minimum, the ionization rates are smaller and fewer atoms are ionized, and more reach closer distances to the Sun, which results in greater ISN density at closer distances to the Sun. During solar maximum, the ionization rates are greater and more ISNs are ionized which results in smaller density at close distances to the Sun. This also results in an apparent shift of the maximum ISN density to greater distances from the Sun (see the top panel in Fig. 12).
ISN (top) and PUI (bottom) density along upwind (left) and downwind (right) directions in space as a function of distance to the Sun for solar minimum (1996, solid lines) and maximum (2001, dashed lines). The densities are normalized to the value of the ISN density in the upwind direction at TS (\(n_{\mathrm{TS,H}}=8.52\times 10^{-2}\) cm−3, \(n_{\mathrm{TS,O}}=5.00\times 10^{-5}\) cm−3, \(n_{\mathrm{TS,Ne}}=5.82\times 10^{-6}\) cm−3, \(n_{\mathrm{TS,He}}=1.50\times 10^{-2}\) cm−3). PUI density are normalized to their densities estimated in the upwind direction at TS (\(n_{\mathrm{TS,H^{+}}}=2.26\times 10^{-4}\) cm−3, \(n_{\mathrm{TS,O^{+}}}=1.19\times 10^{-7}\) cm−3, \(n_{\mathrm{TS,Ne^{+}}}=4.88\times 10^{-9}\) cm−3, \(n_{\mathrm{TS,He^{+}}}=4.42\times 10^{-6}\) cm−3). See more in Sokół et al. (2019b)
In the upwind direction, the density of ISNs is depleted and drops below \(e^{-1}\) of its value assumed for TS at close distances to the Sun marking the so-called density depletion region (known also as an ionization cavity). The depletion due to ionization spans around the Sun at different distances (closer to the Sun in the upwind direction, and farther away from the Sun in the downwind direction). Also, the cavity location varies between species because of differences in the total ionization rates and a non-negligible radiation pressure for H. The ionization cavity reaches out to \(\sim 4\) au from the Sun in the upwind direction for H and O, \(\sim 1.5\) au for Ne, and \(<0.4\) au for He (Sokół et al. 2019b). In the downwind direction it can reach out as far as 20 au in the case of H (Rucinski and Bzowski 1995; Sokół et al. 2019b).
The production of PUI, which is a product of ISN density and ionization rate, is also modulated by the variations of ionization rates (Rucinski et al. 2003; Sokół et al. 2016, 2019b). The maximum densities of interstellar PUIs are expected at distances from the Sun greater than 1 au (see Fig. 12). Exceptions are He+ PUIs and Ne+ PUIs (the latter during solar minimum), for which the greatest densities are expected within 1 au. Similarly, as for the density of ISNs, the maximum of PUIs is at a closer distance to the Sun during solar minimum and at a greater distance during solar maximum.
In addition, the study of heavy atoms from the VLISM provides us with information on the evolution of the interstellar environment close to the Sun. The Milky Way is assumed to be rapidly enriched in Ne and O elements at the time of the formation of the Sun 4.6 Gyr ago. Thus, one expects to find a Ne/O ratio in the contemporary ISM close to the solar ratio. The Ne/O ratio has been also studied through PUI observations (Gloeckler and Fisk 2007) and from X-ray spectroscopy of absorption edges in X-ray binaries (Juett et al. 2006). Moreover, ISN O and Ne have been measured at 1 au by IBEX-Lo instrument (Bochsler et al. 2012; Park et al. 2014). However, derivation of the Ne/O ratio in ISM based on those measurements requires model support and interpretation (Bzowski et al. 2013). It is because Ne and O have very different ionization properties (Sect. 8.1) and their abundance ratio is highly variable spatially and temporally inside the heliosphere. While O undergoes charge exchange with protons in the HP, Ne travels practically unimpeded through the interface between heliosphere and VLISM. This difference leads to different kinetic properties of neutrals (and their respective PUIs) near 1 au. Therefore, comparing the ratio of these heavy ions is a tool to disentangle physical processes in the VLISM, in the boundaries of the heliosphere, or inside the heliosphere close to the Earth.
8.3 Secondary Population of ISNs
In the outer heliosheath (OHS), the interstellar plasma is heated and decelerated while flowing past the heliosphere. Charge exchange of the primary ISNs with the interstellar ions creates a new, secondary, population of the ISNs measurable in the Earth’s orbit. These neutralized ions are decoupled from the very local interstellar magnetic field and then continue to flow away from their birth location. Since charge exchange reactions operate practically without momentum exchange between collision partners, the secondary ISNs inherit the kinematic properties of their parent ions. Thus, the secondary ISNs have slower bulk velocity and higher temperature compared to the primary ISNs. Since the spatial and velocity distribution of the secondary ISNs depends on the plasma properties in the OHS, it is important to measure the secondary ISNs separately from the primary component.
The creation mechanism of the secondary ISNs was anticipated theoretically by Baranov et al. (1981), Baranov and Malama (1993). There are three major species of secondary ISNs: H, He, and O. The existence of secondary ISN H in the heliosphere was confirmed by measurements of the backscattered Lyman-\(\alpha \) radiation (Lallement et al. 2005, 2010). However, the secondary ISN H has not been unambiguously resolved from the primary population in in-situ measurements because the velocity distribution of the secondary ISNs is quite wide due to its higher temperature, and it overlaps the distribution of the primary ISNs (Schwadron et al. 2013; Katushkina et al. 2015). Recently, Katushkina et al. (2021b,a) investigated the possible imprints of the secondary ISN H atoms in the full-sky maps of the H fluxes at the Earth’s orbit. They showed that the maps of the H fluxes with energies 1-20 eV for the solar minimum conditions have two specific features: (1) the main peak of the fluxes is split into two blobs, and (2) there are two tails at high ecliptic latitude near the downwind direction. They claim that these features are pronounced due to a signal of the secondary ISN H.
The secondary ISN He was originally believed to be of negligible abundance compared to the primary population (Müller and Zank 2004). It was because the reaction assumed to be responsible for its creation, \(He^{+} + H \rightarrow He + H^{+}\), has a very low cross-section (Barnett et al. 1990). However, Bzowski et al. (2012) pointed out that the cross-section of the charge exchange reaction between neutral He atoms and He+ ions \((He^{+} + He \rightarrow He + He^{+})\) is comparable to the high cross-section of the charge exchange between H atoms and protons, and interpreted excess He fluxes in the ISN He observations by IBEX as a secondary component (see Fig. 13). Because of the relatively high abundance of He+ ions in the VLISM near the heliosphere (Frisch and Slavin 2003), appreciable amounts of the secondary ISN He atoms should be produced in the OHS. Kubiak et al. (2014) found that the He signal observed by the IBEX-Lo instrument on IBEX is explained as a superposition of the unperturbed ISN He gas and an additional flow component of He atoms, which they called the Warm Breeze (WB).
(a) IBEX-Lo He intensity map. (b) Model result for the ISN He intensity map. (c) Maximum fluxes in the He intensity maps for the IBEX-Lo observations and the model results. Solid curves are fit curves for the primary ISN He, and dashed curves are for the secondary He. (d) IBEX-Lo O intensity map. (e) Simulated ISN O intensity map. (f) Maximum fluxes of O intensity maps for the IBEX-Lo observations and the model results. Figures are adopted from Park et al. (2019)
The existence of secondary ISN O was proposed in the two-shock heliospheric model by Izmodenov et al. (1997). For the secondary ISN O, the most important resonant reaction is the charge exchange between interstellar O+ ion and ambient H atom \((O^{+} + H \rightarrow O_{\mathrm{sec}} + H^{+})\). The sky maps of the IBEX-Lo O fluxes reveal a tail-like emission expanding toward lower longitude and higher latitude from the observational peak of the ISN O and Ne gas flow (Möbius et al. 2009; Park et al. 2015). The extended tail-like emission could be explained as the imprints of the secondary ISN O population. Baliukin et al. (2017) presented the results of modeling ISN O and Ne atoms through the heliospheric interface and inside the heliosphere based on a three-dimensional kinetic-MHD model of the SW interaction with the VLISM. They confirmed that the secondary ISN O population produces a similarly extended tail-like emission, which is seen in the IBEX-Lo O observations. Park et al. (2019) characterized the secondary ISN O flow at the HP with an analytical model for the directional distribution of the inflowing neutral atoms at Earth’s orbit. Figure 13 shows the ISN He and O flux maps from the IBEX-Lo observations and the results of the analytical model by Park et al. (2019). The emissions in the longitude of 150-210∘ result from the secondary ISN populations, which appear as the extended tail-like emission.
One of the key points in the models of the secondary ISNs is the velocity distribution function at the outer boundary. The simplest case assumes that the velocity distribution functions of both the primary and secondary ISNs are non-interacting homogeneous Maxwellian distribution functions. This two-Maxwellian approximation has been used by several previous studies of the IBEX ISN He and O observations (Bzowski et al. 2012; Kubiak et al. 2014, 2016; Park et al. 2019). Since the interstellar ions are decelerated, heated, and deflected in the OHS, this simple approximation does not represent the secondary ISN in the OHS. However, it is a reasonable approximation inside the TS because only a small subset of the whole secondary ISN population can penetrate inside the TS (e.g., Kubiak et al. 2019). On the other hand, the kinetic-MHD model of the SW interaction with the VLISM has been used to determine the distribution of ISN atoms at the outer boundary. Using this global model, Baliukin et al. (2017) calculated the distribution of the combined O atoms (primary and secondary ISN O) as a Maxwellian-like core with a wide plateau. The wide plateau consists of slow atoms (slower than the bulk speed of ISN gas flow, i.e., 26 km s−1) and it is a product of charge exchange in the OHS.
8.4 PUIs Close to the Solar Corona
Interstellar PUIs are omnipresent plasma phenomena connected with the presence of charge exchange reactions between plasma flows and neutral atoms. Fahr et al. (1998, 2000a) have shown that those PUIs also appear in regions close to the solar corona, and they can be seen there in their EUV resonance glow radiations at 304 Å as discussed by Paresce et al. (1981) for He+ PUIs. ISN He atoms pass over the heliosphere and approach the Sun to within less than 10 solar radii before they get ionized. Next, the He+ ions are picked up by the SW plasma flow and are transported out to larger solar distances. The background for this phenomenon was given in early papers by Fahr (1968a,b).
While ISN H atoms are strongly reduced in density by charge exchange processes with SW protons inside ∼3 au, ISN He atoms can penetrate much deeper towards the Sun and finally are extinguished and converted into He+ ions (see Sect. 8.2). Initially, these ions have their original Keplerian velocities, but as ions, they are picked up by the ambient magnetic fields and are incorporated into the SW plasma flow. However, the pick-up process inside of 10 solar radii is very different from how it works at distances of several astronomical units. The main differences are because of the magnetic fields which are nearly unwound, but rather radial, and the magnitude of the B field dominates the kinetic energy of the ions.
These HeII ions are resonantly scattered by the solar EUV radiation at \(\lambda _{0}=\) \(303.8\mathring{A}\) where the solar radiation has a very distinct and strong emission line; however, with a narrow spectral width of only \(\Delta \lambda _{0}=(u_{c}/c)\lambda _{0}=0.1 \mathring{A}\). Thus, the strength of the resonantly scattered radiation by the He+ PUI is strongly dependent on its Doppler-shifting ion velocity \(u_{pui}\). The resonantly scattered radiation at the solar He+ resonance line of \(303.8\mathring{A}\), taking it to be a Gaussian line emission, is given by the following expression:
The calculated intensity of this resonance radiation seen from Earth along a line of sight perpendicular to the upwind-downwind line of the LISM at different solar impact distances in Rayleighs is given in Fig. 14.
Intensity of resonant radiation of He+ PUIs for observations from the Earth’s orbit on lines of sights perpendicular to the upwind-downwind line with different solar impact distances on the upwind and the downwind side. Figure adapted from Fahr et al. (1998)
8.5 Terrestrial ENAs
The shocked SW protons after the passage of the Earth‘s bowshock could act as a diffuse source of H ENAs. However, it requires the terrestrial H-exosphere to extend up to magnetosheath distances of 8 to 10 Earth radii where the shocked SW plasma is present. Recently, Baliukin et al. (2019) derived from SOHO/SWAN Lyman-\(\alpha \) data that the H geocorona extends well beyond the Earth’s Moon. The existence of terrestrial H ENAs from the region ahead of the Earth’s magnetopause has also been studied by measurements carried out by the IBEX satellite (Fuselier et al. 2010, their Fig. 1). Fahr et al. (2018) quantitatively calculate the H ENAs expected from the exosphere of the Earth using the Lyman-\(\alpha \) studies from the TWINS/LAD detector on the H density of the terrestrial exosphere (see Zoennchen et al. 2011; Bailey and Gruntman 2011; Zoennchen et al. 2013). They modeled the magnetosheath plasma flow ahead of the solar part of the Earth’s magnetopause and determined the source flow of H ENAs originating from the charge exchange collisions of terrestrial H atoms with magnetosheath protons. As a result, they obtained a quasi-isotropic source of H ENAs with keV-energies that partly bombard the exobase, elastically collide with the most abundant O atoms, and with a probability of \(93\%\) are reflected from the exobase with typical energies of \(\tilde{E}_{H_{ENA}}\simeq (16/17)\) keV. With such super-escape energies, these reflected ENAs leave the exobase to outer space along straight trajectories, and their local densities fall off like \(n_{H_{ENA}}\sim (r_{ex}/r)^{2}\). Since the density of the normal exobase H atoms at the upper border of the exosphere falls off like \(n_{H}(r)=n_{H0}\cdot (r/r_{0})^{-2.7}\), the relative abundance of H ENAs over H atoms permanently increases with height. This reveals that the (H ENAs/H atoms) cross over point is dependent on the location of the magnetopause \(r_{MP}\) (it is further into the Earth for a low, and further out for a high magnetopause location; see e.g. Baumjohann and Treumann (1996)).
8.6 Inner Source PUIs
Inner source PUIs are a population of PUIs produced close to the Sun. Three main features differentiate them from interstellar PUIs. First, observations of C+ PUIs – a species mainly ionized in the interstellar medium due to its high ionization rate (Geiss et al. 1994). Second, observations of the radial profile of inner source C+ decreasing with radial distance from the Sun (Geiss et al. 1995). Whereas the radial profile of interstellar species such as O+ has been shown to increase with radial distance (see, e.g., Fig. 12). Third, the velocity distribution function of inner source C+ has a thermalized distribution that peaks near the SW speed (Schwadron and Gloeckler 2007). This indicates that they are picked up close to the Sun and cooled with the expanding SW. Compared to interstellar PUIs, inner source PUIs are still poorly understood.
The composition of inner source PUIs resembles the composition of the SW (Gloeckler et al. 2000; Allegrini et al. 2005; Schwadron and Gloeckler 2007). However, being single or double charged excludes them from being produced directly from the Sun. Instead, SW ions reduce their ionization through the interaction with interplanetary dust particles (IDPs). IDPs are dust grains from sources such as the asteroid belt, Edgeworth-Kuiper belt, comets, planets, and the VLISM. They are distributed throughout the heliosphere by a combination of fragmentation, electromagnetic forces, gravity, radiation pressure, and SW pressure.
The production of inner source PUIs is highly dependent on the composition, size, velocity, and density of the IDPs they interact with. The size distribution of the IDP population increases with smaller grain size due to the amount of dust-dust collisions (Ishimoto 2000). There is a large deficiency of IDPs of about \(10^{-15}\) g to \(10^{-12}\) g (i.e., beta-meteoroids) due to following hyperbolic orbits because of radiation pressure. However, grains smaller than beta-meteoroids (i.e., nanograins) have stable orbits close to the Sun (Mann et al. 2007).
There are five proposed mechanisms for inner source PUI production due to the interaction of SW ions with IDPs: SW neutralization (Wimmer-Schweingruber and Bochsler 2003), SW recycling (Schwadron et al. 1999), backscattering, sputtering, and sputtering-induced recycling (Quinn et al. 2018). In neutralization, SW ions gain electrons as they pass through nanograins and the edges of larger IDPs. In recycling, SW ions are implanted within larger IDPs and neutralized in the process. The surface of the IDP becomes saturated and the atoms eventually desorb from the grain, then become ionized and picked up by the interplanetary magnetic field (IMF). In backscattering, charge exchange occurs when SW ions reflect off the surface of IDPs. In sputtering, bombarding SW ions remove atoms that compose the IDP. Lastly, in sputtering-induced recycling, bombarding SW ions instead remove SW ions that were previously implanted into the IDP.
Which production mechanism is dominant is still uncertain. Observations of inner source C+ and O+ show that \(C^{+}/O^{+}>1\) and decreases with SW speed (Taut et al. 2015). Simulations of neutralization, backscattering, and sputtering-induced recycling tend to reflect these observations (Quinn et al. 2019). However, observations of the radial profile, latitudinal profile, size distribution, composition, and morphology of IDPs close to the Sun are necessary to gain more insight.
9 Theory and Interpretation of Measurements: Part 2
9.1 Modeling the PUI-Mediated Supersonic SW
The NH Solar Wind Around Pluto (SWAP) instrument (McComas et al. 2008a) observed interstellar H+ and He+ PUIs in the distant heliosphere, reporting observations at distances between \(\sim 11.26\) and 38 au in the SW (McComas et al. 2017) and out to \(\sim 47\) au McComas et al. (2021). Plasma observations well beyond the hydrogen ionization cavity show that the distant SW is mediated by PUIs. The observed PUI distributions, particularly H+ PUI, should have had sufficient time to evolve into a stable nearly-isotropic distribution. Observations of PUIs by the Ulysses Solar Wind Ion Composition Spectrometer (SWICS) instrument (Gloeckler et al. 1992) within the H ionization cavity, from about 1.4 to 5.4 au, identified numerous PUI species (H+, He+, N+, O+, Ne+) (e.g., Gloeckler and Geiss (1998)). The distributions tended to be highly anisotropic (Gloeckler et al. 1995), suggesting that the PUI scattering mfp was unusually long, although the precise reason for this is somewhat unclear. It is possible that the nature of the underlying turbulence responsible for the scattering of PUIs, being a superposition of a majority quasi-2D and a minority slab component, might be responsible for the long mfps.
The initial ring-beam PUI distribution is unstable to the excitation of Alfvénic modes (Lee and Ip 1987; Williams and Zank 1994; Zank 1999; Cannon et al. 2014b; Aggarwal et al. 2016; Fisher et al. 2016; Smith et al. 2017; Hollick et al. 2018a), and therefore modifies the underlying low-frequency turbulence field responsible for scattering PUIs. The excitation of Alfvénic fluctuations by PUIs is key to understanding the observed radial evolution of magnetic turbulence in the distant SW (Zank et al. 1996a; Matthaeus et al. 1999; Smith et al. 2001; Breech et al. 2008; Isenberg et al. 2010; Oughton et al. 2011; Zank et al. 2012; Adhikari et al. 2014, 2015; Wiengarten et al. 2016; Shiota et al. 2017; Zank et al. 2017; Adhikari et al. 2017). Furthermore the dissipation of low-frequency magnetic fluctuations heats the SW plasma and results in a non-adiabatic SW temperature profile and a slow temperature increase beyond \(\sim 30\) au (Williams et al. 1995; Smith et al. 2001; Zank et al. 2017). PUI generation of low-frequency turbulence in the outer heliosphere also affects cosmic ray mfps (Zank et al. 1998; Florinski et al. 2003; Engelbrecht and Burger 2013; Chhiber et al. 2017; Engelbrecht 2017; Zhao et al. 2018).
There is an intimate coupling of PUIs, thermal SW plasma, and the evolution of low-frequency turbulence throughout the SW. The first PUI-mediated models of the SW assumed instantaneous assimilation and equilibration of newly created PUIs with the SW plasma (Wallis 1971; Holzer 1972; Holzer and Leer 1973; Isenberg et al. 1985) i.e., the combined thermal SW and PUI plasma was treated as a single Maxwellian (or at least isotropic) distribution. The early models predicted a dramatic SW temperature increase with the increasing heliocentric distance that was not observed. Isenberg (1986) pointed out that the SW plasma and PUIs could not form a single equilibrated distribution because the Coulomb collision time scale between suprathermal pickup protons and SW protons (and electrons) far exceeds the fluid advection time for a heliospheric supersonic flow of radial extent less than 100 au (i.e., the distance to the heliospheric TS). Instead the total distribution comprises a cold thermal SW core and a tenuous energetic pickup proton halo (Isenberg 1986; Zank et al. 1996b; Zank 1999; Zank et al. 2010; Burrows et al. 2010; Zank et al. 2014; Zank 2015). As discussed by Isenberg (1986), Zank et al. (2014), Zank (2016), a PUI-mediated model of the supersonic SW must include the thermal SW and the suprathermal pickup protons as distinct plasma components.
Zank et al. (2018) extended the models of Holzer (1972) and Isenberg (1986) by coupling a detailed model of turbulence transport and dissipation to a multi-fluid description of the SW plasma. This allowed them to examine the feedback between SW plasma heating, the modified large-scale SW velocity due to the creation of PUIs, and the driving of turbulence by SW and interstellar PUI sources.
The derivation of the equations for a PUI-mediated SW, including the structure of the TS, presented by Zank et al. (2014), Zank (2016), Zank et al. (2018) assumes that pre-existing and self-generated Alfvén waves scatter PUIs and a form of collisionless Chapman-Enskog expansion is then used to derive model equations describing the evolution of the PUI density \(\rho _{p}\), velocity, and pressure \(P_{p}\). Since the scattered PUI distribution is nearly isotropic, the fluid description for PUIs contains both a heat conduction term \(\propto {\mathbf{K}}_{p} \cdot \nabla P_{p}\), where \({\mathbf{K}}_{p}\) is the collisionless PUI “thermal conduction” tensor and a stress tensor due to the collisionless viscosity \(\eta _{ij}\). The heat conduction term is the first-order anisotropy and the viscosity is the second-order anisotropy in the PUI distribution. Although the scale lengths introduced by both PUI heat conduction and viscosity are much smaller than the large-scale supersonic SW, where they can safely be neglected, they are important in determining the structure of the TS (Mostafavi et al. 2017b; Zank et al. 2018). The PUI-mediated model of the supersonic SW is completed with the inclusion of turbulence, both pre-existing and excited by the creation of PUIs. The coupled model equations can be found in Zank et al. (2018).
An important distinction between earlier PUI-mediated SW models and the Zank et al. (2018) model is in the 1D thermal plasma temperature transport equation, expressed as Adhikari et al. (2015)
Here \(r\) is the radial distance, \(T_{s}\) is SW temperature, \(\gamma _{s} = 5/3\) is the adiabatic index, \(n_{s}\) is the SW density, \(k\) Boltzmann’s constant, \(U\) is the large-scale radial flow velocity, and the turbulent heating term \(S_{t}\) for the thermal plasma and the charge exchange-related term \(\nu _{c}^{s}\) is given by Equations (31) and (12), respectively, in Zank et al. (2018). The heating term \(S_{t}\) expresses the dissipation of turbulent energy as measured in the quasi-2D and slab components (Zank et al. 2017).
Zank et al. (2018) solve the PUI-mediated SW model numerically and restrict attention to a simple spherically symmetric steady-state model. This describes the evolution of the bulk SW and the associated turbulence from 1–75 au. The predicted steady-state solutions are compared to both Voyager 2 plasma and magnetometer data and NH plasma data. The large-scale SW and PUI plasma number densities, pressures, and corresponding temperature, as well as the SW radial component of the flow velocity, are plotted in Fig. 15 as a function of heliocentric distance \(r\). Each panel shows the theoretically predicted results together with Voyager 2 data from 1–75 au and NH SWAP data from 11.26-38 au. The two data sets are independent, being separated by three decades, but we show the spatial region of overlap. The same theoretical model curves are used in all plots. The Voyager 2 observations are taken from 1983–1992 and those of NH from 2008–2017 for the radial heliocentric distance interval 11–38 au, and the SC observed by NH was much weaker than that observed over this distance interval by Voyager 2 (e.g., Lockwood et al. 2011).
Comparison of a theoretical PUI-mediated SW model and observed bulk plasma observations for Voyager 2 data between 1 and 75 au (top plots of each panel) and NH SWAP data between 11.26 and 38 au. Top left: Solid lines show model predictions of the large-scale thermal plasma number density \(n_{s}\) (black curve) and the PUI number density \(n_{p}\) (red curve) together with Voyager 2 observations of \(n_{s}\) (blue symbols, top plot) and NH SWAP observations of \(n_{s}\) (green) and \(n_{p}\) (red) (bottom plot). Top right: Same as previously, but for thermal plasma and PUI pressure for Voyager 2(top) and NH SWAP (bottom). The dotted curves show the pressure without turbulent heating. Bottom left: Thermal temperature (black line, blue symbols) and PUIs (red line). The dotted curves show the temperature without turbulent heating. Bottom right: Predicted and observed SW radial speed \(U\). See more in Zank et al. (2018)
The SW density decays as usual according to \(n_{s} \propto r^{-2}\), whereas \(n_{p}\) increases to a maximum value at \(\sim 12\) au and then very slowly decreases as the SW expands radially outward. The model and Voyager 2 and NH SWAP observations exhibit a good correspondence, although some SC dependence is present in the thermal plasma density. This is more apparent in the Voyager 2 radial velocity plot. The PUI density observations exhibit shorter time scale variation, most likely associated with interplanetary shocks or streams.
The theoretical thermal and PUI pressures and temperatures plotted in Fig. 15 exhibit a change in the cooling rate at \(\sim 20\) au, which has been attributed to the additional dissipation of turbulence driven by PUIs. The effect of heating by turbulence is quite striking as can be seen from the dashed (no dissipative heating) and solid line (dissipative heating included) curves plotted in the pressure and temperature panels of Fig. 15. The agreement between the theoretical and observed Voyager 2 pressure and temperature is very good with the slow flattening/increase in the thermal pressure/temperature profile. A corresponding flattening/increase in the NH SWAP thermal plasma data appears to be consistent with predictions but more data is needed to confirm this. The PUI pressure and temperature profiles are consistent with NH SWAP observations, the PUI temperature being more than two orders of magnitude higher than that of the thermal pressure.
An interesting assumption about the temperature plots in the Zank et al. (2018) model is that the dissipation of PUI-driven turbulence occurs only in the thermal plasma i.e., the dissipation of low-frequency turbulence does not heat the PUIs. However, the PUI temperature and pressure plots do indicate a turn-up in the PUI temperature near 38 au, and this is not consistent with the model presented by Zank et al. (2018). McComas et al. (2021) confirm that the PUIs do appear to increase in temperature with increasing heliocentric distance. The reason for the heating is not entirely obvious. There are several possible explanations for this. The first is that we do not understand the nature of turbulent heating in a non-equilibrated plasma system, and it may be entirely possible that the hotter PUI distribution may experience some heating despite their already high temperature. A second, and perhaps more plausible, the explanation may be that the PUIs are further energized by some form of second-order Fermi acceleration related to counter-propagating Alfvén waves (Bogdan et al. 1991; Le Roux and Ptuskin 1998). A third possibility is that some form of further acceleration of PUIs related to the preferential reflection and subsequent energization of PUIs by interplanetary shocks (Zank et al. 1996b), as has been observed by the SWAP instrument (Zirnstein et al. 2018c), may account for the observed increase in the PUI temperature.
The SW radial velocity plot is highly variable compared to the steady-state solutions in Fig. 15. This is due to both SC variation in flow speeds, as well as the presence of shock waves and stream structure. The theoretical radial velocity plots exhibit a gradual deceleration of the SW due to charge exchange (Holzer 1972; Wallis 1971; Isenberg et al. 1985; Khabibrakhmanov et al. 1996; Zank 1999), which is not easily observed, although see the analysis by Richardson et al. (2004).
9.2 Waves Due to Interstellar PUIs
ISNs which cross the heliosphere and get ionized represent a suprathermal energy source moving through the SW along the mean-field at the SW speed. They resonantly excite sunward propagating, right-hand polarized waves which become left-hand polarized in the spacecraft frame (Lee and Ip 1987). As the waves propagate at the Alfvén speed and the ions are scattered in pitch angle, the waves are seen at spacecraft-frame frequencies \(f_{sc} \ge f_{i,c}\) where \(f_{i,c}\) is the ion cyclotron frequency. While the process of scattering interstellar PUIs excites magnetic wave energy that drives the turbulence, it is not possible to observe that wave energy when it is absorbed by the turbulent cascade. When the turbulent cascade is sufficiently weak to allow the wave energy to accumulate to observable levels over many hours, the waves can be observed in the magnetic field data.
Waves due to newborn interstellar PUIs have been observed by magnetometers on numerous spacecraft including ACE (Argall et al. 2015; Fisher et al. 2016), Ulysses (Murphy et al. 1995; Cannon et al. 2013, 2014b,a; Aggarwal et al. 2016; Cannon et al. 2017; Argall et al. 2017), and Voyager (Joyce et al. 2010, 2012; Hollick et al. 2018a,b,c) and are reviewed by Smith et al. (2017). Figure 16 shows an example of Voyager 1 spectra exhibiting waves due to newborn interstellar \({\mathrm{H^{+}}}\) and He+ PUIs when the spacecraft was at 6.2 au. The waves due to H+ offer the stronger signal, but the ellipticity at \(f_{sc} > f_{He,c}\) does show the expected polarization signature. Both PUI species produce waves with \(E_{lip} < 0\) (left-hand polarized in the spacecraft frame) as expected from theory (Lee and Ip 1987). While waves due to interstellar He+ PUIs can be seen at 1 au, interstellar neutral H does not penetrate inside 3 au in sufficient number to excite waves to an observable level. Waves due to newborn interstellar H+ PUIs are seen in the Ulysses and Voyager data beyond 3 au.
Spectral analysis of Voyager 1 magnetic field data. (top to bottom) The trace of the power spectral density matrix and spectrum of the magnitude time series (indicative of low compression) with the cyclotron frequency of \({\mathrm{He^{+}}}\) and \({\mathrm{H^{+}}}\) shown, degree of polarization and coherence, ellipticity showing the traditional (signed) polarization of the fluctuations, and the angle between the minimum variance direction and the mean magnetic field. The waves are seen at \(f_{sc} > f_{i,c}\) with a high degree of polarization and coherence, are left-hand polarized in the spacecraft frame, and have minimum variance directions parallel to the mean magnetic field. See more in Hollick et al. (2018a)
The computed polarization in the spacecraft frame for wave intervals arising from \({\mathrm{H^{+}}}\) PUIs in the Voyager 2 data (Hollick et al. 2018a) is shown in Fig. 17. The results are obtained by averaging the ellipticity spectrum over the frequency range \(f_{p,c} < f_{sc} < 2f_{p,c}\) where \(f_{p,c}\) is the proton cyclotron frequency. Approximately, half of the wave events are right-hand polarized beginning at 5 au which is contrary to the standard theory and most like attributable to incomplete or modified scattering of the PUI. Approximately 10\(\%\) of the waves due to He+ PUI seen by the ACE spacecraft and those excited by H+ seen by the Ulysses spacecraft are found to be right-hand polarized in the spacecraft frame. The observation of right-hand polarized waves becomes more prominent beyond 5 au. This is thought to be due to incomplete or modified scattering of the PUI, but this has not been proven. The waves observed inside \(\sim 3\) au are unlikely to be due to interstellar PUIs and are thought to originate either from an inner source such as dust grains (see also Sect. 8.6) or ENAs. That study is ongoing.
Spectral ellipticity averaged over the frequency range \(f_{p,c} < f_{sc} < 2f_{p,c}\) as a function of the heliocentric distance. See more in Hollick et al. (2018a)
The results of analysis of the ellipticity of waves due to H+ PUI as seen by the Ulysses spacecraft (top) and Voyager 2 spacecraft (bottom) is combined in Fig. 18. The ellipticity is plotted as a function of the angle between the mean magnetic field and the radial direction, \(\Theta _{BR}\). Waves of both polarizations are consistently seen over the full range of field orientations, although the Ulysses results are a bit more limited in extent showing few right-handed waves at ellipticities \(< 25^{\circ }\) and \(> 75^{\circ }\). It has been speculated that the waves are most often seen when the mean field is radial, owing in part to an approximation made in Lee and Ip (1987). Figure 18 shows that this is not the case, although right-hand polarized waves are not generally seen for nearly radial mean fields. The source of right-hand polarized waves is not yet determined.
Computed wave ellipticity as a function of the angle between the mean field and the radial direction. (top) For waves due to interstellar H+ PUIs seen by the Ulysses spacecraft (Cannon et al. 2014b). Only about 10% of the observations are right-hand polarized as is the case for waves due to He+ seen by ACE (Fisher et al. 2016). (bottom) Same as top but for Voyager 2 data (Hollick et al. 2018a)
9.3 Acceleration and Global Energy Distribution of PUIs
Although PUIs are born to have their thermal speeds nearly equal to the SW speed, observations by experiments on various spacecraft, e.g., ACE, WIND, Ulysses, Cassini, and NH, have shown that the speed of PUIs can go much higher even in periods of low SW disturbance. Quite often, an energetic tail of PUIs with a power-law distribution function close to \(\propto p^{-5}\) can be observed (e.g., Zhang et al. 2019). PUIs are accelerated in the interplanetary space and the mechanisms for the acceleration are still under active discussion. Interplanetary shocks are one of the possible explanation (Giacalone et al. 1997; Summerlin and Baring 2006; Giacalone 2010). However, only a few interplanetary shocks were observed, and thus cannot be used to explain the more prevalent acceleration of PUIs in the quiet SW. The small-scale plasma waves or turbulence, which is ubiquitous in the SW, are another source to accelerate PUIs (Isenberg 1987; Schwadron et al. 1996; Le Roux and Ptuskin 1998; Chalov et al. 2006; Gamayunov et al. 2015).
Fluctuations of electric fields in plasma turbulence appear to be random. If its amplitude is small enough, the effect of fluctuating fields leads to particle diffusion in momentum. It is called the second-order stochastic acceleration, similarly to the mechanism proposed initially by Fermi (1949). The mechanism can accelerate particles to higher energies as well as cause particles to lose energy. Because we have more low-energy particles in typical space plasma or the gradient of particle distribution as a function of particle momentum is negative, the mechanism can cause a flow of particles towards higher energies, thus making the system gain energies statistically.
In the SW plasma, most of the plasma fluctuations are in the form of incompressible Alfvénic turbulence. The momentum diffusion coefficient \(D_{pp}\) is related to particle pitch angle diffusion and parallel spatial diffusion coefficient \(\kappa _{\parallel }\) through
where \(V_{A}\) is Alfvén speed, and the constant \(A\) is of the order 1/9. Chalov et al. (2004) and Gamayunov et al. (2013) considered plasma waves generation by PUIs and acceleration of PUIs self-consistently. They found that the acceleration of PUIs by Alfvén fluctuations is not fast enough to overcome the adiabatic cooling effect in the expanding SW, thus producing an insignificant number of particles above the SW speed. Zhang and Lee (2013) pointed out that the particle’s parallel spatial diffusion coefficient \(\kappa _{\parallel }\) is so large for PUIs that the momentum diffusion time \(p^{2}/D_{pp}\) is longer than adiabatic cooling time in the SW \(3/\bigtriangledown \cdot \mathbf{V}\), where \(\mathbf{V}\) is the SW velocity. The mechanism, however, can heat up the core SW somewhat presumably due to a smaller particle diffusion coefficient at these low energies.
Stochastic acceleration of particles can also occur when there are plasma motions that exhibit random compressions or expansions. If the particles can cause diffusion relative to the plasma, some particles may gain substantial energies by repeatedly going through plasma compression regions. The mechanism was investigated by Bykov and Toptygin (1982, 1993) and Ptuskin (1988), who obtain a momentum diffusion equation using a quasilinear approximation. Ptuskin (1988) dismissed it as an effective mechanism to accelerate or reaccelerate cosmic rays in the interstellar medium based on an estimate of acceleration time using a typical cosmic ray spatial diffusion coefficient. Using an alternative term of “pumping mechanism,” Fisk and Gloeckler (2006, 2008) and Fisk et al. (2010) suggested that it can automatically produce the \(p^{-5}\) distribution of particles commonly observed in the heliosphere. But the quasilinear calculation by Jokipii and Lee (2010) disputes their claims. Zhang (2010, 2011) simulated particles going through trains of compressible plasma waves by solving the Parker transport equation. He found that particle acceleration by this mechanism can be fast and efficient even with amplitudes of plasma compression waves. It is particularly true for those particles with low energies. Significant particle acceleration occurs when the particle diffusion length is greater than the size of the individual plasma compression region but smaller than the entire plasma fluctuation region. In some of the simulations where shock wavelets are prescribed, it is found that particles need to go through as low as a few shocklets with small compression of a few percent to get accelerated a steady-state solution of a power-law distribution function.
Compressible plasma fluctuations tend to propagate in the direction perpendicular to the magnetic field. The spatial diffusion coefficient should be much smaller than the parallel one. That is the main reason why acceleration by compressible plasma fluctuation is much faster than that by Alfvénic fluctuations. If the fluctuation is left to develop fully into many shocklets at compression fronts, the wave power spectrum becomes \(S(k) \propto k^{2}\) in a certain range of \(k\) between \(k_{min}=1/L_{0}\) and \(k_{max}=1/L_{1}\).
The momentum diffusion rate \(D_{0}\) is independent of particle momentum. With this momentum dependence of \(D_{pp}\), the momentum diffusion equation has a steady-state solution of the distribution function for accelerated particles of the form \(\propto p^{-3}\). Such a distribution, if left unmodified, contains an infinity amount of energy density and particle density. In reality, because particles suffer adiabatic energy loss and other possible loss mechanisms, the accelerated particles can never achieve this distribution over a wide range of particle momentum. As a result of acceleration, the pressure contained in accelerated particles can decrease the amplitude and wavenumber of compressible plasma waves, which in turn limits the momentum diffusion rate \(D_{0}\). Zhang (2010) and Zhang and Lee (2013) showed that the momentum diffusion and adiabatic cooling settle at some equilibrium rates so that the pressure of accelerated particles approaches a steady maximum value. At that point, a \(\sim p^{-5}\) power-law distribution function is established without details of wave or particle parameters.
Based on the above mechanism of particle acceleration by compressible plasma fluctuations, Zhang and Schlickeiser (2012) built a bi-modal model for PUI acceleration throughout the heliosphere. The model considers that intense compressible plasma fluctuations only exist in a limited percentage of volume in the heliosphere. At the same time, the accelerated particles can populate other regions of the heliosphere without the presence of compressible plasma fluctuation through some kind of particle transport process or due to propagation of the regions. Most likely, regions of particle acceleration by compressible plasma fluctuations can form and disappear frequently. It is because compressible plasma fluctuations can rapidly convert energies to the internal energy of accelerated particles. That requires the generation of plasma compressible plasma fluctuations regularly through shear flows or conversion from Alfvenic turbulence. In Zhang and Schlickeiser (2012) model of PUIs acceleration, particles also experience various loss mechanisms.
With the condition that particles in particle acceleration regions can only produce a limit pressure in PUIs, Zhang and Schlickeiser (2012) established a maximum stochastic acceleration rate without an explosive increase of particle pressure. They showed under the maximum acceleration rate how particles could automatically establish a \(~\sim p^{-5}\) distribution function in suprathermal energy tails. Figure 19 shows the calculation results of the omnidirectional PUI distribution function at 1 au, 5 au, and near the TS, compared with observations by ACE and Ulysses. Figure 20 shows radial dependence of PUI density and pressure calculated from the model and comparison to those expected radial variations of the SW. The slow down of the SW due to the mass loading of PUIs is neglected. As can be deduced from Fig. 20, the ratio of PUI to SW density and pressure increase with radial distances. By radial distances around 10 to 20 au, the pressure in PUIs dominates all magnetic field pressure, solar thermal pressure, and turbulence pressure all combined. It is only less than SW ram pressure. By the time it reaches the TS, the Mach number of the entire composite, which is equal to the square root of the ratio of SW ram pressure to PUI+SW internal pressure, is only around 3-4 at \(\sim 80\) au even with unaccelerated PUI pressure (Fig. 21). As a result, the TS is no longer a supercritical shock. Particle acceleration of PUIs during their propagation through the interplanetary space partially contributes to PUI pressure buildup, thus further reducing the SW Mach number to below 2 in the quiet SW (Zone 1) at \(\sim 80\) au. In regions of active particle acceleration (Zone 2), the Mach number could dip below 1 outside 60 au. These numbers suggest that the TS is rather weak.
The omnidirectional distribution function of PUI protons in the spacecraft reference frame in the SW at 1, 5, and 80 au and their comparison with measurements by ACE and Ulysses. Zone 2 is the region where active stochastic particle acceleration occurs in the presence of compressible plasma fluctuations. Zone 1 does not accelerate particles, but it receives accelerated particles through leakage from Zone. The calculation assumes that stochastic particle acceleration in Zone 2 is so intense that the back-reactions of particle pressure can moderate the amplitude of plasma fluctuation and hence particle acceleration rate. The velocity of the slow SW is 400 km s−1, and the fast SW has 800 km s−1. Figure adapted from Zhang and Schlickeiser (2012)
Radial dependence of PUI protons, the SW, ISN H, and magnetic field parameters. The Parker model is used in the calculation of SW and magnetic field parameters up to the TS. The rate of PUI injection is calculated from the charge exchange between interstellar neutral and SW ions. PUI proton pressure is calculated without stochastic acceleration. The core SW (thermal) pressure is from adiabatic calculation assuming no interplanetary heating. The 2D turbulence pressure is assumed to follow the WKB approximation. The sound wave speed is calculated from the sum of core SW pressure and pickup proton pressure. Figure adapted from Zhang and Schlickeiser (2012)
9.4 Shocks in the Inner Heliosheath
Nonthermal PUIs in the IHS introduce a large collisionless heat flux and viscosity by their pitch-angle scattering, and thus their contribution cannot be ignored (Mostafavi et al. 2018). The theory estimated that the PUI number density is about \(25\%\) of the thermal gas density in the IHS (Zank et al. 2010), which leads to a significant PUI pressure (i.e., about 25 times than the thermal gas pressure; Mostafavi et al. (2018)). The comparison between the ENA spectra computed from Zank et al. (2010) model with the IBEX observations showed that transmitted and reflected PUI downstream of the TS contribute to the ENA flux with 0.5-5 keV, and above 5 keV energy ranges, respectively (Desai et al. 2012). Later, Desai et al. (2014) showed a significant increase in the ENA fluxes with energies below 0.5 keV by including the ENA production from the charge exchange between an ISN atom with a PUI outside the HP. Zirnstein et al. (2014) improved the multi-component treatment of the IHS plasma by accounting for the loss of PUIs through charge exchange as they propagate in the IHS. Their results suggested that the significant number of ENAs between 0.02 to 10 keV originate from outside the HP. However, there is a large discrepancy between these models and IBEX ENA observations, suggesting that they miss some PUI energization in the IHS. Zirnstein et al. (2018a,b) showed that including turbulence in IHS could increase the PUI energy and account for some part of the missing ENA flux.
Interplanetary shock waves generated by coronal mass ejections or corotating interaction regions (Pizzo 1978; Gosling and Pizzo 1999) propagate in the heliosphere, collide with the TS, and eventually produce one or more weakened transmitted shocks propagating in the IHS (Story and Zank 1997; Zank et al. 2001; Washimi et al. 2011; Provornikova et al. 2012). Any shock waves propagating in the IHS can be a significant source of PUI energization, and one should not ignore their presence in analyzing IBEX observations.
Mostafavi et al. (2019) used a two-fluid (i.e., thermal gas and nonthermal PUIs) model presented by Zank et al. (2014) to study the structure of IHS shock waves and their effect on the ENA flux. As at the TS, shocks in the IHS are mediated by energetic PUIs, and the PUI diffusion length scale determines their thickness. They assumed two shocks propagating in the IHS to calculate the ENA flux. The simulation results were compared with the first five-year average of IBEX observations (McComas et al. 2014) in the Voyager 1 direction. Figure 22 compares the shock model results and IBEX observations at 1 au. The presence of transmitted interplanetary shocks in the IHS increases the IHS PUI temperature primarily (Mostafavi et al. 2019). Thus, it leads to the more effective production of ENAs from the IHS. The extra production of the ENA flux due to the IHS shocks yields a better consistency with the ENA flux observed by IBEX at 1 au.
10 Summary
The Voyager 1 and Voyager 2 missions opened a window to characterize the outer solar system environment and search for the heliosphere boundary, the outer limits of the Sun’s magnetic field, and the outward flow of the SW. IBEX was the next step to extensively explore the interstellar space by remote observations. And NH added significantly to the knowledge about the PUI mediation of the SW inside the heliosphere. They all greatly contributed to our understanding of the heliosphere and the development of the physics of PUIs and ENAs. However, still many questions remain open, especially when theory and models meet the measurements, as discussed here. More observational data is needed to advance and guide the theoretical picture of the heliosphere, its interior, and the processes at its boundary offered by the present-day models. The last decades show again that for such a complex system like the heliosphere modeling and measurement must coexist to satisfy progress in both.
NASA is preparing to launch the Interstellar Mapping and Acceleration Probe (IMAP) in 2025 (McComas et al. 2018), which goal is to better understand the boundary of the heliosphere, the role of PUIs, and the physics of ENAs. The concept of an interstellar probe that would leave our solar system and could make in-situ measurements in interstellar space would be the next huge and needed step in exploring our stellar environment. Several missions have been considered, like, e.g., the Interstellar ExpressFootnote 2 (Wu et al. 2019; Song 2021), the Interstellar ProbeFootnote 3 (McNutt et al. 2019; Brandt et al. 2019), and the Interstellar Heliopause ProbeFootnote 4 (Lyngvi et al. 2005). The coming decades with the new and innovative studies will bring answers to many questions and, for sure, will reveal new unknowns.
Change history
04 May 2022
The original online version of this article was revised due to a retrospective Open Access order.
05 May 2022
A Correction to this paper has been published: https://doi.org/10.1007/s11214-022-00897-0
Abbreviations
- au:
-
astronomical unit
- BS:
-
bow shock
- ENA:
-
energetic neutral atom
- EUV:
-
extreme ultraviolet
- GDF:
-
globally distributed flux
- HP:
-
heliopause
- IBEX:
-
Interstellar Boundary Explorer
- IDP:
-
interplanetary dust particles
- IHS:
-
inner heliosheath
- IMAP:
-
Interstellar Mapping and Acceleration Probe
- ISM:
-
interstellar medium
- ISN:
-
interstellar neutral
- mfp:
-
mean free path
- MS-FLUKSS:
-
Multi-Scale Fluid-Kinetic Simulation Suite
- NH:
-
New Horizons
- OHS:
-
outer heliosheath
- PUI:
-
pickup ion
- SC:
-
solar cycle
- SHIELD:
-
Solar wind with Hydrogen Ion charge Exchange and Large-Scale Dynamics
- SHOIR:
-
Sun-Heliosphere Observation-based Ionization Rates
- SW:
-
solar wind
- TS:
-
termination shock
References
L. Adhikari, G.P. Zank, Q. Hu, A. Dosch, Turbulence transport modeling of the temporal outer heliosphere. Astrophys. J. 793(1), 52 (2014). https://doi.org/10.1088/0004-637X/793/1/52
L. Adhikari, G.P. Zank, R. Bruno, D. Telloni, P. Hunana, A. Dosch, R. Marino, Q. Hu, The transport of low-frequency turbulence in astrophysical flows. II. Solutions for the super-Alfvénic solar wind. Astrophys. J. 805(1), 63 (2015). https://doi.org/10.1088/0004-637X/805/1/63
L. Adhikari, G.P. Zank, P. Hunana, D. Shiota, R. Bruno, Q. Hu, D. Telloni, II. Transport of nearly incompressible magnetohydrodynamic turbulence from 1 to 75 au. Astrophys. J. 841(2), 85 (2017). https://doi.org/10.3847/1538-4357/aa6f5d
P. Aggarwal, D.K. Taylor, C.W. Smith, C.J. Joyce, M.K. Fisher, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, B.E. Cannon, J.D. Richardson, Voyager observations of magnetic waves due to newborn interstellar pickup ions: 2-6 AU. Astrophys. J. 822(2), 94 (2016). https://doi.org/10.3847/0004-637X/822/2/94
F. Allegrini, N.A. Schwadron, D.J. McComas, G. Gloeckler, J. Geiss, Stability of the inner source pickup ions over the solar cycle. J. Geophys. Res. Space Phys. 110, A05105 (2005). https://doi.org/10.1029/2004JA010847
M.R. Argall, M.K. Fisher, C.J. Joyce, C.W. Smith, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, R.M. Skoug, ACE observations of magnetic waves arising from newborn interstellar pickup helium ions. Geophys. Res. Lett. 42(22), 9617–9623 (2015). https://doi.org/10.1002/2015GL066374
M.R. Argall, S.J. Hollick, Z.B. Pine, C.W. Smith, C.J. Joyce, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, J.M. Sokół, M. Bzowski, L.F. Burlaga, Observation of magnetic waves excited by newborn interstellar pickup He+ observed by the Voyager 2 spacecraft at 30 au. Astrophys. J. 849(1), 61 (2017). https://doi.org/10.3847/1538-4357/aa8ee2
W.I. Axford, The Interaction of the Solar Wind with the Interstellar Medium, vol. 308 (1972), p. 609
J. Bailey, M. Gruntman, Experimental study of exospheric hydrogen atom distributions by Lyman-alpha detectors on the TWINS mission. J. Geophys. Res. Space Phys. 116(A9), A09302 (2011). https://doi.org/10.1029/2011JA016531
I.I. Baliukin, V.V. Izmodenov, E. Möbius, D.B. Alexashov, O.A. Katushkina, H. Kucharek, Secondary interstellar oxygen in the heliosphere: numerical modeling and comparison with IBEX-Lo data. Astrophys. J. 850(2), 119 (2017). https://doi.org/10.3847/1538-4357/aa93e8
I.I. Baliukin, J.L. Bertaux, E. Quémerais, V.V. Izmodenov, W. Schmidt, SWAN/SOHO Lyman-\(\alpha \) mapping: the hydrogen geocorona extends well beyond the Moon. J. Geophys. Res. Space Phys. 124(2), 861–885 (2019). https://doi.org/10.1029/2018JA026136
I.I. Baliukin, V.V. Izmodenov, D.B. Alexashov, Heliospheric energetic neutral atoms: non-stationary modelling and comparison with IBEX-Hi data. Mon. Not. R. Astron. Soc. 499(1), 441–454 (2020). https://doi.org/10.1093/mnras/staa2862. 2009.14062
I.I. Baliukin, V.V. Izmodenov, D.B. Alexashov, Energetic pickup proton population downstream of the termination shock as revealed by IBEX-Hi data. Mon. Not. R. Astron. Soc. 509(4), 5437–5453 (2022). https://doi.org/10.1093/mnras/stab3214. 2110.15930
V.B. Baranov, Y.G. Malama, Model of the solar wind interaction with the local interstellar medium numerical solution of self-consistent problem. J. Geophys. Res. 98(A9), 15157–15164 (1993). https://doi.org/10.1029/93JA01171
V.B. Baranov, K.V. Krasnobaev, A.G. Kulikovskii, A model of the interaction of the solar wind with the interstellar medium. Sov. Phys. Dokl. 15, 791 (1971)
V.B. Baranov, M.K. Ermakov, M.G. Lebedev, A three-component model of solar wind - interstellar medium interaction - some numerical results. Sov. Astron. Lett. 7, 206–209 (1981)
C.F. Barnett, H.T. Hunter, M.I. Fitzpatrick, I. Alvarez, C. Cisneros, R.A. Phaneuf, Atomic data for fusion. Volume 1: Collisions of H, H2, He and Li atoms and ions with atoms and molecules. NASA STI/Recon Technical Report N (1990)
W. Baumjohann, R.A. Treumann, Basic Space Plasma Physics (Imperial College Press, London, 1996). https://doi.org/10.1142/p015
P. Blum, H.J. Fahr, Interaction between interstellar hydrogen and the solar wind. Astron. Astrophys. 4, 280–290 (1970)
P. Bochsler, L. Petersen, E. Möbius, N.A. Schwadron, P. Wurz, J.A. Scheer, S.A. Fuselier, D.J. McComas, M. Bzowski, P.C. Frisch, Estimation of the neon/oxygen abundance ratio at the heliospheric termination shock and in the local interstellar medium from IBEX observations. Astrophys. J. Suppl. 198(2), 13 (2012). https://doi.org/10.1088/0067-0049/198/2/13
T.J. Bogdan, M.A. Lee, P. Schneider, Coupled quasi-linear wave damping and stochastic acceleration of pickup ions in the solar wind. J. Geophys. Res. 96(A1), 161–178 (1991). https://doi.org/10.1029/90JA02096
P.C. Brandt, R.L. McNutt, M.V. Paul, K.E. Mandt, C.M. Lisse, M. Zemcov, C.A. Beichman, E.A. Provornikova, K.D. Runyon, A.M. Rymer, Interstellar probe: a cross-divisional mission in to the galaxy, in The Space Astrophysics Landscape for the 2020s and Beyond, vol. 2135 (2019), p. 5053
B. Breech, W.H. Matthaeus, J. Minnie, J.W. Bieber, S. Oughton, C.W. Smith, P.A. Isenberg, Turbulence transport throughout the heliosphere. J. Geophys. Res. Space Phys. 113(A8), A08105 (2008). https://doi.org/10.1029/2007JA012711
L.F. Burlaga, N.F. Ness, Interstellar magnetic fields observed by Voyager 1 beyond the heliopause. Astrophys. J. Lett. 795(1), L19 (2014). https://doi.org/10.1088/2041-8205/795/1/L19
L.F. Burlaga, N.F. Ness, D.B. Berdichevsky, J. Park, L.K. Jian, A. Szabo, E.C. Stone, J.D. Richardson, Magnetic field and particle measurements made by Voyager 2 at and near the heliopause. Nat. Astron. 3, 1007–1012 (2019). https://doi.org/10.1038/s41550-019-0920-y
R.H. Burrows, G.P. Zank, G.M. Webb, L.F. Burlaga, N.F. Ness, Pickup ion dynamics at the heliospheric termination shock observed by Voyager 2. Astrophys. J. 715(2), 1109–1116 (2010). https://doi.org/10.1088/0004-637X/715/2/1109
A.M. Bykov, I.N. Toptygin, The theory of particle acceleration in astrophysical objects containing shock waves and turbulent plasma motions. J. Geophys./Z. Geophys. 50(3), 221–226 (1982)
A.M. Bykov, I. Toptygin, Reviews of topical problems: particle kinetics in highly turbulent plasmas (renormalization and self-consistent field methods). Phys. Usp. 36(11), 1020–1052 (1993). https://doi.org/10.1070/PU1993v036n11ABEH002179
M. Bzowski, Survival probability and energy modification of hydrogen energetic neutral atoms on their way from the termination shock to Earth orbit. Astron. Astrophys. 488(3), 057 (2008). https://doi.org/10.1051/0004-6361:200809393. 0801.2190
M. Bzowski, M.A. Kubiak, E. Möbius, P. Bochsler, T. Leonard, D. Heirtzler, H. Kucharek, J.M. Sokół, M. Hłond, G.B. Crew, N.A. Schwadron, S.A. Fuselier, D.J. McComas, Neutral interstellar helium parameters based on IBEX-Lo observations and test particle calculations. Astrophys. J. Suppl. 198(2), 12 (2012). https://doi.org/10.1088/0067-0049/198/2/12. 1202.0415
M. Bzowski, J.M. Sokół, M.A. Kubiak, H. Kucharek, Modulation of neutral interstellar He, Ne, O in the heliosphere. Survival probabilities and abundances at IBEX. Astron. Astrophys. 557, A50 (2013). https://doi.org/10.1051/0004-6361/201321700. 1306.4463
M. Bzowski, J.M. Sokół, M. Tokumaru, K. Fujiki, E. Quémerais, R. Lallement, S. Ferron, P. Bochsler, D.J. McComas, Solar Parameters for Modeling the Interplanetary Background. ISSI Scientific Report, vol. 13 (Springer, Berlin, 2013b), pp. 67–138. https://doi.org/10.1007/978-1-4614-6384-9_3
B.E. Cannon, C.W. Smith, P.A. Isenberg, B.J. Vasquez, C.J. Joyce, N. Murphy, R.G. Nuno, Preliminary analysis of magnetic waves due to newborn interstellar pickup ions, in Solar Wind 13. American Institute of Physics Conference Series, vol. 1539, ed. by G.P. Zank, J. Borovsky, R. Bruno, J. Cirtain, S. Cranmer, H. Elliott, J. Giacalone, W. Gonzalez, G. Li, E. Marsch, E. Moebius, N. Pogorelov, J. Spann, O. Verkhoglyadova (2013), pp. 334–337. https://doi.org/10.1063/1.4811055
B.E. Cannon, C.W. Smith, P.A. Isenberg, B.J. Vasquez, C.J. Joyce, N. Murphy, R.G. Nuno, Ulysses observations of magnetic waves due to newborn interstellar pickup ions. II. Application of turbulence concepts to limiting wave energy and observability. Astrophys. J. 787(2), 133 (2014a). https://doi.org/10.1088/0004-637X/787/2/133
B.E. Cannon, C.W. Smith, P.A. Isenberg, B.J. Vasquez, N. Murphy, R.G. Nuno, Ulysses observations of magnetic waves due to newborn interstellar pickup ions. I. New observations and linear analysis. Astrophys. J. 784(2), 150 (2014b). https://doi.org/10.1088/0004-637X/784/2/150
B.E. Cannon, C.W. Smith, P.A. Isenberg, B.J. Vasquez, C.J. Joyce, N. Murphy, R.G. Nuno, Listing of 502 times when the Ulysses magnetic fields instrument observed waves due to newborn interstellar pickup protons. Astrophys. J. 840(1), 13 (2017). https://doi.org/10.3847/1538-4357/aa6c2f
S.V. Chalov, Helium pickup ion focusing cone as an indicator of the interstellar flow direction. Mon. Not. R. Astron. Soc. 443, L25–L28 (2014). https://doi.org/10.1093/mnrasl/slu074
S.V. Chalov, H.J. Fahr, Reflection of pre-accelerated pick-up ions at the solar wind termination shock: the seed for anomalous cosmic rays. Sol. Phys. 168(2), 389–411 (1996). https://doi.org/10.1007/BF00148064
S.V. Chalov, H.J. Fahr, The role of solar wind electrons at the solar wind termination shock. Mon. Not. R. Astron. Soc. 433, L40–L43 (2013). https://doi.org/10.1093/mnrasl/slt052
S.V. Chalov, H.J. Fahr, V.V. Izmodenov, Evolution of pickup proton spectra in the inner heliosheath and their diagnostics by energetic neutral atom fluxes. J. Geophys. Res. Space Phys. 108(A6), 1266 (2003). https://doi.org/10.1029/2002JA009492
S.V. Chalov, V.V. Izmodenov, H.J. Fahr, Spatial variation of pickup proton energy spectra in the inner heliosheath and fluxes of energetic neutral atoms. Adv. Space Res. 34(1), 99–103 (2004). https://doi.org/10.1016/j.asr.2003.02.065
S.V. Chalov, D.B. Alexashov, H.J. Fahr, Interstellar pickup protons and solar wind heating in the outer heliosphere. Astron. Lett. 32(3), 206–213 (2006). https://doi.org/10.1134/S106377370603008X
S.V. Chalov, Y.G. Malama, D.B. Alexashov, V.V. Izmodenov, Acceleration of interstellar pickup protons at the heliospheric termination shock: Voyager 1/2 energetic proton fluxes in the inner heliosheath. Mon. Not. R. Astron. Soc. 455(1), 431–437 (2016). https://doi.org/10.1093/mnras/stv2323
R. Chhiber, P. Subedi, A.V. Usmanov, W.H. Matthaeus, D. Ruffolo, M.L. Goldstein, T.N. Parashar, Cosmic-ray diffusion coefficients throughout the inner heliosphere from a global solar wind simulation. Astrophys. J. Suppl. 230(2), 21 (2017). https://doi.org/10.3847/1538-4365/aa74d2
M.I. Desai, F.A. Allegrini, M.A. Dayeh, B. De Majistre, H. Funsten, J. Heerikhuisen, D.J. McComas, N. Pogorelov, N.A. Schwadron, G.P. Zank, Spectral properties of ∼0.5-6 keV energetic neutral atoms measured by the interstellar boundary explorer (IBEX) along the lines of sight of Voyager. Astrophys. J. Lett. 749, L30 (2012). https://doi.org/10.1088/2041-8205/749/2/L30
M.I. Desai, F.A. Allegrini, M. Bzowski, M.A. Dayeh, H. Funsten, S.A. Fuselier, J. Heerikhuisen, M.A. Kubiak, D.J. McComas, N.V. Pogorelov, N.A. Schwadron, J.M. Sokół, G.P. Zank, E.J. Zirnstein, Energetic neutral atoms measured by the interstellar boundary explorer (IBEX): evidence for multiple heliosheath populations. Astrophys. J. 780, 98 (2014). https://doi.org/10.1088/0004-637X/780/1/98
A.M. DeStefano, Ion-atom charge-exchange collisions and their effect on plasma-neutral coupling. PhD thesis, The University of Alabama in Huntsville (2019)
A.M. DeStefano, J. Heerikhuisen, Charge-exchange source terms in magnetohydrodynamic plasmas. J. Phys. Conf. Ser., 837, 012013 (2017). https://doi.org/10.1088/1742-6596/837/1/012013
J.F. Drake, M. Swisdak, M. Opher, A model of the heliosphere with jets. Astrophys. J. Lett. 808(2), L44 (2015). https://doi.org/10.1088/2041-8205/808/2/L44. 1505.01451
N.E. Engelbrecht, On the effects of pickup ion-driven waves on the diffusion tensor of low-energy electrons in the heliosphere. Astrophys. J. Lett. 849(1), L15 (2017). https://doi.org/10.3847/2041-8213/aa9372
N.E. Engelbrecht, R.A. Burger, An ab initio model for cosmic-ray modulation. Astrophys. J. 772(1), 46 (2013). https://doi.org/10.1088/0004-637X/772/1/46
H.J. Fahr, Charge-transfer interactions between solar wind protons and neutral particles in the vicinity of the Sun. Nature 219(5153), 473–474 (1968a). https://doi.org/10.1038/219473a0
H.J. Fahr, Neutral corpuscular energy flux by charge-transfer collisions in the vicinity of the Sun. Astrophys. Space Sci. 2(4), 496–503 (1968b). https://doi.org/10.1007/BF02175924
H.J. Fahr, The interplanetary hydrogen cone and its solar cycle variations. Astron. Astrophys. 14, 263 (1971)
H.J. Fahr, S.V. Chalov, Supersonic solar wind ion flows downstream of the termination shock explained by a two-fluid shock model. Astron. Astrophys. 490(3), L35–L38 (2008). https://doi.org/10.1051/0004-6361:200810679
H.J. Fahr, R. Dutta-Roy, Concerning pressure and entropy of shock-accelerated heliosheath electrons. Mon. Not. R. Astron. Soc. 484(3), 3537–3543 (2019). https://doi.org/10.1093/mnras/stz182
H.J. Fahr, M. Siewert, Anisotropic unstable ion distribution functions downstream of the solar wind termination shock. Astrophys. Space Sci. Trans. 3(1), 21–27 (2007). https://doi.org/10.5194/astra-3-21-2007
H.J. Fahr, M. Siewert, Isotropic ion distribution functions triggered by consecutive solar wind bulk velocity jumps: a new equilibrium state. Astron. Astrophys. 527, A125 (2011). https://doi.org/10.1051/0004-6361/201015619
H.J. Fahr, M. Siewert, Revisiting the role of magnetic moments in heliospheric plasmas. Astron. Astrophys. 552, A38 (2013a). https://doi.org/10.1051/0004-6361/201220965
H.J. Fahr, M. Siewert, The multi-fluid pressures downstream of the solar wind termination shock. Astron. Astrophys. 558, A41 (2013b). https://doi.org/10.1051/0004-6361/201322262
H.J. Fahr, D. Verscharen, Electrons under the dominant action of shock-electric fields. Astron. Astrophys. 587, L1 (2016). https://doi.org/10.1051/0004-6361/201527901
H.J. Fahr, D. Rucinski, H.U. Nass, Modelling of the interplanetary helium EUV-resonance glow for time-dependent solar radiation conditions. Ann. Geophys. 5, 255–263 (1987)
H.J. Fahr, H. Fichtner, H. Scherer, Extreme-ultraviolet diagnostics of pick-up ions in regions close to the solar corona. I. Feasibility of new observations. Astron. Astrophys. 335, 724–732 (1998)
H.J. Fahr, H. Fichtner, H. Scherer, Diagnostics of the solar corona using EUV radiation back-scattered by pick-up ions close to the Sun. Adv. Space Res. 25(9), 1969–1972 (2000a). https://doi.org/10.1016/S0273-1177(99)00612-2
H.J. Fahr, T. Kausch, H. Scherer, A 5-fluid hydrodynamic approach to model the solar system-interstellar medium interaction. Astron. Astrophys. 357, 268–282 (2000b)
H.J. Fahr, M. Siewert, I. Chashei, Phasespace transport of a quasi-neutral multi-fluid plasma over the solar wind MHD termination shock. Astrophys. Space Sci. 341(2), 265–276 (2012). https://doi.org/10.1007/s10509-012-1126-2
H.J. Fahr, J.D. Richardson, D. Verscharen, The electron distribution function downstream of the solar-wind termination shock: where are the hot electrons? Astron. Astrophys. 579, A18 (2015). https://doi.org/10.1051/0004-6361/201525710
H.J. Fahr, U. Nass, R. Dutta-Roy, J.H. Zoennchen, Neutralized solar wind ahead of the Earth’s magnetopause as contribution to non-thermal exospheric hydrogen. Ann. Geophys. 36(2), 445–457 (2018). https://doi.org/10.5194/angeo-36-445-2018
E. Fermi, On the origin of the cosmic radiation. Phys. Rev. 75(8), 1169–1174 (1949). https://doi.org/10.1103/PhysRev.75.1169
M.K. Fisher, M.R. Argall, C.J. Joyce, C.W. Smith, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, R.M. Skoug, J.M. Sokół, M. Bzowski, T.H. Zurbuchen, J.A. Gilbert, A survey of magnetic waves excited by newborn interstellar He+ observed by the ACE spacecraft at 1 au. Astrophys. J. 830(1), 47 (2016). https://doi.org/10.3847/0004-637X/830/1/47
L.A. Fisk, G. Gloeckler, The common spectrum for accelerated ions in the quiet-time solar wind. Astrophys. J. Lett. 640(1), L79–L82 (2006). https://doi.org/10.1086/503293
L.A. Fisk, G. Gloeckler, Thermodynamic constraints on stochastic acceleration in compressional turbulence. Proc. Natl. Acad. Sci. 104(14), 5749–5754 (2007). https://doi.org/10.1073/pnas.0700881104
L.A. Fisk, G. Gloeckler, Acceleration of suprathermal tails in the solar wind. Astrophys. J. 686(2), 1466–1473 (2008). https://doi.org/10.1086/591543
L.A. Fisk, G. Gloeckler, N.A. Schwadron, On theories for stochastic acceleration in the solar wind. Astrophys. J. 720(1), 533–540 (2010). https://doi.org/10.1088/0004-637X/720/1/533
V. Florinski, G.P. Zank, N.V. Pogorelov, Galactic cosmic ray transport in the global heliosphere. J. Geophys. Res. Space Phys. 108(A6), 1228 (2003). https://doi.org/10.1029/2002JA009695
V. Florinski, R.B. Decker J.A. Le Roux, Pitch angle distributions of energetic particles near the heliospheric termination shock. J. Geophys. Res. Space Phys. 113(A7), A07103 (2008). https://doi.org/10.1029/2007JA012859
F. Fraternale, N.V. Pogorelov, Waves and turbulence in the very local interstellar medium: from macroscales to microscales. Astrophys. J. 906(2), 75 (2021). https://doi.org/10.3847/1538-4357/abc88a
P.C. Frisch, J.D. Slavin, The chemical composition and gas-to-dust mass ratio of nearby interstellar matter. Astrophys. J. 594(2), 844–858 (2003). https://doi.org/10.1086/376689. astro-ph/0306590
S.A. Fuselier, H.O. Funsten, D. Heirtzler, P. Janzen, H. Kucharek, D.J. McComas, E. Möbius, T.E. Moore, S.M. Petrinec, D.B. Reisenfeld, N.A. Schwadron, K.J. Trattner, P. Wurz, Energetic neutral atoms from the Earth’s subsolar magnetopause. Geophys. Res. Lett. 37(13), L13101 (2010). https://doi.org/10.1029/2010GL044140
S.A. Fuselier, F. Allegrini, M. Bzowski, H.O. Funsten, A.G. Ghielmetti, G. Gloeckler, D. Heirtzler, P. Janzen, M. Kubiak, H. Kucharek, D.J. McComas, E. Möbius, T.E. Moore, S.M. Petrinec, M. Quinn, D. Reisenfeld, L.A. Saul, J.A. Scheer, N. Schwadron, K.J. Trattner, R. Vanderspek, P. Wurz, Heliospheric neutral atom spectra between 0.01 and 6 keV from IBEX. Astrophys. J. 754(1), 14 (2012). https://doi.org/10.1088/0004-637X/754/1/14
K.V. Gamayunov, M. Zhang, N.V. Pogorelov, J. Heerikhuisen, H.K. Rassoul, Self-consistent model of the interstellar pickup protons, Alfvénic turbulence, and core solar wind in the outer heliosphere. Astrophys. J. 757(1), 74 (2012). https://doi.org/10.1088/0004-637X/757/1/74
K. Gamayunov, M. Zhang, N. Pogorelov, J. Heerikhuisen, H. Rassoul, Alfvénic turbulence generated by the interstellar pickup protons in the outer heliosphere, in American Institute of Physics Conference Series, ed. by G.P. Zank, J. Borovsky, R. Bruno, J. Cirtain, S. Cranmer, H. Elliott, J. Giacalone, W. Gonzalez, G. Li, E. Marsch, E. Moebius, N. Pogorelov, J. Spann, O. Verkhoglyadova. Solar Wind 13, vol. 1539 (2013), pp. 171–174. https://doi.org/10.1063/1.4811015
K.V. Gamayunov, M.J. Engebretson, M. Zhang, H.K. Rassoul, Source of seed fluctuations for electromagnetic ion cyclotron waves in Earth’s magnetosphere. Adv. Space Res. 55(11), 2573–2583 (2015). https://doi.org/10.1016/j.asr.2015.02.024
M. Gedalin, N.V. Pogorelov, V. Roytershteyn, Rankine-Hugoniot relations including pickup ions. Astrophys. J. 889(2), 116 (2020). https://doi.org/10.3847/1538-4357/ab6660
M. Gedalin, N.V. Pogorelov, V. Roytershteyn, Backstreaming pickup ions. Astrophys. J. 910(2), 107 (2021a). https://doi.org/10.3847/1538-4357/abe62c
M. Gedalin, N.V. Pogorelov, V. Roytershteyn, Boundary conditions at the heliospheric termination shock with pickup ions. Astrophys. J. 916(1), 57 (2021b). https://doi.org/10.3847/1538-4357/ac05b7
J. Geiss, G. Gloeckler, U. Mall, R. von Steiger, A.B. Galvin, K.W. Ogilvie, Interstellar oxygen, nitrogen and neon in the heliosphere. Astron. Astrophys. 282, 924–933 (1994)
J. Geiss, G. Gloeckler, L.A. Fisk, R. von Steiger, C+ pickup ions in the heliosphere and their origin. J. Geophys. Res. 100, 23373–23378 (1995). https://doi.org/10.1029/95JA03051
J. Giacalone, The acceleration of inner-source pickup ions by a propagating interplanetary shock, in Pickup Ions Throughout the Heliosphere and Beyond, ed. by J. Le Roux, G.P. Zank, A.J. Coates, V. Florinski. American Institute of Physics Conference Series, vol. 1302 (2010), pp. 119–124. https://doi.org/10.1063/1.3529958
J. Giacalone, D. Burgess, S.J. Schwartz, D.C. Ellison, L. Bennett, Injection and acceleration of thermal protons at quasi-parallel shocks: a hybrid simulation parameter survey. J. Geophys. Res. 102(A9), 19789–19804 (1997). https://doi.org/10.1029/97JA01529
G. Gloeckler, L.A. Fisk, Johannes Geiss’ investigations of solar, heliospheric and interstellar matter. Space Sci. Rev. 130(1–4), 489–513 (2007). https://doi.org/10.1007/s11214-007-9226-y
G. Gloeckler, J. Geiss, Interstellar and inner source pickup ions observed with SWICS on ULYSSES. Space Sci. Rev. 86, 127–159 (1998). https://doi.org/10.1023/A:1005019628054
G. Gloeckler, J. Geiss, H. Balsiger, P. Bedini, J.C. Cain, J. Fischer, L.A. Fisk, A.B. Galvin, F. Gliem, D.C. Hamilton, J.V. Hollweg, F.M. Ipavich, R. Joos, S. Livi, R.A. Lundgren, U. Mall, J.F. McKenzie, K.W. Ogilvie, F. Ottens, W. Rieck, E.O. von Tums, R. Steiger, W. Weiss, B. Wilken, The solar wind ion composition spectrometer. Astron. Astrophys. Suppl. 92(2), 267–289 (1992)
G. Gloeckler, J. Geiss, E.C. Roelof, L.A. Fisk, F.M. Ipavich, K.W. Ogilvie, L.J. von Lanzerotti, R. Steiger, B. Wilken, Acceleration of interstellar pickup ions in the disturbed solar wind observed on Ulysses. J. Geophys. Res. 99(A9), 17637–17644 (1994). https://doi.org/10.1029/94JA01509
G. Gloeckler, N.A. Schwadron, L.A. Fisk, J. Geiss, Weak pitch angle scattering of few MV rigidity ions from measurements of anisotropies in the distribution function of interstellar pickup H+. Geophys. Res. Lett. 22(19), 2665–2668 (1995). https://doi.org/10.1029/95GL02480
G. Gloeckler, L.A. Fisk, J. Geiss, N.A. Schwadron, T.H. Zurbuchen, Elemental composition of the inner source pickup ions. J. Geophys. Res. 105, 7459–7464 (2000). https://doi.org/10.1029/1999JA000224
J.T. Gosling, V.J. Pizzo, Formation and evolution of corotating interaction regions and their three dimensional structure. Space Sci. Rev. 89, 21–52 (1999). https://doi.org/10.1023/A:1005291711900
J. Heerikhuisen, V. Florinski, G.P. Zank, Interaction between the solar wind and interstellar gas: a comparison between Monte Carlo and fluid approaches. J. Geophys. Res. Space Phys. 111(A6), A06110 (2006). https://doi.org/10.1029/2006JA011604
J. Heerikhuisen, N.V. Pogorelov, G.P. Zank, V. Florinski, The effects of global heliospheric asymmetries on energetic neutral atom sky maps. Astrophys. J. Lett. 655(1), L53–L56 (2007). https://doi.org/10.1086/511764
J. Heerikhuisen, E. Zirnstein, N. Pogorelov, \(\kappa \)-distributed protons in the solar wind and their charge-exchange coupling to energetic hydrogen. J. Geophys. Res. Space Phys. 120(3), 1516–1525 (2015). https://doi.org/10.1002/2014JA020636
J. Heerikhuisen, E.J. Zirnstein, N.V. Pogorelov, G.P. Zank, M. Desai, The effect of suprathermal protons in the heliosheath on the global structure of the heliosphere and heliotail. Astrophys. J. 874(1), 76 (2019). https://doi.org/10.3847/1538-4357/ab05e3
S.J. Hollick, C.W. Smith, Z.B. Pine, M.R. Argall, C.J. Joyce, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, J.M. Sokół, M. Bzowski, M.A. Kubiak, Magnetic waves excited by newborn interstellar pickup ions measured by the Voyager spacecraft from 1 to 45 au. I. Wave properties. Astrophys. J. 863(1), 75 (2018a). https://doi.org/10.3847/1538-4357/aac83b
S.J. Hollick, C.W. Smith, Z.B. Pine, M.R. Argall, C.J. Joyce, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, J.M. Sokół, M. Bzowski, M.A. Kubiak, Magnetic waves excited by newborn interstellar pickup ions measured by the Voyager spacecraft from 1 to 45 au. II. Instability and turbulence analyses. Astrophys. J. 863(1), 76 (2018b). https://doi.org/10.3847/1538-4357/aac839
S.J. Hollick, C.W. Smith, Z.B. Pine, M.R. Argall, C.J. Joyce, P.A. Isenberg, B.J. Vasquez, N.A. Schwadron, J.M. Sokół, M. Bzowski, M.A. Kubiak, Magnetic waves excited by newborn interstellar pickup ions measured by the Voyager spacecraft from 1 to 45 au. III. Observation times. Astrophys. J. Suppl. 237(2), 34 (2018c). https://doi.org/10.3847/1538-4365/aac83a
T.E. Holzer, Interaction of the solar wind with the neutral component of the interstellar gas. J. Geophys. Res. 77(28), 5407 (1972). https://doi.org/10.1029/JA077i028p05407
T.E. Holzer, E. Leer, Solar wind heating beyond 1 AU. Astrophys. Space Sci. 24(2), 335–347 (1973). https://doi.org/10.1007/BF02637160
P.A. Isenberg, Interaction of the solar wind with interstellar neutral hydrogen: three-fluid model. J. Geophys. Res. 91(A9), 9965–9972 (1986). https://doi.org/10.1029/JA091iA09p09965
P.A. Isenberg, Evolution of interstellar pickup ions in the solar wind. J. Geophys. Res. 92(A2), 1067–1074 (1987). https://doi.org/10.1029/JA092iA02p01067
P.A. Isenberg, P.P. Chih, L.A. Fisk, The heating of the solar wind by the interstellar neutral gas. J. Geophys. Res. 90(A12), 12040–12046 (1985). https://doi.org/10.1029/JA090iA12p12040
P.A. Isenberg, C.W. Smith, W.H. Matthaeus, J.D. Richardson, Turbulent heating of the distant solar wind by interstellar pickup protons in a decelerating flow. Astrophys. J. 719(1), 716–721 (2010). https://doi.org/10.1088/0004-637X/719/1/716
H. Ishimoto, Modeling the number density distribution of interplanetary dust on the ecliptic plane within 5 AU of the Sun. Astron. Astrophys. 362, 1158–1173 (2000)
V.V. Izmodenov, D.B. Alexashov, Three-dimensional kinetic-MHD model of the global heliosphere with the heliopause-surface fitting. Astrophys. J. Suppl. 220(2), 32 (2015). https://doi.org/10.1088/0067-0049/220/2/32. 1509.08685
V. Izmodenov, D. Alexashov, On the problem of two-tail heliosphere/astrospheres. J. Phys. Conf. Ser. 1031, 012014 (2018). https://doi.org/10.1088/1742-6596/1031/1/012014
V.V. Izmodenov, D.B. Alexashov, Magnitude and direction of the local interstellar magnetic field inferred from Voyager 1 and 2 interstellar data and global heliospheric model. Astron. Astrophys. 633, L12 (2020). https://doi.org/10.1051/0004-6361/201937058. 2001.03061
V. Izmodenov, Y.G. Malama, R. Lallement, Interstellar neutral oxygen in a two-shock heliosphere. Astron. Astrophys. 317, 193–202 (1997)
V.V. Izmodenov, Y.G. Malama, A.P. Kalinin, M. Gruntman, R. Lallement, I.P. Rodionova, Hot neutral H in the heliosphere: elastic H-H, H-p collisions. Astrophys. Space Sci. 274, 71–76 (2000). https://doi.org/10.1023/A:1026531519864
V. Izmodenov, D. Alexashov, A. Myasnikov, Direction of the interstellar H atom inflow in the heliosphere: role of the interstellar magnetic field. Astron. Astrophys. 437(3), L35–L38 (2005). https://doi.org/10.1051/0004-6361:200500132
V.V. Izmodenov, Y.G. Malama, M.S. Ruderman, S.V. Chalov, D.B. Alexashov, O.A. Katushkina, E.A. Provornikova, Kinetic-gasdynamic modeling of the heliospheric interface. Space Sci. Rev. 146(1–4), 329–351 (2009). https://doi.org/10.1007/s11214-009-9528-3
S. Jaeger, H.J. Fahr, The heliospheric plasma tail under the influence of charge exchange processes with interstellar H-atoms. Sol. Phys. 178(1), 193–219 (1998). https://doi.org/10.1023/A:1004953013428
J.R. Jokipii, M.A. Lee, Compression acceleration in astrophysical plasmas and the production of f(v) vprop v −5 spectra in the heliosphere. Astrophys. J. 713(1), 475–483 (2010). https://doi.org/10.1088/0004-637X/713/1/475
C.J. Joyce, C.W. Smith, P.A. Isenberg, N. Murphy, N.A. Schwadron, Excitation of low-frequency waves in the solar wind by newborn interstellar pickup ions H+ and He+ as seen by Voyager at 4.5 AU. Astrophys. J. 724(2), 1256–1261 (2010). https://doi.org/10.1088/0004-637X/724/2/1256
C.J. Joyce, C.W. Smith, P.A. Isenberg, S.P. Gary, N. Murphy, P.C. Gray, L.F. Burlaga, Observation of Bernstein waves excited by newborn interstellar pickup ions in the solar wind. Astrophys. J. 745(2), 112 (2012). https://doi.org/10.1088/0004-637X/745/2/112
A.M. Juett, N.S. Schulz, D. Chakrabarty, T.W. Gorczyca, High-resolution X-ray spectroscopy of the interstellar medium. II. Neon and iron absorption edges. Astrophys. J. 648(2), 1066–1078 (2006). https://doi.org/10.1086/506189. astro-ph/0605674
O.A. Katushkina, V.V. Izmodenov, D.B. Alexashov, N.A. Schwadron, D.J. McComas, Interstellar hydrogen fluxes measured by IBEX-Lo in 2009: numerical modeling and comparison with the data. Astrophys. J. Suppl. 220(2), 33 (2015). https://doi.org/10.1088/0067-0049/220/2/33. 1509.08754
O.A. Katushkina, I.I. Baliukin, V.V. Izmodenov, D.B. Alexashov, Imprints of the secondary interstellar hydrogen atoms at 1 AU. Mon. Not. R. Astron. Soc. 504(2), 2501–2508 (2021a). https://doi.org/10.1093/mnras/stab944
O.A. Katushkina, A. Galli, V.V. Izmodenov, D.B. Alexashov, Analysis of the IBEX-Lo interstellar hydrogen fluxes collected in 2009-2018 as a tool for sensing of the solar radiation pressure and the hydrogen ionization rate. Mon. Not. R. Astron. Soc. 501(2), 1633–1643 (2021b). https://doi.org/10.1093/mnras/staa3780
I.K. Khabibrakhmanov, D. Summers, G.P. Zank, H.L. Pauls, Solar wind flow with hydrogen pickup. Astrophys. J. 469, 921 (1996). https://doi.org/10.1086/177839
T. Kim, I. Kryukov, N. Pogorelov, H. Elliott, G.P. Zank, A data-driven model of the solar wind, interstellar pickup ions, and turbulence throughout interplanetary space (Earth and Space Science Open Archive, 2018), p. 1. https://doi.org/10.1002/essoar.b60497724eca58de.7C985d5380f54d2b.1. https://www.essoar.org/doi/abs/10.1002/essoar.b60497724eca58de.7C985d5380f54d2b.1
M. Kornbleuth, M. Opher, A.T. Michael, J.F. Drake, Globally distributed energetic neutral atom maps for the “Croissant” heliosphere. Astrophys. J. 865(2), 84 (2018). https://doi.org/10.3847/1538-4357/aadbac. 1808.05997
M. Kornbleuth, M. Opher, A.T. Michael, J.M. Sokół, G. Tóth, V. Tenishev, J.F. Drake, The confinement of the heliosheath plasma by the solar magnetic field as revealed by energetic neutral atom simulations. Astrophys. J. Lett. 895(2), L26 (2020). https://doi.org/10.3847/2041-8213/ab922b. 2005.06643
M. Kornbleuth, M. Opher, I. Baliukin, M.A. Dayeh, E. Zirnstein, M. Gkioulidou, K. Dialynas, A. Galli, J.D. Richardson, V. Izmodenov, G.P. Zank, S. Fuselier, Signature of a heliotail organized by the solar magnetic field and the role of nonideal processes in modeled IBEX ENA maps: a comparison of the BU and Moscow MHD models. Astrophys. J. 921(2), 164 (2021a). https://doi.org/10.3847/1538-4357/ac1e2a
M. Kornbleuth, M. Opher, I. Baliukin, M. Gkioulidou, J.D. Richardson, G.P. Zank, A.T. Michael, G. Tóth, V. Tenishev, V. Izmodenov, D. Alexashov, S. Fuselier, J.F. Drake, K. Dialynas, The development of a split-tail heliosphere and the role of non-ideal processes: a comparison of the BU and Moscow models. Astrophys. J. 923(2), 179 (2021b). https://doi.org/10.3847/1538-4357/ac2fa6
I. Kowalska-Leszczynska, M. Bzowski, J.M. Sokół, M.A. Kubiak, Evolution of the solar Ly\(\alpha \) line profile during the solar cycle. Astrophys. J. 852(2), 115 (2018). https://doi.org/10.3847/1538-4357/aa9f2a
I. Kowalska-Leszczynska, M.A. Kubiak, M. Bzowski, Absorption of the Ly\(\alpha \) radiation in the heliosphere. Astrophys. J. 926(1), 27 (2022). https://doi.org/10.3847/1538-4357/ac4092. 2111.15412
M.A. Kubiak, M. Bzowski, J.M. Sokół, P. Swaczyna, S. Grzedzielski, D.B. Alexashov, V.V. Izmodenov, E. Möbius, T. Leonard, S.A. Fuselier, P. Wurz, D.J. McComas, Warm breeze from the starboard bow: a new population of neutral helium in the heliosphere. Astrophys. J. Suppl. 213(2), 29 (2014). https://doi.org/10.1088/0067-0049/213/2/29. 1405.7742
M.A. Kubiak, P. Swaczyna, M. Bzowski, J.M. Sokół, S.A. Fuselier, A. Galli, D. Heirtzler, H. Kucharek, T.W. Leonard, D.J. McComas, E. Möbius, J. Park, N.A. Schwadron, P. Wurz, Interstellar neutral helium in the heliosphere from IBEX observations. IV. Flow vector, Mach number, and abundance of the warm breeze. Astrophys. J. Suppl. 223(2), 25 (2016). https://doi.org/10.3847/0067-0049/223/2/25. 1603.01741
M.A. Kubiak, M. Bzowski, J.M. Sokół, Distribution function of neutral helium outside and inside the heliopause. Astrophys. J. 882(2), 114 (2019). https://doi.org/10.3847/1538-4357/ab3404
R. Lallement, E.Q.J.L. Bertaux, D. Koutroumpa, R. Pellinen, Deflection of the interstellar neutral hydrogen flow across the heliospheric interface: an interstellar magnetic compass? in Solar Wind 11/SOHO 16, Connecting Sun and Heliosphere, ed. by B. Fleck, T.H. Zurbuchen, H. Lacoste. ESA Special Publication, vol. 592 (2005), p. 47
R. Lallement, E. Quémerais, P. Lamy, J.L. Bertaux, S. Ferron, W. Schmidt, The solar wind as seen by SOHO/SWAN since 1996: comparison with SOHO/LASCO C2 coronal densities, in SOHO-23: Understanding a Peculiar Solar Minimum, ed. by S.R. Cranmer, J.T. Hoeksema, J.L. Kohl. Astronomical Society of the Pacific Conference Series, vol. 428 (2010), p. 253. 1003.4243
J.A. Le Roux, V.S. Ptuskin, Self-consistent stochastic preacceleration of interstellar pickup ions in the solar wind including the effects of wave coupling and damping. J. Geophys. Res. 103(A3), 4799–4808 (1998). https://doi.org/10.1029/97JA03177
J.A.le Roux, G.M. Webb, Time-dependent acceleration of interstellar pickup ions at the heliospheric termination shock using a focused transport approach. Astrophys. J. 693(1), 534–551 (2009). https://doi.org/10.1088/0004-637X/693/1/534
J.A. le Roux, G.M. Webb, V. Florinski, G.P. Zank, A focused transport approach to pickup ion shock acceleration: implications for the termination shock. Astrophys. J. 662(1), 350–371 (2007). https://doi.org/10.1086/517601
M.A. Lee, W.H. Ip, Hydromagnetic wave excitation by ionized interstellar hydrogen and helium in the solar wind. J. Geophys. Res. 92(A10), 11041–11052 (1987). https://doi.org/10.1029/JA092iA10p11041
B. Lembège, Z. Yang, Physical roles of interstellar-origin pickup ions at heliospheric termination shock. II. Impact of the front nonstationary on the energy partition and particle velocity distribution. Astrophys. J. 860, 84 (2018). https://doi.org/10.3847/1538-4357/aabe85
B.G. Lindsay, R.F. Stebbings, Charge transfer cross sections for energetic neutral atom data analysis. J. Geophys. Res. Space Phys. 110(A12), A12213 (2005). https://doi.org/10.1029/2005JA011298
M. Lockwood, M.J. Owens, L. Barnard, C.J. Davis, F. Steinhilber, The persistence of solar activity indicators and the descent of the Sun into Maunder minimum conditions. Geophys. Res. Lett. 38(22), L22105 (2011). https://doi.org/10.1029/2011GL049811
A. Lyngvi, P. Falkner, A. Peacock, The interstellar heliopause probe technology reference study. Adv. Space Res. 35(12), 2073–2077 (2005). https://doi.org/10.1016/j.asr.2005.07.083
Y.G. Malama, V.V. Izmodenov, S.V. Chalov, Modeling of the heliospheric interface: multi-component nature of the heliospheric plasma. Astron. Astrophys. 445(2), 693–701 (2006). https://doi.org/10.1051/0004-6361:20053646. astro-ph/0509329
I. Mann, E. Murad, A. Czechowski, Nanoparticles in the inner solar system. Planet. Space Sci. 55, 1000–1009 (2007). https://doi.org/10.1016/j.pss.2006.11.015
W.H. Matthaeus, G.P. Zank, C.W. Smith, S. Oughton, Turbulence, spatial transport, and heating of the solar wind. Phys. Rev. Lett. 82(17), 3444–3447 (1999). https://doi.org/10.1103/PhysRevLett.82.3444
D.J. McComas, B.L. Barraclough, H.O. Funsten, J.T. Gosling, E. Santiago-Muñoz, R.M. Skoug, B.E. Goldstein, M. Neugebauer, P. Riley, A. Balogh, Solar wind observations over Ulysses’ first full polar orbit. J. Geophys. Res. 105(A5), 10419–10434 (2000). https://doi.org/10.1029/1999JA000383
D. McComas, F. Allegrini, F. Bagenal, P. Casey, P. Delamere, D. Demkee, G. Dunn, H. Elliott, J. Hanley, K. Johnson, J. Langle, G. Miller, S. Pope, M. Reno, B. Rodriguez, N. Schwadron, P. Valek, S. Weidner, The Solar Wind Around Pluto (SWAP) instrument aboard New Horizons. Space Sci. Rev. 140(1–4), 261–313 (2008a). https://doi.org/10.1007/s11214-007-9205-3
D.J. McComas, R.W. Ebert, H.A. Elliott, B.E. Goldstein, J.T. Gosling, N.A. Schwadron, R.M. Skoug, Weaker solar wind from the polar coronal holes and the whole Sun. Geophys. Res. Lett. 35(18), L18103 (2008b). https://doi.org/10.1029/2008GL034896
D.J. McComas, F. Allegrini, P. Bochsler, M. Bzowski, E.R. Christian, G.B. Crew, R. DeMajistre, H. Fahr, H. Fichtner, P.C. Frisch, H.O. Funsten, S.A. Fuselier, G. Gloeckler, M. Gruntman, J. Heerikhuisen, V. Izmodenov, P. Janzen, P. Knappenberger, S. Krimigis, H. Kucharek, M. Lee, G. Livadiotis, S. Livi, R.J. MacDowall, D. Mitchell, E. Möbius, T. Moore, N.V. Pogorelov, D. Reisenfeld, E. Roelof, L. Saul, N.A. Schwadron, P.W. Valek, R. Vanderspek, P. Wurz, G.P. Zank, Global observations of the interstellar interaction from the Interstellar Boundary Explorer (IBEX). Science 326(5955), 959 (2009). https://doi.org/10.1126/science.1180906
D.J. McComas, M.A. Dayeh, H.O. Funsten, G. Livadiotis, N.A. Schwadron, The heliotail revealed by the interstellar boundary explorer. Astrophys. J. l771(2), 77 (2013). https://doi.org/10.1088/0004-637X/771/2/77
D.J. McComas, F. Allegrini, M. Bzowski, M.A. Dayeh, R. DeMajistre, H.O. Funsten, S.A. Fuselier, M. Gruntman, P.H. Janzen, M.A. Kubiak, H. Kucharek, E. Möbius, D.B. Reisenfeld, N.A. Schwadron, J.M. Sokół, M. Tokumaru, IBEX: the first five years (2009-2013). Astrophys. J. Suppl. 213, 20 (2014). https://doi.org/10.1088/0067-0049/213/2/20
D.J. McComas, E.J. Zirnstein, M. Bzowski, H.A. Elliott, B. Randol, N.A. Schwadron, J.M. Sokół, J.R. Szalay, C. Olkin, J. Spencer, A. Stern, H. Weaver, Interstellar pickup ion observations to 38 au. Astrophys. J. Suppl. 233(1), 8 (2017). https://doi.org/10.3847/1538-4365/aa91d2. 1710.05194
D.J. McComas, E.R. Christian, N.A. Schwadron, N. Fox, J. Westlake, F. Allegrini, D.N. Baker, D. Biesecker, M. Bzowski, G. Clark, C.M.S. Cohen, I. Cohen, M.A. Dayeh, R. Decker, G.A. de Nolfo, M.I. Desai, R.W. Ebert, H.A. Elliott, H. Fahr, P.C. Frisch, H.O. Funsten, S.A. Fuselier, A. Galli, A.B. Galvin, J. Giacalone, M. Gkioulidou, F. Guo, M. Horanyi, P. Isenberg, P. Janzen, L.M. Kistler, K. Korreck, M.A. Kubiak, H. Kucharek, B.A. Larsen, R.A. Leske, N. Lugaz, J. Luhmann, W. Matthaeus, D. Mitchell, E. Moebius, K. Ogasawara, D.B. Reisenfeld, J.D. Richardson, C.T. Russell, M.J. Sokół, H.E. Spence, R. Skoug, Z. Sternovsky, P. Swaczyna, J.R. Szalay, M. Tokumaru, M.E. Wiedenbeck, P. Wurz, G.P. Zank, E.J. Zirnstein, Interstellar Mapping and Acceleration Probe (IMAP): a new NASA mission. Space Sci. Rev. 214(8), 116 (2018). https://doi.org/10.1007/s11214-018-0550-1
D.J. McComas, P. Swaczyna, J.R. Szalay, E.J. Zirnstein, J.S. Rankin, H.A. Elliott, K. Singer, J. Spencer, S.A. Stern, H. Weaver, Interstellar pickup ion observations halfway to the termination shock. Astrophys. J. Suppl. 254(1), 19 (2021). https://doi.org/10.3847/1538-4365/abee76
R.L. McNutt, R.F. Wimmer-Schweingruber, M. Gruntman, S.M. Krimigis, E.C. Roelof, P.C. Brandt, S.R. Vernon, M.V. Paul, B.W. Lathrop, D.S. Mehoke, D.H. Napolillo, R.W. Stough, Near-term interstellar probe: first step. Acta Astronaut. 162, 284–299 (2019). https://doi.org/10.1016/j.actaastro.2019.06.013
E. Möbius, M. Bzowski, S. Chalov, H.J. Fahr, G. Gloeckler, V. Izmodenov, R. Kallenbach, R. Lallement, D. McMullin, H. Noda, M. Oka, A. Pauluhn, J. Raymond, D. Ruciński, R. Skoug, T. Terasawa, W. Thompson, J. Vallerga, R. von Steiger, M. Witte, Synopsis of the interstellar He parameters from combined neutral gas, pickup ion and UV scattering observations and related consequences. Astron. Astrophys. 426, 897–907 (2004). https://doi.org/10.1051/0004-6361:20035834
E. Möbius, P. Bochsler, M. Bzowski, G.B. Crew, H.O. Funsten, S.A. Fuselier, A. Ghielmetti, D. Heirtzler, V.V. Izmodenov, M. Kubiak, H. Kucharek, M.A. Lee, T. Leonard, D.J. McComas, L. Petersen, L. Saul, J.A. Scheer, N. Schwadron, M. Witte, P. Wurz, Direct observations of interstellar H, He, and O by the interstellar boundary explorer. Science 326(5955), 969 (2009). https://doi.org/10.1126/science.1180971
P. Mostafavi, G.P. Zank, G.M. Webb, Shock wave structure in the presence of energetic particles. J. Phys. Conf. Ser. 900(1), 012016 (2017a). http://stacks.iop.org/1742-6596/900/i=1/a=012016
P. Mostafavi, G.P. Zank, G.M. Webb, Structure of energetic particle mediated shocks revisited. Astrophys. J. 841, 4 (2017b). https://doi.org/10.3847/1538-4357/aa6f10
P. Mostafavi, G.P. Zank, G.M. Webb, The mediation of collisionless oblique magnetized shocks by energetic particles. Astrophys. J. 868(2), 120 (2018). http://stacks.iop.org/0004-637X/868/i=2/a=120
P. Mostafavi, G.P. Zank, E.J. Zirnstein, D.J. McComas, Inner heliosheath shocks and their effect on energetic neutral atom observations by IBEX. Astrophys. J. 878(1), L24 (2019). https://doi.org/10.3847/2041-8213/ab25f4
H.R. Müller, G.P. Zank, Heliospheric filtration of interstellar heavy atoms: sensitivity to hydrogen background. J. Geophys. Res. Space Phys. 109(A7), A07104 (2004). https://doi.org/10.1029/2003JA010269
N. Murphy, E.J. Smith, B.T. Tsurutani, A. Balogh, D.J. Southwood, Further studies of waves accompanying the solar wind pick-up of interstellar hydrogen. Space Sci. Rev. 72(1–2), 447–452 (1995). https://doi.org/10.1007/BF00768819
M. Oka, G.P. Zank, R.H. Burrows, I. Shinohara, Energy dissipation at the termination shock: 1D PIC simulation, in American Institute of Physics Conference Series, ed. by V. Florinski, J. Heerikhuisen, G.P. Zank, D.L. Gallagher. American Institute of Physics Conference Series, vol. 1366 (2011), pp. 53–59. https://doi.org/10.1063/1.3625589
M. Opher, E.C. Stone, P.C. Liewer, The effects of a local interstellar magnetic field on Voyager 1 and 2 observations. Astrophys. J. Lett. 640(1), L71–L74 (2006). https://doi.org/10.1086/503251
M. Opher, J.F. Drake, B. Zieger, T.I. Gombosi, Magnetized jets driven by the Sun: the structure of the heliosphere revisited. Astrophys. J. Lett. 800(2), L28 (2015). https://doi.org/10.1088/2041-8205/800/2/L28. 1412.7687
M. Opher, J.F. Drake, M. Swisdak, B. Zieger, G. Toth, The twist of the draped interstellar magnetic field ahead of the heliopause: a magnetic reconnection driven rotational discontinuity. Astrophys. J. Lett. 839(1), L12 (2017). https://doi.org/10.3847/2041-8213/aa692f. 1702.06178
M. Opher, A. Loeb, J. Drake, G. Toth, A small and round heliosphere suggested by magnetohydrodynamic modelling of pick-up ions. Nat. Astron. 4, 675–683 (2020). https://doi.org/10.1038/s41550-020-1036-0
M. Opher, J.F. Drake, G. Zank, E. Powell, W. Shelley, M. Kornbleuth, V. Florinski, V. Izmodenov, J. Giacalone, S. Fuselier, K. Dialynas, A. Loeb, J. Richardson, A turbulent heliosheath driven by the Rayleigh-Taylor instability. Astrophys. J. 922(2), 181 (2021). https://doi.org/10.3847/1538-4357/ac2d2e
S. Oughton, W.H. Matthaeus, C.W. Smith, B. Breech, P.A. Isenberg, Transport of solar wind fluctuations: a two-component model. J. Geophys. Res. Space Phys. 116(A8), A08105 (2011). https://doi.org/10.1029/2010JA016365
F. Paresce, H. Fahr, G. Lay, A search for interplanetary He ii, 304-A emission. J. Geophys. Res. 86(A12), 10038–10049 (1981). https://doi.org/10.1029/JA086iA12p10038
J. Park, H. Kucharek, E. Möbius, T. Leonard, M. Bzowski, J.M. Sokół, M.A. Kubiak, S.A. Fuselier, D.J. McComas, The Ne-to-O abundance ratio of the interstellar medium from IBEX-Lo observations. Astrophys. J. 795(1), 97 (2014). https://doi.org/10.1088/0004-637X/795/1/97
J. Park, H. Kucharek, E. Möbius, A. Galli, G. Livadiotis, S.A. Fuselier, D.J. McComas, Statistical analysis of the heavy neutral atoms measured by IBEX. Astrophys. J. Suppl. 220(2), 34 (2015). https://doi.org/10.1088/0067-0049/220/2/34
J. Park, H. Kucharek, N. Paschalidis, A. Szabo, D. Heirtzler, E. Möbius, N.A. Schwadron, S.A. Fuselier, D.J. McComas, The characterization of secondary interstellar neutral oxygen beyond the heliopause: a detailed analysis of the IBEX-Lo oxygen observations. Astrophys. J. 880(1), 4 (2019). https://doi.org/10.3847/1538-4357/ab264a
E.N. Parker, The stellar-wind regions. Astrophys. J. 134, 20 (1961). https://doi.org/10.1086/147124
H.L. Pauls, G.P. Zank, L.L. Williams, Interaction of the solar wind with the local interstellar medium. J. Geophys. Res. 100(A11), 21595–21604 (1995). https://doi.org/10.1029/95JA02023
T.D. Phan, J.T. Gosling, G. Paschmann, C. Pasma, J.F. Drake, M. Øieroset, D. Larson, R.P. Lin, M.S. Davis, The dependence of magnetic reconnection on plasma \(\beta \) and magnetic shear: evidence from solar wind observations. Astrophys. J. Lett. 719(2), L199–L203 (2010). https://doi.org/10.1088/2041-8205/719/2/L199
T.D. Phan, G. Paschmann, J.T. Gosling, M. Oieroset, M. Fujimoto, J.F. Drake, V. Angelopoulos, The dependence of magnetic reconnection on plasma \(\beta \) and magnetic shear: evidence from magnetopause observations. Geophys. Res. Lett. 40(1), 11–16 (2013). https://doi.org/10.1029/2012GL054528
V. Pizzo, A three-dimensional model of corotating streams in the solar wind. I - Theoretical foundations. J. Geophys. Res. 83, 5563–5572 (1978). https://doi.org/10.1029/JA083iA12p05563
N.V. Pogorelov, G.P. Zank, T. Ogino, Three-dimensional features of the outer heliosphere due to coupling between the interstellar and interplanetary magnetic fields. II. The presence of neutral hydrogen atoms. Astrophys. J. 644(2), 1299–1316 (2006). https://doi.org/10.1086/503703
N.V. Pogorelov, G.P. Zank, S.N. Borovikov, V. Florinski, J. Heerikhuisen, I.A. Kryukov, MHD-neutral model of the outer heliosphere, in Numerical Modeling of Space Plasma Flows, ed. by N.V. Pogorelov, E. Audit, G.P. Zank. Astronomical Society of the Pacific Conference Series, vol. 385 (2008), p. 180
N.V. Pogorelov, S.N. Borovikov, J. Heerikhuisen, M. Zhang, The heliotail. Astrophys. J. Lett. 812(1), L6 (2015). https://doi.org/10.1088/2041-8205/812/1/L6
N.V. Pogorelov, M.C. Bedford, I.A. Kryukov, G.P. Zank, Pickup ion effect of the solar wind interaction with the local interstellar medium. J. Phys. Conf. Ser. 767, 012020 (2016). https://doi.org/10.1088/1742-6596/767/1/012020
E. Provornikova, M. Opher, V. Izmodenov, G. Toth, Do corotating interaction region associated shocks survive when they propagate into the heliosheath? Astrophys. J. Lett. 756(2), L37 (2012). http://stacks.iop.org/2041-8205/756/i=2/a=L37
V.S. Ptuskin, The acceleration of cosmic rays by long-wave turbulence. Pisma Astron. Zh. 14, 599–605 (1988)
P. Quinn, N. Schwadron, E. Möbius, A. Taut, L. Berger, Inner source c + /o + pickup ions produced by solar wind recycling, neutralization, backscattering, sputtering, and sputtering-induced recycling. Astrophys. J. 861, 98 (2018). https://doi.org/10.3847/1538-4357/aac6ca
P. Quinn, N. Schwadron, E. Möbius, Inner source pickup ions from chondritic smooth interplanetary dust particles. Astrophys. J. 877, 156 (2019). https://doi.org/10.3847/1538-4357/ab1486
F. Rahmanifard, E. Möbius, N.A. Schwadron, A. Galli, N. Richards, H. Kucharek, J.M. Sokół, D. Heirtzler, M.A. Lee, M. Bzowski, I. Kowalska-Leszczynska, M.A. Kubiak, P. Wurz, S.A. Fuselier, D.J. McComas, Radiation pressure from interstellar hydrogen observed by IBEX through solar cycle 24. Astrophys. J. 887(2), 217 (2019). https://doi.org/10.3847/1538-4357/ab58ce
J.D. Richardson, E.C. Stone, The solar wind in the outer heliosphere. Space Sci. Rev. 143(1–4), 7–20 (2009). https://doi.org/10.1007/s11214-008-9443-z
J.D. Richardson, C. Wang, L.F. Burlaga, The solar wind in the outer heliosphere. Adv. Space Res. 34(1), 150–156 (2004). https://doi.org/10.1016/j.asr.2003.03.066
J.D. Richardson, J.C. Kasper, C. Wang, J.W. Belcher, A.J. Lazarus, Cool heliosheath plasma and deceleration of the upstream solar wind at the termination shock. Nature 454(7200), 63–66 (2008). https://doi.org/10.1038/nature07024
D. Ruciński, Model rozkładu galaktycznego gazu neutralnego w heliosferze. PhD thesis, Centrum Badań Kosmicznych PAN (1985)
D. Rucinski, M. Bzowski, Modulation of interplanetary hydrogen density distribution during the solar cycle. Astron. Astrophys. 296, 248 (1995)
D. Ruciński, H.J. Fahr, The influence of electron impact ionization on the distribution of interstellar helium in the inner heliosphere: possible consequences for determination of interstellar helium parameters. Astron. Astrophys. 224, 290–298 (1989)
D. Rucinski, M. Bzowski, H.J. Fahr, Imprints from the solar cycle on the helium atom and helium pickup ion distributions. Ann. Geophys. 21(6), 1315–1330 (2003). https://doi.org/10.5194/angeo-21-1315-2003
K. Scherer, H. Fichtner, M. Lazar, Regularized \(\kappa \)-distributions with non-diverging moments. Europhys. Lett. 120(5), 50002 (2017). https://doi.org/10.1209/0295-5075/120/50002
K. Scherer, H. Fichtner, H.J. Fahr, M. Lazar, On the applicability of \(\kappa \)-distributions. Astrophys. J. 881(2), 93 (2019). https://doi.org/10.3847/1538-4357/ab2df9
N.A. Schwadron, G. Gloeckler, Pickup ions and cosmic rays from dust in the heliosphere. Space Sci. Rev. 130, 283–291 (2007). https://doi.org/10.1007/s11214-007-9166-6
N.A. Schwadron, L.A. Fisk, G. Gloeckler, Statistical acceleration of interstellar pick-up ions in co-rotating interaction regions. Geophys. Res. Lett. 23(21), 2871–2874 (1996). https://doi.org/10.1029/96GL02833
N.A. Schwadron, G. Gloeckler, L.A. Fisk, J. Geiss, T.H. Zurbuchen, The inner source for pickup ions, in American Institute of Physics Conference Series, ed. by S.R. Habbal, R. Esser, J.V. Hollweg, P.A. Isenberg. American Institute of Physics Conference Series, vol. 471 (1999), pp. 487–490. https://doi.org/10.1063/1.58680
N.A. Schwadron, E. Moebius, H. Kucharek, M.A. Lee, J. French, L. Saul, P. Wurz, M. Bzowski, S.A. Fuselier, G. Livadiotis, D.J. McComas, P. Frisch, M. Gruntman, H.R. Mueller, Solar radiation pressure and local interstellar medium flow parameters from interstellar boundary explorer low energy hydrogen measurements. Astrophys. J. 775(2), 86 (2013). https://doi.org/10.1088/0004-637X/775/2/86
N.A. Schwadron, E. Moebius, S.A. Fuselier, D.J. McComas, H.O. Funsten, P. Janzen, D. Reisenfeld, H. Kucharek, M.A. Lee, K. Fairchild, F. Allegrini, M. Dayeh, G. Livadiotis, M. Reno, M. Bzowski, J.M. Sokół, M.A. Kubiak, E.R. Christian, R. DeMajistre, P. Frisch, A. Galli, P. Wurz, M. Gruntman, Separation of the ribbon from globally distributed energetic neutral atom flux using the first five years of IBEX observations. Astrophys. J. Suppl. 215(1), 13 (2014). https://doi.org/10.1088/0067-0049/215/1/13
S.J. Schwartz, M.F. Thomsen, S.J. Bame, J. Stansberry, Electron heating and the potential jump across fast mode shocks. J. Geophys. Res. 93, 12923–12931 (1988). https://doi.org/10.1029/JA093iA11p12923
D. Shiota, G.P. Zank, L. Adhikari, P. Hunana, D. Telloni, R. Bruno, Turbulent transport in a three-dimensional solar wind. Astrophys. J. 837(1), 75 (2017). https://doi.org/10.3847/1538-4357/aa60bc
C.W. Smith, W.H. Matthaeus, G.P. Zank, N.F. Ness, S. Oughton, J.D. Richardson, Heating of the low-latitude solar wind by dissipation of turbulent magnetic fluctuations. J. Geophys. Res. 106(A5), 8253–8272 (2001). https://doi.org/10.1029/2000JA000366
C.W. Smith, P. Aggarwal, M.R. Argall, L.F. Burlaga, M. Bzowski, B.E. Cannon, S.P. Gary, M.K. Fisher, J.A. Gilbert, S.J. Hollick, P.A. Isenberg, C.J. Joyce, N. Murphy, R.G. Nuno, Z.B. Pine, J.D. Richardson, N.A. Schwadron, R.M. Skoug, J.M. Sokół, D.K. Taylor, B.J. Vasquez, Observations of low-frequency magnetic waves due to newborn interstellar pickup ions using ACE, Ulysses, and Voyager data. J. Phys. Conf. Ser. 900, 012018 (2017). https://doi.org/10.1088/1742-6596/900/1/012018
J.M. Sokół, Modulation of selected species of neutral interstellar gas and their derivative populations in the heliosphere due to solar activity cycle effects. PhD thesis, Space Research Centre Polish Academy of Sciences (CBK PAN), Warsaw, Poland (2016)
J.M. Sokół, M. Bzowski, M. Tokumaru, K. Fujiki, D.J. McComas, Heliolatitude and time variations of solar wind structure from in situ measurements and interplanetary scintillation observations. Sol. Phys. 285(1–2), 167–200 (2013). https://doi.org/10.1007/s11207-012-9993-9. 1112.5249
J.M. Sokół, M.A. Kubiak, M. Bzowski, P. Swaczyna, Interstellar neutral helium in the heliosphere from IBEX observations. II. The Warsaw Test Particle Model (WTPM). Astrophys. J. Suppl. 220(2), 27 (2015a). https://doi.org/10.1088/0067-0049/220/2/27. 1510.04869
J.M. Sokół, P. Swaczyna, M. Bzowski, M. Tokumaru, Reconstruction of helio-latitudinal structure of the solar wind proton speed and density. Sol. Phys. 290(9), 2589–2615 (2015b). https://doi.org/10.1007/s11207-015-0800-2. 1510.04092
J.M. Sokół, M. Bzowski, M. Kubiak, E. Möbius, Interstellar neutral He, Ne, O density and pick-up ion flux variation along the Earth’s orbit. Mon. Not. R. Astron. Soc. 458, 3691–3704 (2016). https://doi.org/10.1093/mnras/stw515. 1603.01186
J.M. Sokół, M. Bzowski, M. Tokumaru, Interstellar neutral gas species and their pickup ions inside the heliospheric termination shock. Ionization rates for H, O, Ne, and He. Astrophys. J. 872(1), 57 (2019a). https://doi.org/10.3847/1538-4357/aafdaf. 1809.09823
J.M. Sokół, M.A. Kubiak, M. Bzowski, Interstellar neutral gas species and their pickup ions inside the heliospheric termination shock: the large-scale structures. Astrophys. J. 879(1), 24 (2019b). https://doi.org/10.3847/1538-4357/ab21c4. 1903.06425
J.M. Sokół, D.J. McComas, M. Bzowski, M. Tokumaru, Sun-heliosphere observation-based ionization rates model. Astrophys. J. 897(2), 179 (2020). https://doi.org/10.3847/1538-4357/ab99a4
J. Song, “Interstellar Express”: a possible successor of voyagers. Focus Chin. Acad. Sci. 33(4) (2021)
E.C. Stone, A.C. Cummings, F.B. McDonald, B.C. Heikkila, N. Lal, W.R. Webber, Voyager 1 observes low-energy galactic cosmic rays in a region depleted of heliospheric ions. Science 341(6142), 150–153 (2013). https://doi.org/10.1126/science.1236408
T.R. Story, G.P. Zank, Response of the termination shock to interplanetary disturbances 2. MHD. J. Geophys. Res. 102, 17381–17394 (1997). https://doi.org/10.1029/97JA00225
E.J. Summerlin, M.G. Baring, Modeling accelerated pick-up ion distributions at an interplanetary shock. Adv. Space Res. 37(8), 1426–1432 (2006). https://doi.org/10.1016/j.asr.2005.05.116. astro-ph/0505569
P. Swaczyna, M. Bzowski, Modeling emission of heavy energetic neutral atoms from the heliosphere. Astrophys. J. 846(2), 128 (2017). https://doi.org/10.3847/1538-4357/aa862b. 1709.03443
M. Swisdak, B.N. Rogers, J.F. Drake, M.A. Shay, Diamagnetic suppression of component magnetic reconnection at the magnetopause. J. Geophys. Res. Space Phys. 108(A5), 1218 (2003). https://doi.org/10.1029/2002JA009726. physics/0305021
M. Swisdak, M. Opher, J.F. Drake, F. Alouani Bibi, The vector direction of the interstellar magnetic field outside the heliosphere. Astrophys. J. 710(2), 1769–1775 (2010). https://doi.org/10.1088/0004-637X/710/2/1769. 1001.0589
A. Taut, L. Berger, C. Drews, R.F. Wimmer-Schweingruber, Composition of inner-source heavy pickup ions at 1 AU: SOHO/CELIAS/CTOF observations. Implications for the production mechanisms. Astron. Astrophys. 576, A55 (2015). https://doi.org/10.1051/0004-6361/201425139
T. Terasawa, Energy spectrum and pitch angle distribution of particles reflected by MHD shock waves of fast mode. Planet. Space Sci. 27(2), 193–201 (1979). https://doi.org/10.1016/0032-0633(79)90050-3
G.E. Thomas, The interstellar wind and its influence on the interplanetary environment. Annu. Rev. Earth Planet. Sci. 6, 173–204 (1978)
A.V. Usmanov, M.L. Goldstein, A three-dimensional MHD solar wind model with pickup protons. J. Geophys. Res. Space Phys. 111(A7), A07101 (2006). https://doi.org/10.1029/2005JA011533
A.V. Usmanov, M.L. Goldstein, W.H. Matthaeus, Three-dimensional magnetohydrodynamic modeling of the solar wind including pickup protons and turbulence transport. Astrophys. J. 754(1), 40 (2012). https://doi.org/10.1088/0004-637X/754/1/40
V.M. Vasyliunas, G.L. Siscoe, On the flux and the energy spectrum of interstellar ions in the solar system. J. Geophys. Res. 81(7), 1247 (1976). https://doi.org/10.1029/JA081i007p01247
M. Wallis, Shock-free deceleration of the solar wind? Nat. Phys. Sci. 233(37), 23–25 (1971). https://doi.org/10.1038/physci233023a0
H. Washimi, G.P. Zank, Q. Hu, T. Tanaka, K. Munakata, H. Shinagawa, Realistic and time-varying outer heliospheric modelling. Mon. Not. R. Astron. Soc. 416, 1475–1485 (2011). https://doi.org/10.1111/j.1365-2966.2011.19144.x
C.S. Weller, R.R. Meier, Characteristics of the helium component of the local interstellar medium. Astrophys. J. 246, 386–393 (1981). https://doi.org/10.1086/158936
T. Wiengarten, S. Oughton, N.E. Engelbrecht, H. Fichtner, J. Kleimann, K. Scherer, A generalized two-component model of solar wind turbulence and ab initio diffusion mean-free paths and drift lengthscales of cosmic rays. Astrophys. J. 833(1), 17 (2016). https://doi.org/10.3847/0004-637X/833/1/17
L.L. Williams, G.P. Zank, Effect of magnetic field geometry on the wave signature of the pickup of interstellar neutrals. J. Geophys. Res. 99(A10), 19229–19244 (1994). https://doi.org/10.1029/94JA01657
L.L. Williams, G.P. Zank, W.H. Matthaeus, Dissipation of pickup-induced waves: a solar wind temperature increase in the outer heliosphere? J. Geophys. Res. 100(A9), 17059–17068 (1995). https://doi.org/10.1029/95JA01261
R.F. Wimmer-Schweingruber, P. Bochsler, On the origin of inner-source pickup ions. Geophys. Res. Lett. 30, 1077 (2003). https://doi.org/10.1029/2002GL015218
F.M. Wu, D.L. Judge, Temperature and flow velocity of the interplanetary gases along solar radii. Astrophys. J. 231, 594–605 (1979). https://doi.org/10.1086/157221
P. Wu, D. Winske, S.P. Gary, N.A. Schwadron, M.A. Lee, Energy dissipation and ion heating at the heliospheric termination shock. J. Geophys. Res. Space Phys. 114(A8), A08103 (2009). https://doi.org/10.1029/2009JA014240
W. Wu, D. Yu, J. Huang, Q. Zong, C. Wang, G. Yu, R. He, Q. Wang, Y. Kang, L. Meng, K. Wu, J. He, H. Li, Exploring the solar system boundary. Sci. Sin. Inform. 49(1), 1–16 (2019). https://doi.org/10.1360/N112018-00273
Z. Yang, Y.D. Liu, J.D. Richardson, Q. Lu, C. Huang, R. Wang, Impact of pickup ions on the shock front nonstationarity and energy dissipation of the heliospheric termination shock: two-dimensional full particle simulations and comparison with Voyager 2 observations. Astrophys. J. 809, 28 (2015). https://doi.org/10.1088/0004-637X/809/1/28. 1506.08492
G.P. Zank, Interaction of the solar wind with the local interstellar medium: a theoretical perspective. Space Sci. Rev. 89, 413–688 (1999). https://doi.org/10.1023/A:1005155601277
G.P. Zank, Faltering steps into the galaxy: the boundary regions of the heliosphere. Annu. Rev. Astron. Astrophys. 53, 449–500 (2015). https://doi.org/10.1146/annurev-astro-082214-122254
G.P. Zank, Pickup ion-mediated plasma physics of the outer heliosphere and very local interstellar medium. Geosci. Lett. 3(1), 22 (2016). https://doi.org/10.1186/s40562-016-0055-2
G.P. Zank, W.H. Matthaeus, C.W. Smith, Evolution of turbulent magnetic fluctuation power with heliospheric distance. J. Geophys. Res. 101(A8), 17093–17108 (1996a). https://doi.org/10.1029/96JA01275
G.P. Zank, H.L. Pauls, I.H. Cairns, G.M. Webb, Interstellar pickup ions and quasi-perpendicular shocks: implications for the termination shock and interplanetary shocks. J. Geophys. Res. 101(A1), 457–478 (1996b). https://doi.org/10.1029/95JA02860
G.P. Zank, H.L. Pauls, L.L. Williams, D.T. Hall, Interaction of the solar wind with the local interstellar medium: a multifluid approach. J. Geophys. Res. 101(A10), 21639–21656 (1996c). https://doi.org/10.1029/96JA02127
G.P. Zank, W.H. Matthaeus, J.W. Bieber, H. Moraal, The radial and latitudinal dependence of the cosmic ray diffusion tensor in the heliosphere. J. Geophys. Res. 103(A2), 2085–2098 (1998). https://doi.org/10.1029/97JA03013
G.P. Zank, W.K.M. Rice, I.H. Cairns, J.W. Bieber, R.M. Skoug, C.W. Smith, Predicted timing for the turn-on of radiation in the outer heliosphere due to the Bastille Day shock. J. Geophys. Res. 106, 29363–29372 (2001). https://doi.org/10.1029/2000JA000401
G.P. Zank, J. Heerikhuisen, N.V. Pogorelov, R. Burrows, D. McComas, Microstructure of the heliospheric termination shock: implications for energetic neutral atom observations. Astrophys. J. 708(2), 1092–1106 (2010). https://doi.org/10.1088/0004-637X/708/2/1092
G.P. Zank, A. Dosch, P. Hunana, V. Florinski, W.H. Matthaeus, G.M. Webb, The transport of low-frequency turbulence in astrophysical flows. I. Governing equations. Astrophys. J. 745(1), 35 (2012). https://doi.org/10.1088/0004-637X/745/1/35
G.P. Zank, P. Hunana, P. Mostafavi, M.L. Goldstein, Pickup ion mediated plasmas. I. Basic model and linear waves in the solar wind and local interstellar medium. Astrophys. J. 797(2), 87 (2014). https://doi.org/10.1088/0004-637X/797/2/87
G.P. Zank, L. Adhikari, P. Hunana, D. Shiota, R. Bruno, D. Telloni, Theory and transport of nearly incompressible magnetohydrodynamic turbulence. Astrophys. J. 835(2), 147 (2017). https://doi.org/10.3847/1538-4357/835/2/147
G.P. Zank, L. Adhikari, L.L. Zhao, P. Mostafavi, E.J. Zirnstein, D.J. McComas, The pickup ion-mediated solar wind. Astrophys. J. 869(1), 23 (2018). https://doi.org/10.3847/1538-4357/aaebfe
M. Zhang, Acceleration of suprathermal particles by compressional plasma wave trains in the solar wind. J. Geophys. Res. Space Phys. 115(A12), A12102 (2010). https://doi.org/10.1029/2010JA015723
M. Zhang, Acceleration of energetic particles by compressive plasma waves of arbitrary scale sizes, in International Cosmic Ray Conference, vol. 10 (2011), p. 244. https://doi.org/10.7529/ICRC2011/V10/0907
M. Zhang, M.A. Lee, Stochastic acceleration of energetic particles in the heliosphere. Space Sci. Rev. 176(1–4), 133–146 (2013). https://doi.org/10.1007/s11214-011-9754-3
M. Zhang, N. Pogorelov, The heliosphere as seen in TeV cosmic rays. J. Phys. Conf. Ser. 767, 012027 (2016). https://doi.org/10.1088/1742-6596/767/1/012027
M. Zhang, R. Schlickeiser, A theory of bimodal acceleration of pickup ions by compressive solar wind turbulence under pressure balance. Astrophys. J. 756(2), 129 (2012). https://doi.org/10.1088/0004-637X/756/2/129
M. Zhang, L. Zhao, R. von Steiger, R.F. Wimmer-Schweingruber, G.M. Gloeckler, M. Desai, N.V. Pogorelov, Determination of plasma, pickup ion, and suprathermal particle spectrum in the solar wind frame of reference. Astrophys. J. 871(1), 60 (2019). https://doi.org/10.3847/1538-4357/aaf509
L.L. Zhao, L. Adhikari, G.P. Zank, Q. Hu, X.S. Feng, Influence of the solar cycle on turbulence properties and cosmic-ray diffusion. Astrophys. J. 856(2), 94 (2018). https://doi.org/10.3847/1538-4357/aab362
E.J. Zirnstein, J. Heerikhuisen, G.P. Zank, N.V. Pogorelov, D.J. McComas, M.I. Desai, Charge-exchange coupling between pickup ions across the heliopause and its effect on energetic neutral hydrogen flux. Astrophys. J. 783, 129 (2014). https://doi.org/10.1088/0004-637X/783/2/129
E.J. Zirnstein, H.O. Funsten, J. Heerikhuisen, D.J. McComas, N.A. Schwadron, G.P. Zank, Geometry and characteristics of the heliosheath revealed in the first five years of interstellar boundary explorer observations. Astrophys. J. 826(1), 58 (2016). https://doi.org/10.3847/0004-637X/826/1/58
E.J. Zirnstein, J. Heerikhuisen, G.P. Zank, N.V. Pogorelov, H.O. Funsten, D.J. McComas, D.B. Reisenfeld, N.A. Schwadron, Structure of the heliotail from interstellar boundary explorer observations: implications for the 11-year solar cycle and pickup ions in the heliosheath. Astrophys. J. 836(2), 238 (2017). https://doi.org/10.3847/1538-4357/aa5cb2
E.J. Zirnstein, R. Kumar, J. Heerikhuisen, D.J. McComas, A. Galli, Stochastic acceleration of ∼0.1-5 keV pickup ions in the heliotail. Astrophys. J. 860(2), 170 (2018a). https://doi.org/10.3847/1538-4357/aac3de
E.J. Zirnstein, R. Kumar, J. Heerikhuisen, D.J. McComas, A. Galli, Constraining the evolution of the proton distribution function in the heliotail. Astrophys. J. 865, 150 (2018b). https://doi.org/10.3847/1538-4357/aadb98
E.J. Zirnstein, D.J. McComas, R. Kumar, H.A. Elliott, J.R. Szalay, C.B. Olkin, J. Spencer, S.A. Stern, L.A. Young, In situ observations of preferential pickup ion heating at an interplanetary shock. Phys. Rev. Lett. 121(7), 075102 (2018c). https://doi.org/10.1103/PhysRevLett.121.075102
J.H. Zoennchen, J.J. Bailey, U. Nass, M. Gruntman, H.J. Fahr, J. Goldstein, The TWINS exospheric neutral H-density distribution under solar minimum conditions. Ann. Geophys. 29(12), 2211–2217 (2011). https://doi.org/10.5194/angeo-29-2211-2011
J.H. Zoennchen, U. Nass, H.J. Fahr, Exospheric hydrogen density distributions for equinox and summer solstice observed with TWINS1/2 during solar minimum. Ann. Geophys. 31(3), 513–527 (2013). https://doi.org/10.5194/angeo-31-513-2013
P. Zuo, M. Zhang, K. Gamayunov, H. Rassoul, X. Luo, Energy spectrum of energetic particles accelerated by shock waves: from focused transport to diffusive acceleration. Astrophys. J. 738(2), 168 (2011). https://doi.org/10.1088/0004-637X/738/2/168
Acknowledgements
Authors would like to thank Tae K. Kim for providing Fig. 4. C.W.S. is supported by Advanced Composition Explorer Mission as well as NASA grants NNX17AB86G, 80NSSC17K0009, and 80NSSC18K1215. J.M.S. acknowledges support by IBEX grant 80NSSC20K0719, NASA LWS grant 80NSSC19K0079, and O2R grant 80NSSC20K0290. N.P. at UAH was supported, in part, by NASA grants 80NSSC19K0260, 80NSSC18K1649, 80NSSC18K1212, NSF-BSF grant PHY-2010450, and by the IBEX mission as a part of NASA’s Explorer program. N.P. acknowledges the Texas Advanced Computing Center (TACC) at The University of Texas at Austin for providing HPC resources on Frontera supported by NSF LRAC award 2031611. Supercomputer time allocations were also provided on SGI Pleiades by NASA High-End Computing Program award SMD-17-1537 and Stampede2 by XSEDE project MCA07S033. The contribution from Tae K. Kim was additionally supported by NASA grant 80NSSC20K1453. P.M. acknowledges the support by Johns Hopkins University Applied Physics Laboratory independent R\(\&\)D funds.
Author information
Authors and Affiliations
Contributions
This chapter is a result of a joint effort of all authors who agreed to contribute and all contributions should be considered equal.
Corresponding author
Ethics declarations
Conflict of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The Heliosphere in the Local Interstellar Medium: Into the Unknown
Edited by John D. Richardson, Andrei Bykov, Frederic Effenberger, Klaus Scherer, Veerle Sterken, Rudolf von Steiger and Gary P. Zank
The original online version of this article was revised due to a retrospective Open Access order.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Sokół, J.M., Kucharek, H., Baliukin, I.I. et al. Interstellar Neutrals, Pickup Ions, and Energetic Neutral Atoms Throughout the Heliosphere: Present Theory and Modeling Overview. Space Sci Rev 218, 18 (2022). https://doi.org/10.1007/s11214-022-00883-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-022-00883-6