Abstract
The magnetometer instrument MPO-MAG on-board the Mercury Planetary Orbiter (MPO) of the BepiColombo mission en-route to Mercury is introduced, with its instrument design, its calibration and scientific targets. The instrument is comprised of two tri-axial fluxgate magnetometers mounted on a 2.9 m boom and are 0.8 m apart. They monitor the magnetic field with up to 128 Hz in a \(\pm 2048\) nT range. The MPO will be injected into an initial \(480 \times 1500\) km polar orbit (2.3 h orbital period). At Mercury, we will map the planetary magnetic field and determine the dynamo generated field and constrain the secular variation. In this paper, we also discuss the effect of the instrument calibration on the ability to improve the knowledge on the internal field. Furthermore, the study of induced magnetic fields and field-aligned currents will help to constrain the interior structure in concert with other geophysical instruments. The orbit is also well-suited to study dynamical phenomena at the Hermean magnetopause and magnetospheric cusps. Together with its sister instrument Mio-MGF on-board the second satellite of the BepiColombo mission, the magnetometers at Mercury will study the reaction of the highly dynamic magnetosphere to changes in the solar wind. In the extreme case, the solar wind might even collapse the entire dayside magnetosphere. During cruise, MPO-MAG will contribute to studies of solar wind turbulence and transient phenomena.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Planet Mercury possesses a weak axial dipole moment that interacts with a dense solar wind. Through this interaction, a magnetosphere is created that shows a lot of similarities with the terrestrial counterpart but also differs in several ways. Both spacecraft of the BepiColombo mission carry magnetometers to Mercury in order to survey the planet’s magnetic field. This mission will build on a legacy from previous space missions to the innermost planet in our solar system.
Mariner 10 carried out Mercury flybys on March 29, 1974, September 21, 1974, and March 16, 1975 (see reviews by Ness (1979), Russell et al. (1988a) and Slavin (2004)). All flybys occurred at a heliocentric distance of 0.46 AU, but only the first and third encounters passed close enough to Mercury to return observations of the solar wind interaction and the planetary magnetic field. The first encounter targeted the planetary “wake” and returned surprising observations that indicate a significant intrinsic magnetic field. The closest approach to the surface during this passage was 723 km where a peak magnetic field intensity of 98 nT was observed (Ness et al. 1974). Clear bow shock and magnetopause boundaries were observed along with the north and south lobes of the tail and the cross-tail current sheet (Ness et al. 1974). The third flyby observations were of great importance because they confirmed that the magnetosphere was indeed produced by the interaction of the solar wind with an intrinsic largely dipolar planetary magnetic field. Magnetic field models derived using different subsets of the Mariner 10 data and assumptions concerning the external magnetospheric magnetic field indicate that the tilt of the dipole relative to the planetary rotation axis was less than \(10~^{\circ }\), but the longitude angle of the dipole is very poorly constrained (Ness et al. 1976).
The MErcury Surface, Space ENvironment, GEochemistry, and Ranging (MESSENGER) spacecraft was inserted into a 12 h period, \(82^{\circ }\) inclination, high eccentricity (\(200... 15,000\) km altitude) orbit about Mercury on 18 March 2011 (Solomon et al. 2007). The period of the orbit was reduced on 16 April 2012 to 8 h by lowering the apoapsis altitude to \(10,000\) km. This change in apoapsis part way through the mission resulted in rather complete sampling of Mercury’s magnetosphere and its principal current layers from the nose region and 3 to \(4~R_{M}\) (\(1~R_{M} = 2440\) km) downstream of the center of the planet. As originally found by Mariner 10, and greatly expanded upon by the MESSENGER mission, the structure of Mercury’s magnetosphere is quite similar in many ways to that of the Earth (see reviews Korth et al. (2018); Slavin et al. (2018)). The mean distance from the internal dipole to the nose of Mercury’s magnetopause is only \(1.4~R_{M}\) (Slavin et al. 2009b; Winslow et al. 2013; Zhong et al. 2015b). However, features such as the radiation belt of the Earth’s magnetosphere map to the interior of Mercury due to its large size relative to its magnetosphere and are thus not present at Mercury. Particles may be captured close to the planet but their azimuthal gradient drift paths will lead them to the magnetopause.
Mercury’s magnetic dipole is offset to the north by 0.196 RM (Alexeev et al. 2010; Anderson et al. 2012), which introduces significant north/south asymmetries in the polar magnetic fields, the size of the polar caps, the loss cones and other phenomena. Numerical simulations of the solar wind interaction with Mercury’s magnetic field have reproduced much of the magnetospheric structure and dynamics observed by Mariner 10 and MESSENGER (e.g. Trávníček et al. 2009; Benna et al. 2010; Müller et al. 2012; Jia et al. 2019; Exner et al. 2018; Dong et al. 2019b; Exner et al. 2020). These simulations give a global picture of the magnetosphere but particular results should be treated with caution, because numerical schemes as well as the treatment of boundary conditions may lead to physical behavior that may not be immediately visible. It is evident, that the large gyro radius of ions make it necessary to further conduct at least hybrid studies (electrons as fluid, ions as particles) to enhance our knowledge about the Hermean magnetosphere. Much of our understanding about the southern hemisphere stems from the above-mentioned simulations with the exception of Winslow et al. (2014) who indirectly probe a small region on the planet using proton reflectrometry.
The planetary orbiter (MPO) from BepiColombo will be injected into an initially \(480 \times 1500\) km polar orbit around the planet and carries two 3D fluxgate magnetometers mounted on a boom. These magnetic field measurement will allow us to determine the main field, provide measurements about the magnetospheric structure and its dynamics and further constrain the interior structure as well as the dynamo process that generates the internal magnetic field.
This paper gives an introduction to the instrument and data structure in Sect. 2. An overview on science goals featuring solar-wind—magnetospheric interactions, the magnetic main field and the interior structure is given in Sect. 3. In Sect. 4 the on-going cruise measurements are described, covering solar-wind measurements and the plethora of planetary fly-bys at Earth, Venus and Mercury. Finally, this paper is summarized in Sect. 5 and an outlook to the mission’s future is given.
2 Instrument Description & Characteristics
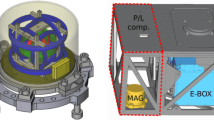
MPO-MAG consists of two vector fluxgate magnetometers mounted on a 2.87 m boom with 0.80 m sensor separation. The instruments comprise identical digital fluxgate sensors (Auster et al. 1995), which have been successfully flown on the Rosetta lander (Auster et al. 2007b), Venus Express (Zhang et al. 2006) and Themis (Auster et al. 2008). The sensors and their electronics were manufactured in a collaboration between the Institute for Geophysics and extraterrestrial Physics, TU Braunschweig, Germany (IGEP), the Space Research Institute of the Austrian Academy of Sciences (IWF) and the Imperial College, London, UK (ICL). A picture of the flight model including the electronics is shown in Fig. 1 and an illustration of the sensor locations on the satellite is depicted in Fig. 2.
2.1 Measurement Principle and Instrument Characteristics
MPO-MAG consists of two digital, triaxial fluxgate magnetometers. The basic principle of a fluxgate magnetometer is known and well-documented (Auster et al. 1995). The basic sensor design was documented by Glassmeier et al. (2010). A toroidal soft magnetic core is wound with a coil and driven to saturation with a high frequency alternating current (square wave, 10 kHz). The external magnetic field (which is to be measured) distorts the symmetry of the magnetic field in the core. As result, a signal with the second harmonic of the excitation frequency is generated and induced into a secondary coil. An external feedback coil compensates the environmental field and the sensor operates in null mode, improving linearity and sensitivity. Typically, the second harmonic of the drive frequency is bandpass filtered, amplified, synchronously detected, integrated, and used to drive the feedback. The feedback current is then proportional to the environmental magnetic field. This current is immediately converted into a voltage and digitized by an AD converter. Likewise, the sensor current in the secondary coil is converted. Since no analog circuits are used here, the magnetometer is less susceptible to temperature changes (compare to e.g. Auster et al. (2007b)). Furthermore, this approach offers maximum flexibility as all processing parameters can be customized by software commands. The instrument characteristics are summarized in Table 1. At Mercury, we expect a maximum operating temperature of about \(180{\ }^{\circ }\)C when the sensor is illuminated. As the orbital period is only 2.3 h, flying from the hot dayside to the cold eclipse happens very fast. In order to cope with this situation, we thermally shielded the sensors against solar and planetary radiation. Furthermore, we thermally isolated the sensors against the spacecraft as best as possible. Details to this may be found in Glassmeier et al. (2010). The expected temperature decrease after entering eclipse is only \(0.42{\ }\)K/min. If this thermal strategy proves to be inadequate, MPO-MAG possesses a heater to help keeping the sensor in a hot operating state. Eventually, one must weigh up the offset change due to a temperature change with the additional DC disturbances caused by the heater.
2.2 Instrument Calibration
During cruise MPO-MAG is expected to experience low temperatures down to \(-106{\ }^{\circ }\)C whereas at the dayside of Mercury very high operating temperatures up to \(+180{\ }^{\circ }\)C of the sensors will be reached. In order to guarantee that the instrument performance is flawless and well-characterized under all these environmental conditions a comprehensive ground test campaign has been conducted. These ground tests are split into
-
a ground calibration campaign
-
ground functional checks
-
noise measurements
The pure instrument characteristics determined isolated on ground can differ significantly from the results obtained in flight, as especially the varying s/c bias field affects the absolute value of the magnetic field components. Furthermore, the AC disturbance generated on the s/c has to be taken into account for a proper interpretation of the data. Therefore, a detailed in-flight calibration and disturbance analysis has to be conducted in order to generate proper magnetic field data.
The following sections give an overview about the different facets of the ground and in-flight calibration.
2.3 Ground Calibration
The ground calibration for the BepiColombo MPO magnetometer MPO-MAG has been conducted at the MAGNETSRODE magnetic calibration facility operated by the Institute for Geophysics and extraterrestrial Physics at the Technische Universität Braunschweig, Germany. This facility has a 50 year heritage of spaceflight magnetometer calibrations for space missions like e.g. HELIOS, CLUSTER, CASSINI, DEEP SPACE 1, DOUBLE STAR, OERSTED, CHAMP, VENUS EXPRESS, ROSETTA, MMS and SOLARORBITER.
The calibration facility consists of a 2.5 m diameter three-axes-Braunbek coilsystem which is connected to computer controlled field generation devices. Equipped with this hardware it is possible to provide artificial DC and AC magnetic fields in three dimensions in the range of \(\pm 100000\) nT with an absolute accuracy better than 0.8 nT. Furthermore, frequency response functions from mHz up to kHz can be recorded. All these calibration measurements can be conducted in a wide temperature range from \(-196{\ }^{\circ }\)C up to \(+200{\ }^{\circ }\)C using a computer-controlled nonmagnetic thermal box. Also offset measurements in the mentioned temperature range can be performed using a sophisticated rotation mechanism inside the box.
The major purpose of the ground calibration is the determination of the temperature dependent transfer function \(\underline{\underline{\varPhi }} \) which defines the relation between the known calibration field \(\mathbf{B}^{\text{c}}\) and the measured field \(\mathbf{B}^{\text{m}}\)
The measured field \(\mathbf{B}^{\text{m}}\) comprises the real raw data \(\mathbf{B}^{\text{r}}\), the coil system residual field \(\mathbf{B}^{\text{res}}\) and the instrument offset \(\mathbf{B}^{\text{off}}\) as
The complete calibration transfer matrix \(\underline{\underline{ \varPhi }}\) is defined by
where \(\underline{\underline{ \sigma }}(T)\) represents the temperature dependent sensor sensitivity, \(\underline{\underline{ \omega }}(T)\) describes the temperature dependent internal sensor misalignment (orthogonalisation matrix), and \(\underline{\underline{ \rho }}(T)\) describes the real rotation of the sensor against the coil axes. The latter matrix \(\underline{\underline{ \rho }}\), which is only a setup but not an instrument characterizing parameter, can be determined by the calibration analysis software and separated from the transfer function, yielding the reduced transfer matrix \(\underline{\underline{ \tilde{\phi }}} = \underline{\underline{ \omega }} \ \underline{\underline{ \sigma }}\).
The sensitivity matrix represents the sensitivities of the 3 sensor axes as diagonal matrix
and the remaining orthogonalisation matrix can be written as
with
Here \(\xi _{xy}, \xi _{xz}, \xi _{yz} \) represent the three sensor characterizing misalignment angles. The reduced transfer function has been determined for various temperatures in the expected operation range from \(-75{\ }^{\circ }\)C to \(+180{\ }^{\circ }\)C by application of sets of three subsequent linear step functions (\(x,y,z\)) in the range of \(\pm 2000\) nT each. Figure 3 displays the temperature behavior of the three sensitivities \(\sigma _{x}, \sigma _{y}, \sigma _{z}\) as calibration result for the Inboard Sensor (IB). Figure 4 depicts the temperature dependence of the three misalignment angles \(\xi _{xy} \), \(\xi _{xz}\), and \(\xi _{yz}\) of the IB sensor. During the ground calibration also the sensor offset \(\mathbf{B}^{\text{off}} \) has been determined for the wide operational temperature range. This could be achieved by taking measurements at zero field conditions in two different sensor orientations, at \(0^{\circ }\) and in a \(180^{\circ }\) turned orientation relative to all three main axes. Doing this for various temperatures leads to the results displayed Fig. 5. In addition to all these static DC characteristics also the frequency response of the magnetometer is crucial for a proper interpretation of plasma observations. Therefore, sinusoidal signals with constant amplitude and discretely varying frequencies (10 frequencies per decade) ranging from 10 mHz to 1 kHz have been applied to the instrument. The resulting response function for the OB sensor, operated at 128 Hz sampling rate at a temperature of \(76{\ }^{\circ }\)C is exemplary displayed in Fig. 6. The calculated 3 dB corner frequency is located at 60 Hz. This corner frequency is higher than the one calculated for the MESSENGER magnetometer (11.3 Hz, Anderson et al. (2007)). The data from the space-borne sensor is currently collected without a correction for the transfer function. For science applications involving burst mode data (i.e. 128 Hz), the attenuation effect should be accounted for by reversing the transfer function.
2.4 Instrument Operation, Processing Pipeline and Data Products
The complete process of instrument commanding, data retrieval and data pipelining up to the ingestion into the public data archives is visualized schematically in Fig. 7. The following three sections describe the complex up- and downlink branches and the generated data products in detail.
2.4.1 Instrument Operation
In order to gain proper scientific observations the instrument has to be set up in right way. There are two ways to control the MPO-MAG instrument on-board the BepiColombo Planetary Orbiter (MPO). As a simple way the MPO-MAG team can send low level commands as Payload Direct Operation Requests (PDOR) to the mission operation control (MOC) located at the European Space Operation Centre (ESOC) in Darmstadt. The second and preferred way is the involvement of the Science Ground Segment (SGS) located at the European Space Astronomy Centre (ESAC) in Spain. Here the Science Planning Operation Tool (SPOT) processes predefined macro command sequences as Payload Operation Requests (POR) jointly from ALL instrument teams. This is done in order to generate a common operation approach considering the power and telemetry (TM) budget available to optimize the overall scientific return of the mission. The result of this scheduling is the instrument timeline (ITL) acting as input to complex, iterative multistage planning process. This is separated into long-term planning (LTP)- several months, midterm planning (MTP) - one month, and short term planning (STP) - one week, providing a tweaked trajectory and attitude profile facilitating the best possible observations. Thus optimal scheduled operations will take everybody’s wishes into account in order to achieve the mission wide science goals.
2.4.2 Data Processing Pipeline
Independently of the described operation request branches ESOC provides the necessary interface to send the commands to the Deep Space Network (DSN) antennas of ESA/NASA which transmit the Telecommands (TC) to the MPO Spacecraft (s/c). After the successful observation the measured magnetic field science (SC) and instrument housekeeping (HK) data have to be downlinked to Earth. Transmitted from MPO and received by any of the DSN antennas, binary data will be transferred and stored in the EGOS (=ESA Ground Operation System) Data Dissemination System (EDDS) located at ESOC. From here all binary s/c data can be retrieved directly by specific requests of the instrument teams or - in case of MPO-MAG data - by the SGS servers. At SGS the first stage of the data conversion is performed routinely. The Tm2Raw s/w (telemetry to raw data software) extracts all relevant binary data packets (SC and HK), generates proper UTC time stamps, and converts the data to daily ASCII SC and HK RAW data files. Additionally PDS4 (Planetary Data System, Version 4) compliant *.xml label files are generated in order to provide useful context. All files are sent to the instrument team for further processing as well as directly to the public archive for permanent storage of the RAW data. The public archive is called Planetary Science Archive (PSA) and is operated by ESA and the Planetary Data System (PDS) maintained by NASA. It can be accessed via https://www.cosmos.esa.int/web/psa.
As next step the important calibration and data cleaning is done at IGEP using specific software and manual means. Routinely the Raw2Cal s/w (raw to calibrated data conversion) reads the RAW ASCII data provided by SGS, applies the results of the ground calibration (temperature dependent sensitivity & misalignment matrices and temperature dependency of the instrument offset), adds a mission phase related constant s/c-magnetic field and generates the needed PDS4 *.xml label files. This is a completely automated process providing the so called CALIBRATED data. The needed transformation into various coordinate systems is accomplished using the SPICE s/w (Acton (1996), Acton et al. (2018)) provided by the NAIF-team (NASA’s Navigation and Ancillary Information Facility) and the actual SPICE kernels provided by ESA’s SPICE and Auxiliary Data Support team at SGS.
In a further, semi-automatic process, the Cal2Der s/w (calibrated to derived data conversion software) generates a best effort cleaned and inflight calibrated magnetic field data product as well as averaged magnetic field data. Here, s/c disturbances like e.g. reaction wheel interference, magnetic thruster signatures, solar panel rotations and the influence of the ion engine are eliminated on best effort basis or at least flagged in the data files.
All CALIBRATED and DERIVED data files are sent back to SGS, which cares about the proper ingestion into the public archive. Additionally browse plots for a quick data overview and useful information for the data end-user can be found in the archived datasets.
2.4.3 Data Products
Various kinds of data products are available at PSA for different purposes. The directory structure of the MPO-MAG data is displayed in Fig. 8. All data are available as ASCII data and grouped in RAW, CALIBRATED & DERIVED data, stored in the directories data_raw, data_calibrated & data_derived accordingly. Below this layer data are grouped by mission phases e.g. near_earth_commissioning or cruise. The next logical layer separates the data by housekeeping hk and science sc data. And finally the real data can be found in the ib and ob folders for the inboard and outboard sensor data, respectively. According to the PDS4 regulations *.tab files with the data tables and related *.xml context label files are written to the archive. The data tables all contain at least UTC time stamps, onboard time entries (OBT) and specific data columns (positions, magnetic field, temperatures,…).
The RAW data comprises unprocessed (ADC counts) HK and SC data for the inboard (IB) and outboard (OB) sensor in instrument coordinates (URF) only. They are used mainly for diagnosis purposes.
The CALIBRATED data represent observations in physical units made by the IB and OB sensor after application of the described ground calibration process. These data are available in URF, spacecraft (SCF) and suitable celestial coordinate frames. Dependent on the actual mission phase data will routinely be provided in the following frames:
FRAME | FOLDER | DESCRIPTION |
MPO_MPO-MAG_IBS | URF | IB sensor unit reference frame |
MPO_MPO-MAG_OBS | URF | OB sensor unit reference frame |
MPO_SPACECRAFT | SCF | MPO spacecraft frame |
ECLIPJ2000 | E2K | Mean ecliptic and equinox of J2000 |
BC_MSO | MSO | Mercury-Centric Solar Orbital |
BC_MSM | MSM | Mercury-Centric Solar Magnetospheric |
BC_MBF | MBF | Mercury Body Fixed |
BC_MME_IAU2009_J2000 | MME | BC_MME_IAU2009_OF_DATE frame frozen at J2000 TDB |
BC_MPO_RTN | RTN | MPO Radial-Tangential-Normal Heliocentric |
BC_GSE | GSE | Geocentric Solar Ecliptic |
BC_GSM | GSM | Geocentric Solar Magnetospheric |
BC_VSO | VSO | Venus Solar Orbital |
The DERIVED data contain an inflight calibrated data product (inflightcal_sc), representing the magnetic field as best as possible. Thus, all known s/c disturbances have been eliminated or at least flagged here. No distinction between IB and OB is made here anymore, there is only one magnetic field data product. Possible inflight calibration techniques have been applied in order to improve the data quality.
Furthermore averaged data can be found in the derived_data folder, for the ground calibrated (avg_cal_sc) as well as for the inflight calibrated data (avg_inflightcal_sc).
For a more detailed data product description refer to the Experiment to Archive Interface Control Document (EAICD) which is part of every delivered dataset.
2.5 Magnetic Interference Analysis
The science goals of MPO-MAG require an outstanding measurement precision. Special care about spacecraft generated magnetic disturbances is therefore required. Already in the design phase of BepiColombo, the so-called Magnetic Review Board was established that could assess potential problems at an early stage. It monitored the spacecraft development and ensured the magnetic design goals. A standardized unit level test was performed on-ground during assembly, integration and verification phase. Only for one unit with a particular strong magnetic moment, a compensation magnet was installed. After integration, potential sources were tested that are known to interfere with low frequency magnetometers. No interference sources were found that could not be coped with in-flight. After launch and with the boom deployed, MPO-MAG monitored other instrument commissionings. Measuring the differences component by component using the two sensors offer the possibility to detect interferences in space. Assuming the natural background magnetic field \(\mathbf{B}_{\scriptsize\mathrm{sw}}\) does not vary between the sensors we have
Taking the differences (component by component), we achieve a measure for the spacecraft induced field:
A lot of spacecraft units may not fully operate until MPO separates from the transfer module. Thus, a full in-space assessment of magnetic interferences will only be possible after orbit injection.
2.6 Boom Deployment
On 25/10/2018, MPO-MAG became fully operational with the deployment of the magnetometer boom. During the commissioning of other instruments the magnetometer was kept on to monitor possible magnetic disturbances. The magnetic field times series is shown in Fig. 9 together with images from MCAM in which the boom visually deploys. The static as well as the dynamic spacecraft induced fields decrease as the boom deploys. In this figure, it is readily seen that especially the oscillations in the \(B_{x}\)-component decrease. The residual static fields from the spacecraft are 21 nT at most on the outboard sensor. The decrease in spacecraft induced magnetic interference is also shown in Fig. 10 which displays the dynamic Fourier-spectrum during the boom deployment for the magnetic field differences between the two MPO-MAG sensors. In this figure, it can be seen, that the flywheel disturbances at about 11 Hz (and higher) decrease drastically after 12:40 (boom deployment).
The dynamic spacecraft field amplitude depend on the source. For example, 5N-thrusters, flywheels, solar array drive mechanisms and Phebus scanner motion cause signals of \(15, 1, 0.3, 0.1\) nT on the outboard sensor, respectively. The solar arrays of the Mercury Transfer Module causes a signal of about 30 nT on the outboard sensor, but this module will be detached from MPO before the orbital mission begins. All these disturbances must be dealt with using in-flight calibration and data cleaning methods.
For measurements during cruise, we determine the magnetometer offset vectors every 12 hours (see Sect. 2.8). So, slowly changing magnetic fields caused by e.g. solar arrays are captured by this. Any higher offset determination rate was found to be too uncertain, which may either be the result of insufficient data or highly varying magnetic disturbers on the spacecraft.
For the in-orbit phase, we plan to use calibration methods such as the one proposed by Schmid et al. (2020). For this we can only determine long term offsets and it is unknown how much e.g. flywheels affect the calibration.
2.7 Mutual Sensor Attitude Determination in Space
In order to take advantage of the dual sensor set-up, measurements of the IB and OB sensor need to be transformed into one common coordinate system. Here, we choose to transform the IB-URF (Unit Reference Frame) to the OB-URF. To determine the transform matrix, we employ the method by Heinisch et al. (2016). Assuming magnetic field measurements made at the same time but at different locations \(P\) and \(Q\) in space are almost identical, the mutual sensor orientation can be determined by rotating the sensor coordinate system associated with the measurement \(Q\) until the correlation coefficient \(\rho \) between both time series maximizes. Let \(\mathbf{B}_{P}\) and \(\mathbf{B'}_{Q}\) be the measured magnetic field vectors at locations \(P\) and \(Q\) respectively and \(\mathbf{B}_{Q}\) the field vector at \(Q\) after transforming into the coordinate system of the measurements at \(P\). The coordinate transformation is as follows
The rotation matrix
is constructed from the Euler angles \(\alpha \), \(\beta \) and \(\gamma \). The correlation coefficient between all components is defined as
where \(\mathrm{Cov}\left (X\right )\) denotes the covariance of \(X\) and \(\mathrm{\sigma }\left (X\right )\) the standard deviation of \(X\). To maximize \(\rho \), a computational grid search method is used testing for all possible angle combination until a maximum is found.
We apply the correlation technique to a two hours measurements interval on 10 November 2018 between 18:00 and 20:00 UTC. This time range bares the advantage of having simultaneous magnetic field measurements by MMO-MGF. The rotation by three Euler angles around fixed axes can be translated into a single rotation around an arbitrary axis. We find such single angles between MPO-IB and MPO-OB of \(1.478^{\circ }\) and \(117.278^{\circ }\) between MMO-OB and MPO-OB. Figure 11 displays the data in the MPO-MAG-OB unit reference frame. It is clearly seen, that the MPO data correlate well whereas the MMO data deviate slightly from the MPO data. This is probably due to the fact that the MMO sensor boom is still stowed and receives stronger magnetic interference from the composite satellites.
Simultaneous magnetic field measurements of MPO and MMO sensors on 10 November 2018 between 18:00 and 20:00 UTC. Data is shown in the MPO-MAG-OB sensor coordinate system. The three panels show top to bottom the \(B_{x}\), \(B_{y}\) and \(B_{z}\) component for each measurement, respectively. For better visibility, OB data is offset by \(+5\) nT, IB data by 0 nT and MMO-OB data by −5 nT. A Gaussian-weighted 30 s moving average filter has been applied for smoother data display
A final check on the absolute sensor attitude was feasible during the Earth swingby of BepiColombo, where we compared our magnetic field measurements to the well-known terrestrial magnetic field. Using these data we were able to calculate the absolute orientations of our IB and OB sensors with respect to the MPO spacecraft frame and to provide the proper assembly angles for usage in the SPICE frame kernels.
2.8 Inflight Calibration
The measured magnetic field value of a sensor in vanishing ambient field is called instrument offset. In case of space missions, the absolute reading of a magnetometer in external zero-field conditions is constantly changing over time due to varying spacecraft induced interferences or instrument drifts. Due to lingual simplicity hereafter sensor offset always means the sum of spacecraft disturbance field and instrument offset. To transform a raw magnetic field measurement \(\mathbf{B}_{\mathrm{Raw}}\) into a calibrated measurement \(\mathbf{B}\) the offset vector \(\mathbf{O}\) needs to be determined along with a coupling matrix \(\underline{\underline{ C}}\). This leads to the expression
In principle, two methods exist to determine a sensor offset using only the magnetic field of the surrounding space plasma. First, the so called Hedgecock-method, originally published by Hedgecock (1975). A few variations of this method exist, described in Leinweber et al. (2008). For this method, pure rotations of the solar wind magnetic field that leave the magnitude unchanged are used to determine the sensor offset. Second, the mirror mode method, as published by Plaschke and Narita (2016) and Plaschke et al. (2017). The maximum variance direction of a compressional fluctuation should match the average magnetic field direction. Deviations are assumed to originate from sensor offsets. Other methods of offset calibration exist but either require further instruments, to measure the magnetic field magnitude, a spinning spacecraft (Auster et al. 2002) or detailed prior knowledge of the ambient magnetic field. Because the MPO satellite will be quasi-nadir pointing in the orbital phase and fast rotations will not be possible due to operational constraints, we will be unable to employ the rotational method in this mission phase.
As solar wind measurements during the BepiColombo cruise phase are available we apply the Davis-Smith-Method, a variation of the Hedgecock-method, to determine the offset values. The Davis-Smith-Method minimizes the variance of the squared magnetic field magnitude. For each sensor axis, an offset value is calculated every minute from data within a five minute sliding window. The one minute values are highly scattered due to short time variations in the spacecraft magnetic field and need further averaging. For a time range of interest one minute offset values are then averaged using a kernel density estimator (KDE) which leads to a probability density function (PDF) for the offset value during that time range. The PDF usually has a clear maximum likelihood value with small standard deviation and in general follows a Gaussian-like distribution.
For almost the first year of the mission phase, Fig. 12 shows the static field estimates of each sensor axis. These estimates contain true sensor offsets as well as more or less static magnetic disturbance fields originating from the spacecraft and its instruments. The annual variation is most likely due to temperature dependent magnetic moments on board. Their true origin has to be verified during the remaining mission with a broader temperature variation.
Besides long time variations, Fig. 12 also shows highly fluctuating short time changes of the static field estimates. The cause of those variations are mostly electrical switching operations causing different current flows. Disturbances like this will be identified and corrected for in the future.
After a correction of these offsets, a comparison with other spacecraft becomes reasonable. From 30/10/2018 until 4/11/2018, BepiColombo was close to the Lagrange 1 point between Earth and the Sun. The Advanced Composition Explorer (ACE) resides at that position to provide continuous solar wind measurements. Figure 13 compares the time series between the ACE- and the MPO-magnetometer (with corrected offsets). It can be seen that these two magnetometers provide roughly the same data during this time period. The small lag between the time series is caused by the spatial displacement of the two probes.
3 Science Goals of MPO-MAG
The MESSENGER probe was first to orbit planet Mercury and also carried a magnetometer. Due to thermal reasons, the polar orbit with a high apocenter altitude was chosen. In consequence, the region close to the planet was only covered in the northern hemisphere. Nevertheless, we have learned a lot about the dynamic Hermean magnetosphere. But the knowledge is incomplete and BepiColombo will extend it. There are a lot of questions that remain to be solved. The following extensive list demonstrates questions of high interest but is still far from complete.
3.1 Magnetospheric Structure
Mercury possesses only a relatively weak magnetic field and is subject to a dense solar wind pressure. It thus carves out only a small magnetosphere with an average subsolar magnetopause distance of about \(1.45~R_{M}\) (Winslow et al. 2013). Therefore, Mercury itself occupies a large fraction of the magnetospheric volume. Because the escape speed from the surface is low and the average surface temperature is so high, no significant atmosphere is retained. Without a neutral atmosphere a significant ionosphere cannot exist there. So, the inner boundary of the magnetosphere is the planet itself. Due to the magnetospheric smallness, the Dungey-Cycle time is also small (Slavin et al. 2010) and thus, the Hermean magnetosphere readily adjusts to changes in the upstream solar wind. It has also been shown that magnetopause reconnection seems to be the rule rather than the exception (DiBraccio et al. 2013). Because of the small Dungey-Cycle time and the prevalence of reconnection, the Hermean magnetosphere is quite dynamic.
In addition to the short-time solar wind dynamics, Mercury is subject to seasonal changes upstream plasma characteristics. Along with these seasonal changes, the magnetospheric system is altered in size. With the crossing of various plasma boundaries, such as bow shock, magnetopause and northern cusp, the boundary reaction to a change in solar wind parameters may be constrained with the BepiColombo mission consisting of two orbits crossing these boundary and regions regularly. More details on the Hermean magnetosphere dynamics and what to expect from BepiColombo may be found in Milillo et al. (2020) and Baumjohann et al. (2020).
3.2 Hermean Bow Shock
Mercury is embedded into a supersonic solar wind flow. Thus, a bow shock forms ahead of the planet. Winslow et al. (2013) determined the bow shock crossings of MESSENGER based on in-situ magnetic field data. These crossings were fitted against a model by Slavin et al. (2009b). The bow shock is modeled with a conic section given by:
Here, \(\rho =\sqrt{Y^{2}+Z^{2}}\) is the distance to the \(x\)-axis, \(\epsilon \) stands for the eccentricity and \(p\) is the focal parameter. \(\theta \) is the angle between the \(x\)-axis and the locations on the bow shock. The parameters of the fit are \(X_{0}=0.5~R_{M}\), \(\epsilon = 1.04\), and \(p=2.75~R_{M}\). With this definition the subsolar (\(\rho =0\) and \(\theta =0\)) bow shock distance is
Depending on the Alfvén-Mach number the control parameters of the bow shock model differ as shown in Table 2. These values were obtained under the assumption that the bow shock shape does not change (constant \(X_{0}\) and \(\epsilon \) parameters). From the fitting of the parameters, relationship for the \(p\)-parameter was established:
which shows quite large errors. These might be due to the \(M_{A}\) estimation which was not based on measurements but on heliospheric model results. If the magnetic field and the mass density have a relationship
it follows that
with \(r_{h}\) as heliocentric distance of Mercury. So, we assume \(M_{A} (\text{perihelion}) \approx 4.12\) and \(M_{A} (\text{aphelion}) \approx 11.8\). Note, that \(R_{\text{BS}} \propto \frac{1}{r_{h}}\). With its large apoherm, the MMO spacecraft equipped with the magnetometer Mio-MGF (Baumjohann et al. 2020) will make further measurements of the bow shock locations and improve our understanding of e.g. foreshock region. With the low orbit of MPO, it is unlikely that it will ever cross the bow shock after orbit injection. However, MPO-MAG will record some Hermean bow shock crossing during the 6 Mercury flybys.
3.3 Hermean Magnetopause
Three different models have been proposed to describe the shape and size of the Hermean magnetopause. To first order, the magnetopause position is given by a pressure balance between the shocked magnetosheath plasma outside and the magnetic pressure inside the boundary. Because Mercury has an eccentric orbit around the sun with \(0.308< r_{h}<0.467\) AU the upstream solar wind conditions change significantly during a Hermean year. As the solar wind dynamic pressure varies with heliocentric distance, the average magnetopause subsolar distance \(R_{\text{SS}}\) will also vary. Of course, transient events change the upstream conditions as well. These short-time variations are statistically captured in the dependence of \(R_{\text{SS}}\) on the magnetospheric disturbance index defined by Anderson et al. (2013). The BepiColombo spacecraft orbits are particularly suited to study the subsolar magnetopause shape and response to solar wind changes. Here, we give an overview about the different magnetopause models that have been proposed and put the BepiColombo orbit trajectories into perspective.
Johnson et al. (2012) used orbital MESSENGER data and fitted a parabolic model magnetopause to observation. This model magnetopause is given by:
with
A flaring parameter of \(\gamma =1\) was assumed. The sub-solar magnetopause standoff distance was found to be in the range \(1.4< R_{\text{SS}}<1.5~R_{M}\). Unfortunately, Johnson et al. (2012) did not specify the exact relation in their work.
Korth et al. (2015) propose to model the magnetopause with a Shue-type model:
Here, \(\theta \) refers to the angle between the \(x\)-axis and the position vector. Best fit values for the parameters are: \(R_{\text{SS}} = 1.42\ R_{M}\) and \(\alpha =0.5\). Korth et al. (2015) scale the subsolar magnetopause distance as
Based on more data Johnson et al. (2016a) determined a slightly different scaling
and attributed this change in the exponent to be due to induction in the Hermean core. Later, Korth et al. (2017) find a scaling factor for the dependence of the subsolar magnetopause distance on the magnetospheric disturbance index \(0\leq \text{DI}\leq 100\) introduced by Anderson et al. (2013):
Here, the small induction effect discussed above was ignored.
In reality, the magnetopause shape is not rotational symmetric and indentions near the cusps must be taken into account. For these reasons, Zhong et al. (2015b) proposed the model magnetopause shape:
This model is based on the work by Lin et al. (2010) on the terrestrial magnetopause. Here, the average subsolar magnetopause stand-off distance is \(R_{\text{SS}} = 1.51\ R_{M}\). The other parameters are given in Table 3. The transformation to the MSM coordinate system is given by
Zhong et al. (2015a) used the model by Zhong et al. (2015b) and determined the change in magnetopause standoff distance with heliocentric distance. For this analysis, they constrained the locations of the magnetopause crossings to lie within a cone close to the subsolar point (\(\arccos (X_{\text{MSM}}/r) < 30^{\circ }\)). They found
It is important to note, that Zhong et al. (2015a) calculated their error using only \(1\sigma \). Recently, Philpott et al. (2020) cast some doubt about the shape of the cusp indentions.
Figure 14 shows a comparison of the subsolar magnetopause distance as a function of heliocentric distance of Mercury derived from the three magnetopause models mentioned above. Although, the magnetopause model used by Winslow et al. (2013) and Korth et al. (2015) are the same, the latter is based on more MESSENGER boundary crossings than the former. Zhong et al. (2015b) used a more elaborated magnetopause model. From this figure, there is a quantifiable uncertainty in the subsolar magnetopause distance. So, a resampling of this subsolar magnetopause region is clearly a science goal of MPO-MAG.
Sub-solar magnetopause distance to the center of the planet as a function of heliocentric distance of Mercury. The red line shows the modeling result of Winslow et al. (2013) using a scaled terrestrial magnetopause model which was also used by Korth et al. (2015) and is shown as a green line. The orange line shows the result by Zhong et al. (2015b) who used a more elaborated magnetopause shape model.
Figure 15 and Fig. 16 depict the orbits of the MPO as well as Mio (MMO in the figure) with respect to the magnetopause model by Zhong et al. (2015b). At aphelion, Mio’s orbit will cross the southern magnetopause and less likely the northern counterpart. The orbit of MPO will only dwell inside the magnetosphere and cross only the cusp regions but not the magnetopause under average solar wind conditions. Only during intense solar wind events, when \(R_{\mathrm{SS}}\) is greatly reduced, MPO has the chance to cross the magnetopause boundary. After ca. one Earth year later, the orbits only shift slightly, leaving this situation basically unchanged. At perihelion, the MPO apoherm is at the dayside and thus, MPO-MAG should observe a lot of dayside magnetopause crossings as well as cusp crossings. Mio will enter/exit the magnetosphere at higher latitudes and, due to its high apoherm, serves as upstream monitor for changes in the solar wind. Then, MPO can observe the resulting changes in the dayside magnetopause.
The orbits of both BepiColombo s/c at aphelion together with a 3D-model of Zhong et al. (2015b) which includes indentions for the cusp regions. The thick line is after orbit insertion and the dashed line is app. 1 Earth year later. The variability of the magnetopause position is expressed by plotting a region instead of a thin line for this boundary. It is important to note, that here only the 1\(\sigma \)-error is displayed, so the average magnetopause variability is expected to be greater.
Same as 15 but with Mercury at perihelion
3.4 Internal Field Models After MESSENGER
In absence of local currents, the planetary magnetic field may be described as the gradient of two scalar potentials, one for the internal part and another for the external part:
In spherical coordinates, it is convenient to expand these potentials in spherical harmonics:
Here, \(R_{M}\) is the mean planetary radius of Mercury and \(P_{l}^{m}\) are the Schmidt semi-normalized, associated Legendre polynomials.
The Mauersberger-Lowes spectrum is defined by:
and represents the energy content for each spherical harmonic degree \(l\). Summing over all \(l\) for given a \(m\) yields the respective expression for each spherical harmonic order.
The internal magnetic field co-rotates with the planet and thus the Mercury-Body Fixed (MBF) coordinate system should be used. The external field, however, should be ordered in a solar reference frame and thus the usage of the Mercury-Solar-Orbital (MSO) reference frame is reasonable. This planetocentric coordinate system is defined by the \(x\)-axis pointing from the planet towards the Sun, the \(y\)-axis pointing against the Herman orbital motion tangentially to the orbital plane and the \(z\)-axis completes the right-handed system pointing north.
In the following, we give a short overview about several approaches to model the average (with respect to time) Hermean magnetic field. The authors of the different model approaches employed different schemes of data reduction and filtering. In consequence, a direct comparison of the average misfits to the magnetic field data might be biased. As the measurements by MESSENGER were confined to the northern hemisphere, they were partially taken in non current-free regions and strong time-variable external fields from the magnetosphere were present. Hence, different approaches were taken into account to guide the inversions.
From the analysis of the data taken during the Mariner 10 flybys, Ness et al. (1974) already concluded that a weak axial dipole dominates the internal magnetic field, but its center is shifted northwards. Connerney and Ness (1988) discussed several other analysis attempts making different assumptions about the internal field geometry and the structure of the external field. The internal axial dipole coefficient was estimated to range from 170 to 350 nT. Strong axial quadrupole contributions were also identified which demonstrates the non-uniqueness of the inversion before the arrival of MESSENGER caused by a limited spatial measurement coverage. After two MESSENGER flybys, Alexeev et al. (2010) employed a relatively simple magnetospheric model to avoid the correlation between internal and external fields. They combined the Mariner 10 measurements with the newly measured flyby data by MESSENGER and found an axial dipole moment of −196 nT \(R_{M}^{3}\) and a northward dipole offset of \(0.165\ R_{M}\). Analysis of early orbital MESSENGER data by Anderson et al. (2011) confirmed the dipole moment but corrected the offset slightly to \(0.198\ R_{M}\).
3.4.1 The Offset Dipole
In the following, we explain why the expression offset dipole must be treated with caution. For the science regarding the magnetosphere it seems sufficient to only model the internal field as a single offset dipole. With respect to the modeling of the Hermean interior, this simple representation is highly problematic.
The offset between the magnetic and geographic equators was assessed by Anderson et al. (2011) for \(\rho _{z} = \sqrt{x^{2}+y^{2}}> 1.29\ R_{M}\). But an extrapolation of this offset dipole model towards the Hermean core is not advisable as harmonic contributions decay with the distance from the planet, and the decay rate increases with the spherical harmonic degree (see Eq. (32)-(33)). Thus, in general, the magnetic field complexity is expected to increase towards the planet’s interior. When the field is axisymmetric, for very large distances to the rotation axis (\(\rho _{z} \gg 0\)), the magnetic equator is offset in \(z\)-direction by a constant value \(d\):
At these large distances, this field then appears to be the field of a pure axial dipole that is offset by \(d\). The internal field in the dynamo region, however, can look completely different, e.g. with more pronounced higher harmonics in the magnetic field.
Alexeev et al. (2010) showed that Eq. (35) can be generalized to include all axial harmonics:
Here, \(\gamma _{1}^{0}\) denotes the Gauss coefficient of the pure offset dipole. Equation (36) describes a field where the offset \(d\) is constant at any distance to the planet. In theory, this equation allows us to calculate any axial harmonic for a given axial dipole contribution, once \(d\) is known. In practice, however, the determination of the magnetic equator is not precise enough to constrain the tiny contributions of higher harmonics.
In their analysis, Anderson et al. (2011) determined each single magnetic equator crossing and calculated the average \(d\). Then, they analyzed for deviations from the specific offset dipole series given by Eq. (36) using all available data within the Hermean magnetosphere to this date. The resulting axisymmetric Gauss coefficients are (in ascending degrees): −190, −74.6, −22.0, 5.7 nT. Non-axisymmetric Gauss coefficients are all below 3 nT. Thus, the Hermean magnetic field is relatively weak and very axisymmetric. The dipole tilt appears to be below \(1^{\circ }\). This series of axisymmetric Gauss coefficients is close to the specific offset dipole coefficient series give by Eq. (36) but shows noticeable differences.
In the following, we discuss several alternative internal field models with respect to the dipole offset (or the quadrupole-to-dipole ratio \(g_{2}^{0} / g_{1}^{0}\) as in Eq. (35)), but it must be kept in mind, that this represents a certain centered multipole series. These model approaches are taking the orbital restriction of the MESSENGER probe and the resulting Gauss coefficient correlation into account in different ways.
In order to enhance the uniqueness of the inversion, Johnson et al. (2018) employed a semi-empirical magnetospheric model by Korth et al. (2014) to describe the external field. For this external field model, an internal field model consisting of an offset axial dipole was sufficient. Johnson et al. (2018) found an offset of \(0.195 \ R_{M}\) and a slightly weaker dipole moment of −188 nT \(R_{M}^{3}\). The average misfit between their model and observations is only 9.6 nT, when one only considers magnetically quiet orbits (minor magnetospheric activity as defined by Anderson et al. (2013)).
Other authors developed local field models, for the northern hemisphere where MESSENGER data provide plenty information. Oliveira et al. (2015) adapted a crustal field modeling technique to the core field of Mercury. They employed Equivalent Source Dipoles (ESD), located deep inside the planet, to model the core field during the first six months of the mission. The ESD technique is a discrete approach and allows to model only the field in the northern hemisphere where ample data are available. The authors used measurements below 1000 km altitude and modeled the field by placing magnetic sources at a depth of 640 km below the surface. This model was used to predict the Hermean core field at 200 km altitude, with a lateral resolution of \(9.6^{\circ }\), or about 410 km. Their model did not show any significant non-axisymmetric magnetic fields. This model predicts \(g_{2}^{0}/g_{1}^{0} = 0.212\) (Oliveira et al. 2015) which is equivalent to \(d= 0.106 \ R_{M}\).
Thébault et al. (2018) considered another localized approach and used revised spherical cap analysis (R-SCA) in order to model the field in the northern hemisphere. As spherical harmonic (SH) techniques, R-SCA is continuous, but models and describes the field onto a spherical cap. They used a similar data selection scheme as Oliveira et al. (2015), but considered the entire mission duration. Their local model is associated with a total root mean square misfit of about 30 nT. It can be downward continued to the top of the core assumed at 400 km depth. As this field model has a maximum degree of \(l = 5\), very little small scale features emerge there.
For comparison to other models, they further converted their local R-SCA model into a global SH mode up to degree and order 5. Higher degrees were subject to strong model parameter correlations. Degree 4 terms were left out from the analysis, because they were shown to destabilize the conversion to global spherical harmonic multipoles. They obtained a significantly lower quadrupole-to-dipole ratio of 0.27 (which results in \(d=0.135\ R\)). The axial external dipole field is estimated to \(G_{1}^{0} = -37 \) nT.
A similar result was obtained by Wardinski et al. (2019), who used a global SH approach, with some a-priori regularization constraints. They restricted the data to the night side and from locations below 1000 km (\(=1.41 \ R\)) above the surface in order to minimize the strongly time-varying magnetospheric field. They chose to regularize the internal field spatially. There are many possible regularization choices (see e.g. Holme and Bloxham 1996, for a discussion). Wardinski et al. (2019) used a regularization norm, which seeks to minimize the complexity of the modeled radial field morphology at the top of the core. The model is truncated to degree \(l=3\) for the internal field, and \(l=1\) for the external field. Their primary motivation was to estimate a static, mean field model for Mercury, but focused also on time-varying fields (see below). As Thébault et al. (2018), they obtained a quadrupole-to-dipole ratio at 0.27. This lower ratio translates into a less important equivalent dipole offset of \(d=0.135 \ R_{M}\). However, and as pointed out by Thébault et al. (2018), this dipole offset is mainly constrained by high altitude, low latitude measurements.
How will the BepiColombo mission improve on the magnetic field measurement and analysis? The MPO spacecraft will enter into an almost circular polar orbit around Mercury, which is suitable to measure the magnetic field also on the southern hemisphere that has been inaccessible to MESSENGER. The Gauss coefficient correlation matrix for the MPO spacecraft is shown Fig. 25, bottom (see Sect. 3.7 for discussion). From this figure, it is clear that the more circular orbit of MPO eliminates most of the internal parameter correlations except for the (weak) \(g_{1}^{0} \leftrightarrow g_{3}^{0}\) correlation.
3.4.2 Comparison of Magnetic Equator Detections to Model Predictions
With the end of the MESSENGER mission, more data on the magnetic equator locations became available than were used by e.g. Anderson et al. (2012). Therefore, we compare these locations with the internal field model predictions (partially created before the mission end). Following Anderson et al. (2011), we linearly fitted the measured \(B_{\rho }\) component in the equatorial vicinity (\(200 < Z_{\text{MSO}} < 800\) km). From this linear fit, we calculated the zero crossing positions which correspond to the magnetic equator \(z\)-location. Figure 17 displays these equator crossings in the \(Z_{\text{MSO}}\text{-}\rho _{z}\)-plane and compares them to various internal field models. It is evident, that the magnetic equator \(z\)-locations increase with increasing \(\rho _{z}\). The high altitude crossings beyond \(\rho _{z}=1.45\ R\) are much more disturbed than the low altitude ones, which may be due to the neutral sheet current reacting to upstream solar wind variations (Rong et al. 2018). A restriction of the input data to lower altitudes results in probably too low dipole offsets. It must be stressed here, that a pure offset dipole seems unable to describe the magnetic equator locations.
Location of the \(Z_{\text{MSO}}\)-coordinate of the magnetic equator as function of distance from the rotational axis (\(\rho \)). Grey plus signs mark the locations of the magnetic equator in the magnetic field data. The red line shows the averaged equator locations in \(\rho \)-bins (“histogram”). The green line displays the equator location for a pure offset dipole (\(Z_{ \text{offset}} = 0.196\ R\)). The purple, orange and yellow lines depict the equator locations for the internal field models of Anderson et al. (2011) and Thébault et al. (2018).
3.4.3 Influence of Local Currents
As mentioned above, local currents cannot be described using the scalar potential ansatz in Eq. (31). Conversely, local currents may cause the spherical harmonic analysis of the magnetic field to deviate from estimating the true Gauss coefficients. In a future analysis, one should account for the presence of local currents such as the field-aligned current (FAC) system (Anderson et al. 2018), that violate the basic assumption that the region of analysis is current-free. At Earth, the FACs are grouped in three different regions. At Mercury, only the region-1 FAC analogue has been observed so far. The region-1 FACs flow from the dawn-side magnetopause along the magnetic field lines towards the planet and re-emerge on the dusk-side to flow again towards the magnetopause. These local currents are quasi-steady and may produce a magnetic signature pole-ward of \(60^{\circ }\) N of up to 60 nT. Sub-surface Pederson-like currents within the planet’s interior (primarily the lower mantle and the core-mantle boundary) may provide current closure. The magnetic fields from these closure currents are also visible at low satellite altitude with an amplitude up to 50 nT and more. How much from the FAC is intercepted and closed via the magnetosphere is currently under debate (Exner et al. 2020). Furthermore, Pederson-like closure currents within the planet’s interior produce magnetic fields that must appear as internal multipoles in the field analysis. More in-situ measurements are required to adequately model the effect of these current systems.
3.4.4 Conclusions
Though the various main field models differ, they nevertheless suggest some unique properties of Mercury’s dynamo field. In essence, the key characteristics of the Hermean main field are thus:
-
1.
The field is particularly weak.
-
2.
The field is highly rotational symmetric and the dipole tilt is only one degree or smaller.
-
3.
Dipole and quadrupole contributions dominate, and the quadrupole-to-dipole ratio is relatively large.
3.5 Planetary Structure & Dynamo Models
The dynamo process in Mercury’s partially liquid core, which is the origin of its magnetic field, has been puzzling the community for decades. Thereby models of the planetary dynamo should at least be able to explain the three main characteristics of the magnetic field (Sect. 3.4) which were determined by the analysis of the MESSENGER data. However, this has remained a challenging task to this day. Nevertheless, there are important constrains for modeling Mercury’s dynamo that can help to understand this process. This includes modelling Mercury’s interior structure, its material properties and its thermal evolution. For that reason, these aspects will be discussed briefly before an overview on Mercury’s dynamo models is given.
3.5.1 Mercury’s Core State
To better understand Mercury’s internal structure, geodetic measurements, e.g. the planet’s obliquity and libration, provide a significant constraint for the interior models, since they are strongly connected to the radial density variations and the physical state (solid or liquid) of the single layers (see Genova et al. (2021), in this issue). Additionally, equations of state describing the behavior of the constituent materials are also needed for interior modelling.
A sufficient amount of light elements must be present in the core to sufficiently decrease the melting temperature of the iron alloy, such that the core can be at least partially liquid. The candidates for the light elements are mainly sulfur and silicon, because both elements have a high solubility in metal for a broad pressure range. Analyses of Mercury’s surface composition indicates, that the planet formed under highly reduced formation conditions (Nittler et al. 2011; McCubbin et al. 2012), such that Si could have entered the liquid iron in a sufficient amount and prevented the dissolution of S in the iron alloy. A small amount of sulfur (around 1.5 wt% (Namur and Charlier 2017; Cartier et al. 2020)) means that a large silicon content of at least 10 wt% must be present to keep the core liquid (Hauck et al. 2013). Considering this kind of distribution of light elements in the interior, the resulting models agree with the estimated polar moment of inertia (Mann et al. 2009; Malavergne et al. 2014; Chabot et al. 2014; Namur et al. 2016; Margot et al. 2018).
Further studies of Fe-S-Si alloys revealed, that they can show immiscible behavior for pressure and temperature conditions which are realistic for the upper part of Mercury’s core (Morard and Katsura 2010; Margot et al. 2018). Hence, there is the possibility that a lighter FeS alloy could accumulate right beneath the core-mantle-boundary (Hauck et al. 2013; Knibbe and van Westrenen 2015), which could be additionally solid (Smith et al. 2012). Underneath the immiscible layer of FeS would than be the heavier FeSi layer.
The existence of an inner core is still not entirely clarified. The two light elements in the core allow for different internal configurations with and without an inner core. If there is a solid inner core, its chemical composition and radial extent remain unclear. An iron alloy with sulfur, which does almost not partition in the solid phase, would be denser compared to an FeSi core. With silicon as light alloying material the core would be less dense but the light element equally partitions into the solid and liquid phase of the core. Thermal evolution models show, that with silicon an inner core would be larger in size than with sulfur (Knibbe and van Westrenen 2018; Rivoldini et al. 2018). Additionally, the radial contraction of the planet, which is caused by cooling of the body, serves as an upper bound of the inner core size (Byrne et al. 2014; Klimczak 2015; Crane and Klimczak 2017). Besides the possibility for both end-members of light constituents that no inner core exists, a recent gravitational model for Mercury predicts its existence (Genova et al. 2019).
The before mentioned partitioning of the light elements in the solid phase plays a significant role for driving the dynamo. Since silicon equally partitions in the solid and liquid phase, a release of the light element due to core solidification would not be possible and compositional convection would not be supported. Instead, the release of latent heat at the inner core boundary can drive thermal convection and power the dynamo (Desai 1986; Knibbe and van Westrenen 2018). With sulfur on the other hand as dominant light element, compositional convection is a realistic driving mechanism.
One-dimensional thermal evolution models which consider a global energy balance of the mantle and core by parameterizing the convective heat transport via scaling laws are also necessary to understand the formation of Mercury’s interior. For the core dynamics, it is important to understand how the heat flux can escape through the core-mantle-boundary. The heat flux is controlled by the convection state of the relatively thin region of the mantle lying above the core, if the convection has not stopped already (Tosi et al. 2013). Consequently, the heat flux through the core-mantle-boundary is rather small and lies below the core adiabatic heat flux. A subadiabatic heat flux can then lead to a thermally stably stratified layer at the upper part of the core (Christensen and Wicht 2008; Knibbe and van Westrenen 2018). Figure 18 shows a sketch of Mercury’s possible internal structure. However, the thickness of such a layer and the degree of stratification is not well constrained. At least for a weak thermal stratification, it is possible for compositional convection to penetrate through the thermally stratified layer and destabilize it (Manglik et al. 2010).
3.5.2 A Survey Through Models for Mercury’s Dynamo
As mentioned before, the special characteristics of Mercury’s magnetic field provide a challenging task to the modelling of the core dynamo. However, several attempts have been made trying to explain at least one striking feature of Mercury’s magnetic field in the dynamo models. In the following part, we give a short overview about important models, which are considering most recent knowledge about Mercury’s interior structure or its external environment.
Involving the external environment, Mercury’s weak magnetic field strength can be explained by a negative coupling of the internally generated magnetic field and the magnetic field originating from the solar wind. Due to the close distance to the sun, Mercury is exposed to a strong solar wind, which carries a magnetic field of high field strength. So-called Chapman-Ferraro currents occur at the magnetopause and induce a magnetic field which is anti-parallel to internally generated magnetic field. Therefore, Glassmeier et al. (2007) proposed that the long-term components of the externally generated magnetic field can diffuse down to the core-mantle-boundary, where it interacts with the dynamo field by reducing its field strength, which results in a less efficient dynamo, a so-called feedback dynamo.
Reduced kinematic dynamo models and also self-consistent dynamo models including the influence of an externally generated magnetic field showed that for a weakly driven dynamo and an initially weak seed magnetic field (e.g. after a field reversal), the weak magnetic field configuration can be maintained (Heyner et al. 2010, 2011a,b). For this effect an external field strength for roughly 10% relative to the internal magnetic field is needed. An earlier study by Gómez-Pérez and Wicht (2010) showed by imposing an external field with constant field strength and orientation on their fully developed dynamo models, that the external field is weakening the internal dynamo field until a reversal is triggered, however, without the external magnetic field a change in polarity would not occur. In this case, depending on the set of control parameters of the dynamo model, only 2 % of the external is sufficient to yield this effect. What is not considered in this study is the fact that after a field reversal the magnetosphere would rearrange itself and thus external magnetic field would return to an anti-parallel orientation. This reconfiguration of the magnetosphere would happen on much faster time scales than the dynamo process and therefore another field reversal would be triggered. What influence such a scenario has on the overall magnetic field strength, though, has yet to be investigated.
Vilim et al. (2010) proposed a dynamo model for Mercury’s core which relies on another type of feedback-mechanism. Assuming that the core temperature profile can cross the core material solidus twice somewhere in the middle of the core, a stably stratified iron snow region could form. This stably stratified layer would separate the core into two convecting regions both with an active dynamo process. Vilim et al. (2010) showed in their study, that these two separated dynamos enable a negative coupling of their generated magnetic fields, resulting in an overall weak magnetic field.
For both types of feedback dynamos, the models can not accurately reproduce the quadrupole-to-dipole (Heyner et al. 2011b) or octupole-to-dipole ratio (Vilim et al. 2010) given by the measurements of Mercury’s magnetic field. This shown by Fig. 19, which depicts the Mauersberger-Lowes spectrum (Eq. (34)) in terms of the spherical harmonic degree \(l\) of different dynamo models compared to results given by internal field models, which were discussed in the previous section. Of course, since only a limited data set in the available parameter space of the dynamo models was investigated, there is the possibility that the models could somehow manage to capture the right spectrum. Even if stronger convection would promote a more Mercury-like quadrupole-to-dipole ratio, it would also lead to a higher time variability, larger dipole tilts and stronger non-axisymmetric field contributions (Wicht and Heyner 2014).
Mauersberger-Lowes spectrum normalized to the dipole part for the three different field models of Anderson et al. (2011), Thébault et al. (2018) (model: M2) and Wardinski et al. (2019) (model: MB_a-n). As a comparison different dynamo models are also shown. Thick lines represent the field models and thin lines are the dynamo models.
As introduced in the previous subsection, there is the possibility of a stably stratified layer (thermally or compositionally) at the upper part of Mercury’s core. For that reason Christensen (2006) and Christensen and Wicht (2008) investigated the influence of such a layer in dynamo simulations as possible explanation for the weak and axisymmetric magnetic field of Mercury. In their models they assumed a thermally driven and stratified model with an inner core size up to 50% of the core volume which is in agreement with recent interior models (Knibbe and van Westrenen 2018; Genova et al. 2019). Since Olson and Christensen (2006) estimated that Mercury’s dynamo operates in a multipolar regime, where a magnetic dipole field is not dominant anymore, the typical parameters were chosen to set the dynamo in that regime. A threshold between the dipolar regime and multipolar regime can be quantified by the local Rossby number
where \(d\) is the typical flow length scale, \(\varOmega \) the rotation rate and \(U\) the rms flow amplitude (Christensen and Aubert 2006). In the dynamo models by Christensen (2006) and Christensen and Wicht (2008), the local Rossby number was \(Ro_{l} > 3\). With a stably stratified layer which occupied 28% of the upper part of the core the models showed a realistic magnetic field amplitude. Temporarily the dipole tilt was low and the right quadrupole-to-dipole ratio was reached, however, the system stayed strongly time-dependent and other contributions besides the dipolar field remained present.
Comparing the magnetic field at the surface with the field right beneath the stably stratified layer revealed, a magnetic skin effect due to the conducting layer is responsible for damping the strongly time-varying parts of the magnetic field. Studies by Christensen and Tilgner (2004) and Lhuillier et al. (2011) derived a scaling law for a spectral representation of the magnetic field which gives their typical time scales. These are roughly inversely proportional to the spherical harmonic degree, so \(\tau _{l} \sim \tau _{0}/l\), which would imply in the case of the magnetic skin effect, that small scale contributions would be damped more efficiently. From this scaling law, the axial dipole is excluded since it has a much longer time scale, than the simple rule would predict.
In addition to the magnetic skin effect, azimuthal flows in the stably stratified layer, which are triggered by lateral temperature differences (thermal winds) or the Lorentz force, can enhance the damping of non-axisymmetric contributions. The dynamo simulation clearly demonstrates that a stably stratified layer is an important component for explaining Mercury’s dynamo process.
Since a stably stratified layer is not sufficient enough to make the quadrupole-to-dipole ratio or a possible ‘dipole offset’ more persistent (cf. Fig. 19), three different studies proposed a solution to this problem. Cao et al. (2014) imposed a heat flux pattern at the core-mantle-boundary in their dynamo model which allows more heat to escape at low latitudes than in high latitudes. A symmetry-breaking between the northern and southern hemisphere is not caused by the choice of thermal boundary conditions itself, however, it leads to a convective flow which is much stronger in the northern hemisphere than in the southern one. Consequently, the type of convection generates a magnetic field which also breaks the north-south-symmetry and posses a persistent Mercury-like quadrupole-to-dipole ratio. Since the dynamo simulations do not include a stably stratified layer, other features of Mercury’s magnetic field, like the weak field strength, are not matched (cf. Fig. 19). Therefore, Tian et al. (2015) included a large stably stratified layer in their model, covering 35% of the core radius. Different to Cao et al. (2014), they assumed a heat flux pattern at the core-mantle-boundary where more heat escapes in the north than in south. Overall their results show a Mercury-like magnetic field which has a persistent quadrupole-to-dipole ratio, a realistic field strength and dipole tilt (cf. Fig. 19).
A weak point of the dynamo models by Cao et al. (2014) and Tian et al. (2015) is that, mantle convection models do not support the assumed heat flux patterns at the core-mantle-boundary, since they would be of small scale. Also, when mantle convection would have stopped long ago, the time-averaged insolation pattern could have diffused down to the core-mantle-boundary in roughly 500 Myr (Tosi et al. 2015). However, this insolation pattern would allow more heat to escape at high latitudes than in low latitudes, so opposite to the configuration of Cao et al. (2014).
With the more recent publication by Takahashi et al. (2019) another model is presented for Mercury’s dynamo process in the core. In their model, the authors consider a double-diffusive approach, where convection is driven by a mixture of thermal and compositional convection. Therefore two separate evolution equations are solved for those transport properties with a contrast of the molecular diffusivities of order 10. In planetary cores, however, the pure molecular diffusivities can differ up to a factor 1000 (Braginsky and Roberts 1995), which cannot be reached in their model due to numerical limitations. Like Christensen and Wicht (2008) and Tian et al. (2015) a thick thermally stratified layer is included on top of the liquid core, extending down to \(r_{s} = 0.5 \ R_{CMB}\). Different to Tian et al. (2015) a uniform heat flux is assumed overall at the core-mantle-boundary, but still the models show a similar, Mercury-like solution of the magnetic field.
To understand what causes the north-south-symmetry-breaking, it is helpful to look at the helicity \(h=\mathbf{u} \cdot (\boldsymbol{\nabla }\times \mathbf{u})\), particularly the axial helicity component \(h_{z} = u_{z} \cdot (\boldsymbol{\nabla }\times \mathbf{u})_{z}\), where \(z\) denotes the direction along the rotation axis, which is an important ingredient in dynamo simulations. Takahashi et al. (2019) showed that indeed the axial kinetic helicity is stronger in the northern hemisphere than in the southern, which is an explanation of the different dynamo action in the hemispheres. A purely kinematic dynamo simulation shows, that without the Lorentz force influencing the core flow, the magnetic field would have been a quadrupole dominated field with no distinct offset. Therefore, only the feedback of the magnetic field on the flow by the Lorentz force causes an asymmetry in the axial helicity between both hemispheres and hence a Mercury-like quadrupole-to-dipole ratio.
How the Lorentz force is triggering the symmetry-breaking is not clarified by Takahashi et al. (2019). Sreenivasan and Jones (2011) have shown that the Lorentz force can promote local helicity generation. This would in turn intensify the local magnetic field thus the Lorentz force, setting off a runaway growth, which could start with natural fluctuations and result in the stronger asymmetry found by Takahashi et al. (2019). This would also be possible in other dynamo simulations, but has not been reported so far.
A promoting feature could be the double-diffusive treatment of the core convection. The authors show that, indeed, the co-density approach (setting the thermal and compositional molecular diffusivities to equal values) gives a different convection pattern and therefore a different magnetic field structure, which is nevertheless dipolar but has no significant dipole offset. Without question, the double-diffusive treatment is a realistic treatment for core convection, since varying the thermal or compositional forcing results in different flow properties (Trümper et al. 2012). Therefore, it must be clarified if the presented type of convection and the symmetry-breaking dynamo is only achieved with a double-diffusive approach of the core convection or whether purely thermal (or codensity) driven convection is sufficient. The only other Mercury dynamo model using the double-diffusive approach have not shown the characteristic magnetic field structure (Manglik et al. 2010). However, Manglik et al. (2010) used a different set of parameters and so the main source of these discrepancies remain unclear.
In summary, BepiColombo will offer a better global coverage and separation of the different field contributions constraining the details of internally generated magnetic field. The magnetic field spectra beyond the spherical harmonic degree \(l=3\), maybe \(l=4\), will help to distinguish between the different dynamo models, hopefully limiting the variety of possible models. We may even be able to constrain the size of the inner core or the thickness of the stable layer based on magnetic observations. A comprehensive geophysical interpretation of magnetic and geodetic constraints on Mercury’s internal structure will be then fundamental to enhance our knowledge of its deep interior.
3.6 Influence of Instrument Calibration on the Hermean Main Field Determination
One of the major instrument science goals is to extend our knowledge about the internal field geometry represented by Gauss coefficients. In this section, the impact of different error sources on the determination of the Hermean internal magnetic field during the BepiColombo mission is analyzed. For this purpose, a parameter study is performed, in which the effect of instrument offset and orientation errors on the Gauss coefficient determination are examined. A synthetic magnetic field is computed at realistic MPO satellite positions by means of a spectrally extrapolated main field model. These virtual measurements are disturbed with an offset as well as orientation errors. From these data, an inversion is performed and the result is compared with the original Gauss coefficients.
Realistic positions of the BepiColombo MPO spacecraft are derived starting from 15 March 2026 until 14 March 2027 with 1 s resolution, using SPICE.Footnote 1 This results in about 31.5 million positions, covering a distance to the planetary surface of about \(331...1649\) km.
The internal magnetic field representation is defined with respect to the Mercury-Body-Fixed coordinate system. The MBF is defined as a co-rotating (with respect to the planetary rotation) and planetocentric frame with radius \(r_{\mathrm{MBF}}\), the co-latitude, \(\theta _{\mathrm{MBF}}\), and the longitude, \(\varphi _{\mathrm{MBF}}\) as spherical coordinates. The latitude is measured positive northward from the equator and the longitude positive eastward from the prime meridian.
From these positions defined in both coordinate systems, a random subset of \(1/3\) of the data points is selected to account for general magnetic quiet conditions. Furthermore, the subset is reduced to positions on the night side of Mercury as it is expected that the magnetic field is more quiet there.
In order to calculate the magnetic field for each position, the Gauss coefficients given by Anderson et al. (2012) are extended to a degree of \(l = 6\) by linearly (in log-space) extrapolating the Mauersberger-Lowes-spectrum (Mauersberger 1956; Lowes 1966; Olsen et al. 2009). Between the \(g\) and \(h\) coefficients each contribution is distributed with a ratio of about \({100:1}\), roughly following the ratio given by Anderson et al. (2012). The resulting coefficients are shown in Table 4. Each coefficient not shown is set to zero.
For each position the resulting internal magnetic field in spherical coordinates is then calculated using the standard spherical harmonic expansion in Eq. (32)-(33).
Two types of errors are added to the calculated field: measurement offsets in each sensor axis as well as a fixed sensor rotation around one of the sensors axes. These errors are added to data in a MPO_MAG_BOOM coordinate system as a representative for the sensor coordinate system. A rotation angle of \(1^{\circ }\) is motivated by a very conservative estimate of the design accuracy by ESA. The offset accuracy of 1 nT is a conservative design goal.
After adding these different types of errors the magnetic field data is transformed back into MBF coordinates, then to spherical coordinates and finally the new Gauss coefficients are determined using a standard singular value decomposition method (Aster et al. 2013) without regularization. Figures 21 – 24 show the results of our analysis. In Fig. 21 the undisturbed case is shown. All of the Gauss coefficients are resolved with an absolute difference of less than 0.01 pT.
Adding a sensor misrotation around the \(x\)-axis of \(1^{\circ }\) results in absolute differences of up to a few 100 pT for higher orders of \(m\), Fig. 22. Coefficients with \(m<2\) show differences to the model of only a few 10 pT. The relative error lies in the range of \(60-100\)% for higher \(l\) (and \(m = 1\)).
Figure 23 shows the impact of only the offset errors of 1 nT on each sensor axis. The absolute difference to the model lies between sub-pT and mostly a few 10 pT. The coefficients \(g_{6}^{1}\) and \(h_{6}^{1}\) show relative differences of about 100%. Taking into account that these coefficients have values of less than 1 pT in our model, the inaccuracy is almost negligible.
Combining both error sources as in Fig. 24 again results in absolute differences of about 0.8 nT and relative differences of about 100% for the high \(g_{l \geq 5}^{m=1}\) coefficients. For better comparison of the more dominant \(g_{l}^{0}\) coefficients Fig. 20 shows the relative difference of these coefficients to the model separately. Our analysis shows what to expect for the Hermean main magnetic field determination from the upcoming BepiColombo mission in the first Earth year of operation. Using our described model Gauss coefficients up to a degree of \(l = 6\) can be resolved with a relative difference of about 100% but an absolute difference of a few pT.
So far the magnetic field of the planet Mercury is only well-known to a degree of \(l = 4\) in a spherical harmonics representation. Beyond this, we can only deduce an upper limit. To what degree we will be able to resolve the magnetic field is not possible to determine yet, as this depends on the strength of the coefficients as well as the yet to be determined attitude knowledge. But assuming a reasonable model as presented, we can expect to extend our knowledge of the Hermean main magnetic field at least to a degree of \(l = 6\) during the main mission phase.
In conclusion, the ability to constrain the time-dependent instrument and spacecraft induced offsets during the orbital mission phase will have an impact on the inversion results. It has to be stressed here, that the attitude knowledge can have the same impact on the inversion results as the offset knowledge. Including more data from MMO and from a larger time interval (including data from a possible mission extension) could improve the outcome of the inversion. If we assume, that there is no significant secular variation of the internal field, we could also involve the MESSENGER magnetic field data in the inversion.
3.7 Influence of the BepiColombo Orbit on the Hermean Main Field Determination
A unique expansion of the field in spherical harmonic functions requires dense and evenly distributed data. Any departure from this ideal distribution of measurement points means that alternative representations with different sets of Gauss coefficients are possible. These coefficients appear to be correlated. The orbit of MESSENGER only permits planetary magnetic field measurements in the northern hemisphere, which means that equatorially symmetric and anti-symmetric contributions are difficult to distinguish. In consequence, different field models may explain the observations equally well.
The Gauss coefficient correlation due to orbital restrictions may be quantified as follows. The spherical harmonic representation may be written as a linear vector transform:
Here, \(\underline{\underline{A}}\), \(\underline{m}\) and \(\underline{b}\) stand for the design matrix (only depending on the measurement locations), the Gauss coefficient vector and the magnetic field measurements vector, respectively. As the internal and external magnetic fields are ordered in different coordinate systems, we need to split the design matrix \(\underline{\underline{A}}= \left (\underline{\underline{A}}_{\mathrm{int}}\bigg |\underline{\underline{A}}_{\mathrm{ext}}\right )\) and the coefficient vector \(\underline{m}= \begin{pmatrix} \underline{m}_{\mathrm{int}} \\ \underline{m}_{\mathrm{ext}} \\ \end{pmatrix}\). The internal part is defined with respect to the MBF frame.
The external magnetic field is represented in the MSO-frame as the magnetospheric field is expected to be ordered in this frame (rather than in the MBF frame mentioned above). This frame is also planetocentric, but the \(X\)-axis points towards the sun, the \(Z\)-axis is anti-parallel with respect to the dipole axis and the \(Y\)-axis completes the right-handed system. Because the dipole axis of Mercury is almost perfectly aligned with the rotational axis, the \(Z\)-axis is chosen to point along the rotational axis.
The correlation matrix \(\underline{\underline{R}}\) is derived from the model parameter covariance matrix \(Cov(\underline{m}) =: \underline{\underline{\varSigma }}\). Following Menke (2018), this matrix is defined as
Here, \(\sigma _{d}\) stands for the data a-priori variance, that may be derived from the, e.g., measurement uncertainty. Then, Fahrmeir et al. (2003) define the correlation matrix:
According to this definition, the model parameter correlation matrix only depends on the measurement locations (and not e.g. on the measurement error).
Despite a large number of measurements of the in-situ magnetic field, strong correlations of the Gauss coefficients are expected, because of MESSENGER’s highly eccentric orbit with its pericenter in the northern hemisphere. Johnson et al. (2018) and Thébault et al. (2018) analyzed the model parameter correlation. If one would only rely on the standard spherical harmonic representation of internal and external fields, this yields strong and important correlations (or anti-correlations) between the following coefficient pairs (up to a degree of 4):
-
\(g_{1}^{0} \leftrightarrow g_{2}^{0}\)
-
\(g_{1}^{0} \leftrightarrow g_{3}^{0}\)
-
\(g_{1}^{0} \leftrightarrow g_{4}^{0}\)
-
\(g_{1}^{0} \leftrightarrow G_{1}^{0}\)
-
\(g_{1}^{0} \leftrightarrow G_{2}^{0}\)
-
\(g_{2}^{0} \leftrightarrow G_{1}^{0}\).
Other correlations not stated here may be strong but at the same time irrelevant as the respective coefficients are negligible in the case of the Hermean magnetic field assessed by the MESSENGER mission. The correlation matrices for the internal Gauss coefficients up to degree six for the MESSENGER mission is shown in Fig. 25 (top). In the case of the MPO orbit, the internal correlation is negligible except for weak correlations between coefficients with a difference of 2 in the coefficient’s degrees. A further complication in the Gauss coefficient determination arises from the presence of relatively strong external fields from the magnetosphere. These may correlate with the internal field in the field inversion. Due to the orbital restrictions of MESSENGER, there are strong correlations between the internal and external fields as shown in Fig. 26. In contrast to this, the respective correlation in the case of the MPO orbit seems much weaker but noticeable. From this result, it is clear that a determination of the low-degree Gauss coefficients must involve additional information on the external field contributions, such as magnetospheric models.
3.8 Crustal Magnetic Fields
The characterization of the present-day temporal evolution (if any) of the Hermean internal magnetic field is difficult. During the MESSENGER mission, no clear secular variation was observed. The comparison of the field measured between 2011 and 2015 and that measured with Mariner 10 in \(1974-75\) is also inconclusive: the dipole coefficient \(g_{1}^{0}\) may have remained constant or varied by up to 10% (Philpott et al. 2014). Its past behavior, on longer time scales, can however be assessed by looking at the signature the ancient magnetic field of Mercury left into the superficial Hermean rocks and minerals, as done on the Earth, Mars or on the Moon (Langlais et al. 2010). The low altitude measurements of MESSENGER at the end of its mission around Mercury provided the opportunity to study these signatures, expected to be associated with short wavelengths and small amplitudes. This precluded such studies before MESSENGER reached a periapsis lower than 100 km, which happened in August 2014, eight months before the end of the mission. During this period MESSENGER orbit was corrected several times, to extend the duration of the mission as long as possible. Its periapsis remained under 100 km altitude between August 2014 and October 2014, and then from January 2015 until the end of April 2015 when MESSENGER crashed into the surface (Johnson et al. 2016b). Because the crustal magnetic field is small, the measurements needed first to be corrected for other magnetic contributions, such those from internal (main field) and external (magnetosphere) origins. Two slightly different techniques have been considered and are described below. Johnson et al. (2016a) corrected the measurements by using different models, first for the shifted dipole core field (Johnson et al. 2012) and then for the magnetospheric field Korth et al. (2015). The remaining field components, or residuals, have amplitudes reaching 10 s of nT, with associated wavelengths at ca. 1500 km. Johnson et al. (2016b) observed that the residual fields changed significantly from one orbit to the next adjacent one, revealing the temporal and dynamic characteristics of these residuals. This is inconsistent with magnetic field sources located in the crust of Mercury, and required additional corrections. They further high pass filtered the residuals in a frequency band, to remove long wavelength (\(<0.002\) Hz, or about \(> 1900\) km at periapsis) and to retain all short wavelength (\(> 0.0075\) Hz, or \(< 500\) km) signals. Very rapid fluctuations, \(> 1\) Hz (or about 4 km at periapsis) were attributed to be of external origin and not considered in their crustal field maps. They compared measurements acquired during two different periods above the same area but at slightly different altitudes. These are shown on Fig. 27, for a small region of the planet extending from 180 to \(240^{\circ }\) E and from 50 to \(80^{\circ }\) N. Alternate bands of radial polarities are found, with a SW-NE main direction. In a series of papers, Hood (2015, 2016), and Hood et al. (2018) considered MESSENGER measurements without making any a priori on the otherwise modeled contributions. They instead applied a two-step filtering techniques to isolate the radial crustal field. First, they fitted a cubic polynomial to each orbit independently to identify and subtract the long wavelength signal, of internal (core) and external origin. Next they computed along-track running averages, to filter out the smallest scale variations of external origin. A maximum wavelength of \(5^{\circ }\) (or about 200 km) is kept. They manually screened the remaining residuals and eliminated those features not repeating on adjacent tracks (i.e., associated with transient features of external origin). Their result is also shown on Fig. 27, right panel, adapted from a larger area shown in Hood (2016). In order to build their map, field residuals are binned and smoothed on a geographic mesh. As a result, magnetic features can be longitudinally interpolated, even though the altitude may vary across the mapped area. The visual comparison of the two maps, produced by two different approaches, shows a very good correlation. There are what seems to be longitudinally elongated features, reaching slightly over 10 nT at the minimum spacecraft altitude. Over Fig. 27 (right), this minimum altitude is below 15 km, at an almost constant latitude slightly south of \(60^{\circ }\) N, between 180 and \(220^{\circ }\) E longitudes. At this altitude, the crustal field represents a few percent of the core field. This is stronger than the Earth’s crustal magnetic field at comparable relative altitude (Thébault et al. 2016). In terms of absolute values, it is similar to the Lunar magnetic field anomalies (e.g. Purucker and Nicholas 2010), but 2 orders of magnitude lower than the Martian crustal magnetic field (Langlais et al., 2019). Globally, the strongest fields are found over a wide area which extends from 120 to \(210^{\circ }\) E. This area is marked by numerous smooth crater terrains, and comprises the northern rim of Caloris basin, the largest impact geological feature on Mercury. On the other side of the planet, where weaker fields are found (Hood et al. 2018), the topography is marked by volcanic plains and cratered terrain. These anomaly field measurements have been further analyzed, first to construct altitude-normalized maps, second to characterize the properties of the crustal magnetic field sources, and third to derive constraints on the ancient Hermean magnetic field which was present when those crustal sources acquired their magnetization. This is because these crustal sources are not associated with induced magnetic fields (Johnson et al. 2015; Hood et al. 2018). Altitude-normalized maps essentially rely on the Equivalent Source Dipoles (ESD) technique, which has been extensively used to model the Martian crustal magnetic field (Purucker et al. 2000; Langlais et al. 2004). In this approach, the field measured at some altitude is assumed to result from magnetized sources homogeneously located below the surface. The magnetization direction can be a priori assumed in any direction, although it can be also be let free and inverted during the modelling process. The dipole mesh has to be as equi-surface as possible. Inversion is highly non unique, and it is necessary to carefully monitor the evolution of the solution as well as that of the remaining unmodelled fields to ensure model convergence. Hood (2015, 2016), Hood et al. (2018) used a mesh resolution with \(1^{\circ }\) (42 km) latitudinal and \(2^{\circ }\) (between 20 and 75 km) longitudinal separations, between \(35^{\circ }\) and \(75^{\circ }\) N, and over all longitudes in their different studies. Johnson et al. (2016b, 2018) used instead a spherical-triangle mesh, with a finer lateral resolution of 20 km. They all assumed a constant depth of 20 km. The thickness was set to 10 km, but this parameter is not a critical one, as only the product of the thickness by the magnetization can be assessed. These studies generally agree on the large scale distribution of the crustal field magnetic anomalies. At 40-km constant altitude, and for the available latitude band (north of \(35^{\circ }\) N) the magnetic field peaks at 8 nT in the vicinity of the Caloris basin, between 120 and \(180^{\circ }\) E. On the other side, the magnetic field is weaker, up to 6 nT, and more patchy too. There is no broad scale correlation with gravity field anomalies, with magnetic anomalies found above both positive and negative free-air gravity anomalies (Hood et al. 2018). Some magnetic features are located above or very close to impact craters. The most preeminent ones are located close to the northern rim of Caloris basin, but their spatial scales are much lower than the diameter of the basin, at 1550 km. A few other smaller craters, between 130 and 300 km diameter, are associated with magnetic field anomalies of comparable scales. Hood et al. (2018) investigated whether these fields could be related to stronger-than-average induced magnetic fields, caused by local enrichment of iron brought by the impactor. They concluded that this is very unlikely, confirming the results of Johnson et al. (2015) at the global scale. More recently, Oliveira et al. (2019) examined five magnetic field anomalies located above impact craters, and focused on magnetization directions, using a method previously used on the Moon and on Mars (Oliveira and Wieczorek 2017; Thomas et al. 2018). This can indeed be used to infer properties about the magnetic field which was present when the magnetization was acquired, when the rock cooled down. Assuming the directions are homogeneous throughout the magnetized body (Merrill and McFadden 2003), one can indeed compute the location of the magnetic paleopole. If different from the current magnetic pole, one generally interpret this as an evidence of a temporal evolution of the magnetic field and/or movements (translation or rotation, usually known by true polar wander) of the magnetized unit since it was put into place. Their results are two-fold. First the studied magnetic field anomalies are not aligned onto the current magnetic field, as each anomaly points towards a magnetic pole which is distinct from the rotation pole. Second, and taking into account uncertainties, it is possible that this anomalies are aligned onto a unique paleopole, which would lie between 30 and \(80^{\circ }\) N latitude, and 0 and \(120^{\circ }\) E longitude. These results strongly suggest that the Hermean magnetic field evolved in the past, possibly in association with polar wander. The difficulty to unambiguously interpret these results highlights the needs for additional measurements and analyses.
left: Along-track magnetic field measurements of the radial crustal field, corrected from model contributions and filtered. Orbits are from September 2014 and March 2015, with altitudes varying from 14 to 60 km. The rim of the Shakespeare basin is plotted. Dark and light gray colors denote smooth and intercrater plains, respectively. Reproduced from Johnson et al. (2016b). right: Average radial magnetic field intensity at the spacecraft altitude. Measurements were acquired in April 2015, detrended and filtered. Contour interval is 2 nT, negative contours are dashed blue, positive contours are red. Adapted from Hood (2016).
The resolution of local magnetic anomalies critically depends on the spacecraft distance from the planetary surface. The pericenter evolution of the two BepiColombo probes is shown in Fig. 28. Beginning of 2027, the MPO pericenter is still expected to be more than 300 km, which strongly limits the detectability of magnetic anomalies with spatial scales below this, if the magnitudes are similar to those observed by MESSENGER. Interestingly, the Mio orbit declines faster and in 2028 we expect Mio to have a lower pericenter altitudes than MPO which puts Mio in the position to detect crustal anomalies, provided that the satellite survives the extreme temperature conditions this long.
3.9 Induction
Mercury has the highest uncompressed density of any known body in the Solar System due to its very large, ca. 2000 km radius, predominantly iron core (Hauck et al. 2013; Johnson et al. 2016a). Beyond the generation of a planetary magnetic field, Mercury’s interior has major impacts upon its interaction with the solar wind due to its thin, low-conducting mantle (ca. 400 km thick) and huge, highly-conducting iron core. This creates a situation with changes in the magnetospheric magnetic field at Mercury’s surface can diffuse down through the mantle in ca. 1 to 10 min, but they are effectively shielded from the iron core where the time for such a change to diffuse to the center of the planet is estimated to be of the order of \(10^{4}\) yr (equivalent to \(3 \cdot 10^{-12}\) Hz) (Heyner et al. 2011b). Given this general interior electrical conductivity profile, it can be concluded that there is only very weak “line-tying” of magnetic fields in Mercury’s crust, but very strong line-tying within 2000 km of the center of the planet. The first theoretical models of induction currents driven by such rapid increases in solar pressure and their ability to compress Mercury’s dayside magnetosphere were due to Hood and Schubert (1979) and Suess and Goldstein (1979) predicted that step-like solar wind pressure increases to ca. 50 to 200 nPa might be needed to compress the dayside magnetopause to Mercury’s surface (i.e. trapping the closed magnetic flux in the crust between the solar wind at higher altitude and the highly conducting core below). Figure 29 depicts the effect of such a sudden solar wind pressure increase with the closed dipolar magnetic fields in the dayside magnetosphere colored according to their source. The dipolar magnetic fields due to the core dynamo are shown in yellow while the magnetic fields due to induction are in green. In this manner the net effect of the induction currents in the interior is to “stiffen” the closed magnetic fields due to dynamo action deep in the core through the addition of closed magnetic flux due to due to shallow induction currents on the surface of Mercury’s core that must act to oppose any change in the magnetic field in the core.
(a) Increases in solar wind pressure drive induction currents (green loops) at the top of Mercury’s large iron core. The sense of these currents is to oppose the compression of the intrinsic magnetic field (yellow) by generating additional magnetic flux (green field lines) that, when added to the intrinsic flux, acts to balance the increased solar wind pressure. (b) Magnetic reconnection between the interplanetary magnetic field and the intrinsic planetary magnetic field opposes the effectiveness of induction by removing magnetic flux from the dayside magnetosphere and transporting it to the tail (from Slavin (2004)).
However, as illustrated in Fig. 29, magnetic reconnection at the dayside magnetopause transfers magnetic flux to the nightside magnetosphere and reduces the distance from the center of the nose of magnetosphere where the solar wind is “stood-off” by the planetary magnetic field. Slavin and Holzer (1981) scaled Earth observations of the reduction in the radius of the dayside magnetosphere due to reconnection to Mercury. This study, which predated the induction analysis of Hood and Schubert (1979), predicted that the dayside magnetopause might be frequently eroded to the surface when the IMF was southward and reconnection rate maximized (see also Heyner et al. (2016)). Slavin et al. (2014) and Jia et al. (2019) investigated electromagnetic response of Mercury’s interior to solar wind pressure increases and the effects of magnetopause reconnection using analytical and global magnetohydrodynamic simulations. As shown in Fig. 30 these studies found only 8 passes through Mercury’s dayside magnetosphere for which the magnetic field just inside of the magnetopause exceeded 300 nT, as compared with more typical values of about 150 nT in the absence of CMEs or HSSs. The upstream solar wind ram pressures were estimated to range from app. 40 to 90 nPa and they appeared due primarily to coronal mass ejections. CMEs at Mercury carry about 3 to 5 times the mean ram pressure observed at Mercury (i.e. about 10 to 15 nPa; see Winslow et al. (2013)). For this reason, Jia et al. (2019) termed these Highly Compressed Magnetospheres (HCM) passes.
The extrapolated standoff distance of the nose of the magnetopause, \(R_{\text{ss}}\), is plotted against the upstream solar wind dynamic pressure, \(p_{\text{sw}}\), for each of the eight highly compressed dayside magnetosphere (HCM) and four disappearing dayside magnetosphere (DDM) intervals. The individual magnetopause crossings are displayed as square symbols with the size of box proportional to the dimensionless reconnection rate. A Chapman-Ferraro (CF) sixth root of \(p_{\text{sw}}\)-curve intersecting the mean \(10-15\) nPa standoff distance determined by Winslow et al. (2013) is the lower dashed line. The upper dashed line (black) is a theoretical model of the compression of Mercury’s dayside magnetosphere by Glassmeier et al. (2007) that includes the effects of induction in Mercury’s interior (from Slavin et al. (2019))
In Fig. 30, the solar wind dynamic pressure is shown on the vertical axis and the distance to the nose of the magnetopause, \(R_{ss}\), is on the horizontal axis (see Slavin et al. (2014)). The \(p_{sw}-R_{ss}\) relationship derived by Glassmeier et al. (2007), which includes the effects of induction, but not reconnection in Mercury’s interior, is shown as a bold dashed line to the right of the Chapman-Ferraro curve. The Chapman-Ferraro model predicts that the nose of the magnetopause should be compressed down to Mercury’s surface for a solar wind dynamic pressure of 90 nPa. This pressure increases to 200 to 250 nPa when the effects of induction currents on the surface of Mercury’s iron core at taken into account (Glassmeier et al. 2007; Hood and Schubert 1979). Jia et al. (2019) found that the induction currents increased the planetary magnetic moment by up to about 25% during these intense solar wind pressure events. These relatively large increases driven by CMEs stand in contrast with the more modest, ca. 5%, increases in total magnetic moment that have been reported in association with the smaller increases in solar wind pressure as Mercury moved from perihelion to aphelion (Zhong et al. 2015a; Johnson et al. 2016a). Finally, Fig. 30 also displays the locations and estimated solar wind ram pressures for the dayside disappearing magnetosphere events recently reported by Slavin et al. (2019). They identified four low-altitude MESSENGER passes over the dayside hemisphere for which no dayside magnetosphere, only magnetosheath plasma was observed. The magnetopause was not crossed during these passes until the spacecraft was at very high-latitudes just forward of the terminator plane. Slavin et al. (2019) termed these intervals “disappearing dayside magnetosphere” (DDM) events. As shown in Fig. 30, the DDM passes correspond to the most extreme solar wind pressures with \(p_{\text{sw}}\) in the range \(140...290\) nPa. Further, the draped interplanetary magnetic field in the magnetosheath during these DDMs were extremely southward with \(B_{z}\) in the range \(- 100...-400\) nT. The size of the boxes in Fig. 30 represent the individual magnetopause crossings and they are proportional to the dimensionless reconnection rate, i.e. \(\alpha =B_{N}/B_{MP}\), determined for each magnetopause crossing from the MVA analysis as described in DiBraccio et al. (2013). As shown, the dimensionless reconnection rates ranged from 0.01 to 0.29 with the lower rates corresponding mostly to the HCM events and the highest rates to the DDM events. The magnetopause crossings in Fig. 30 with the highest reconnection rates, i.e., the larger boxes, are associated with the DDM events and these events are located to the left of the Chapman-Ferraro curve These events have extrapolated subsolar points below the surface, that is, \(R_{\text{ss}}< 1\). In contrast, the HCM events with the highest magnetopause reconnection rates are located closer to the Chapman-Ferraro curve and the crossings with the smallest dimensionless reconnection rates are located closest to the curve on the right-hand side that includes the effects of induction Glassmeier et al. (2007). Overall, these results suggest that reconnection-driven dayside magnetic flux transfer to the magnetotail and the addition of closed magnetic flux to the dayside magnetosphere due to induction currents are in approximate balance for these highly compressed dayside magnetosphere events (see Heyner et al. (2016)). For this reason, the HCM events do not appear to expose the dayside to direct solar wind impact; that is, their \(R_{\text{ss}}\) values are greater than 1. These conclusions are strongly supported by the global MHD simulations of the solar wind interaction with Mercury’s magnetic field and conducting iron core by Jia et al. (2019). Slavin et al. (2019) suggested that these DDM events, which are all associated with CME impacts, are due to extreme solar wind compression and/or reconnection-driven erosion of the dayside magnetosphere. It is likely that the solar wind directly interacts with the surface over much of Mercury’s sunlit hemisphere during DDM intervals. This solar-wind-surface interaction can also be examined with Earth-based telescope observations of emissions from Na-atoms released from the surface by sputtering. Orsini et al. (2018) report about non- standard Na-emissions in equatorial regions during an ICME transit interval – suggesting a disappearing magnetopause. These emissions are as bright as the emissions attributed to the magnetospheric cusps. The dual-spacecraft observations to be returned by this mission will likely provide much new data on the sources of Mercury’s exospheric neutrals and magnetospheric ions.
Induction at planet Mercury at different frequencies may be used to magnetically sound the planetary interior. In order to estimate the ratio of induced to inducing fields (so-called Rikkitake-function) at various inducing frequencies, we use the method described by Seufert et al. (2011). Their expression for the Rikkitake-function was slightly corrected by Heyner et al. (2016). For the internal conductivity structure, we employ two radial conductivity profiles from Zhang and Pommier (2017), who used a multi-anvil apparatus to study metal-olivine systems at Hermean core-mantle boundary pressures. These profiles consist of 5 nested spherical shells of constant conductivity. One profile represents a lower bound of conductivity whereas the other profile stands for an upper bound from the experimental studies by Zhang and Pommier (2017). These two profiles are listed in Table 5. We evaluate the Rikkitake-function by Heyner et al. (2016) for a uniform inducing field at these conductivity profiles for frequencies in the range \(10^{-15}\) Hz to \(10^{4}\) Hz. This vast range is required to explore the full range of inductive responses from the interior conductivities in consideration. The result is shown in Fig. 31. Frequencies below \(10^{-12}\) Hz (inaccessible to the BepiColombo mission) are needed to penetrate through the core. In contrast to this, the 88d and 44d excitation frequencies from the elliptic planetary revolution around the sun have the potential to constrain the conductivity at the core-mantle boundary. A signal could also be expected from the frequent passage through the heliospheric neutral sheet, which should roughly happen with a period comparable to the solar rotation period (642 h). The upper layers of the mantle should be sensitive to excitations with time scales comparable to the magnetospheric Dungey-cycle (2 min) or Kelvin-Helmholtz frequencies at the Herman magnetopause (\(\approx 30\) mHz, see e.g. Liljeblad and Karlsson (2017b)) which have been assumed to drive Field-Line Resonance events in the magnetosphere (James et al. 2019a).
In order to experimentally check parts of the Rikkitake-function with physical processes at certain frequency bands (see above) as induction driver, we need magnetic field measurements of the driver (i.e. far away from the planet) as well as from the inductive response (i.e. close to the planet) within the magnetosphere. Thus, the BepiColombo mission with one satellite far away from the planet (Mio) and one close to the planet (MPO) is particularly well-suited for this endeavor.
3.10 Field-Aligned Currents
Besides other currents, field-aligned currents (FAC) play a vital role in the magnetospheric current structure. At Earth, high latitude, Region-1-FAC (R1) connect the magnetopause region with the ionosphere, while medium latitude, Region-2-FAC (R2) connect the ionosphere with the equatorial ring current / plasmasphere. At the ionospheric foot-points of these R1 and R2, incoming/outgoing currents are closed via lateral Pedersen currents within the dense terrestrial ionosphere (Ganushkina et al. 2015), as depicted in the upper panel of Fig. 32.
Example for Field aligned current system at Earth and Mercury. Adapted from Anderson et al. (2014).
At Mercury, first observations of singular FAC-events were presented by Slavin et al. (1997), who analyzed magnetic field observations of Mariner 10 flybys and estimated electrical current densities of about \(70\ \text{nA}/\text{m}^{2}\) for these events. In the MESSENGER era, a systematic analysis of FAC at Mercury could be carried out in the northern hemisphere using continuous in-situ magnetic field observations. In their analysis, Anderson et al. (2014) found two distinct field-aligned current signatures that are located at high latitudes at dusk and dawn and identified as them as R1. The magnitude of these currents at Mercury vary from \(50~\text{nA}/\text{m}^{2}\) to \(200~\text{nA}/\text{m}^{2}\) and seem to be highly dependent on the disturbance index of the magnetosphere (Anderson et al. 2013, 2018). The apparent absence of R2 in the observations has been attributed to be due to two likely scenarios. Either the sodium exo-ionosphere of Mercury appears to be too tenuous to carry significant currents in the global current structure (Raines et al. 2015), which inhibits the formation of a R2-system in the Hermean magnetosphere. Or the R2-system exists below the altitudes that could be covered by MESSENGER, i.e., in the vicinity of the magnetic equator (Anderson et al. 2014). However, Mercury itself occupies such a large volume within its magnetosphere and Russell et al. (1988a) as well as Baumjohann et al. (2010) argued that the hypothetical Hermean plasmasphere and ring currents would be located beneath the planetary surface. Hence, any R2-FAC connected to the ring current could not exist in the Hermean magnetosphere.
Generally, the R2-system is a necessary part in the global conservation of momentum, plasma transport and closure of the R1-system (Ganushkina et al. 2015). Therefore, understanding how the R1-system is closed without a significant ionosphere is of vital importance for the closure of the global Hermean current system. In order to tackle this problem, Janhunen et al. (2004) and Anderson et al. (2014) proposed a model in which the R1 are penetrating radially through Mercury’s resistive mantle and close by lateral currents along the core-mantle-boundary (CMB), see bottom part of Fig. 32. Such currents at the CMB have been successfully reproduced within global simulation models in MHD by Dong et al. (2019a) and hybrid (kinetic ions, fluid electrons) by Exner et al. (2020).
In the latter study, Exner et al. (2020) presented how the R1-system is formed around Mercury with an IMF that is nearly parallel to the Y-Axis. The global FAC-system in the terminator plane as seen from the tail is shown in panel (a) of Fig. 33. To facilitate a direct comparison to the results of Anderson et al. (2014, 2018) and Dong et al. (2019a), we calculate the field-aligned part of the current density in Fig. 33 as follows:
Thus, red areas/positive values in the upper panel and the middle panel depict field-aligned currents that flow anti-parallel to the local magnetic field, while blue areas/negative values represent field-aligned currents in the same direction as the magnetic field. The currents associated with the R1-system are sketched with black arrows. The formed system is mostly in agreement with the sketch from the bottom panel of Fig. 32, except that it is rotated significantly due to the strong \(B_{y}\)-component of the IMF. The azimuthal movement of the cusp region at Mercury has been empirically modeled by He et al. (2017) and is in agreement with this outcome of the hybrid simulation. One significant difference is the asymmetric feature of the R1 in the equatorial region, as indicated by a green ellipse at dawn. It appears that the rotation of the R1-system is enough to let the southward directed FAC from the northern hemisphere merge with the northward directed FAC of the southern hemisphere. In consequence, a significant portion of the northern current system is directed to the southern dawnside surface. The red dashed line indicates the dawnside section of a MPO trajectory that has its closest approach at dawn. The modeled magnetic field magnitude and FAC along this trajectory are shown in Fig. 33 (c) with black lines. Along the trajectory, only one significant feature in the FAC can be observed near the region of lowest magnetic field, i.e., at a latitude of 10 degrees south. The maximum value of the FAC amounts to \(40\ \text{nA}/\text{m}^{2}\) which is in agreement with values from Anderson et al. (2018) for a minimum disturbance index.
(a) and (b): FAC in the terminator plane as seen from the nightside. The black and green arrows show the direction of the R1 and R2 systems, respectively. The red dashed line denotes the dawnside portion of a MPO trajectory with its periherm at dawn. These panels have been adapted from Exner et al. (2020), in which the MASO coordinate system is used. (c): Magnetic field magnitude and FAC of the model runs without and with a 50-fold exosphere along the red trajectory in black and blue lines, respectively. The orange boxes denote the trajectory sections for R1 and R2 as obtained from the model run with a significant (50-fold) exosphere.
As previously mentioned, direct observations and models of the sodium exosphere yield only tenuous amounts of sodium ions inside the magnetosphere. However, in a recent study of field-line-resonances of MESSENGER MAG data, James et al. (2019a) could derive sodium ion densities at the dayside surface that would amount to values of about \(22\ \text{cm}^{-3}\), which are about three to four orders of magnitude larger than anticipated from MESSENGER FIPS observations (Andrews et al. 2007; Raines et al. 2015).
To investigate how such a dense exosphere affects the global magnetosphere of Mercury, Exner et al. (2020) included an exosphere model that is based on a realistic sodium exosphere model (Gamborino et al. 2019) but with an increased exospheric density to obtain a sodium ionosphere that agrees with the values derived from James et al. (2019a). It has been found, that the presence of such an enhanced exosphere leads to an additional thermal counter-pressure at the magnetopause boundary against the magnetosheath plasma, which results in a significant upstream displacement of the magnetopause location by up to \(0.3R_{M}\) from the average value as obtained by Winslow et al. (2013). The features within the magnetosphere become symmetrized as it seen in panel b of Fig. 33, in which the equatorial asymmetry of the FAC-system at dawn is reduced. The magnetospheric volume increase furthermore allows for the formation of a sodium ring in the equatorial plane (see also Yagi et al. (2010, 2017)). As such, new, R2-currents have emerged below the R1-system, as indicated by green arrows in panel b of Fig. 33 (b). These currents reach an altitude of about \(0.3~R_{M}\) and lie therefore below altitudes covered by MESSENGER in these regions, as Anderson et al. (2014) proposed. However, it seems that the presence of an exosphere is also a necessary factor in the formation of R2-currents.
As the closest approach of the MPO spacecraft lies well below \(0.3~R_{M}\), these additional currents can be observed along the MPO trajectory as seen via the blue lines in panel c of Fig. 33. The orange background boxes denote the trajectory sections in which R1 and R2 can be observed. Here, the two R1-sections exhibit values of \(-20\ \text{nA}/\text{m}^{2}\) and \(40\ \mathrm{nA/m^{2}}\), respectively. The R2-section occupies a range of about 36 degrees and amount to a value of \(20\ \mathrm{nA/m^{2}}\), which is up to a factor of 2 lower than the neighboring R1-system. It may be, that the analysis of FAC by Anderson et al. (2014) could not resolve R2-features as their magnetic fields would be masked by the neighboring R1 currents signatures of larger magnitude.
In conclusion, the FAC-systems at Mercury depend on multiple factors, out of which the \(B_{y}\)-component of the IMF and influence of a sodium exosphere have been presented here. The multi-point observations of the magnetic field with the BepiColombo mission will potentially reveal how the presented factors affect the magnetosphere and is well-suited to provide an answer to open questions regarding the FAC at Mercury.
3.11 Wave-Particle Interactions in the Hermean Magnetosphere
Understanding how energy is transferred between different waves and particle species within a magnetosphere is a critical component of understanding how the system works. This is a rich topic (e.g. the introductory review by Tsurutani and Lakhina 1997), and significant progress is possible in the case of Mercury. In this sub-section we review work on wave activity within the tiny Hermean magnetosphere, focusing on aspects that are unique to this system and with an emphasis on the extensive MESSENGER observations of magnetospheric waves. These studies set the scene for BepiColombo to reveal the full nature of wave-particle interactions, for which MPO-MAG observations will be an important element. MPO-MAG is able to sample the magnetic field at 6 times higher sampling frequencies than MESSENGER. This might lead to new discoveries in the wave physics at Mercury.
Even before the MESSENGER era it was expected that Mercury’s magnetosphere would be the most “kinetic” of any planetary magnetosphere in the Solar System (e.g. Slavin et al. 2007). This is to say that the size of the system would be small when measured in physically meaningful units of typical particle gyroradii. Ultralow-frequency (ULF) waves in the system, which were first identified in magnetic field observations during the Mariner 10 flyby (Russell 1989), have frequencies of order 1 Hz. This is close to expected ion gyrofrequencies, and so the applicability of a magnetohydrodynamic (MHD) approach is far more limited in the context of Mercury’s magnetosphere (Glassmeier et al. 2003, 2004; Blomberg et al. 2007), compared to larger-scale systems like the terrestrial magnetosphere.
Observational evidence for magnetospheric waves at Mercury has been dramatically expanded thanks to the MESSENGER mission. At relatively low frequencies, James et al. (2019b) surveyed \(<0.5\) Hz waves revealed by magnetic field observations, showing that part of the Hermean magnetospheric wave spectrum does lie in the MHD regime. These authors suggested that ULF waves may be predominantly driven by Kelvin-Helmholtz wave activity on the magnetopause, which has also been concluded in similar detailed studies of ULF waves by Liljeblad et al. (2016) and Liljeblad and Karlsson (2017a). These investigations have led to the identification of field line resonances within the system, recently surveyed by James et al. (2019b) and used to shed light on the distribution of plasma.
Higher-frequency waves have also been observed by MESSENGER. Waves at 1 Hz, and thus close to the ion kinetic regime, were surveyed and subsequently interpreted by Boardsen et al. (2012, 2015). Ion cyclotron waves and ion-Bernstein waves are thought to drive some of the wave activity observed at such frequencies. Within this ion kinetic regime it has been proposed that ion-ion hybrid resonance can occur (e.g. Glassmeier et al. 2004; Kim et al. 2015), distinct from the MHD field line resonance phenomenon at lower frequencies mentioned above. The last of the many relevant MESSENGER-based investigations to draw attention to is the work Uritsky et al. (2011), who used magnetic field observations to examine ion- kinetic scale turbulence in different regions of Mercury’s space environment. These authors highlighted the important role of non-MHD, finite-gyroradius effects.
Considerably more work is needed to understand wave-particle interactions in Mercury’s magnetosphere. MESSENGER has effectively set the scene for further progress through the number of careful studies of magnetospheric waves based on MESSENGER data, which we have reviewed in this sub-section. A key motivation in the context of BepiColombo is the question of how ions and electrons are accelerated through their interaction with waves, which is the missing link required for a comprehensive, global understanding of particle acceleration in Mercury’s magnetosphere. Going forward, work based on theory, modelling, and further analysis of MESSENGER data will support major advances in the era of BepiColombo’s orbital tour. MPO-MAG observations will be essential to achieve this future goal, as well as a number of complimentary fields and particles data sets.
3.12 Asymmetries and Dynamics in the Hermean Magnetotail
At a time when much attention is being focused on dawn-dusk asymmetries at the Earth (e.g., see Walsh et al. (2014)), MESSENGER has discovered a number of asymmetries that are both similar and quite different from those observed at Earth. For example, Kelvin-Helmholtz waves on the magnetopause are largely confined to the dusk flank of the magnetopause (Sundberg et al. 2012; Liljeblad et al. 2014), just as predicted by Glassmeier and Espley (2006). Within the magnetotail flux ropes and dipolarization fronts are far more frequently observed on the dawn-side than on the dusk-side (Smith et al. 2017; Sun et al. 2016, 2017) suggesting that magnetic reconnection is also more frequent on this side of the tail. Further, energetic electrons (\(\gtrsim 30\) keV) are observed in the post-midnight region far more frequently than in the pre-midnight region (Ho et al. 2016; Dewey et al. 2017). In contrast, magnetic reconnection observations in Earth’s magnetosphere generally show the very different asymmetries with dipolarization fronts, fast flows and flux rope formation favoring the dusk-side (e.g. Slavin et al. 2005; Imber et al. 2011; Runov et al. 2017).
(Poh et al. 2017) found that the thickness of the dawn-side cross-tail current sheet at Mercury is larger than on the dusk-side by a factor of 3 (see Fig. 34) and the plasma beta is higher suggesting that a thicker current sheet which should be less conducive to reconnection X-line formation. Once again, the Earth observations show the opposite asymmetry with magnetic field strengths in the plasma sheet at dawn exceeding those on the dusk-side (Slavin et al. 1985; Wang 2004) and a thicker plasma sheet on the dawn-side as opposed to the dusk-side (Wang 2004; Rong et al. 2011). More recently, Lu et al. (2018) and Liu et al. (2019) have proposed that the finite length of the reconnection x- lines in their simulations offers an explanation to these apparent contradictions in the spacecraft observations. In particular, Liu et al. (2019) have found a minimum, or intrinsic x-line length to support fast reconnection of about \(10 d_{i}\), where \(d_{i}\) is the local ion inertial length. Outside of this region, especially in the direction of current inflow in the cross-tail current layer, i.e. the duskward direction, reconnection is “suppressed”. Further, these simulations by Lu et al. (2018) and Liu et al. (2019) show that the transport of reconnected \(B_{z}\) magnetic flux moves with the electrons, which goes in the anti-current direction or dawnward. In this manner they argue that the onset of reconnection will still preferentially occur on the side of the tail where the current sheet is thinnest, i.e., the dusk-side, but the “active” portion of the X-line with fast reconnection and exhausts containing high-speed flow that drives dipolarization fronts and carry flux ropes sunward and anti-sunward will be displaced toward the dawn-side of the plasma sheet. This dawn-ward (i.e. anti-current flow direction) skewing of fast reconnection is expected to occur at both Mercury and Earth. However, at Earth the dawnward offset in such a wide tail will not be large enough to shift the peak in high-speed bulk flows and other aspects of the X-line exhausts from the dusk-side where reconnection begins to the dawn-side. However, for Mercury the narrow width of the tail is hypothesized to result in reconnection onset being on the dusk-side, but the region of fast reconnection will only be on the dawn-side (Lu et al. 2018; Liu et al. 2019).
Schematic illustrations of summary and explanation for all asymmetries in Mercury’s current sheet observed in this study. Red dashed line represents the magnetopause. Top and bottom panels on the right represent the post-midnight and pre- midnight views, respectively. The illustration shows that Mercury’s current sheet is thicker and \(B_{z}\) is higher on the post-midnight than the pre-midnight region. The asymmetry in \(B_{z}\) also decreases in strength with increasing downtail distances. Mass loading of ions from the cusp and NMNL farther downtail drift stretches the dusk-side current sheet, while a dawnward preference in reconnection occurrence sends more dipolarized flux tube toward the dawn-side current sheet and thereby thickening the current sheet (from Poh et al. (2017)
3.13 Magnetosheath Dynamics
Due to the orbit of the MPO, it is possible to study the Hermean magnetopause in detail. On the other hand, MMO is able to perform a detailed study of the pristine solar wind and the foreshock region (Milillo et al. 2020; Baumjohann et al. 2020). The nature of the foreshock region modifies the downstream magnetosheath adjacent to the magnetopause as described below.
As the pristine solar wind is super-magnetosonic in Mercury’s frame of reference, a bow shock is created upstream of the magnetopause where deceleration to sub-magnetosonic speeds and plasma heating takes place (e.g. Anderson et al. 2010). The character of the bow shock is highly dependent on the angle between the interplanetary magnetic field and the local shock normal. If that angle exceeds \(45^{\circ }\), the shock is called quasi-perpendicular; in the opposite case, the shock is quasi-parallel. The region upstream of the quasi-parallel shock, that is magnetically connected to the shock, is called the foreshock. Within the foreshock, shock-reflected ions and electrons interact with the incoming solar wind, leading to the growth of waves and magnetic structures (e.g. Burgess et al. 2005). While these may propagate sunward in the solar wind rest frame, they are convected back to the shock by the solar wind flow, leading to much more variable shock and downstream magnetosheath region in comparison to the quasi-perpendicular shock and the adjacent magnetosheath. Within the latter, ion cyclotron or mirror mode waves may yet be frequently observed, driven by the ion temperature anisotropy inherent to the shocked and compressed plasma (e.g. Gary et al. 1993). Although these phenomena can be observed at both Hermean and terrestrial shocks, there are also substantial differences. These arise because the Hermean shock is much weaker, as the solar wind features lower Mach numbers and plasma-\(\beta \) at Mercury than at Earth. Consequently, the stream of ions backstreaming into the incoming solar wind is weaker. In addition, the Hermean shock is much smaller in comparison to the planet, as Mercury’s magnetic field is much weaker than Earth’s while the solar wind dynamic pressure is larger. As a result, the foreshock volume is smaller and structures have less time to evolve and steepen before they are carried to the shock. The foreshock is more often located upstream of the subsolar shock, though, as the interplanetary magnetic field (IMF) cone angle is typically small (about \(20^{\circ }\)). The Parker spiral IMF is, hence, often quasi-radial at Mercury (e.g. Slavin and Holzer 1981). Upstream of the shock, 2 Hz whistler waves are most prevalent at Mercury, which correspond to 1 Hz waves at Earth (Le et al. 2013). Large-amplitude waves with periods of 10 s, corresponding to so-called 30 s waves at Earth (Greenstadt et al. 1981; Eastwood et al. 2005), appear more sporadically in the Hermean foreshock. They can, however, also be observed at the shock, in magnetosheath regions downstream of the quasi-parallel shock, and in the magnetosphere. These waves appear coherent throughout the different regions, suggesting synchronized cyclic shock reformation of the quasi- parallel shock, on global scales (Sundberg et al. 2013, 2015; Karlsson et al. 2016). Cyclic shock reformation means that foreshock waves/structures steepen in the foreshock before they merge into an existing shock, thus becoming the “new shock”. Those structures move toward the shock in the planetary frame, but against the solar wind in the solar wind frame. At Earth, the structures are small in comparison to global scales, and thus the shock reformation process is patchy. At Mercury, the global scales are so small that foreshock structures appear of global scale. Hence, when they merged with the already existing shock, that reformation happens at once for the entire shock and is not as patchy as at Earth (e.g. Burgess et al. 2005). At Earth, the quasi-parallel shock appears to be undulated or rippled, leading to the penetration of less thermalized high-speed jets into the magnetosheath (e.g. Plaschke et al. 2018). Neither foreshock SLAMS nor magnetosheath jets have been observed near Mercury so far, although the identification of jets has also been hindered by the lack of appropriate particle and fields measurements (Karlsson et al. 2016). The list of terrestrial foreshock phenomena not yet observed at Mercury or reported so far also comprises foreshock cavities, i.e. hot ions expanding magnetic flux tubes that are connected to the shock (e.g. Billingham et al. 2008), foreshock cavitons resulting from wave-wave-interactions that may turn into spontaneous hot flow anomalies (Zhang et al. 2013; Omidi et al. 2013), and foreshock bubbles of global scales that form ahead of the shock at IMF rotational discontinuities (Omidi et al. 2010; Turner et al. 2013). IMF discontinuities intersecting with the Hermean shock may, however, lead to signatures similar to those of young hot flow anomalies (HFAs) evolving near the terrestrial bow shock, as reported by Uritsky et al. (2014). Downstream of the quasi-perpendicular shock, mirror mode (MM) structures or ion cyclotron (IC) waves may develop in the magnetosheath, the MM and IC waves being favored under high (Earth) and low (Mercury) plasma beta conditions, respectively. Consequently, IC waves are observed in Mercury’s magnetosheath, while mirror modes have not Sundberg et al. (2015), although they have been predicted to occur, based on global magnetospheric simulations (Herčík et al. 2013). At Earth, both modes are observed, the MM being more prevalent. Low \(\beta \) conditions are enhanced due to the extended plasma depletion layer (PDL) that is commonly present upstream of the Hermean magnetopause (Gershman et al. 2013) for almost all IMF orientations. The PDL thickness should be proportional to \(1 / M_{A}^{2}\) (Zwan and Wolf 1976) and thus thick PDLs are expected at Mercury. This PDL contributes to the high reconnection rate at Mercury in comparison to Earth, leading to rapid successions of flux transfer events (FTEs) at the magnetopause and substorms in the Hermean magnetotail (e.g. Imber and Slavin 2017).
Mariner 10 and, in particular MESSENGER, observations of the Hermean plasma environment have allowed pioneering work in identifying and characterizing foreshock, shock, and magnetosheath waves and structures. Nevertheless, we lack even basic knowledge on the occurrence or not of certain phenomena (cavitons, cavities, spontaneous HFAs, foreshock bubbles, jets, mirror modes) and detailed knowledge on the characteristics, morphologies, and dynamics of already identified waves and boundaries. The BepiColombo spacecraft are expected to revolutionize our understanding of the Hermean plasma environment. During each of the Mercury flybys, Mio-MGF Baumjohann et al. (2020) will gather cross-sectional measurements of the magnetosphere, crossing the bow shock and magnetopause boundaries, as well as the magnetosheath and, likely, the foreshock regions. The inbound and outbound crossings of the shock will probably involve both quasi-parallel and quasi-perpendicular characteristics, allowing for dawn/dusk and quasi- parallel/perpendicular comparative studies of the aforementioned phenomena. Once in orbit, the MPO spacecraft will closely follow the subsolar magnetopause. Thus, we will be able to study how the Hermean magnetosheath conditions and dynamics will affect the magnetopause and thereby the magnetosphere.
4 Measurements During Cruise
Since the boom deployment, MPO-MAG measures the magnetic field in interplanetary space continuously during BepiColombo’s 7-year cruise to Mercury. This will allow us to examine the structure and turbulence of the solar wind, as well as follow transient events in the heliosphere in combination with data from other currently active spacecraft. During the cruise phase, there will be several planetary encounters, where the instrument could also provide useful data.
4.1 Solar Wind
With BepiColombo’s nearly circular orbit-type approach to Mercury around the Sun and the cruise period covering more than half a solar cycle, MPO’s magnetic field measurement in the solar wind is ideal in revealing (1) large-scale structure of solar wind and interplanetary magnetic field, (2) waves and turbulence in the low-frequency domain, (3) transient phenomena crossings such as coronal mass ejections and corotating interaction regions. Furthermore, BepiColombo’s cruise-phase measurements give a unique opportunity to study the inner heliosphere with three spacecraft in a stereographic way together with Parker Solar Probe (covering a wider range in the radial direction from the Sun down to about 10 solar radii) and Solar Orbiter (covering latitudinal dependence up to about 30 degree to the ecliptic plane).
4.1.1 Large-Scale Structure
Large-scale structure of the interplanetary magnetic field is well represented by Archimedian or Parker spiral, yet there a number of models as extensions of the Parker spiral field line such as latitudinal dependence, solar cycle dependence, empirical model, northward component (see, e.g., review by Lhotka and Narita 2019). The MPO magnetometer in the solar wind will be able to validate those models or determine parameters in the models.
4.1.2 Waves and Turbulence
Energy spectra of magnetic field fluctuations in the solar wind often exhibit a power-law with a spectral slope of about −1.5 to −2 up to a frequency of about 1 Hz, and then the spectra become steeper at higher frequencies Bruno and Carbone (2013). The power-law behavior of the interplanetary magnetic field is interpreted as a sign of fully-developed turbulence in the hydrodynamic picture yielding a slope of \(-5/3\), isotropic magnetohydrodynamic picture with a slope of \(-3/2\), or anisotropic magnetohydrodynamic picture with a slope in the range from \(-5/3\) to −2, depending on the projection or sampling angle to the mean magnetic field.
Waves and turbulence properties of the interplanetary magnetic field are known to be associated with two distinct stream types of the solar wind (Dasso et al. 2005). One is the slow solar wind (or the low-speed stream) with a typical flow velocity of 300 to 400 km s−1, and the other is the fast solar wind (or the high-speed stream) with a flow speed of 700 to 800 km s−1 (or even higher). In the former case, the solar wind plasma is considered to originate in the closed field lines in the solar atmosphere, and the solar wind plasma should have a sufficient time to develop into turbulence. In the latter case, the solar wind plasma is considered to originate in the open field lines and the solar wind plasma has little time to develop from Alfvén waves into turbulence. BepiColombo’s cruise data at different heliocentric distances will allow for further studies of the evolution of turbulence with distance to the sun.
4.1.3 Transient Phenomena
Solar transients such as coronal mass ejections (CMEs), solar wind high-speed streams and their associated stream interaction regions (SIRs), solar flares, solar radio emissions or solar energetic particles (SEPs) are sources of extreme and sudden solar wind variability for any spacecraft or solar system body encountered by them. Although these are common features in the solar wind, each of them has near unique properties (energy, velocity, etc.) that makes its forecast complex. Large efforts are being doing by both the heliophysics and planetary communities in order to model their propagation, as well as anticipate their strong effects on different plasma-atmospheric systems.
The long cruise of BepiColombo constitutes an exceptional opportunity for studying the evolution of different solar transients in the most inner heliosphere. This is a region in-situ little explored but of special importance because is where CMEs have their largest deceleration, and where SIR are formed. The BepiColombo cruise phase to Mercury will cover near half solar activity cycle of solar wind observations (which will include both minimum and maximum of solar activity in ∼2019-2020 and ∼2024-2025, respectively). The MPO-MAG instrument is in near-continuous operation for most of the cruise phase at a rate of 4 to 16 Hz. This allows investigations of solar wind variability through the analysis of the interplanetary magnetic field (IMF), as well as investigations on the properties of different solar transient events that hit the spacecraft.
Despite the lower measurement rate during the cruise-phase, MPO-MAG is demonstrating that is very capable of taking great quality observations of the solar wind. All the observations so far have been taken during the minimum of activity of the solar cycle 24-25, which implies that the spacecraft has been mainly hit by SIRs (which have a more dominant role during solar minimum) and slow and small CMEs. Sometimes, these slow CMEs do not have obvious low coronal signatures and are called stealth CMEs or CME-like transients, but can still be geoeffective when hitting Earth (e.g. O’Kane et al. 2019) and other planets (e.g. Sánchez-Cano et al. 2017) and are difficult to track. Figure 35 shows an example of the IMF recorded by MPO-MAG in late May 2020 in ecliptic J2000 coordinates. During this period, BepiColombo was hit by a moderate SIR on 24 May 2020 and by a CME-like transient on 29 May 2020. As can be seen, the shock of both transients is clearly visible as a jump in the IMF magnitude of the three components (marked with a red arrow), as well as the flux ropes (magnetic field rotations) of both transients (marked by green shaded areas). This Figure demonstrates the capability of MPO-MAG for detecting Space Weather events, even during low solar activity conditions. It is expected that MPO-MAG will measure larger and faster CMEs hitting BepiColombo with similar data quality as soon as the ascending phase of the solar cycle is reached.
The good performance of MPO-MAG during the BepiColombo cruise phase, together with the unique opportunity of taking 7 years of solar wind observations at different heliocentric distances, should be used as an example for future missions to perform solar wind and Space Weather science during their cruise science phases, even if at low rates.
4.2 Earth Flyby
BepiColombo encountered Earth again at 10/4/2020. This is a unique opportunity to validate the orientation of the MPO-MAG magnetometers using the well-known terrestrial magnetosphere. The time series of the magnetic field magnitude and the trajectory projected on the equatorial plane is shown in Fig. 36. During the encounter, the solar wind dynamic pressure appeared to be very weak. This is noticeable in the magnetopause crossing that happened around \(X_{\mathrm{GSE}} \approx 11 R_{E}\) (with \(R_{E}\) denoting the Earth radius). Under normal solar wind conditions this would be expected at one \(R_{E}\) less. Also, the magnetosphere was rather quiet during this day, supporting our re-orientation attempt of the MPO-MAG sensors. A conservative estimate (Monte-Carlo approach) using Tsyganenko-Models of the magnetosphere results in an expected accuracy of the sensor re-orientation better than \(1^{\circ }\). This is work in progress and will be reported elsewhere.
BepiColombo flyby trajectory (red) and magnetic field magnitude (green, logarithmic scale) as a projection onto the \(X_{\mathrm{GSE}}-Y_{\mathrm{GSE}}\) plane. The stronger the magnetic field the more the green curve deviates from the red one. Blue marks show the time (UTC) on 10/04/2020. Closest approach happened at 4:24 UTC in the morning. Inbound bow shock and magnetopause crossings are marked with black arrows
4.3 Venus Flybys
During BepiColombo’s cruise phase there will be two Venus flybys, on 12 October 2020 and 11 August 2021, in order to slow the spacecraft down and send it on its way to Mercury. However, these flybys cannot only be used as a course correction, but they can also be used to perform scientific observations of the Venusian environment. Figure 37 shows these two flybys, which differ greatly in their geometry. During the first flyby (2020, green), BepiColombo approaches Venus from the upstream direction, encounters the bow shock near the terminator and leaves Venus along the induced magnetotail. During the second flyby (2021, red), BepiColombo approaches Venus through the induced magnetotail, crossing the bow shock far downstream from the planet, but makes a very close approach, possibly crossing Venus’s ionopause, before crossing the bow shock near the sub-solar point. This means that various regions of the induced Venusian magnetosphere will be sampled by BepiColombo. Below, the two flybys will be discussed in more detail, considering the science that can be done.
The Venus flybys in the XR (top), XY and XZ (bottom left and right) plane. The solid black and gray lines represent the bow shock for solar minimum (Zhang et al. 2008) and maximum (Russell et al. 1988b), respectively, and the blue line represents the ionopause (Zhang et al. 2008). The crosses on the flybys show 10 min tickmarks.
4.3.1 Venus Flyby October 2020
On 15 October 2020, BepiColombo will approach Venus from the sunward side, crossing the bow shock near the terminator at a radial distance of \(\sim 3 R_{\mathrm{V}}\), after which the spacecraft travels along the induced magnetotail away from the planet.
Approaching the planet, the spacecraft will first be in the solar wind proper where turbulence (see e.g., Bruno et al. 2009; Narita et al. 2011) can be studied. Nearing the planet more, the extended hydrogen exosphere of Venus will be encountered (Gunell et al. 2005; Delva et al. 2009), which is prone to photo-ionization and ion pick-up by the solar wind magnetic field. The pick-up creates a ring/ring-beam distribution which, for low plasma-\(\beta \), is unstable to the generation of ion cyclotron waves (Gary 1992). Indeed, these waves have been observed by Venus Express both at solar minimum and maximum, where at maximum there is more activity because of the greater extension of the exosphere (Delva et al. 2015). Ion cyclotron waves are observed in the solar wind upstream of Venus and up to the terminator.
Depending on the direction of the interplanetary magnetic field (IMF), the spacecraft can also enter the foreshock (e.g., Crawford et al. 1993), where ULF waves are indicative of the back-streaming ions along the magnetic field lines from the quasi-parallel bow shock. Also, hot flow anomalies (HFA) are expected upstream of the bow shock when discontinuities in the IMF interact with the bow shock (e.g., Thomsen et al. 1993). These HFAs are characterized by strongly deflected hot plasma and a reduction of the magnetic field strength. They travel at velocities slower than the solar wind and are bounded by regions of enhanced magnetic field and ion temperature (Tjulin et al. 2008). These structures have also been observed by Venus Express (Collinson et al. 2012).
After crossing the bow shock, the spacecraft enters the magnetosheath, where the shocked solar wind plasma flows tailwards. Here, the situation is different from upstream as the plasma-\(\beta \) is large, which means that, depending on the kind of bow shock (quasi-parallel or quasi-perpendicular) different wave modes and turbulence can occur (see e.g., Guicking et al. 2010). One specific mode in the magnetosheath behind the quasi-perpendicular bow shock is the mirror mode, the high plasma-\(\beta \) branch of same instability that generates the ion cyclotron waves in the solar wind (Gary 1992; Volwerk et al. 2016). These non-propagating waves are expected to show a Bohm-like diffusion when they travel along with the plasma flow (Hasegawa and Tsurutani 2011) and thereby create larger structures, as shown by Schmid et al. (2014) at Venus and comet 1P/Halley.
This flyby seems to miss the centre of the induced magnetotail, where magnetic reconnection is expected to take place (Volwerk et al. 2009, 2010; Zhang et al. 2010). However, although the actual reconnection line will not be observed, its effects can be observed at further distances of the centre, such as plasmoids, flux ropes and travelling compression regions, similar as at Earth (e.g. Imber et al. 2011).
4.3.2 Venus Flyby August 2021
The flyby in August 2021 is quite different from that in 2020; in this case BepiColombo will cross the bow shock far behind Venus’s terminator, and it might be questioned if at that location this will be a shock- or a wave-like structure. In the latter case there will be a gradual change in the magnetic field strength from the solar wind to the magnetosheath. Russell et al. (1981) investigated the distant downstream bow shock with Pioneer Venus Orbiter (PVO) and found that up to \(X_{\mathrm{VSO}} \approx -7 R_{\mathrm{V}}\) shock signatures were present in the magnetic field data. As the bow shock is not a stationary structure, but reacts to changes in the solar wind, the long approach phase of BepiColombo, at a slight angle to the model bow shock gives ample opportunity to investigate its nature when multiple crossings would occur.
Inside the bow shock similar investigations as during the first flyby can be made at different locations in the induced magnetotail. Approaching the planet, near the terminator, BepiColombo will get very close to the planet, with an apoapsis of \(\sim 6077\) km (or 555 km above the surface). Based on the model by Zhang et al. (2008) for Venus’s ionosphere, the blue curve in Fig. 37, the spacecraft can enter the ionosphere around 1400 UT. Although the encounter will be less than 10 min, it will be very important to get some new information about this region. Venus’s ionosphere can be described by two different states depending on the solar wind conditions. For normal solar wind conditions the thermal pressure of Venus’s ionosphere is strong enough to keep the magnetic field at bay and is unmagnetized. However, at higher solar wind pressures the magnetic field will penetrate into the ionosphere, magnetizing it (Lumann et al. 1980), displaying numerous small-scale flux ropes. However, with Venus Express another state was found, where there was one giant flux rope in the ionosphere (Zhang et al. 2012).
After closest approach, BepiColombo will enter a basically uncharted region of the induced magnetosphere, as it will cross into the solar wind at almost the subsolar point of the bow shock. The location of the bow shock will show, how well the current models describe this region, as both models are based on measurements at solar zenith angles \(SZA > 20^{\circ }\).
4.4 Mercury Flybys
Before entering orbit, BepiColombo will perform six flybys at Mercury during the cruise phase. Five of them will be close enough to the planet to take measurements within the Hermean magnetosphere. Flyby No. 5 is simply too far away from the planet. Figure 38 shows the flyby geometries in the \(x_{\mathrm{MSM}}-\rho _{x}\) plane in the MSM-frame with \(\rho _{x} = \sqrt{y_{\mathrm{MSM}}^{2}+z_{\mathrm{MSM}}^{2})}\). All close-in flybys (except for flyby No. 4) have pericenters on the nightside of the planet. Figure 39 shows the flyby positions as seen from the sun. Flybys 1-3 are more or less equatorial and flybys 4 and 6 are clearly polar. As a result, BepiColombo flybys in combination with MESSENGER’s equatorial flybys could be used to examine dawn-to-dusk asymmetries in the tail, down-tail evolution of plasma sheet, lobes and the night-side magnetotail radius from direct encounters (e.g Slavin et al. 2010). The BepiColombo M1-3 flybys are also uniquely useful for studying the low-latitude boundaries, including the equatorial diamagnetic depressions expected at the dawn side (Müller et al. 2012), nightside reconnection (including x-line location (Slavin et al. 2009a, 2012) and potentially substorm loading-unloading phases (e.g. Imber and Slavin 2017). In addition to that, Kelvin-Helmholtz vortices at the magnetopause, that had been more challenging from high-latitude MESSENGER orbits may be observed by MPO-MAG On flyby 4, we expect to see quasi-steady region 1 field-aligned currents (Anderson et al. 2018) and also we could study the northern cusp (e.g. He et al. 2017; Zhong et al. 2015b). Flyby 6 could be useful to study a magnetic \(z\)-profile of the Hermean magnetotail. Region 2 field-aligned current systems associated with substorm current wedges (e.g. Glassmeier 2000; Poh et al. 2017) have not been observed so far with MESSENGER data. The BepiColombo flybys 4 and 6 could prove useful to detect these for the first time.
BepiColombo Mercury Flybys in the \(x-\rho _{x}\) plane in the MSM-frame. The black line marks the average magnetopause from Korth et al. (2017)
Figure 40 displays the flybys in a different way: Here, the satellite positions are shown in the \(\rho _{z}-z_{\mathrm{MSO}}\) plane in the MSO-frame with \(\rho _{z}=\sqrt{x_{\mathrm{MSO}}^{2}+y_{\mathrm{MSO}}^{2})}\). In this figure, the BepiColombo flyby coordinates are compared to the MESSENGER positions (light grey area) from its orbital phase. At the pericenters of flybys 1 and 2, it is clearly seen, that we are able to sample the Hermean magnetic field at previously unknown locations within the southern hemisphere. At these points, the Hermean internal field models that were created using MESSENGER magnetic field data (e.g. Wicht and Heyner 2014) can be critically tested. We will also compare these new measurements to the study by Winslow et al. (2014), who used the proton reflectrometry method to assess the surface magnetic field in the southern hemisphere.
BepiColombo Mercury flybys in a \(Z-\rho_{z}\) plane in the MSO-frame. The planet is marked as a black half-circle. The two dashes mark the area studied by Winslow et al. 2014 using proton reflectrometry data. The light grey area indicates the satellite positions of MESSENGER.
5 Summary & Conclusion
MPO-MAG is a very well calibrated instrument that will provide high-precision measurements of the Hermean magnetic field. This will give us deep insights into the planetary structure and the dynamics of the highly dynamic magnetosphere under the influence of the solar wind. The tools for magnetic field analysis and modelling of the planetary interior will have to be continuously advanced until arrival in 2025 in order to evaluate the expected data down to the last detail. The cooperation with the sister instrument Mio-MGF will allow us to take a new look at the Mercury magnetosphere and its reaction as a tightly coupled system to the changing solar wind conditions.
Notes
SPICE planning kernel, version v210_20190801_001, https://www.cosmos.esa.int/web/spice/spice-for-bepicolombo, accessed 26 September 2019.
References
C.H. Acton, Ancillary data services of NASA’s Navigation and Ancillary Information Facility. Planet. Space Sci. 44(1), 65–70 (1996). https://doi.org/10.1016/0032-0633(95)00107-7
C. Acton, N. Bachman, B. Semenov, E. Wright, A look towards the future in the handling of space science mission geometry. Planet. Space Sci. 150, 9–12 (2018). https://doi.org/10.1016/j.pss.2017.02.013
I.I. Alexeev, E.S. Belenkaya, J.A. Slavin, H. Korth, B.J. Anderson, D.N. Baker, S.A. Boardsen, C.L. Johnson, M.E. Purucker, M. Sarantos, S.C. Solomon, Mercury’s magnetospheric magnetic field after the first two MESSENGER flybys. Icarus 209(1), 23–39 (2010). https://doi.org/10.1016/j.icarus.2010.01.024
B.J. Anderson, M.H. Acuna, D.A. Lohr, J. Scheifele, A. Raval, H. Korth, J.A. Slavin, The magnetometer instrument on MESSENGER, in The Messenger Mission to Mercury, ed. by D.L. Domingue, C.T. Russell (Springer, New York, 2007), pp. 417–450
B.J. Anderson, M.H. Acuña, H. Korth, J.a. Slavin, H. Uno, C.L. Johnson, M.E. Purucker, S.C. Solomon, J.M. Raines, T.H. Zurbuchen, G. Gloeckler, R.L. McNutt, The magnetic field of Mercury. Space Sci. Rev. 152(1-4), 307–339 (2010). https://doi.org/10.1007/s11214-009-9544-3
B.J. Anderson, C.L. Johnson, H. Korth, M.E. Purucker, R.M. Winslow, J.A. Slavin, S.C. Solomon, R.L. McNutt, J.M. Raines, T.H. Zurbuchen, The global magnetic field of Mercury from MESSENGER orbital observations. Science 333(6051), 1859–1862 (2011). https://doi.org/10.1126/science.1211001
B.J. Anderson, C.L. Johnson, H. Korth, R.M. Winslow, J.E. Borovsky, M.E. Purucker, J.A. Slavin, S.C. Solomon, M.T. Zuber, R.L. McNutt, Low-degree structure in Mercury’s planetary magnetic field. J. Geophys. Res., Planets 117(E12), E00L12 (2012). https://doi.org/10.1029/2012je004159
B.J. Anderson, C.L. Johnson, H. Korth, A magnetic disturbance index for Mercury’s magnetic field derived from MESSENGER magnetometer data. Geochem. Geophys. Geosyst. 14(9), 3875–3886 (2013). https://doi.org/10.1002/ggge.20242
B.J. Anderson, C.L. Johnson, H. Korth, J.A. Slavin, R.M. Winslow, R.J. Phillips, R.L. McNutt, S.C. Solomon, Steady-state field-aligned currents at Mercury. Geophys. Res. Lett. 41(21), 7444–7452 (2014). https://doi.org/10.1002/2014GL061677
B.J. Anderson, C.L. Johnson, H. Korth, L.C. Philpott, Birkeland currents at Mercury: Review and comparison with Earth, in Electric Currents in Geospace and Beyond, vol. 235 (2018), p. 279
G.B. Andrews, T.H. Zurbuchen, B.H. Mauk, H. Malcom, L.A. Fisk, G. Gloeckler, G.C. Ho, J.S. Kelley, P.L. Koehn, T.W. LeFevere, et al., The energetic particle and plasma spectrometer instrument on the MESSENGER spacecraft. Space Sci. Rev. 131(1-4), 523–556 (2007)
R.C. Aster, B. Borchers, C.H. Thurber, Parameter Estimation and Inverse Problems, 2nd edn. (Academic Press, Amsterdam, 2013), pp. 1–23. https://doi.org/10.1016/B978-0-12-385048-5.00001-X
H.U. Auster, A. Lichopoj, J. Rustenbach, H. Bitterlich, K.H. Fornacon, O. Hillenmaier, R. Krause, H.J. Schenk, V. Auster, Concept and first results of a digital fluxgate magnetometer. Meas. Sci. Technol. 6(5), 477–481 (1995). https://doi.org/10.1088/0957-0233/6/5/007
H.-U. Auster, K.-H. Fornacon, E. Georgescu, K.-H. Glassmeier, U. Motschmann, Calibration of flux-gate magnetometers using relative motion. Meas. Sci. Technol. 13(7), 1124–1131 (2002). https://doi.org/10.1088/0957-0233/13/7/321
H.-U. Auster, I. Apathy, G. Berghofer, A. Remizov, R. Roll, K.-H. Fornacon, K.-H. Glassmeier, G. Haerendel, I. Hejja, E. Kührt, W. Magnes, D. Moehlmann, U. Motschmann, I. Richter, H. Rosenbauer, C.T. Russell, J. Rustenbach, K. Sauer, K. Schwingenschuh, I. Szemerey, R. Waesch, ROMAP: Rosetta magnetometer and plasma monitor. Space Sci. Rev. 128(1-4), 221–240 (2007b). https://doi.org/10.1007/s11214-006-9033-x
H.-U. Auster, K.-H. Glassmeier, W. Magnes, O. Aydogar, W. Baumjohann, D. Constantinescu, D. Fischer, K.-H. Fornacon, E. Georgescu, P. Harvey, O. Hillenmaier, R. Kroth, M. Ludlam, Y. Narita, R. Nakamura, K. Okrafka, F. Plaschke, I. Richter, H. Schwarzl, B. Stoll, A. Valavanoglou, M. Wiedemann, The THEMIS fluxgate magnetometer. Space Sci. Rev. 141(1-4), 235–264 (2008). https://doi.org/10.1007/s11214-008-9365-9
W. Baumjohann, M. Blanc, A. Fedorov, K.H. Glassmeier, Current systems in planetary magnetospheres and ionospheres. Space Sci. Rev. 152(1-4), 99–134 (2010). https://doi.org/10.1007/s11214-010-9629-z ISBN 0038-6308.
W. Baumjohann, A. Matsuoka, Y. Narita, W. Magnes, D. Heyner, K. Glassmeier, R. Nakamura, D. Fischer, F. Plaschke, M. Volwerk, et al., The BepiColombo-mio magnetometer en route to Mercury. Space Sci. Rev. 216(8), 1–33 (2020)
M. Benna, B.J. Anderson, D.N. Baker, S.a. Boardsen, G. Gloeckler, R.E. Gold, G.C. Ho, R.M. Killen, H. Korth, S.M. Krimigis, M.E. Purucker, R.L. McNutt, J.M. Raines, W.E. McClintock, M. Sarantos, J.a. Slavin, S.C. Solomon, T.H. Zurbuchen, Modeling of the magnetosphere of Mercury at the time of the first MESSENGER flyby. Icarus 209(1), 3–10 (2010). https://doi.org/10.1016/j.icarus.2009.11.036
L. Billingham, S. Schwartz, D. Sibeck, The statistics of foreshock cavities: results of a cluster survey, in Annales Geophysicae, vol. 26 (Copernicus GmbH, Göttingen 2008), pp. 3653–3667
L.G. Blomberg, J. Cumnock, K.-H. Glassmeier, R. Treumann, Plasma waves in the Hermean magnetosphere. Space Sci. Rev. 132(2-4), 575–591 (2007)
S.A. Boardsen, J.A. Slavin, B.J. Anderson, H. Korth, D. Schriver, S.C. Solomon, Survey of coherent 1 Hz waves in Mercury’s inner magnetosphere from MESSENGER observations. J. Geophys. Res. Space Phys. 120(A12), A00M05 (2012)
S. Boardsen, E.-H. Kim, J. Raines, J. Slavin, D. Gershman, B. Anderson, H. Korth, T. Sundberg, D. Schriver, P. Travnicek, Interpreting 1 Hz magnetic compressional waves in Mercury’s inner magnetosphere in terms of propagating ion-Bernstein waves. J. Geophys. Res. Space Phys. 120(6), 4213–4228 (2015)
S.I. Braginsky, P.H. Roberts, Equations governing convection in Earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79(1-4), 1–97 (1995). https://doi.org/10.1080/03091929508228992
R. Bruno, V. Carbone, The solar wind as a turbulence laboratory. Living Rev. Sol. Phys. 10(1), 2 (2013)
R. Bruno, V. Carbone, Z. Vörös, R. D’Amicis, B. Bavassano, M.V. Cattaneo, A. Mura, A. Melillo, S. Orsini, P. Veltri, L. Sorriso-Valvo, T. Zahng, H. Biernat, H. Rucker, W. Baumjohann, D. Jankoviccová, P. Vovćs, Coordinated study on solar wind turbulence during the Venus-Express, ACE and Ulysses alignment of August 2007. Earth Moon Planets 104, 101–104 (2009). https://doi.org/10.1007/s11038-008-9272-9
D. Burgess, E. Lucek, M. Scholer, S. Bale, M. Balikhin, A. Balogh, T. Horbury, V. Krasnoselskikh, H. Kucharek, B. Lembège, et al., Quasi-parallel shock structure and processes. Space Sci. Rev. 118(1-4), 205–222 (2005)
P.K. Byrne, C. Klimczak, A.C. Şengör, S.C. Solomon, T.R. Watters, S.A. Hauck, et al., Mercury’s global contraction much greater than earlier estimates. Nat. Geosci. 7(4), 301–307 (2014)
H. Cao, J.M. Aurnou, J. Wicht, W. Dietrich, K.M. Soderlund, C.T. Russell, A dynamo explanation for Mercury’s anomalous magnetic field. Geophys. Res. Lett. 41(12), 4127–4134 (2014). https://doi.org/10.1002/2014GL060196
C. Cartier, O. Namur, L.R. Nittler, S.Z. Weider, E. Crapster-Pregont, A. Vorburger, E.A. Frank, B. Charlier, No FeS layer in Mercury? Evidence from Ti/Al measured by MESSENGER. Earth Planet. Sci. Lett. 534, 116108 (2020). https://doi.org/10.1016/j.epsl.2020.116108
N.L. Chabot, E.A. Wollack, R.L. Klima, M.E. Minitti, Experimental constraints on Mercury’s core composition. Earth Planet. Sci. Lett. 390, 199–208 (2014). https://doi.org/10.1016/j.epsl.2014.01.004
U.R. Christensen, A deep dynamo generating Mercury’s magnetic field. Nature 444(7122), 1056–1058 (2006)
U.R. Christensen, J. Aubert, Scaling properties of convection-driven dynamos in rotating spherical shells and application to planetary magnetic fields. Geophys. J. Int. 166(1), 97–114 (2006). https://doi.org/10.1111/j.1365-246X.2006.03009.x
U.R. Christensen, A. Tilgner, Power requirement of the geodynamo from ohmic losses in numerical and laboratory dynamos. Nature 429(6988), 169–171 (2004)
U.R. Christensen, J. Wicht, Models of magnetic field generation in partly stable planetary cores: applications to Mercury and Saturn. Icarus 196(1), 16–34 (2008). https://doi.org/10.1016/j.icarus.2008.02.013
G.A. Collinson, D.G. Sibeck, A. Masters, N. Shane, J.A. Slavin, A.J. Coates, T.L. Zhang, M. Sarantos, S. Boardsen, T.E. Moore, S. Barabash, Hot flow anomalies at Venus. J. Geophys. Res. 117, A04204 (2012
J.E.P. Connerney, N.F. Ness, Mercury’s Magnetic Field and Interior, ed. by F. Vilas, C.R. Chapman, M.S. Matthews (1988), pp. 494–513
K.T. Crane, C. Klimczak, Timing and rate of global contraction on Mercury. Geophys. Res. Lett. 44(7), 3082–3089 (2017). https://doi.org/10.1002/2017GL072711
G.K. Crawford, R.J. Strangeway, C.T. Russell, VLF imaging of the Venus foreshock. Geophys. Res. Lett. 20, 2801–2804 (1993). https://doi.org/10.1029/93GL01258
S. Dasso, L. Milano, W. Matthaeus, C. Smith, Anisotropy in fast and slow solar wind fluctuations. Astrophys. J. Lett. 635(2), 181 (2005)
M. Delva, M. Volwerk, C. Mazelle, J.Y. Chauffray, J.L. Bertaux, T.L. Zhang, Hydrogen in the extended Venus exosphere. Geophys. Res. Lett. 36, L01203 (2009). https://doi.org/10.1029/2008GL036164
M. Delva, C. Bertucci, M. Volwerk, R. Lundin, C. Mazelle, N. Romanelli, Upstream proton cyclotron waves at Venus near solar maximum. J. Geophys. Res. 120, 344–354 (2015). https://doi.org/10.1002/2014JA020318
P.D. Desai, Thermodynamic properties of iron and silicon. J. Phys. Chem. Ref. Data 15(3), 967–983 (1986). https://doi.org/10.1063/1.555761
R.M. Dewey, J.A. Slavin, J.M. Raines, D.N. Baker, D.J. Lawrence, Energetic electron acceleration and injection during dipolarization events in Mercury’s magnetotail. J. Geophys. Res. Space Phys. 122(12), 12170–12188 (2017). https://doi.org/10.1002/2017JA024617
G.A. DiBraccio, J.a. Slavin, S.a. Boardsen, B.J. Anderson, H. Korth, T.H. Zurbuchen, J.M. Raines, D.N. Baker, R.L. McNutt, S.C. Solomon, MESSENGER observations of magnetopause structure and dynamics at Mercury. J. Geophys. Res. Space Phys. 118(3), 997–1008 (2013). https://doi.org/10.1002/jgra.50123
C. Dong, L. Wang, A. Hakim, A. Bhattacharjee, J.A. Slavin, G.A. DiBraccio, K. Germaschewski, A novel ten-moment multifluid model for Mercury: from the planetary conducting core to the dynamic magnetosphere. Geophys. Res. Lett. 0(ja), 11584–11596 (2019a). https://doi.org/10.1029/2019GL083180
C. Dong, L. Wang, A. Hakim, A. Bhattacharjee, J.A. Slavin, G.A. DiBraccio, K. Germaschewski, Global ten-moment multifluid simulations of the solar wind interaction with Mercury: from the planetary conducting core to the dynamic magnetosphere. Geophys. Res. Lett. 46(21), 11584–11596 (2019b)
J. Eastwood, E. Lucek, C. Mazelle, K. Meziane, Y. Narita, J. Pickett, R. Treumann, The foreshock. Space Sci. Rev. 118(1-4), 41–94 (2005)
W. Exner, D. Heyner, L. Liuzzo, U. Motschmann, D. Shiota, K. Kusano, T. Shibayama, Coronal mass ejection hits Mercury: A.I.K.E.F. hybrid-code results compared to MESSENGER data. Planet. Space Sci. 153, 89–99 (2018). https://doi.org/10.1016/j.pss.2017.12.016
W. Exner, S. Simon, D. Heyner, U. Motschmann, Influence of Mercury’s exosphere on the structure of the magnetosphere. J. Geophys. Res. Space Phys. (2020). https://doi.org/10.1029/2019JA027691
L. Fahrmeir, T. Kneib, S. Lang, B. Marx, Regression: Models, Methods and Applications (Berlin, Heidelberg, 2003)
D. Gamborino, A. Vorburger, P. Wurz, Mercury’s subsolar sodium exosphere: an ab initio calculation to interpret MASCS/UVVS observations from MESSENGER. Ann. Geophys. 37(4), 455–470 (2019). https://doi.org/10.5194/angeo-37-455-2019
N.Y. Ganushkina, M.W. Liemohn, S. Dubyagin, I.A. Daglis, I. Dandouras, D.L. De Zeeuw, Y. Ebihara, R. Ilie, R. Katus, M. Kubyshkina, S.E. Milan, S. Ohtani, N. Ostgaard, J.P. Reistad, P. Tenfjord, F. Toffoletto, S. Zaharia, O. Amariutei, Defining and resolving current systems in geospace. Ann. Geophys. 33(11), 1369–1402 (2015). https://doi.org/10.5194/angeo-33-1369-2015
S.P. Gary, The mirror and ion cyclotron anisotropy instabilities. J. Geophys. Res. 97, 8519–8529 (1992)
S.P. Gary, B.J. Anderson, R.E. Denton, S.A. Fuselier, M.E. McKean, D. Winske, Ion anisotropies in the magnetosheath. Geophys. Res. Lett. 20(17), 1767–1770 (1993)
A. Genova, S. Goossens, E. Mazarico, F.G. Lemoine, G.A. Neumann, W. Kuang, T.J. Sabaka, S.A. Hauck II, D.E. Smith, S.C. Solomon, M.T. Zuber, Geodetic evidence that Mercury has a solid inner core. Geophys. Res. Lett. 46(7), 3625–3633 (2019). https://doi.org/10.1029/2018GL081135
A. Genova, H. Hussmann, T. Van Hoolst, D. Heyner, L. Iess, F. Santoli, N. Thomas, P. Kolhey, B. Langlais, J. Mieth, J.S. Oliveira, A. Stark, N. Tosi, J. Wicht, J. Benkhoff, Geodesy, geophysics and fundamental physics investigations of the BepiColombo mission. Space Sci. Rev. 217(2), 1–62 (2021). https://doi.org/10.1007/s11214-021-00808-9,
D.J. Gershman, J.A. Slavin, J.M. Raines, T.H. Zurbuchen, B.J. Anderson, H. Korth, D.N. Baker, S.C. Solomon, Magnetic flux pileup and plasma depletion in Mercury’s subsolar magnetosheath. J. Geophys. Res. Space Phys. 118(11), 7181–7199 (2013)
K.-H. Glassmeier, Currents in Mercury’s Magnetosphere. Geophysical Monograph, vol. 118 (Am. Geophys. Union, Washington, 2000), pp. 371–380
K.-H. Glassmeier, J. Espley, ULF waves in planetary magnetospheres (2006), pp. 341–359. https://doi.org/10.1029/169GM22
K.-H. Glassmeier, P.N. Mager, D.Y. Klimushkin, Concerning ULF pulsations in Mercury’s magnetosphere. Geophys. Res. Lett. 30(18), 18 (2003)
K.-H. Glassmeier, D. Klimushkin, C. Othmer, P. Mager, ULF waves at Mercury: Earth, the giants, and their little brother compared. Adv. Space Res. 33(11), 1875–1883 (2004)
K.-H. Glassmeier, J. Grosser, H.-U. Auster, D. Constantinescu, Y. Narita, S. Stellmach, Electromagnetic induction effects and dynamo action in the Hermean system. Space Sci. Rev. 132(2-4), 511–527 (2007). https://doi.org/10.1007/s11214-007-9244-9
K.-H. Glassmeier, H.-U. Auster, D. Heyner, K. Okrafka, C. Carr, G. Berghofer, B.J. Anderson, A. Balogh, W. Baumjohann, P. Cargill, U. Christensen, M. Delva, M. Dougherty, K.-H. Fornaçon, T.S. Horbury, E.A. Lucek, W. Magnes, M. Mandea, A. Matsuoka, M. Matsushima, U. Motschmann, R. Nakamura, Y. Narita, H. O’Brien, I. Richter, K. Schwingenschuh, H. Shibuya, J.A. Slavin, C. Sotin, B. Stoll, H. Tsunakawa, S. Vennerstrom, J. Vogt, T. Zhang, The fluxgate magnetometer of the BepiColombo Mercury Planetary Orbiter. Planet. Space Sci. 58(1-2), 287–299 (2010)
N. Gómez-Pérez, J. Wicht, Behavior of planetary dynamos under the influence of external magnetic fields: Application to Mercury and Ganymede. Icarus 209(1), 53–62 (2010). Mercury after Two MESSENGER Flybys. https://doi.org/10.1016/j.icarus.2010.04.006
E. Greenstadt, R. Fredricks, C. Russell, F. Scarf, R. Anderson, D. Gurnett, Whistler mode wave propagation in the solar wind near the bow shock. J. Geophys. Res. Space Phys. 86(A6), 4511–4516 (1981)
L. Guicking, K.-H. Glassmeier, H.-U. Auster, M. Delva, U. Motschmann, Y. Narita, T.L. Zhang, Low-frequency magnetic field fluctuations in Venus’ solar wind interaction region: Venus Express observations. Ann. Geophys. 28, 951–967 (2010)
H. Gunell, M. Holmström, H.K. Biernat, N.V. Erkaev, Planetary ENA imaging: Venus and a comparison with Mars. Planet. Space Sci. 53, 433–441 (2005). https://doi.org/10.1016/j.pss.2004.07.021
A. Hasegawa, B.T. Tsurutani, Mirror mode expansion in planetary magnetosheaths: Bohm-like diffusion. Phys. Rev. Lett. 107, 245005 (2011). https://doi.org/10.1103/PhysRevLett.107.245005
S.a. Hauck, J.L. Margot, S.C. Solomon, R.J. Phillips, C.L. Johnson, F.G. Lemoine, E. Mazarico, T.J. McCoy, S. Padovan, S.J. Peale, M.E. Perry, D.E. Smith, M.T. Zuber, The curious case of Mercury’s internal structure. J. Geophys. Res., Planets 118(6), 1204–1220 (2013). https://doi.org/10.1002/jgre.20091
M. He, J. Vogt, D. Heyner, J. Zhong, Solar wind controls on Mercury’s magnetospheric cusp. J. Geophys. Res. Space Phys. 122(6), 6150–6164 (2017). https://doi.org/10.1002/2016JA023687
P.C. Hedgecock, A correlation technique for magnetometer zero level determination. Space Sci. Instrum. 1, 83–90 (1975)
P. Heinisch, H.U. Auster, I. Richter, D. Hercik, E. Jurado, R. Garmier, C. Güttler, K.H. Glassmeier, Attitude reconstruction of ROSETTA’s Lander PHILAE using two-point magnetic field observations by ROMAP and RPC-MAG. Acta Astronaut. 125, 174–182 (2016). https://doi.org/10.1016/j.actaastro.2015.12.002
D. Herčík, P.M. Trávníček, J.R. Johnson, E.-H. Kim, P. Hellinger, Mirror mode structures in the asymmetric Hermean magnetosheath: hybrid simulations. J. Geophys. Res. Space Phys. 118(1), 405–417 (2013)
D. Heyner, D. Schmitt, J. Wicht, K.-H. Glassmeier, H. Korth, U. Motschmann, The initial temporal evolution of a feedback dynamo for Mercury. Geophys. Astrophys. Fluid Dyn. 104(4), 419–429 (2010). https://doi.org/10.1080/03091921003776839
D. Heyner, D. Schmitt, K.-H. Glassmeier, J. Wicht, Dynamo action in an ambient field. Astron. Nachr. 332(1), 36–42 (2011a). https://doi.org/10.1002/asna.201011466
D. Heyner, J. Wicht, N. Gómez-Pérez, D. Schmitt, H.-U. Auster, K.-H. Glassmeier, Evidence from numerical experiments for a feedback dynamo generating Mercury’s magnetic field. Science 334(6063), 1690–1693 (2011b). https://doi.org/10.1126/science.1207290
D. Heyner, C. Nabert, E. Liebert, K.H. Glassmeier, Concerning reconnection-induction balance at the magnetopause of Mercury. J. Geophys. Res. A, Space Phys. 121, 1–27 (2016). https://doi.org/10.1002/2015JA021484
G.C. Ho, R.D. Starr, S.M. Krimigis, J.D. Vandegriff, D.N. Baker, R.E. Gold, B.J. Anderson, H. Korth, D. Schriver, R.L. McNutt, S.C. Solomon, MESSENGER observations of suprathermal electrons in Mercury’s magnetosphere. Geophys. Res. Lett. 43(2), 550–555 (2016). https://doi.org/10.1002/2015GL066850
R. Holme, J. Bloxham, The magnetic fields of Uranus and Neptune: Methods and models. J. Geophys. Res., Planets 101(E1), 2177–2200 (1996). https://doi.org/10.1029/95JE03437
L.L. Hood, Initial mapping of Mercury’s crustal magnetic field: relationship to the Caloris impact basin. Geophys. Res. Lett. 42(24), 10565–10572 (2015). https://doi.org/10.1002/2015GL066451
L.L. Hood, Magnetic anomalies concentrated near and within Mercury’s impact basins: early mapping and interpretation. J. Geophys. Res., Planets 121(6), 1016–1025 (2016). https://doi.org/10.1002/2016JE005048
L.L. Hood, G. Schubert, Inhibition of solar wind impingement on Mercury by planetary induction currents. J. Geophys. Res. 84(A6), 2641 (1979). https://doi.org/10.1029/JA084iA06p02641
L.L. Hood, J.S. Oliveira, V. Galluzzi, D.A. Rothery, Investigating sources of Mercury’s crustal magnetic field: further mapping of MESSENGER magnetometer data. J. Geophys. Res., Planets 123(10), 2647–2666 (2018). https://doi.org/10.1029/2018JE005683
S.M. Imber, J. Slavin, Messenger observations of magnetotail loading and unloading: implications for substorms at Mercury. J. Geophys. Res. Space Phys. 122(11), 11–402 (2017)
S.M. Imber, J.A. Slavin, H.U. Auster, V. Angelopoulos, A THEMIS survey of flux ropes and traveling compression regions : location of the near-Earth reconnection site during solar minimum. J. Geophys. Res. Space Phys. 116(A2), A02201 (2011). https://doi.org/10.1029/2010ja016026
M.K. James, S.M. Imber, T.K. Yeoman, E.J. Bunce, Field line resonance in the Hermean magnetosphere: structure and implications for plasma distribution. J. Geophys. Res. Space Phys. 124(1), 211–228 (2019a). https://doi.org/10.1029/2018JA025920
M.K. James, S.M. Imber, T.K. Yeoman, E.J. Bunce, Field line resonance in the Hermean magnetosphere: structure and implications for plasma distribution. J. Geophys. Res. Space Phys. 124(1), 211–228 (2019b)
P. Janhunen, E. Kallio, Surface conductivity of Mercury provides current closure and may affect magnetospheric symmetry. Ann. Geophys. 22,1829–1837 (2004)
X. Jia, J.A. Slavin, G. Poh, G.A. DiBraccio, G. Toth, Y. Chen, J.M. Raines, T.I. Gombosi, MESSENGER observations and global simulations of highly compressed magnetosphere events at Mercury. J. Geophys. Res. Space Phys. 124(1), 229–247 (2019). https://doi.org/10.1029/2018JA026166
C.L. Johnson, M.E. Purucker, H. Korth, B.J. Anderson, R.M. Winslow, M.M.H. Al Asad, J.a. Slavin, I.I. Alexeev, R.J. Phillips, M.T. Zuber, S.C. Solomon, MESSENGER observations of Mercury’s magnetic field structure. J. Geophys. Res., Planets 117(12), 1–22 (2012). https://doi.org/10.1029/2012JE004217
C.L. Johnson, R.J. Phillips, M.E. Purucker, B.J. Anderson, P.K. Byrne, B.W. Denevi, J.M. Feinberg, S.A. Hauck, J.W. Head, H. Korth, P.B. James, E. Mazarico, G.A. Neumann, L.C. Philpott, M.A. Siegler, N.A. Tsyganenko, S.C. Solomon, Low-altitude magnetic field measurements by MESSENGER reveal Mercury’s ancient crustal field. Science 348, 892–895 (2015). https://doi.org/10.1126/science.aaa8720
C.L. Johnson, L.C. Philpott, B.J. Anderson, H. Korth, S.A. Hauck, D. Heyner, R.J. Phillips, R.M. Winslow, S.C. Solomon, MESSENGER observations of induced magnetic fields in Mercury’s core. Geophys. Res. Lett. 43(6), 2436–2444 (2016a). https://doi.org/10.1002/2015GL067370
C.L. Johnson, R. Phillips, L. Philpott, B.J. Anderson, P. Byrne, B. Denevi, K. Fan, J. Feinberg, S. Hauck, J. Head, et al., Mercury’s lithospheric magnetic field, in Lunar and Planetary Science Conference, vol. 47, 2016b, p. 1391
C. Johnson, B. Anderson, H. Korth, R. Phillips, L. Philpott, Mercury’s Internal Magnetic Field (Cambridge University Press, Cambridge, 2018)
T. Karlsson, E. Liljeblad, A. Kullen, J.M. Raines, J.A. Slavin, T. Sundberg, Isolated magnetic field structures in Mercury’s magnetosheath as possible analogues for terrestrial magnetosheath plasmoids and jets. Planet. Space Sci. 129, 61–73 (2016)
E.-H. Kim, J.R. Johnson, E. Valeo, C.K. Phillips, Global modeling of ULF waves at Mercury. Geophys. Res. Lett. 42(13), 5147–5154 (2015)
C. Klimczak, Limits on the brittle strength of planetary lithospheres undergoing global contraction. J. Geophys. Res., Planets 120(12), 2135–2151 (2015). https://doi.org/10.1002/2015JE004851
J.S. Knibbe, W. van Westrenen, The interior configuration of planet Mercury constrained by moment of inertia and planetary contraction. J. Geophys. Res., Planets 120(11), 1904–1923 (2015). https://doi.org/10.1002/2015JE004908
J.S. Knibbe, W. van Westrenen, The thermal evolution of Mercury’s Fe–Si core. Earth Planet. Sci. Lett. 482, 147–159 (2018). https://doi.org/10.1016/j.epsl.2017.11.006
H. Korth, B.J. Anderson, D.J. Gershman, J.M. Raines, J.A. Slavin, T.H. Zurbuchen, S.C. Solomon, R.L. McNutt Jr., Plasma distribution in Mercury’s magnetosphere derived from MESSENGER magnetometer and fast imaging plasma spectrometer observations. J. Geophys. Res. Space Phys. 119(4), 2917–2932 (2014). https://doi.org/10.1002/2013JA019567
H. Korth, N.A. Tsyganenko, C.L. Johnson, L.C. Philpott, B.J. Anderson, M.M. Al Asad, S.C. Solomon, R.L. McNutt, Modular model for Mercury’s magnetospheric magnetic field confined within the average observed magnetopause. J. Geophys. Res. Space Phys. 120(6), 4503–4518 (2015). https://doi.org/10.1002/2015JA021022
H. Korth, C.L. Johnson, L. Philpott, N.A. Tsyganenko, B.J. Anderson, A dynamic model of Mercury’s magnetospheric magnetic field. Geophys. Res. Lett. 44, 10,147–10,154 (2017). https://doi.org/10.1002/2017GL074699
H. Korth, B.J. Anderson, C.L. Johnson, J.A. Slavin, J.M. Raines, T.H. Zurbuchen, Structure and configuration of Mercury’s magnetosphere, in Cambridge Planetary Science (Cambridge University Press, Cambridge, 2018), pp. 430–460. https://doi.org/10.1017/9781316650684.017
B. Langlais, M.E. Purucker, M. Mandea, Crustal magnetic field of Mars. J. Geophys. Res. 109, 02008 (2004). https://doi.org/10.1029/2003JE002048
B. Langlais, V. Lesur, M.E. Purucker, J.E. Connerney, M. Mandea, Crustal magnetic fields of terrestrial planets. Space Sci. Rev. 152(1-4), 223–249 (2010)
G. Le, P.J. Chi, X. Blanco-Cano, S. Boardsen, J.A. Slavin, B.J. Anderson, H. Korth, Upstream ultra-low frequency waves in Mercury’s foreshock region: messenger magnetic field observations. J. Geophys. Res. Space Phys. 118(6), 2809–2823 (2013)
H.K. Leinweber, C.T. Russell, K. Torkar, T.L. Zhang, V. Angelopoulos, An advanced approach to finding magnetometer zero levels in the interplanetary magnetic field. Meas. Sci. Technol. 19(5), 055104 (2008). https://doi.org/10.1088/0957-0233/19/5/055104
C. Lhotka, Y. Narita, Kinematic models of the interplanetary magnetic field, in Annales Geophysicae, vol. 37, Copernicus GmbH, 2019, pp. 299–314. Copernicus GmbH
F. Lhuillier, A. Fournier, G. Hulot, J. Aubert, The geomagnetic secular-variation timescale in observations and numerical dynamo models. Geophys. Res. Lett. 38(9) L09306 (2011). https://doi.org/10.1029/2011GL047356
E. Liljeblad, T. Karlsson, Investigation of 20–40 mHz ULF waves and their driving mechanisms in Mercury’s dayside magnetosphere, in Annales Geophysicae, vol. 35, Copernicus GmbH, 2017a, pp. 879–884. Copernicus GmbH
E. Liljeblad, T. Karlsson, Investigation of 20–40 mHz ULF waves and their driving mechanisms in Mercury’s dayside magnetosphere. Ann. Geophys. 35(4), 879–884 (2017b). https://doi.org/10.5194/angeo-35-879-2017
E. Liljeblad, T. Sundberg, T. Karlsson, A. Kullen, Statistical investigation of Kelvin-Helmholtz waves at the magnetopause of Mercury. J. Geophys. Res. Space Phys. 119(12), 9670–9683 (2014). https://doi.org/10.1002/2014JA020614
E. Liljeblad, T. Karlsson, T. Sundberg, A. Kullen, Observations of magnetospheric ULF waves in connection with the Kelvin-Helmholtz instability at Mercury. J. Geophys. Res. Space Phys. 121(9), 8576–8588 (2016)
R.L. Lin, X.X. Zhang, S.Q. Liu, Y.L. Wang, J.C. Gong, A three-dimensional asymmetric magnetopause model. J. Geophys. Res. 115(A4), 1–12 (2010). https://doi.org/10.1029/2009JA014235. ISBN 0148-0227.
Y.H. Liu, T.C. Li, M. Hesse, W.J. Sun, J. Liu, J. Burch, J.A. Slavin, K. Huang, Three-dimensional magnetic reconnection with a spatially confined X-line extent: implications for dipolarizing flux bundles and the dawn-dusk asymmetry. J. Geophys. Res. Space Phys. 124(4), 2819–2830 (2019). https://doi.org/10.1029/2019JA026539
F.J. Lowes, Mean-square values on sphere of spherical harmonic vector fields. J. Geophys. Res. 71(8), 2179 (1966). https://doi.org/10.1029/jz071i008p02179
S. Lu, P.L. Pritchett, V. Angelopoulos, A.V. Artemyev, Formation of dawn-dusk asymmetry in Earth’s magnetotail thin current sheet: a three-dimensional particle-in-cell simulation. J. Geophys. Res. Space Phys. 123(4), 2801–2814 (2018). https://doi.org/10.1002/2017JA025095
J.G. Lumann, R.C. Elphic, C.T. Russell, J.D. Mihalov, J.H. Wolfe, Observations of large scale steady magnetic fields in the dayside Venus ionosphere. Geophys. Res. Lett. 7, 917–920 (1980). https://doi.org/10.1029/GL007i011p00917
V. Malavergne, P. Cordier, K. Righter, F. Brunet, B. Zanda, A. Addad, T. Smith, H. Bureau, S. Surblé, C. Raepsaet, E. Charon, R.H. Hewins, How Mercury can be the most reduced terrestrial planet and still store iron in its mantle. Earth Planet. Sci. Lett. 394, 186–197 (2014). https://doi.org/10.1016/j.epsl.2014.03.028
A. Manglik, J. Wicht, U.R. Christensen, A dynamo model with double diffusive convection for Mercury’s core. Earth Planet. Sci. Lett. 289(3), 619–628 (2010). https://doi.org/10.1016/j.epsl.2009.12.007
U. Mann, D.J. Frost, D.C. Rubie, Evidence for high-pressure core-mantle differentiation from the metal–silicate partitioning of lithophile and weakly-siderophile elements. Geochim. Cosmochim. Acta 73(24), 7360–7386 (2009). https://doi.org/10.1016/j.gca.2009.08.006
J.-L. Margot, S.A. Hauck II, E. Mazarico, S. Padovan, S.J. Peale, Mercury’s internal structure, in Mercury: The View after MESSENGER, ed. by S.C. Solomon, L.R. Nittler, B.J. Anderson vol. 21 (Cambridge University Press, Cambridge, 2018), pp. 85–113. Chap. 4
P. Mauersberger, Das Mittel der Energiedichte des geomagnetischen Hauptfeldes an der Erdoberfläche und seine säkulare Änderung. Gerlands Beitr. Geophys. 65, 207–215 (1956)
F.M. McCubbin, M.A. Riner, K.E. Vander Kaaden, L.K. Burkemper, Is Mercury a volatile-rich planet? Geophys. Res. Lett. 39(9), L09202 (2012). https://doi.org/10.1029/2012GL051711
W. Menke, Geophysical Data Analysis: Discrete Inverse Theory (Academic Press, San Diego, 2018)
R.T. Merrill, P.L. McFadden, The geomagnetic axial dipole field assumption. Phys. Earth Planet. Inter. 139(3), 171–185 (2003). https://doi.org/10.1016/j.pepi.2003.07.016
A. Milillo, M. Fujimoto, G. Murakami, J. Benkhoff, J. Zender, S. Aizawa, M. Dósa, L. Griton, D. Heyner, G. Ho, et al., Investigating Mercury’s environment with the two-spacecraft BepiColombo mission. Space Sci. Rev. 216(5), 1–78 (2020)
G. Morard, T. Katsura, Pressure–temperature cartography of Fe–S–Si immiscible system. Geochim. Cosmochim. Acta 74(12), 3659–3667 (2010). https://doi.org/10.1016/j.gca.2010.03.025
J. Müller, S. Simon, Y.C. Wang, U. Motschmann, D. Heyner, J. Schüle, W.H. Ip, G. Kleindienst, G.J. Pringle, Origin of Mercury’s double magnetopause: 3D hybrid simulation study with A.I.K.E.F. Icarus 218(1), 666–687 (2012). https://doi.org/10.1016/j.icarus.2011.12.028
O. Namur, B. Charlier, Silicate mineralogy at the surface of Mercury. Nat. Geosci. 10(1), 9–13 (2017)
O. Namur, B. Charlier, F. Holtz, C. Cartier, C. McCammon, Sulfur solubility in reduced mafic silicate melts: implications for the speciation and distribution of sulfur on Mercury. Earth Planet. Sci. Lett. 448, 102–114 (2016). https://doi.org/10.1016/j.epsl.2016.05.024
Y. Narita, S.P. Gary, S. Saito, K.-H. Glassmeier, U. Motschmann, Dispersion relation analysis of solar wind turbulence. Geophys. Res. Lett. 38, L05101 (2011). https://doi.org/10.1029/2010GL046588
N.F. Ness, The magnetic field of Mercury. Phys. Earth Planet. Inter. 20(2-4), 209–217 (1979). https://doi.org/10.1016/0031-9201(79)90044-X
N.F. Ness, K.W. Behannon, R.P. Lepping, Y.C. Whang, K.H. Schatten, Magnetic field observations near Mercury: Preliminary results from Mariner 10. Science 185(4146), 151–160 (1974). https://doi.org/10.1126/science.185.4146.151
N.F. Ness, K.W. Behannon, R.P. Lepping, Y.C. Whang, Observations of Mercury’s magnetic field. Icarus 28(4), 479–488 (1976). https://doi.org/10.1016/0019-1035(76)90121-4
L.R. Nittler, R.D. Starr, S.Z. Weider, T.J. McCoy, W.V. Boynton, D.S. Ebel, C.M. Ernst, L.G. Evans, J.O. Goldsten, D.K. Hamara, D.J. Lawrence, R.L. McNutt, C.E. Schlemm, S.C. Solomon, A.L. Sprague, The major-element composition of Mercury’s surface from MESSENGER X-ray spectrometry. Science 333(6051), 1847–1850 (2011). https://doi.org/10.1126/science.1211567
J. O’Kane, L. Green, D.M. Long, H. Reid, Stealth coronal mass ejections from active regions. Astrophys. J. 882(2), L05101 (2019). https://doi.org/10.3847/1538-4357/ab371b
J.S. Oliveira, M.A. Wieczorek, Testing the axial dipole hypothesis for the Moon by modeling the direction of crustal magnetization. J. Geophys. Res., Planets 122, 383–399 (2017). https://doi.org/10.1002/2016JE005199
J.S. Oliveira, B. Langlais, M.A. Pais, H. Amit, A modified Equivalent Source Dipole method to model partially distributed magnetic field measurements, with application to Mercury. J. Geophys. Res., Planets 120(6), 1075–1094 (2015). https://doi.org/10.1002/2014JE004734
J.S. Oliveira, L.L. Hood, B. Langlais, Constraining the early history of Mercury and its core dynamo by studying the crustal magnetic field. J. Geophys. Res., Planets 124(9), 2382–2396 (2019). https://doi.org/10.1029/2019JE005938
N. Olsen, K.-H. Glassmeier, X. Jia, Separation of the magnetic field into external and internal parts. Space Sci. Rev. 152(1-4), 135–157 (2009). https://doi.org/10.1007/s11214-009-9563-0
P. Olson, U.R. Christensen, Dipole moment scaling for convection-driven planetary dynamos. Earth Planet. Sci. Lett. 250(3), 561–571 (2006). https://doi.org/10.1016/j.epsl.2006.08.008
N. Omidi, J. Eastwood, D. Sibeck, Foreshock bubbles and their global magnetospheric impacts. J. Geophys. Res. Space Phys. 115(A6), A06204 (2010)
N. Omidi, H. Zhang, D. Sibeck, D. Turner, Spontaneous hot flow anomalies at quasi-parallel shocks: 2. Hybrid simulations. J. Geophys. Res. Space Phys. 118(1), 173–180 (2013)
S. Orsini, V. Mangano, A. Milillo, C. Plainaki, A. Mura, J.M. Raines, E. De Angelis, R. Rispoli, F. Lazzarotto, A. Aronica, Mercury sodium exospheric emission as a proxy for solar perturbations transit. Sci. Rep. 8(1), 928 (2018). https://doi.org/10.1038/s41598-018-19163-x
L.C. Philpott, C.L. Johnson, R.M. Winslow, B.J. Anderson, H. Korth, M.E. Purucker, S.C. Solomon, Constraints on the secular variation of Mercury’s magnetic field from the combined analysis of MESSENGER and Mariner 10 data. Geophys. Res. Lett. 41(19), 6627–6634 (2014). https://doi.org/10.1002/2014GL061401
L. Philpott, C. Johnson, B. Anderson, R. Winslow, The shape of Mercury’s magnetopause: the picture from messenger magnetometer observations and future prospects for BepiColombo. J. Geophys. Res. Space Phys. 125(5), 2019–027544 (2020)
F. Plaschke, Y. Narita, On determining fluxgate magnetometer spin axis offsets from mirror mode observations. Ann. Geophys. 34(9), 759–766 (2016). https://doi.org/10.5194/angeo-34-759-2016
F. Plaschke, C. Goetz, M. Volwerk, I. Richter, D. Frühauff, Y. Narita, K.-H. Glassmeier, M.K. Dougherty, Fluxgate magnetometer offset vector determination by the 3D mirror mode method. Mon. Not. R. Astron. Soc. 469(Suppl_2), 675–684 (2017). https://doi.org/10.1093/mnras/stx2532
F. Plaschke, H. Hietala, M. Archer, X. Blanco-Cano, P. Kajdič, T. Karlsson, S.H. Lee, N. Omidi, M. Palmroth, V. Roytershteyn, et al., Jets downstream of collisionless shocks. Space Sci. Rev. 214(5), 81 (2018)
G. Poh, J.A. Slavin, X. Jia, J.M. Raines, S.M. Imber, W.-J. Sun, D.J. Gershman, G.A. DiBraccio, K.J. Genestreti, A.W. Smith, Mercury’s cross-tail current sheet: structure, X-line location and stress balance. Geophys. Res. Lett. 44 678–686 (2017). https://doi.org/10.1002/2016GL071612
M.E. Purucker, J.B. Nicholas, Global spherical harmonic models of the internal magnetic field of the Moon based on sequential and coestimation approaches. J. Geophys. Res., Planets 115, 12007 (2010). https://doi.org/10.1029/2010JE003650
M. Purucker, D. Ravat, H. Frey, C. Voorhies, T. Sabaka, M. Acuña, An altitude-normalized magnetic map of Mars and its interpretation. Geophys. Res. Lett. 27, 2449–2452 (2000). https://doi.org/10.1029/2000GL000072
J.M. Raines, G.A. DiBraccio, T.A. Cassidy, D.C. Delcourt, M. Fujimoto, X. Jia, V. Mangano, A. Milillo, M. Sarantos, J.A. Slavin, P. Wurz, Plasma sources in planetary magnetospheres: Mercury. Space Sci. Rev. 192(1-4), 91–144 (2015). https://doi.org/10.1007/s11214-015-0193-4
A. Rivoldini, M. Beuthe, M.H. Deproost, R.M. Baland, T. Van Hoolst, The interior structure of Mercury constrained by geodesy data and present-day thermal state, in AGU Fall Meeting Abstracts, vol. 2018, 2018, pp. 23–3509
Z.J. Rong, W.X. Wan, C. Shen, X. Li, M.W. Dunlop, A.A. Petrukovich, T.L. Zhang, E. Lucek, Statistical survey on the magnetic structure in magnetotail current sheets. J. Geophys. Res. Space Phys. 116(9), 1–17 (2011). https://doi.org/10.1029/2011JA016489
Z.J. Rong, Y. Ding, J.A. Slavin, J. Zhong, G. Poh, W.J. Sun, Y. Wei, L.H. Chai, W.X. Wan, C. Shen, The magnetic field structure of Mercury’s magnetotail. J. Geophys. Res. Space Phys. 123(1), 548–566 (2018). https://doi.org/10.1002/2017JA024923
A. Runov, V. Angelopoulos, A. Artemyev, J. Birn, P.L. Pritchett, X.Z. Zhou, Characteristics of ion distribution functions in dipolarizing flux bundles: event studies. J. Geophys. Res. Space Phys. 122(6), 5965–5978 (2017). https://doi.org/10.1002/2017JA024010
C. Russell, ULF waves in the Mercury magnetosphere. Geophys. Res. Lett. 16(11), 1253–1256 (1989)
C.T. Russell, J.G. Luhmann, R.C. Elphic, F.L. Scarf, The distant bow shock and magnetotail of Venus: magnetic field and plasma wave observations. Geophys. Res. Lett. 8, 843–846 (1981). https://doi.org/10.1029/GL008i007p00843
J.A. Russell, C.T. Baker, D.N. Slavin, The magnetosphere of Mercury, in Mercury, ed. by F. Matthews, M.S. Chapman, C., Vilas (University of Arizona Press, Tucson, 1988a), pp. 514–561
C.T. Russell, E. Chou, J.G. Luhmann, P.G.L.H. Brace, W.R. Hoegy, Solar and interplanetary control of the location of the Venus bow shock. J. Geophys. Res. 93, 5461–5469 (1988b). https://doi.org/10.1029/JA093iA06p05461
B. Sánchez-Cano, B.E.S. Hall, M. Lester, M.L. Mays, O. Witasse, R. Ambrosi, D. Andrews, M. Cartacci, A. Cicchetti, M. Holmström, S. Imber, P. Kajdič, S.E. Milan, R. Noschese, D. Odstrcil, H. Opgenoorth, J. Plaut, R. Ramstad, K.I. Reyes-Ayala, Mars plasma system response to solar wind disturbances during solar minimum. J. Geophys. Res. Space Phys. 122(6), 6611–6634 (2017). https://doi.org/10.1002/2016JA023587
D. Schmid, M. Volwerk, F. Plaschke, Z. Vörös, T.L. Zhang, W. Baumjohann, Y. Narita, Mirror mode structures near Venus and comet P/Halley. Ann. Geophys. 32, 651–657 (2014)
D. Schmid, F. Plaschke, Y. Narita, D. Heyner, J.Z. Mieth, B.J. Anderson, M. Volwerk, A. Matsuoka, W. Baumjohann, Magnetometer in-flight offset accuracy for the BepiColombo spacecraft, in Annales Geophysicae, vol. 38, Copernicus GmbH, 2020, pp. 823–832. Copernicus GmbH
M. Seufert, J. Saur, F.M. Neubauer, Multi-frequency electromagnetic sounding of the Galilean moons. Icarus 214(2), 477–494 (2011). https://doi.org/10.1016/j.icarus.2011.03.017
J.A. Slavin, Mercury’s magnetosphere. Adv. Space Res. 33(11), 1859–1874 (2004). https://doi.org/10.1016/j.asr.2003.02.019. ISBN 1301286583.
J.A. Slavin, R.E. Holzer, Solar wind flow about the terrestrial planets 1. Modeling bow shock position and shape. J. Geophys. Res. Space Phys. 86(A13), 11401–11418 (1981)
J.A. Slavin, E.J. Smith, D.G. Sibeck, D.N. Baker, R.D. Zwickl, S.-I. Akasofu, An ISEE 3 study of average and substorm conditions in the distant magnetotail. J. Geophys. Res. 90(A11), 10875 (1985). https://doi.org/10.1029/JA090iA11p10875
J. Slavin, J. Owen, J. Connerney, S. Christon, Mariner 10 observations of field-aligned currents at Mercury. Planet. Space Sci. 45(1), 133–141 (1997). Mercury: the Planet and its Magnetosphere. https://doi.org/10.1016/S0032-0633(96)00104-3
J.A. Slavin, E.I. Tanskanen, M. Hesse, C.J. Owen, M.W. Dunlop, S. Imber, E.A. Lucek, A. Balogh, K.H. Glassmeier, Cluster observations of traveling compression regions in the near-tail. J. Geophys. Res. Space Phys. 110(A6), 1–19 (2005). https://doi.org/10.1029/2004JA010878
J.A. Slavin, S.M. Krimigis, M.H. Acuña, B.J. Anderson, D.N. Baker, P.L. Koehn, H. Korth, S. Livi, B.H. Mauk, S.C. Solomon, et al., MESSENGER: exploring Mercury’s magnetosphere, in The Messenger Mission to Mercury (Springer, Berlin, 2007), pp. 133–160
J.A. Slavin, M.H. Acuña, B.J. Anderson, D.N. Baker, M. Benna, S.A. Boardsen, G. Gloeckler, R.E. Gold, G.C. Ho, H. Korth, S.M. Krimigis, R.L. McNutt, J.M. Raines, M. Sarantos, D. Schriver, S.C. Solomon, P. Trávníček, T.H. Zurbuchen, Messenger observations of magnetic reconnection in Mercury’s magnetosphere. Science 324(5927), 606–610 (2009a). https://doi.org/10.1126/science.1172011
J.A. Slavin, B.J. Anderson, T.H. Zurbuchen, D.N. Baker, S.M. Krimigis, M.H. Acuña, M. Benna, S.A. Boardsen, G. Gloeckler, R.E. Gold, G.C. Ho, H. Korth, R.L. McNutt, J.M. Raines, M. Sarantos, D. Sehriver, S.C. Solomon, P. Trávníček, MESSENGER observations of Mercury’s magnetosphere during northward IMF. Geophys. Res. Lett. 36(2), 1–6 (2009b). https://doi.org/10.1029/2008GL036158
J.A. Slavin, B.J. Anderson, D.N. Baker, M. Benna, S.A. Boardsen, G. Gloeckler, R.E. Gold, G.C. Ho, H. Korth, S.M. Krimigis, et al., Messenger observations of extreme loading and unloading of Mercury’s magnetic tail. Science 329(5992), 665–668 (2010)
J.A. Slavin, B.J. Anderson, D.N. Baker, M. Benna, S.a. Boardsen, R.E. Gold, G.C. Ho, S.M. Imber, H. Korth, S.M. Krimigis, R.L. McNutt, J.M. Raines, M. Sarantos, D. Schriver, S.C. Solomon, P. Trávníček, T.H. Zurbuchen, MESSENGER and Mariner 10 flyby observations of magnetotail structure and dynamics at Mercury. J. Geophys. Res. Space Phys. 117(1), 1–17 (2012). https://doi.org/10.1029/2011JA016900
J.A. Slavin, G.A. DiBraccio, D.J. Gershman, S.M. Imber, G.K. Poh, J.M. Raines, T.H. Zurbuchen, X. Jia, D.N. Baker, K.-H. Glassmeier, S.A. Livi, S.A. Boardsen, T.A. Cassidy, M. Sarantos, T. Sundberg, A. Masters, C.L. Johnson, R.M. Winslow, B.J. Anderson, H. Korth, R.L. McNutt, S.C. Solomon, MESSENGER observations of Mercury’s dayside magnetosphere under extreme solar wind conditions. J. Geophys. Res. Space Phys. 119(10), 8087–8116 (2014). https://doi.org/10.1002/2014JA020319
J.A. Slavin, D.N. Baker, D.J. Gershman, G.C. Ho, S.M. Imber, S.M. Krimigis, T. Sundberg, Structure and configuration of Mercury’s magnetosphere, in Cambridge Planetary Science (Cambridge University Press, Cambridge, 2018), pp. 461–496. https://doi.org/10.1017/9781316650684.017
J.A. Slavin, H.R. Middleton, J.M. Raines, X. Jia, J. Zhong, W.-J. Sun, S. Livi, S.M. Imber, G.-K. Poh, M. Akavan-Tafti, J. Jasinski, G.A. DiBraccio, C. Dong, R.M. Dewey, M.L. Mays, MESSENGER observations of disappearing dayside magnetosphere events at Mercury. J. Geophys. Res. Space Phys. 124 6613–6635 (2019). https://doi.org/10.1029/2019JA026892
D.E. Smith, M.T. Zuber, R.J. Phillips, S.C. Solomon, S.A. Hauck, F.G. Lemoine, E. Mazarico, G.A. Neumann, S.J. Peale, J.-L. Margot, C.L. Johnson, M.H. Torrence, M.E. Perry, D.D. Rowlands, S. Goossens, J.W. Head, A.H. Taylor, Gravity field and internal structure of Mercury from MESSENGER. Science 336(6078), 214–217 (2012). https://doi.org/10.1126/science.1218809
A.W. Smith, J.A. Slavin, C.M. Jackman, G.K. Poh, R.C. Fear, Flux ropes in the Hermean magnetotail: distribution, properties, and formation. J. Geophys. Res. Space Phys. 122(8), 8136–8153 (2017). https://doi.org/10.1002/2017JA024295
S.C. Solomon, R.L. McNutt, R.E. Gold, D.L. Domingue, MESSENGER mission overview. Space Sci. Rev. 131(1-4), 3–39 (2007). https://doi.org/10.1007/s11214-007-9247-6
B. Sreenivasan, C.A. Jones, Helicity generation and subcritical behaviour in rapidly rotating dynamos. J. Fluid Mech. 688, 5–30 (2011). https://doi.org/10.1017/jfm.2011.233
S.T. Suess, B.E. Goldstein, Compression of the Hermaean magnetosphere by the solar wind J. Geophys. Res. Space Phys. 84(9), 3306–3312 (1979). https://doi.org/10.1029/JA084iA07p03306
W.J. Sun, S.Y. Fu, J.A. Slavin, J.M. Raines, Q.G. Zong, G.K. Poh, T.H. Zurbuchen, Spatial distribution of Mercury’s flux ropes and reconnection fronts: MESSENGER observations. J. Geophys. Res. Space Phys. 121(8), 7590–7607 (2016). https://doi.org/10.1002/2016JA022787
W.J. Sun, J.M. Raines, S.Y. Fu, J.A. Slavin, Y. Wei, G.K. Poh, Z.Y. Pu, Z.H. Yao, Q.G. Zong, W.X. Wan, MESSENGER observations of the energization and heating of protons in the near-Mercury magnetotail. Geophys. Res. Lett. 44(16), 8149–8158 (2017). https://doi.org/10.1002/2017GL074276
T. Sundberg, S.a. Boardsen, J.a. Slavin, B.J. Anderson, H. Korth, T.H. Zurbuchen, J.M. Raines, S.C. Solomon, MESSENGER orbital observations of large-amplitude Kelvin-Helmholtz waves at Mercury’s magnetopause. J. Geophys. Res. Space Phys. 117(4), 1–11 (2012). https://doi.org/10.1029/2011JA017268
T. Sundberg, S.A. Boardsen, J.A. Slavin, V.M. Uritsky, B.J. Anderson, H. Korth, D.J. Gershman, J.M. Raines, T.H. Zurbuchen, S.C. Solomon, Cyclic reformation of a quasi-parallel bow shock at Mercury: Messenger observations. J. Geophys. Res. Space Phys. 118(10), 6457–6464 (2013)
T. Sundberg, S.A. Boardsen, D. Burgess, J.A. Slavin, Coherent wave activity in Mercury’s magnetosheath. J. Geophys. Res. Space Phys. 120(9), 7342–7356 (2015)
F. Takahashi, H. Shimizu, H. Tsunakawa, Mercury’s anomalous magnetic field caused by a symmetry-breaking self-regulating dynamo. Nat. Commun. 10(1), 1–8 (2019)
E. Thébault, P. Vigneron, B. Langlais, G. Hulot, A Swarm lithospheric magnetic field model to SH degree 80. Earth Planets Space 68(1), 126 (2016a). https://doi.org/10.1186/s40623-016-0510-5
E. Thébault, B. Langlais, J.S. Oliveira, H. Amit, L. Leclercq, A time-averaged regional model of the Hermean magnetic field. Phys. Earth Planet. Inter. 276, 93–105 (2018). Special Issue:15th SEDI conference. https://doi.org/10.1016/j.pepi.2017.07.001
P. Thomas, M. Grott, A. Morschhauser, F. Vervelidou, Paleopole reconstruction of martian magnetic field anomalies. J. Geophys. Res., Planets 123(5), 1140–1155 (2018). https://doi.org/10.1002/2017JE005511
M.F. Thomsen, V.A. Thomas, D. Winske, J.T. Gosling, M.H. Harris, C.T. Russell, Observational test of hot flow anomaly formation by the interaction of a magnetic discontinuity with the bow shock. J. Geophys. Res. 89, 15319–15330 (1993). https://doi.org/10.1029/93JA00792
Z. Tian, M.T. Zuber, S. Stanley, Magnetic field modeling for Mercury using dynamo models with a stable layer and laterally variable heat flux. Icarus 260, 263–268 (2015). https://doi.org/10.1016/j.icarus.2015.07.019
A. Tjulin, E.A. Lucek, I. Dandouras, Wave activity inside hot flow anomalies. J. Geophys. Res. 113, A08113 (2008). https://doi.org/10.1029/2008JA013333
N. Tosi, M. Grott, A.-C. Plesa, D. Breuer, Thermochemical evolution of Mercury’s interior. J. Geophys. Res., Planets 118(12), 2474–2487 (2013). https://doi.org/10.1002/jgre.20168
N. Tosi, O. Čadek, M. Běhounková, M. Káňová, A.-C. Plesa, M. Grott, D. Breuer, S. Padovan, M.A. Wieczorek, Mercury’s low-degree geoid and topography controlled by insolation-driven elastic deformation. Geophys. Res. Lett. 42(18), 7327–7335 (2015). https://doi.org/10.1002/2015GL065314
P.M. Trávníček, P. Hellinger, D. Schriver, D. Herčík, J.A. Slavin, B.J. Anderson, Kinetic instabilities in Mercury’s magnetosphere: three-dimensional simulation results. Geophys. Res. Lett. 36(7), L07104 (2009). https://doi.org/10.1029/2008GL036630
T. Trümper, M. Breuer, U. Hansen, Numerical study on double-diffusive convection in the Earth’s core. Phys. Earth Planet. Inter. 194-195, 55–63 (2012). https://doi.org/10.1016/j.pepi.2012.01.004
B.T. Tsurutani, G.S. Lakhina, Some basic concepts of wave-particle interactions in collisionless plasmas. Rev. Geophys. 35(4), 491–501 (1997)
D. Turner, N. Omidi, D. Sibeck, V. Angelopoulos, First observations of foreshock bubbles upstream of Earth’s bow shock: characteristics and comparisons to HFAs. J. Geophys. Res. Space Phys. 118(4), 1552–1570 (2013)
V. Uritsky, J. Slavin, G. Khazanov, E. Donovan, S. Boardsen, B. Anderson, H. Korth, Kinetic-scale magnetic turbulence and finite Larmor radius effects at Mercury. J. Geophys. Res. Space Phys. 116(A9), A09236 (2011)
V. Uritsky, J. Slavin, S. Boardsen, T. Sundberg, J. Raines, D. Gershman, G. Collinson, D. Sibeck, G. Khazanov, B. Anderson, et al., Active current sheets and candidate hot flow anomalies upstream of Mercury’s bow shock. J. Geophys. Res. Space Phys. 119(2), 853–876 (2014)
R. Vilim, S. Stanley, S.A. Hauck II, Iron snow zones as a mechanism for generating Mercury’s weak observed magnetic field. J. Geophys. Res., Planets 115(E11), E11003 (2010). https://doi.org/10.1029/2009JE003528
M. Volwerk, M. Delva, Y. Futaana, A. Retinò, Z. Vörös, T.L. Zhang, W. Baumjohann, S. Barabash, Substorm activity in Venus’s magnetotail. Ann. Geophys. 27, 2321–2330 (2009). https://doi.org/10.5194/angeo-27-2321-2009
M. Volwerk, M. Delva, Y. Futaana, A. Retinò, Z. Vörös, T.L. Zhang, W. Baumjohann, S. Barabash, Corrigendum to “substorm activity in Venus’s magnetotail”. Ann. Geophys., 27, 2321–2330 (2009). https://doi.org/10.5194/angeo-27-2321-2009. Ann. Geophys. 28, 1877–1878 (2010). https://doi.org/10.5194/angeo-28-1877-2010
M. Volwerk, D. Schmid, B.T. Tsurutani, M. Delva, F. Plaschke, Y. Narita, T.L. Zhang, K.-H. Glassmeier, Mirror mode waves in Venus’s magnetosheath: solar minimum vs. solar maximum. Ann. Geophys. 34, 1099–1108 (2016). https://doi.org/10.5194/angeo-34-1099-2016
A.P. Walsh, S. Haaland, C. Forsyth, A.M. Keesee, J. Kissinger, K. Li, A. Runov, J. Soucek, B.M. Walsh, S. Wing, M.G.G.T. Taylor, Dawn–dusk asymmetries in the coupled solar wind–magnetosphere–ionosphere system: a review. Ann. Geophys. 32(7), 705–737 (2014). https://doi.org/10.5194/angeo-32-705-2014
C.-P. Wang, Midnight radial profiles of the quiet and growth-phase plasma sheet: the geotail observations. J. Geophys. Res. 109(A12), 12201 (2004). https://doi.org/10.1029/2004JA010590
I. Wardinski, B. Langlais, E. Thébault, Correlated time-varying magnetic fields and the core size of Mercury. J. Geophys. Res., Planets 124(8), 2178–2197 (2019). https://doi.org/10.1029/2018JE005835
J. Wicht, D. Heyner, Mercury’s magnetic field in the MESSENGER era, in Planetary Geodesy and Remote Sensing (2014), pp. 223–262
R.M. Winslow, B.J. Anderson, C.L. Johnson, J.a. Slavin, H. Korth, M.E. Purucker, D.N. Baker, S.C. Solomon, Mercury’s magnetopause and bow shock from MESSENGER magnetometer observations. J. Geophys. Res. Space Phys. 118(5), 2213–2227 (2013). https://doi.org/10.1002/jgra.50237
R.M. Winslow, C.L. Johnson, B.J. Anderson, D.J. Gershman, J.M. Raines, R.J. Lillis, H. Korth, J.a. Slavin, S.C. Solomon, T.H. Zurbuchen, M.T. Zuber, Mercury’s surface magnetic field determined from proton-reflection magnetometry. Geophys. Res. Lett. 41, 4463–4470 (2014). https://doi.org/10.1002/2014GL060258
M. Yagi, K. Seki, Y. Matsumoto, D.C. Delcourt, F. Leblanc, Formation of a sodium ring in Mercury’s magnetosphere. J. Geophys. Res. Space Phys. 115(A10), A10253 (2010). https://doi.org/10.1029/2009JA015226
M. Yagi, K. Seki, Y. Matsumoto, D.C. Delcourt, F. Leblanc, Global structure and sodium ion dynamics in Mercury’s magnetosphere with the offset dipole. J. Geophys. Res. Space Phys. (2017). https://doi.org/10.1002/2017JA024082
Z. Zhang, A. Pommier, Electrical investigation of metal-olivine systems and application to the deep interior of Mercury. J. Geophys. Res., Planets 122(12), 2702–2718 (2017). https://doi.org/10.1002/2017JE005390
T.L. Zhang, W. Baumjohann, M. Delva, H.U. Auster, A. Balogh, C.T. Russell, S. Barabash, M. Balikhin, G. Berghofer, H.K. Biernat, H. Lammer, H. Lichtenegger, W. Magnes, R. Nakamura, T. Penz, K. Schwingenschuh, Z. Vörös, W. Zambelli, K.H. Fornacon, K.H. Glassmeier, I. Richter, C. Carr, K. Kudela, J.K. Shi, H. Zhao, U. Motschmann, J.P. Lebreton, Magnetic field investigation of the Venus plasma environment: expected new results from Venus Express. Planet. Space Sci. 54(13-14), 1336–1343 (2006). https://doi.org/10.1016/j.pss.2006.04.018
T.L. Zhang, M. Delva, W. Baumjohann, M. Volwerk, C.T. Russell, S. Barabash, M. Balikhin, S. Pope, K.-H. Glassmeier, K. Kudela, C. Wang, Z. Vörös, W. Zambelli, Initial Venus Express magnetic field observations of the Venus bow shock location at solar minimum. Planet. Space Sci. 56, 785–789 (2008). https://doi.org/10.1016/j.pss.2007.09.012
T.L. Zhang, Q. Lu, W. Baumjohann, C.T. Russell, A. Fedorov, S. Barabash, A.J. Coates, A.M. Du, J.B. Cao, R. Nakamura, W.L. Teh, R.S. Wang, X.K. Dou, X. Wang, K.H. Glassmeier, H.U. Auster, M. Balikin, Magnetic reconnection in the near Venusian magnetotail. Science 336, 567–570 (2010). https://doi.org/10.1126/science.1217013
T.L. Zhang, W. Baumjohann, W.L. Teh, R. Nakamura, C.T. Russell, J.G. Luhmann, K.H. Glassmeier, E. Dubinin, H.Y. Wei, A.M. Du, Q.M. Lu, S. Wang, M. Balikhin, Giant flux ropes observed in the magnetized ionosphere at Venus. Geophys. Res. Lett. 39, L23103 (2012). https://doi.org/10.1029/2012GL054236
H. Zhang, D. Sibeck, Q.-G. Zong, N. Omidi, D. Turner, L. Clausen, Spontaneous hot flow anomalies at quasi-parallel shocks: 1. Observations. J. Geophys. Res. Space Phys. 118(6), 3357–3363 (2013)
J. Zhong, W.X. Wan, Y. Wei, J.A. Slavin, J.M. Raines, Z.J. Rong, L.H. Chai, X.H. Han, Compressibility of Mercury’s dayside magnetosphere. Geophys. Res. Lett. 42(23), 10135–10139 (2015a). https://doi.org/10.1002/2015GL067063
J. Zhong, W.X. Wan, J.A. Slavin, Y. Wei, R.L. Lin, L.H. Chai, J.M. Raines, Z.J. Rong, X.H. Han, Mercury’s three-dimensional asymmetric magnetopause. J. Geophys. Res. Space Phys. 120(9), 7658–7671 (2015b). https://doi.org/10.1002/2015JA021425
B. Zwan, R. Wolf, Depletion of solar wind plasma near a planetary boundary. J. Geophys. Res. 81(10), 1636–1648 (1976)
Acknowledgements
D.H. was supported by the German Ministerium für Wirtschaft und Energie and the German Zentrum für Luft- und Raumfahrt under contract 50 QW 1501.
W.E. and D.H. were supported by DFG (German Research Foundation) under contract HE8016/1-1.
A.M. is supported by a Royal Society University Research Fellowship.
J. S. O. is funded by the ESA Research Fellowship programme in Space Science.
B.S.-C. acknowledges support through UK-STFC grants ST/S000429/1 and ST/V000209/1.
J. A. S. is supported by NASA Grants NNX16AJ67G and 80NSSC18K1137.
The Austrian team of the MPO-MAG magnetometer has financially been supported by the Austrian Space Applications Programme (ASAP) which is managed by the Austrian Research Promotion Agency (FFG).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The BepiColombo mission to Mercury
Edited by Johannes Benkhoff, Go Murakami and Ayako Matsuoka
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heyner, D., Auster, HU., Fornaçon, KH. et al. The BepiColombo Planetary Magnetometer MPO-MAG: What Can We Learn from the Hermean Magnetic Field?. Space Sci Rev 217, 52 (2021). https://doi.org/10.1007/s11214-021-00822-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-021-00822-x