The Non-carbonaceous–Carbonaceous Meteorite Dichotomy

Abstract

The isotopic dichotomy between non-carbonaceous (NC) and carbonaceous (CC) meteorites indicates that meteorite parent bodies derive from two genetically distinct reservoirs, which presumably were located inside (NC) and outside (CC) the orbit of Jupiter and remained isolated from each other for the first few million years of the solar system. Here we review the discovery of the NC–CC dichotomy and its implications for understanding the early history of the solar system, including the formation of Jupiter, the dynamics of terrestrial planet formation, and the origin and nature of Earth’s building blocks. The isotopic difference between the NC and CC reservoirs is probably inherited from the solar system’s parental molecular cloud and has been maintained through the rapid formation of Jupiter that prevented significant exchange of material from inside (NC) and outside (CC) its orbit. The growth and/or migration of Jupiter resulted in inward scattering of CC bodies, which accounts for the co-occurrence of NC and CC bodies in the present-day asteroid belt and the delivery of presumably volatile-rich CC bodies to the growing terrestrial planets. Earth’s primitive mantle, at least for siderophile elements like Mo, has a mixed NC–CC composition, indicating that Earth accreted CC bodies during the final stages of its growth, perhaps through the Moon-forming giant impactor. The late-stage accretion of CC bodies to Earth is sufficient to account for the entire budget of Earth’s water and highly volatile species.

1 Introduction

Most meteorites are fragments of asteroids located between Mars and Jupiter. It has traditionally been thought that these bodies formed close to their present-day location, but this view was challenged recently by the discovery of an isotopic dichotomy between non-carbonaceous (NC) and carbonaceous (CC) meteorites (Budde et al. 2016; Warren 2011). These two suites of meteorites derive from distinct reservoirs within the solar protoplanetary disk that remained spatially separated for several million years (Ma), most likely through the presence of Jupiter in between them (Kruijer et al. 2017). Independent of the discovery of the isotope dichotomy, dynamical models aimed at explaining the small mass of Mars suggested that S-type and C-type asteroids represent bodies from inside and outside Jupiter’s orbit, respectively, and that these bodies were implanted into the present-day asteroid belt through the inward-then-outward migration of Jupiter and Saturn (the so-called ‘Grand Tack’ model) (Walsh et al. 2011). Later work showed that planetesimals from beyond Jupiter may have also been implanted into the asteroid belt during the growth of the giant planets, without the need to invoke a specific planetary migration pattern (Raymond and Izidoro 2017). These models are remarkably consistent with the isotopic dichotomy observed among meteorites, and collectively these studies indicate that S-type asteroids and NC meteorites represent inner solar system material, whereas C-type asteroids and CC meteorites derive from the outer solar system.

The purpose of this paper is to review the meteorite dichotomy and its origin, and discuss its implications for understanding the early evolution of the solar accretion disk, the role of Jupiter in the early solar system, the formation of planetesimals, and the accretion history and building blocks of the terrestrial planets.

2 Nucleosynthetic Isotope Anomalies in Meteorites

The distinction between non-carbonaceous (NC) and carbonaceous (CC) meteorites is based on nucleosynthetic isotope anomalies. We will therefore start with briefly reviewing the definition, notation and origin of these isotope anomalies, with a particular focus on those that are fundamental to the definition of the isotope dichotomy. Nucleosynthetic isotope anomalies are characterized by enrichments or depletions in nuclides formed by particular stellar nucleosynthetic processes. As such, these anomalies are distinct from mass-dependent isotope fractionations, which result from physical or chemical processes that separate the isotopes according to their mass. Isotope fractionations can also be non-mass-dependent (sometimes also called mass-independent) when they depart from the accepted mass fractionation law. For instance, O isotope variations among meteorites reveal both mass-dependent and non-mass-dependent isotope fractionations, where the latter are typically expressed as $\Delta ^{17}\text{O}$ as the deviation from the terrestrial mass fractionation line.

Nucleosynthetic isotope anomalies are not the result of isotope fractionation, but instead arise from the heterogeneous distribution of presolar matter derived from multiple nucleosynthetic sources. Some of this material has been identified in the matrix of primitive chondrites as presolar grains, whose isotopic compositions deviate strongly from the solar composition and reflect the particular stellar environment in which these grains formed (Zinner 2014). Isotope anomalies in other meteoritic materials are much smaller than those found in presolar grains, attesting to the near complete homogenization of presolar matter in the parental molecular cloud or the solar nebula itself. Whereas the isotopic composition of presolar grains is commonly reported as absolute isotope ratio, the much smaller isotope anomalies in meteoritic and planetary materials are commonly reported as variations in isotope ratios that are normalized to another ratio of the same element, for which a fixed, terrestrial value is assumed. This normalization is necessary to correct for the effects of natural and instrumental mass fractionation, and it is typically done using the exponential mass fractionation law. Further, as the isotope variations in meteoritic and planetary samples are typically small, they are commonly reported in the $\varepsilon$-unit notation as parts-per-ten-thousand deviations from terrestrial standard values. For instance, Mo isotope anomalies are reported as variations in the $^{i}\text{Mo}/^{96}\text{Mo}$ ratio, which are normalized to the terrestrial $^{98}\text{Mo}/^{96}\text{Mo}$ and are given as $\varepsilon ^{i}\text{Mo}$ values ($i = 92$, 94, 95, 97, 100). Sometimes the anomalies are also given as $\mu$-values ($1\varepsilon = 100\mu$).

For most elements nucleosynthetic anomalies are most prominent in Ca-Al-rich inclusions (CAIs), the solar system’s oldest dated solids (Amelin et al. 2010; Connelly et al. 2012). Of these, FUN (Fractionated and Unknown Nuclear effects) CAIs, platy hibonite crystals (PLACs) and spinel hibonite inclusions (SHIBs) typically have the largest nucleosynthetic anomalies, whereas the more common ‘normal’ CAIs display smaller anomalies (for an overview see Dauphas and Schauble 2016). Most of the initial work on nucleosynthetic anomalies in meteoritic materials was focused on CAIs, because only for these could anomalies be clearly resolved (e.g., Birck and Lugmair 1988; Lee et al. 1978; McCulloch and Wasserburg 1978; Niederer et al. 1981; Niemeyer and Lugmair 1981; Papanastassiou 1986). Nevertheless, some of these earlier studies already provided hints for nucleosynthetic isotope anomalies in other components of primitive chondrites (e.g., chondrules) and also showed that bulk carbonaceous chondrites are characterized by excesses in the neutron-rich isotopes of ⁵⁰Ti and ⁵⁴Cr (Niederer et al. 1985; Niemeyer 1988; Niemeyer and Lugmair 1984; Rotaru et al. 1992). With improvements in analytical techniques over the past two decades, nucleosynthetic isotope anomalies have now been identified for many elements, and it has been shown that they exist not only in bulk carbonaceous chondrites, but also in other groups of meteorites (e.g., Burkhardt et al. 2011; Dauphas et al. 2002; Leya et al. 2008; Regelous et al. 2008; Trinquier et al. 2007, 2009). Because nucleosynthetic isotope anomalies are widespread, they are powerful tracers for inferring genetic relationships between and among meteorites and planets (Burkhardt et al. 2016, 2011; Dauphas 2017; Render et al. 2017; Warren 2011), and for assessing transport and mixing processes in the solar protoplanetary disk (Ebert et al. 2018; Gerber et al. 2017; Olsen et al. 2016; Render et al. 2019; Van Kooten et al. 2016). As such, nucleosynthetic anomalies constitute a powerful tool to constrain models of planet formation.

The processes that led to a heterogeneous distribution of presolar matter in the solar accretion disk are not fully understood and several mechanisms have been proposed. These include inherited heterogeneity from the solar system’s parental molecular cloud (Burkhardt et al. 2019; Dauphas et al. 2002; Nanne et al. 2019), grain type- or size-sorting in the solar protoplanetary disk (Dauphas et al. 2008; Regelous et al. 2008), thermal processing of dust in the disk (Burkhardt et al. 2012; Poole et al. 2017; Trinquier et al. 2009), and late injection of diverse nucleosynthetic components (Brennecka et al. 2013). These processes are not mutually exclusive and may all have played a role.

Although nucleosynthetic anomalies in bulk meteorites and meteorite components have been reported for a considerable number of elements, the anomalies in Ti, Cr, Ni, and Mo are particularly important, because they have been instrumental for identifying the isotope dichotomy of meteorites, and for constraining its origin. The original identification of the NC–CC dichotomy also included O isotopes (Fig. 1b), but we note that for $\Delta^{17}\text{O}$ there is substantial overlap between NC and CC meteorites, and so the dichotomy is essentially defined by isotope variation in the other elements. This paper will therefore largely be focused on isotope anomalies for Ti, Cr, Ni, and Mo. The isotope anomalies in Ti and Cr predominantly reflect variations in the neutron-rich isotopes of these elements (i.e., ⁵⁰Ti, ⁵⁴Cr), both of which are thought to be produced in supernovae (Leya et al. 2008; Trinquier et al. 2007, 2009; Zhang et al. 2012). For Cr, one potential carrier of these anomalies has been identified as ⁵⁴Cr-rich nanospinels that probably condensed in the outflow of supernovae (Dauphas et al. 2010; Qin et al. 2011). Such grains may also be strongly enriched in ⁵⁰Ti (Nittler et al. 2018). Anomalies in Ni appear to have distinct origins in bulk meteorites and CAIs. Whereas the Ni isotope anomalies in CAIs, similar to Cr and Ti, appear to reflect enrichments in the neutron-rich isotopes ⁶²Ni and ⁶⁴Ni (Birck and Lugmair 1988; Render et al. 2018), those in bulk meteorites largely seem to reflect variations in ⁵⁸Ni (Nanne et al. 2019; Steele et al. 2012; Tang and Dauphas 2012).

Fig. 1

(a) $\varepsilon ^{54}\text{Cr}$ versus $\varepsilon ^{50}\text{Ti}$ and (b) $\varepsilon ^{54}\text{Cr}$ versus $\Delta ^{17}\text{O}$. These two plots were instrumental for the original definition of the NC–CC dichotomy. Note that the O isotope anomalies are not thought to be nucleosynthetic in origin, but that they are nevertheless indicative of spatial or temporal changes within the accretion disk (McKeegan et al. 2011). Data taken from the compilations in Burkhardt et al. (2017) and Dauphas and Schauble (2016). (c) $\varepsilon^{94}\text{Mo}$ versus $\varepsilon ^{100}\text{Ru}$ and (d) $\varepsilon ^{94}\text{Mo}$ versus $\varepsilon ^{64}\text{Ni}$. These two plots for siderophile elements are useful for illustrating that the NC–CC dichotomy for iron meteorites extends to several elements. Note that the Ni isotope anomalies most likely reside on ⁵⁸Ni, but they are shown as apparent variations in $\varepsilon ^{64}\text{Ni}$, because for this normalization the apparent anomalies are larger and more precisely measured. Data taken from the compilations in Nanne et al. (2019), Worsham et al. (2019), and Hopp et al. (2020). Importantly, in all plots the NC and CC fields are consistently defined by the same meteorite groups. Note the wide gap between the NC (red) and CC (blue) fields

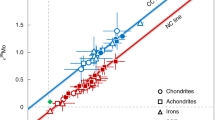
A key element with respect to the NC–CC dichotomy is Mo. The seven stable Mo isotopes are produced by three distinct nucleosynthetic processes, namely the proton ($p$-) process, the slow neutron capture ($s$-) process and the rapid neutron capture ($r$-) process. While the $p$- and $r$-processes are thought to occur in neutron-rich stellar environments such as supernovae or neutron star mergers, the $s$-process takes place in AGB stars. Of the stable Mo nuclides, ⁹²Mo is exclusively produced in the $p$-process, ⁹⁶Mo is only produced in the $s$-process, and ¹⁰⁰Mo is an almost pure $r$-process nuclide. Each of the remaining isotopes is produced by two different nucleosynthetic processes: ⁹⁴Mo ($p$, $s$); ⁹⁵Mo, ⁹⁷Mo, and ⁹⁸Mo ($s$, $r$). An important feature of Mo isotopes is that the $p$-process isotopes ⁹²Mo and ⁹⁴Mo are sufficiently abundant to allow for precise measurement. This in turn makes it possible to distinguish between the heterogeneous distribution of $s$- and $r$-process carriers (Burkhardt et al. 2011), which results in distinctly different Mo isotope patterns (Fig. 2). This feature has been essential for identifying the dichotomy between NC and CC meteorites (Budde et al. 2016).

Fig. 2

Left: Different Mo isotope patterns for $s$-process deficit and $r$-process excess. The differences are most pronounced at $\varepsilon ^{95}\text{Mo}$ and $\varepsilon ^{94}\text{Mo}$. Right: In a plot of $\varepsilon ^{95}\text{Mo}$ versus $\varepsilon ^{94}\text{Mo}$, $s$- and $r$-process variations plot along lines of different slope. Thus, for a given $\varepsilon ^{94}\text{Mo}$, an $r$-process excess results in a much larger $\varepsilon ^{95}\text{Mo}$ than does an $s$-process deficit

3 Isotopic Dichotomy Between Non-carbonaceous and Carbonaceous Meteorites

3.1 Discovery and Characteristic of the NC–CC Dichotomy

The first hint of what now is recognized as the NC–CC dichotomy was observed by Trinquier et al. (2007). These authors showed that in $\Delta^{17}\text{O}$–$\varepsilon ^{54}\text{Cr}$ space, differentiated meteorites and carbonaceous chondrites plot in two distinct fields and on this basis argued that two distinct reservoirs existed in the early solar system. By compiling available isotopic data for Cr, Ti, Ni, and O, Warren (2011) then showed that for these elements meteorites always define two distinct isotopic clusters (Fig. 1a, b). Warren (2011) also introduced the terms non-carbonaceous (NC) and carbonaceous (CC) meteorites to distinguish between these two groups of materials. Importantly, the NC and CC compositional fields are separated by a wide gap, indicating that NC and CC meteorites represent fundamentally distinct materials with little to no mixing between them. On this basis, Warren (2011) suggested that the NC–CC dichotomy may either reflect a temporal change in solar nebula composition (and the later formation of CC bodies), or derivation of NC and CC materials from the inner and outer solar system, respectively.

Budde et al. (2016) subsequently demonstrated that the NC–CC dichotomy also exists for Mo. The dichotomy is most obvious in a plot of $\varepsilon^{95}\text{Mo}$ versus $\varepsilon ^{94}\text{Mo}$, in which the difference between $s$- and $r$-process variability is most clearly resolved (see above and Fig. 2). Budde et al. (2016) showed that in this plot, NC and CC meteorites plot on two distinct and approximately parallel lines (termed the NC- and CC-lines). As will be discussed in more detail below (Sect. 3.2), the isotopic variations along both lines reflect the heterogeneous distribution of $s$-process material, while the offset between these two lines reflects an excess in $r$-process (and possibly $p$-process) Mo in the CC over the NC reservoir (Fig. 3). As a siderophile element, and unlike Cr and Ti, Mo can be analyzed in essentially all meteorites, including chondrites and iron meteorites, which derive from bodies that accreted over a time span of $\sim 4$ million years (Ma) (see below). As such, the discovery of the Mo isotopic dichotomy made it possible to investigate how the compositions of the NC and CC reservoir evolved over time with unprecedented temporal and spatial resolution. The Mo isotope data have, therefore, been key for recognizing that the NC–CC dichotomy reflects the spatial separation of two genetically distinct disk reservoirs, and not merely a temporal change in disk composition (see Sect. 3.4 below). Several subsequent studies have reported high-precision Mo isotopic data for a large set of diverse meteorites, and these studies collectively demonstrate that all known asteroidal meteorites belong to either the NC or the CC group (Bermingham et al. 2018; Budde et al. 2019; Kruijer et al. 2017; Poole et al. 2017; Worsham et al. 2017, 2019; Yokoyama et al. 2019).

Fig. 3

$\varepsilon ^{95}\text{Mo}$ versus $\varepsilon ^{94}\text{Mo}$ for bulk meteorites. In this plot the difference between $s$- and $r$-process isotope variations in most clearly resolved, and so the NC–CC dichotomy for Mo is best illustrated in this plot. Note that the Mo isotope variability along the NC- and CC-lines is predominantly governed by $s$-process variations, whereas the offset between the two lines reflects an approximately constant $r$-process excess in the CC over the NC reservoir. Data are from various sources (Table 1)

Subsequent work demonstrated that the NC–CC dichotomy extends to several other siderophile elements, including W, Ru, and Ni. For instance, CC meteorites are characterized by ⁵⁸Ni (Nanne et al. 2019; Steele et al. 2012) and ¹⁸³W excesses (Budde et al. 2018; Kruijer et al. 2017; Worsham et al. 2019), and they typically also have larger ¹⁰⁰Ru deficits than NC meteorites (Bermingham et al. 2018; Fischer-Gödde et al. 2015; Fischer-Gödde and Kleine 2017; Hopp et al. 2020; Worsham et al. 2019). When the isotope anomalies for these elements are plotted against each other, meteorites can always be subdivided into two clusters (Fig. 1c, d). Importantly, for all these elements a given meteorite always belongs to the same cluster, indicating that the NC–CC dichotomy is consistently present for a wide range of elements (Fig. 1). For some element pairs, the isotope anomalies are correlated in one reservoir but not the other. For instance, Ru and Mo anomalies are correlated in the NC but not the CC reservoir (Fig. 1c), whereas Mo and W anomalies are correlated in the CC but not the NC reservoir (Worsham et al. 2019). The disparate correlations of isotope anomalies most likely reflect different redox and thermal conditions under which presolar carriers have been processed in the two reservoirs, providing further evidence that NC and CC meteorites represent material from fundamentally different areas of the solar protoplanetary disk (Worsham et al. 2019).

In summary, the dichotomy between NC and CC meteorites universally holds for all known meteorite classes. It exists for a large number of elements of different geochemical and cosmochemical behaviour, including lithophile (Cr, Ti, O) and siderophile elements (Ni, Mo, Ru, W), as well as refractory (Ti, Mo, Ru, W) and non-refractory (Cr, Ni) elements. The NC–CC dichotomy, therefore, is a ubiquitous and fundamental characteristic of early-formed planetary objects in the solar system. Compared to the NC reservoir, the CC reservoir exhibits excesses in ⁵⁰Ti, ⁵⁴Cr, ⁵⁸Ni, and $r$-process Mo. The CC reservoir, therefore, is characterized by an enrichment in nuclides produced in neutron-rich stellar environments. Finally, for several element pairs, the isotopic compositions of NC and CC meteorites define two clusters that are separated by a wide gap, indicating that the NC and CC reservoirs represent fundamentally different materials with no or very limited mixing between them (Fig. 1). In contrast to most elements where the NC–CC dichotomy is revealed by distinct anomalies in a single isotope ratio, Mo isotopes are uniquely important, because for them the NC–CC dichotomy is clearly resolved in multiple isotope ratios of a single element (Fig. 3).

3.2 Mo Isotopic Characteristics of the NC and CC Reservoirs

Given the importance of Mo isotopes for the NC–CC dichotomy, we will describe the characteristic Mo isotope systematics of NC and CC meteorites in some more detail. As noted above, the isotopic variations along the NC- and CC-lines are predominantly governed by $s$-process heterogeneity. This conclusion follows from the observation that the slopes of both lines are consistent with the expected slope as derived from isotopic data for presolar mainstream SiC grains. The latter are thought to have condensed in AGB stars, the dominant site of the $s$-process.

Table 1 Summary of Mo isotope data for major groups of meteorites^a

The slope of $s$-process mixing lines in $\varepsilon ^{i}\text{Mo}$–$\varepsilon ^{94}\text{Mo}$ plots can be determined from presolar grain data using the formalism of Dauphas et al. (2004):

$$ m = \frac{\rho ^{i} \text{Mo} - \rho ^{98} \text{Mo} \cdot \mu ^{i} \text{Mo}}{\rho ^{94} \text{Mo} - \rho ^{98} \text{Mo} \cdot \mu ^{94} \text{Mo}} $$

where the parameter $\rho ^{i}\text{Mo}$ represents the $s$-process composition relative to the terrestrial Mo isotope composition:

$$ \rho ^{i} \text{Mo}= \frac{ ( {{}^{i} \text{Mo}} / {{}^{96} \text{Mo}} )_{\mathrm{s}}}{ ( {{}^{i} \text{Mo}} / {{}^{96} \text{Mo}} )} -1 $$

and $\mu ^{i}\text{Mo}$ is the mass difference of the isotope ratio relative to that of the normalizing pair used for correction of instrumental mass fractionation:

$$ \mu ^{i} \text{Mo}= \frac{i -96}{98-96} $$

Information about the $s$-process Mo isotope composition is provided by data for mainstream circumstellar SiC grains, which correspond to $\rho^{i}\text{Mo}$ values of 1, 0.964, 0.615, 0.532, 0.256, and 0.980 for $i = 92$, 94, 95, 97, 98, and 100 (Stephan et al. 2019).

Budde et al. (2019) showed that the slopes of the NC- and CC-lines are indistinguishable from the predicted slopes of $s$-process mixing lines. These authors used a comprehensive set of Mo isotopic data for meteorites, including bulk meteorites, meteorite components from carbonaceous chondrites (i.e., chondrules, matrix, and metal samples from primitive chondrites), and acid leachates of primitive carbonaceous and ordinary chondrites. Linear regression of these data provides $\varepsilon ^{95}\text{Mo}$–$\varepsilon^{94}\text{Mo}$ slopes of $0.596\pm 0.008$ and $0.596\pm 0.006$ for the NC- and CC-lines, respectively. These slopes are in good agreement with a slope of $0.609\pm 0.008$ as calculated from the presolar SiC grain data, demonstrating that the isotopic variations predominantly reflect $s$-process variations.

As noted above, the offset between the NC- and CC-lines is consistent with an excess of $r$-process material in the CC reservoir. This is because for a given $\varepsilon ^{94}\text{Mo}$, a $r$-process excess results in a more positive $\varepsilon ^{95}\text{Mo}$ than an $s$-process deficit (Fig. 2). Further, as the NC- and CC-lines are parallel, all CC meteorites have an approximately constant $r$-process excess compared to NC meteorites, because otherwise the NC- and CC-lines would not be parallel. To quantify the offset between the NC and CC reservoirs it is useful to introduce the $\Delta ^{95}\text{Mo}$ notation as follows (Budde et al. 2019):

$$ \Delta ^{95}\text{Mo} = \bigl(\varepsilon ^{95}\text{Mo} - 0.596 \times \varepsilon ^{94}\text{Mo} \bigr) \times 100 $$

where the slope of 0.596 is the slope of the $s$-process mixing line as obtained from NC and CC meteorites (using the 0.609 slope obtained from SiC grain data would change the $\Delta ^{95}\text{Mo}$ values by less than $\sim1~\text{ppm}$). As such, $\Delta ^{95}\text{Mo}$ provides the parts-per-million deviation of a sample from an $s$-process mixing line that passes through the origin. In other words, $\Delta ^{95}\text{Mo}$ ‘removes’ the $s$-process variations among samples from a given reservoir, and therefore is a measure of any deviation from pure $s$-process variations relative to the composition of the standard. The characteristic values for the NC and CC reservoir are $\Delta ^{95}\text{Mo}_{\text{NC}} = -9\pm 2$ and $\Delta ^{95}\text{Mo}_{\text{CC}} = +26\pm 2$ (Budde et al. 2019). These values are unique isotope signatures of the NC and CC reservoirs, irrespective of the absolute anomaly of a given sample.

The Mo isotopic data allow for small $r$-process (and possibly $p$-process) heterogeneities within the NC- and CC-reservoirs (Budde et al. 2019; Poole et al. 2017; Worsham et al. 2017; Yokoyama et al. 2019). For instance, when only the data for bulk NC meteorites are considered, the slope of the NC-line seems to be slightly shallower (Budde et al. 2019; Yokoyama et al. 2019), suggesting that there are small additional $r$- or $p$-process variations among these samples. However, these heterogeneities are small compared to the $r$-process excess of the CC over the NC reservoir (Fig. 3). Thus, in spite of the heterogeneous distribution of an $s$-process Mo carrier in both reservoirs, the presolar material responsible for the $r$-process offset between the NC and CC reservoirs is fairly homogeneously distributed within both reservoirs. This is not only true for bulk meteorites, but also for most components of primitive chondrites (with the exception of CAI). For instance, chondrule and matrix separates from the CV3 chondrite Allende (Budde et al. 2016), as well as metal and silicate fractions from CR chondrites (Budde et al. 2018) exhibit large $s$-process Mo isotope variations, yet they all plot on the CC-line (not shown in Fig. 3). Collectively, these observations suggest that the excess $r$-process material in the CC reservoir is not hosted in individual presolar carriers, but is characteristic for the bulk isotopic composition of this reservoir (Budde et al. 2019; Burkhardt et al. 2019; Nanne et al. 2019).

3.3 Chronology of NC and CC Meteorites

The dichotomy between NC and CC meteorites may either reflect formation in two spatially separated regions of the solar nebula or distinct formation times of NC and CC meteorites combined with a temporal change of the solar nebula’s isotopic composition (Warren 2011). For instance, because carbonaceous chondrites formed relatively late, up to $\sim 4~\text{Ma}$ after CAI formation (Budde et al. 2018; Schrader et al. 2017), their distinct Ti–Cr–O isotopic composition (Fig. 1a, b) could in principle reflect a change in the solar nebula’s isotopic composition prior to their formation, but after accretion of NC meteorite parent bodies (Warren 2011). Distinguishing between a spatial and temporal origin of the NC–CC dichotomy, therefore, requires knowledge of the timescales of meteorite parent body accretion. Recent summaries of accretion ages can be found in Sugiura and Fujiya (2014), Desch et al. (2018), and Kruijer et al. (2020). Here we will not provide a detailed review of these accretion ages, but focus on those that are most important for understanding the formation of the NC and CC reservoirs, namely the accretion ages of the parent bodies of iron meteorites and chondrites.

The Hf–W chronology of ‘magmatic’ iron meteorites [i.e., iron meteorites from the metallic cores of differentiated bodies (Scott and Wasson 1975)] indicates that core formation in their parent bodies occurred at $\sim0.5\text{--}1.5~\text{Ma}$ (NC irons) and $\sim2\text{--}3~\text{Ma}$ (CC irons) after CAI formation (Kruijer et al. 2017, 2014). Core formation within a few Ma after CAI formation is consistent with decay of ²⁶Al as the dominant heat source facilitating melting and differentiation (Hevey and Sanders 2006), and thermal modeling of planetesimals heated internally by ²⁶Al decay to obtain inferred core formation ages indicates that the NC iron parent bodies accreted within $\sim0.5~\text{Ma}$, whereas the CC iron parent bodies accreted slightly later, at $\sim1~\text{Ma}$ after CAI formation (Kruijer et al. 2017, 2014). Thus, early-formed iron meteorite parent bodies exist in both the NC and CC reservoirs, indicating that the NC–CC dichotomy was already present when the iron meteorite parent bodies formed at $<1~\text{Ma}$ after CAI formation.

The accretion ages for chondrite parent bodies can be inferred from the chronology of chondrules, small igneous spherules that are the dominant component of most chondrites and formed prior to or during the accretion of their host chondrite (Alexander et al. 2008). The Al–Mg chronology of chondrules from ordinary, CV, and CO chondrites provide a narrow interval of formation ages of $\sim2\text{--}3~\text{Ma}$ after CAI formation (Kita and Ushikubo 2012; Kunihiro et al. 2004; Kurahashi et al. 2008; Nagashima et al. 2017; Pape et al. 2019; Rudraswami and Goswami 2007; Rudraswami et al. 2008; Villeneuve et al. 2009), indicating that chondrite parent body accretion in the NC and CC reservoirs occurred mostly within $\sim2\text{--}3~\text{Ma}$. However, Pb–Pb ages for chondrules from ordinary, CV, and CR chondrites are more variable and include chondrules that appear to be as old as CAIs (Bollard et al. 2017; Connelly et al. 2012). The discrepancy between Al–Mg and Pb–Pb ages may reflect local variations of ²⁶Al/²⁷Al in the disk, and, more specifically, a reduced initial ²⁶Al/²⁷Al in the inner disk (Bollard et al. 2019). This interpretation is difficult to reconcile, however, with the good agreement of Hf–W and Al–Mg ages for several meteorites and meteorite components, including samples from the inner and outer disk, and including samples with formation ages varying by almost 5 Ma (Budde et al. 2018; Kleine et al. 2018; Kruijer et al. 2020). Moreover, the Pb–Pb ages for pooled chondrule separates from CV and CR chondrites are also in good agreement with the Al–Mg and Hf–W ages of CV and CR chondrules, in contrast to the Pb–Pb ages for single chondrules (see summary in Kruijer et al. 2020). Altogether, these observations indicate that the discrepancy between Al–Mg and Pb–Pb ages for single chondrules is not due to spatial heterogeneities of ²⁶Al/²⁷Al. As such, the ancient Pb–Pb ages reported for some chondrules do not seem to record the time of chondrule formation. One possibility is that the Pb–Pb ages of some chondrules appear older because of the loss of intermediate decay products within the U–Pb decay chains (Pape et al. 2019), but more work is needed to understand the significance of Pb–Pb ages for single chondrules.

The accretion timescales of chondrite parent bodies can also be inferred by combining ages for processes on the parent body (e.g., aqueous alteration, thermal metamorphism) with thermal modeling of meteorite parent bodies heated internally by ²⁶Al decay. For instance, the cooling history of equilibrated (i.e., thermally metamorphosed) ordinary chondrites as deduced from Pb–Pb and Hf–W chronometry combined with thermal modeling consistently returns an accretion age of $\sim2~\text{Ma}$ after CAI formation (Blackburn et al. 2017; Hellmann et al. 2019; Henke et al. 2012). Likewise, ⁵³Mn–⁵³Cr ages of aqueously formed secondary fayalites, combined with their formation conditions (i.e., temperature, water/rock ratio) and with a thermal model of their parent body provides accretion ages of $\sim2~\text{Ma}$ (ordinary chondrites), $\sim2.2~\text{Ma}$ (CO chondrites), and $\sim 2.5~\text{Ma}$ (CV chondrites), post CAI formation (Doyle et al. 2015; Jogo et al. 2017). Together, these accretion ages are in excellent agreement with the Al–Mg ages for chondrules from these chondrites. This not only provides further evidence that the Al–Mg chondrule ages are chronologically meaningful, but also indicates that the chondrule ages closely approximate the time of chondrite accretion.

In summary, the chronological data for meteorites and meteorite components indicate that chondrite parent bodies accreted later than the iron meteorite parent bodies, starting at $\sim2~\text{Ma}$ in the NC reservoir (i.e., the ordinary chondrites) and continuing until at least $\sim4~\text{Ma}$ after CAI formation in the CC reservoir (i.e., the CR chondrites). Importantly, for both the NC and CC reservoirs, iron meteorites and chondrites plot on single $s$-process mixing lines (i.e., the NC- and CC-lines), demonstrating that CC irons and chondrites have the same characteristic $r$-process excess over the NC irons and chondrites (Fig. 3). This is illustrated in a plot of accretion age versus $\Delta ^{95}\text{Mo}$, which shows that the early- and late-formed NC and CC meteorites have the same, characteristic $\Delta^{95}\text{Mo}$ of their respective reservoir (Fig. 4). Thus, there was only limited influx of CC material into the NC reservoir at least for the period between $\sim0.5~\text{Ma}$ up until $\sim2~\text{Ma}$ (i.e., the accretion period of NC irons and chondrites), and there was no significant influx of NC material into the CC reservoir at least from $\sim 1~\text{Ma}$ to at least $\sim4~\text{Ma}$ (i.e., the accretion period of CC irons and chondrites) (Fig. 4). These observations indicate that the NC and CC reservoirs represent two spatially separated reservoirs of the solar protoplanetary disk that co-existed for several Ma (Kruijer et al. 2017).

Fig. 4

Plot of meteorite accretion ages versus $\Delta ^{95}\text{Mo}$. Only meteorites for which $\Delta ^{95}\text{Mo}$ is known to within better than $\pm20~\text{ppm}$ are shown. The NC–CC dichotomy combined with the accretion ages demonstrates that NC and CC meteorites derive from two spatially separated and contemporaneous reservoirs. The two reservoirs were most plausibly separated by Jupiter. For data sources see Table 1

3.4 The Role of Jupiter

The prolonged spatial separation of the NC and CC reservoirs implies that there was a physical barrier between them, because otherwise the diffusive mixing and radial drift of solids in the disk would have rapidly erased the isotopic difference between the two reservoirs. A plausible mechanism to efficiently separate two disk reservoirs for an extended period of time is the accretion of a giant planet in between them, generating a gap within the disk and inhibiting the inward drift of dust grains (e.g., Morbidelli et al. 2016). Being the largest and nearest gas-giant planet, Jupiter is therefore the most likely candidate for separating the NC and CC reservoirs (Kruijer et al. 2017). Jupiter may have also helped preserving the NC–CC dichotomy by accreting planetesimals with intermediate isotopic compositions (Jacquet et al. 2019). Recently, Brasser and Mojzsis (2020) proposed that the initial separation of the NC and CC reservoirs was not caused by Jupiter itself, but resulted from a pressure maximum in the disk, near the location at which Jupiter later formed. Thus, while these different models differ in the efficiency by which Jupiter itself was responsible for the isolation of the NC and CC reservoirs, they all agree in that the NC and CC reservoirs represent material from inside and outside Jupiter’s orbit and, therefore, the inner and outer solar system, respectively.

The efficiency of the Jupiter barrier depends on the size of the dust grains drifting inwards. In general, the barrier is more efficient for large grains, whereas smaller grains that are well coupled to the gas may pass through the barrier as part of the gas flow. For instance, Weber et al. (2018) showed that the flux of mm-size grains is diminished by seven orders of magnitude by the presence of a gap, whereas there is almost no reduction in the flux of 100 μm-size grains. For comparison, the flux of mm-size grains is reduced by a factor $\sim300$ if the gap is opened by a growing gas giant that has reached half the mass of Jupiter. The filtering is even stronger at small viscosity (deeper gap), reaching a factor of $\sim100$ even for 100 μm-size dust in the case of a gap opened by a Jupiter-mass planet. Thus, while the Jupiter barrier provides an efficient means for preserving an isotopic difference between the NC and CC reservoirs, it likely was permeable for small dust grains, especially when Jupiter had not grown to its full size yet. On this basis, Schiller et al. (2018) argued that CC dust from the outer solar system passed through the Jupiter barrier and continuously changed the isotopic composition of the inner solar system. These authors also speculated that this CC dust was only accreted by larger bodies—such as Vesta, Mars, and Earth—but not by smaller bodies such as the enstatite and ordinary chondrite parent bodies. The preservation of the NC–CC dichotomy may then not only reflect the spatial separation of the two reservoirs, but also the different efficiencies with which CC dust is accreted by planetary bodies. However, in this model the close isotopic link between enstatite chondrites and Earth would be mere coincidence, which seems unlikely. More recently, Spitzer et al. (2020) argued that the isotopic composition of the inner disk may have changed continuously through the addition of CC dust, and that this process affected all meteorite parent bodies, including those of enstatite and ordinary chondrites. Clearly, understanding the efficiency of the Jupiter barrier, and the effect of inward drifting CC dust on the isotopic composition of the inner disk, will be important tasks for future studies.

Regardless of whether Jupiter is responsible for the initial separation of the NC and CC reservoirs, its growth and migration provides a mechanism for the later scattering of CC bodies into the inner solar system to their present-day location in the main asteroid belt between Mars and Jupiter. This inward scattering of CC bodies resulted either from the inward-then-outward migration of Jupiter as proposed in the Grand Tack model (Walsh et al. 2011), or from the runaway growth of Jupiter on a fixed orbit (Raymond and Izidoro 2017). Consequently, the formation of Jupiter can account for both the prolonged spatial separation of the NC and CC reservoirs, and the co-occurrence of NC and CC bodies in the present-day asteroid belt.

4 Early Evolution of the Solar Accretion Disk Inferred from the NC–CC Dichotomy

4.1 Origin of the Dichotomy

The NC–CC dichotomy exists for refractory and non-refractory elements and is consistently present for nuclides produced in neutron-rich stellar environments (i.e., $r$-process Mo, ⁵⁸Ni, ⁵⁰Ti, ⁵⁴Cr). As such it is unlikely that the dichotomy has been produced by thermal processing of presolar carriers within the disk, because this would require the efficient removal of presolar components that were likely hosted in different carriers over a wide range of volatility (Burkhardt et al. 2019; Jacquet et al. 2019; Nanne et al. 2019). Moreover, the efficiency of thermal processing depends on the thermal stability of a carrier and not the particular stellar environment from which this carrier originated, and so there is no reason why thermal processing would preferentially affect presolar carriers from neutron-rich stellar sources.

Many of the isotopic characteristics of the CC reservoir are also found, in more extreme form, in CAIs (Burkhardt et al. 2019; Nanne et al. 2019). This includes enrichments in $r$-process Mo (Brennecka et al. 2013; Burkhardt et al. 2011), ⁵⁴Cr (Papanastassiou 1986), and coupled ⁴⁶Ti–⁵⁰Ti excesses (Davis et al. 2018; Trinquier et al. 2009). Specifically, the isotopic composition of the CC reservoir is intermediate between those of the NC reservoir and CAIs, implying that compared to the NC reservoir, the CC reservoir contains a higher proportion of material with a CAI-like isotopic composition. Nevertheless, the addition of CAIs themselves to the CC reservoir cannot be the sole cause for the NC–CC dichotomy, because this dichotomy exists for non-refractory elements (i.e., Cr, Ni), which are not enriched in CAIs (Burkhardt et al. 2019; Nanne et al. 2019). To affect refractory and non-refractory elements in a similar manner, the formation of the NC–CC dichotomy must, therefore, have involved the addition of isotopically CAI-like material whose bulk chemical composition was broadly chondritic (Burkhardt et al. 2019; Nanne et al. 2019). In this case, CAIs represent only the refractory part of an early disk reservoir, which was enriched in those nuclides that define the NC–CC dichotomy (Burkhardt et al. 2019; Jacquet et al. 2019). Of note, this scenario also accounts for the ⁴⁶Ti–⁵⁰Ti correlation observed among bulk meteorites. Because ⁴⁶Ti and ⁵⁰Ti are produced in distinct stellar sites, the ⁴⁶Ti–⁵⁰Ti correlation was interpreted as evidence for thermal processing during which Ti from distinct presolar carriers evaporated and then re-condensed together into a common Ti-bearing phase, which subsequently was heterogeneously distributed at the bulk meteorite and planetary scale (Trinquier et al. 2009). However, in light of the NC–CC dichotomy the coupled ⁴⁶Ti–⁵⁰Ti excesses of CAIs simply reflect the composition of an early disk reservoir, and the ⁴⁶Ti–⁵⁰Ti correlation is easily understood as the result of mixing of this material to a disk reservoir characterized by ⁴⁶Ti–⁵⁰Ti deficits.

All these observations combined suggest that the NC–CC dichotomy reflects a change in the isotopic composition of the material that is accreted to the disk during infall from the Sun’s collapsing protostellar envelope. The isotopic composition of the infalling material may have changed because material infalling at different times derives from different parts of the parental molecular cloud. Thus, an isotopic heterogeneity within the cloud would have, at least in part, been imparted on the isotopic composition of the disk (Jacquet et al. 2019; Visser et al. 2009). The distance where mass is added to the disk increases with time outwards to several AU (e.g., Hueso and Guillot 2005; Yang and Ciesla 2012), and so different regions of the disk received varying proportions of material infalling at different times. This scenario can readily account for the observation that the dichotomy is consistently present for nuclides produced in neutron-rich stellar environments, exactly because this is the material that is heterogeneously distributed between the two reservoirs (Nanne et al. 2019).

Figure 5, adopted from Nanne et al. (2019) and Burkhardt et al. (2019), is a cartoon illustrating this model for the formation of the NC–CC dichotomy during infall. During the earliest stage of infall, CAIs formed close to the Sun and were transported outwards by rapid radial expansion of the early infalling material, forming an initial disk (Desch et al. 2018; Jacquet et al. 2011, 2019; Pignatale et al. 2018). The isotopic composition of this initial disk is given by that of CAIs, meaning that this disk was enriched in nuclides produced in neutron-rich stellar environments, such as $r$-process Mo, ⁵⁰Ti, and ⁵⁴Cr. Yet, the later infalling material was depleted in these nuclides and, because most of the material in the inner disk derives from this infall, this material likely had a NC-like composition. In the outer disk, beyond the radius at which later material is infalling, the composition of the initial disk is preserved, in diluted form, as the composition of the CC reservoir. Thus, in this model the isotopic composition of the CC reservoir reflects a mixture between that of the earliest disk, which is preserved in CAIs, and later infalling material with an NC-like isotopic composition.

Fig. 5

Formation of the NC and CC reservoirs by late infall of isotopically distinct material (not to scale). Rapid expansion of early infalling material forms an initial disk, whose isotopic composition is represented by CAIs. Later infalling material dominates the composition of the inner disk and has a distinct, NC-like isotopic composition, which compared to the earlier infalling material is depleted in nuclides from neutron-rich stellar environments. Mixing within the disk reduced the isotopic difference between the inner and outer disk, but the rapid formation of Jupiter prevented completed homogenization. Jupiter grew large enough after $\sim2~\text{Ma}$ but before $\sim4\text{--}5~\text{Ma}$ after CAIs to induce scattering of CC bodies into the inner solar system. Figure adapted from Nanne et al. (2019) and Burkhardt et al. (2019)

After the infall of material stopped, the proto-Sun continued to accrete material from its disk, as a result of inward transport of mass and outward movement of angular momentum (Yang and Ciesla 2012). Thus, to maintain an isotopic difference between the CC and NC reservoirs, the inward transport of isotopically distinct outer disk material must have been blocked before planetesimal formation in the NC and CC reservoir had begun (Fig. 4). As argued above, this most likely reflects the presence of a barrier (either Jupiter itself or a pressure bump in the disk where Jupiter later formed) that prohibited significant inward drift of CC material into the inner disk. In brief, “the NC–CC dichotomy reflects an inherited isotopic heterogeneity from the solar system’s parental molecular cloud, which was established during infall from the Sun’s protostellar envelope and has been preserved through the (…) formation of Jupiter” (Nanne et al. 2019).

4.2 Planetesimal Formation in the Inner Solar System

The presence of a barrier against the inward drift of CC dust into the inner solar system likely resulted in the rapid depletion of dust in the inner disk. This is because the available dust either is rapidly accreted into a first generation of planetesimals or drifts into the Sun. Consequently, once most of the dust in the NC reservoir has been incorporated into early-formed planetesimals, the inner disk remains depleted in dust because it cannot be replenished by the inward drift of CC dust (so as to preserve the NC–CC dichotomy), with the exception of the smallest particles ($<100~\upmu \text{m}$), which can pass through the Jupiter barrier (Haugbølle et al. 2019; Weber et al. 2018) but are too small to be efficiently accreted. However, the chronology of NC meteorites indicates that there is more than one generation of planetesimals in the inner disk and that planetesimal formation occurred over a period of at least $\sim2~\text{Ma}$ (Fig. 4). This then raises the question of how there was sufficient dust in the inner disk for this prolonged period of planetesimal formation.

One possibility is that the dust for later-formed planetesimals was produced by collisions among pre-existing planetesimals. As the youngest sampled planetesimals from the NC reservoir are the ordinary and enstatite chondrites (see Fig. 4), this would imply that these chondrites predominantly consist of secondary dust from an earlier generation of planetesimals. Both chondrites contain abundant metal and, in some cases (H and EH chondrites) have approximately solar Fe/Si ratios (Palme et al. 2014). Thus, if these chondrites formed from secondary dust, then this dust must have contained metal and silicate grains in approximately solar proportions. This secondary dust, therefore, probably did not derive primarily from collisions among differentiated planetesimals, because these underwent large-scale metal-silicate separation and core formation. Instead, it is more likely that most secondary dust was produced by collisions among small planetesimals that remained either undifferentiated or partially differentiated, so that no or only minor metal-silicate melt segregation occurred. Alternatively, the secondary dust may also derive from the primitive, undifferentiated crust of larger planetesimals (Elkins-Tanton et al. 2011).

The collisional production of dust would naturally occur in the late stages of the protoplanetary disk, when the damping of the planetesimals’ velocity dispersion exerted by the gas becomes weaker and protoplanets become more massive and can scatter the planetesimals more effectively (Gerbig et al. 2019). The low amount of remaining gas favors the triggering of the streaming instability by the generated dust, because the dust/gas ratio can be large even if the total amount of dust is not so high (Carrera et al. 2017). This would produce in a natural way an asteroid population with a small total mass, as advocated in some models (Hansen 2009; Izidoro et al. 2016).

The NC chondrites, like CC chondrites, contain presolar grains (Huss and Lewis 1995). Although some of these grains may derive from the colliding primitive planetesimals, they may also derive from inward drifting, fine-grained CC dust that was able to pass the Jupiter barrier and mixed into the secondary dust. The amount of this CC dust must have been low, because otherwise the isotopic composition of late- and early-formed NC bodies would be different, but it would likely be a sufficient source for presolar grains in NC chondrites. This would be consistent with the observation that all chondrites, including CC and NC, sampled the same solar-system-wide reservoir of presolar grains (Huss and Lewis 1995).

The formation of NC chondrites from collisionally produced dust does not necessarily imply that these collisions also resulted in the melting that produced NC chondrules. The chondrule-melting events may have occurred at a later time, and they may have been unrelated to the collisions that produced their precursor dust. Nevertheless, it also possible that the same collisions that produced the secondary dust also resulted in chondrule formation (e.g., Stewart et al. 2019).

Clearly, more work is needed to reconcile the early formation of the NC–CC dichotomy with the ‘late’ formation of NC chondrites. The formation of secondary dust by collisions among an earlier generation of planetesimals is one possibility, but requires a more thorough assessment of how well the textural, chemical, and isotopic properties of NC chondrites and chondrules can be reproduced in such a model. Regardless, the NC–CC dichotomy combined with the chronology of chondrite accretion provides a fundamental constraint on models of planetesimal formation in the inner disk.

4.3 Growth History of Jupiter

The standard model for the formation of Jupiter (and other gas giant planets in the solar system) is the core accretion model, in which the planet’s gaseous envelope is accreted onto a pre-existing solid core of about 10–20 Earth masses ($M_{\oplus }$) (Pollack et al. 1996). In this model, gas accretion is not a steady process, but proceeded slowly initially until Jupiter reached a mass of $\sim50~M_{\oplus }$, which was then followed by runaway gas accretion to Jupiter’s final mass of $\sim318~M_{\oplus }$. Depending on the mass reached at different stages of its growth, Jupiter affected bodies inside and outside its orbit in different ways. Specifically, once Jupiter’s core reached a mass of $\sim10\text{--}20~M_{\oplus }$, it would have substantially hampered exchange of material from inside (NC) and outside (CC) its orbit (Lambrechts et al. 2014). When Jupiter reached a mass of $\sim50~M_{\oplus }$, a gap opened in the disk (Crida et al. 2006), leading to inward migration of Jupiter (Walsh et al. 2011). The migration and/or the further growth of Jupiter results in gravitational scattering of bodies from inside and outside Jupiter’s orbit, ultimately leading to dynamical mixing of NC and CC bodies (Raymond and Izidoro 2017). Within this framework, Jupiter’s accretion timescale can be estimated from the formation time and longevity of the NC–CC dichotomy (Kruijer et al. 2017).

A key observation from the Mo isotopic data is that the NC iron meteorites together with ordinary and enstatite chondrites plot on the NC-line (Fig. 2). Thus, there was no significant influx of CC material into the NC reservoir since the formation of the earliest NC bodies at $\sim0.5~\text{Ma}$ after CAI formation, because otherwise early (i.e., NC irons) and late formed NC bodies (i.e., ordinary chondrites) would not plot on a single NC line (i.e., have the same characteristic $\Delta ^{95}\text{Mo}$; Fig. 4). As noted above, the data allow some $r$-process heterogeneity within the NC reservoir, meaning that there might have been some influx of CC material after accretion of the oldest NC bodies. This potential change is small, however, compared to the difference between the NC and CC reservoirs (Spitzer et al. 2020). Both reservoirs were, therefore, probably already separated from each other when the NC iron meteorite parent bodies accreted. Consequently, under the assumption that the formation of Jupiter’s core is responsible for the initial separation of the NC and CC reservoirs, Jupiter reached $\sim10\text{--}20~M_{\oplus }$ within $\sim0.5~\text{Ma}$ after CAI formation. This would probably require formation of Jupiter’s core by pebble accretion (Lambrechts and Johansen 2014; Levison et al. 2015). Brasser and Mojzsis (2020) argued that owing to the inefficiency of the pebble accretion process, a large number of CC pebbles would nevertheless drift past the growing Jupiter, and would then contaminate the NC reservoir. This predicted large influx of CC pebbles into the inner disk is inconsistent with the early preservation of the NC–CC dichotomy, however. To overcome this problem, Brasser and Mojzsis (2020) proposed that there was a pressure maximum in the disk near the location where Jupiter later formed, which limited the inward drift of CC pebbles. In this case, the initial separation of the NC and CC reservoirs may not have been caused by the growth of Jupiter’s core itself, which would make the meteoritic constraints on Jupiter’s early growth more uncertain.

Following accretion of iron meteorite parent bodies in the NC and CC reservoirs, planetesimal formation in both reservoirs continued for an extended period of time, until at least $\sim2~\text{Ma}$ in the NC and $\sim4~\text{Ma}$ in the CC reservoir (Fig. 4). As both NC and CC chondrites plot on their respective NC- and CC-lines together with the NC and CC irons, respectively, there was no substantial mixing between the NC and CC reservoirs at least until after accretion of the youngest chondrite parent body in each reservoir. The formation time of the youngest CC bodies does not provide tight constraints on the early growth of Jupiter, because planetesimal formation in the CC reservoir may have still occurred while Jupiter already scattered earlier-formed CC bodies into the inner solar system (Raymond and Izidoro 2017). A more direct constraint may be obtained from the observation that planetesimal formation in the NC reservoir seems to have stopped at $\sim2~\text{Ma}$, as inferred from the accretion age of the youngest NC meteorites (Fig. 4). For instance, within the framework of the Grand Tack model (Walsh et al. 2011), Jupiter’s migration through the asteroid belt would have terminated planetesimal formation there, implying that the migration occurred at $\sim2~\text{Ma}$ and Jupiter reached a mass of $\sim50~M_{\oplus }$ at about this time. However, if Jupiter did not migrate through the asteroid belt, then the termination of NC planetesimal formation may simply reflect the lack of substantial dust in the inner disk (Sect. 4.2) or the almost complete depletion of gas, which would not allow the dust to clump into new planetesimals. Both possibilities are more difficult to relate to a specific stage of Jupiter’s growth. Nevertheless, there is so far no observational evidence for the inward scattering of CC bodies during the time of NC planetesimal formation, which may mean that Jupiter did not reach $\sim50~M_{\oplus }$ before $\sim2~\text{Ma}$ (Alibert et al. 2018; Kruijer et al. 2020). This conclusion, however, depends on the assumed formation location of the scattered CC bodies and on whether Jupiter’s growth was solely responsible for the inward scattering of CC bodies.

Wang et al. (2017) argued that the final stage of Jupiter’s growth to $\sim318~M_{\oplus }$ was completed by $\sim4\text{--}5~\text{Ma}$ at the latest. This argument is based on the observation that angrites, a class of basaltic achondrites dated at $\sim4\text{--}5~\text{Ma}$ after CAI formation (Amelin 2008; Connelly et al. 2008; Kleine et al. 2012; Spivak-Birndorf et al. 2009), record the absence of a nebular magnetic field, indicating that at this time the nebula gas had dissipated. As Jupiter can only grow to its final size in the presence of nebular gas, its accretion must have been completed by this time. This is consistent with evidence for the addition of CC material to the eucrite and angrite parent bodies (both are NC bodies) at $\sim4\text{--}5~\text{Ma}$ after CAI formation (Sarafian et al. 2017, 2014), which may be related to inward scattering of CC bodies by a nearly fully-formed Jupiter (Raymond and Izidoro 2017).

Taking all these observations together reveals that the meteorite data are consistent with the following growth history of Jupiter: after the rapid initial accretion of its $\sim10\text{--}20~M_{\oplus }$ core within less than $\sim0.5~\text{Ma}$, Jupiter reached $\sim50~M_{\oplus }$ after $\sim2~\text{Ma}$, and its final mass of $\sim318~M_{\oplus }$ before $\sim4\text{--}5~\text{Ma}$ (Kruijer et al. 2017, 2020). This growth history and the distinct rate of gas accretion are approximately consistent with the core accretion model for the formation of Jupiter (Alibert et al. 2018). Nevertheless, as outlined above, the growth history deduced from the meteorite data depends on several assumptions on how Jupiter affected the interaction between material inside and outside its orbit, and so other growth histories are possible.

5 Accretion of Earth

Accretion of Earth, and potentially the other terrestrial planets, continued past the inward scattering of CC bodies resulting from the growth of the gas giants, and so Earth likely accreted CC bodies during its growth (O’Brien et al. 2018; Raymond and Izidoro 2017). These objects are the most likely source of Earth’s water and highly volatiles species (Alexander et al. 2012; Marty 2012). Thus, understanding when, how, and how much CC material was accreted by the growing Earth is of considerable interest (McCubbin and Barnes 2019; O’Brien et al. 2018). It also provides a potential way of discriminating between different models of Earth’s accretion (e.g., Fischer et al. 2018).

Given that NC and CC meteorites have distinct isotopic signatures, the isotopic composition of Earth’s primitive mantle (or bulk silicate Earth, BSE) can be used to reconstruct the accretion of CC material to Earth. For instance, Dauphas (2017) argued that Earth accreted $\sim5\%$ CC material only during the early stages of accretion, and that the later stages consisted entirely of material with an enstatite chondrite-like isotopic composition. This conclusion depends on the assumption that enstatite, ordinary, and carbonaceous chondrites are representative for the building blocks of Earth. If instead a broader range of isotopic compositions is assumed, including those of some achondrites having the lowest $\varepsilon^{50}\text{Ti}$ and $\varepsilon ^{54}\text{Cr}$ values observed among meteorites (Fig. 1), then the Earth may have incorporated a much larger amount of CC material of up to $\sim40\text{--}50\%$ (Schiller et al. 2018; Warren 2011). Thus, the total amount of CC material accreted by Earth is not well known.

Unlike all meteorites analysed to date, the Mo isotopic composition of the bulk silicate Earth (BSE) falls between those of the NC and CC reservoirs ($\Delta ^{95}\text{Mo}_{\text{BSE}} = +7\pm 5$; Fig. 6), indicating that the BSE’s Mo derives from both reservoirs (Budde et al. 2019). This observation may seem unsurprising, given that Earth is expected to have accreted some CC bodies. However, it is important to recognize that Mo, as a siderophile element, only records the late stages of Earth’s growth, probably the last 10–20% of accretion (Dauphas 2017). This is because the Mo from earlier accreted objects was largely removed into Earth’s core. Consequently, the mixed NC–CC Mo isotopic composition of the BSE indicates that Earth accreted CC material in the final 10–20% of its growth, because otherwise the BSE would plot on the NC-line (Fig. 6). Earth may have also accreted CC bodies during earlier stages, but this would not be visible in the BSE’s Mo isotopic composition (Budde et al. 2019; Dauphas 2017; Fischer et al. 2018).

Fig. 6

$\varepsilon ^{95}\text{Mo}$ versus $\varepsilon ^{94}\text{Mo}$ showing the position of the bulk silicate Earth (BSE) relative to the NC-line (red) and CC-line (blue). For clarity, data points for only a few meteorites are shown. Also shown are two hypothetical components, which are characterized by an $s$-process excess relative to the BSE, and are from either the CC or the NC reservoir. At least one $s$-process–enriched component must have been incorporated into the Earth, to accommodate the inclusion of material represented by known meteorites, all of which are characterized by an $s$-process deficit compared to Earth. Figure adapted from Budde et al. (2019)

The position of the BSE among the NC- and CC-lines also reveals that no combination of known meteorites yields the BSE’s Mo isotopic composition, indicating that Earth incorporated material that is distinct from known bulk meteorites (Fig. 6). This material must be enriched in $s$-process Mo, to balance the $s$-process depleted composition of known meteorites, relative to the composition of the BSE. The $s$-process–enriched material may derive from either the NC or the CC reservoir (Fig. 6), but it is noteworthy that for essentially all elements investigated thus far, Earth’s isotopic composition is most similar to that of enstatite chondrites. This suggests that Earth predominantly accreted from material with an enstatite chondrite-like isotopic composition (Dauphas 2017; Dauphas et al. 2014), in which case the BSE’s Mo isotopic composition most likely reflects a mixture of this material with $s$-process–enriched material from the CC reservoir (Fig. 6). In this model, the BSE’s isotopic composition would naturally be similar to enstatite chondrites and would deviate only for elements that were added late, such as Mo (Budde et al. 2019).

Because the NC- and CC-lines are parallel, the BSE composition divides any tie line between them into two segments whose ratio to each other is constant (Fig. 6). Consequently, irrespective of the position of the endmembers on the NC- and CC-lines (i.e., of the absolute Mo isotope anomalies), the resulting mixing ratio between NC and CC material remains the same. The Mo isotopic data, therefore, allow quantifying the fraction of CC material in the BSE irrespective of the NC and CC endmember compositions. Using the $\Delta ^{95}\text{Mo}$ values for the BSE and the NC- and CC reservoirs, the $\text{CC}/(\text{NC}+\text{CC})$ ratio of the BSE is $0.46\pm 0.15$, indicating that between $\sim30\%$ and $\sim60\%$ of the BSE’s Mo derives from the CC reservoir (Budde et al. 2019). This high mass fraction of CC material refers only to the last 10–20% of Earth’s accretion. As such, it should not be confused with the total amount of CC material accreted by Earth, which likely was smaller. For instance, if Earth accreted CC material only during the last $\sim10\text{--}20\%$ of accretion, then it incorporated a total of $\sim3\text{--}6\%$ CC material. Still it seems likely that Earth also accreted some CC material during earlier accretion stages, and so the total amount of CC material is likely higher, and, as noted above, could be as high as $\sim40\text{--}50\%$.

The last 10–20% of Earth’s accretion are dominated by the Moon-forming impactor, which is the last large body thought to collide with Earth (Canup and Asphaug 2001), and the late veneer, the material added to Earth’s mantle after the giant impact and cessation of core formation (e.g., Walker et al. 2015). As such, the Mo in the present-day BSE can be regarded as a mixture of Mo from proto-Earth’s mantle (i.e., the mantle before the giant impact), the Moon-forming impactor, and the late veneer. To quantify the contribution of these components to the observed Mo isotopic composition of the BSE, Budde et al. (2019) calculated the expected $\Delta^{95}\text{Mo}$ of the Earth’s mantle for different assumed compositions of these three components. The results reveal that the CC-derived Mo in the BSE most likely derives from the Moon-forming impactor or the late veneer (Fig. 7). This conclusion holds unless the core of the Moon-forming impactor did not equilibrate even partially with the Earth’s mantle before merging with Earth’s core (Fig. 7). This is because if the impactor core did not equilibrate with Earth’s mantle, then the impactor would not have contributed significantly to the BSE’s Mo isotopic composition. In this case, the CC-derived Mo in the BSE may derive from objects accreted before the Moon-forming impact or from the late veneer (Budde et al. 2019).

Fig. 7

Probability of matching the BSE’s $\Delta ^{95}\text{Mo}$ for different compositions of proto-Earth’s mantle (pE), the Moon-forming impactor (GI), and the late veneer (LV) as a function of impactor core equilibration during formation of the Moon. Scenarios in which the Moon-forming impactor contains CC material have a much higher probability than scenarios in which the Moon-forming impactor has a pure NC composition. A pure CC composition for the LV also provides a good match, but this possibility is ruled out based on Ru isotopes (see text). Figure modified from Budde et al. (2019)

One possibility is that Earth accreted CC material in the form of pebbles, which drifted sunwards and were then captured by the growing proto-Earth (Schiller et al. 2018, 2020). This process requires the presence of gas, implying that most of Earth’s mass accreted within the lifetime of the solar nebula of $\sim5~\text{Ma}$. In this model, the Mo isotopic composition of Earth’s mantle would be entirely dominated by the CC pebbles, and so proto-Earth’s mantle just prior to the Moon-forming impact would have had a CC-like Mo isotopic composition. This is because as a siderophile element, the Mo in the mantle predominantly derives from late-added material (see above). Reproducing the mixed NC–CC Mo isotopic composition of the present-day BSE then requires a very low degree of impactor core re-equilibration during the Moon-forming impact, because otherwise the BSE’s Mo isotopic composition would predominantly reflect that of the impactor (Fig. 7). This poses a problem, however, because the rapid accretion of Earth required in the pebble accretion model is compatible with the ¹⁸²Hf–¹⁸²W chronology of Earth’s core only for a very high degree of core-mantle re-equilibration throughout accretion, and a late ($>50~\text{Ma}$) Moon-forming impact (Kleine and Walker 2017; Rudge et al. 2010). This particularly applies to the pebble accretion model, because the rapid initial accretion of Earth inevitably results in a very radiogenic ¹⁸²W signature of Earth’s mantle. This radiogenic ¹⁸²W must then be removed by a late Moon-forming impact, which in turn requires a high degree of impactor core re-equilibration during this event. Thus, in the pebble accretion model, the BSE would be expected to have a NC-like Mo isotopic composition, because otherwise the previously accumulated CC-derived Mo would be entirely removed into Earth’s core. This problem can only be overcome if the Moon-forming impactor itself already contained appreciable amounts of CC material.

The mixed NC–CC Mo isotopic composition of the BSE may also reflect the accretion of CC planetesimals (instead of pebbles) prior the Moon-forming impact. Again, this would require a low degree impactor core re-equilibration during this impact to avoid complete removal of the CC-derived Mo into Earth’s core (Fig. 7). Unlike for pebble accretion, however, addition of planetesimals to Earth may have occurred over a much longer timescale because it does not require the presence of gas. For this more protracted accretion timescale, the Hf–W systematics of the BSE are compatible with a lower degree of core-mantle re-equilibration (Nimmo et al. 2010; Rudge et al. 2010), and so the accretion of CC planetesimals to Earth would be consistent with the Hf–W chronology of Earth. However, the planetesimal population in the inner disk is dominated by NC planetesimals (Raymond and Izidoro 2017), rendering it unlikely that accretion of planetesimals to Earth prior to the Moon-forming impact produced a CC-like Mo isotopic composition of the proto-Earth’s mantle.

Finally, based on Ru isotope anomalies it seems unlikely that Earth accreted CC material solely through the late veneer. As a highly siderophile element, almost all the Ru in the BSE derives from the late veneer, and so the isotopic composition of Ru solely reflects that of the late veneer. The Ru isotopic composition of the BSE is distinct from all known CC meteorites, but overlaps with some NC meteorites (Bermingham et al. 2018; Fischer-Gödde et al. 2015; Fischer-Gödde and Kleine 2017; Hopp et al. 2020; Worsham et al. 2019). As such, the late veneer most likely had either a pure NC or a mixed NC–CC composition (Hopp et al. 2020). Such a late veneer composition cannot solely account for the observed Mo isotopic composition of the BSE, however (Fig. 7).

Taking all these observations together reveals that the CC-derived Mo in the BSE at least partially derives from the Moon-forming impactor. As such, the impactor may have been a CC embryo from the outer solar system, or it may have been a body with a mixed NC–CC composition itself. Some dynamical models predict that due to the orbital evolution of the giant planets, the final large impactor on Earth (i.e., the Moon-forming impactor) tends to be an embryo from beyond $\sim2.5~\text{AU}$ (O’Brien et al. 2018). Thus, one possibility is that the CC impactor was implanted on a stable orbit in the asteroid belt during the early migration and growth of Jupiter (Raymond and Izidoro 2017; Walsh et al. 2011), and then was destabilized again during a later orbital instability of the gas giants, ultimately resulting in its collision with the Earth. Consistent with this, recent studies suggest that a giant planet instability occurred within the first $\sim100~\text{Ma}$ of the solar system (Morbidelli et al. 2018; Nesvorný et al. 2018) and, therefore, during the likely time of the Moon-forming event (Barboni et al. 2017; Borg et al. 2019; Kleine and Walker 2017).

A final implication of a CC (or mixed NC–CC) heritage for the Moon-forming impactor is that this object may have delivered all of Earth’s water and highly volatile species, which requires at least $2\pm 1\%$ CI chondrite-like material (Alexander et al. 2012; Marty 2012). It is not known if the Moon-forming impactor was as volatile-rich as CI chondrites, but given that it probably delivered about 10% of Earth’s mass (Canup and Asphaug 2001), it seems likely that it contained the equivalent of $\sim2\%$ CI material in terms of water and highly volatiles (Budde et al. 2019).

6 Conclusions

The discovery of an isotopic dichotomy between non-carbonaceous (NC) and carbonaceous (CC) meteorites has fundamentally changed our understanding of early solar system evolution, including the origin of meteorites and how they can be used to constrain the dynamical evolution of the early solar system, and the formation of terrestrial planets. The key observations may be summarized as follows:

• Meteorites derive from two genetically distinct reservoirs that probably were located inside (NC) and outside (CC) Jupiter’s orbit, and remained isolated from each other for the first few million years of the solar system.

• The isotopic difference between the NC and CC reservoirs probably results from a temporal change in the isotopic composition of infalling matter from the Sun’s protostellar envelope, which led to the formation of two early, isotopically distinct disk reservoirs. The outer reservoir had a CAI-like isotopic composition, while the inner reservoir was NC-like. Mixing between these two reservoirs resulted in the formation of the CC reservoir, whose isotopic composition is intermediate between those of the two earlier disk reservoirs.

• The rapid growth of Jupiter prevented significant exchange of material from inside and outside its orbit over several million years, thereby maintaining an isotopic difference between the NC and CC reservoirs. The efficiency of the Jupiter barrier and how it affected the inward drift of CC dust into the inner solar system is subject to further study.

• The chronology of meteorite parent body accretion, combined with the NC–CC dichotomy, may be used to constrain the timescale of Jupiter’s growth. One possible scenario is that Jupiter’s core accreted within the first $\sim0.5~\text{Ma}$ after CAI formation, whereas runaway gas accretion and migration of Jupiter started no earlier than $\sim2~\text{Ma}$, and was completed by $\sim4\text{--}5~\text{Ma}$ after CAI formation. However, other growth scenarios are possible.

• The growth and/or migration of Jupiter resulted in inward scattering of CC bodies, which accounts for the co-occurrence of NC and CC bodies in the present-day asteroid belt. The compositional diversity of bodies in the asteroid belt, therefore, reflects formation of these objects over a wide range of orbital distances. Nevertheless, Earth, and presumably also the other terrestrial planets, also incorporated material that has yet not been identified among meteorites.

• The inward scattering of CC bodies resulted in the incorporation of these objects into the growing terrestrial planets, resulting in a mixed NC–CC composition for the Earth’s mantle, at least for siderophile elements like Mo. The final embryo colliding with Earth and resulting in the formation of the Moon probably had either a CC or a mixed NC–CC composition.

• The late-stage accretion of CC material to Earth is sufficient to account for the entire budget of Earth’s water and highly volatile species, although additional, earlier accretion of CC bodies is also possible.

Collectively, these observations bear testimony to the important role of Jupiter in shaping the architecture of the inner solar system, including the compositional mixture of the asteroid belt, the presence of water and volatile elements on Earth, and perhaps even the very existence of the Moon.