The Origin and Fate of $\mbox{O}_{2}$ in Europa’s Ice: An Atmospheric Perspective

Abstract

The early prediction and subsequent detection of an $\mbox{O}_{2}$ atmosphere on Europa, coupled with the discovery that Europa has an ocean under its ice mantle, has made this moon a prime astrobiologic target, soon to be visited by the JUICE and Europa Clipper spacecraft. In spite of the considerable number of observational, modeling, and laboratory efforts, understanding the physics leading to the observed morphology of Europa’s near-surface $\mbox{O}_{2}$ atmosphere has been problematic. This is the case as the observed emissions depend on the local incident plasma ion flux, the local temperature and composition of the regolith, as well as on the near-surface electron temperature and density. Here we rely heavily on earlier reviews briefly summarizing the observational, laboratory and simulation efforts. Although it is agreed that radiolysis of the surface ice by the incident Jovian plasma is the ultimate source of observed O₂, a recent, simple model of thermal desorption from a regolith permeated with $\mbox{O}_{2}$ has changed the usual paradigm. In that model, the observed orbital dependence of the local source of the near-surface O₂ atmosphere is suggested to be due to the release of $\mbox{O}_{2}$ likely trapped on the ice grains at dangling bonds by the solar flux with a smaller contribution due to direct sputtering. This assumes that Europa’s icy regolith is permeated with trapped $\mbox{O}_{2}$, which could also affect our understanding of the suggestion that the radiolytic products in Europa’s regolith might be a source of oxidants for its underground ocean.

1 Introduction

The photolytic production of $\mbox{O}_{2}$ and H₂ from H₂O sublimated from the surfaces of Jupiter’s icy satellites, along with the preferential escape of H₂, led to the suggestion that the bodies could have accumulated a thin $\mbox{O}_{2}$ atmosphere (Yung and McElroy 1977; Kumar and Hunten 1982). Subsequent laboratory data (Brown et al. 1982) showed that $\mbox{O}_{2}$ is formed much more efficiently in the solid phase by plasma-ion-induced radiolysis of low temperature water ice. This led to the prediction that Europa could have a tenuous $\mbox{O}_{2}$ atmosphere due to the radiolytic decomposition of its icy surface by the incident Jovian plasma particles (Johnson et al. 1982; Johnson 1990). Their rough estimate of the magnitude of the atmosphere has been borne out by extensive Hubble Space Telescope (HST) observations in the UV (e.g., Hall et al. 1995, 1998; McGrath et al. 2004, 2009; Roth et al. 2016) and most recently in the visible during eclipse (de Kleer and Brown 2018). Although the physical processes have also been borne out by additional laboratory data (e.g., see summaries in Johnson 2011; Teolis et al. 2017), a large number of uncertainties remain as to how the laboratory data should be applied at Europa (e.g., see Plainaki et al. 2018). That is, it is agreed upon that $\mbox{O}_{2}$, as well as its concomitant radiolytic product H₂, are produced and ejected by the incident plasma, but a clear, quantitative description of the spatial and temporal distribution of the oxygen aurora based on HST observations remains elusive. This is unfortunate as Europa is a high priority target for exploration by both NASA and ESA. Therefore, it will soon be visited by spacecraft with the principal goal of understanding its potential as a habitable world and the radiation-induced desorption of surface materials might even help in identifying the presence of biologically relevant molecules (e.g., Johnson and Sundqvist 2018). Therefore, there has been a significant recent increase in the observational and modeling studies of the ambient, gas-phase $\mbox{O}_{2}$ at Europa.

It is well established that incident plasma particles and short wavelength solar photons can decompose ice and produce $\mbox{O}_{2}$ and H₂. This is the case not only at Europa, but also at its neighbors Ganymede (e.g., Spencer et al. 1995; Calvin et al. 1996; Turc et al. 2014; Leblanc et al. 2017) and Callisto (Spencer and Calvin 2002; Vorburger et al. 2015), as well as at Saturn’s rings (Johnson et al. 2006; Tseng et al. 2010) and its small icy satellites (e.g., Tokar et al. 2012; Teolis and Waite 2016). The production of oxygen in Europa’s surface ice is especially interesting, as it has been suggested to be important for potential biologic activity by subduction of oxygen rich material into its underground ocean (e.g., Chyba 2000; Johnson et al. 2003; Orlando et al. 2005; Greenberg 2008; Vance et al. 2016; Russell et al. 2017). This possibility depends critically on the state of the O₂ produced in Europa’s icy regolith: that is, on how $\mbox{O}_{2}$ binds in and diffuses through the porous icy regolith and ice mantle. It also depends on the coupling between Europa’s surface ice and its putative ocean. That there is coupling has been discussed for years based on the modeling of the images of its nearly craterless and fractured surface (e.g., Pappalardo et al. 2009; Parro et al. 2016; Kattenhorn and Prockter 2014; Prockter et al. 2017). Recent ground-based observations of Europa point towards the presence of endogenic materials (possibly chlorinated salts) on the surface (Brown and Hand 2013; Fischer et al. 2015, 2016; Ligier et al. 2016), and irradiation experiments by Hand and Carlson (2015) suggest that NaCl-rich material from the sub-surface ocean may explain Europa’s yellow-brownish color at visible wavelengths. In addition, the ambient sodium and potassium emissions observed (Brown and Hill 1996; Brown 2001) also suggest that there is coupling between the surface and the likely ‘salty’ ocean (e.g., Johnson 2000; Leblanc et al. 2002, 2005). Added to these observations, the analysis of Galileo magnetometer measurements has revealed that Europa is a source of Na⁺, Cl⁻ and Cl⁺, and K⁺ pickup ions to the Jovian magnetosphere (Desai et al. 2017; Volwerk et al. 2010, 2001). Finally, recent observations indicating possible plume activity on Europa (e.g., Roth et al. 2014; Sparks et al. 2016, 2017; Jia et al. 2018) has significantly increased interest in the importance of the coupling between its surface and ocean.

Although there is now considerable laboratory data on the sputtering of ice, the surprising inability to carry out a definitive simulation of the observed oxygen aurora is due to the complexity of processes influencing emission. Emission depends on the local plasma ion temperature, composition, precipitation rate and sputtering yield, as well as on the local surface composition affecting the production rate. In addition, it depends critically on local plasma electron temperature and density responsible for dissociation, ionization and excitations. Finally, it is also due to our lack of understanding of the interactions of $\mbox{O}_{2}$ in the porous regolith (e.g., Johnson et al. 2005; Loeffler et al. 2006; Laufer et al. 2017) and our understanding on how the composition and nature of that regolith affect such interactions as discussed below.

There are numerous and even very recent reviews on Europa’s surface properties, the plasma-induced production of $\mbox{O}_{2}$, and on the observational database (e.g., Carlson et al. 2009; Johnson et al. 2009, 2013; McGrath et al. 2004, 2009; Cassidy et al. 2010; Gutipati and Castillo-Rogez 2013; Plainaki et al. 2018). Rather than a new review, we will refer to these in the following focusing on how the modeling of the gas-phase observational data affects our understanding of the likely state of $\mbox{O}_{2}$ in Europa’s regolith. We first give a brief review on the production of $\mbox{O}_{2}$, then summarize the observational data, and, finally, discuss our recent understanding.

2 Radiolysis in Water Ice

As often described, radiation absorbed by gas phase water molecules can directly break bonds, forming H + OH with a smaller fraction of $\mbox{H}_{2}+ \mbox{O}$. It can also cause ionization, with the ionized species eventually recombining with an electron also producing fragment radicals. This is also the case for electron impact excitation producing excited H, which was the basis for the first suggestion of water vapor plumes on Europa (Roth et al. 2014). When H₂O molecules in water ice absorb radiation, the results are more complicated due to trapping (e.g., Johnson et al. 2005) and the rapid reaction of an excited or ionized species with its neighbors. These interactions can depend on the energy density absorbed locally, as closely spaced ionized or excited species interact efficiently (e.g., Johnson 2011). Ignoring the details of these interactions, the net result of irradiation experiments are often given in terms of product yields called G-values: the number of a particular product produced per 100 eV of energy absorption. In addition to the radicals, relatively stable new molecules are produced: H₂, $\mbox{O}_{2}$ and H₂O₂ (e.g., Carlson et al. 2009).

The surprisingly large yield of gas phase $\mbox{O}_{2}$ emanating from irradiated ice seen in early experiments was suggested to be due to the presence of the vacuum interface at the sample’s surface resulting in the loss of the most volatile product, H₂ (e.g., Brown et al. 1982; Haring 1984). That is, prompt production and loss of H₂, even at temperatures well below that of Europa’s surface, leaves an oxidized composition enhancing the efficiency for eventually producing $\mbox{O}_{2}$ by the subsequently absorbed radiation or, if irradiation occurs at very low temperature, by increasing the temperature making the molecules and their products mobile. The former is seen directly in laboratory experiments in terms of the yield vs. irradiation time at low fluences (e.g., Brown et al. 1982; Johnson et al. 1983) and has been confirmed in subsequent work (e.g., Teolis et al. 2017). Depending on the surface temperature, $\mbox{O}_{2}$ is, of course, also volatile. Therefore, it can escape by thermal desorption, be driven from the surface by the radiation flux, and can diffuse into the regolith, as we will discuss shortly.

Although the exact details for the formation of $\mbox{O}_{2}$ in ice is still uncertain and the database is always incomplete, there is now a considerable body of laboratory data on the net yield of $\mbox{O}_{2}$ (number of $\mbox{O}_{2}$ per incident ion) as a function of both the energy density deposited in the icy surface and the temperature of the sample (e.g., Teolis et al. 2017 and references herein). There are also measurements of the amount of H₂O₂ in the ice following a given radiation dose at different temperatures (e.g., Carlson et al. 1999a, 2009; Hand and Carlson 2011). However, one major caveat for application to planetary science is the very limited data on the role of trace contaminants on enhancing or quenching the production of O₂, although recent observations at the icy Saturnian satellites suggest that it is very important (Teolis and Waite 2016).

The irradiation of an icy surface also produces damage in the regolith ice grains (interstitials, vacancies, defects and incomplete bonds) which has been suggested as being detected at Europa as a crystalline to amorphous transition at $\mbox{depths} < 1~\mbox{mm}$ (Hansen and McCord 2004; Paranicas et al. 2018). In addition, the diffusion of radicals and of the molecular products along the damage track vs. temperature and under irradiation is complex and not well understood (e.g., Benit and Brown 1990). It is also true that the release of $\mbox{O}_{2}$ trapped in an ice sample is complex even in the absence of irradiation (e.g., Laufer et al. 2017), as it depends on the thermally-induced structural changes of the ice matrix. All of these issues affect our ability to model, for instance, how strongly bound, on average, an individual $\mbox{O}_{2}$ molecule is in the radiation-damaged ice. However, consistent with laboratory data, $\mbox{O}_{2}$ and H₂O₂ are observed as trapped species in the ice grains on the icy Jovian satellites (Spencer et al. 1995; Carlson et al. 1999a; Spencer and Calvin 2002; Hand and Brown 2013). Such observations are consistent with radiation damage studies in which volatiles, such as $\mbox{O}_{2}$, produced by the irradiation can become trapped in radiation-driven ‘bubbles’ (multiple vacancy sites/voids) in ice grains (Johnson and Jesser 1997) or at defect sites (Loeffler et al. 2006) with the concomitant H₂O₂ being bound as more refractory molecules in an irradiated ice (e.g., Carlson et al. 1999a, 2009). Although a large amount of important work on these topics still needs to be carried out, below we proceed based on our present, but incomplete, understanding.

3 Observations

By observing atomic oxygen emission lines in the UV using HST, Hall et al. (1995, 1998) confirmed that Europa has an ambient gas consisting of both atomic and molecular oxygen. The column density of $\mbox{O}_{2}$ estimated from these observations was roughly consistent with the amount produced as predicted by combining estimated plasma fluxes with the early laboratory data for $\mbox{O}_{2}$ yields (Johnson et al. 1982). These observations have been extensively expanded and are roughly consistent with the more recent observations (e.g., McGrath et al. 2009; Roth et al. 2016) as well as those of the New Horizon spacecraft (Retherford et al. 2007; see also Plainaki et al. 2018, Fig. 4). The average column extracted from observations is $\sim 0.3\mbox{--}2\times 10^{15}$ $\mbox{O}_{2}/\mbox{cm}^{2}$ (Roth et al. 2016). The concomitant ambient H₂ may have also been observed indirectly (e.g., Mauk et al. 2003) as well as the dissociation of ejected gas phase H₂O molecules resulting in Lyman alpha emission from the excited atomic hydrogen. The latter was the first evidence that outgassing of H₂O might be occurring at Europa (Roth et al. 2014) and has been used recently to describe Europa’s hydrogen corona (Roth et al. 2017). Here we focus on $\mbox{O}_{2}$ observations.

The global source and loss rates of oxygen have also been modeled and discussed with the oxygen atmosphere exhibiting a near-surface component dominated by $\mbox{O}_{2}$ and an extended component dominated by O. Unfortunately the near-surface plasma properties are still uncertain, affecting the calculation of both the radiolytic production of oxygen and its emission and loss rates. Therefore, estimates of the global O₂ source rate at Europa have varied due to the uncertainties of in the particle flux and energies as well as the actual physical conditions at Europa’s surface as indicated in Fig. 1. Colors in Fig. 1 indicate the incident charged particle population responsible for producing O₂ in each publication: energetic ions (10’s of keV to MeV), thermal ions ($T \sim 100~\mbox{eV}$), $\mbox{O}_{2} ^{+}$ pickup (ionized atmospheric O₂ re-impacting Europa’s surface), and, in one instance, energetic electrons (10’s of keV to MeV). The gray-striped bars indicate plasma models for which no source rate was specified; the atmosphere in those models is implicit as part of the inner boundary conditions. Black bars indicate that the authors did not specify the responsible charged particle population. Saur et al. (1998) calculated thermal ion flux onto Europa’s surface but also used a source rate calculated for energetic ions (Shi et al. 1995), so we could not determine whether energetic or thermal ions dominate. Therefore, considerable uncertainties remain in the direct, plasma-produced $\mbox{O}_{2}$ source rate.

Fig. 1

Estimates of Europa’s atmospheric $\mbox{O}_{2}$ source processes and rates over the last four decades. Colors indicating the incident radiation type assumed; energetic ions ($>10$’s of keV), thermal ions ($T \sim 100~\mbox{eV}$), $\mbox{O}_{2}^{+}$ pickup (ionized $\mbox{O}_{2}$ re-impacting Europa’s surface); stripped, estimates but plasma parameters not given as discussed in text (earlier version published in Plainaki et al. 2018). The present paper describes the thermally-driven O₂ source suggested analytically and numerically in Oza et al. (2018) and Oza et al. (2019) respectively

What is possibly more interesting, and not yet well understood, is the observed spatial morphology of the observed aurora, which is used to roughly extract the spatial distribution of the atmospheric molecular and atomic oxygen. Experiments indicate that the radiolytically produced O₂ leaves the surface with a speed distribution determined in part by its binding in ice and in part by the surface temperature (Johnson et al. 1983). For this reason it is not easy to observationally distinguish between thermally desorbed $\mbox{O}_{2}$ or $\mbox{O}_{2}$ directly sputtered by photons, electrons or ions. In addition, the distribution of the $\mbox{O}_{2}$ ejection speeds is found to be much less than its escape speed from Europa. This results in an average hop distance of an ejected O₂ that is much smaller than Europa’s radius. In this way the observed surface-bounded atmosphere should reflect, to some degree, the local surface and plasma properties. Since Europa’s surface composition appears to vary with latitude and longitude, as does the incident plasma temperature and flux (e.g., Nordheim et al. 2018), it is unsurprising that the aurora data suggest that its oxygen exosphere is patchy and spatially non-uniform (McGrath et al. 2004; Roth et al. 2016).

Variations in the surface properties seen in reflectance spectra might in part account for the observed spatial variations in the observed column density but these are difficult to separate from variations in the plasma processes. Such compositional variations are due to trace sulfur species (McCord et al. 1999; Carlson et al. 1999b, 2002, 2005) on the trailing hemisphere, whereas in the Polar Regions and leading hemisphere the ice appears to be cleaner with the impurities possibly dominated by trace carbon species and salts (e.g., Carlson et al. 2009; Hand and Brown 2013). Indeed, observations suggest that there may be more atmospheric $\mbox{O}_{2}$ over the regions of cleaner ice (McGrath et al. 2004; Roth et al. 2016) accounting in part for the spatially variable aurora over the disk. The observed north-south differences in the emission rate were shown to be primarily due to the tilt of Jupiter’s dipole field affecting the incident plasma flux onto Europa’s surface as well as the local electron temperature and density (e.g., Roth et al. 2016, Fig. 10). Because of the uncertainties on the influence of the spatial variations in the composition and the incident plasma which affect the $\mbox{O}_{2}$ source, loss and emission rates, carrying out simulations of the atmosphere in order to obtain a detailed description of the emission observations has been problematic. This is not only due to the spatial distribution of radiolytic production and loss, but, as stated earlier, is also due to the uncertainty in the binding state of the $\mbox{O}_{2}$ formed in the ice, and its eventual fate after it is ejected and then returns to the regolith. Due to these complications, in Oza et al. (2018) we took a somewhat different approach to be discussed shortly.

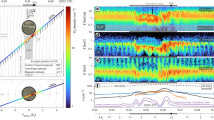
The published HST/STIS images of atomic emissions have a spatial resolution between $\sim 71~\mbox{km}$ and $\sim 95~\mbox{km}$ per pixel depending on Europa’s distance, allowing one to separate emission features originating from the atmosphere within $\sim 500~\mbox{km}$ from the surface from those features originating from an extended corona as analyzed in detail in Roth et al. (2016). The excitation rate depends, of course, on electron temperature, as seen nicely in Fig. 12 of Roth et al. (2016). For the expected electron temperatures near Europa, an intensity ratio of $\sim2$ for the $1356~{\mathring{\mathrm{A}}}/1304~{\mathring{\mathrm{A}}}$ lines is indicative of electron impact dissociation of molecular oxygen. It was estimated that throughout its orbit 95–99% of the near-surface ($r < 1.25r_{E}$) emission is due to electron impact of $\mbox{O}_{2}$, as opposed to electron impact of O (Roth et al. 2016). In addition to north-south asymmetries discussed, hemispheric asymmetries were consistently found at several orbital positions, $\phi_{\mathrm{orb}}$, from the HST dataset spanning from 1999–2015 as seen in Fig. 2. The asymmetries shown were extracted by comparing averaged emission intensity over a range of latitudes and longitudes, but resulted in no clear plasma or surface composition explanation (e.g., Roth et al. 2016). Such asymmetries were difficult to discern from the patterns of individual images obtained over the decades, but orbital and spatial averaging mitigated the uncertainties. One such orbital dependence described in Roth et al. (2016) was subsequently examined in Oza et al. (2018, 2019): the near-surface oxygen emission intensity exhibited a dusk-over-dawn brightening (Fig. 2A) which was shown in the simulations of the near-surface $\mbox{O}_{2}$ column density to be produced when rotation was included.

Fig. 2

Dusk quadrant/Dawn quadrant near surface ($\sim<1.25r_{E}$) brightness ratios for the two oxygen emissions lines: colors indicate observation dates from 1999 to 2015 (from Roth et al. 2016). The $1356~\mathring{\mathrm{A}}/1304~{\mathring{\mathrm{A}}}$ ratio at each sub-observer position, $\phi_{\mathrm{orb}}$, varies but is near to 2 suggesting the emission is heavily dominated by the process $\mbox{O}_{2} + \mbox{e} \rightarrow \mbox{O}^{*} + \mbox{O}$ and the data in (A) is used as a proxy for emission from $\mbox{O}_{2}$ (Roth et al. 2016) in our discussion

Although there is considerable scatter in the data, it is seen in Fig. 2 that to first order, the dusk-over-dawn oxygen aurorae intensity ratios are not extremely sensitive to orbital position, $\phi_{\mathrm{orb}}$. Allowing for the considerable uncertainties the rough average in Fig. 2A is $\sim 1.6$ for the 1356 Å line data. This line is often used as a proxy for emission from $\mbox{O}_{2}$, as the effect of direct solar resonance scattering by the ambient O is negligible at this wavelength. That these observations do exhibit considerable scatter about the average is not surprising considering the spatial and temporal variability discussed above as well as the difficulty of observing near eclipse. Because of their significant scatter, the ratios near eclipse ($0^{\circ}/360^{\circ}$ longitude) could be ignored, although de Kleer and Brown (2018) observed an enhanced brightness in the visible aurora on the trailing dusk quadrant after Europa had entered eclipse consistent with an enhanced dusk/dawn emission ratio. Below we consider the implications of the result in Fig. 2. Before proceeding we note that, although the scatter in the data in Fig. 2 is large, especially near eclipse, the near-surface dusk/dawn emission ratio might be slightly larger in the vicinity of $\phi_{\mathrm{orb}} \sim 180^{\circ}$. In this region of the orbit the dawn half-hemisphere is the darker, trailing hemisphere and the dusk half-hemisphere is the leading, brighter hemisphere. This might be consistent with a somewhat enhanced leading hemisphere emission, possibly consistent with an enhanced source in the region of cleaner ice. Or the data in Fig. 2A could be suggestive of a gradual enhancement of the ratio as the trailing hemisphere becomes visible. In the following we ignore these possibilities as more observations would be required to be definitive.

4 Simulations

Based on the estimates of the column densities derived from both observations and the size of the interaction cross sections, Europa’s O₂ atmosphere is predominantly collisionless (e.g., Hall et al. 1998; Roth et al. 2016). This has led to a number of applications of the laboratory data in simulations of this atmosphere (e.g., Smyth and Marconi 2006; Shematovich et al. 2005; Saur et al. 1998; Cassidy et al. 2013; Lucchetti et al. 2016; Oza et al. 2019). Laboratory data indicate there is a surface temperature and irradiation time dependence to the formation and ejection of $\mbox{O}_{2}$ by UV photons (e.g., Westley et al. 1995a, 1995b), by plasma electrons (e.g., Orlando and Kimmel 1997) and by plasma ions (e.g., Brown et al. 1982; Johnson et al. 1983; Teolis et al. 2017). Therefore, it was pointed out that the thermal and irradiation history must be accounted for in determining the radiolytic source rate (e.g., Teolis et al. 2005, 2009; Cassidy et al. 2013).

Unfortunately, it is difficult to carry out laboratory experiments in a sample that accurately represents a porous regolith (Cassidy and Johnson 2005). That is, the vapor deposited laboratory samples have a porosity at the submicron molecular scale, whereas Europa’s regolith exhibits porosities at the 100s of micron scale. In addition, the charged particles used in many of the experiments had penetration depths smaller than the typical regolith grain size, whereas some experiments use incident particles with penetration depths greater than the typical grain size by irradiating relatively thin samples, in which case the substrate might play a role. Therefore, the concept of ‘the surface’ can differ in these experiments from that understood to be present on Europa or any other icy body. In addition, the thermal plasma electrons and ions at Europa primarily bombard the trailing hemisphere while energetic ions with energies above ∼a few hundred keV bombard the surface much more uniformly (Cassidy et al. 2013). Energetic electrons on the other hand, bombard the surface in highly non-uniform patterns, leading to the formation of ‘bombardment lenses’ centered on the leading and trailing hemispheres at low latitudes (Paranicas et al. 2001; Nordheim et al. 2018) as indicated in Fig. 3. As energy deposition by energetic electrons dominates at cm to m depths, this degree of non-uniformity has important implications for the radiolytic production of $\mbox{O}_{2}$ at depth. Convolved with the significant variation in charged particle energy deposition vs. depth and surface location, is the variability of surface materials and trace species at different locations (e.g., as discussed, the leading hemisphere and polar regions appear to contain different trace species than the trailing hemisphere) as well as the possible spatial variability in the thermal inertia (Trumbo et al. 2018) affecting the local surface temperature. For all of these reasons, agreement on the use of the laboratory data in the simulations remains problematic (see also Cassidy 2016; Plainaki et al. 2018).

Fig. 3

Energy deposited by the ambient plasma in Europa’s surface per unit mass per unit time vs. depth for various regions on Europa indicated in the inset: dose rate in Grays/s ($\mbox{J}/\mbox{kg}/\mbox{s} \sim 1.0 \times 10^{-8}~\mbox{eV}/\mbox{amu}$); depth in meters. This rate can be used with the G-values (number of a product per 100 eV deposited) published in a number of papers to estimate the radiation driven alterations. (From: Nordheim et al. 2018)

In spite of such uncertainties, there have been a number of efforts applying models of the laboratory data in collisionless Monte Carlo simulations of Europa’s atmosphere. Based on the success of the simulations of the observed gas-phase distribution of Na ejected from Europa (Leblanc et al. 2005) and the laboratory data on desorption by the plasma and UV photon flux (e.g., Yakshinskiy and Madey 2001), Oza et al. (2019) applied a similar Monte Carlo model to simulate the oxygen exosphere. In doing this, they tested suggested plasma-induced source distributions including and excluding the temperature dependence. They also included the effect of the centrifugal and Coriolis forces due to Europa’s rotation about Jupiter as well as the effect of the varied spatial composition of Europa’s surface on the sputtered $\mbox{O}_{2}$ as well as on its fate when it returned to the surface. In these simulations, the initially desorbed and thermally reemitted $\mbox{O}_{2}$ were tracked as they were ejected and ballistically hopped across the surface subject to gravity and the centripetal and Coriolis forces. Although the range of possible source processes and the range of the surface effects could surely be expanded beyond those used, the conclusion was that Europa’s rotation about Jupiter was critical in generating a dusk-over-dawn asymmetry in the $\mbox{O}_{2}$ column density. However, the fact that the observed dusk/dawn emission ratios in Fig. 2A did not vary strongly with orbital position could not be reproduced simply assuming the local $\mbox{O}_{2}$ column was proportional to observed brightness. That is, the models used gave near-surface ratios of column density that were strongly dependent on the orbital position, differing at some orbital positions from the HST emission ratios by an order of magnitude indicating to them that the role of the surface needed to be re-examined as discussed below. Furthermore, since a simple average global loss rate was used in these simulations, the authors pointed out that one could design a spatially variable loss rate and/or emission rate to force the simulations to produce dusk/dawn ratios more uniform in orbital longitude. Since such a simulation would likely be artificial, a different approach was tried.

Although the physical processes are complex, the observations in Fig. 2A suggest some simple aspect was being overlooked. In order to focus on the role of Europa’s orbital position with respect to the solar illumination and the preferential bombardment of the trailing hemisphere, the longitudinal variation in the latitudinally averaged O₂ column density was modeled. This was done in order to initially avoid spatial variations in the surface properties and thereby focus on the role of the longitudinal, rotational, and thermal dependence of the source rate. Therefore, a simple rate equation, balancing source and loss rates was used. The goal was to describe the dependence on the local longitude, $\phi$, of the time-variable, latitudinally averaged O₂ column density, $N(\phi, t)$, vs. Europa’s orbital position, $\phi_{\mathrm{orb}}$ (Oza et al. 2018).

As Europa rotates with angular speed, $\varOmega$, phase-locked to Jupiter, $\phi_{\mathrm{orb}}$ is simply related to the local time, $\phi_{s}$, on Europa’s surface with noon at $\phi_{s} = 180^{\circ}$ and midnight at $\phi_{s}= 0^{\circ}/360^{\circ}$. For simplicity the diffusive hopping was ignored, since average ballistic hop distance for an ejected O₂ is much smaller than Europa’s radius and its lifetime is such that its diffusion distance is a fraction of the radius. With these simplifications, a rate equation for the latitudinally averaged O₂ column density, $N$, as a function of longitude, $\phi$, can be approximated as

$$\begin{aligned} dN(\phi,t)/dt \approx\ \varPhi(\phi, \phi_{s}) - \nu(\phi, \phi_{s})N(\phi,t) \end{aligned}$$

(1)

Here $\varPhi$ is the local $\mbox{O}_{2}$ flux from the surface and $\nu$ is the probability per unit time for the loss of $\mbox{O}_{2}$. As stated, this ignores the thermal hopping across the surface described in Oza et al. (2019), which could be included by a diffusive term. However, in this form Eq. (1) can be is readily integrated over time as Europa rotates. This allowed us to test the steady state spatial and thermal dependence of $\mbox{O}_{2}$ that is suggested by the spatial and thermal dependence of the source and loss rates. Although diffusion across the surface, as well as the centripetal and Coriolis forces are ignored, using Eq. (1) with the suggested longitudinal and thermally dependent source and loss rates gave near surface $\mbox{O}_{2}$ column densities that depend very strongly on orbital position, as was seen to be the case in the detailed simulations in Oza et al. (2019). Therefore, Eq. (1) can be used to test a number of proposed source processes. Using a spatially and thermally dependent sputter source in Eq. (1) suggested by data from laboratory experiments, it is seen in Fig. 4a that the dusk/dawn ratio versus orbital position disagrees considerably with the ratios in Fig. 2A extracted from the emission observations. This is the case even allowing for the thermal delays in emission suggested by laboratory measurements (Teolis et al. 2005; Cassidy et al. 2013).

Fig. 4

(a) Half-hemisphere averages of the dusk-over-dawn ratio of emission and modeled column densities $\langle R\rangle$ vs. sub-observer longitude (adapted from Oza et al. 2018, Fig. 3). Circles: ratio of HST emission intensities from Roth et al. (2016) as in Fig. 2 (average $\sim 1.6$). Squares: from detailed simulations of the column density (Oza et al. 2019) in which the trailing hemisphere enhancement in the plasma flux (Cassidy et al. 2013) onto the surface determines the source rate. Curves: plasma ram source with (dashed) and without (dotted-dashed) temperature enhancement. Solid & dotted lines: ratio $\langle R\rangle$ from Eq. (3) with $\beta = \varOmega/\nu = 6.7$ (solid; $\nu \sim 1/\tau_{\mathrm{orb}}$) and $= 1$ (dotted; $\nu \sim 6/\tau_{\mathrm{orb}}$) giving $\langle R\rangle\sim 1.2$ and 1.6 respectively. (b) Normalized source rate (Eq. (2a)) (solid curve: right vertical axis) and resulting normalized column densities vs. $\phi_{s}$ (left vertical axis) for two values of $\beta$ indicated giving the two straight lines for $\langle R\rangle$ in (a)

However, $\mbox{O}_{2}$ trapped in an ice regolith can in principle be released thermally, as discussed frequently (e.g., Loeffler et al. 2006; Bar-Nun et al. 2013; Laufer et al. 2017), and as also seen experimentally on warming an irradiated ice sample (Teolis et al. 2005). Therefore, a regolith permeated with $\mbox{O}_{2}$ that can be desorbed by the solar flux, could in principal dominate the $\mbox{O}_{2}$ sputter source. Using an average loss rate, $\nu$, Oza et al. (2018) noted that a source rate depending only on the local time, $\phi_{s}$, would produce no dependence on orbital position. To first order, this is consistent with the weak dependence on orbital position of the observed dusk-over-dawn ratio in Fig. 2. That is, writing the surface desorption flux vs. $\phi_{s}$ in a clearly oversimplified form

$$\begin{aligned} \varPhi(\phi_{s}) \sim\varPhi(0) \bigl[1 - \cos(\phi_{s})\bigr]/2 \end{aligned}$$

(2a)

where $\varPhi(0)$ is maximum at noon, $\phi_{s} = \pi$, and goes to zero at midnight gives the source rate in Fig. 4b (solid line). Such a source rate results in a steady-state, latitudinally-averaged column density that only depends on $\phi_{s}$: $N(\phi) \sim(\varPhi(0)/2\nu)[1-(1+ \beta^{2})^{-1}(\cos(\phi_{s}) - \beta\sin (\phi_{s}))]$. This is also shown in Fig. 4b for two values of $\beta = \varOmega/\nu$, where $\varOmega$ is the angular frequency and $\nu$ is the loss rate (dashed and dotted lines). Using this estimate of the local column density, the calculated half-hemisphere averaged ratio is found to be independent of $\phi_{\mathrm{orb}}$. That is, on substituting Eq. (2a) into Eq. (1), the half-hemisphere average of the dusk/dawn ratio, $\langle R\rangle$, of the near surface, $\mbox{O}_{2}$ column densities is

$$\begin{aligned} \langle R\rangle \sim \bigl[1+ (2/\pi) (\beta +1) + \beta^{2}\bigr] / \bigl[1 - (2/ \pi) (\beta -1) + \beta^{2}\bigr]. \end{aligned}$$

(3)

Since this depends only on $\beta$, the ratio of the rotation rate to the average loss rate, the rotation is critical in determining the dusk/dawn asymmetry at Europa as shown in the detailed simulations in Oza et al. (2019), and as can be seen from the shift towards dusk of the resulting column densities in Fig. 4b. That the rotation plays a critical role in the surface bounded atmospheres was noted much earlier for the lunar atmosphere (Hodges and Johnson 1968) and Mercury’s Na atmosphere (Cassidy et al. 2015; Leblanc and Johnson 2010). It is seen that in this approximation $\langle R\rangle$ is not only constant but is greater than one. That is, for an $\mbox{O}_{2}$ source that is determined primarily by the solar flux, the peak column is shifted from near noon toward dusk simply due to Europa’s rotation as seen in Fig. 4b and shown in general in the appendix.

The scale height of the observed $\mbox{O}_{2}$ atmosphere has been discussed extensively and may be affected on the trailing hemisphere by collisions with sputtered water molecules (Oza 2017). Yet it is generally agreed that the principal $\mbox{O}_{2}$ content of the atmosphere has a scale height much smaller than Europa’s radius. Therefore, assuming the atmosphere is optically thin, it is not unreasonable that the averaged near surface $\mbox{O}_{2}$ column densities are roughly proportional to the averaged near surface component of the observed $\mbox{O}_{2}$ emission. Although that is a significant assumption, in Fig. 4a we compare the ratio in Eq. (3) to the observational ratios from Fig. 2A. Using a loss rate based on photo and electron impact (Turc et al. 2014, Table 2) gives an ionization rate, $\nu \sim 3.1\times 10^{-6}/\mbox{s}$ for an electron density of $70~\mbox{cm}^{-3}$. Using that value for the globally averaged loss rate, which is close to the inverse of the orbital period, $\tau_{\mathrm{orb}}$, with $\varOmega = 2\pi/\tau_{\mathrm{orb}} = 2.1\times 10^{-5}/\mbox{s}$ at Europa, then $\beta\sim 6.7$. Substituting $\beta$ in Eq. (3) gives the half-hemisphere average dusk/dawn ratio of $\langle R\rangle\sim 1.2$ shown in Fig. 4a. Although $\langle R\rangle$ in Eq. (3) is independent of $\phi_{\mathrm{orb}}$, this underestimates the average ratio, $\sim 1.6$, obtained from the HST data. However, the sense of this result is consistent with an emission ratio nearly independent of orbital position. Recent modeling of the plasma flow (Dols et al. 2016) suggests that charge transfer with the ionized component of the atmosphere dominates the near surface loss rate of $\mbox{O}_{2}$. If that is the case, including all $\mbox{O}_{2}$ loss processes (e.g., Lucchetti et al. 2016), the net, globally-averaged loss rate can be as large as $\nu\sim 2.0\times 10^{-5}/\mbox{s}\sim 6/\tau_{\mathrm{orb}}$. This would result in $\beta \sim 1$ and $\langle R\rangle\sim 1.6$ in Fig. 4a. This is, in surprising, and possibly fortuitous, agreement with the average HST result in Fig. 2A.

The source rate in Eq. (2a) is, of course, over simplified as there are leading and trailing differences in composition and albedo resulting in much more complicated temperature profiles (e.g., Spencer et al. 1999; Trumbo et al. 2018) and in Fig. 5. In fact, unlike the case for desorption of Na, the mechanism for the desorption of the $\mbox{O}_{2}$ returning to the surface is not identified. Assuming thermal desorption, the form in Eq. (2a) could be improved by using a source rate that depends on the local temperature. If the dominant source is thermal desorption from a regolith permeated with adsorbed $\mbox{O}_{2}$, the source flux could be approximated locally as $\varPhi(\phi_{s}) \sim\varPhi _{0} \exp(-U_{s}/kT)$ with $U_{s}$ an average activation/binding energy. One can also crudely approximate an equatorial surface temperature, averaged over a range of longitudes and latitudes, as $T = T_{0} (1 - \varepsilon \cos\phi_{s})$ with $\varepsilon = \Delta T/T_{0}$ and $\Delta T$, the temperature excursion. Assuming $\Delta T$ is small relative to $T_{0}$, the average equatorial temperature, one obtains a latitudinally-averaged source rate that is roughly of the form

$$\begin{aligned} \varPhi(\phi_{s}) \sim\ \varPhi(0) \bigl[1 - (U_{s}/kT_{0})\varepsilon \cos \phi_{s}\bigr] \end{aligned}$$

(2b)

This has a dependence like that in the expression in Eq. (2a), justifying the use of the form in Eq. (2a) to approximate a thermal desorption source.

Fig. 5

(a) Orbital modulation of Europa’s equatorial sub-observer temperature, due to its albedo and the Jovian shadow, in degrees K vs. orbital longitude: the albedo was assumed to be independent of latitude varying linearly with longitude from 0.65 at the center of the leading hemisphere to 0.45 at the center of the trailing approximating the results in Rathbun et al. (2014). Inset: near eclipse. (b) Temperature map for a sub-solar longitude $270^{\circ}$ vs. planetographic longitude & latitude: the drop in surface T during eclipse ($\sim 3\%$ of a Europa day) depends on Jupiter’s season; the time-in-shadow used here is roughly consistent with the durations in the Roth et al. measurements. The regolith T in this model is controlled by the thermal inertia ($\sim 2.1\times 10^{2}~\mbox{J}/(\mbox{m}^{2}\mbox{K}\,\mbox{s}^{0.5})$) resulting in a skin depth $\sim 4~\mbox{cm}$ (Spencer 1987) with a thermal conductivity $2.52\times 10^{2}~\mbox{erg}/(\mbox{cm}\,\mbox{K}\,\mbox{s})$ (Abramov and Spencer 2008), emissivity $\sim 0.96$, and ignores a solid state greenhouse effect (from: Oza et al. 2019, Fig. 2)

Due to the thermal inertia of the icy surface, it is seen in Fig. 5 that the peak in the surface temperature of Europa in the near equatorial region is shifted towards dusk. Ignoring the important hemispheric albedo differences, then Eq. (2a) could be replaced by

$$\begin{aligned} \varPhi(\phi_{s}) \sim\varPhi(0)\bigl[1- c \cos(\phi_{s} + \Delta\phi_{s})\bigr]/(1+c) \end{aligned}$$

(2c)

Here $c$ can be used to fit the difference in the noon to midnight temperature difference and $\Delta\phi_{s}$ accounts for the shift in the peak temperature from noon in Fig. 5b. For a thermal source like that suggested here, the shift in the peak temperature towards dusk would slightly increase the averaged dusk/dawn ratio, $\langle R\rangle$, by $\sim 15\%$. In addition, a direct sputter source, which must certainly be occurring, would add to any solar driven source. For instance, adding to Eq. (2a) a global sputter source, $\varPhi_{s}$, as suggested in Cassidy et al. (2013), $\langle R\rangle$ in Eq. (3) would become

$$\begin{aligned} \langle R\rangle \sim \bigl[1+ \delta_{s} + (2/\pi) (\beta+1) + \beta^{2}\bigr]/\bigl[1+ \delta_{s} - (2/\pi) (\beta-1) +\beta^{2}\bigr] \end{aligned}$$

(4)

where $\delta_{s} = \varPhi_{s}/\varPhi(0)$. Not surprisingly, this expression for the dusk/dawn ratio is also independent of orbital position, but is altered by $\delta_{s}$, the ratio of the direct sputter source to the peak-thermal source. Obviously, more realistic expressions for the source rate $\varPhi$ are needed, but only after a good description of the physics that is occurring is obtained. For instance a stimulated desorption process, like that used for Na in Leblanc et al. (2005) could also give an appropriate dusk/dawn ratio. The above discussion simply shows that even with additional complexity a source driven primarily by the solar flux is consistent with a critical aspect of the near-surface observations.

There are, of course, significant uncertainties in the average loss rate, $\nu$, as well as the sputter to thermal source ratio, $\delta_{s}$. Therefore, using the available observations to make a definitive statement on their relative importance is not likely at present. However, most previous simulations have assumed that $\delta_{s}$ dominates and is strongly dependent on orbital longitude. Therefore, a source rate that responds primarily to the local solar flux as in Oza et al. (2018) and not, primarily to an enhanced trailing hemisphere sputtering rate, appears to be a much simpler way to account for the lack of significant variation with Europa’s orbital position of the averaged dusk/dawn emission ratio observed. Such a source would suggest that Europa’s regolith has become permeated with trapped $\mbox{O}_{2}$, which upon thermal or stimulated desorption populates the near-surface atmosphere, with, of course, a smaller contribution from the ultimate plasma source which replaces and redistributes the O₂ lost by the escape, subduction, dissociation and ionization.

Clearly, additional improvements can be made by accounting for the differences in temperature and composition on the leading and trailing hemispheres as discussed. However, as seen from the data in Fig. 2A the fully illuminated trailing hemisphere (orbital longitude $270^{\circ}$) and the fully illuminated leading hemisphere (orbital longitude $90^{\circ}$) exhibit surprisingly similar radially-averaged dusk/dawn emission ratios, though with significant uncertainties. This is consistent with the fact that the difference in dependence of the emission intensity of the 1356 Å line with distance from the disk center at these orbital longitudes is not large, as seen in Fig. 6 (red lines: dashed leading and dotted trailing). Even the off-disk intensity averages in Fig. 6 are surprisingly similar for the 1304 Å line. The similar dependences with distance from the disk center for the illuminated leading and trailing hemispheres, both of which increase over the disk with distance from the subsolar point, is not inconsistent with a predominantly solar driven source. However, the very similar off disk dependences require a super thermal scale height (Roth et al. 2016), that is roughly consistent with the super thermal tail for O₂ ejections seen in the laboratory data (e.g., Oza et al. 2019). The fact that the hemispherical differences seen in Fig. 6 for the 1304 Å line are larger than those seen in the 1356 Å suggests that spatial variation in the plasma, affecting the dissociation of $\mbox{O}_{2}$, and the subsequent ionization and excitation of the dissociation product O, does play a role. Therefore, corrections to the average loss rate, $\nu$, in Oza et al. (2018, 2019), and also used to obtain Eqs. (3) and 4 above need to be accounted for. For this reason, a good description of the plasma ion and electron temperature and flux very close to Europa’s surface is still needed and is critical. Although one could, in principle, reproduce the HST results in Figs. 4 and 6 by designing functions for the source and loss rates that depended on both $\phi$ and $\phi_{s}$, below we discuss the possibility that a solar dominated source, likely due to sublimation, is reasonable.

Fig. 6

Radial brightness profiles of the mean O I 1356 Å (red) and O I 1304 Å (blue) brightness averaged over concentric 0.05 $R _{E}$ wide rings around the disk center (0 km) in all exposures: dashed, fully illuminated leading hemisphere, $\phi_{\mathrm{orb}} \sim 90^{\circ}$; dotted, fully illuminated trailing hemisphere, $\phi_{\mathrm{orb}} \sim 270^{\circ}$. From Roth et al. (2016), Fig. 11a

5 Discussion

As pointed out following the early laboratory measurements of the radiolysis of ice (Brown et al. 1982; Johnson et al. 1983), the preferential loss of the much more volatile H₂, implies that the irradiated ice becomes oxygen rich. At Europa this effect is enhanced by the fact that H₂, produced and desorbed during radiolysis, also readily escapes Europa’s gravitational field, whereas the ejected O₂ primarily returns to the surface, as does a significant fraction of the O formed following dissociation of $\mbox{O}_{2}$ (e.g., Oza et al. 2019). Therefore, it is clear that the regolith is oxygen rich, at least down to the penetration depth of the incident energetic particle radiation, ∼ a meter (e.g., Cooper et al. 2001; Paranicas et al. 2001, 2009; Nordheim et al. 2018). Because the regolith is porous, thermal and radiation-enhanced diffusion over long time periods would suggest that the ice could be oxygen rich to much larger depths (e.g., Johnson et al. 2003).

Although the state of the oxygen-rich ice is not well defined, and likely differs between hemispheres and with depth, $\mbox{O}_{2}$ has been observed as trapped in Europa’s surface ice grains (Spencer and Calvin 2002). That observation was associated with a band from a solid-like, $\gamma$ phase $\mbox{O}_{2}$ at 5773 Å due to excitation of the $\mbox{O}_{2}$ dimer. Because solid $\mbox{O}_{2}$ cannot be sustained in vapor pressure equilibrium at Europa’s surface temperatures (e.g., Fray and Schmidt 2009), it was suggested to be trapped in radiation produced voids (Johnson and Jesser 1997). Recently, that band was observed to exhibit an unexplained spatial and temporal variability at Europa as tentatively suggested by Spencer and Grundy (2017). This is likely related to a combination of plasma irradiation and local temperature affecting trapping (e.g., Shi et al. 2009) and, possibly, water vapor deposition from the plumes.

The size of the grains in Europa’s regolith, which appear to differ by more than a factor of 10 from the trailing to the leading hemisphere (Cassidy et al. 2013, Fig. 10), can influence the $\mbox{O}_{2}/\mbox{H}_{2}\mbox{O}$ ratio inferred from the 5773 Å $\mbox{O}_{2}$ observations. Assuming the band depth is due to $\mbox{O}_{2}$-$\gamma$, based on the expression derived by Hand et al. (2006) and the data in Spencer and Grundy (2017), then the trapped $\mbox{O}_{2}/\mbox{H}_{2}\mbox{O}$ ratio seems, quite surprisingly, to be within a factor of a few of that emitted from Comet 67P/Churyumov–Gerasimenko: $\mbox{O}_{2}/\mbox{H}_{2}\mbox{O}$ (Bieler et al. 2015) and Comet 1P/Halley (Rubin et al. 2015). In addition to the $\mbox{O}_{2}$ observed at Europa in the 5773 Å band, individual $\mbox{O}_{2}$ can be trapped at defect and dangling bond sites produced by the irradiation (e.g., Cassidy and Johnson 2005; Loeffler et al. 2006; Johnson 2011; Johnson et al. 2013) including at grain surfaces (Teolis et al. 2005). Indeed laboratory experiments indicate that the surface properties play a role in controlling the production and subsequent ejection of $\mbox{O}_{2}$ (e.g. Teolis et al. 2006, 2017). The $\mbox{O}_{2}$ is seen to trap in the near surface region of the irradiated laboratory ice samples, which on Europa would be the surface of an ice grain exposed to the incident plasma. This $\mbox{O}_{2}$ is driven into the gas phase with an amount and rate depending on the irradiation history (Teolis et al. 2005). Indeed on irradiation followed by warming, $\mbox{O}_{2}$ is also seen to evolve (e.g., Teolis et al. 2009, 2017) and warming reduces dangling bond sites (Loeffler et al. 2006). Therefore, the production and release of O₂ is clearly temperature dependent, although for the $\sim 135~\mbox{K}$ maximum temperatures expected at Europa, outgassing in laboratory samples in which H₂O and $\mbox{O}_{2}$ are co-deposited was estimated to be small (Teolis et al. 2005). Emission of $\mbox{O}_{2}$ from non-irradiated samples of co-deposited $\mbox{O}_{2}$ and H₂O has been related to the crystalline phase transitions (e.g., Laufer et al. 2017), which occurs due to the rearrangement of hydrogen bonds.

Although the formation and ejection of $\mbox{O}_{2}$ from a laboratory water ice sample due to the incident radiation is initially negligible, it grows with irradiation time (e.g., Brown et al. 1982; Westley et al. 1995a, 1995b; Teolis et al. 2017). Due to the ability of the solid to accumulate trapped precursors the reaction pathways differ from what occurs in the gas phase (e.g., Johnson 2011). Therefore, a significant amount of solid-state chemistry occurs before the $\mbox{O}_{2}$ yield reaches steady state and precursor trapping has been shown to be critical in modeling of the measured thermal and fluence dependences using chemical rate equations (e.g., Johnson et al. 2005; Teolis et al. 2009; Johnson 2011). Since the nature of the trapping of both the chemical precursors and the O₂ is critical, it likely depends on the availability of defects/dangling H bonds, and has been shown, not surprisingly, to be enhanced by irradiation of crystalline ice (Loeffler et al. 2006).

6 $\mbox{O}_{2}$ Desorption Energy

The laboratory measurements of the steady state yield of $\mbox{O}_{2}$ exhibit a roughly exponential temperature dependence with an apparent activation energy $\sim 0.06~\mbox{eV}$ found in a number of experiments (Reimann et al. 1984; Brown et al. 1984; Fama et al. 2008; Teolis et al. 2017). This activation energy, smaller than the typical hydrogen bond energy in ice and even smaller than the sublimation energy for solid $\mbox{O}_{2}$, is not yet explained. Since the result is extracted from particle irradiation measurements, it is likely that the bonding energy and diffusion are modified by the radiation a process often referred to as radiation-enhanced diffusion.

The convenient, but clearly overly simplified, model in Eq. (2a) is seen in Fig. 4a to give a ratio of the column densities averaged over the dusk quadrant and dawn quadrant similar to the quadrant integrated dusk/dawn emission ratio during Europa’s orbit. Assuming that comparison is not fortuitous, then using the form for $\varPhi(\phi_{s}) \sim \varPhi_{0} [1 - (U_{s}/kT_{0}) \varepsilon\cos \phi_{s}]$ in Eq. (2b), suggests that $(U_{s}/kT_{0}) \varepsilon \sim 1$ where $\varepsilon = \Delta T/T_{0}$. For a very rough estimate of the temperature excursion, $\Delta T\sim 10~\mbox{K}$, with $T_{0}\sim 125~\mbox{K}$ suggested by observations (Spencer et al. 1999) and by calculations such those in Fig. 5, a very crude average thermal activation/bond energy can be estimated, $U_{s}\sim 0.14~\mbox{eV}$. This, of course, would vary with surface composition. This value, primarily applicable near the thermal peak, is roughly similar to hydrogen bond energies in ice, which, of course, vary with the ice structure and the presence of trace species. It is roughly 1.5 times as large as the sublimation energy for pure $\mbox{O}_{2}$. In the temperature range of interest on Europa, the laboratory measurements of outgassing from the co-deposited H₂O/O₂ was seen to be slow, as discussed above, until the temperature was increased to the phase transition $\sim 155~\mbox{K}$. However, over the relevant temperature range for Europa co-deposited samples were shown to steadily release $\mbox{O}_{2}$ (Fig. 4 in Laufer et al. 2017). A desorption energy, possibly fortuitously, close to 0.14 eV was extracted from co-deposition experiments in support of the ROSINA measurements (e.g., Laufer et al. 2017; Table I). These crude comparisons suggest that thermal desorption from the regolith of $\mbox{O}_{2}$ attached to dangling H bonds might be the dominant source of the observed near surface atmospheric $\mbox{O}_{2}$ at Europa.

The early measurements of the sputtered $\mbox{O}_{2}$ speed distribution (Johnson et al. 1983; Reimann et al. 1984) indicted that most of the ejected $\mbox{O}_{2}$ returned to Europa’s surface as mentioned earlier. Therefore, in their extensive simulations, Oza et al. (2019) were concerned with the re-condensing $\mbox{O}_{2}$. They showed, not surprisingly, that the heat of adsorption on the re-condensing $\mbox{O}_{2}$ molecules significantly affected their rate of desorption back into Europa’s atmosphere. Because of surface compositional differences, the effective binding can vary, affecting the spatial morphology of local $\mbox{O}_{2}$ column density (e.g., Fig. 4 in Oza et al. 2019). Therefore, new simulations need to be carried out based on the solar driven desorption concept suggested in Oza et al. (2018) in which one treats the nature of the trapping and the temperature vs. depth and time more carefully. That is, based on the above discussion, and as summarized schematically in Fig. 7, the local source is likely dominated by the solar flux possibly causing thermal desorption of O₂ trapped primarily at dangling hydrogen bonds from a regolith permeated with $\mbox{O}_{2}$ and with a smaller contribution from direct sputtering.

Fig. 7

Schematic diagram of $\mbox{O}_{2}$ trapping and thermal desorption: 1) Primary origin of $\mbox{O}_{2}$ (and H₂) is magnetospheric ion radiolysis. 2) Due to preferential loss of H₂, the regolith becomes oxygen rich enhancing the production of $\mbox{O}_{2}$. Formed and returning $\mbox{O}_{2}$ can become trapped at incomplete (dangling) H bonds (shown) as well as in voids (as shown and observed by Spencer and Calvin 2002). 3) The accumulated O₂ can then be thermally desorbed from the weak dangling bonds due to solar heating, maintaining a quasi-vapor pressure equilibrium (Oza et al. 2018), with a smaller gas-phase contribution from direct sputtering of $\mbox{O}_{2}$. A fraction of the trapped $\mbox{O}_{2}$ is likely subducted

7 Summary

As pointed out often, the state of the trapped $\mbox{O}_{2}$ in Europa’s regolith, not only affects the observation of the gas-phase $\mbox{O}_{2}$, but also affects its ability to diffuse downward and permeate the regolith. This is determined by the temperature variation with depth. That is, the local temperature gradient determines how any produced or returning O₂ diffuses through the ice matrix via defect or grain boundary diffusion (Johnson and Quickenden 1997; Johnson 2011) or simply gas-phase diffusion through a porous regolith. The presence of oxygen rich material at depth is also affected by the radiation which modifies roughly the top meter of Europa’s ice mantle as seen in Fig. 3. This radiation not only produces an oxygen rich ice, but also can affect the crystal structure producing dangling bonds and radiation-enhanced diffusion. Since the porosity likely decreases with depth (e.g., Pappalardo et al. 2009), it is critical that the modeling needs to be carried out on the bulk processes and not just the near surface processes.

Although direct diffusion to the depth of the ocean is likely problematic, geologic mixing and subduction of oxygen rich ice have been suggested as a possible source of oxidants for putative ocean biology (Johnson et al. 2003; Grieves and Orlando 2005; Greenberg 2008; Russell et al. 2017). These are also processes which might bring any ocean organics to the surface where they might be detected following ejection by heavy plasma ion impacts (Johnson and Sundqvist 1992, 2018) or by charged grain impacts (Sternovsky et al. 2018). Oxidants transported to the ocean would not only be $\mbox{O}_{2}$, but other related and stable radiation-induced oxidants such as H₂O₂, sulfates, carbonates, carbonic acids, etc. which can yield an ocean with high chemical potential (e.g., Hand et al. 2006; Vance et al. 2016).

The simple paradigm for production of the observed $\mbox{O}_{2}$ atmosphere described here needs to be improved upon to assist in the planning of the observations of the JUICE and Europa Clipper missions. And further observations in eclipse might help in separating the solar driven and plasma driven components of the near surface $\mbox{O}_{2}$ atmosphere. However, the concept considered suggests a fact that should not be surprising. That is, due to the considerable radiolytic processing of Europa’s surface, and Europa’s significant gravity, it is not surprising that Europa’s ice mantle is permeated with oxidants and trapped O₂. This was, of course, the prime motivation for the suggestion that radiolytic processing of the surface ice combined with geologic activity might lead to subduction of oxidants to Europa’s ocean (Chyba 2000; Johnson et al. 2003; Greenberg 2008; Russell et al. 2017).

If Europa’s regolith is permeated with trapped $\mbox{O}_{2}$, this might at first appear inconsistent with the Cassini observations at Dione and Rhea. Teolis and Waite (2016) showed that the effective source of $\mbox{O}_{2}$ was much smaller than expected based on combining laboratory data with Cassini spacecraft measurements of the plasma flux (Johnson et al. 2008). However, the plasma fluxes at these objects are orders of magnitude smaller than at Europa, these bodies are on average far colder, and the surfaces appear to be older, indicating less geologic activity than observed, for instance, at Enceladus (Porco et al. 2008) and Europa (Roth et al. 2014; Sparks et al. 2016, 2017). This indicates that the application of the interesting and useful laboratory data on the production of gas-phase species by radiolysis must be applied carefully at each body, accounting for the local environment and the surface properties—a not very surprising conclusion. Therefore, we suggest new simulations need to be carried out based on the premise that Europa’s near surface regolith, consisting of ice grains sizes that vary with depth, as well as with longitude and latitude, and the surface thermal processing that varies with time and depth, is permeated with trapped $\mbox{O}_{2}$ that is primarily formed by the incident Jovian plasma. That is, in addition to $\mbox{O}_{2}$ produced at depth by penetrating ions and electrons, ejected molecules ejected in to gas phase above Europa’s surface primarily return to the surface, where they can diffuse into the regolith and attach at binding sites of varying strength or react with trace species. Subsequent radiation can, of course, drive the trapped O₂ back into the gas phase. However, as suggested in Oza et al. (2018), desorption by the solar flux of weakly trapped $\mbox{O}_{2}$, likely at dangling H bonds, might dominate the direct plasma-induce production and ejection in determining the observed, near surface, $\mbox{O}_{2}$ atmosphere.

Appendix

For a latitudinally-averaged source rate $\varPhi(\phi,\phi_{s})$ and an average loss rate, $\nu$, the column density is readily calculated as

$$\begin{aligned} N(\phi,t) = \exp(- \nu t)\int_{0}^{t} \exp\bigl(\nu t'\bigr)\varPhi \bigl(\phi, \phi_{s}'\bigr) dt' \end{aligned}$$

(A.1)

when $N(\phi,0) = 0$ at $\phi_{\mathrm{orb}} = 0$. Using this, the column accumulated in one orbit is

$$\begin{aligned} N_{1}(\phi, \phi_{s}) = e^{-2\pi/\beta} \int_{0} ^{2\pi/\beta}\exp \bigl(\nu t'\bigr) \varPhi\bigl(\phi,\phi_{s}'\bigr) dt' \end{aligned}$$

(A.2)

with $\beta= \varOmega/\nu$ and $2\pi/\varOmega$ the orbital period. Assuming the source and loss rates do not change over many orbits, then the steady state column becomes

$$\begin{aligned} N(\phi, \phi_{s}) = N_{1}(\phi, \phi_{s})/ \bigl(1 - e^{-2\pi/\beta}\bigr). \end{aligned}$$

(A.3)

If the source rate depends to first order only on solar illumination, $\varPhi(\phi_{s})$, as in Eqs. (2a) & (2b), then $N_{1}(\phi,\phi_{s}) \rightarrow N_{1}(\phi_{s})$ so that the dusk/dawn ratios, $R$ and $\langle R\rangle$ discussed in the text, do not change with orbital position.