1 Gravitational Lens Time Delays

1.1 Principles of Gravitational Lens Time Delays

Strong gravitational lensing occurs when a foreground mass distribution is located along the line of sight to a background source such that multiple images of the background source appear around the foreground lens. In cases where the background source intensity varies, such as an active galactic nucleus (AGN) or a supernova (SN), the variability pattern manifests in each of the multiple images and is delayed in time due to the different light paths of the different images. The time delay of image \(i\), relative to the case of no lensing, is

$$ t(\boldsymbol{\theta}_{i};\boldsymbol{\beta}) = \frac{D_{\Delta \mathrm{t}}}{c} \phi(\boldsymbol{\theta}_{i};\boldsymbol{\beta}), $$
(1)

up to an additive constant,Footnote 1 where \(\boldsymbol{\theta}_{i}\) is the position of the lensed image \(i\), \(\boldsymbol{\beta}\) is the position of the source, \(D_{\Delta \mathrm{t}}\) is the so-called “time-delay distance”, \(c\) is the speed of light, and \(\phi\) is the “Fermat potential” related to the lens mass distribution. The time-delay distance for a lens at redshift \(z_{\mathrm{d}}\) and a source at redshift \(z_{\mathrm{s}}\) is

$$ D_{\Delta\mathrm{t}}= (1+z_{\mathrm{d}})\frac{D_{\mathrm{d}}D_{\mathrm{s}}}{D_{\mathrm{ds}}}, $$
(2)

where \(D_{\mathrm{d}}\) is the angular diameter distance to the lens, \(D_{\mathrm{s}}\) is the angular diameter distance to the source, and \(D_{\mathrm{ds}}\) is the angular diameter distance between the lens and the source. In the \(\Lambda\)CDM cosmology with density parameters \(\varOmega_{\mathrm{m}}\) for matter, \(\varOmega_{\mathrm{k}}\) for spatial curvature, and \(\varOmega_{\varLambda }\) for dark energy described by the cosmological constant \(\varLambda\), the angular diameter distance between two redshifts \(z_{1}\) and \(z_{2}\) is

$$ D(z_{1},z_{2}) = \frac{1}{1+z_{2}}f_{K} \bigl[\chi(z_{1},z_{2})\bigr] $$
(3)

where

$$ \chi(z_{1},z_{2}) = \frac{c}{H_{0}} \int_{z_{1}}^{z_{2}} \mathrm{d}z' \bigl(\varOmega _{\mathrm{m}}\bigl(1+z'\bigr)^{3} + \varOmega_{\mathrm{k}} \bigl(1+z'\bigr)^{2} + \varOmega_{\varLambda} \bigr)^{-1/2}, $$
(4)

and

$$ f_{K}(\chi) = \left \{ \textstyle\begin{array}{l@{\quad}l} K^{-1/2} \sin (K^{1/2}\chi ) & \text{for $K>0$},\\ \chi& \text{for $K=0$}, \\ (-K)^{-1/2}\sinh [(-K)^{1/2}\chi ] & \text{for $K< 0$} , \end{array}\displaystyle \right . $$
(5)

\(K=-\varOmega_{\mathrm{k}}H_{0}^{2}/c^{2}\) is the spatial curvature, and \(H_{0}\) is the Hubble constant.

By monitoring the variability of the multiple images, we can measure the time delay between the two images \(i\) and \(j\):

$$ \Delta t_{ij} = t(\boldsymbol{\theta}_{i}; \boldsymbol{\beta})- t(\boldsymbol{\theta}_{j};\boldsymbol{\beta}) = \frac{D_{\Delta\mathrm{t}}}{c}\Delta\phi_{ij}. $$
(6)

The Fermat potential \(\phi\) can be determined by modeling the lens mass distribution using observations of the lens system such as the observed lensed image positions, shapes and fluxes. Therefore, with \(\Delta t\) measured and \(\Delta\phi\) determined, we can use (6) to infer the value of \(D_{\Delta\mathrm{t}}\), which is inversely proportional to \(H_{0}\) (\(D_{\Delta\mathrm{t}}\propto H_{0}^{-1}\)) through (2) and (3). Being a combination of three angular diameter distances, \(D_{\Delta\mathrm{t}}\) is mainly sensitive to the Hubble constant \(H_{0}\) and weakly depends on other cosmological parameters (e.g., Refsdal 1964; Schneider et al. 2006; Suyu et al. 2010).

One can further measure \(D_{\mathrm{d}}\) from a lens system by measuring the velocity dispersion of the foreground lens, \(\sigma_{\mathrm{v}}\), and combining it with the time delays (Paraficz and Hjorth 2009; Jee et al. 2015). The measurement of \(D_{\mathrm{d}}\) provides additional constraints on cosmological models (Jee et al. 2016).

In order to measure \(D_{\Delta\mathrm{t}}\) and \(D_{\mathrm{d}}\) from a time-delay lens system for cosmography, we need the following

  1. 1.

    spectroscopic redshifts of the lens \(z_{\mathrm{d}}\) and source \(z_{\mathrm{s}}\)

  2. 2.

    time delays between the multiple images

  3. 3.

    lens mass model to determine the Fermat potential

  4. 4.

    lens velocity dispersion, which is not only required for \(D_{\mathrm{d}}\) inference, but also provides additional constraints in breaking lens mass model degeneracies

  5. 5.

    lens environment studies to break lens model degeneracies, such as the mass-sheet degeneracy

In the next sections, we describe the history behind this approach, and detail the advances in recent years in acquiring these ingredients before presenting the latest cosmographic inferences from this approach.

1.2 A Brief History

In his original paper Refsdal (1964) proposed to use gravitationally lensed supernovae to measure the time delays: the light curves associated to each lensed image of a supernova are expected to be seen shifted in time by a value that depends on the potential well of the lensing object and on cosmology. However, due to the shallow limiting magnitude of the telescopes available at the time and due to their restricted field of view, discovering faint and distant supernovae right behind a galaxy or a galaxy cluster was completely out of reach. But Refsdal’s idea came right when quasars were discovered (Schmidt 1963; Hazard et al. 1963). These bright, distant and photometrically variable point sources were coming timely, offering a new opportunity to implement the time-delay method: light curves of lensed quasars are constantly displaying new features that can be used to measure the delay.

With the increasing discovery rate of quasars, the first cases of multiply imaged ones also started to grow. The first lensed quasar, Q 0951+567, was found by Walsh et al. (1979), displaying two lensed images. This was followed by the quadruple PG 1115+080 (Young et al. 1981), and a few years later by the discovery of the “Einstein Cross” (Huchra et al. 1985) and of the “cloverleaf” (Magain et al. 1988). The first time-delay measurement became available only in the late 80s with the optical monitoring of Q 0951+567 by Vanderriest et al. (1989) and the radio monitoring of the same object by Lehar et al. (1992). Unfortunately, given the two data sets and methods of analysis to measure the delay, the radio and optical values of the time delay remained in disagreement until new optical data came (e.g. Kundić et al. 1997; Oscoz et al. 1997), allowing to confirm and improve the optical delay of Vanderriest et al. (1989). Further improvement was possible with the “round-the-clock” monitoring of Colley et al. (2003), leading to a time-delay determination to a fraction of a day.

Because of the time and effort it took to solve the “Q0957 controversy”, astrophysicists quickly limited their interest in the time-delay method as a cosmological probe. But at least two sets of impressive monitoring data revived the field. The first one is the optical monitoring of the quadruple quasar PG 1115+080 by Schechter et al. (1997), providing time delays to 14% and the second is the radio monitoring, with the VLA, of the quadruple radio source B1608+656 (Fassnacht et al. 1999), reaching similar accuracy. As the uncertainty on the time delay propagates linearly in the error budget on \(H_{0}^{-1}\) this is still not sufficient for precision cosmology to a few percents.

In a large part thanks to the results obtained for PG 1115+080 and B1608+656 several monitoring campaigns were put in place by independent teams in the late 90s and early 2000. Because lensed quasars were more often discovered in the optical and because their variability is faster at these wavelengths due to the smaller source size than in the radio, these new monitoring campaigns took place in the optical. The teams involved used 1 m class telescopes to measure delays to typical accuracies of 10% or slightly better, i.e. a 30% improvement over previous measurements but still too large for cosmological purposes.

Some of the most impressive results were obtained in the years 2000 with the 2.6 m Nordic Optical Telescope (NOT) for FBQ 0951+2635 (Jakobsson et al. 2005), SBS 1520+530 (Burud et al. 2002b), RX J0911+0551 (Hjorth et al. 2002), B1600+434 (Burud et al. 2000), at ESO with the 1.54 m Danish telescope for HE 2149-2745 (Burud et al. 2002a) and at Wise observatory with the 1 m telescope for HE 1104-1805 (Ofek and Maoz 2003). With these new observations and studies it was shown that “mass production” of time delays was possible and not restricted to a few lenses for which the observational situation was particularly favorable. However, the temporal sampling adopted for the observations and the limited signal-to-noise per observing epoch was still limiting the accuracy on the time-delay measurement to 10% in most cases hence limiting \(H_{0}^{-1}\) measurements with individual lenses to this precision.

Fifty years after Refsdal (1964)’s foresight on lensed SN, the first strongly lensed SN was discovered by Kelly et al. (2015) serendipitously in the galaxy cluster MACS J1149.5+2223 with Hubble Space Telescope (HST) imaging. This core-collapse SN was named “SN Refsdal”, and showed 4 multiple images at detection. The predictions (Treu et al. 2016; Grillo et al. 2016; Kawamata et al. 2016; Jauzac et al. 2016) and subsequent detection (Kelly et al. 2016a) of the re-occurrence of the next (time-delayed) image of SN Refsdal provided a true blind test of our understanding of lensing theory and mass modeling. It is reassuring that some teams predicted accurately the re-occurrence (Grillo et al. 2016; Kawamata et al. 2016), and the modeling software GleeFootnote 2 used by Grillo et al. (2016) was also the software employed for cosmography with lensed quasars (e.g., Suyu et al. 2013, 2014; Wong et al. 2017).

In the fall of 2016, the first spatially-resolved multiply-imaged Type Ia SN, iPTF16geu, was discovered by Goobar (2017) in the intermediate Palomar Transient Factory survey. More et al. (2017) independently modeled a single-epoch HST image of the system, finding short model-predicted time delays (\(<1\) day) between the multiple images. Furthermore, More et al. (2017) found anomalous flux ratios of the SN compared to the smooth model prediction, indicating possible microlensing effects, although Yahalomi et al. (2017) showed that microlensing is unlikely to be the sole cause of the anomalous flux ratios.

Both SN Refsdal and iPTF16geu have been monitored for time-delay measurements (Rodney et al. 2016; Goobar 2017), opening a new window to study cosmology with strongly-lensed SN. Recently Grillo et al. (2018) estimated the time delay of the image SX of SN Refsdal based on the detection presented in Kelly et al. (2016b) (image SX has the longest delay compared to other images of SN Refsdal, so image SX will ultimately provide the most precise time-delay measurement for cosmography from this system), and modeled the mass distribution of the galaxy cluster MACS J1149.5+2223 to infer \(H_{0}\). This feasibility study shows that \(H_{0}\) can be measured with \(\sim7\%\) statistical uncertainty, despite the complexity in modeling the cluster lens mass distribution. The full analysis including various systematic uncertainties is forthcoming, after the time delays are measured from the monitoring data. As lensed SNe are only being discovered/observed recently and their utility as a time-delay cosmological probe is just starting, we focus in the rest of the review on the more common lensed quasars as time-delay lenses, but there is a wealth of information to gather with lensed supernovae, both on a cosmological and stellar physics point of view.

1.3 Recent Advances

A 10% error bar on the time delay translates to a similar error on \(H_{0}\). Improving this further and obtaining \(H_{0}\) measurements competitive with other techniques, i.e. of 3–4% currently and 1–2% in the near future, requires several ingredients. Time-delay measurements of individual lenses must reach 5% at most and many more systems must be measured. With such precision on individual time delays, and under the assumption that all sources of systematic errors are controlled or negligible, measuring \(H_{0}\) to 2% is possible with only a handful of lenses and a 1% measurement is not out of reach with of the order of 50 lenses! However, the lens model for the main lensing galaxy must be well constrained and their systematics evaluated and/or mitigated. Third, the contribution of all objects on the line of sight to the overall potential well must be accounted for. Excellent progress has been made on all three fronts in the recent years and there is still room for further (realistic) improvement.

1.3.1 Time Delays

Measuring time delays is hard, but feasible provided telescope time can be guaranteed over long periods of time with stable instrumentation. The main limiting factors are astrophysical, observational or instrumental.

Astrophysical factors include the characteristics of the intrinsic variability of the source quasar and extrinsic variability of its lensed images due to microlensing by stars in the main lensing galaxy. If the source quasar is highly variable intrinsically, both in amplitude and temporal frequency, the time delay is easier to measure. If microlensing variations are strong and/or comparable in frequency to the intrinsic variations then the time-delay value can be degenerate with the properties of the microlensing variations. In some extreme cases microlensing dominates the observed photometric variations to the point the time delay is hardly measurable (e.g. Morgan et al. 2012) even though microlensing itself can be used to infer details properties of the lensed source on micro-arcsec scales, i.e. out of reach of any current and future instrumentation.

The observations needed to measure time delays must be adapted to the intrinsic and extrinsic variations of the selected quasars and of course to the expected time delay for each target. Not surprisingly the shorter the time delay, the finer the temporal sampling is needed. The position of the target on the sky also influences the results: equatorial targets will hardly be visible more than 6 months in a row, but can be followed both from the North and the South, while circumpolar targets can be seen up to 8–9 consecutive months, hence allowing to measure longer time delays and minimizing the effect of the non-visibility gaps between observing seasons.

Finally, instrumental factors strongly impact the results. A key factor with current monitoring campaigns is the availability of telescopes on good sites and with stable instrumentation, i.e. if possible at all with no camera or filter change and with regular temporal sampling. Long gaps in light curves seriously affect the time-delay values in the sense that they make it more difficult to disentangle the microlensing variations from the quasar intrinsic variations. And since angular separation between the lensed images are small, fairly good seeing is required, typically below 1.2 arcsec even though techniques like image deconvolution (e.g. Magain et al. 1998; Cantale et al. 2016) and used, e.g. by the COSMOGRAIL collaboration (see below) help dealing with data sets spanning a broad range of seeing values.

Once long and well-sampled photometric light curves are available, the time delay must be measured. At first glance, this step may be seen as an easy one. However, one has to deal with irregular temporal sampling, gaps in the light curves, variable signal-to-noise and seeing, atmospheric effects (night-to-night calibration) and with microlensing. A number of numerical methods have been devised over the years to carry out the measurement, with different levels of accuracy and precision. They split in different broad categories. Some attempt to cross-correlate the light curves without trying to model/subtract the microlensing variations. Others involve an analytical representation of the intrinsic quasar variations and of the microlensing or involve e.g. Gaussian processes to mimic the microlensing erratic variations. Recent work in this area has been developed in Tewes et al. (2013a), Hojjati et al. (2013), Hojjati and Linder (2014), Rathna Kumar et al. (2015).

These methods (and others, so far unpublished) were tested in an objective way using simulated light curves proposed to the community in the context of the “Time Delay Challenge” (TDC; Dobler et al. 2015). In the TDC, thousands of light curves of different lengths, sampling rate, signal-to-noise, and visibility gaps are proposed to the participants. Once all participants have submitted their time-delay evaluations to the challenge organizers, the time-delay values are revealed and the results are compared objectively using a metrics common to all participating methods. This metrics was known before the start of the challenge. The results of this TDC are summarized in Liao et al. (2015) as well as in individual papers (e.g. Bonvin et al. 2016). A general conclusion of the TDC was that with current lens monitoring data, curve-shifting technique so far in use are sufficient to extract precise and accurate time delays, given the temporal sampling and signal-to-noise of the data.

Following the encouraging results obtained at NOT, ESO and Wise, long-term monitoring campaigns were organized to measure time delays in a systematic way. Two main teams invested effort in this research: the OSU group lead by C.S. Kochanek (OSU, USA) and the COSMOGRAIL (COSmological MOnitoring of GRAvItational Lenses) program led by F. Courbin and G. Meylan at EPFL, Switzerland (e.g. Courbin et al. 2005; Eigenbrod et al. 2005). Both monitoring programs involve 1-m class telescopes with a temporal sampling of 2 to 3 observing epochs per week and a signal-to-noise of typically 100 per quasar image and per epoch. Both projects started in 2004 and are so far the main (but not only) source of time-delay measurements. Early results from the OSU program were obtained in 2006 for HE 0435-1223 (Kochanek et al. 2006) while COSMOGRAIL delivered its first results starting in 2007 for SDSS J1650+4251 (Vuissoz et al. 2007), WFI J2033-4723 (Vuissoz et al. 2008) and HE 0435-1223 (Courbin et al. 2011a). More recent time-delay measurements from COSMOGRAIL were obtained for RX J1131-1231 (Tewes et al. 2013b), HE 0435-1223 (Bonvin et al. 2017) as well as SDSS J1206+4332 and HS 2209+1914 (Eulaers et al. 2013) and SDSS J1001+5027 (Rathna Kumar et al. 2013). An example of COSMOGRAIL light curve is given in Fig. 1. These data are analysed jointly with the H0LiCOW program (see Sect. 1.4).

Fig. 1
figure 1

From top to bottom: example of light curves produced and exploited by the COSMOGRAIL and H0LiCOW programs, here for the quadruply imaged quasar HE 0435-1223. The original light curves are shown on the top. The second panel shows spline fitting to the data including the intrinsic and extrinsic quasar variations. Crucially, long light curves are needed to extract properly the extrinsic variation (microlensing). The residuals to the fit and the journal of the observations with 5 instruments are displayed in the two lower panels (reproduced with permission from Bonvin et al. 2017)

Full size image

Other recent studies for specific objects include Giannini et al. (2017) for WFI 2033-4723 and HE 0047-1756, and Shalyapin and Goicoechea (2017) reporting a delay for SDSS J1515+1511. Hainline et al. (2013) measure a tentative time delay for SBS 0909+532, although the curves suffer from strong microlensing. Finally, two (long) time delays have been estimated for two quasars lensed by a galaxy group/cluster: SDSS J1029+2623 (Fohlmeister et al. 2013) and SDSSJ1004+4112 (Fohlmeister et al. 2008). These may not be ideal for cosmological applications though, as a complex lens model for a cluster is harder to constrain than models at galaxy-scale, unless the cluster has additional constraints coming from multiple background sources at different redshifts being strongly lensed.

With the observing cadence of 1 point every 3–4 nights and an SNR of 100 per epoch, the current data can catch quasar variations of the order of 0.1 mag in amplitude, arising on time-scales of months. These time scales are unfortunately of the same order of magnitude as the microlensing variations (see 2nd panel of Fig. 1) making it hard to disentangle between intrinsic and extrinsic variations. For this reason, lensed quasars must be monitored for extended periods of time, typically a decade, to infer any reliable time-delay measurement.

Going beyond current monitoring campaigns like COSMOGRAIL and others is possible, but measuring massively time delays for dozens of lensed quasars requires a new observing strategy to minimize the effect of microlensing and to measure time delays in individual objects in less than 10 years! One solution is to observe at high cadence (1 day−1) and high SNR, of the order of 1000. In this way, very small quasar variations can be caught, on time scales much shorter than microlensing hence allowing the separation of the two signals in frequency. We show with 1000 mock light curves that mimic those of HE 0425-1223 (Fig. 1) that time delays can be measured precisely in only 1 observing season. In doing the simulation, we include realistic microlensing and fast quasar variations with a few mmag amplitude. We then run PyCS, the COSMOGRAIL curve-shifting algorithm (Tewes et al. 2013a; Bonvin et al. 2016), to recover the fiducial time delay of 14 days. Figure 2 summarizes our results and provides the length of the monitoring campaign needed to reach a desired relative precision on the time delay, assuming daily observations and an SNR of 1000 per epoch. It appears that a typical 2% precision is achievable in 1 observing season with a 10% failure rate. Doing two seasons allows one to reach the percent precision and a failure rate below 3%. At the time this paper is being written, an intensive lens monitoring program has been started at the 2.2 m MPI telescope at La Silla Observatory, with the above characteristics. Three targets have been observed for 1 semester and time delays have been measured to a few percents for all three! The first of these is presented in Courbin et al. (2017) and features a 1.8% measurement of one of the delays in the newly discovered quadruple lens DES J0408-5354 (Lin et al. 2017; Agnello et al. 2017).

Fig. 2
figure 2

Expected relative precision on a time delay measurement as a function of the length of the campaign. High-cadence (1 day−1) monitoring is assumed and the fiducial delay in this simulations mimics the longer delay of HE 0435-1223, i.e. 14 days. Clearly, 2% precision can be reached in only 1 observing season. The color code shows the catastrophic failure rate, i.e. the probability of getting a measurement wrong by more than 5%. This probability is about 10% for a 1-season campaign and 3% for a 2-season campaign. (Courtesy: Vivien Bonvin)

Full size image

Finally, we note that although quasars have been used so far to implement the time delay method, the original idea of Refsdal was to use lensed supernovae. The first systems have finally be found, as mentioned in Sect. 1.2: SN Refsdal (e.g. Kelly et al. 2015, 2016a; Rodney et al. 2016) and iPTF16geu (e.g. Goobar 2017; More et al. 2017). With the advent of large imaging surveys such as the Zwicky Transient Facility and the Large Synoptic Survey Telescope, prospects to find lensed supernovae are excellent (e.g. Goldstein and Nugent 2017). As supernovae have known light curves, one can measure the time delay by fitting a template to the observed light curves in the lensed images, hence giving much more constraining power than quasars whose photometric variations are close to a random walk. In addition, if the lensed supernova is a Type Ia, then two cosmological probes are available in the same object, hence provide a fantastic cross-check of otherwise completely different methods: standard candles and a geometrical method, provided microlensing effects could be corrected (Dobler and Keeton 2006; Yahalomi et al. 2017; Goldstein et al. 2018).

For all the above reasons, we believe that the future of time-delay cosmography resides in lensed supernovae and in high-cadence monitoring of lensed quasars. However, Tie and Kochanek (2018) recently pointed out that microlensing by stars in the lensing galaxy can introduce a bias in the time-delay measurements. This is due to a combination of differential magnification of different parts of the source and the source geometry itself. The net result is that cosmological time delays can be affected both in a statistical and a systematic way by microlensing. The effect is absolute, with biases on time delays of the order of a day for lensed quasars and tenths of a day for lensed supernovae. Mitigation strategies have been successfully devised (Chen et al. 2018) for lensed quasars and the effect seems less pronounced in lensed supernovae than in lensed quasars (Goldstein et al. 2018; Foxley-Marrable et al. 2018; Bonvin et al. 2018), but clearly this new effect must be accounted for in any future work in the field.

1.3.2 Lens Mass Modeling

To convert the time delays into a measurement of the time-delay distance via (1), one needs to determine the Fermat potential \(\phi(\boldsymbol{\theta}_{i};\boldsymbol{\beta})\), which depends both on the mass distribution of the main strong-lens galaxy and the mass distribution of other galaxies along the line of sight.

The mass distribution of the main strong-lens galaxy can be modeled using either simply parametrized profiles (e.g., Kormann et al. 1994; Barkana 1998; Golse and Kneib 2002) or grid-based approaches (e.g., Williams and Saha 2000; Blandford et al. 2001; Suyu et al. 2009; Vegetti and Koopmans 2009). The total mass distribution of galaxies appear to be well described by profiles close to isothermal (e.g., Koopmans et al. 2006; Barnabè et al. 2011; Cappellari et al. 2015), even though neither the baryons nor the dark matter distribution follow isothermal profiles. Even in the complex case of the gravitational lens B1608+656 with two interacting lens galaxies, simply parametrized profiles provide a remarkably good description of the galaxies when compared to the pixelated lens potential reconstruction (Suyu et al. 2009). Therefore, most of the current mass modeling for time-delay cosmography use simply parametrized profiles, either for the total mass distribution (e.g., Koopmans et al. 2003; Fadely et al. 2010; Suyu et al. 2010, 2013; Birrer et al. 2015b) or for separate components of baryons and dark matter (e.g., Courbin et al. 2011b; Schneider and Sluse 2013; Suyu et al. 2014; Wong et al. 2017).

The source (quasar) properties need to be modeled simultaneously with the lens mass distribution to predict the observables. In particular, source position and intensity are needed to predict the positions, fluxes and time delays of the lensed quasar images, whereas the source surface brightness distribution (of the quasar host galaxy) is needed to predict the lensed arcs. These observables (image positions, fluxes and delays of the multiple quasar images, and lensed arcs) are then used to constrain the parameters of the lens mass model and the source. Several softwares are available publicly for modeling lens systems, including Gravlens (Keeton 2001), lenstool (Jullo et al. 2007), glafic (Oguri 2010) and Lensview (Wayth and Webster 2006).

Observed quasar image positions, fluxes and delays provide around a dozen of constraints for quads (four-image systems) and even fewer constraints for doubles (two-image systems). Thus lens mass models using only these quasar observables are often not precisely constrained. In particular, the radial profile slope of the lens galaxy is strongly degenerate with \(D_{\Delta\mathrm{t}}\) (e.g., Wucknitz 2002; Suyu 2012). The time delays depend primarily on the average surface mass density between the multiple images, and thus provide information on the radial profile slope (Kochanek 2002). Nevertheless, even with multiple time delays from quad systems, it is difficult to infer the slope precisely to better than \(\sim10\%\) precision.Footnote 3 While mass distribution of massive early-type galaxies, which are the majority of lens galaxies, are close to being isothermal, there is an intrinsic scatter in the slope of about \(\sim15\%\)3 (Koopmans et al. 2006; Barnabè et al. 2011). For precise and accurate \(D_{\Delta\mathrm{t}}\) measurement of a lens system, it is important to measure directly, at the few percent level, the radial profile slope of the lens galaxy near the lensed images of the quasars. This requires more observations of the lens system, beyond just the multiple point images of lensed quasars.

Over the past decade, multiple methods have been developed to make use of the lensed arcs (lensed host galaxies of the quasars) to constrain the lens mass distribution. The source intensity distribution can be described by simply parametrized profiles, such as Gaussians or Sersic (e.g., Brewer and Lewis 2008; Oguri 2010; Marshall et al. 2007; Oldham et al. 2017), or on a grid of pixels, either regular (e.g., Wallington et al. 1996; Warren and Dye 2003; Koopmans 2005; Suyu et al. 2006) or adaptive (e.g., Dye and Warren 2005; Vegetti and Koopmans 2009; Tagore and Keeton 2014; Nightingale and Dye 2015), or based on basis functions (e.g., Birrer et al. 2015a, Joseph et al. in prep.). These lensed arcs, when imaged with HST or ground-based telescopes assisted with adaptive optics, contain thousands of intensity pixels and thus allow the measurement of the radial profile slope of the lens galaxies with a precision of a few percent (e.g., Dye and Warren 2005; Suyu 2012; Chen et al. 2016), that are required for cosmography. In Fig. 3, we show an example of the mass modeling using the full surface brightness distributions of quasar host galaxy.

Fig. 3
figure 3

Illustration of lens mass modeling of the gravitational lens RXJ1131-1231. Top left is the observed HST image. Top middle panel is the modeled surface brightness of the lens system, which is composed of three components shown in the second row: lensed AGN images (left), lensed AGN host galaxy (middle), and foreground lens galaxies (right). The bottom row shows that a mass model is required together with the AGN source position and AGN host galaxy surface brightness, to model the lensed AGN and lensed AGN host images. See the text and Suyu et al. (2013, 2014) for more details

Full size image

Once a model of the surface mass density \(\kappa\) is obtained, lens theory states that the following family of models \(\kappa_{\lambda}\) fits equally well to the observed lensing data:

$$ \kappa_{\lambda} = \lambda+ (1-\lambda) \kappa, $$
(7)

where \(\lambda\) is a constant. This transformation is analogous to adding a constant mass sheet \(\lambda\) in convergence, and rescaling the mass distribution of the strong lens (to keep the same mass within the Einstein radius); it is therefore called the “mass-sheet degeneracy” (Falco et al. 1985; Schneider and Sluse 2013, 2014; Schneider 2014). Such a transformation corresponds to a rescaling of the background source coordinate by a factor \((1-\lambda)\), leaving the observed image morphology and brightness invariant. Furthermore, the Fermat potential transforms as

$$ \phi_{\lambda}(\boldsymbol{\theta};\boldsymbol{\beta}) = (1- \lambda ) \phi(\boldsymbol{\theta}; \boldsymbol{\beta}) + \text{constant that depends only on }\boldsymbol{\beta}. $$
(8)

Therefore, for given observed time delays \(\Delta t_{ij}\), (6) and (8) imply that the time-delay distance \(D_{\Delta\mathrm{t}}\) would be scaled by \((1-\lambda)\). The mass-sheet degeneracy has thus a direct impact on cosmography in measuring \(D_{\Delta\mathrm{t}}\).

While \(\lambda\) so far is simply a constant in this mathematical transformation (7), we can identify it with the physical external convergence, \(\kappa_{\mathrm{ext}}\), due to mass structures along the sight line to the lens system. By gathering additional data sets beyond that of the strong lens system, we can infer \(\kappa_{\mathrm{ext}}\) and thus measure \(D_{\Delta\mathrm{t}}\). Two practical ways to break the mass-sheet degeneracy are (1) studies of the lens environment, to estimate \(\kappa_{\mathrm{ext}}\) based on the density of galaxies in the strong-lens line of sight in comparison to random lines of sight (e.g., Momcheva et al. 2006; Fassnacht et al. 2006; Hilbert et al. 2007; Suyu et al. 2010; Greene et al. 2013; Collett et al. 2013; Rusu et al. 2017; Sluse et al. 2017; McCully et al. 2017), and (2) stellar kinematics of the strong lens galaxy, which provides an independent mass measurement within the effective radius to complement the lensing mass enclosed within the Einstein radius (e.g., Grogin and Narayan 1996; Koopmans and Treu 2002; Barnabè et al. 2009; Suyu et al. 2014). The time-delay distance can then be inferred via

$$ D_{\Delta\mathrm{t}}= \frac{D_{\Delta\mathrm{t}}^{\mathrm{model}}}{(1-\kappa_{\mathrm{ext}})}, $$
(9)

where \(D_{\Delta\mathrm{t}}^{\mathrm{model}}\) is the modeled time-delay distance without accounting for the presence of \(\kappa_{\mathrm{ext}}\). In practice, both lens environment characterisations and stellar kinematics are employed to infer \(D_{\Delta\mathrm{t}}\) for cosmography (e.g., Suyu et al. 2010, 2013; Birrer et al. 2015b; Wong et al. 2017). The stellar kinematic data further help constrain the strong-lens mass profile (e.g., Suyu et al. 2014).

Lens systems that have massive galaxies close in projection (within \(\sim10''\)) to the strong lens, but at a different redshift from the strong lens, will need to be accounted for explicitly in the strong lens model. In such cases, multi-lens plane modeling is needed (e.g., Blandford and Narayan 1986; Schneider et al. 1992; Gavazzi et al. 2008; Wong et al. 2017, Suyu et al., in preparation), but (1) for single-lens plane is then not directly valid. In particular, there is not a single time-delay distance, but rather there are multiple combination of distances between the multiple planes. Nonetheless, for some cases, one could obtain an effective time-delay distance as if it were a single-lens plane system (see, e.g., Wong et al. 2017, for details).

As noted in Sect. 1.1, with stellar kinematic and time-delay data, we can infer the angular diameter distance to the lens, \(D_{\mathrm{d}}\), in addition to \(D_{\Delta\mathrm{t}}\) (Paraficz and Hjorth 2009; Jee et al. 2015; Birrer et al. 2015b; Shajib et al. 2017). Measurement of \(D_{\mathrm{d}}\) is often more sensitive to the dark energy parameters (for typical lens redshifts \(\lesssim 1\), see e.g., Fig. 2 of Jee et al. 2016), and can also be used as an inverse distance ladder to infer \(H_{0}\) (Jee et al., submitted). Currently, the precision in \(D_{\mathrm{d}}\) is limited by the uncertainty in the single-aperture averaged velocity dispersion measurement and the unknown anisotropy of stellar orbits (Jee et al. 2015). Nonetheless, we anticipate that spatially resolved kinematic data will help to constrain more precisely \(D_{\mathrm{d}}\).

We have focussed here on the advances in getting \(D_{\Delta\mathrm{t}}\) and \(D_{\mathrm{d}}\) from individual lenses with exquisite follow-up data to control the systematic uncertainties. Alternatively, one could analyse a sample of lenses and constrain a global \(H_{0}\) parameter that is common to all the lenses (e.g., Saha et al. 2006; Oguri 2007; Sereno and Paraficz 2014), assuming that the systematic effects for the lenses average out. For small samples, this assumption might not be valid. Nonetheless, in the future where thousands of lensed quasars are expected (Oguri and Marshall 2010) but most of which will not have exquisite follow-up observations, this large sample of lenses could provide information on the population of lens galaxies as a whole for cosmography (P. J. Marshall & A. Sonnenfeld, priv. comm.). We therefore advocate getting exquisite follow-up observations of a sample of \(\sim40\) lenses to reach an \(H_{0}\) measurement with 1% uncertainty (Jee et al. 2016; Shajib et al. 2017), with the other lenses providing information on the profiles of galaxies to use in the mass modeling.

1.4 Distance Measurements and Cosmological Inference

There are so far only a few lensed quasars for which all required data exist to do time-delay cosmography, i.e., with time-delay measurements to a few percent, deep HST images showing the lensed image of the host galaxy, deep spectra of the lens to measure the velocity dispersion, and multiband data to map the line of sight contribution to the lensing potential.

Some of the best time-delay measurements available to date include the radio time delay for B1608+656 (Fassnacht et al. 1999, 2002) and the two optical measurements of COSMOGRAIL for RX J1131-1231 (Tewes et al. 2013b), and HE 0435-1223 (Bonvin et al. 2017). These 3 quadruply imaged quasars, for which all the ancillary imaging and spectroscopic data are also available, gave birth to the H0LiCOW program (Suyu et al. 2017), which capitalizes on more than a decade of COSMOGRAIL monitoring as its name reflects: H0 Lenses in COMOGRAIL’s Wellspring. With the precise time-delay measurements of COSMOGRAIL, H0LiCOW addresses what has been so far limiting the effectiveness of strong lensing in delivering reliable \(H_{0}\) measurements: the different systematics at work at each step leading to a value for the Hubble constant.

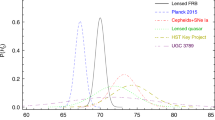
The most recent work by H0LiCOW is summarized in the left panel of Fig. 4 (Bonvin et al. 2017), based on state-of-the-art lens mass modeling and characterisations of mass structures along the line of sight (Sluse et al. 2017; Rusu et al. 2017; Wong et al. 2017; Tihhonova et al. 2017). In the right panel of Fig. 4, we compare the value of \(H_{0}\) from H0LiCOW with other fully independent cosmological probes such as Type Ia supernovae, Cepheids, and CMB(+BAO) for a \(\Lambda\)CDM cosmology. With the current error bars claimed by each probe there exist a tension between local measurements of \(H_{0}\) (e.g., Freedman et al. 2012; Efstathiou 2014; Riess et al. 2018) and the value by the Planck team. When completed, H0LiCOW will feature 5 lenses, with an accuracy on \(H_{0}\) of the order of 3% (Suyu et al. 2017), but reaching close to 1% precision is possible. This will be enabled by working on several fronts simultaneously, by finding more lenses, measuring up to 50 new time delays, and refining the lens modeling tools to mitigate degeneracies between model parameters. Chapter 8 on “Towards a self-consistent astronomical distance scale” provides more details about the (expected) future of quasar time delay cosmography.

Fig. 4
figure 4

Left: Latest \(H_{0}\) measurement from quasar time delays from H0LiCOW and COSMOGRAIL for 3 lenses and for their combination in a \(\Lambda\)CDM Universe (reproduced with permission from Bonvin et al. 2017). Right: comparison between time delay \(H_{0}\) measurements and other methods such as CMB shown in yellow (Planck; Ade et al. 2016) and gray (WMAP; Bennett et al. 2013) or local distance estimators such as Cepheids (green; Freedman et al. 2012) and Type Ia supernovae (blue; Riess et al. 2016b). Quasar time delays are so far in agreement with local estimators but higher than Planck. Measurements for 40–50 new time delays will allow one to confirm (or not) the current tension with Planck to more than \(5\sigma\)

Full size image

2 Baryon Acoustic Oscillations

2.1 BAO as a Standard Ruler

The universe has been expanding, and thus the universe in the earlier stage was much smaller, denser and hotter than today. In such an early universe, electrons interacted with photons via Compton scattering and with protons via Coulomb scattering. Thus, the three components acted as a mixed fluid (Peebles and Yu 1970). They were in the equilibrium state due to the gravity of protons and pressure of photons, and oscillated as sound modes. These oscillations are called baryon acoustic oscillations (BAO) (see Bassett and Hlozek (2010) and Weinberg et al. (2013) for a comprehensive review). It moved with the speed of sound \(c_{\mathrm{s}} = c\sqrt{\frac {1}{3(1+R)}}\), where the ratio of photon density (\(\rho_{\mathrm{r}}\)) to baryon density (\(\rho_{\mathrm{b}}\)) is defined as \(1/R=4\rho_{\mathrm{r}} / 3\rho_{\mathrm{b}}\).

At recombination (\(z\sim1100\)), photons decouple from the baryons and start to free stream. We observe the photons as a map of cosmic microwave background (CMB). The left panel of Fig. 5 shows the angular power spectrum of the latest data of the CMB anisotropy probe, Planck satellite (Adam et al. 2016). One can see a clear oscillation feature in the power spectrum, which is characterized by the sound horizon scale at recombination, expressed as (Hu and Sugiyama 1996; Eisenstein and Hu 1998)

$$ r_{\mathrm{d}}= \int^{\infty}_{z_{*}} \frac{c_{\mathrm{s}}(z)}{H(z)} dz, $$
(10)

where \(z_{*}\) is the redshift at recombination. \(H(z)\) is the Hubble parameter,

$$ H(z)= H_{0} \bigl[ \varOmega_{\mathrm{m}} (1+z)^{3} + \varOmega_{\mathrm{r}}(1+z)^{4} +\varOmega_{\mathrm{DE}}(1+z)^{1+w} \bigr]^{1/2}, $$
(11)

where \(\varOmega_{\mathrm{m}}\) (previously introduced in Sect. 1.1), \(\varOmega_{\mathrm{r}}\) and \(\varOmega_{\mathrm{DE}}\) are the matter, radiation and dark energy density parameters, respectively, and \(w\) is the equation-of-state parameter of dark energy and the simplest candidate for dark energy, the cosmological constant \(\varLambda\), gives \(w=-1\). With standard cosmological models, \(r_{\mathrm{d}} \simeq150\) Mpc. From the Planck observation, it is constrained to \(r_{\mathrm{d}}=144.61 \pm 0.49\) Mpc.

Fig. 5
figure 5

(Left) Angular power spectrum of CMB anisotropies measured from the latest Planck satellite data (© ESA and the Planck Collaboration). The wiggles seen in the spectrum are the feature of BAO, and the oscillation scale corresponds to the sound horizon at recombination. The best-fitting \(\Lambda\)CDM theoretical spectrum is plotted as the solid line in the upper panel. Residuals of the measurement with respect to this model are shown in the lower panel. (Right) BAO feature detected in large-scale correlation function of the galaxy distribution of the SDSS (reproduced with permission from Eisenstein et al. 2005). The bump seen at \(105h^{-1}~\text{Mpc}~(\simeq150~\text{Mpc})\) corresponds to the sound horizon scale at recombination. The solid lines are the theoretical models with \(\varOmega_{\mathrm{m}}h^{2}=0.12\) (top line), 0.13 (second line) and 0.14 (third line). The bottom line shows a pure CDM model with \(\varOmega_{\mathrm{m}}h^{2}=0.105\), which lacks the acoustic peak. The inset zooms into the BAO peak position

Full size image

2.2 Probing BAO in Galaxy Distribution

After the recombination, motion of the baryons becomes non-relativistic. The perturbation of baryons then starts to grow at their locations and interact with the perturbation of dark matter. Thus the baryon acoustic feature should be imprinted onto the late-time large-scale structure of the Universe. Theoretically it is predicted to produce the overdensity at the sound horizon scale, \(\sim150\) Mpc. It is, however, observationally not easy because the observation of BAO signal requires the number of tracers of matter overdensity field to be large enough at the scale to overcome the cosmic variance.

In 2005, detection of the BAO was reported almost simultaneously by two independent groups using the Sloan Digital Sky Survey (SDSS) (Eisenstein et al. 2005) and the 2dF Galaxy Redshift Survey (2dFGRS) (Cole et al. 2005). The right panel of Fig. 5 shows the two-point correlation function obtained from the SDSS galaxy sample by Eisenstein et al. (2005). The 2-point correlation function \(\xi(s)\) is defined as an excess of the probability that one can find pairs of galaxies at a given scale \(s\) from the case of a random distribution. Thus the scales where \(\xi>0\) and \(\xi<0\) correspond to the statistically overdense and underdense regions respectively. The bump seen around \(s\simeq105h^{-1}~\text{Mpc}\) (\(\simeq150\) Mpc) is the feature of BAO, and the scale of the bump corresponds to the sound horizon scale at recombination. The inset of the right panel of Fig. 5 zooms into the feature. Unlike observations of the CMB, galaxy redshift surveys are the observation of 3 dimensional space. The peak scale of BAO should be isotropic because the scale corresponds to the sound horizon at recombination. On the other hand, the BAO scale along the line of sight depends on \(H^{-1}(z)\) while the BAO scale perpendicular to the line of sight depends on the comoving angular diameter distance \(D_{\mathrm{M}}=(1+z)D_{\mathrm{A}}(z)\), where \(D_{\mathrm{A}}(z)\) is expressed in flat universe as (3) with \(z_{1}=0\), or,

$$ D_{\mathrm{A}}(z)=\frac{1}{1+z} \int^{z}_{0} \frac{c\mathrm{d}z'}{H(z')}. $$
(12)

Thus, the scale of BAO probed by a galaxy correlation function has a cosmology dependence of

$$ D_{\mathrm{V}}(z)= \bigl[ (1+z)D_{\mathrm{A}}(z) \bigr]^{2/3} \biggl[\frac {cz}{H(z)} \biggr]^{1/3}. $$
(13)

The BAO scale probed by the CMB anisotropy at high redshift and the galaxy distribution at low redshift should be the same. Moreover, the power spectrum with the acoustic features has been precisely determined for the CMB and interpreted using linear cosmological perturbation theory (see the left panel of Fig. 5). Thus the detection of BAO in the galaxy distribution enables us to constrain \(D_{\mathrm{V}}\), and hence the geometric quantities such as \(H_{0}\), \(w\), and \(\varOmega_{\mathrm{DE}}\) in (11) (Eisenstein et al. 2005).

2.3 Anisotropy of BAO and Alcock-Paczynski

The method presented above does not use all of the information encoded in BAO. To maximally extract the cosmological information, we need to measure the correlation function as functions of separations of galaxy pairs perpendicular (\(s_{\perp}\)) and parallel (\(s_{\parallel}\)) to the line of sight, \(\xi(s_{\perp},s_{\parallel})\), where \(s=\sqrt{s_{\perp}^{2}+s_{\parallel}^{2}}\). In this way, in principle we can constrain \(D_{\mathrm{A}}(z)\) and \(H(z)\) using the transverse and radial BAO measurements, respectively. Given the cosmological dependence of angular and radial distances ((11) and (12)), the shape of the BAO peak is distorted if the wrong cosmology is assumed. This effect was first pointed out by Alcock and Paczynski (1979, AP).

In fact, the AP test using the anisotropy of BAO has additional advantages. Since the BAO scale should correspond to the sound horizon at recombination, it should be a constant. Thus, we can determine the geometric quantities by requiring that the radial BAO scale equals to the angular BAO scale. We no longer need to know the exact value of \(r_{\mathrm{d}}\) nor need to rely on the CMB experiment (see e.g., Seo and Eisenstein 2003; Matsubara 2004). This is particularly important in the context of measuring \(H_{0}\) given the tension in \(H_{0}\) between the local measurements and the inference by the Planck team in flat \(\Lambda\)CDM (see Sect. 1.4).

In galaxy surveys, the distance to each galaxy is measured through redshift, thus it gives the sum of the true distance and the contribution from the peculiar motion of the galaxies and it produces an anisotropy in galaxy distribution along the line of sight, which are called redshift-space distortions (RSD). Since the velocity field of a galaxy is caused by gravity, the anisotropy contains additional cosmological information. This effect is called the Kaiser effect, named after Kaiser (1987) who proposed RSD as a cosmological probe in the linear perturbation theory limit. Since the velocity field is related to the density field through the continuity equation, the anisotropy constrains the quantity \(f\), defined as the logarithmic derivative of the density perturbation, \(f=\mathrm{d}\ln{\delta}/\mathrm{d}\ln{a}\). See Okumura et al. (2016) for the constraint on \(f\) from RSD as a function of \(z\) including the high-\(z\) measurement.

By simultaneously measuring the BAO and RSD and combining them with the CMB anisotropy power spectrum, we can obtain a further constraint on additional geometric quantities, such as the time evolution of \(w\), the neutrino mass \(m_{\nu}\), etc. The cosmological results, presented below, correspond to this case.

The correlation function in 2D space including the BAO scales has been measured by Okumura et al. (2008) for the first time using the same galaxy sample as Eisenstein et al. (2005). The right-hand side of the left panel in Fig. 6 shows the measured correlation function, while the left-hand side shows the best fitting model based on linear perturbation theory (Matsubara 2004). The circle shown at the scale \(s=(s_{\perp}^{2} + s_{\parallel}^{2})^{1/2}\simeq105h^{-1}~\text{Mpc}\) again corresponds to the sound horizon at recombination. The distorted, anisotropic contours shown at the smaller scales are the RSD effect caused by the velocity field.

Fig. 6
figure 6

(Left) Contour plots of the correlation function measured from the SDSS galaxy sample as functions of transverse (\(s_{\perp}\)) and line-of-sight (\(s_{\parallel}\)) separations (right half) and the corresponding theoretical prediction (left half) (reproduced with permission from Okumura et al. 2008). The dashed thin black lines show \(\xi<-0.01\) increasing logarithmically with 0.25 and \(-0.01\leq\xi<0\) linearly with 0.0025. The solid thin lines colored red show \(0\leq\xi<0.01\) increasing linearly with 0.0025 and the solid thick ones colored red are \(\xi\geq 0.01\) logarithmically with 0.25. The baryonic feature slightly appears as ridge structures around the scale \(s=(s_{\perp}^{2} + s_{\parallel}^{2})^{1/2} \simeq100h^{-1}~\text{Mpc}\) (\(= 150\) Mpc), and the dashed circle traces the peaks of the baryon ridges. (Right) Similar to the left panel, but the correlation function from currently the largest galaxy sample from BOSS survey (reproduced with permission from Alam et al. 2016). The correlation function is multiplied by the square of the distance, \(s^{2}\xi\), in order to emphasize the BAO feature

Full size image

The right panel of Fig. 6 is the latest measurement of the correlation function using the SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS) DR12 sample (Alam et al. 2016). The anisotropic feature of BAO is more clearly detected due to the improvement of the data, both in the number of galaxies and the survey volume: the data of the DR12 sample used in Alam et al. (2016) comprised 1.2 million galaxies over the volume of \(18.7~\text{Gpc}^{3} \), whose numbers are respectively 25 times and 9 times larger than those of the DR3 sample used in Okumura et al. (2008).

2.4 Constraints on BAO Distance Scales and \(H_{0}\)

The left panel of Fig. 7 shows the summary of the three distance measures obtained by BAO in various galaxy surveys (Aubourg et al. 2015). The \(y\)-axis is the ratio of each distance and \(r_{\mathrm{d}}\), divided by \(\sqrt{z}\). The blue points are the measurement of \(D_{\mathrm{V}}\) from the angularly-averaged BAO, while the red and green points are respectively the measurements of \(D_{\mathrm{M}}\) and \(D_{\mathrm{H}}\) obtained from the anisotropy of BAO, where \(D_{\mathrm{H}}\) is the radial distance defined as \(D_{\mathrm{H}}(z)=c/H(z)\). The three lines with the same color as the points are the corresponding predictions of the \(\Lambda\)CDM model obtained by Planck (Adam et al. 2016). Nice agreement between BAO measurements from galaxy surveys and Planck cosmology can be seen. However, the agreement with the WMAP cosmology is equivalently good in terms of distance measures (Anderson et al. 2014).

Fig. 7
figure 7

(Left) Three distance measures obtained by BAO in various galaxy surveys (reproduced with permission from Aubourg et al. 2015). The \(y\)-axis is the ratio of each distance to \(r_{\mathrm{d}}\), divided by \(\sqrt{z}\). The top-red, middle-blue and bottom-green curves correspond to the distances \(D_{\mathrm{M}}(z)\), \(D_{\mathrm{V}}(z)\) and \(zD_{\mathrm{H}}(z)\), respectively. (Right) Joint constraints on the angular diameter distance \(D_{\mathrm{A}}(z)\) and the Hubble parameter \(H(z)\) obtained from the correlation analysis of the BOSS galaxy sample at \(z=0.5\) (reproduced with permission from Anderson et al. 2014). The inner and outer contours correspond to the 68% and 95% confidence levels, respectively. The gray and orange contours are the constraints from 1D and 2D BAO analyses, respectively, while the blue and green contours are from CMB experiments (Planck and WMAP)

Full size image

The right panel of Fig. 7 focuses on currently the largest survey, the BOSS survey at \(z=0.5\) (Anderson et al. 2014). Here the joint constraints on \(H(z)\) and \(D_{\mathrm{A}}(z)\) are shown. The gray contours are obtained from the 1D BAO analysis (see Sect. 2.2). Because the 1D BAO constrains \(D_{\mathrm{V}}\propto D_{\mathrm{A}}^{2/3}H^{-1/3}\), there is a perfect degeneracy between \(D_{\mathrm{A}}\) and \(H\). On the other hand, the solid orange contours are from the 2D BAO analysis where the degeneracy is broken to some extent (Sect. 2.3). The obtained constraints on the distance scales are as tight as the flat \(\lambda\)CDM constraints from the CMB experiments, Planck (dashed blue) and WMAP (dot-dashed green). Future galaxy surveys will enable us to measure BAO more accurately and determine the cosmic distance scales with higher precision (see Sect. 2.5).

Let us move onto the constraints on cosmological models using BAO observations. The left panel of Fig. 8 shows the joint constraints on the matter density parameter \(\varOmega_{\mathrm{m}}\) and the Hubble constant \(h=H_{0}/(100~\text{km}\,\text{s}^{-1}\,\text{Mpc}^{-1})\) obtained from the measurements of BAO anisotropy (Aubourg et al. 2015). The red and blue contours are the constraints from the BAO measured from the various galaxy samples at \(z<1\) and from the Ly\(\alpha\) forest at \(z\sim2\), respectively, as shown in the left panel of Fig. 7. Since these constraints are not very tight, the constrained \(H_{0}\) from either galaxy BAO or Ly\(\alpha\) BAO is consistent with other probes including the local measurements. The combination of these two BAO probes largely tightens the constraint on \(H_{0}\) and causes a slight, \(2\sigma\) tension as we will see below. With \(\varOmega_{\mathrm{m}}\) being marginalized over, the Hubble constant is constrained to \(h=0.67\pm0.013\) (\(1\sigma\) C. L.) (Aubourg et al. 2015).

Fig. 8
figure 8

(Left) Joint constraints on the matter density parameter \(\varOmega _{\mathrm{m}}\) and the Hubble constant \(h\) in a flat cosmology (reproduced with permission from Aubourg et al. 2015). Each contour shows the 68%, 95% and 99% confidence levels from inward. Galaxy BAO constraints (red) show strong correlations between \(\varOmega _{\mathrm{m}}\) and \(h\), whereas that of Ly-\(\alpha\) BAO (blue) show strong anti-correlations. The combination of the two (“Combined BAO” in green) thus breaks the degeneracies, resulting in constraints located at the intersection of the two. Planck CMB constraints (black) show also anti-correlation between \(\varOmega_{\mathrm{m}}\) and \(h\), but are substantially narrower than that of Combined BAO. (Right) Comparison of the constraints on \(H_{0}\) (reproduced with permission from Aubourg et al. 2015) from the distance ladder probes (local measurements, red), the CMB anisotropies (green), and the inverse distance ladder analysis (combination of BAO and supernovae; blue)

Full size image

The right panel of Fig. 8 summarizes the comparison of \(H_{0}\) constraints from the BAO measurement and other probes. Augmenting Fig. 4, the top three points are obtained from the distance ladder analysis, showing constraints from the local universe from three independent teams (Riess et al. 2016a; Freedman et al. 2012; Efstathiou 2014). The green, two middle points are the constraints from the two CMB satellite probes, WMAP and Planck. The bottom two points are from the inverse distance ladder analysis, namely the combination of BAO and SN distance measures. As seen from the figure, those from the Planck and the inverse ladder measurements have a mild but non-negligible tension with the distance-ladder measurements, about \(\sim2\sigma\). The discrepancy could be due to just systematics, or a hint of new physics. We will need further observational constraints to resolve these discrepancies.

2.5 Future BAO Surveys

BAO are considered as a probe least affected by systematic biases to measure distance scales, even beyond the local universe (\(z> 0\)), and thus are a promising tool to reveal the expansion history of the universe and constrain the cosmological model. To improve the precision of the distance measurement, a dominant source of error on BAO observations is the cosmic variance. There are larger, ongoing and planned galaxy redshift surveys, such as extended BOSS (eBOSS) (Dawson et al. 2016), Subaru Prime Focus Spectrograph (PFS) (Takada et al. 2014), and Dark Energy Spectroscopic Instrument (DESI) (Aghamousa et al. 2016). With the larger survey volumes, these surveys will measure distance scales using BAO with percent-level precisions. These surveys are also deep and can reveal fainter sources, and hence enable us to extend the distance scales to more distant parts of the universe.

As an example, Fig. 9 presents the accuracies of constraining the angular diameter distance and Hubble expansion rate expected from the analysis of anisotropic BAO (see Sect. 2.3) of the PFS survey at the Subaru Telescope. The PFS will observe the universe at \(0.8< z<2.4\) by using [OII] emitters as a tracer of the large-scale structure. The survey volume of each redshift slice is on the order of \([h^{-1}~\text{Gpc}]^{3}\) and the number density is larger than \(10^{-4} [h^{-1}~\text{Mpc}]^{-3}\), which are comparable to the existing SDSS and BOSS surveys at \(z<0.7\). Hence, one will be able to achieve a few percent constraints on \(D_{\mathrm{A}}\) and \(H\) at high redshifts, almost the same as those obtained from the low-\(z\) surveys. Deep galaxy surveys such as the PFS allow for constraining not only the expansion history of the universe but also dark energy (see the solid line of Fig. 9).

Fig. 9
figure 9

Fractional errors in the angular diameter distance and the expansion rate through the measurements of BAO (reproduced with permission from Takada et al. 2014). The expected accuracies are compared to the existing SDSS and BOSS surveys at \(z<0.7\). Each panel assumes \(w=-1\) as the fiducial model, and when the model is changed to \(w=-0.9\), the baseline of the fractional errors is systematically shifted from the dashed line to the solid curve

Full size image

Ultimately, we would like to survey the galaxies over the whole sky, which can be achieved by satellite missions, such as Euclid (Amendola et al. 2013) and WFIRST (Spergel et al. 2013). These surveys will measure the cosmic distances with an unprecedentedly high precision.

3 Intensity Mapping

3.1 21cm Intensity Mapping BAO

As we described in Sect. 2, current BAO measurements are enabled by large galaxy spectroscopic surveys, and the resulting constraining power on cosmological parameters generally scales as the effective survey comoving volume. Specifically, the precision of cosmological parameter constraints scales as \(\propto1/\sqrt{N}\), where \(N\) is the number of modes, or in the case of 3D map \(\propto1/\sqrt{k_{\mathrm{max}}^{3}V}\) where \(V\) is the comoving volume and \(k_{\mathrm{max}}\) the maximum useful comoving wavenumber. This scale is often given by the non-linearity scale, \(k_{\mathrm{nl}}(z=0)\sim0.2h/\text{Mpc}\), where the complexity of baryonic astrophysics on galaxy and galaxy-cluster scales limits our ability to extract cosmological parameters. Improving parametric precision will therefore require larger volumes, which requires mapping higher redshift volumes that have the added benefit of increasing \(k_{\mathrm{nl}}(z)\). The emerging technique of 21 cm Intensity Mapping appears to be a very promising way to reach this goal.

Galaxy redshifts can be measured at radio wavelengths using the 21 cm hyperfine emission of atomic neutral hydrogen (HI). The 21 cm line is unique in cosmology because for \(\lambda>21\) cm it is the dominant astronomical line emission, i.e., for all positive redshifts and all cosmological emission. So to a good approximation the wavelength of a spectral feature can be converted to a Doppler redshift without the uncertainty and ambiguity of having to first identify the atomic transition. The direct determination of redshifts using 21 cm data can be compared to the corresponding optical technique, which requires identifying a suitable subset of target galaxies (photometry), then obtaining an optical spectrum, and finally finding some unique combination of emission and absorption lines that allow an unambiguous determination of the redshift for that galaxy (spectroscopy).

The 21 cm signal has been used to conduct galaxy redshift surveys in the local Universe around \(z\sim0.1\) (Martin et al. 2010; Zwaan et al. 2001) and out to \(z\sim0.4\) (Fernández et al. 2016). Beyond this redshift, current radio telescopes do not have sufficient collecting area or sensitivity to make 21 cm surveys using individual galaxies.

A radically different technique, HI intensity mapping (HIM), has been proposed (Chang et al. 2008; Wyithe et al. 2008). It uses maps of 21 cm emission where individual galaxies are not resolved. Instead, it detects the combined emission from the many galaxies that occupy large (\(1000~\text{Mpc}^{3}\)) voxels. The technique allows 100 m class telescopes such as the Green Bank Telescope (GBT), which only have angular resolution of several arc-minutes, to rapidly survey enormous comoving volumes at \(z\sim1\) (Abdalla and Rawlings 2005; Peterson et al. 2006; Wyithe et al. 2007; Chang et al. 2008; Wyithe et al. 2008; Tegmark and Zaldarriaga 2009, 2010; Seo et al. 2010). A number of authors (Seo et al. 2010; Xu et al. 2015; Bull et al. 2015) have studied the overall promise of the intensity mapping technique. Chang et al. (2010), Masui et al. (2013) and Switzer et al. (2013) have reported the first detections in cross-correlations and upper limits to the 21 cm auto-power spectrum using the Green Bank Telescope (GBT).

3.1.1 Challenges

One of the major challenges for 21 cm intensity mapping is the mitigation of radio foregrounds, which are predominantly Galatic and extragalactic synchrotron emissions, and are at least \(\sim10^{4}\) times brighter in intensity than the 21 cm emission. The two can be distinguished because the former have smooth spectra and the latter trace the underlying large-scale structure and have spectral structures. The brightness temperature of the synchrotron foreground typically has a spectral dependence of \(\nu^{-2.6}\), or \((1+z)^{2.6}\), and is thus more severe at higher redshifts. Note it has not yet been demonstrated whether the synchrotron radiation is indeed spectrally smooth down to one part of \(10^{4}\) or higher and therefore can in principle be suppressed by this factor to reveal the 21 cm fluctuation signals. However, since the BAO wiggles have very specific structures, we can potentially select Fourier modes that are observationally accessible in scale and redshifts (Chang et al. 2008; Seo et al. 2010).

The 21 cm features we are most interested in are the relatively non-smooth BAO ‘wiggles’. Unfortunately radio telescopes are diffraction-limited and the beam patterns depend on frequency, which mixes angular and frequency dependence. Since the foregrounds are not smooth in position across the sky it is a nontrivial task to identify and subtract the smooth frequency foregrounds with sufficient accuracy so as to reveal the 21 cm emission. It is easier if we go to very small radial scales, but to get the most cosmological information out of the data we would need to remove the foregrounds over the largest range of scales possible. Shaw et al. (2013, 2015) have demonstrated that this is achievable in principle.

To achieve the foreground subtraction goal and to make accurate 3D maps we need a very accurate model of the beam patterns and characterization of the mapping between the observed and true skies. Liao et al. (2016) have recently demonstrated accurate measurements of the polarized GBT beam to sub-percent level, which is critical for polarized foreground mitigation. Developing and demonstrating the efficacy of methods to model and calibrate large dataset is also necessary to achieve the main objective.

3.1.2 Future Prospects

As discussed in Sect. 2, baryon acoustic oscillations provide a convenient standard ruler in the cosmological large scale structure (LSS) allowing a precise measurement of the distance-redshift relation over cosmic time. This distance redshift relation is measured, whether by BAO, SNe-Ia surveys, or weak lensing, to characterize the dark energy; it is augmented by the growth rate of inhomogeneities as well as redshift-space distortions. All three of these quantities can be measured in HI surveys even though to-date, only optical instruments have detected BAO features in the power spectrum.

Going forward requires the most cost-effective way to map the largest cosmological volume, and this may be radio spectroscopy through intensity mapping. One unique advantage of 21 cm Intensity Mapping is the fact that the 21 cm signal is in principle observable from \(z=0\) up to a redshift of \(\sim100\), when its spin temperature decouples from the Cosmic Microwave Background radiation. The vast majority of the cosmic volume is only visible during the dark ages via the 21 cm radiation from neutral hydrogen, before the onset of galaxy formation. 21 cm Intensity Mapping thus provides a unique access to measuring LSS during this period (Tegmark and Zaldarriaga 2009, 2010). Besides, 21 cm intensity mapping has a set of observational systematics that should be largely uncorrelated with the systematic effects in optical surveys.

The on-going low-z GBT-HIM survey is a step along the way to a dark ages radio survey. We have made BAO forecasts based on the expected performance of the array. We assume the seven-beam array has a 700–850 MHz frequency coverage with a total system temperature of 33 K. The BAO forecasts are consistent with predictions in Masui et al. (2010) and are in reasonable agreement with those of Bull et al. (2015). We consider three scenarios with different observing depth and sky coverage: 500 or 1000 hours of on-sky GBT observations, covering 100 or 1000 deg2 of sky areas. The expected errors on the BAO wiggles and the fractional distance constraints are shown in Fig. 10. We anticipate to yield a 3.5% error on the BAO distance at \(z\sim0.8\) with 1000 hours of GBT observing time. The bottom panel of Fig. 10 also shows recent constraints from WiggleZ (Drinkwater et al. 2010) and the BOSS surveys (Anderson et al. 2014) at lower redshifts, and forecasts for CHIME (Bandura et al. 2014) and WFIRST (Spergel et al. 2015). With the demonstrated results and good understanding of systematic effects at the GBT, and with very different astrophysical and measurement systematics from optical/IR spectroscopic redshift surveys, we anticipate the GBT-HIM array can make a firm detection of the BAO signature at \(z\sim0.8\) with the HI intensity mapping technique, and contribute to the future of large-scale structure surveys and the field of 21-cm cosmology. Other on-going experiments such as CHIME (Bandura et al. 2014) and HIRAX (Newburgh et al. 2016) will reach \(z=0.8\text{--}2.5\) and probe even larger cosmological volume.

Fig. 10
figure 10

Top: Expected errors on the BAO signature at \(z\sim 0.8\) of the GBT-HIM array, assuming different observing depth and sky coverage: (1000 hrs, 1000 deg2), (1000 hrs, 100 deg2), and (500 hrs, 100 deg2). BAO signatures can be detected in all three. Bottom: The expected fractional error on the BAO distance scale of the three scenarios. We anticipate a 3.5% error on the BAO distance at \(z\sim0.8\) with 1000 hours of GBT observing time with the array. A detection of BAO will validate HI intensity mapping as a viable tool for large-scale structure and cosmology, and serve as a systematic check and alternative approach to the optical spectroscopic redshift surveys

Full size image