Impacts of Cosmic Dust on Planetary Atmospheres and Surfaces

Abstract

Recent advances in interplanetary dust modelling provide much improved estimates of the fluxes of cosmic dust particles into planetary (and lunar) atmospheres throughout the solar system. Combining the dust particle size and velocity distributions with new chemical ablation models enables the injection rates of individual elements to be predicted as a function of location and time. This information is essential for understanding a variety of atmospheric impacts, including: the formation of layers of metal atoms and ions; meteoric smoke particles and ice cloud nucleation; perturbations to atmospheric gas-phase chemistry; and the effects of the surface deposition of micrometeorites and cosmic spherules. There is discussion of impacts on all the planets, as well as on Pluto, Triton and Titan.

1 Introduction

Critical to our understanding of how interplanetary dust affects the atmospheres of solar system bodies is an accurate understanding of the mass and velocity distributions of interplanetary dust grains throughout the solar system. These distributions are necessary not only for determining the overall mass influx of exogenous material to planetary atmospheres, but also for accurately quantifying the fraction of the incoming mass that ablates (since not all grains that enter a planetary atmosphere will fully ablate), the altitudes at which ablation occurs, the chemical evolution of the ablated products after injection into an atmosphere, and the degree of modification of the material deposited at the surface. Continual improvements in observations (both in situ and remote) and dynamical modelling have slowly but surely defined these quantities throughout the solar system. In parallel, significant advances in understanding the nature of the ablation process—though a combination of experimental simulation and modelling—means that the injection of individual meteoric constituents into a planetary atmosphere, and the consequent impacts, can be determined with much greater confidence.

In this review, the advances in interplanetary dust modelling are described in Sect. 2, followed by a discussion of meteoric ablation in Sect. 3. The next four sections describe a variety of atmospheric impacts, some observed and others predicted by models: layers of metal atoms and ions (Sect. 4); meteoric smoke particles and cloud nucleation (Sect. 5); perturbations to atmospheric gas-phase chemistry (Sect. 6); and the effects of the surface deposition of meteoric debris (Sect. 7). While this is not an exhaustive review, there is discussion of impacts on all planets with atmospheres, as well as on Pluto, Triton and Titan. Note that this review does not cover impacts on airless bodies, apart from a brief mention of the Moon and Mercury.

2 Astronomical Dust Models

In the inner solar system, observations and models over many decades have striven to define the interplanetary dust distribution, including both the velocity distribution and the overall flux. Early models were often phenomenological or empirical in nature and sometimes created ad hoc interplanetary dust distributions (i.e., not necessarily associated with a definite source) in order to explain discrete sets of observations (e.g., Divine 1993). Later models have used the orbital parameters of potential parent body populations, such as asteroids (ASTs), Jupiter Family Comets (JFCs), Halley Type Comets (HTCs), and Oort Cloud Comets (OCCs), as conditions to fit observations such as the Clementine star tracker zodiacal dust cloud images (Hahn et al. 2002); however, such an approach does not accurately capture the time evolution of dust grains away from their parents bodies. A more detailed understanding of the zodiacal dust cloud at 1 AU, including both its ultimate origin(s) and its contribution to the cosmic dust flux to the Earth, has come from a recent series of dynamical models (e.g., Wiegert et al. 2009; Nesvorný et al. 2010, 2011a,b; Pokorny et al. 2014). By comparison with remote observations from the Infrared Astronomical Satellite (IRAS), the Cosmic Background Explorer (COBE), and the Spitzer Space Telescope (Hauser et al. 1984; Low et al. 1984; Kelsall et al. 1998), and observations from terrestrial-based meteor surveys including the Canadian Meteor Orbit Radar (CMOR) (Campbell-Brown 2008), the Advanced Meteor Orbit Radar (AMOR) (Galligan and Baggaley 2004, 2005), and High Performance Large Aperture (HPLA) radars (e.g., Janches and Chau 2005; Janches and ReVelle 2005; Janches et al. 2006, 2008, 2014), the Nesvorný et al. (2010, 2011a) dynamical models have concluded that a majority (∼85–95%) of the zodiacal dust cloud near 1 AU originates from JFCs (e.g., Levison and Duncan 1997). AST, HTC, and OCC dust sources contribute the remaining 5–15%. Note also that while meteor showers can produce incident fluxes larger than the sporadic background flux for isolated time periods, the net flux at 1 AU from meteor streams contributes at most ∼10% relative to the sporadic background (e.g., Jones and Brown 1993). Additional in situ measurements continue to be made near 1 AU, such as by the IKAROS dust detector (Hirai et al. 2014, 2017) and the Lunar Dust Experiment (LDEX) (Horányi et al. 2015) onboard NASA’s Lunar Atmospheric and Dust Environment Explorer (LADEE) mission.

Recently, Carrillo-Sánchez et al. (2016) used the cosmic spherule accretion rate at the bottom of an ice chamber at the Amundsen-Scott base at South Pole (Taylor et al. 1998), together with recent measurements of the vertical fluxes of Na and Fe atoms above 87 km in the atmosphere (Gardner et al. 2014; Huang et al. 2015; Gardner et al. 2016), to determine the absolute contributions of each of these dust sources to the global input of cosmic dust. This study showed that JFCs contribute ($80 \pm 17$)% of the total input mass of $43 \pm 14~\mbox{t}\,\mbox{d}^{-1}$, in good accord with COBE and Planck observations of the zodiacal cloud (Nesvorný et al. 2010, 2011a,b; Rowan-Robinson and May 2013; Yang and Ishiguro 2015).

Our understanding of dust distributions in the outer solar system has been slower to coalesce, mainly due to the infrequent opportunities for in situ observations. To date, dust measurements in the outer solar system come from the Pioneer 10 and 11 meteoroid detectors (Humes 1980; Dikarev and Grun 2002), the Galileo and Ulysses DDS experiments (e.g., Grün et al. 1995a, 1995b, Grün et al. 1997; Kruger et al. 1999, 2006; Kuchner and Stark 2010), the Cassini Cosmic Dust Analyzer (Altobelli et al. 2007; Hillier et al. 2007), and the New Horizons Student Dust Counter (SDC) (Horanyi et al. 2008; Poppe et al. 2010; Szalay et al. 2013). Plasma wave instrumentation on-board the Voyager 1 and 2 spacecraft has also detected signals best interpreted as interplanetary dust impacts on the spacecraft body (Gurnett et al. 1997). While each of these datasets are valuable in their own right, significant differences between the sensitivity, location, and operational profiles of each instrument present challenges when attempting to construct and/or constrain an overall picture of the dust influx to planetary atmospheres.

One method for estimating the dust fluxes to planetary atmospheres in the outer solar system is to extrapolate the Grün et al. (1985) interplanetary dust flux model, or its subsequent updates (Dikarev et al. 2004, 2005), from 1 AU to the desired heliocentric distance. In the absence of sufficient in situ measurements in the outer solar system, this methodology is perhaps the only recourse; however, there is no a priori reason to justify the assumption that dust dynamics at 1 AU hold throughout the outer solar system, especially given the strongly perturbing presence of the giant planets (e.g., Liou and Zook 1999). Fortunately, on-going measurements and modelling have begun to quantify the outer solar system dust environment in more detail.

The last two decades have seen a progression of increasingly detailed dynamical models for the outer solar system distribution, including those by Liou and Zook (1999), Landgraf et al. (2002), Kuchner and Stark (2010), Vitense et al. (2010, 2012, 2014), and Poppe (2016). The most recent model for the interplanetary dust distribution in the outer solar system comes from Poppe (2016). This model uses a dynamical approach to trace ${>}10^{5}$ individual dust grains from their origin under the influence of forces such as solar and planetary gravity, solar radiation pressure, Poynting-Robertson and solar wind drag, and the electromagnetic Lorentz force. Dust grains are launched with initial conditions representative of four families of parent bodies: JFCs, HTCs, OCCs, and Edgeworth-Kuiper Belt (EKB) objects. After applying a collisional grooming algorithm as developed by Stark and Kuchner (2009), the model is constrained by in situ measurements from Pioneer 10 (Humes 1980), Galileo (Sremcevic et al. 2005), and the New Horizons Student Dust Counter (Poppe et al. 2010; Szalay et al. 2013).

Figure 1 shows the unfocused interplanetary dust mass flux as a function of heliocentric distance for the four individual populations considered (coloured lines) and the total flux (dashed line). For comparison, Fig. 1 also displays the extrapolated Grün et al. (1985) interplanetary dust flux (dash-dot line). The relative contributions of various dust sources are strongly dependent on heliocentric distance. Within 10 AU, JFC dust dominates by more than an order-of-magnitude. Since a significant fraction (∼30–40%) of JFC particles are hydrated, this represents a significant source of hydrous particles into the planetary atmospheres within 10 AU. Between 10 and 30 AU, OCC dust is predicted to be dominant, with some additional contributions (∼10–20%) from both JFC and EKB dust. Finally, at distances greater than 30 AU the EKB dust dominates, reflecting the near-by location of the EKB parent bodies themselves (e.g., Petit et al. 2011). One can also see the very large discrepancy between the extrapolated Grün et al. (1985) model prediction and the total flux found in Poppe (2016), with the latter typically an order-of-magnitude less than the former. This model also provides the mass and velocity distributions for each dust grain family with gravitational focusing taken into account (e.g., Spahn et al. (2006)). A remaining open question is whether dust grains from the distant EKB can reach the inner solar system and contribute to cosmic dust accretion at the terrestrial planets (e.g., Flynn 1994; Liou et al. 1996; Moro-Martin and Malhotra 2003; Ipatov and Mather 2006). Lastly, the mass flux of interstellar dust entering the solar system is approximately $5 \times 10^{-17}~\mbox{g}\,\mbox{m}^{-2}\,\mbox{s}^{- 1}$ (Grün et al. 1994). This is between 2 and 3 orders-of-magnitude lower than the interplanetary dust mass fluxes at the giant planets (Fig. 1), and thus only a minor contribution. Although interstellar dust grains have relatively high velocities compared with interplanetary dust, any differences in ablation behaviour will most likely be obscured by the much higher flux of interplanetary dust grains.

Fig. 1

The unfocused interplanetary dust grain mass flux as a function of heliocentric distance. The black filled circles refer to the four giant planets’ average heliocentric distance. Coloured lines are contributions from the JFC, HTC, OCC and EKB parent sources, while the total flux is the black dashed line. The dot-dash line is the Grün et al. (1985) flux at 1 AU extrapolated outwards for comparison (adapted from Poppe 2016). While not shown, the mass flux of interstellar dust entering the solar system is approximately $5 \times 10^{-17}~\mbox{g}\,\mbox{m}^{-2}\,\mbox{s}^{-1}$ (Grün et al. 1994), and thus only a minor contribution relative to interplanetary dust mass fluxes

3 Meteoric Ablation

In order to assess the impacts of cosmic dust in a planetary atmosphere, it is necessary to model the rate of injection of ablation products (i.e. metal atoms and ions) as a function of height, location and time. This requires combining an ablation model with an astronomical model which predicts the distributions of particle mass, velocity and entry angle from the different dust sources (Sect. 2). Ablation models typically use the “classical” meteor physics equations of momentum and energy conservation as a meteoroid enters the atmosphere, underwritten by several assumptions: the meteoroid is treated as a homogenous spherical particle; radial heat transfer is assumed fast enough so the particle is isothermal along its whole path through the atmosphere; and the interaction with the atmosphere occurs in the free molecular flow regime in which the molecular collision mean free path is larger than the dimension of the meteoroid and thus no shock structure can develop.

A current example of an ablation model which also predicts the injection rates of individual elements is the Chemical Ablation MODel (CABMOD) (Vondrak et al. 2008). This model estimates the elemental ablation rates as a function of height from a meteoroid of specified mass, entry velocity and zenith angle. CABMOD treats mass loss both by physical sputtering, which is the mass loss mechanism before particle melting when individual atoms are displaced from the surface of the meteoroid by collisions with air molecules, and thermal ablation after melting. Sputtering can be modelled using laboratory ion-sputtering data in the absence of appropriate data on high speed neutral-surface collisions (Vondrak et al. 2008), but in any case turns out to be relatively minor except for small ($r< 1~\upmu \mbox{m}$) particles entering at high velocity (${>}40~\mbox{km}\,\mbox{s}^{-1}$).

To model thermal ablation, CABMOD contains the MAGMA chemical equilibrium model (Fegley and Cameron 1987; Schaefer and Fegley 2004, 2005) which calculates the equilibrium vapour pressures of the various melt constituents which are treated as eight metal oxides (SiO₂, MgO, FeO, Al₂O₃, TiO₂, CaO, Na₂O and K₂O). The chemical equilibria in the melt are calculated using their Raoultian activities. The mass loss rate through evaporation is estimated by using Langmuir evaporation through the Hertz-Knudsen equation (Markova et al. 1986; Love and Brownlee 1991; McNeil et al. 1998; Vondrak et al. 2008), which assumes that the rate of evaporation into a vacuum is equal to the rate of evaporation needed to balance the rate of uptake of a species in a closed system. The calculated evaporation rate is formally an upper limit, which is probably correct for pure metals (Safarian and Engh 2013), but may be lower in silicate melts because diffusion from the bulk into the surface film may become rate-limiting (Alexander et al. 2002). Vondrak et al. (2008) assumed that meteoroids are mineralogically CI chondrites with an olivine composition (the elemental atomic ratio Fe:Mg is ∼0.84), with an onset of melting at 1750 K.

Recently, a Meteoric Ablation Simulator (MASI) has been developed to test the predictions of ablation models like CABMOD (Bones et al. 2016; Gómez Martín et al. 2017). The MASI heats a meteoritic particle ($r = 20\mbox{--}200~\upmu \mbox{m}$) over a temperature ramp (up to 2800 K) that is programmed to match atmospheric entry for a specified velocity, and measures the absolute rates of evaporation of pairs of metal atoms (e.g. Na and Fe) using high repetition rate time-resolved laser induced fluorescence. MASI measurements confirm the model prediction of differential ablation i.e. the evaporation of relatively volatile elements such as Na and K before the main elements Fe, Mg and Si, and finally the refractory elements Ca, Ti and Al. However, the ablation profiles of individual species tend to be broader than predicted by a model such as CABMOD because meteorites do not consist of single mineral phases (Gómez Martín et al. 2017).

An important use of differential ablation models is to predict the rate of electron production along the path of a meteor; this occurs as individual elements ablate and then ionize through collisions with air molecules (Janches et al. 2014). The electron production rate is needed to determine the meteor detectability of a particular radar, and hence to correct for the inherent observational bias to fast meteors (which produce electrons much more efficiently) when performing meteor astronomy (Close et al. 2007; Janches et al. 2014). An electrostatic dust accelerator has recently been used to generate metallic particles with velocities of 10–70 km s⁻¹, which are then introduced into a pressurized chamber where the particle partially or completely ablates over a short distance. The deceleration is used to determine the rate of mass loss, and an array of biased electrodes above and below the ablation path collect the ions and electrons produced along the ablation path, from which the ionization efficiency can be determined (Thomas et al. 2016, 2017).

A model like CABMOD can then be used to calculate the height profile of the injection rates of the meteoritic constituents into a planetary atmosphere. This is achieved by sampling individual particles from the mass and velocity distributions of the cosmic dust flux entering the atmosphere, computing each particle’s elemental injection profiles, and performing a weighted sum over the mass/velocity distribution (Carrillo-Sánchez et al. 2015). The left-hand panels of Fig. 2 illustrate the cosmic dust mass flux as a function of entry velocity into the atmospheres of Earth, Mars and Venus, for JFC, AST, and HTC particles (OCC particles are also shown in the case of the Earth). These distributions are derived from the ZoDy model (Nesvorný et al. 2010, 2011a,b; Carrillo-Sánchez et al. 2016). The range of entry velocities are 11.5–71.5 km s⁻¹ for Earth, 5.5–59.5 km s⁻¹ for Mars, and 10.5–85.5 km s⁻¹ for Venus. Most of the JFC and AST mass enters at low velocities (<20 km s⁻¹) compared with the HTC and particularly OCC particles, which therefore experience a much higher degree of ablation (Carrillo-Sánchez et al. 2016). The right-hand panels show the ablation rate profiles of various metals as a function of height; these are produced by integrating the ablation profiles calculated by CABMOD for individual silicate particles over the mass, velocity and entry angle distributions of the particle sources (Carrillo-Sánchez et al. 2016). Note that peak mass loss occurs for all three planets when the pressure is around 10⁻⁶ bar, which is ∼80 km on Mars, 92 km on Earth, and 115 km on Venus, in good agreement with the earlier work of Molina-Cuberos et al. (2008). The volatile alkali metals (Na and K) ablate several km higher, and the refractory elements (Ca, Ti, Al) several km lower. The height over which ablation occurs is narrower on Mars because of the smaller range of entry velocities, and the ablated mass is much smaller than on Earth and Venus.

Fig. 2

Panels a, c, and e: mass flux as a function of entry velocity for interplanetary dust from Jupiter-Family comets (JFC, in yellow), Asteroid belt (AST, in red), Halley-Type comets (HTC, in cyan), and Oort-Cloud comets (OCC, in blue) for Earth, Mars and Venus. Panels b, d, and e: overall ablation rate profiles of individual elements, integrated and weighted for the JFC, AST and HTC particle populations (Carrillo-Sánchez et al. 2016)

There have been a number of studies of ablation in the atmospheres of the giant planets, including at Jupiter (Kim et al. 2001; Pesnell and Grebowsky 2001), Saturn (Moses and Bass 2000; Moses et al. 2000), and Neptune (Moses 1992). See Molina-Cuberos et al. (2008) for a general review. As discussed in Sect. 2, there is a relative lack of measurements in the outer solar system which has necessitated the use of simplifying assumptions regarding the particle mass/velocity distributions; however, the dust model of Poppe (2016) now provides these distributions for ablation modelling. This was recently applied to Saturn’s moon Titan (Frankland et al. 2016). Due to the large masses and hence deep gravitational wells of the giant planets, the minimum meteoroid entry velocities are 59.5, 35.5, 21.3, and 23.5 km s⁻¹ for Jupiter, Saturn, Uranus, and Neptune, respectively. Any variations in the velocity distributions of meteoroids in interplanetary space are compressed during gravitational focusing as all grains are accelerated at minimum to the planetary escape velocity. In the outer solar system, the three primary families of dust grains are JFC, OCC and EKB dust, each with distinct mass and velocity distributions. These distributions are a function of not only the grain mass and velocity, but also heliocentric distance (Fig. 1). The initial mass and velocity distributions of dust entering the atmospheres of each of the giant planets are shown in Fig. 3, calculated from the interplanetary dust distributions of Poppe (2016).

Fig. 3

The mass flux as a function of entry velocity for interplanetary dust grains from three populations (Edgeworth-Kuiper Belt, green; Oort Cloud comets, blue; Jupiter-family comets, orange) for each of the giant planets (adapted from Moses and Poppe 2017)

Figure 4 shows the gas injection rate profiles arising from meteoric ablation in the atmospheres of Jupiter, Saturn, Uranus, and Neptune for three dust grain compositions: silicate, organic (using benzoapyrene as a representative species), and water ice (Moses and Poppe 2017). These model results use the interplanetary dust mass and velocity distributions in Fig. 3. Based on the approximate relative mass fractions in cometary nuclei and dust (Greenberg and Li 1999), the bulk dust influx is assumed to comprise 26% silicate, 32% refractory organic, and 42% ice grains. The dust grain parameters—density, mean molecular mass, vaporization temperature, latent heat of vaporization, emissivity etc.—control the differences in the ablation profiles (Moses and Poppe 2017). Several general trends are notable: (1) larger grains penetrate deeper into any atmosphere for any other combination of parameters; (2) larger grains also tend to ablate more fully, since their greater cross section leads to more impacts with ambient molecules and thus, greater heating; (3) faster particles tend to ablate at higher altitudes and more fully than their slower counterparts; (4) the model predicts that grains of all compositions ablate on Jupiter and Saturn due to higher minimum entry velocities while silicate grains only partially ablate on Uranus and Neptune (organic and water ice grains completely or nearly completely ablate on all the giant planets); (5) the vaporization temperature typically controls the average altitude that a given composition grain ablates, with water ice beginning to ablate at the highest altitude (i.e., lower vaporization temperature), organics at an intermediate altitude, and silicate grains (with higher vaporization temperatures) ablating at typically lower altitudes; and (6) the latent heat of vaporization influences the range of altitudes over which ablation occurs, with low latent heats associated with narrower ablation profiles and high latent heats associated with broad ablation profiles (i.e., low latent heat implies more inefficient cooling from evaporation which in turn leads to higher grain temperatures and relatively rapid ablation and vaporization).

Fig. 4

The gas injection rate due to micrometeoroid ablation in the atmospheres of the giant planets (adapted from Moses and Poppe 2017). Three different dust grain compositions were considered: silicate (gray), organic (orange), and water ice (blue). All panels are scaled identically

4 Metallic Layers in Planetary Atmospheres

4.1 Meteoric Metal Layers on Earth

Layers of metallic atoms and ions occur between about 75 and 200 km in the terrestrial atmosphere, as a result of meteoric ablation. These layers have been the subject of two major reviews which cover the history of their detection, laboratory studies to unravel the chemistry which creates the layers, and the development of models including recent whole atmosphere chemistry-climate models (Plane 2003; Plane et al. 2015). Hence, the discussion here will be comparatively brief.

Metal ions (Fe⁺, Mg⁺, Na⁺, Si⁺ etc.) have been observed since the 1960s mainly by rocket-borne mass spectrometry (Kopp 1997; Grebowsky and Aikin 2002), although Mg⁺ can also be observed by satellite optical spectroscopy (Langowski et al. 2015) and Ca⁺ by lidar (Gerding et al. 2000). Following the invention of the laser in the 1970s, the layers of neutral Na, K, Fe and Ca have been observed by ground-based resonance lidars because these metals have spectroscopic transitions at wavelengths longer than 330 nm, and hence the laser light and resonance fluorescence are not absorbed by the stratospheric ozone layer (unlike Mg). The metal layers peak between 85 and 95 km, and are only 5–10 km wide with sharp top- and bottom-sides (Plane 2003). Although most lidar measurements have focused on these metal layers below 105 km, recent advances in lidar technology have enabled measurements of Fe atoms up to ∼190 km (Chu et al. 2011). Simultaneous lidar measurements of the vertical wind and Na and Fe densities have been used to determine the vertical fluxes of these metals around 87 km (Huang et al. 2015), and hence the absolute inputs into the atmosphere of dust from the different sources discussed in Sect. 2 (Carrillo-Sánchez et al. 2016). Since 2007, satellite optical spectrometers using solar-pumped resonance fluorescence—SCIAMACHY on Envisat (Langowski et al. 2015) and OSIRIS on Odin (Fan et al. 2007; Dawkins et al. 2014), or stellar occultation—GOMOS on Envisat (Fussen et al. 2010)—have provided near-global coverage of the Na, K and Mg layers. We therefore know a great deal about the latitudinal, seasonal and diurnal variations of the neutral metal layers.

Figure 5 is a schematic diagram of the chemistry of Fe in the terrestrial upper atmosphere. Many of the individual reactions in this scheme have been studied in the laboratory under appropriate conditions of temperature, and a sufficient range of pressure to permit confident extrapolation to the low pressures of the upper mesosphere (${<}10^{-5}~\mbox{bar}$) where reaction rate coefficients cannot be measured using the conventional pulsed laser photolysis and fast flow tube techniques. Similarly detailed schemes exist for Na, K, Mg and Ca (Plane et al. 2015), as well as Si (Plane et al. 2016). The ionic species in Fig. 5 are shown in blue boxes. These species tend to dominate above 100 km in the lower $E$ region. Metal ions are produced directly during meteoric ablation: the metals atoms which evaporate are initially travelling with a speed similar to that of the parent meteoroid, and so undergo hyperthermal collisions with air molecules which can lead to ionization. Metallic ions are also produced by charge transfer with the ambient $\text{NO}^{+}$ and $\text{O}_{2} ^{+}$ ions, and photo-ionization. Neutralization occurs through forming molecular ions (for Fe⁺ mostly by reaction with O₃), followed by dissociative recombination with electrons; however, this neutralization pathway is interrupted by atomic oxygen, which reduces metal-containing ions back to the atomic metal ions so that the lifetimes of metal ions can be extended to several days. Above ∼105 km, where there is very little O₃, neutralization occurs via the slow process of radiative recombination with electrons (Bones et al. 2015).

Fig. 5

Schematic diagram of the chemistry of Fe in the terrestrial mesosphere and lower thermosphere (adapted from Plane et al. 2015). Ionized species are shown in blue boxes, neutral gas-phase species in green boxes, and potential precursors of meteoric smoke particles in orange boxes

The neutral species in Fig. 5 are identified in green boxes. All the metal atoms studied to date react rapidly with O₃ to form the metal monoxides, which can then form more stable reservoir species (e.g. hydroxides and carbonates) by further reactions involving O₃, O₂, H₂O and CO₂ (Plane et al. 2015). However, as shown in Fig. 5 these reservoir species are reduced back to neutral metal atoms by atomic O and H. Below 82 km, the concentrations of atomic O and H decrease rapidly, and the reservoir species now survive long enough to polymerize into small particles (orange boxes in Fig. 5) known as Meteoric Smoke Particles (MSPs), which cause permanent removal of the metals from the gas phase (Sect. 5.1). The conversion to MSPs below 82 km, and to ions above 100 km, explains why the metal atoms occur in thin layers that peak between 85 and 95 km in the terrestrial atmosphere. The chemistry for six meteoric metals (Na, K, Fe, Mg, Ca and Si—described by ∼140 reactions) has now been incorporated into a whole atmosphere chemistry-climate model (Plane et al. 2015, 2016).

4.2 Meteoric Metal Layers on Venus and Mars

Until very recently, there was only indirect evidence for metallic layers in other planetary atmospheres. This evidence was obtained from radio occultation measurements, where the attenuation of radio waves transmitted from a spacecraft through a planet’s atmosphere and received at Earth can be used to determine the electron density profile in the atmosphere. Pioneer Venus measurements show that the main ion layer in the Venus night-side ionosphere peaks around 142 km, with a second, intermittent peak around 120 km (Kliore et al. 1979). This is close to the peak of meteoric ablation (Fig. 2), and so was tentatively attributed to a layer of metallic ions and electrons, although it was recognized that direct ionization by energetic electron or proton precipitation could also be responsible (Kliore et al. 1979; Molina-Cuberos et al. 2008). The main ionospheric peak in Titan was located at $1180 \pm 150~\mbox{km}$ during the Voyager I fly-by (Bird et al. 1997). More recently, Cassini radio occultation measurements show that there is a secondary intermittent layer between 500 and 600 km, which coincides with the region where ablation is predicted to occur (Frankland et al. 2016).

The atmosphere of Mars has been sounded in more detail. Fjeldbo et al. (1966) analyzed Mariner IV data and found that the daytime ionosphere is characterized by a main layer produced by solar photo-ionization at an altitude of 140 km, and a secondary layer around 100 km with an electron density approximately one order of magnitude lower. Savich et al. (1976) reported a secondary layer at ∼80 km during nighttime using the Soviet spacecraft Mars 4 and Mars 5. Some years later, these layers were confirmed by Mars Express observations of a layer between 65 and 110 km which appeared sporadically in about 10% of measured electron density profiles (Pätzold et al. 2005). A more extensive set of electron density profiles obtained using Mars Global Surveyor exhibited secondary layers between 70 and 105 km, in ∼4% of cases (Withers et al. 2008; Pandya and Haider 2012). Their sporadic occurrence, width of a few km, and appearance over the height range where ablation occurs (Fig. 2), are in many respects similar to sporadic $E$ layers in the terrestrial ionosophere which are known to consist of metallic ions (Grebowsky and Aikin 2002). Therefore, these studies of the Mars low-lying layers concluded that they were most likely composed of metallic ions deposited by meteoric ablation, although the mechanism for concentrating metallic ions into a narrow layer in the absence of a permanent magnetic field was unclear.

More recently, metallic ions (Mg⁺, Fe⁺ and Na⁺) have been measured in situ above 120 km in the Mars ionosphere by the Neutral Gas Ion Mass Spectrometer (NGIMS) aboard the Mars Atmosphere and Volatile Evolution (MAVEN) spacecraft (Grebowsky et al. 2017). Another instrument on MAVEN, the Imaging Ultraviolet Spectrograph (IUVS), was able to detect Mg⁺ down to around 70 km by observing solar-pumped resonance fluorescence at 280 nm (Crismani et al. 2017b). Several unexpected features were observed. First, the NGIMS observations show that all three metallic ions have the same scale height, in spite of being in a very low pressure region where gravitational separation should occur. Second, the IUVS measurements of the Mg⁺ layer peaking around 95 km are reproduced well by a detailed chemistry model with meteoric ablation (Whalley and Plane 2010); however, the model predicts an ever larger neutral Mg layer peaking around 80 km, which is not observed. Third, no instances of sporadic Mg⁺ layers were observed which would correspond to the sporadic electron density layers recorded by radio occultation, so it appears that they have been wrongly attributed to metallic ion layers in the case of Mars (Crismani et al. 2017b). It is also worth noting that although the IUVS instrument observed Mg, Fe⁺ and Fe in addition to Mg⁺ after the meteor storm following the close encounter between Comet Siding Spring (C/2013 A1) and Mars in October 2014 (Schneider et al. 2015), only Mg⁺ has been observed under background conditions.

5 Meteoric Smoke Particles and Clouds

5.1 Formation of Meteoric Smoke Particles

MSPs form via the polymerization of metal-containing molecules (e.g. FeOH, Mg(OH)₂, MgCO₃, NaHCO₃ and Si(OH)₂), which are the relatively long-lived reservoir species on the underside of the metallic layers (Plane et al. 2015, 2016). In the CO₂-rich atmospheres of Mars and Venus, there is probably a higher fraction of carbonates compared with hydroxides (Whalley and Plane 2010). Laboratory studies have shown that these molecules polymerize rapidly because they have large electric dipole moments and, if they contain Fe, their collisions are also governed by long-range magnetic dipole forces (Saunders and Plane 2006, 2010). However, polymerization occurs over several days because the concentrations of these species are low. In the terrestrial atmosphere, most of the particles around 80 km appear to be just large molecular clusters (∼1 nm in effective radius) (Rapp et al. 2007), which have proved very challenging to capture for compositional analysis (Hedin et al. 2014). This has been frustrating given the potentially important roles that MSPs play in the middle atmospheres of planets: acting as ice nuclei for polar mesospheric clouds (Sect. 5.2); providing a significant component of stratospheric sulphate aerosols and polar stratospheric clouds (Sect. 5.3); and providing a reactive surface which can alter the gas-phase composition of a planetary atmosphere through heterogeneous chemistry (Sect. 6).

Because MSPs form in the $D$ region of the terrestrial ionosphere, a small fraction (∼6%) are charged by uptake of electrons and this enables them to be detected using Faraday cup detectors on sounding rocket payloads (Gelinas et al. 2005; Rapp et al. 2012; Plane et al. 2014). Faraday detectors collect charged particles by using the rocket payload ram velocity to drive the particles through a series of electrically biased screens, which reject thermal electrons and positive ions and allow heavy charged particles to reach the detector. By modelling the MSP size range—typically between 0.5 and 2 nm radius—that will be collected efficiently according to the aerodynamic flow around the payload, and the fraction that are charged, the total concentration of MSPs can be estimated (Rapp et al. 2007).

MSPs have also been detected between 80 and 95 km using high performance large aperture radars such as the 430 MHz dual-beam Arecibo incoherent scatter radar in Puerto Rico (18^∘N). The distinctive line shapes of the incoherent scatter radar spectra result from the different diffusion modes in the $D$ region plasma caused by the presence of positive ions and relatively heavy charged MSPs (Strelnikova et al. 2007). MSP number densities and size can be retrieved, although a monodisperse MSP population has to be assumed. MSPs have been detected optically between 40 and 75 km by the limb-scanning Solar Occultation For Ice Experiment (SOFIE) spectrometer on the Aeronomy of Ice in the Mesosphere (AIM) satellite (Hervig et al. 2009). The extremely small extinctions due to MSPs (${<} 1 \times 10^{-8}~\mbox{km}^{-1}$) are measured by solar occultation over a pathlength of ∼300 km through the atmosphere.

MSPs are deposited at the Earth’s surface 4–5 years after formation in the MLT (Dhomse et al. 2013). Several studies have reported measurements of the MSP deposition flux in polar ice cores. Gabrielli et al. (2004) measured the concentrations of Ir and Pt in the Greenland Ice Core Project (GRIP) ice core from Summit, central Greenland using inductively-coupled plasma sector field mass spectrometry (ICP-MS). The Ir and Pt signals were normalized to Al measured in the ice, which is an element that is a good indicator of crustal dust. This showed that the contribution from crust dust to the fluxes of Ir and Pt during the Holocene was negligible, and that the ratio of these elements was in the expected cosmic abundance ($\mbox{Ir}/\mbox{Pt} = 0.49$), confirming that they were of extra-terrestrial origin. Another method for detecting MSPs in polar ice cores is laboratory-induced remanent magnetization, which measures the magnetization carried by ferromagnetic dust particles in the ice (Lanci et al. 2012). This non-destructive technique provides a way of separating MSPs from larger crustal dust particles, because particles with radii between 3.5 and 10 nm become super-paramagnetic as the ice sample is warmed from 77 K to 255 K. In the case of central Greenland during the Holocene, the concentration of super-paramagnetic Fe was almost identical to that calculated from the Ir and Pt measurements using the relative Fe/Ir and Fe/Pt cosmic abundances. Lanci et al. (2012) demonstrated that wet deposition of the MSPs is more important than dry deposition: the deposition flux is about an order of magnitude higher in central Greenland than the eastern highlands of Antarctica, consistent with the relative snowfall at the two locations. It should be noted, however, that a recent study using a global circulation model to predict the deposition of MSPs over the Earth’s surface has found a much lower deposition flux in these polar locations, by more than an order of magnitude, when using a cosmic dust input to the atmosphere of 43 t d⁻¹ (Brooke et al. 2017).

5.2 Mesospheric Clouds on Earth and Mars

Polar mesospheric clouds (PMCs) on Earth have received a great deal of attention as sensitive indicators of climate change (Thomas and Olivero 2001). The clouds were first reported during June 1885 over middle and northern Europe. When viewed from the ground after sunset they are often referred to as noctilucent clouds (NLCs). PMCs are H₂O-ice clouds which form at the very cold temperatures (<145 K) found at altitudes between 82 and 86 km during summer at high latitudes (${>}55^{\circ}$) (Rapp and Thomas 2006). One explanation for the increasingly bright clouds is the growing emission of methane since the Industrial Revolution, since this relatively inert gas reaches the stratosphere where it is oxidized to H₂O. In fact, H₂O in the stratosphere and mesosphere has been increasing at a rate of ∼1% year⁻¹ since the 1950s (Russell et al. 2014). Temperatures in the mesosphere are also decreasing by around −0.5 to −2.0 K decade⁻¹ because of depletion of the stratospheric ozone layer, and increasing greenhouse gases (particularly CO₂) which act as refrigerants in the middle atmosphere (Lübken et al. 2013). The combined trends of cooling temperatures and increasing H₂O concentrations have almost certainly caused the statistically significant increase in both PMC brightness and occurrence frequency which has been observed using Solar Backscatter Ultraviolet (SBUV) instruments on a sequence of nadir-viewing satellites (DeLand et al. 2007; Shettle et al. 2009). PMCs can also be detected by radar: Polar Mesospheric Summer Echoes (PMSEs) are intense radar backscatter echoes that are caused mainly by small ice particles ($r < 10~\mbox{nm}$). These particles are negatively charged by the attachment of electrons and the radar is then scattered by the resulting plasma inhomogeneities (Lübken et al. 1998). There has also been an upward trend in PMSE since 1994 (Latteck and Bremer 2013).

One remaining question is what provides the ice nuclei for PMC formation, since the clouds are observed to form at temperatures above 120 K, which is the upper limit for homogeneous nucleation in the very dry mesosphere (Murray and Jensen 2010). Proposed ice nuclei include $D$region proton hydrates (Balsiger et al. 1996) and MSPs (Kalashnikova et al. 2000), although nucleation on proton hydrates is challenging because of competition with dissociative electron recombination destroying the nascent ice particle before it grows large enough. Nucleation presumably occurs at the mesopause (∼87 km) and the ice particles then settle gravitationally as they grow to visible clouds with $r = 50\mbox{--}80~\mbox{nm}$, eventually sublimating in the warmer mesosphere below 82 km. Laboratory studies have not yet demonstrated that MSPs of 1–2 nm radius can overcome the Kelvin barrier to nucleation. However, as discussed in Sect. 5.1, around 6% of MSPs should be negatively-charged in above 80 km region, and the presence of even a single charge on a nm-sized particle can make it an effective ice nucleus by reducing the classical free energy barrier associated with the Kelvin effect (Gumbel and Megner 2009). Alternatively, electronic structure theory calculations indicate that metal silicate molecules such as FeSiO₃ and MgSiO₃ should form readily in the upper atmosphere (Plane 2011). These molecules, which are essentially the smallest MSP unit, have enormous electric dipole moments of 9.5 and 12.2 Debye, respectively. H₂O molecules therefore bind very effectively to them, and model calculations show that they should nucleate ice particles efficiently under polar mesospheric conditions at temperatures around 140 K (Plane 2011). Optical extinction measurements by the SOFIE instrument (Sect. 5.1) show that between 0.01 and 3% of the ice particle mass is meteoric material (Hervig et al. 2012).

Martian Mesospheric Clouds (MMCs) are the highest clouds in the Martian atmosphere; they are the counterparts to terrestrial PMCs (Määttänen et al. 2013). Their composition has been identified as mainly CO₂ ice crystals, with a small component of H₂O ice. The former feature is unique for a telluric planet as it results from the condensation of the main atmospheric constituent. The detection of CO₂ cloud ice crystals was first claimed by Herr and Pimentel (1970) using Mariner 6 and 7 infrared observations. The low altitude of the feature (<30 km) pointed rather to CO₂ fluorescence (Lellouch et al. 2000; Lopez-Valverde et al. 2005). Given the CO₂ supersaturations measured around 80 km during the Mars Pathfinder mission’s atmospheric entry (Schofield et al. 1997; Clancy and Sandor 1998) used Earth-based submillimeter observations to infer that the predawn bluish cloud observed by the Imager for Mars Pathfinder (IMP) (Smith et al. 1997) was a CO₂ ice cloud. Four detections of nighttime aerosol layers (90–100 km), at southern mid-latitudes and $L_{\text{s}}= 135^{\circ}$ were made in stellar occultation mode (Montmessin et al. 2006) with the SPICAM spectrometer onboard Mars Express (MEx). They were identified as CO₂ ice clouds due to the simultaneous presence of supersaturations. The first identification of CO₂ ice spectroscopic features in an infrared atmospheric spectrum was presented by Formisano et al. (2006) in their study of non-LTE emission using the Planetary Fourier Spectrometer (PFS) onboard MEx. However, the first unambiguous observations of CO₂ mesospheric clouds (Montmessin et al. 2007) were made using the spectral imager OMEGA (MEx). Very recently, Aoki et al. (2018) performed unambiguous CO₂ MMC detections using the PFS. They achieved the highest resolution cloud spectra to date, which will provide detailed information about crystal shape and composition.

More generally, the first systematic detections of MMCs (65–75 km) over the Martian years $\mbox{MY}=24\mbox{--}26$—without constraints on their composition—were presented by Clancy and co-workers (Clancy et al. 2003, 2007) using limb observations with the Thermal Emission Spectrometer (TES) and the Mars Orbiter Camera (MOC), onboard Mars Global Surveyor (MGS). MMCs were mainly located around the equator (15^∘S–15^∘N), and formed after northern spring equinox ($L_{\mathrm{s}}=0\mbox{--}55^{\circ}$) and during northern summer ($L_{\text{s}}=105\mbox{--}180^{\circ}$), confined between 240^∘E and 30^∘E. Later systematic detection of MMCs largely followed this spatial coverage and seasonality. Määttänen et al. (2010) focused on the systematic detection of CO₂ ice clouds with OMEGA over the years $\mbox{MY}=27\mbox{--}29$, characterising the effective crystal size ($r_{\mathrm{eff}}=1\mbox{--}3~\upmu \mbox{m}$) and opacity at 1 μm (<0.5). The nighttime cloud layers detected by Montmessin et al. (2006a) had crystal sizes of $r_{\mathrm{eff}} = 80\mbox{--}110~\upmu \mbox{m}$ and low opacities (0.01 at 200 nm). The HRSC stereoscopic imager (onboard MEx) allowed for the derivation of the OMEGA daytime CO₂ clouds altitudes (55–85 km), and unique measurements of mesospheric wind speeds (5–40 m s⁻¹) (Määttänen et al. 2010; Scholten et al. 2010). Vincendon et al. (2011) used the imaging spectrometer CRISM onboard the Mars Reconnaissance Orbiter (MRO) to discriminate between CO₂ MMCs, and more infrequent water ice MMCs with similar spatial and seasonal distribution. Water ice was detected as high as 80 km. Systematic detections of aerosol layers have been made using THEMIS onboard Mars Odyssey (McConnochie et al. 2010), and differentiating dust layers from MMCs through radiative transfer analysis led to results consistent with the previous unambiguous MMCs detections. Moreover, numerous detections of MMCs by THEMIS occurred in the northern winter mid-latitudes (McConnochie et al. 2010) where OMEGA had detected very few CO₂ MMCs. Sefton-Nash et al. (2013) used the Mars Climate Sounder (MCS) onboard MRO to detect mesospheric aerosol layers using different wavelength channels and similarities with previous MMCs detections were highlighted, although with less constraints on the cloud composition.

Clancy and Sandor (1998) had suggested that the formation mechanism for CO₂ MMCs required low temperatures created by gravity waves in the temperature minima of the larger scale tidal waves. The correlations between the LMD-GCM-simulated temperature minima in the mesosphere with observations of CO₂ MMCs (Gonzalez-Galindo et al. 2011), and the coincidences between areas where atmospheric conditions are favorable to the upward propagation of gravity waves and those of CO₂ MMCs observations (Spiga et al. 2012), strengthen the case for this proposed formation pathway. In addition, Listowski et al. (2014) validated this scenario with one-dimensional detailed microphysics modelling, arguing for an exogenous source of cloud nuclei—most likely MSPs—to explain the observed MMC opacities. Recently, Nachbar et al. (2016) measured in the laboratory the nucleation and growth of CO₂ ice on small ($r < 4~\mbox{nm}$) iron oxide and silica particles, representing MSPs at conditions close to the mesosphere of Mars. They showed that significant supersaturation is required: the characteristic temperatures for the onset of CO₂ ice nucleation are 8–18 K below the CO₂ frost point temperature, depending on MSP particle size.

5.3 Stratospheric Clouds on Earth and Venus

An aerosol layer of H₂SO₄–H₂O droplets (commonly referred to as the Junge layer) occurs in the Earth’s lower stratosphere between ∼20 and 28 km (Kremser et al. 2016). Single particle analyses of these aerosols at mid-latitudes show that roughly half the particles contain 0.5–1.0 wt% meteoric iron (Cziczo et al. 2001). Inside the Arctic polar vortex up to 75% of aerosol particles can contain refractory material i.e. thermally stable residuals which are almost certainly MSPs, transported downwards by the prevailing meridional circulation during winter (Curtius et al. 2005; Weigel et al. 2014). These large concentrations of refractory aerosol are a regular feature, with the accumulation starting during December and reaching its highest level during March in the Arctic. Balloon-borne measurements above 30 km over Antarctica show that MSPs most likely nucleate the H₂SO₄ droplets above the main Junge layer (Campbell and Deshler 2014).

Polar stratospheric clouds (PSCs) form in the winter polar stratosphere when the temperature falls below 197 K; they are responsible for activating chlorine during the polar night, leading to severe ozone depletion the following spring (Kremser et al. 2016). PSCs consist of frozen nitric acid trihydrate (NAT) particles, and recent modelling of PSC formation shows that heterogeneous nucleation is necessary to produce good agreement with observations (Engel et al. 2013; Hoyle et al. 2013). However, an unsolved problem is the actual nature of the ice nuclei. Saunders et al. (2012) showed that the Fe and Mg in MSP analogue particles dissolves in concentrated H₂SO₄ at low temperatures, leaving insoluble silicate cores. These cores, which have been observed in single particle mass spectrometry measurements of stratospheric aerosols (Murphy et al. 2014), may provide the PSC nuclei. A recent laboratory study has shown that analogues of silica cores and unablated meteoric material both trigger the nucleation of NAT (James et al. 2017a).

The sulfuric acid clouds of Venus are characterized by their high visible albedo (>0.8) and optical thickness (>30), and the nearly total coverage of the planet by their 20 km thick layer. A salient feature of the clouds is the markings or contrasts observed at ultraviolet wavelengths, although the absorber causing these markings has still not been identified. The clouds are essentially a product of atmospheric chemistry, with the photochemical production of sulfuric acid vapor near the cloud tops functioning as the source for formation of the acid droplets. The ensuing microphysics takes care of the cloud droplet growth through condensation and coagulation, and the droplets are redistributed vertically through sedimentation and vertical atmospheric motions, which are particularly vigorous in the lowest, turbulent cloud layers. The three cloud layers are found between 48 and 70 km altitude in the atmosphere, embedded in a haze that surrounds them both above and below.

Most observations show that the clouds are formed mainly of concentrated sulfuric acid solution droplets. One curious phenomenon is the blue absorption (400–500 nm) in the upper clouds between 55 and 70 km, which is responsible for the yellowish appearance of the planet. Krasnopolsky (2006) concluded that the most plausible candidate is a ∼1% solution of ferric chloride (FeCl₃) in H₂SO₄ droplets, which matches well the blue absorption. Support for this comes from observations of Fe and Cl by X-ray Fluorescence Spectroscopy, made by the VENERA 14 and VEGA landers.

The Pioneer Venus probe performed the first and only in situ measurements of cloud particle properties within the cloud layers (Knollenberg and Hunten 1980). This showed that the Venus cloud particle size distributions exhibit two modes of sulfuric acid droplets (mode 1: $r \sim 0.2~\upmu \mbox{m}$; mode 2: $r \sim 1~\upmu \mbox{m}$) throughout the clouds (Knollenberg and Hunten 1980). A mode 3 was deduced from the Pioneer Venus measurements as well, but this remains controversial since the measurements could be explained by a large ($r \sim 3\mbox{--}4~\upmu \mbox{m}$), potentially crystalline particle mode, or by a misinterpretation of the data due to instrument calibration (Toon et al. 1984). The presence of crystalline particles and exotic trace substances such as P₄O₁₀ and Fe₂Cl₆ has also been suggested (Andreychikov et al. 1987; Krasnopolsky 1989, 2017) to explain these controversial mode 3 particles.

Although the photochemical production of H₂SO₄ molecules provides a source of condensable vapour, the pathways for cloud droplet formation are uncertain. Although direct formation of droplets through homogeneous nucleation is possible, heterogeneous or ion-induced nucleation should be energetically favoured. Recent theoretical and experimental studies of H₂SO₄–H₂O particle formation have developed state-of-the-art descriptions of the homogeneous and ion-induced particle formation processes (Duplissy et al. 2016; Merikanto et al. 2016), enabling their application to Venus. Modelling of ionization in Venus’ atmosphere indicates a significant level of ionization at the cloud formation altitudes around 70 km (Michael et al. 2009; Plainaki et al. 2016). Many models have considered heterogeneous nucleation on soluble or insoluble particles (James et al. 1997). The latter could be provided either by: polysulfur (Young 1983), formed through atmospheric chemistry; small particles of FeCl₃, whose source is Fe₂Cl₆ vapour produced by the action of HCl on the hot ferric surface planetary surface (Krasnopolsky 2006); or an exogenous source of nuclei provided by MSPs (Gao et al. 2014).

6 Impacts on Atmospheric Chemistry

6.1 Earth

Apart from their role in cloud formation (Sect. 5), MSPs have the potential to influence gas-phase chemistry in the Earth’s middle atmosphere. Starting in the upper mesosphere, rocket-borne measurements show that between 75 and 95 km the electron density is significantly depleted compared to the positive ion density. While this had long been attributed to the formation of negative ions, recent observations show that the electrons are actually attached to MSPs (e.g. Friedrich et al. 2011), because negative ion formation is shut down in the presence of atomic oxygen (Plane et al. 2014).

During winter, MSPs are rapidly transported down to the stratosphere within the polar vortex, on a timescale of a month or so (Bardeen et al. 2008). It has been proposed that metal-rich MSPs can remove trace acidic vapours such as H₂SO₄ and HNO₃ in the middle atmosphere. Balloon-borne mass spectrometry measurements show unexpectedly low H₂SO₄ concentrations above 40 km (Arijs et al. 1985), which can be explained if the uptake coefficient for H₂SO₄ on MSPs is greater than 0.01 (Saunders et al. 2012). Frankland et al. (2015) used a laboratory measurement of the uptake coefficient of HNO₃ on MSP analogue particles to show that heterogeneous removal on MSPs in the winter polar vortex between 30 and 60 km should provide an important sink for HNO₃. Similarly, heterogeneous uptake of the HO₂ radical on MSPs, which is sensitive to the fraction of Fe in the particles, should significantly alter the general radical chemistry of the nighttime polar vortex (James et al. 2017b).

6.2 Mars

Observations of methane (CH₄) in the Martian atmosphere have received a great deal of attention because of the possibility of a subsurface biological source, although the serpentinization reaction between water and olivinic rocks is a potential abiotic source. In addition, the organic matter deposited by exogenous sources may be a significant source of CH₄, which has been produced in the laboratory by irradiating simple organics such as glycine mixed with Martian analogue surface materials (e.g. Stoker and Bullock 1997), as well as carbonaceous chondrites (e.g. Murchison CM2) (Keppler et al. 2012; Schuerger et al. 2012). Later work quantified the amount of CH₄ produced, indicating that UV irradiation of accreted cosmic dust could explain a portion of the globally averaged CH₄ abundance (Moores and Schuerger 2012). Since CH₄ has a relatively short lifetime on Mars (≤330 yrs) (Atreya et al. 2007), to be observed in the Martian atmosphere it must be resupplied on a geologically continuous timescale and persist long enough to accumulate to detectable concentrations. On a pure mass balance basis, the flux of organic carbon from interplanetary dust (e.g. Flynn 1996) is probably sufficient to produce up to 11 ppbv of CH₄ in the Martian atmosphere, if it does not ablate on entry. The total amount of organic carbon observed mixed with surface materials, measured in the Viking, Phoenix and MSL missions, is consistent with organic delivery via IDPs (Moores and Schuerger 2012).

However, this source does not easily explain the seasonal, temporal, diurnal and plume fluctuations of CH₄ that have been reported (Schuerger et al. 2012). A large number of measurements of Martian CH₄ have been published over the past 20 years, including telescopic observations from Earth, remote sensing from orbiting spacecraft, and in situ surface measurements (Webster et al. 2015). The values reported have ranged from 0.7 ppbv to over 100 ppbv. In some cases the releases that are observed are isolated events (Mumma et al. 2009; Webster et al. 2015), while in other cases a repeating seasonal dependence is reported with CH₄ levels declining to near zero in between spikes. In all telescopic cases, large amounts of CH₄ must be invoked—for instance, the ∼45 ppbv peak plume observed by Mumma et al. (2009) would have required 19,000 tons of CH₄. The smallest (sub-ppb) levels were measured by tunable diode laser spectroscopy on the Mars Science Laboratory at Gale crater (Webster et al. 2015).

While none of these observations are contemporaneous and therefore no single observation explicitly contradicts another, questions have been raised about the reliability of any single result or combination of results (e.g. Zahnle et al. 2011). Additionally, the long lifetime of CH₄ in the Martian atmosphere under normal conditions means that any large release of CH₄ reported should be rapidly mixed throughout the Martian atmosphere and persist for long periods, unless an unknown rapid CH₄ destruction process exists (Lefevre and Forget 2009). This brings into question the high variability reported in the literature: it is not the larger spikes of CH₄ that are most difficult to reconcile with our understanding of Martian CH₄ chemistry, but rather the incidence of low CH₄ observations that are most challenging to explain. This is especially problematic for exogenous sources. In order for the low-CH₄ baseline of 0.7 ppbv (Webster et al. 2015) to be explicable, either: (1) conversion rates of exogenous organic carbon to CH₄ must be surprisingly low (<6%); (2) the rate of organic infall from IDPs is over-estimated by a factor > 15, or much of the incoming carbon ablates and is converted to CO₂; (3) the carbon content of IDPs is overestimated by a similar factor; (4) somehow the in-falling IDPs are rapidly buried or otherwise prevented from being irradiated by UV; (5) the destruction pathway for organic carbon on Mars does not lead to CH₄; or (6) some combination of these effects.

Recently, Fries et al. (2016) have posited that there is a way to reconcile all of the measurements that have been made to date, including the low values of CH₄. They note an apparent strong correlation between the times of high CH₄ observed concentrations and the timing of cosmic dust delivery via meteor streams. They then hypothesize that these meteor stream deliver most of the carbonaceous material to Mars, which is subsequently photolyzed to CH₄ by the mechanism of Schuerger et al. (2012). In this way, seasonally repeating observations are the result of the inherent seasonality of the meteor streams, which recur at the same point in Mars’ orbit. The isolated plumes represent Mars passing through unusually dusty segments of the meteor streams, yielding a higher than usual rate of delivery of organic carbon. In order to prevent all of these events from interfering with one another, Fries et al. (2016) propose that the carbonaceous material is actually converted to CH₄ while still high in the Martian atmosphere where CH₄ photolysis lifetimes are potentially less than a year. However, there have been recent objections to this hypothesis. First, Roos-Serote et al. (2016) have questioned the timing correlation of Fries et al. (2016) by applying statistical methods to a larger catalogue of meteor streams. Second, observations made by the MAVEN spacecraft when Comet Siding Spring passed close to Mars in October 2014 were used to show that between 2700 kg and 16,000 kg of fresh carbon-rich dust entered the Martian atmosphere (Schneider et al. 2015), in only ∼5400 s (Tricarico et al. 2014). This global accretion rate of between 0.5 kg s⁻¹ and 3.0 kg s⁻¹ is at least an order of magnitude higher than the mass delivered by a typical intense meteor stream, and is still too small by ∼3 orders of magnitude to result in a visible CH₄ plume (Crismani et al. 2017a).

The solar wind implants significant concentrations of noble gases (e.g. He and Ne) in cosmic dust particles while they are in interplanetary space (Flynn 1997). During the atmospheric entry of a dust particle, some or all of these implanted noble gases will be released directly into the atmosphere; and, if the particle does not completely ablate and reaches the surface, the remaining noble gases may be released if the particle decomposes, or by episodic surface heating. Because Mars has a much lower atmospheric mass compared with Venus and Earth, the atmosphere of Mars is more significantly influenced by this exogenous source of noble gases: over the past 3.6 billion yr, interplanetary dust particles are estimated to have contributed quantities of ³He, ⁴He, ²⁰Ne and ²²Ne that are comparable to the current total atmospheric inventories of these isotopes; furthermore, the He and Ne isotope ratios are distinctly different than assumed to outgas from the planetary interior (Flynn 1997). See further discussion of this topic in Sect. 7.1.

6.3 The Giant Planets; Titan, Triton and Pluto

The photochemical implications of an influx of external material into the atmospheres of the giant planets are significant. As reported by Feuchtgruber et al. (1997, 1999), all of the giant planets and Titan contain oxygen-bearing species (e.g., H₂O, CO, CO₂) at levels typically too large to be explained by upwelling from the deep interior. Additionally, many other observations of external oxygen-bearing species at the giant planets have been reported, including at Jupiter (from both the Shoemaker-Levy 9 impact and background cosmic dust) (e.g., Prather et al. 1978; Bergin et al. 2000; Bezard et al. 2002; Lellouch et al. 2002, 2006; Cavalie et al. 2008a, 2012, 2013), Saturn (deGraauw et al. 1997; Bergin et al. 2000; Moses and Bass 2000; Moses et al. 2000; Prange et al. 2006; Cavalie et al. 2009; Abbas et al. 2013), Uranus (Marten et al. 1993; Encrenaz et al. 2004; Cavalie et al. 2008b; Teanby and Irwin 2013; Cavalie et al. 2014; Orton et al. 2014), and Neptune (Marten et al. 1993; Naylor et al. 1994; Lellouch et al. 2005; Hesman et al. 2007; Fletcher et al. 2010; Luszcz-Cook and de Pater 2013; Irwin et al. 2014). While each of the giant planets presents unique details with respect to the possible source(s) of the external oxygen and its subsequent chemical processing, observations across all four planets clearly demonstrate both internal and external sources. A more complicated question to answer is the relative contribution amongst these sources, including deep internal oxygen that is upwelled, compared with a variety of exogenous oxygen sources including cometary impacts (e.g., the Shoemaker-Levy 9 impact at Jupiter Zahnle and MacLow 1994), ring sources (e.g., Saturn’s E-ring), and the ablation of interplanetary dust.

To assess the relative importance of the interplanetary dust influx to the giant planets one can either, to first order, compare observational-based calculations of the effective external oxygen influx at each planet with predictions from a dynamical dust model; or, for a more detailed approach, one can use ablation profiles as input to photochemical models. Poppe (2016) performed a first-order comparison of oxygen influx to the giant planets from interplanetary dust modeling while Moses and Poppe (2017) recently conducted a photochemical model study using the interplanetary dust ablation profiles in each of the giant planet atmospheres (Fig. 4). In Fig. 6, the effective oxygen influxes from interplanetary dust grains are shown for each planet in black and observational estimates and/or constraints are shown in colour (Feuchtgruber et al. 1997; Moses and Bass 2000; Moses et al. 2000; Bezard et al. 2002; Lellouch et al. 2002, 2005; Cavalie et al. 2010, 2014; Orton et al. 2014).

Fig. 6

A comparison of effective molecular oxygen influx rates to each of the giant planets from interplanetary dust grains (black) to various observational constraints (colour lines and points) (adapted from Poppe 2016)

Starting at Neptune, the IDP model influx of oxygen is consistent with observations of H₂O and CO₂ (Feuchtgruber et al. 1997); however, measurements by Lellouch et al. (2005), Hesman et al. (2007), and more recently by Luszcz-Cook and de Pater (2013) have shown that CO is highly enriched at in Neptune’s stratosphere, with an estimated influx of ${\sim}5 \times 10^{7}~\mbox{cm}^{-2}\,\mbox{s}^{-1}$ (green triangle, Fig. 6)—far more than can be attributed to the interplanetary dust flux of ${\sim} 7 \times 10^{5}~\mbox{cm}^{-2}\,\mbox{s}^{-1}$. This discrepancy and the facts that CO is enriched in Neptune’s stratosphere relative to its troposphere (e.g., Fletcher et al. 2010; Irwin et al. 2014) and that CO is thermochemically favored at higher temperatures argues strongly for the deposition of oxygen by cometary impacts and formation of CO in the associated high-temperature shock chemistry. At the present moment, interplanetary dust plays a minor role in oxygen-bearing photochemistry at Neptune.

At Uranus, the estimated interplanetary dust influx is consistent with observations by Feuchtgruber et al. (1997), Cavalie et al. (2014), and Orton et al. (2014) for the total amount of exogenous oxygen influx, approximately 10⁵ O atom cm⁻² s⁻¹. This suggests that the dust influx can deliver the observed stratospheric oxygen; indeed, recent modeling by Moses and Poppe (2017) of oxygen photochemistry from ablated dust grains in the Uranian atmosphere provides a satisfactory fit to the relative observed abundances of H₂O, CO, and CO₂ by freely fitting the relative form in which the ablated oxygen is deposited into the atmosphere (i.e., as H₂O, CO, and/or CO₂). The best-fit ratio is 30% H₂O, 69% CO, and 0.8% CO₂. As the influx of interplanetary dust can thus explain not only the overall oxygen influx but also the species-specific observations, one possible conclusion is that dust is the primary source; however, given the direct observations or evidence of cometary impacts at Jupiter, Saturn, and Neptune (Lellouch 1996; Lellouch et al. 2005; Cavalie et al. 2012) and estimates from Poppe (2016) as to the timescales of cometary CO dissipation relative to estimated impact rates from Levison and Duncan (1997) (i.e., a km-sized comet should impact Uranus every ∼700 years whereas eddy diffusion on Uranus would take ∼16,000 years to remove the cometary CO), cometary impacts most likely contribute an oxygen influx at Uranus that is comparable to that of interplanetary dust. Note also that dust of planetary origin (potentially from the rings and/or moons of Uranus) can also affect the Uranian atmosphere (e.g., Rizk and Hunten 1990).

At Saturn, the oxygen influx to the atmosphere is potentially a mix of several sources, including the prodigious amount of water from Enceladus, both in the form of neutral water vapor and E-ring grains (Cassidy and Johnson 2010; Fleshman et al. 2013), the main ring system (i.e., “ring rain”) (O’Donoghue et al. 2013; Moore et al. 2015), and cometary impacts (Cavalie et al. 2010). Thus, as shown in Fig. 6, it is unsurprising that the effective oxygen influx from interplanetary dust estimated by Poppe (2016) falls more than an order-of-magnitude short in explaining the inferred atmospheric oxygen influx based on remote observations (Feuchtgruber et al. 1997; Moses and Bass 2000; Moses et al. 2000; Cavalie et al. 2010). As further concluded by Moses and Poppe (2017), interplanetary dust plays a minor role in the delivery of oxygen and other exogenous species to Saturn’s atmosphere.

Frankland et al. (2016) investigated the role of meteoric material in converting acetylene (C₂H₂) into C₆H₆ in Titan’s atmosphere. Because of the relatively small mass of the moon, dust particles enter at low speeds (<29 km s⁻¹) and encounter an atmosphere with a large scale height (∼40 km, so the pressure increases gradually compared to the Earth or Venus). Much of the incoming mass consists of dust particles between $r = 0.4\mbox{ and }10~\upmu \mbox{m}$ from Kuiper belt and Oort Cloud comets; less than 1% of mass loss occurs through sputtering, and few particles reach a temperature above 1750 K where melting and significant evaporative mass loss would occur (Sect. 3). Hence, a much smaller fraction of the particles ablate compared with the terrestrial planets, and unablated meteoroids—rather than MSPs—provide most of the surface area for heterogeneous chemistry. The kinetics of C₂H₂ uptake and cyclo-trimerization into C₆H₆ were measured at low temperatures in the laboratory and input into a 1D model, which shows that the heterogeneous synthesis of C₆H₆ on cosmic dust is likely to be competitive with the gas-phase production of C₆H₆ between 80 and 120 km (Frankland et al. 2016).

Finally, at Jupiter, a more puzzling situation exists. Since the atmospheric state of Jupiter is strongly perturbed by the Shoemaker-Levy 9 impact in the southern hemisphere, constraints have been derived for non-SL9 input mainly from northern hemispheric observations (e.g., Lellouch et al. 2002). The interplanetary dust model of Poppe (2016) predicts an effective oxygen influx rate of ${\sim}10^{7}~\mbox{cm}^{-2}\,\mbox{s}^{- 1}$; however, Lellouch et al. (2002) have placed a rather stringent limit on the H₂O influx to Jupiter of ${<}10^{5}~\mbox{cm}^{-2}\,\mbox{s}^{-1}$. As the Jupiter dust mass influx estimates are perhaps the most certain of all four of the giant planets due to observations by the Galileo Dust Detection System (e.g., Krivov et al. 2003; Sremcevic et al. 2003), there seems little reason to doubt the Poppe (2016) values. Thus, the incoming oxygen from interplanetary dust must be sequestered in other forms such as CO or CO₂. Bezard et al. (2002) have estimated a CO influx rate of $(1.5\mbox{--}10) \times 10^{6}~\mbox{cm}^{-2}\,\mbox{s}^{- 1}$ (which is consistent with the interplanetary dust influx), but attributed this influx to smaller, km-sized and sub-km sized comets, as the shock chemistry from cometary impacts will thermo-kinetically favor the production of CO over H₂O. While this process could potentially provide the measured CO, Moses and Poppe (2017) provide an alternative solution where interplanetary dust provides the appropriate balance of H₂O, CO, and CO₂ by stipulating relative species deposition fractions from ablated dust grains of 98% CO, 1.4% CO₂, and 0.6% H₂O. The speciation of ablated interplanetary dust grains currently remains an unknown, so this solution provided by Moses and Poppe (2017) awaits confirmation.

Two other objects with atmospheres deserve brief mention here: Triton and Pluto, which both have cold, tenuous, N₂-dominated atmospheres driven in large part by the vapour sublimation of ices on their surfaces (Broadfoot et al. 1989; Elliot et al. 1989; Tyler et al. 1989; Yelle et al. 1991; Krasnopolsky et al. 1993). Both atmospheres also contain other minor species, such as CH₄, CO, and various hydrocarbons (Lellouch et al. 2009, 2010; Gladstone et al. 2016), and both atmospheres are observed to have clouds and/or haze layers (Yelle et al. 1991, 1995). At Triton, observations of ion layers below the main ionospheric peak could be evidence of the presence of metallic ions introduced from meteoric ablation (cf. Sect. 4.2). MSPs could also play a role in the formation of the observed haze layers (Yelle et al. 1995; Pesnell et al. 2004). Pesnell et al. (2004) have to date performed the only study of meteoroid ablation in the atmosphere of Triton. By considering both stony and icy meteoroids at characteristic velocities of 10 and 15 km s⁻¹, they found that stony meteoroids ablate 10–75% of their mass before impacting Triton’s surface, while icy meteoroids ablate at least 70% of their mass before surface impact. Combining an estimate of the mainly EKB dust influx (Poppe 2016) which is assumed to be 42% water ice (Moses and Poppe 2017), with the ablation calculations of Pesnell et al. (2004), yields an equivalent O influx to Triton’s atmosphere of ${\sim}10^{5}~\mbox{cm}^{-2}\,\mbox{s}^{-1}$. Krasnopolsky (2012) included an oxygen influx of $2 \times 10^{6}~\mbox{cm}^{-2}\,\mbox{s}^{-1}$ (a factor of ∼20 higher) in a photochemical model of Triton’s atmosphere and found that meteoric H₂O is efficiently converted to O and ultimately CO via interactions with molecules such as CH _x , CN, and CNN. This production method was found to be higher than loss to space, and so Krasnopolsky (2012) concluded that such CO would condense on the surface of Triton. It is unclear if such a conclusion still holds in the case of the relatively lower meteoric O influx based on the revised dust influx (Poppe 2016).

At Pluto, a similar situation is expected to be present, albeit with less meteoric influx compared to Triton due to the lack of gravitational focusing by a giant parent planet (Triton’s meteoric influx is enhanced by a factor of ∼10 relative to interplanetary space due to its position deep inside Neptune’s gravity well). A preliminary study of meteoric ablation in Pluto’s atmosphere, using EKB dust grain mass and velocity distributions from Poppe (2015), indicates that water ice grains will completely ablate before reaching Pluto’s surface, while silicate grains only partially ablate, similar to the Pesnell et al. (2004) results for Triton. The Krasnopolsky (2012) model predicts that water introduced from meteoric ablation to Pluto’s atmosphere will react (photochemically) with the abundant CO to produce CO₂, which then condenses on the surface. More recently, Wong et al. (2017) have examined a detailed photochemical model of Pluto’s atmosphere constrained by New Horizons observations, including a presumed meteoric dust/water flux from Poppe (2015). This influx leads to predicted values for oxygen-bearing species in Pluto’s atmosphere such as CO (the third-most abundant gas in the atmosphere), H₂O, H₂CO, and CO₂. While the latter three species have yet to be detected, their eventual identification would provide strong constraints on the dust/oxygen influx predicted by Poppe (2015, 2016).

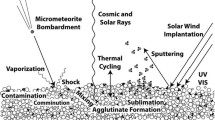
7 Surface Accretion of Dust and Meteorites

The contribution by dust and meteorites to planetary surfaces was demonstrated by the Apollo samples. Elemental analyses showed that the Lunar regolith and regolith breccias had elevated levels of Ir, Au, Zn, Cd, Ag, Br, Bi, and Tl compared to the ordinary Lunar rocks in a pattern that indicated the addition of 1.5% to 2.0% carbonaceous chondrite-like material to the regolith (Keays et al. 1970; Anders et al. 1973). In the case of the Earth, the mass flux at the top of the atmosphere has been estimated by combining results from satellite impact measurements for small particles, radar meteors for intermediate size objects, and the cratering record for large objects, as discussed by Peucker-Ehrenbrink et al. (2016). As shown in Fig. 7, the mass-frequency distribution is bimodal, with peaks corresponding to the continuous, planet-wide input of dust and the infrequent impact of large bodies, with a minimal contribution from objects in the intermediate size range. Measurements of impacts onto the Long Duration Exposure Facility, which was in low-Earth orbit for about 69 months, indicate that the accretion rate of cosmic dust into the Earth’s atmosphere is $110 \pm 55~\mbox{t}\,\mbox{d}^{-1}$ in the current era (Love and Brownlee 1993). This is at least 100 times larger than the annual influx of meteorites (Bland et al. 1996), with particles in the narrow mass range from 10⁻⁸ to 10⁻³ g ($r = {\sim}10\mbox{--}460~\upmu \mbox{m}$) contributing more than 80% of the total mass flux of meteoritic material in the 10⁻¹³ to 10⁶ g mass range incident on the Earth (Hughes 1978; Carrillo-Sánchez et al. 2016). Modeling by Carrillo-Sánchez et al. (2016) of the dust up to 500 μm in diameter indicates that the total mass input is $43\pm 14~\mbox{t}\,\mbox{d}^{-1}$, with 35.4 t d⁻¹ surviving as either unmelted particles or melted spherules, and the remaining 7.9 t d⁻¹ being deposited in the upper atmosphere as ablated atoms. The dust accretion rate was likely much greater during the first 0.6 billion years of Solar System history, when asteroids and comets were more abundant in the inner Solar System as evidenced by the higher impact rate of large objects on the Moon during the Late Heavy Bombardment (Hartmann et al. 2000).

Fig. 7

The estimated mass accretion rates of extraterrestrial objects at the top of the Earth’s atmosphere are dominated by two peaks. The peak at small masses is caused by the continuous accretion of cosmic dust, while the peak at large masses results from the infrequent impacts of large bodies (adapted from Kyte and Wasson 1986)

In the case of planets with atmospheres, some of this extraterrestrial material vaporizes during atmospheric deceleration (Sect. 3). With the exception of the volatile gases released into the atmosphere, all of this material, whether as surviving objects or recondensed MSPs, eventually accretes onto the planet’s surface. Unlike the Lunar case, where the impact of extra-Lunar material is the major regolith-generating mechanism, terrestrial soil is generated by a variety of more rapid weathering mechanisms, which results in a greater dilution of the extraterrestrial component, thus making it more difficult to detect. The most dramatic effects on the surface composition of the terrestrial planets are for the siderophile elements, which are depleted in the surface material and concentrated in the metallic core during planetary differentiation but are abundant in undifferentiated extraterrestrial materials, and a few isotopes that are significantly enriched in extraterrestrial materials, generally by cosmic ray interactions in space. The elemental effects, particularly for Ir, Os, and Pt, and isotopic effects, particularly for He, Re–Os, and Cr, of the meteoritic contributions to the composition of terrestrial sediments have been reviewed in detail by Kyte (2002), Peucker-Ehrenbrink (1996), and Peucker-Ehrenbrink et al. (2016).

7.1 Siderophile and Isotope Contributions to the Earth’s Surface

Pettersson and Rotschi (1950) found that Ni, the most abundant of the siderophile elements, was present in Central Pacific Ocean sediment cores in significantly higher concentrations than in continental rocks and sediments, and they suggested this Ni might be partly derived from cosmic dust settling over the Earth’s surface. Bonner and Lourenqo (1965) attempted to use the Ni abundance in Pacific Ocean cores to measure the accretion rate of extraterrestrial material onto the Earth. However, their value was more than an order of magnitude larger than the currently accepted value, most likely because of Ni mobilization in the oceans.

Iridium has been used most commonly as a tracer of the extraterrestrial component in surface materials because of its high concentration in chondritic material, ${\sim}10^{4}$ times the concentration found in crustal rocks (Palme et al. 1978), and its easy detection by neutron activation analysis. Barker and Anders (1968) used the Ir and Os concentrations in dated deep-sea sediments to infer a value for the infall rate of extraterrestrial material that is in good agreement with the current estimates. The most significant elemental perturbations in both deep-sea sediments and ice cores occur for Ir, Os, and Re (Lal and Jull 2003). The available evidence suggests the input rate has been relatively constant over the past 70 million years (Kyte 2002), allowing the Ir concentration to be used to determine the deposition rates of sediments as well as polar ice and snow layers. As discussed in Sect. 5.1, Ir has also been used to determine the surface deposition rate of MSPs.

One major deviation from this long term average was identified in the clay layer at the Cretaceous-Tertiary boundary. The Ir excesses in deep-sea limestones exposed in Italy, Denmark, and New Zealand, which are 30, 160, and 20 times their respective background levels at the time of the Cretaceous-Tertiary extinctions 65 Myr, were linked to the global deposition of debris from the impact of a ∼10 kilometer diameter asteroid (Alvarez et al. 1980). Clear confirmation of the meteoritic contribution to these boundary clays was presented by Shukolyukov and Lugmair (1998), who found a ⁵³Cr/⁵²Cr ratio consistent with the ratio in carbonaceous meteorites but inconsistent with the terrestrial value. Localized enhancements of Ir and Au, comparable with those at the Cretaceous-Tertiary boundary, were identified in a sediment from the Antarctic Ocean (Kyte et al. 1981), indicating the impact of an asteroid >1 km in diameter ∼2.15 Myr ago (Gersonde et al. 1997).

Because of their high surface area-to-mass ratio compared to larger bodies, interplanetary dust particles have very high concentrations of solar-wind implanted ions, particularly the most abundant solar wind elements, H and He. Since the solar wind ³He/⁴He ratio is much higher than that in any terrestrial material (Nier and Schlutter 1990), interplanetary dust that survives atmospheric entry without outgassing perturbs the He isotopic ratio in deep-sea sediments. Ozima et al. (1984) found an approximately inverse relationship between ³He concentrations and the accumulation rate of Pacific surface sediments, which they attributed to the influx of interplanetary dust. Ozima et al. (1984) calculated an influx rate of only 5 t d⁻¹, nearly an order of magnitude lower than the influx estimates derived from most other techniques (Barker and Anders 1968; Kyte and Wasson 1986; Love and Brownlee 1993; Peucker-Ehrenbrink 1996; Plane 2012; Carrillo-Sánchez et al. 2016). This is because the ³He is most concentrated in the fine fraction of the interplanetary dust, ∼2 to 5 μm radius (Lal and Jull 2005), and is degassed from most larger particles during atmospheric entry, never making it to the sediments. Thus, the ³He content in sediments is not a measure of the total influx of extraterrestrial matter, rather it is a tracer of the fine fraction of the interplanetary dust complex (Fig. 7).

While Ir excesses serve to identify large impacts onto the Earth, the ³He contribution has been used to identify increases in the flux from major, dust-producing events in the past. Farley (1998) measured a factor of 5 increase in the ³He flux over a 2 Myr interval ∼35 Myr ago, and attributed this the accretion of dust from a comet shower. Later work by Mukhopadhyay et al. (2001), covering the interval from 70 to 40 Myr ago, found a factor of 2–4 increase in the ³He accretion rate about 55 Myr ago, but no evidence for variations of more than a factor of 2 over the remainder of that interval. Farley et al. (2006) also identified a factor of 4 increase in the ³He concentration 8.3 Myr ago, which they attributed to the dust produced by the collisional disruption of the 150 km diameter asteroid that created the Veritas family.

Lal and Jull (2003) modeled the contributions of ³He, ¹⁰Be, ¹⁴C, and ²⁶Al to terrestrial sediments by both interplanetary dust and fragments produced by the atmospheric disintegration of larger meteors. They concluded that the rate of production of ¹⁰Be and ¹⁴C in the Earth’s atmosphere by galactic cosmic rays significantly exceeds the contribution from cosmic dust. In contrast, their modelling indicated that ²⁶Al is mostly meteoric, and they suggested that it should be possible to observe high ²⁶Al concentration pulses in sediments during any periods of enhanced meteoroid fluxes in the past (Lal and Jull 2003).

Lastly, Dhomse et al. (2013) and Brooke et al. (2017) have modelled the mass deposition flux of MSPs over the earth’s surface, using two different global circulation models. The strongest deposition occurs over northern and southern mid-latitudes, reflecting the geographical distribution of deep stratosphere-troposphere exchange which is driven both by large mountain ranges and storm tracks over the North Atlantic, North Pacific and Southern Oceans. The Southern Ocean between 50 and 60^∘S is where the supply of bio-available iron to phytoplankton is limited (Johnson 2001). The modelled input of cosmic Fe contained in MSPs is ∼2–5% of the Aeolian dust input into the Southern Ocean. However, unlike continental mineral dust which has a low solubility (estimates vary from <1 to 10%), the MSP Fe should be in the form of highly soluble ferrous/ferric sulfate after processing in the stratospheric sulphate layer (Sect. 5.3) Thus, the input of bio-available Fe from cosmic dust should be 50–400% of the soluble Aeolian dust input. This would have significant climate implications because increased primary production will draw down CO₂ which is then exported to the deep ocean (Dhomse et al. 2013).

7.2 Organics and Water from Dust and Meteoroids

The high temperatures reached during differentiation likely destroyed any organic matter that accreted when the Earth formed from the protoplanetary disk. The presence of solar wind He in $r \sim 5~\upmu \mbox{m}$ interplanetary dust particles captured in the stratosphere (Rajan et al. 1977) demonstrates that small, slow particles survive atmospheric deceleration with minimal heating (Whipple 1950; Fraundorf 1980). The gentle accretion of interplanetary dust to the surface of the primitive Earth could have contributed a layer rich in organic matter, including biologically important compounds that did not form by abiotic synthesis on Earth (Anders 1989). While the organic matter in meteorites has been well characterized (Pizzarello et al. 2006), the small size of the interplanetary dust has precluded full characterization. However, these interplanetary dust particles contain a high abundance of carbon (Thomas et al. 1993), from a few to over 90% by volume, including percent-levels of both carbonyl (C=O) and aliphatic hydrocarbons (C–H₃ and C–H₂) (Flynn et al. 2003). Using the Fraundorf (1980) entry heating model and the C concentration from Thomas et al. (1993), Flynn et al. (2004) estimated that, in the current era, interplanetary dust contributes ∼0.04 t d⁻¹ of unpyrolized organic matter to the surface of the Earth, and this contribution is likely to have been much greater during the Late Heavy Bombardment.

Bradley et al. (2014) demonstrated that solar wind irradiation of the surfaces of interplanetary dust particles deposits H⁺ ions, which then react with oxygen in the minerals to produce water. This result indicates that slow, small interplanetary dust particles can simultaneously deliver organic carbon and water to the surface of the Earth.

7.3 Dust and Meteoritic Contributions to Mars

The accretion rate of cosmic dust in the Martian atmosphere has recently been estimated to be 2–3 tonnes sol⁻¹, based on modelling observations of the Mg⁺ layer around 90 km (Crismani et al. 2017b). However, the MSP and meteorite contribution to the surface of Mars is less well constrained than for Earth. The first in situ elemental analysis of Mars soils, by the Viking landers, indicated that the Mars soil composition was inconsistent with typical basaltic rock fragments but could be fit by a mixture of basaltic rock fragments and meteoritic material (Clark and Baird 1979).

Flynn and McKay (1990) extrapolated from the measured dust accretion rate at Earth, finding that 2–29% of the Martian regolith was contributed by cosmic dust. Morris et al. (2000) found that the compositions of the soils analyzed by the Sojourner Rover were consistent with up to 22% meteoritic material. The Alpha Particle X-ray Spectrometers on the Mars Exploration Rovers measured 16 elements (Na, Mg, Al, Si, P, S, Cl, K, Ca, Ti, Cr, Mn, Fe, Ni, Zn, and Br) in the soils and rocks near the two landing sites. Yen et al. (2006) used the Ni content to indicate that the Mars soil samples and some of the sedimentary rocks contain, on average, 1–3% contamination from chondritic material. As is the case for the Earth, ³He in the regolith should serve as a tracer of the fine interplanetary dust flux, while siderophiles such as Ir are a tracer of the total dust and meteoritic contribution. In the case of planets with thin atmospheres, like Mars, modelling by Lal and Jull (2003) indicates the contribution from meteoroids could be significant for ¹⁰Be, ¹⁴C, and ²⁶Al.

The heating pulse experienced during atmospheric deceleration of dust entering at Mars is less severe than on Earth because of the lower surface gravity ($g = 3.7~\mbox{m}\,\mbox{s}^{-2}$, compared with 9.8 m s⁻² on Earth). This results in both a lower entry speed (Sect. 3) and a somewhat larger scale height in the ablation region (7.2 km on Mars, compared with 5.9 km on Earth) allowing dust to decelerate over a greater distance so that larger dust grains survive atmospheric entry with their organic matter intact (Flynn and McKay 1990). Flynn (1996) modelled the entry heating and found that interplanetary dust delivers an order-of-magnitude higher surface concentration of unpyrolized carbon compounds onto Mars than onto Earth, suggesting interplanetary dust may be an important source of organic carbon on Mars. In the current era, modelling indicates that this organic matter is destroyed relatively rapidly by the ultraviolet radiation that reaches the surface (Stoker and Bullock 1997), explaining the low organic concentration in the Mars regolith samples analyzed by the Viking landers and a potential source of atmospheric CH₄ (Sect. 6.2)

The lower impact speed as well as the relatively gentle accretion of material ejected into the dust torous orbiting with the Martian moons Phobos and Diemos likely leads to a higher concentration of chondritic material in their regoliths than was found on the Moon (Flynn 1991). If this concentration is sufficiently high, the surface reflectance spectra used to infer a chondritic composition may not reflect the actual composition of the underlying material.

7.4 Other Terrestrial Planets

The contributions of dust and meteorites to the surfaces of the other terrestrial planets, Venus and Mercury, have not been studied in any detail. However, the presence of a dense atmosphere on Venus should result in similar conditions for deceleration and accretion to those on Earth (Fig. 2). The global influx of cosmic dust in Venus’ atmosphere was recently estimated to be 32 tonnes per Earth day (Frankland et al. 2017). Impact craters have been identified on Venus, but little or no modelling has been done on the meteoritic contribution to the surface of the planet. Thus far, the soil and rock composition data from the Venera landers (e.g. Surkov et al. 1988) has not included any of the siderophile elements critical for assessing the meteoritic component.

Mercury, lacking a substantial atmosphere, is more similar to the Moon, however the elements detected by the orbiting MESSENGER spacecraft (Mg, Al, Si, S, Ca, Ti and Fe) did not provide a direct measurement of the meteoritic component. Hence, inferences of the meteoritic contribution are based on modelling, which suggests that 50 times as many carbon-rich micrometeorites per unit surface area are delivered to Mercury, compared with the Moon, resulting in approximately 3–6 wt% carbon at Mercury’s surface (Bruck Syal et al. 2015). MESSENGER measurements limit the northern hemisphere C abundance to the range 0–4.1 wt% at the three-sigma significance level (Peplowski et al. 2015). Bruck Syal et al. (2015) suggested the C contributed by micrometeorites could explain Mercury’s globally low reflectance and might also contribute to the darkening of other planetary surfaces. Modelling by Bruno et al. (2007) indicates that the neutral Na “atmosphere” detected on Mercury and the Moon could be produced by the impact of meteoroids and that the mass of meteoroids that have impacted the whole surfaces of the Moon and Mercury in the last 3.8 billion years are $8.9 \times 10^{18}~\mbox{g}$ and $2.7 \times 10^{19}~\mbox{g}$, respectively. Killen and Hahn (2015) estimated the dust deposition rate on Mercury to be around 440 t per Earth day, though this should probably be reduced to ∼170 t d⁻¹ based on the recent estimate of the dust input to the terrestrial atmosphere (Carrillo-Sánchez et al. 2016). Lastly, Christou et al. (2015) demonstrated that the annual, repeatable Ca emission excess in Mercury’s exosphere could result from the impact of millimeter-sized grains that were ejected from Comet 2P/Encke 10,000–20,000 years ago.

7.5 Summary

This review has described the very diverse impacts that interplanetary dust can have throughout a planet’s atmosphere and at its surface. Significant progress has been made recently in quantifying the dust flux throughout the solar system. Models such as those by Nesvorný et al. (2010, 2011a, 2011b) and Poppe (2016) are necessary to connect in situ measurements of dust densities and fluxes at selected positions in the solar system with an overall picture of dust distributions throughout the solar system. In the inner solar system, continued comparison of dynamical models to available datasets will further refine the available models; although, a dedicated orbital mission around Earth for quantifying the terrestrial meteoric input function and resolving existing discrepancies between Earth- and space-based observations (Plane 2012) is crucial for constraining the overall magnitude and variability of the meteoric influx to Earth. Analysis of existing datasets, especially from the Cassini Cosmic Dust Analyzer and the New Horizons Student Dust Counter, will continue to yield information and constraints on the outer solar system distributions. NASA’s forthcoming Europa Clipper mission contains within its payload the Surface Dust Mass Analyzer (SUDA) (Kempf et al. 2015), a powerful dust instrument that, while primarily focused on dust ejected from Europa and the other Galilean moons, will hopefully yield ancillary information regarding the interplanetary dust distribution from its vantage point at Jupiter.

The new laboratory experimental systems for simulating meteoric ablation (Bones et al. 2016; Thomas et al. 2017) are important for testing and improving ablation models, leading to more secure predictions of the fraction of incoming dust that ablates in a planetary atmosphere, the altitudes where different constituents are injected, and the fraction of unablated material that reaches the surface in the form of micrometeorites and cosmic spherules (Carrillo-Sánchez et al. 2016). Future developments in this area should include ablation models that treat multiple mineral phases in a meteoroid, as well as fragmentation during atmospheric entry.

In terms of atmospheric impacts, although the metal atom and ion layers in the terrestrial atmosphere have been studied for decades (Plane 2003), the first direct measurements in another planetary atmosphere have only very recently been obtained for Mars by the MAVEN spacecraft (Crismani et al. 2017b; Grebowsky et al. 2017). There has been a great deal of work in the past decade on meteoric smoke particles. This has included laboratory investigations into MSP formation (Saunders and Plane 2006) and ice-nucleating ability (Nachbar et al. 2016); detection in the terrestrial atmosphere by rocket payloads (Plane et al. 2014), radar (Strelnikova et al. 2007) and optical extinction (Hervig et al. 2009); and modelling impacts through providing a surface for heterogeneous chemistry (Frankland et al. 2016; James et al. 2017b) and ice nuclei for the formation of mesospheric clouds on Earth (Rapp and Thomas 2006; Hervig et al. 2012) and Mars (Määttänen et al. 2013; Listowski et al. 2014). The role of MSPs in the formation of sulphuric acid particles in Venus, and polar stratospheric clouds in the terrestrial atmosphere, still needs to be better understood.

A credible explanation does not yet exist for the low magnitude yet variable nature of CH₄ in the Martian atmosphere (Webster et al. 2015). Following the experience with comet Siding Spring, it is unclear how the photochemical production of CH₄ from cosmic dust settling in the atmosphere (Fries et al. 2016) can be reconciled with the relatively constant delivery of small amounts of dust (Crismani et al. 2017a). With the recent arrival in late 2016 of the ESA Trace Gas Orbiter mission, which will map CH₄ concentrations in the Martian atmosphere with a sensitivity of 20 pptv, the link between Martian CH₄ and the delivery of carbon-rich cosmic dust to the surface is likely to be better understood.

All of the giant planets and Titan are subject to significant fluxes of exogenous material that has profound impacts on their respective chemistry and structure (Moses and Poppe 2017). At Saturn, the main source of this material is the E-ring and Enceladus water vapor torus. Neptune’s atmosphere shows strong evidence of a recent cometary impact that currently swamps any interplanetary dust input. Jupiter, despite the dramatic atmospheric changes wrought by the Shoemaker-Levy 9 impact, still shows evidence for additional exogenous input, whether from km-sized comets or interplanetary dust (or both). Meanwhile, Uranus’ atmospheric composition can currently be explained solely on the basis of the interplanetary dust influx; however, given the evidence of cometary impacts at the other giant planets, delivery of external material from comets remains a possibility in the Uranian system as well (Moses and Poppe 2017). Despite these recent advances in understanding, there are significant areas for further investigation: reconciling the rates of interplanetary dust delivery of oxygen to Jupiter with the measurements of Lellouch et al. (2002) and Bezard et al. (2002); determining whether all the observed O-bearing species in Uranus’ atmosphere originate from interplanetary dust, or these is also evidence of cometary impact; and determining the speciated chemical composition of the ablated vapour in each giant planet’s atmosphere, and the role of metallic species in their atmospheres and ionospheres.