Abstract
The study of GRB prompt emissions (PE) is one of the main goals of the Lomonosov space mission. The payloads of the GRB monitor (BDRG) with the wide-field optical cameras (SHOK) and the ultra-fast flash observatory (UFFO) onboard the Lomonosov satellite are intended for the observation of GRBs, and in particular, their prompt emissions. The BDRG gamma-ray spectrometer is designed to obtain the temporal and spectral information of GRBs in the energy range of 10–3000 keV as well as to provide GRB triggers on several time scales (10 ms, 1 s and 20 s) for ground and space telescopes, including the UFFO and SHOK. The BDRG instrument consists of three identical detector boxes with axes shifted by \(90^{\circ}\) from each other. This configuration allows us to localize a GRB source in the sky with an accuracy of \(\sim 2^{\circ}\).
Each BDRG box contains a phoswich NaI(Tl)/CsI(Tl) scintillator detector. A thick CsI(Tl) crystal in size of \(\varnothing 130 \times 17~\mbox{mm}\) is placed underneath the NaI(Tl) as an active shield in the soft energy range and as the main detector in the hard energy range. The ratio of the CsI(Tl) to NaI(Tl) event rates at varying energies can be employed as an independent metric to distinguish legitimate GRB signals from false positives originating from electrons in near-Earth vicinities.
The data from three detectors are collected in a BA BDRG information unit, which generates a GRB trigger and a set of data frames in output format. The scientific data output is \(\sim 500\) Mb per day, including \(\sim 180\) Mb of continuous data for events with durations in excess of 100 ms for 16 channels in each detector, detailed energy spectra, and sets of frames with \(\sim 5\) Mb of detailed information for each burst-like event. A number of pre-flight tests including those for the trigger algorithm and calibration were carried out to confirm the reliability of the BDRG for operation in space.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Gamma-Ray Bursts (GRBs hereafter) are the most luminous explosions in the universe, emitting high-energy photons, and are detected to the highest redshifts of any discrete source in the universe (Salvaterra et al. 2009). The study of their temporal and spectral properties provides a unique opportunity to understand not only the nature of the universe but fundamental physics as well (Kumar and Zhang 2015; Zhang 2014).
GRBs allow the study of the evolution of stars and stellar populations from redshifts as far back as \(z=0\mbox{--}15\) (Zhang et al. 2009), or over 98% of the age of the Universe. The first stars and galaxies at \(z=10\mbox{--}15\) would be identified with their formation history, and the re-ionization history at \(z\sim 7\). Use of GRBs for early Universe study was discussed by Weimin et al. (2016). GRBs are potential candidates of the next generation cosmological standard candles (Lipunov et al. 2001; Amati et al. 2008; Ghirlanda et al. 2006; Panaitescu and Vestrand 2008); and they are also prime examples for multi-messenger astrophysical observation because their direct photon measurements can be augmented through observations of the air showers that result from the entry of their ultra-high-energy cosmic ray (UHECR) particles into the atmosphere (e.g. TA (Abu-Zayyad et al. 2012; Tokuno et al. 2012), Auger (Abraham et al. 2004), TUS (Panasyuk et al. 2015), JEM-EUSO (Takahashi 2009)), of neutrinos (e.g. ICECUBE (Halzen and Klein 2010), ANITA (Gorham et al. 2009)), and searches for GW (e.g. LIGO (Abramovici et al. 1992), LISA/NGO (Pau et al. 2012)).
GRBs have been observed from space and studied extensively for more than two decades, e.g. by the CGRO instrument (Fishman et al. 1994) which had captured nearly 3000 GRB observations with its four instruments across the wide energy range from 30 keV to 30 GeV. After that, the BeppoSAX satellite (Boella et al. 1997) was another breakthrough mission, accurately situating GRB coordinates to the order of a few arcmin in the X-ray range, while providing additional observations in the gamma range as well as the rapid (within a few hours) dissemination of GRB coordinates for ground-based observation. Following the HETE-2 experiment (Ricker et al. 2002), several missions including KONUS-Wind (Aptekar et al. 1995), Integral (Winkler et al. 2003), Swift (Gehrels et al. 2004) and Fermi (Perna et al. 2003; Oates et al. 2009; Perley et al. 2010) are currently in operation in space.
In spite of the broad knowledge regarding GRBs already acquired, many questions remain unanswered concerning their progenitors and their environment. Despite the abundance of theoretical models, the nature of GRBs is not fully understood. We still do not khow the distribution of GRB sources across the cosmological redshift continuum reflecting the history of the star formation, nor do we have any clear understanding of mechanisms that drive the GRBs and lead to the formation of their relativistic jets. The principal factor in the further progress of research into such matters will be simultaneous multi-wavelength observations of GRBs in the optical, X-ray and gamma ranges, observations of prompt optical emissions from short GRBs, precursor optical emissions, and high temporal resolution optical observations of GRBs.
The Lomonosov satellite allows the simultaneous observation of GRBs in optical and gamma ranges with three onboard payloads: the directed in three axes gamma-ray burst monitors named BDRG; the SHOK wide-field optical cameras; and the UFFO instrument (Park et al. 2009, 2013), which consists of the coding mask X-ray telescope UFFO Burst Alert & Trigger Telescope (UBAT) and a UV/optical Slewing Mirror Telescope (SMT) (Jeong et al. 2013). Thus, the scientific program for the Lomonosov space mission (Sadovnichii et al. 2012; Amelushkin et al. 2013a) includes a multi-wavelength GRB study across a range of time scales. In particular, a complex study of prompt emissions will be provided based on the immediate recording of optical data with a wide-field optical camera as well as the utilization of the UFFO’s slewing mirror system to permit the rapid orientation of its UV/optical detectors to the GRB coordinates. The BDRG package provides an early detection of X- and gamma rays and serves to trigger the other GRB instruments, i.e. the SHOK and the UFFO. Real-time GRB alerts for terrestrial observation will be achieved through the transmission of GRB localization information over the GCN network to ground telescopes, high-energy neutrino facilities such as IceCube and ANTARES, and gravitational wave observatories such as LIGO.
This study provides a description of the BDRG’s gamma-ray monitor, as well as its detector modeling, preflight calibration, GRB trigger criteria, and preliminary analysis results.
2 Observations with BDRG Gamma Ray Burst Monitor
The GRB monitor BDRG/Lomonosov (Amelushkin et al. 2013a, 2013b) is designed to obtain temporal and spectral information about GRBs in the energy range of 10–3000 keV as well as to provide GRB triggering for the SHOK and UFFO instruments. The detection and localization of GRBs by the BDRG is based on the design of the KONUS instrument, which utilized three omni-directional detectors with axes set normal to each other (see Fig. 1) (Mazets et al. 1981). The Konus device was operated successfully onboard the Venus 11-14 interplanetary stations and on the KONUS-Wind mission.
This configuration provides a field of view (FOV) equivalent to at least a half of the entire celestial sphere. Count rates (\(N _{1}\), \(N _{2}\), \(N _{3}\)) from all three detectors are used to determine burst coordinates:
where \(\theta_{i}\) (\(i = 1, \ldots , 3\)) are the angles between the detector axes and the burst direction and \(N _{i}\) are the number of events in the detector \(i\).
The BDRG/Lomonosov consists of 3 identical detector units, BDRG-1, BDRG-2, and BDRG-3, all of which are connected to the electronics unit, BA-BDRG. The BA-BDRG provides an interface with the satellite board system and outputs detector data for preliminary analysis: a functional diagram of BDRG instrument is presented in Fig. 2.
The BDRG detector units, shown in Fig. 3 as orange colored blocks, are mounted on the spacecraft payload platform with their axes oriented 90° to each other. The sensitive area of each detector has a cosine angular dependence which, within \(\sim 60^{\circ}\) of its axis, is not shadowed by any elements of the spacecraft (see Fig. 3). The main advantages in comparison to the KONUS device are the much better time resolution (\(\sim 15\) ms in gamma by gamma mode) and, in place of the KONUS NaI(Tl) crystal detectors, the use of phoswich NaI(Tl)/CsI(Tl) detectors, which provide active shielding against the gamma ray background and the capacity to distinguish GRB signals from electron precipitation and other geophysical phenomena occurring in near-Earth space.
The BDRG instrument operates in two main observational modes: the monitor, or continuous observation, and event modes. In the monitor mode all detector outputs are recorded and stored continuously with a time resolution that can be adjusted via commands from the Earth. On the other hand, the event mode allows the storage of detailed pre-burst, burst, and after-burst data, including gamma by gamma records. The event mode is switched on when triggered by the detection of GRB candidate event, engaging UV/optical data acquisition by the SHOK cameras and the UFFO instrument. The BDRG trigger also provides GRB coordinate estimations and transmits that information along with trigger data to the GCN via the Global Star satellite constellation.
Two detector units (BDRG-1 and BDRG-2) are placed so that their FOVs overlap the FOVs of the SHOK optical cameras: i.e., as shown in Fig. 4, each optical camera FOV is inside of the corresponding BDRG FOV.
As a result of the BDRG and SHOK instrument orientations and corresponding FOVs, it is possible to make observations upon GRB triggering without redirecting the optical instrument. This permits the immediate optical with X-ray observation along with optical light curve measurements not only for prompt emissions but, additionally, for precursor signals. The different combinations of triggers can be used for data fixation for orienting optical cameras, i.e. SHOK-1 data are fixed by the BDRG-1 trigger and the SHOK-2 data by the BDRG-2 trigger, respectively. However, both cameras are fixed by trigger from any BDRG detector.
3 Instrument Description, Preflight Modeling and Calibration
The three identical BDRG instrument units are shown in the photograph in Fig. 5A, and their parameters are given in Table 1. Each detector unit consists of a layer of optically coupled thin (0.3 cm) NaI(Tl) crystals positioned above a considerably thicker (1.7 cm) layer of CsI(Tl) crystals (see Fig. 6). The diameter of each of these scintillators is 13 cm. The NaI(Tl) is placed on top of the CsI(Tl) crystal and both scintillator layers are viewed simultaneously by a single Hammamatsu R877 Photomultiplier Tube (PMT). The thickness of the NaI(Tl) layer is optimized for the soft part of energy range. Working ranges are 0.01–0.5 MeV for the NaI(Tl) scintillator and 0.05–3 MeV for the CsI(Tl) unit. Configured in this way, the NaI(Tl) layer serves as the main detector for hard X-ray timing, while the CsI(Tl) is utilized as an active shield against background gammas, and it can also detect gammas with energies up to a few MeV.
Each detector has a mass of \(\sim 5.5\) kg and power consumption of \(<3\) W. The power consumption of the data analysis unit is \(\sim 15\) W.
The difference in decay times for the NaI(Tl) (\(\sim 0.25\) ms) and CsI(Tl) (\(\sim 2.0\) ms) crystals provides an opportunity to separate light flashes in both scintillators by pulse shapes through the utilization of special electronic circuits. A PMT signal with negative polarity is characterized by fast increase followed by a slower exponential decrease. If signals from a set of crystals are integrated during the first \(\sim 800\) ns (the so-called “fast” component) and during the following \(\sim 3\) ms (the slow component), the ratio of fast to slow components will allow one to separate the cases of interactions in different parts of detector.
The wiring diagram of the BDRG detector block electronics is presented in Fig. 7.
The current pulse generated by the PMT arrives at the amplitude discriminator, generating an “event start” pulse, which initiates a sequence of control signals. One of the control signals changes the SPDT state, so that the two components of the primary PMT output pulse are integrated independently: the first is proportional to the amount of light collected during the first 800 ns of the pulse (so-called “fast component”), and the second is proportional to the amount of light collected during the following \(3~\upmu\mbox{s}\) (so-called “slow component”).
Both signals are digitized by corresponding successive approximation analog to digital converters (ADCs). When the conversion is complete, parallel codes of fast and slow components are sent to the BDRG electronic unit (BA-BDRG) together with a request for an “output strobe.” The BA-BDRG employs the event processing algorithm in order to determine in which of the two scintillators the interaction took place and the value of energy released. Finally, a sequence of several types of data frames generated by the BA-BDRG unit, and the analysis of the data for the GRB trigger condition is produced.
The electronics of the BDRG detector unit consists of two circuit boards. The first board handles amplification, formation, and digitization of the photomultiplier signals. The second board contains low-voltage and high-voltage converters, which provide \(\pm 5\) V for the electronic assemblies, and \(+12\) V for conversion to high-voltage of about 1000 V in typical and up to 2000 V for photomultiplier.
The BA BDRG unit is a box containing two identical copies of the instrument’s computer: one remains active while the other is powered down as a cold reserve for reliability. The computer design includes an Intel Atom processor (1.6 GHz) and contains a computing board, an input/output board, a CAN interface board, and secondary power supplying board.
The computer of the BA BDRG collects the ADC data sent from the 3 detector boxes in response to the request pulse sent by the computer. These data are recorded in a large buffer memory, which contains the amplitude parameters of all events as well as time data accurate to 1 ms. This buffer is used by active processes initiated by the BA BDRG computer in multi-task mode. The processes work independently and generate scientific data sets of several types. Also, several processes are employed to analyze data for the presence of bursts and to determine GRB candidate coordinates when GRB-like bursts occur. Next, if the significance of the burst meets the requisite criteria (according to the “alert” level), a short message with the burst parameters is formed and immediately transferred to the board computer (BI box) for transmission to the Earth. The detailed data of other instruments onboard the Lomonosov satellite are also recorded at this time.
Many parameters including energy thresholds, time intervals and trigger levels are used to control the BDRG’s operation. All of these parameters are remembered in the BA BDRG’s non-volatile memory and can be adjusted by commands sent from the ground.
Modeling of gamma-quantum and electron interactions in BDRG detectors as well as detector calibration was done prior to launch.
Modeling was done with the MEGAlib toolkit v.2.29.01, which utilizes the GEANT4 databases (geant4-10-00-patch-03). For a detailed description of MEGAlib, see Zoglauer (2005) and Zoglauer et al. (2006). The simulation was conducted for the physics of electromagnetic and hadron interactions, with a tracking threshold for all particles and gammas set to 10 keV. The density values and composition of all materials were chosen according to well-known table data; and in particular, with reference to the densities of the PMT (mean density is \(0.11~\mbox{g}/\mbox{cm}^{3}\)) and phoswich package glasses (\(2.2~\mbox{g}/\mbox{cm}^{3}\)).
To obtain the detector response matrix, we ran several dozen simulation sessions of gamma-quantum and electron parallel beam interactions with the DRGE detectors for various beam directions relative to the detector axis. These beam directions were characterized by zenith angle \(\theta\) (i.e. the angle between beam direction and detector axis) and the azimuth angle \(\varphi\) (i.e. between the beam projection on the detector plane and the detector axis). In different sessions, the gamma-quanta flux energy spectrum was chosen for the power law with different power index values, and band models were chosen with different \(E_{c}\), \(\alpha \), \(\beta \) parameter values. As a result, we calculated, in particular, the gamma quantum detection efficiency in NaI(Tl) and CsI(Tl) crystals (see Fig. 8). Our simulations determined the energy threshold to be about 20 keV at \(\sim 20\%\) efficiency for NaI(Tl). Radiation with energy values between 10 and 20 keV can be detected with less efficiency from \(\sim 5\%\) to 20%; and gammas with energy above 200 keV can pass NaI(Tl) layer and penetrate CsI(Tl) crystal. The efficiency of CsI(Tl) detector at 1 MeV is about 30%. Analogous calculations were made for electron fluxes exhibiting power energy spectra. The energy threshold obtained was about 300 keV for NaI(Tl) and about 2 MeV for CsI(Tl) respectively. Both values indicate the primary energy of electrons undiminished by energy losses in the instrument cover.
The phoswich method based on the combination of the two-layer scintillator with different decay time (NaI(Tl)—\(\sim 0.2~\mbox{mcs}\) (\(t_{f}\)), CsI(Tl)—\(\sim 3~\mbox{mcs}\) (\(t_{s}\))) viewed by a given PMT permits the effective separation of events in these scintillators. Such separation can be illustrated clearly in a two-dimensional diagram, which plots the PMT output signal amplitudes, \(U _{f}\) and \(U _{s}\) integrated, respectively, for the decay times \(t_{f}\) and \(t_{s}\). Because the processes of gamma-quantum detection are principally stochastic, the case of mono-energy gamma quantum detection will appear in the diagram as a spot of finite size, which corresponds to the full energy release, and a strip that connects this spot to the zero point, displaying events with partial absorption of energy. Since the scintillation crystals have a different decay time, the events relating to different scintillators have different values of ratio \(U _{f}/U _{s}\), which is plotted on the diagram along straight lines with different slopes.
When observing certain burst-like count increase one can compare numbers of events with energy release in the NaI(Tl) and CsI(Tl) crystals. Gamma-quanta with energies of about several hundreed keV will interact both in NaI(Tl) and CsI(Tl) scintillators. In the case of electrons with identical primary energies, events with energy releases only for CsI(Tl) will be absent. This approach is sufficient for effective identification of real gamma-bursts against the background of electron flux variations including precipitaion-like short, increasing intensity phenomena.
The BDRG detectors were calibrated with the radioactive isotopes listed in Table 2. Additionally, background gamma lines were also used for calibration of the CsI(Tl) part of the detector in a high part of energy range.
Detector calibration was made achieved through the measurement of energy released separately by the NaI(Tl) and CsI(Tl) crystals. The corresponding procedure can be explained using a 2D-diagram where \(x\) and \(y\) values for each event are the fast and slow component amplitudes. An example of such a diagram for 137Cs gamma-source is presented in Fig. 9.
One can see two straight lines for the NaI(Tl) and CsI(Tl) events. Points between these lines correspond to the events in which a Compton interaction of a gamma-quantum took place so the energy was released in both crystals. The spots of events with energy release 662 keV corresponding to the total energy absorption peak of 137Cs source radiation as well as the 1.46 MeV and 2.614 MeV events from background isotopes 40K and 208Tl (from 232Th decay sequence) are seen.
Individual calibrations were made for NaI(Tl) and CsI(Tl) components of each BDRG detector box as well as for the main and redundant high voltage suppliers, because the redundant system provides less voltage for reliability. Sets of calibration lines presented in Fig. 10 demonstrate good linearity for all detectors. Energy resolution at 662 keV for 137Cs is about 13% for both the main and redundant systems, and the main factor limiting the energy resolution is the PMT photocathode sensitivity non-uniformity.
Calibration values obtained in laboratory tests were input into the BA-BDRG ROM, after which the instrument boxes were mounted onto the satellite, connected with each other, and some complex tests of the board systems were undertaken. The stability of energy thresholds and accuracy of correspondence of their values with those in the ROM are crucial factors for measuring quality, in particular for GRB location accuracy. Indeed, any such discrepancy leads to the increasing of GRB coordinate systematic error.
To verify the calibration, in particular, to check the equality of energy channel thresholds for all detector units, different detector outputs were compared, assuming equal background values in the place of detector fixation. For calibration verification, comparison of indentical energy range outputs was accomplished when the main and reserve PMT DC/DC convertors were switched on.
As the result of such verification tests, independent outputs of two detector units in the same energy channel were compared as well as counts in monitor channels when the main and redundant PMT DC/DC convertors were used. In all cases, the output discrepancy was within 10% except for the edge channels that indicate the correctness of instrument calibration.
Because the threshold levels can vary during the flight as a result of changes in temperature and other factors, their adjustment is necessary. In-flight calibration can be accomplished with the 40K background line (1.46 MeV) as a reference: this isotope is present in PMT glass as well as other materials utilized Onboard the Lomonosov satellite. Different control commands for increasing or decreasing the threshold levels by 1, 10, and 100 units increments are foreseen for threshold adjustment.
4 Trigger Formation
If BDRG output monitoring readings demonstrate fast increase in gamma-ray flux, a trigger is produced. Necessary conditions for trigger production are:
-
Presence of a fast rise of hard x-rays readings (50–300 keV channel will be used by the BDRG)
-
A hard X-ray signal that is not excessively high
-
A ratio of actual GRB-like events generated by near-Earth electrons emissions derived from criteria related to NaI(Tl)/CsI(Tl) detection ratios (see below)
An algorithm of the search for the fast rise of gamma-ray readings is illustrated in Fig. 11.
A history of detector readings is stored in memory with temporal step \(\Delta T\) for \(20\times\Delta T\) interval. This sequence of 20 bins is named \(N_{ki}\) (see Fig. 11).
By means of linear and non-linear regression, the expected value for the next interval may be calculated as \(N_{k \mathrm{exp}}\). There are two possible algorithms for an \(N_{k \mathrm{exp}}\) calculation. Simple linear regression is used for fast triggering when random deviation is more important than background variations. In this case sums \(N _{a}\) and \(N _{b}\) are the numbers of events for the calculated first and the second half of history are used for calculation of the slope value used in linear regression formula. Cubic approximation by the least squares method is employed in triggering with a characteristic time \(\Delta T > 1~\mbox{s}\). In all cases if the number of events is very low (\(N _{b}<30\)), the mean value is used as \(N_{k \mathrm{exp}}\).
The standard deviation \(\sigma\) is calculated for the difference between measured sequence \(N_{ki}\) and the regression sequence, after which the values \(N _{k}\) and \(N_{k \mathrm{exp}}\) are compared. The burst trigger is set if
Here the value \(N\) is equivalent to the number of standard deviations when the increase of the BDRG readings is considered significant.
Several time scales are used for independent triggering:
-
(1)
10 ms interval, 1 ms resolution of monitoring data and event data
-
(2)
1 s interval, 10 ms resolution of monitoring data and event data
-
(3)
20 s interval, burst data in event mode added
It is necessary to be certain that the fast rise of BDRG readings resulted from GRB gammas rather than by Bremsstrahlung x-rays emitted by the satellite struck by electrons from some other source. The criterion used by the BDRG is based on a comparison of NaI(Tl) and CsI(Tl) monitor readings in different energy channels. In the event of a GRB radiation arrives at the NaI(Tl) side of the detector. Most of the secondary radiation from electrons comes from the satellite. The parameters for this criterion, including the limits of the energy intervals and NaI(Tl)/CsI(Tl) threshold ratio, were determined through Geant software modeling. They can be also changed by commands transmitted from the ground during the space experiment.
The threshold (the value \(N\) in formula above) can be chosen by an analysis of the empirical distribution of triggers according to their significance. Figure 12 shows an example of such a distribution for triggering at the 20 ms interval collected over a 65 hours period. The criterion for onboard triggering to acquire detailed gamma-ray data can be soft, allowing the transmission to Earth of \(\sim 20\) false bursts per day, while not losing any actual GRB of sufficient amplitude. For the events in Fig. 12, the value is \(N_{\mathrm{sigm}}>9\). The criterion for transfer via world net telegrams or optical data fixation must be harder. The proposed value is \(N_{\mathrm{sigm}}>12\) or even greater, depending on the time scale.
5 Estimation of GRB Coordinates
GRB coordinates can be estimated by comparing the output readings of the 3 BDRG detectors using the cosine function to adjust the beam coordinates. The axes of the detectors are shifted at \(90^{\circ}\) from each other so that the GRB direction coordinates can be calculated from the above formulas. Practically \(N _{i}\) values were estimated for double time intervals, for which triggers were elaborated. These values were estimated from the differences in a given detector between detected gamma-quanta and the expected number of background events, calculated from that detector’s readings immediately prior to the burst beginning. Obviously, the burst source position accuracy depends on GRB fluence and the background level at trigger time. The calibration accuracy of each detector determines the systematic component of the GRB error box. This means that count dispersion across different detectors can be caused by the difference of energy bands and their position in the spectrum.
A computer simulation was used estimate the GRB location accuracy for the BDRG instrument. The GRB source position in the sky was given, after which a gamma-quantum position and interaction parameters in the detectors were simulated, taking into account energy and duration distributions. Thus, the number of detected gamma-quanta in each detector was determined for a given energy range. GRB source coordinates were calculated from the detector outputs. Such simulations were repeated many times for a burst within given energy spectra, flux values, and durations. The RMS of the detection angles of the restored source and hence, its error box, were also determined.
To evaluate the direction reconstruction error, a \(1/6\)th portion of the BDRG field of view (sector 1) was bombarded by gammas, and seventy-nine arrival directions were distributed evenly across the sector. The three BDRG detectors were treated separately for each arrival direction because the incident gamma flux observed them from different aspects. For each detector, all events with non-zero energy contribution to the NaI(Tl) and/or CsI(Tl) crystals were recorded. To make direction error estimates statistically robust, 20 independent samples were simulated for each arrival direction, with different values of spectral index and fluence \(S\).
The accuracy of GRB localization depends on factors such as the brightness and hardness values of the GRB and the background level. The typical error box for bright events (\(S \sim 10^{-5}~\mbox{erg}/\mbox{cm}^{2}\)) is expected in the vicinity of 2–\(3^{\circ}\), while for weak bursts (\(S \sim 10^{-7}~\mbox{erg}/\mbox{cm}^{2}\)) it may exceed \(10^{\circ}\).
To estimate the possible influence of detector calibration inaccuracy on the calculated GRB source coordinates, their deviations caused by the inaccurate count values from one of the detectors were calculated. The result is that the most significant deviations occur if the GRB source is in the center of the detector system FOV. In this case, a 10% deviation of outputs in one of the detectors leads to a systematic error of about \(2.5^{\circ}\).
For experimental estimation of calibration accuracy, background counts in the energy channels of three BDRG detectors were compared. One-hour averaged count rates in each of the eight NaI(Tl) and CsI(Tl) channel were used. The background energy spectra obtained in monitor mode for NaI(Tl) and CsI(Tl) are presented in Fig. 13. As seen from the plotted values, the background counts change equally in all three detectors.
Energy dependences detector count ratios from the same energy channels were used for more detailed analyses. The spread of 1-h averaged background counts across a wide energy range falls within 5–10% limits. A slightly higher difference is observed at the low and high energy boundaries of the range.
Three BDRG detector output deviations from the mean value were calculated within the 20–100 keV range and can be used for GRB error box estimation. These deviations are 2.8%, \(-4.0\%\), 1.2% for BDRG-1, BDRG-2, and BDRG-3, respectively. Thus, such data processing indicates that 1-h mean background outputs in the similar energy ranges differ within the 5% limits that correspond to the sky coordinate systematic error of no more \(1.5^{\circ}\).
The final test for the localization accuracy of the GRB coordinates took into account all factors including systematic and stochastic laboratory modeling of GRBs using the radioactive isotope Am-241, \(E=60\) keV. For GRB simulation the isotope was placed at given points in the three-BDRG unit assembly FOV. The gamma-ray source was placed on a platform on the tripod set at a fixed angle relative to the three-detector assembly axis. The tripod axis coincided with the BDRG instrument axis, thus turning the platform turn did not change the angle between instrument axis and the direction of the source, which was equal to \(\sim 20 ^{\circ}\). It should be noted that gamma-rays from the source were not parallel due to the its small displacement from the instrument which was necessary due to the low intensity of the source. Nevertheless, the gamma-quantum divergence beam did not act significantly on the experimental results because of the setup symmetry.
GRB were simulated with the use of a radioactive isotope for trigger formation with increasing gamma-quantum counts at duration of \(\sim 20\) s. Next, for 40 s intervals, gamma-quantum numbers were summed in the NaI(Tl) 20–100 keV channel of each detector. A gamma-quanta count rate from the isotope placed on the tripod was approximately equal to the background count rate in this channel. The results of the experiment with the GRB simulation were repeated many times, and a \(\sim 5^{ \circ}\) coordinate spread was calculated in the BA BDRG unit and transferred to the other instruments. The observed spread was slightly higher than the modeled values, which may result from the fact that the gamma-ray beam was not strictly parallel. It was also apparent that the mean value position mimics the experimental setup geometry. The comparison of the mean values of the calculated coordinates with the given isotope position indicates that systematic deviations of computed coordinates do not exceed \(1^{\circ}\).
6 Structure and Amount of BDRG Data
Information from the BDRG contains a set of data frames formed continuously and another set of different data frames formed for every trigger. The structure and amount of the data are presented in Table 3.
Continuous data contain 3 main types of frames: “monitoring” (count rate in 8 energy channels for NaI(Tl) and CsI(Tl) from each BDRG detector unit), “spectrum” (724 channel spectra for NaI(Tl) and CsI(Tl) separately) and “event mode” (primary values of fast and slow components for a fixed number of events combined with time data). Information about the main parameters for all GRB triggers is also transferred continuously in “trigger log” frames.
Trigger data contains the standard set of different data frames, which is similar to the “Monitoring”, “Spectrum” and “Event mode” frame set. There are 3 types of triggers - “fast”, “slow” and “super-slow” with characteristic times of 10 ms, 1 s and 20 s, respectively. A sequence of data frames for all 3 mentioned types is formed for “fast” and “slow” triggers, and a large “Event mode” data sequence is formed for “super-slow” trigger. A portion of data collected before the trigger is included for all trigger types.
7 First Results and Conclusion
As the part of Lomonosov mission payload the BDRG instrument was successfully launched on April 28, 2016. The regular observations commenced on May 12, 2016 and more than 50 Gb of data has been obtained up to the present. The example of background count variations along an orbit is presented in Fig. 14. These readings are quite typical for low-altitude satellites with high inclined orbits. We can see the latitude variation in the detection rates for local gamma quanta produced by cosmic rays, very intensive counting rate increases when satellite crosses the outer radiation belt, as well as temporally localized peaks caused by the detection of Bremsstrahlung radiation from precipitated sub-relativistic electrons.
Upper panel: Count rate variations in the BDRG NaI(Tl) monitoring channels along the orbit: BDRG-1 20–35 keV (light red line), 6–10 keV (dark red line), BDRG-2 20–35 keV (light green line), 6–10 keV (dark green line), BDRG-3 20–35 keV (light blue line), 6–10 keV (dark blue line). Lower panel: L-shell coordinate
As one would expect, the minimal background counts are fixed near the geomagnetic equator areas. The typical background energy spectrum collected over 20-min exposure time near the equator is presented in Fig. 15, along with the 1-hour spectrum obtained during the preflight calibrations. A peculiarity in the flight spectra is apparent in the middle of CsI(Tl) spectrum plot. This can be associated with the line from 40K isotope, and shifts slightly with temperature. It could be compared with corresponding peaks on the preflight calibration spectra. From these spectra we can conclude, that detector unit PMT gains did not change significantly, thus, the preflight estimations of NaI(Tl) and CsI(Tl) energy channel thresholds in monitor data frames (see Fig. 13) are valid. The energy thresholds values are presented in Table 4.
Upper panel: the background spectra of energy releases in the BDRG-2 NaI(Tl) and CsI(Tl) crystals obtained during the preflight tests. The main line-type peculiarities (Bi-214, K-40, Tl-208) are marked. Bottom panel: the background spectra of energy releases in the BDRG-2 NaI(Tl) and CsI(Tl) crystals obtained during the flight calibrations
The BDRG detector sensitivity to GRBs can be estimated from the background counts, which are about \(10^{2}\mbox{ s}^{-1}\) near the geomagnetic equator, and \(\sim 10^{3}\mbox{ s}^{-1}\) at the polar caps. These values correspond to the minimal fluence value of \(S \sim 10^{-7}~\mbox{erg}/\mbox{cm}^{2}\) for typical 1 s-long GRBs with Band-type spectra and energies of \(E _{p} = 300\) keV detected at the equator and \(S \sim 5\times 10 ^{-7}\) erg/cm2 for similar bursts detected at the Polar caps. The minimal fluence for similar burst with duration 20 s is \(S \sim 5\times10 ^{-7}~\mbox{erg}/\mbox{cm}^{2}\) for equator and \(S \sim 2.5\times10^{-6}~\mbox{erg}/\mbox{cm} ^{2}\) for Polar caps. It follows from the \(\log N\)–\(\log S\) distribution the expected number of GRBs detectable across the entire sky at sensitivity level \(S \sim 10^{-7}\mbox{--}10^{-6}~\mbox{erg}/\mbox{cm}^{2}\) is about \(6\times10^{2}\) per year. Taking into account that the BDRG FOV is \(\sim 2\pi \) sr, i.e. one half of the sky, and that real observational time is about 30% from the total time at the equator and Polar Regions, the expected number of GRBs that could be detected by any of the three BDRG unit, is \(\sim 10^{2}\) per year. The overlap area of the all three detectors, in which the GRB location is determinable with sufficiently good accuracy (3–\(5^{\circ}\)), is \(1/4\) of the BDRG FOV. Therefore, the expected number of good located events is about 25 per year.
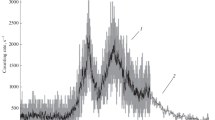
Up to the present (January, 2017), 19 GRBs have been detected and confirmed by other experiments (https://downloader.sinp.msu.ru/grb_catalog/). For all of these GRBs, the GCN circulars were published. The smaller than expected number of detected bursts is due to the reduced time for real observations caused by the satellite testing operations we must perfrom during the initial stage of our work. This also explains the gaps in our data. The time profile of the one of detected GRBs is presented in Fig. 16.
Apart from the 19 observed GRBs, since May, 2014, the BDRG instrument also detected six bursts from SGR1935+2154 as well as a few solar flares at X- and gamma rays.
In comparison with the KONUS experiments the main advantages of the BDRG instrument are the possibility of gamma by gamma reading for detected events and the use of phoswich detectors, which allow effective separation of gamma quanta from electrons. The possibility of such a distinction provides an opportunity to the GRB search as a result of the elimination of electron precipitation-like events that might otherwise be mistaken for GRBs. In comparison with other modern GRB experiments, GBM Fermi, for example, the BDRG payload has comparable sensitivity and temporal resolution, although a slightly smaller effective area. The energy band extending up to 3 MeV, combined with several hundreds cm2 effective area, of the BDRG complement very well the present capabilities of, e.g., Swift/BAT (limited to 150 keV). It is illustrated at Fig. 17 by the energy spectrum of GRB161017A measured by Lomonosov/BDRG and Swift/BAT. The presented spectrum corresponds to the time interval 17:52:07–17:52:09UT, i.e. for 16–18 s after BAT Swift trigger time, when the maximal intensity was observed. Because of the possibility of operative GRB data transfer via the Globalstar network to the GCN, the BDRG GRB monitor on board Lomonosov satellite provides a good input to contemporary GRB observations.
The energy spectrum of GRB161017A measured by Lomonosov/BDRG (empty squares) and Swift/BAT (light-grey filled points). The Swift/BAT data were downloaded from Swift Burst Analyser (Barthelmy et al. 2005) and processed according “BAT Data Analysis Guidelines” (http://swift.gsfc.nasa.gov/docs/swift/analysis/threads/batgrbproductthread.html)
Real-time transmission of data regarding detected events from ground facilities is also foreseen, and the BDRG observations occuring at the moment of the IceCube alert IC-160806 may be considered an example of such an event: no significant GRB was detected by BDRG Lomonosov in the interval \(\pm 50\) s from the moment of IC-160806, i.e. 12:21:33. The upper limit (\(3\sigma\)) for 1 s exposure from BDRG-1 background counts \(<0.23~\mbox{cm}^{-2}\,\mbox{s}^{-1}\) for 20–60 keV is \(<0.13~\mbox{cm}^{-2}\,\mbox{s}^{-1}\) for 60–300 keV (Panasyuk et al. 2016).
Thus, we may now conclude that the BDRG instrument is operating well as a one of the instruments dedicated to the study of GRBs onboard the Lomonosov satellite.
References
J. Abraham et al., Nucl. Instrum. Methods Phys. Res., Sect. A 523, 50 (2004). http://www.auger.org
A. Abramovici et al., Science 256, 325 (1992). http://www.ligo.caltech.edu
T. Abu-Zayyad et al., Nucl. Instrum. Methods Phys. Res., Sect. A 689, 87 (2012)
L. Amati et al., Mon. Not. R. Astron. Soc. 391, 577 (2008)
A.M. Amelushkin, V.V. Bogomolov, V.V. Benghin et al., Space experiments on-board of Lomonosov mission to study gamma-ray bursts and UHECRS, in Gamma-ray Bursts: 15 Years of GRB Afterglows, ed. by A.J. Castro-Tirado, J. Gorosabel, I.H. Park. EAS Publications Series, vol. 61 (2013a), pp. 545–552
A.M. Amelushkin, V.V. Bogomolov, V.I. Galkin, B.V. Goncharov, E.S. Gorbovskoy, V.G. Kornilov, V.M. Lipunov, M.I. Panasyuk, V.L. Petrov, J.F. Smut, S.I. Svertilov, N.N. Vedenkin, I.V. Yashin, The BDRG and SHOK devices for studying gamma ray burst prompt emission on board the Lomonosov spacecraft. Cosm. Res. 51(6), 434–438 (2013b)
R.L. Aptekar, D.D. Frederiks, S.V. Golenetskii, V.N. Ilynskii, E.P. Mazets, V.N. Panov, Konus-W gamma-ray burst experiment for the GGS wind spacecraft. Space Sci. Rev. 71(1–4), 265–272 (1995)
S.D. Barthelmy, L.M. Barbier, J.R. Cummings, E.E. Fenimore, N. Gehrels, D. Hullinger, H.A. Krimm, C.B. Markwardt, D.M. Palmer, A. Parsons, G. Sato, M. Suzuki, T. Takahashi, M. Tashiro, J. Tueller, Space Sci. Rev. 120(3–4), 143–164 (2005)
G. Boella et al., Astron. Astrophys. Suppl. Ser. 122, 299 (1997). http://www.asdc.asi.it/bepposax
G.J. Fishman et al., Astrophys. J. Suppl. Ser. 92, 229 (1994)
N. Gehrels et al., Astrophys. J. 611, 1005 (2004). http://heasarc.gsfc.nasa.gov/docs/swift/swiftsc.html
G. Ghirlanda et al., New J. Phys. 8, 123 (2006)
P.W. Gorham et al., Astropart. Phys. 32, 10 (2009). http://www.ps.uci.edu/~anita/index.html
F. Halzen, S.R. Klein, Rev. Sci. Instrum. 81, 081101 (2010). http://icecube.wisc.edu
S. Jeong et al., Opt. Express 21(2), 2263 (2013)
P. Kumar, B. Zhang, Phys. Rep. 561, 1–109 (2015)
V.M. Lipunov, K.A. Postnov, M.E. Prokhorov, Gamma-ray bursts as standard-energy explosions. Astron. Rep. 45, 236–240 (2001)
E.P. Mazets, S.V. Golenetskii, V.N. Ilinskii, V.N. Panov, R.L. Aptekar, Iu.A. Gurian, M.P. Proskura, I.A. Sokolov, Z.Ia. Sokolova, T.V. Kharitonova, Catalog of cosmic gamma-ray bursts from the KONUS experiment data. Astrophys. Space Sci. 80, 3–83 (1981)
S.R. Oates et al., Mon. Not. R. Astron. Soc. 395, 490 (2009)
A. Panaitescu, W. Vestrand, Mon. Not. R. Astron. Soc. 387, 497 (2008)
M.I. Panasyuk, M. Casolino, G.K. Garipov et al., The current status of orbital experiments for UHECR studies. J. Phys. Conf. Ser. 632(1), 012097 (2015). doi:10.1088/1742-6596/632/1/012097
M.I. Panasyuk, S.I. Svertilov, A.V. Bogomolov et al., GCN Circular No. 19791, 2016
I.H. Park et al., arXiv:0912.0773 (2009)
I.H. Park et al., New J. Phys. 15, 023031 (2013)
A.-S. Pau et al. arXiv:1201.3621 (2012). http://lisa.nasa.gov. http://www.elisa-ngo.org
D.A. Perley et al., Mon. Not. R. Astron. Soc. 406, 2473 (2010)
R. Perna et al., Astrophys. J. 585, 775 (2003)
G. Ricker et al., Astrophys. J. 571, L127 (2002). http://space.mit.edu/HETE/Welcome.html
V.A. Sadovnichii, M.I. Panasyuk, A.M. Amelushkin et al., Study of early universe extreme phenomena on Lomonosov space mission. J. Cosmol. 18, 1437 (2012)
R. Salvaterra et al., Nature 461, 1258 (2009)
Y. Takahashi, New J. Phys. 11, 065009 (2009). http://jemeuso.riken.jp/en
H. Tokuno et al., Nucl. Instrum. Methods Phys. Res., Sect. A 676, 54 (2012)
Weimin et al., Space Sci. Rev. 202(1–4), 235–277 (2016)
C. Winkler et al., Astron. Astrophys. 411, L1 (2003). http://www.isdc.unige.ch/integral
B. Zhang, Int. J. Mod. Phys. D 23(2), 1430002 (2014)
B. Zhang et al., Astrophys. J. 703, 1696 (2009)
A.C. Zoglauer, First Light for the Next Generation of Compton and Pair Telescopes (2005)
A. Zoglauer et al., New Astron. Rev. 50(7–8), 629–632 (2006)
Acknowledgements
The BDRG experiment onboard the Lomonosov satellite was realized with the partial financial support of M.V. Lomonosov Moscow State University within the framework of the “Prospects for Development” program (“Perspektivnye Napravleniya Razvitiya”). The Korean group was supported by the National Research Foundation grants (No. 2015R1A2A1A01006870, and No. 2015R1A2A1A15055344).
Author information
Authors and Affiliations
Corresponding author
Additional information
The Lomonosov Mission
Edited by Yuri Shprits, Hans Bloemen and Jim Burch
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Svertilov, S.I., Panasyuk, M.I., Bogomolov, V.V. et al. Wide-Field Gamma-Spectrometer BDRG: GRB Monitor On-Board the Lomonosov Mission. Space Sci Rev 214, 8 (2018). https://doi.org/10.1007/s11214-017-0442-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11214-017-0442-9