Auroral Substorms: Search for Processes Causing the Expansion Phase in Terms of the Electric Current Approach

Abstract

Auroral substorms are mostly manifestations of dissipative processes of electromagnetic energy. Thus, we consider a sequence of processes consisting of the power supply (dynamo), transmission (currents/circuits) and dissipations (auroral substorms-the end product), namely the electric current line approach. This work confirms quantitatively that after accumulating magnetic energy during the growth phase, the magnetosphere unloads the stored magnetic energy impulsively in order to stabilize itself. This work is based on our result that substorms are caused by two current systems, the directly driven (DD) current system and the unloading system (UL). The most crucial finding in this work is the identification of the UL (unloading) current system which is responsible for the expansion phase. A very tentative sequence of the processes leading to the expansion phase (the generation of the UL current system) is suggested for future discussions.

• (1) The solar wind-magnetosphere dynamo enhances significantly the plasma sheet current when its power is increased above $10^{18}~\mbox{erg}/\mbox{s}$ ($10^{11}$ w).

• (2) The magnetosphere accumulates magnetic energy during the growth phase, because the ionosphere cannot dissipate the increasing power because of a low conductivity. As a result, the magnetosphere is inflated, accumulating magnetic energy.

• (3) When the power reaches $3\mbox{--}5\times 10^{18}~\mbox{erg}/\mbox{s}$ ($3\mbox{--}5\times 10^{11}$ w) for about one hour and the stored magnetic energy reaches $3\mbox{--}5\times10^{22}$ ergs ($10^{15}$ J), the magnetosphere begins to develop perturbations caused by current instabilities (the current density ${\approx}3\times 10^{-12}~\mbox{A}/\mbox{cm}^{2}$ and the total current ${\approx}10^{6}~\mbox{A}$ at 6 Re). As a result, the plasma sheet current is reduced.

• (4) The magnetosphere is thus deflated. The current reduction causes $\partial B/\partial t > 0$ in the main body of the magnetosphere, producing an earthward electric field. As it is transmitted to the ionosphere, it becomes equatorward-directed electric field which drives both Pedersen and Hall currents and thus generates the UL current system.

• (5) A significant part of the magnetic energy is accumulated in the main body of the magnetosphere (the inner plasma sheet) between 4 Re and 10 Re, because the power (Poynting flux $[ \boldsymbol{E} \times \boldsymbol{B} ])$ is mainly directed toward this region which can hold the substorm energy.

• (6) The substorm intensity depends on the location of the energy accumulation (between 4 Re and 10 Re), the closer the location to the earth, the more intense substorms becomes, because the capacity of holding the energy is higher at closer distances. The convective flow toward the earth brings both the ring current and the plasma sheet current closer when the dynamo power becomes higher.

This proposed sequence is not necessarily new. Individual processes involved have been considered by many, but the electric current approach can bring them together systematically and provide some new quantitative insights.

1 Introduction: Auroral and Polar Magnetic Substorms

1.1 Auroral Substorms

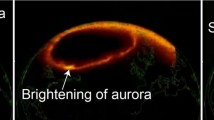
Auroral substorms are a particular global auroral activity, during which auroral displays explosively spread from the midnight sector to the whole dark side of the polar region and beyond (Akasofu 1964); Figs. 1(a) and 1(b). Auroral substorms consist of the growth, expansion and recovery phases and last, on the average, for about 3–4 hours. It is the expansion phase during which the spectacular auroral activities occur for a brief period of about 1.0–1.5 hours.

Fig. 1

Development of the expansion phase of an auroral substorm. (a) A series of auroral images taken by the POLAR satellite (Courtesy G. Parks). (b) Schematic representation of the expansion and recovery phases based on the analysis of all-sky camera images taken during the IGY (Akasofu 1964)

1.2 Three Major Auroral Displays During the Expansion Phase

• (1) Expansion of the auroral oval during the growth phase

During the growth phase, namely prior the onset of the expansion phase, the equatorward boundary of auroral oval expands in the midnight sector and the low latitude boundary of the oval moves equatorwards. The growth phase and its significance are discussed in detail in Sect. 6.1.

• (2) Initial brightening and the poleward expansion

The first indication of the onset of the expansion phase is a sudden brightening (often in a few minutes) of an arc (a curtain-like structure) which is located near the equatorward boundary of the auroral oval.

After the initial brightening for a few minutes, auroral activities spread from the midnight sector to poleward, the evening and morning sides; the speed of the poleward motion (the expansion of the auroral oval in the midnight sector) is about $200~\mbox{m}/\mbox{s}$; Figs. 2(a) and (b) show examples of the poleward expansion recorded by an all-sky camera and a satellite image (DMSP) during an early epoch of the expansion phase. The front of the expanding auroral oval can reach 68°–70° gm lat (geomagnetic latitude) or higher latitude. A possible explanation of the onset and the poleward shift of auroras during the expansion phase is given in Sect. 8.

Fig. 2

(a) Series of all-sky photographs, showing the initial brightening (Fort Yukon, gm. lat. 66.6°). An arc located near the zenith brightened for a few minutes before advancing poleward. (b) A satellite image of an early epoch of the expansion phase (DMSP satellite), showing how the poleward expansion can be seen in the night sector. In Figs. 2, 3 and 5, each snap shot is not simultaneous with the all-sky images

During the recovery phase, the auroral activity continues. Many arcs or their fragments drift equatorward, and then turn eastward, perhaps associated with the large-scale plasma convection (Sect. 6.3).

One of most puzzling aspects of auroral displays during auroral substorms is that they are very different across the midnight meridian, as shown in Figs. 3, 4 and 5. In the evening sky, auroral activities spread in the form of westward traveling surges (Fig. 3), while auroral arcs disintegrate and drift toward the morning sky (Fig. 4) and also form large-scale folds, called ‘torches’ (Fig. 5).

• (3) Westward traveling surges

The poleward expansion of auroral arcs during the expansion phase causes large-scale waves which propagate westward (toward the evening sky) along the aurroal oval with a speed of $2~\mbox{km}/\mbox{s}$. This phenomenon is called the westward travelling surge; Fig. 3. The wave can sometimes reach all the way to the noon sector. Large-scale curling of arcs (a curtain-like structure) occurs within the surge. It is likely that it is the front of the auroral electrojet which flows along the oval (Baumjohann and Opgenoortg 1984); see Sect. 1.3.

• (4) Eastward drifting patches

Auroral arcs disintegrate in the morning sector; Fig. 4. The disintegrated arcs look like cumulus clouds, because it is often difficult to distinguish between the side of arcs and their lower edge; for this reason, they are called ‘patches’, but a careful observation shows the ray structure in them, which indicates the vertical (curtain-like) structure. The patches drift eastward (toward the morning sky) with a speed of $300~\mbox{m}/\mbox{s}$. The patches often pulsate with various periods, say 10 seconds. The disintegration of the arc structure may be related to plasma instabilities in the magnetosphere, but its cause is uncertain.

• (5) Diffuse aurora

There is a wide band of faint light of width of a few hundred km (like the Milky Way brightness) which is called the diffuse aurora (because it does not have a curtain-like structure at least in the evening and midnight sectors) and is located just equatorward of the oval. Its brightness increases during substorms. Often it develops into many faint arcs and/or large-scale wavy structures called ‘torches’ in the morning sector; Fig. 5.

Fig. 3

Westward traveling surge. Top: Visual and all-sky photographs with a schematic illustration westward traveling surge is indicated. Bottom: All-sky images taken at the time of airborne expedition by the NASA plane, Galileo

Fig. 4

Drifting patches. Top: Visual and all-sky photographs; they are not simultaneous. Bottom: Satellite images of patches (both large-scale and local)

Fig. 5

Diffuse aurora and torches. (a) Visual and all-sky photographs. (b) A satellite image (DMSP satellite), together with a schematic oval

It is important note that these auroral features during auroral substorms so far have got little theoretical attention (except westward traveling surges; Baumjohann and Opgenoortg 1984) and should be discussed now on the basis of what we have learned about magnetospheric processes during substorms.

1.3 Polar Magnetic Substorms

Auroral substorms are accompanied by polar magnetic substorms, intense magnetic disturbances caused by ionospheric currents. Figure 6 shows an example, in which an intense magnetic disturbance began at the time of the sudden brightening and poleward advance of an arc. This intense magnetic variation is caused by the intense ionospheric current called the auroral electrojet. Obviously, both auroral substorms (caused by current-carrying electrons) and polar magnetic substorms (the magnetic field produced by the current) are only different aspects caused by the same current system which is discussed in the following section. As shown in Sect. 4.1, the ionospheric current during substorms consists of two components, DD and UL. The DD component flows during the whole period of substorms, while the UL component occurs during the expansion phase. The auroral electrojet is the ionospheric part of the UL current system.

Fig. 6

Simultaneous development of the expansion onset. The all-sky images and the magnetogram was recorded at Poker Flat (64.6°)

In order to find such a current distribution over the whole polar ionosphere, six meridian chains of magnetic observatories were set up by an international effort (International Magnetosphere Study); see Kamide et al. (1982). The magnetic records were analyzed to obtain magnetic disturbance vectors at each station. A computer code, called KRM (the Kamide, Richmond and Matsushita code), was used to determine the ionospheric current distribution on the basis of the distribution of magnetic disturbance vectors with a time resolution of 5 minutes.

Figure 7 shows an example of the growth and decay of the ionospheric currents during a polar magnetic disturbance with the simultaneous auroral substorms. It can be seen that an intense westward current flows in the night sector, the auroral electrojet.

Fig. 7

Distribution and its variations of ionospheric currents during a substorm

Auroral substorms are also accompanied by magnetic disturbances in the magnetosphere. Those disturbances are called magneospheric substorms. These features are described in the whole following sections.

2 Basic Concept and Methodology of the Present Study

2.1 The Electric Current Line Approach

Auroral substorms are various manifestations of electromagnetic energy dissipation. Therefore, it is natural to consider each of them as a sequence of processes, which consists of power supply (dynamo), power transmission (currents and their circuits) and dissipation (auroral substorms); Fig. 8.

Fig. 8

Sequence of processes which will be followed in this paper

However, in the past, these phenomena have almost exclusively studied in terms of magnetic field lines and their motions (namely, the magnetic field line approach). On the other hand, in as early as 1967, Alfven (1967) noted: “In some application we can illustrate essential properties of the electromagnetic state of space either by depicting the magnetic field lines $or$ by depicting the electric current lines. Almost always the first picture is used exclusively. It is important to note that in many cases the physical basis of the phenomena is better understood if the discussion is centered on the picture of the current lines”.

In this paper, we are going to take the electric current line approach. This approach has enabled us to identify quantitatively, though only as a first approximation, two current systems during substorms. The first one is driven directly by the solar wind-magnetosphere dynamo (the directly driven, DD). The second one is caused by unloading of accumulated magnetic energy in the magnetosphere during the growth phase (unloading, UL). This identification of both the DD and UL currents are most crucial in understanding substorms. The two currents are the main basis of the following sections.

2.2 Three Phases of Auroral Substorms

In order to study the overall auroral activity, we consider that auroral substorms consist of three phases, the growth, expansion and recovery phases and last altogether for 3–4 hours. All the auroral displays illustrated in Sect. 1.2 occur during auroral substorms. It is the brief expansion phase (lasting for about one hour or so) which has received much attention, particularly its explosive occurrence.

Auroral substorms occur a few times in 24 hours during a moderately active days. Figure 9 shows an example, in which three auroral substorms occurred during the course of a single night. The upper three all-sky photographs show the pre-onset situation, the expansion and recovery phases. Similarly, the middle and bottom photographs show two following substorms.

Fig. 9

Series of all-sky images, showing the occurrence of three substorm during the course of a night (Saskatoon)

2.3 Bucket Analogy of the Magnetospheric Role

In considering why auroral substorms have the expansion phase, it is instructive to consider, conceptually, the role of the magnetosphere by using a bucket analogy with two spouts as roles of the magnetosphere with a tippy bucket (Fig. 10): Water (energy) from the first spout is proportional to the input from a pipe with a faucet which controls the inflow into the bucket; this portion of energy drives the directly driven current (DD), which will be discussed in detail in Sect. 4.2. Water from the second spout goes first into a tippy bucket. The trippy bucket indicates the role of the magnetosphere for the growth phase and the expansion phase, during which the power is once accumulated as magnetic energy in the magnetospheric circuit and is subsequently unloaded, causing the explosive auroral activity during the expansion phase; this portion of energy drives the unloading current (UL), which will be discussed in detail in Sects. 4.3, 6.1 and 6.2.

Fig. 10

It illustrates how the magnetosphere with a tippy bucket acts when it receives power/energy from the solar wind-magnetosphere dynamo. The magnetic observation records ionospheric currents from both spouts together. An analytical process distinguish the two currents, DD and UL. The DD current system is directly from the magnetosphere, while the UL current from the tippy bucket

A test of the concept of the tippy bucket is to examine geomagnetic storms during which a high level of the power is constantly maintained for at least 18 hours. Fortunately, some of coronal mass ejections (CMEs) have such characteristics. Figure 11 shows an example. It can be seen that substorms of similar intensities occur repeatedly and successively during when the power ($P= \varepsilon$ in Sect. 3.1) is continuously high and lasts for a long time, suggesting that there is a limited amount of energy that the tippy bucket can hold, as illustrated at the bottom of the figure, corresponding to the AL index. One of our tasks is to find the nature of the ‘spring’ attached to the bucket. As we learn in Sect. 4.5, the limiting amount is estimated to be $5.0\times 10^{22}$ ergs for medium intensity substorms on the basis of the Joule heat dissipation in the ionosphere (Sect. 5).

Fig. 11

Geomagnetic storm which are caused by a nearly constant high power for more than 18 hours. Substorms of similar intensities occurred repeatedly during the storm. $\mathrm{EPS} = P = \varepsilon$ (Sect. 3.1), THETA = the latitude angle, and UT = the total energy dissipation

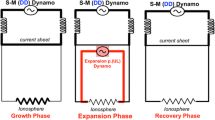
Since we consider substorm processes in terms of the power supply (dynamo), transmission (currents/circuits) and dissipation (auroral substorms), it is worthwhile to consider a conceptual circuit for the three phases. Figure 12 shows the three circuits. The basic circuit for the three phases is the same, consisting of the solar wind-magnetosphere dynamo [(S-M (DD)], the inductance and the ionospheric resistivity. During the expansion phase (the middle one), there occurs an additional circuit (the UL circuit in Sect. 4.3), corresponding to the tippy bucket. The ionospheric resistivity is high during the growth phase. This high resistivity and the inductance of the circuit play a major role for the expansion phase, allowing for the magnetosphere to accumulate magnetic energy during the growth phase (Sect. 6.1). When this energy is unloaded, it generates the UL current system. During the expansion phase, the ionosphere is ionized, so that the resistivity substantially decreases.

Fig. 12

Three conceptual current circuits for the growth, expansion phase and recovery phases, respectively. During the growth phase, the ionospheric resistivity is high, but becomes low during the expansion and recovery phases. An additional circuit appears during the expansion phase circuit, which is the UL circuit (corresponding to the tippy bucket). Note that there is an important difference in the resistivity (or conductivity) of the ionosphere between the growth phase and the expansion/recovery phases

3 Power Generation

3.1 Power Generation: Dynamo Process

Auroral substorms are basically an electromagnetic phenomenon, so that a dynamo as the power supply is needed. The solar wind-magnetosphere interaction constitutes the dynamo. Its power is expressed in terms of the Poynting flux $P$

$$P = \int \boldsymbol{E} \times \boldsymbol{B} \cdot \boldsymbol{dS} = V(B^{2} /8\pi)S, $$

where $V$ and $B$ denote the solar wind speed and the magnitude of the interplanetary magnetic field (IMF), and $S$ denotes the cross-sectional area.

The power $P$ was originally determined empirically (Perreault and Akasofu 1978; also, Akasofu 1977, Sect. 1.4)

$$\varepsilon= VB^{2}\sin^{4} (\theta/2)l^{2}, $$

where $\sin^{4} (\theta/2)l^{2}$ corresponds to the cross-section area $S$; $l$ was taken to be 15 Re by determining the total energy consumption during geomagnetic storms. By considering $\varepsilon$ as the Poynting flux and thus replacing $B^{2}$ by ($B^{2} /8\pi$), $l$ is 5 Re for the newly defined $\varepsilon$. In the future, $l$ should be determined by estimating accurately the energy consumed by substorms (see Sects. 5.1 and 5.2); it may also depends on the solar wind pressure, which determine the cross-sectional size of the magnetosphere. A typical value of $\varepsilon(= P)$ is $3\mbox{--}5\times 10^{18}~\mbox{erg}/\mbox{s}$ during medium substorms.

Microscopically, as the solar wind blows across the merged field between the earth’s dipole field and the IMF, solar wind protons are deflected toward the morning side of the magnetopause, while electrons toward the evening side by $(+,-)e \boldsymbol{V} \times \boldsymbol{B}$ force (Fig. 13(a)). The ‘terminal’ of this dynamo is located on the equatorial plane in the morning side (positive) and evening side (negative) within the magnetospheric boundary (Figs. 17(a), (b)). The location of the terminals is discussed in Sect. 4.2(a). The potential drop across the magnetotail and also across the evening side (positive) and the morning side (negative) of the auroral oval is of about 100 kV; Fig. 13(b).

Fig. 13

(a) Schematic illustration of the solar wind-magnetosphere dynamo; both the meridian cross-section and a vertical cross-section (viewed from the earth) are shown. (b) The potential drop across the morning and evening half of the auroral oval (Courtesy of P. Reiff)

The dynamo generates also two solenoidal currents (including the cross-tail current), which also form the magnetotail (Fig. 14(a)); the current flows across the morning and evening side of the magnetopause. Note that the dayside of the magnetosphere is compressed, while the nightside is extended. Olson (1984) examined the dynamo induced two (northern and southern) solenoidal currents (including the cross-tail current). Figure 14(b) shows the contours of constant magnetic field intensity on the equatorial plane. He noted specifically that the plasma sheet current exists only where these contours intersect the magnetopause. Actually, the magnetopause does not have a clearly defined structure to determine exactly where the dynamo process takes place (Akasofu et al. 1973; see Olson 1984, his Fig. 6); the solar wind blows even a little inside the magnetopause.

Fig. 14

(a) Solenoidal current in the magnetotail. (b) Contours of constant magnetic intensity on the equatorial plane. Adiabatic particles with 90° pitch angle flow along these contour lines (Olson 1984)

The plasma sheet current must be driven by the dynamo. When the power is increased, it is accumulated as magnetic energy in the magnetosphere and then unloaded in causing the expansion phase. These will be discussed in detail in Sects. 4.5 and 6.1.

3.2 Minimum Response of the Magnetosphere to the Dynamo

When the dynamo power $\varepsilon$ is very low (${<} 10^{18}~\mbox{erg}/\mbox{s}$), we can observe its magnetospheric responses as magnetic changes only in high latitudes (>70°). Magnetic records from a set of high latitude stations are used to make the polar cap magnetic index. Figure 15 shows that we can detect magnetospheric responses to changes of the power even as low as $10^{16}~\mbox{erg}/\mbox{s}$. The substorm index AE responds to the power $\varepsilon$ above $10^{18}~\mbox{erg}/\mbox{s}$, so that auroral substorms are a magnetospheric response to increasing dynamo power, when the power is above $10^{18}~\mbox{erg}/\mbox{s}$ for 3–4 hours. This paper is mainly concerned with the situation when the power is above $10^{18}~\mbox{erg}/\mbox{s}$.

Fig. 15

Relationship among the polar cap index, the AE index and the power $\varepsilon$ during a fairly quiet period. The AE index responds to the power $\varepsilon$ when it is above $10^{18}~\mbox{erg}/\mbox{s}$. Note that the unit $\gamma$ is the same as nT

4 Circuits and Currents

4.1 Separation of the DD and UL Current System

As shown in Fig. 10, the magnetosphere has two roles (the two spouts) and produces thus two circuits. The expansion phase requires more than an enhancement of the power; a part of the power is accumulated in the magnetosphere and then unloaded in causing the expansion phase. Thus, it is essential to identify and determine the UL current in understanding the expansion phase. The separation of the DD and UL currents is most crucial in studying substorms and in particular the expansion phase.

Thus, the current distributions were further analyzed in terms of equivalent currents in order to separate the two parts (DD and UL) by a computer code, called MNOC (the Method of Natural Orthogonal Component); it is a sort of ‘two dimensional’ Fourier analysis (Sun et al. 2000). The first component is the UL current which has one eddy, the DD current has two eddies; see Fig. 16. It is shown in Sect. 4.1(b) that the DD current is the large-scale convection current and in Sect. 4.3(b) that it is the current which occurs also during the expansion phase. It is shown in Sect. 4.2 that the contours of the DD current can be identified with SuperDARN observation of the convection contours, while in Sect. 4.3 that the UL occurs only during the expansion phase and agrees with the current system proposed by Bostrom (1964); see Sect. 4.3(c). The successful separation is one of the most important results by taking the electric current approach.

Fig. 16

Separation of the DD and UL in terms of the equivalent currents in the ionosphere by an analytical method (MNOC); Sun et al. (2000)

4.2 Directly Driven Current System (DD)

• (a) Circuit

The potential drop across the magnetotail is communicated to the ionosphere by the field-aligned Region 1 and Region 2 currents. This is schematically shown in Fig. 17. The potential drop across the magnetotail drives the ($\boldsymbol{E} \times \boldsymbol{B}$) drift of plasmas in the magnetosphere and the ionosphere. In the ionosphere, the plasma drift produces the DD current (Axford and Hines 1961). The terminals of the Regions 1 and 2 currents are located just inside the magnetopause (Fig. 18(a)). Axford and Hines (1961) projected the ionospheric current pattern (called the SD current) on the equatorial plane. This process allowed them to infer the location of the terminal in the magnetotail, which is located a little inside of the magnetopause; note that the morning (positive) and evening (negative) sides of the oval is surrounded the convection flow lines (Fig. 18(b)).

• (b) Current

The DD current has a two cell pattern (Figs. 16 and 18(b)). This current pattern is identical to the potential contours. For an ideal situation, it produces two symmetric (with respect the sun-earth line) eddy (isopotential contours) in the ionosphere, along which the ionospheric plasma flows. It is greatly distorted, partially because of non-isotropic conductivity of the ionosphere. The DD convection has been monitored by the SuperDARN network (cf. Bristow 2009; Bristow and Jensen 2007), confirming the distorted pattern (Fig. 18(c)). The ionospheric current flows along the same contours, but in the opposite direction with respect to the plasma flow. The agreement between their results and the DD current pattern is satisfactory. This is one way to confirm even the validity of the KRM and MNOC analyses.

Fig. 17

Circuit connecting the ‘terminals’ on the magnetopause and the ionosphere

Fig. 18

Solar wind-magnetosphere interaction in terms of the DD current. (a) The convection pattern of magnetospheric plasmas associated with the potential drop across the magnetotail (Axford and Hines 1961). (b) The average ionospheric the DD current (convection) deduced from the ground network of magnetometer data. (c) The convection pattern obtained by the SuperDARN network at one particular time (Bristow 2009)

4.3 Unloading Current System (UL)

• (a) Circuit

The unloading circuit proposed by Bostrom (1964) is shown in Fig. 19(a), which consists of the azimuthal and meridional components (or Types 1 and 2). It is quite likely that the actual circuit is more complicated, but it is a useful guide in studying the UL (expansion phase) current system. Furthermore, this current system is the only one among other models (including the current wedge [CW] model), which shows specifically a sheet current (not line currents) which is needed to explain a curtain-like structure of auroral arc; there occurs a potential drop along the sheet current, accelerating auroral electrons in producing the curtain-like structure of arcs.

• (b) Current

The UL current in the ionosphere has a single cell; Figs. 16(b) and 19(b). Both figures show also the electric field, an earthward-directed one in the magnetosphere and equatorward-directed one in the ionosphere. In the UL current circuit (Fig. 19(a)), one can see that $\boldsymbol{J}\cdot \boldsymbol{E}$ is negative only on the equatorial plane, so that the secondary dynamo must exist on the equatorial plane (Fig. 12), in addition to the solar wind-magnetosphere dynamo. Thus, if this field $\boldsymbol{E}$ can occur on the equatorial plane and is transmitted to the ionosphere, it can drive both the azimuthal and merional currents (the 3-D UL current system, including the auroral electrojet); it should be noted that the azimuthal current in the ionosphere is basically the Hall current which is driven by the transmitted equatorward-directed electric field and thus there is no need for an additional dynamo in the ionosphere. It will be shown in Sect. 7.3 that it is this earthward electric field which is essential for the expansion phase. Incoherent scatter radar observations show that the southward electric field in Fig. 19(b) is about $20\mbox{--}50~\mbox{mV}/\mbox{m}$ (Brekke et al. 1974).

• (c) Confirmation

One way to confirm its general validity of the UL current system is to compare the distribution of the ionospheric current with the current distribution on the equatorial plane obtained by a satellite. For this purpose, the distribution of the Pedersen current (mostly the north-south component; Fig. 20(a)) in the ionosphere is projected onto the equatorial plane and is compared it with the distribution of the radial component of the equatorial current determined by a satellite (Iijima et al. 1990; Fig. 20(b)); the current intensity on the equatorial plane is obtained by the relation ($\operatorname{curl}\boldsymbol{B} = \boldsymbol{J}$). The results are satisfactory, in spite of the two entirely different methods used here (Akasofu 1992).

Fig. 19

(a) Bostrom’s 3-D current system which consists of the azimuthal and meridional components. It shows that an earthward-directed electric field can drive the both components and also both the Petersen (iP) and the Hall (iH) currents. (b) The UL current in the ionosphere, together with the driving the equatorward electric field

Fig. 20

Confirmation of Bostrom’s 3-D current system. (a) The Pedersen current vectors (blue arrow) are projected onto the equatorial plane (using Bostrom’s meridional circuit), and compared them with the radial current vectors (red arrow) on the equatorial plane obtained by a satellite (Iijima et al. 1990); this result confirms the validity of the analysis of both methods

In order to infer the equatorial part of the azimuthal component, an example is chosen, in which the westward current was dominant in the night side ionosphere. Using Bostrom’s azimuthal circuit, the distribution of the current in the ionosphere is projected on the equatorial plane and is shown in Fig. 21; obviously, it is a very rough result, but suggests at least some idea about the equatorial current which also develops as the so-called “return current” of the auroral electrojet.

Fig. 21

Distribution of the equatorial current which is connected to the ionospheric currents by the azimuthal circuit. Westward-oriented ionospheric current vectors are in blue, while eastward-oriented current vectors are in red. In the projected vectors on the equatorial plane, they switch the colors

4.4 Relationship Among the Power $\varepsilon$, the DD and UL Currents

Figure 22 shows the relationship among the power $\varepsilon$, the intensity of both the DD and UL currents as a function of time for several moderate substorms, based on the analysis which is described in Sect. 4.1. The results are based on magnetometer records from the international six meridian chains of stations (Kamide et al. 1982) with the two methods KRM and MNOC. This is also one of the most important products of the analyses based on the electric current approach, although it is only a first approximation (Sun et al. 2000; Akasofu 2013).

Fig. 22

Time variations of the power $\varepsilon$, the DD current and the UL current (Sun et al. 2000). Note that current density in the ionosphere is proportional to the Joule heat production rate. It can be seen that the DD current tends to follow the power $\varepsilon$, while UL current is impulsive, unrelated to the power

It is particularly important to note that the DD current tends to follow the power $\varepsilon$ and that the UL current is impulsive and has not directly related to the variations of the power $\varepsilon$. It is emphasized that the UL current occurs only during a brief period of 1–15 hours, coinciding with the expansion phase.

In addition, the above comparison of the trend with $\varepsilon$ (erg/s) is possible because the Joule heat production rate (erg/s) is given by $J^{2} / \sigma$ (where $\sigma$ is the conductivity). Since all the ionospheric currents are connected to the field-aligned current which ionizes the ionosphere, $J$ is approximately proportional to the ionization rate and is thus proportional to the conductivity $\sigma$. Thus, as a first approximation, we can assume the Joule heat production rate $J^{2} /\sigma = J(J/\sigma)$ is proportional to the field-aligned current intensity $J$ in this particular case, namely $J(J/ \sigma) \propto J$. Thus, one can see, at least as the trend, separately how the DD and UL vary with $\varepsilon$, although the DD component is influenced by the increase of ionization during the expansion phase. As shown later in Sect. 8.2, it is suggested that the UL current system results from unloading of the accumulated magnetic energy during the growth phase, so that it is called the unloading current (UL).

It is interesting to note that the impulsive growth of the UL current tends to occur only during an early epoch of substorm. This is an important evidence that the low conductivity of the ionosphere before the expansion onset plays a major role in accumulating the energy of the expansion phase. After the conductivity is sufficiently increased by the expansion phase, the accumulation of the magnetic energy does not occur, except in some cases, including the case when the power is much greater than what the ionosphere can dissipate as the Joule heat (Fig. 11). This is the reason why the expansion phase occurs soon after the growth phase, but in other periods during substorms (with some exceptions, Sect. 10.3).

4.5 Plasma Sheet Current and the Ring Current

• (a) The plasma sheet current and the ring current

The plasma sheet current flows across the magnetopause, while the ring current circles the earth (Olson 1984). The ring current is a byproduct of substorms in two ways; some plasmas are injected into the ring current by the ($\boldsymbol{E} \times \boldsymbol{B}$) drift, while processes related to the UL current inject ionospheric $\mathrm{O}^{+}$ ions into the ring current belt.

• (b) Inflation of the magnetosphere

Figure 23 shows the deformation of the earth’s magnetic field (a second order calculation) for a group of trapped particles centered at 6 Re (Akasofu and Chapman 1961; Akasofu et al. 1961); for details of the distribution of the particles, see the two papers. In this model, the magnetosphere is inflated by trapped particles; the total magnetic energy in this model is $2.9\times 10^{21}$ ergs and the ratio $\beta = ([nkT / B^{2} /8\pi])$ becomes close to 1.0 at the center located at a distance of 6 Re (Fig. 23(a)), suggesting that this amount of magnetic energy centered around 6 Re is close to the limit, since the magnetic field starts to lose controlling the plasma, since $\beta$ becomes close to 1.0. The current density at the center (6 Re) is $3\times10^{-18}~\mbox{A}/\mbox{cm}^{2}$ (Fig. 23(b)). The inflated magnetic configuration is shown in Fig. 23(c).

Fig. 23

Earth’s dipole field distorted by a group of trapped particles centered at 6 Re. (a) Top: the distortion of the earth’s dipole and the magnetic field produced by the group of trapped particles. Bottom: the magnetic field produced by the ring current. (b) The current distribution and its magnetic field vectors. (c) The distorted magnetic field configuration, indicating ‘inflation’ (Akasofu et al. 1961)

Thus, even the main body of the magnetosphere is difficult to accumulate and maintain as much as $10^{23}$ ergs even at a distance of 6 Re. Although this model is based on a group of trapped particles, it can serve in inferring how the plasma sheet current can inflate the magnetic configuration on the basis of Fig. 14.

• (c) Ground effects

The model produces a southward field (Fig. 23(b)) of about −40 nT on the earth’s surface (Fig. 23(a)); including the induction effect of −20 nT, the observed field will be −60 nT. However, the model assumes a symmetric ring current and thus the observed field will be less than −60 nT. The plasma sheet current does not enclose the earth, so that the effect may be less than that of a symmetric ring current. The observed decrease on the ground and at the geosynchronous distance will be discussed in Sect. 6.1.

5 Dissipation: Joule Heat Production

5.1 Joule Heat Production Rate

The final part of the sequence processes is the energy dissipation. The main dissipation is the Joule heating in the ionosphere; it is computed on the basis of the ionospheric current distribution. The other dissipation process, the ionospheric ionization, is about 10% of the Joule dissipation (Ahn et al. 1983). In this calculation, the resistivity (or conductivity) of the ionosphere was determined on the basis of incoherent scatter radar data (the electron density) and the simultaneous ground-based magnetometer data in Alaska. In order to confirm this method, satellite images of the auroral distribution was used in inferring the conductivity (resistivity) distribution, and it was found that the amount of the Joule heat production was about the same order, although different substorms had to be used.

An example of the results is shown in Fig. 24, which shows the distribution of the Joule heat production at different epochs of a substorm (including a quiet period). When it is integrated over the whole polar ionosphere, one can obtain the Joule heat production rate $\delta$. The dissipation rate thus obtained is about $3\mbox{--}5\times10^{18}~\mbox{erg}/\mbox{s}$ for the expansion phase of medium intensity substorms. This value is comparable to the input (power) rate $\varepsilon$ during the growth phase ($\varepsilon \approx \delta$ during the expansion phase). This result tells us why the expansion phase is so short, comparable to the period of the growth phase, because the accumulated energy can be unloaded for the period similar to the period of the growth phase, 40–90 minutes.

Fig. 24

Variations of the Joule heat production in the ionosphere during a substorm time, including a quiet period prior to expansion onset (Ahn et al. 1983)

5.2 Total Energy Consumed by the Expansion Phase

Integrating $\delta$ further during the expansion phase ($\int \delta(t)dt$), we can obtain how much energy medium intensity substorms consume (Fig. 25). It is about $5\times10^{22}$ ergs. This is one of the most the expansion phase crucial values which can so far be obtained only by the ground-based observations.

Fig. 25

Joule heat production rate is integrated over the ionosphere and plotted as a function of time. The AE index is also plotted. The growth, expansion and recovery phases are indicated (Ahn et al. 1983)

6 Substorm Phases

6.1 Growth Phase

• (a) Auroras

During the growth phase of medium intensity auroral substorms, the equatorward boundary of the auroral oval shifts, on the average, from 65° to 64°–62°, an equatorward shift of 1°–3° in latitude. This phenomenon is often difficult to identify and is confused with the southward shift of the polar boundary of the auroral oval, namely the contraction of the width of the auroral oval, not an enlargement of the whole oval. The transferred magnetic flux to the night side of the magnetosphere is roughly estimated to be about $4.0 \times10^{6}~\mbox{G}\,\mbox{km}^{2}$, if the whole oval equally expands. On the basis of satellite images, Frank et al. (1998) estimated it to be about $3 \times 10^{6}~\mbox{G}\,\mbox{km}^{2}$.

• (b) Magnetic changes

• (i) Ground

First of all, it is important to demonstrate that the DD current is very weak before the onset of the expansion phase, because the ionosphere is too resistive to conduct the full DD current before expansion phase onset (namely until a sudden brightening of an arc and the associated ionization occurs); Fig. 25. Figure 26 shows how the DD and UL currents develop during a substorm; the current intensity of the DD and UL currents are shown in Fig. 22. It can be seen that before the onset of the expansion phase (11:35 UT), a very weak two-cell DD current develops first for about one hour or so after the dynamo power increases above $10^{18}~\mbox{erg}/\mbox{s}$. The plasma sheet current is also expected to grow at the same time with $\varepsilon$.

Fig. 26

Time variations of the DD and UL currents. The growth, expansion and recovery phases are indicated, together with the AE index at the top. Note that during the growth phase, a weak DD (two-cell) current develops. The UL current develops suddenly and subsides quickly in one hour period

As shown in Sect. 4.5, the ring current (the accumulation of the magnetic energy) decreases the magnetic field on the earth’s surface. In order to examine the decrease, it is interesting to examine the relationship between weak DD currents (not the UL current) and the Dst index (weak DD currents occur during the growth phase); Fig. 27. Indeed, there is a group of DD current (indicated by a red arrow), which is separated from those proportional to the Dst index (namely, those with a near linear relation with Dst). It is quite likely that many of these points are caused during the growth phase. This figure will also be referred later in discussing the role of both the growth phase and expansion phase on the formation of the ring current.

Fig. 27

(a) Relationship between the DD current and the Dst index. (b) Relationship between the UL current and the Dst index (Sun and Akasofu 2000)

The weakness of the DD current during the growth phase is a good indication that the magnetic energy is accumulated in the inductive circuit of magnetosphere. Thus, it important to examine if the decrease suggested by the model (Fig. 23(a)) can be observed by satellites before the onset of the expansion phase.

• (ii) Geosynchronous distance (6 Re)

Thus, it is instructive to examine the accumulation of the magnetic energy at 6 Re and the resulting decrease (the inflation) of the magnetic field. Figure 28 shows an example of both the magnetic record and particle data taken by the ATS 6 satellite at the geosynchronous distance, together with the AE index. There occurred two substorms in the record, the expansion onset at about 05:30 UT and 06:00 UT. The magnetic record shows clearly a decrease of about 50 nT (often 100 nT) before the expansion onset.

• (c) Role of the growth phase

Thus, the cause of the growth phase is found to be due to the fact that the magnetosphere accumulates the dynamo power as magnetic energy $W (= [1/2]J^{2} L$ where $L =$ inductance) in its inductive circuit of the magnetosphere (causing the inflation of the magnetic field; Fig. 23(c)), because the ionosphere cannot dissipate increasing power; see the inductance in Fig. 12. The limit of the accumulated energy is estimated to be about $5\times10^{22}$ ergs for the expansion phase. Therefore, the growth phase may more appropriately be named the loading phase.

Fig. 28

Both magnetic and particle observations at the geosynchronous distance, together with the AE index. From the top, the $Bz$ component of the magnetic field, electron and proton data and the AE index (Deforest and McIlwain 1971)

(d) The growth phase had been a puzzle for sometime, because auroral activities associated with the expansion phase are delayed for about one hour or so after the power $\varepsilon$ starts to increase. This puzzle was clarified by examining the development of the DD and UL currents.

6.2 Expansion Phase

• (a) Poleward expansion of auroras

During the expansion phase of medium intensity substorms, the front of the expanding oval reaches from 62°–64° to 68°–70° in the midnight sector, Thus, the advance goes well beyond (3°–6°) of the pre-substorm location (65°). An example of a series of all-sky images is shown in Fig. 2(a). The speed of the poleward shift is about 200 m/s. Figure 29 shows that the onset arc located a little north of College (64.6° gm lat) advanced as far as the northern sky of Sachs Harbor (75° gm lat) in about one hour.

• (b) Poleward expansion of the UL current: Auroral electrojet

Figure 30 shows also how far the front of the advancing arcs can reach during the expansion phase. The accompanying westward auroral electrojet also spreads poleward with the aurora; both front arcs and the auroral electrojet reached as far as 77° gm lat (Craven et al. 1984). This fact has an important implication in discussing the cause of the poleward expansion.

Fig. 29

The poleward advance of auroras during the expansion phase, observed by the Alaska meridian chain of all-sky cameras. Note that the sky over Inuvik became cloudy after 10:50 UT (Mould Bay 79°, Sachs Harbor 75°, Inuvik 71°, For Yukon 66.6°, College 64.6 gm lat)

Fig. 30

Simultaneous observation of auroras and ionospheric currents

The satellite of an auroral image is superposed on the distribution of ionospheric currents (Craven et al. 1984).

• (c) Magnetotail

There have been a large number of observations of magnetic field changes in the magnetotail. The most prominent change is a sudden increase of the $Bz$ component called the dipolarization, which is referred to in Sect. 7.1. The $Bz$ changes have been considered in terms of the magnetic field line approach as the result of returning of the stretched field lines during the growth phase. Liou et al. (2002) showed that the expansion area (the auroral bulge) and depolarization closely map.

6.3 Recovery Phase

The recovery phase begins after a brief expansion phase. Auroral substorms and the DD current continue so long as the power $\varepsilon$ is above $10^{18}~\mbox{erg}/\mbox{s}$ (Fig. 22). In fact, the processes during this phase can be explained in terms of the convection. Auroral displays are dominated by equatorward motions of arcs or segmented arcs in the midnight sector, which turn eastward at about 65° (Fig. 4). Figure 31 shows such an example of the equatorward motion. Since this period is driven mainly by the power $\varepsilon$ (Fig. 22) and its consequences can be described by the plasma convection, this phase is more appropriately called the convection phase, instead of the recovery from the expansion phase.

Fig. 31

Southward drifting arc segments during the recover phase after a rapid poleward motion. The onset occurred at 10:15 UT, indicated by a rapid expansion of the oval. Subsequently, arcs and segments of arcs drifted equatorward during the recovery phase; the simultaneous AE index is shown (Snyder and Akasofu 1972)

7 Requirement for the Cause of the Expansion Phase

7.1 Magnetic Energy in the Magnetotail

As shown in Sect. 5.2, the energy consumed by a medium substorm is about $5.0\times10^{22}$ ergs. The total magnetic energy in the magnetotail between 10 Re and 20 Re [where magnetic reconnection has been reported to be observed (Angelopoulos et al. 2008)] is about $6.5\times10^{21}$ ergs (assuming a cylindrical radius of 15 Re and $B=30$ nT—an overestimate), which is less than the energy consumed by a single medium substorm ($\mathrm{AE} = 500\mbox{--}1000$ nT) (cf. Akasofu 2013). The problem becomes more serious for more intense substorms ($\mathrm{AE} =2000$ nT), because more energy must be accumulated.

Miyashita et al. (2012) examined the total energy inflows (BBFs), including the internal energy of plasma, from the magnetotail to the magnetosphere and found that it is $4.3 \times10^{20}$ ergs, which is far less than the needed energy. They conclude: “We deduce that as the energy source of these processes, the energy from the midway region is not sufficient for the early expansion phase”.

7.2 Magnetic Flux in the Magnetotail: Dipolarization?

A distinct change of magnetic field during the expansion phase in the magnetotail (an increase of the $Bz$ component) is commonly referred to as “dipolarization”, implying that the stretched field lines during the growth phase return back to the pre-growth phase configuration (65°) and thus that auroral arcs at the expanding front of the oval is supposed to stop at latitude of 65° at the end of the expansion phase.

This implies that the dipolarization can explain only a part of the expansion phase. As mentioned already in Section 6.2, the expansion front reaches 68°–70° or even farther (77°) in the limited area of the midnight sector during a brief period, so that there is a significant difference of 3°–12° on the range of the expansion phase in terms of latitude (namely, from 62°to 65° and 62° to 68°–77°).

Thus, the expansion phase is not caused by just “returning back” of the stretched field lines during the growth phase. For this reason, the nomenclature “dipolarization” is misleading and incorrect. The expansion goes well beyond the pre-substorm location during the brief period of the poleward expansion. The oval returns back during the life of substorms; westward traveling surges advance toward the evening sector with a speed of only 20 km/s.

The additional area of the poleward expansion is about 500 km (5° in latitude) times $3\times10^{3}$ km (60° in longitude), namely about $2\times10^{9}~\mbox{km}^{2}$, and the needed flux is about $10^{6}~\mbox{G}/\mbox{km}^{2}$. Such flux can be supplied by the azimuthal component of the UL current proposed by Bostrom (1964); Fig. 32(a). It is estimated to be about $1.1\times10^{6}~\mbox{G}\,\mbox{km}^{2}$, assuming a triangular area including the equatorial plane ($[10~\mbox{Re}\times 10~\mbox{Re}/2] \times 50~\mbox{nT}$) in Fig. 32(a). In middle and low latitudes, the magnetic field produced by the UL current system is observed as “positive bays” of magnitude of about 50 nT for medium intensity substorms (Figs. 32(b) and 32(c)) and at the geosynchronous distance, the field increase is also 50 nT or more (Fig. 28). Thus, this amount of magnetic flux of the UL current system can explain the observed poleward expansion beyond 65° (about 600 km).

Fig. 32

(a) Azimuth component of Bostrom’s current produces a northward magnetic field, indicated by an arrow. (b) The ionospheric current during a substorm. (c) The middle and low latitude field produced by the current in (b) is computed. In this case, the field magnitude is about 80 nT

7.3 Need for an Earthward-Directed Electric Field

We have identified the UL current system can explain many aspects of the expansion phase in the earlier sections (Sect. 6). Therefore, the conversion process of the magnetic energy must satisfy the requirement that the process should generate the UL current system and thus the needed earthward electric field (Sect. 4.3(b)). The corresponding ionospheric electric field which can drive the auroral electrojet is about 50 mV/m.

The question is now how the accumulated magnetic energy can be unloaded and be converted for the generation of the UL current system and thus for the needed earthward-oriented electric field; further the expansion phase should last only for about one hour or so. Availability of the converted magnetic energy alone is not enough in explaining the expansion phase.

Thus, one of the most important requirements in considering the cause of the expansion phase is that the conversion process of the magnetic energy must be able to generate an earthward electric field, as shown in Sect.  4.3 (b).

8 Possible Processes

The process leading to the onset of the expansion phase is one of the most interesting, challenging and controversial subjects in magnetospheric physics. A large number of papers have been published on this subjects (cf. Rostoker and Bostrom 1976; Shiokawa et al. 1998; Nakamura et al. 2001; Haerendel 2007, 2008, 2009; Birth et al. 2012). However, it is important to distinguish between the DD and UL currents in explaining the expansion phase. Plasma flows from the magnetotail cannot be the main cause of the UL current system, which do not have enough energy (Sect. 7.1).

The onset of the expansion phase requires a new consideration on the basis of the UL current system. This conclusion is one of the important results in this paper. In this section, a very tentative attempt is made on the basis of what we have learned about magnetospheric and ionospheric processes in terms of the electric current approach, which have been described in the earlier sections. It is hoped that this attempt will initiate a new discussion.

8.1 Inflation: Magnetic Energy Loading

When the magnetic energy is loaded in the main body of the magnetosphere (<10 Re), the magnetosphere is inflated (Sect. 4.5 and Fig. 23(c)). The current causing the inflation is the plasma sheet current (Fig. 14(b) and Sect. 4.5). Another way to understand this process is that a significant part of the power [Poynting flux $( \boldsymbol{E} \times \boldsymbol{B} )]$ is directed toward the equatorial plane of the dipole-like configuration of the inner magnetosphere. The inflated magnetosphere is also shown in Fig. 33.

Fig. 33

Possible cause of the expansion phase as a result of the deflation of the magnetosphere after the magnetosphere is inflated during the growth phase

8.2 Deflation

When the accumulated magnetic energy is unloaded, the magnetosphere is deflated (Fig. 33). Lui and Kamide (2003) and Akasofu (2007, 2013) suggested that electrons and protons are separated during the deflation and produce the needed earthward electric field (Fig. 34). Microscopically, electrons (which are gyrating tightly around the field lines) are brought toward the earth, but protons (which are not tightly gyrating) cannot. This separation process produces an earthward electric field. The generated earthward electric field can drive the UL (3-D) current system (Sect. 4.3 and Fig. 19(a)). The separated electrons are discharged to the ionosphere along the UL current circuit, causing the onset of the expansion phase (a sudden brightening of an arc).

Fig. 34

Schematic illustration suggesting how the charge separation and the eastward electric field might occur during the deflation; blue dots are electrons and red dots are protons

Unfortunately, there is at present no computer code available for simulating this process. This conjecture suggests that the frozen-in field line condition ($\boldsymbol{E} + \boldsymbol{V} \times \boldsymbol{B} = 0$) is violated, so that the ordinary MHD code may not be useful.

The mode of the discharging current is beyond the scope of this paper, but it is emphasized that as mentioned earlier, the acceleration process of the UL electrons is expected to be different from that of the DD current (Karlsson 2012). In this regard, Mende (2003) found that the field-aligned current associated with the poleward advancing arc is carried by superthermal electrons accompanied by waves, which may be related to Pi1B pulsations (Lessard et al. 2011).

The unloading (or releasing) of the magnetic energy causes deflation. Because of the deflation ($\partial Bz > 0$) in the inflated location, an earthward electric field of 5 mV/m [$= (-\partial Bz/\partial t)\partial y) = +50~\mbox{nT}/20~\mbox{min}\times 20$ Re] can be produced; the electric field can be 50 mV/m, depending on the above parameters. This process will continue so long as the magnetosphere is being deflated until the accumulated energy is unloaded.

8.3 A Possible Cause of the Deflation

The fact that the magnetosphere can accumulate only a limited amount of energy $W = ([1/2]J^{2} L)$ [which is roughly estimated to be $5\times 10^{22}$ ergs for medium intensity substorms] means that the current intensity $J$ in the plasma sheet in the main body of the magnetosphere is limited. The amount of the current density in Figs. 23(b) and 23(c) is about $3\times 10^{-12}~\mbox{A}/\mbox{cm}^{2}$ at the maximum location (6 Re). This is the amount of current density, beyond which the current in the plasma sheet current and the magnetosphere may become unstable, as discussed in Sect. 4.5. This is one of the most crucial points to be theoretically discussed in the future, namely how much current the main body of the magnetosphere can hold.

8.4 A Sequence of Processes in Causing the Expansion Phase

It is worthwhile to summarize the suggested sequence of processes leading to the occurrence of the expansion phase. This is obviously a very tentative attempt:

• (1) Increasing dynamo power

• (2) Enhancement of the plasma sheet current, accumulating the magnetic energy leading to the inflation of the magnetosphere

• (3) Initiation of the current (plasma) instabilities

• (4) Reduction of the plasma sheet current and of the magnetic energy, leading to the deflation

• (5) Deflation ($\partial B/\partial t > 0$) induces an earthward electric field

• (6) UL current system is set up by the electric field

• (7) Expansion onset

A supporting observation of the above conjecture is given in the next Sect. 8.5.

8.5 Observation

Lui (2011) observed plasma instabilities, current reduction, plasma instabilities and earthward electric field all simultaneously at a distance of 8.1 Re by the THEMIS satellites, together with an expansion phase onset on the ground; Fig. 35. His observation shows also that the frozen-in field condition ($\boldsymbol{E} + \boldsymbol{V} \times \boldsymbol{B} = 0$) is violated, indicating that the separation of electrons and protons may occur. His observation supports the above conjecture.

Fig. 35

Substorm observation at 8.1 Re. (a) The current reduction; the black line is the X component and the red line is the Y component. (b) Electric field changes; note that the frozen-in field condition is violated; deviations of the red line (defined in the right hand side) from its base line indicates that ($\boldsymbol{E} \times \boldsymbol{B} =0$) is violated. (c) and (d) The simultaneous ground observations (Lui 2011)

Based on the above findings, it may be concluded that the magnetosphere has to unload the accumulated magnetic energy in order to stabilize itself. This process may well be the very reason why the expansion phase does occur. Thus, the expansion phase is more appropriately called the unloading phase, contrasted with loading phase (the growth phase).

9 Intense Auroral Substorms During Geomagnetic Storms: the Relation with the Ring Current

9.1 Latitude of the Substorm Onset Location

During geomagnetic storms, the onset (sudden brightening) location shifts considerably equatorward. Akasofu and Chapman (1962, 1963a) examined auroral activities during a great geomagnetic storm of February 11, 1958. The most important finding was that the latitude of the expansion onset was as low as 48° gm lat (Fig. 36(a)) during the middle of the observed Dst decrease (${\approx} {-}500$ nT). The corresponding $L$ value was 2.4. The front of the poleward expansion reached as high as 68° from 42° with a speed of 1.2 km/s (6 times higher than the average speed) during the expansion phase, so that the latitudinal range of the expansion was as large as 20°, and the corresponding positive bay was greater than 150 nT. Examining several major storms, Fig. 36(b) is constructed to show the onset latitude as a function of the Dst index.

Fig. 36

(a) Auroral substorm observed near the time of the maximum Dst decrease (−500 nT) on February 11, 1958. (b) The expansion onset location as a function of the Dst index (both the observed $\Delta H'$ and the induction-subtracted $\Delta H$)

However, it is not certain if the plasma sheet current can reach a distance of as close as 2.4 Re even during major geomagnetic storms, and thus the distance of 2.4 Re does not necessarily mean that the magnetic energy is located around at $L=2.4$. On the other hand, it is unlikely that the $L= 2.4$ field lines can be stretched out to a distance of 10 Re or even beyond (the magnetotail); well before reaching 10 Re, the magnetosphere may become unstable, causing substorms (Sect. 4.5).

On the basis of this consideration, it is not unreasonable to consider that the location of the magnetic energy is not too far from the location which is connected to the latitude of expansion onset. As will be discussed in Sect. 9.2, the location of the accumulated energy is considered to be about 4 Re for intense substorms of 2000 nT, suggesting that a substorm can occur when field lines at 2.4 Re is stretched to about 4 Re. This value will further discussed in Sect. 9.2.

9.2 Storm Intensity and the Location of the Energy Accumulation

The intensity of substorms ranges from 100 nT to more than 2000 nT in terms of the AE index. The question is why there is such a large range of intensity. When the power is higher, is the tippy bucket larger? In order to understand this question, it is interesting to examine the intensity of substorms during the recovery phase of some geomagnetic storms, during which the power $\varepsilon$ decreases monotonically. During such a period, the intensity of successive substorms decreases toward the end of storms (Fig. 37), suggesting that both the ring current/plasma sheet and the location of the accumulated magnetic energy tend to shift gradually away from the earth during the recovery phase of geomagnetic storms, after advancing during an early epoch of geomagnetic storms.

Fig. 37

Example of geomagnetic storms during which the intensity of substorms tends to decrease as the dynamo power monotonically decreases. In this case, both the IMF $B$ and $Bz$ decreased smoothly

An intense convection can shifts both the ring current and the plasma sheet toward the earth. Indeed, it is known that both the ring current belt and the plasma sheet advance toward the earth at an early epoch of geomagnetic storms and subsequently recede during the recovery phase of geomagnetic storms. Figure 38(a) shows an example (Frank 1970). A simulation study of an imaged ring current shows also that the ring current belt was located between 3 and 7 L during a moderate storm (Fok et al. 2006).

Fig. 38

(a) Earthward advancing and the subsequent receding of the ring current and the plasma sheet during a geomagnetic storm (Frank 1970). (b) Schematic illustration, showing how the location of the accumulated energy might recede from the earth during the recovery phase of geomagnetic storms

Thus, there is an indication that the substorm intensity depends on the location of the accumulated energy, as well as the power $\varepsilon$. Thus, it may be expected that the substorm intensity is higher when the accumulated energy is located closer to the earth, where the intensity of the earth’s magnetic field is higher and thus the capacity of holding the accumulated magnetic energy is greater. In this regard, it is interesting note that the ratio of $B^{2}$ at 4 Re and 10 Re is about 20, a comparable ratio of the AE index (2000 nT/100 nT). This suggests that the location of the accumulated energy varies between 4 Re and 10 Re, depending on the power $\varepsilon$ and thus the intensity of the ($\boldsymbol{E} \times \boldsymbol{B}$) drift, corresponding to $\mathrm{AE} =2000$ nT and 100 nT. This is schematically shown in Fig. 38(b).

9.3 Variety of the Development of Substorms

When one deals with individual substorms, one can find that there is a variety of development. This is likely to be due to, first of all, how the input power as a function of time $\varepsilon(t)$ varies, and to how the ionosphere and the magnetosphere respond before and during the expansion phase, as well as perhaps many others parameters (Akasofu 2013).

10 New Controversial Issues

10.1 Storm-Substorm Relationship

Akasofu and Chapman (1963b) found also that the period of geomagnetic storms is when intense auroral substorms occur frequently. Thus, they suggested that the main phase of geomagnetic storms (namely, the ring current belt) is caused by frequent occurrence of intense substorms. However, there has been a controversy on this storm-substorm relationship, namely questioning the role of substorms on the formation of the ring current belt (Sharma et al. 2003). One of the clues in clarifying the controversy may be to compare the DD-Dst (the main phase intensity, reckoned as the Dst index) relationship and the UL-Dst index relationship. Figure 27 shows these relationships. Both DD and UL have a near linear relationship, although the UL current system is more closely related to the intensity of the ring current (the correlation coefficient = 0.81) than the DD current system (the correlation coefficient, 0.33).

The fact that both DD and UL have a near linear relationship with Dst indicates that the injection occurs in two ways, one is by the convection (proportional to the power $\varepsilon$) and the other by the expansion phase processes which inject ionospheric $\mathrm{O}^{+}$ ions from the ionosphere. The DD-Dst relationship also shows that the potential drop across the magnetotail and thus the ($\boldsymbol{E} \times \boldsymbol{B}$) drift are responsible for bringing both the ring current and the plasma sheet current closer to the earth during geomagnetic storms.

It is actually very clear that substorms are mini-storms. Geomagnetic storms develop because the ring current is anomalously develops when intense substorms inject a large amount of $\mathrm{O}^{+}$ ions into the ring current belt successively and frequently.

10.2 Triggering

There have been many cases of simultaneous occurrences of “northward turning” of the IMF and expansion onset (Lyons et al. 2001); Fig. 39. These cases occur only after “southward turning” for one hour or so (during the growth phase). Once almost enough magnetic energy (close to the unloading quantity) is accumulated during the growth phase, the northward turning of the IMF (decrease of the power) could trigger a reduction of the current, stimulating the unloading and the expansion phase.

Fig. 39

Example of the simultaneous occurrence of “northward turning” of the IMF and substorm onset (Lyons et al. 2001)

There have also been several reports which show the coincidence of magnetotail events and expansion onset (cf. Angelopoulos et al. 2008). Those events may be due to the fact that the unloading is triggered by the observed earthward plasma flows (BBFs) from the magnetotail, although such flows do not have enough energy ($1.2 \times 10^{22}$ ergs) to produce the expansion phase (Miyashita et al. 2012). This could explain why there is no clear one-to-one relationship between the expansion phase and BBFs.

10.3 Auroral Streamers

It has been reported by Nishimura et al. (2010) that auroral ‘streamers’ appear to trigger expansion onset. Streamers tend to occur in the evening sector, when a westward surge is advancing in the evening sky (namely, the recovery phase); Fig. 40 shows a wide view of DMSP image, rather than several ground-based images. The location is where the DD convection changes its direction from the sun-earth direction in the midnight sector to the eastward direction (Fig. 40). Some of such cases may be explained if sufficiently accumulated magnetic energy is left (Sect. 9.3), so that the DD convection might trigger secondary substorms during the recovery phase.

Fig. 40

Relationship between a westward traveling surge and auroral streamers (indicated by red arrows)

11 Concluding Remarks

A study of auroral substorms has so far been a long 50-year journey, but the cause of the expansion phase is still unsolved, but is one of the most challenging problems in space physics.

In this paper, we have attempted to study auroral substorms as a sequence of power generation, transmission and dissipation, the electric current line approach. In the past, this subject has been studied almost exclusively in terms of the magnetic field line approach.

Taking the electric current approach, it is found as suggested by Alfven (1967) that this approach can bring a variety of ground-and satellite-based observations in an orderly and systematic way in order to be able to infer the sequence of physical processes leading the expansion phase and can provide also a somewhat different view from the magnetic field line approach. The important step in making this possible was the separation of the DD and UL currents. In particular, this approach suggests that the converted magnetic energy generates an earthward electric field in the main body of the magnetosphere which is responsible for the expansion phase and that the magnetotail does not play the major role in causing the expansion phase. Thus, it is not certain magnetic reconnection is the main cause of magnetic energy conversion process.

Based on the progresses made in the process in each phase, it is suggested that the terminology based on the morphology, the growth, expansion and recovery phases, may be changed to the loading, unloading and convection phases, respectively, instead of the growth, expansion and recovery phases.