Abstract
The Juno Magnetic Field investigation (MAG) characterizes Jupiter’s planetary magnetic field and magnetosphere, providing the first globally distributed and proximate measurements of the magnetic field of Jupiter. The magnetic field instrumentation consists of two independent magnetometer sensor suites, each consisting of a tri-axial Fluxgate Magnetometer (FGM) sensor and a pair of co-located imaging sensors mounted on an ultra-stable optical bench. The imaging system sensors are part of a subsystem that provides accurate attitude information (to ∼20 arcsec on a spinning spacecraft) near the point of measurement of the magnetic field. The two sensor suites are accommodated at 10 and 12 m from the body of the spacecraft on a 4 m long magnetometer boom affixed to the outer end of one of ’s three solar array assemblies. The magnetometer sensors are controlled by independent and functionally identical electronics boards within the magnetometer electronics package mounted inside Juno’s massive radiation shielded vault. The imaging sensors are controlled by a fully hardware redundant electronics package also mounted within the radiation vault. Each magnetometer sensor measures the vector magnetic field with 100 ppm absolute vector accuracy over a wide dynamic range (to 16 Gauss = \(1.6 \times 10^{6}\mbox{ nT}\) per axis) with a resolution of ∼0.05 nT in the most sensitive dynamic range (±1600 nT per axis). Both magnetometers sample the magnetic field simultaneously at an intrinsic sample rate of 64 vector samples per second. The magnetic field instrumentation may be reconfigured in flight to meet unanticipated needs and is fully hardware redundant. The attitude determination system compares images with an on-board star catalog to provide attitude solutions (quaternions) at a rate of up to 4 solutions per second, and may be configured to acquire images of selected targets for science and engineering analysis. The system tracks and catalogs objects that pass through the imager field of view and also provides a continuous record of radiation exposure. A spacecraft magnetic control program was implemented to provide a magnetically clean environment for the magnetic sensors, and residual spacecraft fields and/or sensor offsets are monitored in flight taking advantage of Juno’s spin (nominally 2 rpm) to separate environmental fields from those that rotate with the spacecraft.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Juno’s primary scientific goal is to understand the origin and evolution of Jupiter (Bolton et al. 2010), an essential prerequisite to understanding the formation of our solar system and planetary systems emergent about other stars. Jupiter is the largest (\(R_{j} = 71{,}492\mbox{ km}\)) and most massive (\(M_{j} = 318 M_{e}\)) planet in the solar system, and as such it captured the lion’s share of the gas component of the solar nebula. It is largely a solar mix of H and He, possibly with a rock and ice core of some tens of Earth masses. Jupiter also boasts the most intense planetary magnetic field, with a dipole moment of ∼20,000 times that of Earth and surface field magnitudes about 20 times greater than Earth’s.
Juno is designed to probe deep inside Jupiter to constrain its interior structure and composition. Juno probes the deep interior by mapping with great precision the gravitational and magnetic fields that arise from the distribution and motion of mass within the planet. Juno’s instrument complement includes a Gravity Science investigation using the X and Ka telecom bands to determine the structure of Jupiter’s interior. The deep interior is also probed by the Magnetic Field Investigation (MAG), using a pair of vector Fluxgate Magnetometers (FGMs) to study the magnetic dynamo at depth in the interior. Juno also carries a Microwave Radiometer (MWR) investigation covering 6 wavelengths between 1.3 and 50 cm to perform deep atmospheric sounding and composition measurements. These measurements taken together will offer constraints on the composition and state of Jupiter’s interior as it exists today. To understand the planet’s origin, we must be able to take the knowledge of its present state back in time to the planet’s formation over 4 billion years ago. This can only be done in the context of detailed models of the planet’s formation and evolution, taking into account the elemental composition of the planet as it grew and the behavior of materials under extreme temperature and pressure conditions.
The Juno Mission Plan and MAG are designed together to acquire a dense net of very accurate measurements of the vector magnetic field close to Jupiter’s surface, well distributed in latitude and longitude, to approximate uniform sampling of space surrounding the planet. This distribution of observations, optimized for constraining Jupiter’s internal field, drives a mission requirement for a complete set of 33 close-in polar orbits, distributed in longitude with ∼12° separation between them. Energetic considerations, and a desire to minimize exposure to Jupiter’s intense radiation environment, led to a mission design with highly elliptical polar orbits that carry the spacecraft beneath the most intense radiation belts, especially early in the mission. The measurements needed to map the magnetic field in close proximity are obtained along the orbit segments that pass over the poles, approaching to within a few thousand kilometers of the atmosphere (1 bar level) near the equator. These orbit segments as originally planned and illustrated in Fig. 1, provide a wealth of observations on a closed surface about Jupiter, approximating the ideal coverage for characterizing Jupiter’s potential fields (gravity, magnetic).
From its unique vantage point above the poles, Juno is the first mission to the giant planet well positioned to explore the polar magnetosphere, sampling Birkeland currents and particle distributions that power the solar system’s most spectacular aurorae. Thus Juno will also conduct an intensive study of the Jovian aurorae and polar magnetosphere, acquiring an impressive set of in-situ and remote observations as it transits the polar region. Juno’s instrument complement thus also includes a suite of fields and particle instruments for in-situ sampling; in addition to the magnetometer, Juno carries an energetic particle detector (JEDI) measuring electrons in the energy range 40–500 keV and ions from 20 keV to >1 MeV (Mauk et al. 2013), a Jovian auroral (plasma) distributions experiment (JADE) measuring electrons with energies of 0.1 to 100 keV and ions from 5 to 50 keV (McComas et al. 2013), and a radio and plasma waves instrument (WAVES) recording Jovian radio emissions to >40 MHz (Kurth et al., this issue). Remote observations of the aurora will be acquired by an ultraviolet spectrometer (UVS) counting individual UV photons (Gladstone et al., 2014) and a Jupiter infrared auroral mapping instrument (JIRAM) supporting imagery and spectrometry (Adriani et al. 2014). Juno also carries a modest imaging system (JunoCam) intended for education and public outreach (Hansen et al. 2014). While not conceived as a science instrument, JunoCam will acquire useful science data that will be archived along with the other mission data in the Planetary Data System (PDS). These instruments are described in detail elsewhere in this volume.
In this paper we describe the Juno MAG investigation, our science objectives, measurement requirements, and the instrumentation developed to acquire the necessary observations. We also briefly describe accommodation of the instrumentation on the spacecraft, and some aspects of the Project’s magnetic control program that we put in place to ensure that the magnetic measurements would not be adversely affected by spacecraft-generated magnetic fields.
2 Science Objectives
The Juno MAG will conduct the first global magnetic mapping of Jupiter and contribute to studies of Jupiter’s polar magnetosphere. The investigation is designed to acquire highly accurate vector measurements of the magnetic field in Jupiter’s environment, mapping the planetary magnetic field with extraordinary accuracy and spatial resolution (orders of magnitude better than current knowledge). Our primary objective is to characterize the Jovian magnetic field with a spherical harmonic model sufficiently detailed as to invite comparisons with the Earth’s dynamo. Simulations suggest that Juno will provide sufficient coverage to determine spherical harmonic coefficients to at least degree and order 14, perhaps beyond. If the harmonic spectrum approximates white noise at the dynamo radius, we will determine the depth to the dynamo surface as well (e.g., Hide and Malin 1979). Finally, with a year of operations about Jupiter it may be possible to detect the secular variation of the Jovian field. If secular variation is detected, an independent measure of the depth to the dynamo may also be obtained by application of the frozen flux theorem (Hide and Malin 1981; Glatzmaier and Roberts 1996).
2.1 Jovian Internal Magnetic Field
Jupiter’s magnetic field was revealed by non-thermal decameter radio emissions (22 MHz) identified with Jupiter’s position in the sky (Burke and Franklin 1955). In subsequent decades, observation of Jovian synchrotron radiation (∼1 GHz) provided geometrical constraints on the magnetic dipole and a precise measurement of the rotation period (9.925 hrs). A more detailed characterization of Jupiter’s magnetic field awaited direct measurement by passing space probes, beginning with Pioneers 10 and 11 the early 1970s (Smith et al. 1974, 1975a, 1975b; Acuña and Ness 1976), followed by Voyagers 1 and 2 (Ness et al. 1979a, 1979b) at the end of the decade (1979).
The Ulysses spacecraft obtained additional observations in 1992, using a Jupiter gravity assist to escape the ecliptic plane (Balogh 1994). The Galileo Orbiter began its study of the Jovian magnetosphere in 1995 (Johnson et al. 1992), but its mission plan, designed to provide multiple satellite encounters, was not well suited for study of Jupiter’s planetary magnetic field. The Cassini and New Horizons spacecraft passed by Jupiter en route to more distant destinations, but neither passed very close to Jupiter. Thus, models of Jupiter’s internal magnetic field are largely based on the early flyby observations, augmented by satellite flux tube footprints (to be discussed later). A more detailed description of the observations and models appears in Connerney (2015).
Jupiter’s magnetic field is most often characterized using a spherical harmonic representation, or for simplicity, its degree 1 approximation, the dipole. In the absence of local currents (\(\boldsymbol{\nabla}\times\mathbf{B} = 0\)), the magnetic field may be obtained from the gradient of a scalar potential \(V\) (\(\mathbf{B} = -\nabla V\)). The potential \(V\) may be expressed in a series expansion of spherical harmonic functions that are solutions to Laplace’s equation in spherical coordinates. The traditional spherical harmonic expansion of \(V\) is given by (e.g., Chapman and Bartels 1940; Langel 1987)
where \(a\) is the planet’s equatorial radius. The first series in increasing powers of \(r\) represents contributions due to external sources, with
The second series in inverse powers of \(r\) represents contributions due to the planetary field or internal sources, with
The \(P_{n}^{m} (\cos \theta )\) are Schmidt quasi-normalized associated Legendre functions of degree \(n\) and order \(m\), and the \(g_{n}^{m}\), \(h_{n}^{m}\) and \(G_{n}^{m}\), \(H_{n}^{m}\), are the internal and external Schmidt coefficients, respectively. These are most often presented in units of Gauss or nanoteslas (\(1\mbox{ G} = 10^{5}\mbox{ nT}\)) for a particular choice of equatorial radius (\(a\)) of the planet. The angles \(\theta \) and \(\phi\) are the polar angles of a spherical coordinate system, \(\theta\) (co-latitude) measured from the axis of rotation and \(\phi\) from the prime meridian. The three components of the magnetic field (internal field only) are obtained from the expression for \(V\) above:
The magnetic field due to external sources may be computed in similar fashion. The expansion in increasing powers of \(r\), representing external fields, is often truncated at \(n = N_{\max} = 1\) corresponding to a uniform external field attributed to magnetopause and tail currents, i.e., sources well beyond the region of interest. A potential field representation is not useful in a region with significant local currents, so in practice local currents are represented with the aid of explicit models. The most significant external source in Jupiter’s magnetosphere is due to an extensive system of ring currents encircling the planet, confined to within a few Jovian radii of the magnetic equator, and extending from the orbit of Io out to 50 \(R_{j}\) or more radial distance (Connerney et al. 1981). A simple model of this equatorial azimuthal current system provides a compact and intuitive representation of the external field, useful in studies of the internal field (e.g., Connerney et al. 1981, 1982) as well.
The maximum degree and order required of the internal field expansion depends on the complexity of the field within the volume of space sampled. The series is often truncated at a maximum degree \(N_{\max}\), where \(N_{\max}\) is large enough to follow variations in the field at the orbital altitude of the measurement. The number of free parameters grows rapidly with increasing \(N_{\max}\), as \(n_{p} = (N_{\max} + 1)^{2} - 1\). Since the spherical harmonics are orthogonal basis functions, if the observations are well distributed on a sphere, the coefficients obtained are independent of the choice \(N_{\max}\). If the observations are poorly distributed or sparse (e.g., a planetary flyby) the spherical harmonic functions do not form an orthogonal set, and it is advisable to construct new orthogonal basis functions. Connerney’s (1981) method, based on the singular value decomposition of Lanczos, involves the construction of partial solutions to the generalized linear inverse problem to obtain estimates of the parameters that are well constrained by the observations; those that are not are readily identified and exploited to characterize model non-uniqueness (see Connerney 1981; Connerney et al. 1991). The observations available prior to the Juno mission have generally limited Jovian spherical harmonic models to degree and order 3 or 4, with some of the degree 3 and 4 coefficients poorly determined as yet.
Jovian observations are rendered in a west longitude system, in which the longitude of a stationary observer (e.g., an Earth-bound observer) increases with time as the planet rotates. (West longitudes are simply related to the angle \(\phi\) by \(\lambda = 360 - \phi\)). For gaseous planets, longitudes must be assigned with knowledge of the rotation rate and time. Observation of Jovian radio emission over several decades provided an accurate determination of the planet’s rotation period, and during all those years, radio astronomers recorded longitudes that by convention increased in time, begetting a west longitude system. One must be aware of the occasional update in rotation period (e.g., \(\lambda_{\mathit{III}}(1957)\) vs \(\lambda_{ \mathit{III}}(1965)\)) that alters the assignment of longitudes for observations obtained at different times, for example. A detailed description of Jovian coordinate systems is given by Dessler (1983) and Bagenal et al. (2014).
The spherical harmonic representation may be extended to accommodate secular variation of the magnetic field, assuming detection of significant time variation. This is usually done by replacing the Schmidt coefficients with time dependent functions, e.g., \(g _{n}^{m}(t) = g_{n}^{ m} + g_{n}^{m} t\).
2.1.1 Models
Table 1 gathers the spherical harmonic coefficients of several models, fit to various subsets of data and using a variety of methods. Estimated parameter errors are available for some models, but not reproduced here, for brevity (original publication should be consulted). The models are organized in the table with more recent models generally appearing on the left. An early comparison of the Voyager 1 model (epoch 1979) with a Pioneer 11 model (GSFC O4; epoch 1973) limited Jovimagnetic secular variation (\(g^{0}_{1}\)) to no more than 0.2 %/yr (Connerney and Acuña 1982). By way of comparison, the Earth’s \(g_{1}^{0}\) term is presently decreasing by about 0.075 %/yr. Differences among the Ulysses era (Ulysses 17 ev) model and those of Voyager (Voyager 1 17 ev) and Pioneer (O4) appear within, or comparable, to estimated parameter errors (Connerney et al. 1996a); so there is little evidence of secular variation of the main field from these data (Connerney and Acuña 1982; Dougherty et al. 1996) or from the more distant observations acquired throughout Galileo’s tour (Yu et al. 2009; Russell and Dougherty 2010). However, a recent and very comprehensive analysis (Ridley and Holme 2016) of all in-situ magnetic field data finds evidence in favor of a modest secular variation (∼0.012 %/yr) of the dipole over the nearly 29 years spanning the observations. Their analysis also finds an improved fit to the observations if a small change in Jupiter’s rotation period (\(+0.015\mbox{ s}\)) is introduced (results in a period of 9 h, 55 m, 29.7258 s), well within the estimated uncertainty (±0.04 s) associated with System III 1965. The Juno mission, particularly as re-planned in late 2014, will provide a good opportunity to detect secular variation during the course of its mission, and an even better opportunity if it is extended beyond the nominal 32 science orbits.
Among the models listed in Table 1, the two leftmost entries are distinguished by the inclusion of geometric constraints, in particular, the observed latitude and longitude of the Io Flux Tube footprint (IFT). The discovery of infrared emission at the foot of the Io Flux Tube (IFT) in Jupiter’s ionosphere (Connerney et al. 1993) provided an extremely valuable geometric constraint on magnetic field models. IFT emission occurs in Jupiter’s polar ionosphere at the base of field lines that pass through the satellite’s orbital plane at an orbital distance of \(5.95~R_{{j}}\). This emission is a visible manifestation of the electrodynamic interaction between Io and the Jovian magnetic field, as originally envisioned to explain the Io phase modulation of Jovian decameter radiation (Goldreich and Lynden-Bell 1969). The Io-related emissions provide an unambiguous reference on Jupiter’s surface through which magnetic field lines with an equatorial crossing distance of \(5.95~{R}_{{j}}\) must pass. Thus observations of the location (latitude, longitude) of the footprint offer a unique constraint on magnetic field models, precisely where it is most needed, on the surface of the planet.
IFT emission is observable from Earth with ground telescopes (e.g., Infrared Telescope Facility on Mauna Kea) in the infrared region of the spectrum (Connerney et al. 1993; Connerney and Satoh 2000), and with the Hubble Space Telescope in the ultraviolet (Clarke et al. 1996, 1998, 2005; Prange et al. 1998; Bonfond et al. 2009). Emission has also been detected at the foot of the Europa and Ganymede flux tubes as well (Clarke et al. 2002; Grodent et al. 2006; 2009), but these offer less useful constraints because these field lines pass through the equator at greater radial distance (9.4 and \(15~{R}_{{j}}\), respectively) where the magnetic field is relatively weak. The mapping of field lines from these more distant satellites is heavily influenced by external fields that are less well constrained and perhaps time-variable.
The “VIP4” model in Table 3 used over 100 IFT footprint locations (north and south) in addition to Pioneer 11 and Voyager in-situ magnetometer data to obtain a partial solution to a 4th degree and order expansion of the internal field (Connerney et al. 1998). This model was designed to fit the position of the IFT footprint very well (within ∼1° latitude), so it has proven particularly useful in analyses of satellite interactions and aurorae; it serves the Juno Project as part of the engineering environment standard. The “VIT4” model (Connerney 2015) is more tightly constrained by the IFT footprints, using over 500 such observations as a geometric constraint, and just enough in-situ magnetometer data (Voyager 1, theta component only) to constrain the magnitude of the field.
These models fit the IFT footprint well, but there remains a systematic and non-negligible residual, particularly in the area of the “kink” that appears in UV observations of satellite footprints and aurorae near 110° Jovian system III longitude. Grodent and colleagues (Grodent et al. 2008) have suggested that a more localized source, or magnetic anomaly, might account for the “kink”. In years past, Alex Dessler and colleagues (Dessler and Sandel 1992) have championed the idea of a “sunspot” analogy for Jupiter’s magnetic field, also know as the “magnetic anomaly” model. Grodent’s putative magnetic anomaly would necessarily be located near the surface in order to modify the satellite and aurora footprints without dramatically altering the field elsewhere.
Hess and coworkers utilized an extensive database of IFT footprints compiled by Bonfond et al. (2009) to obtain a 5th degree and order spherical harmonic model (“VIPAL”) of the Jovian magnetic field (Hess et al. 2011). This model obtains a better fit to the satellite footprints, at the expense of a poorer fit to the in-situ magnetic field observations inward of about \(4~{R}_{{j}}\). This model was also constrained to produce a prescribed surface magnetic field strength along the IFT “footpath”. This was done to better match the local electron gyrofrequency to observations of Jovian decameter radio emissions, under certain assumptions regarding the source location, beaming, and generation of radio emissions. Thus models of this type (e.g., VIPAL) require a measure of confidence in our understanding of the propagation of Alfven waves from Io to Jupiter (longitude constraint), and a degree of confidence in our understanding of the generation and propagation of Jovian radio emissions as the price to be paid for encompassing more observables.
The Juno spacecraft will (July, 2016) enter Jupiter orbit to map the magnetic field much closer to the planet in the northern hemisphere and with much greater accuracy than ever before. We will soon know whether the auroral “kink” is due to the presence of a hidden and localized magnetic anomaly.
2.1.2 Discussion
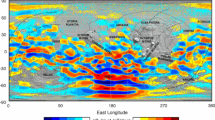
The magnitude of Jupiter’s surface field ranges from just over 3 G at low latitudes to just over 14 G at high (northern) latitudes. The variation of magnetic field magnitude on the surface of Jupiter is illustrated in Fig. 2, which depicts contours of constant field magnitude on the dynamically flattened surface of Jupiter, computed using the VIT4 model. The estimated uncertainty in the surface field magnitude is about ±1 Gauss (Connerney 1981; Connerney et al. 1991), but could be appreciably greater if higher degree and order harmonics are larger than expected, or if magnetic anomalies reveal their presence. Figure 2 also illustrates the foot of the Io flux tube, passing through the region of highest field strength in the northern hemisphere at a longitude of about 150° \(\lambda_{\mathit{III}}\). The maximum surface magnetic field magnitude present along the Io foot is consistent with the maximum frequency extent (39.5 MHz) of Jovian decameter radio emission (DAM), assuming that the emission occurs at the local electron gyrofrequency and at the foot of the Io flux tube (\(f_{c}\mbox{ (MHz)} = 2.8 B~(\mbox{G})\)).
Contours of constant magnetic field magnitude (Gauss) on the dynamically flattened (\(1/15.4\)) surface of Jupiter, computed using the VIT4 model field (see text). The top panel shows the field magnitude in orthographic projections viewed from the north (left) and south (right); below the colorbar is a rectangular latitude-longitude (System 3 west longitude) projection. A trace (dashed) indicates the position of the magnetic equator. Solid lines join points on the surface that trace along field lines to the orbits of the Galilean satellites Io, Europa, and Ganymede, with filled circles for increments of 30° in the satellite’s System 3 longitude
A convenient measure of the complexity of a planetary magnetic field, often used in studies of the magnetic field of the Earth and planets, is the “harmonic spectrum,” sometimes referred to as a “Lowes spectrum,” defined as follows (Lowes 1974; Langel and Estes 1982):
This quantity is equal to the mean squared magnetic field intensity over the planet’s surface produced by harmonics of degree \(n\). Scaled to the core-mantle boundary with the factor \((a/r_{c})^{2n+4}\), this quantity represents the mean squared magnetic field intensity at the dynamo surface. The Earth’s field is well known to high degree and order (\(N_{\max} =23\)). Scaled to the core-mantle boundary, the spectrum becomes almost flat for \(n \leq 14\), suggesting a “white” spectrum for the dynamo at the core-mantle boundary (e.g., Lowes 1974). Harmonic coefficients beyond \(n \sim 14\) are dominated by contributions due to crustal induced and remanent fields, and are not diagnostic of the dynamo.
It has often been assumed that a white spectrum is a common feature of all planetary dynamos (Elphic and Russell 1978), although in the Earth’s case the quadrupole is considerably less than expected. In Fig. 3, we compare the Earth’s \(R_{n}\), calculated using the GSFC 12/83 model (Langel and Estes 1985) with a putative Jovian spectrum calculated for a dynamo simulation that produces a comparable spectrum near the dynamo radius (0.75 and 0.85 \(R_{j}\) illustrated). A dynamo core radius near 0.75 might be expected if the dynamo operates in the metallically conducting hydrogen core (e.g., Stevenson 1983), whereas 0.85 might be appropriate for a dynamo operative in the electrically conducting molecular hydrogen envelope above (Smoluchowski 1975).
2.2 Jupiter’s Magnetosphere and Interaction with the Solar Wind
The interaction of the planetary field and the solar wind forms a multi-tiered interaction region, often approximated as a set of conic sections. The first of which is the bow shock, formed upstream of the obstacle where the supersonic solar wind is slowed (Fig. 4). All of the planets, magnetized or not, interrupt the flow of the solar wind, racing across the solar system at high velocity (∼450 km/s) with the sun’s magnetic field in tow. Magnetized planets carve out a larger cavity in the solar wind, as do more distant planets immersed in a solar wind weakened by virtue of diminished density (\(n\sim 1/r ^{2}\)). Relatively distant Jupiter, with a prodigious magnetic moment, carves out an enormous volume, which, if visible, would appear larger than the Earth’s moon in the sky.
The slowed solar wind flows around the planetary obstacle within the magnetosheath, a turbulent region bounded by the bow shock and the magnetopause, often approximated by a paraboloid of revolution about the planet-sun line. Within the magnetopause is a region dominated by the planetary field, called the magnetosphere (Gold 1959), a term introduced by Tommy Gold in the early 1950s. Jupiter’s magnetosphere assumes a disc-like geometry owing to the extensive washer-shaped region of equatorial azimuthal currents that encircle the planet, analogous to the Earth’s ring current but more extensive and more stable in time. Jupiter’s magnetosphere is described as a rotation-dominated magnetosphere, shaped by the transfer of angular momentum from the planet to outward-flowing plasma (Bagenal et al., this issue), though there is little doubt that rotation and (Earth-like) convection both play a role. The (outward radial) currents that enforce co-rotation in the Jovian magnetosphere cause the field lines that cross the equator at large radial distances to be swept back in a spiral configuration.
The magnetospheric magnetic field extends well downstream in the anti-sunward direction, with field lines drawn out away from the sun as if stretched like an archer’s bowstring, to form the magnetotail. The Jovian magnetotail extends far downstream of Jupiter, and has been observed by spacecraft as far downstream as Saturn, i.e., as distant from Jupiter as Jupiter is from the Sun. The vast spatial scale of the Jovian magnetosphere surely complicates a description of its response to variable solar wind conditions, which are likely to be quite different along the length and girth of the magnetosphere. The Juno approach phase offers a rare opportunity to sample the solar wind ram pressure upstream of Jupiter while remote observations of its infrared and ultraviolet aurorae are obtained. Juno’s remote sensing instruments will be able to image Jupiter during the approach phase along with an impressive array of Earth-bound and Earth-orbiting imaging assets.
Field-aligned, or Birkeland currents, flow between the magnetosphere and the planet’s electrically conducting ionosphere, leading to intense auroral displays. Jovian aurorae are omnipresent and dominated by the transfer of angular momentum necessary to enforce co-rotation of outflowing plasma, but also responsive to variations in the incident solar wind (Baron et al. 1996; Connerney et al. 1996b; Gurnett et al. 2002). Juno’s trajectory affords an opportunity to measure the distribution and intensity of Birkeland currents over both polar regions with every periapsis pass. Juno’s trajectory through the Jovian magnetosphere is illustrated with the aid of Fig. 5, which shows the trajectory in a magnetic equatorial coordinate system for a subset of the orbits, illustrating the evolution of the orbits in time. All orbits pass repeatedly through the polar magnetosphere, traversing field lines illuminated at ionospheric altitudes with auroral emissions. Early in the mission (e.g., orbit #1) the spacecraft remains mostly above and below the extensive equatorial azimuthal current sheet (blue-shaded region); as the orbit evolves in time, Juno penetrates the magnetodisc currents at ever decreasing radial distances. By mission’s end, Juno crosses the magnetic equator in the vicinity of the innermost Galilean satellites (orbit #36). Juno’s exploration of the polar magnetosphere is described in detail in the companion article (Bagenal et al. 2014, this issue).
Juno’s trajectory through the Jovian magnetosphere in a magnetic equatorial coordinate system for a representative set of orbits (\(1,4,19,36\)). Magnetic field lines (purple) are drawn at every 2° co-latitude and contours of magnetic field magnitude (blue) in units of nT as labeled. Radial distances of Galilean satellites Io, Europa, Ganymede, and Callisto indicated as they would appear crossing the magnetic equator
2.3 Satellite Interactions, Flux Tube Footprints
Jupiter’s Galilean satellites (Io, Europa, Ganymede, and possibly Callisto) are electrically conducting obstacles to the magnetoplasma rotating with Jupiter, overtaking the satellites in their Keplerian orbits. Jupiter’s magnetic field sweeps over these satellites, inducing a potential that drives an outward radial current across the satellite body, and a current dipole (Alfven current wings) to and from Jupiter’s polar ionosphere, north and south. These currents produce bright auroral emissions in Jupiter’s ionosphere that can often be observed in association with the foot of the flux tube linking the two, as discussed in the previous section. The electrodynamic interaction between Io and Jupiter was anticipated well before spacecraft arrived at Jupiter (Goldreich and Lynden-Bell 1969). The Voyager 1 spacecraft, arriving in March, 1979, was targeted to pass just south of Io during its flyby and measured a current dipole conducting \(\sim 2.8 \times 10^{6}~\mathrm{A}\) of current between Io and the Jovian ionosphere (Acuña et al. 1981).
While the nominal Juno mission plan does not target close flybys of the Galilean satellites, the Juno spacecraft will pass through L-shells swept by the satellites, albeit often at high magnetic latitudes. The periapsis passes are timed to afford uniform longitude spacing at the Jovigraphic equator, as befits a mapping mission, and thus cannot in general be timed to coincide with a particular satellite orbital phase. However, the Io interaction has been observed (at times) to shed a continuous arc of emission in the Jovian ionosphere downstream of the IFT footprint (along the Io “footpath”). The magnetic field produced by current sheets associated with this emission ought to be directly observable as Juno passes through the polar magnetosphere at longitudes downstream of Io’s orbital position. Charged particle measurements will also be obtained at the same time by the JADE and JEDI experiments, and high-rate wave observations will be sequenced to coincide with traversals of the satellite L-shells.
2.4 En Route to Jupiter: Targets of Opportunity
The lengthy cruise phase provided an opportunity to exercise the instruments and perform periodic instrument calibration and health and safety assessments prior to insertion into orbit about Jupiter. Operation during this phase also granted an opportunity to develop the planning and sequencing processes that will be required during the science phase, and develop experience with the necessary tools. The original mission plan accommodated but a few brief intervals of science instrument operation, as a cost containment strategy, but ultimately a subset of the instruments were able to acquire nearly continuous observations throughout cruise despite the low staffing levels associated with cruise phase. Thus the microwave radiometer (MWR) gathered observations of the cosmic microwave background, the JEDI instrument was primed to detect energetic particle events, the WAVES instrument recorded heliospheric wave activity, while MAG recorded the heliospheric magnetic field at sample rates ranging from 64 vector samples/s to a few (depending on telemetry allocations). The MAG investigation star cameras (ASC) provided measurements of the MAG sensor attitudes throughout cruise at a sample rate of 1 solution per 7 s, and recorded the characteristics of objects that were detected but not found in the on-board star catalog.
2.4.1 Solar System Magnetic Fields
Heliospheric magnetic fields were recorded by the MAG investigation throughout cruise, with the instrument operating almost continuously in the most sensitive of its 6 dynamic ranges (range 0, ±1600 nT). The FGM was designed to operate in strong magnetic fields (to 16 G per axis) and therefore not optimized to measure weak interplanetary magnetic fields, but nonetheless useful data was acquired, in large part aided by the spacecraft spin. With 16 bit quantization, the Least Significant Bit (LSB) in the 1600 nT range corresponds to a quantization step of ∼0.05 nT, a not insignificant fraction of the weak interplanetary field approaching Jupiter (few 10ths of a nT) during this part of the solar cycle. The continuous spin about the spacecraft \(z\) axis allows (inseparable) instrument offsets and spacecraft generated magnetic fields in the \(x\) and \(y\) components to be estimated continuously, but offsets along the spin axis can only be estimated using statistical methods. Nevertheless, we reduced data for each of the interplanetary events (shocks and potential upstream waves) identified by the magnetospheres working group; eventually (6 months post-Jupiter Orbit Insertion (JOI)) all MAG cruise data will be deposited in the Planetary Data System (PDS) repository.
2.4.2 Asteroid Population Characterization
The MAG’s Advanced Stellar Compass (ASC) services the MAG attitude determination requirement by comparison of the star field (imaged by each of its four imagers) with a matching star field generated by an on-board star catalog. As a fully autonomous star tracker, the ASC requires a robust way to distinguish between real stars and other non-stellar objects that might appear in the imager field of view (FOV). These objects (e.g., planets, satellites, asteroids, foreign objects, etc.) might otherwise lead to misidentification of the star field and consequently an inaccurate attitude estimate. The ASC achieves this functionality by accepting the identification of a star field only if all of the luminous objects present in the FOV closely match those in the star catalogue. This implementation has proven extremely robust, and particularly effective when operating the ASC in high radiation environments. Conversely, any luminous object (down to visual magnitude of \(V=7.5\) from O to K type stars) not matched must represent a non-stellar object. This class of objects includes planets, asteroids and other smaller solar system bodies, as well as other spacecraft in close proximity (e.g., orbiting Earth).
The four ASC imagers are oriented on the (spinning) Juno spacecraft with an angular separation of 13° between their optical axis and the spacecraft spin axis, optimized for the attitude determination function. The ASC imagers are referred to as Camera Head Units, CHU-A, B, C, D. As a result, the imagers scan a washer-shaped section of the sky during a rotation, covering about \(1/20\) of the celestial sphere. The ASC is typically limited by command to utilize brighter objects for attitude determination, and the four cameras view the same portion of the sky over a full rotation. Thus only one camera need be commanded to detect, track and register non-stellar objects. The brightness sensitivity of this camera was set to visual magnitude of \(V=8.5\), and this mode of operation, enabled after the Earth flyby, will operate through end of mission. This camera will only be able to detect relatively bright objects with its 250 ms integration time, given its relatively wide FOV (13° by 18°). Large objects may be detected at large distances, whereas small and fast-moving objects may be detected this way only if they are in close proximity to Juno.
Every time the ASC detects a non-stellar object the inertial position and intensity of that object is registered. If the same object is detected in a subsequent observation (e.g., after a full rotation of Juno), its inertial coordinates are compared to the previous coordinates and the apparent tangential angular rate is calculated. If the measured rate of an object falls within a pre-defined range, and if the object is detected at least 5 times, the observation is stored the ASC onboard mass memory for later download. The angular rate range was set to store objects with an apparent tangential rate between 15 arcsec/s to 4800 arcsec/s; this choice excludes most large and well-known asteroids and planets, but allows detection of local objects, even those moving very rapidly in the FOV. To further constrain the nature of objects detected during cruise and hopefully later in science orbit, the ASC automatically captures a thumbnail image of the object being tracked.
The radial velocity of the non-stellar object may be constrained by analysis of the time variation of the measured intensity. Using this technique objects with tangential velocities up to an astonishing 4.5 deg/s were detected and tracked during the cruise phase. A detailed analysis of these remarkable observations, and their implications, is beyond the scope of this paper but will appear in the near future.
2.4.3 Radiation Monitoring with the ASC
The ASC CCD imagers, co-located on the MAG boom with the magnetic sensors, are provided with moderate radiation shielding mass (170 g per camera) in addition to that provided by the magnetometer optical bench that surrounds the small camera head enclosure. Since the camera’s CCDs are sensitive to the passage of energetic particles, they may also be used to monitor the flux of such particles. The majority of the ASC electronics (e.g., computer and associated electronics components) resides within Juno’s massive radiation vault, where ionizing radiation is greatly attenuated.
During the mission, Juno will transit regimes populated by extremely variable fluxes of different types of energetic particles. During most of cruise and probably throughout the more distant reaches of the science orbits, the fluence is primarily comprised of solar protons and cosmic radiation. The shielding level of the CCD is approximately 62 mm equivalent Al, which may be expected to efficiently stop all heavy ions and protons up to about 75 MeV, and all electrons below about 30 MeV. During Juno’s Earth flyby, for example, and beyond a few Jovian radii within the Jovian magnetosphere, trapped protons dominate. During Juno’s periapsis passes, however, energetic electrons prevail.
Energetic protons will generate a line of signal electrons along their path through the active regions of a CCD, with the ionization intensity increasing as they approach thermalization. The ionization path will appear as a bright pixel or line of pixels depending on the incidence angle of the incident proton relative to the plane of the CCD. In contrast, an energetic electron will deposit most of its energy inside a single pixel. The telltale signatures of electron and proton passage will both be evidenced within a single exposure, with no after-effects evident in the ensuing image.
These transient effects are thus distinguished from permanent displacement damage to the CCD caused by radiation. The latter will give rise to an elevated level of thermal electrons being liberated into the conduction-band. These dislocations will appear as permanent hot pixels in all subsequent images. Since the elevated noise in a hot pixel is expressed by thermal electrons, and as such highly sensitive to temperature, the Juno ASC CCDs are operated at a temperature of approximately −55 °C to very effectively (virtually eliminate) suppress this noise.
The Juno ASC is designed to operate in a high radiation environment and is therefore well endowed with several tools to suppress radiation-induced noise sources. The ASC performs this task by means of a suite of morphological filters operating on the image before it is passed to the centroiding algorithms. These filters detect and systematically remove from the image any signal with a signature similar to that expected of a passing energetic proton, electron or neutron. The ASC does, however, maintain a count of the number of such signatures detected in its CCD images.
This information is usually suppressed to better utilize the instrument’s telemetry allocation, and not telemetered to ground. However, in the interest of providing data for radiation environment assessment, we have commanded one of the four MAG ASC camera head units (CHU-D) to return the number of energetic particle events detected at a cadence of 1 Hz. This metric is anticipated to largely reflect the energetic electron flux along Juno’s periapsis passes.
2.4.4 Imaging with the ASC
The ASC cameras are effectively low-light, wide field of view imagers. They may be commanded with great flexibility, allowing for dark-level, gain and shutter control over an impressive dynamic range. During nominal star tracking operations, these levels are all autonomously adjusted for optimal spacecraft attitude determination. However, one or more cameras may be commanded at any time to acquire images at user-specified settings. They may also be commanded to image targets intelligently, with an exposure triggered by the instantaneous inertial orientation in space of the camera boresight. To use this inertial trigger function, the user merely specifies the target’s inertial attitude, and as the spacecraft rotates, the camera being used for imaging will acquire an image when the target appears nearest to the center of that camera’s FOV. This enables automatic targeting of any specific celestial body or target area.
During the course of the mission we’ll target Jupiter’s minor satellites, as well as the Galilean satellites, the tenuous Jovian ring system, and darkened hemisphere of Jupiter. Images planned during Juno’s period reduction maneuver (PRM) will be examined for lightning flashes, and visible emissions associated with the polar aurorae and satellite footprints.
The ASC also took advantage of the Earth flyby image the Earth-moon system upon approach. Juno approached the Earth Moon Barycenter system (EMB) from a sunwards direction in order to perform the necessary gravity assist en route to rendezvous with Jupiter. The ASC CHU-D was commanded into imaging mode, and its exposure time reduced to the extent practical (limited by spacecraft clock considerations), allowing the camera to image of the Earth Moon system repeatedly on approach. The mode was enabled at ∼4 million km distance, and operated through approach to ∼40,000 km. The image sequence obtained during the approach was compiled into a time lapse movie which can be viewed at “https://www.youtube.com/watch?v=_CzBlSXgzqI”.
3 Science Requirements
The magnetometer investigation (MAG) driving requirements benefit from knowledge of the magnetic field environment that Juno will transit, a consequence of the spacecraft missions that preceded Juno. Juno MAG requirements are sourced from the Juno Mission requirements document, Level 3 & 4 functional requirements documents. The most demanding science objective from a measurement perspective is the global magnetic mapping, for which vector measurement accuracy translates directly into estimated parameter uncertainties in the magnetic models derived from the observations. More relaxed measurement requirements would be sufficient to service the needs of the science objectives associated with the exploration of the polar magnetosphere. A relevant subset of the MAG instrument driving requirements are listed as follows:
-
Measure the magnitude and direction of the ambient magnetic field.
-
Encompass a dynamic range of measurement extending from 1 nT to 16 G, per axis (1 G = 100,000 nT).
-
Provide measurement of the vector magnetic field with an absolute accuracy of 0.05 % (goal 0.01 %).
-
Provide the vector magnetic field (via spacecraft C&DH broadcast vector) to other science payloads in flight, in real time, with an accuracy of 1 %.
-
Sample the magnetic field at a (variable) rate of up to 64 vector samples/s.
-
Provide complete hardware redundancy of the magnetic field measurement.
-
Determine the attitude of the sensor platform with an accuracy of 20 arcsec.
-
Sample sensor platform attitude at a rate of up to 4 attitude solutions/s.
-
Provide complete hardware redundancy of the sensor attitude measurement.
-
Provide non-magnetic a/c heaters for sensor thermal control, under operating and non-operating conditions.
-
Operate and meet measurement requirements over environmental conditions per the Juno environmental requirements document.
The measurement system provided by the MAG investigation meets and exceeds the Project requirements with a pair of independent magnetic sensors and associated (co-located) attitude sensors with the performance characteristics listed in Table 2.
4 Investigation Design and Spacecraft Accommodation
The Juno MAG investigation is designed to acquire highly accurate vector measurements of the magnetic field, undisturbed by spacecraft-generated magnetic fields, and to do so with redundancy. This requires the magnetic sensors to be located as far from the body of the spacecraft as is practical. Thus the Juno MAG sensors are remotely mounted (at approximately 10 m and 12 m) along a dedicated MAG boom that extends outward along the spacecraft \(+x\) axis, attached to the outer end of one of the spacecraft’s three solar array structures (Fig. 6). The fully instrumented MAG boom was designed to mimic the outermost solar array panel (of the remaining two solar array structures) in mass and mechanical deployment characteristics, utilizing the same retention and release devices as the other solar array wings. The separated, dual magnetometer sensors provide the capability to monitor (and mitigate) spacecraft-generated magnetic fields, if any, in flight (Ness et al. 1971; Primdahl et al. 2006).
Juno’s magnetometer boom, a carbon-composite, aluminum honeycomb structure supporting the two magnetometer sensor suites. The ∼4 m long structure is affixed to the outermost end of one of Juno’s three solar array wings (“wing 1”), placing the sensors at ∼10 and ∼12 m from the body of the spacecraft for magnetic cleanliness. The structure was designed to mimic the mass of a solar array panel, and deploys using the same retention and release devices as the solar array stack
Magnetic sensors alone would not be sufficient to meet the vector accuracy requirement, however, due to the uncertainty in orientation of the deployed solar array and MAG boom. The (deployed) orientation of the lengthy mechanical assembly is subject to initial deployment uncertainty and to environmental conditions and forces acting upon the assembly, none of which are adequately addressed in the clean room (and in the presence of gravity) prior to launch. It would also be impractical to construct the entire ∼4 m MAG boom with a 20 arcsec stability requirement under all environmental conditions. Therefore, each magnetic sensor is paired with a pair of attitude sensors that continuously monitor its absolute orientation in space.
The magnetic measurement is made with a vector fluxgate magnetometer (FGM) and the attitude measurements are made using non-magnetic star cameras (camera head units, or CHUs) co-located with the FGM sensor. The outboard (OB) and inboard (IB) sensor assemblies are identical. An FGM sensor and two CHUs are mounted on a composite, thermally isolated optical bench (MAG optical bench, or MOB) that is designed to hold all of the sensors in precise alignment. The CHUs measure the attitude of the sensor assembly continuously in flight to better than 20 arcsec and are used to establish, and continuously monitor, the attitude of the sensor assembly with respect to the spacecraft Stellar Reference Units (SRUs) through cruise, orbit insertion at Jupiter, and initial science orbits.
The FGMs and the MOBs were developed at Goddard Space Flight Center, and the attitude determination system (Advanced Stellar Compass, or ASC) was designed and built at the Technical University of Denmark (DTU).
Both systems enjoy ample hardware redundancy, such that no credible single point failure can lead to failure to satisfy measurement requirements. Redundancy in the magnetic measurement is achieved with two identical sensor systems (IB and OB sensors) and shared hardware redundant digital systems and power supplies. Redundancy in the attitude measurement system (ASC) is provided by fully hardware redundant electronics controlling four independent camera heads, any of which may be operated in any combination. The ASC is also cross-strapped to either side of the block redundant spacecraft (A/B).
The ASC provides the most accurate attitude determination for each FGM sensor and as such it is the primary source of attitude information for MAG. However, the investigation is also designed with the capability of meeting measurement requirements (albeit with relaxed vector accuracy) should ASC attitude solutions not be available throughout the duration of the mission. This pathway is available after the spacecraft has settled into the 14-day science orbits and the attitude transformations between spacecraft SRUs and the ASC CHUs have been determined (subsequent to orbit insertion and other disturbances). The relative attitude of the MOBs and the spacecraft SRUs may have a time-dependent component (e.g., thermal response as a function of orbital phase) so a comparison of ASC and SRU attitudes through a few orbits is needed before the spacecraft requirement can be met. Subsequently, the spacecraft can provide (reconstructed) knowledge of the FGM sensor assembly attitude to an accuracy of 200 arcsec throughout the remainder of the mission, using sensors on the body of the spacecraft and knowledge of the attitude transfer between the ASC camera heads and spacecraft SRUs. Thus, stability of the mechanical system (MAG boom, solar array hinges, structure, and articulation strut) linking the body of the spacecraft (SRU reference) to the FGM sensors (and CHUs) is an important element in satisfying the spacecraft requirement, should this pathway be required at any time during the mission.
4.1 Mission Design
The Juno spacecraft was launched promptly on the first day of its 21-day launch window, on 5 August 2011. The spacecraft uses a \(\Delta \)V-EGA trajectory consisting of a deep space maneuver on 12 September 2012 followed by an Earth gravity assist on 9 October 2013 at an altitude of 500 km. The deep space maneuver and Earth flyby were entirely successful if not uneventful: the spacecraft experienced a safe mode entry during the Earth flyby upon detection of a low bus voltage as it passed through the Earth’s shadow. While the spacecraft did successfully transition to safe mode, two additional safe mode entries occurred shortly thereafter, in response to related but unanticipated fault conditions detected by the spacecraft fault protection software. None of these events were of any consequence with respect to the spacecraft trajectory and the spacecraft remained on target for arrival at Jupiter as planned.
Juno will arrive at Jupiter on 4 July 2016 using a lengthy main engine burn to insert into a 53.5-day capture orbit (Fig. 7). The Juno spacecraft approaches Jupiter along the dawn meridian and initially orbits close to the dawn meridian. With each subsequent orbit Juno’s orbit plane drifts in the direction of midnight local time (Fig. 8). Since the mission plan was designed to provide true polar orbits (90° inclination), the orbit evolves in time with the latitude at periapsis gradually shifting northward in time (Fig. 7). As the mission proceeds, apoapsis moves steadily southward, exposing the spacecraft to an ever-increasing radiation dosage.
The original mission plan called for a single 107-day capture orbit prior to execution of a period reduction maneuver (PRM) that would place Juno into a highly elliptical 11-day science orbit with a periapsis altitude of ∼4500 km and apoapsis at ∼20 \(R_{j}\). However, Project has since opted to split the capture orbit into two ∼53.4-day orbits before execution of the PRM to transition to science orbits. This option allows for the science instruments to operate during a periapsis pass to characterize the environment without running afoul of institutional reticence to operate non-essential systems during a critical maneuver (e.g., orbit insertion). It also affords Project the ability to assess instrument and spacecraft performance in this difficult environment before committing to an unrelenting 14-day sequence of periapsis passes once the final orbit is entered via the PRM.
Science orbits are designed to provide a set of close-in periapsis passes spaced evenly in Jovian longitude to approximate uniform coverage of the sphere (Fig. 9). The original mission plan called for a year-long prime mission comprising 32 high-inclination, high-eccentricity orbits of Jupiter, spaced every 12° in longitude at the equator. These polar orbits (90° inclination) would have had a periapsis altitude of ∼4500 km, a semimajor axis of ∼20 \(R_{j}\), and an orbital period of ∼11 days. Here again the Project revised the mission plan, opting instead for 33 science orbits with a 14-day orbital period. This choice affords added time between periapsis passes, if needed, to respond to unanticipated spacecraft events, and it also accumulates longitudes in a more robust sequence compared with the 11-day plan. The original plan completed coarse longitude coverage with 24° spacing between orbits during the first half of the mission, and bisected those longitudes during the second half of the mission. The 14-day plan puts 90° of longitude between successive periapsis passes, sectoring the globe first into 90-degree quadrants, bisecting each of those with the subsequent 4 passes, as illustrated in Figs. 10 and 11. The spacecraft executes a small delta \(v\) maneuver after each set of four orbits to shift the longitude as needed to place subsequent periapsis passes midway between prior passes. In this manner the global coverage of the sphere is built up more evenly in time, with more uniform global coverage provided early in the mission, albeit coarsely.
Orthographic projections of the subspacecraft latitude and longitude for periapsis segments (\(r < 2.5~R_{j}\)) of all orbits, identified by orbit number, against a color-coded contour map of the surface magnetic field as calculated using the VIT4 model magnetic field. Orbit insertion (0) and PRM (2) are targeted to occur at longitudes with relatively less intense magnetic field magnitudes
Subspacecraft latitude and longitude for periapsis segments (\(r < 2.5~R_{j}\)) of Juno’s first 19 orbits, identified by orbit number, against a color-coded contour map of the surface magnetic field as calculated using the VIT4 model magnetic field. The first 4 (red) science orbits (4–7) divide the globe into 90° sectors; after a maneuver, the next 4 (black, solid) orbits (8–11) divide the globe into 45° segments; and the next 8 (dashed), 22.5° segments. Global coverage is accumulated conservatively, with orbits separated by 90°, achieving progressively finer spatial resolution
Subspacecraft latitude and longitude for periapsis segments (\(r < 2.5~R_{j}\)) of Juno’s remaining 17 orbits, identified by orbit number, against a color-coded contour map of the surface magnetic field as calculated using the VIT4 model magnetic field. These orbits are targeted to map longitudes bisecting those already mapped
The primary science is acquired for approximately 6 h centered on each periapsis although fields and particles data are acquired at low rates for the remaining apoapsis portion of each orbit. All orbits will include fields and particles measurements of the planet’s auroral regions. The initial insertion orbit (orbit #0) was selected based upon a number of practical constraints, including ground station coverage; it was also designed to minimize the magnetic field strength to be experienced during the critical maneuver (insertion burn), a consideration related to sensitivity of a critical telecom component. The first 14-day “science” orbit occurs on orbit 4, following a 14-day trajectory “cleanup” orbit and the two 53-day orbits (Fig. 12). This figure shows the predicted field magnitude for each periapsis pass, and illustrates the stepwise accumulation of global coverage with decreasing longitudinal separation between passes. Figure 13 shows predicted field magnitudes for the second half of the mission during which the longitude separation is halved again.
Magnetic field magnitude, in Gauss, for each periapsis during the first half of the mission (for the nominal mission plan) segment, as a function of time (year and day of year) identified by orbit number. Magnetic field magnitudes calculated using the VIP4 magnetic field model. Jupiter orbit insertion (“JOI”), capture orbit (“C”), the period reduction maneuver (“PRM”), and cleanup (“cleanup”) orbits preceding the nominal science orbit phase are indicated (orbits 0–3). Jupiter images illustrate accumulation of global longitude coverage
Currently, five of the first seven periapses are designed to support microwave radiometry of Jupiter’s deep atmosphere with the remaining orbits designed to support gravity measurements to determine the structure of Jupiter’s interior. Juno is spin stabilized with a nominal rotation rate during the science phase of 2 rotations per minute (rpm). (The spacecraft was operated at a reduced spin period of 1 rpm during a portion of the cruise phase, and operates at increased spin rate of 5 rpm during propulsive maneuvers). For the radiometry orbits the spin axis is precisely perpendicular to the orbit plane so that the radiometer fields of view pass through the nadir. For gravity passes, the spin axis is aligned to the Earth direction, allowing for Doppler measurements through the periapsis portion of the orbit. Data acquired during the periapsis passes are either telemetered in near real time or recorded and played back over the subsequent portion of the orbit.
4.2 Spacecraft Requirements and Accommodation
The MAG investigation levied special accommodation requirements on the Juno spacecraft. The most significant requirement stems from the need to separate the magnetic field sensors from the body of the spacecraft, so they may sense an environment free of interference from magnetic fields generated by the spacecraft itself. A minimum separation of 2 meters between the sensor suites was required to preclude interference between them and to allow identification of spacecraft-generated magnetic fields (by virtue of the relative amplitude of such as a function of radial distance from the source). The MAG Boom is an impressive structure crafted with Carbon composite face sheet over Aluminum honeycomb, like much of the mechanical structure of the spacecraft (Fig. 6). It accommodates the two MAG sensor suites at distances of ∼10 m (IB) and ∼12 m (OB) from the center of the spacecraft, radially along the spacecraft payload \(+x\) axis.
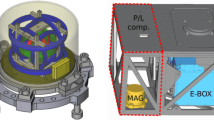
Each MOB (Fig. 14) mounts to the MAG Boom with one Titanium rigid foot under and between the camera heads (called “big foot”) and two fairly stiff Titanium flexure’s at the FGM sensor end of the MOB, on either side of the FGM sensor. The ceramic MOB and the Carbon composite MAG Boom both exhibit a very low coefficient of thermal expansion; the stiff Titanium flexure mounts provide adequate freedom of movement to accommodate differential thermal expansion while satisfying load requirements.
The Carbon Silicon Carbide (CSiC) magnetometer optical bench (MOB) as viewed from above and below, with fluxgate magnetometer (FGM) sensor and camera head units (CHUs) of the Advanced Stellar Compass installed. The master optical cube affixed to the MOB serves to define the coordinate system for the suite of instruments
The two MOB’s mounted on the Sunward, or illuminated side of the Boom so the two ASC camera heads on each MOB look through oval cutouts in the MAG Boom. These oval cutouts were required due to assembly constraints of the inner baffles that are attached to the ASC camera head units. The inner baffles are required to reject stray light between the outer baffle and the camera. The ASC outer light baffles were mounted to the back side of the Lockheed Martin (LM) provided MAG boom. This configuration had both mechanical and thermal benefits. Since the mechanical load could be reacted directly by the MAG boom and the thermal cold load from the baffles could be reacted by the MAG Boom, reducing the heater power needed to keep the MOB’s at designed operating temperature. Mounting the MOB’s and large baffles separately to the MAG Boom did create the need to shim and align the outer baffles to the cameras. This activity was performed cooperatively between LM and NASA GSFC. The FGM sensors protruded through the MAG Boom, placing the FGM sensors precisely in the plane of the (backwired) solar array.
Another significant spacecraft accommodation requirement impacting design of the entire mechanical structure—MAG boom, solar array, spacecraft structure through to Stellar Reference Units—is pointing stability. As stated earlier a pointing allocation for the MOB’s on the end of the solar array were defined. This allocated ∼200 arcsec to the boom and ∼20 arcsec to the MOB’s. This requirement is a post launch requirement that assumes post launch calibration between the spacecraft star sensors and the 2 sets of ASC star cameras. It should also be noted that much work is planned during the cruise, Earth flyby, and early Jupiter operational phases in order to verify that the required pointing accuracy and stability has been met.
The MAG investigation provides a MAG broadcast vector that the spacecraft C&DH system distributes in real time to several instruments that use the magnetic field information to optimize the configuration of their instruments (such as particle pitch angle sorting) and telemetry. The MAG broadcast vector is not intended as a source for scientific quality magnetic field data, as it is distributed using nominal values for scale factors and offsets rather than fully calibrated values. In addition it is important to note that the MAG broadcast vector is produced from the OB sensor by default. The FGM electronics may be reconfigured to use the IB sensor as the source for the MAG broadcast vector, in which case the on board conversion table must be updated since the MOB’s are rotated by 180° (about spacecraft \(z\) axis) on the boom.
4.3 Spacecraft Magnetic Control Plan
A successful Magnetic Field Investigation is not possible without a successful spacecraft magnetic control program to ensure that the vehicle meets magnetic requirements. Juno’s emphasis on high magnetic field strength regions near Jupiter notwithstanding, the science requirements of the Mission led to a system level requirement for no more than 2 nT (static) and 0.5 nT (dynamic) magnetic field from the spacecraft and its systems at the locations of the magnetic field sensors. The most cost-effective tool in a spacecraft magnetic control program is distance: put as much distance between the spacecraft and the MAG sensors as possible, to capitalize on the \(1/r^{3}\) reduction in magnetic fields with distance \(r\) from the source. This led to the placement of the two MAG optical benches on a dedicated magnetometer boom mounted at the end of one (“Wing 1”) of Juno’s three solar array appendages. This placed the inboard MOB about 8 m from the edge of the Juno spacecraft and about 10 m from the spacecraft center. The outboard MOB was by requirements 2 m from the IB MOB, at 12 m from the center of the spacecraft.
Implementation of a successful magnetic control program was the shared responsibility of the spacecraft contractor (Lockheed Martin), the Jet Propulsion Laboratory, and the magnetic field Investigation at Goddard Spaceflight Center. A Magnetics Control Board, co-chaired by JPL’s Pablo Narvaez and the Juno MAG Investigation Lead (and Mission Deputy Principal Investigator) provided oversight and guidance, developing design guidelines, testing facilities and requirements, and management tools. The MAG investigation team worked with LM and their subcontractors, providing specialized test equipment and procedures, performing magnetic tests on critical subsystems (e.g., backwired solar arrays) and systems (e.g., spacecraft magnetic “swing test”).
The spacecraft contractor performed magnetic characterization/degaussing of all spacecraft components. GSFC did provide the spacecraft supplier with two coil systems, one a 7ft Helmholtz system, large enough to characterize virtually any spacecraft part or component, and a 2 ft diameter degaussing coil. In addition, JPL provided a multi-range magnetometer sensitive enough to characterize spacecraft components and a portable screening station that included a GSFC-built screening magnetometer for screening objects that will be close to the flight magnetometer sensors. A many-dipole model of the spacecraft was assembled, using measurements of the Engineering Models and flight systems, as they became available. This model was used as a management tool, tracking progress toward the system level requirement. Wherever practical, multiple components were arranged on the spacecraft in such a way as to null the net magnetic moment of the ensemble (e.g., self-cancellation of the fields due to multiple thruster valves); some systems, notably the sweep magnets on the Traveling Wave Tube Amplifiers (TWTAs) required paired cancellation magnets added to the assembly for cancellation.
Implementation of a magnetic control program within the confines of a cost-controlled project such as Juno requires a pragmatic approach that focuses attention where it will do the most good, i.e., on the few subsystems with significant magnetic materials or current consumption (“tall poles”); and, in particular, systems in close proximity to the MAG sensors. The MAG team designed the backwiring circuits for the solar cell strings used on all three wings of the solar arrays, and worked with LM and the solar array subcontractor (Spectrolab) to verify the designs by test prior to fabrication of the flight arrays. This design provided for individual string by string cancellation of the magnetic fields produced by electrical currents flowing through the solar cells, so cancellation is unaffected by loss of any solar array string. GSFC provided personnel, equipment and analysis support for the testing the Juno solar array panels.
In practice GSFC took responsibility for Magnetic cleanliness and screening on the MAG Boom. GSFC performed a magnetic gradiometer scan of the MAG boom once it was delivered to the launch site. From that point on, all items added to the boom were either magnetically screened by GSFC or verified to have been magnetically screened to the satisfaction of the GSFC MAG investigation team. MAG investigation personnel or Spacecraft magnetics personnel were present for every significant MAG Boom assembly operation at the launch site. Non-magnetic tools were used in the final assembly of the MOB’s to the MAG boom.
5 Juno MAG Instrumentation Suite
The Juno MAG investigation is designed to acquire highly accurate vector measurements of the magnetic field in Jupiter’s environment, mapping the planetary magnetic field with extraordinary accuracy and spatial resolution. Juno accomplishes this with an instrument complement that includes two identical sensor suites, one Inboard (IB) and one Outboard (OB), arranged along a radius vector at about 10 and 12 m from the center of the spacecraft, at the outer end of one of Juno’s three solar array structures. This provides hardware redundancy for the investigation and a means (Ness et al. 1971; Primdahl et al. 2006) of monitoring spacecraft-generated magnetic fields, which one expects to be greater in magnitude at the innermost sensor.
Each sensor suite consists of a fluxgate magnetometer (FGM) to measure the three components of the vector magnetic field and a pair of collocated non-magnetic star cameras (ASC) to provide accurate attitude reference at the FGM sensor. The FGM and the collocated ASC camera heads are maintained in precise alignment by the MAG optical bench, a Carbon-Silicon Carbide (C-SiC) structure to which the three sensors are attached. The MAG optical bench provides enough separation between the FGM sensor and the camera heads to attenuate any magnetic fields generated within the camera heads or their associated heater elements. The FGM is thermally isolated within its own thermal blanket and is temperature controlled via an ac proportional heater to operate at about 0 °C. The ASC camera heads and MOB are thermally controlled via heater elements affixed to the camera head enclosures; the CHUs are temperature controlled to operate at about −54 °C.
The two magnetometer sensor suites are operated continuously throughout flight, but for brief interruptions (e.g., “safe mode” entries, critical spacecraft maneuvers), and both fluxgates are sampled at the same instant in time, referenced to the spacecraft clock. Simultaneous measurement of the magnetic field at the OB and IB sensor locations facilitates analysis of spacecraft-generated magnetic fields, if any. Likewise, all four ASC camera heads are sampled at the same instant in time, referenced to the spacecraft clock. After a successful orbit insertion, the spacecraft response to a safe mode entry will be modified to minimize data loss from the magnetometer investigation. Customarily, when the spacecraft fault protection system detects an uncorrectable problem, or anomaly, and enters “safe mode”, all science instruments are turned off, and restored to operational status only after Project diagnoses the anomaly and determines that it is safe to return to operational status. Thus instruments may be off for a significant time span, depending on the nature of the anomaly. In order to minimize loss of a periapsis pass needed for the global magnetic field map, changes were made to the spacecraft safe mode response (“MAG on in safe mode”) that ensure return of the FGM operational status within minutes of a safe mode entry.
5.1 Fluxgate Magnetometer (FGM)
The GSFC fluxgate magnetometer meets the vector measurement requirement with a simple and reliable instrument with extensive flight heritage. The Juno magnetometer design draws from Mario Acuña’s extensive flight experience, with over 78 space flight magnetometers developed for planetary research and built at GSFC (Voyagers 1 and 2, Pioneer 11, Giotto, Lunar Prospector, Mars Observer, Mars Global Surveyor, MESSENGER, STEREO, WIND, ACE, AMPTE, TRMM, Freja, Viking, UARS, DMSP, Firewheel, MAGSAT, POGS, RBSP, and Maven). Among these prior developments one can find instruments with the extraordinary vector accuracy (e.g., MAGSAT) and large dynamic range (Voyager’s high field magnetometers) needed to satisfy the Juno measurement requirements. However, the Juno instrument is unique, in that it provides both extraordinary vector accuracy (100 ppm) and high dynamic range (to 16 G per axis) in one instrument. The Voyager systems utilized two sets of magnetometers to cover the wide dynamic range: a redundant pair of low field magnetometers and a redundant pair of high field magnetometers, four sensors in all (Behannon et al. 1977). The Juno FGM is an evolved version of the high accuracy MAGSAT sensor, modified to extend the measurement capability to 16 G field magnitudes, without sacrificing performance in low field environments. It was the last of many magnetometers designed by Mario Acuña. The Juno sensor design covers the wide dynamic range with six instrument ranges increasing by factors of 4 in successive steps.
5.1.1 Instrument Description
The FGM functional block diagram (Fig. 15) illustrates the configuration of the Juno FGM sensors and electronics. There are two sensors (Inboard and Outboard) mated to two analog electronics boards (one each Inboard and Outboard). The two sensors and associated analog electronics boards are powered whenever the spacecraft provides power to the instrument via either of the redundant power interfaces. The instrument has two identical power converters and two identical digital electronics sections. At any time only one power converter is powered, along with its associated digital electronics; the other set is cold-spared. Either of these two power converters/digital electronics boards (“A-side” or “B-side”) can service both IB and OB sensors and analog electronics. Likewise, both “A-side” and “B-side” electronics can be powered by and communicate with either of the two redundant sides of the spacecraft command and data handling (C&DH) system. Digital interfaces to the spacecraft are via redundant radiation-tolerant RS-422 driver/receiver pairs; these mirror those on the spacecraft side of the Juno instrument interface. Separate non-magnetic alternating current (AC) heater controllers on independent power switches provide thermal power to the FGM sensors. The system is designed such that no credible single point failure can result in the loss of data from both IB and OB magnetometers.
Functional block diagram of the fluxgate magnetometer systems, showing the electronics (mounted in the spacecraft radiation vault) and remote sensors mounted on the MAG boom. The system is hardware redundant with either power and digital system (red and blue) operational, the other cold spared; both magnetometer analog and A/D cards (green) always powered together
The Juno vector instrument incorporates four single axis analog circuits to measure the three components of the magnetic field; one is measured redundantly (\(R\)). The four component (\(x\), \(y\), \(z\), \(r\)) analog outputs are sampled on the same clock transition 64 times each second by dedicated 16-bit Analog-to-Digital Converters (ADC) that follow anti-aliasing single pole low pass filters (−3 db at 32 Hz). All four ADCs are controlled by, and read by, a digital processor that formats the data for transfer to the spacecraft C&DH, along with housekeeping data (temperatures, voltages, current measurements) sampled sequentially by a fourth dedicated engineering ADC.
Principle of Operation
The fluxgate magnetometer is a simple, robust sensor capable of very high vector accuracy while requiring only modest resources (Acuña 2002). The principle of operation is illustrated with the help of the simplified schematic (Fig. 16) that describes a generic, single axis fluxgate magnetometer utilizing a ring core sensing element. The sensing element is a high permeability ring formed by wrapping a thin tape of 6–81 molybdenum permalloy onto a non-magnetic Inconel hub. This material is nickel-iron alloy with about 81 % nickel and 6 % molybdenum content, the remainder iron, with a magnetic permeability of order 100,000.
Schematic of a single axis fluxgate magnetometer (after Acuña 2002) utilizing a tuned ring core sensor and a shared 2f sense and feedback coil. Each Juno FGM utilizes four such circuits
The “fluxgate” works by driving this sensing element cyclically into saturation by exciting a toroidal winding at a drive frequency of ∼15.4 kHz. The core saturation “gates” the ambient magnetic flux threading the sensing coil, as the core permeability alternates between very high, in the unsaturated state, and very low, in the saturated state. Core saturation occurs at twice the drive frequency, modulating the ambient flux at twice the drive frequency, and inducing a voltage in the sensing coil at 2f, which is amplified and passed to a synchronous detector. The synchronous detector is essentially a lock-in amplifier, using as a reference the second harmonic of the drive frequency, all derived from a stable crystal controlled oscillator. The output of the detector is fed back to the sense coil to drive the field in the sensor to zero, which results in a sensor with very high linearity. The output voltage is linearly related to the ambient field aligned with the axis of the sense/feedback coil. Several dynamic ranges may be implemented by selection of different feedback resistors. The Juno instrument uses miniature relays to perform this switching function, as they are impervious to the effects of radiation.
Each FGM sensor block uses two miniature ring-core fluxgate sensor assemblies to measure all three components of the vector magnetic field. Each ring-core sensor assembly measures the magnetic field in two orthogonal directions in the plane of the ring core. The field in each ring core is both sensed, and nulled, using negative feedback, by a pair of nested coils within which the ring core resides. Each coil nulls the field in one of the two perpendicular axes that define the plane of the ring core. This arrangement nulls the field in the plane of the sensing element, providing excellent linearity over the full dynamic range of the instrument. With two such sensor assemblies, oriented in planes intersecting at 90°, all three components of the vector field are measured (one component measured, redundantly, by both).
The sense and feedback coils, and sensor block, are fabricated using a machinable glass ceramic with low thermal expansion (Macor) and excellent mechanical stability (Fig. 17). A precision optical cube certified to 2 arcsec orthogonality is bonded to each sensor block to facilitate accurate and repeatable calibrations during development and before the sensor assembly is mated to the magnetometer optical bench. The FGM sensor block attaches to the optical bench via a three point kinematic mount to maintain accurate alignment over the range of environments experienced. The FGM sensor block is designed to operate at about 0 °C, whereas the optical bench and CHUs are designed to operate at −54 °C to minimize the effects of radiation. The FGM sensor block is thermally isolated from the optical bench via the three point kinematic mount. The FGM sensor itself is impervious to radiation effects.
A Juno fluxgate sensor block is fabricated using a machinable glass ceramic (MACOR) material with exceptional dimensional stability over temperature. This assembly is shown prior to fitting the kinematic mounts and sensor optical cube. The two outer sense/feedback coils are visible in this image; inside each is another sense/feedback coil oriented at 90° with respect to the outer bobbin such that the magnetic field in each ring core may be nulled in the plane of the ring core
Analog Design
The FGM analog electronics cards for the two magnetometers (IB, OB) each occupy a single electronics circuit board mounted in a shielded, stackable frame. These two analog frames, along with a digital electronics frame and a power converter frame, comprise the four cards in the FGM electronics box (Fig. 18). Cabling internal to the enclosure connects the boards. There is a thin aluminum shield between each slice to limit internal radiated effects. The analog circuitry is isolated from the digital and power circuits to prevent the more sensitive analog circuitry from electromagnetic interference.
The fluxgate control electronics has six available ranges, {1600, 6400, 25600, 102400, 409600, 1638400} nT. After analog signal processing, a voltage proportional to the magnetic field in each axis is digitized to ±15 bits with four dedicated LTC1604 analog-to-digital (ADC) converters. The (nominal) 1600 nT range has resolution of 0.0488 nT/ADU. With a full dynamic range of 16 Gauss per axis, the instrument has a dynamic range of seven orders of magnitude.
There are two ringcores in each fluxgate sensor and these are driven by a common drive frequency of 15.36 kHz which is generated on the analog cards. Using a clock provided by the digital electronics, each card operates at the same frequency and in the same phase. The drive waveform operates continually with a 50 % duty cycle, saturating the ringcores first in one direction and then the other. The drive circuit is of the heritage design, based upon 4000-series CMOS logic, and has been flown on several dozen missions.
The precision solenoid windings on the fluxgate bobbins are utilized for two purposes, typical of a conventional fluxgate design. First, the windings are used as detection coils that transmit the result of the (+) and (−) ringcore saturation down the boom cable to the analog electronics, effectively using the drive frequency as the carrier signal. Second, these windings are used to apply a near-DC magnetic field to the sensor axis parallel with the solenoid and in the plane of the ringcore so that the field at the center of the ringcore in that axis may be nulled. The analog electronics, boom cable, and sensor form the fluxgate servo loop.
The two ringcores in each FGM sensor are each enclosed in an orthogonal bobbin pair. The two bobbin pairs are oriented orthogonally. These four bobbin windings require four individual electronics channels with one channel being a redundant axis. For Juno FGM, each of these channels is active and digitized. For each axis \(\{X, Y, Z, R\}\), the signal transmitted down the boom cable to the electronics is transformer-coupled into the electronics input, band-pass filtered, and amplified. The amplified signal is processed through a synchronous demodulator and integrator, removing the carrier signal at the second harmonic of the drive signal. The integrator sums any offset seen between the (+) and (−) phases over many cycles of the drive. The output of the demodulator/integrator is now near DC (i.e., less than 100 Hz) and passed to both a current source and the ADC. The current source has two switchable ranges and the ADC has three commandable ranges in via a switchable gain buffer. In this way, the analog electronics supports the six ranges. There is little transient when the switchable gain buffers are changed. Whenever the current source range is switched, however, there is a transient recovery time proportional to the bandwidth of the servo loop. The output of the current source is filtered and the near-DC signal driven down the approximately 17 m boom cable to the bobbin solenoid winding. A passive resistive offset trim circuit is incorporated into this servo loop such that any system DC offsets may be nulled just prior to final calibration.
Each analog board (Fig. 19) interfaces to the boom cable via a standard 25 pin D-subminiature connector. The harness incorporates fine gauge non-magnetic coaxial cables and terminates in a non-magnetic D-connector at the sensor end.
Each analog board receives ±13 V from the power converter card. At the card power input, there are foldback limiter circuits which act as resettable circuit breakers. In the event that one of the power rails exceeds the expected power by approximately a factor of three, the limiter will trip and open up the connection. A power cycle is needed to reset the circuit. In the event of a hard short on one analog card, this circuitry acts to prevent the power rail from being loaded, allowing the other analog card to continue in operation.
Each analog card has a thermistor-based board temperature readout circuitry. This voltage, which is proportional to the circuit card temperature, is passed back to the digital card for digitization and inclusion in the FGM analog housekeeping telemetry.
The digital card controls the analog-to-digital conversion process of the LTC1604s. These ADCs return data in a two’s complement format. The conversion rate is 64 Hz and is simultaneous for all four axes. The parallel output data is latched into radiation-hardened shift registers and sent to the digital card serially. The analog card operations are invariant; telemetry downlink rate is controlled by the digital electronics logic.
Power Converter Design
The FGM power converter contains both the low voltage converter for the analog and digital electronics plus two proportional heater controllers. It occupies one slice in the FGM electronics stack. There are two power converter circuits and two heater controllers on the power converter card for redundancy (Fig. 20). Only one of the power converters is powered at a time (primary or redundant), selected by spacecraft switches and responsive to flight rules. The power converter incorporates mechanical relays to route power from either converter A or converter B, depending upon which is powered.
Each power converter has parallel 5 A fuses, an in-rush current limiter, and EMI filtering. The power converter is of the flyback design, based upon the heritage SG1524 pulse width modulator (PWM). It starts with a free-running oscillator until the digital board is operational, at which point it receives a 100 kHz clock so that the converter may be synchronized to the same crystal as the analog drive circuitry. The transformer is custom wound at GSFC for this application. The power converter outputs ±13 V and +5 V to the analog and digital boards.
There is also a current monitor, implemented with a magnetic amplifier operating at roughly 5 kHz. It has an approximate range of 0–300 mA. The voltage output of this current monitor is sent to the digital board for digitization and incorporation into the analog housekeeping telemetry.
Each power converter card has thermistor-based temperature sensing circuitry. The voltage output, which is proportional to the thermistor temperature, is passed to the digital card for digitization and inclusion in the analog housekeeping data.
Proportional Heater Design
There are two alternating current (AC) proportional heater circuits. These reside on the FGM power converter card (Fig. 20). They operate independently and in parallel, one for the IB sensor and one for the OB sensor. The unregulated power received from the spacecraft A or spacecraft B busses is independently diode-OR’ed into each circuit. In this way, the sensor heaters are isolated and have full block redundancy. In flight, the circuits are continually enabled, serving as both survival and operational heaters. During cruise, the heaters have been operating at about 50 % of their full 4.5 W heater authority and maintaining the sensors at approximately 0 °C.
In the event of a transient event where the converters draw more than double their expected maximum current, a foldback-limiter circuit disconnects the heater from the spacecraft bus voltage. These limiters are readily reset by cycling power once the fault is cleared, functioning like a circuit-breaker instead of a fuse.
The heater circuit is based upon a heritage design using the SG1524 regulating pulse width modulator (PWM). A functional block diagram of the proportional heater controller appears in Fig. 21. The 311P18-02A10R thermistor (\(2252~\Omega \) at 25 °C) is mounted internal to the FGM sensor and is used for temperature feedback control. A simple R–C network sets the PWM frequency at approximately 50 kHz, keeping the fundamental and harmonics of the heater switching well outside the bandwidth of the fluxgate’s second harmonic detection circuit. The amount of heater power delivered is set by both the unregulated input voltage and the transformer, which is wound specifically for this purpose at GSFC. Power MOSFETs are used to pull currents through the transformer. The output to the heater is symmetrical and referenced to chassis ground so that there is no DC component in the heater tape. This ensures the heater does not generate a detectable magnetic signature. The heater tape is bonded to the sensor cover. It is constructed of the non-magnetic conductor constantin and is routed such that any DC currents will self-cancel.
Schematic of the fluxgate magnetometer proportional heater circuit. The magnetometer sensors require an a/c heater in order to ensure that no dc currents flow in close proximity to the magnetic sensors (the spacecraft service uses dc current for heaters). Upon application of power, the pulse width modulator (PWM) and field effect transistor (FET) driver circuitry delivers a/c power via an output transformer to the non-inductive (resistive) heater element on the sensor cover. The PWM limits are set to maintain the sensor at a constant temperature near 0 °C, and the power applied to the heater element is monitored by the spacecraft (Heater MON)
An additional winding on the secondary is utilized as a heater monitor; this allows the spacecraft to determine the percentage the PWM is on/off and thereby allowing an inference of the approximate sensor temperature even when the main analog electronics is not powered.
Digital Electronics Design
The digital printed circuit board (Fig. 22) contains two independent digital electronics circuits on the same card, Digital A and Digital B, for redundancy. Each side of the digital electronics has an I/O interface to both the primary and redundant spacecraft data handlers. The FGM digital electronics implementation requires only basic logic functions; it does not require the capability and complexity of a microprocessor or software. The logic design utilizes two low-power Field Programmable Gate Arrays (FPGA) for all logic functions. The logic is contained within radiation-hard (300 krad(Si), 120 MeV-cm2/mg) Aeroflex UT6325 FPGAs and uses +3.3 V input/output (I/O) logic levels. This approach provides for a very robust, radiation tolerant instrument. These devices provide ample logic capability as well as 55 kbits of internal radiation-hard memory, which is sufficient for FGM data processing. Aeroflex UT54ACS164245SEI cold-sparing transceivers are utilized for all signals that interface to the analog boards. This provides isolated cross-strapping for redundancy.
Communication to the spacecraft is asynchronous utilizing standard radiation-hardened 26CLV31RH/26CLV32RH driver/receiver pairs. FGM receives serial commands and a 0.5 Hz synchronization clock from the spacecraft and returns telemetry to the spacecraft Data, Telemetry, and Command Interface (DTCI) via 57.6 kbaud RS-422 UARTs. The FGM digital card contains a 3.6864 MHz crystal used in a Pierce oscillator topology to generate a clock from which all logic functions are synchronized. A derivative of this clock is utilized to create the 15.36 kHz fluxgate drive as well as the demodulator clock for the second harmonic detection.
FGM telemetry packets are sent once every two seconds, synchronized to the spacecraft 0.5 Hz clock. The FGM sends three types of data: a quick-look broadcast vector, an engineering data packet containing analog and digital housekeeping, and a science packet that represents 2 seconds of vector accumulation. Each packet has a frame counter and a time tag. There are 16 analog housekeeping channels and 8 digital housekeeping words that are included in each engineering packet. Each packet conforms to the spacecraft packet scheme, appearing roughly like an IPv4 protocol transmission. A checksum is provided for each packet transmitted. The FGM word is 16 bits in length. All commands and telemetry are send in multiples of 4 bytes to conform to the IPv4 standard.
The FGM has several commands to configure instrument operation but does not require any commands at startup to function. FGM begins telemetering science data within 3 seconds after application of power. At power up, the instrument executes a power-on reset. This reset function may also be executed by instrument command. There are eight science telemetry modes available (as described in the Data Modes section below) that are commandable. There are also multiple engineering data modes. These are used to tailor the amount of IB and OB data telemetered to the overall FGM telemetry allocation. The broadcast vector packet generated is not telemetered to the ground in nominal operations and therefore has no impact on the data rate. The logic also provides control for range changes on the analog board. By default, the instrument autonomously controls ranging (see the discussion below) but may be commanded directly for certain functions, such as zero offset determination. Automatic range control is designed to work with minimal mathematics operations (lacking a microprocessor) by simple inspection of the three components of the measured magnetic field. The algorithm provides adequate hysteresis to prevent multiple transitions (“toggling”) in the vicinity of a threshold and uses a “look back” period to prevent multiple transitions during spacecraft spins. FGM commands and range changes occur only at telemetry packet boundaries (e.g., up to once each two seconds). The spacecraft can direct the FGM digital electronics to monitor either the primary or the redundant interface via a specific discrete side-select command.
The digital electronics provides the power converter board with a synchronization pulse with a period of approximately 100 kHz. This ensures that power converter switching is concurrent with all other logic functions within the FGM. The digital board utilizes local linear regulators to generate the +2.5 V FPGA core voltage and the +3.3 V I/O voltage from the +5 V generated by the power converter board.
Data Modes
The OB and IB FGM sensors sample the field in all component axes simultaneously at an intrinsic sample rate of 64 vector samples per second. It may not be practical, or desirable, to continuously telemeter such a volume of data, so the instrument may perform averaging and decimation of the native 64 vector samples/s telemetry to achieve a desired telemetry allocation (Table 3). This is performed by unweighted averaging over \(2^{n}\) samples (“boxcar average”). Thus sample rates of 64, 32, 16, 8, 4, 2, 1 vector samples/s are available (independently) for each magnetometer, upon selection of the MAG telemetry mode via uplink command, leading to eight data modes (0–7) for each MAG sensor (two distinct modes at 64 samples/s for each sensor).
In mode 0, an infrequently used diagnostic mode, all samples are retained and packaged in the science data packet for transmission to the spacecraft C&DH system; this includes the three components of the magnetic field vector, and a redundant measurement of the \(y\) component provided by the fourth analog channel. In mode 1, the redundant \(y\) measurement is dropped and only the three components of the magnetic field are retained in the science packet, still at the maximum sample rate of 64 vector samples/s. In mode 2, data are averaged by 2 and resampled (decimated by 2) to obtain 32 vector samples/s, before packaging in the science data packet. In mode \(n\), for \(n=2\) to 7, \(2^{(n-1)}\) samples are averaged, and decimated, providing effective sample rates to 1 sample/s, the minimum available.
The instrument sends a science packet to the spacecraft C&DH every time a spacecraft clock is received (every 2 s); the size of that packet varies to accommodate the mode selection for both sensors. Each MAG packet consists of a fixed-size header (frame counter, spacecraft time information, and MAG status words) as well as a (variable) block of science measurements depending on the mode selections for both sensors. Therefore, packet size is determined by the mode pair selected (e.g., 1,1 for IB and OB sensors both at 64 samples/s; or 6,4 for IB at 2 samples/s and OB at 8 samples/s). Any combination may be selected for IB and OB sensors, resulting in 64 distinct telemetry modes, providing flexibility in allocating telemetry between the two sensors and efficiently utilizing the available telemetry.
The FGMs will operate at the maximum sample rate (64 vector samples/s) within about 3 or 4 h of perijove, and at lower effective sample rates elsewhere in orbit, matched to science objectives and requirements of the other particle and fields instruments.
Range Change Algorithm
FGM allows for either automatic (power-on default) or manually-commanded dynamic range selection. Under normal operation the instrument will operate in automatic mode, but manual range control is needed, for example, to force the instrument to operate near the bottom of a dynamic range (e.g., for accurate offset determination). Inboard sensor and Outboard sensor range controls are independent of each other, a concession to the requirement that no single credible failure can result in loss of data from both sensors.
The instrument can change ranges only upon receipt of a spacecraft clock transition, which occurs every 2 s; thus all IB/OB MAG samples in an individual packet are obtained in the same IB/OB dynamic range. In the manual range control mode, the range command bit (3) for the selected sensor is set to “manual” and a selected range is commanded. At the next rising edge of the spacecraft clock (“time tick”), the range bits are latched to the commanded pattern and the instrument changes ranges. The instrument analog outputs will respond immediately and settle to the new output value within a few sample times (\(\mbox{few} \times 1/64\mbox{ s}\)). If the range format is set to “automatic”, then the following algorithm operates and the “manual” range bits are ignored.
An automatic range change algorithm is necessary to optimize the instrument dynamic range to the magnitude of the ambient field, preserving required measurement accuracy. Lacking a programmable microprocessor and the capability to perform complex mathematical functions, the FGM needs a rather simple logic scheme to implement automatic range control within the logic functionality of the FPGA. Therefore, the algorithm is designed to operate on the measured field components. The scheme needs to prevent unnecessary transitions (e.g., “toggling” back and forth between ranges) and it needs to have a measure of noise immunity. The algorithm provides adequate hysteresis to prevent multiple transitions in the vicinity of a range change threshold and uses a “look back” period to prevent unnecessary transitions that would otherwise occur as the spacecraft spins.
Each time the analog to digital converter (ADC) samples a magnetic field vector (each 1/64 second), the data is written to ADC memory. At that time, the ranging algorithm evaluates individually the \(x\), \(y\), and \(z\) components of the measured magnetic field in ADC counts. The components are compared to ranging thresholds for under-range or over-range (in other words, if ADC < lower threshold or ADC > upper threshold). The ranging thresholds are stored in the FPGA memory locations and may be set independently for the two sensors. Each of the six sensor dynamic ranges has its own threshold settings, and any may be altered by ground command if desired. A multiplexer internal to the FPGA selects the appropriate thresholds based upon the current sensor range. The comparison of measured field components with range thresholds is made with sufficient resolution using the 8 most significant bits of the 16-bit ADC value. The default lower thresholds are set to 26 (out of 127) and the default upper thresholds are set to 122 (out of 128). These thresholds correspond to approximately 20 % and 95 % of the ADC full scale, respectively.
The instrument will range up (increasing dynamic range, decreasing sensitivity) in order to prevent saturation of individual components. The ranging algorithm keeps track of how many times a measurement (in each component) exceeds a preset ranging threshold (Fig. 23); if this count exceeds the (programmable) threshold, the instrument will range up at the next opportunity (spacecraft clock transition, every 2 s). This feature provides some noise immunity in that it makes it unlikely that a spurious measurement, or a few spurious measurements, will inadvertently trigger a range change.
Illustration of the Juno FGM automatic range changing behavior in an increasing (blue) and decreasing (red) magnetic field for nominal values of the range limit parameters. The instrument ranges down, to a more sensitive dynamic range when the lower limit (LL) threshold is crossed; likewise, it ranges up when the upper limit (UL) threshold is crossed. Choice of appropriate limits provides ample hysteresis to preclude undesirable “toggling” back and forth between ranges and maintains the required measurement resolution
Each MAG will range down (decreasing dynamic range, increasing sensitivity) to preserve as much measurement resolution as possible. Ranging down works in a similar manner, but threshold comparisons are made over a “look back” interval that is designed to encompass at least one spin period. This is used to prevent undesired range changes that would otherwise occur when all three components of the field drop below a threshold for only a portion of the spacecraft spin period. Noise immunity is provided as above, with the algorithm inhibiting transition to a more sensitive dynamic range if more than a preset number of measurements exceed the lower threshold over the look-back interval.
5.1.2 Radiation Environment and Parts Engineering
The FGM electronics box, containing all active semiconductors used in the design, resides inside the heavily shielded (titanium) radiation vault. Components external to the vault – the FGM sensor assembly and associated passive components – are inherently insensitive to radiation effects. The vault greatly reduces the total dose exposure to parts that are sensitive to radiation effects. The Juno electronics parts radiation requirement is met by parts that are radiation tolerant to total ionizing dose (TID) in excess of 50 krads (Si) @ 100 ml Al; many of the parts used in the design are qualified to 200 krads TID. The 50 krads TID requirement includes a radiation design factor (RDF) of 2, allowing for considerable uncertainty in the radiation environment and the effects of radiation on electronics parts.
Electronic parts are also required to meet a linear energy transfer (LET) threshold against latchup and single event effects (SEE) of 75 MeV-cm2/mg. The Juno parts list meets or exceed these requirements. No additional shielding (e.g., spot shielding) beyond the vault and electronics enclosure was required. Radiation effects were considered in all aspects of the design. For example, we used conventional miniature relays in place of signal JFETs (junction gate field effect transistor) for switching the fluxgate axis current sources. The relays do not exhibit radiation-induced impedance changes that may be expected to occur in the JFETs; an appreciable impedance variation would threaten scale factor stability.
The digital system design specifically targeted fabrication processes that are radiation-hardened. All of the logic functions utilize an epitaxial CMOS (complementary metal-oxide semiconductor) process that far exceeds Juno’s total dose and single event effects requirements. FGM electrical, electronic, and electromechanical (EEE) parts were procured to a class 1 or class 2 standard where possible. In certain instances where no suitable part could be found (e.g., LTC1604, TL431), additional radiation testing and parts screening was performed. Early radiation testing, EEE parts review, and thorough testing/system burn-in were all used to ensure the installed components meet requirements.
5.1.3 Performance
Performance of the magnetometers was monitored throughout the test program (Table 4) using a series of calibration procedures repeated before and after significant environmental tests. A sensor with linear response may be characterized by the sensor model:
Where the true field vector [\(B\)] may be expressed as a linear combination [\(A\)] of the sensor response; here [\(A\)] is a nearly diagonal 3 by 3 matrix. The three components of the sensor response in counts (\(c_{i}\)) are corrected for small offsets (\(o_{i}\)) and scaled to magnetic units with scale factors (\(s_{i}\)). In practice we use near-unity \(s_{i}\) that are slight corrections (<0.5 %) to the nominal scale factors (listed in Table 2). The matrix \(A\) is often called the “orthogonality matrix” and it is a function of the sensor construction and alignment to the reference cube; it is used to express the measured field in the coordinate system defined by the reference cube normal vectors. We compared calibrations (Sect. 5.1.5) performed throughout environmental testing to demonstrate system level alignment stability to 0.003° (∼10 arcsec) or better. Similarly, across all environmental tests, scale factors for both instruments varied by less than \(1 \times 10^{-4}\).
Absolute vector accuracy of the measurements in very weak field environments (few nT) is limited by the most sensitive dynamic range (1600 nT full scale), 16 bit quantization (∼0.05 nT) and knowledge of the spacecraft magnetic field and its variation in time. Static spacecraft fields and/or instrument zero offsets in payload \(x\) and \(y\) may are readily monitored throughout flight using Juno’s spin (about the \(z\) axis), whereas \(z\) axis offsets are estimated using Alfvenic properties of the solar wind
5.1.4 Test Program
The Juno instruments followed the GSFC MAG group’s standard laboratory test procedures. The sensor bobbins and sensor assembly were thermally cycled over a wide temperature range for mechanical stress relief. The sensors were thermally cycled once from +75 °C to −35 °C followed by 12 cycles from +60 °C to −20 °C. The magnetometer electronics progress through resonant tuning of the analog input circuitry and frequency response verification, followed by voltage, temperature, and frequency margin testing (VTFMT) in the laboratory. This involves comprehensive functional testing at hot and cold temperature extremes (+80 °C to −40 °C) while varying voltages and frequencies over their margined envelopes. The electronics and sensor were also assayed for biological contamination prior to delivery.
The magnetometer electronics experienced environmental tests prior to delivery as part of the Juno instrument suite (fully assembled MAG optical benches, ASC camera head units) including thermal vacuum, thermal balance, the full array of electromagnetic compatibility tests, and vibration. Before and after each test element, comprehensive end-to-end functional tests were performed at the GSFC magnetic test facility to provide system-level performance baselines for MAG.
While it is not feasible to perform accurate magnetic calibrations without access to the magnetic test site, functional performance and sensor noise levels were monitored within two four-layer Mu-metal shield cans. These shielded enclosures were designed to protect the sensors from physical damage throughout integration with the spacecraft in the assembly, test, and launch operations (ATLO) environment at Lockheed Martin’s Waterton Canyon facility in Denver. The fully-assembled MAG suite underwent further environmental testing at LM’s facility, where thermal vacuum tests were performed with the MAG instrumentation mounted on a MAG boom proxy (the fully assembled MAG boom was too large to fit within the chamber). The entire spacecraft was fully assembled in launch configuration (Fig. 24) for vibration and acoustic testing after which the spacecraft was shipped to the Kennedy Space Center in parts (solar arrays and MAG boom, MAG instrument suites were re-assembled at the Cape).
5.1.5 Calibration
Calibration of the Juno MAG instrument suite was performed on numerous occasions, and at system and subsystem levels, at several different facilities. We used subsystem level calibrations on the FGMs and ASC sensors to establish performance well in advance of system level calibrations. Later in development, when the flight model (FM) Carbon-Silicon Carbide (C-SiC) MAG Optical Benches (MOBs) were available, system level calibrations were performed before and after each element of the environmental test program (e.g., vibration, thermal vacuum) to establish that exposure to extreme environmental conditions did not alter the instrument response to magnetic fields. At the system level, our reference coordinate system is determined by the non-magnetic reflective optical cube affixed to each MOB (Fig. 14). These optical cubes (0.75 inch on a side) are fabricated to 2 arcsec orthogonality and all cubes were independently measured by the optics branch at GSFC. The magnetometer response is determined relative to this cube as is the response (optical alignment) of the ASC Camera Head Units (CHUs). All sensors—the FGM and the CHUs—are affixed to the MOB via a three point kinematic mounting system described in more detail elsewhere in this report. Thus calibrations relative to the MOB cube include both intrinsic sensor performance and the stability of the mechanical system that serves to bind all elements to each other.
The FGMs were calibrated at the GSFC Mario H. Acuña (MHA) Magnetic Test Facility (MTF), a remote facility located near the GSFC campus. This facility is sufficient to calibrate the FGMs to 100 parts per million (ppm) absolute accuracy for applied fields in all directions and field magnitudes up to about 1 Gauss. The 22 foot facility is large enough to provide applied field uniformity over a large volume, and thus the sensor re-orientations required by the MAGSAT calibration method are easily accomplished without introduction of gradient errors. The facility is operated in a closed loop with a remote reference vector magnetometer to null variations in the Earth’s field so applied fields may be held constant to a fraction of a nT over the duration of the calibration sequence. However, a facility of this size cannot produce fields in excess of a few Gauss at most and indeed large facilities were not designed to produce fields greatly in excess of the Earth’s field magnitude. So scale factor calibration was extended to 16 Gauss using a smaller high field coil to establish sensor linearity, along with measurements in high fields using a nuclear magnetic resonance magnetometer to provide measurements of field strength through the 16 Gauss range.
Two independent methods were used to calibrate the magnetometers. The vector fluxgates are calibrated in the 22′ facility using a method (“MAGSAT method”) developed by Mario Acuña to calibrate the magnetometer flown on the MAGSAT mission. This technique uses precise 90° rotations of the sensing element and a sequence of applied (facility) fields to simultaneously determine the parameters of the magnetometer model response as well as a similar set of parameters that describe the facility coil orthogonality (Acuña 1981). The second calibration method, developed by the DTU researchers (called the “thin shell” method, alternately the “Orsted” method) uses a large set of rotations in a known and stable field to obtain much the same instrument parameters, subject to an arbitrary rotation (Risbo et al. 2002) This method can be performed at a suitable (i.e., magnetically quiet) location using the Earth’s field as a reference, simply by making a sufficient number of measurements of the field measured by the sensor in many orientations relative to the ambient field—thus the name: “thin shell”. The sensor performance is obtained using one applied field in all orientations, approximating a thin shell. This method also employs a Proton Precession reference magnetometer to measure the ambient field magnitude and account for any variations in the field during the test. Of course, this method can also be employed in a magnetic test facility at any desired field magnitude within the dynamic range of the facility. So we have also performed calibrations of the Juno FGMs in our facility at several applied field magnitudes (which we call “thick shell” or “nested shell” calibrations) using this method, as well as in the field, during the inter-calibration activities performed at the Calar Alto magnetic and optical test site near Almeria, Spain.
The “thin shell” method by itself determines the magnetometer sensor response in an unknown coordinate system—an “intrinsic” coordinate system of the magnetometer sensor—the orientation of which needs to be determined by other means. This is equivalent to stating that the parameters of the linear sensor model may be determined subject to an arbitrary rotation, or, that only the symmetric part of the sensor response matrix is established via a “thin shell” calibration. However, if the sensor rotations are measured at the same time, as they are during an inter-calibration of the FGM and the CHU attitude sensors, the rotations taking place under the night sky, then the relative orientation of the magnetometer and CHU frames can also be deduced. For the Juno program, we used two redundant methods to establish relative orientations of the sensors: inter-calibration of the sensor suite in field tests under the night sky at Calar Alto, and FGM to MOB optical cube (via MAGSAT calibrations) and CHU boresights to MOB optical cube (optical calibration). The latter establishes the attitude of each sensor referenced to the MOB master optical cube (reference coordinate system). The inter-calibration method bypasses the MOB reference cube and renders the FGM response in the frame of reference of the CHUs.
GSFC 22′ Calibration Facility
Goddard Space Flight Center has two large magnetic test facilities within the Mario Acuña Magnetic Test Area. The first is the 22 foot (coil diameter) facility built around 1965 and the 40 foot magnetic test facility built a few years later. The GSFC MAG Group and specifically the Juno MAG investigation team uses the 22 foot facility for three reasons: it is a dedicated facility maintained and operated by the GSFC MAG team for sensor development, available exclusively to the Juno activity; it is built on an aluminum en-do skeleton which enables support beams to span the facility, for stable, precise, and repeatable placement of the sensor under test; and the facility was used for development and testing of the MAGSAT instrument, so it was known that the accuracy and stability of the facility was sufficient to meet Juno requirements. The 22 foot MAG facility spans 4 buildings within a radius of 0.25 miles. The first building houses the amplifier/power supply racks that power the coils. The second building is the test building where the 3 axis 22 foot Braunbeck coil system resides (Fig. 25). The third and forth buildings are “out in the woods” and house the environmental control and the reference coil system with a 3-axis Helmholz model coil with a flux gate magnetometer sensor at its center. Field variations sensed at the remote reference are used to null the (presumably identical) field variations at the 22 foot coil facility (the “variation system”) so that applied fields are insensitive to naturally occurring variations in the Earth’s field.
Since the facility was originally designed and built in the mid 1960s the variation system was designed to operate without computers or sophisticated controls. The model coil in the remote reference building is tuned to the 22 foot coils in the main test building to better than 0.1 % by the use of trim coils and potentiometers on the model coil. Thus when the flux gate magnetometer at the center of the Helmholtz is driven to zero field the field in the facility is also driven to zero. Also, as the external field changes a fine variation system holds the fluxgate in the reference facility to zero. This same current flows to the main building compensating for the variation in the Earth’s magnetic field.
These coils were commanded over a range of ±70000 nT with a 1 sigma noise level of 0.6 nT to test and calibrate the Juno magnetometer. A somewhat greater field magnitude (∼1.2 G) may be applied in the direction of the ambient magnetic field (via superposition). An independent measurement of the magnetic field strength is provided by Overhausen Proton Precession magnetometers placed near the unit under test (reference magnetometer). The Proton Precession magnetometers provide an absolute measurement of the applied field over the dynamic range of about 20,000 nT to 1.2 Gauss (120,000 nT). Two proton precession magnetometers were used to monitor the facility. The second proton magnetometer was also used to measure the gradient between the main proton magnetometer (reference) and the center of the facility where the Juno FGM was placed for testing. The proton magnetometers need be separated from the sensor under test by ∼1 m to avoid interference.
The facility uses two Wild T3000 Theodolites with auto-collimation capability to accurately measure alignment of the article under test (to which optical cube(s) are affixed). These units were supported from aluminum beams rigidly connected to the coil support tubes. The theodolites were operated with G compensation turned on thus two axis of bench motion were compensated for. The two units were located 90° apart at the edge of the coils. T1 was used for elevation and azimuth and T2 was used for elevation only providing the Juno team with the ability to determine the attitude of the Juno sensors with an accuracy of a few arcsec. In reality the Juno calibration team actually aligned the cube on the MOB benches to the theodolite zero to a precision of about ±2 arcsec 1 sigma. Thus the cube was always in a known and repeatable angular position relative to the coils. The Juno calibration team also used construction fan lasers aligned to facility reference marks on the wall to locate the cube and therefore the sensor to an accuracy of about ±0.5 cm. Thus when a MOB with its associated FGM sensor was tested the position and orientation of the MOB or sensor cube was highly repeatable.
Since the dynamic range of the MAG test facility is limited to ∼1.2 Gauss, it was necessary to devise an alternative method to extend the calibration up to the full 16 G per axis required. This was done using an auxiliary single-axis high field coil that could produce a linear field from 0 to 16 G. This coil system was installed within the 22 foot Braunbeck system and it used a high precision 0.1 ohm resistor and an Agilent 3458A voltmeter to produce a highly linear field variation by changing the current in a linear way. The basic methodology was to measure the linearity of the sensor relative to full scale and assume that all observed non-linearity was attributed to the flight sensor. The on-axis linearity of the sensor measured in this manner was excellent (10 arcsec).
The 22-foot magnetic test site was used many times during the tuning/trimming, functional, and calibration tests performed on the Juno FGM sensors themselves and then for calibration and functional testing after the FGM sensors were installed on the Carbon-Silicon Carbide MOB’s. This methodology provided a thorough time history of the performance of the sensors throughout the entire program, before and after each of the environmental tests and field operations, over the course of several years of development.
MAGSAT Calibration Method
The MAGSAT calibration method is used to determine the vector response of the fluxgate magnetometer sensor to applied fields relative to a known coordinate system reference (the MOB optical cube). This method also provides, with the same set of measurements, a complete characterization of the facility coil system orthogonality, and orientation, relative to the reference coordinate system. With a series of sensor calibrations performed over a span of time, it is possible to monitor the test repeatability and facility stability as well as the response of the article under test. To achieve, for example, 1 nT vector accuracy with applied fields of ∼70,000 nT, one must have knowledge of the sensor orientation to ∼3 arcsec and comparable knowledge of the facility coil orthogonality.
The method takes advantage of the accuracy with which the orientation of the sensor (reference optical cube) may be determined via autocollimation with a set of precision theodolites or alternately laser autocollimators. We used a pair of T-3000 theodolites permanently affixed to the coil facility structural members as shown in Fig. 26. A primary reference theodolite was positioned south of the facility, and a secondary reference theodolite positioned west of the facility, establishing an orthogonal reference frame centered on and aligned with the facility coil system. The article under test was placed on a leveling platform in the center of the facility that rested atop composite support beams affixed to the facility support structure. With this arrangement, and using mechanical ground support fixtures to position the MOB, we were able to orient the MOB as desired by autocollimating on the optical cube in both theodolites with an accuracy of ∼1 arcsec. This affords the means of achieving very precise 90° rotations that are the basis of the MAGSAT calibration method. The permanent arrangement of the reference theodolites provides a consistent and stable reference coordinate system necessary for test repeatability throughout the program.
Schematic of the coil facility showing placement of the external reference magnetometer, theodolites for precision optical alignment (black squares) and accurate 90° rotations of a test article (sensor under calibration) using a precision optical cube as a reference. The MAGSAT calibration method calibrates the sensor and the facility orthogonality using fields applied in each axis at a set of sensor orientations separated by precisely 90°
The method uses a sequence of applied fields of known magnitude aligned with the coil system symmetry axes (north-south, east-west, up-down) with the sensor oriented in a minimum of 3 orientations, as determined above, representing precise 90° rotations from the initial orientation. The model for the sensor response to applied fields is:
Where is the measured field vector (sensor output) and is the true field vector, where for simplicity what follows assumes that the measured field has been corrected for zero offset. Sensor zero offsets are readily determined prior to each calibration exercise by commanding the facility field to zero and recording the measured field with the sensor aligned parallel and antiparallel to the facility axes. Furthermore, we assume that the sensor scale factors (nT per digital counts) have been chosen such that we may write:
The off diagonal elements are all small (≪1) and represent a slight departure from orthogonality of the sensing elements, or small rotations of the sensor with respect to the reference coordinate system. Similarly, the relationship between the true field vector , and the coil system excitation, \(H_{c}\), is:
where \(H_{c}\) is the coil system excitation and
And again we have assumed that the facility coil constants have been adjusted so that the diagonal elements of \(B\) are unity, and again all off diagonal terms of this matrix are very small (≪1). The off diagonal elements are small enough that an orthonormalized matrix would have diagonal elements essentially indistinguishable from 1.
The measured field in the sensor, or the output of the magnetometer, for facility applied fields, is
so for fields of a chosen magnitude applied in sequence along the facility \(x\), \(y\), and \(z\) axes, e.g.,
we can write
for the response of the sensor in orientation 1, where \(M_{i, j}\) is the \(i\)th component of the field measured when the \(j\)th component of coil system is activated. The first column of \(M^{1}\) is obtained when the facility \(x\) coil is energized, the second column when facility \(y\) is energized, and the third column when facility \(z\) is energized. If we now rotate the sensor we have
where \([ R ] \) is the appropriate rotation matrix. Precise 90° rotations about the optical cube faces correspond to rotations about sensor \(x\), \(y\), or \(z\); the standard form for such rotations (in the positive sense) are:
Some rotations are impractical to implement due to the limited visibility of the MOB cube; both theodolites must be able to view the optical cube. In practice, the axis of rotation and the sense of the rotation angle may be dictated by such practical concerns. In our implementation, the second orientation was obtained by rotating the sensor by −90° about \(z\). Applying facility fields along \(x\), \(y\), and \(z\) as before, and neglecting terms that are products of two small (≪1) numbers, we obtain
These two positions yield 12 equations in 12 unknowns, but four of them are singular. Thus another rotation (this time by −90° about \(x\)) is required, and upon applying fields as before, we obtain
for the response of the system to applied fields in orientation #4 (orientation #3 was skipped as impractical to implement). With fields applied in these three orthogonal sensor orientations, the system of linear equations is overdetermined, and one solution for all elements of \(A\) and \(B\) in terms of the measurements \(M_{i,j}^{n}\) is given in Appendix A1.
Standard MAGSAT method calibrations were performed in the 22-foot facility using the following procedure:
-
(1)
The facility was adjusted to zero field and checked using (reversals of) a magnetic sensor at the origin.
-
(2)
The MOB was positioned in orientation #1 using lasers for coarse alignment and then adjusting the orientation of the MOB until autocollimation with both theodolites was achieved with an accuracy of ∼2 arcsec.
-
(3)
Data was acquired for 20 s in zero applied field in instrument dynamic ranges 6, 5, 4.
-
(4)
A facility field of ∼70,000 nT was applied sequentially in both polarities and along all three facility axes and for each applied field the sensor response, averaged over 20 s, in instrument dynamic ranges (6, 5, 4) was recorded. The field magnitude was also continuously recorded at a reference position ∼1 m from the test article using a reference proton precession magnetometer (PPM1).
-
(5)
A facility field of ∼22,000 nT was applied in both polarities and along all three facility axes and for each applied field the sensor response, averaged over 20 s, in instrument dynamic ranges (4, 2) was recorded. The field magnitude was also continuously recorded at a reference position ∼1 m from the test article using a reference proton precession magnetometer (PPM1).
-
(6)
Steps 3–5 were repeated after repositioning the MOB in orientation #2 using lasers for coarse alignment and then adjusting the orientation of the MOB until autocollimation with both theodolites was achieved with an accuracy of ∼2 arcsec.
-
(7)
Steps 3–5 were repeated after repositioning the MOB in orientation #4 using lasers for coarse alignment and then adjusting the orientation of the MOB until autocollimation with both theodolites was achieved with an accuracy of ∼2 arcsec.
-
(8)
Measurements for sensor zero determination were obtained by commanding the facility back to zero field and performing a series of reversals (180° rotations about sensor \(x\), \(y\), \(z\) axes) of the MOB.
-
(9)
After removal of the MOB, a second proton precession magnetometer (PPM2) was placed in the center of the facility, and the entire sequence of applied fields (steps 4 and 5) was repeated. This allows us to use the reference magnetometer as an absolute measure of the field applied, in each axis, after correcting the reference field for the slight gradient between the position of the reference mag (PPM1) and the position of the test article. (The reference magnetometer needs to be ∼1 m away from the test article to avoid interference.)
These measurements allow determination of the sensor response (sensor zero levels, scale factors, and orthogonality or “\(A\)” matrix elements) in instrument dynamic ranges 6, 5, 4 and 2, with range 4 sensor response determined independently for both low (22,000 nT) and high (77,000 nT) applied fields. Slight adjustments to the scale factors for each axis and range are determined via solution to the overdetermined inverse problem using a singular value decomposition method similar to that described in the following section.
No significant difference in sensor “\(A\)” matrix elements was observed across all instrument dynamic ranges. The range 2, 4, and 5 calibrations, directly referenced to absolute measurements of the applied field (via the proton precession reference magnetometer) are primary; range 0, 1, and 6 scale factors are established by extension of the measured field across dynamic range boundaries, having demonstrated sensor linearity (with the high field coil facility) to a few ppm. A few representative MAGSAT method calibration examples are presented in Appendix A2. These illustrate the accuracy with which sensor response was determined and the stability of the sensor response and calibration facility throughout the qualification program.
“Thin Shell” Calibrations
The thin shell calibration method (Risbo et al. 2002) exploits the fact that the measured magnetic field magnitude ought not vary as the sensor orientation varies. A sensor with linear response may be characterized by a sensor model:
Where the true field vector (\(B\)) may be expressed as a linear combination (\(A\)) of the sensor response; here (\(A\)) is a nearly diagonal 3 by 3 matrix (inverse of the \(A\) matrix discussed in the previous section). The three components of the sensor response in counts (\(c_{i}\)) are corrected for small offsets (\(o_{i}\)) and scaled to magnetic units with scale factors (\(s_{i}\)). In practice we use near-unity \(s_{i}\) that provide slight corrections to the nominal scale factors as given in Table 2.
If the magnetic field is measured with the sensor in numerous orientations, ideally approximating uniform coverage of the sphere, the invariance of the model field magnitude
may be used to constrain the sensor model parameters via inversion (partial solution) of the \(n\) (observations) by \(m\) (parameters) linear system
formed by assembling partial derivatives of the model response \(B_{m}^{2}\) with respect to the model parameters \(p\). The model parameters are the sensor offsets, scale factors, and off-diagonal elements of the \(A\) matrix: \(o_{1}, o_{2}, o_{3}, s_{1}, s_{2}, s_{3}, a _{12}, a_{13}, a_{21}, a_{23}, a_{31}, a_{32}\).
The partial derivatives of \(B_{m}^{2}\) with respect to the model parameters are listed in Appendix A3.
If we let \(y\) represent the \(n\)-length vector of observed minus model field magnitude squared,
then the linear system \(y = {D} p\) may be rewritten as
where the matrix of partial derivatives \(D\) is expressed as the product of three matrices, via the singular value decomposition of Lanczos (Lanczos 1961). \(\varLambda\) is a diagonal matrix whose elements are the singular values (square roots of the eigenvalues) of \(D^{T} D\):
The \(\varLambda\) matrix is assembled with the largest \(\lambda_{i}\) in the upper left position, all elements positive, and in the order \(\lambda_{1} > \lambda_{1} > \cdots \lambda_{M}\). The singular-value decomposition allows us to reparameterize the problem as
And a solution vector may be obtained from
using the \(M - 3\) non-zero elements of \(\varLambda\). The three zero eigenvalues reflect the lack of information regarding the orientation of the sensor and thus the elements of the matrix \(A\) may be determined subject to an arbitrary rotation, or, said another way, only the symmetric part of the \(A\) matrix can be obtained from the thin shell inversion method. When we compare the results of a thin shell calibration with that obtained using the MAGSAT method, we must compare only the symmetric part of the matrices. A few illustrative examples of thin shell calibrations (for the same sensor as in Appendix A2) are presented in Appendix A4. These illustrate the degree to which sensor calibration parameters determined by the two independent calibration methods compare.
5.2 Advanced Stellar Compass (ASC)
The non-magnetic micro Advanced Stellar Compass (μASC) is a fully autonomous high performance non-magnetic star tracker, evolved from the Oersted, SAC-C, CHAMP, and SMART-1 instruments. Despite its miniature size, it implements four fully independent star trackers, backed by a powerful and fully hardware redundant data processing unit (DPU). A block diagram of the system appears in Fig. 27. The μASC requires minimal spacecraft resources (mass, volume and power consumption) and provides accurate attitude solutions with high reliability; consequently, this star tracker is currently found on more than 50 spacecraft.
Schematic block diagram of the ASC electronics. All Camera Head Units (CHUs) may be powered when instrument power is applied, via one of the power converter/digital logic blocks (‘\(A\)’ or ‘\(B\)’); the other is cold spared. Any combination of CHUs (two each reside on each of two magnetometer optical benches) may be operated at any time but in nominal operation all are operated continuously. Each CHU is in a thermal environment maintained by a combination of internal dissipation (0.25 W each when powered on) and the spacecraft thermal service, powered as needed by the spacecraft regardless of instrument power status
The μASC onboard Juno is thus a high heritage instrument with an impressive body of space flight experience to its credit. These instruments have been employed on three axis-stabilized spacecraft and on spinning spacecraft as well (up to 6 rpm). The Juno μASC is a slightly modified version of the instrument in widespread use; it employs additional shielding to mitigate the effects of the harsh radiation environment and it also uses thermal controllers to maintain adequate operating temperature within the imaging systems.
The ASC determines the attitude of the MAG optical bench assembly with respect to an inertial reference frame by imaging the sky and comparing that image with its on-board database of objects. The ASC is capable of an estimated 2 arcsec performance, although operation on a spinning spacecraft (Juno’s nominal spin rate is 2 rpm) and in a challenging radiation environment will degrade performance. To mitigate the relatively rapid motion of stars across the field of view (14° × 20°) due to spacecraft spin, the CHUs are mounted with their optical axes offset from the spacecraft spin axis by about ±13° in the \(y\)-direction (refer to Fig. 6).
5.2.1 Instrument Description
The μASC consist of two separate units, the Data Processing Unit (DPU) and the Camera Head Units (CHU). Thus the DPU may be placed within the body of the spacecraft, while the CHUs may be placed where the attitude measurement is most needed, minimizing attitude transfer biases. Juno’s DPU is comfortably housed in the radiation vault along with the bulk of the spacecraft and instrument subsystems; the CHUs are mounted on the two optical benches, some ∼10 an ∼12 m distant.
The CHUs image the sky with a \(1/4~\mbox{s}\) integration time (4 Hz), synchronized to the spacecraft clock timing reference. The CCD is read out and analog data is transmitted to the DPU in the vault where it is digitized and stored for analysis. Raw images can, by command, be stored and transmitted to ground at a later time if desired. The image is examined for stars, and, depending on the settings and region of the sky imaged, a number of stars (between 20 and a few 100) are detected (among a number of “false stars” and non-stellar objects). The initial attitude acquisition algorithm selects a group of stars, brighter than a set value, for analysis. They are scanned for nearest, and next nearest neighbors. The resulting sets of triplets are matched against a pre-flight compilation of the star catalog, the star database. This match gives a coarse attitude determination (good to approximately \(1/50\)°) and this result can be used to seed an algorithm to determine fine attitude. The quality of the fit is reported along with the attitude.
The ASC time-stamps all attitudes and data with an accuracy of better than 0.1 ms. If the ASC has received a valid spacecraft time, that value appears in the time field; otherwise time is referenced to the internal time kept by the ASC initialized at turn-on. The ASC may be configured to accept both synchronized and non-synchronous timing information.
Each CHU contains a minimum of electronics to service the Charge Coupled Device (CCD) detector. The CHU is fitted with powerful wide-angle optics. The CCD and the lens taken together form a very sensitive optical sensor system, which may operate with essentially unlimited exposure times as commanded. A CHU is shown in Fig. 28. The heritage CHU weights 251 g excluding the pigtail (typically 50 g/m) and external light baffles. The CHU is just 50 mm × 50 mm × 50 mm in size. Each Juno CHU has a mass of 374 g, accounting for additional shielding placed inside the unit in close proximity to the CCD.
The optical system is specifically designed for star tracker operations, with very small field curvature (<0.2 %) and a controlled point spread function (120 μm FWHM) over the entire Field of View (FOV). The optical pass band ranges from 760 nm to 380 nm and the F# = 0.7. The lens elements are made from radiation-hard hard quartz, except for two color corrector elements located deep within the lens stack, and as a result this optical implementation ideally suited for use in high radiation environments. The quartz lens elements are free of Cherenkov ultraviolet (UV) luminescence, which eliminates spurious light due to high energetic electron fluxes.
By minimizing the CHU electronics, a very robust and compact design is realized, minimizing the electromagnetic footprint (allowing for use in close proximity to magnetic sensors) and maximizing shielding efficiency for high radiation tolerance. The fully hardware redundant Juno ASC DPU (Fig. 29) houses the power supplies, processing unit, data and program storage, and a full cross strapping unit that allows either side of the DPU to drive any of the CHUs as desired. The processor has been designed to eliminate bottlenecks in attitude determination to deliver attitude solutions (quaternions) from all four CHUs under extreme operating conditions at a cadence of 4 per second, while consuming little power (6.5 W). The redundant μDPU measures 140 mm × 100 mm × 50 mm and weighs 750 g.
Principle of Operation
Each CHU generates an 8-bit grayscale interlaced image (752 by 580 pixels) of the star field, and sends it to the DPU for processing. The DPU derives the CHU attitude by comparison of the star field with a star catalog and outputs the solution in the form of a quaternion within 200 ms of receipt of the image. Image exposure time is set to 250 ms, which yields 4 attitude solutions for each of the 4 CHUs every second, though not all solutions need be transferred to the spacecraft C&DH.
The detailed processing follows the scheme outlined in Fig. 30. The μASC receives a master clock pulse (2 s time “tic’) from the Juno spacecraft C&DH subsystem. This signal is used to synchronize an internal phase locked loop (PLL) such that the four images from each CHU are acquired with the integration interval centered on exactly 0, 250, 500 and 750 ms relative to the Juno onboard clock.
Each image is stored in the DPU random access memory (RAM). The image from the CHU having priority is processed initially to asses image quality, black level, and blinding conditions and this information is subsequently used for adjusting the drive levels for future images from this particular CHU. The image is next analyzed for larger bright objects, e.g. planets, and these objects are cataloged and removed from the image. The rectified image is the passed through a hot-spot filter to remove transients associated with energetic particles passing through the CCD during the image integration interval. The same filter also removes signatures generated by passing neutrons and any radiation displacement damage effects expressed by the CCD. This filter is adjusted rather aggressively for Juno, to facilitate operations during transit of regions with large fluxes of trapped particles around Jupiter. The cleaned image is then passed to a processing engine (“centroider”) that determines the position of each stellar object visible in the FOV. The centroid list is then stored while an image from the CHU with the next highest priority is processed (as above), repeating until all images are centroid.
Under nominal conditions, a reasonably accurate (better than 0.5 deg) initial estimate of the attitude of each CHU can be derived from the attitude history. Using this seed value, the centroid list of the CHU with the highest priority is passed to a matching engine that compares and link the measured centroids to the expected location derived from the onboard star catalog. The best fit is found using an iterative re-link and linearized least squares fitting routine. If the attitude found results in a robust match to the star catalog, the attitude solution is stored for output and the image next in priority is processed in the same way. However, if no attitude seed exists, or if the match is not successful for some reason, the Lost In Space (LIS) engine is called with the centroid list.
The LIS engine separates the centroid list into bright (visual magnitude > 5) and fainter objects. The bright stars are used to generate triplets, i.e. for each star centroid the nearest and next nearest star is located, and the angular separations between this three are calculated. These triplets of angles are then matched to an onboard triplet database compiled based on the star catalog. This process typically results in some 10–20 potential matches from a single star image, one of which points to the correct location on the sky. These potential attitude solutions are then used as a seed for the nominal processing described above. With Juno operating at 2 rpm, the LIS process will result in acquisition of the correct attitude from one image 95 % of the time, and 100 % of the time from 10 consecutive images.
Some subset of images may become difficult to analyze, e.g. when the FOV contains a planet or many unanticipated objects, real or otherwise. This may increase processing time, and if left unchecked, allow a CHU struggling with complex images to crowd out its brethren. To ensure that this does not happen, an upper limit to the processing time allocated for each CHU is set. When a CHU is timed out, its processing is aborted, an invalid (flagged) attitude is output, and the CHU priority is minimized, thus increasing priority of the other CHU heads. This procedure ensures that the best attitude solutions are output first.
Functionality and Operations
The four CHUs receive power and synchronization signals from the DPU and deliver video information to be processed by the latter. The DPU has a dual redundant communication interface by which the user may send commands to and receive telemetry from the unit. Communication with the μASC is via a full duplex RS422 communication line.
Command and telemetry functionality both adhere to the packet utilization standard. The instrument is synchronized to an onboard hardware (deterministic) clock pulse by means of a spacecraft C&DH broadcast command. All ASC internal processes and telemetry are time stamped in onboard elapsed time for easy comparison to other onboard information.
Upon application of power, the Juno μASC is configured to autonomously switch from the 10 second boot and self-checking mode to attitude determination mode. Therefore, the instrument will autonomously start to generate attitudes after a re-boot, a power cycle or any interruption.
The μASC also provides an image acquisition capability, whereby an image may be acquired at any time, by sending a command to the μASC selecting one of the CHUs and specifying an image compression mode to be used. Those available are: raw (uncompressed) image, JPEG compression (with user-selectable compression rate), Centroid, Non-Stellar objects (see next section) or region of interest (RoI mode, specifying the desired image pixel area around any centroid). The image, or the selected portion of an image, is then transmitted to the spacecraft by a subsequent send image command.
Sequences of images may also be acquired by the μASC. An image sequence is acquired upon command (“auto-imaging mode”), selecting one of the CHUs, and (optionally) a delay time. If no time delay is specified, the next image is acquired as soon as the previous image has been transmitted to the spacecraft. Alternatively, if a time delay (seconds) is specified, the next image will then be acquired as soon as two conditions are satisfied: the previous image transmission has completed, and the required time has elapsed. The delayed image may additionally be delayed until the spacecraft reaches a specific spin-phase. In the latter case, the image will be acquired after the specified time has elapsed and the spacecraft passes a specified rotation angle in inertial space. Thus an image may be ordered to occur when the CHU boresight is most closely associated with a specific target located in inertial right ascension and declination. This function is anticipated to be very useful in orbit around Jupiter, where a phenomenon or object to be imaged may only transit the FOV at specific spacecraft rotation phases.
The μASC transmits housekeeping (HK) packets containing instrument health and safety information, internal voltages, currents, and temperatures at specified intervals. Additional information about the configuration of the instrument is routinely requested by command, downloading the system variable table.
All onboard software and catalogs may be modified in-flight by uploading new software modules and catalogs, excepting a small core loader software which is stored in non-volatile memory. This provides a capability to improve the performance or capabilities of the μASC should inflight experience or conditions warrant. We have exercised this capability during cruise on few occasions, for example, updating the onboard star catalog to improve accuracy for a specific epoch (Jupiter science phase) and improving detection and analysis of non-stellar objects.
All the functions described above may be performed without impact on the proper attitude determination and output.
Bright Object Detection and Obscuration
Normal processing of an image by the DPU involves a filtering operation to mask bright objects. This is necessary because it is not unusual to find a non-stellar luminous object in an image. These bright objects may be planets and moons, asteroids, other spacecraft (near Earth, where many spacecraft orbit) and anything else not in the onboard star catalogs. The image processing locates and determines the extent of bright objects, calculates their effective area circumference and apparent centroid position, prior to removal of the object from the image. Attitude processing continues after bright object removal.
The centroid of the (non-stellar) object thus found will not pose a problem for the linking between observed centroids and those defined by the star-catalog; this greatly improves operational robustness when, for example, operating close to the limb of a planet. If the star field remaining after removal of the object is sufficiently large to allow for proper matching, the attitude is derived and output, albeit with a somewhat decreased accuracy since only a portion of the star field is available for analysis. This situation is noted (flagged), both by an increased attitude noise estimate (fit residual) and by setting the Big Bright Object (BBO) flag in the attitude packet.
Of course, these bright objects may also be imaged, either using RoI, Centroid, JPEG or raw imaging mode, if of sufficient interest.
Autonomous On-board Attitude Solutions
The attitude solution obtained from each image acquired by a CHU is delivered to the spacecraft C&DH expressed in aberrated J2000.0 coordinates. The μASC does have the capability to correct for aberration effects, but since the Juno spacecraft does not deliver to the instruments the (required) heliocentric velocity model, this feature is not used.
With the Juno spacecraft spinning at 1–2 rpm, any star imaged with appreciable integration time (e.g., 0.25 s) will be smeared by some 1.5–3°/s. On a spinning spacecraft, the star will not appear as a point-like object in the image; stellar images will resemble small curved arcs. This smearing results in an asymmetric noise distribution with regard to the attitude solutions, with the highest accuracy (better than 10″ RMS) in the image plane along track of the motion, medium accuracy (better than 15″ RMS) in the image plane across track, and low accuracy (better than 170″ RMS) about the CHU boresight.
The MOB bench attitude solutions can therefore be markedly improved by combining solutions from CHUs that are not co-aligned, i.e., have boresights with angular separation. The CHUs are configured with two CHUs on each magnetometer optical bench and the attitude solution of two CHUs is combined into a single bench attitude solution of high accuracy for all three axes, simply by combining the two attitudes and weighing the individual attitude components by the inverse squares of the noise observed. This process results in a measured attitude accuracy of 7″, 12″ and 20″ RMS respectively. Raw attitude solutions sampled every 7 s from an individual CHU may be plotted over time as shown in Fig. 31.
Since each attitude solution is uniquely derived from the image, time series filtering may be used to further improve the attitude accuracy on ground.
Autonomous Detection of Non-stellar Objects
The μASC uses all of the available stars detected in an image to derive the attitude with the highest possible accuracy. Objects located near a given star may be incorrectly linked to a catalog star, which would result in confused identification and increased measurement error. It is therefore very important to track non-stellar objects (NSOs) in order that any passing near by a star may be removed from consideration. The μASC thus necessarily detects and tracks (autonomously) such objects as long as they persist in an image. The process by which NSOs are identified and tracked is a follows. During the centroiding process, all luminous objects brighter than a specified minimum will be listed in a raw centroid list. After the first linking a crude attitude is found (∼30″ pointing) and any luminous object not listed in the star catalog is moved to a non-stellar objects list. A high accuracy attitude is found, iteratively, and the apparent inertial attitude of the non-stellar objects is calculated.
In the next update cycle a new non-stellar object list is generated. Depending on the distance and apparent trajectory of the object, the centroid will have shifted between the images, and a tangential motion model for each object may be derived. In deep space, the μASC onboard Juno will mostly view planets and planetesimals at great distance resulting in an angular motion of a few arcsec/s. Close to Earth, in the Asteroid belt and in Science orbit around Jupiter, some objects will be much closer, resulting in considerable inertial angular rates up to several hundred of arcsec per second.
The non-stellar object tracker may be used to detect near Earth objects, smaller main belt Asteroids and smaller moons around Jupiter. In order not to load the downlink bandwidth from Juno with known objects, the user may select to download only objects moving within a specified range of angular rates. The operation of this feature was tested when Saturn happened to pass through the FOV of the Juno μASC cameras during real sky tests.
5.2.2 Radiation Environment and Parts Engineering
The μASC, is a high heritage instrument with more than 50 years of accumulated space flight operations of the DPU and more than 200 years of space flight operations for the CHU (as flown onboard Juno). The instrument design and implementation benefits from a comprehensive parts selection program, approval and qualification programs based on the improved version of the INST-0002 standard. The parts program includes batch characterization of flight lots of parts with respect to total ionizing dose (TID), heavy ion, energetic proton and electron irradiation as well as displacement damage characterization of the CCD.
Similarly, the parts program ensures serialization, full X-ray microscopy screening, and full flight lot destructive parts analysis (DPA) for all parts with extremely small rejection rates. In-family behavior of parts within a lot is assessed by means over-testing random samples for all parts lots. All processes and materials are strictly controlled and approved, ensuring the highest craftsmanship and quality standards.
We anticipate that the Juno radiation environment will, at times, challenge the heritage μASC instrument beyond its flight-proven heritage. We therefore designed and conducted a dedicated radiation environment verification program. This analysis demonstrated that the standard DPU, with a 6 mm shielded electronics enclosure, would remain well inside its heritage performance envelope since it is located inside Juno’s heavily shielded radiation vault. The analysis also showed that additional shielding was needed to bring the standard CHU inside its flight heritage performance history, accumulating radiation from launch through Juno’s science orbit 8.
For this reason, additional shielding mass was strategically placed on the magnetometer optical benches as well as within the small CHU electronics enclosure (Fig. 32). With the combined shielding from the magnetometer bench shields (‘collars’ around the base of the lens barrel) and the augmented CHU structural shielding (affixed to the titanium enclosure, inside the enclosure, in close proximity to the CCD), the CHU is well inside its heritage performance envelope for the entire cruise phase and operation through science orbit 9. The modeled electron fluxes, when crossing the lower peaks (‘horns’) of the inner Jovian radiation belts, may disrupt attitude recovery for the (brief) duration of the radiation belt transit. Fortunately, Juno is moving at a rather fast clip during periapsis passes, and will spend very little time transiting this region.
This attitude recovery disruption is caused by the secondary electrons liberated by penetrating energetic electrons in the CCD photoactive layer. Since the displacement damage from passing energetic electrons is low, nominal operation will be restored as soon as the radiation belt is exited. The current best estimate is that proper attitude recovery operation may be briefly disrupted for less than a minute during every science orbit after science orbit 8. However, Juno will be transiting a region about which very little is actually known, as no direct measurements exist. The radiation assessments conducted thus far for Juno science instruments and subsystems are based models of the radiation environment fitted to indirect observations; these inferences may be proven wrong soon after Juno enters polar orbit.
5.2.3 Performance
The μASC has been functionally verified in flight, and it has been established that launch-load effects have had no detrimental effects on any of the ASC hardware. This has partly been verified by checking the inflight electro-optical parameters against the pre-launch values, partly by verifying the centroid quality over the CHU field of view (FOV), and partly by comparing the inflight measured angles between the CHU pairs on each boom to the pre-launch values.
Autonomous attitude generation, accuracy and availability have been validated by analysis of the telemetry from the instrument. Attitude availability from each of the CHUs is virtually 100 % under nominal conditions, as expected. All of the instrument functions have been verified on the nominal side as well as on the (cold-spared) redundant side of the ASC. The redundant side is configured as block redundant so can only be tested when the spacecraft switches to its redundant side. The spacecraft did (of its own accord, in response to fault protection) switch to the “\(B\)” side during cruise, affording the opportunity to verify functionality on the redundant side of the ASC. Both sides have now been updated with the arrival version of the star catalog and both sides of the ASC are configured with identical software, so MAG attitude determination should continue seamlessly should it be necessary to activate the redundant side of the spacecraft.
5.2.4 Test Program
The Juno unit level verification program encompassed full thermal vacuum, thermal cycling (TV/TC) protocols, outgassing, random- and sine-vibration to Juno environmental specifications, as well as a full performance validation testing. The entire flight systems (ASC, CHUs, FGM sensors, electronics, MAG optical benches) as flown were repeatedly operated en-suite during several inter-calibration campaigns whereby the attitude transformation between CHUs and FGM sensors on each MOB were measured.
Engineering qualification models (EQM) were used during unit level testing to demonstrate survivability and performance beyond flight qualification levels. EQMs were subjected to a 400 day highly accelerated stress test (HAST) at 130 deg C and shock testing to 3000 g. Functional end of life (EOL) behavior was verified through a full voltage-temperature-frequency margin (VTFM) test protocol. All tests were passed successfully.
At platform level, the unit was further subjected to flight level thermal vacuum/thermal cycling (TV/TC) and platform level acoustics and vibration testing. It has however been found, that while ground testing were performed to specification, the unit may encounter colder temperatures in case of a heater failure on either one or both CHUs of an optical bench, if the CHU is powered of. It has therefore been decided, to leave the CHU powered for the entire cruise phase to Jupiter.
The Juno μASC has thus been fully qualified for all environmental conditions foreseen for the mission.
5.2.5 Calibration
The calibration program of the Juno μASC consist of a unit level calibration of the electro-optical system, where the internal optical parameters of the unit are established (e.g., the effective focal length, optical distortion and pixel scale). This calibration has been performed on each CHU three times: before environmental testing, once after completion of all environmental tests, and finally inflight. The stability of this calibration demonstrates that the unit has been resilient to flight qualification, launch loads and environmental conditions encountered thus far in flight.
The external calibration of each CHU has been established by two independent means. First the functional coordinate system of each CHU has been established to an optical reference cube (“master cube”) located on each magnetometer bench. Secondly, the functional frame of each CHU has directly been linked to that of the magnetometer sensor on each bench. This procedure (“inter-calibration”) is discussed in detail in a later section.
Timing accuracy has been validated internally by introducing a small optical source placed in the field of view of each CHU. A light emitting diode (LED) is excited periodically to provide an optical reference signal that may be correlated with the electrical reference timing signal issued (by the spacecraft or by ground support equipment) to the CHU. By synchronizing the blinking of the LED to the synchronization pulse (“time tic”) delivered to the μASC, the output telemetry time stamp may be verified with a timing accuracy of better than 2 μs. The timing relative to the magnetometer sensor has likewise been validated using a similar approach in which the CHU was stimulated using the LED source while the magnetometer was stimulated using a small air core solenoid.
We also wanted to demonstrate functionality on a spinning platform, to faithfully replicate the flight operation on a spacecraft spinning about the \(z\) axis with a period of 1 or 2 rpm. We verified functional behavior and calibration using a precision rotation stand capable of turning at very accurate angular rates ranging from 0–4 rpm. These tests, performed at optical test sites (Mauna Kea, Hawaii, and Calar Alto, Spain) under the night sky, afforded an opportunity to validate CHU imaging capabilities and the detection, classification, and tracking of non-stellar objects. The night sky is replete with non stellar objects (satellites launched from Earth) that are ideally suited to such a test.
5.3 Magnetometer Optical Bench
The FGM magnetometer sensor and the two co-located camera heads (CHUs) of the Advanced Stellar Compass (ASC) need to be held in precise alignment throughout the mission, over all environments (thermal, vibrational, shock, etc.) experienced, in order to achieve the required absolute vector accuracy of measurement. To accomplish this task we designed a magnetometer optical bench (MOB), fabricated using a Carbon Silicon Carbide (C/SiC) material commonly employed for optical instruments and telescopes that require extreme mechanical and thermal stability. The sensors, once integrated with a MOB (one MOB for the outboard sensors, another for the inboard sensors), remained assembled throughout all environmental tests and calibrations prior to launch. The fully assembled magnetometer suite instrument mass (each: one OB, one IB), including the FGM and CHU sensors, radiation shielding, and MOB, is ∼5 kg and measures 27 cm × 24 cm × 10 cm. Both flight articles were subjected to a variety of calibration, launch simulation, integration, launch and in-flight environments over a near decade time span (thus far).
5.3.1 Description
The Juno Magnetometer Optical Bench (MOB) was designed to hold a single flux gate magnetometer and two camera head sensors (CHUs) used by the ASC to image the star field. The driving requirements for the MOB were mechanical stability to 20 arcsec over a combination of mechanical launch loads and thermal variations of over 100 C. However, in flight the MOB and its sensors experience a much more benign thermal environment as a result of the active thermal management we employ. The FGM sensor is enclosed individually within a multilayer thermal blanket and thermally stabilized at all times by a non-magnetic resistive heater driven by an alternating current (a/c) proportional controller. The CHUs are individually conditioned with resistive heaters attached to the back of the CHU enclosure and the entire MOB is also enclosed in multilayer thermal blanketing.
Other requirements on MOB design flowed from issues related to fabrication, radiation environment, reliability and maintenance of flight standards. Carbon Silicon Carbide (C/SiC), with its exceptional thermal stability and mechanical stiffness, was used to fabricate the MOBs. For example, the C/SiC structure was formed around the body of the CHU enclosure to provide additional radiation shielding for the imager CCD, and to accommodate a pair of “collars” (Fig. 32) around the lens assembly for additional radiation shielding.
The FGM and the CHUs are mounted to the MOB using three point kinematic mounts in order to reduce rotation due to thermally induced strains between the C/SiC bench and the FGM sensor body (Macor) or CHU body (Titanium). The kinematic mount is a six degree of freedom optimal restraint utilizing a hardened sphere on a cone-groove-flat mount scheme (Fig. 33). The three interface spheres are made from Silicon Nitride and have a very high compressive strength (∼400 kpsi). The kinematic mounts were secured in compression via spring loaded Titanium screws.
The differences between the coefficient of thermal expansion (CTE) of the MOB and the FGM or CHUs could result in unacceptably large (arc-min) rotations if the interface between them were not kinematic. The FGM is heated to keep its operating temperature close to 0 °C. In flight, the temperature gradient between the FGM and the MOB is about 80 °C. The two CHUs run much colder (around −54 °C) and the temperature gradient from sensor to MOB is much smaller. Another advantage of using kinematic mounts is a significant reduction (∼2×) in thermal conductance from the FGM to the MOB when compared with the traditional four cylindrical standoff used on previous missions.
The MOB is attached to the spacecraft MAG boom panel (Carbon face sheet and Aluminum honeycomb construction) with three Titanium flexure “feet”. These are illustrated in Fig. 34. Titanium 6Al-4V was used for the mounts to reduce thermal conduction between the MOB and the panel. The inherent stiffness of these mounts resulted in resonant frequencies of the MOB assembly that are significantly higher than the boom panel (∼600 Hz vs. ∼30 Hz). This greatly reduces the MOB mechanical response to launch vibrational loads propagated through the panel.
The fabrication of the C/SiC bench was a multistep process that takes place over several weeks. The initial step is the machining of a block of carbon/epoxy composite in the “green” (unfired) state. The material is fairly soft and fragile and requires precision machining to ensure the finer features, such as pocket ribs, remain intact. Most of the mechanical features are machined to dimension during this intermediate step as the final C/SiC material is very hard and brittle. The next step is to graphitize the bench at temperatures of up to 2400 °C. This creates a porous carbon structure that is ready for liquid silicon infiltration (LI). The LI process occurs in an autoclave where molten silicon is allowed to wick through the carbon material via capillary action. The molten silicon reacts with some of the carbon producing silicon carbide, a slow process that can take several days. After this process the bench is a gray, moderately electrically conductive ceramic-like structure composed of Carbon, Silicon and Silicon Carbide and is ready for its post-infiltration machining.
The surface of the C/SiC is fairly rough and needs to be prepared before mechanical joining of the foot mounts and instrument attachments. The rough surfaces present concentrated contact areas that can be fracture initiation sites. Thus the interface surfaces are smoothed prior to assembly using a combination of physical material removal (diamond grinding and Electrical Discharge Machining or EDM) and the introduction of a malleable gasketing material (copper foil, 1.5 ml). A Vespel bushing was used in each fastener hole to further reduce concentration of stresses underneath the titanium fasteners. The combination of these methods typically resulted in mechanical interfaces that were virtually unbreakable under the high joint preloads that were used for this instrument (high joint preloads were used to reduce any relative movement between each side of the joint that could concentrate stress and initiate a fracture).
5.3.2 Test and Verification Program
An extensive test and validation plan was executed to ensure the MOBs were qualified for spaceflight. The testing included static and dynamic launch loading for initial screening as well as design qualification and flight acceptance. Thermal stability and survival were also tested. A number of alignment checks were made pre- and post-environmental testing to verify the relative orientations of the FGM and CHUs remained within specification.
Vibration testing included random, quasi-static (sine burst), and shock. Force-limiting random vibration testing (per NASA-HDBK-7004B) was used due to the nature of the design and the brittle properties of the C/SiC. As the MOB was to be mounted to an intrinsically low-mass boom panel (solar panel composite construction) it was well suited for the use of force-limiting in testing. Each MOB was subjected to a random vibration screen test as a preliminary step prior to acceptance. This test was a single axis, full level test run with dummy masses in order to expose any inherent flaws in the structure due to fabrication. The C/SiC material is not susceptible to fatigue so a dynamic loading equal to the level that the MOB was expected to see during the flight environmental testing program was used without compromising MOB cycling life. Sine burst tests were performed in order to verify structural integrity of the MOB. The sine burst tests were run just prior to the random vibration tests and used the same shaker setup.
The Bench was shock qualified on a boom panel simulator designed to allow for the reaction load produced by the MOB when it is driven by mechanical inputs from the panel (see force limiting in the Random section). The MOB was tested at lower levels on both a shaker and the boom panel simulator.
5.3.3 Performance
The MOB exceeded all it mechanical design requirements over the course of the Juno Mag testing program, launch and flight operations. In flight data shows the MOB has maintained the CHU-to-CHU alignment to less than 2 arcsec over the first leg of the Juno mission. The FGM temperatures have been approximately 0–10 °C throughout the first two years after launch. The ASCs have been operating near their design temperature (approximately −53 °C).
5.4 Inter-calibration
Inter-calibration is the process by which the magnetic sensors, attitude sensors, and spacecraft are rendered in a common reference frame. To take full advantage of the accuracy of Juno’s ASC and FGM instruments, accurate knowledge of the relative orientation between the measurement frames of the ASC Camera Head Units and the MAG sensor is needed. The determination of this relative orientation is referred to as inter-calibration. The term is usually reserved for the most demanding alignment requirements that cannot be met with simple mechanical tolerances. The vector accuracy specification for Juno’s magnetic field investigation requires special attention to precise alignment of the magnetic sensors and the camera head sensors of the ASC (on the MAG Optical Bench) as well as those of the spacecraft. During the Juno MAG verification and test phase, we used two independent methods to establish the alignment of these multiple sensors.
The first method, called optical alignment, establishes the orientation of each sensor with respect to a “master” optical cube bonded permanently to each MOB, which serves as a primary reference coordinate system. This may be accomplished by acquiring measurements with each sensor as it is rotated about surface normals of the master reference cube. The master reference cube has surface normals true to within 2 arcsec to facilitate orthogonal rotations via autocollimation. The MAGSAT instrument calibration method (described in Sect. 5.1.5.2) renders a sensor calibration in the reference frame of that master optical cube on the MOB. For the ASC, the orientation of the Camera Head Units relative to the MOB optical cube is determined by the reference cube calibration test, described below. Thus each sensor may then be referenced to another via transformation through the master cube reference frame.
The second method bypasses the transformation to the master reference cube and uses a large set of observations acquired simultaneously by the magnetic sensor and the ASC camera heads as the MOB is articulated to establish the relative alignment of the two sensor types. The co-rotating correlation calibration estimates directly the transformation between each CHU frame and the MAG measurement frame. This is obtained by subjecting the optical bench, carrying the instrument sensors, to a set of rotations relative to the celestial sphere and to the local magnetic field vector of the Earth, while recording simultaneous data from both instruments. This technique was developed by colleagues at the DTU and it allows one to acquire a “thin shell” magnetic calibration in addition to relative alignment knowledge. We describe both methods briefly below.
5.4.1 Optical Alignment
In this section we describe the reference cube calibration for the Advanced Stellar Compass (ASC), which is, in essence, the determination of the surface normal vectors of the reference cube mirror surfaces, expressed in the ASC coordinate frame (shown in Fig. 35). In brief the reference cube is needed to ensure that the accurate attitude measurement of the ASC can be referred accurately to other instrument frames or to the spacecraft coordinate frame. The integration of precision instruments into a spacecraft requires a robust and accurate method of measuring the relative orientation of the instrument reference frame and that of the spacecraft. We need to establish the instrument frame with far greater accuracy than can be supported by typical mechanical tolerances. For example, the optical axis of a telescope or a lens often differs substantially from the mechanical axis of the support structure.
The measurement of the instrument is given with reference to the logical coordinate system defined by the optical axis, and the rotation about this axis. The physical coordinate system is defined by the mechanical properties of the instrument, i.e. casing. Finally the spacecraft coordinate system typically refers to a system chosen such that it may be easy to establish throughout the integration process.
Typically, a reference cube placed on the sensor is used to define the axes of the physical reference system, because the surface normals of the reference cube may be established with reasonable accuracy using a simple auto-collimator. For Juno, we used instead the master optical cube on the MOB as a common reference for each camera head unit (as well as for the magnetic sensor), and determined the surface normal vectors of the master cube, expressed in the logical system of the two camera heads on the MOB. The reference cube calibration is then the determination of the surface normal vectors, expressed in the instrument logical system.
Method of the Reference Cube Calibration
The mechanical stability of the Camera Head Unit (CHU) of the ASC is of the utmost importance for insuring the launch, gravity release and long term accuracy of the instrument. Thus, the design leaves no room for mechanical play or adjustments. The lack of adjustment possibilities will in turn result in small, but stable, discrepancies between the optical and the physical coordinate systems, i.e. between the logical and the physical system as described above.
The relative orientation between the two systems is established via optical calibration measurements that yield the rotation matrix \({M}_{1}\) transforming attitude measurements from the ASC into the reference frame of the master optical cube. The rotation matrix \({M}_{2}\) from the physical to the spacecraft system is established, such that the attitude may be expressed in spacecraft coordinates simply by multiplying the attitude measurement with the combined rotation matrix \({M}_{\mathrm{SC}} = {M}_{2} \cdot {M}_{1}\).
To establish \({M}_{1}\) with reasonable accuracy, real sky measurements are used. Using real star images, calibration errors associated with test pattern generators, auto collimators and focus errors are eliminated. Furthermore, calibration based on real star images will include all offset and bias terms, efficiently delivering an accurate calibration with minimum noise contribution.
Figure 36 shows the procedure: attitude measurements are obtained on points along the great circle having the same surface normal as the mirror face. Recalling that an attitude measurement may be viewed as a rotation from the Inertial Celestial Reference Frame (ICRF) to the attitude measured by the camera, the attitude of two measurements, \(i\) and \(j\), on the great circle may be expressed as \({M}_{{i}}\) and \({M}_{{j}}\) respectively.
The rotation of the CHU between the two measurements may be calculated as
-
\(M_{\mathrm{Rot}} = {M}_{{j}}^{-1} \cdot {M}_{ {i}}\) from which the axis of rotation is easily found from the skew-symmetric elements of \(M_{\mathrm{Rot}}\).
Finally, it is noted that the rotation axis of the CHU was the same as the rotation axis of the mirror, i.e. the surface normal. The mirror normal may be established from any set of two measurements, therefore the measurement noise may be assessed and the accuracy improved by using more measurements. Since the attitude measurements have to be performed over a time interval, correction for the Earth rotation during this interval is required. This task may be performed by transforming all attitudes to the time of the first measurement using the time stamp of each measurement and the Earth rotation speed (the sidereal rate). In order to avoid corrections for atmospheric refraction, the zenith vector at the measurement site should be in the plane of the great circle. Because the refraction only affects the elevation of the measurement, and because only the axis, not the angle, of rotation is needed, this procedure effectively eliminates the need for correction of atmospheric refraction.
The test setup is shown in Fig. 37. In a laboratory environment an autocollimator is typically used to establish the mirror surface normal. For a real sky test, a laser spot may be used for this purpose yielding similar accuracy but enabling a much faster alignment procedure. The distance between the laser source and mirror may be chosen freely as long as the angle between the primary and reflected beam is minimized; 20 cm separation is sufficient.
The laser beam is expanded, passed through a 50 % beam splitter, and is reflected from the reference cube mirror normal, after which it reenters the beam splitter. The part of the beam deflected downwards is reformed to provide a well-defined spot size before being imaged by a CCD camera at 4.7 arcsec per pixel. The centroid of the laser spot is determined with an accuracy of 0.1 pixel, yielding effective resolution of 0.5 arcsec. The reflected laser spot may typically be centered with an accuracy of ∼1 pixel to maintain ∼5 arcsec accuracy of measurement.
Measurements
The reference cube test was performed at the Calar Alto astronomical observatory in Spain on the night of July 02, 2010. Measured were the following normal faces of the optical bench cube:
Outer Bench
-
JN-C001-C2 (CHU2), active faces, (+X) and (+Y) in the CHU frame
-
JN-C001-C6 (CHU6), active faces, (+X) and (+Y) in the CHU frame
Inner Bench
-
JN-C001-C3 (CHU3), active faces, (+X) and (+Y) in the CHU frame
-
JN-C001-C4 (CHU4), active faces, (+X) and (+Y) in the CHU frame
The two active faces of the reference cube (for each CHU) were measured by accumulating measurements at a number of positions. At each position, the CHU attitude was recorded for approximately 2 min corresponding to ∼480 samples at the 4 Hz sample rate of the ASC. Observing conditions were acceptable for reference cube calibration in that the sky was clear and atmospheric conditions were stable, but seeing was not of high astronomical quality.
Data Reduction
Data reduction is performed by calculating the transformation (direction cosines matrix) from the CHU reference frame to a reference system fixed with respect to inertial space. This is performed using the attitude measurements and compensating for precession, nutation and Earth rotation.
Since two CHU’s are located on the same optical bench, attitude data from both CHU’s are combined by transforming attitudes for one CHU (secondary CHU) to the frame of the primary CHU via:
With these transformations, the mirror normal is calculated as the vector (expressed in the CHU system) which under transformation yields the minimum variance in the fixed system.
The result is the mirror normal vector expressed in the CHU reference frame.
Results
1. Mirror Normals
Based on the calculations described above the following mirror normals are found for the second reference cube measurements.
Mirror normal component in the CHU frame | ||||
|---|---|---|---|---|
XCHU | YCHU | ZCHU | Res (″) | |
OB + y-CHU-2 | −0.01115624062617303 | +0.97680850643057193 | −0.21382394641378757 | 10.25 |
OB + x-CHU-2 | +0.99992998181587645 | +0.01002913806204946 | −0.00628075277600665 | 16.26 |
IB + y-CHU-3 | +0.01544319579177291 | +0.97381038782661256 | −0.22683658493443989 | 22.48 |
IB + x-CHU-3 | +0.99987510064430596 | −0.01578936016986364 | +0.00069225498582401 | 21.23 |
OB + y-CHU-6 | −0.00399789281105384 | +0.97427068308642140 | +0.22534562993630328 | 22.32 |
OB + x-CHU-6 | +0.99988502721239458 | +0.00712891268529821 | −0.01338323430245432 | 18.82 |
IB + y-CHU-4 | +0.02509501316704106 | +0.97380965967899014 | +0.22597563370867152 | 18.62 |
IB + x-CHU-4 | +0.99966099184988988 | −0.02276680758436642 | −0.01263225419753013 | 34.01 |
The formal residual (Res) in the table above is less than 26.4 arcsec, in good correspondence with the expected values.
2. CHU to Cube Transformation Matrix
In order to provide a full transformation matrix from the CHU measurement frame to the reference cube frame, the reference cube frame must be constructed based on the two measured reference cube mirror normal determined for each CHU.
Consider the following schematic, Fig. 38, depicting the optical benches from above, with the three coordinate frames Cam A, Cam B and ref. All three \(X\) axis lie approximately in the plane of the optical bench. This is also true for the ref \(Y\) axis. For all three frames the \(Z\) axis completes the triad. Note that the CHU frames are canted approximately 13° outward about \(X\) from the normal to the bench plane.
Known in each CHU frame are the vectors Xref and Yref. To establish the Zref axis it is noted that Xref and Yref spans a plane the normal of which is the natural choice for Zref.
Since Xref and Yref are measured independently, they are not by definition orthogonal. In practice the deviation from an orthogonal system is less than 10″. To establish the orthonormal triad, we retain Xref and adjust Yref as follows:
Thus (Xref, Yref′, Zref) constitutes an orthonormal triad (REF frame triad). Since the components of these vectors are known in each of the CHU frames, the matrix
provides the rotation from the REF frame to a given CHU frame. Likewise the transpose of \(N\) (\(M=N^{T}\)) gives the transformation from a CHU frame to the REF frame.
Below is given the transformation from the CHU to the referenceframe as an orthonormal transformation matrix.
In Board Bench
Transformation from IB optical cube to CHU 3 (CAM port C)
Transformation from IB optical cube to CHU 4 (CAM port D)
Out Board Bench
Transformation from OB optical cube to CHU 2 (CAM port B)
Transformation from OB optical cube to CHU 6 (CAM port A)
For use in the Navigation and Ancillary Information Facility (NAIF) data processing system the above matrices were converted to Euler angles. Below are given the angles Euler angles (3, 2, 1) for the rotation from the bench optical cube to the individual CHU. The values given below were employed in the preliminary Juno Frame Kernel file (juno_v05.txt) produced by NAIF, and verified by DTU.
Rot3 (X) (deg) | Rot2 (Y) (deg) | Rot1 (Z) (deg) | |
|---|---|---|---|
OB to CHU A | +166.98004591 | +0.83914744 | −179.77479685 |
OB to CHU B | −167.65012849 | +0.22864645 | −179.36168926 |
IB to CHU C | −166.89008185 | +0.16658654 | +179.10988258 |
IB to CHU D | +166.92526364 | +0.41005034 | +178.56549108 |
5.4.2 Calar Alto Inter-calibration
The scope of this section is to describe the direct ASC-FGM inter-calibration performed on the Juno MAG optical benches at the Calar Alto Observatory in Spain. This inter-calibration was performed using the co-rotating calibration method originally proposed by Risbo et al. (2002). The co-rotating calibration aims at determining the relative orientation between the FGM magnetometer sensor frame and the ASC’s CHU measurement frame. This relative orientation can be parameterized in a number of ways, e.g. Euler angles, rotation matrix or quaternion.
The basic assumption for the method is that the instrument measurement frames to be calibrated are mounted together on a rigid structure (the optical bench). The two instrument frames (FGM and CHU) on the optical bench are rotated freely together, with the CHUs viewing the night sky and the FGM recording the (relatively stable) vector magnetic field of the Earth. Variations on the magnetic field are corrected for using a nearby reference magnetometer (REF). The FGM and CHU thus simultaneously record the vector magnetic field and the (inertial) attitude relative to the celestial sphere. The relative orientation between FGM and CHU is subsequently derived by using time to correct for Earth rotation.
The magnetic field vector in the FGM frame can be expressed in terms of:
-
The magnetic field in an Earth-fixed frame (Bref).
-
The Earth orientation relative to the inertial frame (Earth rotation theory + time).
-
The orientation of the FGM relative to the inertial frame (CHU measurement + relative orientation between CHU and FGM).
Simultaneous measurements of the Earth magnetic field by REF and FGM shall give the same field (except from local offset in \(B\)).
The transformation between the Earth fixed REF vector magnetometer frame and the rotating FGM magnetometer frame is:
Thus the representation of the REF field in the FGM frame is
Here \(\alpha ,\beta ,\gamma \) are three Euler angles describing the relative orientation between the CHU and FGM frame and (\(\kappa , \lambda ,\mu \)) are the three euler angles describing the orientation of the reference magnetometer (REF) relative to the Earth fixed frame (NEC = North, East, Center). The six orientation parameters (\(\alpha ,\beta ,\gamma ,\kappa ,\lambda ,\mu \)) can be determined by minimizing the residual between \(B_{\text{MAG}}\) and \(B_{\text{REF}}\), via a simulated annealing method.
The Calar Alto Observatory in Spain (Spanish Sierra Nevada) was selected for the inter-calibration. This site offers generally good astronomical observing conditions, low local gradients in the magnetic field, and good accessibility and logistical support.
The Juno inter-calibrations were performed during two nights at the Calar Alto Observatory in Spain:
-
In-Board Bench (IBB) September 08, 2010.
-
Out-Board Bench (OBB) September 09, 2010.
The IB MOB carries CHU 3 and CHU 4, while OB MOB carries CHU 6 and CHU 2.
The IB MOB data set consisted of 270 positions distributed over 10 sweeps at different azimuth settings, while the OB MOB data set has 297 positions distributed over 11 azimuth settings. ASC attitudes were acquired with 0.25 s integration time and sampled at 4 Hz while the FGM and REF data are sampled at 60 and 50 Hz respectively. For each CHU, FGM & REF data were “down-sampled” by averaging all the FGM/REF data within the 0.25 s integration period of the ASC attitude measurement. Samples with high angular rates (as identified by the FGM) are eliminated to eliminate measurements obtained while the test rig is still settling after the last rotation. This is done by removing samples for which the standard deviation of any FGM vector component is larger than 5 nT over the star tracker image integration period. Measurements obtained in excess of 45° from the zenith were eliminated to avoid bias due to high atmospheric refraction. The data will after this filtering is relatively free of systematic noise or bias from the test-setup itself or its operations, but may still contain outliers caused by wind gusts or occasional excessive cloud density. Corrections are applied for the atmospheric refraction (up to 45 arcsec for measurements within <45° of the zenith) and astronomical aberration (up to 21 arcsec).
Results
The inter-calibration directly yields the Euler angles providing the transformation from the CHU measurement frame to the FGM measurement frame. The angles are derived as 3–2–3 Euler angles, and are also expressed below in the 3–2–1 Euler angle format as used by the NAIF at JPL.
EA3 (deg) | EA2 (deg) | EA 3 (deg) | |
|---|---|---|---|
OB to CHU A | 93.846360 | 166.953168 | 93.536740 |
OB to CHU B | 88.913313 | 192.321973 | 88.322915 |
IB to CHU C | 89.062101 | 193.036746 | 90.007455 |
IB to CHU D | 92.014902 | 166.880127 | 93.418814 |
Rot3 (X) (deg) | Rot2 (Y) (deg) | Rot1 (Z) (deg) | |
|---|---|---|---|
OB to CHU A | +166.981554 | +0.867687 | −179.789384 |
OB to CHU B | −167.680175 | +0.231891 | −179.384575 |
IB to CHU C | −166.964941 | +0.211558 | +179.078816 |
IB to CHU D | +166.887958 | +0.457271 | +178.543535 |
The optical calibration (used in the preliminary instrument kernel) and the inter-calibrations yielded substantially different attitude transformation angles, differing by as much as 269 arcsec in the 3–2–1 Euler representation. At the time of launch, it was not obvious (to one of us, at any rate) which of the two calibration methods was superior, so the optical calibration was to be used in the preliminary instrument kernel while the calibration results were studied further.
Instrument operation during the Earth flyby (October 9, 2013, or DOY 282) presented an opportunity to conduct an independent assessment of the relative attitude between the FGM and CHU sensors. Analysis of the EFB observations (described in section below) allowed us to unambiguously identify the results of the inter-calibration as the superior instrument attitude solution, to be used in the instrument kernel post-cruise phase.
5.5 In-flight Verification
Operation of the science instruments during cruise to Jupiter provided an opportunity to acquire instrument and subsystem calibration and performance and gain experience operating the instruments and the spacecraft. Operation of the magnetometers during the cruise phase also provides the first magnetic measurements of the spacecraft and systems, fully integrated and functioning in flight configuration, and operating in a low field environment. In addition, Project conducted several compatibility tests during cruise. During these tests, the science instruments were operated much as intended during science operations once in orbit about Jupiter. None of these activities revealed any significant variations in spacecraft magnetic field or instrument interference.
In-flight calibrations are designed to monitor stability of magnetometer offsets and to provide a capability to diagnose and monitor spacecraft-generated magnetic fields. In most applications, the magnetic sensors are fixed in the spacecraft reference frame, and a constant magnetic field in the sensor (sensor offset or bias) is indistinguishable from a constant (“static”) spacecraft-generated magnetic field. Thus it is common practice to lump them together and estimate the sum of the sensor offset and static or quasi-static spacecraft magnetic field. We will use the term “offset” to describe the combined sensor zeros and spacecraft static field in what follows. Juno’s spin stabilization provides a nearly continuous estimate of offsets in the spin plane (\(x\)–\(y\)) but estimation of the offset oriented along the spacecraft spin axis (\(z\)) requires more attention.
5.5.1 Earth Flyby FGM and CHU Comparison
During the EFB, both FGM sensors and the four CHU’s recorded observations very similar to those obtained during an inter-calibration, with the added benefit of operating simultaneously. Since both IB and OB FGM sensors record the vector magnetic field at the same instant, the field recorded by the two sensors ought to be identical (to within the 100 ppm absolute vector accuracy of measurement, referenced to the MOB master optical cubes). Therefore the rotation between the two MOB frames is determined by comparison of the two. Likewise, since the ASC measures directly the inertial attitude of individual CHUs, the CHU to CHU orientation can be derived directly from simultaneous measurements of any pair of CHUs. By using the in-flight CHU to CHU orientation determined above and the two estimates for the CHU to FGM orientation obtained via pre-flight calibrations (optical calibration versus inter-calibration) the OB MOB to IB MOB transformation can be compared to the one found from the EFB data.
Since the two MAG sensors are rotated approximately 180° about their \(Z\) axis (accommodating packaging considerations in the spacecraft stowed configuration, prior to launch), the signal in the \(X\) and \(Y\) axes of the (spinning) sensor frame is 180° out of phase. The EFB afforded a generous distribution of observations in the sensor frame of reference (Fig. 39). Requiring only that the two FGM sensors observe the same field direction, the following equation expresses the relation between the observed field directions in the two sensor frames:
Where \(\mathbf{E}\) IB is the field direction observed by the IB sensor (\(\mathbf{E}_{\text{IB}} = \mathbf{B}_{\text{IB}} / |\mathbf{B}_{\text{IB}}|\)), \(\mathbf{E}_{\text{OB}}\) is the field direction observed by the OB sensor, and \(R\) OB2IB is the transformation matrix from OB to IB sensor measurement frames. This is the transformation relating the two MOB master alignment optical cubes.
An estimate of rotation the between the two sensor frames is obtained via a singular value decomposition (SVD) inversion of the over-determined matrix using 6579 measurements (every 10th sample). Expressed in the form of 1–2–3 Euler angles the rotation is:
Now we consider the μASC measurements of the CHU to CHU orientation, which may be calculated for any pair of CHUs. Each attitude measurement is corrected for aberration before calculating the transformation. Figure 40 shows an example for the relative attitude between CHUA and CHUB.
The following table summarizes the relative attitude between CHUs as measured on 2013-270 through 282:
CHU-X to CHU-Y | EA1 (deg) | EA2 (deg) | EA3 (deg) | σEA1 (″)σEA2 (″)σEA3 (″) |
|---|---|---|---|---|
CHU-A to CHU-B | +25.32946925 | +0.53146197 | −0.51915934 | 16.66 61.06 202.66 |
CHU-A to CHU-C | −1.15930751 | +0.84158481 | −179.93027341 | 15.90 31.10 215.91 |
CHU-A to CHU-D | +24.97822466 | +1.14937226 | −179.83147505 | 20.10 63.00 264.87 |
CHU-B to CHU-C | −26.48817733 | +0.13462696 | −179.70268029 | 16.39 58.98 202.94 |
CHU-B to CHU-D | −0.35683106 | +0.61357997 | −179.32187406 | 20.09 28.68 276.84 |
CHU-C to CHU-D | −26.13264369 | −0.36134882 | +0.47167148 | 19.97 64.88 265.18 |
The standard deviations of the Euler angle estimates appear in the last three columns of the table, illustrating the larger uncertainty about the optical axis for single CHU solutions.
Using the two estimates for the CHU to FGM orientation obtained from the pre-flight calibrations (from Sects. 5.4.1 and 5.4.2) and the CHU to CHU orientations determined above, the OB MAG to IB MAG orientation can be compared to the one found from the in-flight EFB data. This comparison may be performed using four possible comparison sets for each of the pre-flight calibrations:
-
OB -> CHU-A -> CHU-C -> IB
-
OB -> CHU-A -> CHU-D -> IB
-
OB -> CHU-B -> CHU-C -> IB
-
OB -> CHU-B -> CHU-D -> IB
These four attitude comparison pathways yield four estimates of the MOB to MOB transformation that may be compared with that resulting from the direct (magnetic) IB to OB MAG comparison. The first set of four comparisons are given below using the optical calibration described in Sect. 5.4.1: Inter Mag angles using CAHA optical Ref cube calibration and in-flight 2015-282
EA1 (deg) | EA2 (deg) | EA2 (deg) | dEA1 (″) | dEA2 (″) | dEA3 (″) | |
|---|---|---|---|---|---|---|
OB to IB MAG AC: | +1.069176 | −0.165333 | −178.746960 | (−266.74 | +314.28 | −99.46) |
OB to IB MAG AD: | +1.116267 | −0.162686 | −178.750356 | ( −97.22 | +323.81 | −111.68) |
OB to IB MAG BC: | +1.030376 | −0.184580 | −178.726507 | (−406.42 | +244.99 | −25.83) |
OB to IB MAG BD: | +1.077607 | −0.182154 | −178.722849 | (−236.39 | +253.72 | −12.66) |
The last three columns give the difference between the two in arcseconds.
The next set of four comparisons are given below using the inter-calibration described in Sect. 5.4.2: Inter Mag Euler angles using CAHA intercal and in-flight cal (2013-270 through 282)
OB to IB MAG AC: | +1.142574 | −0.239250 | −178.729055 | (−2.51 +48.17 −35.00) |
OB to IB MAG AD: | +1.152020 | −0.239366 | −178.740379 | (+31.50 +47.76 −75.77) |
OB to IB MAG BC: | +1.135014 | −0.233008 | −178.718215 | (−29.73 +70.65 +4.02) |
OB to IB MAG BD: | +1.144711 | −0.233040 | −178.723215 | (+5.18 +70.53 −13.98) |
From the above comparison we conclude that the pre-flight calibration resulting from the direct inter calibration provides much better agreement with the in-flight (magnetic) MOB to MOB transformation. Therefore, we adopt the (pre-flight) inter-calibration result and have used this in the MAG instrument kernels that encode instrument attitude information. This table is repeated below:
Rot3 (X) (deg) | Rot2 (Y) (deg) | Rot1 (Z) (deg) | |
|---|---|---|---|
OB to CHU A | +166.981554 | +0.867687 | −179.789384 |
OB to CHU B | −167.680175 | +0.231891 | −179.384575 |
IB to CHU C | −166.964941 | +0.211558 | +179.078816 |
IB to CHU D | +166.887958 | +0.457271 | +178.543535 |
We note that a 70 arcsec attitude error in a 24,000 nT field (maximum recorded during the Earth flyby) is equivalent to an error of ∼7 nT in a vector component of the field. This is larger than can be attributed to the magnetic field measurement and as of this writing still under study. One hypothesis under consideration involves an anomalous field of comparable magnitude that might arise from currents induced in the conductive spacecraft structure (thermal blankets and support structure) by virtue of the motional (\(V \times B\)) electric field experienced during the Earth flyby. Preliminary model calculations suggest that currents of sufficient magnitude may be sourced from the plasma environment during the flyby, but this is a difficult problem to model with high fidelity.
5.5.2 Advanced Stellar Compass—Stellar Reference Unit Cross-calibration
The ASC and the SRU both provide the absolute attitude of the respective instrument relative to the inertial reference frame (J2000). The SRU is located on the main body of the spacecraft, whereas the four ASC Camera Head Units are located with the FGM sensors on the MAG boom, at the tip on the \(+X\) solar wing. Since all of these sensors produce attitude quaternions continuously, or nearly so, we are able to compare the orientation of each of these sensors with respect to the others and thereby continuously monitor the mechanical stability of the solar array structure (wing 1) and the MAG boom.
A comparison between the ASC and SRU attitude measurements has been performed to assess the long-term stability of the MAG sensor orientation relative to the main spacecraft body and to establish the relative attitude transfer between ASC and SRU measurement frames. This comparison has been conducted as follows: for each ASC attitude measurement the recorded CHU attitude is corrected for aberration using the Juno spacecraft trajectory information. The SRU attitude (Juno spacecraft orientation) is calculated using the NAIF C-kernels at the exact times corresponding to the ASC attitude solutions. For each pair of attitudes, the relative orientation is calculated and expressed in the form of Euler angles. These Euler angles are reduced to their daily average in order to obtain the long-term relative orientation (SRU to CHU).
Figure 41 shows the variation of that relative orientation throughout all of the cruise phase (for ASC CHU-A and spacecraft SRU). The variation is largely due to the variation in temperature experienced by the solar array (also shown in the middle panel of Fig. 41) as a function of Juno’s heliocentric orbital distance. Please note that the angles are expressed in the spacecraft frame about \(x\), \(y\), and \(z\) axes respectively and that the scale of the theta angle (about spacecraft \(y\) axis) is 10 times the scale of the other two.
Variation of Magnetometer Optical Bench (MOB) attitude in the spacecraft reference frame throughout Juno’s cruise phase. MOB attitude is determined nearly continuously throughout cruise by the MAG investigation star cameras and referenced to the spacecraft attitude provided by a Stellar Reference Unit (SRU) on the body of the spacecraft. The three panels depict rotations about the spacecraft \(x\), \(y\), and \(z\) axes (phi, theta, psi) in degrees; note the vertical scale of the center panel. Also indicated are spacecraft events relevant to attitude disturbances. The attitude variation is largely a rotation about theta (see text) and associated with thermal distortion of the solar array as its temperature (purple curve, right scale) varied en route to Jupiter. Light blue data points between the spacecraft side swap events are as recorded before correction for a bias related to swapping between the A-side and B-side spacecraft SRUs
The majority of the attitude variation (of about 1°) occurs about the spacecraft \(y\)-axis, illustrated in the middle panel. Recall that the plane of the solar array is the \(x\)–\(y\) plane, with \(x\) along the length of the array, and \(y\) along the width (Fig. 42). A rotation about spacecraft \(y\) corresponds to a bending of the solar wing largely due to temperature variation. This is not unexpected. The underlying structure consists of a carbon-composite face sheet material bonded to both sides of an Aluminum honeycomb panel. Solar cells and cover glass bonded to one side of the panel using a room temperature vulcanizing (RTV) Silicone product introduces a thermal expansion mismatch that results in a bending of the panel with temperature. The inflection in the curve in mid-2014, near the second main engine flush, can be recognized as an abrupt change in the tensile properties of the RTV that occurred when the array temperature dropped beneath the bonding agent’s glass transition temperature.
The Juno spacecraft and instrument coordinate frames. The spacecraft \(+z\) axis lies close to the boresight of the high gain antenna and the \(+x\) axis is parallel to the centerline of the solar array (“wing 1”) that is extended by the magnetometer boom assembly. The \(+y\) axis completes the right-handed coordinate system and parallels the hinge axis of the wing 1 solar array
Inter-comparison of ASC and SRU attitudes will continue throughout the mission, with particular emphasis on the mechanical response to events (periapsis passes, propulsive events, large attitude changes) that might be expected to alter the solar array orientation.
5.5.3 MAG Boom Stability
The two MAG instrument suites are located on the four-meter long MAG boom. They are 2 m apart, with one (‘OB’) located at the tip of the MAG boom and one (‘IB’) located near the center of the MAG boom, 2 m removed from the nearest solar cells (refer to Fig. 6). The long-term stability of the MAG boom throughout the mission can be monitored in much the same way by comparison of the attitude solutions for each of the MAG optical benches. All attitude solutions from the individual CHUs were corrected for aberration using the Juno spacecraft trajectory information provided by NAIF. For each point in time, where valid attitude solutions exist for a given pair of CHUs (e.g. CHU A and CHU C) the instantaneous relative attitude is calculated and expressed in the form of Euler angles. The Euler angles are reduced to daily average values and are shown in the Fig. 43.
Variation of the Outboard Magnetometer Optical Bench (MOB) attitude in the frame of reference of the Inboard MOB throughout Juno’s cruise phase. This figure illustrates the (excellent) mechanical stability of the MAG boom, i.e., the structure between the two MOBs, whereas Fig. 41 illustrates the stability of the entire solar array appendage. The three panels depict rotations about the \(x\), \(y\), and \(z\) axes (phi, theta, psi) in degrees (see text). The attitude variation is largely a rather small rotation about theta (see text) associated with thermal distortion of the magnetometer boom as its temperature (purple curve, right scale) varied en route to Jupiter. Light curves depict data before correction for an offset related to an ASC CHU cable impedance adjustment
The angles plotted are (1, 2, 3) Euler angles from CHU A to CHU C. Since CHU A and CHU C boresights (CHU \(Z\) axis) are closely aligned, to within a few degrees, the angles correspond approximately to angles about the CHU A axis \((X,Y,Z)\). Note that the scale is the same on all three panels, and the variation in attitude between the two MOBs throughout cruise is much less than that observed of the solar array. The MAG boom stability appears quite good, well within ∼0.01° angular variation apart from the brief excursion near perihelion. Most of the variation is again about the CHU \(Y\) axis (which is oriented to within 13° of the Juno spacecraft \(y\) axis) and attributed to the thermal response of the mechanical boom structure near perihelion. The MAG boom also uses a Carbon-composite face sheet/Aluminum honeycomb construction, but unlike the solar array, the MAG boom is not bonded to a dissimilar material and it is stiffened via “I-beam” cross-Sectional elements.
5.5.4 Spacecraft-Generated Magnetic Fields
The Juno instrument was designed to measure strong magnetic fields, but it does capably measure the weak fields encountered during cruise (though that was not in the mission plan prior to launch). But for brief periods (in-flight tests and the Earth flyby) the instrument has operated throughout in its most sensitive dynamic range (±1600 nT) with a quantization uncertainty of 0.05 nT. Thus far in cruise, estimated offsets have varied slowly, within the 2 nT static spacecraft field specification. No significant spacecraft-generated magnetic fields have been noted in association with instrument or subsystem operation during in-flight magnetic compatibility tests.
5.5.5 Fluxgate Zeros Determination
We use a statistical least-squares estimation algorithm described by Acuña (2002) to estimate offsets. This method was developed to estimate offsets using the Alfvenic properties of the solar wind, that is, the observation that magnetic field variations in the solar wind tend to be variations in angular direction, preserving the magnitude of the field. The method works very well applied to spacecraft rolls or on a spinning spacecraft where the variations in the vector field ought to preserve the field magnitude as well. The offset vector (\(\boldsymbol{O}\)) is obtained from a series of vector measurements (\(i = 1,2,3,\dots n\)) of the magnetic field,
Where the difference \(\Delta \boldsymbol{B}_{i} = \boldsymbol{B}_{i} - \boldsymbol{B}_{(i+l)}\) may be formed using sequential measurements of the vector field (\(l = 1\)) or measurements separated by \(l\) samples, chosen to provide a suitable vector difference \(\Delta \boldsymbol{B} _{i}\), compared to measurement noise or instrument quantization step size, but not so large that variations in the field magnitude over \(l\) samples arise often. Applied to measurements acquired during spacecraft rolls, \(l\) should be chosen to provide difference point pairs over a small fraction of a roll period.
The inverse of the \(3 \times n\) matrix \([ \Delta \boldsymbol{B}_{i} ] \) is obtained using the singular value decomposition method (Lanczos 1961). Mario Acuña obtained the result above simply by observing that differences in the measured vector field during a pure rotation of the field ought to be orthogonal to the ambient field, which is simply the measured field minus the offset. Leinweber et al. (2008) showed that this result may also be obtained by assuming that variations in the field magnitude are uncorrelated with the variance in differences of the three components. Simply stated, if the offsets are properly estimated, the measured field magnitude will not evidence a spin modulation as the spacecraft rotates (see also Auster et al. 2002). Figure 44 shows the result of the offset estimation methodology applied to Juno magnetometer data obtained in cruise, which provides an estimate of the offsets in \(x\) and \(y\) appropriate to that time (and the state of the spacecraft at that time). These components of the offset are available on a nearly continuous basis owing to the spacecraft’s spin stabilization.
Application of offset estimation to range 0 (±1600 nT dynamic range) observations obtained during cruise. The figure in the upper left is a diagnostic hologram of \(By\) vs. \(Bx\). In the lower figure a time series of the field magnitude and the negative of the field magnitude is shown (dotted lines) demonstrating little spin modulation of the magnetic field magnitude with the estimated offsets applied to the observations. The spin axis component of the field (\(z\) axis) and the spin plane component (rho) are shown, illustrating a few Alfvenic (magnitude-preserving) fluctuations in the solar wind that may be used to estimate offsets in \(z\)
Estimates of the \(z\) component of the offset utilize the same algorithm described above in the manner for which it was originally developed: to utilize Alfvenic fluctuations in the solar wind as a source of rotations that ought to preserve the field magnitude. Figure 44 illustrates application of the method using an interval of time during which several Alfvenic fluctuations were observed. Since fluctuations in the solar wind are often anything but Alfvenic, our practice has been to carefully select for analysis intervals during which both the field rotates through a large angle with minimal variation in magnitude, allowing for a small adjustment to the \(z\) offset.
6 Operations and Data Processing
The MAG investigation provides operations and data processing support for both the FGM instruments and the ASC instruments, handled independently as distinct payloads on the spacecraft. We do, however, provide coordinated operations between FGM and ASC, and with the rest of the instruments of the particles and fields complement aboard Juno. These operations are organized within 14 or 28 day sequences that are coordinated among all payloads, and often subject to test prior to uplink to the spacecraft using a test bed at LM. Communication to the FGMs and the ASC is carried out using telecommands, whereas communication from the instrument is referred to as telemetry. Both telecommands (TCs) and telemetry (TMs) are logically built into packets. These packets follow a CCSDS packet standard.
The FGM is a rather simple and robust instrument built around a radiation-hardened FPGA and as such, without a programmable central processing unit, commanding the FGM is a relatively limited task, exercising various telemetry modes, for example, and setting various system parameters. The ASC, on the other hand, is a fully autonomous star tracker, with a very high degree of built-in autonomy as well as flexibility. The ASC can handle most “anomalies” using built-in failure detection identification and recovery (FDIR) autonomously. Further, like the FGM, on application of power the ASC will automatically enter an operational (attitude) mode and transmit attitude packet after a few seconds of boot-up operation. Operation is therefore in principle limited to change of operation. However, the inherent flexibility of the ASC supports not only attitude determination, but also a host of other functions, many of which of great interest to secondary science opportunities—such as imagery, asteroid detection and characterization, and even radiation detection. As such, the ASC presents an opportunity, via operations support, to implement the following functions:
-
Mode change
-
Memory management (load, dump, check)
-
System parameter management (load, dump)
-
House-keeping, health and safety assessment
-
Imaging (diagnostics, public outreach)
-
Time synchronization functions
-
Connection/aliveness testing
-
Various AIT test modes
The following describes operations conducted during Cruise Phase, and those anticipated for Orbital Phase of Juno’s mission.
6.1 Cruise Operations and Calibrations
The FGM and ASC instruments operated throughout almost all of cruise phase, with the FGM recording vector magnetic field observations at a cadence adjusted by factors of two in response to telemetry constraints. Some measurements were obtained at 64 samples/s but the majority of cruise returned samples obtained at 16 samples/s or less. The ASC operated throughout with attitude solutions transmitted to the spacecraft every 7 , chosen to sample the entire star field available to the CHUs over multiple spins. Both instruments participated in in-flight testing designed to simulate realistic science instrument operation anticipated for science operations at Jupiter.
6.2 Science Orbits Operations
During science orbit operations, a number of ASC activities are planned:
-
Attitude and housekeeping production rate changes to accommodate telemetry allocations and science requirements.
-
Diagnostics imaging to optimize system parameters and performance.
-
Rings imaging.
-
Jovian satellite search.
The attitude packet decimation rate is changed according to the orbit phase, such that the instrument provides a more densely sampled attitude profile near the planet, within a few hours of closest approach, when Juno traverses a region of space characterized by strong magnetic fields. The internal decimation is performed by suppressing individual attitude data packets rather than averaging subsequent attitude measurements. Since the instrument doesn’t have internal information about the orbital phase, the decimation is performed by a stored sequence of commands. A dedicated system parameter controls the decimation rate, which is therefore changed by sending a single command, AscLoadParameterTC.
Instrument housekeeping telemetry includes various temperature measurements and CHU video level information. The temperature of each CHU is measured independently with a sensor mounted as close to the CCD as possible; temperature measurements of the power PCB and the CPU PCB in the DPU are also measured. The video voltage reading is a very efficient, independent way of deriving/proving if foreign objects are obstructing the field of view of the CHUs in case of abnormal performance. Like the decimation rate, the housekeeping generation rate is adjustable by system parameter, i.e. using the AscLoadParameterTC.
The instrument further provides the capabilities to store and transmit the source images used for the attitude determination via the communication interface. The images can optionally be compressed in a number of different forms. The following formats are available:
-
Uncompressed
-
JPEG compressed
-
Region of interest (a 16 × 16 pixel area around each centroid)
-
Centroid list (CCD coordinates and intensity of each centroid)
-
Non Stellar Objects (CCD coordinates, intensity and apparent position of each non-stellar centroid)
The next acquired image is manually latched using the AscStoreImageTC command and it is telemetered using the AscSendImageTC command. The acquired images can be temporarily latched in the instrument’s 8 MByte RAM type mass memory. This memory area can hold a large number of images dependent on compression and can be transmitted at the user’s convenience.
Using an alternative automated operation, referred to as the auto imaging mode, images are stored and transmitted (or send to instrument mass memory) automatically, either:
-
Continuously
-
Periodically (as function of time)
-
Spin locked (as function of spin phase)
During each science orbit, an uncompressed image is acquired from each of the CHUs used for diagnostics health and aging assessment. The images are manually inspected by DTU once reaching ground.
During a couple of the orbit’s perijove phases, when passing the tenuous Rings, a spin locked JPEG imaging sequence is scheduled. (see REF_TO_Jupiter science orbit: Tenuous ring observations). The spin phasing is adjustable via system parameters (i.e. using the AscLoadParameterTC command).
6.3 FGM Data Processing
FGM science data is received from JPL via File Exchange Interface (FEI) client (at GSFC) and server (at JPL). The instrument science data is retrieved in product files spanning 20 min (600 instrument science packets, received every 2 s). Science packets also contain a minimum set of housekeeping data in the science packet header section. The instrument also provides a more thorough summary of engineering information in FGM Engineering packets that are collected by the spacecraft and received in separate files. The science packet housekeeping header word contains one of 16 engineering measurements (temperatures, voltages, currents, etc.) that appear, cyclically, one after the other in sequence (these data are subcommutated within the science packets). Thus, a diagnostic set of instrument engineering data is available from either the engineering packet data stream or the science product data stream. The engineering packets, however, provide a more comprehensive set of measurements and they are available at much higher time resolution, if required, upon command.
The MAG data processing is responsive to the need for rapid turn-around, since other instruments require magnetic field vectors in their preliminary analysis, by design before spacecraft supplementary engineering data is available for archive processing. A preliminary MAG data processing pipeline (Fig. 45) executes prior to receipt of reconstructed spacecraft ephemeris (NAIF SPK kernels) and attitude information (NAIF C-kernels) necessary for archive processing, and without benefit of spacecraft engineering telemetry that may be necessary for detailed analysis. Preliminary processing is conducted to assess the health and safety of the instrument, producing “quicklook” time series magnetic field vectors in either sensor or spacecraft payload coordinates. These data are available to instrument teams (e.g., particle instruments, waves) that may require magnetic field vector data to complete their analysis and are useful in diagnosing instrument offsets and/or spacecraft-generated magnetic fields.
Flow diagram of preliminary MAG data processing. Preliminary processing is done prior to availability of supplementary spacecraft engineering data (e.g., reconstructed spacecraft ephemeris, attitude kernels, spacecraft clock kernels) to assess instrument health and safety and to estimate sensor offsets and/or spacecraft static magnetic fields. Supplementary engineering data and reconstructed kernels are expected to be available within a few weeks after each periapsis
A similar but more comprehensive archive processing pipeline (Fig. 46) incorporates reconstructed spacecraft ephemeris and attitude information, and any supplementary spacecraft engineering information, producing calibrated magnetic field vectors, and spacecraft position vectors, in a variety of coordinate systems of interest. Science products are first concatenated to create one file per day, after which timing errors are flagged and repaired before the science data stream is merged with ancillary engineering data to create a Decommutated Telemetry File (DTL). The DTL file is the primary instrument input to the main processing program, which also accesses a suite of ancillary data files. The timing errors we refer to here (1 s/3 s time “stutter”) are pseudo-random spacecraft clock time tagging errors that MAG is able to detect (as the FGM instrument also keeps track of time). MAG produces a file of these events for use by the rest of the instrument teams.
Flow diagram of MAG final data processing. Final processing is done subsequent to receipt of reconstructed spacecraft ephemeris and attitude kernels using the same program elements. Data files containing time-ordered records of fullycalibrated magnetic field vectors, rendered in several useful coordinate systems, are the archive data products. Each record contains spacecraft position rendered in the appropriate coordinate system along with supplementary engineering data, where useful
Both processing pipelines utilize the same code which is designed to retain the ability to process data when supplementary data is lacking for a complete analysis. The data flow is designed to be extremely flexible in the ability to assimilate unanticipated observations, such as engineering telemetry that may be desired for analysis, and not anticipated early in the mission. This facility is implemented by utilizing a decommutated telemetry file that passes data to the main processing program in a text “keyword = value” format, originally developed for the Mars Observer and Mars Global Surveyor Projects, and currently in use for MAVEN data processing.
ASC quaternions are retrieved by JPL’s NAIF division and used to construct C-kernels for both OB and IB MAG Optical Benches, as well as individual C-kernels for each of the CHUs, subject to data availability.
6.3.1 Telemetry Decommutation
Raw binary MAG packets are checked for errors and decommutated using a bit map appropriate to the instrument mode (sample rates for both magnetometers). Each instrument data packet contains sufficient information within its header to allow processing of the data that it contains, from a magnetometer instrument perspective (i.e., excluding any spacecraft engineering data that may be required). The decom program produces a decommutated telemetry file (“.dtl” extension) that is an ASCII stream of “keyword = value” pairs, utilizing a text format similar to that employed by JPL’s NAIF text kernel readers.
6.3.2 MAG Packet Processing
MAG packet processing operates on the dtl input files, converting instrument counts to magnetic field in nanoteslas, and engineering measurements in counts to engineering units, using calibration files for the instruments and conversion coefficients for engineering quantities (currents, temperatures, voltages, etc.). A SCLK (spacecraft clock) conversion file, provided by NAIF, is required to convert spacecraft clock words to Coordinated Universal Time (UTC), and a leapseconds kernel file (“leap.ker”), also provided by NAIF, is required to maintain accuracy of UTC time conversions. The input files contain sensor data from both of the magnetometers, and as is the case in archive processing, may contain supplementary spacecraft engineering data (e.g., solar array currents, solar array switch states, etc.) for use in spacecraft magnetic field mitigation.
Archive processing requires access to reconstructed spacecraft ephemeris (SPK) and attitude information (C-kernels) that are delivered somewhat later than the instrument science data on a schedule dictated by the Project. The Project currently envisions a bi-weekly delivery of bested C-kernels, spanning a complete orbit, scheduled to be available a few days after each periapsis (14 day orbits). The C-kernels are required to render spacecraft position and magnetic field vectors in the desired coordinate systems. These vectors appear in Cartesian coordinates on output records, one record per observation, at the highest time resolution available, for science data archive. Archive processing may also include spacecraft supplementary engineering data, merged with the instrument science data in dtl files, should that be necessary in processing a correction for time-variable spacecraft-generated magnetic fields. Static spacecraft magnetic fields and/or instrument offsets are compensated via subtraction of a constant that is passed to the analysis program via the input dtl file. Since Juno is a spinning spacecraft (2 rpm nominal rate) the offsets in the spin plane (\(x\) and \(y\) coordinates) are readily computed in most environments from a modest time series. Estimation of the \(z\)-axis offsets, on the other hand, requires more involved analysis (described earlier) and a relatively lengthy time series.
6.3.3 Spacecraft Magnetic Field Mitigation
The MAG data processing pipeline is designed to facilitate inclusion of supplementary engineering data that may be required to mitigate static and time-variable spacecraft-generated magnetic fields. Thus far during cruise phase, we have not identified any significant spacecraft-generated magnetic fields, and apart from routine offset estimation and correction, no corrections to sensor measurements have been needed. This is a welcome outcome, and perhaps not surprising, given the ample separation of sensors and spacecraft body (10 and 12 m) and attention to spacecraft magnetic cleanliness during design and construction of the spacecraft.
6.3.4 Primary/Secondary Attitude Capability
The vector accuracy of the magnetic field measurements can only be fully realized with accurate knowledge of the orientation of the sensors in inertial space. We realized early in the design stage that attitude measurements would be required at each sensor, in order to achieve the required vector accuracy, so the investigation includes a pair of star camera imagers co-located with each MAG sensor. These sensors provide accurate attitude solutions for each MAG sensor at a rate of 4 per second. However, given the uncertainty of the radiation environment that Juno was to endure, and the vulnerability of (even heavily shielded) CCD imagers to radiation, the MAG investigation and data processing pipeline were designed to produce and accommodate attitude information from several different pathways, allowing for graceful degradation in response to instrumental or operational challenges.
A number of attitude solutions are made available in the data processing pipeline using NAIF’s kernel management system. Attitude (“c”) kernels are ordered in a vertical stack, with the best and most accurate solutions at the bottom of the “stack”, and less accurate solutions above. In our example, the c kernels derived for each MOB using the combined output of its two CHUs (the most accurate solution) reside at the bottom of the “stack”. If this kernel contains an attitude solution for the requested time, the processing pipeline selects this solution; if not, the processor works its way up the stack until a solution is found for the requested time. Working upwards in the stack, the second best attitude solution is provided via a single CHU c-kernel on a particular MOB (this may occur if one CHU is temporarily blinded or devoted to another function, such as imaging). If this solution is not available, working further upward in the stack, an attitude solution from the other MOB may be used with a fixed MOB-to-MOB attitude transformation. Working upward still, if no MOB attitude solutions are available, the processor will assign an attitude solution using the spacecraft SRU and a fixed transformation from SRU frame to the MOB frame.
The fixed transformations (MOB to MOB and MOB to spacecraft SRU) are determined in flight by comparison of the ASC CHU and SRU attitude solutions, and may be routinely updated as changes occur. The MOB to MOB attitude transformation is continuously monitored in flight and has been remarkably stable throughout cruise, a testimonial to the excellent mechanical design and fabrication of the MAG boom by engineers at Lockheed Martin. The MOB to SRU attitude transformation has slowly evolved (∼1°) as Juno traveled further from the sun, reflecting the mechanical response of the solar array and MAG boom assemblage as it cooled. The MOB to SRU attitude transformation is also continuously monitored in flight and during special ASC-SRU inter-calibration exercises scheduled to occur during periods of optimal spacecraft stability (avoiding precessions) and more comprehensive SRU attitude telemetry.
6.3.5 MAG Standard Data Products
For immediate use by the science team, and other instrument teams, we provide a quicklook product that consists of time-ordered records of magnetic field vectors in nanoteslas, rendered in spacecraft payload coordinates, along with browse products that are useful in identification of intervals of special interest. These files contain magnetic field processed with a static spacecraft field approximation, but do incorporate the full sensor zeros, calibration scale factors, and sensor orthogonality matrix conversion. They are necessarily produced before reconstructed spacecraft attitude and ephemeris information is available and therefore these quicklook products are intended for preliminary analysis and planning purposes only and are not intended for science archive.
Archive products are produced in a variety of coordinate systems when final reconstructed spacecraft ephemeris and attitude information are available. These include a planet-centered (“pc”) coordinate system, rotating with Jupiter (\(z\) aligned with the spin axis) and with the \(x\) axis through the Jovian IAU prime meridian; and a Sun-state (“ss”) coordinate system wherein the primary reference vector (\(x\) axis) points from the object (Jupiter) to the Sun and the secondary reference vector (\(y\) axis) is in the Jupiter orbit plane (approximately opposite to orbital motion) such that the \(z\) axis is northward. Both of these coordinate systems are also available with respect to any other body (“object”) of interest, for example, the Galilean satellites Io, Europa, Ganymede, and Callisto, should Juno obtain data in the immediate vicinity of these objects. For use during the cruise phase of the mission, prior to JOI, a solar equatorial (“se”) system may be employed, in which the primary reference vector (\(x\) axis) is the vector from the Sun to the spacecraft, the secondary reference vector (\(y\) axis) lies in the Sun’s equator plane, and \(+z\) is aligned with the Sun’s spin axis. Finally, the magnetic field observations are also provided in spacecraft payload (“pl”) coordinates, suitable for use in association with measurements obtained by other instruments on the spacecraft. The spacecraft payload coordinate system and the outboard MAG sensor coordinate systems are nearly aligned. Note that the inner MOB is rotated by 180° (about the spacecraft payload \(z\) axis) with respect to the outboard MOB.
Science archive products are pushed to the Juno Science Operations Center on a regular schedule.
6.4 ASC Data Processing
ASC science and engineering data products are received from JPL via File Exchange Interface (FEI) client (at GSFC) and server (at JPL), and subsequently pushed to DTU (in Copenhagen). The instrument science data is retrieved in product files spanning a variable period of time corresponding to the spacecraft downlink schedule, ranging from one a week during cruise to one a day when Juno enjoys continuous coverage near periapsis and critical events. Each science packet contains the absolute attitude of an individual camera at the time identified by the packet timestamp. Science packets also contain housekeeping data regarding measurement accuracy and information regarding the presence of luminous sources not identified in the star catalog (such as planets). The instrument also provides a more thorough summary of engineering data in ASC Engineering packets, collected by the spacecraft at a programmable cadence, and organized in separate files. Thus, a diagnostic set of instrument engineering data is available from either the engineering or science packet data stream. The engineering packets, however, may contain detailed information on the operational state of the ASC instrument, error logs and calibration values, if desired, upon command.
The ASC data processing is responsive to the need for rapid turn-around, providing the MAG team with accurate and timely attitude information for rendering the magnetic field data in physically relevant coordinate systems. NAIF C-kernels needed for archive processing are generated for each CHU individually (four C-kernels) and for each MAG optical bench (2 more C-kernels) using the combined output of two CHUs for each MOB where available. The MOB kernels are the most accurate attitude determination pathway and are generally available except for brief periods during which one or more cameras is unable to render an attitude estimate, e.g., during obscuration of the FOV by Jupiter. Preliminary processing is also conducted to assess the health and safety of the instrument, producing “quicklook” time series of the CHU attitudes, attitude estimate availability, and performance assessment. These data are immediately available to the MAG team.
6.4.1 ASC Telemetry Decommutation
Each ASC attitude packet telemetered from Juno contains an attitude measurement valid for the spacecraft timestamp of the packet, given in J2000.0 IRF spacecraft centered coordinates in the form of quaternions. Since the heliocentric velocity of Juno is not sent to the ASC, the velocity aberration correction is performed upon reception by DTU.
A report over the spacecraft attitude profile, spin stability and maneuvers is provided on a weekly basis by DTU to the MAG team. Also reported are time evolutions of temperatures, telemetry statistics spin axis statistics.
A separate processing line is maintained constantly calculating the attitude transform between the individual cameras and between the spacecraft coordinate system and each camera. The attitude transform between a given camera and each of the FGMs were established preflight as described in Sects. 5.4.1 and 5.4.2.
Using these attitude-transforms, the attitude of any of a given camera may be transformed into the frame of each FGM at any given time.
Biases and evolution in this over time, between the payload coordinate frame and the individual cameras are being monitored in a special process-line, and the time evolution in these transforms provided to the NAIF system.
6.4.2 MOB Attitude Determination
The MOB orientation in inertial space is determined from the absolute attitude measurements of the ASC, which are transferred to the MOB frame using the attitude transfer described in Sects. 5.4 and 5.5.1. ASC attitudes are corrected for the aberration effect prior usage in order to meet accuracy requirements. The aberration correction is described below in Sect. 6.4.3.
The ASC determines the inertial attitude of each of the four CHUs and transmits each attitude measurement in quaternion representation in a separate telemetry packet. Each of these packets is self-contained, i.e., it contains all relevant information for recovering the sensor attitude. This information includes:
-
The attitude quaternion
-
The timestamp of the center of the integration interval
-
The number of stars used in determination of the attitude estimate
-
A measure of the measurement quality (fit residual)
-
Additional status flags and other information
The four CHUs are all operated synchronously, i.e., they share the same timestamp representing the center of the integration interval. This means that the individual attitude solutions may be readily combined, or merged, to form a combined solution (using two sensor quaternions) that provides an improvement to the accuracy of the attitude solution. Star cameras are relatively insensitive to rotations about the camera boresight, so a combined solution utilizing determinations from cameras with different orientations offers much better accuracy. The following describes the procedure for performing this merging. The basic setup of coordinate frames for up to \(n\) Camera Head Units (\(i =1..n\)) is shown in Fig. 47.
The coordinate frames used are:
-
IRF: Inertial Reference Frame, the reference frame relative to which the star tracker measures the attitude of the sensor heads.
-
CHU1, measurement frame: Camera Head 1 measurement frame.
-
CHUi, measurement frame: Camera Head \(i\) measurement frame.
-
CHU1, fixed frame: Defined to be fixed relative to the common frame C, e.g. the pre-launch or average determined orientation CHU1 relative to C.
-
CHUi, fixed frame: Defined to be fixed relative to the common frame C, e.g. the pre-launch or average determined orientation CHUi relative to C.
-
C: Common frame for the combined attitude, fixed relative to the spacecraft frame.
Transformation between the coordinate frames is performed by rotations, here expressed using quaternions. Generally \(q_{a\text{->}b}\) is the quaternion describing the rotation from coordinate frame \(a\) to coordinate frame \(b\). Specifically:
-
\(q_{\text{IRF->CHU1,mf}}\) is the attitude measurement from CHU1, describing the rotation from the IRF to the CHU1 measurement frame.
-
\(q_{\text{CHU1,mf->CHU1,ff}}\) is the rotation from the CHU1 measurement frame to the CHU1 fixed frame. This rotation describes the current bias state of the actual CHU1 relative to the expected or pre-launch determined CHU1 fixed frame.
-
\(q_{\text{CHU1ff->C}}\) is the expected or pre-launch determined orientation of the CHU1 frame relative to the common frame C.
-
\(q_{\text{IRF->C}}\) is the rotation from the IRF to the common frame C, which is to be determined as a result of the attitude combination
The rotations for the \(i\)’th CHU are defined similarly.
For each CHU, the estimate of the orientation of the combined frame (C) relative to the IRF is found from the following combination of rotations.
where ⊗ denotes quaternion multiplication.
In the ideal case the CHU measurement frame and fixed frame coincide for each CHU, corresponding to a perfect pre-launch alignment determination of all CHUs relative to the common frame. In this case the \(q_{\text{CHU$i$,mf->CHU$i$,ff}}\) is the identity rotation and can be omitted from the equation. From Fig. 40 the \(n\) estimates of the orientation of the common frame are identical, except for measurement noise. In this case the method described in RD1 is applicable and gives the formalism for optimal combination of the quaternions into the common frame. The result will be the optimal estimate of the orientation of the common frame \(q_{\text{IRF->C,Opt}}\).
Depending on the actual design of the spacecraft the validity of the above ideal case will vary. For dedicated high accuracy platforms, e.g. featuring an optical bench with star tracker sensor heads mounted close by the main attitude user (common frame) on a stable structure, the pre-launch values may be a good approximation to the actual value. Stability over orbit will typically be good in such cases. However, launch shifts and gravity release shifts could still occur. In these cases \(q_{\text{CHU$i$,ff->C}}\) should be verified and adjusted to in-flight values. The bias term would in this case be expected to be small.
For spacecraft optimized towards other parameters, the stability of the CHU orientations relative to the common frame may be less and \(q_{\text{CHU$i$,mf->CHUn,ff}}\) is needed to describe variations.
In this case, the deviation in orientation from the fixed frame for each CHU can be estimated every time the combined solution has been estimated and there is a valid attitude measurement for the CHU. The bias for the given CHU is estimated as:
Where \(()^{-1}\) denotes the inverse quaternion.
This estimate will contain bias as well as measurement noise. Since the bias is expected to wary slowly, e.g. as a function of the thermal state of the spacecraft the bias part can be retrieved by low-pass filtering the \(q_{\text{CHU$i$,mf->CHUn,ff}}\).
One practical implementation fulfilling the in-flight implementation requirement of causality is the Z-transform. The next update of the filtered bias state (\(q^{\sim{j+1}}_{\text{CHU$i$,mf->CHUn,ff}} = {q}^{\sim j+1}_{\mathrm{bias}}\)) is found as follows.
Define the stress as the deviation between the current filter estimate of the bias and the current deviation in orientation.
The update to the filtered bias is achieved by taking a fraction (\(\alpha (0..1)\)) of the stress quaternion and multiplying onto the existing bias quaternion. This is found by reducing the rotation angle of the above stress rotation by a factor \(\alpha \) to get \(q^{j}_{\mathrm{stress}}\) (\(\alpha \)). This reduction of rotation angle is found by noting that a quaternion can be described by an axis of rotation (\(e_{x}\), \(e_{y}\), \(e_{z}\)) and a rotation angle \(\gamma \) as follows
Thus
The filtered bias orientation is updated as.
As a final step, to avoid bias drift, any common bias is removed by expressing the filtered biases in the common frame and removing the common bias.
In this manner, estimates for both the stress of the individual CHU relative to the combined solution and of the bias are determined with relatively few calculations. The filter constant \(\alpha \) shall be tuned to match the characteristic timescale of the bias variations for the given spacecraft platform.
6.4.3 Correction for Aberration
The light from the stellar objects observed by the ASC will be affected by astronomical aberration caused by the velocity of the spacecraft. To first order (Kovalevsky 1995) the line of sight (\(\mathbf{r}\)) to an objected will be modified to
where \(\mathbf{r}\) is the unit vector to the object in a rest frame, \(\mathbf{v}\) is the velocity of the observer relative to the rest frame, \(c\) is the velocity of light and \(\mathbf{r}'\) is the direction vector to the object as observed by the moving observer.
The aberrations effect shifts the apparent direction of the received light in the forward direction of motion. Thus when the ASC determines its attitude based on this aberrated light, it will report an attitude which is shifted away from the direction of motion. The correction applied to the attitude shall therefore be in the forward direction. In order to correct to a heliocentric rest frame the spacecraft velocity relative to this frame should be used. The magnitude of the aberration correction varies with the velocity and the angle between \(v\) and \(r\). For the worst case angle (90°) and a velocity of 30 km/s the aberration effect amounts to approximately 20 arcsec.
6.4.4 ASC Image Mode Processing
An ASC camera, operated in image mode, is responsive to a set of user-supplied parameters to control the image acquisition and processing. The effective integration time (shutter) for the image may be specified, along with the ADC dynamic range (dark and full range levels), image output format, and trigger mode. Images may be output in raw form, JPEG compressed, or reduced in size to a to region of interest (ROI). Images may be acquired individually at a specific time or at an unspecified time, triggered by the inertial attitude of the camera (image acquired when the camera attitude is closest to that of the target object). A series of images may also be acquired (“movie mode”), triggered by time or inertial reference, and in the case of the latter, the drift rate across an inertial reference may be specified as well. These modes have been implemented to ease operational complexity when targeting a specific object. For example, when acquiring images for tomographic profiling of the tenuous Jovian rings, the region targeted will constantly change position as seen by the Juno spacecraft as it moves in its orbit. The camera used for imaging the ring system may simply be commanded into movie mode, with the trigger drifting at a rate compensating for Juno’s orbital motion relative to the target.
After acquisition, images are transmitted to the ASC data partition in spacecraft mass memory. This transmission is performed at a lower priority than attitude telemetry packets and housekeeping data, effectively setting a limit on image cadence for raw and JPEG images. A full image takes 43 s to transfer from the ASC memory to the spacecraft memory partition. This bottleneck in image transfer defines the minimum image separation time for time-lapse (movie mode) sequences.
After receipt on the ground, images pass a simple header conversion to transform them into standard 8-bit gray level binary images (raw format) or standard JPEG images (if JPEG output format was selected).
Image timestamps are specified in the same format (spacecraft elapsed time) as the attitude measurements. Consequently, an extremely efficient and accurate image transformation procedure can be used that allows image stacking in inertial coordinates (or another user-selected reference system). This procedure is employed for time lapsed movies and science analyses, and renders the output image with position accuracy errors limited to sub-pixel levels, as described in Pedersen et al. (2016).
6.4.5 Advanced Stellar Compass Standard Data Products
The primary ASC data product is an engineering data product, a stream of time-stamped attitude quaternions that establish the orientation of each of the camera heads in inertial space as a function of time. These quaternions are assimilated by the Navigation and Ancillary Information Facility at JPL and rendered as a set of attitude kernels (“c kernels”) specific to each of the camera heads (CHUs) in much the same way that NAIF handles the spacecraft attitude reference sensors (Stellar Reference Units, or “SRUs”) that establish the attitude of the body of the spacecraft. Thus there are four CHU “c” kernels that are obtained independently for each of the MAG investigation attitude sensors. These individual attitude solutions are less sensitive to a rotation about the CHU boresight, so we combine information from the two CHUs on an optical bench to obtain a more accurate estimate of the attitude of the optical bench. This results in two additional “c” kernels, one for each MAG optical bench, referred to as the Outboard and Inboard “MOB” kernels. They are complete but for times when one or the other CHU on a MOB lacks a quality attitude solution, e.g., when a CHU FOV is obscured, blinded, or devoted to another task such as image acquisition.
7 Summary
The Juno magnetic fields investigation provides accurate vector magnetic field observations throughout all phases of the mission at sample rates of up to 64 vector samples/s. The instrumentation provides two-sensor vector measurements for spacecraft magnetic field mitigation and complete hardware redundancy for risk mitigation. Magnetic field vectors are provided in-flight for use by other science payloads in optimizing data collection, storage, and telemetry utilization. These data, together with the synergistic charged particle observations acquired by the JEDI and JADE investigations, and observations of plasma waves, infrared and ultraviolet emissions, will form the basis of our investigation of Jupiter’s polar magnetosphere. The MAG investigation, together with gravity and the microwave radiometer investigations, will probe Jupiter’s interior to constrain models of its formation and evolution. With a dense net of accurate vector measurements of the magnetic field in close proximity to Jupiter’s dynamo region, MAG may provide the most detailed image of a planetary dynamo, free of the surficial magnetism (induced and remanent) that limits our view of the Earth’s dynamo.
References
M.H. Acuña, MAGSAT—vector magnetometer absolute sensor alignment determination. NASA technical memorandum, 79648 (1981)
M.H. Acuña, Space-based magnetometers. Rev. Sci. Instrum. 73(11), 3717–3736 (2002)
M.H. Acuña, N.F. Ness, Results from the GSFC fluxgate magnetometer on Pioneer 11, in Jupiter, ed. by T. Gehrels (University of Arizona Press, Tucson, 1976), pp. 830–847
M.H. Acuña, F.M. Neubauer, N.F. Ness, Standing Alfvén wave current system at Il: Voyager 1 observations. J. Geophys. Res. 86(A10), 8513–8521 (1981). doi:10.1029/JA086iA10p08513
M.H. Acuña, K.W. Behannon, J.E.P. Connerney, Jupiter’s magnetic field and magnetosphere, in Physics of the Jovian Magnetosphere, ed. by A.J. Dessler (Cambridge University Press, New York, 1983), pp. 1–50
A. Adriani, G. Filacchione, T. Di lorio, D. Turrini, R. Noschese et al., JIRAM, the Jovian infrared auroral mapper. Space Sci. Rev. (2014). doi:10.1007/s11214-014-0094-y
H.U. Auster, K.H. Fornacon, E. Georgescu, K.H. Glassmeier, U. Motschmann, Calibration of fluxgate magnetometers using relative motion. Meas. Sci. Technol. 13, 1124–1131 (2002)
F. Bagenal, A. Adriani, F. Allegrini, S.J. Bolton, B. Bonfond et al., Magnetospheric science objectives of the Juno mission. Space Sci. Rev. (2014). doi:10.1007/s11214-014-0036-8
A. Balogh, The solar-system: a review of results from Space Missions. Philos. Trans.: Phys. Sci. Eng. 349(1690), 227–236 (1994)
R. Baron, T. Owen, J.E.P. Connerney, T. Satoh, J. Harrington, Solar wind control of Jupiter’s H3+ aurorae. Icarus 120, 437–442 (1996)
K.W. Behannon, M.H. Acuña, L.F. Burlaga, R.P. Lepping, N.F. Ness, F.M. Neubauer, Magnetic field experiment for Voyagers 1 and 2. Space Sci. Rev. 21, 235–257 (1977)
S.J. Bolton, The Juno Science Team, The Juno mission. Proc. Int. Astron. Union Symp. 269, 92–100 (2010)
B. Bonfond, D. Grodent, J.-C. Gerard, A. Radioti et al., The Io UV footprint: location, inter-spot distances and tail vertical extent. J. Geophys. Res. 114, A07224 (2009). doi:10.1029/2009JA014312
B.F. Burke, K.L. Franklin, Observations of a variable radio source associated with the planet Jupiter. J. Geophys. Res. 60, 213–217 (1955)
S. Chapman, J. Bartels, Geomagnetism (Oxford University Press, New York, 1940), pp. 639–668
J.T. Clarke, G. Ballester, J. Trauger et al., Far-ultraviolet imaging of Jupiter’s aurora and the Io “footprint” with the Hubble Space Telescope Wide Field Planetary Camera 2. Science 274, 404–409 (1996)
J.T. Clarke, G.E. Ballester, J. Trauger, J. Ajello, W. Pryor, K. Tobiska, J.E.P. Connerney, G.R. Gladstone, J.H. Waite Jr., L.B. Jaffel, J.-C. Gerard, HST imaging of Jupiter’s UV aurora during the Galileo Mission. J. Geophys. Res. 103, 20217–20236 (1998)
J.T. Clarke, J. Ajello, G.E. Ballester et al., Ultraviolet emissions from the magnetic footprints of Io, Ganymede, and Europa on Jupiter. Nature 415, 997–1000 (2002)
J.T. Clarke, D. Grodent, S. Cowley et al., Jupiter’s aurorae, in Jupiter: The Planet, Satellites, and Magnetosphere, ed. by F. Bagenal, T.E. Dowling, W.B. McKinnon (Cambridge University Press, Cambridge, 2005), pp. 639–671
J.E.P. Connerney, The magnetic field of Jupiter: a generalized inverse approach. J. Geophys. Res. 86, 7679–7693 (1981)
J.E.P. Connerney, Planetary magnetism,Volume 10: Planets and Satellites, in Treatise in Geophysics, vol. 10.06, ed. by G. Schubert, T. Spohn (Elsevier, Oxford, 2015), pp. 195–237. ISBN 978-0-444-63803-1
J.E.P. Connerney, T. Satoh, The H3+ ion: a remote diagnostic of the Jovian magnetosphere. Philos. Trans. R. Soc. Lond. 358, 2471–2483 (2000)
J.E.P. Connerney, M.H. Acuña, N.F. Ness, Modeling the Jovian current sheet and inner magnetosphere. J. Geophys. Res. 86, 8370–8384 (1981)
J.E.P. Connerney, M.H. Acuña, Jovimagnetic secular variation. Nature 297, 313–315 (1982)
J.E.P. Connerney, M.H. Acuña, N.F. Ness, Voyager 1 assessment of Jupiter’s planetary magnetic field. J. Geophys. Res. 87, 3623–3627 (1982)
J.E.P. Connerney, M.H. Acuña, N.F. Ness, The magnetic field of Neptune. J. Geophys. Res. 96, 19023–19042 (1991)
J.E.P. Connerney, R. Baron, T. Satoh, T. Owen, Images of excited H3+ at the foot of the Io flux tube in Jupiter’s atmosphere. Science 262, 1035–1038 (1993)
J.E.P. Connerney, M.H. Acuña, N.F. Ness, Octupole model of Jupiter’s magnetic field from Ulysses observations. J. Geophys. Res. 101, 27453–27458 (1996a)
J.E.P. Connerney, T. Satoh, R. Baron, Interpretation of auroral ”light curves” with application to Jupiter’s H3+ aurorae. Icarus 122, 24–35 (1996b)
J.E.P. Connerney, M.H. Acuña, N.F. Ness, T. Satoh, New models of Jupiter’s magnetic field constrained by the Io flux tube footprint. J. Geophys. Res. Space Phys. 103(A6), 11929–11939 (1998)
A.J. Dessler, Coordinate systems, in Physics of the Jovian Magnetosphere, ed. by A.J. Dessler (Cambridge University Press, New York, 1983), pp. 498–504
A.J. Dessler, B. Sandel, System III variations of apparent distance of Io plasma torus from Jupiter. Geophys. Res. Lett. 19(20), 2099–2102 (1992)
M.K. Dougherty, A. Balogh, D.J. Southwood, E.J. Smith, Ulysses assessment of the Jovian planetary field. J. Geophys. Res. Space Phys. 101(A11), 24929–24941 (1996)
R.C. Elphic, C.T. Russell, On the apparent source depth of planetary magnetic fields. Geophys. Res. Lett. 5, 211–214 (1978)
G.R. Gladstone, S.C. Persyn, J.S. Eterno, B.C. Walther, D.C. Slater et al., The untraviolet spectrograph on NASA’s Juno mission. Space Sci. Rev. (2014). doi:10.1007/s11214-014-0040-z
G.A. Glatzmaier, P.H. Roberts, On the magnetic sounding of planetary interiors. Phys. Earth Planet. Inter. 98, 207–220 (1996)
T. Gold, Motions in the magnetosphere of the Earth. J. Geophys. Res. 64(9), 1219–1224 (1959). doi:10.1029/jZ064i009p01219
P. Goldreich, D. Lynden-Bell, Io a Jovian unipolar inductor. Astrophys. J. 156(1P1), 59–78 (1969)
D. Grodent, J.-C. Gerard, J. Gustin et al., Europa’s FUV auroral tail on Jupiter. Geophys. Res. Lett. 33, L06201 (2006). doi:10.1029/2005GL025487
D. Grodent, B. Bonfond, J.-C. Gerard et al., Auroral evidence of a localized magnetic anomaly in Jupiter’s northern hemisphere. J. Geophys. Res. 113, A09201 (2008). doi:10.1029/2008JA013185
D. Grodent, B. Bonfond, A. Radioti et al., Auroral footprint of Ganymede. J. Geophys. Res. 114, A07212 (2009). doi:10.1029/2009JA014289
D.A. Gurnett, W.S. Kurth, G.B. Hospodarsky, A.M. Persoon, P. Zarka, A. Lecacheux, S.J. Bolton, M.D. Desch, W.M. Farrell, M.L. Kaiser, H.-P. Ladreiter, H.O. Rucker, P. Galopeau, P. Louarn, D.T. Young, W.R. Pryor, M.K. Dougherty, Control of Jupiter’s radio emission and aurorae by the solar wind. Nature 415, 985 (2002)
C.J. Hansen, M.A. Caplinger, A. Ingersoll, M.A. Ravine, E. Jensen, S. Bolton, G. Orton, Junocam: Juno’s outreach camera. Space Sci. Rev. (2014). doi:10.1007/s11214-014-0079-x
S.L.G. Hess, B. Bonfond, P. Zarka, T. Grodent, Model of the Jovian magnetic field topology constrained by the Io auroral emissions. J. Geophys. Res. 116, A05217 (2011). doi:10.1029/2010JA016262
R. Hide, S.R.C. Malin, The size of Jupiter’s electrically conducting fluid core. Nature 280, 42–43 (1979). doi:10.1038/280042a0
R. Hide, S.R.C. Malin, On determination of the size of the Earth’s core from observations of the geomagnetic secular variation. Proc. R. Soc. Lond. 374, 15–33 (1981)
T.V. Johnson, C.M. Yeates, R. Young, Space Science Reviews volume on Galileo Mission overview. Space Sci. Rev. 60, 3–21 (1992)
J. Kovalevsky, Modern Astrometry (Springer, Berlin, Heidelberg, 1995). ISBN 3-540-57023-3
C. Lanczos, Linear Differential Operations (Van Nostrand, Princeton, 1961). 564 pp.
R.A. Langel, R.H. Estes, A geomagnetic field spectrum. Geophys. Res. Lett. 9, 250–253 (1982)
R.A. Langel, R.H. Estes, The near-Earth magnetic field at 1980 determined from MAGSAT data. J. Geophys. Res. 90, 2495–2509 (1985)
R.A. Langel, The main field, in Geomagnetism, vol. 1, ed. by J.A. Jacobs (Academic, New York, 1987), pp. 249–513
H.K. Leinweber, C.T. Russell, K. Torkar, T.L. Zhang, V. Angelopoulos, An advanced approach to finding magnetometer zero levels in the interplanetary magnetic field. Meas. Sci. Technol. 19, 055104 (2008). doi:10.1088/0957-0233/19/5/055104
F.J. Lowes, Spatial power spectrum of the main geomagnetic field and extrapolation to the core. Geophys. J. R. Astron. Soc. 36, 717–730 (1974)
B.H. Mauk, D.K. Haggerty, S.E. Jaskulek, C.E. Schlemm, L.E. Brown et al., The Jupiter Energetic Particle Detector Instrument (JEDI) investigation for the Juno Mission. Space Sci. Rev. (2013). doi:10.1007/s11214-013-0025-3
D.J. McComas, N. Alexander, F. Allegrini, F. Bagenal, R. Beebe et al., The Jovian auroral distributions experiment (JADE) on the Juno Mission to Jupiter. Space Sci. Rev. (2013). doi:10.1007/s11214-013-9990-9
N.F. Ness, K.W. Behannon, R.P. Lepping et al., Use of two magnetometers for magnetic field measurements on a spacecraft. J. Geophys. Res. 76(16), 3564–3573 (1971)
N.F. Ness, M.H. Acuña, R.P. Lepping et al., Magnetic field studies at Jupiter by Voyager 1: preliminary results. Science 204, 982–987 (1979a)
N.F. Ness, M.H. Acuña, R.P. Lepping et al., Magnetic field studies at Jupiter by Voyager 2: preliminary results. Science 206, 966–972 (1979b)
D.A.K. Pedersen, A.H. Jorgensen, M. Benn, T. Denver, P.S. Jorgensen, J.B. Bjarno, A. Massaro, J.L. Jorgensen, MicroASC instrument onboard Juno spacecraft utilizing inertially controlled imaging. Acta Astronaut. 118, 308–315 (2016)
R. Prange, D. Rego, L. Pallier, J.E.P. Connerney, P. Zarka, J. Queinnec, Detailed study of FUV Jovian auroral features with the post-COSTAR HST faint object camera. J. Geophys. Res. 103(E9), 20195–20215 (1998)
F. Primdahl, T. Risbo, J.M.G. Merayo et al., In-flight spacecraft magnetic field monitoring using scalar/vector gradiometry. Meas. Sci. Technol. 17, 1563–1569 (2006). doi:10.1088/0957-0233/17/6/038
V.A. Ridley, R. Holme, Modeling the Jovian magnetic field and its secular variation using all available magnetic field observations. J. Geophys. Res. Planets 121 (2016). doi:10.1002/2015JE004951
T. Risbo, P. Brauer, J.M.G. Merayo, O. Nielsen, J.R. Petersen, F. Primdahl, N. Olsen, Ørsted calibration mission: the thin shell method and the spherical harmonic analysis, in Ground and In-flight Space Magnetometer Calibration Techniques, vol. ESA SP-490 (2002)
C.T. Russell, M.K. Dougherty, Magnetic fields of the outer planets. Space Sci. Rev. 152, 251–269 (2010). doi:10.1007/s11214-009-9621-7
E.J. Smith, L. Davis Jr., D.E. Jones et al., The magnetic field of Jupiter and its interaction with the solar wind. Science 183, 305–306 (1974)
E.J. Smith, L. Davis Jr., D.E. Jones et al., Jupiter’s magnetic field, magnetosphere, and its interaction with the solar wind: Pioneer 11. Science 188, 451–455 (1975a)
E.J. Smith, B.V. Connor, G.T. Foster Jr., Measuring the magnetic fields of Jupiter and the outer solar system. IEEE Trans. Magn. MAG-11, 962–980 (1975b)
E.J. Smith, L. Davis Jr., D.E. Jones, Jupiter’s magnetic field and magnetosphere, in Jupiter, ed. by T. Gehrels (University of Arizona Press, Tucson, 1976), pp. 788–829
R. Smoluchowski, Jupiter’s molecular hydrogen layer and the magnetic field. Astrophys. J. Lett. 200, 119–121 (1975)
D.J. Stevenson, Planetary magnetic fields. Rep. Progr. Phys. 46, 555–620 (1983)
Z.J. Yu, H.K. Leinweber, C.T. Russell, Galileo constraints on the secular variation of the Jovian magnetic field. J. Geophys. Res. 115, E03002 (2009). doi:10.1029/2009JE003492
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A1: MAGSAT Calibration Solutions
One set of solutions to the linear equations resulting from the rotations described in Section MAGSAT Calibration Method is listed here:
An alternative set of solutions (though not entirely independent) may also be found which serve as a self-consistency check. Three or more orientations may be used and a solution found by matrix inversion of overdetermined systems as well. Note that the presentation provided here is appropriate to applied fields in only one direction; in practice we apply fields in both polarities.
It can be shown that estimates of all sensor parameters \(a_{i, j}\) are unbiased by errors in facility offsets and by averaging results for both polarities of applied fields, all are unbiased by sensor zero offset errors.
Appendix A2: MAGSAT Method Calibration Example
In the following we provide calibration summary examples for a small subset of the calibrations performed to the MAGSAT method protocol described in the text. The summaries provided here illustrate the sensor calibration in one of the 6 dynamic ranges (range 4), using the “Black” MOB (outboard magnetometer suite), over three calibration runs (August 29, September 5, 16).
IDL> CSUM,DIR='Black/Aug29', RNG=4,/NRM
Magsat Analysis
range: 4 normalized
Fit RMS: 1.58
Run Time: Wed Dec 15 13:41:35 2010
zeros file: idl/cal/Black/Aug29/zeros/ob_tt_ttp.txt
magsat file: idl/cal/Black/Aug29/magsat/ob_tt_ttp.txt
facgrd file: idl/cal/Black/Aug29/fac_grad/ob_tt_ttp.txt
scale factors: 0.997014 0.996692 0.996930
sensor model amx:
1.000000 0.006134 -0.003856
-0.008353 1.000000 -0.008725
0.004784 0.006786 1.000000
symmetric part:
1.000000 -0.001110 0.000464
-0.001110 1.000000 -0.000969
0.000464 -0.000969 1.000000
a-symmetric part:
0.000000 0.007243 -0.004320
-0.007243 0.000000 -0.007756
0.004320 0.007756 0.000000
rotation by: 0.656476 degrees
about unit vector: 0.676888 -0.377037 -0.632191
MAGSAT analysis diagnostics:
facility bmx: 1.000000 -0.000265 -0.000615
0.000226 1.000000 0.000086
0.000594 -0.000115 1.000000
IDL>CSUM,DIR='Black/Sept5',RNG=4,/NRM
Magsat Analysis
range: 4 normalized
Fit RMS: 1.45
Run Time: Wed Dec 15 13:41:57 2010
zeros file: idl/cal/Black/Sept5/zeros/ob_tt_ttp.txt
magsat file: idl/cal/Black/Sept5/magsat/ob_tt_ttp.txt
facgrd file: idl/cal/Black/Sept5/fac_grad/ob_tt_ttp.txt
scale factors: 0.996967 0.996725 0.996963
sensor model amx:
1.000000 0.006151 -0.003859
-0.008357 1.000000 -0.008734
0.004818 0.006786 1.000000
symmetric part: 1.000000 -0.001103 0.000479
-0.001103 1.000000 -0.000974
0.000479 -0.000974 1.000000
a-symmetric part:
0.000000 0.007254 -0.004339
-0.007254 0.000000 -0.007760
0.004339 0.007760 0.000000
rotation by: 0.657428 degrees
about unit vector: 0.676285 -0.378112 -0.632194
MAGSAT analysis diagnostics:
facility bmx:
1.000000 -0.000291 -0.000611
0.000248 1.000000 0.000094
0.000583 -0.000126 1.000000
IDL>CSUM,DIR='Black/Sept16a',RNG=4,/NRM
Magsat Analysis
range: 4 normalized
Fit RMS: 3.50
Run Time: Wed Dec 15 13:42:24 2010
zeros file: idl/cal/Black/Sept16a/zeros/ob_tt_ttp.txt
magsat file: idl/cal/Black/Sept16a/magsat/ob_tt_ttp.txt
facgrd file: idl/cal/Black/Sept16a/fac_grad/ob_tt_ttp.txt
scale factors: 0.996910 0.996776 0.996980
sensor model amx:
1.000000 0.006094 -0.003888
-0.008349 1.000000 -0.008711
0.004824 0.006778 1.000000
symmetric part:
1.000000 -0.001127 0.000468
-0.001127 1.000000 -0.000967
0.000468 -0.000967 1.000000
a-symmetric part:
0.000000 0.007221 -0.004356
-0.007221 0.000000 -0.007745
0.004356 0.007745 0.000000
rotation by: 0.656038 degrees
about unit vector: 0.676390 -0.380439 -0.630684
MAGSAT analysis diagnostics:
facility bmx:
1.000000 -0.000266 -0.000585
0.000227 1.000000 0.000088
0.000564 -0.000122 1.000000
Scale factors for this sensor in range 4 averaged over all MAGSAT calibrations (using “high” and “low” applied fields of ∼70k and ∼20k nT) performed after July are:
( 0.996941, 0.996708, 0.996939)
Scale factors and sensor response matrix elements (amx) estimated from individual calibrations throughout the calibration campaign, and throughout all environmental testing, typically fall within 50 PPM of the average value. We also monitored the facility response matrix (bmx) over the course of the calibration campaign, and found that the 6 off-diagonal matrix elements of the facility bmx varied by ∼20 PPM across all calibration events, exhibiting no discernable trend with time.
An independent pair of (Black bench) calibrations performed on the same day (June 9, 2010) as a repeatability test found even better agreement between subsequent facility matrix estimates:
Facility bmx, June 9, run #1:
facility bmx:
1.000000 -0.000279 -0.000575
0.000233 1.000000 0.000090
0.000523 -0.000134 1.000000
Facility bmx, June 9, run #2:
facility bmx:
1.000000 -0.000278 -0.000584
0.000234 1.000000 0.000090
0.000526 -0.000136 1.000000
Suggesting that independent MAGSAT calibration events conducted under stable conditions on the same day yield an estimated facility response to within a few PPM. The variation observed in the facility matrix estimates over the course of the calibration campaign (∼20 PPM) may well represent minor deformation of the facility from day to day in response to mechanical and/or thermal stresses. The facility coils are isolated from ground motion and stresses on the building surrounding it, by design, and the facility temperature is maintained at comfortable levels; nevertheless, 20 PPM variation represents only ∼4 arcsec shift of a facility coil axis over time.
We also note that while most range 4 MAGSAT calibrations yield fits with an RMS of ∼1.5 nT, the September 16 Black bench calibration yielded an RMS residual that was anomalously large (∼3.5 nT), suggesting relatively poor performance of the facility (or the staff!) on this day. However, an RMS of ∼1.5 nT in range 4 is unlikely to be improved upon, given the quantization step size (3.12 nT) of the 16-bit A/D in this dynamic range (1.024 G).
Appendix A3: Thin Shell Partial Derivatives
The partial derivatives of \(B^{2}\) with respect to the model parameters are
and
Appendix A4: FGM Thin Shell Calibration Examples
In the following we provide calibration summary examples for a small subset of the “thin shell” calibrations performed as described in the text. These thin shell calibrations were performed (range 4) in the GSFC facility, using the “Black” MOB (outboard magnetometer suite). In these calibrations, the facility was held in a fixed field (∼70000 nT) and the sensor assembly was rotated in fixed increments in inclination and azimuth.



The thin shell analysis provides a quick and useful check on sensor linearity and performance, but does not by itself establish the sensor response with respect to an external reference (e.g., MOB cube). The sensor response matrix provided by this analysis is necessarily insensitive to rotation, so only the symmetric part of the response matrix is determined, and may be compared with the symmetric part of the sensor response matrix obtained from the vector MAGSAT calibration method.
The scale factors determined by this method may be compared with those determined via the MAGSAT method, but in doing so one must be cognizant of small differences in coordinate systems. The thin shell method will return a result referenced to the “intrinsic” coordinate system of the sensor assembly, which may differ slightly from that defined by the external reference (MOB cube). So, for example, an equally good fit to the thin shell observations of September 16, with slightly different scale factors, may be found by “seeding” the inverse with a reference coordinate system close to that of the reference cube:


One can readily observe that this fit is equally good and the scale factors referenced this coordinate system compare well with those determined via the vector MAGSAT calibration method (Appendix A2). The thin shell fits typically yield an RMS residual of 0.6–0.7 nT in the magnitude of B for dynamic range 4 (component quantization step size = 3.12 nT).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Connerney, J.E.P., Benn, M., Bjarno, J.B. et al. The Juno Magnetic Field Investigation. Space Sci Rev 213, 39–138 (2017). https://doi.org/10.1007/s11214-017-0334-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-017-0334-z