Abstract
Almost 40 years ago the concept of the substorm current wedge was developed to explain the magnetic signatures observed on the ground and in geosynchronous orbit during substorm expansion. In the ensuing decades new observations, including radar and low-altitude spacecraft, MHD simulations, and theoretical considerations have tremendously advanced our understanding of this system. The AMPTE/IRM, THEMIS and Cluster missions have added considerable observational knowledge, especially on the important role of fast flows in producing the stresses that generate the substorm current wedge. Recent detailed, multi-spacecraft, multi-instrument observations both in the magnetosphere and in the ionosphere have brought a wealth of new information about the details of the temporal evolution and structure of the current system. While the large-scale picture remains valid, the new details call for revision and an update of the original view. In this paper we briefly review the historical development of the substorm current wedge, review recent in situ and ground-based observations and theoretical work, and discuss the current active research areas. We conclude with a revised, time-dependent picture of the substorm current wedge that follows its evolution from the initial substorm flows through substorm expansion and recovery.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Intense auroral displays near midnight are associated with strong and rapidly changing magnetic perturbations. Akasofu (1964) systematically organized the auroral observations in time and space with the concept of an auroral substorm. Horning et al. (1974) used magnetic observations from midlatitudes to deduce that the large-scale current pattern associated with the auroral displays comprised a current from space into the ionosphere at the eastern edge and out from the ionosphere returning to space at the western edge of the auroral activity, connected by a westward horizontal current in the ionosphere. An early picture of this large-scale current system appears in McPherron (1972), but the classic diagram, reproduced here in Fig. 1, was first shown by McPherron et al. (1973a). The term “Substorm Current Wedge” did not appear in the literature until Pytte et al. (1976).
A perspective view of the substorm current wedge is shown in panel (a) where tail current is diverted through the northern and southern midnight ionospheres. An equivalent current representing this diversion is projected into the equatorial plane at the bottom right of panel (b). The north-south (H) and east-west (D) magnetic perturbations of this current at 30° north latitude are shown at the left (McPherron et al. 1973a)
The auroral substorm concept was later expanded into a “magnetospheric substorm” that included the solar wind driver and the magnetotail reconfiguration process into the phenomenological description (Akasofu 1981; McPherron et al. 1973a; Russell and McPherron 1973; Hones 1979). Since then, substorms have been extensively studied due to their importance for regulating energy flow from the solar wind to the magnetosphere—ionosphere system, and as key elements in global reconfiguration processes (Baker et al. 1996). While different models for the onset of the magnetospheric substorm exist, they all include the basic elements of the substorm current wedge, which provides the primary pathway for coupling the magnetospheric reconfiguration with the ionospheric dynamics.
While the original development of the SCW relied upon relatively few measurements obtained from ground magnetometers and primarily geosynchronous spacecraft observations, the ensuing decades have seen a rapid increase in not only the quantity of data available, but in types of measurements routinely obtained. Large, integrated networks of radars provide insight into plasma convection; all-sky imager data can be stitched together to yield high temporal and spatial resolution observations of auroral dynamics; the AMPERE project provides global field-aligned current (FAC) measurements; and numerical techniques now enable routine generation of equivalent current maps characterizing the ionospheric current systems. When combined, these new observations enable an unprecedented picture of the electrodynamic coupling between the ionosphere and magnetosphere. New data qualitatively reconfirm the original SCW picture while simultaneously raising a number of important questions related to the structuring, physical processes, and connectivity of the ionospheric and magnetospheric processes. In this review, we address both the large-scale features of the SCW and the local physics and smaller scale phenomena associated with the global current wedge formation and evolution.
This paper provides a review of the phenomenology of the substorm current wedge and an update of the model based on recent simulation and observational results. We start in Sect. 2 with a brief history of the ionospheric and magnetotail observations that lead to the SCW concept, then place these in the context of solar wind—magnetosphere coupling and energy conversion in Sect. 3. In Sect. 4, we discuss the magnetotail driver of the SCW, starting with insights gleaned from MHD simulations, followed by a review of magnetotail flow bursts and transient coupling with the ionosphere. The SCW as seen in the ionosphere is reviewed in Sect. 5, and includes discussions of the Westward Traveling Surge (WTS), the Cowling channel, and local vs. remote current closure. Finally, we synthesize these new insights of the magnitude, spatial extent, and structure of the SCW obtained from observations and simulation results into a revised phenomenological picture of the SCW, including both magnetospheric and ionospheric components.
2 Historical Remarks
Measurements of Earth’s magnetic field reveal that it is frequently disturbed by the effects of electrical currents flowing in and above the ionosphere. These currents are produced by the interaction of the solar wind with Earth’s geomagnetic field. The two most important processes responsible for these currents are the viscous drag of the solar wind as it flows over the boundary of Earth’s field (Axford and Hines 1961), and magnetic reconnection, which directly connects the solar wind magnetic field to Earth’s field (Dungey 1961). Magnetic reconnection at the dayside depends on the relative orientation of the solar wind magnetic field with respect to Earth’s field at the magnetopause. When the solar wind magnetic field is southward (IMF B z <0), the two fields are antiparallel and reconnection is rapid, allowing the solar wind to transfer substantial energy to the magnetosphere. When the fields are parallel, reconnection ceases, little energy is transferred, and magnetic disturbances vanish. Arnoldy (1971) and Burton et al. (1975) demonstrated this quantitatively using B z and VB s respectively to predict the AE and Dst indices responses to geomagnetic activity.
A variety of geomagnetic phenomena occur at different times and locations within the magnetosphere in response to solar wind energy input (Pulkkinen and Wiltberger 1999; Pulkkinen et al. 2007b, 2010; McPherron et al. 2008). The most dramatic such phenomena are the dynamic auroras that occur during the expansion phase of the magnetospheric substorm (Akasofu 1964). After 30–50 minutes of southward magnetic field, an auroral arc near midnight and near the equatorward boundary of the auroral oval suddenly brightens and expands poleward. At the same time, a strong westward current develops in the ionosphere in the region covered by bright aurora. The space-time development of this current was initially termed the “polar magnetic substorm” (Akasofu et al. 1965a), while the dynamical auroral evolution was separately termed the “auroral substorm”. Note the original usage of “substorm” comes from Akasofu and Chapman (1961), and was used to describe the short-term magnetic variations during the main phase of a magnetic storm. The current definition did not develop until a decade later, after it became clear that substorms and storms were distinctly different geomagnetic phenomena. The research of Jelly and Brice (1967), McPherron et al. (1967) and Coroniti et al. (1968) extended the substorm concept out from the ionosphere with the realization that changes occur throughout the magnetosphere in association with the auroral substorm. Because of this, the collection of phenomena that includes auroral breakup and expansion, the substorm current wedge, near-Earth dipolarization, and Pi2 pulsations, became collectively known as the magnetospheric substorm. Akasofu (1968) provides a lengthy description of many of the phenomena that occur during a substorm. It is not evident that all these phenomena can be observed during the storm-time, short-term magnetic variations.
The interpretation of the magnetic signatures associated with the dynamic aurora has a long history, going back for more than 100 years. Changes in the ground magnetic field measured during auroral activity were reported by Birkeland in his seminal book, The Norwegian Aurora Polaris Expedition, 1902–1903 (Birkeland 1908), but a detailed description of the relation is more recent. Early attempts to understand the cause of magnetic variations during substorms were handicapped by the scarcity of magnetic observatories, and initially focused on current systems confined to just the ionosphere—so-called “equivalent current systems” (Chapman 1918, 1927; Kamide et al. 1976). Statistical analysis of the data from a few stations suggested that the ground observations could be explained by an ionospheric current system with two cells roughly centered at the dawn and dusk terminators (Chapman 1935; Chapman and Bartels 1962; Obayashi and Nishida 1968). Akasofu et al. (1965a), on the other hand, argued that the substorm current consisted of a single cell centered slightly post midnight. As more data became available, it became clear that both current systems exist at different phases of geomagnetic activity. The two cell system is now known as “disturbance polar of the second type”, or DP-2 (Nishida 1971). It first appears during the substorm growth phase and is related to the general circulation of magnetic field and plasma driven by the solar wind. It is commonly referred to now as the two-cell convection pattern. The one-cell system, DP-1, occurs only during the expansion phase of the auroral substorm. It is associated with the collapse of the tail field and near-Earth dipolarization that occurs during the substorm expansion, and is the ground magnetic perturbation of what we now call the “substorm current wedge”.
The possibility that electric currents could flow from the magnetosphere along field lines to the auroral region was discussed more than 100 years ago by Birkeland (1913). In this work Birkeland suggested that there are two elementary current systems that link the two regions. The first is a system in which current flows down a single field line, runs for a short distance east-west, and then returns along a field line to the magnetosphere. The second consists of sheets of current flowing down at one edge of the auroral oval, closing north or south across the oval, and returning to the magnetosphere from the other edge. These elementary current system geometries are given the name Type I and Type II, after Boström (1964). Boström (1964) and Bonnevier et al. (1970) used the Type I system to model the magnetic perturbations associated with the polar magnetic substorm. The authors recognized that their proposal was only an equivalent current system and that other systems such as the purely ionospheric DP-1 system could also explain the observations. Nonetheless, the model did a very good job of predicting the auroral zone magnetic observations.
The demonstration that the Type 1 field-aligned current system assumed for the expansion phase is truly a three-dimensional system with linkage to the magnetosphere occurred soon after the first magnetometer was placed into synchronous equatorial orbit. McPherron and Coleman (1969), McPherron (1972), and McPherron et al. (1973a) noted that substorm variations in the H-component (the midlatitude positive bay) at Honolulu were correlated with simultaneous positive variations in the H component at the geosynchronous ATS-1 satellite. This could only be the case if the currents responsible for the variations were flowing on field lines further from Earth than the satellite location. McPherron et al. (1973a) suggested that this current was produced by a short-circuit of the dawn-to-dusk tail current along field lines through the ionosphere as illustrated in Fig. 1. Additional support for the existence of a real three dimensional current was provided by McPherron and Barfield (1980) with magnetic data from the synchronous spacecraft ATS-6 at ∼11° magnetic latitude. At this spacecraft, the average signature in the east (D) component during substorms was a positive perturbation premidnight and a negative perturbation post midnight, just as is seen on the ground. A pair of field-aligned currents, towards the ionosphere post midnight, away from the ionosphere pre midnight, with a source tailward of geosynchronous would explain the D component signatures. Clauer and McPherron (1974) named this system the “current wedge” because of its shape in a polar projection.
The substorm current wedge shown in Fig. 1 produces a distinctive pattern of changes in the midlatitude magnetic field as illustrated at the bottom left of the figure. Everywhere within the wedge, and to some distance either side, the north component of the magnetic field (H) is positive and symmetric about the central meridian of the wedge. The east component (D) is antisymmetric about the central meridian. In the northern hemisphere the east component is positive premidnight and negative postmidnight, with extremes at the locations of the inward and outward current. In the southern hemisphere, the northern component is also positive, but the pre and post midnight perturbations in the D component are reversed. The most probable width for the current wedge at the end of the substorm expansion phase is about six hours of local time (90°) (Gjerloev et al. 2007), with a typical total current as seen at midlatitudes of about 200 kA (1 MA during large substorms).
The concept of the substorm current wedge has played an important role in understanding the coupling of the magnetotail to the ionosphere during substorms. It provides a simple explanation for the magnetic perturbations observed at mid and low latitudes during substorms, and is useful in understanding the magnetic variations seen in the auroral zone. In its simplest form, a model of the current wedge consists of a single loop with line currents into and out of the ionosphere on dipole field lines connected by a westward ionospheric line current and by an eastward magnetospheric line current (Fig. 1). This model can be inverted to determine the optimum L-shell of the currents, their location in local time, and the strength of the currents. Horning et al. (1974) developed an inversion procedure that utilized ground magnetometer data to obtain the parameters defining the wedge, such as the longitude of the upward and downward FACs and the total current. More recent versions of the algorithm (Cramoysan et al. 1995; Sergeev et al. 1996c) provide a tool suitable for the statistical and event studies of wedge parameters and its dynamics. The wedge model with realistic tail-like field lines and distributed currents, suitable for accurate computations of SCW effects in both the ionosphere and the magnetosphere, is now available (Sergeev et al. 2011). Still better models include changes in the ring current and take into account ground induced currents (e.g., Chu et al. 2014).
This substorm current wedge model is only a crude approximation to the currents that actually exist in space. It is generally believed that the upward current is localized in the premidnight sector while the downward current is more broadly distributed along the auroral oval post-midnight (Untiedt and Baumjohann 1993; Baumjohann 1982; Lester et al. 1983). Upward currents are carried by downward moving electrons, while the downward current is a combination of upward flowing electrons and precipitating ions. The actual currents probably do not flow on the same L-shells. There is evidence that the upward and downward current segments overlap in longitude (Clauer and Kamide 1985) and that the locations of the line currents simply approximate the centers of these sheets. It has also been suggested that the current wedge includes currents closing in meridian planes (Birn et al. 1999; Ritter and Lühr 2008; Sergeev et al. 2011). In this more complex model there is a second current wedge of opposite sense flowing on a lower L-shell with a different current strength. The effect of this loop on the ground is to reduce the apparent strength of the higher latitude current wedge. A demonstration of the existence of a second wedge requires satellite observations in space between the two current loops.
Recently, the combination of Geotail, Cluster, and THEMIS spacecraft probing the magnetotail and inner magnetosphere has made it possible to investigate the properties of the current wedge in space. Improvements in ground observations from a large network of magnetometers in the auroral zone have provided better resolution of the currents closing the current wedge in the ionosphere. It is the purpose of this paper to review recent observations and simulations and to suggest modifications to the original concept of a current wedge that makes it more representative of the physical processes taking place in the magnetosphere.
3 Solar Wind—Magnetosphere—Ionosphere Coupling
3.1 Coupling Modes
Magnetospheric dynamics are driven by energy derived from the solar wind and its magnetic field. This energy is transferred to the magnetosphere by two processes: magnetic reconnection (Dungey 1961) and viscous interaction (Axford and Hines 1961). Of these two processes, magnetic reconnection is by far the dominant driver of activity. Reconnection opens dayside dipole magnetic field lines and the solar wind transports this flux to the tail lobes where it is temporarily stored (Aubry and McPherron 1971). The viscous interaction moves closed field lines and plasma in equatorial boundary layers to the nightside of the magnetosphere (Eastman et al. 1976). Both processes create a reduction in pressure on the dayside relative to the nightside plasma sheet that drives large-scale convection of plasma that returns closed field lines from the boundary layer and plasma sheet to the dayside (Siscoe and Huang 1985).
The amount of energy coupled to the magnetosphere via magnetic reconnection at the dayside varies substantially. The rate at which the magnetic fields connect depends on the rate at which southward magnetic flux is transported by the solar wind. This is given by the dawn-dusk component of the solar wind electric field E y =VB s , where V is the solar wind speed and B s is the strength of the magnetic field anti-parallel to Earth’s field. High speed and strong southward magnetic field cause strong solar wind—magnetosphere coupling, and consequently large magnetic disturbances both in the magnetotail and in the ionosphere. The magnetosphere transports and processes this energy through different modes of response, which sporadically lead to reconfiguration of the nightside magnetosphere and activation of fast flow bursts in the magnetotail. These modes, while they share some common properties, occur on vastly different temporal and spatial scales, and have quite distinct characteristics of their own. These sequences of events were originally defined phenomenologically, but later work has shown that the event categories may overlap and separating one type of event from another may be difficult at times. In order of increasing activity level, the basic response modes can be divided into pseudobreakups, magnetospheric substorms, steady magnetospheric convection (SMC) intervals, sawtooth events and geomagnetic storms (e.g., Koskinen et al. 1993; Baker et al. 1996; Sergeev et al. 1996b; Henderson et al. 2006a; Pulkkinen et al. 2007a; McPherron et al. 2008).
Each of these responses of the magnetosphere to solar wind driving is a core elements of the Dungey Cycle. Dungey (1961) was the first to propose a cycle of magnetospheric convection driven by magnetic reconnection at the dayside magnetosphere. Magnetic field connected on the dayside of Earth is transported by the solar wind to the night side where it forms a long tail behind the Earth. This transfer of flux to the nightside forces the magnetosphere to undergo systematic changes in configuration that eventually lead to nightside magnetic reconnection, which returns flux to the dayside along the flanks of the magnetosphere via the different response modes. This basic process is the source of the two-cell (DP-2) ionospheric convection pattern. Intervals of steady magnetospheric convection, where the dayside and nightside reconnection rates are roughly balanced, approach the idealized state originally envisioned by Dungey (1961) (Sergeev et al. 1996b; Milan et al. 2007; DeJong et al. 2009). Yet reconnection is not a steady process, and even during intervals of SMC, when the solar wind driver is relatively constant, plasmasheet convection can be intermittent and bursty.
Detailed examination of these response modes reveals that a pair of field-aligned currents in the form of a current wedge forms during each of the phenomenological modes. Thus, the substorm current wedge system is a key phenomenon across all magnetospheric dynamics related to the Dungey cycle, present from weak to extreme activity conditions, and is the link between magnetospheric dynamics and the ionosphere. During pseudobreakups, the current wedge has limited local time extent and weak intensity, and during most events connects to the fairly distant magnetotail, beyond the quasi-dipolar region (Koskinen et al. 1993). At the other end of the activity range, sawtooth events contain a very wide and intense current wedge mapping to the inner magnetosphere close to the outer edge of an intensified ring current (Henderson et al. 2006b). Magnetic storms also contain substorm-like activations, which show intense current wedges with varying local time and temporal extent (Kubyshkina et al. 2008). Moreover, the current wedge expands as the dynamic events progress, concurrently with the expansion of the auroral bulge in the ionosphere (Fig. 2).
Comparison of auroral intensification and substorm current wedge signatures (magnetic field dipolarization) in the magnetotail. The red shading illustrates auroral intensity mapped using a field model developed specifically for this event to the magnetotail at the times indicated in the figure. The yellow shadings illustrate the radial section of the tail where the magnetic field dipolarization has occurred based on in-situ magnetic field measurements in the magnetotail. It is evident that the increase of the region with intense auroral precipitation is well correlated with the opening of the substorm current wedge as observed in the magnetotail (after Pulkkinen et al. 1995)
3.2 Magnetospheric Substorms
Although the substorm current wedge exists during the different magnetospheric transport modes, it has been most studied and was initially developed within the context of magnetospheric substorms. Magnetospheric substorms arise due to an imbalance between the dayside and nightside reconnection rates. As a simple example, this can arise during a sudden rotation of the IMF from northward to southward. Reconnection will immediately occur at the dayside magnetosphere, but these newly reconnected flux tubes will take many 10s of minutes to convect to the tail. Without an increase in the nightside reconnection rate, the amount of open flux in the polar cap increases, as indicated by an increase of the magnetic flux content in the tail lobes (McPherron 1972; McPherron et al. 1973a,b; Caan et al. 1973, 1978; Hsu and McPherron 2004) and an increase in the polar cap area (Frank and Craven 1988; Milan et al. 2003, 2008; Taylor et al. 1996). This storage of energy in the magnetotail is termed the substorm growth phase. The enhanced convection circulation in the magnetotail leads to the formation of a highly thinned current sheet at the tail center and a very stretched magnetic configuration (McPherron et al. 1987; Sanny et al. 1994; Thompson et al. 2005; Hones 1972; Nishida and Hones 1974). As the configuration becomes increasingly unstable, at some moment magnetic reconnection begins in the magnetotail, which initiates fast flows from the reconnection site both in the Earthward and tailward directions, and leads to dipolarization of the inner portion of the magnetic field (e.g., Nagai 1991; Baumjohann 2002). This sequence of changes, from energy storage through explosive release, is called a magnetospheric substorm (Akasofu 1968; Coroniti et al. 1968). The reconnection process is temporally and spatially varying, which structures the flows in scale sizes of the order of a few RE and time scales of a few minutes (Angelopoulos et al. 1992; Sergeev et al. 1995). Flows from the reconnection region and dipolarization of the magnetic field are associated with field-aligned currents coupling to the ionosphere, whose net effect is then the substorm current wedge.
While the topic of substorm initiation remains controversial, many of the observational aspects of substorm development are well established. In the near-Earth transition region that separates dipolar from stretched tail magnetic field, the beginning of the substorm expansion phase causes a sudden dipolarization of the magnetic field (Baumjohann et al. 1999) and injection of accelerated particles (Parks and Winckler 1968; Belian et al. 1981). Pi2 pulsations (T=40–150 s), discussed in Sect. 4.4, are created via multiple pathways by the energy imparted by this sudden change in magnetospheric configuration. In addition, the Cluster, Geotail and THEMIS missions have shown the critical role fast flows play in substorm development (e.g., Angelopoulos et al. 2008; Baker et al. 2002).
The auroral phenomenology that occurs during a substorm is also well described (see review by Elphinstone et al. 1996). The auroral substorm begins as a localized brightening near the equatorward boundary of nightside auroral precipitation, most commonly at 23 UT, on the poleward shoulder of the proton precipitation (Sergeev et al. 2012b; Donovan et al. 2008). This initial brightening is generally believed to map along field lines to the near-Earth transition region, i.e., to the region of dipolarizing magnetic field (Lui and Burrows 1978; Sergeev et al. 2012b). This brightening expands rapidly azimuthally, often exhibiting folds and beads during the breakup, and then expands poleward within a few minutes. This poleward expansion transforms into a Westward Traveling Surge (WTS), further discussed in Sect. 5.1. Observations of the WTS have shown that it does not expand smoothly, but instead proceeds as a series of steps (Wiens and Rostoker 1975; Pytte et al. 1976), which has interpreted as intensifications of the substorm expansion (Rostoker et al. 1980). Auroral streamers, believed to be the auroral manifestations of magnetotail flow bursts and frequently observed east of the WTS during substorm expansion, are discussed in Sect. 5.4.
A central component of the near-Earth in situ and auroral activity is the substorm current wedge. It links the dynamical changes occurring in the near-Earth transition region with the ionosphere, and serves as a conduit of energy derived from substorm expansion, and any mode of the SCW must include all of the established observational elements. This current system also couples the energy derived from the solar wind—magnetosphere interaction to the ionosphere, as we describe next.
3.3 Energy Flow, Conversion, and Dissipation
Both viscous interaction and direct coupling to the solar wind through magnetic reconnection drive magnetospheric plasma motions. In turn, the electric fields associated with these motions are transmitted along field lines to the ionosphere where they drive currents through the ionosphere. The high latitude FAC are known as region-1 currents, while the lower latitude currents are called region-2 currents (Iijima and Potemra 1978). The ionospheric current connecting these two FAC systems flows parallel to the projected electric field and is called the Pedersen current. Since the Pedersen current flows through a resistive ionosphere in the direction of the electric field it causes Ohmic heating (J⋅E>0). The two shells of FAC form a solenoid so that the magnetic perturbations they create are confined to the region between them and cannot be detected on the ground. Because of the interaction of the motion of ionized gases with the neutral atmosphere, the ions and electrons undergo different drift motion. Ions, due to higher collision rates with the neutral atmosphere, have a component of motion perpendicular to the E×B drift direction, while the electrons generally follow E×B (see review by Pfaff (2012)). The non-dissipative (J⋅E=0) Hall current flows at right angles to both the electric and magnetic fields. The magnetic effects of the Hall current driven by the region 1 and 2 currents can be observed on the ground and are known as the DP-2 current system described in Sect. 2.
In the context of ionospheric energy dissipation, the different current systems can be classified into two types based on how energy is processed. If the ionospheric motion and dissipation is coupled directly to the solar wind, the system is said to be “directly-driven”. The directly-driven process manifests itself as the DP-2 (two cell pattern) ionospheric current system. If magnetic energy is first stored in the tail lobes and then released some time later, driving additional convection and field-aligned and ionospheric currents, it is called “unloading”, and is associated with the DP-1 (SCW) current system. Both processes cause precipitation of charged particles that also deposit energy in the atmosphere.
The characteristic feature of the driven DP-2 current system is the existence of the eastward and westward electrojets flowing toward midnight along the auroral oval. Rough measures of the strength of these currents are the auroral upper (AU) and auroral lower (AL) indices. These are respectively the largest positive northward magnetic perturbation (H) measured on the ground under the eastward electrojet by any magnetic observatory in the afternoon to dusk sector, and the largest negative southward perturbation measured in the late evening to morning sector. Both AU and AL begin to grow in intensity soon after the IMF turns southward and dayside reconnection begins. The characteristic feature of the unloading DP-1 current system is the sudden development of an additional westward current that flows across the bright region of the expanding auroral bulge. This is the ionospheric segment of the substorm current wedge. The onset of this current is recorded in the AL index as a sudden decrease, corresponding to an increase in intensity of the westward current.
To calculate the dissipative effects of the substorm current wedge, it is necessary to examine separately the unloading vs. driven contributions. Typically, this takes the form of correlating measures of magnetospheric activity with solar wind parameters. Early in the space age it was noted that the strength of magnetic activity depended on solar wind speed (V) (Snyder et al. 1963) and the strength of the interplanetary magnetic field (IMF) (Wilcox et al. 1967). Fairfield and Cahill (1966) noted that it was the north-south component of the IMF that is most important and interpreted this as evidence of magnetic reconnection at the dayside magnetopause. Burton et al. (1975) later demonstrated that the rectified solar wind electric field, E s =VB s , is a good predictor of the rate of change of the Dst index. Perreault and Akasofu (1978) and Akasofu and Chao (1979) introduced a different function, ϵ, of solar wind parameters that they argued was a more appropriate predictor of Dst, and began to refer to the function ϵ as a “coupling function”. In units of Watts, this function is given by
where V (m/s) is the solar wind speed, B (T) is the magnitude of the interplanetary magnetic field, l 0 (m) is the length of the dayside interaction region, and θ=arctan(B y /B z ) is the clock angle of the IMF in GSM coordinates.
One can use these coupling functions to measure the amount of energy entering the magnetosphere and compare the result to measures of energy dissipation in the magnetosphere, as represented, e.g., via the auroral indices. Tanskanen et al. (2002) examined the dependence of the amount of energy dissipated in the ionosphere on the amount of energy incident at the magnetopause. They integrated both the input and the output over the substorm growth, expansion and recovery phases and were able to show that during the expansion and recovery phases there was a good correlation between the amount of energy input and output. This was used to argue that the energy input during the growth phase was responsible for the configuration change necessary for the substorm onset to occur, but that the majority of the energy dissipated in the ionosphere during the expansion and recovery phases was drawn directly from the solar wind (Pulkkinen et al. 2006). Similar conclusions were drawn also by Lockwood et al. (2009) based on low altitude satellite measurements and a model for polar cap flux balance as a function of solar wind driving parameters during various phases of geomagnetic activity.
The above discussion shows that over a substorm cycle the amount of energy dissipated in the ionosphere is proportional to the intensity of the solar wind driving; the general result holds regardless of the exact form of the driving function (see, e.g., Pulkkinen et al. 2011; Newell et al. 2007). However, over longer time scales, solar activity affects the ionospheric energy dissipation. Pulkkinen et al. (2011) examined the auroral electrojets and their dependence on solar activity. First, it is clear that the solar wind driver changes over the solar cycle, with the highest level of driving occurring during solar maxima and weakest during solar minima (Lockwood and Owens 2011; Lockwood et al. 1999). Secondly, the electrojet intensity is higher and the electrojets reside at lower latitudes during higher solar activity than during solar minimum conditions (Pulkkinen et al. 2011). Similar statistical results hold for the occurrence frequency and maximum amplitude of substorms as measured by ionospheric electrojet indices (Tanskanen 2009).
These results suggest that the substorm is driven primarily by the solar wind. It must be emphasized, however, that these are integrated results using data at low temporal resolution (see e.g., McPherron et al. 2009, who used hourly averages). When higher resolution data are used it becomes evident that rapid variations during the substorm expansion phase drive ionospheric currents. This suggests that the formation and development of the substorm current wedge is not correlated with the solar wind coupling function, except in an integrated sense. At the present time, too little is known about the physical mechanisms responsible for the formation of the current wedge to be able to predict its detailed development from observations available in the magnetotail.
4 Magnetotail Driver
The field-aligned currents that feed the substorm current wedge flow in response to dynamical changes in the near-Earth magnetotail, associated with the current sheet collapse and dipolarization. Recent simulation results and THEMIS observations have clarified the roles of dipolarization and flow diversion in this process. The plasma flows are the critical drivers that distort the field lines to create magnetic shear that result in FACs. The flows also drive waves and pulsations in the inner magnetosphere. The effects of individual transient flows are accumulated to form a longer-duration dipolarized region with a modified plasma pressure distribution in the inner magnetosphere, which is the driver of the substorm current wedge. In this section we discuss the physical mechanisms that create field-aligned currents, properties of the fast flows that play a crucial role in creating the wedge, and the mechanism(s) that affect the fast flow and their penetration towards Earth.
4.1 Field-Aligned Current Generation: Insights from Simulations
A comprehensive view of the substorm current wedge is difficult to obtain experimentally. In most of space, the field-aligned currents are weak and spread over large volumes making in situ detection difficult. In the ionosphere, the time-dependent and spatially varying distribution of Hall and Pedersen conductivity creates a complex pattern of current. Remote sensing of the SCW both in space and on the ground has provided an integrated picture of the current system, but insight into the build-up of the currents has come primarily from numerical simulations, which have produced details of the physical processes that create the current wedge and its three-dimensional configuration (Birn and Hesse 1991, 1996, 2000, 2013; Scholer and Otto 1991; Raeder and McPherron 1998; Birn et al. 1999).
The build-up of the substorm current wedge is caused by flow bursts transporting magnetic flux from the reconnection site to the near-Earth region. Figure 3 illustrates this relation, which may be applied to individual flow bursts as well as the full current wedges (Amm et al. 2002). In the simplest view (Fig. 3a) a flow burst transports magnetic flux from the reconnection site to the near-Earth region, changing the magnetic configuration in a limited sector of local time from a stretched tail to more dipolar field while regions outside this dipolar region (towards dawn and dusk) still maintain the original stretched configuration, resulting in a magnetic shear corresponding to field-aligned currents of region-1 sense (into the ionosphere post midnight, out of the ionosphere pre midnight). On either side of the plasma sheet, the magnetic field is mainly in the x direction, so that j x is the primary contributor to the field-aligned current, j ∥. The current density j x can be calculated from Ampere’s law,
Moving from dawn towards the dipolarized region centered near midnight, B z increases with increasing y (towards dusk) so the first term in Eq. (2) is positive, indicating an earthward directed field-aligned current. Moving further towards dusk, B z decreases as one leaves the dipolarized region, creating field-aligned current away from the ionosphere. This apparent diversion of the cross-tail current into the ionosphere is consistent with the original SCW picture shown in Fig. 1a.
A perspective view of how magnetotail flows cause the build-up of the substorm current wedge. (a) A finite width earthward flow will create a region of dipolar-like field lines with the field lines outside the flow region remain stretched. (b) Azimuthal flow will bend a field line out of the meridian. In both (a) and (b) the rotation of magnetic field corresponds to field-aligned current. (c) build-up of a region-1/region2 type system resulting from the shear outside and inside the diverted flow. (a) and (b) are from Fig. 3.4 of Amm et al. (2002), while (c) is from Fig. 7.15 of Birn and Hesse (2013)
Closer to Earth, the shear or twist of the magnetic field becomes strongly intensified when the flow gets braked and diverted around Earth by the increased magnetic pressure of the inner dipole field (Figs. 3b, c). In the post midnight sector, the dawnward flow bends the magnetic field, increasing the magnitude of B y . At higher z, field lines extend farther back into the tail, |B y | decreases and the derivative of B y becomes negative so that the second term adds to the earthward FAC on the dawn side (tailward on the dusk side, i.e., of region 1 type).
The combined vorticity of earthward and azimuthal flow is illustrated by the twisting of two flux ropes in Fig. 3c, modified from Birn et al. (2004). In visualizing the effect of the twisting it is important to realize that the effect strongly depends on ionospheric boundary conditions. If field lines were allowed to slip freely at the ionosphere the flux ropes might rotate uniformly without increasing their twist, that is, without increasing the field-aligned currents. Alternatively, effects that increase ionospheric conductivity and thus the field-line tying at the ionosphere contribute to enhanced twist and enhanced field-aligned current. There is in addition a finite propagation time along the flux tubes, discussed further in Sect. 4.4.
The azimuthal flows that generate region-1 type FACs on the tailward/poleward side of the distorted field also cause opposite vorticity on their earthward/equatorward side, as illustrated by Figs. 3c. This, region-2 type, current is represented by a green arrow pointed outward from Earth. The same arguments can be applied to the gradients on the westward edge of the dipolarized region to show that field-aligned current is out of ionosphere at high latitudes and into the ionosphere at lower latitudes. If the high latitude and low latitude currents were of equal strength they would form solenoidal loops with their magnetic effects confined between them and no effects would be seen on the ground. However, midlatitude ground magnetometers observe effects consistent with the sense of the outer currents so we conclude that the lower latitude current loop is weaker than the outer loop. It thus appears that the total current in the traditional substorm current wedge is the difference between the currents in the outer and inner loops.
This flow-based description, based on Faraday’s law, provides a good visualization of the initial buildup of currents in nearly ideal plasmas. The currents, however, persist even when the flows subside, with their decay governed by ionospheric dissipation and relaxation of magnetospheric stresses. The instantaneous flows in the tail, and the associated shear and twist of magnetic field lines, can no longer be used to infer the currents, even though μ 0 J=∇×B is still valid. In that case, one commonly investigates FACs from a combination of current continuity and momentum balance.
Due to current continuity, calculation of the parallel current is equivalent to calculating the diversion of the perpendicular current. From the momentum equation one obtains for isotropic pressure
Equation (3) can be integrated to yield (e.g., Vasyliunas 1970)
where the integral is taken along a field line from a point where j ∥ vanishes (say, the neutral sheet) to a point of interest such as the ionosphere. The first term on the RHS of (4) is termed the ‘inertial current’, and is non-zero only during acceleration or deceleration of the flows. We note here that ‘inertia-driven’ currents associated with the braking might have the sense of region-1 (Shiokawa et al. 1998), but are found to play only a minor role in comparison to ‘pressure-driven’ currents, represented by the second term on the RHS of (4) (Birn et al. 1999).
Figure 4a shows the diversion to parallel currents as obtained from a recent MHD simulation of near-tail reconnection and earthward flow (Birn et al. 2011). Color shows the magnitude of \(\nabla\cdot {\bf j}_{\parallel}\) in the equatorial plane, integrated over z. A plot of \(\nabla\cdot{\bf j}_{\perp}\) would show equivalent diversion, but of the opposite sign, consistent with Eq. (3). The arrows show velocity vectors and the solid lines are contours of constant B z , shown at intervals of 10 nT with the contour to the right representing the neutral line (B z =0) and the contours to the left indicating the dipolarized region. This should be compared with Fig. 3a, as field lines within the pile-up region (higher B z , y=0) are dipolarized, while the field lines outside this region, at large y, remain stretched. The velocity vectors indicate the vortex flows responsible for the twist of the field shown in Fig. 3b and the build-up of the region-1 type current system. The large red area post-midnight in Fig. 4a shows current towards the ionosphere, and the large blue area pre-midnight shows current from ionosphere. This also shows that, at the inner edge where the flow shear is opposite, a diversion to region-2 type currents takes place (opposite polarity of the red and blue regions). Note that the region-2 current system is weaker than the region-1 system.
(a) Diversion of perpendicular into parallel currents, based on an MHD simulation of near-tail reconnection and earthward flow (Birn et al. 2011). Color shows the magnitude of \(\nabla\cdot{\bf j}_{\parallel}\) in the equatorial plane, integrated over z. The arrows show velocity vectors and the solid lines are contours of constant B z , shown at intervals of 0.5 (10 nT) with the contour to the right representing the neutral line B z =0. (b) Field-aligned current sources evaluated from Vasyliunas’ formula (5), for the same state shown in (a). Color shows the magnitude of the plasma pressure P in the equatorial plane. Solid black lines are contours of constant flux tube volume V, and dashed black and white contours outline the regions of enhanced |∇V×∇P|. (c) Contributions to the current diversion from pressure gradients, and (d) from inertia, shown on the same color scale as panel (a)
With approximate force balance in the absence of strong flows, the inertia term can be neglected in (4) and the parallel currents in the magnetosphere can then be expressed by Vasyliunas’ formula (Vasyliunas 1970)
where
is the volume of a flux tube of unit magnetic flux, integrated from the equatorial plane to the ionosphere (assuming, for simplicity, symmetry around the equatorial plane). Equation (5) explicitly shows that field-aligned current, in steady state, is associated with the non-alignment of gradients in pressure and flux tube volume. While Fig. 4a is obtained by directly integrating the diversion to j || along z, an almost identical picture can be obtained by evaluating Eq. (5). This is illustrated by Fig. 4b, which shows, for the same state as Fig. 4a, the color-coded magnitude of the pressure P in the equatorial plane, contours of constant flux tube volume V (solid black contours), and the regions of enhanced |∇P×∇V| (dashed black and white contours).
Figure 4b shows a region of enhanced pressure (red and orange in Fig. 4b). It consists of compressed plasma in front of the flow, which is part of the “scooped up” surrounding plasma. The local minimum of pressure near x≈−11 RE coincides closely with the local minimum of the flux tube volume and the B z enhancement (dipolarization) at the front of the earthward flow (Fig. 4a), to be discussed further in Sect. 4.2. The subsequent pressure increase (green region) tailward of the minimum is related to pressure balance with a decreasing magnetic pressure from decreasing B z . Farther out the pressure decreases again with distance, consistent with the preexisting equilibrium structure.
The regions of enhanced |∇P×∇V| agree closely with the regions of enhanced diversion to parallel currents, shown in Fig. 4a. The figure shows clearly that the diversion to region-1 type currents, part of the original SCW, is associated with earthward directed pressure gradients and azimuthally outward directed gradients of V, resulting from the reduction of flux tube volume by reconnection. In contrast, the diversion to region-2 type currents is related to (largely unperturbed) radially outward directed gradients of V and gradients of P directed towards midnight, associated with a pressure enhancement resulting from the braking of the earthward flow. Thus, both region-1 type and region-2 type systems are essentially “pressure gradient driven”.
The dominant contribution to the current diversion stems from the pressure gradient term in Eq. (4). This is demonstrated by Figs. 4c and 4d, which show the pressure gradient and inertial contributions to ∫∇⋅j ∥ dz, respectively, on the same color scale as Fig. 4a. In the region where the flow speeds, and hence the inertial terms, are more significant, they are largely compensated by pressure gradient terms, such that the net contribution to ∫∇⋅j ∥ dz is small.
The consistency between the instantaneous flow pattern shown in Fig. 4a and the results from evaluating the current diversion directly or via Vasyliunas’ formula (5), underlying Fig. 4b, may seem surprising in view of the fact that the flow pattern relates to the build-up, while the pressure gradient evaluation describes the established current system. It is an indication that the build-up occurs in a quasi-static fashion, such that inertia terms are negligible in the momentum balance, despite appreciable flow speeds.
We stress here that, in general, the flows that are necessary to build up a field-aligned current system can be quite different from, or even opposite to, the flows that would result from the acceleration or deceleration of the plasma in a stressed system after the build-up of the currents. This can be easily demonstrated if we consider the stretching of a closed field line by tailward flow. If pressure gradient forces were negligible, the Lorentz stress of the stretched field line would result in earthward acceleration and hence earthward flow after the plasma has come to rest. In that case, the buildup flow pattern and the acceleration pattern differ. However, as supported by simulations of magnetotail dynamics, the near magnetotail is typically governed by an approximate balance between pressure gradient and Lorentz forces, such that the inertia term can be neglected in (4).
The simulations also suggest a modified picture of current loops involving both region-1 and region-2 type field-aligned currents as well as local loops confined to the tail. This is illustrated by Fig. 5, which is modified from Plate 4 of Birn et al. (1999), particularly by adding loop 4, which is confined to the vicinity of the equatorial plane in the tail. This loop is evident in the simulation results shown in Plate 1 of Birn and Hesse (2000), near x=−10. If this loop (or part of it) is combined with loops 2 it suggests a magnetotail closure of the region-2 type currents in loops 2 through a westward partial ring current rather than radial currents. This modification to the original SCW, discussed near the end of Sect. 2, has recent observational support. Sergeev et al. (2014) demonstrated that a second region-2 type current was required to match the observational constraints provided by distributed in situ measurements inside the dipolarized region. The relative magnitudes of the region-1 and region-2 type currents were found to vary from event to event. Both the simulation and observational results demonstrate that the current closure in the tail is not a unique property, but depends on how the total current is split up into various loops. Similar statements can be made about the ionospheric closure, to be discussed in Sect. 5.
Current loops associated with the SCW as suggested by MHD simulations of magnetotail reconnection and field collapse. Modified after Fig. 7.12 of Birn et al. (1999)
So far we have considered only the effects of a single flow channel, its braking and diversion. However, magnetotail simulations, as well as global MHD simulations, frequently show the development of multiple flow channels. In addition, in situ observations of flow bursts and ground measurements of Pi2 pulsations suggest multiple flow bursts occur during substorms. Birn et al. (2011) attributed the occurrence of multiple flow channels to the fact that reconnection and the ejection of a plasmoid creates a decrease in the flux tube entropy. This reduced entropy creates a ballooning/interchange unstable configuration near the reconnection site, which can result in cross-tail structure and multiple flow bursts (e.g., Panov et al. 2012). Multiple individual flow bursts, associated with entropy depleted flux tubes, each drive a dipolarization front and generate a small current wedge, but collectively cause a tailward and azimuthal expansion of the dipolarized region.
In situ observations have firmly established that one consequence of magnetic reconnection in the tail is the generation of fast earthward plasma flows. Simulations have greatly expanded our understanding of how these plasma flows interact with the inner magnetosphere and lead to the development of the substorm current wedge. The flows carry plasma with reduced entropy and enhanced magnetic flux that penetrate deep into the magnetosphere. The pressure distribution in the inner magnetosphere deflects the flows creating magnetic shears and pressure distributions that generate field-aligned currents. These fast flows are observed in the tail during virtually every substorm, and have been associated observationally with the formation of Pi2 pulsations and the current wedge. In the next section we describe the properties of these flows.
4.2 Bursty Bulk Flows
It is now well established that the onset of the substorm expansion phase is associated with a large increase in plasmasheet flow velocity (Hones et al. 1973; Hones 1977; Miyashita et al. 2009; McPherron et al. 2011). While these convective plasma flows can occur at any level of magnetic activity (Angelopoulos et al. 1992), their occurrence rate increases significantly in proportion to auroral electrojet activity (Angelopoulos et al. 1994; Baumjohann et al. 1990, 1989). These Earth-directed transient, fast, convective plasma flows have been identified as ‘bursty bulk flows’ (BBFs), and they carry the majority (70–80 %) of flux transport in the magnetotail (Baumjohann et al. 1989; Angelopoulos et al. 1992). BBFs typically have a duration of 10-minutes of enhanced flow, with embedded velocity peaks of 1-min duration that are called ‘flow bursts’. The spatial scale of BBFs has been determined to lie in the range 1–5 RE in the azimuthal (y) direction (Sergeev et al. 1996a; Angelopoulos et al. 1997; Nakamura et al. 2001, 2004; Sergeev et al. 2004).
Superposed epoch studies of flow bursts have yielded the average properties of these flows and how they interact with the inner magnetosphere (Angelopoulos et al. 1992; Baumjohann 1993; Ohtani et al. 2004; Liu et al. 2013). Figure 6, from Ohtani et al. (2004), shows that an individual flow burst generally has a thin (ion scale, about 800–2000 km) frontside boundary, called the dipolarization front (DF). Behind the DF the magnetic field B z component sharply increases whereas the plasma density and pressure decrease. The flow burst then, is a plasma depleted and dipolarized magnetic flux tube with heated plasma carried by the fast flow. The growth in flow begins about 1–2 minutes before the DF arrival, demonstrating plasma compression in front of the approaching dipolarized tube. The comprehensive statistical view of the geometrical properties and the plasma and field variations around the dipolarization fronts obtained in recent studies (Liu et al. 2013; Fu et al. 2012) is remarkably consistent with the simulation results described in Sect. 4.1 and illustrated in Fig. 4. Both theoretical analyses and simulations have demonstrated that the underpopulated plasma content of dipolarized plasma tubes is the parameter that controls its penetration distance into the inner magnetosphere (see Dubyagin et al. (2011) for observational confirmation). Such underpopulated plasma tubes are the natural result of the magnetic reconnection process in the mid tail region, which reconnects the outer plasma sheet boundary layer and lobe magnetic field.
The magnetic field and ion plasma parameters superposed for 818 fast Earthward flow events observed in the CPS by Geotail spacecraft with the start of a B z increase used as the zero time (Ohtani et al. 2004)
The flow burst front (DF) itself takes the form of a thin current sheet on the Earthward side of the dipolarizing flux tubes, while the background plasma in the region ahead is compressed, on average by 20–50 % or more, depending on the distance (Dubyagin et al. 2010). The motion of the flow burst through the plasmasheet creates azimuthal flows at the leading edge, which then distorts the magnetic field and introduces B y shear. These closely associated azimuthal plasma flows and quadrupolar B y magnetic shears are clearly observed in a superposed study of the narrow (∼ 1 RE) compressed plasma layer at the flanks of the flow burst DFs, shown in Fig. 7 (Liu et al. 2013). The magnetic shear at the DFs are observed to create FAC with region-1 sense of 4–20 nA/m2, corresponding to about 7–36 μA/m2 in the ionosphere (Nakamura et al. 2005; Snekvik et al. 2007; Sun et al. 2013; Forsyth et al. 2008). These values are comparable to the 25 μA/m2 FAC values in the ionosphere obtained from the ground magnetic field perturbation associated with an auroral streamer (Amm et al. 1999). Recent studies have further resolved a region-2 sense current system ahead of the DF front with a magnitude of 0.6–10 nA/m2 (Liu et al. 2013; Sun et al. 2013). Multipoint THEMIS observations of flows obtained a vortex pattern with a scale of several RE (Keika et al. 2009; Panov et al. 2010) similar to those observed in MHD simulations. Keiling et al. (2009) estimated a current density of 2.8 nA/m2 for such plasma flow vortices. In situ observations of BBFs therefore obtain field-aligned current patterns and magnitudes of both region-1 and region-2 sense that are consistent with the simulated flows reviewed in Sect. 4.1.
Superposed epoch analysis of B y component (a)–(d) and detrended B y (e)–(h) for earthward-normal dipolarization front events (Liu et al. 2013). The three curves in each panel are the upper quartile (dotted), the median (solid), and the lower quartile (dotted). According to the discontinuity normal direction ’Morning’ stands for n y <−0.2; ‘Evening’ stands for n y >0.2. ‘North’ stands for B x0/B lobe >0.3 (north of the neutral sheet); ‘South’ stands for B x0/B lobe <−0.3 (south of the neutral sheet). The number in each panel is the total number of events used in that panel
The statistical picture of the individual flow burst reviewed above characterizes the propagation state of a BBF, which can be considered a dipolarizing flux tube. The propagating flow burst carries a field-aligned current system, which is similar in geometry to that of the substorm current wedge, with FAC into the ionosphere at the dawnward edge and out of the ionosphere at the duskward edge. The closure path as well as the connection to the strong duskward cross-tail current of 5–20 nA/m2 flowing at the dipolarization front are not understood. For example, Liu et al. (2013) inferred the region-1 sense field-aligned current component flowing in high-latitude portions of the dipolarization front, but argued that the equatorial portion of the DF cross-tail current may be entirely closed in the equatorial plane, similar to the Current Loop 4 in Fig. 5 (but with opposite sense). Birn and Hesse (2014) recently included a new Loop 5 at the Earthward edge of Loop 4, and related it to the intense DF current. In this manner, part of the ‘disrupted’ current may not actually be diverted to the ionosphere and may not be recorded by ground measurements, providing a challenge in understanding the possible direct contribution of the flow burst to the substorm current wedge. Given the ability of flow bursts to sustain field-aligned currents and possibly feed those currents to the ionosphere, they function as individual pieces of a substorm current wedge, and have been called “wedgelets” (Rostoker 1998; Liu et al. 2013; Nakamura et al. 2005).
Statistical maps of flow speed and direction show a general pattern of rapidly decreased flow speed, deflection away from midnight, and decreased flux transport near the inner magnetosphere (e.g., Angelopoulos et al. 1993; Schödel et al. 2001; McPherron et al. 2011), suggesting that the interaction of the flow burst with the high pressure inner magnetosphere generates the strong currents of the substorm current wedge. As discussed above, the total current carried by an individual flow burst is an order of magnitude smaller (about a few 0.1 MA on average) than the total current carried by the SCW, and the width (<1 hour MLT, corresponding to <3 RE cross-tail size in the tail) is several times smaller than the 6 hours wide SCW (see Sect. 2). These differences suggest that the substorm current wedge and sustained near-Earth dipolarization are due to the accumulated effects of multiple, separate, BBFs.
Three factors are important to recognize when discussing the contribution of BBFs and wedgelets to the SCW. First is the long duration effect of these flow bursts on the inner magnetospheric density and pressure that remains well after the flow has stopped. Figure 6 shows that the flow burst passage results in a significant modification of the plasma sheet and current sheet on at least a 5–10 minute timescale (compare especially the B z and T i pre- and post-onset values). This local modification remains even after the flow has returned to background levels. The second important factor is the multiplicity of successive or multiple flow bursts and associated auroral streamers (see Sect. 5.4) that are well documented observationally (e.g., Kauristie et al. 2003; Sergeev et al. 2001; Forsyth et al. 2008; Lyons et al. 2012). In addition to the 1–2 minute repetition rate of flow bursts common within the BBF structure, magnetotail flow bursts have recurrent 5–20 minute activation timescales. These are manifested, e.g., in the repetitive generation of energetic particle injections, new auroral arcs or streamers, near-Earth dipolarizations, and ground midlatitude Pi2 pulsations etc. (Pytte et al. 1976; Lyons et al. 2012; Nagai 1982; Sergeev et al. 1996a,b; Hsu and McPherron 2007). Multiple Earthward moving dipolarization fronts and tailward progressing dipolarized regions due to flux pileup have both been detected within a substorm (Nakamura et al. 2009). Tailward progression of the dipolarized region maps to poleward expansion of the active aurora. The long duration dipolarized region that drives the substorm current wedge is due to the superposition of these multiple flow bursts, each of which creates an enhanced region of dipolarized field that remains after the flow has ceased. Finally, there is an open question on how these wedgelets contribute to the filamentation of the SCW. Recently, Forsyth et al. (2014) studied the filamentary nature of the currents composing the SCW and suggested that the small scale structure of the SCW is not imposed by the structure of flow bursts, in contrast to the ‘wedgelet’ model. Unraveling the details of the filamentary current systems will likely require multiple, low-altitude spacecraft that are capable of separating spatial from temporal effects.
The cumulative effect of these flow bursts is the modification of the pressure distribution in the inner magnetosphere that sustains the substorm current wedge via the ∇P×∇V mechanism discussed in Sect. 4.1. The accumulated stresses also lead to the substorm time scale profiles obtained from statistical studies of the plasmasheet. Baumjohann et al. (1991) showed that the ensemble average bulk speed reached a maximum 20 minutes after substorm expansion onset, while the decrease in B z and flow speed occurred after 45 minutes. This picture essentially agrees with recent simulations of multiple flow bursts by Birn and Hesse (2013), which show that intrusions of new flow bursts at different meridians causes the high-pressure, dipolarized region to expand azimuthally, resembling the current wedge expansion during substorms (Fig. 2).
4.3 Generation of Flow Bursts and the Role of Entropy Depletion
The accumulated effects of flow bursts impinging on the high pressure inner magnetosphere create the substorm current wedge. Theoretical analysis, MHD simulations and multipoint in situ measurements have combined to produce a detailed understanding of how these flow bursts are created. On the basis of ISEE-1 observations near x≈−20 RE , Sergeev and Lennartsson (1988) first pointed out the apparent close relation between strongly concentrated earthward plasma jets and reduced density with enhanced B z , indicating low entropy content, as measured (in near equilibrium) by PV γ. Here P is the plasma pressure, V is the flux tube volume defined by Eq. (6), and γ=5/3. (The fact that these events were found during intervals of steady magnetospheric convection (SMC) shows that fast localized flows, despite their relevance for substorms, are by no means exclusive to substorms.) Pontius and Wolf (1990) then pointed to a possible connection between a reduced plasma content flux tube, called a “bubble”, and fast earthward motion via an interchange mode; Chen and Wolf (1993) subsequently interpreted observations of BBFs as “bubbles” in the plasma sheet. Such bubbles are propelled earthward by a buoyancy force until they come into equilibrium with the surroundings. Characteristic features of the initial bubble include high velocity, low plasma pressure, and strong magnetic field as compared to surrounding flux tubes. Observations of high speed flows with these characteristics were reported by Sergeev et al. (1996a). The authors found that although the plasma pressure in the bubble is lower than the surroundings, it is compensated by a higher magnetic pressure, yielding approximately the same total pressure as the surroundings.
Another factor to be recognized is that each flow burst provides a different distortion of the inner magnetosphere and contributes differently to the dipolarization and current wedge formation. Geotail observations (Shue et al. 2008) have indicated that the penetration of fast earthward flows to inside of x≈−10 RE appears to be crucial in enabling substorm initiation and the formation of an auroral bulge. MHD simulation studies (Birn et al. 2009; Birn and Hesse 2013), as well as observations (Dubyagin et al. 2011), demonstrate that the depth of penetration of bubbles depends on the amount of entropy reduction. Only those most depleted (and most dipolarized) plasma tubes can reach the inner magnetosphere. This occurs most often during the early substorm expansion phase, when magnetic reconnection can operate in the relatively near-Earth (X>−20–25 RE) region (Miyashita et al. 2009), effectively reconnecting the plasma-depleted lobe field lines. At other times, such as quiet, steady convection or substorm recovery, the relatively distant x-line location does not allow for the production of short flux tubes having sufficiently low flux tube volume and entropy (PV 5/3 less than the 0.05 nPa (RE/nT)5/3) that is required to reach the geostationary orbit (Sergeev et al. 2012a). Flow bursts with insufficiently low entropy are braked far away and flow around the inner magnetosphere. This suggests an explanation for why flow bursts that occur during substorm expansion are efficient in the generating the SCW, in comparison to BBF activity at other times.
The most plausible mechanism for the generation of flow bursts, as well as the reduction of entropy, is localized reconnection in the mid tail region, which severs portions of the closed field lines and ejects them as plasmoids. The cross-tail localization of reconnection may result from a pre-onset structure, localization of the kinetic mechanism that breaks the frozen-flux condition of ideal MHD, or an interchange mode that is enabled by the entropy reduction (Birn et al. 2011). Alternatively, an interchange/ballooning type mode in the mid tail plasma sheet may be initiated under suitable magnetotail conditions prior to reconnection (e.g., Pritchett and Coroniti 2013). Conditions favoring the onset of ballooning in the tail region consist particularly in a reversal of the gradient of the entropy PV γ as function of distance, which is monotonically increasing for a typical tail model (Schindler and Birn 2004). It is not clear, however, how such a configuration modification can be obtained from an initial state that is ballooning stable. The consequences of flow bursts in generating field-aligned current systems are similar, independent of the generation mechanism.
4.4 Ionospheric Feedback Processes and Magnetic Pulsations
From the creation of the flow burst at the mid tail reconnection site through the initiation and decay of the substorm current wedge, the changed magnetospheric configurations are communicated to the ionosphere via the currents carried by Alfvén waves (Scholer 1970; Southwood and Kivelson 1991). For simplicity, the SCW is often studied as a quasi-static structure, and for the majority of this review we have treated it as such. Yet the transient coupling of the conductive ionosphere with magnetospheric stresses leads to a strongly coupled system that impacts the time-dependent development of the currents.
The most commonly studied transient magnetosphere-ionosphere responses are the pulsations associated with impulsive movements of magnetotail field lines, principally the braking of BBFs in the near-tail region. Magnetospheric substorms have long been associated with transient pulsations in the Pi2 band (40–150 s, f=6.6–25 mHz) (see reviews by Yumoto (1986) and Keiling and Takahashi (2011)). Although they share a common frequency band, there are at least three distinct types of Pi2 pulsations, organized both by the location where they occur and by the physical processes driving them. Low-latitude Pi2 pulsations are associated with the rapid deceleration of flow bursts in the near-Earth region. This broadband flow braking energy is thought to couple to plasmaspheric cavity modes (Allan et al. 1996; Takahashi et al. 1995, 2003; Lee and Lysak 1989) or directly drive Pi2 pulsations (Kepko and Kivelson 1999; Kepko et al. 2001). These pulsations tend to lie in the shorter period band, due to the comparatively short field lines and high Alfvén speed of the inner magnetosphere. At higher latitudes, pulsations are irregular, large amplitude, and typically have periods near the long period edge of the Pi2 band. Neither low-latitude nor high-latitude Pi2 are associated directly with the SCW, so we will not discuss them further. (see Keiling and Takahashi (2011) for a recent review).
Nightside Pi2 pulsations at midlatitudes are directly associated with the sudden switching-on and development of the substorm current wedge at substorm onset. Using data from an azimuthally extended array of mid latitude ground magnetometers, Lester et al. (1983, 1984) demonstrated that the azimuthal patterns of polarization and phase characteristics of Pi2 pulsations at mid latitudes were related to the substorm current wedge. The pattern of the polarization ellipse of the wave in the H−D plane is schematically illustrated in Fig. 8a, adapted from Lester et al. (1984). Although the wave polarization pattern illustrated in Fig. 8a was consistent from event to event, in about 30 % of cases the pattern was displaced from the substorm current wedge mid-latitude H and D component bays (Lester et al. 1983). This was partially attributed to the fact that the substorm current wedge system is not as simple as first envisaged, for example the upward field aligned current is more localized while the downward field aligned current more distributed longitudinally (e.g., Baumjohann et al. 1981). These initial observations were then supported by a number of subsequent studies involving both ground and geosynchronous magnetometer observations (see e.g. Gelpi et al. (1985b,a), Lester et al. (1989)). A model for the polarization, wave phase and propagation characteristics was proposed by Southwood and Hughes (1985) which consisted of two circularly polarized waves propagating westwards and eastwards, with the larger amplitude wave being the westward propagating wave.
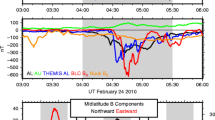
(a) Schematic of the magnetic perturbations in the H and D components and the polarization of Pi2 pulsations measured by nightside, mid latitude ground magnetometers as a result of the substorm current wedge. The Pi2 polarization azimuth rotates in relation to the location of the FAC. Adapted from Lester et al. (1984). (b) Example of a classic midlatitude SCW signature of a small to moderate substorm. Ukiah, located near the central meridian of the SCW, observed primarily a positive ΔH perturbation, while Shawano, located further east, was beneath the downward FAC and observed primarily a negative ΔD perturbation. Transient response Pi2s are evident at the onset of the SCW, with additional intensifications observed later in the recovery
The strong observational foundation linking nightside, mid latitude Pi2 pulsations to the substorm current wedge is accompanied by a wide body of theoretical and numerical research into the time dependent coupling of the magnetosphere and ionosphere via FACs. The sudden switching-on of the substorm current wedge system leads to a complicated interplay between the ionosphere and magnetosphere as the two regions attempt to reach an equilibrium state. Mid latitude Pi2 pulsations, now commonly referred to as transient Pi2 pulsations, are one result of this transitional response (Baumjohann and Glassmeier 1984).
The time dependent nature of the transient response depends on the interaction of the Alfvén waves carrying the current from the magnetosphere source region with the ionosphere. This interaction is controlled by the relative conductances of the ionosphere (Σ P ) and magnetosphere (Σ A =1/μ 0 v A ). We can understand the consequences by looking at how the Alfvén waves carrying current are reflected in a simple scenario (Fig. 3b). The equatorial portion of a flux tube initially at rest is pulled azimuthally by magnetospheric flow. This kink in the field line is a current loop and is carried by an Alfvén wave to the ionosphere. The current flows in the direction to provide a J×B force in the ionosphere to force the footpoints to move in the direction of magnetospheric driving. What happens next depends on a ratio (R) of the conductances (Scholer 1970; Glassmeier 1983):
This reflection coefficient, R, determines the sign and amplitude of the imposed and reflected electric fields. A highly conducting ionosphere (R∼−1) would reflect most of the electric field, which would counteract the original electric field and attempt to move the magnetospheric end of the field line to its original position (this is effectively loop 2 in Fig. 5). In the opposite limit, an ionosphere with low conductivity (R∼1) does not reflect the electric field back to the magnetosphere, and hence the magnetospheric motion can proceed.
This framework is also used to describe the build up of the SCW field-aligned current. As a function of the reflection coefficient, the FAC after an infinite number of Alfvénic bounces is
where j ∥,i is the current carried by the initial pulse (Glassmeier 1984). For a highly conducting ionosphere the FAC builds up. This current closes across the ionosphere, and represents the J×B force necessary to move the ionospheric footprints. If R∼1, corresponding to a weakly conductive ionosphere, the ionosphere moves freely, the reflected current cancels the incoming current, and no FAC is built up. This build up of current is illustrated in Fig. 8b, which shows the midlatitude magnetic field signature of the SCW from a moderate substorm. Note that the increase in ΔB occurs over ∼20 minutes, accompanied by damped Pi2 pulsations.
In addition to transient currents that form in response to changes in magnetospheric configuration, changes in ionosphere conductivity lead to time-dependent coupling of the ionosphere to the magnetosphere. Ionosphere conductivity increases due to particle precipitation, in particular, in regions of upward field-aligned current, where electrons are accelerated into the ionosphere. The increased ionospheric conductivity leads to increased line-tying of the field lines, and a corresponding larger FAC for a given flow. Under a constant electric field, an increase in the conductivity drives an increase in current to overcome the increased line-tying. At some threshold, the magnetosphere may be unable to overcome the increased line-tying. The field-aligned current increases to the point that E parallel becomes non-zero, accelerating particles, and decoupling magnetospheric from ionospheric motion.
5 Ionospheric Perspective
The large scale ionospheric features observed during substorms are largely a response to the dynamic changes in the magnetotail discussed in Sect. 4. Ionospheric properties, principally conductivity, provide boundary conditions for magnetospheric convection, and the ionosphere is often treated as a passive part of the system. Especially during substorms, however, the boundary conditions change in a time-dependent and spatially localized fashion, allowing ionospheric feedback that can alter the magnetospheric dynamics. We discussed previously some aspects of this coupling from a magnetospheric perspective in Sects. 4.1 and 4.4. The coupling from the ionospheric perspective differs primarily in that the ionospheric conductance is anisotropic due to the influence of the neutral atmosphere, involving Hall as well as Pedersen conductivity. These conductivities are altered both by the connecting currents and the precipitating electrons associated with upward field-aligned currents, which increase Pedersen conductivity and field line tying. An important role is also played by field-aligned electric fields, set up locally, primarily in upward field-aligned current regions, which are the cause of auroral intensifications and, specifically auroral arcs. In the following sections we describe some of the ionospheric features directly or indirectly associated with the SCW.
5.1 The Westward Traveling Surge (WTS)
One of the most well defined features of the auroral substorm is the Westward Travel Surge (WTS) (Akasofu et al. 1966, 1965b). The WTS is a bulge of discrete aurora that represents the westward and poleward expansion of the auroral substorm. At the largest scale, the WTS is the visual manifestation of the upward current at the duskward edge of SCW (Akasofu and Meng 1969; Kamide and Akasofu 2012; Hoffman et al. 1994; Marklund et al. 1998), and represents a region of converging horizontal electric fields in the ionosphere (e.g., Weimer et al. 1994). In the WTS, as within any complex physical system, different processes are revealed depending on the spatio-temporal scale on which the system is examined. In situ and ground-based observations have revealed the WTS to be far more complicated than a single region of upward field-aligned current. Since the WTS is a crucial place for the current closure of the SCW, small-scale physics may also affect on the larger-scale properties of the wedge. Here we mention two mechanical processes related to the WTS that are relevant to the scale of individual auroral arcs, i.e., on scales of about 100 km and below.
Using data from the Freja satellite UV imager and electric field instrument, Marklund et al. (1998) were able to resolve the auroral fine-structure associated with the WTS, while at the same time having a full view over the larger-scale auroral display of the substorm bulge. They showed that the WTS consists of a complex configuration of wound-up auroral arcs, separated by regions of lower luminosity, filled with diffuse aurora. The most poleward of these wound-up arcs continues eastward as the poleward boundary of the substorm auroral bulge. When the Freja satellite passed over the individual wound-up arcs and entered into the diffuse auroral regions in between them, it recorded very strong electric fields, up to several hundreds of mV/m. The authors interpreted the electric field in these boundary regions, which have an extent of only a few km, as polarization electric fields. Strong and localized field-aligned currents of magnitudes up to 30 A/km2 were observed associated with the electric field, flowing both upward and downward. However, the majority of the strong electric field structures converge, and are associated with intense high-energy electron precipitation and upward FAC. These observations clearly indicate that the WTS is not a uniform region of upward FAC, but contains complex upward and downward current substructure on the scales of individual auroral arcs.
Another process that becomes relevant in the vicinity of the WTS is induction within the ionosphere. Sharp gradients of ionospheric electrodynamic parameters, especially conductances, and the fast westward motion of the surge up to about 10 km/s (Rothwell et al. 1984; Pytte et al. 1976), create significant temporal gradients for an observer in the Earth’s frame of reference. Vanhamäki et al. (2007) found for their model that although the induced electric field inside the WTS is small in absolute terms (about 3 mV/m), it maps into an area that is characterized by a small potential electric field and high conductances. Hence, the induced electric field contributed up to 30 % of the total electric field and up to almost 100 % of the total FAC (with absolute magnitude of 1.5×10−3 mA/m2) in a small region at the trailing edge of the surge. Ionospheric induction may contribute significantly to the horizontal current and FAC distribution in the central region of the WTS (Vanhamäki et al. 2007). Since this effect is not included in either MHD models or ionospheric solvers, this may explain the discrepancy between model output predictions and measurements.
In summary, these results show that on the largest scale, the WTS is a region of intense aurora at the western edge of the SCW created by a net upward current carried by accelerated electrons. Detailed observations show that this net current contains significant substructure, containing highly localized upward and downward current regions.
5.2 Current Closure
One of the most extensively studied data sets concerning auroral substorm electrodynamics on the scale of the auroral bulge comes from the combined Dynamics Explorer (DE) 1 and 2 spacecraft (Frank et al. 1981; Hoffman and Schmerling 1981). While DE-2 measured electrodynamic parameters between 300 and 1000 km, DE-1 at a higher orbit simultaneously imaged the aurora, which allowed the DE-2 observations to be placed into the context of the substorm auroral bulge. Several studies binned a large amount of satellite data along meridional tracks into different sectors of the bulge to compose an overall model of the SCW in terms of FAC (Fujii et al. 1994), conductances (Gjerloev and Hoffman 2000a,b), and horizontal currents (Gjerloev and Hoffman 2002). A synthesis of the results of these studies is shown in Fig. 9.
For the ionospheric part of the SCW and its divergences, the results show southward Pedersen currents and westward Hall currents inside the bulge, superimposed upon a southwestward overall current system, generally in agreement with previous models (e.g., Kamide et al. 1996; Lu 2000). However, in contrast to these models, the feeding of these currents by downward FAC is largely provided by a “region 0” FAC layer located just poleward of the poleward boundary of the auroral bulge. The majority of the FAC closure takes place in the meridional direction, between this “region 0” and the “region 1” layer of upward FAC located within the substorm auroral bulge. The region 0 FAC is simply a consequence of the conductance gradients at the auroral boundary. We note that the MHD simulation results presented in Fig. 4 do not include an ionosphere. Similarly, the current loops shown in Fig. 5 were derived from examination of the magnetospheric drivers of the current. Exactly how these currents flow in the ionosphere will depend greatly on local ionospheric conditions, primarily the spatial distribution of conductance. Therefore, linking these R0 currents directly to a magnetospheric source is difficult, and remains an open question.
Changes in the amplitude of the westward substorm electrojet in this model are moderated by associated imbalances between the region 0 and the region 1 FAC in each sector of the bulge. This type of current closure is called “local current closure”, in contrast to the “remote current closure” of the original SCW picture, where a downward FAC area on the eastern flank of the SCW is zonally connected via a westward electrojet to an upward FAC area (around the WTS) on its western flank. As shown in Fig. 9, the upward field-aligned currents of the SCW, localized to the active area of the surge, are principally fed by the R0 currents at the poleward boundary, rather than closed by horizontal current of the classical SCW picture. Using a single-event satellite pass through an auroral bulge eastward of a surge, Marklund et al. (2001) concluded that the local current closure model is more suitable to explain the observations for their case. However, it needs to be mentioned that studies that are composed of data from satellite passes that are nearly meridional are unable to unambiguously resolve the dependence of the observed parameters in zonal direction. Therefore, conclusions about zonal current closure drawn from such studies have to be taken with care.
Models and observations are generally in agreement that there is a region of intense upward FAC collocated with the westward traveling surge (WTS) at the westward edge of the auroral bulge, in accordance with the original SCW picture (see Sect. 5.1). Are the currents diverted to the magnetosphere mostly provided by local or by remote current closure? This question was addressed by Amm and Fujii (2008), using spatially distributed optical, electric field, and ground magnetic field data from the MIRACLE network for a substorm breakup spiral event. Taking advantage of the specific geometry of the spiral, the authors were able to quantitatively separate the contribution of the two current closure parts to the upward FAC in the spiral. For their event, about two-thirds of the upward FAC were provided by local current closure, and about one-third by remote current closure. However, in a certain region at the western edge of the spiral, the contribution of the remote closure was more than 80 %. This region, coinciding with steep zonal conductance gradients, was also clearly discriminated in the auroral display.
5.3 The Cowling Channel
Early models of the WTS and of the substorm bulge in its wake suggested that the remote current closure is enhanced by something called “the Cowling effect” (e.g., Coroniti and Kennel 1972; Baumjohann et al. 1981; Opgenoorth et al. 1983). The Cowling effect introduces secondary electric fields that alter the relationship between the primary electric field, created by magnetospheric motions, and the final current flow direction and magnitude in the ionosphere. Given a fixed primary electric field from the magnetosphere and an ionospheric conductance structure, the Cowling effect will force the total currents to flow in a different direction, and be stronger (or weaker) than without the effect. This also allows the ionospheric currents to “decouple” to some extent from the magnetosphere, and therefore complicates the linkage of ionospheric currents (Sect. 5.2) to magnetospheric drivers (Sect. 4.1). Note that the revised ionospheric portion of the SCW discussed later in Sect. 6.1.2 includes this Cowling effect.
The effect is most easily described in the case of the substorm current bulge, which lies in the wake of the WTS and is bounded north and south by regions of sharp conductivity gradients, leading to a channel of high conductivity. The initial westward component of the electric field, as frequently observed in the wake of the WTS, drives a primary meridional Hall current within the channel. Since J=ΣE, stronger currents flow in the high conductivity channel than outside, for the same electric field, leading to an imbalance of current. To maintain current continuity, the extra current must either close as FACs or be reduced. In steady state, the strength of the FAC is determined by the magnetospheric generator, and therefore only a fraction of the excess current can flow upwards along field lines. The excess current leads to a buildup of charge on the boundaries of the conducting strip, leading to a polarizing electric field directed southward, which acts to solve the current closure imbalance. This polarization electric field in turn drives a secondary westward Hall current. This mechanism was also anticipated by Amm and Fujii (2008) for the remote current closure part. Even though a multitude of observations have been shown to be in accordance with a potential Cowling effect, it is not possible to prove the effectiveness of this mechanism for a single event study from ground-based data alone, and single satellite passes miss the required information about zonal gradients. Amm et al. (2011) were the first to prove the existence of the Cowling effect in the auroral electrojet using a statistical approach, analyzing about 1600 electrojet-type situations observed by the MIRACLE network and the EISCAT radar. They found that the probability of the Cowling effect being active in the auroral ionosphere is monotonically increasing with increasing geomagnetic activity, and that the region of highest probability for this effect to be strong is the early morning sector. Their results thus support the hypothesis that the Cowling effect is active in the substorm auroral bulge to increase the zonal (remote) current closure, especially in the eastern part of the bulge.
5.4 Continuity of the SCW as Seen from Ionospheric Observations
An important element of the traditional picture of the SCW is the ionospheric closure of the eastern (downward) and western (upward) FACs via the westward electrojet. In light of extensive ground- and space-based observations of ionospheric current closure, it is apparent that such a direct closure current path is simplified, and that there are significant divergences of the westward current in between. We focus here on two types of typical mesoscale auroral forms that frequently occur within the substorm auroral bulge, for which this question of remote vs. local current closure has recently been addressed in detailed studies: Auroral omega bands and auroral streamers.
Auroral omega bands are periodic, wave-like undulations of the poleward boundary of the morning side diffuse aurora occurring in the recovery phase of substorms. The name “omega bands” was originally chosen by Akasofu and Kimball (1964) to describe the dark areas between the poleward extending auroral waves or tongues, which resemble the form of the inverted capital Greek letter Ω (Fig. 10a). The luminous tongues tend to be narrower with larger latitudinal extent for more intense substorms, and may occasionally develop into auroral torches, which are narrow, finger-like auroral forms that extend several degrees of latitude poleward from the auroral oval (Henderson et al. 2002). The typical longitudinal and latitudinal extent of the tongues is ∼400–500 km (4–5°). Omega bands have been found to grow simultaneously over a longitudinal range of several magnetic local time (MLT) hours, covering a wide range of the central to eastern portion of the SCW (e.g., Paschmann et al. 2003, Sect. 6.3; Yamamoto et al. 1993). It should be noted that although auroral omega bands are regularly observed within substorms, principally during the recovery phase, similar type of structures also exist during periods of steady magnetospheric convection and sawtooth intervals (Sergeev et al. 1995; Henderson et al. 2006a,b).
(a) Omega bands observed by the Polar VIS camera, courtesy of M. Henderson. (b) The structure of the FACs associated with omega bands, and the geometry of the westward electrojet. A significant portion of the westward substorm electrojet is diverted by the alternating sheets of FAC associated with the omega bands. Adapted from Amm et al. (2005)
Amm et al. (2005) used ground-based data from the MIRACLE network in northern Scandinavia together with UV and X-ray observations from the Polar satellite to infer in detail the spatial distributions of the electric field, conductances, currents and FAC inside an omega band structure. In accordance with previous models (e.g., Amm 1996; Buchert et al. 1990), this purely data-based analysis found the auroral tongues of the omega bands to be collocated with sheets of intense upward FAC, and the dark regions in between the tongues to be collocated with downward FAC sheets. The integrated upward FAC in one of the tongues was found to amount to be 2.3 MA, which is comparable to the typical integrated upward westward traveling surge FAC of 2.5 MA found by Gjerloev and Hoffman (2002). In comparison, the integrated westward current that is not connected with FAC but flows continuously in the zonal direction over the omega band, mostly along its equatorward base, is of the order of 500 kA for the Amm (1995) event. This result implies that a majority of the FAC (∼80 %) in omega bands must close locally.
Therefore, it is obvious that for omega bands a significant part of the current in the substorm auroral bulge is not flowing continuously westward, but is diverted away from and towards the ionosphere by alternating sheets of FAC (Fig. 10b). In the classical remote closure picture, all ionospheric current flows horizontally westward, from the downward FAC at the eastern edge of the bulge to the WTS at the western edge. But in the case of omega bands, only a minor fraction of the current is flowing continuously westward. The largest portion of the current is organized as mesoscale “wedgelets” of a few hundred km zonal scale size. The SCW ground magnetic signature, which is a measure of the integrated perturbation fields, could be explained by an equivalent current system flowing continuously westward. This interpretation is misleading, however, as the true currents are highly fragmented (Baumjohann 1982; Opgenoorth et al. 1983; Amm et al. 2005).
Auroral streamers are thought to be the ionospheric counterparts of the magnetospheric flow bursts discussed in Sect. 4.2 (Fairfield et al. 1999; Lyons et al. 1999; Sergeev et al. 1999, 2001; Zesta et al. 2000). They are observed as finger-like, meridionally elongated auroral forms that protrude equatorward inside the substorm auroral bulge, starting from its poleward boundary (Elphinstone et al. 1995, 1996; Henderson et al. 1998). When the streamers reach the equatorward portion of the bulge, they often form blobs of aurora there that can persist for several tens of minutes. The zonal extent of the auroral streamers is typically of the order of 100–150 km but can be as narrow as 20 km. In many cases, several streamers evolve simultaneously with an azimuthal separation of 150–500 km (e.g., Amm and Kauristie 2002, and references therein), covering a significant portion of the western to central portion of the SCW. Studies have also shown that it is the duskside of a bursty bulk flow in the magnetosphere that is conjugate to the auroral activations identified in the ionosphere (Nakamura et al. 2001). This is consistent with the measured electron precipitation in that region, which corresponds to the upward field-aligned currents and is the source of the auroral emissions (Sergeev et al. 2004).
Using data from the Scandinavian Magnetometer Array (SMA), the STARE radar, and all-sky cameras, Amm et al. (1999) were able to infer the detailed spatial distributions of the ionospheric electrodynamic parameters associated with an auroral streamer. Not unlike the omega band case, the auroral streamer current system consists of a localized current wedge with intense upward FAC at the southwestern border of the auroral form, and a more distributed area of downward FAC at its northeastern flank, connected by southwestward flowing horizontal currents. Nakamura et al. (2005) later confirmed this current configuration with combined ionospheric and magnetospheric observations. For the Amm et al. (1999) event, the integrated upward FAC was ∼830 kA, compared to an integrated westward current of about 650 kA that flowed continuously in the westward direction over the analysis area. As for the case of the auroral streamers, a large portion of the westward current in the substorm auroral bulge is not part of the large-scale SCW, but closed by more narrow systems of alternating FAC that exist within the SCW. Further supporting evidences of the existence of a small current wedge pattern associated with magnetospheric flows have been obtained by comparing satellite observations of BBFs with equivalent current (Kauristie et al. 2000; Nakamura et al. 2005) and ionospheric convection patterns (Grocott et al. 2004).
In summary, the results discussed here show that a significant substructure consisting of mesoscale zonal current wedges may exist within the traditional SCW. In fact, the total current flowing within these substructures may be comparable to or even larger than that of the large-scale SCW. This also means that measurements of the westward electrojet current at a meridional intersection of the bulge, as occurs with a low-orbiting satellite, could be dominated largely by the currents of these substructures. We note that the magnetic effects of the narrow current wedges of these substructures are not visible to mid-latitude magnetometers that were used originally to define the SCW.
6 Synthesis of Current Understanding
As originally envisioned, the substorm current wedge is a simple line current model that represents the integrated effects of a diversion of the cross-tail current along magnetic field lines into the auroral ionosphere post midnight and out of the ionosphere pre midnight, connected in the ionosphere by a westward current (McPherron et al. 1973a). This current begins to flow at the onset of the substorm and persists for somewhat less than an hour. The large scale pattern of the SCW is best observed by midlatitude magnetometer stations, which are far from the wedge currents and thus record the overall pattern rather than local details. These magnetometers measure a net effect of the current systems that make up the SCW, and show that the wedge may form almost anywhere in the night sector and may be very narrow or as large as the entire nighttime sector.
In the 40 years since the SCW concept was originally developed, a multitude of in situ and remote measurements, numerical simulations, and theoretical studies have greatly expanded our knowledge of the SCW. Although the original line current picture of the substorm current wedge explains reasonably well the large-scale magnetic signatures observed on ground and in space, these new observations and insights must be incorporated in a revised representation. In the previous sections, we highlighted the important observational and theoretical constraints that must be included an any updated view of the substorm current wedge. The current wedge links changes in nightside magnetotail convection and plasma sheet properties to the ionosphere via field-aligned currents. While smaller wedges appear in conjunction with, for example, pseudobreakups or auroral streamers, the majority of the current wedges are associated with magnetospheric substorms. The original picture illustrated a snapshot of the SCW during its peak expansion. Based on a significant body of work focusing on magnetosphere—ionosphere coupling processes, we now present a time-dependent view of the SCW, showing its association to the initial reconnection site, how it intensifies and spreads during the substorm expansion, and how the currents decay during the substorm recovery.
6.1 Modifications to the Original Picture
6.1.1 Stage 1—Wedgelet
At the end of the growth phase, the magnetotail magnetic field is highly stretched. The substorm begins with reconnection in the midtail plasmasheet, creating opposing jets of flow. The earthward flow burst is the genesis of the SCW, and the Earthward propagation of the flow represents Stage 1 of the SCW. The flow burst itself can be considered a dipolarizing, low entropy flux tube (Sect. 4.3). It moves Earthward to a region where the buoyancy of the flux tube, as represented by the entropy, matches the surroundings. This occurs typically near the transition between stretched and dipolar field lines near the inner edge of the tail current sheet, but can vary depending on the intensity of geomagnetic activity.
This system can be decomposed into time dependent and quasi steady-state components. The time dependent aspects derive from the propagation of the electric and magnetic perturbations generated by the dipolarizing flux tube and their interactions with the ionosphere (Sect. 4.4). Each flow burst is associated with a channel of high speed flow relative to the surroundings. Consequently, the electric field across the channel is higher than that in the adjacent plasma. This elevated electric field is carried to the ionosphere by an Alfvén wave where it drives a westward current in the auroral ionosphere, accelerating ionospheric plasma in an equatorward direction. Due to the inertia of the ionospheric plasma, the wave is reflected and bounces several times as the ionospheric flow is slowly established. This wave is the likely cause of the irregular, high-latitude Pi2 pulsations. After a few minutes, the flow reaches the inner magnetosphere, and the impact generates Pi2 pulsations at mid and low latitudes.
In addition to this transient coupling, the flow burst carries a quasi-static current system, as reviewed in Sect. 4.2 and shown in Fig. 11. The shape of this current loop is identical to that of the substorm current wedge, but because of the narrow width of the channel its width is much smaller so we refer to this pattern as a“wedgelet”. The current carried by this wedgelet is much smaller and has a shorter lifetime than in the current wedge. The ionospheric signatures of these wedgelets are the auroral streamers that appear at the poleward auroral boundary and move equatorward (see Sect. 5.4). The wedgelet contains the region 1-sense current of the original SCW, but contains a new element, the opposite-sense (region 2-sense) loop with westward current at the earthward edge of dipolarized region.
The ‘wedgelet’ current system associated with an earthward propagating dipolarizing flux tube in the ionosphere (a) and equatorial magnetosphere (b). Field-aligned currents connect the region-1 sense currents (blue) at the edge of the flow channel with the ionosphere. This current closes at least partially via a horizontal Pedersen current. The auroral streamer occurs on the westward edge of the system, in association with the upward field-aligned current. The Hall current flows northward, although the closure of this current is still an open question. This wedgelet current system is superimposed upon the existing ionospheric current system of Fig. 9, principally a westward electrojet, so that the full ionospheric SCW current system is the sum of the large scale currents and these smaller wedgelet systems, in addition to localized filamentary systems. Recent observations and simulation results suggest a region-2 sense current at the leading edge of the flow burst (red) in the magnetosphere, although it is unclear if this current closes in the ionosphere or locally in the magnetosphere. An intense dipolarization front (DF) current flows between the R1 and R2 currents, as shown here, although the exact closure of this current is unknown. The magnetospheric wedgelet system shown here is based on MHD simulation results, and represents a snapshot of the dipolarizing flux bundle as it nears Earth. The geometry and spatial extent of the currents further away from the braking region are likely extended further radially than indicated here, as suggested for example in Nakamura et al. (2001)
The importance of these new additions is that they are closely related to the interaction of the flow burst with the inner magnetosphere, and manifested in important substorm phenomena like injections and dipolarization fronts. The substorm current wedge develops during the expansion phase as an accumulation of stresses created by multiple flow bursts. The detailed evolution of the SCW is determined by the pressure gradients and magnetic shear that develops in response to these flow bursts. In addition, this explicit link to flow bursts leads to a natural explanation of substorm intensifications as being associated with, and driven by, new flow bursts.
6.1.2 Stage 2—Pile-up and Initiation
The Earthward traveling flow burst slows rapidly as it approaches the transition region between dipolar and stretched field lines. The braking and diversion of the fast flow around the high pressure inner magnetosphere creates magnetic shear, and is the dynamo that powers the substorm current wedge. The inertial current generated by the decelerating flow lasts a few tens of seconds, and is only a minor constituent of the total current. Once decelerated and deflected, the plasma and field carried by the flow burst joins a general flow around the obstacle created by the inner magnetospheric pressure distribution. It is this slower, but more extensive, flow around the obstacle that produces the entire current wedge. A velocity shear between the inner and outer magnetosphere extending over large distances on the evening and morning sides is the primary source of the currents driving the substorm current wedge. This velocity shear maintains the non-alignment of flux tube volume and pressure gradients that is necessary to sustain the FAC.
While the SCW is often described in terms of a “short-circuiting” of the cross-tail current, it is preferable to view the system in terms of currents driven by stresses within and at the boundaries of the dipolarized region. Returning to Fig. 5, the traditional SCW is represented by loop 1, and consists of a dusk-dawn segment in the magnetotail and an east-west segment in the ionosphere connecting the two FACs. Loop 2 is a consequence of MI coupling, and represents the ‘kickback’ from the ionosphere, attempting to slow the azimuthal expansion. Note that for Loop 2, J×B points towards the center of the dipolarized region in the magnetosphere, while J×B points outward, away from the center of the wedge, in the ionosphere. The magnetospheric portion of this loop is created by the ionosphere attempting to slow azimuthal expansion, while the ionospheric section is created by the magnetosphere attempting to move the ionospheric footprints azimuthally in the direction of the sunward return flow. Loop 4 bounds the dipolarized region, and represents the expansion force created by the difference in pressure between the high magnetic pressure dipolarized region and the still-stretched region outside the loop. In the magnetotail equatorial plane, the sunward/anti-sunward currents at the boundaries of loops 2 and 4 flow in opposite directions. The slight imbalance of these segments possibly relates to the rate of azimuthal expansion—higher ionospheric conductivity would lead to higher currents within loop 2, for example, and thereby slower expansion. Loop 3 is due to off equatorial gradients that arise from the transient magnetic kink as the plasmasheet field lines contract to a quasi-dipolar state.
The SCW, then, is an integral of several different current loops, each with a specific physical driver. The equivalent current loops shown in Fig. 5 are a useful way to gain insight into the physics that underlie the SCW, at the expense of the simplicity of the original McPherron et al. (1973a) diagram. Combining the net effects of the different current loops, we present a revision to the original SCW model in Fig. 12. A major change from the original picture is the addition of a region 2 sense current at the earthward boundary of the SCW, which has support in both observations and numerical simulations. The diversion of the Earthward flow creates two areas of magnetic twist with opposite sense: a region-1 type current tailward of the twist, and a region-2 type Earthward of the twist. The relative strength (I 2/I 1) of each of the current loops can vary substantially across events, ranging from 0.2 to 0.6, and can change during the evolution of an individual event (Sergeev et al. 2014).
We emphasize that midlatitude magnetometers, which are traditionally used to monitor the evolution of the SCW, cannot resolve this two loop current system. There are two ways the two current loops can close in the ionosphere. If the total current in the outer (R1) loop closes along a meridian in the ionosphere, then there would be no westward current in the auroral bulge and the magnetic effects of the two loops would cancel each other at midlatitudes. On the other hand, if the current in the outer loop closes horizontally, which is likely, the current in the lower (R2) loop will partially cancel the effects of the outer loop. The total inferred current flowing in the ionosphere, as determined from mid latitude magnetic field measurements, will be the difference in current between the two loops.
The ionospheric portion of the SCW also requires significant updating. The currents within the substorm current wedge have complex substructure, which is not captured by the original picture (Fig. 13a). The complex and rapidly varying ionospheric conductivity pattern re-distributes the currents in multiple sheets and filaments that couple the ionosphere to the magnetospheric tail. The original SCW model closes two field-aligned currents with a westward electrojet in the ionosphere (Fig. 13a). As reviewed in Sect. 5, current closure is more complicated than this simple line current. Horizontal current closure between the downward eastern and upward western field-aligned currents is complemented by substantial meridional current closure, which reduces the net integrated total current.
The original picture (a) of the ionospheric closure of the SCW connected the upward and downward FAC pair via an enhanced westward electrojet. The updated picture (b) of ionospheric closure adds a meridional system (red), fed by region-0 currents at the poleward boundary, and significant local closure of the upward FAC within the auroral bulge. As with the magnetospheric currents shown in Fig. 12, the relative intensities of current closure via the different pathways changes from event to event
The updated diagram showing the distribution of total currents in the ionosphere during a substorm is shown in Fig. 13b. As with the magnetospheric current loops, the relative intensities of the ionospheric currents likely vary substantially across events. The original upward and downward FAC pair is still evident, with the eastern component distributed, while the western component is localized to the active bulge. The upward R1 FAC is fed by a combination of local closure from R0 currents at the auroral boundary (red), remote closure flowing via the Cowling mechanism as westward electrojet (blue), and some meridional closure from the R2 current system.
Linking the magnetospheric perspective of the SCW obtained from numerical simulations (Fig. 4) and the ionospheric perspective obtained from satellite measurements (Fig. 9) perspectives of the SCW is not straightforward. The structure of the FACs flowing into and out of the ionosphere will depend strongly on gradients in conductivity, which can change substantially during a substorm, as well as the relative intensities of the horizontal currents. In addition, the magnetospheric drivers of these FACs will not be as smooth as indicated in Fig. 4, and will contain localized pressure gradients that would lead to current filamentation. And yet, the average of the FACs in Fig. 9 corresponds to a strong downward current on the westward edge, and a strong upward current at the eastward edge, within the auroral bulge, as shown in Fig. 13a. Similarly, the FAC inside the primary wedge average to the meridional FAC pattern shown in Fig. 13b. How this meridional pattern links to the magnetospheric driver is still an open question.
6.1.3 Stage 3—Intensifications and Decay
After the initial onset, additional flow bursts, auroral brightenings, and Pi2 generation occur every ∼10–20 minutes, even for the smallest substorms, until the recovery phase. These are called substorm intensifications, and are often associated with new auroral activations moving to progressively higher latitudes, and further in longitude from the initial brightening. Flow bursts that penetrate the inner magnetosphere are decelerated and deflected either towards dawn or dusk depending on the pressure gradients. These additional flow bursts do not alter the large scale-scale picture of the SCW summarized in Fig. 12. Rather, plasma and magnetic field deposited by the flow burst extends the pressure distribution in azimuthal and radial distance, growing both the region of dipolarization and the ionospheric extent of the auroral bulge. Additional flow bursts may be deflected away from the high pressure region, or may add to the existing pressure distribution, depending on their width, entropy, and point of impact. This accretion of magnetic flux on the dipolarized region expands higher pressure boundary, which when mapped to the ionosphere corresponds to poleward and azimuthal expansion of the active aurora.
Eventually, as the flow burst generation subsides (presumably when the dayside energy transfer and mid-tail reconnection subsides), the system relaxes the accumulated stresses. The substorm current wedge starts to dissipate (Fig. 8b), as the magnetic flux flows around the system to the dayside as part of the Dungey cycle. Newly reconnected flux from the dayside is added to the nightside to form the new tail-like field, and the cycle begins anew.
6.2 Alternative Mechanisms
The scenario described above is a complete end-to-end description for SCW formation and evolution, and has strong theoretical and observational support. Alternative explanations for different components of the SCW, such as the root cause of dipolarization, have been described in the literature, most often in the context of substorm initiation. However, none of those alternative models present a complete end-to-end description of the formation, growth, and decay of the SCW that are consistent with the suite of ground-based and in situ observations. Below, we review the leading alternative mechanisms for components of the SCW. These alternative mechanisms generally take two forms: (1) suggesting that the SCW system does not exist as described, or is of a different geometry than described here, and (2) arguing that current disruption, rather than convective plasma flows, are responsible for dipolarization.
Rostoker and Friedrich (2005) argued that the ground magnetic perturbations attributed to the SCW are due to a new perturbation on the existing driven component (i.e., the DP-2 current system), and not due to the development of a new current system. The SCW as a three-dimensional wedge shaped system is described in their paper as an “equivalent current system”, which is capable of explaining the characteristic ground perturbations but does not represent a physical current system. Instead, Rostoker and Friedrich (2005) argues that spatial changes in the upward FAC of the electrojets, associated with changes in transition region thermal pressure distributions during the growth phase, create the magnetic perturbation typically ascribed to the SCW. While the model of Rostoker and Friedrich (2005) is capable of explaining the magnetic perturbations observed on the ground, it does not link dipolarization, particle injections, low-latitude Pi2 pulsations and flow bursts to the SCW, all of which now have substantial observational and theoretical support. Gjerloev and Hoffman (2014), building upon their previous statistical studies (Gjerloev et al. 2007, 2008; Gjerloev and Hoffman 2002), recently proposed a two current wedge system, offset in azimuth and separated in latitude, and different than the two current system proposed here (see their Fig. 8). The observational results are in terms of equivalent currents which, in theory, can be explained by an infinite number of real current systems; the one that Gjerloev and Hoffman (2014) are proposing is only one out of many possible solutions. Critically, although the three-dimensional current system proposed here differs from that proposed in Gjerloev and Hoffman (2014), our description of the ionospheric closure of the SCW presented in Fig. 13 is compatible with their observational results. One can see a transition region between the area where the local closure current system (red) reaches the equatorward part of the oval (eastern bulge), and where it gets diverged around the WTS head (western bulge). This will mean that the equivalent currents will shift poleward here, and the current densities also typically intensify towards the WTS. As with Rostoker and Friedrich (2005), there is no discrepancy with the observations, only with the interpretation of the observations.
One set of models that deserve particular attention are those that can generally be classified as ‘current disruption’ models. These models explain the short-circuiting of the near-Earth cross-tail current as being driven by ballooning or cross-field current instabilities (Roux et al. 1991; Lui 1996). While this class of models is capable of explaining dipolarization and low-latitude Pi2 driven by cavity-modes, some aspects of substorm initiation that are observationally linked with SCW development, such as near-Earth particle injections, are left unexplained. Additionally, these models do not currently have strong observational support from either the THEMIS or Cluster missions. Still, the end-to-end model of the SCW described above could be modified to replace the flow burst with ‘current disruption’, and the SCW development would then proceed as described, although the foundational physical mechanisms driving the current and the processes driving the temporal evolution would differ from the MHD framework (see e.g., Lui and Kamide 2003).
7 Conclusions and Open Questions
As a conceptual model, the original description of the substorm current wedge still serves as a large-scale description of the current system at the peak of the substorm expansion phase. However, in order to understand the growth and decay of the currents and the physical processes driving and sustaining the currents, it is necessary to look into the smaller scale details. Synthesizing insights learned from new observations and numerical simulations, we propose key new elements to the substorm current wedge:
-
Description of the formation and decay of the SCW as a three-stage process;
-
Addition of a region 2 sense current Earthward of the region 1 sense loop;
-
Addition of meridional current closure in the ionosphere and structuring of the field-aligned currents.
Still, open issues regarding further details of the processes remain:
-
The initiation of the current wedge through flow bursts and the small-scale wedgelets still contain uncertainties as to the detailed current pattern of the wedgelets and the source of the current near the poleward boundary of the bulge. If driven by the ionosphere, the R0 currents may be associated with the conductivity gradient at the edge of the auroral bulge. On the other hand, if this region connects to the magnetosphere, it may be driven by field stresses near the open-closed boundary after plasmoid release.
-
The details of the formation of the region 2 sense current during the pile-up phase in front of the larger-scale region 1 sense current wedge are still open.
-
While we have discussed the principles of the magnetosphere—ionosphere coupling processes that give rise to the magnetospheric and ionospheric currents, there still remains the rather large issue of how these currents thread together.
-
The relative roles of the local and remote current closure as well as the roles of the longitudinal and meridional current closure determine the dynamics internal to the current wedge. It is already now evident that the eastern edge of the SCW contains a smaller and more distributed current than that within the westward traveling surge, which contains highly structured upward and downward flowing current filaments. What processes determine the relative strength of this current structuring and filamentation, and what role(s) local conductivity gradients play, is as yet an open question, as are the details of how these filaments connect to the magnetotail processes.
Midlatitude magnetograms were originally used over 40 years ago to define the substorm current wedge. As remote sensing instruments, they provide an integral effect of a multitude of smaller-scale currents driven by a variety of processes. Multi-spacecraft in situ measurements in the magnetotail near the location of magnetic reconnection as well as within the pileup region together with dense instrument optical and magnetic instrument networks in the auroral ionosphere have brought and continue to bring enhanced understanding of the physical processes underlying SCW development. The open questions related to the substorm current wedge highlighted above further emphasize the need to obtain accurate multipoint measurements in the magnetosphere in the 0.1–5 RE scales, as well as multipoint observations in the few tens to few hundreds km scales in the ionosphere.
References
S.-I. Akasofu, The development of the auroral substorm. Planet. Space Sci. 12, 273 (1964)
S.-I. Akasofu, Polar and magnetosphere substorms. Astrophys. Space Sci. Libr. 11 (1968)
S.-I. Akasofu, Energy coupling between the solar wind and the magnetosphere. Space Sci. Rev. 28, 121–190 (1981)
S.-I. Akasofu, J.K. Chao, Prediction of the occurrence and intensity of magnetospheric substorms. Geophys. Res. Lett. 6, 897 (1979). ISSN 0094-8276
S.-I. Akasofu, S. Chapman, The ring current, geomagnetic disturbance, and the Van Allen radiation belts. J. Geophys. Res. 66, 1321 (1961)
S.-I. Akasofu, D.S. Kimball, The dynamics of the aurora. I. J. Atmos. Terr. Phys. 26, 205 (1964)
S.-I. Akasofu, C.-I. Meng, A study of polar magnetic substorms. J. Geophys. Res. 74, 293 (1969)
S.-I. Akasofu, S. Chapman, C.I. Meng, The polar electrojet. J. Atmos. Terr. Phys. 27, 1275 (1965a)
S.-I. Akasofu, D.S. Kimball, C.-I. Meng, The dynamics of the aurora. II. Westward traveling surges. J. Atmos. Terr. Phys. 27, 173 (1965b)
S.-I. Akasofu, C.I. Meng, D.S. Kimball, Dynamics of the aurora. IV. Polar magnetic substorms and westward traveling surges. J. Atmos. Terr. Phys. 28, 489 (1966)
W. Allan, F.W. Menk, B.J. Fraser, Y. Li, S.P. White, Are low-latitude Pi2 pulsations cavity/waveguide modes? Geophys. Res. Lett. 23, 765 (1996). ISSN 0094-8276
O. Amm, Direct determination of the local ionospheric Hall conductance distribution from two-dimensional electric and magnetic field data: Application of the method using models of typical ionospheric electrodynamic situations. J. Geophys. Res. 100, 21473 (1995)
O. Amm, Improved electrodynamic modeling of an omega band and analysis of its current system. J. Geophys. Res. 101(A), 2677–2684 (1996)
O. Amm, R. Fujii, Separation of Cowling channel and local closure currents in the vicinity of a substorm breakup spiral. J. Geophys. Res. 113, 06304 (2008)
O. Amm, K. Kauristie, Ionospheric signatures of bursty bulk flows. Surv. Geophys. 23, 1 (2002)
O. Amm, A. Pajunpää, U. Brandström, Spatial distribution of conductances and currents associated with a north-south auroral form during a multiple-substorm period. Ann. Geophys. 17, 1385 (1999). ISSN 0992-7689
O. Amm, J. Birn, J. Bonnell, J.E. Borovsky, J.F. Carbary, C.W. Carlson, C.A. Cattell, R.E. Ergun, A. Eriksson, Y.I. Galperin, S.E. Haaland, T. Hallinan, G. Haerendel, B. Hultqvist, T. Karlsson, D.J. Knudsen, H.E.J. Koskinen, W. Lotko, G. Lu, K.A. Lynch, R.L. Lysak, G. Marklund, J.P. McFadden, A. Masson, C.-I. Meng, H. Opgenoorth, G. Paschmann, R. Pottelette, T.I. Pulkkinen, V.A. Sergeev, Y. Song, R.A. Treumann, Auroral plasma physics. Space Sci. Rev. 103, 1–475 (2002)
O. Amm, A. Aksnes, J. Stadsnes, N. Østgaard, R.R. Vondrak, G.A. Germany, G. Lu, A. Viljanen, Mesoscale ionospheric electrodynamics of omega bands determined from ground-based electromagnetic and satellite optical observations. Ann. Geophys. 23, 325 (2005). ISSN 0992-7689
O. Amm, R. Fujii, K. Kauristie, A. Aikio, A. Yoshikawa, A. Ieda, H. Vanhamäki, A statistical investigation of the Cowling channel efficiency in the auroral zone. J. Geophys. Res. 116(A), 02304 (2011)
V. Angelopoulos, W. Baumjohann, C.F. Kennel, F.V. Coronti, M.G. Kivelson, R. Pellat, R.J. Walker, H. Luehr, G. Paschmann, Bursty bulk flows in the inner central plasma sheet. J. Geophys. Res. 97, 4027 (1992)
V. Angelopoulos, C.F. Kennel, F.V. Coroniti, R. Pellat, H.E. Spence, M.G. Kivelson, R.J. Walker, W. Baumjohann, W.C. Feldman, J.T. Gosling, Characteristics of ion flow in the quiet state of the inner plasma sheet. Geophys. Res. Lett. 20, 1711 (1993). ISSN 0094-8276
V. Angelopoulos, C.F. Kennel, F.V. Coroniti, R. Pellat, M.G. Kivelson, R.J. Walker, C.T. Russell, W. Baumjohann, W.C. Feldman, J.T. Gosling, Statistical characteristics of bursty bulk flow events. J. Geophys. Res. 99, 21257 (1994)
V. Angelopoulos, T.D. Phan, D.E. Larson, F.S. Mozer, R.P. Lin, K. Tsuruda, H. Hayakawa, T. Mukai, S. Kokubun, T. Yamamoto, D.J. Williams, R.W. McEntire, R.P. Lepping, G.K. Parks, M. Brittnacher, G. Germany, J. Spann, H.J. Singer, K. Yumoto, Magnetotail flow bursts: association to global magnetospheric circulation, relationship to ionospheric activity and direct evidence for localization. Geophys. Res. Lett. 24, 2271 (1997). ISSN 0094-8276
V. Angelopoulos, J.P. McFadden, D. Larson, C.W. Carlson, S.B. Mende, H. Frey, T. Phan, D.G. Sibeck, K.-H. Glassmeier, U. Auster, E. Donovan, I.R. Mann, I.J. Rae, C.T. Russell, A. Runov, X.-Z. Zhou, L. Kepko, Tail reconnection triggering substorm onset. Science 321(5891), 931–935 (2008)
R.L. Arnoldy, Signature in the interplanetary medium for substorms. J. Geophys. Res. 76, 5189 (1971)
M.P. Aubry, R.L. McPherron, Magnetotail changes in relation to the solar wind magnetic field and magnetospheric substorms. J. Geophys. Res. 76, 4381 (1971)
W.I. Axford, C.O. Hines, A unifying theory of high-latitude geophysical phenomena and geomagnetic storms. Can. J. Phys. 39, 1433 (1961)
D.N. Baker, T.I. Pulkkinen, V. Angelopoulos, W. Baumjohann, R.L. McPherron, Neutral line model of substorms: past results and present view. J. Geophys. Res. 101, 12975 (1996)
D.N. Baker, W.K. Peterson, S. Eriksson, X. Li, J.B. Blake, J.L. Burch, P.W. Daly, M.W. Dunlop, A. Korth, E. Donovan, R. Friedel, T.A. Fritz, H.U. Frey, S.B. Mende, J. Roeder, H.J. Singer, Timing of magnetic reconnection initiation during a global magnetospheric substorm onset. Geophys. Res. Lett. 29, 43 (2002). ISSN 0094-8276
W. Baumjohann, Ionospheric and field-aligned current systems in the auroral zone—a concise review. Adv. Space Res. 2, 55–62 (1982)
W. Baumjohann, The near Earth plasma sheet—an AMPTE/IRM perspective. Space Sci. Rev. 64(1), 141–163 (1993)
W. Baumjohann, Modes of convection in the magnetotail. Phys. Plasmas 9(9), 3665 (2002)
W. Baumjohann, K.-H. Glassmeier, The transient response mechanism and Pi2 pulsations at substorm onset—review and outlook. Int. Assoc. Geomagn. Aeron. 32, 1361–1370 (1984)
W. Baumjohann, R.J. Pellinen, H.J. Opgenoorth, E. Nielsen, Joint two-dimensional observations of ground magnetic and ionospheric electric fields associated with auroral zone currents—current systems associated with local auroral break-ups. Planet. Space Sci. 29, 431 (1981)
W. Baumjohann, G. Paschmann, C.A. Cattell, Average plasma properties in the central plasma sheet. J. Geophys. Res. 94, 6597 (1989)
W. Baumjohann, G. Paschmann, H. Luehr, Characteristics of high-speed ion flows in the plasma sheet. J. Geophys. Res. 95, 3801 (1990)
W. Baumjohann, G. Paschmann, T. Hagai, H. Luehr, Superposed epoch analysis of the substorm plasma sheet. J. Geophys. Res. 96, 11605 (1991)
W. Baumjohann, M. Hesse, S. Kokubun, T. Mukai, T. Nagai, A.A. Petrukovich, Substorm dipolarization and recovery. J. Geophys. Res. 104(A), 24995–25000 (1999)
R.D. Belian, D.N. Baker, E.W.J. Hones, P.R. Higbie, S.J. Bame, J.R. Asbridge, Timing of energetic proton enhancements relative to magnetospheric substorm activity and its implication for substorm theories. J. Geophys. Res. 86, 1415–1421 (1981)
K. Birkeland, The Norwegian Aurora Polaris Expedition, 1902–1903, Sect. 1. (Christiania, Aschehoug, 1908)
K. Birkeland, The Norwegian Aurora Polaris Expedition, 1902–1903, Sect. 2. (Christiania, Aschehoug, 1913)
J. Birn, M. Hesse, The substorm current wedge and field-aligned currents in MHD simulations of magnetotail reconnection. J. Geophys. Res. 96, 1611 (1991)
J. Birn, M. Hesse, Details of current disruption and diversion in simulations of magnetotail dynamics. J. Geophys. Res. 101, 15345 (1996)
J. Birn, M. Hesse, The current disruption myth, in Magnetospheric Current Systems, ed. by S. Ohtani, R. Fujii, M. Hesse, R.L. Lysak, Geophys. Monogr., vol. 118 (Am. Geophys. Union, Washington, 2000), p. 285
J. Birn, M. Hesse, The substorm current wedge in MHD simulations. J. Geophys. Res. 118, 3364 (2013). doi:10.1002/jgra.50187
J. Birn, M. Hesse, The substorm current wedge: further insights from MHD simulations. J. Geophys. Res. 119 (2014)
J. Birn, M. Hesse, G. Haerendel, W. Baumjohann, K. Shiokawa, Flow braking and the substorm current wedge. J. Geophys. Res. 104, 19895 (1999)
J. Birn, J. Raeder, Y.L. Wang, R.A. Wolf, M. Hesse, On the propagation of bubbles in the geomagnetic tail. Ann. Geophys. 22, 1773 (2004)
J. Birn, M. Hesse, K. Schindler, S. Zaharia, Role of entropy in magnetotail dynamics. J. Geophys. Res. 114 (2009). doi:10.1029/2008JA014015
J. Birn, R. Nakamura, E. Panov, M. Hesse, Bursty bulk flows and dipolarization in MHD simulations of magnetotail reconnection. J. Geophys. Res. 116, 01210 (2011). doi:10.1029/2010JA016083
B. Bonnevier, R. Boström, G. Rostoker, A three-dimensional model current system for polar magnetic substorms. J. Geophys. Res. 75, 107 (1970)
R. Boström, A model of the auroral electrojets. J. Geophys. Res. 69, 4983 (1964)
S. Buchert, G. Haerendel, W. Baumjohann, A model for the electric fields and currents during a strong Ps6 pulsation event. J. Geophys. Res. 95, 3733–3743 (1990). ISSN 0148-0227
R.K. Burton, R.L. McPherron, C.T. Russell, The terrestrial magnetosphere—a half-wave rectifier of the interplanetary electric field. Science 189, 717 (1975)
M.N. Caan, R.L. McPherron, C.T. Russell, Solar wind and substorm-related changes in the lobes of the geomagnetic tail. J. Geophys. Res. 78(3), 8087 (1973)
M.N. Caan, R.L. McPherron, C.T. Russell, The statistical magnetic signature of magnetospheric substorms. Planet. Space Sci. 26, 269–279 (1978)
S. Chapman, An outline of a theory of magnetic storms, in Proceedings of the Royal Society of London. Series A (1918), pp. 61–83
S. Chapman, On certain average characteristics of world wide magnetic disturbance, in Proceedings of the Royal Society of London. Series A (1927), pp. 242–267
S. Chapman, The electric current-systems of magnetic storms. Terr. Magn. Atmos. Electr. 40(4), 349 (1935)
S. Chapman, J. Bartels, Geomagnetism, vol. 1 (Clarendon Press, Oxford, 1962)
C.X. Chen, R.A. Wolf, Interpretation of high-speed flows in the plasma sheet. J. Geophys. Res. 98, 21409 (1993)
X. Chu, T.-S. Hsu, R.L. McPherron, V. Angelopoulos, Z. Pu, J. Weygand, K. Khurana, M. Connors, J. Kissinger, H. Zhang, O. Amm, Development and validation of inversion technique for substorm current wedge using ground magnetic field data. J. Geophys. Res. 119 (2014)
C.R. Clauer, Y. Kamide, DP 1 and DP 2 current systems for the March 22, 1979 substorms. J. Geophys. Res. 90, 1343 (1985)
C.R. Clauer, R.L. McPherron, Mapping the local time—universal time development of magnetospheric substorms using mid-latitude magnetic observations. J. Geophys. Res. 79, 2811 (1974)
F.V. Coroniti, C.F. Kennel, Polarization of the auroral electrojet. J. Geophys. Res. 77, 2835 (1972)
F.V. Coroniti, R.L. McPherron, G.K. Parks, Studies of the magnetospheric substorm. 3. Concept of the magnetospheric substorm and its relation to electron precipitation and micropulsations. J. Geophys. Res. 73(5), 1715 (1968)
M. Cramoysan, R. Bunting, D. Orr, The use of a model current wedge in the determination of the position of substorm current systems. Ann. Geophys. 13(6), 583–594 (1995)
A.D. DeJong, A.J. Ridley, X. Cai, C.R. Clauer, A statistical study of BRIs (SMCs), isolated substorms, and individual sawtooth injections. J. Geophys. Res. 114, 08215 (2009)
E. Donovan, W. Liu, J. Liang, E. Spanswick, I. Voronkov, M. Connors, M. Syrjäsuo, G. Baker, B. Jackel, T. Trondsen, M. Greffen, V. Angelopoulos, C.T. Russell, S.B. Mende, H.U. Frey, A. Keiling, C.W. Carlson, J.P. McFadden, K.-H. Glassmeier, H.U. Auster, K. Hayashi, K. Sakaguchi, K. Shiokawa, J.A. Wild, I.J. Rae, Simultaneous THEMIS in situ and auroral observations of a small substorm. Geophys. Res. Lett. 35 (2008). ISSN 0094-8276
S. Dubyagin, V. Sergeev, S. Apatenkov, V. Angelopoulos, R. Nakamura, J.P. McFadden, D. Larson, J. Bonnell, Pressure and entropy changes in the flow-braking region during magnetic field dipolarization. J. Geophys. Res. 115(A10), 10225 (2010)
S. Dubyagin, V. Sergeev, S. Apatenkov, V. Angelopoulos, A. Runov, R. Nakamura, W. Baumjohann, J. McFadden, D. Larson, Can flow bursts penetrate into the inner magnetosphere? Geophys. Res. Lett. 38(A10) (2011). doi:10.1029/2011GL047016
J.W. Dungey, Interplanetary magnetic field and the auroral zones. Phys. Rev. Lett. 6, 47 (1961)
T.E. Eastman, E.W.J. Hones, S.J. Bame, J.R. Asbridge, The magnetospheric boundary layer—site of plasma, momentum and energy transfer from the magnetosheath into the magnetosphere. Geophys. Res. Lett. 3, 685–688 (1976)
R.D. Elphinstone, D.J. Hearn, L.L. Cogger, J.S. Murphree, H. Singer, V. Sergeev, K. Mursula, D.M. Klumpar, G.D. Reeves, M. Johnson, Observations in the vicinity of substorm onset: implications for the substorm process. J. Geophys. Res. 100, 7937–7969 (1995). ISSN 0148-0227
R.D. Elphinstone, J.S. Murphree, L.L. Cogger, What is a global auroral substorm? Rev. Geophys. 34(2), 169–232 (1996). ISSN 8755-1209
D.H. Fairfield, L.J. Cahill, Transition region magnetic field and polar magnetic disturbances. J. Geophys. Res. 71, 155 (1966)
D.H. Fairfield, T. Mukai, M. Brittnacher, G.D. Reeves, S. Kokubun, G.K. Parks, T. Nagai, H. Matsumoto, K. Hashimoto, D.A. Gurnett, T. Yamamoto, Earthward flow bursts in the inner magnetotail and their relation to auroral brightenings, AKR intensifications, geosynchronous particle injections and magnetic activity. J. Geophys. Res. 104, 355 (1999)
C. Forsyth, M. Lester, S.W.H. Cowley, I. Dandouras, A.N. Fazakerley, R.C. Fear, H.U. Frey, A. Grocott, A. Kadokura, E. Lucek, H. Rème, S.E. Milan, J. Watermann, Observed tail current systems associated with bursty bulk flows and auroral streamers during a period of multiple substorms. Ann. Geophys. 26, 167 (2008). ISSN 0992-7689
C. Forsyth, A.N. Fazakerley, I.J. Rae, C. Watt, K. Murphy, J.A. Wild, T. Karlsson, R. Mutel, C.J. Owen, R. Ergun, In-situ spatio-temporal measurements of the detailed azimuthal substructure of the substorm current wedge. J. Geophys. Res. (2014)
L.A. Frank, J.D. Craven, Imaging results from Dynamics Explorer 1. Rev. Geophys. 26, 249–283 (1988). ISSN 8755-1209
L.A. Frank, J.D. Craven, K.L. Ackerson, M.R. English, R.H. Eather, R.L. Carovillano, Global auroral imaging instrumentation for the Dynamics Explorer mission. Space Sci. Instrum. 5, 369–393 (1981)
H.S. Fu, Y.V. Khotyaintsev, A. Vaivads, M. André, S.Y. Huang, Occurrence rate of earthward-propagating dipolarization fronts. Geophys. Res. Lett. 39(10) (2012). ISSN 0094-8276
R. Fujii, R.A. Hoffman, P.C. Anderson, J.D. Craven, M. Sugiura, L.A. Frank, N.C. Maynard, Electrodynamic parameters in the nighttime sector during auroral substorms. J. Geophys. Res. 99, 6093 (1994). ISSN 0148-0227
C. Gelpi, W.J. Hughes, H.J. Singer, Longitudinal phase and polarization characteristics in mid-latitude Pi2 pulsations. J. Geophys. Res. 90, 9905–9909 (1985a). ISSN 0148-0227
C. Gelpi, W.J. Hughes, H.J. Singer, M. Lester, Mid-latitude Pi2 polarization pattern and synchronous orbit magnetic activity. J. Geophys. Res. 90, 6451–6458 (1985b). ISSN 0148-0227
J.W. Gjerloev, R.A. Hoffman, Height-integrated conductivity in auroral substorms. 1. Data. J. Geophys. Res. 105(A), 215–226 (2000a)
J.W. Gjerloev, R.A. Hoffman, Height-integrated conductivity in auroral substorms. 2. Modeling. J. Geophys. Res. 105(A), 227–236 (2000b)
J. Gjerloev, R.A. Hoffman, Currents in auroral substorms. J. Geophys. Res. 107, 1163 (2002)
J.W. Gjerloev, R.A. Hoffman, The large-scale current system during auroral substorms. J. Geophys. Res. 119(6), 4591–4606 (2014)
J.W. Gjerloev, R.A. Hoffman, J.B. Sigwarth, L.A. Frank, Statistical description of the bulge-type auroral substorm in the far ultraviolet. J. Geophys. Res. 112, 07213 (2007)
J. Gjerloev, R.A. Hoffman, J.B. Sigwarth, L.A. Frank, J.B.H. Baker, Typical auroral substorm: a bifurcated oval. J. Geophys. Res. 113, 03211 (2008)
K.-H. Glassmeier, Reflection of MHD-waves in the PC4-5 period range at ionospheres with non-uniform conductivity distributions, in Chapman Conference on Waves in Magnetospheric Plasmas vol. 10 (1983), pp. 678–681
K.-H. Glassmeier, On the influence of ionospheres with non-uniform conductivity distribution on hydromagnetic waves. J. Geophys. 54(2), 125–137 (1984)
A. Grocott, T.K. Yeoman, R. Nakamura, S.W.H. Cowley, H.U. Frey, H. Rème, B. Klecker, Multi-instrument observations of the ionospheric counterpart of a bursty bulk flow in the near-Earth plasma sheet. Ann. Geophys. 22, 1061 (2004). ISSN 0992-7689
M.G. Henderson, G.D. Reeves, J.S. Murphree, Are north-south aligned auroral structures an ionospheric manifestation of bursty bulk flows? Geophys. Res. Lett. 25, 3737 (1998). ISSN 0094-8276
M. Henderson, L. Kepko, H.E. Spence, M. Connors, J.B. Sigwarth, L.A. Frank, H.J. Singer, K. Yumoto, The evolution of north-south aligned auroral forms into auroral torch structures: the generation of omega bands and Ps6 pulsations via flow bursts, in Proceedings of the Sixth International Conference on Substorms, Seattle, Washington, ed. by R.M. Winglee (2002), pp. 169–174
M.G. Henderson, G.D. Reeves, R. Skoug, M.F. Thomsen, M.H. Denton, S.B. Mende, T.J. Immel, P.C. Brandt, H.J. Singer, Magnetospheric and auroral activity during the 18 April 2002 sawtooth event. J. Geophys. Res. 111(A1), 15 (2006a)
M.G. Henderson, R. Skoug, E. Donovan, M.F. Thomsen, G.D. Reeves, M.H. Denton, H.J. Singer, R.L. McPherron, S.B. Mende, T.J. Immel, J.B. Sigwarth, L.A. Frank, Substorms during the 10–11 August 2000 sawtooth event. J. Geophys. Res. 111(A6), 32 (2006b)
R.A. Hoffman, E.R. Schmerling, Dynamics Explorer program: an overview. Space Sci. Instrum. 5, 345–348 (1981)
R.A. Hoffman, R. Fujii, M. Sugiura, Characteristics of the field-aligned current system in the nighttime sector during auroral substorms. J. Geophys. Res. 99, 21303 (1994). ISSN 0148-0227
E.W. Hones Jr., J.R. Asbridge, S.J. Bame, S. Singer, Magnetotail plasma flow measured by Vela 4A. J. Geophys. Res. 78(25), 5463–5476 (1973)
E.W.J. Hones, Plasma sheet variations during substorms. Planet. Space Sci. 20(9), 1409–1431 (1972)
E.W.J. Hones, Substorm processes in the magnetotail—comments on ‘On hot tenuous plasmas, fireballs, and boundary layers in the earth’s magnetotail’ by L.A. Frank, K.L. Ackerson, and R.P. Lepping. J. Geophys. Res. 82, 5633–5640 (1977)
E.W.J. Hones, Transient phenomena in the magnetotail and their relation to substorms. Space Sci. Rev. 23, 393–410 (1979)
B.L. Horning, R.L. McPherron, D.D. Jackson, Application of linear inverse theory to a line current model of substorm current systems. J. Geophys. Res. 79, 5202 (1974)
T.-S. Hsu, R.L. McPherron, Average characteristics of triggered and nontriggered substorms. J. Geophys. Res. 109, 07208 (2004)
T.-S. Hsu, R.L. McPherron, A statistical study of the relation of Pi2 and plasma flows in the tail. J. Geophys. Res. 112, 05209 (2007)
T. Iijima, T.A. Potemra, Large-scale characteristics of field-aligned currents associated with substorms. J. Geophys. Res. 83, 599 (1978)
D. Jelly, N. Brice, Changes in Van Allen radiation associated with polar substorms. J. Geophys. Res. 72(2), 5919–5931 (1967)
Y. Kamide, S.-I. Akasofu, The auroral electrojet and global auroral features. J. Geophys. Res. 80(25), 3585–3602 (2012)
Y. Kamide, M. Kanamitsu, S.-I. Akasofu, A new method of mapping worldwide potential contours for ground magnetic perturbations—equivalent ionospheric current representation. J. Geophys. Res. 81, 3810–3820 (1976)
Y. Kamide, W. Sun, S.-I. Akasofu, The average ionospheric electrodynamics for the different substorm phases. J. Geophys. Res. 101(A), 99–110 (1996)
K. Kauristie, V.A. Sergeev, M. Kubyshkina, T.I. Pulkkinen, V. Angelopoulos, T. Phan, R.P. Lin, J.A. Slavin, Ionospheric current signatures of transient plasma sheet flows. J. Geophys. Res. 105, 10677 (2000)
K. Kauristie, V.A. Sergeev, O. Amm, M.V. Kubyshkina, J. Jussila, E. Donovan, K. Liou, Bursty bulk flow intrusion to the inner plasma sheet as inferred from auroral observations. J. Geophys. Res. 108, 1040 (2003)
K. Keika, R. Nakamura, M. Volwerk, V. Angelopoulos, W. Baumjohann, A. Retinò, M. Fujimoto, J.W. Bonnell, H.J. Singer, H.U. Auster, J.P. McFadden, D. Larson, I. Mann, Observations of plasma vortices in the vicinity of flow-braking: a case study. Ann. Geophys. 27(8), 3009–3017 (2009). ISSN 0992-7689
A. Keiling, K. Takahashi, Review of Pi2 models. Space Sci. Rev. 161(1), 63–148 (2011)
A. Keiling, V. Angelopoulos, A. Runov, J. Weygand, S.V. Apatenkov, S. Mende, J. McFadden, D. Larson, O. Amm, K.-H. Glassmeier, H.U. Auster, Substorm current wedge driven by plasma flow vortices: THEMIS observations. J. Geophys. Res. 114(A1), A00C22 (2009). doi:10.1029/2009JA014114
L. Kepko, M. Kivelson, Generation of Pi2 pulsations by bursty bulk flows. J. Geophys. Res. 104(A), 25021–25034 (1999)
L. Kepko, M.G. Kivelson, K. Yumoto, Flow bursts, braking, and Pi2 pulsations. J. Geophys. Res. 106(A), 1903–1916 (2001)
H.E.J. Koskinen, R.E. Lopez, R.J. Pellinen, T.I. Pulkkinen, D.N. Baker, T. Bösinger, Pseudobreakup and substorm growth phase in the ionosphere and magnetosphere. J. Geophys. Res. 98, 5801–5813 (1993). ISSN 0148-0227
M. Kubyshkina, T.I. Pulkkinen, N.Y. Ganushkina, N. Partamies, Magnetospheric currents during sawtooth events: event-oriented magnetic field model analysis. J. Geophys. Res. 113, 08211 (2008)
D.-H. Lee, R.L. Lysak, Magnetospheric ULF wave coupling in the dipole model—the impulsive excitation. J. Geophys. Res. 94, 17097–17103 (1989). ISSN 0148-0227
M. Lester, W.J. Hughes, H.J. Singer, Polarization patterns of Pi2 magnetic pulsations and the substorm current wedge. J. Geophys. Res. 88, 7958–7966 (1983). ISSN 0148-0227
M. Lester, W.J. Hughes, H.J. Singer, Longitudinal structure in Pi2 pulsations and the substorm current wedge. J. Geophys. Res. 89, 5489–5494 (1984). ISSN 0148-0227
M. Lester, H.J. Singer, D.P. Smits, W. Jeffrey Hughes, Pi2 pulsations and the substorm current wedge—low-latitude polarization. J. Geophys. Res. 94, 17133 (1989)
V. Liu, V. Angelopoulos, A. Runov, X.-Z. Zhou, On the current sheets surrounding dipolarizing flux bundles in the magnetotail: the case for wedgelets. J. Geophys. Res. 118 (2013). doi:10.1002/jgra.50092
M. Lockwood, M.J. Owens, Centennial changes in the heliospheric magnetic field and open solar flux: the consensus view from geomagnetic data and cosmogenic isotopes and its implications. J. Geophys. Res. 116(A), 04109 (2011)
M. Lockwood, R. Stamper, M.N. Wild, A doubling of the Sun’s coronal magnetic field during the past 100 years. Nature 399(6), 437–439 (1999)
M. Lockwood, M. Hairston, I. Finch, A. Rouillard, Transpolar voltage and polar cap flux during the substorm cycle and steady convection events. J. Geophys. Res. 114(A1), 01210 (2009)
G. Lu, A synthetic view of the magnetospheric-ionospheric current system associated with substorms, in Magnetospheric Current Systems, ed. by S. Ohtani, Geophys. Monogr., vol. 118 (2000), p. 199
A.T.Y. Lui, Current disruption in the Earth’s magnetosphere: observations and models. J. Geophys. Res. 101, 13067 (1996)
A.T.Y. Lui, J.R. Burrows, On the location of auroral arcs near substorm onsets. J. Geophys. Res. 83, 3342 (1978)
A.T.Y. Lui, Y. Kamide, A fresh perspective of the substorm current system and its dynamo. Geophys. Res. Lett. 30 (2003). ISSN 0094-8276
L.R. Lyons, T. Nagai, G.T. Blanchard, J.C. Samson, T. Yamamoto, T. Mukai, A. Nishida, S. Kokobun, Association between geotail plasma flows and auroral poleward boundary intensifications observed by CANOPUS photometers. J. Geophys. Res. 104, 4485 (1999)
L.R. Lyons, Y. Nishimura, X. Xing, A. Runov, V. Angelopoulos, E. Donovan, T. Kikuchi, Coupling of dipolarization front flow bursts to substorm expansion phase phenomena within the magnetosphere and ionosphere. J. Geophys. Res. 117(A2), 02212 (2012)
G.T. Marklund, T. Karlsson, L.G. Blomberg, P.-A. Lindqvist, C.-G. Fälthammar, M.L. Johnson, J.S. Murphree, L. Andersson, L. Eliasson, H.J. Opgenoorth, L.J. Zanetti, Observations of the electric field fine structure associated with the westward traveling surge and large-scale auroral spirals. J. Geophys. Res. 103, 4125 (1998)
G.T. Marklund, T. Karlsson, P. Eglitis, H. Opgenoorth, Astrid-2 and ground-based observations of the auroral bulge in the middle of the nightside convection throat. Ann. Geophys. 19, 633 (2001). ISSN 0992-7689
R.L. McPherron, Substorm related changes in the geomagnetic tail: the growth phase. Planet. Space Sci. 20, 1521 (1972)
R.L. McPherron, J.N. Barfield, A seasonal change in the effect of field-aligned currents at synchronous orbit. J. Geophys. Res. 85, 6743 (1980)
R.L. McPherron, P.J. Coleman, Magnetic field variations at ATS 1, in Proceedings of ESRO Colloquium on Geostationary Magnetospheric Satellite (1969), pp. 119–144
R.L. McPherron, G.K. Parks, F.V. Coroniti, Relation of correlated magnetic micropulsations and electron precipitation to the auroral substorm, in Proceedings of the Conjugate Point Symposium, Boulder, CO ITSA Mem., vol. 72 (1967)
R.L. McPherron, C.T. Russell, M.P. Aubry, Satellite studies of magnetospheric substorms on August 15, 1968. 9. Phenomenological model for substorms. J. Geophys. Res. 78, 3131 (1973a)
R.L. McPherron, C.T. Russell, M.G. Kivelson, P.J. Coleman, Substorms in space: the correlation between ground and satellite observations of the magnetic field. Radio Sci. 8, 1059 (1973b)
R.L. McPherron, A. Nishida, C.T. Russell, Is near-earth current sheet thinning the cause of auroral substorm expansion onset? (extended abstract), in Quantitative Modeling of Magnetosphere-Ionosphere Coupling Processes, ed. by Y. Kamide, R.A. Wolf, Geophys. Monogr., vol. 118 (Kyoto Sangyo University, Kyoto, 1987), pp. 252–257
R.L. McPherron, J.M. Weygand, T.-S. Hsu, Response of the Earth’s magnetosphere to changes in the solar wind. J. Atmos. Sol.-Terr. Phys. 70, 303–315 (2008)
R.L. McPherron, L. Kepko, T.I. Pulkkinen, T.S. Hsu, J.W. Weygand, L.F. Bargatze, Changes in the response of the AL index with solar cycle and epoch within a corotating interaction region. Ann. Geophys. 27, 3165 (2009). ISSN 0992-7689
R.L. McPherron, T.S. Hsu, J. Kissinger, X. Chu, V. Angelopoulos, Characteristics of plasma flows at the inner edge of the plasma sheet. J. Geophys. Res. 116 (2011). doi:10.1029/2010JA015923
S.E. Milan, M. Lester, S.W.H. Cowley, K. Oksavik, M. Brittnacher, R.A. Greenwald, G. Sofko, J.-P. Villain, Variations in the polar cap area during two substorm cycles. Ann. Geophys. 21, 1121 (2003). ISSN 0992-7689
S.E. Milan, G. Provan, B. Hubert, Magnetic flux transport in the Dungey cycle: a survey of dayside and nightside reconnection rates. J. Geophys. Res. 112(A), 01209 (2007)
S.E. Milan, P.D. Boakes, B. Hubert, Response of the expanding/contracting polar cap to weak and strong solar wind driving: implications for substorm onset. J. Geophys. Res. 113(A), 9215 (2008)
Y. Miyashita, S. Machida, Y. Kamide, D. Nagata, K. Liou, M. Fujimoto, A. Ieda, M.H. Saito, C.T. Russell, S.P. Christon, M. Nosé, H.U. Frey, I. Shinohara, T. Mukai, Y. Saito, H. Hayakawa, A state-of-the-art picture of substorm-associated evolution of the near-Earth magnetotail obtained from superposed epoch analysis. J. Geophys. Res. 114(A1), 20 (2009)
T. Nagai, Observed magnetic substorm signatures at synchronous altitude. J. Geophys. Res. 87, 4405 (1982)
T. Nagai, An empirical model of substorm-related magnetic field variations at synchronous orbit, in Magnetospheric Substorms, vol. 64 (1991), pp. 91–95
R. Nakamura, W. Baumjohann, R. Schödel, M. Brittnacher, V.A. Sergeev, M. Kubyshkina, T. Mukai, K. Liou, Earthward flow bursts, auroral streamers, and small expansions. J. Geophys. Res. 106, 10791 (2001)
R. Nakamura, W. Baumjohann, C. Mouikis, L.M. Kistler, A. Runov, M. Volwerk, Y. Asano, Z. Vörös, T.L. Zhang, B. Klecker, H. Rème, A. Balogh, Spatial scale of high-speed flows in the plasma sheet observed by Cluster. Geophys. Res. Lett. 31, 09804 (2004). ISSN 0094-8276
R. Nakamura, O. Amm, H. Laakso, N.C. Draper, M. Lester, A. Grocott, B. Klecker, I.W. McCrea, A. Balogh, H. Rème, M. André, Localized fast flow disturbance observed in the plasma sheet and in the ionosphere. Ann. Geophys. 23, 553 (2005). ISSN 0992-7689
R. Nakamura, A. Retinò, W. Baumjohann, M. Volwerk, N. Erkaev, B. Klecker, E.A. Lucek, I. Dandouras, M. André, Y. Khotyaintsev, Evolution of dipolarization in the near-Earth current sheet induced by Earthward rapid flux transport. Ann. Geophys. 27(4), 1743–1754 (2009). ISSN 0992-7689
P.T. Newell, T. Sotirelis, K. Liou, C.-I. Meng, F.J. Rich, A nearly universal solar wind-magnetosphere coupling function inferred from 10 magnetospheric state variables. J. Geophys. Res. 112, 1206 (2007)
A. Nishida, DP2 and polar substorm. Planet. Space Sci. 19, 205 (1971)
A. Nishida, E.W.J. Hones, Association of plasma sheet thinning with neutral line formation in the magnetotail. J. Geophys. Res. 79(4), 535 (1974)
T. Obayashi, A. Nishida, Large-scale electric field in the magnetosphere. Space Sci. Rev. 8, 3 (1968)
S.-i. Ohtani, M.A. Shay, T. Mukai, Temporal structure of the fast convective flow in the plasma sheet: Comparison between observations and two-fluid simulations. J. Geophys. Res. 109, 03210 (2004)
H.J. Opgenoorth, R.J. Pellinen, W. Baumjohann, E. Nielsen, G. Marklund, L. Eliasson, Three-dimensional current flow and particle precipitation in a westward travelling surge/observed during the barium-GEOS rocket experiment. J. Geophys. Res. 88, 3138–3152 (1983)
E.V. Panov, R. Nakamura, W. Baumjohann, V. Angelopoulos, A.A. Petrukovich, A. Retinò, M. Volwerk, T. Takada, K.-H. Glassmeier, J.P. McFadden, D. Larson, Multiple overshoot and rebound of a bursty bulk flow. Geophys. Res. Lett. 37(8), 08103 (2010). ISSN 0094-8276
E.V. Panov, V.A. Sergeev, P.L. Pritchett, F.V. Coroniti, R. Nakamura, W. Baumjohann, V. Angelopoulos, H.U. Auster, J.P. McFadden, Observations of kinetic ballooning/interchange instability signatures in the magnetotail. Geophys. Res. Lett. 39(8), 08110 (2012). ISSN 0094-8276
G.K. Parks, J.R. Winckler, Acceleration of energetic electrons observed at the synchronous altitude during magnetospheric substorms. J. Geophys. Res. 73(1), 5786–5791 (1968)
G. Paschmann, S. Haaland, R. Treumann, in Auroral Plasma Physics, vol. 1, ed. by S. Ohtani (2003)
P. Perreault, S.-I. Akasofu, A study of geomagnetic storms. Geophys. J. 54, 547–573 (1978)
R.F. Pfaff, The near-Earth plasma environment. Space Sci. Rev. 168(1), 23–112 (2012)
D. Pontius, R.A. Wolf, Transient flux tubes in the terrestrial magnetosphere. Geophys. Res. Lett. 17, 49 (1990)
P.L. Pritchett, F. Coroniti, Structure and consequences of the kinetic ballooning/interchange instability in the magnetotail. J. Geophys. Res. 118, 146 (2013). doi:10.1029/2012JA018143
T. Pulkkinen, M. Wiltberger, Global magnetospheric response to IMF driving: ISTP observations, empirical modeling, and MHD simulations. Phys. Chem. Earth 24, 153–162 (1999)
T.I. Pulkkinen, D.N. Baker, R.J. Pellinen, J.S. Murphree, L.A. Frank, Mapping of the auroral oval and individual arcs during substorms. J. Geophys. Res. 100, 21987 (1995)
T.I. Pulkkinen, M. Palmroth, E.I. Tanskanen, P. janhunen, H.E.J. Koskinen, T.V. Laitinen, New interpretation of magnetospheric energy circulation. Geophys. Res. Lett. 33(7) (2006)
T.I. Pulkkinen, C.C. Goodrich, J.G. Lyon, Solar wind electric field driving of magnetospheric activity: is it velocity or magnetic field? Geophys. Res. Lett. 34, 21101 (2007a). ISSN 0094-8276
T.I. Pulkkinen, M. Palmroth, E.I. Tanskanen, N.Y. Ganushkina, M.A. Shukhtina, N.P. Dmitrieva, Solar wind—magnetosphere coupling: a review of recent results. J. Atmos. Sol.-Terr. Phys. 69, 256 (2007b)
T.I. Pulkkinen, M. Palmroth, H.E.J. Koskinen, T.V. Laitinen, C.C. Goodrich, V.G. Merkin, J.G. Lyon, Magnetospheric modes and solar wind energy coupling efficiency. J. Geophys. Res. 115(A3), 03207 (2010)
T.I. Pulkkinen, E.I. Tanskanen, A. Viljanen, N. Partamies, K. Kauristie, Auroral electrojets during deep solar minimum at the end of solar cycle 23. J. Geophys. Res. 116, 04207 (2011)
T. Pytte, R.L. McPherron, S. Kokubun, The ground signatures of the expansion phase during multiple onset substorms. Planet. Space Sci. 24, 1115 (1976)
J. Raeder, R.L. McPherron, Global MHD simulations of the substorm current wedge and dipolarization, in Substorms-4, ed. by S. Kokubun, Y. Kamide (Kluwer, Dordrecht, 1998), p. 343
P. Ritter, H. Lühr, Near-Earth magnetic signature of magnetospheric substorms and an improved substorm current model. Ann. Geophys. 26, 2781 (2008). ISSN 0992-7689
G. Rostoker, On the place of the pseudo-breakup in a magnetospheric substorm. Geophys. Res. Lett. (1998). ISSN 0094-8276
G. Rostoker, E. Friedrich, Creation of the substorm current wedge through the perturbation of the directly driven current system: a new model for substorm expansion. Ann. Geophys. 23, 2171 (2005). ISSN 0992-7689
G. Rostoker, S.-I. Akasofu, J. Foster, R.A. Greenwald, A.T.Y. Lui, Y. Kamide, K. Kawasaki, R.L. McPherron, C.T. Russell, Magnetospheric substorms—definition and signatures. J. Geophys. Res. 85, 1663 (1980)
P.L. Rothwell, M.B. Silevitch, L.P. Block, A model for the propagation of the westward traveling surge. J. Geophys. Res. 89, 8941 (1984). ISSN 0148-0227
A. Roux, S. Perraut, P. Robert, A. Morane, A. Pedersen, A. Korth, G. Kremser, B. Aparicio, D. Rodgers, R. Pellinen, Plasma sheet instability related to the westward traveling surge. J. Geophys. Res. 96, 17697 (1991)
C.T. Russell, R.L. McPherron, The magnetotail and substorms. Space Sci. Rev. 15, 205 (1973)
J. Sanny, R.L. McPherron, C.T. Russell, D.N. Baker, T.I. Pulkkinen, A. Nishida, Growth-phase thinning of the near-Earth current sheet during the CDAW 6 substorm. J. Geophys. Res. 99, 5805 (1994)
K. Schindler, Birn, MHD stability of magnetotail equilibria including a background pressure. J. Geophys. Res. 109 (2004). doi:10.1029/2004JA010537
R. Schödel, R. Nakamura, W. Baumjohann, T. Mukai, Rapid flux transport and plasma sheet reconfiguration. J. Geophys. Res. 106, 8381 (2001)
M. Scholer, On the motion of artificial ion clouds in the magnetosphere. Planet. Space Sci. 18, 977 (1970)
M. Scholer, A. Otto, Magnetotail reconnection: current diversion and field-aligned currents. Geophys. Res. Lett. 18, 7331 (1991)
V.A. Sergeev, W. Lennartsson, Plasma sheet at x≈−20r e during steady magnetospheric convection. Planet. Space Sci. 36, 353 (1988)
V.A. Sergeev, D.A. Yahnin, K. Liou, M.F. Thomsen, G.D. Reeves, Narrow Plasma Streams as a Candidate to Populate the Inner Magnetosphere (Am. Geophys. Union, Washington, 1995), pp. 55–60
V.A. Sergeev, V. Angelopoulos, J.T. Gosling, C.A. Cattell, C.T. Russell, Detection of localized, plasma-depleted flux tubes or bubbles in the midtail plasma sheet. J. Geophys. Res. 101, 10817 (1996a)
V.A. Sergeev, R.J. Pellinen, T.I. Pulkkinen, Steady magnetospheric convection: a review of recent results. Space Sci. Rev. 75, 551 (1996b)
V.A. Sergeev, L.I. Vagina, R.D. Elphinstone, J.S. Murphree, D.J. Hearn, L.L. Cogger, M.L. Johnson, Comparison of UV optical signatures with the substorm current wedge as predicted by an inversion algorithm. J. Geophys. Res. 101, 2615 (1996c)
V.A. Sergeev, K. Liou, C.-I. Meng, P.T. Newell, M. Brittnacher, G. Parks, G.D. Reeves, Development of auroral streamers in association with localized impulsive injections to the inner magnetotail. Geophys. Res. Lett. 26(3), 417–420 (1999)
V.A. Sergeev, M.V. Kubyshkina, K. Liou, P.T. Newell, G. Parks, R. Nakamura, T. Mukai, Substorm and convection bay compared: auroral and magnetotail dynamics during convection bay. J. Geophys. Res. 106(A), 18843–18856 (2001)
V.A. Sergeev, K. Liou, P.T. Newell, S.-I. Ohtani, M.R. Hairston, F. Rich, Auroral streamers: characteristics of associated precipitation,convection and field-aligned currents. Ann. Geophys. 22, 537 (2004). ISSN 0992-7689
V.A. Sergeev, N.A. Tsyganenko, M.V. Smirnov, A.V. Nikolaev, H.J. Singer, W. Baumjohann, Magnetic effects of the substorm current wedge in a “spread-out wire” model and their comparison with ground, geosynchronous, and tail lobe data. J. Geophys. Res. 116(A7), 07218 (2011)
V.A. Sergeev, I.A. Chernyaev, S.V. Dubyagin, Y. Miyashita, V. Angelopoulos, P.D. Boakes, R. Nakamura, M.G. Henderson, Energetic particle injections to geostationary orbit: relationship to flow bursts and magnetospheric state. J. Geophys. Res. 117(A10), 10207 (2012a)
V. Sergeev, Y. Nishimura, M. Kubyshkina, V. Angelopoulos, R. Nakamura, H.J. Singer, Magnetospheric location of the equatorward prebreakup arc. J. Geophys. Res. 117(A1) (2012b)
V.A. Sergeev, A.V. Nikolaev, N.A. Tsyganenko, V. Angelopoulos, A.V. Runov, H.J. Singer, J. Yang, Testing a two-loop pattern of the substorm current wedge (SCW2L). J. Geophys. Res. 947–963 (2014). doi:10.1002/2013JA019629
K. Shiokawa, W. Baumjohann, G. Haerendel, G. Paschmann, J.F. Fennell, E. Friis-Christensen, H. Lühr, G.D. Reeves, C.T. Russell, P.R. Sutcliffe, K. Takahashi, High-speed ion flow, substorm current wedge, and multiple Pi2 pulsations. J. Geophys. Res. 103(A), 4491–4508 (1998)
J.-H. Shue, A. Ieda, A.T.Y. Lui, G.K. Parks, T. Mukai, S. Ohtani, Two classes of earthward fast flows in the plasma sheet. J. Geophys. Res. 113, 02205 (2008). doi:10.1029/2007JA012456
G.L. Siscoe, T.S. Huang, Polar cap inflation and deflation. J. Geophys. Res. 90, 543–547 (1985). ISSN 0148-0227
K. Snekvik, S. Haaland, N. Østgaard, H. Hasegawa, R. Nakamura, T. Takada, L. Juusola, O. Amm, F. Pitout, H. Rème, B. Klecker, E.A. Lucek, Cluster observations of a field aligned current at the dawn flank of a bursty bulk flow. Ann. Geophys. 25, 1405 (2007). ISSN 0992-7689
C.W. Snyder, M. Neugebauer, U.R. Rao, The solar wind velocity and its correlation with geomagnetic, solar and cosmic ray activity, in Proceedings from the 8th International Cosmic Ray Conference on Solar Particles and Sun-Earth Relations (1963), p. 185
D.J. Southwood, W.J. Hughes, Concerning the structure of Pi2 pulsations. J. Geophys. Res. 90, 386 (1985)
D.J. Southwood, M.G. Kivelson, An approximate description of field-aligned currents in a planetary magnetic field. J. Geophys. Res. 96, 67 (1991)
W.J. Sun, S.Y. Fu, G.K. Parks, J. Liu, Z.H. Yao, Q.Q. Shi, Q.-G. Zong, S.Y. Huang, Z.Y. Pu, T. Xiao, Field-aligned currents associated with dipolarization fronts. Geophys. Res. Lett. 40(1), 4503–4508 (2013)
K. Takahashi, S.-i. Ohtani, B.J. Anderson, Statistical analysis of Pi2 pulsations observed by the AMPTE CCE spacecraft in the inner magnetosphere. J. Geophys. Res. 100, 21929 (1995)
K. Takahashi, D.-H. Lee, M. Nosé, R.R. Anderson, W. Jeffrey Hughes, CRRES electric field study of the radial mode structure of Pi2 pulsations. J. Geophys. Res. 108, 1210 (2003)
E.I. Tanskanen, A comprehensive high-throughput analysis of substorms observed by IMAGE magnetometer network: years 1993–2003 examined. J. Geophys. Res. 114, 05204 (2009)
E. Tanskanen, T.I. Pulkkinen, H.E.J. Koskinen, J.A. Slavin, Substorm energy budget during low and high solar activity: 1997 and 1999 compared. J. Geophys. Res. 107, 1086 (2002)
J.R. Taylor, T.K. Yeoman, M. Lester, B.A. Emery, D.J. Knipp, Variations in the polar cap area during intervals of substorm activity on 20–21 March 1990 deduced from AMIE convection patterns. Ann. Geophys. 14(9), 879–887 (1996)
S.M. Thompson, M.G. Kivelson, K.K. Khurana, R.L. McPherron, J.M. Weygand, A. Balogh, H. Réme, L.M. Kistler, Dynamic Harris current sheet thickness from cluster current density and plasma measurements. J. Geophys. Res. 110, 02212 (2005)
J. Untiedt, W. Baumjohann, Studies of polar current systems using the IMS Scandinavian magnetometer array. Space Sci. Rev. 63, 245 (1993)
H. Vanhamäki, O. Amm, A. Viljanen, Role of inductive electric fields and currents in dynamical ionospheric situations. Ann. Geophys. 25, 437 (2007). ISSN 0992-7689
V.M. Vasyliunas, Mathematical models of magnetospheric convection and its coupling to the ionosphere, in Particles and Fields in the Magnetosphere, ed. by B.M. McCormac (Reidel, Dordrecht, 1970), p. 60
D.R. Weimer, J.D. Craven, L.A. Frank, W.B. Hanson, N.C. Maynard, R.A. Hoffman, J.A. Slavin, Satellite measurements through the center of a substorm surge. J. Geophys. Res. 99, 23639 (1994). ISSN 0148-0227
R.G. Wiens, G. Rostoker, Characteristics of the development of the westward electrojet during the expansive phase of magnetospheric substorms. J. Geophys. Res. 80, 2109 (1975)
J.M. Wilcox, K.H. Schatten, N.F. Ness, Influence of interplanetary magnetic field and plasma on geomagnetic activity during quiet-sun conditions. J. Geophys. Res. 72(1), 19–26 (1967)
T. Yamamoto, K. Makita, M. Ozaki, C.I. Meng, A particle simulation of auroral omega bands and torch-like structures. J. Geomagn. Geoelectr. 45(8), 619–648 (1993)
K. Yumoto, Generation and propagation mechanisms of low-latitude magnetic pulsations—a review. J. Geophys. 60, 79–105 (1986). ISSN 0340-062X
E. Zesta, L.R. Lyons, E. Donovan, The auroral signature of earthward flow bursts observed in the magnetotail. Geophys. Res. Lett. 27, 3241 (2000). ISSN 0094-8276
Acknowledgements
This publication is the result of “The Substorm Current Wedge” International Space Science Institute (ISSI) team selected in 2010, and we are grateful to ISSI for their hospitality during three in-person meetings, and for their support that made them possible. L. Kepko thanks the team for their dedication and patience as this review paper was written, and for their insight, knowledge and camaraderie. J. Birn acknowledges support through NASA grants NNX13AD10G and NNX13AD21G and NSF grant 1203711, as well as support from Los Alamos National Laboratory under a Guest Scientist agreement. M. Lester acknowledges support from STFC on grant ST/K001000/1. The work by R. Nakamura is supported by Austrian Science Fund FWF I429-N16 and P23862-N16. The work of T. Pulkkinen was supported by the Academy of Finland under the grant 267073/2013. V. Sergeev and S. Apatenkov thank support from RSF grant 14-17-00072. The team also thanks S. Cowley for providing helpful comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Kepko, L., McPherron, R.L., Amm, O. et al. Substorm Current Wedge Revisited. Space Sci Rev 190, 1–46 (2015). https://doi.org/10.1007/s11214-014-0124-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-014-0124-9