Abstract
The Magnetospheric Multiscale (MMS) mission will provide measurement capabilities, which will exceed those of earlier and even contemporary missions by orders of magnitude. MMS will, for the first time, be able to measure directly and with sufficient resolution key features of the magnetic reconnection process, down to the critical electron scales, which need to be resolved to understand how reconnection works. Owing to the complexity and extremely high spatial resolution required, no prior measurements exist, which could be employed to guide the definition of measurement requirements, and consequently set essential parameters for mission planning and execution. Insight into expected details of the reconnection process could hence only been obtained from theory and modern kinetic modeling. This situation was recognized early on by MMS leadership, which supported the formation of a fully integrated Theory and Modeling Team (TMT). The TMT participated in all aspects of mission planning, from the proposal stage to individual aspects of instrument performance characteristics. It provided and continues to provide to the mission the latest insights regarding the kinetic physics of magnetic reconnection, as well as associated particle acceleration and turbulence, assuring that, to the best of modern knowledge, the mission is prepared to resolve the inner workings of the magnetic reconnection process. The present paper provides a summary of key recent results or reconnection research by TMT members.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Magnetic reconnection is often recognized to be the most important plasma transport and energy conversion process in space physical plasmas. Magnetic reconnection is a likely contributor to the formation and ejection of coronal mass ejecta (e.g., Gosling et al. 1995; Antiochos et al. 1999) and to coronal heating (e.g., Forbes and Priest 1987; Cargill and Klimchuk 1997), and facilitates the entry of solar wind plasma and electromagnetic energy into the magnetosphere by either low- or high-latitude magnetopause reconnection (e.g., Paschmann et al. 1979; Sonnerup et al. 1981). In the magnetosphere proper magnetic reconnection converts energy stored in the magnetotail lobes to plasma internal and kinetic energy. It is also believed to play a role in the formation of the auroral acceleration region (Atkinson 1978; Haerendel 1987). Therefore, magnetic reconnection constitutes a fundamental and ubiquitous element of the Sun-Earth connected system.
Magnetic reconnection relies on the presence of a diffusion region, where collisionless or collisional plasma processes facilitate the changes in magnetic connection through the generation of dissipative electric fields. This diffusion region is strongly localized, extending at most to typical ion Larmor radii. Typical indirect reconnection signatures (contrasted with direct observations of the diffusion region) include the presence of fast flows and plasma heating associated with magnetic field signatures indicative of the establishment of new magnetic connections. Such indirect signatures are observed remotely in the solar corona, in the solar wind by the magnetic topology of CMEs, and by direct spacecraft observations at the magnetopause and in the magnetotail of the Earth.
To-date, however, spacecraft instrumentation has been insufficient to measure the internal structure of magnetic reconnection, particularly on electron scales. This recognition has motivated NASA to consider the Magnetospheric Multiscale Mission, which would remedy the lack of empirical evidence and include the required measurement capabilities. The successful MMS mission proposal included a Theory and Modeling team, which provided throughout the proposal, a knowledge framework and measurement requirements based on the latest insights into current understanding of the physics of collisionless magnetic reconnection.
The Theory and Modeling Team (TMT) continues to be comprised of experts in basic reconnection physics, the interaction of reconnection and particle acceleration, and in the relation between turbulent processes and magnetic reconnection. After selection, the TMT team has continued to play a key role in mission design, focusing on detailed instrument requirements, and continually infusing new scientific knowledge into mission planning. For this purpose, TMT continued and continues to advance the frontier of scientific knowledge, to prepare the path for a successful MMS science phase.
Since selection, TMT has therefore produced numerous new scientific results. A complete summary of these within this review is impossible. Instead, the present paper provides a concise overview of some of the recent advances achieved by research of TMT members. The paper is divided into subsections, which are written by the appropriate TMT lead. Following this introduction, the paper’s structure is as follows:
-
Section 2: Energy Release and Particle acceleration during Reconnection
-
Section 3: Particle acceleration in the magnetotail
-
Section 4: Reconnection and turbulence
-
Section 5: Observations and simulation of plasma heating and acceleration during reconnection
-
Section 6: Determining the orientation, velocity, and structure of a reconnection region
-
Section 7: Reconnection observations at the magnetopause
-
Section 8: Electron diffusion region signatures
-
Section 9: Global MHD modeling for MMS
-
Section 10: Dissipation measures
-
Section 11: Studying Asymmetric Magnetic Reconnection at Earth’s Magnetopause with MMS
-
Section 12: Electron nongyrotropy in the context of collisionless magnetic reconnection
-
Section 13: Summary
We emphasize that the present paper is intended to be a broad overview of science topics, the pursuit of which will be excellently supported by the MMS mission. A heretofore inaccessible capability such as MMS naturally attracts an unusually wide range of scientific topics, even when centered around the kinetic physics of magnetic reconnection. The present paper presents a view from the vantage point of the Theory and Modeling Team. It is therefore, while broad, not intended to be comprehensive or exhaustive in all of its various elements.
The following section will explore two topics related to magnetic reconnection: energy release and particle acceleration. The former is of particular interest as we expect the energy release to be considerably less localized than the actual diffusion region, and the latter is not only of academic interest, but also important for other interests, such as particle impact on spacecraft and other assets in space.
2 Energy Release and Particle Acceleration During Reconnection
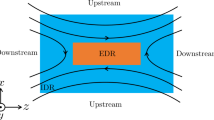
Magnetic reconnection is responsible for the release of magnetic energy into high-speed flows, electron and ion heat and energetic particles in the Earth’s magnetosphere. While the dissipation region plays a central role in breaking magnetic field lines and therefore facilitating magnetic reconnection, the volume occupied by the dissipation region is typically small in large-scale reconnection events in the magnetosphere. Most of the release of magnetic energy during reconnection therefore takes place in the outflow exhaust where newly reconnected field lines expand outwards to release their magnetic tension. During reconnection of anti-parallel magnetic fields, in the MHD model switch-off slow shocks (SSSs) are predicted to both drive both the Alfvenic exhaust and heat the ambient plasma (Petschek 1964). While slow shocks are occasionally observed during reconnection (Feldman et al. 1984; Saito et al. 1998), they are typically not measured during reconnection in the magnetosphere. On the other hand, the outflow velocity of the exhaust is consistent with the Walén relation (Sonnerup et al. 1981), with observations typically falling below the predictions by about 30 % (Phan et al. 2006). Further counter-streaming ions are widely observed in reconnection exhausts both in the magnetosphere (Hoshino et al. 1998; Phan et al. 2007) and in solar wind events (Gosling et al. 2005). Such distributions naturally develop as a result of the slingshot-like acceleration of ions in the exhaust, producing an effective temperature jump \(\Delta T_{\parallel}\sim m_{i}c^{2}_{A}\). Counterstreaming distributions, however, indicate that thermalization of ions is not complete in the collisionless environments of the 1 AU solar wind and magnetosphere. The pressure anisotropy from counter-streaming ions with p ∥>p ⊥ causes the core of the exhaust to bump against the firehose stability boundary ε=1−β ∥/2+β ⊥/2<0 (Fig. 1). Further, since the velocity of the intermediate wave goes to zero at firehose marginal stability, the strong pressure anisotropy within the exhaust prevents the formation of SSSs (Liu et al. 2012; Higashimori and Hoshino 2012), which require that the intermediate modes stand in the inflow into the exhaust. The formation of SSSs is prevented if ε<ε c ≡(5β u +2)/(5β u +5) is violated anywhere within the exhaust, where β u is the upstream ratio of plasma to magnetic pressure. The development of this anisotropy is likely the reason that SSSs are not more widely observed but a careful evaluation of ε within the reconnection exhaust is required to test such a hypothesis.
The results of a PIC simulation of anti-parallel magnetic fields showing (a) the out-of-plane current, (b) the firehose stability parameter ε=1−β ∥/2+β ⊥/2 and (c) cuts of ε at the locations marked by the lines in (b). Note the tendency for a plateau at ε∼0.25 at the edges of the exhaust and the firehose unstable region in the exhaust core. The distinct wobbling of the current in (a) arises from the firehose instability
The partition of energy released during magnetic reconnection has been explored from a data-base of magnetotail reconnection encounters from Cluster (Eastwood et al. 2013). The ions through their enthalpy flux and bulk flow carry the most energy with the electron enthalpy flux and the Poynting flux associated with the Hall fields at comparable levels. The latter suggests that the Poynting flux associated with kinetic Alfven waves is a significant contributor to the energy flux into the auroral acceleration region (Keiling et al. 2003; Shay et al. 2011).
In the presence of an ambient guide magnetic field, which is the typical case during magnetopause reconnection (Sonnerup et al. 1981; Phan et al. 2013a, 2013b), the SSSs bounding the reconnection exhaust are replaced by rotational discontinuities followed by slow shocks (Levy et al. 1964; Lin and Lee 1993). The slow shocks form as counterstreaming, out-of-plane flows produced at the RD compress at a contact discontinuity in the exhaust core. However, there is no evidence for such slow shocks in the satellite observations. This is perhaps not surprising since the interpenetration of ion beams suggests that the contact discontinuities that drive the slow shocks in the MHD model do not develop in collisionless systems. On the other hand in the kinetic description of reconnection with a guide field, the rotational discontinuity collapses to the scale of the ion sound Larmor radius ρ s and can strongly heat the ions if the time scale for ions crossing the exhaust boundary is shorter than the local ion cyclotron time. In this regime the ions effectively behave like pickup particles in the high speed exhaust and gain dominantly perpendicular energy in contrast with the dominant increase in the parallel energy in anti-parallel reconnection (Drake et al. 2009a, 2009b). There is a threshold in the ratio of mass-to-charge to behave like a pickup particle and gain significant energy,
where \(\beta_{pr} = 2\mu_{0}nT_{p}/B_{0r}^{2}\) is the ratio of the proton pressure to that of the reconnecting magnetic field B 0r and M/Q have been normalized to that of protons. This threshold for pickup behavior has been confirmed in PIC simulations where protons were below and helium ions were above the pickup threshold (Fig. 2) (Knizhnick et al. 2011a). Tests of such heating at RDs at the magnetopause have not yet been carried out.
The results of a PIC simulation of magnetic reconnection with a guide field that is twice the reconnection magnetic field and which contains 1 % of fully stripped He ions (Knizhnik et al. 2011a, 2011b). The parameters are chosen so that the He ions are in the pickup regime while the protons are in the adiabatic regime as defined by Eq. (2.1). In (a) is the electric field E y , which drives the flow outflow from the x-line in guide field reconnection. Example trajectories of a proton (black) and He ion (green) are shown. The proton immediately movies downstream as it enters the exhaust, following the local E×B drift. The He ion movies across the exhaust in the direction of the electric field, gaining energy. In (b) are the magnetic moments \(\mu=mv^{2}_{\bot}/2B\) versus time for the two ions in (a) showing the rapid increase in μ for He. In (c) are the initial and late time values of μ for protons (black) and He ions (green) in the white box in (a). The values of μ of protons are conserved while they typically increase strongly for He. Other data (not shown) demonstrates that it is dominantly the He perpendicular temperature that increases on entry into the exhaust
Electron heating is not as well understood as ion heating. While the single reflection of an ion from a newly reconnected magnetic field can produce a substantial energy increment, such a reflection produces negligible electron heating. As a result, electron heating in PIC simulations of slow shocks is much smaller than that of the ions (Liu et al. 2012). On the other hand, because of their high mobility electrons can often have multiple interactions with reconnection exhausts and gain substantial energy. In the magnetotail energetic electrons can undergo multiple interactions with an Earthward propagating reconnection exhaust by reflecting from the converging magnetic field in the near-Earth region (Birn et al. 2004). Within the Earth’s magnetosphere reconnection often develops a multi-island structure in the form of flux-transfer-events (FTEs) at the magnetopause (Russell and Elphic 1979; Oieroset et al. 2011) and flux ropes in the magnetotail (Slavin et al. 2003; Chen et al. 2008a, 2008b). Electrons circulating within contracting or merging magnetic islands rapidly gain energy. The energy gain is again dominantly parallel to the ambient magnetic field and can be described as a Fermi reflection from the Alfvenic exhaust or equivalently by the curvature drift in the direction of the reconnection electric field (Drake et al. 2006; Oka et al. 2011). During the growth of small islands electron heating quickly increases the parallel electron temperature until the marginal firehose condition is reached. Figure 3 shows that, at marginal firehose, the tension force driving reconnection goes away and island growth halts (Karimabadi et al. 2005; Schoeffler et al. 2011). The consequence is that only very long islands \(L>L_{c}=10d_{i}\sqrt{\beta_{e}m_{i}/m_{e}}\), where significant growth can occur before electrons can bounce, reach finite amplitude.
The results of PIC simulations of anti-parallel reconnection for two different mass ratios with islands growing from noise and β e0=0.2 (Schoeffler et al. 2011). In the run with m i /m e =100 strong parallel electron heating caused the island cores to bump against the firehose condition, which saturated short wavelength islands at small amplitude. Only much longer islands were able to continue to grow
Recent observations of 79 magnetopause reconnection events from the THEMIS spacecraft revealed that increment of the electron temperature ΔT e within the reconnection exhaust is given by
where V AL is the effective exhaust velocity during reconnection in an asymmetric system with the subscripts “sph” and “sh” denoting magnetosphere and magnetosheath values, respectively, the subscript “L” indicating that it is the reconnecting components of B in the equation (Phan et al. 2013a). This expression indicates that the electrons gain a specific fraction of the upstream magnetic energy per particle. Whether this energy gain arises from a Fermi mechanism (Drake et al. 2006) or from the development of an electrostatic potential (Egedal et al. 2012) or a combination of the two processes remains unclear. Recent models have been developed to explore both ion and electron acceleration in a system with large numbers of interacting magnetic islands (Drake et al. 2013) but whether such models apply to the magnetosphere has not been established.
We are now, in the next section, moving to the larger-scale effects magnetic reconnection has on particle acceleration. Particle acceleration discussed here is generated by and large by the magnetic and electric field changes on much larger scales than the electron diffusion region, but enabled by the latter’s existence.
3 Particle Acceleration in the Magnetotail
The acceleration of charged particles to high, non-thermal energies and the corresponding flux increases of energetic particles are an important consequence of plasma activity, transport, and magnetic reconfiguration in space and astrophysical plasmas. Major sites of particle acceleration in the Earth’s magnetosphere include the bow shock, the magnetotail, the auroral acceleration region, and the radiation belts.
A central role in energetic particle events in the magnetotail is played by magnetospheric substorms (Akasofu 1968) or, more generally, impulsive dissipation events (Sergeev et al. 1996) and spatially and temporally localized flow bursts (Baumjohann et al. 1990; Angelopoulos et al. 1992). The most common acceleration processes considered within this context include the direct acceleration by the electric field, particularly along a magnetic neutral line or separator, or by a component along the magnetic field, betatron, and Fermi-type acceleration, all primarily involving large-scale electric fields, as well as wave-particle interactions associated with smaller-scale electric fields. Here we consider primarily the effects of (relatively) large-scale electric fields associated with magnetotail reconfigurations in substorms and dipolarization events in the near-tail region, which are a focus of MMS. The insights are based on a recent review of magnetotail acceleration processes (Birn et al. 2012).
3.1 Acceleration in the Vicinity of a Reconnection Site
In order to understand the particle acceleration in the vicinity of a reconnection site, the nonlinear time evolution of a reconnecting thin current sheet has been studied primarily using particle-in-cell (PIC) simulations (e.g., Hoshino et al. 2001; Drake et al. 2003; Pritchett 2008a, 2008b; Oka et al. 2010). Several acceleration mechanisms have been identified, operating in various different regions: (1) the X-type region, which basically coincides with the magnetic diffusion region, (2) magnetic field pileup region where the reconnection jets interact with the pre-existing plasmas at rest, (3) magnetic island formed in a long current sheet, (4) the coalescence region of two magnetic islands, and (5) the boundary layer between the lobe and the plasma sheet.
Some particle acceleration mechanisms suggested by PIC simulations are illustrated in Fig. 4.
Particle acceleration models suggested by PIC simulations: the multi-step acceleration model consisting of Speiser motion in the diffusion region, the chaotic, gradient/curvature B drift motion in the magnetic field pileup region, and the surfing/surfatron acceleration in the boundary region; adapted from (Hoshino 2005a, 2005b)
3.2 Acceleration in Dipolarization Fronts
In addition to the acceleration processes near a reconnection site, particles can be accelerated, even more efficiently, in the outflow regions, particularly in the electric field associated with flow bursts ejected from the reconnection site, which are closely related to earthward propagating “dipolarization fronts” (Nakamura et al. 2002; Runov et al. 2012). Observations of energetic particle injections at geosynchronous orbit and by Cluster and THEMIS satellites in the near tail have put stringent conditions on the possible acceleration sites and mechanisms, indicating near-tail source regions, the importance of induced electric fields, associated with magnetic field dipolarization, and a strong azimuthal localization of the acceleration region (Reeves et al. 1991).
Insights into, and clarification of the relative importance of acceleration mechanisms have been obtained particularly from investigating test particle orbits in time dependent electromagnetic fields, simulating substorm effects and flow bursts in the near tail. Recent results, based on test particle simulations in three-dimensional, time-dependent electric and magnetic fields of MHD simulations of magnetotail reconnection (Birn et al. 2012, 2013) are summarized below.
Figure 5 illustrates typical orbits of accelerated protons and electrons and the associated energy gain. Figure 5a shows characteristic electron and proton orbits, projected into the x,y plane, overlaid on snapshots of the cross-tail electric field (color). The electric field exhibits the properties of a spatially localized, earthward propagating flow burst. As shown by Birn et al. (2011), this is associated with an enhancement of B z (dipolarization front). The instantaneous locations of protons and electrons are shown as orange and yellow dots, respectively. The red dashed contours show the instantaneous location of the near-Earth X-line (B z =0 line). Figure 5b shows the temporal evolution of the kinetic energy of the particles (red for the electron, orange for the proton).
Snapshots of the cross-tail electric field (color) from an MHD simulation of tail reconnection and earthward flow (Birn et al. 2011), with overlaid trajectories of a proton (orange) and electron (yellow), accelerated to a final energy of 80 keV. The instantaneous locations of protons and electrons are shown as orange and yellow dots, respectively. The red dashed contours show the instantaneous location of the near-Earth X-line (B z =0). The time unit is 10 s. (b) Temporal evolution of the kinetic energy of the two particles (red: electron; orange: proton). (After Birn et al. (2012))
Both particles show complementary behavior with similar energization. The electron, which satisfied the drift approximation during the final part of the orbit, drifts eastward toward the acceleration site from the dusk flank plasma sheet. When it reaches the region of strong electric field it participates in the earthward collapse and experiences primarily betatron acceleration, associated with the increase of B z under conservation of the magnetic moment.
The proton does not satisfy the drift approximation, and the full orbit was integrated throughout. Nevertheless, its acceleration is quite similar. It initially drifts toward the acceleration region from the dawn flank, exhibiting “Speiser orbits,” that is, bounces along field lines with mirroring closer to Earth and half-gyration around the B z field near the equatorial plane (only the last part of such an orbit is shown). At t∼122 this part of the orbit is close to the neutral line and the proton experiences acceleration in the direction of the electric field. However, about half of that energy is lost during the eastward motion after exit from that region. Subsequently, the proton essentially gyrates around the increasing magnetic field dominated by B z and becomes accelerated by the fact that the energy gain during the westward part of the orbit exceeds the energy loss during the eastward motion (which is the essence of betatron acceleration). Thus the mechanism and the net energy gain is quite similar to that of the electron, although the proton does not conserve its magnetic moment. The dominant acceleration stems from this last part of the evolution (Fig. 5b).
Two typical source regions for accelerated particles were identified in these simulations: the near-tail plasma sheet flank regions and the closed field line region with equatorial crossing points tailward of the reconnection site. There can also be very effective acceleration of particles that are originally on open field lines (lobes). However, due to their very low density, they cannot contribute significantly to the flux enhancement observed in the near tail and at geosynchronous orbit. The primary acceleration mechanisms for both species can be understood as betatron and first-order Fermi acceleration of type B (Northrop 1963), although ions do not conserve adiabatic invariants during acceleration. Due to pitch angle scattering during neutral sheet crossings, individual ions and electrons may actually experience both during their history.
Figure 6 provides a comprehensive view of energetic electron fluxes at a particular instant of time, which is impossible to obtain observationally without a large fleet of satellites. Color shows the regions of enhanced electron fluxes in the equatorial plane and at the inner, near-Earth, boundary of the simulation box. Black lines in the x,y plane represent contours of constant cross-tail electric field, showing the extent of the flow burst and acceleration site at this time. Colored lines are magnetic field lines within the injection front.
Energetic electron (83.5 keV, 5∘ pitch angle) fluxes at t=130, shown in the z=0 plane and at the near-Earth boundary, x=−7.5. The black contours in the x,y plane show the magnitude of the cross-tail electric field. The colored lines connecting the near-Earth boundary with the x,y plane represent magnetic field lines. The dashed white line represents the open-closed boundary. Modified after Birn et al. (2013)
In summary, test particle orbits in the dynamic fields of MHD simulations have very successfully reproduced qualitatively, and even quantitatively, significant injection features:
-
(1)
the fast rise of the fluxes by one or even more orders of magnitude, which is simultaneous and dispersionless in a central region around midnight,
-
(2)
the limitations of the energy range of flux increases of a few keV to hundreds of keV for electrons, and a few tens of keV to hundreds of keV for protons, and
-
(3)
the difference between the lower limits of flux enhancements for ions and electrons.
Important questions remain: What determines the cross-tail extent of the flow bursts and injections? What affects anisotropies of both species? What is the cause of the occasional events that show injections of one or several MeV particles. One conclusion can be drawn from the fact that in the simulations the maximum energy gain is related to the cross-tail electric field, integrated along the particle path across the acceleration region: higher energy gains require stronger, or more extended, electric fields. Consistent with that conclusion is the fact that MeV proton events occur under strongly stressed conditions with higher impact from the solar wind.
In addition to the more laminar evolution discussed so far, turbulence is also believed to play a role in particle acceleration—in addition to playing a role in magnetic reconnection. While kinetic turbulence may play a role in facilitating reconnection itself, lower frequency turbulence—such as MHD or Hall-MHD turbulence, may be driven by reconnection, or may be facilitating reconnection through the formation of thin current sheets. There is some debate as to how important MHD turbulence will be to drive reconnection in the magnetosphere. In lieu of the answers MMS will provide, the following section presents ways turbulence may be indeed be important for reconnection, and how turbulence and reconnection may be connected to each other. It will furthermore include a look at kinetic turbulence as well.
4 Reconnection and Turbulence
Reconnection has often been seen in relation to turbulent processes. Connections between turbulence and reconnection can involve reconnection driven by turbulence, turbulence generated by reconnection, or kinetic turbulence enabling magnetic reconnection. The relationship between reconnection and turbulence has this been studied for a number a years, in several different guises and using a variety of approaches (Mathaeus and Lamkin 1986; Strauss 1988). One very familiar example of the interplay between turbulence and reconnection is found in the so-called Parker problem (Parker 1972). This is a kind of turbulence problem—coronal flux tubes are twisted and braided by photospheric motions, leading eventually to a kind of zero-frequency driven reconnection, described by a cascade in reduced magnetohydrodynamics (Einaudi et al. 1996; Gomez et al. 2000). In this problem nonlinear stresses build up and relax due to intermittent dissipation events that have the statistical character of nanoflares. Originally viewed as a counterpoint to turbulence descriptions, the nanoflare scenario is now accepted more as a type of turbulence that relaxes through reconnection events (Rappazzo et al. 2010; Rappazzo and Parker 2013). Since is problem is weakly three dimensional, transverse cross sections (see Fig. 1) have an appearance very close to that of the two dimensional (2D) paradigm that has had a dominant role in guiding study of reconnection for fifty years.
In fact most models, identification methods (Gosling et al. 2007) and observational studies (Phan et al. 2006, 2010; Retino et al. 2007) of reconnection have adopted an essentially 2D picture. Because of the relative tractability of the 2D case, both conceptually and computationally, most of what we have to say here will be in that simpler context. Nevertheless, three dimensionality may be an essential feature (Schindler et al. 1988) and may impact the essential defining properties of reconnection, and issue to which we return later below. Even within the context of the simpler 2D or nearly 2D case, it becomes fruitful to consider the array of possible effects of turbulence and nonlinear couplings, as some of these are dramatic, even to the point of being “game changing.” It clearly will be important for the MMS mission analyses to take into account these features, which we now review briefly. It is convenient to discuss separately cases in which either turbulence or reconnection are the dominant feature even though ultimately there are a continuum of such possible relationships (e.g., Matthaeus and Velli 2012).
4.1 Reconnection Effects in Turbulence
Magnetohydrodynamic (MHD) turbulence can take many forms, and therefore reconnection can play diverse roles in the cascade of turbulent fluctuations. In the nanoflare scenario described above there is a buildup of magnetic energy due to a slow stirring process, and the system sporadically destabilizes and relaxes through reconnection to locally lower energy states. Such turbulence is magnetically dominated with patches of rapid (Alfvenic) flows produced in quasi-random bursts. The dissipation also occurs in random “events”, the nanoflares, so that reconnection is a central player in the intermittency and relaxation of coronal flux tubes. Concentration of dissipation at current sheets is a defining signature of intermittent turbulence. In some cases, e.g. the magnetosheath (Sundqvist et al. 2007) the heating at current sheets may be a large fraction of the total plasma heating.
A very different picture of the role of reconnection is found in the turbulent dynamo. In standard dynamo scenarios, the flow energy dominates and the magnetic energy is it initially generated weakly and at small scales (e.g., Brandenberg 2001). For magnetic energy to persist and become dominant, it must be transferred to very long wavelengths. This requires that the reconnection process occurs fast enough to allow the magnetic energy to be “back transferred” to long wave length before it can dissipate. Then it can survive as a dynamo generated large scale field.
While there are some analogous features of the nanoflare and dynamo scenarios, it is clear that they may operate in very different ranges of parameters, and therefore that MHD turbulence and its associated reconnection processes can occur in very different varieties. Not only may the ratio of kinetic energy to magnetic energy differ greatly in various problems, but also the effective dissipation coefficients (magnetic and flow Reynolds numbers), may vary widely and independently. There’s more. The turbulence may have high or low cross helicity, and large or small magnetic helicity. It may evolve in the presence of a large scale externally supported mean magnetic field, which produces global anisotropy, or it may be locally in a near-isotropic state. This variety of parameters can also influence the nature of the reconnection that can occur. For example in the right circumstances strong magnetic helicity enhances back transfer and dynamo action (e.g., Brandenberg 2001) and thus reconnection must be enhanced in such cases in order to allow the topology of the magnetic field fluctuations to evolve. This sensitivity of reconnection to handedness of flux tubes is experimentally known, and has been called “co-helicity” and “counter-helicity” reconnection in the SSX experiment (Ji et al. 1999).
The potentially large number of variations of controlling parameters in MHD turbulence means among other things that MHD turbulence is unlikely to be “universal” in the sense that isotropic homogeneous hydrodynamic turbulence can be under controlled circumstances. In fact it has been argued that there may be a very large number of possible behaviors for MHD turbulence (Lee et al. 2010; Wan et al. 2012). Given that magnetic reconnection is a dynamical process inevitably embedded in MHD turbulence, it seems also likely that there are numerous variations of the type, quality and rates of reconnection in different MHD parameters ranges.
A particularly well studied type of turbulence is Alfvenic MHD turbulence, meaning that the turbulence is incompressible with fluctuations perpendicular to an imposed DC magnetic field. RMHD and 2D MHD are special cases. The 2D case is highly studied both from the perspective of turbulence (Kraichnan and Montgomery 1980) and the role of reconnection in turbulence (Matthaeus and Montgomery 1980; Servidio et al. 2010). Initialized at near-equipartition of MHD-scale kinetic and magnetic fluctuation energies, this system evolves through interaction if magnetic flux structures or magnetic “islands” along with an analogous eddy-structure of the velocity field. It is well known that in this case current sheets and filaments form between adjacent interacting islands. This forms a direct cascade pathway to localized dissipation, while the merger of islands fuels the growth of large scales associated with back transfer (Matthaeus and Montgomery 1980). Only recently has the available computational power been adequate to investigate quantitatively the rates of reconnection in this scenario (Servidio et al. 2010). A glimpse of this complex role of reconnection in active MHD turbulence is provided in Figs. 7 and 8, which show a sea of interacting magnetic islands, their associated X-points, and current sheet-like boundaries. In these numerical experiments (with spectral resolutions up to 163842) it was necessary to monitor accuracy carefully, as inadequate resolution (too high Reynolds no.) causes a reduction in intermittency, lower reconnection rates, and Gausssianization of the small scales. A wide distribution of reconnection rates is found. Most are very low <0.01 in Alfven units, but a few are strong, with rates up to several times 0.1. Ordinary resistivity is used. But the reconnection in this case is driven by turbulent fluctuations. Since the accelerations are intermittent, a few extreme events drive the fast reconnection rates. The idea that reconnection properties may be determined in concert with other stochastic turbulence processes is a relatively new view of triggering and the control of the rate of reconnection, and likely warrants further attention.
(Left) Field lines from a reduced MHD coronal loop simulation; (Right) sheets of electric current density, from the same simulation. (Fron Rappazzo et al. (2010))
In-plane magnetic field lines with X-points and O-points identified (left), and the associated current sheets (right) from a small section of a high resolution 2D MHGD simulation. There are many active reconnection sites, with widely distributed reconnection rates and shapes of reconnection zones. (From Servidio et al. (2010))
4.2 Turbulence Effects on Reconnection
Another approach is to allow small scale turbulence to perturb large scale reconnection problem, such as a sheet pinch. This has been done by adding a spectrum of initial turbulence (Matthaeus and Montgomery 1980; Matthaeus and Lamkin 1986), or by imposing a localized random driving force (Kowal et al. 2009). More recently turbulence triggering of reconnection this has been achieved by initializing a kinetically unstable proton distribution (Matteini et al. 2013); the instability produces waves that provide a turbulent perturbation of the current sheet, accelerating reconnection. Evidently turbulence has a profound effect on a background reconnection process.
There are three types of effects on the reconnection process caused by MHD scale turbulence: (i) the current sheet can be collapsed to thinner dimension by large scale nonlinear (feedback) effect (e.g., Matthaeus and Lamkin 1986; LaPenta 2008); (ii) a turbulent resistivity can be produced by small scale fluctuations, which acts to increase the effective diffusion (e.g., Kim and Diamond 2001); and (iii) the current sheet can become unsteady, break apart into secondary islands, and produce bursty reconnection. All of these might elevate reconnect rates acting collectively in this highly nonlinear process. It remains an open question as to whether MHD reconnection rates become independent of resistivity in a complex turbulent environment. The situation becomes even more complex at higher Reynolds numbers, when the number of X points and flux tubes proliferates due to cascade (Wan et al. 2013), producing increasing numbers if secondary flux tubes and critical points. This effect is very similar to what is called “plasmoid instability” (Loureiro et al. 2007) except that it does not begin with a steady state and is nonlinear. Proliferation of secondary islands is probably best viewed as an impulsive or convective instability that accelerates the reconnection process (Matthaeus and Lamkin 1985).
4.3 The Challenge of Three Dimensionality
Researchers have clung to 2D reconnection models in part because 2D can be modeled with higher resolution (or system size) to attain higher Reynolds numbers Rm, and also because 2D is easier to understand. The first point is amply justified by noting that secondary islands can occur at modest Rm∼1000 (Matthaeus and Lamkin 1985) but occur copiously due to cascade or instability when Rm>10000 or so (Loureiro et al. 2007; Wan et al. 2013). Apart from enabling scaling studies, higher Rm reconnection is more turbulent and therefore of great interest, given that natural systems are typically at vary large effective Rm. (A practical definition is Rm∼[outer scale/inner scale](4/3).)
The second issue—the complexity of 3D reconnection—is potentially more daunting. Reconnection can in effect be defined as magnetic topology change (global at the flux surface level) or as breakdown of the frozen-in condition (local) (Schindler et al. 1988). The former definition requires that surfaces separating regions of differing topology (separatrices) be identified, and an electric field found on the line of their intersection (separator). This involves defining the magnetic flux surfaces, and in 3D this can become a very difficult task as flux surfaces grow in complexity through space when fluctuations are present (Matthaeus et al. 1995; Servidio et al. 2013). It appears that the identification of flux surfaces in 3D is a problem that in general is formally incomputable, being exponentially difficult using classical methods. The local definition is easier to implement, but leaves the ambiguous the connectivity of the field lines. Furthermore following field lines in time in a non-ideal medium is not a well-defined procedure (Schindler et al. 1988; Eyink and Shi 2012). Evidently, a full understanding of reconnection in 3D will face serious difficulties, except in very special cases.
4.4 Kinetic Turbulence, Reconnection and MMS
Most literature on reconnection is either in the context of MHD, or in very simple kinetic problems having sufficient symmetry to suppress or avoid turbulence. Only recently has fully nonlinear kinetic simulation of turbulence and reconnection been reported (Bowers and Li 2007; Daughton et al. 2011; Karimabadi et al. 2013), as kinetic codes and computing capabilities have grown powerful enough to examine these processes simultaneously in the kinetic regime. Figure 9 shows the distribution of electric current intensity from a simulation driven by large scale shear after it reaches a fully developed turbulent state. The results demonstrate that the cascade proceeds into kinetic scales, forming intermittent coherent current structures down to electron inertial and gyroscales. It is apparent that very thin current structures are formed, suggestive of secondary tearing and kinetic scale reconnection. The similarity of this plasma cascade to hydro and MHD shear driven cascades is evident. The complexity of interaction of reconnection and turbulence apparently persists into the kinetic electron scales, which should make the MMS mission investigations all the more important and interesting.
Illustration of out of plane electric current intensity in the fully developed turbulent stage of a shear driven 2.5D PIC simulation of a collisionless electron proton plasma (from Karimabadi et al. 2013). Fine scale sheet like current structures are observed at all scales down to the electron scales, indicating intermittent plasma turbulence, and sites of heating, reconnection and particle energization
The following section will continue the topic of reconnection-turbulence interactions. In particular, it will explore how turbulence generated in association with magnetic reconnection can play a role in plasma heating and particle acceleration.
5 Observations and Simulation of Plasma Heating and Acceleration During Reconnection
This subsection focuses on the interplay of particle acceleration and turbulence in the course of magnetic reconnection. Dynamics of magnetic reconnection in magnetotail involves a variety of plasma processes across many scales from a several 10 R E down to ion/electron inertia scales, and the excited waves in many scales show more or less turbulent behavior (e.g., Russell 1972). Several processes, operating in this multi-scale environment, are candidates to facilitate particle acceleration.
As examples of the broad spectral nature of turbulence, Fig. 10 shows power spectra for magnetic field turbulence observed in the Earth’s magnetotail by the Geotail satellite (Hoshino et al. 1994). Panels (a) and (b) are obtained in the time interval in association with turbulent magnetic fields without bipolar signature of B z , while Panel (c) is the case with bipolar signature, suggesting the passage of the plasmoid. For Panels (a) and (b), we observe that the spectral density of B x , B y and B z has almost the same wave power in high frequency regime, while that of B z is lower than other two component in low frequency regime. We find clearly that the spectrum of B z can be approximated by a “kink” power-law spectrum with a slop changing around 0.04 Hz, which exhibits multi-scale nature of magnetic field fluctuations. The spectral behavior of the kink power-law spectrum is often observed in the magnetotail (e.g., Baure et al. 1995). The spectral features of B x and B y shown in Panel (c) are almost same as those in Panels (a) and (b), but B z has a distinct difference, and the spectrum can be approximated by a single power law function without the kink behavior. From these results, the kink is suggested to correspond to injection region at the wavelength corresponding to the most unstable reconnection/tearing mode in association with direct and inverse cascade of reconnection/tearing islands. While the turbulence in the magnetotail shows often complex behavior with the kink power law spectrum, the magnetotail seems to be in a state of the well-developed turbulence having at least two different scales (Hoshino et al. 1994, Vörös et al. 2007).
Fourier power spectra for magnetic field turbulence observations in magnetotail (adapted from Hoshino et al. 1994)
MHD turbulence is often postulated as an important agent of plasma heating and acceleration. The turbulence is ubiquitous in space, and numerous researchers have discussed about the influence of turbulence to magnetic reconnection. It was suggested that the presence of MHD turbulence could dramatically enhance the reconnection rate through a rapid cascade of turbulent fluctuations into a dissipation scale (Matthaeus and Lamkin 1985). By using MHD simulation, it has been investigated that an externally driven turbulence imposed in the system can enhance the reconnection rate (Loureiro et al. 2009). While the self-generated turbulence remain an open question, Higashimori et al. (2013) have recently demonstrated for the first time that turbulence can be self-consistently generated in the course of reconnection, resulting in a rapid growth of reconnection by using a newly developed Reynolds-averaged Magneto-Hydrodynamics model. In their model, physical quantities are decomposed into mean and turbulent quantities, and they solved self-consistently a set of coupled time evolutional equations of the mean field MHD equations and the turbulent equations. The essential turbulent effect comes from the Ohm’s law given by E=ηJ−V×B−〈v′×b′〉, where 〈v′×b′〉 is the electromotive force due to the effects of an ensemble average of turbulence, where the capital letter and the small letter with prime stand for the mean and the turbulent quantities, respectively. The electromotive force can be modeled by a combination of turbulent kinetic energy and turbulent cross helicity, i.e., 〈v′×b′〉=−βJ−γ∇×V, where β and γ can be related to the turbulent energy K=〈v′2+b′2〉 and the turbulent cross helicity W=〈v′⋅b′〉, respectively (e.g., Yokoi and Hoshino 2011).
Shown in Fig. 11 is the Reynolds-averaged MHD simulation result, and is the comparison of the plasma sheet structure for three different turbulent levels with weak, intermediate, and strong fluctuations. In the case of the intermediate turbulence, the magnitude of turbulence is of order of the background magnetic field energy. The intensity of the electric currents and the flow vectors are depicted. In the case of the laminar reconnection with the weak initial turbulent fluctuations (Run A), a Sweet-Parker-type reconnection in association with an elongated current sheet is formed, while in the intermediate turbulent case (Run B) a Petschek-type reconnection with two pairs of the localized current sheets can been clearly seen. The Alfvenic reconnection jets accelerated at the shock shocks can be observed in the plasma sheet as well. The strong turbulent case (Run C), however, the initial current sheet quickly broadens and the magnetic field energy can be dissipated by the turbulent dissipation process, and no reconnection takes place. From these simulation results, Higashimori et al. (2013) concluded that the self-consistently generated turbulence in the course of reconnection can lead to the rapid growth of reconnection.
Profiles of mean electric current (color contour) and mean flow vectors (black arrows). From top to bottom, a laminar reconnection (Run A), a turbulent, Petschek-type reconnection with a fast magnetic energy conversion (Run B), and a magnetic field diffusing current sheet with a strong turbulence (Run C) (adapted from Higashimori et al. 2013)
The generation mechanism of turbulence is not explicitly mentioned in the model. The turbulence can be generated by several different processes: the outward propagating Alfvenic waves generated by the PSBL ion beams at the plasma sheet boundary layer, the small scale plasmoid ejection around an elongated X-type current sheet, and the collision of the intrinsic reconnection jet motion and the pre-existing plasma sheet plasma, and so on. It would be extremely interesting to study where and how turbulence is generated, and to understand the effect of turbulence to the dynamical evolution of reconnection by using multi-satellite observations such as MMS.
Turbulence is also an important agent for particle acceleration and plasma heating. If the grow of reconnection can be enhanced by turbulence, the stronger inductive electric field is generated, as a result the production of energetic particles can be expected. In the Earth’s magnetosphere, the energetic ions and electrons are observed in a quiet phase without fast plasma flows as well as in an active phase during magnetic reconnection (e.g., Christon et al. 1989; Artemyev et al. 2013). It is believed that not only magnetic reconnection but also turbulence/large-amplitude wave fluctuations may be responsible for energization of hot plasma in the plasma sheet.
The particle acceleration of reconnection has multi-scale behavior of energization, and several different processes are proposed for different acceleration sites. For initial energization, the meandering/Speiser acceleration in and around the X-type region plays an important role, and the interaction of the reconnection jets with the magnetic field pileup region provides further energization (e.g., Hoshino 2005a, 2005b; Priechett 2006). In addition to these processes, the trapped particles inside the magnetic islands, i.e., the O-type region, can gain their energy (e.g., Kliem 1994; Drake et al. 2006). If their gyro-radii becomes larger than the size of the islands, the particles cannot be trapped inside the islands, and as a result the energization may cease. In order to explain the higher energetic particle acceleration, Hoshino (2012) proposed an idea of particle acceleration in an action of turbulent reconnection. Panel (a) in Fig. 12 is the original Fermi acceleration. During the stochastic acceleration, the increase in particle energy is second order of V c /c, where V c and c are the velocity of the random motion of the magnetic cloud and the speed of light, respectively. And this acceleration is known to be a slow process. Panels (b) and (c) have the multiple interaction of the energetic particles with reconnecting islands, instead of the magnetic clouds. In Panel (b) reconnection islands are assumed to be distributed randomly in space, while Panel (c) is for the magnetotail case where the islands are aligned along the tail axis. Based on the PIC simulation result, Hoshino (2012) discussed that the thermal plasma can be confined inside the islands, while the energetic particles have a tendency to be distributed outside the islands, the energetic particles can preferentially interact with the reconnection outflow jets during coalescent magnetic islands. The acceleration efficiency is thus strongly enhanced relative to that of the original Fermi acceleration. In the case of the magnetotail shown in Panel (c), as inferred from the turbulent magnetic field shown in Fig. 10, and as suggested by the Geotail observation about the existence of two active reconnection regions in magnetotail (Hoshino et al. 1996), multiple interaction of the energetic particles can be possible. The higher energetic particles could be observed in the boundary between the lobe and the plasma sheet.
Even though we believe to have a basic understanding of the basic geometry of magnetic and electric fields associated with a reconnection region, unpredictable spatial orientation, motion, or even turbulent effects may make it difficult to properly identify a reconnection region in spacecraft observations. The methods discussed in the following sections are designed to be a tool for this very purpose: maximizing the correct identification of reconnection sites in MMS observations.
6 Determining the Orientation, Velocity, and Structure of a Reconnection Region
In space, the location and orientation of the magnetic reconnection region is often less than obvious. Undulating current sheets, turbulent environments, and moving reconnection regions are some of the effects, which may conspire to complicate identification of a reconnection process. In order to properly interpret the data from MMS we therefore need to determine the large-scale orientation and structure of the reconnection region. To investigate how this could be done, the SMART Theory Team created data sets from MHD and full dynamics kinetic simulations of reconnection. Then this data was analyzed to find out how well the orientation and structure could be determined.
The methods described in this section assume that the reconnection structure is at least approximately time stationary and two-dimensional. The full dynamics kinetic simulation (Shay et al. 2007; Drake et al. 2009a, 2009b) was two dimensional. The MHD simulations (Birn and Hesse 2009) were three dimensional on the large-scale, but were approximately two-dimensional at the central region of the simulation used to study the reconnection structure.
Four virtual spacecraft in a tetrahedral formation were flown through a snapshot of these simulations (with trajectory schematically represented by “S” in Fig. 13). Then other members of the team analyzed the virtual spacecraft data to determine the orientation of the reconnection region as a blind test (Denton et al. 2010, 2012; Sonnerup et al. 2013).
Sketch of the reconnection geometry. The X point is at the origin of the X-Y coordinate system. The reconnecting magnetic field and outflow are oriented in the X direction, while the inflow is in the Y direction. The width d of the diffusion region (rectangular box), is less than its length L, corresponding to greater gradient in the Y direction. The path of the centroid of the array of virtual spacecraft is schematically represented by the path S. (The spacecraft separation is small on this scale.) From Denton et al. (2012)
The first approach we tried for determining the orientation of the reconnection region was the method of Sonnerup and Hasegawa (2005) based on Faraday’s Law. This method uses a time series of electric and magnetic field values and can be used with a single spacecraft. The method seeks to find an invariant (“out of plane”) direction and structure velocity such that one component of the electric field (assumed to be the invariant component) is nearly constant. This is based on the time stationarity. If the in plane components of ∂ B/∂t are zero, then the in plane components of ∇×E must also be zero; but this can only be the case if the out of plane component of E is constant. While this method has proven successful for determining the orientation of flux ropes, it was not successful for determining the orientation of the simulation reconnection regions (Sonnerup et al. 2013, and references therein). For antiparallel MHD reconnection, the out of plane component of E is exactly 0, and the method picks another direction for which time dependence or noise determines the variation. Sonnerup et al. (2013) show also that the method fails for a simple model of component MHD or Hall MHD reconnection. For the full dynamics kinetic simulation, the method gives a roughly correct value of the invariant direction (within about 10∘), but the structure velocity is greatly in error.
Another possibility for single spacecraft data is to use minimum and maximum variance directions. Sonnerup et al. (2013) argue that the invariant direction is usually the intermediate variance direction of B because the maximum variance direction is usually the direction of the reconnection magnetic field while the minimum variance direction is usually the maximum gradient direction across the current sheet. Another option is to use the maximum variance eigenvector of the Sonnerup and Hasegawa (2005) method (which is usually in the direction of the Hall E component across the current sheet) crossed with the maximum variance direction of B.
But results by Denton et al. (2010, 2012) suggest that when four spacecraft are available, such as for MMS, the best method for determining the reconnection region orientation and structure velocity is that of Shi et al. (2005, 2006) based on the gradient of B. The gradient of B, ∇B, is calculated and expressed as the matrix M ∇B, where \(\mathbf{M}^{\nabla B}_{ik} = \partial_{i}B_{k}\), and ∂ i is the spatial partial derivative in the ith direction. Then the symmetric matrix M ∇B⋅(M ∇B)T is formed, where the superscript “T” indicates a transpose. The three eigenvalues of this matrix are the maximum, intermediate, and minimum squared directional derivative (gradient), with the eigenvectors indicating the corresponding directions. Thus the Y direction in Fig. 13 would be the maximum gradient direction, and the Z (out of plane) direction would be the minimum gradient direction. One significant advantage of the Shi et al. method is that it can in principle be implemented point by point as the spacecraft crosses the reconnection region.
Figure 14 shows results for an anti-parallel MHD simulation. The eigenvalues must be well separated in order for eigenvector directions to be well differentiated. In the middle region of the plot, about t=−20 s to 20 s, the eigenvalues are well separated (Fig. 14a) and the eigenvector directions (Fig. 14b–d) are fairly steady. During this time interval, Denton et al. (2010) found values accurate to within about 1∘, verifying that the Shi et al. (2005) algorithm can well determine the reconnection geometry.
(a) Eigenvalues from the Shi et al. (2005) method applied to an anti-parallel MHD simulation with black, blue, and green color corresponding to maximum, intermediate, and minimum gradient, respectively, (b) maximum gradient direction \(\hat{e}_{G{\scriptsize\mbox{-}}\max}\), (c) intermediate gradient direction \(\hat{e}_{G{\scriptsize\mbox{-}}\mathrm{int}}\), and (d) minimum gradient direction \(\hat{e}_{G{\scriptsize\mbox{-}}\min}\), all versus time for an antiparallel MHD simulation. The gradient directions are specified by the direction cosines with respect to the arbitrary x (black), y (blue), and z (green) directions. From Denton et al. (2010)
Assuming time stationary so that ∂ B/∂t=0, Shi et al. (2006) went on to use d B/dt and ∇B observed by the four spacecraft to determine the velocity of the structure relative to the spacecraft, V str =−V sc , where V sc is the velocity of the spacecraft relative to the structure,
Again, this can be evaluated point by point. Figure 15 shows results for the structure velocity for the same MHD simulation used for Fig. 14. The accuracy of the values of V str are not very sensitive to the time intervals; the direction of V str was determined to within 1∘, and the magnitude of V str was determined to within 1 % (Denton et al. 2010).
The curves show components of the structure velocity V str in the arbitrary x (black), y (blue), and z (green) directions. The left pointing triangles at the right of the plot are vertically centered on the median values of each component; the horizontal lines are located vertically at the exact values of the components. From Denton et al. (2010)
The aim in this section is to determine the orientation of the large-scale structure, and there will be many measurements over this scale, so time averaging can eliminate the effect of random noise errors (Denton et al. 2012). Systematic calibration errors, however, could potentially have a serious effect on results from the Shi et al. (2005, 2006) algorithm as shown by Denton et al. (2010, 2012). Systematic calibration errors can lead to a systematic error in ∇B, from which all the results of the method are derived. Denton et al. showed how this problem could be dealt with. Instead of using ∇B, one can use δ∇B=∇B−〈∇B〉0, where 〈∇B〉0 is the average of ∇B evaluated near the central current sheet crossing. This totally eliminates the effect of systematic errors, since the time independent systematic errors will lead to a constant contribution to ∇B.
Denton et al. (2010, 2012) tested the modified Shi et al. (2005, 2006) method using δ∇B for three different MHD simulations and the full dynamics kinetic simulation with various spacecraft trajectories. The accuracy of the directions found varied depending on the simulation and spacecraft trajectory, but all the directions could be found within about 10∘ for all cases.
The structure velocity was found with magnitude accurate to 2 % and direction accurate to within 5∘.
Having determined the orientation and velocity of the structure, it is possible to reconstruct the structure of the region surrounding the spacecraft trajectory if one has a set of fluid equations that adequately describe the plasma. Basically, the procedure is to start with a set of fluid equations expressed as a function of a coordinate x sc along the spacecraft trajectory and y sc normal to the spacecraft trajectory but in the reconnection plane, then drop the explicit time-dependent terms, and then use the derivatives with respect to y sc to step quantities away from the spacecraft trajectory (Sonnerup et al. 2006). Figure 16 shows results for reconstruction of B for the MHD simulation with anti-parallel reconnecting magnetic field using reconstruction equations based on resistive MHD (Teh et al. 2010). Note the fairly accurate determination of the island structure and X point location.
Plot of magnetic field lines (black) and axial field B z in color in the reconstruction (x sc -y sc ) plane for (a) the original MHD simulation, and (b) the reconstructed fields. The most significant difference in color in (a) occurs mostly because the out of plane direction used was that from the Shi et al. analysis, 1.3∘ off from the exact direction. The map was obtained from the spacecraft 3 (green) trajectory. Spacecraft 1, 2, and 4 were used to constrain the resistivity model, while 5 and 6 were used only for testing the reconstruction results. From Teh et al. (2010)
Work is in progress to reconstruct the fields for the full dynamics kinetic simulation. A scalar pressure does not provide an adequate description for the pressure tensor, and it appears that off diagonal pressure elements need to be included in the reconstruction equations in addition to differing diagonal elements. (The ions are not even gyrotropic near the central current sheet.) Thus for the reconstruction equations we will need to use higher moment equations including off-diagonal pressure terms, or model these terms from lower moments using a formalism such as that of Hesse et al. (2011).
The Earth’s magnetopause is a region, in which reconnection has been identified early and reconnection signatures are ubiquitous. The magnetopause is therefore also a prime target for MMS during the first part of the mission. As a preparation, the following section sums up what is presently known about reconnection at the magnetopause, focusing on the analysis of data from earlier space missions.
7 Reconnection Observations at the Magnetopause
7.1 Reconnection Signatures
Due to its ubiquity the consequences of magnetic reconnection have long been observed remotely. Statistical studies of many different global magnetospheric phenomena indicating a strong dependence upon the interplanetary magnetic field (IMF) orientation reveal that reconnection is the dominant process controlling the flow of solar wind mass, energy, and momentum through the Earth’s magnetosphere. Consistent with models for enhanced reconnection on the equatorial magnetopause, the dayside magnetopause moves inward (Aubry et al. 1971), the cusps move equatorward (Newell et al. 1989), open flux in the polar caps and magnetotail grows (Holzworth and Meng 1975), geomagnetic activity intensifies (Fairfield and Cahill 1966), the cross-polar potential drop (a measure of ionospheric convection) increases (Reiff et al. 1981), field-aligned currents into and out of the ionosphere intensify (Weimer 2001), magnetotail magnetic field strengths increase (Caan et al. 1973), the magnetotail magnetopause moves outward (Maezawa 1975), and the chances of an auroral substorm occurring increase (Arnoldy 1971) during periods of southward interplanetary magnetic field (IMF) orientation. Magnetic reconnection then releases the energy that dayside reconnection stores within the magnetotail (Aubry and McPherron 1971), generating bursty bulk flows and dipolarization fronts that transport energy Earthward (Angelopoulos et al. 1994), injecting energized particles into the Earth’s ring current and outer radiation belt (Akasofu 1968; Kamide 1992), driving intense field-aligned currents into the nightside ionosphere (Weimer 2001), releasing plasmoids that travel down the magnetotail (Hones 1979), and enhancing nightside auroral activity (Liou et al. 1998). By demonstrating the importance of magnetic reconnection, these global case and statistical studies have prompted an ongoing effort to identify the in situ microphysical signatures of reconnection and determine the parameters that govern this fundamental process.
Studies employing in situ observations have answered many questions about reconnection (Paschmann et al. 2013), but raised many more. A recently selected National Science Foundation sponsored Geospace Environment Modeling (GEM) focus group outlined several of the topics currently under discussion (see http://aten.igpp.ucla.edu/gemwiki/index.php/FG:_Magnetic_Reconnection_in_the_Magnetosphere). These include the location and extent of reconnection, the proximate cause for reconnection, the extent of the electron diffusion region, the roles played by asymmetries, pressure anisotropies, and shear flows, the nature of the three-dimensional structures that reconnection generates, the manner by which steady and transient reconnection on kinetic scales couples to mesoscale structures like bursty bulk flows, dipolarization fronts, entropy bubbles and flux transfer events, and the structures/processes (e.g. reconnection electric fields and bubbles) that energize particles. These questions, and many others, motivate NASA’s Magnetospheric Multiscale Mission (MMS).
This section summarizes the in situ signatures predicted and observed for magnetic reconnection, primarily at the dayside magnetopause, but with some references to the magnetotail. It begins with a discussion of steady-state microphysical and mesoscale signatures, takes note of the transient signatures predicted when reconnection is unsteady, and then addresses when and where reconnection occurs. For more details, please refer to Paschmann et al. (2013).
7.2 Microscale Structures
Figure 17 provides a microscale view of the geometry around a reconnection line that lies perpendicular to the plane of the figure. A single current layer separates oppositely directed magnetosheath and magnetospheric (or north and south lobe) magnetic fields at locations far from the reconnection line. At the reconnection line within the electron diffusion region, the magnetic field strength exhibits a depression (in the presence of a guide field) or a null (in the absence of a guide field). The sense of the magnetic field component normal to the magnetopause reverses across the reconnection line. The magnitude of this component should be small (∼0.1) compared to that of the magnetic fields on either side of the magnetopause. Reconnection launches pairs of standing slow mode shocks and/or Alfvén mode waves on either side of the reconnection region that not only heat and accelerate electrons but also enable magnetic field lines to rotate from orientations on one side of the current layer to those on the other (Liu et al. 2012). These pairs of standing waves cause the magnetopause current layer to bifurcate. Magnetic field strengths should peak, while plasma densities and pressures pass through minima along the standing slow mode shocks, which lie near the separatrices (Shay and Drake 1998).
The geometry of the reconnection region (adopted from Mozer et al. 2002). The x-axis points normal to the magnetopause, the z-axis northward and the y-axis dusk ward. Ions decouple from the electrons and magnetic field in the ion diffusion region, creating the hall magnetic and electric field patterns. Electrons are demagnetized in the electron diffusion region
Out-of-plane electric fields associated with outward-propagating fast rarefaction waves convect magnetic fields and plasmas on both sides of the current layer inwards towards the reconnection line. First ions, and then electrons, become demagnetized as they drift inward towards the weak magnetic field strengths and curved magnetic field lines within the immediate vicinity of the reconnection line (Mandt et al. 1994). Tied to the magnetic field lines, the electrons stream into the ion diffusion region and out through the outflow region [see Sect. 8]. The ions cannot keep up with the electrons and retain much smaller, nearly constant velocities within the electron diffusion region. Because the ions are left behind, Hall electric fields point inward towards the reconnection line within the ion diffusion region on both sides of the current layer (Shay and Drake 1998; Pritchett 2005). These electric fields cause both electrons and magnetic field lines to move out of the plane of the figure. Equivalently, Hall currents associated with the streaming electrons generate a quadrupole magnetic field pattern into and out of the plane of the figure. A whistler mode wave carries these magnetic field perturbations outward along the separatrices. Whistler dynamics at the separatrices accelerate electrons moving into the outflow region [see Sect. 5]. Non-gyrotropic elements of the electron pressure tensor enable the electrons to decouple from the magnetic field at the reconnection line (Hesse et al. 2002). High-speed electron jets carry a strong current along the reconnection line (Shay and Drake 1998; Hesse et al. 1999, see Sect. 12). High speed electron jets also carry magnetic field lines away from the reconnection site in the plane containing the ambient magnetic fields.
This simple picture needs modification when reconnection is asymmetric or guide fields are present [see Sect. 11]. When reconnection is asymmetric, the Hall fields attain greater magnitudes on the low-density side of the current sheet (Pritchett 2008a, 2008b). Even when reconnection is symmetric, guide fields must be added to the Hall fields, making them appear asymmetric (Karimabadi et al. 1999a, 1999b; Pritchett and Coroniti 2004). Asymmetries, i.e. gradients, in the plasma pressure cause a diamagnetic drift of the reconnection line. When the speed of this drift exceeds that of the plasma outflow Alfvén velocity, reconnection is suppressed (Swisdak et al. 2003a, 2003b). Swisdak et al. (2010) showed that reconnection is possible for small shears in the magnetic field for small jumps in plasma beta across the magnetopause, but large shears are required for large jumps. Pressure anisotropies associated with counterstreaming ions on reconnected magnetic field lines within the ion diffusion region lead to a firehose instability which reduces the Alfvén velocity below the slow mode speed and diminishes ion outflow velocities below those predicted for rotational discontinuities by the Walén relationship (Liu et al. 2012). Large flow shears at the magnetopause sweep reconnection lines antisunward, making steady reconnection impossible (Gosling et al. 1991). Component, but not antiparallel, reconnection favors the energization of high mass-to-charge ions (Knizhnik et al. 2011a, 2011b).
Now consider the observations that support this microscale reconnection model. Identifying the component of the magnetic field normal to the nominal magnetopause requires an extremely accurate determination of the magnetopause normal, which is sometimes possible (Sonnerup and Cahill 1967; Aubry et al. 1971; Sonnerup and Ledley 1974; 1979; Phan et al. 2001; Mozer et al. 2011), but often difficult due to uncertainties in the boundary orientation (Paschmann et al. 2013). As discussed in Sect. 6, MMS will employ multipoint observations to determine the orientation of the boundary and the normal component more accurately than has proven possible in the past. By contrast, the low or null magnetic field strengths that mark the reconnection line embedded within the magnetic field rotations at the bifurcated magnetopause current layer corresponding to standing rotational discontinuities and/or slow mode shocks are readily identifiable (e.g., Dunlop et al. 2011a; Mozer et al. 2011). Nagai et al. (2001), Øieroset et al. (2001), and Mozer et al. (2002) have reported evidence for the quadrupole Hall magnetic field perturbations at the magnetopause and in the magnetotail.
Neither tangential electric fields nor the particle drift velocities into the reconnection region that they drive are easily determined because they are small and must be measured in the frame of the (possibly) moving current sheet. However, Hall electric fields have been identified at the magnetopause and in the magnetotail (Mozer et al. 2002; Wygant et al. 2005). Mozer et al. (2011) reported observations indicating that the parallel component of the electric field is spiky, while the perpendicular component differs from −U i ×B, where U i is the ion flow speed. Fujimoto et al. (1997), Nagai et al. (2001), and Mozer et al. (2011) have reported observations of low energy electrons streaming into the reconnection region along the separatrices, while higher energy electrons streamed away. Chen et al. (2008a, 2008b) reported observations of anisotropic electron distributions and the predicted Hall electric fields normal to the magnetopause in the immediate vicinity of the electron current sheet, while Nagai et al. (2011) and Mozer et al. (2011) reported observations of the predicted super-Alfvénic in-plane jet outflow from the reconnection line and into-the-plane jet along the reconnection line. As predicted by the model, there were no significant enhancements in the ion velocity. Within the current layer, outflowing electrons are heated (Øieroset et al. 2002; Lavraud et al. 2006; Retino et al. 2008; Dunlop et al. 2011a; Mozer et al. 2011). Phan et al. (2013a, 2013b) report THEMIS observations demonstrating that reconnection shuts down for low magnetic field shears and large jumps in plasma beta across the current layer
7.3 Mesoscale Structures
Reconnection launches Alfvén mode waves parallel to magnetic field lines and enables the transmission of energized ions and electrons through the current layer. The transmitted Alfvén waves and particles are confined to the vicinity of the current layer and therefore create boundary layers on either side of this layer. At the magnetopause, these boundary layers exhibit accelerated flows and densities, temperatures, magnetic field strengths and magnetic field orientations intermediate between those of the magnetosheath and magnetosphere (Lin and Lee 1993). In the magnetotail, they correspond to the plasma sheet and/or plasma sheet boundary layer, a region of enhanced densities and temperatures (in comparison to values in the lobes), often accelerated flows, and weak magnetic field strengths that bounds the current layer. Once reconnection occurs, the boundary layers fill with streaming transmitted, reflected, and energized ions and electrons on reconnected magnetic field lines (Lockwood et al. 1996). Because a finite time is required for these particles to reach any given point along the field lines, which themselves are convecting towards the current sheet, only those particles with the highest velocities are seen furthest from the current sheet along any cross-section through the current sheet. A spacecraft moving towards the current layer therefore observes particle dispersion: sequentially detecting the more energetic electrons, the less energetic electrons, the more energetic ions and then the less energetic ions. Since there is a minimum velocity parallel to the magnetic field for particles to reach any given location, reconnection creates characteristic D-shaped particle distributions in the boundary layers (Cowley 1982). Having passed through a rotational discontinuity, the velocity of the particles in the boundary layers should satisfy the Walén relationship, increasing (or decreasing) by one Alfvén velocity depending on position relative to the reconnection line.
Boundary layers exhibiting accelerated flows and densities and temperatures intermediate between those of the magnetosheath and magnetosphere are often observed at the dayside magnetopause. The flow speeds often approach the values predicted for the Walén relationship (Paschmann et al. 1979), but are frequently significantly (∼50 %) lower (Sonnerup et al. 1981). The discrepancy may result from temporal effects, the presence of obstacles in the path of the flow, or the effects of the firehouse instability in the current layer, as discussed above. The accelerated flows may initiate a Kelvin-Helmholtz instability, driving small-scale waves on the current layer (Saunders 1989). Many researchers have reported D-shaped ion distributions in the boundary layers (Fuselier et al. 1991) and the velocity dispersion expected at the edge of the boundary layer (Richardson and Cowley 1985; Gosling et al. 1990). Phan et al. (2000) reported simultaneous observations of outflow on both sides of the reconnection line.
Standing slow mode shocks bound the outflow region in the Earth’s magnetotail (Feldman et al. 1984). The nearly colocated plasma sheet boundary layer often exhibits streaming and counter streaming ion beams (Lui et al. 1978; Krimigis et al. 1978), even during geomagnetically quiet intervals (Eastman et al. 1984). Energized ions stream sunward through the outermost edges of the plasma sheet boundary layer at locations Earthward of the reconnection line (Sarris and Axford 1979; Richardson and Cowley 1985). The ions reflect at low-altitude mirrors. Convection electric fields cause these ions to stream antisunward on magnetic field lines somewhat closer to the center of the current sheet within plasma sheet, where they may encounter other sunward streaming ions, resulting in counterstreaming populations. Tailward of the reconnection line, the sequential layering from the plasma sheet to the lobe side of the PBSL is low energy protons, energetic protons, energetic electrons, while at a fixed energy the layering is oxygen, alphas, and protons (Sarafopoulos et al. 1997).
7.4 Transient Reconnection
The conditions governing the occurrence of steady and transient reconnection remain unknown, as do the conditions that trigger transient reconnection. Perhaps it occurs in response to the tearing instability, or to the Kelvin-Helmholtz instability driven by electron outflow from the reconnection region along the separatrices (Fermo et al. 2012). Whatever the cause, there is much evidence indicating that transient reconnection is common and that it plays an important role in the overall solar wind-magnetosphere interaction.
Transient reconnection at a single reconnection line generates pairs of interconnected magnetic field line bubbles that move away from the reconnection line (Lee and Fu 1985). Transient reconnection at two or more parallel reconnection lines generates true flux ropes bounded by bubbles, both at micro- (Swisdak et al. 2003a, 2003b) and meso-scales (Southwood et al. 1988; Scholer et al. 1988). As they move away from the reconnection line at speeds approaching the Alfvén velocity, the bubbles/flux ropes expand and generate transient bipolar magnetic field signatures normal to the nominal magnetopause in the ambient media. The sense of these signatures depends on the motion of the structures relative to the background magnetic fields. The strong core magnetic fields that are sometimes seen within the events may result from particles streaming outward from within the events (Hesse et al. 1996) or coalescing Hall magnetic fields (Karimabadi et al. 1999a, 1999b). The events themselves contain a heated and accelerated mixture of plasmas from both sides of the current layer.
On the magnetopause, the bubbles/flux ropes are known as flux transfer events or FTEs. In the magnetotail, transient reconnection launches localized sunward and antisunward bursty bulk flows that pile up magnetic flux as they plough into the ambient media. The sunward-moving fronts cause magnetic fields to assume more dipolar magnetic field configurations, while the antisunward-moving fronts represent the first step in the initiation of larger-scale plasmoids (Imber et al. 2011). Observations indicate that the events are common in both regions. At the magnetopause, FTEs may account for 30 (Lockwood et al. 1990) to 100 % of the overall solar wind-magnetosphere interaction. Fermo et al. (2011) invoked island/flux rope growth due to quasi-steady reconnection and merging to successfully explain the distribution of sizes in the spatial regime where spacecraft observations exist, and concluded that the magnetopause is populated by many FTEs too small to be recognized by existing spacecraft instrumentation. Within the magnetotail, the spatially and temporally limited reconnection-initiated bursty bulk flows are the most efficient transporters of flux and energy (Angelopoulos et al. 1994).
Collapsing flux ropes provide an opportunity for efficient electron acceleration. Drake et al. (2006) show how Fermi acceleration within such islands can transfer up to 50 % of the lost magnetic energy to the electrons, resulting in power spectra distributions similar to those observed in the Earth’s magnetotail. The predictions are consistent with observations of isotropic energetic electrons exhibiting a power law spectrum with an index of 3.8 and energies up to 300 keV in the magnetotail diffusion region, as reported by Øieroset et al. (2002).
The reconnection lines that generate flux ropes need not appear simultaneously (Raeder 2006). Observationally, Hasegawa et al. (2010) invoked sequentially-generated reconnection lines to explain observations of converging jets within a magnetopause flux rope and bidirectional field-aligned streams of electrons in the nearby magnetosheath. Likewise, Oieroset et al. (2011) reported observations of converging flows within a magnetopause flux rope and enhanced fluxes of superthermal electrons. Nevertheless, Zhang (2012) reported that only 41 of 3701 low-latitude flux ropes exhibit evidence for converging flows.
The sunward moving bursty bulk flows launched by reconnection in the magnetotail (Angelopoulos et al. 1994) must brake when they encounter the region of dipolar magnetic fields in the near-Earth magnetotail, causing magnetic field strengths to pile up and perhaps initiating Pi2 oscillations in both the magnetic field strength and field-aligned currents (Shiokawa et al. 1997; 1998). However, even in the absence of the dipolar magnetic field region, the onset of reconnection launches sunward (and antisunward) moving dipolarization fronts marked by a preliminary negative dip and then a strong sharp increase in B z (Runov et al. 2009; Sitnov et al. 2009). The energy dissipation in these fronts should be dominated by ions, as observed (Zhou et al. 2010). Once the flow stops near Earth, the region of dipolarization expands azimuthally and tailward, resulting in reversed vortices on the outside of the flow (Panov et al. 2010; Birn et al. 2011).
7.5 Global Occurrence Patterns
Reconnection may occur in patches, along single extended reconnection lines, or along parallel reconnection lines. To take place along an extended line, reconnection must first occur at a microscale patch and then spread (e.g., Shay et al. 2003). In weak guide fields, spreading is due to the motion of current carriers in the direction of the current carriers (Lapenta et al. 2006). In strong guide fields, the spreading is bidirectional due to the excitation of Alfvén waves along the guide field (Shepherd and Cassak 2012). Consistent with exceptions for the reconnection line to spread in the direction of the primary current carrier (ions in this case) when there is little to no guide field, reconnection spreads westward in the Earth’s magnetotail (McPherron et al. 1973). The direction(s) in which it spreads on the magnetopause remains unknown, but the existence of extended reconnection lines on the magnetopause has been inferred from near simultaneous observations of reconnection over extended regions (e.g., Phan et al. 2000).
The location and orientation of the single or multiple reconnection lines on the dayside magnetopause remain to be determined. Component reconnection models predict tilted lines that follow current streamlines and pass through the subsolar point on the magnetopause (Gonzalez and Mozer 1974; Sonnerup 1974). Although the original component reconnection models maintained that reconnection ceases on the dayside magnetopause for strong northward magnetosheath magnetic fields, Cowley (1976) reported that it might continue. Swisdak and Drake (2007a, 2007b) proposed a model for asymmetric reconnection with arbitrary jumps in plasma and magnetic field parameters across the magnetopause in which the X-line lies in the direction that maximizes the Alfvén speed characterizing the reconnection outflow. When the density ratio lies near unity, the model predicts reconnection lines that approximately bisect the angle between the magnetosheath and magnetospheric magnetic fields, thereby approximating results for the component reconnection model, but extending this model to the low shear regime. Maximum shear models predict reconnection lines that lie along the locus of points where shears between the magnetosheath and magnetospheric magnetic fields peak (Trattner et al. 2007). These lines are often displaced away from subsolar point towards the winter hemisphere. At high latitudes, the line lies along the locus of points where magnetosheath and magnetospheric magnetic fields lie antiparallel, i.e. the locations where antiparallel models predict reconnection (Crooker 1979). Enhanced current densities may depress normal magnetic fields and electron magnetization, enabling reconnection. For all but due northward and southward IMF orientations, current driven reconnection occurs on both the dayside and the high latitude magnetopause (Alexeev et al. 1998).
While all the models predict the nearly equatorial reconnection line observed during intervals of strongly southward IMF orientations (e.g., Phan et al. 2000), the maximum shear model has proven remarkably successful in predicted the locations where reconnection is observed in situ (Trattner et al. 2012; Dunlop et al. 2011a, 2011b) or inferred from remote observations for other IMF orientations (Trattner et al. 2007). The distribution of bipolar magnetic field signatures and streaming suprathermal electron anisotropies within FTEs is consistent with reconnection along a tilted component reconnection line passing through the vicinity of the subsolar point on the magnetopause (Daly et al. 1984).
Finally, although the solar wind-magnetosphere interaction intensifies for southward IMF orientations, this should not be taken as evidence for its complete absence on the dayside magnetopause for northward, even strongly northward, IMF orientations. The various component line reconnection models predict reconnection along highly tilted lines running across the dayside magnetopause even during these conditions, while Nishida (1989) predicted the occurrence of reconnection at random sites on the dayside magnetopause under similar circumstances. Observations seem to confirm these predictions. Fuselier et al. (2000) reported evidence for reconnection on the magnetopause equatorward of the cusps during intervals of northward IMF orientation. Contrary to expectations, these observations favored reconnection for nearly parallel magnetosheath and magnetospheric magnetic fields rather than sheared configurations. Chandler and Avanov (2003) reported evidence for a flux transfer event generated under similar circumstances.
Whether in the magnetotail or the magnetopause, reconnection is facilitated by diffusion regions, one for each ion species, and one for electrons. Since electrons are lighter and thus more easily magnetized, the question of how electrons become unmagnetized has galvanized a substantial amount of research. Even though we note that other ideas, particularly around the role of kinetic turbulence have been discussed, the following section presents a summary of a view held by a large part of theorists and modelers regarding the expected structure of the electron diffusion region.
8 Electron Diffusion Region Signatures
8.1 Introduction
Magnetic reconnection relies on the presence of a diffusion region, where collisionless or collisional plasma processes facilitate the changes in magnetic connection through the generation of dissipative electric fields. This diffusion region is strongly localized, extending at most to typical ion Larmor radii. In collisionless plasmas, collisions are sufficiently infrequent to provide the necessary dissipation on the time and spatial scales under consideration. Under this premise, the electron momentum equation can, in the absence of classical collisions, be derived from the Vlasov equations (e.g., Hesse and Winske 1994):
This expression shows that the nonideal mechanism has to be based either on thermal, i.e., pressure based (first term on right-hand-side (RHS) of (8.1)), or inertial effects (second term on RHS of (8.1)). Of these, the pressure based dissipation might rely on nongyrotropies of the distribution function (Vasyliunas 1975; Lyons and Pridmore-Brown 1990; Hesse and Winske 1993). Assuming here and in the following that the reconnecting magnetic field components lie in the x-y plane, the reconnection electric field becomes:
There are two important scenarios to investigate: “guide-field” magnetic reconnection, or anti-parallel magnetic reconnection.
8.2 Guide Field Reconnection
In principle, it is to be expected that the presence of a guide magnetic field, i.e., the presence of a magnetic field that is aligned with the current direction, may destroy the bounce motion of the electrons (and ions) in the inner dissipation region. For simplicity, we again focus on the electrons—similar results can readily be derived for the ions also.
Notionally, the effect of the guide magnetic field is noticeable if the Larmor radius in the guide magnetic field is less or equal to the bounce width in the reconnecting magnetic field component. The electron bounce width in the reconnecting magnetic field component B x is given by (Biskamp and Schindler 1971)
Electron orbits become strongly modified once the thermal electron Larmor radius r L =v the /Ω e equals the bounce width (8.3). After a small amount of algebra, one finds that this condition is equivalent to:
In a situation where B y exceeds the threshold (8.4), electron nongyrotropies need to be based on perturbations of the dominant Larmor motion about the guide magnetic field. In the wake of earlier results pertaining to electron thermal dissipation (Hesse et al. 1999, 2002; Pritchett 2001), Hesse et al. (2004) showed that magnetic reconnection with a guide field can produce scales substantially smaller than the local electron inertial length, and the pressure nongyrotropies remain dominant in providing the reconnection electric field. Hesse (2006) further discovered that electron distributions in the diffusion region are composed of a mixture of particles with different levels of acceleration. In fact, the diffusion region could be understood as a mixture of particles transiently encountering the reconnection electric field. In this way the inertia provided by these particles provides an effective balance to the accelerative force of the reconnection electric field.
Hesse (2006) suggested a gedankenexperiment, where the accelerative force of the reconnection electric field is turned off. Then the replenishment of lost accelerated particles would cease and the current layer would decay. We can assume that the decay would approximately follow some diffusion law:
The role of the reconnection electric field is to maintain the current density. Therefore, we expect:
or:
in the diffusion region. In the following we will use analytic theory to derive this expression including a functional form of the diffusion coefficient k.
Hesse et al. (2004) found that heat flux tensor effects had to be considered when calculating the pressure nongyrotropies in the electron diffusion region. In the immediate vicinity of the poloidal magnetic field reversal, the y-z component of the electron pressure tensor becomes:
Hesse et al. (2011) undertook a comprehensive analysis of the heat flux tensor evolution equation, and succeeded in identifying a suitable set of simplifying assumptions. After some lengthy calculation, they found:
Equation (8.9) offers interesting insight into the physics of the underlying reconnection process. Based on distribution function analysis we argued above that accelerated particles preferentially leave the reconnection region, whereas particles, which have, on average, been accelerated less tend to enter. In the absence of acceleration of the reconnection electric field the current density would therefore decay—which validates our gedankenexperiment above.
Comparison with (8.7) reveals that the coefficient k (analogous to a diffusion coefficient) is:
This expression shows the following. First of all, the square of the Larmor radius indicates that the electric field scales with the square of the ratio of critical length scale and Larmor radius in the guide field. Clearly, this implies that the actual current layer is close to the Larmor radius in thickness in order to facilitate an appreciable reconnection rate.
The velocity derivative in Eq. (8.10) is dimensionally an inverse time scale. This time scale is closely related to the average time a plasma element (or a particle) spends in the diffusion region, i.e., the time it is subjected to acceleration by the reconnection electric field. A short such residence time leaves little time for the reconnection electric field to accelerate in the y-direction and heat the plasma population. Consequently, the reconnection electric field is larger to satisfy the maintenance of current density and pressure. This physical expectation is mirrored exactly in the inverse dependence on the average particle residence time in (8.10).
It should be noted that the electron based electric field expression (8.9) may equally well be expressed through the ions, which exhibit similar dynamics, albeit on the larger scale of an ion Larmor radius—provided the guide field is strong enough. The result is the same as (8.9), but with an index and sign change.
8.3 Anti-parallel Reconnection
Hesse et al. (1999) investigated the effect of different electron masses on the collisionless dissipation process in the reconnection region for anti-parallel configurations. The target of the investigation was to study whether different physics in the diffusion region might lead to different dissipation, thereby influencing and potentially changing the larger scale behavior of the system under investigation. Hesse et al. approximated the reconnection electric field using bounce widths defined above:
Here the values of the pressure tensors are to be taken at the edges of the current sheet, where electrons begin to become magnetized. In these regions, the pressure tensor components can be approximated by (Kuznetsova et al. 1998):
and
Here the cyclotron frequencies are evaluated in the z and x components of the magnetic field, at the diffusion region boundary in the x and z direction, respectively. The two velocity derivatives are related via an approximate, incompressible, equation of continuity. By relating, e.g., \(B_{x} = B_{x}'\lambda_{z}\), a small amount of algebra leads to
for the electric field in the electron diffusion region.
Hesse et al. (2011) succeeded in showing that (8.14) can be cast into a quasi-diffusion form, similar to the corresponding expression for guide field reconnection. In particular, they found:
establishing a potential universal equation for the reconnection electric field.
Regardless of the actual dissipation mechanism, however, the diffusion region process has to satisfy a number of requirements (Hesse et al. 2009). In particular, the reconnection electric field has to fulfill the following functions:
-
1.
The reconnection electric field must sustain the current density in the diffusion region. Incoming plasma typically does not exhibit drift velocities, which support the current flow required by the external magnetic field. At the same time, losses through convection and outflow reduce the current density. The reconnection electric field thus serves to accelerate the incoming plasma such that sufficient current is flowing in the diffusion region.
-
2.
The reconnection electric field must heat the incoming plasma populations such that pressure balance with the outside system is maintained. The reconnection electric field must have this role in order to replace the convective loss of hot plasma through the reconnection outflow.
8.4 Expected Physical Dimensions of the Electron Diffusion Region
The universal equation:
where L is the electron bounce width, the local electron Larmor radius, or whichever other scale length may provide effective mixing of accelerated with not-yet accelerated particles, allows us to make predictions regarding the size of the diffusion region in the magnetosphere of the Earth.
For anti-parallel reconnection, likely to be predominant in the magnetotail, the bounce width (8.3) can be written:
where B xo is the value of the magnetic field at the edge of the electron current layer and be is to β e evaluated at the same location. Equation (8.17) demonstrates that the thickness of the electron diffusion region will be close to or somewhat smaller than the collisionless skin depth as β e ≤1 is a reasonable assumption for the edge of the diffusion region.
For typical magnetotail plasma densities of n e =0.01–0.1 cm−3, we therefore expect:
The lateral dimension ℓ x is more difficult to determine, as it self-consistently adjusts to the reconnection rate. However, for a typical reconnection rate of E=0.1, a good assumption would place the aspect ratio of the electron diffusion region to the same numerical value, yielding.
It should be noted that extraordinary condition, such as the superdense plasma sheet (Borovsky et al. 1997), may yield considerably smaller diffusion region sizes.
At the magnetopause, the above scaling will likely only apply in the rare event where reconnecting magnetic fields are very close to planar. More often, the local electron Larmor radius will be defining the diffusion region thickness. Estimates regarding typical plasma and magnetic field parameters vary significantly and depend strongly on solar wind conditions and the location of the reconnection region. As a sample, we will here a guide field magnitude of B y =20 nT, and an electron energy of E=100 eV, we find for the electron Larmor radius:
We note that substantially different values are possible as both guide field magnitudes and electron energies can vary widely.
Finally, we note that the above estimates are applicable primarily to symmetric reconnection scenarios. Despite a number of recent research activities (e.g., Mozer et al. 2011; Pritchett 2008a, 2008b; Swisdak et al. 2003a, 2003b), asymmetric reconnection remains poorly understood. Even though some recent results (Hesse et al. 2013) indicate that guide field magnetization may play an essential role here also, the underlying theoretical concepts are far less developed than what is presented here. Without a doubt, these will remain a focal point of research, and here, as well as in symmetric reconnection, MMS will provide both unprecedented ground truth and new insights.
One of the big challenges of magnetic reconnection research is to develop both sufficient understanding and technical capability to properly include kinetic reconnection effects into large-scale models, such as global MHD models, which describe the entire magnetosphere. The TM team has thus included a strong activity—described in the following section, which develops a modeling framework to facilitate the coupling between regional and large-scale models. The goal is to translate the scientific insight gleaned from MMS into an implementation, which will permit much more accurate modeling capabilities also on the larger, global scale for the magnetosphere.
9 Global MHD Modeling for MMS
Magnetic reconnection is at the core of a nested set of processes, which determine magnetospheric structure and dynamics. By combining Multiscale modeling of magnetospheric reconnection with the unprecedented observational capabilities of MMS we will significantly advance our understanding of the role of magnetic reconnection in cross-scale coupling and in large space weather events. Reconnection takes place on scales that are orders of magnitude smaller than the system size, yet they play a controlling role in global scale dynamics. The goal of our numerical simulations is to improve the description of magnetic reconnection in global space weather simulations by way of capturing the necessary cross-scale coupling in space plasma systems.
The richness of spatial and temporal scales represents a fundamental challenge in modeling magnetospheric reconnection. The most appropriate (and physically correct) methods to simulate space plasmas depend on the physical processes we want to include and the spatial scales we want to describe. Consequently, we need to address two unresolved challenges:
-
1.
Within a single integrated framework concurrently solve microphysics (kinetic description) and macrophysics (continuum description). The need to couple fluid and kinetic models is without doubt the most burning and crucial challenge not only for space weather modeling but also for many other aspects of computational physics.
-
2.
Resolve a wide range of spatial and temporal scales in a single integrated simulation.
The key to address the multiple scale challenge is the use of the most advanced algorithms to deal with the computational implementation of the proposed multi-scale, multiphysics simulations. We will use a combination of magnetofluid, hybrid and Particle-in-Cell (PIC) methods.
Global magnetospheric simulations have already significantly contributed to our understanding of magnetospheric physics. Global MHD simulations are solving conservation laws for the transport of mass, momentum, energy and magnetic flux. They are able to capture the large-scale configuration and dynamics of the magnetosphere. Figure 18 shows an example of global magnetosphere simulation for one of the biggest space weather, the Halloween storms.
Three-dimensional structure of the magnetosphere during the Halloween storms 1 hour after the shock arrives at the Earth (0700 UT on October 29, 2003). The colored tubes show the last-closed magnetic field lines. The color contours on the planes are electric current density. The 100 nPa pressure isosurface that intersects this boundary is shown in dark red. The figure also shows the locations of magnetospheric satellites (Toth et al. 2007)
9.1 Study of Dayside Reconnection
A long standing fundamental question in magnetospheric physics is “To what extent are the properties (location, intensity, etc.) of reconnection driven by external boundary conditions as opposed to internal instabilities?” We will carry out a series of controlled numerical experiments varying solar wind parameters and investigate the onset and evolution of reconnection in the dayside magnetopause and cross-tail current layer.
Using a coupled kinetic/magnetofluid model at the dayside magnetopause, we will run a variety of idealized solar wind IMF input conditions to measure the locations and rates of reconnection as a function of IMF direction and magnetosheath plasma beta. Global maps of reconnection location will be made as a function of IMF direction for a range of solar wind/magnetosheath conditions to explore the nature of magnetopause reconnection, the interplay between antiparallel and component reconnection and the formation and motion of flux transfer events. These investigations will guide the interpretation of MMS observations.
9.2 Study of Magnetotail Reconnection
Using actual solar wind and IMF data as input to the coupled kinetic/magnetofluid global magnetosphere model, we will investigate the time history of mass, momentum and energy flow into the magnetosphere and its effect on the development of reconnection and storm and substorm dynamics in the magnetotail. The coupled kinetic/magnetofluid tail model will allow resolution of the very poorly understood, complex, highly time dependent changes that the thinned cross-tail current sheet undergoes leading up to the onset of fast reconnection (Karimabadi et al. 2004; Raeder et al. 2010; Pritchett and Coroniti 2011; Sitnov and Schindler 2010; Sitnov and Swisdak 2011; Vapirev et al. 2013). Once reconnection commences, this new tail model will allow the effects of the time dependent growth in the length of the X-line, only captured to date in highly restricted regions, upon the entire tail to be recovered. This will allow the first meaningful investigations of the factors controlling the thinning of the plasma sheet and growth and final width of the fast bursty bulk flow (BBF) channels that transport plasma and magnetic flux to the inner magnetosphere (Angelopoulos et al. 1994; Slavin et al. 1997) and the dawn-dusk asymmetries in the location where reconnection commences (Slavin et al. 2005). We will also investigate the interaction of reconnection regions during formation of multiple X-lines as well as the topology and structure of BBFs and flux ropes.
The kinetic/magnetofluid code with Hall physics should allow, for example, tracking of the entropy of the individual flux tubes convecting sunward out of the tail and the effect of their “buoyancy” relative to adjacent flux tubes on their ability to be transported into the inner magnetosphere (Wolf et al. 2006). Once this code is coupled to the various inner magnetosphere models (such as the radiation belt and ring current models), we will investigate the role of reconnection flows on the dynamics and energy state of the inner magnetosphere.
9.3 Magnetospheric Impacts
The transient and unbalanced reconnection on the dayside and nightside of the magnetosphere leads to a system-wide evolution of geospace topology (e.g., Dungey 1961; Lundin and Dubinin 1985; Milan et al. 2007). There is also significant nonlinear feedback within geospace, with the conditions within the magnetosphere-ionosphere-thermosphere system altering the expected progression of the disturbed-time activity (e.g., Jaggi and Wolf 1973; Ridley et al. 2004; Liemohn et al. 2005). It is known that there are nonlinear limitations on the electric potential imposed on geospace (e.g., Siscoe et al. 2002; Kivelson and Ridley 2008; Brambles et al. 2011; Welling and Zaharia 2012), and the timing and intensity of substorms is related to internal conditions within geospace (Lui 2001; Milan 2009). A hysteresis effect has been reported in the energy supply to the magnetosphere (Palmroth et al. 2006), and many studies have been devoted to the difference in magnetospheric response to different types of solar wind driving (e.g., Tsurutani and Gonzales 1997; Denton et al. 2006; Lu 2013; Borovsky and Denton 2006; Liemohn and Jazowski 2008; Turner et al. 2009).
MMS will address several specific questions regarding the flow of mass and energy through the geospace system. First, we will resolve the relative contributions of potential and inductive electric field control of the large-scale plasma flow (e.g., Katus et al. 2013). The Multiscale simulations will allow for a more realistic descriptions of rapid magnetic distortions, which will allow for a quantitative assessment of these two electric field terms on plasma sheet and ring current dynamics. This will allow for a robust analysis of space weather conditions and impacts within geospace.
9.4 Energetic Particle Transport
A consequence of magnetospheric magnetic reconnection is the acceleration of charged particles. Electrons in particular are energized by the reconfiguration of the magnetic field at X-lines and in the surrounding separatrices reaching energies of 0.1–10 MeV (Kirsh et al. 1980; Richardson et al. 1996; Øieroset et al. 2004). More recent theoretical studies have suggested that these electrons may be adiabatically accelerated while trapped in plasmoid or flux rope structures in the plasma sheet which are contracting (Drake et al. 2006) or interacting with slow shocks emanating from X-lines (Hoshino et al. 2006). In the inner magnetosphere betatron processes accelerate the ions and electrons as they adiabatically gain energy at depolarization fronts and while being convected sunward from the weaker magnetic fields in the near-tail to the stronger magnetic fields in the inner magnetosphere. We plan to study the influence of dayside and nightside reconnection on the flow of energetic particles through the magnetosphere.
9.5 Simulation Tools
The main elements of our global simulations in support of the MMS mission are the following:
SWMF
The foundation for the proposed investigation is our Space Weather Modeling Framework (SWMF) (Toth et al. 2005, 2012), a fully functional, documented technology that provides a high-performance computational capability to simulate the space-weather environment from the sun to the Earth. Figure 19 shows the present structure of the SWMF. There are about a dozen components or physics domains represented by the red boxes. The SWMF has a layered architecture. The top layer is an optional graphical user interface. The second layer contains the control module, which is responsible for distributing the active components over the parallel machine, executing the models, and coupling them at the specified frequencies. The third layer contains the physics domain components. Each component can have multiple versions. Each component version consists of a physics model with a wrapper and one or more couplers. The wrapper is an interface with the control module, while each coupler is an interface with another component. The physics models can also be compiled into stand-alone executables. The fourth and lowest layer contains the shared library and the utilities that can be used by the physics models as well as by the SWMF core.
BATS-R-US
The BATS-R-US code (Powell et al. 1999; Toth et al. 2012) plays a central role in the SWMF. It is a versatile, high-performance, generalized magnetohydrodynamics code with AMR that can be configured to solve the governing equations of ideal and resistive MHD, semi-relativistic, Hall, multispecies and multi-fluid extended magnetofluid equations (XMHD) and most recently XMHD with anisotropic ion pressure. BATS-R-US is used to model several physics domains (see Fig. 20). The state variables of the equation system are defined by the equation modules, while the rest of the application dependent details are implemented into user modules. There are currently 37 equation modules and 42 user modules (obviously not all combinations are possible) which means that BATS-R-US can be configured for quite a few different applications. The major features of BATS-R-US are summarized in Fig. 20.
iPIC3D (Markidis et al. 2010)
is a 3D implicit PIC code. It solves the full set of Maxwell’s equations for the electromagnetic fields, coupled with the equations of motion for electrons and ions on 3D Cartesian grids. It is based on the implicit moment (IMPiC) formulation of the kinetic model that allows us to select the local level of resolution according to the scales of the local processes (Brackbill and Forslund 1982). The IMPiC method solves the plasma moment and Maxwell’s equations self-consistently using implicit time integration (Brackbill and Forslund 1982, 1986; Lapenta et al. 2006; Brackbill and Lapenta 2008). Implicit differencing extends plasma simulations to larger scales and longer times while retaining the contributions of kinetic electrons (Mason 1981; Denavit 1981; Brackbill and Forslund 1982; Langdon et al. 1983). The solutions give good approximations to the fields that would have resulted from taking into account kinetic particle motions. The implicit moment method can be run as a hybrid code when only the resolution at the ion-scale is desired (Lapenta and Brackbill 1996; Cohen et al. 2010). Hybrid simulations model a plasma with kinetic ions and fluid electrons. Typically, the electron fluid model comprises an Ohm’s law and an equation of state. Electron mass is assumed to be negligible, the plasma is charge neutral, and a resistivity is included to remove a singularity. IMPiC becomes a hybrid code when the electron moment solutions are not replaced by particle data at the end of each cycle. In support of MMS we will take advantage of the flexible simulation capabilities of iPIC3D. It will be coupled to SWMF both as a PIC and a hybrid code and it will give the users the option to use it in either mode.
AMPS
Simulating the motion of test particles in electric and magnetic fields is a capability that can be used for a variety of studies ranging from shock acceleration to the energization of particles in the magnetosphere and the entry of solar wind to the magnetosphere. This module simultaneously tracks a large number of particles as they move in the time-varying electric and magnetic fields. In order to ensure good statistics, the particle tracker is able to follow about 109 particles on ∼103 cores. The Adaptive-Mesh-Particle-Simulator (AMPS) (Tenishev et al. 2008) is a Monte Carlo particle model that solves the motion of a large number of test particles. The collision model incorporated into AMPS makes it applicable to study collision-dominated as well as collisionless plasmas. Adaptive mesh refinement (AMR), variable particle weight, and local time stepping methodologies make the code useful in simulations that involve physical processes characterized with significantly different time and spatial scales. The parallel implementation of the code includes both static and dynamic load balancing, which allows us to perform simulations using high performance supercomputers. One of the unique features of the code is the direct run-time access of AMPS to SPICE routines, which is needed to simulate distribution functions observed by individual instruments.
Guided by the MHD picture, magnetic reconnection is expected to involve raising entropy in some form, i.e., to be irreversible. While this association is easy to make in MHD, kinetic plasmas present substantial challenges. While a number of proposals have involved mixing of particle populations, or strong dependence of particle orbits on initial conditions, a comprehensive answer remains illusive. The following section explores the idea that reconnection should involve some kind of nonideal energy conversion—an approach, which offers the additional benefit of being valuable for identifying a reconnection region.
10 Dissipation Measures
At the core of magnetic reconnection is a nested set of diffusion regions, ranging in size from scales associated with the most massive ions involved in the process down to those associated with electrons. Electrons are most difficult to disconnect from the magnetic field they are frozen to; the identification of the electron diffusion region (EDR) where this takes place is therefore very important for the MMS mission. Without accurate identification, it will not be able to deliver the high-resolution EDR data to the ground with top priority. It has been thought that the EDR is identified by the violation of the electron ideal condition, E+v e ×B≠0, but recent researches have revealed that the nonidealness is not a good marker of the EDR. This is because the nonidealness is necessary but not sufficient for breaking the magnetic field lines. Several alternative markers have been proposed such as an agyrotropy, the asymmetry of the electron transverse pressure (Scudder and Daughton 2008).
Let us first examine the literal meaning of the EDR. The term “diffusion region” originally comes from magnetic diffusion in the resistive MHD. A constant uniform resistivity brings a diffusion term in the induction equation,
where V is the MHD velocity. Inside the EDR, we expect similar diffusion of magnetic flux with respect to the electron flow velocity, v e . In analogy to Eq. (10.1), we consider
where the last term contains all the electron kinetic effects. If diffusion-like effects take place, we expect the following relation,
except for singular points. This is the violation of the flux preservation condition (Newcomb 1958). One can see that the nonidealness E+v e ×B≠0 does not always lead to the diffusion of magnetic field lines.
Here we introduce a measure to identify the EDR, from a different viewpoint of energy conversion. In the resistive MHD, the energy transfer from the field to plasmas can be decomposed in the following way (Birn and Hesse 2005),
The terms in the right hand side stand for the work rate by the Lorentz force and Ohmic dissipation D=η j 2≥0. In a kinetic plasma, in the simplest neutral case, the Ohmic dissipation term is replaced by D=j⋅(E+v e ×B). This reads a product of an electric current density in the observer’s frame (j) and the electric field in the comoving frame of the electron bulk flow (E+v e ×B).
Let us advance this idea. Evaluating both two quantities in the comoving frame of electrons, we obtain the energy transfer in the electron frame. This leads to a generalized electron-frame dissipation measure (Zenitani et al. 2011),
This is frame-independent even in a relativistic non-neutral plasma. The Lorentz factor γ e ≈1 and the last term on the right hand side are negligible in the Earth’s magnetosphere. This measure can be either positive or negative, however, in our experience, it tends to be positive in a time-averaged sense. This suggests that the measure could be related to the irreversible energy conversion from the electromagnetic energy to the plasma energy. Since D e is related to the magnetic dissipation by nonideal energy conversion, it would be more appropriate to call the region “dissipation region (DR),” rather than the EDR.
Figure 21 demonstrates the D e measure in PIC simulations without [with] a guide-field. Quantities are averaged over a short interval (a fraction of \(\varOmega_{ci}^{ - 1}\)) to remove electron-scale kinetic noises. The measure is positive in compact regions about the X-line. In the energy balance, these localized regions play a similar role as a localized dissipation region in the MHD. The length and width of the regions are on the electron kinetic scale. The ion counterpart of D e gives similar electron-scale pictures, as mentioned by Zenitani et al. (2011).
The D e measure was recently applied to Geotail observation of a reconnection event in the magnetotail (Zenitani et al. 2012). The left panel of Fig. 22 shows plasma perpendicular velocities (blue for ions and red for electrons). Both of them reverse their signs around the possible X-line at 1055:44 UT. The measure is computed in an approximate form (gray histogram) for magnetotail-like configuration. As indicated by the arrow, one can see a compact DR around the flow reversals. The observed picture is in good agreement with a profile in 2D PIC simulation in the right panel of Fig. 22.
(a) Geotail observations on 15 May 2003. Ion perpendicular velocity (blue), electron perpendicular velocity (red), and an approximate dissipation measure (gray) are presented. (b) The same quantities in a PIC simulation. Reproduced from Zenitani et al. (2012)
Using MMS’s high-resolution data, we hope to see a clearer picture of the DR, so that we can understand the breaking mechanism of field lines.
This dissipation measure applies to both symmetric and asymmetric reconnection configurations. We know even now that there are notable differences between these two scenarios. Also because MMS will begin its scientific journey at the magnetopause, it is of value to review what we know about the theory of asymmetric reconnection. This is the topic of the following section.
11 Studying Asymmetric Magnetic Reconnection at Earth’s Magnetopause with MMS
Magnetic reconnection manifests itself in very different ways in the magnetotail and at the dayside magnetopause. In particular, in the magnetotail, the lobe magnetic field strengths and the densities of the plasmas are often very similar, so reconnection is “symmetric”; in contrast, reconnection at the dayside magnetopause is usually marked by strong asymmetries in magnetic field strengths and plasma densities. In this section, we discuss puzzles about asymmetric reconnection that MMS will help solve, and how theoretical studies of reconnection will help MMS identify dayside reconnection.
The dissipation region in asymmetric reconnection is sketched as the dotted rectangle in Fig. 23. The magnetic fields B and densities ρ in the upstream regions are denoted with “1” and “2” subscripts, which refer to the magnetospheric and magnetosheath sides of the dissipation region for reconnection at the dayside. In asymmetric reconnection |B 1|≠|B 2| and/or ρ 1≠ρ 2. For example, typical magnetospheric conditions at the dayside are magnetic fields of about 50 nT with a density of about 0.5 cm−3, while magnetosheath conditions vary considerably with solar wind conditions but are often between 20–30 nT with a density of 20–30 cm−3 (Phan and Paschmann 1996). A vast majority of dayside reconnection is asymmetric (Mozer and Retinó 2007). Understanding asymmetric reconnection, in particular at the dayside magnetopause, is important for developing a predictive understanding of space weather. Reconnection at the dayside plays a critical role in the coupling of solar wind plasma to the magnetosphere, which affects magnetospheric convection and the associated dynamics of the radiation belts. The energy transferred to the magnetopause ends up in the magnetotail which gets released by substorms and transient events, which drive aurora and potentially deleterious space weather effects.
Sketch of the dissipation region during asymmetric magnetic reconnection. Reprinted from Cassak and Shay (2007)
Much has been learned both observationally and theoretically about asymmetric reconnection at the large scales (ion scales and larger), and how it differs from symmetric reconnection; the present focus is on theoretical contributions. Early studies concentrated on structures at the largest scales, namely the structure of shocks that border the outflow jet (Levy et al. 1964). It was argued that slow shocks bound the exhaust in symmetric reconnection (Petschek 1964), and many studies addressed how asymmetries affect the shock structure (Petschek and Thorne 1967; Sonnerup 1974; Semenov et al. 1983; Heyn et al. 1988). Recent studies have found that kinetic effects alter the simple Petschek slow shock picture from fluid theory for symmetric reconnection (Karimabadi et al. 1995; Liu et al. 2011). How kinetic effects alter the shock structure of asymmetric reconnection remains an open question.
More recent studies addressed the efficiency of asymmetric reconnection and the effect of asymmetries on the structure of the dissipation region at or near ion scales. A classical Sweet-Parker (Parker 1957) control volume analysis based on conservation laws was implemented for asymmetric systems (Cassak and Shay 2007), revealing that the outflow speed goes from being the Alfvén speed based on upstream fields and densities to a hybrid Alfvén speed (see also Swisdak and Drake 2007a, 2007b). The rate of reconnection goes from being a product of the upstream field and the Alfvén speed to a product of a hybrid magnetic field and a hybrid Alfvén speed. These results have been tested in many studies (Borovsky and Hesse 2007; Birn et al. 2008; Cassak and Shay 2008; Malakit et al. 2010). The effect of compression was later included (Birn et al. 2010). For the dissipation region, in symmetric reconnection the X-line (where the magnetic field changes directions) and the stagnation point (where the inflow stops) are at the same point, but in asymmetric reconnection the two points are not colocated (Cassak and Shay 2007, 2009). Many previous observational studies had observed this effect.
At the scale of the electrons, a major question of import both to understanding reconnection and to identifying reconnection sites with MMS is “What are the physical characteristics that define the electron dissipation region?” This is especially important for asymmetric reconnection at the dayside where the structure of the dissipation is modified by asymmetries. A number of candidate measures of the diffusion region have been employed, but most do not faithfully find the electron dissipation region in numerical simulations (Pritchett and Mozer 2009a). As a result, a new measure was determined, and it was shown to be effective for both symmetric and asymmetric reconnection (Zenitani et al. 2011).
What will MMS help to answer about reconnection in general, and asymmetric reconnection in particular? The unprecedented spatial and temporal resolution that MMS will afford will make measurements of the substructure (at electron scales) of the dissipation region possible. A result of this will be a determination of how fast reconnection proceeds and the relation of the rate to the nearby plasma parameters. Other questions include the following: How does the asymmetry present at the dayside affect the acceleration and heating of particles by the reconnection process? What physically happens on electron scales in the dissipation region to allow magnetic reconnection to occur, and can an asymmetric system such as the dayside be a test case for theories that could not otherwise be tested in symmetric systems? What are the ramifications of the non-colocation of the X-line and stagnation point on magnetosheath particle transport into the magnetosphere? By getting a better understanding of these questions, the capability to determine the how reconnection impacts magnetospheric convection and the effect of energetic particles within the magnetosphere can be addressed.
How can theory and observations be used in the run-up to MMS to help MMS be successful? Simulation studies make predictions of what signatures to look for to identify dissipation regions. Two-dimensional fully kinetic particle-in-cell (PIC) simulations have been useful in this regard. For example, asymmetries alter the structure of the Hall electric and magnetic fields (Karimabadi et al. 1999a, 1999b; Pritchett 2008a, 2008b; Mozer et al. 2008; Malakit 2012). Diamagnetic effects make reconnection slower and possibly stop and make the reconnection site move (Swisdak 2003a, 2003b). A dip in density on the magnetospheric side of the dissipation region was seen both in simulations and observations (Tanaka et al. 2008). Electrons are unmagnetized predominantly on the magnetospheric side of the dissipation region (Pritchett and Mozer 2009a). Pressure anisotropies of electrons near asymmetric reconnection sites have been studied (Egedal et al. 2011). There is an in-plane electric field in asymmetric reconnection that is not present in symmetric reconnection (Malakit et al. 2013). Many studies of asymmetric reconnection assumed perfectly anti-parallel magnetic fields undergoing reconnection, but reconnection at the dayside is likely to have a “guide” magnetic field normal to the plane of reconnection. Recent efforts (Pritchett and Mozer 2009b). Tanaka et al. (2010), Aunai et al. (2013), Hesse et al. (2013) have addressed the effect of a guide field. Efforts are now being made to study three-dimensional asymmetric reconnection in PIC simulations. For example, the three-dimensional structure of the electric fields (Pritchett et al. 2012) and the excitation of the lower-hybrid drift instability by the density gradient in asymmetric reconnection (Roytershteyn et al. 2012) have recently been studied.
The MMS mission provides an excellent opportunity to study electron scale physics of magnetic reconnection. The differences between reconnection in the magnetotail and dayside reconnection due to the asymmetries provide a natural technique to test models and determine ramifications of reconnection in multiple settings.
Electron nongyrotropy is expected to play a key role in the electron diffusion region. It is hence of value to define a measure of nongyrotropy, based on first principles, and independent of the selected coordinate system. The topic of the following section is the derivation of the, to-date, most general way of defining electron nongyrotropy.
12 Electron Nongyrotropy in the Context of Collisionless Magnetic Reconnection
Collisionless magnetized plasmas tend to have velocity distribution functions locally symmetric around the magnetic field direction, i.e. to be gyrotropic. In this case, the symmetry implies that the pressure tensor P s of the population s can be written
where P ∥=bPb is the thermal pressure along the magnetic field direction given by the unit vector \(\mathbf{b}, \mathrm{P}_{\bot} = E_{ths} - \mathrm{P}_{|} /2 = (\operatorname{Tr}(\mathbf{P}_{s})-P_{\parallel})/2\) with E ths the thermal energy. Although gyrotropy is generally observed, nongyrotropic distributions are also sometimes met. They are the consequence of either temporal or spatial inhomogeneities on the order of the particle Larmor scale, and a proxy of regions where the bulk of the species is not magnetized. Magnetic reconnection is one of the most important plasma process involving nongyrotropic distributions, of both ions and electrons. In the region surrounding the reconnection site in particular, electrons need to be demagnetized for reconnection to occur and a significant electron nongyrotropy is then expected. Reconnection also create sharp connectivity boundaries between the reconnected flux and the not-yet-reconnected flux, where nongyrotropy might also appear. This work aims in understanding in what regions electron nongyrotropies develop in the context of collisionless magnetic reconnection, what is the kinetic origin of the observed nongyrotropies and how do these regions relate to the fluid behavior of the electrons. In the context of preparation to the analysis of the NASA/MMS data, we use data from fully kinetic simulations to address these questions.
12.1 Measuring the Degree of Nongyrotropy
A prerequisite to characterizing nongyrotropic regions is to actually have a reliable way of quantifying how much nongyrotropic a velocity distribution function is, with respect to another. We propose a new way to quantify the degree of nongyrotropy based on the knowledge of the full distribution function, as opposed to previous methods, using limited information based on symmetries (Scudder and Daughton 2008). The full pressure tensor P s of a particle species s can always be decomposed as P s =G+N, where N defines the nongyrotropic part of the full pressure tensor P s . Physically, G represents the pressure tensor of a virtual gyrotropic distribution function that would have the same thermal energy as the real distribution, from which N can be seen as the deviation. A natural choice for the degree of nongyrotropy is to calculate the Frobenius norm of N, which in the case of a real symmetric tensor is given by \(\sqrt{(\sum_{i} \lambda_{i}^{2})}\), where λ i are the eigenvalues of the tensor N. Although the 3×3 eigenvalue problem is easily solved analytically and thus leads to a vectorized algorithm, one can show the Frobenius norm can also be written as \(\sqrt{(\sum_{ij} N_{ij}^{2})}\), which leads to even faster computations. The local degree of nongyrotropy D ng is obtained by normalizing this norm by the local thermal energy E ths . We obtain,
We model symmetric collisionless magnetic reconnection using a 2.5D partially implicit fully kinetic simulation code (Hesse et al. 2011). The data presented here is normalized to the usual ion scale quantities. The initial state is a simple Harris-like configuration, where the magnetic field is given by B=tanh((z−z 0)/L)e x , where L=0.5 and z 0 is the simulation mid-plane. The density is n(z)=0.2+1/cosh2((z−z 0)/L). The plasma temperature is constant so is the electron to ion temperature ratio T e /T i =0.2. The electron to ion mass ratio is m e /m i =100 and the ratio between the electron plasma frequency and the electron cyclotron frequency is ω pe /Ω ce =4. The domain size is L x =64 and L z =30 in the downstream and upstream directions, respectively, represented by (n x ,n z )=(4096,1600) cells. The downstream boundaries are periodic and the upstream ones reflecting perfect conductors. A centered and localized perturbation is used to trigger magnetic reconnection. Figure 24 shows, in color, the degree nongyrotropy D ng obtained from the simulation. One can see D ng ≈0 in almost all regions except in a narrow band around the midplane extending from x≈24 to x≈40. The upper right panel of Fig. 24 represents a zoom in the area surrounding the X line and delimited by the white rectangle. This zoom reveals the nongyrotropic layer is slightly thicker than the electron bounce width represented on the figure by the two solid black lines and defined as the location where the distance from the neutral line (B x =0) equals the local thermal Larmor radius, based on a local proxy of the temperature \(\operatorname{Tr}(\mathbf{P}_{e})/(3n_{e})\), where n e is the local electron density. The grey solid lines represent the contours of this local thermal Larmor radius and indicate it is much smaller where the nongyrotropy is maximum, probably resulting from the inconsistency between this isotropic electron temperature proxy and the real shape of the (nongyrotropic) distribution. Let us remark that, overall, nongyrotropic regions do not locate the X line region specifically nor they map topological boundaries (separatrices).
Color representation of the nongyrotropy D ng . The dashed gray lines represent the in-plane magnetic field lines. The upper right panel corresponds to a zoom in the reconnection site region where solid gray lines represent the isocontour of the thermal electron Larmor radius, which values are indicated in red. The two solid black lines represent the thermal electron bounce width. The left panel is a zoom in the region inside the white rectangle at x=29. It shows, as small white rectangles, the 6 boxes where particles are selected to make the distribution in Fig. 25
12.2 Kinetic Origin of the Nongyrotropy
Analyzing the velocity distribution functions of the particles picked in the small white rectangles of the left panel of Fig. 24 reveals the kinetic origin of the observed nongyrotropy. From bottom to top, distributions are labelled a to f and are shown in Fig. 25 in a projection onto the plane (V y ,V z ) which shows the most significant variation. Distributions a to d span from outside to inside the reconnection exhaust, and although most are clearly anisotropic, they are well fitted by a gyrotropic ellipse which axis is mostly unchanged; their bulk velocity is close to the E×B drift speed. Distributions e and f are evaluated within the nongyrotropic region. Their shape evolves into a mixing of counterstreaming electrons and is not fitted anymore by the gyrotropic ellipse, which axis rotate with the magnetic field and eccentricity changes with the shape of the distribution.
Velocity distribution functions in the plane (v y ,v z ). Distributions a to f are associated to the white rectangles on the left panel of Fig. 1, from bottom to top. The grey intensity represents the number of macroparticles in the velocity bin. The blue circle represents the in-plane E×B/B 2. The red dashed horizontal and vertical lines indicate the position of the average in-plane velocity which direction is also indicated by the red arrow. The solid green line represents V y =V z =0. The purple arrow represents the direction of the in-plane (B y ,B z ) magnetic field, and the axis of the yellow ellipse correspond to the three times the thermal velocities parallel and perpendicular to the magnetic field
12.3 Nongyrotropic Regions as Seen from the Fluid Viewpoint
It is instructive to look at the fluid signatures in the regions of high nongyrotropy. Figure 26 consists of four panels, showing, from top to bottom, the degree of nongyrotropy D ng , the electron bulk velocity in the x direction V ex , the same component of the electron bulk velocity to which has been subtracted the x component of the electromagnetic E×B/B 2 and diamagnetic drift velocities, and finally a measure of non-ideal energy transfer (Zenitani et al. 2011) D e =j⋅(E+v×B)−ρ v e ⋅E. Consistently with several previous studies (Karimabadi et al. 2007; Hesse et al. 2008; Zenitani et al. 2011; Shay et al. 2007), we observe an elongated electron jet layer. The jet disappears when the electromagnetic and diamagnetic drift velocity are subtracted. This v ex bulk flow is associated with the current sustaining the reversal of the Hall quadrupolar and out-of-plane component of the magnetic field (Hesse et al. 2008), which consistently stops at the same locations x≈24 and x≈40. The non-ideal energy transfer occurs only in the internal part of the layer, consistently with previous studies (Zenitani et al. 2011). The clear evolution in the electron fluid behavior as one gets away from the X line is however not reflected in a variation of the degree of nongyrotropy seen in Fig. 24, which stays roughly uniform. In other words, a significant degree of nongyrotropy does not seem to be a proxy of a specific fluid behavior. On the other hand, a specific fluid behavior like the diamagnetic drift, often presented in textbooks as the result of gyrating particles in an inhomogeneous plasma pressure, may be a degenerate macroscopic viewpoint of multiple kinetic mechanisms, including significantly nongyrotropic ones.
From top to bottom: The degree of nongyrotropy already shown in Fig. 24 is reported here for comparison with other panels. The second panel shows the electron bulk velocity v ex . The third panel shows v ex from which has been subtracted the x component of the electromagnetic E×B/B 2 and diamagnetic drift velocities. The fourth panel shows a measure of non-ideal energy transfer D e =j⋅(E+v×B)−ρ v e ⋅E. The bottom panel shows the out-of-plane magnetic field component. For each panel, the snapshot is made at t=30 and the solid lines represent the in-plane magnetic field lines
12.4 Conclusion
We have presented a new method to measure the degree of nongyrotropy based on the full distribution function of a given plasma species. We focused on the electrons, and revealed the regions where significant nongyrotropy can be expected to be measure by in situ spacecraft. Nongyrotropic electron distributions are observed both at the X line, sustaining the reconnection electric field, and in the electron outflow, and result from the mixing of several demagnetized electron populations. Nongyrotropic distributions cannot be associated to a specific fluid behavior as they are they are observed in both the dissipative region and the diamagnetic current layer sustaining the magnetic field reversal. Besides, the X line itself or the separatrices are not the location of specifically enhanced nongyrotropy. The rareness of regions with significant degree of nongyrotropy for the electrons however still make their localization in numerical models and correlation with other observable quantities interesting, as they can surely help in a better identification/characterization of spatial structures in spacecraft data. The NASA Magnetospheric Multiscale mission will have the resolution to measure electron scale variations of the pressure tensor, which makes the degree of nongyrotropy measurable.
13 Summary
The Magnetospheric Multiscale mission offers an unprecedented opportunity to dive deep into the scientific foundations of arguably the most important plasma process in existence: magnetic reconnection. Owing to the complexity of this process, traditional spacecraft-based investigations of magnetic reconnection have been confined to research of the associated larger scale features, with resolution down to at most ion kinetic scales in missions such as GEOTAIL and CLUSTER. Understanding magnetic reconnection requires much higher time and spatial resolution than what was possible before MMS.
The lack of empirical knowledge at these small scales mandated early on a tight integration of mission planning and development with the latest theoretical and modeling predictions of the basic mechanisms underlying magnetic reconnection, as well as with the latest insights into associated turbulent and particle acceleration processes. This function has been and continues to be provided by the MMS Theory and Modeling Team.
The Theory and Modeling team has thus, among many results, provided measurement requirements for particle and field instrumentations, has provided analysis tools for recognizing magnetic and electric field geometry during the mission data analysis phase, has predicted signatures in energetic particle measurements, has developed general means to identify diffusion regions, and, even today, updates information based on recent research advances. This integrative approach to mission planning, and, after launch, to mission execution is both new and innovative, and MMS is likely to demonstrate the highly efficient synergy between mission planning, data analysis, and accompanying theory and modeling.
References
S.-I. Akasofu, Polar and Magnetospheric Substorms (Springer, New York, 1968)
I.I. Alexeev, D.G. Sibeck, S.Y. Bobrovnikov, J. Geophys. Res. 103 (1998)
V. Angelopoulos, W. Baumjohann, C.F. Kennel, F.V. Coroniti, M.G. Kivelson, R. Pellat, R.J. Walker, H. Lühr, G. Paschmann, J. Geophys. Res. 97 (1992)
V. Angelopoulos, C.F. Kennel, F.V. Coroniti, R. Pellat, M.G. Kivelson, R.J. Walker, C.T. Russell, W. Baumjohann, W.C. Feldman, J.T. Gosling, J. Geophys. Res. 99 (1994)
S.K. Antiochos, C.R. DeVore, J.A. Klimchuk, A model for solar coronal mass ejections. Astrophys. J. 510, 485 (1999)
R.L. Arnoldy, J. Geophys. Res. 76 (1971)
A.V. Artemyev, M. Hoshino, V.N. Lutsenko, A.A. Petrukovich, S. Imada, L.M. Zeleny, Ann. Geophys. 31 (2013)
G. Atkinson, Field-line merging and slippage. Geophys. Res. Lett. 5, 465 (1978)
M.P. Aubry, R.L. McPherron, J. Geophys. Res. 76 (1971)
M.P. Aubry, M.G. Kivelson, C.T. Russell, J. Geophys. Res. 76 (1971)
N. Aunai, M. Hesse, M. Kuznetsova, Electron nongyrotropy in the context of collisionless magnetic reconnection. Phys. Plasmas 20(9), 092903 (2013). doi:10.1063/1.4820953
W. Baumjohann, G. Paschmann, H. Lühr, J. Geophys. Res. 95 (1990)
J. Birn, M. Hesse, Ann. Geophys. 23 (2005)
J. Birn, M. Hesse, Ann. Geophys. 27 (2009)
J. Birn, M.F. Thomsen, M. Hesse, Phys. Plasmas 11 (2004)
J. Birn, J.E. Borovsky, M. Hesse, Phys. Plasmas 15 (2008)
J. Birn, J.E. Borovsky, M. Hesse, K. Schindler, Phys. Plasmas 17 (2010)
J. Birn, R. Nakamura, E.V. Panov, M. Hesse, J. Geophys. Res. (2011). doi:10.1029/2010JA016083
J. Birn, A.V. Artemyev, D.N. Baker, M. Echim, M. Hoshino, L.M. Zelenyi, Space Sci. Rev. (2012). doi:10.1007/s11214-012-9874-4
J. Birn, R. Nakamura, E.V. Panov, M. Hesse, S. Zaharia, J. Geophys. Res. (2013). doi:10.1002/jgra.50132
D. Biskamp, K. Schindler, Plasma Phys. 13 (1971)
J.E. Borovsky, M.H. Denton, J. Geophys. Res. (2006). doi:10.1029/2005JA011447
J.E. Borovsky, M. Hesse, Phys. Plasmas 14 (2007)
J.E. Borovsky, M.F. Thomsen, D.J. McComas, J. Geophys. Res. 102 (1997)
K. Bowers, H. Li, Phys. Rev. Lett. 98 (2007)
J.U. Brackbill, D. Forslund, J. Comput. Phys. 46 (1982)
J.U. Brackbill, D.W. Forslund, Simulation of low-frequency electromagnetic phenomena in plasmas, in Multiple Time Scales (Academic Press, New York, 1986)
J.U. Brackbill, G. Lapenta, Commun. Comput. Phys. 4 (2008)
O.J. Brambles, W. Lotko, B. Zhang, M. Wiltberger, J. Lyon, R.J. Strangeway, Science 332 (2011)
A. Brandenberg, Astrophys. J. 550 (2001)
M.N. Caan, R.L. McPherron, C.T. Russell, J. Geophys. Res. 78 (1973)
P.A. Cargill, J.A. Klimchuk, A nanoflare explanation for the heating of coronal loops observed by Yohkoh. Astrophys. J. 478, 799 (1997)
P.A. Cassak, M.A. Shay, Phys. Plasmas 14 (2007)
P.A. Cassak, M.A. Shay, Geophys. Res. Lett. 35 (2008)
P.A. Cassak, M.A. Shay, Phys. Plasmas 16 (2009)
M.O. Chandler, L.A. Avanov, J. Geophys. Res. (2003). doi:10.1029/2003JA009852
L.-J. Chen et al., Nat. Phys. 4 (2008a)
L.-J. Chen et al., J. Geophys. Res. (2008b). doi:10.1029/2008JA013385
S.P. Christon, D.J. Williams, D.G. Mitchell, L.A. Frank, C.Y. Huang, Spectral characteristics of plasma sheet ion and electron populations during undisturbed geomagnetic conditions. J. Geophys. Res. 94 (1989). doi:10.1029/89JA01069. ISSN:0148-0227
B.I. Cohen, A.J. Kemp, L. Divol, J. Comput. Phys. (2010). doi:10.1016/j.jcp.2010.03.001
S.W.H. Cowley, J. Geophys. Res. 81 (1976)
S.W.H. Cowley, Rev. Geophys. 20 (1982)
N.U. Crooker, J. Geophys. Res. 84 (1979)
P.W. Daly, R.P. Rijnbeek, N. Sckopke, C.T. Russell, M.A. Saunders, J. Geophys. Res. 89 (1984)
W. Daughton et al., Nat. Phys. 7 (2011)
J. Denavit, J. Comput. Phys. 42 (1981)
M.H. Denton, J.E. Borovsky, R.M. Skoug, M.F. Thomsen, B. Lavraud, M.G. Henderson, R.L. McPherron, J.C. Zhang, M.W. Liemohn, J. Geophys. Res. (2006). doi:10.1029/2005JA011436
R.E. Denton, B.U.Ö. Sonnerup, J. Birn, W.-L. Teh, J.F. Drake, M. Swisdak, M. Hesse, W. Baumjohann, J. Geophys. Res. (2010). doi:10.1029/2010JA015420
R.E. Denton, B.U.Ö. Sonnerup, M. Swisdak, J. Birn, J.F. Drake, M. Hesse, J. Geophys. Res. (2012). doi:10.1029/2012JA017877
J.F. Drake, M. Swisdak, C. Cattell, M.A. Shay, B.N. Rogers, A. Zeiler, Science (2003). doi:10.1126/science.1080333
J.F. Drake, M. Swisdak, H. Che, M.A. Shay, Nature (2006). doi:10.1038/nature05116
J.F. Drake, P.A. Cassak, M.A. Shay, M. Swisdak, E. Quataert, Astrophys. J. 700 (2009b)
J.F. Drake, M. Swisdak, T.D. Phan, P.A. Cassak, M.A. Shay, S.T. Lepri, R.P. Lin, E. Quataert, T.H. Zurbuchen, J. Geophys. Res. (2009a). doi:10.1029/2008JA013701
J.F. Drake, M. Swisdak, R. Fermo, Astrophys. J. 763 (2013)
J.W. Dungey, Phys. Rev. Lett. 6 (1961)
M.W. Dunlop et al., Phys. Rev. Lett. 107 (2011a)
M.W. Dunlop et al., Ann. Geophys. 29 (2011b)
T.E. Eastman, L.A. Frank, W.K. Peterson, W. Lennartsson, J. Geophys. Res. 89 (1984)
J.P. Eastwood, T.D. Phan, J.F. Drake, M.A. Shay, A.L. Borg, B. Lavraud, M.G.G.J.T. Taylor, Phys. Rev. Lett. 110 (2013)
J. Egedal, A. Le, P.L. Pritchett, W. Daughton, Phys. Plasmas 18 (2011)
J. Egedal, W. Daughton, A. Le, Nat. Phys. 8 (2012)
G. Einaudi et al., Astrophys. J. 457 (1996)
G.L. Eyink, Y.-K. Shi, Physica D (2012). doi:10.1016/j.physd.2012.05.015
D.H. Fairfield, L.J. Cahill Jr., J. Geophys. Res. 71 (1966)
W.C. Feldman et al., Geophys. Res. Lett. 11 (1984)
R.L. Fermo, J.F. Drake, M. Swisdak, K.-J. Hwang, J. Geophys. Res. (2011). doi:10.1029/2010JA016271
R.L. Fermo, J.F. Drake, M. Swisdak, Phys. Rev. Lett. (2012). doi:10.1103/PhysRevLett.108.255005
T.G. Forbes, E.R. Priest, A comparison of analytical and numerical models for steadily driven magnetic reconnection. Rev. Geophys. 25, 1583 (1987)
M. Fujimoto et al., Geophys. Res. Lett. 24 (1997)
S.A. Fuselier, D.M. Klumpar, E.G. Shelley, Geophys. Res. Lett. 18 (1991)
S.A. Fuselier, K.J. Trattner, S.M. Petrinec, J. Geophys. Res. 105 (2000)
D. Gomez et al., Sol. Phys. 195 (2000)
W.D. Gonzalez, F.S. Mozer, J. Geophys. Res. 79 (1974)
J.T. Gosling, M.F. Thomsen, S.J. Bame, T.G. Onsager, C.T. Russell, Geophys. Res. Lett. 17 (1990)
J.T. Gosling, M.F. Thomsen, S.J. Bame, T.G. Onsager, C.T. Russell, J. Geophys. Res. 96 (1991)
J.T. Gosling, J. Birn, M. Hesse, Geophys. Res. Lett. 22, 869 (1995)
J.T. Gosling, R.M. Skoug, D.J. McComas, Geophys. Res. Lett. 110 (2005)
J.T. Gosling et al., Geophys. Res. Lett. 34 (2007)
G. Haerendel, On the potential role of field-aligned currents in solar physics, in Proceedings of 21st ESLAB Symposium, Bolkesjo, Norway (European Space Agency, Paris, 1987)
H. Hasegawa, J. Wang, M.W. Dunlop, Z.Y. Pu, Q.H. Zhang, B. Lavraud, M.G.T. Taylor et al., Evidence for a flux transfer event generated by multiple X-line reconnection at the magnetopause. Geophys. Res. Lett. 37(1), 16101 (2010). doi:10.1029/2010GL044219
M. Hesse, Phys. Plasmas 13 (2006)
M. Hesse, D. Winske, Hybrid simulations of collisionless ion tearing. Geophys. Res. Lett. 20(June), 1207–1210 (1993). doi:10.1029/93GL01250. ISSN:0094-8276.
M. Hesse, D. Winske, J. Geophys. Res. 99 (1994)
M. Hesse, J. Birn, M.M. Kuznetsova, J. Dreher, J. Geophys. Res. 101 (1996)
M. Hesse, K. Schindler, J. Birn, M. Kuznetsova, Phys. Plasmas 6 (1999)
M. Hesse, M. Kuznetsova, M. Hoshino, Geophys. Res. Lett. 29(12) (2002)
M. Hesse, M. Kuznetsova, J. Birn, Phys. Plasmas 11 (2004)
M. Hesse, S. Zenitani, A. Klimas, The structure of the electron outflow jet in collisionless magnetic reconnection. Phys. Plasmas 15(11), 112102 (2008). doi:10.1063/1.3006341
M. Hesse, S. Zenitani, M. Kuznetsova, A. Klimas, Phys. Plasmas 16 (2009)
M. Hesse, T. Neukirch, K. Schindler, M. Kuznetsova, S. Zenitani, The diffusion region in collisionless magnetic reconnection. Space Sci. Rev. 160(1–4), 3–23 (2011). doi:10.1007/s11214-010-9740-1
M. Hesse, N. Aunai, S. Zenitani, M. Kuznetsova, J. Birn, Phys. Plasmas 20 (2013)
M.F. Heyn, H.K. Biernat, R.P. Rijnbeek, V.S. Semenov, J. Plasma Phys. 40 (1988)
K. Higashimori, M. Hoshino, J. Geophys. Res. 117 (2012)
K. Higashimori, N. Yokoi, M. Hoshino, Phys. Rev. Lett. 110 (2013)
R.H. Holzworth, C.-I. Meng, Geophys. Res. Lett. 2 (1975)
E.W. Hones Jr., Space Sci. Rev. 23 (1979)
M. Hoshino, J. Geophys. Res. (2005a). doi:10.1029/2005JA011229
M. Hoshino, J. Geophys. Res. 110 (2005b)
M. Hoshino, Phys. Rev. Lett. 108 (2012)
M. Hoshino, A. Nishida, T. Yamamoto, S. Kokubun, Geophys. Res. Lett. 21 (1994)
M. Hoshino, T. Mukai, A. Nishida, Y. Saito, T. Yamamoto, S. Kokubun, J. Geomagn. Geoelectr. 49 (1996)
M. Hoshino, T. Mukai, T. Yamamoto, J. Geophys. Res. 103 (1998)
M. Hoshino, T. Mukai, T. Terasawa, I. Shinohara, J. Geophys. Res. (2001). doi:10.1029/2001JA900052
M. Hoshino, T. Mukai, T. Terasawa, I. Shinohara, J. Geophys. Res. 106 (2006)
S.M. Imber, J.A. Slavin, H.U. Auster, V. Angelopoulos, J. Geophys. Res. (2011). doi:10.1029/2010JA016026
R.K. Jaggi, R.A. Wolf, Self-consistent calculation of the motion of a sheet of ions in the magnetosphere. J. Geophys. Res. 78(1), 2852 (1973). doi:10.1029/JA078i016p02852
H. Ji et al., Phys. Plasmas 6 (1999)
Y. Kamide, J. Geomagn. Geoelectr. 44 (1992)
H. Karimabadi, D. Krauss-Varban, N. Omidi, Geophys. Res. Lett. 22 (1995)
H. Karimabadi, D. Krauss-Varban, N. Omidi, H.X. Vu, J. Geophys. Res. (1999a). doi:10.1029/1999JA900089
H. Karimabadi, D. Krauss-Varban, N. Omidi, H.X. Vu, J. Geophys. Res. 104 (1999b)
H. Karimabadi, D. Krauss-Varban, J. Huba, H. Vu, J. Geophys. Res. (2004). doi:10.1029/2004JA010478
H. Karimabadi, W. Daughton, K.B. Quest, J. Geophys. Res. 110 (2005)
H. Karimabadi, W. Daughton, J. Scudder, Multi-scale structure of the electron diffusion region. Geophys. Res. Lett. 34(13), L13104 (2007). doi:10.1029/2007GL030306
H. Karimabdi et al., Phys. Plasmas 20 (2013)
R.M. Katus, M.W. Liemohn, D.L. Gallagher, S. Zou, J. Geophys. Res. (2013). doi:10.1029/2012JA017915
A. Keiling et al., Science 299 (2003)
E.-J. Kim, P.H. Diamond, Astrophys. J. 556 (2001)
E. Kirsh, E.T. Sarris, S.M. Krimigis, Planet. Space Sci. 28 (1980)
M.G. Kivelson, A.J. Ridley, J. Geophys. Res. (2008). doi:10.1029/2007JA012302
B. Kliem, Astrophys. J. Suppl. 90 (1994)
K. Knizhnik, M. Swisdak, J.F. Drake, Astrophys. J. 743 (2011a)
K. Knizhnik, M. Swisdak, J.F. Drake, Astrophys. J. Lett. 743, L35 (2011b)
G. Kowal, A. Lazarian, E.T. Vishniac, K. Otmianowska-Mazur, Numerical tests of fast reconnection in weakly stochastic magnetic fields. Astrophys. J. 700, 63–85 (2009). doi:10.1088/0004-637X/700/1/63
R.H. Kraichnan, D. Montgomery, Rep. Prog. Phys. 43 (1980)
S.M. Krimigis, D. Venkatesan, J.C. Barichello, E.T. Sarris, Simultaneous measurements of energetic protons and electrons in the distant magnetosheath, magnetotail, and upstream in the solar wind. Geophys. Res. Lett. 5(November), 961–964 (1978). doi:10.1029/GL005i011p00961
M. Kuznetsova, M. Hesse, D. Winske, J. Geophys. Res. 103 (1998)
A.B. Langdon, B.I. Cohen, A. Friedman, J. Comput. Phys. 51 (1983)
G. LaPenta, Phys. Rev. Lett. 100 (2008)
G. Lapenta, J.U. Brackbill, Contact discontinuities in collisionless plasmas: a comparison of hybrid and kinetic simulations. Geophys. Res. Lett. 23(1), 1713–1716 (1996). doi:10.1029/96GL01845
G. Lapenta, D. Krauss-Varban, H. Karimabadi, J.D. Huba, L.I. Rudakov, P. Ricci, Geophys. Res. Lett. (2006). doi:10.1029/2005GL025124
B. Lavraud et al., J. Geophys. Res. (2006). doi:10.1029/2005JA011266
L.-C. Lee, Z.-F. Fu, Geophys. Res. Lett. 12 (1985)
E. Lee, M.E. Brachet, A. Pouquet, P.D. Mininni, D. Rosenberg, Lack of universality in decaying magnetohydrodynamic turbulence. Phys. Rev. E (2010). doi:10.1103/PhysRevE.81.016318
R.H. Levy, H.E. Petschek, G.L. Siscoe, AIAA J. 2 (1964)
M.W. Liemohn, M. Jazowski, J. Geophys. Res. (2008). doi:10.1029/2008JA013466
M.W. Liemohn, A.J. Ridley, P.C. Brandt, D.L. Gallagher, J.U. Kozyra, D.M. Ober, D.G. Mitchell, E.C. Roelof, R. DeMajistre, J. Geophys. Res. (2005). doi:10.1029/2005JA011109
Y. Lin, L.-C. Lee, J. Geophys. Res. 98 (1993)
K. Liou, P.T. Newell, C.-I. Meng, M. Brittnacher, G. Parks, J. Geophys. Res. 103 (1998)
Y.H. Liu, J.F. Drake, M. Swisdak, Phys. Plasmas 18 (2011)
Y.-H. Liu, J.F. Drake, M. Swisdak, Phys. Plasmas 19 (2012)
M. Lockwood, S.W.H. Cowley, P.E. Sandholt, R.P. Lepping, J. Geophys. Res. 95 (1990)
M. Lockwood, S.W.H. Cowley, T.G. Onsager, J. Geophys. Res. 101 (1996)
N.F. Loureiro et al., Phys. Plasmas 14 (2007)
N.F. Loureiro, D.A. Uzdensky, A.A. Schekochihin, S.C. Cowley, T.A. Yousel, Mon. Not. R. Astron. Soc. 399 (2009)
G. Lu, in Recurrent Magnetic Storms: Corotating Solar Wind Streams (American Geophysical Union, Washington, 2013), p. 97. doi:10.1029/167GM10
A.T.Y. Lui, Rev. Geophys. (2001). doi:10.1029/2000RG000090
A.T.Y. Lui, L.A. Frank, K.L. Ackerson, C.-I. Meng, S.-I. Akasofu, J. Geophys. Res. 83 (1978)
R. Lundin, E.M. Dubinin, Solar wind energy transfer regions inside the dayside magnetopause—accelerated heavy ions as tracers for MHD-processes in the dayside boundary layer. Planet. Space Sci. 33(August), 891–907 (1985). doi:10.1016/0032-0633(85)90103-5. ISSN:0032-0633
L.R. Lyons, D.C. Pridmore-Brown, J. Geophys. Res. 95 (1990)
K. Maezawa, J. Geophys. Res. 80 (1975)
K. Malakit, Asymmetric magnetic reconnection: a particle-in- cell study. PhD Thesis, University of Delaware, 2012
K. Malakit, M.A. Shay, P.A. Cassak, C. Bard, J. Geophys. Res. 115 (2010)
K. Malakit, M.A. Shay, P.A. Cassak, D. Ruffolo, Phys. Rev. Lett. 111 (2013)
M.E. Mandt, R.E. Denton, J.F. Drake, Geophys. Res. Lett. 21 (1994)
S. Markidis, G. Lapenta, Rizwan-Uddin, Math. Comput. Simul. (2010). doi:10.1016/j.matcom.2009.08.038
R.J. Mason, J. Comput. Phys. 41 (1981)
W.H. Mathaeus, S.L. Lamkin, Phys. Fluids 29 (1986)
W.H. Mathaeus et al., Phys. Rev. Lett. 75 (1995)
L. Matteini et al., Astrophys. J. 763 (2013)
W.H. Matthaeus, S.L. Lamkin, Phys. Fluids 28 (1985)
W.H. Matthaeus, D. Montgomery, Ann. N. Y. Acad. Sci. 357, 203–222 (1980)
W.H. Matthaeus, D. Montgomery, Selective decay hypothesis at high mechanical and magnetic Reynolds numbers. Ann. N.Y. Acad. Sci. 357, 203–222 (1980)
W. Matthaeus, M. Velli, Who needs turbulence? A review of turbulence effects in the heliosphere and on the fundamental process of reconnection. Space Sci. Rev. (2012). doi:10.1007/s11214-011-9793-9
R.L. McPherron, C.T. Russell, M.P. Aubry, J. Geophys. Res. 78 (1973)
S.E. Milan, Geophys. Res. Lett. (2009). doi:10.1029/2009GL039997
S.E. Milan, G. Provan, B. Hubert, J. Geophys. Res. (2007). doi:10.1029/2006JA011642
F.S. Mozer, A. Retinó, J. Geophys. Res. 112 (2007)
F.S. Mozer, S.D. Bale, T.-D. Phan, Phys. Rev. Lett. (2002). doi:10.1103/PhysRevLett.89.015002
F.S. Mozer, V. Angelopoulos, J. Bonnell, K.H. Glassmeier, J.P. McFadden, Geophys. Res. Lett. 35 (2008)
F.S. Mozer, D. Sundkvist, J.P. McFadden, P.L. Pritchett, I. Roth, J. Geophys. Res. (2011). doi:10.1029/2011JA017109
T. Nagai, I. Shinohara, M. Fujimoto, M. Hoshino, Y. Saito, S. Machida, T. Mukai, J. Geophys. Res. 106 (2001)
T. Nagai, I. Shinohara, M. Fujimoto, A. Matsuoka, Y. Saito, T. Mukai, J. Geophys. Res. (2011). doi:10.1029/2010JA016283
R. Nakamura et al., Geophys. Res. Lett. (2002)
W.A. Newcomb, Ann. Phys. 3 (1958)
P.T. Newell, C.-I. Meng, D.G. Sibeck, R. Lepping, J. Geophys. Res. 94 (1989)
A. Nishida, Geophys. Res. Lett. 16 (1989)
T.G. Northrop, The Adiabatic Motion of Charged Particles (Interscience, New York, 1963)
M. Øieroset, T.-D. Phan, M. Fujimoto, R.P. Lin, R.P. Lepping, Nature 412 (2001)
M. Øieroset, R.P. Lin, T.-D. Phan, D.E. Larson, S.D. Bale, Phys. Rev. Lett. (2002). doi:10.1103/PhysRevLett.89
M. Øieroset, T. Phan, M. Fujimoto, Geophys. Res. Lett. (2004). doi:10.1029/2004GL019958
M. Oieroset et al., Phys. Rev. Lett. 107 (2011)
M. Oka, T.D. Phan, S. Krucker, M. Fujimoto, I. Shinohara, Astrophys. J. (2010). doi:10.1088/0004-637X/714/1/915
M. Oka, T.D. Phan, J.P. Eastwood, V. Angelopoulos, N.A. Murphy, M. Øieroset, Y. Miyashita, M. Fujimoto, J. McFadden, D. Larson, Geophys. Res. Lett. 38, L20105 (2011). doi:10.1029/2011GL049350
M. Palmroth, P. Janhunen, T.I. Pulkkinen, Geophys. Res. Lett. (2006). doi:10.1029/2005GL025188
E.V. Panov et al., Geophys. Res. Lett. (2010). doi:10.1029/2009GL041971
E.N. Parker, J. Geophys. Res. 62 (1957)
E.N. Parker, Astrophys. J. 174 (1972)
G. Paschmann et al., Nature 282 (1979)
G. Paschmann, M. Øieroset, T. Phan, Space Sci. Rev. (2013). doi:10.1007/s11214-012-9957-2
H.E. Petschek, Magnetic field annihilation, in AAS/NASA Symposium on the Physics of Solar Flares (NASA, Washington, 1964)
H.E. Petschek, R.M. Thorne, Astrophys. J. 147 (1967)
T.-D. Phan, G. Paschmann, J. Geophys. Res. 101 (1996)
T.-D. Phan et al., Nature 404 (2000)
T.-D. Phan, B.U.Ö. Sonnerup, R.P. Lin, J. Geophys. Res. 106 (2001)
T.D. Phan et al., Nature 439 (2006)
T.D. Phan, J.F. Drake, M.A. Shay, F.S. Mozer, J.P. Eastwood, Phys. Rev. Lett. 99, 255002 (2007)
T. Phan et al., Astrophys. J. 719 (2010)
T.-D. Phan, G. Paschmann, J.T. Gosling, M. Øieroset, M. Fujimoto, J.F. Drake, V. Angelopoulos, Geophys. Res. Lett. (2013a). doi:10.1029/2012GL054528
T.D. Phan, M.A. Shay, J.T. Gosling, M. Fujimoto, J.F. Drake, V. Angelopoulos, Geophys. Res. Lett. 40 (2013b)
K.G. Powell, P.L. Roe, T.J. Linde, T.I. Gombosi, D.L. De Zeeuw, J. Comput. Phys. 154(2) (1999)
P.L. Pritchett, J. Geophys. Res. 106 (2001)
P.L. Pritchett, Phys. Plasmas (2005). doi:10.1063/1.1914309
P.L. Pritchett, J. Geophys. Res. 111 (2006)
P.L. Pritchett, J. Geophys. Res. (2008a). doi:10.1029/2007JA012930
P.L. Pritchett, J. Geophys. Res. 113 (2008b)
P.L. Pritchett, F.V. Coroniti, J. Geophys. Res. (2004). doi:10.1029/2003JA009999
P.L. Pritchett, F.V. Coroniti, Plasma sheet disruption by interchange-generated flow intrusions. Geophys. Res. Lett. 38(1), 10102 (2011). doi:10.1029/2011GL047527
P.L. Pritchett, F.S. Mozer, Phys. Plasmas 16 (2009a)
P.L. Pritchett, F.S. Mozer, J. Geophys. Res. 114 (2009b)
P.L. Pritchett, F.S. Mozer, M. Wilber, Intense perpendicular electric fields associated with three-dimensional magnetic reconnection at the subsolar magnetopause. J. Geophys. Res. 117(A), 6212 (2012). doi:10.1029/2012JA017533
J. Raeder, Ann. Geophys. 24 (2006)
J. Raeder, P. Zhu, Y. Ge, G. Siscoe, J. Geophys. Res. (2010). doi:10.1029/2010JA015876
F. Rappazzo, E.N. Parker, Astrophys. J. Lett. 773 (2013)
F. Rappazzo, M. Velli, G. Einaudi, Astrophys. J. 722 (2010)
G.D. Reeves, D.N. Baker, T.A. Fritz, J. Geophys. Res. 96 (1991)
P.H. Reiff, R.W. Spiro, T.W. Hill, J. Geophys. Res. 86 (1981)
A. Retino et al., Nat. Phys. 3 (2007)
A. Retino et al., J. Geophys. Res. (2008). doi:10.1029/2008JA013511
I.G. Richardson, S.W.H. Cowley, J. Geophys. Res. 90 (1985)
I.G. Richardson, C.J. Owen, J.A. Slavin, J. Geophys. Res. 101 (1996)
A.J. Ridley, T.I. Gombosi, D.L. DeZeeuw, Ann. Geophys. 22 (2004)
V. Roytershteyn, W. Daughton, H. Karimabadi, F.S. Mozer, Influence of the lower-hybrid drift instability on magnetic reconnection in asymmetric configurations. Phys. Rev. Lett. 108(1), 185001 (2012). doi:10.1103/PhysRevLett.108.185001
A. Runov et al., Geophys. Res. Lett. (2009). doi:10.1029/2009GL038980
A. Runov, V. Angelopoulos, X.-Z. Zhou, J. Geophys. Res. (2012). doi:10.1029/2011JA017361
C.T. Russell, Planet. Space Sci. 20, 1541 (1972)
C.T. Russell, R.C. Elphic, ISEE observations of flux transfer events at the dayside magnetopause. Geophys. Res. Lett. 6, 33 (1979)
Y. Saito, R. Mukai, T. Terasawa, New Perspectives on the Earth’s Magnetotail (AGU, Washington, 1998)
D.V. Sarafopoulos, E.T. Sarris, V. Angelopoulos, T. Yamamoto, S. Kokubun, Ann. Geophys. 15 (1997)
E.T. Sarris, W.I. Axford, Nature 277 (1979)
M.A. Saunders, Geophys. Res. Lett. 16 (1989)
K. Schindler et al., J. Geophys. Res. 93 (1988)
K.M. Schoeffler, J.F. Drake, M. Swisdak, Astrophys. J. 743 (2011)
J.D. Scudder, W. Daughton, J. Geophys. Res. 113 (2008)
V.S. Semenov, I.V. Kubyshkin, M.F. Heyn, H.K. Biernat, J. Plasma Phys. 30 (1983)
V.A. Sergeev, T.I. Pulkkinen, R.J. Pellinen, J. Geophys. Res. 101 (1996)
S. Servidio, W.H. Matthaeus, M.A. Shay, P. Dmitruk, P.A. Cassak, M. Wan, Statistics of magnetic reconnection in two-dimensional magnetohydrodynamic turbulence. Phys. Plasmas 17(3), 032315 (2010). doi:10.1063/1.3368798. http://link.aip.org/link/?PHP/17/032315/1
S. Servidio et al., Phys. Rev. Lett. (2013, submitted)
M.A. Shay, J.F. Drake, The role of electron dissipation on the rate of collisionless magnetic reconnection. Geophys. Res. Lett. 25(2), 3759–3762 (1998). doi:10.1029/1998GL900036
M.A. Shay, J.F. Drake, M. Swisdak, W. Dorland, B.N. Rogers, Geophys. Res. Lett. (2003). doi:10.1029/2002GL016267
M.A. Shay, J.F. Drake, M. Swisdak, Phys. Rev. Lett. (2007). doi:10.1103/PhysRevLett.99.155002
M.A. Shay, J.F. Drake, J.P. Eastwood, T.D. Phan, Phys. Rev. Lett. 107 (2011)
L.S. Shepherd, P.A. Cassak, J. Geophys. Res. (2012). doi:10.1029/2012JA017867
Q.Q. Shi, C. Shen, Z.Y. Pu, M.W. Dunlop, Q.G. Zong, H. Zhang, C.J. Xiao, Z.X. Liu, A. Balogh, Geophys. Res. Lett. (2005). doi:10.1029/2005GL022454
Q.Q. Shi, C. Shen, M.W. Dunlop, Z.Y. Pu, Q.G. Zong, Z.X. Liu, E. Lucek, A. Balogh, Geophys. Res. Lett. (2006). doi:10.1029/2005GL025073
K. Shiokawa, W. Baumjohann, G. Haerendel, Geophys. Res. Lett. 24 (1997)
K. Shiokawa et al., J. Geophys. Res. 103 (1998)
G.L. Siscoe, G.M. Erickson, B.U.O. Sonnerup, N.C. Maynard, J.A. Schoendorf, K.D. Siebert, D.R. Weimer, W.W. White, G.R. Wilson, J. Geophys. Res. (2002). doi:10.1029/2001JA000,109
M.I. Sitnov, K. Schindler, Tearing stability of a multiscale magnetotail current sheet. Geophys. Res. Lett. 37(8), 8102 (2010). doi:10.1029/2010GL042961
M.I. Sitnov, M. Swisdak, Onset of collisionless magnetic reconnection in two-dimensional current sheets and formation of dipolarization fronts. J. Geophys. Res. 116(A), 12216 (2011). doi:10.1029/2011JA016920
M.I. Sitnov, M. Swisdak, A.V. Divin, J. Geophys. Res. (2009). doi:10.1029/2008JA013980
J.A. Slavin, D.H. Fairfield, R.P. Lepping, A. Szabo, M.J. Reiner, M. Kaiser, C.J. Owen, T. Phan, R. Lin, S. Kokubun, T. Mukai, T. Yamamoto, H. Singer, S. Romanov, J. Buechner, T. Iyemori, G. Rostoker, Geophys. Res. Lett. 24 (1997)
J. Slavin et al., Geophys. Res. Lett. 30 (2003)
J. Slavin, E. Tanskanen, M. Hesse, C. Owen, M. Dunlop, S. Imber, E. Lucek, A. Balogh, K. Glassmeier, J. Geophys. Res. (2005). doi:10.1029/2004JA010878
B.U.Ö. Sonnerup, J. Geophys. Res. 79 (1974)
B.U.Ö. Sonnerup, L.J. Cahill Jr., J. Geophys. Res. 72 (1967)
B.U.Ö. Sonnerup, H. Hasegawa, J. Geophys. Res. (2005). doi:10.1029/2004JA010853
B.U.Ö. Sonnerup, B.G. Ledley, J. Geophys. Res. 79 (1974)
B.U.Ö. Sonnerup, B.G. Ledley, J. Geophys. Res. 84 (1979)
B.U.Ö. Sonnerup et al., J. Geophys. Res. 86 (1981)
B.U.Ö. Sonnerup, H. Hasegawa, W.-L. Teh, L.-N. Hau, J. Geophys. Res. (2006). doi:10.1029/2006JA0117
B.U.Ö. Sonnerup, R.E. Denton, H. Hasegawa, M. Swisdak, J. Geophys. Res. (2013). doi:10.1002/jgra.50211
D.J. Southwood, C.J. Farrugia, M.A. Saunders, Planet. Space Sci. 36 (1988)
H. Strauss, Astrophys. J. 326 (1988)
D. Sundqvist et al., Phys. Rev. Lett. 99 (2007)
M. Swisdak, J.F. Drake, Geophys. Res. Lett. (2007a). doi:10.1029/2007GL029815
M. Swisdak, J.F. Drake, Geophys. Res. Lett. 34 (2007b)
M. Swisdak, B.N. Rogers, J.F. Drake, M.A. Shay, J. Geophys. Res. (2003a). doi:10.1029/2002JA009726
M. Swisdak, B.N. Rogers, J.F. Drake, M.A. Shay, J. Geophys. Res. 108 (2003b)
M. Swisdak, M. Opher, J.F. Drake, F. Alouani Bibi, Astrophys. J. 710(2), 1769 (2010)
K.G. Tanaka, A. Retinó, Y. Asano, M. Fujimoto, I. Shinohara, A. Vaivads, Y. Khotyaintsev, M. Andre, M.B. Bavassano-Cattaneo, S.C. Buchert, C.J. Owen, Ann. Geophys. 26 (2008)
K.G. Tanaka, M. Fujimoto, I. Shinohara, Int. J. Geophys. 2010 (2010)
W.-L. Teh, B.U.O. Sonnerup, J. Birn, R.E. Denton, Ann. Geophys. 28 (2010)
V. Tenishev, M. Combi, B. Davidsson, Astrophys. J. 685 (2008)
G. Toth, I.V. Sokolov, T.I. Gombosi, D.R. Chesney, C.R. Clauer, D.L. De Zeeuw, K.C. Hansen, K.J. Kane, W.B. Manchester, R.C. Oehmke, K.G. Powell, A.J. Ridley, I.I. Roussev, Q.F. Stout, O. Volberg, R.A. Wolf, S. Sazykin, A. Chan, B. Yu, J. Geophys. Res. (2005). doi:10.1029/2005JA011126
G. Toth, D.L.D. Zeeuw, T.I. Gombosi, W.B. Manchester, A.J. Ridley, I.V. Sokolov, I.I. Roussev, Space Weather J. (2007). doi:10.1029/2006SW000272
G. Toth, B. van der Holst, I.V. Sokolov, D.L. De Zeeuw, T.I. Gombosi, F. Fang, W.B. Manchester, X. Meng, D. Najib, K.G. Powell, Q.F. Stout, A. Glocer, Y.-J. Ma, M. Opher, J. Comput. Phys. (2012). doi:10.1016/j.jcp.2011.02.006
K.J. Trattner, J.S. Mulcock, S.M. Petrinec, S.A. Fuselier, J. Geophys. Res. (2007). doi:10.1029/2007JA012270
K.J. Trattner, S.M. Petrinec, S.A. Fuselier, T.-D. Phan, J. Geophys. Res. (2012). doi:10.1029/2011JA016959
B.T. Tsurutani, W.D. Gonzalez, Geophys. Monogr. Ser., vol. 98 (AGU, Washington, 1997)
N.E. Turner, W.D. Cramer, S.K. Earles, B.A. Emery, J. Atmos. Sol.-Terr. Phys. (2009). doi:10.1016/j.jastp.2009.02.005
A.E. Vapirev, G. Lapenta, A. Divin, S. Markidis, P. Henri, M. Goldman, D. Newman, J. Geophys. Res. (2013). doi:10.1002/jgra.50136
V.M. Vasyliunas, Rev. Geophys. Space Phys. 13 (1975)
Z. Vörös, W. Baumjohann, R. Nakamura, A.V. Runov, M. Volwerk, Y. Asano, D. Jankovičová, E.A. Lucek, H. Reme, Spectral scaling in the turbulent Earth’s plasma sheet revisited. Nonlinear Proc. Geophys. 14, 535–541 (2007)
M. Wan et al., J. Fluid Mech. 697 (2012)
M. Wan et al., Phys. Plasmas 20 (2013)
D.R. Weimer, J. Geophys. Res. 106 (2001)
D.T. Welling, S.G. Zaharia, Geophys. Res. Lett. (2012). doi:10.1029/2012GL054228
R.A. Wolf, V. Kumar, F.R. Toffoletto, G.M. Erickson, A.M. Savoie, C.X. Chen, C.L. Lemon, J. Geophys. Res. (2006). doi:10.1029/2006JA012010
J.R. Wygant et al., J. Geophys. Res. 110 (2005)
N. Yokoi, M. Hoshino, Phys. Plasmas 18 (2011)
S. Zenitani, M. Hesse, A. Klimas, M. Kuznetsova, Phys. Rev. Lett. 106 (2011)
S. Zenitani, I. Shinohara, T. Nagai, Geophys. Res. Lett. 39 (2012)
H. Zhang, Generation and properties of in vivo flux transfer events. J. Geophys. Res. 117 (2012). doi:10.1029/2011JA017166
X.-Z. Zhou, V. Angelopoulos, V.A. Sergeev, A. Runov, J. Geophys. Res. (2010). doi:10.1029/2010JA015481
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hesse, M., Aunai, N., Birn, J. et al. Theory and Modeling for the Magnetospheric Multiscale Mission. Space Sci Rev 199, 577–630 (2016). https://doi.org/10.1007/s11214-014-0078-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-014-0078-y