Abstract
The Relativistic Proton Spectrometer (RPS) on the Radiation Belt Storm Probes spacecraft is a particle spectrometer designed to measure the flux, angular distribution, and energy spectrum of protons from ∼60 MeV to ∼2000 MeV. RPS will investigate decades-old questions about the inner Van Allen belt proton environment: a nearby region of space that is relatively unexplored because of the hazards of spacecraft operation there and the difficulties in obtaining accurate proton measurements in an intense penetrating background. RPS is designed to provide the accuracy needed to answer questions about the sources and losses of the inner belt protons and to obtain the measurements required for the next-generation models of trapped protons in the magnetosphere. In addition to detailed information for individual protons, RPS features count rates at a 1-second timescale, internal radiation dosimetry, and information about electrostatic discharge events on the RBSP spacecraft that together will provide new information about space environmental hazards in the Earth’s magnetosphere.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Scientific Goals
Within two Earth radii of the Earth’s surface there is an unexplored region of trapped particles that are a challenge to accurately measure, a challenge to engineer for spacecraft design, and a challenge to understand given particle lifetimes that can exceed decades or even centuries. The inner Van Allen belt is a nearby reservoir of charged particles from a multitude of sources. We know the existence of trapped protons with energies beyond 1 GeV, secondary particles such as positrons, electrons, and light ions 4He, 3He, and 2H, electrons that diffuse inward from the outer magnetosphere, and heavy ions that originate as interstellar neutral particles. These particles execute their gyration, bounce, and drift motions in a region with a relatively strong and stable magnetic field that shelters them from transients in the geomagnetic field, yielding the longest trapping lifetimes for particles in the Earth’s magnetosphere. The tenuous upper atmosphere is both a source and sink of these populations, whose influence varies over the solar cycle and episodically during times of rapid atmospheric joule heating.
Sorting out the various sources and losses in the Inner belt is challenging but there are particle characteristics that aid the process such as: extremely high proton energies that distinguish these particles as having a galactic cosmic ray origin; heavy ion composition that identifies these as being anomalous cosmic rays whose access to the inner belt is only afforded by their being mostly singly-ionized; and antimatter composition that identifies another branch the products of nuclear collisions between galactic cosmic rays and atmospheric atoms. For electrons the picture is less clear since there is little information about the electron energy spectrum and no identifiable characteristics of an electron that originates from a nuclear interaction versus one that diffused inwards from the outer Van Allen belt.
This paper describes the Relativistic Proton Spectrometer (RPS) whose purpose is to answer scientific and applied questions about the inner Van Allen belt proton population. RPS is government furnished equipment for the RBSP mission. As part of the scientific payload, RPS will measure protons in the energy range of ∼60 to 2000 MeV with good energy resolution and with a design that accommodates the challenges of measuring a foreground proton population with a large background due to penetrating protons. It is strictly a proton spectrometer focused on the primary constituent of the inner belt. RPS complements the other energetic proton measurements on RBSP (Baker et al. 2012; Blake et al. 2012) by extending the proton capability of the mission into the GeV range beyond previous investigations from the near-geosynchronous transfer orbit of CRRES (Johnson and Kierein 1992).
The measurement difficulties in a high-background environment of penetrating particles, along with the mission challenges of operating in the inner belt, have allowed us to obtain only glimpses of the entire inner belt proton population, either at the bottom of the field lines in low-Earth orbit (e.g. Baker et al. 1993) or only up to ∼100 MeV at higher altitudes (Albert and Ginet 1998). By sampling the protons near where their intensities are greatest and by monitoring outer trapping boundaries on two RBSP vehicles, RPS will provide new insights into this unexplored territory of the inner Van Allen belt.
1.1 Inner Belt Origins
The RPS instrument objectives stem from a modern interest in the dominant inner Van Allen belt proton component. One can trace the RPS investigation to the beginning of the modern space age with the flight of Explorer-1 (Van Allen 1960). There are several compelling historical accounts of the first Explorer missions and the concurrent hypotheses about what later investigations determined were high-energy protons stably trapped in the inner belt (e.g. Chudakov and Gortchakov 1959). Reviews such as Hess (1963, 1968) provide a glimpse of these early measurements and the open questions, some of which remain unanswered today. Ludwig (2011) relates a more recent description of those path-finding space discoveries. An early hypothesis held that the trapped radiation was related to the aurorae, while others found a natural link to albedo particles formed from nuclear interactions of galactic cosmic rays with the upper atmosphere (Singer 1958). The relevant facts to remember here are: the trapped inner belt proton environment saturated the Explorer-1 measurement in 1958 with high penetrating rates; and there was an early appreciation for the stability of the inner magnetosphere to form a strong magnetic bottle for natural and artificial injections of high-energy particles.
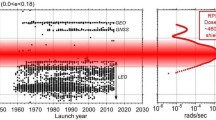
The dominant source for protons above ∼50 MeV in the inner belt is the decay of albedo neutrons from galactic cosmic ray protons that collide with nuclei in the atmosphere and ionosphere (Cosmic Ray Albedo Neutron Decay, or CRAND); e.g., Singer (1958); Freden and White (1962); Farley and Walt (1971). Free neutrons undergo beta decay with a mean lifetime of ∼885 seconds or ∼14.75 minutes (Paul 2009). A small fraction of neutrons above 50 MeV decay and, within the strong magnetic field inside a MacIIwain L-shell of 2, leave a stably trapped proton with approximately the same kinetic energy as the parent neutron (Fig. 1). The energy spectrum is known to extend beyond 1 GeV, but the spectral details are not well established. These are the highest-energy trapped ions in the inner solar system; their fluxes are orders of magnitude more intense than the galactic cosmic ray protons, which are their ultimate source.
In contrast to the steady and weak source for CRAND protons, there are transient events wherein new radiation belts form above and within the inner belt when interplanetary shocks collide with the magnetosphere as shown in Fig. 2 (Looper et al. 2005). The particle sources in these events can be residual magnetospheric ions and electrons as well as interplanetary solar particles including heavy ions up to Fe. An often-cited example is the 1991 March shock event that created >15 MeV electrons and >50 MeV protons above the inner belt within seconds of its impact on the magnetosphere (Blake et al. 1992; Li et al. 1993; Hudson et al. 1995). Recent measurements have also shown newly trapped radiation belts within L∼2 that are created from solar energetic particles (Mazur et al. 2006; Lorentzen et al. 2002). There may be multiple mechanisms at work in creating these new belts. It has also become clear that the new belts can be lost quickly during subsequent geomagnetic activity (Selesnick et al. 2010). Below ∼100 MeV, the disagreement between observations and CRAND models suggest the existence of additional sources such as radial diffusion of newly injected solar protons, although the details of these processes have not been established (e.g. Albert and Ginet 1998).
Monthly averaged count rate of 19–28 MeV protons in the inner belt that mirror at the SAMPEX altitude (Looper et al. 2005). Note the changes in the outer trapping boundary between L=2 and L=3. Episodic solar particle events in 1998 through 2003 created new transient belts inside L=3
1.2 Highlights of Inner Belt Measurements
We highlight a few studies of inner belt protons from ∼10 to ∼100 MeV. One quickly finds that the research interest in the inner belt peaked decades ago with only a few successful attempts at quantifying the inner belt proton spectrum over the past 20 years. Sawyer and Vette (1976) listed the missions that operated in the inner belt including observations from Explorer 4 in 1958 through the Azur mission in 1970. While the examples we highlight here reinforce the existence of a high-energy proton population, the next steps in quantifying the details of that population will require the RBSP mission. What was the case decades ago still obtains today: few satellites have spent significant time near the magnetic equator and at the peak intensities of the inner belt. These research examples added to our motivation to settle the unknowns of the proton energy spectrum: its shape, maximum energy, and time dependence.
The 1971-067 mission was a US Air Force Space Test Program mission with 8 space vehicles. The propulsion module called OV1-20 included a Cherenkov counter telescope that orbited for ∼21 days in a 130 km by 1950 km polar orbit. The counter itself operated for about 8 days in August 1971 using an on-board battery for power. A pair of thin scintillators defined the geometry and a Lucite Cherenkov radiator yielded an energy range of ∼65 to >550 MeV (Kolasinski 2012). The limited OV1-20 measurements were not consistent with the AP-8 model of the inner belt (see the model discussion below). There were plans for follow-on missions to measure the inner belt for longer time periods, although those missions did not occur.
RBSP will be the first mission since the Combined Radiation and Release Effects Satellite (Vampola 1992; Johnson and Kierein 1992) to survey the inner belt using a near-equatorial orbit and suites of particle and fields experiments. Although the CRRES orbit itself was sufficient for investigations of the inner belt, the vehicle did not have instruments to measure protons above ∼100 MeV and many relevant CRRES instruments did not perform well in the inner belt because of large backgrounds from penetrating protons (e.g. Gussenhoven et al. 1993).
After the end of the CRRES mission 1992, the only other relevant science data originated from low-Earth orbit (LEO). Continuing LEO observations, though important for situational awareness and refinement of our understanding of atmospheric losses, cannot obtain the information we need to validate our understanding of the inner belt proton sources and losses. The steep flux gradients caused by the atmosphere introduce large uncertainty in the modeling (e.g. Heynderickxs et al. 1999).
The SAMPEX mission provided a long baseline of inner belt proton measurements below ∼600 km (Baker et al. 1993). The PET instrument was a cosmic-ray sensor design that monitored the outer belt electron population in LEO, solar energetic particle precipitation over the polar caps, and the trapped protons in the inner belt. Figure 2 shows changes in the outer boundary of the trapping region from SAMPEX/PET.
The PAMELA magnetic spectrometer is another example of obtaining information about the inner belt from a cosmic ray detector placed in low-Earth orbit, in this case an elliptical 350–650 km orbit (Adriani et al. 2008). PAMELA benefits from a large geometry factor and an extensive energy range designed to address galactic cosmic ray antiparticle abundances. Similar to SAMPEX, their measurements indicate an inner belt energy spectrum above ∼100 MeV that is harder than the AP8 model discussed below.
1.3 Inner Belt Proton Models
Models of the inner belt protons have been developed to predict the penetrating backgrounds in science and engineering instrumentation, for science analysis, and for spacecraft engineering. We briefly discuss them here because they represent an efficient way of comparing new measurements to prior data sets and because we designed RPS to meet the needs of future models.
A host of LEO models address the low-altitude fringes of the Inner Belt, but only two sets of specification models describe the heart of the Inner Belt environment: AE-8/AP-8 (Vette 1991; Sawyer and Vette 1976) and models from the CRRES mission (Brautigham and Bell 1995; Meffert and Gussenhoven 1994).
From 1966 to 1976 there were a series of publications that compiled the available trapped proton (and electron) measurements in empirical models for applications and space science. The last versions called “AP-8” and “AE-8” for protons and electrons respectively are the de-facto standard for spacecraft engineering and are commonly used references for new measurements. We briefly discuss AP-8 and select a few inner belt proton studies since the creation of AP-8. See Ginet et al. (2012) for further details of the AP & AE models and their follow-ons.
The goal of the trapped proton and electron modeling effort by Vette and others was to synthesize a number of datasets with different coverage in energy and spatial location into a single reference model for engineering and research. Episodic updates using short-term datasets of that era, sometimes only a few months in duration, kept the models in step with the new measurements. There were 43 separate missions that contributed to the last version of the proton model, most of which provided little or no coverage of the inner belt.
The actual model took the form of least squares fits to integral energy spectra at various B and L coordinates. The authors drew smooth curves by hand through the data if there were too few points for a least squares fit, sometimes missing the data by a factor of 2 or more in order to constrain the fit to be smooth. The authors remarked that “the spectrum in the inner zone for energies above 150 MeV is not well supported by data in these models” and in fact above 150 MeV the model consists only of extrapolations of the least squares fits. They anticipated using the data from new missions to populate the higher energies but this addition never occurred. Another problem is that the mapping to B-L space for AP-8 took place in a static 1960 Jensen-Cain magnetic field model (Jensen and Cain 1962), limiting its usefulness today given the secular changes in the geomagnetic field.
Data from the CRRES spacecraft were the basis for the CRRESELE/CRRESPRO models. As mentioned above, the relevant instruments did not perform well in the inner belt. The proton datasets extend from 1.1 to 90.4 MeV and are therefore insufficient for questions relating to the exact shape and energy extent of the CRAND energy spectrum.
Heynderickxs et al. (1999) created an inner belt model for LEO using SAMPEX measurements that extended to 500 MeV and found that the SAMPEX data were higher than the AP-8 model by factors of ∼2 at several hundred MeV. The authors noted that the secular drift in the geomagnetic field means that data of different epochs such as SAMPEX and the 1970’s era AP-8 cannot be compared without transforming both data sets into the same magnetic field model.
Selesnick et al. (2007) reexamined the CRAND with a modern set of tools and knowledge about the process. This theoretical model is the most up to date reference for CRAND and solar energetic particle contributions to the inner belt and forms the hypothesis that the RPS data seeks to test experimentally. They considered two sources for inner belt protons: the neutron albedo using galactic cosmic ray H and He incident on the neutral atmosphere (specified in the NRLMSISE-00 model); and solar energetic particle trapping based upon empirical trapped proton intensities and records of the solar proton fluence during the space age and inferred from polar ice samples for dates prior to 1956. Their use of polar ice proxies indicates a novel challenge for this theoretical treatment of the inner belt: an accurate specification of the current inner belt population must account for histories of the sources, losses, and the trapping field on timescales of hundreds of years or more (e.g. Farley and Walt 1971). Figure 3 is an example of equatorial energy spectra from the Selesnick et al. (2007) model at L=1.3 along with the AP-8 solar minimum model. Most of the energy spectra in the 2007 model (and AP-8) have components below ∼50 MeV from solar proton trapping. The 2007 model predicts harder spectra (i.e. smaller spectral slope) above several 100 MeV, but one must realize that the AP-8 model had no data to justify its spectral rollovers. Figure 3 also shows the energy ranges for the relevant RBSP instrumentation that will form the basis of new models and understanding of the inner belt.
Comparison of model inner belt energy spectra at L=1.3. AD2005 refers to the model of Selesnick et al. (2007). The boxes at the bottom of the figure show the energy ranges of proton instruments onboard the RBSP mission (energy ranges placed at arbitrary proton intensity)
1.4 Inner Belt Engineering Hazards
Many space vehicles have inadvertently detected the inner belt though anomalies and performance impacts from the intense penetrating proton environment. Most often these operational problems have occurred in LEO where the weaker geomagnetic field in the region of the southern Atlantic Ocean and South America allows the trapped protons to mirror at lower altitudes than other portions of their drift orbits. For other missions, the impacts had been anticipated. For example, Fig. 4 shows the position of the SAMPEX satellite during re-tries of its MIL-STD-1773 optical fiber bus. The retries occurred when an energetic proton produced secondary particles (multiple delta rays, nuclear fragments, or both) that upset an optical signal receiver (Crabtree et al. 1993). Other reports (e.g. Bedingfield et al. 1996; LaBel 2009) show the same type of impact, namely single event upsets from secondaries when vehicles transit the inner belt.
Location of single-event transients in the optical data bus of the SAMPEX satellite from 1995 to 1996 (solid symbols). The background image is the count rate of >0.5 MeV protons and electrons, showing the extent of the inner belt at ∼600 km altitude as well as the outer electron belt and higher galactic cosmic ray flux over the polar caps
There have also been documented cases of induced radioactivity in materials. This is a potential problem for LEO spacecraft with astrophysics instrumentation that includes large volumes of scintillator material such as sodium iodide (Peterson 1965; Fowler et al. 1968; Fishman 1977). The effect is a tail on the background count rate that impacts the primary measurement for minutes after leaving the inner belt. The mechanism is photon and electron emission as the transmuted nuclei decay into stable elements. See O’Brien et al. (2006) for more details of these and other engineering concerns.
1.5 Primary RPS Science Questions
The instantaneous inner belt proton spectrum therefore is the result of a wide variety of particle source and loss processes that operate over timescales from minutes to centuries. Fundamental questions remain about these processes and the links between them, in part because what we see today in the trapped particles is a snapshot of a longer-term history. Our primary science questions about the inner belt protons are:
-
1.
What is the energy spectrum of the inner belt protons?
-
2.
How does the spectrum compare with the CRAND mechanism above 100 MeV?
-
3.
What are the major sources for protons below ∼100 MeV?
-
4.
Can we account for long-lifetime protons of ∼GeV energy using our current knowledge of the CRAND process and the secular variations of the geomagnetic field?
-
5.
What are the causes of changes to the outermost limits of the proton-trapping region?
-
6.
What determines whether an interplanetary shock forms a new proton radiation belt?
-
7.
What geomagnetic activity determines how these transient-related belts are lost?
2 RPS Requirements
The RPS instrument requirements flow from the science questions and from the need for a new model of the trapped radiation environment that includes the inner belt protons from ∼100 keV to beyond 100 MeV (Ginet et al. 2012). Figure 5 shows what we define as the level-1 AP-9 model requirements mapped to the RPS instrument. Accommodation of RPS on RBSP provides the spatial coverage and the ability to sample the proton pitch angle distribution for the duration of the RBSP mission.
RPS requirements flow. The Level-1 model requirements for AP-9 (Ginet et al. 2012) as well as the science objectives listed in the text defined the RPS instrument performance parameters
The prime concern for the RPS development is the clean separation of foreground events from the larger rate of penetrating background events. Some previous proton instruments have suffered from insufficient appreciation of the background in the inner belt, hence our need for an instrument that has the minimization of background as a fundamental part of its design. Other major concerns were sufficient margin for particle intensity, both to prevent instrument saturation and to insure sufficient statistics on the spatial scale of 0.1 L; accurate monitoring of instrument deadtime; and accurate in-flight calibration to monitor any changes in the instrument response. Our flux accuracy requirement applies when sufficiently high proton intensity is present so that the error from Poisson counting statistics is negligible and the remaining uncertainty in the flux originates from systematic uncertainties in the instrument itself. This will obtain over short (minutes) timescales in some regions of the RBSP coverage in magnetic coordinates, and over longer (several days) timescales in others.
Figure 5 also indicates the mapping from the higher-level instrument requirements to the detailed RPS attributes captured in level-3 requirements. The following section describes how we addressed these requirements.
3 RPS Instrument Description
3.1 Design Overview
A traditional method of discriminating a penetrating background from desired coincidence events in charged particle telescopes is to use an anticoincidence detector that surrounds the primary detecting elements (e.g. Krimigis et al. 1977). An anticoincidence cup would not work in the inner belt because its trigger rate would be much larger than the rate of valid events leading to a crippling deadtime. Another method is to discriminate against background in the time domain using fast timing coincidence to define valid events; the timing requires fast detectors such as scintillators and corrections for timing walk. The Cherenkov counter on OV1-20 used this timing method. The fast timing method does work in an inner belt environment; however it requires careful and potentially challenging coupling of the scintillator detectors to their light amplifiers and the latter will have gain changes in the environment if one uses traditional photomultiplier tubes, or there may be impacts from single event effects if one uses solid-state photon detectors.
In order to balance the interest in using standard charged particle detection techniques against a large instrument deadtime, the RPS concept requires a 10-fold coincidence in a stack of silicon solid-state detectors for a valid measurement. RPS is therefore not a standard range telescope because it does not measure the range of particles in a silicon stack; rather, we only analyze events that penetrate the entire silicon stack.
Figure 6 is a sketch of the RPS operational principle. Event analysis only occurs after a forward-going proton penetrates a stack of silicon detectors each of whose thickness is sufficient for accurate pulse-height analysis. The energy resolution steadily degrades with increasing proton energy if one only used the silicon detectors, hence the need for another incident energy measurement above several hundred MeV. We employ the proven technique of amplification of Cherenkov light in a solid radiator (Tamm 1939; Getting 1947) to complement the silicon detector measurement at moderate energies in the inner belt and to be the primary measurement up to and beyond ∼1 GeV. Non-ideal response of the Cherenkov system arises from knock-on electrons (e.g. Evenson 1975; Grove and Mewaldt 1992) and scintillation in the radiator. As discussed below, these sub-threshold light sources exist in the RPS flight instruments. However they do not impact the resolution of the spectrometer because they occur in an energy range where the dominant source of information is the array of solid-state detectors.
The RPS measurement principle. Valid coincidence events penetrate all detectors in a series of 1-mm thick silicon detectors. A Cherenkov system provides the incident proton energy for the highest-energies in the RPS range. Non-ideal responses from scintillation and from delta-rays (shown here schematically) in the Cherenkov radiator contribute to photons below the nominal threshold for Cherenkov light (in this case ∼423 MeV for an index of refraction of 1.38)
Figure 7 is a cross section schematic of RPS. Forward-going protons must penetrate and deposit at least 200 keV in each of the 8 energy-measuring detectors labeled D in order to generate a valid event. Pairs of geometry-defining detectors labeled A in the figure are threshold-only detectors with a smaller diameter to guarantee that valid event trajectories are well away from the edges of the D detectors where incomplete charge collection distorts the energy deposits (see Appendix D for more details on edge effects). A front-back pair of A’s is also required in the coincidence of a valid event. We use only one pair (A1A3 or A2A4) in the coincidence definition to define the geometry, leaving the other unused pair as a redundant backup. The microchannel plate photomultiplier tube (MCP/PMT) assembly detects and photoconverts the Cherenkov light from the proton’s passage through an optical grade conical magnesium fluoride radiator.
3.2 System Block Diagram
Figure 8 shows the primary functional components of RPS. The physics package consists of the 4 geometry-defining detectors, the 8 energy-sensing detectors, and the Cherenkov system. A single high-voltage power supply provides the detector bias voltage and the higher voltage required for the Cherenkov system. Analog detector signals flow from the physics package through the Analog Signal Processing (ASP) boards. A single Digital Processing and Interface Electronics board (DPIE) contains the digital signal conversion, event coincidence, and serves as the interface with the RBSP telemetry and command lines. Figure 9 is a photograph of one of the RPS flight models with the top cover removed with labels for the locations of the major subsystems discussed in more detail below. Figure 10 is a photograph of the completed flight model 1. Both flight models have identical design and function.
3.3 Solid-State Detector Assembly
The solid-state detector assembly (SSDA) consists of a total of twelve silicon solid-state detectors, their mechanical mountings, in-flight alpha sources (for the energy-sensing detectors), and a shielding housing to limit the singles rates due to penetrating protons and electrons. We procured the detectors from Micron Semiconductors, LTD. The technology uses ion-implanted doping to form a p+ junction on n-type silicon with nominal thickness of 1000±50 microns. The junction window is a continuous aluminum layer 0.1 micron thick; the ohmic window is continuous aluminum but 0.3 microns thick. Full depletion obtains at a nominal 70 to 90 volts for the flight RPS detectors; we employed a common bias voltage of 170 volts to insure full depletion of the silicon for all the flight detectors. Leakage currents are typically 100 to 200 nA.
The active area diameters are 20 mm and 23 mm for the collimating and energy-sensing detectors, respectively. Figure 11 is a close view of one pair of energy-sensing detectors. To minimize the potential for external noise pickup we mounted the detectors in pairs with their ohmic (signal) sides facing each other. The design also accommodated the potential need to replace a noisy detector at some time during the instrument or spacecraft-level testing, so we made their access relatively simple. To date no detector in either flight instrument has needed replacement.
We also made a provision for continuous alpha particle stimulus of the D detectors during instrument testing, integration, and in-flight, hence the 4-mm diameter extension of the active area outside the circular active area. We attached holders for the alpha sources to either side of the central aluminum detector mounts. The in-flight calibration section has more specifics on the in-flight alpha sources.
All the paired detector housings mount to a 3 mm thick Mallory base. The SSDA base attaches to an aluminum plate that is electrically and thermally coupled to the RPS chassis. A 3 mm thick Mallory cover fits over the remaining 3 sides of the SSDA providing electromagnetic shielding for the detectors and particle shielding corresponding to the range of 53 MeV protons and 5.3 MeV electrons; these approximate energies include the RPS mechanical housing of 350 mils aluminum.
3.4 Cherenkov Subsystem
The Cherenkov subsystem contains the Cherenkov radiator, its mechanical support, and the microchannel plate photomultiplier tube (MCP/PMT) for conversion of the Cherenkov light to an amplified electronic signal, and the bias network for the MCP/PMT. We refer to the entire subsystem as CRA. The radiator is optical-grade magnesium fluoride (MgF2). We chose MgF2 for its index of refraction of 1.38 which yields a threshold energy of ∼432 MeV for protons to generate light in the medium. The actual index of refraction depends on wavelength as described in the Geant4 modeling section below.
The conical shape of the radiator matches the field of view defined by the SSDA geometry. We suppressed internal reflections of light from backwards-going protons by painting the topmost surface of the radiator with a space qualified conducting black paint. A spring-loaded assembly holds the radiator in place; we used this method of pre-loading to mount detectors in the LRO/CRaTER instrument (Spence et al. 2010) and it proved itself useful for RPS. Here the primary concern was possible mechanical damage to the radiator crystal in the vibroacoustic launch environment.
An early design trade considered using a monolithic radiator and conventional PMT in order to eliminate any vacuum gaps or interfaces where internal reflections might cut the light intensity. However there was not sufficient time to pursue development for the RBSP mission, so we procured a UV-sensitive MCP/PMT assembly from Burle Industries. Their 85001 device incorporates a bialkali photocathode deposited onto the backside of a fused silica window; the nominal spectral response is 185 to 660 nm. The window area is 51 mm square. Inside the “tube” is a chevron pair of microchannel plates that amplify the photoelectrons and an anode with 4 equal area quadrants to collect the resulting charge cloud. We did not use the position information that the separate anodes provide, deciding instead to add the 4 quadrants together with a coupler printed circuit board since the prime measurement for RPS is the total light amplitude.
The Burle design allows for a smaller Cherenkov system than a conventional PMT would require, but there is a vacuum gap between the MgF2 radiator and the photocathode. Our early design simulations using the Geant4 tool indicated that there would be a negligible loss due to the gap for incident energies near ∼600 MeV, but that this loss would occur well below the 185 nm threshold of the Burle device. The result is that we capture the bulk of the light output from the radiator and the design is insensitive to cutoffs due to total internal reflections.
We potted the tube into an aluminum housing that also houses the resistor divider network that provides the correct bias voltages to the photocathode and to the MCPs. With 500 MeV protons we measured the flight model tube gains to be on the order of 105 at nominal high voltage of −1950 volts.
3.5 Analog Signal Processing
The Analog Signal Processing (ASP) subsystem accurately collects the pulse height amplitudes of detection events and provides in-flight electronic stimulus of each of the signal processing chains. There are a total of 13 ASP printed circuit boards in each RPS with one ASP dedicated to one detector element (12 for SSDA and 1 for CRA). Our analog processing follows the standard approaches of modern nuclear signal processing with these attributes: a hybrid charge sensitive preamplifier with a low-noise junction field-effect transistor; pole zero cancellation; active multi-pole shaping amplifier; a gated active baseline restorer; a gated peak stretcher; and a synchronous Wilkinson rundown for the pulse height conversion.
Another feature of the ASP system is the use of a dual-threshold detection. A low 50 keV threshold for the D detectors determines whether a deposit in a detector might be a candidate for pulse-height conversion. A higher threshold of 200 keV must then be triggered for actual pulse height analysis. We discuss the coincidence method more in Appendix A. The use of a lower threshold minimizes the walk in the timing coincidence window that is 260 nsec wide. The full range for energy loss measurement in the D detectors is 0.2 to 10 MeV with approximately 20 keV FWHM of system noise.
The ASPs for the D energy sensing detectors incorporate the full circuitry for the PHA conversion. Each valid deposit is digitized with the Wilkinson rundown circuitry in an Amptek PH300 hybrid with a maximum rundown time of 61.44 microseconds and 10 bit conversion, yielding a channel width of ∼10 keV. We perform the rundown simultaneously on all ASPs. Logic within the programmable gate array on the DPIE (next section) controls the PH300 devices.
The ASPs for the four A collimation detectors do not include the PHA circuitry. The single ASP that is dedicated to the CRA required that we attenuate the input by a factor of 18 in order to make the anode charge pulse amplitudes match the range of charge pulses seen from the SSDA, thus enabling all the critical components for signal amplification and processing to be duplicated across the physics package.
3.6 Digital Processing and Interface Electronics
The digital processing and interface electronics subsystem (DPIE) is the data processing unit for the multiple subsystems within RPS. DPIE is a single printed circuit board that contains the command and telemetry interface to the RBSP spacecraft, the power and logic interfaces to the ASP subsystem, and the main coincidence event processing logic. DPIE also creates the RPS CCSDS data packets that include pulse height and rate scaler data from the SSDA and CRA as well as all of the instrument voltage, current, temperature, and radiation dose monitoring.
The field programmable gate array contains the detector scalers, the coincidence logic, and the interfaces to the ASP system for the start of the rundown of valid events. The singles counters tally the number of low-threshold (50 keV) triggers in each active detector; there is a unique double coincidence counter for the selected pair of geometry-defining A detectors. When a valid coincidence event occurs (the nominal case is the 2 active A detectors and 8 D detectors), DPIE sends a signal to the ASPs to begin the rundown of stored charge in the PH300 PHA devices. The gate array latches the event time at the time of the coincidence, inserts the peak amplitudes and other information into the event packet, and transmits the packet to the RBSP spacecraft on a 1-second boundary. An internal counter monitors the time spent processing events and reports it every second as the total system deadtime.
DPIE processes all RPS commands received over the RBSP low-voltage differential signal command interface and uses the 1 pulse per second (PPS) interface for packet creation. RPS does not use any other instrument data or spacecraft housekeeping for autonomous operation, nor does RPS contain any software. One last feature worth noting here is that DPIE gate array monitors the command and PPS interfaces for fast (<120 nsec width) pulses that might be induced on these lines from electrostatic discharge (ESD) events somewhere on the space vehicle. RPS reports accumulated counts of these fast transients in its routine telemetry. Ground-based testing of RPS with a human-body-model ESD gun verified that the instrument had no anomalies from 5 kV pulses, and that the DPIE counted and rejected the induced pulses on the PPS and command interfaces.
3.7 Power Supplies
The RPS low voltage power supply (LVPS) is the power interface between the instrument and the RBSP spacecraft. A space-qualified EMI filter provides the first interface to the spacecraft LVDS power system, followed by three 5-watt DC to DC converters and other power conditioning and filtering to limit inrush currents on the power return and to satisfy the observatory electromagnetic cleanliness requirements. Typical efficiency for the LVPS is 55 %. The rear of the RPS mechanical structure houses the power supply on a single printed circuit board in its own cavity.
The high voltage power supply (HVPS) provides the SSDA bias and the higher voltage for the CRA on a single printed circuit board. The SSDA bias is 170 volts using a custom transformer and a two-stage Cockroft-Walton voltage multiplier. Note that all silicon detectors derive their bias from a single power supply. On the same board separate circuitry using a four-stage Cockroft-Walton series provides the −1650 volts to −2200 volts required for the CRA. A digital to analog converter on the DPIE provides the control signal for the MCP/PMT bias enabling us to compensate for changes in the MCP/PMT gain on the ground and in orbit with 0.14 volts per command step of 0 to 4095. When the HVPS is armed, then all outputs are nominally 2 volts; a disarm command sets the outputs to 0 volts.
3.8 Mechanical & Thermal Systems
The RPS mechanical housing conforms to the RBSP mission requirement of a minimum of 350 mils Aluminum shielding for internal components. Therefore the instrument is much stiffer than typical particle spectrometers with a fundamental resonance mode of the structure about 1.3 kHz. We designed the mechanical housing and its components around the main subsystems to allow for easy bench testing and integration of the engineering and flight subassemblies. For example, the SSDA is a self-contained mechanical housing that can be assembled and tested independently of the rest of the instrument.
We were concerned about the mounts for the Cherenkov radiator and the MCP/PMT because of the housing stiffness. For the former, we captured the radiator in an aluminum cone-shaped housing using 8 springs to pre-load the assembly. For the latter, analysis was of little use because of the complexity of the MCP/PMT stack. Phase-A vibration testing of a similar MCP/PMT led the manufacturer to stiffen the washers that hold the MCPs in place. Subsequent vibration testing on the flight models showed increased gains after shaking, which suggested some movement of the MCPs themselves might still be taking place with our design (see Appendix E for further details).
A single purge port allowed for purge during instrument testing and while on the RBSP spacecraft. A vent hole 0.1 inch in diameter vents the instrument via the LVPS cavity with a characteristic venting time of ∼1 second.
RPS is thermally isolated from the bottom deck of the RBSP spacecraft with insulating washers at each of the six mounting feet. A single thermal blanket, designed and provided by JHU/APL, isolates the bottom of RPS from radiation from the spacecraft. There is no direct solar loading of RPS since it sits on the anti-sunward side of the spacecraft. To control its temperature, RPS uses an operational heater located directly under the SSDA, a survival heater under the DPIE cavity, and a passive germanium black-kapton radiator on the space-facing top of RPS. Predicted temperatures for the SSDA on-orbit are between −20 to −10 degrees C.
One unique aspect of the RPS thermal subsystem was a thermal balance test that occurred before we built the flight model instruments. This earlier-than-usual balance test used a flight-like housing, circuit boards, and power dissipation. We performed the test to gain confidence in the thermal design and the thermal model before the flight model construction.
3.9 In-Flight Calibration System
RPS has internal calibration systems that enable us to monitor the SSDA and ASP performance. The first system is a commandable electronic pulser that sends precision amplitude pulses simultaneously to each of the 13 ASP boards equivalent up to 5 MeV deposit into the charge-sensitive amplifiers at a rate of 10 kHz. With the pulser we are able to monitor the 200 keV thresholds of the SSDA ASPs and simultaneously quantify the system noise by differentiating the curve of system rate versus input amplitude. The DPIE board houses the pulser; we can command the pulser on and off and adjust its amplitude with a 12-bit digital command level. Part of the routine on-orbit calibration will include stimulating the ASPs with the pulser as has been done with our ground-based functional test procedures.
We wanted a way to monitor the complete SSDA performance throughout the integration and testing of the instrument and observatories. As noted in Sect. 3.3, the detector design and mounts accommodate a holder for an alpha particle emitter to directly stimulate the 1 mm detectors. We procured a custom set of muti-nuclide alpha sources that contain approximately equal activities of 148 Gadolinium (3.18 MeV alpha, 74.6 year half life) and 244 Curium (5.76 MeV and 5.80 MeV alphas, 18.1 year half-life). The sources were unsealed and deposited onto 4 mm diameter titanium-platinum foils. The set of sources had an average activity of ∼3700 decays per second (90 nCi) which we scaled down with a small aperture in the source holder to yield approximately 8 events per second per detector in the flight models.
The alpha sources have been useful for monitoring the end-to-end performance of SSDA, ASP, and DPIE throughout the instrument environmental testing and will provide a useful benchmark for flight operations. It is important to note that only when RPS is commanded into its “alpha” operational mode do we pulse-height analyze the alpha events. The normal mode of operation sees no coincidences between any of the alpha triggers due to their low rates. Also note that the alpha sources will always be present in the quiet-time singles rates of the D detectors and will likely dominate those rates when RPS is not inside the inner belt.
3.10 Microdosimeters
Each RPS contains two micro dosimeters that measure the total ionizing dose and dose rate inside the RPS mechanical housing. These dosimeters are the second generation of the design first flown on board the Lunar Reconnaissance Orbiter (Mazur et al. 2011). For RPS, we telemeter the low and medium ranges that have 13.6 microRad and 895 milliRad resolution, respectively. We tested all four RPS dosimeters using a cobalt-60 gamma irradiator to confirm their dose equivalent gains, and have tested the design with 50 MeV protons (Mazur et al. 2011). The dosimeters accumulate the dose as long as RPS is powered on, requiring ground-based processing in the RPS Science Operations Center to accurately derive the dose rate and account for power-off intervals for the calculation of total mission dose. The dose rate and total dose information will be useful for monitoring the performance of RPS, of other systems on the RBSP vehicles, and for direct comparison with calculations of the dose derived from RPS and the other science measurements.
Within the DPIE cavity, one micro dosimeter has its silicon detector in the same plane as the SSDA detectors and facing the front RPS window, while the other is oriented 90 degrees away to explore for systematic pitch angle effects. To penetrate the RPS housing and micro dosimeter package and trigger the nominal 100 keV dosimeter thresholds it will require protons above ∼53 MeV and electrons above ∼5.3 MeV. The effective shielding is ∼3.25 g/cm2 for normal incidence, corresponding to an aluminum thickness of 474 mils.
3.11 Resource Summary
Table 1 lists the RPS mass, volume, power, and data resources.
3.12 Geometry Factors
Table 2 lists the RPS geometry factor as calculated from the active areas of the SSDA. We also list the geometry factors (and energy thresholds) of the PEN and CHE coincidence rates that we derived from bow tie analyses of the modeled instrument response. The bow tie method (Fillius and McIlwain 1974) factors an assumed energy spectrum (here a power law) through the instrument response to derive a consistent geometry factor along with a consistent threshold energy.
4 Calibration
The goal of the RPS calibration is to develop quantitative procedures for converting the RPS data (rates, direct events, & housekeeping) into estimates of the proton energy spectrum and angular distribution. Calibration procedures consist of stimulating the instrument with electronic pulsers, particle sources, and particle beams. Calibration for RPS also consists of iterating the instrument Geant4 model to reproduce the particle data and to refine algorithms for extracting incident proton energy versus incident angle. Finally, in-flight calibration will use internal RPS stimulus and the modeled galactic cosmic ray proton energy spectrum. Hence, calibration for RPS will not stop after launch but is at a sufficiently high level of accuracy prior to the RBSP launch to allow for immediate RPS operations after instrument commissioning. This section briefly reviews the pre-launch and post-launch calibration techniques and their results.
The Level-2 requirements that drive the calibration work for RPS are those for energy resolution (50 % at 100 MeV) and for flux accuracy (≤50 % at 100 MeV). Together these two requirements impact almost every aspect of the RPS design, and we used all aspects of our calibration to verify that the sensors meet the requirements, and to monitor the constituent subsystems so that the instruments always satisfy these performance metrics. We meet the spin-plane angular resolution requirement of 10 degrees via mechanical accommodation on the RBSP vehicle, the RBSP MAG angular accuracy, and the 1/64 second fine time tags of the RPS direct events relative to the MAG data. Those uncertainties in angular response add to ∼4.3 degrees and are not expected to change with time.
As discussed above in Sect. 3.9, the internal pulser and SSDA alpha emitters allow us to routinely monitor the threshold and noise performance of all 13 ASPs as well as the end-to-end performance of the SSDA (e.g. Fig. 12). Another less frequent yet important calibration effort is the collection of atmospheric muons as a means of monitoring the gain and performance of the CRA. We collected atmospheric muons with RPS during the instrument test phase and periodically during the integration and test phase with the RBSP vehicle. The latter required tilting the vehicles 90 degrees on their test stands which was a unique attitude for the spacecraft ground support equipment and normally used only for the tests of the solar array and boom deployments. Muons with ∼19 MeV penetrate the SSDA and the Cherenkov light threshold is ∼50 MeV. Our observed rate near sea level was approximately 7 muons per hour, which was consistent with a convolution of the sea-level muon energy spectrum (Hagmann et al. 2007) with the RPS geometry factor. Figure 13 shows an example of a muon collect during spacecraft integration and test.
RPS FM1 alpha source deposit history over 14 months prior to and after integration on the RBSP spacecraft A. The standard deviations were ∼10 keV and all the other detectors had similar histories. There was no systematic trend with time thus verifying the stability of the SSDA system. Measured deposits in air as shown are on the order of ∼10 % lower that those in vacuum due to energy loss in the 2.7 mm gap between the alpha source and the detector
Example of an RPS collect of atmospheric muons while RPS was integrated with the RBSP-B spacecraft. The figure shows the minimum ionizing SSDA deposits and the Cherenkov light peak. Muons of energies greater than ∼49 MeV will emit Cherenkov light and the sea-level spectrum peaks near ∼500 MeV, hence most events have maximum light output. For this particular HVPS setting some muons saturated the CRA as seen in the highest CRA bin
4.1 Geant4 Model
Our algorithm for identification of the energy of incident protons after launch relies on a library of simulated responses of the sensor to well-characterized incident particles against which we compare the observed response of the sensor to real particles whose characteristics we wish to determine. We simulated RPS using the Geant4 (GEometry ANd Tracking) radiation-transport code version 9.4 (Agostinelli et al. 2003; Allison et al. 2006). Geant4 models the three-dimensional transport of individual particles of arbitrary species and energy through arbitrary material geometries, allowing the user to log information such as energy deposit and the generation of secondary particles along the trajectory of each primary or secondary particle.
The detector coincidence conditions required to be satisfied in order for a particle event to undergo pulse-height analysis result in a well-collimated response restricted to particles arriving near the axis of the detector stack; thus the geometric model whose response we simulated, shown in Fig. 14, has good fidelity for the physics package of the active elements (SSDA and CRA). We represented the shielding of the surrounding mechanical housing as a simple rectangular box for approximate calculation of the off-axis response of individual detectors.
Geant4 has great flexibility with regard to the choice of physical processes modeled during runs. Often this flexibility can hinder its usefulness. Table 3 lists the physical processes that we selected to capture the relevant physics in RPS. These components, taken together, successfully reproduced the RPS response to protons at the TRIUMF accelerator and to atmospheric muons.
In order to ensure that our simulation represents the response of the actual instrument, ideally we would expose the real sensor to unidirectional, monoenergetic particle beams and compare the observations with models of the response. In practice, our primary proton calibrations used two proton beamlines at TRIUMF (Blackmore 2000). In the first, we used un-degraded 500 MeV and 350 MeV primary beams as well as the same beams degraded to lower energies with stacks of aluminum slabs up to 12″ thick. The other TRIUMF line provided 116 MeV primary beams degraded with Lucite up to 4 cm thick. In both cases a lead scatterer a few mm thick was also in the beamline upstream to lower the event rate. The beamlines included collimators and other inert material near the beam axis for focusing and intensity. This additional material resulted in proton spectra at the sensor that were broadened rather than monoenergetic. We therefore found it necessary to model the entire beamlines from the points where they entered the test area, placing the RPS sensor model shown above in the appropriate position. Thus the results we show below reflect the accuracy of not only the RPS model but also our models of the TRIUMF beamlines.
Figure 15 compares the measured and modeled distributions of the average energy deposits in SSDA for valid coincidence events. The average energy deposit increased as proton energy decreased as one expects; the curves from left to right represent test conditions (combinations of primary beam energy and set of degraders in the beam) producing energy distributions at the sensor location that peaked at energies from 444 MeV to 80.5 MeV. Note that using the average of the energy deposits in all eight D detectors discards much of the information available from the variation of deposits between the individual detectors, especially for lower-energy protons. The full particle-identification algorithm uses all the SSDA deposit information but we show just the average in Fig. 15 for brevity. Silicon detectors respond in a very nearly ideal manner, efficiently collecting charge from electromagnetic energy deposit throughout their active volumes. Thus, not surprisingly, our simulations were able to accurately reproduce the measured shapes of the SSD responses. The primary differences were for the lowest-energy beams where the simulation was most sensitive to minor errors in the thickness and distribution of inert material such as degraders and beam deflectors in the TRIUMF beamline.
Our simulations had enough fidelity that, for example, we identified a contamination of ∼250 MeV and ∼450 MeV protons in the 500 MeV beam. Consultations with TRIUMF staff suggested non-nominal paths of some protons through the bulk of the collimators rather than through their apertures likely caused the observed lower-energy populations.
The CRA subsystem has a relatively more complex response as seen by the difference between the widths of the simulated and observed peaks for the highest energies in Fig. 16. As examples we show the CRA amplitude for two TRIUMF beam tests in which the dominant CRA signal was from the Cherenkov light. The test reality was a bit more complex as noted above with the presence of lower-energy protons from the beam collimators. Figure 16a shows the main components of the CRA signal: two distributions from the primary protons and a low-amplitude signal from scintillation in the radiator (discussed below). Figure 16b is the response at an energy near the optical wavelength threshold for light generation. In both cases the simulations have enough fidelity that we are able to see the effects of variation of the CRA refractive index with wavelength, which results in Cherenkov response at the shortest transmitted ultraviolet wavelengths to lower-energy protons than at optical wavelengths. The model predicts Cherenkov response at proton energies somewhat below the threshold of about 432 MeV that would be calculated from the optical-wavelength refractive index, and we observed this sub-threshold response in the TRIUMF calibration. Another source for sub-threshold Cherenkov light is the generation of electron delta-rays in SSDA and the radiator (e.g. Grove and Mewaldt 1992); we include this effect in the Geant4 model.
Figure 16 makes clear the presence of a CRA signal at proton energies well below the Cherenkov threshold. These photons result from proton-induced scintillation in the MgF2 radiator with an intensity of about 5 photons per MeV of energy deposit in our model. Viehmann et al. (1975) estimated a yield of about 20 photons per MeV for UV-grade MgF2. The lower scintillation yield for RPS suggests that the RPS radiator has a higher purity than the material that Viehmann et al. tested. We use the scintillation photon signal as an additional input to the algorithm that calculates the incident proton energy.
Combining the SSDA and CRA signals together is the essence of the RPS measurement. Figure 17 compares the TRIUMF measurements of these detector signals with the Geant4 model for the TRIUMF beams. We show the 8-detector averaged SSDA amplitude and the mean CRA amplitude. The largest discrepancy appears where the model predicts slightly less light from delta rays than observed, but the difference does not warrant further revision because the algorithm to derive incident proton energy is sufficient to meet our requirements across the entire RPS energy range as we discuss below. We attribute the 10–20 % offset in the SSDA responses below 100 MeV to uncertainties in our model of the TRIUMF beam degraders.
Lastly we note that the RPS development schedule prevented a calibration of the flight models at energies higher than 500 MeV. However, early on in the requirements development process we did calibrate an RPS prototype that included the same CRA assembly design as the flight models. There we were able to confirm the roll over of the CRA response, both actual and modeled, to 1 GeV.
4.2 Incident Energy Algorithm
Our process for deriving the incident proton energy from the RPS measurements relies on a pre-computed database of Geant4 test particle interactions with the RPS sensor. Using the modeled event rates as functions of incident energy and angles, we can accurately estimate the energy-angle response of the sensor. To estimate the energy of a single incident particle we constructed an algorithm (called “Enigma”) to perform a nearest-neighbors lookup against the database of modeled proton coincidence events. Specifically, we find a variable k nearest neighbors (k∼10) from the database in a 9-dimensional space defined by the energy deposits in each of D1 through D8 of SSDA and the number of photons detected by the CRA. From these nearest neighbors, we compute an average incident energy and an error metric. We implemented this computation scheme in the RPS Science Operations Center and hence all of what follows occurs in the ground-based processing of the data. We briefly discuss the steps in the Enigma algorithm below
Conversion from pulse heights to MeV for D1–D8 in SSDA is a necessary step to account for the slightly different gains of the ASPs and the few percent dependence on instrument temperature. Similarly, we convert the CRA pulse height to a count of photons using a gain factor established with the TRIUMF beam tests and the Geant4 simulations.
We transform each dimension of the 9-dimensional space (8 dimensions are MeV and the 9th is photons) onto [0,1] domains. The algorithm orders the values for each dimension using the Geant4 model event database: the smallest value maps to 1/(N+1), the largest value maps to N/(N+1), and the middle value maps to 0.5, where N is the number of samples in the database. If an observed event falls below the smallest value then the algorithm sets it to zero; events above the largest value get set to 1. The entire transformation follows the empirical cumulative distribution function (or percentile function) of the values in the database for each individual dimension. Therefore, distances in this transformed domain approximate differences in probability or percentile, given the assumed spectrum and angular distribution used to generate the database.
Using the 9 numbers from the observed event transformed onto the [0,1] domains, we find the k events in the database that are closest in response to the observed event. The algorithm applies a scalable weight to the distance in the D9 (photon) axis that is currently set to a factor of 20 to make the CRA response have the same weight as SSDA. The time it takes the algorithm to find the closest event in the Geant4 model database scales with log(N). Because k is much less than N, the set of neighbors is independent of the choice of the incident spectrum for the Geant4 particle simulations.
Once the algorithm identifies the k nearest neighbors, it queries the database to determine the original incident energy of those k simulated events and computes the average. We then assign this average incident energy to be the estimated energy for the observed event. Figure 18 illustrates how the Enigma algorithm uses nearest neighbors to estimate the incident energy. In the figure we show only the D1–D2 plane of the look-up space so that the nearest neighbors in the figure were nearest in the total space but not necessarily closest in this plane. Also note that while the spread of events in the D1–D2 plane increases for energies above several hundred MeV (yellow to red in the figure), it is at these high energies that the CRA signal plays the larger role in determining incident energy.
Example of the incident energy look-up technique. For this illustration we show only the D1–D2 events. The particle of interest had an incident energy of 394 MeV (a 500 MeV incident beam degraded with 6 inches of aluminum), and the algorithm estimated 421 MeV which is well within the RPS Level-2 requirements for energy resolution
We chose the standard error as the error measurement for the incident energy; this is the sample standard deviation of the k incident energies, divided by the square root of k. This k 1/2 factor reduces the dependence of the error metric on the choice of k. Figure 19 shows the results of numerous beam tests at TRIUMF. The straight lines correspond to the RPS level-2 energy resolution requirement (e.g. 50 % at 100 MeV) and demonstrate the as-built resolution meets the requirement. Also note the improved energy resolution above several hundred MeV where the Cherenkov light amplitude has the dominant role in energy determination.
As noted above, we were able to inadvertently test the Enigma algorithm at the TRIUMF facility when the efforts to reduce the beam intensity produced near-monoenergetic contaminants in the 500 MeV beam at the level of a few percent of the primary beam intensity. We found the estimated contaminant energies to be consistent with material thicknesses upstream of the instrument.
We lastly note that the Enigma approach of using a nearest-neighbors look-up against a database of simulated events has applications to a broad class of particle sensors.
5 Flight Operations
We designed RPS to require minimal operations support. We rely on the extensive calibration efforts discussed above to produce RPS science in the Science Operations Center (SOC) instead of on-board processing of events. There is no on-board software. Choices such as these simplified the development, test, and integration of the flight models. We also recognize that we benefited from the targeted goal of only measuring inner belt protons. In this section we summarize the RPS telemetry, the main components and functions of the RPS SOC, and the primary data products.
5.1 Telemetry and Commands
RPS telemetry consists of two CCSDS packet types; Appendix B contains the details of both. The instrument produces a 304 bit long rate and housekeeping packet once per second whenever RPS is powered on and the instrument receives the 1 pulse per second signal; no command is necessary to start the flow of these packets. When integrated with RBSP, we have detailed information about all the RPS operations parameters, including SSDA and CRA rates as well as internal voltages, currents, and the micro dosimetry. Table 5 in Appendix B lists the contents of the rate and housekeeping packet. In addition to its use in RPS science, the RBSP spacecraft will include the entire RPS rate and housekeeping packet in its real-time space weather broadcast.
The second packet type contains the direct events which are the pulse heights for the valid coincidence events. Table 6 in Appendix B lists the contents of the direct event packet. Each event consists of nine 10-bit pulse heights and a 6-bit sub-second counter for more detailed timing analysis. The packet size is variable depending on the incident flux with up to 339 events per packet. RPS creates direct event packets when one or more valid coincidences occur in a second and when the on-board event quotas allow for transmission of the direct events to the RBSP spacecraft. The direct event packets follow the corresponding 1-second rate and housekeeping packet in the telemetry.
The ability of RPS to control its telemetry via event quotas was a simplification for on-orbit operations. A typical orbit will include two passes through the inner belt lasting 10 s of minutes, followed by quiet-time galactic cosmic rays above L∼2. RPS has a telemetry allocation of 2 kbps averaged across the orbit, and during quiet times we expect that RPS will not exceed this allocation. Of course, RBSP is in some aspects a discovery mission, so the exact nature of the inner belt proton intensity near the magnetic equator will not be known until after launch. However, during intense solar energetic particle events, it is likely that solar protons would exceed our orbital telemetry allocation. These will be scientifically interesting times to monitor the penetration of solar protons to low altitudes and to search for new radiation belts; we do not want to miss collections inside L=2 due to higher-altitude solar particles which will be measured with other sensors. Hence, we implemented 1-second quotas on the coincidence rates of events that trigger the SSDA and those that also have a valid CRA signal. These quotas are commandable in the range of 0 to 650 events per second for the sum of both SSDA and CRA events. The RBSP instrument telemetry data message format limits the size of a packet to 4086 bytes; the result is that RPS cannot send more than 339 direct events per second and quotas larger than 339 events per second will not telemeter more events. Routine operations will use the RBSP ephemeris predictions to estimate the times when each vehicle will cross an L shell of 2.0. On outbound passes at L=2.0 we will lower the event quotas to give priority to the direct events within the inner belt.
RPS has 36 distinct commands. RPS transmits a maximum of one RPS specific command following the spacecraft time and status information within the second. Appendix C lists the RPS commands. Two commands refer to the coincidence mode of the instrument, namely the normal mode in which a pair of A detectors defines the geometry and all D detectors are required for a valid event, and the alpha mode in which any trigger of a D detector creates a valid event. The latter mode is the only means of using the in-flight alpha emitters to create valid events. We can also enable or disable the in-flight pulser, enable and disable the high voltage, and set the CRA high voltage level. The remaining commands are for enabling and disabling individual detectors in SSDA, including the CRA, in order to remove any noisy detector from the nominal coincidence mode.
5.2 Science Operations Center
The RPS Science Operations Center (SOC) is a set of computer algorithms, ground-support equipment software, databases, and desktop computers that operate the RPS instruments in a near-autonomous way and process the RPS telemetry into scientifically useful products. Figure 20 diagrams the two primary SOC components. The console is the interface between the SOC and the RBSP Mission Operations Center (MOC). Functions such as maintaining network connections to the MOC and routine command scheduling occur automatically. We have used the RBSP mission-standard ground support software GSEOS (Hauck 1998–2007) for instrument development, pre and post-delivery testing, and will use the same routines for on-orbit operations.
A governing concern in constructing the SOC was the need to keep the RPS science team aware of the RPS instrument states of health and the status of the SOC data processing. We added a series of scripts that routinely check the instrument status and the volume and contents of the various level-N data against tables and that announce anomalies or abnormalities via emails and text messages to pagers. Fault detection for RPS thus relies on the monitoring of housekeeping and performance in the SOC. Part of the warning message system includes a dead-man timer to insure that a human inspects the top-level functions of the SOC at least once every 2 days. The warnings scripts also automatically construct simple displays of the on-orbit proton flux compared with the AP-8 and -9 models for commissioning and early orbit operations.
5.3 Data Products
The SOC backend is mainly a set of IDL routines that process the RPS telemetry into various data levels as defined in Table 4. All levels of RPS data will be in the form of Common Data Formatted files that conform, as appropriate, to the Panel on Radiation Belt Environment Modeling (PRBEM) standard file format guidelines (http://irbem.svn.sourceforge.net/viewvc/irbem/docs/Standard_File_Format.pdf), which is itself compliant with the ISTP guidelines (http://spdf.gsfc.nasa.gov/sp_use_of_cdf.html).
We will perform the initial data processing with orbit, attitude, and universal time predictions and a model magnetic field. Reprocessing will occur as needed when we obtain the input parameters that global magnetic field models require and when the MOC publishes updates or revisions to attitude, time, and magnetic field vectors. We note that we can meet all the RPS science requirements entirely in the absence of external data because pseudo-static (e.g., Olson-Pfitzer quiet) magnetic field models are adequate organizers of the inner zone protons.
For science analysis, the SOC will routinely push the processed data to a location such as the NASA virtual radiation belt observatory. The daily data volume will be approximately 154 Mbytes for each RPS instrument. This yields an estimated data volume for the 60-day checkout plus a 2-year mission of approximately 300 Gb. The RPS SOC will also work with NASA personnel to transfer the RPS data to a long-term archive that NASA will provide.
6 Summary
The RPS instrument is focused on answering decades-old questions about the inner belt proton environment: the proton energy spectrum across a broad energy range and how it compares to the CRAND process, its maximum energy, and how it changes during geomagnetic activity. The observations from RBSP will foster new interest in this nearby yet relatively unexplored region of trapped particles and will raise new questions and insights about the processes that occur there.
We have implemented a robust instrument design that accommodates the lessons from previous measurements in this challenging penetrating background. RPS also incorporates in-flight calibration and subsystem diagnostics so that we can track its performance on-orbit and make any corrections its response. The RPS calibration and modeling efforts proceeded in pace with the instrument design and test, yielding a pre-flight model that meets our requirements for understanding the instrument performance and for producing useful science products immediately after on-orbit commissioning.
Abbreviations
- ASP:
-
Analog Signal Processing
- CCSDS:
-
Consultative Committee for Space Data Systems
- CRA:
-
Cherenkov subsystem within RPS
- CRAND:
-
Cosmic Ray Albedo Neutron Decay
- CRaTER:
-
Cosmic Ray Telescope for the Effects of Radiation
- CRRES:
-
Combined Release and Radiation Effects Satellite
- CRRESELE:
-
CRRES electrons (model)
- CRRESPRO:
-
CRRES protons (model)
- DPIE:
-
Digital Processing and Interface Electronics
- EMI:
-
Electro-Magnetic Interference
- ESD:
-
Electro-Static Discharge
- Geant4:
-
Geometry and Tracking (4)
- HVPS:
-
High Voltage Power Supply
- ISTP:
-
International Solar-Terrestrial Physics
- JHU/APL:
-
Johns Hopkins University/Applied Physics Laboratory
- LEO:
-
Low Earth Orbit
- LRO:
-
Lunar Reconnaissance Orbiter
- LTD:
-
Limited
- LVPS:
-
Low Voltage Power Supply
- MAG:
-
Magnetometer
- MCP/PMT:
-
Micro-Channel Plate/Photo-Multiplier Tube
- MIL-STD:
-
Military Standard
- MOC:
-
Mission Operations Center
- NASA:
-
National Aeronautics and Space Administration
- NRLMSISE:
-
Naval Research Laboratory Mass Spectrometer Incoherent Scatter Radar
- NRO:
-
National Reconnaissance Office
- PAMELA:
-
Payload for Antimatter Matter Exploration and Light-nuclei Astrophysics
- PET:
-
Proton Electron Telescope
- PMT:
-
Photo-Multiplier Tube
- PPS:
-
Pulse Per Second
- PRBEM:
-
Panel on Radiation Belt Environment Modeling
- RBSP:
-
Radiation Belt Storm Probes
- RPS:
-
Relativistic Proton Spectrometer
- SAMPEX:
-
Solar, Anomalous, and Magnetospheric Explorer
- SOC:
-
Science Operations Center
- SSDA:
-
Solid State Detector Assembly
- TRIUMF:
-
Tri-University Meson Facility
- UV:
-
Ultra-violet
References
O. Adriani et al., in Proc. 21st European Cosmic Ray Symp. (2008)
S. Agostinelli et al., Geant4—a simulation toolkit. Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 506(3), 250–303 (2003). doi:10.1016/S0168-9002(03)01368-8
J.M. Albert, G.P. Ginet, J. Geophys. Res. (1998). doi:10.1029/98JA00290
J. Allison et al., Geant4 developments and applications. IEEE Trans. Nucl. Sci. 53(1), 270–278 (2006). doi:10.1109/TNS.2006.869826
D.N. Baker, G.M. Mason, O. Figueroa, G. Colon, J.G. Watzin, R.M. Aleman, IEEE Trans. Geosci. Remote Sens. 31, 531–541 (1993)
Baker et al., The Relativistic Electron-Proton Telescope (REPT) instrument on board the radiation belt storm probes (RBSP) spacecraft: characterization of Earth’s radiation belt high-energy particle populations. Space Sci. Rev. (2012, this issue)
K.L. Bedingfield, R.D. Leach, M.B. Alexander, NASA Ref. Publ. 1390, 1996
E.W. Blackmore, in Radiation Effects Data Workshop (2000). doi:10.1109/REDW.2000.896260
J.B. Blake, W.A. Kolasinski, R.W. Fillius, E.G. Mullen, Geophys. Res. Lett. (1992). doi:10.1029/92GL00624
Blake et al., MagEIS paper. Space Sci. Rev. (2012, this issue)
D.H. Brautigam, J.T. Bell, CRRESELE Documentation, PL-TR-95-2128, Phillips Laboratory, 1995
A.E. Chudakov, E.V. Gortchakov, Repts. Acad. Sci. USSR 124, 5 (1959)
C.M. Crabtree, K.A. LaBel, E.G. Stassinopoulos, J.T. Miller, Proc. SPIE (1993). doi:10.1117/12.156592
P. Evenson, in 14th Int. Cosmic Ray Conf, vol. 9 (1975), p. 3177
T.A. Farley, M. Walt, J. Geophys. Res. (1971). doi:10.1029/JA076i034p08223
R.W. Fillius, C.E. McIlwain, Measurements of the Jovian radiation belts. J. Geophys. Res. 79(25), 3589–3599 (1974). doi:10.1029/JA079i025p03589
G.J. Fishman, Proton-induced radioactivity in NaI (Tl) scintillation detectors. (NASA CR-150237, 1977). http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/19770016962_1977016962.pdf. Accessed 16 January 2012
W.B. Fowler, E.I. Reed, J.E. Blamont, NASA TM X-63419, 1968
S.C. Freden, R.S. White, J. Geophys. (1962). doi:10.1029/JZ067i001p00025
I. Getting, Phys. Rev. 71, 123 (1947)
G. Ginet et al., Space Sci. Rev. (2012, this issue)
J.E. Grove, R.A. Mewaldt, Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 314, 495 (1992)
M.S. Gussenhoven, E.G. Mullen, M.D. Violet, C. Hein, J. Bass, D. Madden, IEEE Trans. Nucl. Sci. 40, 1450 (1993)
C. Hagmann, D. Lange, D. Wright, Monte Carlo simulation of proton-induced cosmic-ray cascades in the atmosphere. (UCRL-TM-229452, 2007). http://nuclear.llnl.gov/simulation/cry_physics.pdf. Accessed 16 January 2012
T. Hauck, GSEOS 6.0 user manual. (GSE Software, 1998–2007). http://www.gseos.com/doc/Gseos6.0/Gseos.pdf. Accessed 16 January 2012
W.N. Hess, NASA Technical Note D-1749, 1963
W.N. Hess, The Radiation Belt and Magnetosphere (Blaisdell, Boston, 1968)
D. Heynderickx, M. Kruglansk, V. Piercard, J. Lemaire, M.D. Looper, J.B. Blake, IEEE Trans. Nucl. Sci. 46(6), 1475 (1999)
M.K. Hudson, A.D. Kotelnikov, X. Li, I. Roth, M. Temerin, J. Wygant, J.B. Blake, M.S. Gussenhoven, Simulation of proton radiation belt formation during the March 24, 1991 SSC. Geophys. Res. Lett. 22(3), 291–294 (1995). doi:10.1029/95GL00009
D.C. Jensen, J.C. Cain, J. Geophys. Res. 67, 3568 (1962)
M.H. Johnson, J. Kierein, J. Spacecr. Rockets 29, 556 (1992)
A. Kolasinski, Energetic Proton Analyzer. (NSSDC, 2012). http://nssdc.gsfc.nasa.gov/nmc/experimentDisplay.do?id=1971-067A-01. Accessed 16 January 2012
S.M. Krimigis, T.P. Armstrong, W.I. Axford, C.O. Bostrom, C.Y. Fan, G. Gloeckler, L.J. Lanzerotti, Space Sci. Rev. (1977). doi:10.1007/BF00211545
K.A. LaBel, In-flight anomalies and radiation performance of NASA missions—selected lessons learned. (NASA Technical Reports Server, 2009). http://ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20090004168_2008049644.pdf. Accessed 16 January 2012
X. Li, I. Roth, M. Temerin, J.R. Wygant, M.K. Hudson, J.B. Blake, Geophys. Res. Lett. (1993). doi:10.1029/93GL02701
M.D. Looper, J.B. Blake, R.A. Mewaldt, J. Geophys. Res. (2005). doi:10.1029/2004GL021502
K.R. Lorentzen, J.E. Mazur, M.D. Looper, J.F. Fennell, J.B. Blake, J. Geophys. Res. (2002). doi:10.1029/2001JA000276
G.H. Ludwig, Opening Space Research: Dreams, Technology, and Scientific Discovery (AGU, Washington, 2011). doi:10.1029/062SP
D.L. Margolies, T. von Rosenvinge, Advanced Composition Explorer (ACE) lessons learned and final report. (Caltech ACE Science Center, 1998). http://www.srl.caltech.edu/ACE/ASC/DATA/pdf_docs/LessonsLearned.pdf. Accessed 16 January 2012
J.E. Mazur, J.B. Blake, P.L. Slocum, M.K. Hudson, AGU Geophys. Monogr. Ser., vol. 165 (2006), p. 345
J.E. Mazur, W.R. Crain, M.D. Looper, D.J. Mabry, J.B. Blake, A.W. Case, M.J. Golightly, J.C. Kasper, H.E. Spence, Space Weather (2011). doi:10.1029/2010SW000641
J.D. Meffert, M.S. Gussenhoven, CRRESPRO Documentation, PL-TR-94-2218, ADA 284578, Phillips Laboratory, Hanscom AFB, MA (1994)
T.P. O’Brien, J.E. Mazur, J.B. Blake, M.D. Looper, J.T. Bell, G.P. Ginet, A.B. Campbell, Aerospace Report No. ATR-2006(8377)-1, 2006
S. Paul, Nucl. Instrum. Methods Phys. Res., Sect. A, Accel. Spectrom. Detect. Assoc. Equip. 611, 157 (2009)
L.E. Peterson, J. Geophys. Res. (1965). doi:10.1029/JZ070i007p01762
D.N. Sawyer, J.I. Vette, NSSDC WDC-A-R&S 76-06, 1976
R.S. Selesnick, M.D. Looper, R.A. Mewaldt, Space Weather (2007). doi:10.1029/2006SW000275
R.S. Selesnick, M.K. Hudson, B.T. Kress, J. Geophys. Res. (2010). doi:10.1029/2010JA015247
S.F. Singer, Phys. Rev. Lett. 1(5), 171 (1958)
H.E. Spence, A.W. Case, M.J. Golightly, T. Heine, B.A. Larsen, J.B. Blake, P. Caranza, W.R. Crain, J. George, M. Lalic, A. Lin, M.D. Looper, J.E. Mazur, D. Salvaggio, J.C. Kasper, T.J. Stubbs, M. Doucette, P. Ford, R. Foster, R. Goeke, D. Gordon, B. Klatt, J. O’Connor, M. Smith, T. Onsager, C. Zeitlin, L.W. Townsend, Y. Charara, Space Sci. Rev. 150, 243–284 (2010). doi:10.1007/s11214-009-9584-8
I. Tamm, J. Phys. USSR 1, 439 (1939)
A.L. Vampola, J. Spacecr. Rockets 29, 555 (1992)
J.A. Van Allen, State Univ. of Iowa S/ui60-13, 1960
J.I. Vette, NSSDC/WDC-A-R&S 91-24, 1991
W. Viehmann et al., Photomultiplier window materials under electron irradiation: fluorescence and phosphorescence. Appl. Opt. 14(9), 2104–2115 (1975)
Acknowledgements
We thank Colonel C. Groves for architecting the PSBR program of which RPS is the space hardware component. R. Selesnick (AFRL) conceived of the RPS measurement concept. W. Olson managed the early phases of the PSBR project for the National Reconnaissance Office (NRO) and D. Byers (NRL/NRO) led PSBR at the NRO through flight model construction and delivery of the RPS flight models. C. Pritt managed the PSBR program office support for The Aerospace Corporation and B. Klatt provided quality assurance guidance for RPS. We thank T. Alsruhe for his contributions to the early project management and E. Blackmore of TRIUMF for his support of the RPS proton calibrations. We greatly appreciate the efforts of the NASA and JHU/APL RBSP mission partners for their cooperation, support, and participation in accommodating RPS on the RBSP spacecraft, specifically: K. Cooper, A. Reiter, D. Myers, J. Stratton, R. Fitzgerald, B. Williams, J. Troll, C. Herrman, N. Mosavi, D. Jones, A. Dolbow, and E. Rodberg (all at JHU/APL); S. Himes, S. Aloezos, and D. Sibeck (all at NASA/Goddard Space Flight Center); and D. Brewer and M. Kessel (NASA/Headquarters).
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix A: Event Processing Logic and Count Rates
Each of RPS detectors (A1 through A4 and D1 through D9) provides fast timing logic used in singles counting, pulse height digitization, and deadtime determination. The fast timing logic is found on the associated ASP board, with levels set to approximately 50 keV (low threshold) and 200 keV (high threshold). On the ASP/DPIE interface, these signals are active low; however to simplify the discussion, “low/high threshold triggered” will mean that the input signal is over the associated threshold.
1.1 A.1 Normal Mode
This is the nominal operating mode for RPS that requires the 10 or 11-fold coincidence for valid event determination. RPS coincidence event processing in normal mode consists of 5 states: idling, window, gate, valid, and rundown. Below we describe each state and its transition conditions.
- Idling::
-
This is the default start-up state for the event processing logic. When in this state, the logic monitors all enabled detectors (nominally a front/back pair of A detectors and D1 through D8 and D9) while watching for a low threshold trigger on any detector. RPS transitions to the window state when DPIE detects any low threshold trigger.
- Window::
-
The window state is active while the coincidence window is open. In this state, DPIE checks if all enabled detectors trigger the low threshold within the coincidence window; the maximum window length is 260 ns. If the full window period passes without a full coincidence, then processing logic returns to the idling state with no event generated. An immediate transition to gate state occurs when all enabled detectors trigger their low thresholds within the 260 ns window.
- Gate::
-
DPIE logic enters the gate state when fast trigger logic (low thresholds) indicates that an event candidate exists in the signal path. While in this state, DPIE sends a signal to the PH300s pulse-height analysis hybrids on the ASPs to track the input waveform for each of D1–D9 detectors. The gate period is fixed at 800 ns and guarantees that the peak amplitudes will be tracked and stored at conclusion of the interval. At the end of the 800 ns interval, transition to the valid state occurs.
- Valid::
-
The valid state tests whether all the enabled detectors had their high thresholds triggered to determine if the PH300s captured a valid event. On the valid condition, the next state will be rundown. If the event is not a valid coincidence, then the DPIE logic returns to the idling mode with no rundown. When transitioning to the rundown state, the D9 high threshold condition dictates the type of event to be handled (CHE if D9 active, or PEN if not). DPIE increments the PEN scaler if the event is valid and of type PEN and the CHE scaler if the event is valid and of type CHE (that is, if D9 was triggered). In this way we can separately tally events that have Cherenkov light and those that do not. Note that a CHE event cannot be identified in the logic unless the D9 coincidence mask bit is enabled, therefore the D9 coincidence enable bit should always be enabled.
- Rundown::
-
DPIE logic enters the rundown state when the PH300s store a valid event. Here the purpose is to perform the Wilkinson rundown on each ASP as the conversion from pulse height to a digital signal. The “PeakHeld” output from the PH300s is initially asserted on all detectors to show that a peak is held for readout. When the logic transitions to the Rundown state, the gate is released at the PH300s, and ASP logic begins the rundown process. We discharge the pulse peak voltage held by the PH300 at a fixed rate (following a 400 ns delay) and de-assert the PeakHeld when the stored level returns to zero, thereby preparing for the next event. The rundown state lasts a fixed period of 61.84 μs: 400 ns pre-rundown delay +61.44 μs rundown. In the rundown state, the RPS logic monitors the state of all PeakHeld signals while incrementing the rundown count at 25 MHz; de-assertion of a detector’s PeakHeld causes the current rundown count to be latched as the pulse height value for that detector.
1.2 A.2 Alpha Mode
Alpha mode is a special operational mode designed to allow collection of the energy deposits in the eight D detectors from the in-flight alpha sources. We use alpha mode as discussed above, primarily for calibration and monitoring of the SSDA subsystem. RPS event processing in alpha mode consists of 4 states: idling, gate, valid, and rundown. We describe each state and the transition conditions here:
- Idling::
-
this is the default start-up state for the event processing logic in alpha mode. When in this state, the DPIE logic monitors any enabled D detector for a low threshold trigger whereupon the state transitions to the gate state to capture pulse peaks for all of the D detectors.
- Gate::
-
DPIE logic enters the gate state when fast trigger logic (low thresholds) indicates that an event exists in the signal path. While in this state, the PH300s on the ASPs are enabled to track the input waveform for each of D1–D9 detectors. The gate period is fixed at 800 ns and guarantees that the peak amplitude will be tracked and stored at conclusion of this interval. At the end of the 800 ns interval, transition to the valid state occurs.
- Valid::
-
In alpha mode, the logic always follows a valid event with an immediate transition to the rundown state.
- Rundown::
-
The rundown in alpha mode is identical to the rundown process in normal mode, with the exception that typically only one D detector has a measurable pulse height.
1.3 A.3 Discriminator Rates
We monitor each detector with a “singles” counter, that is a scaler that increments whenever the high threshold is triggered for the associated detector. Singles counters operate regardless of the state of the associated bit in the coincidence mask. The scalers are 24 bits, allowing for maximum rates of greater than 107 counts per second. We also monitor the event rate of particles that are in coincidence as defined by a front/back pair of selected A collimation detectors. We included this doubles coincidence as a consistency check on the total rate of 10 or 11-fold coincidence events. We specify this coincidence rate with commands that enable or disable detectors with the nominal pair being A1A3 and the backup pair being A2A4. If both pairs are not available because of detector noise or other problems, the D1 becomes the front detector and D8 the back element.
1.4 A.4 Deadtime Monitor
RPS deadtime occurs whenever any enabled detector triggers its low threshold. The deadtime counter increments on the rising edge of a 12.5 MHz clock using a 24-bit floating point format with 3 exponent bits (most significant portion of output) and 21 mantissa bits (least significant portion of output). Hence the resolution of the deadtime scaler is 80 nsec. RPS reports the deadtime value in the rate and housekeeping packet as a 16-second accumulation that is sufficient for ground-based corrections to the incident particle intensity. The reported value is the number of 80 nsec intervals within 16 seconds during which RPS was busy transitioning from the idle state, hence the time during which new events would not be analyzed.
Appendix B: RPS Data Packet Formats
The RPS rate and housekeeping packet is a total of 38 bytes long and contains all detector scalers, coincidence rate scalers, micro dosimeter values, and other housekeeping information. RPS creates these packets once per second when power is applied and the 1 pulse per second signal exists from ground support equipment or the RBSP spacecraft. Hence the baseline data rate is 304 bits per second. Table 5 lists the contents of the rate and housekeeping packet.
Direct event packets have variable size depending on the number of coincidence events within the second. Table 6 lists the detailed packet contents.
Appendix C: RPS Commands
Table 7 summarizes the RPS commands.
Appendix D: Design Trades and Analyses
During the RPS development we addressed several questions regarding the RPS measurements technique and possible hazards to achieving the Level 1 instrument requirements. We focus here on one effect in order to document some interesting test results regarding the charge collection at the edges of silicon detector active volumes. For future reference, Table 8 summarizes all the major measurement questions that we considered and their answers.
4.1 D.1 Silicon Detector Edge Effects
Early in the RPS design we recognized the need to obtain as accurate a measurement of SSDA energy deposits as feasible. Unlike typical range telescopes, RPS analyzes small (<few MeV) deposits from only Z=1 particles, some of which are near minimum ionizing. Therefore one potential source of uncertainty in the determination of incident proton energy is incomplete charge collection in the SSDA silicon detectors at the edges of their active areas. We took two approaches to address potential edge effects.
The first was to quantify the spatial scale over which incomplete collection occurs at the detector edge. One could use actual particle beams that are sufficiently collimated to probe the energy deposit versus location, but it is challenging to collimate an alpha source to a few microns and expensive to use an accelerator facility. Instead we chose to deposit energy within a test detector using a pulsed ultraviolet (800 nm wavelength) laser whose spot size on the silicon was less than 2 microns wide; this same facility is used for single-event effect testing on bare microcircuits. Another benefit to probing the detector with the UV laser was the visual information about where the energy deposit was relative to the complex guard ring structure; one can image the spot with a video camera. The 1/e penetration depth in the silicon was ∼12 microns. We probed a detector design that uses a metallized grid to establish the electric field in the silicon thus allowing a direct stimulation of the bulk silicon except where the thicker guard rings stopped the laser beam. This detector design and the accurate laser spot placement yielded the transect shown in Fig. 21. The relative signal amplitude fell to 30 % of its nominal value at a radial distance equal to the detector thickness, a result consistent with the rule-of-thumb that the incomplete charge collection occurs over a distance comparable to the detector thickness. At twice the detector thickness, the deposit was only about 4 % of its true value.
Signal amplitude in a 146-micron thick Si solid-state detector versus position along the radius of the circular detector. We stimulated the detector with a pulsed UV laser and measured the location of the energy deposition to within a few microns (solid symbols) as referenced from the edge of the active area. The dashed curve is to guide the eye. The transect shown indicates a 30 % reduction of the energy deposit at a radial distance equal to the detector thickness with non-trivial signal amplitude up to twice the detector thickness
We thus used the UV laser test data to establish the need for collimation detectors in SSDA and to choose the diameters of the collimators (20 mm) and the energy-sensing detectors (23 mm). The difference in their radii is 1.5 mm corresponding to 1.5 times the nominal detector thickness, thus allowing for 50 % margin away from the detector edge.
4.2 D.2 Summary of Other Design Analyses
Table 8 lists the most significant questions that influenced the RPS design.
Appendix E: RPS Performance Lessons
We highlight here two RPS performance issues that we discovered prior to and during the flight model environmental testing. The issues had been solved before integration on the RBSP space vehicles, but we felt their stories were interesting enough to include in this instrument paper. They may be relevant for future instruments that use similar components.
5.1 E.1 MCP/PMT Response During Instrument Environmental Testing
The 85001 Burle MCP/PMT had no spaceflight heritage prior to its use in RPS. We subjected engineering model MCP/PMTs to thermal cycling and vibration prior to the final instrument design to assess their performance before instrument-level testing. We monitored two of the MCP/PMTs with adjustable light inputs and neutral density filters and found that the 28 thermal cycles revealed no performance changes. During early design trades we also vibrated an engineering model device to qualification vibration levels and found, in coordination with the vendor, that there was a slight (<1 mm) movement of one of the MCP mounting clips. The vendor ruggedized the clips for the flight devices and therefore we proceeded with their integration into the engineering and flight models for further testing.
However, during instrument-level vibration testing we found stepwise increases in the dark current noise of the MCP/PMTs. We conducted functional instrument tests during the switch between vibration axes that allowed us to document the instrument status using the 1-second rate and housekeeping packet information. This method proved to us the usefulness of quick functional tests during a vibration test campaign, not only before and after all the tests, but also between the various vibration directions. We found that the MCP/PMT in flight model 2 showed increases in the dark count rate by factors of ∼10 after each of the last 2 of 3 axis vibrations. After subsequent operation the dark count rate gradually dropped a factor of 10 in one month. Follow-on muon collects verified that the system worked adequately for flight. Also, we saw a more modest increase of a factor of 2 in the dark count rate after spacecraft-level vibration.
For RPS flight model 1, the dark count rate dropped by a factor of ∼1000 after the first instrument-level vibration test and a follow-on muon collect showed that the device had lost most of its gain. We replaced the MCP/PMT and the replacement had a similar pattern of increased dark counts after each vibration test.
Our hypothesis was that there was some material being loosened after each vibration within the sealed MCP/PMT, thus accounting for the increased gain that gradually decays with a month timescale. We were unable to discern a root cause for the failed unit. Most importantly, the decreased sensitivity of the devices to the spacecraft-level vibration testing enforces the view that subsystem-level tests are the most stressing due to extreme margins that programs routinely place on the vibration environment (e.g. Margolies and von Rosenvinge 1998). A contributing factor to the RPS design is the robust housing of 350 mils; other less rigid housings may dissipate the vibrational energy although the details would have to be determined through testing because of the mechanical complexity of the MCP/PMT.
5.2 E.2 LVPS Microphonics
Another effect of the rigid RPS housing came into play in the thermal sink for the 3 DC to DC converters on the LVPS circuit board. Upon assembly of the flight models we discovered an unacceptable noise level well above the 50 keV fast timing threshold on the ASPs. The noise had a specific frequency of 500 kHz. The root cause was vibrational energy emitted from the DC-to-DC converters.
Magnetic components on the converter hybrid oscillate at 500 kHz causing a subtle mechanical vibration of the entire part. This mechanical energy coupled through the converter heat sink to the RPS chassis, which being as rigid as it is, efficiently transmitted the energy to the detector coupling capacitor for each of the 13 ASPs. Those input capacitors are ceramic of type XR7 that are known to have piezoelectric properties. Hence, the desire to thermally couple the converters to the chassis had the unintended effect of causing unacceptable electronic noise. We note that the effect was not present in the RPS engineering model likely because of the different thermal coupling used there and the apparent lesser response of the non-flight coupling capacitors to microphonics.
It would have been a large schedule and cost impact to switch the capacitors to a type without any microphonics sensitivity. Instead, we successfully mitigated the problem in the flight models by (1) using a thermally conducting staking compound to fasten the converters, transfer their thermal energy into the chassis, and dampen much of the vibration at its source; (2) further dampen vibration by using compliant washers on the feet of the converter assembly; and (3) changing the ASP card guides that were closest to the coupling capacitors from beryllium-copper to a spaceflight-qualified polymer which was less efficient at transmitting any residual mechanical energy but provided the necessary clamping force for the printed circuit boards.
The problem was an interesting confluence of a part with a known sensitivity to microphonics and an unknown source of the mechanical energy. Finally, we note that spacecraft-level testing showed that there is no external source of similar high-frequency mechanical energy on the RBSP vehicles.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mazur, J., Friesen, L., Lin, A. et al. The Relativistic Proton Spectrometer (RPS) for the Radiation Belt Storm Probes Mission. Space Sci Rev 179, 221–261 (2013). https://doi.org/10.1007/s11214-012-9926-9
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11214-012-9926-9