Study of the Relationship Between Sunspot Number and the Duration of the ≈ 1.6 – 2.2 Year Period in Neutron Monitor Counting Rates

Abstract

Neutron monitor counting rates show periodicities in the ≈ 1.6 – 2.2-year range. These periodicities have been associated with a solar origin affecting the cosmic ray propagation conditions through the heliosphere. Our hypothesis is that the periodicities in the ≈ 1.6 – 2.2-years range correspond to a single periodicity that changes its duration over time.

López-Comazzi and Blanco (Astrophys. J. 927(2), 155, 2022) found that the duration of the ≈ 1.6 – 2.2-year period ($\tau$) is linearly related to the average sunspot number ($SSN_{a}$) in each solar cycle. The relationship shows that shorter ≈ 1.6 – 2.2-year periods occur during stronger cycles when $SSN_{a}$ is higher. Therefore, the duration of this period varies from one solar cycle to another. This study focuses on this relation. For obtaining this relation, the values of the duration of the ≈ 1.6 – 2.2-year period in global neutron monitor counting rates (a virtual station determined by averaging of the different neutron monitor counting rates along the world) along the Solar Cycles 20 – 24 have been used. We extend the sample by adding the duration of the ≈ 1.6 – 2.2-year period in Huancayo neutron monitor counting rates along Solar Cycle 19 to this linear relationship. Once the linear relationship is extended, $\tau$ for the current Solar Cycle 25 is computed giving ≈ 2.24 years. Drawing on this more accurate relationship given by $SSN_{a} = (-120 \pm 10) \: \tau + (320 \pm 20)$, we computed $\tau$ for the cycles previous to the existence of neutron monitors (Solar Cycles 7 – 18).

These ≈ 1.6 – 2.2-year periodicities in neutron monitor counting rates could be produce by variations in the solar magnetic field due to an internal mechanism of the solar dynamo called Rossby waves. Concretely, the harmonic of fast Rossby waves with $m=1$ and $n=8$ fit with the detected ≈ 1.6 – 2.2-year periodicity. In addition, the variation of the solar magnetic-field strength from weaker to stronger solar cycles could explain the different periods detected in each cycle. Based on the detected periodicities using the dispersion relation for fast Rossby waves, a solar tachocline magnetic-field strength of ≈ 7 – 25 kG has been estimated.

1 Introduction

Quasi-biennial oscillation (QBOs) periodicities, ranging from ≈ 0.6 years to 4 years, are detected in ground level neutron monitor (NM) counting rates, sunspot number, solar neutrino flux, and heliospheric magnetic-field strength, among others.

QBOs are detected in magnitudes (sunspots, flares, radio, and X-ray fluxes data) related with different levels of the solar atmosphere, with stronger spectral power around the solar maximum. For this reason, QBOs could be connected with the temporal weakening of solar activity around the solar maximum, called Gnevyshev Gap (Feminella and Storini, 1997; Bazilevskaya et al., 2014). Vecchio et al. (2010) detected the QBOs in the solar neutrino flux and they observed a strong correlation between solar neutrino flux and cosmic ray data during the period 1974 – 2001. The QBOs are also present in the solar interior, since they have been observed in different helioseismic data with good correlation (Broomhall et al., 2011). The QBOs have also been widely observed in the sunspot number (SSN) and sunspot area. Periodicities around 1.3, 1.7, and 2 – 4 years have been observed in large-scale solar photospheric magnetic field data (Knaack, Stenflo, and Berdyugina, 2005; Kane, 2011; Laurenza et al., 2012). A period around 1.6 years has been detected in X-ray flares along Solar Cycles (SCs) 20 – 22 by Antalová (1994). Wang and Sheeley (2003) concluded that stochastic processes associated with the emergence of active regions provide a valid explanation for the existence of ≈ 1 – 3 yr periodicities. Other important periodicity among the QBOs is the Rieger-type period (≈ 151 days), observed by Rieger (1985) in the gamma-ray flares for the first time and subsequently by Kudela et al. (2002) in the cosmic ray intensity.

Using the cosmic ray intensity and solar magnetic data respectively, the dependence between the QBOs and solar cycles has been concluded by Kudela et al. (2002) and Knaack, Stenflo, and Berdyugina (2005). In relation with this, Khramova, Kononovich, and Krasotkin (2002) stated that the features of QBOs depend on the length and power of the particular solar cycle. In agreement with these works, Okhlopkov (2011) investigated the QBOs in the range 1.6 – 2.0 years using data from cosmic rays and various parameters of solar activity, interplanetary medium, and the geomagnetic Ap index along SCs 20 – 23 for individual cycles. He obtained an average period of 1.7 years in the odd cycles (SC 21 and 23) and a 1.81 – 1.93 yr period in the even cycles (SC 20 and 22). Recently, López-Comazzi and Blanco (2022) obtained a relationship between the duration of this period (≈ 1.6 – 2.2 years) and the average of SSN in each SC, therefore, according to this work, the duration of the ≈ 1.6 – 2.2 yr period depends on the strength of the solar activity (measured in averaged SSN).

Many studies indicate the solar origin of the 1.7 yr period that affects the propagation conditions of cosmic rays through the heliosphere. Valdés-Galicia, Pérez-Enríquez, and Otaola (1996) reported a 1.7 yr period in NM counting rates using the maximum entropy method correlated with similar periodicities in southern coronal holes and large active regions (zones where the magnetic flux is generated) for the period 1947 – 1990. Most recently, Tsichla, Gerontidou, and Mavromichalaki (2019) found the 1.7 yr period in the cosmic ray flux, SSN, and geomagnetic index Ap in the time interval 1965 – 2018, while Velasco Herrera et al. (2018) found ground level enhancement (GLE) occurrences with the 1.7 yr period. The authors of this paper studied 56 GLEs along the period 1966 – 2014 finding that all these events occur in coincidence with the positive phase of the 1.7 yr oscillation determined by wavelet analysis.

QBOs have also been observed by detectors on board satellites. For example, Kato et al. (2003) applied the wavelet analysis to the cosmic ray flux at Voyager spaceship in the outer heliosphere and they found a significant periodicity of ≈ 1.7 years.

Bazilevskaya et al. (2014) showed that the QBOs in the cosmic ray flux are correlated with those detected in the heliospheric magnetic field strength (correlation coefficient of $R=-0.68$). On the other hand, the authors of this paper obtained a large correlation $R=-0.82$ between the QBOs in the geomagnetic Dst index and the QBOs in the product of the solar wind velocity and the heliospheric magnetic field strength during the interval 1967 – 2009. The QBOs are variable and intermittent in all the aforementioned magnitudes.

Solar dynamo mechanism properties could probably produce QBOs (Chowdhury et al., 2019). Concretely, the 1.6 – 2.2 yr period has been associated with the instabilities of the $m=1$ fast magnetic Rossby waves in the solar tachocline (Zaqarashvili et al., 2007; Zaqarashvili, Oliver, and Ballester, 2009; Silva and Lopes, 2017). Using the dispersion relation of the magnetic Rossby waves (Gurgenashvili et al., 2016) with $m=1$ and $n=8$, periodicities in the interval ≈ 1.6 – 2.2 years have been computed.

2 Data and Analysis Methods

Before applying the Morlet wavelet analysis to the NM counting rates time series, an outlier detection (box and whiskers) and a linear interpolation to replace outlier and missing values have been applied to the data. By the box and whiskers method, we considered outliers as the points out of the range $\left [Q_{1}-1.5\left (Q_{3}-Q_{1}\right ),Q_{3}+1.5\left (Q_{3}-Q_{1} \right )\right ]$, being $Q_{1}$ and $Q_{3}$ the first and third quartile, respectively. For more details about the analysis method and outlier detection, see the Section 2.4 in López-Comazzi and Blanco (2022).

Morlet wavelet analysis (Torrence and Compo, 1998; Roesch and Schmidbauer, 2018) is a useful tool that allows to detect periodicities within a time series by decomposing it into a sum of wavelets, which come from the Morlet function ($\Psi ( \eta )= \pi ^{-1/4} e^{i \omega _{0} \eta } e^{- \eta ^{2}/2}$, with $\eta = s \cdot t$ and the dimensionless frequency $\omega _{0}=6$).

The normalized wavelet transform applied to a discrete time series ($x_{n}$ are the points of the time series with time index $n$) with equal temporary spacing $\delta t$ and time index $n=0,\ldots, N-1$ is given by:

$$ W_{n}(s) = \sqrt {\frac{\delta t}{s}} \sum _{n'=0}^{N-1} x_{n} \cdot \Psi ^{*} \left [ \frac{(n'-n)\delta t}{s} \right ], $$

(1)

where $\Psi ^{*}$ is the complex conjugate of the mother wavelet function and the coefficient $s$ is the frequency.

Two types of spectra can be derived from this analysis: the Wavelet Power Spectrum (WPS) and the Global Wavelet Spectrum (GWS).

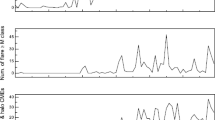
The WPS is presented as a heat map, where higher values of the spectral power $P$ (the square of the wavelet transform $P=|W_{n}(s)|^{2}$ being $W_{n}(s)$ the Morlet wavelet transform) are in red, intermediate values are depicted by green and yellow, and the lower values are shown in blue in Figure 1. The shaded area in the WPS of Figure 1a (top of the figure) shows a zone influenced by edge effects, named the cone of influence.

Figure 1

The Wavelet Power Spectrum (a) and Global Wavelet Spectrum (b) of the Huancayo NM in SC19. The red line in the GWS shows the 95% confidence level and the peaks above this line are significant periodicities.

The GWS is represented by a curve that shows the averaged spectral power associated to each period for the considered interval. A reference background signal is modeled to determine whether the significant periodicities represent a real characteristic of the time series. We considered the univariate lag-1 autoregressive AR(1) process as reference background signal. The Fourier spectrum of this model for red noise is given by

$$ P_{k} = \frac{1-\alpha ^{2}}{1+\alpha ^{2}-2\alpha \cos{(2 \pi k/ m)}}, $$

where $k=0,..,m/2$ is the frequency index and

$$ \alpha = \frac {\sum _{n=0}^{N-2}{(x_{n}-\bar{x})(x_{n+1}-\bar{x})/(N-2)}}{\sum _{n=0}^{N-1}{(x_{n}-\bar{x})^{2}/(N-1)}}. $$

$N$ is the number of points and $\bar{x}$ the value averaged of these time series.

Finally, we multiplied this background spectrum by the half of the 95th percentile value for a chi-squared ($\chi ^{2}$) distribution function with two degrees of freedom following the approach of Torrence and Compo (1998) to determine the 95% confidence level of the periodicities.

We considered a frequency as significant when its confidence level is above the 95%. The red line in Figure 1b marks this significance level. The WPS and GWS of the Huancayo NM counting rates in SC19 are presented in Figure 1a and 1b, upper and lower panels, respectively. The periodicities with 95% confidence level are listed in Table 1.

The data used in the next section are one-hour pressure corrected NM counting rates from the NMDB web page (http://www01.nmdb.eu/) and http://cr0.izmiran.ru/common/links.htm and the daily observations of SSN from https://www.ngdc.noaa.gov/stp/SOLAR/. SSN data have been used as a solar activity measure considering the strong solar cycles as intervals with higher than average SSN ($SSN_{a}$) and weak SCs with lower than average SSN (lower than $SSN_{a}$).

The limits of each solar cycle are selected according to the following time intervals: SC19 (from 1954-04-01 to 1964-09-30), SC20 (from 1964-10-01 to 1976-02-29), SC21 (from 1976-03-01 to 1986-08-31), SC22 (from 1986-09-01 to 1996-07-31), SC23 (from 1996-08-01 to 2008-11-30), and SC24 (from 2008-12-01 to 2019-11-30), where dates are written as year-month-day. For SC25, we consider an interval from 2019-12-01 to 2030-12-31.

3 Results and Discussion

López-Comazzi and Blanco (2022) detected a ≈ 1.6 – 2.2 yr period, among other periodicities, in NM counting rates and SSN in the interval 1964 – 2019 (five solar cycles). They found that the duration of this periodicity in NM counting rates changes from one SC to the other and concluded that shorter ≈ 1.6 – 2.2 yr periods occur during stronger SCs. This conclusion was quantified by a linear relationship between duration of ≈ 1.6 – 2.2 yr period and SSN. The linear relationship is

$$ SSN_{a} = C \: \tau + b $$

(2)

being $C=-130 \pm 10$ sunspots/year the Comazzi’s coefficient (taken from López-Comazzi and Blanco, 2022) and $b = 330 \pm 30$ sunspots, $SSN_{a}$ is the average sunspot number, and $\tau$ denotes the length of the ≈ 1.6 – 2.2 yr period detected in Global Neutron Monitor counting rates in years for each SC. This equation was computed by using the global neutron monitor (GNM) counting rates. This virtual NM was determined by averaging the selected NMs that satisfy a quality criteria proposed by López-Comazzi and Blanco (2020). As verified in that research, the behavior of the GNM reproduces the behavior of the selected NMs. For more details about GNM and Equation 2, see López-Comazzi and Blanco (2022). The linear fit of Equation 2 shows a coefficient of determination of $R^{2}=0.97$.

3.1 Huancayo Neutron Monitor Along Solar Cycle 19

The wavelet analysis was applied to the Huancayo NM counting rates along SC19 (1954 – 1964) in order to check if the duration of the periodicity around ≈ 1.6 – 2.2 yr matches with the predicted value by Equation 2. The Huancayo NM was not included into the analysis performed in López-Comazzi and Blanco (2022). During the SC 19, there are few NMs with available and reliable data, being the Huancayo NM the only one that follows the quality criteria.

SC 19 coincides with the highest average SSN in the last eighteen SCs, therefore following Equation 2, we expected the shortest value of $\tau$. Figure 1a shows the Wavelet Power Spectrum of the Huancayo NM in SC19. One can observe a significant periodicity in 1.57 years in the GWS (Figure 1b). This periodicity appears throughout the whole cycle, but is specially relevant around the solar maximum from 1957 to 1960 (Figure 1a). The duration of the ≈ 1.6 – 2.2 yr period was 1.57 years. On the other hand, the estimated duration using Equation 2 was 1.61 years. This confirms a great degree of concordance between the observation and the estimation by Equation 2. Therefore, the duration of the ≈ 1.6 – 2.2 yr period found in Huancayo NM during SC 19 supports the empirical Equation 2.

3.2 Estimation of $\tau$ in Solar Cycles 7 – 18

In order to expand the statistical sample, we added the duration of the period of the Huancayo NM in SC 19 to the data for the ≈ 1.6 – 2.2 yr periodicities detected in GNM counting rates from SC 20 – 24. The linear fit with this new point decreases the error giving a coefficient of determination of $R^{2}=0.98$. We could linked the results in Huancayo NM counting rates and GNM counting rates because the GNM reproduces the behavior of any NM (López-Comazzi and Blanco, 2020).

The behavior of the averaged SSN versus the duration of the ≈ 1.6 – 2.2 yr period along the SCs is shown in Figure 2.

Figure 2

Mean of the SSN in each solar cycle vs. the duration of the ≈ 1.6 – 2.2 yr period ($\tau$) detected in the GNM counting rates (SCs 20 – 24) and Huancayo NM counting rates (SC 19).

Adding the duration of the ≈ 1.6 – 2.2 yr period of Huancayo NM along the SC19 to the linear fit, Equation 2 becomes

$$ SSN_{a} = \alpha \: \tau + \beta $$

(3)

being $\alpha = -120 \pm 10$ sunspots/year and $\beta = 320 \pm 20$ sunspots. This linear fit shows a coefficient of determination of $R^{2}=0.98$.

The duration of the ≈ 1.6 – 2.2 yr period in NM counting rates, and therefore cosmic ray flux along the SCs prior to the existence of NMs, could be determined assuming that Equation 3 is correct. Under this assumption, a reconstructed duration of the ≈ 1.6 – 2.2 yr period ($\tau _{rec}$) in NM counting rates during the SCs 7 – 19 have been computed. In Table 1, we depict the average of SSN for each SC ($SSN_{a}$), the empirical duration of the ∼1.6 – 2.2 yr period computed by wavelet analysis, $\tau _{wav}$, and the reconstructed value ($\tau _{rec}$) computed by Equation 3. The error of the reconstructed ≈ 1.6 – 2.2 yr periodicity is given by $\epsilon _{\tau _{rec}} = \pm 0.2$ years.

Table 1 From left to right: the SC number, the averaged SSN for each SCs ($SSN_{a}$), the empirical duration of the ≈ 1.6 – 2.2 yr period computed by wavelet analysis applied to the GNM counting rates, $\tau _{wav}$, and the reconstructed value, $\tau_{rec}$, computed by Equation 3 having an error $\epsilon _{\tau _{rec}} = \pm 0.2$ years.

The values of $\tau _{wav}$ detected in GNM counting rates from SCs 20 – 24 have been taken from López-Comazzi and Blanco (2022) (for more details see that article).

3.3 Estimation of $\tau$ in Solar Cycle 25

It is interesting to check if Equation 3 shows real physical properties or if it is just a statistical bias. In order to check this, we made an estimation of $\tau$ for the current SC25. We computed the duration of the ≈ 1.6 – 2.2 yr period based on the expected SSN average for the SC25. When the SC25 ends around the year 2030, the predicted value should be verified.

To model the shape of the sunspot cycle, the approach given by Volobuev (2009) has been considered. The sunspot number has been approximated to the following model of only one parameter

$$ SSN_{x}(t)= C_{x} \left ( \frac{t-T_{0,x}}{A_{x}}\right ) ^{2}e^{- \left ( \frac{t-T_{0,x}}{B_{x}}\right ) ^{2},} $$

(4)

where $x$ indicates the solar cycle number, $T_{0,x}$ is the initial time of the $x$-cycle, and $A_{x}$, $B_{x}$ and $C_{x}$ are free parameters. Volobuev (2009) determined two relationships between these two parameters given by $B_{x}=0.022A_{x}+2.98$ and $A_{x,odd}=0.69A_{x,even}+11$ that allow us to compute the values of these parameters for the SC25: $A_{25}=55.85$ and $B_{25}=4.21$. The parameter $C_{25}=55048.16$ transforms the fractional area into the SSN.

Figure 3 shows the sunspot number model for SC25. The maximum is given by 115 sunspots in early 2024, in agreement with https://www.swpc.noaa.gov/news/solar-cycle-25-forecast-update and Maddanu and Proietti (2022).

Figure 3

The sunspot number model for Solar Cycle 25, the maximum of which is given by 115 sunspots.

An average of ≈ 53 sunspots/day have been estimated along the SC25 and a 2.24 yr period is determined according to Equation 3. As a result, we anticipate that the duration of the 1.6 – 2.2 yr period will be 2.24 years, making it the weakest SC.

3.4 The ≈ 1.6 – 2.2 yr Period in Rossby Waves

The ≈ 1.6 – 2.2 yr period, and QBOs in general, are not persistent during the whole SC (Sykora and Rybak, 2010) and change from cycle to cycle (Vecchio and Carbone, 2009), as noticed by many researchers. The cause is probably the variations of the magnetic field ($B_{max}^{tach}$) and differential rotation in the solar tachocline (Zaqarashvili et al., 2010). The fact that the ≈ 1.6 – 2.2 yr period amplitude is higher around the solar maxima (during the polarity reversal intervals) could be an evidence that this period is related to the solar dynamo (López-Comazzi and Blanco, 2022).

We have measured a period ranging from 1.6 – 2.2 years in NM counting rates along the SCs 19 – 24. As it has been shown above, the duration of the ≈ 1.6 – 2.2 yr period is longer when solar activity is lower. For example, in SC19 the average of the SSN is 129.16 and we detected a 1.57 yr period, a 1.77 yr period in SC21 ($SSN_{a} = 111.31$) and 1.81 yr period in SC22 ($SSN_{a} = 106.26$). While a period closer to ≈ 2.2 years has been observed in SC24, with a lower solar activity ($SSN_{a} = 49.48$). On the other hand, an intermediate period between ≈ 1.6 – 1.8 yr period and ≈ 2.2 yr period has been detected in cycles with moderate solar activity (SC20 and SC23).

The origin of this variation in the ≈ 1.6 – 2.2 yr period could be linked to variations in the global solar magnetic field. Thus, these periodicities could be related with a solar dynamo mechanism (Rossby waves). The angular frequency of fast Rossby waves according to Zaqarashvili, Oliver, and Ballester (2009) is given by

$$ \omega =-\frac{2\Omega _{0}m}{n(n+1)}, $$

(5)

where $\Omega _{0}$ is the system rotational velocity, $n$ and $m$ are integer numbers defined as toroidal and poloidal wave number, respectively ($n=1,2,3,\ldots$ and $m=0,1,2,\ldots,n$). Considering $\Omega _{0}=2.6 \cdot 10^{-6}~\mbox{s}^{-1}$, $m=1$ and $n=6,7$, waves with 1.6– and 2.1 yr period are obtained. A value of $m=1$ has been taken because the poloidal magnetic field component is practically zero. However, this model does not take into account neither differential rotation nor the solar magnetic field strength. In order to have a more realistic approximation to the problem, we have used the model developed by Gurgenashvili et al. (2016).

Gurgenashvili et al. (2016) derive the dispersion relation of the magnetic Rossby waves in the presence of a toroidal magnetic field and differential rotation. In addition, they detected the Rieger period (150 – 197 days) in SSN along the SCs 14 – 24 and used these periods to estimate the dynamo magnetic field strength during these SCs using the dispersion relation. A field strength range of 20 – 40 kG for weaker and stronger cycles, respectively, were estimated in that work.

The dispersion relation for fast Rossby waves is given by

$$ \omega = -m \Omega _{0} \frac{1+s_{2}+\sqrt{(1+s_{2})^{2} +\frac{B_{0}^{2}}{4\pi \rho \Omega _{0}^{2} R_{0}^{2}}n(n+1) }}{n(n+1)} $$

(6)

where $\rho$ is the density perturbation, $R_{0}$ the distance from the center to the dynamo layer, $B_{0}$ the amplitude of the magnetic field strength, and $s_{2}$ is the differential rotation rate. Therefore, the period of the spherical harmonics with fixed $m$ and $n$ depends on the magnitudes above mentioned.

We are considering the values given by $\Omega _{0} = 2.6 \cdot 10^{-6}\text{ s}^{-1}$, $s_{2} = 0.17$, $\rho = 0.2~\mbox{g}\,\text{cm}^{-3}$ and $R_{0} = 5 \cdot 10^{10}\text{ cm}$. With these values for the base of convection zone, fast Rossby waves with $m=1$ and $n=8$ exhibit a ≈ 1.6 – 2.2 yr period. $n=8$ has been taken because the range of the detected periodicities is given for this value.

Zaqarashvili et al. (2010) suggest that the behavior of the ≈ 1.6 – 2.2 yr period could depend on the magnetic field strength and the differential rotation parameters. This hypothesis has been used in the next section to determine a possible relationship between the duration of the ≈ 1.6 – 2.2 yr period in NM counting rates ($\tau$) and the solar dynamo magnetic field strength.

3.5 Modeling the Solar Tachocline Magnetic Field Strength by Using $\tau$

From Equation 6, we derived the solar tachocline magnetic field strength, $\left(B_{max}^{tach}=\frac{B_{0}}{2}\right)$, in function of $\tau _{c} = \frac{2\pi}{\omega}$ and other parameters above mentioned. This equation is given by:

$$ B_{max}^{tach} = 2 \pi R_{0} \sqrt{\frac{\rho}{m\tau _{c}}\left [ \frac{\pi n (n+1)}{m \tau _{c}} - \Omega _{0} (1+s_{2})\right ].} $$

(7)

If the variation of $B_{max}^{tach}$ through different SCs would be responsible for the different duration of ≈ 1.6 – 2.2 yr periods in NM counting rates, then $\tau _{c} = \tau$ and $B_{max}^{tach}$ could be estimated using the observed $\tau$. Therefore, Equation 7 could explain the empirical relationship between the duration of the ≈ 1.6 – 2.2 yr period and the averaged SSN (Equation 3), because the latter magnitude is directly affected by the solar dynamo magnetic field. Furthermore, the detected periodicities in NM counting rates in this range could be used to estimate the magnetic field strength in the solar tachocline or solar dynamo layer using Equation 7.

Figure 4 shows the solar dynamo magnetic field strength $B_{max}^{tach}$ of the Rossby magnetic wave $m=1$ and $n=8$ as function of $\tau$ obtained according with Equation 7. Red points correspond to empirical periodicities and blue points are estimated periodicities. The highest value of the solar tachocline magnetic field strength ($B_{max}^{tach} \approx$25 kG) has been obtained for the shortest period (≈ 1.57 years) in SC 19. The lower values for $B_{max}^{tach} \approx$7 kG has been computed for the longer periods ≈ 2.2 years given in SCs 14, 24, and 25. Therefore, the ≈ 1.6 – 2.2 yr oscillations could be formed in the tachocline with a magnetic field between 7 – 25 kG.

Figure 4

Solar dynamo magnetic field strength, ($B_{max}^{tach}$ in kG), of the magneto Rossby wave m = 1 spherical harmonics with n = 8 vs. the duration of ≈ 1.6 – 2.2 yr period ($\tau$ in years). The observed periods detected in NM counting rates in different solar cycles are marked by dots. Blue points corresponding to estimated periods (SCs 7 – 18 and 25) and red points correspond to empirical values obtained by wavelet analysis for SCs 19 – 24. The following values have been assumed: $\Omega _{0}=2.6\ 10^{-6}\text{ s}^{-1}$, $s_{2} = 0.17$, $\rho =0.2~\mbox{g}\,\mbox{cm}^{-3}$ and $R_{0} = 5 \cdot 10^{10}\text{ cm}$.

Figure 5 shows a summary of the evolution of $\tau$ and $B_{max}^{tach}$ along the SCs 7 – 25. The value of $\tau$ in function of the SC is shown in Figure 5a where blue points correspond to estimated periods (SCs 7 – 18 and SC 25) and red points are associated with the ≈ 1.6 – 2.2 yr periodicities in GNM counting rates computed by wavelet analysis (SCs 19 – 24). As we defined above, SSN data have been associated as the solar activity measure. Equation 3 gives a connection between solar activity and the ≈ 1.6 – 2.2 yr period ($\tau$) in NM counting rates along the different SCs.

Figure 5

(a) The duration of the ≈ 1.6 – 2.2 yr period ($\tau$) vs. the solar cycle number (SC). Blue points correspond to estimated periods (SCs 7 – 18 and 25) and red points correspond to empirical values obtained by wavelet analysis for SCs 19 – 24. (b) Solar tachocline magnetic field strength $B_{max}^{tach}$ (in kG) vs. the solar cycle number.

Figure 5a shows a relative minimum around SCs 8 – 9, $\tau \approx 1.88$ years, then its duration increases to ≈ 2.21 years in SC 14, later the duration of the period decreases again reaching a new minimum in SC 19. From SC 19 onwards there is a gradual increase in $\tau$ (with the exception of SC 20, which shows an atypical behavior) until reaching a relative maximum around SCs 24 – 25.

Figure 5b shows the solar tachocline magnetic field strength vs. the solar cycle number. $B_{max}^{tach}$ shows an inverse correlation with $\tau$. When the solar tachocline magnetic field strength is lower than 10 kG, we observed the longer periods ($\tau \approx 2.2$ years). On the other hand, for the highest value of the $B_{max}^{tach} \approx$ 25 kG (in SC 19 concretely), the lowest value of the duration of $\tau \approx 1.6$ years has been observed.

4 Conclusions

We have considered that the periods ranging from 1.6 years to 2.2 years ($\tau$) in neutron monitor counting rates are a unique period which shows variations of its duration as a function of SSN and of the strength of the each SC. The duration of the ≈ 1.6 – 2.2 yr period in NM counting rates varies over cycles and even through a particular solar cycle. We have observed that this periodicity changes with the average sunspot number $SSN_{a}$ in each solar cycle according with Equation 3. Shorter periods (≈ 1.6 – 1.7 years) occur during stronger solar cycles when $SSN_{a}$ is higher and longer periods (≈ 2.1 – 2.2 years) are observed when $SSN_{a}$ is lower.

We have checked the validity of Equation 2 along the Solar Cycle 19 by means of the Huancayo neutron monitor counting rates. An empirical value of 1.57 yr period was obtained by applying Morlet wavelet analysis to the Huancayo NM counting rates along the Solar Cycle 19. This result is in agreement with the expected value $\tau \approx 1.61$ years computed following Equation 2.

In order to expand the statistical sample, we added the duration of the ≈ 1.6 – 2.2 yr period in Huancayo NM counting rates along SC 19 to the data from SCs 20 – 24. The evolution of $\tau$ along the different solar cycles was reconstructed in function of the average SSN according to the new Equation 3. From this equation, a sunspot number model allowed us to estimate a value of $\tau \approx 2.24$ years for the current Solar Cycle 25.

Finally, a possible explanation for the origin and behavior of these periodicities has been proposed. This explanation hypothesizes that the ≈ 1.6 – 2.2 yr period is due to variations of the global solar magnetic field and is related with the solar dynamo mechanism in the form of Rossby magnetic waves. Rossby waves could explain the intermittency and variable duration of the ≈ 1.6 – 2.2 yr period. Using the dispersion relation for fast Rossby waves with $m=1$ and $n=8$ with the values of $\tau$, a solar dynamo magnetic-field strength $B_{max}^{tach}$ of ≈ 7 – 25 kG has been estimated.