Solar Electron Beam Velocities That Grow Langmuir Waves in the Inner Heliosphere

Abstract

Solar accelerated electron beams, a component of space weather, are emitted by eruptive events at the Sun. They interact with the ambient plasma to grow Langmuir waves, which subsequently produce radio emission, changing the electrons’ motion through space. Solar electron beam–plasma interactions are simulated using a quasilinear approach to kinetic theory to probe the variations in the maximum electron velocity [$\Xi$] responsible for Langmuir wave growth between the Sun’s surface and 50 R_⊙ above the surface. We find that it peaks at 5 R_⊙ at 0.38 c and decreases as $r^{-0.5}$ to 0.16 c at 50 R_⊙. The role of the initial beam density [$n_{\mathrm{beam}}$] and velocity spectral index [$\alpha$] on the energy density of the beam and $\Xi$ is extensively studied. We show that a high spectral index yields a lower $\Xi$, while a high $n_{\mathrm{beam}}$ yields a higher $\Xi$, and vice versa. We observe at different energy channels that below 60 keV, electrons arrive up to 0.75 minutes earlier than expected at 13 R_⊙ while higher energy electrons propagate scatter free in the plasma. A special focus on the associated Type III radio burst shows that the energy range [$\Delta E$] of electrons producing Langmuir waves evolves from 7 keV to 1 keV between 0 and 28 R_⊙. Understanding the transport effect on the electron beam kinetics and arrival time at Earth has space weather implications. The results of this simulation can be tested against readily available in-situ data from Solar Orbiter and Parker Solar Probe.

1 Introduction

Eruptive events near the Sun’s surface, such as solar flares, accelerate beams of energetic particles through the solar corona and out in the solar system. A component of space weather, these electron beams travel along the magnetic field, interacting resonantly with Langmuir waves in the ambient background plasma, which in turn produce solar radio emission (Ginzburg and Zhelezniakov, 1958; Lin, 1974; Gurnett et al., 1981; Reiner, 2001; White et al., 2011). Solar radio emission is a tool used to probe the electron beams they originate from and to understand their characteristics and dynamics (Bastian, Benz, and Gary, 1998).

The recent launches of ESA’s Solar Orbiter’s and NASA’s Parker Solar Probe (PSP) have opened a new era of solar physics, probing the solar corona, as close as 10 R_⊙ above our star. These measurements will revolutionise our understanding of wave–particle interactions in the solar corona and solar wind, as well as of different kinds of emission such as Type III solar radio bursts. The first observations by Solar Orbiter’s Energetic Particle Detector (EPD) during the first perihelion at 0.51 AU (Gómez-Herrero et al., 2021) have shown similar results as at 1 AU, where non-thermal electrons (sub-10 keV) arrive simultaneously to Langmuir waves, earlier than expected from their respective velocities if a scatter free approach is used to analyse their transport.

Other comparative work combining observations of non-thermal electrons by the Advanced Composition Explorer (ACE) and simulations of the observed events, this time at deca-keV energies without beam–plasma interactions or associated Langmuir wave growth show non-thermal electrons in this regime propagating scatter free up to 1 AU (Dröge and Kartavykh, 2009; Agueda et al., 2010). This indicates that there is a limit in the deca-keV range of electron energies where the beam ceases to propagate scatter free, which needs to be investigated further.

It has been shown through previous simulation work that for a Maxwellian electron beam (Li and Cairns, 2013a), or a velocity dependency with a power–law spectrum with spectral index 8 (Reid and Kontar, 2018), the velocity of the subsequent Type III radio emission source cannot exceed 0.3 c. It has also been demonstrated that the Type III velocity highly depends on the initial electron beam parameters, such as the spectral index of the velocity distribution (Li, Robinson, and Cairns, 2008; Li, Cairns, and Robinson, 2009, 2011; Li et al., 2011; Li and Cairns, 2012, 2013b, 2014; Ratcliffe, Kontar, and Reid, 2014; Reid and Kontar, 2018).

The maximum electron velocity responsible for Langmuir wave growth, which is hypothesised to evolve as the beam propagates away from the Sun, into the solar corona and further into the solar wind, and the mechanisms driving this change have not yet been fully investigated. Solar accelerated transport simulation work has looked at the dynamics of electron beams travelling through plasma in the solar corona (e.g. Takakura and Shibahashi, 1976; Kontar, 2001a,b), in the solar wind (e.g. Magelssen and Smith, 1977; Krafft, Volokitin, and Krasnoselskikh, 2013, 2015; Krafft and Volokitin, 2017; Reid and Kontar, 2013, 2015, 2017), and at electron onsets near Earth (e.g. Kontar and Reid, 2009). However, how Langmuir waves change the motion of non-thermal electrons through the solar wind, and how beam–plasma interactions affect the electron beam kinetics is still not well understood. More specifically understanding the causes of this change in velocity will allow for better predictions of the solar electron onset at the Sun as well as arrival times at Earth.

What causes electrons with a certain energy to arrive co-temporally with Langmuir waves at certain distances from the Sun? Are the characteristics of the electron distribution function playing a role in determining which velocity electrons grow Langmuir waves at these distances? Since the low energy electrons arrive simultaneously with the Langmuir waves close to the Sun (e.g. Lin, 1974; Haggerty and Roelof, 2002; Roelof, 2008; Gómez-Herrero et al., 2021), we want to understand what happens during the electrons’ transport for their arrival time to differ from predictions and to analyse what velocity electrons arrive with the Langmuir waves closer to the Sun than 0.51 AU.

$\mathit{Wind}$ observations of Type III radio emission at MHz frequencies show deceleration of CMEs and associated solar energetic particles in the corona (Maia and Pick, 2004). An analysis of Type III solar radio bursts frequencies enables us to probe for solar electron velocities and reveals that the electron beam velocity distribution displays a decelerating trend the further the electrons propagate from the Sun (Krupar et al., 2015). Closer to the Sun, simulations have shown a potential increasing trend in electron velocity (Reid and Kontar, 2018) although this is yet to be inferred observationally by Type III bursts, on account of uncertainties in the background electron density distribution. These results shows that different energy ranges of the electron beam interact with the background plasma as the beam propagates through the corona and the solar wind.

Solar accelerated electrons travel as a distribution of velocities with faster ones outpacing the slower ones as the beam propagates away from the Sun. This outpacing creates an instability that is referred to as the bump-on-tail instability (Ginzburg and Zhelezniakov, 1958). This instability gives rise to a positive gradient in velocity space of the electron distribution function, making the background plasma susceptible to Langmuir waves’ growth above the thermal level. As the electron beam interacts resonantly with the plasma and loses energy to it (Fainberg, Evans, and Stone, 1972; Dulk et al., 1987; Malaspina, Cairns, and Ergun, 2011), the velocity gradient gradually attenuates and the appearance of a plateau is observed (Ginzburg and Zhelezniakov, 1958; Drummond and Pines, 1962; Vedenov, 1963). Energy lost by the beam to the plasma is then reabsorbed by the back of the beam (Kontar, 2001a,b), fueling its transport as a beam–plasma structure (Mel’nik, Lapshin, and Kontar, 1999; Sturrock and Coppi, 1964) through the solar corona and beyond into the solar wind and the interplanetary medium. The position of the bump in the electron velocity distribution determines what are the velocities of electrons that interact resonantly with the plasma and make Langmuir waves susceptible to growth.

Remote sensing observations of beam–plasma interactions via subsequent radio emission (Harvey, 1976; Reid, Vilmer, and Kontar, 2011a; Zharkova and Siversky, 2011) by spacecraft such as STEREO/Waves (Krupar et al., 2015) and $\mathit{Wind}$ (Krucker et al., 2007; Krucker, Oakley, and Lin, 2009) as well as wave–particle interaction simulations (Kontar and Reid, 2009) both display a broken power law in velocity space in the deca-keV range. The simulations (Kontar and Reid, 2009) compare a free-streaming electron beam with one interacting with the background plasma. Figure 1 from Kontar and Reid (2009) shows the simulated electron energy spectrum for the initially injected free-streaming electron beam propagating away from the Sun and the electron energy spectrum for an electron beam resonantly interacting with the Langmuir waves. Kontar and Reid (2009) fit a power law in velocity with spectral index $\alpha$ to the electron energy spectra, showing that for the electron beam interacting with the Langmuir waves, there is a break at 35 keV. The superposition of both electron energy spectra shows clearly that it is the Langmuir wave growth from wave–particle interactions that cause the spectral break. Whilst Langmuir wave energy can be re-absorbed by the back of the beam, refraction off density gradients moves the wave energy to lower phase velocities, where it is re-absorbed by the background plasma, depleting the electron beam of energy and causing the decrease in the electron beam peak flux spectral index below a certain break energy. If we understand that it is the Langmuir wave growth that causes the breaking of the velocity power law, it is not yet known at what electron velocity it happens, at different distances from the Sun.

In this article, we simulate a solar accelerated electron beam propagating through the solar corona and interacting with the background plasma of the solar wind. In particular, we look at the solar electron beam distribution function and the corresponding spectral energy density of the Langmuir waves it grows up to 50 R_⊙. From this, we calculate the range of electron energies growing Langmuir waves and therefore the maximum electron velocity responsible for Langmuir wave growth as a function of distance from the Sun. We examine the electron arrival times and also investigate the role of the spectral index of the velocity distribution [$\alpha$] and the beam density [$n_{\mathrm{beam}}$] on both the beam–plasma interactions and the maximum velocity responsible for Langmuir wave growth. Lastly, we analyse the Type III solar radio burst associated with the simulated electron beam and extract from it information about the velocity range of electrons interacting resonantly with the plasma. The interactions are simulated using quasilinear theory (Drummond and Pines, 1962; Vedenov, 1963) in the weak-turbulence regime combined with the Van Leer numerical scheme (van Leer, 1974, 1977a,b) as this has proven to be an accurate finite difference method for the modelling of the beam–plasma structure interactions and propagation (Ziebell et al., 2008, 2011, 2012).

2 Modelling the Beam–Plasma Interactions

Different processes regulate the transport of energetic electrons in the corona and solar wind plasma (Melrose, 1990). It is assumed that the transport can be modelled in one dimension as the solar accelerated electrons escape from the Sun along open magnetic field lines (Brown and Kontar, 2005).

2.1 The Electron Distribution Function

The electron distribution is injected as a source function

$$ S(v,r,t) = g(v)h(r)i(t), $$

(1)

with three dependencies: velocity, space, and time. $g(v) = A_{v}v^{-\alpha}$ models the velocity dependency as a power law with spectral index $\alpha$. $\alpha$ governs the initial velocity dependence of the injection.

The spatial distribution is modelled by a Gaussian, which describes a beam with width $d$ in position space, $h(r) = \exp \Big(-\frac{r^{2}}{d^{2}}\Big)$. The temporal profile also displays Gaussian characteristics with width $\tau$, the characteristic time of the temporal profile, and is described by $i(t) = A_{t}\exp \Big(-\frac{(t-t_{ \mathrm{inj}})^{2}}{\tau ^{2}}\Big)$ where $t_{\mathrm{inj}}$ is the injection time of the electrons. $A_{v} = n_{b} \frac{(\alpha - 1)}{v_{\mathrm{min}}^{1-\alpha}-v_{\mathrm{max}}^{1-\alpha}}$ is a normalisation constant included to determine the beam density $n_{\mathrm{beam}}$, and $A_{t} = (\tau \sqrt{\pi})^{-1}$ is a normalisation constant that sets the integral of the Gaussian temporal profile to 1.

The electron velocity distribution has a spectral index $\alpha = 8$ (from X-ray observations (Krucker et al., 2007; Holman et al., 2011)) and a density $n_{\mathrm{beam}}={10}^{\text{7}}\text{ cm}$ ^-3. The electron velocities range from $v_{\min }={10}^{\text{9}}$ cm s^-1 to $v_{\max }=2\times {10}^{\text{10}}$ cm s^-1. We inject a beam of width 10⁹ cm at $r = 0$ with an injection height of $r_{\mathrm{inj}} =$ 3 × 10⁹ cm (1.04 R_⊙) from the centre of the Sun (Reid and Kontar, 2015). These values are representative of the size and height of a flare acceleration region as calculated from both radio and X-ray emission observations (Reid, Vilmer, and Kontar, 2011b, 2014).

2.2 The Electron Transport and Propagation

$$ \frac{\partial f}{\partial t} + \frac{v}{M(r)} \frac{\partial}{\partial r}M(r)f = \frac{4\pi ^{2}\mathrm{e}^{2}}{\mathrm{m_{e}}^{2}} \frac{\partial}{\partial v}\Big(\frac{W}{v} \frac{\partial f}{\partial v}\Big) + \frac{4\pi n_{\mathrm{e}}\mathrm{e}^{4}}{\mathrm{m_{e}}^{2}}\ln (\Lambda ) \frac{\partial }{\partial v}\frac{f}{v^{2}} + S(v,r,t) $$

(2)

$$ \frac{\partial W}{\partial t} + \frac{\partial \omega _{\mathrm{L}}}{\partial k} \frac{\partial W}{\partial r} - \frac{\partial \omega _{\mathrm{pe}}}{\partial r} \frac{\partial W}{\partial k} = \frac{\pi \omega _{\mathrm{pe}}}{n_{\mathrm{e}}}v^{2}W \frac{\partial f}{\partial v} - (\gamma _{\mathrm{L}} + \gamma _{\mathrm{c}})W + \mathrm{e}^{2}\omega _{\mathrm{pe}}\mathit{vf}\ln \Big(\frac{v}{v_{\mathrm{Te}}}\Big) $$

(3)

Quasilinear theory and a self-consistent kinetic Fokker Planck approach in Equations 2 and 3 (Reid and Kontar, 2018) model the temporal evolution of the electron beam (e.g. Melrose, 1980; Cairns, 1987a,b; Robinson and Cairns, 1998) and the Langmuir waves where the electron beam dynamics are represented by an electron distribution function $f(x,v,t)$ [cm^-4s] and those of the Langmuir waves by their spectral energy density $W(x,v,t)$ [erg cm^-2].

Equations 2 and 3 include terms modelling the expansion of the beam in space as it propagates along magnetic field lines away from the Sun ($\frac{v}{M(r)}$ $\frac{\partial}{\partial r}M(r)f$) in Equation 2, with $M(r) \propto r^{2}$, the spherically symmetric expansion of the flux tube in space. The total number of electrons in the beam stays constant throughout the beam’s journey due to the $M(r)$ term. The 1D simulated beam propagates along a 3D flux tube with parameters only varying in the direction of propagation. The cross section of the beam increases with the expansion of the beam, resulting in a lower electron beam density as a function of distance from the Sun. The expansion of the Langmuir waves as a function of distance is considered negligible since they do not propagate far enough without being reabsorbed by the electron beam for this effect to be considered significant.

There is a constant thermal level of Langmuir waves present in the background plasma, which can be spontaneously emitted ($\mathrm{e}^{2}\omega _{ \mathrm{pe}}\mathit{v\,f}\ln (\frac{v}{v_{\mathrm{Te}}})$). The spontaneous emission varies with the angular plasma frequency $\omega _{\mathrm{pe}} = \mathit{kv}_{\mathrm{ph}}$ and the natural logarithm of the ratio of the electron velocities to their thermal velocity ($v_{ \mathrm{Te}} = \sqrt{\frac{\mathrm{k_{B}} T}{\mathrm{m_{e}}}}$).

Inhomogeneities in the background plasma lead to refraction ($\partial \omega _{\mathrm{pe}}/\partial r$) of the Langmuir waves up or down in velocity space, depending on the sign of $\frac{\partial n_{\mathrm{e}}}{\partial r}$ (down if $< 0$, up if $> 0$) (Kontar and Reid, 2009). In the simulation $\frac{\partial n_{\mathrm{e}}}{\partial r} < 0$. After being refracted down, like all waves in the plasma, the Langmuir waves undergo Landau damping at low velocities ($\gamma _{\mathrm{L}} = 2 \sqrt{\pi} \omega _{ \mathrm{pe}}(r)\Big(\frac{v}{v_{\mathrm{Te}}}\Big)^{3}\exp ( \frac{-v^{2}}{v^{2}_{\mathrm{Te}}})$). Landau damping is highly dependent on the thermal velocity of electrons, which plays a leading role in the propagation of Langmuir oscillations.

Other particles present along the path of the beam are responsible for collisions. The collisions are modelled by two different terms:

$$ \frac{4\pi n_{\mathrm{e}}\mathrm{e}^{4}}{\mathrm{m_{e}}^{2}}\ln ( \Lambda )\frac{\partial }{\partial v}\frac{f}{v^{2}} $$

(4)

and $\gamma _{\mathrm{c}}$, in Equations 2 and 3, respectively. The first collision term, Equation 4, is related to the gradient in velocity of the electron distribution function to the velocity squared and to the electron density. It represents the Coulomb collisions of electrons with protons in the background plasma where $n_{\mathrm{e}}$ is the electron density of the background plasma, $\mathrm{m_{e}}$ is the mass of the electron, and $\mathrm{ln}(\Lambda )$ is the Coulomb logarithm, which is the natural logarithm of the plasma parameter: of constant value 20. In our simulations, Langmuir waves are treated in the approximation of geometrical optics (the WKB approximation). The second collision term,

$$ \gamma _{\mathrm{c}} = \frac{\pi n_{\mathrm{e}} \mathrm{e}^{4} \ln (\Lambda )}{\mathrm{m_{e}}^{2} v_{\mathrm{Te}}^{3}}, $$

(5)

represents the collisional absorption of Langmuir waves when they collide with ions in the plasma. Collisions happen at a higher rate in denser media, which is the case closer to the Sun where a higher density of electrons is observed. As for all oscillations, Langmuir waves have a group velocity $v_{\mathrm{gr}}=\frac{\partial \omega _{\mathrm{L}}}{\partial k}$.

2.3 The Associated Radio Emission

The dynamic spectrum of the fundamental radio emission associated with the electron beam–plasma interaction in this simulation is calculated using the spectral energy density of the Langmuir waves (Reid and Kontar, 2018). Langmuir wave growth originating from electron beam–plasma interactions results in the spectral energy density of the Langmuir waves [${W_{\mathrm{L}}}$] being substantially greater than the spectral energy density of the ion-sound waves present in the plasma [$W_{\mathrm{S}}$]. When Langmuir waves decay non-linearly into an electromagnetic wave and an ion-sound wave ($L \rightarrow T + S$), the ion-sound wave grows exponentially (Melrose, 1980; Cairns, 1984, 1987a,b), resulting in an increase in ${W_{\mathrm{S}}}$ and the associated brightness temperature $T_{\mathrm{B}}$.

$$ T_{\mathrm{B}}(k,r,t) = \omega _{\mathrm{T}}(r) \frac{\eta}{k_{\mathrm{s}}(r)^{2}\mathrm{k_{ \mathrm{B}}}} \frac{W_{\mathrm{L}}(k,r,t)}{\omega _{\mathrm{L}}(r)} $$

(6)

The brightness temperature [$T_{\mathrm{B}}$] (Equation 6) is calculated using the angular frequencies of the electromagnetic [$\omega _{\mathrm{T}}$] and Langmuir waves [$\omega _{\mathrm{L}}$], the wavenumber of the ion-sound waves [$k_{\mathrm{s}}$], and the Boltzmann constant [$\mathrm{k_{\mathrm{B}}}$]. We approximate that both $\omega _{\mathrm{T}} \approx \omega _{\mathrm{L}}$ and $k_{\mathrm{T}} \approx k_{\mathrm{L}}$ and use $\eta = 2\pi ^{2}$. The brightness temperature as a function of position or frequency $T_{\mathrm{B}}(r,t)$ is calculated by integrating $T_{\mathrm{B}}$ over wavenumber, taking the peak of $T_{\mathrm{B}}(k,r,t)$ at each point in both space and time.

2.4 Density Modelling

The beam–plasma interactions depend highly on the electron density [$n_{ \mathrm{e}}(r)$] upon which several terms in Equations 2 and 3 themselves depend, specifically the refraction.

In our simulation, the normalised Parker density model models the background plasma and its density considering a uniform Maxwellian plasma and neglecting Coulomb collisions (Parker, 1958; Mann et al., 1999). This uniform Maxwellian background plasma is susceptible to spontaneously emitting Langmuir waves present at the thermal level. Following previous simulation work (Reid and Kontar, 2013, 2017), we set the thermal level of Langmuir waves to

$$ W_{\mathrm{thermal}}(t=0,r,v) = \frac{\mathrm{k}_{\mathrm{B}}T_{\mathrm{e}}}{4\pi ^{2}} \frac{\omega _{\mathrm{pe}}^{2}}{v^{2}}\ln \Bigg(\frac{v}{v_{\mathrm{Te}}} \Bigg) $$

(7)

using an electron temperature $T_{\mathrm{e}} = 10^{6}$ K.

3 Results and Discussion

3.1 Electron Flux and Langmuir Wave Growth

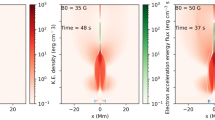
We inject an electron beam into the solar corona and model propagation out through the solar corona and solar wind plasma using the model in Section 2. A snapshot of the electron flux and the associated Langmuir wave spectral energy density is shown in Figure 1. Striations on both the top and bottom panels are due to the resolution in velocity. The top panel on Figure 1 is a contour plot of the electron beam distribution function $f(x,v,t)$ (Equation 1) at 13 R_⊙, normalised in each velocity channel to the peak value. The black dotted line on this plot goes through the maximum of $f$ in time for each velocity channel and is extrapolated back to find the time where this black line crosses the $y = 0$ line, giving us the expected injection time of electrons.

Figure 1

Top: Contour plot of the electron distribution function [$f$] normalised to the maximum value in each velocity channel at 13 R_⊙. Bottom: Spectral energy density of Langmuir waves [$W$] normalised by the thermal level $W_{\mathrm{Th}}$ at 13 R_⊙ at different times. The black dotted line is an interpolation of the maximum of $f$ in time for each velocity channel, analogous to being a line of constant distance (13 R_⊙) on a $v$ vs. $t$ plot. The blue dotted line is the left bound of the full width at 10% maximum of $f$ in time for each velocity channel, a fit to the onset flux. The black + identifies $\Xi$ the maximum electron velocity responsible for Langmuir wave growth.

All the electrons situated to the left of this black dotted line arrive earlier than expected with respect to the velocity at which we measure them at 13 R_⊙. The blue dotted line is the left bound of the full width at 10% maximum of $f$ in time for each velocity channel, analogous to the black dotted line, but to calculate the electron onset times. It is used to probe for the arrival time of the first electrons at 13 R_⊙. This calculation replicates the work shown in Figure 1 in the first EPD observational article (Gómez-Herrero et al., 2021). The point where the black and blue lines cross the $x$-axis gives the estimated time when the electrons are injected at the Sun. If we probe the arrival of the beam at 13 R_⊙ using the electrons on the blue dotted line at each energy channel, they seem to be emitted 46.8 seconds later than the time that we inject them. The transport effects, especially diffusion in velocity space due to the electron beam interaction with the Langmuir waves, directly influences the velocity of the electron beam as it propagates away from the Sun. The electron distribution function $f$ is modified by the electron beam’s resonant interactions with the background plasma it travels through (Drummond and Pines, 1962; Vedenov, 1963). The black cross identifies $\Xi =0.35\mbox{ c}$, the maximum velocity beyond which electrons do not interact with the background plasma to grow a significant amount of Langmuir waves.

The bottom panel on Figure 1 displays the spectral energy density of the Langmuir waves $W(x,v,t)$, normalised to the maximum value of $W$ over all velocity channels. The increase in $W$ shows that Langmuir waves are observed to grow above the thermal level from the beam–plasma resonant interactions at corresponding velocities to those of the diffusion observed in $f$ on the top plot. Figure 1 shows the reduced amount of Langmuir waves stimulated at velocities above $\Xi$, indicated by the black cross.

Figure 2 is similar to Figure 1, except that the snapshot of the simulation is taken at 33 R_⊙. Diffusion is observed to occur for electrons with velocities up to 0.23 c, again indicated by the black cross. Modelling the electron arrival times with the left bound of the full width at 10% maximum of $f$ (blue dashed line), the electron beam looks like it was emitted up to 68.4 seconds earlier than they are injected into the simulation. This diffusion is observed at 13 R_⊙ in Figure 1 for velocities c/$v$ ranging between 8 to 2.8, corresponding to $v$ between 0.13 c and 0.35 c and energies between 3.7 and 31.4 keV, respectively. In Figure 2, diffusion ranges between velocities c/$v$ ranging between 8 to 4.2, corresponding to velocities of 0.13 to 0.23 c or energies of 13.5 to 3.7 keV, respectively. The faster electrons are the ones first interacting with the plasma and growing Langmuir waves, while the slower electrons are slowed down, and their energy is given by the collisionally damped term ($\frac{4\pi n_{\mathrm{e}}\mathrm{e}^{4}}{\mathrm{m_{e}}^{2}}\ln ( \Lambda )\frac{\partial }{\partial v}\frac{f}{v^{2}}$ in Equation 2). Between Figures 1 (13 R_⊙) and 2 (33 R_⊙), the maximum velocity of electrons growing Langmuir waves decreases.

Figure 2

Top: Electron distribution function [$f$] normalised to the maximum value in each velocity channel at 33 R_⊙, Bottom: Spectral energy density of Langmuir waves [$W$] normalised by the thermal level $W_{\mathrm{Th}}$ at 33 R_⊙ at different times. The black dotted line is an interpolation of the maximum of $f$ in time for each velocity channel, analogous to being a line of constant distance (33 R_⊙) on a $v$ vs. $t$ plot. The blue dotted line is the left bound of the full width at 10% maximum of $f$ in time for each velocity channel, a fit to the onset flux. The black + identifies $\Xi$ the maximum electron velocity responsible for Langmuir wave growth.

3.2 Evolution of the Maximum Electron Velocity Responsible for Langmuir Wave Growth

We are interested in looking at how the maximum electron beam velocity responsible for Langmuir wave growth evolves as a function of distance from the Sun. Figure 3 shows this maximum velocity from the beam injection point at 0.014 R_⊙ ($10^{9}\mbox{ cm}$) up to 50 R_⊙, extrapolating on the values at 13 and 33 R_⊙ given in Section 3.1. At each distance, $\Xi$ is calculated by first finding the velocity $\Xi$ at which the maximum in $f$ occurs as a function of $v$, for each point in distance [$r$] and time [$t$]. We then find the ratio of $W(\Xi ,r,t)$ to the thermal level of Langmuir waves $W(\Xi ,r,t=0)$ and check whether this ratio is above our defined threshold of $10^{2}$ that indicates a significant level of Langmuir waves. Figure 3 presents the largest value of $\Xi$ at each distance $r$ over all time.

Figure 3

Maximum electron velocity [$\Xi$] responsible for Langmuir wave growth from the Sun’s surface to 50 R_⊙. $\Xi$ peaks at R_⊙ at 0.38 c. In red is a fit showing $\Xi$ decreases as $r^{-0.5}$ over the maximum velocity data in blue.

Close to the Sun ($r = 0.014$ to 5 R_⊙), we observe in Figure 3 that $\Xi$ first increases to peak at 0.38 c (31.2 keV) at 5 R_⊙ and then decreases to reach 0.16 c (5.6 keV) at 50 R_⊙. The growth of Langmuir waves is proportional to $n_{\mathrm{e}}^{-0.5}v^{2}\frac{\partial f}{\partial r}$, and so the value of $\Xi$ depends upon the terms that govern these variables.

The initial power-law energy distribution means the beam is initially stable to Langmuir wave growth. The growth of Langmuir waves is caused by velocity dispersion from the electron propagation term generating a negative gradient in velocity space. The farther the electron beam propagates, the more the electrons at different velocities separate in space, and the larger the value of $\frac{\partial f}{\partial r}$. Additionally, the value of $n_{\mathrm{e}}^{-0.5}$ increases exponentially, relating to the density profile in the solar corona. These two factors result in higher and higher velocity electrons producing Langmuir waves up to the threshold $W/W_{\mathrm{Th}}=10^{2}$. Owing to the initial negative power-law index of the electron distribution function in velocity space, fewer waves are generated at higher velocities, and hence the threshold is only reached by velocities of 0.38 c at 5 R_⊙.

At farther distances from the Sun, beyond 15 R_⊙, fitting the value of $\Xi$, we find that $\Xi \propto r^{-0.5}$. Looking at the Langmuir wave growth term again, the value of $\frac{\partial f}{\partial r}$ is related to the beam density $n_{\mathrm{beam}}$. The main component that modifies $n_{\mathrm{beam}}$ is the expansion term $M(r)$ (Equation 2), which governs how the beam cross-section increases, and hence the beam density decreases, as a function of distance from the Sun. The beam cross-section increases as $r^{2}$ and hence $n_{\mathrm{beam}}\propto r^{-2}$. However, beyond 10 R_⊙, $n_{\mathrm{e}} \propto r^{-2}$, and hence $n_{\mathrm{e}}^{-0.5} \propto r$, giving a radial dependence of Langmuir wave growth as $r^{-1}$. With a $v^{2}$ dependence also in the growth rate, it follows that the value of $\Xi$ might be expected to decrease as $r^{-0.5}$.

3.3 Role of $\alpha$ and $n_{\mathrm{beam}}$ on the Beam–Plasma Interactions

In the first simulation of this article shown in Section 3.1, beyond 50 R_⊙ we do not observe any Langmuir growth such that $W/W_{\mathrm{Th}}>10^{2}$. This lack of significant Langmuir wave levels beyond 50 R_⊙ is entirely dependent upon our initial electron beam parameters. In particular, the initial velocity spectral index [$\alpha$] and the initial beam density [$n_{\mathrm{beam}}$] control the initial beam energy density [$U$], which heavily influences the amount of Langmuir waves that are produced by a propagating electron beam (Reid and Kontar, 2018).

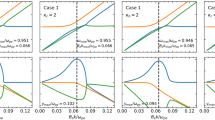
Since $\Xi$ decreases as the beam energy density $U$ decreases as a function of distance from the Sun, we look in more detail at the parameters governing the initial value of $U$, namely $\alpha$ and $n_{\mathrm{beam}}$. First, we vary the value of $\alpha$ between 7 and 9 in steps of 1 while keeping $n_{\mathrm{beam}}$ constant to identify how this parameter affects the value of $\Xi$. Figure 4 shows $\Xi$ from 0 to 4 R_⊙ for $\alpha = 7$, 8, and 9. It is clear from Figure 4 that for a smaller value of $\alpha$, in this case $\alpha = 7$, $\Xi$ is overall larger and plateaus close to 0.6 c. For higher values at $\alpha = 8$, we see $\Xi$ plateau at just under 0.4 c, and for $\alpha = 9$, we see $\Xi$ plateau around 0.25 c before very subtly decreasing again. The increase in $\Xi$ for lower values of $\alpha$ is related to the increased beam energy density $U$ at higher velocities producing more Langmuir waves (Li, Cairns, and Robinson, 2008; Li, Robinson, and Cairns, 2008; Li, Cairns, and Robinson, 2009, 2011; Li et al., 2011; Li and Cairns, 2012, 2013b, 2014; Reid and Kontar, 2018).

Figure 4

Maximum electron velocity [$\Xi$] [c] growing Langmuir waves between 0 and 5 R_⊙ altitude for different values of the spectral index of the electron velocity distribution $\alpha$. $\alpha = 7$ (green), $\alpha = 8$ (blue), and $\alpha = 9$ (red).

We additionally see that the peak of $\Xi$ happens further away from the Sun for a higher value of $\alpha$: 5 R_⊙, 3 R_⊙, and 2.5 R_⊙ for $\alpha = 7$, 8, and 9, respectively. This dependence relates to the beam energy density $U$ being less at higher velocities when $\alpha$ is larger. Consequently, the highest velocity that can produce significant Langmuir waves is reached closer to the Sun.

For increasing values of $\alpha$, we observe $\Xi$ increasing at farther distances from the Sun. This is related to the electron beam instability distance depending upon $\alpha$ (Reid, Vilmer, and Kontar, 2011b; Reid and Ratcliffe, 2014). It is also dependent upon the fixed magnitude of $W/W_{\mathrm{Th}}$, which we require to estimate $\Xi$.

We perform the same study as above but setting $\alpha$ to 8 (from observations; e.g. Krucker et al., 2007) and varying $n_{\mathrm{beam}}$ between 10⁶ and 10⁷ cm^-3 in steps of 0.5 in the exponent, again observing the effects on the simulations. Figure 5 shows $\Xi$ for an initial $n_{\mathrm{beam}}={10}^{\text{6}}$, 10^6.5, and 10⁷. In Figure 5, we see that for a smaller value of $n_{\mathrm{beam}}$, in this case $n_{\mathrm{beam}}={10}^{\text{6}}$ cm^-3, the peak $\Xi$ is smaller (0.25 c) at 2.73 R_⊙ than for $n_{\mathrm{beam}}={10}^{\text{6.5}}$ cm^-3 where the peak $\Xi$ is 0.3 c at 3 R_⊙ and $n_{\mathrm{beam}}={10}^{\text{7}}$ cm^-3 where the peak $\Xi$ is 0.4 c at 4 R_⊙. Similar to modifying the value if $\alpha$, the increase in $\Xi$ for higher values of $n_{\mathrm{beam}}$ is related to the increased beam energy density $U$ at higher velocities producing more Langmuir waves (Reid and Kontar, 2018).

Figure 5

Maximum electron velocity [$\Xi$] [c] growing Langmuir waves between 0 and 5 R_⊙ for different values of beam density $n_{\mathrm{beam}}$. $n_{\mathrm{beam}}={10}^{\text{6}}$ cm^-3 (green), $n_{\mathrm{beam}}={10}^{\text{6.5}}$ cm^-3 (blue), and $n_{\mathrm{beam}}={10}^{\text{7}}$ cm^-3 (red).

It is important to note that varying the threshold used to calculate the amount of Langmuir waves being grown above the thermal level, $W/W_{\mathrm{Th}}>10^{2}$ modifies the values that we obtain for $\Xi$. Increasing the threshold decreases the values of $\Xi$ and causes the peak of $\Xi$ to happen closer to the Sun. As we have shown, increasing the beam density or decreasing the spectral index would cause significant levels of Langmuir waves to be generated past 50 R_⊙ (Li and Cairns, 2013b, 2014), which is required to explain large levels of Langmuir waves at farther distances from the Sun (e.g. Gómez-Herrero et al., 2021).

3.4 Predicted Electron Onset Times Based upon Their Arrival Times

As was shown by Kontar and Reid (2009) the predicted electron beam onset times are modified by the advent of Langmuir wave growth. We show the predicted onset times in different velocity channels in Figure 6 based upon the electron distribution function arriving at $r_{13} = 13\,R_{\odot}$. On the $x$-axis is the time from the simulation from which we subtract $t_{A}$, the analytical time calculated from $r_{13}/v$, which is the time the electrons would have taken to travel a distance $r_{13}$ had their velocities been constant. The dotted line over-plotted for each velocity channel is the analytical solution $n_{\mathrm{beam}}(\alpha - 1) \frac{v^{-\alpha}}{v_{\mathrm{min}}^{-(\alpha -1)} - v_{\mathrm{max}}^{-(\alpha - 1)}} \exp{\bigl(-\frac{t_{\mathrm{inj}}^{2}}{(\frac{d}{v})^{2}}\bigl)}$ of the electron distribution function. We can see that there is no difference between the predicted onset time and the analytical onset time at the highest energies, where a significant level of Langmuir waves is not grown. Whilst it might be tempting to estimate that electron propagation at these highest energies can be described by the scatter free approximation (Wang, Lin, and Krucker, 2006; Roelof, 2008; Agueda et al., 2010), the effect of pitch-angle scattering, not included in our simulations, is likely to modify electron propagation and result in the highest energy electrons not propagating scatter free (Dresing et al., 2021).

Figure 6

Normalised electron flux coloured lines vs. time showing the predicted electron onset times based upon their arrival times at 13 R_⊙ for different energy (velocity) channels. Dotted lines are the analytical solution of the electron flux.

The analytical solution does not change much in energy whereas we observe the inferred initial normalised electron flux to be heavily modified at lower energies. It is essential to use a reliable reference to track the electron arrival time at a given distance. The left bound of the full width at 10% maximum, which is seen to move to the left with decreasing energy Figure 6 due to the electron distribution function $f$ being highly affected by the beam–plasma interactions at low energies (e.g. at 10 keV). This point captures the effect of the diffusion of $f$ in time making it the most effective way to calculate the electron arrival time at a given distance.

3.5 Energy Ranges of Electrons Interacting with Langmuir Waves

Figure 7 shows the Type III solar radio burst in fundamental emission (found using Equation 6) associated with the electron beam simulated in this work, with frequencies ranging between 50 and 0.16 MHz (0.59 to 35 R_⊙, respectively). Figure 7 shows a faint Type III solar radio burst with low brightness temperature, reaching a maximum at $T_{\mathrm{B}}=10^{9}\mbox{ K}$. The parameters for $n_{\mathrm{beam}}$, $\alpha$, and $v_{\mathrm{min}}$ used to create the electron beam producing this Type III explain the faintness of the radio emission. The initial beam density [$n_{\mathrm{beam}}={10}^{\text{7}}$ cm^-3] above $v_{\mathrm{min}}=10^{9}~\mbox{cm}\,\mbox{s}^{-1}$ coupled with a relatively high value of the spectral index $\alpha = 8$ translate into a high number of low velocity electrons that were collisionally damped close to the Sun, and a lower number of high velocity electrons. The low magnitude of the Langmuir waves being grown corresponds directly to weak Type III radio emission even at the highest frequencies. This is directly linked to a higher spectral index $\alpha$, which means more slow electrons injected and thus having less free energy in the beam (Li and Cairns, 2013a).

Figure 7

Brightness temperature of a Type III solar radio burst (fundamental emission) associated with the simulated electron beam in Figures 1 and 2 with frequencies ranging between 0.15 and 50 MHz between 0 and 38 R_⊙.

Previous Type III solar radio burst analyses (e.g. Wild, 1950; Suzuki and Dulk, 1985; Dulk et al., 1987, 1998; Bastian, Benz, and Gary, 1998; Klassen, Karlický, and Mann, 2003; Krupar et al., 2015) use the frequency drift to calculate the associated bulk electron velocity by fitting a straight line through the maximum flux on a frequency as a function of time (for example Figure 7). If we estimate the bulk velocity for our simulated Type III burst, we find a bulk velocity of 0.12 c at 10 R_⊙ that decreases to 0.10 c at 30 R_⊙. This decrease is proportional to $r^{-0.5}$.

Whilst typical predictions of bulk velocity are useful, our work offers to link each frequency with a range of electron velocities interacting with the background plasma to produce Langmuir waves as a function of frequency (Figure 8) rather than just a bulk electron velocity and therefore provide more information about the parent electron beam than has been shown before.

Figure 8

Minimum (bottom curve) and maximum (top curve) electron velocities [c] (energies [keV]) growing Langmuir waves as a function of frequency [MHz] (distance [R_⊙]) as extracted from the Type III solar radio burst in Figure 7. This corresponds to the range of electron velocities (energies) interacting with Langmuir waves as a function of distance from the Sun.

At each frequency in Figure 7 (which corresponds to an altitude above the Sun in R_⊙), we identify the maximum brightness temperature and the time at which this maximum occurs. This gives us a time and distance at which to take a slice in the electron distribution function [$f(v)$]. We then calculate the full width at 10% maximum of this distribution to find the range of velocities of electrons interacting with the background plasma to grow Langmuir waves. The choice of using the full width at 10% maximum is motivated by the shape of a slice of the electron distribution function in time. We observe the evolution of $f$, namely its flattening over time at the top of Figure 1 in Reid and Kontar (2013). The difference between the full width at 1% and 10% maximum is negligible, while the full width at half maximum (50%) does not fully encompass the diffusion of $f$ due to the beam–plasma interactions. Taking the full width at 10% maximum enables us to accurately identify the velocity (energy) range of electrons growing Langmuir waves at the given frequency (distance) over time.

Figure 8 shows the range of velocities of electrons interacting with the background plasma to grow Langmuir waves as a function of Type III solar radio burst frequency (distance). Close to the Sun, the range of velocities is 0.12 c to 0.19 c around 50 MHz. As we go to lower frequencies (farther distances), the maximum velocity of electrons (top curve in Figure 8) decreases. This is as expected given the decreasing bulk electron velocity inferred from the Type III burst. The minimum velocity also decreases but plateaus at 0.08 c around 10 MHz. We believe that this plateau is not physical but caused by the constant value of $v_{\mathrm{Th}}$ in the simulations owing to the constant electron and ion temperature of $10^{6}\mbox{ K}$. In reality, the background temperature would decrease as a function of distance from the Sun, decreasing $v_{\mathrm{Th}}$ and allowing electrons with smaller velocities to interact with Langmuir waves without these waves being Landau damped.

4 Conclusions

We study the solar accelerated electron beam–plasma interactions from the Sun’s surface through the solar wind and solar corona up to 50 R_⊙ through numerical simulations using a quasilinear approach (Reid and Kontar, 2018) to identify for the first time the maximum electron velocity responsible for Langmuir wave growth as a function of distance from the Sun. For our simulation parameters, we find this maximum velocity first increases to peak at 0.38 c at 5 R_⊙ from the Sun then decreases proportional to $r^{-0.5}$ to 0.17 c at 50 R_⊙.

The maximum velocity of electrons that produce Langmuir waves is directly linked to $U$, the initial energy density of the beam. Changing the parameters that modify $U$ such as the initial beam density [$n_{\mathrm{beam}}$] or the initial velocity distribution spectral index [$\alpha$] affects this maximum velocity of electron growing Langmuir waves. A lower spectral index or higher beam density corresponds to more high-velocity electrons and hence larger maximum velocities of electrons that grow Langmuir waves. We predict that Solar Orbiter and Parker Solar Probe will detect Langmuir waves that are co-temporal with higher velocity electrons closer to the Sun, where electron fluxes are larger. Moreover, we expect that at a given distance, Langmuir waves should be detected that are co-temporal with electrons of higher velocities when electron beam fluxes are higher.

Whilst we do not simulate a turbulent background electron density, the presence of such turbulence has been shown to reduce the amount of Langmuir waves generated by electron beams and affect the stopping frequency of Type III bursts (e.g. Li and Cairns, 2012; Reid and Kontar, 2015; Voshchepynets et al., 2017). We estimate that higher turbulence levels would reduce the amount of Langmuir waves produced, as turbulence suppresses the Langmuir wave growth.

Analysing electron arrival times at 13 R_⊙ for increasing energy channels as a function of time shows that at low energies, electrons arrive earlier than expected (e.g. Wang et al., 2006) and the electron distribution function experiences substantial diffusion in time, in line with previous results (Kontar and Reid, 2009). When using observational data, even though there are no Langmuir waves detected co-temporally with higher energy electrons, it does not mean their distribution function has not been modified by wave–particle interactions closer to the Sun. If onset times are being predicted from observational data, we recommend that one should use the time of electron peak flux, and not the electron rise time, to obtain a more accurate result, as shown in Section 3.1.

Looking at the Type III solar radio burst associated with the electron beam simulated in this work, rather than calculating one electron velocity from the Type III drift rate, we identify the range of electron velocities interacting with the plasma. We found a range of about $\Delta v=0.1c$ for the simulation parameters we used. This range is likely to be dependent upon the initial beam parameters, increasing for beams with a larger initial energy density. In our simulation, this range decreased at farther distance from the Sun. However, we think this result was erroneous and related to the constant background electron temperature that we assumed. It would be interesting to measure this range of electron velocities using in-situ data from Solar Orbiter and Parker Solar Probe at different distances from the Sun and test this theory.