1 Introduction

The hypothesis that the solar dynamo may have been synchronized by planetary harmonics has today attracted the attention of an increasing number of scientists and is hotly debated (Charbonneau, 2013; Scafetta and Bianchini, 2022).

The existence of specific solar oscillations (like the 11-year Schwabe sunspot cycle, the 22-year Hale solar magnetic cycle, the 80 – 100-year Gleissberg cycle, the 203 – 208-year Suess-De Vries cycle, and the roughly 1000-year Eddy and 2300-year Hallstatt cycles) is today uncontroversial. Commenting on them, Callebaut, de Jager, and Duhau (2012) made the surprising statement that it “should be remarked ... that virtually none of the papers on planetary influences on solar variability succeeded in identifying these ... periodicities in the planetary attractions”. Callebaut, de Jager, and Duhau (2013) were later forced to correct their position in response to Scafetta et al. (2013) rebuttal, and admitted that “it is well-known that there are some periodicities that are common to solar activity and planetary motions”; they were unable to explain the observed spectral coherence. In fact, all observed solar activity oscillations from the monthly to the millennial scales can be associated with specific planetary tidal and resonant harmonics (e.g.: Scafetta, 2020; Scafetta and Bianchini, 2022).

In a recent study, Nataf (2022) criticized Stefani, Giesecke, and Weier (2019). Regarding the hypothesis that the planets could have synchronized the solar dynamo, Nataf “built synthetic tidal forcings to illustrate the lack of evidence for” a quasi 11 “years periodicity”, stated that it was “therefore surprising that this idea has received a renewed attention”, and concluded that “the astrological quest for a link between solar cycles and planetary tides remains as unfounded as ever”.

However, Nataf (2022) only cited a few pro and contra publications (Okal and Anderson, 1975; De Jager and Versteegh, 2005; Scafetta, 2012a; Okhlopkov, 2016; Baidolda, 2017; Courtillot, Lopes, and Le Mouël, 2021; Charbonneau, 2022) without truly commenting their findings and he based his analysis on a tidal planetary model (see his Appendix A) that has already been demonstrated to be inadequate by Scafetta (2012a,b).

Nataf (2022) primarily focused his criticism of Stefani, Giesecke, and Weier (2019) on the selected solar-cycle record (649 B.C. to A.D. 2000) proposed by Schove (1955), which could have an impact on some of the qualities that were important for Stefani’s study. Additionally, Nataf showed DTS-Omega experiment findings demonstrating the possibility of internally timed oscillations in magnetized fluid without the need for external forcing: I will briefly comment on this result too. However, my main subsequent rebuttal refers to the section of Nataf’s paper regarding his claim that the function of the tides induced by the planets on the Sun does not contain any evidence of a periodicity compatible with the Schwabe 11-year solar cycle.

Given that the aforementioned topic has been already discussed in academic literature and that there are many signs that the variation in solar activity could be modulated by the planets, I found that the analysis proposed by Nataf (2022) was lacking from a number of physical and mathematical perspectives and required the present rebuttal. The interested reader will find an extended review on this field of research in Scafetta and Bianchini (2022) and in their references, where it is shown that there are signs that all main periodicities observed in the solar activity from the monthly to the multi-millennial scales are present in the planetary tidal oscillations, in the planetary conjunction cycles, and in their beats.

2 The Venus-Earth-Jupiter-Saturn Model

Nataf (2022) critiqued Stefani, Giesecke, and Weier (2019) on the grounds that Venus, Earth, and Jupiter would be unable to produce tides with periods compatible with those of the Schwabe 11-year solar cycle. In his Appendix A, Nataf (2022) adopted the following inadequate tidal forcing function

$$ \mathrm{Tide_{1}}(t)=\sum _{\mathrm{P}} \frac{m_{\mathrm{P}}}{d_{\mathrm{P}}^{3}}\left [\cos ^{2}\left (2\pi \frac{t}{T_{\mathrm{S}}}-2\pi \frac{t}{T_{\mathrm{P}}}\right )- \frac{1}{3}\right ], $$
(1)

where \(d_{\mathrm{P}}\) is the distance of the planet P from the Sun, \(m_{\mathrm{P}}\) is its mass and \(T_{\mathrm{S}}=27\) days is the solar rotation period. The orbits were assumed circular (\(d_{\mathrm{P}}=\) mean orbital radius of the planet P) with a period of \(T_{\mathrm{P}}\) expressed in the same units of \(T_{\mathrm{S}}\). In Equation 1, the variable t is in units of days.

Nataf (2022) imitated Okal and Anderson (1975), and restricted his analysis to Mercury, Venus, Earth, and Jupiter. He found that the power spectrum of the tidal signal given by his Equation 1 did not show any peak around 11 years. He could only find harmonics associated with the spring tidal cycles between the four adopted planets. All these tides have periods shorter than 1 year.

However, according to Wolf (1859), Venus, Earth, Jupiter, and Saturn had to constitute the foundation of any minimum model that could account for the Schwabe 11-year solar cycle, because these are the four most important tidal planets (Scafetta, 2012a). Moreover, Johannes Kepler (1571 – 1630) discovered that the orbits of the planets are not circular.

Curiously, Nataf (2022) mentioned Scafetta (2012a) without acknowledging that this study carried on a more accurate study of the planetary tidal function, utilizing all the planets and their actual orbits derived from accurate ephemeris programs. Scafetta’s results have already rebutted Nataf’s present conclusion.

In fact, the accurate modeling of the tidal function makes simple to find a strong and clear correlation between the planetary tides and the observed sunspot spectrum. Scafetta (2012a) specifically found two significant peaks of the planetary tidal function at 9.93 and 11.86 years that optimally match the spectral range of the Schwabe 11-year sunspot cycle. These two peaks are actually present in the power spectra of the sunspot record (Scafetta, 2012a,b, 2014b). The implications of this finding were also discussed in other works (Scafetta, 2012b, 2014a), where it was shown that the modulation of the Schwabe solar cycle induced by these two harmonics yields to the generation of other multidecadal, secular, and millennial cycles observed in solar activity.

Thus, Equation 1 is clearly inadequate since there are other planets, including Saturn, and because the orbits are eccentric, rather than circular. A more realistic tidal function could be written as

$$\begin{aligned} \mathrm{Tide_{2}}(t) & =\sum _{\mathrm{P}} \frac{m_{\mathrm{p}}}{\left [d_{\mathrm{P}}+(d_{\mathrm{Pa}}-d_{\mathrm{P}})\cos \left (2\pi \frac{t-t_{\mathrm{Pa}}}{T_{\mathrm{P}}/365.25}\right )\right ]^{3}} \cdot \\ & \qquad \left [\cos ^{2}\left (2\pi \frac{t-2000}{T_{\mathrm{S}}/365.25}-2\pi \frac{t-2000}{T_{\mathrm{P}}/365.25}-2\pi \frac{\alpha _{\mathrm{PJ},\,2000}}{360{^{\circ}}}\right )- \frac{1}{3}\right ], \end{aligned}$$
(2)

where, \(d_{\mathrm{Pa}}\) and \(t_{\mathrm{Pa}}\) are the aphelion distance and one of its occurrence epochs, respectively, while \(\alpha _{\mathrm{PJ},\,2000}\) is the angular separation of the planet \(P\) from Jupiter on 01/01/2000 00:00. In Equation 2 the variable t is in units of years.

Scafetta (2012a) also asserted that what physically matters is the work done by the tides inside the Sun in a time unit, which is defined by the following function

$$ f(t)=\left |\frac{d\mathrm{Tide}(t)}{dt}\right |\approx \left | \frac{\mathrm{Tide}(t)-\mathrm{Tide}(t-1\,\mathrm{day})}{1\,\mathrm{day}} \right |. $$
(3)

By adopting Equation 2, Equation 3 approximates the theoretical full luminosity function induced by the tides proposed by Scafetta (2012a), which was given as

$$\begin{aligned} I_{P}(t) = & \frac{3~G~R_{\mathrm{S}}^{5}}{2~Q~\Delta t}\int _{0}^{1}K( \chi )~\chi ^{4}\rho (\chi )~\mathtt{d}\chi \cdot \\ & \int _{\theta =0}^{\pi}\int _{\phi =0}^{2\pi}\left |\sum _{ \mathrm{P}}~m_{P} \frac{\cos ^{2}(\alpha _{\mathrm{P},t})-\frac{1}{3}}{R_{\mathrm{SP}}^{3}(t)}-~m_{P} \frac{\cos ^{2}(\alpha _{\mathrm{P},t-\Delta t})-\frac{1}{3}}{R_{\mathrm{SP}}^{3}(t-\Delta t)} \right |~\sin (\theta )~\mathtt{d}\theta \mathtt{d}\phi , \end{aligned}$$
(4)

where the actual physical orbits of the eight planets of the solar system from Mercury to Neptune were obtained from the JPL Horizons solar system data and ephemeris computation programs. Scafetta (2012a) provides explanations of the many parameters and functions of Equation 4: \(G\) is the universal gravitational constant; \(Q^{-1}\) is the effective tidal dissipation factor; \(R_{\mathrm{S}}\) is the radius of the Sun; \(\Delta t\) is the integration time interval of 1 day; \(K(\chi )\) is the function for converting gravitational power into TSI at a distance of 1 AU from the Sun; \(\rho (\chi )\) is the solar density function; \(\chi =r/R_{\mathrm{S}}\) is a normalized distance from the center of the Sun; \(R_{\mathrm{SP}}(t)\) is the distance of a planet from the Sun; \(m_{P}\) is the mass of the planet \(\mathrm{P}\); \(\alpha _{\mathrm{P},t}\) are angles indicating the position of the planet \(\mathrm{P}\) relative to the angular position \(\phi \) on the Sun.

Figure 1 shows the tidal function \(\mathrm{Tide_{1}}(t)\) (Equation 1) and the function \(f(t)\) (Equation 3) adopting Equation 1 which uses Mercury, Venus, Earth, and Jupiter and assumes circular orbits. Several fast oscillations are visible, which are mostly related to the spring tides among the four planets. However, no clear oscillation at a periodicity of about 11 years appears. This is essentially the result found by Charbonneau (2022).

Figure 1
figure 1

(a) Tidal function Equation 1 which assumes circular orbits for Mercury, Venus, Earth and Jupiter. (b) \(f(t)\) (Equation 3) using Equation 1.

Full size image

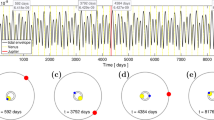
Figure 2a shows the function \(f(t)\) (Equation 3) using Equation 2 with only Jupiter, and Saturn. A quasi 11.86 year oscillation, related to the orbital period of Jupiter, is seen. However, such an oscillation is also modulated by the 9.93-year spring-tidal cycle between Jupiter and Saturn. Consequently, at the decadal timescale, the tidal signal is characterized by two periodicities equal to 9.93 and 11.86 years, whose average is close to 11 years. Figure 2b adopts the planetary set suggested by Wolf (1859) and shows the function \(f(t)\) (Equation 3) using Equation 2 with Venus, Earth, Jupiter, and Saturn. The same 10 – 12 year oscillation is easily observed in the synthetic record. Figure 2c shows that the patterns of the fast tidal fluctuations rather well repeat every about 11 years. This is the recurring pattern linked with the Venus-Earth-Jupiter triple syzygies tidal alignments of 11.07 years discussed by Scafetta (2012a), in the works by Stefani and by other authors (e.g.: Hung, 2007; Tattersall, 2013). Finally, Figure 2d shows the hypothetical luminosity signal stimulated by all planetary tides as calculated in Scafetta (2012a), using Equation 4.

Figure 2
figure 2

(a) Equation 3 assuming ecliptic orbits for Jupiter and Saturn. (b) Equation 3 assuming ecliptic orbits for Venus, Earth, Jupiter, and Saturn. (c) Equation 3 versus itself with an 11 years time-lag. (d) Hypothetical tidal luminosity signal calculated in Scafetta (2012a).

Full size image

Figure 3A shows the power spectrum of the tidal function \(f(t)\) depicted in Figure 1b using circular orbits of Mercury, Venus, Earth, and Jupiter, as assumed by Charbonneau (2022). There is no evidence of any periodicity within the 11-year solar-activity-cycle band, which approximately falls between 9 and 13 years. On the contrary, Figure 3B shows the power spectrum of the tidal function \(f(t)\) depicted in Figure 2b, using the actual orbits of Venus, Earth, Jupiter, and Saturn. Figure 3C shows the power spectrum of the tidally induced luminosity function (Equation 4) using all the planets, as calculated by Scafetta (2012a) and displayed in Figure 2d. The latter two power spectra have in common a number of harmonics, including the spring tides among the planets. In addition, there is a noticeable rise in the power at the decadal period between 9 and 13 years. This range is characterized by two peaks that are clearly generated by the 9.93-year spring-tidal cycle between Jupiter and Saturn and the 11.86-year orbital period of Jupiter. The two tidal cycles perfectly cover the observed Schwabe cycle spectral band and are actually observed in the power spectrum of the sunspot number (Scafetta, 2012a,b, 2014b). They seem to modify the primary Schwabe solar cycle in order to replicate other lengthy solar cycles that are the cause of the extended secular epoch of grand solar maxima and minima (which are known as the Oort, Wolf, Spörer, Maunder, and Dalton grand solar minima) as well as of the quasi-millennial solar activity cycle (which is known as the Eddy solar cycle) (Scafetta, 2012b, 2014a).

Figure 3
figure 3

(a) Power spectrum of the tidal function \(f(t)\) depicted in Figure 1b. (b) Power spectrum of the tidal function \(f(t)\) depicted in Figure 2b. (c) The power spectrum of the tidal luminosity function calculated in Scafetta (2012a) and shown in Figure 2d. VJ, EJ, VE, and JS are the spring tides between Venus and Jupiter, Earth and Jupiter, Venus and Earth, and Jupiter and Saturn; J is the orbital tide of Jupiter. The figure highlights the 11-year solar-activity-cycle band.

Full size image

Therefore, it is essential to use the actual orbits of Jupiter and Saturn to appropriately connect the planetary tide power spectrum to the 11-year sunspot cycle. Nataf (2022) briefly acknowledged that there might exist an oscillation with the period of Jupiter (\(P_{J}=11.86\) years), but he did not appear to be aware of the role of Saturn, which would have added to the power spectrum its spring tide with Jupiter with a period of \(P_{SJ}=9.93\) years and generated a 10 – 12-year tidal-cycle band which is perfectly compatible with the 11-year solar-activity-cycle band. Nataf (2022) made the same mistake Okal and Anderson (1975) did by neglecting Saturn.

The main fast tidal oscillations are instead associated with the spring tides between Venus and Jupiter (\(P_{VJ}=\) 0.3244 year), Venus and Earth (\(P_{VE}=\) 0.7993 year) and Earth and Jupiter (\(P_{EJ}=\) 0.5460 year). Thus, using the planetary set originally suggested by Wolf (1859), the five strongest tidal spectral peaks are \(P_{VJ}\), \(P_{EJ}\), \(P_{VE}\), \(P_{SJ}\), and \(P_{J}\). As we have seen, the last two (\(P_{SJ}\) and \(P_{J}\)) clearly fit the Schwabe 11-year sunspot cycle. Moreover, all fast spring tidal and synodical cycles with periods shorter than 1.5 years are actually observed in total solar irradiance records (Scafetta and Willson, 2013a,b).

The mentioned three fast tidal oscillations exhibit a recurring pattern linked with the triple syzygies tidal alignments of Venus, Earth, and Jupiter which has a period of 11.07 years (Scafetta, 2012a). This periodicity requires careful examination. Different approaches can be adopted.

For example, it is possible to look for combinations of integers \(\eta _{1}\), \(\eta _{2}\), and \(\eta _{3}\) such that the following identity holds

$$ P_{JS}< \eta _{1}\cdot P_{VJ}\approx \eta _{2}\cdot P_{EJ}\approx \eta _{3}\cdot P_{VE}< P_{J}, $$
(5)

so that the recurrence times are as close to each other as possible. The three best combinations \((\eta _{1},\eta _{2},\eta _{3})\) are \((32,19,13)=10.38\pm 0.01\) years, \((34,20,14)=11.05\pm 0.1\) years and \((35,21,14)=11.34\pm 0.1\) years. Of the three combination sets, the one that is best centered between \(P_{JS}\) and \(P_{J}\) is \((34,20,14)\). Finally, by averaging all the five main tidal periods, we get

$$ \frac{P_{JS}+34P_{VJ}+20P_{EJ}+14P_{VE}+P_{J}}{5}=11.0\pm 0.6\; \mbox{year}. $$
(6)

It was also found that the combination \((\eta _{1},\eta _{2},\eta _{3})=(32,19,13)=10.38\pm 0.01\) years is the best case fulfilling the more general condition \(\eta _{1}\cdot P_{VJ}\approx \eta _{2}\cdot P_{EJ}\approx \eta _{3} \cdot P_{VE}\), where the integers vary between 1 and 50. Indeed, a quasi 10.4-year cycle appears in quite a number of climatic records (Scafetta, 2010; Scafetta et al., 2013) and even in the meteorite fall (Scafetta, Milani, and Bianchini, 2020).

In general, the primary recurrent period of the Venus, Earth, and Jupiter triple-syzygies tidal alignment model is given by

$$ P_{VEJ}=\frac{1}{2}\left (\frac{3}{P_{V}}-\frac{5}{P_{E}}+ \frac{2}{P_{J}}\right )^{-1}=11.07\:\mbox{year}, $$
(7)

which is also a planetary invariant inequality (Scafetta, 2012a, 2020). Equation 7 can be also rewritten as

$$ P_{VEJ}=\frac{1}{2}\left [3\left (\frac{1}{P_{V}}-\frac{1}{P_{E}} \right )-2\left (\frac{1}{P_{E}}-\frac{1}{P_{J}}\right )\right ]^{-1}, $$
(8)

which means that the tidal beats of Equation 7 can be simulated by the function

$$ f(t)=\cos \left (2\pi \cdot \frac{t-t_{VE}}{P_{VE}/3}\right )+\cos \left (2\pi \cdot \frac{t-t_{EJ}}{P_{EJ}/2}\right ), $$
(9)

where \(t_{VE}=2002.8327\) is the epoch of one Venus-Earth conjunction and \(t_{EJ}=2003.0887\) is the epoch of one Earth-Jupiter conjunction. For each spring tide, the cosine function is used to predict the spring tidal maxima during the conjunction epochs. Figure 4 shows schematic representations of the Venus-Earth-Jupiter triple-syzygies tidal alignment model versus the average annual number of sunspots from 1700 to 2021: panel A shows Equation 9; panel B shows the model proposed by Hung (2007); and panel C shows the alternative model proposed by Tattersall (2013) by modifying the planetary index devised by Hung (2007) to test alignment along the curve of the Parker spiral, adjusted for solar-wind velocity. All three models are entirely based on astronomical data alone and a clear frequency and phase matching with the Schwabe 11-year cycle since 1700 is observed.

Figure 4
figure 4

(a) Equation 9 Schematic representation of the Venus-Earth-Jupiter model versus the average annual number of sunspots from 1700 to 2021. (b) The model proposed by Hung (2007). (c) The model proposed by Tattersall (2013) by modifying the planetary index devised by Hung (2007) to test alignment along the curve of the Parker spiral, adjusted for solar wind velocity.

Full size image

As a result, the 11-year sunspot cycle is fairly compatible with the five primary tides produced by Venus, Earth, Jupiter, and Saturn. In fact, Equation 6 exactly matches the Schwabe 11-year sunspot cycle.

According to the presented empirical evidence, it is plausible to hypothesize that the Schwabe 11-year solar activity oscillation could be induced by a dual simultaneous clocking of the solar dynamo with the \(P_{JS}\) and \(P_{J}\) decadal tides as well as with the best recurrent patterns of the fast \(P_{VJ}\), \(P_{EJ}\), and \(P_{VE}\) monthly tides. This result clearly implies that the main planetary tidal harmonics perfectly match the frequency band of the Schwabe 11-year sunspot cycle, which refutes the claim by Nataf (2022).

3 Conclusion

The aforementioned calculations show that a proper writing and understanding of the planetary tidal forcing acting on the Sun invalidates the criticism of Nataf (2022). In fact, the planets’ orbits are not circular, and the role of Saturn cannot be ignored. Additionally, it is important to consider how the fast tidal recurrence patterns are synchronized.

The actual planetary tidal forcing function clearly presents multiple spectral characteristics that appear to perfectly fit the Schwabe 11-year sunspot cycle. Planetary harmonics also fit all features observed in the solar activity records, as more extensively demonstrated in the comprehensive review on the planetary theory of solar activity change proposed by Scafetta and Bianchini (2022) and references therein. These studies contradict Nataf (2022) by showing that the hypothesis of a planetary modulation of solar activity is supported by a large number of empirical and theoretical evidences, although several issues remain open in particular regarding the actual involved physical mechanisms.

The aforementioned finding does not refute the observation in Nataf (2022) that "magnetohydrodynamic instabilities can produce quasi-periodic fluctuations that appear almost clocked". However, the solar activity is not oscillating at some type of arbitrary frequency, which is the issue here. The actual solar-activity periodicities and their timing (including the fast monthly and annual cycles, the 11-year Schwabe sunspot cycle, the 22-year Hale solar magnetic cycle, the 88-year Gleissberg cycle, the 100 – 150-year cycles, the 203 – 208-year Suess-De Vries cycle, and the roughly 1000-year Eddy and 2300-year Bray-Hallstatt solar cycles) seem to match the harmonics inferred from the planetary motions on timescales ranging from the monthly to the multi-millennial scales (e.g.: Scafetta, 2020; Scafetta and Bianchini, 2022). The present author proposes that the solar dynamo’s capacity to create quasi-periodic fluctuations that seem nearly clocklike is one of the primary physical factors that could enable their synchronization with the planetary harmonics. That is, the dynamics of solar activity might be an instance of synchronization of forced quasi-periodic coupled oscillators (Pikovsky, Rosemblum, and Kurths, 2001), where a weak external periodic forcing could be able to synchronize an entire system of coupled oscillators: see appendix in Scafetta (2010). Thus, the result by Nataf (2022) does not contradict the planetary theory of solar-activity change.

The actual physical mechanisms that would allow for this synchronization are still unclear, and the present author is well aware that numerous studies have indicated that the planetary tidal accelerations on the Sun seem to be insignificant (De Jager and Versteegh, 2005; Callebaut, de Jager, and Duhau, 2012; Scafetta, 2012a). However, it should also be remembered that Scafetta (2012a) proposed a solar mechanism that could physically enable the synchronization of the solar dynamo oscillators by tidal modulation of the solar luminosity production, which could increase the effect of the tidal gravitational forcing by 4 million times. Scafetta (2012a) also proposed that the issue of the lengthy Kelvin-Helmholtz time-scale required for the thermal energy to travel within the radiative zone could be solved by a quick g-wave transport mechanism of the tidally generated signal through the radiative region toward the tachocline, whose perturbations would synchronize the solar dynamo to the tidal frequencies at the bottom of the convective zone. A strong signal amplification occurring in the solar core and a g-wave fast signal-transport from the core to the tachocline could solve the tiny-tidal problem. In any case, there may exist alternative physical mechanisms, which are still unknown, as more extensively discussed in Scafetta and Bianchini (2022).