1 Introduction

The heliospheric magnetic field (HMF) is rooted in the Sun’s photosphere and extends out into the solar system, where it enables the Sun to interact with planetary magnetospheres. The HMF is the fraction of the magnetic flux that threads the solar photosphere and extends to a sufficient heliocentric distance that it is dragged out by the solar wind (e.g. Levine, Altschuler, and Harvey, 1977; Owens and Forsyth, 2013). Since the majority of the photospheric magnetic flux results in closed loops relatively near to the Sun – which do not contribute to the HMF – it is useful to define a “source surface” where the HMF begins. Magnetic loops that return to the Sun without extending beyond the solar corona are called “closed” and more distended loops that enter the heliosphere are called “open”: the distinction between the two is that open field lines thread the coronal source surface (Wang and Sheeley, 1995). Thus, the total unsigned magnetic flux threading the source surface is referred to as the open solar flux (OSF). However, there are no abrupt changes in the plasma or field parameters that mark the location of the source surface and a number of definitions have been used. The simplest is that the source surface is a heliocentric sphere of a fixed radius (Schatten, 1968a,b). The choice of that radius is arbitrary (typically placed around 2 to 3 solar radii) and it is therefore important when we compare different OSF estimates that they employ the same definition of the source surface.

As described by \(\nabla \cdot \mathbf{B} = 0\), magnetic fields always form closed loops and there is no net source of magnetic flux. Thus, positive (outward) and negative (inward) fluxes cancel over any closed surface. Therefore, for a perfect Parker spiral HMF (Parker, 1958), the unsigned magnetic flux threading the source surface (the OSF) equals that threading a sphere of heliocentric radius \(R\), here referred to as the total heliospheric magnetic flux (total HMF) and denoted \(\Phi _{R}\). What is observed, however, is that OSF estimates derived from remote-sensing observations (magnetograms) are around a factor of two lower than \(\Phi _{R}\). This discrepancy is partially due to local HMF inversions (or ‘switchbacks’) (Kahler and Lin, 1994; Crooker et al., 1996; Kahler, Crocker, and Gosling, 1996; Balogh et al., 1999; Crooker et al., 2004; Owens, Crooker, and Lockwood, 2013; Bale et al., 2019; Horbury et al., 2020), which result in magnetic flux threading a 1-AU sphere (and contributing to \(\Phi _{R = 1~\textrm{AU}}\)) but not the source surface (and thus not contributing to the OSF). However, even using methods to correct for inverted HMF (Owens et al., 2017) in \(\Phi _{R}\), in-situ based estimates of OSF are still systematically larger than those obtained from photospheric observations (Linker et al., 2017; Wallace et al., 2019).

1.1 Methods of Estimating OSF

In order to understand the differences between OSF estimates from magnetograms and in-situ measurements, it is first important to understand how these estimates are obtained. Magnetograms are measurements of the photospheric magnetic field (Beckers, 1968) derived from magnetograph observations. Until the very recent Solar Orbiter mission (Mueller et al., 2013), these observations were limited entirely to the Earth-facing side of the Sun and captured from the ecliptic plane, resulting in poor viewing geometry for the polar field. To obtain an estimate of OSF, photospheric magnetic field observations are collected over a complete solar rotation (approximately 27 days from Earth’s point of view) to give full longitudinal coverage, assumptions are made about the polar fields (and other factors), then the resulting photospheric magnetic field synoptic map is extrapolated to the top of the corona to estimate the OSF. This extrapolation is achieved using a coronal magnetic field model, such as a potential-field source surface (PFSS: Schatten, Wilcox, and Ness, 1969) model. These methods necessarily contain arbitrary choices that affect the OSF, most notably, the assumed radius of the source surface. Model-free estimates of OSF have also been derived from magnetograms by assuming all the OSF resides within coronal holes (e.g. Linker et al., 2017; Wallace et al., 2019), dark regions in extreme ultraviolet (EUV) and X-ray images (Cranmer, 2009). Using this assumption of all OSF residing in these regions, the radius of the source surface can be calibrated by matching OSF foot-points with observed coronal hole area, with the assumption that it is a heliocentric sphere.

Total HMF estimates are derived from in-situ spacecraft measurements by integrating the observed radial magnetic field (\(B_{r}\)) over a heliocentric sphere of radius equal to the observation distance. Smith and Balogh (1995) outlined a key finding enabling the estimation of total HMF from single-point in-situ measurements: Using the Ulysses spacecraft they found that the magnitude of the \(B_{r}\), corrected for heliocentric distance, was independent of latitude. This result was explained by Suess and Smith (1996) and Suess et al. (1996) who noted that close to the Sun the plasma beta is low, so magnetic pressure dominates. Thus, the solar wind flows will be slightly non-radial in this region until tangential (and hence latitudinal) magnetic pressure is equalised, resulting in constancy of radial magnetic field magnitude over a heliocentric sphere. Thereafter, radial flow means that the latitudinal invariance of \(|B_{r}|\) is preserved out into the heliosphere.

Longitudinal coverage is then obtained by integrating over a solar rotation, expressed as \(\langle |B_{r}| \rangle _{27 \textrm{day}}\). The total heliospheric flux threading the heliocentric sphere at the radius of observation, \(R\), can then be calculated as \(\Phi _{R} = 4 \pi R^{2} \langle |B_{r}| \rangle _{27 \textrm{day}}\). Note that while we here use \(4 \pi R^{2} |B_{r}|\), the total unsigned HMF, sometimes the total signed HMF (\(2 \pi R^{2} B_{r}\)) is used instead, such as in Lockwood, Stamper, and Wild (1999).

A subtle, but critical, point is that the time resolution at which one performs the modulus of \(B_{r}\) makes a significant difference to the total HMF estimate, and this is something of a free parameter (Lockwood, Owens, and Rouillard, 2009b). Note that Smith and Balogh avoided this by not actually using the modulus but, rather, averaging (signed) \(B_{r}\) over what they defined by eye to be toward and away sectors of the HMF. However, as pointed out by Lockwood and Owens (2013), using \(B_{r}\) averaged over sectors raises a problem of objectively distinguishing what is a genuine sector boundary (a change in \(B_{r}\) polarity that maps all the way back to the coronal source surface) from inverted HMF flux (a.k.a. “switchbacks” or “folded flux”) in the heliosphere (which do not map back to the source surface). Making that distinction is a key issue addressed in the present paper.

In order to estimate OSF from in-situ observations, it is necessary to relate the total HMF to the OSF. It is often implicitly assumed that the two properties are identical, i.e. \(\mathrm{OSF} = \Phi _{R}\). As previously mentioned, this is true for an ideal Parker spiral, but not for the “real” solar wind. Using observations from a wide range of heliospheric spacecraft, Owens et al. (2008) reported that \(\Phi _{R}\) estimates increased with \(R\). This indicates that the assumption \(\mathrm{OSF} = \Phi _{R}\) cannot be valid. The “flux excess” with heliospheric distance was also addressed by Lockwood, Owens, and Rouillard (2009b,c) using a “kinematic correction” to account for the effect of the large-scale longitudinal structure of the solar wind flow that could generate inverted HMF. Applying this correction gives a result in reasonable agreement with Owens et al. (2017), described below.

Erdos and Balogh (2014) described an alternative method aimed at correcting for \(R\)-dependence of total HMF estimates. Their approach was to consider only the HMF component along the ideal Parker spiral direction. This method showed very good agreement between total HMF estimated from spacecraft at different latitudes and distances. However, this does not necessarily mean that the total HMF values provide accurate OSF estimates. HMF inversions are not explicitly removed by this procedure, as they are often aligned with the Parker spiral orientation. More importantly, an arbitrary time averaging for \(B_{r}\) of 6 hours was used without justification. Using different time averaging reveals the same free-parameter issue that plagues the standard \(\Phi _{R} = 4 \pi R^{2} \langle |B_{r}| \rangle _{27~\textrm{day}}\) method (Owens et al., 2017).

1.2 Magnetic Field Inversion and Suprathermal Electrons

As outlined in the previous section, one possible source of OSF overestimation from in-situ observations are magnetic field inversions (also known as switchbacks or folded flux), where the open field lines locally fold back on themselves (Kahler and Lin, 1994; Crooker et al., 1996; Kahler, Crocker, and Gosling, 1996; Crooker et al., 2004). Since these inversions are often thought to have their origins in the upstream solar wind or corona, they are of great interest in studies on the solar wind origins (e.g. Owens et al., 2018; Macneil et al., 2020). These inversions can be routinely identified using suprathermal electron (STE) data.

Solar wind electron distributions can be separated into three components: a thermal core, a suprathermal near-isotropic halo and a suprathermal field-aligned “strahl” (Feldman et al., 1975). The strahl component carries heat flux outward (away) from the Sun’s hot corona, therefore the presence of this field-aligned beam can be taken as evidence of connectivity to the Sun (Lin and Kahler, 1992; Kahler and Lin, 1994). Thus, using the strahl, it is possible to determine if a magnetic field line is directly connected to the Sun’s surface or is locally inverted. Figure 1 shows how the combination of electron strahl and magnetic field data can be used to distinguish between: open flux (points 1 and 3), recently emerged open flux (i.e. open flux that emerged through the source surface relatively recently and forms loops that are less distended into the heliosphere) (point 2), inverted flux (4) and flux that has been disconnected from the Sun (5).

Figure 1
figure 1

Schematic modified from Owens and Forsyth (2013) displaying the topology of the HMF as inferred from STE observations. Panel (a), on the left, shows the heliographic equatorial plane, with heliospheric magnetic field lines (black arrows) and the STE flux (red arrows) for different magnetic topologies. Panel (b), on the right, shows the suprathermal electron pitch-angle distribution and (c) shows the radial magnetic field time series for the topologies shown on the left. The combination of electron and magnetic data can be used to distinguish between: open flux (points 1 and 3), newly emerged open flux (point 2), inverted flux (4), and flux that has been disconnected from the Sun (5).

Full size image

For point ‘1’ the radial magnetic field is positive in an away-field sector, so the magnetic field is directed towards the Sun: the strahl is directed anti-parallel to the direction of the magnetic field because it is directed away from the Sun. Thus, the field is open and does not show evidence of local inversion. The equivalent case for a toward-field (negative \(B_{r}\) sector) is shown in ‘3’.

Point ‘2’ gives an example of counterstreaming strahl, where the strahl is travelling in both parallel and anti-parallel directions. In the literature, field lines with counterstreaming electron fluxes have often been referred to as “closed” (e.g. Gosling et al., 1987). There are two problems with using this terminology here. First, there is no topological difference between these field lines with counterstreaming strahl and field lines that carry only unidirectional strahl (for example, strahl does not distinguish field lines that penetrate the heliopause, and so enter interstellar space, from those that do not). Secondly, we here use the term “closed” to mean field lines that do not extend beyond the solar corona when defining the coronal source surface. It is more than a matter of convenient definition that we class field lines with counterstreaming electrons as “open”. The reason is that they contribute to the tangential pressure in the heliosphere near to the Sun that gives the latitudinal independence of the radial field (Suess and Smith, 1996; Suess et al., 1996) that is employed when estimating OSF from in-situ data. In this paper, we refer to field lines with counterstreaming strahl as “newly opened” because the counterstreaming reveals that they have been open for a shorter time (i.e. they first emerged through the source surface relatively recently), such that the field-aligned distance to both of the loop’s foot-points in the solar corona is short enough that strahl electrons from both can reach the spacecraft with sufficient fluxes to be detected. The evolution from newly opened to open by this definition is therefore not sudden and described by a time constant, and could be treated in the same way that Lockwood and Owens (2014) accounted for the evolution of streamer belt flux into coronal hole flux.

Point ‘4’ gives an example of a HMF inversion, where the field is positive (directed towards the Sun) and the strahl is parallel to the magnetic field (so also directed towards the Sun in the folded region, even though its ultimate direction of travel is away from the Sun).

Finally, point ‘5’ gives an example of magnetic field that is disconnected from the Sun, which would give a complete absence of strahl, or a “heat-flux dropout” (McComas et al., 1989; Pagel, Crooker, and Larson, 2005; Pagel et al., 2005). Note that in some cases the strahl may be missing although the field line is not completely disconnected from the Sun. This usually occurs when the loop has been disconnected at the nearer foot-point but is still connected topologically by the other foot-point. If the field-aligned distance to the still-connected foot-point is large enough the strahl will be scattered to undetectable low fluxes and no strahl is seen.

Using a combination of strahl and magnetic field data, as outlined in Figure 1, the magnetic topology of each data point observed by a heliospheric spacecraft can be determined in most cases. As each inverted field line at a heliocentric distance \(R\) must thread the spherical surface of radius \(R\) three times, double the amount of flux that corresponds to inverted flux is subtracted from \(\Phi _{R}\) to give the OSF estimate (to account for the measured inverted point and the undetected return of the field). This is explained further in Section 3.1.

1.3 Previous Studies

Wang and Sheeley (1995) used PFSS models (with \(R_{\textrm{SS}}=2.5~R\)) to compute \(|B_{R}|\). They were able to approximately match \(|B_{R}|_{\textrm{IMF}}\) using Wilcox Solar Observatory (WSO) photospheric magnetic maps, but only if they used a correction factor. Using a latitude-dependent correction factor, derived for the Mount Wilson Observatory (MWO), that multiplies low-latitude fields by about 4.5, produced a closer match to \(|B_{R}|_{\textrm{IMF}}\) than using a correction factor based on the WSO magnetograph. See also Wang, Ulrich, and Harvey (2022).

Linker et al. (2017) calculated magnetohydrodynamic (MHD) and PFSS solutions of the coronal magnetic field using 14 different magnetic maps produced from 5 different observatories for a single Carrington rotation. They looked at two classes of method for computing OSF from each map. First, the magnetic flux contained within observationally derived coronal holes was integrated, computing a model-independent estimate of OSF under the assumption that all OSF is rooted in photospheric regions that are dark in extreme ultraviolet emission. Secondly, OSF was estimated using both MHD and PFSS extrapolations. All methods and maps produced OSF estimates in reasonable agreement with each another, but around a factor two lower than the in-situ estimate, even when accounting for inverted HMF using the Owens et al. (2017) methodology. For the PFSS models, the source surface radius is a free parameter, which can be lowered to raise the OSF estimate until it matches that produced from in-situ observations. However, the open magnetic foot-points derived from PFSS then covered a much greater fraction of the photosphere than the observed coronal holes. Thus, Linker et al. (2017) concluded that either the photospheric magnetic field maps underestimate the Sun’s true photospheric magnetic flux, or that a significant amount of OSF does not originate in regions that are dark in EUV. In a recent study, Linker et al. (2021) investigated the errors within detection methods used to identify coronal holes for the purpose of inferring OSF. They applied 6 common detection methods to a single coronal hole, where the uncertainty in coronal hole area, expressed as the standard deviation of the mean of all coronal hole areas, was found to be 26%. This further contributes to the underestimation of OSF from photospheric observations, but cannot alone account for the difference in photospheric and heliospheric OSF estimates.

Wallace et al. (2019) applied similar methods to approximately 20 years of observations. They used heliospheric OSF estimates from 1-day averages of \(|B_{r}|\), which provides a reasonable approximation to the Owens et al. (2017) method (see also Section 4.4). The results were in broad agreement with Linker et al. (2017), with the largest discrepancy between photospheric and in-situ OSF estimates at solar maximum around a factor two.

More recently, Badman et al. (2021) investigated OSF in the inner heliosphere using data from the Parker Solar Probe (PSP: Fox et al., 2016). At these locations too, the observed \(\Phi _{R}\) value was found to be significantly higher than implied by PFSS models, unless the height of the source surface was significantly lowered. This study concluded that this difference in OSF is most likely to be found in new modelling techniques or by our improved knowledge of the photospheric field.

2 Data

The data used in this study come from three sources:

  1. i)

    ACE SWEPAM data link:

    www.srl.caltech.edu/ACE/ASC/DATA/level3/swepam/data/

  2. ii)

    ACE MAGSWE data link:

    ftp://mussel.srl.caltech.edu/pub/ace/level2/magswe/

  3. iii)

    Wind 3DP data link (which also contains the magnetic field data):

    cdaweb.gsfc.nasa.gov/pub/data/wind/3dp/3dp_elpd/

We use the near-continuous magnetic field and STE data from the Advanced Composition Explorer (ACE) (McComas et al., 1998; Smith et al., 1998) and the Global Geoscience International Physics Laboratory (commonly known as Wind) (Lin et al., 1995). The 1998 – 2017 data set for ACE and 1994 – 2021 for Wind are used, following processing, to calibrate between the spacecraft and obtain a best estimate for the OSF, accounting for data gaps.

ACE magnetic field data are obtained from the MAG magnetometer (magnetic fields experiment, Smith et al., 1998) and electron data from SWEPAM (solar wind electron, proton and alpha monitor, McComas et al., 1998). We obtain electron pitch-angle distribution (PAD) data from the SWEPAM data set (data link 1) at an energy of 272 eV, well into the suprathermal energy range, and radial magnetic field data from the MAGSWE data set from the MAG instrument (data link 2). The first 20 months of the MAGSWE data set has a resolution of 128 s; however, the remaining data has a 64 s resolution. In addition to this resolution difference, the SWEPAM data (with a native 128 s resolution) was offset from MAGSWE by 15 s. To correct this offset and to ensure a consistent resolution, the SWEPAM and MAGSWE data was re-sampled to a resolution of 128 s at a consistent time step. This re-sampling was carried out by first up-sampling the data to 1 s resolution by forward filling the values, and then down-sampling the data to the 128 s resolution by averaging the groups of 1 s intervals. By re-sampling the data in this way, the correct weighting of each data point was taken into consideration.

Wind data are obtained from the 3DP (three-dimensional plasma analyser, Lin et al., 1995) EESA-Low (low-energy electron electrostatic analyser). We obtain the electron PAD data set (data link 3) with an energy of 292 eV and radial magnetic field data from the data set. To allow a direct comparison between the two spacecraft for their 19 years of overlap, the Wind data set was re-sampled from the native 98 s resolution to the same 128 s time step.

Interplanetary coronal mass ejections (ICMEs) are not removed from the data. It has been noted that ICMEs can make up a significant fraction of the total magnetic flux threading the 1 AU sphere (Riley, 2007). However, we here treat ICMEs as part of the solar wind flow and note that an ICME encountered at 1 AU will previously have threaded the source surface and therefore have also (temporarily) contributed to the OSF (Owens and Crooker, 2006).

2.1 Wind Bow-Shock Identification

During the first 10 years of the mission, Wind’s orbit routinely took it inside the bow shock of the Earth. As we are only interested in the undisturbed solar wind observations, we remove these periods, as summarised by Figure 2. In geocentric solar ecliptic (GSE) coordinates, any data Sunward of the \(x=0\) line (positive \(x\)) with a radial distance from Earth of less than \(30~R_{\textrm{E}}\) is flagged for removal, and any data to anti-Sunward of the \(x=0\) line (negative \(x\)) that falls within the condition of \(\sqrt{y^{2} + z^{2}} = 50~R_{\textrm{E}}\) is also flagged for removal. These conditions were deemed to be relatively conservative according to the Shue model (Shue et al., 1997), which gives the bow-shock stand-off distance from Earth at approximately \(11R_{\textrm{E}}\) and described by \(\sqrt{y^{2} + z^{2}} = 28~R_{\textrm{E}}\) (Lin et al., 2010). The result of removing this data is shown in Figure 2, which displays the percentage of data that has been removed over each Carrington rotation (27.27-day period). The figure cuts off at 2005, beyond which Wind had no further bow-shock encounters.

Figure 2
figure 2

(a) A schematic of the conditions used to remove Wind data from within the magnetosheath (shocked solar wind) or magnetosphere in GSE coordinates. The solid black line represents the shape of the bow shock (not to scale) and the red dashed lines represent the conditions used to remove the undisturbed solar wind data. (b) The percentage of Wind data removed per Carrington rotation due to the encounter with the bow shock. (c) Comparison of missing data from spacecraft. The percentage of missing ACE (red line) and Wind (black line) data in each Carrington rotation between 1994 and 2021. The Wind missing data includes both data missing from the electron and magnetic fields data sets, and data subsequently removed from within the bow shock.

Full size image

3 Methods

3.1 Calculations

We next computed the OSF using the method outlined by Owens et al. (2017), though with modifications detailed here. We first compute \(\Phi _{R}\), the total unsigned magnetic flux threading the sphere at the radius of observation (approximately \(R =~\text{AU}\)):

$$ \Phi _{R} = 4 \pi R^{2} \langle |B_{r}| \rangle _{27~\text{days}}, $$
(1)

where the averaging interval indicated by the angled brackets is one solar synodic rotation period (\(\approx 27.27\) days for spacecraft in near-Earth space), in order to average over all solar longitudes. However, there is a question of the time resolution at which \(|B_{r}|\) is computed: increasing the time period over which \(|B_{r}|\) is computed increases the degree to which inward and outward fields cancel (see Section 1.2). Computing \(|B_{r}|\) on 1-day resolution data can reduce \(\Phi _{r}\) by around 30% compared with using 64-second data. This choice of averaging interval is arbitrary, since there is no clear choice of time averaging that will necessarily result in \(\Phi _{R} = \text{OSF}\) and, as shown later in Section 4.4, the optimum time averaging may vary with the solar cycle in a complex manner.

Instead, the approach outlined by Owens et al. (2017) is to use the highest-resolution data available to compute \(\Phi _{R}\). The difference between 1 or 2 minutes (as used in this study) and 1-second data is small (\(\sim 1\%\)) compared with the difference between 1 minute and 1-day data (∼ 30%) (e.g. Figure 2 in Lockwood, Owens, and Rouillard, 2009a). Intervals that do not contribute to OSF are then individually identified and subtracted from \(\Phi _{R}\).

STE data is used to identify inverted HMF intervals that have no direct connection to the Sun. Within a given Carrington rotation, the total magnetic flux contained within inverted HMF is designated \(\Phi _{I}\) and subtracted from \(\Phi _{R}\). In fact, as explained earlier, 2 \(\Phi _{I}\) is removed to include the magnetic flux from inverted HMF intervals and the (unidentifiable) return HMF topology. As displayed in Figure 1, disconnected flux (topology e) is identified due to an absence of a strahl signature. Therefore, the flux, \(\Phi _{D}\), that we determine to be unclassified is assumed to be disconnected, so will not contribute to the OSF. This was not explicitly accounted for in Owens et al. (2017), where unclassified strahl intervals were treated in the same manner as data gaps, and assumed to contain magnetic-flux topologies in the same proportions as the classified data. Thus, in this study, we compute OSF as:

$$ \mathrm{OSF} = \Phi _{R} - 2 \Phi _{I} -\Phi _{D}. $$
(2)

The factor of 2 applied to \(\Phi _{I}\) is readily understood in three dimensions because a folded open magnetic-flux tube crosses a sphere of radius \(R\) three times but only crosses the source surface once. However, our observations are all taken close to the ecliptic plane and so are two dimensional. In a Parker spiral configuration, the inverted flux and the two return parts of the folded flux are all in the same plane: this is the most probable configuration, and is illustrated in part (a) of Figure 2 of Lockwood and Owens (2013). However, the other parts of that figure show some of the other potential configurations in which one of more of the three segments of the folded flux is out of the plane in which the spacecraft measurement is made (i.e. at a different heliographic latitude). If we take all of the potential non-coplanar configurations as being of equal probability, their net effect cancels out in Equation 2 and the factor 2 remains valid for our two-dimensional observations.

For each Carrington rotation, the average \(|B_{r}|\) for anti-Sunward strahl (uninverted HMF), Sunward strahl (inverted HMF), closed, unclassified and all HMF types, referred to as \(\langle |B_{r}|\rangle _{\textrm{AS}}\), \(\langle |B_{r}|\rangle _{\textrm{SS}}\), \(\langle |B_{r}|\rangle _{\textrm{CL}}\), \(\langle |B_{r}|\rangle _{\textrm{U}}\) and \(\langle |B_{r}|\rangle _{\textrm{ALL}}\), respectively, as well as the number of 128 s intervals of each type, \(N_{\textrm{AS}}\), \(N_{\textrm{SS}}\), \(N_{\textrm{CL}}\), \(N_{\textrm{U}}\) and \(N_{\textrm{ALL}}\) are determined. From this, Equation 1 can be written as:

$$\begin{aligned} \Phi _{R} = & \frac{4 \pi R^{2}}{N_{\mathrm{ALL}}} [N_{\mathrm{ALL}} \langle |B_{r}|\rangle _{\mathrm{ALL}}] \\ = & \frac{4 \pi R^{2}}{N_{\mathrm{ALL}}} [N_{\mathrm{AS}} \langle |B_{r}| \rangle _{\mathrm{AS}} + N_{\mathrm{SS}} \langle |B_{r}|\rangle _{ \mathrm{SS}} + N_{\mathrm{CS}} \langle |B_{r}|\rangle _{\mathrm{CS}} + N_{\mathrm{U}} \langle |B_{r}|\rangle _{\mathrm{U}}], \end{aligned}$$
(3)

where \(N_{\textrm{ALL}} = N_{\textrm{AS}} + N_{\textrm{SS}} + N_{\textrm{CL}} + N_{ \textrm{U}}\).

The inverted HMF component, \(\Phi _{I}\), is given by:

$$ \Phi _{I} = \frac{4 \pi R^{2}}{N_{\mathrm{ALL}}} [N_{\mathrm{SS}} \langle |B_{r}|\rangle _{\mathrm{SS}}]. $$
(4)

Thus, OSF is given by:

$$ \mathrm{OSF} = \frac{4 \pi R^{2}}{N_{\mathrm{ALL}}} [N_{\mathrm{AS}} \langle |B_{r}|\rangle _{\mathrm{AS}} - N_{\mathrm{SS}} \langle |B_{r}| \rangle _{\mathrm{SS}} + N_{\mathrm{CS}} \langle |B_{r}|\rangle _{ \mathrm{CS}}]. $$
(5)

3.2 Strahl Directions and Topology

To carry out the above calculations, HMF topologies need to be determined from in-situ magnetic field and strahl data algorithmically for each 128 s interval. Figure 3 shows a schematic of a single time-step of Wind suprathermal electron pitch angle data, e.g. at 272 eV and in 8 pitch-angle (PA) bins (ACE contains 20 PA bins) equally spaced between 0 and 180 degrees in relation to the direction of the local magnetic field. First, the background flux is calculated from the average of the centre 2 PA bins, \(F_{90}\), and the parallel flux is calculated from the average of the first 2 PA bins, giving \(F_{0}\). The same method is applied for the anti-parallel flux, \(F_{180}\). Next, the existence of a strahl or strahls is determined. To check for the existence of a parallel strahl, we compute the percentage by which \(F_{0}\) exceeds \(F_{90}\), termed the percentage above background, \(PAB_{0}\). The same condition, \(PAB_{180}\), is computed for the anti-parallel strahl. If neither \(PAB_{0}\) or \(PAB_{180}\) meet the required threshold, the interval is unclassified. If only \(PAB_{0}\) or \(PAB_{180}\) meets the threshold, the interval is HMF with a single (direct) connection to the Sun and will be either inverted or uninverted HMF, depending on the HMF polarity.

Figure 3
figure 3

A schematic of a suprathermal electron pitch-angle distribution and the criteria used to algorithmically determine the strahl direction. \(F_{90}\) is the background flux (taken from the blue shaded bars), \(F_{0}\) is the flux at pitch-angle 0 degrees (taken from the grey shaded bars), and \(F_{180}\) is the flux at pitch-angle 180 degrees (taken from the yellow shaded bars). PAB is the percentage above the background flux, and PAO is the percentage above the opposite direction. These are percentages of linear flux. Thresholds on these values are used to classify the existence of strahl.

Full size image

When both \(PAB_{0}\) and \(PAB_{180}\) meet the required threshold to define strahl, there arises the possibility that the interval should be classified as counterstreaming (CS) strahl, suggesting newly emerged loops in the heliosphere (however, see also Gosling, Skoug, and Feldman, 2001). An additional threshold is introduced, comparing the magnitudes of the two strahl, in terms of the percentage above the opposite (PAO). If both \(PAO_{0}\) and \(PAO_{180}\) are below the required threshold, the interval is CS. As CS is interpreted as recently opened magnetic flux, it is assumed to contribute to the OSF. Otherwise, if \(PAO_{0}\) or \(PAO_{180}\) exceeds the required threshold, the interval represents a single connection in the direction of the highest flux and will be either inverted or uninverted HMF, depending on the HMF polarity.

Optimisation of \(PAB\) and \(PAO\) thresholds to agree with previous studies and the impact of the choice of these values on OSF estimation will be investigated in more detail in the next section.

3.3 Calibration Between Spacecraft

Prior to carrying out calculations of OSF, the topology classifications derived from ACE and Wind were compared to find optimal conditions to give a good agreement between the two. We compared ACE and Wind topologies over the period 1998 – 2011, when there is good data coverage from both spacecraft. In Figure 2c, between 1998 – 2011, the ACE data has mostly complete data and Wind has less than 10% missing data from most CRs. In order to apply the same \(PAB\) and \(PAO\) criteria to both spacecraft for strahl identification, we need to account for the different pitch-angle (PA) resolution of the data.

A number of different PA bin combinations and weightings were attempted to give consistent strahl identification across both spacecraft. The closest agreement is found by using two PA bins for Wind to define \(F_{0}\), \(F_{90}\) and \(F_{180}\), as shown in Figure 3, and four PA bins for ACE.

4 Results and Discussion

4.1 Constraining the Strahl Conditions

In order to automatically and reproducibly classify each data point in the approximately 27-year data set, we require an algorithmic method to identify suprathermal electron strahl and the resulting magnetic field topologies. As discussed above, Owens et al. (2017) used a simple method based on the electron flux close to the 0- and 180-degree pitch-angle bins and applied a threshold as a percentage of the “background” flux, taken to be the flux close to a 90-degree pitch-angle bin. A (somewhat arbitrary) threshold of 30% was then used as a threshold to identify strahl and counterstreaming intervals. That same basic approach is adopted here but, in addition to the pitch-angle bin choices detailed in the previous section, we investigate the choice of the strahl thresholds. In particular, we seek to select values that replicate previous studies that have utilised classification by expert observers.

Figure 4a shows the average OSF computed over the whole 1994 to 2021 interval for different PAO and PAB thresholds. Understanding the general variation is best approached by considering the limiting cases.

Figure 4
figure 4

Selecting strahl-identification criteria. (a) Average OSF over the interval 1994 to 2021 as a function of strahl-identification criteria, PAO and PAB. (b) Values of PAO and PAB that are consistent with four previous studies: Gosling et al. (1992) (red and blue lines corresponding to ACE and Wind, respectively), Anderson et al. (2012) (magenta line), Skoug et al. (2000) (black lines) and Pagel, Crooker, and Larson (2005) (yellow horizontal lines). See main article for more detail. The variation in OSF within the remaining PAO-PAB parameter space is very small.

Full size image

The top portion of Figure 4a shows high values of PAB, which mean the criterion for strahl is more restrictive. This increases the occurrence of unclassified intervals, which are subtracted from \(\Phi _{R}\) to compute OSF. Thus, the lowest OSF estimates are produced in this region of parameter space. The bottom-left corner is low PAB and low PAO. Low PAB means that more strahl intervals will be identified at both 0- and 180-degree pitch angles. This reduces the unclassified (and hence disconnected) flux and increases OSF. However, the low PAO means that both strahl need to be nearly identical to be classed as CS (which would contribute to the OSF). Since the PAO condition is difficult to meet, this will result in fewer CS intervals, which will instead be classified as either uninverted or inverted HMF. As uninverted and CS HMF add to the OSF, and only inverted HMF and unclassified subtract, the possibility of increasing inverted HMF at the expense of CS can only serve to decrease the OSF. Moving to the bottom right of Figure 4a means increasing PAO. High PAO allows the strahl in opposite directions to be categorised as CS even when one strahl is up to double the flux of the other. This increases CS and reduces the occurrence of inverted HMF, increasing the OSF.

Thus, the choice of PAB and PAO, even within fairly conservative limits, can vary the OSF by approximately 50%. In order to constrain PAO and PAB thresholds, we use the results from four previously published observational studies.

Using IMP8 data, Gosling et al. (1992) reported an average CS occurrence of 14.7% for each year around solar maximum from August 1978 to December 1990. Skoug et al. (2000) reported an occurrence of 16% of CS for a 9-month period, days 34 – 300 of 1998, using ACE data. Using an automated identification method, Anderson et al. (2012) gave a CS occurrence of 10% from ACE data between 1998 to 2002.

For each of these studies, we determine the PAB and PAO thresholds that are consistent with the reported CS occurrence rate to within \(\pm 33\%\) (i.e. a 1-sigma range about the reported percentage). For the Skoug et al. (2000) and Anderson et al. (2012) studies, we can reproduce the exact periods of study here. The black lines in the right-hand panel of Figure 4 show the parameter space consistent with Skoug et al. (2000), i.e. PAB and PAO values that produce a CS occurrence rate between 10.7% and 21.3% over days 34 – 300 of 1998. The magenta lines show the parameter space consistent with Anderson et al. (2012), i.e. producing a CS occurrence rate between 7.7% and 13.3% over the period 1998 – 2002.

For Gosling et al. (1992), the actual period of study is not present in our data set. Since the CS occurrence rate is reported for the years around solar maximum, we take an equivalent period from ACE and Wind. Explicitly, we isolate one year of data from the peaks of Solar Cycles 23 and 24, namely 2000 and 2014 (peak of solar maximum as identified by sunspot number SILSO World Data Center, 1994 – 2019), for each spacecraft and use that to constrain the CS occurrence. The red and blue lines show the PAO and PAB values that give a CS rate between 9.8% and 19.5% in ACE and Wind data, respectively.

Finally, Pagel, Crooker, and Larson (2005) reported a 10% occurrence of disconnected flux from 1995 to 1998 using data from Wind. Using the same period of study, we assume this as a proxy for the unclassified flux and take thresholds of \(\pm 33\%\), which results in the yellow horizontal lines in Figure 4b.

The shaded region in Figure 6b shows where all observational constraints are met. As “best estimates” we take PAB and PAO values from the centre of this region as 45% and 140%, respectively, instead of the 30% and 30% values used for PAB and PAO in Owens et al. (2017). The average OSF varies very little (\(\pm 0.22 \times 10^{14}\) Wb or 3.5%) in this interval, suggesting it is not a major source of uncertainty in OSF estimation in comparison with data gaps, as discussed below.

4.2 Data Gaps

In this section we aim to assess whether differences between ACE and Wind estimates of OSF can be attributed to the data gaps in one or both data sets, and to quantify the expected OSF uncertainty for a given level of data coverage. Two approaches are taken. First, we compute the “actual error”, which is the difference between ACE and Wind OSF estimates for the same Carrington rotation. This will incorporate the effect of any data gaps, as well as differences in the pitch-angle bins used to define strahl, the small differences in spacecraft position and instrumental differences. Given the data availability for the period of overlap, we compute the error in the Wind OSF estimate for CRs where there is more than 95% of data available for ACE.

Figure 5a shows the actual errors as black crosses. As expected, there is a general trend for larger errors when there is less data available. This is seen more clearly in the binned data in Figure 5b, where the mean actual errors are binned in 5% intervals. In Figure 5a, there are noticeable outliers in the actual errors between 80% and 100% data coverage.

Figure 5
figure 5

The effect of data gaps on OSF estimate. (a) The percentage error in OSF with changing data availability. The “actual errors” (black crosses), are given by direct comparison of simultaneous ACE and Wind data. Ranges for the 5th/95th (blue), 25th/75th (red) and 33rd/66th (black) percentiles of “predicted errors” are obtained by applying Wind data gaps for a given Carrington rotation to the whole 27-year dataset. (b) “Actual errors” binned in 5% intervals of data availability (black crosses) with a best fit polynomial (black line).

Full size image

To investigate this, we also compute a “predicted error” based purely on the data coverage (rather than also including spacecraft differences) by introducing synthetic data gaps. This is achieved in the following manner. For each CR of Wind data, the distribution of data gaps in time is found. In each instance, this data-gap “mask” is applied to every CR within the ACE data set where there is more than 95% data availability. The change in OSF from the complete ACE estimate as a result of the data-gap mask is recorded, giving a distribution of OSF errors for each CR. This predicted OSF error distribution is shown in Figure 5a in terms of percentiles. Again, there is a general trend for both the mean and the width of the predicted error distribution to decrease with data coverage. However, there are clear exceptions to this, which are the result of different-sized data gaps (e.g. one big data gap versus lots of small data gaps). By inspection, we confirm that CRs with large contiguous data gaps result in larger errors than CRs with smaller frequent data gaps resulted in much smaller errors, even when the total data coverage is comparable. This disparity in data-gap sizes also affects the “actual” errors, especially at higher percentages of available Wind data, where many of the actual errors are higher than the predicted error range. In addition, the “predicted” errors, which only account for data gaps, are systematically lower than the actual error, which suggests there are small spacecraft-specific differences too.

In order to quantify uncertainty in the final OSF estimate, we fit the binned “actual error” data, shown in Figure 5b, with a third-order polynomial:

$$ y = -0.0002135 x^{3} + 0.04825 x^{2} - 3.566 x + 92.17, $$
(6)

where \(y\) is the percentage error in OSF and \(x\) is the percentage of data available. This captures the general trend in the data, which is all we seek to do, of a fairly constant error for data availability above 50%.

4.3 OSF Best Estimate

We now combine the ACE and Wind data sets to produce a best estimate of OSF over the entire period of 1994 – 2021, corresponding to the entire length of the Wind mission. During the period of overlap, for each CR we select the spacecraft with the greatest data coverage, using a minimum data availability of 50%. This threshold corresponds to an expected 10% in OSF. Where data coverage is equal, we take an average of the Wind and ACE estimates. Figure 6a shows the individual spacecraft estimates of OSF and the resulting best estimate. In general, the OSF estimates from the two spacecraft are in very close agreement, but there are two intervals of note. During the early period of overlap, around 1998 – 2002, Wind had poorer HMF coverage owing to its excursions into the magnetosphere and the best estimate is largely the ACE value. Conversely, a significant proportion of ACE data was missing during 2012 – 2014, and the coverage remains around 80% after this period, so the Wind estimate is preferable from 2012 onward. Figure 6b displays the OSF best estimate with corresponding percentage errors extrapolated from Figure 5b.

Figure 6
figure 6

Time series of OSF estimates over the period of study. (a) The individual ACE (red line) and Wind (blue line) OSF estimates. The black line shows the best estimate derived from taking the highest data coverage on a CR by CR basis (b) The best estimate of OSF (black line) with error bars computed from the available data coverage.

Full size image

With the implementation of the method outlined above, the full 1994 – 2021 best estimate data consisted of 14.97% inverted flux by occurrence. Of the remainder, 65.47% was open flux, 11.29% newly opened flux (i.e. counterstreaming) and 8.27% unclassified flux. Compared to Owens et al. (2017) (17.04% inverted flux, 68.65% open flux, 4.18% newly opened flux, and 10.13% unclassified), the values reported here agree well, aside from the higher newly opened flux that is likely the result of the different conditions we used. Another key difference is the assumption we made about the unclassified flux being a proxy for disconnected flux. Despite the different topologies, the OSF calculated here agrees well and is slightly higher than the Owens et al. (2017) result, see Figure 9. The average OSF from Owens et al. (2017) is \(6.45^{+0.28}_{-1.21} \times 10^{14}~\textrm{Wb}\) and our method, for the same period, gave an average OSF of \(6.59\pm 0.35 \times 10^{14}~\textrm{Wb}\). Thus, there is agreement within the estimated uncertainty. The results outlined here also generally agree with Badman et al. (2021), which reports an occurrence of 25% inverted flux, compared to our best estimate of 15% inverted flux for the same time period. Since PSP data is at a much higher resolution that the combined ACE/Wind data set, PSP likely detects rapid inversions that are missing from our data set, which results in a higher percentage from Badman et al. (2021).

We note that the occurrence of inverted HMF appears to show an anticorrelation with sunspot number, peaking in solar minimum and lowest just after solar maximum. This trend, and the association of inverted HMF with different types of solar wind structure, will form the basis of a future study. Here, we focus on the OSF implications.

4.4 Time-Averaging Approximation

Previous studies (Wang and Sheeley, 1995; Wallace et al., 2019; Wang, Ulrich, and Harvey, 2022) have used 1-day averages of \(B_{r}\) to estimate OSF from in-situ data. Owens et al. (2017) showed that this approximates the more complex strahl method, at least on average. Figure 7 shows the best estimate of OSF from the strahl method compared to Equation 1, \(\Phi _{R} = 4\pi R^{2} \langle |B_{r}| \rangle \). The shaded regions show \(\Phi _{R}\) calculated using \(B_{r}\) computed from different averaging interval durations. From lightest to darkest, \(\Phi _{R}\) was computed with averaging intervals of: 1 hour, 10 hours, 18 hours, 20 hours, 24 hours and 48 hours. From these estimates, the 20-hour \(B_{r}\) averages give the closest agreement to the best estimate from the Strahl method, shown in Figure 7 as the red line, with an average difference of 0.72%. The OSF calculated by Owens et al. (2017) are able to be approximated by 35-hour averaged data. This 35-hour averaging gives an OSF estimate 7.29% higher than the results reported here.

Figure 7
figure 7

OSF yearly time series from different time averages of \(B_{r}\) used in the standard OSF calculation (i.e. \(\Phi _{R} = 4\pi R^{2} \langle |B_{r}|\rangle \)). The shaded regions display the different time averages of \(|B_{r}|\) between 1 – 48 hours. The red line shows the best estimate of OSF calculated from the strahl method. A 20-hour time average of \(B_{r}\) provides the closest agreement.

Full size image

Figure 8 shows scatter plots of the best time-averaging approach (i.e. \(\Phi _{R}\) computed from 20-hour averages of \(B_{r}\)) compared to the best OSF estimate from the strahl method, computed in over 1 year (panel a) and 27 day (panel b) intervals. Panels (c) and (d) show the histograms of the percentage difference between the two methods. At both the annual and 27-day resolution, there is clearly a strong correlation between OSF computed by both methods. At annual time scales, there is comparatively low scatter (\(\pm 12.2\)%), which demonstrates the ability of the standard method to accurately represent the true OSF at annual timescales, if the estimates are constructed from 20-hour averages of \(|B_{r}|\). Panel (b) shows that there is a much larger spread at the 27-day resolution (\(\pm 56.3\)%), which demonstrates the difficulty in representing the corrected OSF on CR timescales without using the strahl method.

Figure 8
figure 8

Comparisons of OSF calculated via the standard method (\(\Phi _{R} = 4\pi R^{2} \langle |B_{r}|\rangle \)) computed using 20-hour averages of \(|B_{r}|\) with the best estimate from the strahl method. (a) A scatter plot of yearly averages. The solid black line shows \(y=x\), and the dashed black line is a linear best fit. (b) A scatter plot of CR averages. (c) A histogram of the percentage errors between the strahl method and \(\Phi _{R}\) computed with 20-hour averaged data for yearly intervals, where a positive error signifies an overestimation. (d) The same as panel c, but for CR intervals.

Full size image

Using 20-hour averages of \(B_{r}\), \(\Phi _{R}\) can be corrected to more closely match the Strahl method using the best fits from Figures 8a and b. In order to correct yearly OSF values, the correction is:

$$ \mathrm{OSF}_{\mathrm{corrected}} = 1.04\, \mathrm{OSF}_{\text{20-hour}} - 0.28. $$
(7)

To correct CR OSF values, the correction is:

$$ \mathrm{OSF}_{\mathrm{corrected}} = 0.94\, \mathrm{OSF}_{\text{20-hour}} - 0.36. $$
(8)

These equations correct for the tendency for the time-averaging method to overestimate the OSF at low values (and hence solar minimum), and underestimate OSF at high values (and hence solar maximum).

4.5 In-Situ and Magnetogram OSF Comparisons

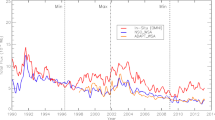
Figure 9 shows the best in-situ estimate of OSF compared with the OSF estimates derived from magnetograms (Wallace et al., 2019). These are either potential-field source surface (PFSS) estimates, or observational coronal hole identification methods applied to magnetograms. The solid black line is the best estimate of OSF using the strahl method, as detailed in Section 4.3. In general, and echoing the result of Owens et al. (2017), our estimate gives lower OSF than simply computing \(\Phi _{R=1~\text{AU}}\), bringing the in-situ estimate of OSF into a closer agreement with the photospheric magnetic field-based OSF estimates, as highlighted by Figure 9. On average, the discrepancy for the period of overlap between our best estimate and WSA (1994 – 2013) is now a factor 1.6 compared to a factor 2 or higher for \(\Phi _{R=1~\text{AU}}\) computed from 1-hour magnetic field data.

Figure 9
figure 9

Comparison of in-situ and photospheric magnetogram estimates of OSF. The best estimate from the current study is shown in black with errors as the grey shaded region, which is displayed as CR averages. The dashed magenta line shows the OSF calculated from Owens et al. (2017), also as CR averages. The coloured lines are magnetogram estimates from KPVT (red line), ADAPT (orange line), EUV (cyan line), Harvey (blue line), displayed as 3 CR averages, from Wallace et al. (2019).

Full size image

5 Conclusions

This study has aimed to improve upon the method outlined in Owens et al. (2017) for estimating open solar flux (OSF) from in-situ spacecraft observations, and to extend the period of study from 13 to 27 years. We have investigated the robustness of the method and the choice of free parameters that can affect the resulting OSF estimate. The “best estimate” OSF values found here are slightly higher than the Owens et al. (2017) estimates. As stated in Section 4.3, the average OSF from Owens et al. (2017) is \(6.45\pm 1.21 \times 10^{14}~\text{Wb}\) for the period 1998 – 2011, and the average OSF from the strahl method used here is \(6.59 \pm 0.35 \times 10^{14}~\text{Wb}\), which agree within the uncertainties. However, a large discrepancy remains between the in-situ and magnetogram OSF estimates, indicating that factors in addition to inverted flux must contribute also. These are likely to be either problems with measuring the photospheric magnetic field (Riley et al., 2019; Wang, Ulrich, and Harvey, 2022) or methods of determining OSF from the magnetograms, such as assuming all OSF is in observable coronal holes. Indeed, outflows mapping to active regions suggest this may not be accurate (e.g. van Driel-Gesztelyi et al., 2012).

A major outstanding assumption that remains in the OSF estimates from in-situ data is that the measurements made at one latitude are representative of all latitudes. \(R^{2} |B_{r}|\) is expected to be constant with latitude due to the equalisation of tangential magnetic pressure. This is expected to occur relatively close to the Sun, inside the Alfvén point, within \(\approx 10~R_{\odot}\) (Suess et al., 1996; Suess and Smith, 1996; Suess et al., 1998). While a latitudinal invariance in \(R^{2} |B_{r}|\) has been observed in the heliosphere (Smith and Balogh, 1995), the uncertainty introduced to OSF estimates is nevertheless difficult to directly quantify. In particular, HMF inversions have been observed close to the Sun (Badman et al., 2021) and tend to increase in occurrence with \(R\) (Macneil et al., 2020), but maybe not equally at all latitudes (Lockwood and Owens, 2009). If inversions are being created in the heliosphere and preferentially in the slow solar wind (Owens, Crooker, and Lockwood, 2013), then \(R^{2} |B_{r}|\) may vary inside/outside the streamer belt. While \(R^{2} |B_{r}|\) may be different at the equator and poles, the actual OSF per unit latitude should be fixed at the near-Sun value (as it cannot easily equilibrate in the supersonic solar wind). However, this merits further investigation.

The strahl-based estimate of OSF presented in this study can be approximated by the use of 20-hour averages of \(B_{r}\) in the standard total heliospheric flux calculation \(4 \pi R^{2} |B_{r}|\). This is useful for studies interested in longer-term variations; however, this is not suitable for CR variations. The time-averaging approximation is likely to slightly underestimate the solar cycle variation in OSF, by overestimating OSF during solar minimum and underestimating during solar maximum.