Exploring the Origin of Stealth Coronal Mass Ejections with Magnetofrictional Simulations

Abstract

Coronal mass ejections (CMEs) – among the most energetic events originating from the Sun – can cause significant and sudden disruption to the magnetic and particulate environment of the heliosphere. Thus, in the current era of space-based technologies, early warning that a CME has left the Sun is crucial. Some CMEs exhibit signatures at the solar surface and in the lower corona as the eruption occurs, thus enabling their prediction before arriving at near-Earth satellites. However, a significant fraction of CMEs exhibit no such detectable signatures and are known as “stealth CMEs”. Theoretical and observational studies aiming to understand the physical mechanism behind stealth CMEs have identified coronal streamers as potential sources. In this paper, we show that such streamer-blowout eruptions – which do not involve the lift-off of a low-coronal magnetic flux rope – are naturally produced even in the quasi-static magnetofrictional model for the coronal magnetic field. Firstly, we show that magnetofriction can reproduce in this way a particular stealth CME event observed during 1 – 2 June 2008. Secondly, we show that the magnetofrictional model predicts the occurrence of repeated eruptions without clear low-coronal signatures from such arcades, provided that the high, overlying magnetic field lines are sufficiently sheared by differential rotation. A two-dimensional parameter study shows that such eruptions are robust under variation of the parameters, and that the eruption frequency is primarily determined by the footpoint shearing. This suggests that magnetofrictional models could, in principle, provide early indication – even pre-onset – of stealth eruptions, whether or not they originate from the eruption of a low-coronal flux rope.

1 Introduction

Through Coronal Mass Ejections (CMEs), an enormous amount of magnetised solar plasma is ejected to the outer solar atmosphere – the solar corona. Observations suggest that on average $10^{14}\,\text{--}\,10^{16}~\text{g}$ of plasma material is suddenly released at radial speeds of $300\,\text{--}\,500\,\text{km}\,\text{s}^{-1}$ (maximum up to $3000~\text{km}\,\text{s}^{-1}$) during CMEs (Vourlidas et al., 2011; Lamy et al., 2019). Hence, CMEs have a tremendous impact on the magnetic and particulate environment in the interplanetary medium (Schrijver et al., 2015; Temmer, 2021). Thus, with the increasing relevance of space weather, numerous theoretical and observational studies have been conducted to investigate various aspects of CMEs (Klimchuk, 2001; Forbes et al., 2006; Chen, 2011; Webb and Howard, 2012).

The occurrence rate of CMEs follows the sunspot cycle with more CMEs during Solar Maximum ($\ge10~\text{day}^{-1}$) compared to Solar Minimum ($\le1~\text{day}^{-1}$) (Webb and Howard, 2012; Lamy et al., 2019). Thus, the characteristics and dynamics of CMEs are considered to be inherently related to their corresponding near-surface magnetic field distribution. These source regions of CMEs often consist of either complex active region clusters or coronal filaments (also known as prominences), or both (Hudson and Cliver, 2001; Gopalswamy et al., 2006; Green et al., 2018). The commonality between these source locations is the presence of polarity inversion lines (PILs) on the solar surface, which are favourable locations for magnetic reconnection. Magnetic diffusion and continuous shearing motion on the photosphere lead to the generation of magnetic helicity and non-potential magnetic energy (with a non-zero electric current) in the vicinity of the PILs (Mackay et al., 2010). This excess storage of magnetic energy exceeding a certain threshold drives the system towards loss of equilibrium between the magnetic forces (pressure and tension) acting on the structure. It leads to a drastic release of the free magnetic energy associated with the local structure, resulting in eruptive phenomena like solar flares and CMEs.

According to coronagraph observations of CMEs in the outer solar corona, the “typical” structure of a CME has three parts: a leading edge, followed by a dark void (cavity), and finally a bright core (for a typical example see Figure 1 of Vourlidas et al., 2013). The leading edge is compressed CME-overlying material, piled together during the initial expansion phase through the ambient interplanetary medium. The void is assumed to correspond to a flux-rope-like structure formed by a bundle of magnetic field lines twisting themselves around a common axis. The magnetic force within the flux rope supports the energised plasma material of the filament which appears as the bright core of the CME. The concept that any CME must consist of a flux-rope-like structure in its core has been discussed in various observational and computational studies (Gilbert et al., 2000; Gopalswamy et al., 2003; Chen, 2011; Schmieder, Démoulin, and Aulanier, 2013; Webb, 2015 and the references within).

Vourlidas et al. (2013) performed a detailed analysis of CME observations with the Large Angle and Spectrometric Coronagraph (LASCO) onboard the Solar and Heliospheric Observatory (SOHO) during 1996 – 2012. Their study also included 3-D magnetohydrodynamic (MHD) simulations and EUV and coronagraphic observations from the Solar Terrestrial Relations Observatory (STEREO) and Solar Dynamics Observatory (SDO) to investigate how many of the observed CMEs were associated with flux ropes. They found that $40\%$ of the total 2403 CMEs during Cycle 23 had the standard three-part structure with flux ropes in their cores. However, a significant number of events ($40\%$) did not have any detectable flux rope cavity.

A major subset of CMEs have no signature at the surface or in the lower corona, and are often classified as “stealth CMEs” or “CMEs from nowhere” (Robbrecht, Patsourakos, and Vourlidas, 2009; Webb and Howard, 2012). A statistical study of stealth CME events by Ma et al. (2010) concluded that the speed of stealth CMEs corresponds to the low end of the CME speed distribution ($\le300\,\text{km}\,\text{s}^{-1}$). However, the absence of usual solar eruption warning signs and detectable low coronal features makes them difficult to predict (Richardson and Cane, 2010). Thus, despite their low speed, stealth CMEs are potential candidates for causing sudden problematic geomagnetic storms and missed space weather events (Nitta et al., 2021). Stealth CMEs are also observed during the Solar Minimum (Ma et al., 2010; Kilpua et al., 2014), indicating that the origin of these CMEs is likely to be linked with the large-scale diffused but non-potential magnetic field distribution. However, D’Huys et al. (2014) identified 40 stealth CMEs without any low-coronal signatures during 2012, which is close to Cycle 24 Maximum.

Howard and Harrison (2013), in their review paper on the history and observations of stealth CMEs, argued that stealth CMEs are merely the subset of the slow, streamer-blowout type of CMEs (Sheeley, Warren, and Wang, 2007). Coronal streamers are helmet-shaped structures with cusp-like bases narrowing into long spikes that extend radially outward from the Sun. Streamers contain closed magnetic loops that confine the hot coronal plasma. When such structures become unstable, the associated coronal loops start swelling up and expand more into the outer corona – eventually leading to a drastic opening up of those coronal loops. The whole process is regarded as the streamer-blowout. An extensive study by Vourlidas and Webb (2018) of more than 900 streamer-blowout events in the LASCO-C2 observations between 1996 and 2015 found that streamer-blowout events are often associated with large-scale PILs, and some without signatures of helical flux ropes. Such magnetic field configurations are more probable during Solar Minimum. One such well-studied stealth CME during Cycle 23 Minimum occurred on 1 – 2 June 2008 (Robbrecht, Patsourakos, and Vourlidas, 2009; Möstl et al., 2009; Bisi et al., 2010; Lynch et al., 2010; Wood, Howard, and Socker, 2010; Nieves-Chinchilla et al., 2011; Rollett et al., 2012). More recently, Lynch et al. (2016) performed a 3-D numerical MHD simulation of this slow streamer blowout event and were able to achieve a comparable agreement with the multi-viewpoint SOHO/LASCO and STEREO coronagraph observations of the same CME.

Full-MHD simulations (with certain approximations) have been utilised for some time to study the coronal magnetic field dynamics associated with streamer-blowout events (Mikic and Linker, 1994; Linker and Mikic, 1995; Antiochos, DeVore, and Klimchuk, 1999; Linker et al., 2003). In the general setup of these MHD simulations, gradual shearing motion at the footpoints of the coronal arcades energises the magnetic configuration, which leads to instabilities associated with the rapid transition to a catastrophic, runaway eruption of coronal fields and plasma. In the presence of resistivity, magnetic reconnection at the radial/vertical current sheet that forms above the PIL allows disconnection and ejection of a plasmoid structure. However, since the driving mechanism in these streamer-blowout models is purely magnetic, we propose that such events could be studied also in a simpler coronal model that does not require the full-MHD framework.

In the present work, we utilise the magnetofrictional approach, which solves only part of the full set of MHD equations. Dissimilar to the full-MHD model, the magnetofrictional model is quasi-static rather than fully dynamic (Mackay and Yeates, 2012). However, unlike static non-linear force-free coronal models, it is capable of capturing the coronal field evolution dictated by the slowly-evolving photospheric-field distribution over time along with the magnetic reconnection (Mackay and Yeates, 2012, and, for a detailed comparison, Yeates et al., 2018). The basic idea of the magnetofrictional approach is that the plasma velocity within the corona is proportional to the Lorentz force. Under such conditions, the coronal magnetic field relaxes towards a force-free equilibrium (Yang, Sturrock, and Antiochos, 1986). The technique was initially introduced by van Ballegooijen, Priest, and Mackay (2000) and was later utilised (with the necessary modifications and improvements) in many studies on the evolution of the non-potential coronal magnetic field (Mackay and van Ballegooijen, 2006; Yeates, Mackay, and van Ballegooijen, 2008b; Yeates and Mackay, 2012; Mackay and Yeates, 2012; Yeates, 2014; Guo, Xia, and Keppens, 2016; Lowder and Yeates, 2017).

Magnetofrictional models have been shown to generate the eruption of twisted magnetic flux ropes that form in the low corona (e.g., Mackay and van Ballegooijen, 2006; Lowder and Yeates, 2017; Yardley, Mackay, and Green, 2018; Yardley et al., 2021). The linear stability properties of force-free equilibria are expected to be similar under both magnetofriction and full-MHD (Craig and Sneyd, 1986), and indeed it has been shown that flux ropes generated by magnetofriction can produce CMEs when their magnetic fields are used to initialise full-MHD simulations (Kliem et al., 2013; Pagano, Mackay, and Poedts, 2014). Thus, with sufficiently accurate input data, the magnetofrictional method offers a possible route for predicting eruptions before onset, without the expense of full-MHD simulations. Notably, the magnetofrictional method was recently used by Yardley et al. (2021) to explain the origin of a stealth CME observed on 3 January 2015, where the obtained magnetic field was also used to initialise a full-MHD model following the eruption dynamics.

In this case, the modelling suggested that the stealth CME originated not from a streamer blowout, but rather from the near-simultaneous eruption of three separate magnetic flux ropes: two directed away from Earth and one directed Earthward that caused a geomagnetic storm. In the observations, there was no clearly attributable low coronal source, likely due to the fact that the Earthward flux rope eruption came from a high-latitude region with a relatively weak magnetic field.

In contrast, our aim here is to investigate whether magnetofriction can also produce stealth eruptions without the lift-off of a pre-eruption magnetic flux rope from the low corona at all. This is motivated by our recent global coronal magnetofrictional simulation for 180 days near Cycle 24 Minimum (Bhowmik and Yeates, 2021). This showed that the corona can still be significantly dynamic even during Solar Minimum when there is no emergence, leading to the formation and disappearance of non-potential coronal structures. Interestingly, the evolution of those structures exhibited quite distinct properties. One class consisted of a pre-existing flux rope which lost equilibrium and disappeared entirely through the outer boundary of the computational domain. In the other class, the magnetic field associated with the non-potential structure underwent partial helicity shedding through reconnection in the overlying arcades with the surrounding magnetic field before settling down to a relatively more stable state. But no magnetic helicity was removed from lower heights in the corona. In fact, the evolution of the coronal magnetic field in this second class of events significantly resembled streamer-blowout dynamics. This motivates us to try reproducing the stealth CME on 1 – 2 June 2008 with the same magnetofrictional model. Apart from this, we also explore different stages of the continuous evolution of a more general streamer-like coronal structure using 3-D and 2-D magnetofrictional simulations, to clarify the basic evolution of such magnetic configurations.

In the following, we first provide in Section 2 a brief description of the computational models (both 3-D and 2-D), along with details of the period of our study and the choice of the initial conditions in our simulations. Section 3 comprises the obtained results, which we further divide into several subsections to address different aspects of our findings obtained from both 3-D and 2-D simulations. Finally, we summarise and interpret our results in Section 4.

2 Computational Models

Two separate computational models have been utilised in this study: one three-dimensional magnetofrictional model (Yeates, 2014; Bhowmik and Yeates, 2021) and another simplified two-dimensional (more like 2.5-D, see Section 2.2) magnetofrictional model. We briefly describe each of the models in the following.

2.1 Three-Dimensional Coronal Magnetic Field Model

The magnetofrictional model is a combination of a surface flux transport model and a non-potential coronal model. The magnetic field [${\boldsymbol {B}}$] within the corona evolves in response to the changing surface boundary. Large-scale shearing velocities on the solar surface play a crucial role in the evolution at the photospheric level – thus, consequently, these govern the dynamics of the coronal magnetic field. The magnetofrictional approach was introduced by van Ballegooijen, Priest, and Mackay (2000), and later Yeates, Mackay, and van Ballegooijen (2008a) extended it to cover the global corona. In this approach, the non-ideal form of the induction equation is solved for the coronal part in terms of a magnetic vector potential [${\boldsymbol {B}} = \boldsymbol {\nabla } \times {\boldsymbol {A}}$],

$$ \frac{\partial {\boldsymbol {A}}}{\partial t} = -{\boldsymbol {E}}, $$

(1)

where ${\boldsymbol {E}} = - {\boldsymbol {v}} \times {\boldsymbol {B}} + {\boldsymbol {N}}$. Here, ${\boldsymbol {E}}$ and ${\boldsymbol {N}}$ represent the electric field and the non-ideal part of Ohm’s law, respectively. Although the corona is highly conducting, the non-ideal term reflects the fact that we are modelling the large-scale mean magnetic field: thus ${\boldsymbol {N}}$ describes the effect of unresolved smaller-scale turbulent motions (van Ballegooijen, Priest, and Mackay, 2000). The velocity [${\boldsymbol {v}}$] is modelled primarily according to the magnetofrictional approach (discussed in the following paragraph). The computational domain is radially extended within $\text{R}_{\odot } \le r \le 2.5~\text{R}_{\odot }$ and includes the full extent of co-latitude, $\theta = 0^{\circ }$ to $\theta = 180^{\circ }$ and longitude, $\phi = 0^{\circ }$ to $\phi = 360^{\circ }$. We solve Equation 1 using a finite-difference method on an equally-spaced grid of $60 \times 180 \times 360$ cells in $\log (r/\text{R}_{\odot })$, sine(latitude) and longitude.

This non-potential coronal model is a simplified version of full-scale MHD models, where we do not solve the full momentum equation to simulate the velocity evolution. Rather we employ a “frictional” velocity [${\boldsymbol {v}}$] that is proportional to the Lorentz force. Such an artificial velocity field drives the coronal magnetic field towards a force-free equilibrium [${\boldsymbol {j}} \times {\boldsymbol {B}} = 0$] (${\boldsymbol {j}}$ being the current density). The velocity field within the corona is modelled accordingly,

$$ {\boldsymbol {v}} = \frac{{\boldsymbol {j}} \times {\boldsymbol {B}}}{\nu ^{\mathrm{3d}}} + v_{ \mathrm{out}}(r)\,\hat{{\boldsymbol {e}_{r}}}, $$

(2)

where $\nu ^{\mathrm{3d}} = \nu _{0}^{\mathrm{3d}}\,|{\boldsymbol {B}}|^{2} /(r^{2} \sin ^{2} \theta )$ is the friction coefficient, with $\nu _{0}^{\mathrm{3d}} =2.8 \times 10^{5}~\text{s}$. On the photosphere, the frictional velocity is set to be zero. Through the second term in Equation 2, where $v_{\mathrm{out}}(r) = v_{0}(r/\text{R}_{\odot })^{11.5}$, we model the effect of the solar wind in the upper corona (Rice and Yeates, 2021). Such a profile ensures that the magnetic field lines become radial beyond $2.5~\text{R}_{\odot }$. For most of our simulations, we consider a maximum solar wind speed $v_{0} = 100~\text{km}\,\text{s}^{-1}$. All components of ${\boldsymbol {B}}$ are periodic in $\phi$. At the inner ($1.0~\text{R}_{\odot }$) and outer ($2.5~\text{R}_{\odot }$) boundaries, the transverse current density [${\boldsymbol {j}}$] is set to zero so that the Lorentz force is always tangential to the boundaries. The non-ideal term [${\boldsymbol {N}}$] can be modelled using either uniform (like ohmic) diffusion or fourth-order hyperdiffusion, where the latter is more preferable in the context of preserving magnetic helicity density [${\boldsymbol {A}}.{\boldsymbol {B}}$] in the volume (van Ballegooijen and Cranmer, 2008). For ohmic diffusion, the functional form is ${\boldsymbol {N}} = \eta _{0} \left ( 1 + c\,|{\boldsymbol {j}}|/{\mathrm{max}|{\boldsymbol {B}}|} \right )\,{\boldsymbol {j}}$ and for hyperdiffusion, we use, ${\boldsymbol {N}} = - ({\boldsymbol {B}}/{|{\boldsymbol {B}}|^{2}}) \nabla (\eta _{\mathrm{h}} | {\boldsymbol {B}}|^{2} \nabla \alpha )$ (where $\alpha = {\boldsymbol {j}}\cdot {\boldsymbol {B}}/|{\boldsymbol {B}}|^{2}$). The other details regarding the constants used in the functional forms of ${\boldsymbol {N}}$ can be found in Bhowmik and Yeates (2021).

Although coronal evolution leads towards the force-free equilibrium of the magnetic field distribution, this is never reached due to the large-scale shearing flows on the surface. In particular, a surface flux transport model operates at the inner photospheric boundary ($r = \text{R}_{\odot }$), incorporating two large-scale velocity fields – differential rotation and meridional circulation – along with supergranular diffusion (for more details, see Section 2.2 of Yeates, 2014). The differential rotation uses the Snodgrass (1983) profile with angular velocity

$$ \Omega (\theta ) = 0.18 - 2.34\, \cos ^{2}\theta -1.72\,\cos ^{4} \theta , $$

(3)

in degrees per day in the Carrington frame. The meridional flow takes the form $v_{\theta }(\theta )=-v_{0}\sin ^{p}\theta \cos \theta$ with $p=2.05$ and $v_{0}$ chosen to give a maximum speed of $8.2~\text{m}\,\text{s}^{-1}$, while the constant surface diffusivity is $455~\text{km}\,\text{s}^{-1}$. These values were chosen according to the standard values suggested by Whitbread et al. (2017).

2.2 Two-Dimensional Coronal Magnetic Field Model

Apart from the 3-D model, we have also utilised a simplified 2-D magnetofrictional model solving the induction Equation 1 in a Cartesian domain. The Cartesian domain can be thought of as representing the local meridional cutout consisting of an arcade of coronal loops with their initial footpoints along the same longitude. We consider the ratio between the width and the height of the 2-D plane to be 1 : 2.75. This is motivated by the horizontal extent of the large overlying arcades typically observed in the solar corona: $30^{\circ }$ degrees (latitude-wise) on the solar surface (equivalent to $0.52~\text{R}_{\odot }$ length-wise), combined with the vertical extent of our 3-D domain: $1.0~\text{R}_{\odot }\,\text{--}\,2.5~\text{R}_{\odot }$.

We again solve Equation 1 for the vector potential, $A(x,z,t) = A_{x}(x,z,t)\hat{\textbf{e}_{x}} + A_{y}(x,z,t)\hat{ \textbf{e}_{y}} + A_{z}(x,z,t)\hat{\textbf{e}_{z}}$, with $x$ and $z$ corresponding to the horizontal and vertical directions in the Cartesian domain, respectively. In this 2-D model, we consider uniform diffusion only, such that ${\boldsymbol {E}} = -{\boldsymbol {v}} \times {\boldsymbol {B}} + \eta {\boldsymbol {j}}$. Similar to the 3-D model, ${\boldsymbol {v}}$ corresponds to the frictional velocity in addition to an outflow mimicking the solar wind,

$$ {\boldsymbol {v}} = \frac{{\boldsymbol {j}} \times {\boldsymbol {B}}}{\nu ^{\mathrm{2d}}} + v_{ \mathrm{out}}(z)\,\hat{\textbf{e}_{z}}. $$

(4)

In the equation above, the friction coefficient is set to $\nu ^{\mathrm{2d}} = \nu _{0}^{\mathrm{2d}}\,(B^{2} + \epsilon \, \mathrm{e}^{-B^{2}/\epsilon })/z^{2}$, with $\nu ^{\mathrm{2d}}_{0} = 2.8 \times 10^{5}~\text{s}$ and $\epsilon = 0.01$. The height $z$ varies between $1.0~\text{R}_{\odot }$ and $2.5~\text{R}_{\odot }$. Unlike in $\nu ^{\mathrm{3d}}$, we do not include a factor $\sin \theta$ in the denominator of $\nu ^{\mathrm{2d}}$ since the horizontal extent in the 2-D model corresponds to a relatively narrow latitudinal domain compared to the 3-D model. The second term, $v_{\mathrm{out}}(z) = v_{0} (z/\text{R}_{\odot })^{10}$ with $v_{0} = 100~\text{km}\,\text{s}^{-1}$, approximates the solar wind profile used in the 3-D simulations and effectively opens up the magnetic field near the outer boundary. We suppose the centre of the arcade is at $20^{\circ }$ latitude and the two footpoints of the outermost loop are positioned at $5^{\circ }$ and $35^{\circ }$ latitudes. The shearing velocity profile at the inner boundary is chosen according to the observed surface differential rotation between $5^{\circ }\,\text{--}\,35^{\circ }$ latitudes with its direction along $\hat{{\boldsymbol {e}}_{y}}$. The functional form uses the profile in Equation 3.

We consider a constant diffusion coefficient ($\eta = 6\times10^{11}~\text{cm}^{2}\,\text{s}^{-1}$) for the coronal magnetic field, but unlike in the 3-D model, we set the photospheric (supergranular) diffusivity to zero. This allows us to clearly isolate surface shearing as the cause of the eruptions – for technical reasons, it is difficult to turn off surface diffusion in the same way in the 3-D code. Since the computational domain is Cartesian, we require appropriate boundary conditions to apply along the horizontal and vertical boundaries. Assuming ${\boldsymbol {j}} \times {\boldsymbol {n}} = \mathbf{{0}}$ along the four boundaries prevents flux of magnetic energy through the boundaries due to either friction or diffusion.

2.3 Initial Condition and Duration of Simulation

2.3.1 3-D Simulation

Our first main objective is to test whether the magnetofrictional model can reproduce the stealth CME event on 2 June 2008. This event occurred during Solar Cycle 23 Minimum, at a location away from the recent active region emergence, so we are justified in neglecting flux emergence in the simulation. To initiate the 3-D simulation, we require three-dimensional magnetic field information in the corona. Accordingly, the simulation starts on 7 April 2008 with a potential field source surface (PFSS) extrapolation (Schatten, Wilcox, and Ness, 1969; Altschuler and Newkirk, 1969) to the radial component of the observed surface magnetic field from the Michelson Doppler Imager onboard SOHO (SOHO/MDI). It corresponds to the Carrington rotation 2068, covering dates between 20 March 2008 and 16 April 2008. The PFSS extrapolation was obtained using our finite-difference code (Yeates, 2018). The 3-D simulation continues till 5 September 2008, i.e. for 150 days without considering any sunspot emergence and produces 3-D coronal magnetic field maps with a daily cadence. In general, the global corona takes about 50 days to evolve away from its initial potential configuration, hence the initialisation on 7 April. Significant dynamics due to the non-potential nature of the coronal magnetic field can be noticed after this initial phase (Bhowmik and Yeates, 2021).

2.3.2 2-D Simulation

Similar to the 3-D simulation, we start with a potential arcade in the 2-D simulation. Imposing $B_{x} = 0$ and $B_{y} = 0$ at the outer boundary ensures that the magnetic field becomes purely radial (or vertical in this case) mimicking the effect of the solar wind. The vector potential corresponding to the initial magnetic field is given by

$$ A_{y}(x,z) = A_{0}\cos \left (\frac{\pi x}{l_{x}}\right )\cosh \left ( \frac{\pi (l_{z} -z)}{l_{z}}\right ), $$

(5)

where $A_{0} = 7 \times 10^{-4}~\text{G}\,\text{R}_{\odot }$, the length along the horizontal direction is $l_{x} = 0.52~\text{R}_{\odot }$ (equivalent to $30^{\circ }$ on the solar surface) and the domain height is $l_{z} = 1.5~\text{R}_{\odot }$ (as in the 3-D case). The domain ratio is 1:2.75 and we take 100 and 275 grid points along the horizontal [$x$] and vertical [$z$] directions, respectively. With $A_{x} = 0$ and $A_{z} = 0$, this profile generates an initial magnetic field [${\boldsymbol {B}} = \boldsymbol {\nabla } \times {\boldsymbol {A}}$] with a maximum amplitude of about 10 G. The initial distribution of $A_{y} (x,z)$ is presented in Figure 1. We follow the evolution for 300 days for this 2-D simulation.

Figure 1

The initial distribution of $A_{y}$ in the 2-D simulation (solid lines are magnetic field lines). Colours show $A_{y}$ in $\text{G}\,\text{R}_{\odot }$. This distribution corresponds to a magnetic field [${\boldsymbol {B}}$] with a maximum strength of 10 G.

3 Results

3.1 3-D Simulation

3.1.1 Stealth CME on 2 June 2008

Our first aim is to study the coronal magnetic field evolution during 1 – 2 June 2008, when a stealth CME originated from the blowout of a streamer. We use our 3-D magnetofrictional simulation and focus primarily on the south-west limb of the Sun, which was estimated as the location of the streamer (Robbrecht, Patsourakos, and Vourlidas, 2009). Now, blowout of a streamer would cause a significant redistribution of the surrounding magnetic field higher up in the corona. This change would primarily be visible in the increased number of open magnetic field lines. Thus we concentrate on the distribution of coronal holes, which are regions of open magnetic field lines having one end in the photosphere and the other beyond $2.5~\text{R}_{\odot }$. The first row in Figure 2 represents the coronal hole distribution on 1 and 3 June 2008. In the second row of the same figure, we can see that the coronal-hole area starts increasing at the initial phase of the event on 1 June 2008 (see the green patch within the rectangle). During the event, the streamer loses some of its stored non-potential magnetic energy and attains a new stable structure. In the process, some of the open magnetic field lines close down again, resulting in decreased coronal-hole area (see the dark purple patch on the right side of the middle-row of Figure 2).

Figure 2

Spatial distribution of the magnetic field at two nearby dates. The footpoints of the radial open-field lines with upward (green) and downward (violet) directions are shown on the top row. The middle row represents the change in coronal-hole area compared to the previous day; dark green and dark purple suggest opening up and closing down of the field lines, i.e. increase and decrease in coronal-hole area, respectively. The distribution of the horizontal component of the magnetic field in G at the outer boundary is depicted in the last row. The rectangle encompasses the location of the streamer above the south-west limb of the Sun.

Alongside the changes in the radial magnetic field component associated with open field lines, the signature of such streamer-blowout events is also captured through the horizontal magnetic field component in the upper corona (e.g. at $2.5~\text{R}_{\odot }$). Solar wind present in the corona forces the field to align along the radial direction at higher heights. However, any non-potential coronal structure will have a significant amount of sheared magnetic field lines along the horizontal direction. When such a structure becomes unstable and passes through the upper corona, it should cause a localised and short-lived enhancement in $B_{\perp } = (B_{\theta }^{2} + B_{\phi }^{2})^{1/2}$. We notice a clear concentration of $B_{\perp }$ at $2.5~\text{R}_{\odot }$ in a similar location as the streamer on 1 June, which later disappeared on 3 June 2008 (see the bottom row of Figure 2).

We might expect the sheared arcade prior to the blowout to have a substantial amount of magnetic helicity (Berger and Field, 1984). Especially field-line helicity has proved to be an excellent tool to assess local magnetic helicity information associated with non-potential magnetic structures with twisted and sheared field lines in the corona (Yeates and Hornig, 2016; Lowder and Yeates, 2017). The field-line helicity is defined as the normalised magnetic helicity within an infinitesimally thin tube around a field line and is calculated through the line integral

$$ \mathcal{A}(x) = \int _{L(x)} \frac{{\boldsymbol {A}}\cdot {\boldsymbol {B}}}{|{\boldsymbol {B}}|}\,\mathrm{d}l. $$

(6)

Here $l$ represents the arc length along the field line $L(x)$ through the point $x$, and ${\boldsymbol {A}}$ is a vector potential for the magnetic field ${\boldsymbol {B}}$. The quantity $\mathcal{A}$ is almost equivalent to the flux linked with the field line, where contributions come from two factors: first, the twisting of the magnetic field lines with height, and second, the winding around the centres of the strong flux on the boundary. Yeates and Hornig (2016) and Yeates and Page (2018) have discussed the theoretical basis of this quantity in detail. They have shown that if the footpoints of the field line on the solar surface remained fixed in time, $\mathcal{A}$ would be an ideal invariant. However, surface motions continuously inject helicity into the global corona; thus we can expect a continuous evolution of field-line helicity and its likelihood to accumulate near non-potential structures. The other details (e.g. the choice of gauge) regarding our field-line helicity calculation can be found in Bhowmik and Yeates (2021).

In Figure 3, we see a concentration of negative field-line helicity in the arcade that would be over the south-west limb of the Sun on 1 June 2008. The set of blue field lines within the rectangle (in the top row) as well as the photospheric projection of field-line helicity (the middle row) indicate the presence of highly sheared magnetic fields in the south-west limb of the Sun. In the bottom row, we further implement a thresholding technique (Bhowmik and Yeates, 2021) based on the intensity of the field-line helicity to detect footpoints of non-potential structures. We, in particular, focus on how those field lines associated with the bottom structure within the rectangle evolve over time.

Figure 3

Field-line helicity on 1 June 2008. In the first row, the grey background corresponds to $B_{r}$ at $1.0~\text{R}_{\odot }$ with a maximum amplitude saturated to 10 G. Here, the projected magnetic field lines in the corona are colour-coded according to their field-line helicity (positive helicity in red and negative in blue, units in Mx). The second row shows the field-line helicity at the field-line footpoints on the photosphere ($1.0~\text{R}_{\odot }$). The last row represents the footprint of the non-potential structures selected after applying a certain threshold. The darker and lighter shades correspond to the cores and extensions of the structures, respectively.

In Figure 4, the 3-D plots represent different stages of its evolution. We track a set of field lines connected to the same set of footpoints on the photosphere as in the bottom row of Figure 3. In Figure 4, these field lines are coloured in the left and right columns based on field-line helicity and radial height, respectively. The top row corresponds to the configuration when the structure was still stable on 28 May 2008. The overlying sheared arcades with substantial negative field line helicity start opening up on 1 June 2008. The process continues during the early hours of 2 June (see the second and third rows with the green arrows). Such an opening up of the field lines naturally increases coronal-hole area locally, which we noticed in the dark green patch in the middle-left of Figure 2. However, due to reconnection in the current sheet that forms at the top of the arcade, new connectivity starts forming in the later hours of 2 June 2008 on the top of the low lying sheared field lines. By 3 June 2008, we can notice a substantial number of such overlying closed field lines, which causes a decrease in coronal-hole area (see the dark purple patch in the middle-right panel of Figure 2). These newly-formed overlying arcades have a relatively less field-line helicity and are closer to the potential than the structure underneath. Interestingly, most of these dynamics happened in the upper corona, whereas the structure in the lower corona remained almost unaltered. Using 3-D MHD simulations, Lynch et al. (2016) found quite a similar dynamics of the structure associated with the streamer-blowout causing the stealth CME on 1 – 2 June 2008 (see Figure 7 in their paper).

Figure 4

Evolution of the magnetic field lines associated with the structure above the south-west limb of the Sun. The magnetic field distribution on the solar disk is depicted in shades of grey (within $\pm 5~\text{G}$). The colour of the field lines on the left and right columns are according to their field-line helicity (within $\pm 5 \times 10^{21}~\text{Mx}$) and radial distance from the Sun’s centre (within $1.0~\text{R}_{\odot }\,\text{--}\,2.5~\text{R}_{\odot }$), respectively. The green and magenta arrows indicate opening up and closing down of overlying arcades, respectively.

This set of sheared magnetic field lines, which later became unstable and erupted, must have had substantial associated electric current density [${\boldsymbol {j}} = {\boldsymbol { \nabla }} \times {\boldsymbol {B}}$]. To verify this, we choose a longitudinal cross-section of the structure at $\phi = 45^{\circ }$ and compare the distribution of current density [$|{\boldsymbol {j}}|$] and $\alpha = {\boldsymbol {j}}\cdot {\boldsymbol {B}}/B^{2}$ between 1 and 3 June 2008. Both are measures of the non-potentiality stored in the coronal magnetic field within the structure. We notice in Figure 5, on 1 June, that a region of current-carrying field lines extends up to $2.5~\text{R}_{\odot }$, incorporating the overlying highly-sheared arcades. After the eruption of these overlying arcades, the tip of the current-carrying region starts descending and comes down to a relatively low height of the corona on 3 June 2008 (indicated by the arrows in the right column of Figure 5).

Figure 5

Distribution of current density [$|{\boldsymbol {j}}|$] and $\alpha$ in the meridional cut across the structure at $45^{\circ }$ longitude. These are shown one day before (left column) and one day after (right column) the eruptive event of 2 June 2008.

We further perform a quantitative analysis on how different measures related to the structure located in the south-west limb change over time. These measures are calculated based on the local magnetic field distribution. The top row in Figure 6 depicts the evolution of the total $B_{\perp }$ at $2.5~\text{R}_{\odot }$ within certain latitudinal and longitudinal extents (roughly shown by the rectangle in Figure 2, latitude: $-55^{\circ }$ to $20^{\circ }$, longitude: $0^{\circ }$ to $120^{\circ }$). A clear peak can be seen on 2 June 2008 marked by the vertical magenta line (labelled P1). In the second row, we integrate $|B_{r}|$ locally (within the same rectangular patch) at $2.5~\text{R}_{\odot }$ which corresponds to the open magnetic flux. We again notice a peak in the open flux on 2 June 2008, which coincides with the increase in the coronal-hole area reported in Figure 2.

Figure 6

Temporal evolution of different quantities with signatures of eruption. The first row shows the total amplitude of $B_{\perp }$ at $2.5~\text{R}_{\odot }$ within the rectangular patch shown in Figure 2. The second and third rows represent temporal evolution of open flux and helicity flux, respectively, through the outer boundary at $2.5~\text{R}_{\odot }$ (within the same rectangular patch). The last row depicts the evolution of the maximum current density near $2.5~\text{R}_{\odot }$ as described in the text.

Figures 3 and 4 indicate that the structure consists of a substantial number of sheared arcades with significant field-line helicity, which were shed through reconnection at the outer boundary during the evolution. Thus, an ejection of helicity flux through $2.5~\text{R}_{\odot }$ is expected. Now, shearing motion at the photospheric level continuously injects helicity into the coronal magnetic field. Any depletion of helicity happens through either volume dissipation or ejection of unstable non-potential structures with high helicity content through the outer boundary. Bhowmik and Yeates (2021) found that the former is negligible compared to the latter in a similar study on the evolution of the global coronal magnetic field during Solar Cycle 24 Minimum. According to Yeates and Hornig (2016), the evolution equation for the relative helicity [$H$], which is the signed integral of the field-line helicity, may be written as

$$ \frac{\mathrm{d}H}{\mathrm{d}t} = -2 \int _{V} {\boldsymbol {N}}\cdot {\boldsymbol {B}} \,\mathrm{d}V + \oint _{S} {\boldsymbol {A}} \times \big[ 2 {\boldsymbol {E}} + \frac{\partial {\boldsymbol {A}}}{\partial t}\big] \,\mathrm{d}{\boldsymbol {S}}. $$

(7)

The first term on the right corresponds to the overall volume dissipation of helicity. The second term captures the eruption of structures with significant helicity, where, in particular, the flux of ${\boldsymbol {A}} \times 2\,{\boldsymbol {E}}$ through $2.5~\text{R}_{\odot }$ has the highest contribution. The third row in Figure 6 shows the temporal evolution of the second term in Equation 7 through $2.5~\text{R}_{\odot }$ integrated over the same rectangular domain. Here again, we notice a clear peak in the helicity flux on 2 June 2008.

Lastly, we study how the maximum amplitude of current changes near the outer boundary ($2.5~\text{R}_{\odot }$) at $45^{\circ }$ longitude within $-28^{\circ }$ and $-10^{\circ }$ latitudinal range (i.e. roughly the location of the tip of the current sheet in the left column in Figure 5). In the last row of Figure 6, the maximum current density shows a peak on 2 June 2008, coinciding with the peaks in other quantities. Bhowmik and Yeates (2021) have found that the eruption of a flux rope exhibits similar signatures in the temporal evolution of these quantities. However, the primary difference between a flux rope eruption and an overlying arcade eruption is the presence of a positive radial tension force in the case of a flux rope with a helical magnetic field distribution. The same measure has also been utilised to identify flux ropes in previous studies (e.g., Yeates, 2014). For the CME on 2 June 2008, we found that it did not contain any positive radial tension force. Thus, we can infer that the stealth CME originated from the eruption of highly sheared overlying arcades and certainly not from destabilisation of any preexisting flux rope.

Despite the successful matching of the timing of the stealth CME on 2 June 2008, it is comparatively difficult to establish a one-to-one correspondence between the simulated 3-D coronal magnetic field distribution and other coronal observations, such as STEREO observations of the streamer blowout or extreme-ultraviolet emission profiles of the corona. Robbrecht, Patsourakos, and Vourlidas (2009) were the first to provide detailed observational analysis of the 2 June streamer blowout event and the associated stealth CME (see Figure 1 in their paper). Similar to their observational evidence, our magnetofrictional simulations also show that the magnetic field lines associated with the helmet streamer in the south-west changed substantially during 1 – 2 June 2008 (Figure 4). Nonetheless, a detailed comparison between the simulated magnetic field and the observed plasma emission profile is worth a separate full-scale study and is beyond the scope of this presented work. As stated before, our primary focus here is gaining a physical understanding of the driver of such events in general.

3.1.2 Repetitive Nature of Streamer Eruptions

The primary driver for overlying arcade eruptions is the shearing motion at the photospheric level. Solar differential rotation on the surface continuously imparts helicity into the field lines anchored to the surface. Thus, although the structure attains a relatively stable configuration after losing some of its non-potentiality during the 2 June 2008 CME, we expect it to evolve towards instability again. Therefore, we continue the global magnetofrictional simulation beyond the 2 June event for an additional 95 days (until 5 September 2008) and closely monitor the evolution of magnetic field distribution in the same location. Indeed, we find that the continuous shearing at the footpoints of the structure leads to multiple instances when its highly sheared overlying arcades erupt. These eruptions cause similar peaks in the integrated (or total) quantities as depicted by P2, P3 and P4 in Figure 6 (marked by the vertical grey lines) during 13 June, 1 July and 3 August 2008, respectively.

Each of these instances are associated with changes in coronal-hole area and $B_{\perp }$ at $2.5~\text{R}_{\odot }$ (like in Figure 2). The magnetic field lines undergo the same opening up and closing down stages as occurred during the 2 June 2008 event (like Figure 4). In particular, Figure 7 provides a qualitative representation of how the extent of the current density associated with the same structure oscillates between a higher ($2.5~\text{R}_{\odot }$) and a lower corona ($\sim 2.0~\text{R}_{\odot }$) repetitively during these events. We note that there was another small peak on 21 July 2008, which is mostly visible in the top three rows of Figure 6. This increment was not associated with the structure; instead, it was related to some other dynamics happening near $120^{\circ }$ longitude which got included within the rectangular domain. However, if we minimise the area of the domain, for example, while calculating the maximum current density, we do not observe any peak on that day (see the last row of Figure 6).

Figure 7

Change in current density associated with each of the peaks (P2, P3 and P4) in Figure 6, where the left and right column correspond to the distribution on the day before and after each of eruptive events took place, respectively. The units in the colour bar are in $10^{-12}~\text{G}\,\text{cm}^{-1}$.

Comparing the difference between the timing of the first two adjacent peaks (P1 and P2), we find that the time between eruptions is about 20 days. However, a noticeable feature in Figure 6 is the increasing gap between each successive pair of peaks. Since in our simulation, we do not consider any photospheric active region emergence, the magnetic field in the photosphere is gradually weakened due to surface diffusion (leading to flux cancellation at the PIL). Thus, it is not surprising that the arcades take more time in the later period to attain enough non-potentiality leading to instability.

The structure in Figure 4 resembles a typical helmet streamer observed in the solar corona. Linker and Mikic (1995) studied the evolution of a two-dimensional (azimuthally symmetric) helmet streamer in a time-dependent MHD setup. Velocity fields in their coronal simulation included solar wind and a continuous photospheric shearing flow. Thus, their simulation setup is comparable to our magnetofrictional setup, particularly if we consider the local evolution of the set of arcades associated with the structure only and not the global corona. Indeed, Linker and Mikic (1995) also found similar repetitive eruptive behaviour of the helmet streamer (see Figure 3 in their paper) with a rough periodicity of 21 days which was primarily driven by the photospheric shearing motion. The agreement between their 2-D MHD and our 3-D magnetofriction simulations are noteworthy. However, in the following section, we further use a simplistic 2-D setup, both to test the robustness of this kind of eruption within the magnetofrictional framework and also to allow further comparison to the simpler magnetic geometry of Linker and Mikic (1995).

3.2 2-D Simulation

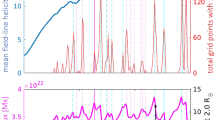
In the 2-D magnetofrictional simulation (see Section 2.2), we start with the initial magnetic field distribution discussed in Section 2.3. This initial configuration is quite similar to the longitudinal cross-section of the structure in our 3-D magnetofrictional simulation (see the left column in Figure 5). Due to the continuous shearing velocity at the footpoints (lower boundary), the overlying arcades (or loops) start rising upwards gradually while evolving away from their initial potential-field configuration. When the top-most loops reach near the outer boundary ($2.5~\text{R}_{\odot }$), the solar wind compels the field lines to open up. This causes a sudden and sharp increase in the open magnetic flux and current near the outer boundary. Then reconnection occurs within the current sheet near the top, and closed field lines start re-forming, which leads to a temporary stable configuration. However, the steady shearing motion at the inner boundary forces the structure to become unstable again and the same dynamics continues repetitively.

The first two rows in Figure 8 represent the evolution of the magnetic field [$B_{y}$] and current density [$J_{y}$] associated with the sheared arcades. In the bottom three rows, the temporal evolution of total magnetic energy, open magnetic flux and the maximum of total current density at the outer boundary ($2.5~\text{R}_{\odot }$) are depicted. The series of maps in the first two rows shows how the configuration becomes unstable on Day 152, changing from its relatively stable form on Day 140. The eruption causes simultaneous peaks in total magnetic energy, open magnetic flux and maximum current density at the outer boundary ($2.5~\text{R}_{\odot }$), marked by vertical magenta lines in the bottom three rows. By Day 155, the tip of the current-carrying region descends to a lower height, and the structure again attains a relatively stable form. Simultaneously, we notice temporary decreases in the integrated quantities. In our 300-days-long 2-D simulation, this oscillatory dynamics of the structure continues, as demonstrated by those multiple repetitive peaks in energy, open flux and maximum current density in Figure 8.

Figure 8

Evolution in the 2-D magnetofriction simulation. The top row depicts the distribution of magnetic field [$B_{y}$] in shades of blue with vector potential [$A_{y}$] denoted by the black contour lines, and the second row represents the current density [$J_{y}$] on Day 140, 152 and 155. The eruption on Day 152 corresponds to the peak (indicated by magenta vertical lines) in the temporal evolution of total magnetic energy, open flux and maximum current in the domain shown by the bottom three rows. We observed multiple such peaks during the 300-day-long simulation.

We can see a qualitative agreement between the evolution of the sheared arcades in our 2-D and 3-D magnetofrictional simulations, which in turn are quite similar to the streamer evolution studied by Linker and Mikic (1995). The periodicity in the 2-D simulation is roughly 22 days, which is calculated based on five peaks around the magenta line in Figure 8. Interestingly, this period increases somewhat during the course of the 2-D simulation, even though – different from the 3-D model – there is no surface (supergranular) diffusion. However, unlike in the 3-D model, this increasing period is a transient effect and the period eventually becomes regular (to be shown in Section 3.3). All these resemblances emphasise the fundamental nature of the dynamics of coronal magnetic arcades subjected to continuous shearing motion at their footpoints.

3.3 Dependency on Model Parameters

To test the robustness of our results, we changed a few parameters used in our simulations. As demonstrated so far, the fast dynamics occur in the upper part of the corona. Since surface diffusion on the photosphere causes reconnection primarily in the lower coronal magnetic field (leading to the formation of flux ropes), we hypothesise that the eruption of a sheared arcade higher up ($> 2.0~\text{R}_{\odot }$) in the corona is caused by shearing of these arcade field-lines themselves, so it should not depend on the amplitude of the surface diffusion. Indeed, we find in a new simulation that reducing the surface magnetic diffusivity to $100~\text{km}^{2}\,\text{s}^{-1}$ from $455~\text{km}^{2}\,\text{s}^{-1}$ does not have any significant impact on the nature of those evolving sheared arcades (at least for the initial 87 days, see, the cyan and magenta curves in Figure 9). Beyond that period, those two simulations start to diverge, and we find that the frequency of eruption is a little higher in the lower surface diffusion simulation (magenta curve).

Figure 9

3-D parameter space study: evolution of the maximum current density [j] near $2.5~\text{R}_{\odot }$ for separate 3-D magnetofrictional simulations with different parameter settings. In the standard simulation (cyan curve), we use hyperdiffusion (HD) with a surface diffusivity $455~\text{km}^{2}\,\text{s}^{-1}$. In the low surface diffusivity case (magenta curve), we set the amplitude to $100~\text{km}^{2}\,\text{s}^{-1}$. The vertical-dashed line denotes the epoch of the event on 2 June 2008.

Arcade eruptions are primarily happening in the upper corona close to $2.5~\text{R}_{\odot }$ in our original simulation. In a new 3-D simulation, we move the outer boundary from $2.5~\text{R}_{\odot }$ to $4.0~\text{R}_{\odot }$ while keeping all other particulars unaltered, so as to check whether our results are an artefact of the imposed numerical boundary conditions at the outer boundary. In this particular simulation, too, we observe an overlying arcade eruption on 2 June 2008 and repetitive successive eruptions on the same south-west limb of the Sun (see the maroon curve in Figure 9). However, the current density in the simulation with the outer boundary at $4.0~\text{R}_{\odot }$ has higher values compared to the original simulation. While examining the distribution of current density across the structure (similar to Figure 7), we found that the extended current sheet caused the excess amplitude in the $4.0~\text{R}_{\odot }$ case. See the Appendix for more details.

Lastly, in a third new 3-D magnetofrictional simulation, we model the non-ideal term in Ohm’s law based on uniform (Ohmic) diffusion instead of hyperdiffusion. This third simulation starts with the same initial Carrington map and produces results similar to the hyperdiffusion case. First, we see an eruption in the overlying arcades on 2 June 2008, followed by repetitive eruptions of the same structure. The evolution of the current density near $2.5~\text{R}_{\odot }$ shows that the periodicity of these successive events is comparable (see the black curve in Figure 9). In summary, our choices of different model parameters or outflow profiles in the 3-D simulations did not have any significant effect on reproducing the stealth CME event during 1 – 2 June 2008. Although each simulation starts diverging from each other after the initial ≈80 days, the structure associated with the CME continues erupting repeatedly. Despite the difference in the epoch of eruptions in different simulations, the average periodicity of the recurring eruptions is roughly 20 – 30 days in all cases – further supporting the generality of such dynamics.

In a series of 2-D magnetofrictional simulations, we explore which parameter controls the frequency of these eruptions. Figure 10 depicts the epochs of eruptions in the 2-D arcades for different values of the friction coefficient [$\nu ^{\mathrm{2d}}_{0}$]. Fluctuations in open flux are used to determine the time of the eruptions, where the size of the dots is proportional to the decrease in open flux associated with the individual eruption. In Figure 10, the first column corresponds to a 2-D simulation with $\nu ^{\mathrm{2d}}_{0} = 4 \times 10^{5}~\text{s}$. We can see more small peaks with higher frequency in the initial phase of the evolution. In the later stage (beyond Day 200), the size of dots increases and the eruptions become less frequent but more regular, which agrees with the nature of evolution depicted in Figure 8. Increasing $\nu^{\mathrm{2d}}_{0}$ delays the start of the periodic eruptions, and beyond $\nu ^{\mathrm{2d}}_{0} = 8 \times 10^{6}~\text{s}$ there are no eruptions even after Day 1000. Such high values of $\nu ^{\mathrm{2d}}_{0}$ are quite different from the $\nu ^{\mathrm{3d}}_{0}$ used in 3-D simulations ($2.8 \times 10^{5}~\text{s}$). Thus, focusing on the data points for $\nu^{\mathrm{2d}}_{0} \le 10^{6}~\text{s}$, we can conclude that the friction coefficient does not have any significant effect on the periodicity of such eruptions. Again in another set of 2-D simulations with slower outflow speeds, the frequency remained almost the same, with a rough periodicity varying between 20 – 30 days during the first 300 days. Reducing the maximum magnetic field strength of initial arcades also did not affect the periodicity. We find that the primary factor controlling the frequency is the shearing flow speed at the arcade footpoints, which agrees with the other MHD simulations (Mikic and Linker, 1994).

Figure 10

2-D parameter space study: variation in the arcade behaviour depending on the friction coefficient $\nu _{0}^{\mathrm{2d}}$. This figure shows the times of arcade eruptions during 50 simulations, with the eruptions from each simulation are represented by blue dots, running vertically from the horizontal axis. The size of the dots is proportional to the decrease in open flux during each eruption.

4 Concluding Discussion

To summarise, in this work, utilising magnetofrictional simulations, we have investigated the evolution of large-scale coronal arcades subjected to continuous photospheric shearing motion (due to the differential rotation) at their footpoints. The first part of our results shows a qualitative agreement with the stealth CME event during 1 – 2 June 2008, which has been well studied both observationally and computationally. Similar to other stealth CMEs, it lacked clear low coronal signatures like disappearing filaments, flare ribbons, post-eruption arcades, etc. Despite having relatively lower speed ($300~\text{km}\,\text{s}^{-1}$), stealth CMEs can cause potential geomagnetic storms when directed towards the Earth (Zhang et al., 2007). Thus estimating the probable source regions of such CMEs based on the Sun’s magnetic field distribution is crucial in the context of space weather.

The differential rotation of plasma on the solar surface acts as a steady source for injecting non-potentiality in the coronal magnetic field. Magnetic arcades will experience stronger shear if the distance between their footpoints is larger. Thereby, large-scale coronal structures such as streamers with their opposite footpoints anchored hundreds of megametres apart can store a substantial amount of magnetic helicity. Even if an unstable magnetic flux rope does not form, once the amount of stored non-potential magnetic energy (i.e. free energy) reaches a certain limit, the structure will eject the excess energy to the outer corona through a streamer-blowout event. However, the time to reach the first epoch of instability requires roughly 50 days from the initial potential magnetic field configuration (Bhowmik and Yeates, 2021). This ‘ramp-up time’ is inversely proportional to the amplitude of the shearing flow. In the same context, we note that the timing of the streamer blowout on Day 56 in our magnetofrictional simulation (which started on 7 April 2008), matching precisely with the event observed on 1 June 2008, is to some extent coincidental. In fact, starting the simulation on an earlier (or later) date, but using the same initial Carrington map 2068, would have caused the event to occur earlier (or later) than 1 June 2008.

Despite the ambiguity in predicting the exact epoch of instability in a particular streamer, we can precisely identify the associated magnetic structure and its location. Such magnetic configurations will have associated PILs at the photospheric level and a substantial amount of field-line helicity in the coronal arcades accumulated over many days (see, Figure 3). This is where magnetofrictional simulations have an advantage over full-MHD simulations since the latter are computationally more expensive for studying the long-term evolution of such structures in the global corona. Vourlidas and Webb (2018), in an extensive study with 19 years of LASCO/C2 data (1996 – 2015), found that streamer blowouts arise from extended PILs outside active regions. Such long, long-lived PILs on the photosphere are common in the less active period of the sunspot cycle, especially during the Solar Minimum. This is a reasonable explanation for why past observational studies (Ma et al., 2010; Kilpua et al., 2014) have found many stealth CMEs during the Minimum. However, the presence of coronal streamers is not exclusive to the Sun’s minimum activity period. Thus, we can expect stealth CMEs associated with destabilisation of coronal streamers during the other phases of the solar cycle (D’Huys et al., 2014).

Lynch et al. (2016) argued that the cause of stealth CMEs is not fundamentally different from the standard filament erupting CMEs (Chen, 2011) and the small-scale plasmoids observed to be continuously emitted from streamer tops in the slow solar wind (Sheeley et al., 2009; Higginson and Lynch, 2018). In a generalised perspective, all these phenomena are driven by excess storage of magnetic stress, followed by its ejection into the heliosphere via reconnection. However, in stealth CMEs, this stress injected by differential rotation gets accumulated at higher coronal heights (like streamers) above the photosphere ($> 2.0~\text{R}_{\odot }$). Thus, stealth CMEs with streamer origin are unlikely to have any clear signatures of magnetic reconnection close to the solar surface. Instead, the crucial reconfiguration of the coronal magnetic field occurs at higher altitudes in overlying magnetic arcades, where the low density makes the observation of plasma heating challenging for detection. The most likely observational signature on the surface would be temporary enlarging of coronal holes, accompanied by coronal dimming.

Another interesting factor we have explored here is the repetitive eruptions of the overlying arcades associated with the streamer. Our results from 3-D magnetofrictional simulations suggest that an individual large-scale magnetic configuration (similar to a streamer) with significant helicity can be the origin of multiple consecutive blowout events. And the dynamics is primarily governed by the surface differential rotation – demonstrating the basic interaction between a large scale magnetic field and shearing plasma motion. The evolution of such structures is so fundamental and generic that a much simpler 2-D magnetofrictional model successfully simulated the repetitive eruptive nature of sheared arcades.

Our parameter space study using the 3-D model reveals that using Ohmic diffusion (instead of hyperdiffusion), or extending the outer boundary beyond $2.5~\text{R}_{\odot }$, or changing the surface diffusivity, still reproduces the stealth CME event on 1 – 2 June 2008. However, in later stages, individual simulations start diverging from each other, which has been seen previously in simulations with no new flux emergence (Bhowmik and Yeates, 2021). Nonetheless, irrespective of our choice of parameters, in each of the simulations, the non-potential structure undergoes repetitive eruptions at higher coronal height in the overlying arcades with an approximate periodicity of 20 – 30 days. From our parameter space study with 2-D simulations, we find that the frequency of eruptions in the arcades is primarily controlled by the shearing speed. Other factors, such as the friction coefficient and outflow speed, do not significantly affect the periodicity. One would expect therefore that a similar periodicity would be observed in full-MHD simulations.

Finally, in the context of space weather studies, stealth CMEs hold significant importance. The absence of any low coronal counterparts makes them hard to detect. Unlike other Earth-directed CMEs with clear surface signatures, which allow a 2 – 5 day precursor warning of potential geomagnetic storms, Earth-directed stealth CMEs can cause unforeseen space weather hazards. Thus they are often labelled as the source of ‘geomagnetic storms from nowhere’. Since helmet streamer-like, large-scale structures act as a potential source of stealth CMEs, modelling their evolution over a long period of time is required. The global magnetofrictional simulation performs well in two major aspects. Firstly, it captures the slow build-up of non-potentiality in the coronal magnetic structures, which can be identified through the distribution of magnetic field-line helicity, at the least a few days before eruptions. Secondly, magnetofrictional simulations are less computationally expensive than full-MHD simulations, yet they can reproduce the fundamental quasi-static development of large-scale coronal magnetic configurations. Therefore, with sufficiently accurate input data, we anticipate that magnetofrictional simulations could potentially provide advance prediction of stealth CMEs whether caused by eruption of low coronal magnetic flux ropes or high-altitude streamer-blowout events.

Appendix

Figure 11 shows further details of the 3-D magnetofrictional simulation, with the outer boundary moved out to $4.0~\text{R}_{\odot }$ instead of $2.5~\text{R}_{\odot }$.

Figure 11

Magnetofrictional simulation with outer boundary at $4.0~\text{R}_{\odot }$. The figure on the left shows the solar wind profile used in this particular simulation (black-dashed curve) in comparison to the standard one with outer boundary at $2.5~\text{R}_{\odot }$ (red curve). Figures on the right depict the distributions of current density (units are in $10^{-12}~\text{G}\,\text{cm}^{-1}$) before and after the stealth CME event on 2 June 2008.