Calibrating GONG Magnetograms with End-to-End Instrument Simulation II: Theory of Calibration

Abstract

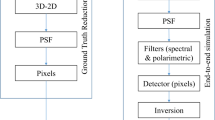
This is the second of three papers describing an ‘absolute’ calibration of the GONG magnetograph using an end-to-end simulation of its measurement process. In the first paper, we described the GONG instrument and our ‘end-to-end’ simulation of its measurement process. In this paper, we consider the theory of calibration, and magnetograph comparison in general, identifying some of the significant issues and pitfalls. The calibration of a magnetograph is a function of whether or not it preserves flux, independent of its spatial resolution. However, we find that the one-dimensional comparison methods most often used for magnetograph calibration and comparison will show dramatic differences between two magnetograms with differing spatial resolution, even if they both preserve flux. Some of the apparent disagreement between magnetograms found in the literature are likely a result of these instrumental resolution differences rather than any intrinsic calibration differences. To avoid them, spatial resolution must be carefully matched prior to comparing magnetograms or making calibration curves. In the third paper, we apply the lessons learned here to absolute calibration of GONG using our ‘end-to-end’ measurement simulation.

Appendix: Curve Fitting Methods and Resolution Mismatch Issues

In the ensuing derivations, we use $a$ (for actual) in place of $\phi ^{0}$ (ground truths), $m$ for $\phi ^{m}$ (measurements), $c$ for $\phi ^{c}$ (calibrated measurements), and so on. This makes the math somewhat less cumbersome.

1.1 A.1 Forcing Flux Conservation by Curve Fitting?

Suppose we attempt to overtly enforce flux conservation in the scatter plot curve fitting procedure, while still including the PSF on the $m_{ij}$ and omitting it from the $a_{ij}$. One suggestion has been looking for a curve where we split the point cloud into bins in $m_{ij}$, and for each bin, set the calibration factor such that the net flux of the $c_{ij}$ in the bin is equal to the net flux of the $a_{ij}$ in the bin. That is, for each measured value bin, $m_{l}$, we take the calibration factor $\gamma _{l}$ to be

$$ \gamma _{l} = \biggl(\sum _{m_{l} \leq m_{ij} < m_{l+1}} a_{ij} \biggr)/ \biggl(\sum _{m_{l} \leq m_{ij} < m_{l+1}} m_{ij} \biggr), $$

(28)

where the summation is over all $i$ and $j$ such that $b_{l} \leq m_{ij} < b_{l+1}$. We then interpolate the $\gamma _{l}$ and $m_{l}$ to obtain the calibration factor for any given value of $m$, $\gamma (m)$. The calibrated values are then

$$ c_{ij} = m_{ij}\gamma (m_{ij}). $$

(29)

We begin, as before, with an analytic example. If there are issues with a proposed calibration scheme in an ideal test case, they will persist in more general cases. The example is chosen for its simplicity and (relatively) easy analytic treatment, which has the advantage that the dependence of the calibration on its inputs can be seen algebraically. In this example, $a_{ij}$ are determined by probability density functions, in terms of which $\gamma _{l}$ can be written

$$ \gamma _{l} = \frac{\int a p(a|m_{l} < m < m_{l+1}) da}{\int m p(m|m_{l} < m < m_{l+1}) dm}. $$

(30)

These probabilities can be computed with the help of Bayes’ theorem:

$$\begin{aligned} &p(a|m_{l} < m < m_{l+1}) = \frac{p(m_{l} < m < m_{l+1}|a)p_{a}(a)}{ p(m_{l} < m < m_{l+1})} \end{aligned}$$

(31)

$$\begin{aligned} &p(m|m_{l} < m < m_{l+1}) = \frac{p(m_{l} < m < m_{l+1}|m)p_{m}(m)}{ p(m_{l} < m < m_{l+1})} \end{aligned}$$

(32)

$$\begin{aligned} &\gamma _{l} = \frac{\int a p(m_{l} < m < m_{l+1}|a)p_{a}(a) da}{\int p(m_{l} < m < m_{l+1}|m)p_{m}(m)dm} = \frac{\int a p(m_{l} < m < m_{l+1}|a)p_{a}(a) da}{\int _{m_{l}}^{m_{l+1}} p_{m}(m)dm}. \end{aligned}$$

(33)

Here, $p_{a}(a)$ and $p_{m}(m)$ are the marginal probabilities of the ‘actual’ and ‘measured’ values, $a$ and $m$. We will once again assume a normal probability density function for the $a_{ij}$:

$$ p_{a}(a) = \frac{1}{2\pi \sigma _{a}^{2}}e^{-(a-a_{0})^{2}/(2\sigma _{a}^{2})} .$$

(34)

And as before, the $m_{ij}$ are related to the $a_{ij}$ by a scaling factor, $c_{m}$, a convolution. Now, we will also assume that the measurement errors are of the form $m_{0}+\Delta m_{ij}$, where $\Delta m_{ij}$ is normal distributed with mean 0 and standard deviation $\sigma _{\Delta m}$:

$$ m_{ij} = m_{0}+\Delta m_{ij} + c_{m} \sum_{kl}w_{ij,kl}a_{kl} .$$

(35)

Consider that each $m$ is the weighted sum (the weights are given by the kernel) of a set of random numbers with probability density function $p(a)$ plus $m_{0}+\Delta m_{ij}$. Since the sum of normal random variables is itself a normal random variable (with terms of the sum adding their standard deviations in quadrature), the errors in each of the $m_{ij}$ will also be normal distributed, with mean

$$ \mu _{m} = a_{0} c_{m} + m_{0}, $$

(36)

and standard deviation equal to

$$ \sigma _{m} =\sqrt{\sigma _{\Delta m}^{2} + c_{m}^{2}\sigma _{a}^{2} \sum_{ij}K_{ij}^{2}} = \sqrt{\sigma _{\Delta m}^{2} + c_{m}^{2} \frac{\sigma _{a}^{2}}{n_{\mathrm{eff}}}}, $$

(37)

where

$$ n_{\mathrm{eff}} \equiv 1/\sum_{ij}K_{ij}^{2} $$

(38)

is the ‘effective’ number of points in the kernel. If the kernel is a two-dimensional top hat ($n_{\mathrm{kernel}}$ nonzero points, all equal to $1/n_{\mathrm{kernel}}$), for instance, then $n_{\mathrm{eff}} = n_{\mathrm{kernel}}$. If almost all of the weight comes from the central point ($1-K_{00}\ll 1$), then $n_{\mathrm{eff}}\approx 1$. In any case, $p_{m}(m)$ is then

$$ p_{m}(m) =\frac{1}{\sqrt{2\pi \sigma _{m}^{2}}} e^{- \frac{(m-\mu _{m})^{2}}{2\sigma _{m}^{2}}}. $$

(39)

The most challenging piece of these expressions is $p(m_{l} < m < m_{l+1}|a)$. To compute it, we must consider a modified version of $p_{m}(m)$, which we call $p_{m'}(m')$. This is the probability distribution of $m_{ij}-a_{ij}$, that is, $m_{ij}$ computed with the central value of the kernel ($K_{00}$) zeroed out. This is also normally distributed, but because the new kernel is missing the $K_{00}$ term it only sums to $(1-K_{00})$. The mean is instead

$$ \mu _{m}' = a_{0}c_{m}(1-K_{00})+ m_{0}, $$

(40)

and the standard deviation is

$$ \sigma _{m'} = \sqrt{\sigma _{\Delta m}^{2}+ \frac{c_{m}^{2}\sigma _{a}^{2}}{n_{\mathrm{eff}}'}}, $$

(41)

where $n_{\mathrm{eff}}'$ is defined similarly to $n_{\mathrm{eff}}$ (e.g., if the kernel is a two-dimensional top hat, then $n_{\mathrm{eff}}'=n_{\mathrm{kernel}}-1$):

$$ n_{\mathrm{eff}}' = \frac{1}{\sum_{ij} K_{ij}^{2}-K_{00}^{2}} = \frac{n_{\mathrm{eff}}}{1-n_{\mathrm{eff}}K_{00}^{2}} .$$

(42)

The probability density function of $p_{m'}(m')$ is

$$ p_{m'}\bigl(m'\bigr) = \frac{1}{\sqrt{2\pi \sigma _{m'}^{2}}}e^{-(m'-\mu _{m}')/(2 \sigma _{m'}^{2})}. $$

(43)

Since this is the probability distribution of $m$ with the central pixel omitted from the convolution, it follows that the probability $m$ for a given central pixel value $a$ is the probability that $m'$ is equal to $m$ minus the central pixel’s contribution, $ac_{m}K_{00}$:¹

$$ p(m|a) = p_{m'}(m - ac_{m}K_{00}) .$$

(44)

Then

$$ p(m_{l} < m < m_{l+1}|a) = \int _{m_{l}}^{m_{l+1}} p_{m'}(m - aK_{00})dm .$$

(45)

The calibration factors are then

$$ \gamma _{l} = \frac{ \int a\int _{m_{l}}^{m_{l+1}} p_{m'}(m - aK_{00})dm p(a) da}{\int _{m_{l}}^{m_{l+1}} m p(m) dm} .$$

(46)

If the bins are chosen to be small (e.g., the continuum limit) compared to the variation in $p_{m}(m)$ and $p_{m'}(m')$, then the $m$ integrands become their values at $m=m_{l}$ and the $dm$ ones with $m_{l+1}-m_{l}$ (the latter factors cancel):

$$ \gamma _{l} = \frac{ \int a p_{m'}(m_{l} - aK_{00})p(a) da}{m_{l} p_{m}(m_{l})} .$$

(47)

With the probability densities defined as above, evaluating this expression is laborious but straightforward. The result is

$$ \gamma _{l} = \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}}+ \frac{1}{m_{l}} \biggl(a_{0}-(a_{0}c_{m}+m_{0}) \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}}\biggr). $$

(48)

The result is more clear when expressed in terms of the calibrated values, $c_{ij}$, as we can see by applying Equation 29 and rearranging:

$$ c_{ij} = (m_{ij}-m_{0}) \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}}+a_{0} \biggl[1-c_{m} \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}} \biggr]. $$

(49)

We encounter here the same issue that we found earlier—the calibration only ‘works’ when the average flux of the region in question exactly matches the average flux (flux bias) of the ground truth ($\Phi '_{\mathrm{net}}/n'_{\mathrm{tot}}=a_{0}$). This is true even if the calibration data set has no flux bias (again, mirroring does not solve the problem): consider when $a_{0}=0$ and $m_{0}=0$ (no flux bias in ‘actual’ values or observations); then,

$$ c_{ij} = \gamma (m_{ij})m_{ij} = m_{ij} \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}}. $$

(50)

So the calibrated net fluxes for some data set ($m_{ij}'$, actual values $a_{ij}'$) other than the one used to produce the calibration would be

$$ \sum_{ij\ \mathrm{region}} c_{ij}' = \sum_{ij\ \mathrm{region}} m_{ij}' \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}} = \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}} \sum_{ij\ c_{m}\mathrm{region}} \sum_{kl} w_{ij,kl}a_{kl}'. $$

(51)

As before, the normalization of the PSF implies that

$$ \sum_{ij\ \mathrm{region}}\sum_{kl} w_{ij,kl}a_{kl}' = \sum _{ij\ \mathrm{region}} a_{ij}' = \Phi _{\mathrm{region}}' $$

(52)

modulo edge effects. Therefore, this time we have

$$ \sum_{ij\ \mathrm{region}} c_{ij}' = \Phi _{\mathrm{region}}' \frac{K_{00}c_{m}}{\frac{c_{m}^{2}}{n_{\mathrm{eff}}}+\frac{\sigma _{\Delta m}^{2}}{\sigma _{a}^{2}}} $$

(53)

for the case where there is no flux bias in the values used to produce the calibrations, which is correct only if $\Phi _{\mathrm{region}}=0$, or there is a lucky coincidence between the PSF, the measurement error, the ‘true’ calibration factor ($c_{m}$), and the variation in the ‘actual’ values used to produce the calibration. Remarkably, even if the kernel is a delta function ($K_{00}=1$, $n_{\mathrm{eff}}=1$), the correct region flux is obtained only if the measurement errors are much smaller than the variation in the ground truth field values ($\sigma _{\Delta m}^{2}\ll \sigma _{a}^{2}$)!

Returning to our previous example case—no measurement errors, but the kernel is not a delta function (it is a Gaussian of width one pixel), while $c_{m}=1$—Equation 51 reduces to just

$$ c_{ij}' = m_{ij}' \frac{K_{00}}{\sum_{kl}K_{kl}^{2}}, $$

(54)

and the ‘calibrated’ net flux would be

$$ \sum_{ij\ \mathrm{region}} c_{ij}' = \Phi _{\mathrm{region}}' \frac{K_{00}}{\sum_{kl}K_{kl}^{2}}. $$

(55)

The size of the factor $K_{00}/(\sum_{kl} K_{kl}^{2})$ depends on the shape of the PSF. For the 1-pixel width Gaussian used as example previously (e.g., Figure 4), that factor is 1.5, so this calibration method (using this calibration ground truth) will also lead to an overestimation of the flux by a factor of 1.5. We have implemented the method and find exactly the same theoretical predicted slope. For Gaussian PSFs much larger than a pixel, the slope is instead 2. There is one type of PSF that would result in a factor of one with this proposed calibration scheme—a top hat—however, such PSFs are not normally encountered in reality (GONG’s certainly is not one) and this is only true if the measurement errors are small ($\sigma _{\Delta m}^{2} \ll \sigma _{a}^{2}$).

Enforcing bin-wise flux conservation has not solved the resolution mismatch problem. It only ensures flux conservation for regions whose properties match those of the simulated flux values used to produce the calibration. As before, it does so by mixing terms between the correction factor and the offset, which means that the correction factors derived in this fashion cannot be relied upon—in general, they are only correct if the PSF is a delta function and the measurement error is much smaller than the variation in the flux values. The idea of explicitly incorporating flux preservation into the curve fitting is not a bad one, however (we will return to it in the final paper when computing our GONG calibration curves): the issue is with the resolution mismatch and not the fitting procedure.

1.2 A.2 Comparing Magnetograms by Histogram Equating

In the interests of completeness, let us also consider another method of comparing two magnetograms, often used in the literature (e.g., Riley et al., 2014; Wenzler et al., 2004; Jones and Ceja, 2001). It has the advantage that the magnetograms being compared do not need to be coregistered, resized to the same scale, or otherwise put on any kind of direct correspondence. However, we will show that this method has an implicit dependence on the relative resolutions of the instrument if the solar magnetic fields being observed have structure smaller than the resolution of either instrument.

This comparison method is most clearly described in Wenzler et al. (2004), and we base our description on that work. In it, the two magnetograms to be compared are each split onto positive and negative halves. Then, each of these ranges is split into bins by their quantiles—for example, the 0 to 0.01999…quantile (i.e., 0 to 1.999…percentile) of the positive flux in magnetogram a might be assigned to positive magnetogram bin 1, 0.02 to 0.039999…to bin 2, and so forth. There results four sets of bins, for a given magnetogram comparison:

• i) positive magnetogram a,

• ii) positive magnetogram b,

• iii) negative magnetogram a,

• iv) negative magnetogram b.

The histogram equating value for each bin is then set to the mean of the magnetogram values within the bin for that set, positive and negative halves are combined, and the resulting two sets of values (one for magnetogram a, one for magnetogram b) are plotted against each other, bin for bin.

Let us see what this procedure results in for the linear measurement model and Gaussian random ‘ground truth’ example distribution discussed in Section 2.1. In that case, we are comparing ‘ground truth’ $a_{ij}$, which have mean $a_{0}$ and standard deviation $\sigma _{a}$, with ‘measurements’ $m_{ij}$ resulting from the linear measurement model, which will consequently have mean and standard deviation given by Equations 36 and 37, respectively. As discussed in Section A.1, both are normal distributed according to Equations 34 and 39. The locations of the bins ($a_{i}^{+}$, $a_{i}^{-}$, $m_{i}^{+}$, and $m_{i}^{-}$) are therefore defined according to normal probability density functions ($p_{a}$ for the ground truth and $p_{m}$ for the measurements) and the quantile values ($q_{i}$):

$$ \frac{\int _{0}^{a_{i}^{+}} p_{a}(a) da}{\int _{0}^{\infty }p_{a} da} = q_{i} = \frac{\int _{0}^{m_{i}^{+}} p_{m}(m) dm}{\int _{0}^{\infty }p_{m} dm} $$

(56)

for the positive bins, and

$$ \frac{\int _{a_{i}^{-}}^{0} p_{a}(a) da}{\int _{-\infty }^{0} p_{a} da} = q_{i} = \frac{\int _{a_{m}^{-}}^{0} p_{m}(m) dm}{\int _{-\infty }^{0} p_{m} dm} $$

(57)

for negative bins. As implemented, the values used to compute the curves are set to the average of the magnetogram values within the bin. However, the bins are much smaller than the width of the distribution ($p_{a}$ and $p_{m}$) so these averages can be replaced with the bin locations ($a_{i}^{+}$, $a_{i}^{-}$, $m_{i}^{+}$, and $m_{i}^{-}$) for purposes of this example; bin widths are usually chosen to be $\sim 1$ percentile, which is much less than a standard deviation ($\sim 30$ percentiles).

Thus, the bin averages can be found by simply inverting the quantile formulas above. These can be made more clear by expressing them in terms of error functions:

$$ \frac{{\mathrm{erf} (\frac{a_{i}^{+}-a_{0}}{\sigma _{a}\sqrt{2}} )}-{\mathrm{erf} (\frac{a_{0}}{\sigma _{a}\sqrt{2}} )}}{1-{\mathrm{erf} (\frac{a_{0}}{\sigma _{a}\sqrt{2}} )}} = q_{i} = \frac{{\mathrm{erf} (\frac{m_{i}^{+}-\mu _{m}}{\sigma _{m}\sqrt{2}} )}-{\mathrm{erf} (\frac{\mu _{m}}{\sigma _{m}\sqrt{2}} )}}{1-{\mathrm{erf} (\frac{\mu _{m}}{\sigma _{m}\sqrt{2}} )}} .$$

(58)

And similarly for the negative bins. We can invert this equation using the inverse error function to express $a_{i}^{+}$ in terms of $m_{i}^{+}$ (or vice versa):

$$ a_{i}^{+} = a_{0}+\sigma _{a} \sqrt{2} {\mathrm{erf}^{-1}} \biggl[ { \mathrm{erf}} \biggl( \frac{a_{0}}{\sigma _{a}\sqrt{2}} \biggr) + \frac{1-{\mathrm{erf}} (\frac{a_{0}}{\sigma _{a}\sqrt{2}} )}{1-{\mathrm{erf}} (\frac{\mu _{m}}{\sigma _{m}\sqrt{2}} )} \biggl( {\mathrm{erf}} \biggl( \frac{m_{i}^{+}-\mu _{m}}{\sigma _{m}\sqrt{2}} \biggr) - { \mathrm{erf}} \biggl( \frac{\mu _{m}}{\sigma _{m}\sqrt{2}} \biggr) \biggr) \biggr]. $$

(59)

This expression is not restricted to comparing a measurement to the specific ground truth from which it was obtained, since the derivation makes no assumption about any correspondence between the $a$ and $m$: it can be modified for comparison between any pair of measurements ($m$ and $m'$), provided the histograms of each can be reasonably characterized by a normal distribution, by simply replacing $a_{i}^{+}$ with $m_{i}^{\prime \,+}$, $a_{0}$ with $\mu _{m'}$, and $\sigma _{a}$ with $\sigma _{m}'$.

In the simplest non-trivial case comparing measurements with ground truth, $c_{m}=1$, $a_{0}=0$, $m_{0}=0$, and $\sigma _{a}^{2}/n_{\mathrm{eff}} \gg \sigma _{\Delta m}$ (again, see Equations 34 and 39), this cumbersome expression is drastically simplified:

$$ a_{i}^{+} = m_{i}^{+} \sqrt{n_{\mathrm{eff}}} $$

(60)

and comparison between two sets of measurements is similarly

$$ m_{i}^{\prime \,+} = m_{i}^{+}\sqrt{ \frac{n_{\mathrm{eff}}}{n_{\mathrm{eff}}'}}. $$

(61)

This results in a similar slope to the other comparison methods previously described—for the 1-pixel width Gaussian PSF, The slope ($\sqrt{n_{\mathrm{eff}}}$) is 1.56. We have verified that this analytical result is replicated when the same comparison is made numerically.

1.3 A.3 Resolution Mismatch in the Literature

A variety of articles have compared magnetograms, and not all of them appear (from their text) to be fully cognizant of this resolution mismatch issue. With respect to the histogram equating method in general, Wenzler et al. (2004) say

‘The basic underlying assumption of this method is that SPM and MDI magnetograms differ only in the scale of the magnetic field. By comparing the relative number of pixels (as opposed to absolute numbers) with a certain magnetic field the two data sets become directly comparable despite the different pixel size.’

Here it appears that the ‘scale of the magnetic field’ refers not to the spatial scale of the field measurements, but rather to the flux scaling of the magnetographs going from solar flux to measured flux. In the language of previous sections of this paper, this is the magnetogram calibration factor $c_{m}$. The assumption in the first sentence is reasonable, but the assertion in the second sentence is incorrect—two magnetic flux data sets which differ in their pixel size (or PSF size) do not differ only in their flux scale (i.e., the flux scaling of the magnetic field measurements), because they are measuring fluxes integrated over different areas. This is true even if the fluxes are each divided by their areas.

Histogram equating can be used to compare any two quantitative data sets, no matter how heterogeneous; that, in and of itself, does not make the data sets ‘directly comparable’. In this case, the results of the comparison depend on the pixel size and the resolution in general, and can show an apparent calibration difference even if the instruments are both perfectly calibrated (see Section A.2). Although the method has no explicit dependence on the spatial resolution of the instruments, it does have an implicit one.

Wenzler et al. (2004) also make comparisons with a more direct comparison method (their Section 3.2). However, although in this section they rebin the SPM data to match the pixel size of MDI, ‘to ensure that no bias due to the different pixel sizes enters the analysis’, they do nothing to ensure that no bias due to the different PSF sizes enters the same analysis. And we have shown that there is indeed a bias due to different PSF sizes. Figure 7 shows a similar curve to the one minute average curve of Wenzler et al. (2004) Figure 6 (except that the axes are reversed). It therefore seems likely that at least some of the differences they find are due to the different resolutions (both pixel size and PSF size) of their instruments, not to intrinsic calibration differences of the instruments (i.e., different flux scaling).

Similarly, when Riley et al. (2014) perform per-pixel comparisons between magnetographs, the higher resolution magnetograph is resampled to the pixel size of the lower resolution one, but the resolution differences due to the PSFs are not taken into account. They also perform histogram equating comparisons; the pixel and PSF size differences are not taken into account here either. Consequently, these results are also likely to be affected by the resolution mismatch issue.

Some other means of comparison will not be affected by resolution difference issues. Virtanen and Mursula (2017), for example, directly compare the coefficients of the multipole expansions. Due to their central role in potential field extrapolations, those comparisons directly show where the calibration effects (including resolution) enter into the comparison and where they do not. They do not need to match resolutions in their comparison because they use an explicitly spatially aware method: the resolution differences only show up in the very high order terms, where they are genuine (and where they have very little effect on the extrapolation, as described by Virtanen and Mursula, 2017; Koskela, Virtanen, and Mursula, 2017). The drawback is that their results are much more complex than a handful of calibration curves.

This is a likely explanation for why Riley et al. (2014) find highly variable correction factors (for HMI vs SOLIS, for instance), even though Virtanen and Mursula (2017) find ‘The mutual scaling between SOLIS and HMI is very good, and one single overall coefficient of approximately 0.8 would be a reasonable choice for those data sets.’: In the former case, the per-pixel resolution difference causes an apparent difference between the magnetograms across the board (because the comparison method is not spatially aware), while the latter is only affected by the resolution differences at those resolutions (because it is spatially aware).

Other papers comparing magnetographs have found a need to degrade the resolution of one magnetograph beyond matching pixel sizes (this is another way of ensuring the resolutions match). For example, Pietarila et al. (2013) found that, when comparing space-based magnetograms with those from SOLIS/VSM, they needed to spatially smooth the space-based magnetograms in order to counter the effects of bad seeing in the VSM magnetograms. Similarly, when Lamb et al. (2010) compare SOHO MDI and Hinode-NFI magnetograms, they convolve both with a spatial Gaussian, reducing both of instruments to a common (lower) resolution. And when Liu et al. (2012) compare SoHO/MDI with SDO/HMI, they carefully reduce the HMI data to MDI’s resolution, including the difference in PSF sizes (which they estimate); that comparison should therefore be unaffected by the resolution mismatch issue. So, while these effects have not been noticed by some in the literature, others have taken them into account. In this paper, we supplement this by clearly demonstrating the issue, why it arises, and how to correct for it. Lamb et al. (2010), Liu et al. (2012), and Pietarila et al. (2013) demonstrate that this means of correction already has a peer-reviewed track record.