Abstract
Sunspots and their dynamics dominate the magnetic topology and evolution of both the photosphere and the overlying coronal active regions. Thus a comprehensive understanding of their behaviour is essential to understanding the solar magnetic field. A new technique is presented for applying multiple ellipse fits as a method for rotation tracking of sunspot umbrae. The method is applied to a sunspot in NOAA active region AR 12158 during an X-class flare event and the resulting rotation rate correlates well with other measurements from literature. The method also reveals an apparent difference in rotation rate between the edge and the innermost region of the sunspot umbra of up to 2 degrees per hour. Such differential rotation must lead to the large-scale twisting of sunspot magnetic flux tubes with implications for models of coronal loops and the build-up of instabilities that may lead to eruptions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Sunspots are a key feature of study on the solar photosphere, as tracers of magnetic flux tubes and a major driver of solar flares and coronal mass ejections. It has been known since at least the start of the previous century (Evershed, 1910; St. John, 1913; Hale and Luckey, 1915) that sunspots can rotate both about their centre and relative to companion spots. It has also been long established that the motions of sunspots are related to flaring activity (Gopasyuk, 1965; Stenflo, 1969), particularly in sunspot groups containing opposite-polarity umbrae (also known as \(\delta \) spots Künzel, 1959; McCloskey, Gallagher, and Bloomfield, 2016). While it is typically the faster rotating spots in shearing motions with opposite-polarity spots that produce the largest flares (Gopasyuk, 1965), slower rotating spots also contribute to flaring activity (Régnier and Canfield, 2006). More recently, Yan, Qu, and Kong (2008) produced a catalogue of sunspot groups that are classified by how they move around each other on the photosphere, and observed the correlation between specific types of rotation and flare productivity. They found that in addition to the rotation rate and presence of opposite-polarity umbrae, the rotation direction of the sunspot relative to the differential rotation direction of the surrounding plasma plays an important role in the strength of a flare. There have also been several papers over the past decades that use data from continual observation instruments—such as the Heliospheric Magnetic Imager (HMI, Scherrer et al., 2012) on the Solar Dynamics Observatory (SDO, Pesnell, Thompson, and Chamberlin, 2012)—to analyse the motions of sunspot umbrae in the lead-up to flaring events (Ruan et al., 2014; Wang et al., 2014, 2016; Li and Liu, 2015; Bi et al., 2016; Zheng et al., 2017). A number of these papers find evidence of an abrupt change in rotation speed in the moments leading up to (and during) large X-class solar flares (e.g. Li and Liu, 2015; Bi et al., 2016).
A common way to determine the rotation of a sunspot—as used by some of the papers cited above—is to fit an ellipse to the umbral–penumbral boundary and track the angle of the major axis to the normal over the course of several hours before and after a flare event. This is a reliable method in cases where the sunspot umbra can be defined well by an ellipse. Often, the ellipse is fit to the boundary region of the umbra, which is found at around 50% quiet-Sun intensity (Jurčák et al., 2018). In this paper we describe a technique that uses ellipses at multiple levels of quiet-Sun intensity, making it possible to investigate how distance from the darkest point affects the rotation rate as measured by the ellipse fitting method.
Section 2 introduces and describes the analysis method, Section 3 outlines the process being applied to an example sunspot. Conclusions are summarised in Section 4.
2 Method: Multi-Layer Thresholding
Analysis of sunspot rotation is often performed on continuum intensity images taken over the course of several hours of observation of a sunspot group (Brown et al., 2003; Yan, Qu, and Kong, 2008; Ruan et al., 2014; Li and Liu, 2015; Bi et al., 2016; Yan et al., 2018). In this study full-disk continuum intensity images from HMI/SDO are obtained at 4096 × 4096 pixel resolution (\(0.5''\) per pixel) and a cadence of 45 s. Images are sent through a standard pre-processing pipeline that removes effects from limb darkening and applies compensation for solar differential rotation to keep the target sunspot in the centre of the solar disk.
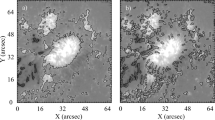
The Multi-Layer Thresholding (MLT) method works by applying a binary thresholding operation to the continuum HMI images at a range of pre-defined intensity levels. Each of the pre-defined thresholds produces a binary image output (or ‘layer’) that defines a cross-section of the sunspot at a specific brightness. Within this layer, pixels below the threshold are grouped together into clusters with the Ordering Points To Identify the Clustering Structure (OPTICS) clustering algorithm. OPTICS is a density-based clustering algorithm that uses the concept of a reachability distance to sort points into groups without the need to know how many groups are present beforehand (Ankerst et al., 1999). This allows the program to determine how many ‘spots’ are in each layer based on the distribution of the points in the binary image. Figure 1 gives an example layer which is split into several different clusters by the OPTICS algorithm.
a A continuum intensity image from HMI of the sunspot in NOAA 12158. b The same sunspot after a thresholding pass at 55% quiet-Sun intensity—all pixels that are less than or equal to this threshold are coloured in black. c The same layer after the OPTICS algorithm is applied, separating the concentrations of pixels into clusters. d A selection of layers at thresholds between 55% and 15% quiet-Sun intensity showing how the spot is represented at each layer.
Each cluster within a layer is treated as a separate spot and as long as the cluster’s perimeter is longer than 10 pixels, an ellipse fit is performed and the orientation of the major axis relative to the solar equator is recorded. The minimum length is required so that there are enough data points to calculate the best fitting ellipse, though typically clusters that are small enough to be close to this limit are ignored in the final analysis.
The thresholds for the process are defined as ratios of the average quiet-Sun intensity on a per image basis. An average intensity of the solar disk is computed and all thresholds are defined as a percentage of the average. This is to ensure that fluctuations in the overall intensity of the images due to external factors do not affect the cluster selection process. The upper bound for the umbral-penumbral boundary is chosen to be at 55% quiet-Sun intensity and the lower bound as 12.5% on the basis that smaller values produced clusters that are not sufficiently large to produce a reliable ellipse fit measurement. Intermediate steps between the two bounds are calculated at steps of 0.5%. These values were determined empirically for the case study presented in this paper and will change for different sunspots; the lower bound in particular is restricted by sunspot size.
Tracking clusters between sequential images is an important step of the process. The naïve approach is to simply pair the clusters in one image with clusters in the next image that have the same geometric centre (to within a few pixels) and are on the same layer. This constant-threshold approach encounters problems due to the underlying assumption that the pixel intensities within the umbra are constant relative to the quiet sun. This is not the case during large flare events where the effects of the flare can be visible in white light images, leading to a sudden localised increase in brightness over the sunspot (Yan et al., 2018). To account for this, the threshold level is not used when attempting to track clusters across images. Instead, each cluster looks for the next cluster that is most similar in area and position regardless of threshold layer. By allowing the threshold value of the cluster to change, the program has the ability to adapt to localised brightenings. Without this ability, these localised brightenings disrupt the clustering approach, and lead to a tracking of the brightening rather than the underlying photospheric plasma. This method of tracking is referred to as the adaptive-threshold approach.
Once all clusters have been tracked, the perimeter of each cluster can be extracted and a least-squares ellipse-fitting technique (as described in Fitzgibbon, Pilu, and Fisher, 1996; Halir and Flusser, 1998) can be applied to extract the orientation of the cluster. This then provides the basis for the sunspot rotation analysis.
3 Results
3.1 Applying MLT to a Flare Event in NOAA AR 12158
Between 17:21 and 18:21 UT on the 10th September 2014, an X1.6 flare was recorded in the southern region of NOAA 12158. The dynamics of the spot during this time are of particular interest. Initial application of the MLT technique shows two distinct clusters within the sunspot: a small region in the north of the spot, and a much larger southern region, as shown in Figure 2a. The larger region contained the flare site and was the area studied by Bi et al. (2016).
Application of the MLT process to a sunspot. A range of threshold values between 12.5% (green) and 23% (purple) were chosen to evaluate the rotation. The top two graphs show the major axis angle and angular velocity of the larger southern spot, respectively. The bottom two graphs show the major axis angle and angular velocity of the smaller northern spot.
Figure 2 shows the sunspot at the peak of the flare (at 17:45 UT) alongside graphs of the major axis orientation and angular velocity of each cluster. The velocity profile clearly shows a change in the rotation of all clusters at three key times: immediately preceding the flare (17:20 UT), during the flare peak (17:45 UT), and after the flare (18:30 UT). Approximately 20 minutes prior to the flare, all the clusters undergo a positive (clockwise) angular acceleration before suddenly reversing rotation direction as the flare begins. The velocity of the rotation gradually decreases over the course of the flare from –6 degrees per hour towards –4 degrees per hour, which is within the range of –4 to –10 degrees per hour that Bi et al. (2016) obtained from their helicity flux model and ellipse fitting methods, respectively. At the end of the flare, the clusters reverse their rotation again, and eventually settle to almost zero angular speed. This velocity profile is indicative of the magnetic flux tube arising from the sunspot becoming twisted over a long period of time, and then suddenly releasing the stored magnetic energy during a flare event.
The rotation profile for the northern region of the spot (bottom graphs of Figure 2) is more erratic due to its comparatively small size to the southern region; however, a rotation profile can be extracted from a range of layers that show similar rotation curves. There is a general downward trend in the rotation profile of the northern region which is seemingly unaffected by the flare until approximately 20 minutes before the end of the flare at 18:00 UT where there is a sudden increase in the clockwise rotation, which then continues at a similar rate as it was at before. Being far from the flare site, it is perhaps unsurprising that this region is not directly affected by the flare; however, in sunspots with more complicated and evolved structure, the capability to track each region independently is advantageous.
When tracking the intensity of the darkest pixel in the sunspot, it becomes apparent that this flare also has an effect on the HMI continuum images. Figure 3c shows the intensity value of the darkest pixel for the duration of the flare, which undergoes a rapid increase in brightness before the flare peak and then gradually reduces back down to pre-flare levels. The effect this has on the constant-threshold approach to cluster tracking is shown in the cluster area plot in Figure 3b. The constant-threshold clusters shrink in response to the brightening, with inner (darker) clusters affected the most. This issue is avoided then tracking using the area rather than the threshold as shown in Figure 3d–e. The area is kept constant and instead the clusters adapt their threshold level to match the variation in the intensity of the darkest pixel. This effect is not visible to the eye in the raw images—the brightening is localised within the umbra and the intensity increase is small. However, we have shown that the change is substantial enough to cause a measurable effect within the umbra. From this, we can conclude that thresholding alone is not enough to accurately track the motion of umbral plasma parcels in continuum intensity data during substantial flare events.
a and b show the variation in threshold value of layers and area of clusters, respectively, for the constant-threshold process. During the flare a large dip can be seen in the area graphs due to localised image brightening. The black line in c shows the variation in intensity value of the darkest pixel. d–f show the same parameters when using the adaptive-threshold method to mitigate the effects of the brightening.
3.2 Radial Variation in Angular Speed
A notable observation in the major axis orientation and angular velocity graphs is an apparent stratification between inner and outer layers after the flare event. With the exception of the innermost layers (below 14%), the layers appear to show a consistent positive angular velocity gradient extending from the darkest point to the umbral boundary. Figure 4 is a scatter plot of the velocities of each layer against the distance from the darkest point. This distance is characterised by the radius of equivalent circle \(R_{\textrm{eq}}\), a parameter that describes the size of a best-fit ellipse in terms of the radius of a circle that has the same area. This parameter can then be used to describe the distance from the umbral centre. Each frame from 13:00 UT to 20:00 UT was sampled, with each frame contributing 13 points to the plot (one for each threshold value).
Distribution of velocities for each cluster within the southern spot umbra for the 7 hours surrounding the flare. Red circles indicate velocities sampled from the hours leading up to the flare event, black crosses were sampled during the flare, and blue triangles were sampled after the flare. The dashed, solid, and dotted lines represent the median angular velocity for before/during/after the flare event, respectively. Smaller values of the radius of equivalent circle correspond to clusters closer to the centre of the umbra.
The distribution shows distinct bands of angular speeds during the three key stages of the flare event. The pre-flare clusters (red circles) show a slightly positive (anti-clockwise) angular velocity of approximately 1 \(\deg \textrm{h}^{-1}\), consistent with previous estimations. During the flare, the clusters undergo a substantial, rapid change in velocity, as indicated by the black crosses. During this time, a trend emerges in the clusters with \(R_{\textrm{eq}}\) greater than 4”, whereby the inner clusters (lower \(R_{\textrm{eq}}\)) show a much greater angular velocity than clusters on the umbral edge. This shows that the centre of the umbra is rotating faster than the outer edge of the umbra, perhaps by as much as 2 degrees per hour. During the post-flare stage (blue triangles), a different pattern emerges in the data as the outer edges of the umbra show the larger angular speeds, while the inner regions show velocities much closer to 0. This pattern is opposite to what is observed during the flare; however, as the differential between the inner and outer clusters is preserved this might suggest the presence of a large-scale oscillation within the umbra.
The reason for this difference in angular velocity with radius is difficult to determine from this dataset alone. While differential rotation within a sunspot umbra during a flare has been observed before in Liu et al. (2016), there are significant differences in the way it has been observed in this instance. The differential rotation observed in Liu et al. (2016) appeared in the wake of the flare ribbon as it passed over the sunspot; however, here the evidence for differential rotation is seen in both the slow divergence of the angular velocity profiles in Figure 2c, and more dramatically in the flare-time velocity data in Figure 4. One possible explanation is the outer regions of the umbra experience resistance from the surrounding photospheric plasma, which attenuates the angular velocity at the edge of the umbra faster than the inner regions.
If this attenuation of the angular velocity with increasing radius were seen before the flare, it would have indicated a possible mechanism by which the flux ropes are twisted. However, as the differential rotation is only seen during and after the flare, it is likely that the phenomenon is an untwisting of the flux rope as a result of the flare. Analysing the differential nature of the rotation of more sunspots during nearby flare events will certainly shed more light on the cause of this phenomenon.
4 Conclusion
A method is presented for determining the rotation rate of a sunspot umbra at multiple threshold levels and applied to a sunspot which rotates during an X1.9 class flare event. The MLT method provides a range of rotation rates consistent with other measurements of rotation and reveals evidence of differential rotation within the umbra. The method is resilient to changes in brightness caused by the flare, further increasing accuracy over a traditional ellipse fit. The method is also able to investigate the impact of the flare on nearby regions of the sunspot group. This ability to track multiple regions simultaneously is a target for future work and allows for more complicated sunspot groups to be analysed in greater detail than before. The differential rotation measure offered by this new method is a novel observational characteristic that may aid understanding of sunspot groups and their dynamics, including the relationship between flares and eruptive events.
References
Ankerst, M., Breunig, M.M., Kriegel, H.P., Sander, J.: 1999, OPTICS: Ordering Points to Identify the Clustering Structure. SIGMOD Rec.28(2), 49. DOI.
Bi, Y., Jiang, Y., Yang, J., Hong, J., Li, H., Yang, B., Xu, Z.: 2016, Observation of a reversal of rotation in a sunspot during a solar flare. Nat. Commun.7, 13798. DOI.
Brown, D.S., Nightingale, R.W., Alexander, D., Schrijver, C.J., Metcalf, T.R., Shine, R.A., Title, A.M., Wolfson, C.J.: 2003, Observations of rotating sunspots from TRACE. Solar Phys.216(1–2), 79. DOI.
Evershed, J.: 1910, Radial movement in sun-spots. (Second paper). Mon. Not. Roy. Astron. Soc.70(3), 217. DOI.
Fitzgibbon, A.W., Pilu, M., Fisher, R.B.: 1996, Direct least squares fitting of ellipses. In: Proceedings – International Conference on Pattern Recognition1, 253. DOI. ISBN: 081867282X. www.dai.ed.ac.ukgroupssmvuuellipse-demo.html.
Gopasyuk, S.I.: 1965, Temporal variations of structure of cross magnetic field in sunspot groups and optical phenomena. Izv. Krym. Astrofiz. Obs.33, 100.
Hale, G.E., Luckey, G.P.: 1915, Some vortex experiments bearing on the nature of sun-spots and flocculi. Proc. Natl. Acad. Sci.1(6), 385. DOI.
Halir, R., Flusser, J.: 1998, Numerically stable direct least squares fitting of ellipses. http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.1.7559.
Jurčák, J., Rezaei, R., González, N.B., Schlichenmaier, R., Vomlel, J.: 2018, The magnetic nature of umbra-penumbra boundary in sunspots. Astron. Astrophys.611, L4. DOI. arXiv.
Künzel, H.: 1959, Die Flare-Häufigkeit in Fleckengruppen unterschiedlicher Klasse und magnetischer Struktur (Mitteilungen des Astrophysikalischen Observatoriums Potsdam Nr. 87). Astron. Nachr.285(5–6), 271. DOI.
Li, A., Liu, Y.: 2015, Sunspot rotation and the M-class flare in solar active region NOAA 11158. Solar Phys.290(8), 2199. DOI.
Liu, C., Xu, Y., Cao, W., Deng, N., Lee, J., Hudson, H.S., Gary, D.E., Wang, J., Jing, J., Wang, H.: 2016, Flare differentially rotates sunspot on Sun’s surface. Nat. Commun.7(1), 13104. DOI.
McCloskey, A.E., Gallagher, P.T., Bloomfield, D.S.: 2016, Flaring rates and the evolution of sunspot group McIntosh classifications. Solar Phys.291(6), 1711. DOI.
Mumford, S.J., Christe, S., Pérez-Suárez, D., Ireland, J., Shih, A.Y., Inglis, A.R., Liedtke, S., Hewett, R.J., Mayer, F., Hughitt, K., Freij, N., Meszaros, T., Bennett, S.M., Malocha, M., Evans, J., Agrawal, A., Leonard, A.J., Robitaille, T.P., Mampaey, B., Campos-Rozo, J.I., Kirk, M.S.: 2015, SunPy – Python for solar physics. Comput. Sci. Discov.8(1), 014009. DOI.
Mumford, S., Christe, S., Mayer, F., Freij, N., Hughitt, K., DanRyanIrish, Liedtke, S., Shih, A.Y., Pérez-Suárez, D., Chakraborty, P., Vishnunarayan, K.I., Aringlis, Pattnaik, P., Sipocz, B., Sharma, R., Leonard, D., Rhewett, Alex-Ian-Hamilton, Panda, A., Earnshaw, M., Choudhary, N., Stansby, D., Kumar, A., Chanda, P., Konge, S., Mdmueller, Haathi, Kirk, M., Jain, Y., Bennett, S.: 2019, sunpy/sunpy: v0.9.6. DOI.
Pesnell, W.D., Thompson, B.J., Chamberlin, P.C.: 2012, The Solar Dynamics Observatory (SDO). Solar Phys.275(1–2), 3. DOI.
Régnier, S., Canfield, R.C.: 2006, Evolution of magnetic fields and energetics of flares in active region 8210. Astron. Astrophys.451(1), 319. DOI.
Ruan, G., Chen, Y., Wang, S., Zhang, H., Li, G., Jing, J., Su, J., Li, X., Xu, H., Du, G., Wang, H.: 2014, A solar eruption driven by rapid sunspot rotation. Astrophys. J.784(2), 165. DOI.
Scherrer, P.H., Schou, J., Bush, R.I., Kosovichev, A.G., Bogart, R.S., Hoeksema, J.T., Liu, Y., Duvall, T.L., Zhao, J., Title, A.M., Schrijver, C.J., Tarbell, T.D., Tomczyk, S.: 2012, The Helioseismic and Magnetic Imager (HMI) investigation for the Solar Dynamics Observatory (SDO). Solar Phys.275(1–2), 207. DOI.
St. John, C.E.: 1913, Radial motion in sun-spots. Astrophys. J.37, 322. DOI.
Stenflo, J.O.: 1969, A mechanism for the build-up of flare energy. Solar Phys.8(1), 115. DOI.
Wang, R., Liu, Y.D., Wiegelmann, T., Cheng, X., Hu, H., Yang, Z.: 2016, Relationship between sunspot rotation and a major solar eruption on 12 July 2012. Solar Phys.291(4), 1159. DOI.
Wang, S., Liu, C., Deng, N., Wang, H.: 2014, Sudden photospheric motion and sunspot rotation associated with the X2.2 flare on 2011 February 15. Astrophys. J. Lett.782(2), L31. DOI.
Yan, X.L., Qu, Z.Q., Kong, D.F.: 2008, Relationship between rotating sunspots and flare productivity. Mon. Not. Roy. Astron. Soc.391(4), 1887. DOI.
Yan, X.L., Wang, J.C., Pan, G.M., Kong, D.F., Xue, Z.K., Yang, L.H., Li, Q.L., Feng, X.S.: 2018, Successive X-class flares and coronal mass ejections driven by shearing motion and sunspot rotation in active region NOAA 12673. Astrophys. J.856(1), 79. DOI.
Zheng, J.C., Yang, Z.L., Guo, J.P., Guo, K.M., Huang, H., Song, X., Wan, W.X.: 2017, Sunspot rotation and magnetic transients associated with flares in NOAA AR 11429. Res. Astron. Astrophys.17(8), 081. DOI.
Acknowledgements
Data collection and analysis made use of Supercomputing Wales computation facilities under project code scw1463. This research has made use of SunPy v0.9.6 Mumford et al. (2019), an open-source and free community-developed solar data analysis Python package Mumford et al. (2015). The data in this work are courtesy of NASA/SDO and the AIA, EVE, and HMI science teams.
Funding
Grimes is supported by an STFC studentship (ST/N503915/1) to Aberystwyth University. Morgan acknowledges STFC grant ST/S000518/1 to Aberystwyth University.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Disclosure of Potential Conflicts of Interest
The authors declare that they have no conflict of interest.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Grimes, R., Pintér, B. & Morgan, H. Observation of Differential Rotation Within a Sunspot Umbra During an X-Class Flare. Sol Phys 295, 87 (2020). https://doi.org/10.1007/s11207-020-01657-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11207-020-01657-5