On the Pulse Shape of Ground-Level Enhancements

Abstract

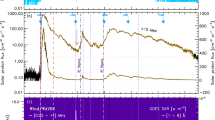
We study the temporal intensity profile, or pulse shape, of cosmic ray ground-level enhancements (GLEs) by calculating the rise $( \tau_{\mathrm{r}})$ and decay $(\tau_{\mathrm{d}})$ times for a small subset of all available events. Although these quantities show very large inter-event variability, a linear dependence of $\tau_{ \mathrm{d}} \approx 3.5 \tau_{\mathrm{r}}$ is found. We interpret these observational findings in terms of an interplanetary transport model, thereby including the effects of scattering (in pitch-angle) as these particles propagate from (near) the Sun to Earth. It is shown that such a model can account for the observed trends in the pulse shape, illustrating that interplanetary transport must be taken into account when studying GLE events, especially their temporal profiles. Furthermore, depending on the model parameters, the pulse shape of GLEs may be determined entirely by interplanetary scattering, obscuring all information regarding the initial acceleration process, and hence making a classification between impulsive and gradual events, as is traditionally done, superfluous.

Appendices

Appendix A: Notes on the Numerical Model

Following Strauss and Fichtner (2015), we integrate Equation (1) numerically by first transforming it into a set of three 1D convection and diffusion equations using a first-order operator splitting method, to obtain

$$\begin{aligned} \frac{1}{3}\frac{\partial f}{\partial t'} + \mu v \frac{\partial f}{ \partial z} =& 0 \end{aligned}$$

(13)

$$\begin{aligned} \frac{1}{3}\frac{\partial f}{\partial t'} + \frac{1-\mu^{2}}{2L} v \frac{ \partial f}{\partial \mu } =& 0 \end{aligned}$$

(14)

$$\begin{aligned} \frac{1}{3}\frac{\partial f}{\partial t'} =& \frac{\partial }{\partial \mu } \biggl( D_{\mu \mu } \frac{\partial f}{\partial \mu } \biggr) , \end{aligned}$$

(15)

where $\mathrm{d}t' = \mathrm{d}t/3$. The diffusion equation (Equation (15)) is solved by an explicit Euler method, while the convection/advection equations (Equations (13) and (14)) are solved by a flux-limiter-corrected upwind scheme. For all equations, flux conserving boundary conditions are applied (see the discussion by Strauss and Fichtner (2015)). To validate this modelling approach, we compare our results to those of Dröge et al. (2010) in this section. These simulations, using exactly the same transport parameters as given by Dröge et al. (2010), are for 4 MeV protons with the results shown as a function of time at Earth’s position. In Figure 8 our model results are labelled as the finite-difference (FD) solutions, while the Dröge et al. (2010) results, computed by making use of stochastic differential equations (SDEs), are labelled accordingly. The left panel compares the omni-directional intensity, and the right panel the first-order anisotropy, defined as

$$ A = 3 \frac{\int_{-1}^{1} \mu f \mathrm{d}\mu }{\int_{-1}^{1} f \,\mathrm{d}\mu } . $$

(16)

The excellent agreement between the two independent models validates our modelling approach and gives us confidence in our calculated temporal profiles.

Figure 8

A comparison between our numerical solver (FD model; indicated by the red lines) and that of Dröge et al. (2010) (SDE model; indicated by the blue symbols). The left panel compares the calculated omni-directional intensity, and the right panel the corresponding first-order anisotropy.

Appendix B: (Semi-) Analytical Approximations

If the particle distribution can be approximated to be nearly isotropic, we can follow Moraal, McCracken, and Caballero-Lopez (2016) and obtain $f$ by solving the spherical symmetric diffusion equation

$$ \frac{\partial f}{\partial t} = \frac{1}{r^{2}} \frac{\partial }{ \partial r} \biggl( r^{2} \kappa_{rr} \frac{\partial f}{\partial r} \biggr) . $$

(17)

Assuming that the effective radial diffusion coefficient, $\kappa_{rr}$, can be parametrised as

$$ \kappa_{rr} = \kappa_{0} \biggl[ \frac{r}{r_{0}} \biggr] ^{\alpha }, $$

(18)

the solution of $f$ for impulsive injection at $r=0$ and $t=0$ is (Duggal, 1979)

$$ f \propto t^{3/(\alpha - 2)} \exp \biggl[ \frac{-r^{2} ( r_{0}/r ) ^{\alpha }}{ (2 - \alpha )^{2} \kappa_{0} t} \biggr] . $$

(19)

The time of peak, or maximum, intensity is evaluated as

$$ t_{\max } = \frac{r^{2} ( r_{0}/r ) ^{\alpha }}{3 (2 - \alpha ) \kappa_{0}}, $$

(20)

with a corresponding peak intensity of

$$ f_{\max } \propto \bigl( \exp ( 1 ) \cdot t_{\max } \bigr) ^{3/(\alpha - 2)} , $$

(21)

so that Equation (19) may be rewritten, in terms of these quantities, as

$$ \frac{f}{f_{\max }} = \biggl[ \frac{t}{t_{\max }} \exp \biggl( \frac{t _{\max }}{t} - 1 \biggr) \biggr] ^{3/(\alpha - 2)}. $$

(22)

This analytical approximation is shown for a variety of different parameters, and is discussed in more detail in Moraal, McCracken, and Caballero-Lopez (2015, 2016). Here, however, we are only interested in times where the distribution obtains a half of its maximum value, i.e. we are interested in finding $t^{a}_{1/2}$ and $t^{b}_{1/2}$ as defined in Figure 3. By setting $2f=f_{\max }$ in Equation (22), we obtain the required transcendental equation

$$ \frac{t_{1/2}}{t_{\max }} = 2 ^{(2 - \alpha )/3} \exp \biggl( 1 - \frac{t _{\max }}{t_{1/2}} \biggr) $$

(23)

that must be solved numerically to obtain the two values of $t^{a}_{1/2} < t_{\max }$ and $t^{b}_{1/2} > t_{\max }$. Note also that this expression is independent of the magnitude of the diffusion coefficient and depends only on its radial dependence through $\alpha$. Figure 9 illustrates how to find the roots (values of $x$ where $y=0$) of Equation (23) for different values of $\alpha$ by setting

$$\begin{aligned} x :=& \frac{t_{1/2}}{t_{\max }}, \end{aligned}$$

(24)

$$\begin{aligned} y(x, \alpha ) := & x - 2 ^{(2 - \alpha )/3} \exp \biggl( 1 - \frac{1}{x} \biggr) . \end{aligned}$$

(25)

For example, $\alpha = 0$ gives $t^{a}_{1/2} \approx 0.44 t_{\max }$ and $t^{b}_{1/2} \approx 3.13 t_{\max }$, which, substituted into our definitions of the rise and decay times (see again Section 2), leads to $\tau_{\mathrm{d}} \approx 3.8 \tau_{\mathrm{{r}}}$. Our results are summarised as

$$\begin{aligned} \alpha = -2 :& \tau_{\mathrm{{d}}} \approx 6.8 \tau_{\mathrm{{r}}} \end{aligned}$$

(26)

$$\begin{aligned} \alpha = -1 :& \tau_{\mathrm{{d}}} \approx 5.2 \tau_{\mathrm{{r}}} \end{aligned}$$

(27)

$$\begin{aligned} \alpha = 0 :& \tau_{\mathrm{{d}}} \approx 3.8 \tau_{\mathrm{{r}}} \end{aligned}$$

(28)

$$\begin{aligned} \alpha = 1 :& \tau_{\mathrm{{d}}} \approx 2.5 \tau_{\mathrm{{r}}} \end{aligned}$$

(29)

with the special case of $\tau_{\mathrm{{d}}} = \tau_{\mathrm{{r}}}$ for $\alpha = 2$ describing a free-streaming scenario. Note that for all values of $\alpha$, we obtain a linear relationship between $\tau_{\mathrm{{d}}}$ and $\tau_{\mathrm{{r}}}$. These resulting estimates, referred to as the isotropic solutions, are included in Figure 7 as the dashed lines.

Figure 9

Finding the roots of Equation (23) for different values of $\alpha$.