1 Introduction

The activity of the Sun is expressed through various solar indices, but the daily International Sunspot Number (ISN) is the key indicator used due to the length of the available record (Hathaway 2010). Until 1980 the ISN was compiled by the Swiss Federal Observatory, the ISN being better known as the Wolf or Zürich number. Since 1981 the Royal Observatory of Belgium (Solar Influences Data Center – SIDC) has computed ISN ( sidc.omea.be ).

In 1844, Schwabe, after 18 years of observations of the number of sunspot groups and spotless days, found that his data indicated the presence of sunspot periodicity, measuring about 11 years in length (Schwabe 1844). The process of determining the dates and values describing solar cycles depends on the methods and input data used to find them (Hathaway 2010). The idea of using spotless days to find the minimum of activity appeared in the papers of Waldmeier (1961) and McKinnon (1987). In 1995, Wilson (1995) proposed to use the first spotless day as a predictor for the sunspot minimum. The possible connections of spotless days with the timing and size of the solar cycle were more accurately examined by Wilson and Hathaway (2005, 2006a, 2007). In 2006, Hamid and Galal (2006) proposed to use the number of spotless events prevailing in the minimum preceding the new cycle as a prediction precursor of new cycle characteristics. Recently, Nielsen and Kjeldsen (2011) discussed the ongoing accumulation of spotless days in different solar cycles.

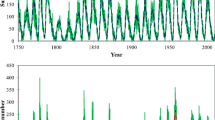
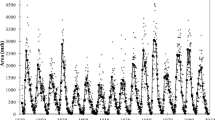
In this work we use the daily ISN series covering the period between January 1818 and May 2011 provided by the SIDC as the basis for characterizing intervals with low solar activity. This period included the decline phase of Cycle 6, Cycles 7 – 23 and the initial rise of Cycle 24. The intrinsic nature and accuracy for four main eras of sunspot number observations are different in the ISN time series (Clette et al. 2007). For example, Cycles 7 – 9 include the era of Schwabe’s records with a large number of days without observations (Wilson 1998). Cycles 10, 11 and the rise of Cycle 12 belong to Wolf’s era (years 1848 – 1882), while those of Cycles 13 – 21 belong to the Zürich era. Since 1981, when the IAU World Data Center for sunspot numbers was transferred from the Zürich Observatory to Brussels, a new approach for calculation of the sunspot number has been established (Clette et al. 2007). However, in the papers of Hathaway, Wilson, and Reichmann (2002), Wilson and Hathaway (2006b, 2008), Li and Liang (2010), these authors determined that the ISN data are reliable from Cycle 12 to the present. Comparison of the ISN time series with sunspot group numbers, devised by Hoyt and Schatten (1998), indicates only ∼ 1% discrepancy between them for the period 1874 – 1995 (Hathaway and Wilson 2004; Hathaway 2010; Usoskin 2008).

The main purpose of this work is to study relations determined from the position of the longest spotless segment (LSS, the longest sequence of consecutive days when no spots were observed) with respect to locations of some characteristic points in the ISN series. We analyze these relations for three different sets of data. The first set includes Cycles from 8 to 23 (all cycles present in the SIDC daily ISN series; Cycle 7 is excluded because there are too many days without data in its minimum), the second spanning Cycles 10 to 23, and the last covering Cycles 13 to 23. As both the position and the length of the LSS are observables, which can be determined without doing any averaging of the data, we use these parameters to determine various predictive characteristics of the sunspot cycles. Using these preferential relations, we also make some predictions regarding Cycle 24.

2 Definitions of Some Characteristic Intervals

In our previous paper (Zięba et al. 2006) we introduced the concept of the passive interval, which we defined as the time distance (denoted d00) from the first spotless day after an old cycle maximum to the last spotless day before the next new cycle maximum. All spotless days occur within the passive intervals. For each passive interval we have a minimum of activity (cycle minimum) and occurrence of the LSS. The position of the LSS can then be determined relative to the positions of different distinctive points within the ISN time series.

We measure distances to the middle of each LSS from the beginning of its passive interval and relative to two differently defined maxima (daily peak maximum and the daily peak Gaussian maximum) located before the first spotless day. The peak maximum is identified as the day having the maximal sunspot number, while the Gaussian maximum is identified as the day having the maximal sunspot number after smoothing the ISN time series using an 810-day Gaussian filter.

The Gaussian filter, having a full width at half maximum (FWHM) equal to 810 days, effectively removes short-term variations of solar activity on time scales of about two years that can produce double peaked maxima. The size of this filter is similar to 24-month Gaussian filter used when monthly averaged sunspot numbers are considered (Hathaway, Wilson, and Reichmann 1999; Hathaway 2010).

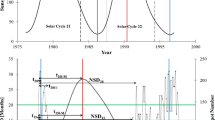
Definitions of all the time intervals (distances) used in our paper are given in Table 1. They are calculated as differences between the aforementioned characteristic points of solar cycles. Figure 1 shows these points for the passive interval 16, while the computed values of the relevant distances are given in the last column of Table 1. Knowing these distances, the following six ratios can be calculated for passive interval 16: r0s=d0s/d00=0.605, rps=dps/dpx=0.681, rGs=dGs/dGx=0.612, r0m=d0m/d00=0.497, rpm=dpm/dpx=0.609, and rGm=dGm/dGx=0.544.

Figure 1
figure 1

The daily values of ISN drawn for the time interval between Solar Cycles 15 and 16. The black curve represents the data smoothed with the Gaussian filter of full width at half maximum (FWHM) of 810 days. Positions of the characteristic extreme points near sunspot minimum and maxima are denoted as the numbers enumerated from 1 January 1918 (for dates see Table 2).

Full size image
Table 1 Definitions of the time intervals used. The last column presents values of the relevant distances calculated for the passive interval 16.
Full size table

The analyzed ISN time series allows us to determine the positions of the characteristic points within each solar cycle, thereby allowing for a determination of the distances and ratios for the 16 known passive intervals (Cycles 8 – 23). These values are summarized in Table 2. Figure 2 displays the values of the calculated ratios (r0s, r0m, rps, rpm, rGs, and rGm). Because the ratios display rather small fluctuations over time (i.e., the passive intervals), this suggests that possible linear relations exist between the various related distances that could prove to be of predictive value (e.g., determination of the expected times for the last spotless day and the maximum for an ongoing sunspot cycle).

Figure 2
figure 2

Variation of six ratios (a) r0s=d0s/d00, r0m=d0m/d00, (b) rps=dps/dpx, rpm=dpm/dpx, (c) rGs=dGs/dGx, rGm=dGm/dGx describing the position of LSS (d0s, dps, dGs) or the Gaussian minimum (d0m, dpm, dGm) with respect to relevant distances (d00, dpx, dGx) for the passive intervals from 8 to 23. The mean value (m) and standard deviation (sd) are also presented.

Full size image
Table 2 Dates defining passive intervals, positions of LSS, cycles maxima and minima together with computed characteristic distances and ratios r0s=d0s/d00, r0m=d0m/d00, rps=dps/dpx, rpm=dpm/dpx, rGs=dGs/dGx, rGm=dGm/dGx. Days are calculated from 1 January 1818.
Full size table

Figures 3, 4 and 5, respectively, show the scatter plots of d00 v. d0s, dpx v. dps and dGx v. dGs. Also shown are the inferred linear regressions for the three different cycle groupings (All, > 9 and > 12) and the position along the x-axis for Cycle 24.

Figure 3
figure 3

Scatter plot of distances between the first and the last spotless days (d00) versus the elapsed time from the first spotless day to LSS (d0s) for the indicated intervals. The determined equation of the best linear fit, the correlation coefficient (r) and the standard error of estimation (SEE) for each of the discussed data sets are also given.

Full size image
Figure 4
figure 4

Scatter plot of distances between the two successive peak maxima (dpx) versus the elapsed time from the first maximum to LSS (dps) for the indicated intervals. The determined equation of the best linear fit, the correlation coefficient (r) and the standard error of estimation (SEE) for each of the discussed data set are also given.

Full size image
Figure 5
figure 5

Scatter plot of distances between the two successive Gaussian maxima (dGx) versus the elapsed time from the first maximum to LSS (dGs) for the indicated intervals. The determined equation of the best linear fit, the correlation coefficient (r) and the standard error of estimation (SEE) for each of the discussed data set are also given.

Full size image

The relations d00 v. d0s (Figure 3) and dGx v. dGs (Figure 5) do not indicate any significant statistical differences among the best linear fits to the three considered data sets. However, in the case of the relation dpx v. dps (Figure 4) the best linear fit to the data set “> 12” (Cycles 13 – 23) deviates clearly from those obtained for the other two. The deviation is caused mainly by the data points for Cycle 22. When we ignore Cycle 22, which has three practically equal peak maxima 300, 295 and 296 occurring almost at yearly intervals, the correlation coefficient between dpx and dps increases from 0.62 to 0.84.

Figure 6 displays similar scatter plots, but using the position of the Gaussian minimum (d0m, dpm and dGm). All three relations d00 v. d0m, dpx v. dpm, and dGx v. dGm are statistically significant. The best agreement among the fits for the three discussed sets of data is seen in the case of the relation dGx v. dGm (Figure 6(c)). Again, the position along the x-axis for Cycle 24 is shown. Previously, Wilson and Hathaway (2005) have analyzed a relation similar to d00 v. d0m using the smoothed monthly mean sunspot number and found these variables strongly correlated (correlation coefficient r=0.95 with the standard error of estimate (SEE) equal to 9.9 months for the data set covering Cycles 10 – 23). Our data give for these cycles the correlation coefficient between d00 and d0m equal to 0.94 and SEE=321 days. Its value grows to 0.98 with SEE=159 days for Cycles 13 – 23.

Figure 6
figure 6

The plots in panels (a), (b) and (c) are similar to those in Figures 3, 4 and 5, respectively, but instead of considering positions of LSS inside of sunspot series positions of Gaussian minima are used.

Full size image

3 Results and Discussion

Using the linear relations depicted in Figures 3, 4 and 5, we find that the occurrences of the last spotless day and sunspot maximum for an ongoing sunspot cycle can be predicted given determination of the LSS for the ongoing cycle. The same is possible using the relations given in Figure 6 based on the 810-day Gaussian minimum. However, as the position of the LSS is known earlier than the Gaussian minimum and its location does not result from any smoothing procedure (thus, reflecting a real physical process), we will concentrate on using those relations based on LSS rather than on using those relations based on the Gaussian minimum.

As we do not find any significant statistical differences among relations calculated for the three discussed data sets, in further work we concentrate on relations obtained from the longest data set (Cycles 8 – 23). In Table 3 we present the parameters of these simple linear regressions and the successive steps leading to determination of the occurrence time of the last spotless day and the maximum of the ongoing Cycle 24. Predictions coming from positions of LSS and Gaussian minima are given.

Table 3 Parameters of the simple linear regression (SEE – standard error of estimation) and predictions for the occurrence time of some extreme points of the ongoing Cycle 24.
Full size table

According to Table 3 the last spotless day for Cycle 24 should be about August 2012, derived from the d00 v. d0s relation. However, using the relation d00 v. d0m, the last spotless day is expected to occur about August 2011. The overlap between the 90% confidence intervals of these two estimates gives for the last spotless day occurrence the time interval between May 2011 and March 2013.

Applying Wilson and Hathaway’s (2005) relation between the time from the first to the last spotless day and the time elapsed from the first spotless day to sunspot minimum occurrence (for Cycle 24 this is 60 months), the last spotless day is expected to occur about July 2011. This is in agreement with our prediction (August 2011) based on d00 v. d0m relation, which is similar to those found by Wilson and Hathaway. Also, according to Nielsen and Kjeldsen (2011), who discuss the ongoing accumulation of spotless days in different solar cycles, the last spotless day before the maximum of Cycle 24 will be about December 2012. This prediction too is close to our result calculated from the d00 v. d0s relation. Up to now the last spotless day for Cycle 24 occurred on 14 August 2011.

The occurrence of the maximum daily sunspot number for Cycle 24 is predicted to be about January 2014 and the occurrence of the peak Gaussian maximum is predicted to be about July 2014, these dates having an uncertainty of about 287 and 125 days, respectively. Using the relations shown in Figure 7 between maximal sunspot values of an ongoing cycle and the relevant passive interval d00 it is possible to estimate how large these maxima might be. A similar relation (having r=−0.67), but one based on the smoothed monthly mean sunspot number, was given by Wilson and Hathaway (2005) for Cycles 10 – 23.

Figure 7
figure 7

Scatter plot of the maximal sunspot numbers (peak – square points and Gaussian – diamonds points) versus the time distance from the first to the last spotless day (d00) for the indicated intervals. The regression equations, the correlation coefficients (r) and standard errors of estimation (SEE) are also given.

Full size image

The d00 value of the passive interval 24, according to Table 3, equals 3136 days, so the sunspot number peak maximum for Cycle 24 is predicted to be about 227±50, and about 87±25 for Cycle 24’s Gaussian maximum. The inferred correlations between maximal sunspot numbers and the d00 time from the first to the last spotless day (see Figure 7) are not particularly strong, with regressions explaining only a part of the observed variance (∼ 25% for the peak maximum and ∼ 50% for the Gaussian one). Consequently, the occurrence of the maximal daily value can vary over a considerable range. Assuming that 14 August 2011 is the last spotless day for Cycle 24, d00 cannot be shorter than 2756 days, leading us to infer that there is only a 5% chance that its peak maximum and the Gaussian maximum will exceed 321 and 139, respectively. Because large values of d00 are associated with weaker cycles, the predicted maxima for Cycle 24 seems likely to be located near the maximal values of Cycles 10, 14 and 15. Usoskin (2008) has suggested that Cycles 14 and 15 are associated with the time of the modern minimum in solar activity. Since Cycle 24 appears likely to be of a similar nature as Cycles 14 and 15, could this be a strong indication that Cycle 24 heralds the start of another minimum in solar activity in the sunspot record?

Figure 8 (left) shows the temporal plots of mGx and mpx, both displaying similar behavior. While true, even- and odd-cycle differences are more clearly discerned in the peak maxima than in the Gaussian maxima. All values, except for even-odd-cycle pairs 8 – 9 and 22 – 23, are found to follow the Gnevyshev–Ohl rule, which states that the odd-following cycle tends to be the stronger cycle (Gnevyshev and Ohl 1948; Kopecky 1950). Presuming the Gnevyshev–Ohl rule still applies, we infer that Cycle 25 should be somewhat stronger than Cycle 24. The right portion of Figure 8 presents ratios between Gaussian and peak maximal sunspot values for Cycles 8 – 23 and the best-fitted sinusoid for these data (coefficient of determination, R-squared=0.901). The value of this ratio for Cycle 24 calculated from the best-fitted sinusoid equals 0.414, while that computed from the predicted peak and Gaussian maximal sunspot numbers for Cycle 24 (Figure 8 left) is 0.383±0.19. As the two different and independent ways used to calculate the ratio between Gaussian and peak maximal sunspot numbers for Cycle 24 give almost the same value, we suppose that our predictions for maximal sunspot numbers are highly probable.

Figure 8
figure 8

(Left) Scatter plot of maximal sunspot numbers for peak and Gaussian cycle maxima, (right) the plot of ratios between Gaussian to peak maximal sunspot numbers and the best-fitted sinusoid for data of Cycles 8 – 23. For Cycle 24 the predicted values are drawn.

Full size image

The best-fitted sinusoid indicates a period of ∼ 150 years, which can be associated with the upper limit of the Gleissberg-cycle period (Gleissberg 1939; Ogurtsov et al. 2002; Duhau 2003; Duhau and de Jager 2008; De Jager, Duhau, and van Geel 2010). The predicted value of Cycle 24 suggests that the Sun may be at the start of a new Gleissberg minimum.

The agreement of conclusions coming from plots presented in Figure 8 with some characteristic features of solar activity known from various review papers (Usoskin 2008; Hathaway 2010; De Jager and Duhau 2011) indicates that the parameters we used might be useful for studying physical processes responsible for solar variability. Future studies of passive interval properties continue.

4 Conclusions

The results obtained in this work can be summarized as follows:

  1. i)

    Recognizing the longest spotless segment (LSS) localized somewhere in an epoch of solar minimum we have attained three new linear relations, shown in Figures 3, 4 and 5. The strong correlation (r=0.96, Figure 5) between the time elapsed from the previous maximum to LSS and the time distance between successive maxima including the LSS suggests that the LSS can provide insight toward understanding variations in solar activity.

  2. ii)

    All inferred relations are statistically significant and allow the time of the last spotless day and the maximum of the ongoing cycle to be predicted on the basis of identifying the LSS.

  3. iii)

    The inferred relations, calculated independently for three different groupings of solar cycles (Cycles 8 – 23, 10 – 23 and 13 – 23), do not differ significantly, thereby indicating that the daily ISN time series gives consistent results from Cycle 8 to the present.

  4. iv)

    For Cycle 24, we predict the last spotless day to occur in August 2012 and the epoch of sunspot maximum to occur during the first half of 2014 based on the non-Gaussian-filtered data.

  5. v)

    The maximal daily sunspot number during the epoch of sunspot maximum should be about 227±50, and the smoothed maximal value using the 810-day Gaussian filter should be about 87±25.

  6. vi)

    Using the Gaussian-filtered values, we predict August 2011 and March 2013 for the occurrences of the last spotless day and sunspot maximum for Cycle 24, respectively.

  7. vii)

    Our predictions for Cycle 24 are consistent with those recently published by Wilson (2011) and allow us to conclude that Cycle 24 will be a low solar activity cycle (Pesnell 2008).

  8. viii)

    Cycle 24 likely represents the start of another minimum in solar activity, like Cycles 14 and 15, which occurred early in the twentieth century.