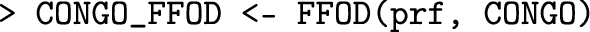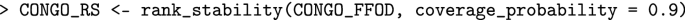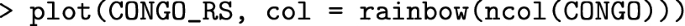Abstract
In this paper, we develop a new statistical procedure for the comparison of frequency distributions on systems of ordinal indicators, based on a multidimensional fuzzy extension of the first order dominance (FOD) criterion. The procedure, named fuzzy-first order dominance (F-FOD), employs concepts and tools from partially ordered set theory and from fuzzy relational calculus and is designed to overcome the main limitations of previously developed algorithms for FOD analysis. In particular, F-FOD produces full pairwise comparison matrices, allows for partial orderings and rankings of the statistical units to be derived from the input data, is computationally sufficiently light to be applied in most cases of practical interest and is freely available in the R package PARSEC. To illustrate its effectiveness, we also show F-FOD in action on two real datasets concerning health in Denmark and child well-being in the Democratic Republic of Congo.











Similar content being viewed by others
Notes
We stress, however, that the problem of information loss and dimensionality reduction on partially ordered domains is not confined to the study of ordinal MISes; in fact, the same issue occurs whenever evaluation and ranking involve multidimensional profiles built on systems of weakly interrelated variables, even of a cardinal type.
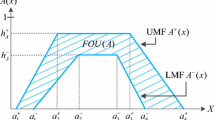
A partially ordered set is a set endowed with a reflexive, anti-symmetric and transitive binary relation Davey and Priestley (2002).
A down-set\(\delta\) of a poset \(\pi\) is a subset of \(\pi\) such that if \(\varvec{p}\in \delta\) and \(\varvec{q}\le \varvec{p}\), then \(\varvec{q}\in \delta\). Dually, an up-setu of a poset \(\pi\) is a subset of \(\pi\) such that if \(\varvec{p}\in u\) and \(\varvec{p}\le \varvec{q}\), then \(\varvec{q}\in u\). The down-set\(\downarrow \!\!\varvec{p}\) of an element \(\varvec{p}\) of \(\pi\) is the same as the set of elements equal to or smaller than \(\varvec{p}\): \(\downarrow \!\!\varvec{p}=\{x\in \pi : x\le \varvec{p}\}\); similarly, the up-set\(\uparrow \!\!\varvec{p}\) of \(\varvec{p}\) is the same as the subset of elements equal to or higher than \(\varvec{p}\): \(\uparrow \!\!\varvec{p}=\{x\in \pi : x\ge \varvec{p}\}\). In Arndt et al. (2012), down-sets are called comprehensive sets, but this is not standard posetic terminology.
By “ equivalent position” of two poset elements, we mean that the poset is invariant upon exchanging their labels.
The length of a chain is defined as the number of edges in it Davey and Priestley (2002).
Dealing with discrete variables, it is in general not possible to build rank intervals covering exactly the desired probability level.
The Bubley-Dyer algorithm is, to our knowledge, the most efficient algorithm for quasi-uniform sampling from the set of linear extensions of a poset. Based on it, an algorithm for quasi-uniform sampling of LLEs could be easily derived.
References
Annoni, P., Fattore, M., & Bruggemann, R. (2011). A multi-criteria fuzzy approach for analyzing poverty structure. Statistica & Applicazioni - Special Issue, 2011, 7–30.
Arcagni, A. (2017). PARSEC: An R package for partial orders in socio-economics. In M. Fattore & R. Bruggemann (Eds.), Partial order concepts in applied sciences. Cham: Springer.
Arndt C., Distante R., Hussain M. A., Østerdal P. L., Pham L. H., & Ibraimo M. (2012). Ordinal welfare comparisons with multiple discrete indicators: A first order dominance approach and application to child poverty, WIDER Working Paper, 2012/36, ISBN 978-92-9230-499-7.
Arndt, C., Vincent, L., & Kristi, M. (2014). Multi-dimensional poverty analysis for Tanzania: First order dominance approach with discrete indicators, WIDER Working Paper, 2014/146, ISBN 978-92-9230-867-4.
Bandler, W., & Kohout, L. (1988). Special properties, closures and interiors of crisp and fuzzy relations. Fuzzy Sets and Systems, 26, 317–331.
Bruggemann, R., & Patil, G. P. (2011). Ranking and prioritization for multi-indicator systems. New York: Springer.
Bubley, R., & Dyer, M. (1999). Faster random generation of linear extensions. Discrete Mathematics, 201, 81–88.
Davey, B. A., & Priestley, B. H. (2002). Introduction to lattices and order. Cambridge: CUP.
De Baets, B., & De Meyer, H. (2003). Transitive approximation of fuzzy relations by alternating closures and openings. Soft Computing, 7, 210–219.
De Loof, K., De Baets, B., & De Meyer, H. (2006). Exploiting the lattice of ideals representation of a poset. Fundamenta Informaticae, 71(2–3), 309–321.
De Loof, K., De Baets, B., & De Meyer, H. (2008). Properties of mutual rank probabilities in partially ordered sets. In J. W. Owsinski & R. Bruggemann (Eds.), Multicriteria ordering and ranking: Partial orders, ambiguities and applied issues. Warsaw: Polish Academy of Sciences.
De Loof K. (2010). Efficient computation of rank probabilities in posets. Ph.D. dissertation.
De Meyer, H., Naessens, H., & De Baets, B. (2004). Algorithms for computing the min-transitive closure and associated partition tree of a symmetric fuzzy relation. European Journal of Operational Research, 155, 226–238.
Dushnik, B., & Miller, E. W. (1941). Partially ordered sets. American Journal of Mathematics, 63(3), 600–610.
El Sayed T., Zahran A. R. (2016). Multidimensional almost dominance: Child wellbeing in Egypt Social Indicators Reearch, https://doi.org/10.1007/s11205-016-1541-9.
Fattore, M. (2016). Partially ordered sets and the measurement of multidimensional ordinal deprivation. Social Indicators Research, 128(2), 835–858. https://doi.org/10.1007/s11205-015-1059-6.
Fattore, M., & Arcagni, A. (2016). A reduced posetic approach to the measurement of multidimensional ordinal deprivation. Social Indicators Research, 136(3), 1053–1070. https://doi.org/10.1007/s11205-016-1501-4.
Fattore, M. (2017). Functionals and synthetic indicators over finite posets. In M. Fattore & R. Bruggemann (Eds.), Partial order concepts in applied sciences. Springer AG: Cham.
Hussain, M. A., Jørgensen, M. M., & Østerdal, P. L. (2016). Refining population health comparisons: A multidimensional first order dominance approach. Social Indicators Resarch, 129, 739–759.
Lee, K. H. (2005). First course on fuzzy theory and applications. Berlin: Springer.
Mishra, S. U., & Shukla, V. (2016). Welfare comparisons with multidimensional well-being indicators: An Indian illustration. Social Indicators Research, 129, 505–525. https://doi.org/10.1007/s11205-015-1117-0.
Nanivazo, M. (2015). First order dominance analysis: Child wellbeing in the Democratic Republic of Congo. Social Indicators Research, 122, 235–255.
Neggers, J., & Kim, S. H. (1998). Basic posets. Singapore: World Scientific.
Olu A., Afeikhena T. J., Olanrewaju O., Kristi M., & Olufunke A. A. (2014). Multidimensional poverty in Nigeria: First order dominance approach, WIDER Working Paper, No. 2014/143.
Peeva, K., & Kyosev, Y. (2004). Fuzzy relational calculus. Singapore: World Scientific Publishing.
Permanyer I., Hussain M. A. (2017). First order dominance techniques and multidimensional poverty indices: An empirical comparison of different approaches, Social Indicators Research https://doi.org/10.1007/s11205-017-1637-x.
R Core Team (2017). R: A language and environment for statistical computing, R foundation for statistical computing, Vienna, Austria. https://www.R-project.org/. Accessed 30 Nov 2017.
Schröder. (2002). Ordered sets. An introduction. Boston:Birkäuser.
Siersbæk, N., Østerdal, P. L., & Arndt, C. (2016). Multidimensional first-order dominance comparisons of population wellbeing. In C. Arndt & F. Tarp (Eds.), Measuring poverty and wellbeing in developing countries. Oxford: Oxford University Press.
Szpilrajn, E. (1930). Sur l’extension de l’ordre partiel. Fundamenta Mathematicae, 1(16), 386–389.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1
In this Appendix, we provide the proof of the following proposition, which plays a fundamental role in the development of F-FOD (see Sect. 2):
Proposition
Let\(\pi\)beafiniteposet; then\(F\le _{FOD}G\)on\(\pi\)ifandonly if, foreachlinearextension\(\ell\)of\(\pi\), \(F\le _{FOD}G\)on\(\ell\).
Proof
(Necessity) Let \(F\le _{FOD}G\) in \(\pi\) and let \(\ell\) be a linear extension of \(\pi\). Consider an element \(\varvec{q}\) and its down-set \(\delta _q\) in \(\ell\); \(\delta _q\) is the union of two subsets, namely the subset A of elements lower than or equal to \(\varvec{q}\) in \(\pi\) (i.e. the down-set \(\downarrow \!\varvec{q}\) of \(\varvec{q}\) in \(\pi\)) and the subset B of elements of \(\delta _q\) which are incomparable with \(\varvec{q}\) in \(\pi\) (which is possibly empty). As a consequence, \(\delta _q\), as a set, is the same as the down-set C of \(\pi\) generated by \(B\cup \{\varvec{q}\}\) (i.e. the set of elements \(\varvec{p}\) of \(\pi\) such that \(\varvec{p}\le \varvec{y}\), for at least one \(\varvec{y}\in B\cup \{\varvec{q}\}\)). Since \(F\le _{FOD}G\) in \(\pi\), it holds:
Since \(\varvec{q}\) is arbitrary, and \(\ell\) is a linear order, we get \(F\le _{FOD}G\) in \(\ell\). \(\square\)
(Sufficiency) Let \(F\le _{FOD}G\) for each linear extension \(\ell\) of \(\pi\); let \(\delta\) be a down-set of \(\pi\) and let n be the cardinality of \(\delta\). There exists at least one linear extension \(\ell\) such that the elements of \(\delta\) are the first (from below) n elements \(\varvec{q}_1,\ldots \varvec{q}_n\) of \(\ell\). Since \(F\le _{FOD}G\) in \(\ell\), it holds
Since this holds for any down-set \(\delta\), it is proved that \(F\le _{FOD} G\) in \(\pi\).
Appendix 2
In this appendix, we report the R code used to elaborate the example pertaining to child well-being in the Democratic Republic of Congo (Sect. 4). Readers may easily replicate the computations and use the following scripts for further applications.
-
1.
Definition of the set of binary profiles.

-
2.
Data reported in Table 9 are put into the data.frameCONGO (notice that the profiles in CONGO must be listed in the same order as in prf).
-
3.
Application of the F-FOD procedure.
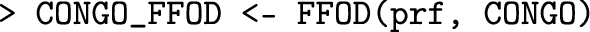
-
4.
Function FFOD returns several results (e.g. the matrix \(\Delta\) of dominance degrees and the cover matrices of the \(\alpha\)-cut posets) and feeds the function rank_stability, which computes in each \(\alpha\)-cut poset the average rank of each profile and the rank intervals with the chosen least coverage probability.
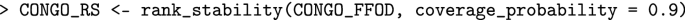
-
5.
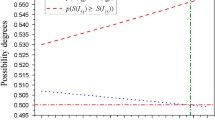
The graphs shown in Fig. 9 are finally produced by:
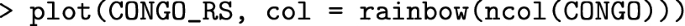
Running the above computations took 5.46 secs on a pc equipped with Intel(R) Core(TM) i7-3632QM CPU @ 2.20GHz, 8GB ram, Windows 10, R version 3.4.3 and R Studio 1.1.382.
Rights and permissions
About this article
Cite this article
Fattore, M., Arcagni, A. F-FOD: Fuzzy First Order Dominance Analysis and Populations Ranking Over Ordinal Multi-Indicator Systems. Soc Indic Res 144, 1–29 (2019). https://doi.org/10.1007/s11205-018-2049-2
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11205-018-2049-2