Abstract
One of the most frequent critiques of the HDI is that is does not take into account inequality within countries in its three dimensions. In this paper, we apply a simply approach to compute the three components and the overall HDI for quintiles of the income distribution. This allows a comparison of the level in human development of the poor with the level of the non-poor within countries, but also across countries. This is an application of the method presented in Grimm et al. (World Development 36(12):2527–2546, 2008) to a sample of 21 low and middle income countries and 11 industrialized countries. In particular the inclusion of the industrialized countries, which were not included in the previous work, implies to deal with a number of additional challenges, which we outline in this paper. Our results show that inequality in human development within countries is high, both in developed and industrialized countries. In fact, the HDI of the lowest quintiles in industrialized countries is often below the HDI of the richest quintile in many middle income countries. We also find, however, a strong overall negative correlation between the level of human development and inequality in human development.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the important short-comings of the United Nations Development Programme’s (UNDP) Human Development Index (HDI) is that it neglects the distribution of achievements within each component of the HDI. It may well be that a country performs well in the aggregate HDI but has a very unequal distribution within the country. The Human Development Report (HDR) 2006 (UNDP 2006) made an important step to address this issue. Based on a method and computations described in detail in Grimm et al. (2008), the HDR presented for a sample of 13 low and middle income and two high income countries a HDI for all five income quintiles of these countries. Households were sorted by income quintile and then for each income quintile, the life expectancy, education, and income indices were calculated to generate an income quintile-specific HDI.Footnote 1 The results showed that across all countries inequality in human development by income quintile was very high, was typically larger in developing countries, and particularly sizable in Africa. This was not only due to an unequal income distribution, but also to substantial differences in education and life expectancy by income quintile. In some middle income developing countries the HDI of the richest income quintile ranked among the high human development countries, whereas the poorest quintile ranked among the low human development countries. But also in rich countries, the differentials were large. For example, the poorest income quintile in the US reaches only position 55 in a general HDI country ranking. Among the low and middle income countries the results showed that in that sample there was no clear relationship between the level of human development and inequality in human development as measured by the ratio of the HDI for the richest and poorest quintiles.
These interesting findings led to the question whether they would extend to other countries as well including also more rich countries. Surprisingly the computation of a comparable quintile-specific HDI is more difficult for rich than for middle and low income countries due to greater difficulties to generate appropriate and harmonized micro data. As discussed below, this required some simplifying assumptions that were not necessary for the low and middle-income countries. This paper describes this extension and presents the main results.Footnote 2 The additional high income countries could be included thanks to the support of the Luxembourg Income Study (LIS) research group. In what follows the general methodology is not described in detail, we just present a short summary. A detailed description can be found in Grimm et al. (2008).
The paper is organized as follows. After a short summary of the general methodology we present our sample of countries and explain how we proceeded in the case of the rich countries. Then we discuss our results and conclude.
2 A Summary of the Methodology
The basic idea of our method is to use household survey data to calculate the three dimension indices which constitute the HDI by quintiles of the income distribution. Thus we are not investigating inequality in each dimension directly, but consider achievements in each dimension by income quintile.Footnote 3 For developing countries, we use a household income survey (‘HIS’ hereafter, e.g. the World Bank’s Living Standard Measurement Surveys) to calculate the quintile specific education and GDP indices and Demographic and Health Surveys (‘DHS’ hereafter, see www.measuredhs.com) to calculate the quintile specific life expectancy index. Given that generally both surveys do not interview the same households and that the DHS does not contain any information on household income or household expenditure, we have first to generate a proxy for household income in the DHS.
2.1 Generating a Proxy for Income for the Households Interviewed in the DHS
To generate a proxy for income for the households interviewed in the DHS we rely on the construction of an asset index as a proxy for income. DHS data generally provides information on the ownership of a radio, TV, refrigerator, bicycle, motorized, vehicle, floor material of housing, type of toilet, type of water source and so on. Using principal component analysis these assets can be aggregated into one single metric index as a proxy for income for each household. This method is relatively standard today. Its shortcomings and alternatives, in particular an approach where we impute incomes for DHS households, are discussed and tested in Grimm et al. (2008). Once households in both surveys can be sorted into “income quintiles” (Q = 1, 2, …, 5), we can calculate the life expectancy index also by income quintiles, even if income is not directly available in the DHS.
2.2 Calculating the Life Expectancy Index by Income Quintiles
To calculate a life expectancy index by income quintile we combine information on child mortality with model life tables. The HIS provides usually no information on mortality. The DHS provides only information on child mortality, but not on mortality by all age groups, which would be necessary to construct a life table and to calculate life expectancy directly. Hence we proceed as follows. In a first step, we calculate under one child mortality rates for each income quintile, \( q_{1}^{Q} \), and for the whole sample. To do this we use the survival status information on all children born in the 5 years preceding the survey. In a next step, we use the estimated under one mortality rates and Ledermann model life tables to calculate quintile specific life expectancy, \( \hat{e}_{0}^{Q} \). Ledermann model life tables are based on historical mortality data for many countries and periods and can reflect the empirical relationship between life-expectancy and the under one mortality rate (Ledermann 1969): In Grimm et al. (2008) we test the robustness of our life-expectancy estimates with respect to alternative life-tables and assumptions.
We calculate the quintile specific life expectancy index, L Q, using the usual minimum and maximum values for life expectancy employed to calculate the general HDI:
The aggregate life expectancy index L can be calculated using \( \hat{e}_{0}^{{}} \) instead of \( \hat{e}_{0}^{Q} \). In a last step, we rescale linearly L Q and L to achieve consistency with the aggregate HDI calculated by UNDP. As rescaling factor we use the ratio between our aggregate life expectancy index L and the aggregate life expectancy index calculated by UNDP (version mid-2008). Consistency is not automatic, given that our approach and UNDP’s approach are based on different data sources. Given that the objective of our approach is first of all to examine the distribution of human development, differences in levels should not present any serious problem.Footnote 4
2.3 Calculating the Education Index by Income Quintiles
To calculate the quintile specific education index, we use the information on literacy and school enrolment provided by the HIS. To compute the adult literacy rate by income quintile, a Q, take the information on literacy status of all adults above the age of 15. Then we calculate the quintile specific adult literacy index, A Q, using again the corresponding usual minimum and maximum values employed in the HDI (which implies A Q = a Q):
The aggregate adult literacy index A can be calculated using a instead of a Q. In a last step, we rescale again linearly A Q and A to achieve consistency with the aggregate HDI calculated by UNDP. As rescaling factor we use the ratio between our aggregate literacy index A and the aggregate literacy index calculated by UNDP.
To calculate the quintile specific gross enrolment index, we calculate first the combined gross enrolment rate for each quintile, g Q. Each individual attending school or university whether general or vocational is considered as enrolled. We define this rate over all individuals of the age group 5- to 23-year-old. Then we calculate the quintile specific gross enrolment index, G Q using the usual minimum and maximum values used for the calculation of the HDI (which implies G Q = g Q):
The aggregate gross enrolment index G can be calculated by using g instead of g Q. Finally, we also rescale G Q and G to the level of the HDI enrolment index.
The quintile specific education index E Q is calculated using the same weighted average as the HDI:
The aggregate education index E can be calculated by using A and G instead of A Q and G Q. Table 3 again illustrates each step for the case of Indonesia.
2.4 Calculating the GDP Index by Income Quintiles
To calculate the GDP index by income quintile, we use our income variable from the HIS (adjusted for regional price differences in each country). One main difference with the two other dimension indices is that mean income calculated from the HIS can be very different from GDP per capita derived from National Accounts data, which is used for the GDP index in the general HDI. This has two reasons: first, because of conceptual differences and, second, because of measurement error on both levels. Hence, we proceed as follows. First, to eliminate differences in national price levels we express household income per capita y h calculated from the HIS, in USD PPP. Second, we rescale \( y_{h}^{\text{PPP}} \) using the ratio between \( \bar{y}_{h}^{\text{PPP}} \)and GDP per capita expressed in PPP (taken from the general HDI):
Once, theses adjustments are done, it is straightforward to calculate the quintile specific GDP index, again using the usual minimum and maximum values of the HDI:
where \( r\bar{y}^{{Q,{\text{PPP}}}} \) is the quintile specific arithmetic mean of the rescaled household income per capita.
It should be noted that in richer countries the GDP per capita measure for the richest quintile, \( r\bar{y}^{5,PPP} \)could easily exceed 40,000 USD PPP and, hence, the index could take a value >1, and this could, in extreme cases, push the overall HDI for the richest quintile also above 1, which would cause problems for interpretation.Footnote 5
2.5 Calculating the Overall HDI and the HDI by Income Quintiles
Once the quintile specific dimension indices have been calculated, determining the QHDI is straightforward. It is the simple average of the three dimension indices:
The aggregate HDI is as usual given by:
Again, a detailed description of that methodology can be found in Grimm et al. (2008). In that paper the interested reader also finds a number of robustness checks of our methodology to alternative assumptions.
3 Sample of Countries
In Grimm et al. (2008) we illustrated our methodology for Finland and the USA as well as eight countries from Sub-Saharan Africa (Burkina Faso, Cameroon, Côte d’Ivoire, Guinea, Madagascar, Mozambique, South-Africa, Zambia), three countries from Latin America (Bolivia, Colombia, Nicaragua) and two countries from Asia (Indonesia, Vietnam). In this paper, we extent our sample by eight additional low and middle income countries and nine industrialized countries. In particular the inclusion of industrialised countries constitutes a methodological challenge as we explain below in detail.
3.1 The Inclusion of Additional Low and Middle Income Countries
In this paper, we extent our initial country sample by the following low and middle income countries: Ghana, Ethiopia, Brazil, Guatemala, Paraguay, Peru, India and the Kyrgyz Republic and apply exactly the same procedure to compute the quintile specific HDI. Table 5 (“in Appendix”) indicates for each country the years in which the household income survey and the Demographic and Health Survey we use were undertaken. We tried of course to take the most recent data available and to keep the time lag between both surveys as short as possible.
3.2 The Inclusion of Additional High Income Countries
Additionally included high income countries are Australia, Canada, France, Germany, Italy, The Netherlands, Poland, Spain, and Sweden. As stated above, the application of our approach to high income countries entails some additional problems. The data availability is very different in developing and industrialized countries. Whereas for a long time access to disaggregated and harmonized income, education and health data was much better in industrialized countries than in developing countries, today it seems to be the other way around. For many developing countries there exist today, as described above, at least roughly comparable income, education and health data thanks to the regular household income surveys and Demographic and Health Surveys. In many industrialized countries, such standardized surveys are either absent or not easily accessible. Moreover, due to very low infant and child mortality levels in rich countries, we could not apply our method of deducing life expectancy from infant or child mortality rates available in household survey data to calculate life expectancies (and its differential by income) with any reliability. Therefore, we had to make some simplifying but reasonable assumptions.
Matters are easiest for the income component. Here we can rely on the Luxemburg Income Study (LIS), which produces harmonized micro data sets on income, demographics, labour market status and expenditures on the level of households and individuals for 30 OECD countries.Footnote 6 These data are of very high quality and probably more reliable than the income/expenditure data available in many developing countries. Hence using LIS data, we computed based on harmonized income data for each of the included high income countries mean household income per capita for each quintile. Then, as for the low and middle income countries, we simply scaled these quintile-specific mean incomes using the ratio between GDP per capita and household income per capita such that the overall mean matched GDP per capita and converted them in USD PPP. In a last step we transformed the mean incomes into logarithms and computed using the usual maximum and minimum values of log(40,000 USD PPP) and log(100 USD PPP) the index number.
To derive the quintile-specific education indices we also used data from the LIS. However, the LIS data sets do not have educational enrolment or adult literacy information. They only provide information on educational achievements by levels of education passed. Therefore, we assume no inequality in adult literacy (based on the presumption of universal adult literacy in those countries)Footnote 7 and use the schooling achievement differential by income for 2000 as reported in the Luxembourg Income Study to estimate income differentials in enrolment ratios.Footnote 8
Hence, we took the LIS information on educational attainment in each quintile, i.e. the percentage of persons in each quintile falling in groups, such as never attended school, “1–4 years of elementary school”, “5–8 years of elementary school”, …, “university certificate”, and derived from this the share of persons attending a first, second, third, etc. year in school. Linking that information to age, it is possible to derive for each quintile an enrolment ratio for the children and adults between 5- and 23-year-old. These ratios were then again rescaled such that the average matched the average reported by UNDP. In a last step we computed the weighted average for each quintile by counting adult literacy with a weight of 2/3 and enrolment with a weight of 1/3.
By far the most difficult issues arise, however, with the life expectancy component. As already stated, using quintile-specific child mortality to derive an estimate of quintile specific life expectancy from household surveys would not be possible as child mortality in most OECD countries is so low that no meaningful differentials by income could be identified. Moreover, child mortality in these countries is much related to premature births, genetic defects, complications during birth and due to accidents all of which not closely related to income. In fact, it is likely that existing income differentials in life expectancy in rich countries are largely due to mortality differentials beyond childhood. In principle, one could try to rely on census or census-like sample surveys with large numbers of observations. An alternative would be to rely on death registrations. These data sources are generally used in rich countries to calculate mortality rates and associated life expectancy statistics. But these data sources usually do not include incomes and cannot be used to calculate income differentials. Two exceptions are the USA and Finland where specialized analyses on the link between incomes and mortality were undertaken. We therefore considered the results from Rogot et al. (1992) and Martikainen et al. (2001) on the life expectancy differential by incomes. These data are based on linked income survey data with vital registration data and are covering the adult mortality experience for 1979–1985 for the USA, and 1991–1996 for Finland. Given that the data for Finland is more recent than the one for the USA, we used the absolute mortality differentials observed for Finland and assumed that those differentials are applicable for the other high income countries as well. More precisely, we matched Finland’s mortality experience by income quintile with the model life tables ‘North’ (Coale and Demeny 1983) and derived quintile specific life expectancy at birth.Footnote 9 These numbers, i.e. the inequality in life expectancy of Finland, were then taken and re-scaled such that we match the overall life expectancy level used by UNDP to construct the HDI.
In a last step we constructed for each quintile the HDI by averaging over the three dimension indices.
4 Results
Table 1 shows the HDI by income quintile, the HDI, and the ratio of the HDI for the richest quintile to the poorest quintile and the HDI ranking for the richest and poorest quintile in the general HDI ranking of all countries (using the latest available HDI ranking). Tables 2, 3, 4 show the components of the HDI by income quintile.
The results reveal very stark differences in human development between the richest and the poorest quintiles. In contrast to comparisons in income inequality (where Latin America is the most unequal region), African countries show more inequality in the HDI by income quintiles than Latin American countries.Footnote 10 This tendency was already visible in the smaller sample analyzed in Grimm et al. (2008). In Latin America, the ratio of the HDI between the richest and the poorest quintile oscillates around 1.4–1.6, while it rangers from 1.7 to 2.5 in most Sub-Saharan African countries.
The reasons for this are twofold. First, due to the logarithmic transformation of income in the HDI, income inequality is particularly attenuated in the richer countries of Latin America compared to poorer African countries. The assumption behind the logarithmic transformation in UNDP’s HDI is that the well-being-effects of higher incomes among the rich are declining with higher incomes. Thus what is being measured here is not the differential in incomes but, in line with the general treatment of the income component in the HDI, the differential in important aspects of quality of life, such as nutrition, housing, clothing, and other aspects that are closely correlated with incomes (UNDP 2006). Hence, richer Latin American countries which have typically a high income inequality appear less unequal as they actually are (cf. Table 2).
Moreover, African countries still have a relatively high degree of inequality in literacy and educational attainment (cf. Table 3). This is not anymore the case in most Latin American countries. One should note, however, that education is only using literacy and enrolment rates and says little about educational quality which is likely to differ much more strongly between the rich and the poor.Footnote 11 Inequality in life expectancy is not significantly different in Latin America and Africa. In both regions inequality is with a few exceptions pronounced, but with an important variance across countries. Some of this may be related to data quality issues and the assumptions that were made in order to derive at these estimates. It appears, however, that in the developing countries inequality in life expectancy is smaller than other forms of inequality (cf. Table 4). However, two countries stand out: South-Africa and Zambia. Both countries are strongly affected by the AIDS epidemic; hence the level of life expectancy is particularly low and the inequality particularly high.
Moreover, regarding the inequality in life expectancy, three additional cautionary notes are important, however. To some extent, smaller inequality is to be expected given that life expectancy is effectively bounded above, i.e. there are limits to life expectancy that even high income populations run up against. Second, the differences in actual life expectancy (rather than the life expectancy index) are still substantial with gaps between the poorest and richest quintile amounting to more than 10 years in several countries. Third, even seemingly smaller differentials in life expectancy may be seen as just as important, or even more important, than larger differentials in the other components. After all, the chance to live and be free from the fear of premature mortality is a fundamental precondition for all other aspects of life (Sen 1998).
Most of the Asian countries included—Indonesia, Vietnam and Kyrgyz Republic—show comparatively lower inequality. The exception is India, where the ratio of the HDI between the richest and the poorest quintile is also about 1.6. But Vietnam for instance shows more or less the same level of human development than Bolivia, but much lower inequality in human development.
As our previous results for Finland and the USA in Grimm et al. (2008) already showed, inequality in human development in high income countries is significantly lower than in middle and low income countries. For most countries included the ratio of the HDI between the richest and the poorest quintile is ‘only’ around 1.1. Exceptions are Poland, Spain and the USA where this ratio comes close to the value of 1.2. In these countries the relative high inequality stems mainly from income inequality and in the case of Poland also from education inequality.Footnote 12 More generally, one may even argue that the HDI is not well adapted to capture differences in human development across and within countries, differences lay not so much in school enrolment or life expectancy per se but rather in the quality of education received and the number of years lived in good health. However, adjustments in that direction should be directed at the aggregate HDI as much as at our inequality-adjusted HDI. Such a discussion, however, is beyond the scope of this paper and requires a more general discussion about the definition of high human development in rich countries.
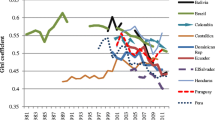
The rank positions of the different quintiles allow further interesting interpretations. Those can be seen in Table 1 again and are also visible in Fig. 1 which shows for each country the overall HDI and the index values for the poorest and richest quintile. For example, the richest quintile in Bolivia is at rank 34, i.e. among the countries with high human development, actually at the same level as Poland, whereas the poorest quintile is at rank 136. The average HDI in Bolivia in last year’s human development report stood at rank 111. In some Sub-Saharan African countries such as Cameroon, Guinea and Madagascar the richest quintile achieves a level similar to those countries with medium human development, i.e. far above the threshold of 0.5. In contrast the poorest quintiles of these countries all rank among the 15 countries with the lowest HDI. Put differently, the differences within countries are as high as the differences between high and medium as well as medium and low human development countries. Also among rich countries, the differences are sizable. While the richest quintile in all included industrialized countries (except Poland) would top the list of human development achievements, the poorest quintiles would only be at rank 34 (Sweden) or lower. In Spain and the USA the poorest quintile would even only occupy position 50 and 55, respectively, considerably worse off than the richest quintile in Guatemala, Colombia, Bolivia, or Indonesia.
Figure 2a shows the relationship between the level of human development and inequality in human development. Whereas, we were not able to derive a clear relationship between both variables with our smaller sample analyzed in Grimm et al. (2008), here we see a relatively pronounced negative correlation. Countries with a higher level of human development also have a lower inequality in human development. The correlation coefficient is about −0.88 across all countries and −0.75 and −0.72 within developing and industrialized countries, respectively. However, the figure clearly shows regional clusters for Sub-Saharan Africa, Latin America and the industrialized countries. Within these regional clusters the correlation between the level and the inequality in human development is close to zero.
Figure 2b–d show the relationship between average achievement and inequality in that achievement for the three sub-indices. For the GDP component we see a clear non-linear relationship with very high inequality in the poor African countries and lower inequality in Latin America and the industrialised countries with only moderate differences between the latter two groups. However, as we explained above would income measured in absolute terms and not in its logarithmic transformation inequality in Latin America would be higher. For the education index we also state a negative relationship but with a huge variance and thus a much lower correlation (−0.82). For the life-expectancy component the graphical representation suggests an inverted-U-shaped patter, i.e. low inequality in life expectancy in countries with low average life-expectancy, high inequality in countries with a middle life-expectancy and, again low inequality in countries with high life expectancy. If interpreted inter-temporally, these different relationships suggest different dynamics of progress from low to high achievements. For income levels, higher incomes generate lower inequality in achievements associated with income inequality (also some of that is by construction and related to the logarithmic transformation discussed above). For education, there is a tendency for educational inequality to decline with higher levels of education, but this is a rather weak relationship and presumably depends greatly on policy interventions to promote education.Footnote 13 In health, the results suggest that as life expectancy improves, those with greater means benefit initially more before inequality declines again, a type of Kuznets Curve relationship. These are tentative interpretations and further research should focus on interpreting these interesting relationships.
To analyse in more depth possible clusters of countries with respect to the inequality in the three HDI components, we also ran a hierarchical cluster analysis using the euclidean distance as a measure of dissimilarity.Footnote 14 The resulting tree diagram (dendrogram) is shown in Fig. 3. Among the industrialised countries one can find a clustering which widely overlaps which geographic closeness. Finland, The Netherlands and Sweden form a cluster. Likewise France and Germany as well as Italy and Spain are grouped together. The USA form an isolated group on the lowest level but are grouped together with Italy and Spain on the next hierarchical level. Poland is the country which differs most from all other industrialized countries that are covered by our sample.
The differences among the developing countries are larger than among the industrialized countries. Closest to the latter one can find a group that comprises Bolivia, India, Colombia Paraguay, Kyrgyz Republic and South-Africa. The group that differs most from the rest is composed by Guinea, Madagascar and Mozambique. These countries are even quite distant from a second cluster of poor African countries in which one can find Burkina Faso, Ethiopia, Ghana and Zambia as well as one Latin American country, Nicaragua.
5 Conclusion
In this paper, we extend and apply an innovative approach to measure inequality in human development to a sample of 32 developing and industrialized countries. The extension allows us to include a large number of industrialized countries for which the data availability is very different from low and middle income countries.
The comparison between low and middle income countries on the one hand and industrialized countries on the other hand provides a number of new insights and interesting results. Inequality in human development seems to be clearly negatively related to the average level of human development. The strength of that relationship is different across the three sub-indices. It is very strong for the GDP component, moderate for the education component and very weak for the life-expectancy component. In the latter case the relationship is rather shaped like an inverted “U”. Another interesting result stemming from our comparisons is that the poorest quintiles in the richer countries fare not much better than the richer quintiles in many poorer countries.
With the approach presented here, we hope to make a useful contribution to the discussion and measurement of human development in its various dimensions. This should sensitize researchers and practitioners to focus not only on the country average level of human development but also on its inequality, which in some countries is substantial.
Notes
Of course, instead of considering inequality in human development by income quintile, one could also consider inequality in human development by studying the inequality within each dimension of the HDI, as proposed, for example, by Hicks (1997); see Grimm et al. (2008) for a more complete discussion of the relative merits and disadvantages of this approach.
A summary of the results were also published in UNDP (2008).
Note that in Grimm et al. (2008), we rescaled indices for each country to the index values published by UNDP for the year in which the household survey data was collected. Thus reference years varied across countries. In this paper, we rescale with respect to the numbers published in 2008 for all countries.
An obvious ‘solution’ to this problem could be to widen the income range for the HDI and the quintile-specific HDI.
For details see: http://www.lisproject.org.
Clearly this is a debatable assumption as a significant share of the population in OECD countries is functionally illiterate (OECD 1997). But unfortunately, these analyses do not provide adult literacy rates by income quintiles. Also, the standard used to measure functional illiteracy in OECD countries was somewhat higher than the standard used in developing countries. As we want to have these measures comparable across countries, it is probably safe to assume that literacy is near universal in OECD countries at the level consistent with literacy information from developing countries (which is often based on having passed 5 or more years of schooling, or self-reported literacy as the basic ability to read and write).
Alternatively, enrolment rates by income quintile could probably be generated from national household income surveys (or co-ordinated surveys such as the European Household Panel Survey) but this would mean that we rely on two different income measures to calculate the two different components (as we had to do with the HIS and the DHS for developing countries).
The ‘income’ that is referred to in these studies does not closely match annual household per capita income that we would use for the income component which causes a further complication.
Obviously, our measure of inequality is very rudimentary, and is not consistent with some basic axioms of inequality measurement. However, it is easy to understand and interpret which makes it suitable for this kind of exercise. Users can easily apply an axiomatic approach to derive an alternative inequality measure using our approach.
We also examine the unconditional inequality in education in each country, i.e. compare the educational achievement of the best educated with the worst educated education quintile. In countries where overall educational levels are rather large, the differences in educational achievements between the best and worst is also small, such as the industrialized countries, the South American countries, and some South–East Asian countries. In each of these cases, the ratio of the best educated to worst educated quintile is <2. In some African countries where the worst educated households have very low education levels, this unconditional inequality can be much larger. Since the households in the worst educational quintile are not identical to the households which are the poorest (or have the poorest health), one cannot combine the achievements of these unconditional quintiles to form a HDI this way.
However, inequality in the industrialized countries would be a bit higher if the HDI allowed index values larger than 1, i.e. if we would not assume (as does UNDP) that the implied welfare function is flat for incomes above the threshold of USD 40,000.
We thank the anonymous referee for this suggestion.
References
Coale, A. J., & Demeny, P. (1983). Regional model life tables and stable populations (2nd ed.). New York/London: Academic Press.
Grimm, M., Harttgen, K., Klasen, S., & Misselhorn, M. (2008). A human development index by income groups. World Development, 36(12), 2527–2546. doi:10.1016/j.worlddev.2007.12.001.
Grosse, M., Harttgen, K., & Klasen, S. (2008). Economic growth and poverty reduction: Measurement issues in income and non-income dimensions. World Development, 36(3), 420–445. doi:10.1016/j.worlddev.2007.03.008.
Hicks, D. A. (1997). The inequality-adjusted human development index: A constructive proposal. World Development, 28(8), 1283–1298. doi:10.1016/S0305-750X(97)00034-X.
Klasen, S. (2008). Economic growth and poverty reduction: Measurement issues in income and non-income dimensions. World Development, 36(6), 1021–1047. doi:10.1016/j.worlddev.2007.10.009.
Ledermann, S. (1969). Nouvelles tables-types de mortalité. Travaux et documents, Cahier n. 53. Paris: INED and PUF.
Martikainen, P., Mäkelä, P., Koskinen, S., & Valkonen, T. (2001). Income differences in mortality: A register-based follow-up study of three million men and women. International Journal of Epidemiology, 30, 1397–1405. doi:10.1093/ije/30.6.1397.
OECD. (1997). Literacy skills for the knowledge society. Further results from the international adult literacy survey. Paris: OECD.
Rogot, E., Sorlie, P. D., & Johnson, N. J. (1992). Life expectancy by employment status, income, and education in the national longitudinal mortality study. Public Health Reports, 107(4), 457–481.
Sen, A. (1998). Development as freedom. New York: Knopf.
United Nations Development Programme (UNDP). (2006). Human development report 2006. New York: Palgrave Macmillan.
United Nations Development Programme (UNDP). (2008). Human development indices—A statistical update 2008. New York: UNDP.
Acknowledgments
We thank the editor, an anonymous referee, Angus Deaton, Ricardo Gomez, Claes Johannsson, Martin Ravallion, Tim Smeeding, Kevin Watkins and participants at seminars at the Universities of Bogor, Osnabrück, and at ISS, and at conferences in Berlin (PEGNet), Göttingen (VfS), and Klagenfurt (NOeG) for helpful comments and discussion. Funding from UNDP in support of this work is gratefully acknowledged.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Grimm, M., Harttgen, K., Klasen, S. et al. Inequality in Human Development: An Empirical Assessment of 32 Countries. Soc Indic Res 97, 191–211 (2010). https://doi.org/10.1007/s11205-009-9497-7
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11205-009-9497-7