The continuous-time hidden Markov model based on discretization. Properties of estimators and applications

Abstract

In this paper we consider continuous-time hidden Markov processes (CTHMM). The model considered is a two-dimensional stochastic process $(X_t,Y_t)$, with $X_t$ an unobserved (hidden) Markov chain defined by its generating matrix and $Y_t$ an observed process whose distribution law depends on $X_t$ and is called the emission function. In general, we allow the process $Y_t$ to take values in a subset of the q-dimensional real space, for some q. The coupled process $(X_t,Y_t)$ is a continuous-time Markov chain whose generator is constructed from the generating matrix of X and the emission distribution. We study the theoretical properties of this two-dimensional process using a formulation based on semi-Markov processes. Observations of the CTHMM are obtained by discretization considering two different scenarii. In the first case we consider that observations of the process Y are registered regularly in time, while in the second one, observations arrive at random. Maximum-likelihood estimators of the characteristics of the coupled process are obtained in both scenarii and the asymptotic properties of these estimators are shown, such as consistency and normality. To illustrate the model a real-data example and a simulation study are considered.

1 Introduction

Hidden Markov Models (HMM) appear in a large number of real-world estimation problems where a process with unobservable states produce observable outputs normally referred as signals. Mor et al. (2021) conduct a review of the published work on HMM during the last few decades, and the different application areas of these models, e.g., Pattern recognition, Bioinformatics, Economy and Finance, Network security, Meteorology, Reliability engineering, etc.

The problem is presented as follows. Consider a coupled process, (X, Y), in discrete or continuous time, where X is an unobserved process, a hidden process, and Y is the observed process. Based on the observations, the law of the coupled process has to be estimated. In general, the hidden process X is a Markov chain, and Y is a process whose distribution depends on the value of $X_t$, i.e., ${{\mathbb {P}}}(Y_t \in B \vert Y_s, X_s; s \le t) ={{\mathbb {P}}}(Y_t \in B \vert X_t)$, or ${{\mathbb {P}}}(Y_t \in B \vert Y_s, X_s; s \le t) ={{\mathbb {P}}}(Y_t \in B \vert Y_t, X_t)$. In the first case we have an M1-M0 model and in the second an M1-M1 model, where M means Markov order 1 or 0. These are the most used orders, but in general we can consider more general orders.

In the literature, the considered Markov chain is a finite-state space process with transition probability $P_{ij}$ being a function of a parameter $\theta$ (in general a vector). It is written as $P_{ij}(\theta )$. Therefore, the estimation of the parameter vector $\theta$, i.e., $\widehat{\theta }$, gives us a plug-in estimator of the transition probability, i.e., $\widehat{P}_{ij}:=P_{ij}(\widehat{\theta })$.

Basic theoretical results concerning HMM in discrete time are given in Baum and Petrie (1966), and Leroux (1992) where consistency of estimators is proven, as well as in Bickel et al. (1998) that prove asymptotic normality of the estimator for a stationary process. These results concerning discrete-time hidden Markov models (DTHMM) case are used in our CTHMM in order to provide asymptotic results for our estimators.

Here, a continuous-time HMM (CTHMM) is considered, where X is defined by its generating matrix $\textbf{A}$ and Y by its probability law, with conditional distribution G(i, B) given $\{X_t=i\}$, and B a measurable set in ${\mathbb {R}}^q$, i.e., ${{\mathbb {P}}}(Y_t \in B \vert X_t=i) =G(i,B)$, so the considered model is an M1-M0.

Our results concern the consistency and asymptotic normality of the estimator of the parameter $\theta$ and applications to a real data set and simulated data.

It is assumed that the generator $\textbf{A}$ of X is a matrix depending on the parameter ${\theta }$, i.e., $\textbf{A}= {A}({\theta })$ as well as the probability distribution of Y, i.e., $G=G_{\theta }$. Let us denote $g_{\theta }$ the density of $G_{\theta }$ with respect to some dominating measure $\mu$.

The methodology to tackle the problem is based on results in DTHMM, as Bickel et al. (1998), Baum and Petrie (1966), Leroux (1992) and also on our results in Gamiz et al. (2023). In the present paper the CTHMM is approached by discretization, so that previous results can be applied here, and the parameter ${\theta }$ can be estimated by the EM-algorithm. From the estimator $\widehat{\theta }$ we obtain an estimator of the generating matrix $\widehat{\textbf{A}}$ and prove the asymptotic properties of this estimator such as normality and consistency.

We consider two different scenarii.

1.1 Scenario 1: Regular inspections in time

The true state of the system at time $t, X_{t}$ is non-observable. However, at regular intervals of length $h, 0<h<T$, certain information related to the system is observed.

Let us show an example of the type of problems that can be treated with this approach. Let us consider a continuous-time Markov chain (CTMC) $\{X_t, t>0\}$ with generating matrix given by

$$\begin{aligned} \textbf{A}=\left( \begin{array}{ccc} -2\lambda &{} 2 \lambda &{} 0 \\ \mu &{} -(\lambda +\mu ) &{} \lambda \\ 0 &{} 2\mu &{}-2 \mu \\ \end{array} \right) . \end{aligned}$$

This model is a typical description of the functioning of a system with two units identical and independent. The units fail at a constant rate equal to $\lambda$. Once a unit fails is sent for repair. The repair system has capacity for the two units and the repair rate is also constant and equal to $\mu$. The state of the system is expressed as the number of units functioning, then the state space is $E=\{0,1,2\}$. For assessing the system performance, we focus on certain functionals $\phi (\textbf{A},t)$, such as the reliability of the system (the probability that the system has not suffered from failure before a given time), the availability function (the probability that the system is operative at a given time) or the expected hitting times (the expected time a particular class of states is reached by the system), among others. The usual procedure is to take a sample of identical systems that work under similar conditions and to estimate the unknown parameters $\lambda$ and $\mu$ from the data. The main problem here is that we consider that the system is not directly observable and then we are not able to register information regarding the number of units that are functioning in the system at any given time. In contrast, at some regular times, $t_0=0$, $t_1=h$, $t_2=2h$, $\ldots$, $t_n=nh$, $\ldots$, we have access to certain indicators that provide useful, though partial, information about the state of the system. Let us denote by $Y_n$ the accessible information about the system that we can observe at time $t_n$, for $n>0$. We assume that $\{Y_0, Y_1, \ldots , Y_n\}$ are (conditionally) independent and that for each n the distribution of the random variable $Y_n$ is determined by a parameter that depends on the current state of the system, that is, at time $t_n=nh$.

Let us define ${ Q}_h(i,j)={{\mathbb {P}}}(X_{h}=j \vert X_0=i)$, for $i, j \in E$, and denote $\textbf{Q}_h$ the corresponding matrix. Using basic properties of CTMC we have that $\textbf{Q}_h = \textbf{I} + \textbf{A} h + o(h)$, with $\textbf{I}$ the identity matrix and $o(h)/h \rightarrow 0$ for $h \rightarrow 0$, then we can approximate $\textbf{Q}_h$, for a fixed small enough h, by the following

$$\begin{aligned} \textbf{Q}_h=\left( \begin{array}{ccc} 1-2\lambda h &{} 2 \lambda h &{} 0 \\ \mu h &{} 1-(\lambda +\mu )h &{} \lambda h \\ 0 &{} 2\mu h &{}1-2 \mu h \\ \end{array} \right) . \end{aligned}$$

In this situation, $\{Y_0, Y_1, \ldots , Y_n\}$ can be seen as a sample from a DTHMM whose parameters can be written as a vector ${\varvec{\theta }}$ that includes $\lambda$, $\mu$ and some other parameters that determine the distribution of $Y_n$ given $\hat{X}_n=X_{nh}=i$, for $i \in E$.

In general, we define $\textbf{A}_h=h^{-1}(\textbf{Q}_h-\textbf{I})$. As $h \rightarrow 0$, $\textbf{A}_h \rightarrow \textbf{A}$, uniformly. As $\textbf{Q}=Q(\theta )$, then $\textbf{A}=A(\theta )$. We estimate $\widehat{\theta }_n$ from observations of the hidden Markov model at times $\{t_{n}=n h, n\ge 0\}$. Leroux (1992) showed the strong consistency of this estimator, that is $\widehat{\theta }_n \rightarrow \theta$, and in Bickel et al. (1998) the weak convergence of the estimator to a Normal law is proven, that is, $\sqrt{n} (\widehat{\theta }_n - \theta ) \rightarrow N(0, \Sigma _{0})$, in the case of HMM.

Subsequently, for the plug-in estimator of the transition matrix $\textbf{Q}_h$, that is $\widehat{\textbf{Q}}_{h,n}={Q}_h(\widehat{\theta }_n)$, the strong consistency and asymptotic normality are proven. At the same time the strong consistency and the asymptotic normality of the plug-in estimator of $\textbf{A}_h$, that is $\widehat{\textbf{A}}_{h,n}= A(\widehat{\textbf{Q}}_{h,n})$, is also demonstrated in this paper.

And as a consequence, for any functional within the following class $H(t)=\Phi (\textbf{A},t)$, $H_{h}(t)=\Phi (\textbf{A}_{h},t)$ is defined. Then the plug-in estimator for $H_{h}(t)$, $\widehat{H}_{h,n}$, is shown to be strongly consistent and asymptotically normal. As an application of this result, the transition matrix function, $H(t)=\textbf{P}(t)=e^{\textbf{A}t}$, can be considered, as well as other functions such as reliability, availability, etc.

1.2 Scenario 2: Random inspections in time

For a given interval length T, the true state of the system at time $t, X_{t}$ is non-observable. Observations related to the underlying state are received at random times following an Homogenous Poisson Process (HPP), N(t), with intensity $\lambda$, unknown and estimated from the data. We consider the embedded Markov chain obtained from the visited states of X at the successive arrival times of the HPP. We denote Q its transition probability matrix and A the generating matrix of the CTMC. We assume that $\lambda \ge$ max$\{a_{i}, i \in E\}$. Using the uniformization method, see, e.g., Kulkarni (2011), we define $\textbf{Q} = (1/{\lambda }) \textbf{A} + \textbf{I}$. Using the HMM, an estimator $\widehat{\textbf{Q}}$, of $\textbf{Q}$ is obtained, and subsequently the corresponding estimator of the generating matrix $\textbf{A}$ is obtained as $\widehat{ \textbf{A}}= \widehat{\lambda } \left( \widehat{\textbf{Q}}- \textbf{I}\right)$. It is demonstrated that these estimators $\widehat{\textbf{Q}}$ and $\widehat{ \textbf{A}}$ are strongly consistent and asymptotically normal.

The model discussed in this scenario should not be confused with the so called Markov-modulated Poisson process, which consists of a Poisson process whose rate is controlled by a non-observable continuous-time Markov chain. In Freed and Shepp (1982) it is considered a switched Poisson process, i.e., with only two states for the hidden chain. The authors assume that the rate of one of the states is zero and derive a simple formula for the asymptotic likelihood ratio that allows to estimate the state at any time from a stream of past events. In our case, a Poisson process is assumed to deal with the number of signals registered by an external observer but it is not responsible for the number of signals emitted by the hidden source nor for the nature of such signals, as it is the case of the Poisson process involved in a Markov-modulated Poisson process.

The results summarized here can be utilized in different areas, such as system reliability, biology, etc., e.g., in Wei et al. (2002) a CTHMM is proposed for evaluating network performance considering discrete time observations. Zhou et al. (2020) proposed as well a CTHMM where the observations can be collected regularly, irregularly or continuously. The number of states is unknown. They apply this model to bladder cancer data. In Verma et al. (2018) the authors develop a CTHMM under a generalized linear modeling framework to model the evolution of chronic obstructive pulmonary disease (COPD), again, the model considers discrete-time observations although they are irregularly-spaced observations. Similarly Hulme et al. (2021) proposed a CTHMM to estimate health conditions of patients that are monitored by wearable and mobile technology, the observations are as well irregularly-spaced. Finally, Liu et al. (2016) considers the use of CTHMM for modeling disease progression as well.

This paper is organized as follows. In Sect. 2 the model and its main characteristics are defined. The generator of the two-dimensional process is defined and obtained in terms of the generating matrix $\textbf{A}$ and the emission distribution G. The basic properties of the model are obtained using a formulation based on semi-Markov processes. In Sect. 3, maximum-likelihood estimators for the parameters of the model are obtained based on data observed under two different time discretization schemes. That is, scenario 1, where observations arrive at times regularly pre-specified; and, scenario 2, where observations arrive randomly according to a homogeneous Poisson process. Some applications and particular cases of the model are described in Sect. 3.6.1. Some numerical examples are presented in Sect. 5 and the conclusions are given in Sect. 6.

2 The model

We follow the formulation of Bickel et al. (1998) and consider the “usual parametrization” of the model. Specifically, let $\{X_t;t\ge 0\}$ be a continuous-time Markov chain with finite state space $E=\{1,\ldots , d\}$ and generating matrix $\textbf{A}=(a_{ij},; i, j \in E)$. Let $\{Y_t; t \ge 0\}$ an $\mathcal {Y}$-valued sequence such that given $X_t=i$, $Y_t$ is conditionally distributed with density g(i, y) with respect to some $\sigma$-finite measure $\mu$ on $\mathcal {Y}$, and fixed $i \in E$.

All processes are defined on a complete probability space $(\Omega , \mathcal {F}, {{\mathbb {P}}})$, are right continuous and then progressively measurable. This will imply also a family of probabilities $\{{{\mathbb {P}}}_i; i\in E\}$, where ${{\mathbb {P}}}_i(\cdot )= {{\mathbb {P}}}(\cdot \vert X_0=i)$, and expectations $\{{{\mathbb {E}}}_{(i,y)}; i \in E, \ y \in \mathcal {Y}\}$, where ${{\mathbb {E}}}_{(i,y)} [\cdot ]={\mathbb {E}}[\cdot \vert X_0=i, Y_0=y]$, which are defined with respect to a family of probabilities $\{{{\mathbb {P}}}_{(i,y)}; i \in E, \ y \in \mathcal {Y}\}$, where ${{\mathbb {P}}}_{(i,y)}(\cdot )= {{\mathbb {P}}}(\cdot \vert X_0=i, Y_0=y)$.

Both, the generating matrix $\textbf{A}$ as well as the family of densities $\{g(i,\cdot );i \in E\}$, depend on a vector of parameters $\theta$, that is $A(i,j)=a_{ij}(\theta )$ and $g(i,\cdot )= g_{\theta }(i,\cdot )$, for all $i, j \in E$. The set of possible values of the vector $\theta$ is denoted $\Theta \subset {\mathbb {R}}^k$, and $\theta$ has to be estimated from a set of observations of the process $\{Y_t\}$.

The vector ${\theta }$ usually includes the transition rates and also some parameters characterizing the densities g. As a particular case, it can be assumed that g(i, y) denotes a concrete parametric family of distributions with parameters ${\varvec{\beta }}=(\beta _1,\beta _2,\ldots , \beta _s)$, then we can write $\theta =(\textbf{A}^*,{\varvec{\beta }})$, with $\textbf{A}^*$ the matrix $\textbf{A}$ without its principal diagonal, since the diagonal entries are functions of the off diagonal entries. In our previous example of a 3-state MC, if we have that $g(i,\cdot )$ is the Normal distribution $N(\kappa _i, \sigma _i^2)$, $i \in E$; the parameter vector $\theta$ will be: $\theta =(\lambda , \mu ,\kappa _1,\sigma _1^2, \kappa _2,\sigma _2^2, \kappa _3,\sigma _3^2)$.

In general $\mathcal {Y}$ can be seen as a subset in ${\mathbb {R}}^q$ for some q. If $Y_t$ has density function $g(i,\cdot )$, given that $X_t=i$, then ${{\mathbb {P}}}(Y_t\in B \vert X_t=i)=\int _{B} g(i,y)\mu (dy)$, for $B \subset \mathcal {Y}$, is the probability that the process $Y_t$ takes values in a subset B given $X_t=i$, for $i \in E$. We also denote $G(i,B)={{\mathbb {P}}}(Y_t \in B \vert X_t=i)$.

At some points of the paper we will discuss the simpler case that $Y_t$ takes values in a finite set, that is $\mathcal {Y}=\{y_1,\ldots , y_s\}$ and then the emission function will be a $d \times s$-dimensional matrix $\textbf{G}$, with elements $G(i,y)=G(i,\{y\})={{\mathbb {P}}}(Y_t=y \vert X_t=i)$, for all $i \in E$ and $y \in \mathcal {Y}$, and all $t >0$ (see Gamiz et al. 2023).

For the rest of the paper we will consider the process (X, Y) defined as follows.

Definition 1

Let $X=\{X_t; t\ge 0\}$ be an irreducible homogeneous Markov process in a finite set E and with generating matrix $\textbf{A}=(a_{ij})_{i,j \in E}$, and $Y=\{Y_t; t\ge 0\}$ is a homogeneous process in a general set $\mathcal {Y}\subset {\mathbb {R}}^q$, with $q \ge 1$ such that, for $t >0$, the distribution of $Y_t$ is determined $G(i, \cdot )$, over the event $X_t=i$, for $i \in E$. Then we say that (X, Y) is a two-dimensional process with dependence structure M1-M0. That is, if ${\mathcal {B}}_{\mathcal {Y}}$ denotes the set of Borel subsets of $\mathcal {Y}$, then for any $i, j \in E$, $y \in \mathcal {Y}$ and $B \in {\mathcal {B}}_{\mathcal {Y}}$, and for all $s, t>0$,

$$\begin{aligned} {{\mathbb {P}}}(X_{t+s}= & {} j,Y_{t+s} \in B \vert X_u, Y_u, 0 \le u \le s)\nonumber \\= & {} {{\mathbb {P}}}(X_{t+s}=j, Y_{t+s} \in B \vert X_s)\\= & {} {{\mathbb {P}}}(X_{t}=j, Y_{t} \in B \vert X_0),\nonumber \end{aligned}$$

(1)

where we also use homogeneity of the processes X and Y. Moreover, for $t>0$,

$$\begin{aligned} {{\mathbb {P}}}(X_t=j, Y_t \in B \vert X_0 =i, Y_0=y)= P_{ij}(t) G(j,B), \end{aligned}$$

and, for $t=0$, ${{\mathbb {P}}}(X_t=j, Y_t \in B \vert X_0 =i, Y_0=y)= 1$ if $i=j$ and $y \in B$; and, 0 otherwise.

2.1 Generators

Let us focus on the two-dimensional process $\{(X_t,Y_t); t\ge 0\}$, where, as above, X is a continuous-time Markov chain taking values in the set $E=\{1,2, \ldots , d\}$, with generating matrix $\textbf{A}$ and initial law $\alpha$; and Y is a stochastic process taking values in a set $\mathcal {Y}\subset {\mathbb {R}}^q$ whose distribution depends on $X_t$.

First we recall the concept of generator operator for a two-dimensional process with a general state space.

Definition 2

(Generator of two-dimensional process with general state space) Let $(X,Y)=\{(X_t, Y_t); t>0\}$ a two-dimensional process, with X taking values in a set $E \subset {\mathbb {R}}^d$ and Y taking values in a set $\mathcal {Y}\subset {\mathbb {R}}^q$ and let $f \in {\mathbb {C}}(E \times \mathcal {Y})$, where ${\mathbb {C}}(E \times \mathcal {Y})$ denotes the set of all continuous bounded functions defined on $E \times \mathcal {Y}$. We define the generator $\widetilde{\textbf{A}}$ of (X, Y) as follows

$$\begin{aligned} \widetilde{\textbf{A}} f (x,y) = \underset{t \rightarrow 0}{\lim } \frac{1}{t} E_{x,y} \left[ f(X_t,Y_t) -f(x,y)\right] , \end{aligned}$$

for $(x, y) \in E \times \mathcal {Y}$.

We consider that X is a MC with finite state space E, while Y is a process taking values in a subset $\mathcal {Y}\subset {\mathbb {R}}^q$, for $q\ge 1$. Since X is a CTMC then its generator is a matrix $\textbf{A}= (a_{ij}; i, j \in E)$, where $a_{ij} \ge 0$, $i \ne j$ and $a_{ii}=-\sum _{j \ne i} a_{ij}$ for all $i \in E$. On the other hand, $\{Y_t\}$ is a sequence conditionally independent, where the law of $Y_t$ depends on the value of $X_t$.

Proposition 1

Let (X, Y) be a stochastic process where X is a CTMC with finite state space E and generating matrix $\textbf{A}= (a_{ij}; i, j \in E)$, and let the transition probabilities of the process (X, Y) be given by (1). The generator of the two-dimensional MC $(X_t, Y_t)$ can be written as

$$\begin{aligned} \widetilde{\textbf{A}} f (i,y)= \sum _{j \in E\setminus {\{i\}}} a_{ij} \int _{\mathcal {Y}} G(j,du) \left[ f(j,u)-f(i,y)\right] \end{aligned}$$

for all $i \in E$ and $y \in \mathcal {Y}$.

Proof

From definition 2 we have, for $i \in E$ and $y \in \mathcal {Y}$,

$$\begin{aligned} \widetilde{\textbf{A}} f (i,y) = \underset{t \rightarrow 0}{\lim } \frac{1}{t} \sum _{j \in E}\int _{\mathcal {Y}} \left[ f(j,u) -f(i,y)\right] {{\mathbb {P}}}(X_t=j, Y_t \in du \vert X_0=i,Y_0=y) \end{aligned}$$

From the expression in (1) we get

$$\begin{aligned} \widetilde{\textbf{A}} f (i,y)= & {} \underset{t \rightarrow 0}{\lim } \frac{1}{t} \sum _{j \in E}\int _{\mathcal {Y}} (f(j,u) -f(i,y))P_{ij}(t) G(j,du) \\= & {} \sum _{j \in E} \int _{\mathcal {Y}}f(j,u)G(j,du)\left( \underset{t \rightarrow 0}{\lim } \frac{P_{ij}(t)-\delta _{ij}\delta _{yu}}{t}\right) \\= & {} a_{ii}f(i,y) +\sum _{j \ne i} a_{ij}\int _{\mathcal {Y}} f(j,u)G(j,du) \end{aligned}$$

$\square$

In particular, when $\mathcal {Y}$ is a finite set, the generator is given by a matrix ${\widetilde{\textbf{A}}}$ as we show next. The general expression in definition 2 becomes

$$\begin{aligned} \widetilde{\textbf{A}} f =\sum _{i \in E} \sum _{y_2 \in \mathcal {Y}} f(j,y_2) \left( \underset{t \rightarrow 0}{\lim }\ \frac{{{\mathbb {P}}}(X_t=j, Y_t=y_2 \vert X_0=i, Y_0=y_1)-\delta _{ij}\delta _{y_1y_2}}{t} \right) \end{aligned}$$

We have that ${{\mathbb {P}}}(X_t=j, Y_t=y_2 \vert X_0=i, Y_0=y_1) = P_{ij}(t) G(j,y_2)$, and we assume that ${{\mathbb {P}}}(X_t=j, Y_t=y_2 \vert X_0=i, Y_0=y_1) \rightarrow 0$ as $t \rightarrow 0$ when $y_1 \ne y_2$. We consider the following cases:

• If $i=j$, $y_1=y_2$, $(1/{t}) \left[ P_{ij}(t) G(j,y_2)-1\right] \rightarrow a_{ii}$;

• If $i=j$, $y_1\ne y_2$, $({1}/{t}) \left[ P_{ij}(t) G(j,y_2)\right] \rightarrow 0$; and,

• If $i\ne j$, $({1}/{t}) \left[ P_{ij}(t) G(j,y_2)\right] \rightarrow a_{ij} G(j,y_2)$

Then the generator can be written as a matrix whose elements are

$$\begin{aligned} {{\widetilde{a}}} ((i,y_1),(j,y_2))= \left\{ \begin{array}{ll} a_{ii}, &{} i=j, y_1=y_2 \\ 0, &{} i=j, y_1\ne y_2 \\ a_{ij}G(j,y_2), &{} i\ne j \end{array} \right. \end{aligned}$$

(2)

Moreover, we have

$$\begin{aligned} \sum _{j \in E} \sum _{y_2 \in \mathcal {Y}} \widetilde{a} ((i,y_1),(j,y_2))= & {} a_{ii}+\sum _{j \ne i}\sum _{y_2 \in \mathcal {Y}} a_{ij} G(j,y_2) \\= & {} a_{ii}+\sum _{j \ne i} a_{ij}=0 \end{aligned}$$

Example 1

For illustrative purposes, let us construct the 2-dimensional generator for a simple case where $E=\{1,2\}$ and ${{\mathcal {Y}}}=\{y_1,y_2,y_3\}$. Then, the state space of the coupled process is $\widetilde{E}=\{(1,y_1),(1,y_2),(1,y_3),(2,y_1),(2,y_2),(2,y_3)\}$, and the corresponding generating matrix is

$$\begin{aligned} \widetilde{\textbf{A}}=\left( \begin{array}{cccccc} a_{11} &{} 0 &{}0 &{} a_{12}G(2,y_1) &{} a_{12}G(2,y_2) &{} a_{12}G(2,y_3) \\ 0 &{} a_{11} &{}0 &{} a_{12}G(2,y_1) &{} a_{12}G(2,y_2) &{} a_{12}G(2,y_3) \\ 0 &{} 0 &{}a_{11} &{} a_{12}G(2,y_1) &{} a_{12}G(2,y_2) &{} a_{12}G(2,y_3) \\ a_{21}G(1,y_1) &{} a_{21}G(1,y_2) &{} a_{21}G(1,y_3) &{} a_{22} &{}0 &{} 0 \\ a_{21}G(1,y_1) &{} a_{21}G(1,y_2) &{} a_{21}G(1,y_3) &{} 0 &{}a_{22} &{} 0 \\ a_{21}G(1,y_1) &{} a_{21}G(1,y_2) &{} a_{21}G(1,y_3) &{} 0&{}0 &{} a_{22} \\ \end{array} \right) \end{aligned}$$

where $a_{\cdot \cdot }$ denote the elements of the generating matrix $\textbf{A}$ of X, and $G(\cdot , \cdot )$ denote the emission probabilities.

From the generator in Proposition 1 we obtain the semigroup

$$\begin{aligned} P(t)=\exp (\widetilde{\textbf{A}} t). \end{aligned}$$

(3)

2.2 Markov renewal equation for Markov processes

The above semigroup is difficult to handle numerically. For this reason we will consider another equivalent formulation via semi-Markov processes (see for example Limnios and Oprisan 2001). In fact, Markov processes are particular cases of semi-Markov processes and we may use the Markov renewal equation in order to obtain the above formulation (3) in a much easier numerical scheme.

Let us define the semi-Markov kernel of the Markov process $X_t$ in the following way.

Let the process (X, Y) defined as in Definition 1.

For $i, j \in E$ and $B \in \mathcal {B}_{\mathcal {Y}}$, we define the following functions

• $M(i,j,B,t)=G(i,B) e^{-a_i t} \delta _{ij}$,

• $L(i,j,t)=({a_{ij}}/{a_i}) (1-e^{-a_i t})$, and,

• $\widetilde{P}(i,j,B,t)={{\mathbb {P}}}_i(X_t=j,Y_t \in B)$,

where ${{\mathbb {P}}}_i(X_t=j,Y_t\in B)={{\mathbb {P}}}(X_t=j,Y_t \in B \vert X_0=i)$, and $\delta _{ij}$ denotes the Kronecker delta and $a_i=-a_{ii}$.

Note that the function L(i, j, t) is the semi-Markov kernel of the Markov process $\{X_t\}$.

In particular, when $Y_t$ takes values in a finite set of size s, we can define the matrix of transition functions of the process (X, Y), $\widetilde{\textbf{P}}_t$ with dimension $(d\cdot s)\times (d \cdot s)$ and elements

$$\begin{aligned} \widetilde{P}_t((i,y'),(j,y))=P_{ij}(t)G(j,y), \ i,j \in E, \ y', y \in \mathcal {Y}, \ \textrm{and} \ t \ge 0. \end{aligned}$$

(4)

In the same way we can construct matrices $\textbf{M}_t$ and $\textbf{L}_t$ whose elements are given above.

Given $\phi$ a measurable function defined on $E \times R_+$ we define its convolution by L as follows

$$\begin{aligned} (L *\phi )(i,t)= \sum _{j \in E} \int _0^t L(i,j,ds)\phi (j,t-s), i \in E, t \ge 0. \end{aligned}$$

(5)

Proposition 2

(Markov renewal equation) The function $\widetilde{P}(i,j,B,t)$ verifies the following Markov renewal equation

$$\begin{aligned} \widetilde{P}(i,j,B,t) = M(i,j,B, t) +\sum _{k \in E} \int _0^t L(i,k,ds) \widetilde{P}(k,j,B,t-s), \end{aligned}$$

(6)

where $i, j \in E$, $B \in \mathcal {B}_{\mathcal {Y}}$, and $t \ge 0$.

Proof

We have that

$$\begin{aligned} {{\mathbb {P}}}_{i}(X_t=j, Y_t\in B)= & {} G(i,B)e^{-a_i t} \delta _{ij} \\{} & {} +\sum _{k \in E} \int _0^t {{\mathbb {P}}}_i(X_t=j,Y_t \in B, J_1=k, T_1 \in ds) \end{aligned}$$

where $(J_1,T_1)$ describes the first jump of the Markov renewal process $\{(J_n,T_n), n>0\}$ associated to the process X, that is $J_1=X_{T_1}$.

Then

$$\begin{aligned} {{\mathbb {P}}}_{i}(X_t=j, Y_t\in B)= & {} G(i,B)e^{-a_i t} \delta _{ij} \\{} & {} +\sum _{k \in E} \int _0^t {{\mathbb {P}}}_{i}(X_t=j,Y_t \in B \vert J_1=k, T_1=s){{\mathbb {P}}}_{i}(J_1=k,T_1 \in ds) \\= & {} G(i,B)e^{-a_i t} \delta _{ij} \\{} & {} +\sum _{k \in E} \int _0^t {{\mathbb {P}}}_{i}(X_{t-s}=j,Y_{t-s} \in B) a_{ik}e^{-a_is}ds \\= & {} M(i,j,B,t)+ \sum _{k \in E} \int _0^t L(i,k,ds) \widetilde{P}(k,j,B, t-s) \\= & {} M(i,j,B,t)+ (L * \widetilde{P})(i,j,B,t) \end{aligned}$$

$\square$

It has been proven that $\widetilde{P}(i,j,B,t)=M(i,j,B,t) + (L*\widetilde{P})(i,j,B,t)$, where $*$ denotes the convolution operation defined in (5).

For the case that $Y_t$ takes values in a finite set we can write Eq. (6) in matrix notation as follows

$$\begin{aligned} {\widetilde{\textbf{P}}}_t = \textbf{M}_t + \textbf{L}_t* {\widetilde{\textbf{P}}}_t \end{aligned}$$

Let us define $\Psi$ the Markov renewal function of the process X, that is $\Psi (t) = \sum _{n \ge 0} \textbf{L}^{(n)}_t$, where $\textbf{L}^{(n)}_t$ denotes the nth fold-convolution of $\textbf{L}_t$, that is, the (i, j)-element given by

$$\begin{aligned} L^{(n)}(i,j,t)=\sum _{k \in E}\int _0^t L(i,k,ds)L^{(n-1)}(k,j,t-s), \ i,j \in E, \ t >0, \end{aligned}$$

being $L^{(0)}(i,j,t)=\delta _{ij} 1_{{{\mathbb {R}}}^+}(t)$, and $L^{(1)}(i,j,t)=L(i,j,t)$.

Then the solution of Eq. (6) is given by ${\widetilde{ P}}(i,j,B,t) = ( \Psi *M)(i,j,B,t)$, see for example Limnios (2012).

Using the Markov renewal theorem (MRE), see Shurenkov (1984), the stationary distribution of the process (X, Y) can be obtained in the following proposition.

Proposition 3

(Stationarity) Under the conditions above and if X is irreducible, we have

$$\begin{aligned} \underset{t \rightarrow \infty }{\lim } \widetilde{P}(i,j,B,t) = \pi _j G(j,B), \ j \in E, \ B\in {{\mathcal {B}}_{\mathcal {Y}}}. \end{aligned}$$

So we have that the probability distribution $\widetilde{\pi }$ whose elements are $\widetilde{\pi }(j,B)= \pi _j G(j,B)$, for $j \in E$, and $B\in {{\mathcal {B}}_{\mathcal {Y}}}$ is the limit distribution of the process (X, Y).

Moreover, $\widetilde{\pi }(i,B)$ is the stationary distribution of the process (X, Y), that is, it verifies that

$$\begin{aligned} \widetilde{\pi } \widetilde{A} f =0, f \in {\mathbb {C}}(E\times \mathcal {Y}). \end{aligned}$$

Proof

For the first part of the proposition, let $\rho$ denote the stationary distribution of the embedded Markov chain $J_n$ associated to the MC $X_t$, with transition probabilities $p_{ij}={a_{ij}(1-\delta _{ij})}/{a_i}$.

Let $\pi$ be the row vector of stationary probabilities of the CTMC $X_t$, that is, verifying that $\pi \textbf{A}= \textbf{0}$. It is satisfied that $\pi _i= {m_i\rho _i}/{m}$, with $m_i=1/a_i$, the mean sojourn time in state i and $m=\sum _{j \in E} m_i \rho _i$.

Then, by the irreducibility of X and, as $\widetilde{P}(i,j,B,t)=(\Psi * M)(i,j,B,t)$ by MRT, we have that

$$\begin{aligned} \underset{t \rightarrow \infty }{\lim } (\Psi * M)(i,j,B,t)= & {} \frac{1}{m} \sum _{k \in E} \rho _k \int _0^{\infty } M(k,j,B,t)dt \\= & {} \frac{1}{m} \sum _{k \in E} \rho _k \int _0^{\infty } G(k,B)e^{-a_k t} \delta _{kj}dt \\= & {} \frac{1}{m} \rho _j G(j,B) \frac{1}{a_j}= \pi _j G(j,B) \end{aligned}$$

Then we define $\widetilde{\pi }(j,B)= \pi _j G(j,B)$, for $j \in E$ and $B \in \mathcal {B}_{\mathcal {Y}}$ the stationary distribution of the coupled process (X, Y).

For the second part, we can write

$$\begin{aligned} \widetilde{\pi } \widetilde{\textbf{A}} f = \sum _{j \in E} \int _{\mathcal {Y}} \widetilde{\pi }(j,dy) \widetilde{A} f(j,y), \end{aligned}$$

and, from the definition of the generator $\widetilde{\textbf{A}}$ and the definition of $\widetilde{\pi }$, we get

$$\begin{aligned} \widetilde{\pi } \widetilde{\textbf{A}} f= & {} \sum _{j \in E} \int _{\mathcal {Y}} \pi _j G(j,dy) \sum _{i \in E} a_{ji}\int _{\mathcal {Y}} G(i,du)\left[ f(i,u)-f(j,y)\right] \\= & {} \sum _{i \in E} \sum _{j \in E} \pi _j a_{ji} \int _{\mathcal {Y}} \int _{\mathcal {Y}} G(j,dy) G(i,du)\left[ f(i,u)-f(j,y)\right] \\= & {} 0 \end{aligned}$$

where the last equality is deduced from the fact that $\pi \textbf{A}=0$. $\square$

Remark 1

As the component G(j, B) does not depend on the time, we can also use relation (4) to derive directly the limit in the first part of Proposition 3.

3 Estimation

As described in Sect. 2, the two-dimensional process (X, Y) is fully specified by the generating matrix of the continuous-time MC X, $\textbf{A}$ and the emission distribution G. Let us assume that $\textbf{A}={A} (\theta )$, and that $G=G_{\theta }$, that is, they both depend on a vector of unknown parameters $\theta$. The problem here is to obtain estimators of the parameter from data. Let us consider that the MC X is unobservable while we can register information about the state of the process Y. In other words, consider that our data come from a continuous-time HMM $(X_t,Y_t)$, where $X_t$ is the hidden process and we aim at estimating $\theta$ from a sample of observations of the process $Y_t$ in an interval of time [0, T].

3.1 Time discretization

3.2 Scenario 1. Regular inspections in time

In this section, observations emitted by a CTHMM are recorded at regular time points.

Let us consider a stochastic system according to a continuous-time Markov chain $\{X_t; t \ge 0\}$ with state space $E=\{1,2,\ldots , d\}$ as above; generating matrix $\textbf{A}$, that is $\textbf{P}(t)= e^{\textbf{A} t}$, for all $t>0$.

The true state of the system $X_t$ is non observable at any time $t \in (0, T]$. However, at n regular pre-specified times denoted by $0<h< 2h< \cdots < nh = T$, observations of a random process $\{Y_t; t \ge 0\}$ are available providing certain information about the true state of the system. Let us denote $\hat{Y}_k=Y_{kh}$ the k-th observed signal, which is recorded at time kh, for $k\in \{0,1,\ldots , n\}$.

Associated to (or embedded in) the continuous-time process we can consider the following discrete time Markov chain $\hat{X}_k=X_{kh}$, with transition matrix $\textbf{Q}_{h}=e^{\textbf{A}h}$, whose (i, j)-element is given by $Q_{h}(i,j)={{\mathbb {P}}}(X_h=j \vert X_0=i)$. The discrete Markov chain $\hat{X}_k$ is called the discrete skeleton (at scale h) of $X_t$, (see Kingman 1963) for ergodicity properties of Markov chains based on discrete skeletons).

Consider the sequence of times $0< h<2h< \cdots <nh$, then $\hat{Y}_{0}$, $\hat{Y}_{1}$, $\ldots$, $\hat{Y}_{n}$ can be seen as a realization of the embedded discrete hidden Markov model that we denote by $(\hat{X},\hat{Y})$. We can use the results in Bickel et al. (1998) to estimate the transition matrix of this embedded hidden Markov chain $\{\hat{X}_n\}$, that is we obtain $\widehat{\textbf{Q}}_{h}$, as well as the emission functions $G(i,dy)={{\mathbb {P}}}(\hat{Y}_k \in dy \vert \hat{X}_k=i)$, for $i \in E$.

For an interval of length h, we have $\textbf{Q}_h=\textbf{P}(h)= e^{\textbf{A} h}$; where $\textbf{A}=(a_{ij}; i,j \in E)$ is the generating matrix of the hidden continuous-time Markov chain; $\textbf{P}(h)$ is the corresponding transition function matrix; and, $\textbf{Q}_h$ is the transition matrix of the Markov chain $\hat{X}_k$. Then, using Taylor expansion, we approximate

$$\begin{aligned} a_{ij}= \frac{1}{h} \left( {Q}_{h}(i,j)-\delta _{ij}\right) + o(1) \end{aligned}$$

where $o(h)/h \rightarrow 0$ as $h \rightarrow 0$, and $\delta _{ij}$ equal to 1 if $i=j$ and 0 otherwise. Then, we define the estimator of the generating matrix as

$$\begin{aligned} \widehat{\textbf{A}}_h:=\frac{1}{h}\left( \widehat{\textbf{Q}}_h-\textbf{I}\right) , \end{aligned}$$

(7)

where $\widehat{\textbf{Q}}_h$ is the maximum likelihood estimator of the transition matrix corresponding to the discrete-time chain $\hat{X}$, obtained as in Gamiz et al. (2023), and $\textbf{I}$ the identity matrix.

Note that since we write $\textbf{A}=A(\theta )$ we also have that $\textbf{Q}$ is a function of the parameter vector $\theta$, that is, $\textbf{Q}=Q(\theta )$.

3.3 Scenario 2. Random inspections in time

In this case, we consider that the observations of the process $\{Y_t\}$ are received at random times following a Poisson process N(t), independent of $X_t$ and $Y_t$, with intensity $\lambda$, which is unknown and can be estimated from the data.

The number of observations into the interval (0, T) is finite, random and equal to N(T), where N(t), $t \ge 0$ is a HPP with intensity $\lambda \ge \max \{a_i\}$, and $a_i=-a_{ii}>0$, for all $i=1,\ldots , d$.

Let us denote ${\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_n$ the observations registered in an interval (0, T]. The states visited by the Markov process X at the successive arrival times of the Poisson process can be seen as an embedded discrete-time hidden Markov chain $Z_n$ with transition probability matrix denoted by $\textbf{Q}$. The generating matrix of the hidden process is denoted by $\textbf{A}$ already given before, then, using the uniformization method (see, e.g., Kulkarni 2011, or Girardin and Limnios 2018), we have that

$$\begin{aligned} \textbf{Q}= \frac{1}{\lambda } \textbf{A} +\textbf{I} \end{aligned}$$

where $\textbf{I}$ is the identity matrix.

Using the HMM model we estimate again the transition matrix of the embedded Markov chain, $\widehat{\textbf{Q}}$. So we can define the following estimator

$$\begin{aligned} \widehat{\textbf{A}}= \widehat{\lambda } \left( \widehat{\textbf{Q}}- \textbf{I}\right) , \end{aligned}$$

(8)

where ${\lambda }$ can be estimated by $\widehat{\lambda }=N(T)/T$.

3.4 Assumptions

In order to establish consistency and asymptotic normality of the estimators, we need the following assumptions.

Let us define $G_\theta (i,dy):= {{\mathbb {P}}}_\theta (Y_t \in dy \vert X_t=i)= g_\theta (i,y)\mu (dy)$, $i\in E$ and $\theta \in \Theta \subset {\mathbb {R}}^k$, with $\Theta$ an open set, and where $\mu$ is some reference measure dominating all $G_\theta (i,\cdot )$.

Denote by $\Vert {\cdot }\Vert$ the euclidean norm in ${\mathbb {R}}^k$, and $\theta =(\theta _1,\ldots ,\theta _k)$. The true value of the vector of parameters is denoted as $\theta _0=(\theta _{01},\ldots ,\theta _{0k})$.

• A1: The MP X is irreducible, i.e., ergodic. We consider moreover that X is stationary.

• A2: The mixtures of $G_\theta (i,\cdot )$ are identifiable.

• A3: The functions $\theta \mapsto P_\theta (i,j)$ and $\theta \mapsto G_\theta (i,\cdot )$ belongs to $C^2(\Theta )$.

• A4: For some $\delta >0$, and all $i\in E$,

  $$\begin{aligned}{} & {} {\mathbb {E}}_{\theta _0}\Vert {\ln g_\theta (i,Y_0)}\Vert< + \infty ,\\{} & {} {\mathbb {E}}_{\theta _0}[\sup _{\Vert {\theta -\theta _0}\Vert<\delta }(\ln g_\theta (i,Y_0))^+]< +\infty . \end{aligned}$$

• A5: For some $\delta >0$

  $$\begin{aligned}{} & {} {\mathbb {E}}_{\theta _0}\Big [\sup _{\Vert {\theta -\theta _0}\Vert<\delta }\Vert {\frac{\partial }{\partial \theta _i}\ln g_\theta (i,Y_0)}\Vert ^2\Big ]< +\infty \\{} & {} {\mathbb {E}}_{\theta _0}\Big [\sup _{\Vert {\theta -\theta _0}\Vert<\delta }\Vert {\frac{\partial ^2}{\partial \theta _i \partial \theta _j}\ln g_\theta (i,Y_0)}\Vert ^2\Big ]< +\infty \\{} & {} \int \sup _{\Vert {\theta -\theta _0}\Vert<\delta }\Vert {\frac{\partial ^k}{\partial \theta _{i_1}\cdots \partial \theta _{i_k}}\ln g_\theta (i,y)}\Vert \mu (dy)< +\infty . \end{aligned}$$

• A6: $k(y):= \sup _{\Vert {\theta -\theta _0}\Vert <\delta } \max _{i,j\in E}\frac{g_\theta (i,y)}{g_\theta (j,y)}$ for some $\delta >0$, and ${{\mathbb {P}}}_{\theta _0}(k(Y_0)= +\infty \vert X_0 =i)< 1$, for any $i\in E$.

3.5 Asymptotic properties

Let (X, Y) be the two-dimensional process as defined in Definition 1 in Sect. 2. Let $\textbf{A}=(a_{ij})$ denote the generating matrix of $X_t, t\ge 0$, with state space $E=\{1,2,\ldots ,d\}$.

Consider the related Markov chains:

Scenario 1: $\hat{X}_n = X_{nh}$, with transition probability matrix $Q_h= e^{\textbf{A}_h}$.

Scenario 2: $Z_n =X_{T_n}$ where $T_n$, $n\ge 1$, are the arrival times of a $HPP (\lambda )$, with $\lambda \ge \max \{a_i, i=1,\ldots ,d\}$, and $T_0=0$, where $a_i:= -a_{ii}$. Its transition probability is $\textbf{Q}= \textbf{I} + {\lambda }^{-1}{} \textbf{A}$.

Lemma 1

• (i) If the Markov process X is irreducible then the above Markov chains, $\hat{X}$ and Z, are irreducible and aperiodic, i.e., ergodic.

• (ii) The Markov process X, and the Markov chains $\hat{X}$ and Z have the same stationary probability, say $\pi$.

• (iii) If the Markov process X is stationary, then the Markov chains $\hat{X}$ and Z are also stationary, and the sequence ${\hat{Y}}$ is stationary with the stationary distribution $\pi G(\cdot )=\sum _{j \in E} \pi _j G(j,\cdot )$ in both scenarii.

• (iv) In our case $M1-M0$, if $\{X_n\}$ is ergodic, the Markov chain $(X_n,Y_n)$ is ergodic with stationary probability ${\tilde{\pi }}(j,B)= \pi _jG(j,B)$, with $j\in E$ and $B \in {\mathcal {B}}_{{\mathcal {Y}}}$, Borel sets in ${{\mathcal {Y}}}$.

Proof

• (i) By construction the ${\hat{X}}$ and Z are irreducible too as X. Moreover they are aperiodic since $Q_{h}(i,i)>0$ and $Q(i,i)>0$.

• (ii) The stationary probability $\pi$ of the MP X is given by the solution of the equation $\pi e^{A h} =\pi$ which is the same as for ${\hat{X}}$. Moreover this is the same for Z too (see, e.g., Ross 1996).

• (iii) If the MP X is stationary, it means that ${{\mathbb {P}}}(X_t=j)=\pi _j$, for all $t \ge 0$ and all $j\in E$, and we have ${{\mathbb {P}}}(X_{kh}=j)={{\mathbb {P}}}({\hat{X}}_{k}=j)=\pi _j$, so that ${\hat{X}}$ is stationary too. The same applies for Z.

• (iv) The transition probability for the Markov process $(X_t,Y_t)$ is obtained by the limit of the transition probability. We showed in Sect. 2.2 that the transition probabilities for the process $(X_t,Y_t)$ are given by ${{\mathbb {P}}}(X_t=j,Y_t \in B \vert X_0=i, Y_0=y)= P_{ij}(t) G(j,B)$, for $i,j \in E$, $B \in \mathcal {B}_{\mathcal {Y}}$ and $y \in {{\mathcal {Y}}}$. Also we proved in Sect. 2.2 that $\widetilde{\pi }(j,B)=\pi _j G(j,B)$.

$\square$

3.6 Scenario 1. Regular inspections in time

In this section we establish asymptotic properties of the estimators. Let $h>0$, and let ${\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_n$ observations of a HMM as described in Sect. 3.2 for Scenario 1.

We extend the sequence $\{Y_n, n \ge 0\}$ to the sequence $\{Y_n, n \in {\mathbb {Z}}\}$.

3.6.1 Notation

• 1. Likelihood:

  $$\begin{aligned} p_{\theta }({\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_n)= \sum _{(i_0, \ldots , i_n)\in E^{n+1}} \pi _{\theta } (i_0)\prod _{k=1}^n P_{\theta }(i_{k-1},i_k) \prod _{l=0}^n G_{\theta }(i_{l},{\hat{Y}}_l). \end{aligned}$$

• 2. Fisher information matrix: $I_n(\theta _0)=- E_{\theta _0}\left[ \frac{\partial ^2\ln p_{\theta }({\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_n)}{\partial \theta _i \partial \theta _j} \biggr |_{\theta =\theta _0} \right] _{ij}$.

• 3. Asymptotic Fisher information matrix; $I(\theta _0)=- E_{\theta _0}\left[ \frac{\partial ^2\ln {{\mathbb {P}}}_{\theta }({\hat{Y}}_0 \vert {\hat{Y}}_{-1}, {\hat{Y}}_{-2} \ldots )}{\partial \theta _i \partial \theta _j} \biggr |_{\theta =\theta _0} \right] _{ij}$. This matrix is nonsingular provided that there exists an integer $n \in {\mathbb {N}}$ such that $I_n(\theta _0)$ is nonsingular.

Under assumptions A1, A2, A3, A4, Leroux (1992) proves that the maximum-likelihood estimator is strongly consistent in euclidean norm. Given consistency and under assumptions A1, A3, A5, A6, Bickel et al. (1998) prove asymptotic normality. Specifically they prove the following theorem.

Theorem 1

(Bickel et al. (1998). Theorem 1.) Assume that A1, A3, A5, A6 hold, that the maximum-likelihood estimator $\widehat{\theta }_n$ is consistent and that $I(\theta _0)$ is nonsingular. Then

$$\begin{aligned} \sqrt{n} \left( \widehat{\theta }_n- \theta _0\right) {\mathop {\longrightarrow }\limits ^{d}} N(0, \Sigma _{0}), \end{aligned}$$

as $n\rightarrow +\infty$, with $\Sigma _{0}=I(\theta _0)^{-1}$.

Now for the processes $X_t$, $Y_t$ in continuous time, we get the following results.

Proposition 4

(Consistency) Let $h>0$ be fixed. Under assumptions A1–A4, given a sample of observations $\{ {\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_{n}\}$, the estimator given in (7) is uniformly strongly consistent, that is

$$\begin{aligned} \max _{i,j \in E}\vert \widehat{\textbf{A}}_{h,n}(i,j) -\textbf{A}_h(i,j)\vert {\mathop {\longrightarrow }\limits ^{a.s.}}0, \ \ \textrm{as} \ n \rightarrow \infty . \end{aligned}$$

Proof

Uniform consistency of $\widehat{\theta }_n$ implies uniform consistency of $\widehat{\textbf{Q}}_{h,n}$, since $\widehat{\textbf{Q}}_{h,n}=Q(\widehat{\theta }_n)$ is a continuous transformation of $\widehat{\theta }_n$, and so is $\widehat{\textbf{A}}_{h,n}$, since we define $\widehat{\textbf{A}}_{h,n}=A(\widehat{\theta }_n)=h^{-1} \left( Q(\widehat{\theta }_n)-\textbf{I}\right)$, then $\widehat{\textbf{A}}_{h,n}$ is a uniform consistent estimator of $\textbf{A}_h$. $\square$

Proposition 5

(Asymptotic normality) Under assumptions A1, A3, A5, A6, given a sample of observations $\{ {\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_n\}$, where for each $k\ge 0$, ${\hat{Y}}_{k}=Y_{kh}$, for $h>0$ fixed, the random matrix $\sqrt{n} \left( \widehat{\textbf{A}}_{h,n} -\textbf{A}_h\right)$ is asymptotically Normal, as $n \rightarrow \infty$, with mean $\textbf{0}$ and variance-covariance matrix $\Sigma _\textbf{A}=\nabla A^{\top } \Sigma _0 \nabla A$, with $\nabla A$ the gradient of function $A (\theta )=\textbf{A}$ evaluated at $\theta _0$.

Proof

For a fixed $h>0$, and $T=nh$, we have, as $T \rightarrow \infty$, $n \rightarrow \infty$, and we can use Therorem 1 of Bickel et al. (1998).

Let $\textbf{A}$ be the generating matrix of $\{X_t\}$, with $\textbf{A}= A(\theta )$; then for $h >0$ fixed, define $\textbf{Q}_h= \textbf{A} h +\textbf{I}$, then $\textbf{Q}_h= Q(\theta )=A(\theta ) h + \textbf{I}$, and $\nabla Q= h \nabla A$. Then

$$\begin{aligned} \sqrt{n} (\widehat{\textbf{Q}}_{h,n}-\textbf{Q}_h) \rightarrow N(0,\Sigma _{\textbf{Q}_h}), \end{aligned}$$

with $\Sigma _{\textbf{Q}_h}= h^2 \Sigma _\textbf{A}= h^2 \nabla A^{\top } \Sigma _0 \nabla A$.

Now, we define $\textbf{A}_h=\frac{\textbf{Q}_h-\textbf{I}}{h}$, for $h>0$ fixed. The estimator of the matrix $\textbf{A}_h$ defined in (7) leads to

$$\begin{aligned} \sqrt{n}(\widehat{\textbf{A}}_{h,n}-\textbf{A}_h)=\frac{\sqrt{n}}{h}\left( \widehat{\textbf{Q}}_{h,n}-\textbf{Q}_h\right) \end{aligned}$$

and then, again using the Delta method, we obtain $\Sigma _{\textbf{A}}=h^{-2}\Sigma _{ \textbf{Q}_h}=\nabla A^{\top } \Sigma _0 \nabla A$, which does not depend on h. $\square$

In this scenario, it is important to check the accuracy, in terms of the value of h, of the approximation of $\textbf{A}$ by $\textbf{A}_h$. The following proposition proves that $\widehat{\textbf{A}}_{h,n}$ converges uniformly to $\textbf{A}$, when h goes to 0 and n goes to $\infty$, for fixed T.

Proposition 6

Under assumptions A1–A4, given a sample of observations $\{ {\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_{n}\}$, it is true that:

• (a) $\widehat{\textbf{A}}_{h,n}$ is an estimator of $\textbf{A}$ uniformly strongly consistent. That is:

  $$\begin{aligned} \underset{i, j \in E}{\max }\ \vert \widehat{\textbf{A}}_{h,n}(i,j) -\textbf{A}(i,j)\vert {\mathop {\longrightarrow }\limits ^{a.s.}}0, \ \ \textrm{as} \ n\rightarrow \infty , \ h\rightarrow 0, \end{aligned}$$

• (b) $\sqrt{n} (\widehat{\textbf{A}}_{h,n}- \textbf{A}) {\mathop {\longrightarrow }\limits ^{d}} N(0, \Sigma _{\textbf{A}})$

Proof

For any $h>0$, as $\textbf{A}_h=\frac{1}{h} \left( \textbf{Q}_h-\textbf{I}\right)$, strong consistency is deduced because $\widehat{\textbf{A}}_{h,n}$ is a continuous transformation of $\widehat{\theta }$, which gives us (a).

For (b) we have

$$\begin{aligned} \sqrt{n}(\widehat{\textbf{A}}_{h,n} - \textbf{A})= \sqrt{n}(\widehat{\textbf{A}}_{h,n} - \textbf{A}_h)+\sqrt{n}(\textbf{A}_{h} - \textbf{A}). \end{aligned}$$

(9)

From Proposition 5, $\sqrt{n}(\widehat{\textbf{A}}_{h,n} - \textbf{A}_h) {\mathop {\longrightarrow }\limits ^{d}} N(0, \Sigma _{\textbf{A}})$, for any h as $n\rightarrow +\infty$ and $T \rightarrow +\infty$. We can take $h_n=(n\ln n)^{-1/2}$ in order that $T=nh_n\rightarrow +\infty$ as $n \rightarrow +\infty$ so we can apply Proposition 5 in the first term of the right hand side of (9). On the other hand, $\textbf{Q}_h=e^{\textbf{A}h}$, and, by the definition of $\textbf{A}_h$, we have that $\textbf{A}_{h_n}-\textbf{A} = \frac{\textbf{A}^2}{2}h_n+o(h_n)$, then, for the second term in the right hand side of (9) we have that $\sqrt{n}(\textbf{A}_{h_n} - \textbf{A})= \frac{\textbf{A}^2}{2}\frac{1}{\sqrt{\ln n}}+o(1/\sqrt{\ln n})$, and the conclusion follows from the uniqueness of the limit. $\square$

3.6.2 Applications

Proposition 6 allows us to prove the almost sure convergence of the plug-in estimators of functionals of type $H(t)=\Phi (\textbf{A},t)$. That is, let $h>0$, then we can define the $H_h(t)= \Phi (\textbf{A}_h,t)$ as H but based on $\textbf{A}_h$. If a sample of size n of the HMM is available, we can define the plug-in estimator of $H_h(t)$ and deduce the properties of this estimator as above. Moreover, we have that

$$\begin{aligned} \widehat{H}_{h,n} (t){\mathop {\longrightarrow }\limits ^{a.s.}} H(t), \ \ \textrm{as} \ n \rightarrow \infty , \ h \rightarrow 0 \end{aligned}$$

and also

$$\begin{aligned} \sqrt{n}\left( \widehat{H}_{n}-H\right) {\mathop {\longrightarrow }\limits ^{d}} N(0, \Sigma _{H}), \ \ \textrm{as} \ n \rightarrow \infty , \ h \rightarrow 0. \end{aligned}$$

As an example let us consider the reliability or survival function. Let $\textbf{A}_0$ and $\alpha _0$ the restrictions of $\textbf{A}$ and $\alpha$ on the up states. Then we can write the reliability formula

$$\begin{aligned} R(t)=\alpha _0 e^{\textbf{A}_0 t}{} \textbf{1}, \end{aligned}$$

and in discrete time, for $t=n h$,

$$\begin{aligned} R_h(t)=\alpha _0 \left( \textbf{Q}_{h,0}\right) ^n\textbf{1}, \end{aligned}$$

where $\textbf{Q}_{h,0}$ is the restriction of $\textbf{Q}_h$ on the up states, and $\textbf{1}$ is a column-vector of 1 s with the appropriate dimension.

Proposition 7

For any arbitrary but fixed $t >0$, such that $t=n h$, we have

$$\begin{aligned} R_{h}(t) \longrightarrow R(t), \ \textrm{as} \ n \longrightarrow \infty \ (h \rightarrow 0). \end{aligned}$$

Proof

This comes from the well known result

$$\begin{aligned} \left( \textbf{Q}_{h,0}\right) ^n = \left( \textbf{I} + n^{-1} \textbf{A}_0 + o(h)\right) ^n \underset{n \rightarrow \infty }{\longrightarrow } e^{\textbf{A}_0t}. \end{aligned}$$

$\square$

3.7 Scenario 2. Random inspections in time

In this section we establish asymptotic properties for $T \rightarrow +\infty$.

Proposition 8

(Consistency) Under assumptions A1-A4, given a sample of observations $\{N(T), {\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_{N(T)}\}$, the estimator given in (8) is strongly consistent, that is $\widehat{A}_T \rightarrow A$ (a.s.), as $T \rightarrow +\infty$.

Proof

We have that $\widehat{\lambda } = \frac{N(T)}{T} \underset{ T \rightarrow +\infty }{\longrightarrow }\ \lambda$, a.s. (see for example Ross 1996). Also from the results in Gamiz et al. (2023) we have that $\widehat{\textbf{Q}}_T \longrightarrow \textbf{Q}$. Then using Slutsky theorem (Gut 2013), we get

$$\begin{aligned} \widehat{\textbf{A}}_T = \widehat{\lambda }_T \left( \widehat{\textbf{Q}}_T-\textbf{I}\right) \underset{ T \rightarrow +\infty }{\longrightarrow }\ \lambda (\textbf{Q}-\textbf{I}) = \textbf{A}; (a.s.). \end{aligned}$$

$\square$

Proposition 9

(Asymptotic normality) Under assumptions A1, A3, A5, A6, given a sample of observations $\{N(T), {\hat{Y}}_0, {\hat{Y}}_1, \ldots , {\hat{Y}}_{N(T)}\}$, the random matrix $\sqrt{T} \left( \widehat{\textbf{A}} -\textbf{A}\right)$ is asymptotically Normal as $T \rightarrow +\infty$, with mean $\textbf{0}$ and variance-covariance matrix $\Sigma _\textbf{A}=\Sigma _{1}+ \Sigma _2$, where $\Sigma _{1}=\lambda \nabla { \textbf{Q}}^{\top } \Sigma _{0}\nabla \textbf{Q}$, and $\Sigma _2=\vec {{\textbf {B}}} \vec {{\textbf {B}}}^{\top }$, where $\textbf{B}=\sqrt{\lambda }\left( \textbf{Q}-\textbf{I}\right)$ and $\vec {{\textbf {B}}}$ is a vector representation of the matrix $\textbf{B}$.

Proof

We can write

$$\begin{aligned} \sqrt{T} \left( \widehat{\textbf{A}}-\textbf{A}\right) =\sqrt{T} \widehat{\lambda } \left( \widehat{\textbf{Q}}_T-\textbf{Q}\right) + \sqrt{T} \left( \widehat{\lambda }-\lambda \right) (\textbf{Q}-\textbf{I}). \end{aligned}$$

(10)

To check the convergence to a Normal distribution we consider the two terms of expression (10) separately. First, we have

$$\begin{aligned} \sqrt{T} \ \widehat{\lambda } \left( \widehat{\textbf{Q}}_T-\textbf{Q}\right) = \sqrt{\frac{N(T)}{T}} \sqrt{N(T)} \left( \widehat{\textbf{Q}}_T-\textbf{Q}\right) , \end{aligned}$$

(11)

where we use that $\widehat{\lambda } =N(T)/T$.

From the results in Bickel et al. (1998) and the fact that $N(T) \rightarrow \infty$ (a.s.) as $T \rightarrow \infty$, we have that

$$\begin{aligned} \sqrt{N(T)}\left( \widehat{\textbf{Q}}_T-\textbf{Q}\right) {\mathop {\longrightarrow }\limits ^{d}} N(0,\Sigma _\textbf{Q}), \ \ \textrm{as} \ T \rightarrow \infty , \end{aligned}$$

with variance-covariance matrix $\Sigma _\textbf{Q}$ obtained by the Delta method applied to the function $Q(\theta )=\textbf{Q}$, similar to proposition 5.

Using that ${N(T)/T} \rightarrow \lambda$, almost surely, as $T \rightarrow +\infty$, we get that the first term of the sum converges to a Normal distribution, that is

$$\begin{aligned} \sqrt{T}\ \widehat{\lambda }\left( \widehat{\textbf{Q}}_T-\textbf{Q}\right) {\mathop {\longrightarrow }\limits ^{d}} N(0,\lambda \Sigma _1), \end{aligned}$$

with $\Sigma _1=\lambda \Sigma _\textbf{Q}$, a matrix of dimension $d^2 \times d^2$.

On the other hand, N(T) has Poisson distribution with mean $\lambda T$, which can be approximated by a Normal distribution with both mean and variance equal to $\lambda T$, that is

$$\begin{aligned} \sqrt{T}\left( \widehat{\lambda }_T -\lambda \right) {\mathop {\longrightarrow }\limits ^{d}} N(0,\lambda ). \end{aligned}$$

Then, the second term in the sum is also asymptotically Normal with variance-covariance matrix $\Sigma _2=\vec {{\textbf {B}}} \vec {{\textbf {B}}}^{\top }$, where $\textbf{B}=\sqrt{\lambda }\left( \textbf{Q}-\textbf{I}\right)$, that is

$$\begin{aligned} \sqrt{T} \left( \lambda _T-\lambda \right) (\textbf{Q}-\textbf{I}) {\mathop {\longrightarrow }\limits ^{d}} N(0,\Sigma _2). \end{aligned}$$

Specifically $\vec {{\textbf {B}}}$ is a $d^2$-dimensional vector obtained by stacking the columns of $\textbf{B}$ into a column vector, then $\Sigma _2$ is also a matrix of dimension $d^2 \times d^2$, and then $\Sigma = \Sigma _1+ \Sigma _2$ is well defined. $\square$

4 Applications

4.1 Reliability for CTHMM with discrete state space

In this section we consider that Y takes values in a finite set, that is $\mathcal {Y}=\{y_1,\ldots , y_s\}$, then the corresponding two-dimensional process $(X_t,Y_t)$ has a finite number of states.

We can write the set of states for the two-dimensional process as $\widetilde{E}= E \times \mathcal {Y}$, with $\widetilde{E}=\{(1,y_1),\ldots ,$ $(d,y_1),(1,y_2),\ldots ,$ $(d,y_2), \ldots , (1,y_s),$ $(2,y_s),\ldots ,(d,y_s)\}$.

Then $\{(X_t,Y_t); t>0\}$ is a two-dimensional continuous-time Markov chain with state-space $\widetilde{E}=E \times \mathcal {Y}$ and transition matrix $\widetilde{\textbf{P}}$ with elements

$$\begin{aligned} \widetilde{P}_t((i,y'),(j,y))=P_{ij}(t)G(j,y), \end{aligned}$$

for $i,j \in E$ and $y', y \in \mathcal {Y}$. In matrix form, we have

$$\begin{aligned} \widetilde{\textbf{P}}(t)=\left( \begin{array}{c|c|c|c} \textbf{B}_{1}(t) &{} \textbf{B}_2(t) &{} \cdots &{}\textbf{B}_s(t) \\ \hline \textbf{B}_{1}(t) &{} \textbf{B}_2(t) &{} \cdots &{}\textbf{B}_s(t) \\ \hline \cdots &{} \cdots &{} \cdots &{}\cdots \\ \hline \textbf{B}_{1}(t) &{} \textbf{B}_2(t) &{} \cdots &{}\textbf{B}_s(t) \\ \end{array} \right) \end{aligned}$$

where for each $k=1,\ldots , s$, the corresponding block is a $d \times d$ sub-matrix $\textbf{B}_k(t)=\textbf{P}(t) \cdot diag(G_k)$, where $diag(G_k)$ is a d-dimensional diagonal matrix with the kth column of the matrix $\textbf{G}$. The generator $\textbf{A}$ is a matrix of dimension $(d\cdot s) \times (d \cdot s)$ with elements $\widetilde{a}((i,y')(j,y))$ as detailed in (2).

Following similar arguments as in Gamiz et al. (2023), we consider that the state-space of the process X is split into two subsets $U:= \{1,\ldots ,r\}$, the working states, and $D:= \{r+1,\ldots ,d\}$, the down states. Additionally, the system up states can be defined not only by $U \subset E$ but also by some subset of $\mathcal {Y}$. Then we consider also a partition in the set of possible observations, that is $\mathcal {Y}=\mathcal {Y}_1 \cup \mathcal {Y}_2$, where in $\mathcal {Y}_1$ we consider indicators of good performance of the system, and in $\mathcal {Y}_2$ we consider the indicators warning of some serious problem in the system.

Let us denote $\tau$ the first time the system visits the set of down states D, i.e., the hitting time of set D. Let us consider $\widetilde{{\mathcal {U}}}=U\times \mathcal {Y}_1$ and $\widetilde{{\mathcal {D}}}=\widetilde{{\mathcal {E}}}\setminus \widetilde{{\mathcal {U}}}$, being ${\widetilde{E}}=E\times \mathcal {Y}$. Then $\tau =\inf \{t> 0: \widetilde{{\mathcal {X}}}=(X_t,Y_t) \in \widetilde{{\mathcal {D}}}\}$. Therefore the reliability of the system can be defined as $\widetilde{R}(t)=\mathbb {P}(\tau >t)$, for $t \ge 0$. Conditioning on the initial state $(i,y) \in \widetilde{U}=U \times \mathcal {Y}_1$, we write

$$\begin{aligned} \widetilde{R}_{(i,y)}(t)= & {} {{\mathbb {P}}}_i(\tau >t) = {{\mathbb {P}}}_i( X_s \in U, Y_s \in \mathcal {Y}_1, 0<s\le t)\nonumber \\= & {} {{\mathbb {P}}}_i( (X_t,Y_t) \in \widetilde{U}, 0<s\le t), \end{aligned}$$

(12)

and then

$$\begin{aligned} \widetilde{R}(t)=\sum _{(i,y) \in \widetilde{U}}\widetilde{R}_{(i,y)}(t), \end{aligned}$$

for $t >0$. Using matrix notation, we can write

$$\begin{aligned} \widetilde{R}(t)=\widetilde{\alpha }e^{\widetilde{\textbf{A}}_{\widetilde{U}} t} \textbf{1}_{\widetilde{U}} \end{aligned}$$

where $\widetilde{\textbf{A}}_{\widetilde{U}}$ denotes the sub-matrix of $\widetilde{\textbf{A}}$ with all transition rates among states of subset $\widetilde{U}$.

4.2 Reliability for CTHMM with a general state space

When the Y process takes values in a finite set, the formula in (12) can be applied because the generator $\textbf{A}_{\widetilde{U}}$ is a matrix, but when Y takes values in a subset of ${\mathbb {R}}^q$, $\textbf{A}_{\widetilde{U}}$ is an operator and we can not make use of the formula in (12). In that case we propose to work by Markov renewal equations (in the semi-Markov way) in this section. Let us define $H(i,t)=e^{-a_i t }G(i,\mathcal {Y}_1)$, for $i \in U$, and let $\Psi _U$ be the Markov renewal function corresponding to the sub semi-Markov kernel $L_U(i,j,t)= \frac{a_{ij}}{a_i}(1-e^{-a_it})$, for $i, j \in U$. The following result can be proved similarly to Proposition 2.

Proposition 10

(Reliability) The conditional reliability function $\widetilde{R}_{(i,y)}(t)$ satisfies the Markov renewal equation (MRE)

$$\begin{aligned} \widetilde{R}(i,t)=H(i,t)+\sum _{j \in U}\int _0^t \widetilde{R}(k,t-s)L(i,k,ds) \end{aligned}$$

Therefore, the conditional reliability is given by the only solution of the above equation, i.e.,

$$\begin{aligned} \widetilde{R}(i,t)=(\Psi _U *H)(i,t) \end{aligned}$$

5 Numerical examples

In this section we illustrate the two scenarii discussed in the rest of the paper. In the first example, a real dataset is considered whereas in the second example a simulation study is carried out. In both cases, we discretize the continous-time problem, and then estimate using our algorithms in Gamiz et al. (2023), and finally we establish estimator properties in continuous-time, our initial problem.

5.1 Scenario 1. Regular inspections in time

As a illustration we consider a comparison study of the suicide-rate in the US and Japan during the period 1985–2015. The data have been taken from the data platform https://www.kaggle.com/. We focus on the following variables: the Suicide Rate, which is measured as the number of suicides/100k population, and, the Gross Domestic Product per capita ($GDP\_per\_capita$).

5.1.1 Preliminary

Although the data registry provides information from a total of 94 countries we limit ourselves to the US and Japan. We have chosen two of the most developed countries in the world with the aim of comparing them with respect to the number of suicides per year.

Fig. 1

Overview of the situation in the US (top panel) and Japan (bottom panel) during the period 1995–2015

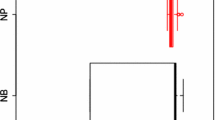
In Fig. 1 we give a graphical description of the situation. On the top panel we describe the case of US while on the bottom panel we represent the information from Japan.

Looking at the figure from left to right we have the following. The plots on the left display the suicide-rate per year for US (top) and Japan (bottom) from 1995 to 2015, respectively. The suicide-rate has been calculated as the number of suicides registered in the country every year per 100,000 inhabitants. In each graph it is shown the value calculated every year as well as a smoothed curve obtained from these values and that helps in visualizing the tendency of the suicide-rate along the period of observation. As we can see from the curves, not only suicides occur in Japan at a significantly higher rate than in US, also it is remarkable the existence of a high variability in the rate of suicides in Japan over the years, which is not appreciated in the case of US where the tendency is more steady.

On the right-side panels, a scatterplot is given representing the GDP per capita from 1995 until 2015 in US (top) and Japan (bottom). What catches our attention is that again the situation in US seems to be more stable and suggests an increasing trend, with an almost constant slope, of the population standard of living in the US. We can see just one abrupt decay coinciding with the period of the economical crisis around 2008. However the GDP curve in Japan, although suggests a slightly increasing tendency from 1995 onwards, it shows high variability at the same period of time when the highest suicide rate is seen in the corresponding plot (on the left panel).

Fig. 2

Density curve of suicide rate in the US (left) and in Japan (right)

Figure 2 shows smooth density estimations of the rate of suicides all along the observation period for both countries, US on the left panel, and Japan on the right one. As we can see, the curves in both cases seem to suggest two different “regimes” (hidden or latent) in the country. These regimes could be the result of the interaction of the country’s wealth (measured in terms of the GDP) and possibly many other intrinsic factors which in conjunction can explain, to a certain extent, the observed rate of suicides at any particular time.

With this in mind, we propose to study this phenomenon using a CTHMM with the following specifications.

• $\{X(t); t>0\}$ is the CTMC that represents the internal regime that is not directly observable. Let us assume that X takes values in $E=\{1,2\}$;

• $\{Y(t), t>0\}$ is the observable process. We define Y(t) as the rate of suicides at time t. Considering the plots in Fig. 2, we assume that Y(t) conditioned to the event $\{X(t)=i\}$ follows a Normal distribution with mean $\mu _i$ and standard deviation $\sigma _i$, for $i \in \{1,2\}$;

We do not have a continuous-time follow-up of the process. We rather have annual observations, so we use the methodology presented in this paper and estimate the model considering Scenario 1 where observations arrive regularly in time, specifically with $h=1$. Regarding the DTHMM for each case study (US and Japan), the following parameters have to be estimated

$$\begin{aligned} {\varvec{\theta }}=\left( Q_{h}(1,1), Q_{h}(2,1), \mu _1, \mu _2, \sigma _1,\sigma _2\right) , \end{aligned}$$

where $Q_{h}(i,1)={\mathbb {P}}(X_h=1 \vert X_0=i)$, for $i \in \{1,2\}$. Then an estimator $\widehat{\textbf{A}}_h$ is obtained as explained in Sect. 3.1.

5.1.2 Results

We use the EM-Algorithm. The function $Q(\theta \vert \theta ^{(m)})= \mathbb {E}_{\theta ^{(m)}}[\ln f(\hat{X},\hat{\textbf{Y}} \vert \theta )]$ will give us by successive iterations an approximation of the estimate of ${\varvec{\theta }}$, where $\ln f(\hat{X},\hat{\textbf{Y}} \vert \theta )$ is the log-likelihood corresponding to the complete dataset, which would be obtained from the bivariate process $({\hat{X}}, {\hat{Y}})$.

$$\begin{aligned} Q(\theta \vert \theta ^{(m)})= & {} \sum _{n=1}^{N-1} \sum _{i,j\in E}\mathbb {P}_{\theta ^{(m)}}(\hat{X}_{n}=i,\hat{X}_{n+1}=j\vert \hat{\textbf{Y}})\ln P_{\theta }(i,j) \nonumber \\{} & {} + \sum _{n=1}^N \sum _{i\in E}\mathbb {P}_{\theta ^{(m)}}(\hat{X}_n=i\vert \hat{\textbf{Y}})\sum _{k=1}^K\ln g(\hat{Y}_{kn}; \phi _i). \end{aligned}$$

(13)

• E-Step For given $\theta ^{(m)}$, compute the probabilities:

  $$\begin{aligned} \mathbb {P}_{\theta ^{(m)}}(\hat{X}_{n}=i,\hat{X}_{n+1}=j\vert \hat{\textbf{Y}}),\quad n \in \{1,\ldots ,N-1\};\quad i,j\in E \end{aligned}$$

  and

  $$\begin{aligned} \mathbb {P}_{\theta ^{(m)}}(\hat{X}_{n}=i\vert \hat{\textbf{Y}}),\quad n \in \{1,\ldots ,N\};\quad i\in E. \end{aligned}$$

  To solve this step we use of the forward-backward probabilities defined as in Gamiz et al. (2023).

• M-Step

Update $\theta ^{(m)}$ to $\theta ^{(m+1)}$. The maximization step M is realized directly by

$$\begin{aligned} {\widehat{P}}^{(m+1)}(i,j) = \frac{\sum _{n=1}^N \mathbb {P}_{\theta ^{(m)}}(\hat{X}_{n}=i,\hat{X}_{n+1}=j\vert \hat{\textbf{Y}}) }{\sum _{n=1}^N \mathbb {P}_{\theta ^{(m)}}(\hat{X}_{n}=i\vert \hat{\textbf{Y}})}. \end{aligned}$$

(14)

Considering that the emission function follows a Normal law, $g_{\theta }(i,y)= (\sigma _i\sqrt{2 \pi })^{-1} \exp \left( {-(y-\mu _i)^2}/(2\sigma _i^2)\right)$, for $i= 1,2$. The optimal value of the second term $Q_2((\phi _i; i\in E) \vert \theta ^{(m)})$ is obtained for

$$\begin{aligned} \widehat{\mu }_i=\frac{\sum _{n=1}^N {{\mathbb {P}}}_{\theta ^{(m)}}({\hat{X}}_n =i \vert \hat{\textbf{Y}}) {\hat{Y}}_n }{\sum _{n=1}^N {{\mathbb {P}}}_{\theta ^{(m)}}({\hat{X}}_n =i \vert \hat{\textbf{Y}})}; \end{aligned}$$

and,

$$\begin{aligned} \widehat{\sigma }_i^2=\frac{\sum _{n=1}^N {{\mathbb {P}}}_{\theta ^{(m)}}({\hat{X}}_n =i \vert \hat{\textbf{Y}})({\hat{Y}}_n-\widehat{\mu }_i)^2 }{\sum _{n=1}^N {{\mathbb {P}}}_{\theta ^{(m)}}({\hat{X}}_n =i \vert \hat{\textbf{Y}})}, \end{aligned}$$

for $i\in \{1,2\}$.

We have estimated the model in both cases, i.e., with data from US as well as Japan. The estimated values reported in Table 1 are the following: the transition matrix $\textbf{Q}_h$; the parameters of the emission law, $\{G(i,\cdot ) \rightarrow N(\mu _i, \sigma _i); i= 1,2\}$; the initial distribution, $\alpha$; the generating matrix $\textbf{A}$ and the stationary distribution of the continuous MC $\pi$.

Table 1 Estimated parameters of the hidden model

Figure 3 represents the transition probability functions between hidden states.

Fig. 3

Transition-function matrix of the hidden MC governing the suicide rate observed in Japan (solid red line) and in US (solid blue line)

5.2 Scenario 2. Random inspections in time

To illustrate this approach we present a simulation study. In particular, we consider a system with four possible states, that is $E=\{1,2,3,4\}$, with $\{1,2\}$ the functioning states whereas $\{3,4\}$ are the down states. The observed output may vary in the set ${{\mathcal {Y}}}=\{y_1,y_2,y_3,y_4\}$. The true generating and the emission matrices are given by

$$\begin{aligned} \mathbb {A}=\left( \begin{array}{cccc} -6 &{} 4 &{} 1 &{} 1 \\ 3 &{} -5&{} 1 &{} 1 \\ 1 &{} 2&{} -5 &{} 2 \\ 0 &{} 2&{} 2 &{}-4 \\ \end{array}\right) ,\textrm{and, } \mathbb {G}=\left( \begin{array}{cccc} 0.5 &{} 0.5&{} 0&{}0 \\ 0.3 &{} 0.5&{} 0.2&{}0 \\ 0.1 &{} 0.2&{} 0.5&{}0.2 \\ 0 &{} 0.2&{} 0.3&{}0.5 \\ \end{array}\right) . \end{aligned}$$

Besides, we assume that the system is inspected at times that follow a Poisson process with intensity $\lambda$. Let us assume that $X_0=1$ and $Y_0=y_1$.

We have simulated a total of 500 samples of size $N=100$ each according to the following algorithm.

• 1. Generate a sample trajectory $(X_1,T_1),\ldots , (X_N,T_N)$ of the MC X from the generating matrix $\textbf{A}$, where $X_n$ is the nth state visited by the process and $T_n$ the sojourn time of the system in the $n-1$ for $n \in \{1, \ldots , N\}$. Denote ${Z}_n= \sum _{k=1}^n T_{n}$, the successive jump times of the MC.

• 2. Generate a sample $Y_1, \ldots , Y_N$ of the process Y, following the rule ${{\mathbb {P}}}(Y=y\vert X=i)=G_{i,y}$, with $i \in \{1,2,3,4\}$ and $y \in {{\mathcal {Y}}}$.

• 3. Generate a sample trajectory of the PP with rate $\lambda$, that is, $S_1< S_2< \ldots < S_{N_0}$. Simulate arrival times until $S_{N_0}\ge {Z}_N$.

• 4. Put ${\hat{Y}}_0=Y_0$. For each $r\in \{ 1,\ldots , N_0\}$, find $n > 0$ such that $Z_n \le S_r <Z_{n+1}$ and define $\hat{Y}_r=Y_n$.

We have considered three cases, $\lambda \in \{6.5, 8, 9\}$

Again we use the EM-algorithm, as in Gamiz et al. (2023), to fit the discrete HMM $({\hat{X}}, {\hat{Y}})$ and estimate the corresponding parameters $\widehat{Q}$ and $\widehat{G}$. Also, for each repetition of the experiment, estimate $\widehat{\lambda }=\frac{n_0}{S_{n_0}}$. Then, obtain an estimation of the generating matrix $\widehat{\textbf{A}}$ as explained in Sect. 3.1. Using the estimation of the emission matrix $\widehat{\textbf{G}}$ we construct the generating matrix of the 2-dimensional process (X, Y) and following 4.1 we can obtain the estimation of the reliability function, which is shown in Fig. 4.

Fig. 4

Scenario 2: Observations follow a Poisson process

Notice that $N_0 \ge N$, since we choose $\lambda > \max \{-a_{ii}, i \in E\}$. In our case we have obtained the statistics displayed in Table 2.

Table 2 Mean values of sample sizes for different values of $\lambda$

6 Conclusion

Continuous-time hidden Markov processes can be seen as a two-dimensional continuous-time Markov process $(X_t,Y_t)$ where the first component $X_t$ is an unobservable continuous-time Markov chain and the second one $Y_t$ is an observable process whose distribution law depends on $X_t$ through a function called the emission function. In this paper, we have defined the generator function corresponding to the coupled process in terms of the generating matrix of $X_t$ and the emission function. The theoretical properties of this type of processes have been obtained using a semi-Markov formulation of the model. To estimate the characteristics of the process we have considered two different discretization schemes under which observations can arrive. On the one hand, we assume that observations arrive regularly in time, and on the other hand, we assume that observations arrive at random. In both cases, maximum-likelihood estimator of the parameters of the CTHMM have been obtained and their asymptotic properties have been proven.

To our knowledge, the approach to HMM models considered in this paper, basing on Markov renewal theory, is completely new and provides a powerful tool to get other insights in this context of HMMs.

With respect to the estimation problem, as pointed out in Liu et al. (2017), when discretization is too coarse, many transitions of the hidden states can occur between two consecutive observations and the dynamics of the hidden process might be poorly caught by the model. This situation may happen in our first scenario when the time-span between observations (h) is not fine enough. Then, more flexible models are required and it is suitable a continuous follow-up of the process that will be considered in a future work.

In the applications discussed in this paper we have assumed that the set of hidden states is finite and the number of states is pre-specified. Generalizations of our work can be to consider selecting the optimal number of hidden states, as in Lin and Song (2022) where the number of states is unknown and to be determined by the data. Another approach that will be considered in future works, consists of defining the state space of the hidden chain, in general as a measurable set. See for example, Dorea and Zhao (2002) where kernel density estimation is discussed for the observed process in the context of DTHMM.